ବିବିଧ ପ୍ରଶ୍ନ ୪୬
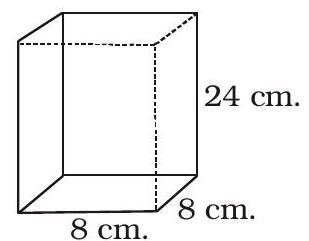
- ପରିମାଣ I: ଏକ ବର୍ଗ ଆଧାର ବକ୍ସ ଯାହାର ପାର୍ଶ୍ବ 8 ସେ.ମି. ଓ ଉଚ୍ଚତା 24 ସେ.ମି., ତା’ ଭିତରେ ରଖାଯାଇପାରିବାକୁ ଥିବା ସବୁଠାରୁ ଲମ୍ବା ଦଣ୍ଡର ଦୈର୍ଘ୍ୟ।
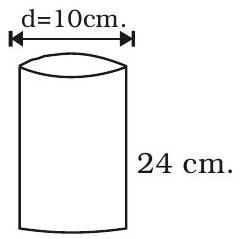
ପରିମାଣ II: ଏକ ବେଳଣା ବକ୍ସ ଯାହାର ବ୍ୟାସ 10 ସେ.ମି. ଓ ଉଚ୍ଚତା 24 ସେ.ମି., ତା’ ଭିତରେ ରଖାଯାଇପାରିବାକୁ ଥିବା ସବୁଠାରୁ ଲମ୍ବା ଦଣ୍ଡର ଦୈର୍ଘ୍ୟ।
(1) ପରିମାଣ I > ପରିମାଣ II
(2) ପରିମାଣ I < ପରିମାଣ II
(3) ପରିମାଣ I ≤ ପରିମାଣ II
(4) ପରିମାଣ I ≥ ପରିମାଣ II
(5) ପରିମାଣ I = ପରିମାଣ II କିମ୍ବା କୌଣସି ସମ୍ବନ୍ଧ ନାହିଁ।
(IBPS Bank PO/MT CWE (Main Exam) 26.11.2017)
Show Answer
ସଠିକ ଉତ୍ତର: 46. (1)
ସମାଧାନ: 46. I. $ \mathrm{L}_{1}=\sqrt{8^{2}+8^{2}+24^{2}}$
$=\sqrt{2 \times 8^{2}+24^{2}}$
$=\sqrt{(8 \sqrt{2})^{2}+24^{2}}$
II. $\mathrm{L}_{2}=\sqrt{10^{2}+24^{2}}$
ଯେହେତୁ, $(8 \sqrt{2})>10$,
$\mathrm{L} {1}>\mathrm{L}{2}$
$\therefore$ ପରିମାଣ I > ପରିମାଣ II।



