ମାପ ପ୍ରଶ୍ନ ୨୯
ପ୍ରଶ୍ନ
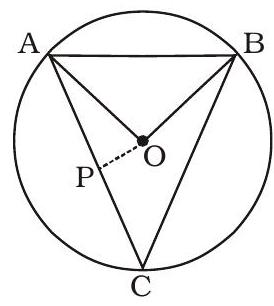
ତଳେ ଦିଆଯାଇଥିବା ଚିତ୍ରରେ, $O$ ବୃତ୍ତର କେନ୍ଦ୍ର। $\triangle AOB$ ଏକ ସମବାହୁ ତ୍ରିଭୁଜ ଅଟେ ଯେପରିକି $\triangle ACB$ ଏକ ସମଦ୍ୱିବାହୁ ତ୍ରିଭୁଜ ଯେଉଁଥିରେ $AC=BC$। OP କୁ $AC$ ଉପରେ ଲମ୍ବ ଭାବେ ଅଙ୍କନ କରାଯାଇଛି।
ପରିମାଣ I : $\angle AOP$
ପରିମାଣ II : $\angle BAP$
(1) $ I > II $
(2) $ I < II $
(3) $ I = II $
(4) $ 1 \leq II $
(5) ସମ୍ପର୍କ ସ୍ଥାପିତ କରିହେବନାହିଁ
(IBPS Bank PO/MT CWE (Main) 18.11.2016)
Show Answer
ସଠିକ ଉତ୍ତର: (3)
ସମାଧାନ: (3)
$\angle AOB=60^{\circ}[\because \Delta$ ସମବାହୁ]
$\angle ACB=30^{\circ}[\angle AOB$ କେନ୍ଦ୍ରୀୟ କୋଣ $\angle ACB$ ପାଇଁ]
ସମଦ୍ୱିବାହୁ $\triangle$ ACB ରେ,
$AC=BC$
$\Rightarrow \quad \angle BAC=\angle ABC$ $=\frac{1}{2}\left(180^{\circ}-30^{\circ}\right)=75^{\circ}$
$\therefore \quad \angle BAP=75^{\circ}$
$\therefore \quad \angle OAP=\angle BAP-\angle BAO$ $=75^{\circ}-60^{\circ}=15^{\circ}$
ଏବେ, ସମକୋଣୀୟ AOP ରେ,
$\angle AOP=180^{\circ}-\left(90^{\circ}+15^{\circ}\right)$ $=75^{\circ}$
(i) ଓ (ii) ଠାରୁ ଆମେ ପାଉଛୁ
$\angle AOP=\angle BAP$ ଅର୍ଥାତ୍, $I=II$



