अध्याय 14 प्रायिकता
प्रायिकताओं के सिद्धांत और त्रुटियों के सिद्धांत अब अति गणितीय रुचि का तथा अति व्यावहारिक महत्व का एक विशाल समूह स्थापित करते हैं।
R.S. Woodward
14.1 प्रायिकता — एक सैद्धांतिक दृष्टिकोण
आइए निम्नलिखित स्थिति पर विचार करें :
मान लीजिए एक सिक्के को यादृच्छया उछाला जाता है।
जब हम एक सिक्के की बात करते हैं, तब हम यह कल्पना करते हैं कि वह न्यायसंगत (fair) है। अर्थात् वह सममित (symmetrical) है, ताकि कोई कारण न हो कि वह एक ही ओर, दूसरी ओर की अपेक्षा, अधिक गिरे। हम सिक्के के इस गुण को उसका अपक्षपातपूर्ण (unbiased) होना कहते हैं। ‘यादृच्छया उछाल’ (random toss) से हमारा तात्पर्य है कि सिक्के को बिना किसी पक्षपात (bias) या रुकावट के स्वतंत्रतापूर्वक गिरने दिया जाता है।
हम पहले से जानते हैं कि सिक्का दो संभव विधियों में से केवल एक ही विधि से गिर सकता है - या तो चित ऊपर होगा या फिर पट ऊपर होगा [हम सिक्के के, उसके किनारे (edge) के अनुदिश गिरने की संभावना को अस्वीकार करते हैं, जो उदाहरणार्थ, तब संभव है जब सिक्का रेत पर गिरे]। हम यह तर्कसंगतरूप से मान सकते हैं कि प्रत्येक
परिणाम, चित या पट, का प्रकट होना उतनी ही बार हो सकता है जितना कि अन्य परिणाम का। दूसरे शब्दों में हम कहते हैं कि परिणाम चित और पट समप्रायिक (equally likely) हैं। समप्रायिक परिणामों के एक अन्य उदाहरण के लिए मान लीजिए कि हम एक पासे को फेंकते हैं। हमारे लिए, एक पासे का अर्थ सदैव एक न्यायसंगत पासे से होगा। संभव परिणाम क्या है? ये $1,2,3,4,5,6$ हैं। प्रत्येक संख्या के ऊपर आने की समान संभावना है। अतः, पासे को फेंकने से प्राप्त होने वाले समप्रायिक परिणाम $1,2,3,4,5$ और 6 हैं।
क्या प्रत्येक प्रयोग के परिणाम समप्रायिक होते हैं? आइए देखें।
मान लीजिए एक थैले में 4 लाल गेंदें और 1 नीली गेंद है तथा आप इस थैले में से, बिना थैले के अंदर कुछ देखें, एक गेंद निकालते हैं। इसके क्या परिणाम हैं? क्या एक लाल गेंद और एक नीली गेंद के परिणाम समप्रायिक हैं? चूँकि यहाँ 4 लाल गेंदें हैं और नीली गेंद केवल एक ही, अतः आप यह अवश्य स्वीकार करेंगे कि आपके द्वारा एक नीली गेंद की अपेक्षा एक लाल गेंद निकालने की संभावना अधिक है। अतः ये परिणाम (एक लाल गेंद और एक नीली गेंद) समप्रायिक नहीं हैं। परंतु थैले में से किसी भी रंग की गेंद निकालने के परिणाम समप्रायिक हैं।
अतः, सभी प्रयोगों के परिणामों का समप्रायिक होना आवश्यक नहीं है। परंतु, इस अध्याय में, हम आगे यह मानकर चलेंगे कि सभी प्रयोगों के परिणाम समप्रायिक हैं।
कक्षा IX में, हमने एक घटना $\mathrm{E}$ की प्रयोगात्मक या आनुभविक प्रायिकता $\mathrm{P}(\mathrm{E})$ को निम्नलिखित रूप में परिभाषित किया था :
$$ \mathrm{P}(\mathrm{E})=\frac{\text { अभिप्रयोगों की संख्या जिनमें घटना घटित हुई है }}{\text { अभिप्रयोगों की कुल संख्या }} $$
प्रायिकता की आनुभविक व्याख्या का बड़ी संख्या में दोहराए जा सकने वाले किसी भी प्रयोग से जुड़े प्रत्येक घटना के लिए अनुप्रयोग किया जा सकता है। किसी प्रयोग को दोहराने की आवश्यकता एक गंभीर परिसीमा है, क्योंकि अनेक स्थितियों में यह अधिक व्यय वाला हो सकता है या यह भी हो सकता है कि ऐसा करना संभव ही न हो। निस्संदेह, सिक्का उछालने या पासा फेंकने के प्रयोगों में, इसमें कोई कठिनाई नहीं हुई। परंतु एक उपग्रह (satellite) छोड़ने के प्रयोग को यह परिकलित करने के लिए बार-बार दोहराने की छोड़ते समय उसकी असफलता की आनुभवित प्रायिकता क्या है, के बारे में आप क्या सोचते हैं अथवा यह कि एक भूकंप के कारण कोई बहुमंजिली इमारत नष्ट होगी या नहीं, की आनुभविक प्रायिकता परिकलित करने के लिए भूकंप की परिघटना के दोबारा घटित होने के बारे में आप क्या कह सकते हैं?
ऐसे प्रयोगों में, जहाँ हम कुछ कल्पनाओं को सही मानने को तैयार हो जाएँ, हम एक प्रयोग के दोहराने से बच सकते हैं, क्योंकि वे कल्पनाएँ सीधे सही (सैद्धांतिक) प्रायिकता परिकलित करने में हमारी सहायता करती हैं। परिणामों के समप्रायिक होने की कल्पना (जो अनेक प्रयोगों में मान्य होती है, जैसे कि ऊपर सिक्का उछालने और पासा फेंकने के दोनों उदाहरणों में है) इन कल्पनाओं में से एक है जो हमें किसी घटना की प्रायिकता की निम्नलिखित परिभाषा की ओर अग्रसर करती है।
किसी घटना $\mathrm{E}$ की सैद्धांतिक प्रायिकता (theoretical probability) [ जिसे परंपरागत प्रायिकता (classical probability) भी कहा जाता है।] $\mathrm{P}(\mathrm{E})$ निम्नलिखित रूप में परिभाषित की जाती है
$$ \mathrm{P}(\mathrm{E})=\frac{\mathrm{E} \text { के अनुकूल परिणामों की संख्या }}{\text { प्रयोग के सभी संभव परिणामों की संख्या }} $$
यहाँ हम यह कल्पना करते हैं कि प्रयोग के परिणाम समप्रायिक हैं।
हम संक्षिप्त रूप में, सैद्धांतिक प्रायिकता को केवल प्रायिकता ही कहेंगे।
प्रायिकता की उपरोक्त परिभाषा 1795 में पियरे-साइमन लाप्लास (Pierre-Simon Laplace) ने दी थी।
प्रायिकता सिद्धांत का सूत्रपात 16 वीं शताब्दी में हुआ, जब एक इतालवी भौतिकशास्त्री एवं गणितज्ञ जे. कार्डन ने इस विषय पर पहली पुस्तक लिखी, जिसका नाम था : The Book on Games of Chance अपने प्रादुर्भाव से ही, प्रायिकता के अध्ययन को महान गणितज्ञों का ध्यान अपनी ओर आकर्षित किया। इन गणितज्ञों में जेम्स बर्नूली (1654-1705), ए.ड़ी मोइवरे (1667-1754) और पियरे-साइमन लाप्लास ऐसे लोग हैं जिन्होंने इस क्षेत्र में एक सार्थक योगदान दिया। लाप्लास द्वारा 1812 में लिखी गई कृति (Theorie Analytiquedes Probabilities) को एक अकेले व्यक्ति द्वारा प्रायिकता के सिद्धांत के लिए किया गया सबसे बड़ा योगदान माना जाता है। हाल ही के कुछ वर्षों में, प्रायिकता का अनेक क्षेत्रों, जैसे कि जैविकी, अर्थशास्त्र, वंश संबंधी शास्त्र (genetics), भौतिकी, समाजशास्त्र इत्यादि क्षेत्रों में प्रचुर मात्रा में उपयोग किया जा रहा है।

पियरे-साइमन लाप्लास (1749 - 1827)
आइए ऐसे प्रयोगों से संबंधित कुछ घटनाओं की प्रायिकता ज्ञात करें, जिनमें समप्रायिक होने की कल्पना मान्य है।
उदाहरण 1 : एक चित प्राप्त करने की प्रायिकता ज्ञात कीजिए, जब एक सिक्के को एक बार उछाला जाता है। साथ ही, एक पट प्राप्त करने की भी प्रायिकता ज्ञात कीजिए।
हल : एक सिक्के को एक बार उछालने के प्रयोग में, संभव परिणामों की संख्या 2 है चित $(\mathrm{H})$ और पट $(\mathrm{T})$ । मान लीजिए घटना $\mathrm{E}$ ‘चित प्राप्त करना’ है। तब, $\mathrm{E}$ के अनुकूल (अर्थात् चित प्राप्त करने के अनुकूल) परिणाम 1 है। अतः,
$$ \mathrm{P}(\mathrm{E})=\mathrm{P}(\text { चित })=\frac{\mathrm{E} \text { के अनुकूल परिणामों की संख्या }}{\text { सभी संभव परिणामों की संख्या }}=\frac{1}{2} $$
इसी प्रकार, यदि घटना $\mathrm{F}$ पट प्राप्त करना है, तो
$$ \mathrm{P}(\mathrm{F})=\mathrm{P}(\text { पट })=\frac{1}{2} \text { (क्यों?) } $$
उदाहरण 2 : एक थैले में एक लाल गेंद, एक नीली गेंद और एक पीली गेंद है तथा सभी गेंदे एक ही साइज की हैं। कृतिका बिना थैले के अंदर झाँके, इसमें से एक गेंद निकालती है। इसकी क्या प्रायिकता है कि वह गेंद
(i) पीली होगी? $\quad$
(ii) लाल होगी? $\quad$
(iii) नीली होगी?
हल : कृतिका थैले में से, उसमें बिना झाँके, गेंद निकालती है। अतः, उसके द्वारा कोई भी गेंद निकालना समप्रायिक है।
माना ‘पीली गेंद निकालना’ घटना $\mathrm{Y}$ है, ‘लाल गेंद निकालना’ घटना $\mathrm{R}$ है तथा ‘नीली गेंद निकालना’ घटना $\mathrm{B}$ है।
अब, सभी संभव परिणामों की संख्या $=3$ है।
(i) घटना $\mathrm{Y}$ के अनुकूल परिणामों की संख्या $=1$
अत: $\quad \mathrm{P}(\mathrm{Y})=\frac{1}{3}$
इसी प्रकार,
$$\mathrm{P}(\mathrm{R})=\frac{1}{3} \text{ और } \mathrm{P}(\mathrm{B})=\frac{1}{3}$$
टिप्पणी :
(1) किसी प्रयोग की वह घटना जिसका केवल एक ही परिणाम हो प्रारंभिक घटना (elementary event) कहलाती है। उदाहरण 1 में दोनों घटनाएँ $\mathrm{E}$ और $\mathrm{F}$ प्रारंभिक घटनाएँ हैं। इसी प्रकार, उदाहरण 2 में, घटना $\mathrm{Y}, \mathrm{R}$ और $\mathrm{B}$ में प्रत्येक एक प्रारंभिक घटना है।
(2) उदाहरण 1 में, हम देखते हैं कि $\mathrm{P}(\mathrm{E})+\mathrm{P}(\mathrm{F})=1$
उदाहरण 2 में, हम देखते हैं कि $\mathrm{P}(\mathrm{Y})+\mathrm{P}(\mathrm{B})+\mathrm{P}(\mathrm{R})=1$
ध्यान दीजिए कि किसी प्रयोग की सभी प्रारंभिक घटनाओं की प्रायिकताओं का योग 1 है। यह व्यापक रूप में भी सत्य है।
उदाहरण 3 : मान लीजिए हम एक पासे को एक बार फेंकते हैं। (i) 4 से बड़ी संख्या प्राप्त होने की प्रायिकता क्या है? (ii) 4 से छोटी या उसके बराबर संख्या प्राप्त होने की प्रायिकता क्या है?
हल : (i) यहाँ मान लीजिए कि ’ 4 से बड़ी संख्या प्राप्त करना’ घटना $\mathrm{E}$ है। सभी संभव परिणाम छः हैं, ये $1,2,3,4,5$ और 6 हैं। स्पष्टतः, घटना $\mathrm{E}$ के अनुकूल परिणाम 5 और 6 हैं। अतः $\mathrm{E}$ के अनुकूल परिणामों की संख्या 2 है। इसलिए
$$ P(E)=P(4 \text { से बड़ी संख्या })=\frac{2}{6}=\frac{1}{3} $$
(ii) मान लीजिए ’ 4 से छोटी या उसके बराबर संख्या प्राप्त करना’ घटना $\mathrm{F}$ है।
सभी संभव परिणाम $=6$ हैं।
घटना $\mathrm{F}$ के अनुकूल परिणाम $1,2,3$ और 4 हैं।
अतः $F$ के अनुकूल परिणामों की संख्या 4 है।
इसलिए
$$ P(F)=\frac{4}{6}=\frac{2}{3} $$
क्या उपरोक्त उदाहरण में दी हुई घटना $\mathrm{E}$ और $\mathrm{F}$ प्रारंभिक घटनाएँ हैं? नहीं, ये प्रारंभिक घटनाएँ नहीं हैं, क्योंकि घटना $\mathrm{E}$ के 2 परिणाम हैं तथा घटना $\mathrm{F}$ के 4 परिणाम हैं।
टिप्पणी : उदाहरण 1 से, हम देखते हैं कि
$$ \begin{equation*} \mathrm{P}(\mathrm{E})+\mathrm{P}(\mathrm{F})=\frac{1}{2}+\frac{1}{2}=1 \tag{1} \end{equation*} $$
जहाँ घटना $\mathrm{E}$ ‘एक चित प्राप्त करना’ है तथा घटना $\mathrm{F}$ ‘एक पट प्राप्त करना’ है।
उदाहरण 3 के (i) और (ii) से भी हम देखते हैं कि
$$ \begin{equation*} \mathrm{P}(\mathrm{E})+\mathrm{P}(\mathrm{F})=\frac{1}{3}+\frac{2}{3}=1 \tag{2} \end{equation*} $$
जहाँ घटना $\mathrm{E}^{\prime} 4$ से बड़ी संख्या प्राप्त करना’तथा घटना $\mathrm{F}^{\prime} 4$ के बराबर या कम संख्या प्राप्त करना’ है।
ध्यान दीजिए कि 4 से बड़ी संख्या नहीं प्राप्त करने का अर्थ वही है जो 4 से छोटी या उसके बराबर संख्या प्राप्त करने का है और इसी प्रकार इसका विलोम भी यही प्रकट करता है।
उपरोक्त (1) और (2) में, क्या घटना ‘F’, ’ $E$ नहीं’ (not E) के समान नहीं है। हाँ, ऐसा ही है। हम घटना ’ $E$ नहीं, को $\overline{\mathrm{E}}$ से व्यक्त करते हैं।
अतः,
$$ P(E)+P(\text { नहीं } E)=1 $$
अर्थात्
$\mathrm{P}(\mathrm{E})+\mathrm{P}(\overline{\mathrm{E}})=1$ है, जिससे $\mathrm{P}(\overline{\mathrm{E}})=1-\mathrm{P}(\mathrm{E})$ प्राप्त होता है।
व्यापक रूप में, किसी घटना $\mathrm{E}$ के लिए यह सत्य है कि
$$ \mathbf{P}(\overline{\mathbf{E}})=1-\mathbf{P}(\mathbf{E}) $$
घटना ’ $\mathrm{E}$ नहीं’ को निरूपित करने वाली घटना $\overline{\mathrm{E}}$ घटना $\mathrm{E}$ की पूरक (complement) घटना कहलाती है। हम यह भी कहते हैं कि $\mathrm{E}$ और $\overline{\mathrm{E}}$ परस्पर पूरक घटनाएँ हैं।
आगे बढ़ने से पहले, आइए निम्नलिखित प्रश्नों के उत्तर ज्ञात करने का प्रयत्न करें:
(i) पासे को एक बार फेंकने पर संख्या 8 प्राप्त करने की क्या प्रायिकता है?
(ii) पासे को एक बार फेंकने पर 7 से छोटी संख्या प्राप्त करने की क्या प्रायिकता है?
आइए (i) का उत्तर दें :
हम जानते हैं कि पासे को एक बार फेंकने पर केवल छः ही संभावित परिणाम हैं। ये परिणाम $1,2,3,4,5$ और 6 हैं। चूँकि पासे के किसी भी फलक पर 8 अंकित नहीं है, इसलिए 8 के अनुकूल कोई भी परिणाम नहीं है, अर्थात् ऐसे परिणामों की संख्या शून्य $(0)$ है। दूसरे शब्दों में, पासे को एक बार फेंकने पर, संख्या 8 प्राप्त करना असंभव (impossible) है।
अतः
$$\mathrm{P}(8 प्राप्त करना )=\frac{0}{6}=0$$
अर्थात् उस घटना, जिसका घटित होना असंभव है, की प्रायिकता 0 होती है। ऐसी घटना को एक असंभव घटना (impossible event) कहते हैं।
आइए (ii) का उत्तर दें :
चूँकि पासे के प्रत्येक फलक पर ऐसी संख्या लिखी है जो 7 से छोटी है, इसलिए पासे को एक बार फेंकने पर यह निश्चित है कि प्राप्त संख्या सदैव 7 से छोटी होगी। अतः, घटना के अनुकूल परिणामों की संख्या सभी संभावित परिणामों की संख्या के बराबर होगी, जो 6 है।
इसलिए
$$ \mathrm{P}(\mathrm{E})=\mathrm{P}(7 \text { से छोटी संख्या प्राप्त करना })=\frac{6}{6}=1 $$
अतः उस घटना, जिसका घटित होना निश्चित (sure) है, की प्रायिकता 1 होती है। ऐसी घटना को एक निश्चित (sure) या निर्धारित (certain) घटना कहते हैं।
टिप्पणी : प्रायिकता $\mathrm{P}(\mathrm{E})$ की परिभाषा से, हम देखते हैं कि अंश (घटना $\mathrm{E}$ के अनुकूल परिणामों की संख्या) सदैव हर (सभी संभव परिणामों की संख्या) से छोटा होता है या उसके बराबर होता है। अतः,
$$ 0 \leq \mathrm{P}(\mathrm{E}) \leq \mathbf{1} $$
आइए अब एक उदाहरण, ताशों (playing cards) से संबंधित लें। क्या आपने ताशों की एक गड्डी देखी है? इसमें 52 पत्ते (cards) होते हैं, जो 4 समूहों में बँटे होते हैं। प्रत्येक समूह में 13 पत्ते होते हैं। ये 4 समूह हुकुम (spades) ( $\spadesuit$ ), पान (hearts) ( $\heartsuit$), ईंट (diamonds) $(\diamondsuit)$ और चिड़ी (clubs) $(\clubsuit)$ हैं। चिड़ी और हुकुम काले रंग के होते हैं तथा पान और ईंट लाल रंग के होते हैं। प्रत्येक समूह के पत्ते : इक्का (ace), बादशाह (king), बेगम (queen), गुलाम (jack), 10, 9, 8, 7, 6, 5, 4, 3 और 2 होते हैं। बादशाह, बेगम और गुलाम वाले पत्ते फेस कार्ड (face cards) कहलाते हैं।
उदाहरण 4 : अच्छी प्रकार से फेटी गई 52 पत्तों की एक गड्डी में से एक पत्ता निकाला जाता है। इसकी प्रायिकता परिकलित कीजिए कि यह पत्ता :
(i) एक इक्का होगा।
(ii) एक इक्का नहीं होगा।
हल : गड्डी को अच्छी प्रकार से फेटने से परिणामों का समप्रायिक होना सुनिश्चित हो जाता है।
(i) एक गड्डी में 4 इक्के होते हैं। मान लीजिए घटना $\mathrm{E}$ ‘एक इक्का होना’ है।
$\mathrm{E}$ के अनुकूल परिणामों की संख्या $=4$
सभी संभव परिणामों की संख्या $=52$ (क्यों?)
अत : $\mathrm{P}(\mathrm{E})=\frac{4}{52}=\frac{1}{13}$
(ii) मान लीजिए घटना $F$ ‘एक इक्का नहीं’ है।
माना $\mathrm{F}$ के अनुकूल परिणामों की संख्या $=52-4=48$ (क्यों?)
सभी संभव परिणामों की संख्या $=52$
अत :
$$ P(F)=\frac{48}{52}=\frac{12}{13} $$
टिप्पणी : ध्यान दीजिए कि $\mathrm{F}$ और कुछ नहीं बल्कि $\overline{\mathrm{E}}$ ही है। अतः, हम $\mathrm{P}(\mathrm{F})$ को इस प्रकार भी परिकलित कर सकते हैं : $\mathrm{P}(\mathrm{F})=\mathrm{P}(\overline{\mathrm{E}})=1-\mathrm{P}(\mathrm{E})=1-\frac{1}{13}=\frac{12}{13}$.
उदाहरण 5 : दो खिलाड़ी संगीता और रेशमा टेनिस का एक मैच खेलते हैं। यह ज्ञात है कि संगीता द्वारा मैच जीतने की प्रायिकता 0.62 है। रेशमा के जीतने की क्या प्रायिकता है?
हल : मान लीजिए $\mathrm{S}$ और $\mathrm{R}$ क्रमशः संगीता के जीतने और रेशमा के जीतने की घटनाएँ व्यक्त करते हैं।
संगीता के जीतने की प्रायिकता $=\mathrm{P}(\mathrm{S})=0.62$ (दिया है)
रेशमा के जीतने की प्रायिकता $=\mathrm{P}(\mathrm{R})=1-\mathrm{P}(\mathrm{S})$
[ चूँकि घटनाएँ $\mathrm{R}$ और $\mathrm{S}$ पूरक हैं]
$$ =1-0.62=0.38 $$
उदाहरण 6 : सविता और हमीदा दो मित्र हैं। इसकी क्या प्रायिकता है कि दोनों (i) के जन्म-दिन भिन्न-भिन्न हों? (ii) का जन्मदिन एक ही हो? [लीप का वर्ष (Leap year)को छोड़ते हुए]
हल : दोनों मित्रों में से किसी एक लड़की, मान लीजिए, सविता का जन्मदिन वर्ष का कोई भी दिन हो सकता है। इसी प्रकार, दूसरी लड़की हमीदा का जन्मदिन भी वर्ष के 365 दिनों में से कोई एक दिन हो सकता है।
#missing
(i) यदि हमीदा का जन्मदिन सविता के जन्मदिन से भिन्न है, तो उसके जन्मदिन के अनुकूल परिणामों की संख्या $365-1=364$ होगी।
अतः $\mathrm{P}$ (हमीदा का जन्मदिन सविता के जन्मदिन से भिन्न है) $=\frac{364}{365}$
(ii) $\mathrm{P}$ (सविता और हमीदा का जन्मदिन एक ही हो)
$$ \begin{aligned} & =1-\mathrm{P} \text { (दोनों का जन्मदिन भिन्न है) } \\ & =1-\frac{364}{365} \quad[\mathrm{P}(\overline{\mathrm{E}})=1-\mathrm{P}(\mathrm{E}) \text { के प्रयोग से }] \\ & =\frac{1}{365} \end{aligned} $$
उदाहरण 7 : किसी स्कूल की कक्षा $\mathrm{X}$ में 40 विद्यार्थी हैं जिनमें से 25 लड़कियाँ हैं और 15 लड़के हैं। कक्षा अध्यापिका को एक विद्यार्थी कक्षा-प्रतिनिधि के रूप में चुनना है। वह प्रत्येक विद्यार्थी का नाम एक अलग कार्ड पर लिखती है, जबकि कार्ड एक जैसे हैं। फिर वह इन कार्डों को एक थैले में डालकर अच्छी तरह से हिला देती है। इसके बाद वह थैले में से एक कार्ड निकालती है। इसकी क्या प्रायिकता है कि कार्ड पर लिखा हुआ नाम एक (i) लड़की का है? (ii) लड़के का है?
हल : कुल 40 विद्यार्थी हैं और इनमें से केवल एक नाम का कार्ड चुनना है।
(i) सभी संभव परिणामों की संख्या $=40$
कार्ड पर लड़की का नाम होने के अनुकूल परिणामों की संख्या $=25$ (क्यों?)
अब, $\mathrm{P}$ (कार्ड पर लड़की का नाम है $)=\mathrm{P}($ लड़की $)=\frac{25}{40}=\frac{5}{8}$
(ii) कार्ड पर लड़के का नाम होने के अनुकूल परिणामों की संख्या $=15$ (क्यों?)
अतः, $\mathrm{P}$ (कार्ड पर लड़के का नाम है $)=\mathrm{P}($ लड़का $)=\frac{15}{40}=\frac{3}{8}$
टिप्पणी : हम $\mathrm{P}$ (लड़का) को इस प्रकार भी निर्धारित कर सकते हैं :
$$ \mathrm{P}(\text { लड़का })=1-\mathrm{P}(\text { लड़का नहीं })=1-\mathrm{P}(\text { लड़की })=1-\frac{5}{8}=\frac{3}{8} $$
उदाहरण 8 : एक बक्से में 3 नीले, 2 सफेद और 4 लाल कंचे (marbles) हैं। यदि इस बक्से में से एक कंचा यादृच्छया निकाला जाता है तो इसकी क्या प्रायिकता है कि यह कंचा
(i) सफेद है? $\quad$
(ii) नीला है? $\quad$
(iii) लाल है? $\quad$
हल : यह कहना कि कंचा यादृच्छया रूप से निकाला गया है, संक्षिप्त में यह कहने के बराबर है कि सभी परिणाम समप्रायिक हैं। अतः,
सभी संभव परिणामों की संख्या $=3+2+4=9$ (क्यों?)
मान लीजिए घटना $\mathrm{W}$ ‘कंचा सफेद है’ को, घटना $\mathrm{B}$ ‘कंचा नीला है’ को तथा घटना $\mathrm{R}$ ‘कंचा लाल है’ को व्यक्त करता है।
(i) घटना $\mathrm{W}$ के अनुकूल परिणामों की संख्या $=2$
अत:
$\mathrm{P}(\mathrm{W})=\frac{2}{9}$
इसी प्रकार,
(ii) $\mathrm{P}(\mathrm{B})=\frac{3}{9}=\frac{1}{3}$ और
(iii) $\mathrm{P}(\mathrm{R})=\frac{4}{9}$
ध्यान दीजिए कि $\mathrm{P}(\mathrm{W})+\mathrm{P}(\mathrm{B})+\mathrm{P}(\mathrm{R})=1$ है।
उदाहरण 9 : हरप्रीत दो भिन्न-भिन्न सिक्कों को एक साथ उछालती है (मान लीजिए एक सिक्का ₹ 1 का है और दूसरा सिक्का ₹ 2 का है)। इसकी क्या प्रायिकता है कि वह कम से कम एक चित प्राप्त करेगी?
हल : हम ‘चित’ के लिए $\mathrm{H}$ और ‘पट’ के लिए $\mathrm{T}$ लिखते हैं। जब दो सिक्कों को एक साथ उछाला जाता है, तो संभावित परिणाम $(\mathrm{H}, \mathrm{H}),(\mathrm{H}, \mathrm{T}),(\mathrm{T}, \mathrm{H}),(\mathrm{T}, \mathrm{T})$ हैं तथा ये सभी समप्रायिक हैं। यहाँ $(\mathrm{H}, \mathrm{H})$ का अर्थ है कि पहले सिक्के (मान लीजिए ₹ 1 के सिक्के) पर ‘चित’ आएगा और दूसरे सिक्के (₹ 2 के सिक्के) पर ‘चित’ आएगा। इसी प्रकार, $(\mathrm{H}, \mathrm{T})$ का अर्थ है कि पहले सिक्के पर ‘चित’ आएगा और दूसरे सिक्के पर ‘पट’ आएगा, इत्यादि।
घटना $\mathrm{E}$ ‘कम से कम एक चित आना’ के अनुकूल परिणाम $(\mathrm{H}, \mathrm{H}),(\mathrm{H}, \mathrm{T})$ और ( $\mathrm{T}, \mathrm{H})$ हैं। (क्यों?)
अतः $\mathrm{E}$ के अनुकूल परिणामों की संख्या $=3$
इसलिए $\quad \mathrm{P}(\mathrm{E})=\frac{3}{4}$
अर्थात् हरप्रीत द्वारा कम से कम एक चित प्राप्त करने की प्रायिकता $\frac{3}{4}$ है।
टिप्पणी : आप $\mathrm{P}(\mathrm{E})$ इस प्रकार भी ज्ञात कर सकते हैं:
$$ \mathrm{P}(\mathrm{E})=1-\mathrm{P}(\overline{\mathrm{E}})=1-\frac{1}{4}=\frac{3}{4} \text { चूँकि } \mathrm{P}(\overline{\mathrm{E}})=\mathrm{P}(\text { कोई चित नहीं })=\frac{1}{4} $$
क्या आपने यह देखा कि अब तक के सभी उदाहरणों में, प्रत्येक प्रयोग के सभी संभव परिणामों की संख्या परिमित थी? यदि नहीं, तो अब इसकी जाँच कर लीजिए।
अनेक प्रयोग ऐसे हैं, जहाँ परिणाम दो संख्याओं के बीच में कोई भी संख्या हो सकती है या जिनमें परिणाम एक वृत्त या आयत के अंदर का प्रत्येक बिंदु होता है, इत्यादि। क्या अब आप सभी संभव परिणामों को गिन सकते हैं? जैसाकि आप जानते हैं, यह संभव नहीं है, क्योंकि दो संख्याओं के बीच में अपरिमित रूप से अनेक संख्याएँ होती हैं, या यह कि एक वृत्त के अंदर अपरिमित रूप से अनेक बिंदु होते हैं। अतः, आपके द्वारा अध्ययन की गई (सैद्धांतिक) प्रायिकता की परिभाषा को वर्तमान रूप में यहाँ प्रयोग नहीं किया जा सकता। इस समस्या का फिर हल क्या है? इसके उत्तर के लिए, आइए निम्नलिखित उदाहरण पर विचार करें।
उदाहरण 10 : एक म्यूज़िकल चेयर (musical chair) खेल में, जो महिला संगीत बजा रही थी उसे सलाह दी गई कि वह संगीत प्रारंभ करने के बाद 2 मिनट के अंदर कभी भी संगीत बंद कर दे। इसकी क्या प्रायिकता है कि संगीत प्रारंभ होने के पहले आधे मिनट के अंदर बंद हो जाएगा?
हल : यहाँ संभव परिणाम 0 और 2 के बीच की सभी संख्याएँ हैं। यह संख्या रेखा का 0 से 2 तक का भाग है (देखिए आकृति 14.1)।

आकृति 14.1
मान लीजिए घटना $\mathrm{E}$ ‘संगीत प्रारंभ होने के पहले आधे मिनट में बंद हो जाता है’।
$\mathrm{E}$ के अनुकूल परिणाम संख्या रेखा पर 0 से $\frac{1}{2}$ के बीच के सभी बिंदु हैं।
#missing
चूँकि सभी परिणाम समप्रायिक हैं, इसलिए हम यह तर्क दे सकते हैं कि कुल दूरी 2 में से दूरी $\frac{1}{2}$ घटना $\mathrm{E}$ के अनुकूल है।
अतः $\mathrm{P}(\mathrm{E})=\frac{\text { घटना } \mathrm{E} \text { के अनुकूल दूरी }}{\text { पूरी दूरी जिसमें परिणाम स्थित हो सकते हैं }}=\frac{\frac{1}{2}}{2}=\frac{1}{4}$
क्या हम उदाहरण 10 की अवधारणा को किसी घटना की प्रायिकता उसके अनुकूल क्षेत्रफल और संपूर्ण क्षेत्रफल के अनुपात के रूप में विस्तृत कर सकते हैं।
उदाहरण 11 : एक लापता हेलीकॉप्टर के बारे में सूचना मिलती है कि वह आकृति 14.2 में दर्शाए आयताकार क्षेत्र में कहीं गिर गया है। इसकी क्या प्रायिकता है कि वह आकृति में दर्शाई गई झील में गिरा है?[^4]

आकृति 14.2
हल : हेलीकॉप्टर का आयताकार क्षेत्र में कहीं भी गिरना समप्रायिक है।
संपूर्ण क्षेत्र का क्षेत्रफल, जहाँ हेलीकॉप्टर गिर सकता है
$$ =(4.5 \times 9) \mathrm{km}^{2}=40.5 \mathrm{~km}^{2} $$
झील का वास्तविक क्षेत्रफल $=(2.5 \times 3) \mathrm{km}^{2}=7.5 \mathrm{~km}^{2}$
अत: $\mathrm{P}$ ( हेलीकॉप्टर झील में गिरा है) $=\frac{7.5}{40.5}=\frac{75}{405}=\frac{5}{27}$ है।
उदहारण 12 : एक डिब्बे में 100 कमीजें हैं, जिसमें से 88 अच्छी हैं तथा 8 में थोड़ी सी खराबी है और 4 में अधिक खराबी है। एक व्यापारी जिम्मी वे ही कमीजें स्वीकार करता है जो अच्छी हैं, जबकि एक अन्य व्यापारी सुजाता उन्हीं कमीजों को अस्वीकार करती है जिनमें खराबी अधिक है। इस डिब्बे में से एक कमीज को यादृच्छया रूप से निकाला जाता है। इसकी क्या प्रायिकता है कि वह कमीज
(i) जिम्मी को स्वीकार हो?
(ii) सुजाता को स्वीकार हो?
हल : 100 कमीजों के डिब्बे में से एक कमीज यादृच्छया रूप से निकाली जाती है। अतः यहाँ 100 समप्रायिक परिणाम हैं।
(i) जिम्मी के अनुकूल (को स्वीकार) परिणामों की संख्या $=88$ (क्यों?)
अतः, $\mathrm{P}$ (कमीज जिम्मी को स्वीकार है) $=\frac{88}{100}=0.88$
(ii) सुजाता के अनुकूल परिणामों की संख्या $=88+8=96$ (क्यों?)
अत: $\mathrm{P}$ (कमीज सुजाता को स्वीकार है) $=\frac{96}{100}=0.96$
उदाहरण 13 : एक सलेटी पासे और एक नीले पासे को एक साथ फेंका जाता है। सभी संभावित परिणामों को लिखिए। इसकी क्या प्रायिकता है कि दोनों पासों की संख्याओं का योग
(i) 8 है।
(ii) 13 है।
(iii) 12 से छोटी या उसके बराबर है।
हल : जब नीला पासा ’ 1 ’ दर्शाता है, तो सलेटी पासे पर संख्याओं $1,2,3,4,5,6$ में से कोई भी संख्या हो सकती है। यही तब भी होगा, जब नीले पासे पर ’ 2 ‘, ’ 3 ‘, ’ 4 ‘, ’ 5 ’ या ’ 6 ’ होगा। इस प्रयोग के संभावित परिणामों को नीचे सारणी में दिया गया है। प्रत्येक क्रमित युग्म की पहली संख्या नीले पासे पर आने वाली संख्या है तथा दूसरी संख्या सलेटी पासे पर आने वाली संख्या है।

आकृति 14.3
ध्यान दीजिए कि युग्म $(1,4)$ युग्म $(4,1)$ से भिन्न है ( क्यों?)
अतः, संभावित परिणामों की संख्या $=6 \times 6=36$ है।
(i) $\mathrm{E}$ द्वारा व्यक्त घटना ‘संख्याओं का योग 8 है’ के अनुकूल परिणाम $(2,6),(3,5)$, $(4,4),(5,3)$ और $(6,2)$ हैं (देखिए आकृति 14.3)।
अर्थात् $\mathrm{E}$ के अनुकूल परिणाम $=5$
इसलिए $\quad \mathrm{P}(\mathrm{E})=\frac{5}{36}$
(ii) जैसा कि आप आकृति 15.3 से देख सकते हैं, घटना $\mathrm{F}$, ‘संख्याओं का योग 13 है’ के अनुकूल कोई भी परिणाम नहीं है।
अत :
$$ P(F)=\frac{0}{36}=0 $$
(iii) जैसा कि आप आकृति 14.3 से देख सकते हैं, घटना $G$ ‘संख्याओं का योग $\leq 12$ से छोटा या उसके बराबर है’ के अनुकूल सभी परिणाम हैं।
अत :
$$ P(G)=\frac{36}{36}=1 $$
प्रश्नावली 14.1
1. निम्नलिखित कथनों को पूरा कीजिए :
(i) घटना $\mathrm{E}$ की प्रायिकता + घटना ’ $\mathrm{E}$ नहीं’ की प्रायिकता = __________ है।
(ii) उस घटना की प्रायिकता जो घटित नहीं हो सकती _______ है। ऐसी घटना _______ कहलाती है।
(iii) उस घटना की प्रायिकता जिसका घटित होना निश्चित है ________ है। ऐसी घटना ________ कहलाती है।
(iv) किसी प्रयोग की सभी प्रारंभिक घटनाओं की प्रायिकताओं का योग _________ है।
(v) किसी घटना की प्रायिकता _________ से बड़ी या उसके बराबर होती है तथा __________ से छोटी या उसके बराबर होती है।
Show Answer
#missing2. निम्नलिखित प्रयोगों में से किन-किन प्रयोगों के परिणाम समप्रायिक हैं? स्पष्ट कीजिए।
(i) एक ड्राइवर कार चलाने का प्रयत्न करता है। कार चलना प्रारंभ हो जाती है या कार चलना प्रारंभ नहीं होती है।
(ii) एक खिलाड़ी बास्केटबॉल को बास्केट में डालने का प्रयत्न करती है। वह बास्केट में बॉल डाल पाती है या नहीं डाल पाती है।
(iii) एक सत्य-असत्य प्रश्न का अनुमान लगाया जाता है। उत्तर सही है या गलत होगा।
(iv) एक बच्चे का जन्म होता है। वह एक लड़का है या एक लड़की है।
Show Answer
#missing3. फुटबॉल के खेल को प्रारंभ करते समय यह निर्णय लेने के लिए कि कौन-सी टीम पहले बॉल लेगी, इसके लिए सिक्का उछालना एक न्यायसंगत विधि क्यों माना जाता है?
Show Answer
#missing4. निम्नलिखित में से कौन सी संख्या किसी घटना की प्रायिकता नहीं हो सकती?
(A) $\frac{2}{3}$
(B) -1.5
(C) $15 %$
(D) 0.7
Show Answer
#missing5. यदि $\mathrm{P}(\mathrm{E})=0.05$ है, तो ’ $\mathrm{E}$ नहीं’ की प्रायिकता क्या है?
Show Answer
#missing6. एक थैले में केवल नीबू की महक वाली मीठी गोलियाँ हैं। मालिनी बिना थैले में झाँके उसमें से एक गोली निकालती है। इसकी क्या प्रायिकता है कि वह निकाली गई गोली
(i) संतरे की महक वाली है?
(ii) नीबू की महक वाली है?
Show Answer
#missing7. यह दिया हुआ है कि 3 विद्यार्थियों के एक समूह में से 2 विद्यार्थियों के जन्मदिन एक ही दिन न होने की प्रायिकता 0.992 है। इसकी क्या प्रायिकता है कि इन 2 विद्यार्थियों का जन्मदिन एक ही दिन हो?
Show Answer
#missing8. एक थैले में 3 लाल और 5 काली गेंदे हैं। इस थैले में से एक गेंद यादृच्छया निकाली जाती है। इसकी प्रायिकता क्या है कि गेंद
(i) लाल हो?
(ii) लाल नहीं हो?
Show Answer
#missing9. एक डिब्बे में 5 लाल कंचे, 8 सफेद कंचे और 4 हरे कंचे हैं। इस डिब्बे में से एक कंचा यादृच्छया निकाला जाता है। इसकी क्या प्रायिकता है कि निकाला गया कंचा
(i) लाल है?
(ii) सफेद है?
(iii) हरा नहीं है?
Show Answer
#missing10. एक पिग्गी बैंक (piggy bank) में, 50 पैसे के सौ सिक्के हैं, ₹ 1 के पचास सिक्के हैं, ₹ 2 के बीस सिक्के और ₹ 5 के दस सिक्के हैं। यदि पिग्गी बैंक को हिलाकर उल्टा करने पर कोई एक सिक्का गिरने के परिणाम समप्रायिक हैं, तो इसकी क्या प्रायिकता है कि वह गिरा हुआ सिक्का (i) 50 पैसे का होगा? (ii) ₹ 5 का नहीं होगा?
Show Answer
#missing11. गोपी अपने जल-जीव कुंड (aquarium) के लिए एक दुकान से मछली खरीदती है। दुकानदार एक टंकी, जिसमें 5 नर मछली और 8 मादा मछली हैं, में से एक मछली यादृच्छया उसे देने के लिए निकालती है (देखिए आकृति 14.4)। इसकी क्या प्रायिकता है कि निकाली गई मछली नर मछली है?

आकृति 14.4
Show Answer
#missing12. संयोग (chance) के एक खेल में, एक तीर को घुमाया जाता है, जो विश्राम में आने के बाद संख्याओं $1,2,3,4,5,6,7$ और 8 में से किसी एक संख्या को इंगित करता है (देखिए आकृति 14.5)। यदि ये सभी परिणाम समप्रायिक हों तो इसकी क्या प्रायिकता है कि यह तीर इंगित

आकृति 14.5
(i) 8 को करेगा?
(ii) एक विषम संख्या को करेगा?
(iii) 2 से बड़ी संख्या को करेगा?
(iv) 9 से छोटी संख्या को करेगा?
Show Answer
#missing13. एक पासे को एक बार फेंका जाता है। निम्नलिखित को प्राप्त करने की प्रायिकता ज्ञात कीजिए:
(i) एक अभाज्य संख्या
(ii) 2 और 6 के बीच स्थित कोई संख्या
(iii) एक विषम संख्या
Show Answer
#missing14. 52 पत्तों की अच्छी प्रकार से फेटी गई एक गड्डी में से एक पत्ता निकाला जाता है। निम्नलिखित को प्राप्त करने की प्रायिकता ज्ञात कीजिए :
(i) लाल रंग का बादशाह
(ii) एक फेस कार्ड अर्थात् तस्वीर वाला पत्ता
(iii) लाल रंग का तस्वीर वाला पत्ता
(iv) पान का गुलाम
(v) हुकुम का पत्ता
(vi) एक ईंट की बेगम
Show Answer
#missing15. ताश के पाँच पत्तों-ईंट का दहला, गुलाम, बेगम, बादशाह और इक्का-को पलट करके अच्छी प्रकार फेटा जाता है। फिर इनमें से यादृच्छया एक पत्ता निकाला जाता है।
(i) इसकी क्या प्रायिकता है कि यह पत्ता एक बेगम है?
(ii) यदि बेगम निकल आती है, तो उसे अलग रख दिया जाता है और एक अन्य पत्ता निकाला जाता है। इसकी क्या प्रायिकता है कि दूसरा निकाला गया पत्ता(a) एक इक्का है? (b) एक बेगम है?
Show Answer
#missing16. किसी कारण 12 खराब पेन 132 अच्छे पेनों में मिल गए हैं। केवल देखकर यह नहीं बताया जा सकता है कि कोई पेन खराब है या अच्छा है। इस मिश्रण में से, एक पेन यादृच्छया निकाला जाता है। निकाले गए पेन की अच्छा होने की प्रायिकता ज्ञात कीजिए।
Show Answer
#missing17. (i) 20 बल्बों के एक समूह में 4 बल्ब खराब हैं। इस समूह में से एक बल्ब यादृच्छया निकाला जाता है। इसकी क्या प्रायिकता है कि यह बल्ब खराब होगा?
(ii) मान लीजिए (i) में निकाला गया बल्ब खराब नहीं है और न ही इसे दुबारा बल्बों के साथ मिलाया जाता है। अब शेष बल्बों में से एक बल्ब यादृच्छया निकाला जाता है। इसकी क्या प्रायिकता है कि यह बल्ब खराब नहीं होगा?
Show Answer
#missing18. एक पेटी में 90 डिस्क (discs) हैं, जिन पर 1 से 90 तक संख्याएँ अंकित हैं। यदि इस पेटी में से एक डिस्क यादृच्छया निकाली जाती है तो इसकी प्रायिकता ज्ञात कीजिए कि इस डिस्क पर अंकित होगी : (i) दो अंकों की एक संख्या (ii) एक पूर्ण वर्ग संख्या (iii) 5 से विभाज्य एक संख्या।
Show Answer
#missing19. एक बच्चे के पास ऐसा पासा है जिसके फलकों पर निम्नलिखित अक्षर अंकित हैं :
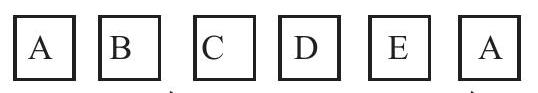
इस पासे को एक बार फेंका जाता है। इसकी क्या प्रायिकता है कि (i) $\mathrm{A}$ प्राप्त हो? (ii) $\mathrm{D}$ प्राप्त हो?
Show Answer
#missing20. मान लीजिए आप एक पासे को आकृति 14.6 में दर्शाए आयताकार क्षेत्र में यादृच्छया रूप से गिराते हैं। इसकी क्या प्रायिकता है कि वह पासा $1 \mathrm{~m}$ व्यास वाले वृत्त के अंदर गिरेगा?
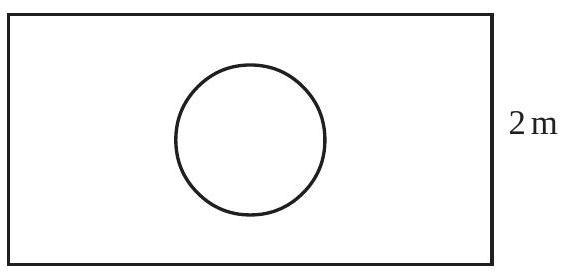
आकृति 14.6
Show Answer
#missing21. 144 बॉल पेनों के एक समूह में 20 बॉल पेन खराब हैं और शेष अच्छे हैं। आप वही पेन खरीदना चाहेंगे जो अच्छा हो, परंतु खराब पेन आप खरीदना नहीं चाहेंगे। दुकानदार इन पेनों में से, यादृच्छया एक पेन निकालकर आपको देता है। इसकी क्या प्रायिकता है कि
(i) आप वह पेन खरीदेंगे?
(ii) आप वह पेन नहीं खरीदेंगे?
Show Answer
#missing22. उदाहरण 13 को देखिए। (i) निम्नलिखित सारणी को पूरा कीजिए :
| घटना दोनों पासों की संख्याओं का योग |
2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| प्रायिकता | $\frac{1}{36}$ | $\frac{5}{36}$ | $\frac{1}{36}$ |
(ii) एक विद्यार्थी यह तर्क देता है कि ‘यहाँ कुल 11 परिणाम $2,3,4,5,6,7,8,9,10,11$ और 12 हैं। अतः, प्रत्येक की प्रायिकता $\frac{1}{11}$ है।’ क्या आप इस तर्क से सहमत हैं? सकारण उत्तर दीजिए।
Show Answer
#missing23. एक खेल में एक रुपए के सिक्के को तीन बार उछाला जाता है और प्रत्येक बार का परिणाम लिख लिया जाता है। तीनों परिणाम समान होने पर, अर्थात् तीन चित या तीन पट प्राप्त होने पर, हनीफ खेल में जीत जाएगा, अन्यथा वह हार जाएगा। हनीफ के खेल में हार जाने की प्रायिकता परिकलित कीजिए।
Show Answer
#missing24. एक पासे को दो बार फेंका जाता है। इसकी क्या प्रायिकता है कि
(i) 5 किसी भी बार में नहीं आएगा?
(ii) 5 कम से कम एक बार आएगा?
[संकेत : एक पासे को दो बार फेंकना और दो पासों को एक साथ फेंकना एक ही प्रयोग माना जाता है।]
Show Answer
#missing25. निम्नलिखित में से कौन से तर्क सत्य हैं और कौन से तर्क असत्य हैं? सकारण उत्तर दीजिए।
(i) यदि दो सिक्कों को एक साथ उछाला जाता है, तो इसके तीन संभावित परिणाम- दो चित, दो पट या प्रत्येक एक बार हैं। अतः, इनमें से प्रत्येक परिणाम की प्रायिकता $\frac{1}{3}$ है।
(ii) यदि एक पासे को फेंका जाता है, तो इसके दो संभावित परिणाम-एक विषम संख्या या एक सम संख्या हैं। अतः एक विषम संख्या ज्ञात करने की प्रायिकता $\frac{1}{2}$ है।
Show Answer
#missing14.2 सारांश
इस अध्याय में, आपने निम्नलिखित तथ्यों का अध्ययन किया है :
1. घटना $\mathrm{E}$ की सैद्धांतिक (या परंपरागत) प्रायिकता $\mathrm{P}(\mathrm{E})$ को निम्नलिखित रूप में परिभाषित किया जाता है:
$$ \mathrm{P}(\mathrm{E})=\frac{\mathrm{E} \text { के अनुकूल परिणामों की संख्या }}{\text { प्रयोग के सभी संभावित परिणामों की संख्या }} $$
जहाँ हम कल्पना करते हैं कि प्रयोग के सभी परिणाम समप्रायिक हैं।
2. एक निश्चित (या निर्धारित) घटना की प्रायिकता 1 होती है।
3. एक असंभव घटना की प्रायिकता 0 होती है।
4. घटना $\mathrm{E}$ की प्रायिकता एक ऐसी संख्या $\mathrm{P}(\mathrm{E})$ है कि
$$ 0 \leq \mathrm{P}(\mathrm{E}) \leq 1 $$
5. वह घटना जिसका केवल एक ही परिणाम हो एक प्रारंभिक घटना कहलाती है। किसी प्रयोग की सभी प्रारंभिक घटनाओं की प्रायिकता का योग 1 होता है।
6. किसी भी घटना $\mathrm{E}$ के लिए $\mathrm{P}(\mathrm{E})+\mathrm{P}(\overline{\mathrm{E}})=1$ होता है, जहाँ $\mathrm{E}$ घटना ’ $\mathrm{E}$ नहीं’ को व्यक्त करता है। $\mathrm{E}$ और $\mathrm{E}$ पूरक घटनाएँ कहलाती हैं।
पाठकों के लिए विशेष
एक घटना की प्रायोगिक या आनुभविक प्रायिकता वास्तविक रूप से घटना के घटित होने पर आधारित होती है, जबकि उस घटना की सैद्धांतिक प्रायिकता में कुछ कल्पनाओं के आधार पर यह प्रागुक्ति की जाती है कि क्या घटना घटेगी। जैसे-जैसे एक प्रयोग में अभिप्रयोगों की संख्या बढ़ती जाती है, वैसे-वैसे प्रायोगिक और सैद्धांतिक प्रायिकताओं की लगभग बराबर होने की प्रत्याशा की जा सकती है।





