अध्याय 11 वृत्तों से संबंधित क्षेत्रफल
11.1 त्रिज्यखंड और वृत्तखंड के क्षेत्रफल
आप पिछली कक्षाओं में शब्दों त्रिज्यखंड (sector) और वृत्तखंड (segment of a circle) से पूर्व परिचित हैं। आपको याद होगा कि एक वृत्तीय क्षेत्र का वह भाग जो दो त्रिज्याओं और संगत चाप से घिरा (परिबद्ध) हो, उस वृत्त का एक त्रिज्यखंड कहलाता है तथा वृत्तीय क्षेत्र का वह भाग जो एक जीवा और संगत चाप के बीच में परिबद्ध हो एक वृत्तखंड कहलाता है। इस प्रकार, आकृति 11.1 में, छायांकित भाग $O A P B$ केंद्र $O$ वाले वृत्त का एक त्रिज्यखंड है। $\angle A O B$ इस त्रिज्यखंड का कोण कहलाता है। ध्यान दीजिए कि इसी आकृति में अछायांकित भाग $O A Q B$ भी वृत्त का त्रिज्यखंड है। स्पष्ट कारणों से OAPB एक लघु त्रिज्यखंड (minor sector) कहलाता है तथा $\mathrm{OAQB}$ एक दीर्घ त्रिज्यखंड (major sector) कहलाता है। आप यह भी देख सकते हैं कि इस दीर्घ त्रिज्यखंड का कोण $360^{\circ}-\angle \mathrm{AOB}$ है।
आवृति 11.1
अब आकृति 11.2 को देखिए, जिसमें $\mathrm{AB}$ केंद्र $\mathrm{O}$ वाले वृत्त की एक जीवा है। अतः छायांकित भाग APB एक वृत्तखंड है। आप यह भी देख सकते हैं कि अछायांकित आकृति 11.2 भाग $A Q B$ भी जीवा $A B$ द्वारा निर्मित एक अन्य वृत्तखंड है। स्पष्ट कारणों से, $\mathrm{APB}$ लघु वृत्तखंड कहलाता है तथा $\mathrm{AQB}$ दीर्घ वृत्तखंड कहलाता है।
आकृति 11.2
टिप्पणी: जब तक अन्यथा न कहा जाए, ‘वृत्तखंड’ और ‘त्रिज्यखंड’ लिखने से हमारा तात्पर्य क्रमशः लघु वृत्तखंड और लघु त्रिज्यखंड से होगा।
आइए उपरोक्त ज्ञान के आधार पर, इनके क्षेत्रफलों के परिकलित करने के कुछ संबंध (या सूत्र) ज्ञात करने का प्रयत्न करें।
मान लीजिए OAPB केंद्र $\mathrm{O}$ और त्रिज्या $r$ वाले वृत्त का एक त्रिज्यखंड है (देखिए आकृति 11.3)। मान लीजिए $\angle \mathrm{AOB}$ का अंशीय (degree) माप $\theta$ है।

आकृति 11.3
आप जानते हैं कि एक वृत्त [वस्तुतः एक वृत्तीय क्षेत्र या चकती (disc)] का क्षेत्रफल $\pi r^{2}$ होता है।
एक तरीके से, हम इस वृत्तीय क्षेत्र को केंद्र $\mathrm{O}$ पर $360^{\circ}$ का कोण बनाने वाला (अंशीय माप 360) एक त्रिज्यखंड मान सकते हैं। फिर ऐकिक विधि (Unitary Method) का प्रयोग करके, हम त्रिज्यखंड OAPB का क्षेत्रफल नीचे दर्शाए अनुसार ज्ञात कर सकते हैं:
जब केंद्र पर बने कोण का अंशीय माप 360 है, तो त्रिज्यखंड का क्षेत्रफल $=\pi r^{2}$
अतः, जब केंद्र पर बने कोण का अंशीय माप 1 है, तो त्रिज्यखंड का क्षेत्रफल $=\frac{\pi r^{2}}{360}$
इसलिए जब केंद्र पर बने कोण का अंशीय माप $\theta$ है, तो त्रिज्यखंड का क्षेत्रफल $=\frac{\pi r^{2}}{360} \times \theta=\frac{\theta}{360} \times \pi r^{2}$
इस प्रकार, हम वृत्त के एक त्रिज्यखंड के क्षेत्रफल के लिए, निम्नलिखित संबंध (या सूत्र) प्राप्त करते हैं :
कोण $\theta$ वाले त्रिज्यखंड का क्षेत्रफल $=\frac{\theta}{360} \times \pi r^{2}$,
जहाँ $r$ वृत्त की त्रिज्या है और $\theta$ त्रिज्यखंड का अंशों में कोण है।
अब एक स्वाभाविक प्रश्न उठता है: क्या हम इस त्रिज्यखंड की संगत चाप APB की लंबाई ज्ञात कर सकते हैं। हाँ, हम ऐसा कर सकते हैं। पुनः, ऐकिक विधि का प्रयोग करने तथा संपूर्ण वृत्त ( $360^{\circ}$ कोण वाले) की लंबाई $2 \pi r$ लेने पर, हम चाप APB की वांछित लंबाई $\frac{\theta}{360} \times 2 \pi r$ प्राप्त करते हैं।
अतः कोण $\theta$ वाले त्रिज्यखंड के संगत चाप की लंबाई $=\frac{\theta}{360} \times 2 \pi r$

आकृति 11.4
आइए अब केंद्र $\mathrm{O}$ और त्रिज्या $r$ वाले वृत्तखंड $\mathrm{APB}$ के क्षेत्रफल पर विचार करें (देखिए आकृति 11.4)। आप देख सकते हैं कि
वृत्तखंड $\mathrm{APB}$ का क्षेत्रफल $=$ त्रिज्यखंड $\mathrm{OAPB}$ का क्षेत्रफल $-\triangle \mathrm{OAB}$ का क्षेत्रफल
$$ =\frac{\theta}{360} \times \pi r^{2}-\Delta \mathrm{OAB} \text { का क्षेत्रफल } $$
टिप्पणी : क्रमशः आकृति 11.3 और आकृति 11.4 से, आप देख सकते हैं कि
दीर्घ त्रिज्यखंड $\mathrm{OAQB}$ का क्षेत्रफल $=\pi r^{2}$ - लघु त्रिज्यखंड $\mathrm{OAPB}$ का क्षेत्रफल
तथा
दीर्घ वृत्तखंड $\mathrm{AQB}$ का क्षेत्रफल $=\pi r^{2}$ - लघु वृत्तखंड $\mathrm{APB}$ का क्षेत्रफल
अब आइए इन अवधारणाओं (या परिणामों) को समझने के लिए कुछ उदाहरण लें।
उदाहरण 1 : त्रिज्या $4 \mathrm{~cm}$ वाले एक वृत्त के त्रिज्यखंड का क्षेत्रफल ज्ञात कीजिए, जिसका कोण $30^{\circ}$ है। साथ ही, संगत दीर्घ त्रिज्यखंड का क्षेत्रफल भी ज्ञात कीजिए। ( $\pi=3.14$ का प्रयोग कीजिए)।
हल : दिया हुआ त्रिज्यखंड OAPB है (देखिए आकृति 11.5)।

आकृति 11.5
त्रिज्यखंड का क्षेत्रफल $=\frac{\theta}{360} \times \pi r^{2}$
$$ \begin{aligned} & =\frac{30}{360} \times 3.14 \times 4 \times 4 \mathrm{~cm}^{2} \\ & =\frac{12.56}{3} \mathrm{~cm}^{2}=4.19 \mathrm{~cm}^{2} \text { (लगभग) } \end{aligned} $$
संगत दीर्घ त्रिज्यखंड का क्षेत्रफल
$$ \begin{aligned} & =\pi r^{2}-\text { त्रिज्यखंड OAPB का क्षेत्रफल } \\ & =(3.14 \times 16-4.19) \mathrm{cm}^{2} \\ & \left.=46.05 \mathrm{~cm}^{2}=46.1 \mathrm{~cm}^{2} \quad \text { (लगभग }\right) \end{aligned} $$
वैकल्पिक रूप से, दीर्घ त्रिज्यखंड का क्षेत्रफल $=\frac{(360-\theta)}{360} \times \pi r^{2}$
$$ \begin{aligned} & =\left(\frac{360-30}{360}\right) \times 3.14 \times 16 \mathrm{~cm}^{2} \\ & =\frac{330}{360} \times 3.14 \times 16 \mathrm{~cm}^{2}=46.05 \mathrm{~cm}^{2} \\ & =46.1 \mathrm{~cm}^{2}(\text { लगभग) } \end{aligned} $$
उदाहरण 2 : आकृति 11.6 में दर्शाए गए वृत्तखंड का क्षेत्रफल ज्ञात कीजिए, यदि वृत्त की त्रिज्या $21 \mathrm{~cm}$ है और $\angle \mathrm{AOB}=120^{\circ}$ है। $\left[\pi=\frac{22}{7}\right.$ लीजिए $]$

आकृति 11.6
हल : वृत्तखंड AYB का क्षेत्रफल
$$ =\text { त्रिज्यखंड OAYB का क्षेत्रफल }- \Delta \mathrm{OAB}\text { का क्षेत्रफल } \tag{1} $$
$$ \text{ अब, त्रिज्यखंड OAYB का क्षेत्रफल } =\frac{120}{360} \times \frac{22}{7} \times 21 \times 21 \mathrm{~cm}^{2}=462 \mathrm{~cm}^{2} \tag{2}$$
$\triangle \mathrm{OAB}$ का क्षेत्रफल ज्ञात करने के लिए $\mathrm{OM} \perp \mathrm{AB}$ खींचिए, जैसाकि आकृति 11.7 में दिखाया गया है।

आकृति 11.7
ध्यान दीजिए कि $\mathrm{OA}=\mathrm{OB}$ है। अतः, $\mathrm{RHS}$ सर्वांगसमता से, $\triangle \mathrm{AMO} \cong \triangle \mathrm{BMO}$ है।
इसलिए $\mathrm{M}$ जीवा $\mathrm{AB}$ का मध्य-बिंदु है तथा $\angle \mathrm{AOM}=\angle \mathrm{BOM}=\frac{1}{2} \times 120^{\circ}=60^{\circ}$ है।
मान लीजिए
$$ \mathrm{OM}=x \mathrm{~cm} \text { है। } $$
इसलिए $\triangle$ OMA से,
$$ \frac{\mathrm{OM}}{\mathrm{OA}}=\cos 60^{\circ} $$
या
$$ \frac{x}{21}=\frac{1}{2} \quad\left(\cos 60^{\circ}=\frac{1}{2}\right) $$
या
$$ x=\frac{21}{2} $$
अत:
$$ \mathrm{OM}=\frac{21}{2} \mathrm{~cm} $$
साथ ही
$$ \frac{\mathrm{AM}}{\mathrm{OA}}=\sin 60^{\circ}=\frac{\sqrt{3}}{2} $$
अत:
$$ \mathrm{AM}=\frac{21 \sqrt{3}}{2} \mathrm{~cm} $$
इसलिए
$$ \mathrm{AB}=2 \mathrm{AM}=\frac{2 \times 21 \sqrt{3}}{2} \mathrm{~cm}=21 \sqrt{3} \mathrm{~cm} $$
अत:
$$ \begin{align*} \Delta \mathrm{OAB} \text { का क्षेत्रफल } & =\frac{1}{2} \mathrm{AB} \times \mathrm{OM}=\frac{1}{2} \times 21 \sqrt{3} \times \frac{21}{2} \mathrm{~cm}^{2} \end{align*} $$
$$ =\frac{441}{4} \sqrt{3} \mathrm{~cm}^{2}\tag{3}$$
इसलिए वृत्तखंड AYB का क्षेत्रफल $=\left(462-\frac{441}{4} \sqrt{3}\right) \mathrm{cm}^{2}$
$[(1),(2)$ और (3) से]
$$ =\frac{21}{4}(88-21 \sqrt{3}) \mathrm{cm}^{2} $$
अभ्यास 11.1
(जब तक अन्यथा न कहा जाए, $\pi=\frac{22}{7}$ का प्रयोग कीजिए।)
1. $6 \mathrm{~cm}$ त्रिज्या वाले एक वृत्त के एक त्रिज्यखंड का क्षेत्रफल ज्ञात कीजिए, जिसका कोण $60^{\circ}$ है।
Show Answer
#missing2. एक वृत्त के चतुर्थांश (quadrant) का क्षेत्रफल ज्ञात कीजिए, जिसकी परिधि $22 \mathrm{~cm}$ है।
Show Answer
#missing3. एक घड़ी की मिनट की सुई जिसकी लंबाई $14 \mathrm{~cm}$ है। इस सुई द्वारा 5 मिनट में रचित क्षेत्रफल ज्ञात कीजिए।
Show Answer
#missing4. 10 सेमी त्रिज्या वाले एक वृत्त की कोई जीवा केंद्र पर एक समकोण अंतरित करती है। निम्नलिखित के क्षेत्रफल ज्ञात कीजिए :
(i) संगत लघु वृत्तखंड
(ii) संगत दीर्घ त्रिज्यखंड ( $\pi=3.14$ का प्रयोग कीजिए)।
Show Answer
#missing5. त्रिज्या $21 \mathrm{~cm}$ वाले वृत्त का एक चाप केंद्र पर $60^{\circ}$ का कोण अंतरित करता है। ज्ञात कीजिए :
(i) चाप की लंबाई
(ii) चाप द्वारा बनाए गए त्रिज्यखंड का क्षेत्रफल
(iii) संगत जीवा द्वारा बनाए गए वृत्तखंड का क्षेत्रफल
Show Answer
#missing6. $15 \mathrm{~cm}$ त्रिज्या वाले एक वृत्त की कोई जीवा केंद्र पर $60^{\circ}$ का कोण अंतरित करती है। संगत लघु और दीर्घ वृत्तखंडों के क्षेत्रफल ज्ञात कीजिए।
$(\pi=3.14$ और $\sqrt{3}=1.73$ का प्रयोग कीजिए।)
Show Answer
#missing7. त्रिज्या $12 \mathrm{~cm}$ वाले एक वृत्त की कोई जीवा केंद्र पर $120^{\circ}$ का कोण अंतरित करती है। संगत वृत्तखंड का क्षेत्रफल ज्ञात कीजिए।
( $\pi=3.14$ और $\sqrt{3}=1.73$ का प्रयोग कीजिए।)
Show Answer
#missing8. $15 \mathrm{~m}$ भुजा वाले एक वर्गाकार घास के मैदान के एक कोने पर लगे खूँटे से एक घोड़े को $5 \mathrm{~m}$ लंबी रस्सी से बाँध दिया गया है (देखिए आकृति 11.8)। ज्ञात कीजिए:
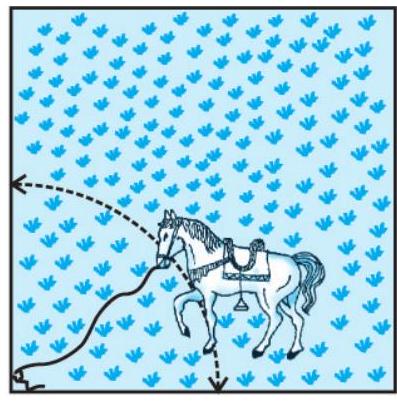
आकृति 11.8
(i) मैदान के उस भाग का क्षेत्रफल जहाँ घोड़ा घास चर सकता है।
(ii) चरे जा सकने वाले क्षेत्रफल में वृद्धि, यदि घोड़े को $5 \mathrm{~m}$ लंबी रस्सी के स्थान पर $10 \mathrm{~m}$ लंबी रस्सी से बाँध दिया जाए। ( $\pi=3.14$ का प्रयोग कीजिए।)
Show Answer
#missing9. एक वृत्ताकार ब्रूच (brooch) को चाँदी के तार से बनाया जाना है जिसका व्यास $35 \mathrm{~mm}$ है। तार को वृत के 5 व्यासों को बनाने में भी प्रयुक्त किया गया है जो उसे 10 बराबर त्रिज्यखंडों में विभाजित करता है जैसा कि आकृति 11.9 में दर्शाया गया है। तो ज्ञात कीजिए:
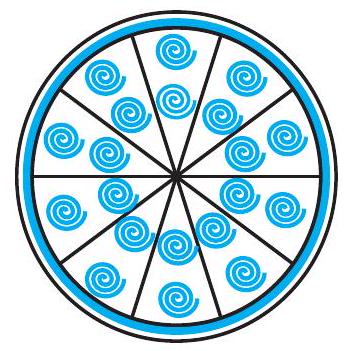
आवृति 11.9
(i) कुल वांछित चाँदी के तार की लंबाई
(ii) ब्रूच के प्रत्येक त्रिज्यखंड का क्षेत्रफल
Show Answer
#missing10. एक छतरी में आठ ताने हैं, जो बराबर दूरी पर लगे हुए हैं (देखिए आकृति 11.10)। छतरी को $45 \mathrm{~cm}$ त्रिज्या वाला एक सपाट वृत्त मानते हुए, इसकी दो क्रमागत तानों के बीच का क्षेत्रफल ज्ञात कीजिए।
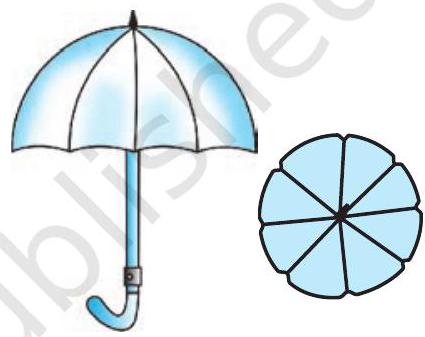
आवृति 11.10
Show Answer
#missing11. किसी कार के दो वाइपर (Wipers) हैं, परस्पर कभी आच्छादित नहीं होते हैं। प्रत्येक वाइपर की पत्ती की लंबाई $25 \mathrm{~cm}$ है और $115^{\circ}$ के कोण तक घूम कर सफाई कर सकता है। पत्तियों की प्रत्येक बुहार के साथ जितना क्षेत्रफल साफ हो जाता है, वह ज्ञात कीजिए।
Show Answer
#missing12. जहाज़ों को समुद्र में जलस्तर के नीचे स्थित चट्टानों की चेतावनी देने के लिए, एक लाइट हाउस (light house) $80^{\circ}$ कोण वाले एक त्रिज्यखंड में $16.5 \mathrm{~km}$ की दूरी तक लाल रंग का प्रकाश फैलाता है। समुद्र के उस भाग का क्षेत्रफल ज्ञात कीजिए जिसमें जहाज़ों को चेतावनी दी जा सके। ( $\pi=3.14$ का प्रयोग कीजिए।)
Show Answer
#missing13. एक गोल मेज़पोश पर छः समान डिज़ाइन बने हुए हैं जैसाकि आकृति 11.11 में दर्शाया गया है। यदि मेज़पोश की त्रिज्या $28 \mathrm{~cm}$ है, तो ₹ 0.35 प्रति वर्ग सेंटीमीटर की दर से इन डिज़ाइनों को बनाने की लागत ज्ञात कीजिए। ( $\sqrt{3}=1.7$ का प्रयोग कीजिए)
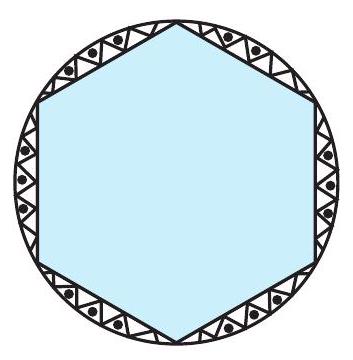
आकृति 11.11
Show Answer
#missing14. निम्नलिखित में सही उत्तर चुनिए:
त्रिज्या $\mathrm{R}$ वाले वृत्त के उस त्रिज्यखंड का क्षेत्रफल जिसका कोण $p^{\circ}$ है, निम्नलिखित है :
(A) $\frac{p}{180} \times 2 \pi \mathrm{R}$
(B) $\frac{p}{180} \times \pi \mathrm{R}^{2}$
(C) $\frac{p}{720} \times 2 \pi \mathrm{R}^{2}$
(D) $\frac{p}{360} \times 2 \pi \mathrm{R}$
Show Answer
#missing11.2 सारांश
इस अध्याय में, आपने निम्नलिखित बिंदुओं का अध्ययन किया है:
1. त्रिज्या $r$ वाले वृत्त के एक त्रिज्यखंड, जिसका कोण अंशों में $\theta$ है, के संगत चाप की लंबाई $\frac{\theta}{360} \times 2 \pi r$ होती है।
2. त्रिज्या $r$ वाले वृत्त के एक त्रिज्यखंड, जिसका कोण अंशों में $\theta$ है, का क्षेत्रफल $\frac{\theta}{360} \times \pi r^{2}$ होता है।
3. एक वृत्तखंड का क्षेत्रफल $=$ संगत त्रिज्यखंड का क्षेत्रफल-संगत त्रिभुज का क्षेत्रफल





