10.1 भूमिका

आपने कक्षा IX में पढ़ा है कि वृत्त एक तल के उन बिंदुओं का समूह होता है जो एक नियत बिंदु (केंद्र) से अचर दूरी (त्रिज्या) पर होते हैं। आपने वृत्त से संबंधित अवधारणाओं जैसे जीवा, वृत्तखंड, त्रिज्यखंड, चाप आदि के बारे में भी पढ़ा है। आइए अब एक तल में स्थित एक वृत्त तथा एक रेखा की विभिन्न स्थितियों पर विचार करें।

आइए, हम एक वृत्त तथा एक रेखा $\mathrm{PQ}$ पर ध्यान दें। दी गई निम्न आकृति 10.1 में तीन संभावनाएँ हो सकती हैं।

आकृति 10.1

आकृति 10.1 (i) में, रेखा $\mathrm{PQ}$ तथा वृत्त में कोई उभयनिष्ठ बिंदु नहीं है। इस दशा में $\mathrm{PQ}$ को वृत्त के सापेक्ष अप्रतिच्छेदी रेखा कहते हैं। आकृति 10.1 (ii) में रेखा $\mathrm{PQ}$ और वृत्त में दो उभयनिष्ठ बिंदु $\mathrm{A}$ और $\mathrm{B}$ हैं। इस दशा में हम रेखा $\mathrm{PQ}$ को वृत्त की छेदक रेखा कहते हैं। आकृति 10.1 (iii) में रेखा $\mathrm{PQ}$ और वृत्त में एक और केवल एक उभयनिष्ठ बिंदु $\mathrm{A}$ है। इस दशा में रेखा वृत्त की स्पर्श रेखा कहलाती है।

आपने कुएँ के ऊपर स्थिर की हुई एक घिरनी को देखा होगा जिसका उपयोग कुएँ से पानी निकालने के लिए किया जाता है। आकृति 10.2 को देखिए। यहाँ घिरनी के दोनों ओर की रस्सी को यदि किरण की तरह समझें तो वह घिरनी द्वारा निरूपित वृत्त पर स्पर्श रेखा की तरह होगी।

आकृति 10.2

ऊपर दी गई स्थितियों के अतिरिक्त क्या वृत्त के सापेक्ष रेखा की कोई अन्य स्थिति हो सकती है? आप देख सकते हैं कि इन स्थितियों के अतिरिक्त रेखा की वृत्त के सापेक्ष कोई अन्य स्थिति नहीं हो सकती है। इस अध्याय में हम वृत्त की स्पर्श रेखा के अस्तित्व के बारे में पढ़ंगे तथा उनके कुछ गुणों का भी अध्ययन करेंगे।

10.2 वृत्त की स्पर्श रेखा

पिछले परिच्छेद में आपने देखा है कि किसी वृत्त की स्पर्श रेखा वह रेखा है जो वृत्त को केवल एक बिंदु पर प्रतिच्छेद करती है।

वृत्त के किसी बिंदु पर स्पर्श रेखा के अस्तित्व को समझने के लिए आइए हम निम्न क्रियाकलाप करें।

क्रियाकलाप 1 : एक वृत्ताकार तार लीजिए तथा वृत्ताकार तार के एक बिंदु $P$ पर एक सीधा तार $\mathrm{AB}$ इस प्रकार जोड़िए कि वह बिंदु $\mathrm{P}$ के परितः एक समतल में घूम सके। इस प्रणाली को एक मेज़ पर रखिए तथा तार $A B$ को बिंदु $P$ के परितः धीमे-धीमे घुमाइए जिससे सीधे तार की विभिन्न अवस्थाएँ प्राप्त हो सकें [देखिए आकृति 10.3(i)]।

विभिन्न स्थितियों में तार, वृत्ताकार तार को बिंदु $\mathrm{P}$ एवं एक अन्य बिंदु $Q _{1}$ या $Q _{2}$ या $Q _{3}$ आदि पर प्रतिच्छेदित करता है। एक स्थिति में, आप देखेंगे कि वह वृत्त को केवल एक बिंदु $\mathrm{P}$ पर ही प्रतिच्छेदित करेगा ( $\mathrm{AB}$ की स्थिति $\mathrm{A}^{\prime} \mathrm{B}^{\prime}$ को देखिए)। ये यह दर्शाता है कि वृत्त के एक बिंदु पर एक स्पर्श रेखा का अस्तित्व है। पुन: घुमाने पर आप प्रेक्षण कर सकते हैं कि $\mathrm{AB}$ की अन्य सभी स्थितियों में वह वृत्त को बिंदु $P$ तथा एक अन्य बिंदु $R _{1}$ या $R _{2}$ या $R _{3}$ आदि पर प्रतिच्छेद करता है। इस प्रकार आप प्रेक्षण कर सकते हैं कि वृत्त के एक बिंदु पर एक और केवल एक स्पर्श रेखा होती है।

आकृति 10.3 (i)

उपर्युक्त क्रियाकलाप करते हुए आपने अवश्य प्रेक्षण किया होगा कि जैसे-जैसे स्थिति $\mathrm{AB}$ से स्थिति $\mathrm{A}^{\prime} \mathrm{B}^{\prime}$ की ओर बढ़ती है, रेखा $\mathrm{AB}$ और वृत्त का उभयनिष्ठ बिंदु $\mathrm{Q} _{1}$, उभयनिष्ठ बिंदु $P$ की ओर निकट आता जाता है। अंततः, $A B$ की स्थिति $A^{\prime} B^{\prime}$ में वह बिंदु $P$ के संपाती हो जाता है। पुनः ध्यान दीजिए कि क्या होता है जब $\mathrm{A}^{\prime \prime} \mathrm{B}^{\prime \prime}, \mathrm{P}$ के परितः दक्षिणावर्त घुमाया जाता है? उभयनिष्ठ बिंदु $\mathrm{R} _{3}$ धीरे-धीरे बिंदु $\mathrm{P}$ की ओर अग्रसर होता है तथा अंततः $\mathrm{P}$ से संपाती हो जाता है। इस प्रकार हम देखते हैं:

किसी वृत्त की स्पर्श रेखा छेदक रेखा की एक विशिष्ट दशा है जब संगत जीवा के दोनों सिरे संपाती हो जाएँ।

क्रियाकलाप 2 : एक कागज पर एक वृत्त और वृत्त की छेदक रेखा $\mathrm{PQ}$ खींचिए। छेदक रेखा के समांतर दोनों ओर अनेक रेखाएँ खींचिए। आप पाएँगे कि कुछ चरणों के बाद रेखाओं द्वारा काटी गई जीवा की लंबाई धीरे-धीरे कम हो रही है अर्थात् रेखा तथा वृत्त के दोनों प्रतिच्छेद बिंदु पास आ रहे हैं [देखिए आकृति 10.3(ii)]। एक स्थिति में छेदक रेखा के एक ओर यह लंबाई तथा दूसरी स्थिति में यह दूसरी ओर शून्य हो जाती है। छेदक रेखा की स्थितियों $\mathrm{P}^{\prime} \mathrm{Q}^{\prime}$ तथा $\mathrm{P}^{\prime \prime} \mathrm{Q}^{\prime \prime}$ की आकृति 10.3 (ii) में अवलोकन कीजिए। ये दोनों रेखाएँ दी गयी छेदक रेखा $\mathrm{PQ}$ के समांतर दो स्पर्श रेखाएँ हैं इससे आपको यह जानने में सहायता मिलती है कि एक छेदक रेखा के समांतर वृत्त की दो से अधिक स्पर्श रेखाएँ नहीं होती हैं।

आकृति 10.3(ii)

इस क्रियाकलाप से यह निष्कर्ष भी निकलता है कि स्पर्श रेखा छेदक रेखा की एक विशेष स्थिति है जब उसकी संगत जीवा के दोनों सिरे संपाती हो जाएँ।

स्पर्श रेखा और वृत्त के उभयनिष्ठ बिंदु को स्पर्श बिंदु [आकृति 10.1 (iii) में बिंदु A] कहते हैं तथा स्पर्श रेखा को वृत्त के उभयनिष्ठ बिंदु पर स्पर्श करना कहते हैं।

अब आप अपने चारों ओर देखिए। क्या आपने एक साइकिल अथवा एक बैलगाड़ी को चलते देखा है? इनके पहियों की ओर देखिए। एक पहिए की सभी तीलियाँ इसकी त्रिज्याओं के अनुरूप हैं। अब पहिए की स्थिति का धरती पर गति करने के सापेक्ष व्याख्या कीजिए। क्या आपको कहीं स्पर्श रेखा दिखती है? (देखिए आकृति 10.4)। वास्तव में पहिया एक रेखा के अनुदिश गति करता है जो पहिये को निरूपित करने वाले वृत्त पर स्पर्श रेखा है। यह भी देखिए कि सभी स्थितियों में आकृति 10.4 धरती के स्पर्श बिंदु से जाने वाली त्रिज्या स्पर्श रेखा पर लंब दृष्टिगोचर होती है (देखिए आकृति 10.4)। अब हम स्पर्श रेखा के इस गुण को सिद्ध करेंगे।

आकृति 10.4

प्रमेय 10.1 : वृत्त के किसी बिंदु पर स्पर्श रेखा स्पर्श बिंदु से जाने वाली त्रिज्या पर लंब होती है।

उपपत्ति : हमें केंद्र $\mathrm{O}$ वाला एक वृत्त दिया है और एक बिंदु $\mathrm{P}$ पर स्पर्श रेखा $\mathrm{XY}$ दी है। हमें सिद्ध करना है कि $\mathrm{OP}, \mathrm{XY}$ पर लंब है।

$\mathrm{XY}$ पर $\mathrm{P}$ के अतिरिक्त एक बिंदु $\mathrm{Q}$ लीजिए और $\mathrm{OQ}$ को मिलाइए (देखिए आकृति 10.5)।

बिंदु $\mathrm{Q}$ वृत्त के बाहर होना चाहिए (क्यों? ध्यान दीजिए कि यदि $\mathrm{Q}$ वृत्त के अंदर है तो $\mathrm{XY}$ वृत्त की एक छेदक रेखा हो जाएगी और वह वृत्त की स्पर्श रेखा नहीं होगी)। अतः, $\mathrm{OQ}$ त्रिज्या $\mathrm{OP}$ से बड़ी है। अर्थात्

$$ \mathrm{OQ}>\mathrm{OP} $$

क्योंकि यह बिंदु $\mathrm{P}$ के अतिरिक्त $\mathrm{XY}$ के प्रत्येक बिंदु के लिए सत्य है, $O P$ बिंदु $O$ से $X Y$ के अन्य बिंदुओं की न्यूनतम दूरी है। इसलिए $\mathrm{OP}, \mathrm{XY}$ पर लंब है (जैसा कि प्रमेय $\mathrm{A} 1.7$ में दर्शाया गया है)।

आकृति 10.5

टिप्पणी :

1. उपर्युक्त प्रमेय से हम यह भी निष्कर्ष निकाल सकते हैं कि वृत्त के किसी बिंदु पर एक और केवल एक स्पर्श रेखा होती है।

2. स्पर्श बिंदु से त्रिज्या को समाहित करने वाली रेखा को वृत्त के उस बिंदु पर ‘अभिलंब’ भी कहते हैं।

प्रश्नावली 10.1

1. एक वृत्त की कितनी स्पर्श रेखाएँ हो सकती हैं?

2. रिक्त स्थानों की पूर्ति कीजिए:

(i) किसी वृत्त की स्पर्श रेखा उसे __________ बिंदुओं पर प्रतिच्छेद करती है।

(ii) वृत्त को दो बिंदुओं पर प्रतिच्छेद करने वाली रेखा को __________ कहते हैं।

(iii) एक वृत्त की _________ समांतर स्पर्श रेखाएँ हो सकती हैं।

(iv) वृत्त तथा उसकी स्पर्श रेखा के उभयनिष्ठ बिंदु को __________ कहते हैं।

3. 5 सेमी त्रिज्या वाले एक वृत्त के बिंदु $\mathrm{P}$ पर स्पर्श रेखा $\mathrm{PQ}$ केंद्र $\mathrm{O}$ से जाने वाली एक रेखा से बिंदु $\mathrm{Q}$ पर इस प्रकार मिलती है कि $\mathrm{OQ}=12$ सेमी। $\mathrm{PQ}$ की लंबाई है:

(A) 12 सेमी $\quad$

(B) 13 सेमी $\quad$

(C) 8.5 सेमी $\quad$

(D) $\sqrt{119}$ सेमी

4. एक वृत्त खींचिए और एक दी गई रेखा के समांतर दो ऐसी रेखाएँ खींचिए कि उनमें से एक स्पर्श रेखा हो तथा दूसरी छेदक रेखा हो।

10.3 एक बिंदु से एक वृत्त पर स्पर्श रेखाओं की संख्या

किसी बिंदु से वृत्त पर खींची गई स्पर्श रेखाओं की संख्या के बारे में जानने के लिए निम्न क्रियाकलाप करें:

क्रियाकलाप 3 : एक कागज़ पर एक वृत्त खींचिए। एक बिंदु $P$ इसके अंदर लीजिए। उस बिंदु से वृत्त पर स्पर्श रेखा खींचने का प्रयत्न कीजिए। आप क्या पाते हैं? आप पाते हैं कि इससे खींची गई प्रत्येक रेखा वृत्त को दो बिंदुओं पर परिच्छेद करती है इसलिए इन रेखाओं में से कोई स्पर्श रेखा नहीं हो सकती [देखिए आकृति 10.6 (i)]।

पुनः, वृत्त पर एक बिंदु $\mathrm{P}$ लीजिए तथा इस बिंदु से स्पर्श रेखाएँ खींचिए। आपने पहले से ही प्रेक्षण किया है कि वृत्त के इस बिंदु पर एक ही स्पर्श रेखा होती है [देखिए आकृति 10.6 (ii)]।

अंत में वृत्त के बाहर एक बिंदु $P$ लीजिए और वृत्त पर इस बिंदु से स्पर्श रेखाएँ खींचने का प्रयत्न करिए। आप क्या प्रेक्षण करते हैं? आप पाएँगे कि इस बिंदु से वृत्त पर दो और केवल दो स्पर्श रेखाएँ खींच सकते हैं (देखिए आकृति 10.6 (iii)]।

आकृति 10.6

संक्षेप में हम इन यथार्थों को निम्न स्थितियों में प्रकट कर सकते हैं।

स्थिति 1 : वृत्त के अंदर स्थित किसी बिंदु से जाने वाली वृत्त पर कोई स्पर्श रेखा नहीं है।

स्थिति 2 : वृत्त पर स्थित किसी बिंदु से वृत्त पर एक और केवल एक स्पर्श रेखा है।

स्थिति 3 : वृत्त के बाहर स्थित किसी बिंदु से जाने वाली वृत्त पर दो और केवल दो स्पर्श रेखाएँ हैं।

आकृति 10.6 (iii) में स्पर्श रेखाओं $\mathrm{PT} _{1}$ तथा $\mathrm{PT} _{2}$ के क्रमशः $\mathrm{T} _{1}$ तथा $\mathrm{T} _{2}$ स्पर्श बिंदु हैं।

वाह्य बिंदु $\mathrm{P}$ से वृत्त के स्पर्श बिंदु तक स्पर्श रेखा खंड की लंबाई को बिंदु $\mathrm{P}$ से वृत्त पर स्पर्श रेखा की लंबाई कहते हैं।

ध्यान दीजिए कि आकृति 10.6 (iii) में $\mathrm{PT} _{1}$ और $\mathrm{PT} _{2}$ बिंदु $\mathrm{P}$ से वृत्त पर स्पर्श रेखाओं की लंबाइयाँ हैं। लंबाइयों $\mathrm{PT} _{1}$ और $\mathrm{PT} _{2}$ में एक उभयनिष्ठ गुण है। क्या आप इसे प्राप्त कर सकते हैं? $\mathrm{PT} _{1}$ और $\mathrm{PT} _{2}$ को मापिए। क्या ये बराबर हैं? वास्तव में सदैव ऐसा ही है। आइए इस तथ्य की एक उपपत्ति निम्न प्रमेय में दें।

प्रमेय 10.2 : वाह्य बिंदु से वृत्त पर खींची गई स्पर्श रेखाओं की लंबाइयाँ बराबर होती है।

उपपत्ति : हमें केंद्र $\mathrm{O}$ वाला एक वृत्त, वृत्त के बाहर का एक बिंदु $\mathrm{P}$ तथा $\mathrm{P}$ से वृत्त पर दो स्पर्श रेखाएँ $\mathrm{PQ}$, $\mathrm{PR}$ दी है (देखिए आकृति 10.7)। हमें सिद्ध करना है कि $\mathrm{PQ}=\mathrm{PR}$

आकृति 10.7

इसके लिए हम $\mathrm{OP}, \mathrm{OQ}$ और $\mathrm{OR}$ को मिलाते हैं। तब $\angle \mathrm{OQP}$ तथा $\angle \mathrm{ORP}$ समकोण हैं क्योंकि ये त्रिज्याओं और स्पर्श रेखाओं के बीच के कोण हैं और प्रमेय 10.1 से ये समकोण है। अब समकोण त्रिभुजों OQP तथा ORP में,

OQ $=$ OR $\quad \quad \quad \quad \quad \quad \quad $(एक ही वृत्त की त्रिज्याएँ)

OP $=$ OP $\quad \quad \quad \quad \quad \quad \quad $ (उभयनिष्ठ)

अत:

$\Delta \mathrm{OQP} \cong \triangle \mathrm{ORP}$ (RHS सर्वांगसमता द्वारा)

इससे प्राप्त होता है

$P Q=P R\quad \quad \quad \quad \text{(CPCT)}$

टिप्पणी :

1. प्रमेय को पाइथागोरस प्रमेय का प्रयोग करके भी निम्न प्रकार से सिद्ध किया जा सकता है:

$\mathrm{PQ}^{2}=\mathrm{OP}^{2}-\mathrm{OQ}^{2}=\mathrm{OP}^{2}-\mathrm{OR}^{2}=\mathrm{PR}^{2}$ (क्योंकि $\mathrm{OQ}=\mathrm{OR}$ )

जिससे प्राप्त होता है कि $\mathrm{PQ}=\mathrm{PR}$

2. यह भी ध्यान दीजिए कि $\angle \mathrm{OPQ}=\angle \mathrm{OPR}$ । अतः $\mathrm{OP}$ कोण $\mathrm{QPR}$ का अर्धक है, अर्थात् वृत्त का केंद्र स्पर्श रेखाओं के बीच के कोण अर्धक पर स्थित होता है।

आइए, अब कुछ उदाहरण लें।

उदाहरण 1 : सिद्ध कीजिए कि दो सकेंद्रीय वृत्तों में बड़े वृत्त की जीवा जो छोटे वृत्त को स्पर्श करती है, स्पर्श बिंदु पर समद्विभाजित होती है।

हल : हमें केंद्र $\mathrm{O}$ वाले दो सकेंद्रीय वृत्त $\mathrm{C} _{1}$ और $\mathrm{C} _{2}$ तथा बड़े वृत्त $C _{1}$ की जीवा $A B$, जो छोटे वृत्त $C _{2}$ को बिंदु $P$ पर स्पर्श करती है, दिए हैं (देखिए आकृति 10.8)। हमें सिद्ध करना है कि $\mathrm{AP}=\mathrm{BP}$

आकृति 10.8

आइए $\mathrm{OP}$ को मिलाएँ। इस प्रकार $\mathrm{AB}, \mathrm{C} _{2}$ के बिंदु $\mathrm{P}$ पर स्पर्श रेखा है और $\mathrm{OP}$ त्रिज्या है। अतः प्रमेय 10.1 से

$$ \mathrm{OP} \perp \mathrm{AB} $$

अब $\mathrm{AB}$ वृत्त $\mathrm{C} _{1}$ की एक जीवा है और $\mathrm{OP} \perp \mathrm{AB}$ है। अतः, $\mathrm{OP}$ जीवा $\mathrm{AB}$ को समद्विभाजित करेगी क्योंकि केंद्र से जीवा पर खींचा गया लंब उसे समद्विभाजित करता है,

अर्थात्

$$ \mathrm{AP}=\mathrm{BP} $$

उदाहरण 2 : केंद्र $\mathrm{O}$ वाले वृत्त पर बाह्य बिंदु $\mathrm{T}$ से दो स्पर्श रेखाएँ $\mathrm{TP}$ तथा $\mathrm{TQ}$ खींची गई हैं। सिद्ध कीजिए कि $\angle \mathrm{PTQ}=2 \angle \mathrm{OPQ}$ है।

हल : हमें केंद्र $\mathrm{O}$ वाला एक वृत्त, एक बाह्य बिंदु $\mathrm{T}$ तथा वृत्त पर दो स्पर्श रेखाएँ $\mathrm{TP}$ और $\mathrm{TQ}$, जहाँ $\mathrm{P}, \mathrm{Q}$ स्पर्श बिंदु हैं, दिए हैं (देखिए आकृति 10.9)। हमें सिद्ध करना है कि

आकृति 10.9

$$ \angle \mathrm{PTQ}=2 \angle \mathrm{OPQ} $$

माना

$$ \angle \mathrm{PTQ}=\theta $$

अब प्रमेय 10.2 से $\mathrm{TP}=\mathrm{TQ}$ । अतः $\mathrm{TPQ}$ एक समद्विबाहु त्रिभुज है।

इसलिए

$$ \angle \mathrm{TPQ}=\angle \mathrm{TQP}=\frac{1}{2}\left(180^{\circ}-\theta\right)=90^{\circ}-\frac{1}{2} \theta $$

प्रमेय 10.1 से

$$\angle \mathrm{OPT}=90^{\circ} \text {है।} $$

अत:

$$ \begin{aligned} \angle \mathrm{OPQ}=\angle \mathrm{OPT}-\angle \mathrm{TPQ} & =90^{\circ}-\left(90^{\circ}-\frac{1}{2} \theta\right) \\ & =\frac{1}{2} \theta=\frac{1}{2} \angle \mathrm{PTQ} \end{aligned} $$

इससे प्राप्त होता है।

$$ \angle \mathrm{PTQ}=2 \angle \mathrm{OPQ} $$

उदाहरण 3: $ 5 \mathrm{~cm}$ त्रिज्या के एक वृत्त की $8 \mathrm{~cm}$ लंबी एक जीवा $P Q$ है। $P$ और $Q$ पर स्पर्श रेखाएँ परस्पर एक बिंदु $\mathrm{T}$ पर प्रतिच्छेद करती हैं (देखिए आकृति 10.10)। TP की लंबाई ज्ञात कीजिए।

हल : OT को मिलाएँ। माना यह $\mathrm{PQ}$ को बिंदु $\mathrm{R}$ पर प्रतिच्छेदित करती है। तब $\triangle \mathrm{TPQ}$ समद्विबाहु है और $\mathrm{TO}, \angle \mathrm{PTQ}$ का कोणार्धक है। इसलिए $\mathrm{OT} \perp \mathrm{PQ}$ और इस प्रकार $\mathrm{OT}, \mathrm{PQ}$ का अर्धक है जिससे प्राप्त होता है $\mathrm{PR}=\mathrm{RQ}=4 \mathrm{~cm}$

आकृति 10.10

साथ ही $\mathrm{OR}=\sqrt{\mathrm{OP}^{2}-\mathrm{PR}^{2}}=\sqrt{5^{2}-4^{2}} \mathrm{~cm}=3 \mathrm{~cm}$

अब $\angle \mathrm{TPR}+\angle \mathrm{RPO}=90^{\circ}=\angle \mathrm{TPR}+\angle \mathrm{PTR}$( क्यों?)

अत: $\quad \angle \mathrm{RPO}=\angle \mathrm{PTR}$

इसलिए समकोण त्रिभुज TRP और समकोण त्रिभुज PRO, AA समरूपता द्वारा समरूप हैं।

इससे प्राप्त होता है।

$\frac{\mathrm{TP}}{\mathrm{PO}}=\frac{\mathrm{RP}}{\mathrm{RO}}$ अर्थात् $\frac{\mathrm{TP}}{5}=\frac{4}{3}$ अर्थात् $\mathrm{TP}=\frac{20}{3} \mathrm{~cm}$

टिप्पणी: TP को पाइथागोरस प्रमेय द्वारा निम्न प्रकार से भी प्राप्त कर सकते हैं:

माना

$$ \begin{array}{rlrl} \mathrm{TP} & =x \text { और } \mathrm{TR}=y . \quad \text { तो } \end{array} $$

$$ \begin{array}{rlrl} x^{2} & =y^{2}+16 & & \quad(\text {समकोण } \Delta \mathrm{PRT}\text{लेकर}) \tag{1} \end{array} $$

$$ \begin{array}{rlrl} x^{2}+5^{2} & =(y+3)^{2} & & \quad(\text { समकोण } \Delta \mathrm{OPT}\text{लेकर}) \tag{2} \end{array} $$

(1) को (2) में से घटाकर, हम पाते हैं

इसलिए

$$ \begin{aligned} 25 & =6 y-7 \text { या } y=\frac{32}{6}=\frac{16}{3} \\ x^{2} & =\left(\frac{16}{3}\right)^{2}+16=\frac{16}{9}(16+9)=\frac{16 \times 25}{9} \quad \quad \quad \text{[ (1)से]}\\ x & =\frac{20}{3} \end{aligned} $$

प्रश्नावली 10.2

प्रश्न सं. $1,2,3$ में सही विकल्प चुनिए एवं उचित कारण दीजिए।

1. एक बिंदु $\mathrm{Q}$ से एक वृत्त पर स्पर्श रेखा की लंबाई $24 \mathrm{~cm}$ तथा $\mathrm{Q}$ की केंद्र से दूरी $25 \mathrm{~cm}$ है। वृत्त की त्रिज्या है:

(A) $7 \mathrm{~cm}$ $\quad$

(B) $12 \mathrm{~cm}$ $\quad$

(C) $15 \mathrm{~cm}$ $\quad$

(D) $24.5 \mathrm{~cm}$

2. आकृति 10.11 में, यदि $\mathrm{TP}, \mathrm{TQ}$ केंद्र $\mathrm{O}$ वाले किसी वृत्त पर दो स्पर्श रेखाएँ इस प्रकार हैं कि $\angle \mathrm{POQ}=110^{\circ}$, तो $\angle \mathrm{PTQ}$ बराबर है:

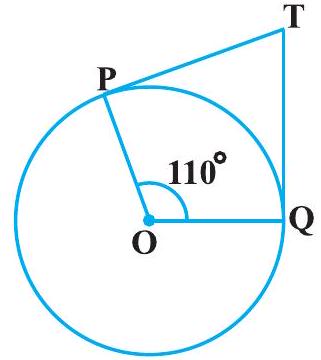
आकृति 10.11

(A) $60^{\circ}$ $\quad$

(B) $70^{\circ}$ $\quad$

(C) $80^{\circ}$ $\quad$

(D) $90^{\circ}$

3. यदि एक बिंदु $\mathrm{P}$ से $\mathrm{O}$ केंद्र वाले किसी वृत्त पर $\mathrm{PA}, \mathrm{PB}$ स्पर्श रेखाएँ परस्पर $80^{\circ}$ के कोण पर झुकी हों, तो $\angle \mathrm{POA}$ बराबर है :

(A) $50^{\circ}$ $\quad$

(B) $60^{\circ}$ $\quad$

(C) $70^{\circ}$ $\quad$

(D) $80^{\circ}$

4. सिद्ध कीजिए कि किसी वृत्त के किसी व्यास के सिरों पर खींची गई स्पर्श रेखाएँ समांतर होती हैं।

5. सिद्ध कीजिए कि स्पर्श बिंदु से स्पर्श रेखा पर खींचा गया लंब वृत्त के केंद्र से होकर जाता है।

6. एक बिंदु $A$ से, जो एक वृत्त के केंद्र से $5 \mathrm{~cm}$ दूरी पर है, वृत्त पर स्पर्श रेखा की लंबाई $4 \mathrm{~cm}$ है। वृत्त की त्रिज्या ज्ञात कीजिए।

7. दो संकेंद्रीय वृत्तों की त्रिज्याएँ $5 \mathrm{~cm}$ तथा $3 \mathrm{~cm}$ हैं। बड़े वृत्त की उस जीवा की लंबाई ज्ञात कीजिए जो छोटे वृत्त को स्पर्श करती हो।

8. एक वृत्त के परिगत एक चतुर्भुज $\mathrm{ABCD}$ खींचा गया है (देखिए आकृति 10.12)। सिद्ध कीजिए :

$$ \mathrm{AB}+\mathrm{CD}=\mathrm{AD}+\mathrm{BC} $$

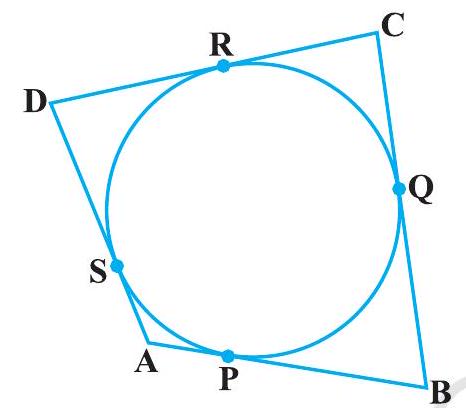
आकृति 10.12

9. आकृति 10.13 में $X Y$ तथा $X^{\prime} Y^{\prime}, O$ केंद्र वाले किसी वृत्त पर दो समांतर स्पर्श रेखाएँ हैं और स्पर्श बिंदु $\mathrm{C}$ पर स्पर्श रेखा $\mathrm{AB}, \mathrm{XY}$ को $\mathrm{A}$ तथा $\mathrm{X}^{\prime} \mathrm{Y}^{\prime}$ को $\mathrm{B}$ पर प्रतिच्छेद करती है। सिद्ध कीजिए कि $\angle \mathrm{AOB}=90^{\circ}$ है।

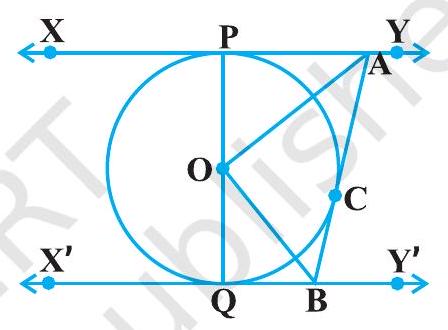
आकृति 10.13

10. सिद्ध कीजिए कि किसी बाह्य बिंदु से किसी वृत्त पर खींची गई स्पर्श रेखाओं के बीच का कोण स्पर्श बिंदुओं को मिलाने वाले रेखाखंड द्वारा केंद्र पर अंतरित कोण का संपूरक होता है।

11. सिद्ध कीजिए कि किसी वृत्त के परिगत समांतर चतुर्भुज समचतुर्भुज होता है।

12. $4 \mathrm{~cm}$ त्रिज्या वाले एक वृत्त के परिगत एक त्रिभुज $\mathrm{ABC}$ इस प्रकार खींचा गया है कि रेखाखंड $\mathrm{BD}$ और $\mathrm{DC}$ (जिनमें स्पर्श बिंदु $\mathrm{D}$ द्वारा $\mathrm{BC}$ विभाजित है) की लंबाइयाँ क्रमशः $8 \mathrm{~cm}$ और $6 \mathrm{~cm}$ हैं (देखिए आकृति 10.14)। भुजाएँ $A B$ और $\mathrm{AC}$ ज्ञात कीजिए।

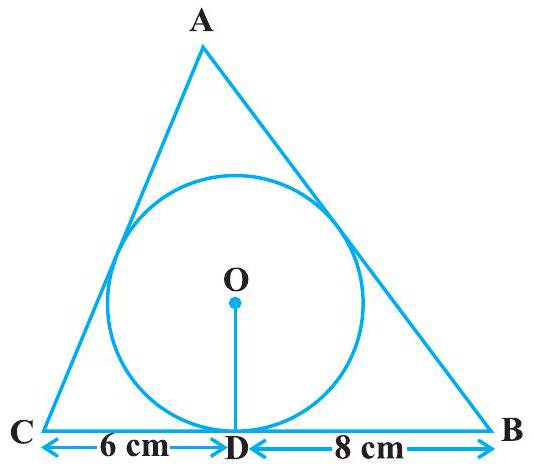
आवृति 10.14

13. सिद्ध कीजिए कि वृत्त के परिगत बनी चतुर्भुज की आमने-सामने की भुजाएँ केंद्र पर संपूरक कोण अंतरित करती हैं।

10.4 सारांश

इस अध्याय में, आपने निम्न तथ्यों का अध्ययन किया है:

1. वृत्त की स्पर्श रेखा का अर्थ।

2. वृत्त की स्पर्श रेखा स्पर्श बिंदु से जाने वाली त्रिज्या पर लंब होती है।

3. बाह्य बिंदु से किसी वृत्त पर खींची गई दोनों स्पर्श रेखाओं की लंबाइयाँ समान होती हैं।