अध्याय 08 त्रिकोणमिति का परिचय
संभवतः त्रिकोणमिति के अतिरिक्त गणणित की कोई ऐसी शाखा नहीं है, जो उसकी मध्य स्थिति का स्थान ले सकी।
J.F. Herbart (1890)
8.1 भूमिका
आप अपनी पिछली कक्षाओं में त्रिभुजों, विशेष रूप से समकोण त्रिभुजों के बारे में अध्ययन कर चुके हैं। आइए हम अपने आस-पास के परिवेश से कुछ ऐसे उदाहरण लें, जहाँ समकोण त्रिभुजों के बनने की कल्पना की जा सकती है। उदाहरण के लिए :
1. मान लीजिए एक स्कूल के छात्र कुतुबमीनार देखने गए हैं। अब, यदि कोई छात्र मीनार के शिखर को देख रहा हो, तो एक समकोण त्रिभुज बनने की कल्पना की जा सकती है जैसाकि आकृति 8.1 में दिखाया गया है। क्या वास्तव में मापे बिना ही छात्र मीनार की ऊँचाई ज्ञात कर सकता है?

आकृति 8.1
2. मान लीजिए एक लड़की नदी के किनारे स्थित अपने मकान की बालकनी पर बैठी हुई है और वह इस नदी के दूसरे किनारे पर स्थित पास ही के मंदिर की एक निचली सीढ़ी पर रखे गमले को देख रही है। इस स्थिति में, एक समकोण त्रिभुज बनने की कल्पना की जा सकती है जैसाकि आकृति 8.2 में दिखाया गया है, यदि आपको वह ऊँचाई ज्ञात हो, जिस पर लड़की बैठी हुई है, तो क्या आप नदी की चौड़ाई ज्ञात कर सकते हैं?

आकृति 8.2
3. मान लीजिए एक गर्म हवा वाला गुब्बारा हवा में उड़ रहा है। आसमान में उड़ने पर आकृति 8.2 इस गुब्बारे को एक लड़की देख लेती है और इस बात को बताने के लिए वह अपनी माँ के पास दौड़कर जाती है। गुब्बारे को देखने के लिए उसकी माँ तुरंत घर से बाहर निकल आती है। अब मान लीजिए कि जब पहले-पहल लड़की गुब्बारे को देखती है, तब गुब्बारा बिंदु $A$ पर था। जब माँ-बेटी दोनों ही गुब्बारे को देखने के लिए बाहर निकलकर आती हैं तब तक गुब्बारा एक अन्य बिंदु $\mathrm{B}$ तक आ चुका होता है। क्या आप जमीन के उस स्थान से, जहाँ माँ और बेटी दोनों खड़ी हैं, $\mathrm{B}$ की ऊँचाई ज्ञात कर सकते हैं?

आकृति 8.3
ऊपर बताई गई सभी स्थितियों में दूरियाँ अथवा ऊँचाईयाँ कुछ गणितीय तकनीकों को, जो त्रिकोणमिति नामक गणित की एक शाखा के अंतर्गत आते हैं, लागू करके ज्ञात किया जा सकता है। अंग्रेजी शब्द ’trigonometry’ की व्युत्पत्ति ग्रीक शब्दों ’tri’ (जिसका अर्थ है तीन), ‘gon’ (जिसका अर्थ है, भुजा) और ‘metron’ (जिसका अर्थ है माप) से हुई है। वस्तुतः त्रिकोणमिति में एक त्रिभुज की भुजाओं और कोणों के बीच के संबंधों का अध्ययन किया जाता है। प्राचीन काल में त्रिकोणमिति पर किए गए कार्य का उल्लेख मिस्र और बेबीलॉन में मिलता है। प्राचीन काल के खगोलविद् त्रिकोणमिति का प्रयोग पृथ्वी से तारों और ग्रहों की दूरियाँ मापने में करते थे। आज भी इंजीनियरिंग और भौतिक विज्ञान में प्रयुक्त अधिकांश प्रौद्योगिकीय उन्नत विधियाँ त्रिकोणमितीय संकल्पनाओं पर आधारित हैं।
इस अध्याय में हम एक समकोण त्रिभुज की भुजाओं के कुछ अनुपातों का उसके न्यून कोणों के सापेक्ष अध्ययन करेंगे जिन्हें कोणों के त्रिकोणमितीय अनुपात कहते हैं। यहाँ हम अपनी चर्चा केवल न्यून कोणों तक ही सीमित रखेंगे। यद्यपि इन अनुपातों का विस्तार दूसरे कोणों के लिए भी किया जा सकता है। यहाँ हम $0^{\circ}$ और $90^{\circ}$ के माप वाले कोणों के त्रिकोणमितीय अनुपातों को भी परिभाषित करेंगे। हम कुछ विशिष्ट कोणों के त्रिकोणमितीय अनुपात परिकलित करेंगे और इन अनुपातों से संबंधित कुछ सर्वसमिकाएँ (identities), जिन्हें त्रिकोणमितीय सर्वसमिकाएँ कहा जाता है, स्थापित करेंगे।
8.2 त्रिकोणमितीय अनुपात
अनुच्छेद 8.1 में आप विभिन्न स्थितियों में बने कुछ समकोण त्रिभुजों की कल्पना कर चुके हैं।
आइए हम एक समकोण त्रिभुज $\mathrm{ABC}$ लें, जैसाकि आकृति 8.4 में दिखाया गया है।
आकृति 8.4
यहाँ, $\angle \mathrm{CAB}$ (या संक्षेप में कोण $\mathrm{A}$ ) एक न्यून कोण है। कोण $\mathrm{A}$ के सापेक्ष भुजा $\mathrm{BC}$ की स्थिति पर ध्यान दीजिए। यह भुजा कोण $\mathrm{A}$ के सामने है। इस भुजा को हम कोण $\mathrm{A}$ की सम्मुख भुजा कहते हैं, भुजा $\mathrm{AC}$ समकोण त्रिभुज का कर्ण है और भुजा $\mathrm{AB}, \angle \mathrm{A}$ का एक भाग है। अतः इसे हम कोण $\mathrm{A}$ की संलग्न भुजा कहते हैं।
ध्यान दीजिए कि कोण $\mathrm{A}$ के स्थान पर कोण $\mathrm{C}$ लेने पर भुजाओं की स्थिति बदल जाती है। (देखिए आकृति 8.5)
आकृति 8.5
पिछली कक्षाओं में आप “अनुपात” की संकल्पना के बारे में अध्ययन कर चुके हैं। यहाँ अब हम समकोण त्रिभुज की भुजाओं से संबंधित कुछ अनुपातों को, जिन्हें हम त्रिकोणमितीय अनुपात कहते हैं, परिभाषित करेंगे।
समकोण त्रिभुज $\mathrm{ABC}$ (देखिए आकृति 8.4) के कोण $\mathrm{A}$ के त्रिकोणमितीय अनुपात निम्न प्रकार से परिभाषित किए जाते हैं:
$$ \begin{aligned} & \angle \mathrm{A} \text { का sine }=\frac{\text { कोण } \mathrm{A} \text { की सम्मुख भुजा }}{\text { कर्ण }}=\frac{\mathrm{BC}}{\mathrm{AC}} \\ & \angle \mathrm{A} \text { का cosine }=\frac{\text { कोण } \mathrm{A} \text { की संलग्न भुजा }}{\text { कर्ण }}=\frac{\mathrm{AB}}{\mathrm{AC}} \end{aligned} $$
$$\angle \mathrm{A}$ का tangent $=\frac{\text { कोण } \mathrm{A} \text { की सम्मुख भुजा }}{\text { कोण } \mathrm{A} \text { की संलग्न भुजा }}=\frac{\mathrm{BC}}{\mathrm{AB}}$$
$$\angle \mathrm{A}$ का cosecant $=\frac{1}{\angle \mathrm{A} \text { का sine }}=\frac{\text { कर्ण }}{\text { कोण } \mathrm{A} \text { की सम्मुख भुजा }}=\frac{\mathrm{AC}}{\mathrm{BC}}$$
$$\angle \mathrm{A}$ का secant $=\frac{1}{\angle \mathrm{A} \text { का cosine }}=\frac{\text { कर्ण }}{\text { कोण } \mathrm{A} \text { की सम्मुख भुजा }}=\frac{\mathrm{AC}}{\mathrm{AB}}$$
$$\angle \mathrm{A}$ का cotangent $=\frac{1}{\angle \mathrm{A} \text { का tangent }}=\frac{\text { कोण } \mathrm{A} \text { की संलग्न भुजा }}{\text { कोण } \mathrm{A} \text { की सम्मुख भुजा }}=\frac{\mathrm{AB}}{\mathrm{BC}}$$
ऊपर परिभाषित किए गए अनुपातों को संक्षेप में क्रमशः $\sin \mathrm{A}, \cos \mathrm{A}, \tan \mathrm{A}, \operatorname{cosec} \mathrm{A}$, $\sec \mathrm{A}$ और $\cot \mathrm{A}$ लिखा जाता है। ध्यान दीजिए कि अनुपात $\operatorname{cosec} \mathrm{A}, \sec \mathrm{A}$ और $\cot \mathrm{A}$ अनुपातों $\sin \mathrm{A}, \cos \mathrm{A}$ और $\tan \mathrm{A}$ के क्रमशः व्युत्क्रम होते हैं।
और आप यहाँ यह भी देख सकते हैं कि $\tan A=\frac{B C}{A B}=\frac{\frac{B C}{A C}}{\frac{A B}{A C}}=\frac{\sin A}{\cos A}$ और $\cot A=\frac{\cos A}{\sin A}$.
अतः एक समकोण त्रिभुज के एक न्यून कोण के त्रिकोणमितीय अनुपात त्रिभुज के कोण और उसकी भुजाओं की लंबाई के बीच के संबंध को व्यक्त करते हैं।
क्यों न यहाँ आप एक समकोण त्रिभुज के कोण $\mathrm{C}$ के त्रिकोणमितीय अनुपातों को परिभाषित करने का प्रयास करें (देखिए आकृति 8.5)?
शब्द “sine” का सबसे पहला प्रयोग जिस रूप में आज हम करते हैं उसका उल्लेख 500 ई. में आर्यभट्ट द्वारा लिखित पुस्तक आर्यभटीयम में मिलता है। आर्यभट्ट ने शब्द अर्ध-ज्या का प्रयोग अर्ध-जीवा के लिए किया था जिसने समय-अंतराल में ज्या या जीवा का संक्षिप्त रूप ले लिया। जब पुस्तक आर्यभटीयम का अनुवाद अरबी भाषा में किया गया, तब शब्द जीवा को यथावत रख लिया गया। शब्द जीवा को साइनस (Sinus) के रूप में अनूदित किया गया, जिसका अर्थ वक्र है, जबकि अरबी रूपांतर को लैटिन में अनूदित किया गया। इसके तुरंत बाद sine के रूप में प्रयुक्त शब्द sinus भी पूरे यूरोप में गणितीय पाठों में प्रयुक्त होने लगा। खगोलविद् के एक अंग्रेजी प्रोफ़ेसर एडमंड गुंटर (1581-1626) ने पहले-पहल संक्षिप्त संकेत ’ $\sin$ ’ का प्रयोग किया था।

आर्यभट्ट $476 - 550$ सा.यु.
शब्दों ‘cosine’ और ’tangent’ का उद्गम बहुत बाद में हुआ था। cosine फलन का उद्गम पूरक कोण के sine का अभिकलन करने को ध्यान में रखकर किया गया था। आर्यभट्ट ने इसे कोटिज्या का नाम दिया था। नाम cosinus का उद्गम एडमंड गुंटर के साथ हुआ था। 1674 में अंग्रेज गणितज्ञ सर जोनास मूरे ने पहले-पहल संक्षिप्त संकेत ‘cos’ का प्रयोग किया था।
टिप्पणी : ध्यान दीजिए कि प्रतीक $\sin \mathrm{A}^{2}$ का प्रयोग कोण $\mathrm{A}^{\prime}$ के $\sin$ के संक्षिप्त रूप में किया गया है। यहाँ $\sin \mathrm{A}, \sin$ और $\mathrm{A}$ का गुणनफल नहीं है। $\mathrm{A}$ से अलग रहकर ’ $\sin$ ’ का कोई अर्थ ही नहीं होता। इसी प्रकार $\cos \mathrm{A}$, ’ $\cos$ ’ और $\mathrm{A}$ का गुणनफल नहीं है। इस प्रकार की व्याख्या अन्य त्रिकोणमितीय अनुपातों के साथ भी की जाती है।
अब, यदि हम समकोण त्रिभुज $\mathrm{ABC}$ के कर्ण $\mathrm{AC}$ पर एक बिंदु $P$ लें या बढ़ी हुई भुजा $A C$ पर बिंदु $Q$ लें और $A B$ पर लंब $\mathrm{PM}$ डालें और बढ़ी हुई भुजा $\mathrm{AB}$ पर लंब $\mathrm{QN}$ डालें (देखिए आकृति 8.6), तो $\triangle \mathrm{PAM}$ के $\angle \mathrm{A}$ के त्रिकोणमितीय अनुपातों और $\triangle \mathrm{QAN}$ के $\angle \mathrm{A}$ के त्रिकोणमितीय अनुपातों में क्या अंतर होगा?

आकृति 8.6
इस प्रश्न का उत्तर ज्ञात करने के लिए आइए पहले हम इन त्रिभुजों को देखें। क्या $\triangle \mathrm{PAM}$ और $\triangle \mathrm{CAB}$ समरूप हैं? आपको याद होगा कि अध्याय 6 में आप AA समरूपता कसौटी के बारे में अध्ययन कर चुके हैं। इस कसौटी को लागू करने पर आप पाएँगे कि त्रिभुज PAM और CAB समरूप हैं। अतः समरूप त्रिभुजों के गुणधर्म के अनुसार इन त्रिभुजों की संगत भुजाएँ आनुपातिक हैं।
अत:
$ \frac{AM}{AB}=\frac{AP}{AC}=\frac{MP}{BC} $
इससे हमें यह प्राप्त होता है
$ \begin{aligned} \frac{\mathrm{MP}}{\mathrm{AP}}=\frac{\mathrm{BC}}{\mathrm{AC}}=\sin \mathrm{A} \end{aligned} $
इसी प्रकार
$ \frac{\mathrm{AM}}{\mathrm{AP}}=\frac{\mathrm{AB}}{\mathrm{AC}}=\cos \mathrm{A}, \frac{\mathrm{MP}}{\mathrm{AM}}=\frac{\mathrm{BC}}{\mathrm{AB}}=\tan \mathrm{A} \text { आदि-आदि } $
इससे यह पता चलता है कि $\triangle \mathrm{PAM}$ के कोण $\mathrm{A}$ के त्रिकोणमितीय अनुपात और $\triangle \mathrm{CAB}$ के कोण $\mathrm{A}$ के त्रिकोणमितीय अनुपातों में कोई अंतर नहीं होता।
इसी प्रकार आप यह जाँच कर सकते हैं कि $\triangle \mathrm{QAN}$ में भी $\sin \mathrm{A}$ का मान (और अन्य त्रिकोणमितीय अनुपातों का मान) समान बना रहता है।
अपने प्रेक्षणों से अब यह स्पष्ट हो जाता है कि यदि कोण समान बना रहता हो, तो एक कोण के त्रिकोणमितीय अनुपातों के मानों में त्रिभुज की भुजाओं की लंबाइयों के साथ कोई परिवर्तन नहीं होता।
टिप्पणी: सुविधा के लिए $(\sin \mathrm{A})^{2},(\cos \mathrm{A})^{2}$, आदि के स्थान पर हम क्रमशः $\sin ^{2} \mathrm{~A}, \cos ^{2} \mathrm{~A}$ आदि लिख सकते हैं। परंतु $\operatorname{cosec} \mathrm{A}=(\sin \mathrm{A})^{-1} \neq \sin ^{-1} \mathrm{~A}$ (इसे साइन इनवर्स $\mathrm{A}$ कहा जाता है)। $\sin ^{-1} \mathrm{~A}$ का एक अलग अर्थ होता है जिस पर चर्चा हम उच्च कक्षाओं में करेंगे। इसी प्रकार की परंपराएँ अन्य त्रिकोणमितीय अनुपातों पर भी लागू होती हैं। कभी-कभी ग्रीक अक्षर $\theta$ (थीटा) का प्रयोग कोण को प्रकट करने के लिए किया जाता है।
यहाँ हमने एक न्यून कोण के छः त्रिकोणमितीय अनुपात परिभाषित किए हैं। यदि हमें कोई एक अनुपात ज्ञात हो, तो क्या हम अन्य अनुपात प्राप्त कर सकते हैं? आइए हम इस पर विचार करें।
यदि एक समकोण त्रिभुज $\mathrm{ABC}$ में $\sin \mathrm{A}=\frac{1}{3}$, तब इसका अर्थ यह है कि $\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{1}{3}$, अर्थात् त्रिभुज $\mathrm{ABC}$ की भुजाओं $\mathrm{BC}$ और $\mathrm{AC}$ की लंबाइयाँ $1: 3$ के अनुपात में हैं (देखिए आकृति 8.7)। अतः यदि $\mathrm{BC}, k$ के बराबर हो, तो $\mathrm{AC}, 3 k$ के बराबर होगी, जहाँ $k$ एक धन संख्या है। कोण $\mathrm{A}$ के अन्य त्रिकोणमितीय अनुपात ज्ञात करने के लिए हमें तीसरी भुजा $\mathrm{AB}$ की लंबाई ज्ञात करनी होती है। क्या आपको पाइथागोरस प्रमेय याद है? आइए हम पाइथागोरस प्रमेय की सहायता से अपेक्षित लंबाई $\mathrm{AB}$ ज्ञात करें।

आकृति 8.7
$ \mathrm{AB}^{2}=\mathrm{AC}^{2}-\mathrm{BC}^{2}=(3 k)^{2}-(k)^{2}=8 k^{2}=(2 \sqrt{2} k)^{2} $
अत:
$ \quad\quad\quad\mathrm{AB}= \pm 2 \sqrt{2} k $
अतः हमें प्राप्त होता है $\mathrm{AB}=2 \sqrt{2} k \quad(\mathrm{AB}=-2 \sqrt{2} k$ क्यों नहीं है? $)$
अब
$ \quad\quad\quad \quad \cos \mathrm{A}=\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{2 \sqrt{2} k}{3 k}=\frac{2 \sqrt{2}}{3} $
इसी प्रकार, आप कोण $\mathrm{A}$ के अन्य त्रिकोणमितीय अनुपात प्राप्त कर सकते हैं।
टिप्पणी: क्योंकि समकोण त्रिभुज का कर्ण, त्रिभुज की सबसे लंबी भुजा होता है, इसलिए $\sin \mathrm{A}$ या $\cos \mathrm{A}$ का मान सदा ही 1 से कम होता है (या विशेष स्थिति में 1 के बराबर होता है।)
आइए अब हम कुछ उदाहरण लें।
उदाहरण 1 : यदि $\tan \mathrm{A}=\frac{4}{3}$, तो कोण $\mathrm{A}$ के अन्य त्रिकोणमितीय अनुपात ज्ञात कीजिए।
हल : आइए सबसे पहले हम एक समकोण $\triangle \mathrm{ABC}$ खींचें (देखिए आकृति 8.8)।

आकृति 8.8
अब, हम जानते हैं कि $\tan \mathrm{A}=\frac{\mathrm{BC}}{\mathrm{AB}}=\frac{4}{3}$
अतः यदि $\mathrm{BC}=4 k$, तब $\mathrm{AB}=3 k$, जहाँ $k$ धन संख्या है।
अब पाइथागोरस प्रमेय लागू करने पर हमें यह प्राप्त होता है
$ \mathrm{AC}^{2}=\mathrm{AB}^{2}+\mathrm{BC}^{2}=(4 k)^{2}+(3 k)^{2}=25 k^{2} $
इसलिए
$ \mathrm{AC}=5 k $
अब हम इनकी परिभाषाओं की सहायता से सभी त्रिकोणमितीय अनुपात लिख सकते हैं।
$ \begin{matrix} \sin A=\frac{BC}{AC}=\frac{4 k}{5 k}=\frac{4}{5} \\ \cos A=\frac{AB}{AC}=\frac{3 k}{5 k}=\frac{3}{5} \end{matrix} $
अत: $\cot \mathrm{A}=\frac{1}{\tan \mathrm{A}}=\frac{3}{4}, \operatorname{cosec} \mathrm{A}=\frac{1}{\sin \mathrm{A}}=\frac{5}{4}$ और $\sec \mathrm{A}=\frac{1}{\cos \mathrm{A}}=\frac{5}{3}$
उदाहरण 2 : यदि $\angle \mathrm{B}$ और $\angle \mathrm{Q}$ ऐसे न्यूनकोण हों जिससे कि $\sin \mathrm{B}=\sin \mathrm{Q}$, तो सिद्ध कीजिए कि $\angle \mathrm{B}=\angle \mathrm{Q}$
हल : आइए हम दो समकोण त्रिभुज $\mathrm{ABC}$ और $\mathrm{PQR}$ लें, जहाँ $\sin \mathrm{B}=\sin \mathrm{Q}$ (देखिए आकृति 8.9)।
आकृति 8.9
यहाँ
$ \sin B=\frac{A C}{A B} $
$ \text{ और } \quad \quad \quad \quad \quad \sin Q=\frac{P R}{P Q} $
तब $ \quad \quad \quad \frac{\mathrm{AC}}{\mathrm{AB}}=\frac{\mathrm{PR}}{\mathrm{PQ}} $
अत :
$$ \begin{equation*} \frac{\mathrm{AC}}{\mathrm{PR}}=\frac{\mathrm{AB}}{\mathrm{PQ}}=k \text { (मान लीजिए) } \tag{1} \end{equation*} $$
अब, पाइथागोरस प्रमेय लागू करने पर हमें ये प्राप्त होते हैं
$ \mathrm{BC}=\sqrt{\mathrm{AB}^{2}-\mathrm{AC}^{2}} $
और
$ \begin{aligned} QR & =\sqrt{PQ^{2}-PR^{2}} \end{aligned} $
अत: $\frac{\mathrm{BC}}{\mathrm{QR}}=\frac{\sqrt{\mathrm{AB}^{2}-\mathrm{AC}^{2}}}{\sqrt{\mathrm{PQ}^{2}-\mathrm{PR}^{2}}}=\frac{\sqrt{k^{2} \mathrm{PQ}^{2}-k^{2} \mathrm{PR}^{2}}}{\sqrt{\mathrm{PQ}^{2}-\mathrm{PR}^{2}}}=\frac{k \sqrt{\mathrm{PQ}^{2}-\mathrm{PR}^{2}}}{\sqrt{\mathrm{PQ}^{2}-\mathrm{PR}^{2}}}=k$
(1) और (2) से हमें यह प्राप्त होता है
$$ \frac{\mathrm{AC}}{\mathrm{PR}}=\frac{\mathrm{AB}}{\mathrm{PQ}}=\frac{\mathrm{BC}}{\mathrm{QR}} $$
तब प्रमेय 6.4 का प्रयोग करने पर $\triangle \mathrm{ACB} \sim \triangle \mathrm{PRQ}$ प्राप्त होता है। अतः $\angle \mathrm{B}=\angle \mathrm{Q}$
उदाहरण 3 : $\triangle \mathrm{ACB}$ लीजिए जिसका कोण $\mathrm{C}$ समकोण है जिसमें $\mathrm{AB}=29$ इकाई, $\mathrm{BC}=21$ इकाई और $\angle \mathrm{ABC}=\theta$ (देखिए आकृति 8.10) हैं तो निम्नलिखित के मान ज्ञात कीजिए।

आकृति 8.10
(i) $\cos ^{2} \theta+\sin ^{2} \theta$
(ii) $\cos ^{2} \theta-\sin ^{2} \theta$.
हल : $\triangle \mathrm{ACB}$ में हमें यह प्राप्त होता है
$$ \begin{aligned} \mathrm{AC} & =\sqrt{\mathrm{AB}^{2}-\mathrm{BC}^{2}}=\sqrt{(29)^{2}-(21)^{2}} \quad \text { आकृति } 8.10 \\ & =\sqrt{(29-21)(29+21)}=\sqrt{(8)(50)}=\sqrt{400}=20 \text { इकाई } \end{aligned} $$
अतः $\quad \sin \theta=\frac{\mathrm{AC}}{\mathrm{AB}}=\frac{20}{29}, \cos \theta=\frac{\mathrm{BC}}{\mathrm{AB}}=\frac{21}{29}$.
अब , (i) $\cos ^{2} \theta+\sin ^{2} \theta=\left(\frac{20}{29}\right)^{2}+\left(\frac{21}{29}\right)^{2}=\frac{20^{2}+21^{2}}{29^{2}}=\frac{400+441}{841}=1$,
और (ii) $\cos ^{2} \theta-\sin ^{2} \theta=\left(\frac{21}{29}\right)^{2}-\left(\frac{20}{29}\right)^{2}=\frac{(21+20)(21-20)}{29^{2}}=\frac{41}{841}$
उदाहरण 4 : एक समकोण त्रिभुज $\mathrm{ABC}$ में, जिसका कोण $\mathrm{B}$ समकोण है, यदि $\tan \mathrm{A}=1$ तो सत्यापित कीजिए कि
$2 \sin \mathrm{A} \cos \mathrm{A}=1$
हल : $\triangle \mathrm{ABC}$ में $\tan \mathrm{A}=\frac{\mathrm{BC}}{\mathrm{AB}}=1$ (देखिए आकृति 8.11) अर्थात्

आकृति 8.11
अर्थात्
$ \mathrm{BC}=\mathrm{AB} $
मान लीजिए $\mathrm{AB}=\mathrm{BC}=k$, जहाँ $k$ एक धन संख्या है।
अब
$$ \begin{aligned} \mathrm{AC} & =\sqrt{\mathrm{AB}^{2}+\mathrm{BC}^{2}} \\ & =\sqrt{(k)^{2}+(k)^{2}}=k \sqrt{2} \end{aligned} $$
अतः
$ \sin \mathrm{A}=\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{1}{\sqrt{2}} \text { और } \cos \mathrm{A}=\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{1}{\sqrt{2}} $
इसलिए $\quad 2 \sin \mathrm{A} \cos \mathrm{A}=2\left(\frac{1}{\sqrt{2}}\right)\left(\frac{1}{\sqrt{2}}\right)=1$, जो कि अपेक्षित मान है।
उदाहरण 5: $ \triangle \mathrm{OPQ}$ में, जिसका कोण $\mathrm{P}$ समकोण है, $\mathrm{OP}=7 \mathrm{~cm}$ और $\mathrm{OQ}-\mathrm{PQ}=1 \mathrm{~cm}$ (देखिए आकृति 8.12), $\sin Q$ और $\cos Q$ के मान ज्ञात कीजिए।

आकृति 8.12
हल : $\triangle \mathrm{OPQ}$ से हमें यह प्राप्त है कि
$ OQ^{2}=OP^{2}+PQ^{2} $
अर्थात्
$ (1+P Q)^{2}=OP^{2}+PQ^{2} $(क्यों?)
अर्थात्
$\quad 1+\mathrm{PQ}^{2}+2 \mathrm{PQ}=\mathrm{OP}^{2}+\mathrm{PQ}^{2}$
अर्थात्
$\quad 1+2 \mathrm{PQ}=7^{2}$(क्यों?)
अर्थात्
$ \mathrm{PQ}=24 \mathrm{~cm} \text { और } \mathrm{OQ}=1+\mathrm{PQ}=25 \mathrm{~cm} $
अत :
$ \quad \sin Q=\frac{7}{25} \text { और } \cos Q=\frac{24}{25} $
प्रश्नावली 8.1
1. $\triangle \mathrm{ABC}$ में, जिसका कोण $\mathrm{B}$ समकोण है, $\mathrm{AB}=24 \mathrm{~cm}$ और $\mathrm{BC}=7 \mathrm{~cm}$ है। निम्नलिखित का मान ज्ञात कीजिए :
(i) $\sin \mathrm{A}, \cos \mathrm{A}$
(ii) $\sin \mathrm{C}, \cos \mathrm{C}$
Show Answer
#missing2. आकृति 8.13 में, $\tan \mathrm{P}-\cot \mathrm{R}$ का मान ज्ञात कीजिए।
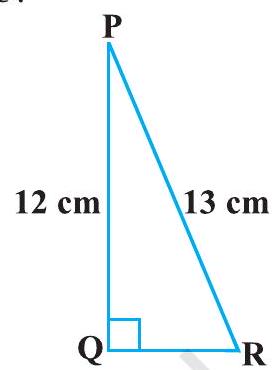
आकृति 8.13
Show Answer
#missing3. यदि $\sin \mathrm{A}=\frac{3}{4}$, तो $\cos \mathrm{A}$ और $\tan \mathrm{A}$ का मान परिकलित कीजिए।
Show Answer
#missing4. यदि $15 \cot \mathrm{A}=8$ हो तो $\sin \mathrm{A}$ और $\sec \mathrm{A}$ का मान ज्ञात कीजिए।
Show Answer
#missing5. यदि $\sec \theta=\frac{13}{12}$, हो तो अन्य सभी त्रिकोणमितीय अनुपात परिकलित कीजिए।
Show Answer
#missing6. यदि $\angle \mathrm{A}$ और $\angle \mathrm{B}$ न्यून कोण हो, जहाँ $\cos \mathrm{A}=\cos \mathrm{B}$, तो दिखाइए कि $\angle \mathrm{A}=\angle \mathrm{B}$
Show Answer
#missing7. यदि $\cot \theta=\frac{7}{8}$, तो
(i) $\frac{(1+\sin \theta)(1-\sin \theta)}{(1+\cos \theta)(1-\cos \theta)}$,
(ii) $\cot ^{2} \theta$ का मान निकालिए?
Show Answer
#missing8. यदि $3 \cot \mathrm{A}=4$, तो जाँच कीजिए कि $\frac{1-\tan ^{2} \mathrm{~A}}{1+\tan ^{2} \mathrm{~A}}=\cos ^{2} \mathrm{~A}-\sin ^{2} \mathrm{~A}$ है या नहीं।
Show Answer
#missing9. त्रिभुज $\mathrm{ABC}$ में, जिसका कोण $\mathrm{B}$ समकोण है, यदि $\tan \mathrm{A}=\frac{1}{\sqrt{3}}$, तो निम्नलिखित के मान ज्ञात कीजिए:
(i) $\sin \mathrm{A} \cos \mathrm{C}+\cos \mathrm{A} \sin \mathrm{C}$
(ii) $\cos \mathrm{A} \cos \mathrm{C}-\sin \mathrm{A} \sin \mathrm{C}$
Show Answer
#missing10. $\triangle \mathrm{PQR}$ में, जिसका कोण $\mathrm{Q}$ समकोण है, $\mathrm{PR}+\mathrm{QR}=25 \mathrm{~cm}$ और $\mathrm{PQ}=5 \mathrm{~cm}$ है। $\sin \mathrm{P}, \cos \mathrm{P}$ और $\tan \mathrm{P}$ के मान ज्ञात कीजिए।
Show Answer
#missing11. बताइए कि निम्नलिखित कथन सत्य हैं या असत्य। कारण सहित अपने उत्तर की पुष्टि कीजिए।
(i) $\tan \mathrm{A}$ का मान सदैव 1 से कम होता है।
(ii) कोण $\mathrm{A}$ के किसी मान के लिए $\sec \mathrm{A}=\frac{12}{5}$
(iii) $\cos \mathrm{A}$, कोण $\mathrm{A}$ के cosecant के लिए प्रयुक्त एक संक्षिप्त रूप है।
(iv) $\cot \mathrm{A}, \cot$ और $\mathrm{A}$ का गुणनफल होता है।
(v) किसी भी कोण $\theta$ के लिए $\sin \theta=\frac{4}{3}$
Show Answer
#missing8.3 कुछ विशिष्ट कोणों के त्रिकोणमितीय अनुपात
ज्यामिति के अध्ययन से आप $30^{\circ}, 45^{\circ}, 60^{\circ}$ और $90^{\circ}$ के कोणों की रचना से आप अच्छी तरह से परिचित हैं। इस अनुच्छेद में हम इन कोणों और साथ ही $0^{\circ}$ वाले कोण के त्रिकोणमितीय अनुपातों के मान ज्ञात करेंगे।
$45^{\circ}$ के त्रिकोणमितीय अनुपात
$\triangle \mathrm{ABC}$ में, जिसका कोण $\mathrm{B}$ समकोण है, यदि एक कोण $45^{\circ}$ का हो, तो अन्य कोण भी $45^{\circ}$ का होगा अर्थात् $\angle \mathrm{A}=\angle \mathrm{C}=45^{\circ}$ (देखिए आकृति 8.14)।

आकृति 8.14
अत:
$ \mathrm{BC}=\mathrm{AB} \quad \text { (क्यों? }) $
अब मान लीजिए $\mathrm{BC}=\mathrm{AB}=a$
तब पाइथागोरस प्रमेय के अनुसार $\mathrm{AC}^{2}=\mathrm{AB}^{2}+\mathrm{BC}^{2}=a^{2}+a^{2}=2 a^{2}$
इसलिए $\quad \mathrm{AC}=a \sqrt{2}$.
त्रिकोणमितीय अनुपातों की परिभाषाओं को लागू करने पर हमें यह प्राप्त होता है :
$$ \begin{aligned} & \sin 45^{\circ}=\frac{45^{\circ} \text { के कोण की सम्मुख भुजा }}{\text { कर्ण }}=\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{a}{a \sqrt{2}}=\frac{1}{\sqrt{2}} \\ & \cos 45^{\circ}=\frac{45^{\circ} \text { के कोण की संलग्न भुजा }}{\text { कर्ण }}=\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{a}{a \sqrt{2}}=\frac{1}{\sqrt{2}} \\ & \tan 45^{\circ}=\frac{45^{\circ} \text { के कोण की सम्मुख भुजा }}{45^{\circ} \text { के कोण की संलग्न भुजा }}=\frac{\mathrm{BC}}{\mathrm{AB}}=\frac{a}{a}=1 \end{aligned} $$
और $\operatorname{cosec} 45^{\circ}=\frac{1}{\sin 45^{\circ}}=\sqrt{2}, \sec 45^{\circ}=\frac{1}{\cos 45^{\circ}}=\sqrt{2}, \cot 45^{\circ}=\frac{1}{\tan 45^{\circ}}=1$
$30^{\circ}$ और $60^{\circ}$ के त्रिकोणमितीय अनुपात
आइए, अब हम $30^{\circ}$ और $60^{\circ}$ के त्रिकोणमितीय अनुपात परिकलित करें। एक समबाहु त्रिभुज $\mathrm{ABC}$ पर विचार करें। क्योंकि समबाहु त्रिभुज का प्रत्येक कोण, $60^{\circ}$ का होता है, इसलिए $\angle \mathrm{A}=\angle \mathrm{B}=\angle \mathrm{C}=60^{\circ}$
$\mathrm{A}$ से भुजा $\mathrm{BC}$ पर लंब $\mathrm{AD}$ डालिए (देखिए आकृति 8.15)।

आकृति 8.15
$ \begin{aligned} \text{अब } \quad \quad \quad & \Delta ABD \cong \Delta ACD \quad(\text{ क्यों? }) \\ \text{इसलिए } \quad \quad \quad & BD =DC \\ \text{ और } \quad \quad \quad & \angle BAD =\angle CAD \quad(CPCT) \end{aligned} $
अब आप यह देख सकते हैं कि:
$\triangle \mathrm{ABD}$ एक समकोण त्रिभुज है जिसका कोण $\mathrm{D}$ समकोण है, और जहाँ $\angle \mathrm{BAD}=30^{\circ}$ और $\angle \mathrm{ABD}=60^{\circ}$ ( देखिए आकृति 8.15)।
जैसा कि आप जानते हैं, कि त्रिकोणमितीय अनुपातों को ज्ञात करने के लिए हमें त्रिभुज की भुजाओं की लंबाइयाँ ज्ञात करने की आवश्यकता होती है। आइए, हम यह मान लें कि $\mathrm{AB}=2 a$
तब
$ \mathrm{BD}=\frac{1}{2} \mathrm{BC}=a $
और
$ \mathrm{AD}^{2}=\mathrm{AB}^{2}-\mathrm{BD}^{2}=(2 a)^{2}-(a)^{2}=3 a^{2} $
इसलिए
$ \mathrm{AD}=a \sqrt{3} $
अब
$$ \begin{aligned} & \sin 30^{\circ}=\frac{\mathrm{BD}}{\mathrm{AB}}=\frac{a}{2 a}=\frac{1}{2}, \cos 30^{\circ}=\frac{\mathrm{AD}}{\mathrm{AB}}=\frac{a \sqrt{3}}{2 a}=\frac{\sqrt{3}}{2} \\ & \tan 30^{\circ}=\frac{\mathrm{BD}}{\mathrm{AD}}=\frac{a}{a \sqrt{3}}=\frac{1}{\sqrt{3}} \end{aligned} $$
और $\quad \operatorname{cosec} 30^{\circ}=\frac{1}{\sin 30^{\circ}}=2, \sec 30^{\circ}=\frac{1}{\cos 30^{\circ}}=\frac{2}{\sqrt{3}}$
$$ \cot 30^{\circ}=\frac{1}{\tan 30^{\circ}}=\sqrt{3} $$
इसी प्रकार
$ \begin{aligned} \sin 60^{\circ}=\frac{\mathrm{AD}}{\mathrm{AB}}=\frac{a \sqrt{3}}{2 a}=\frac{\sqrt{3}}{2}, \cos 60^{\circ}=\frac{1}{2}, \tan 60^{\circ}=\sqrt{3}\\ \operatorname{cosec} 60^{\circ}=\frac{2}{\sqrt{3}}, \sec 60^{\circ}=2 \text{और} \cot 60^{\circ}=\frac{1}{\sqrt{3}} \end{aligned} $
$0^{\circ}$ और $90^{\circ}$ के त्रिकोणमितीय अनुपात
आइए, हम देखें कि यदि समकोण त्रिभुज $\mathrm{ABC}$ के कोण $\mathrm{A}$ को तब तक और छोटा किया जाए जब तक कि यह शून्य नहीं हो जाता है, तब इस स्थिति में कोण $\mathrm{A}$ के त्रिकोणमितीय अनुपातों पर क्या प्रभाव पड़ता है (देखिए आकृति 8.16)। जैसे-जैसे $\angle \mathrm{A}$ छोटा होता जाता है, वैसे-वैसे भुजा $\mathrm{BC}$ की लंबाई कम होती जाती है। बिंदु $\mathrm{C}$, बिंदु $\mathrm{B}$ के निकट आता जाता है और अंत में, जब $\angle \mathrm{A}, 0^{\circ}$ के काफी निकट हो जाता है तब $\mathrm{AC}$ लगभग वही हो जाता है जो कि $\mathrm{AB}$ है (देखिए आकृति 8.17)।

आकृति 8.16
आकृति 8.17
जब $\angle \mathrm{A}, 0^{\circ}$ के अत्यधिक निकट होता है तब $\mathrm{BC}, 0$ के अत्यधिक निकट आ जाता है। तब $\sin \mathrm{A}=\frac{\mathrm{BC}}{\mathrm{AC}}$ का मान 0 के अत्यधिक निकट आ जाता है। और, जब $\angle \mathrm{A}, 0^{\circ}$ के अत्यधिक निकट होता है, तब $\mathrm{AC}$ लगभग वही होता है जो कि $\mathrm{AB}$ होता है और $\cos \mathrm{A}=\frac{\mathrm{AB}}{\mathrm{AC}}$ का मान 1 के अत्यधिक समीप होता है।
इसकी सहायता से हम उस स्थिति में $\sin \mathrm{A}$ और $\cos \mathrm{A}$ के मान परिभाषित कर सकते हैं जबकि $\mathrm{A}=0^{\circ}$, हम $\sin 0^{\circ}=0$ और $\cos 0^{\circ}=1$ परिभाषित करते हैं।
इनका प्रयोग करने पर हमें ये प्राप्त होते हैं:
$\tan 0^{\circ}=\frac{\sin 0^{\circ}}{\cos 0^{\circ}}=0, \cot 0^{\circ}=\frac{1}{\tan 0^{\circ}}$, जो कि परिभाषित नहीं है (क्यों?)
$\sec 0^{\circ}=\frac{1}{\cos 0^{\circ}}=1$ तथा $\operatorname{cosec} 0^{\circ}=\frac{1}{\sin 0^{\circ}}$, और यह भी परिभाषित नहीं है। (क्यों?)
आइए अब हम उस स्थिति में देखें कि $\angle \mathrm{A}$ के त्रिकोणमितीय अनुपातों के साथ क्या होता है जबकि $\triangle \mathrm{ABC}$ के इस कोण को तब तक बड़ा किया जाता है, जब तक कि $90^{\circ}$ का नहीं हो जाता। $\angle \mathrm{A}$ जैसे-जैसे बड़ा होता जाता है, $\angle \mathrm{C}$ वैसे-वैसे छोटा होता जाता है। अतः ऊपर वाली स्थिति की भाँति भुजा $\mathrm{AB}$ की लंबाई कम होती जाती है। बिंदु $\mathrm{A}$, बिंदु $\mathrm{B}$ के निकट होता जाता है और, अंत में जब $\angle \mathrm{A}, 90^{\circ}$ के अत्यधिक निकट आ जाता है, तो $\angle \mathrm{C}, 0^{\circ}$ के अत्यधिक निकट आ जाता है और भुजा $\mathrm{AC}$ भुजा $\mathrm{BC}$ के साथ लगभग संपाती हो जाती है (देखिए आकृति 8.18)।

आकृति 8.18
जब $\angle \mathrm{C}, 0^{\circ}$ के अत्यधिक निकट होता है तो $\angle \mathrm{A}, 90^{\circ}$ के अत्यधिक निकट हो जाता है और भुजा $\mathrm{AC}$ लगभग वही हो जाती है, जो भुजा $\mathrm{BC}$ है। अतः $\sin \mathrm{A}, 1$ के अत्यधिक निकट हो जाता है और, जब $\angle \mathrm{A}, 90^{\circ}$ के अत्यधिक निकट होता है, तब $\angle \mathrm{C}, 0^{\circ}$ के अत्यधिक निकट हो जाता है और भुजा $\mathrm{AB}$ लगभग शून्य हो जाती है। अतः $\cos \mathrm{A}, 0$ के अत्यधिक निकट हो जाता है।
अतः हम यह परिभाषित करते हैं :
$\sin 90^{\circ}=1$ और $\cos 90^{\circ}=0$
अब आप क्यों नहीं $90^{\circ}$ के अन्य त्रिकोणमितीय अनुपात ज्ञात करते हैं?
अब हम तुरंत संदर्भ के लिए एक सारणी 8.1 के रूप में $0^{\circ}, 30^{\circ}, 45^{\circ}, 60^{\circ}$ और $90^{\circ}$ के सभी त्रिकोणमितीय अनुपातों के मान प्रस्तुत करेंगे।
सारणी 8.1
| $\angle \mathrm{A}$ | $\mathbf{0}^{\circ}$ | $\mathbf{3 0 ^ { \circ }}$ | $\mathbf{4 5 ^ { \circ }}$ | $\mathbf{6 0}^{\circ}$ | $\mathbf{9 0}^{\circ}$ |
|---|---|---|---|---|---|
| $\sin \mathrm{A}$ | 0 | $\frac{1}{2}$ | $\frac{1}{\sqrt{2}}$ | $\frac{\sqrt{3}}{2}$ | 1 |
| $\cos \mathrm{A}$ | 1 | $\frac{\sqrt{3}}{2}$ | $\frac{1}{\sqrt{2}}$ | $\frac{1}{2}$ | 0 |
| $\tan \mathrm{A}$ | 0 | $\frac{1}{\sqrt{3}}$ | 1 | $\sqrt{3}$ | अपरिभाषित |
| $\operatorname{cosec} \mathrm{A}$ | अपरिभाषित | 2 | $\sqrt{2}$ | $\frac{2}{\sqrt{3}}$ | 1 |
| $\sec \mathrm{A}$ | 1 | $\frac{2}{\sqrt{3}}$ | $\sqrt{2}$ | 2 | अपरिभाषित |
| $\cot \mathrm{A}$ | अपरिभाषित | $\sqrt{3}$ | 1 | $\frac{1}{\sqrt{3}}$ | 0 |
टिप्पणी : उपर्युक्त सारणी से आप देख सकते हैं कि जैसे-जैसे $\angle \mathrm{A}$ का मान $0^{\circ}$ से $90^{\circ}$ तक बढ़ता जाता है, $\sin \mathrm{A}$ का मान 0 से बढ़कर 1 हो जाता है और $\cos \mathrm{A}$ का मान 1 से घटकर 0 हो जाता है।
आइए, अब हम कुछ उदाहरण लेकर ऊपर की सारणी में दिए गए मानों के प्रयोग को प्रदर्शित करें।
उदाहरण 6: $ \triangle \mathrm{ABC}$ में जिसका कोण $\mathrm{B}$ समकोण है, $\mathrm{AB}=5 \mathrm{~cm}$ और $\angle \mathrm{ACB}=30^{\circ}$ ( देखिए आकृति 8.19)। भुजाओं $\mathrm{BC}$ और $\mathrm{AC}$ की लंबाइयाँ ज्ञात करें।

आकृति 8.19
हल : भुजा $\mathrm{BC}$ की लंबाई ज्ञात करने के लिए हम उस त्रिकोणमितीय अनुपात को लेंगे जिसमें $\mathrm{BC}$ और दी हुई भुजा $\mathrm{AB}$ हो। क्योंकि $\mathrm{BC}$ कोण $\mathrm{C}$ की संलग्न भुजा है, और $\mathrm{AB}$ कोण $\mathrm{C}$ की सम्मुख भुजा है, इसलिए
$ \frac{\mathrm{AB}}{\mathrm{BC}}=\tan \mathrm{C} $
अर्थात्
$ \frac{5}{\mathrm{BC}}=\tan 30^{\circ}=\frac{1}{\sqrt{3}} $
जिससे
$ \mathrm{BC}=5 \sqrt{3} \mathrm{~cm} \text { प्राप्त होता है। } $
भुजा $\mathrm{AC}$ की लंबाई ज्ञात करने के लिए हम
$ \begin{aligned} & \sin 30^{\circ} =\frac{AB}{AC} \quad \quad \quad \text{(क्यों?)} \\ \text{ अर्थात् }\quad \quad \quad & \frac{1}{2} =\frac{5}{AC} \\ \text{ अर्थात् }\quad \quad \quad & AC =10 ~cm \end{aligned} $
ध्यान दीजिए कि ऊपर के उदाहरण में तीसरी भुजा की लंबाई ज्ञात करने के लिए विकल्प के रूप में हम पाइथागोरस प्रमेय को लागू कर सकते थे,
अर्थात्
$$ \mathrm{AC}=\sqrt{\mathrm{AB}^{2}+\mathrm{BC}^{2}}=\sqrt{5^{2}+(5 \sqrt{3})^{2}} \mathrm{~cm}=10 \mathrm{~cm} $$
उदाहरण 7: $ \triangle \mathrm{PQR}$ में, जिसका कोण $\mathrm{Q}$ समकोण है (देखिए आकृति 8.20 ), $\mathrm{PQ}=3 \mathrm{~cm}$ और $\mathrm{PR}=6 \mathrm{~cm}$ है। $\angle \mathrm{QPR}$ और $\angle \mathrm{PRQ}$ ज्ञात कीजिए।

आकृति 8.20
हल : दिया हुआ है $\mathrm{PQ}=3 \mathrm{~cm}$ और $\mathrm{PR}=6 \mathrm{~cm}$
इसलिए
$ \frac{\mathrm{PQ}}{\mathrm{PR}}=\sin \mathrm{R} $
या
$ \sin \mathrm{R}=\frac{3}{6}=\frac{1}{2} $
अत:
$ \angle \mathrm{PRQ}=30^{\circ} $
और, इसलिए
$\angle \mathrm{QPR}=60^{\circ} \quad \quad (क्यों?)$
आप यहाँ यह देख सकते हैं कि यदि एक समकोण त्रिभुज की एक भुजा और कोई एक अन्य भाग (जो या तो न्यून कोण हो या कोई एक भुजा हो) ज्ञात हो, तो त्रिभुज की शेष भुजाएँ और कोण ज्ञात किए जा सकते हैं।
उदाहरण 8 : यदि $\sin (\mathrm{A}-\mathrm{B})=\frac{1}{2}, \cos (\mathrm{A}+\mathrm{B})=\frac{1}{2}, 0^{\circ}<\mathrm{A}+\mathrm{B} \leq 90^{\circ}, \mathrm{A}>\mathrm{B}$, तो $\mathrm{A}$ और $\mathrm{B}$ ज्ञात कीजिए।
हल : क्योंकि $\sin (\mathrm{A}-\mathrm{B})=\frac{1}{2}$, इसलिए, $\mathrm{A}-\mathrm{B}=30^{\circ} \quad$ (क्यों?) $\quad \quad \quad \quad (1)$
और, क्योंकि $\cos (\mathrm{A}+\mathrm{B})=\frac{1}{2}$, इसलिए, $\mathrm{A}+\mathrm{B}=60^{\circ}$ (क्यों?) $\quad \quad \quad \quad (2)$
(1) और (2) को हल करने पर हमें $\mathrm{A}=45^{\circ}$ और $\mathrm{B}=15^{\circ}$ प्राप्त होता है।
प्रश्नावली 8.2
1. निम्नलिखित के मान निकालिए :
(i) $\sin 60^{\circ} \cos 30^{\circ}+\sin 30^{\circ} \cos 60^{\circ}$
(ii) $2 \tan ^{2} 45^{\circ}+\cos ^{2} 30^{\circ}-\sin ^{2} 60^{\circ}$
(iii) $\frac{\cos 45^{\circ}}{\sec 30^{\circ}+\operatorname{cosec} 30^{\circ}}$
(iv) $\frac{\sin 30^{\circ}+\tan 45^{\circ}-\operatorname{cosec} 60^{\circ}}{\sec 30^{\circ}+\cos 60^{\circ}+\cot 45^{\circ}}$
(v) $\frac{5 \cos ^{2} 60^{\circ}+4 \sec ^{2} 30^{\circ}-\tan ^{2} 45^{\circ}}{\sin ^{2} 30^{\circ}+\cos ^{2} 30^{\circ}}$
Show Answer
#missing2. सही विकल्प चुनिए और अपने विकल्प का औचित्य दीजिए:
(i) $\frac{2 \tan 30^{\circ}}{1+\tan ^{2} 30^{\circ}}=$
(A) $\sin 60^{\circ}$
(B) $\cos 60^{\circ}$
(C) $\tan 60^{\circ}$
(D) $\sin 30^{\circ}$
(ii) $\frac{1-\tan ^{2} 45^{\circ}}{1+\tan ^{2} 45^{\circ}}=$
(A) $\tan 90^{\circ}$
(B) 1
(C) $\sin 45^{\circ}$
(D) 0
(iii) $\sin 2 \mathrm{~A}=2 \sin \mathrm{A}$ तब सत्य होता है, जबकि $\mathrm{A}$ बराबर है:
(A) $0^{\circ}$
(B) $30^{\circ}$
(C) $45^{\circ}$
(D) $60^{\circ}$
(iv) $\frac{2 \tan 30^{\circ}}{1-\tan ^{2} 30^{\circ}}$ बराबर है:
(A) $\cos 60^{\circ}$
(B) $\sin 60^{\circ}$
(C) $\tan 60^{\circ}$
(D) $\sin 30^{\circ}$
Show Answer
#missing3. यदि $\tan (\mathrm{A}+\mathrm{B})=\sqrt{3}$ और $\tan (\mathrm{A}-\mathrm{B})=\frac{1}{\sqrt{3}} ; 0^{\circ}<\mathrm{A}+\mathrm{B} \leq 90^{\circ} ; \mathrm{A}>\mathrm{B}$ तो $\mathrm{A}$ और $\mathrm{B}$ का मान ज्ञात कीजिए।
Show Answer
#missing4. बताइए कि निम्नलिखित में कौन-कौन सत्य हैं या असत्य हैं। कारण सहित अपने उत्तर की पुष्टि कीजिए।
(i) $\sin (\mathrm{A}+\mathrm{B})=\sin \mathrm{A}+\sin \mathrm{B}$.
(ii) $\theta$ में वृद्धि होने के साथ $\sin \theta$ के मान में भी वृद्धि होती है।
(iii) $\theta$ में वृद्धि होने के साथ $\cos \theta$ के मान में भी वृद्धि होती है।
(iv) $\theta$ के सभी मानों पर $\sin \theta=\cos \theta$
(v) $\mathrm{A}=0^{\circ}$ पर $\cot \mathrm{A}$ परिभाषित नहीं है।
Show Answer
#missing8.4 त्रिकोणमितीय सर्वसमिकाएँ
आपको याद होगा कि एक समीकरण को एक सर्वसमिका तब कहा जाता है जबकि यह संबंधित चरों के सभी मानों के लिए सत्य हो। इसी प्रकार एक कोण के त्रिकोणमितीय अनुपातों से संबंधित सर्वसमिका को त्रिकोणमितीय सर्वसमिका कहा जाता है। जबकि यह संबंधित कोण (कोणों) के सभी मानों के लिए सत्य होता है।
इस भाग में, हम एक त्रिकोणमितीय सर्वसमिका सिद्ध करेंगे और इसका प्रयोग अन्य उपयोगी त्रिकोणमितीय सर्वसमिकाओं को सिद्ध करने में करेंगे।
$\triangle \mathrm{ABC}$ में, जो $\mathrm{B}$ पर समकोण है (देखिए आकृति 8.21) हमें यह प्राप्त है
$\mathrm{AB}^{2}+\mathrm{BC}^{2}=\mathrm{AC}^{2}$

आकृति 8.21
(1) के प्रत्येक पद को $\mathrm{AC}^{2}$ से भाग देने पर हमें यह प्राप्त होता है
$ \frac{\mathrm{AB}^{2}}{\mathrm{AC}^{2}}+\frac{\mathrm{BC}^{2}}{\mathrm{AC}^{2}}=\frac{\mathrm{AC}^{2}}{\mathrm{AC}^{2}} $
या
$ \left(\frac{\mathrm{AB}}{\mathrm{AC}}\right)^{2}+\left(\frac{\mathrm{BC}}{\mathrm{AC}}\right)^{2}=\left(\frac{\mathrm{AC}}{\mathrm{AC}}\right)^{2} $
अर्थात्
$ (\cos A)^{2}+(\sin A)^{2}=1 $
अर्थात्
$ \cos ^{2} A+\sin ^{2} A=1 \tag{2} $
यह सभी $\mathrm{A}$ के लिए, जहाँ $0^{\circ} \leq \mathrm{A} \leq 90^{\circ}$, सत्य होता है। अतः यह एक त्रिकोणमितीय सर्वसमिका है।
आइए, अब हम (1) को $\mathrm{AB}^{2}$ से भाग दें। ऐसा करने पर हमें यह प्राप्त होता है
$ \frac{\mathrm{AB}^{2}}{\mathrm{AB}^{2}}+\frac{\mathrm{BC}^{2}}{\mathrm{AB}^{2}}=\frac{\mathrm{AC}^{2}}{\mathrm{AB}^{2}} $
या
$ \left(\frac{\mathrm{AB}}{\mathrm{AB}}\right)^{2}+\left(\frac{\mathrm{BC}}{\mathrm{AB}}\right)^{2}=\left(\frac{\mathrm{AC}}{\mathrm{AB}}\right)^{2} $
$ \text{ अर्थात् } \quad 1+\tan ^{2} A=\sec ^{2} A \tag{3} $
क्या यह समीकरण, $\mathrm{A}=0^{\circ}$ के लिए सत्य है? हाँ, यह सत्य है। क्या यह $\mathrm{A}=90^{\circ}$ के लिए भी सत्य है? $\mathrm{A}=90^{\circ}$ के लिए $\tan \mathrm{A}$ और $\sec \mathrm{A}$ परिभाषित नहीं है। अतः (3), ऐसे सभी $\mathrm{A}$ के लिए सत्य होता है, जहाँ $0^{\circ} \leq \mathrm{A}<90^{\circ}$
आइए हम यह देखें कि (1) को $\mathrm{BC}^{2}$ से भाग देने पर हमें क्या प्राप्त होता है।
$ \frac{\mathrm{AB}^{2}}{\mathrm{BC}^{2}}+\frac{\mathrm{BC}^{2}}{\mathrm{BC}^{2}}=\frac{\mathrm{AC}^{2}}{\mathrm{BC}^{2}} $
$ \text{अर्थात्} \quad \quad \quad(\frac{A B}{B C})^{2}+(\frac{B C}{B C})^{2}=(\frac{A C}{B C})^{2}$
$$\text{अर्थात्} \quad \quad \quad \cot^{2} \mathbf{A}+1=cosec^{2} \mathbf{A} \tag{4}$$
ध्यान दीजिए कि $\mathrm{A}=0^{\circ}$ के लिए $\operatorname{cosec} \mathrm{A}$ और $\cot \mathrm{A}$ परिभाषित नहीं है। अतः ऐसे सभी $\mathrm{A}$ के लिए (4) सत्य होता है जहाँ $0^{\circ}<\mathrm{A} \leq 90^{\circ}$
इन सर्वसमिकाओं का प्रयोग करके हम प्रत्येक त्रिकोणमितीय अनुपात को अन्य त्रिकोणमितीय अनुपातों के पदों में व्यक्त कर सकते हैं अर्थात् यदि कोई एक अनुपात ज्ञात हो, तो हम अन्य त्रिकोणमितीय अनुपातों के मान भी ज्ञात कर सकते हैं।
आइए हम यह देखें कि इन सर्वसमिकाओं का प्रयोग करके इसे हम कैसे ज्ञात कर सकते हैं। मान लीजिए हमें $\tan \mathrm{A}=\frac{1}{\sqrt{3}}$ ज्ञात है। तब $\cot \mathrm{A}=\sqrt{3}$
क्योंकि $\sec ^{2} \mathrm{~A}=1+\tan ^{2} \mathrm{~A}=1+\frac{1}{3}=\frac{4}{3}, \sec \mathrm{A}=\frac{2}{\sqrt{3}}$, और $\cos \mathrm{A}=\frac{\sqrt{3}}{2}$
और, क्योंकि $\sin \mathrm{A}=\sqrt{1-\cos ^{2} \mathrm{~A}}=\sqrt{1-\frac{3}{4}}=\frac{1}{2}$. इसलिए $\operatorname{cosec} \mathrm{A}=2$
उदाहरण 9 : अनुपातों $\cos \mathrm{A}, \tan \mathrm{A}$ और $\sec \mathrm{A}$ को $\sin \mathrm{A}$ के पदों में व्यक्त कीजिए।
हल : क्योंकि
$\cos ^{2} \mathrm{~A}+\sin ^{2} \mathrm{~A}=1$, इसलिए
$ \cos ^{2} \mathrm{~A}=1-\sin ^{2} \mathrm{~A} \text {, अर्थात् } \cos \mathrm{A}= \pm \sqrt{1-\sin ^{2} \mathrm{~A}} $
इससे यह प्राप्त होता है
$ \cos \mathrm{A}=\sqrt{1-\sin ^{2} \mathrm{~A}} \quad \text { (क्यों?) } $
अत: $\quad \tan \mathrm{A}=\frac{\sin \mathrm{A}}{\cos \mathrm{A}}=\frac{\sin \mathrm{A}}{\sqrt{1-\sin ^{2} \mathrm{~A}}}$ और $\sec \mathrm{A}=\frac{1}{\cos \mathrm{A}}=\frac{1}{\sqrt{1-\sin ^{2} \mathrm{~A}}}$
उदाहरण 10 : सिद्ध कीजिए कि $\sec \mathrm{A}(1-\sin \mathrm{A})(\sec \mathrm{A}+\tan \mathrm{A})=1$
हल :
वाम पक्ष $=\sec A(1-\sin A)(\sec A+\tan A)=(\frac{1}{\cos A})(1-\sin A)(\frac{1}{\cos A}+\frac{\sin A}{\cos A})$
$ \begin{aligned} & =\frac{(1-\sin A)(1+\sin A)}{\cos ^{2} A}=\frac{1-\sin ^{2} A}{\cos ^{2} A} \\ & =\frac{\cos ^{2} A}{\cos ^{2} A}=1=दाँया पक्ष \end{aligned} $
उदाहरण 11: सिद्ध कीजिए कि $\frac{\cot \mathrm{A}-\cos \mathrm{A}}{\cot \mathrm{A}+\cos \mathrm{A}}=\frac{\operatorname{cosec} \mathrm{A}-1}{\operatorname{cosec} \mathrm{A}+1}$
हल : वाम पक्ष $=\frac{\cot \mathrm{A}-\cos \mathrm{A}}{\cot \mathrm{A}+\cos \mathrm{A}}=\frac{\frac{\cos \mathrm{A}}{\sin \mathrm{A}}-\cos \mathrm{A}}{\frac{\cos \mathrm{A}}{\sin \mathrm{A}}+\cos \mathrm{A}}$
$$ \frac{\cos A\left(\frac{1}{\sin A}-1\right)}{\cos A\left(\frac{1}{\sin A}+1\right)}=\frac{\left(\frac{1}{\sin A}-1\right)}{\left(\frac{1}{\sin A}+1\right)}=\frac{\operatorname{cosec} A-1}{\operatorname{cosec} A+1}=\text { दाँया पक्ष } $$
उदाहरण 12 : सर्वसमिका $\sec ^{2} \theta=1+\tan ^{2} \theta$ का प्रयोग करके सिद्ध कीजिए कि $\frac{\sin \theta-\cos \theta+1}{\sin \theta+\cos \theta-1}=\frac{1}{\sec \theta-\tan \theta}$
हल : क्योंकि हमें $\sec \theta$ और $\tan \theta$ से संबंधित सर्वसमिका प्रयुक्त करनी है, इसलिए आइए हम सबसे पहले सर्वसमिका के वाम पक्ष के अंश और हर को $\cos \theta$ से भाग देकर वाम पक्ष को $\sec \theta$ और $\tan \theta$ के पदों में रूपांतरित करें।
$$ \begin{aligned} \text{ वाम पक्ष } & =\frac{\sin \theta-\cos \theta+1}{\sin \theta+\cos \theta-1}=\frac{\tan \theta-1+\sec \theta}{\tan \theta+1-\sec \theta} \\ & =\frac{(\tan \theta+\sec \theta)-1}{(\tan \theta-\sec \theta)+1}=\frac{{(\tan \theta+\sec \theta)-1}(\tan \theta-\sec \theta)}{{(\tan \theta-\sec \theta)+1}(\tan \theta-\sec \theta)} \\ & =\frac{(\tan ^{2} \theta-\sec ^{2} \theta)-(\tan \theta-\sec \theta)}{{\tan \theta-\sec \theta+1}(\tan \theta-\sec \theta)} \\ & =\frac{-1-\tan \theta+\sec \theta}{(\tan \theta-\sec \theta+1)(\tan \theta-\sec \theta)} \\ & =\frac{-1}{\tan \theta-\sec \theta}=\frac{1}{\sec \theta-\tan \theta} \end{aligned} $$
जो सिद्ध की जाने वाली अपेक्षित सर्वसमिका का दाँया पक्ष है।
प्रश्नावली 8.3
1. त्रिकोणमितीय अनुपातों $\sin \mathrm{A}, \sec \mathrm{A}$ और $\tan \mathrm{A}$ को $\cot \mathrm{A}$ के पदों में व्यक्त कीजिए।
Show Answer
#missing2. $\angle \mathrm{A}$ के अन्य सभी त्रिकोणमितीय अनुपातों को $\sec \mathrm{A}$ के पदों में लिखिए।
Show Answer
#missing3. सही विकल्प चुनिए और अपने विकल्प की पुष्टि कीजिए :
(i) $9 \sec ^{2} \mathrm{~A}-9 \tan ^{2} \mathrm{~A}$ बराबर है:
(A) 1 $\quad$
(B) 9 $\quad$
(C) 8 $\quad$
(D) 0
(ii) $(1+\tan \theta+\sec \theta)(1+\cot \theta-\operatorname{cosec} \theta)$ बराबर है:
(A) 0 $\quad$
(B) 1 $\quad$
(C) 2 $\quad$
(D) -1
(iii) $(\sec \mathrm{A}+\tan \mathrm{A})(1-\sin \mathrm{A})$ बराबर है:
(A) $\sec \mathrm{A}$ $\quad$
(B) $\sin \mathrm{A}$ $\quad$
(C) $\operatorname{cosec} \mathrm{A}$ $\quad$
(D) $\cos \mathrm{A}$
(iv) $\frac{1+\tan ^{2} \mathrm{~A}}{1+\cot ^{2} \mathrm{~A}}$ बराबर है:
(A) $\sec ^{2} \mathrm{~A}$ $\quad$
(B) -1 $\quad$
(C) $\cot ^{2} \mathrm{~A}$ $\quad$
(D) $\tan ^{2} \mathrm{~A}$
Show Answer
#missing4. निम्नलिखित सर्वसमिकाएँ सिद्ध कीजिए, जहाँ वे कोण, जिनके लिए व्यंजक परिभाषित है, न्यून कोण है :
(i) $(\operatorname{cosec} \theta-\cot \theta)^{2}=\frac{1-\cos \theta}{1+\cos \theta}$
(ii) $\frac{\cos \mathrm{A}}{1+\sin \mathrm{A}}+\frac{1+\sin \mathrm{A}}{\cos \mathrm{A}}=2 \sec \mathrm{A}$
(iii) $\frac{\tan \theta}{1-\cot \theta}+\frac{\cot \theta}{1-\tan \theta}=1+\sec \theta \operatorname{cosec} \theta$
[संकेतः व्यंजक को $\sin \theta$ और $\cos \theta$ के पदों में लिख्ए]]
(iv) $\frac{1+\sec A}{\sec A}=\frac{\sin ^2 A}{1-\cos A}$
[संकेत: वाम पक्ष और दाँया पक्ष को अलग-अलग सरल कीजिए।]
(v) सर्वसमिका $\operatorname{cosec}^2 \mathrm{~A}=1+\cot ^2 \mathrm{~A}$ को लागू करके $ \frac{\cos A-\sin A+1}{\cos A+\sin A-1}=\operatorname{cosec} A+\cot A $
(vi) $\sqrt{\frac{1+\sin A}{1-\sin A}}=\sec A+\tan A$
(vii) $\frac{\sin \theta-2 \sin ^3 \theta}{2 \cos ^3 \theta-\cos \theta}-\tan \theta$
(viii) $(\sin \mathrm{A}+\operatorname{cosec} \mathrm{A})^2+(\cos \mathrm{A}+\sec \mathrm{A})^2=7+\tan ^2 \mathrm{~A}+\cot ^2 \mathrm{~A}$
(ix) $(\operatorname{cosec} A-\sin A)(\sec A-\cos A)=\frac{1}{\tan A+\cot A}$
[संकेत : वाम पक्ष और दाँया पक्ष को अलग-अलग सरल कीजिए]
(x) $\left(\frac{1+\tan ^2 \mathrm{~A}}{1+\cot ^2 \mathrm{~A}}\right)=\left(\frac{1-\tan \mathrm{A}}{1-\cot \mathrm{A}}\right)^2=\tan ^2 \mathrm{~A}$
Show Answer
#missing8.5 सारांश
इस अध्याय में, आपने निम्नलिखित तथ्यों का अध्ययन किया है:
1. समकोण त्रिभुज $\mathrm{ABC}$ में, जिसका कोण $\mathrm{B}$ समकोण है,
$$ \begin{aligned} & \sin \mathrm{A}=\frac{\text { कोण } \mathrm{A} \text { की सम्मुख भुजा }}{\text { कर्ण }}, \cos \mathrm{A}=\frac{\text { कोण } \mathrm{A} \text { की संलग्न भुजा }}{\text { कर्ण }} \\ & \tan \mathrm{A}=\frac{\text { कोण } \mathrm{A} \text { की सम्मुख भुजा }}{\text { कोण } \mathrm{A} \text { की संलग्न भुजा }} \end{aligned} $$
2. $\operatorname{cosec} \mathrm{A}=\frac{1}{\sin \mathrm{A}} ; \sec \mathrm{A}=\frac{1}{\cos \mathrm{A}} ; \tan \mathrm{A}=\frac{1}{\cot \mathrm{A}}, \tan \mathrm{A}=\frac{\sin \mathrm{A}}{\cos \mathrm{A}}$
3. यदि एक न्यून कोण का एक त्रिकोणमितीय अनुपात ज्ञात हो, तो कोण के शेष त्रिकोणमितीय अनुपात सरलता से ज्ञात किए जा सकते हैं।
4. $0^{\circ}, 30^{\circ}, 45^{\circ}, 60^{\circ}$ और $90^{\circ}$ के कोणों के त्रिकोणमितीय अनुपातों के मान।
5. $\sin \mathrm{A}$ या $\cos \mathrm{A}$ का मान कभी भी 1 से अधिक नहीं होता, जबकि $\sec \mathrm{A} \operatorname{या} \operatorname{cosec} \mathrm{A}$ का मान सदैव 1 से अधिक या 1 के बराबर होता है।
6. $\sin ^{2} \mathrm{~A}+\cos ^{2} \mathrm{~A}=1$
$\sec ^{2} \mathrm{~A}-\tan ^{2} \mathrm{~A}=1$ जहाँ $0^{\circ} \leq \mathrm{A}<90^{\circ}$
$\operatorname{cosec}^{2} \mathrm{~A}=1+\cot ^{2} \mathrm{~A}$ जहाँ $0^{\circ}<\mathrm{A} \leq 90^{\circ}$





