7.1 भूमिका

कक्षा IX में, आप पढ़ चुके हैं कि एक तल पर किसी बिंदु की स्थिति निर्धारित करने के लिए, हमें निर्देशांक अक्षों के एक युग्म की आवश्यकता होती है। किसी बिंदु की $y$-अक्ष से दूरी उस बिंदु का $x$-निर्देशांक या भुज (abscissa) कहलाती है। किसी बिंदु की $x$-अक्ष से दूरी, उस बिंदु का $y$-निर्देशांक या कोटि (ordinate) कहलाती है। $x$-अक्ष पर स्थित किसी बिंदु के निर्देशांक $(x, 0)$ के रूप के होते हैं तथा $y$-अक्ष पर स्थित किसी बिंदु के निर्देशांक $(0, y)$ के रूप के होते हैं।

यहाँ आपके लिए एक खेल दिया जा रहा है। एक आलेख कागज़ पर लांबिक अक्षों (perpendicular axes) का एक युग्म खींचिए। अब निम्नलिखित बिंदुओं को आलेखित कीजिए और दिए गए निर्देशों के अनुसार उन्हें मिलाइए। बिंदु $\mathrm{A}(4,8)$ को $\mathrm{B}(3,9)$ से, $\mathrm{B}$ को $\mathrm{C}(3,8)$ से, $\mathrm{C}$ को $\mathrm{D}(1,6)$ से, $\mathrm{D}$ को $\mathrm{E}(1,5)$ से, $\mathrm{E}$ को $\mathrm{F}(3,3)$ से, $\mathrm{F}$ को $\mathrm{G}(6,3)$ से, $\mathrm{G}$ को $\mathrm{H}(8,5)$ से, $\mathrm{H}$ को $\mathrm{I}(8,6)$ से, $\mathrm{I}$ को $\mathrm{J}(6,8)$ से, $\mathrm{J}$ को $\mathrm{K}(6,9)$ से, $\mathrm{K}$ को $\mathrm{L}(5,8)$ से और $\mathrm{L}$ को $A$ से मिलाइए। इसके बाद, बिंदुओं $P(3.5,7), Q(3,6)$ और $R(4,6)$ को जोड़ कर एक त्रिभुज बनाइए। साथ ही, एक त्रिभुज बनाने के लिए बिंदुओं $\mathrm{X}(5.5,7), \mathrm{Y}(5,6)$ और $\mathrm{Z}(6,6)$ को मिलाइए। अब एक और त्रिभुज बनाने के लिए, बिंदुओं $\mathrm{S}(4,5), \mathrm{T}(4.5,4)$ और $\mathrm{U}(5,5)$ को मिलाइए। अंत में, बिंदु $S$ को बिंदुओं $(0,5)$ और $(0,6)$ से मिलाइए तथा बिंदु $U$ को बिंदुओं $(9,5)$ और $(9,6)$ से मिलाइए। आपको कौन-सा चित्र प्राप्त होता है?

साथ ही, आप यह भी देख चुके हैं कि $a x+b y+c=0$ (जहाँ $a$ और $b$ एक साथ शून्य न हों) के रूप की दो चरों वाली एक समीकरण को जब आलेखीय रूप से निरूपित करते हैं, तो एक सरल रेखा प्राप्त होती है। साथ ही, अध्याय 2 में आप देख चुके हैं कि $y=a x^{2}+b x+c(a \neq 0)$ का आलेख एक परवलय (parabola) होता है। वस्तुतः, आकृतियों की ज्यामिति का अध्ययन करने के लिए, निर्देशांक ज्यामिति (coordinate geometry) एक बीजीय साधन (algebraic tool) के रूप में विकसित की गई है। यह बीजगणित का प्रयोग करके ज्यामिति का अध्ययन करने में सहायता करती है तथा बीजगणित को ज्यामिति द्वारा समझने में भी सहायक होती है। इसी कारण, निर्देशांक ज्यामिति के विभिन्न क्षेत्रों में व्यापक अनुप्रयोग हैं, जैसे भौतिकी, इंजीनियरिंग, समुद्री-परिवहन (या नौ-गमन) (navigation), भूकंप शास्त्र संबंधी (seismology) और कला।

इस अध्याय में, आप यह सीखेंगे कि दो बिंदुओं, जिनके निर्देशांक दिए हुए हों, के बीच की दूरी किस प्रकार ज्ञात की जाती है तथा तीन दिए हुए बिंदुओं से बने त्रिभुज का क्षेत्रफल किस प्रकार ज्ञात किया जाता है। आप इसका भी अध्ययन करेंगे कि दिए हुए दो बिंदुओं को मिलाने से बने रेखाखंड को एक दिए गए अनुपात में विभाजित करने वाले बिंदु के निर्देशांक किस प्रकार ज्ञात किए जाते हैं।

7.2 दूरी सूत्र

आइए निम्नलिखित स्थिति पर विचार करें:

एक शहर $B$ एक अन्य शहर $A$ से $36 \mathrm{~km}$ पूर्व (east) और $15 \mathrm{~km}$ उत्तर (north) की ओर है। आप शहर $B$ की शहर $A$ से दूरी बिना वास्तविक मापन के किस प्रकार ज्ञात कर सकते हैं? आइए देखें। इस स्थिति को, आलेखीय रूप से, आकृति 7.1 की तरह दर्शाया जा सकता है। अब, आप वांछित दूरी ज्ञात करने के लिए, पाइथागोरस प्रमेय का प्रयोग कर सकते हैं।

आकृति 7.1

अब, मान लीजिए दो बिंदु $x$-अक्ष पर स्थित हैं। क्या हम इनके बीच की दूरी ज्ञात कर सकते हैं? उदाहरणार्थ, आकृति 7.2 के दो बिंदुओं $\mathrm{A}(4,0)$ और $\mathrm{B}(6,0)$ पर विचार कीजिए। बिंदु $\mathrm{A}$ और $\mathrm{B}, x$-अक्ष पर स्थित है।

आकृति से आप देख सकते हैं कि $\mathrm{OA}=$ 4 मात्रक (इकाई) और $\mathrm{OB}=6$ मात्रक हैं।

अतः, $\mathrm{A}$ से $\mathrm{B}$ की दूरी $\mathrm{AB}=\mathrm{OB}-\mathrm{OA}=$ $(6-4)$ मात्रक $=2$ मात्रक है।

इस प्रकार, यदि दो बिंदु $x$-अक्ष पर स्थित हों, तो हम उनके बीच की दूरी सरलता से ज्ञात कर सकते हैं।

अब, मान लीजिए, हम $y$-अक्ष पर स्थित कोई दो बिंदु लेते हैं। क्या हम इनके बीच की दूरी ज्ञात कर सकते हैं? यदि बिंदु $\mathrm{C}(0,3)$ और $\mathrm{D}(0,8), y$-अक्ष पर स्थित हों, तो हम दूरी ऊपर की भाँति ज्ञात कर सकते हैं अर्थात् दूरी $\mathrm{CD}=(8-3)$ मात्रक $=5$ मात्रक है (देखिए आकृति 7.2)।

आकृति 7.2

पुनः, क्या आप आकृति 7.2 में, बिंदु $\mathrm{C}$ से बिंदु $\mathrm{A}$ की दूरी ज्ञात कर सकते हैं? चूँकि $\mathrm{OA}=4$ मात्रक और $\mathrm{OC}=3$ मात्रक हैं, इसलिए $\mathrm{C}$ से $\mathrm{A}$ की दूरी $\mathrm{AC}=\sqrt{3^{2}+4^{2}}=5$ मात्रक है। इसी प्रकार, आप $\mathrm{D}$ से $\mathrm{B}$ की दूरी $\mathrm{BD}=10$ मात्रक ज्ञात कर सकते हैं।

अब, यदि हम ऐसे दो बिंदुओं पर विचार करें, जो निर्देशांक अक्षों पर स्थित नहीं हैं, तो क्या हम इनके बीच की दूरी ज्ञात कर सकते हैं? हाँ! ऐसा करने के लिए, हम पाइथागोरस प्रमेय का प्रयोग करेंगे। आइए एक उदाहरण लेकर देखें।

आकृति 7.3 में, बिंदु $\mathrm{P}(4,6)$ और $\mathrm{Q}(6,8)$ प्रथम चतुर्थांश (first quadrant) में स्थित हैं। इनके बीच की दूरी ज्ञात करने के लिए, हम पाइथागोरस प्रमेय का प्रयोग कैसे करते हैं? आइए $\mathrm{P}$ और $\mathrm{Q}$ से $x$-अक्ष पर क्रमशः लंब $\mathrm{PR}$ और $\mathrm{QS}$ खीचें। साथ ही, $\mathrm{P}$ से $\mathrm{QS}$ पर एक लंब डालिए जो QS को T पर प्रतिच्छेद करे। तब R और $\mathrm{S}$ के निर्देशांक क्रमशः $(4,0)$ और $(6,0)$ हैं। अतः, $\mathrm{RS}=2$ मात्रक है। साथ ही, $\mathrm{QS}=8$ मात्रक और $\mathrm{TS}=\mathrm{PR}=6$ मात्रक है।

आकृति 7.3

स्पष्ट है कि $\mathrm{QT}=2$ मात्रक और $\mathrm{PT}=\mathrm{RS}=2$ मात्रक।

अब, पाइथागोरस प्रमेय के प्रयोग से, हमें प्राप्त होता है:

$ \begin{aligned} \mathrm{PQ}^{2} =\mathrm{PT}^{2}+\mathrm{QT}^{2} \\ =2^{2}+2^{2}=8 \end{aligned} $

अत:

$ \mathrm{PQ}=2 \sqrt{2} \text { मात्रक हुआ। } $

आप दो भिन्न-भिन्न चतुर्थांशों में स्थित बिंदुओं के बीच की दूरी कैसे ज्ञात करेंगे?

बिंदुओं $\mathrm{P}(6,4)$ और $\mathrm{Q}(-5,-3)$ पर विचार कीजिए (देखिए आकृति 7.4)। $x$-अक्ष पर लंब $\mathrm{QS}$ खींचिए। साथ ही, बिंदु $\mathrm{P}$ से बढ़ाई हुई $\mathrm{QS}$ पर $\mathrm{PT}$ लंब खींचिए जो $y$-अक्ष को बिंदु $\mathrm{R}$ पर प्रतिच्छेद करे।

आकृति 7.4

तब, $\mathrm{PT}=11$ मात्रक और $\mathrm{QT}=7$ मात्रक है (क्यों?)

समकोण त्रिभुज PTQ में, पाइथागोरस प्रमेय के प्रयोग से, हमें प्राप्त होता है: $\mathrm{PQ}=\sqrt{11^{2}+7^{2}}=\sqrt{170}$ मात्रक

आइए, अब किन्हीं दो बिंदुओं $\mathrm{P}\left(x _{1}, y _{1}\right)$ और $\mathrm{Q}\left(x _{2}, y _{2}\right)$ के बीच की दूरी ज्ञात करें। $x$-अक्ष पर लंब $\mathrm{PR}$ और $\mathrm{QS}$ खींचिए। $\mathrm{P}$ से $\mathrm{QS}$ पर एक लंब खींचिए, जो उसे $\mathrm{T}$ पर प्रतिच्छेद करे (देखिए आकृति 7.5)।

आकृति 7.5

तब, $\quad \mathrm{OR}=x _{1}, \mathrm{OS}=x _{2}$ है। अत:, $\mathrm{RS}=x _{2}-x _{1}=\mathrm{PT}$ है।

साथ ही, $\quad \mathrm{SQ}=y _{2}$ और $\mathrm{ST}=\mathrm{PR}=y _{1}$ है। अत:, $\mathrm{QT}=y _{2}-y _{1}$ है।

अब, $\triangle \mathrm{PTQ}$ में, पाइथागोरस प्रमेय के प्रयोग से, हमें प्राप्त होता है:

$ \begin{aligned} PQ^{2} & =PT^{2}+QT^{2} \\ & =(x_2-x_1)^{2}+(y_2-y_1)^{2} \end{aligned} $

अत :

$ P Q=\sqrt{(x_2-x_1)^{2}+(y_2-y_1)^{2}} $

ध्यान दें कि चूँकि दूरी सदैव ऋणेतर होती है, हम केवल धनात्मक वर्गमूल लेते हैं। अत: $\mathrm{P}\left(x _{1}, y _{1}\right)$ और $\mathrm{Q}\left(x _{2}, y _{2}\right)$ के बिंदुओं के बीच की दूरी है

$ \mathrm{PQ}=\sqrt{\left(x _{2}-x _{1}\right)^{2}+\left(y _{2}-y _{1}\right)^{2}} $

जो दूरी सूत्र (distance formula) कहलाता है।

टिप्पणियाँ :

1. विशेष रूप से, बिंदु $\mathrm{P}(x, y)$ की मूल बिंदु $\mathrm{O}(0,0)$ से दूरी

$ \mathrm{OP}=\sqrt{x^{2}+y^{2}} \text { होती है। } $

2. हम $\mathrm{PQ}=\sqrt{\left(x _{1}-x _{2}\right)^{2}+\left(y _{1}-y _{2}\right)^{2}}$ भी लिख सकते हैं (क्यों?)

उदाहरण 1 : क्या बिंदु $(3,2),(-2,-3)$ और $(2,3)$ एक त्रिभुज बनाते हैं? यदि हाँ, तो बताइए कि किस प्रकार का त्रिभुज बनता है।00

हल : आइए $\mathrm{PQ}, \mathrm{QR}$ और $\mathrm{PR}$ ज्ञात करने के लिए दूरी सूत्र का प्रयोग करें, जहाँ $\mathrm{P}(3,2)$, $\mathrm{Q}(-2,-3)$ और $\mathrm{R}(2,3)$ दिए हुए बिंदु हैं। हमें प्राप्त होता है:

$$ \begin{aligned} & \mathrm{PQ}=\sqrt{(3+2)^{2}+(2+3)^{2}}=\sqrt{5^{2}+5^{2}}=\sqrt{50}=7.07 \text { ( लगभग) } \\ & \mathrm{QR}=\sqrt{(-2-2)^{2}+(-3-3)^{2}}=\sqrt{(-4)^{2}+(-6)^{2}}=\sqrt{52}=7.21 \text { (लगभग) } \\ & \mathrm{PR}=\sqrt{(3-2)^{2}+(2-3)^{2}}=\sqrt{1^{2}+(-1)^{2}}=\sqrt{2}=1.41 \text { ( लगभग) } \end{aligned} $$

चूँकि इन तीन दूरियों में से किन्हीं दो का योग तीसरी दूरी से अधिक है, इसलिए इन बिंदुओं $\mathrm{P}, \mathrm{Q}$ और $\mathrm{R}$ से एक त्रिभुज बनता है।

साथ ही, यहाँ $\mathrm{PQ}^{2}+\mathrm{PR}^{2}=\mathrm{QR}^{2}$ है। अतः, पाइथागोरस प्रमेय के विलोम से, हमें ज्ञात होता है कि $\angle \mathrm{P}=90^{\circ}$ है। इसलिए, $\mathrm{PQR}$ एक समकोण त्रिभुज है।

उदाहरण 2 : दर्शाइए कि बिंदु $(1,7),(4,2),(-1,-1)$ और $(-4,4)$ एक वर्ग के शीर्ष हैं।

हल : मान लीजिए दिए हुए बिंदु $\mathrm{A}(1,7), \mathrm{B}(4,2), \mathrm{C}(-1,-1)$ और $\mathrm{D}(-4,4)$ हैं। $\mathrm{ABCD}$ को एक वर्ग दर्शाने की एक विधि यह है कि उसका गुणधर्म जैसा कि वर्ग की सभी भुजाएँ बराबर तथा दोनों विकर्ण बराबर होती हैं, का प्रयोग किया जाए। अब,

$ \begin{aligned} & AB=\sqrt{(1-4)^{2}+(7-2)^{2}}=\sqrt{9+25}=\sqrt{34} \\ & BC=\sqrt{(4+1)^{2}+(2+1)^{2}}=\sqrt{25+9}=\sqrt{34} \\ & CD=\sqrt{(-1+4)^{2}+(-1-4)^{2}}=\sqrt{9+25}=\sqrt{34} \\ & DA=\sqrt{(1+4)^{2}+(7-4)^{2}}=\sqrt{25+9}=\sqrt{34} \\ & AC=\sqrt{(1+1)^{2}+(7+1)^{2}}=\sqrt{4+64}=\sqrt{68} \\ & BD=\sqrt{(4+4)^{2}+(2-4)^{2}}=\sqrt{64+4}=\sqrt{68} \end{aligned} $

यहाँ, $\mathrm{AB}=\mathrm{BC}=\mathrm{CD}=\mathrm{DA}$ है और $\mathrm{AC}=\mathrm{BD}$ है, अर्थात् चतुर्भुज $\mathrm{ABCD}$ की चारों भुजाएँ बराबर हैं और दोनों विकर्ण भी बराबर हैं। अतः चतुर्भुज $\mathrm{ABCD}$ एक वर्ग है।

वैकल्पिक हल : हम चारों भुजाएँ और एक विकर्ण, मान लीजिए $\mathrm{AC}$ ऊपर की तरह ज्ञात करते हैं। यहाँ $\mathrm{AD}^{2}+\mathrm{DC}^{2}=34+34=68=\mathrm{AC}^{2}$ है। अतः, पाइथागोरस प्रमेय के विलोम द्वारा $\angle \mathrm{D}=90^{\circ}$ है। चारों भुजाएँ बराबर होने और एक कोण समकोण होने से चतुर्भुज एक वर्ग हो जाता है। अतः $\mathrm{ABCD}$ एक वर्ग है।

उदाहरण 3 : आकृति 7.6 किसी कक्षा में रखे डेस्कों (desks) की व्यवस्था दर्शाती है। आशिमा, भारती और कैमिला क्रमश: $\mathrm{A}(3,1), \mathrm{B}(6,4)$ और $\mathrm{C}(8,6)$ पर बैठी हैं। क्या आप सोचते हैं कि वे एक ही सीध (in a line) में बैठी हैं? सकारण उत्तर दीजिए।

आकृति 7.6

हल : दूरी सूत्र के प्रयोग से, हमें प्राप्त होता है :

$ \begin{aligned} & AB=\sqrt{(6-3)^{2}+(4-1)^{2}}=\sqrt{9+9}=\sqrt{18}=3 \sqrt{2} \\ & BC=\sqrt{(8-6)^{2}+(6-4)^{2}}=\sqrt{4+4}=\sqrt{8}=2 \sqrt{2} \\ & AC=\sqrt{(8-3)^{2}+(6-1)^{2}}=\sqrt{25+25}=\sqrt{50}=5 \sqrt{2} \end{aligned} $

चूँकि $\mathrm{AB}+\mathrm{BC}=3 \sqrt{2}+2 \sqrt{2}=5 \sqrt{2}=\mathrm{AC}$ है, अतः हम कह सकते हैं कि $\mathrm{A}, \mathrm{B}$ और $\mathrm{C}$ संरेखी (collinear) हैं। अर्थात्, वे तीनों एक ही सीध में बैठी हैं।

उदाहरण 4: $ x$ और $y$ में एक संबंध ज्ञात कीजिए, ताकि बिंदु $(x, y)$ बिंदुओं $(7,1)$ और $(3,5)$ से समदूरस्थ (equidistant) हो।

हल : मान लीजिए $\mathrm{P}(x, y)$ बिंदुओं $\mathrm{A}(7,1)$ और $\mathrm{B}(3,5)$ से समदूरस्थ है।

हमें $\mathrm{AP}=\mathrm{BP}$ दिया है। अत: $\mathrm{AP}^{2}=\mathrm{BP}^{2}$ है।

अर्थात् $\quad (x-7)^{2}+(y-1)^{2}=(x-3)^{2}+(y-5)^{2}$

अर्थात् $\quad x^{2}-14 x+49+y^{2}-2 y+1=x^{2}-6 x+9+y^{2}-10 y+25$

अर्थात् $\quad x-y=2$

यही $x$ और $y$ में वांछित संबंध है।

टिप्पणी : ध्यान दीजिए कि समीकरण $x-y=2$ का आलेख एक रेखा होता है। आप अपने पिछले अध्ययन से यह जानते हैं कि वह बिंदु जो दो दिए हुए बिंदुओं $\mathrm{A}$ और $\mathrm{B}$ से समदूरस्थ होता है रेखाखंड $\mathrm{AB}$ के लंब समद्विभाजक पर स्थित होता है। अतः, $x-y=2$ का आलेख रेखाखंड $\mathrm{AB}$ का लंब समद्विभाजक है (देखिए आकृति 7.7)।

आकृति 7.7

उदाहरण 5: $ y$-अक्ष पर एक ऐसा बिंदु ज्ञात कीजिए, जो बिंदुओं $\mathrm{A}(6,5)$ और $\mathrm{B}(-4,3)$ से समदूरस्थ हो।

हल : हम जानते हैं कि $y$-अक्ष पर स्थित कोई भी बिंदु $(0, y)$ के रूप का होता है। अतः, मान लीजिए कि बिंदु $\mathrm{P}(0, y)$ बिंदुओं $\mathrm{A}$ और $\mathrm{B}$ से समदूरस्थ है। तब,

$$ (6-0)^{2}+(5-y)^{2}=(-4-0)^{2}+(3-y)^{2} $$

या $\quad 36+25+y^{2}-10 y=16+9+y^{2}-6 y$

या $\quad 4 y=36$

या $\quad y=9$

अतः, वांछित बिंदु $(0,9)$ है।

आइए अपने हल की जाँच करें: $\mathrm{AP}=\sqrt{(6-0)^{2}+(5-9)^{2}}=\sqrt{36+16}=\sqrt{52}$

$$ \mathrm{BP}=\sqrt{(-4-0)^{2}+(3-9)^{2}}=\sqrt{16+36}=\sqrt{52} $$

टिप्पणी: ऊपर दी गई टिप्पणी का प्रयोग करने से, हम देखते हैं कि $(0,9), y$-अक्ष और रेखाखंड $\mathrm{AB}$ के लंब समद्विभाजक का प्रतिच्छेद बिंदु है।

प्रश्नावली 7.1

1. बिंदुओं के निम्नलिखित युग्मों के बीच की दूरियाँ ज्ञात कीजिए:

(i) $(2,3),(4,1)$

(ii) $(-5,7),(-1,3)$

(iii) $(a, b),(-a,-b)$

2. बिंदुओं $(0,0)$ और $(36,15)$ के बीच की दूरी ज्ञात कीजिए। क्या अब आप अनुच्छेद 7.2 में दिए दोनों शहरों $\mathrm{A}$ और $\mathrm{B}$ के बीच की दूरी ज्ञात कर सकते हैं?

3. निर्धारित कीजिए कि क्या बिंदु $(1,5),(2,3)$ और $(-2,-11)$ संरेखी हैं।

4. जाँच कीजिए कि क्या बिंदु $(5,-2),(6,4)$ और $(7,-2)$ एक समद्विबाहु त्रिभुज के शीर्ष हैं।

5. किसी कक्षा में, चार मित्र बिंदुओं $\mathrm{A}, \mathrm{B}, \mathrm{C}$ और $\mathrm{D}$ पर बैठे हुए हैं, जैसाकि आकृति 7.8 में दर्शाया गया है। चंपा और चमेली कक्षा के अंदर आती हैं और कुछ मिनट तक देखने के बाद, चंपा चमेली से पूछती है, ‘क्या तुम नहीं सोचती हो कि $\mathrm{ABCD}$ एक वर्ग है?’ चमेली इससे सहमत नहीं है। दूरी सूत्र का प्रयोग करके, बताइए कि इनमें कौन सही है।

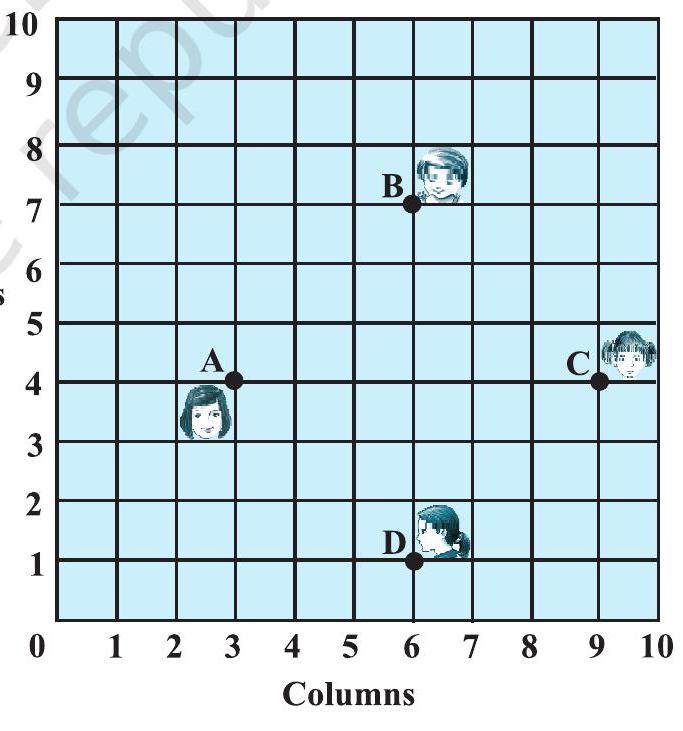
आकृति 7.8

6. निम्नलिखित बिंदुओं द्वारा बनने वाले चतुर्भुज का प्रकार (यदि कोई है तो) बताइए तथा अपने उत्तर के लिए कारण भी दीजिए:

(i) $(-1,-2),(1,0),(-1,2),(-3,0)$

(ii) $(-3,5),(3,1),(0,3),(-1,-4)$

(iii) $(4,5),(7,6),(4,3),(1,2)$

7. $x$-अक्ष पर वह बिंदु ज्ञात कीजिए जो $(2,-5)$ और $(-2,9)$ से समदूरस्थ हैं।

8. $y$ का वह मान ज्ञात कीजिए, जिसके लिए बिंदु $\mathrm{P}(2,-3)$ और $\mathrm{Q}(10, y)$ के बीच की दूरी 10 मात्रक है।

9. यदि $\mathrm{Q}(0,1)$ बिंदुओं $\mathrm{P}(5,-3)$ और $\mathrm{R}(x, 6)$ से समदूरस्थ है, तो $x$ के मान ज्ञात कीजिए। दूरियाँ $\mathrm{QR}$ और PR भी ज्ञात कीजिए।

10. $x$ और $y$ में एक ऐसा संबंध ज्ञात कीजिए कि बिंदु $(x, y)$ बिंदुओं $(3,6)$ और $(-3,4)$ से समदूरस्थ हो।

7.3 विभाजन सूत्र

आइए अनुच्छेद 7.2 में दी हुई स्थिति को याद करें। मान लीजिए कि टेलीफोन कंपनी शहरों $\mathrm{A}$ और $\mathrm{B}$ के बीच में एक प्रसारण टॉवर (relay tower) ऐसे स्थान $\mathrm{P}$ पर स्थापित करना चाहती है कि टॉवर की $\mathrm{B}$ से दूरी उसकी $\mathrm{A}$ से दूरी की दुगुनी हो। यदि $\mathrm{P}$ रेखाखंड $\mathrm{AB}$ पर स्थित है, तो यह $\mathrm{AB}$ को $1: 2$ के अनुपात में विभाजित करे। (देखिए आकृति 7.9)। यदि हम $\mathrm{A}$ को मूलबिंदु $\mathrm{O}$ मानें तथा $1 \mathrm{~km}$ को दोनों अक्षों पर 1 मात्रक मानें, तो $\mathrm{B}$ के निर्देशांक $(36,15)$ होंगे। $\mathrm{P}$ की स्थिति जानने के लिए हमें $\mathrm{P}$ के निर्देशांक ज्ञात करने चाहिए। ये निर्देशांक हम किस प्रकार ज्ञात करें?

आकृति 7.9

मान लीजिए $\mathrm{P}$ के निर्देशांक $(x, y)$ हैं। $\mathrm{P}$ और $\mathrm{B}$ से $x$-अक्ष पर लंब खींचिए जो इसे क्रमशः $\mathrm{D}$ और $\mathrm{E}$ पर मिलें। $\mathrm{BE}$ पर लंब $\mathrm{PC}$ खींचिए जो उससे $\mathrm{C}$ पर मिले। तब, अध्याय 6 में, पढ़ी गई $\mathrm{AA}$ समरूपता कसौटी के प्रयोग से, $\triangle \mathrm{POD}$ और $\triangle \mathrm{BPC}$ समरूप हैं।

अतः $\frac{\mathrm{OD}}{\mathrm{PC}}=\frac{\mathrm{OP}}{\mathrm{PB}}=\frac{1}{2}$ तथा $\frac{\mathrm{PD}}{\mathrm{BC}}=\frac{\mathrm{OP}}{\mathrm{PB}}=\frac{1}{2}$ है।

अत: $\frac{x}{36-x}=\frac{1}{2}$ तथा $\frac{y}{15-y}=\frac{1}{2}$ है।

इन समीकरणों से $x=12$ और $y=5$ प्राप्त होता है।

आप इसकी जाँच कर सकते हैं कि $\mathrm{P}(12,5)$ प्रतिबंध $\mathrm{OP}: \mathrm{PB}=1: 2$ को संतुष्ट करता है।

आइए अब उपरोक्त उदाहरण से प्राप्त की गई समझ के आधार पर विभाजन का व्यापक सूत्र प्राप्त करने का प्रयत्न करें।

किन्हीं दो बिंदुओं $\mathrm{A}\left(x _{1}, y _{1}\right)$ और $\mathrm{B}\left(x _{2}, y _{2}\right)$ पर विचार कीजिए और मान लीजिए बिंदु $\mathrm{P}(x, y)$ रेखाखंड $\mathrm{AB}$ को $m _{1}: m _{2}$ के अनुपात में आंतरिक रूप से (internally) विभाजित करता है, अर्थात् $\frac{\mathrm{PA}}{\mathrm{PB}}=\frac{m _{1}}{m _{2}}$ है (देखिए आकृति 7.10)।

आकृति 7.10

$x$-अक्ष पर $\mathrm{AR}, \mathrm{PS}$ और $\mathrm{BT}$ लंब खींचिए। $x$-अक्ष के समांतर $\mathrm{AQ}$ और $\mathrm{PC}$ खींचिए। तब AA समरूपता कसौटी से,

$ \Delta \mathrm{PAQ} \sim \Delta \mathrm{BPC} $

अत :

$ \frac{PA}{BP}=\frac{AQ}{PC}=\frac{PQ}{BC} \tag{1} $

अब

$ \begin{aligned} & AQ=RS=OS-OR=x-x_1 \\ & PC=ST=OT-OS=x_2-x \\ & PQ=PS-QS=PS-AR=y-y_1 \\ & BC=BT-CT=BT-PS=y_2-y \end{aligned} $

इन मानों को (1) में प्रतिस्थापित करने पर, हमें प्राप्त होता है:

$ \frac{m_1}{m_2}=\frac{x-x_1}{x_2-x}=\frac{y-y_1}{y_2-y} $

$ \text{लेने पर हमें} \quad \quad \frac{m_1}{m_2}=\frac{x-x_1}{x_2-x} \text{प्राप्त होता है। } x=\frac{m_1 x_2+m_2 x_1}{m_1+m_2} $

$$ \text{इसी प्रकार} \quad \quad \frac{m_1}{m_2}=\frac{y-y_1}{y_2-y}, \text{ प्राप्त होता है। } y=\frac{m_1 y_2+m_2 y_1}{m_1+m_2} $$

अतः, दो बिंदुओं $\mathrm{A}\left(x _{1}, y _{1}\right)$ और $\mathrm{B}\left(x _{2}, y _{2}\right)$ को जोड़ने वाले रेखाखंड $\mathrm{AB}$ को $m _{1}: m _{2}$ के अनुपात में आंतरिक रूप से विभाजित करने वाले बिंदु $\mathrm{P}(x, y)$ के निर्देशांक हैं :

$$ \begin{equation*} \left(\frac{m _{1} x _{2}+m _{2} x _{1}}{m _{1}+m _{2}}, \frac{m _{1} y _{2}+m _{2} y _{1}}{m _{1}+m _{2}}\right) \tag{2} \end{equation*} $$

उपरोक्त को विभाजन सूत्र (section formula) कहते हैं।

इसी सूत्र को $\mathrm{A}, \mathrm{P}$ और $\mathrm{B}$ से $y$-अक्ष पर लंब डालकर और ऊपर की भाँति प्रक्रिया अपनाकर भी प्राप्त किया जा सकता है।

यदि $\mathrm{P}$ रेखाखंड $\mathrm{AB}$ को $k: 1$ के अनुपात में विभाजित करे, तो बिंदु $\mathrm{P}$ के निर्देशांक

$ \frac{k x _{2}+x _{1}}{k+1}, \frac{k y _{2}+y _{1}}{k+1} \text { होंगे। } $

विशिष्ट स्थिति : एक रेखाखंड का मध्य-बिंदु उसे $1: 1$ के अनुपात में विभाजित करता है। अतः, बिंदुओं $\mathrm{A}\left(x _{1}, y _{1}\right)$ और $\mathrm{B}\left(x _{2}, y _{2}\right)$ को जोड़ने वाले रेखाखंड $\mathrm{AB}$ के मध्य-बिंदु के निर्देशांक

$$ (\frac{1 \cdot x_1+1 \cdot x_2}{1+1}, \frac{1 \cdot y_1+1 \cdot y_2}{1+1})=(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}) \text{ होंगे। } $$

आइए अब विभाजन सूत्र पर आधारित कुछ उदाहरण हल करें।

उदाहरण 6 : उस बिंदु के निर्देशांक ज्ञात कीजिए जो बिंदुओं $(4,-3)$ और $(8,5)$ को जोड़ने वाले रेखाखंड को आंतरिक रूप से $3: 1$ के अनुपात में विभाजित करता है।

हल : मान लीजिए $\mathrm{P}(x, y)$ वांछित बिंदु है। विभाजन सूत्र का प्रयोग करने पर हमें

$ x=\frac{3(8)+1(4)}{3+1}=7, y=\frac{3(5)+1(-3)}{3+1}=3 $

प्राप्त होता है। अतः $(7,3)$ ही वांछित बिंदु है।

उदाहरण 7 : बिंदु $(-4,6)$, बिंदुओं $\mathrm{A}(-6,10)$ और $\mathrm{B}(3,-8)$ को जोड़ने वाले रेखाखंड को किस अनुपात में विभाजित करता है?

हल : मान लीजिए $(-4,6)$ रेखाखंड $\mathrm{AB}$ को आंतरिक रूप से $m _{1}: m _{2}$ के अनुपात में विभाजित करता है। विभाजन सूत्र के प्रयोग से, हमें प्राप्त होता है:

$$ \begin{equation*} (-4,6)=\left(\frac{3 m _{1}-6 m _{2}}{m _{1}+m _{2}}, \frac{-8 m _{1}+10 m _{2}}{m _{1}+m _{2}}\right) \tag{1} \end{equation*} $$

याद कीजिए कि यदि $(x, y)=(a, b)$ हो, तो $x=a$ और $y=b$ होता है।

अत :

$$ -4=\frac{3 m_1-6 m_2}{m_1+m_2} \text{ और } 6=\frac{-8 m_1+10 m_2}{m_1+m_2} $$

$$\text{अब }\quad-4=\frac{3 m_1-6 m_2}{m_1+m_2} \quad \text{से प्राप्त होता है:}$$

$ -4 m_1-4 m_2=3 m_1-6 m_2 $

अर्थात्

$$ 7 m_1=2 m_2 $$

अर्थात्

$$ m_1: m_2=2: 7 $$

आपको इसकी जाँच कर लेनी चाहिए कि यह अनुपात $y$-निर्देशांक को भी संतुष्ट करता है।

अब $\quad \frac{-8 m _{1}+10 m _{2}}{m _{1}+m _{2}}=\frac{-8 \frac{m _{1}}{m _{2}}+10}{\frac{m _{1}}{m _{2}}+1} \quad\left(m _{2}\right.$ से ऊपर नीचे भाग देने पर $)$

$ =\frac{-8 \times \frac{2}{7}+10}{\frac{2}{7}+1}=6 $

अतः बिंदु $(-4,6)$, बिंदुओं $\mathrm{A}(-6,10)$ और $\mathrm{B}(3,-8)$ को जोड़ने वाले रेखाखंड को $2: 7$ के अनुपात में विभाजित करता है।

वैकल्पिक हल : अनुपात $m _{1}: m _{2}$ को $\frac{m _{1}}{m _{2}}: 1$, या $k: 1$ के रूप में लिखा जा सकता है। मान लीजिए बिंदु $(-4,6)$ रेखाखंड $\mathrm{AB}$ को आंतरिक रूप से $k: 1$ के अनुपात में विभाजित करता है। विभाजन सूत्र द्वारा, हमें प्राप्त होता है:

$ \begin{align*} (-4,6) & =(\frac{3 k-6}{k+1}, \frac{-8 k+10}{k+1}) \tag{2} \end{align*} $

$ \begin{aligned} \text{अत : } \quad \quad & -4 =\frac{3 k-6}{k+1} \\ \text{या } \quad \quad & -4 k-4 =3 k-6 \\ \text{या } \quad \quad & 7 k =2 \\ \text{या } \quad \quad & k: 1 =2: 7 \end{aligned} $

आप $y$-निर्देशांक के लिए भी इसकी जाँच कर सकते हैं।

अतः, बिंदु $(-4,6)$, बिंदुओं $\mathrm{A}(-6,10)$ और $\mathrm{B}(3,-8)$ को जोड़ने वाले रेखाखंड को $2: 7$ के अनुपात में विभाजित करता है।

टिप्पणी : आप इस अनुपात को दूरियाँ $\mathrm{PA}$ और $\mathrm{PB}$ ज्ञात करके और फिर उनके अनुपात लेकर भी प्राप्त कर सकते हैं, जबकि आपको यह जानकारी हो कि बिंदु $\mathrm{A}, \mathrm{P}$ और $\mathrm{B}$ संरेखी हैं।

उदाहरण 8 : बिंदुओं $\mathrm{A}(2,-2)$ और $\mathrm{B}(-7,4)$ को जोड़ने वाले रेखाखंड को सम-त्रिभाजित करने वाले बिंदुओं के निर्देशांक ज्ञात कीजिए।

हल : मान लीजिए रेखाखंड $\mathrm{AB}$ को सम-त्रिभाजित करने वाले बिंदु $\mathrm{P}$ और $\mathrm{Q}$ हैं, अर्थात् $\mathrm{AP}=\mathrm{PQ}=$ $\mathrm{QB}$ है (देखिए आकृति 7.11)।

Fig. 7.11

अतः, $\mathrm{P}$ रेखाखंड $\mathrm{AB}$ को आंतरिक रूप से $1: 2$ के अनुपात में विभाजित करता है। अतः, $\mathrm{P}$ के निर्देशांक सूत्र द्वारा, निम्नलिखित हैं:

$ \left(\frac{1(-7)+2(2)}{1+2}, \frac{1(4)+2(-2)}{1+2}\right), \text { अर्थात् }(-1,0) $

अब, $\mathrm{Q}$ रेखाखंड $\mathrm{AB}$ को आंतरिक रूप से $2: 1$ के अनुपात में विभाजित करता है। अतः $Q$ के निर्देशांक हैं:

$ \left(\frac{2(-7)+1(2)}{2+1}, \frac{2(4)+1(-2)}{2+1}\right), \text { अर्थात् }(-4,2) $

अतः, बिंदुओं $\mathrm{A}$ और $\mathrm{B}$ को जोड़ने वाले रेखाखंड को सम-त्रिभाजित करने वाले बिंदुओं के निर्देशांक $(-1,0)$ और $(-4,2)$ हैं।

टिप्पणी: हम $\mathrm{Q}$ के निर्देशांक उसे $\mathrm{PB}$ का मध्य-बिंदु मानते हुए भी ज्ञात कर सकते थे। इसमें हमें मध्य-बिंदु वाले सूत्र का प्रयोग करना पड़ता।

उदाहरण 9 : बिंदुओं $(5,-6)$ और $(-1,-4)$ को जोड़ने वाले रेखाखंड को $y$-अक्ष किस अनुपात में विभाजित करती है? इस प्रतिच्छेद बिंदु के निर्देशांक भी ज्ञात कीजिए।

हल : मान लीजिए वांछित अनुपात $k: 1$ है। तब, विभाजन सूत्र द्वारा, उस रेखाखंड को $k: 1$ के अनुपात में विभाजित करने वाले बिंदु के निर्देशांक हैं : $\frac{-k+5}{k+1}, \frac{-4 k-6}{k+1}$

यह बिंदु $y$-अक्ष पर स्थित है और हम जानते हैं कि $y$-अक्ष पर भुज 0 होता है। अत :

इसलिए

$ \frac{-k+5}{k+1}=0 $

So,

$ k=5 $

अर्थात् वांछित अनुपात $5: 1$ है। $k$ का मान 5 रखने पर हमें प्रतिच्छेद बिंदु $\left(0, \frac{-13}{3}\right)$ प्राप्त होता है।

उदाहरण 10 : यदि बिंदु $\mathrm{A}(6,1), \mathrm{B}(8,2), \mathrm{C}(9,4)$ और $\mathrm{D}(p, 3)$ एक समांतर चतुर्भुज के शीर्ष इसी क्रम में हों, तो $p$ का मान ज्ञात कीजिए।

हल : हम जानते हैं कि समांतर चतुर्भुज के विकर्ण परस्पर समद्विभाजित करते हैं।

अतः, विकर्ण $\mathrm{AC}$ के मध्य बिंदु के निर्देशांक = विकर्ण $\mathrm{BD}$ के मध्य-बिंदु के निर्देशांक

$\text{अर्थात्}\quad \quad(\frac{6+9}{2}, \frac{1+4}{2})=(\frac{8+p}{2}, \frac{2+3}{2})$

$\text{या}\quad \quad(\frac{15}{2}, \frac{5}{2})=(\frac{8+p}{2}, \frac{5}{2})$

$\text{अत : }\quad \quad \frac{15}{2}=\frac{8+p}{2} $

$\text{या}\quad \quad p=7$

प्रश्नावली 7.2

1. उस बिंदु के निर्देशांक ज्ञात कीजिए, जो बिंदुओं $(-1,7)$ और $(4,-3)$ को मिलाने वाले रेखाखंड को $2: 3$ के अनुपात में विभाजित करता है।

2. बिंदुओं $(4,-1)$ और $(-2,-3)$ को जोड़ने वाले रेखाखंड को सम-त्रिभाजित करने वाले बिंदुओं के निर्देशांक ज्ञात कीजिए।

3. आपके स्कूल में खेल-कूद क्रियाकलाप आयोजित करने के लिए, एक आयताकार मैदान $\mathrm{ABCD}$ में, चूने से परस्पर $1 \mathrm{~m}$ की दूरी पर पंक्तियाँ बनाई गई हैं। $\mathrm{AD}$ के अनुदिश परस्पर $1 \mathrm{~m}$ की दूरी पर 100 गमले रखे गए हैं, जैसा कि आकृति 7.12 में दर्शाया गया है। निहारिका दूसरी पंक्ति में $\mathrm{AD}$ के $\frac{1}{4}$ भाग के बराबर की दूरी दौड़ती है और वहाँ एक हरा झंडा गाड़ देती है। प्रीत आठवीं पंक्ति में $\mathrm{AD}$ के $\frac{1}{5}$ भाग के बराबर की दूरी दौड़ती है और वहाँ एक लाल झंडा गाड़ देती है। दोनों झंडों के बीच की दूरी क्या है? यदि रश्मि को एक नीला झंडा इन दोनों झंडों को मिलाने वाले रेखाखंड पर ठीक आधी दूरी ( बीच में) पर गाड़ना हो तो उसे अपना झंडा कहाँ गाड़ना चाहिए?

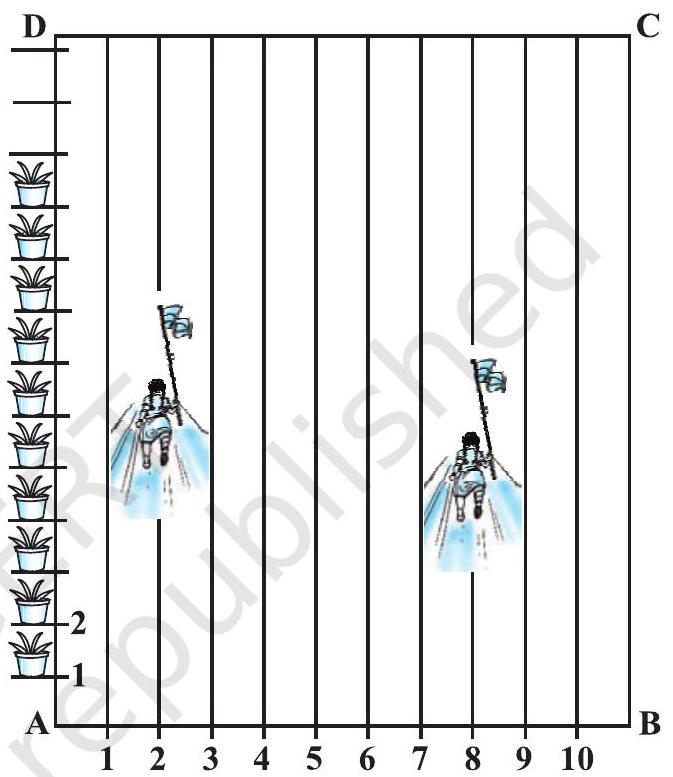
आकृति 7.12

4. बिंदुओं $(-3,10)$ और $(6,-8)$ को जोड़ने वाले रेखाखंड को बिंदु $(-1,6)$ किस अनुपात में विभाजित करता है।

5. वह अनुपात ज्ञात कीजिए जिसमें बिंदुओं $\mathrm{A}(1,-5)$ और $\mathrm{B}(-4,5)$ को मिलाने वाला रेखाखंड $x$-अक्ष से विभाजित होता है। इस विभाजन बिंदु के निर्देशांक भी ज्ञात कीजिए।

6. यदि बिंदु $(1,2),(4, y),(x, 6)$ और $(3,5)$, इसी क्रम में लेने पर, एक समांतर चतुर्भुज के शीर्ष हो तो $x$ और $y$ ज्ञात कीजिए।

7. बिंदु $\mathrm{A}$ के निर्देशांक ज्ञात कीजिए, जहाँ $\mathrm{AB}$ एक वृत्त का व्यास है जिसका केंद्र $(2,-3)$ है तथा $B$ के निर्देशांक $(1,4)$ हैं।

8. यदि $\mathrm{A}$ और $\mathrm{B}$ क्रमशः $(-2,-2)$ और $(2,-4)$ हो तो बिंदु $\mathrm{P}$ के निर्देशांक ज्ञात कीजिए ताकि $\mathrm{AP}=\frac{3}{7} \mathrm{AB}$ हो और $\mathrm{P}$ रेखाखंड $\mathrm{AB}$ पर स्थित हो।

9. बिंदुओं $\mathrm{A}(-2,2)$ और $\mathrm{B}(2,8)$ को जोड़ने वाले रेखाखंड $\mathrm{AB}$ को चार बराबर भागों में विभाजित करने वाले बिंदुओं के निर्देशांक ज्ञात कीजिए।

10. एक समचतुर्भुज का क्षेत्रफल ज्ञात कीजिए जिसके शीर्ष, इसी क्रम में, $(3,0),(4,5),(-1,4)$ और $(-2,-1)$ हैं। [संकेत : समचतुर्भुज का क्षेत्रफल $=\frac{1}{2}$ (उसके विकर्णों का गुणनफल)]

7.4 सारांश

इस अध्याय में, आपने निम्नलिखित तथ्यों का अध्ययन किया है:

1. $\mathrm{P}\left(x _{1}, y _{1}\right)$ और $\mathrm{Q}\left(x _{2}, y _{2}\right)$ के बीच की दूरी $\sqrt{\left(x _{2}-x _{1}\right)^{2}+\left(y _{2}-y _{1}\right)^{2}}$ है।

2. बिंदु $\mathrm{P}(x, y)$ की मूलबिंदु से दूरी $\sqrt{x^{2}+y^{2}}$ होती है।

3. उस बिंदु $\mathrm{P}(x, y)$ के निर्देशांक जो बिंदुओं $\mathrm{A}\left(x _{1}, y _{1}\right)$ और $\mathrm{B}\left(x _{2}, y _{2}\right)$ को जोड़ने वाले रेखाखंड को $m _{1}: m _{2}$ के अनुपात में आंतरिक रूप से विभाजित करता है, निम्नलिखित होते हैं: $\left(\frac{m _{1} x _{2}+m _{2} x _{1}}{m _{1}+m _{2}}, \frac{m _{1} y _{2}+m _{2} y _{1}}{m _{1}+m _{2}}\right)$

4. बिंदुओं $\mathrm{P}\left(x _{1}, y _{1}\right)$ और $\mathrm{Q}\left(x _{2}, y _{2}\right)$ को जोड़ने वाले रेखाखंड $\mathrm{PQ}$ के मध्यबिंदु के निर्देशांक $\left(\frac{x _{1}+x _{2}}{2}, \frac{y _{1}+y _{2}}{2}\right)$ होते हैं।

पाठकों के लिए विशेष

अनुभाग 7.3 में किसी बिंदु $\mathrm{P}$ के लिए जिसके निर्देशांक $(x, y)$ हैं तथा यदि यह बिंदु किन्हीं दो बिंदुओं $\mathrm{A}\left(x _{1}, y _{1}\right)$ और $\mathrm{B}\left(x _{2}, y _{2}\right)$ को मिलाने वाले रेखाखंड को आंतरिक रूप में $m _{1}: m _{2}$ के अनुपात में विभाजित करता है तो

$$ x=\frac{m _{1} x _{2}+m _{2} x _{1}}{m _{1}+m _{2}}, \quad y=\frac{m _{1} y _{2}+m _{2} y _{1}}{m _{1}+m _{2}} $$

ध्यान दीजिए कि $\mathrm{PA}: \mathrm{PB}=m _{1}: m _{2}$

तथापि यदि बिंदु $\mathrm{P}$ बिंदुओं $\mathrm{A}$ और $\mathrm{B}$ के बीच स्थित नहीं है, परंतु यह रेखाखंड के वाह्य में स्थित है जहाँ $\mathrm{PA}: \mathrm{PB}=m _{1}: m _{2}$ है तब हम कहते हैं कि $\mathrm{P}$ बिंदुओं $\mathrm{A}$ और $\mathrm{B}$ को मिलाने वाले रेखाखंड को वाह्यतः विभाजित करता है। ऐसी स्थितियों से संबंधित विभाजन सूत्र का अध्ययन आप उच्चतर कक्षाओं में करेंगे।