अध्याय 05 समांतर श्रेढ़ियाँ
5.1 भूमिका
आपने इस पर अवश्य ध्यान दिया होगा कि प्रकृति में, अनेक वस्तुएँ एक निश्चित प्रतिरूप (pattern) का अनुसरण करती हैं, जैसे कि सूरजमुखी के फूल की पंखुड़ियाँ, मधु-कोष (या मधु-छत्ते) में छिद्र, एक भुट्टे पर दाने, एक अनन्नास और एक पाइन कोन (pine cone) पर सर्पिल, इत्यादि
अब हम अपने दैनिक जीवन में आने वाले प्रतिरूपों की ओर देखते हैं। ऐसे कुछ उदाहरण हैं :
(i) रीना ने एक पद के लिए आवेदन किया और उसका चयन हो गया। उसे यह पद ₹ 8000 के मासिक वेतन और ₹ 500 वार्षिक की वेतन वृद्धि के साथ दिया गया। उसका वेतन (₹ में) पहले वर्ष, दूसरे वर्ष, तीसरे वर्ष, इत्यादि के लिए क्रमशः
$ 8000,8500,9000, \ldots \text { होगा। } $
(ii) एक सीढ़ी के डंडों की लंबाइयाँ नीचे से ऊपर की ओर एक समान रूप से $2 \mathrm{~cm}$ घटती जाती हैं। (देखिए आकृति 5.1)। सबसे नीचे वाला डंडा लंबाई में $45 \mathrm{~cm}$ है। नीचे से, पहले, दूसरे, तीसरे, . . . डंडों की लंबाइयाँ ( $\mathrm{cm}$ में) क्रमशः
$45,43,41,39,37,35,33$ और $31$ हैं।

आकृति 5.1
(iii) किसी बचत योजना में, कोई धनराशि प्रत्येक 3 वर्षों के बाद स्वयं की $\frac{5}{4}$ गुनी हो जाती है। ₹ 8000 के निवेश की $3,6,9$ और 12 वर्षों के बाद परिपक्वता राशियाँ (रुपयों में) क्रमश:
$10000,12500,15625, \text { और } 19531.25 \text { हैं। }$
(iv) भुजाओं $1,2,3, \ldots$ मात्रकों (units) वाले वर्गों में मात्रक वर्गों की संख्याएँ (देखिए आकृति 5.2) क्रमश:
$1^{2}, 2^{2}, 3^{2}, \ldots$ हैं।

आकृति 5.2
(v) शकीला अपनी पुत्री की गुल्लक में ₹ 100 तब डालती है, जब वह एक वर्ष की हो जाती है तथा प्रत्येक वर्ष इसमें ₹ 50 की वृद्धि करती जाती है। उसके पहले, दूसरे, तीसरे, चौथे, … जन्म दिवसों पर उसकी गुल्लक में डाली गई राशियाँ (रुपयों में) क्रमशः
100, 150, 200, 250, $\ldots$ होंगी।
(vi) खरगोशों का एक युग्म अपने पहले महीने में प्रजनन करने के योग्य नहीं है। दूसरे और प्रत्येक आने वाले महीने में वे एक नए युग्म का प्रजनन करते हैं। प्रत्येक नया युग्म अपने दूसरे महीने और प्रत्येक आने वाले महीने में एक नए युग्म का प्रजनन करता है (देखिए आकृति 5.3)। यह मानते हुए कि किसी खरगोश की मृत्यु नहीं होती है, पहले, दूसरे, तीसरे, . . ., छठे महीने के प्रारंभ में खरगोशों के युग्मों की संख्या क्रमशः
$1,1,2,3,5$ और $8$ होगी।

आकृति 5.3
उपरोक्त उदाहरणों में, हम कुछ प्रतिरूप देखते हैं। कुछ में, हम देखते हैं कि उत्तरोत्तर पद अपने से पहले पद में एक स्थिर संख्या जोड़ने से प्राप्त होते हैं; कुछ में ये पद अपने से पहले पद को एक निश्चित संख्या से गुणा करके प्राप्त होते हैं तथा कुछ अन्य में हम यह देखते हैं कि ये क्रमागत संख्याओं के वर्ग हैं, इत्यादि।
इस अध्याय में, हम इनमें से एक प्रतिरूप का अध्ययन करेंगे जिसमें उत्तरोत्तर पद अपने से पहले पदों में एक निश्चित संख्या जोड़ने पर प्राप्त किए जाते हैं। हम यह भी देखेंगे कि इनके $n$ वें पद और $n$ क्रमागत पदों के योग किस प्रकार ज्ञात किए जाते हैं तथा इस ज्ञान का प्रयोग कुछ दैनिक जीवन की समस्याओं को हल करने में करेंगे।
5.2 समांतर श्रेढ़ियाँ
संख्याओं की निम्नलिखित सूचियों (lists) पर विचार कीजिए:
(i) $1,2,3,4, \ldots$
(ii) $100,70,40,10, \ldots$
(iii) $-3,-2,-1,0, \ldots$
(iv) $3,3,3,3, \ldots$
(v) $-1.0,-1.5,-2.0,-2.5, \ldots$.
सूची की प्रत्येक संख्या एक पद (term) कहलाता है।
उपरोक्त सूचियों में से प्रत्येक सूची में, यदि आपको एक पद दिया हो, तो क्या आप उसका अगला पद लिख सकते हैं? यदि हाँ, तो आप ऐसा कैसे करेंगे? शायद, किसी प्रतिरूप या नियम का अनुसरण करते हुए, आप ऐसा करेंगे। आइए, उपरोक्त सूचियों को देखें और इनमें संबद्ध नियम को लिखें।
(i) में प्रत्येक पद अपने पिछले पद से 1 अधिक है।
(ii) में प्रत्येक पद अपने पिछले पद से 30 कम है।
(iii) में प्रत्येक पद अपने पिछले पद में 1 जोड़ने से प्राप्त होता है।
(iv) में सभी पद 3 हैं, अर्थात् प्रत्येक पद अपने पिछले पद में शून्य जोड़कर (या उसमें से शून्य घटा कर प्राप्त होता है।)
(v) में प्रत्येक पद अपने पिछले पद में -0.5 जोड़कर (अर्थात् उसमें से 0.5 घटाकर) प्राप्त होता है।
उपरोक्त सूचियों में से प्रत्येक में हम देखते हैं कि उत्तरोत्तर पदों को इनसे पहले पदों में एक निश्चित संख्या जोड़कर प्राप्त किया जाता है। संख्याओं की ऐसी सूची को यह कहा जाता है कि वे एक समांतर श्रेढ़ी (Arithmetic Progression या A.P.) बना रहे हैं।
अतः, एक समांतर श्रेढ़ी संख्याओं की एक ऐसी सूची है जिसमें प्रत्येक पद ( पहले पद के अतिरिक्त) अपने पद में एक निश्चित संख्या जोड़ने पर प्राप्त होता है।
यह निश्चित संख्या A.P. का सार्व अंतर (common difference) कहलाती है। याद रखिए, यह सार्व अंतर धनात्मक, ऋणात्मक या शून्य हो सकता है।
आइए एक A.P. के पहले पद को $a _{1}$ दूसरे पद को $a _{2}, \ldots, n$ वें पद को $a _{n}$ तथा सार्व अंतर को $d$ से व्यक्त करें। तब, A.P., $a _{1}, a _{2}, a _{3}, \ldots, a _{n}$ हो जाती है।
अत: $a _{2}-a _{1}=a _{3}-a _{2}=\ldots=a _{n}-a _{n-1}=d$ है।
A.P. के कुछ अन्य उदाहरण निम्नलिखित हैं :
(a) किसी स्कूल की प्रातःकालीन सभा में एक पंक्ति में खड़े हुए कुछ विद्यार्थियों की ऊँचाइयाँ ( $\mathrm{cm}$ में ) $147,148,149, \ldots, 157$ हैं।
(b) किसी शहर में, जनवरी मास में किसी सप्ताह में लिए गए न्यूनतम तापमान (डिग्री सेल्सियस में) आरोही क्रम में लिखने पर
$ -3.1,-3.0,-2.9,-2.8,-2.7,-2.6,-2.5 \text { हैं। } $
(c) ₹ 1000 के एक ऋण में से प्रत्येक मास $5 %$ ॠण की राशि वापिस करने पर शेष राशियाँ (₹ में) $950,900,850,800, \ldots, 50$ हैं।
(d) किसी स्कूल द्वारा कक्षाओं I से XII तक के सर्वाधिक अंक पाने वाले विद्यार्थियों को दिए जाने वाले नकद पुरस्कार (₹ में) क्रमशः $200,250,300,350, \ldots, 750$ हैं।
(e) जब प्रति मास ₹ 50 की बचत की जाती है, तो 10 मास के लिए, प्रत्येक मास के अंत में कुल बचत की राशियाँ (₹ में) $50,100,150,200,250,300,350,400,450$ और 500 हैं।
यह आपके अभ्यास के लिए छोड़ा जा रहा है कि आप स्पष्ट करें कि उपरोक्त में प्रत्येक सूची एक A.P. क्यों है।
आप यह देख सकते हैं कि
$ a, a+d, a+2 d, a+3 d, \ldots $
एक समांतर श्रेढ़ी को निरूपित करती है, जहाँ $a$ पहला पद है और $d$ सार्व अंतर है। इसे A.P. का व्यापक रूप (general form) कहते हैं।
ध्यान दीजिए कि उपरोक्त उदाहरणों (a) से (e) में, पदों की संख्या परिमित (finite) है। ऐसी A.P. को एक परिमित A.P. कहते हैं। आप यह भी देख सकते हैं कि इनमें से प्रत्येक A.P. का एक अंतिम पद (last term) है। इसी अनुच्छेद के उदाहरणों (i) से (v) में दी हुई A.P. परिमित A.P. नहीं हैं। ये अपरिमित A.P. (Infinite Arithmetic Progressions) कहलाती है। ऐसी A.P. में अंतिम पद नहीं होते।
अब एक A.P. के बारे में जानने के लिए आपको न्यूनतम किस सूचना की आवश्यकता होती है? क्या इसके प्रथम पद की जानकारी पर्याप्त है? या क्या इसके केवल सार्व अंतर की जानकारी पर्याप्त है? आप पाएँगे कि आपको इन दोनों अर्थात् प्रथम पद $a$ और सार्व अंतर $d$ की जानकारी होना आवश्यक है।
उदाहरणार्थ, यदि प्रथम पद $a=6$ है और सार्व अंतर $d=3$ है तो
$ 6,9,12,15, \ldots \text { A.P. है। } $
तथा यदि $a=6$ है और $d=-3$ है तो
$ 6,3,0,-3, \ldots \text { A.P. है। } $
इसी प्रकार, जब
$ \begin{aligned} & a=-7, \quad d=-2, \quad \text { तो }-7,-9,-11,-13, \ldots \text { A.P. है। } \\ & a=1.0, \quad d=0.1, \quad \text { तो } 1.0,1.1,1.2,1.3, \ldots \text { A.P. है। } \\ & a=0, \quad d=1 \frac{1}{2}, \quad \text { तो } 0,1 \frac{1}{2}, 3,4 \frac{1}{2}, 6, \ldots \text { A.P. है। } \\ & a=2, \quad d=0, \quad \text { तो } 2,2,2,2, \ldots \text { A.P. है। } \end{aligned} $
अतः यदि आपको $a$ और $d$ ज्ञात हों तो A.P. लिख सकते हैं। इसकी विपरीत प्रक्रिया के बारे में आप क्या कह सकते हैं? अर्थात् यदि आपको संख्याओं की एक सूची दी हुई है, तो क्या आप कह सकते हैं कि यह एक A.P. है और फिर इसके $a$ और $d$ ज्ञात कर सकते हैं? क्योंकि $a$ प्रथम पद है, इसलिए इसे सरलता से लिखा जा सकता है। हम जानते हैं कि एक A.P. में, प्रत्येक उत्तरोत्तर पद अपने से पहले पद में $d$ जोड़कर प्राप्त होता है। अतः, एक A.P. के लिए, उसके प्रत्येक पद को उससे अगले पद में से घटाने से प्राप्त $d$ सभी पदों के लिए एक ही होगा।
उदाहरणार्थ, संख्याओं की सूची के लिए :
$ 6,9,12,15, \ldots, \\ $
हमें प्राप्त है
$ \begin{aligned} & a_2-a_1=9-6=3, \\ & a_3-a_2=12-9=3, \\ & a_4-a_3=15-12=3 \end{aligned} $
यहाँ, प्रत्येक स्थिति में, किन्हीं दो क्रमागत पदों का अंतर 3 है। अतः, संख्याओं की उपरोक्त दी हुई चर्चा सूची एक A.P. है, जिसका प्रथम पद $a=6$ है तथा सार्व अंतर $d=3$ है।
संख्याओं की सूची : $6,3,0,-3, \ldots$ के लिए
$ \begin{aligned} & a _{2}-a _{1}=3-6=-3 \\ & a _{3}-a _{2}=0-3=-3 \\ & a _{4}-a _{3}=-3-0=-3 \end{aligned} $
अतः यह भी एक A.P. है जिसका प्रथम पद 6 है और सार्व अंतर -3 है।
व्यापक रूप में, A.P. $a _{1}, a _{2}, \ldots, a _{n}$ के लिए,
$ d=a _{k+1}-a _{k} $
जहाँ $a _{k+1}$ और $a _{k}$ क्रमशः $(k+1)$ वें और $k$ वें पद हैं।
एक दी हुई A.P. का $d$ ज्ञात करने के लिए, हमें $a _{2}-a _{1}, a _{3}-a _{2}, a _{4}-a _{3}, \ldots$ में से सभी को ज्ञात करने की आवश्यकता नहीं है। इनमें से किसी एक का ज्ञात करना ही पर्याप्त है।
संख्याओं की सूची $1,1,2,3,5, \ldots$ पर विचार कीजिए। केवल देखने से ही यह पता चल जाता है कि किन्हीं दो क्रमागत पदों का अंतर सदैव समान नहीं है। अतः यह एक A.P. नहीं है।
ध्यान दीजिए कि A.P. : $6,3,0,-3, \ldots$ का $d$ ज्ञात करने के लिए, हमने 3 में से 6 को घटाया था, 6 में से 3 को नहीं घटाया था। अर्थात् $d$ ज्ञात करने के लिए हमें $(k+1)$ वें पद में से, $k$ वें पद को ही घटाना चाहिए, चाहे $(k+1)$ वाँ पद छोटा ही क्यों न हो।
आइए कुछ उदाहरणों की सहायता से इन अवधारणाओं को और अधिक स्पष्ट करें।
उदाहरण 1 : A.P. : $\frac{3}{2}, \frac{1}{2},-\frac{1}{2},-\frac{3}{2}, \ldots$, के लिए प्रथम पद $a$ और सार्व अंतर $d$ लिखिए।
हल : यहाँ $a=\frac{3}{2}, d=\frac{1}{2}-\frac{3}{2}=-1 \text { है। }$
याद रखिए कि यदि हमें यह ज्ञात हो जाए कि संख्याएँ A.P. में हैं, तो हम किन्हीं भी दो क्रमागत पदों का प्रयोग करके $d$ ज्ञात कर सकते हैं।
उदाहरण 2 : संख्याओं की निम्नलिखित सूचियों में से कौन-कौन से A.P. नहीं हैं? यदि इनसे कोई A.P. है तो उसके अगले दो पद लिखिए।
(i) $4,10,16,22, \ldots$
(ii) $1,-1,-3,-5, \ldots$
(iii) $-2,2,-2,2,-2, \ldots$
(iv) $1,1,1,2,2,2,3,3,3, \ldots$
हल :(i) हमें प्राप्त है $a_2-a_1=10-4=6$
$ \begin{aligned} & a _{3}-a _{2}=16-10=6 \\ & a _{4}-a _{3}=22-16=6 \end{aligned} $
अर्थात्, प्रत्येक बार $a _{k+1}-a _{k}$ एक ही है।
अतः, दी हुई संख्याओं की सूची एक A.P. है जिसका सार्व अंतर $d=6$ है।
इसके अगले दो पद $22+6=28$ और $28+6=34$ हैं।
(ii) $a _{2}-a _{1}=-1-1=-2$
$ \begin{aligned} & a _{3}-a _{2}=-3-(-1)=-3+1=-2 \\ & a _{4}-a _{3}=-5-(-3)=-5+3=-2 \end{aligned} $
अर्थात्, प्रत्येक बार $a _{k+1}-a _{k}$ एक ही है।
अतः, संख्याओं की दी हुई सूची एक A.P. है जिसका सार्व अंतर $d=-2$ है।
इसके अगले दो पद हैं:
$ -5+(-2)=-7 \text { और }-7+(-2)=-9 $
(iii) $a _{2}-a _{1}=2-(-2)=2+2=4$
$ a _{3}-a _{2}=-2-2=-4 $
चूँकि $a _{2}-a _{1} \neq a _{3}-a _{2}$ हैं, इसलिए दी हुई संख्याओं की सूची से एक A.P. नहीं है।
(iv) $a_2-a_1=1-1=0$
$a_3-a_2=1-1=0$
$a_4-a_3=2-1=1$
यहाँ, $a _{2}-a _{1}=a _{3}-a _{2} \neq a _{4}-a _{3}$ है।
अतः, दी हुई संख्याओं की सूची से एक A.P. नहीं है।
प्रश्नावली 5.1
1. निम्नलिखित स्थितियों में से किन स्थितियों में संबद्ध संख्याओं की सूची A.P. है और क्यों?
(i) प्रत्येक किलो मीटर के बाद का टैक्सी का किराया, जबकि प्रथम किलो मीटर के लिए किराया ₹ 15 है और प्रत्येक अतिरिक्त किलो मीटर के लिए किराया ₹ 8 है।
(ii) किसी बेलन (cylinder) में उपस्थित हवा की मात्रा, जबकि वायु निकालने वाला पंप प्रत्येक बार बेलन की शेष हवा का $\frac{1}{4}$ भाग बाहर निकाल देता है।
(iii) प्रत्येक मीटर की खुदाई के बाद, एक कुँआ खोदने में आई लागत, जबकि प्रथम मीटर खुदाई की लागत ₹ 150 है और बाद में प्रत्येक मीटर खुदाई की लागत ₹ 50 बढ़ती जाती है।
(iv) खाते में प्रत्येक वर्ष का मिश्रधन, जबकि ₹ 10000 की राशि $8 %$ वार्षिक की दर से चक्रवृद्धि ब्याज पर जमा की जाती है।
Show Answer
#missing2. दी हुई A.P. के प्रथम चार पद लिखिए, जबकि प्रथम पद $a$ और सार्व अंतर $d$ निम्नलिखित हैं:
(i) $a=10$, $d=10$
(ii) $a=-2, \quad d=0$
(iii) $a=4$, $d=-3$
(iv) $a=-1, \quad d=\frac{1}{2}$
(v) $a=-1.25, d=-0.25$
Show Answer
#missing3. निम्नलिखित में से प्रत्येक A.P. के लिए प्रथम पद तथा सार्व अंतर लिखिए :
(i) $3,1,-1,-3, \ldots$
(ii) $-5,-1,3,7, \ldots$
(iii) $\frac{1}{3}, \frac{5}{3}, \frac{9}{3}, \frac{13}{3}$,
(iv) $0.6,1.7,2.8,3.9, \ldots$
Show Answer
#missing4. निम्नलिखित में से कौन-कौन A.P. हैं? यदि कोई A.P. है, तो इसका सार्व अंतर ज्ञात कीजिए और इनके तीन और पद लिखिए।
(i) $2,4,8,16, \ldots$
(ii) $2, \frac{5}{2}, 3, \frac{7}{2}, \ldots$
(iii) $-1.2,-3.2,-5.2,-7.2, \ldots$
(iv) $-10,-6,-2,2, \ldots$
(v) $3,3+\sqrt{2}, 3+2 \sqrt{2}, 3+3 \sqrt{2}, \ldots$
(vi) $0.2,0.22,0.222,0.2222, \ldots$
(vii) $0,-4,-8,-12, \ldots$
(viii) $-\frac{1}{2},-\frac{1}{2},-\frac{1}{2},-\frac{1}{2}, \ldots$
(ix) $1,3,9,27, \ldots$
(x) $a, 2 a, 3 a, 4 a, \ldots$
(xi) $a, a^{2}, a^{3}, a^{4}, \ldots$
(xii) $\sqrt{2}, \sqrt{8}, \sqrt{18}, \sqrt{32}, \ldots$
(xiii) $\sqrt{3}, \sqrt{6}, \sqrt{9}, \sqrt{12}, \ldots$
(xiv) $1^{2}, 3^{2}, 5^{2}, 7^{2}, \ldots$
(xv) $1^{2}, 5^{2}, 7^{2}, 73, \ldots$
Show Answer
#missing5.3 A.P. का $n$ वाँ पद
आइए अनुच्छेद 5.1 में दी हुई उस स्थिति पर पुनः विचार करें जिसमें रीना ने एक पद के लिए आवेदन किया था और वह चुन ली गई थी। उसे यह पद ₹ 8000 के मासिक वेतन और ₹ 500 वार्षिक की वेतन वृद्धि के साथ दिया गया था। पाँचवें वर्ष में उसका मासिक वेतन क्या होगा?
इसका उत्तर देने के लिए, आइए देखें कि उसका मासिक वेतन दूसरे वर्ष में क्या होगा।
यह $(\text{ ₹ } 8000+\text{ ₹ } 500)=\text{ ₹ } 8500$ होगा। इसी प्रकार, हम तीसरे, चौथे और पाँचवें वर्षों के लिए, उसके मासिक वेतन, पिछले वर्ष के वेतन में ₹ 500 जोड़ कर ज्ञात कर सकते हैं। अतः, उसका तीसरे वर्ष का वेतन $=\text{ ₹ }(8500+500)$
$ \begin{aligned} & =\text{ ₹ }(8000+500+500) \\ & =\text{ ₹ }(8000+2 \times 500) \\ & =\text{ ₹ }[8000+(\mathbf{3}-\mathbf{1}) \times 500] \quad \text { (तीसरे वर्ष के लिए) } \\ & =\text{ ₹ } 9000 \end{aligned} $
चौथे वर्ष का वेतन $=\text{ ₹ }(9000+500)$
$=\text{ ₹ } (8000+500+500+500)$
$=\text{ ₹ } (8000+3 \times 500)$
$=\text{ ₹ } [8000+(4-1) \times 500] \quad$ (चौथे वर्ष के लिए)
$=\text{ ₹ } 9500$
पाँचवें वर्ष का वेतन $=\text{ ₹ }(9500+500)$
$ \begin{aligned} & =\text{ ₹ }(8000+500+500+500+500) \\ & =\text{ ₹ }(8000+4 \times 500) \\ & =\text{ ₹ }[8000+(\mathbf{5}-\mathbf{1}) \times 500] \quad \text { ( पाँचवें वर्ष के लिए ) } \\ & =\text{ ₹ } 10000 \end{aligned} $
ध्यान दीजिए कि यहाँ हमें संख्याओं की निम्नलिखित सूची मिल रही है :
$ 8000,8500,9000,9500,10000, \ldots $
ये संख्याएँ एक A.P. बना रही हैं। (क्यों?)
अब ऊपर बनने वाले प्रतिरूप को देखकर क्या आप उसका छठे वर्ष का मासिक वेतन ज्ञात कर सकते हैं? क्या 15 वें वर्ष का मासिक वेतन ज्ञात कर सकते हैं? साथ ही, यह मानते हुए कि वह इस पद पर आगे भी कार्य करती रहेगी, 25 वें वर्ष के लिए उसके मासिक वेतन के विषय में आप क्या कह सकते हैं? इसका उत्तर देने के लिए, आप पिछले वर्ष के वेतन में ₹ 500 जोड़कर वांछित वेतन परिकलित करेंगे। क्या आप इस प्रक्रिया को कुछ संक्षिप्त कर सकते हैं? आइए, देखें। जिस प्रकार हमने इन वेतनों को ऊपर प्राप्त किया है, उनसे आपको कुछ आभास तो लग गया होगा।
15 वें वर्ष के लिए वेतन
$ \begin{aligned} & =14 \text { वें वर्ष के लिए वेतन }+\text{ ₹ } 500 \\ & =\text{ ₹ }[8000+\underbrace{500+500+500+\ldots+500} _{13 \text { बार }}]+\text{ ₹ } 500 \\ & =\text{ ₹ }[8000+14 \times 500] \\ & =\text{ ₹ }[8000+(\mathbf{1 5}-\mathbf{1}) \times 500]=\text{ ₹ } 15000 \end{aligned} $
अर्थात्, प्रथम वेतन $+(15-1) \times$ वार्षिक वेतन वृद्धि.
इसी प्रकार 25 वें साल में उसका वेतन होगा :
$ \begin{aligned} & \text{ ₹ } [8000+(25-1) \times 500]=\text{ ₹ } 20000 \\ = & \text{ प्रथम वेतन }+(25-\mathbf{1}) \times \text{ वार्षिक वेतन वृद्धि } \end{aligned} $
इस उदाहरण से, आपको कुछ आभास तो अवश्य हो गया होगा कि एक A.P. के 15 वें पद, 25 वें पद और व्यापक रूप में, $n$ वें पद को किस प्रकार लिखा जा सकता है।
मान लीजिए $a _{1}, a _{2}, a _{3}, \ldots$ एक A.P. है, जिसका प्रथम पद $a$ है और सार्व अंतर $d$ है।
तब
दूसरा पद $a_2=a+d=a+(2-1) d$
तीसरा पद $\quad a_3=a_2+d=(a+d)+d=a+2 d=a+(3-1) d$
चौथा पद $\quad a_4=a_3+d=(a+2 d)+d=a+3 d=a+(\mathbf{4 - 1}) d$
इस प्रतिरूप को देखते हुए, हम कह सकते हैं कि $\boldsymbol{n}$ वाँ पद $a _{n}=a+(n-1) d$ है।
अतः, प्रथम पद $a$ और सार्व अंतर $d$ वाली एक A.P. का $n$ वाँ पद $a _{n}=a+(n-1) d$ द्वारा प्राप्त होता है। $\boldsymbol{a} _{n}$ को A.P. का व्यापक पद (general term) भी कहते हैं। यदि किसी A.P. में $m$ पद हैं, तो $a _{m}$ इसके अंतिम पद को निरूपित करता है, जिसे कभी-कभी $l$ द्वारा भी व्यक्त किया जाता है।
आइए अब कुछ उदाहरणों पर विचार करें।
उदाहरण 3 : A.P. : $2,7,12, \ldots$ का 10 वाँ पद ज्ञात कीजिए।
हल : यहाँ $a=2, d=7-2=5$ और $n=10$ है।
चूँकि
$a _{n}=a+(n-1) d$ है,
इसलिए
$ a _{10}=2+(10-1) \times 5=2+45=47 $
अतः दी हुई A.P. का 10 वाँ पद 47 है।
उदाहरण 4 : A.P. : $21,18,15, \ldots$ का कौन-सा पद -81 है? साथ ही क्या इस A.P. का कोई पद शून्य है? सकारण उत्तर दीजिए।
हल : यहाँ, $a=21, d=18-21=-3$ और $a _{n}=-81$ है। हमें $n$ ज्ञात करना है।
चूँकि
$ a _{n}=a+(n-1) d, $
अत :
$ \begin{aligned} -81 & =21+(n-1)(-3) \\ -81 & =24-3 n \\ -105 & =-3 n \end{aligned} $
अत:
$n=35$
इसलिए दी हुई A.P. का 35 वाँ पद -81 है।
आगे, हम यह जानना चाहते हैं कि क्या कोई $n$ ऐसा है कि $a _{n}=0$ हो। यदि ऐसा कोई $n$ है तो
$ \begin{aligned} &21+(n-1)(-3) =0, \\ \text{अर्थात्, } \quad \quad &3(n-1) =21 \\ \text{अर्थात्, } \quad \quad &n =8 \end{aligned} $
अत:, 8 वाँ पद 0 है।
उदाहरण 5 : वह A.P. निर्धारित कीजिए जिसका तीसरा पद 5 और 7 वाँ पद 9 है।
हल : हमें प्राप्त है
और
$$ \begin{align*} & a_3=a+(3-1) d=a+2 d=5 \tag{1} \end{align*} $$
$$ \begin{align*} & a_7=a+(7-1) d=a+6 d=9 \tag{2} \end{align*} $$
समीकरणों (1) और (2) के युग्म को हल करने पर, हमें प्राप्त होता है :
$ a=3, \quad d=1 $
अतः वांछित A.P. : $3,4,5,6,7, \ldots$ है।
उदाहरण 6 : क्या संख्याओं की सूची $5,11,17,23, \ldots$ का कोई पद 301 है? क्यों?
हल : हमें प्राप्त है :
$$ a _{2}-a _{1}=11-5=6, \quad a _{3}-a _{2}=17-11=6, \quad a _{4}-a _{3}=23-17=6 $$
चूँकि $k=1,2,3$, आदि के लिए, $a _{k+1}-a _{k}$ एक समान संख्या होती है, इसलिए दी हुई सूची एक A.P. है।
यहाँ $a=5 \text { और } d=6$
मान लीजिए इस A.P. का $n$ वाँ पद 301 है।
हम जानते हैं कि
$ \begin{aligned} & a_n =a+(n-1) d \\ \text{इसलिए,} \quad \quad& 301 =5+(n-1) \times 6 \\ \text{अर्थात्,} \quad \quad& 301 =6 n-1 \\ \text{अत:,} \quad \quad & n =\frac{302}{6}=\frac{151}{3} \end{aligned} $
परंतु $n$ एक धनात्मक पूर्णांक होना चाहिए (क्यों?)। अतः, 301 संख्याओं की दी हुई सूची का पद नहीं है।
उदाहरण 7 : दो अंकों वाली कितनी संख्याएँ 3 से विभाज्य हैं?
हल : 3 से विभाज्य होने वाली दो अंकों की संख्याओं की सूची है :
$12,15,18, \ldots, 99$
क्या यह एक A.P. है? हाँ, यह है। यहाँ $a=12, d=3$ और $a _{n}=99$ है।
चूँकि
$ a_n=a+(n-1) d, $
इसलिए
$ 99=12+(n-1) \times 3 $
अर्थात्,
$ 87=(n-1) \times 3 $
अर्थात्,
$ \begin{aligned} n-1 & =\frac{87}{3}=29 \end{aligned} $
अर्थात्,
$ \begin{aligned} n & =29+1=30 \end{aligned} $
अतः, 3 से विभाज्य दो अंकों वाली 30 संख्याएँ हैं।
उदाहरण 8 : A.P. : $10,7,4, \ldots,-62$ का अंतिम पद से (प्रथम पद की ओर) 11 वाँ पद ज्ञात कीजिए।
हल : यहाँ, $a=10, d=7-10=-3, l=-62$,
जहाँ
$ l=a+(n-1) d $
अंतिम पद से 11 वाँ पद ज्ञात करने के लिए, हम इस AP के कुल पदों की संख्या ज्ञात करेंगे।
$ \begin{aligned} \text{अतः} \quad \quad & -62 =10+(n-1)(-3) \\ \text{अर्थात्,} \quad \quad & -72 =(n-1)(-3) \\ \text{अर्थात्,} \quad \quad & n-1 =24 \\ \text{या} \quad \quad & n =25 \end{aligned} $
अतः, दी हुई A.P. में 25 पद हैं।
अंतिम पद से 11 वाँ पद $\mathrm{AP}$ का 15 वाँ पद होगा। (ध्यान दीजिए कि यह 14 वाँ पद नहीं होगा। क्यों?)
अतः,
$ a _{15}=10+(15-1)(-3)=10-42=-32 $
इसलिए, अंतिम पद से 11 वाँ पद -32 है।
वैकल्पिक हल:
यदि हम A.P. को विपरीत ओर से देखें, तो इसका प्रथम पद $a=-62$ है और सार्व अंतर $d=3$ है। (क्यों?)
अब, प्रश्न यह बन जाता है कि इस AP का 11 वाँ पद ज्ञात किया जाए।
अत:
$ a _{11}=-62+(11-1) \times 3=-62+30=-32 $
अतः अंतिम पद से 11 वाँ वांछित पद -32 है।
उदाहरण 9 : ₹ 1000 की एक धनराशि $8 %$ वार्षिक साधारण ब्याज पर निवेश की जाती है। प्रत्येक वर्ष के अंत में ब्याज परिकलित कीजिए। क्या ये ब्याज एक A.P. बनाते हैं? यदि ऐसा है, तो इस तथ्य का प्रयोग करते हुए 30 वर्षों के अंत में ब्याज परिकलित कीजिए।
हल : हम जानते हैं कि साधारण ब्याज परिकलित करने के लिए सूत्र निम्नलिखित है:
$ \text { साधारण ब्याज }=\frac{\mathrm{P} \times \mathrm{R} \times \mathrm{T}}{100} $
अतः, प्रथम वर्ष के अंत में ब्याज $=\text{ ₹ } \frac{1000 \times 8 \times 1}{100}=\text{ ₹ } 80$
दूसरे वर्ष के अंत में ब्याज $=\text{ ₹ } \frac{1000 \times 8 \times 2}{100}=\text{ ₹ } 160$
तीसरे वर्ष के अंत में ब्याज $=\text{ ₹ } \frac{1000 \times 8 \times 3}{100}=\text{ ₹ } 240$
इसी प्रकार, हम चौथे, पाँचवें, इत्यादि वर्षों के अंत में ब्याज परिकलित कर सकते हैं।
अतः, पहले, दूसरे, तीसरे, … वर्षों के अंत में ब्याज (₹ में) क्रमशः हैं : $80,160,240, \ldots$
यह एक A.P. है, क्योंकि किन्हीं दो क्रमागत पदों का अंतर 80 है, अर्थात् $d=80$ है। साथ ही, इसमें $a=80$ है।
अतः, 30 वर्षों के अंत में ब्याज ज्ञात करने के लिए हम $a _{30}$ ज्ञात करेंगे।
अब
$ a _{30}=a+(30-1) d=80+29 \times 80=2400 $
अतः 30 वर्षों के अंत में ब्याज ₹ 2400 होगा।
उदाहरण 10 : फूलों की एक क्यारी की पहली पंक्ति में 23 गुलाब के पौधे हैं, दूसरी पंक्ति में 21 गुलाब के पौधे हैं, तीसरी पंक्ति में 19 गुलाब के पौधे हैं, इत्यादि। उसकी अंतिम पंक्ति में 5 गुलाब के पौधे हैं। इस क्यारी में कुल कितनी पंक्तियाँ हैं?
हल : पहली, दूसरी, तीसरी, … पंक्तियों में गुलाब के पौधों की संख्याएँ क्रमशः निम्नलिखित हैं:
$ 23,21,19, \ldots, 5 $
ये एक A.P. बनाती हैं (क्यों?)। मान लीजिए पंक्तियों की संख्या $n$ है।
तब
$ a=23, d=21-23=-2 \text { और } a _{n}=5 \text { है। } $
चूँकि
$ a _{n}=a+(n-1) d $
इसलिए
$ 5=23+(n-1)(-2) $
अर्थात्
$ -18=(n-1)(-2) $
अर्थात्
$ n=10 $
अतः फूलों की क्यारी में 10 पंक्तियाँ हैं।
प्रश्नावली 5.2
1. निम्नलिखित सारणी में, रिक्त स्थानों को भरिए, जहाँ $\mathrm{AP}$ का प्रथम पद $a$, सार्व अंतर $d$ और $n$ वाँ पद $a _{n}$ है:
| $a$ | $d$ | $n$ | $a _{n}$ | |
|---|---|---|---|---|
| (i) | 7 | 3 | 8 | $\ldots$ |
| (ii) | -18 | $\ldots$ | 10 | 0 |
| (iii) | $\ldots$ | -3 | 18 | -5 |
| (iv) | -18.9 | 2.5 | $\ldots$ | 3.6 |
| (v) | 3.5 | 0 | 105 | $\ldots$ |
Show Answer
#missing2. निम्नलिखित में सही उत्तर चुनिए और उसका औचित्य दीजिए:
(i) A.P.: $10,7,4, \ldots$, का 30 वाँ पद है:
(A) 97
(B) 77
(C) -77
(D) -87
(ii) A.P.: $-3,-\frac{1}{2}, 2, \ldots$, का 11 वाँ पद है:
(A) 28
(B) 22
(C) -38
(D) $-48 \frac{1}{2}$
Show Answer
#missing3. निम्नलिखित समांतर श्रेढ़ियों में, रिक्त खानों (boxes) के पदों को ज्ञात कीजिए :
(i) 2 , $\square$, 26
(ii) $\square$, 13, $\square$, 3
(iii) 5, $\square$, $\square$, $9 \frac{1}{2}$
(iv) -4 $\square$, $\square$, $\square$, $\square$, 6
(v) $\square$, 38, $\square$, $\square$, $\square$, -22
Show Answer
#missing4. A.P. : $3,8,13,18, \ldots$ का कौन सा पद 78 है?
Show Answer
#missing5. निम्नलिखित समांतर श्रेढ़ियों में से प्रत्येक श्रेढ़ी में कितने पद हैं?
(i) $7,13,19, \ldots, 205$
(ii) $18,15 \frac{1}{2}, 13, \ldots,-47$
Show Answer
#missing6. क्या A.P., $11,8,5,2 \ldots$ का एक पद -150 है? क्यों?
Show Answer
#missing7. उस A.P. का 31 वाँ पद ज्ञात कीजिए, जिसका 11 वाँ पद 38 है और 16 वाँ पद 73 है।
Show Answer
#missing8. एक A.P. में 50 पद हैं, जिसका तीसरा पद 12 है और अंतिम पद 106 है। इसका 29 वाँ पद ज्ञात कीजिए।
Show Answer
#missing9. यदि किसी A.P. के तीसरे और नौवें पद क्रमशः 4 और -8 हैं, तो इसका कौन-सा पद शून्य होगा?
Show Answer
#missing10. किसी A.P. का 17 वाँ पद उसके 10 वें पद से 7 अधिक है। इसका सार्व अंतर ज्ञात कीजिए।
Show Answer
#missing11. A.P. : $3,15,27,39, \ldots$ का कौन-सा पद उसके 54 वें पद से 132 अधिक होगा?
Show Answer
#missing12. दो समांतर श्रेढ़ियों का सार्व अंतर समान है। यदि इनके 100 वें पदों का अंतर 100 है, तो इनके 1000 वें पदों का अंतर क्या होगा?
Show Answer
#missing13. तीन अंकों वाली कितनी संख्याएँ 7 से विभाज्य हैं?
Show Answer
#missing14. 10 और 250 के बीच में 4 के कितने गुणज हैं?
Show Answer
#missing15. $n$ के किस मान के लिए, दोनों समांतर श्रेढ़ियों $63,65,67, \ldots$ और $3,10,17, \ldots$ के $n$ वें पद बराबर होंगे?
Show Answer
#missing16. वह A.P. ज्ञात कीजिए जिसका तीसरा पद 16 है और 7 वाँ पद 5 वें पद से 12 अधिक है।
Show Answer
#missing17. A.P. : $3,8,13, \ldots, 253$ में अंतिम पद से 20 वाँ पद ज्ञात कीजिए।
Show Answer
#missing18. किसी A.P. के चौथे और 8 वें पदों का योग 24 है तथा छठे और 10 वें पदों का योग 44 है। इस A.P. के प्रथम तीन पद ज्ञात कीजिए।
Show Answer
#missing19. सुब्बा राव ने 1995 में ₹ 5000 के मासिक वेतन पद कार्य आरंभ किया और प्रत्येक वर्ष ₹ 200 की वेतन वृद्धि प्राप्त की। किस वर्ष में उसका वेतन ₹ 7000 हो गया?
Show Answer
#missing20. रामकली ने किसी वर्ष के प्रथम सप्ताह में ₹ 50 की बचत की और फिर अपनी साप्ताहिक बचत ₹ 17.5 बढ़ाती गई। यदि $n$ वें सप्ताह में उसकी साप्ताहिक बचत ₹ 207.50 हो जाती है, तो $n$ ज्ञात कीजिए।
Show Answer
#missing5.4 A.P. के प्रथम $n$ पदों का योग
आइए अनुच्छेद 5.1 में दी हुई स्थिति पर पुन: विचार करें, जिसमें शकीला अपनी पुत्री की गुल्लक में, उसके 1 वर्ष की हो जाने पर ₹ 100 डालती है, उसके दूसरे जन्म दिवस पर ₹ 150 , तीसरे जन्म दिवस पर ₹ 200 डालती है और ऐसा आगे जारी रखती है। जब उसकी पुत्री 21 वर्ष की हो जाएगी, तो उसकी गुल्लक में कितनी धनराशि एकत्रित हो जाएगी?

यहाँ, उसके प्रथम, दूसरे, तीसरे, चौथे, … जन्म दिवसों पर, उसकी गुल्लक में डाली गई राशियाँ (₹ में) क्रमशः $100,150,200,250, \ldots$ हैं तथा यही क्रम उसके 21 वें जन्म दिवस तक चलता रहा। 21 वें जन्म दिवस तक एकत्रित हुई कुल धनराशि ज्ञात करने के लिए, हमें उपरोक्त सूची की संख्याओं को जोड़ने की आवश्यकता है। क्या आप यह नहीं सोचते कि यह एक जटिल प्रक्रिया होगी और इसमें समय भी अधिक लगेगा? क्या हम इस प्रक्रिया को संक्षिप्त बना सकते हैं? यह तभी संभव होगा, जब हम इसका योग निकालने की कोई विधि ज्ञात कर लें। आइए देखें।
हम गॉस (जिसके बारे में आप अध्याय 1 में पढ़ चुके हैं) को दी गई समस्या पर विचार करते हैं, जो उसे हल करने के लिए उस समय दी गई थी, जब वह केवल 10 वर्ष का था। उससे 1 से 100 तक के धन पूर्णांकों का योग ज्ञात करने को कहा गया। उसने तुरंत उत्तर दिया कि योग 5050 है। क्या आप अनुमान लगा सकते हैं कि उसने ऐसा कैसे किया था? उसने इस प्रकार लिखा:
$ \mathrm{S}=1+2+3+\ldots+99+100 $
फिर, उसने उल्टे क्रम संख्याओं को इस प्रकार लिखा:
$ S=100+99+\ldots+3+2+1 $
उपरोक्त को जोड़ने पर उसने प्राप्त किया:
$ \begin{aligned} 2 \mathrm{~S} & =(100+1)+(99+2)+\ldots+(3+98)+(2+99)+(1+100) \\ & =101+101+\ldots+101+101 \quad \text { (100 बार }) \end{aligned} $
अत:
$\mathrm{S}=\frac{100 \times 101}{2}=5050$, अर्थात् योग $=5050$
अब, हम इसी तकनीक का उपयोग करते हुए, एक A.P. के प्रथम $n$ पदों का योग ज्ञात करेंगे। मान लीजिए यह A.P. है :
$ a, a+d, a+2 d, \ldots $
इस A.P. का $n$ वाँ पद $a+(n-1) d$ है। माना $\mathrm{S}$ इस A.P. के प्रथम $n$ पदों के योग को व्यक्त करता है। तब
$$ S=a+(a+d)+(a+2 d)+\ldots+[a+(n-1) d] \tag{1} $$
पदों को विपरीत क्रम में लिखने पर हमें प्राप्त होता है:
$$ S=[a+(n-1) d]+[a+(n-2) d]+\ldots+(a+d)+a \tag{2} $$
अब, (1) और (2) को पदों के अनुसार जोड़ने पर, हमें प्राप्त होता है :
$ 2 \mathrm{~S}=\underbrace{[2 a+(n-1) d]+[2 a+(n-1) d]+\cdots+[2 a+(n-1) d]+[2 a+(n-1) d]} _{n \text { बार }} $
या $\quad 2 \mathrm{~S}=n[2 a+(n-1) d] \quad(\text { चूँकि इसमें } n \text { पद हैं })$
या $\quad \mathrm{S}=\frac{n}{2}[2 a+(n-1) d]$
अतः किसी A.P. के प्रथम $n$ पदों का योग $\mathrm{S}$ निम्नलिखित सूत्र से प्राप्त होता है:
$ S=\frac{n}{2}[2 a+(n-1) d] $
हम इसे इस रूप में भी लिख सकते हैं
$ \mathrm{S}=\frac{n}{2}[a+a+(n-1) d] $
अर्थात्
$$ S=\frac{n}{2}(a+a_n) \tag{3} $$
अब, यदि किसी A.P. में केवल $n$ ही पद हैं, तो $a _{n}$ अंतिम पद $l$ के बराबर होगा।
अतः (3) से हम देखते हैं कि
$$ S=\frac{n}{2}(a+l) \tag{4} $$
परिणाम का यह रूप उस स्थिति में उपयोगी है, जब A.P. के प्रथम और अंतिम पद दिए हों तथा सार्व अंतर नहीं दिया गया हो।
अब हम उसी प्रश्न पर वापस आ जाते हैं, जो प्रारंभ में हमसे पूछा गया था। शकीला की पुत्री की गुल्लक में उसके पहले, दूसरे, तीसरे,…, जन्म दिवसों पर डाली गई धनराशियाँ (₹ में) क्रमशः $100,150,200,250, \ldots$, हैं।
यह एक A.P. है। हमें उसके 21 वें जन्मदिवस तक एकत्रित हुई कुल धनराशि ज्ञात करनी है, अर्थात् हमें इस A.P. के प्रथम 21 पदों का योग ज्ञात करना है।
यहाँ $a=100, d=50$ और $n=21$ है। सूत्र
$ S=\frac{n}{2}[2 a+(n-1) d] $
का प्रयोग करने पर,
$ \begin{aligned} S & =\frac{21}{2}[2 \times 100+(21-1) \times 50]=\frac{21}{2}[200+1000] \\ & =\frac{21}{2} \times 1200=12600 \end{aligned} $
अतः उसके 21 वें जन्म दिवस तक एकत्रित हुई गुल्लक में धनराशि ₹ 12600 है।
क्या सूत्र के प्रयोग से प्रश्न हल करना सरल नहीं हो गया है?
किसी A.P. के $n$ पदों के योग को व्यक्त करने के लिए, हम $\mathrm{S}$ के स्थान पर $\mathrm{S} _{n}$ का भी प्रयोग करते हैं। उदाहरणार्थ, हम A.P. के 20 पदों के योग को व्यक्त करने के लिए $\mathrm{S} _{20}$ का प्रयोग करते हैं। प्रथम $n$ पदों के योग के सूत्र में, चार राशियाँ $\mathrm{S}, a, d$ और $n$ संबद्ध हैं। यदि इनमें से कोई तीन राशियाँ ज्ञात हों, तो चौथी राशि ज्ञात की जा सकती है।
टिप्पणी : किसी A.P. का $n$ वाँ पद उसके प्रथम $n$ पदों के योग और प्रथम $(n-1)$ पदों के योग के अंतर के बराबर है। अर्थात् $a _{n}=\mathrm{S} _{n}-\mathrm{S} _{n-1}$ है।
आइए कुछ उदाहरणों पर विचार करें।
उदाहरण 11 : A.P. : $8,3,-2, \ldots$ के प्रथम 22 पदों का योग ज्ञात कीजिए।
हल : यहाँ $a=8, d=3-8=-5$ और $n=22$ है।
हम जानते हैं कि
$ \begin{aligned} & S=\frac{n}{2}[2 a+(n-1) d] \end{aligned} $
इसलिए
$ \begin{aligned} & S=\frac{22}{2}[16+21(-5)]=11(16-105)=11(-89)=-979 \end{aligned} $
इसलिए दी हुई A.P. के प्रथम 22 पदों का योग -979 है।
उदाहरण 12 : यदि किसी A.P. के प्रथम 14 पदों का योग 1050 है तथा इसका प्रथम पद 10 है तो 20 वाँ पद ज्ञात कीजिए।
हल : यहाँ $\mathrm{S} _{14}=1050, n=14$ और $a=10$ है।
चूँकि
$ \mathrm{S} _{n}=\frac{n}{2}[2 a+(n-1) d] $
इसलिए
$ 1050=\frac{14}{2}[20+13 d]=140+91 d $
अर्थात्
$ 910=91 d $
या
$ d=10 $
अतः
$ a _{20}=10+(20-1) \times 10=200 $ अर्थात् 20 वाँ पद 200 है।
उदाहरण 13 : A.P. : $24,21,18, \ldots$ के कितने पद लिए जाएँ, ताकि उनका योग 78 हो?
हल : यहाँ $a=24, d=21-24=-3$ और $\mathrm{S} _{n}=78$ है। हमें $n$ ज्ञात करना है।
हम जानते हैं कि
$ \mathrm{S} _{n}=\frac{n}{2}[2 a+(n-1) d] $
अत:
$ 78=\frac{n}{2}[48+(n-1)(-3)]=\frac{n}{2}[51-3 n] $
$ \begin{aligned} \text{या} \quad \quad& 3 n^{2}-51 n+156 =0 \\ \text{या} \quad \quad& n^{2}-17 n+52 =0 \\ \text{या} \quad \quad& (n-4)(n-13) =0 \\ \text{या} \quad \quad& n =4 \text{या } 13 \end{aligned} $
$n$ के ये दोनों मान संभव हैं और स्वीकार किए जा सकते हैं। अतः, पदों की वांछित संख्या या तो 4 है या 13 है।
टिप्पणी :
1. इस स्थिति में, प्रथम 4 पदों का योग $=$ प्रथम 13 पदों का योग $=78$ है।
2. ये दोनों उत्तर संभव हैं, क्योंकि 5 वें से 13 वें पदों तक का योग शून्य हो जाएगा। यह इसलिए है कि यहाँ $a$ धनात्मक है और $d$ ॠणात्मक है, जिससे कुछ पद धनात्मक और कुछ पद ऋणात्मक हो जाते हैं तथा परस्पर कट जाते हैं।
उदाहरण 14 : निम्नलिखित का योग ज्ञात कीजिए :
(i) प्रथम 1000 धन पूर्णांक
(ii) प्रथम $n$ धन पूर्णांक
हल :
(i) मान लीजिए $\mathrm{S}=1+2+3+\ldots+1000$ है।
A.P. के प्रथम $n$ पदों के योग के सूत्र $\mathrm{S} _{n}=\frac{n}{2}(a+l)$ का प्रयोग करने पर हमें प्राप्त होता है:
$ S _{1000}=\frac{1000}{2}(1+1000)=500 \times 1001=500500 $
अतः, प्रथम 1000 धन पूर्णांकों का योग 500500 है।
(ii) मान लीजिए $\mathrm{S} _{n}=1+2+3+\ldots+n$ है।
यहाँ $a=1$ और अंतिम पद $l=n$ है।
अत :
$ \mathrm{S} _{n}=\frac{n(1+n)}{2} \quad \text { या } \quad \mathrm{S} _{n}=\frac{n(n+1)}{2} $
इस प्रकार, प्रथम $\boldsymbol{n}$ धन पूर्णांकों का योग सूत्र से प्राप्त किया जाता है।
$ S _{n}=\frac{n(n+1)}{2} $
उदाहरण 15 : संख्याओं की उस सूची के प्रथम 24 पदों का योग ज्ञात कीजिए, जिसका $n$ वाँ पद $a _{n}=3+2 n$ से दिया जाता है।
हल :
चूँकि
$ a_n=3+2 n \text{है } $
इसलिए
$ \begin{aligned} & a_1=3+2=5 \\ & a_2=3+2 \times 2=7 \\ & a_3=3+2 \times 3=9 \end{aligned} $
इस प्रकार प्राप्त संख्याओं की सूची $5,7,9,11, \ldots$ है।
यहाँ
$ 7-5=9-7=11-9=2 \text { इत्यादि हैं। } $
अतः इनसे एक A.P. बनती है, जिसका सार्व अंतर 2 है।
$\mathrm{S} _{24}$ ज्ञात करने के लिए, हमें प्राप्त है: $n=24, a=5, d=2$
अत :
$ S _{24}=\frac{24}{2}[2 \times 5+(24-1) \times 2]=12[10+46]=672 $
इसलिए संख्याओं की दी हुई सूची के प्रथम 24 पदों का योग 672 है।
उदाहरण 16 : टी.वी. सेटों का निर्माता तीसरे वर्ष में 600 टी.वी. तथा 7 वें वर्ष में 700 टी.वी. सेटों का उत्पादन करता है। यह मानते हुए कि प्रत्येक वर्ष उत्पादन में एक समान रूप से एक निश्चित संख्या में वृद्धि होती है, ज्ञात कीजिए:
(i) प्रथम वर्ष में उत्पादन
(ii) 10 वें वर्ष में उत्पादन
(iii) प्रथम 7 वर्षों में कुल उत्पादन
हल: (i) चूँकि प्रत्येक वर्ष उत्पादन में समान रूप से एक निश्चित संख्या में वृद्धि होती है, इसलिए पहले, दूसरे, तीसरे, … वर्षों में उत्पादित टी.वी. सेटों की संख्याएँ एक AP में होंगी।
आइए $n$ वें वर्ष में उत्पादित टी.वी. सेटों की संख्या को $a _{n}$ से व्यक्त करें।
अत:
a _{3}=600 \text { और } a _{7}=700 $
या
$a+2 d=600$
और
$ a+6 d=700 $
इन्हें हल करने पर, हमें $d=25$ और $a=550$ प्राप्त होता है।
अतः प्रथम वर्ष में उत्पादित टी.वी. सेटों की संख्या 550 है।
(ii) अब
$ a _{10}=a+9 d=550+9 \times 25=775 $
अतः 10 वें वर्ष में उत्पादित टी.वी. सेटों की संख्या 775 है।
(iii) साथ ही
$ \begin{aligned} S _{7} & =\frac{7}{2}[2 \times 550+(7-1) \times 25] \\ & =\frac{7}{2}[1100+150]=4375 \end{aligned} $
अतः प्रथम 7 वर्षों में कुल उत्पादित हुए सभी टी.वी. सेटों की संख्या 4375 है।
प्रश्नावली 5.3
1. निम्नलिखित समांतर श्रेढ़ियों का योग ज्ञात कीजिए :
(i) $2,7,12, \ldots, 10$ पदों तक
(ii) $-37,-33,-29, \ldots, 12$ पदों तक
(iii) $0.6,1.7,2.8, \ldots, 100$ पदों तक
(iv) $\frac{1}{15}, \frac{1}{12}, \frac{1}{10}, \ldots, 11$ पदों तक
Show Answer
#missing2. नीचे दिए हुए योगफलों को ज्ञात कीजिए :
(i) $7+10 \frac{1}{2}+14+\ldots+84$
(ii) $34+32+30+\ldots+10$
(iii) $-5+(-8)+(-11)+\ldots+(-230)$
Show Answer
#missing3. एक A.P. में,
(i) $a=5, d=3$ और $a _{n}=50$ दिया है। $n$ और $\mathrm{S} _{n}$ ज्ञात कीजिए।
(ii) $a=7$ और $a _{13}=35$ दिया है। $d$ और $\mathrm{S} _{13}$ ज्ञात कीजिए।
(iii) $a _{12}=37$ और $d=3$ दिया है। $a$ और $\mathrm{S} _{12}$ ज्ञात कीजिए।
(iv) $a _{3}=15$ और $\mathrm{S} _{10}=125$ दिया है। $d$ और $a _{10}$ ज्ञात कीजिए।
(v) $d=5$ और $\mathrm{S} _{9}=75$ दिया है। $a$ और $a _{9}$ ज्ञात कीजिए।
(vi) $a=2, d=8$ और $\mathrm{S} _{n}=90$ दिया है। $n$ और $a _{n}$ ज्ञात कीजिए।
(vii) $a=8, a _{n}=62$ और $\mathrm{S} _{n}=210$ दिया है। $n$ और $d$ ज्ञात कीजिए।
(viii) $a _{\mathrm{n}}=4, d=2$ और $\mathrm{S} _{n}=-14$ दिया है। $n$ और $a$ ज्ञात कीजिए।
(ix) $a=3, n=8$ और $\mathrm{S}=192$ दिया है। $d$ ज्ञात कीजिए।
(x) $l=28, \mathrm{~S}=144$ और कुल 9 पद हैं। $a$ ज्ञात कीजिए।
Show Answer
#missing4. 636 योग प्राप्त करने के लिए, A.P. : $9,17,25, \ldots$ के कितने पद लेने चाहिए?
Show Answer
#missing5. किसी A.P. का प्रथम पद 5 , अंतिम पद 45 और योग 400 है। पदों की संख्या और सार्व अंतर ज्ञात कीजिए।
Show Answer
#missing6. किसी A.P. के प्रथम और अंतिम पद क्रमशः 17 और 350 हैं। यदि सार्व अंतर 9 है, तो इसमें कितने पद हैं और इनका योग क्या है?
Show Answer
#missing7. उस A.P. के प्रथम 22 पदों का योग ज्ञात कीजिए, जिसमें $d=7$ है और 22 वाँ पद 149 है।
Show Answer
#missing8. उस A.P. के प्रथम 51 पदों का योग ज्ञात कीजिए, जिसके दूसरे और तीसरे पद क्रमशः 14 और 18 हैं।
Show Answer
#missing9. यदि किसी A.P. के प्रथम 7 पदों का योग 49 है और प्रथम 17 पदों का योग 289 है, तो इसके प्रथम $n$ पदों का योग ज्ञात कीजिए।
Show Answer
#missing10. दर्शाइए कि $a _{1}, a _{2}, \ldots, a _{n}, \ldots$ से एक A.P. बनती है, यदि $a _{n}$ नीचे दिए अनुसार परिभाषित है :
(i) $a _{n}=3+4 n$
(ii) $a _{n}=9-5 n$
साथ ही, प्रत्येक स्थिति में, प्रथम 15 पदों का योग ज्ञात कीजिए।
Show Answer
#missing11. यदि किसी A.P. के प्रथम $n$ पदों का योग $4 n-n^{2}$ है, तो इसका प्रथम पद (अर्थात् $\mathrm{S} _{1}$ ) क्या है? प्रथम दो पदों का योग क्या है? दूसरा पद क्या है? इसी प्रकार, तीसरे, 10 वें और $n$ वें पद ज्ञात कीजिए।
Show Answer
#missing12. ऐसे प्रथम 40 धन पूर्णांकों का योग ज्ञात कीजिए जो 6 से विभाज्य हैं।
Show Answer
#missing13. 8 के प्रथम 15 गुणजों का योग ज्ञात कीजिए।
Show Answer
#missing14. 0 और 50 के बीच की विषम संख्याओं का योग ज्ञात कीजिए।
Show Answer
#missing15. निर्माण कार्य से संबंधित किसी ठेके में, एक निश्चित तिथि के बाद कार्य को विलंब से पूरा करने के लिए, जुर्माना लगाने का प्रावधान इस प्रकार है : पहले दिन के लिए ₹ 200 , दूसरे दिन के लिए ₹ 250 , तीसरे दिन के लिए ₹ 300 इत्यादि, अर्थात् प्रत्येक उतरोत्तर दिन का जुर्माना अपने से ठीक पहले दिन के जुर्माने से ₹ 50 अधिक है। एक ठेकेदार को जुर्माने के रूप में कितनी राशि अदा करनी पड़ेगी, यदि वह इस कार्य में 30 दिन का विलंब कर देता है?
Show Answer
#missing16. किसी स्कूल के विद्यार्थियों को उनके समग्र शैक्षिक प्रदर्शन के लिए 7 नकद पुरस्कार देने के लिए ₹ 700 की राशि रखी गई है। यदि प्रत्येक पुरस्कार अपने से ठीक पहले पुरस्कार से ₹ 20 कम है, तो प्रत्येक पुरस्कार का मान ज्ञात कीजिए।
Show Answer
#missing17. एक स्कूल के विद्यार्थियों ने वायु प्रदूषण कम करने के लिए स्कूल के अंदर और बाहर पेड़ लगाने के बारे में सोचा। यह निर्णय लिया गया कि प्रत्येक कक्षा का प्रत्येक अनुभाग अपनी कक्षा की संख्या के बराबर पेड़ लगाएगा। उदाहरणार्थ, कक्षा I का एक अनुभाग 1 पेड़ लगाएगा, कक्षा II का एक अनुभाग 2 पेड़ लगाएगा, कक्षा III का एक अनुभाग 3 पेड़ लगाएगा, इत्यादि और ऐसा कक्षा XII तक के लिए चलता रहेगा। प्रत्येक कक्षा के तीन अनुभाग हैं। इस स्कूल के विद्यार्थियों द्वारा लगाए गए कुल पेड़ों की संख्या कितनी होगी?
Show Answer
#missing18. केंद्र $\mathrm{A}$ से प्रारंभ करते हुए, बारी-बारी से केंद्रों $\mathrm{A}$ और $\mathrm{B}$ को लेते हुए, त्रिज्याओं $0.5 \mathrm{~cm}$, $1.0 \mathrm{~cm}, 1.5 \mathrm{~cm}, 2.0 \mathrm{~cm}, \ldots$ वाले उतरोत्तर अर्धवृतों को खींचकर एक सर्पिल (spiral) बनाया गया है, जैसाकि आकृति 5.4 में दर्शाया गया है। तेरह क्रमागत अर्धवृत्तों से बने इस सर्पिल की कुल लंबाई क्या है? ( $\pi=\frac{22}{7}$ लीजिए।)
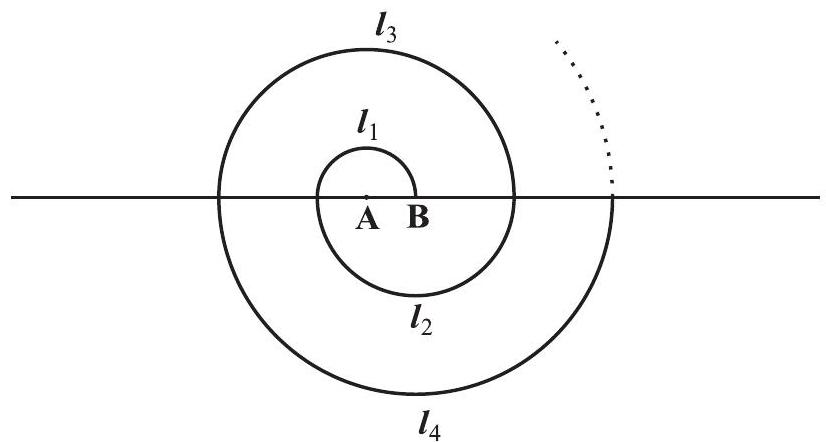
आकृति 5.4
[संकेत : क्रमशः केंद्रों $\mathrm{A}, \mathrm{B}, \mathrm{A}, \mathrm{B}, \ldots$ वाले अर्धवृत्तों की लंबाइयाँ $l _{1}, l _{2}, l _{3}, l _{4}$ हैं। ]
Show Answer
#missing19. 200 लट्ठों $(\log )$ को ढेरी के रूप में इस प्रकार रखा जाता है : सबसे नीचे वाली पंक्ति में 20 लट्ठे, उससे अगली पंक्ति में 19 लट्ठे, उससे अगली पंक्ति में 18 लट्ठे, इत्यादि (देखिए आकृति 5.5)। ये 200 लट्ठे कितनी पंक्तियों में रखे गए हैं तथा सबसे ऊपरी पंक्ति में कितने लट्ठे हैं?

आकृति 5.5
Show Answer
#missing20. एक आलू दौड़ (potato race) में, प्रारंभिक स्थान पर एक बाल्टी रखी हुई है, जो पहले आलू से $5 \mathrm{~m}$ की दूरी पर है, तथा अन्य आलुओं को एक सीधी रेखा में परस्पर $3 \mathrm{~m}$ की दूरियों पर रखा गया है। इस रेखा पर 10 आलू रखे गए हैं (देखिए आकृति 5.6)।

आकृति 5.6
प्रत्येक प्रतियोगी बाल्टी से चलना प्रारंभ करती है, निकटतम आलू को उठाती है, उसे लेकर वापस आकर दौड़कर बाल्टी में डालती है, दूसरा आलू उठाने के लिए वापस दौड़ती है, उसे उठाकर वापस बाल्टी में डालती है, और वह ऐसा तब तक करती रहती है, जब तक सभी आलू बाल्टी में न आ जाएँ। इसमें प्रतियोगी को कुल कितनी दूरी दौड़नी पड़ेगी?
[संकेत : पहले और दूसरे आलुओं को उठाकर बाल्टी में डालने तक दौड़ी गई दूरी $=2 \times 5+2 \times(5+3)$ है। $]$
Show Answer
#missingप्रश्नावली 5.4 (ऐच्छिक )*
1. A.P. : $121,117,113, \ldots$, का कौन-सा पद सबसे पहला ऋणात्मक पद होगा?
[संकेत : $a _{n}<0$ के लिए $n$ ज्ञात कीजिए।]
Show Answer
#missing2. किसी A.P. के तीसरे और सातवें पदों का योग 6 है और उनका गुणनफल 8 है। इस A.P. के प्रथम 16 पदों का योग ज्ञात कीजिए।
Show Answer
#missing3. एक सीढ़ी के क्रमागत डंडे परस्पर $25 \mathrm{~cm}$ की दूरी पर हैं (देखिए आकृति 5.7)। डंडों की लंबाई एक समान रूप से घटती जाती हैं तथा सबसे निचले डंडे की लंबाई $45 \mathrm{~cm}$ है और सबसे ऊपर वाले डंडे की लंबाई $25 \mathrm{~cm}$ है। यदि ऊपरी और निचले डंडे के बीच की दूरी $2 \frac{1}{2} \mathrm{~m}$ है, तो डंडों को बनाने के लिए लकड़ी की कितनी लंबाई की आवश्यकता होगी?
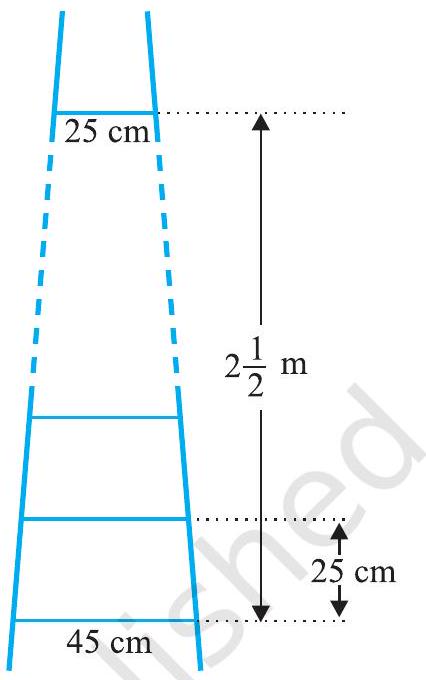
आकृति 5.7
[संकेत : डंडों की संख्या $=\frac{250}{25}+1$ है। ][^3]
Show Answer
#missing4. एक पंक्ति के मकानों को क्रमागत रूप से संख्या 1 से 49 तक अंकित किया गया है। दर्शाइए कि $x$ का एक ऐसा मान है कि $x$ से अंकित मकान से पहले के मकानों की संख्याओं का योग उसके बाद वाले मकानों की संख्याओं के योग के बराबर है। $x$ का मान ज्ञात कीजिए।
[संकेत : $\mathrm{S} _{x-1}=\mathrm{S} _{49}-\mathrm{S} _{x}$ है। ]
Show Answer
#missing5. एक फुटबाल के मैदान में एक छोटा चबूतरा है जिसमें 15 सीढ़ियाँ बनी हुई हैं। इन सीढ़ियों में से प्रत्येक की लंबाई $50 \mathrm{~m}$ है और वह ठोस कंक्रीट (concrete) की बनी है।
प्रत्येक सीढ़ी में $\frac{1}{4} \mathrm{~m}$ की चढ़ाई है और $\frac{1}{2} \mathrm{~m}$ का फैलाव (चौड़ाई) है। (देखिए आकृति 5.8)। इस चबूतरे को बनाने में लगी कंक्रीट का कुल आयतन परिकलित कीजिए।
[संकेत : पहली सीढ़ी को बनाने में लगी कंक्रीट का आयतन $=\frac{1}{4} \times \frac{1}{2} \times 50 \mathrm{~m}^{3}$ है।]
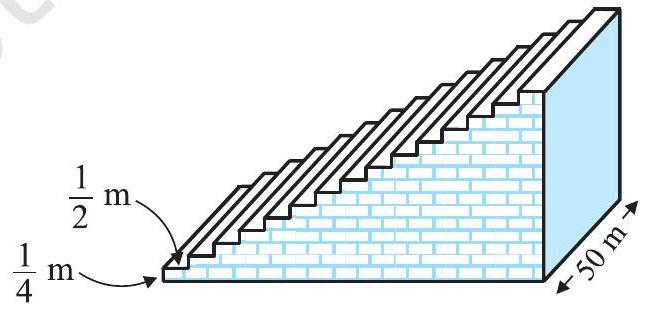
आकृति 5.8
Show Answer
#missing5.5 सारांश
इस अध्याय में, आपने निम्नलिखित तथ्यों का अध्ययन किया है :
1. एक समांतर श्रेढ़ी संख्याओं की ऐसी सूची होती है, जिसमें प्रत्येक पद ( प्रथम पद के अतिरिक्त) अपने से ठीक पहले पद में एक निश्चित संख्या $d$ जोड़कर प्राप्त होता है। यह निश्चित संख्या $d$ इस समांतर श्रेढ़ी का सार्व अंतर कहलाती है।
एक A.P. का व्यापक रूप $a, a+d, a+2 d, a+3 d, \ldots$ है।
2. संख्याओं की एक दी हुई सूची A.P. होती है, यदि अंतरों $a _{2}-a _{1}, a _{3}-a _{2}, a _{4}-a _{3}, \ldots$, से एक ही (समान) मान प्राप्त हो, अर्थात् $k$ के विभिन्न मानों के लिए $a _{k+1}-a _{k}$ एक ही हो।
3. प्रथम पद $a$ और सार्व अंतर $d$ वाली A.P. का $n$ वाँ पद (या व्यापक पद) $a _{n}$ निम्नलिखित सूत्र द्वारा प्राप्त होता है: $a _{n}=a+(n-1) d$
4. किसी A.P. के प्रथम $n$ पदों का योग $\mathrm{S}$ सूत्र
$ \mathrm{S}=\frac{n}{2}[2 a+(n-1) d] \text { से प्राप्त होता है। } $
5. यदि एक परिमित A.P. का अंतिम पद (मान लीजिए $n$ वाँ पद) $l$ है, तो इस A.P. के सभी पदों का योग $\mathrm{S}$ सूत्र
$ \mathrm{S}=\frac{n}{2}(a+l) \text { से प्राप्त होता है। } $
पाठकों के लिए विशेष
यदि $a, b, c$, A.P. में हैं तब $b=\frac{a+c}{2}$ और $b, a$ तथा $c$ का समांतर माध्य कहलाता है।





