अध्याय 7 बर्बाज धारा
अभ्यास
7.1 एक $100 \Omega$ प्रतिरोधक को $220 \mathrm{~V}, 50 \mathrm{~Hz}$ ए.सी. आपूर्ति से जोड़ा गया है।
(a) परिपथ में ए.सी. की औसत मूल्य धारा क्या है?
(b) एक पूर्ण चक्र में नियत शक्ति क्या है?
उत्तर दिखाएं
उत्तर
प्रतिरोधक का प्रतिरोध, $R=100 \Omega$
आपूर्ति वोल्टता, $V=220 \mathrm{~V}$
आवृत्ति, $v=50 \mathrm{~Hz}$
(a) परिपथ में ए.सी. की औसत मूल्य धारा निम्नलिखित द्वारा दी गई है:
$$ \begin{aligned} I & =\frac{V}{R} \\ & =\frac{220}{100}=2.20 \mathrm{~A} \end{aligned} $$
(b) एक पूर्ण चक्र में नियत शक्ति निम्नलिखित द्वारा दी गई है:
$$ P=V I $$
$$\implies P=220 \times 2.2=484 \mathrm{~W}$$
7.2 (a) एक ए.सी. आपूर्ति का शिखर वोल्टता $300 \mathrm{~V}$ है। ए.सी. के औसत मूल्य वोल्टता क्या है?
(b) एक ए.सी. परिपथ में औसत मूल्य धारा का मान $10 \mathrm{~A}$ है। शिखर धारा क्या है?
उत्तर दिखाएं
उत्तर
(a) ए.सी. आपूर्ति का शिखर वोल्टता, $V_{0}=300 \mathrm{~V}$
औसत मूल्य वोल्टता निम्नलिखित द्वारा दी गई है:
$$ \begin{aligned} V & =\frac{V_{0}}{\sqrt{2}} \\ & =\frac{300}{\sqrt{2}}=212.1 \mathrm{~V} \end{aligned} $$
(b) औसत मूल्य धारा निम्नलिखित द्वारा दी गई है:
$I=10 \mathrm{~A}$
अब, शिखर धारा निम्नलिखित द्वारा दी गई है:
$$ \begin{aligned} I_{0} & =\sqrt{2} I \\ & =10 \sqrt{2}=14.1 \mathrm{~A} \end{aligned} $$
7.3 एक $44 \mathrm{mH}$ प्रेरक को $220 \mathrm{~V}, 50 \mathrm{~Hz}$ ए.सी. आपूर्ति से जोड़ा गया है। परिपथ में ए.सी. की औसत मूल्य धारा का मान ज्ञात कीजिए।
उत्तर दिखाएं
उत्तर
प्रेरक का प्रेरकत्व, $L=44 \mathrm{mH}=44 \times 10^{-3} \mathrm{H}$
आपूर्ति वोल्टता, $V=220 \mathrm{~V}$
आवृत्ति, $\nu=50 \mathrm{~Hz}$
कोणीय आवृत्ति, $\omega=2 \pi v$
प्रेरक बाधा, $X_{\mathrm{L}}=\omega L=2 \pi \nu L=2 \pi \times 50 \times 44 \times 10^{-3} \Omega$
ए.सी. की औसत मूल्य धारा निम्नलिखित द्वारा दी गई है:
$$ \begin{aligned} I & =\frac{v}{X_{\mathrm{L}}} \\ & =\frac{220}{2 \pi \times 50 \times 44 \times 10^{-3}}=15.92 \mathrm{~A}
\end{aligned} $$
अतः, परिपथ में विद्युत धारा का rms मान $15.92 \mathrm{~A}$ है।
7.4 एक $60 \mu \mathrm{F}$ कैपेसिटर को $110 \mathrm{~V}, 60 \mathrm{~Hz}$ ए.सी. आपूर्ति के साथ जोड़ा गया है। परिपथ में विद्युत धारा का rms मान ज्ञात कीजिए।
उत्तर दिखाएं
उत्तर
कैपेसिटर की क्षमता, $C=60 \mu \mathrm{F}=60 \times 10^{-6} \mathrm{~F}$
आपूर्ति वोल्टता, $V=110 \mathrm{~V}$
आवृत्ति, $\nu=60 \mathrm{~Hz}$
कोणीय आवृत्ति, $\omega=2 \pi v$
कैपेसिटिव प्रतिरोध $X_{\mathrm{c}}=\frac{1}{\omega C}$
$=\frac{1}{2 \pi v C}$
$=\frac{1}{2 \times 3.14 \times 60 \times 60 \times 10^{-6}} \Omega^{-1}$
विद्युत धारा का rms मान निम्नलिखित द्वारा दिया गया है:
$$ \begin{aligned} I & =\frac{v}{X_{\mathrm{c}}} \\ & =110 \times 2 \times 3.14 \times 60 \times 10^{-6} \times 60=2.49 \mathrm{~A} \end{aligned} $$
अतः, विद्युत धारा का rms मान $2.49 \mathrm{~A}$ है।
7.5 अभ्यास 7.3 और 7.4 में, प्रत्येक परिपथ द्वारा एक पूर्ण चक्र में अवशोषित कुल शक्ति क्या है? अपने उत्तर की व्याख्या कीजिए।
उत्तर दिखाएं
उत्तर
प्रेरक परिपथ में,
विद्युत धारा का rms मान, $I=15.92 \mathrm{~A}$
वोल्टता का rms मान, $V=220 \mathrm{~V}$
अतः, अवशोषित कुल शक्ति को निम्नलिखित संबंध द्वारा प्राप्त किया जा सकता है,
$P=V I \cos \Phi$
जहाँ, $\Phi=$ $V$ और $I$ के बीच चर वोल्टता और धारा के बीच अंतर
एक शुद्ध प्रेरक परिपथ में, चर वोल्टता और धारा के बीच अंतर $90^{\circ}$ होता है, अर्थात $\Phi=90^{\circ}$।
अतः, $P=0$ अर्थात कुल शक्ति शून्य है।
कैपेसिटिव परिपथ में,
विद्युत धारा का rms मान, $I=2.49$ A
वोल्टता का rms मान, $V=110 \mathrm{~V}$
अतः, अवशोषित कुल शक्ति निम्नलिखित द्वारा प्राप्त की जा सकती है:
$P=V I \operatorname{Cos} \Phi$
एक शुद्ध कैपेसिटिव परिपथ में, चर वोल्टता और धारा के बीच अंतर $90^{\circ}$ होता है, अर्थात $\Phi=90^{\circ}$।
अतः, $P=0$ अर्थात कुल शक्ति शून्य है।
7.6 आवेशित $30 \mu \mathrm{F}$ कैपेसिटर को $27 \mathrm{mH}$ प्रेरक के साथ जोड़ा गया है। परिपथ में मुक्त दोलनों की कोणीय आवृत्ति क्या है?
उत्तर दिखाएं
उत्तर
क्षमता, $C=30 \mu \mathrm{F}=30 \times 10^{-6} \mathrm{~F}$
गैल्वेनोमीटर, $L=27 \mathrm{mH}=27 \times 10^{-3} \mathrm{H}$
कोणीय आवृत्ति निम्नलिखित द्वारा दी गई है:
$$ \begin{aligned} \omega_{r} & =\frac{1}{\sqrt{L C}} \\ & =\frac{1}{\sqrt{27 \times 10^{-3} \times 30 \times 10^{-6}}}=\frac{1}{9 \times 10^{-4}}=1.11 \times 10^{3} \mathrm{rad} / \mathrm{s} \end{aligned} $$
अतः, परिपथ के स्वतंत्र दोलन की कोणीय आवृत्ति $1.11 \times 10^{3} \mathrm{rad} / \mathrm{s}$ है।
7.7 एक श्रेणी $L C R$ परिपथ $R=20 \Omega, L=1.5 \mathrm{H}$ और $C=35 \mu \mathrm{F}$ के साथ एक चर आवृत्ति वाले $200 \mathrm{~V}$ ए.सी. आपूर्ति से जुड़ा है। जब आपूर्ति की आवृत्ति परिपथ की प्राकृतिक आवृत्ति के बराबर होती है, तो परिपथ में एक पूर्ण चक्र में औसत शक्ति कितनी होती है?
उत्तर दिखाएं
उत्तर
संतुलन पर, आपूर्ति की आवृत्ति दिए गए LCR परिपथ की प्राकृतिक आवृत्ति के बराबर होती है।
प्रतिरोध, $R=20 \Omega$
गैल्वेनोमीटर, $L=1.5 \mathrm{H}$
क्षमता, $C=35 \mu \mathrm{F}=30 \times 10^{-6} \mathrm{~F}$
ए.सी. आपूर्ति वोल्टेज, $V=200 \mathrm{~V}$
परिपथ के प्रतिघात को निम्नलिखित संबंध द्वारा दिया गया है,
$Z=\sqrt{R^{2}+\left(\omega L-\frac{1}{\omega C}\right)^{2}}$
संतुलन पर, $\omega L=\frac{1}{\omega C}$
$\therefore Z=R=20 \Omega$
परिपथ में धारा की गणना निम्नलिखित द्वारा की जा सकती है:
$$ \begin{aligned} I & =\frac{V}{Z} \\ & =\frac{200}{20}=10 \mathrm{~A} \end{aligned} $$
अतः, परिपथ में एक पूर्ण चक्र में औसत शक्ति $=V I$
$=200 \times 10=2000 \mathrm{~W}$।
7.8 चित्र 7.17 में एक श्रेणी $L C R$ परिपथ एक चर आवृत्ति वाले $230 \mathrm{~V}$ स्रोत से जुड़ा है। $L=5.0 \mathrm{H}, C=80 \mu \mathrm{F}, R=40 \Omega$।
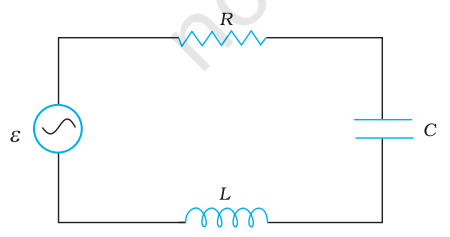
FIGURE 7.17
(a) बर्तन के संरेखण के लिए स्रोत आवृत्ति निर्धारित करें।
(b) संरेखण आवृत्ति पर परिपथ के प्रतिरोध और धारा के आयाम की गणना करें।
(c) परिपथ के तीन तत्वों पर rms विभव पतन की गणना करें। संरेखण आवृत्ति पर $LC$ संयोजन के विभव पतन के शून्य होने को सिद्ध करें।
उत्तर दिखाएं
उत्तर
चोटी के इंडक्टर के प्रेरकत्व, $L=5.0 \mathrm{H}$
कैपेसिटर की क्षमता, $C=80 \mu \mathrm{H}=80 \times 10^{-6} \mathrm{~F}$
रेजिस्टर का प्रतिरोध, $R=40 \Omega$
संचालन वोल्टेज स्रोत के वोल्टेज, $V=230 \mathrm{~V}$
(a) संरेखण कोणीय आवृत्ति निम्न द्वारा दी गई है: $$ \begin{aligned} \omega_R & =\frac{1}{\sqrt{L C}} \ & =\frac{1}{\sqrt{5 \times 80 \times 10^{-6}}}=\frac{10^3}{20}=50 \mathrm{rad} / \mathrm{s} \end{aligned} $$
इसलिए, स्रोत आवृत्ति $50 \mathrm{rad} / \mathrm{s}$ पर परिपथ संरेखण में आएगा।
(b) परिपथ के प्रतिरोध को निम्न द्वारा दिया गया है, $$ Z=\sqrt{R^2+\left(\omega L-\frac{1}{\omega C}\right)^2} $$
संरेखण पर, $$ \begin{aligned} & \omega L=\frac{1}{\omega C} \ & \therefore Z=R=40 \Omega \end{aligned} $$
संरेखण आवृत्ति पर धारा के आयाम को निम्न द्वारा दिया गया है: $I_0=\frac{V_0}{Z}$
जहाँ, $V_0 =\text { Peak voltage }$
$$ \begin{aligned} & V_0 =\sqrt{2} \mathrm{~V} \ \therefore I_0 & =\frac{\sqrt{2} \mathrm{~V}}{Z} \ & =\frac{\sqrt{2} \times 230}{40}=8.13 \mathrm{~A} \end{aligned} $$
इसलिए, संरेखण पर परिपथ के प्रतिरोध $40 \Omega$ है और धारा का आयाम $8.13 \mathrm{~A}$ है।
(c) प्रेरक पर rms विभव पतन, $$ \left(V_L\right)_{\text {rms }}=I \times \omega_R L $$
जहाँ, $I=$ rms धारा $$ \begin{aligned} & =\frac{I_0}{\sqrt{2}}=\frac{\sqrt{2} V}{\sqrt{2} Z}=\frac{230}{40} \mathrm{~A} \ & \therefore\left(V_L\right)_{\text {rms }}=\frac{230}{40} \times 50 \times 5=1437.5 \mathrm{~V} \end{aligned} $$
कैपेसिटर पर विभव पतन, $$ \begin{aligned}
$$ \left(V_c\right)_{\mathrm{rms}} & =I \times \frac{1}{\omega_R C} \ & =\frac{230}{40} \times \frac{1}{50 \times 80 \times 10^{-6}}=1437.5 \mathrm{~V} \end{aligned} $$
विद्युत धारा के माध्यम से रेजिस्टर पर विभव पार, $$ \begin{aligned} & \left(V_R\right)_{\mathrm{rms}}=I R \ & =\frac{230}{40} \times 40=230 \mathrm{~V} \end{aligned} $$
LC संयोजन पर विभव पार, $$ V_{L C}=I\left(\omega_R L-\frac{1}{\omega_R C}\right) $$
संतुलन आवृत्ति पर, $\omega_R L=\frac{1}{\omega_R C}$ $$ \therefore V_{L C}=0 $$
इसलिए, यह सिद्ध होता है कि आवृत्ति के संतुलन पर $L C$ संयोजन पर विभव पार शून्य होता है।





