उत्तर

दो आवेश हैं,

$q_{1}=5 \times 10^{-8} \mathrm{C}$

$q_{2}=-3 \times 10^{-8} \mathrm{C}$

दोनों आवेशों के बीच दूरी, $d=16 \mathrm{~cm}=0.16 \mathrm{~m}$

मान लीजिए कि एक बिंदु $\mathrm{P}$, दोनों आवेशों के बीच रेखा पर स्थित है, जैसा कि दिए गए चित्र में दिखाया गया है।

$r=$ बिंदु $\mathrm{P}$ से आवेश $q_{1}$ की दूरी

मान लीजिए कि बिंदु $\mathrm{P}$ पर वैद्युत विभव $(V)$ शून्य है।

बिंदु $\mathrm{P}$ पर विभव, क्रमशः आवेश $q_{1}$ और $q_{2}$ द्वारा उत्पन्न विभव के योग के बराबर होता है।

$\therefore V=\frac{q_{1}}{4 \pi \epsilon_{0} r}+\frac{q_{2}}{4 \pi \epsilon_{0}(d-r)}$

जहाँ,

$\epsilon_{0}=$ रिक्त स्थान की प्रवैगता

$V=0$ के लिए, समीकरण (i) निम्नलिखित रूप में घटता है

$$ \begin{aligned} & \frac{q_{1}}{4 \pi \epsilon_{0} r}=-\frac{q_{2}}{4 \pi \epsilon_{0}(d-r)} \\ & \frac{q_{1}}{r}=\frac{-q_{2}}{d-r} \\ & \frac{5 \times 10^{-8}}{r}=-\frac{\left(-3 \times 10^{-8}\right)}{(0.16-r)} \\ & \frac{0.16}{r}-1=\frac{3}{5} \\ & \frac{0.16}{r}=\frac{8}{5} \\ & \therefore r=0.1 \mathrm{~m}=10 \mathrm{~cm} \end{aligned} $$

इसलिए, धनावेश के 10 सेमी दूरी पर विभव शून्य होता है।

मान लीजिए बिंदु $\mathrm{P}$, दोनों आवेशों के नकारात्मक आवेश से बाहर एक बिंदु है जहाँ विभव शून्य है, जैसा कि निम्नलिखित चित्र में दिखाया गया है।

इस व्यवस्था के लिए, विभव द्वारा दिया गया है,

$$ \begin{equation*} V=\frac{q_{1}}{4 \pi \epsilon_{0} s}+\frac{q_{2}}{4 \pi \epsilon_{0}(s-d)} \tag{ii} \end{equation*} $$

जब $V=0$ हो, तो समीकरण (ii) निम्नलिखित रूप में घटता है,

$$ \frac{q_{1}}{4 \pi \epsilon_{0} s}=-\frac{q_{2}}{4 \pi \epsilon_{0}(s-d)} $$

$\frac{q_{1}}{s}=\frac{-q_{2}}{s-d}$

$\implies \frac{5 \times 10^{-8}}{s}=-\frac{\left(-3 \times 10^{-8}\right)}{(s-0.16)}$

$\implies 1-\frac{0.16}{s}=\frac{3}{5}$

$\implies \frac{0.16}{s}=\frac{2}{5}$

$\therefore s=0.4 \mathrm{~m}=40 \mathrm{~cm}$

इसलिए, धनात्मक आवेश से बाहर आवेश व्यवस्था के बिंदु पर विभव शून्य होता है।

उत्तर

दिए गए चित्र में षट्कोण के कोनों पर छह बराबर मात्रा में आवेश, $q$, हैं।

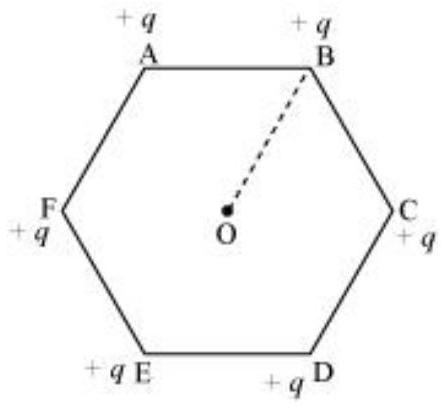
जहाँ, आवेश, (q) $=5 \mu \mathrm{C}=5 \times 10^{-6} \mathrm{C}$

षट्कोण की भुजा, $l=\mathrm{AB}=\mathrm{BC}=\mathrm{CD}=\mathrm{DE}=\mathrm{EF}=\mathrm{FA}=10 \mathrm{~cm}$

केंद्र $\mathrm{O}$ से प्रत्येक कोने की दूरी $\mathrm{d}=10 \mathrm{~cm}$

बिंदु $\mathrm{O}$ पर विद्युत विभव,

$$ V=\frac{6 \times q}{4 \pi \epsilon_{0} d} $$

जहाँ,

$$ \epsilon_{0}=\text { रिक्त स्थान की प्रवैगता } $$

$$ \begin{aligned} & \frac{1}{4 \pi \epsilon_{0}}=9 \times 10^{9} \mathrm{~N} \mathrm{C}^{-2} \mathrm{~m}^{-2} \\

$$ \begin{aligned} & \therefore V=\frac{6 \times 9 \times 10^{9} \times 5 \times 10^{-6}}{0.1} \\ & \quad=2.7 \times 10^{6} \mathrm{~V} \end{aligned} $$

इसलिए, षट्कोण के केंद्र पर विभव $2.7 \times 10^{6} \mathrm{~V}$ है।

उत्तर

दिए गए चित्र में प्रदर्शित स्थिति है।

एक समविभव सतह वह तल या अंतरिक बिंदु होता है जहां सभी बिंदुओं पर विभव समान होता है। यह तल रेखा $\mathrm{AB}$ के लंबवत होता है। यह तल रेखा $\mathrm{AB}$ के मध्य बिंदु पर स्थित है क्योंकि आवेशों के परिमाण समान हैं।

इस सतह पर प्रत्येक बिंदु पर विद्युत क्षेत्र की दिशा तल के लंबवत रेखा $\mathrm{AB}$ की दिशा में होती है।

उत्तर

गोलीय चालक की त्रिज्या, $r=12 \mathrm{~cm}=0.12 \mathrm{~m}$

आवेश चालक के सतह पर समान रूप से वितरित है, $q=1.6 \times 10^{-7} \mathrm{C}$

गोलीय चालक के अंदर विद्युत क्षेत्र शून्य होता है। इसका कारण यह है कि यदि चालक के अंदर क्षेत्र होता तो आवेश इसे निराकरण करने के लिए गति करते।

चालक के बाहर बिंदु पर विद्युत क्षेत्र $E$ के लिए संबंध निम्नलिखित है,

$$ \begin{aligned} & \therefore V=\frac{6 \times 9 \times 10^{9} \times 5 \times 10^{-6}}{0.1} \\ & \quad=2.7 \times 10^{6} \mathrm{~V} \end{aligned} $$

इसलिए, षट्कोण के केंद्र पर विभव $2.7 \times 10^{6} \mathrm{~V}$ है।

उत्तर

दिए गए चित्र में प्रदर्शित स्थिति है।

एक समविभव सतह वह तल या अंतरिक बिंदु होता है जहां सभी बिंदुओं पर विभव समान होता है। यह तल रेखा $\mathrm{AB}$ के लंबवत होता है। यह तल रेखा $\mathrm{AB}$ के मध्य बिंदु पर स्थित है क्योंकि आवेशों के परिमाण समान हैं।

इस सतह पर प्रत्येक बिंदु पर विद्युत क्षेत्र की दिशा तल के लंबवत रेखा $\mathrm{AB}$ की दिशा में होती है।

उत्तर

गोलीय चालक की त्रिज्या, $r=12 \mathrm{~cm}=0.12 \mathrm{~m}$

आवेश चालक के सतह पर समान रूप से वितरित है, $q=1.6 \times 10^{-7} \mathrm{C}$

गोलीय चालक के अंदर विद्युत क्षेत्र शून्य होता है। इसका कारण यह है कि यदि चालक के अंदर क्षेत्र होता तो आवेश इसे निराकरण करने के लिए गति करते।

चालक के बाहर बिंदु पर विद्युत क्षेत्र $E$ के लिए संबंध निम्नलिखित है,

E = \frac{1}{4\pi \varepsilon_0} \cdot \frac{q}{r^2}

$$ E=\frac{q}{4 \pi \epsilon_{0} r^{2}} $$

जहाँ, $ \epsilon_{0}=\text { रिक्त स्थान की प्रवैगता } $

$\frac{1}{4 \pi \epsilon_{0}}=9 \times 10^{9} \mathrm{~N} \mathrm{~m}^{2} \mathrm{C}^{-2}$

$\therefore E=\frac{1.6 \times 10^{-7} \times 9 \times 10^{-9}}{(0.12)^{2}}$

$=10^{5} \mathrm{~N} \mathrm{C}^{-1}$

इसलिए, गोले के बाहर बिंदु पर विद्युत क्षेत्र $10^{5} \mathrm{~N} \mathrm{C}^{-1}$ है।

गोले के केंद्र से 18 मीटर की दूरी पर बिंदु पर विद्युत क्षेत्र $=E_{1}$

केंद्र से बिंदु की दूरी, $d=18 \mathrm{~cm}=0.18 \mathrm{~m}$

$$ \begin{aligned} E_{1} & =\frac{q}{4 \pi \epsilon_{0} d^{2}} \\ & =\frac{9 \times 10^{9} \times 1.6 \times 10^{-7}}{\left(18 \times 10^{-2}\right)^{2}} \\ & =4.4 \times 10^{4} \mathrm{~N} / \mathrm{C} \end{aligned} $$

इसलिए, गोले के केंद्र से 18 सेमी की दूरी पर बिंदु पर विद्युत क्षेत्र $4.4 \times 10^{4} \mathrm{~N} / \mathrm{C}$ है।

संधारित्र के समान्तर प्लेटों के बीच धारिता, $\mathrm{C}=8 \mathrm{pF}$

प्रारंभ में प्लेटों के बीच दूरी $d$ थी और वहाँ वायु भरी हुई थी। वायु का विद्युतशीलक स्थिरांक, $k=1$

धारिता, $C$, निम्न सूत्र द्वारा दी गई है,

$$ \begin{align*} C & =\frac{k \epsilon_{0} A}{d} \\ & =\frac{\epsilon_{0} A}{d} \tag{i} \end{align*} $$

जहाँ, $A=$ प्रत्येक प्लेट का क्षेत्रफल

$ \epsilon_{0}=\text { रिक्त स्थान की प्रवैगता } $

यदि प्लेटों के बीच दूरी आधी कर दी जाए, तो नई दूरी, $d=\frac{d}{2}$

प्लेटों के बीच भरे गए पदार्थ का विद्युतशीलक स्थिरांक, $k^{\prime}=6$

इसलिए, संधारित्र की धारिता बन जाएगी

$$ \begin{equation*} C^{\prime}=\frac{k^{\prime} \in_{0} A}{d^{\prime}}=\frac{6 \in_{0} A}{\frac{d}{2}} \tag{ii}

\end{equation*} $$

समीकरण (i) और (ii) के अनुपात लेने पर हम प्राप्त करते हैं

$$ \begin{aligned} C^{\prime} & =2 \times 6 C \\ & =12 C \\ & =12 \times 8=96 \mathrm{pF} \end{aligned} $$

इसलिए, प्लेट के बीच कैपेसिटेंस $96 \mathrm{pF}$ है।

Answer

तीन कैपेसिटर की कैपेसिटेंस, $C=9 \mathrm{pF}$

कैपेसिटर के संयोजन की समतुल्य कैपेसिटेंस $\left(C^{\prime}\right)$ को निम्न संबंध द्वारा दिया गया है,

$$ \begin{aligned} \frac{1}{C^{\prime}} & =\frac{1}{C}+\frac{1}{C}+\frac{1}{C} \\ & =\frac{1}{9}+\frac{1}{9}+\frac{1}{9}=\frac{3}{9}=\frac{1}{3} \end{aligned} $$

$\therefore C^{\prime}=3 \mu \mathrm{F}$

इसलिए, संयोजन की कुल कैपेसिटेंस $3 \mu \mathrm{F}$ है।

आपूर्ति वोल्टेज, $V=120 \mathrm{~V}$

प्रत्येक कैपेसिटर पर विभवांतर $\left(V^{\prime}\right)$ आपूर्ति वोल्टेज के एक-तिहाई के बराबर होता है।

$$ \therefore V^{\prime}=\frac{V}{3}=\frac{120}{3}=40 \mathrm{~V} $$

इसलिए, प्रत्येक कैपेसिटर पर विभवांतर $40 \mathrm{~V}$ है।

Answer

दिए गए कैपेसिटर की कैपेसिटेंस हैं

$$ \begin{aligned} & C_{1}=2 \mathrm{pF} \\ & C_{2}=3 \mathrm{pF} \\ & C_{3}=4 \mathrm{pF} \end{aligned} $$

कैपेसिटर के समांतर संयोजन के लिए, समतुल्य कैपेसिटेंस $C^{\prime}$ को बीजगणितीय योग द्वारा दिया गया है,

$$ C^{\prime}=2+3+4=9 \mathrm{pF} $$

इसलिए, संयोजन की कुल कैपेसिटेंस $9 \mathrm{pF}$ है।

पाव वोल्टेज, $V=100 \mathrm{~V}$

सभी तीन कैपेसिटरों के माध्यम से वोल्टेज समान होता है $=V=100 \mathrm{~V}$

क्षमता $C$ और विभवांतर $V$ वाले कैपेसिटर पर आवेश के लिए संबंध द्वारा दिया गया है,

$q=V C \ldots$ (i)

एक लेखक के लिए $\mathrm{C}=2 \mathrm{pF}$,

आवेश $=V C=100 \times 2=200 \mathrm{pC}=2 \times 10^{-10} \mathrm{C}$

एक लेखक के लिए $\mathrm{C}=3 \mathrm{pF}$,

आवेश $=V C=100 \times 3=300 \mathrm{pC}=3 \times 10^{-10} \mathrm{C}$

एक लेखक के लिए $\mathrm{C}=4 \mathrm{pF}$,

आवेश $=V C=100 \times 4=200 \mathrm{pC}=4 \times 10^{-10} \mathrm{C}$

उत्तर

समान्तर प्लेट कैपेसिटर के प्रत्येक प्लेट का क्षेत्रफल, $A=6 \times 10^{-3} \mathrm{~m}^{2}$

प्लेटों के बीच दूरी, $d=3 \mathrm{~mm}=3 \times 10^{-3} \mathrm{~m}$

आपूर्ति वोल्टेज, $V=100 \mathrm{~V}$

समान्तर प्लेट कैपेसिटर की क्षमता $C$ द्वारा दिया गया है,

$C=\frac{\in_{0} A}{d}$

जहाँ,

$ \epsilon_{0}=\text { रिक्त स्थान की विद्युतशीलता } $

$\quad =8.854 \times 10^{-12} \mathrm{~N}^{-1} \mathrm{~m}^{-2} \mathrm{C}^{-2}$

$$ \begin{aligned} \therefore C & =\frac{8.854 \times 10^{-12} \times 6 \times 10^{-3}}{3 \times 10^{-3}} \\ & =17.71 \times 10^{-12} \mathrm{~F} \\ & =17.71 \mathrm{pF} \end{aligned} $$

विभव $V$ को आवेश $q$ और क्षमता $C$ के साथ संबंधित करते हैं

$$ \begin{aligned} & V=\frac{q}{C} \\ & \therefore q=V C \\ & =100 \times 17.71 \times 10^{-12} \\ & =1.771 \times 10^{-9} \mathrm{C} \end{aligned} $$

इसलिए, कैपेसिटर की क्षमता $17.71 \mathrm{pF}$ है और प्रत्येक प्लेट पर आवेश $1.771 \times$ $10^{-9} \mathrm{C}$ है।

Answer

मिका शीट के डाइइलेक्ट्रिक नियतांक, $k=6$

प्रारंभिक कैपेसिटेंस, $C=1.771 \times 10^{-11} \mathrm{~F}$

नया कैपेसिटेंस, $C^{\prime}=k C=6 \times 1.771 \times 10^{-11}=106 \mathrm{pF}$

सप्लाई वोल्टेज, $V=100 \mathrm{~V}$

नया चार्ज, $q^{\prime}=C^{\prime} V=6 \times 1.771 \times 10^{-9}=1.06 \times 10^{-8} \mathrm{C}$

प्लेटों के बीच वोल्टेज $100 \mathrm{~V}$ रहता है।

डाइइलेक्ट्रिक नियतांक, $k=6$

प्रारंभिक कैपेसिटेंस, $C=1.771 \times 10^{-11} \mathrm{~F}$

नया कैपेसिटेंस, $C^{\prime}=k C=6 \times 1.771 \times 10^{-11}=106 \mathrm{pF}$

अगर सप्लाई वोल्टेज हटा दिया जाता है, तो प्लेटों में चार्ज की मात्रा पर कोई प्रभाव नहीं होता।

चार्ज $=1.771 \times 10^{-9} \mathrm{C}$

प्लेटों के बीच वोल्टेज निम्नलिखित द्वारा दिया जाता है,

$$ \begin{aligned} \therefore V^{\prime} & =\frac{q}{C^{\prime}} \\ & =\frac{1.771 \times 10^{-9}}{106 \times 10^{-12}} \\ & =16.7 \mathrm{~V} \end{aligned} $$

Answer

कैपेसिटेंस के कैपेसिटर, $C=12 \mathrm{pF}=12 \times 10^{-12} \mathrm{~F}$

विभवांतर, $V=50 \mathrm{~V}$

कैपेसिटर में संग्रहीत विद्युत स्थैतिक ऊर्जा को निम्नलिखित संबंध द्वारा दिया जाता है,

$$ \begin{aligned} E & =\frac{1}{2} C V^{2} \\ & =\frac{1}{2} \times 12 \times 10^{-12} \times(50)^{2} \\ & =1.5 \times 10^{-8} \mathrm{~J} \end{aligned} $$

इसलिए, कैपेसिटर में संग्रहीत विद्युत स्थैतिक ऊर्जा $1.5 \times 10^{-8} \mathrm{~J}$ है।

Answer

कैपेसिटर की कैपेसिटेंस, $C=600 \mathrm{pF}$

संभावित विभवांतर, $V=200 \mathrm{~V}$

कैपेसिटर में संचित विद्युत ऊर्जा निम्नलिखित द्वारा दी जाती है,

$$ \begin{aligned} E & =\frac{1}{2} C V^{2} \\ & =\frac{1}{2} \times\left(600 \times 10^{-12}\right) \times(200)^{2} \\ & =1.2 \times 10^{-5} \mathrm{~J} \end{aligned} $$

यदि कैपेसिटर से आपूर्ति को अलग कर दिया जाता है और इसके साथ एक अन्य कैपेसिटर जुड़ा जाता है जिसकी कैपेसिटेंस $C=600$ $\mathrm{pF}$ है, तो संयोजन की समतुल्य कैपेसिटेंस $(C)$ निम्नलिखित द्वारा दी जाती है,

$$ \begin{aligned} & \frac{1}{C^{\prime}}=\frac{1}{C}+\frac{1}{C} \\ & \quad=\frac{1}{600}+\frac{1}{600}=\frac{2}{600}=\frac{1}{300} \\ & \therefore C^{\prime}=300 \mathrm{pF} \end{aligned} $$

नई विद्युत ऊर्जा निम्नलिखित द्वारा गणना की जा सकती है

$$ \begin{aligned} E^{\prime} & =\frac{1}{2} \times C^{\prime} \times V^{2} \\ & =\frac{1}{2} \times 300 \times(200)^{2} \\ & =0.6 \times 10^{-5} \mathrm{~J} \end{aligned} $$

विद्युत ऊर्जा में कमी $=E-E^{\prime}$

$$ \begin{aligned} & =1.2 \times 10^{-5}-0.6 \times 10^{-5} \\ & =0.6 \times 10^{-5} \\ & =6 \times 10^{-6} \mathrm{~J} \end{aligned} $$

अतः, प्रक्रिया में विद्युत ऊर्जा की हानि $6 \times 10^{-6} \mathrm{~J}$ है।