उत्तर

मान लीजिए $I_{1}$ और $I_{2}$ दोनों प्रकाश तरंगों की तीव्रता है। उनकी परिणामी तीव्रता निम्नलिखित द्वारा प्राप्त की जा सकती है:

$I^{\prime}=I_{1}+I_{2}+2 \sqrt{I_{1} I_{2}} \cos \phi$

जहाँ,

$\phi=$ दोनों तरंगों के बीच अपेक्षा अंतर

एकल रंग वाली प्रकाश तरंगों के लिए,

$$ \begin{aligned} & I_{1}=I_{2} \\ & \begin{aligned} \therefore I^{\prime} & =I_{1}+I_{1}+2 \sqrt{I_{1} I_{1}} \cos \phi \\ & =2 I_{1}+2 I_{1} \cos \phi \end{aligned} \end{aligned} $$

अपेक्षा अंतर $=\frac{2 \pi}{\lambda} \times$ पथ अंतर

क्योंकि पथ अंतर $=\lambda$,

अपेक्षा अंतर, $\phi=2 \pi$

$\therefore I^{\prime}=2 I_{1}+2 I_{1}=4 I_{1}$

दिया गया है,

$I^{\prime}=K$

$\therefore I_{1}=\frac{K}{4}$

जब पथ अंतर $=\frac{\lambda}{3}$,

अपेक्षा अंतर, $\phi=\frac{2 \pi}{3}$

इसलिए, परिणामी तीव्रता, $I_{R}^{\prime}=I_{1}+I_{1}+2 \sqrt{I_{1} I_{1}} \cos \frac{2 \pi}{3}$

$=2 I_{1}+2 I_{1}\left(-\frac{1}{2}\right)=I_{1}$

समीकरण (1) का उपयोग करते हुए, हम लिख सकते हैं:

$I_{R}=I_{1}=\frac{K}{4}$

इसलिए, जहां पथ अंतर $\frac{\lambda}{3}$ है, प्रकाश की तीव्रता $\frac{K}{4}$ इकाई है।

उत्तर

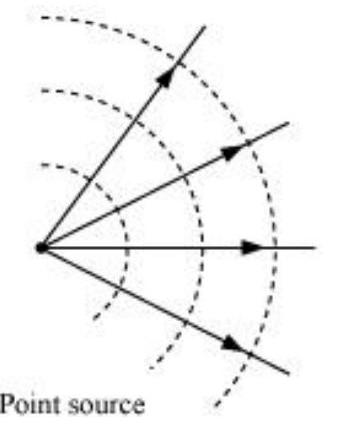
एक बिंदु स्रोत से विस्तारित प्रकाश के मामले में तरंग सामग्री के आकार गोलाकार होता है। बिंदु स्रोत से निकलने वाली तरंग सामग्री को दिए गए चित्र में दिखाया गया है।

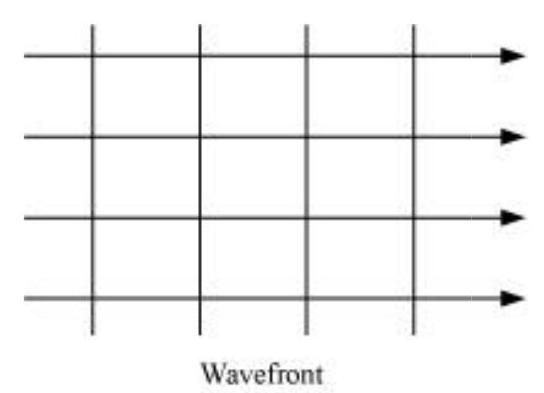
किरण के तरंग सामन्तर जाल के रूप में होता है जब एक बिंदु स्रोत को उत्तल लेंस के फोकस पर रखा जाता है। इसका चित्र दिया गया है।

एक दूर के तारे से आने वाली किरण के तरंग सामन्तर जाल के रूप में होता है जब यह पृथ्वी द्वारा पकड़ लिया जाता है।

Answer काँच का अपवर्तनांक, $\mu=1.5$

प्रकाश की गति, $\mathrm{c}=3 \times 10^{8} \mathrm{~m} / \mathrm{s}$

काँच में प्रकाश की गति के संबंध में,

$$ \begin{aligned} v & =\frac{c}{\mu} \\ & =\frac{3 \times 10^{8}}{1.5}=2 \times 10^{8} \mathrm{~m} / \mathrm{s} \end{aligned} $$

अतः, काँच में प्रकाश की गति $2 \times 10^{8} \mathrm{~m} / \mathrm{s}$ है।

काँच में प्रकाश की गति रंग के अनुसार स्वतंत्र नहीं है।

सफेद प्रकाश के बैंगनी घटक के अपवर्तनांक के बराबर लाल घटक के अपवर्तनांक से अधिक होता है। अतः, बैंगनी प्रकाश की गति काँच में लाल प्रकाश की गति से कम होती है। अतः, बैंगनी प्रकाश एक ग्लास प्रिज्म में लाल प्रकाश की तुलना में धीमी गति से चलता है।

उत्तर

स्लिटों के बीच की दूरी, $d=0.28 \mathrm{~mm}=0.28 \times 10^{-3} \mathrm{~m}$

स्लिटों और स्क्रीन के बीच की दूरी, $D=1.4 \mathrm{~m}$

केंद्रीय झरने और चौथे $(n=4)$ झरने के बीच की दूरी,

$u=1.2 \mathrm{~cm}=1.2 \times 10^{-2} \mathrm{~m}$

निर्माणात्मक अनुसरण के मामले में, हम दो झरनों के बीच दूरी के लिए संबंध के रूप में निम्नलिखित सूत्र होता है:

$u=n \lambda \frac{D}{d}$

जहाँ,

$n=$ झरनों की कोटि $=4$, $\lambda=$ उपयोग किए गए प्रकाश की तरंगदैर्ध्य

$ \therefore \lambda=\frac{u d}{n D} $

$=\frac{1.2 \times 10^{-2} \times 0.28 \times 10^{-3}}{4 \times 1.4}$

$=6 \times 10^{-7}$

$=600 \mathrm{~nm}$

अतः, प्रकाश की तरंगदैर्ध्य $600 \mathrm{~nm}$ है।

उत्तर

मान लीजिए $I_{1}$ और $I_{2}$ दो प्रकाश तरंगों की तीव्रता है। उनकी परिणामी तीव्रता निम्नलिखित रूप में प्राप्त की जा सकती है:

$I^{\prime}=I_{1}+I_{2}+2 \sqrt{I_{1} I_{2}} \cos \phi$

जहाँ,

$\phi=$ दोनों तरंगों के बीच चरण अंतर

एकल तरंगदैर्ध्य वाली प्रकाश तरंगों के लिए,

$$ \begin{aligned} & I_{1}=I_{2} \\ & \begin{aligned} \therefore I^{\prime} & =I_{1}+I_{1}+2 \sqrt{I_{1} I_{1}} \cos \phi \\ & =2 I_{1}+2 I_{1} \cos \phi \end{aligned} \end{aligned} $$

चरण अंतर $=\frac{2 \pi}{\lambda} \times$ पथांतर

क्योंकि पथांतर $=\lambda$,

चरण अंतर, $\phi=2 \pi$

$\therefore I^{\prime}=2 I_{1}+2 I_{1}=4 I_{1}$

दिया गया है,

$I^{\prime}=K$

$\therefore I_{1}=\frac{K}{4}$

जब पथांतर $=\frac{\lambda}{3}$,

चरण अंतर, $\phi=\frac{2 \pi}{3}$

अतः, परिणामी तीव्रता, $I_{R}^{\prime}=I_{1}+I_{1}+2 \sqrt{I_{1} I_{1}} \cos \frac{2 \pi}{3}$

$=2 I_{1}+2 I_{1}\left(-\frac{1}{2}\right)=I_{1}$

समीकरण (1) का उपयोग करते हुए, हम लिख सकते हैं:

$I_{R}=I_{1}=\frac{K}{4}$

इसलिए, वह बिंदु पर प्रकाश की तीव्रता जहां पथान्तर $\frac{\lambda}{3}$ है, $\frac{K}{4}$ इकाई है।

उत्तर

प्रकाश किरण बंडल की तरंगदैर्घ्य, $\lambda_{1}=650 \mathrm{~nm}$

दूसरे प्रकाश किरण बंडल की तरंगदैर्घ्य, $\lambda_{2}=520 \mathrm{~nm}$

स्लिट की स्क्रीन से दूरी $=D$

दो स्लिट के बीच की दूरी $=d$

स्क्रीन पर $n^{\text {th }}$ चमकीले बैंड की केंद्रीय अधिकतम से दूरी को निम्न संबंध द्वारा दिया जाता है,

$x=n \lambda_{1}\left(\frac{D}{d}\right)$

तीसरे चमकीले बैंड के लिए, $n=3$

$\therefore x=3 \times 650 \frac{D}{d}=1950\left(\frac{D}{d}\right) \mathrm{nm}$

मान लीजिए कि तरंगदैर्घ्य $\lambda_{2}$ के कारण $n^{\text {th }}$ चमकीले बैंड और तरंगदैर्घ्य $\lambda_{1}$ के कारण $(n-1)^{\text {th }}$ चमकीले बैंड स्क्रीन पर एक साथ आए। हम चमकीले बैंड के शर्तों को बराबर कर सकते हैं:

$$ \begin{aligned} & n \lambda_{2}=(n-1) \lambda_{1} \\ & 520 n=650 n-650 \\ & 650=130 n \\ & \therefore n=5 \end{aligned} $$

इसलिए, केंद्रीय अधिकतम से सबसे कम दूरी को निम्न संबंध द्वारा प्राप्त किया जा सकता है:

$$ \begin{aligned} x & =n \lambda_{2} \frac{D}{d} \\ & =5 \times 520 \frac{D}{d}=2600 \frac{D}{d} \mathrm{~nm} \end{aligned} $$

नोट: प्रश्न में $d$ और $D$ के मान नहीं दिए गए हैं।