हल

i. आवश्यक क्षेत्रफल द्वारा छायांकित क्षेत्र ADCBA को प्रस्तुत करता है

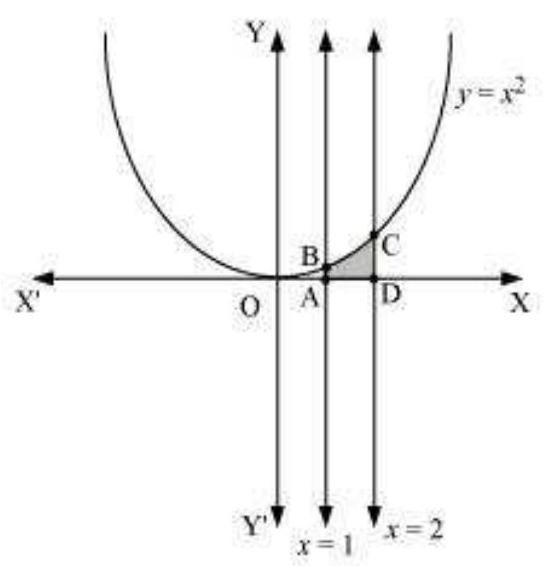
$ \begin{aligned} \text{ क्षेत्रफल ADCBA } & =\int_1^{2} y d x \\ & =\int_1^{2} x^{2} d x \\ & =[\frac{x^{3}}{3}]_1^{2} \\ & =\frac{8}{3}-\frac{1}{3} \\ & =\frac{7}{3} \text{ इकाई } \end{aligned} $

ii. आवश्यक क्षेत्रफल द्वारा छायांकित क्षेत्र ADCBA को प्रस्तुत करता है

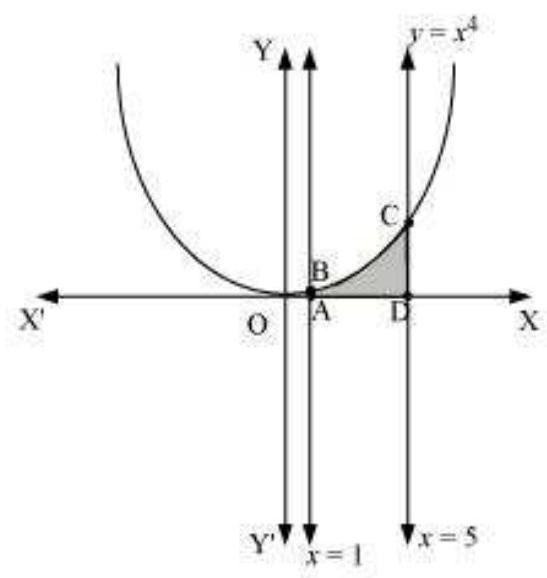
$ \begin{aligned} \text{ क्षेत्रफल ADCBA } & =\int_1^{5} x^{4} d x \\ & =[\frac{x^{5}}{5}]_1^{5} \\ & =\frac{(5)^{5}}{5}-\frac{1}{5} \\ & =(5)^{4}-\frac{1}{5} \\ & =625-\frac{1}{5} \\ & =624.8 \text{ इकाई } \end{aligned} $

हल

दिया गया समीकरण $y=|x+3|$ है

$x$ और $y$ के संगत मान निम्नलिखित तालिका में दिए गए हैं।

इन बिंदुओं को आलेखित करने पर, हमें $y=|x+3|$ के ग्राफ के निम्नलिखित रूप मिलता है।

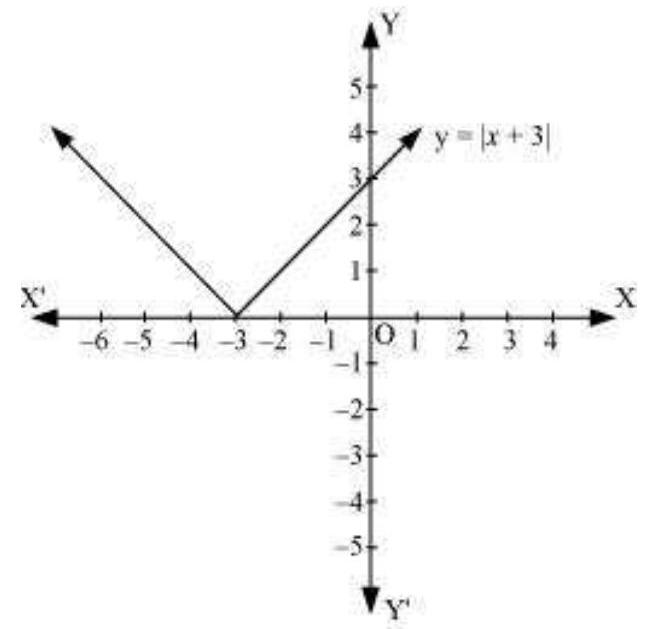
ज्ञात है कि, $(x+3) \leq 0$ जब $-6 \leq x \leq-3$ और $(x+3) \geq 0$ जब $-3 \leq x \leq 0$

$ \begin{aligned} \therefore \int _{-6}^{0}|(x+3)| d x & =-\int _{-6}^{-3}(x+3) d x+\int _{-3}^{0}(x+3) d x \\ & =-[\frac{x^{2}}{2}+3 x] _{-6}^{-3}+[\frac{x^{2}}{2}+3 x] _{-3}^{0} \\ & =-[(\frac{(-3)^{2}}{2}+3(-3))-(\frac{(-6)^{2}}{2}+3(-6))]+[0-(\frac{(-3)^{2}}{2}+3(-3)]] \\ & =-[-\frac{9}{2}]-[-\frac{9}{2}] \\ & =9 \end{aligned} $

हल

$y=\sin x$ के ग्राफ को खींचा जा सकता है

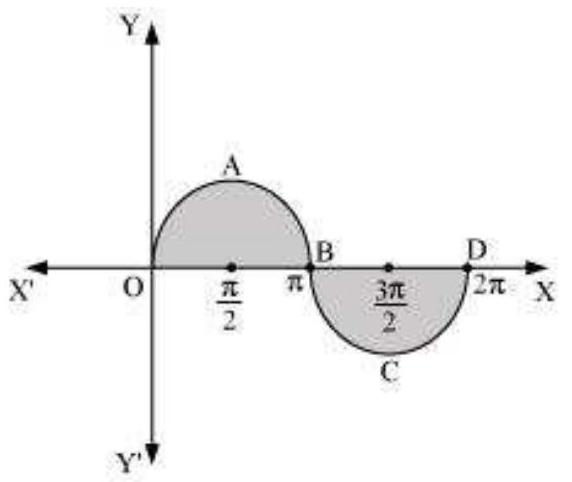
$\therefore$ आवश्यक क्षेत्रफल $=$ क्षेत्र $OABO+$ क्षेत्र $BCDB$

$ \begin{aligned} & =\int_0^{\pi} \sin x d x+|\int _{\pi}^{2 \pi} \sin x d x| \\ & =[-\cos x]_0^{\pi}+|[-\cos x] _{\pi}^{2 \pi}| \\ & =[-\cos \pi+\cos 0]+|-\cos 2 \pi+\cos \pi| \\ & =1+1+|(-1-1)| \\ & =2+|-2| \\ & =2+2=4 \text{ इकाई } \end{aligned} $

हल

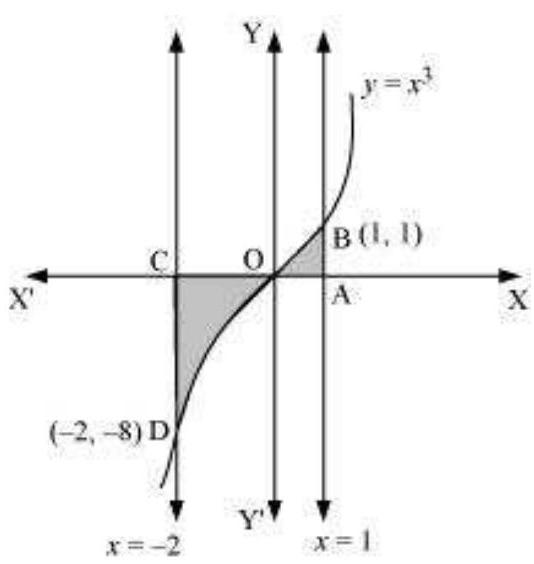
आवश्यक क्षेत्रफल $=\int _{-2}^{1} y d x$

1 धनात्मक और ऋणात्मक क्षेत्र की पहचान करें:

• हम जानते हैं कि वक्र x = -2 और x = 0 के बीच x-अक्ष के नीचे गिर जाता है (लगभग x = -1 के बिंदु पर)।

• इसलिए, हम वक्र के तल के नीचे क्षेत्रफल की गणना दो खंडों में करेंगे:

  • x-अक्ष के ऊपर क्षेत्रफल: x = 0 से x = 1 तक (धनात्मक)
  • x-अक्ष के नीचे क्षेत्रफल: x = -2 से x = 0 तक (ऋणात्मक)

2 सीमित समाकलन बनाएं:

• x-अक्ष के ऊपर क्षेत्रफल: ∫₀¹ (x^3) dx
• x-अक्ष के नीचे क्ष त्रफल: ∫-20 (x^3) dx (यहां ऋणात्मक चिह्न का ध्यान रखें ताकि x-अक्ष के नीचे क्षेत्रफल को गिना जा सके)

3 समाकलन का मूल्यांकन करें: पिछले चरण के जैसे ही शक्ति नियम का उपयोग करते हुए:

• x-अक्ष के ऊपर क्षेत्रफल: [(x^4)/4]₀¹ = (1/4)
• x-अक्ष के नीचे क्षेत्रफल: |[(-x^4)/4]₋²⁰| = (16/4) (धनात्मक क्षेत्रफल को गिनने के लिए अंतर्गत धनात्मक मान लें)

4 समाप्त घिरे क्षेत्रफल की गणना करें:

• समाप्त घिरे क्षेत्रफल = x-अक्ष के ऊपर क्षेत्रफल + x-अक्ष के नीचे क्षेत्रफल = (1/4) + (16/4) = 17/4

सही विकल्प D है।

हल

अभीष्ट क्षेत्रफल $=\int _{-1}^{1} y d x$

$=-\int _{-1}^{1} x|x| d x$

$=\int _{-1}^{0} x^{2} d x+\int_0^{1} x^{2} d x$

$=-[\frac{x^{3}}{3}] _{-1}^{0}+[\frac{x^{3}}{3}]_0^{1}$

$=-(-\frac{1}{3})+\frac{1}{3}$

$=\frac{2}{3}$ इकाई

इसलिए, सही उत्तर C है।