हल

दी गई वृत्त के समीकरण, $\frac{x^{2}}{16}+\frac{y^{2}}{9}=1$, को निम्नलिखित रूप में प्रस्तुत किया जा सकता है

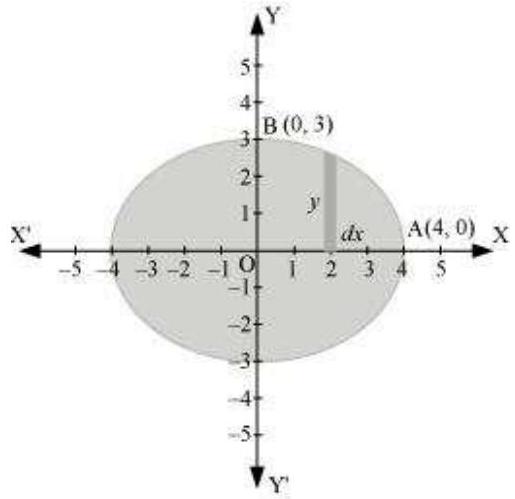
यह देखा जा सकता है कि वृत्त $x$-अक्ष और $y$-अक्ष के संदर्भ में सममित है।

$\therefore$ वृत्त द्वारा घिरे क्षेत्रफल $=4 \times$ OAB क्षेत्रफल

$ \begin{aligned} \text{ OAB क्षेत्रफल } & =\int_0^{4} y d x \\ & =\int_0^{4} 3 \sqrt{1-\frac{x^{2}}{16}} d x \\ & =\frac{3}{4} \int_0^{4} \sqrt{16-x^{2}} d x \\ & =\frac{3}{4}[\frac{x}{2} \sqrt{16-x^{2}}+\frac{16}{2} \sin ^{-1} \frac{x}{4}]_0^{4} \\ & =\frac{3}{4}[2 \sqrt{16-16}+8 \sin ^{-1}(1)-0-8 \sin ^{-1}(0)] \\ & =\frac{3}{4}[\frac{8 \pi}{2}] \\ & =\frac{3}{4}[4 \pi] \\ & =3 \pi \end{aligned} $

इसलिए, वृत्त द्वारा घिरे क्षेत्रफल $=4 \times 3\pi =12 \pi$ इकाई

हल

दी गई वृत्त के समीकरण को निम्नलिखित रूप में प्रस्तुत किया जा सकता है

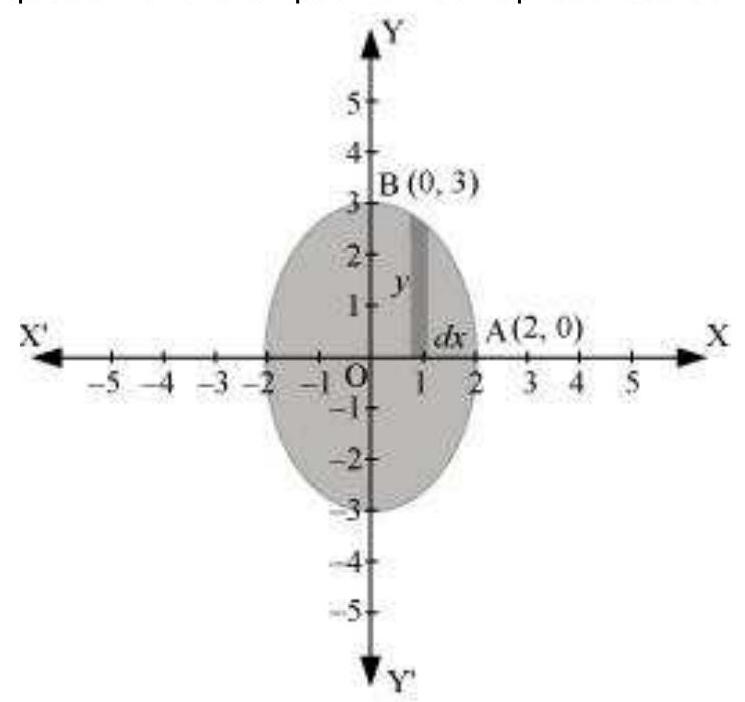
$\frac{x^{2}}{4}+\frac{y^{2}}{9}=1$

$\Rightarrow y=3 \sqrt{1-\frac{x^{2}}{4}}$

यह देखा जा सकता है कि वृत्त $x$-अक्ष और $y$-अक्ष के संदर्भ में सममित है।

$\therefore$ वृत्त द्वारा घिरे क्षेत्रफल $=4 \times$ OAB क्षेत्रफल $\therefore$ OAB क्षेत्रफल $=\int_0^{2} y d x$

$ \begin{aligned} & =\int_0^{2} 3 \sqrt{1-\frac{x^{2}}{4}} d x \quad \text{ [समीकरण (1) का उपयोग करके] } \\ & =\frac{3}{2} \int_0^{2} \sqrt{4-x^{2}} d x \\ & =\frac{3}{2}[\frac{x}{2} \sqrt{4-x^{2}}+\frac{4}{2} \sin ^{-} \frac{x}{2}]_0^{2} \\ & =\frac{3}{2}[\frac{2 \pi}{2}] \\ & =\frac{3 \pi}{2} \end{aligned} $

इसलिए, वृत्त द्वारा घिरे क्षेत्र का क्षेत्रफल $=4 \times \frac{3 \pi}{2}=6 \pi$ इकाई है

हल

वृत्त और रेखाओं $x=0$ और $x=2$ द्वारा पहले चतुर्थांश में घिरे क्षेत्र को निम्नलिखित चित्र द्वारा प्रस्तुत किया गया है

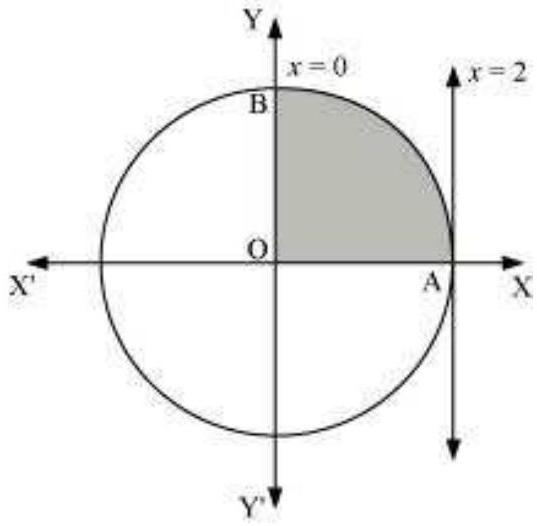
$ \begin{aligned} \therefore \text{ क्षेत्र OAB } & =\int_0^{2} y d x \\ & =\int_0^{2} \sqrt{4-x^{2}} d x \\ & =[\frac{x}{2} \sqrt{4-x^{2}}+\frac{4}{2} \sin ^{-1} \frac{x}{2}]_0^{2} \\ & =2(\frac{\pi}{2}) \\ & =\pi \text{ इकाई } \end{aligned} $

इसलिए, सही उत्तर $A$ है।

हल

वक्र, $y^{2}=4 x$, $y$-अक्ष और $y=3$ द्वारा घिरे क्षेत्र को निम्नलिखित चित्र द्वारा प्रस्तुत किया गया है

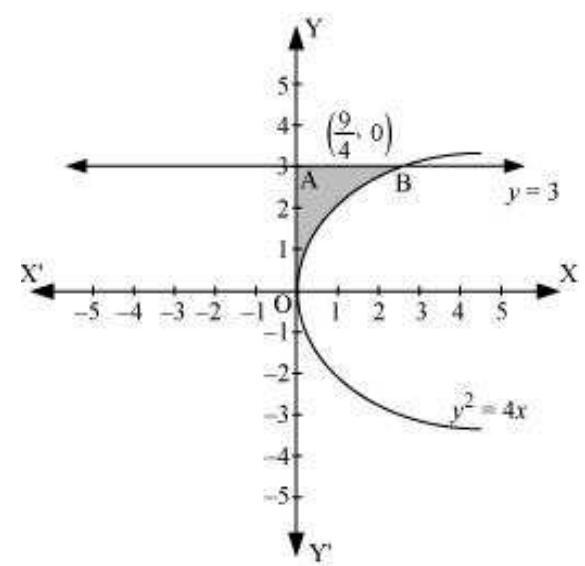
$\therefore$ क्षेत्रफल $OAB=\int_0^{3} x d y$

$ =\int_0^{3} \frac{y^{2}}{4} d y $

$ \begin{aligned} & =\frac{1}{4}[\frac{y^{3}}{3}]_0^{3} \\ & =\frac{1}{12}(27) \\ & =\frac{9}{4} \text{ units } \end{aligned} $

इसलिए, सही उत्तर $B$ है।