हल

दिया गया फलन $f(x)=\frac{\log x}{x}$ है।

$ f^{\prime}(x)=\frac{x(\frac{1}{x})-\log x}{x^{2}}=\frac{1-\log x}{x^{2}} $

अब, $f^{\prime}(x)=0$

$\Rightarrow 1-\log x=0$ $\Rightarrow \log x=1$

$\Rightarrow \log x=\log e$

$\Rightarrow x=e$

अब, $f^{\prime \prime}(x)=\frac{x^{2}(-\frac{1}{x})-(1-\log x)(2 x)}{x^{4}}$

$ \begin{aligned} & =\frac{-x-2 x(1-\log x)}{x^{4}} \\ & =\frac{-3+2 \log x}{x^{3}} \end{aligned} $

अब, $f^{\prime \prime}(e)=\frac{-3+2 \log e}{e^{3}}=\frac{-3+2}{e^{3}}=\frac{-1}{e^{3}}<0$

इसलिए, द्वितीय अवकलज परीक्षण के अनुसार, $f$ का मान $x=e$ पर अधिकतम होता है।

हल

मान लीजिए $\triangle A B C$ एक समद्विबाहु त्रिभुज है जहाँ $B C$ निश्चित लंबाई का आधार $b$ है।

मान लीजिए $\triangle A B C$ की दो बराबर भुजाओं की लंबाई $a$ है।

AD $\square BC$ खींचिए।

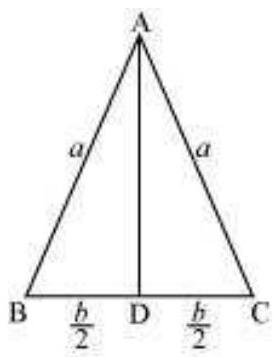
अब, $\triangle A D C$ में पिथागोरस प्रमेय के अनुसार, हमें प्राप्त होता है:

$AD=\sqrt{a^{2}-\frac{b^{2}}{4}}$

त्रिभुज का क्षेत्रफल

$ (A)=\frac{1}{2} b \sqrt{a^{2}-\frac{b^{2}}{4}} $

क्षेत्रफल के संबंध में समय $(t)$ के संबंध में परिवर्तन की दर निम्नलिखित है,

$\frac{d A}{d t}=\frac{1}{2} b \cdot \frac{2 a}{2 \sqrt{a^{2}-\frac{b^{2}}{4}}} \frac{d a}{d t}=\frac{a b}{\sqrt{4 a^{2}-b^{2}}} \frac{d a}{d t}$

दिया गया है कि त्रिभुज की दो बराबर भुजाएँ $3$ सेमी/सेकंड की दर से घट रही हैं।

$ \begin{aligned} & \\ & \square \frac{d a}{d t}=-3\ cm / s \\ & \therefore \frac{d A}{d t}=\frac{-3 a b}{\sqrt{4 a^{2}-b^{2}}} \end{aligned} $

फिर, जब $a=b$ हो, तो हमें प्राप्त होता है:

$\frac{d A}{d t}=\frac{-3 b^{2}}{\sqrt{4 b^{2}-b^{2}}}=\frac{-3 b^{2}}{\sqrt{3 b^{2}}}=-\sqrt{3} b$

इसलिए, यदि दो समान भुजाएँ आधार के बराबर हों, तो त्रिभुज का क्षेत्रफल $\sqrt{3} bm\ cm^{2} / s$ की दर से घट रहा है।

हल

$f(x)=\frac{4 \sin x-2 x-x \cos x}{2+\cos x}$

$\therefore f^{\prime}(x)=\frac{(2+\cos x)(4 \cos x-2-\cos x+x \sin x)-(4 \sin x-2 x-x \cos x)(-\sin x)}{(2+\cos x)^{2}}$

$=\frac{(2+\cos x)(3 \cos x-2+x \sin x)+\sin x(4 \sin x-2 x-x \cos x)}{(2+\cos x)^{2}}$

$=\frac{6 \cos x-4+2 x \sin x+3 \cos ^{2} x-2 \cos x+x \sin x \cos x+4 \sin ^{2} x-2 x \sin x-x \sin x \cos x}{(2+\cos x)^{2}}$

$=\frac{4 \cos x-4+3 \cos ^{2} x+4 \sin ^{2} x}{(2+\cos x)^{2}}$

$=\frac{4 \cos x-4+3 \cos ^{2} x+4-4 \cos ^{2} x}{(2+\cos x)^{2}}$

$=\frac{4 \cos x-\cos ^{2} x}{(2+\cos x)^{2}}=\frac{\cos x(4-\cos x)}{(2+\cos x)^{2}}$

अब, $f^{\prime}(x)=0$

$\Rightarrow \cos x=0$ या $\cos x=4$

लेकिन, $\cos x \neq 4$

$\square \cos x=0$

$\Rightarrow x=\frac{\pi}{2}, \frac{3 \pi}{2}$

अब, $x=\frac{\pi}{2}$ और $x=\frac{3 \pi}{2}$ अंतराल $(0,2 \pi)$ को तीन अलग-अलग अंतराल में विभाजित करते हैं, अर्थात,

$(0, \frac{\pi}{2}),(\frac{\pi}{2}, \frac{3 \pi}{2})$, और $(\frac{3 \pi}{2}, 2 \pi)$।

अंतराल $(0, \frac{\pi}{2})$ और $(\frac{3 \pi}{2}, 2 \pi)$ में $f^{\prime}(x)>0$ है।

इसलिए, $f(x)$ के लिए $0<x<\frac{x}{2}$ और $\frac{3 \pi}{2}<x<2 \pi$ में बढ़ रहा है।

अंतराल $(\frac{\pi}{2}, \frac{3 \pi}{2})$ में $f^{\prime}(x)<0$ है।

इसलिए, $f(x)$ के लिए $\frac{\pi}{2}<x<\frac{3 \pi}{2}$ में घट रहा है।

हल

$f(x)=x^{3}+\frac{1}{x^{3}}$

$\therefore f^{\prime}(x)=3 x^{2}-\frac{3}{x^{4}}=\frac{3 x^{6}-3}{x^{4}}$

फिर, $f^{\prime}(x)=0 \Rightarrow 3 x^{6}-3=0 \Rightarrow x^{6}=1 \Rightarrow x= \pm 1$

अब, बिंदु $x=1$ और $x=-1$ वास्तविक रेखा को तीन अलग-अलग अंतराल में विभाजित करते हैं

अर्थात, $(-\infty,-1),(-1,1)$, और $(1, \infty)$।

अंतराल $(-\infty,-1)$ और $(1, \infty)$ में, अर्थात जब $x<-1$ और $x>1, f^{\prime}(x)>0$ होता है।

इसलिए, जब $x<-1$ और $x>1, f$ बढ़ रहा है।

अंतराल $(-1,1)$ में, अर्थात जब $-1<x<1, f^{\prime}(x)<0$ होता है।

इसलिए, जब $-1<x<1, f$ घट रहा है।

हल

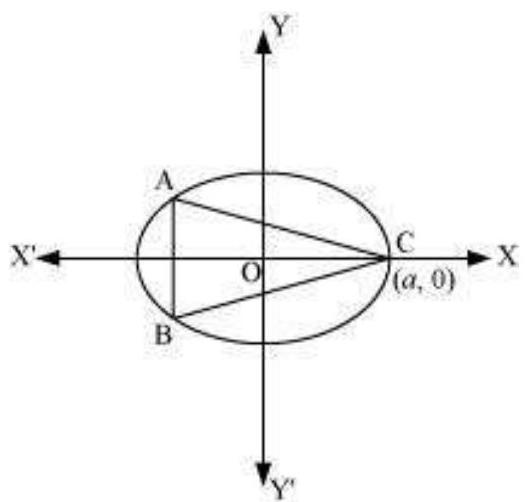
दिया गया वृत्त $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$ है।

मान लीजिए मुख्य अक्ष $x$-अक्ष के अनुदिश है।

मान लीजिए $A B C$ वृत्त में अंकित एक त्रिभुज है जहाँ शीर्ष $C$ बिंदु $(a, 0)$ पर है।

चूंकि वृत्त $x$-अक्ष और $y$-अक्ष के संबंध में सममित है, हम मान सकते हैं कि $A$ के निर्देशांक $(-x_1, y_1)$ हैं और $B$ के निर्देशांक $(-x_1,-y_1)$ हैं।

अब, हमें $y_1= \pm \frac{b}{a} \sqrt{a^{2}-x_1^{2}}$ है।

$\square$ $A$ के निर्देशांक $(-x_1, \frac{b}{a} \sqrt{a^{2}-x_1^{2}})$ हैं और $B$ के निर्देशांक $(x_1,-\frac{b}{a} \sqrt{a^{2}-x_1^{2}})$ हैं।

जब बिंदु $(x_1, y_1)$ वृत्त पर स्थित होता है, तो त्रिभुज $ABC$ का क्षेत्रफल निम्नलिखित द्वारा दिया जाता है,

$ \begin{aligned} & A=\frac{1}{2}|a(\frac{2 b}{a} \sqrt{a^{2}-x_1^{2}})+(-x_1)(-\frac{b}{a} \sqrt{a^{2}-x_1^{2}})+(-x_1)(-\frac{b}{a} \sqrt{a^{2}-x_1^{2}})| \\

$$ \begin{aligned} & \Rightarrow A=b \sqrt{a^{2}-x_1^{2}}+x_1 \frac{b}{a} \sqrt{a^{2}-x_1^{2}} \\ & \therefore \frac{d A}{d x_1}=\frac{-2 x_1 b}{2 \sqrt{a^{2}-x_1^{2}}}+\frac{b}{a} \sqrt{a^{2}-x_1^{2}}-\frac{2 b x_1^{2}}{a 2 \sqrt{a^{2}-x_1^{2}}} \\ & =\frac{b}{a \sqrt{a^{2}-x_1^{2}}}[-x_1 a+(a^{2}-x_1^{2})-x_1^{2}] \\ & =\frac{b(-2 x_1^{2}-x_1 a+a^{2})}{a \sqrt{a^{2}-x_1^{2}}} \end{aligned} $$

अब, $\frac{d A}{d x_1}=0$

$\Rightarrow-2 x_1^{2}-x_1 a+a^{2}=0$

$\Rightarrow x_1=\frac{a \pm \sqrt{a^{2}-4(-2)(a^{2})}}{2(-2)}$

$=\frac{a \pm \sqrt{9 a^{2}}}{-4}$

$=\frac{a \pm 3 a}{-4}$

$\Rightarrow x_1=-a, \frac{a}{2}$

लेकिन, $x_1$ के मान $a$ के बराबर नहीं हो सकता। $\therefore x_1=\frac{a}{2} \Rightarrow y_1=\frac{b}{a} \sqrt{a^{2}-\frac{a^{2}}{4}}=\frac{b a}{2 a} \sqrt{3}=\frac{\sqrt{3} b}{2}$

अब, $\frac{d^{2} A}{d x_1^{2}}=\frac{b}{a}{\frac{\sqrt{a^{2}-x_1^{2}}(-4 x_1-a)-(-2 x_1^{2}-x_1 a+a^{2}) \frac{(-2 x_1)}{2 \sqrt{a^{2}-x_1^{2}}}}{a^{2}-x_1^{2}}}$

$ =\frac{b}{a}{\frac{(a^{2}-x_1^{2})(-4 x_1-a)+x_1(-2 x_1^{2}-x_1 a+a^{2})}{(a^{2}-x_1^{2})^{\frac{3}{2}}}} $

$ =\frac{b}{a}{\frac{2 x^{3}-3 a^{2} x-a^{3}}{(a^{2}-x_1^{2})^{\frac{3}{2}}}} $

इसके अतिरिक्त, जब $x_1=\frac{a}{2}$, तो

$ \begin{aligned} \frac{d^{2} A}{d x_1^{2}} & =\frac{b}{a}{\frac{2 \frac{a^{3}}{8}-3 \frac{a^{3}}{2}-a^{3}}{(\frac{3 a^{2}}{4})^{\frac{3}{2}}}}=\frac{b}{a}{\frac{\frac{a^{3}}{4}-\frac{3}{2} a^{3}-a^{3}}{(\frac{3 a^{2}}{4})^{\frac{3}{2}}}} \\ & =-\frac{b}{a}{\frac{\frac{9}{4} a^{3}}{(\frac{3 a^{2}}{4})^{\frac{3}{2}}}}<0 \end{aligned} $

इसलिए, जब $x_1=\frac{a}{2}$, तब क्षेत्रफल अधिकतम होता है।

$\square$ त्रिभुज का अधिकतम क्षेत्रफल निम्नलिखित है,

$ \begin{aligned} A & =b \sqrt{a^{2}-\frac{a^{2}}{4}}+(\frac{a}{2}) \frac{b}{a} \sqrt{a^{2}-\frac{a^{2}}{4}} \\ & =a b \frac{\sqrt{3}}{2}+(\frac{a}{2}) \frac{b}{a} \times \frac{a \sqrt{3}}{2} \\ & =\frac{a b \sqrt{3}}{2}+\frac{a b \sqrt{3}}{4}=\frac{3 \sqrt{3}}{4} a b \end{aligned} $

हल

मान लीजिए $l, b$, और $h$ क्रमशः टैंक की लंबाई, चौड़ाई और ऊंचाई को प्रस्तुत करते हैं।

तब, हमें ऊंचाई $(h)=2$ मीटर मिलती है।

टैंक का आयतन $=8$ मीटर³ है।

टैंक का आयतन $=l \times b \times h$

$\square 8=l \times b \times 2$

$\Rightarrow l b=4 \Rightarrow b=\frac{4}{l}$

अब, आधार का क्षेत्रफल $=I b=4$

चार दीवारों का क्षेत्रफल $(A)=2 h(I+b)$

$\therefore A=4(l+\frac{4}{l})$

$\Rightarrow \frac{d A}{d l}=4(1-\frac{4}{l^{2}})$

अब, $\frac{d A}{d l}=0$

$\Rightarrow 1-\frac{4}{l^{2}}=0$

$\Rightarrow l^{2}=4$

$\Rightarrow l= \pm 2$

हालांकि, लंबाई नकारात्मक नहीं हो सकती।

इसलिए, हमें $I=4$ मिलता है।

$\therefore b=\frac{4}{l}=\frac{4}{2}=2$

अब, $\frac{d^{2} A}{d l^{2}}=\frac{32}{l^{3}}$

जब $l=2, \frac{d^{2} A}{d l^{2}}=\frac{32}{8}=4>0$।

इसलिए, दूसरे अवकलज परीक्षण के अनुसार, क्षेत्रफल जब $I=2$ होता है तो न्यूनतम होता है।

हमें $I=b=h=2$ मिलता है।

$\square$ आधार के निर्माण की लागत $=70$ रुपये $\times (I b)=70(4)=280$ रुपये

दीवारों के निर्माण की लागत $=2 h(I+b) \times 45=90(2)(2+2)$

$=8(90)=720$ रुपये

अभीष्ट कुल लागत $=280+720=1000$ रुपये

इसलिए, टैंक की कुल लागत 1000 रुपये होगी।

हल

मान लीजिए $r$ वृत्त की त्रिज्या है और $a$ वर्ग की भुजा है।

तब, हमें दिया गया है:

$2 \pi r+4 a=k$ (जहाँ $k$ नियत संख्या है)

$\Rightarrow a=\frac{k-2 \pi r}{4}$

वृत्त और वर्ग के क्षेत्रफल के योग $(A)$ निम्नलिखित है,

$A=\pi r^{2}+a^{2}=\pi r^{2}+\frac{(k-2 \pi r)^{2}}{16}$

$\therefore \frac{d A}{d r}=2 \pi r+\frac{2(k-2 \pi r)(-2 \pi)}{16}=2 \pi r-\frac{\pi(k-2 \pi r)}{4}$

अब, $\frac{d A}{d r}=0$

$\Rightarrow 2 \pi r=\frac{\pi(k-2 \pi r)}{4}$

$8 r=k-2 \pi r$

$\Rightarrow(8+2 \pi) r=k$

$\Rightarrow r=\frac{k}{8+2 \pi}=\frac{k}{2(4+\pi)}$

अब, $\frac{d^{2} A}{d r^{2}}=2 \pi+\frac{\pi^{2}}{2}>0$

$\therefore$ जब $r=\frac{k}{2(4 \pi)}, \frac{d^{2} A}{d r^{2}}>0$।

जब $r=\frac{k}{2(4 \pi)}, a=\frac{k-2 \pi[\frac{k}{2(4 \pi)}]}{4}=\frac{k(4 \pi) \pi k}{4(\pi)}=\frac{4 k}{4(\pi)}=\frac{k}{\pi}=2 r$।

अतः सिद्ध कर दिया गया है कि वृत्त और वर्ग के क्षेत्रफल के योग कम से कम होता है जब वर्ग की भुजा वृत्त की त्रिज्या के दुगुनी होती है।

हल

मान लीजिए $x$ और $y$ आयताकार खिड़की की लंबाई और चौड़ाई है।

अर्धवृत्ताकार खोल की त्रिज्या $=\frac{x}{2}$

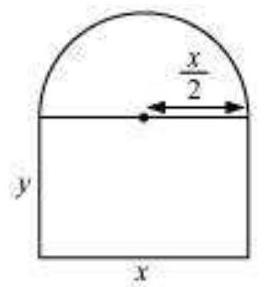
दिया गया है कि खिड़की का परिमाप $10 मीटर$ है।

$\therefore x+2 y+\frac{\pi x}{2}=10$

$\Rightarrow x(1+\frac{\pi}{2})+2 y=10$

$\Rightarrow 2 y=10-x(1+\frac{\pi}{2})$

$\Rightarrow y=5-x(\frac{1 \pi}{2}+\frac{-}{4})$

आवृत्ति क्षेत्रफल $(A)$ निम्नलिखित द्वारा दिया गया है,

$ \begin{aligned} A & =x y+\frac{\pi}{2}(\frac{x}{2})^{2} \\ & =x[5-x(\frac{1 \pi}{2}+\frac{\pi}{4})]+\frac{x^{2}}{8} \\ & =5 x-x^{2}(\frac{1 \pi}{2}+\frac{\pi}{4})+\frac{\pi}{8} x^{2} \\ \therefore & \frac{d A}{d x}=5-2 x(\frac{1 \pi}{2}+\frac{\pi}{4})+\frac{\pi}{4} x \\ & =5-x(1+\frac{\pi}{2})+\frac{\pi}{4} x \\ \therefore & \frac{d^{2} A}{d x^{2}}=-(1+\frac{\pi}{2})+\frac{\pi}{4}=-1-\frac{\pi}{4} \end{aligned} $

अब, $\frac{d A}{d x}=0$

$\Rightarrow 5-x(1+\frac{\pi}{2})+\frac{\pi}{4} x=0$

$\Rightarrow 5-x-\frac{\pi}{4} x=0$

$\Rightarrow x(1+\frac{\pi}{4})=5$

$\Rightarrow x=\frac{5}{(1+\frac{\pi}{4})}=\frac{20}{\pi+4}$

अतः जब $x=\frac{20}{\pi+4}$ तो $\frac{d^{2} A}{d x^{2}}<0$।

इसलिए, द्वितीय अवकलज परीक्षण के अनुसार, क्षेत्रफल अधिकतम होता है जब लंबाई $x=\frac{20}{\pi+4} m$ हो। अब,

$y=5-\frac{20}{\pi+4}(\frac{2+\pi}{4})=5-\frac{5(2+\pi)}{\pi+4}=\frac{10}{\pi+4} m$

इसलिए, अधिकतम प्रकाश प्रवेश करने वाले खिड़की के आवश्यक आयाम द्वारा दिए गए हैं

लंबाई $=\frac{20}{\pi+4} m$ और चौड़ाई $=\frac{10}{\pi+4} m$।

हल

मान लीजिए $\triangle A B C$ बिंदु $B$ पर समकोण है। मान लीजिए $A B=x$ और $B C=y$।

मान लीजिए $P$ त्रिभुज के कर्ण पर एक बिंदु है जैसे कि $P$ भुजा $A B$ और $B C$ से क्रमशः $a$ और $b$ की दूरी पर है।

मान लीजिए $\square C=\theta$।

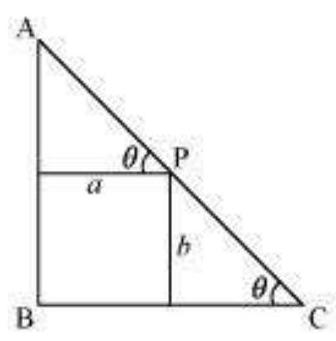
हमारे पास,

$AC=\sqrt{x^{2}+y^{2}}$

अब,

$PC=b cosec \theta$

और, $AP=a \sec \theta$

$\square AC=AP+PC$

$\square AC=b cosec \theta+a \sec \theta \ldots$ (1)

$\therefore \frac{d(AC)}{d \theta}=-b cosec \theta \cot \theta+a \sec \theta \tan \theta$

$\therefore \frac{d(AC)}{d \theta}=0$

$\Rightarrow a \sec \theta \tan \theta=b cosec \theta \cot \theta$

$\Rightarrow \frac{a}{\cos \theta} \cdot \frac{\sin \theta}{\cos \theta}=\frac{b}{\sin \theta} \frac{\cos \theta}{\sin \theta}$

$\Rightarrow a \sin ^{3} \theta=b \cos ^{3} \theta$

$\Rightarrow(a)^{\frac{1}{3}} \sin \theta=(b)^{\frac{1}{3}} \cos \theta$

$\Rightarrow \tan \theta=(\frac{b}{a})^{\frac{1}{3}}$

$\therefore \sin \theta=\frac{(b)^{\frac{1}{3}}}{\sqrt{a^{\frac{2}{3}}+b^{\frac{2}{3}}}}$ और $\cos \theta=\frac{(a)^{\frac{1}{3}}}{\sqrt{a^{\frac{2}{3}}+b^{\frac{2}{3}}}}$

स्पष्ट रूप से दिखाया जा सकता है कि $\frac{d^{2}(AC)}{d \theta^{2}}<0$ जब $\tan \theta=(\frac{b}{a})^{\frac{1}{3}}$।

इसलिए, द्वितीय अवकलज परीक्षण के अनुसार, तीन कोण की लंबाई अधिकतम होती है जब

$\tan \theta=(\frac{b}{a})^{\frac{1}{3}}$.

अब, जब $\tan \theta=(\frac{b}{a})^{\frac{1}{3}}$, हम निम्नलिखित प्राप्त करते हैं:

$ \begin{aligned} AC & =\frac{b \sqrt{a^{\frac{2}{3}}+b^{\frac{2}{3}}}}{b^{\frac{1}{3}}}+\frac{a \sqrt{a^{\frac{2}{3}}+b^{\frac{2}{3}}}}{a^{\frac{1}{3}}} \\ & =\sqrt{a^{\frac{2}{3}}+b^{\frac{2}{3}}}(b^{\frac{2}{3}}+a^{\frac{2}{3}}) \\ & =(a^{\frac{2}{3}}+b^{\frac{2}{3}})^{\frac{3}{2}} \end{aligned} $

इसलिए, अधिकतम तीन कोण की लंबाई $(a^{\frac{2}{3}}+b^{\frac{2}{3}})^{\frac{3}{2}}$ है।

हल

दिया गया फलन $f(x)=(x-2)^{4}(x+1)^{3}$ है।

$ \begin{aligned} \therefore f^{\prime}(x) & =4(x-2)^{3}(x+1)^{3}+3(x+1)^{2}(x-2)^{4} \\ & =(x-2)^{3}(x+1)^{2}[4(x+1)+3(x-2)] \\ & =(x-2)^{3}(x+1)^{2}(7 x-2) \end{aligned} $

अब, $f^{\prime}(x)=0 \Rightarrow x=-1$ और $x=\frac{2}{7}$ या $x=2$

अब, $x$ के मान जो $\frac{2}{7}$ के निकट हों और $\frac{2}{7}$ के बाईं ओर हों, $f^{\prime}(x)>0$ होता है। इसके अतिरिक्त, $x$ के मान जो $\frac{2}{7}$ के निकट हों और $\frac{2}{7}$ के दाईं ओर हों, $f^{\prime}(x)<0$ होता है।

इसलिए, $x=\frac{2}{7}$ स्थानीय उच्चिष्ठ बिंदु है।

अब, $x$ के मान जो 2 के निकट हों और 2 के बाईं ओर हों, $f^{\prime}(x)<0$ होता है। इसके अतिरिक्त, $x$ के मान जो 2 के निकट हों और 2 के दाईं ओर हों, $f^{\prime}(x)>0$ होता है।

इसलिए, $x=2$ स्थानीय निम्निष्ठ बिंदु है।

अब, $x$ के मान जो $-1$ के माध्यम से चलते हैं, $f^{\prime}(x)$ अपना चिह्न बदलता नहीं है।

इसलिए, $x=-1$ वक्रता परिवर्तन बिंदु है।

हल

$ \begin{aligned} f(x) & =\cos ^{2} x+\sin x \\ f^{\prime}(x) & =2 \cos x(-\sin x)+\cos x \\ & =-2 \sin x \cos x+\cos x

\end{aligned} $

अब, $f^{\prime}(x)=0$

$\Rightarrow 2 \sin x \cos x=\cos x \Rightarrow \cos x(2 \sin x-1)=0$

$\Rightarrow \sin x=\frac{1}{2}$ या $\cos x=0$

$\Rightarrow x=\frac{\pi}{6}$, या $\frac{\pi}{2}$ क्योंकि $x \in[0, \pi]$

अब, अंतराल $[0, \pi]$ के क्रिटिकल बिंदुओं $x=\frac{\pi}{2}$ और $x=\frac{\pi}{6}$ तथा अंतिम बिंदुओं (अर्थात $x=0$ और $x=\pi$) पर $f$ के मान का मूल्यांकन करते हैं, हम पाते हैं: $f(\frac{\pi}{6})=\cos ^{2} \frac{\pi}{6}+\sin \frac{\pi}{6}=(\frac{\sqrt{3}}{2})^{2}+\frac{1}{2}=\frac{5}{4}$

$f(0)=\cos ^{2} 0+\sin 0=1+0=1$

$f(\pi)=\cos ^{2} \pi+\sin \pi=(-1)^{2}+0=1$

$f(\frac{\pi}{2})=\cos ^{2} \frac{\pi}{2}+\sin \frac{\pi}{2}=0+1=1$

इसलिए, $f$ का अंतिम अधिकतम मान $\frac{5}{4}$ है जो $x=\frac{\pi}{6}$ पर होता है और $f$ का अंतिम न्यूनतम मान 1 है जो $x=0, \frac{\pi}{2}$ और $\pi$ पर होता है।

हल

एक निश्चित त्रिज्या $(r)$ वाला एक गोला दिया गया है।

मान लीजिए $R$ और $h$ क्रमशः बेलन की त्रिज्या और ऊंचाई है।

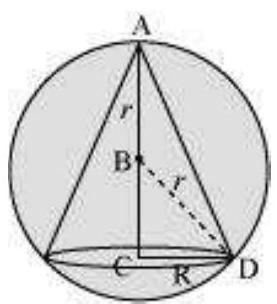
बेलन का आयतन $(V)$ निम्नलिखित द्वारा दिया गया है,

$V=\frac{1}{3} \pi R^{2} h$

अब, समकोण त्रिभुज $BCD$ से हम पाते हैं:

$BC=\sqrt{r^{2}-R^{2}}$

$\square h=r+\sqrt{r^{2}-R^{2}}$

$ \begin{aligned} & \therefore V=\frac{1}{3} \pi R^{2}(r+\sqrt{r^{2}-R^{2}})=\frac{1}{3} \pi R^{2} r+\frac{1}{3} \pi R^{2} \sqrt{r^{2}-R^{2}} \\ & \begin{aligned} \therefore \frac{d V}{d R} & =\frac{2}{3} \pi R r+\frac{2 \pi}{3} \pi R \sqrt{r^{2}-R^{2}}+\frac{R^{2}}{3} \cdot \frac{(-2 R)}{2 \sqrt{r^{2}-R^{2}}} \\ & =\frac{2}{3} \pi R r+\frac{2 \pi}{3} \pi R \sqrt{r^{2}-R^{2}}-\frac{R^{3}}{3 \sqrt{r^{2}-R^{2}}} \\

$$ \begin{aligned} & =\frac{2}{3} \pi R r+\frac{2 \pi R(r^{2}-R^{2})-\pi R^{3}}{3 \sqrt{r^{2}-R^{2}}} \\ & =\frac{2}{3} \pi R r+\frac{2 \pi R r^{2}-3 \pi R^{3}}{3 \sqrt{r^{2}-R^{2}}} \end{aligned} $$ $$ \end{aligned} $$

अब, $\frac{d V}{d R^{2}}=0$

$\Rightarrow \frac{2 \pi r R}{3}=\frac{3 \pi R^{3}-2 \pi R r^{2}}{3 \sqrt{r^{2}-R^{2}}}$

$\Rightarrow 2 r \sqrt{r^{2}-R^{2}}=3 R^{2}-2 r^{2}$

$\Rightarrow 4 r^{2}(r^{2}-R^{2})=(3 R^{2}-2 r^{2})^{2}$

$\Rightarrow 4 r^{4}-4 r^{2} R^{2}=9 R^{4}+4 r^{4}-12 R^{2} r^{2}$

$\Rightarrow 9 R^{4}-8 r^{2} R^{2}=0$

$\Rightarrow 9 R^{2}=8 r^{2}$

$\Rightarrow R^{2}=\frac{8 r^{2}}{9}$

अब, $\frac{d^{2} V}{d R^{2}}=\frac{2 \pi r}{3}+\frac{3 \sqrt{r^{2}-R^{2}}(2 \pi r^{2}-9 \pi R^{2})-(2 \pi R r^{2}-3 \pi R^{3})(-6 R) \frac{1}{2 \sqrt{r^{2}-R^{2}}}}{9(r^{2}-R^{2})}$

$ =\frac{2 \pi r}{3}+\frac{3 \sqrt{r^{2}-R^{2}}(2 \pi r^{2}-9 \pi R^{2})+(2 \pi R r^{2}-3 \pi R^{3})(3 R) \frac{1}{2 \sqrt{r^{2}-R^{2}}}}{9(r^{2}-R^{2})} $

अब, जब $R^{2}=\frac{8 r^{2}}{9}$, तो दिखाया जा सकता है कि $\frac{d^{2} V}{d R^{2}}<0$।

$\square$ जब आयतन अधिकतम होता है, तो

$ R^{2}=\frac{8 r^{2}}{9} $

जब $R^{2}=\frac{8 r^{2}}{9}$, तो शंकु की ऊँचाई $=r+\sqrt{r^{2}-\frac{8 r^{2}}{9}}=r+\sqrt{\frac{r^{2}}{9}}=r+\frac{r}{3}=\frac{4 r}{3}$।

इसलिए, देखा जा सकता है कि त्रिज्या $r$ वाले गोले में अंकित अधिकतम आयतन वाले समकोण वृत्तीय शंकु की ऊँचाई $\frac{4 r}{3}$ होती है।

Solution

हम कोई दो बिंदु $\mathrm{c}_1$ और $\mathrm{c}_2$ लेते हैं ताकि

${\mathrm{c} _1, \mathrm{c} _2} \in(\mathrm{a}, \mathrm{b})$ और

$\mathrm{c} _2=\mathrm{c} _1+\mathrm{h}$,

जहाँ $\mathrm{h} \rightarrow \mathrm{O}$

अब, $f^{\prime}\left(c _1\right)=\lim _{h \rightarrow 0} \frac{f\left(c _1+h\right)-f\left(c _1\right)}{h}=\frac{f\left(c _2\right)-f\left(c _1\right)}{c _2-c _1}$

अब, यह दिया गया है कि $\mathrm{f}^{\prime}(\mathrm{x})>0 \quad \forall \mathrm{x} \in(\mathrm{a}, \mathrm{b})$. इसलिए, $\mathrm{f}^{\prime}\left(\mathrm{c}_1\right)>0$

$\Rightarrow \frac{\mathrm{f}\left(\mathrm{c}_2\right)-\mathrm{f}\left(\mathrm{c}_1\right)}{\mathrm{c}_2-\mathrm{c}_1}>\mathrm{O}$

ऊपर के अंश से, हम निष्कर्ष निकाल सकते हैं कि:

1. $\mathrm{c}_2>\mathrm{c}_1$ के लिए, $\mathrm{f}\left(\mathrm{c}_2\right)>\mathrm{f}\left(\mathrm{c}_1\right)$

2. $c_1>c_2$ के लिए, $f\left(c_1\right)>f\left(c_2\right)$

इसलिए, $\mathrm{f}(\mathrm{x})$ अंतराल $(\mathrm{a}, \mathrm{b})$ में एक बढ़ती फलन है।

हल

एक निश्चित त्रिज्या $(R)$ वाले गोले को दिया गया है।

मान लीजिए $r$ और $h$ क्रमशः बेलन की त्रिज्या और ऊंचाई है।

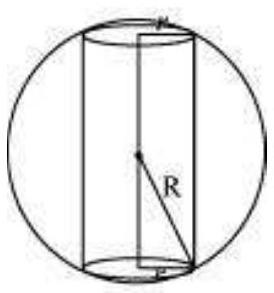
दिए गए चित्र से, हमें $h=2 \sqrt{R^{2}-r^{2}}$ मिलता है।

बेलन के आयतन $(V)$ को निम्नलिखित द्वारा दिया गया है,

$ \begin{aligned} & V=\pi r^{2} h=2 \pi r^{2} \sqrt{R^{2}-r^{2}} \\ & \begin{aligned} \therefore \frac{d V}{d r} & =4 \pi r \sqrt{R^{2}-r^{2}}+\frac{2 \pi r^{2}(-2 r)}{2 \sqrt{R^{2}-r^{2}}} \\ & =4 \pi r \sqrt{R^{2}-r^{2}}-\frac{2 \pi r^{3}}{\sqrt{R^{2}-r^{2}}} \\ & =\frac{4 \pi r(R^{2}-r^{2})-2 \pi r^{3}}{\sqrt{R^{2}-r^{2}}} \\ & =\frac{4 \pi r R^{2}-6 \pi r^{3}}{\sqrt{R^{2}-r^{2}}} \end{aligned} \end{aligned} $

अब, $\frac{d V}{d r}=0 \Rightarrow 4 \pi r R^{2}-6 \pi r^{3}=0$

$\Rightarrow r^{2}=\frac{2 R^{2}}{3}$

अब, $\frac{d^{2} V}{d r^{2}}=\frac{\sqrt{R^{2}-r^{2}}(4 \pi R^{2}-18 \pi r^{2})-(4 \pi r R^{2}-6 \pi r^{3}) \frac{(-2 r)}{2 \sqrt{R^{2}-r^{2}}}}{(R^{2}-r^{2})}$

$ \begin{aligned} & =\frac{(R^{2}-r^{2})(4 \pi R^{2}-18 \pi r^{2})+r(4 \pi r R^{2}-6 \pi r^{3})}{(R^{2}-r^{2})^{\frac{3}{2}}} \\ & =\frac{4 \pi R^{4}-22 \pi r^{2} R^{2}+12 \pi r^{4}+4 \pi r^{2} R^{2}}{(R^{2}-r^{2})^{\frac{3}{2}}} \end{aligned} $

अब, यह देखा जा सकता है कि $r^{2}=\frac{2 R^{2}}{3}$ पर, $\frac{d^{2} V}{d r^{2}}<0$ होता है।

$\square$ जब $r^{2}=\frac{2 R^{2}}{3}$, तब बेलन का आयतन अधिकतम होता है।

जब $r^{2}=\frac{2 R^{2}}{3}$, तब बेलन की ऊँचाई $2 \sqrt{R^{2}-\frac{2 R^{2}}{3}}=2 \sqrt{\frac{R^{2}}{3}}=\frac{2 R}{\sqrt{3}}$ होती है।

अतः, जब बेलन की ऊँचाई $\frac{2 R}{\sqrt{3}}$ होती है, तब बेलन का आयतन अधिकतम होता है।

हल

दिए गए एक निश्चित ऊँचाई $(h)$ और अर्ध-शीर्षकोण $(\alpha)$ वाले समकोण वृताकार शंकु को निम्नलिखित चित्र में बर्क लिया जा सकता है:

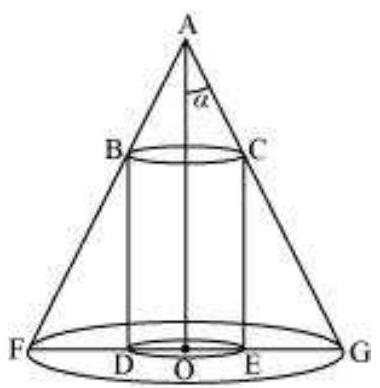
यहाँ, एक बेलन जिसकी त्रिज्या $R$ और ऊँचाई $H$ है, शंकु में आकृति बनाता है।

तब, $\square GAO=a, OG=r, OA=h, OE=R$, और $CE=H$ होता है।

हम जानते हैं,

$r=h \tan a$

अब, क्योंकि $\triangle AOG$ और $\triangle CEG$ समानुपाती हैं, हम लिख सकते हैं:

$\frac{AO}{OG}=\frac{CE}{EG}$

$\Rightarrow \frac{h}{r}=\frac{H}{r-R} \quad[EG=OG-OE]$

$\Rightarrow H=\frac{h}{r}(r-R)=\frac{h}{h \tan \alpha}(h \tan \alpha-R)=\frac{1}{\tan \alpha}(h \tan \alpha-R)$

अब, बेलन का आयतन $(V)$ निम्नलिखित द्वारा दिया जाता है,

$V=\pi R^{2} H=\frac{\pi R^{2}}{\tan \alpha}(h \tan \alpha-R)=\pi R^{2} h-\frac{\pi R^{3}}{\tan \alpha}$

$\therefore \frac{d V}{d R}=2 \pi R h-\frac{3 \pi R^{2}}{\tan \alpha}$

अब, $\frac{d V}{d R}=0$

$\Rightarrow 2 \pi R h=\frac{3 \pi R^{2}}{\tan \alpha}$

$\Rightarrow 2 h \tan \alpha=3 R$

$\Rightarrow R=\frac{2 h}{3} \tan \alpha$

अब, $\frac{d^{2} V}{d R^{2}}=2 \pi h-\frac{6 \pi R}{\tan \alpha}$

और, $R=\frac{2 h}{3} \tan \alpha$ के लिए, हम निम्नलिखित प्राप्त करते हैं:

$\frac{d^{2} V}{d R^{2}}=2 \pi h-\frac{6 \pi}{\tan \alpha}(\frac{2 h}{3} \tan \alpha)=2 \pi h-4 \pi h=-2 \pi h<0$

$\square$ द्वितीय अवकलज परीक्षण के अनुसार, बेलन का आयतन जब $R=\frac{2 h}{3} \tan \alpha$ होता है, तब सबसे अधिक होता है।

जब $R=\frac{2 h}{3} \tan \alpha, H=\frac{1}{\tan \alpha}(h \tan \alpha-\frac{2 h}{3} \tan \alpha)=\frac{1}{\tan \alpha}(\frac{h \tan \alpha}{3})=\frac{h}{3}$।

अतः, जब बेलन का आयतन सबसे अधिक होता है, तब बेलन की ऊँचाई शंकु की ऊँचाई के एक-तिहाई होती है।

अब, बेलन के अधिकतम आयतन को निम्नलिखित तरीके से प्राप्त किया जा सकता है:

$\pi(\frac{2 h}{3} \tan \alpha)^{2}(\frac{h}{3})=\pi(\frac{4 h^{2}}{9} \tan ^{2} \alpha)(\frac{h}{3})=\frac{4}{27} \pi h^{3} \tan ^{2} \alpha$

अतः, दिए गए परिणाम की पुष्टि कर दी गई है।

हल

मान लीजिए $r$ बेलन की त्रिज्या है।

तब, बेलन का आयतन $(V)$ निम्नलिखित द्वारा दिया जाता है,

$V=\pi(\text{ त्रिज्या })^{2} \times$ ऊँचाई

$ \begin{matrix} =\pi(10)^{2} h & (\text{ त्रिज्या }=10 m) \\ =100 \pi h \end{matrix} $

समय $t$ के सापेक्ष अवकलन करने पर, हम निम्नलिखित प्राप्त करते हैं:

$\frac{d V}{d t}=100 \pi \frac{d h}{d t}$

टैंक 314 घन मीटर प्रति घंटा की दर से गेहूँ से भर रहा है।

$ \square \frac{d V}{d t}=314 m^{3} / h $

इसलिए, हम निम्नलिखित प्राप्त करते हैं:

$ \begin{aligned} & 314=100 \pi \frac{d h}{d t} \\ & \Rightarrow \frac{d h}{d t}=\frac{314}{100(3.14)}=\frac{314}{314}=1 \end{aligned} $

इसलिए, गेहूँ की गहराई की वृद्धि दर $1 m / h$ है।

सही उत्तर $A$ है।