हल

(i) दिया गया फलन $f(x)=(2 x-1)^{2}+3$ है।

यह देखा जा सकता है कि $(2 x-1)^{2} \geq 0$ प्रत्येक $x \in \mathbf{R}$ के लिए।

इसलिए, $f(x)=(2 x-1)^{2}+3 \geq 3$ प्रत्येक $x \in \mathbf{R}$ के लिए।

$f$ का न्यूनतम मान जब $2 x-1=0$ होता है।

$2 x-1=0$

$ x=\frac{1}{2} $

$\square$ $f$ का न्यूनतम मान $f(\frac{1}{2})=(2 \cdot \frac{1}{2}-1)^{2}+3=3$

अतः, फलन $f$ का अधिकतम मान नहीं है।

(ii) दिया गया फलन $f(x)=9 x^{2}+12 x+2=(3 x+2)^{2}-2$ है।

यह देखा जा सकता है कि $(3 x+2)^{2} \geq 0$ प्रत्येक $x \in \mathbf{R}$ के लिए।

इसलिए, $f(x)=(3 x+2)^{2}-2 \geq-2$ प्रत्येक $x \in \mathbf{R}$ के लिए।

$f$ का न्यूनतम मान जब $3 x+2=0$ होता है।

$3 x+2=0 \Rightarrow x=\frac{-2}{3}$

$\square$ $f$ का न्यूनतम मान $f(-\frac{2}{3})=(3(\frac{-2}{3})+2)^{2}-2=-2$

अतः, फलन $f$ का अधिकतम मान नहीं है।

(iii) दिया गया फलन $f(x)=-(x-1)^{2}+10$ है।

यह देखा जा सकता है कि $(x-1)^{2} \geq 0$ प्रत्येक $x \in \mathbf{R}$ के लिए।

इसलिए, $f(x)=-(x-1)^{2}+10 \leq 10$ प्रत्येक $x \in \mathbf{R}$ के लिए।

$f$ का अधिकतम मान जब $(x-1)=0$ होता है।

$(x-1)=0 \Rightarrow x=1$

$\square$ $f$ का अधिकतम मान $f(1)=-(1-1)^{2}+10=10$

अतः, फलन $f$ का न्यूनतम मान नहीं है।

(iv) दिया गया फलन $g(x)=x^{3}+1$ है।

अतः, फलन $g$ का अधिकतम और न्यूनतम मान दोनों ही नहीं है।

हल

(i) $f(x)=|x+2|-1$

हम जानते हैं कि $|x+2| \geq 0$ प्रत्येक $x \in \mathbf{R}$ के लिए।

इसलिए, $f(x)=|x+2|-1 \geq-1$ प्रत्येक $x \square \mathbf{R}$ के लिए।

$f$ का न्यूनतम मान जब $|x+2|=0$ होता है।

$|x+2|=0$

$\Rightarrow x=-2$

$\square$ न्यूनतम मान $f=f(-2)=|-2+2|-1=-1$

इसलिए, फलन $f$ का अधिकतम मान नहीं होता।

(ii) $g(x)=-|x+1|+3$

हम जानते हैं कि $-|x+1| \leq 0$ प्रत्येक $x \square \mathbf{R}$ के लिए।

इसलिए, $g(x)=-|x+1|+3 \leq 3$ प्रत्येक $x \square \mathbf{R}$ के लिए।

$g$ का अधिकतम मान जब $|x+1|=0$ होता है।

$|x+1|=0$

$\Rightarrow x=-1$

$\square$ अधिकतम मान $g=g(-1)=-|-1+1|+3=3$

इसलिए, फलन $g$ का न्यूनतम मान नहीं होता। (iii) $h(x)=\sin 2 x+5$

हम जानते हैं कि $-1 \leq \sin 2 x \leq 1$।

$\square-1+5 \leq \sin 2 x+5 \leq 1+5$

$\square 4 \leq \sin 2 x+5 \leq 6$

इसलिए, $h$ के अधिकतम और न्यूनतम मान क्रमशः 6 और 4 हैं।

(iv) $f(x)=|\sin 4 x+3|$

हम जानते हैं कि $-1 \leq \sin 4 x \leq 1$।

$\square 2 \leq \sin 4 x+3 \leq 4$

$\square 2 \leq^{|\sin 4 x+3|} \leq 4$

इसलिए, $f$ के अधिकतम और न्यूनतम मान क्रमशः 4 और 2 हैं।

(v) $h(x)=x+1, x \square(-1,1)$

यहाँ, यदि एक बिंदु $x_0$ -1 के सबसे करीब हो, तो हम जानते हैं कि $\frac{x_0}{2}+1<x_0+1$ सभी $x_0 \square(-1,1)$ के लिए।

इसके अलावा, यदि $x_1$ 1 के सबसे करीब हो, तो $x_1+1<\frac{x_1+1}{2}+1$ सभी $x_1 \square(-1,1)$ के लिए।

इसलिए, फलन $h(x)$ के अंतराल $(-1,1)$ में कोई अधिकतम या न्यूनतम मान नहीं होता।

Solution

(i) $f(x)=x^{2}$

$\therefore f^{\prime}(x)=2 x$

अब,

$f^{\prime}(x)=0 \Rightarrow x=0$

इसलिए, $x=0$ एकमात्र ऐसा क्रिटिकल बिंदु है जो $f$ के लोकल मैक्सिमम या लोकल मिनिमम के बिंदु हो सकता है।

हमें $f^{\prime \prime}(0)=2$ है, जो धनात्मक है।

इसलिए, दूसरे अवकलज परीक्षण के अनुसार, $x=0$ एक स्थानीय न्यूनतम बिंदु है और $f$ के $x=0$ पर स्थानीय न्यूनतम मान $f(0)=0$ है।

(ii) $g(x)=x^{3}-3 x$

$\therefore g^{\prime}(x)=3 x^{2}-3$

अब,

$g^{\prime}(x)=0 \Rightarrow 3 x^{2}=3 \Rightarrow x= \pm 1$

$g^{\prime}(x)=6 x$

$g^{\prime}(1)=6>0$

$g^{\prime}(-1)=-6<0$

दूसरे अवकलज परीक्षण के अनुसार, $x=1$ एक स्थानीय न्यूनतम बिंदु है और $g$ के $x=1$ पर स्थानीय न्यूनतम मान $g(1)=1^{3}-3=1-3=-2$ है। हालांकि, $x=-1$ एक स्थानीय उच्चिष्ठ बिंदु है और $g$ के $x=-1$ पर स्थानीय उच्चिष्ठ मान $g(1)=(-1)^{3}-3(-1)=-1+3=2$ है।

(iii) $h(x)=\sin x+\cos x, 0<x<\frac{\pi}{2}$

$\therefore h^{\prime}(x)=\cos x-\sin x$

$h^{\prime}(x)=0 \Rightarrow \sin x=\cos x \Rightarrow \tan x=1 \Rightarrow x=\frac{\pi}{4} \in(0, \frac{\pi}{2})$

$h^{\prime \prime}(x)=-\sin x-\cos x=-(\sin x+\cos x)$

$h^{\prime \prime}(\frac{\pi}{4})=-(\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}})=-\frac{2}{\sqrt{2}}=-\sqrt{2}<0$

इसलिए, दूसरे अवकलज परीक्षण के अनुसार, $x=\frac{\pi}{4}$ एक स्थानीय उच्चिष्ठ बिंदु है और $h$ के $x=\frac{\pi}{4}$ पर स्थानीय उच्चिष्ठ मान $h(\frac{\pi}{4})=\sin \frac{\pi}{4}+\cos \frac{\pi}{4}=\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}=\sqrt{2}$ है।

(iv) $f(x)=\sin x-\cos x, 0<x<2 \pi$

$\therefore f^{\prime}(x)=\cos x+\sin x$

$f^{\prime}(x)=0 \Rightarrow \cos x=-\sin x \Rightarrow \tan x=-1 \Rightarrow x=\frac{3 \pi}{4}, \frac{7 \pi}{4} \in(0,2 \pi)$

$f^{\prime \prime}(x)=-\sin x+\cos x$

$f^{\prime \prime}(\frac{3 \pi}{4})=-\sin \frac{3 \pi}{4}+\cos \frac{3 \pi}{4}=-\frac{1}{\sqrt{2}}-\frac{1}{\sqrt{2}}=-\sqrt{2}>0$

$f^{\prime \prime}(\frac{7 \pi}{4})=-\sin \frac{7 \pi}{4}+\cos \frac{7 \pi}{4}=\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}=\sqrt{2}>0$

इसलिए, दूसरे अवकलज परीक्षण के अनुसार, $x=\frac{3 \pi}{4}$ एक स्थानीय उच्चिष्ठ बिंदु है और $f$ के $x=\frac{3 \pi}{4}$ पर स्थानीय उच्चिष्ठ मान

$f(\frac{3 \pi}{4})=\sin \frac{3 \pi}{4}-\cos \frac{3 \pi}{4}=\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}=\sqrt{2}$ है। हालांकि, $x=\frac{7 \pi}{4}$ एक स्थानीय न्यूनतम बिंदु है और

the local minimum value of $f$ at $x=\frac{7 \pi}{4}$ is $f(\frac{7 \pi}{4})=\sin \frac{7 \pi}{4}-\cos \frac{7 \pi}{4}=-\frac{1}{\sqrt{2}}-\frac{1}{\sqrt{2}}=-\sqrt{2}$.

(v) $f(x)=x^{3}-6 x^{2}+9 x+15$

$\therefore f^{\prime}(x)=3 x^{2}-12 x+9$

$f^{\prime}(x)=0 \Rightarrow 3(x^{2}-4 x+3)=0$

$\Rightarrow 3(x-1)(x-3)=0$

$\Rightarrow x=1,3$

Now, $f^{\prime \prime}$

$(x)=6 x-12=6(x-2)$

$f^{\prime \prime}(1)=6(1-2)=-6<0$

$f^{\prime \prime}(3)=6(3-2)=6>0$

Therefore, by second derivative test, $x=1$ is a point of local maxima and the local maximum value of $f$ at $x=1$ is $f(1)=1-6+9+15=19$. However, $x=3$ is a point of local minima and the local minimum value of $f$ at $x=3$ is $f(3)=27-54+27+15=$ 15.

(vi) $g(x)=\frac{x}{2}+\frac{2}{x}, x>0$

$\therefore g^{\prime}(x)=\frac{1}{2}-\frac{2}{x^{2}}$

Now,

$g^{\prime}(x)=0$ gives $\frac{2}{x^{2}}=\frac{1}{2} \Rightarrow x^{2}=4 \Rightarrow x= \pm 2$

Since $x>0$, we take $x=2$.

Now,

$g^{\prime \prime}(x)=\frac{4}{x^{3}}$

$g^{\prime \prime}(2)=\frac{4}{2^{3}}=\frac{1}{2}>0$

Therefore, by second derivative test, $x=2$ is a point of local minima and the local

minimum value of $g$ at $x=2$ is $g(2)=\frac{2}{2}+\frac{2}{2}=1+1=2$.

(vii) $g(x)=\frac{1}{x^{2}+2}$

$\therefore g^{\prime}(x)=\frac{-(2 x)}{(x^{2}+2)^{2}}$

$g^{\prime}(x)=0 \Rightarrow \frac{-2 x}{(x^{2}+2)^{2}}=0 \Rightarrow x=0$

Now, for values close to $x=0$ and to the left of $0, g^{\prime}(x)>0$. Also, for values close to $x=$ 0 and to the right of $0, g^{\prime}(x)<0$.

Therefore, by first derivative test, $x=0$ is a point of local maxima and the local maximum value of $g(0)$ is $\frac{1}{0+2}=\frac{1}{2}$.

(viii) $f(x)=x \sqrt{1-x}, x>0$

$\therefore f^{\prime}(x)=\sqrt{1-x}+x \cdot \frac{1}{2 \sqrt{1-x}}(-1)=\sqrt{1-x}-\frac{x}{2 \sqrt{1-x}}$

$=\frac{2(1-x)-x}{2 \sqrt{1-x}}=\frac{2-3 x}{2 \sqrt{1-x}}$

$f^{\prime}(x)=0 \Rightarrow \frac{2-3 x}{2 \sqrt{1-x}}=0 \Rightarrow 2-3 x=0 \Rightarrow x=\frac{2}{3}$

$f^{\prime \prime}(x)=\frac{1}{2}[\frac{\sqrt{1-x}(-3)-(2-3 x)(\frac{-1}{2 \sqrt{1-x}})}{1-x}]$

$=\frac{\sqrt{1-x}(-3)+(2-3 x)(\frac{1}{2 \sqrt{1-x}})}{2(1-x)}$

$=\frac{-6(1-x)+(2-3 x)}{4(1-x)^{\frac{3}{2}}}$

$=\frac{3 x-4}{4(1-x)^{\frac{3}{2}}}$

$f^{\prime \prime}(\frac{2}{3})=\frac{3(\frac{2}{3})-4}{4(1-\frac{2}{3})^{\frac{3}{2}}}=\frac{2-4}{4(\frac{1}{3})^{\frac{3}{2}}}=\frac{-1}{2(\frac{1}{3})^{\frac{3}{2}}}<0$

इसलिए, द्वितीय अवकलज परीक्षण के अनुसार, $x=\frac{2}{3}$ एक स्थानीय उच्चिष्ठ बिंदु है और $f$ के $x=\frac{2}{3}$ पर स्थानीय उच्चिष्ठ मान है $f(\frac{2}{3})=\frac{2}{3} \sqrt{1-\frac{2}{3}}=\frac{2}{3} \sqrt{\frac{1}{3}}=\frac{2}{3 \sqrt{3}}=\frac{2 \sqrt{3}}{9}$.

हल

i. हम जानते हैं,

$f(x)=e^{x}$

$\therefore f^{\prime}(x)=e^{x}$

अब, यदि $f^{\prime}(x)=0$, तो $e^{x}=0$. लेकिन, समाकलन फलन कभी भी किसी भी $x$ के मान के लिए 0 नहीं हो सकता।

इसलिए, कोई भी $c \in \mathbf{R}$ ऐसा नहीं है जैसे कि $f^{\prime}(c)=0$.

इसलिए, फलन $f$ उच्चिष्ठ या निम्निष्ठ नहीं हो सकता।

ii. हम जानते हैं,

$g(x)=\log x$

$\therefore g^{\prime}(x)=\frac{1}{x}$

क्योंकि $\log x$ धनात्मक संख्या $x$ के लिए परिभाषित है, $g^{\prime}(x)>0$ कोई भी $x$ के लिए होता है।

इसलिए, कोई भी $c \in \mathbf{R}$ ऐसा नहीं है जैसे कि $g^{\prime}(c)=0$.

इसलिए, फलन $g$ उच्चिष्ठ या निम्निष्ठ नहीं हो सकता।

iii. हम जानते हैं,

$h(x)=x^{3}+x^{2}+x+1$

$\therefore h^{\prime}(x)=3 x^{2}+2 x+1$

अब,

$h(x)=0 \Rightarrow 3 x^{2}+2 x+1=0 \Rightarrow x=\frac{-2 \pm 2 \sqrt{2} i}{6}=\frac{-1 \pm \sqrt{2} i}{3} \notin \mathbf{R}$

इसलिए, कोई भी $c \in \mathbf{R}$ ऐसा नहीं है जैसे कि $h^{\prime}(c)=0$.

इसलिए, फलन $h$ उच्चिष्ठ या निम्निष्ठ नहीं हो सकता।

Solution

(i) दी गई फलन $f(x)=x^{3}$ है।

$\therefore f^{\prime}(x)=3 x^{2}$

अब,

$f^{\prime}(x)=0 \Rightarrow x=0$

फिर, हम अंतिम बिंदुओं $[-2,2]$ पर फलन $f$ के मान का मूल्यांकन करते हैं।

$f(0)=0$

$f(-2)=(-2)^{3}=-8$

$f(2)=(2)^{3}=8$

इसलिए, हम निष्कर्ष निकाल सकते हैं कि फलन $f$ का अंतिम अधिकतम मान $[-2,2]$ पर 8 है जो $x=2$ पर होता है। इसके अलावा, फलन $f$ का अंतिम न्यूनतम मान $[-2,2]$ पर -8 है जो $x=-2$ पर होता है।

(ii) दी गई फलन $f(x)=\sin x+\cos x$ है।

$\therefore f^{\prime}(x)=\cos x-\sin x$

अब,

$f^{\prime}(x)=0 \Rightarrow \sin x=\cos x \Rightarrow \tan x=1 \Rightarrow x=\frac{\pi}{4}$

फिर, हम अंतिम बिंदुओं $[0, \pi]$ पर फलन $f$ के मान का मूल्यांकन करते हैं।

Solution

लाभ फलन निम्नलिखित द्वारा दिया गया है $p(x)=41-24 x-18 x^{2}$।

$\therefore p^{\prime}(x)=-24-36 x$

$p^{\prime \prime}(x)=-36$

अब,

$p^{\prime}(x)=0 \Rightarrow x=\frac{-24}{36}=-\frac{2}{3}$

इसके अलावा,

$p^{\prime \prime}(\frac{-2}{3})=-36<0$

द्वितीय अवकलज परीक्षण के अनुसार, $x=-\frac{2}{3}$ फलन $p$ के लोकल अधिकतम बिंदु है।

$\therefore$ अधिकतम लाभ $=p(-\frac{2}{3})$

$ \begin{aligned} & =41-24(-\frac{2}{3})-18(-\frac{2}{3})^{2} \\ & =41+16-8 \\ & =49 \end{aligned} $

इसलिए, कंपनी द्वारा किए जाने वाले अधिकतम लाभ 49 इकाई है।

Solution

$f(x)=3 x^4-8 x^3+12 x^2-48 x+25$

$f^{\prime}(x)=0$ के लिए अंतर बिंदुओं का खोज करें

$f^{\prime}(x)=12 x^3-24 x^2+24 x-48$

$12 x^3-24 x^2+24 x-48=0$

$12 x^2(x-2)+24(x-2)=0$

$\left(12 x^2+24\right)(x-2)=0$

क्योंकि $12 x^2+24 \neq 0$ और $x-2=0 \Longrightarrow x=2$

हमें $x=0,2,3$ पर जांच करनी होगी $f(0)=25$

$f(2)=-39$

$f(3)=16$

$\therefore$ $f(x)$ का अधिकतम मान $x=0$ पर 25 है

$f(x)$ का न्यूनतम मान $x=2$ पर -39 है

Solution

मान लीजिए $f(x)=\sin 2 x$.

$\therefore f^{\prime}(x)=2 \cos 2 x$

अब,

$ \begin{aligned} & f^{\prime}(x)=0 \Rightarrow \cos 2 x=0 \\ & \Rightarrow 2 x=\frac{\pi}{2}, \frac{3 \pi}{2}, \frac{5 \pi}{2}, \frac{7 \pi}{2} \\ & \Rightarrow x=\frac{\pi}{4}, \frac{3 \pi}{4}, \frac{5 \pi}{4}, \frac{7 \pi}{4} \end{aligned} $

फिर, हम अंतराल $[0,2 \pi]$ के सीमा बिंदुओं $x=\frac{\pi}{4}, \frac{3 \pi}{4}, \frac{5 \pi}{4}, \frac{7 \pi}{4}$ पर $f$ के मान का मूल्यांकन करते हैं।

$f(\frac{\pi}{4})=\sin \frac{\pi}{2}=1, f(\frac{3 \pi}{4})=\sin \frac{3 \pi}{2}=-1$

$f(\frac{5 \pi}{4})=\sin \frac{5 \pi}{2}=1, f(\frac{7 \pi}{4})=\sin \frac{7 \pi}{2}=-1$

$f(0)=\sin 0=0, f(2 \pi)=\sin 2 \pi=0$

इसलिए, हम निष्कर्ष निकाल सकते हैं कि $f$ का अंतराल $[0,2 \pi]$ पर अधिकतम मान निम्नलिखित बिंदुओं पर हो रहा है

$x=\frac{\pi}{4}$ और $x=\frac{5 \pi}{4}$ पर।

Solution

मान लीजिए $f(x)=\sin x+\cos x$.

$\therefore f^{\prime}(x)=\cos x-\sin x$

$f^{\prime}(x)=0 \Rightarrow \sin x=\cos x \Rightarrow \tan x=1 \Rightarrow x=\frac{\pi}{4}, \frac{5 \pi}{4} \ldots$,

$f^{\prime \prime}(x)=-\sin x-\cos x=-(\sin x+\cos x)$

अब, $f^{\prime \prime}(x)$ नकारात्मक होगा जब $(\sin x+\cos x)$ धनात्मक हो, अर्थात जब $\sin x$ और $\cos x$ दोनों धनात्मक हों। हम जानते हैं कि $\sin x$ और $\cos x$ दोनों पहले चतुर्थांश में धनात्मक होते हैं। तब, $f^{\prime \prime}(x)$ नकारात्मक होगा जब $x \in(0, \frac{\pi}{2})$।

इसलिए, हम $x=\frac{\pi}{4}$ को ध्यान में रखते हैं।

$f^{\prime \prime}(\frac{\pi}{4})=-(\sin \frac{\pi}{4}+\cos \frac{\pi}{4})=-(\frac{2}{\sqrt{2}})=-\sqrt{2}<0$ $\square$ द्वितीय अवकलज परीक्षण के अनुसार, $f$ का अधिकतम मान $x=\frac{\pi}{4}$ पर होगा और $f$ का अधिकतम मान $f(\frac{\pi}{4})=\sin \frac{\pi}{4}+\cos \frac{\pi}{4}=\frac{1}{\sqrt{2}} \times \frac{1}{\sqrt{2}}=\frac{2}{\sqrt{2}}=\sqrt{2}$ होगा।

हल

मान लीजिए $f(x)=2 x^{3}-24 x+107$।

$\therefore f^{\prime}(x)=6 x^{2}-24=6(x^{2}-4)$

अब,

$f^{\prime}(x)=0 \Rightarrow 6(x^{2}-4)=0 \Rightarrow x^{2}=4 \Rightarrow x= \pm 2$

हम पहले अंतराल $[1,3]$ को ध्यान में रखते हैं।

फिर, हम अंतराल $[1,3]$ के क्रिटिकल बिंदु $x=2 \square[1,3]$ और अंतराल $[1,3]$ के सीमा बिंदुओं पर $f$ के मान का मूल्यांकन करते हैं।

$f(2)=2(8)-24(2)+107=16-48+107=75$

$f(1)=2(1)-24(1)+107=2-24+107=85$

$f(3)=2(27)-24(3)+107=54-72+107=89$

इसलिए, अंतराल $[1,3]$ में $f(x)$ का अंतराल अधिकतम मान 89 है जो $x=3$ पर होता है।

अब, हम अंतराल $[-3,-1]$ को ध्यान में रखते हैं।

अंतराल $[-3,-1]$ के क्रिटिकल बिंदु $x=-2 \square[-3,-1]$ और अंतराल $[1,3]$ के सीमा बिंदुओं पर $f$ के मान का मूल्यांकन करते हैं।

$f(-3)=2(-27)-24(-3)+107=-54+72+107=125$

$f(-1)=2(-1)-24(-1)+107=-2+24+107=129$

$f(-2)=2(-8)-24(-2)+107=-16+48+107=139$

इसलिए, अंतराल $[-3,-1]$ में $f(x)$ का अंतराल अधिकतम मान 139 है जो $x=-2$ पर होता है।

हल

मान लीजिए $f(x)=x^{4}-62 x^{2}+a x+9$।

$\therefore f^{\prime}(x)=4 x^{3}-124 x+a$

यह दिया गया है कि फलन $f$ अंतराल $[0,2]$ में $x=1$ पर अपना अधिकतम मान प्राप्त करता है।

$\therefore f^{\prime}(1)=0$

$\Rightarrow 4-124+a=0$

$\Rightarrow a=120$

इसलिए, $a$ का मान 120 है।

हल

मान लीजिए $f(x)=x+\sin 2 x$।

$\therefore f^{\prime}(x)=1+2 \cos 2 x$

अब, $f^{\prime}(x)=0 \Rightarrow \cos 2 x=-\frac{1}{2}=-\cos \frac{\pi}{3}=\cos (\pi-\frac{\pi}{3})=\cos \frac{2 \pi}{3}$

$2 x=2 \pi \pm \frac{2 \pi}{3} \quad n \in \mathbf{Z}$

$\Rightarrow x=n \pi \pm \frac{\pi}{3}, n \in \mathbf{Z}$

$\Rightarrow x=\frac{\pi}{3}, \frac{2 \pi}{3}, \frac{4 \pi}{3}, \frac{5 \pi}{3} \in[0,2 \pi]$

तब, हम अंतराल $[0,2 \pi]$ के क्रिटिकल बिंदुओं $x=\frac{\pi}{3}, \frac{2 \pi}{3}, \frac{4 \pi}{3}, \frac{5 \pi}{3}$ और अंतराल के सीमा बिंदुओं $[0,2 \pi]$ पर $f$ के मान का मूल्यांकन करते हैं। $f(\frac{\pi}{3})=\frac{\pi}{3}+\sin \frac{2 \pi}{3}=\frac{\pi}{3}+\frac{\sqrt{3}}{2}$

$f(\frac{2 \pi}{3})=\frac{2 \pi}{3}+\sin \frac{4 \pi}{3}=\frac{2 \pi}{3}-\frac{\sqrt{3}}{2}$

$f(\frac{4 \pi}{3})=\frac{4 \pi}{3}+\sin \frac{8 \pi}{3}=\frac{4 \pi}{3}+\frac{\sqrt{3}}{2}$

$f(\frac{5 \pi}{3})=\frac{5 \pi}{3}+\sin \frac{10 \pi}{3}=\frac{5 \pi}{3}-\frac{\sqrt{3}}{2}$

$f(0)=0+\sin 0=0$

$f(2 \pi)=2 \pi+\sin 4 \pi=2 \pi+0=2 \pi$

इसलिए, हम निष्कर्ष निकाल सकते हैं कि अंतराल $[0,2 \pi]$ में $f(x)$ का अंतराल अधिकतम मान $2 \pi$ है जो $x=2 \pi$ पर होता है और अंतराल का अंतराल न्यूनतम मान 0 है जो $x=0$ पर होता है।

हल

मान लीजिए एक संख्या $x$ है। तब, दूसरी संख्या $(24-x)$ होती है।

मान लीजिए $P(x)$ दोनों संख्याओं के गुणनफल को दर्शाता है। इसलिए, हम निम्नलिखित रखते हैं:

$ \begin{aligned} & P(x)=x(24-x)=24 x-x^{2} \\ & \therefore P^{\prime}(x)=24-2 x \\ & P^{\prime \prime}(x)=-2 \end{aligned} $

अब,

$P^{\prime}(x)=0 \Rightarrow x=12$

इसके अतिरिक्त,

$P^{\prime \prime}(12)=-2<0$

$\square$ द्वितीय अवकलज परीक्षण के अनुसार, $x=12$ $P$ के लोकल मैक्सिमा के बिंदु है। इसलिए, जब संख्याएं 12 और $24-12=12$ होती हैं तब उत्पाद अधिकतम होता है।

हल

दो संख्याएं $x$ और $y$ जैसे कि $x+y=60$ हैं।

$\square y=60-x$

मान लीजिए $f(x)=x y^{3}$.

$\Rightarrow f(x)=x(60-x)^{3}$

$\therefore f^{\prime}(x)=(60-x)^{3}-3 x(60-x)^{2}$

$=(60-x)^{2}[60-x-3 x]$

$=(60-x)^{2}(60-4 x)$

और, $f^{\prime \prime}(x)=-2(60-x)(60-4 x)-4(60-x)^{2}$

$ \begin{aligned} & =-2(60-x)[60-4 x+2(60-x)] \\ & =-2(60-x)(180-6 x) \\ & =-12(60-x)(30-x) \end{aligned} $

अब, $f^{\prime}(x)=0 \Rightarrow x=60$ या $x=15$

जब $x=60, f^{\prime \prime}(x)=0$ है।

जब $x=15, f^{\prime \prime}(x)=-12(60-15)(30-15)=-12 \times 45 \times 15<0$ है।

$\square$ द्वितीय अवकलज परीक्षण के अनुसार, $x=15$ फलन $f$ के एक लोकल मैक्सिमा बिंदु है। अतः, फलन $x y^{3}$ का मान $x=15$ और $y=60-15=45$ के लिए अधिकतम होता है।

अतः, आवश्यक संख्याएँ 15 और 45 हैं।

हल

मान लीजिए एक संख्या $x$ है। तब, दूसरी संख्या $y=(35-x)$ है।

मान लीजिए $P(x)=x^{2} y^{5}$. तब, हमारे पास है:

$ \begin{aligned} & P(x)=x^{2}(35-x)^{5} \\ & \begin{aligned} \therefore P^{\prime}(x) & =2 x(35-x)^{5}-5 x^{2}(35-x)^{4} \\ & =x(35-x)^{4}[2(35-x)-5 x] \\ & =x(35-x)^{4}(70-7 x) \\ & =7 x(35-x)^{4}(10-x) \end{aligned} \end{aligned} $

और, $P^{\prime \prime}(x)=7(35-x)^{4}(10-x)+7 x[-(35-x)^{4}-4(35-x)^{3}(10-x)]$

$ \begin{aligned} & =7(35-x)^{4}(10-x)-7 x(35-x)^{4}-28 x(35-x)^{3}(10-x) \\ & =7(35-x)^{3}[(35-x)(10-x)-x(35-x)-4 x(10-x)] \\ & =7(35-x)^{3}[350-45 x+x^{2}-35 x+x^{2}-40 x+4 x^{2}] \\ & =7(35-x)^{3}(6 x^{2}-120 x+350) \end{aligned} $

अब, $P^{\prime}(x)=0 \Rightarrow x=0, x=35, x=10$

जब $x=35, P^{\prime}(x)=f(x)=0$ और $y=35-35=0$ है। यह उत्पाद $x^{2} y^{5}$ को शून्य बनाएगा।

जब $x=0, y=35-0=35$ और उत्पाद $x^{2} y^{5}$ शून्य होगा।

$\square x=0$ और $x=35$ के संभावित मान नहीं हो सकते।

जब $x=10$, हमारे पास है:

$ \begin{aligned} P^{\prime \prime}(x) & =7(35-10)^{3}(6 \times 100-120 \times 10+350) \\ & =7(25)^{3}(-250)<0 \end{aligned} $

$\square$ द्वितीय अवकलज परीक्षण के अनुसार, $P(x)$ का मान $x=10$ और $y=35-10=25$ के लिए अधिकतम होता है।

अतः, आवश्यक संख्याएँ 10 और 25 हैं।

हल

मान लीजिए एक संख्या $x$ है। तब, दूसरी संख्या $(16-x)$ होगी।

इन संख्याओं के घनों के योग को $S(x)$ से नोट करते हैं। तब,

$S(x)=x^{3}+(16-x)^{3}$

$\therefore S^{\prime}(x)=3 x^{2}-3(16-x)^{2}, S^{\prime \prime}(x)=6 x+6(16-x)$

अब, $S^{\prime}(x)=0 \Rightarrow 3 x^{2}-3(16-x)^{2}=0$

$\Rightarrow x^{2}-(16-x)^{2}=0$

$\Rightarrow x^{2}-256-x^{2}+32 x=0$

$\Rightarrow x=\frac{256}{32}=8$

अब, $S^{\prime \prime}(8)=6(8)+6(16-8)=48+48=96>0$

$\square$ द्वितीय अवकलज परीक्षण के अनुसार, $x=8$ $S$ के लोकल मिनिमा बिंदु है।

इसलिए, संख्याओं के घनों का योग जब संख्याएँ 8 और $16-8=8$ होती हैं तब न्यूनतम होता है।

हल

मान लीजिए काटे गए वर्ग की भुजा $x$ सेमी है। तब, बॉक्स की लंबाई और चौड़ाई $(18-2 x)$ सेमी होगी और बॉक्स की ऊंचाई $x$ सेमी होगी।

इसलिए, बॉक्स का आयतन $V(x)$ निम्नलिखित द्वारा दिया जाता है,

$V(x)=x(18-2 x)^{2}$ $\therefore V^{\prime}(x)=(18-2 x)^{2}-4 x(18-2 x)$

$=(18-2 x)[18-2 x-4 x]$

$=(18-2 x)(18-6 x)$

$=6 \times 2(9-x)(3-x)$

$=12(9-x)(3-x)$

और, $V^{\prime \prime}(x)=12[-(9-x)-(3-x)]$

$=-12(9-x+3-x)$

$=-12(12-2 x)$

$=-24(6-x)$

अब, $V^{\prime}(x)=0 \Rightarrow x=9$ या $x=3$

यदि $x=9$, तो लंबाई और चौड़ाई शून्य हो जाएगी।

$\therefore x \neq 9$.

$\Rightarrow x=3$.

अब, $V^{\prime \prime}(3)=-24(6-3)=-72<0$

$\therefore$ द्वितीय अवकलज परीक्षण के अनुसार, $x=3$ $V$ के अधिकतम बिंदु है।

इसलिए, यदि हम वर्ग टिन के प्रत्येक कोने से 3 सेमी भुजा वाला वर्ग काट दें और बचे हुए शीट से बॉक्स बनाएं, तो प्राप्त बॉक्स का आयतन अधिकतम होगा।

हल

मान लीजिए वर्ग के काटे गए किनारे की लंबाई $x cm$ है। तब, बॉक्स की ऊंचाई $x$, लंबाई $45-2 x$ और चौड़ाई $24-2 x$ है।

इसलिए, बॉक्स का आयतन $V(x)$ निम्नलिखित द्वारा दिया जाता है,

$ \begin{aligned} V(x) & =x(45-2 x)(24-2 x) \\ & =x(1080-90 x-48 x+4 x^{2}) \\ & =4 x^{3}-138 x^{2}+1080 x \end{aligned} $

$\therefore V^{\prime}(x)=12 x^{2}-276 x+1080$

$ =12(x^{2}-23 x+90) $

$ =12(x-18)(x-5) $

$V^{\prime \prime}(x)=24 x-276=12(2 x-23)$

अब, ${ }^{V^{\prime}}(x)=0 \Rightarrow x=18$ और $x=5$

एक आयताकार शीट के प्रत्येक कोने से $18 cm$ के वर्ग काटना संभव नहीं है। इसलिए, $x$ 18 के बराबर नहीं हो सकता।

$\square x=5$

अब, $V^{\prime \prime}(5)=12(10-23)=12(-13)=-156<0$

$\therefore$ द्वितीय अवकलज परीक्षण के अनुसार, $x=5$ अधिकतम बिंदु है।

इसलिए, बॉक्स के आयतन को अधिकतम करने के लिए काटे गए वर्ग के किनारे की लंबाई $5 cm$ है।

हल

मान लीजिए एक आयत जिसकी लंबाई $l$ और चौड़ाई $b$ है, दिए गए वृत्त में आकर्षित है जिसकी त्रिज्या $a$ है। तब, विकर्ण केंद्र से गुजरता है और इसकी लंबाई $2 a cm$ है।

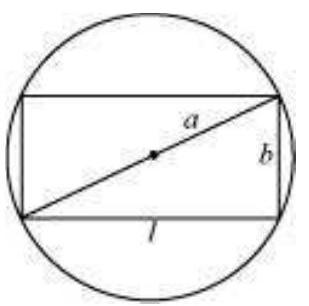
अब, पिथागोरस प्रमेय के द्वारा हम निम्नलिखित प्राप्त करते हैं:

$ \begin{aligned} & (2 a)^{2}=l^{2}+b^{2} \\ & \Rightarrow b^{2}=4 a^{2}-l^{2} \\ & \Rightarrow b=\sqrt{4 a^{2}-l^{2}} \end{aligned} $

$\square$ आयत का क्षेत्रफल, $A=l \sqrt{4 a^{2}-l^{2}}$

$\therefore \frac{d A}{d l}=\sqrt{4 a^{2}-l^{2}}+l \frac{1}{2 \sqrt{4 a^{2}-l^{2}}}(-2 l)=\sqrt{4 a^{2}-l^{2}}-\frac{l^{2}}{\sqrt{4 a^{2}-l^{2}}}$

$ =\frac{4 a^{2}-2 l^{2}}{\sqrt{4 a^{2}-l^{2}}} `

$

$\frac{d^{2} A}{d l^{2}}=\frac{\sqrt{4 a^{2}-l^{2}}(-4 l)-(4 a^{2}-2 l^{2}) \frac{(-2 l)}{2 \sqrt{4 a^{2}-l^{2}}}}{(4 a^{2}-l^{2})}$

$ =\frac{(4 a^{2}-l^{2})(-4 l)+l(4 a^{2}-2 l^{2})}{(4 a^{2}-l^{2})^{\frac{3}{2}}} $

$ =\frac{-12 a^{2} l+2 l^{3}}{(4 a^{2}-l^{2})^{\frac{3}{2}}}=\frac{-2 l(6 a^{2}-l^{2})}{(4 a^{2}-l^{2})^{\frac{3}{2}}} $

अब, $\frac{d A}{d l}=0$ देता है $4 a^{2}=2 l^{2} \Rightarrow l=\sqrt{2} a$

$ \Rightarrow b=\sqrt{4 a^{2}-2 a^{2}}=\sqrt{2 a^{2}}=\sqrt{2} a $

अब, जब $l=\sqrt{2} a$,

$\frac{d^{2} A}{d l^{2}}=\frac{-2(\sqrt{2} a)(6 a^{2}-2 a^{2})}{2 \sqrt{2} a^{3}}=\frac{-8 \sqrt{2} a^{3}}{2 \sqrt{2} a^{3}}=-4<0$

$\therefore$ द्वितीय अवकलज परीक्षण के अनुसार, जब $l=\sqrt{2} a$, तो आयत का क्षेत्रफल अधिकतम होता है।

क्योंकि $l=b=\sqrt{2} a$, तो आयत एक वर्ग होता है।

इसलिए, साबित कर दिया गया है कि दिए गए निश्चित वृत्त में आयत के सभी आकृतियों में वर्ग का क्षेत्रफल अधिकतम होता है।

हल

मान लीजिए $r$ और $h$ बेलन की त्रिज्या और ऊंचाई हैं।

तब, बेलन के सतह क्षेत्रफल $(S)$ द्वारा दिया गया है,

$ \begin{aligned} & S=2 \pi r^{2}+2 \pi r h \\ & \Rightarrow h=\frac{S-2 \pi r^{2}}{2 \pi r} \\ &=\frac{S}{2 \pi}(\frac{1}{r})-r \end{aligned} $

मान लीजिए $V$ बेलन का आयतन है। तब,

$V=\pi r^{2} h=\pi r^{2}[\frac{S}{2 \pi}(\frac{1}{r})-r]=\frac{S r}{2}-\pi r^{3}$

तब, $\frac{d V}{d r}=\frac{S}{2}-3 \pi r^{2}, \frac{d^{2} V}{d r^{2}}=-6 \pi r$

अब, $\frac{d V}{d r}=0 \Rightarrow \frac{S}{2}=3 \pi r^{2} \Rightarrow r^{2}=\frac{S}{6 \pi}$

जब $r^{2}=\frac{S}{6 \pi}$, तब $\frac{d^{2} V}{d r^{2}}=-6 \pi(\sqrt{\frac{S}{6 \pi}})<0$।

द्वितीय अवकलज परीक्षण के अनुसार, जब $r^{2}=\frac{S}{6 \pi}$, तो आयतन अधिकतम होता है।

अब, जब $r^{2}=\frac{S}{6 \pi}$, तब $h=\frac{6 \pi r^{2}}{2 \pi}(\frac{1}{r})-r=3 r-r=2 r$।

इसलिए, आयतन तब अधिकतम होता है जब ऊंचाई त्रिज्या के दुगुनी हो, अर्थात जब ऊंचाई व्यास के बराबर हो।

हल

मान लीजिए $r$ और $h$ क्रमशः बेलन की त्रिज्या और ऊंचाई है।

तब, बेलन का आयतन $(V)$ निम्नलिखित है,

$V=\pi r^{2} h=100 \quad$ (दिया गया)

$\therefore h=\frac{100}{\pi r^{2}}$

बेलन के सतह क्षेत्रफल $(S$ ) निम्नलिखित है,

$S=2 \pi r^{2}+2 \pi r h=2 \pi r^{2}+\frac{200}{r}$

$\therefore \frac{d S}{d r}=4 \pi r-\frac{200}{r^{2}}, \frac{d^{2} S}{d r^{2}}=4 \pi+\frac{400}{r^{3}}$

$\frac{d S}{d r}=0 \Rightarrow 4 \pi r=\frac{200}{r^{2}}$

$\Rightarrow r^{3}=\frac{200}{4 \pi}=\frac{50}{\pi}$

$\Rightarrow r=(\frac{50}{\pi})^{\frac{1}{3}}$

अब, यह देखा जाता है कि जब $r=(\frac{50}{\pi})^{\frac{1}{3}}, \frac{d^{2} S}{d r^{2}}>0$ है।

$\square$ द्वितीय अवकलज परीक्षण द्वारा, सतह क्षेत्रफल न्यूनतम होता है जब बेलन की त्रिज्या $(\frac{50}{\pi})^{\frac{1}{3}} cm$ हो।

जब $r=(\frac{50}{\pi})^{\frac{1}{3}}, h=\frac{100}{\pi(\frac{50}{\pi})^{\frac{2}{3}}}=\frac{2 \times 50}{(50)^{\frac{2}{3}}()^{1-\frac{2}{3}}}=2(\frac{50}{\pi})^{\frac{1}{3}} cm$ होता है।

इसलिए, न्यूनतम सतह क्षेत्रफल वाली टंकी की आवश्यक विमाएं त्रिज्या $=(\frac{50}{\pi})^{\frac{1}{3}} cm$ और ऊंचाई $=2(\frac{50}{\pi})^{\frac{1}{3}} cm$ है।

हल

मान लीजिए दिए गए तार से एक टुकड़े की लंबाई $l$ हो।

तब, वृत्त के रूप में बनाने के लिए दूसरे टुकड़े की लंबाई $(28 - l) m$ होती है।

अब, वर्ग की भुजा $=\frac{l}{4}$।

$ r $ के वृत्त की त्रिज्या होने दें। तब,

$ 2 \pi r=28-l \Rightarrow r=\frac{1}{2 \pi}(28-l) \text{. } $

वर्ग और वृत्त के संयुक्त क्षेत्रफल $(A)$ निम्नलिखित द्वारा दिया जाता है,

$A=(\text{ वर्ग की भुजा })^{2}+r^{2}$

$=\frac{l^{2}}{16}+\pi[\frac{1}{2 \pi}(28-l)]^{2}$

$=\frac{l^{2}}{16}+\frac{1}{4 \pi}(28-l)^{2}$

$\therefore \frac{d A}{d l}=\frac{2 l}{16}+\frac{2}{4 \pi}(28-l)(-1)=\frac{l}{8}-\frac{1}{2 \pi}(28-l)$

$\frac{d^{2} A}{d l^{2}}=\frac{1}{8}+\frac{1}{2 \pi}>0$

अब, $\frac{d A}{d l}=0 \Rightarrow \frac{l}{8}-\frac{1}{2 \pi}(28-l)=0$

$\Rightarrow \frac{\pi l-4(28-l)}{8 \pi}=0$

$\Rightarrow(\pi+4) l-112=0$

$\Rightarrow l=\frac{112}{\pi+4}$

इसलिए, जब $l=\frac{112}{\pi+4}, \frac{d^{2} A}{d l^{2}}>0$ होता है।

$\therefore$ द्वितीय अवकलज परीक्षण के अनुसार, क्षेत्रफल $(A)$ जब $l=\frac{112}{\pi+4}$ होता है, तब न्यूनतम होता है।

इसलिए, जब वर्ग के निर्माण के तार की लंबाई $\frac{112}{\pi+4} cm$ होती है, तब संयुक्त क्षेत्रफल न्यूनतम होता है। वृत्त के निर्माण के तार की लंबाई $28-\frac{112}{\pi+4}=\frac{28 \pi}{\pi+4} cm$ होती है।

हल

मान लीजिए $r$ और $h$ क्रमशः एक गोले के त्रिज्या $R$ के अंतर्गत अंतर्विष्ट शंकु की त्रिज्या और ऊँचाई हो।

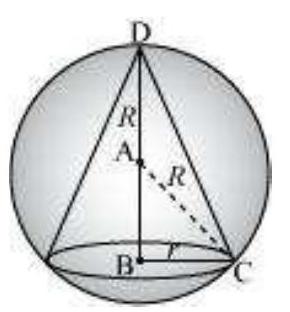
मान लीजिए $V$ शंकु का आयतन हो।

तब, $V=\frac{1}{3} \pi r^{2} h$

शंकु की ऊँचाई निम्नलिखित द्वारा दी जाती है,

$h=R+AB=R+\sqrt{R^{2}-r^{2}} \quad$ [ $ABC$ एक समकोण त्रिकोण है]

$ \begin{aligned} & \therefore V=\frac{1}{3} \pi r^{2}(R+\sqrt{R^{2}-r^{2}}) \\ & =\frac{1}{3} \pi r^{2} R+\frac{1}{3} \pi r^{2} \sqrt{R^{2}-r^{2}} \\ & \therefore \frac{d V}{d r}=\frac{2}{3} \pi r R+\frac{2}{3} \pi r \sqrt{R^{2}-r^{2}}+\frac{1}{3} \pi r^{2} \cdot \frac{(-2 r)}{2 \sqrt{R^{2}-r^{2}}} \\

$$ \begin{aligned} & =\frac{2}{3} \pi r R+\frac{2}{3} \pi r \sqrt{R^{2}-r^{2}}-\frac{1}{3} \pi \frac{r^{3}}{\sqrt{R^{2}-r^{2}}} \\ & =\frac{2}{3} \pi r R+\frac{2 \pi r(R^{2}-r^{2})-\pi r^{3}}{3 \sqrt{R^{2}-r^{2}}} \\ & =\frac{2}{3} \pi r R+\frac{2 \pi r R^{2}-3 \pi r^{3}}{3 \sqrt{R^{2}-r^{2}}} \\ & \frac{d^{2} V}{d r^{2}}=\frac{2 \pi R}{3}+\frac{3 \sqrt{R^{2}-r^{2}}(2 \pi R^{2}-9 \pi r^{2})-(2 \pi r R^{2}-3 \pi r^{3}) \cdot \frac{(-2 r)}{6 \sqrt{R^{2}-r^{2}}}}{9(R^{2}-r^{2})} \\ & =\frac{2}{3} \pi R+\frac{9(R^{2}-r^{2})(2 \pi R^{2}-9 \pi r^{2})+2 \pi r^{2} R^{2}+3 \pi r^{4}}{27(R^{2}-r^{2})^{\frac{3}{2}}} \end{aligned} $$

अब, $\frac{d V}{d r}=0 \Rightarrow \frac{2}{3} \quad r R=\frac{3 \pi r^{3}-2 \pi r R^{2}}{3 \sqrt{R^{2}-r^{2}}}$

$\Rightarrow 2 R=\frac{3 r^{2}-2 R^{2}}{\sqrt{R^{2}-r^{2}}} \Rightarrow 2 R \sqrt{R^{2}-r^{2}}=3 r^{2}-2 R^{2}$

$\Rightarrow 4 R^{2}(R^{2}-r^{2})=(3 r^{2}-2 R^{2})^{2}$

$\Rightarrow 4 R^{4}-4 R^{2} r^{2}=9 r^{4}+4 R^{4}-12 r^{2} R^{2}$

$\Rightarrow 9 r^{4}=8 R^{2} r^{2}$

$\Rightarrow r^{2}=\frac{8}{9} R^{2}$

जब $r^{2}=\frac{8}{9} R^{2}$, तो $\frac{d^{2} V}{d r^{2}}<0$।

द्वितीय अवकलज परीक्षण के अनुसार, शंकु का आयतन जब $r^{2}=\frac{8}{9} R^{2}$ होता है, तब अधिकतम होता है।

जब $r^{2}=\frac{8}{9} R^{2}, h=R+\sqrt{R^{2}-\frac{8}{9} R^{2}}=R+\sqrt{\frac{1}{9} R^{2}}=R+\frac{R}{3}=\frac{4}{3} R$।

इसलिए,

$=\frac{1}{3} \pi(\frac{8}{9} R^{2})(\frac{4}{3} R)$

$=\frac{8}{27}(\frac{4}{3} \pi R^{3})$

$=\frac{8}{27} \times($ गोले का आयतन $)$

इसलिए, गोले में अंकित सबसे बड़े शंकु का आयतन गोले के आयतन के $\frac{8}{27}$ होता है।

हल

मान लीजिए $r$ और $h$ क्रमशः शंकु की त्रिज्या और ऊँचाई (ऊंचाई) है।

तब, शंकु का आयतन $(V)$ निम्नलिखित द्वारा दिया गया है:

$V=\frac{1}{3} \pi r^{2} h \Rightarrow h=\frac{3 V}{r^{2}}$

अपकेंद्री शंकु के सतह क्षेत्रफल $(S)$ द्वारा दिया जाता है,

$S=\pi r l$ (जहाँ $/$ झुकाव ऊंचाई है)

$=\pi r \sqrt{r^{2}+h^{2}}$

$=\pi r \sqrt{r^{2}+\frac{9 \hbar^{2}}{\pi^{2} r^{4}}} \stackrel{\pi}{=} \frac{r \sqrt{9^{2} r^{6}+V^{2}}}{\pi r^{2}}$

$=\frac{1}{r} \sqrt{\pi^{3} r^{6}+9 V^{2}}$

$ \begin{aligned} \therefore \frac{d S}{d r} & =\frac{r \cdot \frac{6 \pi^{2} r^{5}}{2 \sqrt{{ }^{2} r^{6} 9 V^{2}}}-\sqrt{\pi^{2} r^{6}+9 V^{2}}}{r^{2}} \\ & =\frac{3 \pi^{2} r^{6}-\pi^{2} r^{6}-9 V^{2}}{r^{2} \sqrt{\pi^{2} r^{6}+9 V^{2}}} \\ & =\frac{2 \pi^{2} r^{6}-9 V^{2}}{r^{2} \sqrt{\pi^{2} r^{6}+9 V^{2}}} \\ & =\frac{2 \pi^{2} r^{6}-9 V^{2}}{r^{2} \sqrt{\pi^{2} r^{6}+9 V^{2}}} \end{aligned} $

अब, $\frac{d S}{d r}=0 \Rightarrow 2 \pi^{2} r^{6}=9 V^{2} \Rightarrow r^{6}=\frac{9 V^{2}}{2 \pi^{2}}$

इसलिए, यह आसानी से जांचा जा सकता है कि जब $r^{6}=\frac{9 V^{2}}{2 \pi^{2}}, \frac{d^{2} S}{d r^{2}}>0$ होता है।

$\square$ द्वितीय अवकलज परीक्षण के अनुसार, शंकु के सतह क्षेत्रफल न्यूनतम होता है जब $r^{6}=\frac{9 V^{2}}{2 \pi^{2}}$ हो।

जब $r^{6}=\frac{9 V^{2}}{2 \pi^{2}}, h=\frac{3 V}{\pi r^{2}}=\frac{3}{\pi r^{2}}(\frac{2 \pi^{2} r^{6}}{9})^{\frac{1}{2}}=\frac{3}{\pi r^{2}} \cdot \frac{\sqrt{2} \pi r^{3}}{3}=\sqrt{2} r$।

इसलिए, दिए गए आयतन के लिए, न्यूनतम वक्र सतह वाले सम वृत्तीय शंकु की ऊंचाई आधार की त्रिज्या के $\sqrt{2}$ गुना होती है।

हल

मान लीजिए $\theta$ शंकु का अर्ध-शीर्ष कोण है।

स्पष्ट रूप से,

$ \theta \in[0, \frac{\pi}{2}] $

मान लीजिए $r, h$, और $/$ क्रमशः शंकु की त्रिज्या, ऊंचाई और झुकाव ऊंचाई है। शंकु की झुकाव ऊंचाई निर्धारित की गई है।

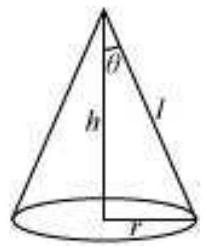
अब, $r=I \sin \theta$ और $h=I \cos \theta$

शंकु का आयतन $(V)$ निम्नलिखित द्वारा दिया जाता है,

$ \begin{aligned} & V=\frac{1}{3} \pi r^{2} h \\ & =\frac{1}{3} \pi(l^{2} \sin ^{2} \theta)(l \cos \theta) \\ & =\frac{1}{3} \pi l^{3} \sin ^{2} \theta \cos \theta \\ & \begin{aligned} \therefore \frac{d V}{d \theta} & =\frac{l^{3} \pi}{3}[\sin ^{2} \theta(-\sin \theta)+\cos \theta(2 \sin \theta \cos \theta)] \\ & =\frac{l^{3} \pi}{3}[-\sin ^{3}+2 \sin \theta \cos ^{2} \theta] \end{aligned} \\ & \begin{aligned} \frac{d^{2} V}{d \theta^{2}} & =\frac{l^{3} \pi}{3}[-3 \sin ^{2} \theta \cos \theta+2 \cos ^{3} \theta-4 \sin ^{2} \theta \cos \theta] \\ & =\frac{l^{3} \pi}{3}[2 \cos ^{3} \theta-7 \sin ^{2} \theta \cos \theta] \end{aligned} \end{aligned} $

अब, $\frac{d V}{d \theta}=0$

$\Rightarrow \sin ^{3} \theta=2 \sin \theta \cos ^{2} \theta$

$\Rightarrow \tan ^{2} \theta=2$

$\Rightarrow \tan \theta=\sqrt{2}$

$\Rightarrow \theta=\tan ^{-1} \sqrt{2}$

अब, जब $\theta=\tan ^{-1} \sqrt{2}$, तो $\tan ^{2} \theta=2$ या $\sin ^{2} \theta=2 \cos ^{2} \theta$।

तब, हम निम्नलिखित प्राप्त करते हैं:

$\frac{d^{2} V}{d \theta^{2}}=\frac{l^{3} \pi}{3}[2 \cos ^{3} \theta-14 \cos ^{3} \theta]=-4 \pi l^{3} \cos ^{3} \theta<0$ जब $\theta \in[0, \frac{\pi}{2}]$

$\square$ द्वितीय अवकलज परीक्षण के अनुसार, आयतन $(V)$ अधिकतम होता है जब $\theta=\tan ^{-1} \sqrt{2}$।

इसलिए, दिए गए झुकाव ऊँचाई के लिए, अधिकतम आयतन वाले शंकु के अर्ध-शीर्षकोण $\tan ^{-1} \sqrt{2}$ होता है।

हल

मान लीजिए $\mathrm{r}, \mathrm{h}, \mathrm{l}$ क्रमशः एक सम वृत्तीय शंकु की त्रिज्या, ऊँचाई और झुकाव ऊँचाई हो। मान लीजिए $S$ शंकु के दिए गए सतह क्षेत्रफल हो। हम जानते हैं, $l^2=\mathrm{r}^2+\mathrm{h}^2 \ldots .(1)$

$\begin{aligned} & S=\pi r l+\pi r^2 \ & S-\pi r^2=\pi r l \ & \Rightarrow l=\frac{S-\pi r^2}{\pi r} \ldots . . \end{aligned}$

$\begin{aligned} & \mathrm{V}=\frac{1}{3} \pi \mathrm{r}^2 \mathrm{~h} \\ & \Rightarrow \mathrm{V}=\frac{1}{3} \pi \mathrm{r}^2 \sqrt{1^2-\mathrm{r}^2}(\mathrm{by}(1)) \\ & \Rightarrow \mathrm{V}^2=\frac{1}{9} \pi^2 \mathrm{r}^4\left(\mathrm{l}^2-\mathrm{r}^2\right) \end{aligned}$

$\begin{aligned} & \Rightarrow \mathrm{V}^2=\frac{1}{9} \pi^2 \mathrm{r}^4\left[\left(\frac{\mathrm{S}-\pi \mathrm{r}^2}{\pi \mathrm{r}}\right)^2-\mathrm{r}^2\right] \\ & \Rightarrow \mathrm{V}^2=\frac{1}{9} \pi^2 \mathrm{r}^4\left[\frac{\left(\mathrm{S}-\pi \mathrm{r}^2\right)^2-\pi^2 \mathrm{r}^4}{\pi^2 \mathrm{r}^2}\right] \\ & \Rightarrow \mathrm{V}^2=\frac{1}{9} \mathrm{r}^2\left[\left(\mathrm{~S}-\pi \mathrm{r}^2\right)^2-\pi^2 \mathrm{r}^4\right] \\ & \Rightarrow \mathrm{V}^2=\frac{1}{9} \mathrm{r}^2\left[\mathrm{~S}^2-2 \pi \mathrm{Sr}^2+\pi^2 \mathrm{r}^4-\pi^2 \mathrm{r}^4\right] \\ & \Rightarrow \mathrm{V}^2=\frac{1}{9}\left(\mathrm{r}^2 \mathrm{~S}^2-2 \pi \mathrm{Sr}^4\right) \\ \end{aligned}$

$2 \mathrm{~V} \frac{\mathrm{dV}}{\mathrm{dr}}=\frac{\mathrm{S}^2}{9} 2 \mathrm{r}-\frac{2 \pi \mathrm{S}}{9} 4 \mathrm{r}^3$

$2 \mathrm{~V} \frac{\mathrm{dV}}{\mathrm{dr}}=\frac{2 \mathrm{rS}}{9}\left(\mathrm{~S}-4 \pi \mathrm{r}^2\right)$

अधिकतम आयतन के लिए, $\frac{\mathrm{dV}}{\mathrm{dr}}=0$

$\begin{aligned} & \Rightarrow \frac{2 \mathrm{rS}}{9}\left(\mathrm{~S}-4 \pi \mathrm{r}^2\right)=0 \\ & \Rightarrow \mathrm{r}=\mathrm{o} \text { or } \mathrm{S}-4 \pi \mathrm{r}^2=0 \end{aligned}$

क्योंकि, $r$ शून्य नहीं हो सकता

$\begin{aligned} & \Rightarrow \mathrm{S}=4 \pi \mathrm{r}^2 \ & \Rightarrow \mathrm{r}^2=\frac{\mathrm{S}}{4 \pi} \ & \Rightarrow \mathrm{r}^2=\frac{\pi \mathrm{rl}+\pi \mathrm{r}^2}{4 \pi} \end{aligned}$

$\begin{aligned} & \Rightarrow 4 \pi r^2=\pi r l+\pi r^2 \ & \Rightarrow 3 \pi r^2=\pi r l \ & \Rightarrow l=3 r \end{aligned}$

मान लीजिए $\alpha$ अर्ध-शीर्षकोण है।

$\begin{aligned} & \sin \alpha=\frac{r}{l} \\ & \sin \alpha=\frac{r}{3 r} \\ & \Rightarrow \alpha=\sin ^{-1}\left(\frac{1}{3}\right)

\end{aligned}$

हल

दिया गया वक्र $x^{2}=2 y$ है।

प्रत्येक $x$ के मान के लिए बिंदु की स्थिति $(x, \frac{x^{2}}{2})$ होगी।

बिंदु $(x, \frac{x^{2}}{2})$ और $(0,5)$ के बीच दूरी $d(x)$ निम्नलिखित द्वारा दी गई है,

$d(x)=\sqrt{(x-0)^{2}+(\frac{x^{2}}{2}-5)^{2}}=\sqrt{x^{2}+\frac{x^{4}}{4}+25-5 x^{2}}=\sqrt{\frac{x^{4}}{4}-4 x^{2}+25}$

$\therefore d^{\prime}(x)=\frac{(x^{3}-8 x)}{2 \sqrt{\frac{x^{4}}{4}-4 x^{2}+25}}=\frac{(x^{3}-8 x)}{\sqrt{x^{4}-16 x^{2}+100}}$

अब, $d^{\prime}(x)=0 \Rightarrow x^{3}-8 x=0$

$\Rightarrow x(x^{2}-8)=0$

$\Rightarrow x=0, \pm 2 \sqrt{2}$

$ \begin{aligned} & \begin{aligned} & \text{ और, } d^{\prime \prime}(x)= \frac{\sqrt{x^{4}-16 x^{2}+100}(3 x^{2}-8)-(x^{3}-8 x) \cdot \frac{4 x^{3}-32 x}{2 \sqrt{x^{4}-16 x^{2}+100}}}{(x^{4}-16 x^{2}+100)} \\ &=\frac{(x^{4}-16 x^{2}+100)(3 x^{2}-8)-2(x^{3}-8 x)(x^{3}-8 x)}{(x^{4}-16 x^{2}+100)^{\frac{3}{2}}} \\ &=\frac{(x^{4}-16 x^{2}+100)(3 x^{2}-8)-2(x^{3}-8 x)^{2}}{(x^{4}-16 x^{2}+100)^{\frac{3}{2}}} \\ & \text{ जब, } x=0 \text{, तो } d^{\prime \prime}(x)=\frac{36(-8)}{6^{3}}<0 . \end{aligned} \\ & \text{ जब, } x= \pm 2 \sqrt{2}, d^{\prime \prime}(x)>0 . \end{aligned} $

$\square$ दूसरे अवकलज परीक्षण द्वारा, $d(x)$ का मान $x= \pm 2 \sqrt{2}$ पर न्यूनतम होता है।

जब $x= \pm 2 \sqrt{2}, y=\frac{(2 \sqrt{2})^{2}}{2}=4$ होता है।

अतः, वक्र $x^{2}=2 y$ पर बिंदु $(0,5)$ से सबसे निकटस्थ बिंदु $( \pm 2 \sqrt{2}, 4)$ है। सही उत्तर है $A$।

हल

मान लीजिए $f(x)=\frac{1-x+x^{2}}{1+x+x^{2}}$।

$ \begin{aligned} \therefore f^{\prime}(x) & =\frac{(1+x+x^{2})(-1+2 x)-(1-x+x^{2})(1+2 x)}{(1+x+x^{2})^{2}} \\

$$ & =\frac{-1+2 x-x+2 x^{2}-x^{2}+2 x^{3}-1-2 x+x+2 x^{2}-x^{2}-2 x^{3}}{(1+x+x^{2})^{2}} \\ & =\frac{2 x^{2}-2}{(1+x+x^{2})^{2}}=\frac{2(x^{2}-1)}{(1+x+x^{2})^{2}} \end{aligned} $

$\therefore f^{\prime}(x)=0 \Rightarrow x^{2}=1 \Rightarrow x= \pm 1$

अब, $f^{\prime \prime}(x)=\frac{2[(1+x+x^{2})^{2}(2 x)-(x^{2}-1)(2)(1+x+x^{2})(1+2 x)]}{(1+x+x^{2})^{4}}$

$ =\frac{4(1+x+x^{2})[(1+x+x^{2}) x-(x^{2}-1)(1+2 x)]}{(1+x+x^{2})^{4}} $

$ \begin{aligned} & =\frac{4[x+x^{2}+x^{3}-x^{2}-2 x^{3}+1+2 x]}{(1+x+x^{2})^{3}} \\ & =\frac{4(1+3 x-x^{3})}{(1+x+x^{2})^{3}} \end{aligned} $

और, $f^{\prime \prime}(1)=\frac{4(1+3-1)}{(1+1+1)^{3}}=\frac{4(3)}{(3)^{3}}=\frac{4}{9}>0$

भी, $f^{\prime \prime}(-1)=\frac{4(1-3+1)}{(1-1+1)^{3}}=4(-1)=-4<0$

$\square$ द्वितीय अवकलज परीक्षण के अनुसार, $f$ का न्यूनतम मान $x=1$ पर है और न्यूनतम मान द्वारा दिया गया है

$f(1)=\frac{1-1+1}{1+1+1}=\frac{1}{3}$.

सही उत्तर है $D$.

हल

मान लीजिए $f(x)=[x(x-1)+1]^{\frac{1}{3}}$.

$\therefore f^{\prime}(x)=\frac{2 x-1}{3[x(x-1)+1]^{\frac{2}{3}}}$

अब, $f^{\prime}(x)=0 \Rightarrow x=\frac{1}{2}$

फिर, हम अंतिम बिंदुओं $x=0$ और $x=1$ के अंतराल $[0,1]$ पर $f$ के मान का मूल्यांकन करते हैं।

$f(0)=[0(0-1)+1]^{\frac{1}{3}}=1$

$f(1)=[1(1-1)+1]^{\frac{1}{3}}=1$

$f(\frac{1}{2})=[\frac{1}{2}(\frac{-1}{2})+1]^{\frac{1}{3}}=(\frac{3}{4})^{\frac{1}{3}}$

इसलिए, हम निष्कर्ष निकाल सकते हैं कि अंतराल $[0,1]$ में $f$ का अधिकतम मान 1 है।

सही उत्तर है $C$.