हल

मान लीजिए ${ }^{x_1}$ और $x_2$ कोई दो संख्याएँ हैं $\mathbf{R}$ में।

तब, हम निम्नलिखित के अनुसार हैं:

$x_1<x_2 \Rightarrow 3 x_1<3 x_2 \Rightarrow 3 x_1+17<3 x_2+17 \Rightarrow f(x_1)<f(x_2)$

अतः, $f$ फलन $\mathbf{R}$ पर सख्त रूप से बढ़ता है।

अल्टरनेट विधि:

$f(x)=3>0$, $\mathbf{R}$ के प्रत्येक अंतराल में।

अतः, फलन $\mathbf{R}$ पर सख्त रूप से बढ़ता है।

हल

मान लीजिए ${ }^{x_1}$ और $x_2$ कोई दो संख्याएँ हैं $\mathbf{R}$ में।

तब, हम निम्नलिखित के अनुसार हैं:

$x_1<x_2 \Rightarrow 2 x_1<2 x_2 \Rightarrow e^{2 x_1}<e^{2 x_2} \Rightarrow f(x_1)<f(x_2)$

अतः, $f$ फलन $\mathbf{R}$ पर सख्त रूप से बढ़ता है।

हल

दिया गया फलन $f(x)=\sin x$ है।

$\therefore f^{\prime}(x)=\cos x$ (a) प्रत्येक $x \in(0, \frac{\pi}{2})$ के लिए, $\cos x>0$, हमें $f^{\prime}(x)>0$ प्राप्त होता है।

अतः, $f$ फलन $(0, \frac{\pi}{2})$ में सख्त रूप से बढ़ता है।

(b) प्रत्येक $x \in(\frac{\pi}{2}, \pi)$ के लिए, $\cos x<0$, हमें $f^{\prime}(x)<0$ प्राप्त होता है।

अतः, $f$ फलन $(\frac{\pi}{2}, \pi)$ में सख्त रूप से घटता है।

(c) (a) और (b) में प्राप्त नतीजों से स्पष्ट है कि $f$ फलन $(0, \pi)$ में न बढ़ता है और न ही घटता है।

हल

दिया गया फलन $f(x)=2 x^{2}-3 x$ है।

$f^{\prime}(x)=4 x-3$

$\therefore f^{\prime}(x)=0 \Rightarrow x=\frac{3}{4}$

अब, बिंदु $\frac{3}{4}$ वास्तविक रेखा को दो अलग-अलग अंतराल में विभाजित करता है अर्थात, $(-\infty, \frac{3}{4})$ और $(\frac{3}{4}, \infty)$।

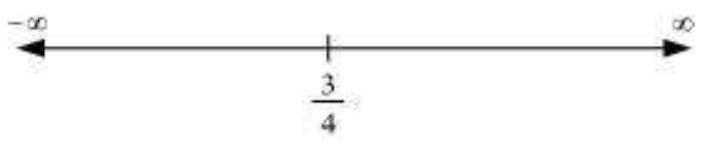
अंतराल $(-\infty, \frac{3}{4}), f^{\prime}(x)=4 x-3<0$।

अतः, दी गई फलन $(f)$ अंतराल $(-\infty, \frac{3}{4})$ में सख्त घटता है।

अंतराल $(\frac{3}{4}, \infty), f^{\prime}(x)=4 x-3>0$।

अतः, दी गई फलन $(f)$ अंतराल $(\frac{3}{4}, \infty)$ में सख्त बढ़ता है।

हल

दिया गया फलन $f(x)=2 x^{3}-3 x^{2}-36 x+7$ है।

$f^{\prime}(x)=6 x^{2}-6 x-36=6(x^{2}-x-6)=6(x+2)(x-3)$

$\therefore f^{\prime}(x)=0 \Rightarrow x=-2,3$

बिंदु $x=-2$ और $x=3$ वास्तविक रेखा को तीन अलग-अलग अंतराल में विभाजित करते हैं अर्थात, $(-\infty,-2),(-2,3)$, और $(3, \infty)$।

अंतराल $(-\infty,-2)$ और $(3, \infty), f^{\prime}(x)$ धनात्मक होता है जबकि अंतराल $(-2,3), f^{\prime}(x)$ ऋणात्मक होता है।

अतः, दिया गया फलन $(f)$ अंतराल $(-\infty,-2)$ और $(3, \infty)$ में सख्त बढ़ता है, जबकि फलन $(f)$ अंतराल $(-2,3)$ में सख्त घटता है।

हल

(a) हमें दिया गया है,

$f(x)=x^{2}+2 x-5$

$\therefore f^{\prime}(x)=2 x+2$

अब,

$f^{\prime}(x)=0 \Rightarrow x=-1$

बिंदु $x=-1$ वास्तविक रेखा को दो अलग-अलग अंतराल में विभाजित करता है, अर्थात $(-\infty,-1)$ और $(-1, \infty)$।

अंतराल $(-\infty,-1)$ में, $f^{\prime}(x)=2 x+2<0$।

$\therefore f$ अंतराल $(-\infty,-1)$ में सख्त घटती है।

इसलिए, $f$ बिंदु $x<-1$ के लिए सख्त घटती है।

अंतराल $(-1, \infty)$ में, $f^{\prime}(x)=2 x+2>0$।

$\therefore f$ अंतराल $(-1, \infty)$ में सख्त बढ़ती है।

इसलिए, $f$ बिंदु $x>-1$ के लिए सख्त बढ़ती है।

(b) हमें दिया गया है,

$f(x)=10-6 x-2 x^{2}$

$\therefore f^{\prime}(x)=-6-4 x$

अब,

$f^{\prime}(x)=0 \Rightarrow x=-\frac{3}{2}$

बिंदु $x=-\frac{3}{2}$ वास्तविक रेखा को दो अलग-अलग अंतराल में विभाजित करता है

अर्थात $(-\infty,-\frac{3}{2})$ और $(-\frac{3}{2}, \infty)$।

अंतराल $(-\infty,-\frac{3}{2})$ अर्थात जब $x<-\frac{3}{2}, f^{\prime}(x)=-6-4 x<0$।

$\therefore f$ बिंदु $x<-\frac{3}{2}$ के लिए सख्त बढ़ती है।

अंतराल $(-\frac{3}{2}, \infty)$ अर्थात जब $x>-\frac{3}{2}, f^{\prime}(x)=-6-4 x<0$।

$\therefore f$ बिंदु $x>-\frac{3}{2}$ के लिए सख्त घटती है।

(c) हमें दिया गया है,

$f(x)=-2 x^{3}-9 x^{2}-12 x+1$

$\therefore f^{\prime}(x)=-6 x^{2}-18 x-12=-6(x^{2}+3 x+2)=-6(x+1)(x+2)$

अब,

$f^{\prime}(x)=0 \Rightarrow x=-1$ और $x=-2$

बिंदु $x=-1$ और $x=-2$ वास्तविक रेखा को तीन अलग-अलग अंतराल में विभाजित करते हैं

अर्थात $(-\infty,-2),(-2,-1)$, और $(-1, \infty)$।

अंतराल $(-\infty,-2)$ और $(-1, \infty)$ अर्थात जब $x<-2$ और $x>-1$,

$f^{\prime}(x)=-6(x+1)(x+2)<0$। $\therefore f$ बिंदु $x<-2$ और $x>-1$ के लिए सख्त घटती है।

अब, अंतराल $(-2,-1)$ अर्थात जब $-2<x<-1, f^{\prime}(x)=-6(x+1)(x+2)>0$।

$\therefore f$ बिंदु $-2<x<-1$ के लिए सख्त बढ़ती है।

(d) हमें दिया गया है,

$ \begin{aligned} & f(x)=6-9 x-x^{2} \\ & \therefore f^{\prime}(x)=-9-2 x \end{aligned} $

अब, $f^{\prime}$

$(x)=0$ देता है $x=-\frac{9}{2}$

बिंदु $x=-\frac{9}{2}$ वास्तविक रेखा को दो अलग-अलग अंतराल में विभाजित करता है अर्थात,

$(-\infty,-\frac{9}{2})$ और $(-\frac{9}{2}, \infty)$।

अंतराल $(-\infty,-\frac{9}{2})$ अर्थात, $x<-\frac{9}{2}$ के लिए, $f^{\prime}(x)=-9-2 x>0$।

$\therefore f$ $x<-\frac{9}{2}$ के लिए सख्त रूप से बढ़ती है।

अंतराल $(-\frac{9}{2}, \infty)$ अर्थात, $x>-\frac{9}{2}$ के लिए, $f^{\prime}(x)=-9-2 x<0$। $\therefore f$ $x>-\frac{9}{2}$ के लिए सख्त रूप से घटती है।

(e) हमारे पास,

$ \begin{aligned} f(x)= & (x+1)^{3}(x-3)^{3} \\ f^{\prime}(x) & =3(x+1)^{2}(x-3)^{3}+3(x-3)^{2}(x+1)^{3} \\ & =3(x+1)^{2}(x-3)^{2}[x-3+x+1] \\ & =3(x+1)^{2}(x-3)^{2}(2 x-2) \\ & =6(x+1)^{2}(x-3)^{2}(x-1) \end{aligned} $

अब,

$f^{\prime}(x)=0 \Rightarrow x=-1,3,1$

बिंदु $x=-1, x=1$, और $x=3$ वास्तविक रेखा को चार अलग-अलग अंतराल में विभाजित करते हैं

अर्थात, $(-\infty,-1),(-1,1),(1,3)$, और $(3, \infty)$।

अंतराल $(-\infty,-1)$ और $(-1,1)$ में, $f^{\prime}(x)=6(x+1)^{2}(x-3)^{2}(x-1)<0$।

$\therefore f$ अंतराल $(-\infty,-1)$ और $(-1,1)$ में सख्त रूप से घटती है।

अंतराल $(1,3)$ और $(3, \infty)$ में, $f^{\prime}(x)=6(x+1)^{2}(x-3)^{2}(x-1)>0$।

$\therefore f$ अंतराल $(1,3)$ और $(3, \infty)$ में सख्त रूप से बढ़ती है।

Solution

हमारे पास,

$ \begin{aligned} & y=\log (1+x)-\frac{2 x}{2+x} \\ & \therefore \frac{d y}{d x}=\frac{1}{1+x}-\frac{(2+x)(2)-2 x(1)}{(2+x)^{2}}=\frac{1}{1+x}-\frac{4}{(2+x)^{2}}=\frac{x^{2}}{(2+x)^{2}} \end{aligned} $

अब, $\frac{d y}{d x}=0$

$\Rightarrow \frac{x^{2}}{(2+x)^{2}}=0$

$\Rightarrow x^{2}=0 \quad[(2+x) \neq 0$ क्योंकि $x>-1]$

$\Rightarrow x=0$

क्योंकि $x>-1$, बिंदु $x=0$ डोमेन $(-1, \infty)$ को दो अलग-अलग अंतराल में विभाजित करता है अर्थात, $-1<$ $x<0$ और $x>0$।

जब $-1<x<0$, हमारे पास:

$x<0 \Rightarrow x^{2}>0$

$x>-1 \Rightarrow(2+x)>0 \Rightarrow(2+x)^{2}>0$

$\therefore y^{\prime}=\frac{x^{2}}{(2+x)^{2}}>0$

इसके अलावा, जब $x>0$:

$x>0 \Rightarrow x^{2}>0,(2+x)^{2}>0$

$\therefore y^{\prime}=\frac{x^{2}}{(2+x)^{2}}>0$

इसलिए, फलन $f$ इस डोमेन में बढ़ता है।

हल

हमारे पास,

$y=[x(x-2)]^{2}=[x^{2}-2 x]^{2}$

$\therefore \frac{d y}{d x}=y^{\prime}=2(x^{2}-2 x)(2 x-2)=4 x(x-2)(x-1)$

$\therefore \frac{d y}{d x}=0 \Rightarrow x=0, x=2, x=1$।

बिंदु $x=0, x=1$, और $x=2$ वास्तविक रेखा को चार अलग-अलग अंतराल में विभाजित करते हैं, अर्थात $(-\infty, 0),(0,1)(1,2)$, और $(2, \infty)$।

अंतराल $(-\infty, 0)$ और $(1,2)$ में $\frac{d y}{d x}<0$।

$\therefore y$ अंतराल $(-\infty, 0)$ और $(1,2)$ में सख्ती से घटता है।

हालांकि, अंतराल $(0,1)$ और $(2, \infty)$ में $\frac{d y}{d x}>0$।

$\therefore y$ अंतराल $(0,1)$ और $(2, \infty)$ में सख्ती से बढ़ता है।

$\therefore y$ $0<x<1$ और $x>2$ के लिए सख्ती से बढ़ता है।

हल

हमारे पास,

$ \begin{aligned} & y=\frac{4 \sin \theta}{(2+\cos \theta)}-\theta \\ & \begin{aligned} \therefore \frac{d y}{d x} & =\frac{(2+\cos \theta)(4 \cos \theta)-4 \sin \theta(-\sin \theta)}{(2+\cos \theta)^{2}}-1 \\ \quad & \frac{8 \cos \theta+4 \cos ^{2} \theta+4 \sin ^{2} \theta}{(2+\cos \theta)^{2}}-1 \\ \quad & \frac{8 \cos \theta+4}{(2+\cos \theta)^{2}}-1 \end{aligned} \end{aligned} $

अब, $\frac{d y}{d x}=0$।

$\Rightarrow \frac{8 \cos \theta+4}{(2+\cos \theta)^{2}}=1$

$\Rightarrow 8 \cos \theta+4=4+\cos ^{2} \theta+4 \cos \theta$

$\Rightarrow \cos ^{2} \theta-4 \cos \theta=0$

$\Rightarrow \cos \theta(\cos \theta-4)=0$

$\Rightarrow \cos \theta=0$ या $\cos \theta=4$

क्योंकि $\cos \theta \neq 4, \cos \theta=0$।

$\cos \theta=0 \Rightarrow \theta=\frac{\pi}{2}$

अब,

$\frac{d y}{d x}=\frac{8 \cos \theta+4-(4+\cos ^{2} \theta+4 \cos \theta)}{(2+\cos \theta)^{2}}=\frac{4 \cos \theta-\cos ^{2} \theta}{(2+\cos \theta)^{2}}=\frac{\cos \theta(4-\cos \theta)}{(2+\cos \theta)^{2}}$

अंतराल $(0, \frac{\pi}{2})$ में, हमें $\cos \theta>0$ मिलता है। अतः, $4>\cos \theta \Rightarrow 4-\cos \theta>0$।

$\therefore \cos \theta(4-\cos \theta)>0$ और भी $(2+\cos \theta)^{2}>0$ है

$\Rightarrow \frac{\cos \theta(4-\cos \theta)}{(2+\cos \theta)^{2}}>0$

$\Rightarrow \frac{d y}{d x}>0$

अतः, $y$ अंतराल $(0, \frac{\pi}{2})$ में सख्त रूप से बढ़ती है।

इसके अतिरिक्त, दी गई फलन $x=0$ और $x=\frac{\pi}{2}$ पर सतत है।

अतः, $y$ अंतराल $[0, \frac{\pi}{2}]$ में बढ़ती है।

हल

दिया गया फलन $f(x)=\log x$ है।

$\therefore f^{\prime}(x)=\frac{1}{x}$

स्पष्ट रूप से, $x>0$ के लिए $f^{\prime}(x)=\frac{1}{x}>0$ है।

अतः, $f(x)=\log x$ अंतराल $(0, \infty)$ में सख्त रूप से बढ़ता है।

हल

दिया गया फलन $f(x)=x^{2}-x+1$ है।

$\therefore f^{\prime}(x)=2 x-1$

अब, $f^{\prime}(x)=0 \Rightarrow x=\frac{1}{2}$ है।

बिंदु $\frac{1}{2}$ अंतराल $(-1,1)$ को दो अलग-अलग अंतरालों में विभाजित करता है

अर्थात, $(-1, \frac{1}{2})$ और $(\frac{1}{2}, 1)$।

अब, अंतराल $(-1, \frac{1}{2})$ में, $f^{\prime}(x)=2 x-1<0$ है।

अतः, $f$ अंतराल $(-1, \frac{1}{2})$ में सख्त रूप से घटता है।

हालांकि, अंतराल $(\frac{1}{2}, 1)$ में, $f^{\prime}(x)=2 x-1>0$ है।

अतः, $f$ अंतराल $(\frac{1}{2}, 1)$ में सख्त रूप से बढ़ता है।

अतः, $f$ अंतराल $(-1,1)$ में न तो सख्त रूप से बढ़ता है और न ही घटता है।

हल

(A) मान लीजिए $f_1(x)=\cos x$।

$\therefore f_1^{\prime}(x)=-\sin x$

अंतराल $(0, \frac{\pi}{2})$ में, $f_1^{\prime}(x)=-\sin x<0$ है।

$\therefore f_1(x)=\cos x$ अंतराल $(0, \frac{\pi}{2})$ में सख्त रूप से घटता है।

(B) मान लीजिए $f_2(x)=\cos 2 x$.

$\therefore f_2^{\prime}(x)=-2 \sin 2 x$

अब, $0<x<\frac{\pi}{2} \Rightarrow 0<2 x<\pi \Rightarrow \sin 2 x>0 \Rightarrow-2 \sin 2 x<0$

$\therefore f_2^{\prime}(x)=-2 \sin 2 x<0$ अंतराल $(0, \frac{\pi}{2})$ पर

$\therefore f_2(x)=\cos 2 x$ अंतराल $(0, \frac{\pi}{2})$ में सख्त घटती है।

(C) मान लीजिए $f_3(x)=\cos 3 x$.

$\therefore f_3^{\prime}(x)=-3 \sin 3 x$

अब, $f_3^{\prime}(x)=0$.

$\Rightarrow \sin 3 x=0 \Rightarrow 3 x=\pi$, क्योंकि $x \in(0, \frac{\pi}{2})$

$\Rightarrow x=\frac{\pi}{3}$

बिंदु $x=\frac{\pi}{3}$ अंतराल $(0, \frac{\pi}{2})$ को दो अलग-अलग अंतराल में विभाजित करता है

अर्थात, $0(0, \frac{\pi}{3})$ और $(\frac{\pi}{3}, \frac{\pi}{2})$।

अब, अंतराल $(0, \frac{\pi}{3}), f_3(x)=-3 \sin 3 x<0[.$ क्योंकि $.0<x<\frac{\pi}{3} \Rightarrow 0<3 x<\pi]$.

$\therefore f_3$ अंतराल $(0, \frac{\pi}{3})$ में सख्त घटती है।

हालांकि, अंतराल $(\frac{\pi}{3}, \frac{\pi}{2}), f_3(x)=-3 \sin 3 x>0[.$ क्योंकि $.\frac{\pi}{3}<x<\frac{\pi}{2} \Rightarrow \pi<3 x<\frac{3 \pi}{2}]$. $\therefore f_3$ अंतराल $(\frac{\pi}{3}, \frac{\pi}{2})$ में सख्त बढ़ती है।

इसलिए, $f_3$ अंतराल $(0, \frac{\pi}{2})$ में न तो बढ़ती है और न ही घटती है।

(D) मान लीजिए $f_4(x)=\tan x$.

$\therefore f_4^{\prime}(x)=\sec ^{2} x$

अंतराल $(0, \frac{\pi}{2}), f_4^{\prime}(x)=\sec ^{2} x>0$.

$\therefore f_4$ अंतराल $(0, \frac{\pi}{2})$ में सख्त बढ़ती है।

इसलिए, फलन $\cos x$ और $\cos 2 x$ अंतराल $(0, \frac{\pi}{2})$ में सख्त घटते हैं। इसलिए, सही उत्तर A और B हैं।

हल

हम जानते हैं, $f(x)=x^{100}+\sin x-1$

$\therefore f^{\prime}(x)=100 x^{99}+\cos x$

अंतराल $(0,1), \cos x>0$ और $100 x^{99}>0$.

$\therefore f^{\prime}(x)>0$.

इसलिए, फलन $f$ अंतराल $(0,1)$ में सख्त बढ़ती है।

अंतराल $(\frac{\pi}{2}, \pi), \cos x<0$ और $100 x^{99}>0$ है। इसके अलावा, $100 x^{99}>\cos x$ भी है।

$\therefore f^{\prime}(x)>0$ अंतराल $(\frac{\pi}{2}, \pi)$ में है।

इसलिए, फलन $f$ अंतराल $(\frac{\pi}{2}, \pi)$ में सख्त रूप से बढ़ रहा है।

अंतराल $(0, \frac{\pi}{2}), \cos x>0$ और $100 x^{99}>0$ है।

$\therefore 100 x^{99}+\cos x>0$

$\Rightarrow f^{\prime}(x)>0$ अंतराल $(0, \frac{\pi}{2})$ पर है

$\therefore f$ अंतराल $(0, \frac{\pi}{2})$ में सख्त रूप से बढ़ रहा है।

इसलिए, फलन $f$ कोई भी अंतराल में सख्त रूप से घट रहा नहीं है।

सही उत्तर D है।

हल

हम जानते हैं, $f(x)=x^{2}+a x+1$

$\therefore f^{\prime}(x)=2 x+a$

अब, फलन $f$ अंतराल $(1,2)$ में बढ़ रहा होगा, यदि $f^{\prime}(x)>0$ अंतराल $(1,2)$ में है।

$f^{\prime}(x)>0$

$\Rightarrow 2 x+a>0$

$\Rightarrow 2 x>-a$

$\Rightarrow \quad x>\frac{-a}{2}$

इसलिए, हमें ऐसे न्यूनतम मान का पता लगाना होगा जिसके लिए

$x>\frac{-a}{2}$, जब $x \in(1,2)$ हो।

$\Rightarrow x>\frac{-a}{2}$ (जब $1<x<2)$

इसलिए, फलन $f$ के लिए अंतराल $(1,2)$ पर बढ़ता होने के लिए $a$ का न्यूनतम मान निम्नलिखित द्वारा दिया गया है,

$\frac{-a}{2}=1$

$\frac{-a}{2}=1 \Rightarrow a=-2$

इसलिए, $a$ के आवश्यक मान -2 है।

हल

हम जानते हैं,

$f(x)=x+\frac{1}{x}$

$\therefore f^{\prime}(x)=1-\frac{1}{x^{2}}$

अब,

$f^{\prime}(x)=0 \Rightarrow \frac{1}{x^{2}}=1 \Rightarrow x= \pm 1$

बिंदु $x=1$ और $x=-1$ वास्तविक रेखा को तीन अलग-अलग अंतराल में विभाजित करते हैं, अर्थात,

$(-\infty,-1),(-1,1)$, और $(1, \infty)$।

अंतराल $(-1,1)$ में यह देखा जाता है कि:

$-1<x<1$

$\Rightarrow x^{2}<1$

$\Rightarrow 1<\frac{1}{x^{2}}, x \neq 0$

$\Rightarrow 1-\frac{1}{x^{2}}<0, x \neq 0$

$\therefore f^{\prime}(x)=1-\frac{1}{x^{2}}<0$ अंतराल $(-1,1) \sim{0}$ पर है।

$\therefore f$ अंतराल $(-1,1) \sim{0}$ पर सख्त घटती है।

अंतराल $(-\infty,-1)$ और $(1, \infty)$ में, यह देखा गया है कि: $x<-1$ या $1<x$

$\Rightarrow x^{2}>1$

$\Rightarrow 1>\frac{1}{x^{2}}$

$\Rightarrow 1-\frac{1}{x^{2}}>0$

$\therefore f^{\prime}(x)=1-\frac{1}{x^{2}}>0$ अंतराल $(-\infty,-1)$ और $(1, \infty)$ पर।

$\therefore f$ अंतराल $(-\infty, 1)$ और $(1, \infty)$ पर सख्त बढ़ती है।

इसलिए, फलन $f$ अंतराल $\mathbf{I}$ पर सख्त बढ़ती है जो $(-1,1)$ से अलग है। इसलिए, दिए गए परिणाम की साबित कर दिया गया है।

हल

हम जानते हैं,

$f(x)=\log \sin x$

$\therefore f^{\prime}(x)=\frac{1}{\sin x} \cos x=\cot x$

अंतराल $(0, \frac{\pi}{2})$ में, $f^{\prime}(x)=\cot x>0$।

$\therefore f$ अंतराल $(0, \frac{\pi}{2})$ में सख्त बढ़ती है।

अंतराल $(\frac{\pi}{2}, \pi)$ में, $f^{\prime}(x)=\cot x<0$।

$\therefore f$ अंतराल $(\frac{\pi}{2}, \pi)$ में सख्त घटती है।

हल

हम जानते हैं,

$f(x)=\log \cos x$

$\therefore f^{\prime}(x)=\frac{1}{\cos x}(-\sin x)=-\tan x$

अंतराल $(0, \frac{\pi}{2})$ में, $\tan x>0 \Rightarrow-\tan x<0$।

$\therefore f^{\prime}(x)<0$ अंतराल $(0, \frac{\pi}{2})$ पर

$\therefore f$ अंतराल $(0, \frac{\pi}{2})$ पर सख्त घटती है।

अंतराल $(\frac{\pi}{2}, \pi)$ में, $\tan x<0 \Rightarrow-\tan x>0$।

$\therefore f^{\prime}(x)>0$ अंतराल $(\frac{\pi}{2}, \pi)$ पर $\therefore f$ अंतराल $(\frac{\pi}{2}, \pi)$ पर सख्त बढ़ती है।

हल

हम जानते हैं,

$f(x)=x^{3}-3 x^{2}+3 x-100$

$ \begin{aligned} f^{\prime}(x) & =3 x^{2}-6 x+3 \ \end{aligned} `

& =3(x^{2}-2 x+1) \\ & =3(x-1)^{2} \end{aligned} $

किसी भी $x \in \mathbf{R},(x-1)^{2}>0$।

अतः, $f^{\prime}(x)$ वास्तविक संख्या में हमेशा धनात्मक होता है।

इसलिए, दी गई फलन $(f)$ वास्तविक संख्या में बढ़ता है।

हल

हमें दिया गया है,

$y=x^{2} e^{-x}$ $\therefore \frac{d y}{d x}=2 x e^{-x}-x^{2} e^{-x}=x e^{-x}(2-x)$

अब, $\frac{d y}{d x}=0$.

$\Rightarrow x=0$ और $x=2$

बिंदु $x=0$ और $x=2$ वास्तविक रेखा को तीन अलग-अलग अंतराल में विभाजित करते हैं

अर्थात, $(-\infty, 0),(0,2)$, और $(2, \infty)$।

अंतराल $(-\infty, 0)$ और $(2, \infty)$ में $f^{\prime}(x)<0$ क्योंकि $e^{-x}$ हमेशा धनात्मक होता है।

$\therefore f$ अंतराल $(-\infty, 0)$ और $(2, \infty)$ पर घटता है।

अंतराल $(0,2)$ में $f^{\prime}(x)>0$।

$\therefore f$ अंतराल $(0,2)$ पर सख्ती से बढ़ता है।

इसलिए, $f$ अंतराल $(0,2)$ में सख्ती से बढ़ता है।

सही उत्तर D है।