अध्याय 11 त्रिविमीय ज्यामिति अभ्यास 11.1
अभ्यास 11.1
1. यदि एक रेखा x, y और z-अक्ष के साथ क्रमशः $90^{\circ}, 135^{\circ}, 45^{\circ}$ के कोण बनाती है, तो इसके दिशा अनुपात ज्ञात कीजिए।
उत्तर दिखाएं
हल
मान लीजिए रेखा के दिशा अनुपात $l, m$, और $n$ हैं।
$l=\cos 90^{\circ}=0$
$m=\cos 135^{\circ}=-\frac{1}{\sqrt{2}}$
$n=\cos 45^{\circ}=\frac{1}{\sqrt{2}}$
इसलिए, रेखा के दिशा अनुपात $0,-\frac{1}{\sqrt{2}}$, और $\frac{1}{\sqrt{2}}$ हैं।
2. एक रेखा जो निर्देशांक अक्षों के साथ समान कोण बनाती है, के दिशा अनुपात ज्ञात कीजिए।
उत्तर दिखाएं
हल
मान लीजिए रेखा के दिशा अनुपात निर्देशांक अक्षों के प्रत्येक साथ कोण $a$ बनाते हैं।
$\therefore I=\cos a, m=\cos a, n=\cos a$
$ \begin{aligned} & l^{2}+m^{2}+n^{2}=1 \\ & \Rightarrow \cos ^{2} \alpha+\cos ^{2} \alpha+\cos ^{2} \alpha=1 \\ & \Rightarrow 3 \cos ^{2} \alpha=1 \\ & \Rightarrow \cos ^{2} \alpha=\frac{1}{3} \\ & \Rightarrow \cos \alpha= \pm \frac{1}{\sqrt{3}} \end{aligned} $
इसलिए, निर्देशांक अक्षों के साथ समान कोण बनाने वाली रेखा के दिशा अनुपात,
$\pm \frac{1}{\sqrt{3}}, \pm \frac{1}{\sqrt{3}}$, और $\pm \frac{1}{\sqrt{3}}$ हैं।
3. यदि एक रेखा के दिशा अनुपात $-18,12,-4$ हैं, तो इसके दिशा अनुपात ज्ञात कीजिए।
उत्तर दिखाएं
हल
यदि एक रेखा के दिशा अनुपात $-18,12$, और -4 हैं, तो इसके दिशा अनुपात हैं
$\frac{-18}{\sqrt{(-18)^{2}+(12)^{2}+(-4)^{2}}}, \frac{12}{\sqrt{(-18)^{2}+(12)^{2}+(-4)^{2}}}, \frac{-4}{\sqrt{(-18)^{2}+(12)^{2}+(-4)^{2}}}$
अर्थात, $\frac{-18}{22}, \frac{12}{22}, \frac{-4}{22}$
$\frac{-9}{11}, \frac{6}{11}, \frac{-2}{11}$
इसलिए, दिशा अनुपात $-\frac{9}{11}, \frac{6}{11}$, और $\frac{-2}{11}$ हैं।
4. दिखाइए कि बिंदु $(2,3,4),(-1,-2,1),(5,8,7)$ संरेख हैं।
उत्तर दिखाएं
हल
दिए गए बिंदु $A(2,3,4), B(-1,-2,1)$, और $C(5,8,7)$ हैं।
यह ज्ञात है कि बिंदुओं $(x_1, y_1, z_1)$ और $(x_2, y_2, z_2)$ को मिलाने वाली रेखा के दिशा अनुपात $x_2-x_1, y_2-y_1$, और $z_2-z_1$ द्वारा दिए जाते हैं।
$A B$ के दिशा अनुपात $(-1-2),(-2-3)$, और $(1-4)$ अर्थात $-3,-5$, और -3 हैं। $BC$ के दिशा अनुपात $(5-(-1)),(8-(-2))$, और $(7-1)$ अर्थात 6,10 , और 6 हैं। यह देखा जा सकता है कि $B C$ के दिशा अनुपात $A B$ के दिशा अनुपात के -2 गुना है अर्थात वे समानुपाती हैं।
इसलिए, $A B$ $B C$ के समान्तर है। क्योंकि बिंदु $B$ दोनों $A B$ और $B C$ के सामान्य बिंदु है, अतः बिंदु $A, B$, और $C$ संरेख हैं।
5. त्रिभुज के तीनों भुजाओं के दिशा कोसाइन ज्ञात कीजिए जिनके शीर्ष $(3,5,-4),(-1,1,2)$ और $(-5,-5,-2)$ हैं।
उत्तर दिखाएं
हल
$\triangle A B C$ के शीर्ष $A(3,5,-4), B(-1,1,2)$, और $C(-5,-5,-2)$ हैं।
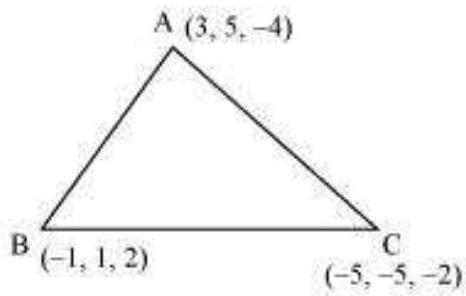
भुजा $A B$ के दिशा अनुपात $(-1-3),(1-5)$, और $(2-(-4))$ अर्थात $-4,-4$, और 6 हैं।
तब, $\sqrt{(-4)^{2}+(-4)^{2}+(6)^{2}}=\sqrt{16+16+36}$
$ \begin{aligned} & =\sqrt{68} \\ & =2 \sqrt{17} \end{aligned} $
इसलिए, $A B$ के दिशा कोसाइन हैं
$ \begin{aligned} & \frac{-4}{\sqrt{(-4)^{2}+(-4)^{2}+(6)^{2}}}, \frac{-4}{\sqrt{(-4)^{2}+(-4)^{2}+(6)^{2}}}, \frac{6}{\sqrt{(-4)^{2}+(-4)^{2}+(6)^{2}}} \\ & \frac{-4}{2 \sqrt{17}},-\frac{4}{2 \sqrt{17}}, \frac{6}{2 \sqrt{17}} \\ & \frac{-2}{\sqrt{17}}, \frac{-2}{\sqrt{17}}, \frac{3}{\sqrt{17}} \end{aligned} $
$BC$ के दिशा अनुपात $(-5-(-1)),(-5-1)$, और $(-2-2)$ अर्थात $-4,-6$, और -4 हैं। इसलिए, $B C$ के दिशा कोसाइन हैं
$ \begin{aligned} & \frac{-4}{\sqrt{(-4)^{2}+(-6)^{2}+(-4)^{2}}}, \frac{-6}{\sqrt{(-4)^{2}+(-6)^{2}+(-4)^{2}}}, \frac{-4}{\sqrt{(-4)^{2}+(-6)^{2}+(-4)^{2}}} \\
& \text{ अर्थात, } \frac{-4}{2 \sqrt{17}}, \frac{-6}{2 \sqrt{17}}, \frac{-4}{2 \sqrt{17}} \end{aligned} $
CA के दिशा अनुपात $(-5-3),(-5-5)$, और $(-2-(-4))$ अर्थात, $-8,-10$, और 2 हैं। अतः, $A C$ के दिशा कोसाइन हैं
$ \begin{aligned} & \frac{-8}{\sqrt{(-8)^{2}+(10)^{2}+(2)^{2}}}, \frac{-5}{\sqrt{(-8)^{2}+(10)^{2}+(2)^{2}}}, \frac{2}{\sqrt{(-8)^{2}+(10)^{2}+(2)^{2}}} \\ & \text{ अर्थात, } \frac{-8}{2 \sqrt{42}}, \frac{-10}{2 \sqrt{42}}, \frac{2}{2 \sqrt{42}} \end{aligned} $





