अध्याय 9 सरल रेखाएँ अतिरिक्त अभ्यास
अध्याय 9 पर अतिरिक्त अभ्यास
1. उस के मान ज्ञात कीजिए $k$ जिसके लिए रेखा $\left(k-3\right) x-(4-k^{2}) y+k^{2}-7 k+6=0$ है
(a): $x$-अक्ष के समानांतर,
(b): $y$-अक्ष के समानांतर,
(c): मूल बिंदु से गुजरती है।
उत्तर दिखाएँ
उत्तर :
दी गई रेखा का समीकरण $(k - 3) x - (4 - k^{2}) y+k^{2} - 7 k+6=0$ है
(a): यदि दी गई रेखा $x$-अक्ष के समानांतर है, तो
दी गई रेखा का ढलान $=$ $x$-अक्ष का ढलान
दी गई रेखा को लिखा जा सकता है $( 4 - k^{2}) y=(k -3 ) x+k^{2}- 7 k+6=0$
$y=\dfrac{(k-3)}{(4-k^{2})} x+\dfrac{k^{2}-7 k+6}{(4-k^{2})}$ , जो $y=m x+c$ के रूप में है।
$\therefore \quad $ दी गई रेखा का ढलान $=\dfrac{(k-3)}{(4-k^{2})}$
$x$-अक्ष का ढलान $=0$
$\therefore \quad \dfrac{(k-3)}{(4-k^{2})}=0$
$\Rightarrow k-3=0$
$\Rightarrow k=3$
इसलिए, यदि दी गई रेखा $x$-अक्ष के समानांतर है, तो $k$ का मान $3$ है।
(b): यदि दी गई रेखा $y$-अक्ष के समानांतर है, तो यह ऊर्ध्वाधर है। इसलिए, इसका ढलान अनिर्धारित होगा।
दी गई रेखा का ढलान $\dfrac{(k-3)}{(4-k^{2})}$ है।
अब, $\dfrac{(k-3)}{(4-k^{2})}$ तब अनिर्धारित होता है जब $k^{2}=4$
$\Rightarrow k^{2}=4$
$\Rightarrow k= \pm 2$
इसलिए, यदि दी गई रेखा $y$-अक्ष के समानांतर है, तो $k$ का मान $\pm 2$ है।
(c): यदि दी गई रेखा मूल बिंदु से गुजरती है, तो बिंदु $(0,0)$ दी गई रेखा के समीकरण को संतुष्ट करता है।
$(k-3)(0)-(4-k^{2})(0)+k^{2}-7 k+6=0$
$k^{2}-7 k+6=0$
$k^{2}-6 k-k+6=0$
$(k-6)(k-1)=0$
$k=1$ या 6
इसलिए, यदि दी गई रेखा मूल बिंदु से गुजरती है, तो $k$ का मान या तो $1$ या $6$ है।
2. उन रेखाओं के समीकरण ज्ञात कीजिए जो अक्षों पर अंत: खंड काटती हैं जिनके योग और गुणनफल क्रमशः $1$ और $-6$ हैं।
उत्तर दिखाएँ
उत्तर :
मान लीजिए दी गई रेखाओं द्वारा अक्षों पर काटे गए अंत: खंड $a$ और $b$ हैं।
दिया गया है
$a+b=1 \qquad\ldots(1)$
$a b=- 6 \qquad\ldots(2)$
समीकरण $(1)$ और $(2)$ को हल करने पर, हम प्राप्त करते हैं
$a=3$ और $b= - 2$ या $a=-2$ और $b=3$
यह ज्ञात है कि एक रेखा का समीकरण जिसके अक्षों पर अपवाह बिंदु $a$ और $b$ हों, होता है
$\dfrac{x}{a}+\dfrac{y}{b}=1$ या $b x+a y-a b=0$
केस I:
$a=3$ और $b= - 2$
इस स्थिति में, रेखा का समीकरण $3 x - 2 y-6=0$, अर्थात $3 x-2 y=6$ है।
केस II:
$a= - 2$ और $b=3$
इस स्थिति में, रेखा का समीकरण $-2 x+3 y-6=0$, अर्थात $2 x - 3 y=6$ है।
इस प्रकार, आवश्यक रेखाओं के समीकरण $2 x - 3 y=6$ और $3 x-2 y=6$ हैं।
3. $y$-अक्ष पर वह बिंदु कौन से हैं जिनकी दूरी रेखा $\dfrac{x}{3}+\dfrac{y}{4}=1$ से 4 इकाई है।
उत्तर दिखाएं
उत्तर :
मान लीजिए $(0, b)$ वह बिंदु है जो $y$-अक्ष पर स्थित है और जिसकी दूरी रेखा $\dfrac{x}{3}+\dfrac{y}{4}=1$ से 4 इकाई है।
दी गई रेखा को $4 x+3 y- 12=0$ के रूप में लिखा जा सकता है।
समीकरण (1) को रेखा के सामान्य समीकरण $A x+B y+C=0$ के साथ तुलना करने पर, हम प्राप्त करते हैं $A=4, B=3$, और $C= -12$।
यह ज्ञात है कि बिंदु $(x_1, y_1)$ से रेखा $A x+B y+C=0$ की लम्ब दूरी $(d)$ द्वारा दी गई है
$d=\dfrac{|A x_1+B y_1+C|}{\sqrt{A^{2}+B^{2}}}$।
इसलिए, यदि $(0, b)$ वह बिंदु है जो $y$-अक्ष पर स्थित है और जिसकी दूरी रेखा $\dfrac{x}{3}+\dfrac{y}{4}=1$ से 4 इकाई है, तो:
$\quad 4=\dfrac{|4(0)+3(b)-12|}{\sqrt{4^{2}+3^{2}}}$
$\Rightarrow 4=\dfrac{|3 b-12|}{5}$
$\Rightarrow 20=|3 b-12|$
$\Rightarrow 20= \pm(3 b-12)$
$\Rightarrow 20=(3 b-12)$ या $20=-(3 b-12)$
$\Rightarrow 3 b=20+12$ या $3 b=-20+12$
$\Rightarrow b=\dfrac{32}{3}$ या $b=-\dfrac{8}{3}$
इस प्रकार, आवश्यक बिंदु $\left(0, \dfrac{32}{3}\right)$ और $\left(0,-\dfrac{8}{3}\right)$ हैं।
4. बिंदुओं $(\cos \theta, \sin \theta)$ और $(\cos \phi, \sin \phi)$ को मिलाने वाली रेखा के मूल बिंदु से लम्ब दूरी ज्ञात कीजिए।
उत्तर दिखाएं
उत्तर :
बिंदुओं $(\cos \theta, \sin \theta)$ और $(\cos \phi, \sin \phi)$ को मिलाने वाली रेखा का समीकरण निम्नलिखित है
$$ \frac{x}{\cos \theta} + \frac{y}{\sin \theta} = 1 $$
इस रेखा के मूल बिंदु से लम्ब दूरी निम्नलिखित है:
$$ \frac{|0 \cdot \cos \theta + 0 \cdot \sin \theta - 1|}{\sqrt{\cos^2 \theta + \sin^2 \theta}} = \frac{1}{\sqrt{1}} = 1 $$
इस प्रकार, मूल बिंदु से रेखा की लम्ब दूरी 1 इकाई है।
$ \begin{aligned} & y-\sin \theta=\left(\dfrac{\sin \phi-\sin \theta}{\cos \phi-\cos \theta}\right)(x-\cos \theta) \\ \\ & y(\cos \phi-\cos \theta)-\sin \theta(\cos \phi-\cos \theta)=x(\sin \phi-\sin \theta)-\cos \theta(\sin \phi-\sin \theta) \\ \\ & x(\sin \theta-\sin \phi)+y(\cos \phi-\cos \theta)+\cos \theta \sin \phi-\cos \theta \sin \theta-\sin \theta \cos \phi+\sin \theta \cos \theta=0 \\ \\ & x(\sin \theta-\sin \phi)+y(\cos \phi-\cos \theta)+\sin (\phi-\theta)=0 \\ \\ & A x+B y+C=0, \text{ where } A=\sin \theta-\sin \phi, B=\cos \phi-\cos \theta, \text{ and } C=\sin (\phi-\theta) \end{aligned} $
यह ज्ञात है कि एक रेखा $A x+B y+C=0$ के बिंदु $(x_1, y_1)$ से लंब दूरी $(d)$ निम्नलिखित द्वारा दी जाती है $d=\dfrac{|A x_1+B y_1+C|}{\sqrt{A^{2}+B^{2}}}$.
इसलिए, दिए गए रेखा से बिंदु $(x_1, y_1)=(0,0)$ की लंब दूरी $(d)$ है
$ \begin{aligned} d & =\dfrac{|(\sin \theta-\sin \phi)(0)+(\cos \phi-\cos \theta)(0)+\sin (\phi-\theta)|}{\sqrt{(\sin \theta-\sin \phi)^{2}+(\cos \phi-\cos \theta)^{2}}} \\ \\ & =\dfrac{|\sin (\phi-\theta)|}{\sqrt{\sin ^{2} \theta+\sin ^{2} \phi-2 \sin \theta \sin \phi+\cos ^{2} \phi+\cos ^{2} \theta-2 \cos \phi \cos \theta}} \\ \\ & =\dfrac{|\sin (\phi-\theta)|}{\sqrt{(\sin ^{2} \theta+\cos ^{2} \theta)+(\sin ^{2} \phi+\cos ^{2} \phi)-2(\sin \theta \sin \phi+\cos \theta \cos \phi)}} \\ \\ & =\dfrac{|\sin (\phi-\theta)|}{\sqrt{1+1-2(\cos (\phi-\theta))}} \\ \\ & =\dfrac{|\sin (\phi-\theta)|}{\sqrt{2(1-\cos (\phi-\theta))}} \\ \\ & =\dfrac{|\sin (\phi-\theta)|}{\sqrt{2(2 \sin ^{2}(\dfrac{\phi-\theta}{2}))}} \\ \\ & =\dfrac{|\sin (\phi-\theta)|}{|2 \sin (\dfrac{\phi-\theta}{2})|} \end{aligned} $
5. बिंदुओं के प्रतिच्छेद बिंदु से गुजरने वाली एक रेखा का समीकरण ज्ञात कीजिए जो $y$-अक्ष के समानांतर हो। जो रेखाएँ $x-7 y+5=0$ और $3 x+y=0$ के प्रतिच्छेद बिंदु से गुजरती है।
उत्तर दिखाएँ
उत्तर :
किसी भी रेखा का समीकरण जो $y$-अक्ष के समानांतर होती है, निम्नलिखित रूप में होता है
$x=a\qquad \ldots(1)$
दी गई दो रेखाएँ हैं
x - 7y + 5 = 0 \qquad \ldots(2) 3x + y = 0 \qquad \ldots(3)
अब, दोनों रेखाओं के प्रतिच्छेद बिंदु को ज्ञात करने के लिए समीकरण (2) और (3) को हल करें।
समीकरण (3) से $y = -3x$ लें और इसे समीकरण (2) में बदल दें:
$$ x - 7(-3x) + 5 = 0 $$
$$ x + 21x + 5 = 0 $$
$$ 22x + 5 = 0 $$
$$ x = -\dfrac{5}{22} $$
अब, $x = -\dfrac{5}{22}$ को समीकरण (3) में बदलें:
$$ y = -3\left(-\dfrac{5}{22}\right) = \dfrac{15}{22} $$
अतः, प्रतिच्छेद बिंदु है: $\left(-\dfrac{5}{22}, \dfrac{15}{22}\right)$
अब, इस बिंदु से गुजरने वाली रेखा का समीकरण ज्ञात करें जो $y$-अक्ष के समानांतर हो। रेखा का समीकरण निम्नलिखित रूप में होता है:
$$ x = a $$
इस रेखा के लिए, बिंदु $\left(-\dfrac{5}{22}, \dfrac{15}{22}\right)$ से गुजरती है, इसलिए:
$$ x = -\dfrac{5}{22} $$
अतः, अभीष्ट रेखा का समीकरण है:
$$ x = -\dfrac{5}{22} $$
$x- 7 y+5=0\qquad \ldots(2)$
$3 x+y=0\qquad \ldots(3)$
समीकरण $(2)$ और $(3)$ को हल करने पर, हमें $x=-\dfrac{5}{22}$ और $y=\dfrac{15}{22}$ प्राप्त होते हैं।
इसलिए, $\left(-\dfrac{5}{22}, \dfrac{15}{22}\right)$ रेखाओं $\left(2\right)$ और $\left(3\right)$ के प्रतिच्छेद बिंदु है।
क्योंकि रेखा $x=a$ बिंदु $\left(-\dfrac{5}{22}, \dfrac{15}{22}\right)$ से गुजरती है, इसलिए $a=-\dfrac{5}{22}$
इसलिए, अभीष्ट रेखा का समीकरण $x=-\dfrac{5}{22}$ है।
6. रेखा $\dfrac{x}{4}+\dfrac{y}{6}=1$ के लंब रेखा का समीकरण ज्ञात कीजिए, जो इस रेखा के $y$-अक्ष के बिंदु पर गुजरती है।
उत्तर दिखाएं
Answer :
दी गई रेखा का समीकरण $\dfrac{x}{4}+\dfrac{y}{6}=1$ है।
इस समीकरण को भी लिखा जा सकता है $3 x+2 y - 12=0$
$y=\dfrac{-3}{2} x+6$, जो $y=m x+c$ के रूप में है।
$\therefore \quad $ दी गई रेखा की प्रतिलोम ढलान $=-\dfrac{3}{2}$
$\therefore \quad $ दी गई रेखा के लंब रेखा की ढलान $ =-\dfrac{1}{\left(-\dfrac{3}{2}\right)}=\dfrac{2}{3} $
मान लीजिए दी गई रेखा $y$-अक्ष के बिंदु $\left(0, y\right)$ पर प्रतिच्छेद करती है।
दी गई रेखा के समीकरण में $x$ को 0 से बदल देने पर, हमें $\dfrac{y}{6}=1 \Rightarrow y=6$ प्राप्त होता है।
$\therefore \quad $ दी गई रेखा $y$-अक्ष के बिंदु $\left(0,6\right)$ पर प्रतिच्छेद करती है।
ढलान $\dfrac{2}{3}$ और बिंदु $\left(0,6\right)$ से गुजरने वाली रेखा का समीकरण है
$\left(y-6\right)=\dfrac{2}{3}\left(x-0\right)$
$3 y-18=2 x$
$2 x-3 y+18=0$
इसलिए, अभीष्ट रेखा का समीकरण $2 x-3 y+18=0$ है।
7. रेखाओं $y-x=0, x+y=0$ और $x-k=0$ द्वारा बने त्रिभुज का क्षेत्रफल ज्ञात कीजिए।
उत्तर दिखाएं
Answer :
दी गई रेखाओं के समीकरण हैं
$y- x=0\qquad \ldots(1)$
$x+y=0\qquad \ldots(2)$
$x- k=0\qquad \ldots(3)$
रेखाओं $\left(1\right)$ और $\left(2\right)$ के प्रतिच्छेद बिंदु के निर्देशांक निम्नलिखित हैं
$x=0$ और $y=0$
रेखाओं $\left(2\right)$ और $\left(3\right)$ के प्रतिच्छेद बिंदु के निर्देशांक निम्नलिखित हैं
$x=k$ और $y= -k$
बिंदुओं $\left(3\right)$ और $\left(1\right)$ के प्रतिच्छेद बिंदु के निर्देशांक निम्नलिखित हैं
$x=k$ और $y=k$
इसलिए, तीन दिए गए रेखाओं द्वारा बने त्रिभुज के शीर्ष $\left(0,0\right),\left(k, -k\right) $, और $\left(k, k\right)$ हैं।
हम जानते हैं कि एक त्रिभुज के शीर्ष $\left(x_1, y_1\right),\left(x_2, y_2\right)$, और $\left(x_3, y_3\right)$ वाले त्रिभुज का क्षेत्रफल है
$\dfrac{1}{2}|x_1\left(y_2-y_3\right)+x_2\left(y_3-y_1\right)+x_3\left(y_1-y_2\right)|$
इसलिए, तीन दिए गए रेखाओं द्वारा बने त्रिभुज का क्षेत्रफल
$=\dfrac{1}{2}|0\left(-k-k\right)+k\left(k-0\right)+k\left(0+k\right)|$ वर्ग इकाई
$=\dfrac{1}{2}|k^{2}+k^{2}|$ वर्ग इकाई
$=\dfrac{1}{2}|2 k^{2}|$ वर्ग इकाई
$=k^{2}$ वर्ग इकाई
8. $p$ का मान ज्ञात कीजिए ताकि रेखाएँ $3 x+y-2=0, p x+2 y-3=0$ और $2 x-y-3=0$ एक बिंदु पर प्रतिच्छेद कर सकें।
उत्तर दिखाएं
Answer :
दिए गए रेखाओं के समीकरण हैं
$3 x+y-2=0\qquad \ldots(1)$
$p x+2 y-3=0\qquad \ldots(2)$
$2 x-y-3=0\qquad \ldots(3)$
समीकरण $\left(1\right)$ और $\left(3\right)$ को हल करने पर, हम प्राप्त करते हैं
$x=1$ और $y=-1$
चूंकि ये तीन रेखाएँ एक बिंदु पर प्रतिच्छेद कर सकती हैं, रेखाओं $\left(1\right)$ और $\left(3\right)$ के प्रतिच्छेद बिंदु रेखा $\left(2\right)$ को भी संतुष्ट करेंगे
$p\left(1\right)+2\left(-1\right)-3=0$
$p-2-3=0$
$p=5$
इसलिए, आवश्यक $p$ का मान 5 है
9. यदि तीन रेखाओं के समीकरण $y=m_1 x+c_1, y=m_2 x+c_2$ और $y=m_3 x+c_3$ संगत हों, तो सिद्ध कीजिए कि $m_1\left(c_2-c_3\right)+m_2\left(c_3-c_1\right)+m_3\left(c_1-c_2\right)=0$।
उत्तर दिखाएं
Answer :
दिए गए रेखाओं के समीकरण हैं
$y=m_1 x+c_1 \qquad \ldots(1)$
$y=m_2 x+c_2 \qquad \ldots(2)$
$y=m_3 x+c_3\qquad \ldots(3)$
समीकरण $\left(1\right)$ को $\left(2\right)$ से घटाने पर, हम प्राप्त करते हैं
$0=\left(m_2-m_1\right) x+\left(c_2-c_1\right)$
$\Rightarrow\left(m_1-m_2\right) x=c_2-c_1$
$\Rightarrow x=\dfrac{c_2-c_1}{m_1-m_2}$
उपरोक्त मान के $x$ को समीकरण $\left(1\right)$ में बदल देने पर हम प्राप्त करते हैं
$ \begin{aligned} & y=m_1\left(\dfrac{c_2-c_1}{m_1-m_2}\right)+c_1 \\ \\ & y=\dfrac{m_1 c_2-m_1 c_1}{m_1-m_2}+c_1 \\ \\ & y=\dfrac{m_1 c_2-m_1 c_1+m_1 c_1-m_2 c_1}{m_1-m_2} \\ \\ & y=\dfrac{m_1 c_2-m_2 c_1}{m_1-m_2} \end{aligned} $
$ \therefore \quad \left(\dfrac{c_2-c_1}{m_1-m_2}, \dfrac{m_1 c_2-m_2 c_1}{m_1-m_2}\right) \text{ रेखाओं (1) और (2) के प्रतिच्छेद बिंदु है। } $
दिया गया है कि रेखाएँ $\left(1\right), \left(2\right),$ और $\left(3\right)$ संगत हैं। अतः, रेखाओं $\left(1\right)$ और $\left(2\right)$ के प्रतिच्छेद बिंदु समीकरण $\left(3\right)$ को भी संतुष्ट करेगा।
$ \begin{aligned} & \dfrac{m_1 c_2-m_2 c_1}{m_1-m_2}=m_3\left(\dfrac{c_2-c_1}{m_1-m_2}\right)+c_3 \\ \\ & \dfrac{m_1 c_2-m_2 c_1}{m_1-m_2}=\dfrac{m_3 c_2-m_3 c_1+c_3 m_1-c_3 m_2}{m_1-m_2} \\ \\ & m_1 c_2-m_2 c_1-m_3 c_2+m_3 c_1-c_3 m_1+c_3 m_2=0 \\ \\ & m_1\left(c_2-c_3\right)+m_2\left(c_3-c_1\right)+m_3\left(c_1-c_2\right)=0 \\ \\ & \text{ अतः, } m_1\left(c_2-c_3\right)+m_2\left(c_3-c_1\right)+m_3\left(c_1-c_2\right)=0 \end{aligned} $
10. बिंदु $\left(3,2\right)$ से गुजरने वाली रेखाओं का समीकरण ज्ञात कीजिए जो रेखा $x-2 y=3$ के साथ $45^{\circ}$ का कोण बनाती हों।
उत्तर दिखाएं
Answer :
अभीष्ट रेखा की ढलान $m_1$ हो।
दी गई रेखा को $y=\dfrac{1}{2} x-\dfrac{3}{2}$ लिखा जा सकता है, जो $y=m x+c$ के रूप में है।
$\therefore \quad $ दी गई रेखा की ढलान $=m_2=\dfrac{1}{2}$
दिया गया है कि अभीष्ट रेखा और रेखा $x - 2 y=3$ के बीच का कोण $45^{\circ}$ है।
हम जानते हैं कि यदि $\theta$ रेखाओं $I_1$ और $I_2$ के बीच न्यून कोण हो जिनकी ढलान क्रमशः $m_1$ और $m_2$ हो, तो
$\tan \theta=\left|\dfrac{m_2-m_1}{1+m_1 m_2}\right|$
$\therefore \quad \tan 45^{\circ}=\dfrac{\big|m_1-m_2\big|}{1+m_1 m_2}$
$\Rightarrow 1=\left|\dfrac{\dfrac{1}{2}-m_1}{1+\dfrac{m_1}{2}}\right|\Rightarrow 1 =\left|\dfrac{\left(\dfrac{1-2 m_1}{2}\right)}{\dfrac{2+m_1}{2}}\right|$
$\Rightarrow 1 =\left|\dfrac{1-2 m_1}{2+m_1}\right|\Rightarrow 1 = \pm\left(\dfrac{1-2 m_1}{2+m_1}\right)$
$\Rightarrow 1 =\dfrac{1-2 m_1}{2+m_1}$ or $1=-\left(\dfrac{1-2 m_1}{2+m_1}\right)$
$\Rightarrow 2+m_1=1-2 m_1$ or $2+m_1=-1+2 m_1$
$\Rightarrow m_1=-\dfrac{1}{3}$ or $m_1=3$
केस I:
$m_1=3$
उस रेखा का समीकरण जो बिंदु $\left(3,2\right)$ से गुजरती है और ढलान $3$ के साथ होती है:
$y - 2 = 3\left(x - 3 \right)$
$y - 2=3 x - 9$
$3 x -y=7$
केस II:
$m_1=-\dfrac{1}{3}$
उस रेखा का समीकरण जो बिंदु $\left(3,2\right)$ से गुजरती है और ढलान $-\dfrac{1}{3}$ के साथ होती है:
$y-2=-\dfrac{1}{3}\left(x-3\right)$
$3 y-6=-x+3$
$x+3 y=9$
इस प्रकार, रेखाओं के समीकरण $3 x - y=7$ और $x+3 y=9$ हैं
11. बिंदु प्रतिच्छेदन के माध्यम से रेखा का समीकरण ज्ञात कीजिए जो रेखाओं $4 x+7 y-3=0$ और $2 x-3 y+1=0$ के प्रतिच्छेदन बिंदु से गुजरती है और अक्षों पर समान प्रतिच्छेद बिंदु बनाती है।
उत्तर दिखाएं
उत्तर :
मान लीजिए अक्षों पर समान प्रतिच्छेद बिंदु बनाने वाली रेखा का समीकरण $\dfrac{x}{a}+\dfrac{y}{a}=1$ है
या $ ~ x+y=a\qquad \ldots(1)$
समीकरण $4 x+7 y - 3=0$ और $2 x - 3 y+1=0$ को हल करने पर, हमें $x=\dfrac{1}{13}$ और $y=\dfrac{5}{13}$ प्राप्त होता है
$\therefore \quad \left(\dfrac{1}{13}, \dfrac{5}{13}\right)$ दो दी गई रेखाओं के प्रतिच्छेद बिंदु है।
क्योंकि समीकरण $\left(1\right)$ बिंदु $\left(\dfrac{1}{13}, \dfrac{5}{13}\right)$ से गुजरता है, $\dfrac{1}{13}+\dfrac{5}{13}=a$
$\Rightarrow a=\dfrac{6}{13}$
$\therefore \quad $ समीकरण $\left(1\right)$ बन जाता है
$ x+y=\dfrac{6}{13} \text{, अर्थात } 13 x+13 y=6 $
इस प्रकार, अभीष्ट रेखा का समीकरण $13 x+13 y=6$ है
12. दिखाइए कि रेखा का समीकरण जो मूल बिंदु से गुजरती है और रेखा $y=m x+c$ के साथ कोण $\theta$ बनाती है, है $ \ \ \dfrac{y}{x}=\dfrac{m \pm \tan ,}{1 \mp m \tan ,}$
उत्तर दिखाएं
उत्तर :
मान लीजिए मूल बिंदु से गुजरने वाली रेखा का समीकरण $y=m_1 x$ है।
यदि यह रेखा रेखा $y=m x+c$ के साथ कोण $\theta$ बनाती है, तो कोण $\theta$ द्वारा दिया जाता है
$\therefore \quad \tan \theta=\bigg|\dfrac{m_1-m}{1+m_1 m}\bigg|$
$\Rightarrow\quad \tan \theta=\left|\dfrac{\dfrac{y}{x}-m}{1+\dfrac{y}{x} m}\right|$
$\Rightarrow\quad \tan \theta= \pm\left(\dfrac{\dfrac{y}{x}-m}{1+\dfrac{y}{x} m}\right)$
$\Rightarrow\quad \tan \theta=\left(\dfrac{\dfrac{y}{x}-m}{1+\dfrac{y}{x} m}\right) \ $ or $ \ \tan \theta=-\left(\dfrac{\dfrac{y}{x}-m}{1+\dfrac{y}{x} m}\right)$
केस I:
$ \tan \theta=\left(\dfrac{\dfrac{y}{x}-m}{1+\dfrac{y}{x} m}\right)$
$ \tan \theta=\left(\dfrac{\dfrac{y}{x}-m}{1+\dfrac{y}{x} m}\right) $
$\Rightarrow \quad \left(1+\dfrac{y}{x} m\right) \tan \theta=\dfrac{y}{x}-m$
$\Rightarrow \quad\tan \theta + \dfrac{y}{x} \ m \ \tan \theta=\dfrac{y}{x}-m$
$\Rightarrow\quad m+\tan \theta=\dfrac{y}{x}\left(1-m \tan \theta\right)$
$\Rightarrow\quad \dfrac{y}{x}=\dfrac{m+\tan \theta}{1-m \tan \theta}$
केस II:
$ \tan \theta=-\left(\dfrac{\dfrac{y}{x}-m}{1+\dfrac{y}{x} m}\right) $
$\tan \theta=-\left(\dfrac{\dfrac{y}{x}-m}{1+\dfrac{y}{x} m}\right)$
$\Rightarrow\quad \tan \theta+\dfrac{y}{x} m \tan \theta=-\dfrac{y}{x}+m$
$\Rightarrow\quad \dfrac{y}{x}\left(1+m \tan \theta\right)=m-\tan \theta$
$\Rightarrow\quad \dfrac{y}{x}=\dfrac{m-\tan \theta}{1+m \tan \theta}$
इसलिए, आवश्यक रेखा के समीकरण है $\dfrac{y}{x}=\dfrac{m \pm \tan \theta}{1 \mp m \tan \theta}$
13. $\left(-1,1\right)$ और $\left(5,7\right)$ को जोड़ने वाली रेखा को $x+y=4$ रेखा द्वारा किस अनुपात में विभाजित करती है?
उत्तर दिखाएं
उत्तर :
बिंदुओं $\left( -1,1\right)$ और $\left(5,7\right)$ को जोड़ने वाली रेखा का समीकरण निम्नलिखित है
$y-1=\left(\dfrac{7-1}{5+1}\right)\left(x+1\right)$
$y-1=\left(\dfrac{6}{6}\right)\left(x+1\right)$
$x-y+2=0\qquad \ldots(1)$
दी गई रेखा का समीकरण है
$x +y -4 =0\qquad \ldots(2)$
रेखाओं $\left(1\right)$ और $\left(2\right)$ के प्रतिच्छेद बिंदु के निर्देशांक निम्नलिखित हैं
$x=1$ और $y=3$
मान लीजिए बिंदु $\left(1,3\right)$ बिंदुओं $\left(- 1,1\right)$ और $\left(5,7\right)$ को जोड़ने वाले रेखाखंड को अनुपात $1: k$ में विभाजित करता है।
अतः, अनुपात के अनुसार,
$\left(1,3\right)=\left(\dfrac{k\left(-1\right)+1\left(5\right)}{1+k}, \dfrac{k\left(1\right)+1\left(7\right)}{1+k}\right)$
$\Rightarrow\left(1,3\right)=\left(\dfrac{-k+5}{1+k}, \dfrac{k+7}{1+k}\right)$
$\Rightarrow \dfrac{-k+5}{1+k}=1, \dfrac{k+7}{1+k}=3$
$\therefore \quad \dfrac{-k+5}{1+k}=1$
$\Rightarrow-k+5=1+k$
$\Rightarrow 2 k=4$
$\Rightarrow k=2$
अतः, बिंदुओं $\left( -1,1\right)$ और $\left(5,7\right)$ को जोड़ने वाली रेखा रेखा $x+y=4$ द्वारा $1: 2$ के अनुपात में विभाजित होती है।
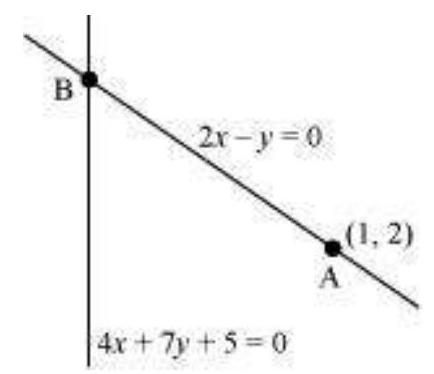
14. बिंदु $\left(1,2\right)$ से रेखा $4 x+7 y+5=0$ की दूरी ज्ञात कीजिए जो रेखा $2 x-y=0$ के अनुदिश है।
उत्तर दिखाएं
Answer :
दी गई रेखाएँ हैं
$2 x - y=0\qquad \ldots(1)$
$4 x+7 y+5=0\qquad \ldots(2)$
$A \left(1,2\right)$ रेखा $\left(1\right)$ पर एक बिंदु है
मान लीजिए $B$ रेखाओं $\left(1\right)$ और $\left(2\right)$ के प्रतिच्छेद बिंदु है
समीकरण $\left(1\right)$ और $\left(2\right)$ को हल करने पर हम प्राप्त करते हैं,
$ x=\dfrac{-5}{18} \text{ और } y=\dfrac{-5}{9} $
$\therefore \quad $ बिंदु $B$ के निर्देशांक $\left(\dfrac{-5}{18}, \dfrac{-5}{9}\right)$ हैं
दूरी सूत्र का उपयोग करके बिंदुओं $A$ और $B$ के बीच की दूरी निम्नलिखित रूप में प्राप्त की जा सकती है
$AB=\sqrt{\left(1+\dfrac{5}{18}\right)^{2}+\left(2+\dfrac{5}{9}\right)^{2}}$ इकाई
$\qquad=\sqrt{\left(\dfrac{23}{18}\right)^{2}+\left(\dfrac{23}{9}\right)^{2}}$ इकाई
$\qquad=\sqrt{\left(\dfrac{23}{2 \times 9}\right)^{2}+\left(\dfrac{23}{9}\right)^{2}}$ इकाई
$\qquad=\sqrt{\left(\dfrac{23}{9}\right)^{2}\left(\dfrac{1}{2}\right)^{2}+\left(\dfrac{23}{9}\right)^{2}}$ इकाई
$\qquad=\sqrt{\left(\dfrac{23}{9}\right)^{2}\left(\dfrac{1}{4}+1\right)}$ इकाई $=\dfrac{23}{9} \sqrt{\dfrac{5}{4}}$ इकाई
$\qquad=\dfrac{23}{9} \times \dfrac{\sqrt{5}}{2}$ इकाई $=\dfrac{23 \sqrt{5}}{18}$ इकाई
इसलिए, आवश्यक दूरी है $\dfrac{23 \sqrt{5}}{18}$ इकाई
15. बिंदु $\left(-1,2\right)$ से गुजरने वाली एक सीधी रेखा की दिशा ज्ञात कीजिए जिसके बिंदु एवं रेखा $x+y=4$ के प्रतिच्छेद बिंदु की दूरी इस बिंदु से 3 इकाई हो।
उत्तर दिखाएं
उत्तर :
मान लीजिए $y=m x+c$ बिंदु $\left(- 1,2\right)$ से गुजरने वाली रेखा है
इसलिए, $2=m\left(- 1\right)+c$.
$\Rightarrow 2=- m+c$
$\Rightarrow c=m+2$
$\therefore \quad y=m x+m+2\qquad \ldots(1)$
दी गई रेखा है $ ~ x+y=4\qquad \ldots(2)$
समीकरण $\left(1\right)$ और $\left(2\right)$ को हल करने पर, हम प्राप्त करते हैं
$ \begin{aligned} & x=\dfrac{2-m}{m+1} \text{ और } y=\dfrac{5 m+2}{m+1} \\ \\ & \therefore \quad \left(\dfrac{2-m}{m+1}, \dfrac{5 m+2}{m+1}\right) \text{ रेखाओं (1) और (2) के प्रतिच्छेद बिंदु है। } \end{aligned} $
क्योंकि यह बिंदु बिंदु $\left(- 1,2 \right)$ से 3 इकाई की दूरी पर है, दूरी सूत्र के अनुसार,
$ \begin{aligned} & \sqrt{\left(\dfrac{2-m}{m+1}+1\right)^{2}+\left(\dfrac{5 m+2}{m+1}-2\right)^{2}}=3 \\ \\ \Rightarrow & \left(\dfrac{2-m+m+1}{m+1}\right)^{2}+\left(\dfrac{5 m+2-2 m-2}{m+1}\right)^{2}=3^{2} \\ \\ \Rightarrow & \dfrac{9}{\left(m+1\right)^{2}}+\dfrac{9 m^{2}}{\left(m+1\right)^{2}}=9 \\ \\ \Rightarrow & \dfrac{1+m^{2}}{\left(m+1\right)^{2}}=1 \\ \\ \Rightarrow & 1+m^{2}=m^{2}+1+2 m \\ \\ \Rightarrow & 2 m=0 \\ \\ \Rightarrow & m=0 \end{aligned} $
इसलिए, आवश्यक रेखा की ढलान शून्य होनी चाहिए, अर्थात रेखा x-अक्ष के समानांतर होनी चाहिए।
16. समकोण त्रिभुज के कर्ण के सिरे बिंदु $\left(1,3\right)$ और $\left(-4,1\right)$ पर हैं। त्रिभुज के लंब भुजाओं (लम्ब भुजाओं) के समीकरण ज्ञात कीजिए जो अक्षों के समानांतर हों।
उत्तर दिखाएं
उत्तर :
मान लीजिए $A\left(1,3\right)$ और $B\left(-4,1\right)$ कर्ण के सिरों के निर्देशांक हैं।
अब, बिंदुओं $A\left(1,3\right)$ और $B\left(-4,1\right)$ को जोड़ने वाले रेखाखंड को निर्देशांक तल पर खींचने पर, हमें दो समकोण त्रिभुज मिलते हैं जिनका कर्ण $AB$ है। अब आरेख से स्पष्ट है कि समकोण त्रिभुज के अन्य दो भुजाओं के प्रतिच्छेद बिंदु $P$ या $Q$ हो सकते हैं।
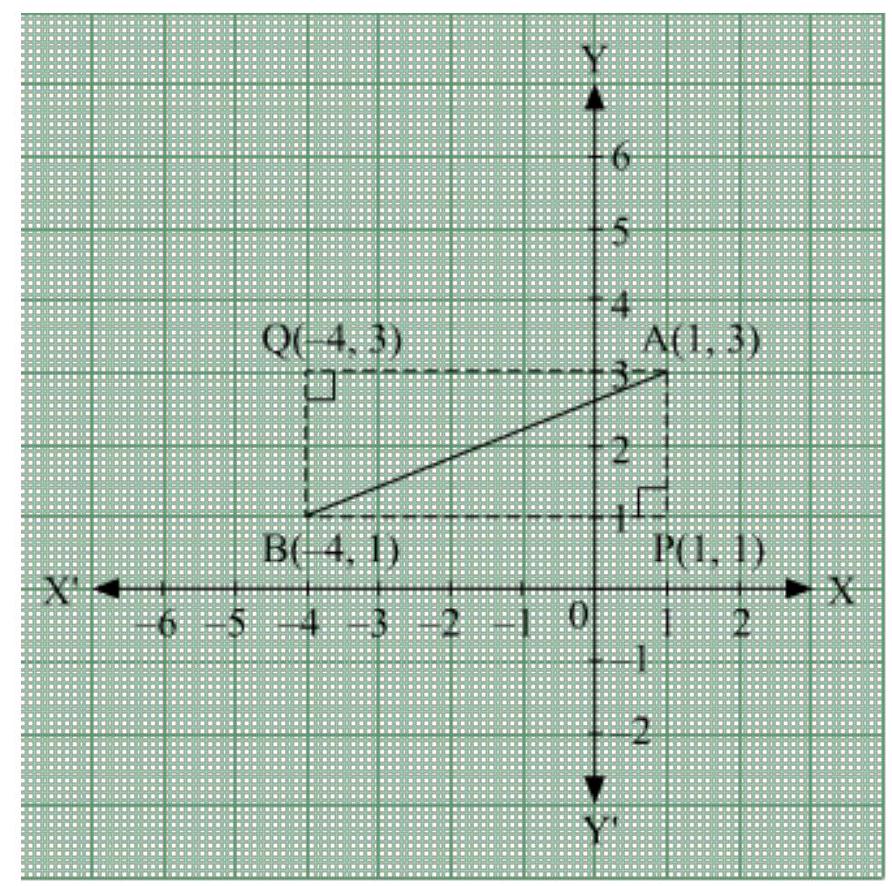
केस 1: जब ∠APB लिया जाता है।
∠APB में लम्ब भुजाएँ AP और PB हैं।
अब, भुजा PB, x-अक्ष के समानांतर है और x-अक्ष से 1 इकाई की दूरी पर है।
इसलिए, PB का समीकरण, y=1 या y-1=0 है।
भुजा AP, y-अक्ष के समानांतर है और y-अक्ष के दाहिने ओर 1 इकाई की दूरी पर है।
इसलिए, AP का समीकरण x=1 या x-1=0 है।
केस 2: जब ∠AQB लिया जाता है।
∠AQB में लम्ब भुजाएँ AQ और QB हैं।
अब, भुजा AQ, x-अक्ष के समानांतर है और x-अक्ष से 3 इकाई की दूरी पर है।
इसलिए, AQ का समीकरण, y=3 या y-3=0 है।
भुजा QB, y-अक्ष के समानांतर है और y-अक्ष के बाईं ओर 4 इकाई की दूरी पर है।
इसलिए, QB का समीकरण x=-4 या x+4=0 है।
इसलिए, भुजाओं के समीकरण हैं:
x=1, y=1 या x=-4, y=3
17. बिंदु (3,8) के संदर्भ में रेखा x+3y=7 के प्रतिबिम्ब को ज्ञात कीजिए, मान लीजिए रेखा एक तलीय दर्पण है।
उत्तर दिखाएँ
उत्तर :
दी गई रेखा का समीकरण है
x + 3y = 7 …(1)
मान लीजिए बिंदु B(a, b), बिंदु A(3,8) का प्रतिबिम्ब है।
इसलिए, रेखा (1) AB के लंब समद्विभाजक है।
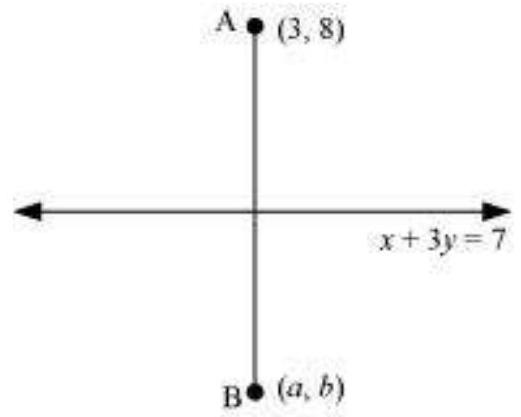
AB की ढलान = (b-8)/(a-3), जबकि रेखा (1) की ढलान = -1/3
क्योंकि रेखा (1) AB के लंबवत है, (b-8)/(a-3) × (-1/3) = -1
⇒ (b-8)/(3a-9) = 1
⇒ b-8 = 3a-9
⇒ 3a - b = 1 …(2)
AB का मध्य बिंदु = ((a+3)/2, (b+8)/2)
में रेखा $A B$ के मध्य बिंदु रेखा $\left(1\right)$ को भी संतुष्ट करेगा।
इसलिए, समीकरण $\left(1\right)$ से हमें प्राप्त होता है
$\left(\dfrac{a+3}{2}\right)+3\left(\dfrac{b+8}{2}\right)=7$
$\Rightarrow a+3+3 b+24=14$
$\Rightarrow a+3 b=-13\qquad \ldots(3)$
समीकरण $\left(2\right)$ और $\left(3\right)$ को हल करने पर हमें $a=$ $- 1$ और $b=$ $-4$ प्राप्त होते हैं।
इसलिए, दी गई रेखा के संबंध में दिए गए बिंदु के प्रतिबिम्ब के निर्देशांक $\left(-1, -4\right)$ हैं।
18. यदि रेखाएँ $y=3 x+1$ और $2 y=x+3$ रेखा $y=m x+4$ के समान कोण पर झुकी हुई हैं, तो $m$ का मान ज्ञात कीजिए।
उत्तर दिखाएं
Answer :
दी गई रेखाओं के समीकरण हैं
$y=3 x+1 \qquad \ldots(1)$
$2 y=x+3\qquad \ldots(2)$
$y=m x+4 \qquad \ldots(3)$
रेखा $\left(1\right)$ का ढलान, $m_1=3$
रेखा $\left(2\right)$ का ढलान, $m_2=\dfrac{1}{2}$
रेखा $\left(3\right)$ का ढलान, $m_3=m$
दिया गया है कि रेखाएँ $\left(1\right)$ और $\left(2\right)$ रेखा $\left(3\right)$ के समान कोण पर झुकी हुई हैं। इसका अर्थ है कि रेखा $\left(1\right)$ और $\left(3\right)$ के बीच का कोण रेखा $\left(2\right)$ और $\left(3\right)$ के बीच के कोण के बराबर है।
$\therefore \quad \ \ \bigg|\dfrac{m_1-m_3}{1+m_1 m_3}\bigg|=\bigg|\dfrac{m_2-m_3}{1+m_2 m_3}\bigg|$
$\Rightarrow\bigg|\dfrac{3-m}{1+3 m}\bigg|=\bigg|\dfrac{\dfrac{1}{2}-m}{1+\dfrac{1}{2} m}\bigg|$
$\Rightarrow\bigg|\dfrac{3-m}{1+3 m}\bigg|=\bigg|\dfrac{1-2 m}{m+2}\bigg|$
$\Rightarrow \dfrac{3-m}{1+3 m}= \pm\left(\dfrac{1-2 m}{m+2}\right)$
$\Rightarrow \dfrac{3-m}{1+3 m}=\dfrac{1-2 m}{m+2}$ या $\dfrac{3-m}{1+3 m}=-\left(\dfrac{1-2 m}{m+2}\right)$
यदि $ ~ \dfrac{3-m}{1+3 m}=\dfrac{1-2 m}{m+2}$, तो
$\left(3-m\right)\left(m+2\right)=\left(1-2 m\right)\left(1+3 m\right)$
$\Rightarrow-m^{2}+m+6=1+m-6 m^{2}$
$\Rightarrow 5 m^{2}+5=0$
$\Rightarrow\left(m^{2}+1\right)=0$
$\Rightarrow m=\sqrt{-1}$, जो वास्तविक नहीं है
इसलिए, यह स्थिति संभव नहीं है।
यदि $\dfrac{3-m}{1+3 m}=-\left(\dfrac{1-2 m}{m+2}\right)$, तो
$\Rightarrow\left(3-m\right)\left(m+2\right)=-\left(1-2 m\right)\left(1+3 m\right)$
$\Rightarrow-m^{2}+m+6=-\left(1+m-6 m^{2}\right)$
$\Rightarrow 7 m^{2}-2 m-7=0$
$\Rightarrow m=\dfrac{2 \pm \sqrt{4-4\left(7\right)\left(-7\right)}}{2\left(7\right)}$
$\Rightarrow m=\dfrac{2 \pm 2 \sqrt{1+49}}{14}$
$\Rightarrow m=\dfrac{1 \pm 5 \sqrt{2}}{7}$
इसलिए, $m$ का अभीष्ट मान $\dfrac{1 \pm 5 \sqrt{2}}{7}$ है।
19. यदि एक चर बिंदु $P\left(x, y\right)$ के रेखाओं $x+y-5=0$ और $3 x-2 y+7=0$ से लंब दूरी का योग हमेशा $10$ होता है। दिखाइए कि $P$ एक सीधी रेखा पर गति करता है।
उत्तर दिखाएं
उत्तर :
दी गई रेखाओं के समीकरण हैं
$x+y - 5=0\qquad \ldots(1)$
$3 x- 2 y+7=0\qquad \ldots(2)$
बिंदु $P\left(x, y\right)$ के रेखाओं $\left(1\right)$ और $\left(2\right)$ से लंब दूरियाँ निम्नलिखित द्वारा दी गई हैं
$ d_1=\dfrac{|x+y-5|}{\sqrt{\left(1\right)^{2}+\left(1\right)^{2}}} \text{ और } d_2=\dfrac{|3 x-2 y+7|}{\sqrt{\left(3\right)^{2}+\left(-2\right)^{2}}} $
अर्थात, $d_1=\dfrac{|x+y-5|}{\sqrt{2}}$ और $d_2=\dfrac{|3 x-2 y+7|}{\sqrt{13}}$
दिया गया है कि $d_1+d_2=10$
$\therefore \quad \dfrac{|x+y-5|}{\sqrt{2}}+\dfrac{|3 x-2 y+7|}{\sqrt{13}}=10$
$\Rightarrow \sqrt{13}|x+y-5|+\sqrt{2}|3 x-2 y+7|-10 \sqrt{26}=0$
$\Rightarrow \sqrt{13}\left(x+y-5\right)+\sqrt{2}\left(3 x-2 y+7\right)-10 \sqrt{26}=0$
$\big[$ मान लीजिए $\left(x+y-5\right)$ और $\left(3 x-2 y+7\right)$ धनात्मक हैं $\big]$
$\Rightarrow \sqrt{13} x+\sqrt{13} y-5 \sqrt{13}+3 \sqrt{2} x-2 \sqrt{2} y+7 \sqrt{2}-10 \sqrt{26}=0$
$\Rightarrow x\left(\sqrt{13}+3 \sqrt{2}\right)+y\left(\sqrt{13}-2 \sqrt{2}\right)+\left(7 \sqrt{2}-5 \sqrt{13}-10 \sqrt{26}\right)=0$
जो कि एक रेखा का समीकरण है।
इसी तरह, हम किसी भी चिन्ह के लिए $\left(x+y-5=0\right)$ और $\left(3 x-2 y+7=0\right)$ के लिए रेखा का समीकरण प्राप्त कर सकते हैं
इसलिए, बिंदु $P$ एक रेखा पर गति करता है।
20. समांतर रेखाओं $9 x+6 y-7=0$ और $3 x+2 y+6=0$ से बराबर दूरी पर स्थित रेखा का समीकरण ज्ञात कीजिए।
उत्तर दिखाएं
उत्तर :
दिए गए रेखाओं के समीकरण हैं
$9 x+6 y - 7=0\qquad \ldots(1)$
$3 x+2 y+6=0\qquad \ldots(2)$
मान लीजिए $P\left(h, k\right)$ वह अस्थायी बिंदु है जो रेखाओं $\left(1\right)$ और $\left(2\right)$ से समान दूरी पर है। $P\left(h, k\right)$ की रेखा $\left(1\right)$ से लंब दूरी निम्नलिखित है
$ d_1=\dfrac{|9 h+6 k-7|}{\left(9\right)^{2}+\left(6\right)^{2}}=\dfrac{|9 h+6 k-7|}{\sqrt{117}}=\dfrac{|9 h+6 k-7|}{3 \sqrt{13}} $
$P\left(h, k\right)$ की रेखा $\left(2\right)$ से लंब दूरी निम्नलिखित है
$ d_2=\dfrac{|3 h+2 k+6|}{\sqrt{\left(3\right)^{2}+\left(2\right)^ {2}}}=\dfrac{|3 h+2 k+6|}{\sqrt{13}} $
क्योंकि $P\left(h, k\right)$ रेखाओं $\left(1\right)$ और $\left(2\right)$ से समान दूरी पर है, $d_1=d_2$
$ \begin{aligned} & \therefore \quad \dfrac{|9 h+6 k-7|}{3 \sqrt{13}}=\dfrac{|3 h+2 k+6|}{\sqrt{13}} \\ \\ & \Rightarrow |9 h+6 k-7|=3| 3 h+2 k+6 \mid \\ \\ & \Rightarrow (9 h+6 k-7 )= \pm 3\left(3 h+2 k+6\right) \\ \\ & \Rightarrow 9 h+6 k-7=3\left(3 h+2 k+6\right) \text{ or } 9 h+6 k-7=-3\left(3 h+2 k+6\right) \end{aligned} $
स्थिति $ \ \ 9 h+6 k-7=3\left(3 h+2 k+6\right)$ संभव नहीं है क्योंकि
$9 h+6 k-7=3\left(3 h+2 k+6\right) $
$\Rightarrow-7=18$ (जो असंभव है)
$\therefore \quad h+6 k-7=-3\left(3 h+2 k+6\right)$
$9h + 6k -7 = -9h-6k-18$
$\Rightarrow 18 h+12 k+11=0$
इसलिए, आवश्यक रेखा का समीकरण $18 x+12 y+11=0$ है
21. एक किरण बिंदु $\left(1,2\right)$ से गुजरती है, $x$-अक्ष पर बिंदु $A$ पर परावर्तित होती है और परावर्तित किरण बिंदु $\left(5,3\right)$ से गुजरती है। $A$ के निर्देशांक ज्ञात कीजिए।
उत्तर दिखाएं
Answer :

मान लीजिए बिंदु $A$ के निर्देशांक $\left(a, 0\right)$ हैं
एक रेखा $\left(AL\right)$ खींचिए जो $x$-अक्ष के लंबवत हो।
हम जानते हैं कि प्रतिविम्बन कोण आपतित कोण के बराबर होता है।
इसलिए, बराबर करें $ \ \ \angle BAL=\angle CAL=\varnothing$
मान लें $ \ \ \angle CAX=\theta$
$ \ \therefore \quad \angle OAB=180^{\circ} - \left(\theta+2 \varnothing\right)=180^{\circ} - [\theta+2\left(90^{\circ} - \theta\right)]$
$ \begin{aligned} \therefore \quad \angle OAB & =180^{\circ} - \left(\theta+2 \varnothing\right)=180^{\circ} - \big[\theta+2\left(90^{\circ} - \theta\right)\big] \\ \\ & =180^{\circ} - \theta - 180^{\circ}+2 \theta \\ \\ & =\theta \end{aligned} $
$ \therefore \quad \angle B A X=180^{\circ} - \theta$
अब, रेखा $AC$ की प्रतिशत दर $=\dfrac{3-0}{5-a}$
$\Rightarrow \tan \theta=\dfrac{3}{5-a}\qquad \ldots(1)$
रेखा $AB$ की प्रतिशत दर $=\dfrac{2-0}{1-a}$
$\Rightarrow \tan \left(180^{\circ}-\theta\right)=\dfrac{2}{1-a}$
$\Rightarrow-\tan \theta=\dfrac{2}{1-a}$
$\Rightarrow \tan \theta=\dfrac{2}{a-1}\qquad \ldots(2)$
समीकरण $\left(1\right)$ और $\left(2\right)$ से, हम प्राप्त करते हैं
$ \begin{aligned} & \dfrac{3}{5-a}=\dfrac{2}{a-1} \\ \\ & \Rightarrow 3 a-3=10-2 a \\ \\ & \Rightarrow a=\dfrac{13}{5} \end{aligned} $
इसलिए, बिंदु $A$ के निर्देशांक $\left(\dfrac{13}{5}, 0\right)$ हैं
22. सिद्ध करें कि बिंदु $\left(\sqrt{a^{2}-b^{2}}, 0\right)$ और $\left(\sqrt{a^{2}-b^{2}}, 0\right)$ से रेखा $\dfrac{x}{a} \cos \theta+\dfrac{y}{b} \sin \theta=1$ पर खींचे गए लम्बों की लंबाई का गुणनफल $b^{2}$ होता है
उत्तर दिखाएं
उत्तर :
दी गई रेखा का समीकरण है
$\dfrac{x}{a} \cos \theta+\dfrac{y}{b} \sin \theta=1$
या, $b x \cos \theta+a y \sin \theta-a b=0\qquad \ldots(1)$
बिंदु $\left(\sqrt{a^{2}-b^{2}}, 0\right)$ से रेखा $\left(1\right)$ पर खींचे गए लम्ब की लंबाई है
$p_1=\dfrac{|b \cos \theta\left(\sqrt{a^{2}-b^{2}}\right)+a \sin \theta\left(0\right)-a b|}{\sqrt{b^{2} \cos ^{2} \theta+a^{2} \sin ^{2} \theta}}=\dfrac{|b \cos \theta \sqrt{a^{2}-b^{2}}-a b|}{\sqrt{b^{2} \cos ^{2} \theta+a^{2} \sin ^{2} \theta}}\qquad \ldots(2)$
बिंदु $\left(-\sqrt{a^{2}-b^{2}}, 0\right)$ से रेखा $\left(2\right)$ पर खींचे गए लम्ब की लंबाई है
$p_2=\dfrac{|b \cos \theta\left(-\sqrt{a^{2}-b^{2}}\right)+a \sin \theta\left(0\right)-a b|}{\sqrt{b^{2} \cos ^{2} \theta+a^{2} \sin ^{2} \theta}}=\dfrac{|b \cos \theta \sqrt{a^{2}-b^{2}}+a b|}{\sqrt{b^{2} \cos ^{2} \theta+a^{2} \sin ^{2} \theta}}\qquad \ldots(3)$
समीकरण $\left(2\right)$ और $\left(3\right)$ को गुणा करने पर, हम प्राप्त करते हैं
$ \begin{aligned} p_1 p_2 & =\dfrac{|b \cos \theta \sqrt{a^{2}-b^{2}}-a b|\left(b \cos \theta \sqrt{a^{2}-b^{2}}+a b\right) \mid}{\left(\sqrt{b^{2} \cos ^{2} \theta+a^{2} \sin ^{2} \theta}\right)^{2}} \\ \\ & =\dfrac{|\left(b \cos \theta \sqrt{a^{2}-b^{2}}-a b\right)\left(b \cos \theta \sqrt{a^{2}-b^{2}}+a b\right)|}{\left(b^{2} \cos ^{2} \theta+a^{2} \sin ^{2} \theta\right)} \\ \\ & =\dfrac{|\left(b \cos \theta \sqrt{a^{2}-b^{2}}\right)^{2}-\left(a b\right)^{2}|}{\left(b^{2} \cos ^{2} \theta+a^{2} \sin ^{2} \theta\right)} \\ \\ & =\dfrac{|b^{2} \cos ^{2} \theta\left(a^{2}-b^{2}\right)-a^{2} b^{2}|}{\left(b^{2} \cos ^{2} \theta+a^{2} \sin ^{2} \theta\right)} \\ \\ & =\dfrac{|a^{2} b^{2} \cos ^{2} \theta-b^{4} \cos ^{2} \theta-a^{2} b^{2}|}{b^{2} \cos ^{2} \theta+a^{2} \sin ^{2} \theta} \\ \\ & =\dfrac{b^{2}|a^{2} \cos ^{2} \theta-b^{2} \cos ^{2} \theta-a^{2}|}{b^{2} \cos ^{2} \theta+a^{2} \sin ^{2} \theta} \\ \\ & =\dfrac{b^{2}|a^{2} \cos ^{2} \theta-b^{2} \cos ^{2} \theta-a^{2} \sin ^{2} \theta-a^{2} \cos ^{2} \theta|}{b^{2} \cos ^{2} \theta+a^{2} \sin ^{2} \theta} \qquad\big[\because\sin ^{2} \theta+\cos ^{2} \theta=1\big] \\ \\ & =\dfrac{b^{2}|-\left(b^{2} \cos ^{2} \theta+a^{2} \sin ^{2} \theta\right)|}{b^{2} \cos ^{2} \theta+a^{2} \sin ^{2} \theta} \\ \\ & =\dfrac{b^{2}\left(b^{2} \cos ^{2} \theta+a^{2} \sin ^{2} \theta\right)}{\left(b^{2} \cos ^{2} \theta+a^{2} \sin ^{2} \theta\right)} \\ \\ & =b^{2} \end{aligned} $
इसलिए, सिद्ध किया गया।
23. दो सीधी रेखाओं, जिनके समीकरण $2 x-3 y+4=0$ और $3 x+4 y-5=0$ हैं, के क्रॉसिंग (जunction) पर खड़े एक व्यक्ति को एक रेखा, जिसका समीकरण $6 x-7 y+8=0$ है, तक सबसे कम समय में पहुँचना है। उसके द्वारा अनुसरण किए जाने वाले पथ का समीकरण ज्ञात कीजिए।
उत्तर दिखाएं
}
उत्तर :
दिए गए रेखाओं के समीकरण हैं
$2 x- 3 y+4=0\qquad \ldots(1)$
$3 x+4 y- 5=0\qquad \ldots(2)$
$6 x- 7 y+8=0\qquad \ldots(3)$
व्यक्ति रेखाओं $\left(1\right)$ और $\left(2\right)$ द्वारा प्रतिनिधित्व किए गए मार्गों के संगम पर खड़ा है।
समीकरण $\left(1\right)$ और $\left(2\right)$ को हल करने पर हम प्राप्त करते हैं
$ x=-\dfrac{1}{17} \text{ और } y=\dfrac{22}{17} $
इस प्रकार, व्यक्ति बिंदु $\left(-\dfrac{1}{17}, \dfrac{22}{17}\right)$ पर खड़ा है
व्यक्ति बिंदु $\left(-\dfrac{1}{17}, \dfrac{22}{17}\right)$ से रेखा $\left(3\right)$ के लम्बवत रेखा के अनुदिश चलने पर रेखा $\left(3\right)$ तक सबसे कम समय में पहुँच सकता है
रेखा $\left(3\right)$ की प्रतिलोम ढलान $-\dfrac{7}{6}$ है
$\therefore \quad $ रेखा $\left(3\right)$ के लम्बवत रेखा की ढलान $ =-\dfrac{1}{\left(\dfrac{6}{7}\right)}=-\dfrac{7}{6} $
बिंदु $\left(-\dfrac{1}{17}, \dfrac{22}{17}\right)$ से गुजरने वाली रेखा जिसकी ढलान $-\dfrac{7}{6}$ है, निम्नलिखित द्वारा दी जाती है
$ \begin{aligned} & \left(y-\dfrac{22}{17}\right)=-\dfrac{7}{6}\left(x+\dfrac{1}{17}\right) \\ \\ & 6\left(17 y-22\right)=-7\left(17 x+1\right) \\ \\ & 102 y-132=-119 x-7 \\ \\ & 119 x+102 y=125 \end{aligned} $
इस प्रकार, व्यक्ति के अनुसरण करने वाला मार्ग $119 x+102 y=125$ है





