उत्तर :

(i): दी गई समीकरण $x+7 y=0$ है

इसे लिखा जा सकता है

$y=-\dfrac{1}{7} x+0\qquad\ldots (1)$

इस समीकरण के रूप $y=m x+c$ है, जहाँ

$ m=-\dfrac{1}{7} \text{ और } c=0 $

इसलिए, समीकरण $(1)$ ढलान-अपवार्ति रूप में है, जहाँ ढलान और $y$-अपवार्ति क्रमशः $-\dfrac{1}{7}$ और $0$ हैं।

(ii): दी गई समीकरण $6 x+3 y -5=0$ है

इसे लिखा जा सकता है

$y=\dfrac{1}{3}(-6 x+5)$

$y=-2 x+\dfrac{5}{3}\qquad\ldots (2)$

इस समीकरण के रूप $y=m x+c$ है, जहाँ $m=-2$ और $c=\dfrac{5}{3}$

इसलिए, समीकरण $(2)$ ढलान-अपवार्ति रूप में है, जहाँ ढलान और $y$-अपवार्ति क्रमशः $-2$ और $\dfrac{5}{3}$ हैं।

(iii): दी गई समीकरण $y=0$ है।

इसे लिखा जा सकता है

$y=0 . x+0 \qquad\ldots (3)$

इस समीकरण के रूप $y=m x+c$ है, जहाँ $m=0$ और $c=0$।

इसलिए, समीकरण $(3)$ ढलान-अपवार्ति रूप में है, जहाँ ढलान और $y$-अपवार्ति क्रमशः $0$ और $0$ हैं।

उत्तर :

(i): दी गई समीकरण $3 x+2 y- 12=0$ है

इसे लिखा जा सकता है

$3 x+2 y=12$

$\dfrac{3 x}{12}+\dfrac{2 y}{12}=1$

अर्थात, $ \quad \dfrac{x}{4}+\dfrac{y}{6}=1\qquad\ldots (1)$

इस समीकरण के रूप $\dfrac{x}{a}+\dfrac{y}{b}=1$ है, जहाँ $a=4$ और $b=6$।

इसलिए, समीकरण $(1)$ अपवार्ति रूप में है, जहाँ $x$ और $y$ अक्षों पर अपवार्ति क्रमशः $4$ और $6$ हैं।

(ii): दी गई समीकरण $4 x - 3 y=6$ है।

यह लिखा जा सकता है

$\dfrac{4 x}{6}-\dfrac{3 y}{6}=1$

$\dfrac{2 x}{3}-\dfrac{y}{2}=1$

अर्थात, $ \quad \dfrac{x}{(\frac{3}{2})}+\dfrac{y}{(-2)}=1\qquad\ldots (2)$

इस समीकरण के रूप $\dfrac{x}{a}+\dfrac{y}{b}=1$ है, जहाँ $a=\dfrac{3}{2}$ और $b=-2$ है।

इसलिए, समीकरण $(2)$ कटाव रूप में है, जहाँ $x$ और $y$ अक्षों पर कटाव क्रमशः $\dfrac{3}{2}$ और $-2$ हैं।

(iii): दिया गया समीकरण $3 y+2=0$ है।

इसे लिखा जा सकता है $3 y=-2$

अर्थात, $\dfrac{y}{\left(-\dfrac{2}{3}\right)}=1\qquad\ldots (3)$

इस समीकरण के रूप $\dfrac{x}{a}+\dfrac{y}{b}=1$ है, जहाँ $a=0$ और $b=-\dfrac{2}{3}$ है।

इसलिए, समीकरण $(3)$ कटाव रूप में है, जहाँ $y$-अक्ष पर कटाव $-\dfrac{2}{3}$ है और इसका $x$-अक्ष पर कटाव नहीं है।

Answer :

रेखा का दिया गया समीकरण $12(x+6)=5(y - 2)$ है

$\Rightarrow 12 x+72=5 y - 10$

$\Rightarrow 12 x - 5 y+82=0$

समीकरण $(1)$ को रूप $A x+B y+C=0$ के सामान्य रूप से तुलना करने पर, हमें $A=12, B= - 5$ , और $C=82$ प्राप्त होते हैं।

ज्ञात है कि रेखा $A x+B y+C=0$ के बिंदु $(x_1, y_1)$ से लंब दूरी $( d )$ निम्नलिखित द्वारा दी जाती है

$d=\dfrac{\big|A x_1+B y_1+C\big|}{\sqrt{A^{2}+B^{2}}}$.

दिया गया बिंदु $(x_1, y_1)=(- 1,1)$ है।

इसलिए, बिंदु $( - 1,1 )$ की दी गई रेखा से दूरी

$=\dfrac{\big|12(-1)+(-5)(1)+82\big|}{\sqrt{(12)^{2}+(-5)^{2}}}$ इकाई $=\dfrac{\big|-12-5+82\big|}{\sqrt{169}}$ इकाई $=\dfrac{\big|65\big|}{13}$ इकाई $=5$ इकाई

Answer :

दिया गया रेखा का समीकरण $\dfrac{x}{3}+\dfrac{y}{4}=1$

या, $4 x+3 y-12=0$

समीकरण $(1)$ को रूप $A x+B y+C=0$ के सामान्य रूप से तुलना करने पर, हमें $A=4, \ B=3$, और $C= - 12$ प्राप्त होते हैं

मान लीजिए $(a, 0)$ वह बिंदु है जो $x$-अक्ष पर स्थित है जिसकी दी गई रेखा से दूरी 4 इकाई है।

ज्ञात है कि एक रेखा $A x+B y+C=0$ के बिंदु $(x_1, y_1)$ से लंब दूरी $(d)$ निम्नलिखित द्वारा दी जाती है

$d=\dfrac{\big|A x_1+B y_1+C\big|}{\sqrt{A^{2}+B^{2}}}$

इसलिए,

$ \quad 4=\dfrac{\big|4 a+3 \times 0-12\big|}{\sqrt{4^{2}+3^{2}}}$

$\Rightarrow 4=\dfrac{\big|4 a-12\big|}{5}$

$\Rightarrow\big|4 a-12\big|=20$

$\Rightarrow \pm(4 a-12)=20$

$\Rightarrow(4 a-12)=20$ या $-(4 a-12)=20$

$\Rightarrow 4 a=20+12$ या $4 a=-20+12$

$\Rightarrow a=8$ या $-2$

इसलिए, $x$-अक्ष पर आवश्यक बिंदु $(-2,0)$ और $(8,0)$ हैं।

उत्तर :

ज्ञात है कि समानांतर रेखाओं $A x+B y+C_1=0$ और $A x+B y+C_2=0$ के बीच की दूरी $(d)$ निम्नलिखित द्वारा दी जाती है $d=\dfrac{\big|C_1-C_2\big|}{\sqrt{A^{2}+B^{2}}}$

(i): दी गई समानांतर रेखाएँ $15 x+8 y - 34=0$ और $15 x+8 y+31=0$ हैं

यहाँ, $A=15, \ B=8, \ C_1= - 34 ,$ और $C_2=31$ हैं।

इसलिए, समानांतर रेखाओं के बीच की दूरी है $d=\dfrac{\big|C_1-C_2\big|}{\sqrt{A^{2}+B^{2}}}=\dfrac{\big|-34-31\big|}{\sqrt{(15)^{2}+(8)^{2}}}$ $=\dfrac{\big|-65\big|}{17}$ $=\dfrac{65}{17}$ इकाई

(ii): दी गई समानांतर रेखाएँ $l(x+y)+p=0$ और $l(x+y) - r=0$ हैं।

$l x+l y+p=0$ और $l x+l y - r=0$

यहाँ,

$A=l, \ B=l, \ C_1=p$, और $C_2=- r$ हैं।

इसलिए, समानांतर रेखाओं के बीच की दूरी है

$d=\dfrac{\big|C_1-C_2\big|}{\sqrt{A^{2}+B^{2}}}=\dfrac{\big|p+r\big|}{\sqrt{l^{2}+l^{2}}}$ $=\dfrac{\big|p+r\big|}{\sqrt{2 l^{2}}}$ $=\dfrac{\big|p+r\big|}{l \sqrt{2}}$ $=\dfrac{1}{\sqrt{2}}\big|\dfrac{p+r}{l}\big|$ इकाई

उत्तर :

दी गई रेखा का समीकरण है

$3 x-4 y+2=0$

या $y=\dfrac{3 x}{4}+\dfrac{2}{4}$

या $y=\dfrac{3}{4} x+\dfrac{1}{2}$, जो $y=m x+c$ के रूप में है

$\therefore \ \ $ दी गई रेखा की ढलान $ =\dfrac{3}{4} $

ज्ञात है कि समानांतर रेखाओं की ढलान समान होती है।

$\therefore$ दूसरी रेखा की ढलान $ m=\dfrac{3}{4} $

अब, ढलान $\dfrac{3}{4}$ वाली रेखा का समीकरण जो बिंदु $(-2,3)$ से गुजरती है, है

$ \begin{aligned} & (y-3)=\dfrac{3}{4}\lbrace x-(-2) \rbrace \\ \\ & 4 y-12=3 x+6 \\ \\ & \text{ अर्थात, } 3 x-4 y+18=0 \end{aligned} $

उत्तर :

दी गई रेखा का समीकरण $x-7 y+5=0$

या, $ \ y=\dfrac{1}{7} x+\dfrac{5}{7}$, जो $y=m x+c$ के रूप में है

$\therefore \ \ $ दी गई रेखा की ढलान $ =\dfrac{1}{7} $

ढलान $\dfrac{1}{7}$ वाली रेखा के लम्ब रेखा की ढलान $m=-\dfrac{1}{\left(\frac{1}{7}\right)}=-7$ है

ढलान $- 7$ वाली रेखा का समीकरण जो $x$-अक्ष प्रतिच्छेदन 3 हो है

$\quad y=m(x - d)$

$\Rightarrow y=- 7(x - 3)$

$\Rightarrow y=- 7 x+21$

$\Rightarrow 7 x+y=21$

उत्तर :

दी गई रेखाएँ $\sqrt{3} x+y=1$ और $x+\sqrt{3} y=1$ हैं।

$y=-\sqrt{3} x+1 \qquad \ldots(1) \quad$

और $y=-\dfrac{1}{\sqrt{3}} x+\dfrac{1}{\sqrt{3}}\qquad\ldots\mathrm{(2)}$

रेखा $(1)$ की ढलान $m_1=-\sqrt{3}$ है, जबकि रेखा $(2)$ की ढलान $m_2=-\dfrac{1}{\sqrt{3}}$ है

दोनों रेखाओं के बीच न्यून कोण अर्थात, $\theta$ द्वारा दिया गया है $\tan \theta=\left|\dfrac{m_1-m_2}{1+m_1 m_2}\right|$

$\tan \theta=\left|\dfrac{-\sqrt{3}+\dfrac{1}{\sqrt{3}}}{1+(-\sqrt{3})(-\dfrac{1}{\sqrt{3}})}\right|$

$\tan \theta=\left|\dfrac{\dfrac{-3+1}{\sqrt{3}}}{1+1}\right|=\left|\dfrac{-2}{2 \times \sqrt{3}}\right|$

$\tan \theta=\dfrac{1}{\sqrt{3}}$

$\quad \ \theta=30^{\circ}$

इसलिए, दी गई रेखाओं के बीच कोण या तो $30^{\circ}$ है या $180^{\circ} - 30^{\circ}=150^{\circ}$

उत्तर :

बिंदुओं $(h, 3)$ और $(4,1)$ से गुजरने वाली रेखा की ढलान $m_1=\dfrac{1-3}{4-h}=\dfrac{-2}{4-h}$ है।

रेखा $7 x$ - $9 y$ - $19=0$ या $y=\dfrac{7}{9} x-\dfrac{19}{9}$ की ढलान $m_2=\dfrac{7}{9}$ है।

दिया गया है कि दोनों रेखाएँ लंबवत हैं।

$\therefore \ m_1 \times m_2=-1$

$\Rightarrow \left(\dfrac{-2}{4-h}\right) \times\left(\dfrac{7}{9}\right)=-1$

$\Rightarrow \dfrac{-14}{36-9 h}=-1$

$\Rightarrow 14=36-9 h$

$\Rightarrow 9 h=36-14$

$\Rightarrow h=\dfrac{22}{9}$

अतः, $h$ का मान $\dfrac{22}{9}$ है।

उत्तर :

रेखा $A x+B y+C=0$ या $y=\left(\dfrac{-A}{B}\right) x+\left(\dfrac{-C}{B}\right)$ की ढलान $\quad m=-\dfrac{A}{B}$ है।

ज्ञात है कि समांतर रेखाओं की ढलान समान होती है।

$\therefore \ \ $ दूसरी रेखा की ढलान $ ~ m=-\dfrac{A}{B}$ है।

बिंदु $(x_1, y_1)$ से गुजरने वाली रेखा के लिए जिसकी ढलान $m=-\dfrac{A}{B}$ है, उसका समीकरण है:

$y-y_1=m(x-x_1)$

$y-y_1=-\dfrac{A}{B}(x-x_1)$

$B(y-y_1)=-A(x-x_1)$

$A(x-x_1)+B(y-y_1)=0$

अतः, बिंदु $(x_1, y_1)$ से गुजरने वाली रेखा जो रेखा $A x+B y+C=0$ के समांतर है, उसका समीकरण है:

$A(x - x_1)+B(y - y_1)=0$

उत्तर :

दिया गया है कि पहली रेखा की ढलान, $m_1=2$ है।

मान लीजिए दूसरी रेखा की ढलान $m_2$ है।

दोनों रेखाओं के बीच कोण $60^{\circ}$ है।

$\therefore \ \tan 60^{\circ}=\left|\dfrac{m_1-m_2}{1+m_1 m_2}\right|$

$\Rightarrow \sqrt{3}=\left|\dfrac{2-m_2}{1+2 m_2}\right|$

$\Rightarrow \sqrt{3}= \pm\left(\dfrac{2-m_2}{1+2 m_2}\right)$

$\Rightarrow \sqrt{3}=\dfrac{2-m_2}{1+2 m_2}$ या $\sqrt{3}=-\left(\dfrac{2-m_2}{1+2 m_2}\right)$

$\Rightarrow \sqrt{3}(1+2 m_2)=2-m_2$ या $\sqrt{3}(1+2 m_2)=-(2-m_2)$

$\Rightarrow \sqrt{3}+2 \sqrt{3} m_2+m_2=2$ या $\sqrt{3}+2 \sqrt{3} m_2-m_2=-2$

$\Rightarrow \sqrt{3}+(2 \sqrt{3}+1) m_2=2$ या $\sqrt{3}+(2 \sqrt{3}-1) m_2=-2$

$\Rightarrow m_2=\dfrac{2-\sqrt{3}}{(2 \sqrt{3}+1)}$ या $m_2=\dfrac{-(2+\sqrt{3})}{(2 \sqrt{3}-1)}$

केस I: $\quad m_2=\left(\dfrac{2-\sqrt{3}}{2 \sqrt{3}+1}\right)$

बिंदु $(2,3)$ से गुजरने वाली रेखा के ढलान के $\left(\dfrac{2-\sqrt{3}}{2 \sqrt{3}+1}\right)$ के साथ समीकरण है

$(y-3)=\dfrac{2-\sqrt{3}}{2 \sqrt{3}+1}(x-2)$

$(2 \sqrt{3}+1) y-3(2 \sqrt{3}+1)=(2-\sqrt{3}) x-2(2-\sqrt{3})$

$(\sqrt{3}-2) x+(2 \sqrt{3}+1) y=-4+2 \sqrt{3}+6 \sqrt{3}+3$

$(\sqrt{3}-2) x+(2 \sqrt{3}+1) y=-1+8 \sqrt{3}$

इस मामले में, दूसरी रेखा का समीकरण $(\sqrt{3}-2) x+(2 \sqrt{3}+1) y=-1+8 \sqrt{3}$ है।

केस II : $\quad m_2= -\left(\dfrac{2+\sqrt{3}}{2 \sqrt{3}-1}\right)$

बिंदु $(2,3)$ से गुजरने वाली रेखा के ढलान के $-\left(\dfrac{2+\sqrt{3}}{2 \sqrt{3}-1}\right)$ के साथ समीकरण है

$ \begin{aligned} & (y-3)=-\left(\dfrac{2+\sqrt{3}}{2 \sqrt{3}-1}\right)(x-2) \\ \\ & (2 \sqrt{3}-1) y-3(2 \sqrt{3}-1)=-(2+\sqrt{3}) x+2(2+\sqrt{3}) \\ \\ & (2 \sqrt{3}-1) y+(2+\sqrt{3}) x=4+2 \sqrt{3}+6 \sqrt{3}-3 \\ \\ & (2+\sqrt{3}) x+(2 \sqrt{3}-1) y=1+8 \sqrt{3} \end{aligned} $

इस मामले में, दूसरी रेखा का समीकरण $(2+\sqrt{3}) x+(2 \sqrt{3}-1) y=1+8 \sqrt{3}$ है।

इसलिए, दूसरी रेखा का अभीष्ट समीकरण $(\sqrt{3}-2) x+(2 \sqrt{3}+1) y=-1+8 \sqrt{3}$

या $(2+\sqrt{3}) x+(2 \sqrt{3}-1) y=1+8 \sqrt{3}$ है।

उत्तर :

एक रेखाखंड के दाईं ओर लंब रेखा रेखाखंड को $90^{\circ}$ पर बराबर विभाजित करती है।

रेखाखंड के सिरे बिंदु $A (3,4)$ और $B(-{ } 1,2)$ दिए गए हैं।

इसलिए, $A B$ के मध्य बिंदु $ =\left(\dfrac{3-1}{2}, \dfrac{4+2}{2}\right)=(1,3) $

$A B$ की ढलान $=\left(\dfrac{2-4}{-1-3}\right)=\left(\dfrac{-2}{-4}\right)=\dfrac{1}{2}$

$\therefore \ $ $A B$ के लंब रेखा की ढलान $ =-\dfrac{1}{\left(\dfrac{1}{2}\right)}=-2 $

बिंदु $(1,3)$ से गुजरने वाली रेखा का समीकरण जो ढलान $- 2$ है निम्नलिखित है

$(y - 3)= -2 (x - 1)$

$y - 3=- 2 x+2$

$2 x+y=5$

इसलिए, अभीष्ट रेखा का समीकरण $2 x+y=5$ है।

उत्तर :

मान लीजिए $(a, b)$ बिंदु $(- 1,3)$ से रेखा $3 x - 4 y - 16=0$ पर लंब के पाद के निर्देशांक हैं।

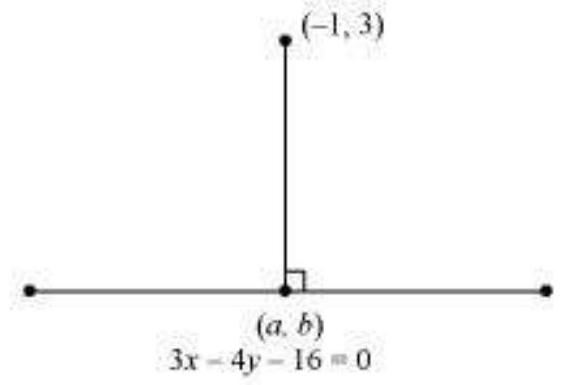
बिंदुओं $(- 1,3)$ और $(a, b)$ को जोड़ने वाली रेखा की ढलान, $m_1=\dfrac{b-3}{a+1}$

रेखा $3 x$- $4 y$- $16=0$ या $y=\dfrac{3}{4} x-4$ की ढलान, $m_2=\dfrac{3}{4}$

चूंकि ये दोनों रेखाएँ लंब हैं, $m_1 m_2= - 1$

$\therefore\left(\dfrac{b-3}{a+1}\right) \times\left(\dfrac{3}{4}\right)=-1$

$\Rightarrow \dfrac{3 b-9}{4 a+4}=-1$

$\Rightarrow 3 b-9=-4 a-4$

$\Rightarrow 4 a+3 b=5\qquad\ldots\mathrm{(1)}$

बिंदु $(a, b)$ रेखा $3 x$ - $4 y=16$ पर स्थित है।

$\therefore \ \ 3 a$ - $4 b=16\qquad\ldots\mathrm{(2)}$

समीकरण (1) और (2) को हल करने पर हम प्राप्त करते हैं

$a=\dfrac{68}{25}$ और $b=-\dfrac{49}{25}$

इसलिए, अभीष्ट लंब के पाद के निर्देशांक $\left(\dfrac{68}{25},-\dfrac{49}{25}\right)$ हैं।

उत्तर :

दी गई रेखा का समीकरण $y=m x+c$ है।

दिया गया है कि मूल बिंदु से लंब रेखा दी गई रेखा को बिंदु $(-1,2)$ पर मिलती है।

इसलिए, बिंदुओं $(0,0)$ और $(- 1,2)$ को मिलाने वाली रेखा दी गई रेखा के लंबवत है।

$\therefore \ $ बिंदुओं $(0,0)$ और $( - 1,2)$ को मिलाने वाली रेखा की ढलान $ =\dfrac{2}{-1}=-2 $

दी गई रेखा की ढलान $m$ है।

$\therefore \ \ m \times -2=-1 \qquad $ [दोनों रेखाएँ लंबवत हैं]

$\Rightarrow m=\dfrac{1}{2}$

क्योंकि बिंदु $( - 1,2)$ दी गई रेखा पर स्थित है, इसलिए यह समीकरण $y=m x+c$ को संतुष्ट करता है।

$\therefore 2=m(-1)+c$

$\Rightarrow 2=\dfrac{1}{2}(-1)+c$

$\Rightarrow c=2+\dfrac{1}{2}=\dfrac{5}{2}$

इसलिए, $m$ और $c$ के संगत मान $\dfrac{1}{2}$ और $\dfrac{5}{2}$ हैं।

Answer :

दी गई रेखाओं के समीकरण हैं

$x \cos \theta - y \sin \theta=k \cos 2 \theta \qquad\ldots\mathrm{(1)}$

$x \sec \theta+y cosec \theta=k$.

एक रेखा $A x+B y+C=0$ के बिंदु $(x_1, y_1)$ से लंबवत दूरी $(d)$ निम्नलिखित होती है

$ d=\dfrac{\big|A x_1+B y_1+C\big|}{\sqrt{A^{2}+B^{2}}} \qquad \ldots {(2)} $

समीकरण $(1)$ को एक व्यापक रेखा समीकरण $A x+B y+C=0$ के रूप में तुलना करने पर, हमें $A=\cos \theta, \ B= -\sin \theta$, और $C=- k \cos 2 \theta$ प्राप्त होते हैं।

दिया गया है कि $p$ बिंदु $(0,0)$ से रेखा $(1)$ पर लंबवत दूरी है।

$\therefore \ \ p=\dfrac{\big|A(0)+B(0)+C\big|}{\sqrt{A^{2}+B^{2}}}=\dfrac{\big|C\big|}{\sqrt{A^{2}+B^{2}}}=\dfrac{\big|-k \cos 2 \theta\big|}{\sqrt{\cos ^{2} \theta+\sin ^{2} \theta}}=\big|-k \cos 2 \theta\big|$

समीकरण $(2)$ को एक व्यापक रेखा समीकरण $A x+B y+C=0$ के रूप में तुलना करने पर, हमें $A=\sec \theta, \ B=cosec \theta$, और $C= -k.$ प्राप्त होते हैं।

दिया गया है कि $q$ बिंदु $(0,0)$ से रेखा $(2)$ पर लंबवत दूरी है।

$\therefore \quad q=\dfrac{\big|A(0)+B(0)+C\big|}{\sqrt{A^{2}+B^{2}}}=\dfrac{\big|C\big|}{\sqrt{A^{2}+B^{2}}}=\dfrac{\big|-k\big|}{\sqrt{\sec ^{2} \theta+cosec^{2} \theta}}$

$(3)$ और $(4)$ से, हमें प्राप्त है

$ \begin{aligned} p^{2}+4 q^{2} & =(-k \cos 2 \theta)^{2}+4\left(\dfrac{\big|-k\big|}{\sqrt{\sec ^{2} \theta+cosec^{2} \theta}}\right)^{2} \\ \\ & =k^{2} \cos ^{2} 2 \theta+\dfrac{4 k^{2}}{(\sec ^{2} \theta+cosec^{2} \theta)} \\ \\ & =k^{2} \cos ^{2} 2 \theta+\dfrac{4 k^{2}}{\left(\dfrac{1}{\cos ^{2} \theta}+\dfrac{1}{\sin ^{2} \theta}\right)} \\ \\ & =k^{2} \cos ^{2} 2 \theta+\dfrac{4 k^{2}}{\left(\dfrac{\sin ^{2} \theta+\cos ^{2} \theta}{\sin ^{2} \theta \cos ^{2} \theta}\right)} \\ \\ & =k^{2} \cos ^{2} 2 \theta+\dfrac{4 k^{2}}{\left(\dfrac{1}{\sin ^{2} \theta \cos ^{2} \theta}\right)} \\ \\ & =k^{2} \cos ^{2} 2 \theta+4 k^{2} \sin ^{2} \theta \cos ^{2} \theta \\ \\ & =k^{2} \cos ^{2} 2 \theta+k^{2}(2 \sin \theta \cos \theta)^{2} \\ \\ & =k^{2} \cos ^{2} 2 \theta+k^{2} \sin ^{2} 2 \theta \\ \\ & =k^{2}(\cos ^{2} 2 \theta+\sin ^{2} 2 \theta) \\ \\ & =k^{2} \end{aligned} $

इसलिए, हमने सिद्ध कर दिया कि $p^{2}+4 q^{2}=k^{2}$।

उत्तर :

मान लीजिए $AD$ त्रिभुज $ABC$ की शीर्ष $A$ से लंब है।

इसलिए, $AD \perp BC$

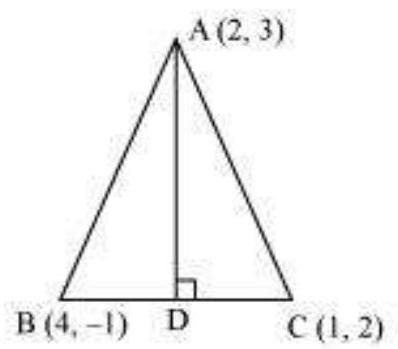
बिंदु $(2,3)$ से गुजरने वाली रेखा की ढलान 1 होने वाली समीकरण है

$(y - 3)=1(x -2 )$

$\Rightarrow x - y+1=0$

$\Rightarrow y - x=1$

इसलिए, शीर्ष $A$ से लंब की समीकरण

$y - x=1$

$AD$ की लंबाई = बिंदु $A(2,3)$ से रेखा $BC$ पर लंब की लंबाई है

रेखा $BC$ की समीकरण है

$(y+1)=\left(\dfrac{2+1}{1-4}\right)(x-4)$

$\Rightarrow(y+1)=-1(x-4)$

$\Rightarrow y+1=-x+4$

$\Rightarrow x+y-3=0$

एक बिंदु $(x_1, y_1)$ से रेखा $Ax + By + C = 0$ की लंब दूरी $(d)$ निम्नलिखित द्वारा दी जाती है $\sqrt{A^{2}+B^{2}}$।

समीकरण $(1)$ को रेखा के सामान्य समीकरण $A x+B y+C=0$ के साथ तुलना करने पर, हमें $A=1, B=1$, और $C= - 3$ प्राप्त होता है।

$\therefore \ \ $ $A D$ की लंबाई $ =\dfrac{\big|1 \times 2+1 \times 3-3\big|}{\sqrt{1^{2}+1^{2}}} =\dfrac{\big|2\big|}{\sqrt{2}} =\dfrac{2}{\sqrt{2}} =\sqrt{2} \text{ इकाई } $

इस प्रकार, शीर्ष $A$ से लंब की समीकरण और लंबाई क्रमशः $y - x=1$ और $\sqrt{2}$ इकाई है।

उत्तर :

यह ज्ञात है कि एक रेखा के अक्षों पर अपवाह $a$ और $b$ होने पर रेखा का समीकरण $\dfrac{x}{a}+\dfrac{y}{b}=1 $ होता है।

$\text{ या } ~ b x+a y-a b=0 \qquad \ldots {(1)}$

एक बिंदु $(x_1, y_1)$ से रेखा $A x+B y+C=0$ की लंबवत दूरी $(d)$ निम्नलिखित द्वारा दी जाती है

$ d=\dfrac{\big|A x_1+B y_1+C\big|}{\sqrt{A^{2}+B^{2}}} $

समीकरण $(1)$ को रेखा के सामान्य समीकरण $A x+B y+C=0$ के साथ तुलना करने पर, हमें $A=b, \ B=a$, और $C=a -a b$ प्राप्त होता है।

इसलिए, यदि $p$ बिंदु $(x_1, y_1)=(0,0)$ से रेखा $(1)$ की लंबवत दूरी है, तो हमें प्राप्त होता है

$p=\dfrac{\big|A(0)+B(0)-a b\big|}{\sqrt{b^{2}+a^{2}}}$

$\Rightarrow p=\dfrac{\big|-a b\big|}{\sqrt{a^{2}+b^{2}}}$

दोनों ओर वर्ग करने पर, हमें प्राप्त होता है

$p^{2}=\dfrac{(-a b)^{2}}{a^{2}+b^{2}}$

$\Rightarrow p^{2}(a^{2}+b^{2})=a^{2} b^{2}$

$\Rightarrow \dfrac{a^{2}+b^{2}}{a^{2} b^{2}}=\dfrac{1}{p^{2}}$

$\Rightarrow \dfrac{1}{p^{2}}=\dfrac{1}{a^{2}}+\dfrac{1}{b^{2}}$

इस प्रकार, हम दिखाए हैं कि $\dfrac{1}{p^{2}}=\dfrac{1}{a^{2}}+\dfrac{1}{b^{2}}$