उत्तर :

एक समांतर चतुर्भुज $A B C D$ के तीन शीर्ष $ A\left(3, - 1, 2 \right), B\left(1,2,- 4\right),$ और $C \left(-1, 1, 2\right).$ चौथे शीर्ष के निर्देशांक $D\left(x, y, z\right)$ हों।

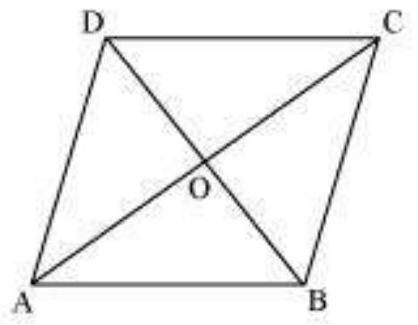
हम जानते हैं कि समांतर चतुर्भुज के विकर्ण एक दूसरे को समद्विभाजित करते हैं।

इसलिए, समांतर चतुर्भुज $A B C D$ में $A C$ और $B D$ एक दूसरे को समद्विभाजित करते हैं।

$\therefore \ \ $ $A C$ का मध्य-बिंदु = $B D$ का मध्य-बिंदु

$\Rightarrow \ \ \left(\dfrac{3-1}{2}, \dfrac{-1+1}{2}, \dfrac{2+2}{2}\right)=\left(\dfrac{x+1}{2}, \dfrac{y+2}{2}, \dfrac{z-4}{2}\right)$

$\Rightarrow \ \ \left(1,0,2\right)=\left(\dfrac{x+1}{2}, \dfrac{y+2}{2}, \dfrac{z-4}{2}\right)$

$\Rightarrow \ \ \dfrac{x+1}{2}=1, \dfrac{y+2}{2}=0$, और $\dfrac{z-4}{2}=2$

$\Rightarrow \ \ x=1, y=- 2$ , और $z=8$

इसलिए, चौथे शीर्ष के निर्देशांक $\left(1, -2, 8\right)$ हैं।

उत्तर :

मान लीजिए $A D, B E$, और $C F$ दिए गए त्रिभुज $A B C$ की माध्यिकाएं हैं।

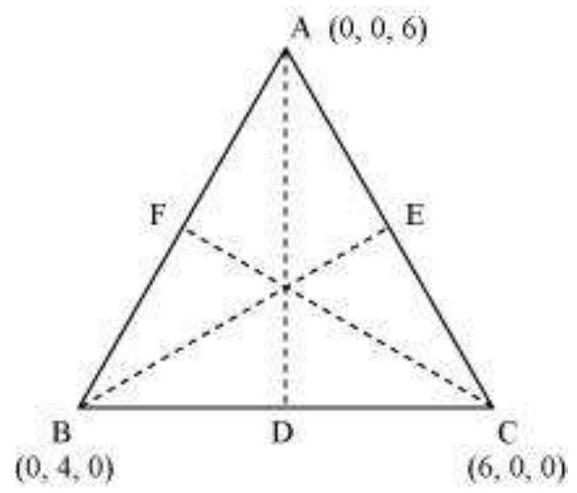
क्योंकि $A D$ माध्यिका है, तो $D$ बिंदु $B C$ का मध्य-बिंदु है।

$\therefore \ \ $ बिंदु $D$ के निर्देशांक $\left(\dfrac{0+6}{2}, \dfrac{4+0}{2}, \dfrac{0+0}{2}\right)=\left(3,2,0\right)$

$AD=\sqrt{\left(0-3\right)^{2}+\left(0-2\right)^{2}+\left(6-0\right)^{2}}=\sqrt{9+4+36}=\sqrt{49}=7$

क्योंकि $BE$ माध्यिका है, $E$ $AC$ का मध्य-बिंदु है।

$\therefore \ \ $ बिंदु $E$ के निर्देशांक $\left(\dfrac{0+6}{2}, \dfrac{0+0}{2}, \dfrac{6+0}{2}\right)=\left(3,0,3\right)$

$BE=\sqrt{\left(3-0\right)^{2}+\left(0-4\right)^{2}+\left(3-0\right)^{2}}=\sqrt{9+16+9}=\sqrt{34}$

क्योंकि $CF$ माध्यिका है, $F$ $AB$ का मध्य-बिंदु है।

$\therefore \ \ $ बिंदु $F$ के निर्देशांक $\left(\dfrac{0+0}{2}, \dfrac{0+4}{2}, \dfrac{6+0}{2}\right)=\left(0,2,3\right)$

$CF$ की लंबाई $\sqrt{\left(6-0\right)^{2}+\left(0-2\right)^{2}+\left(0-3\right)^{2}}=\sqrt{36+4+9}=\sqrt{49}=7$

इस प्रकार, $\triangle ABC$ की माध्यिकाओं की लंबाई $7, \sqrt{34}$, और $7$ है।

Answer :

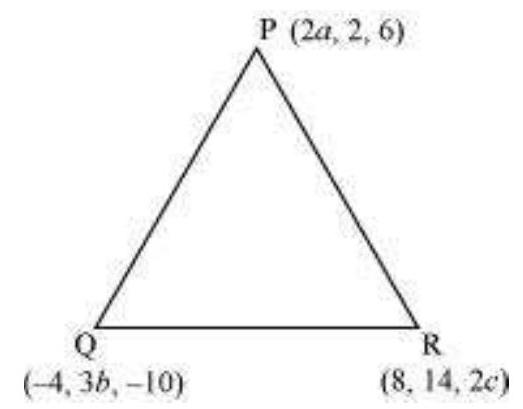
यह ज्ञात है कि त्रिभुज के शीर्ष $\left(x_1, y_1, z_1\right),\left(x_2, y_2, z_2\right)$ और $\left(x_3, y_3, z_3\right)$ के लिए केंद्रक के निर्देशांक $\left(\dfrac{x_1+x_2+x_3}{3}, \dfrac{y_1+y_2+y_3}{3}, \dfrac{z_1+z_2+z_3}{3}\right)$ होते हैं।

इसलिए, $\Delta PQR$ के केंद्रक के निर्देशांक $\left(\dfrac{2 a-4+8}{3}, \dfrac{2+3 b+14}{3}, \dfrac{6-10+2 c}{3}\right)=\left(\dfrac{2 a+4}{3}, \dfrac{3 b+16}{3}, \dfrac{2 c-4}{3}\right)$

यह दिया गया है कि मूल बिंदु त्रिभुज $PQR$ का केंद्रक है।

$\therefore \ \ \left(0,0,0\right)=\left(\dfrac{2 a+4}{3}, \dfrac{3 b+16}{3}, \dfrac{2 c-4}{3}\right)$

$\Rightarrow \ \ \dfrac{2 a+4}{3}=0, \dfrac{3 b+16}{3}=0$ और $\dfrac{2 c-4}{3}=0$

$\Rightarrow \ \ a=-2, b=-\dfrac{16}{3}$ और $c=2$

इस प्रकार, $a, b$, और $c$ के संगत मान हैं

$ -2,-\dfrac{16}{3}, \text{ और } 2 $

उत्तर :

बिंदुओं $A$ और $B$ के निर्देशांक क्रमशः $\left(3,4,5\right)$ और $(-1,3,-7)$ दिए गए हैं।

मान लीजिए बिंदु $P$ के निर्देशांक $\left(x, y, z\right)$ हैं।

दूरी सूत्र का उपयोग करते हुए, हम प्राप्त करते हैं

$ \begin{aligned} PA^{2} & =\left(x-3\right)^{2}+\left(y-4\right)^{2}+\left(z-5\right)^{2} \\ \\ & =x^{2}+9-6 x+y^{2}+16-8 y+z^{2}+25-10 z \\ \\ & =x^{2}-6 x+y^{2}-8 y+z^{2}-10 z+50 \\ \\ PB^{2} & =\left(x+1\right)^{2}+\left(y-3\right)^{2}+\left(z+7\right)^{2} \\ \\ & =x^{2}+2 x+y^{2}-6 y+z^{2}+14 z+59 \end{aligned} $

अब, यदि $PA^{2}+PB^{2}=k^{2}$,

तो,

$ \begin{aligned} & \left(x^{2}-6 x+y^{2}-8 y+z^{2}-10 z+50\right)+\left(x^{2}+2 x+y^{2}-6 y+z^{2}+14 z+59\right)=k^{2} \\ \\ & \Rightarrow \ \ 2 x^{2}+2 y^{2}+2 z^{2}-4 x-14 y+4 z+109=k^{2} \\ \\ & \Rightarrow \ \ 2\left(x^{2}+y^{2}+z^{2}-2 x-7 y+2 z\right)=k^{2}-109 \\ \\ & \Rightarrow \ \ x^{2}+y^{2}+z^{2}-2 x-7 y+2 z=\dfrac{k^{2}-109}{2} \\ \\ & \qquad x^{2}+y^{2}+z^{2}-2 x-7 y+2 z=\dfrac{k^{2}-109}{2} . \end{aligned} $