प्रकाश के रेखीय प्रकाशिकी एवं प्रकाशिक यंत्र
बहुविकल्पीय प्रश्न (MCQs)
1. एक प्रिज्म के विवर्तन तल पर कोण $\theta$ पर प्रकाश की किरण आपतित होती है और दूसरे तल से नॉर्मल रूप से निर्गत होती है। यदि प्रिज्म का कोण $5^{\circ}$ है और प्रिज्म के पदार्थ का विवर्तनी अपवर्तनांक 1.5 है, तो आपतन कोण है
(a) $7.5^{\circ}$
(b) $5^{\circ}$
(c) $15^{\circ}$
(d) $2.5^{\circ}$
उत्तर दिखाएं
सोचने की प्रक्रिया
पहले सतह से अपवर्तित किरण दूसरे सतह पर नॉर्मल रूप से प्रतिगत होती है, ताकि दूसरे तल से नॉर्मल रूप से निर्गत हो सके।
उत्तर
(a) क्योंकि, विवर्तन $\delta=(\mu-1) A=(1.5-1) \times 5^{\circ}=2.5^{\circ}$
ज्यामिति के अनुसार, पहले सतह से अपवर्तन कोण $5^{\circ}$ है।
लेकिन $\delta=\theta-r$, इसलिए, हमें $2.5^{\circ}=\theta-5^{\circ}$ पर हल करने पर $\theta=7.5^{\circ}$ प्राप्त होता है।
-
विकल्प (b) $5^{\circ}$: यह विकल्प गलत है क्योंकि यदि आपतन कोण $5^{\circ}$ होता, तो विवर्तन शून्य होता, जो $2.5^{\circ}$ के दिए गए विवर्तन के विरोधाभास होता है।
-
विकल्प (c) $15^{\circ}$: यह विकल्प गलत है क्योंकि यदि आपतन कोण $15^{\circ}$ होता, तो विवर्तन $2.5^{\circ}$ से बहुत अधिक होता, जिसके लिए अपवर्तनांक और प्रिज्म के कोण के आधार पर यह संभव नहीं होता।
-
विकल्प (d) $2.5^{\circ}$: यह विकल्प गलत है क्योंकि यदि आपतन कोण $2.5^{\circ}$ होता, तो विवर्तन नकारात्मक होता, जो इस संदर्भ में संभव नहीं होता।
2. एक छोटी पल्स श्वेत प्रकाश वायु से ग्लास के टुकड़े में अभिलम्ब आपतन के साथ आपतित होती है। टुकड़े के माध्यम से गुजरने के बाद पहले निर्गत होने वाला रंग है $\newline$
(a) नीला $\newline$
(b) हरा $\newline$
(c) बौछारा $\newline$
(d) लाल $\newline$
उत्तर दिखाएं
सोचने की प्रक्रिया
जब प्रकाश की किरण एक माध्यम से दूसरे माध्यम में जाती है, तो प्रकाश की आवृत्ति अपरिवर्तित रहती है।
उत्तर
(d) क्योंकि $v \propto \lambda$, लाल रंग की किरण सबसे अधिक तरंगदैर्ध्य वाली होती है और इसलिए सबसे अधिक चाल वाली होती है। इसलिए, टुकड़े के माध्यम से गुजरने के बाद लाल रंग पहले निर्गत होता है।
-
(a) नीला: नीले प्रकाश की तरंगदैर्घ्य लाल प्रकाश की तुलना में छोटी होती है, जिसका अर्थ है कि यह काँच के प्लेट में धीमी गति से चलता है। इसलिए, यह पहले निकलने वाला नहीं होगा।
-
(b) हरा: हरे प्रकाश की तरंगदैर्घ्य लाल प्रकाश की तुलना में छोटी होती है लेकिन नीले और बैंगनी की तुलना में लंबी होती है। यह काँच के प्लेट में लाल प्रकाश की तुलना में धीमी गति से चलता है, इसलिए यह पहले निकलने वाला नहीं होगा।
-
(c) बैंगनी: बैंगनी प्रकाश दिए गए विकल्पों में सबसे छोटी तरंगदैर्घ्य वाला होता है, जिसका अर्थ है कि यह काँच के प्लेट में सबसे धीमी गति से चलता है। इसलिए, यह पहले निकलने वाला नहीं होगा।
3. एक वस्तु लेंस के बाईं ओर से एक समान गति $5 m / s$ के साथ लेंस की ओर आती है और फोकस पर रुक जाती है। छवि
(a) लेंस से दूर एक समान गति $5 m / s$ के साथ चलती है
(b) लेंस से दूर एक समान त्वरण के साथ चलती है
(c) लेंस से दूर एक असमान त्वरण के साथ चलती है
(d) लेंस की ओर एक असमान त्वरण के साथ चलती है
उत्तर दिखाएं
सोचने की प्रक्रिया
इस समस्या का संबंध वस्तु के विभिन्न स्थितियों में छवि के निर्माण से है।
उत्तर
(c) जब एक वस्तु लेंस के बाईं ओर से $5 m / s$ की एक समान गति के साथ लेंस की ओर आती है, तो छवि लेंस से दूर एक असमान त्वरण के साथ चलती है।
-
विकल्प (a): छवि $5 m / s$ की एक समान गति के साथ लेंस से दूर नहीं चलती क्योंकि संग्रहण लेंस में वस्तु दूरी और छवि दूरी के बीच संबंध रैखिक नहीं होता। जैसे ही वस्तु फोकस बिंदु की ओर आती है, छवि दूरी असमान रूप से बदलती है, जिसके कारण असमान गति होती है।
-
विकल्प (b): छवि लेंस से दूर एक समान त्वरण के साथ नहीं चलती क्योंकि छवि दूरी के परिवर्तन की दर निरंतर नहीं होती। छवि दूरी लेंस सूत्र के अनुसार बदलती है, जिसके कारण वस्तु फोकस बिंदु की ओर आते हुए छवि दूरी में असमान त्वरण होता है।
-
विकल्प (d): छवि लेंस की ओर एक असमान त्वरण के साथ नहीं चलती क्योंकि संग्रहण लेंस में जब वस्तु लेंस की ओर आती है, तो छवि लेंस से दूर चलती है। इसलिए, छवि के गति की दिशा लेंस से दूर होती है, न कि लेंस की ओर।
4. एक विमान में यात्री के लिए
(a) कभी भी बादल के रंग नहीं दिखाई देंगे
(b) मुख्य और द्वितीयक बादल के रंग के रूप में संकेंद्रित वृत्त दिखाई दे सकते हैं
(c) मुख्य और द्वितीयक बादल के रंग के रूप में संकेंद्रित चाप दिखाई दे सकते हैं
(d) कभी भी द्वितीयक बादल के रंग नहीं दिखाई देंगे
उत्तर दिखाएँ
उत्तर
(b) एक विमान में यात्री मुख्य और द्वितीयक बादल के रंग के रूप में संकेंद्रित वृत्त देख सकते हैं।
-
(a) कभी भी बादल के रंग नहीं दिखाई देंगे: यह गलत है क्योंकि एक विमान में यात्री यदि सही शर्तों हों तो बादल के रंग देख सकते हैं, जैसे कि वायुमंडल में पानी के बूंद हों और सूरज प्रेक्षक के पीछे चमक रहा हो।
-
(c) मुख्य और द्वितीयक बादल के रंग के रूप में संकेंद्रित चाप दिखाई दे सकते हैं: यह गलत है क्योंकि एक उच्च स्थिति से, जैसे विमान में, बादल के रंग एक पूर्ण वृत्त के रूप में दिखाई देते हैं। जमीन आमतौर पर वृत्त के निचले हिस्से को अवरोधित कर देती है जब जमीन से देखा जाता है, जिसके कारण वे चाप के रूप में दिखाई देते हैं।
-
(d) कभी भी द्वितीयक बादल के रंग नहीं दिखाई देंगे: यह गलत है क्योंकि द्वितीयक बादल के रंग उचित शर्तों में दिखाई दे सकते हैं। वे पानी के बूंदों में सूरज के प्रकाश के दो बार परावर्तन के कारण बनते हैं और विमान से भी जमीन से एक तरह से देखे जा सकते हैं, हालांकि वे मुख्य बादल के रंग के विपरीत रंग वाले होते हैं और कम तीव्रता के होते हैं।
5. आपको चार प्रकाश के स्रोत दिए गए हैं, जो प्रत्येक एक रंग के प्रकाश के रूप में उपलब्ध हैं - लाल, नीला, हरा और पीला। मान लीजिए कि एक विशिष्ट प्रकार के प्रतिगामी कोण के लिए पीले प्रकाश के लिए दो माध्यमों के संपर्क बिंदु पर प्रकाश के अपवर्तन कोण $90^{\circ}$ है। यदि पीले प्रकाश के स्रोत को अन्य प्रकाश के स्रोत के साथ बदल दिया जाए बिना प्रतिगामी कोण को बदले बिना, निम्नलिखित में से कौन सा कथन सही है?
(a) लाल प्रकाश की किरण के अंतर्निहित पूर्ण परावर्तन होगा
(b) लाल प्रकाश की किरण द्वितीय माध्यम में प्रकाश के द्वारा अपवर्तित होकर अभिलंब की ओर मुड़ेगी
(c) नीले प्रकाश की किरण के अंतर्निहित पूर्ण परावर्तन होगा
(d) हरे प्रकाश की किरण द्वितीय माध्यम में प्रकाश के द्वारा अपवर्तित होकर अभिलंब से दूर मुड़ेगी
उत्तर दिखाएँ
सोच-समझ प्रक्रिया
इस समस्या के आधार पर कुल आंतरिक प्रतिबिंब के न्यूनतम कोण के बारे में है।
उत्तर
(c) वीबीगीओआर के अनुसार, सभी दिए गए प्रकाश स्रोतों में नीले प्रकाश की तरंगदैर्घ्य सबसे कम होती है। कौशी संबंध के अनुसार, छोटी तरंगदैर्घ्य वाले प्रकाश के लिए अपवर्तनांक अधिक होता है और इसलिए न्यूनतम कोण होता है।
इसलिए, नीले रंग के लिए न्यूनतम कोण होता है जो नीले प्रकाश के बeam के लिए कुल आंतरिक प्रतिबिंब को संभव बनाता है। हरा प्रकाश का बeam भी कुल आंतरिक प्रतिबिंब के अंतर्गत आएगा।
-
(a) लाल प्रकाश का बeam कुल आंतरिक प्रतिबिंब के अंतर्गत आएगा: यह कथन गलत है क्योंकि लाल प्रकाश की तरंगदैर्घ्य पीले प्रकाश की तुलना में लंबी होती है, जिसका अर्थ है कि इसका अपवर्तनांक कम होता है और न्यूनतम कोण बड़ा होता है। क्योंकि आपतन कोण समान है, तो लाल प्रकाश आवश्यक कुल आंतरिक प्रतिबिंब के न्यूनतम कोण तक पहुंच नहीं सकता है।
-
(b) लाल प्रकाश का बeam दूसरे माध्यम में अपवर्तित होते समय अभिलंब की ओर मुड़ जाएगा: यह कथन गलत है क्योंकि यदि पीले प्रकाश के लिए अपवर्तन कोण $90^{\circ}$ है, तो आपतन कोण पीले प्रकाश के लिए न्यूनतम कोण होता है। लाल प्रकाश के लिए न्यूनतम कोण बड़ा होता है, इसलिए आपतन कोण इसके न्यूनतम कोण से कम होता है, जिसके कारण यह अभिलंब से दूर मुड़ता है, न कि अभिलंब की ओर।
-
(d) हरा प्रकाश का बeam दूसरे माध्यम में अपवर्तित होते समय अभिलंब से दूर मुड़ जाएगा: यह कथन गलत है क्योंकि हरा प्रकाश की तरंगदैर्घ्य पीले प्रकाश की तुलना में छोटी होती है, जिसका अर्थ है कि इसका अपवर्तनांक अधिक होता है और न्यूनतम कोण छोटा होता है। क्योंकि आपतन कोण समान है, तो हरा प्रकाश कुल आंतरिक प्रतिबिंब के अंतर्गत आएगा न कि अभिलंब से दूर मुड़ जाएगा।
6. एक वातावरण-उत्तल लेंस के वक्र तल की वक्रता त्रिज्या $20 , \text{cm}$ है। यदि लेंस के पदार्थ का अपवर्तनांक 1.5 हो, तो यह
(a) केवल उन वस्तुओं के लिए उत्तल लेंस के रूप में कार्य करे जो इसके वक्र तल पर स्थित हों
(b) उन वस्तुओं के लिए अवतल लेंस के रूप में कार्य करे जो इसके वक्र तल पर स्थित हों
(c) वस्तु के स्थिति के अतिरिक्त उत्तल लेंस के रूप में कार्य करे
(d) वस्तु के स्थिति के अतिरिक्त अवतल लेंस के रूप में कार्य करे
उत्तर दिखाएँ
सोचने की प्रक्रिया
प्लेनो-उत्तल लेंस के लेंस निर्माता सूत्र के अनुसार, फोकस दूरी $f=\dfrac{R}{\mu-1}$ द्वारा दी जाती है। यह वस्तु के लेंस के माध्यम के ऑप्टिकल घनत्व बराबर या अधिक होने पर हमेशा धनात्मक होती है या वायु में रखे गए लेंस के माध्यम के ऑप्टिकल घनत्व बराबर या अधिक होने पर हमेशा धनात्मक होती है।
उत्तर
(c) यहाँ, $R=20 cm, \mu=1.5$, मान लेंस सूत्र $f=\dfrac{R}{\mu-1}=\dfrac{20}{1.5-1}=40 cm$ में उपस्थित करने पर धनात्मक फोकस दूरी के कारण अपसारी प्रकृति के रूप में लेंस उत्तल लेंस के रूप में कार्य करता है चाहे वस्तु कहीं भी स्थित हो।
-
(a) केवल उन वस्तुओं के लिए उत्तल लेंस के रूप में कार्य करे जो इसके वक्र तल पर स्थित हों: यह विकल्प गलत है क्योंकि लेंस की फोकस दूरी धनात्मक है, जिससे यह अपसारी लेंस (उत्तल लेंस) के रूप में कार्य करता है चाहे वस्तु कहीं भी स्थित हो। वस्तु के तल के आधार पर लेंस की प्रकृति बदल नहीं सकती।
-
(b) उन वस्तुओं के लिए अवतल लेंस के रूप में कार्य करे जो इसके वक्र तल पर स्थित हों: यह विकल्प गलत है क्योंकि लेंस की धनात्मक फोकस दूरी इसे अपसारी लेंस (उत्तल लेंस) के रूप में बताती है। एक अवतल लेंस के लिए नकारात्मक फोकस दूरी होती है, जो यहाँ नहीं है।
-
(d) वस्तु के स्थिति के अतिरिक्त अवतल लेंस के रूप में कार्य करे: यह विकल्प गलत है क्योंकि लेंस की धनात्मक फोकस दूरी इसे अपसारी लेंस (उत्तल लेंस) के रूप में बताती है। एक अवतल लेंस के लिए नकारात्मक फोकस दूरी होती है, जो यहाँ नहीं है।
7. आयनमंडल द्वारा रेडियो तरंगों के परावर्तन के घटना के समान है
(a) तल दर्पण द्वारा प्रकाश के परावर्तन
(b) एक दुर्दृश्य के दौरान हवा में प्रकाश के कुल आंतरिक परावर्तन
(c) बर्फ के बरसात के दौरान पानी के अणु द्वारा प्रकाश के विस्थापन
(d) हवा के कणों द्वारा प्रकाश के प्रकीर्णन
उत्तर दिखाएँ
उत्तर
(b) आयनमंडल द्वारा रेडियो तरंगों के परावर्तन की घटना वायु में एक दृग्गोल के दौरान प्रकाश के कुल आंतरिक परावर्तन के समान होती है, अर्थात आपतन कोण आंतरिक क्रांतिक कोण से अधिक होता है।
-
(a) प्रकाश के तल दर्पण द्वारा परावर्तन: यह एक सरल परावर्तन है जहाँ आपतन कोण परावर्तन कोण के बराबर होता है। यह क्रांतिक कोण या कुल आंतरिक परावर्तन की अवधारणा के बिना होता है, जो आयनमंडल द्वारा रेडियो तरंगों के परावर्तन में महत्वपूर्ण है।
-
(c) वर्षा के निर्माण के दौरान पानी के अणुओं द्वारा प्रकाश का विस्थापन: विस्थापन प्रकाश के विभिन्न तरंगदैर्घ्यों के लिए विभिन्न अपवर्तनांक के कारण विभिन्न रंगों में विभाजन के कारण होता है। यह आयनमंडल में होने वाले कुल आंतरिक परावर्तन से भिन्न घटना है।
-
(d) हवा के कणों द्वारा प्रकाश का प्रसार: प्रसार विभिन्न दिशाओं में प्रकाश के पुनः निर्देशन के कारण होता है। यह कुल आंतरिक परावर्तन या क्रांतिक कोण की अवधारणा से संबंधित नहीं है, जो आयनमंडल द्वारा रेडियो तरंगों के परावर्तन में महत्वपूर्ण है।
8. अवतल दर्पण पर प्रकाश के किरण के आपतन दिशा को $P Q$ द्वारा दिखाया गया है जबकि आपतन के बाद परावर्तित किरण की दिशा को चार किरणों द्वारा दिखाया गया है जिन्हें 1, 2, 3 और 4 द्वारा चिह्नित किया गया है (चित्र)। चारों किरणों में से कौन सी किरण परावर्तित किरण की सही दिशा को दिखाती है?
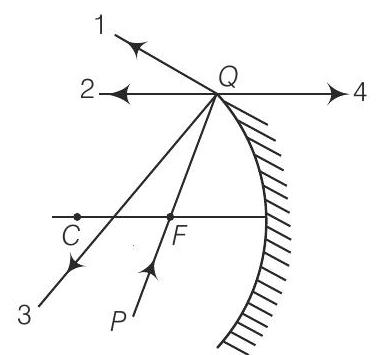
(a) 1 $\newline$
(b) 2 $\newline$
(c) 3 $\newline$
(d) 4 $\newline$
उत्तर दिखाएँ
उत्तर
(b) $P Q$ किरण प्रकाश फोकस $F$ से गुजरती है और अवतल दर्पण पर आपतित होती है, परावर्तन के बाद यह मुख्य अक्ष के समानांतर चलेगी और चित्र में किरण-2 द्वारा दिखाई गई है।
-
विकल्प (a): 1 द्वारा दिखाई गई किरण अवतल दर्पण के प्रतिबिम्ब नियम का पालन नहीं करती है। यदि आपतित किरण फोकस से गुजरती है, तो परावर्तित किरण मुख्य अक्ष के समानांतर चलेगी, न कि 1 द्वारा दिखाई गई दिशा में।
-
विकल्प (c): 3 द्वारा दिखाए गए किरण की दिशा अवतल दर्पण में प्रकाश किरणों के व्यवहार के साथ समान नहीं है। यदि प्रतिविम्बित किरण फोकस से गुजरती है, तो प्रतिविम्बित किरण मुख्य अक्ष के समानांतर होनी चाहिए, न कि 3 द्वारा दिखाए गए दिशा में।
-
विकल्प (d): 4 द्वारा दिखाए गए किरण की दिशा अवतल दर्पण के लिए सही प्रतिबिम्ब पैटर्न के अनुरूप नहीं है। यदि प्रतिविम्बित किरण फोकस से गुजरती है, तो प्रतिविम्बित किरण मुख्य अक्ष के समानांतर होनी चाहिए, न कि 4 द्वारा दिखाए गए दिशा में।
9. टर्पेंटाइन का प्रकाश घनत्व पानी के अपेक्षाकृत अधिक होता है जबकि इसका द्रव्यमान घनत्व कम होता है। चित्र में एक टंकी में टर्पेंटाइन की एक परत पानी के ऊपर तैर रही है। चित्र में टर्पेंटाइन पर आपतित चार किरणों में से किसके पथ का चित्रित पथ सही है?
(a) 1 $\newline$
(b) 2 $\newline$
(c) 3 $\newline$
(d) 4 $\newline$
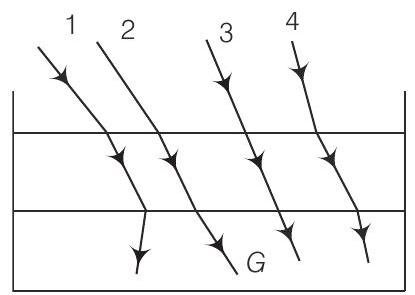
उत्तर दिखाएं
सोचने की प्रक्रिया
जब प्रकाश किरण एक (प्रकाशिक) कम घनत्व वाले माध्यम से एक (प्रकाशिक) अधिक घनत्व वाले माध्यम में जाती है, तो यह अभिलम्ब की ओर मुड़ जाती है, अर्थात i>r और विपरीत।
उत्तर
(b) यहाँ प्रकाश किरण हवा (प्रकाशिक रूप से कम घनत्व वाले माध्यम) से टर्पेंटाइन (प्रकाशिक रूप से अधिक घनत्व वाले माध्यम) में जाती है, तो यह अभिलम्ब की ओर मुड़ जाती है, अर्थात $i>r$ जबकि जब यह टर्पेंटाइन (प्रकाशिक रूप से अधिक घनत्व वाले माध्यम) से पानी (प्रकाशिक रूप से कम घनत्व वाले माध्यम) में जाती है, तो यह अभिलम्ब से दूर मुड़ जाती है, अर्थात $i<r$।
-
विकल्प (a): विकल्प (a) में दिखाए गए पथ गलत है क्योंकि जब प्रकाश हवा (प्रकाशिक रूप से कम घनत्व वाले माध्यम) से टर्पेंटाइन (प्रकाशिक रूप से अधिक घनत्व वाले माध्यम) में जाती है, तो यह अभिलम्ब की ओर मुड़ जानी चाहिए। हालांकि, चित्र में प्रकाश किरण अभिलम्ब की ओर मुड़ती नहीं दिखाई देती है, जो प्रकाश के अपवर्तन के सिद्धांत के उलट है।
-
विकल्प (c): विकल्प (c) में दिखाए गए पथ गलत है क्योंकि जब प्रकाश टर्पेंटाइन (प्रकाशिक रूप से अधिक घनत्व वाले माध्यम) से पानी (प्रकाशिक रूप से कम घनत्व वाले माध्यम) में जाती है, तो यह अभिलम्ब से दूर मुड़ जानी चाहिए। चित्र में प्रकाश किरण अभिलम्ब से दूर मुड़ती नहीं दिखाई देती है, जो प्रकाश के अपवर्तन के सिद्धांत के उलट है।
-
विकल्प (d): विकल्प (d) में दिखाए गए पथ की गलती है क्योंकि जब प्रकाश हवा (प्रकाशिक रूप से कम घनत्व वाला माध्यम) से टर्पेंटाइन (प्रकाशिक रूप से घनत्व वाला माध्यम) में चलता है, तो यह अभिलम्ब की ओर मुड़ जाता है। चित्र में, प्रकाश की किरण अभिलम्ब की ओर मुड़ती नहीं दिखाई देती, जो अपवर्तन के सिद्धांत के उल्टा है।
10. $A$ कार एक सीधी सड़क पर $60 km h^{-1}$ की निरंतर गति से चल रही है। पीछे के दृश्य दर्पण में देखकर ड्राइवर जानता है कि उसके पीछे चल रही कार $100 m$ की दूरी पर है और $5 kmh^{-1}$ की गति से आ रही है।
अपने कार के पीछे वाली कार के पीछे रहने के लिए ड्राइवर अपनी कार के पीछे और ओर दर्पण के बीच दो सेकंड के अंतराल पर अपनी नजर बदलता रहता है जब तक दूसरी कार उसे पार नहीं कर लेती। यदि दोनों कारें अपनी गति को बरकरार रखती हैं, तो निम्नलिखित में से कौन सा कथन सही है?
(a) पीछे वाली कार की गति $65 km h^{-1}$ है
(b) ओर दर्पण में पीछे वाली कार अग्रगामी कार के ड्राइवर के लिए $5 kmh^{-1}$ की गति से आ रही दिखाई देगी
(c) पीछे वाली कार की गति पीछे वाली कार के बीच दूरी कम होने के साथ-साथ पीछे वाली कार के दृश्य में कम हो जाएगी
(d) ओर दर्पण में पीछे वाली कार की गति पीछे वाली कार के बीच दूरी कम होने के साथ-साथ बढ़ जाएगी
उत्तर दिखाएं
सोचने की प्रक्रिया
उत्तल दर्पण द्वारा बनाए गए छवि के आकार वस्तु के संबंध में दर्पण के स्थान पर निर्भर नहीं करता है।
उत्तर
(d) कार के छवि की गति दोनों कारों के बीच दूरी कम होने के साथ-साथ बढ़ जाएगी।
-
(a) पीछे वाली कार की गति $65 km h^{-1}$ है: यह कथन गलत है क्योंकि पीछे वाली कार की गति वास्तव में $60 km h^{-1}$ + $5 km h^{-1}$ अग्रगामी कार के संबंध में है। पीछे वाली कार अग्रगामी कार के प्रति $5 km h^{-1}$ की सापेक्ष गति से आ रही है, न कि $65 km h^{-1}$ के अभिलक्षण गति में।
-
(b) ओर दर्पण में पीछे वाली कार अग्रगामी कार के ड्राइवर के लिए $5 kmh^{-1}$ की गति से आ रही दिखाई देगी: यह कथन गलत है क्योंकि ओर दर्पण अप्रत्यक्ष गति को प्रभावित नहीं करता है। $5 km h^{-1}$ की सापेक्ष गति यही रहती है, चाहे ड्राइवर पीछे के दृश्य दर्पण में देखे या ओर दर्पण में देखे।
-
(सी) पीछे के दृश्य में, आगंतुक कार की गति कम लगती है जैसे कि कारों के बीच की दूरी कम होती जाती है: यह कथन गलत है क्योंकि आगंतुक कार की सापेक्ष गति $5 km h^{-1}$ के नियत रहती है जब तक कि दोनों कारें अपनी गति बनाए रखती हैं। कारों के बीच की दूरी एक स्थिर दर पर कम होती जाती है, इसलिए गति कम नहीं लगती।
11. कुछ ऐसे पदार्थ लैब में विकसित किए गए हैं जिनका अपवर्तनांक ऋणात्मक होता है। हवा (माध्यम 1) से ऐसे माध्यम (माध्यम 2) में आगंतुक किरण के पथ के अनुसार होगा:
(a)
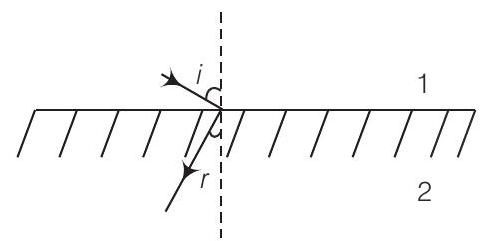
(c)
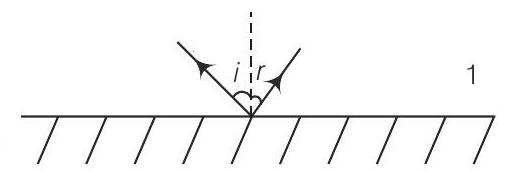
2 (ब)
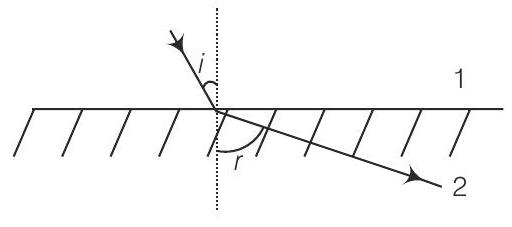
(डी)
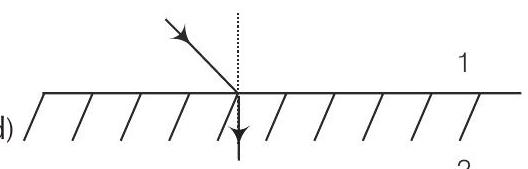
उत्तर दिखाएं
उत्तर
(ए) ऋणात्मक अपवर्तनांक बहुआयामी पदार्थ वे होते हैं जिनमें हवा (माध्यम 1) से उनमें आगंतुक किरण धनात्मक अपवर्तनांक माध्यम के तुलना में अलग ढंग से अपवर्तित या मोड़ लेती है।
-
विकल्प (ब): यह विकल्प एक धनात्मक अपवर्तनांक माध्यम में किरण के एक ही दिशा में मोड़ दिखाता है। ऋणात्मक अपवर्तनांक पदार्थ में, किरण विपरीत दिशा में मोड़ लेती है।
-
विकल्प (c): यह विकल्प एक किरण के सीधे चलते रहने का चित्रण करता है बिना कोई अपवर्तन। यह गलत है क्योंकि एक नकारात्मक अपवर्तन निशाला वाले पदार्थ के कारण किरण भी मुड़ेगी, लेकिन धनात्मक अपवर्तन निशाला वाले पदार्थ के विपरीत दिशा में।
-
विकल्प (d): यह विकल्प दिखाता है कि किरण धनात्मक अपवर्तन निशाला वाले माध्यम में वैसे ही दिशा में मुड़ती है जैसे कि वह एक धनात्मक अपवर्तन निशाला वाले माध्यम में मुड़ती है। विकल्प (b) के जैसे, यह गलत है क्योंकि एक नकारात्मक अपवर्तन निशाला वाले पदार्थ के कारण किरण विपरीत दिशा में मुड़ेगी।
बहुविकल्पीय प्रश्न (एक से अधिक विकल्प)
12. एक विस्तारित वस्तु को एक तल गड्डी में जल में डूबाया गया है। जब इस वस्तु को गड्डी के किनारे के पास से देखा जाता है तो वस्तु विकृत दिखाई देती है क्योंकि
(a) किनारे के पास बिंदुओं की आभासी गहराई जल के सतह से दूर बिंदुओं की तुलना में निकट होती है
(b) वस्तु के छवि के द्वारा आंख में बने कोण वास्तविक कोण की तुलना में छोटा होता है जो हवा में वस्तु द्वारा बनाया गया होता है
(c) किनारे से दूर बिंदुओं के कुछ बिंदु दृश्य नहीं हो सकते हैं क्योंकि पूर्ण आंतरिक परावर्तन के कारण
(d) गड्डी में जल लेंस के रूप में कार्य करता है और वस्तु को बढ़ा देता है
उत्तर दिखाएं
सोचने की प्रक्रिया
इस समस्या के आधार घनत्व बर्तन से दुर्लभ माध्यम में चलने पर परावर्तन की घटना पर है
उत्तर
$(a, b, c)$
जब डूबी हुई वस्तु को गड्डी के किनारे के पास से देखा जाता है तो वस्तु विकृत दिखाई देती है क्योंकि किनारे के पास बिंदुओं की आभासी गहराई जल के सतह से दूर बिंदुओं की तुलना में निकट होती है।
वस्तु के छवि के द्वारा आंख में बने कोण वास्तविक कोण की तुलना में छोटा होता है जो हवा में वस्तु द्वारा बनाया गया होता है और किनारे से दूर बिंदुओं के कुछ बिंदु दृश्य नहीं हो सकते हैं क्योंकि पूर्ण आंतरिक परावर्तन के कारण।
- विकल्प (d) गलत है क्योंकि गड्डी में जल लेंस के रूप में कार्य नहीं करता है जो वस्तु को बढ़ा देता है। देखे गए विकृति के कारण जल-हवा संपर्क तल पर प्रकाश के अपवर्तन है, लेंस प्रभाव के कारण नहीं।
13. एक आयताकार काँच के ब्लॉक $ABCD$ का अपवर्तनांक 1.6 है। एक नाखून फलक $AB$ के मध्य बिंदु पर रखा गया है चित्र में। जब इसे फलक $AD$ से देखा जाता है, तो नाखून का
(a) $A$ के पास दिखाई देना
(b) $D$ के पास दिखाई देना
(c) $AD$ के केंद्र में दिखाई देना
(d) कोई भी दिखाई नहीं देना
उत्तर दिखाएं
सोचने की प्रक्रिया
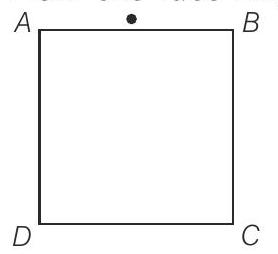
इस समस्या के साथ तीव्र आंतरिक परावर्तन की घटना संबंधित है।
उत्तर
(d) जब $\mu=1.6$ हो, तो तीव्र कोण, $\mu=1 / \sin C$, हमें $C=38.7^{\circ}$ प्राप्त होता है, जब नाखून से निकले किरण के फलक $AD$ पर आपतन कोण तीव्र कोण से अधिक होता है, तो किरण तीव्र आंतरिक परावर्तन के कारण नहीं निकलती है और फलक $AD$ से देखी नहीं जा सकती है।
-
(a) $A$ के पास दिखाई देना: यह विकल्प गलत है क्योंकि यदि नाखून $A$ के पास दिखाई देता, तो यह इंगित करता कि किरणें काँच से गुजरते हुए $A$ की ओर मुड़ जाती हैं। हालांकि, उच्च अपवर्तनांक और तीव्र कोण के अधिक होने के कारण किरणें तीव्र आंतरिक परावर्तन के कारण नहीं निकलती हैं और फलक $AD$ से बाहर नहीं निकलती हैं।
-
(b) $D$ के पास दिखाई देना: यह विकल्प गलत है क्योंकि यदि नाखून $D$ के पास दिखाई देता, तो यह इंगित करता कि किरणें काँच से गुजरते हुए $D$ की ओर मुड़ जाती हैं। विकल्प (a) के समान रूप से, किरणें तीव्र कोण के अधिक होने के कारण तीव्र आंतरिक परावर्तन के कारण नहीं निकलती हैं और फलक $AD$ से बाहर नहीं निकलती हैं।
-
(c) $AD$ के केंद्र में दिखाई देना: यह विकल्प गलत है क्योंकि यदि नाखून $AD$ के केंद्र में दिखाई देता, तो यह इंगित करता कि किरणें काँच से गुजरते हुए बिना बहुत विचलित होए सीधे निकल जाती हैं। हालांकि, अपवर्तनांक और तीव्र कोण के कारण किरणें तीव्र आंतरिक परावर्तन के कारण नहीं निकलती हैं और फलक $AD$ से बाहर नहीं निकलती हैं।
14. प्राथमिक और द्वितीयक चमकदार वृष्टि के बीच एक गहरा बैंड होता है जिसे एलेक्जैंडर के गहरा बैंड कहा जाता है। इसके कारण है
(a) इस क्षेत्र में प्रकाश के प्रतिस्थापित विक्षेपित रेखा नष्ट करने वाला अवतल अपवर्तन करते हैं
(b) इस क्षेत्र में कोई भी प्रकाश विक्षेपित नहीं होता
(c) इस क्षेत्र में प्रकाश अवशोषित हो जाता है
(d) सूर्य के प्रकाश के संबंध में विक्षेपित किरणों द्वारा आंख के कोण के बीच लगभग $42^{\circ}$ और $50^{\circ}$ के बीच होता है
उत्तर दिखाएं
Answer
$(a, d)$
एलेक्जैंडर के गहरा बैंड प्राथमिक और द्वितीयक चमकदार वृष्टि के बीच होता है, जो इस क्षेत्र में प्रकाश के विक्षेपित रेखा नष्ट करने वाला अवतल अपवर्तन करते हैं के कारण बनता है।
क्योंकि, प्राथमिक चमकदार वृष्टि द्वारा अवलोकनकर्ता की आंख के लगभग $41^{\circ}$ से $42^{\circ}$ के कोण पर बनती है, जबकि द्वितीयक चमकदार वृष आंख के लगभग $51^{\circ}$ से $54^{\circ}$ के कोण पर बनती है।
इसलिए, सूर्य के प्रकाश के संबंध में विक्षेपित किरणों के बीच लगभग $42^{\circ}$ और $50^{\circ}$ के बीच होता है।
-
(b) इस क्षेत्र में कोई भी प्रकाश विक्षेपित नहीं होता: यह विकल्प गलत है क्योंकि प्राथमिक और द्वितीयक चमकदार वृष्टि के बीच इस क्षेत्र में विक्षेपित प्रकाश होता है। एलेक्जैंडर के गहरा बैंड इस क्षेत्र में विक्षेपित प्रकाश के नष्ट करने वाला अवतल अपवर्तन के कारण बनता है, न कि विक्षेपित प्रकाश की अनुपस्थिति।
-
(c) इस क्षेत्र में प्रकाश अवशोषित हो जाता है: यह विकल्प गलत है क्योंकि गहरा बैंड अवशोषण के कारण नहीं बनता। बजाए इसके, यह इस क्षेत्र में विक्षेपित प्रकाश के नष्ट करने वाला अवतल अपवर्तन के कारण बनता है। प्रकाश के अवशोषण का अर्थ होता है कि प्रकाश की ऊर्जा माध्यम द्वारा ली जाती है, जो यहां नहीं है।
15. एक आवर्धक चश्मा का उपयोग किया जाता है, क्योंकि देखे जाने वाले वस्तु को आंख के सामने अधिक निकट लाया जा सकता है। इसके परिणामस्वरूप होता है
(a) वस्तु आंख के लिए एक बड़ा कोण बनाती है और इसलिए, अधिक विस्तार से देखा जाता है
(b) एक आभासी उल्टा छवि के निर्माण
(c) दृश्य क्षेत्र में वृद्धि
(d) निकट बिंदु पर अपरिमित आवर्धन
उत्तर दिखाएं
सोचने की प्रक्रिया
समस्या वह स्थिति है जब एक वस्तु अभिसारी (मोटापेटा) लेंस के प्रकाशिक केंद्र और फोकस के बीच रखी जाती है।
उत्तर
$(a, b)$
एक मोटापेटा चश्मा का उपयोग किया जाता है, क्योंकि देखे जाने वाली वस्तु को आम निकट बिंदु से कम दूरी पर लाया जा सकता है। इसके परिणामस्वरूप वस्तु के आंख पर बने कोण बड़ा हो जाता है और इस प्रकार वस्तु को अधिक विस्तार से देखा जा सकता है। इसके अतिरिक्त, एक आभासी, उल्टा और बड़ा छवि के निर्माण की प्रक्रिया होती है।
-
विकल्प (c): दृश्य क्षेत्र में वृद्धि गलत है क्योंकि एक मोटापेटा चश्मा आमतौर पर दृश्य क्षेत्र को कम करता है। जब एक वस्तु बढ़ाई जाती है, तो एक समय में वस्तु के केवल छोटा हिस्सा देखा जा सकता है, जिसके कारण समग्र दृश्य क्षेत्र कम हो जाता है।
-
विकल्प (d): निकट बिंदु पर अपरिमित बढ़ाई गलत है क्योंकि कोई भी प्रकाशिक उपकरण, चश्मा सहित, अपरिमित बढ़ाई प्रदान नहीं कर सकता। बढ़ाई लेंस के प्रकाशिक गुणों और वस्तु के रखे गए दूरी पर आधारित होती है।
16. एक खगोखगी अपवर्ती टेलीस्कोप के अपरिवर्तक की फोकस दूरी $20 m$ है और एपिरिस की फोकस दूरी $2 cm$ है।
(a) टेलीस्कोप ट्यूब की लंबाई $20.02 m$ है
(b) बढ़ाई $1000$ है
(c) बनी छवि उल्टी है
(d) एक बड़े अपरिवर्तक के अपवर्तक बर्तन छवि की चमक को बढ़ाएगा और रंगीन अपसामानता को कम करेगा
उत्तर दिखाएं
सोचने की प्रक्रिया
बढ़ाई शक्ति $m$ अंतिम छवि द्वारा आंख पर बने कोण $\beta$ के अनुपात में वस्तु द्वारा लेंस या आंख पर बने कोण $\boldsymbol{\alpha}$ के अनुपात में होती है। इसलिए, सामान्य समायोजन में
$$ m \approx \dfrac{\beta}{\alpha} \approx \dfrac{h}{f_{e}} \dfrac{f_{o}}{h}=\dfrac{f_{o}}{f_{e}} $$
इस स्थिति में, टेलीस्कोप ट्यूब की लंबाई $f_{o}+f_{e}$ होती है।
उत्तर
$(a, b, c)$
टेलीस्कोप ट्यूब की लंबाई $f_{o}+f_{e}=20+(0.02)=20.02 m$ है
इसके अतिरिक्त,
$m=20 / 0.02=1000$
इसके अतिरिक्त, बनी छवि उल्टी होती है।
- एक बड़े अपवर्तन कोण के लेंस का उद्देश्य चमक को बढ़ाएगा लेकिन छवि के रंगीन अपसार को कम नहीं करेगा। रंगीन अपसार लेंस के पदार्थ और डिज़ाइन पर निर्भर करता है, न कि अपवर्तन कोण के आकार पर।
बहुत छोटे उत्तर प्रकार प्रश्न
17. लेंस के लिए लाल प्रकाश के फोकल लंबाई नीले प्रकाश के फोकल लंबाई से अधिक, समान या कम होगी?
उत्तर दिखाएं
उत्तर
क्योंकि लाल प्रकाश के अपवर्तनांक नीले प्रकाश के अपवर्तनांक से कम होता है, एक लेंस पर आपतित समान बीम प्रकाश नीले प्रकाश के लिए अक्ष के तरफ अधिक मुड़ेगा जबकि लाल प्रकाश के लिए नहीं।
अन्य शब्दों में, $\mu_{b}>\mu_{r}$
लेंस निर्माता के सूत्र के अनुसार
$$ \dfrac{1}{f}=(n_{21}-1) \dfrac{1}{R_1}-\dfrac{1}{R_2} $$
इसलिए, $f_{b}<f_{r}$।
अतः, नीले प्रकाश के लिए फोकल लंबाई लाल प्रकाश के लिए फोकल लंबाई से कम होगी।
18. $ \text{एक औसत व्यक्ति के निकट दृष्टि की दूरी 25 सेमी होती है}$. एक वस्तु को 10 कोणीय आवर्धन के साथ देखने के लिए माइक्रोस्कोप की शक्ति कितनी होनी चाहिए?
उत्तर दिखाएं
उत्तर
एक औसत व्यक्ति के निकट दृष्टि की दूरी (अर्थात, $D$ ) $25$ सेमी होती है, एक वस्तु को 10 आवर्धन के साथ देखने के लिए,
यहाँ, $v=D=25$ सेमी और $u=f$
लेकिन आवर्धन $m=v / u=D / f$
$$ \begin{aligned} & m=\dfrac{D}{f} \\ & f=\dfrac{D}{m}=\dfrac{25}{10}=2.5=0.025 मीटर \\ & P=\dfrac{1}{0.025}=40 D \end{aligned} $$
इसकी आवश्यक लेंस की शक्ति है
19. एक असममित दो अपवर्तक वृत्ताकार पतला लेंस एक बिंदु वस्तु के अक्ष पर छवि बनाता है। यदि लेंस को उलट दिया जाए तो छवि की स्थिति बदलेगी या नहीं?
उत्तर दिखाएं
सोचने की प्रक्रिया
एक लेंस के एक विशिष्ट फोकल लंबाई होती है, जो उसके चेहरे या ज्यामिति के आधार पर निर्भर नहीं करती।
उत्तर
नहीं, लेंस निर्माता के सूत्र की उलटनीयता।
20. तीन अमिशिबल तरल पदार्थ जिनके घनत्व $d_1>d_2>d_3$ और अपवर्तनांक $\mu_1>\mu_2>\mu_3$ हैं, एक बीकर में रखे गए हैं। प्रत्येक तरल के स्तंभ की ऊंचाई $\dfrac{h}{3}$ है। बीकर के तल पर एक बिंदु बनाया गया है। निकट अभिनेता दृष्टि के लिए, बिंदु की आभासी गहराई ज्ञात कीजिए।
उत्तर दिखाएं
सोचने की प्रक्रिया
पहले माध्यम द्वारा बने चित्र को दूसरे माध्यम के लिए वस्तु के रूप में कार्य करता है।
उत्तर
मान लीजिए वस्तु की आभासी गहराई $O_1$ है जो $m_2$ से देखी जाती है, तो
$$ O_1=\dfrac{\mu_2}{\mu_1} \dfrac{h}{3} $$
किरण प्रकाशिकी और प्रकाश यंत्र
क्योंकि, आभासी गहराई = वास्तविक गहराई / अपवर्तनांक $\mu$।
क्योंकि, माध्यम 1 द्वारा बने चित्र $O_2$ को माध्यम 2 के लिए वस्तु के रूप में कार्य करता है।
यदि $\mu_3$ से देखा जाए, तो आभासी गहराई $O_2$ है।
उसी तरह, माध्यम 2 द्वारा बने चित्र $O_2$ को माध्यम 3 के लिए वस्तु के रूप में कार्य करता है
$$ \begin{aligned} O_2 & =\dfrac{\mu_3}{\mu_2} \dfrac{h}{3}+O_1 \\ & =\dfrac{\mu_3}{\mu_2} \dfrac{h}{3}+\dfrac{\mu_2 h}{\mu_1 3}=\dfrac{h}{3} \dfrac{\mu_3}{\mu_2}+\dfrac{\mu_2}{\mu_1} \end{aligned} $$
बाहर से देखे जाने पर आभासी ऊंचाई है
$$ \begin{aligned} O_3 & =\dfrac{1}{\mu_3} \dfrac{h}{3}+O_2=\dfrac{1}{\mu_3} \dfrac{h}{3}+\dfrac{h}{3} \dfrac{\mu_3}{\mu_2}+\dfrac{\mu_3}{\mu_1} \\ & =\dfrac{h}{3} \dfrac{1}{\mu_1}+\dfrac{1}{\mu_2}+\dfrac{1}{\mu_3} \end{aligned} $$
यह आभासी गहराई का आवश्यक व्यंजक है।
21. एक काँच के प्रिज्म $(\mu=\sqrt{3})$ के लिए, न्यूनतम विचलन कोण प्रिज्म के कोण के बराबर है। प्रिज्म के कोण का पता लगाएं।
उत्तर दिखाएं
उत्तर
अपवर्तनांक, प्रिज्म कोण $A$ और न्यूनतम विचलन कोण के बीच संबंध निम्नलिखित है
$$ \mu=\dfrac{\sin \dfrac{(A+D_{m})}{2}}{\sin \dfrac{A}{2}} $$
यहाँ,
$\therefore$ दिया गया है,
$$ D_{m}=A $$
मान लें, तो हमें प्राप्त होता है
$\therefore \quad \mu=\dfrac{\sin A}{\sin \dfrac{A}{2}}$
हल करने पर हमें प्राप्त होता है
$$ \begin{aligned} & =\dfrac{2 \sin \dfrac{A}{2} \cos \dfrac{A}{2}}{\sin \dfrac{A}{2}}=2 \cos \dfrac{A}{2} \\ \mu & =\dfrac{\sin A}{\sin \dfrac{A}{2}}=\dfrac{2 \sin \dfrac{A}{2} \cos \dfrac{A}{2}}{\sin \dfrac{A}{2}}=2 \cos \dfrac{A}{2} \end{aligned} $$
दिए गए अपवर्तनांक के मान के लिए,
हमें प्राप्त होता है
$$ \therefore \cos \dfrac{A}{2} =\dfrac{\sqrt{3}}{2} $$ $$ \text{या} \quad \quad s\dfrac{A}{2} =30^{\circ}$$
$$\therefore A =60^{\circ}$$
यह प्रिज्म कोण का आवश्यक मान है।
22. एक छोटी वस्तु जिसकी लंबाई $L$ है, एक अवतल दर्पण के मुख्य अक्ष पर फोकस से दूर रखी गई है। वस्तु की दूरी $u$ है। यदि दर्पण की फोकस दूरी $f$ है, तो छवि की लंबाई क्या होगी? आप $L«|v-f|$ लें सकते हैं।
उत्तर दिखाएं
सोचने की प्रक्रिया
छवि की लंबाई वस्तु के सिरों द्वारा दर्पण द्वारा बनाए गए छवियों के बीच की दूरी होती है।
उत्तर
क्योंकि, वस्तु की दूरी $u$ है। मान लीजिए वस्तु के दो सिरों की दूरी क्रमशः $u_1=u-L / 2$ और $u_2=u+L / 2$ है ताकि $|u_1-u_2|=L$ हो। मान लीजिए दोनों सिरों की छवियाँ क्रमशः $v_1$ और $v_2$ पर बनती हैं ताकि छवि की लंबाई होगी
$$ L^{\prime}=|v_1-v_2| $$
दर्पण सूत्र के अनुसार, हम लिख सकते हैं
$$ \dfrac{1}{u}+\dfrac{1}{v}=\dfrac{1}{f} \text { या } v=\dfrac{f u}{u-f} $$
हल करने पर, दोनों छवियों के स्थान निम्नलिखित हैं
$$ v_1=\dfrac{f(u-L / 2)}{u-f-L / 2}, v_2=\dfrac{f(u+L / 2)}{u-f+L / 2} $$
लंबाई के लिए, समीकरण (i) में मान रखने पर हम प्राप्त करते हैं
$$ L^{\prime}=|v_1-v_2|=\dfrac{f^{2} L}{(u-f)^{2} \times L^{2} / 4} $$
क्योंकि, वस्तु छोटी है और फोकस से दूर रखी गई है, हम लिख सकते हैं
$$ L^{2} / 4«(u-f)^2 \\ \text {अतः, अंत में} L^{\prime}=\dfrac{f^2}{(u-f)^2} $$
यह छवि की लंबाई का आवश्यक व्यंजक है।
23. एक वृत्ताकार डिस्क जिसकी त्रिज्या $R$ है, एक अपारगम्य अर्धगोलीय बाउल के अक्ष के समानांतर और क्षैतिज रूप से रखी गई है। बाउल के किनारे से देखने पर डिस्क का दूर सिरा ठीक दिखाई देता है। बाउल में पारगम्य तरल है जिसका अपवर्तनांक $\mu$ है और डिस्क का निकट सिरा ठीक दिखाई देता है। डिस्क को बाउल के शीर्ष से कितनी दूर रखा गया है?
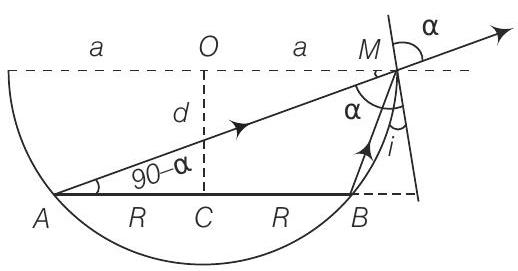
उत्तर दिखाएँ
सोचने की प्रक्रिया
इस समस्या में ज्यामिति और स्नेल के नियम के व्यापक उपयोग की आवश्यकता होती है।
उत्तर
चित्र के अनुसार, $AM$ तरंग के प्रतिगमन के दिशा रेखा है जब तरल भरा नहीं होता। जब तरल भरा जाता है, $BM$ तरंग के प्रतिगमन के दिशा रेखा होती है। दोनों मामलों में प्रकाश के अपवर्तित रेखा एक ही रहती है जो $AM$ के अनुदिश होती है।
मान लीजिए डिस्क $O$ से $d$ की दूरी पर अलग है जैसा कि चित्र में दिखाया गया है। अतिरिक्त रूप से, कोण के बारे में विचार करें।
यहाँ, चित्र में
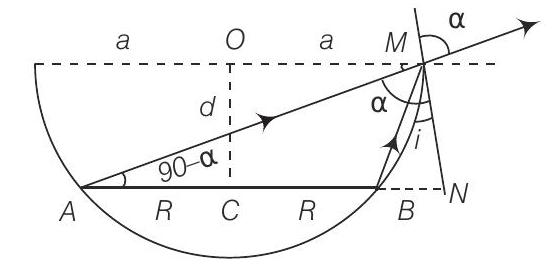
$$ N=90^{\circ}, OM=a, CB=NB=a-R, AN=a+R $$
और
$$ \begin{aligned} \sin t & =\dfrac{a-R}{\sqrt{d^{2}+(a-R)^{2}}} \\ \sin \alpha & =\cos (90-\alpha)=\dfrac{a+R}{\sqrt{d^{2}+(a+R)^{2}}} \end{aligned} $$
लेकिन स्नेल के नियम के अनुसार,
$$ \dfrac{1}{\mu}=\dfrac{\sin t}{\sin r}=\dfrac{\sin t}{\sin \alpha} $$
मान लें कि मूल्यों को बदलकर हमें अलग करने के लिए अलग करना होगा
$$ d=\dfrac{\mu(a^{2}-b^{2})}{\sqrt{(a+r)^{2}-\mu(a-r)^{2}}} $$
यह आवश्यक व्यंजक है।
24. एक पतला उत्तल लेंस जिसकी फोकल लंबाई $25 cm$ है, मुख्य अक्ष से $0.5 cm$ ऊपर काट लिया जाता है। ऊपरी भाग $ (0,0) $ पर रखा जाता है और एक वस्तु $ (-50 cm, 0) $ पर रखी जाती है। छवि के निर्देशांक ज्ञात कीजिए।
उत्तर दिखाएँ
सोचने की प्रक्रिया
प्रश्न में दिए गए अनुसार लेंस काटने पर इसकी फोकल लंबाई पर कोई प्रभाव नहीं होता।
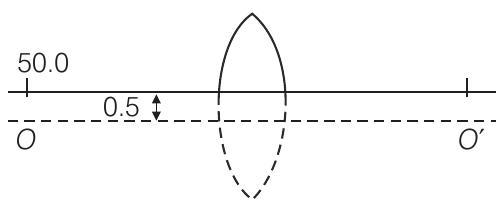
उत्तर
अगर काट नहीं लिया गया होता, तो वस्तु मुख्य अक्ष $OO^{\prime}$ से $0.5 cm$ की ऊंचाई पर होती।
लेंस सूत्र के अनुसार, हमें इस प्रकार मिलता है
$$ \begin{aligned} & & \dfrac{1}{v}-\dfrac{1}{u} & =\dfrac{1}{f} \\
$$ \therefore \dfrac{1}{v} =\dfrac{1}{u}+\dfrac{1}{f}=\dfrac{1}{-50}+\dfrac{1}{25}=\dfrac{1}{50} \\ \text { Mangnification is } m =\dfrac{v}{u}=-\dfrac{50}{50}=-1 \end{aligned} $$
इसलिए, चित्र $50 cm$ की दूरी पर ध्रुव से बनेगा और मुख्य अक्ष के नीचे $0.5 cm$ पर। इसलिए, $X$-अक्ष के अतिरिक्त छेद के किनारे से गुजरते हुए, चित्र के निर्देशांक $(50 cm,-1 cm)$ होंगे।
25. कई प्रयोगात्मक सुविधाओं में, स्रोत और पर्दा एक निश्चित दूरी, कहलाती है $D$ पर निश्चित होते हैं और लेंस गतिशील होता है। दिखाइए कि लेंस के दो स्थितियाँ होती हैं जहाँ चित्र पर्दे पर बनता है। इन बिंदुओं के बीच दूरी और इन दो बिंदुओं के लिए चित्र के आकार के अनुपात को ज्ञात कीजिए।
उत्तर दिखाएं
सोचने की प्रक्रिया
यह भी लेंस के फोकल दूरी को प्रयोगशाला में ज्ञात करने के एक तरीके के रूप में जाना जाता है और इसे विस्थापन विधि के रूप में जाना जाता है।
उत्तर
प्रतिस्थापन के सिद्धांत के अनुसार, वस्तु और चित्र के स्थान आपस में बदल जाते हैं। इसलिए, लेंस के सूत्र के द्वारा $u$ और $v$ के विस्थापन के कारण, देखा जाता है।
$$ \dfrac{1}{f}=\dfrac{1}{v}-\dfrac{1}{u} $$
स्पष्ट रूप से, दो स्थितियाँ होती हैं जहाँ चित्र बनता है।
पर्दे पर, पहली स्थिति जब लेंस $O$ पर होता है। $u$ और $v$ को ज्ञात करके लेंस सूत्र में प्रतिस्थापित करें।
दिया गया है,
$\Rightarrow$
लेंस सूत्र में रखें
$$ \dfrac{1}{D-v}+\dfrac{1}{v}=\dfrac{1}{f} $$
हल करने पर, हमें प्राप्त होता है
$$ \begin{aligned} \Rightarrow \dfrac{v+D-v}{(D-v) v} =\dfrac{1}{f} \newline \newline\\ \Rightarrow v^{2}-D v+D f =0 \newline \newline\\ \Rightarrow v =\dfrac{D}{2} \pm \dfrac{\sqrt{D^{2}-4 D f}}{2} \end{aligned} $$
इसलिए, $u$ को ज्ञात करें
$$ u=-(D-v)=-\dfrac{D}{2} \pm \dfrac{\sqrt{D^{2}-4 D f}}{2} $$
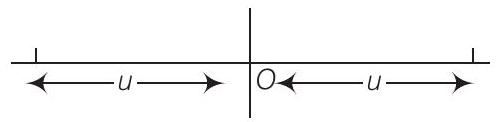
जब, वस्तु की दूरी $\quad \dfrac{D}{2}+\dfrac{\sqrt{D^{2}-4 D f}}{2}$
तो प्रतिबिम्ब बनता है
$$ \dfrac{D}{2}-\dfrac{\sqrt{D^{2}-4 D f}}{2} $$
उसी तरह, जब वस्तु की दूरी हो
प्रतिबिम्ब बनता है
$$ \begin{aligned} & \dfrac{D}{2}-\dfrac{\sqrt{D^{2}-4 D f}}{2} \\ & \dfrac{D}{2}+\dfrac{\sqrt{D^{2}-4 D f}}{2} \end{aligned} $$
इन दो वस्तु दूरियों के ध्रुवों के बीच दूरी है
$$ \dfrac{D}{2}+\dfrac{\sqrt{D^{2}-4 D f}}{2}-\dfrac{D}{2}-\dfrac{\sqrt{D^{2}-4 D f}}{2}=\sqrt{D^{2}-4 D f} $$
$$ \begin{aligned} & \text { मान लीजिए } \\ & \text { यदि } u=\dfrac{D}{2}+\dfrac{d}{2} \text {, तो प्रतिबिम्ब } v=\dfrac{\sqrt{D^{2}-4 D f}}{2}-\dfrac{d}{2} \text { पर होता है } . \\ & \therefore \quad \text { आवर्धन } m_1=\dfrac{D-d}{D+d} \\ & \text { यदि } u=\dfrac{D-d}{2} \text {, तो } v=\dfrac{D+d}{2} \\ & \therefore \text { आवर्धन } m_2=\dfrac{D+d}{D-d} \\ & \text { इस प्रकार, } \quad \dfrac{m_2}{m_1}=\dfrac{D+d}{D-d} . \end{aligned} $$
यह आवर्धन का आवश्यक व्यंजक है।
26. एक जार की ऊँचाई $h$ है जो एक पारगमन निर्वात द्रव के साथ भरा है जिसका अपवर्तनांक $\mu$ है चित्र। जार के तल पर केंद्र पर एक बिंदु है। ज्ञात कीजिए एक डिस्क का न्यूनतम व्यास जिसे जार के ऊपरी सतह पर केंद्र के सममित रूप से रखने पर बिंदु दृष्य रहे बिना रह जाए।
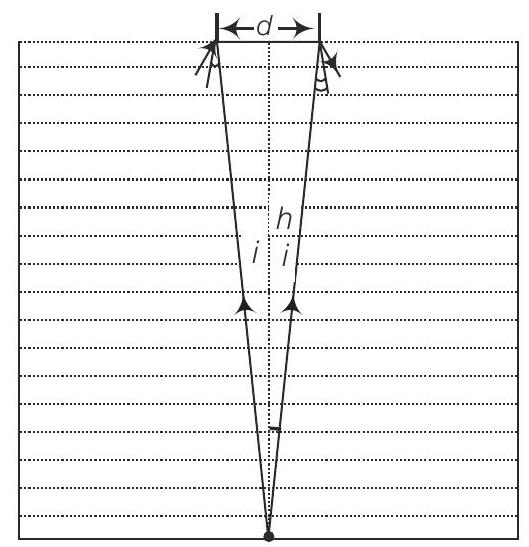
उत्तर दिखाएं
सोचने की प्रक्रिया
इस समस्या के पीछे के सिद्धांत को पूर्ण आंतरिक परावर्तन और दृश्यता क्षेत्र के क्षेत्र के सिद्धांत के आधार पर आधारित है।
उत्तर
मान लीजिए $d$ डिस्क का व्यास है। यदि बिंदु $O$ से बिंदु के तीव्र कोण पर आपतित किरणें तल पर $d / 2$ पर बिंदु दृश्य रहे बिना रह जाए तो बिंदु अदृश्य हो जाएगा।
मान लीजिए $i$ आपतन कोण है।
अपवर्तनांक और तीव्र कोण के बीच संबंध का उपयोग करते हुए,
तब,
$$ \sin t=\dfrac{1}{\mu}
$$
ज्यामिति और त्रिकोणमिति का उपयोग करते हुए।
अब,
$$ \begin{aligned} \dfrac{d / 2}{h} & =\tan i \\ \dfrac{d}{2} & =h \tan i=h[\sqrt{\mu^{2}-1}]^{-1} \\ d & =\dfrac{2 h}{\sqrt{\mu^{2}-1}} \end{aligned} $$
यह $d$ का आवश्यक व्यंजक है।
27. एक निकट दृष्टि वाले व्यक्ति के दूर बिंदु $0.1$ मीटर है। उसकी अनुकूलन क्षमता $4 D$ है।
(i) दूर के वस्तुओं को देखने के लिए कितनी शक्ति के लेंस की आवश्यकता है?
(ii) चश्मा के बिना उसका निकट बिंदु क्या है?
(iii) चश्मा के साथ उसका निकट बिंदु क्या है? (आंख के लेंस से रेटिना तक छवि दूरी को $2$ सेमी मान लीजिए।)
उत्तर दिखाएं
सोचने की प्रक्रिया
दो पतले लेंस जिनकी फोकल लंबाई $f_1$ और $f_2$ है, एक दूसरे के संपर्क में हों, तो संयोजन की प्रभावी फोकल लंबाई निम्नलिखित द्वारा दी जाती है,
शक्ति के संदर्भ में $P=P_1+P_2$
$$ \dfrac{1}{f}=\dfrac{1}{f_1}+\dfrac{1}{f_2} $$
उत्तर
(i) एक औसत व्यक्ति के आरामपूर्वक आंख के लिए दूर बिंदु पर शक्ति $P_{f}$ होती है। आवश्यक शक्ति
$$ P_{f}=\dfrac{1}{f}=\dfrac{1}{0.1}+\dfrac{1}{0.02}=60 D $$
संशोधक लेंस के कारण दूर बिंदु पर वस्तु की दूरी $\infty$ होती है।
आवश्यक शक्ति है
$$ P_f^{\prime}=\dfrac{1}{f^{\prime}}=\dfrac{1}{\infty}+\dfrac{1}{0.02}=50 D $$
आंख + लेंस प्रणाली के लिए,
हमें आंख और चश्मा की शक्ति के योग $P_{g}$ के लिए निम्नलिखित है
$$ \begin{matrix} \therefore & P_f^{\prime}=P_{f}+P_{g} \\ \therefore & P_{g}=-10 D \end{matrix} $$
(ii) उसकी अनुकूलन क्षमता आम आंख के लिए $4 D$ है। आम आंख के निकट दृष्टि के लिए शक्ति $P_{n}$ होती है।
$$ \text { तब, } \quad 4=P_{n}-P_{f} \text { या } P_{n}=64 D $$
उसके निकट बिंदु को $x_{n}$ मान लीजिए, तो
$$ \begin{aligned} \dfrac{1}{x_{n}}+\dfrac{1}{0.02} & =64 \text { या } \dfrac{1}{x_{n}}+50=64 \\ \dfrac{1}{x_{n}} & =14, \\ \therefore \quad x_{n} & =\dfrac{1}{14} = 0.07 m \end{aligned} $$
(iii) चश्मा के साथ $P_n^{\prime}=P_f^{\prime}+4=54$
$$ \begin{aligned} 54 & =\dfrac{1}{x_n^{\prime}}+\dfrac{1}{0.02}=\dfrac{1}{x_n^{\prime}}+50 \\ \dfrac{1}{x_n^{\prime}} & =4 \\ \therefore \quad x_n^{\prime} & =\dfrac{1}{4}=0.25 m
\end{aligned} $$
28. सिद्ध करें कि एक पदार्थ के लिए जिसका अपवर्तनांक $\mu \geq \sqrt{2}$ है, कोई भी प्रकाश किरण अपवर्तन कोण पर आपतित होने पर आपतित फलक के लंबवत दिशा में चलने के लिए दिशा बदल देगी।
उत्तर दिखाएं
उत्तर
कोई भी किरण $i$ कोण पर प्रवेश करती है तो यह $A C$ के अनुदिश चलेगी यदि किरण द्वारा फलक $A C(\varphi)$ के साथ बना कोण अपवर्तन के नियम के अनुसार क्रांतिक कोण से अधिक हो, अतः $\varphi + r = 90^{\circ}$, इसलिए $\sin \varphi = \cos r$
$\begin{aligned} \Rightarrow \qquad \sin \varphi & \geq \dfrac{1}{\mu} \\ \Rightarrow \qquad \cos r & \geq \dfrac{1}{\mu} \\ \text{या} \qquad 1-\cos ^2 r & \leq 1-\dfrac{1}{\mu^2} \\ \text{i.e.,} \qquad \sin ^2 r & \leq \dfrac{1}{\mu^2} \end{aligned}$
$\begin{aligned} & \text { अर्थात } \qquad \sin ^2 r \leq 1-\dfrac{1}{\mu^2} \\ \qquad & \text { क्योंकि, } \qquad \sin i=\mu \sin r \\ & \dfrac{1}{\mu_2} \sin ^2 i \leq 1-\dfrac{1}{\mu^2} \\ & \text { जब } \qquad i=\dfrac{\pi}{2} \\ & \end{aligned}$
तब, हमें न्यूनतम कोण $\varphi$ मिलता है।
यदि वह क्रांतिक कोण से अधिक हो, तो सभी अन्य क्रांतिक कोण भी होंगे।
$\begin{array}{ll} \text { इसलिए, }\qquad & 1 \leq \mu^2-1 \\ \text { या } & \mu^2 \geq 2 \\ \Rightarrow & \mu \geq \sqrt{2} \end{array}$
यह आवश्यक परिणाम है।
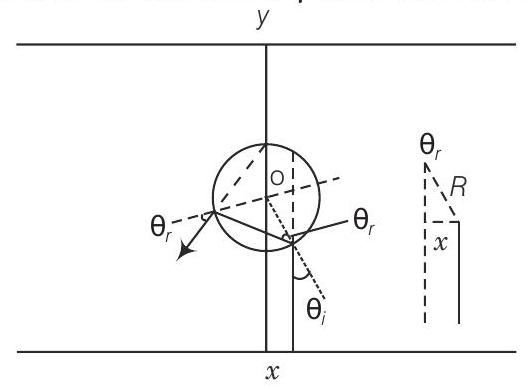
31. एक असामान्य विशेष सामग्री से बना अपरिमित लंबाई का बेलन त्रिज्या $R$ के बराबर है (चित्र)। बेलन दो तलों के बीच रखा गया है जिनके अभिलम्ब $y$-दिशा में हैं। बेलन के केंद्र 0 $y$-अक्ष पर है। एक संकीर्ण लेजर किरण $y$-दिशा में नीचे के तल से दिशात्मक है। लेजर स्रोत $y$ दिशा में व्यास के संबंध में क्षैतिज दूरी $x$ पर है। ऐसे $x$ के विस्तार का खोज करें जिसमें नीचे के तल से उत्सर्जित प्रकाश ऊपर के तल तक पहुँचे बिना रह सके।
उत्तर दिखाएँ
उत्तर
चूंकि, पदार्थ का अपवर्तनांक $-1$ है, तो $\theta_{r}$ नकारात्मक होगा और $\theta_r^{\prime}$ धनात्मक होगा।
अब,
$$ |\theta_{t}|=|\theta_{r}|=|\theta_r^{\prime}| $$
निर्गमन किरण के प्रारंभिक किरण से कुल विचलन $4 \theta$ है। यदि
$$ .\dfrac{\pi}{2} \leq 4 \theta_{t} \leq \dfrac{3 \pi}{2} \quad \text { [y-अक्ष से घड़ी के विपरीत दिशा में मापे गए कोण]} $$
हो तो प्राप्त करने वाले प्लेट पर किरण पहुँच नहीं सकती है।
हल करने पर,
$$ \dfrac{\pi}{8} \leq \theta_{t} \leq \dfrac{3 \pi}{8} $$
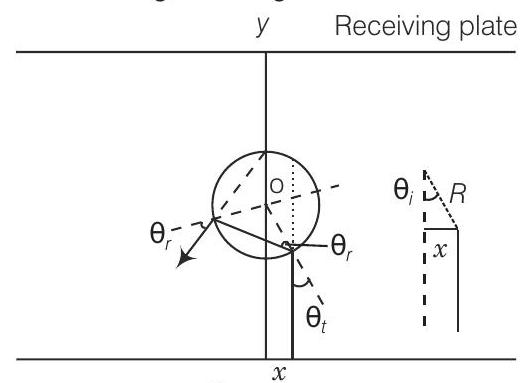
अब,
या
$$ \begin{aligned} \sin \theta_{t} & =\dfrac{x}{R} \\ \dfrac{\pi}{8} & \leq \sin ^{-1} \dfrac{x}{R} \leq \dfrac{3 \pi}{8} \\ \dfrac{\pi}{8} & \leq \dfrac{x}{R} \leq \dfrac{3 \pi}{8} \end{aligned} $$
इसलिए, स्रोत से निकली लाइट प्राप्त करने वाले प्लेट तक पहुँच नहीं सकती है। यदि $\dfrac{R \pi}{8} \leq x \leq \dfrac{R 3 \pi}{8}$ हो।
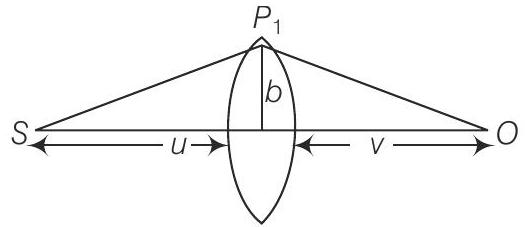
32. (i) एक तीव्र लेंस को स्रोत $(S)$ और अवलोकक $( O )$ के बीच रखा गया है (चित्र)। मान लीजिए कि लेंस की मोटाई $w(b)=w_0-\dfrac{b^{2}}{\alpha}$ के रूप में बदलती है, जहाँ $b$ ध्रुव से ऊर्ध्वाधर दूरी है, $w_0$ एक स्थिरांक है। फर्मेट के सिद्धांत का उपयोग करके, एक किरण के स्रोत से अवलोकक तक समय यात्रा एक अतिस्थिर होता है, तो यह शर्त ज्ञात कीजिए कि सभी पारस्परिक किरणें स्रोत से एक बिंदु 0 पर अक्ष पर संगत हों। फोकल लंबाई ज्ञात कीजिए।
(ii) गुरुत्वाकर्षण लेंस को एक विशिष्ट रूप में बदलती चौड़ाई के रूप में माना जा सकता है
$$ \begin{aligned} w(b) & =k_1 \ln \dfrac{k_2}{b} \quad b_{\text {min }}<b<b_{\max } \\
& =k_1 \ln \dfrac{k_2}{b_{\text {min }}} \quad b<b_{\text {min }} \end{aligned} $$
दिखाइए कि एक प्रेक्षक एक बिंदु वस्तु के छवि को लेंस के केंद्र के चारों ओर एक वृत्त के रूप में देखेगा जिसकी कोणीय त्रिज्या होगी
$$ \beta=\sqrt{\dfrac{(n-1) k_1 \dfrac{u}{v}}{u+v}} $$
उत्तर दिखाएं
उत्तर
(i) $S$ से $P_1$ तक यात्रा के लिए लगने वाला समय है
$$ t_1=\dfrac{S P_1}{c}=\dfrac{\sqrt{u^{2}+b^{2}}}{c} $$
या
$$ \dfrac{u}{c} +\dfrac{1}{2} \dfrac{b^{2}}{u^{2}} \text { माना कि } b«u_0 \text {. } $$
$P_1$ से $O$ तक यात्रा के लिए लगने वाला समय है
$$ t_2=\dfrac{P_1 O}{c}=\dfrac{\sqrt{v^{2}+b^{2}}}{c} = \dfrac{v}{c} 1+\dfrac{1}{2} \dfrac{b^{2}}{v^{2}} $$
लेंस के माध्यम से यात्रा के लिए लगने वाला समय है
$$ t_1=\dfrac{(n-1) w(b)}{c} $$
जहाँ $n$ अपवर्तनांक है।
इसलिए, कुल समय है
$$ t=\dfrac{1}{c} (u+v)+\dfrac{1}{2} b^{2} \left(\dfrac{1}{u}+\dfrac{1}{v}\right)+(n-1) w(b) $$
मान लीजिए
$$ \dfrac{1}{D}=\dfrac{1}{u}+\dfrac{1}{v} $$
तब,
$$ t=\dfrac{1}{c} (u+v)+\dfrac{1}{2} \dfrac{b^{2}}{D}+(n-1) w_0+\dfrac{b^{2}}{\alpha} $$
फेर्मेट के सिद्धांत के अनुसार समय न्यूनतम होना चाहिए।
इसके लिए पहले अवकलज शून्य होना चाहिए।
$$ \begin{aligned} \dfrac{d t}{d b} & =0=\dfrac{b}{C D}-\dfrac{2(n-1) b}{c \alpha} \\ \alpha & =2(n-1) D \end{aligned} $$
इसलिए, यदि $\alpha=2(n-1) D$ तो एक संग्रहणी लेंस बनता है। यह एवं से स्वतंत्र है और इसलिए, सभी पारस्परिक किरणें $S$ से $O$ पर संग्रहित होंगी अर्थात, किरणों के लिए
और
$$ (b«v .) $$
क्योंकि, $\dfrac{1}{D}=\dfrac{1}{u}+\dfrac{1}{V}$, फोकल लंबाई $D$ है।
(ii) इस मामले में, समय लेने वाले व्यंजक के संबंध में $b$ के संदर्भ में अवकलन करें
$$ t =\dfrac{1}{c} u+v+ \dfrac{1}{2} \dfrac{b^2}{D}+(n-1) k_1 \ln \dfrac{k_2}{b} \newline $$
$$ \Rightarrow \dfrac{d t}{d b} =0=\dfrac{b}{D}-(n-1) \dfrac{k_1}{b} $$
$$ \therefore b^{2} =(n-1) k_1 D$$
$$ \therefore b =\sqrt{(n-1) k_1 D} \newline $$
इसलिए, सभी किरणें जो ऊंचाई $b$ पर गुजरती हैं, छवि के लिए योगदान करती हैं। किरण पथ एक कोण बनाते हैं।
$$ \beta = \dfrac{b}{v}=\dfrac{\sqrt{(n-1) k_1 D}}{v^{2}}=\sqrt{\dfrac{(n-1) k_1 u v}{v^{2}(u+v)}}=\sqrt{\dfrac{(n-1) k_1 u}{(u+v) v}} $$
$$
यह आवश्यक अभिव्यक्ति है।





