न्यूक्लियस
बहुविकल्पीय प्रश्न (MCQs)
1. मान लीजिए हम एक बड़ी संख्या के बर्तनों को विचार करते हैं, जिनमें प्रारंभ में एक रेडियोएक्टिव पदार्थ के 10000 परमाणु होते हैं जिसका अर्ध्जीवन काल 1 वर्ष है। 1 वर्ष के बाद,
(a) सभी बर्तन में पदार्थ के 5000 परमाणु होंगे
(b) सभी बर्तन में पदार्थ के समान संख्या के परमाणु होंगे लेकिन वह संख्या केवल लगभग 5000 होगी
(c) बर्तन आमतौर पर पदार्थ के अलग-अलग संख्या के परमाणु होंगे लेकिन उनका औसत लगभग 5000 के पास होगा
(d) कोई भी बर्तन में 5000 परमाणु से अधिक नहीं हो सकते
उत्तर दिखाएं
सोचने की प्रक्रिया
$T_{\frac{1}2}=\frac{\ln 2}{\lambda}, \lambda \rightarrow$ विघटन नियतांक
उत्तर
(c) रेडियोएक्टिवता एक प्रक्रिया है जिसके कारण एक रेडियोएक्टिव पदार्थ स्वतंत्र रूप से विघटित होता है। पदार्थ के अर्ध्जीवन काल $(t=1 वर्ष)$ में, औसतन परमाणुओं की संख्या के आधा विघटित हो जाता है।
इसलिए, बर्तन आमतौर पर पदार्थ के अलग-अलग संख्या के परमाणु होंगे लेकिन उनका औसत लगभग 5000 के पास होगा।
-
(a) यह विकल्प गलत है क्योंकि रेडियोएक्टिव विघटन एक यादृच्छिक प्रक्रिया है, और निश्चित रूप से सभी बर्तन में 1 वर्ष के बाद 5000 परमाणु नहीं होंगे। विघटन की संख्या विघटन के यादृच्छिक प्रकृति के कारण बर्तन के बीच भिन्न हो सकती है।
-
(b) यह विकल्प गलत है क्योंकि, यद्यपि औसत रूप से बचे हुए परमाणुओं की संख्या लगभग 5000 होगी, पर वास्तविक संख्या प्रत्येक बर्तन में भिन्न हो सकती है। विघटन प्रक्रिया यादृच्छिक है, इसलिए बर्तन के बीच परमाणुओं की सटीक संख्या भिन्न हो सकती है।
-
(d) यह विकल्प गलत है क्योंकि कुछ बर्तन में 1 वर्ष के बाद 5000 परमाणु से अधिक बचे हुए परमाणु हो सकते हैं। अर्ध्जीवन काल औसत विघटन दर को दर्शाता है, लेकिन विघटन के यादृच्छिक प्रकृति के कारण व्यक्तिगत बर्तन में अधिक या कम परमाणु हो सकते हैं।
2. $H$-परमाणु और दूसरे कण के बीच गुरुत्वाकर्षण बल न्यूटन के नियम द्वारा दिया जाता है
$$ F=G \frac{M \cdot m}{r^{2}} \text {, जहाँ } r \text { किमी में होता है और } $$
(a) $M=m_{\text {proton }}+m_{\text {electron }}$
(b) $M=m_{\text {proton }}+m_{\text {electron }}-\frac{B}{c^{2}}(B=13.6 eV)$.
(c) $M$ हाइड्रोजन परमाणु के द्रव्यमान से संबंधित नहीं है।
(d) $M=m_{\text {proton }}+m_{\text {electron }}-\frac{|V|}{c^{2}}(|V|=$ इलेक्ट्रॉन के $H$-परमाणु में संभावना ऊर्जा के मापदंड के बराबर है।
उत्तर दिखाएं
Answer
(b) दिया गया है, $F=\frac{G M m}{r^{2}}$
$$ \begin{aligned} M & =\text { हाइड्रोजन परमाणु के प्रभावी द्रव्यमान } \\ & =\text { इलेक्ट्रॉन के द्रव्यमान }+ \text { प्रोटॉन के द्रव्यमान }-\frac{B^{2}}{C} \end{aligned} $$
जहाँ $B$ हाइड्रोजन परमाणु के बंधन ऊर्जा $B E$ है $=13.6 eV$।
-
(a) गलत है क्योंकि यह हाइड्रोजन परमाणु के बंधन ऊर्जा को गणना में शामिल नहीं करता है। हाइड्रोजन परमाणु का द्रव्यमान प्रोटॉन और इलेक्ट्रॉन के द्रव्यमान के योग से थोड़ा कम होता है क्योंकि बंधन ऊर्जा के कारण।
-
(c) गलत है क्योंकि गुरुत्वाकर्षण बल की गणना के लिए हाइड्रोजन परमाणु के द्रव्यमान की आवश्यकता होती है, जो प्रोटॉन और इलेक्ट्रॉन के द्रव्यमान और बंधन ऊर्जा से संबंधित होता है।
-
(d) गलत है क्योंकि शब्द $\frac{|V|}{c^{2}}$ हाइड्रोजन परमाणु में इलेक्ट्रॉन की संभावना ऊर्जा को निरूपित करता है, न कि बंधन ऊर्जा। सही शब्द $\frac{B}{c^{2}}$ होना चाहिए, जहाँ $B$ बंधन ऊर्जा है।
3. जब एक परमाणु के नाभिक में रेडियोएक्टिव विघटन होता है, तो परमाणु के इलेक्ट्रॉन ऊर्जा स्तर
(a) किसी भी प्रकार के रेडियोएक्टिवता के लिए बदल नहीं जाते
(b) $\alpha$ और $\beta$-रेडियोएक्टिवता के लिए बदल जाते हैं लेकिन $\gamma$-रेडियोएक्टिवता के लिए नहीं
(c) $\alpha$-रेडियोएक्टिवता के लिए बदल जाते हैं लेकिन अन्य के लिए नहीं
(d) $\beta$-रेडियोएक्टिवता के लिए बदल जाते हैं लेकिन अन्य के लिए नहीं
उत्तर दिखाएं
Answer
(b) $\alpha-\beta$ कण एक इकाई नकारात्मक आवेश ले जाते हैं, $\alpha$-कण दो इकाइयों धनात्मक आवेश ले जाते हैं और $\gamma$ (कण) आवेश नहीं ले जाते, इसलिए परमाणु के इलेक्ट्रॉन ऊर्जा स्तर $\alpha$ और $\beta$ विघटन के लिए बदल जाते हैं, लेकिन $\gamma$-विघटन के लिए नहीं।
- (अ) यह विकल्प गलत है क्योंकि इलेक्ट्रॉनिक ऊर्जा स्तर $\alpha$ और $\beta$-पराग्रहण के कारण बदल जाते हैं क्योंकि परमाणु के नाभिकीय आवेश और इलेक्ट्रॉन की संख्या में परिवर्तन होता है।
- (स) यह विकल्प गलत है क्योंकि $\beta$-पराग्रहण भी इलेक्ट्रॉनिक ऊर्जा स्तर को बदलता है, न केवल $\alpha$-पराग्रहण।
- (द) यह विकल्प गलत है क्योंकि $\alpha$-पराग्रहण भी इलेक्ट्रॉनिक ऊर्जा स्तर को बदलता है, न केवल $\beta$-पराग्रहण।
4. $M_{x}$ और $M_{y}$ क्रमशः विघटनशील परमाणु और पुत्र परमाणु के परमाणु द्रव्यमान को नोट करते हैं। $\beta^{-}$ विघटन के लिए $Q$-मान $Q_1$ है और $\beta^{+}$ विघटन के लिए $Q_2$ है। यदि $m_{e}$ एक इलेक्ट्रॉन के द्रव्यमान को नोट करता है, तो निम्नलिखित में से कौन सा कथन सही है?
(a) $Q_1=(M_{x}-M_{y}) c^{2}$ और $Q_2=[M_{x}-M_{y}-2 m_{e}] c^{2}$
(b) $Q_1=(M_{x}-M_{y}) c^{2}$ और $Q_2=(M_{x}-M_{y}) c^{2}$
(c) $Q_1=(M_{x}-M_{y}-2 m_{e}) c^{2}$ और $Q_2=(M_{x}-M_{y}+2 c_{e}) c^{2}$
(d) $Q_1=(M_{x}-M_{y}+2 m_{e}) c^{2}$ और $Q_2=(M_{x}-m_{y}+2 m_{e}) c^{2}$
उत्तर दिखाएं
उत्तर
(a) मान लीजिए कि नाभिक $ _{z} X^{A} $ है। $\beta^{+}$ विघटन को इस प्रकार नोट किया जाता है:
$${}_z X^A \rightarrow _{z-1} Y^A+ _ {+1} e^0 +v+Q_2 \newline $$
$$\therefore \quad Q_2 =[m( {} _z X^A) - m_n ({} _{z-1} Y^A) - m _{e}] c^{2} $$
$$ =[m( {} _z X^A) + zm _e - m_n ({} _{z-1} Y^A) -(z-1) m_e - 2m_e]c^{2} $$
$$ =[m( {} _z X^A) -m({} _{z-1} Y^A)-2 m _{e}] c^{2} $$
$$ =(M _{x}- M _{y} -2 m _{e}) c^{2} $$
$\beta^{-}$ विघटन को इस प्रकार नोट किया जाता है:
$$ \therefore \quad {}_z X^A \rightarrow _{z-1} y^A+ _ {+1} e^0 +v+Q_2 \newline $$
$$ \alpha_1 =[m( {} _z X^A) - m_n ({} _{z-1} Y^A) - m _{e}] c^{2} $$
$$ =[m( {} _z X^A) + zm _e - m_n ({} _{z+1} Y^A) -(z-1) m_e ] c^2 $$
$$ =[m( {} _z X^A) -m({} _{z-1} Y^A)] c^{2} $$
$$ =(M _{x}- M _{y} ) c^{2} $$
-
विकल्प (ब): यह विकल्प बताता है कि $\beta^{-}$ विघटन और $\beta^{+}$ विघटन के लिए $Q$-मान $(M_{x} - M_{y}) c^{2}$ है। यह गलत है क्योंकि $\beta^{+}$ विघटन के लिए दो इलेक्ट्रॉन (एक धनावेशी इलेक्ट्रॉन और एक इलेक्ट्रॉन) के द्रव्यमान को गिना जाना चाहिए, जिसके कारण $Q$-मान के व्यंजक में $-2m_{e}$ का अंश आता है। अतः $\beta^{+}$ विघटन के लिए सही $Q$-मान $(M_{x} - M_{y} - 2m_{e}) c^{2}$ है, न केवल $(M_{x} - M_{y}) c^{2}$।
-
विकल्प (c): यह विकल्प बताता है कि $\beta^{-}$ विघटन के लिए Q-मान $(M_{x} - M_{y} - 2m_{e}) c^{2}$ होता है और $\beta^{+}$ विघटन के लिए $(M_{x} - M_{y} + 2c_{e}) c^{2}$ होता है। यह गलत है क्योंकि, $\beta^{-}$ विघटन के लिए सही Q-मान $(M_{x} - M_{y}) c^{2}$ होता है, क्योंकि इलेक्ट्रॉन के द्रव्यमान की गणना करने की आवश्यकता नहीं होती। इसके अतिरिक्त, $\beta^{+}$ विघटन के Q-मान में $2c_{e}$ का शब्द गलत है; इसके बजाय $-2m_{e}$ होना चाहिए, नहीं $+2c_{e}$।
-
विकल्प (d): यह विकल्प बताता है कि $\beta^{-}$ विघटन के लिए Q-मान $(M_{x} - M_{y} + 2m_{e}) c^{2}$ होता है और $\beta^{+}$ विघटन के लिए $(M_{x} - m_{y} + 2m_{e}) c^{2}$ होता है। यह गलत है क्योंकि, $\beta^{-}$ विघटन के लिए सही Q-मान $(M_{x} - M_{y}) c^{2}$ होता है, और $2m_{e}$ के जोड़ की आवश्यकता नहीं होती। $\beta^{+}$ विघटन के लिए सही Q-मान $(M_{x} - M_{y} - 2m_{e}) c^{2}$ होता है, नहीं $(M_{x} - m_{y} + 2m_{e}) c^{2}$।
5. ट्रिटियम हाइड्रोजन का एक समस्थानिक है जिसके नाभिक ट्रिटन में 2 न्यूट्रॉन और 1 प्रोटॉन होते हैं। स्वतंत्र न्यूट्रॉन $p+\bar{e}+\bar{n}$ में विघटित हो जाते हैं। यदि ट्रिटन के एक न्यूट्रॉन विघटित हो जाए, तो यह $^{3}$ हीलियम नाभिक में परिवर्तित हो जाएगा। यह नहीं होता। इसका कारण है
(a) ट्रिटन की ऊर्जा $^{3}_{\alpha}$ हीलियम नाभिक की तुलना में अधिक होती है
(b) बीटा विघटन प्रक्रिया में उत्पन्न इलेक्ट्रॉन नाभिक में रह नहीं सकता
(c) ट्रिटन के दोनों न्यूट्रॉन एक साथ विघटित होना पड़ते हैं, जिसके परिणामस्वरूप नाभिक में 3 प्रोटॉन होते हैं, जो $^{3}$ हीलियम नाभिक नहीं होता।
(d) स्वतंत्र न्यूट्रॉन बाह्य प्रभावों के कारण विघटित होते हैं, जो ट्रिटन नाभिक में अस्तित्व में नहीं होते।
उत्तर दिखाएं
सोचने की प्रक्रिया
एक तत्व के समस्थानिक एक ही परमाणु संख्या और भिन्न परमाणु द्रव्यमान संख्या वाले होते हैं।
उत्तर
(a) ट्रिटियम $^{3} _ {2}$ He में 1 प्रोटॉन और 2 न्यूट्रॉन होते हैं। एक न्यूट्रॉन विघटित होकर $n \rightarrow P+\bar{e}+\bar{v}$ बनता है, नाभिक में 2 प्रोटॉन और एक न्यूट्रॉन हो सकते हैं, जिसके परिणामस्वरूप ट्रिटियम $^{3} _ {2}$ He (2 प्रोटॉन और 1 न्यूट्रॉन) में परिवर्तित हो जाएगा।
ट्रिटन की ऊर्जा $^{3} _ {2}$ He नाभिक की तुलना में कम होती है, अर्थात परिवर्तन ऊर्जा के दृष्टिकोण से अनुमत नहीं होता।
-
(ब) बीटा अपघटन प्रक्रिया में बने इलेक्ट्रॉन के नाभिक में रहे रहने के लिए असंभव है: यह गलत है क्योंकि बीटा अपघटन में उत्पन्न इलेक्ट्रॉन के नाभिक में रहे रहने की आवश्यकता नहीं होती। यह उत्सर्जित हो जाता है और नाभिक से बाहर जाता है, इसलिए इसके द्वारा परिवर्तन को रोका नहीं जा सकता।
-
(स) ट्रिटन में दोनों न्यूट्रॉन एक साथ अपघटित होना आवश्यक है, जिसके परिणामस्वरूप एक नाभिक में 3 प्रोटॉन होंगे, जो $^{3}$ He नाभिक नहीं है: यह गलत है क्योंकि ट्रिटन में एक न्यूट्रॉन के अपघटन से $^{3}$ He नाभिक (2 प्रोटॉन और 1 न्यूट्रॉन) बनता है। दोनों न्यूट्रॉन के एक साथ अपघटन के लिए कोई आवश्यकता नहीं होती।
-
(द) स्वतंत्र न्यूट्रॉन बाहरी अस्थिरताओं के कारण अपघटित होते हैं, जो ट्रिटन नाभिक में नहीं होती है: यह गलत है क्योंकि स्वतंत्र न्यूट्रॉन दुर्बल नाभिकीय बल के कारण स्वतंत्र रूप से अपघटित होते हैं, बाहरी अस्थिरताओं के कारण नहीं। ट्रिटन नाभिक में बाहरी अस्थिरताओं की अनुपस्थिति नाभिक में न्यूट्रॉन के अपघटन को रोकने के लिए आवश्यक नहीं है।
6. भारी स्थायी नाभिक में प्रोटॉन की तुलना में अधिक न्यूट्रॉन होते हैं। इसके कारण है
(a) न्यूट्रॉन प्रोटॉन से भारी होते हैं
(b) प्रोटॉन के बीच विद्युत चालक बल प्रतिकर्षण बल होता है
(c) न्यूट्रॉन बीटा अपघटन के माध्यम से प्रोटॉन में अपघटित होते हैं
(d) न्यूट्रॉन के बीच नाभिकीय बल प्रोटॉन के बीच नाभिकीय बल से कम होते हैं
उत्तर दिखाएं
Answer
(b) स्थायी भारी नाभिक में प्रोटॉन की तुलना में अधिक न्यूट्रॉन होते हैं। इसके कारण प्रोटॉन के बीच विद्युत चालक बल प्रतिकर्षण बल होता है, जो स्थायित्व को कम कर सकता है।
-
(a) न्यूट्रॉन प्रोटॉन से भारी होते हैं: न्यूट्रॉन और प्रोटॉन के द्रव्यमान के अंतर स्थायी भारी नाभिक में न्यूट्रॉन-प्रोटॉन अनुपात के कारण नहीं होता। स्थायित्व नाभिकीय बल और विद्युत चालक प्रतिकर्षण के बीच संतुलन के कारण अधिक प्रभावित होता है।
-
(c) न्यूट्रॉन बीटा अपघटन के माध्यम से प्रोटॉन में अपघटित होते हैं: यही बात है कि न्यूट्रॉन प्रोटॉन में अपघटित हो सकते हैं, लेकिन यह प्रक्रिया स्थायी भारी नाभिक में अधिक न्यूट्रॉन के कारण बताने के लिए उपयोगी नहीं है। बीटा अपघटन एकल न्यूट्रॉन के स्थायित्व के लिए अधिक जिम्मेदार है, न कि भारी नाभिक में न्यूट्रॉन-प्रोटॉन अनुपात के लिए।
-
(d) न्यूट्रॉन के बीच नाभिकीय बल प्रोटॉन के बीच नाभिकीय बल से कम होते हैं: यह गलत है क्योंकि नाभिकीय बल (मजबूत अंतरक्रिया) वास्तव में किसी भी न्यूक्लिऑन (प्रोटॉन या न्यूट्रॉन) के बीच समान शक्ति के होते हैं। स्थायित्व के अंतर के कारण प्रोटॉन के बीच प्रतिकर्षण विद्युत स्थैतिक बल हैं, नाभिकीय बल की शक्ति नहीं।
7. एक नाभिकीय रिएक्टर में, मॉडरेटर न्यूट्रॉन को विखंडन प्रक्रिया में निकले न्यूट्रॉन को धीमा करते हैं। उपयोग किए जाने वाले मॉडरेटर हल्के नाभिक रखते हैं। भारी नाभिक इस कार्य के लिए उपयोगी नहीं होंगे, क्योंकि
(a) वे टूट जाएंगे
(b) न्यूट्रॉन के भारी नाभिक के साथ अप्रतिस्थापन टकराव न्यूट्रॉन को धीमा नहीं करेंगे
(c) रिएक्टर का कुल भार असहनीय हो जाएगा
(d) भारी नाभिक वाले पदार्थ कमरे के तापमान पर तरल या गैसीय अवस्था में नहीं होते
उत्तर दिखाएं
सोचने की प्रक्रिया
दो समान द्रव्यमान वाले दो वस्तुओं के बीच अप्रतिस्थापन टकराव होने पर उनके वेग आपस में बदल जाते हैं।
उत्तर
(b) प्रश्न के अनुसार, उपयोग किए जाने वाले मॉडरेटर हल्के नाभिक (जैसे प्रोटॉन) रखते हैं। जब प्रोटॉन न्यूट्रॉन के उत्सर्जित होने के साथ अप्रतिस्थापन टकराव करते हैं तो उनके वेग आपस में बदल जाते हैं, अर्थात न्यूट्रॉन विराम में आ जाते हैं और प्रोटॉन न्यूट्रॉन के वेग के साथ चलते हैं। भारी नाभिक इस कार्य के लिए उपयोगी नहीं होंगे क्योंकि न्यूट्रॉन के भारी नाभिक के साथ अप्रतिस्थापन टकराव न्यूट्रॉन को धीमा नहीं करेंगे।
- (a) भारी नाभिक न्यूट्रॉन टकराव के तहत आसानी से टूट नहीं पाएंगे; वे सामान्यतः स्थायी होते हैं और इस प्रकार के संपर्क का सामना कर सकते हैं।
- (c) रिएक्टर का कुल भार मॉडरेटर के चयन में प्राथमिक चिंता नहीं है; न्यूट्रॉन को धीमा करने में प्रभावशीलता निर्णायक कारक है।
- (d) भारी नाभिक वाले पदार्थ कमरे के तापमान पर ठोस अवस्था में भी मौजूद हो सकते हैं, और पदार्थ की अवस्था उनके मॉडरेटर के रूप में उपयोग के निर्णायक कारक नहीं है।
बहुविकल्पीय प्रश्न (एक से अधिक विकल्प)
8. फ्यूजन प्रक्रियाएं, जैसे दो ड्यूटेरॉन के संयोजन से हीलियम नाभिक बनाना, सामान्य तापमान और दबाव पर संभव नहीं होती हैं। इसके कारण निम्नलिखित हो सकते हैं
(a) परमाणु बल छोटी दूरी तक कार्य करते हैं
(b) नाभिक धनावेशित होते हैं
(c) प्रारंभिक नाभिक पूरी तरह से आयनित होना चाहिए ताकि फ्यूजन हो सके
(d) प्रारंभिक नाभिक एक दूसरे के साथ मिलने से पहले टूट जाना चाहिए
उत्तर दिखाएँ
उत्तर
$(a, b)$
फ्यूजन प्रक्रियाएँ सामान्य तापमान और दबाव पर संभव नहीं हो सकती। कारण यह है कि नाभिक धनावेशित होते हैं और परमाणु बल छोटी दूरी तक सबसे मजबूत बल होते हैं।
-
विकल्प (c) गलत है क्योंकि फ्यूजन के लिए प्रारंभिक नाभिक पूरी तरह से आयनित होना आवश्यक नहीं होता। फ्यूजन वही हो सकता है जब नाभिक पहले से आयनित या आंशिक रूप से आयनित हों, जब तक वे एक दूसरे के बीच विद्युत स्थैतिक प्रतिकर्षण को पार करने के लिए पर्याप्त गतिज ऊर्जा रखते हों।
-
विकल्प (d) गलत है क्योंकि फ्यूजन के लिए प्रारंभिक नाभिक एक दूसरे के साथ मिलने से पहले टूट जाना आवश्यक नहीं होता। फ्यूजन नाभिकों के सीधे संयोजन के बारे में होता है, न कि उनके पहले विघटन।
9. दो रेडियोएक्टिव न्यूक्लियस $A$ और $B$ के नमूने लिए गए हैं $\lambda_{A}$ और $\lambda_{B}$ क्रमशः $A$ और $B$ के विघटन नियतांक हैं। निम्नलिखित में से किस स्थिति में, दो नमूने कोई भी समय पर समान विघटन दर रख सकते हैं?
(a) $A$ की प्रारंभिक विघटन दर $B$ की प्रारंभिक विघटन दर की दोगुनी है और $\lambda_{A}=\lambda_{B}$
(b) $A$ की प्रारंभिक विघटन दर $B$ की प्रारंभिक विघटन दर की दोगुनी है और $\lambda_{A}>\lambda_{B}$
(c) $B$ की प्रारंभिक विघटन दर $A$ की प्रारंभिक विघटन दर की दोगुनी है और $\lambda_{A}>\lambda_{B}$
(d) $B$ की प्रारंभिक विघटन दर $A$ की विघटन दर के समान है $t=2$ घंटे पर और $\lambda_{B}<\lambda_{A}$
उत्तर दिखाएँ
उत्तर
$(b, d)$
दो रेडियोएक्टिव न्यूक्लियस $A$ और $B$ के दो नमूने कोई भी समय पर समान विघटन दर रख सकते हैं यदि $A$ की प्रारंभिक विघटन दर $B$ की प्रारंभिक विघटन दर की दोगुनी हो और $\lambda_{A}>\lambda_{B}$ हो। इसके अलावा, जब $B$ की प्रारंभिक विघटन दर $t=2$ घंटे पर $A$ की विघटन दर के समान हो और $\lambda_{B}<\lambda_{A}$ हो।
-
विकल्प (a): यह विकल्प यह कहता है कि $A$ के विघटन की शुरुआती दर $B$ की शुरुआती विघटन दर के दोगुनी है और $\lambda_{A}=\lambda_{B}$. यदि विघटन नियतांक समान हैं, तो विघटन दर हमेशा अपनी शुरुआती दर के समान अनुपात में रहेगी। इसलिए, कोई भी समय पर वे एक समान विघटन दर नहीं रख सकते क्योंकि $A$ की शुरुआती विघटन दर $B$ की दोगुनी है।
-
विकल्प (c): यह विकल्प यह कहता है कि $B$ की शुरुआती विघटन दर $A$ की शुरुआती विघटन दर के दोगुनी है और $\lambda_{A}>\lambda_{B}$. चूंकि $\lambda_{A}>\lambda_{B}$, $A$ $B$ से तेजी से विघटित होगा। चूंकि $B$ के प्रारंभिक विघटन दर अधिक है, विघटन दर $A$ और $B$ के बीच समय के साथ अलग हो जाएगी और वे एक साथ एक समान विघटन दर नहीं रख सकते।
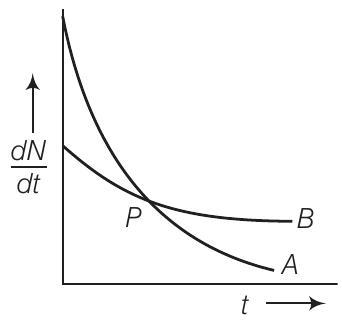
10. दो रेडियोएक्टिव नमूनों $A$ और $B$ के विघटन दर के समय के साथ परिवर्तन को चित्र में दिखाया गया है।
निम्नलिखित में से कौन से कथन सत्य हैं?
(a) $A$ का विघटन नियतांक $B$ के विघटन नियतांक से अधिक है, इसलिए $A$ हमेशा $B$ से तेजी से विघटित होता है
(b) $B$ का विघटन नियतांक $A$ के विघटन नियतांक से अधिक है लेकिन इसकी विघटन दर हमेशा $A$ की विघटन दर से कम है
(c) $A$ का विघटन नियतांक $B$ के विघटन नियतांक से अधिक है लेकिन यह हमेशा $B$ से तेजी से विघटित नहीं होता
(d) $B$ का विघटन नियतांक $A$ के विघटन नियतांक से कम है लेकिन बाद में इसकी विघटन दर $A$ के विघटन दर के बराबर हो जाती है
उत्तर दिखाएं
$(c, d)$
दिए गए चित्र से स्पष्ट है कि वक्र $A$ की ढलान वक्र $B$ की ढलान से अधिक है। इसलिए $A$ की विघटन दर $B$ की विघटन दर से तेज है।
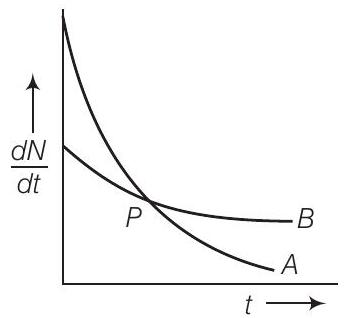
हम जानते हैं कि $(\frac{d N}{d t}) \propto, \lambda$, किसी भी समय के अंतराल में इसलिए हम कह सकते हैं कि $\lambda_{A}>\lambda_{B}$. चित्र में दिखाए गए बिंदु $P$ पर दोनों वक्र प्रतिच्छेद करते हैं।
इसलिए बिंदु $P$ पर, $A$ और $B$ दोनों के विघटन की दर समान है।
-
(a) $ A $ का विघटन नियतांक $ B $ के विघटन नियतांक से अधिक है, इसलिए $ A $ हमेशा $ B $ से तेजी से विघटित होता है: यह कथन गलत है क्योंकि यद्यपि $ A $ का विघटन नियतांक $ B $ के विघटन नियतांक से अधिक है, $ A $ हमेशा $ B $ से तेजी से विघटित नहीं होता। विघटन दर विघटन नियतांक और अविघटित नाभिकों की संख्या दोनों पर निर्भर करती है। बिंदु $P$ पर $ A $ और $ B $ के विघटन दर समान है, जिससे स्पष्ट होता है कि $ A $ हमेशा $ B $ से तेजी से विघटित नहीं होता।
-
(b) $ B $ का विघटन नियतांक $ A $ के विघटन नियतांक से अधिक है लेकिन इसकी विघटन दर हमेशा $ A $ की विघटन दर से कम होती है: यह कथन गलत है क्योंकि $ B $ का विघटन नियतांक $ A $ के विघटन नियतांक से अधिक नहीं है। दिए गए चित्र में दिखाया गया है कि वक्र $ A $ की ढलान वक्र $ B $ की ढलान से अधिक है, जिससे स्पष्ट होता है कि $ A $ का विघटन नियतांक $ B $ के विघटन नियतांक से अधिक है। इसके अतिरिक्त, $ B $ की विघटन दर हमेशा $ A $ की विघटन दर से कम नहीं होती; बिंदु $P$ पर दोनों की विघटन दर समान है।
बहुत छोटे उत्तर प्रकार प्रश्न
11. $^{3} _ {2}$ He और $^{3} _ {1}$ He नाभिकों के समान द्रव्यमान संख्या है। क्या उनके बंधन ऊर्जा समान है?
उत्तर दिखाएं
उत्तर
नाभिक $^{3} _ {2}$ He और $^{3} _ {1}$ He के समान द्रव्यमान संख्या है। $^{3} _ {2}$ He में दो प्रोटॉन और एक न्यूट्रॉन होते हैं। $^{3} _ {1}$ He में एक प्रोटॉन और दो न्यूट्रॉन होते हैं। $^{3} _ {1}$ He में प्रोटॉन के बीच प्रतिकर्षण बल की कमी होती है इसलिए $^{3} _ {1}$ He के बंधन ऊर्जा $ ^{3} _ {2}$ He के बंधन ऊर्जा से अधिक होती है।
12. सक्रिय नाभिकों की संख्या के साथ विघटन दर के परिवर्तन को दर्शाने वाली एक ग्राफ बनाएं।
उत्तर दिखाएं
उत्तर
हम जानते हैं कि, विघटन दर $=\frac{-d N}{d t}=\lambda N$
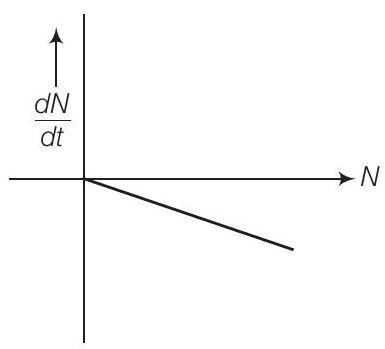
जहाँ विघटन नियतांक $(\lambda)$ एक दिए गए रेडियोएक्टिव पदार्थ के लिए नियत रहता है। अतः $N$ और $\frac{d N}{d t}$ के बीच ग्राफ एक सीधी रेखा होती है जैसा कि चित्र में दिखाया गया है।
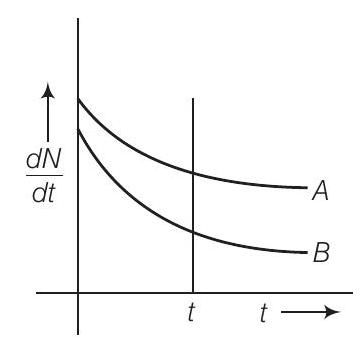
13. चित्र में दिखाए गए नमूने $A$ या $B$ में से कौन सा औसत आयु कम होती है?
उत्तर दिखाएं
Answer
दिए गए चित्र से हम कह सकते हैं कि
$$ \text { जब } t=0, $$
$$ (\frac{d N}{d t})_{A}=(\frac{d N}{d t}) _{B} $$
$$ \Rightarrow \qquad(N_0)_A=(N_0)_B $$
किसी भी क्षण $t$ को लेते हुए समय अक्ष के लंब रेखा खींचकर हम देखते हैं कि $(\frac{d N}{d t})_A>(\frac{d N}{d t})_B$
$$ \begin{matrix} \Rightarrow & \lambda_{A} N_{A}>\lambda_{B} N_{B} & \\ \because & N_{A}>N_{B} & \text { (B के विघटन की दर धीमी है) } \\ \therefore & \lambda_{B}>\lambda_{A} & \\ \Rightarrow & \tau_{A}>\tau_{B} & [\because \text { औसत आयु } \tau=\frac{1}{\lambda}] \end{matrix} $$
14. निम्नलिखित में से कौन विकिरण उत्सर्जित नहीं कर सकता और क्यों? उत्तेजित नाभिक, उत्तेजित इलेक्ट्रॉन।
उत्तर दिखाएं
Answer
उत्तेजित इलेक्ट्रॉन विकिरण उत्सर्जित नहीं कर सकता क्योंकि इलेक्ट्रॉनिक ऊर्जा स्तर की ऊर्जा $eV$ के रेंज में होती है और नहीं $MeV$ (मेगा इलेक्ट्रॉन वोल्ट)। $\gamma$-विकिरण की ऊर्जा $MeV$ के क्रम में होती है।
15. युग्म विघटन में, एक इलेक्ट्रॉन और एक पॉजिट्रॉन एक दूसरे को नष्ट करके गामा विकिरण उत्पन्न करते हैं। संवेग कैसे संरक्षित होता है?
उत्तर दिखाएं
Answer
युग्म विघटन में, एक इलेक्ट्रॉन और एक पॉजिट्रॉन एक दूसरे को नष्ट करके $2 \gamma$ फोटॉन उत्पन्न करते हैं जो विपरीत दिशाओं में चलते हैं ताकि रैखिक संवेग संरक्षित रहे। विघटन को नीचे दिखाया गया है $ _0 e^{-1}+ _0 e^{+1}\rightarrow 2 \gamma$ राइ फोटॉन।
छोटे उत्तर प्रकार प्रश्न
16. क्यों स्थायी नाभिक न्यूट्रॉनों की संख्या के बराबर या अधिक प्रोटॉन नहीं रखते?
उत्तर दिखाएं
उत्तर
क्योंकि प्रोटॉन धनावेशित होते हैं और इलेक्ट्रिक रूप से एक दूसरे को बहिष्कृत करते हैं। ऐसा बहुत बड़ा प्रतिकर्षण उन नाभिकों में होता है जिनमें 10 प्रोटॉन से अधिक होते हैं, इसलिए स्थायित्व के लिए अतिरिक्त न्यूट्रॉन आवश्यक होते हैं जो केवल आकर्षण बल उत्पन्न करते हैं।
19. न्यूक्लिऑन बुनियादी कण हैं, या वे अभी भी छोटे भागों से बने हैं? जांच करने के एक तरीके के रूप में रदरफोर्ड ने परमाणु की जांच की थी। एक इलेक्ट्रॉन के लिए किस गतिज ऊर्जा की आवश्यकता होगी ताकि वह एक न्यूक्लिऑन की जांच कर सके? मान लीजिए एक न्यूक्लिऑन का व्यास लगभग $10^{-15} m$ है।
उत्तर दिखाएं
सोचने की प्रक्रिया
हमें डी-ब्रोग्ली सूत्र $(\boldsymbol{\lambda}=h / p)$ का उपयोग करके कण के संवेग की गणना करनी होगी।
उत्तर
परमाणु के भीतर उपस्थित प्रत्येक कण (न्यूट्रॉन और प्रोटॉन) को न्यूक्लिऑन कहते हैं।
मान लीजिए $\boldsymbol{\lambda}$ तरंगदैर्ध्य हो, $\boldsymbol{\lambda}=10^{-15} m$
एक न्यूक्लिऑन के भीतर अलग-अलग भागों की जांच करने के लिए इलेक्ट्रॉन के तरंगदैर्ध्य कम से कम $10^{-15} m$ होना चाहिए।
हम जानते हैं कि
ऊर्जा
$$ \begin{aligned} \lambda & =\frac{h}{p} \text { और } KE=PE \\ & =\frac{h c}{\lambda} \end{aligned} $$
$$ \begin{aligned} \text { इलेक्ट्रॉन की गतिज ऊर्जा } & =P E=\frac{h c}{\lambda}-\frac{6.6 \times 10^{-34} \times 3 \times 10^{8}}{10^{-15} \times 1.6 \times 10^{-19}} eV \\ KE & =12.375 \times 10^{8} eV \end{aligned} $$
20. यदि न्यूक्लिड 1, न्यूक्लिड 2 के दर्पण इसोबार है तो $Z_1=N_2$ और $Z_2=N_1$ होता है। (a) $^{23} _ {11} Na$ के दर्पण इसोबार कौन है? (b) दो दर्पण इसोबार में से कौन सा न्यूक्लिड बंधन ऊर्जा में अधिक होगा और क्यों?
उत्तर दिखाएं
सोचने की प्रक्रिया
दर्पण इसोबार और बंधन ऊर्जा के अवधारणा पर आधारित।
उत्तर
(a) प्रश्न के अनुसार, यदि न्यूक्लिड 1, न्यूक्लिड 2 के मिरर आइसोबार होता है, तो $Z_1=N_2$ और $Z_2=N_1$ होता है।
अब $^{23}_{11} Na$ में $Z_1=11$, $N_1=23-11=12$
$\therefore$ $^{23}{11} Na$ का मिरर आइसोबार $^{23}{12} Mg$ है, जिसके लिए $Z_2=12=N_1$ और $N_2=23-12=11=Z_1$ होता है।
(b) क्योंकि $^{23}{12} Mg$ में प्रोटॉन की संख्या (12) सम संख्या है जबकि $^{23}{11} Na$ में प्रोटॉन की संख्या (11) विषम संख्या है, इसलिए $^{23}{11} Mg$ की बंधन ऊर्जा $^{23}{11} Na$ की बंधन ऊर्जा से अधिक होती है।
लंबा उत्तर प्रकार प्रश्न
21. कभी-कभी एक रेडियोएक्टिव न्यूक्लियस अपने आप रेडियोएक्टिव न्यूक्लियस में विघटित हो जाता है। एक उदाहरण है
$^{38}\text{सल्फर} \quad \quad \substack{\text{अर्ध-जीवन} \\ \\ =2.48\text{ घंटा}}{\longrightarrow} {\quad} ^{38}Cl \quad \substack{\text{अर्ध-जीवन} \\ \\ =0.62\text{ घंटा}} {\longrightarrow} {\quad} ^{38}Ar(\text{स्थायी})$
मान लीजिए कि हम $t=0$ के समय $1000{ }^{38} S$ न्यूक्लियस से शुरू करते हैं। $t=0$ पर $^{38} Cl$ की संख्या शून्य होती है और $t=\infty$ पर भी शून्य होती है। उस समय $t$ के किस मान पर गिनती की संख्या अधिकतम होगी?
उत्तर दिखाएं
सोचने की प्रक्रिया
इस समस्या को हल करने के लिए दो विघटन प्रक्रियाओं के श्रृंखला के अवधारणा का उपयोग किया जाएगा। प्रक्रिया के लिए,
$A \rightarrow B \rightarrow C$, विघटन कानून है $\frac{d N_{B}}{d t}=\lambda_{B} N_{B}+\lambda_{A} N_{A}$।
उत्तर
दो विघटन प्रक्रियाओं के श्रृंखला को ध्यान में रखते हुए
$$ { }^{38} \mathrm{~S} \xrightarrow[2.48 \mathrm{~h}]{ }{ }^{38} \mathrm{Cl} \xrightarrow[0.62 \mathrm{~h}]{ }^{38} \mathrm{Ar} $$
समय $t$ पर, $^{38} S$ में $N_1(t)$ सक्रिय न्यूक्लियस होते हैं और $^{38} Cl$ में $N_2(t)$ सक्रिय न्यूक्लियस होते हैं।
इसके अलावा,
$$ \begin{aligned} \frac{d N_1}{d t} & =-\lambda_1 N_1=\text { Cl}^{38} \text{ के निर्माण की दर} . \\ \frac{d N_2}{d t} & =-\lambda_2 N_2+\lambda_1 N_1 \\ N_1 & =N_0 e^{-\lambda_1 t} \\ \frac{d N_2}{d t} & =\lambda_1 N_0 e^{-\lambda_1 t}-\lambda_2 N_2 \end{aligned} $$
$$ \text { लेकिन } \quad N_1=N_0 e^{-\lambda_1 t} $$
$e^{\lambda z^{\star}} d t$ से गुणा करके और व्यवस्थित करके
$$ e^{\lambda_2 t} d N_2+\lambda_2 N_2 e^{\lambda_2 t} d t=\lambda_1 N_0 e^{(\lambda_2-\lambda_1) t} d t $$
दोनों ओर समाकलन करने पर
$$ \begin{aligned} & N_2 e^{\lambda_2 t}=\frac{N_0 \lambda_1}{\lambda_2-\lambda_1} e^{(\lambda_2-\lambda_1) t}+C \\ & \text { क्योंकि, } \\ & \text { जब } t=0, N_2=0, C=-\frac{N_0 \lambda_1}{\lambda_2-\lambda_1} \\ & N_2 e^{\lambda_2 t}=\frac{N_0 \lambda_1}{(\lambda_2-\lambda_1)}(e^{(\lambda_2-\lambda_1) t}-1) \\ & N_2=\frac{N_0 \lambda_1}{\lambda_2-\lambda_1}(e^{-\lambda_1 t}-e^{-\lambda_2 t}) \\ & \frac{d N_2}{d t}=0 \\ & \text { अधिकतम संख्या के लिए, } \quad \text {.. (ii) } \\ & \lambda_1 N_0 e^{-\lambda_1 t}-\lambda_2 N_2=0 \\ & e^{\lambda_2 t}-\frac{\lambda_2}{\lambda_1} \cdot \frac{\lambda_1}{N_2}=\frac{\lambda_2}{\lambda_1} e^{\lambda_1 t} \\ & e^{\lambda_2 t}-\frac{.\lambda_2)}{\lambda_2} e^{\lambda_1 t}[e^{(\lambda_2-\lambda_1) t}-1]=0 \text { [समीकरण (i) से] } \\ & \text { या } e^{\lambda_2 t}+\frac{\lambda_2}{(\lambda_2-\lambda_1)} e^{\lambda_1 t}=0 \end{aligned} $$
$$ 1-\frac{\lambda_2}{(\lambda_2-\lambda_1)}+\frac{\lambda_2}{(\lambda_2-\lambda_1)} e^{(\lambda_1-\lambda_2) t}=0 \newline $$ $$\frac{\lambda_2}{(\lambda_2-\lambda_1)} e^{(\lambda_1-\lambda_2) t}=\frac{\lambda_2}{(\lambda_2-\lambda_1)}-1 \newline$$
$$e^{(\lambda_1-\lambda_2) t}=\frac{\lambda_1}{\lambda_2} \newline t=\log _{e} \frac{\lambda_1}{\lambda_2} /(\lambda_1-\lambda_2) \newline$$ $$=\frac{\log _e \frac{2.48}{0.62}}{2.48-0.62} \newline $$ $$=\frac{\log _e 4}{1.86}=\frac{2.303 \times 2 \times 0.3010}{1.86} \newline $$
$$=0.745 s \qquad [\because \lambda=\frac{0.693}{T_{1 / 2}}] $$
नोट रेडियोएक्टिव फॉर्मूला के सीधे उपयोग करें नहीं। चैन डिकेज आधारित सूत्रों का उपयोग करें।
22. ड्यूटेरॉन एक न्यूट्रॉन और प्रोटॉन के बंधन अवस्था है जिसकी बंधन ऊर्जा $B=2.2 MeV$ है। एक $\gamma$-किरण ऊर्जा $E$ के साथ ड्यूटेरॉन नाभिक पर लक्षित किया जाता है ताकि इसे न्यूट्रॉन + प्रोटॉन में तोड़ दिया जा सके जैसे कि न्यूट्रॉन और प्रोटॉन लक्षित $\gamma$-किरण की दिशा में गति करें। यदि $E=B$, तो दिखाइए कि यह घटना घट नहीं सकती। इसलिए, ऐसी प्रक्रिया के लिए ऐसी ऊर्जा $E$ के लिए बताइए कि यह $B$ से कितना अधिक होना चाहिए।
उत्तर दिखाएं
सोचने की प्रक्रिया
ऊर्जा संरक्षण और संवेग संरक्षण के नियम को लागू करें।
उत्तर
दिया गया बंधन ऊर्जा
$$ B=2.2 MeV $$
ऊर्जा संरक्षण के नियम से,
$$ E-B=K_{n}+K_{p}=\frac{p_n^{2}}{2 m}+\frac{p_p^{3}}{2 m} \qquad …(i) $$
संवेग संरक्षण से,
$$ p_{n}+p_{p}=\frac{E}{C} \qquad …(ii) $$
क्योंकि
$$ E=B \Rightarrow p_n^{2}+p_p^{2}=0 $$
यह केवल तभी हो सकता है जब $p_{n}=p_{p}=0$
इसलिए, समीकरण (ii) की संतुष्टि नहीं हो सकती और प्रक्रिया नहीं हो सकती।
मान लीजिए $E=B+X$, जहाँ $X«B$ प्रक्रिया के लिए।
समीकरण (ii) से $p_{n}$ के मान को समीकरण (i) में रखने पर, हम प्राप्त करते हैं
$$ X=\frac{(\frac{E}{c}-p_{p})}{2 m}+\frac{p_p^{2}}{2 m} $$
$$ या \qquad 2 p_p^{2}-\frac{2 E p_{p}}{c}+\frac{E^{2}}{c^{2}}-2 m X=0 $$
द्विघात समीकरण के सूत्र का उपयोग करने पर, हम प्राप्त करते हैं
$$ p_{p}=\frac{\frac{2 E}{c} \pm \sqrt{\frac{4 E^{2}}{c^{2}}-8 (\frac{E^{2}}{c^{2}}-2 m X})}{4} $$
समान वास्तविक मान $p_{p}$ के लिए, विविक्तकरण धनात्मक होना चाहिए
$$ \begin{aligned} \frac{4 E^{2}}{c^{2}} & =8 (\frac{E^{2}}{c^{2}}-2 m X) \\ 16 m X & =\frac{4 E^{2}}{c^{2}} \\ X & =\frac{E^{2}}{4 m c^{2}} \approx \frac{B^{2}}{4 m c^{2}} \qquad[\because X < < B \Rightarrow E \cong B] \end{aligned} $$
23. ड्यूटेरियम नाभिकीय बलों द्वारा बंधा होता है जैसे $H$-परमाणु $p$ और $e$ द्वारा विद्युत बलों द्वारा बंधा होता है। यदि हम ड्यूटेरियम में न्यूट्रॉन और प्रोटॉन के बीच बल को कूलॉम विभव के रूप में लें लेकिन एक प्रभावी आवेश $e^{\prime}$ के साथ
$$ F=\frac{1}{4 \pi \varepsilon_0} \cdot \frac{e^{2}}{r} $$
दिया गया है, तो ड्यूटेरियम के बंधन ऊर्जा $2.2 MeV$ के दिए गए आधार पर $(e^{\prime} / e)$ का मान अनुमानित करें।
उत्तर दिखाएं
उत्तर
बंधन ऊर्जा $H$-परमाणु के लिए
$$ E=\frac{m e^{4}}{\pi \varepsilon_0^{2} h^{2}}=13.6 eV \quad …(i) $$
यदि प्रोटॉन और न्यूट्रॉन के प्रत्येक के आवेश $e^{\prime}$ हो और वे एक ही विद्युत बल द्वारा नियंत्रित हों, तो उपरोक्त समीकरण में हमें इलेक्ट्रॉनिक द्रव्यमान $m$ को प्रोटॉन-न्यूट्रॉन के घटित द्रव्यमान $m^{\prime}$ और इलेक्ट्रॉनिक आवेश $e$ को $e^{\prime}$ से बदलना होगा।
$$ \begin{aligned} m^{\prime} & =\frac{M \times N}{M+N}=\frac{M}{2} \\ & =\frac{1836 m}{2}=918 m \end{aligned} $$
यहाँ, $M$ न्यूट्रॉन/प्रोटॉन के द्रव्यमान को प्रदर्शित करता है
$$ \therefore \quad \text { बंधन ऊर्जा }=\frac{918 m(e^{\prime})^{4}}{8 \varepsilon_0^{2} h^{2}}=2.2 MeV \quad …(ii) $$
समीकरण (ii) और (i) को विभाजित करने पर हमें प्राप्त होता है
$$ \begin{aligned} 918 (\frac{e^{\prime}}{e})^4 & =\frac{2.2 MeV}{13.6 eV}=\frac{2.2 \times 10^{6}}{13.6} \\ (\frac{e^{\prime}}{e})^4 & =\frac{2.2 \times 10^{6}}{13.6 \times 918}=176.21 \\ \frac{e^{\prime}}{e} & =(176.21)^{1 / 4}=3.64 \end{aligned} $$
24. न्यूट्रिनो अनुमान के पहले, बीटा विघटन प्रक्रिया को एक संक्रमण के रूप में माना जाता था।
$$ n\rightarrow p+e $$
यदि यह सत्य होता, तो दिखाइए कि यदि न्यूट्रॉन विराम में होता, तो प्रोटॉन और इलेक्ट्रॉन निश्चित ऊर्जा से बाहर निकलेंगे और उन्हें गणना कीजिए। प्रयोग में इलेक्ट्रॉन ऊर्जा के बड़ी श्रेणी में पाया गया था।
उत्तर दिखाएं
उत्तर
बीटा विघटन से पहले न्यूट्रॉन विराम में होता है। अतः, $E_{n}=m_{n} c^{2}, p_{n}=0$
$$p_{n}=p_{p}+p_{e}$$
$$या \qquad p_{p} + p_{e} = 0 \Rightarrow |p_p|=|p_{e}|=p $$
इसके अतिरिक्त,
$$E_{p} =(m_p^{2} c^{4}+p_p^{2} c^{2})^{\frac{1}{2}}, \\ E_{e} =(m_e^{2} c^{4}+p_p^{2} c^{2})^{\frac{1}{2}} \\ =(m_e^{2} c^{4}+p_e^{2} c^{2})^{\frac{1}{2}} $$
ऊर्जा संरक्षण से,
$$ \begin{aligned} (m_p^{2} c^{4}+p^{2} c^{2})^{\frac{1}{2}}+ & =(m_e^{2} c^{4}+p^{2} c^{2})^{\frac{1}{2}}=m_{n} c^{2} \\ m_{p} c^{2} \approx 936 MeV, m_{n} c^{2} & \approx 938 MeV, m_{e} c^{2}=0.51 MeV \end{aligned} $$
क्योंकि, $n$ और $p$ के बीच ऊर्जा अंतर छोटा है, $p c$ छोटा होगा, $p c«<m _ {p} c^{2}$, जबकि $p c$ $m _ {e} c^{2}$ से अधिक हो सकता है
$$(m^{2} _ {p}c^{4} + p^{2}c^{2})^{\frac{1}{2}}=m _ {n}c^{2} - pc$$
$$m _ {p}c^{2} \left(1 + \frac{p^{2}c^{2}}{m^{2} _ {p}c^{4}}\right)^{\frac{1}{2}}= m _ {n}c^{2} - pc$$
$$m _ {p}c^{2} \left(1 + \frac{p^{2}c^{2}}{2m^{2} _ {p}c^{4}}\right)^{\frac{1}{2}}=m _ {n}c^{2} - pc$$
$$ \Rightarrow \quad m _ {p} c^{2}+\frac{p^{2} c^{2}}{2 m _ p^{2} c^{4}}=m _ {n} c^{2}-p c $$
$$
पहले कोटि के अनुसार $\quad p c \simeq m _ {n} c^{2}-m _ {p} c^{2}=938 MeV-936 MeV=2 MeV$
इससे प्रोटॉन या न्यूट्रॉन के संवेग को प्राप्त कर सकते हैं। फिर,
$$ \begin{aligned} E _ {p} & =(m _ p^{2} c^{4}+p^{2} c^{2})^{\frac{1}{2}}=\sqrt{936^{2}+2^{2}} \\ & \simeq 936 MeV \\ E _ {e} & =(m _ e^{2} c^{4}+p^{2} c^{2})^{\frac{1}{2}}=\sqrt{(0.51)^{2}+2^{2}} \\ & \simeq 2.06 MeV \end{aligned} $$
लंबे उत्तर प्रकार प्रश्न
25. अज्ञात रेडियोएक्टिव न्यूक्लिड की गतिविधि $R$ को घंटे के अंतराल पर मापा जाता है। परिणाम नीचे दिए गए तालिका में दिए गए हैं
| $\boldsymbol{t}(h)$ | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| $\boldsymbol{R}(MB_{q})$ | 100 | 35.36 | 12.51 | 4.42 | 1.56 |
(i) $R$ के विरुद्ध $t$ के ग्राफ का चित्र बनाएं और ग्राफ से अर्ध-आयु की गणना करें।
(ii) $\ln \frac{R}{R_0}$ के विरुद्ध $t$ के ग्राफ का चित्र बनाएं और ग्राफ से अर्ध-आयु का मान प्राप्त करें।
उत्तर दिखाएं
सोचने की प्रक्रिया
अपघटन कानून और अर्ध-आयु पर आधारित।
उत्तर
नीचे दिए गए तालिका में हमने $R(MB_{q})$ और $\ln \frac{R}{R_0}$ के मानों को सूचित किया है।
| $\boldsymbol{t}(h)$ | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| $\boldsymbol{R}(MB_q)$ | 100 | 35.36 | 12.51 | 4.42 | 1.56 |
| $\frac{R}{R_0}$ | - | -1.04 | -2.08 | -3.11 | -4.16 |
(i) जब हम $R$ के विरुद्ध $t$ के ग्राफ बनाते हैं, तो हमें एक अपसारी वक्र प्राप्त होता है जैसा कि नीचे दिखाया गया है।
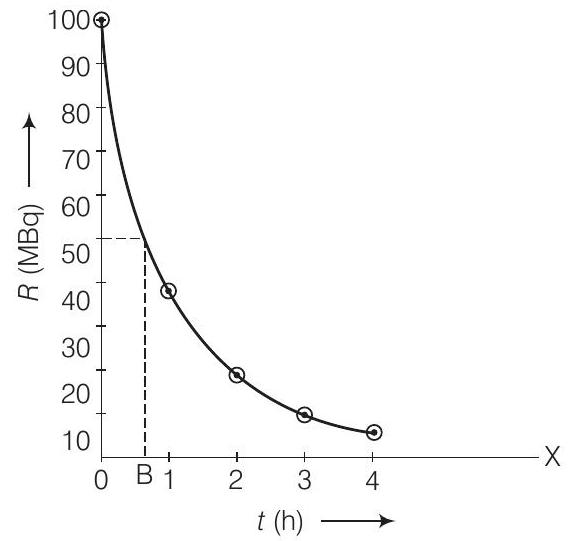
ग्राफ से हम कह सकते हैं कि गतिविधि $R$ $t=O B \approx 40 min$ में $50 %$ तक कम हो जाती है। इसलिए, $t_{1 / 2} \approx 40 min$ है।
(ii) अगला चित्र $\ln (R / R_0)$ के विरुद्ध $t$ के ग्राफ को दिखाता है।
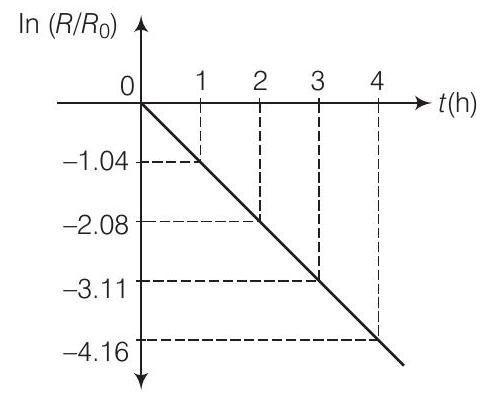
ढलान इस ग्राफ के $=-\lambda$
ग्राफ से,
अर्ध-आयु
$$ \begin{aligned} \lambda & =-\frac{-4.16-(-3.11)}{1} \Rightarrow=1.05 h^{-1} \\ T_{1 / 2} & =\frac{0.693}{\lambda}=\frac{0.693}{1.05}=0.66 h \\ & =39.6 \text{ मिनट} \approx 40 \text{ मिनट} \end{aligned} $$
ग्राफ से हम कह सकते हैं कि क्रियाशीलता $R$ $t=O B \approx 40 \text{ मिनट}$ में $50 %$ तक घट जाती है। इसलिए, $t_{1 / 2} \approx 40 \text{ मिनट}$।
26. प्रोटॉन की मैगिक संख्या $Z=2,8,20,28,50,52$ और न्यूट्रॉन की मैगिक संख्या $N=2,8,20,28,50,82$ और 126 वाले नाभिक बहुत स्थिर पाए जाते हैं।
(i) इसकी जांच करें द्वारा प्रोटॉन के अलग करने की ऊर्जा $S_{p}$ की गणना करके ${ }^{120} Sn(Z=50)$ और ${ }^{121} Sb(Z=51)$ के लिए।
एक न्यूक्लिड के लिए प्रोटॉन अलग करने की ऊर्जा उस न्यूक्लिड के नाभिक से सबसे कम बंधे प्रोटॉन को अलग करने के लिए आवश्यक न्यूनतम ऊर्जा होती है। यह द्वारा दिया गया है
दिया गया है,
$$ \begin{aligned} S_{p} & =(M_{Z-1, N}+M_{H}-M_{Z, N}) c^{2} . \\ { }^{119} \ln & =118.9058 u,{ }^{120} S n=199.902199 u, \\ { }^{121} S b & =120.903824 u,{ }^{1} H=1.0078252 u . \end{aligned} $$
(ii) मैगिक संख्या के अस्तित्व का क्या अर्थ है?
उत्तर दिखाएं
Answer
(i) प्रोटॉन अलग करने की ऊर्जा द्वारा दिया गया है
$$ \begin{aligned} S_{p S n} & =(M_{119.70}+M_{H}-M_{120,70}) c^{2} \\ & =(118.9058+1.0078252-119.902199) c^{2} \\ & =0.0114362 c^{2} \\ S_{p S p} & =(M_{120,70}+M_{H}-M_{121,70}) c^{2} \\ & =(119.902199+1.0078252-120.903822) c^{2} \\ & =0.0062022 c^{2} \end{aligned} $$
इसी तरह
क्योंकि, $S_{pSn}>S_{pSb}$, Sn नाभिक Sb नाभिक से अधिक स्थिर है।
(ii) मैगिक संख्या के अस्तित्व का अर्थ है कि नाभिक के शेल संरचना परमाणु के शेल संरचना के समान है। यह बinging ऊर्जा/न्यूक्लियन वक्र में पिक्स की व्याख्या भी करता है।





