गति करते चार्ज और चुंबकत्व
बहुविकल्पीय प्रश्न (MCQs)
1. दो चार्जित कण एक समान चुंबकीय क्षेत्र $\mathbf{B}=\mathrm{B}_{0} \hat{\mathbf{k}}$ में एक दूसरे के विपरीत दिशा में एक जैसी हेलिकल पथ तय करते हैं।
(a) उनके z-अक्ष के घटक आवेग समान होते हैं
(b) उनके चार्ज समान होने चाहिए
(c) वे आवश्यक रूप से एक कण और उसके विपरीत कण के जोड़े को निरूपित करते हैं
(d) आवेश और द्रव्यमान के अनुपात के लिए
$$ \frac{e}{m_{1}}+\frac{e}{m_{2}}=0 $$
उत्तर दिखाएं
सोचने की प्रक्रिया
हेलिकल पथ के अद्वितीयता को इसके झुकाव द्वारा निर्धारित किया जाता है, जो निम्नलिखित द्वारा दिया जाता है
$$ \text { झुकाव }=\frac{2 \pi m v \cos \theta}{q B} $$
उत्तर
(d) दिए गए झुकाव d के लिए आवेशित कण के लिए, हम निम्नलिखित प्राप्त करते हैं
$$ \frac{q}{m}=\frac{2 \pi v \cos \theta}{q B}=\text { स्थिरांक } $$
चूंकि, आवेशित कण एक समान चुंबकीय क्षेत्र B में एक दूसरे के विपरीत दिशा में एक जैसी हेलिकल पथ तय करते हैं, तो दो कणों के लिए बाएं ओर के भाग समान होना चाहिए और विपरीत चिह्न के होना चाहिए। अतः,
$$ \frac{e}{m_{1}}+\frac{e}{m_{2}}=0 $$
ध्यान दें: समाधान में e के स्थान पर $q$ का उपयोग करें।
-
(a) वे आवेशित कणों के z-अक्ष के घटक आवेग समान होते हैं: यह गलत है क्योंकि z-अक्ष के घटक आवेग के लिए कण के आवेश और वेग दोनों पर निर्भर करता है। चूंकि कण एक दूसरे के विपरीत दिशा में एक जैसी हेलिकल पथ तय करते हैं, उनके z-दिशा में वेग अलग हो सकते हैं, जिसके कारण z-अक्ष के घटक आवेग अलग हो सकते हैं।
-
(b) वे आवश्यक रूप से समान आवेश वाले होने चाहिए: यह गलत है क्योंकि कणों के आवेश अलग हो सकते हैं जब तक उनके आवेश-द्रव्यमान अनुपात ऐसा हो कि वे एक दूसरे के विपरीत दिशा में एक जैसी हेलिकल पथ तय करते हैं। एक जैसी हेलिकल पथ विपरीत दिशा में तय करने के लिए आवश्यक शर्त यह है कि आवेश-द्रव्यमान अनुपात के मापदंड समान आकार के हों लेकिन विपरीत चिह्न के हों, आवेश खुद समान नहीं होना आवश्यक है।
-
(c) वे आवश्यक रूप से एक कण और उसके विपरीत कण के जोड़े को निरूपित करते हैं: यह गलत है क्योंकि चुंबकीय क्षेत्र में विपरीत हेलिकल पथ के अस्तित्व के लिए आवश्यक रूप से कण और उसके विपरीत कण के जोड़े के अस्तित्व का अर्थ नहीं होता। वे बस दो अलग-अलग कण हो सकते हैं जिनके आवेश-द्रव्यमान अनुपात के मापदंड समान आकार के हों लेकिन विपरीत चिह्न के हों।
2. बियो-सावर्ट कानून बताता है कि गतिशील इलेक्ट्रॉन (गति $v$ ) एक चुंबकीय क्षेत्र $\mathbf{B}$ उत्पन्न करते हैं जैसे कि
(a) $B$ लम्बवत होता है
(b) $B$ $v$ के समानांतर होता है
(c) यह व्युत्क्रम घन नियम का पालन करता है
(d) यह इलेक्ट्रॉन और प्रेक्षण बिंदु को जोड़ने वाली रेखा के अनुदिश होता है
उत्तर दिखाएँ
चिंतन प्रक्रिया
यहाँ बियो-सावर्ट कानून के उपयोग की महत्वपूर्ण भूमिका निभाती है।
उत्तर
(a) बियो-सावर्ट के कानून में, चुंबकीय क्षेत्र $\mathbf{B}= \mathrm{i|dl} \times \mathbf{r|}$ और इलेक्ट्रॉन के प्रवाह के कारण idl विपरीत दिशा में $\mathbf{v}$ के अनुदिश होता है और दो सदिशों के क्रॉस उत्परिण की दिशा द्वारा
$$ B \perp v $$
-
(b) $B$ $v$ के समानांतर होता है: यह गलत है क्योंकि, बियो-सावर्ट कानून के अनुसार, चुंबकीय क्षेत्र $\mathbf{B}$ धारा तत्व $\mathbf{idl}$ और स्थिति सदिश $\mathbf{r}$ के क्रॉस उत्परिण द्वारा दिया जाता है। दो सदिशों के क्रॉस उत्परिण हमेशा उन सदिशों के समतल के लम्बवत होता है, इसलिए $\mathbf{B}$ $v$ के समानांतर नहीं हो सकता।
-
(c) यह व्युत्क्रम घन नियम का पालन करता है: यह गलत है क्योंकि बियो-सावर्ट कानून कहता है कि धारा तत्व द्वारा उत्पन्न चुंबकीय क्षेत्र $\mathbf{B}$ दूरी के वर्ग के व्युत्क्रमानुपाती होता है, न कि घन। गणितीय रूप से, $\mathbf{B} \propto \frac{1}{r^2}$, जहाँ $r$ धारा तत्व से प्रेक्षण बिंदु तक की दूरी है।
-
(d) यह इलेक्ट्रॉन और प्रेक्षण बिंदु को जोड़ने वाली रेखा के अनुदिश होता है: यह गलत है क्योंकि गतिशील आवेश या धारा तत्व द्वारा उत्पन्न चुंबकीय क्षेत्र $\mathbf{B}$ इलेक्ट्रॉन और प्रेक्षण बिंदु को जोड़ने वाली रेखा के अनुदिश नहीं होता। बजाय इसके, यह धारा की दिशा (या इलेक्ट्रॉन की गति की दिशा) और इलेक्ट्रॉन से प्रेक्षण बिंदु तक जाने वाली रेखा के लम्बवत होता है, जैसा कि क्रॉस उत्परिण के दाहिने हाथ नियम द्वारा निर्धारित होता है।
3. एक वैद्युत धारा वाले वृत्ताकार लूप जिसकी त्रिज्या $\mathrm{R}$ है, $x$-$y$ तल में रखा है और केंद्र मूल बिंदु पर है। अब लूप के आधा हिस्सा $x>0$ के लिए बनाया गया है जो अब $y$-$z$ तल में रखा है।
(a) चुंबकीय आघूर्ण के परिमाण अब कम हो जाता है
(b) चुंबकीय आघूर्ण बदलता नहीं है
(c) $ (0,0, z) $ पर $ z > R $ के लिए $ B $ के परिमाण में वृद्धि होती है
(d) $ (0,0, z) $ पर $ z \gg R $ के लिए $ B $ के परिमाण में कोई बदलाव नहीं होता
उत्तर दिखाएँ
सोचने की प्रक्रिया
वृताकार लूप के चुंबकीय आघूर्ण और प्रत्येक अर्धवृत्तीय लूप के चुंबकीय आघूर्ण के नेट परिमाण की तुलना $ x-y $ तल और $ y-z $ तल में की जाती है।
उत्तर
(a) त्रिज्या $ R $ के वृताकार लूप के चुंबकीय आघूर्ण की दिशा $ x-y $ तल में होती है और यह $ z $-दिशा में होती है और इसे $ M = I(\pi^{2}) $ द्वारा दिया जाता है। जब लूप के $ x > 0 $ भाग को बन्ध कर दिया जाता है ताकि यह अब $ y-z $ तल में रह जाए, तो प्रत्येक अर्धवृत्तीय लूप के चुंबकीय आघूर्ण के परिमाण $ x-y $ तल और $ y-z $ तल में $ M^{\prime} = \dfrac{I(\pi^{2})}{4} $ होते हैं और इनकी दिशा क्रमशः $ z $-दिशा और $ x $-दिशा में होती है।
इनके परिणामी
$$ M_{\text {net }} = \sqrt{M^{\prime 2} + M^{\prime 2}} = \sqrt{2} M^{\prime} = \dfrac{\sqrt{2} I(\pi^{2})}{4} $$
इसलिए, $ M_{\text {net }} < M $ या $ M $ कम हो जाता है।
-
(b) चुंबकीय आघूर्ण बदलता नहीं है: यह विकल्प गलत है क्योंकि जब लूप बन्ध कर दिया जाता है तब चुंबकीय आघूर्ण बदल जाता है। प्रारंभ में चुंबकीय आघूर्ण $ z $-दिशा में होता है। बन्ध करने के बाद दो अर्धवृत्तीय लूप के चुंबकीय आघूर्ण क्रमशः $ x-y $ और $ y-z $ तल में होते हैं, जिसके कारण नेट चुंबकीय आघूर्ण आरंभिक चुंबकीय आघूर्ण के कम हो जाता है।
-
(c) $ (0,0, z) $ पर $ z > R $ के लिए $ B $ के परिमाण में वृद्धि होती है: यह विकल्प गलत है क्योंकि $ z $-अक्ष पर बिंदु (जहाँ $ z > R $) पर चुंबकीय क्षेत्र मुख्य रूप से लूप के नेट चुंबकीय आघूर्ण पर निर्भर करता है। जब लूप बन्ध कर दिया जाता है तब नेट चुंबकीय आघूर्ण कम हो जाता है, इसलिए $ (0,0,z) $ पर $ z > R $ के लिए चुंबकीय क्षेत्र कम हो जाता है, न कि बढ़ता है।
-
(d) $ (0,0, z) $ पर $ z \gg R $ के लिए $ B $ के परिमाण में कोई बदलाव नहीं होता: यह विकल्प गलत है क्योंकि $ z $-अक्ष पर बिंदु (जहाँ $ z \gg R $) पर चुंबकीय क्षेत्र लूप के नेट चुंबकीय आघूर्ण पर आनुपातिक होता है। जब लूप बन्ध कर दिया जाता है तब नेट चुंबकीय आघूर्ण कम हो जाता है, इसलिए $ (0,0,z) $ पर $ z \gg R $ के लिए चुंबकीय क्षेत्र कम हो जाता है, न कि अपरिवर्तित रहता है।
4. एक इलेक्ट्रॉन को धारावाही लंबे सोलेनॉइड के अक्ष के अनुदिश समान वेग से प्रक्षेपित किया जाता है। निम्नलिखित में से कौन सा सत्य है?
(a) इलेक्ट्रॉन अक्ष के अनुदिश त्वरित होगा
(b) इलेक्ट्रॉन का पथ अक्ष के चारों ओर वृत्ताकार होगा
(c) इलेक्ट्रॉन को अक्ष के सापेक्ष $45^{\circ}$ के कोण पर बल अनुभव होगा और इसलिए एक घुमावदार पथ अपनाएगा
(d) इलेक्ट्रॉन लंबे धारावाही सोलेनॉइड के अक्ष के अनुदिश समान वेग से चलता रहेगा
उत्तर दिखाएं
सोचने की प्रक्रिया
यहाँ, जब एक आवेश एक समान चुंबकीय क्षेत्र में गति करता है जो धारावाही लंबे सोलेनॉइड द्वारा उत्पन्न होता है, तो चुंबकीय लॉरेंज बल उत्पन्न होता है।
उत्तर
(d) चुंबकीय लॉरेंज बल इलेक्ट्रॉन को धारावाही लंबे सोलेनॉइड के अक्ष के अनुदिश समान वेग से प्रक्षेपित किया जाता है $F=-\operatorname{ev} B \sin 180^{\circ}=0\left(\theta=0^{\circ}\right)$ चुंबकीय क्षेत्र और वेग अक्ष के समान्तर होते हैं। इलेक्ट्रॉन लंबे धारावाही सोलेनॉइड के अक्ष के अनुदिश समान वेग से चलता रहेगा।
-
(a) इलेक्ट्रॉन अक्ष के अनुदिश त्वरित नहीं होगा क्योंकि इलेक्ट्रॉन के वेग और चुंबकीय क्षेत्र के बीच लॉरेंज बल इलेक्ट्रॉन के वेग और चुंबकीय क्षेत्र के लंबवत कार्य करता है। चूंकि इलेक्ट्रॉन का वेग सोलेनॉइड के अक्ष के समान्तर होता है, बल शून्य होता है और अक्ष के अनुदिश त्वरण नहीं होता।
-
(b) इलेक्ट्रॉन का पथ अक्ष के चारों ओर वृत्ताकार नहीं होगा क्योंकि वृत्ताकार पथ के लिए वेग के चुंबकीय क्षेत्र के सापेक्ष लंबवत घटक की आवश्यकता होती है। इस मामले में, इलेक्ट्रॉन का वेग चुंबकीय क्षेत्र के समान्तर होता है, जिसके कारण चुंबकीय क्षेत्र के लंबवत बल नहीं होता जो वृत्ताकार गति के लिए आवश्यक होता है।
-
(c) इलेक्ट्रॉन को अक्ष के सापेक्ष $45^{\circ}$ के कोण पर बल अनुभव नहीं होगा और इसलिए एक घुमावदार पथ अपनाएगा क्योंकि चार्ज के कण पर चुंबकीय क्षेत्र में बल लॉरेंज बल द्वारा दिया जाता है, जो वेग और चुंबकीय क्षेत्र के बीच कोण के ज्या पर निर्भर करता है। यहाँ, कोण $0^{\circ}$ है, जिसके कारण बल शून्य होता है, इसलिए इलेक्ट्रॉन घुमावदार पथ अपनाएगा।
5. एक साइक्लोट्रॉन में एक आवेशित कण
(a) सदैव त्वरित होता रहता है
(b) डी के बीच चुंबकीय क्षेत्र के कारण त्वरित होता है
(c) डी में त्वरित होता है
(d) डी में धीमा होता है और डी के बीच त्वरित होता है
उत्तर दिखाएं
सोचने की प्रक्रिया
यहां साइक्लोट्रॉन के कार्य के समझने की आवश्यकता होती है।
उत्तर
(a) आवेशित कण त्वरित होता है क्योंकि
(i) डी के बीच चुंबकीय क्षेत्र के कारण त्वरित होता है और
(ii) डी के भीतर चुंबकीय क्षेत्र के कारण गति की दर समान रहती है लेकिन दिशा निरंतर बदलती रहती है।
-
(b) आवेशित कण डी के बीच चुंबकीय क्षेत्र के कारण त्वरित नहीं होता; यह डी के बीच उपस्थित झूलते विद्युत क्षेत्र के कारण त्वरित होता है। चुंबकीय क्षेत्र केवल डी के भीतर कण की दिशा को बदलता है।
-
(c) आवेशित कण डी में त्वरित नहीं होता; यह डी के भीतर निरंतर गति बनाए रखता है क्योंकि चुंबकीय क्षेत्र केवल इसकी दिशा को बदलता है, न कि इसकी गति।
-
(d) आवेशित कण डी में धीमा नहीं होता; यह डी के भीतर चुंबकीय क्षेत्र के कारण निरंतर गति बनाए रखता है। यह केवल डी के बीच झूलते विद्युत क्षेत्र के कारण त्वरित होता है।
6. एक वृत्ताकार विद्युत धारा लूप जिसका चुंबकीय आघूर्ण $M$ है, एक बाह्य चुंबकीय क्षेत्र $\mathbf{B}$ में अप्रत्यक्ष रूप से रखा गया है। लूप को अपने तल के लंबवत अक्ष के चारों ओर $30^{\circ}$ घुमाने में किया गया कार्य है
(a) $M B$ $ \newline $
(b) $\sqrt{3} \frac{M B}{2}$ $ \newline $
(c) $\frac{M B}{2}$ $ \newline $
(d) शून्य $ \newline $
उत्तर दिखाएं
सोचने की प्रक्रिया
लूप के $30^{\circ}$ घुमाने के अक्ष के लंबवत अक्ष के चारों ओर इसके तल के लंबवत अक्ष के साथ लूप के अक्ष की झुकाव को बरकरार रखता है।
उत्तर
(a) लूप के $30^{\circ}$ घुमाने के अक्ष के लंबवत अक्ष के चारों ओर लूप के अक्ष के चुंबकीय क्षेत्र के दिशा के साथ बने कोण में कोई परिवर्तन नहीं होता, इसलिए लूप को घुमाने में किया गया कार्य शून्य होता है।
ध्यान दें: चालक लूप को चुंबकीय क्षेत्र में घुमाने के कार्य $W=M B\left(\cos \theta_{1}-\cos \theta_{2}\right)$ होता है। जहाँ चिह्न सामान्य रूप से होते हैं।
-
विकल्प (b) $\sqrt{3} \frac{M B}{2}$: यह विकल्प गलत है क्योंकि इसका अर्थ यह होता है कि लूप को $30^{\circ}$ घुमाने के लिए शून्य नहीं होता। हालांकि, क्योंकि घुमाने की धुरी लूप के तल के लंबवत होती है, चुंबकीय आघूर्ण और चुंबकीय क्षेत्र के बीच कोण नहीं बदलता, जिसके कारण कार्य शून्य होता है।
-
विकल्प (c) $\frac{M B}{2}$: यह विकल्प विकल्प (b) के लिए उतना ही गलत है। इसका अर्थ यह होता है कि कार्य शून्य नहीं होता, लेकिन घुमाने के दौरान चुंबकीय आघूर्ण और चुंबकीय क्षेत्र के बीच कोण अपरिवर्तित रहता है, जिसके कारण कार्य शून्य होता है।
-
विकल्प (d) शून्य: यह विकल्प वास्तव में सही है, जैसा कि उत्तर में बताया गया है। लूप को इसके तल के लंबवत धुरी के चारों ओर $30^{\circ}$ घुमाने के लिए कार्य वास्तव में शून्य होता है क्योंकि चुंबकीय आघूर्ण और चुंबकीय क्षेत्र के बीच कोण नहीं बदलता।
7. बोहर मॉडल के अनुसार, एक इलेक्ट्रॉन के एच-परमाणु में गायरो-चुंबकीय अनुपात है
(a) इसके कक्षा के अनुसार स्वतंत्र
(b) नकारात्मक
(c) धनात्मक
(d) क्वांटम संख्या $n$ के साथ बढ़ता है।
उत्तर दिखाएं
सोचने की प्रक्रिया
एच-परमाणु में एक इलेक्ट्रॉन के गायरो-चुंबकीय अनुपात इलेक्ट्रॉन के चुंबकीय आघूर्ण और कोणीय संवेग के अनुपात के बराबर होता है।
उत्तर
(a) यदि $I$ इलेक्ट्रॉन के केंद्रीय नाभिक के चारों ओर कोणीय संवेग के परिमाण को दर्शाता है (कक्षीय कोणीय संवेग)। सदिश रूप में,
$$ \mu_{l}=-\frac{e}{2 m_{e}} l $$
ऋणात्मक चिह्न इलेक्ट्रॉन के कोणीय संवेग की दिशा के विपरीत चुंबकीय आघूर्ण की दिशा को दर्शाता है।
-
(b) नकारात्मक: गायरो-चुंबकीय अनुपात को चुंबकीय आघूर्ण और कोणीय संवेग के अनुपात के रूप में परिभाषित किया गया है। जबकि चुंबकीय आघूर्ण नकारात्मक होता है (इलेक्ट्रॉन के नकारात्मक आवेश के कारण), गायरो-चुंबकीय अनुपात एक अदिश राशि है और धनात्मक होता है क्योंकि यह दो सदिशों (चुंबकीय आघूर्ण और कोणीय संवेग) के अनुपात के परिमाण को दर्शाता है।
-
(c) positive: यह विकल्प गलत नहीं है। गाय्रो-चुंबकीय अनुपात वास्तव में धनात्मक होता है क्योंकि यह चुंबकीय आघूर्ण के अनुपात के परिमाण को दर्शाता है।
-
(d) चुंबकीय अनुपात $ n $ के साथ बढ़ता है: बोहर मॉडल के अनुसार, गाय्रो-चुंबकीय अनुपात $\frac{e}{2m_e}$ द्वारा दिया जाता है, जो एक स्थिरांक है और $ n $ के अनुसार निर्भर नहीं करता। इसलिए, यह $ n $ के साथ बढ़ता नहीं है।
बहुविकल्पीय प्रश्न (एक से अधिक विकल्प)
8. एक तार जो स्थिर धारा $I$ को ले रहा है, एक समान चुंबकीय क्षेत्र $\mathbf{B}$ में रखा गया है जो इसकी लंबाई के लंबवत है। तार के अंदर के आवेशों के बारे में विचार करें। यह ज्ञात है कि चुंबकीय बल कार्य नहीं करता। इसका अर्थ है कि,
(a) चालक के अंदर आवेशों की गति $\mathbf{B}$ के द्वारा प्रभावित नहीं होती, क्योंकि वे ऊर्जा अवशोषित नहीं करते
(b) $\mathbf{B}$ के कारण तार के अंदर कुछ आवेश सतह तक बढ़ जाते हैं
(c) यदि तार $\mathbf{B}$ के प्रभाव से गति करता है, तो बल द्वारा कार्य नहीं किया जाता
(d) यदि तार $\mathbf{B}$ के प्रभाव से गति करता है, तो आयनों पर चुंबकीय बल द्वारा कार्य नहीं किया जाता, आयन तार के अंदर निश्चित माने गए होते हैं।
उत्तर दिखाएँ
उत्तर
$(b, d)$
एक तार जो स्थिर धारा $I$ को ले रहा है, एक समान चुंबकीय क्षेत्र $B$ में रखा गया है, तार जो स्थिर धारा $I$ को ले रहा है, एक समान चुंबकीय क्षेत्र $\mathbf{B}$ में रखा गया है जो इसकी लंबाई के लंबवत है, तार पर बल निम्नलिखित द्वारा दिया जाता है
$$ F=I l B $$
बल की दिशा फ्लेमिंग के बाएँ हाथ नियम द्वारा दी जाती है और $F$ चुंबकीय क्षेत्र $\mathbf{B}$ की दिशा के लंबवत होता है। इसलिए, आयनों पर चुंबकीय बल द्वारा कार्य शून्य होता है।
-
(a) चालक के अंदर आवेशों की गति $\mathbf{B}$ के द्वारा प्रभावित होती है क्योंकि चुंबकीय क्षेत्र गतिशील आवेशों पर बल लगाता है, जिसके कारण आवेश अपनी वेग और चुंबकीय क्षेत्र के लंबवत बल का अनुभव करते हैं। यह चालक के अंदर आवेशों के पुनर्वितरण के लिए जिम्मेदार हो सकता है, हालांकि चुंबकीय बल कार्य नहीं करता।
-
(c) यदि तार $\mathbf{B}$ के प्रभाव में गति करता है, तो बल द्वारा कार्य किया जा सकता है। चुंबकीय बल तार को गति करने में सक्षम हो सकता है, और यदि तार बल की दिशा में गति करता है, तो यांत्रिक कार्य किया जाता है। हालांकि, यह कार्य चुंबकीय बल द्वारा चार्ज पर सीधे नहीं किया जाता है, बल्कि चुंबकीय क्षेत्र और तार में वर्तमान के अंतरक्रिया के माध्यम से किया जाता है।
9. दो समान वर्तमान वाहक सह-अक्षीय लूप, वर्तमान $I$ के विपरीत दिशा में ले रहे हैं। एक सरल अम्पियन लूप दोनों के माध्यम से एक बार गुजरता है। लूप को $C$ कहते हैं,
(a) $\oint \mathbf{B} \cdot \mathbf{d I}=m \mu_{0} I$
(b) $\oint \mathbf{B} . \mathbf{d I}={\pm} 2 \mu_{0} I$ का मान $C$ की दिशा के संगत निरपेक्ष होता है
(c) $C$ पर किसी बिंदु पर, $\mathbf{B}$ और $\mathbf{d l}$ लंबवत हो सकते हैं
(d) $C$ पर सभी बिंदुओं पर $\mathbf{B}$ शून्य होता है
उत्तर दिखाएं
Thinking Process
दिए गए स्थिति पर अम्पियन परिपथ के कानून के अनुप्रयोग करना होता है।
Answer
( $b, c$ )
अम्पियन परिपथ के कानून के अनुप्रयोग से हमें प्राप्त होता है,
$$ \int_{C} \mathrm{~B} \cdot \mathrm{dl}=\mu_{0}(I-I)=0 \quad \text { (क्योंकि वर्तमान विपरीत दिशा में है।) } $$
इसके अलावा, $ \mathbf{C} $ पर किसी बिंदु पर $ \mathbf{B} $ और $ \mathbf{d l} $ लंबवत हो सकते हैं और इसलिए,
$$ \int_{c} \mathrm{~B} \cdot \mathrm{dl}=0 $$
-
विकल्प (a) गलत है: $\oint \mathbf{B} \cdot \mathbf{dI} = m \mu_{0} I$ का व्यंजक गलत है क्योंकि इस स्थिति में वर्तमान विपरीत दिशा में है, इसलिए अम्पियन परिपथ के कानून के सही अनुप्रयोग से नेट वर्तमान शून्य होता है। इसलिए, $\oint \mathbf{B} \cdot \mathbf{dI} = \mu_{0}(I - I) = 0$, नहीं $m \mu_{0} I$।
-
विकल्प (d) गलत है: $\mathbf{B}$ सभी बिंदुओं पर शून्य होता है यह कथन गलत है। विपरीत वर्तमान के कारण नेट समाकल $\oint \mathbf{B} \cdot \mathbf{dI}$ शून्य होता है, लेकिन इसका अर्थ यह नहीं होता कि $C$ पर सभी बिंदुओं पर $\mathbf{B}$ शून्य होता है। $\mathbf{B}$ का अस्तित्व $C$ पर कई बिंदुओं पर रह सकता है, लेकिन दोनों लूप के योग के योग के अंतर के कारण इसके समाकल शून्य होता है।
10. एक घनाकार क्षेत्र में कुछ समान विद्युत और चुंबकीय क्षेत्र भरे हुए हैं। एक इलेक्ट्रॉन एक फलक से वेग $v$ के साथ प्रवेश करता है और एक पॉजिट्रॉन विपरीत फलक से वेग $-v$ के साथ प्रवेश करता है। इस क्षण,
(a) दोनों कणों पर विद्युत बल समान त्वरण उत्पन्न करते हैं
(b) दोनों कणों पर चुंबकीय बल समान त्वरण उत्पन्न करते हैं
(c) दोनों कण एक ही दर से ऊर्जा लेते या खोते हैं
(d) केंद्र बिंदु (CM) के गति केवल चुंबकीय क्षेत्र द्वारा निर्धारित होती है
उत्तर दिखाएं
सोचने की प्रक्रिया
कुछ समान विद्युत और चुंबकीय क्षेत्र भरे हुए अंतरिक अंतरिक एक गतिशील आवेश पर लोरेंज बल द्वारा अनुभव किया जाता है जो द्वारा दिया जाता है $\mathbf{F}=\mathbf{q} \mathbf{E}+q(\mathbf{v} \times \mathbf{B})$।
उत्तर
$(b, c, d)$
चुंबकीय बल $\mathbf{F}=q(\mathbf{v} \times \mathbf{B})$, आवेशित कण पर या तो शून्य होता है या $\mathbf{F}$ वेग $\mathbf{v}$ (या वेग के घटक) के लंबवत होता है जो फिर कण को एक समान वेग के साथ वृत्ताकार पथ पर घूमने के लिए ले जाता है। दोनों स्थितियों में कणों के समान त्वरण होते हैं।
दोनों कण एक ही दर से ऊर्जा लेते या खोते हैं क्योंकि दोनों के एक ही विद्युत बल $(\mathbf{F}=q \mathbf{E})$ के विपरीत दिशा में उत्पन्न होते हैं।
केंद्र बिंदु (CM) के लिए कोई परिवर्तन नहीं होता है, इसलिए केंद्र बिंदु (CM) के गति केवल $\mathbf{B}$ द्वारा निर्धारित होती है।
-
(a) दोनों कणों पर विद्युत बल समान त्वरण उत्पन्न करते हैं
यह विकल्प गलत है क्योंकि आवेशित कण पर विद्युत बल $\mathbf{F} = q \mathbf{E}$ द्वारा दिया जाता है। इलेक्ट्रॉन और पॉजिट्रॉन के विपरीत आवेश होते हैं ($q$ और $-q$), इसलिए उन पर विद्युत बल विपरीत दिशा में होते हैं। इसलिए त्वरण भी विपरीत दिशा में होते हैं, न कि समान।
-
(b) दोनों कणों पर चुंबकीय बल समान त्वरण उत्पन्न करते हैं
यह विकल्प सही है, इसलिए यहां कारण की आवश्यकता नहीं है।
-
(c) दोनों कण एक ही दर से ऊर्जा लेते या खोते हैं
इस विकल्प के अनुसार सही है, इसलिए यहाँ कारण की आवश्यकता नहीं है।
-
(d) केंद्र गति (CM) केवल B द्वारा निर्धारित होती है
इस विकल्प के अनुसार सही है, इसलिए यहाँ कारण की आवश्यकता नहीं है।
11. एक आवेशित कण एक क्षेत्र में एक स्थिर वेग के साथ गति करता रहेगा जहाँ,
(a) $\mathbf{E}=0, \mathbf{B} \neq 0$
(b) $\mathbf{E} \neq 0, \mathbf{B} \neq 0$
(c) $\mathbf{E} \neq 0, \mathbf{B}=0$
(d) $\mathbf{E}=0, \mathbf{B}=0$
उत्तर दिखाएं
सोचने की प्रक्रिया
कुछ समान विद्युत और चुंबकीय क्षेत्र भरे अंतराल में एक गतिशील आवेश के द्वारा अनुभव किया गया लोरेंज बल $\mathbf{F}=q \mathbf{E}+q(\mathbf{v} \times \mathbf{B})$ द्वारा दिया जाता है।
उत्तर
$(a, b, d)$
यहाँ, विद्युत क्षेत्र के कारण आवेशित कण पर बल $\mathrm{F}_{\mathrm{E}}=q \mathrm{E}$ होता है।
आवेशित कण पर चुंबकीय क्षेत्र के कारण बल, $\mathbf{F}_{m}=q(\mathbf{v} \times \mathbf{B})$
अब, $F_{E}=0$ यदि $E=0$ और $F_{m}=0$ यदि $\sin \theta=0$ या $\theta^{\circ}=0^{\circ}$ या $180^{\circ}$
इसलिए, $B \neq 0$ होता है।
इसके अतिरिक्त, $E=0$ और $B=0$ और परिणामी बल $q \mathbf{E}+q(\mathbf{v} \times \mathbf{B})=0$ होता है। इस स्थिति में $E \neq 0$ और $B \neq 0$ होता है।
- विकल्प (c) $\mathbf{E} \neq 0, \mathbf{B}=0$: एक गैर-शून्य विद्युत क्षेत्र $\mathbf{E}$ की उपस्थिति आवेशित कण पर बल $\mathbf{F}_{\mathbf{E}} = q\mathbf{E}$ लगाती है, जिसके कारण कण एक स्थिर वेग के साथ गति नहीं करता बल्कि त्वरित हो जाता है।
बहुत छोटे उत्तर प्रकार प्रश्न
12. यह सत्यापित करें कि चक्रवती आवृत्ति $\omega=e B / m$ के आयाम $[\mathrm{T}]^{-1}$ के सही हैं।
उत्तर दिखाएं
उत्तर
एक आवेशित कण चुंबकीय क्षेत्र के लंबवत गति करता है, तो चुंबकीय लोरेंज बल घूर्णन के आवश्यक केंद्रापाती बल के लिए आवश्यक होता है।
$$ \frac{m v^{2}}{R}=q v B $$
पदों को सरल करने पर हमें प्राप्त होता है
$$ \therefore \quad \frac{q B}{m}=\frac{v}{R}=\omega $$
कोणीय आवृत्ति के आयामी सूत्र की गणना करें
$$ \begin{array}{ll}
\therefore & {[\omega]=\frac{q B}{m}=\frac{v}{R}=[T]^{-1}} \end{array} $$
13. सिद्ध करें कि एक बल जो कार्य नहीं करता है, वह वेग पर निर्भर बल होना चाहिए।
उत्तर दिखाएं
उत्तर
मान लीजिए कोई बल द्वारा कार्य नहीं किया जाता है, इसलिए हम लिख सकते हैं:
$$ \begin{array}{rlrl} \mathrm{d} \mathbf{W}=\mathbf{F} \cdot \mathbf{d l}=0 \ \Rightarrow & \text { F.v } d t & =0 \ \Rightarrow & \text { F.v } & =0 & \end{array} $$
इसलिए, $F$ वेग पर निर्भर होना चाहिए जो इसके वेग $v$ के साथ कोण $90^{\circ}$ होने का अर्थ है। यदि $v$ बदल जाता है (दिशा), तो (दिशा) में $F$ भी बदल जाना चाहिए ताकि उपरोक्त स्थिति संतुष्ट हो सके,
14. चुंबकीय बल $v$ पर निर्भर करता है जो अभिलक्षणीय दृश्य के अनुसार बदल सकता है। तो अभिलक्षणीय दृश्य से दृश्य के बीच चुंबकीय बल अलग होता है? अलग अभिलक्षणीय दृश्य में त्वरण के मान के अलग होने के लिए क्या तर्कसंगत है?
उत्तर दिखाएं
उत्तर
हाँ, अभिलक्षणीय दृश्य से दृश्य के बीच चुंबकीय बल अलग होता है। चुंबकीय बल दृश्य पर निर्भर होता है।
इस त्वरण के नेट त्वरण जो अभिलक्षणीय दृश्य में अस्तित्व में आता है लेकिन अभिलक्षणीय दृश्यों के लिए त्वरण अस्तित्व में आता है (अ-सापेक्षतात्मक भौतिकी)।
15. यदि रेडियो आवृत्ति (rf) क्षेत्र की आवृत्ति दोगुनी हो जाए, तो आवेशित कण के चक्रत्मक चुंबक में आवेशित कण के गति का वर्णन करें।
Show, Answer
चिंतन प्रक्रिया
चक्रत्मक में आवेशित कण के बीच रेडियो आवृत्ति और आवेशित कण की आवृत्ति के बीच संबंध बराबर होना चाहिए ताकि आवेशित कण को चक्रत्मक के दी बीच त्वरित किया जा सके।
उत्तर
यहाँ, चुंबकीय अनुरोध की शर्त के उल्टा हो जाता है।
जब रेडियो आवृत्ति (rf) क्षेत्र की आवृत्ति दोगुनी हो जाती है, तो रेडियो आवृत्ति (rf) क्षेत्र की आवृत्ति आधा हो जाती है। इसलिए, दी के बीच आवेशित कण के आधे चक्र के दौरान रेडियो आवृत्ति (rf) क्षेत्र एक चक्र पूरा कर लेता है।
इसलिए, आवेशित कण एक बार तेजी से त्वरित होता है और फिर धीमा हो जाता है। इसलिए, दी के बीच आवेजित कण के पथ की त्रिज्या एक ही रहती है।
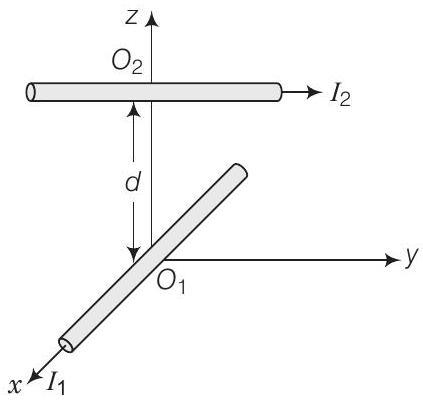
16. दो लंबे तार, जो $I_{1}$ और $I_{2}$ धारा वहन करते हैं, चित्र में दिखाए गए अनुसार व्यवस्थित हैं। जो धारा $I_{1}$ वाला तार $x$-अक्ष के अनुदिश है। दूसरा जो धारा $I_{2}$ वाला तार $x=0$ और $z=d$ द्वारा दिए गए रेखा के अनुदिश है। $x$-अक्ष के अनुदिश वाले तार के कारण $\mathrm{O}_{2}$ पर बल क्या होगा?
उत्तर दिखाएं
सोचने की प्रक्रिया
यहाँ, चुंबकीय क्षेत्र और विद्युत धारा वाले तार पर चुंबकीय बल के दिशा के नियम के अनुप्रयोग की समझ को बहुत अच्छे तरीके से परीक्षण किया गया है।
उत्तर
बियो-सावर्ट के नियम में, चुंबकीय क्षेत्र $\mathbf{B}$, $i \mathrm{dl} \times \mathbf{r}$ के समानुपाती होता है और $i \mathbf{d l}$ की दिशा धारा के प्रवाह की दिशा के अनुदिश होती है।
यहाँ, चुंबकीय क्षेत्र की दिशा के लिए, $I_{1}$ वाले तार के कारण चुंबकीय क्षेत्र की दिशा होगी:
$$ \text { B }_ | =i \text { dl } \times r \text { या } \hat{\mathbf{i}} \times \hat{\mathbf{k}} \text {, लेकिन } \hat{\mathbf{i}} \times \hat{\mathbf{k}}=-\hat{\mathbf{j}} $$
इसलिए, $\mathrm{O}_{2}$ पर दिशा $Y$-अक्ष के अनुदिश होगी।
$\mathrm{O}_{2}$ पर चुंबकीय बल की दिशा $x$-अक्ष के अनुदिश वाले तार के कारण होगी।
$$ \mathrm{F}=I l \times \mathrm{B} \approx \hat{\mathbf{j}} \times(-\hat{\mathbf{j}})=0 $$
इसलिए, $l_{1}$ के कारण चुंबकीय क्षेत्र $y$-अक्ष के अनुदिश है। दूसरा तार $y$-अक्ष के अनुदिश है और इसलिए, बल शून्य है।
छोटे उत्तर प्रकार प्रश्न
17. एक धारा वाला लूप 3 समान चतुर्थांश वृत्तों के बना है, जिनकी त्रिज्या $R$ है, जो $x-y$, $y-z$ और $z-x$ तलों के धनात्मक चतुर्थांश में स्थित हैं और उनके केंद्र उत्पत्ति पर हैं, जो एक साथ जुड़े हुए हैं। उत्पत्ति पर $\mathbf{B}$ की दिशा और मात्रा ज्ञात कीजिए।
उत्तर दिखाएं
सोचने की प्रक्रिया
विद्युत धारा वाले कुंडल के एक चाप द्वारा केंद्र पर $\theta$ कोण बनाये जाने पर चुंबकीय क्षेत्र के कारण चुंबकीय क्षेत्र $\mathbf{B}=\frac{\mu_{0}}{4 \pi} \frac{I \theta}{R}$ द्वारा दिया जाता है।
उत्तर
विद्युत धारा वाले लूप के चौथाई वृत्ताकार चाप जो $x$-$y$ तल के धनात्मक चतुर्थांश में स्थित हैं
$$ B_1=\frac{\mu_{0}}{4 \pi} \frac{I(\pi / 2)}{R} \hat{k}=\frac{\mu_{0}}{4} \frac{I}{2 R} \hat{{k}} $$
विद्युत धारा वाले लूप के चौथाई वृत्ताकार चाप जो $y$-$z$ तल के धनात्मक चतुर्थांश में स्थित हैं
$$ B_2=\frac{0}{4} \frac{I}{2R} \hat{i} $$
विद्युत धारा वाले लूप के चौथाई वृत्ताकार चाप जो $z$-$x$ तल के धनात्मक चतुर्थांश में स्थित हैं
$$ B_{3}=\frac{\mu_{0}}{4} \frac{I}{2 R} \hat{i} $$
विद्युत धारा वाले लूप में 3 समान चौथाई वृत्ताकार चाप जो $x$-$y, y$-$y$ और $z$-$z$ तल के धनात्मक चतुर्थांश में स्थित हैं और उनके केंद्र उत्सर्जन बिंदु पर हैं, जो एक साथ जुड़े हैं तो चुंबकीय क्षेत्र के कारण प्रत्येक चौथाई के चुंबकीय क्षेत्र के सदिश योग के बराबर होता है और निम्नलिखित द्वारा दिया जाता है
$$ \mathbf{B}=\frac{1}{4 \pi}(\hat{\mathbf{i}}+\hat{\mathbf{j}}+\hat{\mathbf{k}}) \frac{\mu_{0} I}{2 R} . $$
18. आवेश $e$ और द्रव्यमान $m$ वाले एक आवेशित कण विद्युत क्षेत्र $\mathbf{E}$ और चुंबकीय क्षेत्र $\mathbf{B}$ में गति कर रहा है। आवेशहीन मात्राएँ और आयाम $[T]^{-1}$ वाली मात्राएँ बनाएं।
उत्तर दिखाएँ
उत्तर
दिए गए मात्राओं से आवेशहीन मात्रा बनाई नहीं जा सकती।
एक आवेशित कण चुंबकीय क्षेत्र के लंबवत गति करता है, तो चुंबकीय लॉरेंज बल घूर्णन के आवश्यक केंद्रापाती बल के लिए आवश्यक होता है।
$$ \frac{m v^{2}}{R}=q v B $$
पदों को सरल करने पर हमें प्राप्त होता है
$$ \therefore \quad \frac{q B}{m}=\frac{v}{R}=\omega $$
कोणीय आवृत्ति के आयामी सूत्र की खोज
$$ \begin{array}{ll} \therefore & {[\omega]=\frac{q B}{m}=\frac{v}{R}=[T]^{-1}} \end{array} $$
यह आवश्यक सूत्र है।
19. एक इलेक्ट्रॉन $x$-$y$ तल के समानांतर तल में एक घनाकार क्षेत्र में (निर्देशांक तलों के समानांतर फलक) प्रवेश करता है जहां एक समान विद्युत और चुंबकीय क्षेत्र होते हैं। इलेक्ट्रॉन का वृत्त घन के अंदर घुमते हुए नीचे जाता है। विद्युत और चुंबकीय क्षेत्र $\mathbf{E}$ और $\mathbf{B}$ की व्यवस्था का सुझाव दें जो इसके कारण हो सकती है।
उत्तर दिखाएं
सोचने की प्रक्रिया
चुंबकीय क्षेत्र आवेशित कण को $x-y$ तल में एकसमान वृत्तीय गति में घूमाता है और विद्युत क्षेत्र $x$-दिशा में गति की दर को बढ़ाता है, जिसके परिणामस्वरूप वृत्तीय पथ की त्रिज्या बढ़ जाती है और इसलिए कण घुमावदार पथ पर गति करता है।
उत्तर
मान लीजिए चुंबकीय क्षेत्र $\mathbf{B}=B_{0} \hat{\mathbf{k}}$ है, और एक इलेक्ट्रॉन $x-y$ तल में एक घन वर्गीय क्षेत्र में (निर्देशांक तलों के समानांतर फलक वाला) $v_{0} \hat{\mathbf{i}}$ वेग के साथ प्रवेश करता है।
इलेक्ट्रॉन पर बल, चुंबकीय लोरेंज बल के द्वारा दिया गया है:
$$ F=-e\left(v_{0} \hat{i} \times B_{0} \hat{k}\right)=e v_{0} B_{0} \hat{j} $$
जो इलेक्ट्रॉन को $x$ - $y$ तल में घूमाता है।
विद्युत बल $\mathbf{F}=-\mathbf{e} \mathrm{E}_{0} \hat{\mathbf{j}}$ इलेक्ट्रॉन को $y$-अक्ष के अनुदिश त्वरित करता है, जिसके परिणामस्वरूप वृत्तीय पथ की त्रिज्या बढ़ जाती है और इसलिए कण घुमावदार पथ पर गति करता है।
20. क्या चुंबकीय बल न्यूटन के तीसरे नियम का पालन करते हैं? दो धारा तत्व $dl_1=dl \hat{i}$ के लिए जो मूल बिंदु पर स्थित है और $dl_2=dl \hat{j}$ के लिए जो $(0, R, 0)$ पर स्थित है, दोनों में धारा $I$ है।
उत्तर दिखाएं
सोचने की प्रक्रिया
यहां, चुंबकीय क्षेत्र की दिशा निर्धारित करने के नियमों और चुंबकीय क्षेत्र में धारा वाले तार पर चुंबकीय बल की दिशा निर्धारित करने के नियमों के अनुप्रयोग के बारे में समझना आवश्यक है।
उत्तर
बियो-सावार के नियम में, चुंबकीय क्षेत्र $\mathbf{B}$, $i \mathbf{d l} \times \mathbf{r}$ के समानुपाती (||) होता है और $i d$ की दिशा धारा के प्रवाह की दिशा के समान होती है।
यहां, चुंबकीय क्षेत्र की दिशा के लिए, $dl_2$ जो $(0, R, 0)$ पर स्थित है, तार $d_1$ के कारण दिया गया चुंबकीय क्षेत्र $B = i |dl \times r|$ या $\hat {i} \times \hat{j}$ (क्योंकि बिंदु $(0, R, 0)$ $y$-अक्ष पर स्थित है), लेकिन $\hat{i} \times \hat{j}=\hat{k}$
इसलिए, $d_{2}$ पर चुंबकीय क्षेत्र की दिशा $z$-दिशा में होती है।
$F=i(I \times B)$ अर्थात $F |(i \times k)$ या $-\hat{\mathbf{j}}$ दिशा में होता है।
इसलिए, $dl_1$ के कारण $dl_2$ पर बल शून्य नहीं है।
अब, चुंबकीय क्षेत्र की दिशा के लिए, बिंदु $d_{1}$ पर, बिंदु $(0, R, 0)$ के संदर्भ में $y$-दिशा में स्थित $(0,0,0)$ पर तार $d_{2}$ के कारण द्वारा दिया गया $B = i \mathbf{|d l} \times \mathbf{r|}$ या $\hat{\mathbf{j}} \times \hat{\mathbf{j}}$ (क्योंकि मूल बिंदु $y$-दिशा में है) लेकिन $\mathbf{j} \times \mathbf{j} = 0$ है।
इसलिए, $d_{1}$ पर चुंबकीय क्षेत्र नहीं है।
$dl_2$ के कारण $dl_1$ पर बल शून्य है।
इसलिए, चुंबकीय बल न्यूटन के तीसरे नियम का पालन नहीं करते हैं।
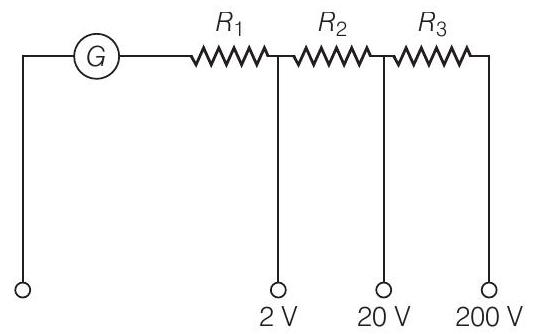
21. एक बहुमापी वोल्टमीटर को चित्र में दिखाए गए गैल्वेनोमीटर परिपथ का उपयोग करके बनाया जा सकता है। हम एक वोल्टमीटर बनाना चाहते हैं जो $10 \Omega$ प्रतिरोध के गैल्वेनोमीटर का उपयोग करते हुए $2 \mathrm{~V}, 20 \mathrm{~V}$ और $200 \mathrm{~V}$ को माप सके और जो धारा के $1 \mathrm{~mA}$ के लिए अधिकतम विस्थापन उत्पन्न करे। $R_{1}, R_{2}$ और $R_{3}$ के मान ज्ञात कीजिए जो उपयोग किए जाने वाले हैं।
उत्तर दिखाएं
सोचने की प्रक्रिया
एक गैल्वेनोमीटर को वोल्टमीटर में बदला जा सकता है जब इसके साथ एक बहुत उच्च प्रतिरोध के तार को श्रेणीक्रम में जोड़ दिया जाए। संबंध द्वारा $I_{g}(G+R)=V$ दिया गया है जहाँ $I_{g}$ गैल्वेनोमीटर की सीमा है, $G$ गैल्वेनोमीटर का प्रतिरोध है और $R$ श्रेणीक्रम में जोड़े गए तार का प्रतिरोध है।
उत्तर
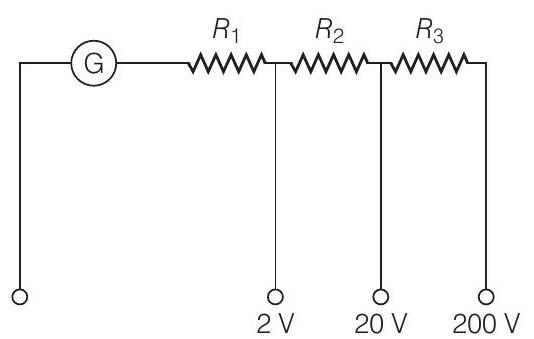
अलग-अलग स्थितियों में समीकरण के उपयोग करते हुए
$$ \begin{array}{lll} \text { लिए } & i_{G}\left(G+R_{1}\right)=2 & \text { 2V के माप के लिए } \\ \text { लिए } & i_{G}\left(G+R_{1}+R_{2}\right)=20 & \text { 20V के माप के लिए } \\ \text { लिए } & i_{G}\left(G+R_{1}+R_{2}+R_{3}\right)=200 & \text { 200V के माप के लिए }
\end{array} $$
हल करने पर, हमें $R_{1}=1990 \Omega, R_{2}=18 \mathrm{k} \Omega$ और $R_{3}=180 \mathrm{k} \Omega$ मिलते हैं।
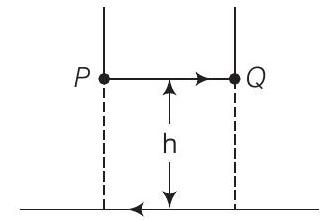
22. एक लंबी सीधी तार, जो $25 \mathrm{~A}$ की धारा ले रही है, एक मेज पर रखी हुई है जैसा कि चित्र में दिखाया गया है। एक अन्य तार $P Q$ जिसकी लंबाई $1 \mathrm{~m}$ और द्रव्यमान $2.5 \mathrm{~g}$ है, उसी धारा को विपरीत दिशा में ले रही है। तार $P Q$ ऊपर और नीचे गति कर सकती है। $P Q$ कितनी ऊँचाई तक उठेगी?
उत्तर दिखाएं
सोचने की प्रक्रिया
लंबी सीधी तार जो $25 \mathrm{~A}$ की धारा ले रही है और मेज पर रखी हुई है, द्वारा तार $P Q$ पर लगाए गए बल को छोटी धारा ले रही तार के भार के संतुलन करना पड़ेगा।
उत्तर
लंबी सीधी तार जो $25 \mathrm{~A}$ की धारा ले रही है और मेज पर रखी हुई है, छोटी तार पर उत्पन्न चुंबकीय क्षेत्र है
$$ B=\frac{\mu_{0} I}{2 \pi h} $$
छोटे चालक पर चुंबकीय बल है
$$ F=B I l \sin \theta=B I l $$
तार $P Q$ पर लगाए गए बल छोटी धारा ले रही तार के भार के संतुलन करता है।
$$ \begin{aligned} F & =m g=\frac{\mu_{0} I^{2} l}{2 \pi h} \ h & =\frac{\mu_{0} I^{2} l}{2 \pi m g}=\frac{4 \pi \times 10^{-7} \times 25 \times 25 \times 1}{2 \pi \times 2.5 \times 10^{-3} \times 9.8}=51 \times 10^{-4} \ h & =0.51 \mathrm{~cm} \end{aligned} $$
लंबा उत्तर प्रकार प्रश्न
23. एक 100 चक्र वाला आयताकार कुंडल $ABCD$ (X-Y तल में) एक तुला के एक हाथ के अंत पर लटकाया गया है। दूसरे हाथ पर 500 ग्राम का द्रव्यमान जोड़कर कुंडल के भार को संतुलित किया गया है। कुंडल में 4.9 एम्पियर की धारा प्रवाहित हो रही है और एक स्थिर चुंबकीय क्षेत्र 0.2 टेसला है जो आंतरिक दिशा में (x-z तल में) कार्य करता है। इस चुंबकीय क्षेत्र को चालू कर दिया जाता है जिसके कारण केवल लंबाई 1 सेंटीमीटर के अंत $CD$ क्षेत्र में रहता है। संतुलन के लिए कितना अतिरिक्त द्रव्यमान $m$ जोड़ना पड़ेगा?
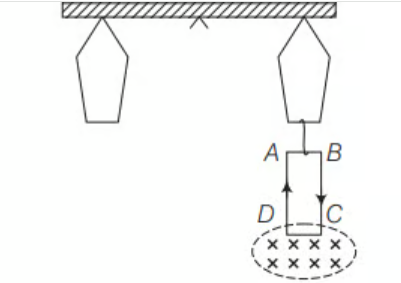
उत्तर दिखाएं
सोचने की प्रक्रिया
चुंबकीय क्षेत्र द्वारा CD पर लगाए गए चुंबकीय बल को वजन के संतुलन के लिए बराबर करना आवश्यक है।
उत्तर
संतुलन के लिए, बराबर बलाघूर्ण भी शून्य होना चाहिए।
जब क्षेत्र बंद हो जाता है $\Sigma t=0$ और प्रत्येक लटके मध्य बिंदु से अलग होने की दूरी $I$ होती है।
$$ \begin{aligned} M g l & =W_{\text {coil }} l \newline \ 500 g l & =W_{\text {coil }} l \newline \ W_{\text {coil }} & =500 \times 9.8 \mathrm{~N} \end{aligned} $$
मध्य बिंदु के संबंध में बल के आघूर्ण की गणना करते हुए, हम चुंबक के वजन को पाएंगे जब चुंबकीय क्षेत्र सक्रिय होता है
$$ \begin{aligned} M g l+m g l & =W_{\text {coil }} l+I B L \sin 90^{\circ} I \newline \ m g l & =B I L l \newline \ m & =\frac{B I L}{g}=\frac{0.2 \times 4.9 \times 1 \times 10^{-2}}{9.8}=10^{-3} \mathrm{~kg}=1 \mathrm{~g} \end{aligned} $$
इसलिए, संतुलन बराबर करने के लिए $1 \mathrm{~g}$ अतिरिक्त द्रव्यमान को जोड़ना आवश्यक है।
24. एक आयताकार चालक लूप में दो तार होते हैं जो दो विपरीत भुजाओं की लंबाई $l$ के होते हैं जो एक दूसरे से लंबाई $d$ के छड़ों द्वारा जुड़े होते हैं। तार एक ही सामग्री के होते हैं लेकिन अनुप्रस्थ काट के क्षेत्रफल में एक गुणक के अंतर होता है। मोटा तार का प्रतिरोध $R$ होता है और छड़ें निम्न प्रतिरोध के होते हैं, जो एक स्थिर वोल्टता स्रोत $V_{0}$ के साथ जुड़े होते हैं। लूप को एक समान चुंबकीय क्षेत्र $\mathbf{B}$ में रखा जाता है जो इसके तल के साथ $45^{\circ}$ का कोण बनाता है। लूप पर चुंबकीय क्षेत्र द्वारा लगाए गए आघूर्ण $\tau$ की गणना करें जो छड़ों के केंद्रों के माध्यम से अक्ष के संबंध में होता है।
उत्तर दिखाएं
सोचने की प्रक्रिया
दोनों तारों में धारा के बाद, चुंबकीय बल और आघूर्ण की गणना करके शुद्ध आघूर्ण की गणना करनी होती है।
उत्तर
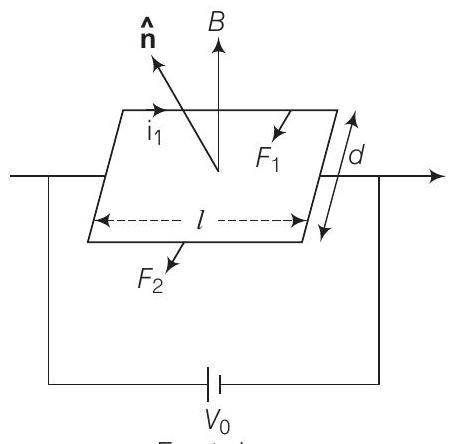
पहली दृष्टि
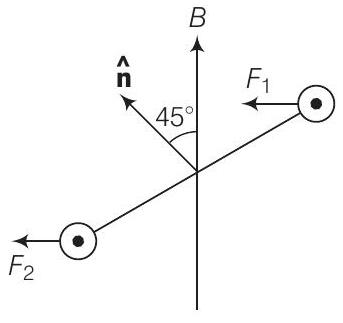
पार्श्व दृश्य
मोटा तार के प्रतिरोध $R$ है, तो दूसरे तार के प्रतिरोध $2 R$ होगा क्योंकि तार समान पदार्थ के हैं लेकिन अनुपात 2 के अनुसार अनुप्रस्थ काट के अलग हैं।
अब, पहले तार पर बल तथा आघूर्ण निम्नलिखित द्वारा दिया जाता है
$$ F_{1}=i_{1} l B=\frac{V_{0}}{2 R} l B, \tau_{1}=\frac{d}{2 \sqrt{2}} F_{1}=\frac{V_{0} l d B}{2 \sqrt{2} R} $$
इसी तरह, दूसरे तार पर बल तथा आघूर्ण निम्नलिखित द्वारा दिया जाता है
$$ F_{2}=i_{2} l B=\frac{V_{0}}{2 R} l B, \tau_{2}=\frac{d}{2 \sqrt 2} F_{2}=\frac{V_{0} l d B}{4 \sqrt{2} R} $$
अतः, कुल आघूर्ण, $\quad \tau=\tau_{1}-\tau_{2}$
$$ \tau=\frac{1}{4 \sqrt{2}} \frac{V_{0} l d B}{R} $$
25. एक इलेक्ट्रॉन और एक पॉजिट्रॉन को एक समान चुंबकीय क्षेत्र $\mathbf{B}=B_{0} \hat{\mathbf{i}}$ में $(0,0,0)$ और $(0,0,1.5 R)$ के बिंदु से छोड़ा जाता है, जिनके प्रत्येक के परिमाण में समान संवेग $p=e B R$ है। संवेग के दिशा के किस शर्त पर वृत्त असंकरण वृत्त होंगे?
उत्तर दिखाएं
सोचने की प्रक्रिया
इलेक्ट्रॉन और पॉजिट्रॉन के वृत्त अतिव्यापन नहीं करेंगे यदि दो केंद्रों के बीच की दूरी $2 R$ से अधिक हो।
उत्तर
क्योंकि, $B$ x-अक्ष के अनुदिश है, एक वृत्तीय कक्षा के लिए दो कणों के संवेग $y-z$ तल में होंगे। मान लीजिए $p_{1}$ और $p_{2}$ इलेक्ट्रॉन और पॉजिट्रॉन के संवेग हैं, क्रमशः। दोनों कक्षा के त्रिज्या $R$ के वृत्त पर घूमते हैं लेकिन विपरीत दिशा में। मान लीजिए $p_{1}$ को $y$-अक्ष के साथ कोण $\theta$ बनाता है, तो $p_{2}$ भी उसी कोण के साथ बनाएगा।
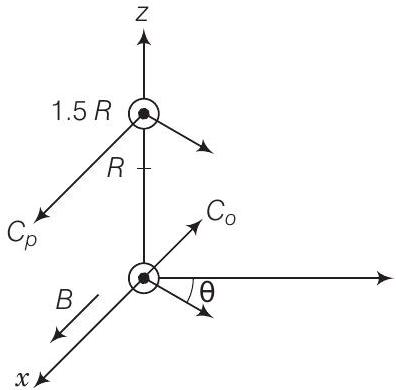
संगत वृत्त के केंद्र ताकत के लंबवत होंगे और दूरी $R$ पर होंगे। मान लीजिए इलेक्ट्रॉन के केंद्र को $C_{e}$ और पॉजिट्रॉन के केंद्र को $C_{p}$ के रूप में लें। इलेक्ट्रॉन के केंद्र के निर्देशांक हैं
$$ C_{e} \equiv(0,-R \sin \theta, R \cos \theta) $$
पॉजिट्रॉन के केंद्र के निर्देशांक हैं
$$ C_{p} \equiv(0,-R \sin \theta, R \cos \theta) $$
$$ C_{p} \equiv\left(0,-R \sin \theta, \frac{3}{2} R-R \cos \theta\right) $$
दोनों के वृत्त एक दूसरे को नहीं काटेंगे यदि दोनों केंद्रों के बीच की दूरी $2 R$ से अधिक हो।
मान लीजिए $d$ दोनों $C_{p}$ और $C_{e}$ के बीच की दूरी है।
तब,
$$ \begin{aligned} d^{2} & =(2 R \sin \theta)^{2}+\frac{3}{2} R-2 R \cos \theta \newline \ & =4 R^{2} \sin ^{2} \theta+\frac{9^{2}}{4} R-6 R^{2} \cos \theta+4 R^{2} \cos ^{2} \theta \newline \ & =4 R^{2}+\frac{9}{4} R^{2}-6 R^{2} \cos \theta \end{aligned} $$
क्योंकि, $d$ के मान $2 R$ से अधिक होना चाहिए
$$ \begin{array}{rlrl} d^{2} >4 R^{2} \newline \ \Rightarrow 4 R^{2}+\frac{9}{4} R^{2}-6 R^{2} \cos \theta >4 R^{2} \newline \ \Rightarrow \frac{9}{4} >6 \cos \theta \newline \ \text { या, } \cos \theta <\frac{3}{8} \end{array} $$
26. एक समान चालक तार जिसकी लंबाई $12 a$ और प्रतिरोध $R$ है, को एक विद्युत धारा वाले कुंडल के रूप में बांधा जाता है जो निम्नलिखित आकारों में हो सकता है: (i) एक समबाहु त्रिकोण जिसकी भुजा $a$ है, (ii) एक वर्ग जिसकी भुजा $a$ है और, (iii) एक नियमित षट्कोण जिसकी भुजा $a$ है। कुंडल को एक वोल्टेज स्रोत $V_{0}$ के साथ जोड़ा जाता है। प्रत्येक मामले में कुंडल के चुंबकीय आघूर्ण की गणना कीजिए।
उत्तर दिखाएं
सोचने की प्रक्रिया
अलग-अलग आकार अलग-अलग क्षेत्रफल के आकार बनाते हैं और इसलिए उनके चुंबकीय आघूर्ण भिन्न होते हैं।
उत्तर
हम जानते हैं कि कुंडल के चुंबकीय आघूर्ण $m=n / A$ होता है।
क्योंकि, तीनों मामलों में समान तार का उपयोग किया गया है और समान विभव पर, तीनों मामलों में समान धारा प्रवाहित होती है।
(i) एक भुजा $a$ वाले समबाहु त्रिकोण के लिए,
$n=4$ क्योंकि कुल तार की लंबाई $=12 a$
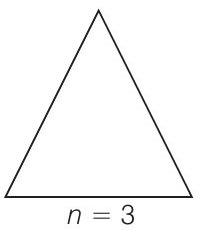
कुंडल के चुंबकीय आघूर्ण $m=n I A=4 I \quad \frac{\sqrt{3}}{4} a^{2}$
$\therefore \quad m=I a^{2} \sqrt{3}$
(ii) भुजा $a$ वाले वर्ग के लिए,

$$ A=a^{2} $$
$n=3$ के कुल तार की लंबाई $=12 a$
कुंडलों के चुंबकीय आघूर्ण $m=n I A=3 I\left(a^{2}\right)=3 I a^{2}$
(iii) एक नियमित षट्कोण के लिए जिसकी भुजा $a$ है,
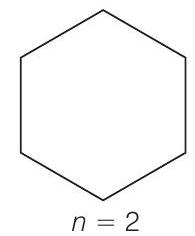
$n=2$ के कुल तार की लंबाई $=12 a$
कुंडलों के चुंबकीय आघूर्ण $m=n \left\lvert, A=21 \frac{6 \sqrt{3}}{4} a^{2}\right.$
$$ m=3 \sqrt{3} a^{2} I $$
$m$ एक ज्यामितीय श्रेणी में है।
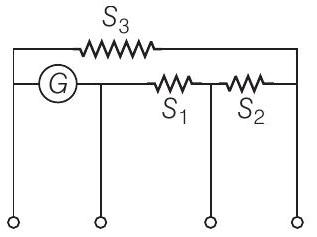
28. चित्र में दिखाए गए गैल्वेनोमीटर परिपथ का उपयोग करके एक बहुमापी धारा मापी का निर्माण किया जा सकता है। हमें एक धारा मापी बनाना है जो $10 \mathrm{~mA}, 100 \mathrm{~mA}$ और $1 \mathrm{~mA}$ की धारा माप सके जिसके लिए एक $10 \Omega$ प्रतिरोध के गैल्वेनोमीटर का उपयोग किया जाए और जो $1 \mathrm{~mA}$ की धारा के लिए अधिकतम विक्षेपण उत्पन्न करे। $S_{1}, S_{2}$ और $S_{3}$ के मान ज्ञात कीजिए जिनका उपयोग किया जाए।
उत्तर दिखाएं
चिंतन प्रक्रिया
एक गैल्वेनोमीटर को एम्पियरमीटर बनाया जा सकता है दो बराबर विद्युत प्रतिरोध वाले तार के साथ शंट (S) के समानांतर में जोड़कर। संबंध द्वारा $I_{g} G=\left(I-I_{g}\right)$ S दिया गया है, जहां $I_{g}$ गैल्वेनोमीटर की सीमा है, $G$ गैल्वेनोमीटर का प्रतिरोध है।
उत्तर
$$ \begin{aligned} I_{G} \cdot G & =\left(I_{1}-I_{G}\right)\left(S_{1}+S_{2}+S_{3}\right) \text { for } I_{1}=10 \mathrm{~mA} \newline \ I_{G}\left(G+S_{1}\right) & =\left(I_{2}-I_{G}\right)\left(S_{2}+S_{3}\right) \text { for } I_{2}=100 \mathrm{~mA} \newline \
$$ I_{G}\left(G+S_{1}+S_{2}\right) & =\left(I_{3}-I_{G}\right)\left(S_{3}\right) \text { for } I_{3}=1 \mathrm{~A} \newline \ S_{1} & =1 \mathrm{~W}, S_{2}=0.1 \mathrm{~W} \newline \ S_{3} & =0.01 \mathrm{~W} \end{aligned} $$
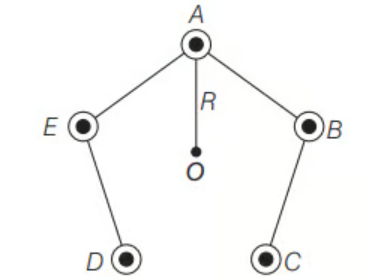
29. पांच लंबे तार $A, B, C, D$ और $E$, प्रत्येक को धारा $I$ ले रहे हैं, जो चित्र में दिखाए गए एक पंचकोणीय प्रिज्म के किन्हीं किन्हीं किन्हीं के रूप में व्यवस्थित हैं। प्रत्येक तार तार के कागज के तल से बाहर धारा ले रहे हैं।
(a) एक बिंदु पर चुंबकीय आघूर्ण जो अक्ष $O$ पर है, क्या होगा? अक्ष प्रत्येक तार से $R$ दूरी पर है।
(b) यदि एक तार (मान लीजिए $A$) में धारा बंद कर दी जाए तो क्षेत्र क्या होगा?
(c) यदि एक तार (मान लीजिए $A$) में धारा उलट दी जाए तो क्षेत्र क्या होगा?
उत्तर दिखाएं
Thinking Process
प्रत्येक तार द्वारा $O$ पर उत्पन्न चुंबकीय क्षेत्र के सदिश योग शून्य होता है।
Answer
(a) मान लीजिए पांच तार $A, B, C, D$ और $E$ कागज के तल के लंब रेखा में चित्र में दिखाए गए स्थान पर हैं।
इसलिए, पांच तारों के कारण चुंबकीय आघूर्ण कागज के तल में एक बंद पंचकोण के विभिन्न भुजाओं के रूप में प्रस्तुत किया जाता है। इसलिए, इसका मान शून्य होता है।
(b) चूंकि प्रत्येक तार द्वारा $O$ पर उत्पन्न चुंबकीय क्षेत्र के सदिश योग शून्य होता है। इसलिए, एक धारा ले रहे तार द्वारा उत्पन्न चुंबकीय आघूर्ण का मान चार तारों के परिणामी के बराबर होता है और विपरीत दिशा में होता है।
इसलिए, यदि एक तार (मान लीजिए $A$) में धारा बंद कर दी जाए तो क्षेत्र $\frac{\mu_{0}}{2 \pi} \frac{i}{R}$ होता है जो $AO$ के लंबवत बाएं दिशा में होता है।
(c) यदि तार $A$ में धारा उलट दी जाए तो
$O$ पर कुल चुंबकीय आघूर्ण
$=$ तार $A$ द्वारा उत्पन्न चुंबकीय आघूर्ण + तार $B, C, D$ और $E$ द्वारा उत्पन्न चुंबकीय आघूर्ण
$$ =\frac{\mu_{0}}{4 \pi R} \frac{2 I}{R} $$
(जो $AO$ के लंबवत बाएं दिशा में कार्य करता है) $+\frac{\mu_{0}}{\pi} \frac{2 I}{R}$ (जो $AO$ के लंबवत बाएं दिशा में कार्य करता है) $=\frac{\mu_{0} I}{\pi R}$ जो $AO$ के लंबवत बाएं दिशा में कार्य करता है।





