चुंबकत्व एवं पदार्थ
बहुविकल्पीय प्रश्न (MCQs)
2. पृथ्वी के चुंबकीय क्षेत्र को पृथ्वी के केंद्र पर स्थित एक बिंदु डाइपोल के चुंबकीय क्षेत्र द्वारा मॉडल किया जा सकता है। डाइपोल अक्ष पृथ्वी के अक्ष के सापेक्ष $11.3^{\circ}$ का कोण बनाता है। मुंबई में विवर्तन लगभग शून्य है। तब,
(a) विवर्तन $11.3^{\circ} \mathrm{W}$ से $11.3^{\circ} \mathrm{E}$ के बीच बदलता रहता है
(b) न्यूनतम विवर्तन $0^{\circ}$ है
(c) डाइपोल अक्ष और पृथ्वी अक्ष द्वारा निर्मित समतल ग्रिनिच के माध्यम से गुजरता है
(d) पृथ्वी के विवर्तन का औसत हमेशा नकारात्मक होना चाहिए
उत्तर दिखाएं
उत्तर
(a) पृथ्वी के चुंबकीय क्षेत्र के चुंबकीय रेखाएँ एक अतिकल्पनात्मक चुंबकीय डाइपोल के चुंबकीय क्षेत्र के समान दिखाई देती हैं, जो पृथ्वी के केंद्र पर स्थित होता है।
डाइपोल अक्ष पृथ्वी के घूर्णन अक्ष के साथ समान नहीं होता है, बल्कि इसके सापेक्ष लगभग $11.3^{\circ}$ का कोण बनाता है। इसके कारण आगे दिए गए चित्र में दिखाए गए दो स्थितियाँ उत्पन्न होती हैं।
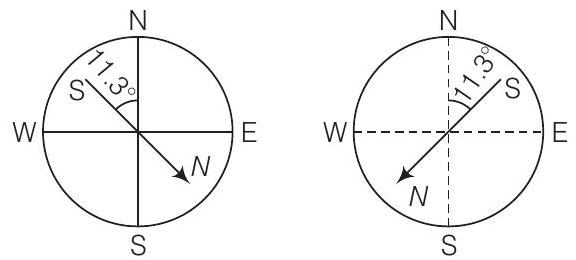
इसलिए, विवर्तन $11.3^{\circ} \mathrm{W}$ से $11.3^{\circ} \mathrm{E}$ के बीच बदलता रहता है।
-
(b) न्यूनतम विवर्तन $0^{\circ}$ है: यह विकल्प गलत है क्योंकि मुंबई में विवर्तन लगभग शून्य है, लेकिन इसका अर्थ यह नहीं होता कि विवर्तन के न्यूनतम मान शून्य है। विवर्तन का मान पृथ्वी के सतह पर स्थिति और चुंबकीय डाइपोल अक्ष के भौगोलिक अक्ष के संबंध के आधार पर बदल सकता है।
-
(c) डाइपोल अक्ष और पृथ्वी अक्ष द्वारा निर्मित समतल ग्रिनिच के माध्यम से गुजरता है: यह विकल्प गलत है क्योंकि डाइपोल अक्ष और पृथ्वी अक्ष द्वारा निर्मित समतल ग्रिनिच के माध्यम से गुजरने के लिए कोई विशिष्ट कारण नहीं है। इस संदर्भ में ग्रिनिच की स्थिति अस्पष्ट है और इसका कोई सीधा संबंध भौगोलिक डाइपोल मॉडल के साथ नहीं है।
-
(d) ध्रुवता पृथ्वी के औसत पर हमेशा नकारात्मक होती है: यह विकल्प गलत है क्योंकि ध्रुवता स्थान पर निर्भर करके धनात्मक और ऋणात्मक दोनों हो सकती है। ध्रुवता चुंबकीय उत्तर और वास्तविक उत्तर के बीच कोण होता है, और यह भिन्न-भिन्न पृथ्वी के क्षेत्रों में धनात्मक से ऋणात्मक मान तक बदल सकती है। इसलिए, पूरी पृथ्वी पर ध्रुवता का औसत आवश्यक रूप से नकारात्मक होना आवश्यक नहीं है।
4. दो आदर्शी तंत्रों को विचार करें (i) एक समान प्लेट धारिता जिसमें बड़े प्लेट और छोटी अलगाव हो और (ii) एक लंबी सॉलेनॉइड जिसकी लंबाई $L \gg R$ हो, ताल अनुप्रस्थ काट की त्रिज्या है। (i) में $\mathbf{E}$ को प्लेट के बीच में आदर्श रूप से एक स्थिर माना जाता है और बाहर शून्य माना जाता है। (ii) में चुंबकीय क्षेत्र को सॉलेनॉइड के भीतर एक स्थिर माना जाता है और बाहर शून्य माना जाता है। इन आदर्शी धारणाओं के बावजूद, निम्नलिखित मूल नियमों के विरोध करती हैं:
(a) मामला (i) विद्युत क्षेत्र के गॉस के नियम के विरोध करता है
(b) मामला (ii) चुंबकीय क्षेत्र के गॉस के नियम के विरोध करता है
(c) मामला (i) $\oint \mathrm{E}$. dl $=0$ के साथ सहमत होता है।
(d) मामला (ii) $\oint \mathrm{H} \cdot \mathrm{dl}=I_{\mathrm{e}}$ के विरोध करता है
उत्तर दिखाएं
सोचने की प्रक्रिया
विद्युत क्षेत्र रेखाएं, एक लगातार बंद पथ बनाती हैं जबकि चुंबकीय क्षेत्र रेखाएं बंद पथ बनाती हैं।
उत्तर
(b) गॉस के नियम के अनुसार, विद्युत क्षेत्र के लिए $\int_{S} E \cdot d s=\frac{q}{\varepsilon_{0}}$ होता है। विद्युत क्षेत्र के लिए यह विरोध नहीं करता क्योंकि विद्युत क्षेत्र रेखाएं लगातार बंद पथ बनाती हैं नहीं।
चुंबकीय क्षेत्र में गॉस के नियम के अनुसार,
$$ \int_{S} \mathrm{E} \cdot \mathrm{ds}=0 $$
चुंबकीय क्षेत्र के लिए यह विरोध करता है क्योंकि सॉलेनॉइड के भीतर चुंबकीय क्षेत्र होता है और सॉलेनॉइड के बाहर धारा वाहक नहीं होता लेकिन चुंबकीय क्षेत्र रेखाएं बंद पथ बनाती हैं।
-
(a) मामला (i) विद्युत क्षेत्र के गॉस के नियम के विरोध नहीं करता क्योंकि गॉस के नियम कहता है कि एक बंद सतह के माध्यम से विद्युत फ्लक्स उस सतह के भीतर बंद आवेश के समानुपाती होता है। समान प्लेट धारिता के मामले में, प्लेट के बीच विद्युत क्षेत्र समान रूप से होता है और बाहर शून्य होता है, जो उन प्लेटों पर आवेश के साथ संगत होता है और गॉस के नियम के विरोध नहीं करता।
-
(c) मामला (i) $\oint \mathrm{E} \cdot \mathrm{dl} = 0$ के साथ आवश्यक रूप से सहमत नहीं होता। यह समीकरण विद्युत चुंबकत्व की स्थिति को प्रस्तुत करता है जहां बंद लूप के चारों ओर विद्युत क्षेत्र के रेखीय समाकल शून्य होता है, जो विद्युत चुंबकत्व में सत्य होता है। हालांकि, यह विद्युत क्षेत्र के टाँकों के बीच स्थिर और बाहरी शून्य होने के आदर्शीकरण के बारे में कोई अतिरिक्त जानकारी नहीं प्रदान करता।
-
(d) मामला (ii) $\oint \mathrm{H} \cdot \mathrm{dl} = I_{\mathrm{e}}$ के विरोधाभास नहीं होता। यह समीकरण ऐम्पियर के नियम को प्रस्तुत करता है, जो बताता है कि बंद लूप के चारों ओर चुंबकीय क्षेत्र के रेखीय समाकल लूप द्वारा घेरे गए विद्युत धारा के बराबर होता है। लंबे सोलेनॉइड के मामले में, चुंबकीय क्षेत्र आंतरिक एकसमान होता है और बाहरी क्षेत्र शून्य होता है, जो ऐम्पियर के नियम के साथ संगत होता है और इसे उल्लंघन नहीं करता।
5. प्रामाणिक नमूना 0.6 टेसला के बाह्य चुंबकीय क्षेत्र में 4 केल्विन तापमान पर रखे जाने पर 8 एमपीर वर्ग मीटर के विपरीत चुंबकीय प्रेरण को दर्शाता है। जब उसी नमूना को 0.2 टेसला के बाह्य चुंबकीय क्षेत्र में 16 केल्विन तापमान पर रखा जाता है, तो चुंबकीय प्रेरण होगा $\newline$
(a) $\frac{32}{3} \mathrm{Am}^{-1}$ $\newline$
(b) $\frac{2}{3} \mathrm{Am}^{-1}$ $\newline$
(c) $6 \mathrm{Am}^{-1}$ $\newline$
(d) $2.4 \mathrm{Am}^{-1}$ $\newline$
उत्तर दिखाएं
Thinking Process
चुंबकीय नियम के अनुसार, हम जानते हैं कि चुंबकीय प्रेरण चुंबकीय क्षेत्र और तापमान के व्युत्क्रमानुपाती होता है।
Answer
(b) चुंबकीय नियम के अनुसार, हम चुंबकीय क्षेत्र, तापमान और चुंबकीय प्रेरण के बीच संबंध के लिए एक सूत्र निकाल सकते हैं।
अर्थात, $\quad I$ (चुंबकीय प्रेरण $) \propto \frac{B \text { (चुंबकीय क्षेत्र इंडक्शन })}{t \text { (केल्विन में तापमान })}$
$\begin{array}{rlrl} \Rightarrow & \frac{I_2}{I_1} =\frac{B_2}{B_1} \times \frac{t_1}{t_2} \\ \text { मान लीजिए, यहां } & I_1 =8 \mathrm{Am}^{-1} \\ B_1 & =0.6 \mathrm{~T}, t_1=4 \mathrm{~K} \\
B_2 & =0.2 \mathrm{~T}, t_2=16 \mathrm{~K} \\ I_2=? \\ \Rightarrow \quad & \frac{0.2}{0.6} \times \frac{4}{16} =\frac{I_2}{8} \\ \Rightarrow \quad & I_2 =8 \times \frac{1}{12}=\frac{2}{3} \mathrm{Am}^{-1} \end{array}$
-
विकल्प (a) $\frac{32}{3} \mathrm{Am}^{-1}$: यह विकल्प गलत है क्योंकि यह एक चुंबकीय प्रेरण के मूल्य के बहुत अधिक मूल्य को सुझाता है, जो $8 \mathrm{Am}^{-1}$ के आरंभिक चुंबकीय प्रेरण से बहुत अधिक है, जो कर्य नियम के साथ संगत नहीं है। कर्य नियम के अनुसार, चुंबकीय क्षेत्र कम हो जाने और तापमान बढ़ जाने पर चुंबकीय प्रेरण कम होना चाहिए।
-
विकल्प (c) $6 \mathrm{Am}^{-1}$: यह विकल्प गलत है क्योंकि यह कर्य नियम द्वारा निर्धारित समानुपातिक संबंध का पालन नहीं करता है। चुंबकीय क्षेत्र कम हो जाने और तापमान बढ़ जाने के कारण चुंबकीय प्रेरण $8 \mathrm{Am}^{-1}$ से बहुत कम होना चाहिए, न कि केवल थोड़ा कम होना चाहिए।
-
विकल्प (d) $2.4 \mathrm{Am}^{-1}$: यह विकल्प गलत है क्योंकि यह घटे हुए चुंबकीय क्षेत्र और बढ़े हुए तापमान के संयुक्त प्रभाव को सही तौर पर प्रतिबिम्बित नहीं करता है। कर्य नियम का सही गणना दर्शाता है कि चुंबकीय प्रेरण $\frac{2}{3} \mathrm{Am}^{-1}$ होना चाहिए, जो $2.4 \mathrm{Am}^{-1}$ से बहुत कम है।
बहुविकल्पीय प्रश्न (एक से अधिक विकल्प)
6. $S$ एक चुंबकीय पदार्थ के खंड की सतह है।
(a) $\mathbf{B}$ के रेखाएँ $S$ के द्वारा आवश्यक रूप से अंतर्गत रहती हैं
(b) कुछ $\mathbf{B}$ के रेखाएँ $S$ के द्वारा अंतर्गत रहती हैं
(c) $\mathbf{H}$ के रेखाएँ $S$ के द्वारा आवश्यक रूप से अंतर्गत रहती हैं
(d) $\mathbf{H}$ के रेखाएँ $S$ के द्वारा अंतर्गत रहती हैं
उत्तर दिखाएं
सोचने की प्रक्रिया
चुंबकीय क्षेत्र रेखाओं (B) के गुणों के अनुसार, किसी भी चुंबक के लिए, ये बंद लूप बनाती हैं। यह विद्युत द्विध्रुव के विपरीत नहीं है, जहाँ इन क्षेत्र रेखाएँ धनात्मक आवेश से शुरू होती हैं और ऋणात्मक आवेश पर समाप्त होती हैं या अनंत तक बिखर जाती हैं।
साथ ही, चुंबकीय तीव्रता $(H)$ किसी भी चुंबक के बाहर $H=B / \mu_{0}$ होती है और चुंबक के भीतर $H=B / \mu_{0} \mu_{r}$ होती है, जहाँ $\mu_{r}$ पदार्थ (चुंबकीय) की सापेक्ष प्रवेश्यियता है।
उत्तर
$(a, d)$
चुंबकीय बल रेखाएँ चुंबकीय आघूर्ण (B) के लिए अंतर्विरोधी रेखाएँ बनाती हैं। इसलिए, B के रेखाएँ $S$ के लिए आवश्यक रूप से अंतर्विरोधी होती हैं।
इसके अलावा, चुंबकीय तीव्रता $\mathbf{( H )}$ घन के भीतर और बाहर भिन्न होती है। इसलिए, $\mathbf{H}$ के रेखाएँ $S$ के लिए सभी अंतर्विरोधी नहीं हो सकतीं।
-
(b) कुछ $\mathbf{B}$ के रेखाएँ $S$ के लिए अंतर्विरोधी होनी चाहिए: यह गलत है क्योंकि चुंबकीय आघूर्ण ($\mathbf{B}$) के लिए चुंबकीय बल रेखाएँ हमेशा अंतर्विरोधी होती हैं। वे अचानक शुरू या समाप्त नहीं होतीं; वे बंद लूप बनाती हैं।
-
(c) $\mathbf{H}$ के रेखाएँ $S$ के लिए आवश्यक रूप से अंतर्विरोधी होती हैं: यह गलत है क्योंकि चुंबकीय तीव्रता ($\mathbf{H}$) चुंबकीय पदार्थ के घन के सीमा के पार बदल सकती है। पदार्थ की उपस्थिति चुंबकीय क्षेत्र को प्रभावित करती है, जिसके कारण $\mathbf{H}$ के रेखाएँ सतह $S$ के लिए अंतर्विरोधी हो सकती हैं।
7. चुंबकत्व के मुख्य मूल (s) निम्नलिखित में से हैं
(a) परमाणु धाराएँ
(b) पॉली अपवर्जन सिद्धांत
(c) अणुओं की ध्रुवी प्रकृति
(d) इलेक्ट्रॉन की अंतर्निहित घूर्णन
उत्तर दिखाएँ
उत्तर
$(a, d)$
चुंबकत्व के मुख्य मूल यह है कि इलेक्ट्रॉन परमाणु के नाभिक के चारों ओर घूम और घूमते हैं, जो एक धारा के रूप में जानी जाती है, जिसे परमाणु धारा कहा जाता है।
इस परमाणु धारा के कारण चुंबकत्व उत्पन्न होता है। परमाणु के नाभिक के चारों ओर घूम और घूमना इलेक्ट्रॉन की अंतर्निहित घूर्णन कहलाता है।
-
(b) पॉली अपवर्जन सिद्धांत: पॉली अपवर्जन सिद्धांत कहता है कि कोई भी दो इलेक्ट्रॉन एक परमाणु में एक ही क्वांटम संख्या के सेट के साथ नहीं हो सकते। यह सिद्धांत परमाणुओं में इलेक्ट्रॉन के व्यवस्था और आवर्त सारणी की संरचना के लिए महत्वपूर्ण है, लेकिन यह चुंबकत्व के मूल के लिए सीधे योगदान नहीं देता।
-
(c) अणुओं की ध्रुवी प्रकृति: अणुओं की ध्रुवी प्रकृति अणु के परमाणुओं में विद्युत आवेश के वितरण को संदर्भित करती है, जिससे द्विध्रुव आघूर्ण उत्पन्न होता है। यह गुण विद्युत क्षेत्र में अणुओं के व्यवहार से संबंधित है और चुंबकत्व के मूल के लिए सीधे योगदान नहीं देता।
8. एक लंबे सोलेनॉइड में 1000 वोल्ट टर्न प्रति मीटर होते हैं और इसमें $1 \mathrm{~A}$ की धारा प्रवाहित होती है। इसका एक नरम लोहा कोर होता है जिसका $\mu_{r}=1000$ होता है। कोर को एक शीतल तापमान से ऊपर तापमान पर गरम कर दिया जाता है, $T_{c}$।
(a) सोलेनॉइड में $\mathbf{H}$ क्षेत्र लगभग अपरिवर्तित रहता है लेकिन $\mathbf{B}$ क्षेत्र बहुत तेजी से कम हो जाता है
(b) सोलेनॉइड में $\mathbf{H}$ और $\mathbf{B}$ क्षेत्र लगभग अपरिवर्तित रहते हैं
(c) कोर में चुंबकीय बल दिशा में विपरीत हो जाता है
(d) कोर में चुंबकीय बल लगभग $10^{8}$ के कारक द्वारा कम हो जाता है
उत्तर दिखाएं
चिंतन प्रक्रिया
चुंबकीय तीव्रता $\mathbf{H}$ क्षेत्र $=n \boldsymbol{I}$, जहाँ $n=$ सोलेनॉइड के प्रति मीटर टर्न की संख्या
और $I=$ धारा और $B=\mu_{0} \mu_{r} n I$ होता है।
इसके अलावा, सामान्य तापमान पर, एक सोलेनॉइड एक लोहा चुंबकीय ठोस के रूप में व्यवहार करता है और तापमान के शीतल तापमान से ऊपर जब यह एक पैरामैग्नेटिक पदार्थ के रूप में व्यवहार करता है।
उत्तर
(a, $d)$
यहाँ, सोलेनॉइड में $\mathbf{H}=n I$ होता है।
$\Rightarrow \quad \mathrm{H}=1000 \times 1=1000 \mathrm{Am}$
इसलिए, $\mathbf{H}$ एक स्थिरांक है, इसलिए यह लगभग अपरिवर्तित रहता है।
लेकिन
$$ \begin{aligned} B & =\mu_{0} \mu_{r} n I \\ & =\mu_{0} n I \mu_{r} \\ & =k \text { (स्थिरांक) } \mu_{r} . \end{aligned} $$
इसलिए, ऊपर दिए गए समीकरण से हम जानते हैं कि $\mathbf{B}$, $\mu_{r}$ में परिवर्तन के साथ परिवर्तित होता है।
अब, कोर में चुंबकीय बल के लिए, जब सोलेनॉइड के लोहा कोर का तापमान शीतल तापमान से ऊपर बढ़ा दिया जाता है, तो यह पैरामैग्नेटिक पदार्थ के रूप में व्यवहार करता है, जहाँ
$\begin{aligned} \text{और} \quad (\chi_m) _{\text {Fero }} & \approx 10^3 \\ \text{और} \quad (\chi_m) _{\text {Para }} & \approx 10^{-5} \\ \Rightarrow \quad\frac{(\chi_mt) _{\text {Fero }}}{(\chi_m)} & =\frac{10^3}{10^{-5}}=10^8 \end{aligned}$
-
विकल्प (b): यह कथन कहता है कि सोलेनॉइड में दोनों $\mathbf{H}$ और $\mathbf{B}$ क्षेत्र लगभग अपरिवर्तित रहते हैं। यह गलत है क्योंकि जबकि $\mathbf{H}$ क्षेत्र लगभग अपरिवर्तित रहता है, $\mathbf{B}$ क्षेत्र परमानुसारीयता $\mu_r$ पर निर्भर करता है। जब कोर को शीतल तापमान से ऊपर तापमान पर गरम कर दिया जाता है, तो $\mu_r$ बहुत तेजी से कम हो जाता है, जिसके कारण $\mathbf{B}$ क्षेत्र में बहुत बड़ा कमी हो जाती है।
-
विकल्प (c): कथन यह दावा करता है कि लोहे के नाले में चुंबकीय प्रेरण की दिशा उलट जाती है। यह गलत है क्योंकि नाले को एक बर्नोली तापमान से अधिक गरम करने पर वस्तु अपने चुंबकीय गुणों को खो देती है और पैरामैग्नेटिक बन जाती है। इस परिवर्तन में चुंबकीय प्रेरण की दिशा के उलटने के बजाए चुंबकीय प्रेरण के एक महत्वपूर्ण कमी के कारण होता है।
9. चालक खोल द्वारा विद्युत चुंबकीय छाया बनाने और चुंबकीय छाया बनाने के बीच मूलभूत अंतर के कारण है
(a) विद्युत क्षेत्र रेखाएँ आवेशों पर समाप्त हो सकती हैं और चालक आवेशों के साथ रह सकते हैं
(b) $\mathbf{B}$ की रेखाएँ भी समाप्त हो सकती हैं लेकिन चालक उन्हें समाप्त नहीं कर सकते
(c) $\mathbf{B}$ की रेखाएँ कोई भी सामग्री पर समाप्त नहीं हो सकती हैं और पूर्ण छाया बनाना संभव नहीं है
(d) उच्च पारगम्यता वाले सामग्री के खोल का उपयोग $\mathbf{B}$ की रेखाओं को आंतरिक क्षेत्र से दूर ले जाने के लिए किया जा सकता है
उत्तर दिखाएं
उत्तर
$(a, c, d)$
विद्युत छाया बनाना वह घटना है जो विद्युत क्षेत्र के प्रभावों को रोकती है। चालक खोल बाहरी क्षेत्र के प्रभावों को अंतर्निहित सामग्री पर रोक सकता है या आंतरिक क्षेत्र के प्रभावों को बाहरी वातावरण से रोक सकता है।
चुंबकीय छाया बनाना उच्च पारगम्यता वाले चुंबकीय सामग्री से बने एक बंद बर्तन का उपयोग करके किया जाता है ताकि बाहरी चुंबकीय क्षेत्र बंद बर्तन के अंतर्गत वस्तुओं तक पहुंच न सके या चुंबकीय क्षेत्र को बंद बर्तन के अंतर्गत सीमित रखा जा सके।
- विकल्प (b) गलत है क्योंकि $\mathbf{B}$ की रेखाएँ कोई भी सामग्री पर समाप्त नहीं हो सकती हैं। चुंबकीय रेखाएँ लगातार लूप होती हैं और आवेशों या चालकों पर समाप्त नहीं होती हैं, जैसे कि विद्युत क्षेत्र रेखाएँ आवेशों पर समाप्त हो सकती हैं।
10. पृथ्वी के चुंबकीय क्षेत्र को एक बिंदु चुंबकीय द्विध्रुव के केंद्र पर रखे गए चुंबकीय द्विध्रुव के क्षेत्र के रूप में मॉडल किया जा सकता है। भौगोलिक विषुवत रेखा पर एक बिंदु पर चुंबकीय झुकाव कोण
(a) हमेशा शून्य होता है
(b) विशिष्ट बिंदुओं पर शून्य हो सकता है
(c) धनात्मक या ऋणात्मक हो सकता है
(d) सीमित होता है
उत्तर दिखाएं
उत्तर
$(b, c, d)$
यदि धरती के कुल चुंबकीय क्षेत्र को धरती के केंद्र पर एक बिंदु चुंबकीय द्विध्रुव के रूप में मॉडल किया जाता है, तो यह भौगोलिक विषुवत वृत के समान तल में होता है, इसलिए भौगोलिक विषुवत वृत पर एक बिंदु पर ध्रुव कोण धनात्मक से नकारात्मक मान के बीच बदल सकता है।
-
विकल्प (a) गलत है क्योंकि भौगोलिक विषुवत वृत पर ध्रुव कोण हमेशा शून्य नहीं होता। ध्रुव कोण स्थान और चुंबकीय क्षेत्र के अनुपात के आधार पर बदल सकता है।
-
विकल्प (b) आंशिक रूप से सही है लेकिन पूर्ण रूप से नहीं। जबकि ध्रुव कोण कुछ बिंदुओं पर शून्य हो सकता है, लेकिन यह हमेशा शून्य नहीं होता, जिसके कारण विकल्प (a) गलत है।
-
विकल्प (c) सही है, इसलिए इसके गलत होने के लिए कोई कारण नहीं है।
-
विकल्प (d) सही है, इसलिए इसके गलत होने के लिए कोई कारण नहीं है।
बहुत छोटे उत्तर प्रकार प्रश्न
11. एक प्रोटॉन के घूर्णन और चुंबकीय आघूर्ण इलेक्ट्रॉन के जैसे होते हैं। तब भी इसका प्रभाव सामग्री के चुंबकत्व में नगण्य क्यों होता है?
उत्तर दिखाएं
सोचने की प्रक्रिया
प्रोटॉन का द्रव्यमान इलेक्ट्रॉन के द्रव्यमान से बहुत अधिक होता है, इसलिए इसका घूर्णन इलेक्ट्रॉन के घूर्णन की तुलना में नगण्य होता है।
उत्तर
प्रोटॉन और इलेक्ट्रॉन के घूर्णन की तुलना उनके चुंबकीय द्विध्रुव आघूर्ण की तुलना करके की जा सकती है, जो निम्नलिखित द्वारा दिया जा सकता है:
$$ M =\frac{e h}{4 \pi m} \text { या } M \propto \frac{1}{m}$$
$$\therefore \frac{M_{p}}{M_{e}} =\frac{m_{e}}{m_{p}}$$
$$=\frac{M_{e}}{1837 M_{e}}\left(\because \frac{e h}{4 \pi}=\text { constant }\right)$$
$$\Rightarrow \frac{M_{p}}{M_{e}} =\frac{1}{1837} \ll 1$$
$$\Rightarrow M_{p} \ll M_{e} \left(\because M_{p}=1837 m_{e}\right) $$
इसलिए, प्रोटॉन के चुंबकीय आघूर्ण का प्रभाव इलेक्ट्रॉन के चुंबकीय आघूर्ण की तुलना में नगण्य होता है।
12. एक चालू चुंबक के रूप में एक पतली सिलिंडर के आकार में एक चालू चुंबक की लंबाई $10 \mathrm{~cm}$ है और इसका $M=10^{6} \mathrm{~A} / \mathrm{m}$ है। चुंबकीय आघूर्ण धारा $I_{M}$ की गणना करें।
उत्तर दिखाएं
उत्तर
दिया गया, $M$ (चुंबकीय अनुप्रस्थता) $=10^{6} \mathrm{~A} / \mathrm{m}$.
$$ \begin{aligned} l \text { (लंबाई) } & =10 \mathrm{~cm}=10 \times 10^{-2} \mathrm{~m}=0.1 \mathrm{~m} \\ I_{M} & =\text { चुंबकीय अनुप्रस्थता धारा } \\ M & =\frac{I_{M}}{l} \\ I_{M} & =M \times l \\ & =10^{6} \times 0.1=10^{5} \mathrm{~A} \end{aligned} $$
13. $\mathrm{N}_{2}\left(\sim 5 \times 10^{-9}\right)$ (स्थिर ताप और दबाव पर) और $\mathrm{Cu}\left(\sim 10^{-5}\right)$ के विद्युत चुंबकीय प्रतिरोधकता में कोटि के अंतर को गणितीय रूप से समझाइए।
उत्तर दिखाएं
चिंतन प्रक्रिया
चुंबकीय प्रतिरोधकता एक बाहरी क्षेत्र के लिए एक चुंबकीय पदार्थ के प्रतिक्रिया के माप को दर्शाती है।
उत्तर
हम जानते हैं कि
इसके अलावा,
$$ \begin{array}{r} \text { नाइट्रोजन का घनत्व } \rho_{N2}=\frac{28 ~g}{22.4 ~L}=\frac{28 ~g}{22400 cc} \\ \text { कॉपर का घनत्व } \rho_{Cu}=\frac{8 ~g}{22.4 L}=\frac{8 ~g}{22400 cc} \end{array} $$
अब, दोनों घनत्व की तुलना करें
इसके अलावा दिया गया है
$$ \begin{aligned} \frac{\rho_{N_2}}{\rho_{{Cu}}} & =\frac{28}{22400} \times \frac{1}{8}=1.6 \times 10^{-4} \newline \ \frac{\chi_{N_{2}}}{\chi_{{Cu}}} & =\frac{5 \times 10^{-9}}{10^{-5}}=5 \times 10^{-4} \newline \ \chi & =\frac{\text { चुंबकीय अनुप्रस्थता }(M)}{\text { चुंबकीय तीव्रता }(H)} \newline \ & =\frac{\text { चुंबकीय आघूर्ण }(M) / \text { आयतन }(V)}{H} \newline \ & =\frac{M}{H V}=\frac{M}{H \text { (द्रव्यमान / घनत्व) }}=\frac{M \rho}{H m} \end{aligned} $$
हम जानते हैं कि, $\quad \chi=\frac{\text { चुंबकीय अनुप्रस्थता }(M)}{\text { चुंबकीय तीव्रता }(H)}$
$\therefore \quad \chi \propto \rho \quad\left(\because \frac{M}{H m}=\right.$ स्थिरांक $)$
अतः,
$$ \frac{{N_2}}{{{Cu}}}=\frac{\rho_{N_2}}{\rho_{Cu}}=1.6 \times 10^{-4} $$
इस प्रकार, हम कह सकते हैं कि ${N}_{2}$ और ${Cu}$ के विद्युत चुंबकीय प्रतिरोधकता में मात्रा के अंतर या मुख्य अंतर।
14. अणुओं के दृष्टिकोण से, विद्युत चुंबकीयता, प्रामाणिक चुंबकीयता और अपमाण चुंबकीयता के तापमान पर निर्भरता के बारे में चर्चा करें।
उत्तर दिखाएँ
उत्तर
चुंबकीय पदार्थ की संवेदनशीलता $\chi=\frac{I}{H}$, जहाँ $I$ वस्तु में प्रेरित चुंबकीय तीव्रता है और $H$ चुंबकीय बल है।
प्रतिचुंबकत्व एक परमाणु में इलेक्ट्रॉन के कक्षीय गति के कारण होता है, जो आवेशित क्षेत्र के विपरीत दिशा में चुंबकीय क्षेत्र उत्पन्न करता है। इसलिए, प्रतिचुंबकीय पदार्थ के परिणामी चुंबकीय क्षेत्र क्षेत्र शून्य होता है और इसलिए, प्रतिचुंबकीय पदार्थ की संवेदनशीलता $\chi$ तापमान के साथ बहुत कम प्रभावित होती है।
प्रामाणिक चुंबकत्व और अपरिवर्तनीय चुंबकत्व आवेशित क्षेत्र की दिशा में परमाणु चुंबकीय क्षेत्र के समानांतर व्यवस्था के कारण होता है। जब तापमान बढ़ता है, तो व्यवस्था विक्षेपित हो जाती है, जिसके परिणामस्वरूप दोनों की संवेदनशीलता तापमान के बढ़ने के साथ कम हो जाती है।
15. एक सुपरकंडक्टिंग पदार्थ के गेंद को तरल नाइट्रोजन में डूबाकर एक बार मैग्नेट के पास रखा जाता है।
(i) यह किस दिशा में गति करेगी?
(ii) इसके चुंबकीय क्षेत्र की दिशा क्या होगी?
उत्तर दिखाएँ
सोचने की प्रक्रिया
एक सुपरकंडक्टिंग पदार्थ और नाइट्रोजन दोनों प्रतिचुंबकीय प्रकृति के होते हैं।
उत्तर
जब कोई प्रतिचुंबकीय पदार्थ तरल नाइट्रोजन में डूबाया जाता है, तो यह फिर से प्रतिचुंबकीय पदार्थ के रूप में व्यवहार करता है। इसलिए, सुपरकंडक्टिंग पदार् फिर से प्रतिचुंबकीय पदार्थ के रूप में व्यवहार करेगा। जब यह प्रतिचुंबकीय पदार्थ बार मैग्नेट के पास रखा जाता है, तो यह चुंबकीय क्षेत्र के विपरीत दिशा में अल्प चुंबकीय बन जाएगा।
(i) इसलिए, यह विपरीत दिशा में विस्थापित होगा।
(ii) इसके चुंबकीय क्षेत्र की दिशा भी चुंबक के चुंबकीय क्षेत्र की विपरीत दिशा में होगी।
छोटे उत्तर प्रकार प्रश्न
16. एक बिंदु डाइपोल के चुंबकीय क्षेत्र के लिए गॉस के नियम की जांच करें, जहाँ डाइपोल का डाइपोल आघूर्ण $\mathbf{m}$ मूल बिंदु पर है और सतह एक गोला है जिसकी त्रिज्या $R$ है।
उत्तर दिखाएँ
उत्तर
दिए गए स्थिति के लिए चित्र बनाएं,
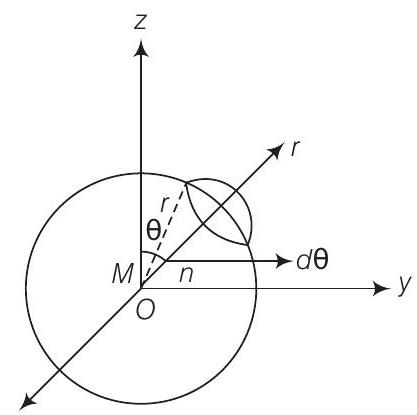
हमें सिद्ध करना है कि $\int \mathbf{B} \cdot d \mathbf{S}=0$। इसे चुंबकत्व में गॉस के नियम के रूप में जाना जाता है।
प्रश्न के अनुसार,
उत्पत्ति $O$ पर द्विध्रुव के चुंबकीय आघूर्ण के लिए
$$ \mathbf{M}=M \hat{k} $$
मान लीजिए $P$ एक बिंदु है जो $O$ से $r$ दूरी पर है और $O P$ एक कोण $\theta$ बनाता है जो $z$-अक्ष के साथ है। $\mathbf{M}$ के $O P$ के अनुदिश घटक $M \cos \theta$ है।
अब, द्विध्रुव आघूर्ण $\mathbf{M} \cos \theta$ के कारण $P$ पर चुंबकीय क्षेत्र अपवर्तन है
$$ \mathbf{B}=\frac{\mu_{0}}{4 \pi} \frac{2 M \cos \theta}{r^{3}} \hat{r} $$
चित्र से, $r$ एक गोले की त्रिज्या है जो $O$ केंद्र वाला है और जो yz-समतल में स्थित है। $P$ पर सतह के एक छोटे क्षेत्र $\mathbf{S}$ के लिए, तो
$$ \begin{aligned} d \mathbf{S} & =r(r \sin \theta d \theta) \hat{\mathbf{r}}=r^{2} \sin \theta d \theta \hat{\mathbf{r}} \\ \int \mathbf{B} \cdot d \mathbf{S} & =\oint \frac{\mu_{0}}{4 \pi} \frac{2 M \cos \theta}{r^{3}} \hat{\mathbf{r}}\left(r^{2} \sin \theta d \theta \hat{\mathbf{r}}\right) \\ & =\frac{\mu_{0}}{4 \pi} \frac{M}{r} \int_{0}^{2 \pi} 2 \sin \theta \cdot \cos \theta d \theta \\ & =\frac{\mu_{0}}{4 \pi} \frac{M}{r} \int_{0}^{2 \pi} \sin 2 \theta d \theta \\ & =\frac{\mu_{0}}{4 \pi} \frac{M}{r} \frac{-\cos 2 \theta}{2} 0 \\ & =-\frac{\mu_{0}}{4 \pi} \frac{M}{2 r}[\cos 4 \pi-\cos 0] \\ & =\frac{\mu_{0}}{4 \pi} \frac{M}{2 r}[1-1]=0 \end{aligned} $$
17. तीन समान छड़ चुंबक केंद्र पर एक ही समतल में जुड़े हुए हैं जैसा कि चित्र में दिखाया गया है। यह प्रणाली धीरे-धीरे बदलते चुंबकीय क्षेत्र में शांति में रखा गया है। यह पाया गया है कि चुंबक के प्रणाली कोई गति नहीं दिखाती है। एक चुंबक के उत्तर-दक्षिण ध्रुव चित्र में दिखाए गए हैं। बचे हुए दो चुंबकों के ध्रुवों की निर्धारण करें।
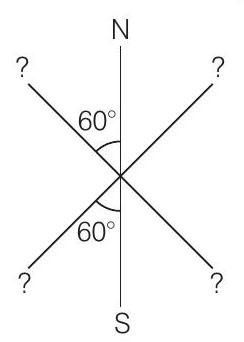
उत्तर दिखाएं
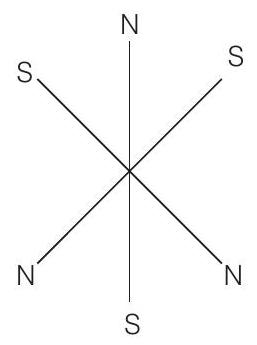
Answer
यदि प्रणाली पर नेट बल शून्य है और प्रणाली पर नेट बलाघूर्ण भी शून्य है तो प्रणाली स्थायी संतुलन में होगी। यह संभव है केवल जब बचे हुए दो चुंबकों के ध्रुव चित्र में दिखाए गए हैं।
18. मान लीजिए हम एक स्पष्ट प्रयोग के माध्यम से विद्युत स्थैतिक और चुंबक स्थैतिक के अनुपात की जांच करना चाहते हैं। (i) विद्युत द्विध्रुव $\mathbf{p}$ के विद्युत स्थैतिक क्षेत्र $\mathbf{E}$ में गति और (ii) चुंबकीय द्विध्रुव $\mathbf{M}$ के चुंबकीय क्षेत्र $\mathbf{B}$ में गति के बारे में विचार करें। $\mathbf{E}, \mathbf{B}, \mathbf{p}, \mathbf{M}$ पर एक सेट की शर्तें लिखें ताकि दोनों गतियों को समान ठहराया जा सके। (मान लीजिए समान प्रारंभिक स्थितियाँ हैं।)
उत्तर दिखाएं
चिंतन प्रक्रिया
$E(r)=c B(r)$, मान लीजिए $\mathbf{p}$ और $\mathbf{E}$ के बीच कोण $\boldsymbol{\theta}$ है। विद्युत द्विध्रुव के पल के लिए,
$\mathbf{p}$ के विद्युत क्षेत्र $\mathbf{E}$ में बलाघूर्ण,
$\tau=p E \sin \theta$।
उत्तर
अब, मान लीजिए $\mathbf{M}$ और $B$ के बीच कोण $\theta$ है।
चुंबकीय द्विध्रुव के पल के लिए $\mathbf{M}$ के चुंबकीय क्षेत्र $\mathbf{B}$ में बलाघूर्ण,
$$ \tau^{\prime}=M B \sin \theta $$
दोनों गतियाँ समान होंगी, यदि
लेकिन,
$$ \begin{aligned} p E \sin \theta & =M B \sin \theta \\ p E & =M B \\ E & =c B \end{aligned} $$
$\therefore$ इस मान को E(i) में रखने पर,
$$ \begin{gathered} p c B=M B \\ p=\frac{M}{c} \end{gathered} $$
लंबे उत्तर प्रकार प्रश्न
21. चुंबकीय द्विध्रुव के चुंबकीय क्षेत्र के लिए अम्पियर के नियम की जांच करें जिसका द्विध्रुव आघूर्ण $\mathbf{M}=M \hat{\mathbf{k}}$ है। $C$ को बंद वक्र मान लें जो घड़ी के विपरीत दिशा में चलता है
(i) $z$-अक्ष पर $z=a>0$ से $z=R$ तक,
(ii) $x z$-समतल के पहले चतुर्थांश में केंद्र मूल बिंदु पर त्रिज्या $R$ के चतुर्थांश वृत्त के अनुदिश,
(iii) $x$-अक्ष पर $x=R$ से $x=a$ तक, और
(iv) $x z$-समतल के पहले चतुर्थांश में केंद्र मूल बिंदु पर त्रिज्या $a$ के चतुर्थांश वृत्त के अनुदिश
दिखाओ उत्तर
सोचने की प्रक्रिया
हम नीचे दिए गए चित्र को ध्यान में रखते हैं
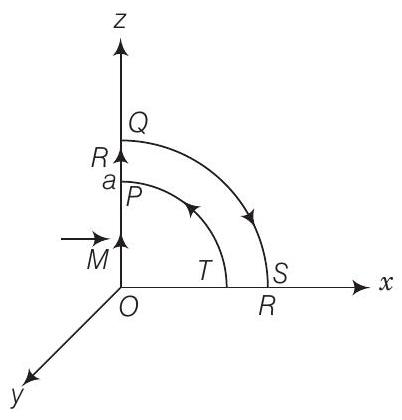
उत्तर
$P$ से $Q$ तक, $z$-अक्ष पर स्थित हर बिंदु चुंबकीय द्विध्रुव के आघूर्ण $\mathbf{M}$ की अक्ष पर स्थित है। चुंबकीय द्विध्रुव के आघूर्ण के दूरी $z$ पर चुंबकीय क्षेत्र के परिमाण के लिए,
$$ |\mathbf{B}|=\frac{\mu_{0}}{4 \pi} \frac{2|\mathbf{M}|}{z^{3}}=\frac{\mu_{0} M}{2 \pi z^{3}} $$
(i) $z$-अक्ष पर $P$ से $Q$ तक।
$$ \begin{aligned} \int_{P}^{Q} B \cdot d l & =\int_{P}^{Q} B \cdot d l \cos 0^{\circ}=\int_{P}^{Q} B d z \\
& =\int_{a}^{R} \frac{\mu_{0}}{2 \pi} \frac{M}{z^{3}} d z=\frac{\mu_{0} M}{2 \pi} \frac{-1}{2} \frac{1}{R^{2}}-\frac{1}{a^{2}} \\ & =\frac{\mu_{0} M}{4 \pi} \frac{1}{a^{2}}-\frac{1}{R^{2}} \end{aligned} $$
(ii) चित्र में दिए गए त्रिज्या $R$ के चतुर्थांश वृत्त $QS$ के अनुदिश
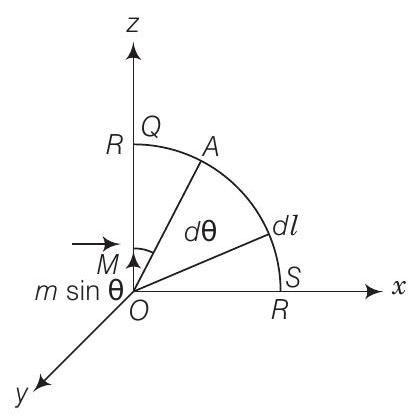
बिंदु $A$ चुंबकीय द्विध्रुवी आघूर्ण $M \sin \theta$ के ध्रुवीय रेखा पर स्थित है। बिंदु $A$ पर वृत्तीय चाप पर चुंबकीय क्षेत्र है
$$ \begin{aligned} B & =\frac{\mu_{0}}{4 \pi} \frac{M \sin \theta}{R^{3}} ; \mathrm{dl}=R d \theta \\ \therefore \quad & \int \mathrm{B} \cdot \mathrm{dl}=\int \mathrm{B} \cdot \mathrm{dl} \cos \theta=\int_{0}^{\frac{\pi}{2}} \frac{\mu_{0}}{4 \pi} \frac{M \sin \theta}{R^{3}} R d \theta \end{aligned} $$
वृत्तीय चाप $=\frac{\mu_0}{4 \pi} \frac{M}{R}(-\cos \theta)_{0}^{\pi / 2}=\frac{\mu_0}{4 \pi} \frac{M}{R^{2}}$
(iii) $x$-अक्ष के अनुदिश पथ $ST$ पर, आगे दिए गए चित्र को ध्यान में रखें
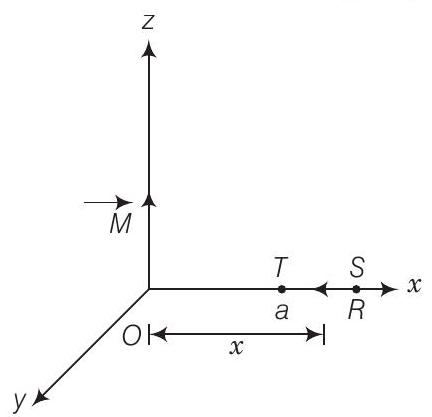
चित्र से, प्रत्येक बिंदु चुंबकीय द्विध्रुवी के ध्रुवीय रेखा पर स्थित है। द्विध्रुवी से $x$ दूरी पर बिंदु पर चुंबकीय क्षेत्र प्रेरण है
$$ \begin{aligned} & B=\frac{\mu_{0}}{4 \pi} \frac{M}{x^{3}} \\ & \therefore \quad \int_{\beta}^{T} \cdot \mathbf{d l}=\int_{R}^{a}-\frac{\mu_{0} \mathbf{M}}{4 \pi x^{3}} \cdot d \mathbf{d l}=0\left[\because \text { angle between }(-\mathbf{M}) \text { and } \mathbf{d l} \text { is } 90^{\circ}\right] \end{aligned} $$
(iv) त्रिज्या $a$ के चतुर्थांश वृत्त $TP$ के अनुदिश। नीचे दिए गए चित्र को ध्यान में रखें
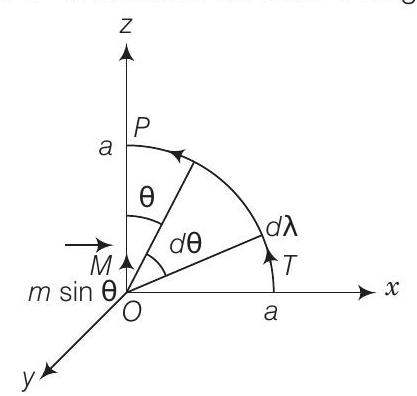
स्थिति (ii) से, हमें वृत्तीय वृत्त के चतुर्थांश $TP$ पर $\mathbf{B}$ के लिनियर समाकलन प्राप्त होता है
$$ \begin{aligned} & \int B \cdot dl = \int_{\pi / 2}^0 \frac{\mu_0}{4 \pi} \frac{M \sin \theta}{a^{3}} a d \theta \\ & =\frac{\mu_0}{4 \pi} \frac{M}{a^{2}} \int_{\pi / 2}^0 \sin \theta d \theta = \frac{\mu_0}{4 \pi} \frac{M}{a^{2}}[-\cos \theta]_{\pi / 2}^0 \\ & =\frac{-\mu_0}{4 \pi} \frac{M}{a^{2}} \\ & =\frac{\mu_0 M}{4} \frac{1}{a^{2}} - \frac{1}{R^{2}} + \frac{\mu_0}{4 \pi} \frac{M}{R^{2}} + 0 - \frac{\mu_0}{4 \pi} \frac{M}{a^{2}} = 0 \end{aligned} $$
$$ \therefore \quad \oint_{P Q S T} B \cdot d l = \int_{P}^{Q} B \cdot d l + \int_{Q}^{S} B \cdot d l + \int_{S}^{T} B \cdot d l + \int_{T}^{P} B \cdot d l $$
22. $\chi$, चुंबकीय प्रतिस्थापन के विमाएं क्या हैं? एक $\mathrm{H}$-एटम को ध्यान में रखते हुए, एक अचर के अतिरिक्त $\chi$ के विमाओं के लिए एक राशि का व्यंजक दें, जो परमाणु के पैरामीटर $e, m, v, R$ और $\mu_{0}$ से बनाई गई हो। यहाँ, $m$ इलेक्ट्रॉन के द्रव्यमान, $v$ इलेक्ट्रॉन की चाल, $R$ बोहर त्रिज्या है। इस तरह प्राप्त संख्या का अनुमान लगाएं और अनेक ठोस पदार्थों के लिए $|X| \sim 10^{-5}$ के मान के साथ तुलना करें।
उत्तर दिखाएं
चिंतन प्रक्रिया
चुंबकीय प्रतिस्थापन एक बाहरी क्षेत्र के लिए एक चुंबकीय पदार्थ के प्रतिक्रिया के माप के रूप में होता है। अर्थात, चुंबकीय प्रतिस्थापन
$$ \chi_{m} = \frac{I}{H} = \frac{(\text{चुंबकीय तीव्रता})}{(\text{चुंबकीय बल}) $$
उत्तर
क्योंकि $I$ और $H$ दोनों के एक ही इकाई और विमा होते हैं, इसलिए $\chi$ विमाहीन होता है। इस प्रश्न में $\chi$ को $e, m, v, R$ और $\mu_{0}$ से संबंधित करना है। हम जानते हैं कि $\mu_{0}$ के विमा $\left[\mathrm{ML} \theta^{-2}\right]$ होते हैं
बियॉट-सावार्ट के नियम से,
$$ \begin{aligned} d B & = \frac{\mu_{0}}{4 \pi} \frac{I d l \sin \theta}{r^{2}} \\ \Rightarrow \quad \mu_{0} & = \frac{4 \pi r^{2} d B}{I d l \sin \theta} = \frac{4 \pi r^{2}}{I d l \sin \theta} \times \frac{f}{q v \sin \theta} \quad \because d B = \frac{F}{q v \sin \theta} \\
$$ \therefore \quad \text { } \mu_{0} \text{ के } \text{ आयाम } & =\frac{L^{2} \times\left(\mathrm{MLT}^{-2}\right)}{\left(\mathrm{QT}^{-1}\right)(\mathrm{L}) \times 1 \times(\mathrm{Q})\left(\mathrm{LT}^{-1}\right) \times(1)} \newline=\left[\mathrm{MLQ}^{-2}\right] \end{aligned} $$
$$ \end{aligned} $$
जहाँ $Q$ आवेश के आयाम है।
क्योंकि $\chi$ आयामहीन है, इसके आयामी सूत्र में आवेश $Q$ की भाग नहीं लेनी चाहिए। यदि $\mu_{0}$ और $e$ मिलकर $\mu_{0} e^{2}$ के मान को देंगे, तो इस तरह होगा, क्योंकि $e$ के आयाम आवेश के होते हैं।
मान लीजिए
$$ \chi=\mu_{0} e^{2} m^{a} v^{b} R^{c} $$
जहाँ $a, b, c$ क्रमशः $m, v$ और $R$ के घात हैं, ताकि संबंध (i) संतुष्ट हो।
संबंध (i) के आयामी समीकरण है
$$ \begin{aligned} {\left[\mathrm{M}^{0} \mathrm{~L}^{0} \mathrm{~T}^{0} \mathrm{Q}^{0}\right] } & =\left[\mathrm{ML} \mathrm{Q}^{-2}\right] \times\left[\mathrm{Q}^{2}\right]\left[\mathrm{M}^{a}\right] \times\left(\mathrm{LT}^{-1}\right)^{b} \times[\mathrm{L}]^{c} \\ & =\left[\mathrm{M}^{1+a}+\mathrm{L}^{1+b+c} \mathrm{~T}^{-b} \mathrm{Q}^{0}\right] \end{aligned} $$
$M, L$ और $T$ की घातों की तुलना करने पर हम प्राप्त करते हैं
$$ \begin{aligned} & 0=1+a \Rightarrow a=-1,0=1+b+c \\ & 0=-b \Rightarrow b=0,0=1+0+c \text { या } c=-1 \end{aligned} $$
समीकरण (i) में मान रखने पर हम प्राप्त करते हैं
$$ \begin{aligned} \chi & =\mu_{0} e^{2} m^{-1} v^{2} R^{-1}=\frac{\mu_{0} e^{2}}{m R} \\ \mu_{0} & =4 \pi \times 10^{-7} \mathrm{Tm} \mathrm{A}{ }^{-1} \\ e & =1.6 \times 10^{-19} \mathrm{C} \\ m & =9.1 \times 10^{-31} \mathrm{~kg}, R=10^{-10} \mathrm{~m} \\ \chi & =\frac{\left(4 \pi \times 10^{-7}\right) \times\left(1.6 \times 10^{-19}\right)^{2}}{\left(9.1 \times 10^{-31}\right) \times 10^{-10}} \approx 10^{-4} \end{aligned} $$
$$ \therefore \quad \frac{\chi}{\chi_{\text {(given solid) }}}=\frac{10^{-4}}{10^{-5}}=10 $$
23. मान लीजिए पृथ्वी के चुंबकीय क्षेत्र $B$ के लिए द्विध्रुव मॉडल का उपयोग करें जो $B_{V}=$ चुंबकीय क्षेत्र के ऊर्ध्वाधर घटक $=\frac{\mu_{0}}{4 \pi} \frac{2 m \cos \theta}{r^{3}}$ द्वारा दिया गया है।
$B_{H}=$ चुंबकीय क्षेत्र का क्षैतिज घटक $=\frac{\mu_{0}}{4 \pi} \frac{\sin \theta m}{r^{3}}$
$\theta=90^{\circ}$-चुंबकीय विषुवत रेखा के रूप में मापी गई अक्षांश।
ज्ञात कीजिए बिंदुओं के बिंदु जहां (a) $|B|$ न्यूनतम है (b) झुकाव कोण शून्य है और (c) झुकाव कोण $45^{\circ}$ है।
उत्तर दिखाएं
उत्तर
(a)
$$ \begin{aligned} B_{V} & =\frac{\mu_{0}}{4 \pi} \frac{2 m \cos \theta}{r^{3}} \\ B_{H} & =\frac{\mu_{0}}{4 \pi} \frac{\sin \theta m}{r^{3}} \end{aligned} $$
दोनों समीकरणों के वर्ग करके जोड़ने पर हम प्राप्त करते हैं
$$ \begin{aligned} B_{V}^{2}+B_{H}^{2} & =\frac{\mu_{0}}{4 \pi} \frac{m^{2}}{r^{6}}\left[4 \cos ^{2} \theta+\sin ^{2} \theta\right] \\ B & =\sqrt{B_{V}^{2}+B_{H}^{2}}=\frac{\mu_{0}}{4 \pi} \frac{m}{r^{3}}\left[3 \cos ^{2} \theta+1\right]^{1 / 2} \end{aligned} $$
समीकरण (iii) से, $B$ का मान न्यूनतम होगा यदि $\cos \theta=\frac{\pi}{2}$
$\theta=\frac{\pi}{2}$. इसलिए, चुंबकीय विषुवत रेखा बिंदुओं का बिंदु है। (b) झुकाव कोण,
$$ \begin{aligned} & \tan \delta=\frac{B_{V}}{B_{H}}=\frac{\frac{\mu_{0}}{4 \pi} \cdot \frac{2 m \cos \theta}{r^{3}}}{\frac{\mu_{0}}{4 \pi} \cdot \frac{\sin \theta \cdot m}{r^{3}}}=2 \cot \theta \\ & \tan \delta=2 \cot \theta \end{aligned} $$
जब झुकाव कोण शून्य होता है अर्थात $\delta=0$
$$ \begin{aligned} \cot \theta & =0 \\ \theta & =\frac{\pi}{2} \end{aligned} $$
इसका अर्थ है कि बिंदु फिर से चुंबकीय विषुवत रेखा है।
(c) $\tan \delta=\frac{B_{V}}{B_{H}}$
झुकाव कोण अर्थात $\delta= \pm 45$
$$ \begin{aligned} \frac{B_{V}}{B_{H}} & =\tan \left( \pm 45^{\circ}\right) \\ \frac{B_{V}}{B_{H}} & =1 \\ 2 \cot \theta & =1 \\ \cot \theta & =\frac{1}{2} \\ \Rightarrow \quad \tan \theta & =2 \\ \quad \theta & =\tan ^{-1}(2) \end{aligned} $$
इसलिए, $\theta=\tan ^{-1}(2)$ बिंदु है।
24. चुंबकीय अक्ष और पृथ्वी के अक्ष द्वारा बने तल $S$ को विचार करें। मान लीजिए $P$ चुंबकीय विषुवत रेखा पर और $S$ में स्थित बिंदु है। $Q$ भौगोलिक और चुंबकीय विषुवत रेखा के प्रतिच्छेद बिंदु है। $P$ और $Q$ पर विवरण और झुकाव कोण ज्ञात कीजिए।
उत्तर दिखाएँ
उत्तर
$P$ समतल $S$ में है, सुई उत्तर दिशा में है, इसलिए विस्थापन शून्य है।
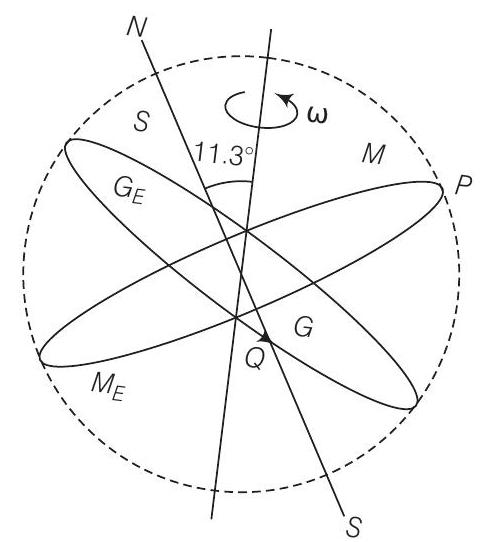
$P$ चुंबकीय भू-ध्रुव भी है, इसलिए झुकाव कोण $=0$, क्योंकि भू-ध्रुव पर झुकाव कोण का मान शून्य होता है। $Q$ भी चुंबकीय भू-ध्रुव पर है, इसलिए झुकाव कोण शून्य है। पृथ्वी अपने अक्ष पर $11.3^{\circ}$ झुकी हुई है, इसलिए $Q$ पर विस्थापन कोण $11.3^{\circ}$ है।
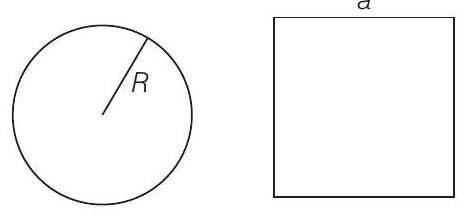
25. दो धारा वाहक समतल कुंडल हैं, जो प्रत्येक एक समान तार के बने हैं जिसकी लंबाई $L$ है। $C_{1}$ वृत्ताकार है (त्रिज्या $R$) और $C_{2}$ वर्गाकार है (भुजा $a$)। ये इस तरह बनाए गए हैं कि जब वे एक ही समान एकसमान $\mathbf{B}$ में रखे जाते हैं और एक ही धारा वाहक होते हैं, तो उनका आवर्तन आवृत्ति समान होती है। $a$ को $R$ के अनुसार ज्ञात कीजिए।
उत्तर दिखाएँ
उत्तर
$C_{1}=$ त्रिज्या $R$ के वृत्ताकार कुंडल, लंबाई $L$, इकाई लंबाई पर फेरों की संख्या
$$ n_{1}=\frac{L}{2 \pi R} $$
$C_{2}=$ भुजा $a$ के वर्ग और परिमाप $L$, इकाई लंबाई पर फेरों की संख्या $n_{2}=\dfrac{L}{4 a}$
$C_{1}$ का चुंबकीय आघूर्ण
$$ m_{1}=n_{1} I A_{1} $$
$\Rightarrow$ $C_{2}$ का चुंबकीय आघूर्ण
$$ \begin{aligned} m_{2} & =n_{2} I A_{2} \\ m_{1} & =\frac{L \cdot I \cdot \pi R^{2}}{2 \pi R} \\ m_{2} & =\frac{L}{4 a} \cdot I \cdot a^{2} \\ m_{1} & =\frac{L I R}{2} \\ m_{2} & =\frac{L I a}{4} \end{aligned} $$
$C_{1}$ के जड़त्व आघूर्ण $\Rightarrow I_{1}=\frac{M R^{2}}{2}$
$C_{2}$ के जड़त्व आघूर्ण $\Rightarrow I_{2}=\frac{M a^{2}}{12}$
$C_{1}$ की आवृत्ति $\Rightarrow t_{1}=2 \pi \sqrt{\frac{I_{1}}{m_{1} B}}$
$C_{2}$ की आवृत्ति $\Rightarrow f_{2}=2 \pi \sqrt{\frac{I_{2}}{m_{2} B}}$
प्रश्न के अनुसार, $f_{1}=f_{2}$
$$ \begin{aligned} 2 \pi \sqrt{\frac{I_{1}}{m_{1} B}} & =2 \pi \sqrt{\frac{I_{2}}{m_{2} B}} \\ \frac{I_{1}}{m_{1}} & =\frac{I_{2}}{m_{2}} \text { या } \frac{m_{2}}{m_{1}}=\frac{I_{2}}{I_{1}} \end{aligned} $$
समीकरण (i), (ii), (iii) और (iv) के मान उपयोग करके प्रतिस्थापित करने पर
$$ \begin{aligned} \frac{L I a \cdot 2}{4 \times L I R} & =\frac{M a^{2} \cdot 2}{12 \cdot M R^{2}} \\ \frac{a}{2 R} & =\frac{a^{2}}{6 R^{2}} \\ 3 R & =a \end{aligned} $$
इस प्रकार, $a$ का मान $3 R$ है।





