बहुविकल्पीय प्रश्न (MCQs)
1. कार्बन मोनोऑक्साइड अणु को कार्बन और ऑक्सीजन परमाणु में विखंडित करने के लिए $11 eV$ ऊर्जा की आवश्यकता होती है। विखंडन के लिए उपयुक्त विद्युत चुम्बकीय विकिरण की न्यूनतम आवृत्ति निम्नलिखित में से किस क्षेत्र में होगी?
(a) दृश्य क्षेत्र
(c) अवरक्त क्षेत्र
(b) अवलोकनी क्षेत्र
(d) माइक्रोवेव क्षेत्र
उत्तर दिखाएं
उत्तर
(c) दिया गया है, कार्बन मोनोऑक्साइड अणु को कार्बन और ऑक्सीजन परमाणु में विखंडित करने के लिए आवश्यक ऊर्जा $E=11 eV$
हम जानते हैं कि, $E=h \nu$, जहाँ $h=6.62 \times 10^{-34} J$-s
$$ \begin{aligned} \Rightarrow \quad 11 eV & =h \nu \\ v & =\dfrac{11 \times 1.6 \times 10^{-19}}{h} J \\ & =\dfrac{11 \times 1.6 \times 10^{-19}}{6.62 \times 10^{-34}} J \\ & =2.65 \times 10^{15} Hz \end{aligned} $$
इस आवृत्ति के विकिरण क्षेत्र अवरक्त क्षेत्र में होते हैं।
-
दृश्य क्षेत्र: विद्युत चुम्बकीय विकिरण के दृश्य क्षेत्र की आवृत्ति लगभग $4 \times 10^{14}$ Hz से $7.5 \times 10^{14}$ Hz के बीच होती है। गणना की गई आवृत्ति $2.65 \times 10^{15}$ Hz इस श्रेणी से बहुत अधिक है, इसलिए विकिरण दृश्य क्षेत्र में नहीं होगा।
-
अवरक्त क्षेत्र: विद्युत चुम्बकीय विकिरण के अवरक्त क्षेत्र की आवृत्ति लगभग $3 \times 10^{11}$ Hz से $4 \times 10^{14}$ Hz के बीच होती है। गणना की गई आवृत्ति $2.65 \times 10^{15}$ Hz इस श्रेणी से बहुत अधिक है, इसलिए विकिरण अवरक्त क्षेत्र में नहीं होगा।
-
माइक्रोवेव क्षेत्र: विद्युत चुम्बकीय विकिरण के माइक्रोवेव क्षेत्र की आवृत्ति लगभग $3 \times 10^{9}$ Hz से $3 \times 10^{11}$ Hz के बीच होती है। गणना की गई आवृत्ति $2.65 \times 10^{15}$ Hz इस श्रेणी से बहुत अधिक है, इसलिए विकिरण माइक्रोवेव क्षेत्र में नहीं होगा।
2. एक रैखिक ध्रुवीकृत विद्युत चुम्बकीय तरंग $\mathbf{E}=E_0 \hat{\mathbf{i}} \cos (k z-\omega t)$ दी गई है जो $z=a$ पर एक पूर्णतः प्रतिध्वनि देने वाली अपरिमित दीवार पर अभिलम्बवत आपतित होती है। मान लीजिए कि दीवार के पदार्थ का अपवर्णन गुण नहीं है, तो प्रतिध्वनित तरंग को निम्नलिखित में से कौन देगी?
$\newline$
(a)$ r=E_{o} \hat{i}(k z-\omega t)$ $\newline$
(b)$ r=E_{o} \hat{i} \cos (k z+\omega t)$ $\newline$
(c)$ r=-E_{o} \hat{i} \cos (k z+\omega t)$ $\newline$
(d)$ r=E_{o} \hat{i} \sin (k z-\omega t)$ $\newline$
उत्तर दिखाएँ
सोचने की प्रक्रिया
जब एक तरंग घनत्व अधिक माध्यम से परावर्तित होती है, तो इसका चरण $180^{\circ}$ या $\pi$ के द्वारा बदल जाता है।
उत्तर
(b) जब एक तरंग घनत्व अधिक माध्यम से परावर्तित होती है, तो तरंग का प्रकार बदल नहीं जाता लेकिन इसका केवल चरण $180^{\circ}$ या $\pi$ रेडियन द्वारा बदल जाता है।
इसलिए, परावर्तित तरंग के लिए $\hat{\mathbf{z}}=-\hat{\mathbf{z}}, \hat{\mathbf{i}}=-\hat{\mathbf{i}}$ और आपतित तरंग में अतिरिक्त चरण $\pi$ होता है।
दिया गया है, यहाँ आपतित विद्युत चुंबकीय तरंग है,
$$ \mathbf{E}=E_0 \hat{\mathbf{i}} \cos (k z-\omega t) $$
परावर्तित विद्युत चुंबकीय तरंग द्वारा दिया गया है
$$ \begin{aligned} r & =E_0(\hat{i}) \cos [k(-z)-\omega t+\pi] \\ & =-E_0 \hat{i} \cos [-(k z+\omega t)+\pi] \\ & =E_0 \hat{i} \cos [-(k_{z}+\omega t)=E_0 \hat{\mathbf{i}} \cos (k z+\omega t)] \end{aligned} $$
-
विकल्प (a): दी गई अभिव्यक्ति $r=E_{o} \hat{i}(k z-\omega t)$ है। यह गलत है क्योंकि इसमें कोसाइन फलन का प्रतिनिधित्व नहीं होता है और परावर्तन के दौरान चरण परिवर्तन के लिए गणना नहीं की गई है। परावर्तित तरंग में कोसाइन फलन के साथ चरण परिवर्तन $\pi$ होना चाहिए।
-
विकल्प (c): दी गई अभिव्यक्ति $r=-E_{o} \hat{i} \cos (k z+\omega t)$ है। यह गलत है क्योंकि $E_0 \hat{i}$ के सामने नकारात्मक चिह्न आवश्यक नहीं है। सही परावर्तित तरंग में आपतित तरंग के समान आयाम और दिशा होनी चाहिए लेकिन चरण परिवर्तन $\pi$ होता है, जो कोसाइन फलन में शामिल हो चुका है।
-
विकल्प (d): दी गई अभिव्यक्ति $r=E_{o} \hat{i} \sin (k z-\omega t)$ है। यह गलत है क्योंकि परावर्तित तरंग अभी भी कोसाइन फलन होना चाहिए, न कि साइन फलन। परावर्तन के दौरान तरंग का रूप बदल नहीं जाता, केवल चरण बदल जाता है।
3. एक ऊर्जा फ्लक्स वाली प्रकाश तरंग $20 W / cm^{2}$ के अनुप्रस्थ आपतन पर एक अप्रतिध्वनि सतह पर आपतित होती है। यदि सतह का क्षेत्रफल $30 cm^{2}$ है, तो $30 min$ के लिए पूर्ण अवशोषण के दौरान दिया गया कुल संवेग है
$\newline$
(a) $36 \times 10^{-5} kg-m / s$ $\newline$
(b) $36 \times 10^{-4} kg-m / s$ $\newline$
(c) $108 \times 10^{4} kg-m / s$ $\newline$
(d) $1.08 \times 10^{7} kg-m / s$ $\newline$
उत्तर दिखाएं
उत्तर
(b) दिया गया, ऊर्जा फ्लक्स $\phi=20 W / cm^{2}$
क्षेत्रफल, $\quad A=30 cm^{2}$
समय, $\quad t=30 min=30 \times 60 s$
अब, समय $t$ में सतह पर पड़ने वाली कुल ऊर्जा, $U=\phi A t=20 \times 30 \times(30 \times 60) J$
आपतित प्रकाश का संवेग $=\dfrac{U}{C}$
$$ =\dfrac{20 \times 30 \times(30 \times 60)}{3 \times 10^{8}} \Rightarrow=36 \times 10^{-4} kg-ms^{-1} $$
प्रतिबिंबित प्रकाश का संवेग $=0$
$\therefore$ सतह को स्थानांतरित संवेग
$$ =36 \times 10^{-4}-0=36 \times 10^{-4} kg-ms^{-1} $$
-
विकल्प (a): मान $36 \times 10^{-5} kg-m / s$ गलत है क्योंकि यह कुल संवेग के अंतर को अति अल्प अनुमानित करता है। सही गणना दर्शाती है कि संवेग के अंतर $36 \times 10^{-4} kg-m / s$ है, जो एक आदेश अधिक है।
-
विकल्प (c): मान $108 \times 10^{4} kg-m / s$ गलत है क्योंकि यह कुल संवेग के अंतर को बहुत अधिक अनुमानित करता है। सही गणना दर्शाती है कि संवेग के अंतर $36 \times 10^{-4} kg-m / s$ है, जो कई आदेश अधिक छोटा है।
-
विकल्प (d): मान $1.08 \times 10^{7} kg-m / s$ गलत है क्योंकि यह भी कुल संवेग के अंतर को बहुत अधिक अनुमानित करता है। सही गणना दर्शाती है कि संवेग के अंतर $36 \times 10^{-4} kg-m / s$ है, जो कई आदेश अधिक छोटा है।
4. $100 W$ बल्ब से आने वाले विकिरणों द्वारा एक $3 m$ दूरी पर उत्पन्न विद्युत क्षेत्र तीव्रता $E$ है। $50 W$ बल्ब से आने वाले विकिरणों द्वारा एक ही दूरी पर उत्पन्न विद्युत क्षेत्र तीव्रता है:
(a) $\dfrac{E}{2}$
(b) $2 E$
(c) $\dfrac{E}{\sqrt{2}}$
(d) $\sqrt{2} E$
उत्तर दिखाएं
सोचने की प्रक्रिया
किसी सतह पर आपतित विकिरणों के कारण विद्युत क्षेत्र तीव्रता है,
$$ \begin{aligned}
I_{av} \propto E_o^2 \\ \dfrac{P_{av .}}{A} \propto E_o^2 \\ \end{aligned} $$
यहाँ,
$$ P_{a v} \propto E_0^{2} \quad[\because A \text { दोनों मामलों में समान है }] $$
उत्तर
(c) हम जानते हैं कि,
$$ E_0 \propto \sqrt{P_{av}} $$
$\dfrac{(E_O)_1}{(E_O)_2} = \sqrt{\dfrac{(P_a{av})_1} {(P_a{av})_2} \Rightarrow \dfrac{E}{E_O}_2} = \sqrt{\dfrac{1000}{5}} \\ $
प्रश्न के अनुसार, P=50 W, P=100 W
$\therefore \quad$ समीकरण (i) में इन मानों को रखने पर, हम प्राप्त करते हैं
$$ \dfrac{E^{\prime}}{E}=\dfrac{50}{100} \Rightarrow \dfrac{E^{\prime}}{E}=\dfrac{1}{2} \Rightarrow E^{\prime}=\dfrac{E}{2} $$
-
विकल्प (a) $\dfrac{E}{2}$: यह विकल्प गलत है क्योंकि इसका सुझाव है कि विद्युत क्षेत्र की तीव्रता शक्ति के सीधे अनुपात में होती है। हालांकि, विद्युत क्षेत्र की तीव्रता शक्ति के वर्गमूल के अनुपात में होती है, न कि शक्ति के अनुपात में। अतः शक्ति को आधा करने से विद्युत क्षेत्र की तीव्रता के आधा नहीं होता।
-
विकल्प (b) $2E$: यह विकल्प गलत है क्योंकि इसका सुझाव है कि विद्युत क्षेत्र की तीव्रता शक्ति के सीधे अनुपात में होती है। विद्युत क्षेत्र की तीव्रता शक्ति के वर्गमूल के अनुपात में होती है, अतः शक्ति को दोगुना करने से विद्युत क्षेत्र की तीव्रता के दोगुना नहीं होता।
-
विकल्प (d) $\sqrt{2}E$: यह विकल्प गलत है क्योंकि इसका सुझाव है कि विद्युत क्षेत्र की तीव्रता शक्ति के वर्गमूल के अनुपात में होती है जिसके परिणामस्वरूप एक $\sqrt{2}$ गुना कारक होता है। हालांकि, 50 W के बल्ब के तुलनात्मक रूप से 100 W के बल्ब के लिए सही कारक $\dfrac{1}{\sqrt{2}}$ होता है, न कि $\sqrt{2}$।
5. यदि $\mathbf{E}$ और $\mathbf{B}$ विद्युत तथा चुंबकीय क्षेत्र वेक्टर हों, तो विद्युत चुंबकीय तरंग के प्रसार की दिशा किस दिशा में होती है?
(a) $\mathbf{E}$
(b) $\mathbf{B}$
(c) $\mathbf{B} \times \mathbf{E}$
(d) $\mathbf{E} \times \mathbf{B}$
उत्तर दिखाएं
उत्तर
(d) विद्युत चुंबकीय तरंग के प्रसार की दिशा विद्युत क्षेत्र वेक्टर $\mathbf{E}$ और चुंबकीय क्षेत्र वेक्टर $\mathbf{B}$ दोनों के लंबवत होती है, अर्थात $\mathbf{E} \times \mathbf{B}$ की दिशा में।
इसे नीचे दिए गए चित्र द्वारा देखा जा सकता है
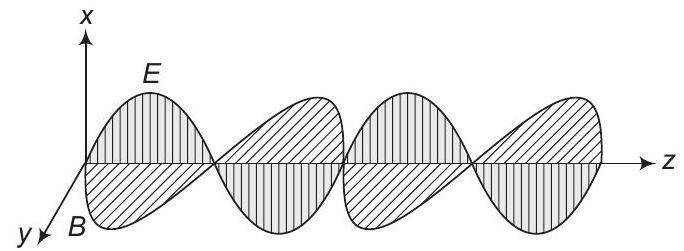
यहाँ, विद्युतचुम्बकीय तरंग $z$-दिशा में है जो $\mathbf{E}$ और $\mathbf{B}$ के क्रॉस गुणनफल द्वारा दिया गया है।
-
(a) $\mathbf{E}$: विद्युतचुम्बकीय तरंग की चलन दिशा विद्युत क्षेत्र सदिश $\mathbf{E}$ के समान नहीं होती। विद्युत क्षेत्र सदिश $\mathbf{E}$ तरंग के चलन दिशा के लंबवत दोलन करता है।
-
(b) $\mathbf{B}$: विद्युतचुम्बकीय तरंग की चलन दिशा चुम्बकीय क्षेत्र सदिश $\mathbf{B}$ के समान नहीं होती। चुम्बकीय क्षेत्र सदिश $\mathbf{B}$ तरंग के चलन दिशा के लंबवत दोलन करता है।
-
(c) $\mathbf{B} \times \mathbf{E}$: विद्युतचुम्बकीय तरंग की चलन दिशा $\mathbf{B} \times \mathbf{E}$ के समान नहीं होती। चलन दिशा देने वाला सही क्रॉस गुणनफल $\mathbf{E} \times \mathbf{B}$ होता है, न कि $\mathbf{B} \times \mathbf{E}$।
6. विद्युतचुम्बकीय तरंग की तीव्रता के लिए विद्युत क्षेत्र और चुम्बकीय क्षेत्र के घटकों द्वारा किए गए योग का अनुपात है
(a) $c: 1$
(b) $c^{2}: 1$
(c) $1: 1$
(d) $\sqrt{c}: 1$
उत्तर दिखाएं
सोचने की प्रक्रिया
विद्युतचुम्बकीय तरंग की तीव्रता, $I=U_{a v} c$
जहाँ, $\quad U_{a v}=$ औसत ऊर्जा
और $\quad c=$ प्रकाश की चाल
उत्तर
(c) विद्युत क्षेत्र के अनुसार तीव्रता $U_{av}=\dfrac{1}{2} \varepsilon_0 E_0^{2}$
चुम्बकीय क्षेत्र के अनुसार तीव्रता $U_{av}=\dfrac{1}{2} \dfrac{B_0^{2}}{\mu_0}$
अब विद्युत क्षेत्र के अनुसार तीव्रता लेते हैं।
$$ \quad(U_{\text{av}}) \text{ विद्युत क्षेत्र } =\dfrac{1}{2} E_0^{2} $$ $$=\dfrac{1}{2} (c B_0)^{2} \quad(\because E_0=c B_0) =\dfrac{1}{2} \times c^{2} B^{2} $$
$$\text { लेकिन, } \quad =\dfrac{1}{\sqrt{\mu_0 }} \therefore\quad(U_{\text{av}})_{\text {विद्युत क्षेत्र }}$$
इसलिए, विद्युत चुंबकीय तरंग के ऊर्जा के बीच विद्युत क्षेत्र सदिश और चुंबकीय क्षेत्र सदिश के बीच समान विभाजित होती है।
इसलिए, विद्युत क्षेत्र और चुंबकीय क्षेत्र के घटकों द्वारा विद्युत चुंबकीय तरंग की तीव्रता के योगदान के अनुपात $1: 1$ होता है।
-
विकल्प (a) $c: 1$: यह विकल्प गलत है क्योंकि इसका अर्थ है कि विद्युत क्षेत्र के योगदान की तीव्रता चुंबकीय क्षेत्र के योगदान की तीव्रता के $c$ गुना होती है। हालांकि, विद्युत चुंबकीय तरंग में विद्युत और चुंबकीय क्षेत्र के योगदान बराबर होते हैं, न कि प्रकाश की गति $c$ के अनुपात में।
-
विकल्प (b) $c^{2}: 1$: यह विकल्प गलत है क्योंकि इसका अर्थ है कि विद्युत क्षेत्र के योगदान की तीव्रता चुंबकीय क्षेत्र के योगदान की तीव्रता के $c^2$ गुना होती है। यह सत्य नहीं है, क्योंकि योगदान बराबर होते हैं। $c^2$ कारक विद्युत और चुंबकीय क्षेत्र के परिमाण के बीच संबंध में आता है, लेकिन तीव्रता के योगदान में नहीं।
-
विकल्प (d) $\sqrt{c}: 1$: यह विकल्प गलत है क्योंकि इसका अर्थ है कि विद्युत क्षेत्र के योगदान की तीव्रता चुंबकीय क्षेत्र के योगदान की तीव्रता के $\sqrt{c}$ गुना होती है। यह सही नहीं है, क्योंकि योगदान बराबर होते हैं। विद्युत चुंबकीय तरंग की तीव्रता के योगदान के संदर्भ में $\sqrt{c}$ का कोई संबंध नहीं होता।
7. एक डायोड एंटीना से विद्युत चुंबकीय तरंग बाहर फैलती है, जिसके विद्युत क्षेत्र सदिश के आम्प्लीट्यूड को $E_{o}$ के रूप में दर्शाया जाता है। विद्युत क्षेत्र $E_0$ जो उत्सर्जन के स्रोत से महत्वपूर्ण ऊर्जा को पहुंचाता है, दूरी $(r)$ के व्युत्क्रमानुपाती रूप से घटता है।
(a) $\dfrac{1}{r^{3}}$ $\newline$
(b) $\dfrac{1}{r^{2}}$ $\newline$
(c) $\dfrac{1}{r}$ $\newline$
(d) निरंतर रहता है $\newline$
उत्तर दिखाएं
उत्तर
(c) एक डायोड एंटीना से विद्युत चुंबकीय तरंग बाहर फैलती है।
स्रोत से महत्वपूर्ण ऊर्जा को पहुंचाने वाले विद्युत क्षेत्र सदिश $(E_0)$ के आम्प्लीट्यूड का घटता हुआ तीव्रता एंटीना से दूरी $(r)$ के व्युत्क्रमानुपाती होती है, अर्थात $E_0 \propto \dfrac{1}{r}$.
-
(a) $\dfrac{1}{r^{3}}$: यह विकल्प गलत है क्योंकि एक डाइपोल एंटीना से विस्तारित विद्युत चुंबकीय तरंग के विद्युत क्षेत्र का मान दूरी के घन के व्युत्क्रमानुपाती नहीं होता। $\dfrac{1}{r^3}$ आश्रितता आमतौर पर एंटीना के पास क्षेत्र (near-field region) से संबंधित होती है, जहां प्रतिक्रिया क्षेत्र बहुत महत्वपूर्ण होते हैं, न कि ऊर्जा के दूर तक पहुंचने वाले विस्तारित क्षेत्रों से।
-
(b) $\dfrac{1.}{r^{2}}$: यह विकल्प गलत है क्योंकि $\dfrac{1}{r^2}$ आश्रितता विद्युत चुंबकीय तरंग के शक्ति घनत्व (क्षमता घनत्व) की विशेषता होती है, न कि विद्युत क्षेत्र के आयाम। शक्ति घनत्व दूरी के वर्ग के व्युत्क्रमानुपाती होता है, लेकिन विद्युत क्षेत्र के आयाम दूरी के रेखीय रूप से घटते हैं।
-
(d) स्थिर रहता है: यह विकल्प गलत है क्योंकि इसका अर्थ है कि विद्युत क्षेत्र के आयाम दूरी के साथ घटते नहीं हैं, जो तरंग प्रसार के मूल सिद्धांतों के विरोधाभास है। जब तरंग बाहर फैलती है, तो ऊर्जा बड़े क्षेत्र में फैल जाती है, जिसके कारण विद्युत क्षेत्र के आयाम दूरी के साथ घटते हैं।
8. एक विद्युत चुंबकीय तरंग निर्वात में $z$-दिशा में चलती है $\mathbf{E}=(E_1 \hat{\mathbf{i}} + E_2 \hat{\mathbf{j}}) \cos (k z-\omega t)$. निम्नलिखित में से सही विकल्प चुनें
(a) संबद्ध चुंबकीय क्षेत्र निम्नलिखित द्वारा दिया जाता है
$$ \mathbf{B}=\dfrac{1}{C}(E_1 \hat{\mathbf{i}}-E_2 \hat{\mathbf{j}}) \cos (k z-\omega t) $$
(b) संबद्ध चुंबकीय क्षेत्र निम्नलिखित द्वारा दिया जाता है
$$ \mathbf{B}=\dfrac{1}{C}(E_1 \hat{\mathbf{i}}-E_2 \hat{\mathbf{j}}) \cos (k z-\omega t) $$
(c) दिया गया विद्युत चुंबकीय क्षेत्र वृत्तीय ध्रुवीय है
(d) दिया गया विद्युत चुंबकीय तरंग तल ध्रुवीय है
उत्तर दिखाएं
सोचने की प्रक्रिया
मैक्सवेल के समीकरणों से यह देखा जा सकता है कि एक विद्युत चुंबकीय तरंग में विद्युत और चुंबकीय क्षेत्र के मान निम्नलिखित रूप में संबंधित होते हैं
$$ B_0=\dfrac{E_0}{c} $$
उत्तर
(d) यहां, विद्युत चुंबकीय तरंग में विद्युत क्षेत्र सदिश निम्नलिखित द्वारा दिया गया है,
$$ \mathbf{E}=(E_1 \hat{\mathbf{i}}+E_2 \hat{\mathbf{j}}) \cos (k z-\omega t)
$$
विद्युत चुम्बकीय तरंग में संगत चुम्बकीय क्षेत्र सदिश,
$$ \mathbf{B}=\dfrac{E}{C}=\dfrac{E_1 \hat{i}+E_2 \hat{j}}{c} \cos (k z-\omega t) $$
इसके अतिरिक्त, $\mathbf{E}$ और $\mathbf{B}$ एक दूसरे के लंबवत होते हैं और विद्युत चुम्बकीय तरंग का प्रसार $\mathbf{E}$ और $\mathbf{B}$ दोनों के लंबवत होता है, इसलिए दी गई विद्युत चुम्बकीय तरंग समतल ध्रुवीय होती है।
-
विकल्प (a) गलत है क्योंकि चुम्बकीय क्षेत्र सदिश $\mathbf{B}$ विद्युत क्षेत्र सदिश $\mathbf{E}$ और प्रसार की दिशा के लंबवत होना चाहिए। विकल्प (a) में दिए गए चुम्बकीय क्षेत्र के व्यंजक इस शर्त को संतुष्ट नहीं करता है।
-
विकल्प (b) विकल्प (a) के समान कारणों से गलत है। चुम्बकीय क्षेत्र सदिश $\mathbf{B}$ विद्युत क्षेत्र सदिश $\mathbf{E}$ और प्रसार की दिशा के लंबवत होना चाहिए, जो दिए गए व्यंजक में नहीं है।
-
विकल्प (c) गलत है क्योंकि दिए गए विद्युत क्षेत्र सदिश $\mathbf{E}=(E_1 \hat{\mathbf{i}}+E_2 \hat{\mathbf{j}}) \cos (k z-\omega t)$ दो लंबवत घटकों के एक रैखिक संयोजन को प्रस्तुत करता है, जिनके अम्प्लीट्यूड $E_1$ और $E_2$ स्थिर हैं। यह इंगित करता है कि तरंग रैखिक ध्रुवीय है, न कि वृत्तीय ध्रुवीय। वृत्तीय ध्रुवीयता के लिए विद्युत क्षेत्र घटकों के बीच अंतर फेज अंतर $\pi/2$ होना चाहिए और अम्प्लीट्यूड बराबर होना चाहिए, जो इस मामले में नहीं है।
बहुविकल्पीय प्रश्न (एक से अधिक विकल्प)
9. $z$-अक्ष के अनुदिश चल रही एक विद्युत चुम्बकीय तरंग को $\mathbf{E}=\mathbf{E}_{0} \cos (k z-\omega t)$ दिया गया है। निम्नलिखित में से सही विकल्प चुनें
(a) संगत चुम्बकीय क्षेत्र दिया गया है $B=\dfrac{1}{C} \hat{\mathbf{k}} \times \mathbf{E}=\dfrac{1}{\omega}(\hat{\mathbf{k}} \times \mathbf{E})$
(b) विद्युत चुम्बकीय क्षेत्र को संगत चुम्बकीय क्षेत्र के रूप में लिखा जा सकता है $\mathbf{E}=c(\mathbf{B} \times \hat{\mathbf{k}})$
(c) $\hat{\mathbf{k}} \cdot \mathbf{E}=0, \hat{\mathbf{k}} \cdot \mathbf{B}=0$
(d) $\hat{\mathbf{k}} \times \mathbf{E}=0, \hat{\mathbf{k}} \times \mathbf{B}=0$
उत्तर दिखाएँ
सोचने की प्रक्रिया
दिया गया है, $E=E_{0} \cos (k z-w t)$. इसलिए, यह नकारात्मक y-दिशा में कार्य करता है।
उत्तर
$(a, b, c)$
मान लीजिए एक विद्युत चुम्बकीय तरंग नकारात्मक z-दिशा में चल रही है। इसके विद्युत क्षेत्र को निम्न द्वारा दिया गया है
$$ \mathbf{E}=E_{0} \cos (k z-\omega t) $$
जो $z$-अक्ष के लंबवत है। यह नकारात्मक $y$-दिशा में कार्य करता है।
विद्युत चुम्बकीय तरंग में संगत चुम्बकीय क्षेत्र $\mathbf{B}$ x-अक्ष के अनुदिश होता है, अर्थात $\hat{\mathbf{k}} \times \mathbf{E}$ के अनुदिश होता है।
$$ \begin{array}{ll} \text { जैसे कि, } & B_{0}=\dfrac{E_{0}}{C} \\ \therefore & B=\dfrac{1}{C}(\hat{\mathbf{k}} \times \mathbf{E}) \end{array} $$
संगत विद्युत क्षेत्र को चुम्बकीय क्षेत्र के रूप में लिखा जा सकता है
$$ \mathbf{E}=c(\mathbf{B} \times \hat{\mathbf{k}}) $$
$\hat{\mathbf{k}}$ और $\mathbf{E}$ के बीच कोण $90^{\circ}$ है, $\hat{\mathbf{k}}$ और $\mathbf{B}$ के बीच कोण $90^{\circ}$ है। इसलिए, $\mathbf{E}=1 E \cos 90^{\circ}=0$ और $\hat{\mathbf{k}} \cdot \mathbf{B}=1 E \cos 90^{\circ}=0$
- विकल्प (d) गलत है क्योंकि एक विद्युत चुम्बकीय तरंग में, विद्युत क्षेत्र $\mathbf{E}$ और चुम्बकीय क्षेत्र $\mathbf{B}$ दोनों प्रसार दिशा $\hat{\mathbf{k}}$ के लंबवत होते हैं। इसलिए, $\hat{\mathbf{k}} \times \mathbf{E}$ और $\hat{\mathbf{k}} \times \mathbf{B}$ निरा नहीं होते। वास्तव में, $\hat{\mathbf{k}} \times \mathbf{E}$ चुम्बकीय क्षेत्र $\mathbf{B}$ की दिशा देता है, और $\hat{\mathbf{k}} \times \mathbf{B}$ विद्युत क्षेत्र $\mathbf{E}$ की दिशा देता है।
10. एक समतल विद्युत चुम्बकीय तरंग जो x-दिशा में चल रही है, के लिए निम्नलिखित $\mathbf{E}$ और $\mathbf{B}$ के युग्म हो सकते हैं। $\newline$
उत्तर दिखाएँ
उत्तर
$(b, d)$ $\newline$
(a) $E_{x}, B_{y}$ $\newline$
(b) $E_{y}, B_{z}$ $\newline$
(c) $B_{x}, E_{y}$ $\newline$
(d) $E_{z}, B_{y}$ $\newline$
विद्युत और चुम्बकीय क्षेत्र वेक्टर $\mathbf{E}$ और $\mathbf{B}$ एक दूसरे के लंबवत होते हैं और विद्युत चुम्बकीय तरंग के प्रसार दिशा के लंबवत होते हैं।
यहाँ प्रश्न में विद्युत चुम्बकीय तरंग $x$-दिशा में चल रही है। इसलिए, विद्युत और चुम्बकीय क्षेत्र वेक्टर या तो $y$-दिशा या $z$-दिशा में होने चाहिए। $\newline$
-
(a) $E_{x}, B_{y}$: यह विकल्प गलत है क्योंकि विद्युत क्षेत्र वेक्टर $\mathbf{E}$ $x$-दिशा में है, जो विद्युत चुम्बकीय तरंग के प्रसार दिशा के समान है। एक समतल विद्युत चुम्बकीय तरंग के लिए, विद्युत क्षेत्र वेक्टर $\mathbf{E}$ प्रसार दिशा के लंबवत होना चाहिए।
-
(c) $B_{x}, E_{y}$: यह विकल्प गलत है क्योंकि चुम्बकीय क्षेत्र वेक्टर $\mathbf{B}$ $x$-दिशा में है, जो विद्युत चुम्बकीय तरंग के प्रसार दिशा के समान है। एक समतल विद्युत चुम्बकीय तरंग के लिए, चुम्बकीय क्षेत्र वेक्टर $\mathbf{B}$ प्रसार दिशा के लंबवत होना चाहिए।
11. एक आवेशित कण अपने माध्य संतुलन स्थिति के चारों ओर $10^{9} \mathrm{~Hz}$ की आवृत्ति से आवर्ती गति करता है। उत्पन्न विद्युत चुम्बकीय तरंग $\newline$
(a) $10^{9} \mathrm{~Hz}$ की आवृत्ति रखेंगी $\newline$
(b) $2 \times 10^{9} \mathrm{~Hz}$ की आवृत्ति रखेंगी $\newline$
(c) $0.3 \mathrm{~m}$ की तरंगदैर्ध्य रखेंगी $\newline$
(d) रेडियो तरंग के क्षेत्र में पड़ेंगी $\newline$
उत्तर दिखाएं
सोचने की प्रक्रिया
एक आवेशित कण द्वारा उत्पन्न विद्युत चुम्बकीय तरंग की आवृत्ति उस कण के अपने माध्य संतुलन स्थिति के चारों ओर आवर्ती गति की आवृत्ति के बराबर होती है।
उत्तर
$(a, c, d)$
दिया गया है, आवेशित कण द्वारा अपने माध्य संतुलन स्थिति के चारों ओर आवर्ती गति करने की आवृत्ति $=10^{9} \mathrm{~Hz}$।
इसलिए, आवेशित कण द्वारा उत्पन्न विद्युत चुम्बकीय तरंग की आवृत्ति $v=10^{9} \mathrm{~Hz}$ है।
$$ \text { तरंगदैर्ध्य } \lambda=\dfrac{c}{v}=\dfrac{3 \times 10^{8}}{10^{9}}=0.3 \mathrm{~m} $$
इसके अलावा, $10^{9} \mathrm{~Hz}$ की आवृत्ति रेडियो तरंग के क्षेत्र में पड़ती है।
- विकल्प (b) गलत है क्योंकि आवेशित कण द्वारा उत्पन्न विद्युत चुम्बकीय तरंग की आवृत्ति उस कण के आवर्ती गति की आवृत्ति के बराबर होती है, जो $10^{9} \mathrm{~Hz}$ है, न कि $2 \times 10^{9} \mathrm{~Hz}$।
12. विद्युत चुम्बकीय तरंगों के स्रोत एक आवेश हो सकता है
(a) नियत वेग से गति करता है
(b) एक वृत्ताकार कक्षा में गति करता है
(c) विराम में होता है
(d) विद्युत क्षेत्र में गिरता है
उत्तर दिखाएं
सोचने की प्रक्रिया
एक विद्युत चुम्बकीय तरंग तेजी से या त्वरित आवेश द्वारा उत्पन्न हो सकती है।
उत्तर
( $b, d)$
यहाँ, विकल्प (b) में आवेश एक वृत्ताकार कक्षा में गति करता है।
वृत्ताकार गति में, आवेश के गति की दिशा निरंतर बदलती रहती है, इसलिए यह एक त्वरित गति है और यह विकल्प सही है।
हम जानते हैं कि एक आवेश जब विद्युत क्षेत्र में गिरता है तब यह त्वरित हो जाता है।
-
विकल्प (a) में नियत वेग से गति करता है: नियत वेग से गति करते हुए आवेश पर कोई त्वरण नहीं होता। विद्युत चुम्बकीय तरंग त्वरित आवेश द्वारा उत्पन्न होती है, न कि नियत वेग से गति करते हुए आवेश द्वारा।
-
विकल्प (c) में विराम में होता है: विराम में आवेश विद्युत चुम्बकीय तरंग उत्पन्न नहीं करता क्योंकि इसकी गति या स्थिति में कोई परिवर्तन नहीं होता। विद्युत चुम्बकीय तरंग आवेश के त्वरण द्वारा उत्पन्न होती है, और एक स्थिर आवेश में कोई त्वरण नहीं होता।
13. एक विद्युत चुम्बकीय तरंग जिसकी तीव्रता $I$ है, एक रिक्त अंतरिका में रखे गए सतह पर आपतित होती है और इस पर विकिरण दबाव $p$ लगता है। निम्नलिखित में से कौन से कथन सत्य हैं?
(a) यदि तरंग पूर्ण रूप से अवशोषित होती है तो विकिरण दबाव $\dfrac{I}{\mathrm{C}}$ होता है
(b) यदि तरंग पूर्ण रूप से प्रतिबिंबित होती है तो विकिरण दबाव $\dfrac{I}{\mathrm{C}}$ होता है
(c) यदि तरंग पूर्ण रूप से प्रतिबिंबित होती है तो विकिरण दबाव $\dfrac{2 I}{\mathrm{C}}$ होता है
(d) वास्तविक सतहों के लिए विकिरण दबाव $\dfrac{I}{\mathrm{C}}<p<\dfrac{2 I}{\mathrm{C}}$ के बीच होता है
उत्तर दिखाएं
उत्तर
$(a, c, d)$
विकिरण दबाव $(p)$ विद्युत चुम्बकीय तरंग द्वारा सतह के एक इकाई क्षेत्र पर लगाए गए बल को कहते हैं, अर्थात सतह के एक इकाई क्षेत्र पर आवेश के पल के परिवर्तन की दर।
इकाई क्षेत्र पर इकाई समय में आवेश
$$ =\dfrac{\text { तीव्रता }}{\text { तरंग की चाल }}=\dfrac{I}{\mathrm{c}}
$$
क्षमता परिवर्तन प्रति इकाई समय प्रति इकाई क्षेत्रफल $=\dfrac{\Delta I}{C}=$ विकिरण दबाव $(p)$ अर्थात,
$$ p=\dfrac{\Delta I}{c} $$
प्रति इकाई समय प्रति इकाई क्षेत्रफल पर आगंतुक तरंग की क्षमता $=\dfrac{I}{c}$
जब तरंग सतह द्वारा पूरी तरह अवशोषित होती है, तो प्रति इकाई समय प्रति इकाई क्षेत्रफल पर परावर्तित तरंग की क्षमता $=0$।
विकिरण दबाव $(p)=$ प्रति इकाई समय प्रति इकाई क्षेत्रफल पर क्षमता परिवर्तन $=\dfrac{\Delta I}{c}=\dfrac{I}{c}-0=\dfrac{I}{c}$।
जब तरंग पूरी तरह परावर्तित होती है, तो प्रति इकाई समय प्रति इकाई क्षेत्रफल पर परावर्तित तरंग की क्षमता $=-\dfrac{I}{\mathrm{c}}$, विकिरण दबाव $p=\dfrac{I}{\mathrm{c}}–\dfrac{I}{\mathrm{c}}=\dfrac{2 I}{\mathrm{c}}$।
यहाँ, $p$ $\dfrac{I}{c}$ और $\dfrac{2 I}{c}$ के बीच होता है।
- विकल्प (b) गलत है क्योंकि यदि तरंग पूरी तरह परावर्तित होती है, तो विकिरण दबाव $\dfrac{I}{\mathrm{C}}$ नहीं होता। जब तरंग पूरी तरह परावर्तित होती है, तो क्षमता परिवर्तन आगंतुक क्षमता के दुगुना होता है, जिसके कारण विकिरण दबाव $\dfrac{2I}{\mathrm{C}}$ होता है, न कि $\dfrac{I}{\mathrm{C}}$।
बहुत छोटे उत्तर प्रकार प्रश्न
14. पोर्टेबल रेडियो के संबंध में प्रसार स्टेशन के संबंध में आवश्यकता क्यों होती है?
उत्तर दिखाएं
उत्तर
पोर्टेबल रेडियो के संबंध में प्रसार स्टेशन के संबंध में आवश्यकता होती है क्योंकि विद्युत चुंबकीय तरंगें तल ध्रुवित होती हैं, इसलिए ग्राहक एंटीना विद्युत या चुंबकीय क्षेत्र के तरंग के झंकार के समानांतर होना चाहिए।
15. माइक्रोवेव ओवन क्यों जलते हुए जल अणु वाले खाद्य पदार्थ को सबसे कुशल तौर पर गरम करता है?
उत्तर दिखाएं
उत्तर
माइक्रोवेव ओवन जल अणु वाले खाद्य पदार्थ को सबसे कुशल तौर पर गरम करता है क्योंकि माइक्रोवेव की आवृत्ति जल अणु की अनुनाद आवृत्ति के साथ मेल खाती है।
16. समांतर प्लेट कैपेसिटर पर आवेश $q=q_{0} \cos 2 \pi v t$ के रूप में बदलता है। प्लेट बहुत बड़ी हैं और एक दूसरे के निकट हैं (क्षेत्रफल $=A$, अलगाव $=d$)। किन्तु किनारे के प्रभाव को नगण्य मानते हुए, कैपेसिटर के माध्यम से विस्थापन धारा ज्ञात कीजिए।
उत्तर दिखाएँ
उत्तर
कैपेसिटर के माध्यम से विस्थापन धारा है,
यहाँ,
इस मान को समीकरण (i) में रखने पर हम प्राप्त करते हैं
$$ I_{d}=I_{C}=\dfrac{d q}{d t} $$
$$ \begin{aligned} & I_{d}=I_{c}=-q_{0} \sin 2 \pi v t \times 2 \pi v \\ & I_{d}=I_{c}=-2 \pi v q_{0} \sin 2 \pi v t \end{aligned} $$
17. एक परिवर्तनीय आवृत्ति का ए.सी. स्रोत एक कैपेसिटर के साथ जुड़ा हुआ है। आवृत्ति कम होने पर विस्थापन धारा में क्या परिवर्तन होगा?
उत्तर दिखाएँ
सोचने की प्रक्रिया
कैपेसिटेंस प्रतिरोध $X_{c}$ विस्थापन धारा के व्युत्क्रमानुपाती होता है, अर्थात $X_{c} \propto \dfrac{1}{I}$।
उत्तर
कैपेसिटिव प्रतिरोध $X_{C}=\dfrac{1}{2 \pi f C}$,
$\therefore \quad X_{c} \propto \dfrac{1}{f}$
जब आवृत्ति कम होती है, $X_{C}$ बढ़ता है और सं conduction धारा $X_{c}$ के व्युत्क्रमानुपाती होती है क्योंकि $I \propto \dfrac{1}{X_{c}}$
इसलिए, विस्थापन धारा कम होती है क्योंकि conduction धारा विस्थापन धारा के बराबर होती है।
18. एक फ़िल्टर से निकले बीम के चुंबकीय क्षेत्र को एक बारिश के बल्ब के सामने दिया गया है जो द्वारा दिया गया है
$$ B_{0}=12 \times 10^{-8} \sin \left(1.20 \times 10^{7} z-3.60 \times 10^{15} t\right) \mathrm{T} \text {. } $$
बीम की औसत तीव्रता क्या है?
उत्तर दिखाएँ
उत्तर
चुंबकीय क्षेत्र $\mathbf{B}=B_{0}$ sin $\omega t$
दिया गया, समीकरण $B=12 \times 10^{-8} \sin \left(1.20 \times 10^{7} z-3.60 \times 10^{15} t\right) \mathrm{T}$.
इस समीकरण को मानक समीकरण के साथ तुलना करने पर हम प्राप्त करते हैं
$$ B_{0}=12 \times 10^{-8} $$
बीम की औसत तीव्रता $I_{\mathrm{av}}=\dfrac{1}{2} \dfrac{B_{0}^{2}}{\mu_{0}} \cdot \mathrm{C}=\dfrac{1}{2} \times \dfrac{\left(12 \times 10^{-8}\right)^{2} \times 3 \times 10^{8}}{4 \pi \times 10^{-7}}$
$$ =1.71 \mathrm{~W} / \mathrm{m}^{2} $$
19. पॉइंटिंग वेक्टर $S$ एक वेक्टर है जिसके मान के बराबर तरंग की तीव्रता होती है और जिसकी दिशा तरंग के प्रसार की दिशा के समान होती है। गणितीय रूप से, इसे $\mathbf{S}=\dfrac{1}{\mu_{0}} \mathbf{E} \times \mathbf{B}$ द्वारा दिया गया है। $\mathbf{S}$ के लेख ग्राफ की प्रकृति दिखाइए।
उत्तर दिखाएँ
उत्तर
एक विद्युतचुम्बकीय तरंग की अवलोकन करें, मान लीजिए $\mathbf{E}$ $y$-अक्ष के अनुदिश बदल रहा है, $\mathbf{B}$ $z$-अक्ष के अनुदिश है और तरंग का प्रसार $x$-अक्ष के अनुदिश है। तब $\mathbf{E} \times \mathbf{B}$ विद्युतचुम्बकीय तरंग में ऊर्जा प्रवाह की दिशा बताएगा, जो $x$-अक्ष के अनुदिश होगी।
मान लीजिए
$$ \begin{aligned} \mathbf{E} & =E_{0} \sin (\omega t-k x) \hat{\mathbf{j}} \\ \mathbf{B} & =B_{0} \sin (\omega t-k x) \hat{\mathbf{k}} \\ \mathbf{S} & =\dfrac{1}{\mu_{0}}(\mathbf{E} \times \mathbf{B})=\dfrac{1}{\mu_{0}} E_{0} B_{0} \sin ^{2}(\omega t-k x)[\hat{\mathbf{j}} \times \hat{\mathbf{k}}] \\ & =\dfrac{E_{0} B_{0}}{\mu_{0}} \sin ^{2}(\omega t-k x) \hat{\mathbf{i}} \end{aligned} $$
समय $t$ के साथ $|\mathbf{S}|$ के परिवर्तन को नीचे दिए गए चित्र में दिखाया गया है
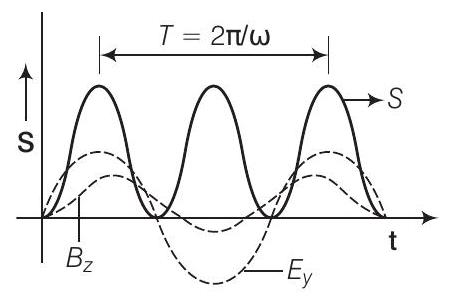
20. प्रोफेसर सी वी रमन ने एक पारदर्शी वैक्यूम कमरे में एक छोटे से प्रकाश गेंद को आवेग देकर आवेग देकर अनुमति देकर अपने छात्रों को आश्चर्यचकित किया। वह विद्युतचुम्बकीय तरंग के किस गुण को प्रदर्शित कर रहे थे? इस गुण का एक और उदाहरण दीजिए।
उत्तर दिखाएँ
उत्तर
एक विद्युतचुम्बकीय तरंग अन्य तरंगों की तरह ऊर्जा और संवेग ले जाती है।
क्योंकि यह संवेग ले जाती है, एक विद्युतचुम्बकीय तरंग भी एक दबाव के रूप में दबाव लगाती है जिसे विकिरण दबाव कहते हैं। विद्युतचुम्बकीय तरंग के इस गुण ने प्रोफेसर सी वी रमन को अपने छात्रों को आश्चर्यचकित करने के लिए एक पारदर्शी वैक्यूम कमरे में एक छोटे से प्रकाश गेंद को आवेग देकर अनुमति देकर एक लेजर किरण के बल पर लटकाया। चमत्कार के ताल भी विकिरण दबाव के कारण होते हैं।
छोटे उत्तर प्रकार के प्रश्न
21. सिद्ध करें कि समानांतर प्लेट कैपेसिटर के प्लेट के बीच के बिंदु पर चुंबकीय क्षेत्र $B$ का मान $\dfrac{\mu_{o} \varepsilon_{0} r}{2} \dfrac{d E}{d t}$ होता है (चिह्नों के सामान्य अर्थ हैं)।
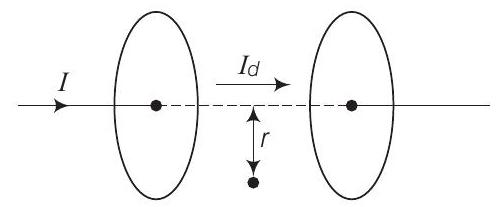
उत्तर दिखाएँ
उत्तर
चित्र के आधार पर सिद्ध करें कि समानांतर प्लेट कैपेसिटर के प्लेट के बीच बिंदु पर चुंबकीय क्षेत्र $\mathrm{B}$ का मान $\dfrac{\varepsilon_{0} \mu_{0} r}{2} \dfrac{d E}{d t}$ होता है।
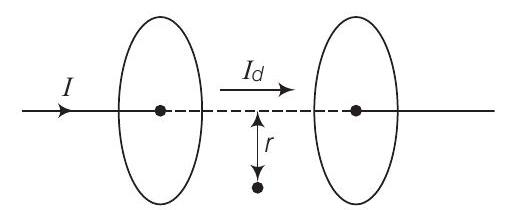
मान लीजिए $I_{d}$ दो प्लेट के बीच क्षेत्र में विस्थापन धारा है, जैसा कि चित्र में दिखाया गया है।
कैपेसिटर के दो प्लेट के बीच क्षेत्र में एक बिंदु पर चुंबकीय क्षेत्र तीव्रता जो अक्ष से दूरी $r$ पर होती है, निम्नलिखित है:
$$ \begin{array}{rlrl} B & =\dfrac{\mu_{0} 2 I_{d}}{4 \pi r}=\dfrac{\mu_{0}}{2 \pi r} I_{d}=\dfrac{\mu_{0}}{2 \pi r} \times \varepsilon_{0} \dfrac{d \varphi_{E}}{d t} & & \because I_{d}=\dfrac{E_{0} d \varphi_{E}}{d t} \\ & =\dfrac{\mu_{0} \varepsilon_{0}}{2 \pi r} \dfrac{d}{d t}\left(E r^{2}\right)=\dfrac{\mu_{0} \varepsilon_{0}}{2 \pi r} \pi^{2} \dfrac{d E}{d t} & \\ B & =\dfrac{\mu_{0} \varepsilon_{0} r}{2} \dfrac{d E}{d t} & & {\left[\because \varphi_{E}=E r^{2}\right]} \end{array} $$
22. विद्युत चुंबकीय तरंगों के तरंगदैर्ध्य के संबंध में
(i) $\lambda_{1}$ उपग्रह संचार में उपयोग किया जाता है।
(ii) $\lambda_{2}$ पानी के शुद्धिकरण में जीरो की बीमारियों को मारने के लिए उपयोग किया जाता है।
(iii) $\lambda_{3}$ भू-संचार पाइपलाइन में तेल की रिसाव का पता लगाने के लिए उपयोग किया जाता है।
(iv) $\lambda_{4}$ धुंआ और धूल के शर्मा वाले स्थानों में दृश्यता को सुधारने के लिए उपयोग किया जाता है।
(a) इन विकिरणों के विद्युत चुंबकीय विकिरण के किस भाग के लिए और नाम बताएँ।
(b) इन तरंगदैर्ध्यों को उनके मान के बढ़ते क्रम में व्यवस्थित करें।
(c) प्रत्येक के एक अतिरिक्त उपयोग लिखें।
उत्तर दिखाएँ
उत्तर
(a) (i) माइक्रोवेव सैटेलाइट संचार में प्रयोग किया जाता है।
इसलिए, $\lambda_{1}$ माइक्रोवेव की तरंगदैर्घ्य है।
(ii) अल्ट्रावॉल्टा रेडियों का प्रयोग पानी के शुद्धिकरण में बैक्टीरिया को मारने के लिए किया जाता है। इसलिए, $\lambda_{2}$ UV रेडियों की तरंगदैर्घ्य है।
(iii) $X$-रेडियों का प्रयोग भूमिगत पाइपलाइन में तेल की रिसाव की जांच के लिए किया जाता है। इसलिए, $\lambda_{3}$ $X$-रेडियों की तरंगदैर्घ्य है।
(iv) इन्फ्रारेड का प्रयोग धुंआ और धूल के शर्तों में विमान विमानकरण के रनवे पर दृश्यता को सुधारने के लिए किया जाता है। इसलिए, इसकी तरंगदैर्घ्य इन्फ्रारेड तरंगों की है।
(b) $X$-रेडियों की तरंगदैर्घ्य $<$ UV की तरंगदैर्घ्य $<$ इन्फ्रारेड की तरंगदैर्घ्य $<$ माइक्रोवेव की तरंगदैर्घ्य।
$$ \Rightarrow \quad \lambda_{3}<\lambda_{2}<\lambda_{4}<\lambda_{1} $$
(c) (i) माइक्रोवेव रेडियों का प्रयोग रेडार में किया जाता है।
(ii) UV रेडियों का प्रयोग LASIK आंख की चिकित्सा में किया जाता है।
(iii) $X$-रेडियों का प्रयोग बोने में टूट जाने की जांच के लिए किया जाता है।
(iv) इन्फ्रारेड रेडियों का प्रयोग प्रकाश संचार में किया जाता है।
23. सिद्ध करें कि एक चक्र $T$ के दौरान विकिरण तीव्रता घनत्व $S$ का औसत मान $S=\dfrac{1}{2 c \mu_{0}} E_{0}^{2}$ द्वारा दिया जाता है।
उत्तर दिखाएँ
उत्तर
विकिरण तीव्रता घनत्व $S=\dfrac{1}{\mu_{0}}(\mathbf{E} \times \mathbf{B})=c^{2} \varepsilon_{0}(\mathbf{E} \times \mathbf{B})$
$$ \because c=\dfrac{1}{\sqrt{\mu_{0} \varepsilon_{0}}} $$
मान लीजिए कि विद्युतचुंबकीय तरंग $x$-अक्ष के अनुदिश चल रही है। विद्युत क्षेत्र वेक्टर विद्युतचुंबकीय तरंग के $y$-अक्ष के अनुदिश है और चुंबकीय क्षेत्र वेक्टर $z$-अक्ष के अनुदिश है। इसलिए,
और $$ E =E_0 \cos(k x-\omega t) $$ $$ {B} =B_0 \cos(k x-\omega t) \\ $$
$$E \times B =\left(E_0 \times B_0\right) \cos^{2}(k x-\omega t) \\ $$ $$S =c^{2}{0}(E \times B) \\ =c^{2}{0}\left(E_0 \times B_0\right) \cos^{2}(k x-\omega t) $$
पूरे चक्र के दौरान विकिरण तीव्रता घनत्व के मान का औसत मान है
$$ \begin{array}{rlrl} S_{av} =c^{2}{0}\left|E_0 \times B_0\right| \dfrac{1}{T} \int{0}^{T} \cos ^{2}(k x-\omega t) d t \newline \\ =c^{2}{0} E{0} B_{0} \times \dfrac{1}{T} \times \dfrac{T}{2} \because \int_{0}^{T} \cos ^{2}(k x-\omega t) d t=\dfrac{T}{2} \newline \\
\Rightarrow S_{av}=c^{2}{0} E{0} \dfrac{E_{0}}{c} \text { जैसे, } c=\dfrac{E_{0}}{B_{0}} \newline \\ =c^{2}{0} E{0}^{2}=\dfrac{c}{2} \times \dfrac{1}{c^{2} \mu_{0}} E_{0}^{2} c=\dfrac{1}{\sqrt{\mu_{0} 0}} \text { या } 0=\dfrac{1}{c^{2} \mu_{0}} \newline \\ \Rightarrow \quad S_{av} =\dfrac{E_{0}^{2}}{2 \mu_{0} c} \end{array} $$
24. आपको एक $2 \mu \mathrm{F}$ समान्तर प्लेट कैपेसिटर दिया गया है। आपको इसके प्लेट के बीच अंतराल में एक आविष्कृत धारा $1 \mathrm{~mA}$ स्थापित करनी है।
उत्तर दिखाएं
उत्तर
दिया गया, कैपेसिटर की क्षमता $C=2 \mu \mathrm{F}$,
अपवर्जित धारा $I_{d}=1 \mathrm{~mA}$ आवेश
या
$$ \begin{aligned} q & =C V \\ I_{d} d t & =C d V \\ I_{d} & =C \dfrac{d V}{d t} \\ 1 \times 10^{-3} & =2 \times 10^{-6} \times \dfrac{d V}{d t} \\ \dfrac{d V}{d t} & =\dfrac{1}{2} \times 10^{+3}=500 \mathrm{~V} / \mathrm{s} \end{aligned} \quad[\because q=i t] $$
$$ \text { या } $$
इसलिए, एक विशिष्ट विभवान्तर के परिवर्तन के द्वारा $500 \mathrm{~V} / \mathrm{s}$ के विभवान्तर के परिवर्तन के द्वारा हम अभीष्ट अपवर्जित धारा उत्पन्न कर सकते हैं।
27. एक विद्युत क्षेत्र $\mathrm{E}$ एक आवेशित कण पर बल $q \mathrm{E}$ लगाता है, लेकिन विद्युत चुंबकीय तरंग के विद्युत क्षेत्र के लिए विकिरण दबाव के लिए योगदान नहीं देता है (लेकिन ऊर्जा परिवहन करता है)। समझाइए।
उत्तर दिखाएँ
उत्तर
क्योंकि, विद्युत चुंबकीय तरंग का विद्युत क्षेत्र एक आवर्ती क्षेत्र होता है और इसके कारण आवेशित कण पर लगने वाला बल भी आवर्ती होता है। इस बल का औसत मान एक पूर्ण चक्र के लिए शून्य होता है, क्योंकि इसकी दिशा प्रत्येक आधा चक्र में बदल जाती है।
इसलिए, विद्युत क्षेत्र विकिरण दबाव के लिए जिम्मेदार नहीं होता है।
लंबा उत्तर प्रकार प्रश्न
28. एक अनंत लंबाई के तंतु के रूप में एक समान रूप से वितरित स्थैतिक आवेश घनत्व $\lambda$ के साथ एक तार $z$-अक्ष के अक्ष के अनुदिश रखा गया है (चित्र)। तार को अपने अक्ष के अनुदिश एक समान वेग $v = v \hat{k}_{z}$ से गति कराई जाती है। बताइए कि बीम वेक्टर $S = \dfrac{1}{0}(E \times B)$ की गणना कीजिए।
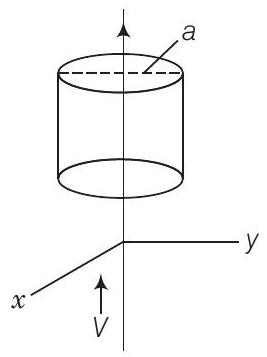
उत्तर दिखाएँ
उत्तर
दिया गया है,
$$ \begin{aligned} B & =\dfrac{\mu_{0} i}{2 \pi a} \hat{i}=\dfrac{\mu_{0} \lambda v}{2 \pi a} \hat{i} \newline\\ \therefore \quad S & =\dfrac{1}{\mu_{0}}[E \times B]=\dfrac{1}{\mu_{0}} \dfrac{\lambda_{\hat{j}}}{2 \pi \varepsilon_{0} a} \times \dfrac{\mu_{0}}{2 \pi a} \lambda \sqrt{\hat{i}} \newline\\
& =\dfrac{\lambda^{2} v}{4 \pi^{2} \varepsilon_{0} a^{2}}(\hat{j} \times \hat{i})=-\dfrac{\lambda^{2} V}{4 \pi^{2} \varepsilon_{0} a^{2}} \hat{k} \end{aligned} \quad\left[\because I=\lambda_{V}\right] $$
$$ E=\dfrac{\lambda \hat{e}{s}}{2 \pi \varepsilon{0} a} \hat{j} $$
29. समुद्री जल की आवृत्ति $v=4 \times 10^{8} \mathrm{~Hz}$ पर परमेट्टिविटी $\varepsilon \approx 80 \varepsilon_{0}$, प्रवाहियता $\mu \approx \mu_{0}$ और प्रतिरोधकता $\rho=0.25 \mathrm{~m}$ है। कल्पना करें कि एक समान्तर प्लेट कैपेसिटर समुद्री जल में डूबा हुआ है और एक विन्यास वोल्टेज स्रोत $V(t)=V_{0} \sin (2 \pi v t)$ द्वारा चलाया जा रहा है। सं conduction धारा घनत्व के एक भिन्न के विस्थापन धारा घनत्व क्या है?
उत्तर दिखाएं
conduction धारा घनत्व को ओहम के नियम द्वारा दिया गया है = प्लेट के बीच विद्युत क्षेत्र।
Answer
मान लीजिए समान्तर प्लेट के बीच दूरी $d$ है और आवेश वोल्टेज $V_{(t)}=V_{0} 2 \pi v t$ है।
इसलिए, विद्युत क्षेत्र
अब ओहम के नियम का उपयोग करते हुए,
$$ \begin{aligned} E=\dfrac{V_{0}}{d} \sin (2 \pi v t) \newline \\ J_{c} =\dfrac{1}{\rho} \dfrac{V_{0}}{d} \sin (2 \pi v t) \newline \\ =\dfrac{V_{0}}{\rho d} \sin (2 \pi v t) \newline \end{aligned} $$
$$J_{0}^{c} =\dfrac{V_{0}}{\rho d}$$
$$ \Rightarrow \quad\dfrac{V_{0}}{\rho d} \sin (2 \pi v t)=J_{0}^{c} \sin 2 \pi v t $$
यहाँ,
अब विस्थापन धारा घनत्व निम्नलिखित द्वारा दिया गया है
$$ \begin{array}{rlrl} J_{d} =\varepsilon \dfrac{\delta E}{d t}=\dfrac{\varepsilon \delta}{d t} \newline \\ =\dfrac{\varepsilon 2 \pi v V_{0}}{d} \cos (2 \pi v t) \newline \\ \Rightarrow =J_{0}^{d} \cos (2 \pi v t) \newline \\ \text { where, } J_{0}^{d} =\dfrac{2 \pi V \varepsilon V_{0}}{d} \newline \\ \Rightarrow \dfrac{J_{0}^{d}}{J_{0}^{c}} =\dfrac{2 \pi v \varepsilon V_{0}}{d} \cdot \dfrac{\rho d}{V_{0}}=2 \pi v \varepsilon \rho \newline \\ =2 \pi \times 80 \varepsilon_{0} v \times 0.25=4 \pi \varepsilon_{0} v \times 10 \newline \\ =\dfrac{10 v}{9 \times 10^{9}}=\dfrac{4}{9}
\end{array} $$
30. एक लंबी सीधी केबल जिसकी लंबाई $l$ है, $z$-अक्ष के सममित रूप से रखी गई है और इसकी त्रिज्या $a(«l)$ है। केबल में एक चोटी तार और एक सह-अक्षीय चालक ट्यूब होता है। एक अल्टरनेटिंग धारा $I(t)=I_{0} \sin (2 \pi v t)$ केंद्रीय चोटी तार में बहती है और इसे सह-अक्षीय चालक ट्यूब के माध्यम से वापस ले जाती है। केबल के भीतर तार से $s$ दूरी पर प्रेरित विद्युत क्षेत्र है
$$ E(s, t)=\mu_0 I_0 v \cos (2 \pi v t) \ln \dfrac sa \hat{k} $$
(i) केबल के भीतर विस्थापन धारा घनत्व की गणना करें।
(ii) केबल के काट के क्षेत्रफल के बराबर विस्थापन धारा घनत्व के समाकलन करके विस्थापन धारा के कुल मान $I^{d}$ ज्ञात करें।
(iii) चालन धारा $I_{0}$ को विस्थापन धारा $I_{0}^{d}$ के साथ तुलना करें।
उत्तर दिखाएं
सोचने की प्रक्रिया
विस्थापन धारा घनत्व
$$ J_{d}=\varepsilon_{0} \dfrac{dE}{d t} $$
उत्तर
(i) दिया गया है, तार से $r$ दूरी पर केबल के भीतर प्रेरित विद्युत क्षेत्र है
$$ \mathbf{E}(s, t)=\mu_{0} I_{0} v \cos (2 \pi v t) \ln \dfrac sa \hat{\mathbf{k}} $$
अब, विस्थापन धारा घनत्व,
$$ Jd=\varepsilon_{0} \dfrac{d \mathbf{E}}{d t}=\varepsilon_{0} \dfrac{d}{d t} \mu_{0} I_{0} v \cos (2 \pi v t) \ln \dfrac{s}{a} \hat{\mathbf{k}} $$
(ii)
$\begin{aligned} I _d & =\int J _d s d s d \theta=\int _{s=0}^a J _d s d s \int _0^{2 \pi} d \theta=2\pi \int _{s=0}^a J _d s d s \\ & =\int _{s=0}^a[\dfrac{2 \pi}{\lambda^2} I_0 \log _e(\dfrac{a}{s}) s d s \sin 2 \pi v t] \times 2 \pi \\ & =(\dfrac{2 \pi}{\lambda})^2 I _0 \int _{s=0}^a(\dfrac{a}{s}) s d s \sin 2 \pi v t \\ \Rightarrow \qquad & =(\dfrac{2 \pi}{\lambda})^2 I _0 \int _{s=0}^a \ln (\dfrac{a}{s}) \dfrac{1}{2} d(s^2) \cdot \sin 2 \pi v t \end{aligned}$
$\begin{aligned} & =\dfrac{a^2}{2}\left(\dfrac{2 \pi}{\lambda}\right)^2 I_0 \sin 2 \pi v t \int_{s=0}^a \ln \left(\dfrac{a}{s}\right) \cdot d\left(\dfrac{s}{a}\right)^2 \\ & =\dfrac{a^2}{4}\left(\dfrac{2 \pi}{\lambda}\right)^2 I_0 \sin 2 \pi v t \int_{s=0}^a \ln \left(\dfrac{a}{s}\right)^2 \cdot d\left(\dfrac{s}{a}\right)^2 \\
& =-\dfrac{a^2}{4}\left(\dfrac{2 \pi}{\lambda}\right)^2 I_0 \sin 2 \pi v t \int_{s=0}^a \ln \left(\dfrac{s}{a}\right)^2 \cdot d\left(\dfrac{s}{a}\right)^2 \end{aligned}$
$\begin{array}{rlrl} & =-\dfrac{a^2}{4}\left(\dfrac{2 \pi}{\lambda}\right)^2 I_0 \sin 2 \pi v t \times(-1) & {\left[\because \int_{s=0}^a \ln \left(\dfrac{s}{a}\right)^2 d\left(\dfrac{s}{a}\right)^2=-1\right]} \\ \therefore & I_d =\dfrac{a^2}{4}\left(\dfrac{2 \pi}{\lambda}\right)^2 I_0 \sin 2 \pi v t \\ \Rightarrow \qquad & =\left(\dfrac{2 \pi a}{2 \lambda}\right)^2 I_0 \sin 2 \pi v t & \end{array}$
(iii) विस्थापन धारा,
$$ \begin{aligned} & I_{d}=\dfrac{2 \pi a^{2}}{2 \lambda} I_{0} \sin 2 \pi v t=I_{0 d} \sin 2 \pi v t \\ \text { यहाँ, } & I_{0 d}=\dfrac{2 \pi a}{2 \lambda}^{2} I_{0}=\dfrac{a \pi^{2}}{\lambda} I_{0} \\ \therefore & \dfrac{I_{0 d}}{I_{0}}=\dfrac{a \pi^{2}}{\lambda} \end{aligned} $$
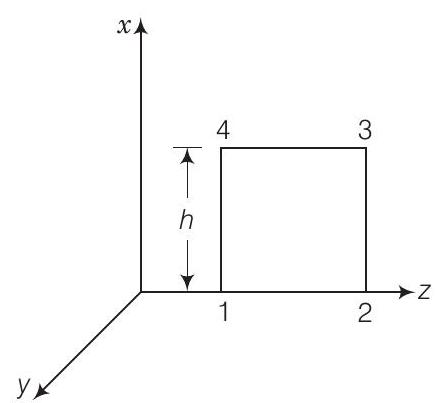
31. एक समतल $E M$ तरंग वैक्यूम में $z$-दिशा के अनुदिश दी गई है $\mathbf{E}=E_{0} \sin (k z-\omega t) \hat{\mathbf{i}}$ और $\mathbf{B}=B_{0} \sin (k z-\omega t) \hat{\mathbf{j}}$।
(i) चित्र में दिखाए गए आयताकार लूप 1234 के लिए $\int \mathbf{E} \cdot \mathbf{d l}$ का मूल्यांकन करें।
(ii) लूप 1234 द्वारा सीमित सतह पर $\int \mathbf{B} \cdot \mathbf{d s}$ का मूल्यांकन करें।
(iii) समीकरण $\int \mathbf{E} \cdot \mathbf{d} \mathbf{l}=\dfrac{-d \varphi_{B}}{d t}$ का उपयोग करके $\dfrac{E_{0}}{B_{0}}=c$ सिद्ध करें।
(iv) समान प्रक्रिया और समीकरण के उपयोग द्वारा
$$ \int \mathbf{B} \cdot \mathbf{d l}=\mu_{0} I+\varepsilon_{0} \dfrac{d \varphi_{E}}{d t}, \text { सिद्ध करें कि } c=\dfrac{1}{\sqrt{\mu_{0} \varepsilon_{0}}} $$
उत्तर दिखाएं
Answer
(i) नीचे दिए गए चित्र को ध्यान में रखें
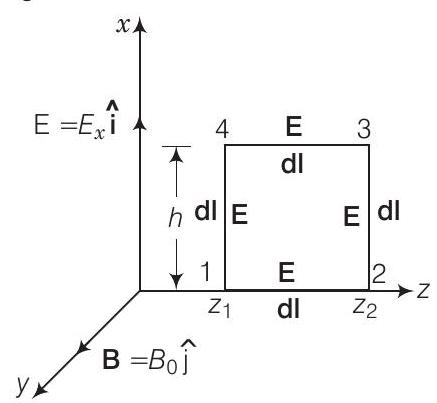
दूर तक विद्युत चुम्बकीय तरंग के प्रसार के दौरान, मान लीजिए विद्युत क्षेत्र सदिश $(\mathbf{E})$ $x$-अक्ष के अनुदिश और चुम्बकीय क्षेत्र सदिश $\mathbf{B}$ $y$-अक्ष के अनुदिश हो, अर्थात $\mathbf{E}=E_{0} \hat{\mathbf{i}}$ और $\mathbf{B}=B_{0} \hat{\mathbf{j}}$।
चित्र में $x$-$z$ तल में बंद आयताकार पथ 1234 के लिए $E$ के लिनियर समाकलन
$$ \begin{aligned} \int \mathbf{E} \cdot \mathbf{d l} & =\int_{1}^{2} E \cdot d l+\int_{2}^{3} E \cdot d l+\int_{3}^{4} E \cdot d l+\int_{4}^{1} E \cdot d l \newline \\ & =\int_{1}^{2} E \cdot d l \cos 90+\int_{2}^{3} E \cdot d l \cos 0+\int_{3}^{4} E \cdot d l \cos 90+\int_{4}^{1} E \cdot d l \cos 180^{\circ} \newline \\ & =E_{0} h\left[\sin \left(k z_{2}-\omega t\right)-\sin \left(k z_{1}-g \omega t\right)\right] \end{aligned} $$
(ii) $\boldsymbol{\beta} \mathbf{B} \cdot \mathbf{d s}$ का मूल्यांकन करने के लिए, मान लीजिए आयत 1234 को एरिया $d s=h d z$ के बैंडों से बनाया गया हो।
$$ \begin{aligned} \int \mathbf{B} \cdot \mathbf{d} \mathbf{s}=\int \mathbf{B} \cdot \mathbf{d} \mathbf{s} \cos 0 & =\int \mathbf{B} \cdot \mathbf{d} \mathbf{s}=\int_{z_{1}}^{z_{2}} B_{0} \sin (k z-\omega t) h d z \\ & =\dfrac{-B_{0} h}{k}\left[\cos \left(k z_{2}-\omega t\right)-\cos \left(k z_{1}-\omega t\right)\right] \end{aligned} $$
(iii) दिया गया है, $g \mathbf{E} \cdot dl=\dfrac{-d \varphi_{B}}{d t}=-\dfrac{d}{d t} g \mathbf{B} \cdot \mathbf{d s}$
समीकरण (i) और (ii) से मान रखने पर, हम प्राप्त करते हैं
$$ E_{0} h [\sin (k z_{2}-\omega t)-\sin (k z_{1}-\omega t)] \\ $$
$$= \dfrac{-d}{d t} \dfrac{B_{y} h}{k}\cos (k z_{2}-\omega t)-\cos (k z_{1}-\omega t) \\ $$ $$= \dfrac{B_y h}{k} \omega [\sin (k z_2-\omega t)-\sin (k z_{1}-\omega t) ]$$
$$\Rightarrow \quad E_{0}=\dfrac{B_{0} \omega}{k}=B_{y} c \because \dfrac{\omega}{k}=c$$
$$\Rightarrow \quad \dfrac{E_0}{B_0}= C$$
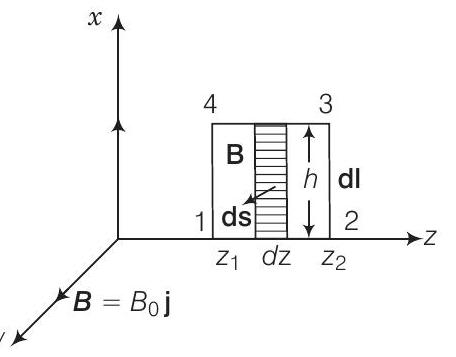
(iv) $\int{\mathbf{B}} \cdot \mathbf{d l}$ का मूल्यांकन करने के लिए, हम नीचे दिए गए चित्र में दिखाए गए $y$-z तल में लूप 1234 को विचार करें
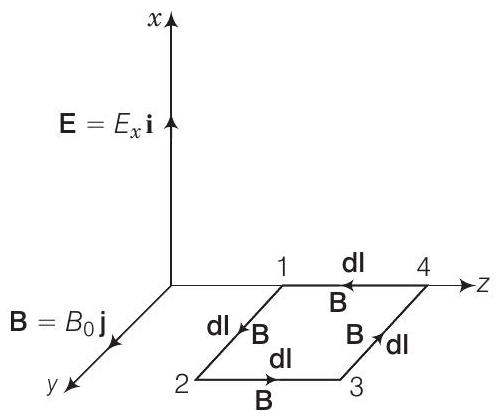
$$ \begin{aligned} \int \mathbf{B} \cdot \mathbf{d l} & =\int_{1}^{2} \mathbf{B} \cdot \mathbf{d l}+\int_{2}^{3} \mathbf{B} \cdot \mathbf{d l}+\int_{3}^{4} \mathbf{B} \cdot \mathbf{d l}+\int_{4}^{1} \mathbf{B} \cdot \mathbf{d l}\newline \\ & =\int_{1}^{2} \mathbf{B} \cdot \mathbf{d l} \cos 0+\int_{2}^{3} \mathbf{B} \cdot \mathbf{d l} \cos 90^{\circ}+\int_{3}^{4} \mathbf{B} \cdot \mathbf{d l} \cos 180^{\circ}+\int_{4}^{1} \mathbf{B} \cdot \mathbf{d l} \cos 90^{\circ}\newline \\ & =B_{0} h\left[\sin \left(k z_{1}-\omega t\right)-\sin \left(k z_{2}-\omega t\right)\right] \end{aligned} $$
अब $\varphi_{E}=\int \mathbf{E} \cdot \mathbf{d s}$ का मूल्यांकन करने के लिए, हम लूप 1234 को $h d_{2}$ क्षेत्रफल के बैंडों से बना हुआ मानें।
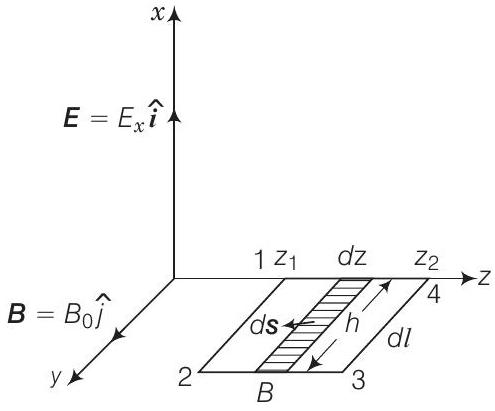
$$ \begin{aligned} \varphi_{E} & =\int E \cdot d s=\int E d s \cos 0=\int E d s=\int_{z_{1}}^{z_{0}^{2}} E_{0} \sin \left(k z_{1}-\omega t\right) h d z \\ & =-\dfrac{E_{0} h}{k}\left[\cos \left(k z_{2}-\omega t\right)-\cos \left(k z_{1}-\omega t\right)\right] \\ \therefore \quad \dfrac{d \varphi_{E}}{d t} & =\dfrac{E_{0} h \omega}{k}\left[\sin \left(k z_{1}-\omega t\right)-\sin \left(k z_{2}-\omega t\right)\right] \end{aligned} $$
$$ \begin{aligned} \text { In } \quad \int \mathbf{B} \cdot \mathbf{d l} & =\mu_{0} I+\dfrac{\varepsilon_{0} d \varphi_{E}}{d t}, I=\text { conduction current } \\ & =0 \text { in vacuum } \\ \therefore \quad \quad \quad \int \mathbf{B} \cdot \mathrm{dl} & =\mu_{0} \varepsilon \dfrac{d \varphi_{E}}{d t} $$
\end{aligned} $$
समीकरण (iii) और (iv) से प्राप्त संबंधों का उपयोग करके सरलीकरण करने पर हम प्राप्त करते हैं
$$ \begin{array}{rlrl} B_{0} =E_{0} \dfrac{\omega \mu_{0} \varepsilon_{0}}{k} \newline \\ \Rightarrow \dfrac{E_{0}}{B_{0}} \dfrac{\omega}{k} =\dfrac{1}{\mu_{0} \varepsilon_{0}} \newline \\ \text { लेकिन } \dfrac{E_{0}}{B_{0}} =c \text { और } \omega=c k \newline \\ \Rightarrow c \cdot c =\dfrac{1}{\mu_{0} \varepsilon_{0}}, \text { अतः } c=\dfrac{1}{\sqrt{\mu_{0} \varepsilon_{0}}} \end{array} $$
32. $\mathrm{~A}$ समतल $E M$ तरंग $z$-दिशा में चल रही है जो $\mathbf{E}=E_{0} \sin (k z-\omega t) \hat{\mathbf{i}}$ और $\mathbf{B}=B_{0} \sin (k z-\omega t) \hat{\mathbf{j}}$ द्वारा वर्णित है। दिखाइए कि
(i) तरंग की औसत ऊर्जा घनत्व द्वारा दिया जाता है
$$ u_{\mathrm{av}}=\dfrac{1}{4} \varepsilon_{0} E_{0}^{2}+\dfrac{1}{4} \dfrac{B_{0}^{2}}{\mu_{0}} $$
(ii) तरंग की समय के औसत तीव्रता द्वारा दिया जाता है
$$ I_{\mathrm{av}}=\dfrac{1}{2} c \varepsilon_{0} E_{0}^{2} . $$
उत्तर दिखाएं
Answer
(i) विद्युतचुंबकीय तरंग ऊर्जा ले जाती है जो विद्युत क्षेत्र वेक्टर और चुंबकीय क्षेत्र वेक्टर के कारण होती है। विद्युतचुंबकीय तरंग में, $E$ और $B$ बिंदु से बिंदु और क्षण से क्षण बदलते रहते हैं। मान लीजिए $E$ और $B$ उनके समय औसत हैं।
विद्युत क्षेत्र $E$ के कारण ऊर्जा घनत्व है
$$ u_{E}=\dfrac{1}{2} \varepsilon_{0} E^{2} $$
चुंबकीय क्षेत्र $B$ के कारण ऊर्जा घनत्व है
$$ u_{B}=\dfrac{1}{2} \dfrac{B^{2}}{\mu_{0}} $$
विद्युतचुंबकीय तरंग की कुल औसत ऊर्जा घनत्व
$$ u_{a v}=u_{E}+u_{B}=\dfrac{1}{2} \varepsilon_{0} E^{2}+\dfrac{1}{2} \dfrac{B^{2}}{\mu_{0}} $$
मान लीजिए विद्युतचुंबकीय तरंग $z$-दिशा में चल रही है। विद्युत क्षेत्र वेक्टर और चुंबकीय क्षेत्र वेक्टर को निम्नलिखित द्वारा प्रस्तुत किया जाता है
$$ \begin{aligned} & E=E_{0} \sin (k z-\omega t) \\ & B=B_{0} \sin (k z-\omega t) \end{aligned} $$
पूरे चक्र के लिए $E^{2}$ का समय औसत मान $=\dfrac{E_{0}^{2}}{2}$
और पूरे चक्र के लिए $B^{2}$ का समय औसत मान $=\dfrac{B_{0}^{2}}{2}$
$$ \begin{aligned} u_{\mathrm{av}} & =\dfrac{1}{2} \dfrac{\varepsilon_{0} E_{0}^{2}}{2}+\dfrac{1}{2} \mu_{0} \dfrac{B_{0}^{2}}{2} \\ & =\dfrac{1}{4} \varepsilon_{0} E_{0}^{2}+\dfrac{B_{0}^{2}}{4 \mu_{0}} \end{aligned} $$
(ii) हम जानते हैं कि $E_{0}=c B_{0}$ और $c=\dfrac{1}{\sqrt{\mu_{0} \varepsilon_{0}}}$
$$ \begin{array}{rlrl} \therefore \dfrac{1}{4} \dfrac{B_{0}^{2}}{\mu_{0}} =\dfrac{1}{4} \dfrac{E_{0}^{2} / c^{2}}{\mu_{0}}=\dfrac{E_{0}^{2}}{4 \mu_{0}} \times \mu_{0} \varepsilon_{0}=\dfrac{1}{4} \varepsilon_{0} E_{0}^{2} \newline\\ \therefore u_{B} =u_{E} \newline\\ \text { अतः, } u_{\mathrm{av}} =\dfrac{1}{4} \varepsilon_{0} E_{0}^{2}+\dfrac{1}{4} \dfrac{B_{0}^{2}}{\mu_{0}} \newline\\ =\dfrac{1}{4} \varepsilon_{0} E_{0}^{2}+\dfrac{1}{4} \varepsilon_{0} E_{0}^{2} \newline\\ =\dfrac{1}{2} \varepsilon_{0} E_{0}^{2}=\dfrac{1}{2} \dfrac{B_{0}^{2}}{\mu_{0}} \end{array} $$
तरंग की समय औसत तीव्रता
$$ I_{\mathrm{av}}=u_{\mathrm{av}} \mathrm{c}=\dfrac{1}{2} \varepsilon_{0} E_{0}^{2} \mathrm{C}=\dfrac{1}{2} \varepsilon_{0} E_{0}^{2} $$





