विद्युत आवेश एवं क्षेत्र
बहुविकल्पीय प्रश्न (MCQs)
1. चित्र में दो धनात्मक आवेश $q_{2}$ और $q_{3}$ y-अक्ष के अनुदिश निश्चित हैं, जो एक निश्चित आवेश $q_{1}$ (जो x-अक्ष के अनुदिश निश्चित है) पर एक नेट विद्युत बल धनात्मक x-अक्ष की दिशा में लगाते हैं। यदि बिंदु $(x, 0)$ पर एक धनात्मक आवेश $Q$ जोड़ दिया जाए, तो $q_{1}$ पर बल
(i)
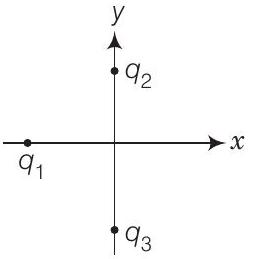
(ii)
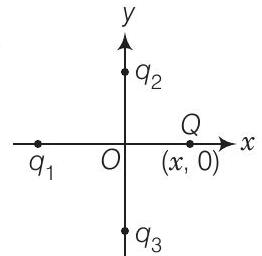
(a) धनात्मक x-अक्ष के अनुदिश बढ़ेगा
(b) धनात्मक x-अक्ष के अनुदिश कम हो जाएगा
(c) ऋणात्मक x-अक्ष के अनुदिश बिंदु करेगा
(d) बल बढ़ेगा लेकिन दिशा बदल जाएगी क्योंकि $Q$ के साथ $q_{2}$ और $q_{3}$ के प्रतिकर्षण के कारण
उत्तर दिखाएं
सोचने की प्रक्रिया
$q_{1}-q_{2}$ और $q_{1}-q_{3}$ के बीच बल की प्रकृति को ज्ञात करें। बल की प्रकृति $q_{1}$ के आवेश के प्रकार को बताएगी। नए आवेश के साथ $q_{1}$ के बीच बल की प्रकृति को ज्ञात करें।
उत्तर
(a) $q_{2}$ और $q_{3}$ द्वारा $q_{1}$ पर लगने वाला नेट बल धनात्मक x-अक्ष की दिशा में है, इसलिए $q_{1}, q_{2}$ और $q_{1}, q_{3}$ के बीच बल आकर्षण प्रकृति का है। इसको नीचे दिए गए चित्र द्वारा प्रदर्शित किया जा सकता है
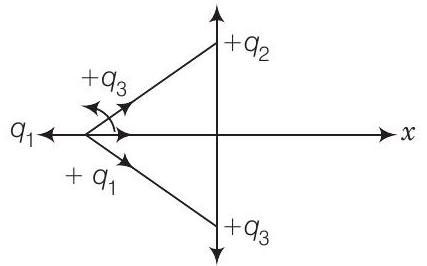
इन आवेशों के बीच आकर्षण बल के कारण यह स्पष्ट होता है कि $q_{1}$ एक ऋणात्मक आवेश है (क्योंकि $q_{2}$ और $q_{3}$ धनात्मक हैं)।
इसलिए $q_{1}$ और नए आवेश $Q$ (धनात्मक) के बीच बल आकर्षण प्रकृति का है और $q_{2}, q_{3}$ और $Q$ द्वारा $q_{1}$ पर लगने वाला नेट बल आरेख में दिए गए दिशा में एक ही दिशा में होगा।
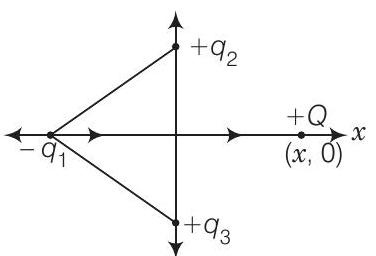
ऊपर दिए गए चित्र से स्पष्ट रूप से दिखाई दे रहा है कि $q_{1}$ पर बल धनात्मक $x$-अक्ष के अनुदिश बढ़ेगा क्योंकि धनात्मक आवेश $Q$ के कारण होता है।
ध्यान दें: विपरीत आवेश एक दूसरे को बहिष्कृत करते हैं और समान आवेश एक दूसरे को आकर्षित करते हैं।
-
(b) धनात्मक $x$-अक्ष के अनुदिश घटेगा: यह विकल्प गलत है क्योंकि $ (x, 0) $ पर धनात्मक आवेश $Q$ के उपस्थिति के कारण नकारात्मक आवेश $q_{1}$ पर अतिरिक्त आकर्षण बल लगेगा, जिसके कारण धनात्मक $x$-अक्ष के अनुदिश नेट बल बढ़ेगा न कि घटे।
-
(c) ऋणात्मक $x$-अक्ष के अनुदिश बिंदु बताएगा: यह विकल्प गलत है क्योंकि नकारात्मक आवेश $q_{1}$ और नए उपस्थित धनात्मक आवेश $Q$ के बीच बल आकर्षण होगा, जिसके कारण बल $Q$ की ओर धनात्मक $x$-अक्ष के अनुदिश दिशा लेगा, न कि ऋणात्मक $x$-अक्ष के अनुदिश।
-
(d) बल बढ़ेगा लेकिन $Q$ के $q_{2}$ और $q_{3}$ के साथ प्रतिच्छेदन के कारण दिशा बदल जाएगी: यह विकल्प गलत है क्योंकि धनात्मक आवेश $Q$ के प्रवर्तन से $q_{1}$ पर नेट बल की दिशा में कोई परिवर्तन नहीं होता। $Q$ के कारण बल धनात्मक $x$-अक्ष के अनुदिश होगा, और क्योंकि $q_{2}$ और $q_{3}$ $y$-अक्ष पर स्थिर हैं, उनके बल $Q$ के बल से प्रतिच्छेद नहीं करते। इसलिए, नेट बल की दिशा धनात्मक $x$-अक्ष के अनुदिश बनी रहती है।
2. एक बिंदु धनात्मक आवेश को एक अनुनादित चालक गोले के पास लाया जाता है (चित्र)। विद्युत क्षेत्र निम्नलिखित में से किसके द्वारा बेस्ट दिया जाता है?
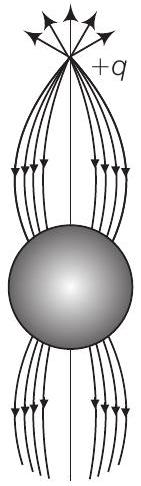
(a)
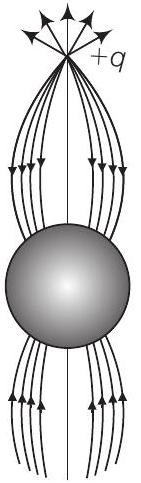
(b)
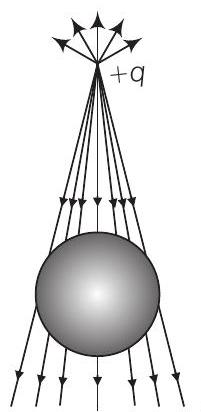
(c)
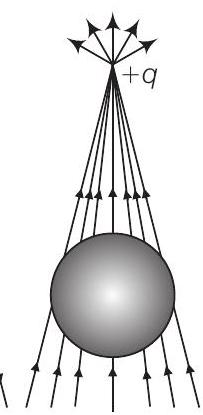
उत्तर दिखाएं
सोचने की प्रक्रिया
एक धनावेशित बिंदु आवेश को एक चालक गोले के पास लाने से गोला प्रेरण प्रक्रिया द्वारा आवेशित हो जाता है। आवेशित वस्तु में विद्युत क्षेत्र रेखाएँ कुछ नियमों के अनुसार गुजरती हैं।
उत्तर
(a) जब एक धनावेशित बिंदु आवेश को एक अलग रखे गए चालक गोले के संपर्क के बिना लाया जाता है, तो गोले में मुक्त इलेक्ट्रॉन धनावेशित आवेश की ओर आकर्षित हो जाते हैं। इससे गोले के पिछले (दाहिने) सतह पर अतिरिक्त धनावेश बच जाता है।
मेटल गोले में दोनों प्रकार के आवेश बंधे होते हैं और बाहर निकल नहीं सकते। इसलिए, वे सतह पर रहते हैं।
इसलिए, गोले के बाएँ सतह पर नकारात्मक आवेश और दाएँ सतह पर धनावेश अतिरिक्त होता है, जैसा कि नीचे चित्र में दिखाया गया है।
आकर्षित नकारात्मक
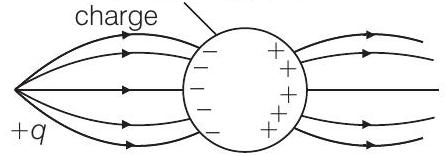
एक धनावेशित आवेश से विद्युत क्षेत्र रेखाएँ शुरू होती हैं और नकारात्मक आवेश पर समाप्त होती हैं (इस मामले में बिंदु धनावेशित आवेश से गोले के अंदर उत्पन्न नकारात्मक आवेश पर)।
इसके अलावा, एक अकेले आवेश के मामले में विद्युत क्षेत्र रेखाएँ धनावेशित आवेश से शुरू होती हैं और अनंत तक समाप्त होती हैं।
यहाँ, चित्र (a) में सभी इन शर्तों को पूरा किया गया है।
-
विकल्प (b): इस विकल्प में विद्युत क्षेत्र रेखाएँ गोले पर आवेश के वितरण को सही तरीके से प्रतिनिधित्व नहीं करती हैं। रेखाएँ धनावेशित आवेश से शुरू होनी चाहिए और गोले पर प्रेरित नकारात्मक आवेश पर समाप्त होनी चाहिए। इस चित्र में विद्युत क्षेत्र रेखाएँ इस सही व्यवहार को दर्शाती हैं।
-
विकल्प (c): यह विकल्प गलत रूप से दिखाता है कि गोला स्वयं धनात्मक आवेश का स्रोत है, जो वास्तव में नहीं है। गोले के धनात्मक बिंदु आवेश के निकट ओर ऋणात्मक आवेश और दूर ओर धनात्मक आवेश uced होने चाहिए, जो यहां दिखाया गया नहीं है।
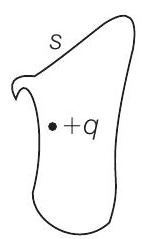
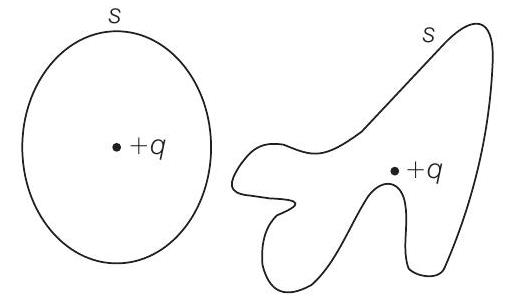
3. सतह के माध्यम से विद्युत फ्लक्स
(i)

(ii)
(iv)
(a) चित्र (iv) में सबसे बड़ा है
(b) चित्र (iii) में सबसे कम है
(c) चित्र (ii) में चित्र (iii) के समान है लेकिन चित्र (iv) से कम है
(d) सभी चित्रों के लिए समान है
उत्तर दिखाएं
उत्तर
(d) विद्युत चुंबकत्व के गॉस के नियम के अनुसार, बंद सतह से बाहर निकलने वाले विद्युत फ्लक्स का कुल मान सतह के भीतर बंद किए गए आवेश के बराबर होता है, अर्थात, $Q$ विद्युत $=\dfrac{Q}{\varepsilon_{0}}$।
इसलिए, एक सतह के माध्यम से विद्युत फ्लक्स सतह के आकार, आकृति या क्षेत्रफल पर निर्भर नहीं करता, बल्कि इसके भीतर बंद किए गए आवेश की संख्या पर निर्भर करता है।
इस प्रश्न में, सभी चित्रों में समान विद्युत फ्लक्स है क्योंकि उनमें से प्रत्येक में एक धनात्मक आवेश है।
-
(a) चित्र (iv) सबसे बड़ा है: यह विकल्प गलत है क्योंकि एक बंद सतह के माध्यम से विद्युत फ्लक्स केवल सतह के बाहर बंद किए गए आवेश पर निर्भर करता है, न कि सतह के आकार या आकृति पर। क्योंकि सभी चित्र एक ही धनावेश को बंद करते हैं, इसलिए सभी के लिए विद्युत फ्लक्स समान है।
-
(b) चित्र (iii) में सबसे कम है: यह विकल्प उपरोक्त कारणों के लिए गलत है। एक बंद सतह के माध्यम से विद्युत फ्लक्स सतह के आकार या आकृति पर निर्भर नहीं करता, बल्कि उस सतह के बाहर बंद किए गए आवेश पर निर्भर करता है। सभी चित्र एक ही धनावेश को बंद करते हैं, इसलिए सभी के लिए विद्युत फ्लक्स समान है।
-
(c) चित्र (ii) में चित्र (iii) के समान है लेकिन चित्र (iv) से छोटा है: यह विकल्प गलत है क्योंकि यह इस बात की ओर इशारा करता है कि विद्युत फ्लक्स आवेश के आकार या आकृति पर निर्भर कर सकता है। गॉस के नियम के अनुसार, एक बंद सतह के माध्यम से विद्युत फ्लक्स केवल उस सतह के बाहर बंद किए गए आवेश पर निर्भर करता है। क्योंकि सभी चित्र एक ही धनावेश को बंद करते हैं, इसलिए सभी के लिए विद्युत फ्लक्स समान है।
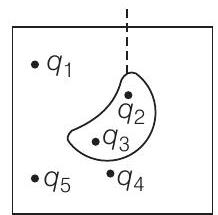
4. पांच आवेश $q_{1}, q_{2}, q_{3}, q_{4}$, और $q_{5}$ चित्र में दिखाए गए स्थानों पर स्थिर हैं, $S$ एक गॉसीय सतह है। गॉस के नियम को $\int_{5} E . d S=\dfrac{q}{\varepsilon_{0}}$ द्वारा दिया गया है। निम्नलिखित में से कौन सा कथन सही है?
(a) उपरोक्त समीकरण के बाईं ओर $\mathbf{E}$ के योगदान $q_{1}, q_{5}$ और $q_{1}, q_{5}$ और $q_{3}$ से होगा जबकि दाईं ओर $q$ के योगदान केवल $q_{2}$ और $q_{4}$ से होगा
(b) उपरोक्त समीकरण के बाईं ओर $\mathbf{E}$ के योगदान सभी आवेशों से होगा जबकि दाईं ओर $q$ के योगदान केवल $q_{2}$ और $q_{3}$ से होगा
(c) उपरोक्त समीकरण के बाईं ओर $\mathbf{E}$ के योगदान सभी आवेशों से होगा जबकि दाईं ओर $q$ के योगदान केवल $q_{1}, q_{3}$ और $q_{5}$ से होगा
(d) दोनों $\mathbf{E}$ बाईं ओर और $q$ दाईं ओर केवल $q_{2}$ और $q_{4}$ से योगदान प्राप्त करेंगे
उत्तर दिखाएं
उत्तर
(b) गॉस के नियम के अनुसार, समीकरण $\int_{S} E \cdot d S=\dfrac{q}{\varepsilon_{0}}$ के दाईं ओर $q$ का अंश तल के भीतर स्थित सभी आवेशों के योग को शामिल करता है।
आवेश तल के कहीं भी भीतर स्थित हो सकते हैं, यदि तल इस तरह चुना जाए कि कुछ आवेश भीतर और कुछ बाहर हों, तो समीकरण के बाईं ओर विद्युत क्षेत्र भीतर और बाहर दोनों आवेशों के कारण होता है।
इसलिए, उपरोक्त समीकरण के बाईं ओर $\mathrm{E}$ के योगदान सभी आवेशों से होगा जबकि दाईं ओर $q$ के योगदान केवल $q_{2}$ और $q_{3}$ से होगा।
-
विकल्प (a): यह विकल्प गलत है क्योंकि गॉस के नियम के समीकरण के बाईं ओर विद्युत क्षेत्र $\mathbf{E}$ दोनों भीतर और बाहर के आवेशों के कारण होता है। हालांकि, कथन का दावा करता है कि $\mathbf{E}$ केवल $q_1$, $q_5$ और $q_3$ से योगदान प्राप्त करेगा, जो सही नहीं है। इसके अलावा, दाईं ओर के आवेश $q$ सभी आवेशों के योग को शामिल करता है जो तल के भीतर हैं, जो $q_2$ और $q_4$ हैं, लेकिन कथन इस भाग को सही रूप से पहचानता है।
-
विकल्प (c): यह विकल्प गलत है क्योंकि गॉस के नियम के समीकरण के दाईं ओर आवेश $q$ सभी आवेशों के योग को शामिल करता है जो तल $S$ के भीतर हैं, जो $q_2$ और $q_4$ हैं। कथन गलत रूप से दावा करता है कि $q$ केवल $q_1$, $q_3$ और $q_5$ से योगदान प्राप्त करेगा, जो गॉसीय तल के बाहर हैं।
-
विकल्प (d): यह विकल्प गलत है क्योंकि गॉस के नियम के समीकरण के बाईं ओर विद्युत क्षेत्र $\mathbf{E}$ दोनों भीतर और बाहर के आवेशों के कारण होता है। कथन गलत रूप से दावा करता है कि $\mathbf{E}$ केवल $q_2$ और $q_4$ से योगदान प्राप्त करेगा, जो तल के भीतर हैं।
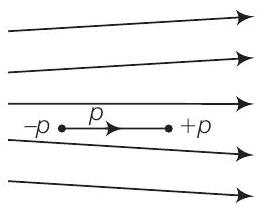
5. चित्र में विद्युत क्षेत्र रेखाएँ दिखाई गई हैं जिनमें एक विद्युत द्विध्रुव $P$ दिखाया गया है। निम्नलिखित में से कौन सा कथन सही है?
(a) डाइपोल को कोई बल अनुभव नहीं होगा
(b) डाइपोल को दाहिने ओर बल अनुभव होगा
(c) डाइपोल को बाएँ ओर बल अनुभव होगा
(d) डाइपोल को ऊपर ओर बल अनुभव होगा
उत्तर दिखाएँ
सोचने की प्रक्रिया
डाइपोल के आवेशों पर विद्युत क्षेत्र की तीव्रता ज्ञात कीजिए।
बल विद्युत क्षेत्र की तीव्रता के सीधे अनुपात में होता है, अर्थात अधिक विद्युत क्षेत्र की तीव्रता अधिक बल का कारण होती है और विपरीत भी।
उत्तर
(c) विद्युत क्षेत्र रेखाओं के बीच अंतर बढ़ रहा है, यहाँ बाएँ से दाएँ तक और इसकी विशेषता यह है कि विद्युत क्षेत्र की तीव्रता विद्युत क्षेत्र रेखाओं के बीच अंतर के बढ़ने के साथ घटती जाती है। इस कारण आवेशों पर बल बाएँ से दाएँ घटता जाता है।
इसलिए, आवेश $-q$ पर बल $+q$ पर बल से अधिक होता है, जिसके कारण डाइपोल को बाएँ ओर बल अनुभव होता है।
-
(a) डाइपोल को कोई बल अनुभव नहीं होगा: यह गलत है क्योंकि विद्युत क्षेत्र असमान है, अर्थात डाइपोल के धनावेश और नकारात्मक आवेश पर बल बराबर और विपरीत नहीं होते, जिसके कारण डाइपोल पर एक संतुलित बल होता है।
-
(b) डाइपोल को दाहिने ओर बल अनुभव होगा: यह गलत है क्योंकि विद्युत क्षेत्र की तीव्रता बाएँ से दाएँ घटती जाती है। नकारात्मक आवेश (जो अधिक मजबूत होता है) डाइपोल को बाएँ ओर खींचेगा, न कि दाहिने ओर।
-
(d) डाइपोल को ऊपर ओर बल अनुभव होगा: यह गलत है क्योंकि विद्युत क्षेत्र रेखाएँ क्षैतिज होती हैं, जिसका अर्थ है कि डाइपोल पर कार्य करने वाले बल भी क्षैतिज होते हैं। विद्युत क्षेत्र में कोई ऊर्ध्वाधर घटक नहीं होता जो ऊपर की दिशा में बल का कारण हो सके।
6. एक बिंदु आवेश $+q$ एक अनुनादित चालक सतह से दूरी $d$ पर रखा गया है। चालक सतह के दूसरी ओर बिंदु $P$ पर विद्युत क्षेत्र है
(a) तल के तल के लम्बवत तथा तल से दूर
(b) तल के लम्बवत लेकिन तल की ओर
(c) बिंदु आवेश से दूर तथा त्रिज्या के अनुदिश
(d) बिंदु आवेश की ओर तथा त्रिज्या के अनुदिश
उत्तर दिखाएँ
उत्तर
(a) जब एक बिंदु धनावेश एक अनुनादित चालक तल के पास लाया जाता है, तो तल के सतह पर ऋणावेश उत्पन्न होता है जो आवेश की ओर होता है और तल के विपरीत ओर बराबर धनावेश उत्पन्न होता है। इस प्रक्रिया को आवेशन द्वारा आकर्षण कहते हैं।
-
(b) तल के दूसरी ओर बिंदु $ P $ पर विद्युत क्षेत्र तल की ओर नहीं दिशा ले सकता क्योंकि तल के विपरीत ओर उत्पन्न धनावेश तल के दूर दिशा में विद्युत क्षेत्र उत्पन्न करता है।
-
(c) बिंदु $ P $ पर विद्युत क्षेत्र बिंदु आवेश की ओर त्रिज्या के अनुदिश नहीं दिशा ले सकता क्योंकि चालक तल विद्युत क्षेत्र वितरण को बदल देता है और क्षेत्र रेखाएँ चालक के सतह के लम्बवत होनी चाहिए।
-
((d) बिंदु $ P $ पर विद्युत क्षेत्र बिंदु आवेश की ओर त्रिज्या के अनुदिश नहीं दिशा ले सकता क्योंकि चालक तल पर उत्पन्न आवेशों के प्रभाव विद्युत क्षेत्र रेखाओं की दिशा को बदल देता है, जिसके कारण वे तल के लम्बवत हो जाती हैं।
7. एक अर्धगोला एकसमान रूप से धनावेशित है। एक बिंदु पर अर्धगोले के व्यास के अनुदिश दूर दिशा में विद्युत क्षेत्र की दिशा है
(a) व्यास के लम्बवत
(b) व्यास के समानांतर
(c) व्यास की ओर झुकी एक कोण पर
(d) व्यास से दूर झुकी एक कोण पर
उत्तर दिखाएँ
उत्तर
(a) जब बिंदु अर्धगोले के व्यास के अनुदिश दूर दिशा में स्थित होता है जो एकसमान रूप से धनावेशित होता है, तो विद्युत क्षेत्र व्यास के लम्बवत होता है। विद्युत तीव्रता के घटक जो व्यास के समानांतर होते हैं, एक दूसरे को बर्बाद कर देते हैं।
-
(b) व्यास के समानांतर: यह विकल्प गलत है क्योंकि सममिति के कारण विद्युत क्षेत्र के घटक जो व्यास के समानांतर होते हैं, एक दूसरे को बर्बाद कर देते हैं। अतः विद्युत क्षेत्र की नेट दिशा व्यास के समानांतर नहीं हो सकती।
-
(स) व्यास के तिरछे कोण पर: यह विकल्प गलत है क्योंकि अर्धगोले पर आवेश वितरण की सममिति बरकरार रखती है, जिसके कारण व्यास के अनुदिश विद्युत क्षेत्र के घटक उलट जाते हैं। विद्युत क्षेत्र व्यास के लंबवत होता है, न कि इसकी ओर झुका होता है।
-
(द) व्यास के दूर तिरछे कोण पर: इस विकल्प के लिए (स) के लिए दिए गए कारण के लिए यह भी गलत है। आवेश वितरण की सममिति के कारण व्यास के अनुदिश विद्युत क्षेत्र के घटक उलट जाते हैं, जिसके कारण विद्युत क्षेत्र व्यास के लंबवत होता है, न कि इससे दूर तिरछा होता है।
बहुविकल्पीय प्रश्न (एक से अधिक विकल्प)
8. यदि $\int_{5} E . d S=0$ एक सतह पर हो, तो
(अ) सतह के अंदर और इस पर विद्युत क्षेत्र शून्य होता है
(ब) सतह के अंदर विद्युत क्षेत्र आवश्यक रूप से समान होता है
(स) सतह के माध्यम से प्रवाह रेखाओं की संख्या प्रवाह रेखाओं की संख्या के बराबर होनी चाहिए जो सतह से बाहर जाती हैं
(द) सभी आवेश आवश्यक रूप से सतह के बाहर होना चाहिए
सोचने की प्रक्रिया
गॉस के नियम के बारे में विस्तार से चर्चा करें।
उत्तर दिखाएं
उत्तर
(स, द)
$\oint_{S} E . d S=0$ एक बंद सतह पर विद्युत प्रवाह को दर्शाता है।
सामान्य रूप से, $\oint_{S} E . d S$ एक सतह के माध्यम से प्रवाह रेखाओं की संख्या के बीजगणितीय योग को दर्शाता है, जो सतह के अंदर आती हैं और जो सतह के बाहर जाती हैं।
जब $\oint_{S} E . d S=0$ होता है, तो यह बताता है कि सतह के माध्यम से प्रवाह रेखाओं की संख्या बराबर होती है जो सतह के अंदर आती हैं और जो सतह के बाहर जाती हैं।
अब, गॉस के नियम से हम जानते हैं कि $\oint_{S} E . d S=\dfrac{q}{\varepsilon_{0}}$ जहां $q$ सतह के अंदर आवेश होता है। जब $\int_{S} E \cdot d S=0$ होता है, तो $q=0$ अर्थात सतह के अंदर कुल आवेश शून्य होता है। इसलिए, सभी अन्य आवेश आवश्यक रूप से सतह के बाहर होना चाहिए। इसका कारण यह है कि सतह के बाहर के आवेश विद्युत प्रवाह में योगदान नहीं देते हैं।
-
(अ) सतह के अंदर और इस पर विद्युत क्षेत्र शून्य होता है: यह गलत है क्योंकि सतह के अंदर विद्युत क्षेत्र आवश्यक रूप से शून्य नहीं होता है। शर्त $\int_{S} E \cdot dS = 0$ केवल यह बताती है कि सतह के माध्यम से कुल प्रवाह शून्य होता है, जो विद्युत क्षेत्र के अंदर शून्य न होने के बावजूद भी हो सकता है, जब तक कि प्रवाह रेखाओं की संख्या जो सतह के अंदर आती हैं और जो सतह के बाहर जाती हैं बराबर न हों।
-
(ब) सतह के अंदर विद्युत क्षेत्र आवश्यक रूप से समान होता है: यह गलत है क्योंकि सतह के अंदर विद्युत क्षेत्र आवश्यक रूप से समान नहीं होता। स्थिति $\int_{S} E \cdot dS = 0$ केवल इस बात को दर्शाती है कि सतह के माध्यम से शुद्ध फ्लक्स शून्य होता है, जो असमान विद्युत क्षेत्र के लिए भी सत्य हो सकता है। विद्युत क्षेत्र के समान होना शुद्ध फ्लक्स के लिए आवश्यक नहीं होता।
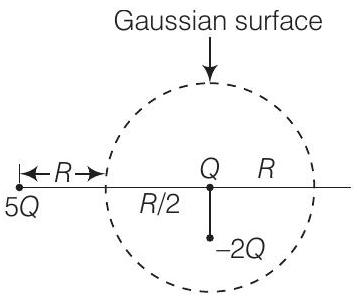
12. चित्र में आवेशों के व्यवस्था के संदर्भ में और एक गैस गुरुत्व त्रिज्या $R$ के साथ $Q$ केंद्र में हो। तब,
(a) गोले के सतह के माध्यम से कुल फ्लक्स $\dfrac{-Q}{\varepsilon_{0}}$ होता है
(b) गोले के सतह पर क्षेत्र $\dfrac{-Q}{4 \pi \varepsilon_{0} R^{2}}$ होता है
(c) $5 Q$ के कारण गोले के सतह के माध्यम से फ्लक्स शून्य होता है
(d) $-2 \mathrm{Q}$ के कारण गोले के सतह पर क्षेत्र सभी स्थानों पर समान होता है
उत्तर दिखाएं
Answer
$(a, c)$
गॉस के नियम के अनुसार, एक बंद सतह के कुल विद्युत फ्लक्स $\dfrac{q}{\varepsilon_{0}}$ होता है, जहां $q$ सतह के भीतर बंद आवेश होता है। इसलिए, चित्र से,
सतह के भीतर कुल आवेश $= Q - 2 Q = -Q$
$\therefore$ गोले के सतह के माध्यम से कुल फ्लक्स $= \dfrac{-Q}{\varepsilon_{0}}$
अब, $5 Q$ के आवेश के बारे में सोचें। $5 Q$ आवेश सतह के बाहर होता है, इसलिए इसका दिए गए सतह के माध्यम से विद्युत फ्लक्स पर कोई योगदान नहीं होता।
-
विकल्प (ब): गोले के सतह पर विद्युत क्षेत्र $\dfrac{-Q}{4 \pi \varepsilon_{0} R^{2}}$ द्वारा दिया गया नहीं है। यह व्यंजक यदि $-Q$ ही एकमात्र आवेश हो और एकसमान रूप से वितरित हो, तो सही होता। हालांकि, गॉसीय सतह के बाहर अन्य आवेशों की उपस्थिति विद्युत क्षेत्र के वितरण को प्रभावित करती है, जिसके कारण इस व्यंजक के लिए दिए गए विन्यास में अमान्य हो जाता है।
-
विकल्प (द): $-2Q$ के कारण गोले के सतह पर विद्युत क्षेत्र सभी स्थानों पर समान नहीं है। $-2Q$ गॉसीय सतह के संदर्भ में सममित रूप से रखा गया नहीं है, जिसके कारण गोले के सतह पर विद्युत क्षेत्र असमान हो जाता है।
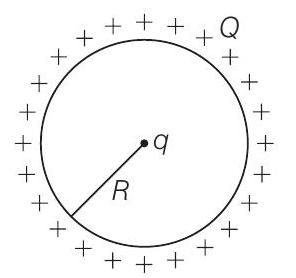
13. एक धनात्मक आवेश $Q$ त्रिज्या $R$ के एक वृत्ताकार वलय के अक्ष के अनुदिश एकसमान रूप से वितरित है। एक छोटा परीक्षण आवेश $q$ वलय के केंद्र पर रखा गया है। तब,
(a) यदि $q>0$ और केंद्र से वलय के तल में दूर बह जाता है, तो यह केंद्र की ओर वापस लौटेगा
(b) यदि $q<0$ और कें द्र से वलय के तल में दूर बह जाता है, तो यह केंद्र में वापस नहीं आएगा और वलय तक जाते हुए चलता रहेगा
(c) यदि $q<0$, तो वलय के अक्ष के अनुदिश छोटे विस्थापन के लिए यह सरल आवर्त गति करेगा
(d) $q$ वलय के केंद्र पर धनात्मक आवेश के लिए वलय के तल में अस्थायी संतुलन में है
उत्तर दिखाएं
उत्तर
$(a, b, c)$
धनात्मक आवेश $Q$ बंद गोले के बाहरी सतह पर एकसमान रूप से वितरित है। इसलिए, गोले के भीतर विद्युत क्षेत्र शून्य होता है।
इसलिए, धनात्मक आवेश $Q$ के कारण आवेश $q$ पर विद्युत क्षेत्र का प्रभाव शून्य होता है।
अब, आवेशों के बीच आकर्षण और प्रतिकर्षण बल ही नियंत्रक कारक होते हैं।
$(Q$ और $q)$ के बीच दो स्थितियाँ उत्पन्न होती हैं।
केस I जब आवेश $q>0$ अर्थात $q$ एक धनात्मक आवेश है, तो आवेश $q$ और $Q$ के बीच प्रतिकर्षण बल उत्पन्न होता है।
आवेश $Q$ के सभी ओर से आकर्षण बल आवेश $q$ को वलय के केंद्र की ओर खींचेगा यदि यह वलय के केंद्र से विस्थापित हो जाए।
केस II जब आवेश $q<0$ अर्थात् $q$ एक नकारात्मक आवेश हो तो आवेश $Q$ और $q$ के बीच आकर्षण बल होता है।
यदि $q$ केंद्र से विस्थापित हो जाए तो इस आवेश के पास निकटतम धनावेश इसे अपनी ओर खींचेगा और आवेश $q$ केंद्र वापस नहीं लौटेगा।
-
विकल्प (d) गलत है क्योंकि:
कथन कहता है कि एक धनावेशित परीक्षण आवेश $q$ वलय के केंद्र पर वलय के तल में अस्थायी संतुलन में होता है जब $q > 0$। हालांकि, यह सत्य नहीं है। एक धनावेशित परीक्षण आवेश $q$ वलय के केंद्र पर, वलय पर एकसमान रूप से वितरित धनावेश $Q$ के विपरीत बल एक दूसरे को बराबर कर देंगे, जिसके परिणामस्वरूप स्थायी संतुलन होगा। यदि आवेश $q$ थोड़ा विस्थापित हो जाए तो शुद्ध बल इसे केंद्र की ओर ले जाएगा, जो स्थायी संतुलन को दर्शाता है, न कि अस्थायी संत नहीं।
बहुत छोटे उत्तर प्रकार प्रश्न
14. एक अस्थिर सतह एक द्विध्रुव को घेरती है। इस सतह के माध्यम से विद्युत फ्लक्स क्या होगा?
उत्तर दिखाएं
उत्तर
गॉस के नियम के अनुसार, बंद सतह के माध्यम से विद्युत फ्लक्स निम्नलिखित द्वारा दिया जाता है $\oint_{s} E \cdot d S=\dfrac{q}{\varepsilon_{0}}$। यहाँ, $q$ उस बंद सतह के अंदर कुल आवेश है।
अब, द्विध्रुव के अंतर्गत कुल आवेश $-q+q=0$ द्वारा दिया जाता है।
$\therefore$ एक द्विध्रुव को घेरने वाली सतह के माध्यम से विद्युत फ्लक्स $=\dfrac{-q+q}{\varepsilon_{0}}=\dfrac{0}{\varepsilon_{0}}=0$
15. एक धातु के गोलीय खोल के आंतरिक त्रिज्या $R_{1}$ और बाहरी त्रिज्या $R_{2}$ है। एक आवेश $Q$ गोलीय रिक्त स्थान के केंद्र पर रखा गया है। आंतरिक सतह और बाहरी सतह पर क्रमशः क्षेत्रफल आवेश घनत्व क्या होगा? $\newline$
(i) आंतरिक सतह $\newline$
(ii) बाहरी सतह? $\newline$
उत्तर दिखाएं
सोचने की प्रक्रिया
हम दिए गए स्थिति के अनुसार चित्र बनाएं। आवेश के प्रेरण प्रक्रिया का उपयोग करके पूरे गोलीय खोल पर आवेश के वितरण को निर्धारित करें। अब, आवश्यक सतह आवेश घनत्व को खोजें।
उत्तर
यहाँ, गोलीय खाली स्थान के केंद्र में रखे आवेश का धनात्मक आवेश है। अतः, आवेश के कारण गोले के आंतरिक सतह पर उत्पन्न आवेश $-Q$ होगा और इस आवेश के कारण बाहरी सतह पर उत्पन्न आवेश $+Q$ होगा।
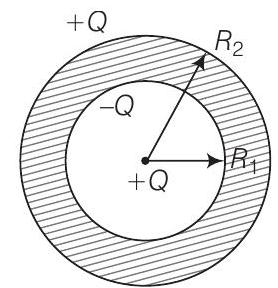
अब, आंतरिक सतह पर सतह आवेश घनत्व $=\dfrac{-Q}{4 \pi R_{1}^{2}}$ और
आंतरिक सतह पर सतह आवेश घनत्व $=\dfrac{+Q}{4 \pi R_{2}^{2}}$
16. परमाणु के आयाम एंगस्ट्रॉम के क्रम के होते हैं। अतः, प्रोटॉन और इलेक्ट्रॉन के बीच बड़े विद्युत क्षेत्र होना चाहिए। तब भी चालक के भीतर विद्युत क्षेत्र शून्य क्यों होता है?
उत्तर दिखाएं
उत्तर
प्रोटॉन और इलेक्ट्रॉन परमाणु में अलग-अलग और स्वतंत्र रूप से बंधे होते हैं और आवेश के अंतर में उदासीन होते हैं।
विद्युत क्षेत्र अतिरिक्त आवेश की उपस्थिति के कारण होता है।
लेकिन एक अलग चालक के बाहरी सतह पर कोई अतिरिक्त आवेश नहीं हो सकता। अतः, चालक के भीतर विद्युत क्षेत्र शून्य होता है चाहे परमाणु के आयाम एंगस्ट्रॉम के क्रम के हों।
17. यदि किसी सतह के भीतर आवेश के कुल आवेश शून्य हो, तो यह क्या अर्थ है कि सतह पर सभी बिंदुओं पर विद्युत क्षेत्र शून्य होता है? विपरीत, यदि किसी सतह पर सभी बिंदुओं पर विद्युत क्षेत्र शून्य हो, तो यह क्या अर्थ है कि सतह के भीतर कुल आवेश शून्य होता है।
उत्तर दिखाएं
उत्तर
गॉस के नियम के अनुसार, जब सतह के भीतर आवेश हो और बाहर आवेश भी हो, तो ऐसी सतह के चयन के लिए यह भी कहा जा सकता है।
ऐसी स्थिति में फ्लक्स निम्न द्वारा दिया जाता है $\oint_{s} E . d S=\dfrac{q}{\varepsilon_{0}}$।
ऐसी स्थितियों में, बाएँ पक्ष में विद्युत क्षेत्र आवेश के दोनों भीतर और बाहर आवेश के कारण होता है। गॉस के नियम के समीकरण के दाएँ पक्ष में $q$ शब्द केवल सतह के भीतर आवेश को प्रतिनिधित्व करता है।
Thus, चालू आवेश के एक सतह के बाहर शून्य होने के बावजूद, यह बताने की आवश्यकता नहीं है कि सतह पर सभी बिंदुओं पर विद्युत क्षेत्र शून्य है, विद्युत क्षेत्र सतह के लंब रेखा के अनुदिश हो सकता है।
इसके विपरीत, यदि किसी सतह पर सभी बिंदुओं पर विद्युत क्षेत्र शून्य है, तो इसका अर्थ यह नहीं है कि इसके भीतर कुल आवेश शून्य है।
अर्थात,
हम प्राप्त करते हैं
$$ \text { रखें } E=0 \text { तो } \oint_{s} E . d S=\dfrac{q}{\varepsilon_{0}} $$
$$ q=0 . $$
18. चित्र में दिखाए गए समान आवेश वाले खोखले सिलेंडर के लिए विद्युत क्षेत्र रेखाओं का चित्र बनाएं।
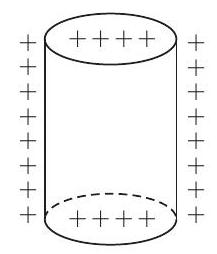
उत्तर दिखाएं
सोचने की प्रक्रिया
सामान्य गुणों के अनुसार, विद्युत क्षेत्र रेखाएं धनात्मक आवेश से शुरू होती हैं और ऋणात्मक आवेश पर समाप्त होती हैं। यदि एक अकेला आवेश हो, तो वे अनंत तक शुरू या समाप्त हो सकती हैं।
उत्तर
इसलिए, विद्युत क्षेत्र रेखाएं धनात्मक आवेश से शुरू होंगी और अनंत की ओर बढ़ेंगी, जैसा कि चित्र में दिखाया गया है।
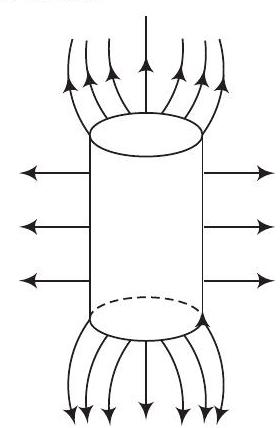
पार्श्व दृश्य
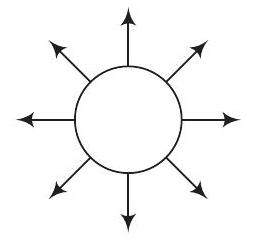
ऊपरी दृश्य
19. चित्र में दिखाए गए घन के फलकों के माध्यम से कुल फ्लक्स क्या होगा, जिसकी भुजा की लंबाई $a$ है, यदि आवेश $q$ निम्नलिखित स्थानों पर रखा गया है?
(a) $A$ घन के कोने पर
(b) $B$ घन के एक किनारे के मध्य बिंदु पर
(c) $C$ घन के एक फलक के केंद्र पर
(d) $D$ $B$ और $C$ के मध्य बिंदु पर
$K$ सोचने की प्रक्रिया
ऐसी सममिति वाली आकृति के बारे में तर्क करें जहां रखा गया आवेश केंद्र में आ जाए। इसलिए,
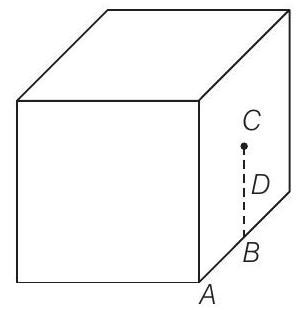
गॉस के प्रमेय के उपयोग द्वारा कल्पनात्मक आकृति से संबंधित फ्लक्स की गणना करें। उसके बाद दी गई आकृति से संबंधित फ्लक्स की गणना करें।
उत्तर दिखाएं
उत्तर
(a) एक घन के आठ कोने होते हैं, इसलिए घन के कुल आवेश $\dfrac{q}{8}$ होता है।
इसलिए, बिंदु $A$ पर विद्युत फ्लक्स $=\dfrac{q}{8 \varepsilon_{0}}$ होता है।
(b) जब आवेश $q$ घन के किसी किनारे के मध्य बिंदु $B$ पर रखा जाता है, तो यह 4 घनों के बीच बराबर बांट दिया जाता है। इसलिए, दिए गए घन के फलकों के माध्यम से कुल फ्लक्स $=q / 4 \varepsilon_{0}$ होता है।
(c) जब आवेश $q$ घन के किसी फलक के केंद्र $C$ पर रखा जाता है, तो यह 2 घनों के बीच बराबर बांट दिया जाता है। इसलिए, दिए गए घन के फलकों के माध्यम से कुल फ्लक्स $=q / 2 \varepsilon_{0}$ होता है।
(d) इसी तरह, जब आवेश $q$ बिंदु $Q$ पर रखा जाता है, जो $B$ और $C$ के मध्य बिंदु है, तो यह 2 घनों के बीच बराबर बांट दिया जाता है। इसलिए, दिए गए घन के फलकों के माध्यम से कुल फ्लक्स $=q / 2 \varepsilon_{0}$ होता है।
छोटे उत्तर प्रकार प्रश्न
20. एक पैसा सिक्का एल्यूमिनियम-मैग्नीशियम मिश्र धातु से बना होता है और इसका भार $0.75 \mathrm{~g}$ होता है। यह एक वर्ग आकार का होता है और इसके विकर्ण की लंबाई $17 \mathrm{~mm}$ होती है। यह विद्युत उदासीन होता है और धनात्मक और ऋणात्मक आवेश के बराबर मात्रा में रहता है।
उत्तर दिखाएं
सोचने की प्रक्रिया
एल्यूमिनियम से बने पैसा सिक्के के बारे में सोचें, एक समान संख्या में धनात्मक और ऋणात्मक आवेश के मात्रा की गणना करें। आप इस मात्रा से क्या निष्कर्ष निकालते हैं?
उत्तर
यहाँ दिए गए मात्राएँ हैं
पैसा सिक्के का भार $=0.75 \mathrm{~g}$
एल्यूमिनियम का परमाणु भार $=26.9815 \mathrm{~g}$
आवोगाड्रो संख्या $=6.023 \times 10^{23}$
इसलिए, एक पैसा सिक्के में एल्यूमिनियम परमाणुओं की संख्या,
$$ N=\dfrac{6.023 \times 10^{23}}{26.9815} \times 0.75=1.6742 \times 10^{22} $$
एल्यूमिनियम के आवेश संख्या 13 है, इसलिए प्रत्येक एल्यूमिनियम परमाणु में 13 प्रोटॉन और 13 इलेक्ट्रॉन होते हैं।
$\therefore \quad$ एक पैसे के सिक्के में धनात्मक और नकारात्मक आवेश के मापदंड $=\mathrm{N}$ ze
$$ \begin{aligned} & =1.6742 \times 10^{22} \times 13 \times 1.60 \times 10^{-19} \mathrm{C} \ & =3.48 \times 10^{4} \mathrm{C}=34.8 \mathrm{kC} \end{aligned} $$
यह एक बहुत बड़ा आवेश है। इसलिए, हम निष्कर्ष निकाल सकते हैं कि सामान्य उदासीन पदार्थ में बहुत बड़ी मात्रा में $\pm$ आवेश होते हैं।
21. प्रश्न 20 के सिक्के के बारे में विचार करें। यह विद्युत उदासीन है और धनात्मक और नकारात्मक आवेश के बराबर मात्रा में शामिल है जिसके मापदंड $34.8 \mathrm{kC}$ है। मान लीजिए कि इन बराबर आवेशों को दो बिंदु आवेशों में संकेंद्रित कर दिया जाता है जो निम्नलिखित दूरी पर अलग हैं:
(i) $1 \mathrm{~cm} \sim \dfrac{1}{2} \times$ एक पैसे के सिक्के के विकर्ण के आधा
(ii) $100 \mathrm{~m}$ (एक लंबे इमारत की लंबाई)
(iii) $10^{6} \mathrm{~m}$ (पृथ्वी की त्रिज्या)।
तीनों मामलों में प्रत्येक बिंदु आवेश पर बल ज्ञात कीजिए। आप इन परिणामों से क्या निष्कर्ष निकालते हैं?
उत्तर दिखाएं
सोचने की प्रक्रिया
एक बिंदु आवेश पर बल $=\dfrac{|q|^{2}}{4 \pi \varepsilon_{0} r^{2}}$। यहाँ, $q=$ एक आवेश के मापदंड, $r=$ दो आवेशों के बीच की दूरी।
उत्तर
यहाँ,
$$ \begin{aligned} q= \pm 34.8 \mathrm{RC}= \pm 3.48 \times 10^{4} \mathrm{C} \newline\ r_{1}=1 \mathrm{~cm}=10^{-2} \mathrm{~m}, r_{2}=100 \mathrm{~m}, r_{3}=10^{6} \mathrm{~m} \newline \quad \quad \quad \quad \quad \quad \text { and } \dfrac{1}{4 \pi \varepsilon_{0}}=9 \times 10^{9} \newline \ F_{1}=\dfrac{|q|^{2}}{4 \pi \varepsilon_{0} r_{1}^{2}}=\dfrac{9 \times 10^{9}\left(3.48 \times 10^{4}\right)^{2}}{\left(10^{-2}\right)^{2}}=1.09 \times 10^{23} \mathrm{~N} \newline \ F_{2}=\dfrac{|q|^{2}}{4 \pi \varepsilon_{0} r_{2}^{2}}=\dfrac{9 \times 10^{9}\left(3.48 \times 10^{4}\right)^{2}}{(100)^{2}}=1.09 \times 10^{15} \mathrm{~N} \newline \ F_{3}=\dfrac{|q|^{2}}{4 \pi \varepsilon_{0} r_{3}^{2}}=\dfrac{9 \times 10^{9}\left(3.48 \times 10^{4}\right)^{2}}{\left(10^{6}\right)^{2}}=1.09 \times 10^{7} \mathrm{~N} \end{aligned} \newline
$$
इस परिणाम से हम देखते हैं कि जब सामान्य रूप से तटस्थ पदार्थ में $\pm$ चार्ज बिंदु चार्ज के रूप में अलग किए जाते हैं, तो वे एक विशाल बल लगाते हैं। इसलिए, पदार्थ के विद्युत तटस्थता को बिगाड़ना बहुत कठिन होता है।
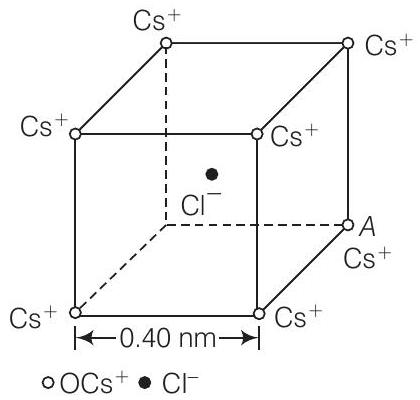
22. चित्र एक सीजियम क्लोराइड, $\mathrm{CsCl}$ के क्रिस्टल इकाई को प्रस्तुत करता है। सीजियम परमाणु, जो खाली वृत्तों द्वारा प्रस्तुत किए गए हैं, एक घन के कोनों पर स्थित हैं जिसकी भुजा $0.40 \mathrm{~nm}$ है, जबकि एक $\mathrm{Cl}$ परमाणु घन के केंद्र पर स्थित है। सीजियम परमाणु एक इलेक्ट्रॉन के अभाव में हैं जबकि $\mathrm{Cl}$ परमाणु एक अतिरिक्त इलेक्ट्रॉन के साथ है।
(i) आठ $\mathrm{Cs}$ परमाणुओं के कारण $\mathrm{Cl}$ परमाणु पर शुद्ध विद्युत क्षेत्र क्या होगा?
(ii) मान लीजिए कि कोने $A$ पर स्थित $\mathrm{Cs}$ परमाणु गायब हो गया है। अब छह शेष $\mathrm{Cs}^{2}$ परमाणुओं के कारण $\mathrm{Cl}$ परमाणु पर शुद्ध बल क्या होगा?
उत्तर दिखाएं
सोचने की प्रक्रिया
(i) दो बराबर और विपरीत चार्जों के कारण एक चार्ज पर शुद्ध बल शून्य होता है। एक चार्ज पर विद्युत क्षेत्र निम्न द्वारा दिया जाता है $E=\dfrac{F}{q}$ जहाँ $E=$ विद्युत क्षेत्र, $F=$ विद्युत क्षेत्र के कारण चार्ज $q$ पर बल, $q=$ चार्ज $q$ के परिमाण है।
(ii) यदि कोने $A$ पर एक $\mathrm{Cs}$ परमाणु बर्बाद हो जाता है तो एक एकल चार्जित नकारात्मक $\mathrm{Cs}$ आयन $A$ पर उपस्थित हो जाएगा।
उत्तर
(i) दिए गए चित्र से हम विश्लेषण कर सकते हैं कि क्लोरीन परमाणु घन के केंद्र पर है अर्थात घन के सभी आठ कोनों पर स्थित सीजियम परमाणुओं से बराबर दूरी पर है। इसलिए, सममिति के कारण सभी $\mathrm{Cs}$ परमाणुओं के कारण $\mathrm{Cl}$ परमाणु पर बल शून्य हो जाएगा।
इसलिए,
$$ E=\dfrac{F}{q} \text { जहाँ } F=0 $$
$$ \therefore \quad E=0 $$
(ii) इसलिए, कोने $A$ पर $\mathrm{Cl}$ परमाणु पर शुद्ध बल होगा,
$$ F=\dfrac{e^{2}}{4 \pi \varepsilon_{0} r^{2}} $$
जहाँ, $\quad r=$ $\mathrm{Cl}$ आयन और $\mathrm{Cs}$ आयन के बीच की दूरी।
पाइथागोरस प्रमेय के अनुसार, हमें प्राप्त होता है
अब,
$$ \begin{aligned} r & =\sqrt{(0.20)^{2}+(0.20)^{2}+(0.20)^{2}} \times 10^{-9} \mathrm{~m} \newline \ & =0.346 \times 10^{-9} \mathrm{~m} \newline \ F & =\dfrac{q^{2}}{4 \pi \varepsilon_{0} r^{2}}=\dfrac{e^{2}}{4 \pi \varepsilon_{0} r_{2}} \newline \ & =\dfrac{9 \times 10^{9}\left(1.6 \times 10^{-19}\right)^{2}}{\left(0.346 \times 10^{-9}\right)^{2}}=1.92 \times 10^{-9} \mathrm{~N} \newline \end{aligned} $$
23. दो आवेश $q$ और $-3 q$ एक स्थिर अवस्था में $x$-अक्ष पर दूरी $d$ के अलग-अलग रखे गए हैं। एक तीसरा आवेश $2 q$ कहाँ रखा जाना चाहिए ताकि यह कोई बल अनुभव न करे?
उत्तर दिखाएं
सोचने की प्रक्रिया
कोई आवेश पर बल शून्य होगा केवल तभी जब सभी बल संतुलित हों, अर्थात, आकर्षण बल के द्वारा बल द्वारा प्रतिकर्षण बल संतुलित हो।
उत्तर
यहाँ, हम आवेश $2 q$ को $A$ से दूरी $r$ पर रखते हैं।
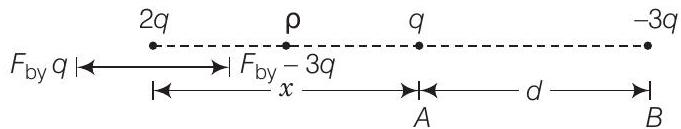
इसलिए, आवेश $2 q$ कोई बल अनुभव नहीं करेगा।
जब, इस पर $q$ के कारण प्रतिकर्षण बल $-3 q$ के कारण आकर्षण बल द्वारा संतुलित होता है, तो बिंदु $B$ पर, जहाँ $AB = d$ है।
इसलिए, $-3 q$ द्वारा आकर्षण बल = $q$ द्वारा प्रतिकर्षण बल
$$ \begin{array}{rlrl} \Rightarrow & & \dfrac{2 q \times q}{4 \pi \varepsilon_{0} x^{2}} & =\dfrac{2 q \times 3 q}{4 \pi \varepsilon_{0}(x+d)^{2}} \ \Rightarrow & & (x+d)^{2} & =3 x^{2} \ \Rightarrow & x^{2}+d^{2}+2 x d & =3 x^{2} \ \Rightarrow & & =2 x^{2}-d^{2} \end{array} $$
$$ \begin{aligned} \therefore \quad 2 x^{2}-2 d x-d^{2} & =0 \ x & =\dfrac{d}{2} \pm \dfrac{\sqrt{3} d}{2} \end{aligned} $$
(ऋणात्मक चिह्न $q$ और $-3 q$ के बीच होता है और इसलिए अनुपयुक्त है।)
$$ \begin{aligned} x & =-\dfrac{d}{2}+\dfrac{\sqrt{3} d}{2} \ & =\dfrac{d}{2}(1+\sqrt{3}) \text { बिंदु } q \text{ के बाईं ओर }. \end{aligned} $$
24. चित्र में तीन बिंदु आवेश $A, B$ और $C$ के आसपास विद्युत क्षेत्र रेखाएँ दिखाई गई हैं
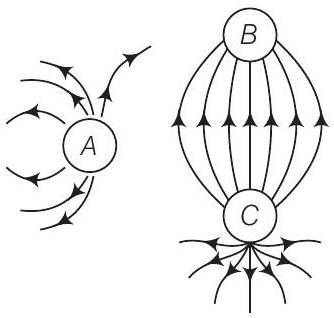
(i) कौन से आवेश धनात्मक हैं?
(ii) कौन सा आवेश सबसे बड़े परिमाण का है? क्यों?
(iii) चित्र के किस क्षेत्र या क्षेत्रों में विद्युत क्षेत्र शून्य हो सकता है? अपने उत्तर की व्याख्या करें। $\newline$
(a) $A$ के पास $\newline$
(b) $B$ के पास $\newline$
(c) $C$ के पास $\newline$
(d) कहीं नहीं $\newline$
उत्तर दिखाएँ
सोचने की प्रक्रिया
(i) विद्युत बल रेखाएँ हमेशा धनात्मक आवेश से शुरू होती हैं और नकारात्मक आवेश में समाप्त होती हैं। एक अकेले आवेश के मामले में, विद्युत बल रेखाएँ धनात्मक आवेश से शुरू होती हैं और अनंत में समाप्त होती हैं।
(ii) आवेश के परिमाण की तीव्रता आवेश से निकलने वाली बल रेखाओं की संख्या पर निर्भर करती है। अर्थात, बल रेखाओं की संख्या अधिक होने पर आवेश का परिमाण अधिक होता है और विपरीत।
उत्तर
(i) चित्र में, विद्युत बल रेखाएँ $A$ और $C$ से निकलती हैं। अतः, आवेश $A$ और $C$ धनात्मक होंगे।
(ii) यहाँ आवेश $C$ से निकलने वाली विद्युत बल रेखाओं की संख्या सबसे अधिक है, अतः $C$ का परिमाण सबसे अधिक होगा।
(iii) दो समान आवेशों के बीच विद्युत बल शून्य होने वाले बिंदु को उदासीन बिंदु कहते हैं। अतः, उदासीन बिंदु केवल $A$ और $C$ के बीच ही हो सकता है।
अब, उदासीन बिंदु की स्थिति आवेशों के बल की तीव्रता पर निर्भर करती है। यहाँ, विद्युत बल रेखाओं की संख्या अधिक होने से आवेश $C$ का बल आवेश $A$ के बल से अधिक होता है। अतः, उदासीन बिंदु $A$ के पास होगा।
25. प्रत्येक कोर पर $q$ आवेश रखे गए एक सम षट्भुज के कोरों पर पांच आवेश रखे गए हैं।
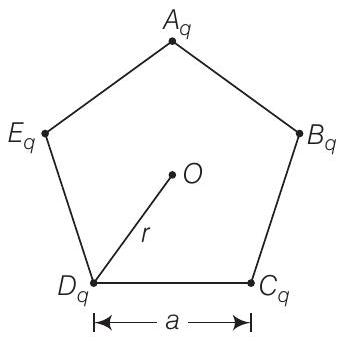
(a) (i) पेंटागन के केंद्र 0 पर विद्युत क्षेत्र क्या होगा?
(ii) यदि किसी कोने (मान लीजिए $A$) का आवेश हटा दिया जाए तो बिंदु $0$ पर विद्युत क्षेत्र क्या होगा?
(iii) यदि कोने $A$ पर आवेश $q$ को $-q$ से बदल दिया जाए तो बिंदु $0$ पर विद्युत क्षेत्र क्या होगा?
(b) यदि पेंटागन को $n$-भुजा नियमित बहुभुज से बदल दिया जाए जिसके प्रत्येक कोने पर आवेश $q$ हो, तो आपके उत्तर (a) में क्या प्रभाव पड़ेगा?
उत्तर दिखाएं
सोचने की प्रक्रिया
सभी आवेशों के कारण बल सममिति के कारण विपरीत दिशा में बरकरार रहते हैं और वियोजित हो जाते हैं।
उत्तर
(a) (i) बिंदु $O$ पेंटागन के सभी आवेशों से समान दूरी पर है। अतः सममिति के कारण सभी आवेशों के कारण बल विपरीत दिशा में बरकरार रहते हैं और वियोजित हो जाते हैं। फलस्वरूप बिंदु $O$ पर विद्युत क्षेत्र शून्य होगा।
(ii) जब आवेश $q$ हटा दिया जाए तो बिंदु $A$ पर एक नकारात्मक आवेश विकसित होगा जिसके कारण विद्युत क्षेत्र $E=\dfrac{q \times 1}{4 \pi \varepsilon_{0} r^{2}}$ होगा और यह $O A$ के अनुदिश होगा।
(iii) यदि कोने $A$ पर आवेश $q$ को $-q$ से बदल दिया जाए तो बिंदु $A$ पर दो नकारात्मक आवेश $-2 q$ विकसित होंगे। अतः विद्युत क्षेत्र का मान $E=\dfrac{2 q}{4 \pi \varepsilon_{0} r^{2}}$ होगा और यह $O A$ के अनुदिश होगा।
(b) जब पेंटागन को $n$-भुजा नियमित बहुभुज से बदल दिया जाए जिसके प्रत्येक कोने पर आवेश $q$ हो, तो बिंदु $O$ पर विद्युत क्षेत्र फिर भी शून्य बरकरार रहेगा क्योंकि आवेशों की सममिति बहुभुज की नियमितता के कारण होती है। यह बहुभुज के भुजाओं की संख्या या आवेशों की संख्या पर निर्भर नहीं करता।
लंबे उत्तर प्रकार प्रश्न
26. 1959 में Lyttleton और Bondi ने सुझाव दिया कि ब्रह्मांड के विस्तार को समझने के लिए वस्तुओं पर एक नेट आवेश हो सकता है। मान लीजिए कि ब्रह्मांड हाइड्रोजन अणुओं से बना है जिसकी संख्या घनत्व $N$ है जो नियत रहता है। मान लीजिए कि प्रोटॉन पर आवेश $e_{p}=-(1+y) e$ है जहाँ $e$ इलेक्ट्रॉनिक आवेश है।
(a) विस्तार शुरू हो सके ऐसे $y$ के न्यूनतम मान को ज्ञात कीजिए।
(b) दिखाइए कि विस्तार की गति विस्तार केंद्र से दूरी के समानुपाती होती है।
उत्तर दिखाएं
सोचने की प्रक्रिया
ब्रह्मांड के विस्तार शुरू होगा यदि एक हाइड्रोजन अणु पर दूरी $R$ पर कूलॉम प्रतिकर्षण गुरुत्वाकर्षण आकर्षण से बड़ा हो।
उत्तर
(a) मान लीजिए कि ब्रह्मांड एक त्रिज्या $R$ के पूर्ण गोले के रूप में है और इसके संघटक हाइड्रोजन परमाणु गोले में समान रूप से वितरित हैं।
हाइड्रोजन परमाणु में एक प्रोटॉन और एक इलेक्ट्रॉन होते हैं, इसलिए प्रत्येक हाइड्रोजन परमाणु पर आवेश होता है।
$$ e_{H}=e_{P}+e=-(1+Y) e+e=-Y e=(Y e) $$
यदि $E$ गोले के सतह पर दूरी $R$ पर विद्युत क्षेत्र की तीव्रता है, तो गॉस के प्रमेय के अनुसार,
$$ \begin{aligned} \text { g. E.ds } & =\dfrac{q}{\varepsilon_{0}} \text { अर्थात, } E\left(4 \pi R^{2}\right)=\dfrac{4}{3} \dfrac{\pi R^{3} N|Y e|}{\varepsilon_{0}} \newline\ E & =\dfrac{1}{3} \dfrac{N|Y e| R}{\varepsilon_{0}} \newline \end{aligned} $$
अब, मान लीजिए कि प्रत्येक हाइड्रोजन परमाणु के द्रव्यमान $\simeq m_{P}=$ प्रोटॉन के द्रव्यमान, $G_{R}=$ गोले के सतह पर दूरी $R$ पर गुरुत्वीय क्षेत्र है।
तब
$$ -4 \pi R^{2} G_{R}=4 \pi G m_{P} \times \dfrac{4}{3} \pi R^{3} N $$
$$ \Rightarrow \quad G_{R}=\dfrac{-4}{3} \pi G m_{P} N R $$
$\therefore$ इस परमाणु पर गुरुत्वीय बल $F_{G}=m_{P} \times G_{R}=\dfrac{-4 \pi}{3} G m_{P}^{2} N R$
हाइड्रोजन परमाणु पर $R$ पर कूलॉम बल $F_{C}=(Y e) E=\dfrac{1}{3} \dfrac{N Y^{2} e^{2} R}{\varepsilon_{0}}$
अब, विस्तार शुरू करने के लिए $F_{C}>F_{G}$ होना चाहिए और विस्तार शुरू करने के लिए $Y$ के क्रिटिकल मान के लिए जब
$$ \begin{aligned} F_{C} & =F_{G} \newline \ \Rightarrow \quad \dfrac{1}{3} \dfrac{N Y^{2} e^{2} R}{\varepsilon_{0}} & =\dfrac{4 \pi}{3} G m_{P}^{2} N R \newline \ \Rightarrow \quad Y^{2} & =\left(4 \pi \varepsilon_{0}\right) G \dfrac{m_{P}{ }^{2}}{e} \newline \ & =\dfrac{1}{9 \times 10^{9}} \times\left(6.67 \times 10^{-11}\right) \dfrac{\left(1.66 \times 10^{-27}\right)^{2}}{\left(1.6 \times 10^{-19}\right)^{2}}=79.8 \times 10^{-38} \newline \ \Rightarrow \quad Y & =\sqrt{79.8 \times 10^{-38}}=8.9 \times 10^{-19} \simeq 10^{-18} \end{aligned} $$
इसलिए, $10^{-18}$ ब्रह्मांड के विस्तार के शुरू होने के लिए आवश्यक क्रिटिकल मान है। (b) हाइड्रोजन परमाणु द्वारा अनुभव किया गया नेट बल निम्नलिखित है
$$ F=F_{C}-F_{G}=\dfrac{1}{3} \dfrac{N Y^{2} e^{2} R}{\varepsilon_{0}}-\dfrac{4 \pi}{3} G m_{P}^{2} N R $$
$$
यदि हाइड्रोजन परमाणु के त्वरण को $d^{2} R / d t^{2}$ से प्रस्तुत किया जाए, तो
$$ \begin{aligned} m_{p} \dfrac{d^{2} R}{d t^{2}} & =F=\dfrac{1}{3} \dfrac{N Y^{2} e^{2} R}{\varepsilon_{0}}-\dfrac{4 \pi}{3} G m_{p}^{2} N R \newline \ & =\dfrac{1}{3} \dfrac{N Y^{2} e^{2}}{\varepsilon_{0}}-\dfrac{4 \pi}{3} G m_{p}^{2} N R \newline \ \therefore \quad \dfrac{d^{2} R}{d t^{2}} & =\dfrac{1}{m_{p}} \dfrac{1}{3} \dfrac{N Y^{2} e^{2}}{\varepsilon_{0}}-\dfrac{4 \pi}{3} G m_{p}^{2} N R=\alpha^{2} R \end{aligned} $$
जहाँ, $\quad \alpha^{2}=\dfrac{1}{m_{p}} \dfrac{1}{3} \dfrac{N Y^{2} e^{2}}{\varepsilon_{0}}-\dfrac{4 \pi}{3} G m_{p}^{2} N$
समीकरण (iv) का सामान्य हल $R=A e^{\alpha t}+B e^{-\alpha t}$ है। हम विस्तार की ओर ध्यान दे रहे हैं, इसलिए $B=0$ और $R=A e^{\alpha t}$ है।
$\Rightarrow \quad$ विस्तार की गति, $v=\dfrac{d R}{d t}=A e^{\alpha t}(\alpha)=\alpha A e^{\alpha t}=\alpha R$
इसलिए, $v \propto R$ अर्थात विस्तार की गति केंद्र से दूरी के समानुपाती है।
27. एक गोले के व्यास $R$ और आवेश घनत्व $p(r)=k r$ के रूप में वितरित है जहाँ $r \leq R=0$ जहाँ $r>R$ है।
(a) सभी बिंदुओं $r$ पर विद्युत क्षेत्र को ज्ञात कीजिए।
(b) मान लीजिए गोले पर कुल आवेश $2 e$ है जहाँ $e$ इलेक्ट्रॉन आवेश है। दो प्रोटॉन कहाँ स्थापित किए जा सकते हैं ताकि प्रत्येक पर बल शून्य हो। मान लीजिए कि प्रोटॉन के प्रस्तुत करने से नकारात्मक आवेश वितरण बदल नहीं जाता।
उत्तर दिखाएं
सोचने की प्रक्रिया
दिए गए गोले के व्यास $R$ के आवेश घनत्व वितरण के अनुसार, अर्थात $p(r)=K r$ जहाँ $r \leq R=0$ जहाँ $r>R$ है, यह स्पष्ट है कि विद्युत क्षेत्र वृत्तीय है।
उत्तर
(a) मान लीजिए एक गोला $S$ व्यास $R$ के रूप में और दो कल्पनात्मक गोले व्यास $r<R$ और $r>R$ के रूप में हैं।
अब, बिंदु $r<R$ पर विद्युत क्षेत्र की तीव्रता निम्नलिखित द्वारा दी जाएगी,
$$\phi=\int E.ds = \dfrac{1}{\varepsilon_0} \int pdV $$
$ [dV के लिए, V = \dfrac{4}{3} \Pi r^3 \Rightarrow dV = 3 $ $\times \dfrac{4}{3} \Pi r^3dr = 4 \pi r^2] \newline $
$$\phi = \int E.ds = \dfrac{1}{\varepsilon_0} 4 \pi K \int 0^r r^3dr $$ $$E = \dfrac{1}{4\varepsilon{0}}Kr^2$$
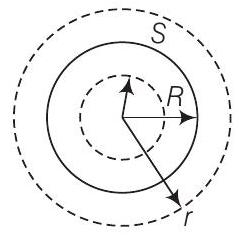
$(\because p(r)=K r)$
यहाँ, आवेश घनत्व धनात्मक है।
इसलिए, $\mathrm{E}$ की दिशा त्रिज्या के बाहर की ओर है।
बिंदु $r>R$ पर, विद्युत क्षेत्र तीव्रता निम्नलिखित द्वारा दी जाएगी
$$ \begin{array}{rlrl} \int \text { E.dS } =\dfrac{1}{\varepsilon_{0}} \int \rho . d V \newline \ \Rightarrow E\left(4 \pi^{2}\right) =\dfrac{4 \pi K}{\varepsilon_{0}} \int_{0}^{R} r^{3} d r=\dfrac{4 \pi K}{\varepsilon_{0}} \dfrac{R^{4}}{4} \newline \ \Rightarrow E =\dfrac{K}{4 \varepsilon_{0}} \dfrac{R^{4}}{r^{2}} \newline \end{array} $$
आवेश घनत्व फिर भी धनात्मक है। इसलिए, $\mathrm{E}$ की दिशा त्रिज्या के बाहर की ओर है।
(b) दो प्रोटॉन केंद्र के विपरीत ओर एक व्यास के अनुदिश सममिति के नियम के अनुसार स्थित होंगे। इसको नीचे दिए गए चित्र द्वारा दिखाया जा सकता है। गोले पर आवेश,
$$ \begin{aligned} q & =\int_{0}^{R} \rho d V=\int_{0}^{R}(K r) 4 \pi r^{2} d r \newline \ q & =4 \pi K \dfrac{R^{4}}{4}=2 e \newline \ \therefore \quad K & =\dfrac{2 e}{\pi R^{4}} \end{aligned} $$
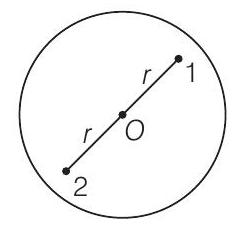
यदि प्रोटॉन 1 और 2 को गोले के केंद्र से दूरी $r$ पर स्थित किया जाए जैसा कि चित्र में दिखाया गया है, तो प्रोटॉन 1 पर आवेश वितरण के कारण आकर्षण बल है
$$ F_{1}=e E=\dfrac{-e K r^{2}}{4 \varepsilon_{0}} $$
प्रोटॉन 2 के कारण प्रोटॉन 1 पर प्रतिकर्षण बल है
प्रोटॉन 1 पर शुद्ध बल,
$$ F_{2}=\dfrac{e^{2}}{4 \pi \varepsilon_{0}(2 r)^{2}} $$
इसलिए,
$$ \begin{aligned} & F=F_{1}+F_{2} \newline \ & F=\dfrac{-e K r^{2}}{4 \varepsilon_{0}}+\dfrac{e^{2}}{16 \pi \varepsilon_{0} r^{2}} \newline \ \end{aligned} $$
& F=\dfrac{-r^{2}}{4 \varepsilon_{0}} \dfrac{Z e}{\pi R^{4}}+\dfrac{e^{2}}{16 \pi \varepsilon_{0} r^{4}} \end{aligned} $$
इसलिए, प्रोटॉन 1 पर शुन्य बल कार्य करेगा, जब
$$ \begin{array}{rlrl} & & \dfrac{e r^{2} 2 e}{4 \varepsilon_{0} \pi R^{4}} & =\dfrac{e^{2}}{16 \pi \varepsilon_{0} r} \ \Rightarrow & r^{4} & =\dfrac{R^{4}}{8} \ \Rightarrow & r & =\dfrac{R}{(8)^{1 / 4}} \end{array} $$
यह दोनों प्रोटॉनों के केंद्र से दूरी है।
28. दो स्थिर, समान चालक प्लेटें $(\alpha$ और $\beta)$, प्रत्येक क्षेत्रफल $S$ है और इन्हें क्रमशः $-Q$ और $q$ आवेश दिया गया है, जहाँ $Q>q>0$ है। एक तीसरी समान प्लेट $(\gamma)$, जो गति कर सकती है, आवेश $q$ वाली प्लेट के दूसरी ओर दूरी $d$ पर स्थित है (चित्र)। तीसरी प्लेट को छोड़ दिया जाता है और यह प्लेट $\beta$ से टकराती है। मान लीजिए कि टकराव आदर्श बर्बादी रहित है और टकराव के समय $\beta$ और $\gamma$ के बीच आवेश का पुनः वितरण हो जाता है।
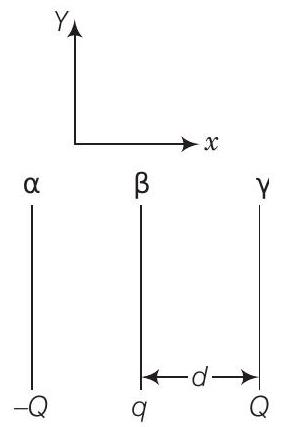
(a) टकराव से पहले प्लेट $\gamma$ पर कार्य करने वाले विद्युत क्षेत्र को खोजें।
(b) टकराव के बाद $\beta$ और $\gamma$ पर आवेश को खोजें।
(c) टकराव के बाद प्लेट $\gamma$ की गति और एक दूरी $d$ पर प्लेट $\beta$ से दूरी पर गति को खोजें।
उत्तर दिखाएं
Answer
(a) टकराव से पहले प्लेट $\gamma$ पर शुद्ध विद्युत क्षेत्र प्लेट $\alpha$ और $\beta$ के कारण प्लेट $\gamma$ पर विद्युत क्षेत्र के योग के बराबर होता है।
प्लेट $\gamma$ पर प्लेट $\alpha$ के कारण विद्युत क्षेत्र $E_{1}=\dfrac{-Q}{S\left(2 \varepsilon_{0}\right)}$, बाईं ओर होता है।
प्लेट $\gamma$ पर प्लेट $\beta$ के कारण विद्युत क्षेत्र $E_{2}=\dfrac{q}{S\left(2 \varepsilon_{0}\right)}$, दाईं ओर होता है।
इसलिए, टकराव से पहले प्लेट $\gamma$ पर शुद्ध विद्युत क्षेत्र।
$$ E=E_{1}+E_{2}=\dfrac{q-Q}{S\left(2 \varepsilon_{0}\right)} \text {, बाईं ओर, यदि } Q>q
$$
(b) टक्कर के समय, प्लेट $\beta$ और $\gamma$ एक साथ होते हैं। उनके विभव समान हो जाते हैं।
मान लीजिए प्लेट $\beta$ पर आवेश $q_{1}$ है और प्लेट $\gamma$ पर आवेश $q_{2}$ है। दो प्लेट के बीच किसी बिंदु $O$ पर विद्युत क्षेत्र शून्य होना चाहिए।
प्लेट $\alpha$ के कारण $O$ पर विद्युत क्षेत्र $=\dfrac{-Q}{S\left(2 \varepsilon_{0}\right)}$, बाईं ओर
प्लेट $\beta$ के कारण $O$ पर विद्युत क्षेत्र $=\dfrac{q_{1}}{S\left(2 \varepsilon_{0}\right)}$, दाईं ओर
प्लेट $\gamma$ के कारण $O$ पर विद्युत क्षेत्र $=\dfrac{q_{2}}{S\left(2 \varepsilon_{0}\right)}$, बाईं ओर
क्योंकि $O$ पर विद्युत क्षेत्र शून्य है, इसलिए
$$ \begin{aligned} \dfrac{Q+q_{2}}{S\left(2 \varepsilon_{0}\right)} & =\dfrac{q_{1}}{S\left(2 \varepsilon_{0}\right)} \\ Q+q_{2} & =q_{1} \\ Q & =q_{1}-q_{2} \end{aligned} $$
कोई आवेश टक्कर के कारण खो नहीं जाता है, इसलिए
$$ Q+q=q_{1}+q_{2} $$
समीकरण (i) और (ii) को हल करने पर हम प्राप्त करते हैं
$$ \begin{aligned} & q_{1}=(Q+q / 2)=\text { प्लेट } \beta \text{ पर आवेश} \\ & q_{2}=(q / 2)=\text { प्लेट } \gamma \text{ पर आवेश} \end{aligned} $$
(c) टक्कर के बाद, प्लेट $\beta$ से दूरी $d$ पर,
मान लीजिए प्लेट $\gamma$ की गति $v$ है। टक्कर के बाद प्लेट $\gamma$ पर विद्युत क्षेत्र है
$$ E_{2}=\dfrac{-Q}{2 \varepsilon_{0} S}+\dfrac{(Q+q / 2)}{2 \varepsilon_{0} S}=\dfrac{q / 2}{2 \varepsilon_{0} S} \text { दाईं ओर। } $$
टक्कर से पहले प्लेट $\gamma$ पर विद्युत क्षेत्र $E_{1}=\dfrac{Q-q}{2 \varepsilon_{0} S}$ है।
यदि $F_{1}$ टक्कर से पहले प्लेट $\gamma$ पर बल है, तो $F_{1}=E_{1} Q=\dfrac{(Q-q) Q}{2 \varepsilon_{0} S}$
विद्युत क्षेत्र द्वारा किया गया कुल कार्य प्लेट $\gamma$ के चक्कर लगाने के लिए है
$$ \begin{aligned} W & =\left(F_{1}+F_{2}\right) d \ & =\dfrac{\left[(Q-q) Q+(q / 2)^{2}\right] d}{2 \varepsilon_{0} S}=\dfrac{(Q-q / 2)^{2} d}{2 \varepsilon_{0} S} \end{aligned} $$
यदि $m$ प्लेट $\gamma$ का द्रव्यमान है, तो प्लेट $\gamma$ द्वारा प्राप्त किया गया गतिज ऊर्जा $=\dfrac{1}{2} m v^{2}$
कार्य-ऊर्जा सिद्धांत के अनुसार, $\dfrac{1}{2} m v^{2}=W=\dfrac{(Q-q / 2)^{2} d}{2 \varepsilon_{0} S}$
$$ Y=(Q-q / 2){\dfrac{d}{m \varepsilon_{0} S}}^{1 / 2} $$
29. एक अन्य उपयोगी इकाई प्रणाली, SI/MKS के अलावा, है। इस प्रणाली को CGS (सेंटीमीटर-ग्राम-सेकंड) प्रणाली कहते हैं। इस प्रणाली में, कूलॉम के नियम को $\mathbf{F}=\dfrac{Q q}{r^{2}} \hat{\mathbf{r}}$ द्वारा दिया जाता है।
जहाँ दूरी $r$ को सेंटीमीटर में मापा जाता है $\mathrm{cm}\left(=10^{-2} m \right), F$ डाइन में $\left(=10^{-5} \mathrm{~N}\right)$ और आवेश को विद्युत स्थैतिक इकाइयों (es इकाइयों) में मापा जाता है, जहाँ 1 es इकाई का आवेश $=\dfrac{1}{3^2} \times 10^{-9} \mathrm{C}$ होता है। संख्या [3] वाक्यांश रूप से निर्वात में प्रकाश की गति से उत्पन्न होती है जो अब ठीक रूप से $c=2.99792458 \times 10^{8} \mathrm{~m} / \mathrm{s}$ के बराबर होती है। तब एक अनुमानित मान $c$ के लिए $c=3 \times 10^{8} \mathrm{~m} / \mathrm{s}$ होता है।
(i) दिखाएं कि CGS इकाइयों में कूलॉम के नियम के अनुसार 1 esu आवेश $=1(\text { dyne })^{1 / 2} \mathrm{~cm}$ होता है। द्रव्यमान $M$, लंबाई $L$ और समय $T$ के अनुसार आवेश की इकाइयों के आयाम प्राप्त करें। दिखाएं कि यह $M$ और $L$ के भिन्न घातों के रूप में दिया जाता है।
(ii) 1 esu आवेश $=x C$ लिखें, जहाँ $x$ एक विमाही नंबर है। दिखाएं कि यह $\dfrac{1}{4 \pi \varepsilon_{0}}=\dfrac{10^{-9}}{x^{2}} \dfrac{\mathrm{Nm}^{2}}{\mathrm{C}^{2}}$ देता है। $x=\dfrac{1}{[3]} \times 10^{-9}$ के साथ, हमें $\dfrac{1}{4 \pi \varepsilon_{0}}=[3]^{2} \times 10^{9} \dfrac{\mathrm{Nm}^{2}}{\mathrm{C}^{2}}, \dfrac{1}{4 \pi \varepsilon_{0}}=(2.99792458)^{2} \times 10^{9} \dfrac{\mathrm{Nm}^{2}}{\mathrm{C}^{2}}$ (ठीक) मिलता है।
उत्तर दिखाएं
Answer
(i) संबंध से, $F=\dfrac{Q q}{r^{2}}=1$ डाइन $=\dfrac{[1 \text { esu of charge }]^{2}}{[1 \mathrm{~cm}]^{2}}$
इसलिए, 1 esu आवेश $=(1 \text { डाइन })^{1 / 2} \times 1 \mathrm{~cm}=F^{1 / 2} \cdot L=\left[\mathrm{MLT}^{-2}\right]^{1 / 2} \mathrm{~L}$
$\Rightarrow 1$ esu आवेश $=\mathrm{M}^{1 / 2} \mathrm{~L}^{3 / 2} \mathrm{~T}^{-1}$.
इस प्रकार, esu आवेश को $M$ के $\dfrac{1}{2}$ घात और $L$ के $\dfrac{3}{2}$ घात के रूप में प्रस्तुत किया जाता है।
(ii) मान लीजिए 1 esu आवेश $=x C$, जहाँ $x$ एक विमाहीन संख्या है। दो आवेश, जिनके परिमाण 1 esu हैं और उनके बीच की दूरी $1 \mathrm{~cm}$ है, के बीच कूलॉम बल डाइन होता है जो $10^{-5} \mathrm{~N}$ के बराबर है। यह स्थिति दो आवेशों के बराबर परिमाण $x C$ और उनके बीच की दूरी $10^{-2} \mathrm{~m}$ के बराबर है।
$$ \begin{array}{ll} \therefore F=\dfrac{1}{4 \pi \varepsilon_{0}} \dfrac{x^{2}}{\left(10^{-2}\right)^{3}}=1 \text { dyne }=10^{-5} \mathrm{~N} \newline \newline \ \therefore \dfrac{1}{4 \pi \varepsilon_{0}}=\dfrac{10^{-9}}{x^{2}} \dfrac{\mathrm{Nm}^{2}}{\mathrm{C}^{2}} \newline \newline \ \text { लेते हुए, } x=\dfrac{1}{|3| \times 10^{9}}, \newline \newline \ \text { हम प्राप्त करते हैं, } \dfrac{1}{4 \pi \varepsilon_{0}}=10^{-9} \times|3|^{2} \times 10^{18} \dfrac{\mathrm{Nm}^{2}}{\mathrm{C}^{2}}=9 \times 10^{9} \dfrac{\mathrm{Nm}^{2}}{\mathrm{C}^{2}} \newline \newline \ \text { यदि }|3| \rightarrow 2.99792458 \text {, हम प्राप्त करते हैं } \dfrac{1}{4 \pi \varepsilon_{0}}=8.98755 \times 10^{9} \mathrm{Nm}^{2} \mathrm{C}^{-2} . \end{array} $$
30. दो आवेश $-q$ प्रत्येक दूरी $2 d$ के अलग-अलग स्थिर रखे गए हैं। एक तीसरा आवेश $q$ जिसके द्रव्यमान $m$ है, मध्य बिंदु पर रखा गया है और चित्र में दिखाए गए अनुसार दो स्थिर आवेशों के बीच रेखा के लंब दिशा में थोड़ा विस्थापित हो जाता है। दिखाइए कि $q$ सरल आवर्त गति करेगा जिसका समय अवधि है।
$$ T={\dfrac{8 \pi^{3} \varepsilon_{0} m d^{3}}{q^{2}}}^{1 / 2} $$
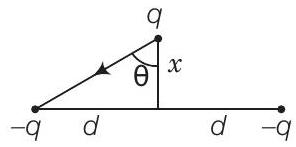
उत्तर दिखाएं
Thinking Process
आवेश a के गति के लिए सरल आवर्त गति होने के लिए, आवेश q पर बल उसकी केंद्र $\mathrm{O}$ से दूरी के अनुपाती होना चाहिए और वह केंद्र $\mathrm{O}$ की ओर दिशा में होना चाहिए।
Answer
हम पहले चित्र को विस्तार से समझें।
दिया गया है, दो आवेश $-q$ बिंदु $A$ और $B$ पर हैं
$$ A B=A O+O B=2 d $$
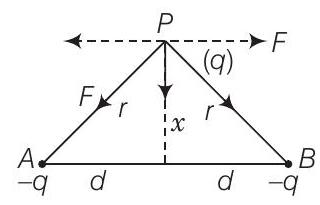
$x=$ छोटी दूरी $O$ के लंबवत है।
अर्थात, $x<d$ आवेश $q$ के द्रव्यमान के लिए। इसलिए, $P$ पर $A$ और $B$ की ओर आकर्षण बल $F=\dfrac{q(q)}{4 \pi \varepsilon_{0} r^{2}}$ है, जहाँ $AP=BP=r$
इन बलों के क्षैतिज घटक $F_{n}$ विपरीत दिशा में बरकरार रहते हैं। ऊर्ध्वाधर घटक $PO$ के अनुदिश जोड़ देते हैं।
यदि $\angle APO=O$, तो $q$ के लिए $PO$ अक्ष के अनुदिश नेट बल $F^{\prime}=2 F \cos Q$ है
$$ \begin{aligned} & =\dfrac{2 q^{2}}{4 \pi \varepsilon_{0} r^{3}} \newline \ & =\dfrac{2 q^{2} x}{4 \pi \varepsilon_{0}\left(d^{2}+x^{2}\right)^{3 / 2}} \end{aligned} $$
जब,
$$ x«d, F^{\prime}=\dfrac{2 q^{2} x}{4 \pi \varepsilon_{0} d^{3}}=K x $$
जहाँ,
$$ K=\dfrac{2 q^{2}}{4 \pi \varepsilon_{0} d^{3}} $$
$\Rightarrow$
$$ F \propto x $$
अर्थात, आवेश $q$ पर बल इसके केंद्र $\mathrm{O}$ से विस्थापन के अनुपाती है और यह केंद्र $\mathrm{O}$ की ओर दिशा में है।
इसलिए, आवेश $q$ का गति सरल आवर्त गति होगी, जहाँ
और
$$ \begin{aligned} \omega & =\sqrt{\dfrac{K}{m}} \newline \ T & =\dfrac{2 \pi}{\omega}=2 \pi \sqrt{\dfrac{m}{K}} \newline \ & =2 \pi \sqrt{\dfrac{m \cdot 4 \pi \varepsilon_{0} d^{3}}{2 q^{2}}}=\dfrac{8 \pi^{3} \varepsilon_{0} m d^{3}}{q^{2}} \end{aligned} $$
31. कुल आवेश $-Q$ एक वृत्त के परिधि के लंबाई पर समान रूप से वितरित है, जिसकी त्रिज्या $R$ है। एक छोटा परीक्षण आवेश $+q$ जिसका द्रव्यमान $m$ है, वृत्त के केंद्र पर रखा गया है और इसे वृत्त के अक्ष के अनुदिश एक नुकसान दिया जाता है।
(a) दिखाएं कि कण सरल आवर्त गति करता है।
(b) इसके समय अवधि का प्राप्त करें।
सोचने की प्रक्रिया
सरल आवर्त गति के लिए, $q$ पर बल इसके विस्थापन के ऋणात्मक अनुपाती होता है।
उत्तर दिखाएं
उत्तर
प्रश्न के अनुसार चित्र बनाएं,
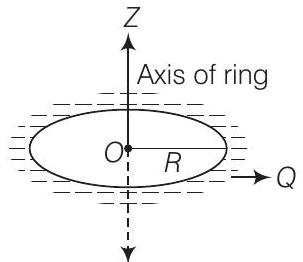
वृत्त के अक्ष के अनुदिश $q$ पर एक नुकसान देने से चित्र में दिखाए गए स्थिति के उत्पादन होता है।
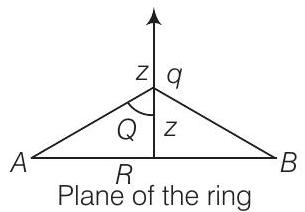
$A$ और $B$ पर आवेश के रेखा तत्व लेते हुए, जिनकी लंबाई एक इकाई है, तो प्रत्येक तत्व पर आवेश।
$$ d F=2\times \dfrac{Qq}{2 \pi R} \times \dfrac{1}{4 \pi \varepsilon_{0}} \dfrac{1}{r^{2}} \cos \theta $$
पूरे वृत्त के कारण आवेश $q$ पर कुल बल
$$ \begin{aligned} F & =-\dfrac{Q q}{\pi R}(\pi R) \cdot \dfrac{1}{4 \pi \varepsilon_{0}} \dfrac{1}{r^{2}} \cdot \dfrac{2}{r} \ F & =-\dfrac{Q q z}{4 \pi \varepsilon_{0}\left(Z^{2}+R^{2}\right)^{3 / 2}} \end{aligned} $$
यहाँ, $Z<R, \quad F=-\dfrac{Q q z}{4 \pi \varepsilon_{0} R^{3}}=-K z$
जहाँ
$$ \dfrac{Q q}{4 \pi \varepsilon_{0} R^{3}}=\text { constant } $$
$F \propto-Z$
$\Rightarrow$
स्पष्ट रूप से, $q$ पर बल इसके विस्थापन के ऋणात्मक अनुपात में है। अतः $q$ की गति सरल आवर्त गति है।
$\Rightarrow \quad T=2 \pi \sqrt{\dfrac{4 \pi \varepsilon_{0} m R^{3}}{Q q}}$
$$ \begin{aligned} \omega=\sqrt{\dfrac{K}{m}} \text { and } T=\dfrac{2 \pi}{\omega}=2 \pi \sqrt{\dfrac{m}{K}} \newline \ T=2 \pi \sqrt{\dfrac{m 4 \pi \varepsilon_{0} R^{3}}{Q q}} \newline \ T=2 \pi \sqrt{\dfrac{4 \pi \varepsilon_{0} m R^{3}}{Q q}} \end{aligned} $$





