प्रकाश का द्विप्रकृति एवं पदार्थ
बहुविकल्पीय प्रश्न (MCQs)
1. एक कण को ऊँचाई $H$ से गिराया जाता है। कण के देब्रोगली तरंगदैर्ध्य के ऊँचाई के फलन के रूप में समानुपातित होता है
(a) $H$
(b) $H^{1 / 2}$
(c) $H^{0}$
(d) $H^{-1 / 2}$
उत्तर दिखाएं
सोचने की प्रक्रिया
देब्रोगली तरंगदैर्ध्य $\boldsymbol{\lambda}$ द्वारा दिया जाता है $\boldsymbol{\lambda}=\dfrac{h}{m v}$।
उत्तर
(d) ऊँचाई $H$ से गिरने वाले एक वस्तु की चाल द्वारा दिया जाता है
$$ v=\sqrt{2 g H} $$
हम जानते हैं कि देब्रोगली तरंगदैर्ध्य
$$ \lambda=\dfrac{h}{m v}=\dfrac{h}{m \sqrt{2 g H}} \Rightarrow=\dfrac{h}{m \sqrt{2 g} \sqrt{H}} $$
यहाँ, $\dfrac{h}{m \sqrt{2 g}}$ एक नियतांक $\phi$ कहलाता है ’ $K$ ‘।
इसलिए,
$$ \begin{aligned} & \lambda=K \dfrac{1}{\sqrt{H}} \Rightarrow \lambda \propto \dfrac{1}{\sqrt{H}} \\ & \lambda \propto H^{-1 / 2} \end{aligned} $$
-
विकल्प (a) $H$: यह विकल्प गलत है क्योंकि देब्रोगली तरंगदैर्ध्य ऊँचाई $H$ के वर्गमूल के व्युत्क्रमानुपाती होती है, न कि $H$ के सीधे अनुपाती। अर्जित संबंध दिखाता है कि $\lambda \propto H^{-1/2}$, न कि $\lambda \propto H$।
-
विकल्प (b) $H^{1 / 2}$: यह विकल्प गलत है क्योंकि देब्रोगली तरंगदैर्ध्य ऊँचाई $H$ के वर्गमूल के व्युत्क्रमानुपाती होती है। सही संबंध $\lambda \propto H^{-1/2}$ है, न कि $\lambda \propto H^{1/2}$।
-
विकल्प (c) $H^{0}$: यह विकल्प गलत है क्योंकि $H^0$ इंगित करता है कि देब्रोगली तरंगदैर्ध्य ऊँचाई $H$ के स्वतंत्र होती है। हालांकि, अर्जित संबंध दिखाता है कि तरंगदैर्ध्य $H$ पर निर्भर होती है और इसके वर्गमूल के व्युत्क्रमानुपाती होती है, $\lambda \propto H^{-1/2}$।
2. एक नाभिक से एक प्रोटॉन को हटाने के लिए आवश्यक फोटॉन की तरंगदैर्ध्य लगभग $\newline$
(a) $1.2 nm$ $\newline$
(b) $1.2 \times 10^{-3} nm$ $\newline$
(c) $1.2 \times 10^{-6} nm$ $\newline$
(d) $1.2 \times 10 nm$ $\newlin
सोचने की प्रक्रिया
एक फोटॉन की ऊर्जा $E=\dfrac{h c}{\lambda}$ होती है, जहाँ $\lambda$ वह न्यूनतम तरंगदैर्ध्य है जिसके द्वारा प्रोटॉन को नाभिक से बाहर निकाला जा सकता है।
उत्तर दिखाएं
उत्तर
(b) प्रश्न में दिया गया है,
एक फोटॉन की ऊर्जा, $E=1 MeV \Rightarrow=10^{6} eV$
अब,
$h c=1240 eVnm$
अब,
$E=\dfrac{h c}{\lambda}$
$\Rightarrow$
$$ \lambda=\dfrac{h c}{E}=\dfrac{1240 eVnm}{10^{6} eV} $$
$$ =1.24 \times 10^{-3} nm $$
-
विकल्प (a) $1.2 nm$: यह विकल्प गलत है क्योंकि नाभिक से प्रोटॉन को बाहर निकालने के लिए आवश्यक तरंगदैर्ध्य बहुत छोटी है। $1 MeV$ की ऊर्जा वाला फोटॉन $10^{-3} nm$ के क्रम की तरंगदैर्ध्य के संगत होता है, न कि $1.2 nm$।
-
विकल्प (c) $1.2 \times 10^{-6} nm$: यह विकल्प गलत है क्योंकि इसकी तरंगदैर्ध्य गणना की गई मान की तुलना में बहुत छोटी है। सही तरंगदैर्ध्य $1.24 \times 10^{-3} nm$ है, जो $1.2 \times 10^{-6} nm$ की तुलना में तीन आदेशों के अधिक है।
-
विकल्प (d) $1.2 \times 10 nm$: यह विकल्प गलत है क्योंकि इसकी तरंगदैर्ध्य गणना की गई मान की तुलना में बहुत बड़ी है। सही तरंगदैर्ध्य $1.24 \times 10^{-3} nm$ है, जो $1.2 \times 10 nm$ की तुलना में चार आदेशों के कम है।
3. एक धातु सतह पर एक वाक्सुम कमरे में रखे गए धातु सतह पर ऊर्जा $E_0$ वाले इलेक्ट्रॉनों की किरण डाली जाती है। तब,
(a) कोई इलेक्ट्रॉन निकलेंगे क्योंकि केवल फोटॉन इलेक्ट्रॉन निकाल सकते हैं
(b) इलेक्ट्रॉन निकल सकते हैं लेकिन सभी ऊर्जा $E_0$ के साथ
(c) इलेक्ट्रॉन निकल सकते हैं किसी भी ऊर्जा के साथ, अधिकतम $E_0-\phi$ ( $\phi$ वर्क फंक्शन है)
(d) इलेक्ट्रॉन निकल सकते हैं किसी भी ऊर्जा के साथ, अधिकतम $E_0$ ऊर्जा के साथ
उत्तर दिखाएं
उत्तर
(d) ऊर्जा $E_0$ वाले इलेक्ट्रॉनों की किरण एक धातु सतह पर डाली जाती है जो एक वाक्सुम कमरे में रखी गई है, तो इलेक्ट्रॉन निकल सकते हैं अधिकतम ऊर्जा $E_0$ (गैर-संघटित टकराव के कारण) और इलेक्ट्रॉन के निकलने के लिए धातु के सतह से इलेक्ट्रॉन को छुड़ाने के लिए इलेक्ट्रॉन की ऊर्जा के कुछ हिस्सा उपयोग करने के कारण इलेक्ट्रॉन के ऊर्जा के कम अधिकतम $E_0$ के साथ।
-
(a) कोई इलेक्ट्रॉन उत्सर्जित नहीं होंगे क्योंकि केवल फोटॉन इलेक्ट्रॉन उत्सर्जित कर सकते हैं: यह गलत है क्योंकि इलेक्ट्रॉन भी एक धातु सतह से अन्य इलेक्ट्रॉनों के उत्सर्जन के लिए तापीय अपघटन या द्वितीय इलेक्ट्रॉन उत्सर्जन जैसी प्रक्रियाओं के माध्यम से इलेक्ट्रॉन उत्सर्जित कर सकते हैं। केवल फोटॉन ही इलेक्ट्रॉन उत्सर्जित कर सकते हैं यह गलत है।
-
(b) इलेक्ट्रॉन उत्सर्जित हो सकते हैं लेकिन सभी एक ऊर्जा, $E_0$ पर होंगे: यह गलत है क्योंकि सभी उत्सर्जित इलेक्ट्रॉन $E_0$ ऊर्जा के साथ नहीं होंगे। कुछ आपतित इलेक्ट्रॉनों की ऊर्जा धातु के कार्य फलन को पार करने में खरच हो सकती है या अनुप्रस्थ टकराव में खो जाती है, जिसके कारण उत्सर्जित इलेक्ट्रॉनों की ऊर्जा के एक श्रेणी में हो सकती है।
-
(c) इलेक्ट्रॉन कोई भी ऊर्जा से उत्सर्जित हो सकते हैं, जिसका अधिकतम मान $E_0-\phi$ ( $\phi$ कार्य फलन है): यह गलत है क्योंकि उत्सर्जित इलेक्ट्रॉनों की अधिकतम ऊर्जा $E_0$ हो सकती है जब आपतित इलेक्ट्रॉन अपनी ऊर्जा को उत्सर्जित इलेक्ट्रॉन में पूरी तरह से स्थानांतरित करते हैं बिना किसी खोए बिना अनुप्रस्थ टकराव में। कार्य फलन $\phi$ फोटोइलेक्ट्रिक उत्सर्जन के लिए अपेक्षित है, न कि इलेक्ट्रॉन-उत्सर्जन के लिए।
4. नीचे दिए गए चित्र को ध्यान से देखें। मान लीजिए $A$ पर लगाए गए वोल्टेज को बढ़ा दिया जाता है। अपवर्तित किरण के अधिकतम मान वाली किरण के लिए कोण $\theta$ का मान
(a) पहले के मान से बड़ा होगा
(b) पहले के मान के समान होगा
(c) पहले के मान से कम होगा
(d) लक्ष्य पर निर्भर करेगा
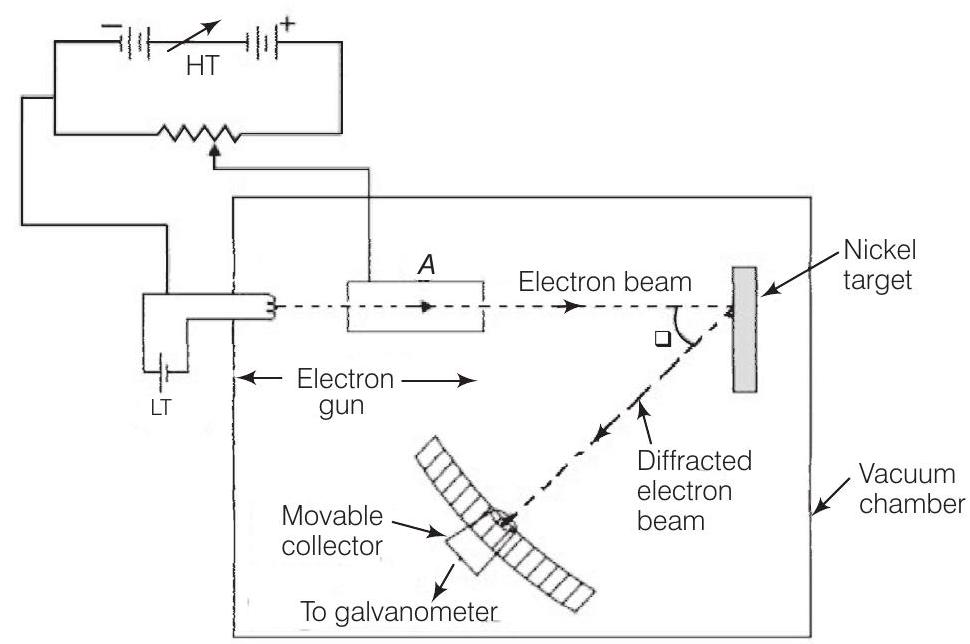
उत्तर दिखाएं
सोचने की प्रक्रिया
यहां दिया गया चित्र डेविसन-जर्मर प्रयोग को दर्शाता है जिसे इलेक्ट्रॉन के तरंग प्रकृति की जांच के लिए किया गया था।
उत्तर
(c) डेविसन-जर्मर प्रयोग में, इलेक्ट्रॉन के साथ संबद्ध डी-ब्रोग्ली तरंग दैर्ध्य है
$$ \lambda=\dfrac{12.27}{\sqrt{V}} \AA $$
जहां $V$ लगाए गए वोल्टेज है।
यदि अपवर्तित इलेक्ट्रॉनों के अधिकतम मान एक कोण $\theta$ पर होता है, तो
$$ 2 d \sin \theta=\lambda $$
(i) से, हम यह ध्यान रखते हैं कि यदि $V$ तरंगदैर्ध्य $\lambda$ के व्युत्क्रमानुपाती होता है। अर्थात, $V$ के बढ़ने के साथ-साथ $\lambda$ कम होता है।
समीकरण (ii) से, हम यह ध्यान रखते हैं कि तरंगदैर्ध्य $\lambda$ $\sin \theta$ के सीधे अनुपाती होती है और इसलिए $\theta$ भी। अतः $\lambda$ कम होने पर $\theta$ भी कम हो जाएगा।
इस प्रकार, जब $A$ पर आवेश लगाए गए वोल्टेज को बढ़ा दिया जाएगा, तो विवर्तन बीम के अधिकतम मान एक ऐसे $\theta$ के मान पर होगा जो पहले के मान से कम होगा।
-
विकल्प (a) पहले के मान से बड़ा होगा: यह विकल्प गलत है क्योंकि, डेविसन-जर्मर प्रयोग के अनुसार, लगाए गए वोल्टेज $ V $ के बढ़ने के साथ-साथ डी-ब्रोग्ली तरंगदैर्ध्य $ \lambda $ कम होती है। चूंकि $ \lambda $ $\sin \theta$ के सीधे अनुपाती होती है, इसलिए $ \lambda $ के कम होने के कारण $ \theta $ भी कम हो जाएगा। अतः $ \theta $ पहले के मान से बड़ा नहीं होगा।
-
विकल्प (b) पहले के मान के समान होगा: यह विकल्प गलत है क्योंकि लगाए गए वोल्टेज $ V $ और डी-ब्रोग्ली तरंगदैर्ध्य $ \lambda $ के बीच संबंध इस प्रकार है कि $ V $ के बढ़ने के साथ-साथ $ \lambda $ कम होती है। चूंकि $ \lambda $ $\sin \theta$ के सीधे अनुपाती होती है, इसलिए $ \lambda $ के परिवर्तन के कारण $ \theta $ का परिवर्तन होता है। अतः $ \theta $ पहले के मान के समान नहीं रहेगा।
-
विकल्प (d) लक्ष्य पर निर्भर करेगा: यह विकल्प गलत है क्योंकि विवर्तन बीम के अधिकतम मान वाले कोण $ \theta $ डी-ब्रोग्ली तरंगदैर्ध्य $ \lambda $ और क्रिस्टल के लैटिस अंतर्राश के बीच संबंध द्वारा निर्धारित होता है, न कि लक्ष्य पदार्थ के आधार पर। संबंध $ 2d \sin \theta = \lambda $ से स्पष्ट है कि $ \theta $ $ \lambda $ पर निर्भर करता है, जो वोल्टेज $ V $ पर निर्भर करता है। अतः $ \theta $ लक्ष्य पर निर्भर नहीं करता है।
5. एक प्रोटॉन, एक न्यूट्रॉन, एक इलेक्ट्रॉन और एक $\alpha$-कण के समान ऊर्जा हो। तब, उनके डी-ब्रोग्ली तरंगदैर्ध्य की तुलना करें।
(a) $\lambda_{p}=\lambda_{n}>\lambda_{e}>\lambda_{\alpha}$ $\newline$
(b) $\lambda_{\alpha}<\lambda_{p}=\lambda_{n}>\lambda_{e}$ $\newline$
(c) $\lambda_{e}<\lambda_{p}=\lambda_{n}>\lambda_{\alpha}$ $\newline$
(d) $\lambda_{e}=\lambda_{p}=\lambda_{n}=\lambda_{\alpha}$ $\newline$
उत्तर दिखाएं
Thinking Process
किसी भी कण की ऊर्जा को $K=\dfrac{1}{2} m v^{2}$ द्वारा दिया जा सकता है
$\Rightarrow \quad m v=\sqrt{2 m k}$
इसके अतिरिक्त, डी-ब्रोग्ली तरंगदैर्ध्य को निम्नलिखित द्वारा दिया जाता है
$$ \lambda=\dfrac{h}{m v} $$
अब, किसी भी कण की ऊर्जा और तरंगदैर्ध्य के बीच संबंध को द्वारा समीकरण (i) के मान को समीकरण (ii) में रखकर दिया जाता है
$$ \lambda=\dfrac{h}{\sqrt{2 m k}} $$
Answer
(b) हम जानते हैं कि $\lambda$ और $K$ के बीच संबंध निम्नलिखित द्वारा दिया जाता है
$$ \lambda=\dfrac{h}{\sqrt{2 m k}} $$
यहाँ, दी गई ऊर्जा $K$ के लिए, $\dfrac{h}{\sqrt{2 k}}$ एक स्थिरांक है।
अतः, $\quad \lambda \propto \dfrac{1}{\sqrt{m}}$
$\therefore \quad \lambda_{p}: \lambda_{n}: \lambda_{e}: \lambda_{\alpha}$
$\Rightarrow \quad=\dfrac{1}{\sqrt{m_{p}}}: \dfrac{1}{\sqrt{m_{n}}}: \dfrac{1}{\sqrt{m_{e}}}: \dfrac{1}{\sqrt{m_{\alpha}}}$
क्योंकि, $\quad m_{p}=m_{n}$, अतः $\boldsymbol{\lambda}{p}=\lambda{n}$
जबकि, $\quad m_{\alpha}>m_{p}$, अतः $\lambda_{\alpha}<\lambda_{p}$
और, $\quad m_{e}<m_{n}$, अतः $\lambda_{e}>\lambda_{n}$
अतः, $\quad \lambda_{\alpha}<\lambda_{p}=\lambda_{n}<\lambda_{e}$
-
विकल्प (a) गलत है क्योंकि इसका अर्थ है कि प्रोटॉन और न्यूट्रॉन के डी-ब्रोग्ली तरंगदैर्ध्य इलेक्ट्रॉन के तरंगदैर्ध्य से अधिक है, जो सत्य है, लेकिन यह भी अस्वीकृति करता है कि प्रोटॉन और न्यूट्रॉन के डी-ब्रोग्ली तरंगदैर्ध्य अल्फा कण के तरंगदैर्ध्य से अधिक है। अल्फा कण के द्रव्यमान प्रोटॉन और न्यूट्रॉन के द्रव्यमान से अधिक है, इसलिए इसका डी-ब्रोग्ली तरंगदैर्ध्य छोटा होना चाहिए, न कि बड़ा।
-
विकल्प (c) गलत है क्योंकि इसका अर्थ है कि इलेक्ट्रॉन के डी-ब्रोग्ली तरंगदैर्ध्य प्रोटॉन और न्यूट्रॉन के तरंगदैर्ध्य से कम है। इलेक्ट्रॉन का द्रव्यमान प्रोटॉन और न्यूट्रॉन के द्रव्यमान की तुलना में बहुत कम है, इसलिए इसका डी-ब्रोग्ली तरंगदैर्ध्य अधिक होना चाहिए, न कि कम।
-
विकल्प (d) गलत है क्योंकि इसका अर्थ है कि प्रोटॉन, न्यूट्रॉन, इलेक्ट्रॉन और अल्फा कण के डी-ब्रोग्ली तरंगदैर्ध्य सभी बराबर हैं। डी-ब्रोग्ली तरंगदैर्ध्य द्रव्यमान के वर्गमूल के व्युत्क्रमानुपाती होती है, इसलिए भले ही वे समान ऊर्जा के हों, अलग-अलग द्रव्यमान वाले कणों के डी-ब्रोग्ली तरंगदैर्ध्य अलग-अलग होंगे।
6. एक इलेक्ट्रॉन की आरंभिक वेग $\mathbf{v}=v_0 \hat{\mathbf{i}}$ है और इसके चारों ओर एक चुंबकीय क्षेत्र $\mathbf{B}=B_0 \hat{\mathbf{j}}$ है। तब, इसके डी-ब्रोग्ली तरंगदैर्ध्य
(a) स्थिर रहता है
(b) समय के साथ बढ़ता है
(c) समय के साथ घटता है
(d) समय के साथ आवर्ती रूप से बढ़ता और घटता है
उत्तर दिखाएं
उत्तर
(a) दिया गया है,
$$ \mathbf{v}=v_0 \hat{\mathbf{i}} \Rightarrow \mathbf{B}=B_0 \hat{\mathbf{j}} $$
चुंबकीय क्षेत्र के कारण गतिशील इलेक्ट्रॉन पर बल, $F=-e(v \times B)$ होता है
$$ =-e[v_0 \hat{\mathbf{i}} \times B_0 \hat {\mathbf{j}}] \Rightarrow=-e v_0 B_0 \hat{\mathbf{k}} $$
इस बल के लंबवत $\mathbf{v}$ और $\mathbf{B}$ होते हैं, इसलिए $\mathbf{v}$ के परिमाण में कोई परिवर्तन नहीं होता, अर्थात, संवेग $(=m v)$ के परिमाण में कोई परिवर्तन नहीं होता। इसलिए,
डी-ब्रोग्ली तरंगदैर्ध्य $\lambda=\dfrac{h}{m v}$ स्थिर रहता है।
-
(b) डी-ब्रोग्ली तरंगदैर्ध्य समय के साथ बढ़ता नहीं है क्योंकि इलेक्ट्रॉन के वेग के परिमाण में कोई परिवर्तन नहीं होता। चूंकि डी-ब्रोग्ली तरंगदैर्ध्य संवेग (जो द्रव्यमान और वेग के गुणनफल होता है) के व्युत्क्रमानुपाती होती है, एक स्थिर वेग के कारण एक स्थिर तरंगदैर्ध्य होती है।
-
(c) डी-ब्रोग्ली तरंगदैर्ध्य समय के साथ घटता नहीं है कारण ऊपर के कारण बराबर है। इलेक्ट्रॉन के वेग के परिमाण में कोई परिवर्तन नहीं होता, इसलिए संवेग स्थिर रहता है, और इसलिए तरंगदैर्ध्य स्थिर रहती है।
-
(d) डी-ब्रोग्ली तरंगदैर्ध्य समय के साथ आवर्ती रूप से बढ़ता और घटता नहीं है क्योंकि इलेक्ट्रॉन के वेग के परिमाण में कोई परिवर्तन नहीं होता। चुंबकीय क्षेत्र के कारण बल केवल वेग की दिशा को बदलता है, न कि इसके परिमाण को, इसलिए तरंगदैर्ध्य आवर्ती रूप से नहीं बदलती।
7. एक इलेक्ट्रॉन (द्रव्यमान $m$ ) के आरंभिक वेग $\mathbf{v}=v_0 \mathbf{i}(v_0>0)$ है और इसमें विद्युत क्षेत्र $\mathbf{E}=-E_0 \hat{\mathbf{i}}(E_0=.$ स्थिर $.>0)$ है। समय $t$ पर इसकी डी-ब्रोग्ली तरंगदैर्ध्य दी गई है $\newline$
(a) $\dfrac{\lambda_0}{1+\dfrac{e E_0}{m} \dfrac{t}{v_0}}$ $\newline$
(b) $\lambda_0 1+\dfrac{e E_0 t}{m v_0}$ $\newline$
(c) $\lambda_0$ $\newline$
(d) $\lambda_0 t $ $\newline $
उत्तर दिखाएं
सोचने की प्रक्रिया
डी-ब्रोग्ली तरंगदैर्ध्य $\boldsymbol{\lambda}=\dfrac{h}{m v}$ द्वारा दी गई है।
उत्तर
(a) इलेक्ट्रॉन की आरंभिक डी-ब्रोग्ली तरंगदैर्ध्य,
$$ \lambda_0=\dfrac{h}{m v_0} $$
विद्युत क्षेत्र में इलेक्ट्रॉन पर बल,
$$ \mathbf{F}=-e \mathbf{E}=-e[-E_0 \hat{\mathbf{i}}]=e E_0 \hat{\mathbf{i}} $$
इलेक्ट्रॉन के त्वरण
$$ a=\dfrac{\mathbf{F}}{m}=\dfrac{e E_0 \hat{\mathbf{i}}}{m} $$
समय $t$ पर इलेक्ट्रॉन का वेग,
$$ \begin{aligned} v & =v_0 \hat{\mathbf{i}}+\dfrac{e E_0 \hat{\mathbf{i}}}{m} t=(v_0+\dfrac{e E_0}{m} t) \hat{\mathbf{i}} \end{aligned} $$
समय $t$ पर इलेक्ट्रॉन के साथ संबंधित डी-ब्रोग्ली तरंगदैर्ध्य है
$$ \begin{aligned} & \lambda=\dfrac{h}{m v} \\ & =\dfrac{h}{m (v_0 +\dfrac{e E_0}{m v_0} t)}\\ & =\dfrac{\lambda_0}{1+\dfrac{e E_0}{m v_0} t} \\ & \because \lambda_0=\dfrac{h}{m v_0} \end{aligned} $$
-
विकल्प (b): विकल्प (b) में दी गई अभिव्यक्ति गलत है क्योंकि यह समय के साथ डी-ब्रोग्ली तरंगदैर्ध्य के रूप में रैखिक वृद्धि के बारे में बताती है, जो वास्तविक व्यवहार के विपरीत है। सही अभिव्यक्ति यह दर्शाती है कि इलेक्ट्रॉन के वेग में वृद्धि के कारण डी-ब्रोग्ली तरंगदैर्ध्य कम होती जाती है।
-
विकल्प (c): यह विकल्प गलत है क्योंकि यह समय के साथ डी-ब्रोग्ली तरंगदैर्ध्य के अचर रहने के बारे में बताता है। हालांकि, विद्युत क्षेत्र के कारण इलेक्ट्रॉन त्वरित हो रहा है, जिसके कारण इसका वेग बदल रहा है, इसलिए इसकी डी-ब्रोग्ली तरंगदैर्ध्य भी बदल रही है।
-
विकल्प (d): यह विकल्प गलत है क्योंकि यह डी-ब्रोग्ली तरंगदैर्ध्य के समय के साथ अनुपातिक होने के बारे में बताता है। यह इलेक्ट्रॉन के वेग और इसकी डी-ब्रोग्ली तरंगदैर्ध्य के बीच संबंध को नहीं लेता है, जो वेग के विपरीत अनुपाती होता है।
8. एक इलेक्ट्रॉन (द्रव्यमान $m$ ) के आरंभिक वेग $\mathbf{v}=v_0 \hat{\mathbf{i}}$ है और इसमें विद्युत क्षेत्र $\mathbf{E}=E_0 \hat{\mathbf{j}}$ है। यदि $\lambda_0=h / m v_0$, तो समय $t$ पर इसकी डी-ब्रोग्ली तरंगदैर्ध्य द्वारा दिया गया है $\newline$
(a) $\lambda_0$ $\newline$
(b) $\lambda_0 \sqrt{1+\dfrac{e^{2} E_0^{2} t^{2}}{m^{2} v_0^{2}}}$ $\newline$
(c) $\dfrac{\lambda_0}{\sqrt{1+\dfrac{e^{2} E_0^{2} t^{2}}{m^{2} v_0^{2}}}}$ $\newline$
(d) $\dfrac{\lambda_0}{1+\dfrac{e^{2} E_0^{2} t^{2}}{m^{2} v_0^{2}}}$ $\newline$
उत्तर दिखाएं
Answer
(c) इलेक्ट्रॉन की आरंभिक डी-ब्रोग्ली तरंगदैर्ध्य,
$$ \lambda_0=\dfrac{h}{m v_0} $$
विद्युत क्षेत्र में इलेक्ट्रॉन पर बल,
$$ F=-e E=-e E_0 \hat{j} $$
इलेक्ट्रॉन के त्वरण,
$$ a=\dfrac{F}{m}=\dfrac{e E_0 \hat{j}}{m} $$
यह नकारात्मक $y$-अक्ष के अनुदिश कार्य करता है।
इलेक्ट्रॉन के आरंभिक वेग $x$-अक्ष के अनुदिश, $x_0=v_0 \hat{\mathbf{i}}$ है। इलेक्ट्रॉन के आरंभिक वेग $y$-अक्ष के अनुदिश,
$$ y_0=0 . $$
समय $t$ के बाद इलेक्ट्रॉन के $x$-अक्ष के अनुदिश वेग, $x =_0 \hat{\mathbf{i}}$
समय $t$ के बाद इलेक्ट्रॉन के $y$-अक्ष के अनुदिश वेग,
$$ y=0+-\dfrac{e E_0}{m} \hat{\mathbf{j}} t=-\dfrac{e E_0}{m} t \hat{\mathbf{j}} $$
समय $t$ के बाद इलेक्ट्रॉन के वेग के परिमाण,
$$ v =\sqrt{v_x^{2}+v_y^{2}}=\sqrt{v_0^{2}+(\dfrac{-e E_0}{m} t)^{2}} \newline $$ $$\Rightarrow =v_0 \sqrt{1+\dfrac{e^{2} E_0^{2} t^{2}}{m^{2} v_0^{2}}} \newline $$ $$\text { डी-ब्रोग्ली तरंगदैर्ध्य, } \lambda^{\prime} =\dfrac{h}{m v} \newline $$ $$ =\dfrac{h}{m v_0 \sqrt{\dfrac{1+e^{2} E_0^{2} t^{2}}{(m^{2} v_0^{2})}}} \newline $$ $$ =\dfrac{\lambda_0}{\sqrt{\dfrac{1+e^{2} E_0^{2} t^{2}}{m^{2} v_0^{2}}}} $$
-
विकल्प (a): यह विकल्प बताता है कि डी-ब्रोग्ली तरंगदैर्ध्य समय के साथ अपरिवर्तित रहती है। हालांकि, इलेक्ट्रॉन के वेग विद्युत क्षेत्र के कारण समय के साथ बदलता है, जो इसकी डी-ब्रोग्ली तरंगदैर्ध्य को प्रभावित करता है, इसलिए यह गलत है।
-
विकल्प (b): यह विकल्प बताता है कि डी-ब्रोग्ली तरंगदैर्ध्य समय के साथ बढ़ती है। हालांकि, डी-ब्रोग्ली तरंगदैर्ध्य इलेक्ट्रॉन के संवेग (और इसलिए वेग) के व्युत्क्रमानुपाती होती है। विद्युत क्षेत्र के कारण वेग बढ़ता है, इसलिए तरंगदैर्ध्य घटती होनी चाहिए, न कि बढ़ती।
-
विकल्प (d): यह विकल्प बताता है कि डी-ब्रोग्ली तरंगदैर्ध्य $1 + \dfrac{e^{2} E_0^{2} t^{2}}{m^{2} v_0^{2}}$ के व्युत्क्रमानुपाती होती है। हालांकि, इस रूप में वेग और तरंगदैर्ध्य के बीच संबंध को सही तरीके से दर्शाया नहीं जाता है। सही संबंध नामकरण के अंश में शब्द के वर्गमूल के साथ होता है, जैसा कि विकल्प (c) में दिया गया है।
बहुविकल्पीय प्रश्न (एक से अधिक विकल्प)
9. जब कण के गतिज ऊर्जा के व्यंजक $\dfrac{1}{2} m v^{2}$, $m c^{2}$ के समान या उसके पास हो जाता है, तब सापेक्षता के संशोधन आवश्यक हो जाते हैं, जहां $m$ कण के द्रव्यमान है। एक इलेक्ट्रॉन के लिए सापेक्षता के संशोधन महत्वपूर्ण होंगे जब डी-ब्रोग्ली तरंगदैर्ध्य कितनी होगी?
(a) $\lambda=10 nm$
(b) $\lambda=10^{-1} nm$
(c) $\lambda=10^{-4} nm$
(d) $\lambda=10^{-6} nm$
उत्तर दिखाएँ
सोचने की प्रक्रिया
सापेक्षता के संशोधन महत्वपूर्ण होंगे जब डी-ब्रोग्ली तरंगदैर्ध्य प्रकाश की गति से अधिक हो। अर्थात, $3 \times 10^{8} m / s$ से अधिक हो।
उत्तर
$(c, d)$
डी-ब्रोग्ली तरंगदैर्ध्य
यहां,
$$ \begin{aligned} & \lambda=\dfrac{h}{m v} \Rightarrow v=\dfrac{h}{m \lambda} \\ & h=6.6 \times 10^{-34} Js \end{aligned} $$
और इलेक्ट्रॉन के लिए,
अब प्रत्येक विकल्प के बारे में अलग-अलग सोचें
(a)
$$ \lambda_1=10 nm=10 \times 10^{-9} m=10^{-8} m $$
$$ \begin{matrix} \Rightarrow & v_1=\dfrac{6.6 \times 10^{-34}}{(9 \times 10^{-31}) \times 10^{-8}} \\ \Rightarrow & =\dfrac{2.2}{3} \times 10^{5} \approx 10^{5} m / s \end{matrix} $$
(b) $\lambda_2=10^{-1} nm=10^{-1} \times 10^{-9} m=10^{-10} m$
$\Rightarrow \quad v_2=\dfrac{6.6 \times 10^{-34}}{(9 \times 10^{-31}) \times 10^{-10}} \approx 10^{7} m / s$
(c) $\lambda_3=10^{-4} nm=10^{-4} \times 10^{-9} m=10^{-13} m$
$\Rightarrow \quad v_3=\dfrac{6.6 \times 10^{-34}}{(9 \times 10^{-31}) \times 10^{-13}} \approx 10^{10} m / s$
(d) $\lambda_4=10^{-6} nm=10^{-6} \times 10^{-9} m=10^{-15} m$
$\Rightarrow \quad v_4=\dfrac{6.6 \times 10^{-34}}{9 \times 10^{-31} \times 10^{-15}} \approx 10^{12} m / s$
इसलिए, विकल्प (c) और (d) सही हैं क्योंकि $v_3$ और $v_4$ $3 \times 10^{8} m / s$ से अधिक हैं।
-
विकल्प (a) $\lambda=10 \ \text{nm}$:
- गणना की गई वेग $v_1 \approx 10^5 \ \text{m/s}$ उच्च वेग $c = 3 \times 10^8 \ \text{m/s}$ से कहाँ भी कम है। इसलिए, सापेक्षतांत्रिक संशोधन आवश्यक नहीं हैं।
-
विकल्प (b) $\lambda=10^{-1} \ \text{nm}$:
- गणना की गई वेग $v_2 \approx 10^7 \ \text{m/s}$ अभी भी उच्च वेग $c = 3 \times 10^8 \ \text{m/s}$ से कहाँ भी कम है। इसलिए, सापेक्षतांत्रिक संशोधन आवश्यक नहीं हैं।
10. दो कण $A_1$ और $A_2$ जिनके द्रव्यमान $m_1, m_2(m_1>m_2)$ हैं, के एक ही डी-ब्रोग्ली तरंगदैर्ध्य है। तब,
(a) उनके संवेग समान हैं
(b) उनकी ऊर्जा समान है
(c) $A_1$ की ऊर्जा $A_2$ की ऊर्जा से कम है
(d) $A_1$ की ऊर्जा $A_2$ की ऊर्जा से अधिक है
उत्तर दिखाएं
Answer
(a, c)
डी-ब्रोग्ली तरंगदैर्ध्य $\lambda=\dfrac{h}{m v}$
जहाँ, $m v=p$ (संवेग)
$\Rightarrow$
$$ \lambda=\dfrac{h}{p} \Rightarrow p=\dfrac{h}{\lambda} $$
यहाँ, $h$ एक स्थिरांक है।
इसलिए,
$$ \begin{gathered} p \propto \dfrac{1}{\lambda} \Rightarrow \dfrac{p_1}{p_2}=\dfrac{\lambda_2}{\lambda_1} \\ (\lambda_1=\lambda_2)=\lambda \\ \dfrac{p_1}{p_2}=\dfrac{\lambda}{\lambda}=1 \Rightarrow p_1=p_2 \end{gathered} $$
लेकिन
तब,
इसलिए, उनके संवेग समान हैं।
इसके अलावा,
$$ \begin{aligned} E & =\dfrac{1}{2} m v^{2}=\dfrac{1}{2} \dfrac{m v^{2} \times m}{m} \\ & =\dfrac{1}{2} \dfrac{m^{2} v^{2}}{m}=\dfrac{1}{2} \dfrac{p^{2}}{m} \end{aligned} $$
यहाँ, $p$ एक स्थिरांक है
$$ E \propto \dfrac{1}{m} $$
$$ \dfrac{E_1}{E_2}=\dfrac{m_2}{m_1}<1 \Rightarrow E_1<E_2 $$
(b) उनकी ऊर्जा समान है
कारण: कणों की ऊर्जा समान नहीं है क्योंकि ऊर्जा कणों के द्रव्यमान और वेग दोनों पर निर्भर करती है। दिया गया है कि डी-ब्रोग्ली तरंगदैर्ध्य समान है, इसलिए संवेग समान है, लेकिन क्योंकि द्रव्यमान अलग है ($m_1 > m_2$), वेग भी अलग होना चाहिए। गतिज ऊर्जा, जो $E = \dfrac{p^2}{2m}$ द्वारा दी गई है, दोनों कणों के लिए अलग होगी। विशेष रूप से, बड़े द्रव्यमान ($m_1$) वाले कण की ऊर्जा छोटे द्रव्यमान ($m_2$) वाले कण की ऊर्जा से कम होगी।
(d) $A_1$ की ऊर्जा $A_2$ की ऊर्जा से अधिक है
कारण: यह विकल्प गलत है क्योंकि, जैसा कि अवलोकन किया गया है, जब संवेग स्थिर रहता है, तो कण की ऊर्जा उसके द्रव्यमान के व्युत्क्रमानुपाती होती है। क्योंकि $m_1 > m_2$ और संवेग समान है, तो $A_1$ (जिसका द्रव्यमान अधिक है) की ऊर्जा $A_2$ (जिसका द्रव्यमान कम है) की ऊर्जा से कम होगी। अतः $E_1 < E_2$।
11. एक फोटॉन की डी-ब्रोग्ली तरंगदैर्ध्य एक इलेक्ट्रॉन की डी-ब्रोग्ली तरंगदैर्ध्य की दोगुनी है। इलेक्ट्रॉन की चाल $v_{e}=\dfrac{c}{100}$ है। तब, $\newline$
(a) $\dfrac{E_{e}}{E_{p}}=10^{-4}$ $\newline$
(b) $\dfrac{E_{e}}{E_{p}}=10^{-2}$ $\newline$
(c) $\dfrac{p_{e}}{m_{e} c}=10^{-2}$ $\newline$
(d) $\dfrac{p_{e}}{m_{e} c}=10^{-4}$ $\newline$
उत्तर दिखाएं
Answer
( $b, c$ )
मान लीजिए, इलेक्ट्रॉन का द्रव्यमान $=m_{e}$
फोटॉन का द्रव्यमान $=m_{p}$,
इलेक्ट्रॉन की चाल $=v_{e}$
फोटॉन की चाल $=v_{p}$
इसलिए, इलेक्ट्रॉन के लिए डी-ब्रोग्ली तरंगदैर्ध्य
$$ \begin{aligned} \lambda_{e} & =\dfrac{h}{m_{e} v_{e}} \\ & =\dfrac{h}{m_{e}(c / 100)}=\dfrac{100 h}{m_{e} c} \text { (दिया गया) } \end{aligned} $$
किण्वी ऊर्जा,
$$ E_{e}=\dfrac{1}{2} m_{e} v_e^{2} $$
$\Rightarrow \quad m_{e} v_{e}=\sqrt{2 E_{e} m_{e}}$
$$ \text { इसलिए, } \quad \lambda_{e}=\dfrac{h}{m_{e} v_{e}}=\dfrac{h}{\sqrt{2 m_{e} E_{e}}} $$
$\Rightarrow \quad E_{e}=\dfrac{h^{2}}{2 \lambda_e^{2} m_{e}}$
फोटॉन के लिए तरंगदैर्ध्य $\lambda_{p}$, ऊर्जा
$$ E_{p}=\dfrac{h c}{\lambda_{p}}=\dfrac{h c}{2 \lambda_{e}} $$
$$ \begin{aligned} & \therefore \quad \dfrac{E_{p}}{E_{e}}=\dfrac{h c}{2 \lambda_{e}} \times \dfrac{2 \lambda_e^{2} m_{e}}{h^{2}} \\ & =\dfrac{\lambda_{e} m_{e} c}{h}=\dfrac{100 h}{m_{e} c} \times \dfrac{m_{e} c}{h}=100 \\ & \text { इलेक्ट्रॉन के लिए, } \\ & \dfrac{E_{e}}{E_{p}}=\dfrac{1}{100}=10^{-2} \\ & p_{e}=m_{e} v_{e}=m_{e} \times c / 100 \\ & \dfrac{p_{e}}{m_{e} c}=\dfrac{1}{100}=10^{-2} \end{aligned} $$
-
विकल्प (a): $\dfrac{E_{e}}{E_{p}}=10^{-4}$
यह विकल्प गलत है क्योंकि, समाधान में जैसा कि अवलोकन किया गया है, इलेक्ट्रॉन की ऊर्जा और फोटॉन की ऊर्जा के अनुपात के लिए $\dfrac{E_{e}}{E_{p}}=10^{-2}$ है, न कि $10^{-4}$. गणना दिखाती है कि $\dfrac{E_{e}}{E_{p}}=\dfrac{1}{100}=10^{-2}$.
-
विकल्प (d): $\dfrac{p_{e}}{m_{e} c}=10^{-4}$
यह विकल्प गलत है क्योंकि, समाधान में जैसा कि निर्धारित किया गया है, इलेक्ट्रॉन के संवेग के अपने द्रव्यमान और प्रकाश की गति के गुणनफल के अनुपात के रूप में $\dfrac{p_{e}}{m_{e} c}=10^{-2}$ होता है, न कि $10^{-4}$. गणना दिखाती है कि $\dfrac{p_{e}}{m_{e} c}=\dfrac{1}{100}=10^{-2}$।
12. पदार्थ में अवशोषित फोटॉन ऊष्मा में बदल जाते हैं। एक स्रोत जो $n$ फोटॉन/सेकंड की आवृत्ति $v$ के साथ उत्सर्जन करता है, का उपयोग $1$ किग्रा बर्फ के $0^{\circ} C$ पर पानी में बदलने के लिए किया जाता है। तब, परिवर्तन के लिए लिया गया समय $T$
(a) $n$ के बढ़ने के साथ घटता है, $v$ निश्चित रहता है
(b) $n$ निश्चित रहता है, $v$ बढ़ने के साथ घटता है
(c) $n$ और $v$ बदलते हैं जैसे कि $n v =$ निश्चित रहता है, तो निश्चित रहता है
(d) जब उत्पाद $n v$ बढ़ता है तो बढ़ता है
उत्तर दिखाएं
उत्तर
$(a, b, c)$
बर्फ को पानी में बदलने के लिए खर्च की ऊर्जा
$$ \begin{aligned} & =\text { द्रव्यमान } \times \text { छिपी ऊष्मा } \\ & =m L=(1000 g) \times(80 cal / g) \\ & =80000 cal \end{aligned} $$
उपयोग की गई फोटॉन की ऊर्जा $=n T \times E=n T \times h \nu$
इसलिए,
$$ n T h \nu=m L \Rightarrow T=\dfrac{m L}{n h v} $$
$\therefore \quad T \propto \dfrac{1}{n}$, जब $v$ निश्चित रहता है।
$T \propto \dfrac{1}{v}$, जब $n$ निश्चित रहता है।
$\Rightarrow \quad T \propto \dfrac{1}{n v}$।
इसलिए, यदि $n v$ निश्चित रहता है, तो $T$ निश्चित रहता है।
- विकल्प (d) गलत है: परिवर्तन के लिए लिया गया समय $ T $ बढ़ते उत्पाद $ n v $ के साथ घटता है, न कि बढ़ता है। इसका कारण यह है कि $ T $, जैसा कि संबंध $ T = \dfrac{m L}{n h v} $ द्वारा दिखाया गया है, $ n v $ के विपरीत अनुपात में होता है। अतः, यदि $ n v $ बढ़ता है, $ T $ घटता है।
13. एक कण मूल बिंदु के चारों ओर एक बंद कक्षा में घूमता है, क्योंकि एक बल जो मूल बिंदु की ओर बलपूर्वक दिशा में होता है। कण के डी-ब्रोग्ली तरंगदैर्ध्य चक्रीय रूप से दो मानों $\lambda_1, \lambda_2$ के बीच बदलता है जहां $\lambda_1>\lambda_2$। निम्नलिखित में से कौन से कथन सत्य हैं?
(a) कण एक वृत्ताकार कक्षा में घूम सकता है जिसका केंद्र मूल बिंदु होता है
(b) कण एक अतिपरवलयी आवर्त पथ पर गति कर सकता है जिसका केंद्र इसका फोकस है
(c) जब डी-ब्रोग्ली तरंगदैर्ध्य $\lambda_1$ होती है, तो कण मूल बिंदु से कम दूरी पर होता है जब इसका मान $\lambda_2$ होता है
(d) जब डी-ब्रोग्ली तरंगदैर्ध्य $\lambda_2$ होती है, तो कण मूल बिंदु से कम दूरी पर होता है जब इसका मान $\lambda_1$ होता है
उत्तर दिखाएं
उत्तर
($b, d)$
यदि कण एक अतिपरवलयी आवर्त पथ पर गति कर रहा है जिसका मूल बिंदु इसका एक फोकस है, तो कण की डी-ब्रोग्ली तरंगदैर्ध्य $\lambda_1$ और $\lambda_2$ के बीच चक्रीय रूप से बदल सकती है।
नीचे दिए गए चित्र को ध्यान में रखें
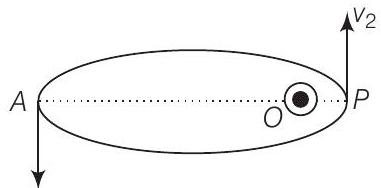
मान लीजिए $v_1, v_2$ कण के बिंदु $A$ और $B$ पर चाल है और मूल बिंदु $O$ पर फोकस है। यदि $\lambda_1, \lambda_2$ कण के बिंदु $A$ और $B$ पर गति करते समय संगत डी-ब्रोग्ली तरंगदैर्ध्य हैं, तो,
और
$$ \begin{aligned} & \lambda_1=\dfrac{h}{m v_1} \\ & \lambda_2=\dfrac{h}{m v_2} \end{aligned} $$
$$ \begin{matrix} \therefore & \dfrac{\lambda_1}{\lambda_2}=\dfrac{v_2}{v_1} \\ \text { क्योंकि } & \lambda_1>\lambda_2 \\ \therefore & v_2>v_1 \end{matrix} $$
कोणीय संवेग के संरक्षण के नियम के अनुसार, कण जब फोकस से निकट होता है तब तेजी से गति करता है।
चित्र से हम देख सकते हैं कि मूल बिंदु $O$ बिंदु $P$ के बराबर निकट है जबकि $A$ के बराबर नहीं।
-
विकल्प (a): कण मूल बिंदु केंद्र के चारों ओर एक वृत्तीय पथ पर गति कर सकता है।
कारण: एक वृत्तीय पथ में मूल बिंदु (केंद्र) से कण की दूरी स्थिर रहती है। अतः कण की चाल और इसलिए डी-ब्रोग्ली तरंगदैर्ध्य भी स्थिर रहती है। यह दिया गया शर्त कि डी-ब्रोग्ली तरंगदैर्ध्य दो मानों के बीच चक्रीय रूप से बदलती है इसके विरोधाभासी है।
-
विकल्प (c): जब डी-ब्रोग्ली तरंगदैर्ध्य $\lambda_1$ होती है, तो कण मूल बिंदु से कम दूरी पर होता है जब इसका मान $\lambda_2$ होता है।
कारण: डी-ब्रोग्ली संबंध के अनुसार, $\lambda = \dfrac{h}{mv}$, एक बड़े तरंगदैर्ध्य $\lambda_1$ के लिए छोटा वेग $v_1$ और एक छोटे तरंगदैर्ध्य $\lambda_2$ के लिए बड़ा वेग $v_2$ संबंधित होता है। कोणीय संवेग के संरक्षण के अनुसार, कण जब फोकस से निकट होता है तब तेज गति करता है। इसलिए, कण जब डी-ब्रोग्ली तरंगदैर्ध्य $\lambda_2$ (छोटा मान) होता है तब उसके उत्पति बिंदु से निकट होता है और जब डी-ब्रोग्ली तरंगदैर्ध्य $\lambda_1$ (बड़ा मान) होता है तब उसके उत्पति बिंदु से दूर होता है। इस कारण, विकल्प (c) गलत है।
बहुत छोटे उत्तर प्रकार प्रश्न
14. एक प्रोटॉन और एक $\alpha$-कण को समान विभवांतर का उपयोग करके त्वरित किया जाता है। डी-ब्रोग्ली तरंगदैर्ध्य $\lambda_{p}$ और $\lambda_{\alpha}$ के बीच कैसा संबंध होता है?
उत्तर दिखाएं
सोचने की प्रक्रिया
यहाँ, क्योंकि प्रोटॉन और $\boldsymbol{\alpha}$-कण दोनों समान विभवांतर का उपयोग करते हैं, इसलिए उन्हें नियत मान लिया जाता है।
उत्तर
क्योंकि,
$$ \begin{aligned} \lambda & =\dfrac{h}{\sqrt{2 m q v}} \\ \lambda & \propto \dfrac{1}{\sqrt{m q}} \\ \dfrac{\lambda_{p}}{\lambda_{\alpha}} & =\dfrac{\sqrt{m_{\alpha} q_{\alpha}}}{\sqrt{m_{p} q_{p}}}=\dfrac{\sqrt{4 m_{p} \times 2 e}}{\sqrt{m_{p} \times e}}=\sqrt{8} \end{aligned} $$
$$ \therefore \quad \lambda_{p}=\sqrt{8} \lambda_{\alpha} $$
अर्थात, प्रोटॉन की तरंगदैर्ध्य $\alpha$-कण की तरंगदैर्ध्य के $\sqrt{8}$ गुना होती है।
15. (i) फोटोइलेक्ट्रिक प्रभाव की व्याख्या में, हम एक फोटॉन आवृत्ति $v$ के एक फोटॉन के साथ एक इलेक्ट्रॉन के टकराव की अवधारणा करते हैं और इसकी ऊर्जा को स्थानांतरित करते हैं। इससे उत्सर्जित इलेक्ट्रॉन की अधिकतम ऊर्जा $E_{\max }$ के लिए समीकरण होता है
$$ E_{\max }=h \nu-\phi_0 $$
जहाँ $\phi_0$ धातु के कार्य फलन है। यदि एक इलेक्ट्रॉन 2 फोटॉन (प्रत्येक की आवृत्ति $\nu$) अवशोषित करता है, तो उत्सर्जित इलेक्ट्रॉन के अधिकतम ऊर्जा क्या होगी?
(ii) दो फोटॉन अवशोषण की इस तथ्य को हम अपने विभवांतर विपरीत विभव के चर्चा में क्यों नहीं लेते हैं?
उत्तर दिखाएँ
उत्तर
(i) यहाँ दिया गया है कि, एक इलेक्ट्रॉन 2 फोटॉन अवशोषित करता है, जिनकी आवृत्ति $v$ है तो $v^{\prime}=2 v$ जहाँ, $v^{\prime}$ उत्सर्जित इलेक्ट्रॉन की आवृत्ति है।
दिया गया है, $\quad E_{\max }=h \nu-\phi_0$
अब, उत्सर्जित इलेक्ट्रॉन के अधिकतम ऊर्जा के लिए
$$ E_{\max }^{\prime}=h(2 v)-\phi_0=2 h \nu-\phi_0 $$
(ii) एक ही इलेक्ट्रॉन द्वारा 2 फोटॉन अवशोषित करने की प्रायिकता बहुत कम होती है। इसलिए, ऐसी उत्सर्जन नगण्य होगी।
16. ऐसे अवस्थाएँ हो सकती हैं जिनमें कुछ पदार्थ छोटी तरंगदैर्घ्य के फोटॉन अवशोषित करते हैं और लंबी तरंगदैर्घ्य के फोटॉन उत्सर्जित करते हैं। क्या कोई स्थायी पदार्थ हो सकता है जो लंबी तरंगदैर्घ्य के फोटॉन अवशोषित करे और छोटी तरंगदैर्घ्य के प्रकाश के रूप में उत्सर्जन करे?
उत्तर दिखाएँ
उत्तर
पहले कथन के अनुसार, जब छोटी तरंगदैर्घ्य के फोटॉन अवशोषित करने वाले पदार्थ के आपतित फोटॉन की ऊर्जा उच्च होती है और उत्सर्जित फोटॉन की ऊर्जा लंबी तरंगदैर्घ्य के कारण कम होती है।
लेकिन दूसरे कथन में, जब लंबी तरंगदैर्घ्य के फोटॉन अवशोषित करने वाले पदार्थ के आपतित फोटॉन की ऊर्जा कम होती है और उत्सर्जित फोटॉन की ऊर्जा छोटी तरंगदैर्घ्य के कारण उच्च होती है। इसका अर्थ है कि इस कथन में पदार्थ को उत्सर्जन के लिए ऊर्जा प्रदान करनी पड़ती है।
लेकिन एक स्थायी पदार्थ के लिए ऐसा संभव नहीं है।
17. जो इलेक्ट्रॉन फोटॉन अवशोषित करते हैं उनमें से सभी फोटोइलेक्ट्रॉन के रूप में बाहर आते हैं?
उत्तर दिखाएँ
उत्तर
प्रकाश विद्युत प्रभाव में हम देख सकते हैं कि अधिकांश इलेक्ट्रॉन एक फोटॉन अवशोषित करके धातु में बिखर जाते हैं।
इसलिए, जो इलेक्ट्रॉन फोटॉन अवशोषित करते हैं वे सभी फोटोइलेक्ट्रॉन के रूप में बाहर नहीं आते हैं। केवल वे इलेक्ट्रॉन धातु से बाहर आते हैं जिनकी ऊर्जा धातु के कार्य फलन से अधिक हो जाती है।
18. दो लाइट स्रोत हैं, जो प्रत्येक 100 W के शक्ति के साथ उत्सर्जन करते हैं। एक एक्स-रे के तरंगदैर्घ्य $1 nm$ के फोटॉन उत्सर्जित करता है और दूसरा 500 nm के दृश्य प्रकाश के फोटॉन उत्सर्जित करता है। दिए गए तरंगदैर्घ्य के एक्स-रे फोटॉन और दृश्य प्रकाश के फोटॉन की संख्या के अनुपात को ज्ञात कीजिए?
उत्तर दिखाएँ
उत्तर
मान लीजिए $X$-किरणों की तरंगदैर्ध्य $\lambda_1$ है और दृश्य प्रकाश की तरंगदैर्ध्य $\lambda_2$ है।
दिया गया है, $\quad P=100 W$
और
$\lambda_1=1 nm$
$\lambda_2=500 nm$
इसके अतिरिक्त, $n_1$ और $n_2$ क्रमशः दोनों स्रोतों से प्रति सेकंड उत्सर्जित $X$-किरणों और दृश्य प्रकाश के फोटॉनों की संख्या को प्रदर्शित करते हैं।
इसलिए,
$\dfrac{E}{t}=P=n_1 \dfrac{h c}{\lambda_1}=n_2 \dfrac{h c}{\lambda_2}$
$\Rightarrow$
$\dfrac{n_1}{\lambda_1}=\dfrac{n_2}{\lambda_2}$
$\Rightarrow$
$\dfrac{n_1}{n_2}=\dfrac{\lambda_1}{\lambda_2}=\dfrac{1}{500}$
छोटे उत्तर प्रकार के प्रश्न
19. फोटोइमिशन के चित्र को ध्यान में रखते हुए, आप गति संरक्षण के साथ कैसे समझाएंगे? ध्यान दें कि प्रकाश (फोटॉन) के संवेग की दिशा उत्सर्जित इलेक्ट्रॉन की दिशा से अलग होती है।
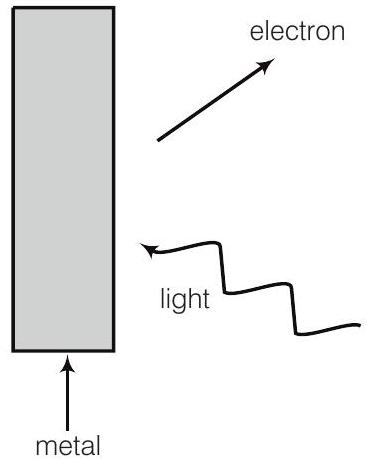
उत्तर दिखाएँ
उत्तर
फोटोइलेक्ट्रिक उत्सर्जन के दौरान, आपतित फोटॉन के संवेग को धातु में स्थानांतरित किया जाता है। माइक्रोस्कोपिक स्तर पर, धातु के परमाणु फोटॉन को अवशोषित करते हैं और इसका संवेग मुख्य रूप से नाभिक और इलेक्ट्रॉन को स्थानांतरित किया जाता है।
उत्सर्जित इलेक्ट्रॉन निर्गत होता है। इसलिए, संवेग के संरक्षण को ध्यान में रखते हुए, आपतित फोटॉन के संवेग को नाभिक और इलेक्ट्रॉन को स्थानांतरित किया जाता है।
20. एक धातु को 600 nm तरंगदैर्ध्य के प्रकाश के अनुरक्षण के लिए चित्र को ध्यान में रखते हुए, आप गति संरक्षण के साथ कैसे समझाएंगे? ध्यान दें कि प्रकाश (फोटॉन) के संवेग की दिशा उत्सर्जित इलेक्ट्रॉन की दिशा से अलग होती है।

उत्तर दिखाएँ
सोचने की प्रक्रिया
अधिकतम ऊर्जा $=h \nu-\phi$
उत्तर
दिया गया है,
पहली स्थिति के लिए,
प्रकाश की तरंगदैर्ध्य $\lambda=600 nm$
और दूसरी स्थिति के लिए,
प्रकाश की तरंगदैर्ध्य $\lambda^{\prime}=400 nm$
इसके अतिरिक्त, दूसरी स्थिति के अधिकतम कार्य ऊर्जा पहली स्थिति के कार्य ऊर्जा के दोगुना होता है।
$$\text { अर्थात, } K_{\max }^{\prime} =2 K_{\max }$$ $$\text { यहाँ, } K_{\max }^{\prime} =\dfrac{h c}{\lambda}-\phi$$ $$\Rightarrow 2 K_{\max } =\dfrac{h c}{\lambda^{\prime}}-\phi_0$$ $$\Rightarrow 2 \dfrac{1230}{600}-\phi =\dfrac{1230}{400}-\phi$$ $$\Rightarrow \phi =\dfrac{1230}{1200}=1.02 eV$$
21. मान लीजिए एक इलेक्ट्रॉन को 1 nm चौड़े क्षेत्र में सीमित कर दिया गया है, हाइजेनबर्ग अनिश्चितता सिद्धांत का उपयोग करके आवेग में अनिश्चितता ज्ञात कीजिए $(\Delta x \times \Delta p \approx h)$. आप अवस्थिति में अनिश्चितता $\Delta x$ को $1 nm$ मान सकते हैं। मान लीजिए $p \approx \Delta p$, इलेक्ट्रॉन की ऊर्जा इलेक्ट्रॉन वोल्ट में ज्ञात कीजिए।
उत्तर दिखाएं
Answer
यहाँ, $\Delta x=1 nm=10^{-9} m, \Delta p=$ ?
जैसे $\Delta x \Delta p \approx h$
$$\therefore \Delta p =\dfrac{h}{\Delta x}=\dfrac{h}{4 \pi \Delta x}$$
$$\Rightarrow =\dfrac{6.62 \times 10^{-34} Js}{2 \times(22 / 7)(10^{-9}) m}$$
$$=0.526 \times 10^{-25} kg m / s$$
$$\text { ऊर्जा, } E =\dfrac{p^{2}}{2 m}=\dfrac{(\Delta p)^{2}}{2 m}$$
$$=\dfrac{(1.05 \times 10^{-25})^{2}}{2 \times 9.1 \times 10^{-31}} J$$
$$\Rightarrow =\dfrac{(1.05 \times 10^{-25})^{2}}{2 \times 9.1 \times 10^{-31} \times 1.6 \times 10^{-19}} eV$$
$$=0.009501 \times 10^{-2} eV .$$
22. दो एकरूपता वाले प्रकाश के पुंज $A$ और $B$ बराबर तीव्रता $I$ के साथ एक पर्दे पर प्रहार करते हैं। प्रकाश पुंज $A$ द्वारा पर्दे पर प्रहार करने वाले फोटॉन की संख्या पुंज $B$ की दो गुनी है। तब, आप उनकी आवृत्तियों के बारे में क्या निष्कर्ष निकाल सकते हैं?
उत्तर दिखाएं
Answer
मान लीजिए $n_{A}$ पुंज $A$ के प्रति सेकंड आते हुए फोटॉन की संख्या है और $n_{B}$ पुंज $B$ के प्रति सेकंड आते हुए फोटॉन की संख्या है।
इसलिए,
$$ \begin{gathered} n_{A}=2 n_{B} \\ A=h v_{A} \\ B=h v_{B} \end{gathered} $$
प्रकाश के फोटॉन की ऊर्जा प्रकाश के फोटॉन की ऊर्जा
अब, प्रश्न के अनुसार,
तीव्रता के $A=$ तीव्रता के $B$
$$ \begin{aligned} & \therefore \quad n_{A} h \nu_{A}=n_{B} h v_{E} \\ & \Rightarrow \quad \dfrac{v_{A}}{v_{B}}=\dfrac{n_{B}}{n_{A}}=\dfrac{n_{B}}{2 n_{B}}=\dfrac{1}{2} \\
$$ & \Rightarrow \quad v_{B}=2 v_{A} \end{aligned} $$
अतः, इस संबंध से हम निष्कर्ष निकाल सकते हैं कि किरण $B$ की आवृत्ति किरण $A$ की आवृत्ति की दुगुनी है।
23. दो कण $A$ और $B$ के डी-ब्रोग्ली तरंगदैर्ध्य $\lambda_1$ और $\lambda_2$ हैं जो मिलकर कण $C$ बनाते हैं। प्रक्रिया संवेग के संरक्षण के नियम का पालन करती है। कण $C$ के डी-ब्रोग्ली तरंगदैर्ध्य का निर्धारण कीजिए। (गति एक-विमीय है)
उत्तर दिखाएँ
उत्तर
संवेग के संरक्षण के आधार पर दिया गया है,
$$ \begin{matrix} |C|=|A|+|B| = \dfrac{h}{\lambda_{C}}=\dfrac{h}{\lambda_{A}}+\dfrac{h}{\lambda_{B}} \quad \newline \because \lambda=\dfrac{h}{m v}=\dfrac{h}{p} \Rightarrow p=\dfrac{h}{\lambda} \newline \\ \Rightarrow \dfrac{h}{\lambda_{C}}=\dfrac{h \lambda_{B}+h \lambda_{A}}{\lambda_{A} \lambda_{B}} \newline \\ \Rightarrow \dfrac{\lambda_{C}}{h}=\dfrac{\lambda_{A} \lambda_{B}}{h \lambda_{A}+h \lambda_{B}} \Rightarrow \lambda_{C}=\dfrac{\lambda_{A} \lambda_{B}}{\lambda_{A}+\lambda_{B}} \end{matrix} $$
केस I मान लीजिए कि दोनों $p_{A}$ और $p_{B}$ धनात्मक हैं, तो
$$ \lambda_{C}=\dfrac{\lambda_{A} \lambda_{B}}{\lambda_{A}+\lambda_{B}} $$
केस II जब दोनों $p_{A}$ और $p_{B}$ नकारात्मक हैं, तो
$$ \lambda_{C}=-\dfrac{\lambda_{A} \lambda_{B}}{\lambda_{A}+\lambda_{B}} $$
केस III जब $p_{A}>0, p_{B}<0$ अर्थात $p_{A}$ धनात्मक और $p_{B}$ नकारात्मक है, तो
$$ \begin{aligned} & \dfrac{h}{\lambda_{C}}=\dfrac{h}{\lambda_{A}}-\dfrac{h}{\lambda_{B}}=\dfrac{(\lambda_{B}-\lambda_{A}) h}{\lambda_{A} \lambda_{B}} \\ & \Rightarrow \quad \lambda_{C}=\dfrac{\lambda_{A} \lambda_{B}}{\lambda_{B}-\lambda_{A}} \end{aligned} $$
केस IV $\quad$ $p_{A}<0, p_{B}>0$, अर्थात $p_{A}$ नकारात्मक और $p_{B}$ धनात्मक है,
$$ \begin{matrix} \therefore \dfrac{h}{\lambda_{C}} =\dfrac{-h}{\lambda_{A}}+\dfrac{h}{\lambda_{B}} \newline \\ \Rightarrow =\dfrac{(\lambda_{A}-\lambda_{B}) h}{\lambda_{A} \lambda_{B}} \Rightarrow \lambda_{C}=\dfrac{\lambda_{A} \lambda_{B}}{\lambda_{A}-\lambda_{B}} \end{matrix} $$
24. एक न्यूट्रॉन बीम ऊर्जा $E$ के साथ एक सतह पर विस्थापित होती है जिसके परमाणुओं के बीच दूरी $d=0.1 nm$ है। परावर्तित बीम में तीव्रता के पहले अधिकतम मान $\theta=30^{\circ}$ पर होता है। बीम की गतिज ऊर्जा $E$ किलोवोल्ट में कितनी है?
उत्तर दिखाएं
उत्तर
दिया गया है, $d=0.1 nm$,
अब, ब्रैग के नियम के अनुसार
$$ \begin{matrix} \Rightarrow 2 d \sin \theta =n \lambda \Rightarrow 2 \times 0.1 \times \sin 30=1 \lambda \newline \\ \text { अब, } \lambda =0.1 nm \Rightarrow=10^{-10} m \newline \\ \Rightarrow \lambda =\dfrac{h}{m v}=\dfrac{h}{p} \newline \\ \Rightarrow p=\dfrac{h}{\lambda} =\dfrac{6.62 \times 10^{-34}}{10^{-10}} \newline \\ \text { अब, } =6.62 \times 10^{-24} kg-m / s \newline \\ KE =\dfrac{1}{2} m v^{2}=\dfrac{1}{2} \dfrac{m^{2} v^{2}}{m}=\dfrac{1}{2} \dfrac{p^{2}}{m} \newline \\ =\dfrac{1}{2} \times \dfrac{(6.62 \times 10^{-24})^{2}}{1.67 \times 10^{-27}} J \newline \\ =0.21 eV \end{matrix} $$
लंबा उत्तर प्रकार प्रश्न
26. एक इलेक्ट्रॉन को धातु के सतह के सामने दूरी $d$ पर मान लीजिए (जिसे अनंत तल के रूप में मान लिया गया है)। मान लीजिए प्लेट द्वारा आकर्षण बल $\dfrac{1}{4} \dfrac{q^{2}}{4 \pi \varepsilon_0 d^{2}}$ द्वारा दिया गया है। आवेश को प्लेट से अनंत दूरी तक ले जाने में किया गया कार्य की गणना कीजिए। $d=0.1 nm$ लेकर इलेक्ट्रॉन वोल्ट में कार्य की गणना कीजिए।
उत्तर दिखाएँ
सोचने की प्रक्रिया
$$ \text { बाह्य एजेंसी द्वारा किया गया कार्य }=+\dfrac{1}{4 \pi \varepsilon_0} \cdot \dfrac{1}{4} \int_0^{\infty} \dfrac{q^{2}}{x^{2}} d x $$
उत्तर
प्रश्न के अनुसार, नीचे दिए गए चित्र को ध्यान में रखें। चित्र से, $d=0.1 nm=10^{-10} m$,
$$ F=\dfrac{q^{2}}{4 \times 4 \pi \varepsilon_0 d^{2}} $$
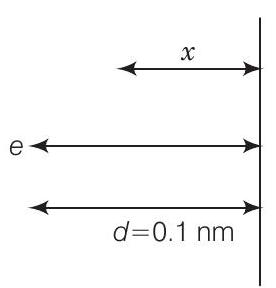
मान लीजिए इलेक्ट्रॉन धातु सतह से दूरी $x$ पर है। तब, इस पर आकर्षण बल है
$$ F_{x}=\dfrac{q^{2}}{4 \times 4 \pi \varepsilon_0 x^{2}} $$
बाह्य एजेंसी द्वारा इलेक्ट्रॉन को दूरी $d$ से अनंत तक ले जाने में किया गया कार्य है
$$ \begin{aligned} W & =\int_1^{\infty} F_{x} d x=\int_1^{\infty} \dfrac{q^{2} d x}{4 \times 4 \pi \varepsilon_0} \dfrac{1}{x^{2}} \\ & =\dfrac{q^{2}}{4 \times 4 \pi \varepsilon_0} \dfrac{1}{d} \\ & =\dfrac{(1.6 \times 10^{-19})^{2} \times 9 \times 10^{9}}{4 \times 10^{-10}} J \\ & =\dfrac{(1.6 \times 10^{-19})^{2} \times(9 \times 10^{9})}{(4 \times 10^{-10}) \times(1.6 \times 10^{-19})} eV=3.6 eV \end{aligned} $$
27. एक छात्र फोटोइलेक्ट्रिक प्रभाव पर एक प्रयोग करता है, दो सामग्रियों $A$ और $B$ का उपयोग करता है। चित्र में $V_{\text {stop }}$ के विरुद्ध $v$ के आलेख को दिया गया है।
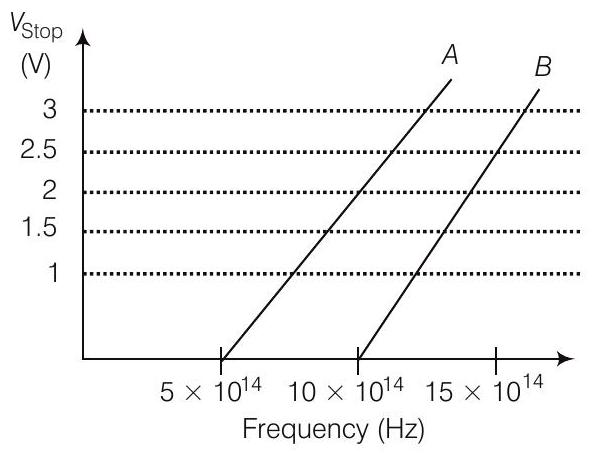
(i) कौन सा सामग्री $A$ या $B$ अधिक कार्य फलन का रखता है?
(ii) इलेक्ट्रॉन के विद्युत आवेश $=1.6 \times 10^{-19} C$ दिया गया है, दोनों $A$ और $B$ के लिए प्रयोग से प्राप्त $h$ के मान की गणना करें।
ईश्वर के सिद्धांत के साथ यह सांतर है या नहीं टिप्पणी करें।
उत्तर दिखाएँ
उत्तर
(i) दिया गया है, अधिकतम आवृत्ति $A$ के लिए $\nu_{O A}=5 \times 10^{14} Hz$ और $B$ के लिए,
$ \nu_{O B}=10 \times 10^{14} Hz $
हम जानते हैं कि
कार्य फ़ंक्शन,
$$ \phi=h v_0 \text { या } \phi_0 \propto v_0 $$
$$ \begin{aligned} \phi_0 & \propto \nu_0 \\ \dfrac{\phi_{D A}}{\phi_{O B}} & =\dfrac{5 \times 10^{14}}{10 \times 10^{14}}<1 \\ \phi_{D A} & <\phi_{O B} \end{aligned} $$
इसलिए,
अतः, $B$ का कार्य फ़ंक्शन $A$ के अपेक्षा अधिक है।
(ii) धातु $A$ के लिए, ढलान $=\dfrac{h}{e}=\dfrac{2}{(10-5) 10^{14}}$
या
$$ \begin{aligned} h & =\dfrac{2 e}{5 \times 10^{14}}=\dfrac{2 \times 1.6 \times 10^{-19}}{5 \times 10^{14}} \\ & =6.4 \times 10^{-34} Js \end{aligned} $$
धातु $B$ के लिए, ढलान $=\dfrac{h}{e}=\dfrac{2.5}{(15-10) 10^{14}}$
या
$$ \begin{aligned} h & =\dfrac{2.5 \times e}{5 \times 10^{14}}=\dfrac{2.5 \times 1.6 \times 10^{-19}}{5 \times 10^{14}} \\ & =8 \times 10^{-34} Js \end{aligned} $$
क्योंकि, धातुओं $A$ और $B$ के लिए प्रयोग से प्राप्त $h$ का मान अलग-अलग है। अतः, प्रयोग सिद्धांत से संगत नहीं है।
28. एक कण $A$ जिसका द्रव्यमान $m_{A}$ है, वेग $v$ से गति करते हुए एक दूसरे कण $B$ (द्रव्यमान $m_{B}$) के जो विराम में है उस पर टकराता है (एक-विमीय गति)। कण $A$ के डी-ब्रोग्ली तरंगदैर्ध्य में परिवर्तन ज्ञात कीजिए। टकराव को आदर्श टकराव मान लीजिए।
उत्तर दिखाएं
उत्तर
क्योंकि टकराव आदर्श है, अतः संवेग और कार्य ऊर्जा के संरक्षण के नियम पूरा किए जाते हैं।
संवेग के संरक्षण के अनुसार,
$\Rightarrow$
$$ \begin{aligned} m_{A} v+m_{B} 0 & =m_{A} v_1+m_{B} v_2 \\ m_{A}(v-v_1) & =m_{B} v_2 \end{aligned} $$
कार्य ऊर्जा के संरक्षण के अनुसार,
$$ \begin{matrix} \Rightarrow \dfrac{1}{2} m_{A} v^{2} =\dfrac{1}{2} m_{A} v_1^{2}+\dfrac{1}{2} m_{B} v_2^{2} \\ \Rightarrow m_{A}(v-v_1^{2}) =m_{B} v_2^{2} \\ \Rightarrow m_{A}(v-v_1)(v+v_1) =m_{B} v_2^{2} \end{matrix} $$
समीकरण (ii) को समीकरण (i) से विभाजित करने पर,
हमें प्राप्त होता है, $\quad v+v_1=v_2$ या $v=v_2-v_1$
समीकरण (i) और (iii) को हल करने पर हमें प्राप्त होता है
$$ \begin{aligned} v_1 & =\dfrac{m_{A}-m_{B}}{m_{A}+m_{B}} \quad v \text { और } v_2=\dfrac{2 m_{A}}{m_{A}+m_{B}} v \\
$$ \lambda_{\text {initial }} & =\dfrac{h}{m_{A} v} \\ \lambda_{\text {final }} & =\dfrac{h}{m_{A} v_1}=\dfrac{h(m_{A}+m_{B})}{m_{A}(m_{A}-m_{B}) v} \\ \Delta \lambda & =\lambda_{\text {final }}-\lambda_{\text {initial }}=\dfrac{-2h{m_{B}}}{m_{A} (m_{A}+m_{B})v} \end{aligned} $$
29. एक $20 W$ के बल्ब को लाल लाइट जो $5000 \AA$ तरंगदैर्ध्य की होती है और एक धातु के सतह पर रखे गए दूरी $2 m$ पर चमकाया जाता है। मान लीजिए कि धातु की सतह के कार्यफलन $2 eV$ है और धातु की सतह पर प्रत्येक परमाणु को एक वृत्ताकार डिस्क के रूप में ले लिया जा सकता है जिसकी त्रिज्या $1.5 \AA$ है।
(i) बल्ब द्वारा प्रति सेकंड उत्सर्जित फोटॉन की संख्या का अनुमान लगाएं।
[मान लीजिए कि कोई अन्य खोई नहीं होती है]
(ii) फोटोइलेक्ट्रॉन उत्सर्जन होगा या नहीं?
(iii) धातु के परमाणु डिस्क को कार्यफलन के बराबर ऊर्जा प्राप्त करने में कितना समय लगेगा?
(iv) (iii) में गणना किए गए समय अवधि के भीतर परमाणु डिस्क को कितने फोटॉन प्राप्त होंगे?
(v) आप बता सकते हैं कि फोटोइलेक्ट्रॉन प्रभाव कैसे तुरंत देखा गया था?
उत्तर दिखाएं
Answer
दिया गया, $P=20 W, \lambda=5000 \AA=5000 \times 10^{-10} m$
$$ d=2 m, \phi_0=2 eV, r=1.5 A=1.5 \times 10^{-10} m $$
(i) बल्ब द्वारा प्रति सेकंड उत्सर्जित फोटॉन की संख्या $n^{\prime}=\dfrac{p}{h c / \lambda}=\dfrac{p \lambda}{h c}$
$\Rightarrow$
$$ \begin{aligned} & =\dfrac{20 \times(5000 \times 10^{-10})}{(6.62 \times 10^{-34}) \times(3 \times 10^{8})} \\ & =5 \times 10^{19} s^{-1} \end{aligned} $$
(ii) आपतित फोटॉन की ऊर्जा $=\dfrac{h c}{\lambda}=\dfrac{(6.62 \times 10^{-34})(3 \times 10^{8})}{5000 \times 10^{-10} \times 1.6 \times 10^{-19}}$
$$ =2.48 eV $$
क्योंकि यह ऊर्जा $2 eV$ से अधिक है (अर्थात धातु के सतह के कार्यफलन), इसलिए फोटोइलेक्ट्रॉन उत्सर्जन होता है।
(iii) मान लीजिए $\Delta t$ वह समय है जिसमें ऊर्जा $\phi=$ (धातु के कार्यफलन) प्राप्त करने के लिए लगता है।
Consider the figure,
$$ \Rightarrow \quad \begin{aligned} \dfrac{P}{4 \pi d^{2}} \times \pi r^{2} \Delta t & =\phi_0 \\ \Delta t & =\dfrac{4 \phi_0 d^{2}}{P r^{2}} \\ & =\dfrac{4 \times(2 \times 1.6 \times 10^{-19}) \times 2^{2}}{20 \times(1.5 \times 10^{-10})^{2}} \approx 28.4 s \end{aligned} $$
(iv) समय $\Delta t$ में परमाणु डिस्क द्वारा प्राप्त फोटॉन की संख्या है
$$ \begin{aligned} N & =\dfrac{n^{\prime} \times \pi^{2}}{4 \pi d^{2}} \times \Delta t \\ & =\dfrac{n^{\prime} r^{2} \Delta t}{4 d^{2}} \\ & =\dfrac{(5 \times 10^{19}) \times(1.5 \times 10^{-10})^{2} \times 28.4}{4 \times(2)^{2}} \approx 2 \end{aligned} $$
(v) इलेक्ट्रॉन के उत्सर्जन के समय $11.04 s$ है।
इस समस्या में फोटोइलेक्ट्रॉन उत्सर्जन तात्कालिक नहीं होता।
फोटोइलेक्ट्रॉन उत्सर्जन में, आपतित फोटॉन और धातु सतह के मुक्त इलेक्ट्रॉन के बीच टकराव होता है, जो बहुत छोटे समय अंतराल में $(\approx 10^{-9} s)$ चलता है, इसलिए हम फोटोइलेक्ट्रॉन उत्सर्जन को तात्कालिक मानते हैं





