बहुविकल्पीय प्रश्न (MCQs)
1. तीन तरंगों $A, B$ और $C$ के आवृत्ति क्रमशः $1600 kHz, 5 MHz$ और $60 MHz$ हैं, जो एक स्थान से दूसरे स्थान तक प्रसारित की जानी है। निम्नलिखित में से कौन सा संचार के सबसे उपयुक्त तरीका है?
(a) $A$ को स्पेस तरंग द्वारा प्रसारित किया जाएगा जबकि $B$ और $C$ को स्काई तरंग द्वारा प्रसारित किया जाएगा
(b) $A$ को भू-तरंग द्वारा प्रसारित किया जाएगा, $B$ को स्काई तरंग द्वारा और $C$ को स्पेस तरंग द्वारा प्रसारित किया जाएगा
(c) $B$ और $C$ को भू-तरंग द्वारा प्रसारित किया जाएगा जबकि $A$ को स्काई तरंग द्वारा प्रसारित किया जाएगा
(d) $B$ को भू-तरंग द्वारा प्रसारित किया जाएगा जबकि $A$ और $C$ को स्पेस तरंग द्वारा प्रसारित किया जाएगा
उत्तर दिखाएं
सोचने की प्रक्रिया
तरंग के संचार के तरीका तरंग की आवृत्ति पर निर्भर करता है।
उत्तर
(b) संचार के तरीका आवृत्ति सीमा
भू-तरंग प्रसारण $-530 kHz$ से $1710 kHz$ तक
स्काई तरंग प्रसारण $-1710 kHz$ से $40 MHz$ तक
स्पेस तरंग प्रसारण $-54 MHz$ से $4.2 GHz$ तक
-
विकल्प (a) गलत है:
- तरंग $A$ (1600 kHz) भू-तरंग प्रसारण के बराबर रेंज (530 kHz से 1710 kHz) में है, न कि स्पेस तरंग रेंज में।
- तरंग $C$ (60 MHz) स्पेस तरंग प्रसारण के बराबर रेंज (54 MHz से 4.2 GHz) में है, न कि स्काई तरंग रेंज में।
-
विकल्प (c) गलत है:
- तरंग $B$ (5 MHz) स्काई तरंग प्रसारण के बराबर रेंज (1710 kHz से 40 MHz) में है, न कि भू-तरंग रेंज में।
- तरंग $C$ (60 MHz) स्पेस तरंग प्रसारण के बराबर रेंज (54 MHz से 4.2 GHz) में है, न कि भू-तरंग रेंज में।
- तरंग $A$ (1600 kHz) भू-तरंग प्रसारण के बराबर रेंज (530 kHz से 1710 kHz) में है, न कि स्काई तरंग रेंज में।
-
विकल्प (d) गलत है:
- तरंग $B$ (5 MHz) स्काई तरंग प्रसारण के बराबर रेंज (1710 kHz से 40 MHz) में है, न कि भू-तरंग रेंज में।
- तरंग $A$ (1600 kHz) भू-तरंग प्रसारण के बराबर रेंज (530 kHz से 1710 kHz) में है, न कि स्पेस तरंग रेंज में।
2. एक $100 m$ लंबा एंटीना $500 m$ ऊंचे इमारत पर लगाया गया है। इमारत तरंगों के लिए एक प्रसारक टावर बन सकती है जिसकी $\lambda$ $\newline`
(a) $\sim 400 m$ $\newline$
(b) $\sim 25 m$ $\newline$
(c) $\sim 150 m$ $\newline$
(d) $\sim 2400 m$ $\newline$
उत्तर दिखाएँ
Answer
(a) दिया गया, भवन की लंबाई $(l)$ निम्नलिखित द्वारा दी गई है
$$ l=500 m $$
हम जानते हैं कि, वह तरंग जो द्वारा प्रसारित की जा सकती है
$$ \lambda \sim 4 l=4 \times 100=400 m $$
-
विकल्प (b) $\sim 25 m$: तरंग दैर्घ्य $\lambda \sim 25 m$ एंटीना की लंबाई (100 m) की तुलना में बहुत छोटी है। प्रसार के लिए तरंग दैर्घ्य एंटीना की लंबाई के समान या उससे लंबी होनी चाहिए।
-
विकल्प (c) $\sim 150 m$: तरंग दैर्घ्य $\lambda \sim 150 m$ एंटीना की लंबाई (100 m) के पूर्णांक गुणक नहीं है। प्रसार के लिए तरंग दैर्घ्य आमतौर पर एंटीना की लंबाई के पूर्णांक गुणक होनी चाहिए।
-
विकल्प (d) $\sim 2400 m$: तरंग दैर्घ्य $\lambda \sim 2400 m$ एंटीना की लंबाई (100 m) की तुलना में बहुत लंबी है। यहां तक कि लंबी तरंग दैर्घ्य कभी-कभी प्रसार के लिए उपयोग की जा सकती है, लेकिन इस लंबाई के एंटीना के लिए यह अनुकूल नहीं है।
3. एक $1 kW$ संकेत को एक संचार चैनल के माध्यम से प्रसारित किया जाता है जो प्रति $km$ $-2 dB$ की धुंआई प्रदान करता है। यदि संचार चैनल की कुल लंबाई $5 km$ है, तो प्राप्त संकेत की शक्ति है
[gain in $dB=10 \log \frac{P_0}{P_{j}}$ ] $\newline$
(a) $900 W$ $\newline$
(b) $100 W$ $\newline$
(c) $990 W$ $\newline$
(d) $1010 W$ $\newline$
उत्तर दिखाएँ
Answer
(b) दिया गया, प्रसारित संकेत की शक्ति $P_{i}=1 kW=1000 W$ है
संकेत के धुंआई की दर $=-2 dB / km$ है
कुल पथ की लंबाई $=5 km$ है
इसलिए,
$$ \text { gain in } d B=5 \times(-2)=-10 dB $$
इसके अलावा,
$$ \text { gain in } d B=10 \log \frac{P_0}{P_{i}} $$
यहां $P_0$ प्राप्त संकेत की शक्ति है।
समीकरण (i) में दिए गए मान रखने पर,
$$ -10=10 \log \frac{P_0}{P_{i}}=-10 \log \frac{P_{i}}{P_0} $$
$$ \Rightarrow \log \frac{P_{i}}{P_0}=1 \Rightarrow \log \frac{P_{i}}{P_0}=\log 10 $$
$$ \Rightarrow \frac{P_{i}}{P_0}=10 \Rightarrow 1000 W=10 P_0 $$
$$ \Rightarrow P_0=100 W $$
-
विकल्प (a) $900 W$: यह विकल्प गलत है क्योंकि 5 किमी की दूरी पर संकेत के अवमन्दन के कारण शक्ति में बहुत बड़ा कमी होती है, न कि केवल 900 W तक की छोटी कमी। गणना दिखाती है कि प्राप्त शक्ति बहुत कम होती है, विशेषकर 100 W होती है।
-
विकल्प (c) $990 W$: यह विकल्प गलत है क्योंकि इसका अर्थ है कि 5 किमी की दूरी पर संकेत के अवमन्दन के लगभग नगण्य होता है। दिया गया अवमन्दन दर -2 डेसीबेल प्रति किमी है, इसलिए शक्ति की हानि बहुत अधिक होती है, जिसके कारण प्राप्त शक्ति 100 W होती है, न कि 990 W होती है।
-
विकल्प (d) $1010 W$: यह विकल्प गलत है क्योंकि इसका अर्थ है कि प्राप्त शक्ति प्रसारित शक्ति से अधिक है, जो चैनल में अवमन्दन के कारण संभव नहीं है। सही गणना दिखाती है कि प्राप्त शक्ति 100 W होती है, न कि 1010 W होती है।
4. एक बोलने वाले संकेत के $3 kHz$ को एक $1 MHz$ आवृत्ति वाले कैरियर संकेत के साथ आयाम वैकल्पिकता द्वारा प्रसारित किया जाता है। ओर ओर बैंड की आवृत्तियाँ होंगी $\newline$
(a) $1.003 MHz$ और $0.997 MHz$ $\newline$
(b) $3001 kHz$ और $2997 kHz$ $\newline$
(c) $1003 kHz$ और $1000 kHz$ $\newline$
(d) $1 MHz$ और $0.997 MHz$ $\newline$
उत्तर दिखाएं
सोचने की प्रक्रिया
आयाम वैकल्पिकता वाले संकेत में कैरियर तरंग की आवृत्ति $\omega_{c}$ होती है जिसके साथ दो अतिरिक्त वृत्तीय तरंगें होती हैं, एक की आवृत्ति $(\omega_{c}-\omega_{m})$ और दूसरी की आवृत्ति $(\omega_{c}+\omega_{m})$ होती है। ये दोनों तरंगें ओर ओर बैंड कहलाती हैं और उनकी आवृत्तियाँ ओर ओर बैंड आवृत्ति कहलाती हैं।
उत्तर
(a) दिया गया, कैरियर संकेत की आवृत्ति $\omega_{c}=1 MHz$
$\quad$ बोलने वाले संकेत की आवृत्ति $=3 kHz=3 \times 10^{-3} MHz$
$$ \begin{aligned} & =0.003 MHz \end{aligned} $$
अब, हम जानते हैं कि,
ओर ओर बैंड की आवृत्तियाँ $=(\omega_{c} \pm \omega_{m})$
$$ =(1 \pm 0.003) $$
$$ =1.003 MHz \text { और } 0.997 MHz $$
-
विकल्प (b): आवृत्तियाँ $3001 kHz$ और $2997 kHz$ गलत हैं क्योंकि वे सही इकाई में नहीं हैं। सही ओर ओर बैंड आवृत्तियाँ MHz में होनी चाहिए, न कि kHz में। इसके अतिरिक्त, मान भी $1.003 MHz$ और $0.997 MHz$ होने चाहिए, न कि $3001 kHz$ और $2997 kHz$ होने चाहिए।
-
विकल्प (c): आवृत्तियाँ $1003 kHz$ और $1000 kHz$ गलत हैं क्योंकि ये सही ओर बैंड आवृत्तियों का प्रतिनिधित्व नहीं करती हैं। सही ओर बैंड आवृत्तियाँ $1.003 MHz$ और $0.997 MHz$ हैं। इस विकल्प में दी गई मान गणना किए गए ओर बैंड आवृत्तियों से मेल नहीं खाती हैं।
-
विकल्प (d): आवृत्तियाँ $1 MHz$ और $0.997 MHz$ गलत हैं क्योंकि एक ओर बैंड आवृत्ति अनुपस्थित है। सही ओर बैंड आवृत्तियाँ $1.003 MHz$ और $0.997 MHz$ हैं। इस विकल्प में केवल एक सही ओर बैंड आवृत्ति दी गई है और दूसरी अनुपस्थित है।
5. एक संदेश संकेत की आवृत्ति $\omega_{m}$ एक वाहक तरंग की आवृत्ति $\omega_{c}$ पर अधिकृत करके एक आयाम वैकल्पिक तरंग (AM) प्राप्त की जाती है। AM तरंग की आवृत्ति होगी $\newline$
(a) $\omega_{m}$ $\newline$
(b) $\omega_{c}$ $\newline$
(c) $\frac{\omega_{c}+\omega_{m}}{2}$ $\newline$
(d) $\frac{\omega_{c}-\omega_{m}}{2}$ $\newline$
उत्तर दिखाएं
सोचने की प्रक्रिया
आयाम वैकल्पिकता में, वैकल्पिक तरंग की आवृत्ति वाहक तरंग की आवृत्ति के बराबर होती है।
उत्तर
(b) यहाँ, प्रश्न के अनुसार, वाहक तरंग की आवृत्ति $\omega_{c}$ है।
इसलिए आयाम वैकल्पिक तरंग की आवृत्ति भी $\omega_{c}$ होती है।
-
विकल्प (a) $\omega_{m}$: यह विकल्प गलत है क्योंकि $\omega_{m}$ संदेश संकेत की आवृत्ति का प्रतिनिधित्व करता है, न कि आयाम वैकल्पिक तरंग की आवृत्ति। आयाम वैकल्पिक तरंग की आवृत्ति मुख्य रूप से वाहक तरंग की आवृत्ति द्वारा निर्धारित होती है, न कि संदेश संकेत की आवृत्ति।
-
विकल्प (c) $\frac{\omega_{c}+\omega_{m}}{2}$: यह विकल्प गलत है क्योंकि आयाम वैकल्पिक तरंग की आवृत्ति वाहक तरंग और संदेश संकेत की आवृत्तियों के औसत के बराबर नहीं होती। आयाम वैकल्पिक तरंग में वाहक आवृत्ति $\omega_{c}$ और ओर बैंड आवृत्तियाँ $\omega_{c} \pm \omega_{m}$ होती हैं, लेकिन केंद्रीय आवृत्ति $\omega_{c}$ बनी रहती है।
-
विकल्प (d) $\frac{\omega_{c}-\omega_{m}}{2}$: यह विकल्प गलत है क्योंकि आयाम वैकल्पिक तरंग की आवृत्ति वाहक और संदेश संकेत की आवृत्तियों के अंतर के आधे के बराबर नहीं होती। आयाम वैकल्पिक तरंग की आवृत्ति वाहक आवृत्ति $\omega_{c}$ के चारों ओर केंद्रित होती है, और ओर बैंड आवृत्तियाँ $\omega_{c} \pm \omega_{m}$ पर होती हैं।
6. चार उपकरणों के I-V विशेषताएं चित्र में दिखाई गई हैं।
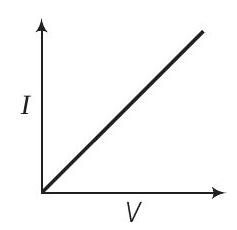
(i)
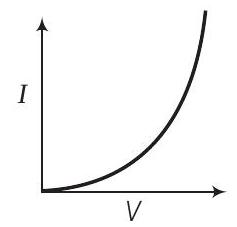
(ii)
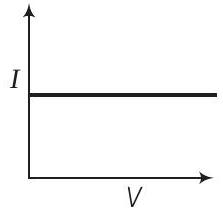
(iii)
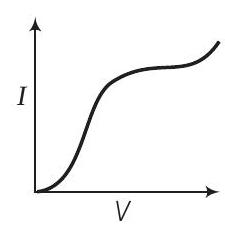
(iv)
मॉडुलेशन के लिए उपयोग किए जा सकने वाले उपकरणों की पहचान करें
(a) (i) और (iii)
(b) केवल (iii)
(c) (ii) और (iv) के कुछ क्षेत्र
(d) सभी उपकरणों का उपयोग किया जा सकता है
उत्तर दिखाएं
सोचने की प्रक्रिया
एक वर्ग नियम उपकरण वह होता है जहां या तो धारा या वोल्टेज दूसरे के वर्ग पर निर्भर करती है।
उत्तर
(c) वह उपकरण जो वर्ग नियम का पालन करता है, मॉडुलेशन के लिए उपयोग किया जाता है। (i) और (iii) द्वारा दिखाई गई विशेषताएं रैखिक उपकरणों के लिए हैं।
(ii) द्वारा दिखाई गई विशेषताएं वर्ग नियम उपकरण के लिए हैं। (i) के कुछ हिस्सा भी वर्ग नियम का पालन करता है।
इसलिए, (ii) और (iv) मॉडुलेशन के लिए उपयोग किए जा सकते हैं।
-
विकल्प (a) (i) और (iii): यह विकल्प गलत है क्योंकि (i) और (iii) रैखिक उपकरण हैं जो वर्ग नियम का पालन नहीं करते हैं। मॉडुलेशन के लिए वर्ग नियम का पालन करने वाले उपकरण की आवश्यकता होती है।
-
विकल्प (b) केवल (iii): यह विकल्प गलत है क्योंकि (iii) एक रैखिक उपकरण है और वर्ग नियम का पालन नहीं करता है। मॉडुलेशन के लिए वर्ग नियम का पालन करने वाले उपकरण की आवश्यकता होती है।
-
विकल्प (d) सभी उपकरणों का उपयोग किया जा सकता है: यह विकल्प गलत है क्योंकि सभी उपकरण वर्ग नियम का पालन नहीं करते हैं। उपकरण (i) और (iii) रैखिक उपकरण हैं और वे मॉडुलेशन के लिए उपयोग नहीं किए जा सकते हैं। केवल उपकरण (ii) और (iv) के कुछ क्षेत्र वर्ग नियम का पालन करते हैं और मॉडुलेशन के लिए उपयोग किए जा सकते हैं।
7. मॉडुलेशन-प्रसारण के बाद एक पुरुष की आवाज ग्राहक के लिए एक महिला की आवाज जैसी सुनाई देती है। समस्या के कारण है
(a) मॉडुलेशन सूचकांक के चुनाव की कमी (चुना गया $0<m<1$ )
(b) एम्प्लीफायर के बैंडविड्थ के चुनाव की कमी
(c) कैरियर आवृत्ति के चुनाव की कमी
(d) प्रसारण में ऊर्जा की हानि।
उत्तर दिखाएं
सोचने की प्रक्रिया
पुरुष की आवाज की आवृत्ति महिला की आवाज की आवृत्ति से कम होती है।
उत्तर
(b) इस प्रश्न में, प्राप्त मॉडुलित संकेत की आवृत्ति अधिक हो जाती है, जो एम्प्लीफायर के बैंडविड्थ के चुनाव की कमी के कारण संभव होता है।
इसके कारण आमप्लीट्यूड मॉडुलेशन में बैंडविड्थ आवृत्ति के मॉडुलेटिंग संकेत के दोगुनी होती है।
लेकिन, पुरुष की आवाज की आवृत्ति महिया की आवाज की आवृत्ति से कम होती है।
-
(a) मॉडुलेशन सूचकांक के चुनाव की कमी (चुना गया $0<m<1$): मॉडुलेशन सूचकांक मॉडुलित संकेत के आयाम को प्रभावित करता है न कि आवृत्ति। $0<m<1$ के बराबर मॉडुलेशन सूचकांक अंतर्गत अंतर्गत मॉडुलेशन के अंतर्गत होता है, जो एक कमजोर संकेत के रूप में परिणाम होता है लेकिन आवाज की आवृत्ति के अनुभव को बदलने के लिए आवश्यक नहीं होता।
-
(c) कैरियर आवृत्ति के चुनाव की कमी: कैरियर आवृत्ति तय करती है जिस आवृत्ति पर संकेत प्रसारित किया जाता है, लेकिन इसका मॉडुलेटिंग संकेत (आवाज) की आवृत्ति विशेषताओं पर प्रभाव नहीं होता। इसलिए, कैरियर आवृत्ति के चुनाव की कमी के कारण पुरुष की आवाज महिला की आवाज जैसी सुनाई नहीं देती।
-
(d) प्रसारण में ऊर्जा की हानि: प्रसारण में ऊर्जा की हानि ग्राहक पर एक कमजोर संकेत के रूप में परिणाम होती है, जो संकेत की गुणवत्ता या समझदारी में कमी के कारण हो सकती है। लेकिन, इसके कारण प्राप्त संकेत की आवृत्ति विशेषताओं में परिवर्तन नहीं होता, इसलिए यह पुरुष की आवाज को महिला की आवाज जैसी नहीं बनाता।
8. एक मूलभूत संचार प्रणाली में निम्नलिखित होता है
A. प्रेषक।
B. सूचना स्रोत।
C. सूचना का उपयोगकर्ता।
D. चैनल।
E. प्राप्तकर्ता।
इनको मूलभूत संचार प्रणाली में कौन सी क्रम में व्यवस्थित किया जाता है। $\newline$
(a) ABCDE $\newline$
(b) BADEC $\newline$
(c) BDACE $\newline$
(d) BEADC $\newline$
उत्तर दिखाएं
उत्तर
(b) एक संचार प्रणाली एक स्थान से दूसरे स्थान तक सूचना के प्रसारण और प्राप्ति के लिए उपयोग किया जाने वाला संगठन होता है।
पूरी प्रणाली एक क्रम में कई तत्वों से बनी होती है। इसे नीचे दिए गए चित्र के रूप में प्रस्तुत किया जा सकता है
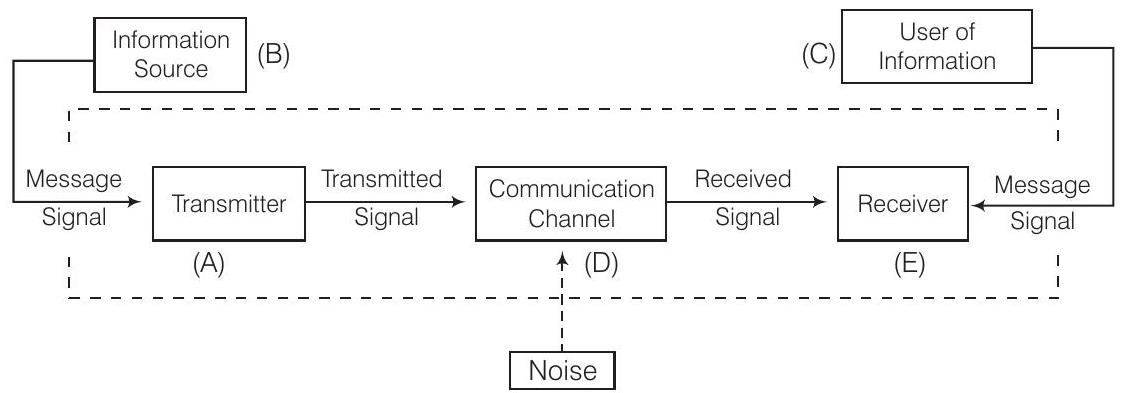
-
विकल्प (a) ABCDE: यह क्रम गलत है क्योंकि यह प्रेषक (A) से शुरू होता है, जबकि सूचना स्रोत (B) से शुरू होना चाहिए। मूलभूत संचार प्रणाली में सूचना स्रोत प्रारंभिक बिंदु होता है, न कि प्रेषक।
-
विकल्प (c) BDACE: यह क्रम गलत है क्योंकि यह चैनल (D) के बाद प्रेषक (A) को रखता है। सही क्रम में प्रेषक के पहले चैनल होना चाहिए, क्योंकि प्रेषक चैनल के माध्यम से सूचना को प्रसारित करता है।
-
विकल्प (d) BEADC: यह क्रम गलत है क्योंकि यह चैनल (D) के बाद प्राप्तकर्ता (E) को रखता है। मूलभूत संचार प्रणाली में प्राप्तकर्ता के बाद चैनल होना चाहिए, क्योंकि यह चैनल के माध्यम से प्रसारित सूचना को प्राप्त करता है।
9. आयाम वर्णित तरंग के गणितीय व्यंजक की पहचान करें $\newline$
(a) $A_{c} \sin [{\omega_{c}+k_1 V_{m}(t)} t+\phi]$ $\newline$
(b) $A_{c} \sin {\omega_{c} t+\phi+k_2 V_{m}(t)}$ $\newline$
(c) ${A_{c}+k_2 V_{m}(t)} \sin (\omega_{c} t+\phi)$ $\newline$
(d) $A_{c} V_{m}(t) \sin (\omega_{c} t+\phi)$ $\newline$
उत्तर दिखाएं
सोचने की प्रक्रिया
एक असंगत चरण कोण के परिवर्तन को $\phi$ द्वारा दर्शाया जाता है।
उत्तर
(c) एक वृत्तीय विस्पति संकेत को निम्नलिखित द्वारा प्रस्तुत किया जाता है:
$$ m(t)=A_{m} \sin \omega_{m} t $$
जहाँ, $A_{m}=$ विस्पति संकेत के आयाम $\omega_{m}=$ कोणीय आवृत्ति $=2 \pi V_{m}=\phi V_{m}$
इसके अतिरिक्त, एक वृत्तीय वाहक तरंग को निम्नलिखित द्वारा प्रस्तुत किया जाता है $C(t)=A_{c} \sin \omega_{c} t$
इसलिए, संकेतित तरंग को निम्नलिखित द्वारा दिया जाता है:
यहाँ,
$$ \begin{aligned} C_{m}(t) & =(A_{c}+A_{m} \sin \omega_{m} t) \sin \omega_{c} t \\ & =A_{c}[1+\frac{A_{m}}{A_{c}} \sin \omega_{m} t) \sin \omega_{c} t \end{aligned} $$
$\Rightarrow$
$$ \frac{A_{m}}{A_{c}}=M $$
$\Rightarrow \quad C_{m}(t)=(A_{c}+A_{c} \times \mu \sin \omega_{m} t) \sin \omega_{c} t$
अब, हम जानते हैं कि $A_{c} \times \mu=K$ [तरंग नियतांक] और $\sin \omega_{m} t=V_{m}$ [तरंग वेग]
इसलिए, समीकरण (iii) निम्नलिखित रूप में बन जाता है:
$$ C_{m}(t)=(A_{c}+K \times V_{m}) \sin \omega_{c} t $$
अब, चरण कोण में एक परिवर्तन $\phi$ के बाद $\sin \omega_{c} t$ के स्थान पर $\sin (\omega_{c} t+\phi)$ आ जाता है
इसलिए,
$$ C_{m}(t)=(A_{c}+K V_{m})(\sin \omega_{c}+\phi) $$
-
विकल्प (a): व्यंजक $ A_{c} \sin [{\omega_{c}+k_1 V_{m}(t)} t+\phi] $ एक आवृत्ति-संकेतित तरंग को निरूपित करता है न कि आयाम-संकेतित तरंग। आयाम-संकेतित तरंग में वाहक आवृत्ति $\omega_{c}$ स्थिर रहती है, और यह आयाम विस्पति संकेत $V_{m}(t)$ के साथ बदलता है।
-
विकल्प (b): व्यंजक $ A_{c} \sin {\omega_{c} t+\phi+k_2 V_{m}(t)} $ एक चरण-संकेतित तरंग को निरूपित करता है न कि आयाम-संकेतित तरंग। आयाम-संकेतित तरंग में चरण $\phi$ स्थिर रहता है, और यह आयाम विस्पति संकेत $V_{m}(t)$ के साथ बदलता है।
-
विकल्प (d): व्यंजक $ A_{c} V_{m}(t) \sin (\omega_{c} t+\phi) $ गलत रूप से यह सुझाव देता है कि वाहक तरंग के आयाम को विस्पति संकेत $V_{m}(t)$ के साथ गुणा किया जाता है। आयाम-संकेतित तरंग में सही रूप वाहक आयाम में विस्पति संकेत को जोड़ना होता है, न कि गुणा करना।
बहुविकल्पीय प्रश्न (एक से अधिक विकल्प)
10. 15 किलोहर्ट्ज आवृत्ति के एक ऑडियो सिग्नल को लंबी दूरी तक अनुपातित किए बिना प्रसारित नहीं किया जा सकता, क्योंकि
(a) आवश्यक एंटीना के आकार कम से कम 5 किमी होगा जो असुविधाजनक है
(b) ऑडियो सिग्नल को आकाश तरंगों के माध्यम से प्रसारित नहीं किया जा सकता
(c) आवश्यक एंटीना के आकार कम से कम 20 किमी होगा जो असुविधाजनक है
(d) यदि एंटीना का आकार 5 किमी से कम हो, तो प्रसारित क्षमता बहुत कम होगी
उत्तर दिखाएं
सोचने की प्रक्रिया
एक सिग्नल के प्रसारित होने पर तीन कारकों पर निर्भर करता है। ये एंटीना के आकार, प्रसारित किए जाने वाले माध्यम और प्रसारित तरंग की क्षमता है।
उत्तर
$(a, b, d)$
दिया गया, प्रसारित किए जाने वाले तरंग की आवृत्ति है
$$ \begin{aligned} v_{m} & =15 kHz=15 \times 10^{3} Hz \\ \text { तरंगदैर्घ्य } \lambda_{m} & =\frac{c}{v_{m}}=\frac{3 \times 10^{8}}{15 \times 10^{3}}=\frac{1}{5} \times 10^{5} m \end{aligned} $$
आवश्यक एंटीना के आकार, $\quad l=\frac{\lambda}{4}=\frac{1}{4} \times \frac{1}{5} \times 10^{5}$
$$ =5 \times 10^{3} m=5 km $$
ऑडियो सिग्नल कम आवृत्ति के तरंग होते हैं। इसलिए, वे आकाश तरंगों के माध्यम से प्रसारित नहीं किए जा सकते क्योंकि वे वातावरण द्वारा अवशोषित हो जाते हैं।
यदि एंटीना का आकार 5 किमी से कम हो, तो प्रसारित क्षमता बहुत कम होगी क्योंकि तरंग के अनुनाद तरंगदैर्घ्य और एंटीना के आकार से विचलन होता है।
- विकल्प (c) गलत है क्योंकि 15 किलोहर्ट्ज आवृत्ति के सिग्नल के लिए आवश्यक एंटीना का आकार 5 किमी होता है, न कि 20 किमी।
11. 3 किलोहर्ट्ज आवृत्ति के ऑडियो साइन तरंगों का उपयोग एक 1.5 MHz वाले कैरियर सिग्नल के आयाम वर्णक्रम के लिए किया जाता है। निम्नलिखित में से कौन से कथन सत्य हैं?
(a) ओर आवृत्ति 1506 किलोहर्ट्ज और 1494 किलोहर्ट्ज हैं
(b) आयाम वर्णक्रम के लिए आवश्यक बैंडविड्थ 6 किलोहर्ट्ज है
(c) आयाम वर्णक्रम के लिए आवश्यक बैंडविड्थ 3 MHz है
(d) ओर आवृत्ति 1503 किलोहर्ट्ज और 1497 किलोहर्ट्ज हैं
उत्तर दिखाएं
सोच-समझ
यहाँ, इस प्रश्न में आप्शन एम्प्लीट्यूड मॉड्यूलेशन के साइड बैंड आवृत्ति और बैंडविड्थ के मान देते हैं। इसलिए, सबसे पहले इन मानों की गणना करें।
उत्तर
$(b, d)$
दिया गया,
$$ \begin{aligned} \omega_{m} & =3 \text{kHz} \\ \omega_{c} & =1.5 \text{MHz}=1500 \text{kHz} \end{aligned} $$
अब, साइड बैंड आवृत्तियाँ
$$ \begin{aligned} \omega_{c} \pm \omega_{m} & =(1500 \pm 3) \\ & =1503 \text{kHz} \text{ और } 1497 \text{kHz} \end{aligned} $$
साथ ही, बैंडविड्थ $=2 \omega_{m}=2 \times 3=6 \text{kHz}$
-
आप्शन (a) गलत है क्योंकि साइड बैंड आवृत्तियाँ $\omega_{c} \pm \omega_{m} = 1500 \pm 3 = 1503 \text{kHz}$ और $1497 \text{kHz}$ होती हैं, न कि $1506 \text{kHz}$ और $1494 \text{kHz}$।
-
आप्शन (c) गलत है क्योंकि एम्प्लीट्यूड मॉड्यूलेशन के लिए आवश्यक बैंडविड्थ $2 \omega_{m} = 2 \times 3 \text{kHz} = 6 \text{kHz}$ होती है, न कि $3 \text{MHz}$।
12. एक टीवी प्रसारण टॉवर की ऊंचाई $240 \text{m}$ है। इस टॉवर से प्रसारित संकेत एलओएस (लाइन ऑफ़ साइट) संचार के माध्यम से किस दूरी तक प्राप्त होंगे? (पृथ्वी की त्रिज्या $6.4 \times 10^{6} \text{m}$ मान लें)
(a) $100 \text{km}$
(b) $24 \text{km}$
(c) $55 \text{km}$
(d) $50 \text{km}$
उत्तर दिखाएं
सोच-समझ
$$ \text { रेंज } d_{T}=\sqrt{2 R h_{T}} $$
उत्तर
$(b, c, d)$
दिया गया, $\quad$ टॉवर की ऊंचाई $h=240 \text{m}$
एलओएस (लाइन ऑफ़ साइट) संचार के लिए।
प्रसारक से एक संकेत के अधिकतम दूरी जिस तक यह संकेत प्राप्त हो सकता है, निम्नलिखित द्वारा दी गई है
$$ d=\sqrt{2 R h} $$
यहाँ $R$ पृथ्वी की त्रिज्या है, अर्थात $R=6.4 \times 10^{6} \text{m}$
समीकरण (i) में सभी मान रखने पर, हम प्राप्त करते हैं
$$ \begin{aligned} d & =\sqrt{2 R h}=\sqrt{2 \times 6.4 \times 10^{6} \times 240} \\ & =55.4 \times 10^{3} \text{m}=55.4 \text{km} \end{aligned} $$
इसलिए, $55.4 \text{km}$ की रेंज $24 \text{km}, 55 \text{km}$ और $50 \text{km}$ की दूरी ढकती है।
-
आप्शन (a) $100 \text{km}$: यह आप्शन गलत है क्योंकि टॉवर से एलओएस संचार के अधिकतम दूरी की गणना $55.4 \text{km}$ है। $100 \text{km}$ की दूरी इस अधिकतम रेंज से अधिक है, जिसके कारण इस दूरी पर संकेत प्राप्त नहीं हो सकता।
-
विकल्प (b) $24 किमी$: यह विकल्प सही है क्योंकि $24 किमी$ 55.4 किमी के गणनाएँ किए गए अधिकतम दूरी के भीतर है।
-
विकल्प (c) $55 किमी$: यह विकल्प सही है क्योंकि $55 किमी$ 55.4 किमी के गणनाएँ किए गए अधिकतम दूरी के भीतर है।
-
विकल्प (d) $50 किमी$: यह विकल्प सही है क्योंकि $50 किमी$ 55.4 किमी के गणनाएँ किए गए अधिकतम दूरी के भीतर है।
13. फ़िल्टर परिपथ के आवृत्ति प्रतिक्रिया वक्र (चित्र) के लिए एम तरंग के उत्पादन के लिए निम्नलिखित में से कौन सा सही है?
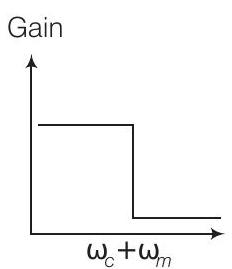
(i)
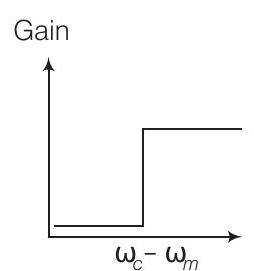
(ii)
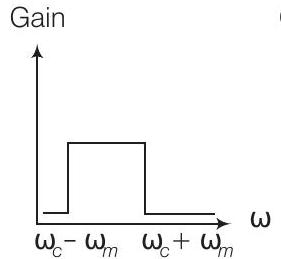
(iii)
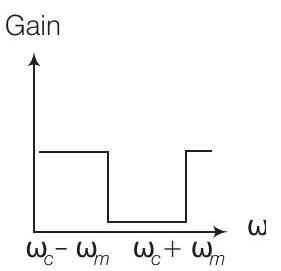
(iv)
(a) (i) के बाद (ii)
(b) (ii) के बाद (i)
(c) (iii)
(d) (iv)
उत्तर दिखाएँ
उत्तर
$(a, b, c)$
यहाँ, आयाम विस्तारित तरंग के उत्पादन के लिए बैंडविड्थ निम्नलिखित द्वारा दिया गया है = ऊपरी ओर बैंड आवृत्ति - निचली ओर बैंड आवृत्ति
$$ =\omega_{USB}-\omega_{LSB}=(\omega_{c}+\omega_{m})-(\omega_{c}-\omega_{m}) $$
-
विकल्प (b) (ii) के बाद (i):
- यह विकल्प बताता है कि आवृत्ति प्रतिक्रिया वक्र पहले (ii) के पैटर्न का अनुसरण करे और फिर (i) का अनुसरण करे। हालाँकि, एम तरंग के उत्पादन के लिए फ़िल्टर को ऊपरी ओर बैंड और निचली ओर बैंड के आवृत्तियों को पास करना चाहिए और अन्य आवृत्तियों को अस्वीकृत करना चाहिए। (ii) के बाद (i) का क्रम इस आवश्यकता के साथ मेल नहीं खाता है क्योंकि यह आवश्यक आवृत्तियों को सही तरीके से फ़िल्टर नहीं करेगा।
-
विकल्प (c) (iii):
- यह विकल्प बताता है कि आवृत्ति प्रतिक्रिया वक्र (iii) के पैटर्न का अनुसरण करना चाहिए। (iii) में वक्र सही एम तरंग के उत्पादन के लिए आवश्यक बैंडपास फ़िल्टर को प्रतिनिधित्व नहीं करता है। यह ऊपरी और नीचली ओर बैंड को सही तरीके से पास नहीं करता है जबकि अन्य आवृत्तियों को अस्वीकृत करता है।
-
विकल्प (d) (iv):
- यह विकल्प बताता है कि आवृत्ति प्रतिक्रिया वक्र (iv) के पैटर्न का अनुसरण करना चाहिए। (iv) में वक्र एम तरंग के उत्पादन के लिए आवश्यक बैंडपास फ़िल्टर विशेषताओं के साथ मेल नहीं खाता है। यह ऊपरी और नीचली ओर बैंड के लिए आवश्यक आवृत्तियों को सही तरीके से फ़िल्टर नहीं करता है।
14. आयाम वर्णन में, वर्णन सूचकांक $m$, को 1 से कम या बराबर रखा जाता है क्योंकि
(a) $m>1$, कार्यकर्ता आवृत्ति और संदेश आवृत्ति के बीच अवरोधन के कारण विकृति होती है
(b) $m>1$, दोनों ओर बैंड के ओवरलैप के कारण सूचना की हानि होती है
(c) $m>1$, कार्यकर्ता संकेत और संदेश संकेत के बीच अवस्थांतर के कारण होता है
(d) $m>1$, संदेश संकेत के आयाम के आयाम के कारण विकृति होती है
उत्तर दिखाएं
उत्तर
$(b, d)$
आयाम वर्णन तरंग के वर्णन सूचकांक $(m)$ है
$$ m=\frac{\text { संदेश संकेत के आयाम }(A_{m})}{\text { कार्यकर्ता संकेत के आयाम }(A_{c})} $$
यदि $m>1$, तो $A_{m}>A_{c}$ होता है।
इस स्थिति में, आयाम वर्णन तरंग के परिणामी संकेत की विकृति होती है। अधिकतम वर्णन आवृत्ति $(m_{f})$ एम तरंग के लिए है
$$ \begin{aligned} m_{f} & =\frac{\Delta v_{\max }}{v_{m}(\max )} \\ & =\frac{\text { आवृत्ति विकृति }}{\text { संदेश तरंग की अधिकतम आवृत्ति मान }} \end{aligned} $$
यदि $m_{f}>1$, तो $\Delta v_{\max }>v_{m}$. इसका अर्थ है कि वर्णन तरंग के दोनों ओर बैंड के ओवरलैप होता है जिसके कारण सूचना की हानि होती है।
-
विकल्प (a) गलत है क्योंकि कार्यकर्ता आवृत्ति और संदेश आवृत्ति के बीच अवरोधन वर्णन सूचकांक $m \leq 1$ रखे रहने का मुख्य कारण नहीं है। $m > 1$ के मुख्य समस्या विकृति और ओर बैंड के ओवरलैप है, न कि कार्यकर्ता और संदेश आवृत्तियों के बीच अवरोधन।
-
विकल्प (c) गलत है क्योंकि वाहक संकेत और संदेश संकेत के बीच एक चरण परिवर्तन एक अप्रत्यक्ष परिणाम नहीं होता है जब मॉड्यूलेशन सूचकांक $m > 1$ होता है। $m > 1$ के मुख्य चिंता बाहरी बैंड के विकृति और ओवरलैप होते हैं, न कि चरण परिवर्तन।
बहुत छोटे उत्तर प्रकार प्रश्न
15. निम्नलिखित में से कौन-कौन एनालॉग संकेत उत्पन्न करेंगे और कौन-कौन डिजिटल संकेत उत्पन्न करेंगे?
(a) एक झंगता वाला स्वरचालित ट्यूनिंग फोर्क
(b) एक झंगता वाले सितार के तार के कारण संगीत संकेत
(c) प्रकाश तरंग
(d) एनडीएन गेट के आउटपुट
उत्तर दिखाएं
उत्तर
एनालॉग और डिजिटल संकेत जानकारी के संचार के लिए उपयोग किए जाते हैं, आमतौर पर विद्युत संकेत के माध्यम से। इन दोनों तकनीकों में, जानकारी जैसे कोई ऑडियो या वीडियो विद्युत संकेत में परिवर्तित कर दिया जाता है।
एनालॉग और डिजिटल तकनीकों के बीच अंतर यह है कि एनालॉग तकनीक में जानकारी को विभिन्न आयाम वाले विद्युत तरंगों में परिवर्तित कर दिया जाता है। डिजिटल तकन के तहत जानकारी को बाइनरी रूप में (शून्य या एक) परिवर्तित कर दिया जाता है, जहां प्रत्येक बिट दो अलग-अलग आयामों का प्रतिनिधित्व करता है।
इसलिए, (a) और (b) एनालॉग संकेत उत्पन्न करेंगे और (c) और (d) डिजिटल संकेत उत्पन्न करेंगे।
16. 60 MHz आवृत्ति के टीवी संकेत के संचार के लिए स्काई तरंगों के उपयोग के लिए क्या उपयुक्त होंगी?
उत्तर दिखाएं
उत्तर
एक संकेत के संचार के लिए जो स्काई तरंगों के माध्यम से भेजा जाए, इसकी आवृत्ति सीमा 1710 केजीएचजी से 40 मेगाहर्ट्ज तक होती है।
लेकिन, यहां टीवी संकेत की आवृत्ति 60 मेगाहर्ट्ज है जो आवश्यक सीमा के बाहर है।
इसलिए, 60 मेगाहर्ट्ज आवृत्ति के टीवी संकेत के संचार के लिए स्काई तरंगों के उपयोग उपयुक्त नहीं होंगी।
17. दो तरंग A और B जिनकी आवृत्ति क्रमशः 2 MHz और 3 MHz है, एक ही दिशा में भेजी जाती हैं ताकि आकाशीय तरंग के माध्यम से संचार हो सके। इनमें से कौन आयनमंडल में अपने अंतर्निहित परावर्तन के लिए लंबी दूरी तक यात्रा करेगा?
उत्तर दिखाएं
उत्तर
क्योंकि तरंग B की आवृत्ति तरंग A की आवृत्ति से अधिक है, इसका अर्थ है कि तरंग B का अपवर्तनांक तरंग A के अपवर्तनांक से अधिक होगा (क्योंकि अपवर्तनांक आवृत्ति के बढ़ने के साथ बढ़ता है)।
उच्च आवृत्ति के तरंग (अर्थात उच्च अपवर्तनांक) के लिए अपवर्तन कोण कम होता है, अर्थात विक्षेपण कम होता है। इसलिए, तरंग $B$ आयनमंडल में कुछ अधिक दूरी तक यात्रा करती है जब तक कि आंतरिक पूर्ण परावर्तन के अधीन नहीं हो जाती।
18. एक $AM$ तरंग के अधिकतम आयाम को $15 V$ पाया गया है जबकि इसके न्यूनतम आयाम को $3 V$ पाया गया है। प्रसार सूचकांक क्या है?
उत्तर दिखाएं
उत्तर
मान लीजिए $A_{c}$ और $A_{m}$ क्रमशः वाहक तरंग और प्रसारित तरंग के आयाम हैं। इसलिए,
$$ \text { अधिकतम आयाम } A_{\max }=A_{c}+A_{m}=15 V $$
$$ \text { न्यूनतम आयाम } A_{\min }=A_{c}-A_{m}=3 V $$
समीकरण (i) और (ii) को जोड़ने पर हमें प्राप्त होता है
$$ \begin{aligned} 2 A_{c} & =18 \\ A_{c} & =9 V \end{aligned} $$
$$ \begin{aligned} A_{m} =15-9=6 V \\ \text { तरंग के प्रसार सूचकांक } \mu & =\frac{A_{m}}{A_{c}}=\frac{6}{9}=\frac{2}{3} \end{aligned} $$
छोटे उत्तर प्रकार के प्रश्न
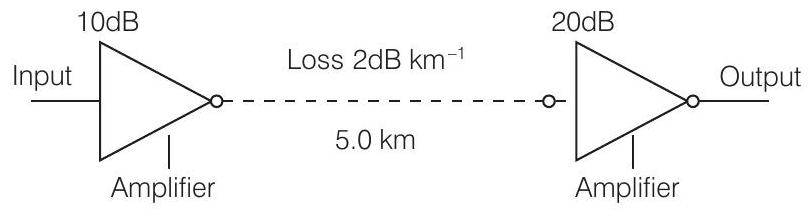
21. चित्र एक संचार प्रणाली को दर्शाता है। जब इनपुट सिग्नल $1.01 \text{ mW}$ होता है तो आउटपुट शक्ति कितनी होती है? [गैन $dB=10 \log _{10}(P _0 / P _{i})$ ]
उत्तर दिखाएं
उत्तर
सिग्नल की यात्रा की दूरी $5 \text{ km}$ है। संचार पथ में हुई हानि $=2 \text{ dB}/\text{km}$
इसलिए, $5 \text{ km}$ में कुल हुई हानि $=-2 \times 5=-10 \text{ dB}$
कुल एम्पलीफायर गैन $=10 \text{ dB}+20 \text{ dB}=30 \text{ dB}$
संकेंद्रित गैन $=30-10=20 \text{ dB}$
प्रश्न के अनुसार, गैन $dB=10 \log _{10} \frac{P_0}{P_j}$
$$
\therefore 20 =10 \log_{10} \frac{P_0}{P_i}
$$
$$
\text {या} \log _{10} \frac{P_0}{P_i}=2
$$
यहाँ, $P_{i}=1.01 \text{ mW}$ और $P_0$ आउटपुट शक्ति है।
$$ \begin{matrix} \therefore & \frac{P_0}{P_{i}}=10^{2}=100 \\ \Rightarrow & P_0=P_{i} \times 100=1.01 \times 100 \\ \text { या } & P_0=101 \text{ mW} \\ \text { इसलिए, आउटपुट शक्ति } 101 \text{ mW} \text{ है }. \end{matrix} $$
22. एक टीवी संचार टॉवर एंटीना की ऊंचाई $20 \text{ m}$ है। यदि प्राप्त करने वाली एंटीना (i) जमीन स्तर पर है, (ii) $25 \text{ m}$ की ऊंचाई पर है, तो इसके द्वारा कवर किया गया सेवा क्षेत्र कितना होगा? मामला (ii) में मामला (i) के तुलना में कवर किए गए क्षेत्र में प्रतिशत वृद्धि की गणना करें।
उत्तर दिखाएं
उत्तर
दिया गया, एंटीना की ऊंचाई $h=20 \text{ m}$
पृथ्वी की त्रिज्या $=6.4 \times 10^{6} \text{ m}$
जमीन स्तर पर,
(i) परिसीमा $=\sqrt{2 h R}=\sqrt{2 \times 20 \times 6.4 \times 10^{6}}$
$$ \begin{aligned} & =16000 \text{ m}=16 \text{ km} \\ \text { कवर किया गया क्षेत्र } A & =\pi(\text { परिसीमा })^{2} \\ & =3.14 \times 16 \times 16=803.84 \text{ km}^{2} \end{aligned} $$
(ii) जमीन स्तर से $H=25 \text{ m}$ की ऊंचाई पर
$$ \begin{aligned} \text { परिसीमा } & =\sqrt{2 h R}+\sqrt{2 H R} \\ & =\sqrt{2 \times 20 \times 6.4 \times 10^{6}}+\sqrt{2 \times 25 \times 6.4 \times 10^{6}} \\
& =16 \times 10^{3}+17.9 \times 10^{3} \\ & =33.9 \times 10^{3} m \\ & =33.9 km \end{aligned} $$
$$ \begin{aligned} \text { क्षेत्रफल ढका } & =\pi(\text { परिसर })^{2} \\ & =3.14 \times 33.9 \times 33.9 \\ & =3608.52 km^{2} \\ \text { क्षेत्रफल में प्रतिशत वृद्धि } & =\frac{\text { क्षेत्रफल में अंतर }}{\text { प्रारंभिक क्षेत्रफल }} \times 100 \\ & =\frac{(3608.52-803.84)}{803.84} \times 100 \\ & =348.9 % \end{aligned} $$
इसलिए, क्षेत्रफल में प्रतिशत वृद्धि $348.9 %$ है
23. यदि पूरी धरती को एक लाइन ऑफ़ साइट (LOS) संचार के माध्यम से जोड़ा जाना है और एंटीना के आकार या टॉवर की ऊंचाई के बारे में कोई बाधा नहीं है, तो आवश्यक न्यूनतम एंटीना की संख्या क्या होगी? इन एंटीना के टॉवर की ऊंचाई को पृथ्वी की त्रिज्या के रूप में गणना करें।
$$ \begin{gathered} K \text { सोचने की प्रक्रिया } \\ \text { परिसर } d_{T}=\sqrt{2 R h t} \end{gathered} $$
उत्तर दिखाएं
उत्तर
इस प्रश्न को हल करने के लिए नीचे दिए गए चित्र को ध्यान में रखें
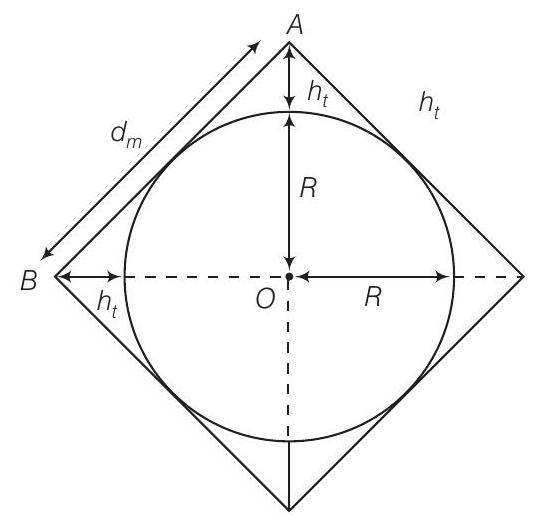
मान लीजिए ट्रांसमिटिंग एंटीना या रिसीविंग एंटीना की ऊंचाई जो पृथ्वी के पूरे सतह को संचार के माध्यम से ढके रहे हो वह $h_{t}$ है और पृथ्वी की त्रिज्या $R$ है
तब, अधिकतम दूरी
$$ \begin{matrix} d_m^{2} =(R+h_{t})^{2}+(R+h_{t})^{2} \newline =2(R+h_{t})^{2} \newline \therefore d_{m} =\sqrt{2 h_{t} R}+\sqrt{2 h_{t} R}=2 \sqrt{2 h_{t} R} \newline \Rightarrow 8 h_{t} R =2(R+h_{t})^{2} \newline \Rightarrow 4 h_{t} R =R^{2}+2 R h_{t}+h_t^{2} \newline \Rightarrow R^{2}-2 h_{t} R+h_t^{2} =0 \newline \Rightarrow (R-h_{t})^{2} =0 \newline \Rightarrow R =h_{t} \end{matrix} $$
क्योंकि, स्पेस वेव आवृत्ति का उपयोग किया जाता है इसलिए $\lambda«h_{t}$, इसलिए केवल टॉवर की ऊंचाई को ध्यान में रखा जाएगा। पृथ्वी के तीन आयामों में, पूरी धरती के सतह को संचार कार्यक्रम के माध्यम से ढकने के लिए ऊंचाई $h_{t}=R$ के प्रत्येक टॉवर के साथ 6 एंटीना टॉवर का उपयोग किया जाएगा।
24. किसी आयनमंडल के एक विशिष्ट स्तर से आकाश तरंगों के परावर्तन की अधिकतम आवृत्ति $f_{\max }=9(N_{\max })^{1 / 2}$ होती है, जहाँ $N_{\max }$ आयनमंडल के उस स्तर पर अधिकतम इलेक्ट्रॉन घनत्व है।
एक निश्चित दिन यह देखा गया है कि $5 MHz$ से अधिक आवृत्ति के संकेत $F_1$ आयनमंडल स्तर से परावर्तन के माध्यम से प्राप्त नहीं होते हैं जबकि $8 MHz$ से अधिक आवृत्ति के संकेत $F_2$ आयनमंडल स्तर से परावर्तन के माध्यम से प्राप्त नहीं होते हैं। उस दिन $F_1$ और $F_2$ आयनमंडल स्तर के अधिकतम इलेक्ट्रॉन घनत्व का अनुमान लगाएं।
उत्तर दिखाएँ
Answer
आकाश तरंगों के परावर्तन की अधिकतम आवृत्ति
$$ f_{\max }=9(N_{\max })^{1 / 2} $$
जहाँ, $N_{\text {max }}$ अधिकतम इलेक्ट्रॉन घनत्व है।
$\text { For } F_1 \text { layer, }$
$$ \begin{aligned} f_{\max } & =5 MHz \\ 5 \times 10^{6} & =9(N_{\max })^{1 / 2} \end{aligned} $$
अधिकतम इलेक्ट्रॉन घनत्व
$$ \begin{aligned} & N_{\max }=\left(\frac{5}{9} \times 10^{6}{ }\right)^{2}=3.086 \times 10^{11} / m^{3} \\ & f_{\max }=8 MHz \\ & 8 \times 10^{6}=9(N_{\max })^{1 / 2} \end{aligned} $$
अधिकतम इलेक्ट्रॉन घनत्व
$$ N_{\max }=\left(\frac{8 \times 10^{6}}{9}\right)^{2}=7.9 \times 10^{11} / m^{3} $$
25. विकिरण (अतिक्रमण) और $A M$ आवृत्ति नियोजित संकेत के लिए, कुल विकिरण शक्ति $\omega_{c}, \omega_{c}-\omega_{m}$ और $\omega_{c}+\omega_{m}$ द्वारा ले जाए गए ऊर्जा के कारण होती है। जानकारी के बिना लागत कम करने के तरीके सुझाएं।
उत्तर दिखाएँ
Answer
अम्प्लीतुड नियोजित संकेत में केवल ओर बैंड आवृत्ति जानकारी को धारण करती है। इसलिए केवल $(\omega_{c}+\omega_{m})$ और $(\omega_{c}-\omega_{m})$ जानकारी को धारण करती है।
अब, प्रश्न के अनुसार, कुल विकिरण शक्ति $\omega_{c},(\omega_{c}-\omega_{m})$ और $(\omega_{c}+\omega_{m})$ द्वारा ले जाए गए ऊर्जा के कारण होती है।
इसलिए जानकारी के बिना लागत कम करने के लिए $\omega_{c}$ को छोड़कर विकिरण कर सकते हैं। $(\omega_{c}+\omega_{m}),(\omega_{c}-\omega_{m})$ या दोनों $(\omega_{c}+\omega_{m})$ और $(\omega_{c}-\omega_{m})$।
लंबा उत्तर प्रकार प्रश्न
26. एक प्रकाश तरंग की तीव्रता एक संचार चैनल के माध्यम से चलते हुए दूरी $x$ के साथ अपसरण के अनुसार $I=I_0 e^{-\alpha x}$ के संबंध में आ экспोनेंशियल रूप से कम होती है, जहाँ $I_0$ $x=0$ पर तीव्रता है और $\alpha$ अपसरण नियतांक है।
(a) दिखाइए कि दूरी $\frac{\ln 4}{\alpha}$ के बाद तीव्रता 75% घट जाती है।
(b) एक संकेत के अपसरण को डेसीबेल (dB) में व्यक्त किया जा सकता है, जो $dB=10 \log _{10} \frac{I}{I_0}$ के संबंध द्वारा दिया गया है। एक प्रकाश तंतु में जहाँ तीव्रता 50 किमी की दूरी पर 50% घट जाती है, तो अपसरण $dB / km$ में कितना होगा?
उत्तर दिखाएँ
उत्तर
(a) दिया गया है, प्रकाश तरंग की तीव्रता $I=I_0 e^{-\alpha x}$
जहाँ, $I_0$ $x=0$ पर तीव्रता है और $\alpha$ नियतांक है।
प्रश्न के अनुसार, $I=25 %$ के $I_0=\frac{25}{100} \cdot I_0=\frac{I_0}{4}$
प्रश्न में उल्लेखित सूत्र का उपयोग करते हुए,
या
$$ \begin{aligned} I & =I_0 e^{-\alpha x} \\ \frac{I_0}{4} & =I_0 e^{-\alpha x} \\ \frac{1}{4} & =e^{-\alpha x} \end{aligned} $$
दोनों ओर लघुगणक लेने पर, हम प्राप्त करते हैं
$$ \begin{aligned} \ln 1-\ln 4 & =-\alpha x \ln e \quad(\because \ln e=1) \\ -\ln 4 & =-\alpha x \\ x & =\frac{\ln 4}{\alpha} \end{aligned} $$
इसलिए, दूरी $x=\frac{\ln 4}{\alpha}$ पर, तीव्रता प्रारंभिक तीव्रता के 75% घट जाती है।
(b) मान लीजिए $\alpha$ डेसीबेल (dB) में अपसरण है। यदि $x$ संकेत की तय की गई दूरी है, तो
$$ 10 \log _{10} \frac{I}{I_0}=-\alpha x $$
जहाँ, $I_0$ प्रारंभिक तीव्रता है।
प्रश्न के अनुसार, $I=50 %$ के $I_0=\frac{I_0}{2}$ और $x=50$ किमी
समीकरण (i) में $x$ के मान को रखने पर, हम प्राप्त करते हैं
$$ \begin{aligned} 10 \log _{10} \frac{I_0}{2 I_0} & =-\alpha \times 50 \\ 10[\log 1-\log 2] & =-50 \alpha \\ \frac{10 \times 0.3010}{50} & =\alpha \end{aligned} $$
$\therefore$ प्रकाश तंतु के लिए अपसरण
$$ \alpha=0.0602 dB / km $$
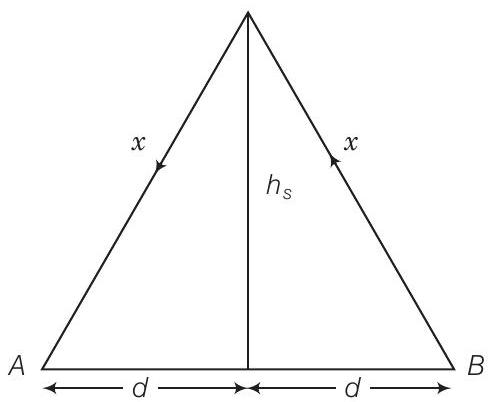
27. 50 MHz आकाश तरंग एक उपग्रह के माध्यम से प्राप्त करने वाले प्राप्तक के लिए 4.04 ms के लिए चलती है, जो पृथ्वी की सतह से 600 किमी ऊपर है। उपग्रह द्वारा पुन: प्रसारण के समय को नगण्य मानते हुए, स्रोत और प्राप्तक के बीच की दूरी ज्ञात कीजिए। यदि दोनों के बीच संचार लाइन ऑफ़ साइट (LOS) विधि के माध्यम से किया जाए, तो प्राप्तक और प्रसारक एंटीना के आकार और स्थान कैसा होना चाहिए?
उत्तर दिखाएं
उत्तर
मान लीजिए प्राप्तक के बिंदु $A$ पर है और स्रोत $B$ पर है।
तरंगों की गति $=3 \times 10^{8} m / s$
एक प्राप्तक तक पहुंचने का समय $=4.04 ms=4.04 \times 10^{-3} s$
मान लीजिए उपग्रह की ऊंचाई है
$h_{s}=600 km$
पृथ्वी की त्रिज्या $=6400 km$
रेडियो ट्रांसमिटर एंटीना के आकार $=h_{T}$
हम जानते हैं कि $\frac{\text { तरंग द्वारा तय की गई दूरी }}{\text { समय }}=$ तरंगों की गति
$$ \begin{aligned} \frac{2 x}{4.04 \times 10^{-3}} & =3 \times 10^{8} \\ x & =\frac{3 \times 10^{8} \times 4.04 \times 10^{-3}}{2} \\ & =6.06 \times 10^{5}=606 km \end{aligned} $$
या
पाइथागोरस प्रमेय का उपयोग करते हुए,
या
$$ d^{2}=x^{2}-h_s^{2}=(606)^{2}-(600)^{2}=7236 $$
इसलिए, स्रोत और प्राप्तक के बीच दूरी $=2 d$
$$ =2 \times 85.06=170 km $$
प्रसारित एम तरंगों द्वारा भू-पृष्ठ पर अधिकतम दूरी
$$ \text { या } $$
$$ d=\sqrt{2 R h_{T}} $$
$$ \frac{d^{2}}{2 R}=h_{T} $$
या
$$ \text { एंटीना के आकार } h_{T}=\frac{7236}{2 \times 6400} $$
$$ =0.565 km=565 m $$
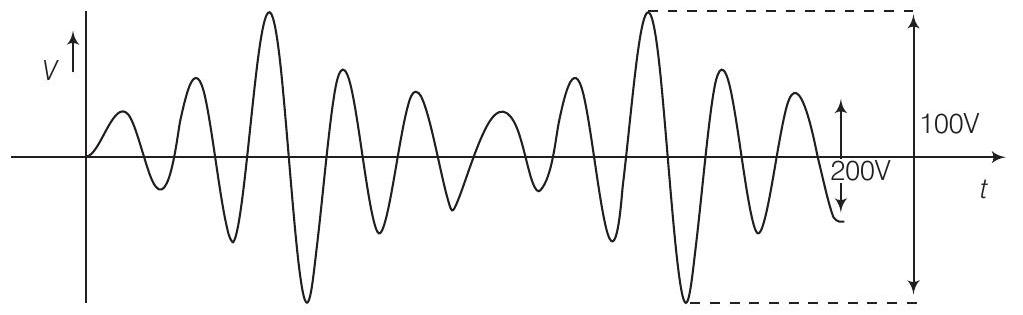
28. एक आयाम वर्णक तरंग चित्र में दिखाई गई है। गणना करें
(i) प्रतिशत आयाम वर्णक,
(ii) शिखर कार्लर वोल्टेज और
(iii) जानकारी वोल्टेज का शिखर मान
उत्तर दिखाएं
उत्तर
चित्र से,
$$ \begin{aligned} & \text { अधिकतम वोल्टेज } V_{\max }=\frac{100}{2}=50 V \\ & \text { न्यूनतम वोल्टेज } V_{\min }=\frac{20}{2}=10 V \end{aligned} $$
(i) प्रतिशत आयाम वर्णक, $\mu=\frac{V_{\max }-V_{\min }}{V_{\max }+V_{\min }} \times 100=\frac{50-10}{50+10} \times 100$
$$ =\frac{40}{60} \times 100=66.67 % $$
(ii) शिखर कार्लर वोल्टेज, $\quad V_{c}=\frac{V_{\max }+V_{\min }}{2}=\frac{50+10}{2}=30 V$
(iii) जानकारी वोल्टेज का शिखर मान,
$$ V_{m}=\mu V_{c}=\frac{66.67}{100} \times 30=20 V $$
29. (i) एम्प्लीटूड वर्सस $\omega$ के ग्राफ को एम्प्लीटूड संचारित तरंग के लिए खींचें जिसकी कार्लर तरंग $(\omega_{c})$ दो संचारित संकेतों $\omega_1$ और $\omega_2$ $(\omega_2>\omega_1)$ को वहन कर रही है।
(ii) ग्राफ $\omega_{c}$ के संदर्भ में सममित है? विशेष रूप से $\omega<\omega_{c}$ क्षेत्र में ग्राफ के बारे में टिप्पणी करें।
(iii) अगर अधिक तरंगों को संचारित करना हो तो अपेक्षित समस्याओं की पूर्वानुमान लगाएं।
(iv) उपरोक्त समस्या के लिए समाधान सुझाएं। इस प्रक्रिया में आप बैंडविड्थ के अतिरिक्त एक लाभ के बारे में भी समझ सकते हैं?
उत्तर दिखाएँ
Answer
(i) एम्प्लीटूड वर्सस $\omega$ के ग्राफ को नीचे चित्र में दिखाया गया है
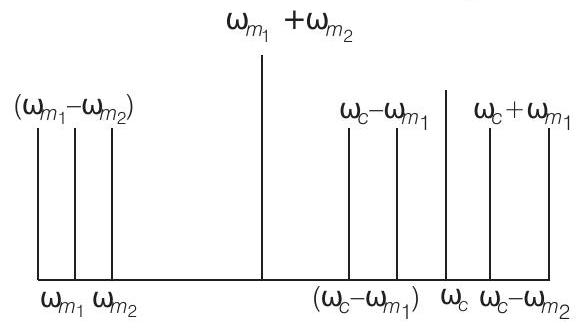
(ii) चित्र से हम यह नोट करते हैं कि आवृत्ति स्पेक्ट्रम $\omega_{c}$ के संदर्भ में असममित है। $\omega<\omega_{t}$ के क्षेत्र में स्पेक्ट्रम के घनीभूत होने के लक्षण उपलब्ध हैं।
(iii) अगर अधिक तरंगों को संचारित करना हो तो $\omega<\omega_{c}$ के क्षेत्र में संचारित संकेत के घनीभूत होने के अधिक अवसर होंगे। इसके परिणामस्वरूप संकेतों के मिश्रण के अधिक अवसर होंगे।
(iv) अधिक संकेतों के लिए बैंडविड्थ बढ़ाएं और आवृत्ति कार्लर तरंग $\omega_{t}$ बढ़ाएं। यह दिखाता है कि बड़ी कार्लर आवृत्ति अधिक जानकारी (अर्थात अधिक $\omega_{m}$) वहन करने में सक्षम होती है और इसके परिणामस्वरूप बैंडविड्थ भी बढ़ जाएगी।
30. एक ऑडियो संकेत को 20 MHz के कार्लर तरंग द्वारा संचारित किया जाता है जिसके लिए संचारण के लिए आवश्यक बैंडविड्थ 3 kHz है। क्या यह तरंग एक डाइऑड डिटेक्टर द्वारा डिमोडुलेट किया जा सकता है जिसके मान $R$ और $C$ के रूप में हैं
(i) $R=1 k \Omega, C=0.01 \mu F$।
(ii) $R=10 k \Omega, C=0.01 \mu F$.
(iii) $R=10 k \Omega, C=0.1 \mu F$.
उत्तर दिखाएँ
उत्तर
दिया गया, कैरियर तरंग आवृत्ति $f_{c}=20 MHz$
$$ =20 \times 10^{6} Hz $$
संचार के लिए आवश्यक बैंडविड्थ है
$$ \begin{aligned} & 2 f_{m}=3 kHz=3 \times 10^{3} Hz \\ \Rightarrow & f_{m}=\frac{3 \times 10^{3}}{2}=1.5 \times 10^{3} Hz \end{aligned} $$
एक डायोड द्वारा डेमोडुलेशन संभव होता है यदि शर्त $\frac{1}{f_{c}} \ll R C<\frac{1}{f_{m}}$ संतुष्ट हो
इसलिए,
$$ \begin{aligned} \frac{1}{f_{c}} & =\frac{1}{20 \times 10^{6}}=0.5 \times 10^{-7} \\ \frac{1}{f_{m}} & =\frac{1}{1.5 \times 10^{3}} Hz=0.6 \times 10^{-3} s \end{aligned} $$
अब, $R$ और $C$ के सभी विकल्पों के माध्यम से एक-एक करके गैन की गणना करते हैं, हम प्राप्त करते हैं
(i) $R C=1 k \Omega \times 0.01 \mu F=10^{3} \Omega \times(0.01 \times 10^{-6} F)=10^{-5} S$
यहाँ, शर्त $\frac{1}{f_{c}} \ll R C<\frac{1}{f_{m}}$ संतुष्ट है।
अतः इसका डेमोडुलेशन संभव है।
(ii) $R C=10 K \Omega \times 0.01 \mu F=10^{4} \Omega \times 10^{-8} F=10^{-4} S$
यहाँ शर्त $\frac{1}{f_{c}} \ll R C<\frac{1}{f_{m}}$ संतुष्ट है।
अतः इसका डेमोडुलेशन संभव है।
(iii) $R C=10 k \Omega \times 1 \mu \mu F=10^{4} \Omega \times 10^{-12} F=10^{-8} S$
यहाँ, शर्त $\frac{1}{f_{c}}>R C$, इसलिए इसका डेमोडुलेशन संभव नहीं है।
$P Q$ के बीच उत्पन्न ईएमएफ इसके गति या चुंबकीय flux के परिवर्तन के कारण होता है, जो लूप के घेरे के क्षेत्र के परिवर्तन के कारण होता है।
एन वें न्यूनतम के बनने के लिए स्क्रीन पर पथ अंतर $S_1$ और $S_2$ से आने वाली किरणों के बीच $(2 n-1) \frac{\lambda}{2}$ होना चाहिए।





