विभिन्न धारा
बहुविकल्पीय प्रश्न (MCQs)
1. यदि 50 हर्ट्ज एसी परिपथ में औसत धारा 5 एम्पियर है, तो जब धारा शून्य हो जाती है तब 1/300 सेकंड बाद धारा का मान होगा
(a) $5 \sqrt{2} \mathrm{~A}$
(b) $5 \sqrt{3 / 2} \mathrm{~A}$
(c) $5 / 6 \mathrm{~A}$
(d) $5 / \sqrt{2} \mathrm{~A}$
उत्तर दिखाएं
उत्तर
(b) दिया गया है,
$$ \begin{aligned} & v=50 \mathrm{~Hz}, I_{\mathrm{rms}}=5 \mathrm{~A} \\ & t=\frac{1}{300} \mathrm{~s} \end{aligned} $$
हमें $I(t)$ ज्ञात करना है
$$ \begin{aligned} I_{0} & =\text { शिखर मान }=\sqrt{2}, I_{\mathrm{rms}}=\sqrt{2} \times 5 \\ & =5 \sqrt{2} \mathrm{~A} \\ I & =I_{0} \sin \omega t=5 \sqrt{2} \sin 2 \pi v t=5 \sqrt{2} \sin 2 \pi \times 50 \times \frac{1}{300} \\ & =5 \sqrt{2} \sin \frac{\pi}{3}=5 \sqrt{2} \times \frac{\sqrt{3}}{2}=5 \sqrt{3 / 2} \mathrm{~A} \end{aligned} $$
-
विकल्प (a): $5 \sqrt{2} \mathrm{~A}$
- यह विकल्प गलत है क्योंकि यह धारा के शिखर मान को दर्शाता है, न कि $t = \frac{1}{300} \mathrm{~s}$ पर क्षणिक मान। शिखर मान $I_0 = 5 \sqrt{2} \mathrm{~A}$ है, लेकिन दिए गए समय पर क्षणिक मान अलग है।
-
विकल्प (c): $5 / 6 \mathrm{~A}$
- यह विकल्प गलत है क्योंकि यह $t = \frac{1}{300} \mathrm{~s}$ पर क्षणिक धारा के सही गणना को दर्शाता नहीं है। सही गणना में त्रिकोणमितीय फलन और कोणीय आवृत्ति का उपयोग किया जाता है, जो एक अलग मान देता है।
-
विकल्प (d): $5 / \sqrt{2} \mathrm{~A}$
- यह विकल्प गलत है क्योंकि यह धारा के औसत मान को दर्शाता है, न कि $t = \frac{1}{300} \mathrm{~s}$ पर क्षणिक मान। औसत मान $I_{\mathrm{rms}} = 5 \mathrm{~A}$ है, और इसे $\sqrt{2}$ से विभाजित करना दिए गए समय पर सही क्षणिक मान नहीं देता है।
2. एक विभव जनित्र के आंतरिक प्रतिरोध $R_{g}$ और आंतरिक प्रतिक्रिया $X_{g}$ है। इसे एक पासिव लोड के लिए ऊर्जा आपूर्ति के लिए उपयोग किया जाता है, जो एक प्रतिरोध $R_{g}$ और प्रतिक्रिया $X_{L}$ के संगठन से बना होता है। जनित्र से लोड तक अधिकतम शक्ति के आपूर्ति के लिए $X_{L}$ का मान किसके बराबर होता है
(a) शून्य (b) $X_{g}$ (c) $-X_{g}$ (d) $R_{g}$
उत्तर दिखाएँ
उत्तर
(c) जनरेटर से लोड तक अधिकतम शक्ति प्रसारित करने के लिए, कुल आंतरिक प्रतिघात को कुल बाहरी प्रतिघात के संयुग्मक के बराबर होना चाहिए।
इसलिए,
$$ \begin{aligned} X_{\text {int }} & ={ }^* X_{\text {ext }} \\ X_g & =\left(X_L\right)^*=-X_{L} \\ X_L & =-X_g \end{aligned} $$
-
विकल्प (a) शून्य: यदि $ X_L $ शून्य हो, तो लोड शुद्ध प्रतिरोधी होगा। इस अवस्था में AC परिपथ में अधिकतम शक्ति प्रसार के लिए आवश्यक शर्त लोड के प्रतिघात को जनरेटर के प्रतिघात के ऋणात्मक होना होता है, जो इस विकल्प के द्वारा संतुष्ट नहीं होता।
-
विकल्प (b) $ X_g $: यदि $ X_L $ के मान $ X_g $ के बराबर हो, तो प्रतिघात एक दूसरे के जोड़ बनेंगे और कुल प्रतिघात अधिक होगा। अधिकतम शक्ति प्रसार के लिए लोड के प्रतिघात को जनरेटर के प्रतिघात के ऋणात्मक होना आवश्यक होता है, जो इस विकल्प के द्वारा संतुष्ट नहीं होता।
-
विकल्प (d) $ R_g $: $ X_L $ के मान $ R_g $ के बराबर होना गलत है क्योंकि $ R_g $ एक प्रतिरोध है, न कि प्रतिघात। AC परिपथ में अधिकतम शक्ति प्रसार की शर्त प्रतिघात के समान होना होता है, न कि प्रतिरोध के।
3. जब एक वोल्टमीटर को $A C$ मेन्स के साथ जोड़ा जाता है, तो मीटर 220 वोल्ट के स्थिर इनपुट वोल्टेज को दिखाता है। इसका अर्थ है
(a) इनपुट वोल्टेज एक एसी वोल्टेज नहीं हो सकता, बल्कि डीसी वोल्टेज होता है
(b) अधिकतम इनपुट वोल्टेज 220 वोल्ट होता है
(c) मीटर $v$ को नहीं, बल्कि $\left\langle v^{2}\right\rangle$ को दिखाता है और इसे ऐसे कैलिब्रेट किया गया है कि इसके द्वारा $\sqrt{\left\langle v^{2}\right\rangle}$ का मान दिखाया जाता है
(d) मीटर के सूचक द्वारा कोई यांत्रिक दोष के कारण अटक गया है
उत्तर दिखाएँ
उत्तर
(c) एसी मेन्स के साथ जोड़े गए वोल्टमीटर के द्वारा माध्य मान $\left(\left\langle v^{2}\right\rangle\right)$ को दिखाया जाता है और इसे ऐसे कैलिब्रेट किया गया है कि इसके द्वारा $\left\langle v^{2}\right\rangle$ के मान को दिखाया जाता है, जिसे रूप गुणक के गुणन के द्वारा औसत मान के रूप में परिवर्तित किया जाता है।
-
(a) इनपुट वोल्टेज एक एसी वोल्टेज नहीं हो सकता, बल्कि डीसी वोल्टेज होता है: यह गलत है क्योंकि मीटर को एसी वोल्टेज मापने के लिए डिज़ाइन किया गया है और इसके द्वारा एसी वोल्टेज के RMS मान को दिखाया जा सकता है। 220 वोल्ट के स्थिर पाठ के कारण वोल्टेज के डीसी होने का अर्थ नहीं होता।
-
(ब) अधिकतम इनपुट वोल्टेज 220 वोल्ट है: यह गलत है क्योंकि मीटर एसी वोल्टेज के एक्सपेक्टेड (रूट मीन स्क्वेयर) मान को दर्शाता है, न कि शिखर या अधिकतम मान। 220 वोल्ट के एसी सिग्नल के लिए अधिकतम (शिखर) वोल्टेज अधिक होगा, विशेष रूप से $220V \times \sqrt{2} \approx 311V$ होगा।
-
(डी) मीटर के इंडिकेटर का बाधा कुछ यांत्रिक त्रुटि के कारण है: यह गलत है क्योंकि एक बाधा वाला इंडिकेटर एक विश्वसनीय या स्थिर रीडिंग नहीं प्रदान करेगा। 220 वोल्ट के स्थिर रीडिंग के कारण मीटर काम कर रहा है और एसी वोल्टेज के एक्सपेक्टेड मान को माप रहा है।
4. एक $L-C-R$ श्रेणी परिपथ में जनरेटर के साथ अनुनाद आवृत्ति को कम करने के लिए
(ए) जनरेटर आवृत्ति को कम करना चाहिए
(ब) पहले के साथ समानांतर में एक अतिरिक्त कैपेसिटर जोड़ना चाहिए
(स) इंडक्टर के लौह नाभिक को हटाना चाहिए
(द) कैपेसिटर में डाइइलेक्ट्रिक को हटाना चाहिए
उत्तर दिखाएं
उत्तर
(ब) हम जानते हैं कि $L-C-R$ परिपथ में अनुनाद आवृत्ति निम्न द्वारा दी जाती है
$$ v_{0}=\frac{1}{2 \pi \sqrt{L C}} $$
अब $v_{0}$ को कम करने के लिए हम या तो $L$ को बढ़ा सकते हैं या $C$ को बढ़ा सकते हैं।
कैपेसिटेंस को बढ़ाने के लिए हमें पहले के साथ समानांतर में एक अतिरिक्त कैपेसिटर जोड़ना चाहिए।
-
(ए) जनरेटर आवृत्ति को कम करना परिपथ के अनुनाद आवृत्ति पर प्रभाव नहीं डालता है, जो इंडक्टर (L) और कैपेसिटर (C) के मान द्वारा निर्धारित होती है, न कि जनरेटर आवृत्ति।
-
(स) इंडक्टर के लौह नाभिक को हटाना इंडक्टेंस (L) को कम करेगा, जो वास्तव में अनुनाद आवृत्ति को बढ़ा देगा, न कि कम करेगा।
-
(द) कैपेसिटर में डाइइलेक्ट्रिक को हटाना कैपेसिटेंस (C) को कम करेगा, जो भी अनुनाद आवृत्ति को बढ़ा देगा, न कि कम करेगा।
5. आवागाही के लिए उपयोग किए जाने वाले $L-C-R$ परिपथ के बेहतर ट्यूनिंग के लिए निम्नलिखित में से कौन से संयोजन का चयन करना चाहिए?
(ए) $R=20 \Omega, L=1.5 \mathrm{H}, C=35 \mu \mathrm{F}$
(ब) $R=25 \Omega, L=2.5 \mathrm{H}, \mathrm{C}=45 \mu \mathrm{F}$
(स) $R=15 \Omega, L=3.5 \mathrm{H}, C=30 \mu \mathrm{F}$
(d) $R=25 \Omega, L=1.5 \mathrm{H}, \mathrm{C}=45 \mu \mathrm{F}$
उत्तर दिखाएँ
एक संचार के लिए उपयोग किए जाने वाले L-C-R परिपथ के बेहतर ट्यूनिंग के लिए परिपथ के गुणवत्ता गुणक को ज्यादा से ज्यादा होना चाहिए।
Answer
(c) एक $L-C-R$ परिपथ के गुणवत्ता गुणक $(Q)$ के लिए,
$$ Q=\frac{1}{R} \sqrt{\frac{L}{C}} $$
जहाँ $R$ प्रतिरोध है, $L$ चुंबकीय प्रेरकत्व है और $C$ संधारित्र की धारिता है। $Q$ को ज्यादा करने के लिए,
$R$ को कम, $L$ को ज्यादा और $C$ को कम होना चाहिए।
इन शर्तों को विकल्प (c) में दिए गए मानों द्वारा सर्वोत्तम रूप से संतुष्ट किया जाता है।
नोट: गुणवत्ता गुणक के सूत्र को लिखते समय हम ध्यान रखें क्योंकि हम श्रेणीक्रम में L-C-R परिपथ के बारे में बात कर रहे हैं।
-
विकल्प (a): प्रतिरोध $ R = 20 \Omega $ विकल्प (c) के प्रतिरोध की तुलना में अधिक है, जो गुणवत्ता गुणक $ Q $ को कम करता है। इसके अलावा, प्रेरकत्व $ L = 1.5 \mathrm{H} $ विकल्प (c) के प्रेरकत्व की तुलना में कम है, जो भी $ Q $ को कम करता है।
-
विकल्प (b): प्रतिरोध $ R = 25 \Omega $ विकल्प (c) के प्रतिरोध की तुलना में अधिक है, जो गुणवत्ता गुणक $ Q $ को कम करता है। हालांकि, प्रेरकत्व $ L = 2.5 \mathrm{H} $ विकल्प (a) के प्रेरकत्व की तुलना में अधिक है, लेकिन यह अभी भी विकल्प (c) के प्रेरकत्व की तुलना में कम है। संधारित्र की धारिता $ C = 45 \mu \mathrm{F} $ विकल्प (c) की धारिता की तुलना में अधिक है, जो भी $ Q $ को कम करता है।
-
विकल्प (d): प्रतिरोध $ R = 25 \Omega $ विकल्प (c) के प्रतिरोध की तुलना में अधिक है, जो गुणवत्ता गुणक $ Q $ को कम करता है। प्रेरकत्व $ L = 1.5 \mathrm{H} $ विकल्प (c) के प्रेरकत्व की तुलना में कम है, और संधारित्र की धारिता $ C = 45 \mu \mathrm{F} $ विकल्प (c) की धारिता की तुलना में अधिक है, जो दोनों एक साथ $ Q $ को कम करते हैं।
6. एक $1 \Omega$ के प्रतिरोधक और $2 \Omega$ के प्रेरक को $6 \mathrm{~V}$ (rms) AC विद्युत आवेश के सिरों पर श्रेणीक्रम में जोड़ा गया है। परिपथ में व्यय ऊर्जा है $\newline$
(a) $8 \mathrm{~W}$ $\newline$
(b) $12 \mathrm{~W}$ $\newline$
(c) $14.4 \mathrm{~W}$ $\newline$
(d) $18 \mathrm{~W}$ $\newline$
उत्तर दिखाएँ
उत्तर
(c) दिया गया है, $X_{L}=1 \Omega, R=2 \Omega$
$$ E_{\mathrm{rms}}=6 \mathrm{~V}, P_{\mathrm{av}}=? $$
परिपथ में औसत शक्ति क्षय
$$ \begin{aligned} P_{\mathrm{av}} & =E_{\mathrm{rms}} I_{\mathrm{rms}} \cos \phi \\ I_{\mathrm{rms}} & =\frac{I_{0}}{\sqrt{2}}=\frac{E_{\mathrm{rms}}}{Z} \\ Z & =\sqrt{R^{2}+X_{L}^{2}} \\ & =\sqrt{4+1}=\sqrt{5} \\ I_{\mathrm{rms}} & =\frac{6}{\sqrt{5}} \mathrm{~A} \\ \cos \phi & =\frac{R}{Z}=\frac{2}{\sqrt{5}} \\ P_{\mathrm{av}} & =6 \times \frac{6}{\sqrt{5}} \times \frac{2}{\sqrt{5}} \\ & =\frac{72}{\sqrt{5} \sqrt{5}}=\frac{72}{5}=14.4 \mathrm{~W} \end{aligned} $$
-
विकल्प (a) $8 \mathrm{~W}$: यह विकल्प गलत है क्योंकि दिए गए प्रतिरोध, प्रतिक्रिया और वोल्टेज के मानों के आधार पर परिपथ में क्षय शक्ति $14.4 \mathrm{~W}$ है, न कि $8 \mathrm{~W}$. शक्ति क्षय सूत्र में rms वोल्टेज, rms धारा और शक्ति गुणक के गुणनफल को शामिल किया जाता है, जो $8 \mathrm{~W}$ से अधिक मान देता है।
-
विकल्प (b) $12 \mathrm{~W}$: यह विकल्प गलत है क्योंकि दिए गए पैरामीटर (प्रतिक्रिया, प्रतिरोध और rms वोल्टेज) के आधार पर वास्तविक शक्ति क्षय $14.4 \mathrm{~W}$ है। शक्ति क्षय की गणना सूत्र $P_{\mathrm{av}} = E_{\mathrm{rms}} I_{\mathrm{rms}} \cos \phi$ के आधार पर की जाती है, जो $12 \mathrm{~W}$ नहीं देता है।
-
विकल्प (d) $18 \mathrm{~W}$: यह विकल्प गलत है क्योंकि दिए गए मानों के आधार पर परिपथ में शक्ति क्षय $14.4 \mathrm{~W}$ है। शक्ति क्षय के सूत्र में प्रतिबाधा और शक्ति गुणक को शामिल किया जाता है, जो $18 \mathrm{~W}$ से कम मान देता है।
7. एक डाउन करने वाले ट्रांसफॉर्मर के आउटपुट को $12 \mathrm{~W}$ के एक बल्ब के संयोजन पर $24 \mathrm{~V}$ मापा जाता है। शिखर धारा का मान है
(a) $1 / \sqrt{2} \mathrm{~A}$
(b) $\sqrt{2} \mathrm{~A}$
(c) $2 \mathrm{~A}$
(d) $2 \sqrt{2} \mathrm{~A}$
उत्तर दिखाएँ
उत्तर
(a) द्वितीयक वोल्टेज $V_{S}=24 \mathrm{~V}$
द्वितीयक के साथ संबद्ध शक्ति $P_{S}=12 \mathrm{~W}$
$$ \begin{aligned} I_{S} & =\frac{P_{S}}{V_{S}}=\frac{12}{24} \\ & =\frac{1}{2} \mathrm{~A}=0.5 \mathrm{~A} \end{aligned} $$
द्वितीयक में धारा का पिक मान
$$ \begin{aligned} I_{0} & =I_{S} \sqrt{2} \\ & =(0.5)(1.414)=0.707=\frac{1}{\sqrt{2}} \mathrm{~A} \end{aligned} $$
-
विकल्प (b) $\sqrt{2} \mathrm{~A}$: यह विकल्प गलत है क्योंकि पिक धारा की गणना $ I_0 = I_S \sqrt{2} $ के द्वारा की जाती है। दिया गया है $ I_S = 0.5 \mathrm{~A} $, तो पिक धारा $ I_0 $ होगी $ 0.5 \sqrt{2} \mathrm{~A} $, जो सरलीकृत रूप में $ \frac{1}{\sqrt{2}} \mathrm{~A} $ होती है, नहीं $ \sqrt{2} \mathrm{~A} $।
-
विकल्प (c) $2 \mathrm{~A}$: यह विकल्प गलत है क्योंकि यह RMS धारा और पिक धारा के बीच संबंध को ध्यान में नहीं लेता। RMS धारा $ I_S $ होती है $ 0.5 \mathrm{~A} $, और पिक धारा $ I_0 $ होती है $ 0.5 \sqrt{2} \mathrm{~A} $, जो $ 2 \mathrm{~A} $ के बराबर नहीं होती।
-
विकल्प (d) $2 \sqrt{2} \mathrm{~A}$: यह विकल्प गलत है क्योंकि यह पिक धारा को बहुत अधिक अनुमानित करता है। सही पिक धारा $ 0.5 \sqrt{2} \mathrm{~A} $ होती है, जो $ 2 \sqrt{2} \mathrm{~A} $ की तुलना में काफी कम होती है।
बहुविकल्पीय प्रश्न (एक से अधिक विकल्प)
8. एक $\mathrm{AC}$ परिपथ की आवृत्ति बढ़ती जाती है, तो धारा पहले बढ़ती है और फिर घटती है। परिपथ के संगठन के लिए सबसे संभावित संयोजन कौन सा हो सकता है?
(a) प्रेरक और संधारित्र
(b) प्रतिरोधक और प्रेरक
(c) प्रतिरोधक और संधारित्र
(d) प्रतिरोधक, प्रेरक और संधारित्र
उत्तर दिखाएँ
सोचने की प्रक्रिया
हम दिए गए परिपथ के तत्वों को निर्धारित कर सकते हैं जो आवृत्ति के साथ उनके प्रतिघात के परिवर्तन की भविष्यवाणी करके।
उत्तर
$(a, d)$
प्रेरकत्व $L$ के प्रेरक के प्रतिघात होता है, $X_{L}=2 \pi \nu L$ जहाँ $v$ एक एसी परिपथ की आवृत्ति होती है।
$$
\begin{aligned} X_{C} & =\text { कैपेसिटिव परिपथ का अप्रत्याधारकता } \\ & =\frac{1}{2 \pi f C} \end{aligned} $$
आवृत्ति $v$ के बढ़ने पर, स्पष्ट रूप से $X_{L}$ बढ़ता है और $X_{C}$ घटता है।
एक $L-C-R$ परिपथ के लिए,
$$ \begin{aligned} Z & =\text { परिपथ का प्रतिबाधा } \\ & =\sqrt{R^{2}+\left(X_{L}-X_{C}\right)^{2}} \\ & =\sqrt{R^{2}+(2 \pi v L-\frac{1}{2 \pi v C}})^2 \end{aligned} $$
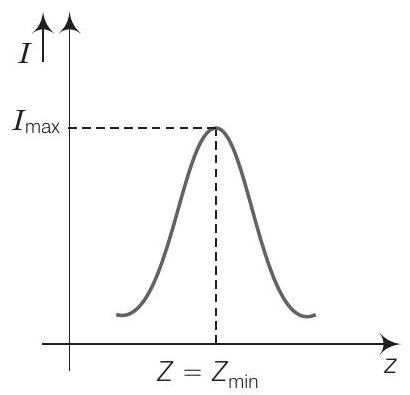
जब आवृत्ति $(v)$ बढ़ती है, तो $Z$ घटता है और एक निश्चित आवृत्ति के मान पर, जिसे संतृप्त आवृत्ति $\left(\nu_{0}\right)$ कहा जाता है, प्रतिबाधा $Z$ न्यूनतम होती है जो $Z_{\min }=R$ होती है। धारा प्रतिबाधा के विपरीत बदलती है और $Z_{\min }$ पर धारा अधिकतम होती है।
-
(b) प्रतिरोधक और प्रेरक:
- केवल एक प्रतिरोधक और एक प्रेरक के संयोजन वाले परिपथ में, आवृत्ति के बढ़ने के साथ प्रतिबाधा बढ़ती है क्योंकि प्रेरक अप्रत्याधारकता $X_L = 2\pi v L$ आवृत्ति के साथ रेखीय रूप से बढ़ती है। अतः, आवृत्ति के बढ़ने के साथ धारा निरंतर घटती रहती है, न कि पहले बढ़े और फिर घटे।
-
(c) प्रतिरोधक और कैपेसिटर:
- केवल एक प्रतिरोधक और एक कैपेसिटर के संयोजन वाले परिपथ में, आवृत्ति के बढ़ने के साथ प्रतिबाधा घटती है क्योंकि कैपेसिटिव अप्रत्याधारकता $X_C = \frac{1}{2\pi v C}$ आवृत्ति के बढ़ने के साथ घटती है। अतः, आवृत्ति के बढ़ने के साथ धारा निरंतर बढ़ती रहती है, न कि पहले बढ़े और फिर घटे।
9. एक अल्टरनेटिंग करंट परिपथ में, जिसमें तत्व श्रेणी के रूप में होते हैं, आवृत्ति के बढ़ने के साथ धारा बढ़ती है। निम्नलिखित में से कौन से तत्व परिपथ के संघटक हो सकते हैं?
(a) केवल प्रतिरोधक
(b) प्रतिरोधक और एक प्रेरक
(c) प्रतिरोधक और एक कैपेसिटर
(d) केवल एक कैपेसिटर
उत्तर दिखाएँ
Answer
$(c, d)$
प्रश्न के अनुसार, आवृत्ति के बढ़ने के साथ धारा बढ़ती है। अतः, परिपथ के अप्रत्याधारकता कम होनी चाहिए जब आवृत्ति बढ़ती है।
एक कैपेसिटिव परिपथ में,
$$ X_{C}=\frac{1}{\omega C}=\frac{1}{2 \pi f C} $$
स्पष्ट रूप से जब आवृत्ति बढ़ती है, $X_{C}$ घटती है।
$R$ - $C$ परिपथ के लिए,
$$ X=\sqrt{R^{2}+(\frac{1}{w C})^{2}} $$
जब आवृत्ति बढ़ती है $X$ घटती है।
-
विकल्प (a) केवल प्रतिरोधक के लिए:
- शुद्ध रूप से प्रतिरोधक परिपथ में, धारा आपूर्ति की आवृत्ति पर निर्भर नहीं करती। प्रतिरोधक के प्रतिरोध को निरंतर रखा जाता है और आवृत्ति पर बदल नहीं जाता। अतः, केवल प्रतिरोधक के परिपथ में आवृत्ति के बढ़ने से धारा पर कोई प्रभाव नहीं होता।
-
विकल्प (b) प्रतिरोधक और एक प्रेरक के लिए:
- एक $R$ - $L$ परिपथ में, प्रेरक अवगत बल $X_L$ निम्नलिखित द्वारा दिया जाता है: $$ X_{L} = \omega L = 2 \pi f L $$ जब आवृत्ति बढ़ती है, प्रेरक अवगत बल $X_L$ बढ़ता है, जो पूरे परिपथ के सामान्य प्रतिरोध को बढ़ा देता है। इसके परिणामस्वरूप, धारा कम हो जाती है, जो प्रश्न में दिए गए शर्त के विपरीत है।
10. विद्युत ऊर्जा बड़ी दूरी तक उच्च अल्टरनेटिंग वोल्टेज पर प्रसारित की जाती है। निम्नलिखित में से कौन सा कथन सही है (हैं)?
(a) एक दिए गए शक्ति स्तर के लिए, धारा कम होती है
(b) कम धारा शक्ति हानि को कम करती है
(c) प्रसार लाइन को छोटा बनाया जा सकता है
(d) आवरण छोर पर वोल्टेज को कम करना स्टेप-डाउन ट्रांसफॉर्मर के उपयोग द्वारा आसान होता है
उत्तर दिखाएँ
सोचने की प्रक्रिया
प्रसार लाइन के प्रतिरोध ( $R$ ) और rms धारा ( $I_{r m s}$ ) के कारण शक्ति हानि $I^{2}{ }_{r m s} R$ होती है
उत्तर
$(a, b, d)$
हम बड़ी दूरी तक उच्च अल्टरनेटिंग वोल्टेज पर ऊर्जा (शक्ति) प्रसारित करते हैं, इसलिए तारों में प्रवाहित धारा कम होती है क्योंकि एक दिए गए शक्ति $(P)$ के लिए,
$$P =E_{rms} I_{rms}$$
$I_{rms} \text { निम्न होता है जब } E_{rms} \text { उच्च होता है }$
$$\text { शक्ति हानि } =I^{2}{ }{\text {rms }} R=\text { निम्न } \quad\left(\because I{rms} \text { निम्न होता है }\right)$$
अब आवरण छोर पर उच्च वोल्टेज को कम करने के लिए स्टेप-डाउन ट्रांसफॉर्मर का उपयोग किया जाता है।
- विकल्प (c) गलत है क्योंकि प्रसार लाइन की मोटाई मुख्य रूप से यांत्रिक शक्ति के आवश्यकताओं और तापीय सीमाओं द्वारा निर्धारित होती है, न केवल धारा। यहां भले ही कम धारा प्रतिरोधी हानि को कम करती हो, लेकिन लाइन अभी भी पर्यावरणीय कारकों जैसे हवा और बर्फ के भार के खिलाफ प्रतिरोध करने के लिए प्रबल होनी चाहिए।
11. $L-C-R$ परिपथ के लिए, चालक स्रोत से चालित विस्पति के ऊर्जा प्रस्तुत करने की शक्ति $P=I^{2} Z \cos \phi$ होती है।
(a) यहाँ, शक्ति गुणक $\cos \phi \geq 0, P \geq 0$
(b) चालक बल कभी-कभी विस्पति को ऊर्जा नहीं दे सकता है $(P=0)$
(c) चालक बल विस्पति से ऊर्जा निकाल नहीं सकता है $(P<0)$
(d) चालक बल विस्पति से ऊर्जा निकाल सकता है
उत्तर दिखाएं
उत्तर
$(a, b, c)$
प्रश्न के अनुसार ऊर्जा प्रस्तुत,
$$ P=I^{2} Z \cos \phi $$
जहाँ $I$ धारा है, $Z=$ प्रतिरोधकता और $\cos \phi$ शक्ति गुणक है
शक्ति गुणक,
जहाँ
$$ \begin{aligned} \cos \phi & =\frac{R}{Z} \\ R & >0 \text { और } Z>0 \\ \cos \phi & >0 \Rightarrow P>0 \end{aligned} $$
- विकल्प (d) गलत है क्योंकि चालक स्रोत से चालित विस्पति के बीच ऊर्जा प्रस्तुत हमेशा गैर-ऋणात्मक होती है ($P \geq 0$)। चालक बल विस्पति से ऊर्जा निकाल नहीं सकता है, क्योंकि इसका अर्थ ऋणात्मक ऊर्जा प्रस्तुत होती है ($P < 0$), जो दिया गया $\cos \phi \geq 0$ के अनुसार संभव नहीं है।
12. जब $A C$ वोल्टेज $220 \mathrm{~V}$ को कैपेसिटर $C$ पर लगाया जाता है
(a) प्लेट के बीच अधिकतम वोल्टेज $220 \mathrm{~V}$ होता है
(b) धारा लगाए गए वोल्टेज के समान चरण में होती है
(c) प्लेट पर आवेश लगाए गए वोल्टेज के समान चरण में होता है
(d) कैपेसिटर के लिए आवेश निर्माण शून्य होता है
उत्तर दिखाएं
उत्तर
(c, $d)$
जब AC वोल्टेज कैपेसिटर पर लगाया जाता है, तो धनात्मक टर्मिनल से जुड़ी प्लेट उच्च विभव पर होती है और ऋणात्मक टर्मिनल से जुड़ी प्लेट निम्न विभव पर होती है।
धनात्मक आवेश वाली प्लेट उच्च विभव पर होती है और ऋणात्मक आवेश वाली प्लेट निम्न विभव पर होती है। इसलिए, हम कह सकते हैं कि आवेश लगाए गए वोल्टेज के समान चरण में होता है।
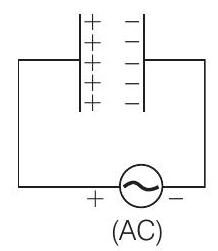
ऊर्जा एक परिपथ में आरोपित $\quad P_av =V_rms I_rms \cos \phi$
कैपेसिटिव परिपथ में, $\quad \phi =90^{\circ}$
$\Rightarrow \quad \cos \phi =0 $
$\Rightarrow \quad P_{\mathrm{av}} =\text { ऊर्जा आपूर्ति }=0$
-
(a) प्लेट के बीच अधिकतम वोल्टेज $220 \mathrm{~V}$ है: यह कथन गलत है क्योंकि एक AC परिपथ में कैपेसिटर के प्लेट के बीच अधिकतम वोल्टेज आवर्ती विद्युत आपूर्ति के RMS वोल्टेज के बराबर आवश्यक नहीं होता। RMS वोल्टेज एक प्रभावी वोल्टेज का माप है, न कि शिखर वोल्टेज। शिखर वोल्टेज $ V_{\text{peak}} $ वास्तव में $ V_{\text{rms}} \times \sqrt{2} $ होता है, जो RMS वोल्टेज से अधिक होता है।
-
(b) धारा आरोपित वोल्टेज के समान चरण में है: यह कथन गलत है क्योंकि शुद्ध कैपेसिटिव AC परिपथ में धारा वोल्टेज के 90 डिग्री आगे होती है। इसका अर्थ है कि धारा अपने अधिकतम मान को एक चौथाई चक्र पहले पहुंचती है, इसलिए वे चरण में नहीं होती।
13. आपके घर के घरेलू उपयोग के लिए विद्युत आपूर्ति के लिए सड़क से जुड़े लाइन के बारे में कौन सा कथन सही है
(a) औसत धारा शून्य है
(b) $220 \mathrm{~V}$ औसत वोल्टेज
(c) वोल्टेज और धारा $90^{\circ}$ के बाहर चरण में है
(d) वोल्टेज और धारा के चरण अंतर $\phi$ ऐसा हो सकता है जहां $|\phi|<\frac{\pi}{2}$
उत्तर दिखाएँ
Answer
$(a, d)$
घरेलू आपूर्ति के लिए AC धारा का उपयोग किया जाता है जो एक चक्र में औसत मान शून्य होता है।
लाइन में कुछ प्रतिरोध होता है इसलिए शक्ति गुणक $\cos \phi=\frac{R}{Z} \neq 0$
इसलिए,
$$ \phi \neq \pi / 2 \Rightarrow \phi,<\pi / 2 $$
अर्थात, चरण 0 और $\pi / 2$ के बीच होता है।
-
(b) $220 \mathrm{~V}$ औसत वोल्टेज: घरेलू आपूर्ति के लिए वोल्टेज आमतौर पर RMS (मूल औसत वर्ग) मान होता है, न कि औसत मान। 220V के RMS मान एक प्रभावी वोल्टेज का माप है, न कि एक चक्र में औसत वोल्टेज।
-
(c) वोल्टेज और धारा $90^{\circ}$ के बाहर चरण में है: एक सामान्य घरेलू विद्युत आपूर्ति में वोल्टेज और धारा $90^{\circ}$ के बाहर चरण में नहीं होती। यदि वे ऐसे होते, तो यह शुद्ध प्रतिरोधी लोड (या शुद्ध प्रेरक या शुद्ध कैपेसिटिव) के लिए बताता। घरेलू उपकरणों में शुद्ध प्रतिरोधी और प्रतिरोधी घटक दोनों होते हैं, जो ऐसा नहीं होता।
बहुत छोटे उत्तर प्रकार प्रश्न
14. यदि एक $L-C$ परिपथ को एक अनुत्क्रमणीय वृत्तीय ब्लॉक प्रणाली के समान बनाया जाता है, तो $L-C$ परिपथ के किस ऊर्जा को स्थितिज ऊर्जा के समान और किस ऊर्जा को गतिज ऊरजा के समान माना जाएगा?
उत्तर दिखाएँ
उत्तर
यदि हम एक $L-C$ परिपथ को एक अनुत्क्रमणीय वृत्तीय ब्लॉक प्रणाली के समान बनाते हैं। विद्युत ऊर्जा $\frac{1}{2} C V^{2}$ स्थितिज ऊर्जा के समान होगी और आवेश गतिमान होने से संबंधित ऊर्जा (विद्युत चालकता) जो $\frac{1}{2} L I^{2}$ होती है, गतिज ऊर्जा के समान होगी।
15. चित्र में दिखाए गए परिपथ के बहुत उच्च आवृत्तियों पर प्रभावी समतुल्य परिपथ को बनाएँ और प्रभावी प्रतिघात को ज्ञात करें।
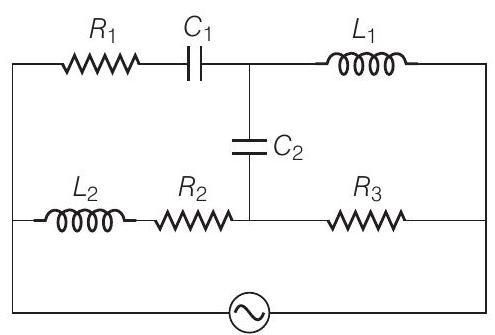
उत्तर दिखाएँ
सोचने की प्रक्रिया
अपरिवर्तनीय प्रतिरोध वाले घटक को खुला घटक माना जाएगा और शून्य प्रतिरोध वाले घटक को बंद घटक माना जाएगा।
उत्तर
हम जानते हैं कि प्रेरकत्व प्रतिघात $X_{L}=2 \pi f L$
और कैपेसिटिव प्रतिघात $X_{C}=\frac{1}{2 \pi f C}$
बहुत उच्च आवृत्तियों के लिए $(f \rightarrow \infty), X_{L} \rightarrow \infty$ और $X_{C} \rightarrow 0$
जब किसी परिपथ का प्रतिघात अपरिमित होता है तो इसे खुला परिपथ माना जाएगा। जब किसी परिपथ का प्रतिघात शून्य होता है तो इसे बंद परिपथ माना जाएगा।
इसलिए, $C_{1}, C_{2} \rightarrow$ बंद और $L_{1}, L_{2} \rightarrow$ खुला।
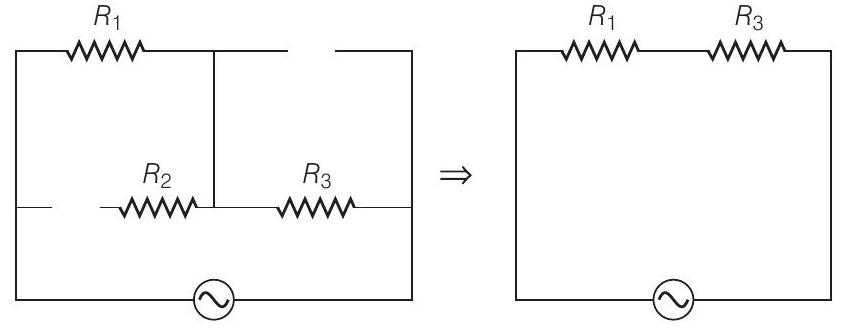
इसलिए, प्रभावी प्रतिघात $=R_{\text {eq }}=R_{1}+R_{3}$
16. चित्र में दिखाए गए परिपथ (a) और (b) का अध्ययन करें और निम्नलिखित प्रश्नों के उत्तर दें।
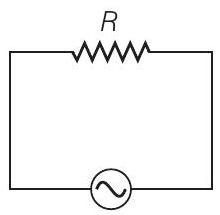
(क)
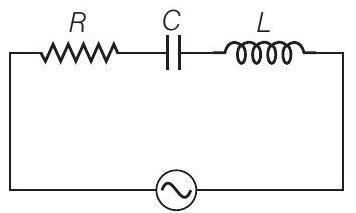
(ख)
(क) दोनों परिपथों में rms धारा समान होने के किन शर्तों के अधीन होगी?
(ख) क्या परिपथ (ख) में rms धारा, परिपथ (क) में rms धारा से अधिक हो सकती है?
उत्तर दिखाएँ
उत्तर
मान लीजिए,
$$ \begin{aligned} & \left(I_{\mathrm{rms}}\right) a=\text { परिपथ }(\mathrm{a}) \text{ में rms धारा} \\ & \left(I_{\mathrm{rms}} $$
(क) जब
$$ \begin{aligned} \left(I_{\mathrm{rms}}\right) a & =\left(I_{\mathrm{rms}}\right) b \\ R & =\sqrt{R^{2}+\left(X_{L}-X_{C}\right)^{2}} \end{aligned} $$
$$ \Rightarrow \quad X_{L}=X_{C} \text{, विचलन शर्त } $$
(ख) चूंकि $Z \geq R$
$$ \begin{array}{rlrl} \Rightarrow \frac{\left(I_{\mathrm{rms}}\right) a}{\left(I_{\mathrm{rms}}\right) b} & =\frac{\sqrt{R^{2}+\left(X_{L}-X_{C}\right)^{2}}}{R} \\ =\frac{Z}{R} \geq 1 \\ \Rightarrow \left(I_{\mathrm{rms}}\right) a & \geq\left(I_{\mathrm{rms}}\right) b \end{array} $$
नहीं, परिपथ (ख) में rms धारा, परिपथ (क) में rms धारा से अधिक नहीं हो सकती।
17. क्या किसी AC स्रोत के क्षणिक शक्ति आउटपुट कभी नकारात्मक हो सकती है? क्या औसत शक्ति आउटपुट नकारात्मक हो सकती है?
उत्तर दिखाएँ
उत्तर
लगाए गए विद्युत वाहक बल
$$ E=E_{0} \sin (\omega t) $$
और विकसित धारा है
$$ I=I_{0} \sin (\omega t \pm \phi) $$
AC स्रोत की क्षणिक शक्ति आउटपुट
$$ \begin{aligned} P & =E I \\ & =E_{0} I_{0} \sin \omega t \cdot \sin (\omega t+\phi) \\ & =\frac{E_{0} I_{0}}{2}[\cos \phi-\cos (2 \omega t+\phi)] \end{aligned} $$
औसत शक्ति
$$ \begin{aligned} P_{\mathrm{av}}= & \frac{V_{0}}{\sqrt{2}} \frac{I_{0}}{\sqrt{2}} \cos \phi \\ & =V_{\mathrm{rms}} I_{\mathrm{rms}} \cos \phi \end{aligned} $$
जहाँ $\phi$ तरंग के दोनों चर विद्युत धाराओं के बीच कलांतर है।
स्पष्ट रूप से, समीकरण (i) से
जब
$$ \begin{gathered} \cos \phi<\cos (2 \omega t+\phi) \\ P<0 \end{gathered} $$
हाँ, एक AC स्रोत की क्षणिक शक्ति नकारात्मक हो सकती है समीकरण (ii) से
$$ \begin{aligned} P_{\mathrm{av}} & >0 \\ \cos \phi & =\frac{R}{Z}>0 \end{aligned} $$
कारण
नहीं, एक AC स्रोत की औसत शक्ति नकारात्मक नहीं हो सकती।
18. श्रेणी क्रम में LCR परिपथ में $I_{\max }$ के विरुद्ध $\omega$ के ग्राफ को चित्र में दिखाया गया है। बैंडविड्थ ज्ञात कीजिए और चित्र में अंकित कीजिए।
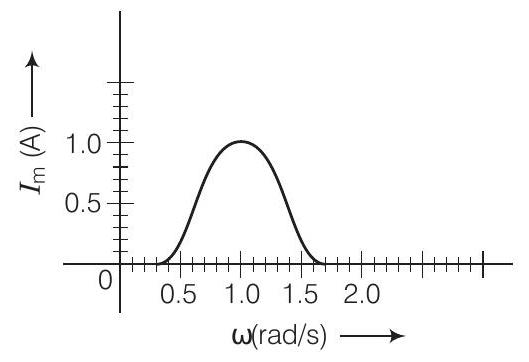
उत्तर दिखाएं
उत्तर
चित्र को ध्यान से देखें ।
बैंडविड्थ $=\omega_{2}-\omega_{1}$
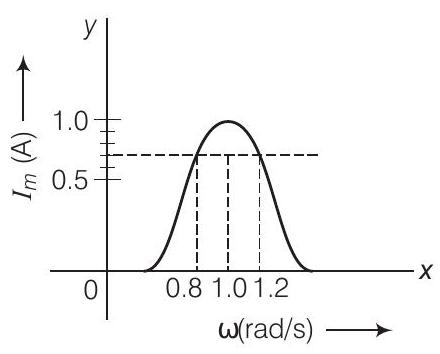
जहाँ $\omega_{1}$ और $\omega_{2}$ वह आवृत्ति है जहाँ धारा के मान का महत्तम मान के $\frac{1}{\sqrt{2}}$ गुना होता है।
$$ I_{\mathrm{rms}}=\frac{I_{\max }}{\sqrt{2}}=\frac{1}{\sqrt{2}} \approx 0.7 \mathrm{~A} $$
चित्र से स्पष्ट रूप से, संगत आवृत्तियाँ $0.8 \mathrm{rad} / \mathrm{s}$ और $1.2 \mathrm{rad} / \mathrm{s}$ हैं।
$$ \Delta \omega=\text { बैंडविड्थ }=1 \cdot 2-0.8=0.4 \mathrm{rad} / \mathrm{s} $$
19. एक परिपथ में अल्टरनेटिंग विद्युत धारा को चित्र में दिखाए गए ग्राफ द्वारा वर्णित किया गया है। इस ग्राफ में rms धारा को दिखाइए।

उत्तर दिखाएँ
उत्तर
$I_{\mathrm{rms}}=\mathrm{rms}$ धारा
$$ =\sqrt{\frac{1^{2}+2^{2}}{2}}=\sqrt{\frac{5}{2}}=1.58 \mathrm{~A} \approx 1.6 \mathrm{~A} $$
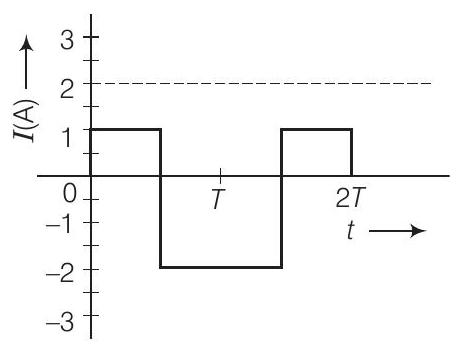
धारा के rms मान $\left(I_{\mathrm{rms}}\right)=1.6 \mathrm{~A}$ चित्र में दिखाया गया है।
20. एक $L-C-R$ श्रेणी परिपथ में, आपूर्ति वोल्टेज के धारा के संबंध में चरण कोण $\phi$ के चिह्न किस प्रकार बदलता है जब आपूर्ति आवृत्ति बहुत कम से बहुत उच्च तक धीरे-धीरे बढ़ाई जाती है।
उत्तर दिखाएँ
उत्तर
$ L-C-R $ श्रेणी परिपथ में वोल्टेज के धारा के संबंध में चरण कोण $(\phi)$ निम्नलिखित द्वारा दिया जाता है
$$ \begin{array}{ll} \tan \phi=\frac{X_{L}-X_{C}}{R}=\frac{2 \pi \nu L-\frac{1}{2 \pi \nu C}}{R} & \\ \tan \phi<0\left(\text { for } \nu<\nu_{0}\right) & \text { for } \nu=\nu_{0}=\frac{1}{2 \pi \sqrt{2 C}} \end{array} $$
छोटे उत्तर प्रकार के प्रश्न
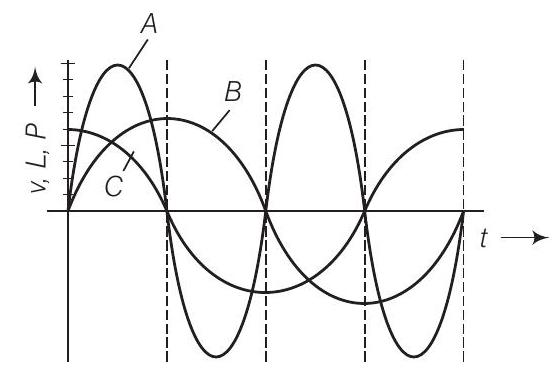
21. एक उपकरण ’ $X$ ’ को एक $A C$ स्रोत से जोड़ा गया है। वोल्टेज, धारा और शक्ति के एक पूर्ण चक्र में परिवर्तन चित्र में दिखाया गया है।
(a) कौन सा वक्र एक पूर्ण चक्र में शक्ति उपयोग को दर्शाता है?
(b) एक चक्र में औसत शक्ति उपयोग क्या है?
(c) उपकरण $X$ की पहचान करें।
उत्तर दिखाएँ
उत्तर
(a) हम जानते हैं कि शक्ति $=P=V I$
अर्थात शक्ति के वक्र के अधिकतम आयाम वोल्टेज $(V)$ और धारा $(I)$ के वक्र के आयाम के गुणनफल के बराबर होता है। इसलिए, वक्र को $A$ द्वारा प्रस्तुत किया जाता है।
(b) चित्र में छायांकित क्षेत्र द्वारा दिखाए गए अनुसार, ग्राफ का पूरा चक्र एक धनात्मक और एक नकारात्मक सममित एरिया के बराबर होता है।
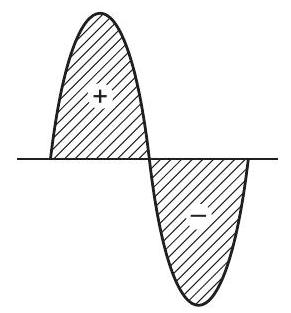
इसलिए, एक चक्र में औसत शक्ति शून्य होती है।
(c) औसत शक्ति शून्य होने के कारण, यह उपकरण एक इंडक्टर $(L)$ या कैपेसिटर $(C)$ या $L$ और $C$ के श्रेणीक्रम संयोजन हो सकता है।
22. विभिन्न प्रकार के विद्युत धारा (एल्टरनेटिंग और डाइरेक्ट) को ऐम्पियर में मापा जाता है। लेकिन एल्टरनेटिंग धारा के लिए ऐम्पियर कैसे परिभाषित किया जाता है?
उत्तर दिखाएँ
Answer
डाइरेक्ट करंट (DC) के लिए,
$$ 1 \text { ऐम्पियर }=1 \text { कूलॉम/सेकंड } $$
एक एल्टरनेटिंग करंट (AC) धारा आवृत्ति के अनुसार दिशा बदलती है और आकर्षण बल औसत रूप से शून्य हो जाता है। इसलिए, एल्टरनेटिंग ऐम्पियर को धारा की दिशा से स्वतंत्र गुण के आधार पर परिभाषित किया जाना चाहिए।
जूल के ऊष्मीय प्रभाव ऐसा गुण है और इसलिए इसका उपयोग AC के औसत मूल्य को परिभाषित करने में किया जाता है।
23. 0.01 H इंडक्टेंस और 1 ओम प्रतिरोध वाला एक कॉइल 200 वोल्ट, 50 हर्ट्ज एल्टरनेटिंग विद्युत आपूर्ति के साथ जुड़ा हुआ है। परिपथ के प्रतिघात और अधिकतम विभव और धारा के बीच समय अंतर ज्ञात कीजिए।
उत्तर दिखाएँ
Answer
दिया गया, इंडक्टेंस $L=0.01 \mathrm{H}$ प्रतिरोध $R=1 \Omega$, वोल्टेज $(V)=200 \mathrm{~V}$
और आवृत्ति $(f)=50 \mathrm{~Hz}$।
परिपथ का प्रतिघात $\quad Z=\sqrt{R^{2}+X_{L}^{2}}=\sqrt{R^{2}+(2 \pi f L)^{2}}$ $$=\sqrt{1^{2}+(2 \times 3.14 \times 50 \times 0.01)^{2}}$$
$$ or \quad Z=\sqrt{10.86}=3.3 \Omega $$
$$ \begin{aligned} \tan \phi & =\frac{\omega L}{R}=\frac{2 \pi f L}{R}=\frac{2 \times 3.14 \times 50 \times 0.01}{1}=3.14 \\ \phi & =\tan ^{-1}(3.14) \approx 72^{\circ} \\ \text{फेज अंतर} \qquad \phi & =\frac{72 \times \pi}{180} \mathrm{rad} . \end{aligned}
$$
वैद्युत वोल्टेज और धारा के बीच समय अंतर
$$ \Delta t=\frac{\phi}{\omega}=\frac{72 \pi}{180 \times 2 \pi \times 50}=\frac{1}{250} \mathrm{~s} $$
24. एक ट्रांसफॉर्मर के द्वितीयक के संगत एक $60 \mathrm{~W}$ की भार जुड़ा हुआ है जिसके प्राथमिक तार लाइन वोल्टेज ले रहा है। यदि भार में $0.54 \mathrm{~A}$ की धारा प्रवाहित हो रही है, तो प्राथमिक कुंडल में धारा कितनी होगी? उपयोग किए गए ट्रांसफॉर्मर के प्रकार के बारे में टिप्पणी करें।
उत्तर दिखाएँ
Answer
दिया गया, $P_{S}=60 \mathrm{~W}, I_{S}=0.54 \mathrm{~A}$
प्राथमिक में धारा $I_{D}=$ ?
लाइन वोल्टेज को $220 \mathrm{~V}$ मान लें।
हम लिख सकते हैं कि,
$$ \begin{array}{ll} \Rightarrow & P_{L}=60 \mathrm{~W}, I_{L}=0.54 \mathrm{~A} \\ \Rightarrow & V_{L}=\frac{60}{0.54}=110 \mathrm{~V} . \end{array} $$
द्वितीयक में वोल्टेज $\left(E_{S}\right)$ प्राथमिक में वोल्टेज $\left(E_{p}\right)$ से कम है।
अतः ट्रांसफॉर्मर एक डायन ट्रांसफॉर्मर है।
क्योंकि, परिवर्तन अनुपात
मान रखने पर,
हल करने पर
$$ \begin{aligned} r & =\frac{V_{s}}{V_{p}}=\frac{I_{p}}{I_{s}} \\ \frac{110 \mathrm{~V}}{220 \mathrm{~V}} & =\frac{I_{p}}{0.54 \mathrm{~A}} \\ I_{p} & =0.27 \mathrm{~A} \end{aligned} $$
25. क्यों एक कैपेसिटर द्वारा एक अल्टरनेटिंग धारा के लिए प्रतिरोध आवृत्ति के बढ़ने के साथ कम हो जाता है?
उत्तर दिखाएँ
Answer
एक कैपेसिटर डायरेक्ट करंट के प्रवाह को अनुमति नहीं देता क्योंकि खाली अंतर के बीच प्रतिरोध अनंत होता है। जब एक अल्टरनेटिंग वोल्टेज कैपेसिटर के प्लेटों पर लगाया जाता है, तो प्लेट एक बार चार्ज होते हैं और फिर डिस्चार्ज होते हैं। कैपेसिटर में धारा इस बदलते वोल्टेज (या चार्ज) के परिणामस्वरूप होती है।
इसलिए, यदि वोल्टेज तेजी से बदल रहा है, तो कैपेसिटर द्वारा अधिक धारा पारित कर सकता है, अर्थात यदि आपूर्ति की आवृत्ति अधिक है। इसका अर्थ है कि कैपेसिटर द्वारा प्रतिरोध आवृत्ति के बढ़ने के साथ कम हो जाता है।
गणितीय रूप से, प्रतिरोध को $X_{C}=\frac{1}{\omega C}$ के रूप में लिखा जा सकता है।
26. बताइए कि एक प्रेरक के द्वारा आवेश के प्रवाह के विरोध को आवृत्ति के बढ़ने के साथ बढ़ता क्यों होता है?
उत्तर दिखाएं
उत्तर
एक प्रेरक लेंज के नियम के अनुसार विपरीत वि. वा. बल (back emf) विकसित करके धारा के प्रवाह के विरोध करता है। उत्पन्न वि. वा. बल की ध्रुवता इस प्रकार होती है कि धारा को अपने वर्तमान मूल्य के स्थायी रखे रहे। यदि धारा कम हो रही है, तो उत्पन्न वि. वा. बल की ध्रुवता धारा को बढ़ाने के लिए होती है और विपरीत रूप से यदि धारा बढ़ रही है, तो उत्पन्न वि. वा. बल की ध्रुवता धारा को कम करने के लिए होती है।
चूंकि, उत्पन्न वि. वा. बल धारा के परिवर्तन की दर के समानुपाती होता है, इसलिए यदि परिवर्तन की दर तेज होती है, तो धारा के प्रवाह के विरोध को अधिक प्रदान करता है, अर्थात यदि आवृत्ति अधिक होती है। इसलिए, प्रेरक के विरोध को आवृत्ति के समानुपाती होता है। गणितीय रूप से, प्रेरक द्वारा प्रदान किए गए विरोध को $X_{L}=\omega L$ द्वारा दिया जाता है।
लंबा उत्तर प्रकार प्रश्न
27. एक विद्युत उपकरण एक एल. सी. एस. (AC) मुख्य (वोल्टेज $223 \mathrm{~V}$ (rms) $=\sqrt{50000} \mathrm{~V}$ ) से $2 \mathrm{~kW}$ शक्ति लेता है। धारा वोल्टेज के तुलना में फेज में अलग होती है और $\phi \tan \phi=\frac{-3}{4}$ होता है। (a) $R_{r}$ (b) $X_{C}-X_{L}$ और (c) $I_{M}$ ज्ञात कीजिए। एक अन्य उपकरण के लिए $R, X_{C}$ और $X_{L}$ के मान दोगुने हैं। उत्तर कैसे प्रभावित होते हैं?
उत्तर दिखाएं
सोचने की प्रक्रिया
हमें फेज संबंध के सूत्र, नेट रेक्टेंस और विद्युत परिपथ के संदर्भ में वोल्टेज और धारा के संबंध में अंतिम शक्ति के सूत्र के लिए फॉर्मूला के उपयोग करना होगा।
उत्तर
दिया गया, शक्ति ली गई $=P=2 \mathrm{~kW}=2000 \mathrm{~W}$
$$ \begin{array}{rlrl} \tan \phi =-\frac{3}{4}, I_{M}=I_{0}=?, R=?, X_{C}-X_{L}=? \\ V_{\mathrm{rms}} =V=223 \mathrm{~V} \\ \text { शक्ति } P =\frac{V^{2}}{Z} \\ \Rightarrow Z =\frac{V^{2}}{P}=\frac{223 \times 223}{2 \times 10^{3}}=25 \\ \text { प्रतिरोधकता } Z =25 \Omega \\ \text { प्रतिरोधकता } Z =\sqrt{R^{2}+\left(X_{L}-X_{C}\right)^{2}} \\ \Rightarrow \qquad 25 =\sqrt{R^{2}+\left(X_{L}-X_{C}\right)^{2}} \\ or \qquad 625 =R^{2}+\left(X_{L}-X_{C}\right)^{2} \\
\text{फिर से,}\qquad \tan \phi =\frac{X_{L}-X_{C}}{R}=\frac{3}{4} \\ या \qquad X_{L}-X_{C} =\frac{3 R}{4} \end{array} $$
समीकरण (ii) से, हम $X_{L}-X_{C}=\frac{3 R}{4}$ को समीकरण (i) में रखते हैं, हम प्राप्त करते हैं
$$ \begin{aligned} & 625=R^{2}+\frac{3 R}{4}^{2}=R^{2}+\frac{9 R^{2}}{16} \\ या \qquad & 625=\frac{25 R^{2}}{16} \end{aligned} $$
(a) प्रतिरोध $R=\sqrt{25 \times 16}=\sqrt{400}=20 \Omega$
(b) $X_{L}-X_{C}=\frac{3 R}{4}=\frac{3}{4} \times 20=15 \Omega$
(c) मुख्य धारा $I_{M}=\sqrt{2} I=\sqrt{2} \frac{V}{Z}=\frac{223}{25} \times \sqrt{2}=12.6 \mathrm{~A}$
जब $R, X_{C}, X_{L}$ सभी दोगुने हो जाते हैं, $\tan \phi$ बदल नहीं। $Z$ दोगुना हो जाता है, धारा आधा हो जाती है। इसलिए, शक्ति भी आधी हो जाती है।
28. $\mathrm{MW}$ शक्ति एक विद्युत स्टेशन से एक शहर तक $10 \mathrm{~km}$ की दूरी पर पहुंचाई जानी है। इसके लिए एक जोड़ा $\mathrm{Cu}$ तार जिनकी त्रिज्या $0.5 \mathrm{~cm}$ है, का उपयोग किया जाता है। यदि
(i) शक्ति $220 \mathrm{~V}$ पर प्रसारित की जाए। इसकी संभावना की चर्चा करें।
(ii) एक ट्रांसफॉर्मर का उपयोग करके वोल्टेज को $11000 \mathrm{~V}$ तक बढ़ा दिया जाए, शक्ति प्रसारित कर दी जाए, फिर एक ट्रांसफॉर्मर का उपयोग करके वोल्टेज को $220 \mathrm{~V}$ तक लाया जाए।
$$ \left(\rho_{c u}=1.7 \times 10^{-8} \text { SI इकाई }\right) $$
उत्तर दिखाएं
उत्तर
(i) शहर $10 \mathrm{~km}$ दूर है, उपयोग किए गए $\mathrm{Cu}$ तार के जोड़े की लंबाई, $L=20 \mathrm{~km}=20000 \mathrm{~m}$ है।
$\mathrm{Cu}$ तार का प्रतिरोध,
$$ \begin{aligned} R & =\frac{l}{A}=\frac{l}{\pi(r)^{2}} \\ & =\frac{1.7 \times 10^{-8} \times 20000}{3.14\left(0.5 \times 10^{-2}\right)^{2}}=4 \Omega \end{aligned} $$
$220 \mathrm{~V}$ पर $I$,
$$ \begin{aligned} V I & =10^{6} \mathrm{~W} ; I=\frac{10^{6}}{220}=0.45 \times 10^{4} \mathrm{~A} \\ R I^{2} & =\text { शक्ति हानि } \\ & =4 \times(0.45)^{2} \times 10^{8} \mathrm{~W} \\ & >10^{6} \mathrm{~W} \end{aligned} $$
इसलिए, इस विधि का उपयोग प्रसारण के लिए नहीं किया जा सकता।
(ii) जब शक्ति $P=10^{6} \mathrm{~W}$ $11000 \mathrm{~V}$ पर प्रसारित की जाती है।
$$ \begin{aligned} V^{\prime} I^{\prime} & =10^{6} \mathrm{~W}=11000 I^{\prime} \\ \text { धारा ली गई, } I^{\prime} & =\frac{1}{1.1} \times 10^{2} \\ \text { शक्ति हानि } & =R I^{2}=\frac{1}{1.21} \times 4 \times 10^{4} \\ & =3.3 \times 10^{4} \mathrm{~W} \\ \text { शक्ति हानि का अंश } & =\frac{3.3 \times 10^{4}}{10^{6}}=3.3 % \end{aligned} $$
30. एक $L-C-R$ परिपथ के लिए आवृत्ति $\omega$ पर चलाने पर समीकरण इस प्रकार होता है
$$ L \frac{d i}{d t}+R i+\frac{q}{C}=V_{i}=V_{m} \sin \omega t $$
(a) समीकरण को $i$ से गुणा करें और संभव हो तो सरल करें।
(b) प्रत्येक पद के भौतिक अर्थ की व्याख्या करें।
(c) समीकरण को ऊर्जा संरक्षण के कथन के रूप में लिखें।
(d) एक चक्र के लिए समीकरण के समाकलन करें ताकि $V$ और $i$ के बीच कल अंतर न्यून कोण होना आवश्यक हो।
उत्तर दिखाएं
सोचने की प्रक्रिया
दिए गए L-C-R श्रेणी परिपथ के लिए KVL का उपयोग करें और आवश्यक संबंधों को खोजें। साथ ही, प्रतिरोधकों के माध्यम से ऊर्जा क्षय के बारे में जानकारी लें ताकि परिपथ में कुल ऊर्जा क्षय के बारे में जानकारी प्राप्त कर सकें।
उत्तर
$ L-C-R $ परिपथ को ध्यान में रखें। लूप के लिए KVL के उपयोग से, हम लिख सकते हैं:
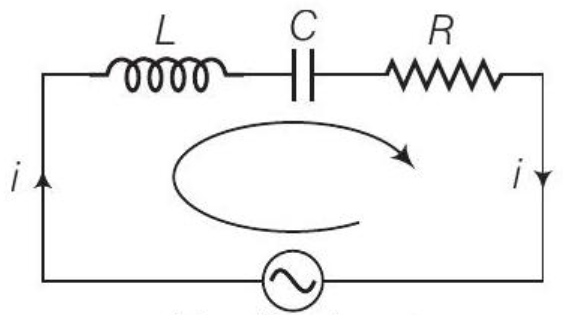
$$ \begin{gathered}V=V_m \sin \omega t \\ L \frac{d i}{d t}+\frac{q}{C}+i R=V_m \sin \omega t\end{gathered} $$
दोनों ओर को $i$ से गुणा करने पर, हम प्राप्त करते हैं:
$$ L i \frac{d i}{d t}+\frac{q}{C} i+i^{2} R=\left(V_{m} i\right) \sin \omega t=V i $$
जहाँ
$$ \begin{aligned} L i \frac{d i}{d t}=\frac{d}{d t} & \frac{1}{2} L i^{2}=\text { एक प्रेरक में संग्रहित ऊर्जा के परिवर्तन की दर। } \\ R i^{2} & =\text { जूल ऊष्मा खोई गई ऊर्जा } \\ \frac{q}{C} i=\frac{d}{d t} & \frac{q^{2}}{2 C}=\text { एक संधारित्र में संग्रहित ऊर्जा के परिवर्तन की दर। } \end{aligned} $$
$V i=$ चालक बल द्वारा ऊर्जा प्रवेश करने की दर। यह (i) ओहमी खोई गई ऊर्जा और (ii) संग्रहित ऊर्जा के वृद्धि में जाता है।
इसलिए समीकरण (ii) ऊर्जा संरक्षण के कथन के रूप में है। समीकरण (ii) के दोनों ओर समय के संदर्भ में एक पूर्ण चक्र $(0 \rightarrow T)$ पर समाकलन करने पर हम लिख सकते हैं:
$$ \begin{array}{r} \int_{0}^{T} \frac{d}{d t} \frac{1}{2} L i^{2}+\frac{q^{2}}{2 C} d t+\int_{0}^{T} R i^{2} d t=\int_{0}^{T} V i d t \\ \Rightarrow 0+(+v e)=\int_{0}^{T} V i d t \\ \Rightarrow \int_{0}^{T} V i d t>0 \text { यदि } V \text { और } i \text { के बीच कल अंतर एक नियत और न्यून कोण हो। } \end{array} $$
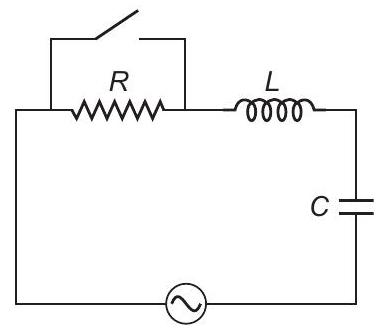
31. चित्र में दिखाए गए $L-C-R$ परिपथ में $AC$ चालक वोल्टेज $V=V_{m}$ $\sin \omega t$ है।
(a) $q(t)$ के गति के समीकरण को लिखें।
(b) $t=t_{0}$ पर, वोल्टेज स्रोत बंद हो जाता है और $R$ शॉर्ट सर्किट कर दिया जाता है। अब लिखें कि प्रत्येक $L$ और $C$ में कितनी ऊर्जा संग्रहित है।
(c) आवेशों के आगे चले गति का वर्णन करें।
K सोचने की प्रक्रिया
हमें KVL के अनुपालन करना होगा, वर्तमान और आवेश के रूप में समीकरण लिखना होगा, समय के सापेक्ष दो बार अवकलन करके आवश्यक संबंध खोजना होगा।
उत्तर दिखाएं
उत्तर
(a) आसन्न चित्र में दिखाए गए R-L-C परिपथ को विचार करें।
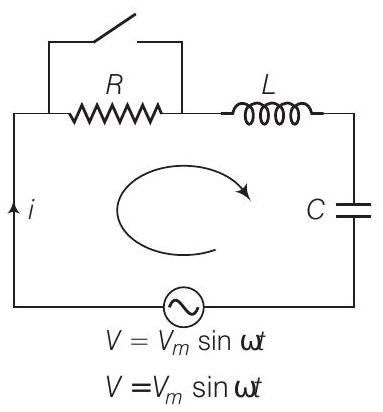
दिया गया किसी भी क्षण वर्तमान $i$ हो।
दिए गए परिपथ में KVL के अनुपालन करें
$$ i R + L \frac{d i}{d t} + \frac{q}{C} - V_{m} \sin \omega t = 0 $$
अब, हम लिख सकते हैं
$$ i = \frac{d q}{d t} \Rightarrow \frac{d i}{d t} = \frac{d^{2} q}{d t^{2}} $$
समीकरण (i) से
$$ \frac{d q}{d t} R + L \frac{d^{2} q}{d t^{2}} + \frac{q}{C} = V_{m} \sin \omega t $$
$$ \Rightarrow \quad L \frac{d^{2} q}{d t^{2}} + R \frac{d q}{d t} + \frac{q}{C} = V_{m} \sin \omega t $$
यह आवेश के परिवर्तन (गति) के आवश्यक समीकरण है। (b) मान लीजिए $\quad q = q_{m} \sin (\omega t + \phi) = -q_{m} \cos (\omega t + \phi)$
$$ \begin{aligned} i & = i_{m} \sin (\omega t + \phi) = q_{m} \omega \sin (\omega t + \phi) \\ i_{m} & = \frac{V_{m}}{Z} = \frac{V_{m}}{\sqrt{R^{2} + \left(X_{C} - X_{L}\right)^{2}}} \\ \phi & = \tan ^{-1} \frac{X_{C} - X_{L}}{R} \end{aligned} $$
जब $R$ को $t = t_{0}$ पर छोटा सर्किट कर दिया जाता है, तो ऊर्जा $L$ और $C$ में संग्रहित होती है।
और
$$ \begin{aligned} U_{L} & = \frac{1}{2} L i^{2} = \frac{1}{2} L \frac{V_{m}}{\sqrt{\left(R^{2} + X_{C} - X_{L}\right)^{2}}} \sin ^{2}\left(\omega t_{0} + \phi\right) \\ U_{C} & = \frac{1}{2} \times \frac{q^{2}}{C} = \frac{1}{2 C}\left[q^{2} m \cos ^{2}\left(\omega t_{0} + \phi\right)\right] \\ & = \frac{1}{2 C} \frac{V_{m}}{\sqrt{R^{2} + \left(X_{C} - X_{L}\right)^{2}}} \\ \end{aligned} $$
$$ \begin{aligned} & =\frac{1}{2 C} \times \frac{i_{m}}{\omega} \cos ^{2}\left(\omega t_{0}+\phi\right) \\ & =\frac{i^{2} m}{2 C \omega^{2}} \cos ^{2}\left(\omega t_{0}+\phi\right) \\ & =\frac{1}{2 C} \frac{V_{m}}{\sqrt{R^{2}+\left(X_{C}-X_{L}\right)^{2}}} \frac{\cos ^{2}\left(\omega t_{0}+\phi\right)}{\omega^{2}} \quad\left[\because i_{m}=q_{m} \omega\right] \\ & =\frac{1}{2 C \omega^{2}} \frac{V_{m}}{\sqrt{R^{2}+\left(X_{C}-X_{L}\right)^
(c) जब $R$ छोटा सर्किट कर दिया जाता है, तो परिपथ एक $L-C$ ऑस्किलेटर बन जाता है। संधारित्र लगातार विस्थापित होता रहेगा और सभी ऊर्जा $L$ में जाएगी और फिर वापस आएगी। इसलिए, ऊर्जा विद्युत चालकता से चुंबकीय और चुंबकीय से विद्युत चालकता में आवर्ती रूप से चलती रहती है।





