ठोसों के यांत्रिक गुण
बहुविकल्पीय प्रश्न (MCQs)
1. आदर्श तरल पदार्थ के झिल्ली प्रतिरोधकता मापांक है
(a) अपरिमित
(b) शून्य
(c) एक
(d) कुछ छोटा अपरिमित निश्चित मान
उत्तर दिखाएं
उत्तर (b) आदर्श तरल पदार्थ में घर्षण (गाढ़ा) बल नहीं होता, इसलिए, स्पर्शरेखीय बल शून्य होते हैं, इसलिए, तनाव का विकास नहीं होता।
-
(a) अपरिमित: यदि झिल्ली प्रतिरोधकता मापांक अपरिमित होता, तो यह बताता कि तरल पदार्थ पूर्ण रूप से अकम्पनी होता है और कोई भी झिल्ली तनाव द्वारा विकृत नहीं हो सकता, जो तरल पदार्थ की प्रकृति के विरोधाभास होता है जो झिल्ली तनाव द्वारा बह सकते हैं और विकृत हो सकते हैं।
-
(c) एक: झिल्ली प्रतिरोधकता मापांक एक होने पर यह बताता कि तरल पदार्िल्ली तनाव द्वारा एक निश्चित, शून्य नहीं वाला प्रतिरोध रखता है, जो आदर्श तरल पदार्थ के लिए नहीं होता है जो झिल्ली तनाव के विरुद्ध कोई प्रतिरोध नहीं रखता है।
-
(d) कुछ छोटा अपरिमित निश्चित मान: यह बताता कि तरल पदार्थ झिल्ली तनाव द्वारा कुछ माप्य प्रतिरोध रखता है, जो आदर्श तरल पदार्थ की परिभाषा के विरुद्ध है जो घर्षण रहित होता है और इसलिए झिल्ली तनाव के विरुद्ध कोई प्रतिरोध नहीं रखता है।
2. तार के लंबाई को अपनी मूल लंबाई के आधा कर देने पर तार के टूटने से पहले उसके वहन कर सकने वाला अधिकतम भार होगा
(a) दुगुना
(b) आधा
(c) चार गुना
(d) अपरिवर्तित रहेगा
उत्तर दिखाएं
उत्तर (d) हम जानते हैं कि, टूटने तनाव $=\frac{\text { टूटने बल }}{\text { काट क्षेत्रफल }}$
जब तार की लंबाई बदलती है, तो काट क्षेत्रफल समान रहता है।
इसलिए, जब लंबाई बदलती है, तो टूटने बल समान रहता है।
-
विकल्प (a) गलत है क्योंकि टूटने बल टूटने तनाव और काट क्षेत्रफल पर निर्भर करता है, जो जब लंबाई को आधा कर दिया जाता है तो अपरिवर्तित रहता है। इसलिए, टूटने बल दुगुना नहीं होता।
-
विकल्प (b) गलत है क्योंकि तार की लंबाई को आधा कर देने पर टूटने तनाव या काट क्षेत्रफल में कोई परिवर्तन नहीं होता। इसलिए, टूटने बल आधा नहीं होता।
-
विकल्प (c) गलत है क्योंकि तनाव बल तार की लंबाई पर निर्भर नहीं करता बल्कि तनाव तन्यता और काट के क्षेत्रफल पर। इसलिए, तनाव बल चार गुना नहीं हो जाता।
3. एक तार के तापमान को दोगुना कर दिया जाता है। यंग के मापांक
(a) भी दोगुना हो जाएगा
(b) चार गुना हो जाएगा
(c) समान रहेगा
(d) घट जाएगा
उत्तर दिखाएँ
Answer (d) हम जानते हैं कि तापमान में वृद्धि के साथ तार की लंबाई बदलती है जैसे कि
$$ L_{t}=L_{o}(1+\alpha \Delta T) $$
जहाँ $\Delta T$ तापमान में परिवर्तन है, $L_0$ मूल लंबाई है, $\alpha$ रैखिक प्रसार गुणांक है और $L_{t}$ तापमान $T$ पर लंबाई है।
अब हम लिख सकते हैं
$$ \Delta L=L_{t}-L_0=L_0 \alpha \Delta T $$
जहाँ $\alpha$ रैखिक प्रसार गुणांक है।
यंग के मापांक $(Y)=\frac{\text { Stress }}{\text { Strain }}=\frac{F L_0}{A \times \Delta L}=\frac{F L_0}{A L_0 \alpha \Delta T} \propto \frac{1}{\Delta T}$
क्योंकि,
$$ Y \propto \frac{1}{\Delta T} $$
जब तापमान बढ़ता है $\Delta T$ बढ़ता है, इसलिए, $Y$ घट जाता है।
-
(a) भी दोगुना हो जाएगा: यह विकल्प गलत है क्योंकि यंग के मापांक तापमान में परिवर्तन के व्युत्क्रमानुपाती होता है। जब तापमान बढ़ता है, तो यंग के मापांक कम हो जाता है, न कि बढ़ता है।
-
(b) चार गुना हो जाएगा: यह विकल्प गलत है क्योंकि यंग के मापांक तापमान के साथ बढ़ता नहीं होता। बल्कि जब तापमान बढ़ता है, तो यह कम हो जाता है। संबंध व्युत्क्रमानुपाती होता है, न कि सीधा या अपसारी होता है।
-
(c) समान रहेगा: यह विकल्प गलत है क्योंकि तापमान के परिवर्तन यंग के मापांक पर प्रभाव डालते हैं। जब तापमान बढ़ता है, तो मापांक कम हो जाता है, इसलिए यह समान नहीं रहता।
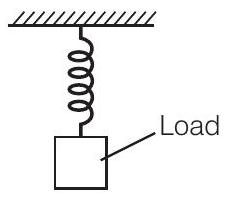
4. एक स्प्रिंग को अपने मुक्त सिरे पर एक भार लगाकर खिंचा जाता है। स्प्रिंग में उत्पन्न तनाव है
(a) आयतनिक
(b) अपसारी
(c) अक्षीय और अपसारी
(d) अक्षीय
उत्तर दिखाएँ
Answer (c) चित्र में एक स्प्रिंग को अपने मुक्त सिरे पर एक भार लगाकर खिंचा जाता है। स्पष्ट रूप से स्प्रिंग की लंबाई और आकृति बदल जाती है।
लंबाई में परिवर्तन अक्षीय तनना के रूप में और आकार में परिवर्तन अपरिवर्तनीय तनना के रूप में संबंधित होता है।
-
(a) आयतनिक: आयतनिक तनना एक सामग्री के आयतन में परिवर्तन को संदर्भित करता है। जब एक स्प्रिंग खिंचा जाता है, तो इसका आयतन बहुत कम परिवर्तन नहीं होता; बजाय इसके, लंबाई और आकार ही मुख्य रूप से प्रभावित होते हैं।
-
(b) अपरिवर्तनीय: अपरिवर्तनीय तनना वास्तव में स्प्रिंग में उत्पन्न होती है, लेकिन यह एकमात्र प्रकार की तनना नहीं है। स्प्रिंग के लंबाई में परिवर्तन के कारण इसमें अक्षीय तनना भी होती है। इसलिए, यह विकल्प अधूरा है।
-
(d) अक्षीय: लंबाई में परिवर्तन के कारण स्प्रिंग में अक्षीय तनना उत्पन्न होती है। हालांकि, यह विकल्प अधूरा है क्योंकि यह स्प्रिंग के आकार में परिवर्तन के कारण उत्पन्न होने वाली अपरिवर्तनीय तनना को गणना में नहीं लेता है।
5. एक द्रव्यमान $M$ के कठोर छड़ को तीन तारों द्वारा सममित रूप से समर्थन दिया जाता है, जिनमें से प्रत्येक की लंबाई $l$ है। दोनों सिरों पर तांबे के तार हैं और मध्य में लोहे का तार है। यदि प्रत्येक के एक ही तनाव होना चाहिए, तो उनके व्यास के अनुपात के बराबर होता है
(a) $Y_{\text {copper }} / Y_{\text {iron }}$
(b) $\sqrt{\frac{Y_{\text {iron }}}{Y_{\text {copper }}}}$
(c) $\frac{Y^{2} \text { iron }}{Y^{2} \text { copper }}$
(d) $\frac{Y_{\text {iron }}}{Y_{\text {copper }}}$
उत्तर दिखाएँ
Answer (b) हम जानते हैं कि यंग के मापांक
$$ \begin{aligned} & Y=\frac{\text { Stress }}{\text { Strain }}=\frac{F / A}{\Delta L / L}=F / A \times \frac{L}{\Delta L} \\ &=\frac{F}{\pi(D / 2)^{2}} \times \frac{L}{\Delta L}=\frac{4 F L}{\pi D^{2} \Delta L} \\ & \Rightarrow \quad D^{2}=\frac{4 F L}{\pi \Delta L Y} \Rightarrow D=\sqrt{\frac{4 F L}{\pi \Delta L Y}} \\ & \text { जैसे कि } F \text { और } \frac{L}{\Delta L} \text { नियतांक हैं। } \end{aligned} $$
इसलिए,
$$ D \propto \sqrt{\frac{1}{Y}}
$$
अब, हम अनुपात ज्ञात कर सकते हैं $\frac{D_{\text {copper }}}{D_{\text {iron }}}=\sqrt{\frac{Y_{\text {iron }}}{Y_{\text {copper }}}}$
-
विकल्प (a) $Y_{\text {copper }} / Y_{\text {iron }}$: यह विकल्प गलत है क्योंकि इसका अर्थ है कि व्यास का अनुपात यंग के मापांक के अनुपात के सीधे अनुपात में है। हालांकि, सही संबंध यह है कि व्यास यंग के मापांक के वर्गमूल के व्युत्क्रम अनुपात में होता है। इसलिए, यह विकल्प वर्गमूल संबंध को सही तरीके से प्रस्तुत नहीं करता है।
-
विकल्प (c) $\frac{Y^{2} \text { iron }}{Y^{2} \text { copper }}$: यह विकल्प गलत है क्योंकि इसका अर्थ है कि व्यास का अनुपात यंग के मापांक के अनुपात के वर्ग के सीधे अनुपात में है। सही संबंध यंग के मापांक के अनुपात के वर्गमूल के अनुपात में होता है, न कि वर्ग के अनुपात में। इसलिए, यह विकल्प अमान्य है।
-
विकल्प (d) $\frac{Y_{\text {iron }}}{Y_{\text {copper }}}$: यह विकल्प गलत है क्योंकि इसका अर्थ है कि व्यास और यंग के मापांक के सीधे अनुपात में है। सही संबंध यह है कि व्यास यंग के मापांक के वर्गमूल के व्युत्क्रम अनुपात में होता है, न कि यंग के मापांक के सीधे अनुपात में। इसलिए, यह विकल्प सही संबंध को सही तरीके से प्रस्तुत नहीं करता है।
6. एक मृदु लोहे के तार की लंबाई $2 L$ और क्रॉस-सेक्शनल क्षेत्रफल $A$ है, जो दो स्तंभों के बीच एक सीधी रेखा में तार के बिंदु पर लटकाया जाता है (चित्र)। एक द्रव्यमान $m$ तार के मध्य बिंदु से लटकाया जाता है। तार में विकृति है
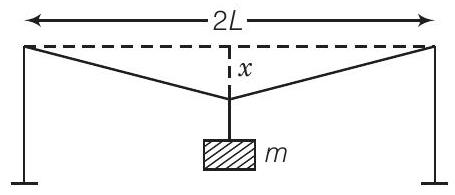
(a) $\frac{x^{2}}{2 L^{2}}$
(b) $\frac{x}{L}$
(c) $x^{2} / L$
(d) $x^{2} / 2 L$
उत्तर दिखाएँ
सोचने की प्रक्रिया
हम मान लेंगे कि क्षैतिज विस्थापन $x$ लंबाई $L$ के तुलना में बहुत छोटा है। . लंबाई में परिवर्तन की गणना शुरूआती लंबाई $2 L$ और अंतिम कुल लंबाई के अंतर के द्वारा की जाएगी।
उत्तर (अ) नीचे दिए गए आरेख को ध्यान में रखें
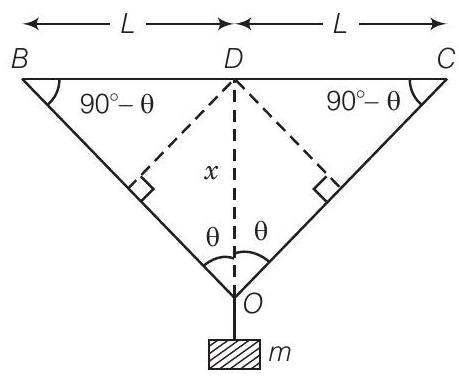
इसलिए, लंबाई में परिवर्तन
$$ \begin{matrix} \Delta L & =B O+O C-(B D+D C) & \\ & =2 B O-2 B D \\ & =2[B O-B D] \\ & =2[(x^{2}+L^{2})^{1 / 2}-L] \\ & =2 L[(1+\frac{x^{2}}{L^{2}})^{1 / 2}-1] \\ & \approx 2 L[1+\frac{1}{2} \frac{x^{2}}{L^{2}}-1]=\frac{x^{2}}{L} & \\ \therefore \quad \text { विकृति } & =\frac{\Delta L}{2 L}=\frac{x^{2} / L}{2 L}=\frac{x^{2}}{2 L^{2}} & {[\because x«L]} \end{matrix} $$
-
विकल्प (ब) $\frac{x}{L}$: यह विकल्प गलत है क्योंकि यह विकृति और क्षैतिज विस्थापन $ x $ के रूप में रैखिक संबंध को सुझाता है। हालांकि, तार में विकृति द्रव्यमान $ m $ के कारण लंबवत विस्थापन के कारण लंबाई में परिवर्तन से निर्मित होती है, जो $ x $ के वर्ग के साथ संबंधित होती है। सही विकृति के व्यंजक में $ x^2 $ होता है, न कि $ x $।
-
विकल्प (स) $x^{2} / L$: यह विकल्प गलत है क्योंकि यह विकृति के व्यंजक में निर्वाचक तार की मूल लंबाई $ 2L $ के कारण उत्पन्न होने वाले विभाजक के गुणक के लिए गौण गुणक को गौण नहीं लेता है। सही विकृति सूत्र के व्यंजक को मूल लंबाई $ 2L $ के बराबर लंबाई में परिवर्तन को विभाजित करके प्राप्त किया जाता है, जिसके कारण विभाजक में एक अतिरिक्त गुणक $ 2 $ आता है।
-
विकल्प (द) $x^{2} / 2 L$: यह विकल्प गलत है क्योंकि यह विकृति के व्यंजक में $ x^2 $ के अनुपात में $ 2L $ के अनुपात में विकृति के सीधे संबंध को सुझाता है। हालांकि, सही विकृति सूत्र में लंबाई में परिवर्तन को मूल लंबाई $ 2L $ के बराबर विभाजित करके प्राप्त किया जाता है, जिसके कारण विभाजक में एक अतिरिक्त गुणक $ L $ आता है, जिसके कारण सही व्यंजक $\frac{x^2}{2L^2}$ होता है।
7. एक आयताकार फ्रेम को दो समान लंबाई के तारों के माध्यम से दो समर्थनों पर सममित रूप से लटकाया जाना है (चित्र)। इसे निम्नलिखित तीन तरीकों में से किसी एक तरीके से किया जा सकता है;
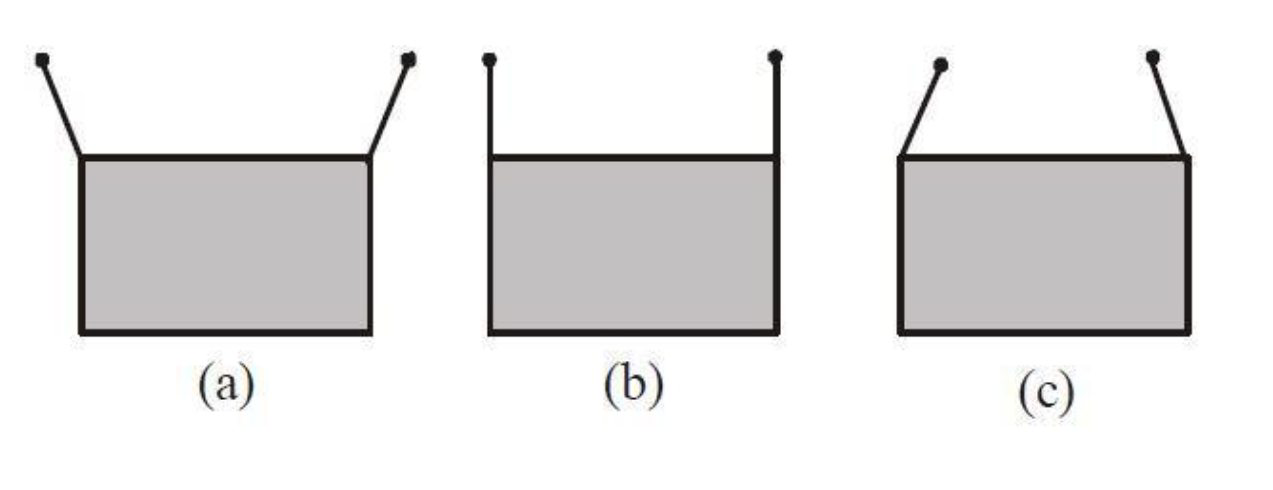
तारों में तनाव होगा
(a) सभी मामलों में समान
(b) (a) में सबसे कम
(c) (b) में सबसे कम
(d) (c) में सबसे कम
उत्तर दिखाएं
उत्तर (c) आयताकार फ्रेम के एफबीडी चित्र को ध्यान में रखें
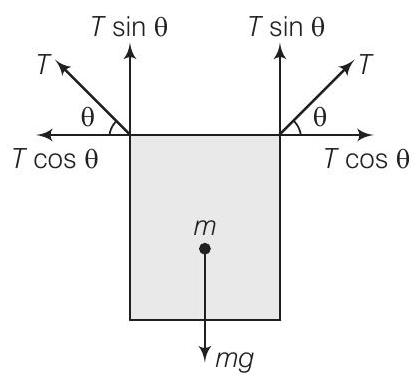
ऊर्ध्वाधर बलों के संतुलन $2 T \sin \theta - m g = 0 $
$2 T \sin \theta = m g $
कुल क्षैतिज बल $= T \cos \theta - T \cos \theta = 0$
अब समीकरण (i) से, $\quad T = \frac{m g}{2 \sin \theta}$
जबकि $m g$ स्थिर है
$$ \begin{aligned} \Rightarrow \quad T \propto \frac{1}{\sin \theta} & \Rightarrow T_{\max }=\frac{m g}{2 \sin \theta_{\text {min }}} \\ \sin \theta_{\text {min }}=0 & \Rightarrow \theta_{\text {min }}=0 \end{aligned} $$
कोई भी विकल्प $\theta=0^{\circ}$ के साथ मेल नहीं खाता है
$$ \begin{aligned} & T_{\min }=\frac{m g}{2 \sin \theta_{\max }} \\ & \sin \theta_{\max }=1 \Rightarrow \theta=90^{\circ} \\ & (\text { क्योंकि, } \sin \theta_{\max }=1) \end{aligned} $$
इसके साथ विकल्प (b) मेल खाता है
अतः, तनाव (b) के मामले में सबसे कम होता है।
नोट - जब हम कोण मापते हैं तो ध्यान रखें, यह चित्र में दिए गए दिशा के अनुरूप होना चाहिए।
-
विकल्प (a): यह विकल्प गलत है क्योंकि तारों में तनाव को तार और ऊर्ध्वाधर के बीच कोण $\theta$ पर निर्भर करता है। जैसे $\theta$ बदलता है, $\sin \theta$ का मान बदलता है, जिसके कारण तनाव $T$ भी बदलता है। अतः, सभी मामलों में तनाव समान नहीं हो सकता।
-
विकल्प (b): यह विकल्प गलत है क्योंकि, समीकरण $T = \frac{mg}{2 \sin \theta}$ से, तनाव $\sin \theta$ के व्युत्क्रमानुपाती होता है। जब $\sin \theta$ अधिकतम होता है, तब तनाव सबसे कम होता है, जो $\theta = 90^\circ$ पर होता है। मामला (b) में $\theta$ $90^\circ$ नहीं है, इसलिए इस मामले में तनाव सबसे कम नहीं होता।
-
विकल्प (d): यह विकल्प गलत है क्योंकि, विकल्प (b) के समान तनाव कम होता है जब $\sin \theta$ अधिकतम होता है। मामला (c) में $\theta$ $90^\circ$ होता है, जिसके कारण $\sin \theta = 1$ होता है, जिससे तनाव सबसे कम होता है। अतः, मामला (d) में तनाव सबसे कम नहीं होता।
8. दो सिलिंडरिकल छड़ों की तुलना करें, जो एक दूसरे के समान आकार और आकृति के हों, एक रबर की और दूसरी स्टील की। दोनों छड़ें छत के एक सिरे पर ठोस रूप से लगाई गई हैं। प्रत्येक छड़ के मुक्त सिरे के केंद्र पर एक द्रव्यमान $M$ लगाया गया है।
(a) दोनों छड़ें खिंचेंगी लेकिन आकृति में कोई चिह्नित परिवर्तन नहीं होगा
(b) स्टील छड़ खिंचेगी और आकृति में परिवर्तन होगा लेकिन रबर छड़ केवल खिंचेगी
(c) स्टील छड़ खिंचेगी बिना कोई चिह्नित आकृति परिवर्तन के, लेकिन रबर छड़ खिंचेगी और नीचले किनारे की आकृति एक वृत्ताकार बन जाएगी
(d) स्टील छड़ खिंचेगी, बिना कोई चिह्नित आकृति परिवर्तन के, लेकिन रबर छड़ खिंचेगी और नीचले किनारे की आकृति केंद्र पर एक छोटी छोटी चोटी बन जाएगी
उत्तर दिखाएँ
उत्तर (d) चित्र को देखें।
केंद्र पर एक द्रव्यमान $M$ लगाया गया है। जैसे द्रव्यमान दोनों छड़ों पर लगाया गया है, दोनों छड़ें खिंचेंगी, लेकिन चूंकि रबर और स्टील के अलग-अलग अनुत्कृत गुण होते हैं, रबर छड़ आकृति में भी परिवर्तन करेगी।
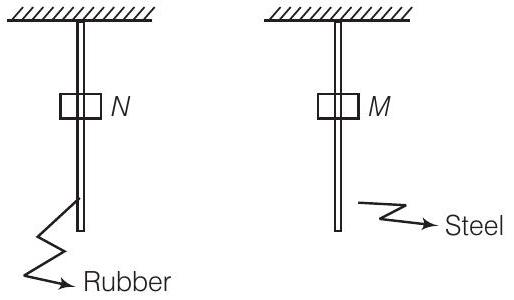
-
विकल्प (a) गलत है: जबकि दोनों छड़ें खिंचेंगी, रबर छड़ अपनी मूल बेलनाकार आकृति को बरकरार न रखेगी क्योंकि इसकी अधिक अनुत्कृत गुण होते हैं।
-
विकल्प (b) गलत है: स्टील छड़ खिंचेगी लेकिन आकृति में कोई बड़ा परिवर्तन नहीं होगा क्योंकि इसकी उच्च अनुत्कृत गुण होते हैं। रबर छड़ खिंचेगी लेकिन आकृति में भी परिवर्तन होगा, जो विकल्प में कहे गए बात के विपरीत है।
-
विकल्प (c) गलत है: रबर छड़ खिंचेगी और आकृति में परिवर्तन होगा, लेकिन नीचले किनारे की आकृति वृत्ताकार नहीं होगी। बजाय इसके, यह केंद्र पर एक छोटी छोटी चोटी बन जाएगी क्योंकि द्रव्यमान के वितरण और रबर के अनुत्कृत गुण के कारण होगा।
बहुविकल्पीय प्रश्न (एक से अधिक विकल्प)
9. दो पदार्थों के तनाव-ऊतक ग्राफ चित्र में दिखाए गए हैं। (एक ही मापदंड मान लें)
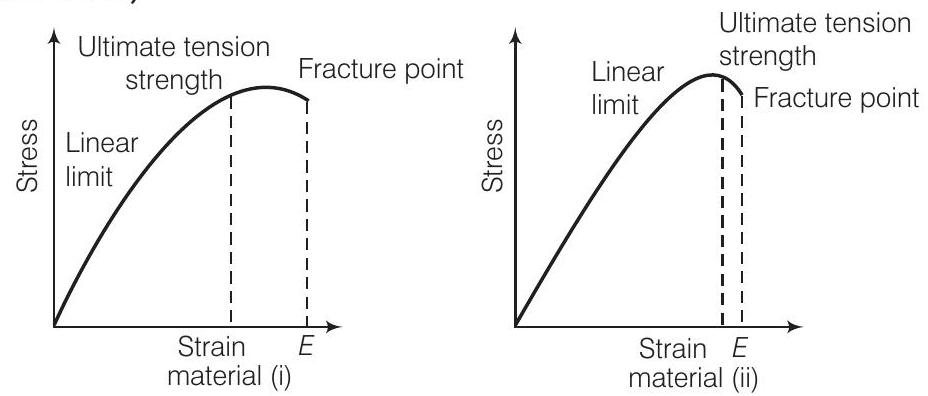
(a) पदार्थ (ii) पदार्थ (i) की तुलना में अधिक लचीला है और इसलिए पदार् (ii) अधिक टूटल लचीला है
(b) पदार्थ (i) और (ii) के एक ही लचीलापन और एक ही टूटल लचीलापन है
(c) पदार्थ (ii) के ऊतक क्षेत्र में पदार्थ (i) की तुलना में अधिक विस्तार है
(d) पदार्थ (ii) पदार्थ (i) की तुलना में अधिक टूटल है
उत्तर दिखाएं
सोचने की प्रक्रिया
हमें प्रत्येक पदार्थ के अंतिम तनाव शक्ति की तुलना करनी होगी। अंतिम तनाव शक्ति अधिक वाला पदार्थ अधिक विस्तार तक लचीला होगा।
उत्तर $(c, $d)$
दो ग्राफ से स्पष्ट है कि पदार्थ (ii) के अंतिम तनाव शक्ति अधिक है, इसलिए पदार्थ (ii) के ऊतक क्षेत्र में पदार्थ (i) की तुलना में अधिक विस्तार है। पदार्थ (ii) के टूटने के बिंदु कम दूरी पर है, इसलिए यह अधिक टूटल है।
-
(a) पदार्थ (ii) पदार्थ (i) की तुलना में अधिक लचीला है और इसलिए पदार्थ (ii) अधिक टूटल है:
- गलत क्योंकि लचीलापन और टूटल लचीलापन के बीच सीधा संबंध नहीं है। लचीलापन एक पदार्थ की विकृति के बाद अपनी मूल आकृति में वापस आने की क्षमता को संदर्भित करता है, जबकि टूटल लचीलापन एक पदार्थ के बिना बड़ी विकृति के बिना टूटने की प्रवृत्ति को संदर्भित करता है। ग्राफ में लचीलापन और टूटल लचीलापन के बीच सीधा संबंध नहीं दिखाया गया है।
-
(b) पदार्थ (i) और (ii) के एक ही लचीलापन और एक ही टूटल लचीलापन है:
- गलत क्योंकि दोनों पदार्थों के तनाव-ऊतक व्यवहार ग्राफ में अलग-अलग दिखाए गए हैं। पदार्थ (ii) के अंतिम तनाव शक्ति अधिक है और पदार्थ (i) के तुलना में अलग टूटने के बिंदु है, जो इस बात को संकेत करता है कि वे एक ही लचीलापन या टूटल लचीलापन नहीं रखते हैं।
10. एक तार छत से लटकाया गया है और इसके दूसरे सिरे से लटकाए गए भार $F$ के कारण खिंचा जाता है। छत द्वारा तार पर लगाए गए बल का परिमाण और दिशा भार के बराबर और विपरीत होता है।
(a) तार के किसी भी काट $A$ पर तनाव $F / A$ होता है
(b) किसी भी काट पर तनाव शून्य होता है
(c) तार के किसी भी काट $A$ पर तनाव $2 F / A$ होता है
(d) तार के किसी भी काट $A$ पर तनाव $F$ होता है
उत्तर दिखाएँ
उत्तर $(a, d)$
चित्र में दिखाए गए अनुसार
स्पष्ट रूप से, प्रत्येक काट पर बल $F$ होता है।
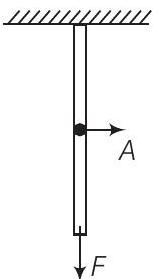
अब सूत्र के उपयोग से,
$$ \begin{aligned} \text { तनाव } & =\frac{\text { तनाव }}{\text { क्षेत्रफल }}=\frac{F}{A} \\ \text { तनाव } & =\text { आवेशित बल }=F \end{aligned} $$
-
(b) किसी भी काट पर तनाव शून्य होता है: यह विकल्प गलत है क्योंकि तनाव को इकाई क्षेत्रफल पर बल के रूप में परिभाषित किया गया है। क्योंकि तार पर बल $ F $ कार्य कर रहा है और तार का काट क्षेत्रफल $ A $ है, तनाव शून्य नहीं हो सकता। यह $ \frac{F}{A} $ द्वारा दिया गया है।
-
(c) तार के किसी भी काट $ A $ पर तनाव $ 2F / A $ होता है: यह विकल्प गलत है क्योंकि तनाव की गणना बल के विभाजन द्वारा क्षेत्रफल के रूप में की जाती है। तार पर कार्य कर रहा बल $ F $ है, नहीं $ 2F $। इसलिए, सही तनाव $ \frac{F}{A} $ है, नहीं $ \frac{2F}{A} $।
11. एक छड़ की लंबाई $l$ और नगण्य द्रव्यमान है, जिसके दो सिरों पर दो तारों द्वारा संलग्न की गई है, स्टील (तार $A$ ) और एल्यूमीनियम (तार $B$ ) के बराबर लंबाई (चित्र)। तार $A$ और $B$ के काट क्षेत्रफल क्रमशः $1.0 mm^{2}$ और $2.0 mm^{2}$ हैं। $\quad(Y_{A l}=70 \times 10^{9} Nm^{-2}$ और $Y_{\text {steel }}=200 \times 10^{9} Nm^{-2})$
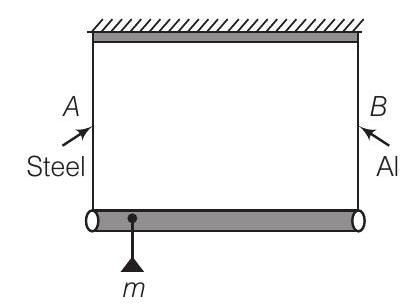
(a) द्रव्यमान $m$ को तार $A$ के पास लटकाया जाना चाहिए ताकि दोनों तारों में समान तनाव हो सके
(b) द्रव्यमान $m$ को $B$ के पास लटकाया जाना चाहिए ताकि दोनों तारों में समान तनाव हो
(c) द्रव्यमान $m$ को तारों के मध्य बिंदु पर लटकाया जाना चाहिए ताकि दोनों तारों में समान तनाव हो
(d) द्रव्यमान $m$ को तार $A$ के पास लटकाया जाना चाहिए ताकि दोनों तारों में समान विकृति हो
उत्तर दिखाएं
उत्तर $(b, d)$
मान लीजिए द्रव्यमान $x$ की दूरी पर $B$ के सिरे से रखा गया है।
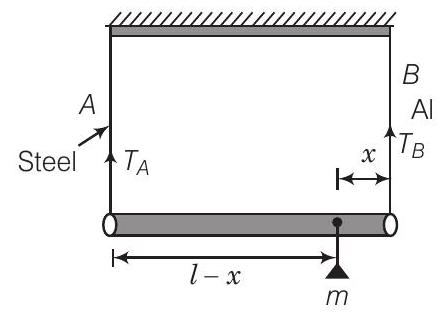
मान लीजिए तार $A$ और $B$ में तनाव क्रमशः $T_{A}$ और $T_{B}$ है।
सिस्टम के घूर्णन संतुलन के लिए,
$$ \begin{aligned} & \sum \tau=0 \\ & \Rightarrow \quad T_{B} x-T_{A}(l-x)=0 \\ & \Rightarrow \quad \frac{T_{B}}{T_{A}}=\frac{l-x}{x} \\ & \text { तार } A में तनाव = S_{A}=\frac{T_{A}}{a_{A}} \\ & \text { तार } B में तनाव = S_{B}=\frac{T_{B}}{a_{B}} \end{aligned} $$
जहाँ $a_{A}$ और $a_{B}$ क्रमशः तार $A$ और $B$ के क्रॉस-सेक्शनल क्षेत्र हैं।
प्रश्न के अनुसार, $a_{B}=2 a_{A}$
अब, समान तनाव के लिए
$$ \begin{aligned} & \Rightarrow \quad \frac{T_{A}}{a_{A}}=\frac{T_{B}}{a_{B}} \Rightarrow \frac{T_{B}}{T_{A}}=\frac{a_{B}}{a_{A}}=2 \\ & \Rightarrow \quad \frac{l-x}{x}=2 \Rightarrow \frac{l}{x}-1=2 \\ & \Rightarrow \quad x=\frac{l}{3} \Rightarrow l-x=l-l / 3=\frac{2 l}{3} \end{aligned} $$
अतः, द्रव्यमान $m$ को $B$ के पास रखना चाहिए।
समान विकृति के लिए, $\quad( strain )_A $= $( strain)_B $
$ \Rightarrow \quad \frac{(Y_{A})}{S_{A}}=\frac{Y_{B}}{S_{B}} \quad \text { (जहाँ } Y_{A} \text { और } Y_{B} \text { यंग प्रतिबल हैं) } $
$ \Rightarrow \quad \frac{Y_{\text {steel }}}{T_{A} / a_{A}}=\frac{Y_{A l}}{T_{B} / a_{B}} $
$ \Rightarrow \quad \frac{Y_{\text {steel }}}{Y_{\text {Al }}}=\frac{T_{A}}{T_{B}} \times \frac{a_{B}}{a_{A}}=(\frac{x}{l-x})(\frac{2 a_{A}}{a_{A}}) $
$ \Rightarrow \quad \frac{200 \times 10^{9}}{70 \times 10^{9}}=\frac{2 x}{l-x} \Rightarrow \frac{20}{7}=\frac{2 x}{l-x} $
$ \Rightarrow \quad \frac{10}{7}=\frac{x}{l-x} \Rightarrow 10 l-10 x=7 x $
$ \Rightarrow \quad 17 x=10 l \quad \Rightarrow \quad x=\frac{10 l}{17} $
$ l-x=l-\frac{10 l}{17}=\frac{7 l}{17}$
इसलिए, द्रव्यमान $m$ को तार $A$ के निकट रखा जाना चाहिए।
-
विकल्प (a) गलत है: द्रव्यमान को तार $A$ के निकट लटकाना दोनों तारों में समान तनाव नहीं बनाएगा। समान तनाव के लिए सही स्थान तार $B$ के निकट होगा, जैसा कि समाधान में निर्धारित किया गया है। इसका कारण यह है कि तार $B$ का क्रॉस-सेक्शनल क्षेत्रफल बड़ा है, और तनाव के संतुलन के लिए तार $B$ में तनाव अधिक होना आवश्यक है, जिसे तार $B$ के निकट द्रव्यमान के लटकाने से प्राप्त किया जा सकता है।
-
विकल्प (c) गलत है: तारों के मध्य बिंदु पर द्रव्यमान लटकाने से दोनों तारों में समान तनाव नहीं होगा। प्रत्येक तार में तनाव तनाव बल पर निर्भर करता है, जो द्रव्यमान के स्थान पर प्रभावित होता है। द्रव्यमान को मध्य बिंदु पर रखने से दोनों तारों के क्रॉस-सेक्शनल क्षेत्रफल और यंग के माड़ूलस के अंतर को ध्यान में नहीं लिया जाएगा, जिसके कारण असमान तनाव होगा।
-
विकल्प (d) सही है: यह विकल्प वास्तव में सही है, जैसा कि समाधान में निर्धारित किया गया है। द्रव्यमान को तार $A$ के निकट लटकाना दोनों तारों में समान विकृति बनाएगा। इसका कारण यह है कि यंग के माड़ूलस और क्रॉस-सेक्शनल क्षेत्रफल के अंतर के कारण द्रव्यमान को इस तरह स्थान देना आवश्यक है कि विकृति (जो तनाव के यंग के माड़ूलस से विभाजित होती है) समान हो।
12. एक आदर्श द्रव के लिए,
(a) आयतन प्रतिरोधकता अपरिमित होती है
(b) आयतन प्रतिरोधकता शून्य होती है
(c) अपसामान्य प्रतिरोधकता अपरिमित होती है
(d) अपसामान्य प्रतिरोधकता शून्य होती है
उत्तर दिखाएँ
उत्तर $(a, d)$
क्योंकि एक आदर्श द्रव अकम्पनी नहीं होता।
इसलिए, आयतन में परिवर्तन, $\quad \Delta V=0$
$$ \begin{aligned} & \text { आयतन प्रतिरोधकता } B=\frac{\text { तनाव }}{\text { आयतन विकृति }}=\frac{F / A}{\Delta V / V}=\frac{F}{A} \times \frac{V}{\Delta V}=\infty \\ & \text { कम्पनीता, } K=\frac{1}{B}=\frac{1}{\infty}=0 \end{aligned} $$
क्योंकि आदर्श द्रव में कोई अपसामान्य बल (गैर-संपीड़न बल) नहीं होता, इसलिए, अपसामान्य प्रतिरोधकता $=0$।
-
विकल्प (b) आयतन प्रतिरोधकता शून्य है: यह गलत है क्योंकि आदर्श तरल के लिए आयतन प्रतिरोधकता वास्तव में अपरिमित होती है। आदर्श तरल अकम्पनीय होता है, जिसका अर्थ है कि कोई आवेग लगाने पर इसका आयतन बदल नहीं जाता। इसलिए, आयतन प्रतिरोधकता, जो संपीड़न के विरोध को मापती है, अपरिमित होती है।
-
विकल्प (c) अपरिमित अपस्थापन प्रतिरोधकता है: यह गलत है क्योंकि आदर्श तरल के लिए अपस्थापन प्रतिरोधकता शून्य होती है। आदर्श तरल अपस्थापन बल के विरुद्ध बल नहीं उत्पन्न कर सकता; यह कोई भी स्पर्शीय बल लगाने पर बहता है, जिसका अर्थ है कि इसकी अपस्थापन विकृति के विरुद्ध अकम्पनीयता नहीं होती।
13. एक समान व्यास के तांबे और स्टील के तार एक दूसरे के संपर्क में जुड़े हुए हैं। इस संयोजन पर एक विकृति बल $F$ लगाया जाता है जो कुल लम्बाई में $1$ सेमी की वृद्धि करता है। दोनों तारों के लिए
(a) समान तनाव
(b) अलग-अलग तनाव
(c) समान विकृति
(d) अलग-अलग विकृति
उत्तर दिखाएं
उत्तर $(a, d)$
एक चित्र में एक विकृति बल $F$ लगाया गया है।
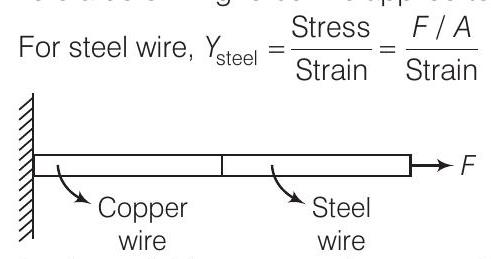
जहाँ $F$ प्रत्येक तार में तनाव है और $A$ प्रत्येक तार का काट क्षेत्रफल है।
क्योंकि $F$ और $A$ दोनों तारों के लिए समान है, इसलिए दोनों तारों के लिए तनाव समान होगा।
क्योंकि,
$( विकृति )_{स्टील } $ = $\frac{ तनाव }{Y _ {स्टील }} $,
$(विकृति ) _ {तांबा} $= $\frac{ तनाव }{Y _ {तांबा }} $
$Y_{\text {स्टील }} \neq Y_{\text {तांबा }}$
इसलिए, दोनों तारों के लिए विकृति अलग-अलग होगी।
-
विकल्प (b) अलग-अलग तनाव: यह विकल्प गलत है क्योंकि दोनों तारों में तनाव समान है। तनाव तार के क्षेत्रफल पर लगाए गए बल के अनुपात में परिभाषित होता है, और क्योंकि बल $F$ और काट क्षेत्रफल $A$ दोनों तारों के लिए समान है, तनाव भी समान होगा।
-
विकल्प (c) समान विकृति: यह विकल्प गलत है क्योंकि दोनों तारों में विकृति अलग-अलग है। विकृति तार के मूल लम्बाई के संबंध में लम्बाई में परिवर्तन के अनुपात में परिभाषित होती है, और इसकी गणना तार के यंग प्रतिरोधकता ($Y$) पर निर्भर करती है। क्योंकि स्टील और तांबे की यंग प्रतिरोधकता अलग-अलग है ($Y_{\text{स्टील}} \neq $ $Y_{\text{तांबा}}$), भले ही तनाव समान हो, दोनों तारों में विकृति अलग-अलग होगी।
बहुत छोटे उत्तर प्रकार के प्रश्न
14. स्टील के यंग प्रत्यास्थता गुणांक रबर के यंग प्रत्यास्थता गुणांक से बहुत अधिक होता है। समान दीर्घाकार विकृति के लिए, किसके तनाव तनाव अधिक होगा?
उत्तर दिखाएं
उत्तर यंग प्रत्यास्थता गुणांक $(Y)=\frac{\text { तनाव }}{\text { दीर्घाकार विकृति }}$
समान दीर्घाकार विकृति के लिए, $Y \propto \text { तनाव }$
$\therefore$ $\frac{Y _ {\text {स्टील }}}{Y _ {\text {रबर }}} =\frac{(\text { तनाव }) _ {\text {स्टील }}}{(\text { तनाव }) _ {\text {रबर }}}$
इसलिए, समीकरण (i) से,
$ \frac{(\text { तनाव }) _ {\text {स्टील }}}{(\text { तनाव }) _ {\text {रबर }}}>1 $ $ \Rightarrow \quad(\text { तनाव }) _ {\text {स्टील }}>\text { (तनाव) } _ {\text {रबर }}$
15. तनाव एक सदिश राशि है?
उत्तर दिखाएं
उत्तर तनाव $=\frac{\text { आंतरिक बल के परिमाण }}{\text { परिसेक्शन क्षेत्रफल }}$
इसलिए, तनाव एक अदिश राशि है।
16. स्टील और कॉपर के समान आकार के तार बराबर खिंचे गए हैं। किस तार पर अधिक कार्य करना पड़ेगा?
उत्तर दिखाएं
उत्तर एक तार को खिंचने में किया गया कार्य निम्न द्वारा दिया जाता है: $W=\frac{1}{2} F \times \Delta l$
[जहाँ $F$ आवेग बल है और $\Delta l$ तार में विस्तार है]। जब स्टील और कॉपर के तार बराबर खिंचे गए हैं। इसलिए, समान बल $(F)$ के लिए,
$$ W \propto \Delta l $$
$$ \text { यंग प्रत्यास्थता गुणांक }(Y)=\frac{F}{A} \times \frac{l}{\Delta l} \Rightarrow \Delta l=\frac{F}{A} \times \frac{l}{Y} $$
क्योंकि दोनों तार समान हैं, $\quad \Delta l \propto \frac{1}{Y}$
समीकरण (i) और (ii) से, हम प्राप्त करते हैं $\quad W \propto \frac{1}{Y}$
$$ \begin{matrix} \therefore & \frac{W_{\text {स्टील }}}{W_{\text {कॉपर }}}=\frac{Y_{\text {कॉपर }}}{Y_{\text {स्टील }}}<1 & \text { (क्योंकि, } .Y_{\text {स्टील }}>Y_{\text {कॉपर }}) \\ \Rightarrow & W_{\text {स्टील }}<W_{\text {कॉपर }} \end{matrix} $$
इसलिए, कॉपर तार को खिंचने में अधिक कार्य करना पड़ेगा।
17. पूर्ण अविश्वासी वस्तु के यंग प्रत्यास्थता मापांक क्या होता है?
उत्तर दिखाएं
उत्तर यंग प्रत्यास्थता मापांक $(Y)=\frac{F}{A} \times \frac{l}{\Delta l}$
एक पूर्ण अविश्वासी वस्तु के लिए, लंबाई में परिवर्तन $\Delta l=0$
$$ Y=\frac{F}{A} \times \frac{l}{0}=\infty $$
अतः, पूर्ण अविश्वासी वस्तु के यंग प्रत्यास्थता मापांक अपरिमित होता है $(\infty)$।
18. पूर्ण अविश्वासी वस्तु के आयतन प्रत्यास्थता मापांक क्या होता है?
उत्तर दिखाएं
उत्तर आयतन प्रत्यास्थता मापांक $(K)=\frac{p}{\Delta V / V}=\frac{p V}{\Delta V}$
पूर्ण अविश्वासी वस्तु के लिए, आयतन में परिवर्तन $\Delta V=0$
$\therefore \quad K=\frac{p V}{0}=\infty$
अतः, पूर्ण अविश्वासी वस्तु के आयतन प्रत्यास्थता मापांक अपरिमित होता है $(\infty)$।
19. एक तार की लंबाई $L$ तथा त्रिज्या $r$ है जो एक सिरे पर अटैच कर दिया गया है। जब दूसरे सिरे पर बल $f$ लगाया जाता है तो इसकी लंबाई $l$ बढ़ जाती है। एक अन्य तार जो उसी सामग्री का है, लंबाई $2 L$ तथा त्रिज्या $2 r$ है, जिस पर बल $2 f$ लगाया जाता है। इस तार की लंबाई में वृद्धि ज्ञात कीजिए।
उत्तर दिखाएं
चिंतन प्रक्रिया
इस समस्या में हम बेल्ट के नियम को लागू करना होगा और तारों में वृद्धि की तुलना करनी होगी।
उत्तर स्थिति चित्र में दिखाई गई है।
अब, यंग प्रत्यास्थता मापांक $(Y)=\frac{f}{A} \times \frac{L}{l}$
पहले तार के लिए,
$Y=\frac{f}{\pi r^{2}} \times \frac{L}{l}$
दूसरे तार के लिए,
$Y=\frac{2 f}{\pi(2 r)^{2}} \times \frac{2 L}{l^{\prime}}$
$=\frac{f}{\pi r^{2}} \times \frac{L}{l^{\prime}}$
समीकरण (i) और (ii) से,
$$
\frac{f}{\pi r^{2}} \times \frac{L}{l}=\frac{f}{\pi r^{2}} \times \frac{L}{l^{\prime}}
$$
$$
l=l^{\prime}
$$

( $\because$ दोनों तार एक ही सामग्री के हैं, अतः यंग प्रत्यास्थता मापांक समान होगा।)
20. एक स्टील छड़ $(Y=2.0 \times 10^{11} N / m^{2}$ तथा $\alpha=10^{-50}{ }^{\circ} C^{-1})$ की लंबाई $1 m$ तथा काट के क्षेत्रफल $1 cm^{2}$ है जिसे $0^{\circ} C$ से $200^{\circ} C$ तक गरम किया जाता है, बिना इसे फैलने या मोड़ने के। छड़ में उत्पन्न तनाव क्या होगा?
उत्तर दिखाएं
सोचने की प्रक्रिया
रॉड के तापमान में वृद्धि के कारण लंबाई बढ़ जाती है। रॉड के रैखिक विस्तार के लिए ऊष्मीय विस्तार के समीकरण का उपयोग किया जाएगा।
उत्तर दिया गया, स्टील का यंग प्रतिबल $Y=2.0 \times 10^{11} N / m^{2}$
ऊष्मीय विस्तार गुणांक $\alpha=10^{-5}{ }^{\circ} C^{-1}$
लंबाई $l=1 m$
काट क्षेत्रफल $A=1 cm^{2}=1 \times 10^{-4} m^{2}$
तापमान में वृद्धि $\Delta t=200^{\circ} C-0^{\circ} C=200^{\circ} C$
स्टील रॉड में उत्पन्न तनाव $(F)=Y A \alpha \Delta t$
$$ \begin{aligned} & =2.0 \times 10^{11} \times 1 \times 10^{-4} \times 10^{-5} \times 200 \\ & =4 \times 10^{4} N \end{aligned} $$
21. गहरे समुद्र में एक रबर के गेंद को कितने गहराई तक ले जाया जाना चाहिए ताकि इसका आयतन 0.1% कम हो जाए। (रबर का आयतन प्रतिबल $9.8 \times 10^{8} N / m^{2}$ है; और समुद्र के पानी का घनत्व $10^{3} kg / m^{3}$ है )
उत्तर दिखाएं
उत्तर दिया गया, रबर का आयतन प्रतिबल $(K)=9.8 \times 10^{8} N / m^{2}$
समुद्र के पानी का घनत्व $(\rho)=10^{3} kg / m^{3}$
आयतन में प्रतिशत कमी, $(\frac{\Delta V}{V} \times 100)=0.1 \Rightarrow \frac{\Delta V}{V}=\frac{0.1}{100}$
$\Rightarrow \quad \frac{\Delta V}{V}=\frac{1}{1000}$
मान लीजिए कि रबर के गेंद को गहराई $h$ तक ले जाया जाता है।
$\therefore \quad$ दबाव में परिवर्तन $(p)=h \rho g$
$\therefore \quad$ आयतन प्रतिबल $(K)=|\frac{p}{\Delta V / V}|=\frac{h \rho g}{(\Delta V / V)}$
$\Rightarrow \quad h=\frac{K \times(\Delta V / V)}{\rho g}=\frac{9.8 \times 10^{8} \times \frac{1}{1000}}{10^{3} \times 9.8}=100 m$
22. एक ट्रक एक स्टील केबल के माध्यम से एक कार को गड्ढे से बाहर खींच रहा है, जो 9.1 मीटर लंबा है और 5 मिमी त्रिज्या का है। जब कार बर्बाद होने लगती है, तो केबल में तनाव 800 एन है। केबल में कितनी लंबाई बढ़ गई है? (स्टील के लिए यंग प्रतिबल $2 \times 10^{11} N / m^{2}$ है )
उत्तर दिखाएं
उत्तर
$$ \begin{aligned} \text { स्टील केबल की लंबाई } l & =9.1 m \\
$$ \text { त्रिज्या } r & =5 , \text{mm}=5 \times 10^{-3} , \text{m} \\ \text { केबल में तनाव } F & =800 , \text{N} \\ \text { स्टील के यंग के मापांक } Y & =2 \times 10^{11} , \text{N}/\text{m}^{2} \\ \text { लंबाई में परिवर्तन } \Delta l & =? \\ \text { यंग के मापांक }(Y) & =\frac{F}{A} \times \frac{l}{\Delta l} \Rightarrow \Delta l=\frac{F}{\pi r^{2}} \times \frac{l}{Y} \\ & =\frac{800}{3.14 \times(5 \times 10^{-3})^{2}} \times \frac{9.1}{2 \times 10^{11}} \\ & =4.64 \times 10^{-4} , \text{m} \end{aligned} $$
23. एक ही आकार के दो ठोस गेंद, एक आईवोरी की और दूसरी नम मिट्टी की, एक ही ऊँचाई से फर्श पर गिराई जाती है। फर्श से टकराने के बाद कौन सी गेंद अधिक ऊँचाई तक उछलेगी और क्यों?
उत्तर दिखाएं
Answer क्योंकि, आईवोरी गेंद नम मिट्टी की गेंद की तुलना में अधिक विरोधी होती है, इसलिए, आईवोरी गेंद अपने मूल आकार को तेजी से पुनः प्राप्त करने की कोशिश करती है। इसलिए, आईवोरी गेंद के तुलना में नम मिट्टी की गेंद में अधिक ऊर्जा और गति परिवर्तन आईवोरी गेंद में होता है और इसलिए, फर्श से टकराने के बाद आईवोरी गेंद अधिक ऊँचाई तक उछलेगी।24. एक लंबी स्टील बार के लंबाई के अनुदिश किनारों पर लगाए गए बल $F$ के कारण बार में तनाव उत्पन्न होता है (चित्र)। एक तल जो लंबाई के साथ कोण $\theta$ बनाता है, इस तल पर तनाव और छेदन तनाव क्या होंगे?
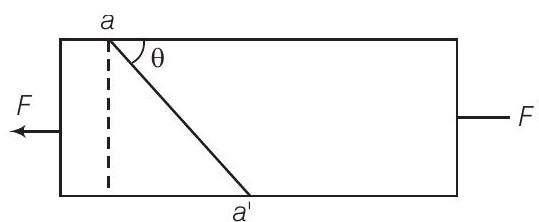
(a) तनाव अधिकतम होने के लिए कोण कौन सा होगा?
(b) छेदन तनाव अधिकतम होने के लिए कोण कौन सा होगा?
उत्तर दिखाएं
Thinking Process
इस प्रश्न को हल करने के लिए, हमें झुके तल के अनुदिश और लंबवत दिशा में बल को विभाजित करना होगा। अब, हम तनाव और छेदन तनाव की गणना आसानी से कर सकते हैं।
Answer निर्मित आरेख को ध्यान में रखें।
मान लीजिए बार के काट क्षेत्र का क्षेत्रफल $A$ है। तल aa’ के संतुलन को ध्यान में रखें। इस तल पर एक बल $F$ कार्य करता है जो अभिलंब $ON$ के साथ कोण $\frac{\pi}{2}-\theta$ बनाता है। बल $F$ को तल के अनुदिश $(F P)$ और तल के लंबवत दिशा में विभाजित करें।
$$ \begin{aligned} & F_{P}=F \cos \theta \\ & F_{N}=F \sin \theta \end{aligned} $$
मान लीजिए फलक aa’ का क्षेत्रफल $A^{\prime}$ है, तो
$$ \begin{aligned} \frac{A}{A^{\prime}} & =\sin \theta \\ \therefore \quad \text { तनाव तन्यता } & =\frac{A}{\sin \theta} \\ & =\frac{\text { अभिलम्ब बल }}{A / \sin \theta}=\frac{F \sin \theta}{A^{\prime}} \\ \text { अपघटन तनाव } & =\frac{\text { समान्तर बल }}{\text { क्षेत्रफल }} \\ & =\frac{F \cos \theta}{A / \sin \theta}=\frac{F}{A} \sin \theta \cdot \cos \theta \\ & =\frac{F}{2 A}(2 \sin \theta \cdot \cos \theta)=\frac{F}{2 A} \sin 2 \theta \end{aligned} $$
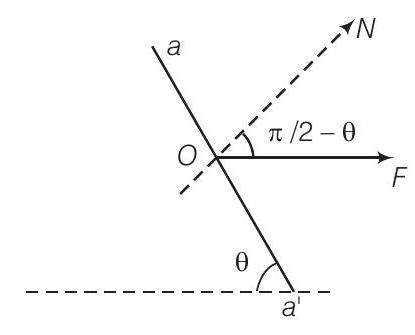
(a) तनाव तन्यता अधिकतम होने के लिए, $\sin ^{2} \theta=1$
$$ \begin{aligned} \Rightarrow & \sin \theta & =1 \\ \Rightarrow & \theta & =\frac{\pi}{2} \end{aligned} $$
(b) अपघटन तनाव अधिकतम होने के लिए,
$$ \begin{matrix} \Rightarrow & & \sin 2 \theta & =1 \\ \Rightarrow & 2 \theta & =\frac{\pi}{2} \\ \Rightarrow & & \theta & =\frac{\pi}{4} \end{matrix} $$
नोट: हम तनाव के सूत्र को सीधे लगाने नहीं चाहिए, बलों को विभाजित करना आवश्यक है।
25. (a) एक स्टील के तार के इकाई लम्बाई पर द्रव्यमान $\mu$ है जिसका एक वृत्ताकार परिच्छेद है और इसकी त्रिज्या $0.1 cm$ है। तार की लम्बाई $10 m$ है जब यह एक दीवार पर लटके हुए मापा जाता है। तार के मुक्त सिरे पर $25 kg$ का द्रव्यमान लटकाया जाता है। मान लीजिए तार समान है और अनुप्रस्थ विकृति $<$ अक्षीय विकृति है, तार की लम्बाई में विस्तार ज्ञात कीजिए। स्टील का घनत्व $7860 kg m^{-3}$ है। (यंग के मापांक $Y=2 \times 10^{11} Nm^{-2}$ है।
(b) यदि स्टील की विक्षेपण शक्ति $2.5 \times 10^{8} Nm^{-2}$ है, तो तार के निचले सिरे पर लटकाए जा सकने वाले अधिकतम द्रव्यमान क्या है?
उत्तर दिखाएँ
सोचने की प्रक्रिया
जब तार लटकता है तो तार के विभिन्न भाग पर विभिन्न बल कार्य करते हैं। तार के सम्पूर्ण भाग के कारण तनाव ज्ञात करने के लिए, एक छोटे तत्व को लेकर उस बिंदु पर तनाव ज्ञात करें और फिर तार के सम्पूर्ण भाग के लिए समाकलन करें।
उत्तर कार्य करते समय एक छोटे तत्व के लंबाई के एक छोटे तत्व $d x$ को $x$ से बर्बाद करते हुए ध्यान दें $(x=0)$।
(a) मान लीजिए $T(x)$ और $T(x+d x)$ दो परिच्छेदों पर तनाव है जो $d x$ की दूरी पर है, तो-$-T(x+d x)+T(x)=d m g=\mu d x g$ (जहाँ $\mu$ द्रव्यमान/लंबाई है)।
$(\because d m=\mu d x)$
$$ \begin{matrix} \Rightarrow T(x) =\mu g x+C \\ \text { जब } x=0, & T(0)=M g \Rightarrow C = M g \\ \therefore T(x) =\mu g x+M g \end{matrix} $$
मान लीजिए $x$ पर $d x$ की लंबाई $d r$ बढ़ जाती है, तो
$$ \begin{aligned} \text { यंग के मापदंड } Y & =\frac{\text { तनाव }}{\text { विकृति }} \\ \frac{T(x) / A}{d r / d x} & =Y \\ \Rightarrow \quad \frac{d r}{d x} & =\frac{1}{Y A} T(x) \\ r & =\frac{1}{Y A} \int_0^{L}(\mu g x+M g) d x \\ & =\frac{1}{Y A}[\frac{\mu g x^{2}}{2}+M g x]_0^{L} \\ & =\frac{1}{Y A}[\frac{m g L^{2}}{2}+M g L] \end{aligned} $$
$$ \begin{matrix} {[\because d T=T(x+d x)-T(x)]} \\ \text { (एकीकरण के बाद) } \end{matrix} $$
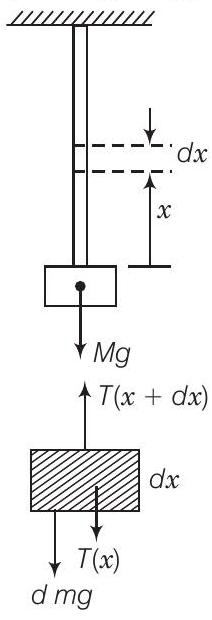
( $m$ तार का द्रव्यमान है)
$$ A=\pi \times(10^{-3})^{2} m^{2} $$
$$ \begin{aligned} & Y=200 \times 10^{9} Nm^{-2} \\ & m=\pi \times(10^{-3})^{2} \times 10 \times 7860 kg \end{aligned} $$
$$ \begin{aligned} \therefore \quad r & =\frac{1}{2 \times 10^{11} \times \pi \times 10^{-6}} \quad[\frac{\pi \times 786 \times 10^{-3} \times 10 \times 10}{2}+25 \times 10 \times 10] \\ & =[196.5 \times 10^{-6}+3.98 \times 10^{-3}] \approx 4 \times 10^{-3} m \end{aligned} $$
(b) स्पष्ट रूप से तनाव $x=L$ पर अधिकतम होगा
$$\therefore T =\mu g L+M g=(m+M) g$$
$$ \text{अपसार बल = (अपसार शक्ति Y) क्षेत्रफल} =250 \times 10^{6} \times \pi \times(10^{-3})^{2}=250 \times \pi N$$
$$ \text{अपसार बिंदु पर} \quad[\because m=\mu L]$$
$$\Rightarrow \quad(m+M) g =250 \times \pi$$
$$\Rightarrow m =\pi \times(10^{-3})^{2} \times 10 \times 7860 \ll M$$
$$\therefore M g \approx 250 \times \pi$$
$\text{अतः}, M =\frac{250 \times \pi}{10}=25 \times \pi \approx 75 kg$.
26. एक स्टील की छड़ जिसकी लंबाई $2 l$, क्रॉस सेक्शनल क्षेत्र $A$ और द्रव्यमान $M$ है, एक क्षैतिज समतल में एक अक्ष के चारों ओर घूम रही है जो छड़ के केंद्र से गुजरता है। यदि $Y$ स्टील के यंग प्रत्यास्थता गुणांक है, तो छड़ की लंबाई में विस्तार ज्ञात कीजिए। (मान लीजिए कि छड़ समान घनत्व की है)
उत्तर दिखाएं
सोचने की प्रक्रिया
इस प्रश्न को हल करने के लिए, हमें एक छोटे तत्व को ध्यान में रखना होगा, इस तत्व पर छड़ में तनाव की गणना करनी होगी और फिर पूरी छड़ के लिए गणना करनी होगी।
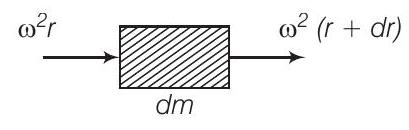
उत्तर चित्र में दिखाए गए रूप में $r$ पर चौड़ाई $d r$ वाले एक तत्व को लें। मान लीजिए $T(r)$ और $T(r+d r)$ क्रमशः $r$ और $r+d r$ पर तनाव है।
तत्व पर कुल अपकेंद्री बल $=\omega^{2} r d m$
(जहाँ $\omega$ छड़ की कोणीय वेग है)
$$ \begin{aligned} & =\omega^{2} r \mu d r \\ & \Rightarrow \quad T(r)-T(r+d r)=\mu \omega^{2} r d r \\ & \Rightarrow \quad-d T=\mu \omega^{2} r d r \\ & {[\because \text { तनाव और अपकेंद्री बल विपरीत दिशा में है]}} \\ & \therefore \quad-\int_{T=0}^{T} d T=\int_{r=l}^{r=r} \mu \omega^{2} r d r \quad[\because T=0 \text { जब } r=l] \\ & \Rightarrow \quad T(r)=\frac{\mu \omega^{2}}{2}(l^{2}-r^{2}) \end{aligned} $$
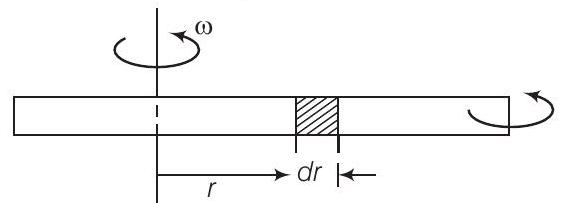
मान लीजिए तत्व $d r$ की लंबाई में वृद्धि $\Delta r$ है
$$ \begin{aligned} & \text { इसलिए }, \quad \text { यंग प्रत्यास्थता गुणांक } Y=\frac{\text { तनाव }}{\text { विकृति }}=\frac{T(r) / A}{\frac{\Delta r}{d r}} \\ & \therefore \quad \frac{\Delta r}{d r}=\frac{T(r)}{A}=\frac{\mu \omega^{2}}{2 Y A}(l^{2}-r^{2}) \\ & \therefore \quad \Delta r=\frac{1}{Y A} \frac{\mu \omega^{2}}{2}(l^{2}-r^{2}) d r \\ & \therefore \quad \Delta=\text { दाहिने हिस्से में लंबाई में परिवर्तन }=\frac{1}{Y A} \frac{\mu \omega^{2}}{2} \int_0^{l}(l^{2}-r^{2}) d r \\ $$
$$ \begin{aligned} & =(\frac{1}{Y A}) \frac{\mu \omega^{2}}{2}[l^{3}-\frac{l^{3}}{3}]=\frac{1}{3 Y A} \mu \omega^{2} l^{2} \\ & \therefore \quad \text { कुल लंबाई में परिवर्तन }=2 \Delta=\frac{2}{3 Y A} \mu \omega^{2} l^{2} \end{aligned} $$
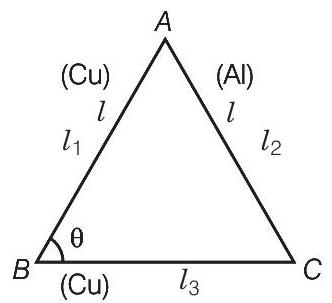
27. एक समबाहु त्रिभुज $A B C$ दो Cu छड़ों $A B$ और $B C$ और एक Al छड़ द्वारा बनाया गया है। इसे इस प्रकार गर्म किया जाता है कि प्रत्येक छड़ के तापमान में $\triangle T$ की वृद्धि होती है। कोण $A B C$ में परिवर्तन ज्ञात कीजिए। [Cu के रैखिक प्रसार गुणांक $\alpha_1$ है, Al के रैखिक प्रसार गुणांक $\alpha_2$ है ]
उत्तर दिखाएं
सोचने की प्रक्रिया
तापमान में वृद्धि के कारण प्रत्येक भुजा की लंबाई बदल जाएगी और इसलिए किसी भी शीर्ष के संगत कोण भी बदल जाएगा।
उत्तर चित्र देखें जो नीचे दिया गया है
मान लीजिए
$$ \begin{aligned} l_1 & =A B, l_2=A C, l_3=B C \\ \cos \theta & =\frac{l_3^{2}+l_1^{2}-l_2^{2}}{2 l_3 l_1} \end{aligned} $$
$$ \Rightarrow \quad 2 l_3 l_1 \cos \theta=l_3^{2}+l_1^{2}-l_2^{2} $$
दोनों ओर के चर संबंधित अवकलन करने पर, हमें प्राप्त होता है:
$$2(l_1 \frac{dl_3}{dt} + l_3 \frac{dl_1}{dt}) \cos \theta - 2l_1l_3 \sin \theta \frac{d\theta}{dt} = 2l_1 \frac{dl_1}{dt} + 2l_3 \frac{dl_3}{dt} - 2l_2 \frac{dl_2}{dt}$$
अब, हमें दिया गया है कि:
$$l_1 = l_2 = l_3 = l$$
$$\frac{dl_1}{dt} = l \alpha_1 \Delta T$$
$$\frac{dl_2}{dt} = l \alpha_2 \Delta T$$
$$\frac{dl_3}{dt} = l \alpha_1 \Delta T$$
इन मानों को समीकरण में बदलने पर, हमें प्राप्त होता है:
$$2(l \cdot l \alpha_1 \Delta T + l \cdot l \alpha_1 \Delta T) \cos \theta - 2l \cdot l \sin \theta \frac{d\theta}{dt} = 2l \cdot l \alpha_1 \Delta T + 2l \cdot l \alpha_1 \Delta T - 2l \cdot l \alpha_2 \Delta T$$
दोनों ओर $2l^2$ से विभाजित करने पर, हम प्राप्त करते हैं:
$$2\alpha_1 \Delta T \cos \theta - \sin \theta \frac{d\theta}{dt} = 2\alpha_1 \Delta T - \alpha_2 \Delta T$$
अब, हमें दिया गया है कि $\theta = 60^\circ$। इस मान को समायोजित करने पर, हम प्राप्त करते हैं:
$$\sin \theta \frac{d\theta}{dt} = 2\alpha_1 \Delta T (\cos \theta - 1) + \alpha_2 \Delta T$$
$$\frac{\sqrt{3}}{2} \frac{d\theta}{dt} = 2\alpha_1 \Delta T (\frac{1}{2} - 1) + \alpha_2 \Delta T$$
$$\frac{\sqrt{3}}{2} \frac{d\theta}{dt} = -\alpha_1 \Delta T + \alpha_2 \Delta T$$
$$\frac{d\theta}{dt} = \frac{2}{\sqrt{3}} (\alpha_2 - \alpha_1) \Delta T$$
इसलिए, अंतिम उत्तर है:
$$\frac{d\theta}{dt} = \frac{2}{\sqrt{3}} (\alpha_2 - \alpha_1) \Delta T$$
या
$$d\theta = \frac{2}{\sqrt{3}} (\alpha_2 - \alpha_1) \Delta T$$
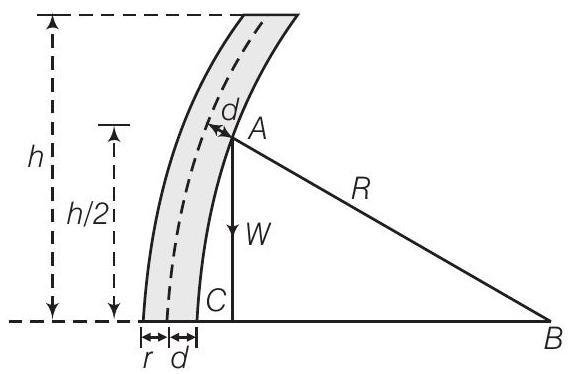
28. प्रकृति में, संरचनात्मक भागों के विफल होने के अधिकांश मामले घूर्णन या झुकाव के कारण बड़े टॉर्क के कारण होते हैं, जो तनाव या संपीड़न तनाव के कारण नहीं होते। इस संरचनात्मक विघटन की प्रक्रिया को झुकाव कहते हैं और ऊंचे बेलनाकार संरचनाओं जैसे पेड़ों के मामले में, टॉर्क अपने भार के कारण होता है जो संरचना को झुकाव देता है। इसलिए, गुरुत्व केंद्र से गुजरने वाली ऊर्ध्वाधर रेखा आधार में नहीं आती है। गुरुत्व के कारण झुकाव के कारण वृक्ष के केंद्रीय अक्ष के चारों ओर उत्पन्न तांत्रिक टॉर्क द्वारा दिया गया है $\frac{Y \pi r^{4}}{4 R}$. $Y$ यंग के मापांक है, $r$ वृक्ष के त्रिज्या है और $R$ वृक्ष के ऊंचाई के अक्ष के अनुदिश झुके सतह की वक्रता त्रिज्या है (गुरुत्व केंद्र वाले तटस्थ सतह)। दिए गए त्रिज्या के लिए वृक्ष की आवश्यक ऊंचाई का अनुमान लगाएं।
उत्तर दिखाएँ
सोचने की प्रक्रिया
इस प्रश्न में, तांत्रिक टॉर्क दिया गया है और हमें भार के कारण झुकाव के कारण उत्पन्न टॉर्क की गणना करनी है और दिए गए मान के साथ तुलना करनी है।
उत्तर प्रश्न के अनुसार आरेख को ध्यान में रखते हुए, वृक्ष के त्रिज्या $r$ के त्रुंग के झुकाव टॉर्क $=\frac{Y \pi r^{4}}{4 R}$
जहां $R$ झुके सतह की वक्रता त्रिज्या है।
जब वृक्ष झुकने के बराबर होता है $W d=\frac{Y \pi r^{4}}{4 R}$
यदि $R \gg h$, तो भूमि से गुरुत्व केंद्र की ऊंचाई $l \approx \frac{1}{2} h$ होती है।
$\quad \triangle A B C$ से, $R^{2} \simeq(R-d)^{2}+(\frac{1}{2} h)^{2}$
यदि $d \ll R$, $R^{2} \simeq R^{2}-2 R d+\frac{1}{4} h^{2}$
$\therefore \quad d=\frac{h^{2}}{8 R}$
यदि $\omega_0$ वजन/आयतन है
$$ \begin{aligned} & \qquad \frac{Y \pi r^{4}}{4 R}=\omega_0(\pi r^{2} h) \frac{h^{2}}{8 R} \quad[\because \text { बल-आघूर्ण वजन द्वारा उत्पन्न होता है }] \\ & \Rightarrow \quad h \simeq(\frac{2 Y}{\omega_0})^{1 / 3} r^{2 / 3} \\ & \text { अतः, आवश्यक ऊंचाई }=h=(\frac{2 Y}{\omega_0})^{1 / 3} r^{2 / 3} . \end{aligned} $$
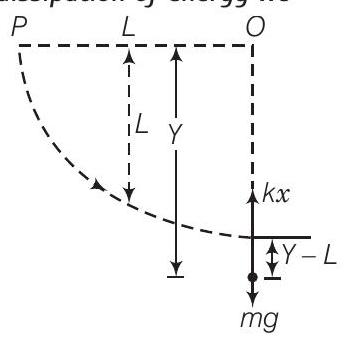
29. एक चट्टान जिसका द्रव्यमान $m$ है, एक तार से बांध दिया गया है जिसका द्रव्यमान नगण्य है और बल नियतांक $k$ है। तार की अतिरिक्त लंबाई $L$ है और इसका द्रव्यमान नगण्य है। तार के दूसरे सिरे को बिंदु $P$ पर लगे नाखून से बांध दिया गया है। आरंभ में चट्टान बिंदु $P$ के समान स्तर पर है। चट्टान को बिंदु $P$ से ऊर्ध्वाधर रूप से गिराया जाता है।
(a) चट्टान एक समय के लिए आवर्त रूप से रुक जाने पर ऊपर से दूरी $y$ ज्ञात कीजिए।
(b) इस गिरावट में चट्टान की अधिकतम चाल क्या होगी?
(c) चट्टान अपने निम्नतम बिंदु तक पहुंच जाने के बाद गति की प्रकृति क्या होगी?
उत्तर दिखाएँ
सोचने की प्रक्रिया
इस समस्या में, दिया गया तार अतिरिक्त है और ऊर्जा का कोई नुकसान नहीं होता है, इसलिए हम यांत्रिक ऊर्जा के संरक्षण को लागू कर सकते हैं।
उत्तर चित्र को ध्यान में रखते हुए, चट्टान को बिंदु $p$ से गिराया जाता है।
(a) चट्टान लंबाई $L$ तक गिरते वक्त यह मुक्त गिरावट में होगी। इसके बाद तार की अतिरिक्तता चट्टान को एक आवर्त गति में बलपूर्वक ले जाएगी। मान लीजिए कि चट्टान बिंदु $y$ पर एक समय के लिए आवर्त रूप से रुक जाती है।
चट्टान की स्थितिज ऊर्जा की कमी तार में तारित ऊर्जा के रूप में होती है।
$$ m g y=\frac{1}{2} k(y-L)^{2} $$
$$ \begin{aligned} \Rightarrow \quad m g y & =\frac{1}{2} k y^{2}-k y L+\frac{1}{2} k L^{2} \Rightarrow \frac{1}{2} k y^{2}-(k L+m g) y+\frac{1}{2} k L^{2}=0 \\ y & =\frac{(k L+m g) \pm \sqrt{(k L+m g)^{2}-k^{2} L^{2}}}{k}=\frac{(k L+m g) \pm \sqrt{2 m g k L+m^{2} g^{2}}}{k} \end{aligned} $$
धनात्मक चिह्न को बरकरार रखें।
$$ \therefore \quad y=\frac{(k L+m g)+\sqrt{2 m g k L+m^{2} g^{2}}}{k} $$
(b) सरल आवर्त गति में, अधिकतम वेग तब प्राप्त होता है जब वस्तु “संतुलन स्थिति” से गुजरती है, अर्थात जब क्षणिक त्वरण शून्य होता है। अर्थात $m g-k x=0$, जहाँ $x$ $L$ से बढ़ी विस्तार है।
$\Rightarrow$ $m g=k x$
मान लीजिए वेग $v$ है। तब,
$$ \begin{aligned} & \frac{1}{2} m v^{2}+\frac{1}{2} k x^{2}=m g(L+x) \quad \text { (ऊर्जा संरक्षण से) } \\ & \frac{1}{2} m v^{2}=m g(L+x)-\frac{1}{2} k x^{2} \end{aligned} $$
$$ \begin{aligned} \therefore \quad \frac{1}{2} m v^{2} & =m g(L+\frac{m g}{k})-\frac{1}{2} k \frac{m^{2} g^{2}}{k^{2}}=m g L+\frac{m^{2} g^{2}}{k}-\frac{1}{2} \frac{m^{2} g^{2}}{k} \\ \frac{1}{2} m v^{2} & =m g L+\frac{1}{2} \frac{m^{2} g^{2}}{k} \\ \therefore \quad v^{2} & =2 g L+m g^{2} / k \\ v & =(2 g L+m g^{2} / k)^{1 / 2} \end{aligned} $$
(c) जब पत्थर सबसे नीचे स्थिति में होता है, अर्थात बिंदु $P$ से क्षणिक दूरी $Y$ पर होता है, तो पत्थर के गति के समीकरण होता है
$$ \frac{m d^{2} y}{d t^{2}}=m g-k(y-L) \Rightarrow \frac{d^{2} y}{d t^{2}}+\frac{k}{m}(y-L)-g=0 $$
चर बदले करें, $z=\frac{k}{m}(y-L)-g$
$$ \therefore \quad \frac{d^{2} z}{d t^{2}}+\frac{k}{m} z=0 $$
यह द्वितीय कोटि के अवकल समीकरण है जो सरल आवर्त गति को प्रस्तुत करता है।
इसे समीकरण $\frac{d^{2} z}{d t^{2}}+\omega^{2} z=0$ के साथ तुलना करें
सरल आवर्त गति की कोणीय आवृत्ति $\omega=\sqrt{\frac{k}{m}}$
ऊपर के समीकरण के हल $z=A \cos (\omega t+\phi)$ के रूप का होगा; जहाँ $\omega=\sqrt{\frac{k}{m}}$
$$ y=(L+\frac{m g}{k})+A^{\prime} \cos (\omega t+\phi) $$
इस प्रकार, पत्थर $y_0=L+\frac{m g}{k}$ के बारे में कोणीय आवृत्ति $\omega=\sqrt{k / m}$ के साथ सरल आवर्त गति करेगा।





