सरल रेखा में गति
बहुविकल्पीय प्रश्न (MCQs)
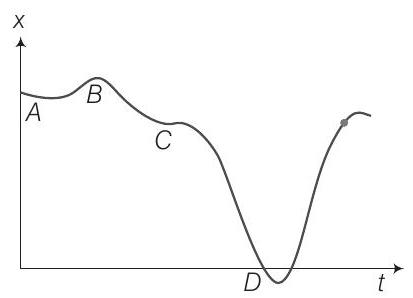
1. चित्र में दिए गए चार ग्राफ में से केवल एक ग्राफ है जिसके लिए समय अंतराल $(0, T)$ पर औसत वेग एक उपयुक्त $T$ के चयन के लिए शून्य हो सकता है। यह कौन सा है?

(c)

उत्तर दिखाएं
सोचने की प्रक्रिया
इस समस्या में हमें ऐसे ग्राफ की पहचान करनी होगी जिसमें दो समय के लिए समान विस्थापन हो। जब एक ही विस्थापन के लिए दो समय होते हैं, तो संगत वेग विपरीत दिशा में होते हैं।
उत्तर (b) ग्राफ (b) में एक विस्थापन के लिए दो अलग-अलग समय के बिंदु होते हैं। इसलिए, एक समय के लिए औसत वेग धनात्मक होता है और दूसरे समय के लिए ऋणात्मक होता है।
अंतराल 0 से $T$ में विपरीत वेग होने के कारण, औसत वेग (b) में शून्य हो सकता है। इसको नीचे दिए गए चित्र में देखा जा सकता है
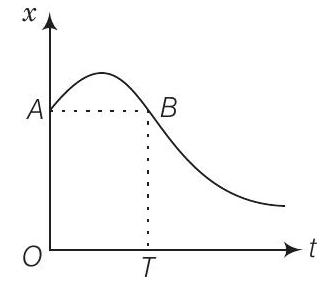
यहाँ, $O A=B T$ (समान विस्थापन) दो अलग-अलग समय के बिंदुओं के लिए होता है।
-
ग्राफ (a): ग्राफ (a) में विस्थापन समय के साथ हमेसा बढ़ता या घटता होता है। इसका अर्थ है कि वेग का चिह्न नहीं बदलता है और इसलिए किसी भी अंतराल में औसत वेग शून्य नहीं हो सकता।
-
ग्राफ (c): ग्राफ (c) में विस्थापन एक सीधी रेखा होती है जिसकी ढलान स्थिर होती है, जिसका अर्थ है कि वेग स्थिर होता है। चूंकि वेग बदलता नहीं है, इसलिए किसी भी अंतराल में औसत वेग इस स्थिर वेग के बराबर होता है और शून्य नहीं हो सकता।
-
ग्राफ (d): ग्राफ (d) में, विस्थापन भी एक सीधी रेखा है जिसका स्थिर ढलान है, जो ग्राफ (c) के समान है। यह एक स्थिर वेग को दर्शाता है और इसलिए किसी भी अंतराल में औसत वेग इस स्थिर वेग के बराबर होगा और शून्य नहीं हो सकता।
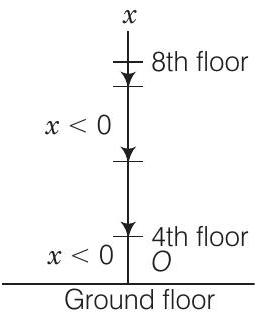
2. एक लिफ्ट 8वीं मंजिल से आ रही है और अब 4वीं मंजिल पर पहुंचने वाली है। जमीन तल को मूल बिंदु मानते हुए और सभी मात्राओं के लिए ऊपर की दिशा को धनात्मक दिशा मानते हुए, निम्नलिखित में से कौन सा सही है?
(a) $x<0, v<0, a>0$
(b) $x>0, v<0, a<0$
(c) $x>0, v<0, a>0$
(d) $x>0, v>0, a<0$
उत्तर दिखाएँ
उत्तर (a) लिफ्ट नीचे की दिशा में आ रही है, इसलिए विस्थापन नकारात्मक होगा। हम देखेंगे कि गति त्वरित या अवतरित है या नहीं।
हम जानते हैं कि नीचे की दिशा में गति के कारण विस्थापन नकारात्मक होगा। जब लिफ्ट 4वीं मंजिल पर पहुंच रही है तो रुकने वाली है, इसलिए गति अवतरित प्रकृति की है, इसलिए $x<0 ; a>0$ होगा।
क्योंकि विस्थापन नकारात्मक दिशा में है, वेग भी नकारात्मक होगा अर्थात, $v<0$ होगा।
इसको आसंजन ग्राफ पर दिखाया जा सकता है।
-
विकल्प (b): $x>0, v<0, a<0$
- कारण: विस्थापन $x$ नकारात्मक होना चाहिए क्योंकि लिफ्ट 8वीं मंजिल से 4वीं मंजिल की ओर नीचे की दिशा में गति कर रही है। इसलिए, $x>0$ गलत है। इसके अतिरिक्त, यदि लिफ्ट रुकने वाली है, तो त्वरण $a$ धनात्मक होना चाहिए, नकारात्मक नहीं।
-
विकल्प (c): $x>0, v<0, a>0$
- कारण: विस्थापन $x$ नकारात्मक होना चाहिए क्योंकि लिफ्ट 8वीं मंजिल से 4वीं मंजिल की ओर नीचे की दिशा में गति कर रही है। इसलिए, $x>0$ गलत है।
-
विकल्प (d): $x>0, v>0, a<0$
- कारण: विस्थापन $x$ नकारात्मक होना चाहिए क्योंकि लिफ्ट 8वीं मंजिल से 4वीं मंजिल की ओर नीचे की दिशा में गति कर रही है। इसलिए, $x>0$ गलत है। इसके अतिरिक्त, वेग $v$ नकारात्मक होना चाहिए क्योंकि लिफ्ट नीचे की दिशा में गति कर रही है, नहीं ऊपर की दिशा में।
3. एक आयामी गति में, तात्कालिक चाल $v$ संतुष्टि करती है $0 \leq v<v_0$.
(a) समय $T$ में विस्थापन हमेशा गैर-ऋणात्मक मान होता है
(b) समय $T$ में विस्थापन $x$ संतुष्टि करता है $-v_0 T<x<v_0 T$
(c) त्वरण हमेशा एक गैर-ऋणात्मक संख्या होती है
(d) गति में कोई भी घूमने बिंदु नहीं होते
उत्तर दिखाएँ
Answer (b) अधिकतम और न्यूनतम विस्थापन के लिए हमें अधिकतम वेग के परिमाण और दिशा को ध्यान में रखना होता है।
अधिकतम धनात्मक दिशा में वेग $v_0$ होता है, अधिकतम विपरीत दिशा में वेग भी $v_0$ होता है।
एक दिशा में अधिकतम विस्थापन $=v_0 T$
विपरीत दिशा में अधिकतम विस्थापन $=-v_0 T$
अतः, $-v_0 T<x<v_0 T$
नोट: हम वेग की दिशा के साथ गलत नहीं होना चाहिए, अर्थात एक दिशा में धनात्मक लिया जाता है और दूसरी दिशा में ऋणात्मक लिया जाता है।
-
(a) समय (T) में विस्थापन यदि गति विपरीत दिशा में हो तो ऋणात्मक मान ले सकता है। अतः, यह हमेशा गैर-ऋणात्मक नहीं होता।
-
(c) यदि वस्तु धीमी हो रही हो तो त्वरण ऋणात्मक हो सकता है। अतः, यह हमेशा एक गैर-ऋणात्मक संख्या नहीं होती।
-
(d) यदि वस्तु दिशा बदल देती है तो गति में घूमने बिंदु हो सकते हैं। अतः, गति में घूमने बिंदु आवश्यक रूप से नहीं होते।
4. एक वाहन दूरी $l$ के आधा भाग $v_1$ की गति से तय करता है और दूसरा आधा भाग $v_2$ की गति से तय करता है, तो औसत गति होगी
(a) $\dfrac{v_1+v_2}{2}$
(b) $\dfrac{2 v_1+v_2}{v_1+v_2}$
(c) $\dfrac{2 v_1 v_2}{v_1+v_2}$
(d) $\dfrac{L(v_1+v_2)}{v_1 v_2}$
उत्तर दिखाएँ
हमें औसत गति की गणना करनी होगी, इसके लिए हम पहले कुल दूरी की गणना करेंगे और फिर कुल समय के बराबर विभाजित करेंगे।
Answer (c) पहले आधा दूरी तय करने में लगा समय $t_1=\dfrac{l / 2}{v_1}=\dfrac{l}{2 v_1}$
दूसरे आधा दूरी तय करने में लगा समय $t_2=\dfrac{l}{2 v_2}$
कुल समय $=t_1+t_2$
$ =\dfrac{l}{2 v_1}+\dfrac{l}{2 v_2}=\dfrac{l}{2}\left[\dfrac{1}{v_1}+\dfrac{1}{v_2}\right]
$
हम जानते हैं कि,
$ \begin{aligned} V_{av}= & \text { औसत गति }=\dfrac{\text { कुल दूरी }}{\text { कुल समय }} \\ = & \dfrac{l}{\dfrac{l}{2}\left[\dfrac{1}{v_1}+\dfrac{1}{v_2}\right]}=\dfrac{2 v_1 v_2}{v_1+v_2} \end{aligned} $
ध्यान दें: हम दूरी और विस्थापन के बीच भ्रम नहीं उत्पन्न करना चाहिए। दूरी $\geq$ विस्थापन।
-
विकल्प (a) $\dfrac{v_1+v_2}{2}$: यह विकल्प दो गतियों के अंकगणितीय औसत का प्रतिनिधित्व करता है। हालांकि, एक यात्रा में विभिन्न खंडों पर विभिन्न गतियों से यात्रा करने पर औसत गति उन गतियों के अंकगणितीय औसत के बराबर नहीं होती। औसत गति की गणना में प्रत्येक गति पर बर्बाद समय को ध्यान में रखना आवश्यक होता है, जो इस विकल्प में नहीं किया गया है।
-
विकल्प (b) $\dfrac{2 v_1+v_2}{v_1+v_2}$: यह विकल्प दूरी, गति और समय के बीच संबंध के सही अंकन के लिए गलत है। औसत गति के सूत्र के लिए जब दूरी समान रूप से विभाजित होती है, तो गतियों के हार्मोनिक औसत को ध्यान में रखना आवश्यक होता है, जो इस विकल्प में नहीं किया गया है।
-
विकल्प (d) $\dfrac{L(v_1+v_2)}{v_1 v_2}$: यह विकल्प दूरी $L$ को अंश में गलत रूप से उपयोग करता है और गतियों के हार्मोनिक औसत का सही प्रतिनिधित्व नहीं करता है। जब विभिन्न गतियों पर समान दूरी तय की जाती है, तो औसत गति के सही सूत्र में गतियों के हार्मोनिक औसत का उपयोग किया जाता है, जो इस व्यंजक में नहीं है।
5. एक कण के विस्थापन को $x=(t-2)^{2}$ द्वारा दिया गया है, जहाँ $x$ मीटर में और $t$ सेकंड में है। पहले 4 सेकंड में कण द्वारा तय की गई दूरी है
(a) $4 m$
(b) $8 m$
(c) $12 m$
(d) $16 m$
उत्तर दिखाएँ
सोचने की प्रक्रिया
ऐसे प्रकार की समस्याओं में हम देखना होता है कि गति त्वरित या अवतरित है। अवतरित यात्रा के दौरान कण के बीच में रुक जाता है।
उत्तर (b) दिया गया है,
$ x=(t-2)^{2} $
गति,
$ v=\dfrac{d x}{d t}=\dfrac{d}{d t}(t-2)^{2}=2(t-2) m / s $
त्वरण,
$ a=\dfrac{d v}{d t}=\dfrac{d}{d t}[2(t-2)] $
$ =2[1-0]=2 m / s^{2} $
जब,
$ \begin{aligned} & t=0 ; \quad v=-4 m / s \\ & t=2 s ; \quad v=0 m / s \\
& t=4 s ; \quad v=4 m / s \end{aligned} $
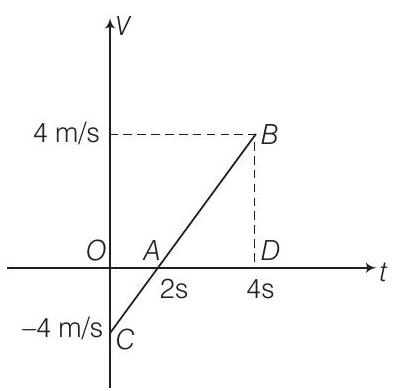
$ v $ - $ t $ ग्राफ आगे के चित्र में दिखाया गया है।
तय की गई दूरी $=$ ग्राफ के क्षेत्रफल के बराबर होती है
$ \begin{aligned} & =\text { क्षेत्रफल } O A C+\text { क्षेत्रफल } A B D \\ & =\dfrac{4 \times 2}{2}+\dfrac{1}{2} \times 2 \times 4=8 m \end{aligned} $
-
विकल्प (a) $4 m$: यह विकल्प गलत है क्योंकि पहले 4 सेकंड में कण द्वारा तय की गई दूरी की गणना, दिए गए विस्थापन फलन और वेग-समय ग्राफ के आधार पर, 8 मीटर निकलती है। वेग-समय ग्राफ के तल के नीचे क्षेत्रफल, जो दूरी को प्रतिनिधित करता है, 8 मीटर होता है, न कि 4 मीटर।
-
विकल्प (c) $12 m$: यह विकल्प गलत है क्योंकि वेग-समय ग्राफ से निर्णय की गई कण द्वारा तय की गई कुल दूरी 8 मीटर है। गणना में वेग-समय ग्राफ में बने दो त्रिभुजों के क्षेत्रफल को जोड़ा जाता है, जो 8 मीटर के बराबर होता है, न कि 12 मीटर।
-
विकल्प (d) $16 m$: यह विकल्प गलत है क्योंकि पहले 4 सेकंड में कण द्वारा तय की गई कुल दूरी 8 मीटर है, जो वेग-समय ग्राफ के तल के नीचे क्षेत्रफल के आधार पर निर्धारित की गई है। ग्राफ में त्रिभुजों के क्षेत्रफल की सही गणना से प्राप्त कुल दूरी 8 मीटर होती है, न कि 16 मीटर।
6. मेट्रो स्टेशन पर, एक लड़की एक स्थिर एस्कलेटर पर समय $t_1$ में चढ़ती है। यदि वह एस्कलेटर पर स्थिर रहती है, तो एस्कलेटर उसे ऊपर ले जाता है समय $t_2$ में। उसके द्वारा गति करके एस्कलेटर पर ऊपर चढ़ने के लिए लिया गया समय होगा
(a) $(t_1+t_2) / 2$
(b) $t_1 t_2 /(t_2-t_1)$
(c) $t_1 t_2 /(t_2+t_1)$
(d) $t_1-t_2$
उत्तर दिखाएँ
उत्तर (c) इस प्रश्न में हमें पृथ्वी के संबंध में शुद्ध वेग निर्धारित करना होगा जो लड़की के वेग और एस्कलेटर के वेग के योग के बराबर होता है।
स्थानांतरण $L$ हो, तो
$ \text { लड़की की गति } v_{g}=\dfrac{L}{t_1} $
एस्कलेटर की गति $v_{e}=\dfrac{L}{t_2}$
लड़की की संयुक्त गति $=v_{g}+v_{e}=\dfrac{L}{t_1}+\dfrac{L}{t_2}$
यदि $t$ दूरी $L$ को तय करने में कुल समय हो, तो
$ \dfrac{L}{t}=\dfrac{L}{t_1}+\dfrac{L}{t_2} \Rightarrow t=\dfrac{t_1 t_2}{t_1+t_2} $
-
विकल्प (a): $(t_1 + t_2) / 2$ गलत है क्योंकि यह दो समयों के अंकगणितीय औसत को प्रस्तुत करता है, जो लड़की की चल गति और एस्कलेटर की गति के संयुक्त प्रभाव को गणना में शामिल नहीं करता है। सही सूत्र अंकगणितीय औसत के बजाय हार्मोनिक औसत को शामिल करता है।
-
विकल्प (b): $t_1 t_2 / (t_2 - t_1)$ गलत है क्योंकि यह दो समयों के अंतर के विपरीत अनुपात में समय के अवलोकन को सुझाता है। यह लड़की की चल गति और एस्कलेटर की गति के संयुक्त प्रभाव को सही रूप से प्रस्तुत नहीं करता है। सही संबंध दो समयों के योग को शामिल करता है, न कि अंतर को।
-
विकल्प (d): $t_1 - t_2$ गलत है क्योंकि यह दो समयों के अंतर को समय के अवलोकन के रूप में सुझाता है, जो लड़की और एस्कलेटर की संयुक्त वेग को गणना में शामिल नहीं करता है। सही सूत्र दो समयों के हार्मोनिक औसत को शामिल करता है, न कि अंतर को।
बहुविकल्पीय प्रश्न (एक से अधिक विकल्प)
7. चित्र में राशि $A$ के राशि $B$ के साथ परिवर्तन का आलेख दिया गया है। यह एक सीधी रेखा में गतिमान कण के गति को वर्णित करता है।
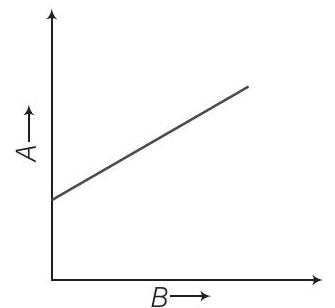
(a) राशि B समय का प्रतिनिधित्व कर सकती है
(b) यदि गति समान रहे तो राशि A वेग हो सकती है
(c) यदि गति समान रहे तो राशि A विस्थापन हो सकती है
(d) यदि गति समान रूप से त्वरित रहे तो राशि A वेग हो सकती है
उत्तर दिखाएँ
उत्तर $(a, c, d)$
एक विस्थापन-समय ग्राफ के लिए वेग की गणना करते समय हम ढलान लेते हैं, इसी तरह हम त्वरण की गणना करते समय वेग-समय ग्राफ के ढलान को लेते हैं। जब ढलान स्थिर रहे तो गति समान रहेगी।
जब हम ग्राफ के माध्यम से गति को प्रस्तुत करते हैं तो यह विस्थापन-समय, वेग-समय या त्वरण-समय ग्राफ हो सकता है, इसलिए $B$ समय का प्रतिनिधित्व कर सकता है। समान गति के लिए वेग-समय ग्राफ एक समय अक्ष के समानांतर सीधी रेखा होनी चाहिए। समान गति के लिए वेग स्थिर होता है, इसलिए ढलान धनात्मक होगा। इसलिए मात्रा $A$ विस्थापन है।
समान त्वरण के लिए ढलान धनात्मक होगा और $A$ वेग का प्रतिनिधित्व करेगा।
- विकल्प (b) गलत है: यदि गति समान है तो मात्रा $A$ वेग नहीं हो सकती क्योंकि समान गति में वेग स्थिर होता है और समय के साथ बदलता नहीं होता। यदि $A$ वेग होता और $B$ समय होता तो ग्राफ एक क्षैतिज रेखा दिखाई देता, जो दिए गए ग्राफ में नहीं दिखाई देता।
8. चित्र में $x$ के विरुद्ध $t$ के ग्राफ दिखाया गया है। नीचे दिए गए सही विकल्प चुनें
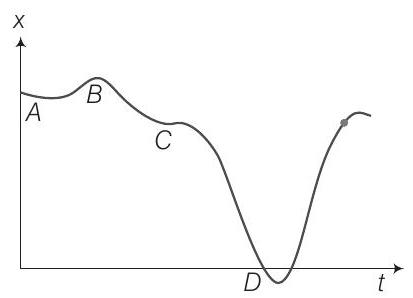
(a) कण $t=0$ पर विराम से छोड़ा गया था
(b) B पर त्वरण $a>0$ है
(c) A और D के बीच गति के औसत वेग धनात्मक है
(d) D पर चाल E पर चाल से अधिक है
उत्तर दिखाएँ
सोचने की प्रक्रिया
इस समस्या में हमें ग्राफ और वेग के लिए ढलान के सूत्र $=\dfrac{d x}{d t}$ का उपयोग करना होगा।
$v=\dfrac{d x}{d t}$।
उत्तर $(a, c, d)$
चित्र के अनुसार, बिंदु $A$ पर ग्राफ समय अक्ष के समानांतर है, इसलिए $v=\dfrac{d x}{d t}=0$। कारण शुरुआती बिंदु $A$ है, इसलिए हम कह सकते हैं कि कण विराम से शुरू होता है।
$C$ पर ग्राफ का ढलान बदल जाता है, इसलिए वेग भी बदल जाता है। चूंकि $C$ पर ग्राफ समय अक्ष के समानांतर है, इसलिए हम कह सकते हैं कि वेग शून्य हो जाता है।
त्वरण की दिशा बदल जाती है, इसलिए हम कह सकते हैं कि बीच में यह शून्य हो सकता है।
ग्राफ से स्पष्ट है कि
$ \mid \text { ढलान } D \mid > \mid \text { ढलान } E \mid $
इसलिए $D$ पर चाल $E$ पर चाल से अधिक होगी।
ध्यान दें: हम ढलान के मान के बारे में बहुत स्पष्ट होना चाहिए। नकारात्मक ढलान का अर्थ निम्न मान नहीं होता। यह वेग के दिशा परिवर्तन का प्रतिनिधित्व करता है।
- विकल्प (b): बिंदु B पर, ग्राफ अवतल नीचे होता है, जिससे ग्राफ के ढलान (वेग) कम हो रहा है। इसका अर्थ है कि त्वरण नकारात्मक है, न कि धनात्मक। अतः, B पर त्वरण $a > 0$ के बारे में कथन गलत है।
9. एक विमानीय गति के लिए, जो $x = t - \sin t$ द्वारा वर्णित है
(a) $x(t) > 0$ सभी $t > 0$ के लिए
(b) $v(t) > 0$ सभी $t > 0$ के लिए
(c) $a(t) > 0$ सभी $t > 0$ के लिए
(d) $v(t)$ 0 और 2 के बीच होता है
उत्तर दिखाएँ
उत्तर $(a, d)$
दिया गया है,
$x = t - \sin t $
$\text{ वेग } v = \dfrac{d x}{d t} = \dfrac{d}{d t}[t - \sin t] $
= $1 - \cos t $
$\text{ त्वरण } a = \dfrac{d v}{d t} = \dfrac{d}{d t}[1 - \cos t] = \sin t $
$a > 0 \text{ सभी } t > 0 $ के लिए
$x(t) > 0 \text{ सभी } t > 0 $ के लिए
$\text{ वेग } v = 1 - \cos t $
$\cos t = 1, \text{ वेग } v = 0 $
$v_{\max } = 1 - (\cos t)_{\min } = 1 - (-1) = 2 $
$v_{\min } = 1 - (\cos t)_{\max } = 1 - 1 = 0$
जैसे त्वरण
अतः,
जब,
अतः, $v$ 0 और 2 के बीच होता है
$ \text { त्वरण } a = \dfrac{d v}{d t} = -\sin t $
जब $t = 0 ; x = 0, x = +1, a = 0$
जब $t = \dfrac{\pi}{2} ; x = 1, v = 0, a = -1$
जब $t = \pi ; x = 0, x = -1, a = 1$
जब $t = 2 \pi ; x = 0, x = 0, a = 0$
ध्यान (i) जब कोई व्यंजक में साइनोइडल फंक्शन शामिल होता है, तो हम साइन और कोसाइन फंक्शन के बारे में ध्यान से रहना चाहिए।
(ii) हम वेग के अधिकतम और न्यूनतम मान की गणना करते समय ध्यान से रहना चाहिए क्योंकि इसमें दिए गए व्यंजक में कोसाइन के साथ व्युत्क्रम संबंध होता है।
-
विकल्प (b) गलत है: वेग ( $v(t) = 1 - \cos t$ ) सभी $t > 0$ के लिए निश्चित रूप से धनात्मक नहीं होता। उदाहरण के लिए, जब $t = 2n\pi$ (जहाँ $n$ एक पूर्णांक है), $ \cos t = 1 $ और इसलिए $v(t) = 0$ होता है। अतः, $v(t)$ सभी समय धनात्मक नहीं होता।
-
विकल्प (c) गलत है: त्वरण ( $a(t) = \sin t$ ) सभी $t > 0$ के लिए निश्चित रूप से धनात्मक नहीं होता। साइन फंक्शन -1 और 1 के बीच दोलन करता है, इसलिए कुछ अंतराल में $ \sin t $ नकारात्मक होता है, जिससे $ a(t) $ उन अंतराल में नकारात्मक होता है। अतः, $ a(t) $ सभी समय धनात्मक नहीं होता।
10. एक स्प्रिंग जिसका एक सिरा एक द्रव्यमान से और दूसरा एक ठोस समर्थन से जुड़ा है, खींचा जाता है और छोड़ दिया जाता है।
(a) जब द्रव्यमान को छोड़े जाने के तुरंत बाद त्वरण के मापदंड का मान अधिकतम होता है
(b) संतुलन स्थिति पर त्वरण के मापदंड का मान अधिकतम होता है
(c) जब द्रव्यमान संतुलन स्थिति पर होता है तब चाल अधिकतम होती है
(d) जब चाल न्यूनतम होती है तब विस्थापन के मापदंड का मान हमेशा अधिकतम होता है
उत्तर दिखाएँ
Answer (a, c)
जब स्प्रिंग को $x$ द्वारा खींचा जाता है, तो पुनर्स्थापन बल $F=-k x$ होता है
खींचे गए स्प्रिंग की संभावित ऊर्जा $=PE=\dfrac{1}{2} k x^{2}$
पुनर्स्थापन बल केंद्रीय होता है, इसलिए जब कण को छोड़ दिया जाता है तो यह संतति गतिशीलता (SHM) के अनुसार संतुलन स्थिति के चारों ओर गति करता है।
त्वरण होगा
$ a=\dfrac{F}{m}=\dfrac{-k x}{m} $
$ \begin{matrix} \text { संतुलन स्थिति पर, } & x=0 \Rightarrow a=0 \\ \text { इसलिए, जब द्रव्यमान को छोड़े जाने के तुरंत बाद } & x=x_{\max } \end{matrix} $
इसलिए, त्वरण अधिकतम होता है। इसलिए विकल्प (a) सही है।
संतुलन स्थिति पर पूरी $PE$ को $KE$ में बदल दिया जाता है, इसलिए $KE$ अधिकतम होता है और चाल अधिकतम होती है।
-
(b) संतुलन स्थिति पर त्वरण के मापदंड का मान अधिकतम होता है: यह गलत है क्योंकि संतुलन स्थिति पर विस्थापन (x) शून्य होता है। त्वरण (a) के मापदंड के लिए $a = \dfrac{-kx}{m}$ होता है, जब $x = 0$ होता है, तो $a$ भी शून्य होता है। इसलिए, संतुलन स्थिति पर त्वरण के मापदंड का मान अधिकतम नहीं होता, बल्कि यह शून्य होता है।
-
(d) जब चाल न्यूनतम होती है तब विस्थापन के मापदंड का मान हमेशा अधिकतम होता है: यह गलत है क्योंकि दोलन के अतिरिक्त स्थितियों पर विस्थापन के मापदंड का मान अधिकतम होता है, जहां चाल वास्तव में शून्य होती है। हालांकि, “हमेशा” के अर्थ में जब चाल न्यूनतम होती है तब विस्थापन के मापदंड का मान अधिकतम होता है, जो सत्य नहीं है। चाल अतिरिक्त स्थितियों पर भी शून्य होती है, लेकिन विस्थापन के मापदंड का मान अधिकतम नहीं होता है। इसलिए, यह कथन सामान्य रूप से सत्य नहीं है।
11. $ A$ गेंद 1 मीटर/सेकंड की गति से रेलवे कमरे के दीवारों के बीच एलास्टिक रूप से टकराती है। रेलवे कमरे की विमाएं 10 मीटर हैं और गति दीवारों के लंबवत दिशा में है। रेलगाड़ी एक स्थिर वेग 10 मीटर/सेकंड से गति कर रही है जो गेंद की गति की दिशा के समान है। जमीन से देखे जाने पर।
(a) गेंद की गति की दिशा हर 10 में बदल जाती है।
(b) गें ड की गति हर 10 में बदल जाती है।
(c) कोई भी 20 के अंतराल में गेंद की औसत गति निश्चित है।
(d) गेंद के त्वरण रेलगाड़ी के दृष्टि से एक ही है।
उत्तर दिखाएँ
Answer $(b, c, d)$
इस समस्या में हमें देखने वाले प्रेक्षक के अंग को ध्यान में रखना होगा। यहां हमें स्पष्ट रूप से यह समझना होगा कि हम जमीन से गति की दृष्टि से गति की जा रही है। ट्रेन के वेग $(10 m / s)$ की तुलना में गेंद की गति कम है $(1 m / s)$।
गेंद के ट्रेन के दीवार के संघटन से पहले गति $10+1=11 m / s$ है।
गेंद के ट्रेन के दीवार के संघटन के बाद गति $=10-1=9 m / s$ है।
गति 10 मीटर यात्रा के बाद बदल जाती है और गति 1 मीटर/सेकंड है, इसलिए गति बदलने के लिए समय अंतराल 10 सेकंड है।
क्योंकि गेंद के संघटन पूर्णतः एलास्टिक है, तो ऊर्जा का कोई वितरण नहीं होता, इसलिए कुल संवेग और कार्य ऊर्जा संरक्षित रहती है।
क्योंकि ट्रेन एक स्थिर वेग से गति कर रही है, इसलिए यह पृथ्वी के जैसा एक अभिन्न अंग के रूप में कार्य करेगी और दोनों अंग में त्वरण समान होगा।
हम अभिन्न और अभिन्न अंग के बीच भ्रम नहीं डालना चाहिए। एक अंग जो तेजी से नहीं चल रहा है वह अभिन्न अंग होगा।
- (a) गेंद की गति की दिशा हर 10 में बदल जाती है: यह विकल्प गलत है क्योंकि गेंद की गति की दिशा रेलवे कमरे की दीवारों के हर टकराव के बाद बदल जाती है। दीवारों के बीच गेंद एलास्टिक रूप से टकराती है और कमरे की चौड़ाई 10 मीटर है, इसलिए ट्रेन के अंग में गेंद की दिशा हर 10 सेकंड में बदल जाती है। हालांकि, जमीन के अंग में गेंद की गति ट्रेन के संबंधी गति के कारण बदल जाती है, लेकिन दिशा के बदलने के लिए यह ठीक 10 सेकंड नहीं होता क्योंकि ट्रेन और गेंद के संयुक्त गति के कारण होता है।
बहुत छोटे उत्तर प्रकार के प्रश्न
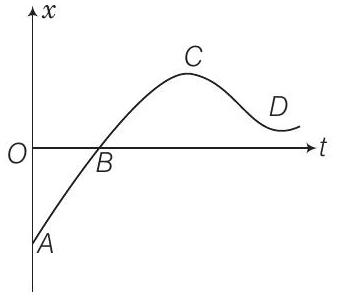
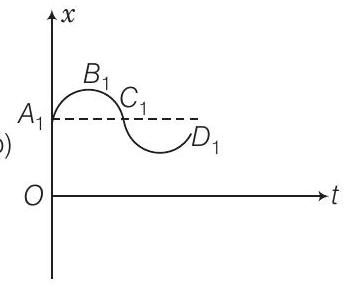
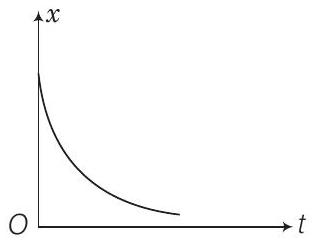
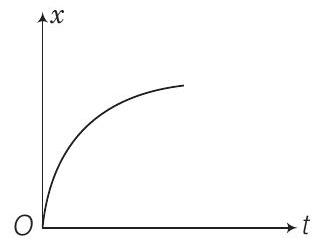
12. आकृति में ग्राफ का संदर्भ लें। निम्नलिखित को मिलाएं
| ग्राफ | विशेषताएं |
|---|---|
| (a) | (i) $\quad$ $v>0$ और $a<0$ दोनों धनात्मक हैं |
| (b) | (ii) $\quad$ $x>0$ दोनों धनात्मक हैं और एक बिंदु पर $v=0$ तथा एक बिंदु पर $a=0$ है |
| (c) | (iii) $\quad$ $t>0$ के लिए शून्य विस्थापन के बिंदु है |
| (d) | (iv) $\quad$ $v<0$ और $a>0$ है |
(b)
(c)
(d)
उत्तर दिखाएं
उत्तर हमें प्रत्येक वक्र के ढलान के विश्लेषण करना होगा अर्थात $\dfrac{d x}{d t}$. शिखर बिंदुओं पर $\dfrac{d x}{d t}$ शून्य होगा क्योंकि शिखर बिंदुओं पर $x$ अधिकतम होता है।
ग्राफ (a) में एक बिंदु (B) है जहां विस्थापन शून्य है। अतः (a) (iii) से मेल खाता है।
ग्राफ (b) में $x$ सदैव धनात्मक है ( $>0$ ) और बिंदु $B_1$ पर $V=\dfrac{d x}{d t}=0$ है। चूंकि वक्रता परिवर्तन के बिंदु पर $a=0$ होता है, अतः (b) (ii) से मेल खाता है।
ग्राफ (c) में ढलान $V=\dfrac{d x}{d t}$ नकारात्मक है अतः वेग नकारात्मक होगा। अतः (c) (iv) से मेल खाता है।
ग्राफ (d) में ढलान $V=\dfrac{d x}{d t}$ धनात्मक है अतः $V>0$ होगा। अतः (d) (i) से मेल खाता है।
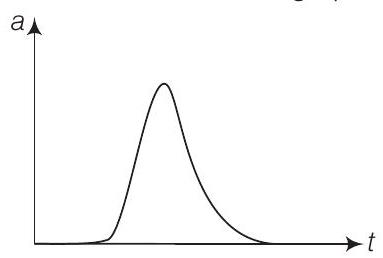
13. एक समान गति में चल रहे क्रिकेट के गेंद को बल के द्वारा बहुत छोटे समय अंतराल में वापस भेज दिया जाता है। इसके त्वरण के समय के साथ परिवर्तन को दिखाइए (त्वरण के पीछे दिशा को धनात्मक मान लीजिए)।
उत्तर दिखाएं
उत्तर गुरुत्वाकर्षण प्रभाव को नगण्य माने तो एक समान गति में चल रहे गेंद को बल के द्वारा बराबर चाल से वापस भेज दिया जाता है। गेंद के बल के संपर्क से पहले त्वरण शून्य होता है। जब गेंद बल के संपर्क में आती है, तो बल द्वारा लगाए गए आवेग बल के कारण गेंद त्वरित हो जाती है।
त्वरण के समय के साथ परिवर्तन ग्राफ में दिखाया गया है
14. एक एक-विमीय गति के उदाहरण दीजिए जहाँ
(a) धनात्मक $x$-दिशा में गति करते हुए कण आवर्ती रूप से विराम में आता है और आगे बढ़ता है।
(b) धनात्मक $x$-दिशा में गति करते हुए कण आवर्ती रूप से विराम में आता है और पीछे जाता है।
उत्तर दिखाएं
उत्तर जब हम आवर्ती प्रकृति वाले समीकरण के लिए लिख रहे होते हैं तो इसमें ज्या या कोज्या फलन शामिल होते हैं।
(a) कण केवल तभी धनात्मक $x$-दिशा में गति करेगा जब $t>\sin t$
इसलिए,
$x(t) =1-\sin t $
$\text { वेग } v(t) =\dfrac{d x(1)}{d t}=1-\cos t$
$\text { त्वरण } a(t) =\dfrac{d v}{d t}=\sin t $
जब $ t =0 ; x(t)=0 $
जब $ t = \pi ; x(t)= \pi > 0 $
जब $ t =0 ; x(t)=2 \pi >0 $
(b) समीकरण को निम्नलिखित रूप में प्रस्तुत किया जा सकता है
$ \begin{aligned} x(t) & =\sin t \\ v & =\dfrac{d}{d t} x(t)=\cos t \end{aligned} $
क्योंकि विस्थापन और वेग में sint और cost शामिल हैं, इसलिए ये समीकरण आवर्ती हैं।
15. एक गति के उदाहरण दीजिए जहाँ $x>0, v<0, a>0$ एक विशिष्ट क्षण पर।
उत्तर दिखाएं
उत्तर मान लीजिए गति निम्नलिखित द्वारा प्रस्तुत की जाती है
(i) $x(t) = A + B e^{-\gamma t}$
Let $A > B$ and $\gamma>0$
$x(t) > 0$
(ii) $v(t) = \dfrac{d x (t)}{d t}$
$v(t) = \dfrac{d}{dt} (A + B e^{- \gamma t})$
$v(t) = -\gamma B e^{-\gamma t}$
as $\quad \gamma > 0 $
$v(t) < 0$
$v < 0$
(iii) $a (t) = \dfrac{dv(t)}{dt}$
$a(t) = \dfrac{d}{dt} (-\gamma B e^{-\gamma t})$
$a(t) = \gamma^2 Be^{-\gamma t}$
as $\quad \gamma > 0$
$a (t) > 0$
$a > 0$
मान लीजिए हम किसी भी क्षण $t$ पर विचार कर रहे हैं, तो समीकरण (i) से हम कह सकते हैं कि
$ x(t)>0 ; v(t)<0 \quad \text { और } \quad a>0 $
16. एक वस्तु तरल में गिरते हुए देखा जाता है जिसका त्वरण $a=g-b v$ द्वारा दिया जाता है जहाँ $g=$ गुरुत्वीय त्वरण और $b$ एक स्थिरांक है। विस्फोट के बाद लंबे समय के बाद यह देखा जाता है कि यह नियत गति के साथ गिरता है। नियत गति का मान क्या होना चाहिए?
उत्तर दिखाएँ
Answer जब गति नियत हो जाती है तो त्वरण $a=\dfrac{d v}{d t}=0$
दिया गया त्वरण
$a=g-b v$
जहाँ, $g$ = गुरुत्वीय त्वरण
ऊपर के समीकरण से स्पष्ट रूप से, जैसे गति बढ़ती है त्वरण कम होता जाता है। एक निश्चित गति कहलाए गए $v_0$ पर त्वरण शून्य हो जाएगा और गति नियत रहेगी।
इसलिए,
$a=g-b v_0=0$
$\Rightarrow$
$v_0=g / b$
छोटे उत्तर प्रकार प्रश्न
17. एक गेंद गिराई जाती है और इसका विस्थापन व समय के ग्राफ नीचे दिखाए गए हैं (विस्थापन $x$ जमीन से और सभी मात्राएँ ऊपर की ओर धनात्मक हैं)।
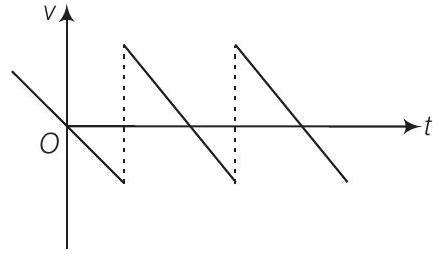
(a) गति व समय के ग्राफ को गुणात्मक रूप से बनाएं
(b) त्वरण व समय के ग्राफ को गुणात्मक रूप से बनाएं
उत्तर दिखाएँ
सोचने की प्रक्रिया
हम वेग की गणना करने के लिए विस्थापन-समय वक्र के लिए ढलान $\dfrac{d x}{d t}$ निकालेंगे और त्वरण की गणना करने के लिए वेग-समय वक्र के ढलान $\dfrac{d V}{d t}$ निकालेंगे।
उत्तर ग्राफ से स्पष्ट है कि विस्थापन $x$ सभी समय धनात्मक है। एक ऊँचाई से गेंद गिराई जाती है और गुरुत्वाकर्षण के कारण इसका वेग नीचे की ओर बढ़ता है। इस स्थिति में $v$ नकारात्मक होता है लेकिन गेंद का त्वरण गुरुत्वाकर्षण के कारण बराबर होता है अर्थात, $a=-g$। जब गेंद ऊपर की ओर वापस लौटती है तो इसका वेग धनात्मक होता है लेकिन त्वरण $a=-g$ होता है।
(a) गेंद का वेग-समय ग्राफ आकृति (i) में दिखाया गया है।
(i)
(b) गेंद का त्वरण-समय ग्राफ आकृति (ii) में दिखाया गया है।

18. एक कण $x(t)=x_0(1-e^{-\gamma t}) ; t \geq 0$, $x_0>0$ के द्वारा वर्णित गति करता है।
(a) कण कहाँ से शुरू होता है और किस वेग से?
(b) $x(t), v(t), a(t)$ के अधिकतम और न्यूनतम मान ज्ञात कीजिए। दिखाइए कि $x(t)$ और $a(t)$ समय के साथ बढ़ते हैं और $v(t)$ समय के साथ घटता है।
उत्तर दिखाएँ
पहले हम वेग और त्वरण की गणना करनी होगी और फिर अधिकतम या न्यूनतम मान के अनुसार निर्धारित कर सकते हैं।
Answer दिया गया है,
$ \begin{aligned} & x(t)=x_0(1-e^{-\gamma t}) \\ & v(t)=\dfrac{d x(t)}{d t}=x_0 \gamma e^{-\gamma t} \\ & a(t)=\dfrac{d v(t)}{d t}=-x_0 \gamma^{2} e^{-\gamma t} \end{aligned} $
(a) जब $t = 0$
$x(t = 0)=x_0(1-e^{-0})=x_0(1-1)=0$
$ v(t=0)=x_0 \gamma e^{-0}=x_0 \gamma(1)=\gamma x_0 $
(b) $x(t)$ जब $t=\infty$ होता है तो अधिकतम होता है; $[x(t)]_{\max }=x_0$
$x(t)$ जब $t=0$ होता है तो न्यूनतम होता है; $[x(t)]_{\text {min }}=0$
$v(t)$ जब $t=0$ होता है तो अधिकतम होता है; $v(0)=x_0 \gamma$
$v(t)$ जब $t=\infty$ होता है तो न्यूनतम होता है; $v(\infty)=0$
$a(t)$ जब $t=\infty$ होता है तो अधिकतम होता है; $a(\infty)=0$
$a(t)$ जब $t=0$ होता है तो न्यूनतम होता है; $a(0)=-x_0 \gamma^{2}$
ध्यान दें हम वक्र के परिवर्तन की प्रकृति के बारे में सावधान रहें और अधिकतम और न्यूनतम मान उसके अनुसार निर्धारित किए जाएंगे।
19. दो कारों के बीच एक पक्षी आगे-पीछे उड़ते हुए एक सीधी सड़क पर एक-दूसरे की ओर गति कर रही है। एक कार की गति $18 km / h$ है जबकि दूसरी कार की गति $27 km / h$ है। पक्षी पहली कार से दूसरी कार की ओर गति करती है और इसकी गति $36 km / h$ है और जब दोनों कारें $36 km$ की दूरी पर थीं। पक्षी द्वारा कुल कितनी दूरी तय की गई?
उत्तर दिखाएं
सोचने की प्रक्रिया
इस समस्या में हम अपेक्षित वेग के अवधारणा का उपयोग करना होगा। एक ही दिशा में वेगों को घटाया जाता है और विपरीत दिशा में वेगों को जोड़ा जाता है।
उत्तर दिया गया, पहली कार की गति $=18 km / h$
दूसरी कार की गति $=27 km / h$
$\therefore$ प्रत्येक कार के संबंध में अपेक्षित गति
$ =18+27=45 km / h $
कारों के बीच दूरी $=36 km$
$\therefore \quad$ कारों के मिलने का समय $(t)=\dfrac{\text { कारों के बीच दूरी }}{\text { कारों की अपेक्षित गति }}=\dfrac{36}{45}=\dfrac{4}{5} h=0.8 h$
पक्षी की गति $(v_{b})=36 km / h$
$\therefore$ पक्षी द्वारा तय की गई दूरी $=v_{b} \times t=36 \times 0.8=28.8 km$
20. एक आदमी एक ऊंचे इमारत के छत पर दौड़ता है और अगली इमारत के छत पर उतरने की आशा के साथ क्षैतिज रूप से छलांग लगाता है, जो पहली इमारत की तुलना में कम ऊंचाई पर होती है। यदि उसकी गति $9 m / s$ है, दो इमारतों के बीच क्षैतिज दूरी $10 m$ है और ऊंचाई के अंतर $9 m$ है, तो वह अगली इमारत पर उतर पाएगा क्या? (ग्राविटेशन बल $g=10 m / s^{2}$ लें)
उत्तर दिखाएं
सोचने की प्रक्रिया
जब आदमी छत पर दौड़ता है तो वेग क्षैतिज होता है। फिर, त्वरण ऊर्ध्वाधर नीचे की ओर होता है जिसे $g$ के रूप में लिया जाता है और फिर गति के समीकरणों का उपयोग किया जाता है।
उत्तर दिया गया, आदमी की क्षैतिज गति $(u_{x})=9 m / s$
दो इमारतों के बीच क्षैतिज दूरी $=10 m$
दो इमारतों के बीच ऊंचाई के अंतर $=9 m$
$ g=10 m / s^{2} $
मान लीजिए आदमी बिंदु $A$ से छलांग लगाता है और अगली इमारत के छत पर बिंदु $B$ पर उतरता है। ऊर्ध्वाधर दिशा में गति की गणना करते हुए,
$ \begin{aligned} & y=u t+\dfrac{1}{2} a t^{2} \\ & 9=0 \times t+\dfrac{1}{2} \times 10 \times t^{2} \\ & 9=5 t^{2} \\ & t=\sqrt{\dfrac{9}{5}}=\dfrac{3}{\sqrt{5}} \end{aligned} $
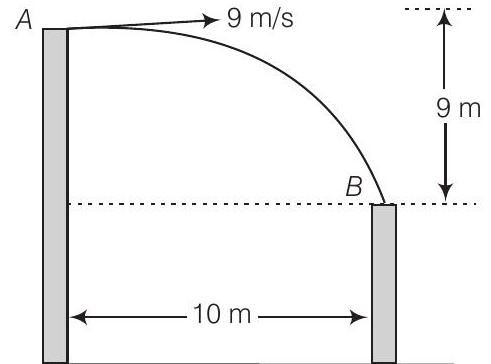
$\therefore$ अनुसूची दूरी $=u_{x} \times t=9 \times \dfrac{3}{\sqrt{5}}=\dfrac{27}{\sqrt{5}} m$ $\approx 12 m$
मनुष्य द्वारा तय की गई अनुसूची दूरी $10 m$ से अधिक है, इसलिए, वह अगले भवन पर उतरेगा।
21. एक गेंद एक 45 मीटर ऊंचे भवन से गिराई जाती है। एक साथ दूसरी गेंद 40 मीटर/सेकंड की गति से ऊपर फेंकी जाती है। समय के फलन के रूप में गेंदों की सापेक्ष गति की गणना कीजिए।
उत्तर दिखाएँ
सोचने की प्रक्रिया
इस समस्या में गेंद गिराई जाती है, इसलिए आरंभिक वेग शून्य माना जाएगा। हम एक विमान में गति के समीकरणों को लागू करेंगे।
उत्तर भवन से गिराई गई गेंद के लिए, $u_1=0, u_2=40 m / s$
समय $t$ के बाद गिराई गई गेंद की गति,
$ \begin{aligned} & v_1=u_1+g t \\ & v_1=g t \end{aligned} $
(नीचे की ओर)
गेंद ऊपर फेंके जाने के लिए, $u_2=40 m / s$
समय $t$ के बाद गेंद की गति
$ \begin{aligned} v_2 & =u_2-g t \\ & =(40-g t) \end{aligned} $
(ऊपर की ओर)
$\therefore$ एक गेंद के संबंध में दूसरी गेंद की सापेक्ष वेग
$ \begin{aligned} & =v_1-v_2 \\ & =g t-[(40-g t)]=-40 m / s \end{aligned} $
ध्यान रखें जब हम रेखीय गति के समीकरणों के लागू करते हैं, तो भौतिक राशियों के चिह्न के लिए ध्यानपूर्वक लिखना चाहिए।
22. एक कण के वेग-स्थिति ग्राफ को चित्र में दिखाया गया है।
(a) $v$ और $x$ के बीच संबंध लिखिए।
(b) त्वरण और स्थिति के बीच संबंध प्राप्त कीजिए और इसे आलेखित कीजिए।
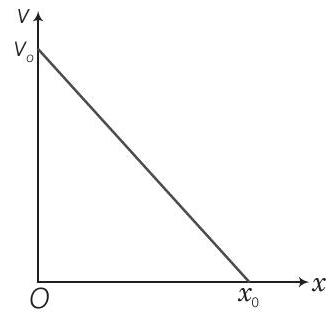
उत्तर दिखाएँ
सोचने की प्रक्रिया
इस समस्या में हम ढलान की अवधारणा का उपयोग करेंगे। मान लीजिए ढलान $m$ है तो समीकरण $y = m x+c$ के रूप में आएगा।
उत्तर दिया गया, आरंभिक वेग $=v_0$
मान लीजिए समय $t$ में तय की गई दूरी $x_0$ है।
ग्राफ के लिए
$ \tan \theta=\dfrac{v_0}{x_0}=\dfrac{v_0-v}{x} \quad \text{(i)} `
$
जहाँ, $v$ वेग है और $x$ कोई भी समय $t$ के अंतराल में विस्थापन है।
$ \begin{aligned} \text { समीकरण (i) से } v_0-v & =\dfrac{v_0}{x_0} x \\ \Rightarrow v & =\dfrac{-v_0}{x_0} x+v_0 \end{aligned} $
हम जानते हैं कि
$ \begin{aligned} \text { त्वरण } a & =\dfrac{d v}{d t}=\dfrac{-v_0}{x_0} \dfrac{d x}{d t}+0 \\ a & =\dfrac{-v_0}{x_0}(v) \\ & =\dfrac{-v_0}{x_0}(\dfrac{-v_0}{x_0} x+v_0) \\ & =\dfrac{v_0^{2}}{x_0^{2}} x-\dfrac{v_0^{2}}{x_0} \end{aligned} $
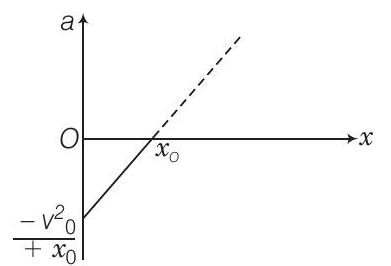
$ x $ के सापेक्ष $ a $ के ग्राफ ऊपर दिया गया है।
लंबा उत्तर प्रकार प्रश्न
23. यह एक सामान्य अवलोकन है कि बारिश के बादल भूमि से लगभग एक किलोमीटर की ऊंचाई पर हो सकते हैं।
(a) ऐसी ऊंचाई से एक बारिश की बूंद गुरुत्वाकर्षण के अंतर्गत मुक्त रूप से गिरती है, तो इसकी गति क्या होगी? इसकी गति की गणना $km/h$ में करें $(g=10 m/s^{2})$।
(b) एक सामान्य बारिश की बूंद का व्यास लगभग $4 mm$ होता है। जब यह भूमि पर टकराती है तो इसका संवेग अनुमानित करें।
(दिया गया है, $\text{संवेग} = \text{द्रव्यमान} \times \text{गति}$)
(c) बूंद को फैलाने में आवश्यक समय का अनुमान लगाएं।
(d) संवेग के परिवर्तन की दर बल होती है। ऐसी एक बूंद आप पर कितना बल लगाएगी?
(e) छत्ते पर बल के कोटि का अनुमान लगाएं। दो बारिश की बूंदों के बीच सामान्य लंबवत अंतर $5 cm$ है।
(मान लें कि छत्ता वृत्ताकार है और इसका व्यास $1 m$ है और कपड़ा नहीं छेदा गया है।)
उत्तर दिखाएँ
सोचने की प्रक्रिया
इस समस्या में गति के समीकरण और न्यूटन के द्वितीय नियम जो है $F_{\text {ext }}=\dfrac{d p}{d t}$ का उपयोग किया जाएगा। जहाँ $d p$ समय $dt$ में संवेग में परिवर्तन है।
उत्तर दिया गया है, ऊंचाई $(h)=1 km=1000 m$
$ g=10 m / s^{2} $
(a) ऊंचाई $h$ के माध्यम से मुक्त रूप से गिरती बारिश की बूंद द्वारा प्राप्त वेग।
$ \begin{aligned} V & =\sqrt{2 g h}=\sqrt{2 \times 10 \times 1000}=100 \sqrt{2} m / s \\
& =100 \sqrt{2} \times \dfrac{60 \times 60}{1000} km / h \\ & =360 \sqrt{2} km / h \approx 510 km / h \end{aligned} $
(b) बूंद का व्यास $(d)=2 r=4 mm$
$\therefore$ बूंद की त्रिज्या $(r)=2 mm=2 \times 10^{-3} m$
बरसात की एक बूंद का द्रव्यमान $(m)=V \times \rho$
$ \begin{aligned} & =\dfrac{4}{3} \pi r^{3} \rho \\ & =\dfrac{4}{3} \times \dfrac{22}{7} \times(2 \times 10^{-3})^{3} \times 10^{3} \quad(\because \text { पानी का घनत्व }=10^{3} kg / m^{3}) \\ & \approx 3.4 \times 10^{-5} kg \end{aligned} $
बरसात की बूंद का संवेग $(p)=m v$
$ \begin{aligned} & =3.4 \times 10^{-5} \times 100 \sqrt{2} \\ & =4.7 \times 10^{-3} kg-m / s \\ & \approx 5 \times 10^{-3} kg-m / s \end{aligned} $
(c) बूंद को चौड़ा करने के लिए आवश्यक समय = धरातल के पास बूंद के व्यास के बराबर दूरी तय करने में लगने वाला समय
$ \begin{aligned} t & =\dfrac{d}{V}=\dfrac{4 \times 10^{-3}}{100 \sqrt{2}}=0.028 \times 10^{-3} s \\ & =2.8 \times 10^{-5} s \end{aligned} $
(d) बरसात की बूंद द्वारा लगाया गया बल
$ \begin{aligned} F & =\dfrac{\text { संवेग में परिवर्तन }}{\text { समय }}=\dfrac{p-0}{t} \\ & =\dfrac{4.7 \times 10^{-3}}{2.8 \times 10^{-5}} \approx 168 N \end{aligned} $
(e) छतरी की त्रिज्या $(R)=\dfrac{1}{2} m$
$\therefore$ छतरी का क्षेत्रफल $(A)=\pi R^{2}=\dfrac{22}{7} \times \left(\dfrac{1}{2}\right)^{2}=\dfrac{22}{28}=\dfrac{11}{14} \approx 0.8 m^{2}$
औसत अंतर के साथ छतरी पर एक साथ बूंदों की संख्या $5 cm$ $=5 \times 10^{-2} m$।
$ =\dfrac{0.8}{(5 \times 10^{-2})^{2}}=320 $
$\therefore$ छतरी पर लगाया गया नेट बल $=320 \times 168=53760 N \approx 54000 N$
नोट: व्यावहारिक रूप से, हवा के घर्षण के कारण बूंदों की गति कम हो जाती है।
24. एक मोटर कार $72 km / h$ की गति से चल रही है जो $3.0 s$ से कम समय में रोक नहीं सकती है जबकि ट्रक के लिए यह समय अंतराल $5.0 s$ है। एक राजमार्ग पर, कार ट्रक के पीछे चल रही है दोनों $72 km / h$ की गति से चल रहे हैं। ट्रक एक आपातकालीन चेतावनी देता है कि यह रोक रहा है। कार को ट्रक से कितनी दूर रहना चाहिए ताकि यह ट्रक के संघटन से बच सके। मानव प्रतिक्रिया समय $0.5 s$ है।
उत्तर दिखाएँ
उत्तर इस समस्या में एक वस्तु के एक विमीय गति संबंधी समीकरणों का उपयोग किया जाएगा। त्वरण के लिए धनात्मक चिह्न का उपयोग किया जाएगा और विलम्बन के लिए ऋणात्मक चिह्न का उपयोग किया जाएगा।
दिया गया, कार और ट्रक की गति $=72 , \text{किमी}/\text{घंटा}$
विलम्बन के लिए ट्रक के लिए $\quad v=u+a_{t} t$
$ =72 \times \dfrac{5}{18} , \text{मी}/\text{सेकंड}=20 , \text{मी}/\text{सेकंड} $
या
$ 0=20+a_{t} \times 5 $
$ a_{t}=-4 , \text{मी}/\text{सेकंड}^{2} $
विलम्बन के लिए कार के लिए
$ \begin{aligned} v & =u+a_{c} t \\ 0 & =20+a_{c} \times 3 \\ a_{c} & =-\dfrac{20}{3} , \text{मी}/\text{सेकंड}^{2} \end{aligned} $
मान लीजिए कार ट्रक से $x$ दूरी पर है, जब ट्रक संकेत देता है और $t$ समय लेता है इस दूरी को तय करने के लिए।
मानव प्रतिक्रिया समय $0.5 , \text{सेकंड}$ है, इसलिए कार के विलम्बन के लिए समय $(t-0.5) , \text{सेकंड}$ है।
समय $t$ के बाद कार की गति,
$ \begin{aligned} v_{c} & =u-a t \\ & =20-(\dfrac{20}{3})(t-0.5) \end{aligned} $
समय $t$ के बाद ट्रक की गति
$ v_{t}=20-4 t $
कार को ट्रक के संघटन से बचने के लिए,
$ \begin{aligned} v_{c} & =v_{t} \\ 20-\dfrac{20}{3}(t-0.5) & =20-4 t \\ 4 t & =\dfrac{20}{3}(t-0.5) \\ t & =\dfrac{5}{3}(t-0.5) \\ 3 t & =5 t-2.5 \\ t & =\dfrac{2.5}{2}=\dfrac{5}{4} , \text{सेकंड} \end{aligned} $
समय $t$ में ट्रक द्वारा तय की गई दूरी,
$ \begin{aligned} s_{t} & =u_{t} t+\dfrac{1}{2} a_{t} t^{2} \\ & =20 \times \dfrac{5}{4}+\dfrac{1}{2} \times(-4) \times\left(\dfrac{5}{4}\right)^{2} \\ & =21.875 , \text{मी} \end{aligned} $
समय $t$ में कार द्वारा तय की गई दूरी = समय $0.5 , \text{सेकंड}$ में कार द्वारा तय की गई दूरी (विलम्बन बिना) + समय $(t-0.5) , \text{सेकंड}$ में कार द्वारा तय की गई दूरी (विलम्बन के साथ)
$s_{c} =(20 \times 0.5)+20\left(\dfrac{5}{4}-0.5\right)-\dfrac{1}{2}\left(\dfrac{20}{3}\right)\left(\dfrac{5}{4}-0.5\right)^{2}$
$ =23.125 , \text{मी} $
$\therefore \quad s_{c}-s_{t} =23.125-21.875=1.250 , \text{मी}$
इसलिए, ट्रक से टकराने से बचने के लिए, कार को ट्रक से अधिक $1.250 , \text{मी}$ की दूरी बनाए रखनी चाहिए।
25. एक बंदर एक फाटक वाले खंबे पर 3 सेकंड तक चढ़ता है और फिर 3 सेकंड तक उतर जाता है। इसकी गति समय $t$ पर $v(t)=2 t(3-t)$; $0<t<3$ और $v(t)=-(t-3)(6-t)$; $3<t<6$ सेकंड में $m/s$ में दी गई है। यह चक्र तब तक दोहराता रहता है जब तक यह 20 मीटर की ऊंचाई पहुंच जाए।
(a) इसकी वेग अधिकतम कब होता है?
(b) इसकी औसत वेग अधिकतम कब होता है?
(c) इसकी त्वरण के परिमाण के अधिकतम कब होता है?
(d) शीर्ष तक पहुँचने के लिए कितने चक्र (भिन्न के रूप में गिने जाते हैं) की आवश्यकता होती है?
उत्तर दिखाएं
उत्तर इस समस्या को हल करते समय अधिकतम वेग की गणना के लिए हम $\dfrac{d v}{d t}=0$ का उपयोग करेंगे, फिर अधिकतम वेग के संगत समय प्राप्त किया जाएगा।
दिया गया वेग
$ v(t)=2 t(3-t)=6 t-2 t^{2} \quad \text{(i)} $
(a) अधिकतम वेग के लिए $\dfrac{d v(t)}{d t}=0$
$\Rightarrow \dfrac{d}{d t}(6 t-2 t^{2}) =0$
$\Rightarrow 6-4 t =0$
$\Rightarrow t =\dfrac{6}{4}=\dfrac{3}{2} s=1.5 s$
(b) समीकरण (i) से $v=6 t-2 t^{2}$
$ \begin{matrix} \Rightarrow & \dfrac{d s}{d t}=6 t-2 t^{2} \\ \Rightarrow & d s=(6 t-2 t^{2}) d t \end{matrix} $
जहाँ, $s$ विस्थापन है
$\therefore$ समय अंतराल 0 से $3 s$ में तय की गई दूरी।
$ \begin{aligned} S & =\int_0^{3}(6 t-2 t^{2}) d t \\ & =\left[\dfrac{6 t^{2}}{2}-\dfrac{2 t^{3}}{3}\right]_0^{3}=\left[3 t^{2}-\dfrac{2}{3} t^{3}\right]_0^{3} \\ & =3 \times 9-\dfrac{2}{3} \times 3 \times 3 \times 3 \\ & =27-18=9 m. \end{aligned} $
$ \begin{aligned} \text { औसत वेग } & =\dfrac{\text { तय की गई दूरी }}{\text { समय }} \end{aligned} $
$=\dfrac{9}{3}=3 m / s$
$x =6 t-2 t^{2} $
$3 =6 t-2 t^{2} $
$2 t^{2}-6 t-3 =0 $
$t =\dfrac{6 \pm \sqrt{6^{2}-4 \times 2 \times 3}}{2 \times 2}=\dfrac{6 \pm \sqrt{36-24}}{4} $
$=\dfrac{6 \pm \sqrt{12}}{4}=\dfrac{3 \pm 2 \sqrt{3}}{2}$
केवल धनात्मक चिह्न को लें
$ t=\dfrac{3+2 \sqrt{3}}{2}=\dfrac{3+2 \times 1.732}{2}=3.232 ~\text{s} $
(c) चक्रीय गति में जब वेग शून्य होता है तब त्वरण अधिकतम होता है। समीकरण (i) में $v=0$ रखकर देखें
$0 =6 t-2 t^{2} $
$\Rightarrow 0 =t(6-2 t) $
$\Rightarrow =t \times 2(3-t)=0 $
t=0 या 3 s
(d) 0 से $3 s$ में तय की गई दूरी $9 m$ है
3 से $6 s$ में तय की गई दूरी $\int_3^{6}(18-9 t+t^{2}) d t$
$ \begin{aligned} & =\left(18 t-\dfrac{9 t^{2}}{2}+\dfrac{t^{3}}{3}\right)_3^{6} \\
$$ \begin{aligned} & =18 \times 6-\dfrac{9}{2} \times 6^{2}+\dfrac{6^{3}}{3}-\left(18 \times 3-\dfrac{9 \times 3^{2}}{2}+\dfrac{3^{3}}{3}\right) \\ & =108-9 \times 18+\dfrac{6^{3}}{3}-18 \times 3+\dfrac{9}{2} \times 9-\dfrac{27}{3} \\ & =108-18 \times 9+\dfrac{216}{3}-54+4.5 \times 9-9=-4.5 m \end{aligned} $$
$$ \therefore $$ कुल दूरी एक चक्र में तय की गई $=s_1+s_2=9-4.5=4.5 m$
कुल दूरी के लिए कवर किए गए चक्रों की संख्या $=\dfrac{20}{4.5} \approx 4.44$।
26. एक आदमी एक 100 मीटर ऊंचे इमारत के शीर्ष पर खड़ा है। वह दो गेंदों को ऊर्ध्वाधर रूप से फेंकता है, एक $t=0$ पर और एक समय अंतर (2 सेकंड से कम) के बाद। बाद की गेंद को पहली गेंद के वेग के आधे वेग से फेंका जाता है। पहली और दूसरी गेंद के बीच ऊर्ध्वाधर अंतर $t=2$ सेकंड पर $+15$ मीटर है। अंतर निरंतर रहता है। गेंदों को फेंकने के वेग और उनके फेंकने के सटीक समय अंतर की गणना करें।
उत्तर दिखाएं
सोचने की प्रक्रिया
इस प्रश्न में गति के समीकरण के साथ सही चिह्न के साथ उपयोग किया जाएगा और समय अंतर की गणना के लिए हम विस्थापन के अंतर के अंतर का उपयोग करेंगे।
उत्तर मान लीजिए दो गेंदों (1 और 2) के वेग $v_1$ और $v_2$ हैं जहां
यदि $v_1=2 v, v_2=v$
यदि $y_1$ और $y_2$ दो गेंदों द्वारा रूकने तक तय की गई दूरी है, तो
$ y_1=\dfrac{v_1^{2}}{2 g}=\dfrac{4 v^{2}}{2 g} \text { और } y_2=\dfrac{v_2^{2}}{2 g}=\dfrac{v^{2}}{2 g} $
$ y_1-y_2=15 m, \dfrac{4 v^{2}}{2 g}-\dfrac{v^{2}}{2 g}=15 m \text { या } \dfrac{3 v^{2}}{2 g}=15 m $
या $\quad v=10 m / s$
स्पष्ट रूप से, $v_1=20 m / s$ और $v_2=10 m / s$
$ \begin{aligned} & y_1=\dfrac{v_1^{2}}{2 g}=\dfrac{(20 m)^{2}}{2 \times 10 m 15}=20 m \\ & y_2=y_1-15 m=5 m \end{aligned} $
यदि $t_2$ दूसरी गेंद द्वारा 5 मीटर की दूरी तय करने के लिए लिया गया समय है, तो
$y_2=v_2 t-\dfrac{1}{2} g t_2^{2}$
$ 5=10 t_2-5 t_2^{2} \text { या } t_2^{2}-2 t_2+1=0 $
जहाँ $\quad t_2=1 ~\text{s}$
क्योंकि $t_1$ (पहली गेंद द्वारा 20 मीटर की दूरी तय करने के लिए लिया गया समय) 2 सेकंड है, दो फेंकों के बीच समय अंतर
$ =t_1-t_2=2 s-1 s=1 s $
ध्यान दें हम जब एकसरणी गति के समीकरण के अनुप्रयोग कर रहे हैं तब हम बहुत सावधानी से काम करना चाहिए।





