यदि संख्या 1 से कम हो, तो दशमलव बिंदु के दाहिने ओर शून्य (ओ) और पहले गैर-शून्य अंक के बीच रखे गए शून्य अंक असांख्यिकीय होते हैं।

उत्तर (b) $\underline{0}$. $\underline{6} 6900$ में अंतर्गत शून्य अंक असांख्यिकीय हैं। अतः सांख्यिकीय अंकों की संख्या चार (6900) है।

• विकल्प (a) गलत है क्योंकि इसमें 5 सांख्यिकीय अंकों की बात कही गई है, लेकिन शुरुआती शून्य अंक असांख्यिकीय है, अतः केवल 4 सांख्यिकीय अंक (6900) हैं।
• विकल्प (c) गलत है क्योंकि इसमें केवल 2 सांख्यिकीय अंकों की बात कही गई है, लेकिन दशमलव बिंदु के बाद रखे गए शून्य अंक सांख्यिकीय हैं, अतः इसकी संख्या 4 (6900) है।
• विकल्प (d) गलत है क्योंकि इसमें 3 सांख्यिकीय अंकों की बात कही गई है, लेकिन दशमलव बिंदु के बाद रखे गए शून्य अंक सांख्यिकीय हैं, अतः इसकी संख्या 4 (6900) है।

उत्तर (b) संख्याओं के योग की गणना 663.821 के अंकगणितीय रूप में की जा सकती है। दशमलव स्थानों की सबसे कम संख्या वाली संख्या 227.2 है जो केवल एक दशमलव स्थान तक सही है।

अतः अंतिम परिणाम को एक दशमलव स्थान तक को घिस देना चाहिए, अर्थात 664 ।

नोट: योग की गणना करते समय हम दशमलव स्थानों की संख्या और सांख्यिकीय अंकों की संख्या के बारे में गलत अंतर कर नहीं चाहिए। परिणाम के दशमलव स्थानों की सबसे कम संख्या होनी चाहिए।

• विकल्प (a) 663.821: यह विकल्प गलत है क्योंकि इसमें दशमलव स्थानों की सबसे कम संख्या के अनुसार घिसने के नियम का पालन नहीं किया गया है। 227.2 में केवल एक दशमलव स्थान है, अतः अंतिम परिणाम को एक दशमलव स्थान तक घिस देना चाहिए, न कि तीन दशमलव स्थान तक।

• विकल्प (c) 663.8: यह विकल्प गलत है क्योंकि योग को एक दशमलव स्थान तक घिसा गया है, लेकिन ठीक घिसने के नियम का पालन नहीं किया गया है। 663.821 को एक दशमलव स्थान तक घिसने पर यह 664 होता है, न कि 663.8।

• विकल्प (d) 663.82: यह विकल्प गलत है क्योंकि यह योग को दो दशमलव स्थान तक करीब ले जाता है। संख्या 227.2 केवल एक दशमलव स्थान तक है, इसलिए अंतिम परिणाम को एक दशमलव स्थान तक करीब ले जाया जाना चाहिए, न कि दो।

उत्तर (c) इस प्रश्न में, घनत्व को दो सांख्यिकीय अंकों तक रिपोर्ट करना चाहिए।

$ \text { घनत्व }=\frac{4.237 g}{2.5 cm^{3}}=1.6948 $

संख्या को घनत्व के रूप में रॉउंड करते हुए, हमें घनत्व $=1.7$ प्राप्त होता है।

• विकल्प (a) $1.6048 g cm^{-3}$: यह विकल्प गलत है क्योंकि यह $1.6948 g cm^{-3}$ के गणना मूल्य से मेल नहीं खाता है और इसमें अतिरिक्त सांख्यिकीय अंक हैं।
• विकल्प (b) $1.69 g cm^{-3}$: यह विकल्प गलत है क्योंकि इसमें तीन सांख्यिकीय अंक हैं, जबकि सही उत्तर को दो सांख्यिकीय अंकों तक रॉउंड करना चाहिए।
• विकल्प (d) $1.695 g cm^{-3}$: यह विकल्प गलत है क्योंकि इसमें चार सांख्यिकीय अंक हैं, जबकि सही उत्तर को दो सांख्यिकीय अंकों तक रॉउंड करना चाहिए।

उत्तर (d) 2.745 को तीन सांख्यिकीय अंकों तक रॉउंड करने पर यह 2.74 होगा। 2.735 को तीन सांख्यिकीय अंकों तक रॉउंड करने पर यह भी 2.74 होगा।

• विकल्प (a) 2.75 और 2.74: यह विकल्प गलत है क्योंकि 2.745 को तीन सांख्यिकीय अंकों तक रॉउंड करने पर 2.74, न कि 2.75 प्राप्त होता है। तीसरे सांख्यिकीय अंक के बाद के अंक 5 है, और रॉउंडिंग के नियमों के अनुसार, यदि अंक ठीक 5 हो, तो आप एक सम संख्या तक रॉउंड करते हैं, जो इस मामले में 4 है।

• विकल्प (ब) 2.74 और 2.73: यह विकल्प गलत है क्योंकि 2.735 को 3 सांख्यिकीय अंकों तक करोड़ करने पर परिणाम 2.74 होना चाहिए, न कि 2.73। तीसरे सांख्यिकीय अंक के बाद के अंक 5 है, और करोड़ करने के नियमों के अनुसार, यदि अंक ठीक 5 हो, तो आपको सबसे करीबी समान अंक तक करोड़ करना होता है, जो इस मामले में 4 है।

• विकल्प (स) 2.75 और 2.73: यह विकल्प दो कारणों से गलत है। पहले, 2.745 को 3 सांख्यिकीय अंकों तक करोड़ करने पर परिणाम 2.74 होना चाहिए, न कि 2.75। दूसरे, 2.735 को 3 सांख्यिकीय अंकों तक करोड़ करने पर परिणाम 2.74 होना चाहिए, न कि 2.73। दोनों मामलों में तीसरे सांख्यिकीय अंक के बाद के अंक 5 है, और करोड़ करने के नियमों के अनुसार, यदि अंक ठीक 5 हो, तो आपको सबसे करीबी समान अंक तक करोड़ करना होता है, जो दोनों मामलों में 4 है।

यदि $\Delta x$ एक भौतिक राशि में त्रुटि है, तो संबंधित त्रुटि की गणना $\frac{\Delta x}{x}$ के रूप में की जाती है।

उत्तर (a) दिया गया है,

$ \begin{aligned} \text { लंबाई } l & =(16.2 \pm 0.1) cm \\ \text { चौड़ाई } b & =(10.1 \pm 0.1) cm \\ \text { क्षेत्रफल } A & =l \times b \\ & =(16.2 cm) \times(10.1 cm)=163.62 cm^{2} \end{aligned} $

तीन सांख्यिकीय अंकों तक करोड़ करने पर, क्षेत्रफल $A=164 cm^{2}$

$ \begin{aligned} \frac{\Delta A}{A} & =\frac{\Delta l}{l}+\frac{\Delta b}{b}=\frac{0.1}{16.2}+\frac{0.1}{10.1} \\ & =\frac{1.01+1.62}{16.2 \times 10.1}=\frac{2.63}{163.62} \\ \Rightarrow \quad \Delta A & =A \times \frac{2.63}{163.62}=163.62 \times \frac{2.63}{163.62}=2.63 cm^{2} \\ \Delta A & =3 cm^{2} \quad \text { (एक सांख्यिकीय अंक तक करोड़ करने पर) } \\ \therefore \quad \text { क्षेत्रफल, } A & =A \pm \Delta A=(164 \pm 3) cm^{2} . \end{aligned} $

• विकल्प (ब): क्षेत्रफल की गणना सही रूप से $163.62 , \text{cm}^2$ है, लेकिन त्रुटि की गणना गलत है। त्रुटि को एक सांख्यिकीय अंक तक करोड़ करना चाहिए, जो $3 , \text{cm}^2$ होता है, न कि $2.6 , \text{cm}^2$।

• विकल्प (c): क्षेत्रफल $163.6 , \text{cm}^2$ के रूप में घुमाया गया है, जो गलत है क्योंकि क्षेत्रफल को तीन सांख्यिक अंकों तक घुमाया जाना चाहिए, जिसके परिणामस्वरूप $164 , \text{cm}^2$ होता है। इसके अलावा, त्रुटि को एक सांख्यिक अंक तक घुमाया जाना चाहिए, जो $3 , \text{cm}^2$ होता है, न कि $2.6 , \text{cm}^2$।

• विकल्प (d): क्षेत्रफल $163.62 , \text{cm}^2$ के रूप में सही ढंग से गणना की गई है, लेकिन त्रुटि की गणना गलत है। त्रुटि को एक सांख्यिक अंक तक घुमाया जाना चाहिए, जो $3 , \text{cm}^2$ होता है, न कि $3 , \text{cm}^2$ (क्योंकि यह पहले से सही है)। हालांकि, क्षेत्रफल को तीन सांख्यिक अंकों तक घुमाया जाना चाहिए, जिसके परिणामस्वरूप $164 , \text{cm}^2$ होता है।

उत्तर (c) (a) कार्य $=$ बल $\times$ दूरी $=[MLT^{-2}][L][ML^{2} T^{-2}]$ बलाघूर्ण $=$ बल $\times$ दूरी $=[ML^{2} T^{-2}]$

(b) कोणीय संवेग $=mvr=[M][LT^{-1}][L]=[ML^{2} T^{-1}]$ प्लैंक के नियतांक $=\frac{E}{V}=\frac{[ML^{2} T^{-2}]}{[T^{-1}]}=[ML^{2} T^{-1}]$

(c) तनाव $=$ बल $=[MLT^{-2}]$

सतह तनाव $=\frac{\text { बल }}{\text { लंबाई }}=\frac{[MLT^{-2}]}{[L]}=[ML^{0} T^{-2}]$

(d) आवेग $=$ बल $\times$ समय $=[MLT^{-2}][T]=[MLT^{-1}]$

संवेग $=$ द्रव्यमान $\times$ वेग $=[M][LT^{-1}]=[MLT^{-1}]$

नोट: एक व्यक्ति को दोनों भौतिक राशियों - सतह तनाव और तनाव के समान रूप के तनाव के साथ गलतफहमी नहीं होनी चाहिए। दोनों के विमीय सूत्र एक नहीं हैं।

• (a) कार्य और बलाघूर्ण: कार्य और बलाघूर्ण के विमीय सूत्र एक ही है, जो $[ML^2 T^{-2}]$ है। इसलिए, यह विकल्प गलत है।

• (b) कोणीय संवेग और प्लैंक के नियतांक: कोणीय संवेग और प्लैंक के नियतांक के विमीय सूत्र एक ही है, जो $[ML^2 T^{-1}]$ है। इसलिए, यह विकल्प गलत है।

• (d) आवेग और रैखिक संवेग: आवेग और रैखिक संवेग के एक ही आयामी सूत्र होता है, जो $[MLT^{-1}]$ होता है। इसलिए, यह विकल्प गलत है।

Answer (a) दिया गया है,

$ \begin{aligned} A & =2.5 ms^{-1} \pm 0.5 ms^{-1}, B=0.10 s \pm 0.01 s \\ x & =A B=(2.5)(0.10)=0.25 m \\ \frac{\Delta x}{x} & =\frac{\Delta A}{A}+\frac{\Delta B}{B} \\ & =\frac{0.5}{2.5}+\frac{0.01}{0.10}=\frac{0.05+0.025}{0.25}=\frac{0.075}{0.25} \end{aligned} $

$\Delta x=0.075=0.08 m$, दो सांख्यिकीय अंकों तक कोण देने पर।

$A B=(0.25 \pm 0.08) m$

• विकल्प (b) $(0.25 \pm 0.5) m$ गलत है क्योंकि गणना किया गया अनिश्चितता $\Delta x$ $0.08 m$ है, न कि $0.5 m$। मान $0.5 m$ वास्तविक अनिश्चितता से बहुत अधिक है।

• विकल्प (c) $(0.25 \pm 0.05) m$ गलत है क्योंकि गणना किया गया अनिश्चितता $\Delta x$ $0.08 m$ है, न कि $0.05 m$। मान $0.05 m$ वास्तविक अनिश्चितता से कम है।

• विकल्प (d) $(0.25 \pm 0.135) m$ गलत है क्योंकि गणना किया गया अनिश्चितता $\Delta x$ $0.08 m$ है, न कि $0.135 m$। मान $0.135 m$ वास्तविक अनिश्चितता से अधिक है।

Answer (d) दिया गया है,

$ \begin{aligned} & A=1.0 m \pm 0.2 m, B=2.0 m \pm 0.2 m \\ & Y=\sqrt{A B}=\sqrt{(1.0)(2.0)}=1.414 m \end{aligned} $

मान लीजिए,

दो सांख्यिकीय अंकों तक कोण देने पर $Y=1.4 m$

$\frac{\Delta Y}{Y}=\frac{1}{2}[\frac{\Delta A}{A}+\frac{\Delta B}{B}]=\frac{1}{2}[\frac{0.2}{1.0}+\frac{0.2}{2.0}]=\frac{0.6}{2 \times 2.0}$

$\Rightarrow \Delta Y=\frac{0.6 Y}{2 \times 2.0}=\frac{0.6 \times 1.4}{2 \times 2.0}=0.212$

एक सांख्यिक अंक के लिए चौड़ाई को गोल करने पर $\Delta Y=0.2 m$

इसलिए, $\sqrt{A B}=r+\Delta r=1.4 \pm 0.2 m$ का सही मान है

• विकल्प (a) $1.4 m \pm 0.4 m$ गलत है क्योंकि अस्थिरता $\pm 0.4 m$ बहुत बड़ी है। सही अस्थिरता की गणना $\pm 0.2 m$ देती है।

• विकल्प (b) $1.41 m \pm 0.15 m$ गलत है क्योंकि मान $1.41 m$ दो सांख्यिक अंकों तक गोल नहीं किया गया है। इसके अलावा, अस्थिरता $\pm 0.15 m$ सही गणना के साथ संगत नहीं है, जो $\pm 0.2 m$ देती है।

• विकल्प (c) $1.4 m \pm 0.3 m$ गलत है क्योंकि अस्थिरता $\pm 0.3 m$ बहुत बड़ी है। सही अस्थिरता की गणना $\pm 0.2 m$ देती है।

उत्तर (a) सभी दिए गए मापन दो दशमलव स्थान तक सही हैं। यहाँ $5.00 mm$ सबसे छोटा इकाई है और $5.00 mm$ में त्रुटि सबसे कम है (अगर निर्दिष्ट नहीं किया गया हो तो आमतौर पर $0.01 mm$ लिया जाता है), इसलिए $5.00 mm$ सबसे सटिक है।

टिप्पणी: इस तरह के प्रश्नों को हल करते समय हम इकाइयों के बारे में सावधान रहना चाहिए भले ही उनके मान एक समान हों।

• $5.00 cm$: यह दो दशमलव स्थान तक सही है, लेकिन इकाई $5.00 mm$ से बड़ी है, जिसके कारण $5.00 cm$ में अधिक अंतर त्रुटि होती है (अगर निर्दिष्ट नहीं किया गया हो तो आमतौर पर $0.01 cm$ लिया जाता है), जिसके कारण यह $5.00 mm$ की तुलना में कम सटिक है।

• $5.00 m$: यह मापन भी दो दशमलव स्थान तक सही है, लेकिन इकाई $5.00 cm$ से भी बड़ी है, जिसके कारण अधिक अंतर त्रुटि होती है (अगर निर्दिष्ट नहीं किया गया हो तो आमतौर पर $0.01 m$ लिया जाता है), जिसके कारण यह $5.00 mm$ और $5.00 cm$ की तुलना में कम सटिक है।

• $5.00 km$: हालांकि यह दो दशमलव स्थान तक सही है, लेकिन इकाई विकल्पों में सबसे बड़ी है, जिसके कारण अधिक अंतर त्रुटि होती है (अगर निर्दिष्ट नहीं किया गया हो तो आमतौर पर $0.01 km$ लिया जाता है), जिसके कारण यह $5.00 mm$, $5.00 cm$ और $5.00 m$ की तुलना में सबसे कम सटिक है।

उत्तर (a) दी गई लंबाई

$ l=5 cm $

अब, प्रत्येक विकल्प के साथ त्रुटि की जांच करते हुए, हमें प्राप्त होता है

त्रुटि $\Delta l_1$ सबसे कम है।

$ \begin{aligned} & \Delta l_1=5-4.9=0.1 cm \\ & \Delta l_2=5-4.805=0.195 cm \\ & \Delta l_3=5.25-5=0.25 cm \\ & \Delta l_4=5.4-5=0.4 cm \end{aligned} $

अतः, $4.9 cm$ सबसे सटीक है।

• विकल्प (b) $4.805 cm$ गलत है क्योंकि त्रुटि $\Delta l_2 = 0.195 cm$ $4.9 cm$ की त्रुटि की अपेक्षा अधिक है।
• विकल्प (c) $5.25 cm$ गलत है क्योंकि त्रुटि $\Delta l_3 = 0.25 cm$ $4.9 cm$ की त्रुटि की अपेक्षा अधिक है।
• विकल्प (d) $5.4 cm$ गलत है क्योंकि त्रुटि $\Delta l_4 = 0.4 cm$ $4.9 cm$ की त्रुटि की अपेक्षा अधिक है।

उत्तर (c) दिया गया, यंग प्रतिबल

$ \begin{aligned} Y & =1.9 \times 10^{11} N / m^{2} \\ 1 N & =10^{5} \text { डाइन } \\ Y & =1.9 \times 10^{11} \times 10^{5} \text { डाइन } / m^{2} \\ 1 m & =100 cm \\ Y & =1.9 \times 10^{11} \times 10^{5} \text { डाइन } /(100)^{2} cm^{2} \\ & =1.9 \times 10^{16-4} \text { डाइन } / cm^{2} \\ Y & =1.9 \times 10^{12} \text { डाइन } / cm^{2} \end{aligned} $

अतः,

हम जानते हैं कि

ध्यान रखें कि इकाई आवर्तन के दौरान हमें इकाइयों के सही संबंध के बारे में ध्यान रखना चाहिए।

• विकल्प (a) $1.9 \times 10^{10}$: यह विकल्प गलत है क्योंकि इसमें आवर्तन गुणक को अतिक्रमित करता है। सही आवर्तन गुणक के गुणन के बराबर $1.9 \times 10^{12}$ होता है, न कि $1.9 \times 10^{10}$.

• विकल्प (b) $1.9 \times 10^{11}$: यह विकल्प गलत है क्योंकि इसमें $N/m^2$ से $dyne/cm^2$ में पूर्ण रूप से बदलाव को ध्यान में नहीं लिया गया है। सही बदलाव गुणांक $10^{16-4}$ होता है, जिसके कारण $1.9 \times 10^{12}$, नहीं $1.9 \times 10^{11}$ प्राप्त होता है।

• विकल्प (d) $1.9 \times 10^{13}$: यह विकल्प गलत है क्योंकि इसमें बदलाव गुणांक को अधिक अनुमानित किया गया है। सही बदलाव के परिणाम $1.9 \times 10^{12}$ dyne/cm^2 होता है, नहीं $1.9 \times 10^{13}$।

उत्तर (d) दिया गया है, मूल राशियाँ संवेग $(p)$, क्षेत्रफल $(A)$ और समय $(T)$ हैं। हम ऊर्जा $E$ को लिख सकते हैं

$ \begin{aligned} & E \propto p^{a} A^{b} T^{c} \\ & E=k p^{a} A^{A} T^{c} \end{aligned} $

जहाँ $k$ अप्रमाणीय अनुपातिक नियतांक है।

विमाएँ हैं

$ \begin{aligned} E & =[E]=[ML^{2} T^{-2}] \text { और }[p]=[MLT^{-1}] \\ {[A] } & =[L^{2}] \\ {[T] } & =[T] \\ {[E] } & =[K][p]^{a}[A]^{b}[T]^{c} \end{aligned} $

सभी विमाओं को रखने पर हमें प्राप्त होता है

$ \begin{aligned} ML^{2} T^{-2} & =[MLT^{-1}]^{a}[L^{2}]^{b}[T]^{c} \\ & =M^{a} L^{2 b+a} T^{-a+c} \end{aligned} $

विमीय समानता के सिद्धांत के अनुसार,

$ a =1,2 b+a=2 $

$\Rightarrow 2 b+1 =2 $

$\Rightarrow b =1 / 2-a+c=-2 $

$\Rightarrow c =-2+a=-2+1=-1 $

$\text{ इसलिए, } E =p A^{1 / 2} T^{-1}$

• विकल्प (a) $[pA^{-1} T^{1}]$: यह विकल्प गलत है क्योंकि विमीय विश्लेषण ऊर्जा की विमाओं के साथ मेल नहीं खाता है। ऊर्जा की विमाएँ $[ML^2 T^{-2}]$ होती हैं, लेकिन दिए गए विकल्प की विमाएँ $[MLT^{-1}][L^{-2}][T] = [ML^{-1}T^0]$ होती हैं, जो ऊर्जा की विमाओं के बराबर नहीं होती हैं।

• विकल्प (b) $[p^{2} AT]$: यह विकल्प गलत है क्योंकि विमीय विश्लेषण ऊर्जा की विमाओं के साथ मेल नहीं खाता है। ऊर्जा की विमाएँ $[ML^2 T^{-2}]$ होती हैं, लेकिन दिए गए विकल्प की विमाएँ $[MLT^{-1}]^2[L^2][T] = [M^2L^4T^{-2}][T] = [M^2L^4T^{-1}]$ होती हैं, जो ऊर्जा की विमाओं के बराबर नहीं होती हैं।

• विकल्प (c) $[p A^{-1 / 2} T]$: यह विकल्प गलत है क्योंकि आयामांकन के अनुरूप ऊर्जा के आयाम नहीं मिलते। ऊर्जा के आयाम $[ML^2 T^{-2}]$ होते हैं, लेकिन दिए गए विकल्प के आयाम $[MLT^{-1}][L^{-1}][T] = [ML^0T^0] = [M]$ होते हैं, जो ऊर्जा के आयाम के बराबर नहीं होते।

हम जानते हैं कि कोण आयामहीन होता है। यहाँ, $a$ विस्थापन है और $y$ भी विस्थापन है, इसलिए दोनों के आयाम समान होते हैं।

उत्तर $(b, c)$

अब, आयाम समानता के सिद्धांत के अनुसार (a) और (d) के बाईं ओर और दाईं ओर के आयाम समान होंगे और यह $L$ होगा।

(के लिए) $ \begin{aligned} & {[LHS]=L} \\ & {[RHS]=\frac{L}{T}=LT^{-1}} \\ & {[LHS] \neq[RHS]} \end{aligned} $

इसलिए, (c) गलत विकल्प है।

विकल्प (b) में कोण के आयाम [vt] है, अर्थात $[L]$ $ \begin{matrix} \Rightarrow & R H S=L . L=L^{2} \text { और } L H S=L \\ \Rightarrow & L H S \neq R H S . \end{matrix} $

इसलिए, विकल्प (b) भी गलत है।

• विकल्प (b) के लिए:

  • साइन फंक्शन में कोण के आयाम [vt] है, जो $[L]$ होता है।
  • इसलिए, दाईं ओर के आयाम $L \cdot L = L^2$ होते हैं।
  • बाईं ओर के आयाम $L$ होते हैं।
  • इसलिए, $[LHS] \neq [RHS]$ होता है।

• विकल्प (c) के लिए:

  • बाईं ओर के आयाम $L$ होते हैं।
  • दाईं ओर के आयाम $\frac{L}{T} = LT^{-1}$ होते हैं।
  • इसलिए, $[LHS] \neq [RHS]$ होता है।

हमें याद रखना चाहिए कि जब दो भौतिक राशियों को जोड़ा या घटाया जाता है तो उनके आयाम समान होने चाहिए।

उत्तर $(a, e)$

इस प्रश्न में दिया गया है कि $P, Q$ और $R$ अलग-अलग आयाम रखते हैं, इसलिए उन्हें जोड़ा या घटाया नहीं जा सकता, इसलिए हम कह सकते हैं कि (a) और (e) अर्थपूर्ण नहीं हैं। हम इन राशियों के गुणनफल के आयाम के बारे में नहीं कह सकते, इसलिए (b), (c) और (d) अर्थपूर्ण हो सकते हैं।

ध्यान रखें: इस प्रश्न में हम एक राशि के बारे में निश्चित हैं जो कभी अर्थपूर्ण नहीं होती है, लेकिन हमें याद रखना चाहिए कि अन्य राशियाँ अर्थपूर्ण हो सकती हैं या नहीं।

• विकल्प (b) $PQ - R$:

  • गुणन $PQ$ एक नई राशि के आयाम के रूप में उत्पन्न होता है जो $P$ और $Q$ के आयाम के संयोजन के बराबर होता है। क्योंकि $R$ के आयाम अलग है, $PQ$ से $R$ को घटाना अर्थपूर्ण नहीं है क्योंकि अलग-अलग आयाम वाली राशियों को जोड़ा या घटाया नहीं जा सकता।

• विकल्प (c) $PQ / R$:

  • $PQ$ के गुणनफल को $R$ से विभाजित करने से एक नई राशि के आयाम के रूप में उत्पन्न होता है जो $P$, $Q$ और $R$ के आयाम के संयोजन के बराबर होता है। इस संयोजन के आधार पर इस राशि के आयाम अर्थपूर्ण हो सकते हैं या नहीं, जो $P$, $Q$ और $R$ के विशिष्ट आयाम पर निर्भर करता है।

• विकल्प (d) $(PR - Q^2) / R$:

  • $PR$ के आयाम $P$ और $R$ के आयाम के संयोजन के बराबर होते हैं, और $Q^2$ के आयाम $Q$ के आयाम के वर्ग के बराबर होते हैं। क्योंकि $P$, $Q$ और $R$ अलग-अलग आयाम रखते हैं, $PR$ और $Q^2$ के बीच घटाव अर्थपूर्ण नहीं हो सकता। हालांकि, पूरे व्यंजक $(PR - Q^2) / R$ के आयाम अर्थपूर्ण हो सकते हैं या नहीं, जो $P$, $Q$ और $R$ के विशिष्ट आयाम पर निर्भर करता है।

• विकल्प (e) $(R + Q) / P$:

  • $R + Q$ के योग अर्थपूर्ण नहीं है क्योंकि $R$ और $Q$ के आयाम अलग हैं और उन्हें जोड़ा नहीं जा सकता। इसलिए, पूरे व्यंजक $(R + Q) / P$ अर्थपूर्ण नहीं है।

उत्तर

( $b, d)$

हम जानते हैं कि विकिरण की ऊर्जा, $E=h v$

$ [h]=\frac{[E]}{[v]}=\frac{[ML^{2} T^{-2}]}{[T^{-1}]}=[ML^{2} T^{-1}] $

रैखिक इम्पलस की विमा = संवेग की विमा $=[MLT^{-1}]$

हम जानते हैं कि रैखिक इम्पलस $J=\Delta P$

$\Rightarrow \quad$ एंगलर इम्पलस $=\tau d t=\Delta L=$ एंगलर संवेग में परिवर्तन

अतः, एंगलर इम्पलस की विमा

$ \begin{aligned} & =\text { एंगलर संवेग की विमा } \\ & =[ML^{2} T^{-1}] . \end{aligned} $

यह प्लैंक नियतांक $h$ की विमा के समान है।

• विकल्प (a) रैखिक इम्पलस: रैखिक इम्पलस की विमा रैखिक संवेग के समान होती है, जो $[MLT^{-1}]$ होती है। यह प्लैंक नियतांक $h$ की विमा $[ML^2T^{-1}]$ से भिन्न है।

• विकल्प (c) रैखिक संवेग: रैखिक संवेग की विमा $[MLT^{-1}]$ होती है। यह प्लैंक नियतांक $h$ की विमा $[ML^2T^{-1}]$ से मेल नहीं खाती है।

उत्तर

$(a, b, d)$

हम जानते हैं कि $h$ की विमा $[h]=[ML^{2} T^{-1}]$

$[c]=[LT^{-1}],[m_{e}]=M$

$[G]=[M^{-1} L^{3} T^{-2}]$

$[e]=[A T],[m_{p}]=[M]$

$[\frac{h c}{G}]=\frac{[ML^{2} T^{-1}][LT^{-1}]}{[M^{-1} L^{3} T^{-2}]}=[M^{2}]$

$M=\sqrt{\frac{h c}{G}}$

उसी तरह,

$\frac{h}{c}=\frac{[ML^{2} T^{-1}]}{[LT^{-1}]}=[ML]$

$L=\frac{h}{c M}=\frac{h}{c} \sqrt{\frac{G}{h c}}=\frac{\sqrt{G h}}{c^{3 / 2}}$

जैसे,

$ c=L T^{-1} $

$\Rightarrow \quad[T]=\frac{[L]}{[c]}=\frac{\sqrt{G h}}{c^{3 / 2} \cdot c}=\frac{\sqrt{G h}}{c^{5 / 2}}$

अतः, (a), (b) या (d) कोई भी तीन चुने गए मूलभूत राशियों के आधार पर $L, M$ और $T$ को व्यक्त करने के लिए उपयोग किया जा सकता है।

• विकल्प (c) इलेक्ट्रॉन के आवेश (e) के लिए गलत है क्योंकि इसका आयाम $[A T]$ होता है, जिसमें विद्युत धारा (A) की इकाई शामिल होती है। चूंकि चुने गए मूल राशियाँ प्लैंक नियतांक $(h)$ और निर्वात में प्रकाश की गति $(c)$ हैं, जो विद्युत धारा की इकाई को शामिल नहीं करती हैं, इसलिए इलेक्ट्रॉन के आवेश का उपयोग तीन चुने गए मूल राशियों के संदर्भ में लंबाई, द्रव्यमान और समय को व्यक्त करने के लिए नहीं किया जा सकता है।

इस प्रकार के प्रश्नों को हल करते समय, हम सबसे पहले एक व्यंजक लिखें और इसे विकल्प में दी गई राशियों के संदर्भ में व्यक्त करने की कोशिश करें।

उत्तर $(a, b)$

हम जानते हैं कि दबाव $=\frac{\text { बल }}{\text { क्षेत्रफल }}$

$ \text { दबाव }=\frac{\text { बल } \times \text { दूरी }}{\text { क्षेत्रफल } \times \text { दूरी }}=\frac{\text { कार्य }}{\text { आयतन }}=\frac{\text { ऊर्जा }}{\text { आयतन }} $

ध्यान दें: यहाँ हमें ध्यान रखना चाहिए कि उपरोक्त मान सटीक रूप से बराबर नहीं हैं, लेकिन इनके इकाइयों के संदर्भ में ये तुलनीय हैं।

• विकल्प (c) ऊर्जा/क्षेत्रफल: इस अनुपात दबाव को व्यक्त नहीं करता है क्योंकि दबाव इकाई क्षेत्रफल पर बल के अनुपात में होता है, न कि ऊर्जा पर इकाई क्षेत्रफल पर। इकाई क्षेत्रफल पर ऊर्जा के अनुपात के रूप में एक अलग भौतिक राशि हो सकती है, जैसे कि सतह पर ऊर्जा घनत्व।

• विकल्प (d) बल/आयतन: इस अनुपात दबाव को व्यक्त नहीं करता है क्योंकि दबाव इकाई क्षेत्रफल पर बल के अनुपात में होता है, न कि बल पर इकाई आयतन पर। इकाई आयतन पर बल के अनुपात के रूप में एक अलग भौतिक राशि हो सकती है, जैसे कि बल घनत्व।

उत्तर $(b, d)$

हम जानते हैं कि 1 प्रकाश वर्ष $=9.46 \times 10^{11} m$

$=$ विद्युत धारा के वेग $3 \times 10^{8} m / s$ के साथ 1 वर्ष में प्रकाश द्वारा तय की गई दूरी।

1 पार्सेक $=3.08 \times 10^{16} m$

$=$ उस दूरी को दर्शाता है जिस पर पृथ्वी के वृत्तीय कक्षा की औसत त्रिज्या 1 पार्सेक कोण के अंतर्गत झुकती है

यहाँ, सेकंड और वर्ष समय को दर्शाते हैं।

• पार्सेक: पार्सेक एक दूरी की इकाई है जो खगोल विज्ञान में उपयोग की जाती है ताकि हम अपने सौर मंडल के बाहर के वस्तुओं की बड़ी दूरी को माप सकें। यह लगभग 3.26 प्रकाश वर्ष या लगभग 3.08 × 10^16 मीटर के बराबर होता है। यह समय की इकाई नहीं है।

• प्रकाश वर्ष: प्रकाश वर्ष एक दूरी की इकाई है, न कि समय की। यह एक वैक्यूम में एक वर्ष में प्रकाश द्वारा तय की गई दूरी को दर्शाता है, जो लगभग 9.46 × 10^12 किलोमीटर या लगभग 5.88 × 10^12 मील के बराबर होता है।

उत्तर किसी भी दी गई भौतिक राशि का मान एक बहुत विस्तार के रेंज में बदल सकता है, इसलिए एक ही भौतिक राशि के लिए विभिन्न इकाइयाँ आवश्यक होती हैं।

उदाहरण के लिए, कलम की लंबाई को $cm$ में आसानी से मापा जा सकता है, पेड़ की ऊंचाई मीटर में मापी जा सकती है, दो शहरों के बीच की दूरी किलोमीटर में मापी जा सकती है और दो आकाशगंगाओं के बीच की दूरी प्रकाश वर्ष में मापी जा सकती है।

उत्तर

$$ \begin{aligned} \text{परमाणु की त्रिज्या} & = 1 \text{Å} = 10^{-10} , \text{m} \ \text{नाभिक की त्रिज्या} & = 1 \text{फर्मी} = 10^{-15} \text{m} \ \text{परमाणु का आयतन} & = V_A = \frac{4}{3} \pi R_A^{3} \ \text{नाभिक का आयतन} & = V_N = \frac{4}{3} \pi R_N^{3} \ \frac{V_A}{V_N} & = \frac{\frac{4}{3} \pi R_A^{3}}{\frac{4}{3} \pi R_N^{3}} = \left(\frac{R_A}{R_N}\right)^{3} = \left(\frac{10^{-10}}{10^{-15}}\right)^{3} = 10^{15} \end{aligned} $$ नोट: ऐसे प्रश्नों में, हमें हमेशा एक ही इकाई में मान बदलना चाहिए।

उत्तर एक परमाणु द्रव्यमान इकाई एक $ _6 C^{12} $ परमाणु के द्रव्यमान का $\frac{1}{12}$ होती है।

एक मोल के $ _6 C^{12} $ परमाणु का द्रव्यमान $=12 g$

एक मोल में परमाणुओं की संख्या $=$ आवोगाड्रो संख्या

$ =6.023 \times 10^{23} $

$ \begin{aligned} \therefore \quad \text { एक } _6 C^{12} \text { परमाणु का द्रव्यमान } & =\frac{12}{6.023 \times 10^{23}} g \\ 1 amu & =\frac{1}{12} \times \text { एक } _6 C^{12} \text { परमाणु का द्रव्यमान } \\ \therefore \quad 1 amu & =(\frac{1}{12} \times \frac{12}{6.023 \times 10^{23}}) g=1.67 \times 10^{-24} g \\ & =1.67 \times 10^{-27} kg \quad(\because 1 g=10^{-3} kg) \end{aligned} $

उत्तर भौतिकी में लंबाई, द्रव्यमान और समय को आधार राशियों के रूप में चुना गया है क्योंकि

(i) लंबाई, द्रव्यमान और समय एक दूसरे से निर्विवाद नहीं निर्मित हो सकते, अर्थात ये राशियाँ स्वतंत्र हैं।

(ii) भौतिकी के सभी अन्य राशियाँ लंबाई, द्रव्यमान और समय के रूप में व्यक्त की जा सकती हैं।

चिंतन प्रक्रिया

इस प्रश्न को हल करने के लिए, हमें पृथ्वी की त्रिज्या को चांद से देखे गए एक चाप के रूप में लेना पड़ेगा।

उत्तर (a) दूरी $r$ पर लंबाई $l$ के कारण बने कोण के लिए:

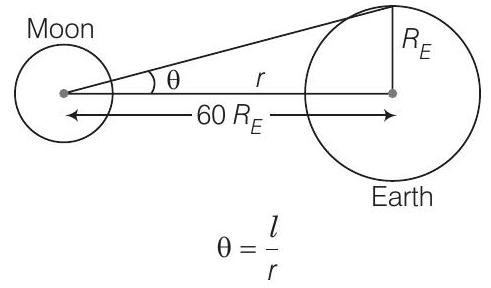
दिया गया है,

$ \begin{aligned} l & =R_{E} ; r=60 R_{E} \\ \theta & =\frac{R_{E}}{60 R_{E}}=\frac{1}{60} rad=\frac{1}{60} \times \frac{180}{\pi} \text { degree } \\ & =\frac{3}{\pi} \approx 1^{\circ} \end{aligned} $

इसलिए, पृथ्वी के व्यास द्वारा बने कोण $=2 \theta=2^{\circ}$।

(b) दिया गया है कि चांद $(\frac{1}{2})^{\circ}$ व्यास के रूप में दिखाई देता है और पृथ्वी $2^{\circ}$ व्यास के रूप में दिखाई देती है।

इसलिए,

$ \frac{\text { पृथ्वी का व्यास }}{\text { चांद का व्यास }}=\frac{(2 / \pi) rad}{(\frac{1}{2 \pi}) rad}=4 $

(c) पार्श्वानुमान मापन से दिया गया है कि सूर्य पृथ्वी-चांद दूरी के लगभग 400 गुना दूर है, इसलिए, $\frac{r_{\text {sun }}}{r_{\text {moon }}}=400$

(यहाँ, $r$ दूरी को और $D$ व्यास को दर्शाता है) पृथ्वी से देखे गए चांद और सूर्य दोनों एक ही कोणीय व्यास के रूप में दिखाई देते हैं।

$ \begin{matrix} \therefore & \frac{D_{\text {sun }}}{r_{\text {sun }}}=\frac{D_{\text {moon }}}{r_{\text {moon }}} \\ \therefore & \frac{D_{\text {sun }}}{D_{\text {moon }}}=400 \\ \text { लेकिन } & \frac{D_{\text {earth }}}{D_{\text {moon }}}=4 \\ \therefore & \frac{D_{\text {sun }}}{D_{\text {earth }}}=100 \end{matrix} $

उत्तर

दिए गए विकल्पों में सबसे अधिक सटीक समय मापन उपकरण है:

(d) परमाणु घड़ी।

स्पष्टीकरण:

• दीवार घड़ी: आमतौर पर सेकंड के अंतर के साथ अधिक सटीक होती है, लेकिन यह मेकैनिज्म (एनालॉग या डिजिटल) पर निर्भर करती है।
• स्टॉपवॉच: आमतौर पर सेकंड के सौवें हिस्से तक समय माप सकता है, जो एक दीवार घड़ी की तुलना में अधिक सटीक होता है।
• डिजिटल घड़ी: आमतौर पर स्टॉपवॉच के समान अधिक सटीकता प्रदान करती है, अक्सर सेकंड या सेकंड के सौवें हिस्से तक समय माप सकती है।
• परमाणु घड़ी: यह उपलब्ध समय मापन उपकरणों में सबसे अधिक सटीक होती है, जो बिलियनवें हिस्से (नैनोसेकंड) या उससे अधिक अंतर के साथ समय माप सकती है। परमाणु घड़ियाँ परमाणुओं (आमतौर पर सीजियम या रबीडियम) के झूले पर आधारित होती हैं और एक सेकंड के परिभाषा के मानक के रूप में उपयोग की जाती हैं।

इसलिए, दिए गए विकल्पों में परमाणु घड़ी सबसे अधिक सटीक समय मापन उपकरण है।

उत्तर दिया गया है, गैलेक्सी की दूरी $=10^{25}$ मीटर

$ \text { प्रकाश की गति }=3 \times 10^{8} \text{ मीटर/सेकंड} $

इसलिए, प्रकाश के गैलेक्सी से हम तक पहुंचने में लगने वाला समय है,

$ \begin{aligned} t & =\frac{\text { दूरी }}{\text { गति }}=\frac{10^{25}}{3 \times 10^{8}} \approx \frac{1}{3} \times 10^{17} \\ & =\frac{10}{3} \times 10^{16}=3.33 \times 10^{16} \text{ सेकंड} \end{aligned} $

असटीकता को मुख्य स्केल विभाजन (MSD) और 1 वर्नियर स्केल विभाजन (VSD) के अंतर द्वारा मापा जाएगा, जहाँ MSD = मुख्य स्केल विभाजन और VSD = वर्नियर स्केल विभाजन है।

उत्तर प्रश्न के अनुसार, यह दिया गया है कि

$ \begin{aligned} 50 VSD & =49 MSD \\ 1 MSD & =\frac{50}{49} VSD \\

1 VSD & =\frac{49}{50} MSD \\ \text { न्यूनतम असटंडर्ड त्रुटि } & =1 MSD-1 VSD \\ & =1 MSD-\frac{49}{50} MSD=\frac{1}{50} MSD \end{aligned} $

$ \begin{aligned} 1 MSD & =0.5 mm \\ \text { न्यूनतम असटंडर्ड त्रुटि } & =\frac{1}{50} \times 0.5 mm=\frac{1}{100}=0.01 mm \end{aligned} $

उत्तर

नीचे दिए गए चित्र को ध्यान में रखिए

$R_{m e}=$ पृथ्वी से चांद की दूरी

$R_{\text {se }}=$ पृथ्वी से सूर्य की दूरी

मान लीजिए सूर्य और चांद द्वारा बनाया गया कोण $\theta$ है, हम लिख सकते हैं

$ \theta=\dfrac{A_{\text {sun }}}{R_{se}^{2}}=\dfrac{A_{\text {moon }}}{R_{\text {me }}^{2}} $

यहाँ,

$A_{\text {sun }}=$ सूर्य का क्षेत्रफल

$A_{\text {moon }}=$ चांद का क्षेत्रफल

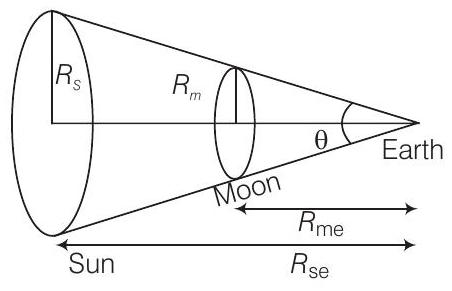
$ \Rightarrow \theta =\dfrac{\pi R_s^{2}}{R_{s e}^{2}}=\dfrac{\pi R_m^{2}}{R_{m e}^{2}}$

$ \Rightarrow (\dfrac{R_{s}}{R_{s e}})^{2} =(\dfrac{R_{m}}{R_{m e}})^{2}$

$ \Rightarrow \dfrac{R_{s}}{R_{s e}} =\dfrac{R_{m}}{R_{m e}}$

$ \Rightarrow \dfrac{R_{s}}{R_{m}} =\dfrac{R_{s e}}{R_{m e}} $

(यहाँ, सूर्य और चांद की त्रिज्या उनके आकार को प्रतिनिधित्व करती है)

चिंतन प्रक्रिया

पहले प्रत्येक राशि की विमा लिखें और फिर उनके बीच संबंध बनाएं।

उत्तर

बल की विमा $F=[MLT^{-2}]=100 N \ldots \text{(1)}$

$\begin{aligned} \text { लंबाई }(L) & =[L]=10 m\ldots \text{(2)} \\ Time(t) & =[T]=100 s \ldots \text{(3)} \end{aligned}$

समीकरण (ii) और (iii) से $L$ और $T$ के मान को समीकरण (i) में बदलकर हमें प्राप्त होता है

F = 100 N = [MLT^{-2}] \Rightarrow 100 = M \times (10)^1 \times (100)^{-2} \Rightarrow 100 = M \times 10 \times \frac{1}{10000} \Rightarrow 100 = \frac{M}{1000} \Rightarrow M = 100 \times 1000 = 100000 \text{ kg}

इस प्रणाली में द्रव्यमान की ईकाई $100000 \text{ kg}$ है।

$ M \times 10 \times(100)^{-2}=100 $

$\Rightarrow \quad \frac{M \times 10}{100 \times 100}=100$

$\Rightarrow \quad M=100 \times 1000 kg$

$M=10^{5} kg$

Answer (a) तल कोण $\theta=\frac{L}{r}$ रेडियन

इसकी इकाई रेडियन है लेकिन विमाओं के बिना है

(b) तनन $\frac{\Delta L}{L}=\frac{\text { लंबाई में परिवर्तन }}{\text { लंबाई }}$

इसकी इकाई और विमाओं दोनों के बिना है

(c) गुरुत्वाकर्षण नियतांक $(G)=6.67 \times 10^{-11} N-m^{2} / kg^{2}$

(d) रेनॉल्ड्स संख्या एक नियतांक है जो इकाई के बिना होती है।

Answer हम जानते हैं कि कोण

$ \begin{aligned} & \theta=\frac{l}{r} \text { रेडियन } \\ & \theta=\frac{\pi}{6}=\frac{l}{31} cm \end{aligned} $

दिया गया है,

अतः,

$ \text { लंबाई }=l=31 \times \frac{\pi}{6} cm=\frac{31 \times 3.14}{6} cm=16.22 cm $

तीन सांख्यिकीय अंकों तक को चारों ओर घुमाने पर यह $16.2 cm$ होगा।

Answer हम जानते हैं कि ठोस कोण $\Omega=\frac{\text { क्षेत्रफल }}{(\text { दूरी })^{2}}$

$ =\frac{1 cm^{2}}{(5 cm)^{2}}=\frac{1}{25}=4 \times 10^{-2} \text { स्टेरियाडियन } $

$(\because$ क्षेत्रफल $=1 cm^{2}$, दूरी $=5 cm)$

नोट: हम ठोस कोण को तल कोण $\theta=\frac{l}{r}$ रेडियन से गलत नहीं समझना चाहिए।

इस प्रकार के प्रश्नों को हल करते समय, हम विमाओं की समानता के सिद्धांत को लागू करेंगे।

उत्तर अब, विमाओं की समानता के सिद्धांत के अनुसार, बाईं ओर वाले पद (LHS) और दाईं ओर वाले पद (RHS) की विमाएँ समान होनी चाहिए, इसलिए

$[LHS]=[RHS]$

$\Rightarrow$

$[L]=[A]=L$

क्योंकि $\omega t - kx$ विमाहीन होना चाहिए, इसलिए $[\omega t]=[k x]=1$

$\begin{matrix} \Rightarrow & {[\omega] T=[k] L=1}\end{matrix} $

$\Rightarrow \quad[\omega]=T^{-1}$ और $[k]=L^{-1}$

हम माध्य मान, अंतर्राष्ट्रीय त्रुटि और माध्य अंतर्राष्ट्रीय त्रुटि के सूत्र को लागू करेंगे।

उत्तर दिया गया है, $\quad t_1=39.6 s, t_2=39.9 s$ और $t_3=39.5 s$

मापन यंत्र की न्यूनतम गणना $=0.1 s$

(क्योंकि मापन में केवल एक दशमलव स्थान है)

मापन में सटीकता $=$ मापन यंत्र की न्यूनतम गणना $=0.1 s$

20 दोलन के लिए समय का माध्य मान निम्नलिखित द्वारा दिया गया है

$ \begin{aligned} t & =\frac{t_1+t_2+t_3}{3} \\ & =\frac{39.6+39.9+39.5}{3}=39.7 s \end{aligned} $

मापन में अंतर्राष्ट्रीय त्रुटि

$ \begin{aligned} & \Delta t_1=t-t_1=39.7-39.6=0.1 s \\ & \Delta t_2=t-t_2=39.7-39.9=-0.2 s \\ & \Delta t_3=t-t_3=39.7-39.5=0.2 s \\ & \text { माध्य अंतर्राष्ट्रीय त्रुटि }= \frac{|\Delta t_1|+|\Delta t_2|+|\Delta t_3|}{3} \\ &= \frac{0.1+0.2+0.2}{3} \\ &= \frac{0.5}{3}=0.17 \approx 0.2 \quad \text { (एक दशमलव स्थान तक कोण चुनाव) } \end{aligned} $

$\therefore \quad$ मापन की सटीकता $= \pm 0.2 s$

इस प्रश्न को हल करते समय, हम इकाई प्रणाली के सूत्र $u, n u=$ अचर को लागू करेंगे।

उत्तर हम जानते हैं कि ऊर्जा की विमा $=[ML^{2} T^{-2}]$

मान लीजिए $M_1, L_1, T_1$ और $M_2, L_2, T_2$ दिए गए दो प्रणालियों में द्रव्यमान, लंबाई और समय की इकाइयाँ हैं।

$\therefore \quad M_1=1 kg, L_1=1 m, T_1=1 s$

$M_2 =\alpha kg, L_2=\beta m, T_2=\gamma s$

एक भौतिक राशि के मान किसी भी मापन प्रणाली में समान रहता है, अर्थात $n_1 u_1=n_2 u_2$

$ \begin{aligned} \Rightarrow \quad n_2 & =n_1 \frac{u_1}{u_2}=n_1 \frac{[M_1 L_1^{2} T_1^{-2}]}{[M_2 L_2^{2} T_2^{-2}]}=5[\frac{M_1}{M_2}] \times[\frac{L_1}{L_2}]^{2} \times[\frac{T_1}{T_2}]^{-2} \\ & =5[\frac{1}{\alpha} kg] \times[\frac{1}{\beta} m]^{2} \times[\frac{1}{\gamma} s]^{-2} \\ & =5 \times \frac{1}{\alpha} \times \frac{1}{\beta^{2}} \times \frac{1}{\gamma^{-2}} \\ n_2 & =\frac{5 \gamma^{2}}{\alpha \beta^{2}} \end{aligned} $

इसलिए, ऊर्जा की नई इकाई $\frac{\gamma^{2}}{\alpha \beta^{2}}$ होगी।

एक समीकरण की विमा यदि दोनों ओर समान हो तो इसे विमीय रूप से सही माना जाता है।

उत्तर एक पाइप के लंबाई $l$ और त्रिज्या $r$ के एक तालुका में एक सेकंड में बाहर निकलने वाली तरल के आयतन को $V=\frac{\pi}{8} \frac{p r^{4}}{\eta l}$ द्वारा दिया गया है।

$V$ की विमा = $\frac{\text { आयतन की विमा }}{\text { समय की विमा }}=\frac{[L^{3}]}{[T]}=[L^{3} T^{-1}]$

$(\because V$ एक सेकंड में बाहर निकलने वाले तरल का आयतन है)

$p$ की विमा = $[ML^{-1} T^{-2}] $

$\eta$ की विमा = $[ML^{-1} T^{-1}] $

$l$ की विमा = [L]

$r$ की विमा = [L]

बायां पक्ष की विमा, $[V]=\frac{[L^{3}]}{[T]}=[L^{3} T^{-1}]$

दायां पक्ष की विमा, $\frac{[ML^{-1} T^{-2}] \times[L^{4}]}{[ML^{-1} T^{-1}] \times[L]}=[L^{3} T^{-1}]$

आकार LHS के आकार RHS के बराबर है।

इसलिए, समीकरण आयाम के अनुसार सही है।

हम राशि $x$ के प्रतिशत त्रुटि के लिए सूत्र के उपयोग करेंगे, जैसा कि $\frac{\Delta x}{x} \times 100$ है।

उत्तर दिया गया, भौतिक राशि $X=a^{2} b^{3} c^{5 / 2} d^{-2}$ है

$X$ में अधिकतम प्रतिशत त्रुटि है

$ \begin{aligned} \frac{\Delta X}{X} \times 100 & = \pm[2(\frac{\Delta a}{a} \times 100)+3(\frac{\Delta b}{b} \times 100)+\frac{5}{2}(\frac{\Delta c}{c} \times 100)+2(\frac{\Delta d}{d} \times 100)] \\ & = \pm[2(1)+3(2)+\frac{5}{2}(3)+2(4)] % \\ & = \pm[2+6+\frac{15}{2}+8]= \pm 23.5 % \end{aligned} $

$\therefore$ राशि $X$ में प्रतिशत त्रुटि $= \pm 23.5 %$

$X$ में माध्य अंतर त्रुटि $= \pm 0.235= \pm 0.24 \quad$ (दो सांख्यिकीय अंकों तक करीब ले जाएं)

$X$ के गणना मान को दो सांख्यिकीय अंकों तक करीब ले जाएं।

$\therefore \quad X=2.8$

एक आयामहीन राशि के आयामी सूत्र $[M^{0} L^{0} T^{0}]$ होता है।

उत्तर दिया गया, व्यंजक है

$ \begin{aligned} P & =E L^{2} m^{-5} G^{-2} \\ {[E] } & =[M L^{2} T^{-2}] \\ {[m] } & =[M] \\ {[L] } & =[M L^{2} T^{-1}] \\ {[G] } & =[M^{-1} L^{3} T^{-2}] \end{aligned} $

जहाँ $E$ ऊर्जा है

$m$ द्रव्यमान है

$L$ कोणीय संवेग है

$G$ गुरुत्वीय नियतांक है

समीकरण में प्रत्येक चर के आयामों के आयामों को बदल दें,

$ \begin{aligned} {[P] } & =[ML^{2} T^{-2}] \times[ML^{2} T^{-1}]^{2} \times[M]^{-5} \times[M^{-1} L^{3} T^{-2}]^{-2} \\ & =[M^{1+2-5+2} L^{2+4-6} T^{-2-2+4}]=[M^{0} L^{0} T^{0}] \end{aligned} $

इसलिए, $P$ एक आयामहीन राशि है।

इस समस्या में हमें आयामों के समानता के सिद्धांत के उपयोग करना होगा, जिसके अनुसार समीकरण के दोनों ओर आयाम समान होंगे।

उत्तर हम जानते हैं कि,

$ \text{Dimensions of }(h) = [ML^{2} T^{-1}], \quad \text{Dimensions of }(c) = [L T^{-1}], \quad \text{Dimensions of }(G) = [M^{-1} L^{3} T^{-2}] \quad \text{(i)} $

मान लीजिए

$m \propto c^{x} h^{y} G^{z}$

$\Rightarrow \quad m=k c^{x} h^{y} G^{z}$

जहाँ, $k$ एक आयामहीन समानुपातिक नियतांक है।

समीकरण (i) में प्रत्येक चर के आयामों को बदल दें, हमें प्राप्त होता है

$ \begin{aligned} {[ML^{0} T^{0}] } & =[LT^{-1}]^{x} \times[ML^{2} T^{-1}]^{y}[M^{-1} L^{3} T^{-2}]^{z} \\ & =[M^{y-z} L^{x+2 y+3 z} T^{-x-y-2 z}] \end{aligned} $

दोनों ओर समान शब्दों के घात की तुलना करने पर हमें प्राप्त होता है

$ \begin{matrix} y-z=1 \quad \text{(ii)}\\ x+2 y+3 z=0 \quad \text{(iii)}\\ -x-y-2 z=0\quad \text{(iv)} \end{matrix} $

समीकरण (ii), (iii) और (iv) को जोड़ने पर हमें प्राप्त होता है

$ 2 y=1 \Rightarrow y=\frac{1}{2} $

$y$ के मान को समीकरण (ii) में रखने पर हमें प्राप्त होता है

$ z=-\frac{1}{2} $

समीकरण (iv) से

$ x=-y-2 z $

$y$ और $z$ के मानों को रखने पर हमें प्राप्त होता है

$ x=-\frac{1}{2}-2(-\frac{1}{2})=\frac{1}{2} $

$x, y$ और $z$ के मानों को समीकरण (i) में रखने पर हमें प्राप्त होता है

$ m=k c^{1 / 2} h^{1 / 2} G^{-1 / 2} $

$ \Rightarrow \quad m=k \sqrt{\frac{c h}{G}} $

(ii) मान लीजिए

$ L \propto c^{x} h^{y} G^{z} $

$ \Rightarrow \quad L=k c^{x} h^{y} G^{z} \quad \text{(v)} $

जहाँ, $k$ एक आयामहीन नियतांक है।

Substituting dimensions of each term in Eq. (v), हमें प्राप्त होता है

$ \begin{aligned} {[M^{0} LT^{0}] } & =[LT^{-1}]^{x} \times[ML^{2} T^{-1}]^{y} \times[M^{-1} L^{3} T^{-2}]^{z} \\ & =[M^{y-z} L^{x+2 y+3 z} T^{-x-y-2 z}] \end{aligned} $

समान पदों के घातों की तुलना करने पर, हमें प्राप्त होता है

$ \begin{matrix} y-z=0 \quad \text{(vi)}\\ x+2 y+3 z=1 \quad \text{(vii)}\\ -x-y-2 z=0\quad \text{(viii)} \end{matrix} $

समीकरण (vi), (vii) और (viii) को जोड़ने पर, हमें प्राप्त होता है

$\begin{matrix} & 2 y=1 \\ \implies & y =\frac{1}{2}\end{matrix} $

समीकरण (vi) में $y$ के मान को रखने पर, हमें प्राप्त होता है

$ z=\frac{1}{2} $

समीकरण (viii) से,

$ x=-y-2 z $

$y$ और $z$ के मान को रखने पर, हमें प्राप्त होता है

$ x=-\frac{1}{2}-2(\frac{1}{2})=-\frac{3}{2} $

$x, y$ और $z$ के मानों को समीकरण (v) में रखने पर, हमें प्राप्त होता है

$ \begin{aligned} & L=k c^{-3 / 2} h^{1 / 2} G^{1 / 2} \\ & L=k \sqrt{\frac{h G}{c^{3}}} \end{aligned} $

(iii) मान लीजिए $T \propto c^{x} h^{y} G^{z}$

$ \Rightarrow \quad T=k c^{x} h^{y} G^{z}\quad \text{(ix)} $

जहाँ, $k$ एक विमाहीन नियतांक है।

समीकरण (ix) में प्रत्येक पद की विमा को रखने पर, हमें प्राप्त होता है

$ \begin{aligned} {[M^{0} L^{0} T.} & =[LT^{-1}]^{x} \times[ML^{2} T^{-1}]^{y} \times[M^{-1} L^{3} T^{-2}]^{z} \\ & =[M^{y-z} L^{x+2 y+3 z} T^{-x-y-2 z}] \end{aligned} $

समान पदों के घातों की तुलना करने पर, हमें प्राप्त होता है

$ \begin{matrix} y-z=0 \quad \text{(x)}\\ x+2 y+3 z=0 \quad \text{(xi)}\\ -x-y-2 z=1\quad \text{(xii)} \end{matrix} $

समीकरण (x), (xi) और (xii) को जोड़ने पर, हमें प्राप्त होता है

$ \begin{aligned} & 2 y & =1 \\ \Rightarrow & y & =\frac{1}{2} \end{aligned} $

समीकरण (x) में $y$ के मान को रखने पर, हमें प्राप्त होता है

$ z=y=\frac{1}{2} $

समीकरण (xii) से,

$ x=-y-2 z-1 $

$y$ और $z$ के मान को रखने पर, हमें प्राप्त होता है

$ x=-\frac{1}{2}-2(\frac{1}{2})-1=-\frac{5}{2} $

$x, y$ और $z$ के मानों को समीकरण (ix) में रखने पर, हमें प्राप्त होता है

$ \begin{aligned} T & =k c^{-5 / 2} h^{1 / 2} G^{1 / 2} \\ T & =k \sqrt{\frac{h G}{c^{5}}} \end{aligned} $

सोच-समझ की प्रक्रिया

इस समस्या में हमें केपलर के तीसरे नियम के अनुपालन करना होगा, $T^{2} \propto a^{3}$ अर्थात, एक ग्रह के चारों ओर घूम रहे उपग्रह के समय अवधि $(T^{2})$ का वर्ग, उसके कक्षा की त्रिज्या $(a^{3})$ के अनुपाती होता है।

उत्तर

केपलर के तीसरे नियम के अनुसार, $\quad T^{2} \propto r^{3} \Rightarrow T \propto r^{3 / 2}$

हम जानते हैं कि $T$, $R$ और $g$ के फ़ंक्शन है।

मान लीजिए

$$ \begin{aligned} & T \propto r^{3 / 2} R^{a} g^{b} \\ & T=k r^{3 / 2} R^{a} g^{ b} \end{aligned} $$

जहाँ, $k$ एक विमाहीन समानुपातिक नियतांक है।

समीकरण (i) में प्रत्येक पद की विमा को बदलकर रखने पर हम प्राप्त करते हैं

$$ \begin{aligned} {[M^{0} L^{0} T]} & =k[L]^{3 / 2}[L]^{a}[LT^{-2}]^{b} \\ & =k[L^{a+b+3 / 2} T^{-2 b}] \end{aligned} $$

समान पदों की घातों की तुलना करने पर हम प्राप्त करते हैं

$$ \begin{aligned} a+b+3 / 2 & =0 \\ -2 b & =1 \Rightarrow b=-1 / 2 \end{aligned} $$

समीकरण (ii) से हम प्राप्त करते हैं

$$ a-1 / 2+3 / 2=0 \Rightarrow a=-1 $$

समीकरण (i) में $a$ और $b$ के मान को रखने पर हम प्राप्त करते हैं

$$ \begin{matrix} \Rightarrow & T & =k r^{3 / 2} R^{-1} g^{-1 / 2} \\ T & =\frac{k}{R} \sqrt{\frac{r^{3}}{g}} \end{matrix} $$

ध्यान रखें: जब हम सूत्रों के उपयोग करते हैं, तो हमें $r$ (कक्षा की त्रिज्या) और $R$ (ग्रह की त्रिज्या) के बारे में सावधान रहना चाहिए।

उत्तर (a) ऑलिक एसिड पानी में घुल नहीं सकता, इसलिए इसे एल्कोहल में घोला जाता है।

(b) लाइकोपोडियम पॉवडर को एकसमान रूप से छिटकने पर यह पानी के सतह पर फैल जाता है। जब एक बूंद तैयार समाधान को पानी पर गिराया जाता है, तो ऑलिक एसिड पानी में घुल नहीं सकता। बजाए इसके, यह पानी के सतह पर फैलता है और लाइकोपोडियम पॉवडर को दूर धकेलता है ताकि बूंद गिरने वाले क्षेत्र को साफ कर दे। इसलिए हम ऑलिक एसिड के फैलने वाले क्षेत्र को माप सकते हैं।

(c) तैयार किए गए प्रत्येक $mL$ समाधान में ऑलिक एसिड का आयतन $=\frac{1}{20} mL \times \frac{1}{20}=\frac{1}{400} mL$

(d) इस ऑलिक एसिड के समाधान के $n$ बूंदों के आयतन की गणना बुर्डे और मापन के बर्तन के माध्यम से और बूंदों की संख्या मापकर की जा सकती है।

(e) यदि समाधान की $n$ बूंदें $1 mL$ बनाती है, तो एक बूंद में ऑलिक एसिड का आयतन $\frac{1}{(400) n} mL$ होगा।

उत्तर (a) परिभाषा के अनुसार,

1 पार्सेक $=$ वह दूरी जहां $1 AU$ लंबे चाप को $1 s$ कोण बनाता है।

$\therefore 1 \text { पार्सेक } =(\frac{1 AU}{1 arcsec})$

$\therefore 1 \text{ डिग्री} =3600 \text{ arcsec}$

$\therefore 1 \text { पार्सेक } =\frac{\pi}{3600 \times 180} rad$

$1 \text { parsec } =\frac{3600 \times 180}{\pi} AU=206265 AU \approx 2 \times 10^{5} AU$

(ब) सूर्य का व्यास $1 AU$ पर $(\frac{1}{2})^{\circ}$ है।

इसलिए, $1$ पैरसेक पर तारा का व्यास $\frac{1 / 2}{2 \times 10^{5}}$ डिग्री होगा $=15 \times 10^{-5}$ ऐर्क मिनिट।

100 गुना आवर्धन के साथ, यह $15 \times 10^{-3}$ ऐर्क मिनिट दिखाई देगा। हालांकि, वातावरण के झूलों के कारण, यह लगभग 1 ऐर्क मिनिट के आकार का दिखाई देगा। तारे के द्वारा आवर्धन नहीं किया जा सकता।

(स) दिया गया है कि

$ \frac{D_{\text {mars }}}{D_{\text {earth }}}=\frac{1}{2} $

जहाँ $D$ व्यास को दर्शाता है।

उत्तर 25(ई) से

$\begin{matrix} \text { हम जानते हैं कि, } & \frac{D_{\text {earth }}}{D_{\text {sun }}}=\frac{1}{100} \\ \therefore & \frac{D_{\text {mars }}}{D_{\text {sun }}}=\frac{1}{2} \times \frac{1}{100}\end{matrix} $

[समीकरण (i) से]

$ \begin{aligned} & \text { 1 AU पर सूर्य का व्यास }=(\frac{1}{2})^{\circ} \\ & \therefore \quad \text { मार्स का व्यास }=\frac{1}{2} \times \frac{1}{200}=\frac{1}{400} \\ & \text { } \frac{1}{2} AU पर मार्स का व्यास }=\frac{1}{400} \times 2^{\circ}=(\frac{1}{200})^{\circ} \end{aligned} $

100 आवर्धन के साथ, मार्स का व्यास $=\frac{1}{200} \times 100^{\circ}=(\frac{1}{2})^{\circ}=30^{\prime}$

इसके कारण वातावरण के झूलों के कारण विभेदक निम्नतम सीमा से अधिक है। इसलिए, यह आवर्धित दिखाई देता है।

उत्तर

(a) हम जानते हैं कि

$ \begin{aligned} 1 \text{ amu} & =1 u=1.67 \times 10^{-27} kg \\ E & =m c^{2} \\ \text { ऊर्जा } & =E=(1.67 \times 10^{-27})(3 \times 10^{8})^{2} J \\ & =1.67 \times 9 \times 10^{-11} J \\ E & =\frac{1.67 \times 9 \times 10^{-11}}{1.6 \times 10^{-13}} MeV=939.4 MeV \approx 931.5 MeV \end{aligned} $

(b) आयाम सही संबंध है

$1 \text{ amu} \times c^{2}=1 u \times c^{2}=931.5 MeV$