तरंगें
बहुविकल्पीय प्रश्न (MCQs)
1. एक मोटर बोट के जहाजी जाने से उत्पन्न जल तरंगें हैं
(a) न तो अनुप्रस्थ न ही अनुदिश
(b) दोनों अनुप्रस्थ और अनुदिश
(c) केवल अनुदिश
(d) केवल अनुप्रस्थ
उत्तर दिखाएं
उत्तर (b) एक मोटर बोट के जहाजी जाने से उत्पन्न जल तरंगें दोनों अनुप्रस्थ और अनुदिश होती हैं, क्योंकि तरंगें माध्यम के कणों में अनुप्रस्थ और अनुदिश दोनों प्रकार के विक्षोभ उत्पन्न करती हैं। अनुप्रस्थ तरंगें जल के सतह पर होती हैं, जबकि अनुदिश तरंगें जल के सतह के नीचे उत्पन्न होती हैं।
-
(a) एक मोटर बोट के जहाजी जाने से उत्पन्न जल तरंगें “न तो अनुप्रस्थ न ही अनुदिश” नहीं होतीं क्योंकि ये दोनों प्रकार के विक्षोभ शामिल होते हैं: अनुदिश (तरंग प्रसार की दिशा के समानांतर) और अनुप्रस्थ (तरंग प्रसार की दिशा के लंबवत)।
-
(c) एक मोटर बोट के जहाजी जाने से उत्पन्न जल तरंगें “केवल अनुदिश” नहीं होतीं क्योंकि ये अनुप्रस्थ विक्षोभ भी शामिल होते हैं, जहां माध्यम के कण तरंग प्रसार की दिशा के लंबवत गति करते हैं।
-
(d) एक मोटर बोट के जहाजी जाने से उत्पन्न जल तरंगें “केवल अनुप्रस्थ” नहीं होतीं क्योंकि ये अनुदिश विक्षोभ भी शामिल होते हैं, जहां माध्यम के कण तरंग प्रसार की दिशा के समानांतर गति करते हैं।
2. तरंगदैर्घ्य $\lambda$ की ध्वनि तरंगें एक माध्यम में $v m / s$ की गति से चल रही हैं जहां इसकी गति $2 v m / s$ हो जाती है। दूसरे माध्यम में ध्वनि तरंगों की तरंगदैर्घ्य है
(a) $\lambda$
(b) $\frac{\lambda}{2}$
(c) $2 \lambda$
(d) $4 \lambda$
उत्तर दिखाएं
उत्तर (c) माध्यम में आवृत्ति $ \nu $ है और दूसरे माध्यम में आवृत्ति $\nu^{\prime}$ है। आवृत्ति दोनों माध्यमों में समान रहती है
इसलिए,
$$ \nu =\nu^{\prime} \Rightarrow \frac{v}{\lambda}=\frac{v^{\prime}}{\lambda^{\prime}} $$
$$ \Rightarrow \quad \lambda^{\prime}=\left(\frac{v^{\prime}}{v}\right) \lambda $$
$\lambda$ और $\lambda^{\prime}, v$ और $v^{\prime}$ पहले और दूसरे माध्यम में क्रमशः तरंगदैर्घ्य और वेग हैं।
इसलिए,
$$ \lambda^{\prime}=\left(\frac{2 v}{v}\right) \lambda=2 \lambda $$
-
विकल्प (a) $\lambda$: यह विकल्प गलत है क्योंकि जब ध्वनि तरंग एक अलग वेग वाले माध्यम में प्रवेश करती है, तो तरंगदैर्घ्य बदल जाती है। चूंकि दूसरे माध्यम में ध्वनि का वेग पहले माध्यम में वेग के दुगुना है, तरंगदैर्घ्य भी आनुपातिक रूप से बदल जाती है। इसलिए, तरंगदैर्घ्य एक ही रह सकती है ($\lambda$)।
-
विकल्प (b) $\frac{\lambda}{2}$: यह विकल्प गलत है क्योंकि इसका अर्थ है कि दूसरे माध्यम में तरंगदैर्घ्य पहले माध्यम में तरंगदैर्घ्य के आधा है। चूंकि दूसरे माध्यम में ध्वनि का वेग पहले माध्यम में वेग के दुगुना है, तरंगदैर्घ्य बढ़ जाती है, न कि घटती है। इसलिए, तरंगदैर्घ्य $\frac{\lambda}{2}$ नहीं हो सकती।
-
विकल्प (d) $4 \lambda$: यह विकल्प गलत है क्योंकि इसका अर्थ है कि दूसरे माध्यम में तरंगदैर्घ्य पहले माध्यम में तरंगदैर्घ्य के चार गुना है। चूंकि दूसरे माध्यम में ध्वनि का वेग पहले माध्यम में वेग के दुगुना है, तरंगदैर्घ्य भी दुगुनी होनी चाहिए, न कि चार गुनी। इसलिए, तरंगदैर्घ्य $4 \lambda$ नहीं हो सकती।
3. हवा में ध्वनि तरंग की गति
(a) तापमान के अतिरिक्त निर्भर नहीं करती
(b) दबाव के बढ़ने के साथ बढ़ती है
(c) आर्द्रता में वृद्धि के साथ बढ़ती है
(d) आर्द्रता में वृद्धि के साथ घटती है
उत्तर दिखाएँ
उत्तर (c) आर्द्रता के उपस्थिति के कारण हवा का घनत्व कम हो जाता है।
हम जानते हैं कि हवा में ध्वनि की गति $v=\sqrt{\frac{\gamma p}{\rho}}$ द्वारा दी जाती है।
हवा के लिए $\gamma$ और $p$ स्थिरांक हैं।
$$ \begin{aligned} & v \propto \frac{1}{\sqrt{\rho}}, \text { जहाँ } \rho \text { हवा का घनत्व है। } \\ & \frac{v_2}{v_1}=\sqrt{\frac{\rho_2}{\rho_1}} \end{aligned} $$
जहाँ $\rho_1$ सूखी हवा का घनत्व है और $\rho_2$ आर्द्र हवा का घनत्व है।
क्योंकि $\quad \rho_2<\rho_1=\frac{v_2}{v_1}>1 \Rightarrow v_2>v_1$
अतः, हवा में ध्वनि तरंग की गति आर्द्रता में वृद्धि के साथ बढ़ती है।
-
(a) हवा में ध्वनि की गति तापमान के स्वतंत्र नहीं होती। वास्तव में, तापमान में वृद्धि के साथ यह बढ़ती है क्योंकि ध्वनि की गति वायु के अंतराल तापमान के वर्गमूल के समानुपाती होती है।
-
(b) सामान्य वायुमंडलीय स्थितियों में हवा में ध्वनि की गति दबाव के बर्बाद नहीं होती क्योंकि दबाव और घनत्व ऊंचाई के साथ आनुपातिक रूप से बदलते हैं, जिससे ध्वनि की गति लगभग स्थिर रहती है।
-
(d) आर्द्रता में वृद्धि के साथ ध्वनि की गति घटती नहीं होती। जैसा कि समझाया गया है, आर्द्रता की उपस्थिति हवा के घनत्व को कम करती है, जिसके परिणामस्वरूप ध्वनि की गति बढ़ती है।
4. माध्यम के तापमान में परिवर्तन निम्नलिखित में से किसको प्रभावित करता है?
(a) ध्वनि तरंगों की आवृत्ति
(b) ध्वनि तरंगों का आयाम
(c) ध्वनि तरंगों की तरंगदैर्घ्य
(d) ध्वनि तरंगों की तीव्रता
उत्तर दिखाएँ
Answer (c) माध्यम में ध्वनि तरंग की गति $v \propto \sqrt{T}$ (जहाँ $T$ माध्यम के तापमान है) स्पष्ट रूप से, जब तापमान बदलता है तो गति भी बदलती है।
जैसा कि,
$$ v= \nu \lambda $$
जहाँ $\nu$ आवृत्ति है और $\lambda$ तरंगदैर्घ्य है।
आवृत्ति $(\nu)$ स्थिर रहती है
$\Rightarrow \quad v \propto \lambda$ या $\lambda \propto v$
क्योंकि आवृत्ति बदलती नहीं है, तरंगदैर्घ्य $(\lambda)$ बदलती है।
-
(a) ध्वनि तरंगों की आवृत्ति: ध्वनि तरंग की आवृत्ति ध्वनि के स्रोत द्वारा निर्धारित होती है और माध्यम के तापमान के साथ बदलती नहीं होती। तापमान ध्वनि की गति को प्रभावित करता है, लेकिन आवृत्ति स्थिर रहती है।
-
(b) ध्वनि तरंगों का आयाम: ध्वनि तरंग का आयाम तरंग की ऊर्जा और तीव्रता से संबंधित होता है, जो स्रोत और माध्यम के गुणों पर निर्भर करता है, लेकिन तापमान के सीधे प्रभाव नहीं होता।
-
(d) ध्वनि तरंगों की तीव्रता: तीव्रता एक अनुभव करने योग्य गुण है जो तरंग के आयाम और तीव्रता से संबंधित होती है। यद्यपि तापमान हवा के घनत्व और अवशोषण में परिवर्तन के कारण ध्वनि के प्रसार और इसकी अनुभूति तीव्रता को प्रभावित कर सकता है, लेकिन ध्वनि तरंग की तीव्रता को सीधे बदलता नहीं है।
5. माध्यम के माध्यम से अनुप्रस्थ तरंगों के प्रसार के साथ, संचारित राशि है
(a) पदार्थ
(b) ऊर्जा
(c) ऊर्जा और पदार्थ
(d) ऊरजा, पदार्थ और गति
उत्तर दिखाएं
उत्तर (b) माध्यम के माध्यम से अनुप्रस्थ तरंगों के प्रसार के कारण माध्यम के माध्यम से ऊर्जा के संचार होता है बिना किसी पदार्थ के संचार के।
माध्यम में कोई गति नहीं होती है (द्रव्यमान) और इसलिए गति भी नहीं होती।
-
(a) पदार्थ: अनुप्रस्थ तरंगें माध्यम के माध्यम से पदार्थ के संचार नहीं करती हैं; वे केवल माध्यम के कणों को अपने संतुलन स्थितियों के चारों ओर आवर्ती रूप से आगे-पीछे गति करने के लिए कारण बनती हैं बिना किसी शुद्ध पदार्थ के गति के।
-
(c) ऊर्जा और पदार्थ: यद्यपि अनुप्रस्थ तरंगें ऊर्जा के संचार करती हैं, लेकिन वे माध्यम के माध्यम से पदार्थ के शुद्ध गति के नतीजे के रूप में नहीं होती हैं। माध्यम के कण केवल अपने संतुलन स्थितियों के चारों ओर आवर्ती रूप से गति करते हैं।
-
(d) ऊर्जा, पदार्थ और गति: अनुप्रस्थ तरंगें ऊर्जा के संचार करती हैं लेकिन माध्यम के माध्यम से पदार्थ या गति के शुद्ध गति के नतीजे के रूप में नहीं होती हैं। कण आगे-पीछे गति करते हैं, लेकिन कोई शुद्ध पदार्थ या गति के संचार नहीं होता है।
6. निम्नलिखित में से कौन से कथन तरंग गति के लिए सही हैं?
(a) यांत्रिक अनुप्रस्थ तरंगें सभी माध्यमों में प्रसारित हो सकती हैं
(b) अनुप्रस्थ तरंगें केवल ठोस में प्रसारित हो सकती हैं
(c) यांत्रिक अनुप्रस्थ तरंगें केवल ठोस में प्रसारित हो सकती हैं
(d) अनुप्रस्थ तरंगें वैक्यूम में प्रसारित हो सकती हैं
उत्तर दिखाएं
उत्तर (c) जब यांत्रिक अनुप्रस्थ तरंग माध्यम के माध्यम से प्रसारित होती है, तो माध्यम के घटक तरंग गति के लंबवत आवर्ती रूप से आगे-पीछे गति करते हैं जिसके कारण आकार में परिवर्तन होता है। यानी प्रत्येक माध्यम के तत्व घर्षण तनाव के अंतर्गत रहते हैं। ठोस और तार घूर्णन प्रतिबल के कारण घूर्णन प्रतिबल को संभाल सकते हैं, इसलिए घूर्णन प्रतिबल को संभाल सकते हैं।
तरल पदार्थ में अपना आकार नहीं होता है, वे घूर्णन प्रतिबल के अंतर्गत आ जाते हैं। इसलिए ठोस और तार में अनुप्रस्थ तरंग संभव होती है लेकिन तरल में नहीं।
-
(a) यांत्रिक अनुप्रस्थ तरंगें सभी माध्यमों में प्रसारित हो सकती हैं: यह गलत है क्योंकि यांत्रिक अनुप्रस्थ तरंगों के लिए एक माध्यम की आवश्यकता होती है जो घूर्णन प्रतिबल को संभाल सके। ठोस और तार घूर्णन प्रतिबल को संभाल सकते हैं क्योंकि उनके घूर्णन प्रतिबल होता है, लेकिन तरल (तरल और गैस) नहीं। इसलिए यांत्रिक अनुप्रस्थ तरंगें सभी माध्यमों में नहीं प्रसारित हो सकती हैं, विशेष रूप से तरल में नहीं।
-
(ब) अनुप्रस्थ तरंगें केवल ठोस में प्रसारित हो सकती हैं: यह गलत है क्योंकि अनुप्रस्थ तरंगें तरंग प्रसार की दिशा में कणों के दोलन के कारण होती हैं, जिसके परिणामस्वरूप संपीड़न और विरलन उत्पन्न होते हैं। ये तरंगें ठोस, तरल और गैस में प्रसारित हो सकती हैं, क्योंकि इन सभी माध्यमों में संपीड़न तनाव को समर्थन किया जा सकता है।
-
(ड) अनुप्रस्थ तरंगें वैक्यूम में प्रसारित हो सकती हैं: यह गलत है क्योंकि अनुप्रस्थ तरंगें यांत्रिक तरंगें होती हैं जिनके प्रसार के लिए माध्यम की आवश्यकता होती है। वैक्यूम में कोई कण नहीं होते हैं जो दोलन कर सकें और तरंग के प्रसार को संचालित कर सकें, इसलिए अनुप्रस्थ तरंगें वैक्यूम में प्रसारित नहीं हो सकती हैं।
7. एक ध्वनि तरंग वायु स्तंभ में संपीड़न और विरलन के रूप में प्रसारित हो रही है। क्रमागत संपीड़न और विरलन में,
(a) घनत्व स्थिर रहता है
(b) बॉयल के नियम का पालन किया जाता है
(c) वायु के आयतन प्रतिरोध दोलन करता है
(d) ऊष्मा के परिवहन के लिए कोई आवश्यकता नहीं होती
उत्तर दिखाएँ
उत्तर (ड)
संपीड़न और विरलन के कारण माध्यम (वायु) के घनत्व में परिवर्तन होता है। संपीड़न क्षेत्र में घनत्व अधिकतम होता है और विरलन क्षेत्र में घनत्व न्यूनतम होता है। संपीड़न और विरलन के समय बहुत छोटा होता है, अर्थात हम एडियाबैटिक प्रक्रम मान सकते हैं और इसलिए ऊष्मा के परिवहन के लिए कोई आवश्यकता नहीं होती।
-
(अ) संपीड़न और विरलन के कारण माध्यम (वायु) के घनत्व में परिवर्तन होता है। संपीड़न क्षेत्र में घनत्व अधिकतम होता है और विरलन क्षेत्र में घनत्व न्यूनतम होता है।
-
(ब) घनत्व में परिवर्तन हो रहा है, इसलिए बॉयल के नियम का पालन नहीं किया जाता है।
-
(स) आयतन प्रतिरोध स्थिर रहता है।
8. एक समतल आगे बढ़ती तरंग का समीकरण $y=0.6 \sin 2 \pi(t-\frac{x}{2})$ द्वारा दिया गया है। एक घन धातु माध्यम से परावर्तन के कारण इसके आयाम के आयाम के $\frac{2}{3}$ हो जाता है। परावर्तित तरंग का समीकरण है
(a) $y=0.6 \sin 2 \pi(t+\frac{x}{2})$
(b) $y=-0.4 \sin 2 \pi(t+\frac{x}{2})$
(c) $y=0.4 \sin 2 \pi(t+\frac{x}{2})$
(d) $y=-0.4 \sin 2 \pi(t-\frac{x}{2})$
उत्तर दिखाएँ
एक घन माध्यम से परावर्तन के कारण परावर्तित तरंग में $180^{\circ}$ का चरण परिवर्तन होता है।
उत्तर (b) परावर्तित तरंग का आयाम
$$ A_{r}=\frac{2}{3} \times A_{i}=\frac{2}{3} \times 0.6=0.4 \text { इकाई } $$
दिया गया आपतित तरंग का समीकरण
$$ y_{i}=0.6 \sin 2 \pi(t-\frac{x}{2}) $$
परावर्तित तरंग का समीकरण है
$$ y_{r}=A_{r} \sin 2 \pi(t+\frac{x}{2}+\pi) $$
[ $\because$ घनत्व अधिक माध्यम में, चरण में $\pi$ का परिवर्तन होता है] धनात्मक चिह्न प्रसार दिशा के उलट होने के कारण है
इसलिए,
$$ y_{r}=-0.4 \sin 2 \pi(t+\frac{x}{2}) \quad[\because \sin (\pi+\theta)=-\sin \theta] $$
-
विकल्प (a): परावर्तित तरंग का आयाम सही रूप से समायोजित नहीं किया गया है। दिया गया आयाम 0.6 है, लेकिन इसे 0.6 के $\frac{2}{3}$ होना चाहिए, जो 0.4 है। इसके अलावा, $\pi$ के चरण परिवर्तन को ध्यान में नहीं लिया गया है, जो एक नकारात्मक चिह्न लाएगा।
-
विकल्प (c): आयाम सही रूप से 0.4 तक समायोजित किया गया है, लेकिन $\pi$ के चरण परिवर्तन को ध्यान में नहीं लिया गया है। चरण परिवर्तन एक नकारात्मक चिह्न लाएगा, जो इस विकल्प में अनुपस्थित है।
-
विकल्प (d): आयाम सही रूप से 0.4 तक समायोजित किया गया है, लेकिन प्रसार दिशा के उलट को ध्यान में नहीं लिया गया है। सही समीकरण में साइन फलन के तर्ग में धनात्मक चिह्न होना चाहिए जो प्रसार दिशा के उलट को दर्शाएगा।
9. 2.5 किग्रा द्रव्यमान की एक स्ट्रिंग को 200 एन के तनाव में रखा गया है। तनी हुई स्ट्रिंग की लंबाई 20.0 मीटर है। यदि स्ट्रिंग के एक सिरे पर अनुप्रस्थ झटका दिया जाता है, तो अवांछित घटना दूसरे सिरे तक पहुंचेगी
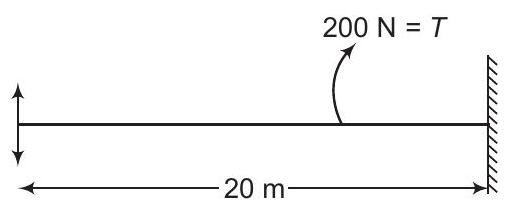
(a) $1 सेकंड$
(b) $0.5 सेकंड$
(c) $2 सेकंड$
(d) दिया गया डेटा पर्याप्त नहीं है
उत्तर दिखाएँ
उत्तर (b)
द्रव्यमान $m=2.5 kg$
$ \mu=\text { इकाई लंबाई पर द्रव्यमान } $
$$ \begin{aligned} & \mu =\frac{m}{l}=\frac{2.5 kg}{20}=\frac{1.25}{10}=0.125 kg / m \\ \text { गति } v & =\sqrt{\frac{T}{\mu}}=\sqrt{\frac{200}{0.125}} \quad \text { [किसी भी स्ट्रिंग में अनुप्रस्थ तरंगों की गति] } \\
$$ \begin{aligned} l & =v \times t \Rightarrow 20=\sqrt{\frac{200}{0.125}} \times t \\ t & =20 \times \sqrt{\frac{125}{2 \times 10^{5}}}=20 \times \sqrt{\frac{25 \times 5}{2 \times 10^{5}}} \\ & =20 \times \sqrt{25 \times \frac{1}{0.4 \times 10^{5}}} \\ & =20 \times 5 \sqrt{\frac{1}{4 \times 10^{4}}}=\frac{20 \times 5}{2 \times 10^{2}} \\ & =\frac{1}{2}=0.5 \end{aligned} $$
-
विकल्प (a) $1 सेकंड$: यह विकल्प गलत है क्योंकि तार के लंबाई के लिए विक्षोभ के यात्रा के समय की गणना $0.5 सेकंड$ है, न कि $1 सेकंड$। तरंग की गति और तार की लंबाई एक $1 सेकंड$ के यात्रा समय को समर्थन नहीं करते हैं।
-
विकल्प (c) $2 सेकंड$: यह विकल्प गलत है क्योंकि तार के लंबाई के लिए विक्षोभ के यात्रा के समय की गणना $0.5 सेकंड$ है, न कि $2 सेकंड$। $2 सेकंड$ के यात्रा समय का अर्थ होता है कि तरंग की गति बहुत धीमी होगी, जो दिए गए तनाव और इकाई लंबाई पर द्रव्यमान के साथ असंगत है।
-
विकल्प (d) दिए गए डेटा पर्याप्त नहीं है: यह विकल्प गलत है क्योंकि तार के द्रव्यमान, तनाव और तार की लंबाई के दिए गए डेटा का उपयोग करके तरंग की गति और विक्षोभ के तार के लंबाई के लिए यात्रा समय की गणना की जा सकती है। समस्या में सही उत्तर निर्धारित करने के लिए सभी आवश्यक जानकारी दी गई है।
10. एक ट्रेन नियत आवृत्ति से बजती है और एक नियत गति $v$ से एक स्टेशन की ओर चल रही है। ट्रेन एक स्थिर अवलोकनकर्ता के पास से गुजरती है। अवलोकनकर्ता द्वारा सुने गए ध्वनि की आवृत्ति $n^{\prime}$ को समय $t$ के फ़ंक्शन के रूप में ग्राफ़ के रूप में दर्शाया गया है (चित्र)। अपेक्षित वक्र को पहचानें।

उत्तर दिखाएँ
अवलोकित आवृत्ति डॉप्लर परिवर्तन के कारण दिखाई देने वाली आवृत्ति है।
उत्तर (c) मान लीजिए स्रोत की मूल आवृत्ति $n_0$ है। माध्यम में ध्वनि तरंग की गति $v$ है।
अवलोकक स्थिर है
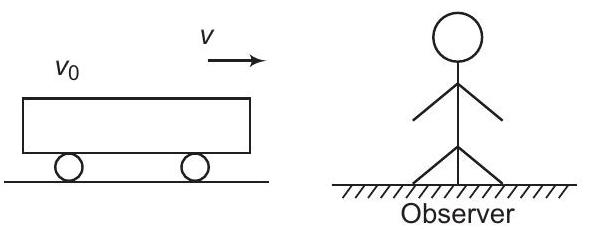
प्रतीत आवृत्ति, $n_{a}=(\frac{v}{v-v_{s}}) n_0$
जब ट्रेन अवलोकक की ओर आ रही है
$$ \implies (\frac{v}{v-v_{s}}) n_0=n_{a}>n_0 $$
जब ट्रेन अवलोकक से दूर जा रही है
प्रतीत आवृत्ति, $n_{a}=(\frac{v}{v+v_{s}}) n_{o}=n_{a}<n_{o}$
इसलिए, अपेक्षित वक्र (c) है।
-
विकल्प (a): यह विकल्प समय के साथ एक स्थिर आवृत्ति को सुझाता है, जो गलत है क्योंकि डॉप्लर प्रभाव अवलोकक के पास ट्रेन आने और फिर दूर जाने के समय आवृत्ति में परिवर्तन कारण बनता है। आवृत्ति ट्रेन अवलोकक की ओर आने पर बढ़ती है और दूर जाने पर कम होती है।
-
विकल्प (b): यह विकल्प समय के साथ एक रैखिक परिवर्तन को सुझाता है, जो गलत है क्योंकि डॉप्लर प्रभाव अवलोकक के पास ट्रेन पास होते समय आवृत्ति में अचानक परिवर्तन कारण बनता है। आवृत्ति रैखिक रूप से नहीं बदलनी चाहिए बल्कि एक तीखा परिवर्तन दिखाए।
-
विकल्प (d): यह विकल्प एक सममित वक्र के साथ एक गुलाबी परिवर्तन को सुझाता है, जो गलत है क्योंकि डॉप्लर प्रभाव अवलोकक के पास ट्रेन पास होते समय आवृत्ति में अचानक परिवर्तन कारण बनता है। आवृत्ति एक विशिष्ट कूद दिखाए बल्कि एक गुलाबी वक्र नहीं दिखाए।
बहुविकल्पीय प्रश्न (एक से अधिक विकल्प)
11. एक तार पर एक अनुप्रस्थ अनुनादी तरंग का वर्णन निम्नलिखित है
$ y(x, t)=3.0 \sin (36 t+0.018 x+\frac{\pi}{4}) $
जहाँ $x$ और $y$ सेंटीमीटर में है और $t$ सेकंड में है। $x$ की धनात्मक दिशा बाएं से दाएं है।
(a) तरंग दाएं से बाएं चल रही है
(b) तरंग की गति $20 m / s$ है
(c) तरंग की आवृत्ति $5.7 Hz$ है
(d) तरंग में दो क्रमागत शिखरों के बीच न्यूनतम दूरी $2.5 cm$ है
उत्तर दिखाएँ
एक तरंग के विशिष्ट पैरामीटर ज्ञात करने के लिए, दी गई तरंग के समीकरण को एक मानक समीकरण के साथ तुलना करें।
उत्तर $(a, b, c)$
दिया गया समीकरण है
$$ y(x, t)=3.0 \sin (36 t+0.018 x+\frac{\pi}{4}) $$
इस समीकरण को मानक रूप से तुलना करें।
$$ y=a \sin (\omega t+k x+\phi) $$
(a) समीकरण में $x$ के साथ धनात्मक चिह्न है, इसलिए तरंग दाहिने से बाएँ बढ़ रही है। इसलिए, विकल्प (a) सही है।
(b) दिया गया है
$\omega=36 \Rightarrow 2 \pi \nu=36$
$\Rightarrow$ $\nu=$ आवृत्ति $=\frac{36}{2 \pi}=\frac{18}{\pi}$
$k=0.018 \Rightarrow \frac{2 \pi}{\lambda}=0.018$
$$ \begin{aligned} & \Rightarrow \quad \frac{2 \pi v}{v \lambda}=0.018 \Rightarrow \frac{\omega}{v}=0.018 \quad[\because 2 \pi v=\omega \text { और } v \lambda=v] \\ & \Rightarrow \quad \frac{36}{V}=0.018=\frac{18}{1000} \\ & \Rightarrow \quad v=2000 cm / s=20 m / s \end{aligned} $$
(c) $2 \pi v=36$
$$ \Rightarrow \quad v=\frac{36}{2 \pi} Hz=\frac{18}{\pi}=5.7 Hz $$
(d) $\frac{2 \pi}{\lambda}=0.018$
$$ \begin{aligned} \Rightarrow \quad \lambda & =\frac{2 \pi}{0.018} cm \\ & =\frac{2000 \pi}{18} cm=\frac{20 \pi}{18} m=3.48 cm \end{aligned} $$
इसलिए, दो क्रमागत चरमों के बीच न्यूनतम दूरी $=\lambda=3.48 m$।
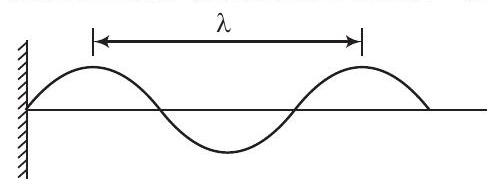
- विकल्प (d) गलत है: तरंग में दो क्रमागत चरमों के बीच न्यूनतम दूरी तरंगदैर्घ्य $\lambda$ द्वारा दी गई है। गणना से, $\lambda = 3.48 , \text{cm}$, नहीं $2.5 , \text{cm}$। इसलिए, दो क्रमागत चरमों के बीच न्यूनतम दूरी $2.5 , \text{cm}$ नहीं है।
12. एक स्ट्रिंग के विस्थापन को निम्नलिखित द्वारा दिया गया है
$$ y(x, t)=0.06 \sin (\frac{2 \pi x}{3}) \cos (120 \pi t) $$
जहाँ $x$ और $y$ मीटर में है और $t$ सेकंड में है। स्ट्रिंग की लंबाई 1.5 $m$ है और इसका द्रव्यमान $3.0 \times 10^{-2} kg$ है।
(a) यह 60 Hz आवृत्ति की एक प्रगतिशील तरंग को प्रस्तुत करता है
(b) यह 60 Hz आवृत्ति की एक स्थैतिक तरंग को प्रस्तुत करता है
(c) यह दो तरंगों के अध्यादि के परिणाम है, जिनकी तरंगदैर्ध्य $3 m$ है, आवृत्ति $60 Hz$ है और वे $180 m / s$ की चाल से विपरीत दिशा में यात्रा कर रही हैं
(d) इस तरंग का आयाम स्थिर है
उत्तर दिखाएं
उत्तर (b, c)
दिया गया समीकरण है
$$ y(x, t)=0.06 \sin (\frac{2 \pi x}{3}) \cos (120 \pi t) $$
(a) एक मानक स्थैतिक तरंग समीकरण के साथ तुलना करते हुए
$$ y(x, t)=a \sin (k x) \cos (\omega t) $$
स्पष्ट रूप से, दिया गया समीकरण स्थैतिक तरंग के अंतर्गत आता है। अतः, विकल्प (a) सही नहीं है।
(b) तुलना करते हुए,
$$ \begin{aligned} & \omega =120 \pi \\ \Rightarrow 2 \pi f & =120 \pi \Rightarrow f=60 Hz \end{aligned} $$
(c) $k=\frac{2 \pi}{3}=\frac{2 \pi}{\lambda}$
$$ \Rightarrow \begin{aligned} \lambda & =\text { तरंगदैर्ध्य }=3 m \\ \text { आवृत्ति } & =f=60 Hz \\ \text { चाल } & =v=f \lambda=(60 Hz)(3 m)=180 m / s \end{aligned} $$
(d) स्थैतिक तरंग में, माध्यम के सभी कण आवर्ती गति करते हैं जिनका आयाम बदलता रहता है।
-
(a) यह एक आगे बढ़ती तरंग है जिसकी आवृत्ति $60 Hz$ है
दिया गया समीकरण $ y(x, t) = 0.06 \sin \left( \frac{2 \pi x}{3} \right) \cos (120 \pi t) $ एक स्थैतिक तरंग समीकरण $ y(x, t) = a \sin (kx) \cos (\omega t) $ के रूप के साथ मेल खाता है। एक आगे बढ़ती तरंग के रूप में $ y(x, t) = A \sin (kx - \omega t) $ या $ y(x, t) = A \sin (kx + \omega t) $ होता है। अतः, दिया गया समीकरण एक आगे बढ़ती तरंग को निरूपित नहीं करता है।
-
(d) इस तरंग का आयाम स्थिर है
एक स्थैतिक तरंग में, तार के लंबाई के अनुसार आयाम बदलता रहता है। आयाम नोड्स पर शून्य और एंटीनोड्स पर अधिकतम होता है। दिया गया समीकरण $ y(x, t) = 0.06 \sin \left( \frac{2 \pi x}{3} \right) \cos (120 \pi t) $ दर्शाता है कि आयाम $ x $ के स्थान पर निर्भर करता है (विशेषकर, यह $ 0.06 \sin \left( \frac{2 \pi x}{3} \right)$ होता है), जिससे स्पष्ट रूप से आयाम स्थिर नहीं है।
13. तरंग की चाल एक तरल में निर्भर करती है
(a) माध्यम के घनत्व पर विपरीत रूप से
(b) माध्यम के आयतन प्रतिबाधा के वर्ग पर
(c) घनत्व के वर्गमूल के व्युत्क्रमानुपाती
(d) माध्यम के बुल्क मॉड्यूलस के वर्गमूल के सीधे अनुपाती
उत्तर दिखाएं
उत्तर $(c, d)$
एक तरल में ध्वनि तरंगों की गति $v=\sqrt{\frac{B}{\rho}}$ द्वारा दी जाती है, जहाँ $B$ बुल्क मॉड्यूलस है और $\rho$ माध्यम के घनत्व है।
स्पष्ट रूप से,
$$ \begin{matrix} v \propto \frac{1}{\sqrt{\rho}} & {[\therefore \text { किसी भी तरल के लिए, } B=\text { स्थिरांक }]} \\ v \propto \sqrt{B} & {[\because \text { माध्यम के लिए, } \rho=\text { स्थिरांक }]} \end{matrix} $$
-
(a) माध्यम के घनत्व के सीधे अनुपाती: यह गलत है क्योंकि तरल में ध्वनि की गति घनत्व के वर्गमूल के व्युत्क्रमानुपाती होती है, न कि घनत्व के सीधे अनुपाती। यदि घनत्व बढ़ता है, तो ध्वनि की गति कम हो जाती है।
-
(b) माध्यम के बुल्क मॉड्यूलस के वर्ग के अनुपाती: यह गलत है क्योंकि तरल में ध्वनि की गति बुल्क मॉड्यूलस के वर्गमूल के सीधे अनुपाती होती है, न कि बुल्क मॉड्यूलस के वर्ग के अनुपाती। यदि बुल्क मॉड्यूलस बढ़ता है, तो ध्वनि की गति बढ़ती है, लेकिन बुल्क मॉड्यूलस के वर्ग के अनुपाती नहीं।
14. एक तलीय आगे बढ़ती यांत्रिक तरंग के प्रसार के दौरान,
(a) सभी कण एक ही चरण में झूल रहे हैं
(b) सभी कणों का आयाम समान है
(c) माध्यम के कण आवर्त गति करते हैं
(d) तरंग वेग माध्यम की प्रकृति पर निर्भर करता है
उत्तर दिखाएं
उत्तर ( $b, c, d)$
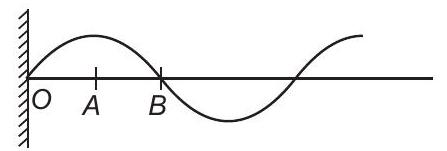
एक तलीय आगे बढ़ती यांत्रिक तरंग के प्रसार के दौरान, जैसा कि चित्र में दिखाया गया है, सभी कणों का आयाम समान है।
(i) स्पष्ट रूप से, कण $O, A$ और $B$ अलग-अलग चरण में हैं।
(ii) चित्र में दिखाए गए तरंग के कण ऊपर नीचे आवर्त गति करते हैं।
(iii) एक आगे बढ़ती तरंग एक तरल में प्रसारित होती है।
अतः,
$$ \begin{aligned}
\text { वेग } & =v=\sqrt{\frac{B}{\rho}} \\ v & \propto \sqrt{\frac{1}{\rho}} \end{aligned} $$
$$ [\because B \text { एक स्थिरांक है }] $$
जबकि $\rho$ माध्यम की प्रकृति पर निर्भर करता है, इसलिए $v$ भी माध्यम की प्रकृति पर निर्भर करता है।
- विकल्प (a) गलत होने के कारण: एक समतल आगे बढ़ते यांत्रिक तरंग के प्रसार के दौरान, सभी कण एक ही चरण में झूल नहीं रहते हैं। विभिन्न कण अपने गति के चक्र के विभिन्न बिंदुओं पर होते हैं, जैसा कि चित्र में दिखाया गया है, जहां कण O, A और B विभिन्न चरणों में हैं।
15. एक स्ट्रिंग (दोनों सिरों पर बंधी) के अनुप्रस्थ विस्थापन को $y(x, t)=0.06 \sin (\frac{2 \pi x}{3}) \cos (120 \pi t)$ द्वारा दिया गया है।
स्ट्रिंग पर दो क्रमागत नोड के बीच सभी बिंदु इस प्रकार झूलते हैं:
(a) समान आवृत्ति
(b) समान चरण
(c) समान ऊर्जा
(d) विभिन्न आयाम
उत्तर दिखाएँ
उत्तर $(a, b, d)$
दिया गया समीकरण है
$$ y(x, t)=0.06 \sin (\frac{2 \pi}{3} x) \cos (120 \pi t) $$
इसे स्थैतिक तरंग के मानक समीकरण के साथ तुलना करें
$$ y(x, t)=a \sin (k x) \cos (\omega t) $$
यह चित्र द्वारा प्रस्तुत किया गया है।
जहां $N$ नोड को और $A$ अन्तर्नोड को दर्शाता है।
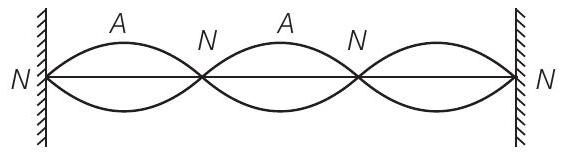
(a) स्पष्ट रूप से, सभी बिंदुओं के लिए आवृत्ति समान है।
(b) दो नोड के बीच सभी कणों के लिए एक ही समय पर $(120 \pi t)$ के चरण समान होते हैं।
लेकिन (c) और (d) के लिए $0.06 \sin (\frac{2 \pi}{3} x)$ के विभिन्न आयाम होते हैं और विभिन्न आयाम के कारण विभिन्न ऊर्जा होती है।
- विकल्प (c) गलत है क्योंकि दो क्रमागत नोड के बीच बिंदुओं के विभिन्न आयाम $0.06 \sin \left(\frac{2 \pi}{3} x\right)$ द्वारा दिया गया है। चूंकि ऊर्जा आयाम के वर्ग के समानुपाती होती है, इसलिए विभिन्न आयाम विभिन्न ऊर्जा के निर्माण के लिए जिम्मेदार होते हैं।
16. एक ट्रेन, स्टेशन यार्ड में खड़ी होकर, चाल वाली हवा में आवृत्ति $400 Hz$ के बजाय ब्लॉस बजाती है। हवा यार्ड से स्टेशन की दिशा में $10 m / s$ की गति से बहने लगती है। दिया गया है कि शांत हवा में ध्वनि की गति $340 m / s$ है। तब
(a) प्लेटफॉर्म पर खड़े प्रेक्षक द्वारा सुनी गई ध्वनि की आवृत्ति $400 Hz$ है
(b) प्लेटफॉर्म पर खड़े प्रेक्षक द्वारा सुनी गई ध्वनि की गति $350 m / s$ है
(c) प्लेटफॉर्म पर खड़े प्रेक्षक द्वारा सुनी गई ध्वनि की आवृत्ति बढ़ जाएगी
(d) प्लेटफॉर्म पर खड़े प्रेक्षक द्वारा सुनी गई ध्वनि की आवृत्ति घट जाएगी
उत्तर दिखाएँ
Thinking Process
जब हवा ध्वनि तरंग की दिशा के समान दिशा में बहती है तो तरंग की नेट गति ध्वनि तरंग की गति और हवा की गति के योग के बराबर होती है।
Answer ( $a, b$ )
दिया गया है,
हवा की गति
$$ \begin{aligned} & v_0=400 Hz, v=340 m / s \\ & v_{w}=10 m / s \end{aligned} $$
(a) क्योंकि स्रोत और प्रेक्षक दोनों स्थिर हैं, इसलिए प्रेक्षक द्वारा देखी गई आवृत्ति स्वाभाविक आवृत्ति के बराबर होगी $v_0=400 Hz$
(b) ध्वनि की गति $v=v+v_{w}$
$$ v =340+10=350 m / s $$
(c) और (d) में आवृत्ति पर कोई प्रभाव नहीं होगा क्योंकि स्रोत और प्रेक्षक के बीच कोई सापेक्ष गति नहीं है और इसलिए (c),(d) गलत हैं।
-
(c) प्लेटफॉर्म पर खड़े प्रेक्षक द्वारा सुनी गई ध्वनि की आवृत्ति बढ़ जाएगी: यह गलत है क्योंकि स्रोत (ट्रेन) और प्रेक्षक (प्लेटफॉर्म पर खड़ा) के बीच कोई सापेक्ष गति नहीं है। हवा ध्वनि की गति पर प्रभाव डालती है लेकिन दोनों स्रोत और प्रेक्षक स्थिर हैं इसलिए आवृत्ति पर कोई प्रभाव नहीं होता।
-
(d) प्लेटफॉर्म पर खड़े प्रेक्षक द्वारा सुनी गई ध्वनि की आवृत्ति घट जाएगी: यह (c) के लिए उतना ही गलत है। स्रोत और प्रेक्षक के बीच कोई सापेक्ष गति नहीं है, इसलिए आवृत्ति अपरिवर्तित रहती है।
17. अप्रगामी तरंगों के लिए निम्नलिखित में से कौन से कथन सत्य हैं?
(a) प्रत्येक कण के एक निश्चित आम्प्लीतुड होता है जो इसके सबसे करीब के कण के आम्प्लीतुड से भिन्न होता है
(b) सभी कण अपने माध्य स्थिति के एक ही समय पार गुजरते हैं
(c) सभी कण एक ही आयाम के साथ आवर्त गति कर रहे हैं
(d) कोई भी तल पर ऊर्जा का नेट परिवहन नहीं होता
(e) कुछ कण हमेशा विराम में रहते हैं
उत्तर दिखाएँ
उत्तर $(a, b, d, e)$
एक स्थैतिक तरंग के समीकरण को विचार करें; $y=a \sin (k x) \cos \omega t$
(a) स्पष्ट रूप से $x$ पर प्रत्येक कण का आयाम $=a \sin k x=$ निश्चित होता है
(b) माध्य स्थिति के लिए $y=0$
$$ \begin {matrix} \Rightarrow & \cos \omega t =0 \\ \Rightarrow \omega t & =(2 n-1) \frac{\pi}{2} \end{matrix} $$
इसलिए, $n$ के निश्चित मान के लिए, सभी कणों के लिए समान समय मान होता है
$$ t =(2 n-1) \frac{\pi}{2 \omega} \quad[\because \omega=\text { निश्चित }] $$
(c) सभी कणों के आयाम $ a \sin (k x)$ होते हैं, जो $x$ के विभिन्न मानों के लिए विभिन्न कणों के लिए भिन्न होते हैं
(d) स्थैतिक तरंग में ऊर्जा दो नोड के बीच सीमित होती है
(e) विभिन्न नोड पर स्थित कण हमेशा विराम में रहते हैं।
- (c) सभी कणों का आयाम $a \sin (kx)$ होता है, जो $x$ के विभिन्न मानों के लिए विभिन्न कणों के लिए भिन्न होता है। इसलिए, सभी कण एक ही आयाम के साथ आवर्त गति नहीं कर रहे हैं।
बहुत छोटे उत्तर प्रकार के प्रश्न
18. एक सोनोमीटर तार एक स्वर घटक के साथ अनुनाद में विभाजित हो रहा है। तनाव को समान रखते हुए तार की लंबाई दुगुनी कर दी जाती है। तार के साथ स्वर घटक के अनुनाद के लिए किन शर्तों में तार के साथ अनुनाद बना रहेगा?
उत्तर दिखाएँ
उत्तर दुगुनी लंबाई के तार अपने द्वितीय अपवर्तन में विभाजित होता है। इसलिए, यदि स्वर घटक $L$ पर अनुनाद करता है, तो यह $2L$ पर भी अनुनाद करता है। इसे नीचे बताया गया है
सोनोमीटर आवृत्ति निम्नलिखित द्वारा दी गई है
$$ \nu=\frac{n}{2 L} \sqrt{\frac{T}{m}} \quad(n=\text { लूप की संख्या }) $$
अब, जब लंबाई $L$ पर विभाजित होता है, हम मान लेते हैं $\nu=\nu_1$
$$ \begin{aligned} n & =n_1 \\ \therefore \quad \nu_1 & =\frac{n_1}{2 L} \sqrt{\frac{T}{m}} \end{aligned} $$
जब लंबाई दुगुनी हो जाती है, तो
$$ \nu_2=\frac{n_2}{2 \times 2 L} \sqrt{\frac{T}{m}} $$
समीकरण (i) को समीकरण (ii) से विभाजित करने पर, हम प्राप्त करते हैं
$$ \frac{\nu_1}{\nu_2}=\frac{n_1}{n_2} \times 2 $$
आवृत्ति के अनुनाद के लिए बनाए रखने के लिए
$$ \begin{aligned} & \frac{\nu_1}{\nu_2}=1=\frac{n_1}{n_2} \times 2 \\ \Rightarrow \quad & n_2=2 n_1 \end{aligned} $$
इसलिए, जब तार दुगुना हो जाता है तो लूप की संख्या भी दुगुनी हो जाती है ताकि अनुनाद उत्पन्न हो सके। अर्थात, यह द्वितीय अधिस्वर अनुनाद में होता है।
19. एक ऑर्गन पाइप जिसकी लंबाई $L$ है और दोनों सिरों पर खुला है, एक ट्यूनिंग फोर्क जिसकी आवृत्ति $480 Hz$ है के उत्तेजन से अपने प्रथम अधिस्वर में झंग उत्पन्न करता है। एक ऐसे पाइप की लंबाई क्या होनी चाहिए जो एक छोर पर बंद हो और उसी ट्यूनिंग फोर्क के उत्तेजन से अपने प्रथम अधिस्वर में झंग उत्पन्न करे?
उत्तर दिखाएँ
Thinking Process
हमें दबाव तरंग और विस्थापन तरंग के बीच भ्रम नहीं होना चाहिए। किसी भी प्रकार की तरंग के बारे में विचार करने पर, परिणाम समान होगा।
Answer चित्र में दिखाए गए स्थिति को ध्यान में रखें
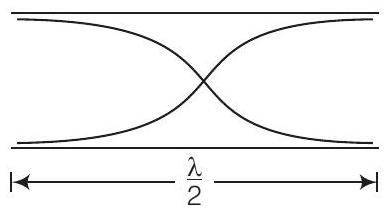
क्योंकि ऑर्गन पाइप दोनों सिरों पर खुला है, इसलिए प्रथम अधिस्वर के लिए
$$ \begin{gathered} l=\frac{\lambda}{2} \\ \Rightarrow \quad \lambda=2 l \Rightarrow \frac{c}{\nu}=2 l \Rightarrow \nu=\frac{c}{2 l} \end{gathered} $$
जहाँ $c$ हवा में ध्वनि तरंग की चाल है।
एक ऐसे पाइप के लिए जो एक छोर पर बंद हो
$$ \nu^{\prime}=\frac{C}{4 L^{\prime}} $$
प्रथम अधिस्वर के लिए $c$
इसलिए,
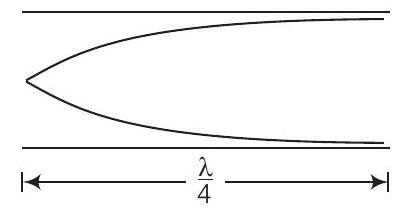
$$ \begin{matrix} \Rightarrow \frac{C}{2 L} =\frac{C}{4 L^{\prime}} \\ \Rightarrow \frac{L^{\prime}}{L} =\frac{2}{4}=\frac{1}{2} \Rightarrow L^{\prime}=\frac{L}{2} \end{matrix} $$
20. एक ट्यूनिंग फोर्क $A$, जिसे $512 Hz$ अंकित किया गया है, एक अनंकित ट्यूनिंग फोर्क $B$ के साथ बजाने पर 5 बीट प्रति सेकंड उत्पन्न करता है। यदि $B$ को वेस के साथ भर दिया जाए तो बीट की संख्या फिर भी 5 प्रति सेकंड होती है। अनलोड करने पर ट्यूनिंग फोर्क $B$ की आवृत्ति क्या होती है?
उत्तर दिखाएँ
उत्तर तार $A$ की आवृत्ति,
$$ \nu_{A}=512 \text{ Hz} $$
संभावित आवृत्ति तार $B$ की,
$$ \nu_{B}=\nu_{A} \pm 5=512 \pm 5=517 \text { या } 507 \text{ Hz} $$
जब $B$ भारित होता है, तो इसकी आवृत्ति कम हो जाती है।
अगर यह $517 \text{ Hz}$ है, तो यह $507 \text{ Hz}$ तक कम हो सकती है और फिर भी $5 \text{ Hz}$ के बीट बन सकता है।
अगर यह $507 \text{ Hz}$ है, तो आवृत्ति कम होने पर बीट आवृत्ति हमेशा बढ़ जाएगी, इसलिए $\nu_{B}=517 \text{ Hz}$
नोट: दोनों तारों के बीट आवृत्ति उत्पन्न करने के लिए उनकी आवृत्तियाँ लगभग समान होनी चाहिए, अर्थात आवृत्तियों में थोड़ा अंतर होना चाहिए।
21. एक इलास्टिक तरंग के विस्थापन को फलन $y=3 \sin \omega t+4 \cos \omega t$ द्वारा दिया गया है, जहाँ $y$ सेंटीमीटर में और $t$ सेकंड में है। परिणामी आयाम की गणना कीजिए।
उत्तर दिखाएँ
उत्तर दिया गया, इलास्टिक तरंग के विस्थापन; $y=3 \sin \omega t+4 \cos \omega t$. मान लीजिए,
$$ 3=a \cos \phi $$
$$ 4=a \sin \phi $$
समीकरण (ii) को समीकरण (i) से विभाजित करने पर, हमें प्राप्त होता है;
$ \tan \phi = \frac {3}{4} $
इसके अतिरिक्त, $\quad a^{2} \cos ^{2} \phi+a^{2} \sin ^{2} \phi=3^{2}+4^{2}$
$\Rightarrow \quad a^{2}(\cos ^{2} \phi+\sin ^{2} \phi)=25$
या,
$$ a^{2} \cdot 1=25 \Rightarrow a=5 $$
अतः, आयाम $=5 \text{ cm}$
22. एक सितार के तार को एक नए तार से बदल दिया जाता है, जो एक ही लंबाई और सामग्री के है लेकिन पहले तार के तीन गुना त्रिज्या का है। यदि तार में तनाव समान रहे, तो आवृत्ति में कितना अंतर आएगा?
उत्तर दिखाएँ
एक सितार के तार में आवर्तन के अनुमानित रूप से दोनों सिरों पर बांधे गए तार के अनुरूप होता है।
उत्तर तनाव वाले तार द्वारा उत्पन्न आवर्तन की आवृत्ति
$$ \begin{aligned} & \nu=\frac{n}{2 l} \sqrt{\frac{T}{\mu}} \\ & \text { इकाई लंबाई का द्रव्यमान, } \mu=\frac{\text { द्रव्यमान }}{\text { लंबाई }}=\frac{\pi r^{2} l \rho}{l}=\pi r^{2} \rho \quad[\because M=\nu p=A l \rho=\pi r^{2} l \rho] \\ & \therefore \quad \nu=\frac{n}{2 l} \sqrt{\frac{T}{\pi r^{2} \rho}} \Rightarrow \nu \propto \sqrt{\frac{1}{r^{2}}} \\ & \nu \propto \frac{1}{r} \\
$$ \begin{aligned} & \text{अतः, जब त्रिज्या तीन गुनी हो जाती है, } \nu \text{ पहले मान के } (\frac{1}{3})^{\text{वां}} \text{ होगा। } \end{aligned} $$
23. किस तापमान $(^{\circ} C)$ पर हवा में ध्वनि की चाल शून्य डिग्री सेल्सियस पर इसके मान के तीन गुना होगी ?
उत्तर दिखाएँ
Answer हम जानते हैं कि हवा में ध्वनि की चाल $v \propto \sqrt{T}$
$ \therefore \frac{v_{T}}{v_0} =\sqrt{\frac{T_{T}}{T_0}}=\sqrt{\frac{T_{T}}{273}}$
$\text { लेकिन } \frac{v_{T}}{v_0} =\frac{3}{1} $
$\therefore \frac{3}{1} =\sqrt{\frac{T_{T}}{T_0}} \Rightarrow \frac{T_{T}}{273}=9 $
[जहाँ $T \text { केल्विन में है] }$
$ T_{T} =273 \times 9=2457 K$
$ =2457-273=2184^{\circ} C$
24. दो तरंगों जिनकी आवृत्तियाँ $n_1$ और $n_2$ लगभग समान हैं, एक बिंदु पर एक साथ पहुँचती हैं, तो लगातार उच्चिष्ठ के बीच समय अंतर क्या होगा?
उत्तर दिखाएँ
Thinking Process
जब दो लगभग समान आवृत्ति वाली तरंगें एक दूसरे के साथ अवतरण करती हैं, तो वे ध्वनि बैंड उत्पन्न करती हैं।
Answer मान लीजिए,
ध्वनि बैंड आवृत्ति
$$ \begin{aligned} & n_1>n_2 \\ & \nu_{b}=n_1-n_2 \end{aligned} $$
ध्वनि बैंड काला $=T_{b}=\frac{1}{\nu_{b}}=\frac{1}{n_1-n_2}$
छोटे उत्तर प्रकार के प्रश्न
25. एक स्टील की तार की लंबाई $12 m$ है और द्रव्यमान $2.10 kg$ है। जब $2.06 \times 10^{4} N$ के तनाव के अनुप्रयोग के बाद इस तार पर अनुप्रस्थ तरंग की चाल क्या होगी?
उत्तर दिखाएँ
Answer दिया गया, तार की लंबाई, $l = 12 m $
तार का द्रव्यमान, $ m =2.10 kg $
तनाव, $T = 2.06 \times 10^{4} N$
अनुप्रस्थ तरंग की चाल
$$ \begin{aligned} v & =\sqrt{\frac{T}{\mu}} \quad \quad \quad[\text { जहाँ } \mu=\text { इकाई लंबाई पर द्रव्यमान] } \\ & =\sqrt{\frac{2.06 \times 10^{4}}{(\frac{2.10}{12})}}=\sqrt{\frac{2.06 \times 12 \times 10^{4}}{2.10}}=343 m / s \end{aligned} $$
26. एक $20 cm$ लंबी नली एक सिरे पर बंद है। एक $1237.5 Hz$ आवृत्ति वाले स्रोत द्वारा नली के किस हारमोनिक मोड को अनुनादित किया जाता है? (हवा में ध्वनि की चाल $=330 ms^{-1}$ )
उत्तर दिखाएं
उत्तर पाइप की लंबाई
$$ \begin{aligned} l & =20 \mathrm{~cm}=20 \times 10^{-2} \mathrm{~m} \\ \nu_{\text {funda }} & =\frac{\nu}{4 L}=\frac{330}{4 \times 20 \times 10^{-2}} \quad \quad \quad \text{(बंद पाइप के लिए)} \\ \nu_{\text {funda }} & =\frac{330 \times 100}{80}=412.5 \mathrm{~Hz} \\ \frac{\nu_{\text {given }}}{\nu_{\text {funda }}} & =\frac{1237.5}{412.5}=3 \end{aligned} $$
इसलिए, दिए गए आवृत्ति के स्रोत द्वारा पाइप के $3^{rd}$ हार्मोनिक नोड को रेजोनेंस के द्वारा उत्प्रेरित किया जाता है।
27. एक ट्रेन रेलवे स्टेशन के बाहरी संकेत बिंदु पर खड़ी होकर 400 Hz आवृत्ति के बुलबुला बजाती है। ट्रेन अपने प्लेटफॉर्म की ओर 10 ms⁻¹ की गति से चलना शुरू करती है। प्लेटफॉर्म पर खड़े अवलोकक के लिए ध्वनि की आवृत्ति क्या होगी? (हवा में ध्वनि की गति = 330 ms⁻¹)
उत्तर दिखाएं
उत्तर कारण स्रोत (ट्रेन) अवलोकक (प्लेटफॉर्म) की ओर गति कर रहा है, इसलिए अवलोकक द्वारा देखी गई आवृत्ति प्राकृतिक आवृत्ति से अधिक होती है।
बुलबुला की आवृत्ति
ट्रेन की गति
हवा में ध्वनि की गति
$$ \begin{aligned} \nu & =400 Hz \\ v_{t} & =10 m / s \\ v & =330 m / s \end{aligned} $$
जब स्रोत गति कर रहा हो, तो दिखाई देने वाली आवृत्ति, $\nu_{app}=(\frac{v}{v-v_{t}}) v$
$$ \begin{aligned} & =(\frac{330}{330-10}) 400 \\ \Rightarrow \quad \nu_{\text {app }} & =\frac{330}{320} \times 400=412.5 Hz \end{aligned} $$
28. एक तनी हुई रस्सी पर तरंग पैटर्न के चित्र दिया गया है। इस तरंग के प्रकार की व्याख्या करें और इसकी तरंगदैर्ध्य ज्ञात करें।
उत्तर दिखाएं
उत्तर हमें विभिन्न बिंदुओं के विस्थापन और स्थिति का अवलोकन करना होता है, फिर दो तरंगों की प्रकृति के अनुसार निर्णय लेना होता है।
बिंदु $x=10,20,30,40$ कभी भी गति के संबंध में मध्य स्थिति में होते हैं, जो नोड बनाते हैं जो एक स्थैतिक तरंग की विशेषता है।
$\because$ दो क्रमागत नोड के बीच दूरी $=\frac{\lambda}{2}$
$\Rightarrow$ $\lambda =2 \times(\text { नोड से नोड दूरी })$
$\quad =2 \times(20-10) $ $=2 \times 10=20 cm$
29. एक तनी गई रस्सी पर दो अलग-अलग समय के लिए बने खड़े तरंगों के पैटर्न को चित्र में दिखाया गया है। दो तरंगों के अध्यावेशन से खड़े तरंग बनते हैं जिनका वेग $360 ms^{-1}$ है और उनकी आवृत्ति $256 Hz$ है।
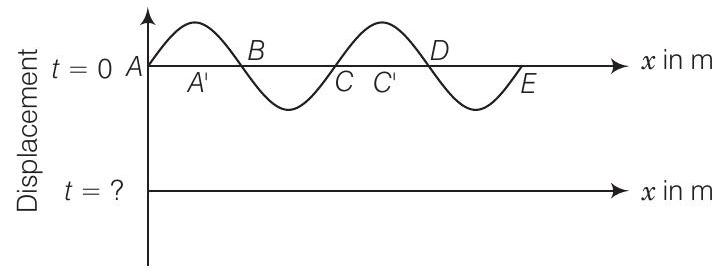
(a) दूसरे वक्र के खींचे जाने के समय की गणना करें।
(b) वक्र पर नोड और अंतर्नोड को चिह्नित करें।
(c) $A^{\prime}$ और $C^{\prime}$ के बीच दूरी की गणना करें।
उत्तर दिखाएँ
Answer दिया गया, तरंग की आवृत्ति $v=256 Hz$
समय अवधि,
$$ T=\frac{1}{v}=\frac{1}{256} S=3.9 \times 10^{-3} S $$
(a) मध्य स्थिति से पार जाने के लिए लिया गया समय
$$ t=\frac{T}{4}=\frac{1}{40}=\frac{3.9 \times 10^{-3}}{4} s=9.8 \times 10^{-4} s $$
(b) नोड $A, B, C, D, E$ (अर्थात शून्य विस्थापन) हैं और अंतर्नोड $A^{\prime}, C^{\prime}$ (अर्थात अधिकतम विस्थापन) हैं
(c) चित्र से स्पष्ट है कि $A^{\prime}$ और $C^{\prime}$ क्रमागत अंतर्नोड हैं, इसलिए अलगाव $=$ तरंगदैर्घ्य $(\lambda)$
$$ =\frac{v}{\nu}=\frac{360}{256}=1.41 m $$ $$\qquad \qquad \qquad[\because v=v \lambda]$$
30. एक ट्यूब में पानी भरा है जिसके खुले सिरे के पास एक स्वर घटक (ट्यूनिंग फोर्क) रखा गया है (चित्र)। ट्यूब में पानी के स्तर को धीरे-धीरे कम करते जाते हैं। जब पानी का स्तर खुले सिरे से $17 cm$ कम होता है, तो ध्वनि की अधिकतम तीव्रता सुनी जाती है। यदि कमरे का तापमान $20^{\circ} C$ है, तो गणना करें
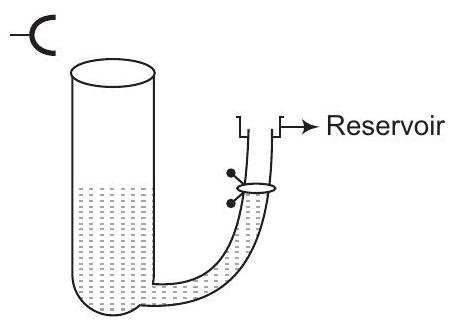
(a) कमरे के तापमान पर हवा में ध्वनि की गति।
(b) $0^{\circ} C$ पर हवा में ध्वनि की गति।
(c) यदि ट्यूब में पानी के स्थान पर पारा लगाया जाए, तो आपके अवलोकन में कोई अंतर होगा या नहीं?
उत्तर दिखाएं
पानी से आंशिक रूप से भरे ट्यूब, बंद आवाज नली के रूप में कार्य करता है। इसके आधार पर, हम संबंधित आवृत्तियों को खोजेंगे।
उत्तर चित्र में दिखाए गए अनुसार, संतूर वादक की आवृत्ति $\nu=512 , \text{Hz}$ है।
पहले तीव्रता के उच्चिष्ठ के अवलोकन के लिए
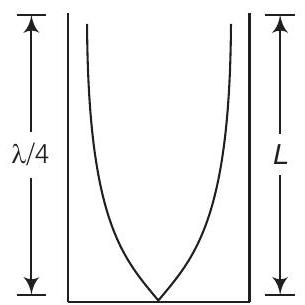
(a) $L=\frac{\lambda}{4} \Rightarrow \lambda=4 L$
[बंद नली के लिए]
$$ \begin{aligned} v & =\nu \lambda=512 \times 4 \times 17 \times 10^{-2} \\ & =348.16 , \text{m/s} \end{aligned} $$
(b) हम जानते हैं कि $v \propto \sqrt{T}$, जहाँ तापमान $(T)$ केल्विन में होता है।
$$ \begin{aligned} \frac{v_{20}}{v_0} & =\sqrt{\frac{273+20}{273+0}}=\sqrt{\frac{293}{273}} \\ \frac{v_{20}}{v_0} & =\sqrt{1.073}=1.03 \\ v_0 & =\frac{v_{20}}{1.03}=\frac{348.16}{1.03}=338 , \text{m/s} \end{aligned} $$
(c) पारे के सतह पर ध्वनि तरंगों के अधिक पूर्ण परावर्तन के कारण ध्वनि की तीव्रता अधिक हो सकती है, केवल हवा के स्तंभ के $17 , \text{cm}$ लंबाई पर अनुनाद देखा जाएगा क्योंकि पारा पानी से घनत्व अधिक होता है।
31. दिखाइए कि एक तार जो अपने दोनों सिरों पर निश्चित है, 1 लूप, 2 लूप, 3 लूप और 4 लूप में झंकर रहता है, तो आवृत्तियाँ $1: 2: 3: 4$ के अनुपात में होती हैं।
उत्तर दिखाएं
उत्तर मान लीजिए तार में $n$ संख्या में लूप हैं।
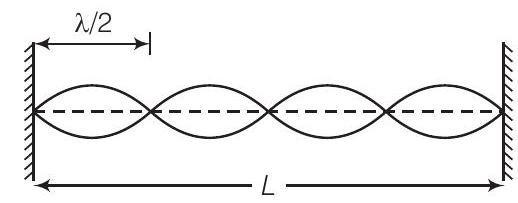
एक दोनों सिरों पर निश्चित तार की झंकर आवृत्तियों के अनुपात $1:2:3:4$ होता है, जो मूल आवृत्ति और उसके हार्मोनिक हैं, हम तरंग गति और अवस्थान तरंगों के नियमों का उपयोग करके दिखा सकते हैं।
मूल आवृत्ति (1 लूप): मूल आवृत्ति में, स्ट्रिंग एक लूप (एक पूर्ण तरंग दैर्घ्य) में झूलती है। स्ट्रिंग की लंबाई $L$ एक तरंग दैर्घ्य $\lambda_1$ के बराबर होती है: $$ L = \lambda_1 $$ आवृत्ति $f_1$ निम्नलिखित द्वारा दी जाती है: $$ f_1 = \frac{v}{\lambda_1} $$ जहाँ $v$ स्ट्रिंग पर तरंग की चाल होती है।
पहला अधिस्वर (2 लूप): पहला अधिस्वर में, स्ट्रिंग दो लूप (दो पूर्ण तरंग दैर्घ्य) में झूलती है। स्ट्रिंग की लंबाई $L$ दो तरंग दैर्घ्य $\lambda_2$ के बराबर होती है: $$ L = 2\lambda_2 \implies \lambda_2 = \frac{L}{2} $$ आवृत्ति $f_2$ निम्नलिखित द्वारा दी जाती है: $$ f_2 = \frac{v}{\lambda_2} = \frac{v}{\frac{L}{2}} = \frac{2v}{L} = 2f_1 $$
दूसरा अधिस्वर (3 लूप): दूसरा अधिस्वर में, स्ट्रिंग तीन लूप (तीन पूर्ण तरंग दैर्घ्य) में झूलती है। स्ट्रिंग की लंबाई $L$ तीन तरंग दैर्घ्य $\lambda_3$ के बराबर होती है: $$ L = 3\lambda_3 \implies \lambda_3 = \frac{L}{3} $$ आवृत्ति $f_3$ निम्नलिखित द्वारा दी जाती है: $$ f_3 = \frac{v}{\lambda_3} = \frac{v}{\frac{L}{3}} = \frac{3v}{L} = 3f_1 $$
तीसरा अधिस्वर (4 लूप): तीसरा अधिस्वर में, स्ट्रिंग चार लूप (चार पूर्ण तरंग दैर्घ्य) में झूलती है।
स्ट्रिंग की लंबाई $L$ चार तरंग दैर्घ्य $\lambda_4$ के बराबर होती है: $$ L = 4\lambda_4 \implies \lambda_4 = \frac{L}{4} $$ आवृत्ति $f_4$ निम्नलिखित द्वारा दी जाती है: $$ f_4 = \frac{v}{\lambda_4} = \frac{v}{\frac{L}{4}} = \frac{4v}{L} = 4f_1 $$ इस प्रकार, आवृत्तियाँ निम्न अनुपात में होती हैं: $$ f_1 : f_2 : f_3 : f_4 = 1 : 2 : 3 : 4 $$
यह दिखाता है कि दोनों सिरों पर बंधी झूलती हुई स्ट्रिंग की आवृत्तियाँ वास्तव में $1:2:3:4$ के अनुपात में होती हैं।
लंबा उत्तर प्रकार प्रश्न
32. पृथ्वी की त्रिज्या $6400$ किमी है। आंतरिक भाग $1000$ किमी त्रिज्या के ठोस है। इसके बाहर, $1000$ किमी से $3500$ किमी तक के क्षेत्र में तरल अवस्था है। फिर $3500$ किमी से $6400$ किमी तक पृथ्वी ठोस है। केवल अनुप्रस्थ $(P)$ तरंगें तरल में चल सकती हैं।
मान लीजिए कि $P$ तरंग की गति $8 km s^{-1}$ की गति से ठोस भागों में और $5 km s^{-1}$ की गति से द्रव भागों में पृथ्वी में होती है। एक भूकंप किसी स्थान पर होता है जो पृथ्वी के सतह के करीब है। गणना कीजिए कि एक सिस्मोमीटर में इसका रिकॉर्ड कितने समय के बाद एक व्यासानुरूपी बिंदु पर दर्ज होगा, यदि तरंग व्यास के अनुदिश यात्रा करती है?
उत्तर दिखाएं
उत्तर ठोस में तरंग की गति $=8 km / s$
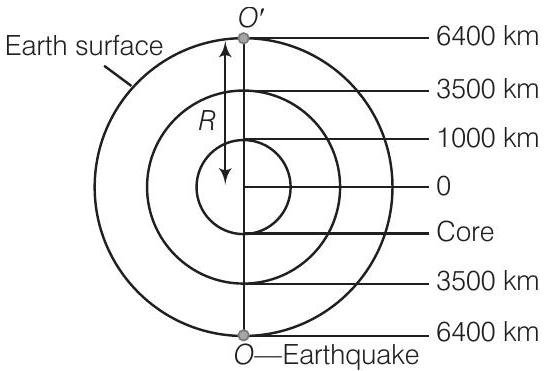
द्रव में तरंग की गति $=5 km / s$
आवश्यक समय $=[\frac{1000-0}{8}+\frac{3500-1000}{5}+\frac{6400-3500}{8}] \times 2 \quad[\because$ व्यास $=$ त्रिज्या $\times 2]$
$$ \begin{matrix} =[\frac{1000}{8}+\frac{2500}{5}+\frac{2900}{8}] \times 2 & {[\text { समय }=\frac{\text { दूरी }}{\text { गति }}]} \\ =[125+500+362.5] \times 2=1975 & \end{matrix} $$
हम व्यासानुरूपी बिंदु पर विचार कर रहे हैं, इसलिए यहां 2 के गुणन के कारण है।
33. यदि $c$ गैस में अणुओं की औसत वर्ग मूल गति है और $v$ गैस में ध्वनि तरंग की गति है, तो दिखाइए कि $c / v$ सभी द्विपरमाणुक गैसों के लिए तापमान स्वतंत्र और नियत होता है।
उत्तर दिखाएं
उत्तर हम जानते हैं कि गैस के अणुओं की औसत वर्ग मूल गति
$$ c=\sqrt{\frac{3 p}{\rho}}=\sqrt{\frac{3 R T}{M}} $$
जहां, $M=$ गैस के मोलर द्रव्यमान है।
गैस में ध्वनि तरंग की गति $v=\sqrt{\frac{\gamma \rho}{\rho}}=\sqrt{\frac{\gamma R T}{M}}$
समीकरण (i) को समीकरण (ii) से विभाजित करने पर हम प्राप्त करते हैं
$$ \frac{c}{v}=\sqrt{\frac{3 R T}{M} \times \frac{M}{\gamma R T}} \Rightarrow \frac{c}{v}=\sqrt{\frac{3}{\gamma}} $$
जहां, $\gamma=$ द्विपरमाणुक गैस के अनुप्रस्थ नियतांक है
इसलिए,
$$ \gamma=\frac{7}{5} $$
$$ [\text { क्योंकि } \gamma=\frac{C_{p}}{C_{V}}] $$
34. नीचे दिए गए कुछ $x$ और $t$ के फ़ंक्शन एक अनुतापी तरंग के विस्थापन को प्रस्तुत करते हैं।
(i) $y=5 \cos (4 x) \sin (20 t)$
(ii) $y=4 \sin (5 x-t / 2)+3 \cos (5 x-t / 2)$
(iii) $y=10 \cos [(252-250) \pi t] \cos [(252+250) \pi t]$
(iv) $y=100 \cos (100 \pi t+0.5 x)$
कहें कि इनमें से कौन-कौन
(a) $x$-दिशा में चलती तरंग को प्रदर्शित करता है
(b) स्थैतिक तरंग को प्रदर्शित करता है
(c) बीट्स को प्रदर्शित करता है
(d) $x$-दिशा में चलती तरंग को प्रदर्शित करता है
अपने उत्तर के लिए कारण दें।
उत्तर दिखाएँ
तरंग की प्रकृति का अनुमान लगाने के लिए हमें मानक समीकरण के साथ तुलना करनी होती है।
उत्तर (a) समीकरण $y=100 \cos (100 \pi t+0.5 x)$, $x$-दिशा में चलती तरंग को प्रदर्शित करता है।
(b) समीकरण $y=5 \cos (4 x) \sin (20 t)$, स्थैतिक तरंग को प्रदर्शित करता है, क्योंकि इसमें sin और cos शब्द हैं, अर्थात दो प्रगतिशील तरंगों के संयोजन को दर्शाता है।
(c) समीकरण $y=10 \cos [(252-250) \pi t] \cdot \cos [(252+250) \pi t]$ दो निकटवर्ती आवृत्तियों 252 और 250 के योग और अंतर के संबंध में है, इसलिए इस समीकरण बीट्स के निर्माण को प्रदर्शित करता है।
(d) समीकरण $y=4 \sin (5 x-t / 2)+3 \cos (5 x-t / 2)$ में $x$ के साथ ऋणात्मक चिह्न है, इसलिए यह $x$-दिशा में चलती तरंग को प्रदर्शित करता है।
नोट: हमें $x$ के साथ जुड़े चिह्न और तरंग के प्रसार की दिशा के बीच गलतफहमी नहीं होनी चाहिए। यह बस उलटा है, $x$ के साथ धनात्मक चिह्न तरंग के नकारात्मक $x$-दिशा में प्रसार को दर्शाता है और विपरीत।
35. दी गई प्रगतिशील तरंग, $y=5 \sin (100 \pi t-0.4 \pi x)$ में $y$ और $x$ मीटर में है, $t$ सेकंड में है। इसके
(a) आयाम?
(b) तरंगदैर्घ्य?
(c) आवृत्ति?
(d) तरंग वेग?
(e) कण वेग का आयाम?
उत्तर दिखाएँ
उत्तर प्रगतिशील तरंग का मानक समीकरण निम्नलिखित है
$$ y=a \sin (\omega t-k x+\phi) $$
यह धनात्मक $x$-दिशा में चलती है।
दी गई समीकरण: $\quad y=5 \sin (100 \pi t-0.4 \pi x)$
मानक समीकरण के साथ तुलना करने पर
(a) आयाम $=5$ मीटर
(b) $k=\frac{2 \pi}{\lambda}=0.4 \pi$
$\therefore$ तरंगदैर्घ्य $\lambda=\frac{2 \pi}{k}=\frac{2 \pi}{0.4 \pi}=\frac{20}{4}=5$ मीटर
(c) $\omega=100 \pi$
$$ \begin{aligned} \omega & =2 \pi \nu=100 \pi \\ \therefore \quad \text { आवृत्ति, } \nu & =\frac{100 \pi}{2 \pi}=50 Hz \end{aligned} $$
(द) तरंग वेग $v=\frac{\omega}{k}$, जहाँ $k$ तरंग संख्या है और $k=\frac{2 \pi}{\lambda}$. $$ \begin{aligned} & =\frac{100 \pi}{0.4 \pi}=\frac{1000}{4} \\ & =250 m / s \\ \end{aligned} $$ (ए) हम देखते हैं;
$y =5 \sin (100 \pi t-0.4 \pi x) $
$\frac{d y}{d t} =\text { कण वेग }$
समीकरण (i) से,
$$ \frac{d y}{d t}=5(100 \pi) \cos [100 \pi t-0.4 \pi x] $$
कण वेग के अधिकतम मान $(\frac{d y}{d t})_{\max }$
जो कि ${\cos [100 \pi t-0.4 \pi x]}_{\max }=1$ के लिए होगा
$\therefore$ कण वेग के अधिकतम मान
$$ \begin{aligned} & =(\frac{d y}{d t})_{\max }=5(100 \pi) \times 1 \\ & =500 \pi m / s \end{aligned} $$
36. अप्रसारी तरंग के लिए $y=2 \cos 2 \pi(10 t-0.0080 x+3.5)$ जहाँ $x$ और $y$ सेंटीमीटर में है और $t$ सेकंड में है। दो बिंदुओं के बीच दोलन गति के बीच कलांतर क्या होगा जो एक दूरी पर हैं
(ए) $4 m$
(ब) $0.5 m$
(स) $\frac{\lambda}{2}$
(द) $\frac{3 \lambda}{4}$ (एक निश्चित समय के लिए)
(ए) एक कण के दोलन के बीच कलांतर क्या होगा जो $x=100 cm$ पर स्थित है, $t=T \sec$ और $t=5$ के लिए?
उत्तर दिखाएँ
उत्तर दिया गया, तरंग फलन हैं
$$ \begin{aligned} y & =2 \cos 2 \pi(10 t-0.0080 x+3.5) \\ & =2 \cos (20 \pi t-0.016 \pi x+7 \pi) \end{aligned} $$
अब, एक गतिशील तरंग के मानक समीकरण को लिखा जा सकता है
$$ y=a \cos (\omega t-k x+\phi) $$
ऊपर के समीकरण के साथ तुलना करने पर, हम प्राप्त करते हैं
$$ \begin{aligned} & a=2 cm \\ & \omega=20 \pi rad / s \\ & k=0.016 \pi \end{aligned} $$
पथ अंतर $=4 cm$
(ए) कलांतर $\Delta \phi=\frac{2 \pi}{\lambda} \times$ पथ अंतर
$$ \begin{aligned} \Delta \phi & =0.016 \pi \times 4 \times 100 \\ & =6.4 \pi rad \end{aligned} $$
(ब) $\Delta \phi=\frac{2 \pi}{\lambda} \times(0.5 \times 100)$
$[\because$ पथ अंतर $=0.5 m]$
$$ \begin{aligned}
& =0.016 \pi \times 0.5 \times 100 \\ & =0.8 \pi rad \end{aligned} $$
(c) $\Delta \phi=\frac{2 \pi}{\lambda} \times(\frac{\lambda}{2})=\pi rad$
(d) $\Delta \phi=\frac{2 \pi}{\lambda} \times \frac{3 \lambda}{4}=\frac{3 \pi}{2} rad$
(e) $T=\frac{2 \pi}{\omega}=\frac{2 \pi}{20 \pi}=\frac{1}{10} s$
$$ \therefore \quad \begin{aligned} \text { At } x & =100 cm \\ t & =T \\ \phi_1 & =20 \pi T-0.016 \pi(100)+7 \pi \\ & =20 \pi(\frac{1}{10})-1.6 \pi+7 \pi=2 \pi-1.6 \pi+7 \pi \end{aligned} $$
Again, at $x=100 cm, t=5 s$
$$ \begin{aligned} \phi_2 & =20 \pi(5)-0.016 \pi(100)+7 \pi \\ & =100 \pi-(0.016 \times 100) \pi+7 \pi \\ & =100 \pi-1.6 \pi+7 \pi \end{aligned} $$
$\therefore$ From Eqs. (i) and (ii), we get
$\Delta \phi=$ phase difference $=\phi_2-\phi_1$
$$ \begin{aligned} & =(100 \pi-1.6 \pi+7 \pi)-(2 \pi-1.6 \pi+7 \pi) \\ & =100 \pi-2 \pi=98 \pi rad \end{aligned} $$





