आवर्त गति
बहुविकल्पीय प्रश्न (MCQs)
1. एक कण के विस्थापन को समीकरण $y=3 \cos (\frac{\pi}{4}-2 \omega t)$ द्वारा प्रस्तुत किया गया है। कण की गति है
(a) सरल आवर्त गति जिसका आवर्तकाल $2 \pi / \omega$ है
(b) सरल आवर्त गति जिसका आवर्तकाल $\pi / \omega$ है
(c) आवर्त लेकिन सरल आवर्त नहीं
(d) अनावर्ती
उत्तर दिखाएं
उत्तर (b) दिया गया, $y=3 \cos (\frac{\pi}{4}-2 \omega t)$
कण का वेग
$$ \begin{aligned} v & =\frac{d y}{d t}=\frac{d}{d t}[3 \cos (\frac{\pi}{4}-2 \omega t)] \\ & =3(-2 \omega)[-\sin (\frac{\pi}{4}-2 \omega t)] \\ & =6 \omega \sin (\frac{\pi}{4}-2 \omega t) \\ \text { त्वरण, } a & =\frac{d v}{d t}=\frac{d}{d t}[6 \omega \sin (\frac{\pi}{4}-2 \omega t)] \\ & =6 \omega \times(-2 \omega) \cos (\frac{\pi}{4}-2 \omega t)=-12 \omega^{2} \cos (\frac{\pi}{4}-2 \omega t) \\ & =-4 \omega^{2}[3 \cos (\frac{\pi}{4}-2 \omega t)] \\ \Rightarrow \quad a & =-4 \omega^{2} y \\ \Rightarrow \text { त्वरण, } a \propto & -y \end{aligned} $$
इसलिए, ऋणात्मक चिह्न के कारण गति सरल आवर्त गति (SHM) है।
स्पष्ट रूप से, समीकरण से
$$ \begin{aligned} & \omega^{\prime}=2 \omega \\ & \Rightarrow \quad \frac{2 \pi}{T^{\prime}}=2 \omega \Rightarrow T^{\prime}=\frac{2 \pi}{2 \omega}=\frac{\pi}{\omega} \quad \text { [और दिया गया समीकरण } y=3 \cos (-2 \omega t+\frac{\pi}{4}) \text { ] } \end{aligned} $$
इसलिए, गति आवर्त गति है जिसका आवर्तकाल $\frac{\pi}{\omega}$ है।
-
विकल्प (a): विकल्प (a) में दिया गया आवर्तकाल $ \frac{2\pi}{\omega} $ है। हालांकि, दिए गए समीकरण $ y = 3 \cos \left( \frac{\pi}{4} - 2\omega t \right) $ से, कोणीय आवृत्ति $ 2\omega $ है। इसलिए, आवर्तकाल $ T $ की गणना $ T = \frac{2\pi}{2\omega} = \frac{\pi}{\omega} $ के रूप में की जाती है, न कि $ \frac{2\pi}{\omega} $।
-
विकल्प (c): समीकरण $ y = 3 \cos \left( \frac{\pi}{4} - 2\omega t \right) $ द्वारा वर्णित गति सरल आवर्त गति (SHM) है क्योंकि इसे $ y = A \cos (\omega’ t + \phi) $ के रूप में व्यक्त किया जा सकता है, जहाँ $ A $ आयाम है, $ \omega’ $ कोणीय आवृत्ति है और $ \phi $ चरण स्थिरांक है। इसलिए, यह बस आवर्त नहीं है, बल्कि विशेष रूप से सरल आवर्त गति है।
-
विकल्प (d): दी गई समीकरण $ y = 3 \cos \left( \frac{\pi}{4} - 2\omega t \right) $ एक आवर्ती फलन को प्रस्तुत करती है, क्योंकि यह नियमित अंतराल पर दोहराती है। इसके कारण यह आवर्ती है और एक सरल आवर्त गति (SHM) के रूप का अनुसरण करती है, इसलिए इसे गैर-आवर्ती गति के रूप में वर्गीकृत नहीं किया जा सकता है।
2. एक कण के विस्थापन को समीकरण $y=\sin ^{3} \omega t$ द्वारा प्रस्तुत किया जाता है। गति है
(a) गैर-आवर्ती
(b) आवर्ती लेकिन सरल आवर्त नहीं
(c) सरल आवर्त गति जिसका आवर्तकाल $2 \pi / \omega$ है
(d) सरल आवर्त गति जिसका आवर्तकाल $\pi / \omega$ है
उत्तर दिखाएँ
उत्तर (b) दी गई गति के समीकरण है
$$ \begin{aligned} & y = \sin ^{3} \omega t \\ &=(3 \sin \omega t-4 \sin 3 \omega t) / 4 \quad[\because \sin 3 \theta=3 \sin \theta-4 \sin ^{3} \theta] \\ & \Rightarrow \quad \frac{d y}{d t}=[\frac{d}{d t}(3 \sin \omega t)-\frac{d}{d t}(4 \sin 3 \omega t)] / 4 \\ & \Rightarrow \quad 4 \frac{d y}{d t}=3 \omega \cos \omega t-4 \times[3 \omega \cos 3 \omega t] \\ & \Rightarrow \quad 4 \times \frac{d^{2} y}{d t^{2}}=-3 \omega^{2} \sin \omega t+12 \omega \sin 3 \omega t \\ & \Rightarrow \quad \frac{d^{2} y}{d t^{2}}=-\frac{3 \omega^{2} \sin \omega t+12 \omega^{2} \sin 3 \omega t}{4} \\ & \Rightarrow \frac{d^{2} y}{d t^{2}} \text { व्युत्पन्न } y \text { के समानुपाती नहीं है।} \\ & \text { अतः, गति सरल आवर्त गति नहीं है।} \end{aligned} $$
क्योंकि व्यंजक में साइन फलन शामिल है, इसलिए यह आवर्ती होगा।
-
(a) गति गैर-आवर्ती नहीं है क्योंकि दी गई समीकरण $ y = \sin^3(\omega t) $ त्रिकोणमितीय फलनों को शामिल करती है, जो मूल रूप से आवर्ती होते हैं। अतः, गति आवर्ती होना चाहिए।
-
(c) गति $ 2\pi / \omega $ आवर्तकाल के साथ सरल आवर्त गति नहीं है क्योंकि सरल आवर्त गति (SHM) के लिए त्वरण (विस्थापन का द्वितीय अवकलज) विस्थापन के समानुपाती होना चाहिए और विपरीत दिशा में होना चाहिए। दी गई समीकरण इस शर्त को संतुष्ट नहीं करती है।
-
(d) गति $ \pi / \omega $ आवर्तकाल के साथ सरल आवर्त गति नहीं है, कारण विकल्प (c) के जैसे ही है। त्वरण विस्थापन के समानुपाती नहीं है, जो SHM के लिए आवश्यक है।
3. चार कणों के त्वरण और विस्थापन के बीच संबंध नीचे दिए गए हैं
(a) $a_{x}=+2 x$
(b) $a_{x}=+2 x^{2}$
(c) $a_{x}=-2 x^{2}$
(d) $a_{x}=-2 x$
कौन सा कण सरल आवर्त गति के अपवाद है?
उत्तर दिखाएं
उत्तर (d) गति सरल आवर्त गति होने के लिए कण के त्वरण को विस्थापन के ऋणात्मक अनुपात में होना चाहिए।
अर्थात, $\quad a \propto-(y$ या $x)$
हम यह स्पष्ट रूप से जानते हैं कि $y$ रैखिक होना चाहिए।
-
(a) $a_{x}=+2 x$: त्वरण विस्थापन के सीधे अनुपात में है, लेकिन यह ऋणात्मक नहीं है। सरल आवर्त गति में त्वरण विस्थापन के ऋणात्मक अनुपात में होना चाहिए।
-
(b) $a_{x}=+2 x^{2}$: त्वरण विस थापन के वर्ग के अनुपात में है, न कि विस्थापन के स्वयं के। इसके अतिरिक्त, यह धनात्मक है, न कि ऋणात्मक। सरल आवर्त गति में त्वरण विस्थापन के ऋणात्मक अनुपात में होना चाहिए।
-
(c) $a_{x}=-2 x^{2}$: त्वरण विस्थापन के वर्ग के अनुपात में है, न कि विस्थापन के स्वयं के। भले ही यह ऋणात्मक है, सरल आवर्त गति के लिए संबंध रैखिक होना चाहिए।
4. U-नलिका में एक द्रव स्तंभ के दोलन गति है
(a) आवर्त लेकिन सरल आवर्त नहीं
(b) अनावर्ती
(c) सरल आवर्त और समय अवधि द्रव के घनत्व से स्वतंत्र है
(d) सरल आवर्त और समय अवधि द्रव के घनत्व के सीधे अनुपात में है
उत्तर दिखाएं
उत्तर (c) चित्र को ध्यान में रखते हुए विचार करें जिसमें एक द्रव स्तंभ दोलन करता है। इस स्थिति में, गुरुत्वाकर्षण के कारण द्रव पर एक पुनर्स्थापन बल कार्य करता है। द्रव स्तंभ के त्वरण को पुनर्स्थापन बल के आधार पर गणना किया जा सकता है।
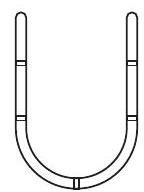
पुनर्स्थापन बल
$f=$ ऊंचाई $2 y$ के द्रव स्तंभ के भार
$\Rightarrow \quad f=-(A \times 2 y \times \rho) \times g=-2 A \rho g y$
$\Rightarrow f \propto-y \Rightarrow$ गति $k=2 A \rho g$ बल नियतांक के साथ SHM है।
$\Rightarrow$ समय अवधि
$$ \begin{aligned} & T=2 \pi \sqrt{\frac{m}{k}}=2 \pi \sqrt{\frac{A \times 2 h \times \rho}{2 A \rho g}}=2 \pi \sqrt{\frac{h}{g}} \\ & T=2 \pi \sqrt{\frac{l}{g}}, \text { जहाँ } l=h \end{aligned} $$
जो द्रव के घनत्व से स्वतंत्र है।
-
(a) आवर्ती लेकिन निम्न अवस्था गति नहीं: यह विकल्प गलत है क्योंकि U-नली में द्रव के स्तंभ की गति एक पुनरावर्ती बल द्वारा नियंत्रित होती है जो विस्थापन के सीधे अनुपाती होता है, जो सरल अवस्था गति (SHM) की विशेषता है। अतः, गति न केवल आवर्ती है बल्कि सरल अवस्था गति भी है।
-
(b) अआवर्ती: यह विकल्प गलत है क्योंकि U-नली में द्रव के स्तंभ की गति आवर्ती होती है। द्रव एक नियमित, पुनरावर्ती पैटर्न में आगे-पीछे झूलता है, जो आवर्ती गति की परिभाषा है।
-
(d) सरल अवस्था गति और समय अवधि द्रव के घनत्व के सीधे अनुपाती है: यह विकल्प गलत है क्योंकि झूले के समय अवधि द्रव के घनत्व से स्वतंत्र होती है। झूले के समय अवधि $ T $ द्वारा दी गई है $ T = 2\pi \sqrt{\frac{l}{g}} $, जहाँ $ l $ द्रव के स्तंभ की लंबाई है और $ g $ गुरुत्वीय त्वरण है। द्रव के घनत्व का इस व्यंजक में कोई भूमिका नहीं है, जो इसके समय अवधि पर कोई प्रभाव नहीं डालता है।
5. एक कण को एक दूसरे के लंबकर्मी सरल अवस्था गति $x=a \cos \omega t$ और $y=a \sin \omega t$ द्वारा एक साथ कार्य करता है। कण की गति के पथ के बारे में क्या कहा जा सकता है?
(a) एक अतिपरवलय
(b) एक परवलय
(c) एक वृत्त
(d) एक सीधी रेखा
उत्तर दिखाएँ
Thinking Process
हमें $x$ और $y$-अक्ष के घटकों को जोड़कर परिणामी विस्थापन ज्ञात करना होगा। $x$ और $y$ के विचरण के आधार पर पथ का अनुमान लगाया जाएगा।
Answer (c) दिया गया है,
$$ \begin{gathered} x=a \cos \omega t \\ y=a \sin \omega t \end{gathered} $$
समीकरण (i) और (ii) को वर्ग करके जोड़ने पर,
$$ \begin{matrix} a^{2} \Rightarrow y^{2} & =a^{2} & (\cos ^{2} \omega t+\sin ^{2} \omega t) \\ x^{2}+y^{2} & =a^{2} & {[\because \cos ^{2} \omega t+\sin ^{2} \omega t=1]} \end{matrix} $$
यह एक वृत्त का समीकरण है
स्पष्ट रूप से, बिंदु का बिंदुपथ एक अचर त्रिज्या a के वृत्त का है।
-
विकल्प (a) एक अतिपरवलय: समीकरण $x = a \cos \omega t$ और $y = a \sin \omega t$ एक वृत्त को वर्णित करते हैं, न कि एक अतिपरवलय। एक अतिपरवलय के लिए, $\cos \omega t$ और $\sin \omega t$ के गुणांक अलग-अलग होने चाहिए, अर्थात, $x = a \cos \omega t$ और $y = b \sin \omega t$ जहाँ $a \neq b$ हो।
-
विकल्प (b) एक परवलय: दिए गए समीकरण एक परवलय नहीं बनाते हैं। एक परवलयीय पथ आमतौर पर $x$ और $y$ के बीच द्विघातीय संबंध के रूप में होता है, जैसे $y = kx^2$ या $x = ky^2$। दिए गए समीकरण एक वृत्तीय गति को वर्णित करते हैं, न कि परवलयीय गति।
-
विकल्प (d) एक सीधी रेखा: समीकरण $x = a \cos \omega t$ और $y = a \sin \omega t$ एक वृत्तीय गति को वर्णित करते हैं, न कि एक रेखीय गति। एक सीधी रेखा के लिए $x$ और $y$ के बीच रेखीय संबंध होना चाहिए, जैसे $y = mx + c$।
6. एक कण के विस्थापन समय के साथ निम्न संबंध द्वारा परिवर्तित होता है $y=a \sin \omega t+b \cos \omega t$.
(a) गति दोलन गति है लेकिन अपरिवर्ती गति नहीं
(b) गति अपरिवर्ती गति है जिसका आयाम $a+b$ है
(c) गति अपरिवर्ती गति है जिसका आयाम $a^{2}+b^{2}$ है
(d) गति अपरिवर्ती गति है जिसका आयाम $\sqrt{a^{2}+b^{2}}$ है
उत्तर दिखाएँ
उत्तर (d) प्रश्न के अनुसार, विस्थापन
$$ \begin{aligned} & \text { मान लीजिए, } \\ & y=a \sin \omega t+b \cos \omega t \\ & \text { मान लीजिए, } \\ & a=A \sin \phi \text { और } b=A \cos \phi \\ & \quad \text { अब, } \quad a^{2}+b^{2}=A^{2} \sin ^{2} \phi+A^{2} \cos ^{2} \phi \\ & =A^{2} \Rightarrow A=\sqrt{a^{2}+b^{2}} \\ & y=A \sin \phi \cdot \sin \omega t+A \cos \phi \cdot \cos \omega t \\ & =A \sin (\omega t+\phi) \\ & \frac{d y}{d t}=A \omega \cos (\omega t+\phi) \\ & \frac{d^{2} y}{d t^{2}}=-A \omega^{2} \sin (\omega t+\phi)=-A y \omega^{2}=(-A \omega^{2}) y \\
$$ \begin{aligned} & \Rightarrow \quad \frac{d^{2} y}{d t^{2}} \propto(-y) \end{aligned} $$
इसलिए, यह एक सरल आवर्त गति (SHM) के समीकरण है जिसका आयाम $A=\sqrt{a^{2}+b^{2}}$ है।
-
(a) गति आवर्त है लेकिन निश्चित आवर्त गति नहीं: दी गई विस्थापन समीकरण $ y = a \sin \omega t + b \cos \omega t $ को $ y = A \sin (\omega t + \phi) $ के रूप में लिखा जा सकता है, जो सरल आवर्त गति (SHM) के मानक रूप है। इसलिए, गति वास्तव में एक SHM है, बस आवर्त नहीं।
-
(b) गति आवर्त गति है और आयाम $ a + b $ है: SHM के आयाम को वैकल्पिक तर्क और कोज्या पदों के गुणांक के परिणाम के रूप में निर्धारित किया जाता है, जो $ \sqrt{a^2 + b^2} $ द्वारा दिया जाता है। योग $ a + b $ गति के आयाम को सही रूप से प्रस्तुत नहीं करता है।
-
((c) गति आवर्त गति है और आयाम $ a^2 + b^2 $ है: SHM के आयाम को वैकल्पिक तर्क और कोज्या पदों के गुणांक के वर्ग के योग के वर्गमूल के रूप में निर्धारित किया जाता है, जो $ \sqrt{a^2 + b^2} $ है। व्यंजक $ a^2 + b^2 $ आयाम के वर्ग को प्रस्तुत करता है,
Through the elastic support the disturbance is transferred to all the pendulums.
$A$ and $C$ are having same length, hence they will be in resonance, because their time period of oscillation.
$$
T=2 \pi \sqrt{\frac{l}{g}}
$$
and hence, frequency is same.
So, amplitude of $A$ and $C$ will be maximum.
Note: In this problem, we have assumed that the support is perfectly elastic and there is no damping. Hence, oscillation is considered as undamped.
-
Option (a) is incorrect: Pendulum $D$ has a different length compared to $A$. Since the time period of oscillation depends on the length of the pendulum, $D$ will not be in resonance with $A$. Therefore, $D$ will not vibrate with maximum amplitude.
-
Option (c) is incorrect: Pendulum $B$ has a shorter length than $A$. This difference in length means that $B$ will have a different time period of oscillation and will not be in resonance with $A$. Consequently, $B$ will not vibrate with maximum amplitude.
-
Option (d) is incorrect: The pendulums have different lengths, which means they have different time periods of oscillation. Only pendulums with the same length (and thus the same time period) will resonate and have maximum amplitude. Therefore, not all four pendulums will oscillate with equal amplitude.
8. Figure shows the circular motion of a particle. The radius of the circle, the period, sense of revolution and the initial position are indicated on the figure. The simple harmonic motion of the $x$-projection of the radius vector of the rotating particle $P$ is
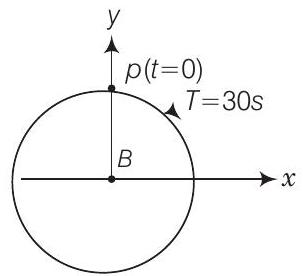
(a) $x(t)=B \sin (\frac{2 \pi t}{30})$
(b) $x(t)=B \cos (\frac{\pi t}{15})$
(c) $x(t)=B \sin (\frac{\pi t}{15}+\frac{\pi}{2})$
(d) $x(t)=B \cos (\frac{\pi t}{15}+\frac{\pi}{2})$
उत्तर दिखाएँ
उत्तर
(a) मान लीजिए कण के वृत्तीय गति के दौरान कोणीय वेग $\omega$ है और जब यह $Q$ पर होता है तो यह चित्र में दिखाए गए कोण $\theta$ बनाता है।
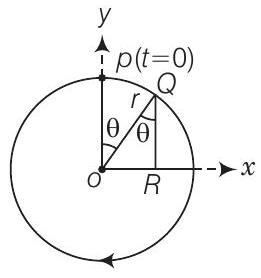
स्पष्ट रूप से,
$\theta=\omega t$
अब, हम लिख सकते हैं
$$ \begin{aligned} & O R=O Q \cos (90-\theta) \\ & =O Q \sin \theta=O Q \sin \omega t \\ & =r \sin \omega t \quad[\because O Q=r] \\ & {[\because r=B]} \\ & =B \sin \frac{2 \pi}{T} t=B \sin (\frac{2 \pi}{30} t) \end{aligned} $$
$$ \Rightarrow \quad x=r \sin \omega t=B \sin \omega t $$
स्पष्ट रूप से, यह समीकरण एक सरल आवर्त गति को प्रस्तुत करता है।
-
विकल्प (b): $x(t)=B \cos (\frac{\pi t}{15})$
- यह विकल्प गलत है क्योंकि इसमें कोसाइन फलन का उपयोग किया गया है जबकि सही फलन साइन होना चाहिए। कण के $t=0$ पर अंतिम धनात्मक विस्थापन एक्स-अक्ष के अनुदिश होता है, जो शून्य से शुरू होने वाले साइन फलन के संगत है। इसके अतिरिक्त, कोणीय आवृत्ति $\frac{\pi}{15}$ सही कोणीय आवृत्ति $\frac{2\pi}{30}$ के आधा है।
-
विकल्प (c): $x(t)=B \sin (\frac{\pi t}{15}+\frac{\pi}{2})$
- यह विकल्प गलत है क्योंकि इसमें $\frac{\pi}{2}$ के फेज विस्थापन का उपयोग किया गया है, जो सही समीकरण में नहीं है। फेज विस्थापन का अर्थ होता है कि कण के प्रारंभिक स्थिति अलग है, जो यहां नहीं है। इसके अतिरिक्त, कोणीय आवृत्ति $\frac{\pi}{15}$ सही कोणीय आवृत्ति $\frac{2\pi}{30}$ के आधा है।
-
विकल्प (d): $x(t)=B \cos (\frac{\pi t}{15}+\frac{\pi}{2})$
- यह विकल्प दो कारणों से गलत है: इसमें कोसाइन फलन का उपयोग किया गया है जबकि सही फलन साइन होना चाहिए, और इसमें $\frac{\pi}{2}$ के फेज विस्थापन का उपयोग किया गया है। कोसाइन फलन के $\frac{\pi}{2}$ के फेज विस्थापन के साथ एक अपरिवर्तित साइन फलन हो सकता है, लेकिन कोणीय आवृत्ति $\frac{\pi}{15}$ अभी भी गलत है क्योंकि यह सही कोणीय आवृत्ति $\frac{2\pi}{30}$ के आधा है।
9. एक कण के गति का समीकरण $x=a \cos (\alpha t)^{2}$ है। गति है
(a) आवर्ती लेकिन दोलन गति नहीं
(b) आवर्ती और दोलन गति
(c) दोलन गति लेकिन आवर्ती नहीं
(d) न तो आवर्ती न ही दोलन गति
उत्तर दिखाएँ
उत्तर (c) चूंकि दिया गया समीकरण
$$ x=a \cos (\alpha t)^{2} $$
एक कोसाइन फलन है। इसलिए, यह एक दोलन गति है।
अब, $t+T$ के स्थान पर $t$ रखें
$$ \begin{aligned} x(t+T) & =a \cos [\alpha(t+T)]^{2} \quad[\because x(t)=acos(\alpha t)^{2}] \\ & =a \cos [\alpha t^{2}+\alpha T^{2}+2 \alpha t T] \neq x(t) \end{aligned} $$
जहाँ, $T$ फलन $\omega(t)$ की आवर्तकाल मान लिया गया है।
इसलिए, यह आवर्ती नहीं है।
-
(a) आवर्ती लेकिन दोलन गति नहीं: दिया गया समीकरण $ x = a \cos (\alpha t)^2 $ एक दोलन गति को व्यक्त करता है क्योंकि इसमें एक कोसाइन फलन है, जो दोलन को प्रतिनिधित करता है। इसलिए, गति आवर्ती लेकिन दोलन गति नहीं हो सकती।
-
(b) आवर्ती और दोलन गति: हालांकि कोसाइन फलन के कारण गति दोलन गति है, लेकिन यह आवर्ती नहीं है। इसका कारण यह है कि समीकरण में $ t + T $ के स्थान पर $ t $ रखने पर फलन $ x(t) $ के समान नहीं प्राप्त होता, जिससे यह स्पष्ट होता है कि कोई निश्चित आवर्तकाल $ T $ नहीं है जिसके कारण गति दोहराई जा सके।
-
(d) न तो आवर्ती न ही दोलन गति: गति दोलन गति है क्योंकि इसमें एक कोसाइन फलन है, जो दोलन को प्रतिनिधित करता है। इसलिए, गति को न तो आवर्ती न ही दोलन गति के रूप में वर्गीकृत नहीं किया जा सकता।
10. एक कण जो $S H M$ में गति कर रहा है, की अधिकतम चाल $30 cm / s$ और अधिकतम त्वरण $60 cm / s^{2}$ है। दोलन काल है
(a) $\pi$ सेकंड
(b) $\frac{\pi}{2}$ सेकंड
(c) $2 \pi$ सेकंड
(d) $\frac{\pi}{t} \sec$
उत्तर दिखाएँ
उत्तर (a) एक SHM के समीकरण को $y=a \sin \omega t$ द्वारा प्रस्तुत किया जाता है
v =$\frac{d y}{d t}=a \omega \cos \omega t $
$\Rightarrow \quad(v)_{\max } =a \omega=30 $
$\text { त्वरण }(A) =\frac{d x^{2}}{d t^{2}}=-a \omega^{2} \sin \omega t $
$A_{\max } =\omega^{2} a=60 $
$\text { समीकरण (i) और (ii) से, हम प्राप्त करते हैं } \omega(\omega a) =60 \Rightarrow \omega(30)=60 $
$\Rightarrow \quad \omega =2 rad / s $
$\Rightarrow \quad \frac{2 \pi}{T} =2 rad / s \Rightarrow T=\pi sec$
-
विकल्प (b) $\frac{\pi}{2}$ sec गलत है क्योंकि दोलन की आवधिकता $T$ द्वारा दी गई है $T = \frac{2\pi}{\omega}$. दिया गया $\omega = 2 , \text{rad/s}$, सही आवधिकता $T = \pi , \text{sec}$ है, नहीं $\frac{\pi}{2} , \text{sec}$.
-
विकल्प (c) $2 \pi$ sec गलत है क्योंकि, उसी सूत्र $T = \frac{2\pi}{\omega}$ का उपयोग करते हुए और दिया गया $\omega = 2 , \text{rad/s}$, आवधिकता $T = \pi , \text{sec}$ है, नहीं $2 \pi , \text{sec}$.
-
विकल्प (d) $\frac{\pi}{t}$ sec गलत है क्योंकि इसके द्वारा दी गई $\omega = 2 , \text{rad/s}$ के लिए एक वैध आवधिकता प्रदान नहीं की जाती है। सही आवधिकता $T = \pi , \text{sec}$ है, और $\frac{\pi}{t}$ इस मान के साथ मेल नहीं खाता है।
बहुविकल्पीय प्रश्न (एक से अधिक विकल्प)
11. जब एक द्रव्यमान $m$ दो स्प्रिंग $S_1$ और $S_2$ के साथ अलग-अलग जुड़ा होता है, तो दोलन आवृत्तियाँ $v_1$ और $v_2$ होती हैं। यदि वही द्रव्यमान चित्र में दिखाए गए दो स्प्रिंगों के साथ जुड़ा होता है, तो दोलन आवृत्ति होगी
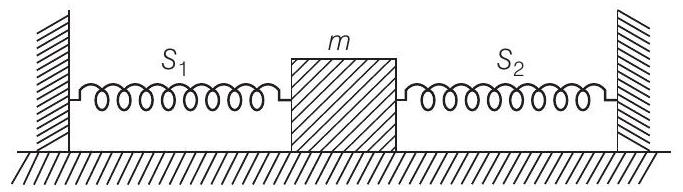
(a) $v_1+v_2$
(b) $\sqrt{v_1^{2}+v_2^{2}}$
(c) $(\frac{1}{v_1}+\frac{1}{v_2})^{-1}$
(d) $\sqrt{v_1^{2}-v_2^{2}}$
उत्तर दिखाएँ
सोचने की प्रक्रिया
इस प्रश्न को हल करने के लिए, हमें जब द्रव्यमान को बीच में जोड़ा जाता है तब प्रणाली के समतुल्य स्प्रिंग नियतांक को खोजना होता है।
उत्तर (b)
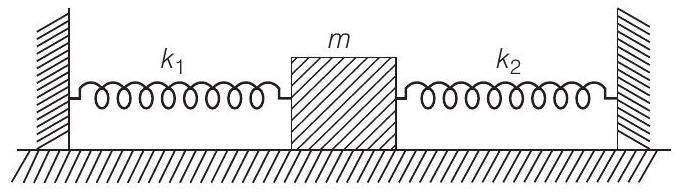
चित्र को ध्यान में रखते हुए, दो स्प्रिंगों को समानांतर में ले सकते हैं।
इसलिए,
$$ \begin{aligned} k_{eq} & =\text { समतुल्य स्प्रिंग नियतांक } \\ & =k_1+k_2 \end{aligned} $$
स्प्रिंग ब्लॉक-सिस्टम के दोलन काल
$$ \begin{aligned} T & =2 \pi \sqrt{\frac{m}{k_{\text {eq }}}}=2 \pi \sqrt{\frac{m}{k_1+k_2}} \\ \Rightarrow \quad v & =\frac{1}{T}=\frac{1}{2 \pi} \times \sqrt{\frac{k_1+k_2}{m}} \\ & =\text { समतुल्य दोलन आवृत्ति। } \end{aligned} $$
जब द्रव्यमान को दो स्प्रिंगों के अलग-अलग संयोजन से जोड़ा जाता है
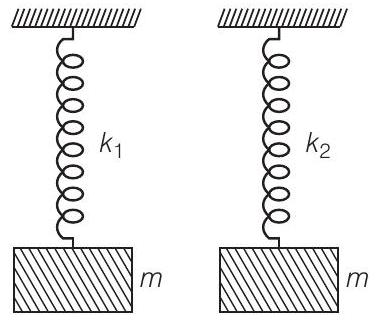
$$ \begin{aligned} & v_1=\frac{1}{2 \pi} \sqrt{\frac{k_1}{m}} \\ & v_2=\frac{1}{2 \pi} \sqrt{\frac{k_2}{m}} \end{aligned} $$
समीकरण (i), (ii) और (iii) से,
$$ \begin{aligned} & v=\frac{1}{2 \pi}[\frac{k_1}{m}+\frac{k_2}{m}]^{1 / 2} \\ & =\frac{1}{2 \pi}[\frac{4 \pi^{2} v_1^{2}}{1}+\frac{4 \pi^{2} v_2^{2}}{1}]^{1 / 2} \\ & {[\because \text { समीकरण (ii) से } \frac{k_1}{m}=4 \pi^{2} v_1^{2} \text { और समीकरण (iii) से } \frac{k_2}{m}=4 \pi^{2} v_2^{2}]} \\ & =\frac{2 \pi}{2 \pi}[v_1^{2}+v_2^{2}]^{1 / 2} \Rightarrow v=\sqrt{v_1^{2}+v_2^{2}} \end{aligned} $$
नोट: स्प्रिंग के समानांतर और श्रेणीक्रम संयोजन के साथ गलत समझ न करें।
-
विकल्प (a) $v_1 + v_2$: यह विकल्प गलत है क्योंकि जब दो स्प्रिंग समानांतर में संयोजित होते हैं तो दोलन आवृत्तियों को सरल रूप से जोड़ा नहीं जाता। सही तरीका संयोजित स्प्रिंग नियतांक और परिणामी आवृत्ति को ध्यान में रखते हुए अपनाया जाता है, जो व्यक्तिगत आवृत्तियों के वर्गों के योग के वर्गमूल से निर्मित होता है।
-
विकल्प (c) $(\frac{1}{v_1} + \frac{1}{v_2})^{-1}$: यह विकल्प गलत है क्योंकि यह श्रेणीक्रम में आवृत्तियों को संयोजित करने के सूत्र को दर्शाता है, न कि समानांतर में। जब स्प्रिंग श्रेणीक्रम में होते हैं, तो प्रभावी स्प्रिंग नियतांक अलग होता है, और परिणामी आवृत्ति की गणना अलग तरीके से की जाती है।
-
विकल्प (d) $\sqrt{v_1^2 - v_2^2}$: यह विकल्प गलत है क्योंकि आवृत्तियों के वर्गों के अंतर के वर्गमूल द्वारा संयोजित प्रणाली के सही भौतिक संबंध को दर्शाया नहीं जाता। सही सूत्र व्यक्तिगत आवृत्तियों के वर्गों के योग के वर्गमूल को दर्शाता है, न कि उनके अंतर के वर्गमूल।
12. पृथ्वी के अपने अक्ष के चारों ओर घूर्णन है
(a) आवर्त गति
(b) सरल अथवा वृत्तीय गति
(c) आवर्त लेकिन सरल अथवा वृत्तीय गति नहीं
(d) अनावर्त गति
उत्तर दिखाएं
उत्तर $(a, c)$
पृथ्वी के अपने अक्ष के चारों ओर घूर्णन आवर्त है क्योंकि यह एक नियत समय अंतराल के बाद दोहराई जाती है।
पृथ्वी की घूर्णन एक निश्चित बिंदु के आसपास आगे-पीछे गति के रूप में स्पष्ट रूप से नहीं है, इसलिए इसकी गति एसएचएम नहीं है।
-
विकल्प (b) सरल अथवा वृत्तीय गति: पृथ्वी के अपने अक्ष के चारों ओर घूर्णन सरल अथवा वृत्तीय गति नहीं है क्योंकि सरल अथवा वृत्जीय गति एक ऐसी गति होती है जिसमें एक वस्तु संतुलन स्थिति के आसपास आगे-पीछे गति करती है। पृथ्वी की घूर्णन एक सतत वृत्तीय गति है, न कि आवर्त गति।
-
विकल्प (d) अनावर्त गति: पृथ्वी के अपने अक्ष के चारों ओर घूर्णन अनावर्त गति नहीं है क्योंकि यह नियमित अंतराल पर होती है। अनावर्त गति नियमित अंतराल पर दोहराई नहीं जाती, जबकि पृथ्वी की घूर्णन प्रतिदिन 24 घंटे के बाद दोहराई जाती है।
13. एक स्मूथ वक्र बाउल में एक गेंद के गति के बारे में जब उसे निम्न बिंदु के ऊपर एक छोटे से बिंदु से छोड़ दिया जाता है तो गति है
(a) सरल अथवा वृत्तीय गति
(b) अनावर्त गति
(c) आवर्त गति
(d) आवर्त लेकिन $SHM$ नहीं
उत्तर दिखाएं
उत्तर $(a, c)$
एक स्मूथ वक्र बाउल में गेंद के अंदर गति के बारे में सोचें।
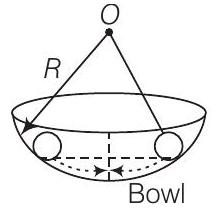
छोटे कोणीय विस्थापन या छोटे से छोड़े गए गति के लिए, इसे एक कोणीय SHM के रूप में ले लिया जा सकता है।
जब गेंद को एक कोण $\theta$ पर रखा जाता है तो वापसी बल $(g \sin \theta) m$ कार्य करता है जैसा कि दिखाया गया है।
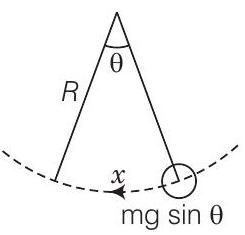
$$ \begin{aligned} \because & m a =m g \sin \theta \\ \Rightarrow & a =g \sin \theta \end{aligned} $$
$$ \Rightarrow \quad \frac{d^{2} x}{d t^{2}}=-g \sin \theta=-g \times \frac{x}{R} \quad[\therefore \sin \theta \simeq \theta=x / R] $$
अतः, गति सरल वृत्तीय गति (SHM) है
$$ \begin{matrix} \Rightarrow d^{2} x / d t^{ 2} \propto(-x) \\ \Rightarrow \omega =\sqrt{g / R} \\ \text { समय अवधि } T=\frac{2 \pi}{\omega}=2 \pi \sqrt{\frac{R}{g} .} . \end{matrix} $$
क्योंकि गति सरल वृत्तीय गति (SHM) है, अतः यह आवर्ती होना चाहिए।
-
(b) अनावर्ती गति: गोलीय गति के अंदर एक चिकनी वक्र बर्तन में गोली की गति आवर्ती है क्योंकि यह एक निश्चित समय अंतराल के बाद दोहराई जाती है। अनावर्ती गति नियमित समय अंतराल पर दोहराई नहीं जाती, जो यहाँ पर नहीं है।
-
(d) आवर्ती लेकिन $SHM$ नहीं: छोटे कोणीय विस्थापन के लिए, गोली की गति को सरल वृत्तीय गति (SHM) के रूप में अपेक्षित किया जा सकता है। बहाव बल विस्थापन के अनुपाती होता है, जो SHM की विशेषता है। अतः, गति न केवल आवर्ती है बल्कि यह भी SHM है।
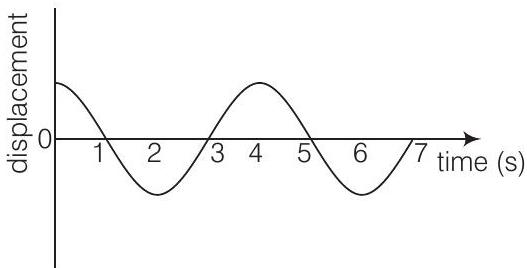
14. एक कण के सरल वृत्तीय गति (SHM) में विस्थापन के समय वक्र को चित्र में दिखाया गया है। सही कथन का चयन करें।
(a) आवर्तक के चरण एक ही है $t=0 s$ और $t=2 s$ के लिए
(b) आवर्तक के चरण एक ही है $t=2 s$ और $t=6 s$ के लिए
(c) आवर्तक के चरण एक ही है $t=1 s$ और $t=7 s$ के लिए
(d) आवर्तक के चरण एक ही है $t=1 s$ और $t=5 s$ के लिए
उत्तर दिखाएँ
Answer $(b, d)$
कक्षा के वक्र से स्पष्ट है कि $t=2 s$ और $t=6 s$ के बिंदु एक समय अवधि के दूरी के बराबर है। अतः, ये बिंदु एक ही चरण में होना चाहिए।
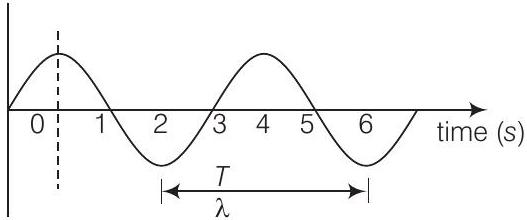
अतः, $t=1 , \text{s}$ और $t=5 , \text{s}$ पर बिंदुओं के बीच एक समय अंतर है, इसलिए ये एक चरण में होना चाहिए।
-
$t = 0 , \text{s}$ और $t = 2 , \text{s}$ पर कण अपने चक्र में अलग-अलग स्थितियों में है। $t = 0 , \text{s}$ स्थिति में अधिकतम विस्थापन है, जबकि $t = 2 , \text{s}$ स्थिति में संतुलन बिंदु है। इसलिए, इन समयों पर आवर्ती निर्माणक का चरण अलग है।
-
$t = 1 , \text{s}$ और $t = 7 , \text{s}$ पर कण अपने चक्र में अलग-अलग स्थितियों में है। $t = 1 , \text{s}$ स्थिति में कण संतुलन बिंदु की ओर गति कर रहा है, जबकि $t = 7 , \text{s}$ स्थिति में कण संतुलन बिंदु से दूर गति कर रहा है। इसलिए, इन समयों पर आवर्ती निर्माणक का चरण अलग है।
15. निम्नलिखित में से कौन-से कथन सरल आवर्त गति के लिए सत्य हैं?
(a) कार्य कर रहे बल औसत स्थिति से विस्थापन के सीधे अनुपाती होता है और इसके विपरीत होता है
(b) गति आवर्त होती है
(c) आवर्ती निर्माणक का त्वरण स्थिर होता है
(d) वेग आवर्त होता है
उत्तर दिखाएँ
सोचने की प्रक्रिया
हमें आवर्त गति के लिए समीकरण लिखना होगा और फिर विस्थापन के संगत वेग और त्वरण निकालना होगा।
उत्तर $(a, b, d)$
आवर्त गति के लिए समीकरण $x = a \sin \omega t$ है।
स्पष्ट रूप से, यह एक आवर्त गति है क्योंकि इसमें साइन फलन है।
$$ \text { वेग } v = \frac{d x}{d t} = \frac{d}{d t}(a \sin \omega t) = a \omega \cos \omega t $$
वेग भी आवर्त है क्योंकि इसमें कोसाइन फलन है।
त्वरण,
$$ A = \frac{d v}{d t} = \frac{d^{2} x}{d t^{2}} = -a \omega^{2} \sin \omega t $$
[ $\because$ त्वरण एक साइन फलन है, इसलिए यह स्थिर नहीं हो सकता]
$$ = -(\omega^{2} a) \sin \omega t = -\omega^{2} x $$
बल,
$$ \begin{aligned} F & = \text { द्रव्यमान } \times \text { त्वरण } \\ & = m A = -m \omega^{2} x \end{aligned} $$
इसलिए, कार्य कर रहे बल औसत स्थिति से विस्थापन के सीधे अनुपाती होता है और इसके विपरीत होता है।
- विकल्प (c): आवर्तक के त्वरण नियत नहीं होता। सरल आवर्त गति में त्वरण $ A = -a \omega^2 \sin \omega t $ द्वारा दिया जाता है, जो एक ज्याफलन है। चूंकि ज्याफलन समय के साथ बदलता रहता है, त्वरण नियत नहीं होता।
16. एक कण के सरल आवर्त गति के विस्थापन-समय ग्राफ को चित्र में दिखाया गया है। निम्नलिखित में से कौन-सा कथन सत्य है/हैं?
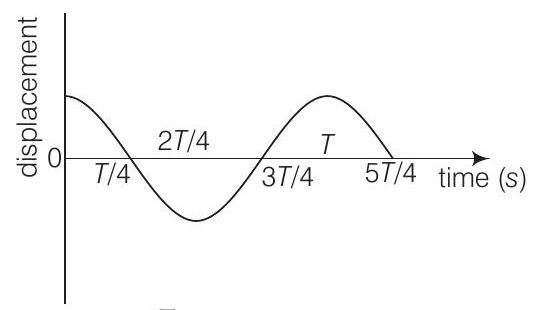
$\text{(a) } t = \frac{3T}{4} \text{ पर बल शून्य है}$
$\text{(b) } t = T \text{ पर त्वरण अधिकतम है}$
$\text{(c) } t = \frac{T}{4} \text{ पर वेग अधिकतम है}$
$\text{(d) } t = \frac{T}{2} \text{ पर संतृप्त ऊर्जा आवर्त गति के गतिज ऊर्जा के बराबर है}$
उत्तर दिखाएँ
उत्तर
$(a, b, c)$
निरीक्षण चित्र को ध्यान में रखते हुए
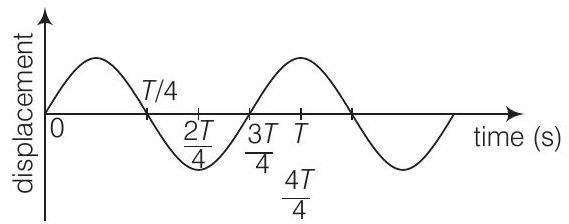
दिए गए चित्र से स्पष्ट है कि
(a) $t=\frac{3 T}{4}$ पर कण का विस्थापन शून्य है। अतः कण सरल आवर्त गति कर रहा है, अतः औसत स्थिति में है अर्थात $x=0$। अतः त्वरण शून्य है तथा बल भी शून्य है।
(b) $t=\frac{4 T}{4}$ पर विस्थापन अधिकतम है अर्थात अंतिम स्थिति है, अतः त्वरण अधिकतम है।
(c) $t=\frac{T}{4}$ पर औसत स्थिति है, अतः इस स्थिति पर वेग अधिकतम होता है।
(d) $t=\frac{2 T}{4}=\frac{T}{2}$ पर अंतिम स्थिति है, अतः $KE=0$ तथा $PE=$ अधिकतम है।
- (d) के असत्य होने के कारण: $ t = \frac{T}{2} $ पर कण अंतिम स्थिति पर है। इस स्थिति पर गतिज ऊर्जा (KE) शून्य है तथा संतृप्त ऊर्जा (PE) अधिकतम है। अतः $ t = \frac{T}{2} $ पर संतृप्त ऊर्जा (PE) आवर्त गति के गतिज ऊर्जा (KE) के बराबर होने के कथन के असत्य होने के कारण यह कथन असत्य है।
17. एक वस्तु दोलन गति कर रही है, तो इसके
(a) एक चक्र में औसत कुल ऊर्जा इसकी अधिकतम किनेटिक ऊर्जा के बराबर होती है
(b) एक चक्र में औसत किनेटिक ऊर्जा इसकी अधिकतम किनेटिक ऊर्जा के आधा होती है
(c) पूरे चक्र में औसत वेग इसके अधिकतम वेग के $\frac{2}{\pi}$ गुना होता है
(d) वर्ग माध्य मूल वेग इसके अधिकतम वेग के $\frac{1}{\sqrt{2}}$ गुना होता है
उत्तर दिखाएँ
उत्तर $(a, b, d)$
एक दोलन गति के समीकरण को $x=a \sin \omega t$ के रूप में प्रस्तुत करें।
मान लीजिए वस्तु का द्रव्यमान $m$ है।
(a) कोई भी समय $t$ पर वस्तु की कुल यांत्रिक ऊर्जा है
$$ E=\frac{1}{2} m \omega^{2} a^{2} $$
कोई भी समय $t$ पर किनेटिक ऊर्जा है
$$ \begin{matrix} K & =\frac{1}{2} m v^{2}=\frac{1}{2} m[\frac{d x}{d t}]^{2} & {[\because v=\frac{d x}{d t}]} \\ & =\frac{1}{2} m \omega^{2} a^{2} \cos ^{2} \omega t & {[\because x=a \sin \omega t]} \\ \Rightarrow \quad K_{\max } & =\frac{1}{2} m \omega^{2} a^{2}=E & {[\because \text { for } k_{\max }, \cos \omega t=1] \ldots \text { (ii) }} \end{matrix} $$
(b) कोई भी समय $t$ पर $KE$ है
K = $\frac{1}{2} m \omega^{2} a^{2} \cos ^{2} \omega t $
$(K_{av}) \text { एक चक्र के लिए } =\frac{1}{2} m \omega^{2} a^{2}[(\cos ^{2} \omega t)_{av}] \text { एक चक्र के लिए } $
$ =\frac{1}{2} m \omega^{2} a^{2}[\frac{0+1}{2}] $
$ =\frac{1}{4} m \omega^{2} a^{2}=\frac{K_{\max }}{2}$
[समीकरण (ii) से]
(c) वेग $=v=\frac{d x}{d t}=a \omega \cos \omega t$
पूरे चक्र के लिए, $$ \begin{aligned} v_{\text {mean }} & =\frac{v_{\text {max }}+v_{\text {min }}}{2} \\ & =\frac{a \omega+(-a \omega)}{2}=0 \end{aligned} $$
(d) $v_{\text {rms }}=\sqrt{\frac{v_{\text {max }}^{2}+v_2^{2}}{2}}=\sqrt{\frac{0+a^{2} \omega^{2}}{2}}=\frac{a \omega}{\sqrt{2}}$
$$ \Rightarrow \quad V_{rms}=\frac{V_{\max }}{\sqrt{2}} $$
-
विकल्प (c) गलत है क्योंकि:
दोलन गति के पूरे चक्र में औसत वेग शून्य होता है, न कि इसके अधिकतम वेग के $\frac{2}{\pi}$ गुना। इसका कारण यह है कि वेग एक वाटिका फलन होता है जो एक पूरे चक्र में शून्य के बराबर औसत करता है।
18. एक कण दो बिंदुओं $A$ और $B$ के बीच रेखीय सरल आवर्त गति में है। $A$ और $B$ 10 सेमी के अलग हैं (चित्र देखें)। $A$ से $B$ की दिशा को धनात्मक दिशा मानें और सही कथन का चयन करें।
$$ \begin{aligned} & \ddot{A} \\ & A O=O B=5 cm \\ & B C=8 cm \end{aligned} $$
(a) जब कण $A$ से 3 सेमी दूर है और $B$ की ओर जा रहा है, तब इसके वेग, त्वरण और बल के चिह्न धनात्मक हैं
(b) जब कण $C$ पर है और $B$ की ओर जा रहा है, तब इसके वेग के चिह्न ऋणात्मक हैं
(c) जब कण $B$ से 4 सेमी दूर है और $A$ की ओर जा रहा है, तब इसके वेग, त्वरण और बल के चिह्न ऋणात्मक हैं
(d) जब कण $B$ पर है, तब इसके त्वरण और बल के चिह्न ऋणात्मक हैं
उत्तर दिखाएं
उत्तर $(a, c, d)$
चित्र को ध्यान से देखें।

(a) जब कण $A$ से 3 सेमी दूर है और $B$ की ओर जा रहा है, तब वेग $AB$ की ओर है, अर्थात धनात्मक है।
सरल आवर्त गति में, त्वरण हमेशा मध्य स्थिति $(O)$ की ओर होता है, इसलिए यह धनात्मक है।
(b) जब कण $C$ पर है, तब वेग $B$ की ओर है, अतः धनात्मक है।
(c) जब कण $B$ से 4 सेमी दूर है और $A$ की ओर जा रहा है, तब वेग ऋणात्मक है और त्वरण मध्य स्थिति $(O)$ की ओर है, अतः ऋणात्मक है।
(d) त्वरण हमेशा मध्य स्थिति $(O)$ की ओर होता है। जब कण $B$ पर है, तब त्वरण और बल $BA$ की ओर होते हैं, अतः ऋणात्मक हैं।
-
(b) जब कण $C$ पर है और $B$ की ओर जा रहा है, तब इसके वेग के चिह्न ऋणात्मक हैं
कारण: जब कण $C$ पर है और $B$ की ओर जा रहा है, तब वेग वास्तव में धनात्मक है क्योंकि यह $A$ से $B$ की धनात्मक दिशा में गति कर रहा है। अतः, वेग के ऋणात्मक कथन गलत है।
बहुत छोटे उत्तर प्रकार के प्रश्न
19. एक कण के सरल आवर्त गति के लिए विस्थापन-समय वक्र चित्र में दिखाया गया है। चित्र में चिह्नित बिंदुओं पर (i) आवर्तक के वेग शून्य है, (ii) आवर्तक की चाल अधिकतम है।
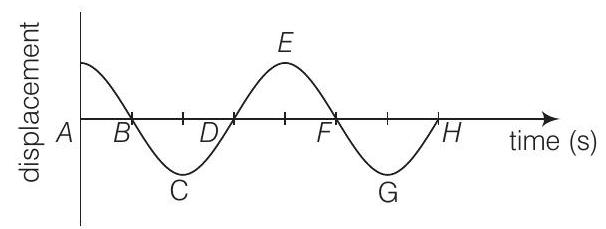
उत्तर दिखाएँ
Answer SHM में y-t ग्राफ में शून्य विस्थापन माध्य स्थिति को दर्शाता है; जहां आवर्तक कण की चाल अधिकतम होती है।
जबकि शिखर और घाट अतिरिक्त स्थितियों को दर्शाते हैं, जहां विस्थापन अधिकतम होता है और आवर्तक कण की चाल न्यूनतम होती है और शून्य होती है। अतः,
(a) $A, C, E, G$ या तो शिखर या घाट होते हैं जहां चाल शून्य होती है।
(b) माध्य स्थितियों, जो $B, D, F, H$ बिंदुओं द्वारा निरूपित होती हैं, पर चाल अधिकतम होती है।
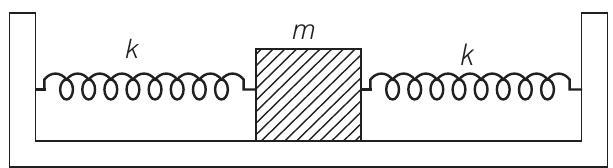
20. दो समान बर्फ के बल नियतांक $k$ वाले स्प्रिंग एक द्रव्यमान $m$ के ब्लॉक और निश्चित समर्थनों के साथ जुड़े हैं जैसा कि चित्र में दिखाया गया है। जब द्रव्यमान संतुलन स्थिति से दूरी $x$ के द्वारा दाईं ओर विस्थापित होता है, तो बहाव बल की गणना कीजिए।
उत्तर दिखाएँ
Answer चित्र में ब्लॉक के दाईं ओर $x$ के द्वारा विस्थापन के बारे में विचार करें।
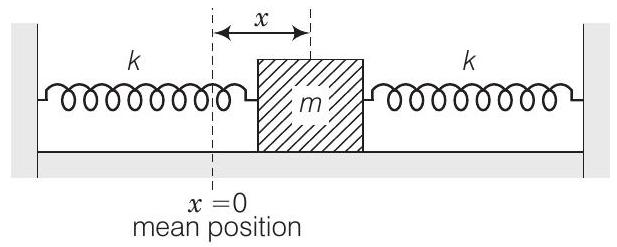
दाईं ओर का स्प्रिंग $x$ के द्वारा संपीड़ित हो जाता है जिसके कारण ब्लॉक पर बहाव बल $k x$ बाईं ओर लगता है। बाईं ओर का स्प्रिंग $x$ के द्वारा खिंच जाता है जिसके कारण ब्लॉक पर बहाव बल $k x$ बाईं ओर लगता है जैसा कि ब्लॉक के मुक्त शरीर आरेख में दिखाया गया है।
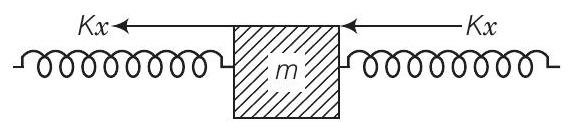
अतः, कुल बल (बहाव बल) $=(k x + k x)$ $=2 k x$ बाईं ओर $\quad[\because$ दोनों बल समान दिशा में हैं]
21. सरल दोलन के दो मूल गुण क्या हैं?
उत्तर दिखाएं
उत्तर सरल दोलन के दो मूल गुण हैं
(i) त्वरण विस्थापन के सीधे अनुपातिक होता है।
(ii) त्वरण की दिशा हमेशा माध्य स्थिति की ओर होती है, अर्थात विस्थापन के विपरीत होती है।
22. सरल लोलक के गति कब सरल दोलन होगी?
उत्तर दिखाएं
उत्तर सरल लोलक के चित्र को ध्यान में रखें।
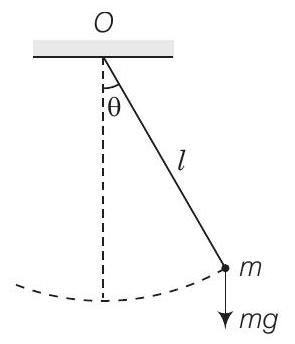
लोलक का बल्ब चित्र में दिखाए गए कोण $\theta$ द्वारा विस्थापित होता है।
स्थायी बलाघूर्ण निश्चित बिंदु $O$ के संबंध में
यदि $\theta$ रेडियन में छोटा कोण है, तो $\sin \theta \approx \theta$
हम जानते हैं, $$ \tau=-m g \sin \theta $$
$\Rightarrow \quad \tau \approx-m g \theta \Rightarrow \tau \propto(-\theta)$
अतः, छोटे कोण के दोलन के लिए सरल लोलक की गति सरल दोलन होती है।
23. सरल दोलन के उत्तेजक के अधिकतम त्वरण के अधिकतम वेग के अनुपात क्या है?
उत्तर दिखाएं
सोचने की प्रक्रिया
हमें वेग को विस्थापन के समीकरण के अवकलज के रूप में खोजना होगा और त्वरण को वेग और समय के समीकरण के अवकलज के रूप में खोजना होगा।
उत्तर मान लीजिए $x=A \sin \omega t$ सरल दोलन का विस्थापन फलन है।
वेग,
$$ \begin{aligned} v & =\frac{d x}{d t}=A \omega \cos \omega t \\ v_{\max } & =A \omega|\cos \omega t|_{\max } \\ & =A \omega \times 1=\omega A \end{aligned} $$
$[\because|\cos \omega t|_{\max }=1] \ldots(i)$
त्वरण, $a=\frac{d v}{d t}=-\omega A \cdot \omega \sin \omega t$
$$ \begin{aligned} & =-\omega^{2} A \sin \omega t \\ |a_{\max }| & =|(-\omega^{2} A)(+1)| \\ |a_{\max }| & =\omega^{2} A \end{aligned} $$
समीकरण (i) और (ii) से, हम प्राप्त करते हैं
$ \frac{v_{\max }}{a_{\max }}=\frac{\omega A}{\omega^{2} A}=\frac{1}{\omega} $
$\Rightarrow \frac{a_{\max }}{v_{\max }}=\omega$
24. एक आवर्तकाल में आवर्तक गति करते वस्तु द्वारा तय की गई दूरी और आम्प्लीतुड के बीच अनुपात क्या होगा?
उत्तर दिखाएँ
Answer चित्र निम्नलिखित को दर्शाता है
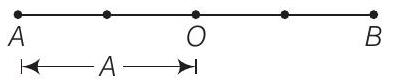
$A$ और $B$ के बीच एक कण के द्वारा निर्वाचक गति करते हुए गति को।
जब यह $A$ से $B$ तक जाता है और फिर $A$ पर वापस आता है तो तय की गई कुल दूरी है
$$ \begin{aligned} & =A O+O B+B O+O A \\ & =A+A+A+A=4 A \quad[\because O A=A] \end{aligned} $$
आम्प्लीतुड $=OA=A$
अतः दूरी और आम्प्लीतुड के अनुपात $=\frac{4 A}{A}=4$
25. चित्र में, संदर्भ कण $P$ के वेग के प्रक्षेपण $P^{\prime}$ के वेग का चिह्न क्या होगा। $P$ एक त्रिज्या $R$ के वृत्त में विपरीत घड़ी की दिशा में गति कर रहा है।
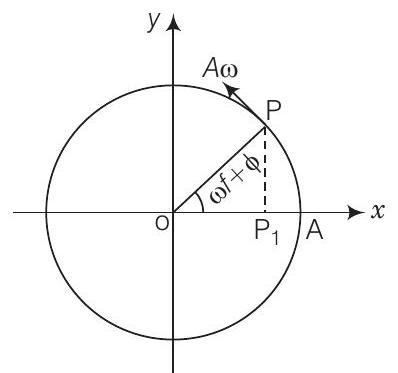
उत्तर दिखाएँ
Answer जैसे संदर्भ वृत्त पर कण विपरीत घड़ी की दिशा में गति करता है। प्रक्षेपण बिंदु $P$ से $O$ की ओर बाईं ओर जाता है।
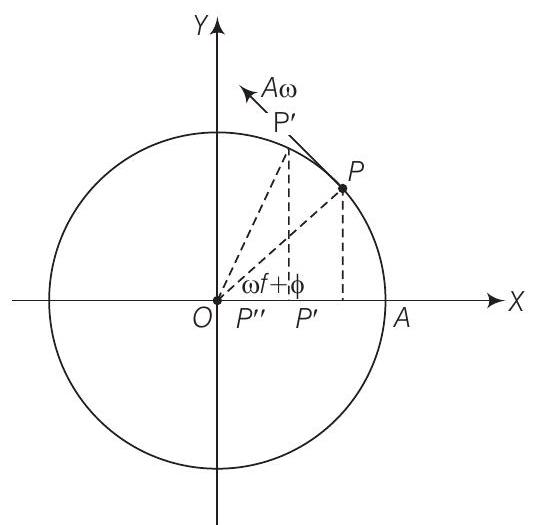
अतः दिखाए गए स्थिति में वेग $P^{\prime} \rightarrow P^{\prime \prime}$ की दिशा में है, अर्थात दाईं से बाईं ओर, अतः चिह्न नकारात्मक है।
26. दिखाइए कि एक कण द्वारा निर्वाचक गति करते हुए वेग और विस्थापन के बीच अपेक्षा अंतर $\pi / 2$ होता है।
उत्तर दिखाएँ
उत्तर मान लीजिए एक सरल आवर्त गति के विस्थापन फलन के बारे में
जहाँ, $ x= a \cos \omega t $
$a =\text { गति का आयाम }$
$ \text { वेग }, v =\frac{d x}{d t} $
या
$$ \begin{aligned} \frac{d x}{d t} & =a(-\sin \omega t) \omega=-\omega a \sin \omega t \\ v & =-\omega a \sin \omega t \\ & =\omega a \cos(\frac{\pi}{2}+\omega t) \quad[\because \sin \omega t=-\cos (\frac{\pi}{2}+\omega t)] \end{aligned} $$
अब, विस्थापन के चरण $=\omega t$
वेग के चरण $=\frac{\pi}{2}+\omega t$
$\therefore$ वेग के चरण और विस्थापन के चरण के बीच अंतर
$$ =\frac{\pi}{2}+\omega t-\omega t=\frac{\pi}{2} $$
27. एक सरल आवर्त गति के विस्थापन के साथ-साथ $P E, K E$ और कुल ऊर्जा के परिवर्तन को दिखाने वाली एक ग्राफ बनाइए।
उत्तर दिखाएं
उत्तर एक सरल आवर्त गति के ential ऊर्जा (PE) होती है
$$ \begin{aligned} & PE =\frac{1}{2} k x^{2}=\frac{1}{2} m \omega^{2} x^{2} \\ k & =\text { बल नियतांक }=m \omega^{2} \end{aligned} $$
जब PE को विस्थापन $x$ के विरुद्ध आलेखित किया जाता है, तो हमें एक परवलय प्राप्त होता है।
जब $x=0, PE=0$
जब $x= \pm A, PE=$ अधिकतम
$$ \begin{aligned} & =\frac{1}{2} m \omega^{2} A^{2} \\ \text { एक सरल आवर्त गति के गतिज ऊर्जा } & =\frac{1}{2} m v^{2} \\ & =\frac{1}{2} m[\omega \sqrt{A^{2}-x^{2}}]^{2} \quad[\because v=\omega \sqrt{A^{2}-x^{2}}] \\ & =\frac{1}{2} m \omega^{2}(A^{2}-x^{2}) \end{aligned} $$
यह भी एक परवलय है, यदि गतिज ऊर्जा को विस्थापन $x$ के विरुद्ध आलेखित किया जाता है।
$$ \begin{matrix} \text { अर्थात, } & KE=0 \text { जब } x= \pm A \\ \text { और } & KE=\frac{1}{2} m \omega^{2} A^{2} \text { जब } x=0 \end{matrix} $$
$$ \begin{aligned} & \begin{matrix} =\frac{1}{2} m \omega^{2} x^{2}+\frac{1}{2} m \omega^{2}(A^{2}-x^{2}) \end{matrix} \\ & =\frac{1}{2} m \omega^{2} x^{2}+\frac{1}{2} m \omega^{2} A^{2}-\frac{1}{2} m \omega^{2} x^{2} \\ & TE=\frac{1}{2} m \omega^{2} A^{2} \end{aligned} $$
जो एक स्थिर राशि है और इसमें $x$ पर निर्भर नहीं होता।
ऊपर दिए गए निर्देशों के अनुसार गतिज ऊर्जा, स्थितिज ऊर्जा और कुल ऊर्जा के विस्थापन $x$ के साथ ग्राफ निम्नलिखित होता है

28. पृथ्वी के सतह पर एक सेकंड के सरल लोलक की लंबाई $1 m$ है। चांद के सतह पर एक सेकंड के सरल लोलक की लंबाई क्या होगी?
उत्तर दिखाएं
उत्तर एक सेकंड के सरल लोलक का अर्थ एक ऐसा सरल लोलक होता है जिसका आवर्तकाल $T=2 s$ होता है।
एक सरल लोलक के लिए, $\quad T=2 \pi \sqrt{\frac{l}{g}}$
जहाँ, $l=$ लोलक की लंबाई और
$g=$ पृथ्वी के सतह पर गुरुत्वीय त्वरण होता है।
$$ T_{e}=2 \pi \sqrt{\frac{l_{e}}{g_{e}}} $$
चांद के सतह पर,
$$ \begin{aligned} & T_{m}=2 \pi \sqrt{\frac{l_{m}}{g_{m}}} \\ & \frac{T_{e}}{T_{m}}=\frac{2 \pi}{2 \pi} \sqrt{\frac{l_{e}}{g_{e}}} \times \sqrt{\frac{g_{m}}{l_{m}}} \end{aligned} $$
$T_{e}=T_{m}$ के लिए सेकंड के लोलक के आवर्तकाल को बनाए रखने के लिए।
$$ \therefore \quad 1=\sqrt{\frac{l_{e}}{l_{m}} \times \frac{g_{m}}{g_{e}}} $$
लेकिन चांद पर गुरुत्वीय त्वरण पृथ्वी पर गुरुत्वीय त्वरण के $1/6$ होता है, अर्थात,
$$ g_{m}=\frac{g_{e}}{6} $$
समीकरण (iii) को वर्ग करके और इस मान को रखकर,
1 = $\frac{l_{e}}{l_{m}} \times \frac{g_{e} / 6}{g_{e}}=\frac{l_{e}}{l_{m}} \times \frac{1}{6} $
$\Rightarrow \frac{l_{e}}{6 l_{m}} =1 \Rightarrow 6 l_{m}=l_{e} $
$\Rightarrow l_{m} =\frac{1}{6} l_{e}=\frac{1}{6} \times 1=\frac{1}{6} m$
छोटे उत्तर प्रकार के प्रश्न
29. चित्र में दिखाए गए तंत्र के लिए द्रव्यमान $M$ के आवर्तकाल की गणना कीजिए जब इसे संतुलन स्थिति से विस्थापित करके छोड़ दिया जाता है।
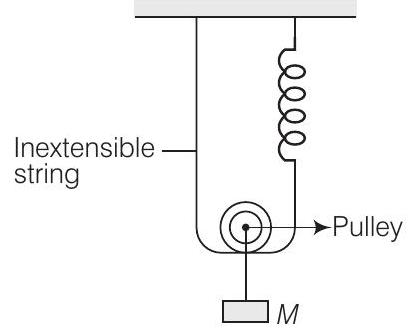
उत्तर दिखाएं
सोचने की प्रक्रिया
हमें द्रव्यमान को थोड़ा विस्थापित करके गति की प्रकृति का अनुमान लगाना होता है और वापसी बल के कारण त्वरण की गणना करनी होती है।
उत्तर गणना के उद्देश्य के लिए, इस स्थिति में हम गुरुत्वाकर्षण को नगण्य मानेंगे क्योंकि यह पूरे तंतु में स्थिर रहता है और सम्पूर्ण पुनर्स्थापन बल को प्रभावित नहीं करता है।
संतुलन स्थिति में, स्प्रिंग के एक राशि $x_0$ तक विस्तार हो जाता है।
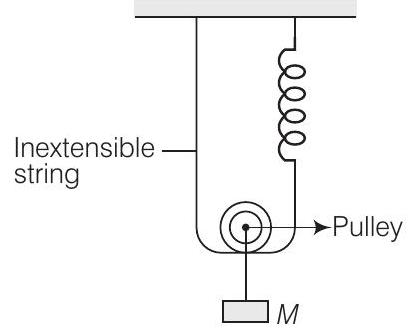
अब, यदि द्रव्यमान को एक और $x$ राशि द्वारा नीचे विस्थापित कर दिया जाए, तो तार और स्प्रिंग दोनों की लंबाई $x$ तक बढ़ जाएगी।
लेकिन, तार विस्तार योग्य नहीं है, इसलिए स्प्रिंग ही कुल विस्तार $x+x=2x$ के लिए ज़िम्मेदार होगी, जिससे द्रव्यमान को आरंभिक संतुलन स्थिति $x_0$ से $x$ राशि द्वारा नीचे ले जाया जाएगा। इसलिए, स्प्रिंग में कुल विस्तार $(=2x + x_0)$ होगा।
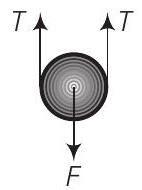
अब, द्रव्यमान के बल पर बल लगता है (जब $x_0$ विस्तार के मामले में)
हालांकि,
$$ \begin{aligned} F & =2 T \\ T & =k x_0 \\ F & =2 k x_0 \end{aligned} $$
[जहां $k$ स्प्रिंग नियतांक है]
जब द्रव्यमान को और भी $x$ राशि द्वारा नीचे ले जाया जाए,
$$ F^{\prime}=2 T^{\prime} $$
लेकिन नए स्प्रिंग की लंबाई $=(2x + x_0)$
$\therefore \quad F^{\prime}=2k(2x + x_0)$
सिस्टम पर पुनर्स्थापन बल।
समीकरण (i) और (ii) का उपयोग करके, हम प्राप्त करते हैं
$$ F_{\text {restoring }}=-[F^{\prime}-F] $$
$$ \begin{aligned} F_{\text {restoring }} & =-[2k(2x + x_0)-2k x_0] \\ & =-[2 \times 2k x + 2k x_0 - 2k x_0] \\ & =-4k x \end{aligned} $$
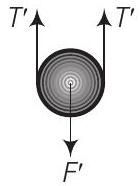
या
$$ M a=-4k x $$
जहां, $ a=\text { त्वरण } $
$\Rightarrow$ $ a=-(\frac{4k}{M}) x$
(क्योंकि, $F=m a)$
$k$, $M$ नियत रहते हैं।
$$ \therefore \quad a \propto -x $$
$$
अतः, गति सरल आवर्त गति है।
ऊपर दिए गए त्वरण के समीकरण को मानक सरल आवर्त गति के समीकरण $a=-\omega^{2} x$ के साथ तुलना करने पर हम प्राप्त करते हैं
$$ \therefore \quad \text { समय अवधि }, T=\frac{2 \pi}{\omega}=\frac{2 \pi}{\sqrt{\frac{4 k}{M}}}=2 \pi \sqrt{\frac{M}{4 k}} $$
30. दिखाइए कि एक कण के गति को $y=\sin \omega t-\cos \omega t$ द्वारा प्रस्तुत किया गया है, जो एक सरल आवर्त गति है जिसका आवर्तकाल $2 \pi / \omega$ है।
उत्तर दिखाएँ
उत्तर हमें दिए गए दो आवर्त फलनों के संयोजन को एकल आवर्त (साइन या कोसाइन) फलन में परिवर्तित करना होगा।
दिया गया, विस्थापन फलन
$$ \begin{aligned} y & =\sin \omega t-\cos \omega t \\ & =\sqrt{2}(\frac{1}{\sqrt{2}} \cdot \sin \omega t-\frac{1}{\sqrt{2}} \cdot \cos \omega t) \\ & =\sqrt{2}[\cos (\frac{\pi}{4}) \cdot \sin \omega t-\sin (\frac{\pi}{4}) \cdot \cos \omega t] \\ & =\sqrt{2}[\sin (\omega t-\frac{\pi}{4})]=\sqrt{2}[\sin (\omega t-\frac{\pi}{4})] \end{aligned} $$
मानक समीकरण के साथ तुलना करने पर
$$ y=a \sin (\omega t+\phi), \text { हम प्राप्त करते हैं }=\omega=\frac{2 \pi}{T} \Rightarrow T=\frac{2 \pi}{\omega} $$
स्पष्ट रूप से, फलन सरल आवर्त गति को प्रस्तुत करता है जिसका आवर्तकाल $T=\frac{2 \pi}{\omega}$ है।
31. एक सरल आवर्त दोलनक के विस्थापन को ज्ञात कीजिए जहाँ इसकी स्थितिज ऊर्जा दोलनक की अधिकतम ऊर्जा के आधा है।
उत्तर दिखाएँ
उत्तर मान लीजिए कि आवश्यक विस्थापन $x$ है।
$\therefore$ सरल आवर्त दोलनक की स्थितिज ऊर्जा $=\frac{1}{2} k x^{2}$
जहाँ,
$$ k=\text { बल नियतांक }=m \omega^{2} $$
$$ PE=\frac{1}{2} m \omega^{2} x^{2} $$
दोलनक की अधिकतम ऊर्जा
$$ TE=\frac{1}{2} m \omega^{2} A^{2} $$
जहाँ, $ A=\text { गति का आयाम } $
दिया गया,
$PE=\frac{1}{2} TE$
$\Rightarrow \quad \frac{1}{2} m \omega^{2} x^{2}=\frac{1}{2}[\frac{1}{2} m \omega^{2} A^{2}]$
$\Rightarrow \quad x^{2}=\frac{A^{2}}{2}$
या
$$ x=\sqrt{\frac{A^{2}}{2}}= \pm \frac{A}{\sqrt{2}} $$
चिह्न $\pm$ माध्य स्थिति के दोनों ओर दर्शाता है।
32. द्रव्यमान $m$ का एक वस्तु $U(x)=U_0(1-\cos \alpha x)$ ential field में स्थित है जबकि, $U_0$ और $\alpha$ स्थिरांक हैं। छोटे दोलन के लिए आवर्तकाल ज्ञात कीजिए।
उत्तर दिखाएँ
उत्तर दिए गए क्षेत्र से संबद्ध संभावित ऊर्जा
$$ U(x)=U_0(1-\cos \alpha x) $$
अब,
$$ \text { बल } F=-\frac{d U(x)}{d x} $$
$$ [\because \text { संरक्षित बल } f, \text { के लिए हम } f=\frac{-d u}{d x} \text { लिख सकते हैं}] $$
[हमने मान लिया कि क्षेत्र संरक्षित है]
$$ \begin{aligned} & F=-U_0 \alpha^{2} x \\ & m \omega^{2}=U_0 \alpha^{2} \\ & \omega^{2}=\frac{U_0 \alpha^{2}}{m} \text { या } \omega=\sqrt{\frac{U_0 \alpha^{2}}{m}} \\ & \text { समय आवर्तकाल } T=\frac{2 \pi}{\omega}=2 \pi \sqrt{\frac{m}{U_0 \alpha^{2}}} \end{aligned} $$
$$ F=-\frac{d}{d x}(U_0-U_0 \cos \alpha x)=-U_0 \alpha \sin \alpha x $$
$[\because$ छोटे दोलन के लिए $\alpha x$ छोटा होता है, $\sin \alpha x \approx \alpha x]$
नोट: छोटे दोलन के लिए ही गति सरल आवर्त गति होती है और इसलिए, समय आवर्तकाल केवल छोटे दोलन के मामले में मान्य है।
33. एक $2 kg$ के द्रव्यमान को एक विस्तार नियतांक $50 Nm^{-1}$ के स्प्रिंग से जोड़ दिया गया है। ब्लॉक को अपने संतुलन स्थिति $x=0$ से $5 cm$ की दूरी पर एक क्षैतिज घर्षणरहित सतह पर $t=0$ से शांति से खींच लिया गया है। किसी भी समय $t$ पर इसके विस्थापन के व्यंजक को लिखिए।
उत्तर दिखाएँ
चिंतन प्रक्रिया
स्प्रिंग-ब्लॉक प्रणाली औसत स्थिति के आसपास सरल आवर्त गति करेगी जिसका आयाम $5 cm$ होगा।
उत्तर स्प्रिंग-ब्लॉक प्रणाली के आरेख को ध्यान में रखें। यह औसत स्थिति के आसपास $5 cm$ के आयाम के साथ सरल आवर्त गति करता है।
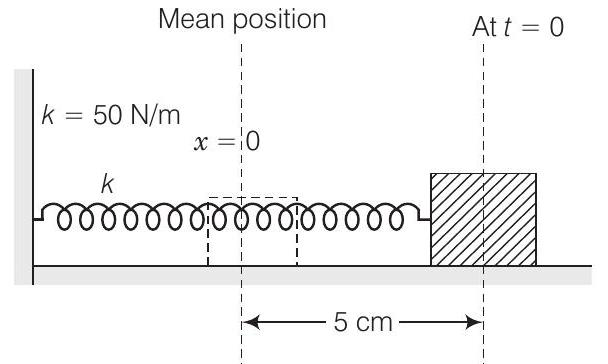
दिया गया है, $\quad \quad$ स्प्रिंग नियतांक $k=50 N / m$
$ m=\text { जुड़े द्रव्यमान }=2 kg $
$\therefore \quad$ कोणीय आवृत्ति $\omega=\sqrt{\frac{k}{m}}=\sqrt{\frac{50}{2}}=\sqrt{25}=5 rad / s$
मान लीजिए विस्थापन फलन
$$ y(t)=A \sin (\omega t+\phi) $$
जहाँ, $\phi=$ आरंभिक कलांतर
लेकिन दिया गया है कि $t=0, y(t)=+A$
या
$$ \begin{aligned} & y(0)=+A=A \sin (\omega \times 0+\phi) \\ & \sin \phi=1 \Rightarrow \phi=\frac{\pi}{2} \end{aligned} $$
$\therefore$ अभीष्ट समीकरण $y(t)=A \sin (\omega t+\frac{\pi}{2})=A \cos \omega t$ है
मान लीजिए $A=5 cm$, $\omega=5 rad / s$
हमें प्राप्त होता है, $y(t)=5 \sin 5 t$
जहाँ, $t$ सेकंड में है और $y$ सेंटीमीटर में है।
34. एक जोड़े के समान पेंडुलम के बारे में सोचें, जो समान आयाम के साथ स्वतंत्र रूप से आवर्त गति करते हैं ताकि जब एक पेंडुलम ऊर्ध्वाधर के सापेक्ष दाहिने ओर $2^{\circ}$ के कोण पर अतिक्रमण के स्थिति में होता है, तो दूसरा पेंडुलम ऊर्ध्वाधर के सापेक्ष बाईं ओर $1^{\circ}$ के कोण पर अतिक्रमण के स्थिति में होता है। पेंडुलमों के बीच कलांतर क्या है?
उत्तर दिखाएं
उत्तर चित्र (i) और (ii) में दिखाए गए स्थितियों को ध्यान में रखें
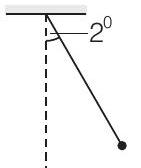
(i)
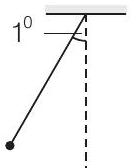
(ii)
मान लीजिए दोनों पेंडुलम अपने कोणीय विस्थापन के निम्न फलनों का पालन करते हैं
और
$$ \begin{aligned} & \theta_1=\theta_0 \sin (\omega t+\phi_1) \\ & \theta_2=\theta_0 \sin (\omega t+\phi_2) \end{aligned} $$
जैसा कि दिया गया है कि आयाम और आवर्तकाल समान है लेकिन कलांतर अलग है।
अब, पहले पेंडुलम के किसी भी समय $t$ पर
समीकरण (i) से हमें प्राप्त होता है
$$ \theta_1=+\theta_0 $$
[दाहिना अतिक्रमण]
$$ \Rightarrow \begin{aligned} \theta_0 & =\theta_0 \sin (\omega t+\phi_1) \text { या } 1=\sin (\omega t+\phi_1) \\ \sin \frac{\pi}{2} & =\sin (\omega t+\phi_1) \\ (\omega t+\phi_1) & =\frac{\pi}{2}
\end{aligned} $$
$$ \Rightarrow \quad \sin \frac{\pi}{2}=\sin (\omega t+\phi_1) $$
या
समान समय $t$ पर द्वितीय सरल लोलक के लिए, हम निम्नलिखित प्राप्त करते हैं:
$$ \theta_2=-\frac{\theta_0}{2} $$
जहाँ $\theta_0=2^{\circ}$ प्रथम लोलक का कोणीय आयाम है। द्वितीय लोलक के लिए कोणीय विस्थापन एक डिग्री है, इसलिए $\theta_2=\frac{\theta_0}{2}$ और ऋणात्मक चिह्न लेना आवश्यक है ताकि इसकी बाईं ओर स्थिति को दर्शाया जा सके।
समीकरण (ii) से, तो
$$ \begin{aligned} -\frac{\theta_0}{2} & =\theta_0 \sin (\omega t+\phi_2) \\ \sin (\omega t+\phi_2) & =-\frac{1}{2} \Rightarrow(\omega t+\phi_2)=-\frac{\pi}{6} \text { या } \frac{7 \pi}{6} \\ (\omega t+\phi_2) & =-\frac{\pi}{6} \text { या } \frac{7 \pi}{6} \end{aligned} $$
समीकरण (iv) और (iii) से, कल्पना के बीच अंतर
$$ \begin{gathered} (\omega t+\phi_2)-(\omega t+\phi_1)=\frac{7 \pi}{6}-\frac{\pi}{2}=\frac{7 \pi-3 \pi}{6}=\frac{4 \pi}{6} \\ (\phi_2-\phi_1)=\frac{4 \pi}{6}=\frac{2 \pi}{3}=120^{\circ} \end{gathered} $$
लंबा उत्तर प्रकार प्रश्न
35. एक व्यक्ति आमतौर पर $50 kg$ वजन वाला होता है जो एक द्रव्यमानहीन प्लेटफॉर्म पर खड़ा होता है जो ऊपर और नीचे के अनुपाती आवर्तन के साथ आवर्ती गति करता है जिसकी आवृत्ति $2.0 s^{-1}$ और आयाम $5.0 cm$ है। प्लेटफॉर्म पर एक वजन मापन यंत्र व्यक्ति के वजन को समय के अनुसार दर्शाता है।
(a) आवर्तन के दौरान शरीर के वजन में कोई परिवर्तन होगा या नहीं?
(b) यदि (a) के उत्तर हाँ है, तो मशीन में अधिकतम और न्यूनतम पाठ क्या होगा और वे किस स्थिति में होंगे?
उत्तर दिखाएँ
उत्तर इस स्थिति में त्वरण अचर नहीं है। त्वरित गति में, शरीर के वजन के त्वरण के आयाम और दिशा पर निर्भर करता है जो ऊपर या नीचे की गति के लिए होता है।
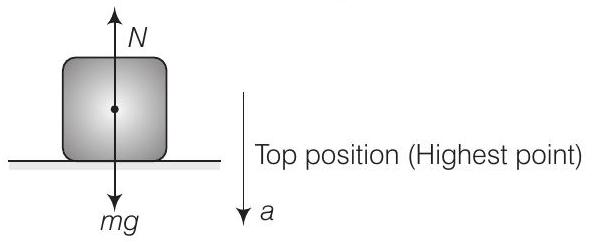
(a) अतः, आवर्तन के दौरान शरीर के वजन में परिवर्तन होता है
(b) दो अतिरिक्त स्थितियों की स्थिति को ध्यान में रखते हुए विचार करें, क्योंकि उनका त्वरण आयाम के अधिकतम मान में होता है।
हमारे पास,
$$ m g-N=m a $$
$\because$ सबसे ऊपर के बिंदु पर, प्लेटफॉर्म नीचे की ओर त्वरित हो रहा है।
$$ \begin{matrix} \Rightarrow & N=m g-m a \\ \text { लेकिन } & a=\omega^{2} A \\ \therefore & N=m g-m \omega^{2} A \\ \text { जहां, } & A=\text { गति का आयाम } \\ \text { दिया गया, } & m=50 kg, \text { आवृत्ति } v=2 s^{-1} \\ \therefore & \omega=2 \pi v=4 \pi rad / s \\ \therefore & A=5 cm=5 \times 10^{-2} m \\ & N=50 \times 9.8-50 \times(4 \pi)^{2} \times 5 \times 10^{-2} \\ & =50[9.8-16 \pi^{2} \times 5 \times 10^{-2}] \\ & =50[9.8-7.89] \\ & =50 \times 1.91 \\ & =95.5 N \end{matrix} $$
$$ \begin{matrix} \text { लेकिन } & a=\omega^{2} A & \text { [मात्रा में] } \end{matrix} $$
जब प्लेटफॉर्म अपने दोलन के सबसे नीचले स्थान पर होता है,
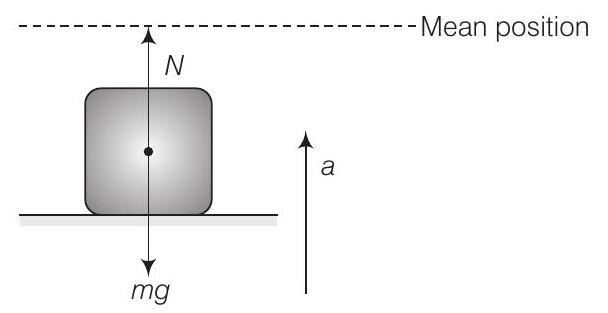
यह औसत स्थिति की ओर त्वरित हो रहा है, जो कि ऊर्ध्वाधर ऊपर की ओर है।
गति के समीकरण के लिए लिखें
या
$$ N-m g=m a=m \omega^{2} A $$
$$ \begin{aligned} N & =m g+m \omega^{2} A \\ & =m[g+\omega^{2} A] \end{aligned} $$
डेटा को रखने पर
$$ \begin{aligned} N & =50[9.8+(4 \pi)^{2} \times 5 \times 10^{-2}] \\ & =50[9.8+(12.56)^{2} \times 5 \times 10^{-2}] \\ & =50[9.8+7.88] \\ & =50 \times 17.68=884 N \end{aligned} $$
अब, मशीन अभिलक्षण बल को पढ़ता है। स्पष्ट है कि
अधिकतम भार $=884 N$ (नीचले बिंदु पर)
न्यूनतम भार $=95.5 N$ (ऊपर के बिंदु पर)
36. एक द्रव्यमान $m$ का एक वस्तु एक द्रव्यमानहीन स्प्रिंग के एक सिरे से जुड़ी है जो एक निश्चित बिंदु से लटका हुआ है। द्रव्यमान को हाथ में रखकर, स्प्रिंग न तो खिंचा है और न ही संपीड़ित है। अचानक, हाथ के समर्थन को हटा दिया जाता है। दोलन के दौरान द्रव्यमान द्वारा प्राप्त सबसे कम ऊंचाई $4 cm$ नीचे है, जहां इसे हाथ में रखा गया था।
(a) दोलन का आयाम क्या है?
(b) दोलन की आवृत्ति ज्ञात कीजिए?
उत्तर दिखाएँ
सोचने की प्रक्रिया
जब हम बल के समर्थन देते हैं, तो नेट बल $=0$ और जब यह छोड़ दिया जाता है, तो इसकी सभी स्थितिज ऊर्जा $KE$ में बदल जाती है।
उत्तर (a) जब हाथ के समर्थन को हटा दिया जाता है, तो वस्तु औसत स्थिति के चारों ओर दोलन करती है।
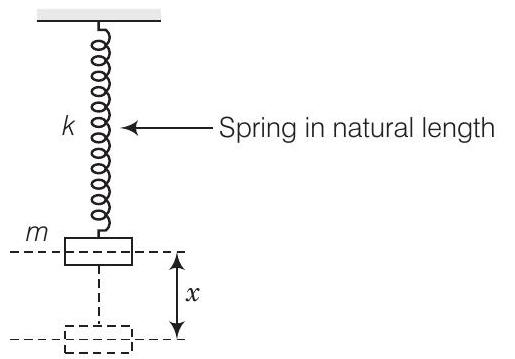
मान लीजिए $x$ वह अधिकतम विस्तार है जब वह दोलन के सबसे नीचले बिंदु पहुँचता है।
ब्लॉक की स्थितिज ऊर्जा में क्षय $=m g x$
जहाँ,
$m=$ ब्लॉक का द्रव्यमान
स्प्रिंग की अतिरिक्त स्थितिज ऊर्जा के लाभ $ =\frac{1}{2} k x^{2} $
क्योंकि दोनों बराबर हैं, यांत्रिक ऊर्जा के संरक्षण के अनुसार,
हम प्राप्त करते हैं,
$ m g x=\frac{1}{2} k x^{2} \text { या } x=\frac{2 m g}{k} $
अब, दोलन के औसत स्थिति होगी, जब ब्लॉक स्प्रिंग द्वारा संतुलित होता है।
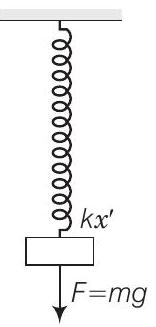
यदि $x^{\prime}$ उस स्थिति में विस्तार है, तो
$$ \begin{aligned} F & =+k x^{\prime} \\ \text { हालाँकि, } F & =m g \\ \Rightarrow m g & =+k x^{\prime} \\ \text { या } x^{\prime} & =\frac{m g}{k} \end{aligned} $$
समीकरण (iii) को समीकरण (iv) से विभाजित करने पर,
$$ \begin{aligned} & & \frac{x}{x^{\prime}} & =\frac{2 m g}{k} / \frac{m g}{k}=2 \\ \Rightarrow & & x & =2 x^{\prime} \end{aligned} $$
लेकिन दिया गया है $x=4 cm$ (अनुत्तरित स्थिति से अधिकतम विस्तार)
$$ \begin{aligned} \therefore & 2 x^{\prime} & =4 \\ \therefore & x^{\prime} & =\frac{4}{2}=2 cm \end{aligned} $$
लेकिन द्रव्यमान के औसत स्थिति से स्प्रिंग के प्राकृतिक लंबाई प्राप्त करने वाली स्थिति तक विस्थापन दोलन के आयाम के बराबर होता है।
$$ \therefore \quad A=x^{\prime}=2 cm $$
जहाँ, $A=$ गति का आयाम।
(b) दोलन करते निकाय के समय अवधि द्रव्यमान और स्प्रिंग नियतांक पर निर्भर करती है, जो द्वारा दी गई है
$$ T=2 \pi \sqrt{\frac{m}{k}} $$
यह आम्प्लीतुड पर निर्भर नहीं करता।
लेकिन समीकरण (iii) से,
$ \frac{2 m g}{k} =x $
$\frac{2 m g}{k} =4 , \text{cm}=4 \times 10^{-2} , \text{m} $
$\therefore \frac{m}{k} =\frac{4 \times 10^{-2}}{2 g}=\frac{2 \times 10^{-2}}{g} $
$\therefore \frac{k}{m} =\frac{g}{2 \times 10^{-2}} $
$ \text { और } \text { (अधिकतम विस्तार) } $
$\therefore \quad \text { आवृति }=\frac{1}{T}=\frac{1}{2 \pi} \sqrt{\frac{k}{m}} $
$ =\frac{1}{2 \times 3.14} \sqrt{\frac{g}{2 \times 10^{-2}}} $
$ =\frac{10}{6.28} \times 2.14 \sqrt{\frac{4.9}{10^{-2}}}=\frac{1}{6.28} \times \sqrt{4.9 \times 100}$
नोट: आवर्त गति के दौरान ब्लॉक उस स्थिति से ऊपर नहीं जा सकता, क्योंकि दिया गया है कि प्रणाली या बाह्य एजेंट द्वारा ऊपर की दिशा में कोई वेग नहीं है।
37. एक बाल्टी लकड़ी के बेलनाकार टुकड़े की ऊंचाई $h$ और काट क्षेत्रफल $A$ है जो पानी में तैरता है। इसे दबाकर फिर छोड़ दिया जाता है। दिखाइए कि लकड़ी एक सरल आवर्त गति करती है जिसका समय अंतराल है।
$$ T=2 \pi \sqrt{\frac{m}{A \rho g}} $$
जहाँ, $m$ वस्तु के द्रव्यमान है और $\rho$ द्रव के घनत्व है।
उत्तर दिखाएँ
सोचने की प्रक्रिया
सरल आवर्त गति के लिए समय अंतराल निकालने के लिए बेलन को संतुलन स्थिति से छोटे विस्थापन द्वारा विस्थापित करें और फिर बहाव बल को निकालें।
उत्तर चित्र को ध्यान में रखें।
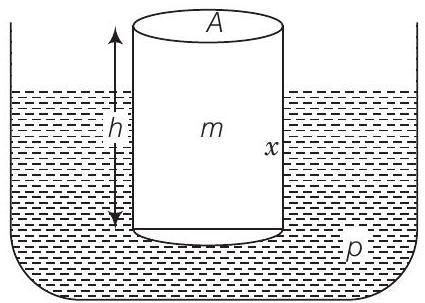
मान लीजिए कि बेलन को दबाया गया है और संतुलन स्थिति में ऊर्ध्वाधर विस्थापन $x_0$ है। संतुलन में,
$$ m g=\text { उत्थान बल }=(\rho A x_0) g \quad[\because m=V \rho=(A x_0) \rho] $$
जब इसे और भी विस्थापन $x$ द्वारा विस्थापित किया जाता है, तो उत्थान बल $A(x_0+x) \rho g$ होता है
$\therefore \quad$ नेट बहाव बल $=$ उत्थान बल - भार
$$ \begin{aligned} & =A(x_0+x) \rho g-m g \\ & =(A \rho g) x \end{aligned}
$$
$$ [\because m g=\rho A x_0 g] $$
जब विस्थापन $x$ नीचे की ओर होता है और बहाव बल ऊपर की ओर होता है, हम लिख सकते हैं
$$ \begin{aligned} F_{\text {restoring }} & =-(A \rho g) x \\ & =-k x \\ k & =\text { constant }=A \rho g \end{aligned} $$
इसलिए, गति सरल आवर्त गति (SHM) है
अब,
$ \text { Acceleration, } a=\frac{F_{\text {restoring }}}{m}=-\frac{k}{m} x $
इसे तुलना करें
$ a=-\omega^{2} x $
$\Rightarrow$ $ \omega^{2}=\frac{k}{m} \Rightarrow \omega=\sqrt{\frac{k}{m}} $
$\Rightarrow$ $ \frac{2 \pi}{T}=\sqrt{\frac{k}{m}} \Rightarrow T=2 \pi \sqrt{\frac{m}{k}} $
$\Rightarrow$ $ T=2 \pi \sqrt{\frac{m}{A \rho g}} $
38. एक $V$-नलिका जिसमें पारा होता है, के एक सिरे को एक छिपे हुए पंप के साथ जोड़ा गया है और दूसरा सिरा वातावरण के साथ जोड़ा गया है। नलिका के दोनों भाग अनुप्रस्थ दिशा में $45^{\circ}$ के कोण पर झुके हुए हैं। जब छिपे हुए पंप हटा दिया जाता है तो दो स्तंभों के बीच एक छोटा दबाव अंतर उत्पन्न होता है। $V$-नलिका में पारा के स्तंभ की सरल आवर्त गति करेगा? कैपिलरी और चिपचिप बल को नगण्य मानें। आवर्तकाल की गणना करें।
उत्तर दिखाएँ
Answer नीचे दिखाए गए चित्र को ध्यान में रखें
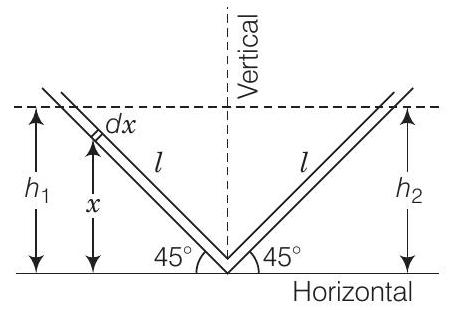
मान लीजिए कि एक अपरिमित द्रव स्तंभ के लंबाई $d x$ एक ऊंचाई $x$ पर है।
यदि $\rho=$ द्रव का घनत्व
$$ A=\text { V-नलिका का काट क्षेत्रफल } $$
एक तत्व $d x$ की स्थितिज ऊर्जा निम्न द्वारा दी जाएगी
$$ PE=d m g x=(A \rho d x) g x \quad[\because d m=p V=p A d x] $$
जहाँ, $A \rho d x=d m=$ तत्व $d x$ के द्रव्यमान
$\therefore$ बाएँ स्तंभ की कुल स्थितिज ऊर्जा
$$ \begin{aligned} & PE_{total}=\int_0^{h_1} A \rho g x d x \\ & =A \rho g \int_0^{h_1} x d x \\ & =A \rho g|\frac{x^{2}}{2}|_0^{h_1}=A \rho g \frac{h_1^{2}}{2} \end{aligned} $$
लेकिन,
$$ \begin{aligned} h_1 & =l \sin 45^{\circ} \\ PE & =\frac{A \rho g}{2} l^{2} \sin ^{2} 45^{\circ}
\end{aligned} $$
उसी तरह,
$$ \begin{aligned} \text { दाहिने स्तंभ की स्थितिज ऊर्जा } & =\frac{A \rho g}{2} l^{2} \sin ^{2} 45^{\circ} \\ \text { कुल स्थितिज ऊर्जा } & =\frac{A \rho g}{2} l^{2} \sin ^{2} 45^{\circ}+\frac{A \rho g}{2} l^{2} \sin ^{2} 45^{\circ} \\ & =2 \times \frac{1}{2} A \rho g l^{2}(\frac{1}{\sqrt{2}})^{2}=\frac{A \rho g l^{2}}{2} \end{aligned} $$
यदि बाएं तरफ के तत्व के कारण दबाव अंतर के कारण दाएं तरफ गति होती है, तो बाएं भाग में द्रव $=l-y$
दाएं भाग में द्रव $=l+y$
$\therefore \quad$ कुल स्थितिज ऊर्जा $=A \rho g(l-y)^{2} \sin ^{2} 45^{\circ}+A \rho g(l+y)^{2} \sin ^{2} 45^{\circ}$
या
स्थितिज ऊर्जा में परिवर्तन $=PE _{final }-P E _{initial }$
$$ \begin{aligned} \Delta PE & =\frac{A \rho g}{2}[(l-y)^{2}+(l+y)^{2}-l^{2}] \\ & =\frac{A \rho g}{2}[l^{2}+y^{2}-2 l y+l^{2}+y^{2}+2 l y-l^{2}] \\ & =\frac{A \rho g}{2}[2(l^{2}+y^{2})] \\ & =A \rho g(l^{2}+y^{2}) \end{aligned} $$
यदि $v$ कुल द्रव स्तंभ के वेग में परिवर्तन है, तो गतिज ऊर्जा में परिवर्तन
$$ \begin{aligned} \Delta KE & =\frac{1}{2} m v^{2} \\ m & =A \rho(2 l) \end{aligned} $$
$\therefore \quad \Delta KE=\frac{1}{2} A \rho 2 l v^{2}=A \rho l v^{2}$
समीकरण (iv) और (v) से,
$$ \Delta PE+\Delta KE=A \rho g(l^{2}+y^{2})+A \rho l v^{2} $$
क्योंकि, प्रणाली संरक्षित है।
$\therefore$ कुल ऊर्जा में परिवर्तन $=0$
समीकरण (vi) से,
$$ A \rho g(l^{2}+y^{2})+A \rho l v^{2}=0 $$
दोनों ओर समय $(t)$ के संदर्भ में अवकलन करने पर, हमें प्राप्त होता है;
$\quad \frac{d y}{d t}=v$ और $\frac{d v}{d t}=a$ [त्वरण]
$\Rightarrow \quad A \rho g(2 y v)+A \rho l(2 v) a=0$
$\Rightarrow \quad(g y+l a) 2 A \rho v=0$
$2 A \rho v=$ स्थिरांक और $2 A \rho v \neq 0$
$\therefore \quad l a+g y=0$
$$ \begin{matrix} a+(\frac{g}{l}) y=0 \\ \frac{d^{2} y}{d t^{2}}+(\frac{g}{l}) y=0 \end{matrix} $$
यह दोलन गति के रूप के मानक अवकल समीकरण है
$ \frac{d^{2} y}{d t^{2}}+\omega^{2} y $ =0
$\therefore \quad =\sqrt{\frac{g}{l}} $
$T=\frac{2 \pi}{\omega} =2 \pi \sqrt{\frac{l}{g}}$
39. पृथ्वी के केंद्र से गुजरने वाला एक सिलेंडर खोदा गया है। दिखाइए कि एक द्रव्यमान $m$ का एक वस्तु जब एक सिलेंडर के एक सिरे से विराम से गिराया जाता है तो यह सरल आवर्त गति करती है।
उत्तर दिखाएं
उत्तर चित्र में दिखाए गए स्थिति को ध्यान में रखें।
पृथ्वी के केंद्र से $r$ दूरी पर एक कण पर गुरुत्वाकर्षण बल पृथ्वी के उस भाग से उत्पन्न होता है जो कण के स्थान से आंतरिक खोलों में होता है। बाहरी खोलें कण पर कोई बल नहीं लगाती हैं।
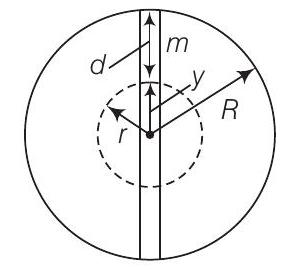
अधिक स्पष्ट रूप से,
मान लीजिए $g^{\prime}$ बिंदु $P$ पर त्वरण है।
इसलिए,
$g^{\prime}=g(1-\frac{d}{R})=g(\frac{R-d}{R})$
चित्र से,
$R-d=y$
$\Rightarrow$ $g^{\prime}=g \frac{y}{R}$
बिंदु $p$ पर वस्तु पर बल,
$F=-m g^{\prime}=\frac{-m g}{R} y$
$\Rightarrow$ $F \propto-y \quad$ [जहाँ, $y$ केंद्र से दूरी है]
इसलिए, गति सरल आवर्त गति है।
समय आवर्तकाल के लिए, हम समीकरण (i) को लिख सकते हैं
क्योंकि
$$ m a=-\frac{M g}{R} y \Rightarrow a=-\frac{g}{R} y $$
$ a=-\omega^{2} y $ के साथ तुलना करते हैं
$$ \begin{aligned} \omega^{2} & =\frac{g}{R} \\ \Rightarrow \quad(\frac{2 \pi}{T}) & =\frac{g}{R} \Rightarrow T=2 \pi \sqrt{\frac{R}{g}} \end{aligned} $$
40. एक सरल लोलक का समय आवर्तकाल $1 s$ और लंबाई $l$ है। इसे बिंदु $0$ पर एक निश्चित समर्थन से लटकाया गया है। ऐसा कि लोलक का बबल भूमि पर बिंदु $A$ से ऊर्ध्वाधर ऊपर $H$ की दूरी पर है (चित्र) अम्प्लीतुड $ \theta_0 $ है तथा रस्सी $ \theta = \theta_0 / 2 $ पर टूट जाती है। बबल भूमि तक पहुंचने में लगने वाला समय ज्ञात कीजिए। भूमि पर बबल द्वारा बिंदु $A$ से टकराने वाली दूरी भी ज्ञात कीजिए। मान लीजिए $ \theta_0 $ छोटा है, ताकि $ \sin \theta_0 \simeq \theta_0 $ और $ \cos \theta_0 \simeq 1 $ हो।
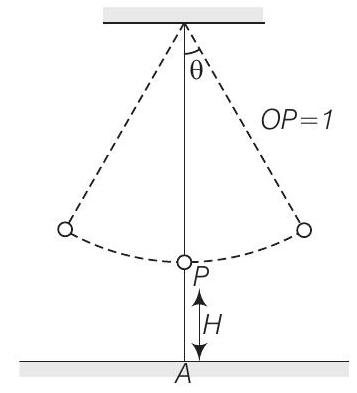
उत्तर दिखाएँ
सोचने की प्रक्रिया
हमें $\theta=\theta_0$ को संदर्भ बिंदु के रूप में लेना होगा, अर्थात जब $\theta=\theta_0$ हो तो समय को $t=0$ मान लें। फिर, सीधी रेखा गति के समीकरण का उपयोग करेंगे।
उत्तर चित्र को ध्यान में रखें।
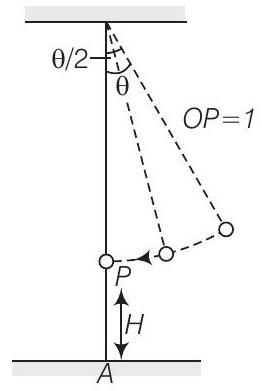
मान लें $t=0$ जब $\theta=\theta_0$, तो $\theta=\theta_0 \cos \omega t$
दिया गया है कि एक सेकंड का स्पर्श्रेखीय घड़ी है, $\omega=2 \pi \Rightarrow \theta=\theta_0 \cos 2 \pi t$
समय $t_1$ पर, मान लें $\theta=\theta_0 / 2$
$$ \begin{matrix} \therefore \cos 2 \pi t_1 =1 / 2 \Rightarrow t_1=\frac{1}{6} \\ \frac{d \theta}{d t} =-(\theta_0 2 \pi) \sin 2 \pi t & {[\because \cos 2 \pi t_1=\cos \frac{\pi}{3} \Rightarrow 2 \pi t_1=\frac{\pi}{3}]} \\ & \text { [समीकरण (i) से] } \end{matrix} $$
जब
$$ \begin{aligned} t & =t_1=\frac{1}{6} \\ \frac{d \theta}{d t} & =-\theta_0 2 \pi \sin \frac{2 \pi}{6}=-\sqrt{3} \pi \theta_0 \end{aligned} $$
ऋणात्मक चिह्न दर्शाता है कि यह बाईं ओर जा रहा है।
इसलिए, रैखिक वेग है
$$ u=-\sqrt{3} \pi \theta_0 l \text { तार के लंबवत। } $$
ऊर्ध्वाधर घटक है
$$ u_{y}=-\sqrt{3} \pi \theta_0 l \sin (\theta_0 / 2) $$
और क्षैतिज घटक है
$$ u_{x}=-\sqrt{3} \pi \theta_0 l \cos (\theta_0 / 2) $$
जब यह टूटता है, तो ऊर्ध्वाधर ऊंचाई है
$$ H^{\prime}=H+l(1-\cos (\theta_0 / 2)) $$
मान लें गिरने के लिए आवश्यक समय $t$ है, तो
$$ \begin{aligned} & H^{\prime}=u_{y} t+(1 / 2) g t^{2} \quad \text { (ध्यान दें } g \text { भी नकारात्मक दिशा में है) } \\ & \text { या } \quad \frac{1}{2} g t^{2}+\sqrt{3} \pi \theta_0 l \sin \frac{\theta_{o}}{2} t-H^{\prime}=0 \\ & \therefore \quad t=\frac{-\sqrt{3} \pi \theta_0 l \sin \frac{\theta_0}{2} \pm \sqrt{3 \pi^{2} \theta_0^{2} l^{2} \sin ^{2} \frac{\theta_0}{2}+2 g H^{\prime}}}{g} \\ & =\frac{-\sqrt{3} \pi l \frac{\theta_o^{2}}{2} \pm \sqrt{3 \pi^{2}(\frac{\theta_o^{4}}{4}) l^{2}+2 g H^{\prime}}}{g}[\because \sin \frac{\theta_0}{2} \simeq \frac{\theta_0}{2} \text { छोटे कोण के लिए }] $$
\end{aligned} $$
$\theta_0$ छोटा है, इसलिए $\theta_0^{2}$ के क्रम के शब्दों को नगण्य मान लें
$$ t=\sqrt{\frac{2 H^{\prime}}{g}} $$
$$ \begin{aligned} & \text { अब, } \quad H^{\prime} \approx H+l(1-1) \quad[\therefore \cos \theta_0 / 2 \approx 1] \\ & \begin{aligned} & =H \\ \Rightarrow \quad t & =\sqrt{\frac{2 H}{g}} \end{aligned} \end{aligned} $$
$x$-दिशा में तय की गई दूरी $u_{x} t$ है, जो बोब के बर्न के स्थान से बाईं ओर है
$$ \begin{aligned} & X=U x t=\sqrt{3} \pi \theta_0 l Cos(\frac{\theta_0}{2}) \sqrt{\frac{2 H}{g}} s \\ & \text { जबकि } \theta_0 \text { छोटा है } \Rightarrow \cos (\frac{\theta_0}{ }{2}) \approx 1 \\ & X=\sqrt{3} \pi \theta_0 l \sqrt{\frac{2 H}{g}}=\sqrt{\frac{6 H}{g}} \theta_0 l \pi \end{aligned} $$
बर्न के समय, बोब $A$ से $l \sin (\theta_0 / 2) \approx l \frac{\theta_0}{2}$ की दूरी पर था।
इसलिए, जमीन पर मिलने वाले बोब की $A$ से दूरी है
$$ \begin{aligned} & =\frac{l \theta_0}{2}-X=\frac{l \theta_0}{2}-\sqrt{\frac{6 H}{g}} \theta_0 l \pi \\ & =\theta_0 l(\frac{1}{2}-\pi \sqrt{\frac{6 H}{g}}) \end{aligned} $$





