किनेटिक सिद्धांत
बहुविकल्पीय प्रश्न (MCQs)
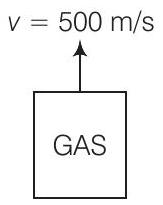
1. एक घन वाला बर्तन (जिसकी फलक क्षैतिज और ऊर्ध्वाधर है) एनटीपी पर आदर्श गैस के साथ भरा है। बर्तन को एक रॉकेट द्वारा ले जाया जा रहा है, जो ऊर्ध्वाधर दिशा में $500 m s^{-1}$ की गति से चल रहा है। बर्तन के अंदर गैस के दबाव को जमीन पर हम देखेंगे
(a) अपरिवर्तित रहेगा क्योंकि $500 ms^{-1}$ गैस के $v_{\text {rms }}$ की तुलना में बहुत कम है
(b) अपरिवर्तित रहेगा क्योंकि बर्तन के सारे गति के कारण गैस अणुओं और दीवारों के संबंधी गति पर प्रभाव नहीं पड़ता
(c) बर्तन के शीर्ष दीवार और तल दीवार पर अलग-अलग होगा जो वहां $v_rms^{2}+(500)^{2}) / v_rms^{2}$ के गुणक से बढ़ जाएगा जहां $v_{rms}$ गैस के मूल औसत वर्ग वेग था
(d) बर्तन के शीर्ष दीवार और तल दीवार पर अलग-अलग होगा
उत्तर दिखाएं
सोचने की प्रक्रिया
इस घटना के पीछे अवलोकन के संबंध में गति के संबंध में अवलोकन होता है जब टकराव होता है, तो यह अवलोकन वेग के बदले हुए होता है।
उत्तर (b) बर्तन के सारे गति के कारण गैस अणुओं के दीवारों के संबंधी गति पर प्रभाव नहीं पड़ता, इसलिए बर्तन के अंदर गैस के दबाव को हम जमीन पर देखेंगे तो यह अपरिवर्तित रहेगा।
-
(a) यह कथन गलत है क्योंकि रॉकेट की गति और गैस अणुओं के वर्ग मूल वेग ($v_{\text{rms}}$) के बीच तुलना दबाव के अवलोकन के लिए संबंधित नहीं है। दबाव बर्तन की दीवारों के संबंध में गैस अणुओं के संबंधी गति द्वारा निर्धारित होता है, जो रॉकेट की गति के बावजूद अपरिवर्तित रहता है।
-
(c) यह विकल्प गलत है क्योंकि यह बताता है कि दबाव रॉकेट की गति के वर्ग और गैस के मूल औसत वर्ग वेग के गुणक से बढ़ जाएगा। हालांकि, आदर्श गैस के दबाव तापमान और आयतन पर निर्भर होता है, न कि बर्तन के बाहरी गति। बर्तन की दीवारों के संबंध में गैस अणुओं के संबंधी गति अपरिवर्तित रहती है, इसलिए दबाव इस गुणक से बढ़ नहीं सकता।
-
(d) यह विकल्प गलत है क्योंकि इसका अर्थ है कि रॉकेट के ऊर्ध्वाधर गति के कारण बरतन के शीर्ष और तल दीवारों पर दबाव अलग-अलग होगा। हालांकि, बरतन के अंदर दबाव आइसोट्रॉपिक (सभी दिशाओं में समान) होता है और यह गैस अणुओं के दीवारों से टकराव से निर्धारित होता है, जो बरतन के समान गति के प्रभाव से प्रभावित नहीं होता है।
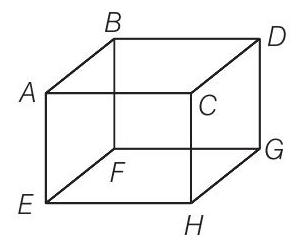
2. 300 K तापमान पर एक आदर्श गैस के 1 मोल को एक घनाकार आयतन $V, A B C D E F G H$ में रखा गया है (चित्र)। घन के एक फलक $(E F G H)$ का निर्माण एक ऐसे पदार्थ से किया गया है जो उस पर आपतित कोई भी गैस अणु को पूरी तरह से अवशोषित कर लेता है। किसी भी समय,
(a) $E F G H$ पर दबाव शून्य होगा
(b) सभी फलकों पर दबाव समान होगा
(c) $E F G H$ पर दबाव $A B C D$ पर दबाव के दोगुना होगा
(d) $E F G H$ पर दबाव $A B C D$ पर दबाव के आधा होगा
उत्तर दिखाएँ
Answer (d) आदर्श गैस में, जब एक अणु एक दीवार से बर्बाद टकराव करता है, तो प्रत्येक अणु को सामान्य गति के मापदंड के दोगुने मापदंड के बराबर आवेग स्थानांतरित किया जाता है। $E F G H$ फलक के लिए, इसके आवेग का केवल आधा हिस्सा स्थानांतरित होता है।
-
(a) $E F G H$ पर दबाव शून्य होगा: यह गलत है क्योंकि भले ही $E F G H$ फलक गैस अणुओं को अवशोषित करता है, लेकिन अणुओं के अवशोषण से पहले वे इस पर कुछ दबाव डालते हैं। दबाव शून्य नहीं होता बल्कि कम हो जाता है।
-
(b) सभी फलकों पर दबाव समान होगा: यह गलत है क्योंकि $E F G H$ फलक गैस अणुओं को अवशोषित करता है, जिसके कारण इस पर दबाव अन्य फलकों के मुकाबले कम हो जाता है, जहां गैस अणु बर्बाद टकराव करते हैं।
-
(c) $E F G H$ पर दबाव $A B C D$ पर दबाव के दोगुना होगा: यह गलत है क्योंकि $E F G H$ फलक द्वारा गैस अणुओं के अवशोषण इस पर दबाव को कम कर देता है। इसके दोगुना दबाव $A B C D$ पर नहीं हो सकता; वास्तव में, यह कम होता है।
3. Boyle’s law is applicable for an
(a) adiabatic process
(b) isothermal process
(c) isobaric process
(d) isochoric process
उत्तर दिखाएँ
Answer
(b) Boyle’s law is applicable when temperature is constant
i.e.,
$p V=n R T=$ constant
$\Rightarrow$ $p V=$ constant (at constant temperature)
i.e., $p \propto \frac{1}{V}$
[where,$p=$ pressure, $V=$ volume $]$
So, this process can be called as isothermal process.
-
Adiabatic process: In an adiabatic process, there is no heat exchange with the surroundings, and the temperature of the gas changes. Boyle’s law requires the temperature to remain constant, which is not the case in an adiabatic process.
-
Isobaric process: In an isobaric process, the pressure remains constant. Boyle’s law describes the relationship between pressure and volume at a constant temperature, not at a constant pressure.
-
Isochoric process: In an isochoric process, the volume remains constant. Boyle’s law involves changes in volume and pressure while keeping the temperature constant, which is not applicable when the volume is fixed.
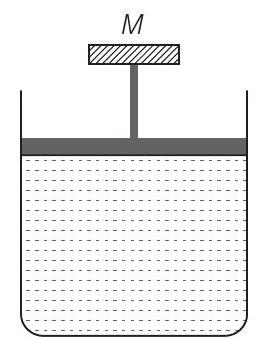
4. A cylinder containing an ideal gas is in vertical position and has a piston of mass $M$ that is able to move up or down without friction (figure). If the temperature is increased
(a) both $p$ and $V$ of the gas will change
(b) only $p$ will increase according to Charles’ law
(c) $V$ will change but not $p$
(d) $p$ will change but not $V$
उत्तर दिखाएँ
Answer (c) Consider the diagram where an ideal gas is contained in a cylinder, having a piston of mass $M$. Friction is absent.
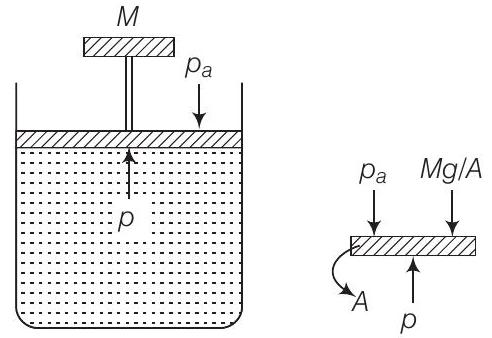
दाब गैस के अंदर होगा
$$ p=p_{a}+M g / A $$
जहाँ, $p_{a}=$ वायुमंडलीय दाब
$A=$ पिस्टन के क्रॉस-सेक्शन क्षेत्रफल।
$M g=$ पिस्टन का भार
इसलिए, $p=$ स्थिर।
जब तापमान बढ़ता है, तो $p V=n R T \Rightarrow$ आयतन $(V)$ नियत दाब पर बढ़ता है।
-
विकल्प (a): यह विकल्प गलत है क्योंकि इसमें गैस के दाब $ p $ और आयतन $ V $ दोनों बदल जाएगे कहा गया है। हालांकि, दिए गए स्थिति में पिस्टन पर बल के संतुलन के कारण दाब $ p $ स्थिर रहता है (वायुमंडलीय दाब प्लस पिस्टन का भार)। केवल तापमान बढ़ने पर आयतन $ V $ बदलता है, आदर्श गैस के नियम $ pV = nRT $ के अनुसार।
-
विकल्प (b): यह विकल्प गलत है क्योंकि इसमें केवल दाब $ p $ बढ़ेगा कहा गया है चार्ल्स के नियम के अनुसार। चार्ल्स के नियम वास्तव में एक गैस के आयतन के तापमान के साथ अनुपातिक होता है जब दाब स्थिर रहता है। इस स्थिति में दाब स्थिर रहता है और तापमान बढ़ने पर आयतन $ V $ बढ़ता है, न कि दाब।
-
विकल्प (d): यह विकल्प गलत है क्योंकि इसमें दाब $ p $ बदलेगा लेकिन आयतन $ V $ नहीं बदलेगा कहा गया है। दिए गए सेटअप में पिस्टन पर बल के संतुलन के कारण दाब $ p $ स्थिर रहता है। जब तापमान बढ़ता है, तो आयतन $ V $ बढ़ेगा ताकि आदर्श गैस के नियम $ pV = nRT $ द्वारा वर्णित संबंध बना रहे।
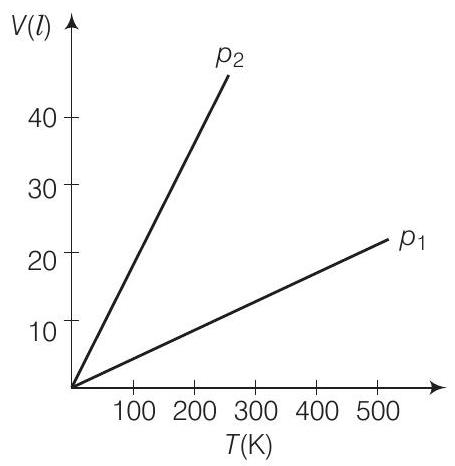
5. एक आदर्श गैस के दिए गए द्रव्यमान के आयतन व तापमान के ग्राफ चित्र में दिए गए हैं। दो अलग-अलग नियत दाब के मानों पर। $p_1$ और $p_2$ के बीच संबंध के बारे में क्या निष्कर्ष निकाला जा सकता है?
(a) $p_1>p_2$
(b) $p_1=p_2$
(c) $p_1<p_2$
(d) डेटा पर्याप्त नहीं है
उत्तर दिखाएँ
सोचने की प्रक्रिया
आवश्यक संबंध खोजने के लिए हमें $V-T$ ग्राफ के ढलान को ध्यान में रखना होगा। आदर्श गैस समीकरण के अनुसार, $V-T$ वक्र के ढलान $V / T=n R / p$ होता है। इसका अर्थ है कि ढलान अधिक होने पर दाब छोटा होता है और विपरीत।
उत्तर (a) हम जानते हैं कि आदर्श गैस के लिए,
$$ \begin{aligned} & p V=n R T \Rightarrow V=(\frac{n R}{p}) T \\ & \text { } V-T \text { ग्राफ के ढलान, } \quad m=\frac{d V}{d T}=\frac{n R}{p} \quad[m=\text { } V-t \text { ग्राफ के ढलान }] \\ & \Rightarrow \quad m \propto \frac{1}{p} \quad[\therefore n R=\text { स्थिरांक }] \\ & \Rightarrow \quad p \propto \frac{1}{m} \\ & \text { इसलिए, } \quad \frac{p_1}{p_2}=\frac{m_2}{m_1}<1 \\ & {[\begin{matrix} P=\text { दबाव } \\ V=\text { आयतन } \\ n=\text { गैस के मोलों की संख्या } \\ R=\text { गैस नियतांक } \\ T=\text { तापमान } \end{matrix} ]} \end{aligned} $$
जहाँ, $m_1$ वह ढलान है जो $p_1$ के संगत ग्राफ के लिए है और इसी तरह $m_2$ वह ढलान है जो $p_2$ के संगत ग्राफ के लिए है।
$$ \Rightarrow \quad p_2<p_1 \text { या } p_1>p_2 $$
-
विकल्प (b) $p_1 = p_2$: यह विकल्प गलत है क्योंकि यदि दबाव समान होता, तो आयतन व तापमान के ग्राफ के ढलान भी समान होते। हालांकि, समस्या में दिया गया है कि ग्राफ दो अलग-अलग नियत दबाव के मानों पर हैं, जिससे अलग-अलग ढलान बनते हैं।
-
विकल्प (c) $p_1 < p_2$: यह विकल्प गलत है क्योंकि, संबंध $ p \propto \frac{1}{m} $ के अनुसार, एक उच्च ढलान (m) एक निम्न दबाव को दर्शाता है। चूंकि $ m_1 $ वह ढलान है जो $ p_1 $ के लिए है और $ m_2 $ वह ढलान है जो $ p_2 $ के लिए है, और दिया गया है कि $ \frac{p_1}{p_2} = \frac{m_2}{m_1} < 1 $, इसलिए $ p_1 > p_2 $ होगा।
-
विकल्प (d) डेटा पर्याप्त नहीं है: यह विकल्प गलत है क्योंकि दिया गया डेटा और आदर्श गैस के नियम पर्याप्त डेटा प्रदान करते हैं जिससे $ p_1 $ और $ p_2 $ के बीच संबंध का निर्धारण किया जा सकता है। ग्राफ के ढलान और निर्धारित संबंध $ p \propto \frac{1}{m} $ पर्याप्त हैं जिससे निष्कर्ष निकाला जा सकता है कि $ p_1 > p_2 $ है।
6. 1 मोल के $H_2$ गैस को $V=1.00 m^{3}$ के बॉक्स में $T=300 K$ तापमान पर रखा गया है। गैस को $T=3000 K$ तक गरम कर दिया जाता है और गैस हाइड्रोजन परमाणुओं की गैस में परिवर्तित हो जाती है। अंतिम दबाव क्या होगा (सभी गैसों को आदर्श मान लें)
(a) आरंभिक दबाव के समान
(b) आरंभिक दबाव के 2 गुना
(c) आरंभिक दबाव के 10 गुना
(d) आरंभिक दबाव के 20 गुना
उत्तर दिखाएँ
उत्तर (d) चित्र को ध्यान से देखें, जब अणु अपने परमाणुओं में विखंडित हो जाते हैं, तो मोल की संख्या दोगुनी हो जाती है।
अब, आदर्श गैस समीकरण के अनुसार
$$ \begin{matrix} P & =\text { गैस का दबाव }, & & n=\text { मोल की संख्या } \\ R & =\text { गैस नियतांक }, & T=\text { तापमान } \\ p V & =n R T & & \end{matrix} $$
कंटेनर का आयतन $(V)$ नियत रहता है।
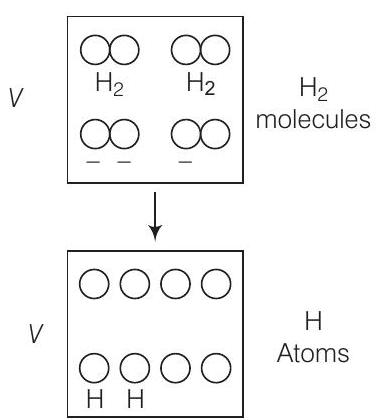
जब गैस विखंडित होती है, मोल की संख्या आरंभिक के दोगुनी हो जाती है, इसलिए $n_2=2 n_1$
इसलिए,
$$ \begin{aligned} & p \propto n T \\ & \frac{p_2}{p_1}=\frac{n_2 T_2}{n_1 T_1}=\frac{(2 n_1)(3000)}{n_1(300)}=20 \end{aligned} $$
$\Rightarrow$
$$ p_2=20 p_1 $$
अतः, गैस के अंतिम दबाव आरंभिक दबाव के 20 गुना हो जाएगा।
-
विकल्प (a) आरंभिक दबाव के समान: यह विकल्प गलत है क्योंकि जब गैस गरम की जाती है और $H_2$ अणु अपने परमाणुओं में विखंडित हो जाते हैं, तो गैस के मोल की संख्या दोगुनी हो जाती है। आदर्श गैस के नियम के अनुसार, दबाव मोल की संख्या और तापमान के सीधे अनुपात में होता है। चूंकि मोल की संख्या और तापमान दोनों बढ़ जाते हैं, दबाव एक ही रहना असंभव है।
-
विकल्प (b) आरंभिक दबाव के 2 गुना: यह विकल्प गलत है क्योंकि जब $H_2$ अपने परमाणुओं में विखंडित हो जाते हैं, तो मोल की संख्या दोगुनी हो जाती है, लेकिन तापमान भी 10 गुना बढ़ जाता है (300 K से 3000 K तक)। इसलिए, दबाव 20 गुना बढ़ जाता है, न कि केवल 2 गुना।
-
विकल्प (c) आरंभिक दबाव के 10 गुना: यह विकल्प गलत है क्योंकि इसमें केवल तापमान में 10 गुना वृद्धि को ध्यान में रखा गया है। यह $H_2$ के विखंडित होने से मोल की संख्या दोगुनी हो जाने को नहीं लेता है। मोल की संख्या और तापमान दोनों के वृद्धि के प्रभाव के कारण दबाव 20 गुना बढ़ जाता है, न कि 10 गुना।
7. एक आयतन $V$ के नाले में 1 मोल हाइड्रोजन और 1 मोल ऑक्सीजन (दोनों को आदर्श गैस माना जाता है) के मिश्रण है। मान लीजिए $f_1(v) d v$, वेग के बीच $v$ और $v + dv$ के अणुओं के अंश को दर्शाता है, तथा $f_2(v) d v$ ऑक्सीजन के लिए इसी तरह। तब,
(a) $f_1(v)+f_2(v)=f(v)$ एमेक्स के वितरण कानून का पालन करता है
(b) $f_1(v), f_2(v)$ अलग-अलग एमेक्स के वितरण कानून का पालन करते हैं
(c) न तो $f_1(v)$, न ही $f_2(v)$ एमेक्स के वितरण कानून का पालन करेंगे
(d) $f_2(v)$ और $f_1(v)$ एक समान होंगे
उत्तर दिखाएं
उत्तर (b) एक फ़ंक्शन $f(v)$ के लिए, वेग के बीच $v$ और $v + dv$ के अणुओं की संख्या $n = f(v)$ होती है।
प्रत्येक फ़ंक्शन $f_1(v)$ और $f_2(v)$ के लिए, $n$ अलग-अलग होगी, इसलिए प्रत्येक फ़ंक्शन $f_1(v)$ और $f_2(v)$ अलग-अलग एमेक्स के वितरण कानून का पालन करेंगे।
-
(a) $f_1(v)+f_2(v)=f(v)$ एमेक्स के वितरण कानून का पालन करता है: यह गलत है क्योंकि $f_1(v)$ और $f_2(v)$ क्रमशः हाइड्रोजन और ऑक्सीजन अणुओं के वेग वितरण को दर्शाते हैं। इन वितरणों के योग एक मिश्रण के लिए एमेक्स के वितरण कानून का पालन आवश्यक नहीं होता, क्योंकि एमेक्स वितरण अणुओं के द्रव्यमान पर निर्भर करता है, और हाइड्रोजन और ऑक्सीजन के अणुओं के द्रव्यमान अलग-अलग होते हैं।
-
(c) न तो $f_1(v)$, न ही $f_2(v)$ एमेक्स के वितरण कानून का पालन करेंगे: यह गलत है क्योंकि हाइड्रोजन और ऑक्सीजन आदर्श गैस हैं, और आदर्श गैस के अणुओं के वेग वितरण एमेक्स-बोल्ट्जमैन वितरण कानून का पालन करते हैं। इसलिए, $f_1(v)$ और $f_2(v)$ अलग-अलग एमेक्स के वितरण कानून का पालन करेंगे।
-
(d) $f_2(v)$ और $f_1(v)$ एक समान होंगे: यह गलत है क्योंकि एमेक्स-बोल्ट्जमैन वितरण अणुओं के द्रव्यमान पर निर्भर करता है। हाइड्रोजन और ऑक्सीजन के अणुओं के द्रव्यमान अलग-अलग होते हैं, इसलिए उनके वेग वितरण $f_1(v)$ और $f_2(v)$ अलग-अलग होंगे।
8. एक फूले हुए रबर के बल्ले में एक मोल आदर्श गैस है, जिसका दबाव $p$, आयतन $V$ और तापमान $T$ है। यदि तापमान $1.1 T$ तक बढ़ जाता है और आयतन $1.05 V$ तक बढ़ जाता है, तो अंतिम दबाव होगा
(a) $1.1 p$
(b) $p$
(c) less than $p$
(d) between $p$ and $1.1p$
उत्तर दिखाएँ
Answer (d) हम जानते हैं कि आदर्श गैस के लिए, $p V=n R T$ (आदर्श गैस समीकरण)
$$ \Rightarrow \quad \begin{aligned} n & =\text { मोल की संख्या, } p=\text { दबाव, } V=\text { आयतन } \\ R & =\text { गैस नियतांक, } \quad T=\text { तापमान } \\ & =\frac{p V}{R T} \end{aligned} $$
क्योंकि गैस के मोल की संख्या निश्चित रहती है, इसलिए हम लिख सकते हैं
$$ \begin{matrix} \frac{p_1 V_1}{R T_1} =\frac{p_2 V_2}{R T_2} & \\ \Rightarrow \quad p_2 =(p_1 V_1)(\frac{T_2}{V_2 T_1}) & \\ =\frac{(p)(V)(1.1 T)}{(1.05) V(T)} \quad[\begin{matrix} p_1=p \\ V_2=1.05 V \text { और } T_2=1.1 T \end{matrix} ] \\ =p \times(\frac{1.1}{1.05}) =p(1.0476) \approx 1.05 p \end{matrix} $$
अतः, अंतिम दबाव $p_2$ $p$ और $1.1 p$ के बीच है।
-
विकल्प (a) $1.1 p$: यह विकल्प गलत है क्योंकि इसमें दबाव के तापमान के बढ़ने के साथ-साथ अनुपातिक रूप से बढ़ने की धारणा है। हालांकि, आयतन भी बढ़ता है, जो दबाव के बढ़ने को धीमा करता है। वास्तविक अंतिम दबाव $1.1 p$ से कम है क्योंकि आयतन और तापमान के बढ़ने के संयोग के कारण है।
-
विकल्प (b) $p$: यह विकल्प गलत है क्योंकि इसमें तापमान और आयतन के बदले होने के बावजूद दबाव के निरंतर रहने की धारणा है। आदर्श गैस के नियम के अनुसार, यदि तापमान बढ़ता है और आयतन भी बढ़ता है, तो दबाव बदल जाता है। इस मामले में, दबाव बढ़ता है लेकिन $1.1 p$ के बराबर नहीं होता।
-
विकल्प (c) less than $p$: यह विकल्प गलत है क्योंकि इसमें तापमान के बढ़ने के साथ-साथ दबाव कम होने की धारणा है। जब तापमान और आयतन दोनों बढ़ते हैं, तो दबाव बढ़ता है लेकिन $1.1 p$ के बराबर नहीं होता। अंतिम दबाव $p$ से अधिक है लेकिन $1.1 p$ से कम है।
बहुविकल्पीय प्रश्न (एक से अधिक विकल्प)
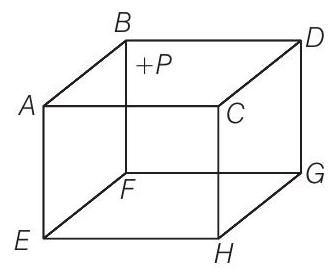
9. A B C D E F G H एक विद्युत अपरिचालक के बने खाली क्यूब है (चित्र) फेस $A B C D$ पर धनात्मक आवेश है। क्यूब के अंदर हमें आयनित हाइड्रोजन है।
सामान्य गतिमान सिद्धांत के व्यंजक के लिए दबाव
(a) सही होगा
(b) सही नहीं होगा, क्योंकि आयन दीवारों के संघटन से अलग बलों के कारण बल अनुभव करेंगे
(c) सही नहीं होगा, क्योंकि दीवारों के संघटन अनुत्क्रमणीय होंगे
(d) सही नहीं होगा क्योंकि सममिति खो जाती है
उत्तर दिखाएं
सोचने की प्रक्रिया
क्योंकि घन के भीतर आयनित हाइड्रोजन उपस्थित है, इनके चार्ज होते हैं। अब, सतह $ABCD$ पर धनात्मक चार्ज के उपस्थिति के कारण हाइड्रोजन आयन विद्युत चार्ज के कारण बल अनुभव करेंगे।
उत्तर $(b, d)$
सतह $ABCD$ पर बाहरी धनात्मक चार्ज के उपस्थिति के कारण, गतिमान सिद्धांत के आधार पर दबाव के सामान्य व्यंजक सही नहीं होगा, क्योंकि आयन दीवारों के संघटन से अलग विद्युत चार् के बल भी अनुभव करेंगे। धनात्मक चार्ज के उपस्थिति के कारण सममिति भी खो जाती है।
-
(a) सही होगा: यह विकल्प गलत है क्योंकि सतह $ABCD$ पर बाहरी धनात्मक चार्ज के उपस्थिति के कारण घन के भीतर आयनों पर अतिरिक्त विद्युत बल लगेंगे। दबाव के सामान्य गतिमान सिद्धांत के व्यंजक मान लेता है कि कणों पर केवल दीवारों के संघटन से बल लगते हैं, जो यहां नहीं है।
-
(c) सही नहीं होगा, क्योंकि दीवारों के संघटन अनुत्क्रमणीय होंगे: यह विकल्प गलत है क्योंकि समस्या में दीवारों के संघटन अनुत्क्रमणीय होने के लिए कोई कारण नहीं दिया गया है। बाहरी चार्ज के उपस्थिति आयनों पर बल के अनुभव को प्रभावित करता है लेकिन दीवारों के संघटन अनुत्क्रमणीय होने का अनुमान लगाने के लिए आवश्यक नहीं है।
10. हाइड्रोजन जैसे द्विपरमाणुक अणु गतिमान सिद्धांत के समीकरण $p V=\frac{2}{3} E$ के अनुसार गतिज ऊर्जा के अलावा घूर्णन गतिज ऊर्जा के कारण ऊर्जा के अधिक रूप में उपलब्ध होते हैं। $E$ है
(a) इकाई आयतन पर कुल ऊर्जा
(b) केवल ऊर्जा के परिवहन भाग क्योंकि घूर्णन ऊर्जा परिवहन ऊर्जा की तुलना में बहुत कम होती है
(c) केवल ऊर्जा के परिवहन भाग क्योंकि दीवारों के साथ टकराव के दौरान दबाव रैखिक संवेग में परिवर्तन से संबंधित होता है
(d) ऊर्जा के परिवहन भाग क्योंकि अणुओं की घूर्णन ऊर्जा धनात्मक या ऋणात्मक दोनों हो सकती है और सभी अणुओं के औसत में यह शून्य होता है
उत्तर दिखाएं
उत्तर (c) गतिक सिद्धांत के अनुसार, हम मान लेते हैं कि दीवारें केवल अणुओं पर लंबवत बल लगाती हैं। वे कोई समानांतर बल नहीं लगाती हैं, इसलिए कोई भी घूर्णन उपस्थित नहीं हो सकती है।
दीवार केवल परिवहन गति में परिवर्तन उत्पन्न करती है।
इसलिए, समीकरण में
$$ p V=\frac{2}{3} E $$
$$\left[\begin{array}{c} \text { जहाँ } P=\text { दबाव } \ V=\text { आयतन } \end{array}\right]$$
$E$ केवल ऊर्जा के परिवहन भाग को प्रतिनिधित करता है।
-
(a) इकाई आयतन पर कुल ऊर्जा: यह विकल्प गलत है क्योंकि समीकरण $ pV = \frac{2}{3} E $ गैस अणुओं की परिवहन गतिज ऊर्जा से संबंधित होता है, न कि कुल ऊर्जा जो घूर्णन और संभवतः विपाटन ऊर्जा के साथ शामिल हो सकती है।
-
(b) केवल ऊर्जा के परिवहन भाग क्योंकि घूर्णन ऊर्जा परिवहन ऊर्जा की तुलना में बहुत कम होती है: यह विकल्प गलत है क्योंकि दिए गए कारण सही नहीं है। घूर्णन ऊर्जा परिवहन ऊर्जा की तुलना में आवश्यक रूप से बहुत कम नहीं होती। सही कारण यह है कि समीकरण $ pV = \frac{2}{3} E $ टकराव के दौरान रैखिक संवेग में परिवर्तन के कारण केवल परिवहन गतिज ऊर्जा को ध्यान में रखते हुए निर्मित किया गया है।
-
(d) ऊर्जा के परिवहन भाग क्योंकि अणुओं की घूर्णन ऊर्जा धनात्मक या ऋणात्मक दोनों हो सकती है और सभी अणुओं के औसत में यह शून्य होता है: यह विकल्प गलत है क्योंकि घूर्णन ऊर्जा धनात्मक या ऋणात्मक दोनों हो सकती है; वे हमेशा धनात्मक होती हैं। सही कारण यह है कि समीकरण $ pV = \frac{2}{3} E $ परिवहन गतिज ऊर्जा से निर्मित होता है, जो दीवारों के साथ टकराव के दौरान रैखिक संवेग में परिवर्तन के माध्यम से दबाव और आयतन से संबंधित होता है।
11. एक द्विपरमाणुक अणु में, दिए गए तापमान पर घूर्णन ऊर्जा
(a) मैक्सवेल के वितरण का पालन करती है
(b) सभी अणुओं के लिए समान मान रखती है
(c) प्रत्येक अणु के लिए परिवहन गतिज ऊर्जा के बराबर होती है
(d) प्रत्येक अणु के लिए परिवहन गतिज ऊर्जा के $(\frac{2}{3})^{rd}$ होती है
उत्तर दिखाएँ
उत्तर $(a, d)$
एक द्विपरमाणुक अणु को चित्र में दिखाया गया है।
अणु के साथ संबंधित कुल ऊर्जा है
$$ E=\frac{1}{2} m v_x^{2}+\frac{1}{2} m v_y^{2}+\frac{1}{2} m v_z^{2}+\frac{1}{2} I_{x} \omega_x^{2}+\frac{1}{2} I_{y} \omega_y^{2} $$
उपरोक्त व्यंजक में परिवहन गतिज ऊर्जा $(\frac{1}{2} m v^{2})$ प्रत्येक $x, y$ और $z$-दिशा में वेग के संगत है तथा घूर्णन गतिज ऊर्जा $(\frac{1}{2} I \omega^{2})$ घूर्णन अक्ष $x$ और $y$ के संगत है।
उपरोक्त व्यंजक में स्वतंत्र पदों की संख्या 5 है।
हम जानते हैं कि अणुओं के वेग को मैक्सवेल के वितरण द्वारा अनुमान लगाया जा सकता है, इसलिए उपरोक्त व्यंजक मैक्सवेल के वितरण का पालन करता है।
$\because$ प्रत्येक अणु के लिए 2 घूर्णन और 3 परिवहन ऊर्जाएँ संबंधित होती हैं।
$\therefore$ दिए गए तापमान पर घूर्णन ऊर्जा प्रत्येक अणु के परिवहन गतिज ऊर्जा के $(\frac{2}{3})^{rd}$ होती है।
-
(b) सभी अणुओं के लिए समान मान रखती है: यह विकल्प गलत है क्योंकि अणुओं की घूर्णन ऊर्जा मैक्सवेल-बोल्ट्जमैन वितरण का पालन करती है और सभी अणुओं के लिए समान मान रखती है। ऊर्जा स्तर संगत और अलग-अलग अणुओं में भिन्न हो सकते हैं।
-
(c) प्रत्येक अणु के लिए परिवहन गतिज ऊर्जा के बराबर होती है: यह विकल्प गलत है क्योंकि घूर्णन ऊर्जा परिवहन गतिज ऊर्जा के बराबर नहीं होती। एक द्विपरमाणुक अणु में घूर्णन ऊर्जा परिवहन गतिज ऊर्जा के एक भिन्न होती है, विशेष रूप से $\frac{2}{3}$ परिवहन गतिज ऊर्जा, जो अणु के संबंधित स्वतंत्र चरों से निर्मित होती है।
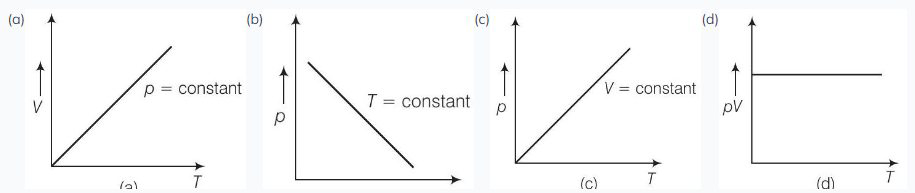
12. निम्नलिखित आरेख (चित्र) में से कौन सा आरेख आदर्श गैस के व्यवहार को दर्शाता है?
उत्तर दिखाएँ
उत्तर
$(a, c)$
हम जानते हैं कि आदर्श गैस समीकरण है
$$ p V=n R T $$
(a) जब दबाव, $p=$ स्थिर है। समीकरण (i) से आयतन $V, \propto$ तापमान $T$
(b) जब $T$ = स्थिर है, समीकरण (i) से $p V=$ स्थिर
इसलिए, ग्राफ आयताकार हाइपरबोला होता है।
(c) जब $V=$ स्थिर है।
समीकरण (i) से $p \propto T$
इसलिए, ग्राफ मूल बिंदु से गुजरने वाली सीधी रेखा होती है।
(d) समीकरण (i) से $p V \propto T$
$\Rightarrow \quad \frac{p V}{T}=$ स्थिर
$\Rightarrow$ इसलिए, ग्राफ मूल बिंदु से गुजरता है।
इसलिए, (d) सही नहीं है।
-
विकल्प (b): जब तापमान $ T $ स्थिर है, तो संबंध $ pV = \text{स्थिर} $ एक आयताकार हाइपरबोला बनाता है। हालांकि, विकल्प (b) में ग्राफ एक आयताकार हाइपरबोला नहीं दिखाता है, इसलिए यह आदर्श गैस के ऊष्मारहित स्थितियों में व्यवहार को प्रतिनिधित्व नहीं करता है।
-
विकल्प (d): संबंध $ \frac{pV}{T} = \text{स्थिर} $ यह बताता है कि ग्राफ मूल बिंदु से गुजरता है। हालांकि, विकल्प (d) में ग्राफ मूल बिंदु से गुजरता नहीं है, इसलिए यह आदर्श गैस के व्यवहार को प्रतिनिधित्व नहीं करता है।
13. जब एक आदर्श गैस ऊष्मारहित रूप से संपीड़ित की जाती है, तो इसका तापमान बढ़ जाता है और अणुओं के औसत रूप से अधिक गतिज ऊर्जा होती है। गतिज ऊर्जा बढ़ती है,
(a) दीवार के गतिशील भाग के संघटन से ही
(b) दीवार के पूरे भाग के संघटन से
(c) अणुओं के अपने आयतन में गति में तेजी से होने से
(d) अणुओं में ऊर्जा के पुनर्वितरण से
उत्तर दिखाएँ
सोचने की प्रक्रिया
अणुओं के दो प्रणाली के गतिशील भाग के साथ अप्रत्यावर्ती संघटन उनकी ऊर्जा बढ़ाता है।
उत्तर (a) जब गैस ऊष्मारहित रूप से संपीड़ित की जाती है, तो गैस पर किए गए कुल कार्य गैस की आंतरिक ऊर्जा को बढ़ा देता है, जिसके परिणामस्वरूप गैस अणुओं की गतिज ऊर्जा बढ़ जाती है और इसलिए, अणुओं के बीच टक्कर भी बढ़ जाती है।
-
(ब) गतिज ऊर्जा दीवार के साथ टक्कर के कारण बढ़ नहींती क्योंकि एक अनुवर्ती प्रक्रम में वातावरण के साथ ऊष्मा का आदान-प्रदान नहीं होता, इसलिए गतिज ऊर्जा के बढ़ने का कारण गैस पर किए गए कार्य होता है, न कि दीवार के साथ टक्कर के कारण।
-
(स) गतिज ऊर्जा बढ़ नहींती क्योंकि अणु आयतन के भीतर अपनी गति में तेजी से चलते हैं। अणुओं के त्वरण का परिणाम गतिज ऊर्जा के बढ़ना होता है, न कि कारण। कारण गैस के संपीड़न के दौरान गैस पर किया गया कार्य होता है।
-
(द) गतिज ऊर्जा बढ़ नहींती क्योंकि अणुओं में ऊर्जा के पुन: वितरण के कारण। अणुओं में ऊर्जा के पुन: वितरण से कुल गतिज ऊर्जा में कोई परिवर्तन नहीं होता, यह केवल ऊर्जा के वितरण को बदलता है। गतिज ऊर्जा के बढ़ने का कारण अनुवर्ती संपीड़न के दौरान गैस पर किया गया कार्य होता है।
बहुत छोटे उत्तर प्रकार के प्रश्न
14. 39.4 ग्राम सोने में अणुओं की संख्या की गणना कीजिए। सोने का मोलर द्रव्यमान $197 g mole^{-1}$ है।
उत्तर दिखाएं
उत्तर हम जानते हैं कि,
$$ \text { मोलर द्रव्यमान } = \text { आवोगाड्रो संख्या के अणुओं के द्रव्यमान (अणु) } $$
$$ = 6.023 \times 10^{23} \text { अणु } $$
दिया गया है, सोने का मोलर द्रव्यमान $= 197 g/mol$
अब,
$\therefore \quad 197 g$ सोने में $= 6.023 \times 10^{23}$ अणु होते हैं
$\therefore \quad 1 g$ सोने में $= \frac{6.023 \times 10^{23}}{197}$ अणु होते हैं
$\therefore \quad 39.4 g$ सोने में $= \frac{6.023 \times 10^{23} \times 39.4}{197} \Rightarrow 1.20 \times 10^{23}$ अणु होते हैं।
15. एक निश्चित द्रव्यमान के गैस का 27°C, 1 atm दबाव पर आयतन 100 cc है। 327°C पर इसका आयतन क्या होगा?
उत्तर दिखाएं
उत्तर हमें दिए गए तापमान को केल्विन में बदलना होगा। यदि गैस के निश्चित द्रव्यमान के दबाव को स्थिर रखा जाए, तो
$$ \begin{aligned} & V \propto T \\ & \Rightarrow \quad \frac{V}{T} = \text { स्थिरांक } \quad[\begin{matrix} V = \text { गैस का आयतन } \\
$$ \begin{aligned} & T=\text { गैस का तापमान } \end{matrix} ] \\ & \Rightarrow \quad \frac{V_1}{T_1}=\frac{V_2}{T_2} \\ & \Rightarrow \quad V_2=V_1(\frac{T_2}{T_1}) \\ & T_1=273+27=300 K \\ & T_2=273+327=600 K \\ & \text { लेकिन } \quad V_1=100 cc \\ & V_2=V_1(\frac{600}{300}) \\ & V_2=2 V_1 \\ & V_2=2 \times 100=200 cc \end{aligned} $$
नोट: आदर्श गैस समीकरण के अनुप्रयोग के लिए, दिए गए तापमान को केल्विन में बदलना आवश्यक है।
16. एक निश्चित द्रव्यमान के गैस के अणु $27^{\circ} C$ तापमान और 1.00 वायुमंडलीय दबाव पर $100 ms^{-1}$ के वर्ग माध्य चाल के होते हैं। $127^{\circ} C$ तापमान और 2.0 वायुमंडलीय दबाव पर गैस के अणु के वर्ग माध्य चाल क्या होगी?
उत्तर दिखाएं
उत्तर हम जानते हैं कि एक निश्चित द्रव्यमान के गैस के लिए
$$ v_{rms}=\sqrt{\frac{3 R T}{M}} $$
जहाँ, $R$ गैस नियतांक है
$T$ केल्विन में तापमान है
$M$ गैस के मोलर द्रव्यमान है।
स्पष्ट रूप से,
$$ V_{rms} \propto \sqrt{T} $$
जबकि $R, M$ नियतांक हैं,
$ \frac{(v _{rms})_1}{(v _{rms})_2} $= $\sqrt \frac{T_1}{T_2} $
दिया गया है,
$\therefore$ समीकरण (i) से
$(v_{\text {rms }})_1=100 m / s $
$ T_1=27^{\circ} C=27+273=300 K $
$ T_2=127^{\circ} C=127+273=400 K$
समीकरण (i) से
$ \frac {100}{(v_{rms})_2}$ = $ \sqrt \frac{300}{400}$ = $ \frac{\sqrt 3}{2}$
$$ \Rightarrow \quad(v_{rms})_2=\frac{2 \times 100}{\sqrt{3}}=\frac{200}{\sqrt{3}} m / s $$
17. एक गैस के दो अणु क्रमशः $9 \times 10^{6} ms^{-1}$ और $1 \times 10^{6} ms^{-1}$ के वेग रखते हैं। इन अणुओं के वर्ग माध्य वेग क्या होगा?
उत्तर दिखाएं
उत्तर $ n $ अणुओं के लिए, हम जानते हैं कि
$$ v_{rms}=\sqrt{\frac{v_1^{2}+v_2^{2}+v_3^{2}+\ldots \ldots+v_n^{2}}{n}} \quad[\begin{matrix} v_{r m s}=\text { वर्ग माध्य } \\ \text { चाल } \end{matrix} ] $$
जहाँ $v_1, v_2, v_3 \ldots \ldots . . v_{n}$ गैस के $n$ अणुओं के व्यक्तिगत वेग हैं।
दो अणुओं के लिए,
दिया गया है,
$$ v_{r m s}=\sqrt{\frac{v_1^{2}+v_2^{2}}{2}} \quad[v_1, v_2, v_3 \ldots \ldots \ldots . . v_{n} \text { व्यक्तिगत वेग }]
$$
और
$$ v_1=9 \times 10^{6} m / s $$
$$ \begin{aligned} v_2 & =1 \times 10^{6} m / s \\ v_{r m s} & =\sqrt{\frac{(9 \times 10^{6})^{2}+(1 \times 10^{6})^{2}}{2}} \\ & =\sqrt{\frac{81 \times 10^{12}+1 \times 10^{12}}{2}} \\ & =\sqrt{\frac{(81+1) \times 10^{12}}{2}} \\ & =\sqrt{\frac{82 \times 10^{12}}{2}} \\ & =\sqrt{41} \times 10^{6} m / s \end{aligned} $$
18. एक गैस मिश्रण में 2.0 मोल ऑक्सीजन और 4.0 मोल नियॉन है तापमान $T$ पर। सभी विपादी तरंगों को नगण्य मानते हुए, प्रणाली की कुल आंतरिक ऊर्जा की गणना कीजिए। (ऑक्सीजन के दो घूर्णन तरंग होते हैं।)
उत्तर दिखाएँ
सोचने की प्रक्रिया
एक गैस के दिए गए अणु के लिए कुल ऊर्जा का सटीक मान जानने के लिए, हमें गैस के अणुओं के साथ संबंधित मोड़ की संख्या जानी होती है।
उत्तर $O_2$ एक द्विपरमाणुक गैस है जिसमें 5 मोड़ होते हैं।
गैस के प्रति मोल कुल आंतरिक ऊर्जा $=\frac{5}{2} R T$
$[\begin{matrix} R=\text { सार्वत्रिक गैस नियतांक } \\ T=\text { तापमान }\end{matrix} ]$
2 मोल गैस के लिए कुल आंतरिक ऊर्जा $=2 \times \frac{5}{2} R T=5 R T$
नियॉन (Ne) एक एकपरमाणुक गैस है जिसमें 3 मोड़ होते हैं।
$\therefore$ प्रति मोल ऊर्जा $=\frac{3}{2} R T$
हमारे पास 4 मोल $Ne$ हैं।
अतः,
$$ \text { ऊर्जा }=4 \times \frac{3}{2} R T=6 R T $$
$$ \begin{aligned} \text { कुल ऊर्जा } & =5 R T+6 R T \\ & =11 R T \end{aligned} $$
19. दो गैसों के अणुओं के औसत मुक्त पथ के अनुपात की गणना कीजिए जिनके अणुओं के व्यास $1 \AA$ और $2 \AA$ हैं। गैसों को तापमान, दबाव और आयतन के समान शर्तों के अंतर्गत लिया जा सकता है।
उत्तर दिखाएँ
उत्तर एक अणु के औसत मुक्त पथ को निम्नलिखित द्वारा दिया जाता है
$$ l=\frac{1}{\sqrt{2} d^{2} n} $$
जहाँ, $n=$ अणुओं की संख्या/आयतन
$d=$ अणु का व्यास
अब, हम लिख सकते हैं $l \propto \frac{1}{d^{2}}$
दिया गया है,
$$ d_1=1 \AA, d_2=2 \AA $$
जैसे कि
$\Rightarrow$ अतः,
$$ l_1 \propto \frac{1}{d_1^{2}} \text { और } l_2 \propto \frac{1}{d_2^{2}}
$$
$\Rightarrow$ इसलिए,
$$ \frac{l_1}{l_2}=(\frac{d_2}{d_1})^{2}=(\frac{2}{1})^{2}=\frac{4}{1} $$
इसलिए,
$$ l_1: l_2=4: 1 $$
छोटे उत्तर प्रकार प्रश्न
20. चित्र में दिखाए गए बरतन में दो कमरे हैं, जो एक विभाजक द्वारा अलग किए गए हैं, जिनके आयतन $V_1=2.0 L$ और $V_2=3.0 L$ हैं। कमरों में $\mu_1=4.0$ और $\mu_2=5.0$ मोल गैस है, जो दबाव $p_1=1.00 atm$ और
| $p _1, V _1$ | $p _2, V _2$ |
|---|---|
| $\mu _1$ | $\mu _2$ |
$p_2=2.00 atm$ पर है। विभाजक हटाने के बाद और मिश्रण संतुलन पर पहुँच जाने के बाद दबाव की गणना करें।
| $V _1, \mu _1$, | $V _2$ |
|---|---|
| $p _1$ | $\mu _2$, |
| $p _2$, |
उत्तर दिखाएं
उत्तर चित्र को ध्यान में रखें,
दिया गया है,
$$ \begin{aligned} V_1 & =2.0 L, V_2=3.0 L \\ \mu_1 & =4.0 mol, \mu_2=5.0 mol \\ p_1 & =1.00 atm, p_2=2.00 atm \end{aligned} $$
कमरा 1 के लिए, $p_1, V_1=\mu_1 R T_1$
कमरा 2 के लिए, $p_2, V_2=\mu_2 R T_2$
जब विभाजक हटा दिया जाता है तो गैसें बिना ऊर्जा की कोई हानि के मिश्रित हो जाती हैं। अब मिश्रण एक सामान्य संतुलन दबाव पर पहुँच जाता है और प्रणाली का कुल आयतन व्यक्तिगत कमरों के आयतन $V_1$ और $V_2$ के योग होता है।
इसलिए,
गैसों के गतिमेंद्रिक सिद्धांत से,
लिए गए $l$ मोल के लिए, $p V=\frac{2}{3} E$ $[\begin{matrix} E=\underset{\text { किनेटिक ऊर्जा }}{\text { परिवहन }}\end{matrix} ]$
लिए गए $\mu_1$ मोल के लिए,
$$ p_1 V_1=\frac{2}{3} \mu_1 E_1 $$
लिए गए $\mu_2$ मोल के लिए,
$$ p_2 V_2=\frac{2}{3} \mu_2 E_2 $$
कुल ऊर्जा है
$$ (\mu_1 E_1+\mu_2 E_2)=\frac{3}{2}(p_1 V_1+p_2 V_2) $$
उपरोक्त संबंध से, $\quad p V=\frac{2}{3} E_{\text {कुल }}=\frac{2}{3} \mu E_{\text {प्रति मोल }}$
$$ \begin{aligned} p(V_1+V_2) & =\frac{2}{3} \times \frac{3}{2}(p_1 V_1+p_2 V_2) \\ p & =\frac{p_1 V_1+p_2 V_2}{V_1+V_2} \\ & =(\frac{1.00 \times 2.0+2.00 \times 3.0}{2.0+3.0}) atm \\ & =\frac{8.0}{5.0}=1.60 atm \end{aligned} $$
21. एक गैस मिश्रण में $A, B$ और $C$ के अणु हैं, जिनके द्रव्यमान $m_{A}>m_{B}>m_{C}$ है। (a) औसत किनेटिक ऊर्जा और (b) rms गति के क्रम में तीन प्रकार के अणुओं की व्यवस्था करें।
उत्तर दिखाएँ
उत्तर (ए) तापमान और दबाव के स्थिति समान होने के कारण औसत कार्य ऊर्जा समान होगी।
अब,
$$ \begin{aligned} v_{rms} & =\sqrt{\frac{3 p V}{M}}=\sqrt{\frac{3 R T}{M}} \\ & =\sqrt{\frac{3 R T}{m N}}=\sqrt{\frac{3 k T}{m}} \end{aligned} $$
जहाँ,
स्पष्ट रूप से,
$$ \begin{aligned} M & =\text { गैस की मोलर द्रव्यमान } \\ m & =\text { गैस के प्रत्येक अणु की द्रव्यमान } \\ R & =\text { गैस नियतांक } \end{aligned} $$
(बी) क्योंकि $k = $ बोल्ट्जमैन नियतांक
$$ v_{rms} \propto \sqrt{\frac{1}{m}} $$
$T$ = अंतराल तापमान (सभी के लिए समान है)
लेकिन $m_{A}>m_{B}>m_{C}$
$(v _ {rms})_A < (v _ {rms})_B < (v _ {rms})_C $
या
$(v _ {rms})_C > (v _ {rms})_B > (v _ {rms})_A$
22. हमें एक घनाकार कमरे में $3 cm$ के आकार के एक घन में $0.5 g$ हाइड्रोजन गैस है जो NTP पर रखे गए हैं। कमरे में गैस को संपीड़ित किया जाता है जबकि तापमान स्थिर रहता है तक अंतिम दबाव $100 atm$ हो जाता है। अंतिम अवस्था में आदर्श गैस के नियम के अनुमान करने के लिए एक व्यक्ति को जस्टिफ़ि रहे हैं? (हाइड्रोजन अणुओं को त्रिज्या $1 \AA$ के गोले के रूप में माना जा सकता है।)
उत्तर दिखाएँ
सोचने की प्रक्रिया
आदर्श गैस के नियम के अनुमान के लिए अणुओं के आयतन और आदर्श गैस द्वारा उपयोग किए गए आयतन की तुलना की जाती है। यदि दोनों में से मेल खाता है, तो नियम ठीक रहता है अन्यथा नहीं।
उत्तर हाइड्रोजन अणुओं को त्रिज्या $1 \AA$ के गोले के रूप में मान लें।
इसलिए, $r=1 \AA=$ त्रिज्या।
हाइड्रोजन अणुओं का आयतन $=\frac{4}{3} \pi r^{3}$
$$ \begin{aligned} =\frac{4}{3}(3.14)(10^{-10})^{3} & \approx 4 \times 10^{-30} m^{3} \\ \text { हाइड्रोजन के मोल की संख्या } & =\frac{\text { द्रव्यमान }}{\text { अणुक द्रव्यमान }} \\ & =\frac{0.5}{2}=0.25 \end{aligned} $$
$H_2$ के अणुओं की संख्या $=$ $H_2$ के मोल की संख्या $\times 6.023 \times 10^{23}$
$$ =0.25 \times 6.023 \times 10^{23} $$
$\therefore$ उपस्थित अणुओं का आयतन $=$ अणुओं की संख्या $\times$ प्रत्येक अणु का आयतन
$$ \begin{aligned} & =0.25 \times 6.023 \times 10^{23} \times 4 \times 10^{-30} \\ & =6.023 \times 10^{23} \times 10^{-30} \\
& \approx 6 \times 10^{-7} m^{3} \end{aligned} $$
अब, यदि आदर्श गैस के नियम को स्थिर माना जाता है।
$$ \begin{aligned} p_{i} V_{i} & =p_{f} V_{f} \\ V_{f} & =(\frac{p_{i}}{p_{f}}) V_{i}=(\frac{1}{100})(3 \times 10^{-2})^{3} \\ & =\frac{27 \times 10^{-6}}{10^{2}} \\ & =2.7 \times 10^{-7} m^{3} \end{aligned} $$
इसलिए, संपीड़न के बाद गैस के आयतन का क्रम अणुक आयतन के समान है [समीकरण (i) और समीकरण (ii) से]। अणुक बल भूमिका निभाएगे और गैस आदर्श गैस व्यवहार से विचलित हो जाएगी।
23. जब एक साइकिल टायर में हवा भरी जाती है तो टायर में हवा का आयतन और दबाव दोनों बढ़ जाते हैं। इस स्थिति में बॉयल के नियम के बारे में क्या कहा जा सकता है?
उत्तर दिखाएँ
उत्तर जब हवा भरी जाती है तो अधिक अणु भरे जाते हैं और बॉयल के नियम उस स्थिति में बताता है जहां अणुओं की संख्या स्थिर रहती है।
इस स्थिति में, हवा के अणुओं की संख्या बढ़ती रहती है। इसलिए, यह एक चर द्रव्यमान की स्थिति है। बॉयल के नियम (और चार्ल्स के नियम भी) केवल उन स्थितियों में लागू होते हैं जहां गैस के अणुओं की संख्या स्थिर रहती है।
इसलिए, इस स्थिति में बॉयल के नियम के अनुपालन नहीं होता है।
24. एक बैलून में हीलियम के 5.0 मोल है $7^{\circ} C$ पर। गणना करें
(a) बैलून में हीलियम के अणुओं की संख्या।
(b) प्रणाली की कुल आंतरिक ऊर्जा।
उत्तर दिखाएँ
सोचने की प्रक्रिया
एक मोनोअटोमिक अणु के साथ संबंधित ऊर्जा $\frac{3}{2} k T$ होती है।
उत्तर दिया गया, हीलियम के मोल की संख्या $=5$
$$ T=7^{\circ} C=7+273=280 K $$
(a) इसलिए, अणुओं की संख्या (हीलियम मोनोअटोमिक होता है)
$$ \begin{aligned} & =\text { मोल की संख्या } \times \text { आवोगाड्रो संख्या } \\ & =5 \times 6.023 \times 10^{23} \\ & =30.015 \times 10^{23} \\ & =3.0 \times 10^{24} \text { अणु } \end{aligned} $$
(b) अब, एक अणु के औसत किनेटिक ऊर्जा $=\frac{3}{2} k_{B} T$
यहां, $k_{B}=$ बोल्ट्जमैन नियतांक है।
(इसमें केवल 3 स्वतंत्रता डिग्री होती है)
$\therefore$ सभी अणुओं की कुल ऊर्जा
$$ \begin{aligned} & =\text { कुल आंतरिक ऊर्जा } \\
$$ \begin{aligned} & =\frac{3}{2} k_{b} T \times \text { number of atoms } \\ & =\frac{3}{2} \times 1.38 \times 10^{-23} \times 280 \times 3.0 \times 10^{24} \\ & =1.74 \times 10^{4} J \end{aligned} $$
25. 1 cc हाइड्रोजन गैस के अणुओं की मोलर ऊर्जा की डिग्री की संख्या गणना करें।
उत्तर दिखाएं
सोच की प्रक्रिया
एक थर्मोडाइनामिक प्रणाली में कुल डिग्री की संख्या $=$ प्रति अणु डिग्री की संख्या × अणुओं की संख्या।
उत्तर दिया गया अणु हाइड्रोजन के हैं।
$\therefore$ 1 मोल गैस द्वारा घेरे गए आयतन
$$ \begin{aligned} & =1 \text { मोल गैस एनटीपी पर } \\ & =22400 mL=22400 cc \end{aligned} $$
$\therefore$ 1 cc हाइड्रोजन में अणुओं की संख्या
$$ =\frac{6.023 \times 10^{23}}{22400}=2.688 \times 10^{19} $$
$H_2$ एक डाइएटोमिक गैस है, जिसकी कुल 5 डिग्री होती है (3 आयामिक + 2 घूर्णन)
$\therefore$ सभी अणुओं द्वारा अधिकृत कुल डिग्री
$$ \begin{aligned} & =5 \times 2.688 \times 10^{19} \\ & =1.344 \times 10^{20} \end{aligned} $$
नोट: कोई आदर्श गैस एनटीपी पर 22400 mL (cc) के मोलर आयतन के रूप में होती है।
26. एक ऊष्मारोधी कंटेनर में मोनोएटोमिक गैस के मोलर द्रव्यमान $m$ है जो वेग $v_{o}$ के साथ गति कर रहा है। यदि कंटेनर अचानक रूप से रोक दिया जाता है, तो तापमान में परिवर्तन ज्ञात करें।
उत्तर दिखाएं
सोच की प्रक्रिया
जब कंटेनर अचानक रूप से रोक दिया जाता है तो ऊष्मा के आदान-प्रदान के लिए कोई समय नहीं होता।
उत्तर तापमान के किनेटिक अनुवाद के अनुसार, एक गैस के नमूने के अंतर्गत अंतर्गत तापमान उसके अणुओं की कुल आयामिक गतिज ऊर्जा के समानुपातिक होता है।
इसलिए, किसी गैस के अंतर्गत तापमान में कोई परिवर्तन उसकी आयामिक गतिज ऊर्जा में संगत परिवर्तन के रूप में देखा जा सकता है और विपरीत रूप से भी।
मान लीजिए $n=$ मोल की संख्या।
दिया गया, $\quad m=$ गैस का मोलर द्रव्यमान।
जब कंटेनर रोक दिया जाता है, तो इसकी कुल गतिज ऊर्जा गैस अणुओं के रूप में आयामिक गतिज ऊर्जा के रूप में स्थानांतरित हो जाती है, जिससे अंतर्गत तापमान बढ़ जाता है।
If $\Delta T$ = change in absolute temperature.
Then, $KE$ of molecules due to velocity $v_0, KE=\frac{1}{2}(m n) v_0^{2}$
Increase in translational $K E=n \frac{3}{3} R(\Delta T)$
According to kinetic theory Eqs. (i) and (ii) are equal
$$ \begin{matrix} \Rightarrow & \frac{1}{2}(m n) v_0^{2} & =n \frac{3}{2} R(\Delta T) \\ \Rightarrow & \Delta T & =\frac{(m n) v_0^{2}}{3 n R} \\ \Rightarrow & n 3 R(\Delta T) = (m n) v_0^{2} \\ \Rightarrow & \Delta T & =\frac{m v_0^{2}}{3 R} \end{matrix} $$
लंबा उत्तर प्रकार प्रश्न
27. स्पष्ट करें कि
(a) चांद पर वायुमंडल नहीं है
(b) ऊंचाई के साथ तापमान कम हो जाता है
उत्तर दिखाएँ
उत्तर (a) चांद पर छोटा गुरुत्वाकर्षण बल है (आकर्षण) और इसलिए, भाप वेग छोटा है। चांद के भाप वेग का मान $4.6 km / s$ है।
चांद सूर्य से दूर नहीं है, इसलिए चांद पर प्रति इकाई क्षेत्र के लिए तापमान पृथ्वी के तापमान के समान है।
वायु के अणुओं के वेग की बहुत बड़ी श्रेणी होती है। भले ही वायु के अणुओं के rms वेग चांद पर भाप वेग से कम होता है, लेकिन कई अणुओं के वेग भाप वेग से अधिक होता है और वे भाप जाते हैं।
अब, शेष अणु तापमान के संतुलन के लिए वेग वितरण को संतुलित करते हैं। फिर भी कई अणुओं के वेग भाप वेग से अधिक हो जाते हैं और वे भाप जाते हैं। इसलिए, लंबे समय बाद चांद अधिकांश वायुमंडल खो बैठता है।
$$ \begin{aligned} \text { At } 300 K, v_{rms}=\sqrt{\frac{3 kT}{m}} & =\sqrt{\frac{3 \times 1.38 \times 10^{-23} \times 300}{7.3 \times 10^{-26}}}=1.7 km / s \\ v_{es} \text { for moon } & =4.6 km / s \quad \quad[v_{es}=\text { escape velocity }] \end{aligned} $$
(b) जैसे अणु ऊंचाई बढ़ते जाते हैं, उनकी संभावित ऊर्जा बढ़ती जाती है और इसलिए, गतिज ऊर्जा कम हो जाती है और तापमान कम हो जाता है।
अधिक ऊंचाई पर अधिक आयतन उपलब्ध होता है और गैस फैलती है और इसलिए, कुछ शीतलन होता है।
नोट: हम तापमान को संभावित ऊर्जा के साथ सीधे संबंध नहीं रखना चाहिए। यह अणुओं की गतिज ऊर्जा के साथ सीधे संबंध होता है।
28. एक आदर्श गैस के वेग के निम्नलिखित वितरण को ध्यान में रखते हुए विचार करें।
| वेग $(m / s)$ | अणुओं का प्रतिशत |
|---|---|
| 200 | 10 |
| 400 | 20 |
| 600 | 40 |
| 800 | 20 |
| 1000 | 10 |
(a) $v_{\text {rms }}$ की गणना करें और फिर $T$ की गणना करें। ($m=3.0 \times 10^{-26} kg$)
(b) यदि सभी वेग $1000 m / s$ वाले अणु प्रणाली से बाहर निकल जाएं, तो नए $v_{\text {rms }}$ और फिर $T$ की गणना करें।
उत्तर दिखाएं
सोचने की प्रक्रिया
इस समस्या में दिखाया गया है कि वाष्पीकरण के बाद ठंडक होती है।
उत्तर (a) हम जानते हैं कि
$$ v_rms^{2}=\frac{\sum_{i} n_{i} v_i^{2}}{\sum n_{i}} $$
यह सभी अणुओं के लिए औसत वर्ग वेग है।
$$ \text { अब, } \begin{aligned} v_{\text {rms }} & =(\frac{\sum_{i} n_{i} v_i^{2}}{\sum n_{i}})^{\frac{1}{2}} \\ & =\sqrt{\frac{n_1 v_1^{2}+n_2 v_2^{2}+n_3 v_3^{2}+\ldots \ldots \ldots+n_{n} v_n^{2}}{n_1+n_2+n_3+\ldots \ldots . .+n_{n}}} \\ & =\sqrt{\frac{n_1 v_1^{2}+n_2 v_2^{2}+n_3 v_3^{2}+n_4 v_4^{2}+n_5 v_5^{2}}{n_1+n_2+n_3+n_4+n_5}} \\ & =\sqrt{\frac{.10 \times(200)^{2}+20 \times(400)^{2}+40 \times 600)^{2}+20 \times(800)^{2}+10 \times(1000)^{2}}{100}} \\ & =\sqrt{1000 \times(4+32+144+128+100)} \\ & =\sqrt{408 \times 1000} \approx 639 m / s . \end{aligned} $$
अब, गैस के गतिज तर्क के अनुसार
$$ \begin{aligned} \frac{1}{2} m v_rms^{2} & =\frac{3}{2} k_{B} T \quad[\begin{matrix} K_{B}=\text { बोल्ट्जमैन नियतांक } \\ m=\text { गैसीय अणुओं का द्रव्यमान } \end{matrix} ] \\ T=\frac{1}{3} \frac{m v_rms^{2}}{k_{B}} & =\frac{1}{3} \times \frac{3.0 \times 10^{-26} \times 4.08 \times 10^{5}}{1.38 \times 10^{-23}} \\ & =2.96 \times 10^{2} K=296 K \end{aligned} $$
(b) यदि सभी वेग $1000 m / s$ वाले अणु प्रणाली से बाहर निकल जाएं, तो
$$ \begin{aligned} v_rms^{2} & =\frac{10 \times(200)^{2}+20 \times(400)^{2}+40 \times(600)^{2}+20 \times(800)^{2}}{90} \\ & =\frac{10 \times 100^{2} \times(1 \times 4+2 \times 16+4 \times 36+2 \times 64)}{90} \\ & =10000 \times \frac{308}{9}=342 \times 1000 m^{2} / s^{2} \\ $$
\text { फिर से } \quad v_{rms} & =584 m / s \\ T & =\frac{1}{3} \frac{mv_{rms}^{2}}{k} \\ & =\frac{1}{3} \times \frac{3 \times 10^{-26} \times 3.42 \times 10^{5}}{1.38 \times 10^{-23}} \\ & =2.478 \times 10^{2} \\ & =247.8 \approx 248 K \end{aligned} $$
नोट: मोलेकुलों के वेग $1000 m / s$ के साथ उत्सर्जन के बाद, भाग (b) में तापमान $248 K$ है जबकि भाग (a) में उत्सर्जन से पहले तापमान 296 K था। इसलिए, वाष्पीकरण शीतलन को सुगम बनाता है।
29. दस छोटे विमान $150 km / h$ की गति से कुल अंधेरे में $20 \times 20 \times 1.5 km^{3}$ आयतन के वायु अंतरिक में उड़ रहे हैं। आप इन विमानों में से एक में हैं, जो इस अंतरिक में यादृच्छिक रूप से उड़ रहे हैं और अन्य विमानों के स्थान के बारे में कोई ज्ञान नहीं है। आपके विमान के साथ निकटतम टकराव के बीच औसतन कितने समय लगेगा? इस लगभग गणना के लिए मान लीजिए कि विमान के आसपास सुरक्षा क्षेत्र को एक त्रिज्या $10 m$ के गोले के रूप में अपेक्षित किया जा सकता है।
उत्तर दिखाएँ
चिंतन प्रक्रिया
इस समस्या को हल करने के लिए हमें आराम काल और औसत मुक्त पथ के बारे में विचार करना होगा।
उत्तर इस स्थिति को गैस के गतिमें आधारित आराम काल के आधार पर विचार किया जा सकता है। औसत मुक्त पथ दो क्रमागत टकराव के बीच दूरी है, जिसे हम यहाँ विमान के द्वारा टकराव से बचने के लिए तय की गई दूरी के रूप में लेंगे, जो परमाणु के त्रिज्या के तुलनात्मक है।
इसलिए, आवश्यक समय
$$ \begin{aligned} t=\frac{l}{V}, l=\text { औसत मुक्त पथ } & =\frac{1}{\sqrt{2} \pi d^{2} n}, n=\text { संख्या घनत्व }=\frac{N}{V} \\ n & =\frac{\text { विमानों की संख्या }(N)}{\text { आयतन }(V)} \\ & =\frac{10}{20 \times 20 \times 1.5}=0.0167 km^{-3} \\ t & =\frac{1}{\sqrt{2} \pi d^{2}(N / V)} \times \frac{1}{V} \quad[V=\text { विमान की गति }] \end{aligned} $$
दिए गए डेटा के साथ,
$$ \begin{aligned} t & =\frac{1}{\sqrt{2} \times 3.14 \times(20)^{2} \times 0.0167 \times 10^{-6} \times 150} \\
$$ \begin{aligned} & =\frac{10^{6}}{1776.25 \times 2.505} \\ & =\frac{10^{6}}{4449.5}=224.74 h \\ & \approx 225 h \end{aligned} $$
30. एक $1.00 m^{3}$ के बॉक्स को $300 K$ तापमान पर $1.50 atm$ दबाव पर नाइट्रोजन से भरा जाता है। बॉक्स में एक छेद है जिसका क्षेत्रफल $0.010 mm^{2}$ है। यदि बाहरी दबाव $1 atm$ है, तो दबाव के $0.10 atm$ तक कम होने में कितना समय लगेगा?
उत्तर दिखाएं
उत्तर दिया गया, बॉक्स का आयतन, $V=1.00 m^{3}$
$$ \begin{gathered} \text { क्षेत्रफल }=a=0.010 mm^{2} \\ =8.01 \times 10^{-6} m^{2} \\ =10^{-8} m^{2} \end{gathered} $$
बाहरी तापमान = आंतरिक तापमान
बॉक्स के आंतरिक शुरुआती दबाव = $1.50 atm$.
बॉक्स के आंतरिक अंतिम दबाव = $0.10 atm$.
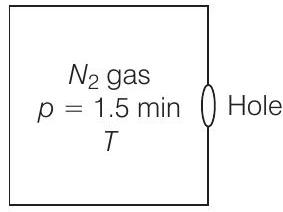
$p_{\text {outside }}=1$ atm मान लें,
$v_{i x}=$ बॉक्स के आंतरिक नाइट्रोजन अणु की $x$-दिशा में गति की चाल।
$n_{i}=$ एक समय अंतराल $\Delta T$ में इकाई आयतन में अणुओं की संख्या, सभी अणु जो दूरी $(v_{i x} \Delta t)$ पर छेद और दीवार से टकराएंगे, अणु जो छेद के माध्यम से बाहर निकलेंगे तो बॉक्स में दबाव कम हो जाएगा।
दीवार के क्षेत्रफल के अंतर्गत, समय में टकराने वाले अणुओं की संख्या
$$ \Delta t=\frac{1}{2} n_{i}(v_{i x} \Delta t) A $$
$\frac{1}{2}$ गुणक इसलिए है कि सभी $x$-दिशा में अणु यादृच्छिक रूप से व्यवहार करते हैं। इसलिए, इनमें से आधे अणु दोनों ओर की दीवारों पर टकराएंगे।
बॉक्स में, $\quad v_{i x}^{2}+v_{i y}^{2}+v_{i z}^{2}=v_{\text {rms }}^{2}$
$$ .\begin{matrix} \therefore & v_{i x}^{2}=\frac{v_rms^{2}}{3} \\ \text { या } & \frac{1}{2} m v_rms^{2} & =\frac{3}{2} k_{B} T \\ \Rightarrow & v_rms^{2} & =\frac{3 k_{B} T}{m} \end{matrix} ] $$
[गैसों के गतिमेंद्रिक सिद्धांत के अनुसार]
अब
$$ v_{i x}^{2}=\frac{v_rms^{2}}{3}=\frac{1}{3} \times \frac{3 k_{B} T}{m} $$
या
$$ v_{i x}^{2}=\frac{k_{B} T}{m}
$$
$\therefore$ समय में टकराने वाले कणों की संख्या
$$ \Delta t=\frac{1}{2} n_{i} \sqrt{\frac{k_{B} T}{m}} \Delta t A $$
यदि कण छेद के माध्यम से टकराते हैं, तो वे बाहर जाते हैं। इसी तरह, बाहरी कण छेद के माध्यम से टकराते हैं तो वे अंदर आते हैं।
यदि $a=$ छेद का क्षेत्रफल है
तो, समय $\Delta t$ में शुद्ध कण प्रवाह $=\frac{1}{2}(n_1-n_2) \sqrt{\frac{k_{B} T}{m}} \Delta t a$
[कॉर्नर के अंदर और बाहर के तापमान समान हैं]
$$ p V=\mu R T \Rightarrow \mu=\frac{p V}{R T} $$
मान लीजिए $n=$ नाइट्रोजन के कण घनत्व $=\frac{\mu N_{A}}{V}=\frac{p N_{A}}{R T}$
मान लीजिए $N_{A}=$ आवोगाड्रो संख्या
यदि समय $\tau$ के बाद बाहर के दबाव के बदले $p$ से $p_1^{1}$ हो जाता है
$$ \therefore \quad \quad n_1^{\prime}=\frac{V N_{A}}{R T} $$
अब, बाहर गए कणों की संख्या $=n_1 V-n_1^{\prime} V$
$ =\frac{1}{2}(n_1-n_2) \sqrt{\frac{k_{B} T}{m}} \tau a $
$\therefore \frac{p_1 N_{A}}{R T} V-\frac{v N_{A}}{R T} V =\frac{1}{2}(p_1-p_2) \frac{N_{A}}{R T} \sqrt{\frac{k_{B} T}{m}} \tau a $
$ \text { या } \frac{p_1 N_{A}}{R T} V-\frac{v N_{A}}{R T} V =\frac{1}{2}(p_1-p_2) \frac{N_{A}}{R T} \sqrt{\frac{k_{B} T}{m}} \tau a $
$ \therefore \tau =2(\frac{p_1-p v_1}{p_1-p_2}) \frac{V}{a} \sqrt{\frac{m}{k_{B} T}}$
दिए गए डेटा से मान रखने पर,
$$ \begin{aligned} \tau & =2(\frac{1.5-1.4}{1.5-1.0}) \frac{1 \times 1.00}{0.01 \times 10^{-6}} \sqrt{\frac{46.7 \times 10^{-27}}{1.38 \times 10^{-23} \times 300}} \\ & =2(\frac{0.1}{0.5}) \frac{1}{10^{-8}} \sqrt{\frac{4.7}{1.38 \times 3} \times 10^{-6}} \\ & =2(\frac{1}{5}) 1 \times 10^{8} \times 10^{-3} \times \sqrt{\frac{46.7}{4.14}}=\frac{2}{5} \times 10^{5} \sqrt{\frac{45.7}{4.14}} \\ & =\frac{2}{5} \times 10^{5} \sqrt{11.28} \\ & =\frac{2}{5} \times 3.358 \times 10^{5}=\frac{6.717}{5} \times 10^{5}=1.343 \times 10^{5} s \end{aligned} $$
31. एक घन लकड़ी के ब्लॉक को गैस के तापमान $T$ और द्रव्यमान घनत्व $\rho$ में वेग $v_0$ के साथ गति करते हुए मान लीजिए। मान लीजिए वेग $x$-अक्ष के अनुदिश है और $v_0$ के लंबवत ब्लॉक के परिसेक्शन क्षेत्रफल $A$ है। दिखाइए कि ब्लॉक पर घर्षण बल $4 r A v_0 \sqrt{\frac{k T}{m}}$ है, जहां $m$ गैस अणु के द्रव्यमान है।
उत्तर दिखाएं
सोचने की प्रक्रिया
यदि एक भारी वस्तु एक हल्की वस्तु के सापेक्ष वेग $v+v_{o}$ से गति कर रही है, तो हल्की वस्तु के संवेग में $2 m(v+v_0)$ का परिवर्तन होता है जो भारी वस्तु में स्थानांतरित हो जाता है।
उत्तर चित्र को ध्यान में रखें
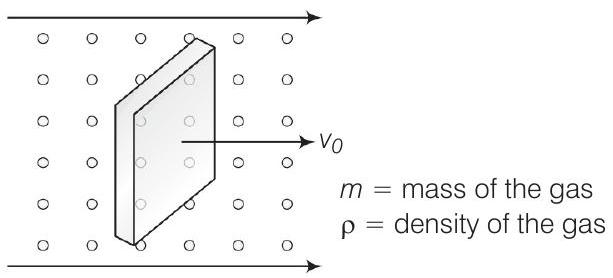
मान लीजिए $n=$ इकाई आयतन में अणुओं की संख्या
$v_{\text {rms }}=$ गैस अणुओं का rms वेग
जब ब्लॉक $v_0$ के वेग से गति कर रही है, तो अणुओं के सापेक्ष आगे के फलक के सापेक्ष वेग $=v+v_0$
मुकाबला करते हुए, प्रति टकराव में संवेग के स्थानांतरण $=2 m(v+v_0)$,
जहाँ, $m=$ अणु का द्रव्यमान है।
समय $\Delta t$ में टकराव की संख्या $=\frac{1}{2}(v+v_0) n \Delta t A$, जहाँ, $A=$ ब्लॉक के परिसेक्शन क्षेत्रफल और $1/2$ कारक ब्लॉक की ओर गति कर रहे कणों के कारण उत्पन्न होता है।
इसलिए, समय $\Delta t$ में संवेग के स्थानांतरण $=m(v+v_0)^{2} n A \Delta t$ आगे के सतह से।
उसी तरह, समय $\Delta t$ में संवेग के स्थानांतरण $=m(v-v_0)^{2} n A \Delta t$ (पीछे के सतह से)
इसलिए, शुद्ध बल
$$ \begin{aligned} (\text { घर्षण बल }) & =m n A[(v+v_0)^{2}-(v-v_0)^{2}] \\ & =m n A(4 v v_0)=(4 m n A v) v_0 \\ & =(4 \rho A v) v_0 \\ \text { शुद्ध } \quad \quad \rho & =\frac{m n}{v}=\frac{M}{V} \end{aligned} $$
जहाँ हमने मान लिया है
[सामने से]
यदि $v=$ $x$-अक्ष के अनुदिश वेग है
तो हम लिख सकते हैं
$$ KE=\frac{1}{2} m v^{2}=\frac{1}{2} k_{B} T $$
$\Rightarrow$ $ v=\sqrt{\frac{k_{B} T}{m}} $
$[\begin{matrix} K_{B} & =\text { बोल्ट्जमैन नियतांक } \\ K E & =\text { गतिज ऊर्जा } \\ T & =\text { तापमान }\end{matrix} ]$
इसलिए, समीकरण (i) से, $\quad$ घर्षण बल $=(4 \rho A v) v_0=4 \rho A \sqrt{\frac{k_{B} T}{m}} v_0$।





