हल

मान लीजिए $\alpha=60^{\circ}, \beta=45^{\circ}$ और $OZ$ अक्ष के सापेक्ष झुकाव को $\gamma$ हो।

हम जानते हैं कि

$\cos ^{2} \alpha+\cos ^{2} \beta+\cos ^{2} \gamma=1$

$\Rightarrow \cos ^{2} 60^{\circ}+\cos ^{2} 45^{\circ}+\cos ^{2} \gamma=1$

$\Rightarrow \quad(\dfrac{1}{2})^{2}+(\dfrac{1}{\sqrt{2}})^{2}+\cos ^{2} \gamma=1 \quad \Rightarrow \quad \dfrac{1}{4}+\dfrac{1}{2}+\cos ^{2} \gamma=1$

$\Rightarrow \quad \dfrac{3}{4}+\cos ^{2}\gamma=1 \Rightarrow \cos ^{2} \gamma=1-\dfrac{3}{4}=\dfrac{1}{4}$

$\therefore \quad \cos \gamma= \pm \dfrac{1}{2}$

$\therefore \quad \overrightarrow{{}OA}=|\overrightarrow{{}OA}|(\dfrac{1}{2} \hat{i}+\dfrac{1}{\sqrt{2}} \hat{j}\pm\dfrac{1}{2} \hat{k})=10(\dfrac{1}{2} \hat{i}+\dfrac{1}{\sqrt{2}} \hat{j}\pm\dfrac{1}{2} \hat{k})$

$=5 \hat{i}+5 \sqrt{2} \hat{j}\pm5 \hat{k}$

अतः, $A$ का स्थिति सदिश $(5 \hat{i}+5 \sqrt{2} \hat{j}\pm5 \hat{k})$ है।

हल

हम जानते हैं कि रेखा का समीकरण होता है

$ \vec{r}=\vec{a}+\vec{b} \lambda $

यहाँ, $\vec{a}=\hat{i}-2 \hat{j}+3 \hat{k}$ और $ \overrightarrow{{}b}= 3\hat{i}-2 \hat{j}+6 \hat{k}$

$\therefore$ रेखा का समीकरण $\vec{r}=(\hat{i}-2 \hat{j}+3 \hat{k})+\lambda(3 \hat{i}-2 \hat{j}+6 \hat{k}) $

$\Rightarrow (x\hat{i} + y \hat{j}+ z \hat{k})= (\hat{i}-2 \hat{j}+3 \hat{k})+\lambda(3 \hat{i}-2 \hat{j}+6 \hat{k})$

$\Rightarrow(x \hat{i}+y \hat{j}+z \hat{k})-(\hat{i}-2 \hat{j}+3 \hat{k})=\lambda(3 \hat{i}-2 \hat{j}+6 \hat{k})$

$\Rightarrow(x-1) \hat{i}+(y+2) \hat{j}+(z-3) \hat{k}=\lambda(3 \hat{i}-2 \hat{j}+6 \hat{k})$

इसलिए, आवश्यक समीकरण है

$(x-1) \hat{i}+(y+2) \hat{j}+(z-3) \hat{k}=\lambda(3 \hat{i}-2 \hat{j}+6 \hat{k})$

हल

दी गई समीकरण हैं

$ \begin{aligned} & \dfrac{x-1}{2}=\dfrac{y-2}{3}=\dfrac{z-3}{4} \text{ और } \dfrac{x-4}{5}=\dfrac{y-1}{2}=z \\ & \text{ मान लीजिए } \quad \dfrac{x-1}{2}=\dfrac{y-2}{3}=\dfrac{z-3}{4}=\lambda \\ & \therefore x=2 \lambda+1, y=3 \lambda+2 \text{ और } z=4 \lambda+3 \\ & \text{ और } \quad \dfrac{x-4}{5}=\dfrac{y-1}{2}=\dfrac{z}{1}=\mu \\ & \therefore x=5 \mu+4, y=2 \mu+1 \text{ और } z=\mu \end{aligned} $

यदि दोनों रेखाएँ एक बिंदु पर प्रतिच्छेद करती हैं,

तो $2 \lambda+1=5 \mu+4 \Rightarrow 2 \lambda-5 \mu=3\quad …$ (i)

$3 \lambda +2=2 \mu+1 \Rightarrow 3 \lambda-2 \mu=-1 \quad …$ (ii)

और $4 \lambda+3=\mu \quad \Rightarrow 4 \lambda-\mu=-3 \quad …$ (iii)

समीकरण (i) और (ii) को हल करने पर हम प्राप्त करते हैं

$\begin{aligned} \Rightarrow 6 \lambda-15 \mu=9 \\ 6 \lambda-4 \mu=-2 \\ (-) \quad (+) \quad (+) \\ \hline \quad -11 \mu =\quad 11 \\ \therefore \quad \mu=-1 \end{aligned}$

$\mu$ के मान को समीकरण (i) में रखने पर हम प्राप्त करते हैं,

$2\lambda -5(-1) =3$

$\Rightarrow \quad 2 \lambda+5 =3$

$\Rightarrow \quad 2 \lambda =-2 \quad \therefore \lambda=-1$

अब $\lambda$ और $\mu$ के मान को समीकरण (iii) में रखने पर हम प्राप्त करते हैं

$ \begin{aligned} 4(-1)-(-1) & =-3 \\ -4+1 & =-3 \\ -3 & =-3 \text{ (संतुष्ट) } \end{aligned} $

$\therefore$ दी गई रेखाएँ प्रतिच्छेद करती हैं और प्रतिच्छेद बिंदु के निर्देशांक हैं

$ \begin{aligned} & x=5(-1)+4=-5+4=-1 \\ & y=2(-1)+1=-2+1=-1 \\ & z=-1 \end{aligned} $

इसलिए, दी गई रेखाएँ एक दूसरे के बराबर $(-1,-1,-1)$ पर प्रतिच्छेद करती हैं।

Solution

यहाँ,

$ \vec{b} _1=2 \hat{i}+\hat{j}+2 \hat{k} \text{ और } \vec{b} _2=6 \hat{i}+3 \hat{j}+2 \hat{k} $

$ \begin{aligned} \therefore \quad \cos \theta & =\dfrac{ \vec{b} _1 \cdot \vec{b} _2}{| \vec{b} _1| \vec{b} _2 \mid}=\dfrac{(2 \hat{i}+\hat{j}+2 \hat{k}) \cdot(6 \hat{i}+3 \hat{j}+2 \hat{k})}{\sqrt{(2)^{2}+(1)^{2}+(2)^{2}} \cdot \sqrt{(6)^{2}+(3)^{2}+(2)^{2}}} \\ & =\dfrac{12+3+4}{\sqrt{4+1+4} \cdot \sqrt{36+9+4}}=\dfrac{19}{\sqrt{9} \cdot \sqrt{49}}=\dfrac{19}{3 \cdot 7}=\dfrac{19}{21} \\ \therefore \quad \theta & =\cos ^{-1}(\dfrac{19}{21}) \end{aligned} $

इसलिए, आवश्यक कोण है $\cos ^{-1}(\dfrac{19}{21})$।

Solution

दिए गए बिंदु $A(0,-1,-1)$ , $B(4,5,1)$, $C(3,9,4) \text{ और } D(-4,4,4)$ हैं

रेखा $AB$ के कार्तीय रूप का समीकरण है

$ \dfrac{x-0}{4-0}=\dfrac{y+1}{5+1}=\dfrac{z+1}{1+1} \Rightarrow \dfrac{x}{4}=\dfrac{y+1}{6}=\dfrac{z+1}{2} $

और इसका सदिश रूप है $\vec{r}=(-\hat{j}-\hat{k})+\lambda(4 \hat{i}+6 \hat{j}+2 \hat{k})$

इसी तरह, रेखा $CD$ का समीकरण है

$ \dfrac{x-3}{-4-3}=\dfrac{y-9}{4-9}=\dfrac{z-4}{4-4} \Rightarrow \dfrac{x-3}{-7}=\dfrac{y-9}{-5}=\dfrac{z-4}{0} $

और इसका सदिश रूप है $\vec{r}=(3 \hat{i}+9 \hat{j}+4 \hat{k})+\mu(-7 \hat{i}-5 \hat{j})$

अब, यहाँ $ \vec{a} _1=-\hat{j}-\hat{k}, \quad \vec{b} _1=4 \hat{i}+6 \hat{j}+2 \hat{k}$

$ \vec{a} _2=3 \hat{i}+9 \hat{j}+4 \hat{k}, \quad \vec{b} _2=-7 \hat{i}-5 \hat{j} $

रेखा $AB$ और $CD$ के बीच न्यूनतम दूरी

$ \begin{aligned} \text{ S.D. } & =|\dfrac{( \vec{a} _2- \vec{a} _1) \cdot( \vec{b} _1 \times \vec{b} _2)}{| \vec{b} _1 \times \vec{b} _2|}| \\ \vec{a} _2- \vec{a} _1 & =(3 \hat{i}+9 \hat{j}+4 \hat{k})-(-\hat{j}-\hat{k})=3 \hat{i}+10 \hat{j}+5 \hat{k} . \\

$$ \vec{b} _1 \times \vec{b} _2 & = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \ 4 & 6 & 2 \ -7 & -5 & 0 \end{vmatrix} \ & =\hat{i}(0+10)-\hat{j}(0+14)+\hat{k}(-20+42) \ & =10 \hat{i}-14 \hat{j}+22 \hat{k} \end{aligned} $$

$$ \begin{aligned} | \vec{b} _1 \times \vec{b} _2| & =\sqrt{(10)^{2}+(-14)^{2}+(22)^{2}} \ & =\sqrt{100+196+484}=\sqrt{780} \ \therefore \quad \quad \text{ S.D } & =\dfrac{(3 \hat{i}+10 \hat{j}+5 \hat{k}) \cdot(10 \hat{i}-14 \hat{j}+22 \hat{k})}{\sqrt{780}} \ & =\dfrac{30-140+110}{\sqrt{780}}=0 \end{aligned} $$

इसलिए, दो रेखाएँ एक दूसरे के लंब हैं।

हल

दिया गया है: $\quad x = py + q \Rightarrow y = \dfrac{x - q}{p}$

और $$ z = ry + s \Rightarrow y = \dfrac{z - s}{r} $$

$\therefore$ समीकरण बनता है

$$ \dfrac{x - q}{p} = \dfrac{y}{1} = \dfrac{z - s}{r} $$ जिसके दिशा अनुपात $a_1 = p, b_1 = 1, c_1 = r$ हैं

इसी तरह

$$ x = p^{\prime} y + q^{\prime} \Rightarrow y = \dfrac{x - q^{\prime}}{p^{\prime}} $$

और $$ z = r^{\prime} y + s^{\prime} \Rightarrow y = \dfrac{z - s^{\prime}}{r^{\prime}} $$

$\therefore$ समीकरण बनता है

$$ \dfrac{x - q^{\prime}}{p^{\prime}} = \dfrac{y}{1} = \dfrac{z - s^{\prime}}{r^{\prime}} \text{ जिसमें } a_2 = p^{\prime}, b_2 = 1, c_2 = r^{\prime} $$

यदि रेखाएँ एक दूसरे के लंब हों, तो

$$ \begin{matrix} a_1 a_2 + b_1 b_2 + c_1 c_2 = 0 \ pp^{\prime} + 1.1 + rr^{\prime} = 0 \end{matrix} $$

इसलिए, $pp^{\prime} + rr^{\prime} + 1 = 0$ आवश्यक शर्त है।

हल

दिया गया है $A(2,3,4)$ और $B(4,5,8)$

तल के मध्य बिंदु $C$ के निर्देशांक $(\dfrac{2+4}{2}, \dfrac{3+5}{2}, \dfrac{4+8}{2}) = (3,4,6)$ हैं

अब तल के अभिलम्ब के दिशा अनुपात

$ \begin{aligned} & =\text{ रेखा AB के दिशा अनुपात } \\ & =4-2,5-3,8-4=(2,2,4) \end{aligned} $

समतल का समीकरण है

$a(x-x_1)+b(y-y_1)+c(z-z_1) =0 $

$\Rightarrow \quad 2(x-3)+2(y-4)+4(z-6) =0 $

$\Rightarrow \quad 2 x-6+2 y-8+4 z-24 =0$

$\Rightarrow \quad 2 x+2 y+4 z =38 \quad \Rightarrow \quad x+y+2 z=19$

अतः, अभीष्ट समतल का समीकरण $x+y+2 z=19 \quad$ या $\quad \vec{r}(\hat{i}+\hat{j}+2 \hat{k})=19$ है।

हल

क्योंकि, समतल का अभिलम्ब निर्देशांक अक्षों के समान झुका हुआ है

$\therefore \cos \alpha=\cos \beta=\cos \gamma$

$\Rightarrow \cos ^{2} \alpha+\cos ^{2} \alpha+\cos ^{2} \alpha=1$

$\begin{aligned} \Rightarrow 3 \cos ^{2} \alpha =1 \Rightarrow \cos \alpha=\dfrac{1}{\sqrt{3}} \\ \Rightarrow \cos \alpha =\cos \beta=\cos \gamma=\dfrac{1}{\sqrt{3}}\end{aligned}$

अतः, अभिलम्ब है

$ \overrightarrow{{}N}=\dfrac{1}{\sqrt{3}} \hat{i}+\dfrac{1}{\sqrt{3}} \hat{j}+\dfrac{1}{\sqrt{3}} \hat{k} $

$\therefore$ समतल का समीकरण $\vec{r} \cdot \vec{N}=d$ है

$ \begin{aligned} & \Rightarrow \quad \vec{r} \cdot \dfrac{\vec{N}}{|\vec{N}|}=d \\ & \Rightarrow \quad \dfrac{\vec{r} \cdot(\dfrac{1}{\sqrt{3}} \hat{i}+\dfrac{1}{\sqrt{3}} \hat{j}+\dfrac{1}{\sqrt{3}} \hat{k})}{1}=3 \sqrt{3} \\ & \Rightarrow \quad \vec{r} \cdot(\dfrac{1}{\sqrt{3}} \hat{i}+\dfrac{1}{\sqrt{3}} \hat{j}+\dfrac{1}{\sqrt{3}} \hat{k})=3 \sqrt{3} \\ & \Rightarrow(x \hat{i}+y \hat{j}+z \hat{k}) \cdot \dfrac{1}{\sqrt{3}}(\hat{i}+\hat{j}+\hat{k})=3 \sqrt{3} \\ & \Rightarrow \quad x+y+z=3 \sqrt{3} \cdot \sqrt{3} \Rightarrow x+y+z=9 \end{aligned} $

अतः, अभीष्ट समतल का समीकरण $x+y+z=9$ है।

हल

समतल के अभिलम्ब के दिशा अनुपात हैं

$(a,b,c)=(1+2,-3+1,3+3) =(3,-2,6)$

एक बिंदु $(x_1, y_1, z_1)$ से गुजरने वाले समतल का समीकरण है

$a(x-x_1)+b(y-y_1)+c(z-z_1) =0 $

$\Rightarrow \quad 3(x-1)-2(y+3)+6(z-3) =0 $

$\Rightarrow \quad 3 x-3-2 y-6+6 z-18 =0$

$\Rightarrow \quad 3 x-2 y+6 z-27 =0 \quad \Rightarrow 3 x-2 y+6 z=27$

अतः, आवश्यक समीकरण $3 x-2 y+6 z=27$ है।

हल

क्योंकि, बिंदुओं $(x_1, y_1, z_1),(x_2, y_2, z_2)$ और $(x_3, y_3, z_3)$ से गुजरने वाले समतल का समीकरण है

$ \begin{aligned} & \begin{vmatrix} x-x_1 & y-y_1 & z-z_1 \\ x_2-x_1 & y_2-y_1 & z_2-z_1 \\ x_3-x_1 & y_3-y_1 & z_3-z_1 \end{vmatrix} =0 \\ & \Rightarrow \begin{vmatrix} x-2 & y-1 & z-0 \\ 3-2 & -2-1 & -2-0 \\ 3-2 & 1-1 & 7-0 \end{vmatrix} =0 \Rightarrow \begin{vmatrix} x-2 & y-1 & z \\ 1 & -3 & -2 \\ 1 & 0 & 7 \end{vmatrix} =0 \\ & \Rightarrow(x-2) \begin{vmatrix} -3 & -2 \\ 0 & 7 \end{vmatrix} -(y-1) \begin{vmatrix} 1 & -2 \\ 1 & 7 \end{vmatrix} +z \begin{vmatrix} 1 & -3 \\ 1 & 0 \end{vmatrix} =0 \\ & \Rightarrow \quad(x-2)(-21)-(y-1)(7+2)+z(3)=0 \\ & \Rightarrow \quad-21(x-2)-9(y-1)+3 z=0 \\ & \Rightarrow \quad-21 x+42-9 y+9+3 z=0 \\ & \Rightarrow \quad-21 x-9 y+3 z+51=0 \Rightarrow 7 x+3 y-z-17=0 \end{aligned} $

अतः, आवश्यक समीकरण $7 x+3 y-z-17=0$ है।

हल

दिया है, $\dfrac{x-3}{2} =\dfrac{y-3}{1}=\dfrac{z}{1}=\lambda$

दी गई रेखा पर कोई बिंदु है

$x =2 \lambda+3, y=\lambda+3$ और $\quad z =\lambda$

मान लीजिए P और Q दो रेखाओं के प्रतिच्छेद बिंदु हैं जो मूल बिंदु से गुजरती हैं और दी गई रेखा को काटती हैं।

मान लीजिए, P के निर्देशांक $P=(2\lambda +3, \lambda+3,\lambda)$

$\therefore$ OP के दिशा अनुपात $(2 \lambda+3-0),(\lambda+3-0)$ और $(\lambda-0) \Rightarrow 2 \lambda+3, \lambda+3, \lambda$

लेकिन PQ रेखा के दिशा अनुपात $2, 1,1$ हैं

$\begin{aligned}\cos \theta =\dfrac{a_1 a_2+b_1 b_2+c_1 c_2}{\sqrt{a_1^{2}+b_1^{2}+c_1^{2}} \cdot \sqrt{a_2^{2}+b_2^{2}+c_2^{2}}}\end{aligned}$

$\begin{aligned}\cos \dfrac{\pi}{3} =\dfrac{2(2 \lambda+3)+1(\lambda+3)+1 . \lambda}{\sqrt{(2)^{2}+(1)^{2}+(1)^{2}} \cdot \sqrt{(2 \lambda+3)^{2}+(\lambda+3)^{2}+\lambda^{2}}}\end{aligned} $

$\begin{aligned}\Rightarrow \quad \dfrac{1}{2} =\dfrac{4 \lambda+6+\lambda+3+\lambda}{\sqrt{6} \cdot \sqrt{4 \lambda^{2}+9+12 \lambda+\lambda^{2}+9+6 \lambda+\lambda^{2}}}\end{aligned} $

$\begin{aligned}\Rightarrow \quad \dfrac{\sqrt{6}}{2} =\dfrac{6 \lambda+9}{\sqrt{6 \lambda^{2}+18 \lambda+18}}=\dfrac{6 \lambda+9}{\sqrt{6} \sqrt{\lambda^{2}+3 \lambda+3}}\end{aligned}$

$ \begin{aligned} & \Rightarrow \quad \dfrac{6}{2}=\dfrac{3(2 \lambda+3)}{\sqrt{\lambda^{2}+3 \lambda+3}} \Rightarrow 3=\dfrac{3(2 \lambda+3)}{\sqrt{\lambda^{2}+3 \lambda+3}} \\ & \Rightarrow \quad 1=\dfrac{2 \lambda+3}{\sqrt{\lambda^{2}+3 \lambda+3}} \Rightarrow \sqrt{\lambda^{2}+3 \lambda+3}=2 \lambda+3 \\ & \Rightarrow \quad \lambda^{2}+3 \lambda+3=4 \lambda^{2}+9+12 \lambda \\ & \Rightarrow \quad 3 \lambda^{2}+9 \lambda+6=0 \quad \Rightarrow \lambda^{2}+3 \lambda+2=0 \\ & \Rightarrow \quad(\lambda+1)(\lambda+2)=0 \\ & \therefore \quad \lambda=-1, \lambda=-2 \\ & \therefore \text{ Direction ratios are }[2(-1)+3,-1+3,-1] \text{ i.e., } 1,2,-1 \text{ when } \\ & \lambda=-1 \text{ and }[2(-2)+3,-2+3,-2] \text{ i.e., }-1,1,-2 \text{ when } \lambda=-2 . \end{aligned} $

इसलिए, मूल बिंदु से गुजरने वाली दो रेखाओं के आवश्यक समीकरण हैं

$ \dfrac{x}{1}=\dfrac{y}{2}=\dfrac{z}{-1} \text{ और } \dfrac{x}{-1}=\dfrac{y}{1}=\dfrac{z}{-2} . $

हल

दिए गए समीकरण हैं

$ \begin{aligned} l+m+n & =0 \qquad…(i)\\ l^{2}+m^{2}-n^{2} & =0 \qquad…(ii) \end{aligned} $

समीकरण (i) से $n=-(l+m)$

समीकरण (ii) में $n$ का मान रखने पर हमें प्राप्त होता है

$ \begin{aligned} & l^{2}+m^{2}-[-(l+m)^{2}]=0 \\ & \Rightarrow \quad l^{2}+m^{2}-l^{2}-m^{2}-2 l m=0 \\ & \Rightarrow \quad-2 lm=0 \\ & \Rightarrow \quad l m=0 \Rightarrow(-m-n) m=0 \quad [\because l=-m-n] \\ & \Rightarrow \quad(m+n) m=0 \Rightarrow m=0 \text{ या } m=-n \\ & \Rightarrow \quad l=-n \text{ या } l=0 \end{aligned} $

$\therefore$ दोनों रेखाओं के दिशा अनुपात हैं

$0,-n, n$ और $-n, 0, n \Rightarrow 0,-1,1$ और $-1,0,1$

$\begin{aligned}\therefore \quad \cos \theta =\dfrac{(0 \hat{i}-\hat{j}+\hat{k}) \cdot(-\hat{i}+0 \hat{j}+\hat{k})}{\sqrt{(-1)^{2}+(1)^{2}} \sqrt{(-1)^{2}+(1)^{2}}}=\dfrac{1}{\sqrt{2} \cdot \sqrt{2}}=\dfrac{1}{2}\end{aligned}$

$\therefore \quad \theta =\dfrac{\pi}{3}$

अतः, अभीष्ट कोण $\dfrac{\pi}{3}$ है।

हल

दिया गया है कि $l, m, n$ और $l+\delta l, m+\delta m, n+\delta n$ एक चर रेखा के दो स्थितियों के दिशा अनुपात हैं

$ \begin{aligned} \therefore \quad l^{2}+m^{2}+n^{2}=1 \qquad…(i) \end{aligned} $

$ \begin{aligned} & \text{ और }(l+\delta l)^{2}+(m+\delta m)^{2}+(n+\delta n)^{2}=1 \qquad…(ii)\\ & \Rightarrow l^{2}+\delta l^{2}+2 l . \delta l+m^{2}+\delta m^{2}+2 m . \delta m+n^{2}+\delta n^{2}+2 n . \delta n=1 \\ & \Rightarrow(l^{2}+m^{2}+n^{2})+(\delta l^{2}+\delta m^{2}+\delta n^{2})+2(l . \delta l+m . \delta m+n . \delta n)=1 \\

$$ \begin{aligned} & \Rightarrow 1+(\delta l^{2}+\delta m^{2}+\delta n^{2})+2(l . \delta l+m . \delta m+n \cdot \delta n)=1 \\ & \Rightarrow l . \delta l+m . \delta m+n . \delta n=-\dfrac{1}{2}(\delta l^{2}+\delta m^{2}+\delta n^{2}) \end{aligned} $$

मान लीजिए $\vec{a}$ और $\vec{b}$ एक रेखा के अनुदिश एक इकाई सदिश हैं जिनके दिशा अनुपात $l, m$, $n$ और $(l+\delta l),(m+\delta m),(n+\delta n)$ हैं।

$\therefore \vec{a}=l \hat{i}+m \hat{j}+n \hat{k}$ और $\vec{b}=(l+\delta l) \hat{i}+(m+\delta m) \hat{j}+(n+\delta n) \hat{k}$

$\cos \delta \theta=\dfrac{\vec{a} \cdot \vec{b}}{|\vec{a}||\vec{b}|}$

$\cos \delta \theta=\dfrac{(l \hat{i}+m \hat{j}+n \hat{k}) \cdot[(l+\delta l) \hat{i}+(m+\delta m) \hat{j}+(n+\delta n) \hat{k}]}{1.1}$ $\qquad [\because|\vec{a}|=|\vec{b}|=1]$

$\Rightarrow \quad \cos \delta \theta=l(l+\delta l)+m(m+\delta m)+n(n+\delta n)$

$\Rightarrow \quad \cos \delta \theta=l^{2}+l . \delta l+m^{2}+m . \delta m+n^{2}+n . \delta n$

$\Rightarrow \quad \cos \delta \theta=(l^{2}+m^{2}+n^{2})+(l . \delta l+m . \delta m+n . \delta n)$

$\Rightarrow \quad \cos \delta \theta=1-\dfrac{1}{2}(\delta l^{2}+\delta m^{2}+\delta n^{2})$

$\Rightarrow 1-\cos \delta \theta=\dfrac{1}{2}(\delta l^{2}+\delta m^{2}+\delta n^{2})$

$\Rightarrow 2 \sin ^{2} \dfrac{\delta \theta}{2}=\dfrac{1}{2}(\delta l^{2}+\delta m^{2}+\delta n^{2})$

$\Rightarrow 4 \sin ^{2} \dfrac{\delta \theta}{2}=\delta l^{2}+\delta m^{2}+\delta n^{2}$

$ \Rightarrow 4(\dfrac{\delta \theta}{2})^{2}=\delta l^{2}+\delta m^{2}+\delta n^{2}\qquad \begin{bmatrix} \because \quad \dfrac{\delta \theta}{2} \text{ बहुत छोटा है इसलिए, } \sin \dfrac{\delta \theta}{2}=\dfrac{\delta \theta}{2} \end{bmatrix} $

$\Rightarrow \quad(\delta \theta)^{2}=\delta l^{2}+\delta m^{2}+\delta n^{2}$

इसलिए सिद्ध किया गया है

Solution

हमें $A(a, b, c)$ और $O(0,0,0)$ दिया गया है

$\therefore$ $OA$ के दिशा अनुपात $a-0, b-0, c-0 =a, b, c$

$\therefore$ रेखा $OA$ के दिशा कोसाइन $=\dfrac{a}{\sqrt{a^{2}+b^{2}+c^{2}}}, \dfrac{b}{\sqrt{a^{2}+b^{2}+c^{2}}}, \dfrac{c}{\sqrt{a^{2}+b^{2}+c^{2}}} $

अब समतल के अभिलम्ब के दिशा अनुपात $(a, b, c)$ हैं।

$\therefore$ बिंदु $A(a, b, c)$ से गुजरने वाले समतल का समीकरण है

$ a(x-a)+b(y-b)+c(z-c)=0 $

$ \begin{aligned} \Rightarrow a x-a^{2}+b y-b^{2}+c z-c^{2} =0 \\ \Rightarrow a x+b y+c z =a^{2}+b^{2}+c^{2} \end{aligned} $

इसलिए, अभीष्ट समीकरण $a x+b y+c z=a^{2}+b^{2}+c^{2}$ है।

हल

OX, OY, OZ और OX’, OY’, OZ’ दो आयतन अक्ष प्रणालियाँ मान लीजिए

दिया गया है कि समतल अक्षों को क्रमशः मूल से $a, b, c$ और $a^{\prime}, b^{\prime}, c^{\prime}$ की दूरी पर काटता है।

$\therefore$ दोनों समतलों के समीकरण हैं

$$ \begin{equation*} \dfrac{x}{a}+\dfrac{y}{b}+\dfrac{z}{c}=1 \ldots(i) \quad \text{ और } \quad \dfrac{x}{a^{\prime}}+\dfrac{y}{b^{\prime}}+\dfrac{z}{c^{\prime}}=1 \ldots(ii) \end{equation*} $$

मूल से समतल $(i)$ की लम्ब दूरी है

$ =\Bigg|\dfrac{\dfrac{0}{a}+\dfrac{0}{b}+\dfrac{0}{c}-1}{\sqrt{\dfrac{1}{a^{2}}+\dfrac{1}{b^{2}}+\dfrac{1}{c^{2}}}}\Bigg|=\dfrac{1}{\sqrt{\dfrac{1}{a^{2}}+\dfrac{1}{b^{2}}+\dfrac{1}{c^{2}}}} $

मूल से समतल (ii) की लम्ब दूरी है

$ =\Bigg|\dfrac{\dfrac{0}{a^{\prime}}+\dfrac{0}{b^{\prime}}+\dfrac{0}{c^{\prime}}-1}{\sqrt{\dfrac{1}{a^{\prime 2}}+\dfrac{1}{b^{\prime 2}}+\dfrac{1}{c^{\prime 2}}}}\Bigg|=\dfrac{1}{\sqrt{\dfrac{1}{a^{\prime 2}}+\dfrac{1}{b^{\prime 2}}+\dfrac{1}{c^{\prime 2}}}} $

प्रश्न के अनुसार स्थिति के अनुसार

$ \dfrac{1}{\sqrt{\dfrac{1}{a^{2}}+\dfrac{1}{b^{2}}+\dfrac{1}{c^{2}}}}=\dfrac{1}{\sqrt{\dfrac{1}{a^{\prime 2}}+\dfrac{1}{b^{\prime 2}}+\dfrac{1}{c^{\prime 2}}}} $

अतः, $\dfrac{1}{a^{2}}+\dfrac{1}{b^{2}}+\dfrac{1}{c^{2}}=\dfrac{1}{a^{\prime 2}}+\dfrac{1}{b^{\prime 2}}+\dfrac{1}{c^{\prime 2}}$

हल

दिया गया है: $\quad \dfrac{4-x}{2}=\dfrac{y}{6}=\dfrac{1-z}{3}$ रेखा का समीकरण है

$ \Rightarrow \quad \dfrac{x-4}{-2}=\dfrac{y}{6}=\dfrac{z-1}{-3}=\lambda $

$\therefore$ रेखा पर किसी बिंदु $Q$ के निर्देशांक $x=-2 \lambda+4, y=6 \lambda$ और $z=-3 \lambda+1$ हैं और दिया गया बिंदु $P(2,3,-8)$ है

PQ के दिशा अनुपात $-2 \lambda+4-2,6 \lambda-3,-3 \lambda+1+8$

अर्थात, $-2 \lambda+2,6 \lambda-3,-3 \lambda+9$

और दी गई रेखा के दिशा अनुपात $-2,6,-3$ हैं।

यदि PQ दी गई रेखा के लंब हो तो,

$-2(-2 \lambda+2)+6(6 \lambda-3)-3(-3 \lambda+9)=0$

$\Rightarrow \quad 4 \lambda-4+36 \lambda-18+9 \lambda-27=0$

$\Rightarrow \quad 49 \lambda-49=0 \Rightarrow \lambda=1$

$\therefore$ लंब का पाद $-2(1)+4,6(1),-3(1)+1$

अर्थात, $2,\ 6,\ -2$

$ \begin{aligned} \text{ अब, दूरी P Q } & =\sqrt{(2-2)^{2}+(3-6)^{2}+(-8+2)^{2}} \\ & =\sqrt{9+36}=\sqrt{45}=3 \sqrt{5} \end{aligned} $

अतः, लंब के पाद के आवश्यक निर्देशांक $2,6,-2$ हैं और आवश्यक दूरी $3 \sqrt{5}$ इकाई है।

हल

दी गई रेखा का समीकरण है

$ \dfrac{x+5}{1}=\dfrac{y+3}{4}=\dfrac{z-6}{-9}=\lambda$ और दिया गया बिंदु $P(2,4,-1)$ है

मान लीजिए $Q$ दी गई रेखा पर कोई बिंदु है

$\therefore$ $Q$ के निर्देशांक $x=\lambda-5, y=4 \lambda-3, z=-9 \lambda+6$ हैं

दिशा अनुपात PQ के $\lambda-5-2,4 \lambda-3-4,-9 \lambda+6+1$ अर्थात $\lambda-7,4 \lambda-7,-9 \lambda+7$ हैं।

रेखा के दिशा अनुपात $1,4,-9$ हैं।

यदि PQ दी गई रेखा के लंब है, तो

$$ \begin{aligned} & 1(\lambda-7)+4(4 \lambda-7)-9(-9 \lambda+7) =0 \\ & \lambda-7+16 \lambda-28+81 \lambda-63 =0 \\ & \Rightarrow \quad 98 \lambda-98 =0 \\ & \therefore \quad \lambda = 1 \end{aligned} $$

इसलिए, $Q$ के निर्देशांक $1-5,4 \times 1-3,-9 \times 1+6$ अर्थात $-4,1,-3$ हैं।

$$ \begin{aligned} \therefore \quad PQ & =\sqrt{(-4-2)^{2}+(1-4)^{2}+(-3+1)^{2}} \\ & =\sqrt{(-6)^{2}+(-3)^{2}+(-2)^{2}}=\sqrt{36+9+4}=\sqrt{49}=7 \end{aligned} $$

इसलिए, अभीष्ट दूरी 7 इकाई है।

हल

दिया गया तल $2 x-2 y+4 z+5=0$ और दिया गया बिंदु $(1, \dfrac{3}{2}, 2)$ है।

तल के अभिलम्ब के दिशा अनुपात 2, -2, 4 हैं।

इसलिए, बिंदु $(1, \dfrac{3}{2}, 2)$ से गुजरने वाली रेखा का समीकरण जो तल के अभिलम्ब के दिशा अनुपात के बराबर है अर्थात $2,-2,4$ है $\dfrac{x-1}{2}=\dfrac{y-\dfrac{3}{2}}{-2}=\dfrac{z-2}{4}=\lambda$

$\therefore$ तल में किसी भी बिंदु के निर्देशांक $\left(2 \lambda+1,-2 \lambda+\dfrac{3}{2}, 4 \lambda+2\right)$ हैं।

लंब के पाद को ज्ञात करने के लिए, मान लीजिए बिंदु $\left(2 \lambda+1,-2 \lambda+\dfrac{3}{2}, 4 \lambda+2\right)$ तल पर स्थित है।

क्योंकि बिंदु तल में स्थित है, तो

$2(2 \lambda+1)-2(-2 \lambda+\dfrac{3}{2})+4(4 \lambda+2)+5=0$

$\Rightarrow 4 \lambda+2+4 \lambda-3+16 \lambda+8+5=0$

$\Rightarrow 24 \lambda+12=0 \quad \therefore \lambda=-\dfrac{1}{2}$

इसलिए, तल में बिंदु के निर्देशांक हैं

$ 2(-\dfrac{1}{2})+1,-2(-\dfrac{1}{2})+\dfrac{3}{2}, 4(-\dfrac{1}{2})+2 \text{ i.e., } 0, \dfrac{5}{2}, 0 $

इसलिए, लंब का पाद $(0, \dfrac{5}{2}, 0)$ है और लंबाई

$$ \begin{aligned} \therefore \text{अभीष्ट लंबाई} \quad & =\sqrt{(1-0)^{2}+(\dfrac{3}{2}-\dfrac{5}{2})^{2}+(2-0)^{2}} \\

& =\sqrt{1+1+4}=\sqrt{6} \text{ इकाई } \end{aligned} $

हल

दिया गया बिंदु $(3,0,1)$ और दिए गए समतल के समीकरण हैं

$$ \quad \begin{aligned} x+2 y & =0 \ldots(i) \\ 3 y-z & =0 \ldots(i) \end{aligned}$$

किसी भी रेखा $l$ के समीकरण जो $(3,0,1)$ से गुजरती हो वह है

$l: \dfrac{x-3}{a}=\dfrac{y-0}{b}=\dfrac{z-1}{c}$

समतल (i) और (ii) के अभिलम्ब के दिशा अनुपात हैं

$(1,2,0)$ और $(0,3,-1)$

चूंकि रेखा दोनों समतलों के समांतर है।

$ \begin{matrix} \therefore & 1 \cdot a+2 \cdot b+0 . c=0 \Rightarrow a+2 b+0 c=0 \\ \text{ और } & 0 \cdot a+3 \cdot b-1 . c=0 \Rightarrow 0 \cdot a+3 b-c=0 \end{matrix} $

इसलिए

$ \dfrac{a}{-2-0}=\dfrac{-b}{-1-0}=\dfrac{c}{3-0}=\lambda $

$\therefore a=-2 \lambda, b=\lambda, c=3 \lambda$

इसलिए, रेखा का समीकरण है

$ \dfrac{x-3}{-2 \lambda}=\dfrac{y}{\lambda}=\dfrac{z-1}{3 \lambda} $

इसलिए, आवश्यक समीकरण है $\dfrac{x-3}{-2}=\dfrac{y}{1}=\dfrac{z-1}{3}$

या सदिश रूप में है

$ (x-3) \hat{i}+y \hat{j}+(z-1) \hat{k}=\lambda(-2 \hat{i}+\hat{j}+3 \hat{k}) $

हल

दो बिंदुओं $(x_1, y_1, z_1)$ और $(x_2, y_2, z_2)$ से गुजरते एक समतल के समीकरण जिसके अभिलम्ब के दिशा अनुपात $(a, b, c)$ हैं, है

$$ \begin{equation*} a(x-x_1)+b(y-y_1)+c(z-z_1)=0 \ldots(i) \end{equation*} $$

यदि समतल $(x_2, y_2, z_2)$ से गुजरता है तो

$$a(x_2-x_1)+b(y_2-y_1)+c(z_2-z_1) =0$$

चूंकि, समतल (2,1,-1) और (-1,3,4) से गुजरता है तो

$$ \begin{align*} & & a(-1-2)+b(3-1)+c(4+1) & =0 \\ \Rightarrow & & -3 a+2 b+5 c & =0 \ldots(ii) \end{align*} $$

चूंकि आवश्यक समतल दिए गए समतल $x-2 y+4 z=10$ के लम्बवत है, तो

$$ \begin{equation*}

1 . a-2 . b+4 . c=10 \ldots(iii) \end{equation*} $$

(iii) और (ii) को हल करने पर, हम प्राप्त करते हैं,

$ \dfrac{a}{8+10}=\dfrac{-b}{-12-5}=\dfrac{c}{6-2}=\lambda $

$a=18 \lambda, b=17 \lambda, c=4 \lambda$

इसलिए, अभीष्ट तल है

$ \begin{matrix} 18 \lambda(x-2)+17 \lambda(y-1)+4 \lambda(z+1) =0 \\ \Rightarrow 18 x-36+17 y-17+4 z+4 =0 \\ \Rightarrow 18 x+17 y+4 z-49 =0 \end{matrix} $

Solution

दिए गए रेखाओं के समीकरण हैं

$$ \begin{align*} \vec{r} & =(8+3 \lambda) \hat{i}-(9+16 \lambda) \hat{j}+(10+7 \lambda) \hat{k} \ldots(i)\\ \text{ और } \quad \vec{r} & =15 \hat{i}+29 \hat{j}+5 \hat{k}+\mu(3 \hat{i}+8 \hat{j}-5 \hat{k}) \ldots(ii) \end{align*} $$

समीकरण (i) को पुन: लिखा जा सकता है

$$ \begin{equation*} \vec{r}=8 \hat{i}-9 \hat{j}+10 \hat{k}+\lambda(3 \hat{i}-16 \hat{j}+7 \hat{k}) \ldots(iii) \end{equation*} $$

यहाँ, $\quad \vec{a} _1=8 \hat{i}-9 \hat{j}+10 \hat{k}$ और $ \vec{a} _2=15 \hat{i}+29 \hat{j}+5 \hat{k}$

$ \begin{aligned} \vec{b} _1 & =3 \hat{i}-16 \hat{j}+7 \hat{k} \text{ और } \vec{b} _2=3 \hat{i}+8 \hat{j}-5 \hat{k} \\ \vec{a} _2- \vec{a} _1 & =7 \hat{i}+38 \hat{j}-5 \hat{k} \\ \vec{b} _1 \times \vec{b} _2 & = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 3 & -16 & 7 \\ 3 & 8 & -5 \end{vmatrix} \end{aligned} $

$ \begin{aligned} & =\hat{i}(80-56)-\hat{j}(-15-21)+\hat{k}(24+48) \\ & =24 \hat{i}+36 \hat{j}+72 \hat{k} \end{aligned} $

$\therefore$ सबसे छोटी दूरी, SD $\begin{aligned}=|\dfrac{( \vec{a} _2- \vec{a} _1) \cdot( \vec{b} _1 \times \vec{b} _2)}{| \vec{b} _1 \times \vec{b} _2|}|\end{aligned}$

$ \begin{aligned} & =|\dfrac{(7 \hat{i}+38 \hat{j}-5 \hat{k}) \cdot(24 \hat{i}+36 \hat{j}+72 \hat{k})}{\sqrt{(24)^{2}+(36)^{2}+(72)^{2}}}| \\

$$ \left|\dfrac{168+1368-360}{\sqrt{576+1296+5184}}\right|=\left|\dfrac{168+1008}{\sqrt{7056}}\right|=\dfrac{1176}{84}=14 \text{ इकाई } $$ $$ \end{aligned} $$

अतः, आवश्यक दूरी 14 इकाई है।

हल

दिए गए समतल हैं

$P_1: \quad 5 x+3 y+6 z+8=0$

$P_2: \quad x+2 y+3 z-4=0$

$P_3: \quad 2 x+y-z+5=0$

$P_2$ और $P_3$ के अखंड रेखा के माध्यम से गुजरने वाले समतल का समीकरण है

$$ (x+2 y+3 z-4)+\lambda(2 x+y-z+5)=0 $$

$$ \begin{aligned} \Rightarrow \quad(1+2 \lambda) x+(2+\lambda) y+(3-\lambda) z-4+5 \lambda=0 \ldots(i) \end{aligned} $$

समतल (i) $P_1$ के लम्बवत है, तो

$5(1+2 \lambda)+3(2+\lambda)+6(3-\lambda) =0 $

$\Rightarrow \quad 5 5+10 \lambda+6+3 \lambda+18-6 \lambda =0$

$\Rightarrow \quad 7 \lambda+29 =0 $

$\therefore \quad \lambda =\dfrac{-29}{7}$

$\lambda$ के मान को समीकरण (i) में रखने पर, हम प्राप्त करते हैं

$$ \begin{aligned} & {\left[1+2\left(\dfrac{-29}{7}\right)\right] x+\bigg[2-\dfrac{29}{7}\bigg] y+\bigg[3+\dfrac{29}{7}\bigg] z-4+5\bigg(\dfrac{-29}{7}\bigg)=0} \\ & \Rightarrow \dfrac{-51}{7} x-\dfrac{15}{7} y+\dfrac{50}{7} z-4-\dfrac{145}{7}=0 \\ & \Rightarrow-51 x-15 y+50 z-28-145=0 \\ & \Rightarrow-51 x-15 y+50 z-173=0 \\ &\Rightarrow 51 x+15 y-50 z+173=0 \end{aligned} $$

हल

दिए गए समतल हैं:

$$ \begin{aligned} a x+b y & =0 \ldots(i)\\ z & =0 \ldots(ii) \end{aligned} $$

समतल (i) और (ii) के अखंड रेखा के माध्यम से गुजरने वाले किसी भी समतल का समीकरण है

$$ \begin{aligned} (a x+b y)+k z=0 \Rightarrow a x+b y+k z=0 \ldots(iii)

\end{aligned} $

दोनों ओर को $\sqrt{a^{2}+b^{2}+k^{2}}$ से विभाजित करने पर, हम प्राप्त करते हैं

$\begin{aligned}\dfrac{a}{\sqrt{a^{2}+b^{2}+k^{2}}} x+\dfrac{b}{\sqrt{a^{2}+b^{2}+k^{2}}} y+\dfrac{k}{\sqrt{a^{2}+b^{2}+k^{2}}} z=0\end{aligned}$

$\therefore$ समतल के लम्ब के दिशा अनुपात हैं

$\begin{aligned}\dfrac{a}{\sqrt{a^{2}+b^{2}+k^{2}}}, \dfrac{b}{\sqrt{a^{2}+b^{2}+k^{2}}}, \dfrac{k}{\sqrt{a^{2}+b^{2}+k^{2}}}\end{aligned}$

और समतल (i) के दिशा अनुपात हैं

$\begin{aligned}\dfrac{a}{\sqrt{a^{2}+b^{2}}}, \dfrac{b}{\sqrt{a^{2}+b^{2}}}, 0\end{aligned}$

क्योंकि, $\alpha$ दो समतलों (i) और (iii) के बीच का कोण है, हम प्राप्त करते हैं

$ \begin{aligned} & \cos \alpha=\dfrac{a \cdot a+b \cdot b+k \cdot 0}{\sqrt{a^{2}+b^{2}+k^{2}} \cdot \sqrt{a^{2}+b^{2}}} \\ & \Rightarrow \quad \cos \alpha=\dfrac{a^{2}+b^{2}}{\sqrt{a^{2}+b^{2}+k^{2}} \cdot \sqrt{a^{2}+b^{2}}} \\ & \Rightarrow \quad \cos \alpha=\dfrac{\sqrt{a^{2}+b^{2}}}{\sqrt{a^{2}+b^{2}+k^{2}}} \Rightarrow \cos ^{2} \alpha=\dfrac{a^{2}+b^{2}}{a^{2}+b^{2}+k^{2}} \\ & \Rightarrow(a^{2}+b^{2}+k^{2}) \cos ^{2} \alpha=a^{2}+b^{2} \\ & \Rightarrow a^{2} \cos ^{2} \alpha+b^{2} \cos ^{2} \alpha+k^{2} \cos ^{2} \alpha=a^{2}+b^{2} \\ & \Rightarrow \quad k^{2} \cos ^{2} \alpha=a^{2}-a^{2} \cos ^{2} \alpha+b^{2}-b^{2} \cos ^{2} \alpha \\ & \Rightarrow \quad k^{2} \cos ^{2} \alpha=a^{2}(1-\cos ^{2} \alpha)+b^{2}(1-\cos ^{2} \alpha) \\ & \Rightarrow \quad k^{2} \cos ^{2} \alpha=a^{2} \sin ^{2} \alpha+b^{2} \sin ^{2} \alpha \\ & \Rightarrow \quad k^{2} \cos ^{2} \alpha=(a^{2}+b^{2}) \sin ^{2} \alpha \\ & \Rightarrow \quad k^{2}=(a^{2}+b^{2}) \dfrac{\sin ^{2} \alpha}{\cos ^{2} \alpha} \Rightarrow k= \pm \sqrt{a^{2}+b^{2}} \cdot \tan \alpha \end{aligned} $

समीकरण (iii) में $k$ का मान रखने पर हम प्राप्त करते हैं

$a x+b y \pm(\sqrt{a^{2}+b^{2}} \cdot \tan \alpha) z=0$ जो समतल का अभीष्ट समीकरण है।

इसलिए सिद्ध किया गया है।

हल

दिए गए समतल हैं;

और $\begin{aligned} \quad \vec{r} \cdot(\hat{i}+3 \hat{j})-6=0 \quad & \Rightarrow \quad x+3 y-6=0 \qquad…(i) \\ \quad \vec{r} \cdot(3 \hat{i}-\hat{j}-4 \hat{k})=0 & \Rightarrow \quad 3 x-y-4 z=0 \qquad…(ii) \end{aligned}$

समतल (i) और (ii) के प्रतिच्छेद रेखा के माध्यम से गुजरने वाले समतल का समीकरण है

$$ \begin{matrix} (x+3 y-6)+k(3 x-y-4 z)=0 \qquad…(iii)\\ (1+3 k) x+(3-k) y-4 k z-6=0 \end{matrix} $$

मूल बिंदु से लंब दूरी

$\begin{aligned}=\bigg|\dfrac{-6}{\sqrt{(1+3 k)^{2}+(3-k)^{2}+(-4 k)^{2}}}\bigg|=1\end{aligned}$

$\begin{aligned}\Rightarrow \dfrac{36}{1+9 k^{2}+6 k+9+k^{2}-6 k+16 k^{2}}=1\end{aligned} \qquad$ [दोनों ओर वर्ग करने पर]

$\begin{aligned}\Rightarrow \quad \dfrac{36}{26 k^{2}+10}=1 \Rightarrow 26 k^{2}+10=36\end{aligned}$

$\Rightarrow \quad 26 k^{2}=26 \quad \Rightarrow \quad k^{2}=1 \quad \therefore k= \pm 1$

समीकरण (iii) में $k$ के मान को रखने पर हमें प्राप्त होता है,

$ (x+3 y-6) \pm(3 x-y-4 z)=0 $

$\Rightarrow x+3 y-6+3 x-y-4 z=0$ और $x+3 y-6-3 x+y+4 z=0$

$\Rightarrow 4 x+2 y-4 z-6=0$ और $-2 x+4 y+4 z-6=0$

इसलिए, आवश्यक समीकरण हैं:

$4 x+2 y-4 z-6=0$ और $-2 x+4 y+4 z-6=0$.

हल

दिए गए बिंदु $P(\hat{i}-\hat{j}+3 \hat{k})$ और $Q(3 \hat{i}+3 \hat{j}+3 \hat{k})$ और समतल $\vec{r} .(5 \hat{i}+2 \hat{j}-7 \hat{k})+9=0$

बिंदु $P(\hat{i}-\hat{j}+3 \hat{k})$ से समतल $\vec{r} .(5 \hat{i}+2 \hat{j}-7 \hat{k})+9=0$ की लंब दूरी

$ \begin{aligned} & =\bigg|\dfrac{(\hat{i}-\hat{j}+3 \hat{k}) \cdot(5 \hat{i}+2 \hat{j}-7 \hat{k})+9}{\sqrt{(5)^{2}+(2)^{2}+(-7)^{2}}}\bigg| \\ & =\bigg|\dfrac{5-2-21+9}{\sqrt{25+4+49}}\bigg|=\bigg|\dfrac{-9}{\sqrt{78}}\bigg| \end{aligned} $

कोण $Q(3 \hat{i}+3 \hat{j}+3 \hat{k})$ के तल $\vec{r} .(5 \hat{i}+2 \hat{j}-7 \hat{k})+9=0$ से लंब दूरी

$ \begin{aligned} & =\bigg|\dfrac{(3 \hat{i}+3 \hat{j}+3 \hat{k}) \cdot(5 \hat{i}+2 \hat{j}-7 \hat{k})+9}{\sqrt{25+4+49}}\bigg| \\ & =\bigg|\dfrac{15+6-21+9}{\sqrt{78}}|=|\dfrac{9}{\sqrt{78}}\bigg| \end{aligned} $

इसलिए, दो बिंदु दिए गए तल से समान दूरी पर हैं। विपरीत चिह्न दर्शाता है कि वे तल के दोनों ओर स्थित हैं।

हल

बिंदु $A$ का स्थिति सदिश $6 \hat{i}+7 \hat{j}+4 \hat{k}$ है और $\overrightarrow{{}AB}=3 \hat{i}-\hat{j}+\hat{k}$

इसलिए, किसी भी रेखा का समीकरण जो $A$ से गुजरती है और $\overrightarrow{{}AB}$ के समानांतर है

$$ \begin{equation*} \vec{r}=(6 \hat{i}+7 \hat{j}+4 \hat{k})+\lambda(3 \hat{i}-\hat{j}+\hat{k}) \qquad…(i) \end{equation*} $$

अब कोई बिंदु $P$ रेखा $\overrightarrow{{}AB}$ पर $(6+3 \lambda, 7-\lambda, 4+\lambda)$ है

इसी तरह, बिंदु $C$ का स्थिति सदिश $-9 \hat{j}+2 \hat{k}$ है

और $\overrightarrow{{}CD}=-3 \hat{i}+2 \hat{j}+4 \hat{k}$

इसलिए, किसी भी रेखा का समीकरण जो $C$ से गुजरती है और $\overrightarrow{{}CD}$ के समानांतर है है

$$ \begin{equation*} \vec{r}=(-9 j+2 \hat{k})+\mu(-3 \hat{i}+2 \hat{j}+4 \hat{k}) \qquad…(ii) \end{equation*} $$

कोई बिंदु $Q$ रेखा $\overrightarrow{{}CD}$ पर $(-3 \mu,-9+2 \mu, 2+4 \mu)$ है

$\overrightarrow{{}PQ}$ के दिशा अनुपात हैं

$ (6+3 \lambda+3 \mu, 7-\lambda+9-2 \mu, 4+\lambda-2-4 \mu) $

$\Rightarrow(6+3 \lambda+3 \mu),(16-\lambda-2 \mu),(2+\lambda-4 \mu)$

अब $\overrightarrow{{}PQ}$, समीकरण (i) के लंबवत है, तो

$3(6+3 \lambda+3 \mu)-1(16-\lambda-2 \mu)+1(2+\lambda-4 \mu)=0$

$\Rightarrow 18+9 \lambda+9 \mu-16+\lambda+2 \mu+2+\lambda-4 \mu=0 $

$\Rightarrow 11 \lambda+7 \mu+4=0\qquad $…(iii)

$\overrightarrow{{}PQ} \text{ भी } \perp \text{ समीकरण }(\text{ ii }) \text{ के } \text{, तब }$

$-3(6+3 \lambda+3 \mu)+2(16-\lambda-2 \mu)+4(2+\lambda-4 \mu)=0 $

$\Rightarrow -18-9 \lambda-9 \mu+32-2 \lambda-4 \mu+8+4 \lambda-16 \mu=0 $

$\Rightarrow -7 \lambda-29 \mu+22=0 $

$\Rightarrow 7 \lambda+29 \mu-22=0 \qquad $…(iv)

समीकरण (iii) और (iv) को हल करने पर हम प्राप्त करते हैं

$ \begin{aligned} 77 \lambda+49 \mu+28=0 \\ 77 \lambda+319 \mu-242=0 \\ (-)\quad(-) \quad (+) \quad (-) \\ \hline -270\mu+270=0 \end{aligned} $

$\therefore \mu=1$

अब समीकरण (iv) में $\mu=1$ का प्रयोग करते हुए हम प्राप्त करते हैं

$ 7 \lambda+29-22=0 \Rightarrow \lambda=-1 $

$\therefore$ $P$ का स्थिति सदिश $[6+3(-1), 7+1,4-1]=(3,8,3)$

और $Q$ का स्थिति सदिश $[-3(1),-9+2(1), 2+4(1)]=(-3,-7,6)$

इसलिए,

$ P=3 \hat{i}+8 \hat{j}+3 \hat{k} \text{ और } Q=-3 \hat{i}-7 \hat{j}+6 \hat{k} $

हल

दिया गया है, $2 l+2 m-n=0\quad \ldots (i)$ और

$\quad m n+n l+l m=0 \quad \ldots (ii)$

समीकरण (i) से, $m=\dfrac{n-2 l}{2}$

समीकरण (ii) में $m$ के मान को प्रतिस्थापित करते हुए हम प्राप्त करते हैं

$ \begin{aligned} & (\dfrac{n-2 l}{2}) n+n l+l(\dfrac{n-2 l}{2})=0 \\ \Rightarrow & \dfrac{n^{2}-2 n l+2 n l+n l-2 l^{2}}{2}=0 \\ \Rightarrow & n^{2}+n l-2 l^{2}=0 \\ \Rightarrow & n^{2}+2 n l-n l-2 l^{2}=0 \\ \Rightarrow & n(n+2 l)-l(n+2 l)=0 \\ \Rightarrow & (n-l)(n+2 l)=0 \\ \Rightarrow & n=-2 l \quad \text{ और } \quad n=l \\ \therefore \quad & m=\dfrac{-2 l-2 l}{2}, \quad m=\dfrac{l-2 l}{2} \\ \Rightarrow & m=-2 l, \quad m=\dfrac{-l}{2} \end{aligned} $

इसलिए, दिशा अनुपात $l,-2 l,-2 l$ और $l, \dfrac{-l}{2}, l$ के अनुपात में हैं।

$\Rightarrow 1,-2,-2$ और $2,-1,2$

अगर दो रेखाएँ एक दूसरे के लंब हैं तो

$ \begin{aligned} 1(2)-2(-1)-2 \times 2 & =0 \\ 2+2-4 & =0 \\ 0 & =0 \end{aligned} $

इसलिए, दोनों रेखाएँ एक दूसरे के लंब हैं।

हल

मान लीजिए $\vec{a}, \vec{b}, \vec{c}$ और $\vec{d}$ ऐसे हैं कि

$ \vec{a}=l_1 \hat{i}+m_1 \hat{j}+n_1 \hat{k} $

$ \begin{aligned} \vec{b} & =l_2 \hat{i}+m_2 \hat{j}+n_2 \hat{k} \\ \vec{c} & =l_3 \hat{i}+m_3 \hat{j}+n_3 \hat{k} \end{aligned} $

और $\vec{d}=(l_1+l_2+l_3) \hat{i}+(m_1+m_2+m_3) \hat{j}+(n_1+n_2+n_3) \hat{k}$

क्योंकि दिए गए दिशा अनुपात आपस में लंब हैं तो

$ \begin{aligned} & l_1 l_2+m_1 m_2+n_1 n_2=0 \\ & l_2 l_3+m_2 m_3+n_2 n_3=0 \\ & l_1 l_3+m_1 m_3+n_1 n_3=0 \\ & l_1^2+m_1^2+n_1=1 \\ & l_2^2+m_2^2+n_2^2=1 \\ & l_3^2+m_3^2+n_3^2=1 \end{aligned} $

$ \begin{array}{l} \therefore\left(l_1+l_2+l_3\right)^2+\left(m_1+m_2+m_3\right)^2+\left(n_1+n_2n_3\right)^2 \ =\left(l_{1}^{2}+m_{1}^{2}+n_{1}^{2}\right)+\left(l_{2}^{2}+m_{2}^{2}+n_{2}^{2}\right)+\left(l_{3}^{2}+m_{3}^{2}+n_{3}^{2}\right)+2\left(l_{1} l_{2}+m_{1} m_{2}\right. \left.+n_{1} n_{2}\right) \+2\left(l_{1} l_{2}+m_{1} m_{3}+n_{1} n_{3}\right)+2\left(l_{2} l_{3}+m_{2} m_{3}+n_{2} n_{3}\right)\ = 1 + 1 + 1 + 2 \times 0+2 \times 0+2 \times 0\ =3 \end{array} $

$$ \Rightarrow \sqrt{\left(l_{1}+l_{2}+l_{3}\right)^{2}+\left(m_{1}+m_{2}+m_{3}\right)^{2}+\left(n_{1}+n_{2}+n_{3}\right)^{2}}=\sqrt{3} $$

मान लीजिए $\alpha, \beta$ और $\gamma$ क्रमशः $\vec{a}$ और $\vec{d}, \vec{b}$ और $\vec{d}, \vec{c}$ और $\vec{d}$ के बीच के कोण हैं।

$$ \cos\alpha=\dfrac{\left\lbrack\left.l_1(l_1+l_2+l_3\right)+m_1(m_1+m_2+m_3)+n_1\left(n_1+n_2+n_3)\right\rbrack\right.}{\sqrt{l_1^2+m_1^2+n_1^2}\sqrt{\left.(l_1+l_2+l_3\right)^2+\left(m_1+m_2+m_3\right)^2+\left(n_1+n_2+n_3\right)^2}^{}} $$

$ \begin{aligned} \therefore \cos \alpha & =\dfrac{\left\lbrack\left.l_1(l_1+l_2+l_3\right)+m_1(m_1+m_2+m_3)+n_1\left(n_1+n_2+n_3)\right\rbrack\right.}{\sqrt{3}\ } \\ & =\dfrac{l_1^{2}+l_1 l_2+l_1 l_3+m_1^{2}+m_1 m_2+m_1 m_3+n_1^{2}+n_1 n_2+n_1 n_3}{\sqrt{3}} \\ & =\dfrac{(l_1^{2}+m_1^{2}+n_1^{2})+(l_1 l_2+m_1 m_2+n_1 n_2)+(l_1 l_3+m_1 m_3+n_1 n_3)}{\sqrt{3}} \\ & =\dfrac{1+0+0}{\sqrt{3}} \\ & = \dfrac{1}{\sqrt{3}} \ \therefore \cos \beta & =\dfrac{l_2(l_1+l_2+l_3)+m_2(m_1+m_2+m_3)+n_2(n_1+n_2+n_3)}{\sqrt{l_2^2+m_2^2+n_2^2}\sqrt{\left.(l_1+l_2+l_3\right)^2+\left(m_1+m_2+m_3\right)^2+\left(n_1+n_2+n_3\right)^2}^{}} \\ & =\dfrac{l_1 l_2+l_2^{2}+l_2 l_3+m_1 m_2+m_2^{2}+m_2 m_3+n_1 n_2+n_2^{2}+n_2 n_3}{\sqrt{3}} \\ & =\dfrac{(l_2^{2}+m_2^{2}+n_2^{2})+(l_1 l_2+m_1 m_2+n_1 n_2)+(l_2 l_3+m_2 m_3+n_2 n_3)}{\sqrt{3}} \\ & = \dfrac{1+0+0}{\sqrt{3}} \ & = \dfrac{1}{\sqrt{3}} \end{aligned} $

इसी तरह,

$ \begin{aligned} \therefore \cos \gamma & =\dfrac{l_3(l_1+l_2+l_3)+m_3(m_1+m_2+m_3)+n_3(n_1+n_2+n_3)}{\sqrt{l_3^2+m_3^2+n_3^2}\sqrt{\left.(l_1+l_2+l_3\right)^2+\left(m_1+m_2+m_3\right)^2+\left(n_1+n_2+n_3\right)^2}^{}} \\ & =\dfrac{l_1 l_3+l_2 l_3+l_3^{2}+m_1 m_3+m_2 m_3+m_3^{2}+n_1 n_3+n_2 n_3+n_3^{2}}{\sqrt{3}} \\ & = \dfrac{(l_3^{2}+m_3^{2}+n_3^{2})+(l_1 l_3+m_1 m_3+n_1 n_3)+(l_2 l_3+m_2 m_3+n_2 n_3)}{\sqrt{3}} \\ & =\dfrac{1+0+0}{\sqrt{3}}\ & = \dfrac{1}{\sqrt{3}} \end{aligned} $

$\therefore \cos \alpha=\cos \beta=\cos \gamma=\dfrac{1}{\sqrt{3}} \Rightarrow \alpha=\beta=\gamma$ जो कि आवश्यक परिणाम है।

हल

दिया गया बिंदु $(\alpha, \beta, \gamma)$ है

$y$-अक्ष पर कोई बिंदु $=(0, \beta, 0)$ है

$\therefore$ आवश्यक दूरी $=\sqrt{(\alpha-0)^{2}+(\beta-\beta)^{2}+(\gamma-0)^{2}}$

$ =\sqrt{\alpha^{2}+\gamma^{2}} `

$

अतः, सही विकल्प (d) है।

हल

यदि $l, m, n$ एक रेखा के दिशा अनुपात हैं, तो

$l^{2}+m^{2}+n^{2} =1 $

$\text{ इसलिए, } \quad k^{2}+k^{2}+k^{2} =1 $

$ \quad \Rightarrow 3 k^{2} =1 \Rightarrow k= \pm \dfrac{1}{\sqrt{3}}$

अतः, सही विकल्प (d) है।

हल

दिया गया है: $\vec{r} \cdot(\dfrac{2}{7} \hat{i}+\dfrac{3}{7} \hat{j}-\dfrac{6}{7} \hat{k})=1$

समतल के उत्सर्जन के बिंदु से दूरी $d$ जो रूप $\vec{r}.\vec{n}=d_0$ में दिया गया है, इस प्रकार गणना की जाती है:

$$d=\left|\dfrac{d_0}{|\vec{n}|}\right|$$

इसलिए, दिए गए समतल के उत्सर्जन के बिंदु से दूरी है

$\begin{aligned}=\bigg|\dfrac{1}{\sqrt{(\dfrac{2}{7})^{2}+(\dfrac{3}{7})^{2}+(\dfrac{-6}{7})^{2}}}\bigg|=\bigg|\dfrac{1}{\sqrt{\dfrac{4}{49}+\dfrac{9}{49}+\dfrac{36}{49}}}\bigg|=\dfrac{1}{1}=1\end{aligned}$

अतः, सही विकल्प $(a)$ है।

हल

दी गई रेखा $\quad l: \dfrac{x-2}{3}=\dfrac{y-3}{4}=\dfrac{z-4}{5}$

और समतल $\quad P: 2 x-2 y+z=5$

रेखा के दिशा अनुपात $3,4,5$ हैं

समतल के अभिलम्ब के दिशा अनुपात $2,-2,1$ हैं

मान लीजिए, $ \theta $ रेखा $ l $ और समतल $ P $ के बीच कोण है। इसलिए, अभिलम्ब और रेखा के बीच कोण $ 90^\circ - \theta $ है।

अब, $\cos (90^{\circ}-\theta)=\sin \theta = \dfrac{\left| a_1 b_1 + a_2 b_2 + a_3 b_3 \right|}{\sqrt{a_1^2 + a_2^2 + a_3^2} \cdot \sqrt{b_1^2 + b_2^2 + b_3^2}}$

यहाँ : $\quad$ $a_1​,a_2​,a_3​$ रेखा के दिशा अनुपात हैं।

$b_1​,b_2​,b_3$​ समतल के अभिलम्ब के दिशा अनुपात हैं।

$ \begin{matrix} \therefore & \sin \theta=\dfrac{3(2)+4(-2)+5(1)}{\sqrt{9+16+25} \cdot \sqrt{4+4+1}} \\ \Rightarrow & \sin \theta=\dfrac{6-8+5}{\sqrt{50} \cdot 3} \Rightarrow \dfrac{3}{5 \sqrt{2} \cdot 3}=\dfrac{1}{5 \sqrt{2}}=\dfrac{\sqrt{2}}{10} \end{matrix} $

इसलिए, सही विकल्प $(d)$ है।

हल

बिंदु $(\alpha,\beta,\gamma)$ के $ x y $-तल में प्रतिबिम्ब ज्ञात करने के लिए, आपको बिंदु के निर्देशांक को $ x y $-तल के प्रभाव के अनुसार विचार करना होगा।

$ x y $-तल $ z=0 $ द्वारा परिभाषित है। इस तल के प्रतिबिम्ब के लिए, आप बिंदु के $ x $ और $ y $ निर्देशांक को समान रखते हैं और $ z $ निर्देशांक को ऋणात्मक करते हैं।

इसलिए, बिंदु $(\alpha,\beta,\gamma)$ के $ x y $-तल में प्रतिबिम्ब $(\alpha,\beta,-\gamma)$ है।

इसलिए, सही विकल्प $(d)$ है।

हल

दिए गए बिंदु $A(0,4,1), B(2,3,-1), C(4,5,0)$ और $D(2,6,2)$ हैं

$AB$ के दिशा अनुपात $2,-1-2$

$DC$ के दिशा अनुपात $2,-1,-2$

$\therefore AB || DC$

इसी तरह, $AD$ के दिशा अनुपात $2,2,1$ और $BC$ के दिशा अनुपात $2,2,1$

$\therefore AD || BC$

इसलिए, चतुर्भुज $ABCD$ एक समांतर चतुर्भुज है।

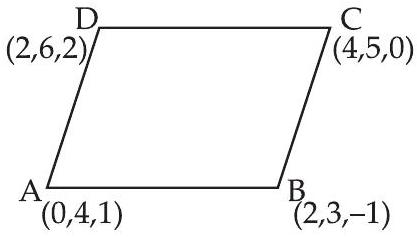
$ \begin{aligned} & \overrightarrow{{}AB}=2 \hat{i}-\hat{j}-2 \hat{k} \\

& \overrightarrow{{}AD}=2 \hat{i}+2 \hat{j}+\hat{k} \end{aligned} $

$\therefore$ समांतर चतुर्भुज $ABCD$ का क्षेत्रफल $|\overrightarrow{{}AB} \times \overrightarrow{{}AD}|$ है

$= \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 2 & -1 & -2 \\ 2 & 2 & 1\end{vmatrix} =\hat{i}(-1+4)-\hat{j}(2+4)+\hat, (4+2)=3 \hat{i}-6 \hat{j}+6 \hat{k}$

$=\sqrt{(3)^{2}+(-6)^{2}+(6)^{2}}=\sqrt{9+36+36}=\sqrt{81}=9$ वर्ग इकाई

इसलिए, सही विकल्प $(a)$ है।

हल

दिया गया है: $\quad xy + yz = 0$

$ \begin{aligned} y \cdot(x+z) & =0 \\ y & =0 \text{ या } x+z=0 \end{aligned} $

यहाँ $y=0$ एक समतल है और $x+z=0$ दूसरा समतल है। इसलिए, यह दो समतलों के एक जोड़ी को निरूपित करता है।

इन समतलों के लंब रेखाओं की जांच करके जांच करें कि ये समतल क्या हैं:

• समतल $y=0$ के लंब वेक्टर $(0,1,0)$ है।

• समतल $x+z=0$ के लंब वेक्टर $(1,0,1)$ है।

इन लंब वेक्टरों के डॉट उत्पाद है: $ (0,1,0) \cdot(1,0,1)=0 \times 1+1 \times 0+0 \times 1=0 $

चूंकि डॉट उत्पाद शून्य है, इसलिए लंब वेक्टर लंब हैं, जिसका अर्थ है कि समतल एक दूसरे के लंब हैं।

इसलिए, सही विकल्प $(d)$ है।

• (a) एक जोड़ी लंब रेखाएँ: समीकरण $xy + yz = 0$ तीन आयामी अंतरिका में एक संबंध है जो समतलों को निरूपित करता है, न कि रेखाओं को। इसलिए, यह एक जोड़ी लंब रेखाओं को निरूपित नहीं कर सकता।

• (b) एक जोड़ी समांतर रेखाएँ: वैसे भी, समीकरण $xy + yz = 0$ तीन आयामी अंतरिका में एक संबंध है जो समतलों को निरूपित करता है, न कि रेखाओं को। इसलिए, यह एक जोड़ी समांतर रेखाओं को निरूपित नहीं कर सकता।

• (c) एक जोड़ी समांतर समतल: समीकरण $xy + yz = 0$ सरल करके $y(x + z) = 0$ होता है, जो दो अलग-अलग समतल $y = 0$ और $x + z = 0$ को दर्शाता है। ये समतल एक रेखा के अनुदिश प्रतिच्छेद करते हैं और एक दूसरे के समांतर नहीं हैं। इसलिए, यह एक जोड़ी समांतर समतल को निरूपित नहीं कर सकता।

हल

समतल $2 x-3 y+6 z-11=0$ के अभिलम्ब के दिशा अनुपात 2, -3, 6 हैं

$x$-अक्ष के दिशा अनुपात $1,0,0$ हैं

एक रेखा और समतल के बीच कोण के लिए सूत्र निम्नलिखित है: $ \sin \theta=\dfrac{\mathbf{d} \cdot \mathbf{n}}{|\mathbf{d}||\mathbf{n}|} $

यहाँ:

• $ \mathbf{d} $ रेखा के दिशा वेक्टर है।
• $ \mathbf{n} $ समतल के अभिलम्ब वेक्टर है।

$ \therefore\ $ समतल और रेखा के बीच कोण है

$ \begin{aligned} \sin \theta & =\dfrac{2(1)-3(0)+6(0)}{\sqrt{(2)^{2}+(-3)^{2}+(6^{2})} \cdot \sqrt{(1)^{2}+(0)^{2}+(0)^{2}}} \\ & =\dfrac{2}{\sqrt{4+9+36}}=\dfrac{2}{7} \end{aligned} $

इसलिए, सही विकल्प (c) है।

हल

दिए गए बिंदु $(2,0,0),(0,3,0)$ और $(0,0,4)$ हैं।

इसलिए, समतल द्वारा x-, y- और z-अक्ष पर काटे गए अंतराल क्रमशः 2, 3, 4 हैं

समतल के समीकरण (अंतराल रूप) है

$\dfrac{x}{a}+\dfrac{y}{b}+\dfrac{z}{c}=1$

यहाँ, $a$, $b$, और $c$ क्रमशः समतल के x-, y- और z-अंतराल हैं।

$\therefore \quad \dfrac{x}{2}+\dfrac{y}{3}+\dfrac{z}{4}=1 $

इसलिए, समतल का समीकरण $\dfrac{x}{2}+\dfrac{y}{3}+\dfrac{z}{4}=1$ है।

हल

मान लीजिए

$ \vec{a}=2 \hat{i}+2 \hat{j}-\hat{k} $

$\vec{a}$ के दिशा अनुपात 2, 2, -1 हैं

सदिश $\vec{a} = a_1 \hat{i} + a_2 \hat{j} + a_3 \hat{k}$ के दिशा अनुपात निम्नलिखित हैं: $\dfrac{a_1}{\left|\vec{a}\right|},\dfrac{a_2}{\left|\vec{a}\right|},\dfrac{a_3}{\left|\vec{a}\right|}$

तो, दिशा अनुपात $\dfrac{2}{\sqrt{4+4+1}}, \dfrac{2}{\sqrt{4+4+1}}, \dfrac{-1}{\sqrt{4+4+1}} \Rightarrow \dfrac{2}{3}, \dfrac{2}{3}, \dfrac{-1}{3}$

इसलिए, दिए गए सदिश के दिशा अनुपात $\dfrac{2}{3}, \dfrac{2}{3}, \dfrac{-1}{3}$ हैं।

हल

दी गई समीकरण है $ \dfrac{x-5}{3}=\dfrac{y+4}{7}=\dfrac{z-6}{2} $

यहाँ, बिंदु $(5, -4, 6)$ रेखा पर एक बिंदु है, जिसे स्थिति सदिश के रूप में व्यक्त किया जा सकता है : $ \vec{a}=(5 \hat{i}-4 \hat{j}+6 \hat{k}) $

दिशा अनुपात $3, 7, 2$ का उपयोग करके रेखा के समीकरण का निर्माण किया जाता है:

$ \vec{b}=(3 \hat{i}+7 \hat{j}+2 \hat{k}) $

रेखा के सदिश समीकरण निम्नलिखित है:

$ \vec{r} = \vec{a} + \lambda \vec{b} $

इसलिए, दी गई रेखा के सदिश समीकरण है $ \vec{r}=(5 \hat{i}-4 \hat{j}+6 \hat{k})+\lambda(3 \hat{i}+7 \hat{j}+2 \hat{k}) $

हल

दिए गए बिंदु $(3,4,-7)$ और $(1,-1,6)$

बिंदु (3,4,−7) हमें एक स्थिति सदिश देता है : $ \vec{a} = 3 \hat{i} + 4 \hat{j} - 7 \hat{k} $

बिंदु (1,−1,6) हमें एक अन्य स्थिति सदिश देता है : $ \vec{b} = \hat{i} - \hat{j} + 6 \hat{k} $

रेखा के सदिश समीकरण निम्नलिखित है :

$ \vec{r} = \vec{a} + \lambda (\vec{b} - \vec{a}) $

$\Rightarrow \vec{r}=(3 \hat{i}+4 \hat{j}-7 \hat{k})+\lambda[(\hat{i}-\hat{j}+6 \hat{k})-(3 \hat{i}+4 \hat{j}-7 \hat{k})]$

$\Rightarrow \vec{r}=(3 \hat{i}+4 \hat{j}-7 \hat{k})+\lambda(-2 \hat{i}-5 \hat{j}+13 \hat{k})$

$\Rightarrow(x \hat{i}+y \hat{j}+z \hat{k})=(3 \hat{i}+4 \hat{j}-7 \hat{k})+\lambda(-2 \hat{i}-5 \hat{j}+13 \hat{k})$

$\Rightarrow(x-3) \hat{i}+(y-4) \hat{j}+(z+7) \hat{k}=\lambda(-2 \hat{i}-5 \hat{j}+13 \hat{k})$

इसलिए, रेखा के सदिश समीकरण है

$ (x-3) \hat{i}+(y-4) \hat{j}+(z+7) \hat{k}=\lambda(-2 \hat{i}-5 \hat{j}+13 \hat{k}) $

हल

दी गई समीकरण $\vec{r} \cdot(\hat{i}+\hat{j}-\hat{k})=2$ है

$\begin{matrix} \Rightarrow & (x \hat{i}+y \hat{j}+z \hat{k}) \cdot(\hat{i}+\hat{j}-\hat{k}) & =2 \\ \Rightarrow & x+y-z & =2\end{matrix} $

इसलिए, समतल का कार्तीय समीकरण $x+y-z=2$ है।

हल

दिया गया समतल $x+2 y+3 z-6=0$ है

समतल के लम्ब सदिश $\vec{n}=\hat{i}+2 \hat{j}+3 \hat{k}$

$\therefore \hat{n}=\dfrac{\vec{n}}{|\vec{n}|}=\dfrac{\hat{i}+2 \hat{j}+3 \hat{k}}{\sqrt{(1)^{2}+(2)^{2}+(3)^{2}}}=\dfrac{1}{\sqrt{14}} \hat{i}+\dfrac{2}{\sqrt{14}} \hat{j}+\dfrac{3}{\sqrt{14}} \hat{k}$

इसलिए, दिए गए कथन के अनुसार ‘सत्य’ है।

हल

समतल का समीकरण $2 x-3 y+5 z+4=0$ है

$\Rightarrow \quad 2 x-3 y+5 z=-4$

$\Rightarrow \dfrac{2}{-4} x-\dfrac{3 y}{-4}+\dfrac{5 z}{-4}=1$

$\Rightarrow \dfrac{x}{-2}+\dfrac{y}{4 / 3}+\dfrac{z}{-4 / 5}=1$

इसलिए, आवश्यक अंतराल $-2, \dfrac{4}{3}$ और $-\dfrac{4}{5}$ हैं

इसलिए, दिए गए कथन के अनुसार ‘सत्य’ है।

हल

रेखा का समीकरण $\vec{r}=(5 \hat{i}-\hat{j}-4 \hat{k})+\lambda(2 \hat{i}-\hat{j}+\hat{k})$ और समतल का समीकरण $\vec{r} \cdot(3 \hat{i}-4 \hat{j}-\hat{k})+5=0$ है

यहाँ, रेखा के दिशा सदिश है: $$ \vec{b}_{1}=2 \hat{i}-\hat{j}+\hat{k} $$

समतल के अभिलम्ब सदिश है: $$ \vec{n}_{2}=3 \hat{i}-4 \hat{j}-\hat{k} $$

रेखा और समतल के बीच कोण के लिए सूत्र निम्नलिखित है:

$ \sin \theta=\dfrac{\mathbf{d} \cdot \mathbf{n}}{|\mathbf{d}||\mathbf{n}|} $

यहाँ:

• $ \mathbf{d} $ रेखा के दिशा सदिश है।
• $ \mathbf{n} $ समतल के अभिलम्ब सदिश है।

$\therefore \quad \sin \theta=\dfrac{b_1 \vec{n} _2}{| \vec{b} _1|| \vec{n} _2|}$

$\Rightarrow \quad \sin \theta=\dfrac{(2 \hat{i}-\hat{j}+\hat{k}) \cdot(3 \hat{i}-4 \hat{j}-\hat{k})}{\sqrt{4+1+1} \cdot \sqrt{9+16+1}}=\dfrac{6+4-1}{\sqrt{6} \cdot \sqrt{26}}=\dfrac{9}{\sqrt{6} \cdot \sqrt{26}}$

$\Rightarrow \quad \sin \theta=\dfrac{9}{2 \sqrt{39}}$

इसलिए, दिए गए कथन ‘गलत’ है।

हल

दिए गए समतल हैं $ \vec{r} \cdot(2 \hat{i}-3 \hat{j}+\hat{k})=1 $ और $ \vec{r} \cdot(\hat{i}-\hat{j})=4 $

यहाँ, पहले समतल के अभिलम्ब सदिश है

$\vec{n}_1=2\hat{i}-3\hat{j}+\hat{k}$ और

दूसरे समतल के अभिलम्ब सदिश है

$\vec{n}_2=(\hat{i}-\hat{j})$

दो समतलों के बीच कोण $ \theta $ के कोसाइन के लिए सूत्र निम्नलिखित है :

$\cos\theta=\dfrac{\vec{n}_1\cdot\vec{n}_2}{|\vec{n}_1||\vec{n}_2|}$

जहाँ, $\vec{n}_1$ और $\vec{n}_2$ समतलों के अभिलम्ब सदिश हैं।

इसलिए, $ \quad\cos\theta=\dfrac{(2 i-3 j+\hat{k}) \cdot(\hat{i}-\hat{j})}{\sqrt{4+9+1} \cdot\sqrt{1+1}}=\dfrac{2+3}{\sqrt{14} \cdot\sqrt{2}}=\dfrac{5}{\sqrt{28}} $

$ \therefore \quad \theta=\cos ^{-1}\left(\dfrac{5}{\sqrt{28}}\right) $

इसलिए, दिए गए कथन ‘गलत’ है।

हल

दिए गए रेखा की दिशा वेक्टर है : $ \vec{d} = \hat{i} - \hat{j} + 2 \hat{k} $

दिए गए समतल के अभिलम्ब वेक्टर है : $ \vec{n} = 3 \hat{i} + \hat{j} - \hat{k} $

समानांतरता की जांच:

रेखा समतल समानांतर होने के लिए, रेखा के दिशा वेक्टर को समतल के अभिलम्ब वेक्टर के लंबवत होना चाहिए।

इसका अर्थ है कि उनका डॉट उत्पाद शून्य होना चाहिए:

$ \vec{d} \cdot \vec{n} = (\hat{i} - \hat{j} + 2 \hat{k}) \cdot (3 \hat{i} + \hat{j} - \hat{k}) = 1 \cdot 3 + (-1) \cdot 1 + 2 \cdot (-1) = 3 - 1 - 2 = 0 $

चूंकि डॉट उत्पाद शून्य है, रेखा विशेष रूप से समतल समानांतर है।

रेखा समतल में निहित होने की जांच:

रेखा समतल में निहित होने के लिए, रेखा पर एक बिंदु समतल के समीकरण को संतुष्ट करना चाहिए।

रेखा के माध्यम से गुजरने वाले बिंदु के स्थिति वेक्टर है : $ \vec{a} = 2 \hat{i} - 3 \hat{j} - \hat{k} $

$\vec{a}$ को समतल के समीकरण में प्रतिस्थापित करें : $ (2 \hat{i} - 3 \hat{j} - \hat{k}) \cdot (3 \hat{i} + \hat{j} - \hat{k}) + 2 = 6 - 3 + 1 + 2 = 6 $

परिणाम शून्य नहीं है, इसलिए बिंदु समतल के समीकरण को संतुष्ट नहीं करता है।

इसलिए, रेखा समतल में नहीं है।

अतः, दिए गए कथन ‘गलत’ है।

हल

दिए गए कार्तीय रूप की रेखा है : $ \dfrac{x-5}{3} = \dfrac{y+4}{7} = \dfrac{z-6}{2} = \lambda $

इस समीकरण एक रेखा को बताता है जो बिंदु $(x_1, y_1, z_1) = (5, -4, 6)$ से गुजरती है और दिशा अनुपात $ (a, b, c) = (3, 7, 2) $ हैं।

कार्तीय रूप को वेक्टर रूप में बदलने के लिए, हम बिंदु और दिशा वेक्टर का उपयोग करते हैं:

स्थिति वेक्टर द्वारा दिया गया है :

$ \vec{r}_0 = 5 \hat{i} - 4 \hat{j} + 6 \hat{k} $

दिशा वेक्टर है:

$ \vec{d} = 3 \hat{i} + 7 \hat{j} + 2 \hat{k} $

रेखा का वेक्टर समीकरण निम्नलिखित है :

$\vec{r}=\vec{r}_0+\lambda\vec{d}$

$ \Rightarrow \vec{r} = (5 \hat{i} - 4 \hat{j} + 6 \hat{k}) + \lambda (3 \hat{i} + 7 \hat{j} + 2 \hat{k}) $

इसलिए, दिए गए कथन “सत्य” है।

हल

कार्तीय रूप में एक रेखा का समीकरण निम्नलिखित होता है : $ \dfrac{x - x_1}{a} = \dfrac{y - y_1}{b} = \dfrac{z - z_1}{c} $

जहाँ $ (x_1, y_1, z_1) $ रेखा गुजरता हुआ बिंदु है और $ (a, b, c) $ दिशा अनुपात हैं।

दिया गया है:

• रेखा गुजरता हुआ बिंदु : $ (5, -2, 4) $

• रेखा के समान्तर सदिश : $ 2 \hat{i} + \hat{j} + 3 \hat{k} $

इसलिए, $ x_1 = 5, y_1 = -2, z_1 = 4 $ और $ a = 2, b = 1, c = 3 $

इसलिए, रेखा का समीकरण होगा : $ \dfrac{x - 5}{2} = \dfrac{y + 2}{1} = \dfrac{z - 4}{3} $

इसलिए, दिए गए कथन “असत्य” है।

हल

एक नॉर्मल सदिश $\vec{n} = (a, b, c)$ के साथ एक समतल का समीकरण निम्नलिखित होता है :

$ a(x - x_0) + b(y - y_0) + c(z - z_0) = 0 $

• मूल बिंदु से एक समतल पर लंब डाले गए लंब का पाद बिंदु एक बिंदु $(x_0, y_0, z_0)$ प्रदान करता है जो समतल पर स्थित है।

• समतल का नॉर्मल सदिश मूल बिंदु और इस बिंदु के बीच वेक्टर के समान होता है $(x_0,y_0,z_0)$।

इसलिए, $\vec{n}=(x_0,y_0,z_0)$।

जब मूल बिंदु से लंब का पाद बिंदु $(x_0,y_0,z_0)$ होता है, तो समतल का समीकरण होता है:

$x_0(x-x_0)+y_0(y-y_0)+z_0(z-z_0)=0$

चूंकि लंब का पाद बिंदु $(5, -3, -2)$ है, तो समतल का समीकरण होगा:

$5(x-5)-3(y+3)-2(z+2)=0$

$\Rightarrow5x-3y-2z=38$

$\Rightarrow\vec{r}\cdot(5\hat{i}-3\hat{j}-2\hat{k})=38$

इसलिए, दिए गए कथन “सत्य” है।