प्रायिकता
छोटे उत्तर प्रकार के प्रश्न
1. एक भारित पासे के निकाले जाने पर निम्नलिखित प्रायिकताएँ दी गई हैं:
$P(1)=P(2)=0.2, P(3)=P(5)=P(6)=0.1$ और $P(4)=0.3$
पासा दो बार उछाला जाता है। मान लीजिए $A$ और $B$ घटनाएँ हैं, जिनके नाम क्रमशः ‘हर बार समान संख्या’ और ‘कुल अंक 10 या अधिक’ हैं। निर्धारित कीजिए कि क्या $A$ और $B$ स्वाेक्ष घटनाएँ हैं या नहीं।
उत्तर दिखाएँ
हल
एक भारित पासा उछाला जाता है जिसके निम्नलिखित प्रायिकताएँ हैं:
$P(1)=P(2)=0.2, P(3)=P(5)=P(6)=0.1$ और $P(4)=0.3$ और पासा दो बार उछाला जाता है। दिया गया है कि:
$A =$ हर बार समान संख्या और
$B =$ कुल अंक 10 या अधिक है।
$ \begin{aligned} & \text{ इसलिए, } P(A)=[P(1,1)+P(2,2)+P(3,3)+P(4,4)+P(5,5)+P(6,6)] \\ & =P(1) \cdot P(1)+P(2) \cdot P(2)+P(3) \cdot P(3)+P(4) \cdot P(4) \\ & +P(5) \cdot P(5)+P(6) \cdot P(6) \\ & =0.2 \times 0.2+0.2 \times 0.2+0.1 \times 0.1+0.3 \times 0.3+0.1 \times 0.1 \\ & +0.1 \times 0.1 \\ & =0.04+0.04+0.01+0.09+0.01+0.01=0.20 \end{aligned} $
अब $B=[(4,6),(6,4),(5,5),(5,6),(6,5),(6,6)]$
$P(B)=[P(4) \cdot P(6)+P(6) \cdot P(4)+P(5) \cdot P(5)+P(5) \cdot P(6)$ $+P(6) \cdot P(5)+P(6) \cdot P(6)$
$=0.3 \times 0.1+0.1 \times 0.3+0.1 \times 0.1+0.1 \times 0.1+0.1 \times 0.1$ $+0.1 \times 0.1$
$=0.03+0.03+0.01+0.01+0.01+0.01=0.10$
$A$ और $B$ दोनों घटनाएँ स्वापेक्ष घटनाएँ होंगी यदि
$$ \begin{equation*} P(A \cap B)=P(A) \cdot P(B) \ldots(i) \end{equation*} $$
यहाँ,
$ (A \cap B)={(5,5),(6,6)} $
$ \therefore \quad P(A \cap B)=P(5,5)+P(6,6)=P(5) \cdot P(5)+P(6) \cdot P(6) $
$ =0.1 \times 0.1+0.1 \times 0.1=0.02 $
$L.H.S=P(A \cap B)=0.02\\ $ $R.H.S=P(A).P(B)=0.20 \times 0.10 = 0.02\\ $ $\therefore L.H.S=R.H.S\\ $ $\therefore P(A \cap B)=P(A).P(B)$
$ \begin{aligned} & 0.02=0.20 \times 0.10 \\ & 0.02=0.02 \end{aligned} $
इसलिए, $A$ और $B$ स्वापेक्ष घटनाएँ हैं।
2. उपरोक्त प्रश्न 1 के संदर्भ में संदर्भित करें। यदि पासा समान रूप से भारित होता, तो निर्धारित कीजिए कि क्या घटनाएँ $A$ और $B$ स्वापेक्ष घटनाएँ हैं या नहीं।
उत्तर दिखाएं
हल
प्रश्न 1 के हल के अनुसार, हमारे पास है
$A={(1,1),(2,2),(3,3),(4,4),(5,5),(6,6)}$
$\therefore n(A)=6$ और $n(S)=6 \times 6=36$
इसलिए, $P(A)=\dfrac{n(A)}{n(S)}=\dfrac{6}{36}=\dfrac{1}{6}$
और $\quad B={(4,6),(6,4),(5,5),(5,6),(6,5),(6,6)}$
$n(B)=6$ और $n(S)=36$
$\therefore \quad P(B)=\dfrac{n(B)}{n(S)}=\dfrac{6}{36}=\dfrac{1}{6}$
$A \cap B={(5,5),(6,6)}$
$\therefore P(A \cap B)=\dfrac{2}{36}=\dfrac{1}{18}$
इसलिए, यदि $A$ और $B$ स्वाधीन घटनाएं हैं, तो
$P(A \cap B)=P(A) \cdot P(B)$
$\Rightarrow \quad \dfrac{1}{18} \neq \dfrac{1}{6} \times \dfrac{1}{6} \Rightarrow \dfrac{1}{18} \neq \dfrac{1}{36}$
इसलिए, $A$ और $B$ स्वाधीन घटनाएं नहीं हैं।
3. दो घटनाओं $A$ और $B$ में से कम से कम एक घटना के घटने की प्रायिकता 0.6 है। यदि $A$ और $B$ एक साथ घटित होने की प्रायिकता 0.3 है, तो $P(\overline{A})+P(\overline{B})$ का मूल्यांकन करें।
उत्तर दिखाएं
हल
हम जानते हैं कि:
$A \cup B$ यह दर्शाता है कि कम से कम एक घटना घटित होती है और $A \cap B$ यह दर्शाता है कि दोनों घटनाएं एक साथ घटित होती हैं।
$ \begin{matrix} \text{ इसलिए, } P(A \cup B) =P(A)+P(B)-P(A \cap B) \\ \Rightarrow 0.6 =P(A)+P(B)-0.3 \\ \Rightarrow 0.9 =P(A)+P(B) \\ \Rightarrow 0.9 =1-P(\overline{A})+1-P(\overline{B}) \\ \Rightarrow P(\overline{A})+P(\overline{B}) =2-0.9=1.1 \end{matrix} $
इसलिए, अभीष्ट उत्तर 1.1 है।
4. एक बरतन में 5 लाल गेंद और 3 काली गेंद हैं। तीन गेंद एक एक करके बिना वापस किए जाने के बिना खींची जाती हैं। यदि पहली गेंद लाल है, तो तीन गेंदों में से कम से कम एक गेंद काली होने की प्रायिकता क्या है?
उत्तर दिखाएं
हल
लाल गेंद को $R$ और काली गेंद को $B$ से निरूपित करें। यदि तीन गेंदों में से कम से कम एक गेंद काली हो और पहली गेंद लाल है, तो निम्नलिखित तीन संभावित स्थितियाँ हो सकती हैं।
(i) $E_1$ : दूसरी गेंद काली है और तीसरी गेंद लाल है
(ii) $E_2$ : दूसरी गेंद काली है और तीसरी गेंद भी काली है
(iii) $E_3:$ दूसरा गेंद लाल और तीसरा काला है
$ \begin{aligned} & \therefore \quad P(E_1)=P(R_1) \cdot P(B_1 / R_1) \cdot P(R_2 / R_1 B_1)=\dfrac{5}{8} \cdot \dfrac{3}{7} \cdot \dfrac{4}{6}=\dfrac{60}{336}=\dfrac{5}{28} \\ & \quad P(E_2)=P(R_1) \cdot P(B_1 / R_1) \cdot P(B_2 / R_1 B_1)=\dfrac{5}{8} \cdot \dfrac{3}{7} \cdot \dfrac{2}{6}=\dfrac{30}{336}=\dfrac{5}{56} \\ & \text{ और } P(E_3)=P(R_1) \cdot P(R_2 / R_1) \cdot B(B_1 / R_1 R_2)=\dfrac{5}{8} \cdot \dfrac{4}{7} \cdot \dfrac{3}{6}=\dfrac{60}{336}=\dfrac{5}{28} \\ & \therefore \quad P(E)=P(E_1)+P(E_2)+P(E_3)=\dfrac{5}{28}+\dfrac{5}{56}+\dfrac{5}{28}=\dfrac{25}{56} \end{aligned} $
इसलिए अभीष्ट प्रायिकता $\dfrac{25}{56}$ है।
5. दो पासे एक साथ फेंके जाते हैं और कुल अंक नोट किए जाते हैं। घटनाएँ $E, F$ और $G$ क्रमशः ‘कुल 4’ ‘कुल 9 या अधिक’, और ‘कुल 5 से विभाज्य’ हैं। $P(E), P(F)$ और $P(G)$ की गणना करें और निर्धारित करें कि कौन से घटनाओं के युग्म, यदि कोई हों, स्वतंत्र हैं।
उत्तर दिखाएँ
हल
दो पासे एक साथ फेंके जाते हैं
$\therefore n(S)=36$
$E=\text{ कुल } 4={(2,2),(1,3),(3,1)} \\ \therefore n(E)=3$
$F=\text{ कुल } 9 \text{ या अधिक } $
$={(3,6),(6,3),(5,4),(4,5),(5,5),(4,6),(6,4),(5,6),(6,5),(6,6)}$
$\therefore n(F)=10 ;\\ G=\text{ कुल } 5 \text{ से विभाज्य } ={(1,4),(4,1),(2,3),(3,2),(4,6),(6,4),(5,5)} \\ \therefore n(G)=7$
यहाँ, हम देखते हैं कि $(E \cap F)=\phi$ और $(E \cap G)=\phi$
और $ (F \cap G)={(4,6),(6,4),(5,5)} $
$ \begin{aligned} \therefore \quad n(F & \cap G)=3 \text{ और } (E \cap F \cap G)=\phi \\ \therefore \quad P(E) & =\dfrac{n(E)}{n(S)}=\dfrac{3}{36}=\dfrac{1}{12} \\ P(F) & =\dfrac{n(F)}{n(S)}=\dfrac{10}{36}=\dfrac{5}{18} ; P(G)=\dfrac{n(G)}{n(S)}=\dfrac{7}{36} \\ P(F \cap G) & =\dfrac{3}{36}=\dfrac{1}{12} \text{ और } P(F) \cdot P(G)=\dfrac{5}{18} \cdot \dfrac{7}{36}=\dfrac{35}{648} \end{aligned} $
क्योंकि, $P(F \cap G) \neq P(F) . P(G)$
इसलिए, कोई भी स्वतंत्र घटनाओं के युग्म नहीं है।
6. एक सिक्का तीन बार उछालने के प्रयोग को द्विपद वितरण के रूप में क्यों कहा जाता है?
उत्तर दिखाएं
हल
हम जानते हैं कि यदि यादृच्छिक चर $X$ मान $0,1,2,3, \ldots, n$ ले लेता है और यदि यह प्रायिकता $P(X=r)={ }^{n} C_r p^{r} q^{n-r}$ द्वारा दी जाती है, जहाँ $q=1-p$ और $r=0,1,2,3, \ldots$ है, तो $X$ द्विपद वितरण के रूप में कहलाता है।
इसी तरह, एक सिक्का तीन बार उछालने के मामले में,
$n=3$ और $X$ के मान $0,1,2,3$ होते हैं, जहाँ $p=\dfrac{1}{2}, q=\dfrac{1}{2}$ है।
इसलिए, इसे द्विपद वितरण के रूप में कहा जाता है।
7. $A$ और $B$ दो घटनाएँ इस प्रकार हैं कि $P(A)=\dfrac{1}{2}, P(B)=\dfrac{1}{3}$ और $P(A \cap B)=\dfrac{1}{4}$. ज्ञात कीजिए:
(i) $P(A / B)$
(ii) $P(B / A)$
(iii) $P(A^{\prime} / B)$
(iv) $P(A^{\prime} / B^{\prime})$
उत्तर दिखाएं
हल
हम जानते हैं $P(A)=\dfrac{1}{2}, P(B)=\dfrac{1}{3}$ और $P(A \cap B)=\dfrac{1}{4}$
$ \begin{aligned} P(A^{\prime}) & =1-\dfrac{1}{2}=\dfrac{1}{2}, P(B^{\prime})=1-\dfrac{1}{3}=\dfrac{2}{3} \\ P(A^{\prime} \cap B^{\prime}) & =1-P(A \cup B)=1-[P(A)+P(B)-P(A \cap B)] \\ & =1-[\dfrac{1}{2}+\dfrac{1}{3}-\dfrac{1}{4}]=1-[\dfrac{6+4-3}{12}]=1-\dfrac{7}{12}=\dfrac{5}{12} \end{aligned} $
(i) $P(A / B)=\dfrac{P(A \cap B)}{P(B)}=\dfrac{1 / 4}{1 / 3}=\dfrac{3}{4}$
(ii) $P(B / A)=\dfrac{P(A \cap B)}{P(A)}=\dfrac{1 / 4}{1 / 2}=\dfrac{1}{2}$
(iii) $P(A^{\prime} / B)=\dfrac{P(A^{\prime} \cap B)}{P(B)}=\dfrac{P(B)-P(A \cap B)}{P(B)}$
$ =1-\dfrac{P(A \cap B)}{P(B)}=1-\dfrac{1 / 4}{1 / 3}=1-\dfrac{3}{4}=\dfrac{1}{4} $
(iv) $P(A^{\prime} / B^{\prime})=\dfrac{P(A^{\prime} \cap B^{\prime})}{P(B^{\prime})}=\dfrac{5 / 12}{2 / 3}=\dfrac{5}{12} \times \dfrac{3}{2}=\dfrac{5}{8}$
8. तीन घटनाएँ $A, B$ और $C$ क्रमशः $\dfrac{2}{5}, \dfrac{1}{3}$ और $\dfrac{1}{2}$ की प्रायिकता हैं। यह दिया गया है कि $P(A \cap C)=\dfrac{1}{5}$ और $P(B \cap C)=\dfrac{1}{4}$, $P(C / B)$ और $P(A^{\prime} \cap C^{\prime})$ के मान ज्ञात कीजिए।
उत्तर दिखाएं
हल
हमें $P(A)=\dfrac{2}{5}, P(B)=\dfrac{1}{3}$ और $P(C)=\dfrac{1}{2}$ दिया गया है
$ \begin{aligned} & P(A \cap C)=\dfrac{1}{5} \text{ और } P(B \cap C)=\dfrac{1}{4} \\ & \therefore \quad P(C / B)=\dfrac{P(B \cap C)}{P(B)}=\dfrac{1 / 4}{1 / 3}=\dfrac{3}{4} \\ & P(A^{\prime} \cap C^{\prime})=1-P(A \cup C) \\ & =1-[P(A)+P(C)-P(A \cap C)] \end{aligned} $
$ =1-[\dfrac{2}{5}+\dfrac{1}{2}-\dfrac{1}{5}]=1-\dfrac{7}{10}=\dfrac{3}{10} $
9. मान लीजिए $E_1$ और $E_2$ दो स्वतंत्र घटनाएँ हैं जैसे कि $P(E_1)=p_1$ और $P(E_2)=p_2$। घटनाओं के कौन से शब्दों की संभावना निम्नलिखित हैं:
(i) $p_1 p_2$
(ii) $(1-p_1) p_2$
(iii) $1-(1-p_1)(1-p_2)$
(iv) $p_1+p_2-2 p_1 p_2$
उत्तर दिखाएं
हल
यहाँ,
$ P(E_1)=p_1 \text{ और } P(E_2)=p_2 $
(i)
$ p_1 p_2=P(E_1) \cdot P(E_2)=P(E_1 \cap E_2) $
इसलिए, $E_1$ और $E_2$ दोनों घटित होते हैं।
(ii)
$ (1-p_1) \cdot p_2=P(E_1)^{\prime} \cdot P(E_2)=P(E_1^{\prime} \cap E_2) $
इसलिए, $E_1$ नहीं घटित होता लेकिन $E_2$ घटित होता है।
(iii) $1-(1-p_1)(1-p_2)=1-P(E_1)^{\prime} P(E_2)^{\prime}=1-P(E_1^{\prime} \cap E_2^{\prime})$
$ =1-[1-P(E_1 \cup E_2)]=P(E_1 \cup E_2) $
इसलिए, $E_1$ या $E_2$ या दोनों घटनाएँ घटित होती हैं।
(iv)
$ \begin{aligned} p_1+p_2-2 p_1 p_2 & =P(E_1)+P(E_2)-2 P(E_1) \cdot P(E_2) \\ & =P(E_1)+P(E_2)-2 P(E_1 \cap E_2) \\ & =P(E_1 \cup E_2)-2 P(E_1 \cap E_2) \end{aligned} $
इसलिए, $E_1$ या $E_2$ घटित होता है लेकिन दोनों नहीं।
10. एक विसंगत यादृच्छिक चर $X$ के संभावना वितरण के नीचे दिया गया है:
$\begin{array}{|l|l|l|l|l|} \hline X & 0.5 & 1 & 1.5 & 2 \ \hline P(X) & k & k^2 & 2k^2 & k \ \hline \end{array}$
(i) $k$ का मान ज्ञात कीजिए।
(ii) वितरण का माध्य ज्ञात कीजिए।
उत्तर दिखाएं
हल
एक संभावना वितरण के लिए, हम जानते हैं कि यदि $P_i \geq 0$
(i) $\sum _{i=1}^{n} P_i=1 \Rightarrow k+k^{2}+2 k^{2}+k=1$
$ \begin{aligned} & \Rightarrow \quad 3 k^{2}+2 k-1=0 \Rightarrow 3 k^{2}+3 k-k-1=0 \\
$$ \begin{aligned} & \Rightarrow \quad 3 k(k+1)-1(k+1)=0 \Rightarrow(3 k-1)(k+1)=0 \\ & \therefore \quad k=\dfrac{1}{3} \text{ और } k=-1 \end{aligned} $$
लेकिन $k \geq 0 \quad \therefore k=\dfrac{1}{3}$
(ii) वितरण का माध्य
$$ \begin{aligned} E(X)&=\sum _{i=1}^{n} X_i P_i=0.5 k+1 . k^{2}+1.5(2 k^{2})+2 k\\ & =\dfrac{k}{2}+k^{2}+3 k^{2}+2 k=4 k^{2}+\dfrac{5}{2} k \\ & =4(\dfrac{1}{3})^{2}+\dfrac{5}{2}(\dfrac{1}{3})=\dfrac{4}{9}+\dfrac{5}{6}=\dfrac{23}{18} \end{aligned} $$
11. सिद्ध कीजिए कि
(i) $P(A)=P(A \cap B)+P(A \cap \overline{B})$
(ii) $P(A \cup B)=P(A \cap B)+P(A \cap \overline{B})+P(\overline{A} \cap B)$
उत्तर दिखाएँ
हल
(i) सिद्ध करना है: $P(A)=P(A \cap B)+P(A \cap \overline{B})\$ दाहिना हाथ की ओर $=P(A \cap B)+P(A \cap \bar{{}B})$
$$ \begin{aligned} & =P(A) \cdot P(B)+P(A) \cdot P(\overline{B})=P(A)[P(B)+P(\overline{B})] \\ & =P(A) \cdot 1 \\ & =P(A)=\text{ बाईं हाथ की ओर। इसलिए सिद्ध कर दिया। } \end{aligned} $$
(ii) सिद्ध करना है: $P(A \cup B)=P(A \cap B)+P(A \cap \overline{B})+P(\overline{A} \cap B)$
दाहिना हाथ की ओर $=P(A) \cdot P(B)+P(A) \cdot P(\bar{{}B})+P(\bar{{}A}) \cdot P(B)$
$$ \begin{aligned} & =P(A) \cdot P(B)+P(A)[1-P(B)]+[1-P(A)] \cdot P(B) \\ & =P(A) \cdot P(B)+P(A)-P(A) \cdot P(B)+P(B)-P(A) \cdot P(B) \\ & =P(A)+P(B)-P(A \cap B) \\ & =P(A \cup B)=\text{ बाईं हाथ की ओर। इसलिए सिद्ध कर दिया। } \end{aligned} $$
12. यदि $X$ एक सिक्के के तीन उछालों में पैदा होने वाले पैंस की संख्या है, तो $X$ के मानक विचलन का निर्धारण कीजिए।
उत्तर दिखाएँ
हल
दिया गया है: $X=0,1,2,3$
$\therefore P(X=r)={ }^{n} C_r p^{r} q^{n-r}$
जहाँ $n=3, p=\dfrac{1}{2}, q=\dfrac{1}{2}$ और $r=0,1,2,3$
$P(X=0)=\dfrac{1}{2} \times \dfrac{1}{2} \times \dfrac{1}{2}=\dfrac{1}{8} ; P(X=1)=3 \times \dfrac{1}{2} \times \dfrac{1}{2} \times \dfrac{1}{2}=\dfrac{3}{8}$
$P(X=2)=3 \times \dfrac{1}{2} \times \dfrac{1}{2} \times \dfrac{1}{2}=\dfrac{3}{8} ; P(X=3)=\dfrac{1}{2} \times \dfrac{1}{2} \times \dfrac{1}{2}=\dfrac{1}{8}$
प्रायिकता वितरण तालिका निम्नलिखित है:
| X | P(X) |
|---|---|
| 0 | 1/8 |
| 1 | 3/8 |
| 2 | 3/8 |
| 3 | 1/8 |
$\begin{array}{|l|l|l|l|l|} \hline X & 0 & 1 & 2 & 3 \ \hline P(X) & \dfrac{1}{8} & \dfrac{3}{8} & \dfrac{3}{8} & \dfrac{1}{8} \ \hline \end{array}$
$ \begin{aligned} & E(X)=0+1 \times \dfrac{3}{8}+2 \times \dfrac{3}{8}+3 \times \dfrac{1}{8}=\dfrac{3}{8}+\dfrac{6}{8}+\dfrac{3}{8}=\dfrac{12}{8}=\dfrac{3}{2} \\ & E(X^{2})=0+1 \times \dfrac{3}{8}+4 \times \dfrac{3}{8}+9 \times \dfrac{1}{8}=\dfrac{3}{8}+\dfrac{12}{8}+\dfrac{9}{8}=\dfrac{24}{8}=3 \end{aligned} $
हम जानते हैं कि $Var(X)=E(X^{2})-[E(X)]^{2}=3-(\dfrac{3}{2})^{2}=3-\dfrac{9}{4}=\dfrac{3}{4}$
$\therefore$ मानक विचलन $=\sqrt{Var(X)}=\sqrt{\dfrac{3}{4}}=\dfrac{\sqrt{3}}{2}$।
13. एक पासा खेल में, खिलाड़ी प्रत्येक पासा फेंकने के लिए ₹ 1 के बदले देती है। यदि पासा पर 3 आता है, तो वह ₹ 5 प्राप्त करती है, यदि पासा पर 1 या 6 आता है, तो वह ₹ 2 प्राप्त करती है, अन्य दशा में कुछ नहीं प्राप्त करती है। एक लंबी श्रृंखला में प्रत्येक फेंक में खिलाड़ी के अपेक्षित लाभ क्या होगा?
उत्तर दिखाएँ
हल
मान लीजिए $X$ प्रत्येक फेंक में लाभ के यादृच्छिक चर है।
$\begin{array}{|l|l|l|l|l|} \hline X & -1 & 1 & 4 \ \hline P(X) & \dfrac{1}{2} & \dfrac{1}{2} & \dfrac{1}{6} \ \hline \end{array}$
क्योंकि, वह 2, 4, 5 पर आने पर ₹ 1 हानि उठाती है।
इसलिए, $P(X=-1)=\dfrac{1}{6}+\dfrac{1}{6}+\dfrac{1}{6}=\dfrac{3}{6}=\dfrac{1}{2}$
$ \begin{matrix} P(X=1)=\dfrac{1}{6}+\dfrac{1}{6}=\dfrac{2}{6}=\dfrac{1}{3} & (\because \text{ पासा पर } 1 \text{ या } 6 \text{ आना}) \\ P(X=4)=\dfrac{1}{6} & (\because \text{ पासा पर केवल } 3 \text{ आना}) \end{matrix} $
खिलाड़ी का अपेक्षित लाभ $=\sum p_1 x_i$
$ =-1 \times \dfrac{1}{2}+1 \times \dfrac{1}{3}+4 \times \dfrac{1}{6}=-\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{2}{3}=\dfrac{1}{2}=₹ 0.50 $
14. तीन पासे एक साथ फेंके जाते हैं। यदि ज्ञात हो कि पासों पर संख्याओं का योग 6 है, तो तीनों पासों पर 2 आने की प्रायिकता ज्ञात कीजिए।
उत्तर दिखाएँ
हल
पासा तीन बार फेंका जाता है
$\therefore$ नमूना अंतर $n(S)=(6)^{3}=216$
मान लीजिए $E_1$ वह घटना है जब पासों पर संख्याओं का योग 6 होता है और $E_2$ वह घटना है जब तीनों पासों पर 2 आते हैं।
$ \begin{aligned} &\Rightarrow E_1={(1,1,4),(1,2,3),(1,3,2),(1,4,1),(2,1,3),(2,2,2),(2,3,1),(3,1,2),(3,2,1),(4,1,1)}\\ & E_2={(2,2,2)} \end{aligned} $
$\begin{aligned}\Rightarrow n(E_1)=10 \text{ and } n(E_2)=1\end{aligned}$
$\begin{aligned}\therefore P(E_2 / E_1)=\dfrac{P(E_1 \cap E_2)}{P(E_1)}=\dfrac{1 / 216}{10 / 216}=\dfrac{1}{10} . \end{aligned} $
15. मान लीजिए कि एक लॉटरी में 10,000 टिकट बेचे जाते हैं जिनमें प्रत्येक की कीमत 1 रुपया है। पहला पुरस्कार 3,000 रुपये का है और दूसरा पुरस्कार 2,000 रुपये का है। तीसरे पुरस्कार के तीन रूप 500 रुपये के हैं। यदि आप एक टिकट खरीदते हैं, तो आपकी आशा क्या है?
उत्तर दिखाएं
हल
मान लीजिए $X$ एक यादृच्छिक चर है जहाँ $X=0,500,2000$ और 3000
$\begin{array}{|l|l|l|l|l|l|} \hline X & 0 & 500 & 2000 & 3000 \ \hline P(X) & \dfrac{9995}{10000} & \dfrac{3}{10000} & \dfrac{1}{10000} & \dfrac{1}{10000} \ \hline \end{array}$
$E(X)=\sum X \cdot P(X) =0 \times \dfrac{9995}{10000} + 500 \times \dfrac{3}{10000} + 2000 \times \dfrac{1}{10000}+ 3000 \times \dfrac{1}{10000} = 0.65 $
इसलिए, आशा की कीमत 0.65 रुपये है।
16. एक बैग में 4 सफेद और 5 काले गेंद हैं। दूसरा बैग में 9 सफेद और 7 काले गेंद हैं। एक गेंद पहले बैग से दूसरे बैग में निकाली जाती है और फिर दूसरे बैग से एक गेंद यादृच्छिक रूप से निकाली जाती है। दूसरे बैग से निकाली गई गेंद के सफेद होने की प्रायिकता ज्ञात कीजिए।
उत्तर दिखाएं
हल
मान लीजिए $W_1$ और $W_2$ दो बैग हैं जो क्रमशः (4 सफेद, 5 काले) और (9 सफेद, 7 काले) गेंद रखते हैं।
मान लीजिए $E_1$ वह घटना है जिसमें गेंद पहले बैग $W_1$ से दूसरे बैग $W_2$ में सफेद गेंद के रूप में स्थानांतरित होती है और $E_2$ वह घटना है जिसमें गेंद पहले बैग $W_1$ से दूसरे बैग $W_2$ में काली गेंद के रूप में स्थानांतरित होती है।
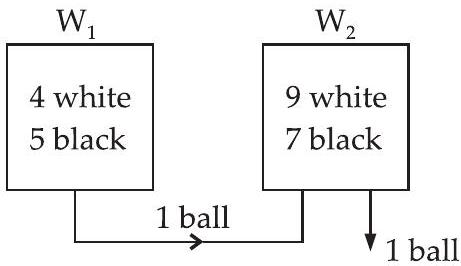
और $E$ वह घटना है जिसमें दूसरे बैग से निकाली गई गेंद सफेद होती है।
$ \begin{aligned} \therefore P(E / E_1) & =\dfrac{10}{17}, \quad P(E / E_2)=\dfrac{9}{17} \\
P(E_1) & =\dfrac{4}{9} \text{ और } P(E_2)=\dfrac{5}{9} \\ \therefore \quad P(E) & =P(E_1) \cdot P(E / E_1)+P(E_2) \cdot P(E / E_2) \\ & =\dfrac{4}{9} \times \dfrac{10}{17}+\dfrac{5}{9} \times \dfrac{9}{17}=\dfrac{40}{153}+\dfrac{45}{153}=\dfrac{85}{153}=\dfrac{5}{9} \end{aligned} $
इसलिए, आवश्यक प्रायिकता है $\dfrac{5}{9}$।
17. बॉक्स I में 3 काले और 2 सफेद गेंद हैं, बॉक्स II में 2 काले और 4 सफेद गेंद हैं। एक बॉक्स और एक गेंद यादृच्छिक रूप से चुनी जाती है। काली गेंद के चुने जाने की प्रायिकता ज्ञात कीजिए।
उत्तर दिखाएँ
हल
दिया गया है $ \text{बॉक्स}\ I={3 B, 2 W}$ और $\quad$ बॉक्स II $={2 B, 4 W}$
मान लीजिए $E_1=$ घटना कि बॉक्स I चुना गया है
$ E_2=\text{ घटना कि बॉक्स II चुना गया है } $
और $E=$ घटना कि एक काली गेंद चुनी गई है
$ \begin{aligned} \therefore \quad P(E_1) & =\dfrac{1}{2}, P(E_2)=\dfrac{1}{2}, P(E {/} E_1)=\dfrac{3}{5} \text{ और } P(E_2 E_2)=\dfrac{1}{3} \\ P(E) & =P(E_1) \cdot P(E / E_1)+P(E_2) \cdot P(E / E_2) \\ & =\dfrac{1}{2} \times \dfrac{3}{5}+\dfrac{1}{2} \times \dfrac{1}{3}=\dfrac{3}{10}+\dfrac{1}{6}=\dfrac{9+5}{30}=\dfrac{14}{30}=\dfrac{7}{15} \end{aligned} $
इसलिए, आवश्यक प्रायिकता है $\dfrac{7}{15}$।
18. एक बॉक्स में 5 बूंद और 4 लाल गेंद हैं। एक गेंद यादृच्छिक रूप से खींची जाती है और बिना वापस रखे जाए। इसका रंग भी नोट किए बिना, फिर एक गेंद यादृच्छिक रूप से खींची जाती है। दूसरी गेंद के बूंद होने की प्रायिकता क्या है?
उत्तर दिखाएँ
हल
दिया गया है कि बॉक्स में 5 बूंद और 4 लाल गेंद हैं।
मान लीजिए $E_1$ घटना है कि पहली गेंद बूंद है $E_2$ घटना है कि पहली गेंद लाल है
और $E$ घटना है कि दूसरी गेंद बूंद है।
$ \begin{aligned} \therefore \quad P(E) & =P(E_1) \cdot P(E / E_1)+P(E_2) \cdot P(E / E_2) \\ & =\dfrac{5}{9} \times \dfrac{4}{8}+\dfrac{4}{9} \times \dfrac{5}{8}=\dfrac{20}{72}+\dfrac{20}{72}=\dfrac{40}{72}=\dfrac{5}{9} \end{aligned} $
इसलिए, आवश्यक प्रायिकता है $\dfrac{5}{9}$।
19. 52 कार्डों के एक डेक से चार कार्ड बिना बदले लगातार खींचे जाते हैं। सभी चार कार्ड किंग होने की प्रायिकता क्या है?
उत्तर दिखाएं
हल
मान लीजिए $E_1, E_2, E_3$ और $E_4$ क्रमशः पहले, दूसरे, तीसरे और चौथे कार्ड किंग होने के घटनाएं हैं।
$\therefore P(E_1 \cap E_2 \cap E_3 \cap E_4)$
$=P(E_1) \cdot P(E_2 / E_1) \cdot P[\dfrac{E_3}{(E_1 \cap E_2)}] \cdot P[\dfrac{E_4}{(E_1 \cap E_2 \cap E_3 \cap E_4)}]$
$=\dfrac{4}{52} \times \dfrac{3}{51} \times \dfrac{2}{50} \times \dfrac{1}{49}=\dfrac{24}{52 \cdot 51 \cdot 50 \cdot 49}=\dfrac{1}{13 \cdot 17 \cdot 25 \cdot 49}=\dfrac{1}{27075}$
इसलिए, अभीष्ट प्रायिकता $\dfrac{1}{27075}$ है।
20. एक पासा 5 बार फेंका जाता है। विषम संख्या तीन बार आने की प्रायिकता ज्ञात कीजिए।
उत्तर दिखाएं
हल
यहाँ, $p=\dfrac{1}{6}+\dfrac{1}{6}+\dfrac{1}{6}=\dfrac{1}{2} \Rightarrow q=1-\dfrac{1}{2}=\dfrac{1}{2}$ और $n=5$
$ \begin{aligned} \therefore \quad P(x & =r)={ }^{n} C_r p^{r} q^{n-r} \\ & ={ }^{5} C_3(\dfrac{1}{2})^{3}(\dfrac{1}{2})^{5-3}=\dfrac{5 !}{3 ! 2 !} \cdot(\dfrac{1}{2})^{3} \cdot(\dfrac{1}{2})^{2}=10 \cdot \dfrac{1}{8} \cdot \dfrac{1}{4}=\dfrac{5}{16} \end{aligned} $
इसलिए, अभीष्ट प्रायिकता $\dfrac{5}{16}$ है।
21. दस सिक्के उछाले जाते हैं। कम से कम 8 सिक्कों पर सिर आने की प्रायिकता क्या है?
उत्तर दिखाएं
हल
यहाँ, $n=10, p=\dfrac{1}{2}, q=-\dfrac{1}{2}=\dfrac{1}{2}$
$ \begin{aligned} & P(X \geq 8)=P(x=8)+P(x=9)+P(x=10) \\ & ={ }^{10} C_8(\dfrac{1}{2})^{8}(\dfrac{1}{2})^{10-8}+{ }^{10} C_9(\dfrac{1}{2})^{9}(\dfrac{1}{2})^{10-9}+{ }^{10} C _{10}(\dfrac{1}{2})^{10}(\dfrac{1}{2})^{0} \\ & =\dfrac{10 !}{8 ! 2 !} \cdot(\dfrac{1}{2})^{8} \cdot(\dfrac{1}{2})^{2}+\dfrac{10 !}{9 ! 1 !}(\dfrac{1}{2})^{9}(\dfrac{1}{2})+(\dfrac{1}{2})^{10} \\ & =45 \cdot(\dfrac{1}{2})^{10}+10 \cdot(\dfrac{1}{2})^{10}+(\dfrac{1}{2})^{10}=(\dfrac{1}{2})^{10} \cdot(45+10+1) \\
$$ =56(\dfrac{1}{2})^{10}=56 \times \dfrac{1}{1024}=\dfrac{7}{128} $$ $$ \end{aligned} $$
अतः, आवश्यक प्रायिकता है $\dfrac{7}{128}$।
22. एक व्यक्ति के लक्ष्य को छूने की प्रायिकता 0.25 है। वह 7 बार गोली चलाता है। उसके कम से कम दो बार लक्ष्य को छूने की प्रायिकता क्या है?
उत्तर दिखाएं
हल
यहाँ $n=7, \quad p=0.25=\dfrac{25}{100}=\dfrac{1}{4} \quad$ और $q=1-\dfrac{1}{4}=\dfrac{3}{4}$
$$ \begin{aligned} P(X \geq 2) & =1-[P(X=0)+P(X=1)] \\ & =1-[{ }^{7} C_0(\dfrac{1}{4})^{0}(\dfrac{3}{4})^{7}+{ }^{7} C_1(\dfrac{1}{4})^{1}(\dfrac{3}{4})^{6}] \\ & =1-[(\dfrac{3}{4})^{7}+\dfrac{7}{4}(\dfrac{3}{4})^{6}]=1-(\dfrac{3}{4})^{6}(\dfrac{3}{4}+\dfrac{7}{4}) \\ & =1-(\dfrac{3}{4})^{6}(\dfrac{10}{4})=1-\dfrac{729}{4096} \times \dfrac{10}{4}=1-\dfrac{7290}{16384} \\ & =\dfrac{16384-7290}{16384}=\dfrac{9094}{16384}=\dfrac{4547}{8192} \end{aligned} $$
अतः, आवश्यक प्रायिकता है $\dfrac{4547}{8192}$।
23. 100 घड़ियों के एक समूह में 10 खराब घड़ियाँ हैं। यदि यादृच्छिक रूप से 8 घड़ियाँ (एक-एक करके प्रतिस्थापन के साथ) चुनी जाती हैं, तो कम से कम एक खराब घड़ियाँ चुनने की प्रायिकता क्या है?
उत्तर दिखाएं
हल
100 घड़ियों में खराब घड़ियों की प्रायिकता $=\dfrac{10}{100}=\dfrac{1}{10}$।
यहाँ, $n=8, p=\dfrac{1}{10}$ और $q=1-\dfrac{1}{10}=\dfrac{9}{10}$ और $r \geq 1$
$P(X \geq 1)=1-P(X=0)=1-{ }^{8} C_0(\dfrac{1}{10})^{0}(\dfrac{9}{10})^{8-0}=1-(\dfrac{9}{10})^{8}$
अतः, आवश्यक प्रायिकता है $1-(\dfrac{9}{10})^{8}$।
24. एक यादृच्छिक चर X के प्रायिकता बटुए को विचार करें:
$$ \begin{array}{|l|l|l|l|l|l|} \hline x & 0 & 1 & 2 & 3 & 4 \ \hline y & 0.1 & 0.25 & 0.3 & 0.2 & 0.15 \ \hline \end{array} $$
गणना करें:
(i) $V(\dfrac{X}{2})$
(ii) $X$ के विचलन।
उत्तर दिखाएं
हल
यहाँ, हमारे पास है
$$ \begin{array}{|l|l|l|l|l|l|} \hline x & 0 & 1 & 2 & 3 & 4 \ \hline y & 0.1 & 0.25 & 0.3 & 0.2 & 0.15 \
\hline \end{array}$
$V(X)=E(X^{2})-[E(X)]^{2}$
जहाँ $E(X)=\sum _{i=1}^{n} x_i p_i$ और $E(X^{2})=\sum _{i=1}^{n} p_i x_i^{2}$
$\therefore \quad E(X)=0 \times 0.1+1 \times 0.25+2 \times 0.3+3 \times 0.2+4 \times 0.15$
$ \qquad\quad\quad=0+0.25+0.6+0.6+0.6=2.05$
$E(X^{2})=0 \times 0.1+1 \times 0.25+4 \times 0.3+9 \times 0.2+16 \times 0.15$
$\quad\qquad=0+0.25+1.2+1.8+2.40=5.65$
(i) $V(\dfrac{X}{2})=\dfrac{1}{4} V(X)=\dfrac{1}{4}[5.65-(2.05)^{2}]=\dfrac{1}{4}[5.65-4.2025]$
$\qquad\qquad=\dfrac{1}{4} \times 1.4475=0.361875$
$[\because V(\dfrac{X}{2})=\dfrac{1}{4} V(X)]$
(ii)
$V(X)=E(X^{2})-[E(X)]^{2}=1.4475$
25. एक यादृच्छिक चर $X$ के प्रायिकता बटुआ नीचे दिया गया है:
$\begin{array}{|l|l|l|l|l|l|} \hline x & 0 & 1 & 2 & 3 \ \hline y & k & \dfrac{k}{2} & \dfrac{k}{4} & \dfrac{k}{8} \ \hline \end{array}$
(i) $k$ का मान ज्ञात कीजिए।
(ii) $P(X \leq 2)$ और $P(X>2)$ ज्ञात कीजिए।
(iii) $P(X \leq 2)+P(X>2)$ ज्ञात कीजिए।
उत्तर दिखाएँ
हल
(i) हम जानते हैं कि $P(0)+P(1)+P(2)+P(3)=1$
$ \begin{matrix} \Rightarrow k+\dfrac{k}{2}+\dfrac{k}{4}+\dfrac{k}{8} =1 \\ \Rightarrow \quad \dfrac{8 k+4 k+2 k+k}{8} =1 \Rightarrow 15 k=8 \\ \therefore \quad k =\dfrac{1}{15} \end{matrix} $
(ii)
$ \begin{aligned} P(X \leq 2) & =P(X=0)+P(X=1)+P(X=2) \\ & =k+\dfrac{k}{2}+\dfrac{k}{4}=\dfrac{7 k}{4}=\dfrac{7}{4} \times \dfrac{8}{15}=\dfrac{14}{15} \end{aligned} $
और $P(X>2)=P(X=3)=\dfrac{k}{8}=\dfrac{1}{8} \times \dfrac{8}{15}=\dfrac{1}{15}$
(iii) $P(X \leq 2)+P(X>2)=\dfrac{14}{15}+\dfrac{1}{15}=\dfrac{14+1}{15}=\dfrac{15}{15}=1$.
26. निम्नलिखित प्रायिकता बटुआ के लिए, यादृच्छिक चर $X$ के मानक विचलन की गणना कीजिए।
$\begin{array}{|l|l|l|l|} \hline x & 2 & 3 & 4 \ \hline y & 0.2 & 0.5 & 0.3 \ \hline \end{array}$
उत्तर दिखाएँ
हल
हम जानते हैं कि: मानक विचलन (S.D.) $=\sqrt{\text{ विचलन }}$
$ \begin{aligned} & \therefore \quad Var(X)=E(X^{2})-[E(X)]^{2} \\
& E(X)=2 \times 0.2+3 \times 0.5+4 \times 0.3=0.4+1.5+1.2=3.1 \\ & E(X^{2})=4 \times 0.2+9 \times 0.5+16 \times 0.3=0.8+4.5+4.8=10.1 \\ & V(X)=10.1-(3.1)^{2}=10.1-9.61=0.49 \\ & \therefore \quad \text{ S.D. }=\sqrt{Var(X)}=\sqrt{0.49}=0.7 \end{aligned} $
27. एक विक्षेपित पासा ऐसा है कि $P(4)=\dfrac{1}{10}$ और अन्य संख्याएँ समान संभावना के हैं। पासा दो बार फेंका जाता है। यदि $X$ देखे गए चौथे की संख्या है, तो यादृच्छिक चर $X$ के विचलन को ज्ञात कीजिए।
उत्तर दिखाएँ
Solution
यहाँ, यादृच्छिक चर $X=0,1,2$
$ \begin{aligned} P(4) & =\dfrac{1}{10}, P(\overline{4})=1-\dfrac{1}{10}=\dfrac{9}{10} \\ P(X=0) & =P(\overline{4}) \cdot P(\overline{4})=\dfrac{9}{10} \times \dfrac{9}{10}=\dfrac{81}{100} \\ P(X=1) & =P(\overline{4}) \cdot P(4)+P(4) \cdot P(\overline{4})=\dfrac{9}{10} \times \dfrac{1}{10}+\dfrac{1}{10} \times \dfrac{9}{10}=\dfrac{18}{100} \end{aligned} $
$P(X=2)=P(4) \cdot P(4)=\dfrac{1}{10} \times \dfrac{1}{10}=\dfrac{1}{100}$
$\begin{array}{|l|l|l|l|} \hline X & 0 & 1 & 2 \ \hline P(X) & \dfrac{81}{100} & \dfrac{18}{100} & \dfrac{1}{100} \ \hline \end{array}$
हम जानते हैं कि $V(X)=E(X^{2})-[E(X)]^{2}$
$ \begin{aligned} E(X) & =0 \times \dfrac{81}{100}+1 \times \dfrac{18}{100}+\dfrac{2}{100}=\dfrac{20}{100}=\dfrac{1}{5} \\ E(X^{2}) & =0 \times \dfrac{81}{100}+1 \times \dfrac{18}{100}+4 \times \dfrac{1}{100}=\dfrac{22}{100}=\dfrac{11}{50} \\ \therefore \quad Var(X) & =\dfrac{11}{50}-(\dfrac{1}{5})^{2}=\dfrac{11}{50}-\dfrac{1}{25}=\dfrac{9}{50}=0.18 \end{aligned} $
इसलिए, आवश्यक विचलन $=0.18$।
28. एक पासा तीन बार फेंका जाता है। मान लीजिए $X$ देखे गए दो की संख्या है, $X$ की अपेक्षा को ज्ञात कीजिए।
उत्तर दिखाएँ
Solution
यहाँ, हमें $X=0,1,2,3 \quad[\because$ पासा तीन बार फेंका जाता है] और $p=\dfrac{1}{6}, q=\dfrac{5}{6}$ है
$\therefore P(X=0)=P(not\ 2) \cdot P(not\ 2) \cdot P(not\ 2)=\dfrac{5}{6} \cdot \dfrac{5}{6} \cdot \dfrac{5}{6}=\dfrac{125}{216}$
$P(X=1)=P(2) \cdot P(not\ 2) \cdot P(not\ 2)+P(not\ 2) \cdot P(2) \cdot P(not\ 2)$
$+P( नहीं 2) . P(नहीं 2) \cdot P(2) $
$=\dfrac{1}{6} \cdot \dfrac{5}{6} \cdot \dfrac{5}{6}+\dfrac{5}{6} \cdot \dfrac{1}{6} \cdot \dfrac{5}{6}+\dfrac{5}{6} \cdot \dfrac{5}{6} \cdot \dfrac{1}{6}=\dfrac{25}{216}+\dfrac{25}{216}+\dfrac{25}{216}=\dfrac{75}{216}$
$P(X=2)=P(2) \cdot P(2) \cdot P(नहीं 2)+P(2) \cdot P(नहीं 2) \cdot P(2)$
$ +P( नहीं 2) \cdot P(2) \cdot P(2) $
$=\dfrac{1}{6} \cdot \dfrac{1}{6} \cdot \dfrac{5}{6}+\dfrac{1}{6} \cdot \dfrac{5}{6} \cdot \dfrac{1}{6}+\dfrac{5}{6} \cdot \dfrac{1}{6} \cdot \dfrac{1}{6}=\dfrac{5}{216}+\dfrac{5}{216}+\dfrac{5}{216}=\dfrac{15}{216}$
$P(X=3)=P(2) \cdot P(2) \cdot P(2)=\dfrac{1}{6} \cdot \dfrac{1}{6} \cdot \dfrac{1}{6}=\dfrac{1}{216}$
अब $E(X)=\sum _{i=1}^{n} p_i x_i$
$ \begin{aligned} & =0 \times \dfrac{125}{216}+1 \times \dfrac{75}{216}+2 \times \dfrac{15}{216}+3 \times \dfrac{1}{216} \\ = & 0+\dfrac{75}{216}+\dfrac{30}{216}+\dfrac{3}{216}=\dfrac{75+30+3}{216}=\dfrac{108}{216}=\dfrac{1}{2} \end{aligned} $
इसलिए, आवश्यक आशा मूल्य है $\dfrac{1}{2}$।
29. दो विस्फोटक पासे एक साथ फेंके जाते हैं। पहले पासे के लिए $P(6)=\dfrac{1}{2}$, अन्य संख्याएँ समान संभावना वाली होती हैं जबकि दूसरे पासे के लिए $P(1)=\dfrac{2}{5}$ होता है और अन्य संख्याएँ समान संभावना वाली होती हैं। ‘एक के देखे गए संख्या’ के प्रायिकता बंटन को ज्ञात कीजिए।
उत्तर दिखाएँ
हल
दिया गया है: पहले पासे के लिए $P(6)=\dfrac{1}{2}$ और $P(\overline{6})=1-\dfrac{1}{2}=\dfrac{1}{2}$
$\Rightarrow P(1)+P(2)+P(3)+P(4)+P(5)=\dfrac{1}{2}$
लेकिन $P(1)=P(2)=P(3)=P(4)=P(5)$
$\therefore 5 . P(1)=\dfrac{1}{2} \Rightarrow P(1)=\dfrac{1}{10}$ और $P(\overline{1})=1-\dfrac{1}{10}=\dfrac{9}{10}$
दूसरे पासे के लिए $P(1)=\dfrac{2}{5}$ और $P(\overline{1})=1-\dfrac{2}{5}=\dfrac{3}{5}$
मान लीजिए $X$ एक के देखे गए संख्या है
$ \begin{aligned} \therefore X=0,1,2 \\ \Rightarrow \quad \begin{aligned} P(X=0) =P(\overline{1}) \cdot P (\overline{1})=\dfrac{9}{10} \cdot \dfrac{3}{5}=\dfrac{27}{50}=0.54 \\ P(X=1) =P(\overline{1}) \cdot P(1)+P(1) \cdot P {(\overline{1})} \\
=\dfrac{9}{10} \cdot \dfrac{2}{5}+\dfrac{1}{10} \cdot \dfrac{3}{5}=\dfrac{18+3}{50}=\dfrac{21}{50}=0.42 \\ P(X=2) =\underset{ \hspace{2mm} }{P(1) \cdot P(1)}=\dfrac{1}{10} \cdot \dfrac{2}{5}=\dfrac{2}{50}=0.04 \end{aligned} \end{aligned} $
इसलिए, आवश्यक प्रायिकता बटुए के वितरण है
$\begin{array}{|l|l|l|l|} \hline X & 0 & 1 & 2 \ \hline P(X) & 0.54 & 0.42 & 0.04 \ \hline \end{array}$
30. असतत यादृच्छिक चर $X$ और $Y$ के दो प्रायिकता वितरण नीचे दिए गए हैं।
$\begin{array}{|l|l|l|l|l|} \hline X & 0 & 1 & 2 & 3 \ \hline P(X) & \dfrac{1}{5} & \dfrac{2}{5} & \dfrac{1}{5} & \dfrac{1}{5} \ \hline \end{array}$
$\begin{array}{|l|l|l|l|l|} \hline (Y) & 0 & 1 & 2 & 3 \ \hline P(Y) & \dfrac{1}{5} & \dfrac{3}{10} & \dfrac{2}{5} & \dfrac{1}{10} \ \hline \end{array}$
सिद्ध करें कि: $E(Y^{2})=2 E(X)$।
उत्तर दिखाएँ
हल
पहला प्रायिकता वितरण नीचे दिया गया है
$\begin{array}{|l|l|l|l|l|} \hline X & 0 & 1 & 2 & 3 \ \hline P(X) & \dfrac{1}{5} & \dfrac{2}{5} & \dfrac{1}{5} & \dfrac{1}{5} \ \hline \end{array}$
हम जानते हैं कि, $E(X)=\sum _{i=1}^{n} P_i X_i$
$\Rightarrow E(X)=0 \cdot \dfrac{1}{5}+1 \cdot \dfrac{2}{5}+2 \cdot \dfrac{1}{5}+3 \cdot \dfrac{1}{5}=0+\dfrac{2}{5}+\dfrac{2}{5}+\dfrac{3}{5}=\dfrac{7}{5}$
दूसरे प्रायिकता वितरण के लिए,
$\begin{array}{|l|l|l|l|l|} \hline Y & 0 & 1 & 2 & 3 \ \hline P(Y) & \dfrac{1}{5} & \dfrac{3}{10} & \dfrac{2}{5} & \dfrac{1}{10} \ \hline \end{array}$
$ \begin{aligned} E(Y^{2}) & =0 \cdot \dfrac{1}{5}+1 \cdot \dfrac{3}{10}+4 \cdot \dfrac{2}{5}+9 \cdot \dfrac{1}{10} \\ & =0+\dfrac{3}{10}+\dfrac{8}{5}+\dfrac{9}{10}=\dfrac{28}{10}=\dfrac{14}{5} \end{aligned} $
अब $E(Y^{2})=\dfrac{14}{5}$ और $2 E(X)=2 \cdot \dfrac{7}{5}=\dfrac{14}{5}$
इसलिए, $E(Y^{2})=2 E(X)$।
31. एक कारखाना बल्ब बनाता है। कोई भी बल्ब खराब होने की प्रायिकता $\dfrac{1}{50}$ है और वे 10 बल्बों के बॉक्स में पैक किए जाते हैं। एक बॉक्स से, निम्नलिखित की प्रायिकता ज्ञात करें (i) कोई भी बल्ब खराब नहीं है (ii) ठीक दो बल्ब खराब हैं (iii) 8 से अधिक बल्ब सही काम करते हैं।
उत्तर दिखाएँ
हल
मान लीजिए $X$ एक चर जो एक बल्ब के खराब होने को दर्शाता है।
यहाँ, $n=10, p=\dfrac{1}{50}, q=1-\dfrac{1}{50}=\dfrac{49}{50}$
हम जानते हैं कि $P(X=r)={ }^{n} C_r p^{r} q^{n-r}$
(i) कोई भी बल्ब खराब नहीं है, अर्थात $r=0$
$ P(X=0)={ }^{10} C_0(\dfrac{1}{50})^{0}(\dfrac{49}{50})^{10-0}=(\dfrac{49}{50})^{10} $
(ii) ठीक दो बल्ब खराब हैं
$ \begin{aligned} \therefore \quad P(X=2) & ={ }^{10} C_2(\dfrac{1}{50})^{2}(\dfrac{49}{50})^{10-2} \\ & =45 \cdot \dfrac{(49)^{8}}{(50)^{10}}=45 \times(\dfrac{1}{50})^{10} \times(49)^{8} \end{aligned} $
(iii) अधिक तक 8 बल्ब सही काम करते हैं
हम कह सकते हैं कि कम से कम 2 बल्ब खराब हैं
$ P(X<2)=P(X=0)+P(X=1) $
$={ }^{10} C_0(\dfrac{1}{50})^{0}(\dfrac{49}{50})^{10}+{ }^{10} C_1(\dfrac{1}{50})^{1}(\dfrac{49}{50})^{9}=(\dfrac{49}{50})^{10}+\dfrac{1}{5}(\dfrac{49}{50})^{9}$
$ =(\dfrac{49}{50})^{9}(\dfrac{49}{50}+\dfrac{1}{5})=(\dfrac{49}{50})^{9}(\dfrac{59}{50})=\dfrac{59(49)^{9}}{(50)^{10}} . $
32. मान लीजिए आपके जेब में दो सिक्के हैं जो आपके लिए एक जैसे दिखते हैं। आप जानते हैं कि एक सिक्का सामान्य है और एक दो चाल वाला है। यदि आप एक निकालते हैं, उसे उछालकर एक सिर आता है, तो इसकी प्रायिकता क्या है कि वह सामान्य सिक्का है?
उत्तर दिखाएँ
हल
मान लीजिए $E_1=$ घटना कि सिक्का सामान्य है
$ E_2=\text{ घटना कि सिक्का दो चाल वाला है } $
और $H=$ घटना कि उछाले गए सिक्के में सिर आता है।
$ P(E_1)=\dfrac{1}{2}, \quad P(E_2)=\dfrac{1}{2}, \quad P(H / E_1)=\dfrac{1}{2}, \quad P(H / E_2)=1 $
$\therefore$ बेयेस प्रमेय का उपयोग करते हुए, हम प्राप्त करते हैं
$ \begin{aligned} P(E_1 / H) & =\dfrac{P(E_1) \cdot P(H / E_1)}{P(E_1) \cdot P(H / E_1)+P(E_2) \cdot P(H / E_2)} \\ & =\dfrac{\dfrac{1}{2} \cdot \dfrac{1}{2}}{\dfrac{1}{2} \cdot \dfrac{1}{2}+\dfrac{1}{2} \cdot 1}=\dfrac{\dfrac{1}{4}}{\dfrac{1}{4}+\dfrac{1}{2}}=\dfrac{\dfrac{1}{3}}{\dfrac{3}{4}}=\dfrac{1}{3} \end{aligned} $
अतः आवश्यक प्रायिकता $\dfrac{1}{3}$ है।
33. मान लीजिए 6% लोगों के रक्त समूह O है और अन्य रक्त समूहों के लोगों में 10% विशेषज्ञ हैं, 30% लोगों के रक्त समूह O है। यदि एक विशेषज्ञ व्यक्ति यादृच्छिक रूप से चुना जाता है, तो उसके रक्त समूह O होने की प्रायिकता क्या है?
उत्तर दिखाएँ
हल
मान लीजिए $E_1=$ एक व्यक्ति के रक्त समूह $O$ होने की घटना, $E_2=$ एक व्यक्ति के रक्त समूह अन्य होने की घटना और $H=$ चुने गए व्यक्ति के बाईं तरफ बैठे होने की घटना है
$ \begin{matrix} \therefore \quad P(E_1) =0.30 \text{ और } & P(E_2)=0.70 \\ P(H / E_1) =0.06 & P(H / E_2)=0.10 \end{matrix} $
इसलिए, बेयेस के प्रमेय से
$ \begin{aligned} & \quad P(\dfrac{E_1}{H})=\dfrac{P(E_1) \cdot P(H / E_1)}{P(E_1) \cdot P(H / E_1)+P(E_2) \cdot P(H / E_2)} \\ & =\dfrac{0.30 \times 0.06}{0.30 \times 0.06+0.70 \times 0.10}=\dfrac{0.018}{0.018+0.070}=\dfrac{0.018}{0.088}=\dfrac{9}{44} \\ & \text{ इसलिए, आवश्यक प्रायिकता } \dfrac{9}{44} \text{ है }. \end{aligned} $
34. दो प्राकृतिक संख्याएँ $r$ और $s$ समुच्चय $S={1,2,3, \ldots, n}$ से बिना प्रतिस्थापन के एक-एक करके निकाली जाती हैं। $P(r \leq p / s \leq p)$ ज्ञात कीजिए, जहाँ $p \in S$।
उत्तर दिखाएँ
हल
दिया गया है: $S={1,2,3, \ldots, n}$
$ \therefore \quad P(r \leq p / s \leq p)=\dfrac{P(p \cap S)}{P(S)}=\dfrac{p-1}{n} \times \dfrac{n}{n-1}=\dfrac{p-1}{n-1} $
इसलिए, आवश्यक प्रायिकता $\dfrac{p-1}{n-1}$ है।
35. एक पासे को दो बार फेंकने पर प्राप्त अधिकतम अंक के प्रायिकता बंटन को ज्ञात कीजिए। वितरण का अपेक्षित मान भी ज्ञात कीजिए।
उत्तर दिखाएँ
हल
मान लीजिए $X$ एक पासे को दो बार फेंकने पर प्राप्त अंक के यादृच्छिक चर है।
$X ={1,2,3,4,5,6}$ और
$ \begin{aligned} S & ={(1,1),(1,2),(2,1),(2,2),(1,3),(2,3),(3,1),(3,2),(3,3),(3,4),(3,5),..,(6,6)} \end{aligned} $
इसलिए, $\quad P(X=1)=\dfrac{1}{6} \cdot \dfrac{1}{6}=\dfrac{1}{36}$
$ \begin{aligned} & P(X=2)=\dfrac{1}{6} \cdot \dfrac{1}{6}+\dfrac{1}{6} \cdot \dfrac{1}{6}+\dfrac{1}{6} \cdot \dfrac{1}{6}=\dfrac{3}{36} \\ & P(X=3)=\dfrac{1}{6} \cdot \dfrac{1}{6}+\dfrac{1}{6} \cdot \dfrac{1}{6}+\dfrac{1}{6} \cdot \dfrac{1}{6}+\dfrac{1}{6} \cdot \dfrac{1}{6}+\dfrac{1}{6} \cdot \dfrac{1}{6}=\dfrac{5}{36}
\end{aligned} $
इसी तरह
$ P(X=4)=\dfrac{7}{36} ;\ P(X=5)=\dfrac{9}{36} \text{ और } P(X=6)=\dfrac{11}{36} $
इसलिए, आवश्यक वितरण है
$\begin{array}{|l|l|l|l|l|l|l|} \hline X & 1 & 2 & 3 & 4 & 5 & 6 \ \hline P(X) & \dfrac{1}{36} & \dfrac{3}{36} & \dfrac{5}{36} & \dfrac{7}{36} & \dfrac{9}{36} &\dfrac{11}{36} \ \hline \end{array}$
अब, माध्य $E(X)=\sum _{i=1}^{n} x_i p_i$
$ \begin{aligned} & =1 \times \dfrac{1}{36}+2 \times \dfrac{3}{36}+3 \times \dfrac{5}{36}+4 \times \dfrac{7}{36}+5 \times \dfrac{9}{36}+6 \times \dfrac{11}{36} \\ & =\dfrac{1}{36}+\dfrac{6}{36}+\dfrac{15}{36}+\dfrac{28}{36}+\dfrac{45}{36}+\dfrac{66}{36}=\dfrac{161}{36} \end{aligned} $
इसलिए, आवश्यक माध्य $=\dfrac{161}{36}$।
36. यादृच्छिक चर $X$ केवल मान $0,1,2$ ले सकता है। यदि $P(X=0)=P(X=1)=p$ और $E(X^{2})=E(X)$, तो $p$ का मान ज्ञात कीजिए।
उत्तर दिखाएं
हल
दिया गया है: $\quad X=0,1,2$ और $X=0$ और 1 पर $P(X)$ का मान $p$ है। मान लीजिए $X=2$ पर $P(X)$ का मान $x$ है
$\Rightarrow \quad p+p+x=1 \quad \Rightarrow \quad x=1-2 p$
अब हमें निम्नलिखित वितरण मिलता है।
$\begin{array}{|l|l|l|l|} \hline X & 0 & 1 & 2 \ \hline P(X) & p & p & 1-2p \ \hline \end{array}$
$\therefore \quad E(X)=0 . p+1 . p+2(1-2 p)=p+2-4 p=2-3 p$
और $\quad E(X^{2})=0 . p+1 . p+4(1-2 p)=p+4-8 p=4-7 p$
दिया गया है: $\quad E(X^{2})=E(X)$
$\therefore \quad 4-7 p=2-3 p \Rightarrow 4 p=2 \Rightarrow p=\dfrac{1}{2}$
इसलिए, आवश्यक $p$ का मान $\dfrac{1}{2}$ है।
37. वितरण के विचलन की गणना कीजिए:
$\begin{array}{|l|l|l|l|l|l|l|} \hline X & 0 & 1 & 2 & 3 & 4 & 5 \ \hline P(X) & \dfrac{1}{6} & \dfrac{5}{18} & \dfrac{2}{9} & \dfrac{1}{6} & \dfrac{1}{9} &\dfrac{1}{18} \ \hline \end{array}$
उत्तर दिखाएं
हल
हम जानते हैं कि:
$ \begin{aligned} & \text{ विचलन }(X)=E(X^{2})-[E(X)]^{2} \\ & E(X)=\sum _{i=1}^{n} p_i x_i \\ &=0 \times \dfrac{1}{6}+1 \times \dfrac{5}{18}+2 \times \dfrac{2}{9}+3 \times \dfrac{1}{6}+4 \times \dfrac{1}{9}+5 \times \dfrac{1}{18} \\
$$ \begin{aligned} &=0+\dfrac{5}{18}+\dfrac{4}{9}+\dfrac{3}{6}+\dfrac{4}{9}+\dfrac{5}{18}=\dfrac{5+8+9+8+5}{18}=\dfrac{35}{18} \\ & E(X^{2})=0 \times \dfrac{1}{6}+1 \times \dfrac{5}{18}+4 \times \dfrac{2}{9}+9 \times \dfrac{1}{6}+16 \times \dfrac{1}{9}+25 \times \dfrac{1}{18} \\ &=\dfrac{5}{18}+\dfrac{8}{9}+\dfrac{9}{6}+\dfrac{16}{9}+\dfrac{25}{18}=\dfrac{5+16+27+32+25}{18}=\dfrac{105}{18} \\ & \therefore \text{ Var }(X)=\dfrac{105}{18}-\dfrac{35}{18} \times \dfrac{35}{18}=\dfrac{1890-1225}{324}=\dfrac{665}{324} \\ & \text{ Hence, the required variance is } \dfrac{665}{324} . \end{aligned} $$
38. A और B एक जोड़ी के पास डायर स्वरलेख उत्पाद वैकल्पिक रूप से फेंकते हैं। A खेल जीतता है यदि उसे 6 का कुल प्राप्त होता है और B खेल जीतती है यदि उसे 7 का कुल प्राप्त होता है। यदि A खेल की शुरुआत करता है, तो ज्ञात कीजिए कि A द्वारा जीत की प्रायिकता क्या है जब जोड़ी के पास डायर स्वरलेख के तीसरे फेंक में।
उत्तर दिखाएं
हल
मान लीजिए $A_1$ घटना है जब 6 का कुल प्राप्त होता है
$ ={(2,4),(4,2),(1,5),(5,1),(3,3)} $
और $B_1$ घटना है जब 7 का कुल प्राप्त होता है
$ ={(2,5),(5,2),(1,6),(6,1),(3,4),(4,3)} $
मान लीजिए $P(A_1)$ घटना है जब A एक फेंक में जीतता है $=\dfrac{5}{36}$
और $P(B_1)$ घटना है जब B एक फेंक में जीतती है $=\dfrac{1}{6}$
$\therefore$ अभीष्ट जीत की प्रायिकता $A$ के अपने तीसरे फेंक में
$ =P(\overline{A}_1) \cdot P(\overline{B}_1) \cdot P(A_1)=\dfrac{31}{36} \cdot \dfrac{5}{6} \cdot \dfrac{5}{36}=\dfrac{775}{7776} . $
39. दो पासे फेंके जाते हैं। निम्नलिखित दो घटनाएं $A$ और $B$ स्वतंत्र हैं या नहीं। $A={(x, y): x+y=11}$ और $B={(x, y): x \neq 5}$ जहां $(x, y)$ एक सामान्य नमूना बिंदु को दर्शाता है।
उत्तर दिखाएं
हल
दिया गया है:
$A={(x, y): x+y=11} \text{ और } B={(x, y): x \neq 5}$
$\therefore \quad A={(5,6),(6,5)},$
$B={(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(2,1),(2,2),(2,3),(2,4),(2,5),(2,6),(3,1),$ $(3,2),(3,3),(3,4),(3,5),(3,6),(4,1),(4,2),(4,3),(4,4),(4,5),(4,6),(6,1),(6,2),$ $ (6,3),(6,4),(6,5),(6,6)}$
$ \begin{aligned} & \Rightarrow n(A)=2, n(B)=30 \text{ और } n(A \cap B)=1 \\ & \therefore \quad P(A)=\dfrac{2}{36}=\dfrac{1}{18} \text{ और } P(B)=\dfrac{30}{36}=\dfrac{5}{6} \\ & \Rightarrow \quad P(A) \cdot P(B)=\dfrac{1}{18} \cdot \dfrac{5}{6}=\dfrac{5}{108} \text{ और } P(A \cap B)=\dfrac{1}{36} \end{aligned} $
क्योंकि $P(A).P(B) \neq P(P \cap B)$
अतः, A और B स्वाधीन नहीं हैं।
40. एक बरतन में $m$ सफेद और $n$ काले गेंद हैं। एक गेंद यादृच्छिक रूप से खींची जाती है और इसे बरतन में वापस डाल दिया जाता है, जिसके साथ-साथ खींची गई गेंद के रंग के बराबर $k$ अतिरिक्त गेंद भी डाल दिए जाते हैं। फिर एक बार फिर से एक गेंद यादृच्छिक रूप से खींची जाती है। दिखाइए कि एक सफेद गेंद खींचने की प्रायिकता $k$ पर निर्भर नहीं करती है।
उत्तर दिखाएँ
हल
मान लीजिए $A$ घटना है जिसमें $m$ सफेद और $n$ काले गेंद हैं
$ \begin{aligned} & E_1={\text{ पहली गेंद लाल रंग की है }} \\ & E_2={\text{ पहली गेंद काली रंग की है }}\\ & E_3={\text{ दूसरी गेंद लाल रंग की है }} \end{aligned} $
$ \begin{aligned} & \therefore \quad P(E_1)=\dfrac{m}{m+n} \text{ और } P(E_2)=\dfrac{n}{m+n} \\ & P(E_3 / E_1)=\dfrac{m+k}{m+n+k} \text{ और } P(E_3 / E_2)=\dfrac{m}{m+n+k} \\ & \text{ अब } P(E_3)=P(E_1) \cdot P(E_3 / E_1)+P(E_2) \cdot P(E_3 / E_2) \\ &=\dfrac{m}{m+n} \times \dfrac{m+k}{m+n+k}+\dfrac{n}{m+n} \times \dfrac{m}{m+n+k} \\ &=\dfrac{m}{m+n+k}[\dfrac{m+k}{m+n}+\dfrac{n}{m+n}] \\ &=\dfrac{m}{m+n+k}[\dfrac{m+n+k}{m+n}]=\dfrac{m}{m+n} \end{aligned} $
अतः, एक सफेद गेंद खींचने की प्रायिकता $k$ पर निर्भर नहीं करती है।
लंबे उत्तर प्रकार प्रश्न
41. तीन बॉग के अंदर लाल और सफेद गेंदों की संख्या इस प्रकार है, बॉग I: 3 लाल गेंद, बॉग II: 2 लाल गेंद और 1 सफेद गेंद और बॉग III: 3 सफेद गेंद। बॉग $i$ के चुने जाने और इससे एक गेंद चुने जाने की प्रायिकता $\dfrac{i}{6}$ है, जहाँ $i=1,2,3$ है।
(क) एक लाल गेंद चुने जाने की प्रायिकता क्या है? (ख) एक सफेद गेंद चुने जाने की प्रायिकता क्या है?
उत्तर दिखाएँ
हल
दिया गया है:
बैग I: 3 लाल गेंद और कोई सफेद गेंद नहीं
बैग II: 2 लाल गेंद और 1 सफेद गेंद
बैग III: कोई लाल गेंद नहीं और 3 सफेद गेंद
मान लीजिए $E_1, E_2$ और $E_3$ क्रमशः बैग I, बैग II और बैग III के चुने जाने के घटनाएँ हैं और इससे एक गेंद निकाली जाती है।
$\therefore P(E_1)=\dfrac{1}{6}, P(E_2)=\dfrac{2}{6}$ और $P(E_3)=\dfrac{3}{6}$
(i) मान लीजिए $E$ वह घटना है जिसमें लाल गेंद चुनी जाती है
$ \begin{aligned} \therefore P(E) & =P(E_1) \cdot P(E / E_1)+P(E_2) \cdot P(E / E_2)+P(E_3) \cdot P(E / E_3) \\ & =\dfrac{1}{6} \cdot \dfrac{3}{3}+\dfrac{2}{6} \cdot \dfrac{2}{3}+\dfrac{3}{6} \cdot 0=\dfrac{3}{18}+\dfrac{4}{18}=\dfrac{7}{18} \end{aligned} $
(ii) मान लीजिए $F$ वह घटना है जिसमें सफेद गेंद चुनी जाती है
$ \begin{matrix} \therefore P(F) =1-P(E) & {[P(E)+P(F)=1]} \\ \qquad\qquad =1-\dfrac{7}{18}=\dfrac{11}{18} \end{matrix} $
इसलिए, आवश्यक प्रायिकताएँ $\dfrac{7}{18}$ और $\dfrac{11}{18}$ हैं।
42. प्रश्न Q. 41 के संदर्भ में संदर्भित करें। यदि एक सफेद गेंद चुनी गई है, तो इसकी प्रायिकता क्या है कि यह (i) बैग II से आई है (ii) बैग III से आई है?
उत्तर दिखाएँ
हल
प्रश्न Q.41 के संदर्भ में, हम यहाँ बेयेस के प्रमेय का उपयोग करेंगे
$ \begin{aligned} \begin{aligned} \text{ (i) } P(E_2 / F) & =\dfrac{P(E_2) \cdot P(F / E_2)}{P(E_1) \cdot P(F / E_1)+P(E_2) \cdot P(F / E_2)+P(E_3) \cdot P(F / E_3)} \\ & =\dfrac{\dfrac{2}{6} \cdot \dfrac{1}{3}}{\dfrac{1}{6} \cdot 0+\dfrac{2}{6} \cdot \dfrac{1}{3}+\dfrac{3}{6} \cdot 1}=\dfrac{\dfrac{2}{18}}{\dfrac{2}{18}+\dfrac{3}{6}}=\dfrac{2}{11} \\ \text{ (ii) } P(E_3 / F) & =\dfrac{P(E_3) \cdot P(F / E_3)}{P(E_1) \cdot P(F / E_1)+P(E_2) \cdot P(F / E_2)+P(E_3) \cdot P(F / E_3)} \\ & =\dfrac{\dfrac{3}{6} \cdot 1}{\dfrac{1}{6} \cdot 0+\dfrac{2}{6} \cdot \dfrac{1}{3}+\dfrac{3}{6} \cdot 1}=\dfrac{\dfrac{3}{6}}{\dfrac{2}{18}+\dfrac{3}{6}}=\dfrac{3}{6} \times \dfrac{18}{11}=\dfrac{9}{11} \end{aligned} \\ \text{ इसलिए, आवश्यक प्रायिकताएँ } \dfrac{2}{11} \text{ और } \dfrac{9}{11} \text{ हैं } . \end{aligned}
$
43. एक दुकानदार तीन प्रकार के फूल के बीज $A_1, A_2$ और $A_3$ बेचता है। वे मिश्रण के रूप में बेचे जाते हैं, जहाँ अनुपात $4: 4: 2$ होता है। तीन प्रकार के बीज के बीजाणु उत्पन्न करने की दर $45 %, 60 %$ और $35 %$ है। बर्न बर्न करने की प्रायिकता गणना करें
(i) एक यादृच्छिक चुने गए बीज के बीजाणु उत्पन्न करने की
(ii) बीज बीजाणु उत्पन्न नहीं करेगा दिया गया है कि बीज प्रकार $A_3$ का है
(iii) एक यादृच्छिक चुने गए बीज बीजाणु उत्पन्न नहीं करता है दिया गया है कि बीज प्रकार $A_2$ का है।
उत्तर दिखाएं
हल
दिया गया है $A_1: A_2: A_3=4: 4: 2$
$\therefore P(A_1)=\dfrac{4}{10}, P(A_2)=\dfrac{4}{10}$ और $P(A_3)=\dfrac{2}{10}$
जहाँ $A_1, A_2$ और $A_3$ तीन प्रकार के बीज हैं।
मान लीजिए $E$ एक घटना है कि बीज बीजाणु उत्पन्न करता है और $\overline{E}$ एक घटना है कि बीज बीजाणु उत्पन्न नहीं करता है
$\therefore P(\dfrac{E}{A_1})=\dfrac{45}{100}, P(\dfrac{E}{A_2})=\dfrac{60}{100}$ और $P(\dfrac{E}{A_3})=\dfrac{35}{100}$
और $P(\dfrac{\overline{E}}{A_1})=\dfrac{55}{100}, P(\dfrac{\overline{E}}{A_2})=\dfrac{40}{100}$ और $P(\dfrac{\overline{E}}{A_3})=\dfrac{65}{100}$
(i)
$ \begin{aligned} P(E) & =P(A_1) \cdot P(\dfrac{E}{A_1})+P(A_2) \cdot P(\dfrac{E}{A_2})+P(A_3) \cdot P(\dfrac{E}{A_3}) \\ & =\dfrac{4}{10} \cdot \dfrac{45}{100}+\dfrac{4}{10} \cdot \dfrac{60}{100}+\dfrac{2}{10} \cdot \dfrac{35}{100} \\ & =\dfrac{180}{1000}+\dfrac{240}{1000}+\dfrac{70}{1000}=\dfrac{490}{1000}=0.49 \end{aligned} $
(ii) $P(\overline{E} / A_3)=1-P(E / A_3)=1-\dfrac{35}{100}=\dfrac{65}{100}=0.65$
(iii) बेयेस प्रमेय का उपयोग करते हुए, हम प्राप्त करते हैं
$ \begin{aligned} & P(A_2 / \overline{E})=\dfrac{P(A_2) \cdot P(\overline{E} / A_2)}{P(A_1) \cdot P(\overline{E} / A_1)+P(A_2) \cdot P(\overline{E} / A_2)+P(A_3) \cdot P(\overline{E} / A_3)} \\ &= \dfrac{\dfrac{4}{10} \cdot \dfrac{40}{100}}{\dfrac{4}{10} \cdot \dfrac{55}{100}+\dfrac{4}{10} \cdot \dfrac{40}{100}+\dfrac{2}{10} \cdot \dfrac{65}{100}} \\ &=\dfrac{\dfrac{160}{1000}}{\dfrac{220}{1000}+\dfrac{160}{1000}+\dfrac{130}{1000}}=\dfrac{160}{220+160+130}=\dfrac{160}{510}=\dfrac{16}{51}=0.314
\end{aligned} $
अतः, आवश्यक प्रायिकता $\dfrac{16}{51}$ या 0.314 है।
44. एक अक्षर ज्ञात है कि यह या तो TATA NAGAR से आया है या CALCUTTA से आया है। एवलेट पर, केवल दो क्रमागत अक्षर TA दिखाई दे रहे हैं। अक्षर के TATA NAGAR से आए होने की प्रायिकता क्या है?
उत्तर दिखाएं
हल
मान लीजिए $E_1$: घटना कि अक्षर TATANAGAR से आता है और
$E_2$: घटना कि अक्षर CALCUTTA से आता है
इसके अतिरिक्त $E_3$: घटना कि अक्षर पर दो क्रमागत अक्षर TA दिखाई देते हैं
$\therefore P(E_1)=\dfrac{1}{2}$ और $P(E_2)=\dfrac{1}{2}$ और $P(\dfrac{E_3}{E_1})=\dfrac{2}{8}$ और $P(\dfrac{E_3}{E_2})=\dfrac{1}{7}$
$[\because$ TATA NAGAR के लिए, दो क्रमागत अक्षर जो दिखाई देते हैं TA, AT, TA, AN, NA, AG, GA, AR हैं]
$\therefore P(E_3 / E_1)=\dfrac{2}{8}$ और
[CALCUTTA के लिए, दो क्रमागत अक्षर जो दिखाई देते हैं $CA, AL, LC, CU, UT, TT$ और TA हैं] इसलिए, $P(E_3 / E_2)=\dfrac{1}{7}$
अब बेयेस के प्रमेय का उपयोग करते हुए, हम निम्नलिखित प्राप्त करते हैं
$ P(E_1 / E_3)=\dfrac{P(E_1) \cdot P(E_3 / E_1)}{P(E_1) \cdot P(E_3 / E_1)+P(E_2) \cdot P(E_3 / E_2)} $
$ =\dfrac{\dfrac{1}{2} \cdot \dfrac{2}{8}}{\dfrac{1}{2} \cdot \dfrac{2}{8}+\dfrac{1}{2} \cdot \dfrac{1}{7}}=\dfrac{\dfrac{1}{8}}{\dfrac{1}{8}+\dfrac{1}{14}}=\dfrac{\dfrac{1}{8}}{\dfrac{7+4}{56}}=\dfrac{7}{11} $
अतः, आवश्यक प्रायिकता $\dfrac{7}{11}$ है।
45. दो बैग हैं, जिसमें से एक में 3 काले और 4 सफेद गेंद हैं जबकि दूसरे में 4 काले और 3 सफेद गेंद हैं। एक पासा फेंका जाता है। यदि यह 1 या 3 दिखाई देता है, तो पहले बैग से एक गेंद ली जाती है लेकिन यदि यह कोई अन्य संख्या दिखाई देती है, तो दूसरे बैग से एक गेंद चुनी जाती है। काली गेंद चुनने की प्रायिकता ज्ञात कीजिए।
उत्तर दिखाएं
हल
मान लीजिए $E_1$ बैग I के चयन की घटना है और $E_2$ बैग II के चयन की घटना है
मान लीजिए $E_3$ काली गेंद के चयन की घटना है
$ \begin{aligned} \therefore \quad P(E_1) & =\dfrac{2}{6}=\dfrac{1}{3} \text{ और } P(E_2)=1-\dfrac{1}{3}=\dfrac{2}{3} \\
P(E_3 / E_1) & =\dfrac{3}{7} \text{ और } P(E_3 / E_2)=\dfrac{4}{7} \\ \therefore \quad P(E_3) & =P(E_1) \cdot P(E_3 / E_1)+P(E_2) \cdot P(E_3 / E_2) \\ & =\dfrac{1}{3} \cdot \dfrac{3}{7}+\dfrac{2}{3} \cdot \dfrac{4}{7}=\dfrac{3+8}{21}=\dfrac{11}{21} \end{aligned} $
इसलिए, आवश्यक प्रायिकता है $\dfrac{11}{21}$।
46. तीन बरतन हैं जिनमें क्रमशः 2 सफेद और 3 काले गेंद, 3 सफेद और 2 काले गेंद, और 4 सफेद और 1 काले गेंद हैं। प्रत्येक बरतन के चुने जाने की समान प्रायिकता है। चुने गए बरतन से एक गेंद यादृच्छिक रूप से खींची गई और यह पाया गया कि गेंद सफेद है। दूसरे बरतन से गेंद खींचे जाने की प्रायिकता ज्ञात कीजिए।
उत्तर दिखाएं
हल
हमारे पास 3 बरतन हैं:
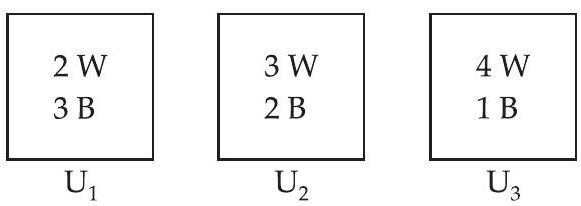
$\therefore$ किसी भी बरतन के चुने जाने की प्रायिकता है
$ P(U_1)=P(U_2)=P(U_3)=\dfrac{1}{3} $
मान लीजिए $H$ चुने गए बरतन से सफेद गेंद खींचे जाने की घटना है।
$ \begin{aligned} & \therefore P(H / U_1)=\dfrac{2}{5}, P(H / U_2)=\dfrac{3}{5} \text{ और } P(H / U_3)=\dfrac{4}{5} \\ & \therefore P(U_2 / H)=\dfrac{P(U_2) \cdot P(H / U_2)}{P(U_1) \cdot P(H / U_1)+P(U_2) \cdot P(H / U_2)+P(U_3) \cdot P(H / U_3)} \\ & \quad=\dfrac{\dfrac{1}{3} \cdot \dfrac{3}{5}}{\dfrac{1}{3} \cdot \dfrac{2}{5}+\dfrac{1}{3} \cdot \dfrac{3}{5}+\dfrac{1}{3} \cdot \dfrac{4}{5}}=\dfrac{\dfrac{3}{5}}{\dfrac{2}{5}+\dfrac{3}{5}+\dfrac{4}{5}}=\dfrac{3}{9}=\dfrac{1}{3} \end{aligned} $
इसलिए, आवश्यक प्रायिकता है $\dfrac{1}{3}$।
47. एक व्यक्ति के द्वारा चेस्ट $X$-रे के माध्यम से टीबी का अनुमान लगाने पर, व्यक्ति वास्तव में टीबी से पीड़ित होने पर टीबी का पता लगने की प्रायिकता 0.99 है। स्वस्थ व्यक्ति के टीबी के रूप में निदान करने की प्रायिकता 0.001 है। एक शहर में 1000 लोगों में से 1 व्यक्ति टीबी से पीड़ित होता है। एक व्यक्ति यादृच्छिक रूप से चुना जाता है और टीबी के रूप में निदान किया जाता है। वह वास्तव में टीबी से पीड़ित होने की प्रायिकता क्या है?
उत्तर दिखाएँ
हल
मान लीजिए $E_1$ : घटना कि एक व्यक्ति में टीबी है
$ E_2 \text{ : घटना कि एक व्यक्ति में टीबी नहीं है } $
और $H$ : घटना कि व्यक्ति के टीबी होने का निदान किया जाता है।
$ \begin{aligned} & \therefore \quad P(E_1)=\dfrac{1}{1000}=0.001, P(E_2)=1-\dfrac{1}{1000}=\dfrac{999}{1000}=0.999 \\ & P(H / E_1)=0.99, P(H / E_2)=0.001 \\ & \therefore P(E_1 / H)=\dfrac{P(E_1) \cdot P(H / E_1)}{P(E_1) \cdot P(H / E_1)+P(E_2) \cdot P(H / E_2)} \\ & =\dfrac{0.001 \times 0.99}{0.001 \times 0.99+0.999 \times 0.001}=\dfrac{0.99}{0.99+0.999} \\ & =\dfrac{0.990}{0.990+0.999}=\dfrac{990}{1989}=\dfrac{110}{221} \end{aligned} $
इसलिए, आवश्यक प्रायिकता है $\dfrac{110}{221}$।
48. एक वस्तु तीन मशीनों A, B और C द्वारा निर्मित की जाती है। निर्धारित अवधि के दौरान निर्मित कुल वस्तुओं में से, $50 %$ मशीन A द्वारा निर्मित होती है, $30 %$ मशीन B द्वारा निर्मित होती है और $20 %$ मशीन C द्वारा निर्मित होती है। मशीन A द्वारा निर्मित वस्तुओं के $2 %$ तथा मशीन B द्वारा निर्मित वस्तुओं के $2 %$ खराब होते हैं और मशीन C द्वारा निर्मित वस्तुओं के $3 %$ खराब होते हैं। सभी वस्तुएँ एक ही भंडार में संग्रहीत हैं। एक वस्तु यादृच्छया निकाली जाती है और यह खराब पाई जाती है। इस वस्तु के मशीन A द्वारा निर्मित होने की क्या प्रायिकता है?
उत्तर दिखाएँ
हल
मान लीजिए $E_1$ : घटना कि वस्तु मशीन A द्वारा निर्मित है
$E_2$ : घटना कि वस्तु मशीन B द्वारा निर्मित है
$E_3$ : घटना कि वस्तु मशीन C द्वारा निर्मित है
मान लीजिए $H$ घटना कि चयनित वस्तु खराब है।
$\therefore$ बेयेस प्रमेय का उपयोग करते हुए,
$ \begin{aligned} & P(E_1)=\dfrac{50}{100}, P(E_2)=\dfrac{30}{100}, P(E_3)=\dfrac{20}{100} \\ & P(H / E_1)=\dfrac{2}{100}, P(H / E_2)=\dfrac{2}{100} \text{ और } P(H / E_3)=\dfrac{3}{100} \\ & \therefore P(E_1 / H)=\dfrac{P(E_1) \cdot P(H / E_1)}{P(E_1) \cdot P(H / E_1)+P(E_2) \cdot P(H / E_2)+P(E_3) \cdot P(H / E_3)} \\ & =\dfrac{\dfrac{50}{100} \times \dfrac{2}{100}}{\dfrac{50}{100} \times \dfrac{2}{100}+\dfrac{30}{100} \times \dfrac{2}{100}+\dfrac{20}{100} \times \dfrac{3}{100}} \\
& =\dfrac{100}{100+60+60}=\dfrac{100}{220}=\dfrac{10}{22}=\dfrac{5}{11} \end{aligned} $
49. मान लीजिए $X$ एक विस्तारित यादृच्छिक चर है जिसकी प्रायिकता वितरण निम्नलिखित तरह पर परिभाषित है:
$ P(X=x)=\begin{cases} k(x+1) & \text{ जब } x=1,2,3,4 \ 2 k x & \text{ जब } x=5,6,7 \ 0, & \text{ अन्यथा } \end{cases} $
जहाँ $k$ एक स्थिरांक है-गणना करें:
(i) $k$ का मान (ii) $E(X)$ (iii) $X$ के मानक विचलन।
उत्तर दिखाएं
हल
(i) यहाँ, $P(X=x)=k(x+1)$ जब $x=1,2,3,4$
इसलिए, $P(X=1)=k(1+1)=2 k ; P(X=2)=k(2+1)=3 k$
$ P(X=3)=k(3+1)=4 k ; P(X=4)=k(4+1)=5 k $
इसके अलावा, $P(X=x)=2 k x$ जब $x=5,6,7$
$ \begin{aligned} & P(X=5)=2(5) k=10 k ; P(X=6)=2(6) k=12 k \\ & P(X=7)=2(7) k=14 k \end{aligned} $
और अन्यथा यह 0 है ।
$\therefore$ प्रायिकता वितरण निम्नलिखित द्वारा दिया गया है
$\begin{array}{|l|l|l|l|l|l|l|l|l|} \hline X & 1 & 2 & 3 & 4 & 5 & 6 & 7 & \text{अन्यथा} \ \hline P(X) & 2k & 3k & 4k & 5k & 10k & 12k & 14k & 0 \ \hline \end{array}$
$ \begin{aligned} & \text{ हम जानते हैं कि } \sum _{i=1}^{n} P(X_i)=1 \\ & \text{ इसलिए, } 2 k+3 k+4 k+5 k+10 k+12 k+14 k=1 \\ & \Rightarrow \quad 50 k=1 \Rightarrow k=\dfrac{1}{50} \\ & \text{ अतः, } k \text{ का मान } \dfrac{1}{50} \text{ है} \end{aligned} $
(ii) अब प्रायिकता वितरण निम्नलिखित है
$\begin{array}{|l|l|l|l|l|l|l|l|} \hline X & 1 & 2 & 3 & 4 & 5 & 6 & 7 \ \hline P(X) & \dfrac{2}{50} & \dfrac{3}{50} & \dfrac{4}{50} & \dfrac{5}{50} & \dfrac{10}{50} & \dfrac{12}{50} &\dfrac{14}{50} \ \hline \end{array}$
$ \begin{aligned} E(X)=1 \times \dfrac{2}{50}+2 \times \dfrac{3}{50}+3 \times \dfrac{4}{50}+4 \times \dfrac{5}{50}+5 \times \dfrac{10}{50}+ 6 \times \dfrac{12}{50} & +7 \times \dfrac{14}{50} \end{aligned} $
$ =\dfrac{2}{50}+\dfrac{6}{50}+\dfrac{12}{50}+\dfrac{20}{50}+\dfrac{50}{50}+\dfrac{72}{50}+\dfrac{98}{50}=\dfrac{260}{50}=\dfrac{26}{5}=5.2 $
(iii) हम जानते हैं कि मानक विचलन (SD) $=\sqrt{\text{ विचलन }}$ $=\sqrt {E(X^{2})-[E(X)]^{2}}$
$
\begin{aligned} & \begin{aligned} & E(X^{2})= 1 \times \dfrac{2}{50}+4 \times \dfrac{3}{50}+9 \times \dfrac{4}{50}+16 \times \dfrac{5}{50}+25 \times \dfrac{10}{50}+36 \times \dfrac{12}{50}+49 \times \dfrac{14}{50} \\ &=\dfrac{2}{50}+\dfrac{12}{50}+\dfrac{36}{50}+\dfrac{80}{50}+\dfrac{250}{50}+\dfrac{432}{50}+\dfrac{686}{50}=\dfrac{1498}{50} \end{aligned} \\ & \therefore \text{ Variance }(X)=\dfrac{1498}{50}-(\dfrac{26}{5})^{2} \\ & =\dfrac{1498}{50}-\dfrac{676}{25}=\dfrac{1498-1352}{50}=\dfrac{146}{50}=2.92 \\ & \therefore \quad \text{ S.D }=\sqrt{2.92}=1.7 \text{ (approx.) } \end{aligned} $
50. एक असतत यादृच्छिक चर $X$ के प्रायिकता बटुआ नीचे दिया गया है:
$\begin{array}{|l|l|l|l|l|l|l|} \hline X & 1 & 2 & 4 & 2A & 3A & 5A \ \hline P(X) & \dfrac{1}{2} & \dfrac{1}{5} & \dfrac{3}{25} & \dfrac{1}{10} & \dfrac{1}{25} & \dfrac{1}{25} \ \hline \end{array}$
गणना करें: (i) $E(X)=2.94$ होने पर $A$ का मान; (ii) $X$ के विचरण
उत्तर दिखाएँ
हल
(i) हम जानते हैं कि: $E(X)=\sum _{i=1}^{n} P_i X_i$
$ \begin{aligned} &\therefore E(X) =1 \times \dfrac{1}{2}+2 \times \dfrac{1}{5}+4 \times \dfrac{3}{25}+2 A \times \dfrac{1}{10} + 3 A \times \dfrac{1}{25}+5 A \times \dfrac{1}{25} \\ & \Rightarrow 2.94 =\dfrac{1}{2}+\dfrac{2}{5}+\dfrac{12}{25}+\dfrac{A}{5}+\dfrac{3 A}{25}+\dfrac{A}{5} \\ &\Rightarrow 2.94 =0.5+0.4+0.48+\dfrac{13 A}{25}=1.38+\dfrac{13 A}{25} \\ &\Rightarrow 2.94 -1.38=\dfrac{13 A}{25} \Rightarrow 1.56=\dfrac{13 A}{25} \\ &\Rightarrow \quad A =\dfrac{1.56 \times 25}{13}=0.12 \times 25 \\ & \therefore \quad A =3 \end{aligned} $
(ii) अब बटुआ इस प्रकार हो जाता है
$\begin{array}{|l|l|l|l|l|l|l|} \hline X & 1 & 2 & 4 & 6 & 9 & 15 \ \hline P(X) & \dfrac{1}{2} & \dfrac{1}{5} & \dfrac{3}{25} & \dfrac{1}{10} & \dfrac{1}{25} & \dfrac{1}{25} \ \hline \end{array}$
$E(X^{2})=1 \times \dfrac{1}{2}+4 \times \dfrac{1}{5}+16 \times \dfrac{3}{25}+36 \times \dfrac{1}{10}+81 \times \dfrac{1}{25}+225 \times \dfrac{1}{25}$
$ \begin{aligned} & =\dfrac{1}{2}+\dfrac{4}{5}+\dfrac{48}{25}+\dfrac{36}{10}+\dfrac{81}{25}+\dfrac{225}{25} \\ & =0.5+0.8+1.92+3.6+3.24+9.00=19.06 \end{aligned} $
विचलन $(X)=E(X^{2})-[E(X)]^{2}$
$ =19.06-(2.94)^{2}=19.06-8.64=10.42 $
51. एक यादृच्छिक चर $X$ के प्रायिकता बटुआ निम्नलिखित है:
जहाँ $k$ एक स्थिरांक है। गणना करें:
$ P(X=x)=\begin{cases} k x^{2} & \text{ जब } x=1,2,3 \\ 2 k x & \text{ जब } x=4,5,6 \\ 0 & \text{ अन्यथा } \end{cases} . $
(i) $E(X)$ (ii) $E(3 X^{2})$ (iii) $P(X \geq 4)$
उत्तर दिखाएँ
हल
दिया गया है: $\quad P(X=x)=\begin{cases} k x^{2} & \text{ जब } x=1,2,3 \\ 2 k x & \text{ जब } x=4,5,6 \\ 0 & \text{ अन्यथा } \end{cases} .$
$\therefore$ यादृच्छिक चर $X$ के प्रायिकता बटुआ निम्नलिखित है
$\begin{array}{|l|l|l|l|l|l|l|l|l|} \hline X & 1 & 2 & 3 & 4 & 5 & 6 & \text{अन्यथा} \ \hline P(X) & k & 4k & 9k & 8k & 10k & 0 \ \hline \end{array}$
हम जानते हैं कि $\sum _{i=1}^{n} P(X_i)=1$
$\therefore k+4 k+9 k+8 k+10 k+12 k=1 \Rightarrow 44 k=1 \Rightarrow k=\dfrac{1}{44}$
(i) $E(X)=\sum _{i=1}^{n} P_i X_i=1 \times k+2 \times 4 k+3 \times 9 k+4 \times 8 k+5 \times 10 k+6 \times 12 k$ $=k+8 k+27 k+32 k+50 k+72 k=190 k$ $=190 \times \dfrac{1}{44}=\dfrac{95}{22}=4.32$ (लगभग)
(ii) $E(3 X^{2})=3[k+4 \times 4 k+9 \times 9 k+16 \times 8 k+25 \times 10 k+36 \times 12 k]$
$=3[k+16 k+81 k+128 k+250 k+432 k]=3[908 k]$
$=3 \times 908 \times \dfrac{1}{44}=\dfrac{2724}{44}=61.9$ (लगभग)
(iii) $P(X \geq 4)=P(X=4)+P(X=5)+P(X=6)$
$=8 k+10 k+12 k=30 k$
$=30 \times \dfrac{1}{44}=\dfrac{15}{22}$.
52. एक बरतन में $(2 n+1)$ सिक्के हैं। यह ज्ञात है कि $n$ सिक्के दोनों ओर सिर के साथ हैं जबकि शेष सिक्के सामान्य हैं। बरतन से एक सिक्का यादृच्छिक रूप से निकाला जाता है और उछाला जाता है। यदि उछाल के परिणाम में सिर के प्रायिकता $\dfrac{31}{42}$ है, तो $n$ का मान ज्ञात करें।
उत्तर दिखाएँ
हल
दिया गया है कि $n$ सिक्के दो चेहरे वाले सिक्के हैं और शेष $(n+1)$ सिक्के अच्छे सिक्के हैं।
मान लीजिए $E_1$ : घटना कि अनुचित सिक्का चुना गया है
$E_2$ : घटना कि सामान्य सिक्का चुना गया है
$E$ : घटना कि उछाल के परिणाम एक सिरा है
$\therefore \quad P(E_1)=\dfrac{n}{2 n+1}$ और $P(E_2)=\dfrac{n+1}{2 n+1}$
$P(E / E_1)=1$ (निश्चित घटना) और $P(E / E_2)=\dfrac{1}{2}$
$\therefore \quad P(E)=P(E_1) \cdot P(E / E_1)+P(E_2) \cdot P(E / E_2)$
$=\dfrac{n}{2 n+1} \cdot 1+\dfrac{n+1}{2 n+1} \cdot \dfrac{1}{2}=\dfrac{1}{2 n+1}(n+\dfrac{n+1}{2})$
$=\dfrac{1}{2 n+1}(\dfrac{2 n+n+1}{2})=\dfrac{3 n+1}{2(2 n+1)}$
लेकिन $\quad P(E)=\dfrac{31}{42}$ (दिया गया है)
$ \begin{aligned} &\therefore \dfrac{3 n+1}{2(2 n+1)}=\dfrac{31}{42} \\ &\Rightarrow \dfrac{3 n+1}{2 n+1} =\dfrac{31}{21} \\ &\Rightarrow 63 n+21 =62 n+31 \\ &\Rightarrow n =10 \end{aligned} $
इसलिए, $n$ का अभीष्ट मान 10 है।
54. एक पासा दो बार उछाला जाता है। एक उछाल में सम संख्या प्राप्त करना एक “सफलता” है। सफलताओं की संख्या के विचलन की गणना कीजिए।
उत्तर दिखाएं
हल
मान लीजिए $E$ एक पासे के उछाल में सम संख्या प्राप्त करने की घटना है।
$\therefore P(E)=\dfrac{3}{6}=\dfrac{1}{2}$ और $P(\overline{E})=1-\dfrac{1}{2}=\dfrac{1}{2}$
यहाँ $X=0,1,2$
$ \begin{gathered} P(X=0)=P(\bar{{}E}) \cdot P(\bar{{}E})=\dfrac{1}{2} \cdot \dfrac{1}{2}=\dfrac{1}{4} \\ P(X=1)=P(E) \cdot P(\bar{{}E})+P(\bar{{}E}) \cdot P(E)=\dfrac{1}{2} \cdot \dfrac{1}{2}+\dfrac{1}{2} \cdot \dfrac{1}{2}=\dfrac{1}{4}+\dfrac{1}{4}=\dfrac{2}{4} \\ P(X=2)=P(E) \cdot P(E)=\dfrac{1}{2} \cdot \dfrac{1}{2}=\dfrac{1}{4} \end{gathered} $
$\therefore$ प्रायिकता बंटन सारणी है
$\begin{array}{|l|l|l|l|} \hline X & 0 & 1 & 2 \ \hline P(X) & \dfrac{1}{4} & \dfrac{2}{4} & \dfrac{1}{4} \ \hline \end{array}$
$ \begin{aligned} E(X) & =0 \times \dfrac{1}{4}+1 \times \dfrac{2}{4}+2 \times \dfrac{1}{4}=\dfrac{2}{4}+\dfrac{2}{4}=1 \\ E(X^{2}) & =0 \times \dfrac{1}{4}+1 \times \dfrac{2}{4}+4 \times \dfrac{1}{4}=\dfrac{3}{2} \end{aligned} $
$\therefore$ विचलन $(X)=E(X^{2})-[E(X)]^{2}=\dfrac{3}{2}-1=\dfrac{1}{2}=0.5$
55. 1 से 5 तक संख्या लिखे गए 5 कार्ड हैं, एक कार्ड पर एक संख्या। बिना प्रतिस्थापन के दो कार्ड यादृच्छिक रूप से खींचे जाते हैं। मान लीजिए $X$ दो खींचे गए कार्डों पर संख्याओं के योग को दर्शाता है। $X$ के माध्य और विचलन की गणना कीजिए।
उत्तर दिखाएं
हल
यहाँ, नमूना अंतरिक्ष $S={(1,2),(2,1),(1,3),(3,1),(2,3),(3,2)$, $(1,4),(4,1),(1,5),(5,1),(2,4),(4,2),(2,5),(5,2),(3,4),(4,3)$, $(3,5),(5,3),(5,4),(4,5)}$
$\therefore n(S)=20$
मान लीजिए $X$ दो कार्डों पर संख्याओं के योग को दर्शाने वाले यादृच्छिक चर है।
$ \therefore \quad X=3,4,5,6,7,8,9 $
इसलिए, $\quad P(X=3)=\dfrac{2}{20}$
$ \begin{aligned} & P(X=4)=\dfrac{2}{20} \\ & P(X=6)=\dfrac{4}{20} \\ & P(X=8)=\dfrac{2}{20} \end{aligned} $
$ \begin{aligned} & P(X=5)=\dfrac{4}{20} \\ & P(X=7)=\dfrac{4}{20} \\ & P(X=9)=\dfrac{2}{20} \end{aligned} $
$ \begin{aligned} &\therefore \text{ माध्य, } E(X)=3 \times \dfrac{2}{20}+4 \times \dfrac{2}{20}+5 \times \dfrac{4}{20}+6 \times \dfrac{4}{20}+7 \times \dfrac{4}{20} +8 \times \dfrac{2}{20}+9 \times \dfrac{2}{20} \\ &=\dfrac{6}{20}+\dfrac{8}{20}+\dfrac{20}{20}+\dfrac{24}{20}+\dfrac{28}{20}+\dfrac{16}{20}+\dfrac{18}{20}=\dfrac{120}{20}=6 \\ &E(X^{2})=9 \times \dfrac{2}{20}+16 \times \dfrac{2}{20}+25 \times \dfrac{4}{20}+36 \times \dfrac{4}{20}+49 \times \dfrac{4}{20}+64 \times \dfrac{2}{20}+81 \times \dfrac{2}{20} \\ &=\dfrac{18}{20}+\dfrac{32}{20}+\dfrac{100}{20}+\dfrac{144}{20}+\dfrac{196}{20}+\dfrac{128}{20}+\dfrac{162}{20}=\dfrac{780}{20}=39 \\ &\therefore \text{ विचलन }(X)=E(X^{2})-[E(X)]^{2}=39-(6)^{2}=39-36=3 \end{aligned} $
वस्तुनिष्ठ प्रश्न
56. यदि $P(A)=\dfrac{4}{5}$ और $P(A \cap B)=\dfrac{7}{10}$, तो $P(B / A)$ किसके बराबर है
(a) $\dfrac{1}{10}$
(b) $\dfrac{1}{8}$
(c) $\dfrac{7}{8}$
(d) $\dfrac{17}{20}$
उत्तर दिखाएं
हल
दिया गया है: $P(A)=\dfrac{4}{5}$ और $P(A \cap B)=\dfrac{7}{10}$
$ \therefore \quad P(B / A)=\dfrac{P(A \cap B)}{P(A)}=\dfrac{7 / 10}{4 / 5}=\dfrac{7}{8} $
इसलिए, सही विकल्प (c) है।
-
विकल्प (a) $\dfrac{1}{10}$: यह विकल्प शर्ती संभावना के सूत्र को संतुष्ट नहीं करता। $P(B / A)$ की सही गणना $P(A \cap B)/P(A)$ होती है, जो $\dfrac{7/10}{4/5} = \dfrac{7}{8}$ होती है, न कि $\dfrac{1}{10}$।
-
विकल्प (b) $\dfrac{1}{8}$: यह विकल्प शर्ती संभावना के सूत्र को संतुष्ट नहीं करता। $P(B / A)$ की सही गणना $P(A \cap B)/P(A)$ होती है, जो $\dfrac{7/10}{4/5} = \dfrac{7}{8}$ होती है, न कि $\dfrac{1}{8}$।
-
विकल्प (d) $\dfrac{17}{20}$: यह विकल्प गलत है क्योंकि इसमें शर्ती संभावना के सही गणना के अनुसार नहीं आता है। $P(B / A)$ के सही गणना के लिए $\dfrac{P(A \cap B)}{P(A)}$ का उपयोग किया जाता है, जो $\dfrac{7/10}{4/5} = \dfrac{7}{8}$ के रूप में आता है, न कि $\dfrac{17}{20}$।
57. यदि $P(A \cap B)=\dfrac{7}{10}$ और $P(B)=\dfrac{17}{20}$, तो $P(A / B)$ के बराबर है
(a) $\dfrac{14}{17}$
(b) $\dfrac{17}{20}$
(c) $\dfrac{7}{8}$
(d) $\dfrac{1}{8}$
उत्तर दिखाएं
हल
दिया गया है: $P(A \cap B)=\dfrac{7}{10}$ और $P(B)=\dfrac{17}{20}$
$ \therefore \quad P(A / B)=\dfrac{P(A \cap B)}{P(B)}=\dfrac{7 / 10}{17 / 20}=\dfrac{14}{17} $
अतः सही विकल्प $(a)$ है।
-
विकल्प (b) $\dfrac{17}{20}$: यह विकल्प गलत है क्योंकि यह घटना B की संभावना को दर्शाता है, न कि शर्ती संभावना $P(A / B)$। शर्ती संभावना $P(A / B)$ की गणना सूत्र $ \dfrac{P(A \cap B)}{P(B)} $ का उपयोग करके की जाती है, जो $\dfrac{17}{20}$ के रूप में सरल नहीं होता।
-
विकल्प (c) $\dfrac{7}{8}$: यह विकल्प गलत है क्योंकि यह $P(A / B)$ की गणना के परिणाम के बराबर नहीं है। सही गणना $ \dfrac{P(A \cap B)}{P(B)} = \dfrac{7/10}{17/20} = \dfrac{14}{17} $ है, न कि $\dfrac{7}{8}$।
-
विकल्प (d) $\dfrac{1}{8}$: यह विकल्प गलत है क्योंकि यह $P(A / B)$ की गणना के परिणाम के बराबर नहीं है। सही गणना $ \dfrac{P(A \cap B)}{P(B)} = \dfrac{7/10}{17/20} = \dfrac{14}{17} $ है, न कि $\dfrac{1}{8}$।
58. यदि $P(A)=\dfrac{3}{10}, P(B)=\dfrac{2}{5}$ और $P(A \cup B)=\dfrac{3}{5}$, तो
$P(B / A)+P(A / B)$ के बराबर है
(a) $\dfrac{1}{4}$
(b) $\dfrac{1}{3}$
(c) $\dfrac{5}{12}$
(d) $\dfrac{7}{12}$
उत्तर दिखाएं
हल
यहाँ, $P(A)=\dfrac{3}{10}, P(B)=\dfrac{2}{5}$ और $P(A \cup B)=\dfrac{3}{5}$
$ \begin{aligned} & P(A \cup B)=P(A)+P(B)-P(A \cap B) \\ & \Rightarrow \quad \dfrac{3}{5}=\dfrac{3}{10}+\dfrac{2}{5}-P(A \cap B) \\
$$ \begin{aligned} & \text{Therefore, } P(A^{\prime} / B^{\prime}) \cdot P(B^{\prime} / A^{\prime})=\dfrac{5}{7} \cdot \dfrac{5}{6}=\dfrac{25}{42} \\ & \text{Hence, the correct option is } (c). \end{aligned} $$
**
-
Option (a) $\dfrac{5}{6}$: This option is incorrect because it does not represent the product of $P(A^{\prime} / B^{\prime})$ and $P(B^{\prime} / A^{\prime})$. The correct value is $\dfrac{25}{42}$, not $\dfrac{5}{6}$.
-
Option (b) $\dfrac{5}{7}$: This option is incorrect because it only represents one of the conditional probabilities, $P(A^{\prime} / B^{\prime})$, but not the product of both probabilities.
-
Option (d) 1: This option is incorrect because the product of the two conditional probabilities is not equal to 1. The correct value is $\dfrac{25}{42}$, not 1.
59. यदि $P(A)=\dfrac{2}{5}, P(B)=\dfrac{3}{10}$ और $P(A \cap B)=\dfrac{1}{5}$, तो $P(A^{\prime} / B^{\prime}) \cdot P(B^{\prime} / A^{\prime})$ किसके बराबर है?
(a) $\dfrac{5}{6}$
(b) $\dfrac{5}{7}$
(c) $\dfrac{25}{42}$
(d) 1
उत्तर दिखाएँ
Solution
दिया गया है: $P(A)=\dfrac{2}{5}, P(B)=\dfrac{3}{10}$ और $P(A \cap B)=\dfrac{1}{5}$
$ \begin{aligned} & P(A^{\prime})=1-\dfrac{2}{5}=\dfrac{3}{5}, P(B^{\prime})=1-\dfrac{3}{10}=\dfrac{7}{10} \\ & \text{ और } P(A^{\prime} \cap B^{\prime})=1-P(A \cup B)=1-[P(A)+P(B)-P(A \cap B)] \\ &=1-[\dfrac{2}{5}+\dfrac{3}{10}-\dfrac{1}{5}]=1-[\dfrac{1}{5}+\dfrac{3}{10}]=1-\dfrac{5}{10}=\dfrac{1}{2} \\ & \therefore \quad P(A^{\prime} / B^{\prime})=\dfrac{P(A^{\prime} \cap B^{\prime})}{P(B^{\prime})}=\dfrac{1 / 2}{7 / 10}=\dfrac{5}{7} \\ & \text{ और } P(B^{\prime} / A^{\prime})=\dfrac{P(A^{\prime} \cap B^{\prime})}{P(A^{\prime})}=\dfrac{1 / 2}{3 / 5}=\dfrac{5}{6} \\
$$ \therefore P(A^{\prime} / B^{\prime}) \cdot P(B^{\prime} / A^{\prime})=\dfrac{5}{7} \times \dfrac{5}{6}=\dfrac{25}{42} $$ $$ \end{aligned} $$
$
अतः, सही विकल्प (c) है।
-
विकल्प (a) $\dfrac{5}{6}$: यह विकल्प गलत है क्योंकि यह केवल $P(B^{\prime} / A^{\prime})$ के मान को दर्शाता है, न कि $P(A^{\prime} / B^{\prime})$ और $P(B^{\prime} / A^{\prime})$ के गुणनफल को।
-
विकल्प (b) $\dfrac{5}{7}$: यह विकल्प गलत है क्योंकि यह केवल $P(A^{\prime} / B^{\prime})$ के मान को दर्शाता है, न कि $P(A^{\prime} / B^{\prime})$ और $P(B^{\prime} / A^{\prime})$ के गुणनफल को।
-
विकल्प (d) 1: यह विकल्प गलत है क्योंकि $P(A^{\prime} / B^{\prime})$ और $P(B^{\prime} / A^{\prime})$ के गुणनफल के बराबर 1 नहीं है। सही गुणनफल $\dfrac{25}{42}$ है।
60. यदि $A$ और $B$ दो घटनाएँ इस प्रकार हैं कि $P(A)=\dfrac{1}{2}, P(B)=\dfrac{1}{3}$ और $P(A / B)=\dfrac{1}{4}$, तो $P(A^{\prime} \cap B^{\prime})$ के बराबर है
(a) $\dfrac{1}{12}$
(b) $\dfrac{3}{4}$
(c) $\dfrac{1}{4}$
(d) $\dfrac{3}{16}$
उत्तर दिखाएँ
हल
दिया गया है: $P(A)=\dfrac{1}{2}, P(B)=\dfrac{1}{3}$ और $P(A / B)=\dfrac{1}{4}$
$$ \begin{aligned} P(A / B) & =\dfrac{P(A \cap B)}{P(B)} \\ \dfrac{1}{4} & =\dfrac{P(A \cap B)}{1 / 3} \Rightarrow P(A \cap B)=\dfrac{1}{4} \times \dfrac{1}{3}=\dfrac{1}{12} \end{aligned} $$
अब $\quad P(A^{\prime} \cap B^{\prime})=1-P(A \cup B)$
$$ =1-[P(A)+P(B)-P(A \cap B)] $$
$$ =1-[\dfrac{1}{2}+\dfrac{1}{3}-\dfrac{1}{12}]=1-[\dfrac{5}{6}-\dfrac{1}{12}]=1-\dfrac{9}{12}=\dfrac{3}{12}=\dfrac{1}{4} $$
अतः, सही विकल्प (c) है।
-
विकल्प (a) $\dfrac{1}{12}$: यह विकल्प गलत है क्योंकि यह घटनाओं $A$ और $B$ के प्रतिच्छेदन की प्रायिकता ($P(A \cap B)$) को दर्शाता है, न कि उनके पूरकों के प्रतिच्छेदन की प्रायिकता ($P(A^{\prime} \cap B^{\prime})$) को।
-
विकल्प (b) $\dfrac{3}{4}$: यह विकल्प गलत है क्योंकि यह $P(A^{\prime} \cap B^{\prime})$ की गणना के लिए सही तरीका नहीं दर्शाता है। सही गणना में $A$ और $B$ के संयोजन को 1 से घटाया जाता है, जिसके परिणामस्वरूप $\dfrac{1}{4}$ होता है, न कि $\dfrac{3}{4}$।
-
विकल्प (d) $\dfrac{3}{16}$: यह विकल्प गलत है क्योंकि यह दिए गए प्रायिकताओं और $P(A^{\prime} \cap B^{\prime})$ के सही सूत्र से निकाला गया नहीं है। सही गणना $\dfrac{1}{4}$ देती है, नहीं $\dfrac{3}{16}$।
61. यदि $P(A)=0.4, P(B)=0.8$ और $P(B / A)=0.6$ तो $P(A \cup B)$ किसके बराबर है
(a) 0.24
(b) 0.3
(c) 0.48
(d) 0.96
उत्तर दिखाएँ
हल
दिया गया है: $P(A)=0.4, P(B)=0.8$ और $P(B / A)=0.6$
$ \begin{aligned} P(B / A)=\dfrac{P(A \cap B)}{P(A)} & \Rightarrow 0.6=\dfrac{P(A \cap B)}{0.4} \\ \therefore \quad P(A \cap B) & =0.6 \times 0.4=0.24 \\ P(A \cup B) & =P(A)+P(B)-P(A \cap B) \\ & =0.4+0.8-0.24=1.20-0.24=0.96 \end{aligned} $
अतः, सही विकल्प (d) है।
-
विकल्प (a) 0.24 गलत है क्योंकि यह घटनाओं A और B के प्रतिच्छेदन की प्रायिकता $ P(A \cap B) $ को दर्शाता है, न कि एकत्रिति $ P(A \cup B) $ को।
-
विकल्प (b) 0.3 गलत है क्योंकि यह दिए गए डेटा के अनुसार किसी भी संबंधित प्रायिकता गणना के साथ मेल नहीं खाता है। यह A, B, या उनके प्रतिच्छेदन या एकत्रिति की प्रायिकता नहीं है।
-
विकल्प (c) 0.48 गलत है क्योंकि यह घटनाओं A और B के एकत्रिति के सही गणना के साथ मेल नहीं खाता है। यह एक गलत गणना या संबंधित प्रायिकता हो सकती है।
62. यदि $A$ और $B$ दो घटनाएँ हैं और $A \neq \phi, B \neq \phi$, तो
(a) $P(A / B)=P(A) \cdot P(B)$
(b) $P(A / B)=\dfrac{P(A \cap B)}{P(B)}$
(c) $P(A / B) \cdot P(B / A)=1$
(d) $P(A / B)=\dfrac{P(A)}{P(B)}$
उत्तर दिखाएँ
हल
दिया गया है: $A=\phi$ और $B \neq \phi$,
तो
$ P(A / B)=\dfrac{P(A \cap B)}{P(B)} $
अतः, सही विकल्प (b) है।
-
विकल्प (a) $P(A / B)=P(A) \cdot P(B)$: यह गलत है क्योंकि शर्ती प्रायिकता $ P(A / B) $ घटना $ A $ के घटना $ B $ के घटने के दिए गए अवस्था में घटना $ A $ के घटने की प्रायिकता को दर्शाती है। यह केवल $ A $ और $ B $ के प्रायिकताओं के गुणनफल नहीं है। शर्ती प्रायिकता का सही सूत्र $ P(A / B) = \dfrac{P(A \cap B)}{P(B)} $ है।
-
विकल्प (c) $P(A / B) \cdot P(B / A)=1$: यह गलत है क्योंकि $ P(A / B) $ और $ P(B / A) $ के गुणनफल के लिए आवश्यक रूप से 1 नहीं होता। इन प्रायिकताओं के सही संबंध बेयेस के प्रमेय द्वारा दिया गया है: $ P(A / B) = \dfrac{P(B / A) \cdot P(A)}{P(B)} $।
-
विकल्प (d) $P(A / B)=\dfrac{P(A)}{P(B)}$: यह गलत है क्योंकि $ P(A / B) $ केवल $ A $ और $ B $ की प्रायिकताओं के अनुपात के रूप में नहीं होता। शर्ती प्रायिकता के सही सूत्र है: $ P(A / B) = \dfrac{P(A \cap B)}{P(B)} $। दिया गया सूत्र केवल तभी सही होगा जब $ A $ और $ B $ स्वतंत्र घटनाएँ हों, जो समस्या में नहीं बताया गया है।
63. A और $B$ ऐसे घटनाएँ हैं कि $P(A)=0.4, P(B)=0.3$ और $P(A \cup B)$ $=0.5$। तब $P(B^{\prime} \cap A)$ के बराबर है
(a) $\dfrac{2}{3}$
(b) $\dfrac{1}{2}$
(c) $\dfrac{3}{10}$
(d) $\dfrac{1}{5}$
उत्तर दिखाएँ
हल
दिया गया है: $P(A)=0.4, P(B)=0.3$ और $P(A \cup B)=0.5$
$ \begin{aligned} P(A \cup B) & =P(A)+P(B)-P(A \cap B) \\ 0.5 & =0.4+0.3-P(A \cap B) \\ P(A \cap B) & =0.4+0.3-0.5=0.2 \\ \therefore \quad P(B^{\prime} \cap A) & =P(A)-P(A \cap B) \\ & =0.4-0.2=0.2=\dfrac{1}{5} \end{aligned} $
अतः सही विकल्प $(d)$ है।
-
विकल्प (a) $\dfrac{2}{3}$: यह विकल्प गलत है क्योंकि $P(B^{\prime} \cap A)$ की गणना दिए गए प्रायिकताओं और सूत्र $P(B^{\prime} \cap A) = P(A) - P(A \cap B)$ के आधार पर की जाती है। सही मान 0.2 है, जो $\dfrac{2}{3}$ के बराबर नहीं है।
-
विकल्प (b) $\dfrac{1}{2}$: यह विकल्प गलत है क्योंकि दिए गए प्रायिकताओं और उपयोग किए गए सूत्र के आधार पर $P(B^{\prime} \cap A) = 0.2$ है। मान $\dfrac{1}{2}$ (या 0.5) गणना किए गए मान 0.2 के बराबर नहीं है।
-
विकल्प (c) $\dfrac{3}{10}$: यह विकल्प गलत है क्योंकि $P(B^{\prime} \cap A)$ की सही गणना 0.2 होती है। मान $\dfrac{3}{10}$ (या 0.3) गणना किए गए मान 0.2 के बराबर नहीं है।
64. यदि $A$ और $B$ दो घटनाएँ इस प्रकार है कि $P(B)=\dfrac{3}{5}, P(A / B)=\dfrac{1}{2}$ और $P(A \cup B)=\dfrac{4}{5}$, तो $P(A)$ के बराबर है
(a) $\dfrac{3}{10}$
(b) $\dfrac{1}{5}$
(c) $\dfrac{1}{2}$
(d) $\dfrac{3}{5}$
उत्तर दिखाएँ
हल
दिया गया है: $P(B)=\dfrac{3}{5}, P(A / B)=\dfrac{1}{2}$ और $P(A \cup B)=\dfrac{4}{5}$
हम जानते हैं कि $P(A / B)=\dfrac{P(A \cap B)}{P(B)} \Rightarrow \dfrac{1}{2}=\dfrac{P(A \cap B)}{3 / 5}$
$\therefore \quad P(A \cap B)=\dfrac{3}{10}$
अब $\quad P(A \cup B)=P(A)+P(B)-P(A \cap B)$
$ \begin{aligned} \dfrac{4}{5} & =P(A)+\dfrac{3}{5}-\dfrac{3}{10} \\ \Rightarrow \quad P(A) & =\dfrac{4}{5}-\dfrac{3}{5}+\dfrac{3}{10}=\dfrac{1}{5}+\dfrac{3}{10}=\dfrac{5}{10}=\dfrac{1}{2} \end{aligned} $
अतः, सही विकल्प (c) है।
-
विकल्प (a) $\dfrac{3}{10}$ गलत है क्योंकि दिए गए प्रायिकताओं और दो घटनाओं के संयोजन के सूत्र का उपयोग करके $P(A)$ की गणना करने पर हमें $P(A) = \dfrac{1}{2}$ प्राप्त होता है, न कि $\dfrac{3}{10}$।
-
विकल्प (b) $\dfrac{1}{5}$ गलत है क्योंकि $P(A)$ की गणना में $P(B)$ को घटाया जाता है और $P(A \cap B)$ को $P(A \cup B)$ में जोड़ा जाता है। इससे $P(A) = \dfrac{1}{2}$ प्राप्त होता है, न कि $\dfrac{1}{5}$।
-
विकल्प (d) $\dfrac{3}{5}$ गलत है क्योंकि $P(A)$ की गणना समीकरण $P(A \cup B) = P(A) + P(B) - P(A \cap B)$ के आधार पर की जाती है। दिए गए मानों के साथ इस समीकरण को हल करने पर $P(A) = \dfrac{1}{2}$ प्राप्त होता है, न कि $\dfrac{3}{5}$।
65. उपरोक्त प्रश्न 64 में, $P(B / A^{\prime})$ के बराबर है
(a) $\dfrac{1}{5}$
(b) $\dfrac{3}{10}$
(c) $\dfrac{1}{2}$
(d) $\dfrac{3}{5}$
उत्तर दिखाएँ
हल
उपरोक्त प्रश्न 64 के अनुसार, हम जानते हैं कि
$ \begin{aligned} & P(B)=\dfrac{3}{5}, P(A / B)=\dfrac{1}{2}, P(A \cup B)=\dfrac{4}{5} \\ & P(B / A^{\prime})=\dfrac{P(B \cap A^{\prime})}{P(A^{\prime})}=\dfrac{P(B)-P(A \cap B)}{1-P(A)}=\dfrac{\dfrac{3}{5}-\dfrac{3}{10}}{1-\dfrac{1}{2}}=\dfrac{\dfrac{3}{10}}{\dfrac{1}{2}}=\dfrac{3}{5} \end{aligned}
$
अतः, सही विकल्प $(d)$ है।
-
विकल्प (a) $\dfrac{1}{5}$ गलत है क्योंकि $P(B / A^{\prime})$ की गणना में $P(B) - P(A \cap B)$ के अंतर और $1 - P(A)$ के विभाजन की आवश्यकता होती है। सही गणना $\dfrac{3}{5}$ देती है, न कि $\dfrac{1}{5}$।
-
विकल्प (b) $\dfrac{3}{10}$ गलत है क्योंकि यह $P(A \cap B)$ का मान है, न कि $P(B / A^{\prime})$। $P(B / A^{\prime})$ की सही गणना $\dfrac{3}{5}$ देती है।
-
विकल्प (c) $\dfrac{1}{2}$ गलत है क्योंकि यह $P(B / A^{\prime})$ की गणना के परिणाम से मेल नहीं खाता। सही गणना $\dfrac{3}{5}$ देती है, न कि $\dfrac{1}{2}$।
66. यदि $P(B)=\dfrac{3}{5}, P(A / B)=\dfrac{1}{2}$ और $P(A \cup B)=\dfrac{4}{5}$, तो
$P(A \cup B)^{\prime}+P(A^{\prime} \cup B)=$
(a) $\dfrac{1}{5}$
(b) $\dfrac{4}{5}$
(c) $\dfrac{1}{2}$
(d) 1
उत्तर दिखाएँ
हल
दिया गया है: $P(B)=\dfrac{3}{5}, P(A / B)=\dfrac{1}{2}$ और $P(A \cup B)=\dfrac{4}{5}$
$ \begin{aligned} P(A / B) & =\dfrac{P(A \cap B)}{P(B)} \\ \Rightarrow \quad \dfrac{1}{2} & =\dfrac{P(A \cap B)}{3 / 5} \Rightarrow P(A \cap B)=\dfrac{3}{10} \\ P(A \cup B) & =P(A)+P(B)-P(A \cap B) \\ \dfrac{4}{5} & =P(A)+\dfrac{3}{5}-\dfrac{3}{10} \\ \therefore \quad P(A) & =\dfrac{4}{5}-\dfrac{3}{5}+\dfrac{3}{10}=\dfrac{1}{5}+\dfrac{3}{10}=\dfrac{5}{10}=\dfrac{1}{2} \end{aligned} $
अब $P(A \cup B)^{\prime}+P(A^{\prime} \cup B)$
$ \begin{aligned} & =1-P(A \cup B)+1-P(A \cap B^{\prime}) \\ & =2-\dfrac{4}{5}-P(A) \cdot P(B^{\prime}) \\ & =\dfrac{6}{5}-\dfrac{1}{2} \cdot(1-\dfrac{3}{5})=\dfrac{6}{5}-\dfrac{1}{2} \times \dfrac{2}{5}=\dfrac{6}{5}-\dfrac{1}{5}=\dfrac{5}{5}=1 \end{aligned} $
अतः, सही विकल्प $(d)$ है।
-
विकल्प (a) $\dfrac{1}{5}$: यह विकल्प गलत है क्योंकि $P(A \cup B)^{\prime} + P(A^{\prime} \cup B)$ की गणना में प्रायिकताओं को घटाया जाता है और संपूरकों को जोड़ा जाता है, जिसके परिणामस्वरूप मान 1 होता है, न कि $\dfrac{1}{5}$।
-
विकल्प (b) $\dfrac{4}{5}$: यह विकल्प गलत है क्योंकि इसमें सही प्रायिकताओं और उनके पूरक के सही संयोजन को ध्यान में नहीं लिया गया है। सही गणना दिखाती है कि योग 1 है, न कि $\dfrac{4}{5}$।
-
विकल्प (c) $\dfrac{1}{2}$: यह विकल्प गलत है क्योंकि इसमें संयुक्त प्रायिकताओं और उनके पूरक के परिणाम को गलत तरीके से प्रस्तुत किया गया है। सही गणना एक कुल दिखाती है, न कि $\dfrac{1}{2}$।
67. मान लीजिए $P(A)=\dfrac{7}{13}, P(B)=\dfrac{9}{13}$ और $P(A \cap B)=\dfrac{4}{13}$. तो $P(A^{\prime} / B)$ किसके बराबर है
(a) $\dfrac{6}{13}$
(b) $\dfrac{4}{13}$
(c) $\dfrac{4}{9}$
(d) $\dfrac{5}{9}$
उत्तर दिखाएँ
हल
दिया गया है: $P(A)=\dfrac{7}{13}, P(B)=\dfrac{9}{13}$ और $P(A \cap B)=\dfrac{4}{13}$
$ P(A^{\prime} / B)=\dfrac{P(A^{\prime} \cap B)}{P(B)}=\dfrac{P(B)-P(A \cap B)}{P(B)}=\dfrac{\dfrac{9}{13}-\dfrac{4}{13}}{\dfrac{9}{13}}=\dfrac{\dfrac{5}{13}}{\dfrac{9}{13}}=\dfrac{5}{9} $
इसलिए, सही विकल्प $(d)$ है।
-
विकल्प (a) $\dfrac{6}{13}$: यह विकल्प गलत है क्योंकि इसमें स्थिति गुणांक प्रायिकता सूत्र को ध्यान में नहीं लिया गया है। सही गणना $P(B)$ और $P(A \cap B)$ के अंतर को $P(B)$ से विभाजित करने के बराबर होती है, जो $\dfrac{5}{9}$ होती है, न कि $\dfrac{6}{13}$।
-
विकल्प (b) $\dfrac{4}{13}$: यह विकल्प गलत है क्योंकि यह $A \cap B$ की प्रायिकता को निरूपित करता है, न कि स्थिति गुणांक $P(A^{\prime} / B)$ को। $P(A^{\prime} / B)$ की सही गणना $P(B) - P(A \cap B)$ को $P(B)$ से विभाजित करने के सूत्र का उपयोग करती है।
-
विकल्प (c) $\dfrac{4}{9}$: यह विकल्प गलत है क्योंकि इसमें गलत गणना होती है। $P(A^{\prime} / B)$ की सही गणना $P(B) - P(A \cap B)$ को $P(B)$ से विभाजित करने के बराबर होती है, जो $\dfrac{5}{9}$ होती है, न कि $\dfrac{4}{9}$।
68. यदि $A$ और $B$ ऐसे घटनाएँ हैं जहाँ $P(A)>0$ और $P(B) \neq 1$ तो $P(A^{\prime} / B^{\prime})$ के बराबर है
(a) $1-P(A / B)$
(b) $1-P(A^{\prime} / B)$
(c) $\dfrac{1-P(A \cup B)}{P(B^{\prime})}$
(d) $\dfrac{P(A^{\prime})}{P(B^{\prime})}$
उत्तर दिखाएँ
Solution
दिया गया है: $P(A)>0$ और $P(B) \neq 1$
$ \therefore \quad P(A^{\prime} / B^{\prime})=\dfrac{P(A^{\prime} \cap B^{\prime})}{P(B^{\prime})}=\dfrac{1-P(A \cup B)}{P(B^{\prime})} $
इसलिए, सही विकल्प (c) है।
-
विकल्प (a): $1 - P(A / B)$ गलत है क्योंकि $P(A^{\prime} / B^{\prime})$ केवल $P(A / B)$ के पूरक नहीं होता। $P(A^{\prime} / B^{\prime})$ और $P(A / B)$ के बीच संबंध $A$ और $B$ के संयुक्त प्रायिकताओं और उनके पूरकों पर निर्भर करता है, न कि केवल एक सीधा पूरक संचालन।
-
विकल्प (b): $1 - P(A^{\prime} / B)$ गलत है क्योंकि $P(A^{\prime} / B^{\prime})$ $P(A^{\prime} / B)$ के पूरक नहीं होता। घटनाओं के पूरकों वाले संतति प्रायिकताओं के बीच यह सरल पूरक नियम लागू नहीं होता।
-
विकल्प (d): $\dfrac{P(A^{\prime})}{P(B^{\prime})}$ गलत है क्योंकि $P(A^{\prime} / B^{\prime})$ $B^{\prime}$ के दिए गए $A^{\prime}$ की संतति प्रायिकता होती है, जो $A^{\prime}$ और $B^{\prime}$ के संयुक्त प्रायिकता पर निर्भर करती है। सही व्यंजक संयुक्त प्रायिकता $P(A^{\prime} \cap B^{\prime})$ को शामिल करता है, न कि केवल $P(A^{\prime})$ के मार्जिनल प्रायिकता।
69. यदि $A$ और $B$ दो स्वतंत्र घटनाएं हैं जिनके $P(A)=\dfrac{3}{5}$ और $P(B)=\dfrac{4}{9}$ हैं, तो $P(A^{\prime} \cap B^{\prime})$ के बराबर है
(a) $\dfrac{4}{15}$
(b) $\dfrac{8}{45}$
(c) $\dfrac{1}{3}$
(d) $\dfrac{2}{9}$
उत्तर दिखाएँ
Solution
दिया गया है: A और B स्वतंत्र घटनाएं हैं
जैसे कि
$ \begin{aligned} & P(A)=\dfrac{3}{5} \quad \therefore P(A^{\prime})=1-\dfrac{3}{5}=\dfrac{2}{5} \\ & P(B)=\dfrac{4}{9} \quad \therefore P(B^{\prime})=1-\dfrac{4}{9}=\dfrac{5}{9} \end{aligned} $
$ \therefore \quad P(A^{\prime} \cap B^{\prime})=P(A^{\prime}) \cdot P(B^{\prime})=\dfrac{2}{5} \cdot \dfrac{5}{9}=\dfrac{2}{9} $
इसलिए, सही विकल्प $(d)$ है।
-
विकल्प (a) $\dfrac{4}{15}$: यह विकल्प गलत है क्योंकि इसमें $A$ और $B$ के पूरक की प्रायिकताओं के गुणनफल को सही तरीके से प्रस्तुत नहीं किया गया है। सही गणना $\dfrac{2}{5} \cdot \dfrac{5}{9} = \dfrac{2}{9}$ है, न कि $\dfrac{4}{15}$।
-
विकल्प (b) $\dfrac{8}{45}$: यह विकल्प गलत है क्योंकि इसमें $A$ और $B$ के पूरक की प्रायिकताओं के गुणनफल को सही तरीके से प्रस्तुत नहीं किया गया है। सही गणना $\dfrac{2}{5} \cdot \dfrac{5}{9} = \dfrac{2}{9}$ है, न कि $\dfrac{8}{45}$।
-
विकल्प (c) $\dfrac{1}{3}$: यह विकल्प गलत है क्योंकि इसमें $A$ और $B$ के पूरक की प्रायिकताओं के गुणनफल को सही तरीके से प्रस्तुत नहीं किया गया है। सही गणना $\dfrac{2}{5} \cdot \dfrac{5}{9} = \dfrac{2}{9}$ है, न कि $\dfrac{1}{3}$।
70. यदि दो घटनाएँ स्वायत्त हैं, तो
(a) वे एक-दूसरे से अपवाद रहित होना चाहिए
(b) उनकी प्रायिकताओं का योग 1 के बराबर होना चाहिए
(c) (a) और (b) दोनों सही हैं
(d) उपरोक्त में से कोई भी सही नहीं है
उत्तर दिखाएँ
हल
स्वायत्त घटनाओं $A$ और $B$ के लिए $P(A) \cdot P(B) = P(A \cap B)$
इसलिए, वे एक-दूसरे से अपवाद रहित नहीं होंगे।
यदि $P(A) + P(B) = 1$, तो वे एक-दूसरे के अपवाद रहित घटनाएँ होंगी और स्वायत्त घटनाओं $A$ और $B$ के लिए $P(A \cap B) \neq 0$ होता है।
इसलिए, सही विकल्प $(d)$ है।
-
विकल्प (a): यदि दो घटनाएँ एक-दूसरे से अपवाद रहित हों, तो यह बताता है कि वे एक साथ घटित नहीं हो सकते, अर्थात $P(A \cap B) = 0$। हालाँकि, स्वायत्त घटनाओं के लिए $P(A \cap B) = P(A) \cdot P(B)$ होता है। अतः, यदि $P(A) \cdot P(B) \neq 0$, तो घटनाएँ एक-दूसरे से अपवाद रहित नहीं हो सकते। इसलिए, स्वायत्तता अपवाद रहितता का अर्थ नहीं देती है।
-
विकल्प (b): दो स्वायत्त घटनाओं की प्रायिकताओं का योग आवश्यक रूप से 1 के बराबर नहीं होता। दो स्वायत्त घटनाओं की प्रायिकताओं का योग घटनाओं की व्यक्तिगत प्रायिकताओं पर निर्भर करके 0 और 2 के बीच कोई भी मान हो सकता है। इसलिए, स्वायत्तता यह नहीं बताती कि $P(A) + P(B) = 1$ हो।
-
विकल्प (c): चूंकि (a) और (b) दोनों गलत हैं, इसलिए यह विकल्प भी गलत है।
71. मान लीजिए $A$ और $B$ दो घटनाएँ इस प्रकार कि $P(A)=\dfrac{3}{8}, P(B)=\dfrac{5}{8}$ और $P(A \cup B)=\dfrac{3}{4}$. तब $P(A / B) \cdot P(A^{\prime} / B)$ किसके बराबर है?
(a) $\dfrac{2}{5}$
(b) $\dfrac{3}{8}$
(c) $\dfrac{3}{20}$
(d) $\dfrac{6}{25}$
उत्तर दिखाएँ
हल
दिया गया है: $P(A)=\dfrac{3}{8}, P(B)=\dfrac{5}{8}$ और $P(A \cup B)=\dfrac{3}{4}$
$ \begin{matrix} \therefore &P(A \cup B) =P(A)+P(B)-P(A \cap B) \ &\dfrac{3}{4} =\dfrac{3}{8}+\dfrac{5}{8}-P(A \cap B) \\ &\Rightarrow P(A \cap B) =\dfrac{3}{8}+\dfrac{5}{8}-\dfrac{3}{4}=\dfrac{1}{4} \end{matrix} $
$ \begin{aligned} \text{ अब } P(A / B) \cdot P(A^{\prime} / B) & =\dfrac{P(A \cap B)}{P(B)} \cdot \dfrac{P(A^{\prime} \cap B)}{P(B)} \\ & =\dfrac{P(A \cap B)}{P(B)} \cdot \dfrac{P(B)-P(A \cap B)}{P(B)} \\ & =\dfrac{\dfrac{1}{5}}{\dfrac{5}{8}} \cdot \dfrac{(\dfrac{5}{8}-\dfrac{1}{4})}{\dfrac{5}{8}}=\dfrac{2}{5} \cdot \dfrac{3}{5}=\dfrac{6}{25} \end{aligned} $
अतः सही विकल्प $(d)$ है।
-
विकल्प (a) $\dfrac{2}{5}$: यह विकल्प गलत है क्योंकि इसमें $ P(A / B) \cdot P(A^{\prime} / B) $ के सही गणना को ध्यान में नहीं लिया गया है। सही गणना $ \dfrac{1/4}{5/8} $ के गुणनफल के रूप में $ \dfrac{(5/8 - 1/4)}{5/8} $ के रूप में होती है, जो $ \dfrac{6}{25} $ के बराबर होती है, न कि $ \dfrac{2}{5} $।
-
विकल्प (b) $\dfrac{3}{8}$: यह विकल्प गलत है क्योंकि इसमें संयोजी प्रायिकता के सूत्र के सही अनुप्रयोग को ध्यान में नहीं लिया गया है। $ P(A / B) $ और $ P(A^{\prime} / B) $ के सही गुणनफल $ \dfrac{6}{25} $ होता है, न कि $ \dfrac{3}{8} $।
-
विकल्प (c) $\dfrac{3}{20}$: यह विकल्प गलत है क्योंकि इसमें शामिल प्रायिकताओं के गलत गणना के कारण होता है। $ P(A / B) $ और $ P(A^{\prime} / B) $ के सही गुणनफल $ \dfrac{6}{25} $ होता है, न कि $ \dfrac{3}{20} $।
72. यदि घटनाएँ $A$ और $B$ स्वायत्त हैं, तो $P(A \cap B)$ किसके बराबर है?
(a) $P(A)+P(B)$
(b) $P(A)-P(B)$
(c) $P(A) \cdot P(B)$
(d) $\dfrac{P(A)}{P(B)}$
उत्तर दिखाएँ
हल
क्योंकि $A$ और $B$ दो स्वतंत्र घटनाएँ हैं
$ \therefore \quad P(A \cap B)=P(A) \cdot P(B) $
इसलिए, सही विकल्प (c) है।
-
विकल्प (a) $P(A) + P(B)$: यह विकल्प गलत है क्योंकि दो घटनाओं के प्रायिकता के योग उनके प्रतिच्छेद को गिनते नहीं है। स्वतंत्र घटनाओं के लिए, दोनों घटनाओं के एक साथ होने की प्रायिकता उनकी व्यक्तिगत प्रायिकताओं के गुणनफल होती है, न कि योग।
-
विकल्प (b) $P(A) - P(B)$: यह विकल्प गलत है क्योंकि एक घटना की प्रायिकता को दूसरी घटना की प्रायिकता से घटाना उनके प्रतिच्छेद की प्रायिकता को नहीं दर्शाता है। दो स्वतंत्र घटनाओं के प्रतिच्छेद की प्रायिकता उनकी प्रायिकताओं के गुणनफल द्वारा गणना की जाती है, न कि घटाव द्वारा।
-
विकल्प (d) $\dfrac{P(A)}{P(B)}$: यह विकल्प गलत है क्योंकि एक घटना की प्रायिकता को दूसरी घटना की प्रायिकता से विभाजित करना उनके प्रतिच्छेद की प्रायिकता को नहीं दर्शाता है। स्वतंत्र घटनाओं के लिए, सही संचालन गुणन होता है, न कि विभाजन।
73. दो घटनाएँ $E$ और $F$ स्वतंत्र हैं। यदि $P(E)=0.3$ और $P(E \cup F)=0.5$, तो $P(E / F)-P(F / E)$ के बराबर है
(a) $\dfrac{2}{7}$
(b) $\dfrac{3}{35}$
(c) $\dfrac{1}{70}$
(d) $\dfrac{1}{7}$
उत्तर दिखाएँ
हल
दिया गया है: $E$ और $F$ स्वतंत्र घटनाएँ हैं जैसे कि $P(E)=0.3$ और $P(E \cup F)=0.5$
$ \begin{aligned} &P(E \cup F) =P(E)+P(F)-P(E \cap F) \\ &0.5 =0.3+P(F)-P(E) \cdot P(F) \\ &\Rightarrow \quad 0.5-0.3 =P(F)[1-P(E)] \Rightarrow 0.2=P(F)(1-0.3) \\ &\Rightarrow \quad 0.2 =P(F) \cdot(0.7) \\ &\therefore \quad P(F) =\dfrac{0.2}{0.7}=\dfrac{2}{7} \\ \\ &\text{ अब } P(E / F)-P(F / E) =\dfrac{P(E \cap F)}{P(F)}-\dfrac{P(E \cap F)}{P(E)} \\ &=\dfrac{P(E) \cdot P(F)}{P(F)}-\dfrac{P(E) \cdot P(F)}{P(E)} =P(E)-P(F)=\dfrac{3}{10}-\dfrac{2}{7}=\dfrac{1}{70} \end{aligned} $
इसलिए, सही विकल्प (c) है।
-
विकल्प (a) $\dfrac{2}{7}$: यह विकल्प गलत है क्योंकि यह $P(F)$ की प्रायिकता को दर्शाता है, न कि $P(E / F) - P(F / E)$ के अंतर को। गणना दिखाती है कि $P(F) = \dfrac{2}{7}$, लेकिन यह हमें खोजने वाला मान नहीं है।
-
विकल्प (b) $\dfrac{3}{35}$: यह विकल्प गलत है क्योंकि यह गणना किए गए अंतर $P(E / F) - P(F / E)$ के साथ मेल नहीं खाता। सही अंतर $\dfrac{1}{70}$ है, और $\dfrac{3}{35}$ एक अलग मान है जो दिए गए समस्या के किसी भी हिस्से से संबंधित नहीं है।
-
विकल्प (d) $\dfrac{1}{7}$: यह विकल्प गलत है क्योंकि यह $P(E / F) - P(F / E)$ के अंतर का परिणाम नहीं है। सही गणना दिखाती है कि अंतर $\dfrac{1}{70}$ है, और $\dfrac{1}{7}$ एक बड़ा मान है जो निर्मित परिणाम से मेल नहीं खाता है।
74. एक बैग में 5 लाल और 3 नीली गेंद हैं। यदि 3 गेंद बिना वापस लेने के यादृच्छिक रूप से खींची जाती हैं, तो ठीक एक लाल गेंद के प्राप्त होने की प्रायिकता है
(a) $\dfrac{45}{196}$
(b) $\dfrac{135}{392}$
(c) $\dfrac{15}{56}$
(d) $\dfrac{15}{29}$
उत्तर दिखाएँ
हल
दिया गया है: बैग में 5 लाल और 3 नीली गेंद हैं।
3 गेंद बिना वापस लेने के यादृच्छिक रूप से खींची जाती हैं तो ठीक एक लाल गेंद के प्राप्त होने की प्रायिकता
$=P(R) \cdot P(B) \cdot P(B)+P(B) \cdot P(R) \cdot P(B)+P(B) \cdot P(B) \cdot P(R)$
$=\dfrac{5}{8} \cdot \dfrac{3}{7} \cdot \dfrac{2}{6}+\dfrac{3}{8} \cdot \dfrac{5}{7} \cdot \dfrac{2}{6}+\dfrac{3}{8} \cdot \dfrac{2}{7} \cdot \dfrac{5}{6}=\dfrac{30}{336}+\dfrac{30}{336}+\dfrac{30}{336}=\dfrac{90}{336}=\dfrac{15}{56}$
अतः, सही विकल्प (c) है।
-
विकल्प (a) $\dfrac{45}{196}$ गलत है क्योंकि सही प्रायिकता गणना $\dfrac{15}{56}$ देती है, न कि $\dfrac{45}{196}$. 196 के अंतर्गत गेंदों के 3 गेंद खींचने के कुल तरीकों की संख्या 56 है, जो अलग है।
-
विकल्प (b) $\dfrac{135}{392}$ गलत है क्योंकि सही प्रायिकता गणना $\dfrac{15}{56}$ देती है। 135 अंश और 392 हर के साथ अंतर गणना के सही मान से मेल नहीं खाते हैं।
-
विकल्प (d) $\dfrac{15}{29}$ गलत है क्योंकि सही प्रायिकता गणना $\dfrac{15}{56}$ देती है। 29 के हर के साथ गेंदों के 3 गेंद खींचने के कुल तरीकों की संख्या 56 है, जो अलग है।
75. ऊपर के प्रश्न 74 को देखें। तीन गेंदों में से ठीक दो गेंद लाल हों, तथा पहली गेंद लाल होने की प्रायिकता है
(a) $\dfrac{1}{3}$
(b) $\dfrac{4}{7}$
(c) $\dfrac{15}{28}$
(d) $\dfrac{5}{28}$
उत्तर दिखाएँ
हल
प्रश्न 74 के अनुसार,
मान लीजिए $E_1$ घटना है जब पहली गेंद लाल हो।
$E_2$ घटना है जब तीन गेंदों में से ठीक दो गेंद लाल हों।
$\therefore \quad P(E_1)=P(R) \cdot P(R) \cdot P(B)+P(R) \cdot P(R) \cdot P(R)+P(R) \cdot P(B) \cdot P(R)$ $+P(R) \cdot P(B) \cdot P(B)$
$=\dfrac{5}{8} \cdot \dfrac{4}{7} \cdot \dfrac{3}{6}+\dfrac{5}{8} \cdot \dfrac{4}{7} \cdot \dfrac{3}{6}+\dfrac{5}{8} \cdot \dfrac{3}{7} \cdot \dfrac{4}{6}+\dfrac{5}{8} \cdot \dfrac{3}{7} \cdot \dfrac{2}{6}$
$=\dfrac{60}{336}+\dfrac{60}{336}+\dfrac{60}{336}+\dfrac{30}{336}=\dfrac{210}{336}$
$P(E_1 \cap E_2)=P(R) \cdot P(B) \cdot P(R)+P(R) \cdot P(R) \cdot P(B)$
$=\dfrac{5}{8} \cdot \dfrac{3}{7} \cdot \dfrac{4}{6}+\dfrac{5}{8} \cdot \dfrac{4}{7} \cdot \dfrac{3}{6}=\dfrac{60}{336}+\dfrac{60}{336}=\dfrac{120}{336}$
$\therefore P(E_2 / E_1)=\dfrac{P(E_1 \cap E_2)}{P(E_1)}=\dfrac{120 / 336}{210 / 336}=\dfrac{4}{7}$
अतः, सही विकल्प $(b)$ है।
-
विकल्प (a) $\dfrac{1}{3}$: यह विकल्प गलत है क्योंकि तीन गेंदों में से ठीक दो गेंद लाल हों, तथा पहली गेंद लाल होने की गणनित प्रायिकता $\dfrac{4}{7}$ है। मान $\dfrac{1}{3}$ इस प्रायिकता के बराबर नहीं है और यह दिए गए शर्तों और गणना से निकाला गया नहीं है।
-
विकल्प (c) $\dfrac{15}{28}$: यह विकल्प गलत है क्योंकि गणना के अनुसार सही प्रायिकता $\dfrac{4}{7}$ है। भिन्न $\dfrac{15}{28}$ अपने रूप में $\dfrac{15}{28}$ है, जो $\dfrac{4}{7}$ के बराबर नहीं है। अतः, यह सही प्रायिकता का प्रतिनिधित्व नहीं करता है।
-
विकल्प (d) $\dfrac{5}{28}$: यह विकल्प गलत है क्योंकि सही प्रायिकता $\dfrac{4}{7}$ है। भिन्न $\dfrac{5}{28}$ गणनित प्रायिकता के बराबर नहीं है और यह दिए गए शर्तों और गणना से निकाला गया नहीं है।
76. तीन व्यक्ति A, B और C एक लक्ष्य पर एक दूसरे के बाद गोली चलाते हैं, शुरू में A से। उनकी लक्ष्य को भेद करने की प्रायिकताएँ क्रमशः $0.4, 0.3$ और 0.2 हैं। दो भेद करने की प्रायिकता है
(a) 0.024
(b) 0.188
(c) 0.336
(d) 0.452
उत्तर दिखाएँ
हल
दिया गया है: $P(A)=0.4, P(B)=0.3$ और $P(C)=0.2$
इसके अतिरिक्त $P(\overline{A})=1-0.4=0.6, P(\overline{B})=1-0.3=0.7$
और $P(\bar{{}C})=1-0.2=0.8$
$\therefore$ दो भेद करने की प्रायिकता
$=P(A) \cdot P(B) \cdot P(\overline{C})+P(A) \cdot P(\overline{B}) \cdot P(C)+P(\overline{A}) \cdot P(B) \cdot P(C)$
$=0.4 \times 0.3 \times 0.8+0.4 \times 0.7 \times 0.2+0.6 \times 0.3 \times 0.2$
$=0.096+0.056+0.036=0.188$
अतः सही विकल्प $(b)$ है।
-
विकल्प (a) 0.024: यह मान दो भेद करने की प्रायिकता को प्रतिनिधित करने के लिए बहुत कम है। दो भेद करने की प्रायिकता की गणना लक्ष्य को भेद करने और नहीं भेद करने के विभिन्न संयोजनों के योग के रूप में होती है, और इन प्रायिकताओं के योग लगभग 0.024 से बहुत अधिक है।
-
विकल्प (c) 0.336: यह मान बहुत अधिक है। सही गणना तीन अलग-अलग स्थितियों के योग के रूप में होती है, जहाँ तीन व्यक्तियों में से दो भेद करते हैं। इन प्रायिकताओं के योग 0.188 है, जो 0.336 से बहुत कम है।
-
विकल्प (d) 0.452: यह मान भी बहुत अधिक है। तीन गोलीबाजों के द्वारा लक्ष्य को भेद करने और नहीं भेद करने की व्यक्तिगत प्रायिकताओं को ध्यान में रखते हुए दो भेद करने की कुल प्रायिकता 0.188 है, जो 0.452 से बहुत कम है।
77. मान लीजिए कि एक परिवार में, प्रत्येक बच्चा लड़का या लड़की होने के बराबर संभावना रखता है। एक तीन बच्चों वाले परिवार को यादृच्छिक रूप से चुना जाता है। दिया गया है कि परिवार में कम से कम एक लड़की है, तो सबसे बड़े बच्चे के लड़की होने की प्रायिकता है
(a) $\dfrac{1}{2}$
(b) $\dfrac{1}{3}$
(c) $\dfrac{2}{3}$
(d) $\dfrac{4}{7}$
उत्तर दिखाएँ
हल
मान लीजिए $G$ दिए गए परिवार की लड़की को दर्शाता है और $B$ दिए गए परिवार की लड़की को दर्शाता है।
$\text{S}={(BGG),(GBG),(GGB),(GBB),(BGB),(BBG),(BBB), (GGG)}$
मान लीजिए $E_1$ वह घटना है जिसमें परिवार में कम से कम एक लड़की हो।
$\therefore E_1={(BGG),(GBG),(GGB),(GBB),(BGB),(BBG),(GGG)}$
मान लीजिए $E_2$ वह घटना है जिसमें सबसे बड़ा बच्चा लड़की हो।
$ \begin{aligned} & \therefore \quad E_2={(GBG),(GGB),(GBB),(GGG)} \\ & (E_1 \cap E_2)={(GBB),(GGB),(GBG),(GGG)} \\ & \therefore P(E_2 / E_1)=\dfrac{P(E_1 \cap E_2)}{P(E_1)}=\dfrac{4 / 8}{7 / 8}=\dfrac{4}{7} \end{aligned} $
इसलिए, सही विकल्प $(d)$ है।
-
विकल्प (a) $\dfrac{1}{2}$: यह विकल्प गलत है क्योंकि यह मान लेता है कि सबसे बड़े बच्चे के लड़की होने की प्रायिकता वह घटना जिसमें परिवार में कम से कम एक लड़की हो इस शर्त के अंतर्गत स्वतंत्र है। हालांकि, यह शर्त नमूना अंतरिक बदल देती है और सही प्रायिकता केवल $\dfrac{1}{2}$ नहीं है।
-
विकल्प (b) $\dfrac{1}{3}$: यह विकल्प गलत है क्योंकि यह परिवार में कम से कम एक लड़की होने के दिए गए शर्त के अंतर्गत प्रायिकता की गलत गणना करता है। सही गणना में वह नमूना अंतरिक जहां कम से कम एक लड़की हो वह शामिल होता है, जो एक अलग प्रायिकता देता है।
-
विकल्प (c) $\dfrac{2}{3}$: यह विकल्प गलत है क्योंकि यह समस्या को गलत तरीके से समझता है या प्रायिकता की गलत गणना करता है। सही तरीका घटनाओं के प्रतिच्छेदन को ढूंढना होता है और फिर कम से कम एक लड़की होने की प्रायिकता से विभाजित करना होता है, जो $\dfrac{4}{7}$ के बजाए $\dfrac{2}{3}$ नहीं होता।
78. यदि एक पासा फेंका जाता है और एक ताश के पत्ते से एक पत्ता यादृच्छिक रूप से चुना जाता है। पासे पर सम संख्या आने और एक चांदी के पत्ते के आने की प्रायिकता है
(a) $\dfrac{1}{2}$
(b) $\dfrac{1}{4}$
(c) $\dfrac{1}{8}$
(d) $\dfrac{3}{4}$
उत्तर दिखाएँ
हल
मान लीजिए $E_1$ वह घटना है जिसमें पासे पर सम संख्या आती है। $E_2$ वह घटना है जिसमें एक चांदी का पत्ता चुना जाता है।
$\therefore P(E_1)=\dfrac{3}{6}=\dfrac{1}{2}$ और $P(E_2)=\dfrac{13}{52}=\dfrac{1}{4}$
So $\quad P(E_1 \cap E_2)=P(E_1) \cdot P(E_2)=\dfrac{1}{2} \cdot \dfrac{1}{4}=\dfrac{1}{8}$
अतः, सुधार विकल्प (c) है।
-
विकल्प (a) $\dfrac{1}{2}$ गलत है क्योंकि इसमें माना गया है कि दोनों घटनाओं के एक साथ होने की प्रायिकता एक घटना के होने की प्रायिकता के बराबर है, जो वास्तव में नहीं है। दो स्वतंत्र घटनाओं की व्यक्तिगत प्रायिकताओं के गुणनफल ही सही प्रायिकता है।
-
विकल्प (b) $\dfrac{1}{4}$ गलत है क्योंकि इसमें केवल एक घटना (स्पाड डिकार्ड के चयन) की प्रायिकता को ध्यान में लिया गया है और दोनों घटनाओं (डाइस पर सम संख्या आना और स्पाड डिकार्ड के चयन) की संयुक्त प्रायिकता को गणना में नहीं लिया गया है।
-
विकल्प (d) $\dfrac{3}{4}$ गलत है क्योंकि इसमें दो स्वतंत्र घटनाओं की संयुक्त प्रायिकता को अधिक अनुमानित किया गया है। दोनों घटनाओं की सही संयुक्त प्रायिकता बहुत कम है, जैसा कि दोनों घटनाओं की व्यक्तिगत प्रायिकताओं के गुणनफल द्वारा गणना किया गया है।
79. एक बॉक्स में 3 संतरे गेंद, 3 हरी गेंद और 2 नीली गेंद हैं। बॉक्स से बिना वापस लेने के तीन गेंद यादृच्छिक रूप से निकाली जाती हैं। 2 हरी गेंद और एक नीली गेंद निकालने की प्रायिकता है
(a) $\dfrac{3}{28}$
(b) $\dfrac{2}{21}$
(c) $\dfrac{1}{28}$
(d) $\dfrac{167}{168}$
उत्तर दिखाएँ
हल
2 हरी गेंद और 1 नीली गेंद निकालने की प्रायिकता $=P(G) \cdot P(G) \cdot P(B)+P(G) \cdot P(B) \cdot P(G)+P(B) \cdot P(G) \cdot P(G)$
$=\dfrac{3}{8} \cdot \dfrac{2}{7} \cdot \dfrac{2}{6}+\dfrac{3}{8} \cdot \dfrac{2}{7} \cdot \dfrac{2}{6}+\dfrac{2}{8} \cdot \dfrac{3}{7} \cdot \dfrac{2}{6}=\dfrac{12}{336}+\dfrac{12}{336}+\dfrac{12}{336}=\dfrac{36}{336}=\dfrac{3}{28}$
अतः, सही विकल्प $(a)$ है।
-
विकल्प (b) $\dfrac{2}{21}$ गलत है क्योंकि 2 हरी गेंद और 1 नीली गेंद निकालने की प्रायिकता $\dfrac{3}{28}$ है, न कि $\dfrac{2}{21}$. मान $\dfrac{2}{21}$ सही प्रायिकता के साथ मेल नहीं खाता है, जो संयोजन और गणना से निकाली गई है।
-
विकल्प (c) $\dfrac{1}{28}$ गलत है क्योंकि 2 हरी गेंद और 1 नीली गेंद निकालने की सही प्रायिकता $\dfrac{3}{28}$ है। मान $\dfrac{1}{28}$ बहुत कम है और सही प्रायिकता के साथ मेल नहीं खाता है, जो संयोजन और गणना से निकाली गई है।
-
विकल्प (d) $\dfrac{167}{168}$ गलत है क्योंकि यह सही प्रायिकता $\dfrac{3}{28}$ की तुलना में बहुत अधिक है। मान $\dfrac{167}{168}$ लगभग 1 है, जो एक लगभग निश्चित घटना को दर्शाता है, जबकि वास्तविक प्रायिकता काफी कम है।
80. एक फ़ॉसफ़ोरस बल्ब में 8 बैटरी हैं, जिनमें से 3 मर गई हैं। यदि दो बैटरी बिना प्रतिस्थापन के चुनकर परीक्षण किए जाते हैं, तो दोनों मर गई होने की प्रायिकता है
(a) $\dfrac{33}{56}$
(b) $\dfrac{9}{64}$
(c) $\dfrac{1}{14}$
(d) $\dfrac{3}{28}$
उत्तर दिखाएँ
हल
अभीष्ट प्रायिकता $=P($ मर गई $) \cdot P($ मर गई $)$
$ =\dfrac{3}{8} \cdot \dfrac{2}{7}=\dfrac{3}{28} $
अतः सही विकल्प $(d)$ है।
-
विकल्प (a) $\dfrac{33}{56}$: यह विकल्प गलत है क्योंकि यह 8 बैटरी में से 3 मर गई होने की प्रायिकता को सही तौर पर प्रकट नहीं करता है। सही गणना में एक बैटरी के चुने जाने की प्रायिकता और बिना प्रतिस्थापन के दूसरी बैटरी के चुने जाने की प्रायिकता को गुणा करना शामिल होता है, जो $\dfrac{3}{28}$ के बराबर होता है, न कि $\dfrac{33}{56}$।
-
विकल्प (b) $\dfrac{9}{64}$: यह विकल्प गलत है क्योंकि यह दोनों मर गई बैटरी के चुने जाने की प्रायिकता को $\dfrac{3}{8}$ और $\dfrac{3}{8}$ के गुणनफल के रूप में मानता है, जो बार बार चुने जाने के मामले में होता है। लेकिन चुने जाने के बिना प्रतिस्थापन के मामले में सही प्रायिकता $\dfrac{3}{8} \cdot \dfrac{2}{7} = \dfrac{3}{28}$ होती है।
-
विकल्प (c) $\dfrac{1}{14}$: यह विकल्प गलत है क्योंकि यह बिना प्रतिस्थापन के दोनों मर गई बैटरी के चुने जाने की प्रायिकता को सही तौर पर प्रकट नहीं करता है। सही प्रायिकता $\dfrac{3}{8} \cdot \dfrac{2}{7} = \dfrac{3}{28}$ होती है, जो $\dfrac{3}{28}$ के बराबर होती है, न कि $\dfrac{1}{14}$।
81. यदि आठ सिक्कों को एक साथ उछाला जाता है, तो तीन सिक्कों में से ठीक 3 सिक्के चित आने की प्रायिकता है
(a) $\dfrac{1}{256}$
(b) $\dfrac{7}{32}$
(c) $\dfrac{5}{32}$
(d) $\dfrac{3}{32}$
उत्तर दिखाएँ
हल
यहाँ, $n=8, p=\dfrac{1}{2}, q=1-\dfrac{1}{2}=\dfrac{1}{2}$ और $r=3$
हम जानते हैं कि $P(x=r)={ }^{n} C_r p^{r} . q^{n-r}$
$ \begin{aligned} \therefore \quad P(x=3) & ={ }^{8} C_3(\dfrac{1}{2})^{3}(\dfrac{1}{2})^{8-3} \\ & =\dfrac{8 !}{3 ! \cdot 5 !} \cdot(\dfrac{1}{2})^{3}(\dfrac{1}{2})^{5}=56 \cdot(\dfrac{1}{2})^{8}=56 \cdot \dfrac{1}{256}=\dfrac{7}{32} \end{aligned} $
इसलिए, सही विकल्प $(b)$ है।
- विकल्प (a) $\dfrac{1}{256}$ गलत है क्योंकि इसका अर्थ 8 सिक्कों के उछालने पर ठीक 0 सिर या 8 सिर प्राप्त करने की प्रायिकता है, न कि 3 सिर।
- विकल्प (c) $\dfrac{5}{32}$ गलत है क्योंकि यह ठीक 3 सिर प्राप्त करने की गणना की प्रायिकता $\dfrac{7}{32}$ के साथ मेल नहीं खाता।
- विकल्प (d) $\dfrac{3}{32}$ गलत है क्योंकि यह भी ठीक 3 सिर प्राप्त करने की गणना की प्रायिकता $\dfrac{7}{32}$ के साथ मेल नहीं खाता।
82. दो पासे फेंके जाते हैं। यदि यह ज्ञात हो कि पासों पर संख्याओं का योग 6 से कम है, तो योग 3 प्राप्त करने की प्रायिकता है
(a) $\dfrac{1}{18}$
(b) $\dfrac{5}{18}$
(c) $\dfrac{1}{5}$
(d) $\dfrac{2}{5}$
उत्तर दिखाएँ
हल
मान लीजिए $E_1$ दो पासों पर संख्याओं के योग के 6 से कम होने की घटना है और $E_2$ दो पासों पर संख्याओं के योग के 3 होने की घटना है।
$ \begin{aligned} & \therefore \quad E_1={(1,1),(1,2),(2,1),(1,3),(3,1),(1,4),(4,1), \\ &(2,2),(2,3),(3,2)} \\ & \text{ और } \quad n(E_1)=10 \\ & E_2={(1,2),(2,1)} \Rightarrow n(E_2)=2 \text{ और } n(E_1 \cap E_2)=2 \end{aligned} $
$\therefore$ आवश्यक प्रायिकता
$ P(E_2 / E_1)=\dfrac{n(E_1 \cap E_2)}{n(E_1)}=\dfrac{2}{10}=\dfrac{1}{5} $
इसलिए, सही विकल्प (c) है।
-
विकल्प (a) $\dfrac{1}{18}$ गलत है क्योंकि यह संख्याओं के योग 6 से कम होने वाले कुल परिणामों के अनुपात को सही रूप से प्रतिनिधित्व नहीं करता। सही अनुपात $\dfrac{2}{10}$ है, जो $\dfrac{1}{5}$ के रूप में सरलीकृत होता है।
-
विकल्प (b) $\dfrac{5}{18}$ गलत है क्योंकि यह संभावना को अधिक अनुमानित करता है। सही संभावना $\dfrac{1}{5}$ है, जो योग 3 के अनुकूल परिणामों के अनुपात से प्राप्त की जाती है जहाँ योग 6 से कम हो।
-
विकल्प (d) $\dfrac{2}{5}$ गलत है क्योंकि यह संभावना को अधिक अनुमानित करता है। सही संभावना $\dfrac{1}{5}$ है, जो योग 3 के अनुकूल परिणामों के अनुपात से प्राप्त की जाती है जहाँ योग 6 से कम हो।
83. बाईनोमियल वितरण के लिए निम्नलिखित में से कौन एक आवश्यकता नहीं है?
(a) प्रत्येक प्रयोग में दो नतीजे होते हैं। (b) प्रयोगों की एक निश्चित संख्या होती है।
(c) परिणाम एक दूसरे पर निर्भर करना चाहिए।
(d) सफलता की संभावना सभी प्रयोगों के लिए समान होनी चाहिए।
उत्तर दिखाएँ
हल
हम जानते हैं कि बाईनोमियल वितरण के लिए परिणाम एक दूसरे पर निर्भर नहीं करना चाहिए।
अतः सही विकल्प (c) है।
-
(a) प्रत्येक प्रयोग में दो नतीजे होते हैं।
- यह बाईनोमियल वितरण की आवश्यकता है क्योंकि प्रत्येक प्रयोग में दो संभावित नतीजों में से एक होना चाहिए, जो आमतौर पर “सफलता” और “असफलता” के रूप में चिह्नित किए जाते हैं।
-
(b) प्रयोगों की एक निश्चित संख्या होती है।
- यह बाईनोमियल वितरण की आवश्यकता है क्योंकि प्रयोगों की संख्या आगे चलकर निर्धारित और स्थिर होनी चाहिए।
-
(d) सफलता की संभावना सभी प्रयोगों के लिए समान होनी चाहिए।
- यह बाईनोमियल वितरण की आवश्यकता है क्योंकि सफलता की संभावना सभी प्रयोगों में समान रहनी चाहिए ताकि प्रयोग समान वितरण वाले हों।
84. एक अच्छी ढंग से मिश्रित 52 कार्ड के खेल के ढेर से दो कार्ड बराबरी के साथ खींचे जाते हैं, तो दोनों कार्ड क्वीन होने की संभावना है
(a) $\dfrac{1}{13} \times \dfrac{1}{13}$
(b) $\dfrac{1}{13}+\dfrac{1}{13}$
(c) $\dfrac{1}{13} \times \dfrac{1}{17}$
(d) $\dfrac{1}{13} \times \dfrac{4}{51}$
उत्तर दिखाएँ
हल
क्वीन प्राप्त करने की संभावना $=\dfrac{4}{52}$
तो, आवश्यक प्रायिकता
$ \begin{aligned} & =P(\text{ राजकुमारी }) \cdot P(\text{ राजकुमारी }) \\ & =\dfrac{4}{52} \cdot \dfrac{4}{52}=\dfrac{1}{13} \cdot \dfrac{1}{13} \quad \text{ (पुनः चयन के साथ) } \end{aligned} $
इसलिए, सही विकल्प है $(a)$।
-
विकल्प (b) $\dfrac{1}{13}+\dfrac{1}{13}$: यह विकल्प गलत है क्योंकि यह प्रायिकताओं के योग को दर्शाता है, न कि गुणन। दो स्वतंत्र घटनाओं के एक साथ होने की प्रायिकता की गणना करते समय, आप उनकी प्रायिकताओं को गुणा करते हैं, न कि जोड़ते हैं।
-
विकल्प (c) $\dfrac{1}{13} \times \dfrac{1}{17}$: यह विकल्प गलत है क्योंकि इसमें दूसरे कार्ड के लिए गलत प्रायिकता का उपयोग किया गया है। दोनों कार्ड के लिए राजकुमारी खींचने की प्रायिकता $\dfrac{1}{13}$ बनी रहती है क्योंकि कार्ड पुनः चयन के साथ खींचे जाते हैं, जिसका अर्थ है कि प्रत्येक खींचे के बाद डेक को अपनी मूल स्थिति में वापस ले जाया जाता है।
-
विकल्प (d) $\dfrac{1}{13} \times \dfrac{4}{51}$: यह विकल्प गलत है क्योंकि इसमें अनुमान लगाया गया है कि कार्ड बिना पुनः चयन के खींचे जाते हैं। यदि कार्ड बिना पुनः चयन के खींचे जाते, तो दूसरे कार्ड के लिए राजकुमारी खींचने की प्रायिकता पहले कार्ड के राजकुमारी खींचने के बाद $\dfrac{3}{51}$ होती। हालांकि, समस्या में दिया गया है कि कार्ड पुनः चयन के साथ खींचे जाते हैं, इसलिए प्रत्येक खींचे के लिए प्रायिकता $\dfrac{1}{13}$ बनी रहती है।
85. सच और गलत प्रकार की परीक्षा में कम से कम 8 उत्तर सही तरह से अनुमान लगाने की प्रायिकता है
(a) $\dfrac{7}{64}$
(b) $\dfrac{7}{128}$
(c) $\dfrac{45}{1024}$
(d) $\dfrac{7}{41}$
उत्तर दिखाएँ
हल
यहाँ, $n=10, p=\dfrac{1}{2}$ और $q=\dfrac{1}{2} \quad$ (सच और गलत प्रश्न के लिए) और $r \geq 8$ अर्थात $8,9,10$
$ \begin{aligned} \therefore P(X \geq 8) & =P(X=8)+P(X=9)+P(X=10) \\ & ={ }^{10} C_8(\dfrac{1}{2})^{8}(\dfrac{1}{2})^{2}+{ }^{10} C_9(\dfrac{1}{2})^{9}(\dfrac{1}{2})+{ }^{10} C _{10}(\dfrac{1}{2})^{10}(\dfrac{1}{2})^{0} \\ & =45 \cdot(\dfrac{1}{2})^{10}+10 \cdot(\dfrac{1}{2})^{10}+(\dfrac{1}{2})^{10}=(\dfrac{1}{2})^{10}(45+10+1) \\
& =56 \times \dfrac{1}{1024}=\dfrac{7}{128} \end{aligned} $
अतः, सही विकल्प (b) है।
-
विकल्प (a) $\dfrac{7}{64}$: यह विकल्प गलत है क्योंकि 10 प्रश्नों में से कम से कम 8 प्रश्नों को सही तरीके से अनुमान लगाने की संभावना $\dfrac{7}{128}$ है, न कि $\dfrac{7}{64}$. मान $\dfrac{7}{64}$ सही संभावना के दोगुना है, जो गणना में त्रुटि को दर्शाता है।
-
विकल्प (c) $\dfrac{45}{1024}$: यह विकल्प गलत है क्योंकि यह केवल 10 प्रश्नों में से 8 प्रश्नों को सही तरीके से अनुमान लगाने की संभावना को दर्शाता है। समस्या में कम से कम 8 प्रश्नों को सही तरीके से अनुमान लगाने की संभावना की आवश्यकता है, जो 8, 9 और 10 प्रश्नों को सही तरीके से अनुमान लगाने की संभावना के योग को शामिल करती है।
-
विकल्प (d) $\dfrac{7}{41}$: यह विकल्प गलत है क्योंकि इसकी संभावना $\dfrac{7}{128}$ के साथ मेल नहीं खाती है। मान $\dfrac{7}{41}$ विलोमी बाइनोमियल संभावना सूत्र का उपयोग नहीं करता है जो समाधान में उपयोग किया गया है और यह सही संभावना के सरल रूप के रूप में नहीं है।
86. एक व्यक्ति के तैराक नहीं होने की संभावना 0.3 है। 5 व्यक्तियों में से 4 तैराक होने की संभावना है
(a) ${ }^{5} C_4(0.7)^{4}(0.3)$
(b) ${ }^{5} C_1(0.7)(0.3)^{4}$
(c) ${ }^{5} C_4(0.7)(0.3)^{4}$
(d) $(0.7)^{4}(0.3)$
उत्तर दिखाएँ
समाधान
दिया गया है: $\overline{P}=0.3 \therefore p=0.7$ और $q=1-0.7=0.3$ $n=5$ और $r=4$
हम जानते हैं कि
$ \begin{aligned} & P(X=r)={ }^{n} C_r(p)^{r} \cdot(q)^{n-r} \\ \therefore \quad & P(X=4)={ }^{5} C_4(0.7)^{4}(0.3)^{5-4}={ }^{5} C_4(0.7)^{4}(0.3) \end{aligned} $
अतः, सही विकल्प (a) है।
-
विकल्प (b) गलत है क्योंकि यह गलत रूप से तैराक नहीं होने की संभावना (0.3) के घात 4 को दर्शाता है बल्कि तैराक होने की संभावना (0.7) के घात 4 को दर्शाना चाहिए। सही सूत्र में तैराक होने की संभावना के घात 4 होना चाहिए।
-
विकल्प (c) गलत है क्योंकि यह गलत रूप से तैराक नहीं होने की संभावना (0.3) के घात 4 को दर्शाता है बल्कि तैराक होने की संभावना (0.7) के घात 4 को दर्शाना चाहिए। सही सूत्र में तैराक होने की संभावना के घात 4 होना चाहिए।
-
विकल्प (d) गलत है क्योंकि इसमें द्विपद गुणांक ${ }^{5} C_4$ शामिल नहीं है, जो 5 व्यक्तियों में से 4 तैराकों के चयन के विभिन्न तरीकों की गणना करने के लिए आवश्यक है।
87. एक असतत यादृच्छिक चर $X$ के प्रायिकता बितौर नीचे दिया गया है:
$\begin{array}{|l|l|l|l|l|} \hline X & 2 & 3 & 4 & 5 \ \hline P(X) & \dfrac{5}{k} & \dfrac{7}{k} & \dfrac{9}{k} & \dfrac{11}{k} \ \hline \end{array}$
$ k $ का मान है
(a) 8
(b) 16
(c) 32
(d) 48
उत्तर दिखाएँ
हल
हम जानते हैं कि $\sum _{i=1}^{n} P(X_i)=1$
$ \begin{aligned} \therefore \quad \dfrac{5}{k}+\dfrac{7}{k}+\dfrac{9}{k}+\dfrac{11}{k} & =1 \\ \dfrac{32}{k} & =1 \Rightarrow k=32 . \end{aligned} $
अतः, सही विकल्प (c) है।
-
विकल्प (a) 8 गलत है क्योंकि यदि $ k = 8 $, तो प्रायिकता के योग का मान $\dfrac{5}{8} + \dfrac{7}{8} + \dfrac{9}{8} + \dfrac{11}{8} = \dfrac{32}{8} = 4 $ होगा, जो 1 के बराबर नहीं है।
-
विकल्प (b) 16 गलत है क्योंकि यदि $ k = 16 $, तो प्रायिकता के योग का मान $\dfrac{5}{16} + \dfrac{7}{16} + \dfrac{9}{16} + \dfrac{11}{16} = \dfrac{32}{16} = 2 $ होगा, जो 1 के बराबर नहीं है।
-
विकल्प (d) 48 गलत है क्योंकि यदि $ k = 48 $, तो प्रायिकता के योग का मान $\dfrac{5}{48} + \dfrac{7}{48} + \dfrac{9}{48} + \dfrac{11}{48} = \dfrac{32}{48} = \dfrac{2}{3} $ होगा, जो 1 के बराबर नहीं है।
88. निम्नलिखित प्रायिकता बितौर के लिए:
$\begin{array}{|l|l|l|l|l|l|} \hline X & -4 & -3 & -2 & -1 & 0\ \hline P(X) & 0.1 & 0.2 & 0.3 & 0.2 & 0.2 \ \hline \end{array}$
$E(X)$ के मान के बराबर है:
(a) 0
(b) -1
(c) -2
(d) -1.8
उत्तर दिखाएँ
हल
हम जानते हैं कि:
$ \begin{aligned} E(X) & =\sum _{i=1}^{n} X_i P_i \\ & =(-4)(0.1)+(-3)(0.2)+(-2)(0.3)+(-1)(0.2)+0(0.2) \\ & =-0.4-0.6-0.6-0.2=-1.8 \end{aligned} $
अतः, सही विकल्प $(d)$ है।
-
विकल्प (a) 0 गलत है क्योंकि $ E(X) $ की गणना $ X $ के मानों के अपने संगत प्रायिकताओं के भारित औसत के रूप में की जाती है। गणना दिखाती है कि योग $-1.8$ है, न कि 0।
-
विकल्प (b) -1 गलत है क्योंकि अपेक्षित मूल्य $ E(X) $ की गणना $-1.8$ के रूप में की जाती है, न कि $-1$। प्रत्येक $ X $ के मान और उसकी प्रायिकता के उत्पादों का योग $-1$ के बराबर नहीं होता।
-
विकल्प (c) -2 गलत है क्योंकि अपेक्षित मूल्य $ E(X) $ की गणना $-1.8$ के रूप में की जाती है, न कि $-2$। प्रत्येक $ X $ के मान और उसकी प्रायिकता के उत्पादों का योग $-2$ के बराबर नहीं होता।
89. निम्नलिखित प्रायिकता वितरण के लिए
$\begin{array}{|l|l|l|l|l|l|} \hline X & 1 & 2 & 3 & 4 \ \hline P(X) & \dfrac{1}{10} & \dfrac{3}{10} & \dfrac{3}{10} & \dfrac{2}{10} \ \hline \end{array}$
$E(X^{2})$ के बराबर है
(a) 3
(b) 5
(c) 7
(d) 10
उत्तर दिखाएँ
हल
हम जानते हैं कि
$ \begin{aligned} E(X^{2}) & =\sum _{i=1}^{n} P_i X_i^{2} \\ & =1 \times \dfrac{1}{10}+4 \times \dfrac{1}{5}+9 \times \dfrac{3}{10}+16 \times \dfrac{2}{5} =\dfrac{1}{10}+\dfrac{4}{5}+\dfrac{27}{10}+\dfrac{32}{5}=\dfrac{28}{10}+\dfrac{36}{5}=\dfrac{100}{10}=10 \end{aligned} $
अतः सही विकल्प (d) है।
-
विकल्प (a) 3: यह विकल्प गलत है क्योंकि $E(X^2)$ की गणना प्रत्येक $X$ के मान के वर्ग को गुणा करके उसकी संगत प्रायिकता से गुणा करके जोड़ने से की जाती है। इन उत्पादों का योग 3 के बराबर नहीं होता। विशेष रूप से, सही गणना के परिणाम 10 होते हैं, न कि 3।
-
विकल्प (b) 5: यह विकल्प गलत है क्योंकि, विकल्प (a) के तरह, $E(X^2)$ की सही गणना प्रत्येक $X$ के मान के वर्ग को गुणा करके उसकी संगत प्रायिकता से गुणा करके जोड़ने से की जाती है। इन उत्पादों का योग 10 होता है, न कि 5।
-
विकल्प (c) 7: यह विकल्प गलत है क्योंकि $E(X^2)$ की सही गणना के परिणाम 10 होते हैं। प्रत्येक $X$ के मान के वर्ग को गुणा करके उसकी संगत प्रायिकता से गुणा करके जोड़ने के उत्पादों का योग 7 के बराबर नहीं होता।
90. मान लीजिए एक यादृच्छिक चर $X$ पैरामीटर $n$ और $p$ के साथ बायनोमियल वितरण का पालन करता है, जहाँ $0 < p < 1$ है। यदि $\dfrac{P(X=r)}{P(X=n-r)}$ $n$ और $r$ के स्वतंत्र है, तो $p$ के बराबर है
(a) $\dfrac{1}{2}$
(b) $\dfrac{1}{3}$
(c) $\dfrac{1}{5}$
(d) $\dfrac{1}{7}$
उत्तर दिखाएँ
हल
$\quad P(X=r)={ }^{n} C_r p^{r} q^{n-r}=\dfrac{n !}{r !(n-r) !} p^{r} \cdot(1-p)^{n-r}$
$ \begin{aligned} P(X=n-r) & ={ }^{n} C _{n-r} p^{n-r} \cdot(q)^{n-(n-r)}={ }^{n} C _{n-r} p^{n-r} \cdot q^{r} \\ & =\dfrac{n !}{(n-r) !(n-n+r) !} p^{n-r} q^{r}=\dfrac{n !}{(n-r) ! r !} \cdot p^{n-r} \cdot q^{r} \end{aligned} $
अब $\dfrac{P(X=r)}{P(X=n-r)}=\dfrac{\dfrac{n !}{r !(n-r) !} \cdot p^{r} \cdot(1-p)^{n-r}}{\dfrac{n !}{r !(n-r) !} \cdot p^{n-r} \cdot(1-p)^{r}}=\dfrac{(\dfrac{1-p}{p})^{n-r}}{(\dfrac{1-p}{p})^{r}}$
उपरोक्त व्यंजक $n$ और $r$ पर निर्भर नहीं होगा यदि
$ (\dfrac{1-p}{p})=1 \Rightarrow \dfrac{1}{p}=2 \Rightarrow p=\dfrac{1}{2} $
इसलिए, सही विकल्प (a) है।
-
विकल्प (b) $\dfrac{1}{3}$: यदि $ p = \dfrac{1}{3} $, तो $ 1 - p = \dfrac{2}{3} $. अनुपात $\dfrac{P(X=r)}{P(X=n-r)}$ होगा $\left(\dfrac{\dfrac{2}{3}}{\dfrac{1}{3}}\right)^{n-2r} = 2^{n-2r}$. यह व्यंजक $n$ और $r$ पर निर्भर है, जो शर्त के विरोधाभास है कि अनुपात $n$ और $r$ पर निर्भर नहीं होना चाहिए।
-
विकल्प (c) $\dfrac{1}{5}$: यदि $ p = \dfrac{1}{5} $, तो $ 1 - p = \dfrac{4}{5} $. अनुपात $\dfrac{P(X=r)}{P(X=n-r)}$ होगा $\left(\dfrac{\dfrac{4}{5}}{\dfrac{1}{5}}\right)^{n-2r} = 4^{n-2r}$. यह व्यंजक $n$ और $r$ पर निर्भर है, जो शर्त के विरोधाभास है कि अनुपात $n$ और $r$ पर निर्भर नहीं होना चाहिए।
-
विकल्प (d) $\dfrac{1}{7}$: यदि $ p = \dfrac{1}{7} $, तो $ 1 - p = \dfrac{6}{7} $. अनुपात $\dfrac{P(X=r)}{P(X=n-r)}$ होगा $\left(\dfrac{\dfrac{6}{7}}{\dfrac{1}{7}}\right)^{n-2r} = 6^{n-2r}$. यह व्यंजक $n$ और $r$ पर निर्भर है, जो शर्त के विरोधाभास है कि अनुपात $n$ और $r$ पर निर्भर नहीं होना चाहिए।
91. एक कॉलेज में, 30% छात्र भौतिकी में असफल होते हैं, 25% गणित में असफल होते हैं और 10% दोनों में असफल होते हैं। एक छात्र को यादृच्छया चुना जाता है। यदि वह गणित में असफल हो गई है, तो वह भौतिकी में असफल होने की प्रायिकता क्या है?
(a) $\dfrac{1}{10}$
(b) $\dfrac{2}{5}$
(c) $\dfrac{9}{20}$
(d) $\dfrac{1}{3}$
उत्तर दिखाएँ
हल
मान लीजिए $E_1$ वह घटना है जिसमें छात्र भौतिक विज्ञान में असफल होता है और $E_2$ वह घटना है जिसमें वह गणित में असफल होती है।
$\therefore \quad P(E_1)=\dfrac{30}{100}, P(E_2)=\dfrac{25}{100}$ और $P(E_1 \cap E_2)=\dfrac{10}{100}$
$\therefore P(E_1 / E_2)=\dfrac{P(E_1 \cap E_2)}{P(E_2)}=\dfrac{10 / 100}{25 / 100}=\dfrac{2}{5}$
अतः, सही विकल्प (b) है।
-
विकल्प (a) $\dfrac{1}{10}$ गलत है क्योंकि यह घटना के शर्तीय प्रायिकता $\dfrac{2}{5}$ के साथ मेल नहीं खाता है जिसमें छात्र भौतिक विज्ञान में असफल होता है जबकि वह गणित में असफल हो चुका होता है। सही गणना $\dfrac{10/100}{25/100} = \dfrac{2}{5}$ है, न कि $\dfrac{1}{10}$।
-
विकल्प (c) $\dfrac{9}{20}$ गलत है क्योंकि यह शर्तीय प्रायिकता की गणना के परिणाम नहीं है। सही प्रायिकता $\dfrac{2}{5}$ है, जो $\dfrac{4}{10}$ के रूप में सरलीकृत होता है, न कि $\dfrac{9}{20}$।
-
विकल्प (d) $\dfrac{1}{3}$ गलत है क्योंकि यह सही शर्तीय प्रायिकता का प्रतिनिधित्व नहीं करता है। सही गणना $\dfrac{2}{5}$ देती है, न कि $\dfrac{1}{3}$।
92. A और B दो छात्र हैं। उनके एक समस्या को सही तरीके से हल करने के अवसर क्रमशः $\dfrac{1}{3}$ और $\dfrac{1}{4}$ हैं। यदि उनके एक साथ त्रुटि करने की प्रायिकता $\dfrac{1}{20}$ है और वे समान उत्तर प्राप्त करते हैं, तो उनके उत्तर के सही होने की प्रायिकता है
(a) $\dfrac{1}{12}$
(b) $\dfrac{1}{40}$
(c) $\dfrac{13}{120}$
(d) $\dfrac{10}{13}$
उत्तर दिखाएँ
हल
मान लीजिए $E_1$ वह घटना है जिसमें दोनों छात्र समस्या को हल करते हैं।
$\therefore \quad P(E_1)=\dfrac{1}{3} \times \dfrac{1}{4}=\dfrac{1}{12}$
और $E_2$ वह घटना है जिसमें दोनों छात्र समस्या को गलत तरीके से हल करते हैं।
$\therefore \quad P(E_2)=(1-\dfrac{1}{3}) \times(1-\dfrac{1}{4})=\dfrac{2}{3} \times \dfrac{3}{4}=\dfrac{1}{2}$
मान लीजिए $H$ वह घटना है जिसमें दोनों छात्र समान उत्तर प्राप्त करते हैं।
यहाँ, $P(H / E_1)=1, P(H / E_2)=\dfrac{1}{20}$
$\therefore P(E_1 / H)=\dfrac{P(E_1) \cdot P(H / E_1)}{P(E_1) \cdot P(H / E_1)+P(E_2) \cdot P(H / E_2)}$
$=\dfrac{\dfrac{1}{12} \times 1}{\dfrac{1}{12} \times 1+\dfrac{1}{2} \times \dfrac{1}{20}}=\dfrac{\dfrac{1}{12}}{\dfrac{1}{12}+\dfrac{1}{40}}=\dfrac{\dfrac{1}{12}}{\dfrac{10+3}{120}}=\dfrac{1 / 12}{13 / 120}=\dfrac{10}{13}$
इसलिए, सही विकल्प (d) है।
-
विकल्प (a) $\dfrac{1}{12}$: यह विकल्प गलत है क्योंकि यह दोनों A और B के समस्या को सही तरीके से हल करने की संभावना को दर्शाता है, न कि दोनों के समान उत्तर प्राप्त करने के दिए गए शर्त पर शर्तित संभावना।
-
विकल्प (b) $\dfrac{1}{40}$: यह विकल्प गलत है क्योंकि यह दोनों A और B के सामान त्रुटि करने की संभावना को दर्शाता है, न कि दोनों के समान उत्तर प्राप्त करने के दिए गए शर्त पर शर्तित संभावना।
-
विकल्प (c) $\dfrac{13}{120}$: यह विकल्प गलत है क्योंकि यह दोनों के समस्या को सही तरीके से हल करने की संभावना और दोनों के सामान त्रुटि करने की संभावना के योग से निर्मित है, लेकिन यह दोनों के समान उत्तर प्राप्त करने के दिए गए शर्त पर शर्तित संभावना को ध्यान में नहीं लेता है।
93. एक बॉक्स में 100 पेन हैं जिनमें से 10 खराब हैं। एक नमूना में 5 पेन एक-एक करके प्रतिस्थापन के साथ खींचे जाते हैं। अधिकतम एक खराब पेन की संभावना क्या है?
(a) $(\dfrac{9}{10})^{5}$
(b) $\dfrac{1}{2}(\dfrac{9}{10})^{4}$
(c) $\dfrac{1}{2}(\dfrac{9}{10})^{5}$
(d) $(\dfrac{9}{10})^{5}+\dfrac{1}{2}(\dfrac{9}{10})^{4}$
उत्तर दिखाएँ
हल
यहाँ, $n=5, p=\dfrac{10}{100}=\dfrac{1}{10}$ और $q=1-\dfrac{1}{10}=\dfrac{9}{10}$ और $r \leq 1$
हम जानते हैं कि
$ \begin{aligned} \text{ इसलिए, } P(X=r) & ={ }^{n} C_r p^{r} q^{n-r} \\ P(X \leq 1) & =P(X=0)+P(X=1) \\ & ={ }^{5} C_0(\dfrac{1}{10})^{0}(\dfrac{9}{10})^{5}+{ }^{5} C_1(\dfrac{1}{10})(\dfrac{9}{10})^{4}\\ &=(\dfrac{9}{10})^{5}+\dfrac{5}{10}(\dfrac{9}{10})^{4}=(\dfrac{9}{10})^{5}+\dfrac{1}{2}(\dfrac{9}{10})^{4} \end{aligned} `
$
अतः, सही विकल्प (d) है।
-
विकल्प (a) $(\dfrac{9}{10})^{5}$ गलत है क्योंकि यह केवल उस संभावना को गिनती है कि खींचे गए 5 कलम सभी अक्षम हों। यह तभी एक कलम क्षम होने के समान दृश्य को शामिल नहीं करता है।
-
विकल्प (b) $\dfrac{1}{2}(\dfrac{9}{10})^{4}$ गलत है क्योंकि यह केवल एक क्षम कलम खींचने की संभावना को ध्यान में रखता है और एक भी क्षम कलम खींचने की संभावना को शामिल नहीं करता है।
-
विकल्प (c) $\dfrac{1}{2}(\dfrac{9}{10})^{5}$ गलत है क्योंकि यह अक्षम कलम खींचने की संभावना को $\dfrac{1}{2}$ से गलत रूप से गुणा करता है, जो सही गणना के हिस्से में नहीं है।
सत्य/असत्य
94. मान लीजिए $P(A)>0$ और $P(B)>0$। तब $A$ और $B$ दोनों एक-दूसरे से अपवाद रहित और स्वतंत्र हो सकते हैं।
उत्तर दिखाएं
हल
गलत
- यदि घटनाएँ $ A $ और $ B $ एक-दूसरे से अपवाद रहित होती हैं, तो इसका अर्थ है कि $ P(A \cap B) = 0 $। हालांकि, घटनाओं के स्वतंत्र होने के लिए उनके प्रतिच्छेदन की संभावना उनकी व्यक्तिगत संभावनाओं के गुणनफल के बराबर होनी चाहिए, अर्थात $ P(A \cap B) = P(A) \cdot P(B) $। चूंकि $ P(A) > 0 $ और $ P(B) > 0 $, तो $ P(A) \cdot P(B) > 0 $। अतः, $ P(A \cap B) $ एक समय शून्य और एक समय धनात्मक हो सकता है। अतः, घटनाएँ $ A $ और $ B $ दोनों एक-दूसरे से अपवाद रहित और स्वतंत्र नहीं हो सकते हैं।
95. यदि $A$ और $B$ स्वतंत्र घटनाएँ हैं, तो $A^{\prime}$ और $B^{\prime}$ भी स्वतंत्र होते हैं।
उत्तर दिखाएं
हल
सत्य
- कथन सत्य है क्योंकि यदि $ A $ और $ B $ स्वतंत्र घटनाएँ हैं, तो उनके पूरक $ A’ $ और $ B’ $ के एक साथ होने की संभावना उनकी व्यक्तिगत संभावनाओं के गुणनफल के बराबर हो सकती है। विशेष रूप से, $ P(A’ \cap B’) = P(A’) \cdot P(B’) $। यह तथ्य इस बात पर आधारित है कि $ P(A’) = 1 - P(A) $ और $ P(B’) = 1 - P(B) $, और $ A $ और $ B $ के स्वतंत्र होने के कारण $ P(A \cap B) = P(A) \cdot P(B) $। अतः, पूरक $ A’ $ और $ B’ $ भी स्वतंत्र होते हैं।
96. यदि A और B परस्पर अपवादी घटनाएँ हैं, तो वे स्वतंत्र घटनाएँ भी होंगी।
उत्तर दिखाएँ
हल
गलत
-
कारण 1: परस्पर अपवादी घटनाएँ स्वतंत्र नहीं हो सकते क्योंकि यदि एक घटना हो जाती है, तो दूसरी घटना के होने की प्रायिकता शून्य हो जाती है। दो घटनाएँ स्वतंत्र होने के लिए, एक घटना के होने से दूसरी घटना के होने की प्रायिकता पर कोई प्रभाव नहीं पड़ना चाहिए।
-
कारण 2: परस्पर अपवादी घटनाओं A और B के लिए, P(A ∩ B) = 0 होता है। हालाँकि, स्वतंत्र घटनाओं के लिए, P(A ∩ B) P(A) * P(B) के बराबर होना चाहिए। क्योंकि परस्पर अपवादी घटनाओं के लिए P(A ∩ B) = 0 होता है, और P(A) * P(B) आमतौर पर शून्य नहीं होता बर्ताव जब तक कि एक घटना की प्रायिकता शून्य नहीं होती, परस्पर अपवादी घटनाएँ स्वतंत्र नहीं हो सकते।
-
कारण 3: स्वतंत्रता का अर्थ यह है कि एक घटना के होने से दूसरी घटना के होने के बारे में कोई जानकारी नहीं होती। विपरीत, यदि घटनाएँ परस्पर अपवादी होती हैं, तो एक घटना के होने से दूसरी घटना के होने की संभावना निरस्त हो जाती है, जिसका अर्थ है कि वे स्वतंत्र नहीं हो सकते।
97. दो स्वतंत्र घटनाएँ हमेशा परस्पर अपवादी होती हैं।
उत्तर दिखाएँ
हल
गलत
- स्वतंत्र घटनाएँ ऐसी घटनाएँ होती हैं जिनके एक घटना के होने से दूसरी घटना के होने की प्रायिकता पर कोई प्रभाव नहीं पड़ता। विपरीत, परस्पर अपवादी घटनाएँ ऐसी घटनाएँ होती हैं जो एक ही समय में नहीं हो सकतीं। यदि दो घटनाएँ परस्पर अपवादी होती हैं, तो एक घटना के होने से दूसरी घटना के होने की संभावना निरस्त हो जाती है, जो स्वतंत्र घटनाओं की परिभाषा के विपरीत है। इसलिए, स्वतंत्र घटनाएँ परस्पर अपवादी नहीं हो सकतीं।
98. यदि $A$ और $B$ दो स्वतंत्र घटनाएँ हैं, तो
$ P(A \text{ और } B)=P(A) \cdot P(B) \text{। } $
उत्तर दिखाएँ
हल
सही
- कथन सही है क्योंकि, परिभाषा के अनुसार, यदि दो घटनाएँ $A$ और $B$ स्वतंत्र हैं, तो दोनों घटनाओं के एक साथ होने की प्रायिकता (अर्थात $P(A \text{ और } B)$) उनकी व्यक्तिगत प्रायिकताओं के गुणनफल के बराबर होती है, $P(A) \cdot P(B)$। यह संभावना सिद्धांत में स्वतंत्र घटनाओं की मूल गुणधर्म है।
99. किसी प्रायिकता वितरण के अपेक्षित मान के एक अन्य नाम अपेक्षित मान है।
उत्तर दिखाएँ
Solution
सत्य $\qquad [\because E(X)=\sum X_i P(X_i)]$
- कथन सत्य है क्योंकि किसी प्रायिकता वितरण के अपेक्षित मान के लिए अपेक्षित मान कहा जाता है। अपेक्षित मान, $ E(X) $ से नोट किया जाता है, जो यादृच्छिक चर $ X $ के प्रत्येक संभावित मान $ X_i $ के संगत प्रायिकता $ P(X_i) $ से गुणा करके जोड़े गए होते हैं। इसे गणितीय रूप से $ E(X) = \sum X_i P(X_i) $ के रूप में प्रस्तुत किया जाता है।
100. यदि $A$ और $B^{\prime}$ स्वतंत्र घटनाएँ हैं, तो $P(A^{\prime} \cup B)=1-P(A) \cdot P(B^{\prime})$
उत्तर दिखाएँ
Solution
सही विकल्प A है। सत्य
$ P\left(A^{\prime} \cup B\right)=1-P\left(A \cap B^{\prime}\right)=1-P(A) P\left(B^{\prime}\right) $

101. यदि $A$ और $B$ स्वतंत्र घटनाएँ हैं, तो
$P($ ठीक एक घटना $A, B$ होती है $)=P(A) \cdot P(B^{\prime})+P(B) \cdot P(A^{\prime})$
उत्तर दिखाएँ
Solution
सत्य
घटना A होती है और B नहीं होती है की प्रायिकता $P(A)⋅P(B^{\prime})$ है।
घटना B होती है और A नहीं होती है की प्रायिकता $P(B)⋅P(A^{\prime})$ है।
क्योंकि घटनाएँ स्वतंत्र हैं, इन प्रायिकताओं को जोड़ सकते हैं:
$ P(\text{ठीक एक घटना } A \text{ या } B \text{ होती है}) = P(A) \cdot P(B’) + P(B) \cdot P(A’) $
102. यदि $A$ और $B$ दो घटनाएँ हैं जैसे कि $P(A)>0$ और $P(A)+P(B)>1$,
तो $P(B / A) \geq 1-\dfrac{P(B^{\prime})}{P(A)}$
उत्तर दिखाएँ
Solution
गलत
$ \begin{matrix} {\because P(B / A)=\dfrac{P(A \cap B)}{P(A)}=\dfrac{P(A)+P(B)-P(A \cup B)}{P(A)}}>\dfrac{1-P(A \cup B)}{P(A)} \end{matrix} $
103. यदि $A, B$ और $C$ तीन स्वतंत्र घटनाएँ हैं जैसे कि
$P(A)=P(B)=P(C)=p$,
तो P (कम से कम दो घटनाएँ $A, B$ और $C$ होती हैं) $=3 p^{2}-2 p^{3}$
उत्तर दिखाएं
हल
सत्य
क्योंकि $P$ (कम से कम दो में से $A, B$ और $C$ हों)
$ \begin{aligned} & =p \times p \times(1-p)+(1-p) \cdot p \cdot p+p(1-p) \cdot p+p \cdot p \cdot p \\ & =3 p^{2}(1-p)+p^{3}=3 p^{2}-3 p^{3}+p^{3}=3 p^{2}-2 p^{3} \end{aligned} $
भरण पदार्थ
104. यदि $A$ और $B$ दो घटनाएं इस प्रकार हैं कि $P(A / B)=p, P(A)=p$,
$ P(B)=\dfrac{1}{3} \text{ और } P(A \cup B)=\dfrac{5}{9} \text{, तो } p \text{ के बराबर है } $ ……
उत्तर दिखाएं
हल
दिया गया है: $P(A)=p, P(B)=\dfrac{1}{3}$ और $P(A \cup B)=\dfrac{5}{9}$
$ \begin{aligned} &P(A / B) =\dfrac{P(A \cap B)}{P(B)}=p\\ &\Rightarrow P(A \cap B)=p \cdot P(B)=p \cdot \dfrac{1}{3} \\ &\text{ और } P(A \cup B) =P(A)+P(B)-P(A \cap B) \\ &\dfrac{5}{9}=p+\dfrac{1}{3} -\dfrac{p}{3}\\ &\Rightarrow \dfrac{5}{9}-\dfrac{1}{3}=\dfrac{2 p}{3}\\ &\Rightarrow \dfrac{2}{9}=\dfrac{2 p}{3}\\ &\Rightarrow p=\dfrac{1}{3} \end{aligned} $
अतः, $p$ के बराबर $\dfrac{1}{3}$ है।
105. यदि $A$ और $B$ इस प्रकार हैं कि $P(A^{\prime} \cup B^{\prime})=\dfrac{2}{3}$ और $P(A \cup B)=\dfrac{5}{9}$, तो $P(A^{\prime})+P(B^{\prime})$ के बराबर है ……
उत्तर दिखाएं
हल
यहाँ,
$ P(A^{\prime} \cup B^{\prime})=\dfrac{2}{3} \text{ और } P(A \cup B)=\dfrac{5}{9} $
$ \begin{aligned} & \therefore & 1-P(A \cap B) & =\dfrac{2}{3} \\ & \Rightarrow & P(A \cap B) & =1-\dfrac{2}{3}=\dfrac{1}{3} \end{aligned} $
अब $\quad P(A^{\prime})+P(B^{\prime})=1-P(A)+1-P(B)=2-[P(A)+P(B)]$
$ \begin{aligned} & =2-[P(A \cup B)+P(A \cap B)] \\ & =2-[\dfrac{5}{9}+\dfrac{1}{3}]=2-\dfrac{8}{9}=\dfrac{10}{9} \end{aligned} $
अतः, भरण पदार्थ का मान $\dfrac{10}{9}$ है।
106. यदि $X$ वितरण के साथ बाइनोमियल वितरण का अनुसरण करता है $n=5, p$ और $P(X=2)=9 P(X=3)$, तो $p$ के बराबर है ……
उत्तर दिखाएं
हल
दिया गया है: $P(X=2)=9 P(X=3)$
$ \Rightarrow{ }^{5} C_2 p^{2} q^{3}=9 .{ }^{5} C_3 p^{3} q^{2} `
$
$ \begin{aligned} &\Rightarrow \dfrac{1}{9} =\dfrac{{ }^{5} C_3 p^{3} q^{2}}{{ }^{5} C_2 p^{2} q^{3}}\\ &\Rightarrow \dfrac{1}{9}=\dfrac{p}{q} \quad[\because{ }^{5} C_3={ }^{5} C_2] \\ &\Rightarrow 9 p =q \\ &\Rightarrow 9 p =1-p\\ &\Rightarrow 9 p+p=1\\ &\Rightarrow 10 p=1\\ &\therefore p=\dfrac{1}{10} \end{aligned} $
इसलिए, भरण पद का मान $\dfrac{1}{10}$ है।
107. मान लीजिए $X$ एक यादृच्छिक चर है जो $x_1, x_2, x_3, \ldots, x_n$ के मान लेता है जिनकी प्रायिकताएँ क्रमशः $p_1, p_2, p_3, \ldots, p_n$ हैं। तब $Var(X)$ के बराबर है ……
उत्तर दिखाएँ
हल
$\quad Var(X)=E(X^{2})-[E(X)]^{2}$
$=\sum X^{2} P(X)-[\sum X . P(X)]^{2}=\sum p_i x_i^{2}-(\sum p_i x_i)^{2}$
इसलिए, $Var(X)$ के बराबर $\sum p_i x_i^{2}-(\sum p_i x_i)^{2}$ है।
108. मान लीजिए $A$ और $B$ दो घटनाएँ हैं। यदि $P(A / B)=P(A)$, तो $A$ $B$ के ….. है।
उत्तर दिखाएँ
हल
$ \begin{aligned} &\because \qquad P(A / B) =\dfrac{P(A \cap B)}{P(B)} \\ &\Rightarrow P(A) =\dfrac{P(A \cap B)}{P(B)} \\ &\Rightarrow P(A \cap B) =P(A) \cdot P(B) \end{aligned} $
इसलिए, $A$ $B$ से स्वाधीन है।





