अवकल समीकरण
छोटे उत्तर प्रकार प्रश्न
1. $\frac{d y}{d x}=2^{y-x}$ के समाधान ज्ञात कीजिए।
उत्तर दिखाएं
हल
दिया गया अवकल समीकरण है
चरों को अलग करने पर, हमें प्राप्त होता है
$ \frac{d y}{d x}=2^{y-x} \Rightarrow \frac{d y}{d x}=\frac{2^{y}}{2^{x}} $
$ \frac{d y}{2^{y}}=\frac{d x}{2^{x}} \Rightarrow 2^{-y} d y=2^{-x} d x $
दोनों ओर समाकलन करने पर, हमें प्राप्त होता है
$ \begin{aligned} \int 2^{-y} d y & =\int 2^{-x} d x \\ & \\ \frac{-2^{-y}}{\log 2} & =\frac{-2^{-x}}{\log 2}+c \quad \Rightarrow-2^{-y}=-2^{-x}+c \log 2 \\ \Rightarrow \quad-2^{-y}+2^{-x} & =c \log 2 \\ \Rightarrow \quad 2^{-x}-2^{-y} & =k \quad \quad \quad \text{जहाँ} \quad c \log 2=k \end{aligned} $
2. एक तल में सभी ऊर्ध्वाधर रेखाओं के अवकल समीकरण ज्ञात कीजिए।
उत्तर दिखाएं
हल
सभी ऊर्ध्वाधर रेखाओं का समीकरण $y=m x+c$ है
$ x $ के संदर्भ में अवकलन करने पर, हमें प्राप्त होता है $\frac{d y}{d x}=m$
फिर दोबारा $ x $ के संदर्भ में अवकलन करने पर हमें प्राप्त होता है $\frac{d^{2} y}{d x^{2}}=0$
इसलिए, अभीष्ट समीकरण $\frac{d^{2} y}{d x^{2}}=0$ है।
3. यह दिया गया है कि $\frac{d y}{d x}=e^{-2 y}$ और $y=0$ जब $x=5$ है। $y=3$ होने पर $x$ का मान ज्ञात कीजिए।
उत्तर दिखाएं
हल
दिया गया समीकरण है
$ \begin{aligned} & \frac{d y}{d x} & =e^{-2 y} \end{aligned} $
चरों को अलग करने पर, हमें प्राप्त होता है
$ \begin{aligned} \Rightarrow \quad \frac{d y}{e^{-2 y}} & =d x \Rightarrow e^{2 y} \cdot d y=d x \end{aligned} $
दोनों ओर समाकलन करने पर, हमें प्राप्त होता है
$ \int e^{2 y} d y=\int d x \Rightarrow \frac{1}{2} e^{2 y}=x+c $
$y=0$ और $x=5$ (दिया गया) रखने पर
$\Rightarrow \frac{1}{2} e^{0}=5+c \Rightarrow c=\frac{1}{2}-5=-\frac{9}{2}$
$\therefore$ समीकरण बनता है $\frac{1}{2} e^{2 y}=x-\frac{9}{2}$
अब $y=3$ रखने पर, हमें प्राप्त होता है
$ \frac{1}{2} e^{6}=x-\frac{9}{2} \Rightarrow x=\frac{1}{2} e^{6}+\frac{9}{2} $
इसलिए, अभीष्ट $x$ का मान $x=\frac{1}{2}(e^{6}+9)$ है।
4. अवकल समीकरण $(x^{2}-1) \frac{d y}{d x}+2 x y=\frac{1}{x^{2}-1}$ को हल कीजिए।
हल दी गई अवकल समीकरण है $
(x^{2}-1) \frac{d y}{d x}+2 x y=\frac{1}{x^{2}-1}
$ $(x^{2}-1)$ से विभाजित करने पर, हमें प्राप्त होता है $
\frac{d y}{d x}+\frac{2x y}{x^{2}-1}=\frac{1}{(x^{2}-1)^{2}}
$ यह एक प्रथम घात और प्रथम कोटि का रैखिक अवकल समीकरण है। यहाँ, $ P=\frac{2 x}{x^{2}-1}$ और $Q=\frac{1}{(x^{2}-1)^{2}}$ समाकलन गुणक I.F. $=e^{\int P d x}=e^{\int \frac{2 x}{x^{2}-1} d x}=e^{\log |(x^{2}-1)|}=(x^{2}-1) , ((x^{2}-1)>0)$ $\therefore$ समीकरण का हल है $
\begin{aligned}
& y \times \text{ I.F. }=\int Q \times \text{ I.F. } d x+\text{ C } \\
& \Rightarrow y \times(x^{2}-1)=\int \frac{1}{(x^{2}-1)^{2}} \times(x^{2}-1) d x+\text{ C } \\
& \Rightarrow y(x^{2}-1)=\int \frac{1}{x^{2}-1} d x+C
\end{aligned}
$ $ \Rightarrow y(x^{2}-1)=\frac{1}{2} \log (|\frac{x-1}{x+1}|)+C$ अतः अभीष्ट हल $y(x^{2}-1)=\frac{1}{2} \log (|\frac{x-1}{x+1}|)+C$ है।उत्तर दिखाएँ
5. अवकल समीकरण $\frac{d y}{d x}+2 x y=y$ को हल कीजिए।
हल दी गई समीकरण $\frac{d y}{d x}+2 x y=y$ है। $
\Rightarrow \quad \frac{d y}{d x}=y-2 x y \quad \Rightarrow \frac{d y}{d x}=y(1-2 x) \\
\Rightarrow \frac{d y}{y}=(1-2 x) d x
$ दोनों ओर समाकलन करने पर, हमें प्राप्त होता है $
\begin{aligned}
& \int \frac{d y}{ y}=\int(1-2 x) d x \Rightarrow \log |y|=x-2 \cdot \frac{x^{2}}{2}+\log |c| \\
& \Rightarrow \quad \log |y|=x-x^{2}+\log |c| \Rightarrow \log |y|-\log |c|=x-x^{2} \\
& \Rightarrow \quad \log |\frac{y}{c}|=x-x^{2} \Rightarrow |{y}|=|{c}|e^{x-x^{2}} \\
\Rightarrow {y}=\pm {c}e^{x-x^{2}} \\
& \therefore \quad y=C \cdot e^{x-x^{2}} (where \quad C=\pm c)
\end{aligned}
$ अतः अभीष्ट हल $y=C \cdot e^{x-x^{2}}$ है।उत्तर दिखाएँ
6. $\frac{d y}{d x}+a y=e^{m x}$ के व्यापक हल को ज्ञात कीजिए।
हल दी गई समीकरण है $\frac{d y}{d x}+a y=e^{m x}$. यहाँ, $P=a$ और $Q=e^{m x}$ $\therefore$ I.F. $=e^{\int P d x}=e^{\int a \cdot d x}=e^{a x}$. समीकरण का हल $y \times$ I.F $=\int Q \times $ I.F. $d x+c$ $
\begin{matrix}
\Rightarrow \quad y \cdot e^{a x}=\int e^{m x} \cdot e^{a x} d x+c \Rightarrow y \cdot e^{a x}=\int e^{(m+a) x} d x+c \\
\Rightarrow \qquad y \cdot e^{a x}=\frac{e^{(m+a) x}}{(m+a)}+c \Rightarrow y=\frac{e^{(m+a) x}}{(m+a)} \cdot e^{-a x}+c \cdot e^{-a x} \\
\therefore \qquad y=\frac{e^{m x}}{(m+a)}+c \cdot e^{-a x}
\end{matrix}
$ $ \Rightarrow (m+a)y = e^{mx}+ c(m+a)e^{-ax}$ $ \Rightarrow (m+a)y = e^{mx}+ Ce^{-ax} (where \quad C= c(m+a))$ इसलिए अभीष्ट हल है $ (m+a)y = e^{mx}+ Ce^{-ax}$उत्तर दिखाएँ
7. अवकल समीकरण $\frac{d y}{d x}+1=e^{x+y}$ को हल करें।
उत्तर दिखाएँ
हल
दिया गया है: $\frac{d y}{d x}+1=e^{x+y}$
$ x+y=t $ रखें
दोनों ओर x के सापेक्ष अवकलन करें, (हम प्राप्त करते हैं)
$ \begin{matrix} \therefore & 1+\frac{d y}{d x} & =\frac{d t}{d x} \\ \therefore & \frac{d t}{d x} & =e^{t} \Rightarrow \frac{d t}{e^{t}}=d x \\ \Rightarrow e^{-t} d t=d x \end{matrix} $
दोनों ओर समाकलन करने पर, हम प्राप्त करते हैं
$ \begin{gathered} \int e^{-t} d t=\int d x \Rightarrow-e^{-t}=x+c \\ \Rightarrow \quad-e^{-(x+y)}=x+c \Rightarrow \frac{-1}{e^{x+y}}=x+c \Rightarrow(x+c) e^{x+y}=-1 \end{gathered} $
इसलिए, अभीष्ट हल है $(x+c) \ e^{x+y} \ +1=0$.
8. हल करें: $y d x-x d y=x^{2} y d x$.
उत्तर दिखाएँ
हल
दी गई समीकरण है $y d x-x d y=x^{2} y d x$.
$ \begin{aligned} & \Rightarrow \quad y d x-x^{2} y d x=x d y \\ & \Rightarrow \quad y(1-x^{2}) d x=x d y \\ & \Rightarrow \quad(\frac{1-x^{2}}{x}) d x=\frac{d y}{y} \Rightarrow(\frac{1}{x}-x) d x=\frac{d y}{y} \end{aligned} $
दोनों ओर समाकलन करने पर हम प्राप्त करते हैं
$ \begin{aligned} & \int(\frac{1}{x}-x) d x=\int \frac{d y}{y} \\ \Rightarrow & \log |x|-\frac{x^{2}}{2}=\log |y|+\log |c| \end{aligned}
$
$ \begin{aligned} & \Rightarrow \log |x|-\frac{x^{2}}{2}=\log |y c| \Rightarrow \log |x|-\log |y c|=\frac{x^{2}}{2} \\ & \Rightarrow \log |\frac{x}{y c}|=\frac{x^{2}}{2} \Rightarrow |\frac{x}{y c}|=e^\frac{x^{2}}{2} \\ & \Rightarrow \quad \frac{x}{y c}=\pm e^{x^{2} / 2} \Rightarrow \frac{y c}{x}=\mp e^{-x^{2} / 2} \Rightarrow y c=\mp x e^{-x^{2} / 2} \\ & \therefore \quad y=\mp \frac{1}{c} \cdot x e^{-x^{2} / 2} \Rightarrow y=k x e^{-x^{2} / 2} \quad[जहाँ \quad k=\mp \frac{1}{c}] \end{aligned} $
इसलिए, आवश्यक हल है $y=k x e^{-x^{2} / 2}$।
9. अवकल समीकरण $\frac{d y}{d x}=1+x+y^{2}+x y^{2}$ को हल करें, जब $y=0, x=0$ हो।
उत्तर दिखाएं
हल
दी गई समीकरण है
$ \begin{aligned} \frac{d y}{d x} & =1+x+y^{2}+x y^{2} \\ \Rightarrow \quad \frac{d y}{d x} & =1(1+x)+y^{2}(1+x) \\ \Rightarrow \quad \frac{d y}{d x} & =(1+x)(1+y^{2})\\ \Rightarrow \quad \frac{d y}{1+y^{2}}=(1+x) d x \end{aligned} $
दोनों ओर समाकलन करने पर, हम प्राप्त करते हैं
$ \int \frac{d y}{1+y^{2}}=\int(1+x) d x \Rightarrow \tan ^{-1} y=x+\frac{x^{2}}{2}+c $
$ x=0 $ और $ y=0 $ रखने पर, हम प्राप्त करते हैं $ \tan ^{-1}(0)=0+0+c \Rightarrow c=0 $
$\therefore \quad \tan ^{-1} y=x+\frac{x^{2}}{2} \Rightarrow y=\tan (x+\frac{x^{2}}{2})$
इसलिए, आवश्यक हल है $y=\tan (x+\frac{x^{2}}{2})$।
10. $(x+2 y^{3}) \frac{d y}{d x}=y$ के सामान्य हल ज्ञात करें।
उत्तर दिखाएं
हल
दी गई समीकरण है $(x+2 y^{3}) \frac{d y}{d x}=y$
$ \begin{aligned} & \Rightarrow \quad \frac{d y}{d x}=\frac{y}{x+2 y^{3}} \Rightarrow \frac{d x}{d y}=\frac{x+2 y^{3}}{y} \\ & \Rightarrow \quad \frac{d x}{d y}=\frac{x}{y}+\frac{2 y^{3}}{y} \Rightarrow \frac{d x}{d y}-\frac{x}{y}=2 y^{2} \end{aligned} $
यह एक प्रथम कोटि और प्रथम डिग्री का रैखिक अवकल समीकरण है।
यहाँ $P=-\frac{1}{y}$ और $Q=2 y^{2}$ है।
$\therefore$ समाकलन गुणक I.F. $=e^{\int P d y}=e^{\int-\frac{1}{y} d y}=e^{-\log |y|}=e^{\log \frac{1}{|y|}}=\frac{1}{|y|}, \quad (y \neq 0)$
$ y > 0 $ के लिए
इस समीकरण का समाधान है
$ \begin{aligned} x \times I . F . & =\int Q \times \text{ I.F. } d y+c \\ x \cdot \frac{1}{y} & =\int 2 y^{2} \cdot \frac{1}{y} d y+c \\ \Rightarrow \quad \frac{x}{y} & =2 \int y d y+c \Rightarrow \frac{x}{y}=2 \cdot \frac{y^{2}}{2}+c \Rightarrow \frac{x}{y}=y^{2}+c \end{aligned} $
इसलिए $x=y(y^{2}+c)$
$ y < 0 $ के लिए
इस समीकरण का समाधान है
$ \begin{aligned} x \times I . F . & =\int Q \times \text{ I.F. } d y+k \\ x \cdot \frac{1}{-y} & =\int 2 y^{2} \cdot \frac{1}{-y} d y+k \\ \Rightarrow \quad \frac{x}{y} & =2 \int y d y-k \Rightarrow \frac{x}{y}=2 \cdot \frac{y^{2}}{2}-k \Rightarrow \frac{x}{y}=y^{2}-k \end{aligned} $
इसलिए $x=y(y^{2}-k)$
इसलिए, आवश्यक समाधान है $x=y(y^{2}+C)$.
11. यदि $y(x)$ समीकरण $(\frac{2+\sin x}{1+y}) \frac{d y}{d x}=-\cos x$ का हल है और $y(0)=1$, तो $y(\frac{\pi}{2})$ का मान ज्ञात कीजिए।
उत्तर दिखाएँ
हल
दिया गया समीकरण है
$ \begin{aligned} & (\frac{2+\sin x}{1+y}) \frac{d y}{d x}=-\cos x \\ \Rightarrow &(\frac{2+\sin x}{\cos x}) \frac{d y}{d x}=-(1+y)\\ \Rightarrow \frac{d y}{(1+y)}=-(\frac{\cos x}{2+\sin x}) d x \end{aligned} $
दोनों ओर समाकलन करने पर, हम प्राप्त करते हैं
$ \begin{aligned} \int \frac{d y}{1+y} & =-\int \frac{\cos x}{2+\sin x} d x \\ \log |1+y| & =-\log |2+\sin x|+\log |c| \\ \Rightarrow \log |1+y|+\log |2+\sin x| & =\log |c| \\ \Rightarrow \quad \log |(1+y)(2+\sin x)| & =\log |c| \Rightarrow |(1+y)(2+\sin x)|=|c| \\ \Rightarrow (1+y)(2+\sin x)=\pm c \\ \Rightarrow (1+y)(2+\sin x)= C, \quad (where \quad C =\pm c) \end{aligned} $
$ x=0 $ और $ y=1 $ रखने पर, हम प्राप्त करते हैं
$(1+1)(2+\sin 0)=C \Rightarrow 4=C$
$\therefore$ समीकरण है $(1+y)(2+\sin x)=4$
अब $ x=\frac{\pi}{2} $ रखने पर
$ \begin{aligned} & \therefore \quad(1+y)(2+\sin \frac{\pi}{2})=4 \\ & \Rightarrow \quad(1+y)(2+1)=4 \Rightarrow 1+y=\frac{4}{3} \Rightarrow y=\frac{4}{3}-1 \Rightarrow y=\frac{1}{3} \end{aligned} $
इसलिए, $y(\frac{\pi}{2})=\frac{1}{3}$
इसलिए, आवश्यक समाधान $y(\frac{\pi}{2})=\frac{1}{3}$ है।
12. यदि $y(t)$ समीकरण $(1+t) \frac{d y}{d t}-t y=1$ का हल है और $y(0)=-1$, तो दिखाइए कि $y(1)=-\frac{1}{2}$ है।
उत्तर दिखाएँ
हल
दी गई समीकरण है
$ (1+t) \frac{d y}{d t}-t y=1 \Rightarrow \frac{d y}{d t}-(\frac{t}{1+t}) y=\frac{1}{1+t} $
यह एक प्रथम कोटि और प्रथम डिग्री का रैखिक अवकल समीकरण है।
यहाँ, $P=\frac{-t}{1+t}$ और $Q=\frac{1}{1+t}$
$\therefore$ समाकलन गुणक I.F. $=e^{\int P d t}=e^{\int \frac{-t}{1+t} d t}=e^{-\int \frac{1+t-1}{1+t} d t}$
$ \begin{aligned} & I.F. =e^{-\int(1-\frac{1}{1+t}) d t}=e^{-[t-\log |(1+t)|]} \\ & =e^{-t+\log |(1+t)|}=e^{-t} \cdot e^{\log (1+t)} , \quad ((1+t)>0) \end{aligned} $
$\therefore$ I.F. $=e^{-t} \cdot(1+t)$
दी गई अवकल समीकरण के आवश्यक समाधान है
$ \begin{matrix} y \times \text{ I.F. } =\int \text Q \times {I.F. } d t+c \\ \Rightarrow \qquad y \cdot e^{-t}(1+t) =\int \frac{1}{(1+t)} \cdot e^{-t} \cdot(1+t) d t+c \\ \Rightarrow \qquad y \cdot e^{-t}(1+t) =\int e^{-t} d t+c \\ \Rightarrow \qquad y \cdot e^{-t}(1+t) =-e^{-t}+c \end{matrix} $
$ \begin{aligned} & \text{ रखें } t=0 \text{ और } y=-1 , [\because y(0)=-1] \\ & \Rightarrow \quad-1 \cdot e^{0} \cdot 1=-e^{0}+c \\ & \Rightarrow \quad-1=-1+c \Rightarrow c=0 \end{aligned} $
इसलिए समीकरण बन जाती है
$ y e^{-t}(1+t)=-e^{-t} $
अब $t=1$ रखें
$\therefore \quad y \cdot e^{-1}(1+1)=-e^{-1}$
$\Rightarrow \quad 2 y=-1 \Rightarrow y=-\frac{1}{2}$
इसलिए $y(1)=-\frac{1}{2}$ की जांच की गई है।
13. बनाइए अवकल समीकरण जिसका $y=(\sin ^{-1} x)^{2}+A$ $\cos ^{-1} x+B$ जहाँ $A$ और $B$ अचर नियतांक हैं, उसका सामान्य हल हो।
उत्तर दिखाएँ
हल
दी गई समीकरण है $y=(\sin ^{-1} x)^{2}+A \cos ^{-1} x+B$
$ \frac{d y}{d x}=2 \sin ^{-1} x \cdot \frac{1}{\sqrt{1-x^{2}}}+A \cdot(\frac{-1}{\sqrt{1-x^{2}}}) $
अब दोनों ओर को $\sqrt{1-x^{2}}$ से गुणा करने पर, हम प्राप्त करते हैं
$$ \sqrt{1-x^{2}} \cdot \frac{d y}{d x} = 2 \sin ^{- $$
$ \sqrt{1-x^{2}} \frac{d y}{d x}=2 \sin ^{-1} x-A $
पुनः $x$ के सापेक्ष अवकलन करने पर, हमें प्राप्त होता है
$ \begin{aligned} & \sqrt{1-x^{2}} \frac{d^{2} y}{d x^{2}}+\frac{d y}{d x} \cdot \frac{1 \times(-2 x)}{2 \sqrt{1-x^{2}}}=\frac{2}{\sqrt{1-x^{2}}} \\ \Rightarrow \quad & \sqrt{1-x^{2}} \frac{d^{2} y}{d x^{2}}-\frac{x}{\sqrt{1-x^{2}}} \frac{d y}{d x}=\frac{2}{\sqrt{1-x^{2}}} \end{aligned} $
दोनों ओर को $\sqrt{1-x^{2}}$ से गुणा करने पर, हमें प्राप्त होता है
$ \Rightarrow \quad(1-x^{2}) \frac{d^{2} y}{d x^{2}}-x \frac{d y}{d x}-2=0 $
जो अभीष्ट अवकल समीकरण है।
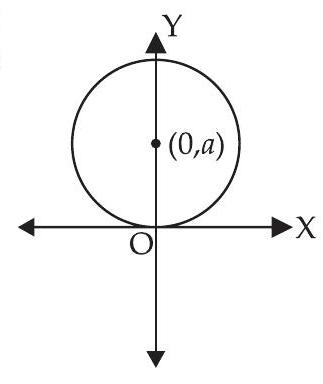
14. ऐसे सभी वृत्तों के अवकल समीकरण बनाइए जो मूल बिंदु से गुजरते हैं और जिनके केंद्र $y$-अक्ष पर स्थित होते हैं।
उत्तर दिखाएँ
हल
मूल बिंदु से गुजरते हुए और जिनके केंद्र $y$-अक्ष पर स्थित होते हैं वाले वृत्त का समीकरण है
$$(x-0)^{2}+(y-a)^{2} =a^{2}$$
$$\Rightarrow \qquad x^{2}+y^{2}+a^{2}-2 a y =a^{2}$$
$$\Rightarrow \qquad x^{2}+y^{2}-2 a y =0 \tag{i}$$
$ x $ के सापेक्ष अवकलन करने पर, हमें प्राप्त होता है
$\Rightarrow \quad 2 x+2 y \cdot \frac{d y}{d x}-2 a \cdot \frac{d y}{d x}=0$
$\Rightarrow \quad x+y \frac{d y}{d x}-a \cdot \frac{d y}{d x}=0 \Rightarrow x+(y-a) \cdot \frac{d y}{d x}=0$
$ y-a=\frac{-x}{d y / d x} $
$ \therefore \quad a=y+\frac{x}{d y / d x} $
समीकरण (i) में $a$ के मान को रखने पर, हमें प्राप्त होता है
$ \begin{aligned} & x^{2}+y^{2}-2(y+\frac{x}{d y / d x}) y=0 \\ & \Rightarrow \quad x^{2}+y^{2}-2 y^{2}-\frac{2 x y}{\frac{d y}{d x}}=0 \Rightarrow x^{2}-y^{2}=\frac{2 x y}{\frac{d y}{d x}} \\ & \therefore \quad(x^{2}-y^{2}) \frac{d y}{d x}-2 x y=0 \end{aligned} $
इसलिए, अभीष्ट अवकल समीकरण है
$ (x^{2}-y^{2}) \frac{d y}{d x}-2 x y=0 $
15. एक वक्र का समीकरण ज्ञात कीजिए जो मूल बिंदु से गुजरता है और अवकल समीकरण $(1+x^{2}) \frac{d y}{d x}+2 x y=4 x^{2}$ को संतुष्ट करता है।
उत्तर दिखाएँ
हल
दी गई समीकरण है
$$ \begin{aligned} & (1+x^{2}) \frac{d y}{d x}+2 x y=4 x^{2} \\ & \Rightarrow \quad \frac{d y}{d x}+\frac{2 x}{1+x^{2}} \cdot y=\frac{4 x^{2}}{1+x^{2}} \end{aligned} $$
यह एक प्रथम कोटि और प्रथम डिग्री की रैखिक अवकल समीकरण है।
यहाँ, $P=\frac{2 x}{1+x^{2}}$ और $Q=\frac{4 x^{2}}{1+x^{2}}$
समाकलन गुणक I.F. $=e^{\int P d x}=e^{\int \frac{2 x}{1+x^{2}} d x}=e^{\log |(1+x^{2})|}=|(1+x^{2})| = (1+ x^{2} ) , \quad (\because \quad (1+ x^{2} ) \quad धनात्मक है) $
$\therefore$ हल है
$$ \begin{align*} & y \times \text{ I.F. }=\int Q \times \text{ I.F. } d x+c \\ & \Rightarrow y(1+x^{2})=\int \frac{4 x^{2}}{1+x^{2}} \times(1+x^{2}) d x+c \\ & \Rightarrow \quad y(1+x^{2})=\int 4 x^{2} d x+c \\ & \Rightarrow \quad y(1+x^{2})=\frac{4}{3} x^{3}+c \tag{i} \end{align*} $$
क्योंकि वक्र मूलबिंदु (0,0) से गुजरता है
$\therefore$ समीकरण (i) में $y=0$ और $x=0$ रखें
$0(1+0)=\frac{4}{3}(0)^{3}+c \Rightarrow c=0$
$\therefore$ समीकरण है $y(1+x^{2})=\frac{4}{3} x^{3} \Rightarrow y=\frac{4 x^{3}}{3(1+x^{2})}$
अतः, अभीष्ट हल $y=\frac{4 x^{3}}{3(1+x^{2})}$ है।
16. हल करें : $x^{2} \cdot \frac{d y}{d x}=x^{2}+x y+y^{2}$
उत्तर दिखाएँ
हल
दी गई समीकरण है $x^{2} \frac{d y}{d x}=x^{2}+x y+y^{2}$
$$ \Rightarrow \quad \frac{d y}{d x}=\frac{x^{2}+x y+y^{2}}{x^{2}} \quad \text{(होमोजीन अवकल समीकरण)} $$
$y=v x$ रखें
$\therefore \quad \frac{d y}{d x}=v+x \cdot \frac{d v}{d x}$
$\therefore \quad v+x \cdot \frac{d v}{d x}=\frac{x^{2}+v x^{2}+v^{2} x^{2}}{x^{2}}$
$\Rightarrow \quad v+x \cdot \frac{d v}{d x}=\frac{x^{2}(1+v+v^{2})}{x^{2}}$
$\Rightarrow \quad v+x \cdot \frac{d v}{d x}=1+v+v^{2} \Rightarrow x \cdot \frac{d v}{d x}=1+v+v^{2}-v$
$$ \Rightarrow \quad x \cdot \frac{d v}{d x}=1+v^{2}\\ \Rightarrow \frac{d v}{1+v^{2}}=\frac{d x}{x} $$
दोनों ओर समाकलन करने पर, हम प्राप्त करते हैं
$$ \begin{aligned} \int \frac{d v}{1+v^{2}} & =\int \frac{d x}{x} \\
\Rightarrow \quad \tan ^{-1} v & =\log |x|+c \Rightarrow \tan ^{-1}(\frac{y}{x})=\log |x|+c \end{aligned} $
अतः, आवश्यक हल है $\tan ^{-1}(\frac{y}{x})=\log |x|+c$।
17. अवकल समीकरण का सामान्य हल ज्ञात कीजिए
$ (1+y^{2})+(x-e^{\tan ^{-1} y}) \frac{d y}{d x}=0 $
उत्तर दिखाएँ
हल
दी गई समीकरण है
$ \begin{aligned} & (1+y^{2})+(x-e^{\tan ^{-1} y}) \frac{d y}{d x}=0 \\ \Rightarrow & (x-e^{\tan ^{-1} y}) \frac{d y}{d x}=-(1+y^{2}) \Rightarrow \frac{d y}{d x}=\frac{-(1+y^{2})}{x-e^{\tan ^{-1} y}} \\ \Rightarrow & \quad \frac{d x}{d y}=\frac{x-e^{\tan ^{-1} y}}{-(1+y^{2})} \Rightarrow \frac{d x}{d y}=-\frac{x}{(1+y^{2})}+\frac{e^{\tan ^{-1} y}}{1+y^{2}} \\ \Rightarrow & \frac{d x}{d y}+\frac{x}{(1+y^{2})}=\frac{e^{\tan ^{-1} y}}{1+y^{2}} \end{aligned} $
यह एक प्रथम कोटि और प्रथम डिग्री का रैखिक अवकल समीकरण है।
यहाँ, $P=\frac{1}{1+y^{2}}$ और $Q=\frac{e^{\tan ^{-1} y}}{1+y^{2}}$
$\therefore$ समाकलन गुणक I.F. $=e^{\int P d y}=e^{\int \frac{1}{1+y^{2}} d y}=e^{\tan ^{-1} y}$
$\therefore$ हल है
$ \begin{aligned} & x \times \text{ I.F. }=\int Q \times \text{ I.F. } d y+c \\ \Rightarrow \quad x \cdot e^{\tan ^{-1} y} & =\int \frac{e^{\tan ^{-1} y}}{1+y^{2}} \cdot e^{\tan ^{-1} y} d y+c \end{aligned} $
मान लीजिए $e^{\tan ^{-1} y}=t$
$\therefore e^{\tan ^{-1} y} \cdot \frac{1}{1+y^{2}} d y=d t$
$\therefore \quad x \cdot e^{\tan ^{-1} y}=\int t \cdot d t+c$
$\Rightarrow x \cdot e^{\tan ^{-1} y}=\frac{1}{2} t^{2}+c$
$ \begin{aligned} & \Rightarrow \quad x \cdot e^{\tan ^{-1} y}=\frac{1}{2}(e^{\tan ^{-1} y})^{2}+c \\ & \Rightarrow 2 x \cdot e^{\tan ^{-1} y}=(e^{\tan ^{-1} y})^{2}+2 c \\ & \Rightarrow 2 x \cdot e^{\tan ^{-1} y}=(e^{2\tan ^{-1} y})+ C, \quad (where \quad C = 2c) \end{aligned} $
अतः, यह आवश्यक सामान्य हल है।
18. $y^{2} d x+(x^{2}-x y+y^{2}) d y=0$ का सामान्य हल ज्ञात कीजिए।
उत्तर दिखाएँ
हल
दी गई समीकरण है $y^{2} d x+(x^{2}-x y+y^{2}) d y=0$.
$ \begin{matrix} \Rightarrow & y^{2} d x=-(x^{2}-x y+y^{2}) d y \\ \Rightarrow & \frac{d x}{d y}=-\frac{x^{2}-x y+y^{2}}{y^{2}} \end{matrix} $
क्योंकि यह एक एकरूप समीकरण है
$\therefore$ रखें $x=v y \Rightarrow \frac{d x}{d y}=v+y \cdot \frac{d v}{d y}$
इसलिए, $\quad v+y \cdot \frac{d v}{d y}=-(\frac{v^{2} y^{2}-v y^{2}+y^{2}}{y^{2}})$
$\Rightarrow \quad v+y \cdot \frac{d v}{d y}=-\frac{y^{2}(v^{2}-v+1)}{y^{2}}$
$\Rightarrow \quad v+y \cdot \frac{d v}{d y}=(-v^{2}+v-1) \Rightarrow y \cdot \frac{d v}{d y}=-v^{2}+v-1-v$
$\Rightarrow \quad y \cdot \frac{d v}{d y}=-v^{2}-1 \Rightarrow \frac{d v}{(v^{2}+1)}=-\frac{d y}{y}$
दोनों ओर समाकलन करने पर, हम प्राप्त करते हैं
$ \begin{aligned} & \Rightarrow \quad \int \frac{d v}{(v^{2}+1)}=-\int \frac{d y}{y} \Rightarrow \tan ^{-1} v=-\log |y|+c \\ & \Rightarrow \quad \tan ^{-1}(\frac{x}{y})+\log |y|=c \end{aligned} $
इसलिए अभीष्ट समाधान है $\tan ^{-1}(\frac{x}{y})+\log |y|=c$.
19. हल करें: $(x+y)(d x-d y)=d x+d y$.
उत्तर दिखाएँ
हल
दी गई अवकल समीकरण है
$\qquad (x+y)(d x-d y) =d x+d y$
$\Rightarrow \quad (x+y) d x-(x+y) d y =d x+d y$
$\Rightarrow \quad -(x+y) d y-d y =d x-(x+y) d x$
$ \begin{aligned} \Rightarrow \quad -(x+y+1) d y =-(x+y-1) d x \\ \Rightarrow \frac{d y}{d x} =\frac{x+y-1}{x+y+1} \end{aligned} $
रखें $x+y=z$
$ \begin{aligned} \therefore \quad 1+\frac{d y}{d x} & =\frac{d z}{d x} \\ \frac{d y}{d x} & =\frac{d z}{d x}-1 \end{aligned} $
इसलिए, $\quad \frac{d z}{d x}-1=\frac{z-1}{z+1}$
$\Rightarrow \quad \frac{d z}{d x}=\frac{z-1}{z+1}+1 \Rightarrow \frac{d z}{d x}=\frac{z-1+z+1}{z+1}$
$\Rightarrow \quad \frac{d z}{d x}=\frac{2 z}{z+1} \quad \Rightarrow \frac{z+1}{z} d z=2 \cdot d x$
दोनों ओर समाकलन करने पर, हम प्राप्त करते हैं
$ \begin{aligned} & \int \frac{z+1}{z} d z=2 \int d x \\ & \Rightarrow \quad \int(1+\frac{1}{z}) d z=2 \int d x \\ & \Rightarrow \quad z+\log |z|=2 x+\log |c| \\
$ x+y=C \cdot e^{x-y} $।
20. हल करें: $2(y+3)-x y \cdot \frac{d y}{d x}=0$, जबकि $y(1)=-2$।
उत्तर दिखाएँ
हल
दी गई अवकल समीकरण है
$ \begin{aligned} 2(y+3)-x y \cdot \frac{d y}{d x} & =0 \\ \Rightarrow \quad x y \cdot \frac{d y}{d x} & =2 y+6 \\ \Rightarrow \quad(\frac{y}{2 y+6}) d y & =\frac{d x}{x} \Rightarrow \frac{1}{2}(\frac{y}{y+3}) d y=\frac{d x}{x} \end{aligned} $
दोनों ओर समाकलन करने पर, हमें प्राप्त होता है
$ \begin{aligned} & \Rightarrow \quad \frac{1}{2} \int \frac{y}{y+3} \cdot d y=\int \frac{d x}{x} \Rightarrow \frac{1}{2} \int \frac{y+3-3}{y+3} d y=\int \frac{d x}{x} \\ & \Rightarrow \quad \frac{1}{2} \int(1-\frac{3}{y+3}) d y=\int \frac{d x}{x} \end{aligned} $
$ \begin{aligned} & \Rightarrow \frac{1}{2} \int 1 \cdot d y-\frac{3}{2} \int \frac{1}{y+3} d y=\int \frac{d x}{x} \\ & \Rightarrow \quad \frac{1}{2} y-\frac{3}{2} \log |y+3|=\log|x|+\log |c| \\ & \Rightarrow \quad \frac{1}{2} y-\frac{3}{2} \log |y+3|=\log|xc| \\ & \Rightarrow \quad y-{3} \log |y+3|=2\log|xc| \\ & \Rightarrow \quad y-{3} \log |y+3|=\log(|xc|)^{2} \\ & \Rightarrow \quad y= \log (|y+3|)^{3}+\log(|xc|)^{2} \\ & \Rightarrow \quad y= \log (|y+3|)^{3}+\log(xc)^{2} \\ & \Rightarrow \quad y= \log ((xc)^{2}(|y+3|)^{3}) \\ & \Rightarrow \quad e^{y}= ((xc)^{2}(|y+3|)^{3}) \\ & \Rightarrow \quad x^{2}|y+3|^{3}=\frac {1}{c^{2}} e^{y} \\ & \Rightarrow \quad x^{2}(y+3)^{3}=\pm \frac {1}{c^{2}} e^{y} \\ & \Rightarrow \quad x^{2}(y+3)^{3}=C e^{y},(where \quad C=\pm \frac {1}{c^{2}}) \end{aligned} `
$
$x=1, y=-2$ रखें
$ \Rightarrow \quad 1^{2}(-2+3)^{3} =C e^{-2} $
$ \Rightarrow \quad C=e^{2}$
$ \therefore$ समीकरण है
$ \Rightarrow x^{2}(y+3)^{3}=e^{y+2}$
इसलिए, अभीष्ट समाधान $x^{2}(y+3)^{3}=e^{y+2}$ है।
21. अवकल समीकरण $d y=cos x \text {(2-y cosec x)} d x$ को हल करें जबकि $y=2$ जब $x=\frac{\pi}{2}$ है।
उत्तर दिखाएँ
हल
दिया गया अवकल समीकरण है
$ d y=\cos x \text{(2-y cosec x)} d x $
$\Rightarrow \frac{d y}{d x}=\cos x\text {(2-y cosec x)} \Rightarrow \frac{d y}{d x}=2 \cos x-y \cos x \cdot \frac{1}{sinx}$
$\Rightarrow \frac{d y}{d x}=2 \cos x-y \cot x \Rightarrow \frac{d y}{d x}+y \cot x=2 \cos x$
यह एक प्रथम कोटि और प्रथम डिग्री का रैखिक अवकल समीकरण है।
यहाँ, $P=\cot x$ और $Q=2 \cos x$ हैं।
$\therefore$ समाकलन गुणक I.F. $=e^{\int P d x}=e^{\int \cot x d x}=e^{\log |\sin x|}=\sin x , \quad (\sin x>0)$
$\therefore$ अभीष्ट समाधान $y \times$ I.F $=\int Q \times$ I.F. $d x+c$ $\Rightarrow y \cdot \sin x=\int 2 \cos x \cdot \sin x d x+c$
$\Rightarrow y \cdot \sin x=\int \sin 2 x d x+c \Rightarrow y \cdot \sin x=-\frac{1}{2} \cos 2 x+c$
$x=\frac{\pi}{2}$ और $y=2$ रखने पर, हमें प्राप्त होता है
$ \begin{aligned} 2 \sin \frac{\pi}{2} & =-\frac{1}{2} \cos \pi+c \\ \Rightarrow \quad 2(1) & =-\frac{1}{2}(-1)+c \Rightarrow 2=\frac{1}{2}+c \Rightarrow c=2-\frac{1}{2}=\frac{3}{2} \end{aligned} $
$\therefore$ समीकरण $y \sin x=-\frac{1}{2} \cos 2 x+\frac{3}{2}$ है।
22. $A x^{2}+B y^{2}=1$ में $A$ और $B$ को आप दूर करके अवकल समीकरण बनाएं।
उत्तर दिखाएँ
हल
दिया गया है $A x^{2}+B y^{2}=1$
$ x $ के संदर्भ में अवकलन करने पर, हमें प्राप्त होता है
$\qquad 2 A \cdot x+2 B y \frac{d y}{d x} =0$
$\Rightarrow \qquad A x+B y \cdot \frac{d y}{d x} =0 \Rightarrow B y \cdot \frac{d y}{d x}=-A x$
$\therefore \qquad \frac{y}{x} \cdot \frac{d y}{d x} =-\frac{A}{B}$
$ x $ के संदर्भ में दोबारा अवकलन करने पर, हमें प्राप्त होता है
$ \begin{aligned}
$$ & \frac{y}{x} \cdot \frac{d^{2} y}{d x^{2}}+\frac{d y}{d x}(\frac{x \cdot \frac{d y}{d x}-y \cdot 1}{x^{2}})=0 \\ \Rightarrow & \frac{y x^{2}}{x} \cdot \frac{d^{2} y}{d x^{2}}+x \cdot(\frac{d y}{d x})^{2}-y \cdot \frac{d y}{d x}=0 \\ \Rightarrow & x y \cdot \frac{d^{2} y}{d x^{2}}+x \cdot(\frac{d y}{d x})^{2}-y \cdot \frac{d y}{d x}=0 \Rightarrow x y \cdot y^{\prime \prime}+x \cdot(y^{\prime})^{2}-y \cdot y^{\prime}=0 \end{aligned} $$
अतः, आवश्यक समीकरण है
$$ x y \cdot y^{\prime \prime}+x \cdot(y^{\prime})^{2}-y \cdot y^{\prime}=0 $$
23. अवकल समीकरण $(1+y^{2}) \tan ^{-1} x d x+2 y(1+x^{2}) d y=0$ को हल कीजिए।
उत्तर दिखाएँ
हल
दिया गया अवकल समीकरण है
$$ \begin{matrix} (1+y^{2}) \tan ^{-1} x d x+2 y(1+x^{2}) d y=0 \\ \Rightarrow \qquad 2 y(1+x^{2}) d y=-(1+y^{2}) \cdot \tan ^{-1} x \cdot d x \\ \Rightarrow \qquad \frac{2 y}{1+y^{2}} d y=-\frac{\tan ^{-1} x}{1+x^{2}} \cdot d x \end{matrix} $$
दोनों ओर समाकलन करने पर, हम प्राप्त करते हैं
$$ \int \frac{2 y}{1+y^{2}} d y =-\int \frac{\tan ^{-1} x}{1+x^{2}} \cdot d x $$
$$ let \quad 1+y^{2} = t $$
$$ 2y dy = dt $$
$$ and \quad \tan ^{-1} x = k $$
$$ \frac{1} {1+x^{2}} dx = dk $$
$$ \therefore \int \frac {dt}{t} = -\int kdk $$
$$ log |t| =- \frac {k^{2}}{2} + c $$
$$ \Rightarrow \quad \log |1+y^{2}| =-\frac{1}{2}(\tan ^{-1} x)^{2}+c $$
$$ \Rightarrow \quad \frac{1}{2}(\tan ^{-1} x)^{2}+\log |1+y^{2}|=c $$
$$ \Rightarrow \quad \frac{1}{2}(\tan ^{-1} x)^{2}+\log (1+y^{2})=c, \quad (\because (1+y)^{2} \quad धनात्मक होता है) $$
इस प्रकार आवश्यक हल प्राप्त होता है।
24. केंद्र $(1,2)$ वाले अकेंद्रिक वृत्तों के प्रणाली के अवकल समीकरण ज्ञात कीजिए।
उत्तर दिखाएँ
हल
केंद्र $(1,2)$ वाले अकेंद्रिक वृत्तों के प्रणाली के लिए समीकरण है
$$ (x-1)^{2}+(y-2)^{2}=r^{2} $$
दोनों ओर $x$ के संदर्भ में अवकलन करने पर हम प्राप्त करते हैं
$$ 2(x-1)+2(y-2) \frac{d y}{d x}=0 \Rightarrow(x-1)+(y-2) \frac{d y}{d x}=0 $$
इस प्रकार आवश्यक समीकरण है।
लंबा उत्तर प्रकार प्रश्न
25. हल करें: $y+\frac{d}{d x}(x y)=x(\sin x+\log x)$
उत्तर दिखाएं
हल
दिया गया अवकल समीकरण है
$ \begin{aligned} & y+\frac{d}{d x}(x y)=x(\sin x+\log x) \\ & \Rightarrow \quad y+x \cdot \frac{d y}{d x}+y=x(\sin x+\log x) \\ & \Rightarrow \quad x \frac{d y}{d x}=x(\sin x+\log x)-2 y \\ & \Rightarrow \quad \frac{d y}{d x}=(\sin x+\log x)-\frac{2 y}{x} \Rightarrow \frac{d y}{d x}+\frac{2}{x} y=(\sin x+\log x) \end{aligned} $
यह एक पहले कोटि और पहले डिग्री का रैखिक अवकल समीकरण है।
यहाँ, $P=\frac{2}{x}$ और $Q=(\sin x+\log x)$
समाकल गुणक I.F. $=e^{\int P d x}=e^{\int \frac{2}{x} d x}=e^{2 \log |x|}=e^{\log |x|^{2}}=|x|^{2}= x^{2}$
$\therefore$ हल है
$$ \begin{align*} y \times \text{ I.F. } & =\int Q \times \text{ I.F. } d x+c \\ \Rightarrow \quad y \cdot x^{2} & =\int(\sin x+\log x) x^{2} d x+c \tag{1}\\ \Rightarrow \quad y \cdot x^{2} & = \text {I +c } \end{align*} $$
मान लीजिए I
$ \begin{aligned} & =\int(\sin x+\log x) x^{2} d x \\ & =\int x^{2} \sin x d x+\int x^{2} \log x d x \\ & (Integration \quad by \quad parts) \\ & \begin{aligned} = & {[x^{2} \cdot \int \sin x d x-\int(D(x^{2}) \cdot \int \sin x d x) d x]+} {[\log x \cdot \int x^{2} d x-\int(D(\log x) \cdot \int x^{2} d x) d x] } \end{aligned} \\ & =[x^{2}(-\cos x)-2 \int-x \cos x d x]+[\log x \cdot \frac{x^{3}}{3}-\int \frac{1}{x} \cdot \frac{x^{3}}{3} d x] \\ & =[-x^{2} \cos x+2(x \sin x-\int 1 \cdot \sin x d x)]+[\frac{x^{3}}{3} \log x-\frac{1}{3} \int x^{2} d x] \\ & =-x^{2} \cos x+2 x \sin x+2 \cos x+\frac{x^{3}}{3} \log x-\frac{1}{9} x^{3} \end{aligned} $
अब समीकरण (1) से हमें प्राप्त होता है,
$ \begin{aligned} y \cdot x^{2} & =-x^{2} \cos x+2 x \sin x+2 \cos x+\frac{x^{3}}{3} \log x-\frac{1}{9} x^{3}+c \\ \therefore \quad & y=-\cos x+\frac{2 \sin x}{x}+\frac{2 \cos x}{x^{2}}+\frac{x \log x}{3}-\frac{1}{9} x+c \cdot x^{-2} \end{aligned} $
इसलिए, आवश्यक हल है
$ y=-\cos x+\frac{2 \sin x}{x}+\frac{2 \cos x}{x^{2}}+\frac{x \log x}{3}-\frac{1}{9} x+c \cdot x^{-2} `
$
26. $(1+\tan y)(d x-d y)+2 x d y=0$ का सामान्य हल ज्ञात कीजिए।
उत्तर दिखाएँ
हल
दिया गया है: $(1+\tan y)(d x-d y)+2 x d y=0$
$\Rightarrow \quad(1+\tan y) d x-(1+\tan y) d y+2 x d y=0$
$ \Rightarrow \quad(1+\tan y) d x-(1+\tan y-2 x) d y=0 $
$ \begin{aligned} & \Rightarrow \quad(1+\tan y) \frac{d x}{d y}=(1+\tan y-2 x) \Rightarrow \frac{d x}{d y}=\frac{1+\tan y-2 x}{1+\tan y} \\ & \Rightarrow \quad \frac{d x}{d y}=1-\frac{2 x}{1+\tan y} \Rightarrow \frac{d x}{d y}+\frac{2 x}{1+\tan y}=1 \end{aligned} $
यह एक प्रथम कोटि और प्रथम डिग्री का रैखिक अवकल समीकरण है।
यहाँ, $P=\frac{2}{1+\tan y}$ और $Q=1$
समाकलन गुणक (I.F.)
$ \begin{aligned} & =e^{\int \frac{2}{1+\tan y} d y}=e^{\int \frac{2 \cos y}{\sin y+\cos y} d y} \\ & =e^{\int \frac{\sin y+\cos y-\sin y+\cos y}{(\sin y+\cos y)} d y}=e^{\int(1+\frac{\cos y-\sin y}{\sin y+\cos y}) d y} \\ & =e^{\int 1 \cdot d y} \cdot e^{\int \frac{\cos y-\sin y}{\sin y+\cos y} d y} \\ & =e^{y} \cdot e^{\log |(\sin y+\cos y)|}=e^{y} \cdot(\sin y+\cos y), \quad ((\sin y+\cos y)>0) \end{aligned} $
इसलिए, हल है $\quad x \times$ I.F. $=\int Q \times$ I.F. $d y+c$
$\Rightarrow x \cdot e^{y}(\sin y+\cos y)=\int 1 \cdot e^{y}(\sin y+\cos y) d y+c$
$\Rightarrow \quad x \cdot e^{y}(\sin y+\cos y)=e^{y} \cdot \sin y+c$
$ [\because \int e^{x}[f(x)+f^{\prime}(x)] d x=e^{x} f(x)+c] $
$\Rightarrow \quad x(\sin y+\cos y)=\sin y+c \cdot e^{-y}$
इसलिए, अभीष्ट हल $x(\sin y+\cos y)=\sin y+c \cdot e^{-y}$ है।
27. हल कीजिए : $\frac{d y}{d x}=\cos (x+y)+\sin (x+y)$. [संकेत: $x+y=z$ के प्रतिस्थापन करें ]
उत्तर दिखाएँ
हल
दिया गया है : $\frac{d y}{d x}=\cos (x+y)+\sin (x+y)$
मान लीजिए $\quad x+y=v$, अब $x$ के सापेक्ष अवकलन करने पर, हमें प्राप्त होता है,
$1+\frac{d y}{d x} =\frac{d v}{d x}$
$\therefore \quad \frac{d y}{d x} =\frac{d v}{d x}-1$
$\therefore \quad \frac{d v}{d x}-1 =\cos v+\sin v$
$\Rightarrow \quad \frac{d v}{d x} =\cos v+\sin v+1$
$\Rightarrow \quad \frac{d v}{\cos v+\sin v+1} = d x $
$\Rightarrow \quad \frac{d v}{(\frac{1-\tan ^{2} \frac{v}{2}}{1+\tan ^{2} \frac{v}{2}}+\frac{2 \tan \frac{v}{2}}{1+\tan ^{2} \frac{v}{2}}+1)} = d x $
$\Rightarrow \quad \frac{(1+\tan ^{2} \frac{v}{2})}{1-\tan ^{2} \frac{v}{2}+2 \tan \frac{v}{2}+1+\tan ^{2} \frac{v}{2}} d v = d x $
इन्टीग्रेट करने पर \quad दोनों \quad ओर, हम \quad पाते हैं $
$\Rightarrow \quad \int \frac{\sec ^{2} \frac{v}{2}}{2+2 \tan \frac {v}{2}} d v =\int 1 . d x $
$\text{ रखें } \quad 2+2 \tan \frac{v}{2} = t$
$2 \cdot \frac{1}{2} \sec ^{2} \frac{v}{2} d v =d t \Rightarrow \sec ^{2} \frac{v}{2} d v=d t $
$\int \frac{d t}{t} =\int 1 \cdot d x $
$\Rightarrow \quad \log |t| =x+c $
$\Rightarrow \quad \log |2+2 \tan \frac{v}{2}| =x+c $
$\Rightarrow \quad \log |2+2 \tan (\frac{x+y}{2})|=x+c \Rightarrow \log 2(|1+\tan (\frac{x+y}{2})|)=x+c $
$\Rightarrow \quad \log 2+\log (|1+\tan (\frac{x+y}{2})|) =x+c $
$\Rightarrow \quad \log (|1+\tan (\frac{x+y}{2})|) =x+c-\log 2$
इसलिए, आवश्यक समाधान है
$ \log (|1+\tan (\frac{x+y}{2})|)=x+K \quad[c-\log 2=K] $
28. $\frac{d y}{d x}-3 y=\sin 2 x$ का सामान्य समाधान ज्ञात कीजिए।
उत्तर दिखाएँ
हल
दी गई समीकरण $\frac{d y}{d x}-3 y=\sin 2 x$ है।
यह एक प्रथम कोटि और प्रथम डिग्री का रैखिक अवकल समीकरण है।
यहाँ, $P=-3$ और $Q=\sin 2 x$
$\therefore$ समाकलन गुणक I.F. $=e^{\int P d x}=e^{\int-3 d x}=e^{-3 x}$
$\therefore$ समाधान है
$ \begin{aligned} & y \times \text{ I.F. }=\int Q \times \text{ I.F. } d x+c \\ & \Rightarrow \quad y \cdot e^{-3 x}=\int \sin 2 x \cdot e^{-3 x} d x+c \\ & \text{ रखें } \quad I=\int \sin 2 x \cdot e^{-3 x} d x \\ \text{ अंतरगत गुणन } \\ & \Rightarrow \quad I=\sin 2 x \cdot \int e^{-3 x} d x-\int(D(\sin 2 x) \cdot \int e^{-3 x} d x) d x \\ & \Rightarrow \quad I=\sin 2 x \cdot \frac{e^{-3 x}}{-3}-\int 2 \cos 2 x \cdot \frac{e^{-3 x}}{-3} d x \\ & \Rightarrow \quad I=\frac{e^{-3 x}}{-3} \sin 2 x+\frac{2}{3} \int {\cos 2 x} \cdot e^{-3 x} d x \\
& \Rightarrow \quad I=\frac{e^{-3 x}}{-3} \sin 2 x+\frac{2}{3}[\cos 2 x \cdot \int e^{-3 x} d x-\int[D (\cos 2 x) \cdot \int e^{-3 x} d x] d x] \end{aligned} $
$ \begin{aligned} \Rightarrow \quad I & =\frac{e^{-3 x}}{-3} \sin 2 x+\frac{2}{3}[\cos 2 x \cdot \frac{e^{-3 x}}{-3}- \int -2 \sin 2 x \cdot \frac{e^{-3 x}}{-3}] d x \\ \Rightarrow \quad I & =\frac{e^{-3 x}}{-3} \sin 2 x-\frac{2}{9} \cos 2 x \cdot e^{-3 x}-\frac{4}{9} \int \sin 2 x \cdot e^{-3 x} d x \\ \Rightarrow \quad & =\frac{e^{-3 x}}{-3} \sin 2 x-\frac{2}{9} e^{-3 x} \cos 2 x-\frac{4}{9} I \\ \Rightarrow \quad I+\frac{4}{9} I & =\frac{e^{-3 x}}{-3} \sin 2 x-\frac{2}{9} e^{-3 x} \cos 2 x \\ \Rightarrow \quad \frac{13 I}{9} & =-\frac{1}{9}[3 e^{-3 x} \sin 2 x+2 e^{-3 x} \cos 2 x] \\ \Rightarrow \quad I & =-\frac{1}{13} e^{-3 x}[3 \sin 2 x+2 \cos 2 x] \end{aligned} $
$\therefore$ समीकरण बन जाता है
$ \begin{aligned} y \cdot e^{-3 x} & =-\frac{1}{13} e^{-3 x}[3 \sin 2 x+2 \cos 2 x]+c \\ \therefore \quad y & =-\frac{1}{13}[3 \sin 2 x+2 \cos 2 x]+c \cdot e^{3 x} \end{aligned} $
इसलिए, आवश्यक हल है
$ y=-[\frac{3 \sin 2 x+2 \cos 2 x}{13}]+c \cdot e^{3 x} $
29. किसी वक्र का समीकरण ज्ञात कीजिए जो बिंदु $(2,1)$ से गुजरता है यदि वक्र के किसी बिंदु $(x, y)$ पर स्पर्श रेखा की प्रवणता $\frac{x^{2}+y^{2}}{2 x y}$ है।
उत्तर दिखाएं
हल
दिया गया है कि वक्र के किसी बिंदु $(x, y)$ पर स्पर्श रेखा की प्रवणता है
$ \frac{d y}{d x}=\frac{x^{2}+y^{2}}{2 x y} $
यह एक एकरूपता अवकल समीकरण है
इसलिए, $y=v x \Rightarrow \frac{d y}{d x}=v+x \cdot \frac{d v}{d x}$
$ v+x \cdot \frac{d v}{d x}=\frac{x^{2}+v^{2} x^{2}}{2 x \cdot v x} $
$ \begin{aligned} & \Rightarrow \quad v+x \cdot \frac{d v}{d x}=\frac{1+v^{2}}{2 v} \\ & \Rightarrow \quad x \cdot \frac{d v}{d x}=\frac{1+v^{2}}{2 v}-v \Rightarrow x \cdot \frac{d v}{d x}=\frac{1+v^{2}-2 v^{2}}{2 v} \\ & \Rightarrow \quad x \cdot \frac{d v}{d x}=\frac{1-v^{2}}{2 v} \Rightarrow \frac{2 v}{1-v^{2}} d v=\frac{d x}{x}
\end{aligned} $
दोनों ओर समाकलन करने पर, हम प्राप्त करते हैं
$ \begin{gathered} \int \frac{2 v}{1-v^{2}} d v=\int \frac{d x}{x} \Rightarrow-\log |1-v^{2}|=\log |x|+\log |C| \\ \Rightarrow-\log |1-\frac{y^{2}}{x^{2}}|=\log |x|+\log |C| \Rightarrow-\log |\frac{x^{2}-y^{2}}{x^{2}}|=\log |x|+\log |C| \\ \Rightarrow \log |\frac{x^{2}}{x^{2}-y^{2}}|=\log |x C| \Rightarrow \frac{x^{2}}{x^{2}-y^{2}}=\pm Cx \\ \Rightarrow \frac{x^{2}}{x^{2}-y^{2}}=cx, \quad (where \quad c = \pm C) \end{gathered} $
क्योंकि, वक्र बिंदु $(2,1)$ से गुजरता है
$ \therefore \quad \frac{(2)^{2}}{(2)^{2}-(1)^{2}}=2 c \Rightarrow \frac{4}{3}=2 c \Rightarrow c=\frac{2}{3} $
इसलिए, अभीष्ट समीकरण है
$ \frac{x^{2}}{x^{2}-y^{2}}=\frac{2}{3} x \Rightarrow 2(x^{2}-y^{2})=3 x $
30. बिंदु $(1,0)$ से गुजरने वाले वक्र का समीकरण ज्ञात कीजिए यदि वक्र के किसी बिंदु $(x, y)$ पर स्पर्श रेखा की प्रवणता $\frac{y-1}{x^{2}+x}$ है।
उत्तर दिखाएं
हल
दिया गया है कि वक्र के बिंदु $(x, y)$ पर स्पर्श रेखा की प्रवणता है
$ \frac{d y}{d x}=\frac{y-1}{x^{2}+x} \Rightarrow \frac{d y}{y-1}=\frac{d x}{x^{2}+x} $
दोनों ओर समाकलन करने पर, हम प्राप्त करते हैं
$ \begin{aligned} & \int \frac{d y}{y-1}=\int \frac{d x}{x^{2}+x} \\ & \Rightarrow \quad \int \frac{d y}{y-1}=\int \frac{d x}{x^{2}+x+\frac{1}{4}-\frac{1}{4}} \text{ [पूर्ण वर्ग बनाने के लिए] } \\ & \Rightarrow \quad \int \frac{d y}{y-1}=\int \frac{d x}{(x+\frac{1}{2})^{2}-(\frac{1}{2})^{2}} \end{aligned} $
$ \begin{matrix} \Rightarrow & \log |y-1|=\frac{1}{2 \times \frac{1}{2}} \log |\frac{x+\frac{1}{2}-\frac{1}{2}}{x+\frac{1}{2}+\frac{1}{2}}|+\log |c| \\ \Rightarrow & \log |y-1|=\log |\frac{x}{x+1}|+\log |c| \\ \Rightarrow & \log |y-1|=\log |c(\frac{x}{x+1})| \\ \therefore & |y-1|=|\frac{c x}{x+1}| \\ \therefore & y-1=\pm \frac{c x}{x+1} \\ \Rightarrow & (y-1)(x+1)=C x , \quad (where \quad C= \pm c) \end{matrix} $
क्योंकि, रेखा बिंदु $(1,0)$ से गुजरती है, तो $(0-1)(1+1)=C(1) \Rightarrow C=-2$।
$(y-1)(x+1)=-2 x$.
अतः, आवश्यक समाधान है $(y-1)(x+1)+2 x=0$.
31. किसी वक्र का समीकरण ज्ञात कीजिए जो मूल बिंदु से होकर गुजरता है, यदि वक्र के किसी बिंदु $(x, y)$ पर स्पर्श रेखा का ढलान बिंदु के भुजा और कोटि के अंतर के वर्ग के बराबर हो।
उत्तर दिखाएं
हल
यहाँ, वक्र के स्पर्श रेखा का ढलान $=\frac{d y}{d x}$ और भुजा और कोटि के अंतर $=x-y$ है।
$\therefore$ दिए गए शर्त के अनुसार, $\frac{d y}{d x}=(x-y)^{2}$
$ x-y=v $ रखें
$ \begin{aligned} & 1-\frac{d y}{d x}=\frac{d v}{d x} \\ & \therefore \quad \frac{d y}{d x}=1-\frac{d v}{d x} \end{aligned} $
$\therefore$ समीकरण बन जाता है
$ 1-\frac{d v}{d x}=v^{2} \Rightarrow \frac{d v}{d x}=1-v^{2} \Rightarrow \frac{d v}{1-v^{2}}=d x $
दोनों ओर समाकलन करने पर, हम प्राप्त करते हैं
$$ \begin{align*} \int \frac{d v}{1-v^{2}} & =\int d x \\ \Rightarrow \quad \frac{1}{2} \log |\frac{1+v}{1-v}| & =x+c \quad \Rightarrow \quad \frac{1}{2} \log |\frac{1+x-y}{1-x+y}|=x+c \\ \Rightarrow \quad |\frac{1+x-y}{1-x+y}|=e^{2(x+c)} \\ \Rightarrow \quad |\frac{1+x-y}{1-x+y}|=e^{2c}e^{2x} \\ \Rightarrow \quad \frac{1+x-y}{1-x+y}=\pm e^{2c}e^{2x} \\ \Rightarrow \quad \frac{1+x-y}{1-x+y}=\pm e^{2c}e^{2x} \\ \Rightarrow \quad \frac{1+x-y}{1-x+y}=Ce^{2x} (where C= \pm e^{2c}) \end{align*} $$
क्योंकि, वक्र मूल बिंदु $(0,0)$ से होकर गुजरता है
$ \Rightarrow \frac{1+0-0}{1-0+0} =Ce^{ 0} $
$ \Rightarrow C=1 $
$ \begin{aligned} & \therefore & \frac{1+x-y}{1-x+y} & =e^{2 x} \\ \Rightarrow & & (1+x-y) & =e^{2 x}(1-x+y) \end{aligned} $
अतः, आवश्यक समीकरण है $(1+x-y)=e^{2 x}(1-x+y)$.
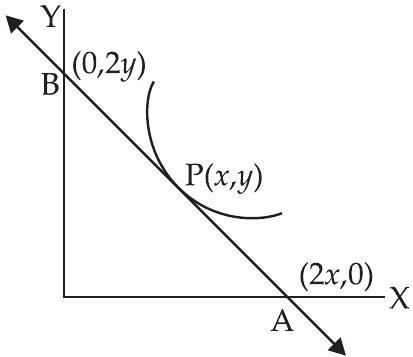
32. एक वक्र का समीकरण ज्ञात कीजिए जो बिंदु $(1,1)$ से होकर गुजरता है, यदि वक्र के किसी बिंदु $P(x, y)$ पर खींची गई स्पर्श रेखा निर्देशांक अक्षों को $A$ और $B$ पर मिलती है ताकि $P$ बिंदु $AB$ का मध्य बिंदु हो।
उत्तर दिखाएं
हल
मान लीजिए $P(x, y)$ वक्र का कोई बिंदु है और $AB$ वक्र के बिंदु $P$ पर खींची गई स्पर्श रेखा है।
$P$ रेखा $AB$ का मध्य बिंदु है (दिया गया)
$\therefore$ $A$ और $B$ के निर्देशांक क्रमशः $(2 x, 0)$ और $(0,2 y)$ हैं।
$\therefore$ स्पर्शरेखा की प्रवणता
$ AB= $
$ \begin{aligned} & \frac{2 y-0}{0-2 x}=-\frac{y}{x} \\ & \therefore \quad \frac{d y}{d x}=-\frac{y}{x} \Rightarrow \frac{d y}{y}=-\frac{d x}{x} \end{aligned} $
दोनों ओर समाकलन करने पर, हम प्राप्त करते हैं
$ \begin{aligned} & \int \frac{d y}{y}=-\int \frac{d x}{x} \Rightarrow \log |y|=-\log |x|+\log |c| \\ & \Rightarrow \quad \log |y|+\log |x|=\log |c| \quad \Rightarrow \log |y x|=\log|c| \\ & \therefore \quad |y x|=|c| \\ & \therefore \quad y x=\pm c \\ & \therefore \quad y x=C , \quad (where \quad C = \pm c) \end{aligned} $
क्योंकि, वक्र $(1,1)$ से गुजरता है
$ \begin{aligned} \therefore & & 1 \times 1 & =C\quad \therefore \quad C=1 \\ \Rightarrow & & y x & =1 \end{aligned} $
इसलिए, अभीष्ट समीकरण $x y=1$ है।
33. हल करें: $x \frac{d y}{d x}=y(\log y-\log x+1)$
उत्तर दिखाएँ
हल
दिया गया है: $x \frac{d y}{d x}=y(\log y-\log x+1)$
$ \Rightarrow \quad x \frac{d y}{d x}=y[\log (\frac{y}{x})+1] \Rightarrow \frac{d y}{d x}=\frac{y}{x}[\log (\frac{y}{x})+1] $
क्योंकि, यह एक एकरूप समीकरण है।
$\therefore$ रखें $y=v x \Rightarrow \frac{d y}{d x}=v+x \cdot \frac{d v}{d x}$
$\therefore \quad v+x \cdot \frac{d v}{d x}=\frac{v x}{x}[\log (\frac{v x}{x})+1]$
$\Rightarrow \quad v+x \cdot \frac{d v}{d x}=v[\log v+1]$
$\Rightarrow \quad x \cdot \frac{d v}{d x}=v[\log v+1]-v \Rightarrow x \cdot \frac{d v}{d x}=v[\log v+1-1]$
$\Rightarrow \quad x \cdot \frac{d v}{d x}=v \cdot \log v \Rightarrow \frac{d v}{v \log v}=\frac{d x}{x}$
दोनों ओर समाकलन करने पर, हम प्राप्त करते हैं
$ \qquad \int \frac{d v}{v \log v}=\int \frac{d x}{x} `
$
$\log v=t$ को बायां ओर लिखें।
$ \begin{matrix} \frac{1}{v} d v =dt \\ \therefore \quad \int \frac{d t}{t} =\int \frac{d x}{x} \\ \log |t| =\log |x|+\log |C| \\ \Rightarrow \quad \log |\log v| =\log |x C| \Rightarrow |\log v|=|x C| \\ \Rightarrow \quad \log (\frac{y}{x}) =\pm Cx\\ \Rightarrow \quad \log (\frac{y}{x}) =cx, \quad where \quad c = \pm C \end{matrix} $
इसलिए, अभीष्ट हल है $\log (\frac{y}{x})=x c$.
वस्तुनिष्ठ प्रश्न
34. अवकल समीकरण की डिग्री
$ (\frac{d^{2} y}{d x^{2}})^{2}+(\frac{d y}{d x})^{2}=x \sin (\frac{d y}{d x}) \text{ है } $
(a) 1
(b) 2
(c) 3
(d) अनिर्धारित
उत्तर दिखाएं
हल
दिए गए अवकल समीकरण की डिग्री अनिर्धारित है क्योंकि $\sin (\frac{d y}{d x})$ के विस्तार के दौरान मान बढ़ती शक्ति में $(\frac{d y}{d x})$ के रूप में होगा।
-
विकल्प (a) 1: यह गलत है क्योंकि अवकल समीकरण की डिग्री को अवकलज के उच्चतम घात के रूप में परिभाषित किया जाता है, जब तक समीकरण अवकलजों में बहुपदीय हो। इस मामले में, समीकरण में अवकलज के त्रिकोणमितीय फलन होता है, जिसके कारण यह बहुपदीय नहीं होता है।
-
विकल्प (b) 2: यह गलत है क्योंकि, हालांकि दूसरे कोटि के अवकलज की उच्चतम घात 2 है, अवकलज के त्रिकोणमितीय फलन $\sin (\frac{d y}{d x})$ के कारण समीकरण अवकलजों में बहुपदीय नहीं होता है, इसलिए डिग्री अनिर्धारित है।
-
विकल्प (c) 3: यह गलत है क्योंकि, हालांकि दूसरे कोटि के अवकलज की उच्चतम घात 2 है, अवकलज के त्रिकोणमितीय फलन $\sin (\frac{d y}{d x})$ के कारण समीकरण अवकलजों में बहुपदीय नहीं होता है, इसलिए डिग्री अनिर्धारित है।
35. अवकल समीकरण $[1+(\frac{d y}{d x})^{2}]^{3 / 2}=\frac{d^{2} y}{d x^{2}}$ की डिग्री है
(a) 4
(b) $\frac{3}{2}$
(c) अनिर्धारित
(d) 2
उत्तर दिखाएं
हल
दिए गए अवकल समीकरण है
$ [1+(\frac{d y}{d x})^{2}]^{3 / 2}=(\frac{d^{2} y}{d x^{2}}) `
$
दोनों ओर वर्ग करने पर, हमें मिलता है
$ [1+(\frac{d y}{d x})^{2}]^{3}=(\frac{d^{2} y}{d x^{2}})^{2} $
इसलिए, दिए गए अवकल समीकरण की डिग्री 2 है ।
इसलिए, सही विकल्प $(d)$ है।
36. अवकल समीकरण $\frac{d^{2} y}{d x^{2}}+(\frac{d y}{d x})^{\frac{1}{4}}+x^{\frac{1}{5}}=0$ का क्रम और डिग्री क्रमशः है
(a) 2 और 4
(b) 2 और अपरिभाषित
(c) 2 और 3
(d) 3 और 3
उत्तर दिखाएँ
हल
दिया गया है, $\quad \frac{d^2 y}{d x^2}+\left(\frac{d y}{d x}\right)^{1 / 4}=-x^{1 / 5}$
$ \begin{aligned} & \Rightarrow \quad \frac{d^2 y}{d x^2}+\left(\frac{d y}{d x}\right)^{1 / 4}=-x^{1 / 5} \ & \Rightarrow \quad\left(\frac{d y}{d x}\right)^{1 / 4}=-\left(x^{1 / 5}+\frac{d^2 y}{d x^2}\right) \end{aligned} $
दोनों ओर वर्ग करने पर, हमें मिलता है
$ \left(\frac{d y}{d x}\right)^{1 / 2}=\left(x^{1 / 5}+\frac{d^2 y}{d x^2}\right)^2 $
फिर दोनों ओर वर्ग करने पर, हमें मिलता है
$ \frac{d y}{d x}=\left(x^{1 / 5}+\frac{d^2 y}{d x^2}\right)^4 $
क्रम $=2$, डिग्री $=4$
इसलिए, सही विकल्प $(a)$ है।
37. यदि $y=e^{-x}(A \cos x+B \sin x)$, तो $y$ निम्नलिखित में से किसका एक हल है
(a) $\frac{d^{2} y}{d x^{2}}+2 \frac{d y}{d x}=0$
(b) $\frac{d^{2} y}{d x^{2}}-2 \frac{d y}{d x}+2 y=0$
(c) $\frac{d^{2} y}{d x^{2}}+2 \frac{d y}{d x}+2 y=0$
(d) $\frac{d^{2} y}{d x^{2}}+2 y=0$
उत्तर दिखाएँ
हल
दिया गया समीकरण है $y=e^{-x}(A \cos x+B \sin x)$
दोनों ओर $x$ के सापेक्ष अवकलन करने पर, हमें मिलता है
$ \begin{aligned} & \frac{d y}{d x}=e^{-x}(-A \sin x+B \cos x)-e^{-x}(A \cos x+B \sin x) \\ & \frac{d y}{d x}=e^{-x}(-A \sin x+B \cos x)-y \end{aligned} $
फिर दोनों ओर $x$ के सापेक्ष अवकलन करने पर, हमें मिलता है
$ \begin{aligned} & \frac{d^{2} y}{d x^{2}}=e^{-x}(-A \cos x-B \sin x)-e^{-x}(-A \sin x+B \cos x)-\frac{d y}{d x} \\ \Rightarrow & \frac{d^{2} y}{d x^{2}}=-e^{-x}(A \cos x+B \sin x)-[\frac{d y}{d x}+y]-\frac{d y}{d x} \\ \Rightarrow & \frac{d^{2} y}{d x^{2}}=-y-\frac{d y}{d x}-y-\frac{d y}{d x} \\
\Rightarrow & \frac{d^{2} y}{d x^{2}}=-2 \frac{d y}{d x}-2 y \Rightarrow \frac{d^{2} y}{d x^{2}}+2 \frac{d y}{d x}+2 y=0 \end{aligned} $
अतः, सही विकल्प (c) है।
38. $y=A \cos \alpha x+B \sin \alpha x$ के लिए अवकल समीकरण, जहाँ $A$ और $B$ अस्थिर नियतांक हैं, है:
(a) $\frac{d^{2} y}{d x^{2}}-\alpha^{2} y=0$
(b) $\frac{d^{2} y}{d x^{2}}+\alpha^{2} y=0$
(c) $\frac{d^{2} y}{d x^{2}}+\alpha y=0$
(d) $\frac{d^{2} y}{d x^{2}}-\alpha y=0$
उत्तर दिखाएँ
हल
दी गई समीकरण है : $y=A \cos \alpha x+B \sin \alpha x$ दोनों ओर $x$ के सापेक्ष अवकलन करने पर, हमें मिलता है
$ \begin{aligned} \frac{d y}{d x} & =-A \sin \alpha x \cdot \alpha+B \cos \alpha x \cdot \alpha \\ & =-A \alpha \sin \alpha x+B \alpha \cos \alpha x \end{aligned} $
फिर दोबारा $x$ के सापेक्ष अवकलन करने पर, हमें मिलता है
$ \begin{aligned} \frac{d^{2} y}{d x^{2}} & =-A \alpha^{2} \cos \alpha x-B \alpha^{2} \sin \alpha x \\ \Rightarrow \quad \frac{d^{2} y}{d x^{2}} & =-\alpha^{2}(A \cos \alpha x+B \sin \alpha x) \\ \Rightarrow \quad \frac{d^{2} y}{d x^{2}} & =-\alpha^{2} y \Rightarrow \frac{d^{2} y}{d x^{2}}+\alpha^{2} y=0 \end{aligned} $
अतः, सही विकल्प (b) है।
39. अवकल समीकरण $x d y-y d x=0$ का हल निम्नलिखित को दर्शाता है:
(a) आयताकार वृत्त
(b) मूल बिंदु पर शीर्ष वाला पराबोला
(c) मूल बिंदु से गुजरने वाली सीधी रेखा
(d) मूल बिंदु केंद्र वाला वृत्त
उत्तर दिखाएँ
हल
दी गई अवकल समीकरण है
$ x d y-y d x=0 $
$ \Rightarrow \quad \frac{d y}{d x}=\frac{y}{x} \Rightarrow \frac{d y}{y}=\frac{d x}{x} $
दोनों ओर समाकलन करने पर, हमें मिलता है
$
\begin{aligned}
& \qquad \int \frac{d y}{y}=\int \frac{d x}{x} \\
& \Rightarrow \quad \log |y|=\log |x|+\log|c| \Rightarrow \log |y|=\log |x c| \\
& \Rightarrow \quad |y|=|x c| \\
& \Rightarrow \quad y =\pm cx \\
& \Rightarrow \quad y =Cx \quad जहाँ \quad C = \pm c
& \text{ जो मूल बिंदु से गुजरने वाली सीधी रेखा है। } \\
& \text{ अतः, सही उत्तर है }(c) \end{aligned} $
40. अवकल समीकरण $\cos x \cdot \frac{d y}{d x}+y \sin x=1$ का समाकलन गुणांक है
(a) $\cos x$
(b) $\tan x$
(c) $\sec x$
(d) $\sin x$
उत्तर दिखाएं
हल
दी गई अवकल समीकरण है
$ \begin{aligned} \cos x \cdot \frac{d y}{d x}+y \sin x =1 \\ \Rightarrow \qquad \frac{d y}{d x}+\frac{\sin x}{\cos x} y =\frac{1}{\cos x} \Rightarrow \frac{d y}{d x}+\tan x y=\sec x \end{aligned} $
यहाँ, $P=\tan x$ और $Q=\sec x$
$\therefore$ समाकलन गुणांक $=e^{\int P d x}=e^{\int \tan x d x}=e^{\log |\sec x|}=\sec x ,\quad (\sec x >0)$
अतः, सही विकल्प (c) है।
41. अवकल समीकरण $\tan y \sec ^{2} x d x+\tan x \sec ^{2} y d y=0$ का हल है
(a) $\tan x+\tan y=k$
(b) $\tan x-\tan y=k$
(c) $\frac{\tan x}{\tan y}=k$
(d) $\tan x \cdot \tan y=k$
उत्तर दिखाएं
हल
दी गई अवकल समीकरण है
$ \tan y \sec ^{2} x d x+\tan x \sec ^{2} y d y=0 $
$\Rightarrow \tan x \sec ^{2} y d y=-\tan y \sec ^{2} x d x$
$\Rightarrow \quad \frac{\sec ^{2} y}{\tan y} \cdot d y=\frac{-\sec ^{2} x}{\tan x} \cdot d x$
दोनों ओर समाकरण करने पर, हमें प्राप्त होता है
$ \begin{aligned} & \Rightarrow \quad \int \frac{\sec ^{2} y}{\tan y} d y=\int \frac{-\sec ^{2} x}{\tan x} d x \\ & \Rightarrow \quad \log |\tan y|=-\log |\tan x|+\log |c| \\ & \Rightarrow \quad \log |\tan y|+\log |\tan x|=\log |c| \\ & \Rightarrow \quad \log |\tan x. \tan y|=\log |c| \\ & \Rightarrow \quad |\tan x. \tan y|= |c| \\ & \Rightarrow \quad \tan x. \tan y= \pm c \\ & \Rightarrow \quad \tan x. \tan y= k \quad (where \quad k = \pm c) \end{aligned} $
अतः, विकल्प (d) सही है।
42. वक्रों का परिवार $y=A x+A^{3}$ निम्न अवकल समीकरण को प्रस्तुत करता है जिसकी डिग्री है
(a) 1
(b) 2
(c) 3
(d) 4
उत्तर दिखाएं
हल
दी गई समीकरण है
$$ \begin{equation*} y=A x+A^{3}\tag{1}
\end{equation*} $$
दोनों ओर अवकलज लेने पर, हमें $\frac{d y}{d x}=A$ मिलता है
समीकरण 1 में A का मान रखें
$y=x \frac{dy}{dx}+ (\frac {dy}{dx})^{3}$
इसलिए, अवकल समीकरण की डिग्री 3 है ।
अतः, सही उत्तर (c) है।
43. $x \frac{d y}{d x}-y=x^{4}-3x$ का अभिनिर्देशक गुणांक है
(a) $x$
(c) $\frac{1}{x}$
(b) $\log x$
(d) $-x$
उत्तर दिखाएँ
हल
दिया गया अवकल समीकरण है
$ x \frac{d y}{d x}-y=x^{4}-3 x \Rightarrow \frac{d y}{d x}-\frac{y}{x}=x^{3}-3 $
यहाँ, $P=-\frac{1}{x}$ और $Q=x^{3}-3$
इसलिए, अभिनिर्देशक गुणांक $=e^{\int P d x}=e^{\int-\frac{1}{x} d x}=e^{-\log| x|}=e^{\log \frac{1}{x}}=\frac{1}{x} , (x>0) $
अतः, सही विकल्प (c) है।
44. $\frac{d y}{d x}-y=1, y(0)=1$ का हल निम्नलिखित में से कौन सा है
(a) $x y=-e^{x}$
(b) $x y=-e^{-x}$
(c) $x y=-1$
(d) $y=2 e^{x}-1$
उत्तर दिखाएँ
हल
दिया गया अवकल समीकरण है
$ \frac{d y}{d x}-y=1 $
यहाँ, $P=-1, Q=1$
$\therefore$ अभिनिर्देशक गुणांक, I.F. $=e^{\int P d x}=e^{\int-1 d x}=e^{-x}$
इसलिए, हल है
$ \begin{aligned} & y \times \text{ I.F. }=\int Q \times \text{ I.F. } d x+c \\ & \Rightarrow \quad y \times e^{-x}=\int 1 . e^{-x} d x+c \\ & \Rightarrow \quad y \cdot e^{-x}=-e^{-x}+c \\ & \text{ Put } x=0, y=1 \\ & \Rightarrow \quad 1 \cdot e^{0}=-e^{0}+c \\ & \Rightarrow \quad 1=-1+c \quad \\ & \therefore c=2 \end{aligned} $
इसलिए समीकरण $y \cdot e^{-x}=-e^{-x}+2$ है
$ \Rightarrow \quad y=-1+2 e^{x}=2 e^{x}-1 $
अतः, सही विकल्प $(d)$ है।
45. $\frac{d y}{d x}=\frac{y+1}{x-1}$ के अवकल समीकरण के हल की संख्या जब $y(1)=2$ है
(a) कोई नहीं
(b) एक
(c) दो
(d) अपरिमित
उत्तर दिखाएँ
हल
दिया गया अवकल समीकरण है $\frac{d y}{d x}=\frac{y+1}{x-1}$
$ \Rightarrow \quad \frac{d y}{y+1}=\frac{d x}{x-1} $
दोनों ओर समाकलन करने पर, हमें मिलता है
$\int \frac{d y}{y+1}=\int \frac{d x}{x-1}$
$\Rightarrow \log |(y+1)|=\log |(x-1)|+\log |c| $
$\Rightarrow \quad \log |(y+1)|-\log |(x-1)|=\log |c|$
$\Rightarrow \log |\frac{y+1}{x-1}|=\log |c| $
$\Rightarrow \frac{y+1}{x-1}=C \text{ Put } x=1 \text{ and } y=2 \quad where \quad C = \pm c$
$\Rightarrow \frac{2+1}{1-1}=C \quad \therefore C=\infty$
$\therefore \frac{y+1}{x-1}=\frac{1}{0} \Rightarrow x-1=0 \Rightarrow x=1$
अतः, सही विकल्प $(b)$ है।
46. निम्नलिखित में से कौन सा द्वितीय कोटि के अवकल समीकरण है?
(a) $(y^{\prime})^{2}+x=y^{2}$
(c) $y^{ \prime}+(y^{ \prime})^{2}+y=0$
(b) $y^{\prime} y^{\prime \prime}+y=\sin x$
(d) $y^{\prime}=y^{2}$
उत्तर दिखाएँ
हल
द्वितीय कोटि का अवकल समीकरण $y^{\prime} y^{\prime \prime}+y=\sin x$
अतः, सही विकल्प $(b)$ है।
47. अवकल समीकरण का समाकलन गुणक
$ (1-x^{2}) \frac{d y}{d x}-x y=1 \text{ है } $
(a) $-x$
(b) $\frac{x}{1+x^{2}}$
(c) $\sqrt{1-x^{2}}$
(d) $\frac{1}{2} \log (1-x^{2})$
उत्तर दिखाएँ
हल
दिया गया अवकल समीकरण है
$ \begin{aligned} & (1-x^{2}) \frac{d y}{d x}-x y=1 \\ \Rightarrow \quad & \frac{d y}{d x}-\frac{x}{1-x^{2}} \cdot y=\frac{1}{1-x^{2}} \end{aligned} $
यहाँ, $P=-\frac{x}{1-x^{2}}$ और $Q=\frac{1}{1-x^{2}}$
$\therefore$ समाकलन गुणक
$ \text{ I.F. }=e^{\int P d x}=e^{\int \frac{-x}{1-x^{2}} d x}=e^{\frac{1}{2} \log |(1-x^{2})|}=\sqrt{1-x^{2}}, \quad ( (1-x^{2})>0) $
अतः, सही विकल्प (c) है।
48. $\tan ^{-1} x+\tan ^{-1} y=c$ अवकल समीकरण का सामान्य समाधान है:
(a) $\frac{d y}{d x}=\frac{1+y^{2}}{1+x^{2}}$
(b) $\frac{d y}{d x}=\frac{1+x^{2}}{1+y^{2}}$
(c) $(1+x^{2}) d y+(1+y^{2}) d x=0$
(d) $(1+x^{2}) d x+(1+y^{2}) d y=0$
उत्तर दिखाएँ
हल
दिया गया समीकरण है $\tan ^{-1} x+\tan ^{-1} y=c$
$ x $ के सापेक्ष अवकलन करने पर, हमें प्राप्त होता है
$ \begin{aligned} \frac{1}{1+x^{2}}+\frac{1}{1+y^{2}} \cdot \frac{d y}{d x} & =0 \\ \Rightarrow \quad(\frac{1}{1+y^{2}}) \frac{d y}{d x}=-(\frac{1}{1+x^{2}}) & \Rightarrow \frac{d y}{d x}=-(\frac{1+y^{2}}{1+x^{2}}) \\
\Rightarrow \quad(1+x^{2}) d y & =-(1+y^{2}) d x \\ \Rightarrow \quad(1+x^{2}) d y+(1+y^{2}) d x & =0 \end{aligned} $
अतः सही विकल्प (c) है।
49. अवकल समीकरण $y \frac{d y}{d x}+x=c$ का प्रतिनिधित्व है:
(a) अतिपरवलय का परिवार
(c) दीर्घवृत्त का परिवार
(b) परवलय का परिवार
(d) वृत्त का परिवार
उत्तर दिखाएँ
हल
दिया गया अवकल समीकरण है
$ \begin{aligned} y \frac{d y}{d x}+x & =c \\ \Rightarrow \quad y \frac{d y}{d x} & =c-x \quad \Rightarrow y d y=(c-x) d x \end{aligned} $
$\therefore$ दोनों ओर समाकलन करने पर, हम प्राप्त करते हैं
$\int y d y =\int(c-x) d x$
$\Rightarrow \frac{y^{2}}{2} =c x-\frac{x^{2}}{2}+k\Rightarrow \frac{x^{2}}{2}+\frac{y^{2}}{2}-c x=k$
$\Rightarrow x^{2}+y^{2}-2 c x =2 k \text{ जो एक वृत्त के परिवार को दर्शाता है। }$
अतः, सही विकल्प (d) है।
50. $e^{x} \cos y d x-e^{x} \sin y d y=0$ का सामान्य हल है:
(a) $e^{x} \cos y=k$
(b) $e^{x} \sin y=k$
(c) $e^{x}=k \cos y$
(d) $e^{x}=k \sin y$
उत्तर दिखाएँ
हल
दिया गया अवकल समीकरण है
$ e^{x} \cos y d x-e^{x} \sin y d y=0 $
$\Rightarrow e^{x}(\cos y d x-\sin y d y)=0$
$\Rightarrow \quad \cos y d x-\sin y d y=0$
$\Rightarrow \quad \sin y d y=\cos y d x \Rightarrow \frac{\sin y}{\cos y} d y=d x$
दोनों ओर समाकलन करने पर, हम प्राप्त करते हैं
$ \begin{aligned} \int \frac{\sin y}{\cos y} d y & =\int d x \\ \Rightarrow \quad-\log |\cos y| & =x+\log k \Rightarrow \log |\frac{1}{\cos y}|-\log k=x \\ \Rightarrow \quad \log (\frac{1}{k |\cos y|}) & =x \Rightarrow \frac{1}{k |\cos y|}=e^{x} \\ \Rightarrow \quad \frac{1}{k} & =e^{x} |\cos y| \Rightarrow e^{x} \cos y= \quad \pm \frac{1}{k} \\ &\Rightarrow e^{x} \cos y= c, \quad (where \quad c = \pm \frac {1}{k} ) \end{aligned} $
अतः, सही विकल्प (a) है।
51. अवकल समीकरण की डिग्री:
$ \frac{d^{2} y}{d x^{2}}+(\frac{d y}{d x})^{3}+6 y^{5}=0 \text{ है } $
(a) 1
(b) 2
(c) 3
(d) 5
उत्तर दिखाएँ
हल
दिए गए अवकल समीकरण की डिग्री 1 है क्योंकि सर्वोच्च कोटि की घात 1 है।
अतः, सही विकल्प $(a)$ है।
52. अवकल समीकरण का हल
$ \frac{d y}{d x}+y=e^{-x}, y(0)=0 \text{ है } $
(a) $y=e^{x}(x-1)$
(c) $y=x e^{-x}+1$
(b) $y=x e^{-x}$
(d) $y=(x+1) e^{-x}$
उत्तर दिखाएँ
हल
दिए गए अवकल समीकरण है
$ \frac{d y}{d x}+y=e^{-x} $
क्योंकि, यह एक प्रथम कोटि का रैखिक अवकल समीकरण है।
$\therefore P=1$ और $Q=e^{-x}$
$\therefore$ I.F $=e^{\int 1 . d x}=e^{x}$
अतः, हल है
$ \begin{aligned} & \quad y \times \text{ I.F. }= \int Q \times \cdot \text{ I.F. } d x+c \Rightarrow y \cdot e^{x}=\int e^{-x} \cdot e^{x} d x+c \\ & \Rightarrow \quad y \cdot e^{x}=\int 1 \cdot d x+c \Rightarrow y \cdot e^{x}=x+c \\ & \text{ Put } x=0, y=0, \text{ हमें प्राप्त होता है } 0=0+c \quad \\ & \therefore c=0 \end{aligned} $
अतः, हल है $y e^{x}=x \Rightarrow y=x \cdot e^{-x}$
अतः, सही विकल्प (b) है।
53. अवकल समीकरण का समाकलन गुणक
$ \frac{d y}{d x}+y \tan x-\sec x=0 \text{ है } $
(a) $\cos x$
(b) $\sec x$
(c) $e^{\cos x}$
(d) $e^{\sec x}$
उत्तर दिखाएँ
हल
दिए गए अवकल समीकरण है
$ \frac{d y}{d x}+y \tan x-\sec x=0 \Rightarrow \frac{d y}{d x}+y \tan x=\sec x $
यहाँ, $P=\tan x$ और $Q=\sec x$
$\therefore$ I.F. $=e^{\int P d x}=e^{\int \tan x d x}=e^{\log |\sec x|}=\sec x , (\sec x>0)$
अतः, सही विकल्प (b) है।
54. अवकल समीकरण का हल
$ \frac{d y}{d x}=\frac{1+y^{2}}{1+x^{2}} \text{ है } $
(a) $y=\tan ^{-1} x$
(b) $y-x=k(1+x y)$
(c) $x=\tan ^{-1} y$
(d) $\tan (x y)=k$
उत्तर दिखाएँ
हल
दिए गए अवकल समीकरण है
$ \frac{d y}{d x}=\frac{1+y^{2}}{1+x^{2}} \Rightarrow \frac{d y}{1+y^{2}}=\frac{d x}{1+x^{2}} `
$
दोनों ओर समाकलन करने पर, हम प्राप्त करते हैं
$\int \frac{d y}{1+y^{2}} =\int \frac{d x}{1+x^{2}}$
$\Rightarrow \tan ^{-1} y =\tan ^{-1} x+c \Rightarrow \tan ^{-1} y-\tan ^{-1} x=c$
$\Rightarrow \tan^{-1}(\frac{y-x}{1+x y}) =c$
$\Rightarrow \frac{y-x}{1+x y} =\tan c \Rightarrow \frac{y-x}{1+x y}=k \quad[k=\tan c]$
$\Rightarrow y-x =k(1+x y)$
इसलिए, सही विकल्प $(b)$ है।
55. अवकल समीकरण का समाकलन गुणक
$ \frac{d y}{d x}+y=\frac{1+y}{x} \text{ है: } $
(a) $\frac{x}{e^{x}}$
(b) $\frac{e^{x}}{x}$
(c) $x e^{x}$
(d) $e^{x}$
उत्तर दिखाएँ
हल
दिया गया अवकल समीकरण है
$ \frac{d y}{d x}+y=\frac{1+y}{x} $
$\begin{matrix} \Rightarrow & \frac{d y}{d x}=\frac{1+y}{x}-y \\ \Rightarrow & \frac{d y}{d x}=\frac{1}{x}+y \frac{(1-x)}{x} \Rightarrow \frac{d y}{d x}-(\frac{1-x}{x}) y=\frac{1}{x}\end{matrix} $
यहाँ, $P=-(\frac{1-x}{x})$ और $Q=\frac{1}{x}$
$\therefore$ समाकलन गुणक I.F. $=e^{\int P d x}=e^{\int \frac{x-1}{x} d x}=e^{\int(1-\frac{1}{x}) d x}$
$ =e^{(x-\log |x|)}=e^{x} \cdot e^{-\log x}, (x>0) $
$ =e^{x} \cdot e^{\log \frac{1}{x}}=e^{x} \cdot \frac{1}{x} $
इसलिए, सही विकल्प $(b)$ है।
56. $y=a e^{m x}+b e^{-m x}$ निम्नलिखित में से किस अवकल समीकरण को संतुष्ट करता है?
(a) $\frac{d y}{d x}+m y=0$
(b) $\frac{d y}{d x}-m y=0$
(c) $\frac{d^{2} y}{d x^{2}}-m^{2} y=0$
(d) $\frac{d^{2} y}{d x^{2}}+m^{2} y=0$
उत्तर दिखाएँ
हल
दिया गया समीकरण है $y=a e^{m x}+b e^{-m x}$
अवकलन करने पर, हम प्राप्त करते हैं $\frac{d y}{d x}=a \cdot m e^{m x}-b \cdot m e^{-m x}$
फिर अवकलन करने पर, हम प्राप्त करते हैं
$ \begin{aligned} & \frac{d^{2} y}{d x^{2}}=a m^{2} e^{m x}+b m^{2} e^{-m x} \\ \Rightarrow & \frac{d^{2} y}{d x^{2}}=m^{2}(a e^{m x}+b e^{-m x}) \Rightarrow \frac{d^{2} y}{d x^{2}}=m^{2} y \Rightarrow \frac{d^{2} y}{d x^{2}}-m^{2} y=0 \end{aligned} $
इसलिए, सही विकल्प (c) है।
57. अवकल समीकरण $\cos x \sin y d x+\sin x \cos y d y=0$ का हल है
(a) $\frac{\sin x}{\sin y}=c$
(b) $\sin x \sin y=c$
(c) $\sin x+\sin y=c$
(d) $\cos x \cos y=c$
उत्तर दिखाएं
हल
दिया गया अवकल समीकरण $\cos x \sin y d x+\sin x \cos y d y=0$
$\Rightarrow \quad \sin x \cos y d y=-\cos x \sin y d x$
$\Rightarrow \frac{\cos y}{\sin y} d y=-\frac{\cos x}{\sin x} d x \Rightarrow \cot y d y=-\cot x d x$
दोनों ओर समाकलन करने पर, हमें प्राप्त होता है
$\Rightarrow \quad \int \cot y d y=-\int \cot x d x$
$ \begin{aligned} & \Rightarrow \quad \log |\sin y|=-\log |\sin x|+\log |C| \\ & \Rightarrow \quad \log |\sin y|+\log |\sin x|=\log |C| \\ & \Rightarrow \quad \log |\sin y \cdot \sin x|=\log |C| \Rightarrow \sin x \sin y=\pm C \\ & \Rightarrow \sin x \sin y=c, \quad (where \quad c= \pm C) \end{aligned} $
अतः सही विकल्प (b) है।
58. $x \frac{d y}{d x}+y=e^{x}$ का हल है:
(a) $y=\frac{e^{x}}{x}+\frac{k}{x}$
(b) $y=x e^{x}+c x$
(c) $y=x \cdot e^{x}+k$
(d) $x=\frac{e^{y}}{y}+\frac{k}{y}$
उत्तर दिखाएं
हल
दिया गया अवकल समीकरण $x \frac{d y}{d x}+y=e^{x}$
$\Rightarrow \quad \frac{d y}{d x}+\frac{y}{x}=\frac{e^{x}}{x}$
यहाँ $P=\frac{1}{x}$ और $Q=\frac{e^{x}}{x}$
$\therefore$ समाकलन गुणक I.F. $=e^{\int \frac{1}{x} d x}=e^{\log |x|}=x, (x>0)$
अतः हल है
$ \begin{aligned} y \times \text{ I.F. } & =\int Q \times \text{ I.F. } d x+k \Rightarrow y \times x=\int \frac{e^{x}}{x} \times x d x+k \\ \Rightarrow y \times x & =\int e^{x} d x+k \Rightarrow y \times x=e^{x}+k \\ \therefore y & =\frac{e^{x}}{x}+\frac{k}{x} \end{aligned} $
अतः सही विकल्प $(a)$ है।
59. वक्रों के परिवार $x^{2}+y^{2}-2 a y=0$ के अवकल समीकरण है, जहाँ $a$ एक अचर नियतांक है:
(a) $(x^{2}-y^{2}) \frac{d y}{d x}=2 x y$
(b) $2(x^{2}+y^{2}) \frac{d y}{d x}=x y$
(c) $2(x^{2}-y^{2}) \frac{d y}{d x}=x y$
(d) $(x^{2}+y^{2}) \frac{d y}{d x}=2 x y$
उत्तर दिखाएँ
Solution
दिए गए समीकरण है
$$ \begin{equation*} x^{2}+y^{2}-2 a y=0 \tag{1} \end{equation*} $$
$ x $ के सापेक्ष अवकलन करने पर, हमें मिलता है
$ \begin{aligned} & 2 x+2 y \cdot \frac{d y}{d x}-2 a \frac{d y}{d x}=0 \\ & \Rightarrow \quad x+y \frac{d y}{d x}-a \frac{d y}{d x}=0 \quad \Rightarrow \quad x+(y-a) \frac{d y}{d x}=0 \\ & \Rightarrow \quad(y-a) \frac{d y}{d x}=-x \quad \Rightarrow y-a=\frac{-x}{d y / d x} \end{aligned} $
$\Rightarrow \quad a=y+\frac{x}{d y / d x} \Rightarrow a=\frac{y \cdot \frac{d y}{d x}+x}{\frac{d y}{d x}}$
समीकरण (1) में $ a $ का मान रखने पर हमें मिलता है
$ \begin{aligned} & x^{2}+y^{2}-2 y[\frac{y \frac{d y}{d x}+x}{\frac{d y}{d x}}]=0 \\ & \Rightarrow \quad(x^{2}+y^{2}) \frac{d y}{d x}-2 y(y \frac{d y}{d x}+x)=0 \\ & \Rightarrow \quad(x^{2}+y^{2}) \frac{d y}{d x}-2 y^{2} \frac{d y}{d x}-2 x y=0 \\ & \Rightarrow \quad(x^{2}+y^{2}-2 y^{2}) \frac{d y}{d x}=2 x y \Rightarrow(x^{2}-y^{2}) \frac{d y}{d x}=2 x y \end{aligned} $
$\therefore$ अतः सही विकल्प $(a)$ है।
60. परिवार $y=A x+A^{3}$ के वक्रों के लिए अवकल समीकरण की कोटि होगी
(a) 3
(b) 2
(c) 1
(d) अनिर्धारित
उत्तर दिखाएँ
Solution
दिए गए समीकरण है
$$ \begin{equation*} y=A x+A^{3}\tag{1} \end{equation*} $$
दोनों ओर अवकलन करने पर, हमें मिलता है $\frac{d y}{d x}=A$
A के मान को समीकरण 1 में रखने पर
$y=x \frac{dy}{dx}+ (\frac {dy}{dx})^{3}$
अतः अवकल समीकरण की कोटि 1 है ।
अतः सही विकल्प $(c)$ है।
61. $\frac{d y}{d x}=2 x e^{x^{2}-y}$ के सामान्य हल है :
(a) $e^{x^{2}-y}=c$
(c) $e^{y}=e^{x^{2}}+c$
(b) $e^{-y}+e^{x^{2}}=c$
(d) $e^{x^{2}+y}=c$
उत्तर दिखाएँ
Solution
दिए गए अवकल समीकरण है
$ \begin{aligned} \frac{d y}{d x} & =2 x \cdot e^{x^{2}-y} \\ \Rightarrow \quad \frac{d y}{d x} & =2 x \cdot e^{x^{2}} \cdot e^{-y} \Rightarrow \frac{d y}{e^{-y}}=2 x \cdot e^{x^{2}} d x
\end{aligned} $
इन्टीग्रल के दोनों ओर समाकलन करने पर, हमें प्राप्त होता है
$ \begin{aligned} \int \frac{d y}{e^{-y}}=\int 2 x \cdot e^{x^{2}} d x \Rightarrow & \int e^{y} d y=\int 2 x \cdot e^{x^{2}} d x \\ & \text{ दाहिनी ओर } x^{2}=t \therefore 2 x d x=d t \end{aligned} $
$ \begin{aligned} \therefore \quad \int e^{y} d y & =\int e^{t} d t \\ \Rightarrow \quad e^{y} & =e^{t}+c \Rightarrow e^{y}=e^{x^{2}}+c \\ \Rightarrow \quad e^{y-x^{2}} = c \end{aligned} $
इसलिए, सही विकल्प (c) है।
62. वक्र जिसके किसी बिंदु पर स्पर्श रेखा की ढलान बिंदु के भुजा और कोटि के अनुपात के बराबर होती है:
(a) एक वृत्ताकार वृत्त
(b) परवलय
(c) वृत्त
(d) आयताकार अतिपरवलय
उत्तर दिखाएँ
हल
क्योंकि, वक्र के स्पर्श रेखा की ढलान $=x: y$
$ \therefore \quad \frac{d y}{d x}=\frac{x}{y} \Rightarrow y d y=x d x $
दोनों ओर समाकलन करने पर हमें प्राप्त होता है $\int y d y=\int x d x$
$ \begin{aligned} & \Rightarrow \quad \frac{y^{2}}{2}=\frac{x^{2}}{2}+c \Rightarrow y^{2}=x^{2}+2 c \\ & \Rightarrow \quad y^{2}-x^{2}=2 c=k \text{ जो आयताकार अतिपरवलय है। } \end{aligned} $
इसलिए, सही विकल्प $(d)$ है।
63. अवकल समीकरण $\frac{d y}{d x}=e^{\frac{x^{2}}{2}}+x y$ का सामान्य हल है:
(a) $y=c \cdot e^{\frac{-x^{2}}{2}}$
(c) $y=(x+c) \cdot e^{{x^{2}}}$
(b) $y=c \cdot e^{\frac{x^{2}}{2}}$
(d) $y=(c-x) e^{\frac{x^{2}}{2}}$
उत्तर दिखाएँ
हल
दिया गया अवकल समीकरण है
$ \frac{d y}{d x}=e^{\frac{x^{2}}{2}}+x y \Rightarrow \frac{d y}{d x}-x y=e^{\frac{x^{2}}{2}} $
क्योंकि यह एक रैखिक अवकल समीकरण है जहाँ $P=-x$ और $Q=e^{\frac{x^{2}}{2}}$
$\therefore$ समाकलन गुणक I.F. $=e^{\int P d x}=e^{\int-x d x}=e^{-\frac{x^{2}}{2}}$
इसलिए, हल है
$ \begin{aligned} & y \times \text{ I.F. }=\int Q \times \text{ I.F. } d x+c \\ & \Rightarrow \quad y \times e^{-\frac{x^{2}}{2}}=\int e^{\frac{x^{2}}{2}} e^{-\frac{x^{2}}{2}} d x+c \\
& \Rightarrow \quad y \times e^{-\frac{x^{2}}{2}}=\int e^{0} d x+c \\ & \Rightarrow \quad y \times e^{-\frac{x^{2}}{2}}=\int 1 . d x+c \Rightarrow y \times e^{-\frac{x^{2}}{2}}=x+c \end{aligned} $
$ \therefore \quad y=(x+c) e^{\frac{x^{2}}{2}} $
अतः सही विकल्प है $(c)$।
बायां पक्ष लें
$\frac{d y}{d x} = \frac{d ((c-x) e^{\frac{x^{2}}{2}})}{d x}$
$=(c-x)\cdot e^\frac {x^{2}}{2} \cdot \frac {2x}{2}+e^\frac {x^{2}}{2} (0-1) $
$=x((c-x)e^\frac {x^{2}}{2})-e^\frac {x^{2}}{2}$
$=xy-e^\frac {x^{2}}{2}$
$\therefore $ बायां पक्ष दायां पक्ष के बराबर नहीं है।
अतः विकल्प (d) गलत है।
64. समीकरण $(2 y-1) d x-(2 x+3) d y=0$ का हल है
(a) $\frac{2 x-1}{2 y+3}=k$
(b) $\frac{2 y+1}{2 x-3}=k$
(c) $\frac{2 x+3}{2 y-1}=k$
(d) $\frac{2 x-1}{2 y-1}=k$
उत्तर दिखाएँ
हल
दी गई अवकल समीकरण है
$ \begin{aligned} (2 y-1) d x-(2 x+3) d y & =0 \Rightarrow(2 x+3) d y=(2 y-1) d x \\ \Rightarrow \quad \frac{d y}{2 y-1} & =\frac{d x}{2 x+3} \end{aligned} $
दोनों ओर समाकलन करने पर, हमें प्राप्त होता है
$ \begin{matrix} \int \frac{d y}{2 y-1} =\int \frac{d x}{2 x+3} \\ \Rightarrow \quad \frac{1}{2} \log |2 y-1| =\frac{1}{2} \log |2 x+3|+\log c \\ \Rightarrow \quad \log |2 y-1| =\log |2 x+3|+2 \log c \\ \Rightarrow \quad \log |2 y-1|-\log |2 x+3| =\log c^{2} \\ \Rightarrow \quad \log |\frac{2 y-1}{2 x+3}| =\log c^{2} \\ \Rightarrow \quad \frac{2 y-1}{2 x+3} = \pm c^{2}\\ \Rightarrow \quad \frac{2 y-1}{2 x+3} = C , \quad जहां \quad C = \pm c^2 \\ \Rightarrow \quad \frac{2 x+3}{2 y-1}=\frac{1}{C} \\ \Rightarrow \quad \frac{2 x+3}{2 y-1} =k \text{, जहां } k=\frac{1}{C} \end{matrix} $
अतः सही विकल्प (c) है।
65. जिस अवकल समीकरण के लिए $y=a \cos x+b \sin x$ एक हल है, वह है:
(a) $\frac{d^{2} y}{d x^{2}}+y=0$
(b) $\frac{d^{2} y}{d x^{2}}-y=0$
(c) $\frac{d^{2} y}{d x^{2}}+(a+b) y=0$
(d) $\frac{d^{2} y}{d x^{2}}+(a-b) y=0$
उत्तर दिखाएँ
हल
दी गई समीकरण है
$ \begin{gathered} y=a \cos x+b \sin x \\ \frac{d y}{d x}=-a \sin x+b \cos x \end{gathered} $
$ \begin{aligned} \frac{d^{2} y}{d x^{2}} & =-a \cos x-b \sin x \\ \Rightarrow \quad \frac{d^{2} y}{d x^{2}} & =-(a \cos x+b \sin x) \Rightarrow \frac{d^{2} y}{d x^{2}}=-y \Rightarrow \frac{d^{2} y}{d x^{2}}+y=0 \end{aligned} $
इसलिए, सही विकल्प है $(a)$।
66. $\frac{d y}{d x}+y=e^{-x}, y(0)=0$ का हल है:
(a) $y=e^{-x}(x-1)$
(b) $y=x \cdot e^{x}$
(c) $y=x e^{-x}+1$
(d) $y=x \cdot e^{-x}$
उत्तर दिखाएँ
हल
दी गई अवकल समीकरण है $\frac{d y}{d x}+y=e^{-x}$
क्योंकि, यह एक रैखिक अवकल समीकरण है तो $P=1$ और $Q=e^{-x}$
समाकलन गुणक I.F. $=e^{\int P d x}=e^{\int 1 . d x}=e^{x}$
$\therefore$ हल है
$ \begin{aligned} y \times \text{ I.F. } & =\int Q \times \text{ I.F. } d x+c \\ \Rightarrow \quad y \times e^{x} & =\int e^{-x} \times e^{x} d x+c \Rightarrow y \times e^{x}=\int e^{0} d x+c \\ \Rightarrow \quad y \times e^{x} & =\int 1 . d x+c \Rightarrow y \times e^{x}=x+c \end{aligned} $
$y=0$ और $x=0$ रखें
$\therefore \quad 0=0+c \quad $
$\therefore \quad c=0$
$\therefore$ समीकरण है $y \times e^{x}=x$
इसलिए $\quad y=x \cdot e^{-x}$
इसलिए, सही विकल्प है $(d)$।
67. अवकल समीकरण
$ [\frac{d^{3} y}{d x^{3}}]^{2}-3 \frac{d^{2} y}{d x^{2}}+2(\frac{d y}{d x})^{4}=y^{4} \text{ का कोटि और स्तर } $
(a) 1,4
(b) 3,4
(c) 2,4
(d) 3,2
उत्तर दिखाएँ
हल
दी गई अवकल समीकरण है
$ [\frac{d^{3} y}{d x^{3}}]^{2}-3 \frac{d^{2} y}{d x^{2}}+2(\frac{d y}{d x})^{4}=y^{4} $
यहाँ सर्वोच्च अवकलज $\frac{d^{3} y}{d x^{3}}$ है।
$\therefore$ अवकल समीकरण की कोटि 3 है और क्योंकि, सर्वोच्च अवकलज की घात 2 है
$\therefore$ इसका स्तर 2 है
इसलिए, सही विकल्प है (d)।
68. अवकल समीकरण का क्रम और घात
$[1+(\frac{d y}{d x})^{2}]=\frac{d^{2} y}{d x^{2}}$ है:
(a) $2, \frac{3}{2}$
(b) 2,3
(c) 2, 1
(d) 3, 4
उत्तर दिखाएं
हल
दिया गया अवकल समीकरण है
$ [1+(\frac{d y}{d x})^{2}]=\frac{d^{2} y}{d x^{2}} $
यहाँ, सर्वोच्च अवकलज की घात 2 है,
$\therefore$ क्रम $=2$
और सर्वोच्च अवकलज की घात 1 है
$\therefore$ घात $=1$
अतः सही विकल्प (c) है।
69. वक्रों के परिवार $y^{2}=4 a(x+a)$ का अवकल समीकरण है:
(a) $y^{2}=4 \frac{d y}{d x}(x+\frac{d y}{d x})$
(b) $2 y \cdot \frac{d y}{d x}=4 a$
(c) $y \cdot \frac{d^{2} y}{d x^{2}}+(\frac{d y}{d x})^{2}=0$
(d) $2 x \cdot \frac{d y}{d x}+y(\frac{d y}{d x})^{2}-y=0$
उत्तर दिखाएं
हल
दिया गया वक्रों के परिवार का समीकरण है
$$ \begin{align*} & y^{2}=4 a(x+a) \\ \Rightarrow \quad & y^{2}=4 a x+4 a^{2} \tag{1} \end{align*} $$
दोनों ओर के संबंध के संबंध में अवकलन करने पर, हम प्राप्त करते हैं
$ \begin{aligned} 2 y \cdot \frac{d y}{d x} & =4 a \\ \Rightarrow \quad y \cdot \frac{d y}{d x} & =2 a \Rightarrow \frac{y}{2} \frac{d y}{d x}=a \end{aligned} $
अब, समीकरण (1) में $a$ के मान को रखने पर हम प्राप्त करते हैं
$ \begin{aligned} y^{2} & =4 x(\frac{y}{2} \frac{d y}{d x})+4(\frac{y}{2} \cdot \frac{d y}{d x})^{2} \\ \Rightarrow \quad y^{2} & =2 x y \frac{d y}{d x}+y^{2}(\frac{d y}{d x})^{2} \Rightarrow y=2 x \frac{d y}{d x}+y(\frac{d y}{d x})^{2} \end{aligned} $
$ \Rightarrow \quad 2 x \cdot \frac{d y}{d x}+y \cdot(\frac{d y}{d x})^{2}-y=0 $
अतः सही विकल्प (d) है।
70. निम्नलिखित में से कौन सा निम्नलिखित का सामान्य हल है
$ \frac{d^{2} y}{d x^{2}}-2 \frac{d y}{d x}+y=0 ? $
(a) $y=(A x+B) \cdot e^{x}$
(b) $y=(A x+B) e^{-x}$
(c) $y=A e^{x}+B e^{-x}$
(d) $y=A \cos x+B \sin x$
उत्तर दिखाएं
हल
दिया गया अवकल समीकरण है
$ \frac{d^{2} y}{d x^{2}}-2 \frac{d y}{d x}+y=0 $
क्योंकि उपरोक्त समीकरण द्वितीय क्रम और प्रथम घात का है
$\therefore \quad D^{2} y-2 D y+y=0$, जहाँ $D=\frac{d}{d x}$
$\Rightarrow(D^{2}-2 D+1) y=0$
$\therefore$ सहायक समीकरण है
$ m^{2}-2 m+1=0 \Rightarrow(m-1)^{2}=0 \Rightarrow m=1,1 $
यदि सहायक समीकरण के मूल वास्तविक और समान हों, जैसे $(m)$ तो $C F=(ax+b) \cdot e^{m x}$
$\therefore \quad C F=(A x+B) e^{x}$
इसलिए $y=(A x+B) \cdot e^{x}$
इसलिए, सही विकल्प है $(a)$।
71. $\frac{d y}{d x}+y \tan x=\sec x$ के सामान्य हल है:
(a) $y \sec x=\tan x+c$
(b) $y \tan x=\sec x+c$
(c) $\tan x=y \tan x+c$
(d) $x \sec x=\tan y+c$
उत्तर दिखाएँ
हल
दी गई अवकल समीकरण है $\frac{d y}{d x}+y \tan x=\sec x$
क्योंकि, यह एक रैखिक अवकल समीकरण है
$\therefore \quad P=\tan x$ और $Q=\sec x$
समाकलन गुणक I.F. $=e^{\int P d x}=e^{\int \tan x d x}=e^{\log |\sec x|}=\sec x, (\sec x>0)$
$\therefore$ हल है
$ \begin{aligned} y \times \text{ I.F. } & =\int Q \times \text{ I.F. } d x+c \\ \Rightarrow \quad y \times \sec x & =\int \sec x \cdot \sec x d x+c \\ \Rightarrow \quad y \sec x & =\int \sec ^{2} x d x+c \Rightarrow y \sec x=\tan x+c \\ \Rightarrow y \sec x=\tan x+c \end{aligned} $
इसलिए, सही विकल्प है (a)।
72. अवकल समीकरण $\frac{d y}{d x}+\frac{y}{x}=\sin x$ का हल है:
(a) $x(y+\cos x)=\sin x+c$
(b) $x(y-\cos x)=\sin x+c$
(c) $x y \cos x=\sin x+c$
(d) $x(y+\cos x)=\cos x+c$
उत्तर दिखाएँ
हल
दी गई अवकल समीकरण है $\frac{d y}{d x}+\frac{y}{x}=\sin x$
क्योंकि, यह एक रैखिक अवकल समीकरण है
$\therefore \quad P=\frac{1}{x}$ और $Q=\sin x$
समाकलन गुणक I.F. $=e^{\int \frac{1}{x} d x}=e^{\log |x|}=x , (x>0)$
$\therefore$ हल है $y \times$ I.F. $=\int Q \times$ I.F. $d x+c$
$ \begin{matrix} y \times x =\int \sin x \cdot x d x+c \Rightarrow y \times x=\int x \sin x d x+c \\ y x =x \cdot \int \sin x d x-\int(D(x) \int \sin x d x) d x+c \\ \Rightarrow y x =x(-\cos x)-\int-\cos x d x \\
\Rightarrow y x=-x \cos x+\int \cos x d x \Rightarrow y x=-x \cos x+\sin x+c \\ \Rightarrow y x+x \cos x =\sin x+c \\ \Rightarrow x(y+\cos x) =\sin x+c \end{matrix} $
इसलिए, सही विकल्प है $(a)$।
73. अवकल समीकरण $(e^{x}+1) y d y=(y+1) e^{x} d x$ का सामान्य हल है:
(a) $(y+1)=k(e^{x}+1)$
(b) $y+1=e^{x}+1+k$
(c) $y=\log [k(y+1)(e^{x}+1)]$
(d) $y=\log {\frac{e^{x}+1}{y+1}}+k$
उत्तर दिखाएँ
हल
दिया गया अवकल समीकरण है
$ \begin{aligned} (e^{x}+1) y d y & =(y+1) e^{x} d x \\ \Rightarrow \quad \frac{y}{y+1} d y & =\frac{e^{x}}{e^{x}+1} d x \end{aligned} $
दोनों ओर समाकलन करने पर, हम प्राप्त करते हैं
$ \begin{aligned} \int \frac{y}{y+1} d y & =\int \frac{e^{x}}{e^{x}+1} d x \\ \Rightarrow \quad \int \frac{y+1-1}{y+1} d y & =\int \frac{e^{x}}{e^{x}+1} d x \\ \Rightarrow \quad \int 1 \cdot d y-\int \frac{1}{y+1} d y & =\int \frac{e^{x}}{e^{x}+1} d x \end{aligned} $
$ \begin{aligned} \Rightarrow \quad y-\log |y+1| =\log |e^{x}+1|+\log |c| \\ \Rightarrow \quad y =\log |y+1|+\log |e^{x}+1|+\log |c| \\ \Rightarrow \quad y =\log |c(y+1)(e^{x}+1)| \\ \Rightarrow \quad y =\log [k(y+1)(e^{x}+1)] , \quad (where \quad k= \pm c) \end{aligned} $
इसलिए, सही विकल्प है (c)।
74. अवकल समीकरण $\frac{d y}{d x}=e^{x-y}+x^{2} e^{-y}$ का हल है:
(a) $y=e^{x-y}-x^{2} e^{-y}+c$
(b) $e^{y}-e^{x}=\frac{x^{3}}{3}+c$
(c) $e^{x}+e^{y}=\frac{x^{3}}{3}+c$
(d) $e^{x}-e^{y}=\frac{x^{3}}{3}+c$
उत्तर दिखाएँ
हल
दिया गया अवकल समीकरण है
$ \begin{aligned} & \frac{d y}{d x}=e^{x-y}+x^{2} e^{-y} \\ & \Rightarrow \quad \frac{d y}{d x}=e^{x} \cdot e^{-y}+x^{2} \cdot e^{-y} \Rightarrow \frac{d y}{d x}=e^{-y}(e^{x}+x^{2}) \\ & \Rightarrow \quad \frac{d y}{e^{-y}}=(e^{x}+x^{2}) d x \Rightarrow e^{y} \cdot d y=(e^{x}+x^{2}) d x \end{aligned} $
दोनों ओर समाकलन करने पर, हम प्राप्त करते हैं
$ \begin{aligned} \int e^{y} d y & =\int(e^{x}+x^{2}) d x \\
\Rightarrow \quad e^{y} & =e^{x}+\frac{x^{3}}{3}+c \Rightarrow e^{y}-e^{x}=\frac{x^{3}}{3}+c \end{aligned} $
अतः, सही विकल्प है $(b)$।
75. अवकल समीकरण का हल
$ \frac{d y}{d x}+\frac{2 x y}{1+x^{2}}=\frac{1}{(1+x^{2})^{2}} \text{ है: } $
(a) $y(1+x^{2})=c+\tan ^{-1} x$
(b) $\frac{y}{1+x^{2}}=c+\tan ^{-1} x$
(c) $y \log (1+x^{2})=c+\tan ^{-1} x$
(d) $y(1+x^{2})=c+\sin ^{-1} x$
उत्तर दिखाएँ
हल
दिया गया अवकल समीकरण है
$ \frac{d y}{d x}+\frac{2 x y}{1+x^{2}}=\frac{1}{(1+x^{2})^{2}} $
क्योंकि, यह एक रैखिक अवकल समीकरण है
$ P=\frac{2 x}{1+x^{2}} \text{ और } Q=\frac{1}{(1+x^{2})^{2}} $
समाकलन गुणक I.F. $=e^{\int P d x}=e^{\int \frac{2 x}{1+x^{2}} d x}=e^{\log |(1+x^{2})|}=|(1+x^{2})|=(1+x^{2}), \quad (\because (1+x^{2}) \quad धनात्मक होता है)
$
$\therefore$ हल $y \times$ I.F. $=\int Q \times$ I.F. $d x+c$
$ \begin{aligned} & \Rightarrow \quad y(1+x^{2})=\int \frac{1}{(1+x^{2})^{2}} \times(1+x^{2}) d x+c \\ & \Rightarrow \quad y(1+x^{2})=\int \frac{1}{(1+x^{2})} d x+c \Rightarrow y(1+x^{2})=\tan ^{-1} x+c \end{aligned} $
अतः, सही विकल्प है $(a)$।
भरों
76. निम्नलिखित के खाली स्थान भरें ( $i$ से $x i$ ):
(i) अवकल समीकरण $\frac{d^{2} y}{d x^{2}}+e^{d y / d x}=0$ की डिग्री ……
(ii) अवकल समीकरण $\sqrt{1+(\frac{d y}{d x})^{2}}=x$ की डिग्री ……
(iii) तीसरे कोटि के अवकल समीकरण के सामान्य हल में अचर अचर नियतांकों की संख्या ……
(iv) $\frac{d y}{d x}+\frac{y}{x \log x}=\frac{1}{x}$ एक ऐसे समीकरण के प्रकार का समीकरण है ……
(v) $\frac{d x}{d y}+P_1 x=Q_1$ प्रकार के अवकल समीकरण के सामान्य हल को ……
(vi) अवकल समीकरण $x \frac{d y}{d x}+2 y=x^{2}$ का हल ……
(vii) $(1+x^{2}) \frac{d y}{d x}+2 x y-4 x^{2}=0$ का हल ……
(viii) अवकल समीकरण $y d x+(x+x y) d y=0$ का हल ……
(ix) $\frac{d y}{d x}+y=\sin x$ के सामान्य हल है ……
( $x$ ) अवकल समीकरण $\cot y d x=x d y$ का हल है ……
(xi) $\frac{d y}{d x}+y=\frac{1+y}{x}$ के समाकलन गुणक है ……
उत्तर दिखाएँ
हल
(i) अवकल समीकरण $\frac{d^{2} y}{d x^{2}}+e^{d y / d x}=0$ की डिग्री परिभाषित नहीं है।
(ii) दिया गया अवकल समीकरण $\sqrt{1+(\frac{d y}{d x})^{2}}=x$ है। दोनों ओर वर्ग करने पर हम प्राप्त करते हैं
$ 1+(\frac{d y}{d x})^{2}=x^{2} $
इसलिए, समीकरण की डिग्री 2 है।
(iii) हल में अनिश्चित अचरों की संख्या 3 है।
(iv) दिया गया अवकल समीकरण $\frac{d y}{d x}+\frac{y}{x \log x}=\frac{1}{x}$ तरह के $\frac{d y}{d x}+P y=Q$ के रूप में है।
(v) $\frac{d x}{d y}+P_1 x=Q_1$ तरह के अवकल समीकरण के सामान्य हल $x \times$ I.F. $=\int Q \times$ I.F. $d y+c$ द्वारा दिया जाता है
$\Rightarrow \quad x \cdot e^{\int P_1 d y}=\int Q_1 \cdot e^{\int P_1 d y} d y+c$.
(vi) दिया गया अवकल समीकरण $x \frac{d y}{d x}+2 y=x^{2}$
$\Rightarrow \quad \frac{d y}{d x}+\frac{2}{x} y=x$.
क्योंकि, यह एक रैखिक अवकल समीकरण है
$\therefore \quad P=\frac{2}{x}$ और $Q=x$
समाकलन गुणक I.F. $=e^{\int P d x}=e^{\int \frac{2}{x} d x}=e^{2 \log |x|}=e^{\log |x^{2}|}=x^{2}$
$\therefore$ हल है
$ \begin{aligned} y \times \text{ I.F. } & =\int Q \times \text{ I.F. } d x+c \\ \Rightarrow \quad y \cdot x^{2} & =\int x \cdot x^{2} d x+c \quad \Rightarrow y \cdot x^{2}=\int x^{3} d x+c \\ \Rightarrow \quad y \cdot x^{2} & =\frac{1}{4} x^{4}+c \quad \Rightarrow y=\frac{1}{4} x^{2}+c \cdot x^{-2} \end{aligned} $
इसलिए, हल $y=\frac{1}{4} x^{2}+c \cdot x^{-2}$ है।
(vii) दिया गया अवकल समीकरण है
$ \begin{aligned} & (1+x^{2}) \frac{d y}{d x}+2 x y-4 x^{2}=0 \\ \Rightarrow \quad & \frac{d y}{d x}+\frac{2 x y}{1+x^{2}}=\frac{4 x^{2}}{1+x^{2}} \end{aligned} $
क्योंकि यह एक रैखिक अवकल समीकरण है
$\therefore \quad P=\frac{2 x}{1+x^{2}}$ और $Q=\frac{4 x^{2}}{1+x^{2}}$
समाकलन गुणांक I.F. $=e^{\int P d x}=e^{\int \frac{2 x}{1+x^{2}} d x}=e^{\log |(1+x^{2})|}=(1+x^{2}) , \quad (\because (1+x^{2}) \quad है \quad धनात्मक )$
$\therefore$ हल $y \times I$.F $=\int Q \times$ I.F. $d x+c$
$ \begin{aligned} \Rightarrow y \times(1+x^{2}) =\int \frac{4 x}{1+x^{2}} \times(1+x^{2}) d x+c \\ \Rightarrow y \times(1+x^{2}) =\int 4 x^{2} d x+c \Rightarrow y \times(1+x^{2})=\frac{4}{3} x^{3}+c \\ \Rightarrow y =\frac{4}{3} \frac{x^{3}}{(1+x^{2})}+c(1+x^{2})^{-1} \end{aligned} $
$\Rightarrow 3y (1+x^{2})= 4x^{3}+3c$
$\Rightarrow 3y (1+x^{2})= 4x^{3}+C , (where \quad C=3c)$
इसलिए, आवश्यक हल $ 3y (1+x^{2})= 4x^{3}+C$ है।
(viii) दिया गया अवकल समीकरण है
$ \begin{gathered} y d x+(x+x y) d y=0 \\ \Rightarrow \quad(x+x y) d y=-y d x \Rightarrow x(1+y) d y=-y d x \\ \Rightarrow \quad \frac{1+y}{y} d y=-\frac{1}{x} d x \end{gathered} $
दोनों ओर समाकलन करने पर हमें प्राप्त होता है
$ \begin{aligned} & \int \frac{1+y}{y} d y=-\int \frac{1}{x} d x \\ & \Rightarrow \quad \int(\frac{1}{y}+1) d y=-\int \frac{1}{x} d x \\ & \Rightarrow \quad \log |y|+y=-\log |x|+\log |c| \\ & \Rightarrow \log |x|+\log |y|=\log |c|-y \\ & \Rightarrow \quad \log |x y |=\log |c|-y \\ & \Rightarrow \quad |x y |=e^{\log|c|}e^{-y} \\ & \Rightarrow \quad x y =\pm e^{\log|c|}e^{-y} \\ & \Rightarrow \quad x y =Ce^{-y} , \quad (where \quad C=\pm e^{\log|c|} )\\ \end{aligned} $
इसलिए, आवश्यक हल $x y=C e^{-y}$ है।
(ix) दिया गया अवकल समीकरण है $\frac{d y}{d x}+y=\sin x$
क्योंकि, यह एक रैखिक अवकल समीकरण है
$\therefore \quad P=1$ और $Q=\sin x$
समाकलन गुणांक I.F. $=e^{\int P d x}=e^{\int 1 . d x}=e^{x}$
$\therefore$ हल $y \times$ I.F. $=\int Q \times$ I.F. $d x+c$
$\Rightarrow \quad y \cdot e^{x}=\int \sin x \cdot e^{x} d x+c$
मान लीजिए $ I=\int \sin x \cdot e^{x} d x$
$ समाकलन \quad द्वारा \quad भाग \quad समाकलन $
$ \begin{aligned} & I=\sin x \cdot \int e^{x} d x-\int(D(\sin x) \cdot \int e^{x} d x) d x \\
& I=\sin x \cdot e^{x}-\int \cos x \cdot e^{x} d x \\ & I=\sin x \cdot e^{x}-[\cos x \cdot \int e^{x} d x-\int(D(\cos x) \int e^{x} d x) d x] \end{aligned} $
$ \begin{aligned} I & =\sin x \cdot e^{x}-[\cos x \cdot e^{x}-\int-\sin x \cdot e^{x} d x] \\ I & =\sin x \cdot e^{x}-\cos x \cdot e^{x}-\int \sin x \cdot e^{x} d x \\ I & =\sin x \cdot e^{x}-\cos x \cdot e^{x}-I \\ \Rightarrow I+I & =e^{x}(\sin x-\cos x) \\ \Rightarrow \quad 2 I & =e^{x}(\sin x-\cos x) \\ \therefore \quad I & =\frac{e^{x}}{2}(\sin x-\cos x) \end{aligned} $
समीकरण (1) से हमें प्राप्त होता है
$ \begin{aligned} y \cdot e^{x} & =\frac{e^{x}}{2}(\sin x-\cos x)+c \\ y & =(\frac{\sin x-\cos x}{2})+c \cdot e^{-x} \end{aligned} $
इसलिए, आवश्यक समाधान है
$ y=(\frac{\sin x-\cos x}{2})+c \cdot e^{-x} $
(x) दिया गया अवकल समीकरण है $\cot y d x=x d y$
$ \Rightarrow \frac{d y}{\cot y}=\frac{d x}{x} \Rightarrow \tan y d y=\frac{d x}{x} $
दोनों ओर समाकलन करने पर हमें प्राप्त होता है
$ \begin{aligned} & \quad \int \tan y d y=\int \frac{d x}{x} \Rightarrow \log |\sec y|=\log |x|+\log |c| \\ \Rightarrow \quad & \log |\sec y|-\log |x|=\log |c| \\ \Rightarrow \quad & \log |\frac{\sec y}{x}|=\log |c| \\ \therefore \quad & |\frac{\sec y}{x}|=|c| \\ \therefore \quad & \frac{\sec y}{x}=\pm c \\ \therefore \quad & \frac{\sec y}{x}=C \quad ( where \quad C = \pm c)\\ \Rightarrow & \frac{x}{\sec y}=\frac{1}{C} \Rightarrow \frac{x}{\sec y}=C \\ \therefore \quad & x=C \sec y \end{aligned} $
इसलिए, आवश्यक समाधान है $x=C \sec y$.
$(x i)$ दिया गया अवकल समीकरण है
$ \begin{aligned} \frac{d y}{d x}+y & =\frac{1+y}{x} \\ \frac{d y}{d x}+y & =\frac{1}{x}+\frac{y}{x} \\ \Rightarrow \quad \frac{d y}{d x}+y-\frac{y}{x} & =\frac{1}{x} \Rightarrow \frac{d y}{d x}+(1-\frac{1}{x}) y=\frac{1}{x} \end{aligned} $
$ \begin{aligned} & \text{ यहाँ } P=(1-\frac{1}{x}) \\ & \therefore \quad \text{ I.F. }=e^{\int P d x}=e^{\int(1-\frac{1}{x}) d x}=e^{(x-\log |x|)} \\ & =e^{x} \cdot e^{-\log |x|}=e^{x} \cdot e^{\log |\frac{1}{x}|}=\frac{e^{x}}{|x|}=\frac{e^{x}}{x},(x>0)
\end{aligned} $
अतः, आवश्यक I.F. $=\frac{e^{x}}{x}$
सत्य/असत्य
77. निम्नलिखित के लिए सत्य या असत्य कहें:
(i) रूप $\frac{d x}{d y}+P_1 x=Q_1$ के अवकल समीकरण का एकाधिक गुणक (I.F.) $e^{\int P_1 d y}$ द्वारा दिया जाता है।
(ii) रूप $\frac{d x}{d y}+P_1 x=Q_1$ के अवकल समीकरण के हल $x$. I.F. $=\int$ (I.F.) $Q_1 d y$ द्वारा दिया जाता है।
(iii) रूप $\frac{d y}{d x}=f(x, y)$ के अवकल समीकरण के हल के लिए सही प्रतिस्थापन वह है जहाँ $f(x, y)$ शून्य डिग्री का समानुपाती फलन है, तो $y=v x$ होता है।
(iv) रूप $\frac{d x}{d y}=g(x, y)$ के अवकल समीकरण के हल के लिए सही प्रतिस्थापन वह है जहाँ $g(x, y)$ शून्य डिग्री का समानुपाती फलन है, तो $x=v y$ होता है।
(v) द्वितीय कोटि के अवकल समीकरण के विशिष्ट हल में अनुकूल नियतांकों की संख्या दो होती है।
(vi) वृत्तों के परिवार $x^{2}+(y-a)^{2}=a^{2}$ को प्रसत्त करने वाले अवकल समीकरण की कोटि दो होगी।
(vii) $\frac{d y}{d x}=(\frac{y}{x})^{1 / 3}$ के अवकल समीकरण का हल $y^{2 / 3}-x^{2 / 3}=c$ होता है।
(viii) वक्रों के परिवार
$ y=e^{x}(A \cos x+B \sin x) \text{ का } \frac{d^{2} y}{d x^{2}}-2 \frac{d y}{d x}+2 y=0 $
(ix) अवकल समीकरण $\frac{d y}{d x}=\frac{x+2 y}{x}$ का हल $x+y=k x^{2}$ होता है।
(x) $\frac{x d y}{d x}=y+x \tan \frac{y}{x}$ के अवकल समीकरण का हल $\sin (\frac{y}{x})=c x$ होता है।
(xi) तल में सभी अनुपाती रेखाओं के अवकल समीकरण $\frac{d^{2} x}{d y^{2}}=0$ होता है।
उत्तर दिखाएँ
हल
(i) सत्य
दिए गए अवकल समीकरण का एकाधिक गुणक (I.F.)
$ \frac{d x}{d y}+P_1 x=Q \text{ है } e^{\int P_1 d y} $
(ii) सत्य
(iii) सत्य
(iv) सत्य
(v) असत्य
क्योंकि अवकल समीकरण के विशिष्ट हल में कोई अनुकूल नियतांक नहीं होता।
(vi) असत्य
हम जानते हैं कि अवकल समीकरण की कोटि अनुकूल नियतांकों की संख्या के बराबर होती है।
(vii) सत्य
दिए गए अवकल समीकरण है
$ \begin{aligned} \frac{d y}{d x} & =(\frac{y}{x})^{1 / 3} \\
\Rightarrow \quad \frac{d y}{d x} & =\frac{y^{1 / 3}}{x^{1 / 3}} \Rightarrow \frac{d y}{y^{1 / 3}}=\frac{d x}{x^{1 / 3}} \end{aligned} $
अतः दोनों ओर समाकलन करने पर, हम प्राप्त करते हैं
$\int \frac{d y}{y^{1 / 3}} =\int \frac{d x}{x^{1 / 3}} \Rightarrow \int y^{-1 / 3} d y=\int x^{-1 / 3} d x$
$\Rightarrow \frac{1}{-\frac{1}{3}+1} y^{-1 / 3+1} =\frac{1}{-1 / 3+1} \cdot x^{-1 / 3+1}+c$
$\Rightarrow \quad \frac{3}{2} y^{2 / 3} =\frac{3}{2} x^{2 / 3}+c$
$\Rightarrow \quad y^{2 / 3} =x^{2 / 3}+\frac{2}{3} c \Rightarrow y^{2 / 3}-x^{2 / 3}=k[k=\frac{2}{3} c]$
(viii) सत्य
दिया गया समीकरण है
$ y=e^{x}(A \cos x+B \sin x) $
दोनों ओर अवकलन करने पर, हम प्राप्त करते हैं
$ \begin{aligned} & \frac{d y}{d x}=e^{x}(-A \sin x+B \cos x)+(A \cos x+B \sin x) e^{x} \\ & \frac{d y}{d x}=e^{x}(-A \sin x+B \cos x)+y \end{aligned} $
फिर अवकलन करने पर $x$ के संदर्भ में, हम प्राप्त करते हैं
$ \begin{aligned} & \frac{d^{2} y}{d x^{2}}=e^{x}(-A \cos x-B \sin x)+(-A \sin x+B \cos x) \cdot e^{x}+\frac{d y}{d x} \\ & \frac{d^{2} y}{d x^{2}}=-e^{x}(A \cos x+B \sin x)+\frac{d y}{d x}-y+\frac{d y}{d x} \\ & \frac{d^{2} y}{d x^{2}}=-y-y+2 \frac{d y}{d x} \quad \therefore \quad \frac{d^{2} y}{d x^{2}}-2 \frac{d y}{d x}+2 y=0 \end{aligned} $
(ix) सत्य
दिया गया अवकलन समीकरण है
$ \begin{aligned} \frac{d y}{d x} & =\frac{x+2 y}{x} \\ \Rightarrow \quad \frac{d y}{d x} & =1+2 \frac{y}{x} \Rightarrow \frac{d y}{d x}-\frac{2 y}{x}=1 \end{aligned} $
यहाँ, $P=\frac{-2}{x}$ और $Q=1$
समाकलन गुणक I.F. $=e^{\int \frac{-2}{x} d x}=e^{-2 \log |x|}=e^{\log |x|^{-2}}=\frac{1}{|x|^{2}} = \frac{1}{x^{2}}$
$\therefore$ हल है $y \times$ I.F. $=\int Q \times$ I.F. $d x+c$
$\Rightarrow y \times \frac{1}{x^{2}}=\int 1 \times \frac{1}{x^{2}} d x+c$
$\Rightarrow \quad \frac{y}{x^{2}}=\int \frac{1}{x^{2}} d x+c \Rightarrow \frac{y}{x^{2}}=-\frac{1}{x}+c$
$\Rightarrow \quad y=-x+c x^{2} \Rightarrow y+x=c x^{2}$
(x) सत्य
दिया गया अवकलन समीकरण है
$ \begin{aligned} & x \frac{d y}{d x}=y+x \tan (\frac{y}{x}) \\ & x \frac{d y}{d x}-x \tan (\frac{y}{x})=y \\ `
& \Rightarrow \frac{d y}{d x}-\tan (\frac{y}{x})=\frac{y}{x} \Rightarrow \frac{d y}{d x}=\frac{y}{x}+\tan (\frac{y}{x}) \\ & \text{ Put } y=v x \Rightarrow \frac{d y}{d x}=v+x \frac{d v}{d x} \\ & \Rightarrow \quad v+x \cdot \frac{d v}{\text{d}x}=\frac{v x}{x}+\tan (\frac{v x}{x}) \end{aligned} $
$ \begin{aligned} & \Rightarrow \quad v+x \frac{d v}{d x}=v+\tan v \Rightarrow x \frac{d v}{d x}=\tan v \\ & \Rightarrow \quad \frac{d v}{\tan v}=\frac{d x}{x} \Rightarrow \cot v d v=\frac{d x}{x} \end{aligned} $
दोनों ओर समाकलन करने पर, हम प्राप्त करते हैं
$ \begin{matrix} \int \cot v d v =\int \frac{d x}{x} \Rightarrow \log |\sin v|=\log |x|+\log |c| \\ \Rightarrow \log |\sin \frac{y}{x}|=\log |x c| \\ \therefore \qquad \sin \frac{y}{x} =\pm cx \\ \therefore \qquad \sin \frac{y}{x} =Cx , \quad (where \quad C= \pm c) \end{matrix} $
(xi) सत्य
मान लीजिए $y=m x+c$ एक तल में अनुप्रस्थ रेखा है
$\therefore \qquad \frac{d y}{d x}=m$ और $\frac{d^{2} y}{d x^{2}}=0$.





