हल

हमें दिया गया है, $y^{2}=9 x, y=3 x$

दोनों समीकरणों को हल करने पर हमें प्राप्त होता है

$(3 x)^{2}=9 x$

$\Rightarrow \quad 9 x^{2}-9 x=0 \Rightarrow 9 x(x-1)=0$

$\therefore \quad x=0,1$

छायांकित क्षेत्र का क्षेत्रफल

$=area($ क्षेत्र $OAB)-area(\triangle OAB)$

$=-\int_0^{1} y_l \cdot d x=\int_0^{1} \sqrt{9 x} d x-\int_0^{1} 3 x d x$

$=3 \int_0^{1} \sqrt{x} d x-3 \int_0^{1} x d x=3 \times \dfrac{2}{3}[x^{3 / 2}]_0^{1}-3[\dfrac{x^{2}}{2}]_0^{1}$

$=2[(1)^{3 / 2}-0]-\dfrac{3}{2}[(1)^{2}-0]=2(1)-\dfrac{3}{2}(1)=2-\dfrac{3}{2}=\dfrac{1}{2}$ वर्ग इकाई

अतः, आवश्यक क्षेत्रफल $=\dfrac{1}{2}$ वर्ग इकाई है।

हल

हमें दिया गया है: $x^{2}=2 p y \ldots(i)$

और $y^{2}=2 p x \ldots(ii)$

समीकरण (i) से हमें $y=\dfrac{x^{2}}{2 p}$ प्राप्त होता है

समीकरण (ii) में $y$ का मान रखने पर हमें प्राप्त होता है

$ \begin{aligned} & (\dfrac{x^{2}}{2 p})^{2}=2 p x \Rightarrow \dfrac{x^{4}}{4 p^{2}}=2 p x \\ & \Rightarrow x^{4}=8 p^{3} x \Rightarrow x^{4}-8 p^{3} x=0 \\ & \Rightarrow x(x^{3}-8 p^{3})=0 \\ &\therefore x=0,2 p \end{aligned} $

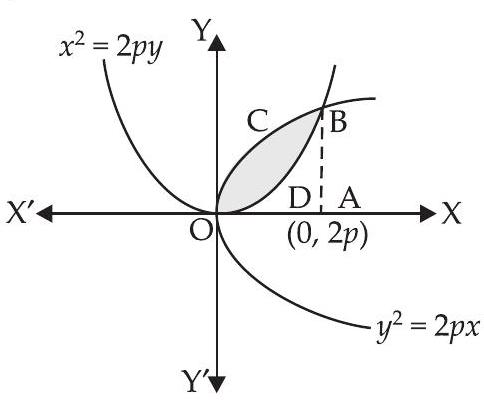
$ \begin{aligned} & \text{ आवश्यक क्षेत्रफल }=\text{ क्षेत्र }(\text{ OCBA - ODBA) } \\ & =\int_0^{2 p} \sqrt{2 p x} d x-\int_0^{2 p} \dfrac{x^{2}}{2 p} d x=\sqrt{2 p} \int_0^{2 p} \sqrt{x} d x-\dfrac{1}{2 p} \int_0^{2 p} x^{2} d x \\

& =\sqrt{2 p} \cdot \dfrac{2}{3}[x^{3 / 2}]_0^{2 p}-\dfrac{1}{2 p} \cdot \dfrac{1}{3}[x^{3}]_0^{2 p} \\ & =\dfrac{2 \sqrt{2}}{3} \sqrt{p}[(2 p)^{3 / 2}-0]-\dfrac{1}{6 p}[(2 p)^{3}-0] \\ & =\dfrac{2 \sqrt{2}}{3} \sqrt{p} \cdot 2 \sqrt{2} p^{\dfrac{3}{2}}-\dfrac{1}{6 p} \cdot 8 p^{3} \\ & =\dfrac{8}{3} \cdot p^{2}-\dfrac{8}{6} p^{2}=\dfrac{8}{6} p^{2}=\dfrac{4}{3} p^{2} \text{ वर्ग इकाई } \end{aligned} $

इसलिए, आवश्यक क्षेत्रफल $=\dfrac{4}{3} p^{2}$ वर्ग इकाई है।

हल

हमें दिया गया है: $y=x^{3}, y=x+6$ और $x=0$

$y=x^{3}$ और $y=x+6$ को हल करने पर, हम प्राप्त करते हैं

$x+6 =x^{3}$

$\Rightarrow x^{3}-x-6 =0$

$\Rightarrow x^{2}(x-2)+2 x(x-2)+3(x-2) =0$

$\Rightarrow (x-2)(x^{2}+2 x+3) =0$

$x^{2}+2 x+3=0$ के कोई वास्तविक मूल नहीं हैं।

$\therefore x=2$

$\therefore$ छायांकित क्षेत्र का आवश्यक क्षेत्रफल

$ \begin{aligned} & =\int_0^{2}(x+6) d x-\int_0^{2} x^{3} d x \\ & =[\dfrac{x^{2}}{2}+6 x]_0^{2}-\dfrac{1}{4}[x^{4}]_0^{2} \end{aligned} $

$ \begin{aligned} & =(\dfrac{4}{2}+12)-(0+0)-\dfrac{1}{4}[(2)^{4}-0] \\ & =14-\dfrac{1}{4} \times 16=14-4=10 \text{ वर्ग इकाई। } \end{aligned} $

हल

हमें $y^{2}=4 x$ और $x^{2}=4 y$ दिया गया है।

$ \begin{aligned} y & =\dfrac{x^{2}}{4} \\ \Rightarrow \quad(\dfrac{x^{2}}{4})^{2} & =4 x \end{aligned} $

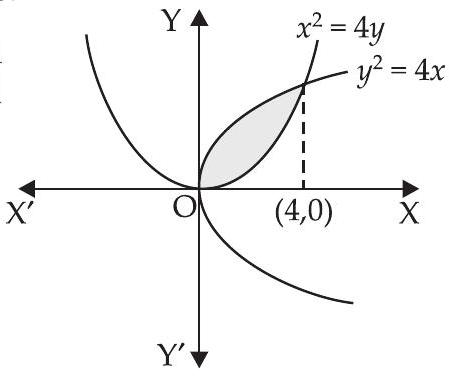
$ \begin{aligned} & \Rightarrow \quad \dfrac{x^{4}}{16}=4 x \\ & \Rightarrow \quad x^{4}=64 x \Rightarrow x^{4}-64 x=0 \\

& \Rightarrow \quad x(x^{3}-64)=0 \\ & \therefore x=0, x=4 \end{aligned} $

अभीष्ट क्षेत्रफल $=\int_0^{4} \sqrt{4 x} d x-\int_0^{4} \dfrac{x^{2}}{4} d x=2 \int_0^{4} \sqrt{x} d x-\dfrac{1}{4} \int_0^{4} x^{2} d x$

$ \begin{aligned} & =2 \cdot \dfrac{2}{3}[x^{3 / 2}]_0^{4}-\dfrac{1}{4} \cdot \dfrac{1}{3}[x^{3}]_0^{4} \\ & =\dfrac{4}{3}[(4)^{3 / 2}-0]-\dfrac{1}{12}[(4)^{3}-0]=\dfrac{4}{3}[8]-\dfrac{1}{12}[64] \\ & =\dfrac{32}{3}-\dfrac{16}{3}=\dfrac{16}{3} \text{ वर्ग इकाई } \end{aligned} $

इसलिए, अभीष्ट क्षेत्रफल $=\dfrac{16}{3}$ वर्ग इकाई है।

हल

दिया गया है: $\quad y^{2}=9 x \ldots(i)$

और $\quad y=x \ldots(ii)$

समीकरण (i) और (ii) को हल करने पर हमें मिलता है

$ \begin{aligned} x^{2} =9 x\\ \Rightarrow x^{2}-9 x=0 \\ \Rightarrow x(x-9) =0 \\ \therefore x=0,9 \end{aligned} $

अभीष्ट क्षेत्रफल

$ \begin{aligned} & =\int_0^{9} \sqrt{9 x} d x-\int_0^{9} x d x=3 \int_0^{9} \sqrt{x} d x-\int_0^{9} x d x \\ & =3 \cdot \dfrac{2}{3}[x^{3 / 2}]_0^{9}-\dfrac{1}{2}[x^{2}]_0^{9} \\ & =2[(9)^{3 / 2}-0]-\dfrac{1}{2}[(9)^{2}-0] \\ & =2(27)-\dfrac{1}{2}(81)=54-\dfrac{81}{2}=\dfrac{108-81}{2} \\ & =\dfrac{27}{2} \text{ वर्ग इकाई } \end{aligned} $

इसलिए, अभीष्ट क्षेत्रफल $=\dfrac{27}{2}$ वर्ग इकाई है।

हल

यहाँ, $x^{2}=y$ और $y=x+2$

$\therefore \quad x^{2}=x+2$

$\Rightarrow \quad x^{2}-x-2=0$

$\Rightarrow \quad x^{2}-2 x+x-2=0$

$\Rightarrow \quad x(x-2)+1(x-2)=0$

$\Rightarrow \quad(x-2)(x+1)=0$

$\therefore x=-1,2$

$y=x+2$ के ग्राफ

$ \begin{array}{|c|c|c|} \hline x & 0 & -2 \\ \hline y & 2 & 0 \\ \hline \end{array} $

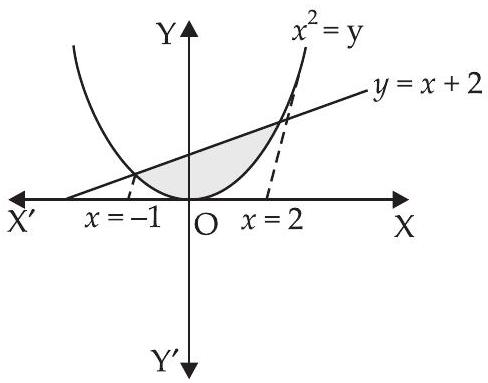
क्षेत्रफल जो आवश्यक क्षेत्र को प्रदर्शित करता है

$ \begin{aligned} & =\int _{-1}^{2}(x+2) d x-\int _{-1}^{2} x^{2} d x=[\dfrac{x^{2}}{2}+2 x] _{-1}^{2}-\dfrac{1}{3}[x^{3}] _{-1}^{2} \\ & =[(\dfrac{4}{2}+4)-(\dfrac{1}{2}-2)]-\dfrac{1}{3}[8-(-1)] \\ & =(6+\dfrac{3}{2})-\dfrac{1}{3}(9)=\dfrac{15}{2}-3=\dfrac{9}{2} \text{ वर्ग इकाई } \end{aligned} $

इसलिए, आवश्यक क्षेत्रफल $=\dfrac{9}{2}$ वर्ग इकाई है।

हल

यहाँ,

$ y^{2}=8 x \text{ और } x=2 $

$ y^{2}=8(2)=16$

$ \therefore \quad y= \pm 4 $

आवश्यक क्षेत्रफल

$=2 \int_0^{2} \sqrt{8 x} d x=2 \times 2 \sqrt{2} \int_0^{2} \sqrt{x} d x$

$=4 \sqrt{2} \times \dfrac{2}{3}[x^{3 / 2}]_0^{2}$

$=\dfrac{8 \sqrt{2}}{3}[(2)^{3 / 2}]=\dfrac{8 \sqrt{2}}{3} \times 2 \sqrt{2}=\dfrac{32}{3}$ वर्ग इकाई

इसलिए, क्षेत्र का क्षेत्रफल $=\dfrac{32}{3}$ वर्ग इकाई है।

हल

दिया गया है ${(x, 0): y=\sqrt{4-x^{2}}}$

$ \begin{matrix} \Rightarrow & y^{2}=4-x^{2} \\ \Rightarrow & x^{2}+y^{2}=4 \text{ जो एक वृत्त है। } \end{matrix} $

आवश्यक क्षेत्रफल

$ =2 \cdot \int_0^{2} \sqrt{4-x^{2}} d x $

[क्योंकि वृत्त $y$-अक्ष के संदर्भ में सममित है]

$ \begin{aligned} & =2 \cdot \int_0^{2} \sqrt{(2)^{2}-x^{2}} d x \\ & =2 \cdot[\dfrac{x}{2} \sqrt{4-x^{2}}+\dfrac{4}{2} \sin ^{-1} \dfrac{x}{2}]_0^{2} \\ & =2[(\dfrac{2}{2} \sqrt{4-4}+2 \sin ^{-1}(1))-(0+0)] \\ & =2[2 \cdot \dfrac{\pi}{2}]=2 \pi \text{ वर्ग इकाई } \end{aligned} $

इसलिए, आवश्यक क्षेत्रफल $=2 \pi$ वर्ग इकाई है।

हल

दिए गए वक्र $y=2 \sqrt{x}, x=0$ और $x=1$ के बीच क्षेत्रफल ज्ञात करें।

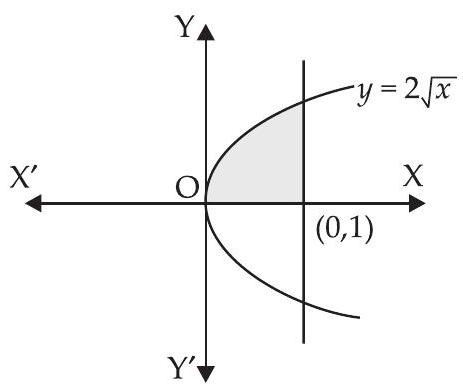
$ \begin{aligned} \text{आवश्यक क्षेत्रफल } & =\int_0^{1}(2 \sqrt{x}) d x \\ & =2 \times \dfrac{2}{3}[x^{3 / 2}]_0^{1} \\ & =\dfrac{4}{3}[(1)^{3 / 2}-0] \\ & =\dfrac{4}{3} \text{ वर्ग इकाई } \end{aligned} $

इसलिए, आवश्यक क्षेत्रफल $=\dfrac{4}{3}$ वर्ग इकाई।

हल

दिया गया है: $2 y=5 x+7, x$-अक्ष, $x=2$ और $x=8$।

मान लीजिए कि हम $2 y=5 x+7 \Rightarrow y=\dfrac{5 x+7}{2}$ के ग्राफ को खींचते हैं।

$ \begin{array}{|c|c|c|} \hline x & 1 & -1 \\ \hline y & 6 & 1 \\ \hline \end{array} $

आवश्यक छायांकित क्षेत्र का क्षेत्रफल

$=\int_2^{8}(\dfrac{5 x+7}{2}) d x=\dfrac{1}{2}[\dfrac{5}{2} x^{2}+7 x]_2^{8}$

$=\dfrac{1}{2}[\dfrac{5}{2}(64-4)+7(8-2)]$

$=\dfrac{1}{2}[\dfrac{5}{2} \times 60+7 \times 6]=\dfrac{1}{2}[150+42]$

$=\dfrac{1}{2} \times 192=96$ वर्ग इकाई

इसलिए, आवश्यक क्षेत्रफल $=96$ वर्ग इकाई।

हल

यहाँ, हमें $y=\sqrt{x-1}$ दिया गया है

$\Rightarrow \quad y^{2}=x-1$ (परबोला)

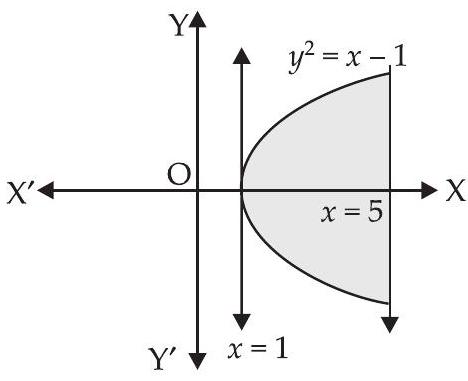
आवश्यक क्षेत्र का क्षेत्रफल

$=\int_1^{5} \sqrt{x-1} d x$

$=\dfrac{2}{3}[(5-1)^{3 / 2}-0]=\dfrac{2}{3} \times(4)^{3 / 2}$

$=\dfrac{2}{3} \times 8=\dfrac{16}{3}$ वर्ग इकाई

इसलिए, आवश्यक क्षेत्रफल $=\dfrac{16}{3}$ वर्ग इकाई है।

हल

यहाँ हमें $y=\sqrt{a^{2}-x^{2}}$ दिया गया है

$ \begin{matrix} \Rightarrow & y^{2}=a^{2}-x^{2} \\ \Rightarrow & x^{2}+y^{2}=a^{2} \end{matrix} $

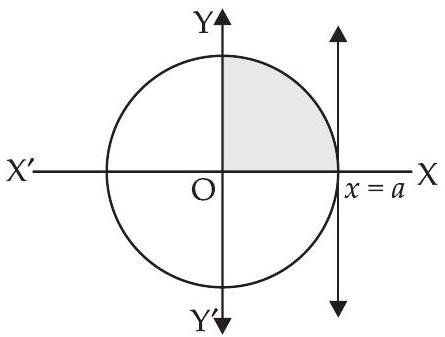
छायांकित क्षेत्र का क्षेत्रफल

$=2[(1)^{3 / 2}-0]-\dfrac{3}{2}[(1)^{2}-0]$

$=[\dfrac{x}{2} \sqrt{a^{2}-x^{2}}+\dfrac{a^{2}}{2} \sin ^{-1} \dfrac{x}{a}]_0^{a}$

$ \begin{aligned} & =[\dfrac{a}{2} \sqrt{a^{2}-a^{2}}+\dfrac{a^{2}}{2} \sin ^{-1} \dfrac{a}{a}-0-0] \\ & =\dfrac{a^{2}}{2} \sin ^{-1}(1)=\dfrac{a^{2}}{2} \cdot \dfrac{\pi}{2}=\dfrac{\pi a^{2}}{4} \end{aligned} $

इसलिए, आवश्यक क्षेत्रफल $=\dfrac{\pi a^{2}}{4}$ वर्ग इकाई है।

हल

हमें वक्र $y=\sqrt{x}$ और रेखा $y=x$ के समीकरण दिया गया है।

$y=\sqrt{x} \Rightarrow y^{2}=x$ और $y=x$ को हल करने पर, हम प्राप्त करते हैं

$ \begin{aligned} x^{2} & =x \Rightarrow x^{2}-x=0 \\ \Rightarrow \quad x(x-1) & =0\\ \therefore x=0,1 \end{aligned} $

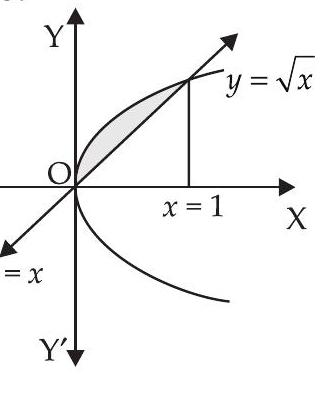
छायांकित क्षेत्र का आवश्यक क्षेत्रफल

$ \begin{aligned} & =\int_0^{1} \sqrt{x} d x-\int_0^{1} x d x \\ & =\dfrac{2}{3}[x^{3 / 2}]_0^{1}-\dfrac{1}{2}[x^{2}]_0^{1} \\ & =\dfrac{2}{3}[(1)^{3 / 2}-0]-\dfrac{1}{2}[(1)^{2}-0] \\ `

& =\dfrac{2}{3}-\dfrac{1}{2} \Rightarrow \dfrac{4-3}{6} \Rightarrow \dfrac{1}{6} \text{ sq. units } \end{aligned} $

अतः, अभीष्ट क्षेत्रफल $=\dfrac{1}{6}$ sq. units.

हल

हमें दिया गया है कि $y=-x^{2}$ या $x^{2}=-y$ और रेखा $x+y+2=0$

दोनों समीकरणों को हल करने पर, हम प्राप्त करते हैं

$x-x^{2}+2 =0$

$\Rightarrow x^{2}-x-2 =0$

$\Rightarrow x^{2}-2 x+x-2 =0$

$\Rightarrow x(x-2)+1(x-2) =0$

$\Rightarrow (x-2)(x+1) =0$

$\therefore x =-1,2$

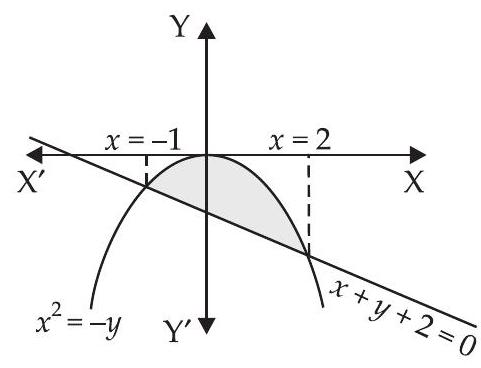
अभीष्ट छायांकित क्षेत्र का क्षेत्रफल

$=|\int _{-1}^{2}(-x-2) d x-\int _{-1}^{2}-x^{2} d x|$

$\Rightarrow \quad |-[\dfrac{x^{2}}{2}+2 x] _{-1}^{2} +\dfrac{1}{3}[x^{3}] _{-1}^{2}|$

$\Rightarrow \quad |-[(\dfrac{4}{2}+4)-(\dfrac{1}{2}-2)]+\dfrac{1}{3}(8+1)|$

$\Rightarrow \quad |-(6+\dfrac{3}{2})+\dfrac{1}{3}(9)|\Rightarrow|-\dfrac{15}{2}+3|$

$\Rightarrow \quad |\dfrac{-15+6}{2}|=|\dfrac{-9}{2}|=\dfrac{9}{2} \text{ sq. units }$

हल

दिए गए वक्रों के समीकरण हैं $ y = \sqrt{x} $ और $ x = 2y + 3 $ पहले चतुर्थांश में।

दोनों समीकरणों को $ y $ के संदर्भ में हल करने पर, हम प्राप्त करते हैं

$ \begin{aligned} & y = \sqrt{2y + 3} \ & \Rightarrow y^2 = 2y + 3 \ & \Rightarrow y^2 - 2y - 3 = 0 \ & \Rightarrow y^2 - 3y + y - 3 = 0 \ & \Rightarrow y(y - 3) + 1(y - 3) = 0 \ & \Rightarrow (y + 1)(y - 3) = 0 \ & \Rightarrow y = -1, 3 \end{aligned} $

$\therefore$ छायांकित क्षेत्र का अभीष्ट क्षेत्रफल,

$ \begin{aligned}

A &= \int_{0}^{3} (2y + 3 - y^2) , dy = \left[ \frac{2y^2}{2} + 3y - \frac{y^3}{3} \right]_{0}^{3} \ &= \left[ \frac{18}{2} + 9 - 9 - 0 \right] \ &= 9 \text{ वर्ग इकाई।} \end{aligned} $

हल

कक्षाओं के समीकरण निम्नलिखित हैं

$$ \begin{equation*} x^{2}+y^{2}=4 x \qquad…(i) \end{equation*} $$

$$ \begin{equation*} \text{ और } \quad y^{2}=2 x \qquad…(ii) \end{equation*} $$

$ \begin{matrix} \Rightarrow & x^{2}-4 x+y^{2}=0 \\ \Rightarrow & x^{2}-4 x+4-4+y^{2}=0 \\ \Rightarrow & (x-2)^{2}+y^{2}=4 \end{matrix} $

स्पष्ट रूप से यह एक वृत्त के समीकरण है जिसके केंद्र $(2,0)$ और त्रिज्या 2 है।

$ x^{2}+y^{2}=4 x $ और $ y^{2}=2 x $ को हल करते हैं

$ x^{2}+2 x=4 x $

$\Rightarrow x^{2}+2 x-4 x=0$

$\Rightarrow \quad x^{2}-2 x=0$

$\Rightarrow \quad x(x-2)=0$

$\therefore \quad x=0,2$

आवश्यक क्षेत्र का क्षेत्रफल

$=2[\int_0^{2} \sqrt{4-(x-2)^{2}} d x-\int_0^{2} \sqrt{2 x} d x]$

[ $\therefore$ पराबोला और वृत्त दोनों $x$-अक्ष के संदर्भ में सममित हैं।]

$=2[\dfrac{x-2}{2} \sqrt{4-(x-2)^{2}}+\dfrac{4}{2} \sin ^{-1} \dfrac{x-2}{2}]_0^{2}-2 \cdot \sqrt{2} \cdot \dfrac{2}{3}[x^{3 / 2}]_0^{2}$

$=2[(0+0)-(0+2 \sin ^{-1}(-1)]-\dfrac{4 \sqrt{2}}{3}[2^{3 / 2}-0].$

$=-2 \times 2 \cdot(-\dfrac{\pi}{2})-\dfrac{4 \sqrt{2}}{3} \cdot 2 \sqrt{2}$

$=2 \pi-\dfrac{16}{3}=2(\pi-\dfrac{8}{3})$ वर्ग इकाई

अतः, आवश्यक क्षेत्र $=2(\pi-\dfrac{8}{3})$ वर्ग इकाई है।

हल

कक्षाओं के समीकरण निम्नलिखित हैं

$y=\sin x$ $x=0$ और $x=2 \pi$ के बीच।

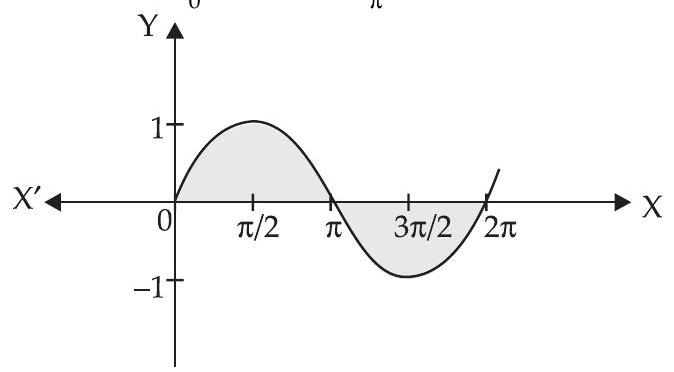
Required area $=\int_0^{\pi} \sin x d x+\int _{\pi}^{2 \pi}|\sin x| d x$

$ \begin{aligned} & =-[\cos x]_0^{\pi}+|(-\cos x)| _{\pi}^{2 \pi}=-[\cos \pi-\cos 0]+[\cos 2 \pi-\cos \pi] \\ & =-[-1-1]+[1+1]=2+2=4 \text{ sq. units } \end{aligned} $

हल

$\triangle ABC$ के शीर्षों के निर्देशांक दिए गए हैं $A(-1,1)$, B $(0,5)$ और $C(3,2)$।

$AB$ का समीकरण है $

$y-1=\dfrac{5-1}{0+1}(x+1)$

$\Rightarrow y-1 =4 x+4$

$\therefore y =4 x+4+1 \Rightarrow y=4 x+5 \qquad…(1)$

$BC\ $ का समीकरण है $ \quad y-5=\dfrac {2-5}{3-0}(x-0)$

$ \Rightarrow \quad y-5=-x $

$ \begin{aligned} \therefore \quad y=5-x \qquad…(ii) \end{aligned} $

$CA$ का समीकरण है

$ \begin{aligned} y-1 & =\dfrac{2-1}{3+1}(x+1) \\ \Rightarrow \quad y-1 & =\dfrac{1}{4} x+\dfrac{1}{4} \Rightarrow y=\dfrac{1}{4} x+\dfrac{1}{4}+1 \\ \therefore \quad y & =\dfrac{1}{4} x+\dfrac{5}{4}=\dfrac{1}{4}(5+x) \end{aligned} $

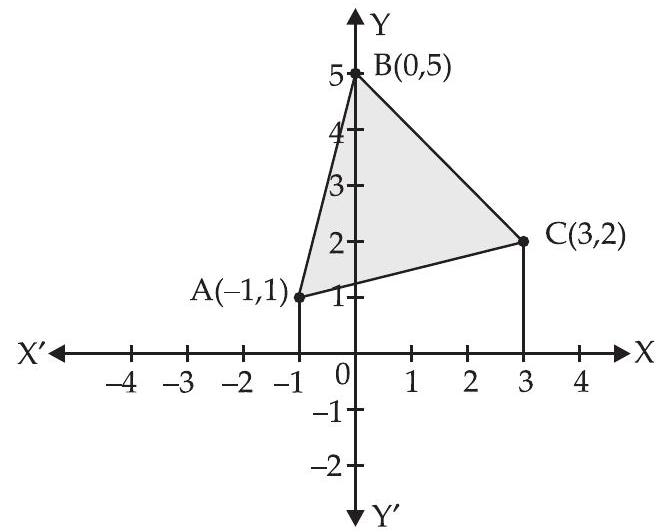
$\triangle ABC$ का क्षेत्रफल

$ \begin{aligned} & =\int _{-1}^{0}(4 x+5) d x+\int_0^{3}(5-x) d x-\int _{-1}^{3} \dfrac{1}{4}(5+x) d x \\ & =\dfrac{4}{2}[x^{2}] _{-1}^{0}+5[x] _{-1}^{0}+5[x]_0^{3}-\dfrac{1}{2}[x^{2}]_0^{3}-\dfrac{1}{4}[5 x+\dfrac{x^{2}}{2}] _{-1}^{3} \end{aligned} $

$ \begin{aligned} & =2(0-1)+5(0+1)+5(3-0)-\dfrac{1}{2}(9-0) \\ & -\dfrac{1}{4}[(15+\dfrac{9}{2})-(-5+\dfrac{1}{2})] \\ & =-2+5+15-\dfrac{9}{2}-\dfrac{1}{4}(\dfrac{39}{2}+\dfrac{9}{2}) \\ & =18-\dfrac{9}{2}-\dfrac{1}{4} \times \dfrac{48}{2}=18-\dfrac{9}{2}-6=12-\dfrac{9}{2}=\dfrac{15}{2} \text{ sq. units } \end{aligned} $

अतः, आवश्यक क्षेत्रफल $=\dfrac{15}{2}$ sq. units।

हल

दिया गया है:

${(x, y): y^{2} \leq 6 a x.$ और $.x^{2}+y^{2} \leq 16 a^{2}}$

पराबोला का समीकरण है

$$ \begin{equation*} y^{2}=6 a x \qquad…(i) \end{equation*} $$

और वृत्त का समीकरण है

$$ \begin{equation*} x^{2}+y^{2} \leq 16 a^{2} \qquad…(ii) \end{equation*} $$

समीकरण (i) और (ii) को हल करने पर हम प्राप्त करते हैं

$ \begin{matrix} \Rightarrow & x^{2}+6 a x-16 a^{2}=0 \\ \Rightarrow & x^{2}+8 a x-2 a x-16 a^{2}=0 \\ \Rightarrow & x(x+8 a)-2 a(x+8 a)=0 \\ \Rightarrow & (x+8 a)(x-2 a)=0 \end{matrix} $

$\therefore x=2 a$ और $x=-8 a$। (इसे अस्वीकृत कर दिया गया है क्योंकि यह क्षेत्र के बाहर है)

आवश्यक छायांकित क्षेत्र का क्षेत्रफल

$ \begin{aligned} & =2[\int_0^{2 a} \sqrt{6 a x} d x+\int _{2 a}^{4 a} \sqrt{16 a^{2}-x^{2}} d x] \\ & =2[\sqrt{6 a} \int_0^{2 a} \sqrt{x} d x+\int _{2 a}^{4 a} \sqrt{(4 a)^{2}-x^{2}} d x] \\ & =2 \sqrt{6 a} \cdot \dfrac{2}{3} \cdot[x^{3 / 2}]_0^{2 a}+2[\dfrac{x}{2} \sqrt{(4 a)^{2}-x^{2}}+\dfrac{16 a^{2}}{2} \sin ^{-1} \dfrac{x}{4 a}] _{2 a}^{4 a} \\ & =\dfrac{4 \sqrt{6}}{3} \cdot \sqrt{a}[(2 a)^{3 / 2}-0]+[x \sqrt{(4 a)^{2}-x^{2}}+16 a^{2} \sin ^{-1} \dfrac{x}{4 a}] _{2 a}^{4 a} \end{aligned} $

$ \begin{aligned} & =\dfrac{4 \sqrt{6}}{3} \sqrt{a} \cdot 2 \sqrt{2} \cdot a^{3 / 2}+[0+16 a^{2} \sin ^{-1}(\dfrac{4 a}{4 a})-2 a \sqrt{16 a^{2}-4 a^{2}}-16 a^{2} \sin ^{-1} \dfrac{2 a}{4 a}] \\ & =\dfrac{8 \sqrt{12}}{3} a^{2}+[16 a^{2} \cdot \sin ^{-1}(1)-2 a \cdot 2 \sqrt{3} a-16 a^{2} \cdot \sin ^{-1} \dfrac{1}{2}] \\ & =\dfrac{16 \sqrt{3}}{3} a^{2}+[16 a^{2} \cdot \dfrac{\pi}{2}-2 a \cdot 2 \sqrt{3} a-16 a^{2} \cdot \dfrac{\pi}{6}] \\ & =\dfrac{16 \sqrt{3}}{3} a^{2}+8 \pi a^{2}-4 \sqrt{3} a^{2}-\dfrac{8}{3} \pi a^{2} \\

$$ \begin{aligned} & =\dfrac{16 \sqrt{3}}{3}-4 \sqrt{3}) a^{2}+\dfrac{16}{3} \pi a^{2}=\dfrac{4 \sqrt{3}}{3} a^{2}+\dfrac{16}{3} \pi a^{2} \\ & =\dfrac{4}{3}(\sqrt{3}+4 \pi) a^{2} \end{aligned} $$

अतः, आवश्यक क्षेत्रफल $=\dfrac{4}{3}(\sqrt{3}+4 \pi) a^{2}$ वर्ग इकाई है।

हल

दिया गया है:

$x+2 y=2 \qquad…(i)$

$ y-x=1 \qquad…(ii) $

$\text{ और } \qquad 2 x+y=7 \qquad…(iii)$

$\begin{array}{|c|c|c|} \hline x & 0 & 2 \\ \hline y & 1 & 0 \\ \hline \end{array}$

$\begin{array}{|c|c|c|} \hline x & 0 & -1 \\ \hline y & 1 & 0 \\ \hline \end{array}$

$\begin{array}{|c|c|c|} \hline x & 0 & 7 / 2 \\ \hline y & 7 & 0 \\ \hline \end{array}$

समीकरण (ii) और (iii) को हल करने पर हम प्राप्त करते हैं:

$y =1+x$

$\therefore 2 x+1+x =7$

$3 x =6$

$\Rightarrow x =2$

$\therefore y =1+2$

$=3$

$B$ के निर्देशांक $(2,3)$ हैं।

समीकरण (i) और (iii) को हल करने पर हम प्राप्त करते हैं:

$x +2 y =2$

$\therefore x =2-2 y$

$2 x+y =7$

$ 2(2-2 y)+y =7$

$\Rightarrow 4-4 y+y =7 \Rightarrow-3 y=3$

$\therefore y =-1 \text{ और } x=4$

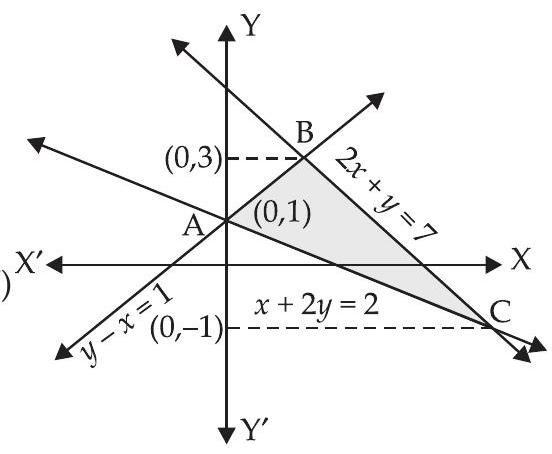
$\therefore$ $C$ के निर्देशांक $(4,-1)$ और $A$ के निर्देशांक $(0,1)$ हैं।

y-अक्ष पर सीमाएँ लेने पर हम प्राप्त करते हैं:

$ \begin{matrix} \int _{-1}^{3} x _{BC} d y-\int _{-1}^{1} x _{AC} d y-\int_1^{3} x _{AB} d y \\ =\int _{-1}^{3} \dfrac{7-y}{2} d y-\int _{-1}^{1}(2-2 y) d y-\int_1^{3}(y-1) d y \\ =\dfrac{1}{2}[7 y-\dfrac{y^{2}}{2}] _{-1}^{3}-2[y-\dfrac{y^{2}}{2}] _{-1}^{1}-[\dfrac{y^{2}}{2}-y]_1^{3} \\ =\dfrac{1}{2}[(21-\dfrac{9}{2})-(-7-\dfrac{1}{2})]-2[(1-\dfrac{1}{2})-(-1-\dfrac{1}{2})] -[(\dfrac{9}{2}-3)-(\dfrac{1}{2}-1)] \\ =\dfrac{1}{2} \times 24-2 \times 2-2 \Rightarrow 12-4-2=6 \text{ वर्ग इकाई } \end{matrix} $

अतः, आवश्यक क्षेत्रफल $=6$ वर्ग इकाई है।

हल

दिया गया है

और

$ \begin{aligned} & y =4 x+5 \qquad…(i)\\ & y =5-x \qquad…(ii)\\ & 4 y =x+5 \qquad…(iii) \end{aligned} $

$\begin{array}{|c|c|c|} \hline x & 0 & -5 / 4 \\ \hline y & 5 & 0 \\ \hline \end{array}$

$\begin{array}{|c|c|c|} \hline x & 0 & 5 \\ \hline y & 5 & 0 \\ \hline \end{array}$

$\begin{array}{|c|c|c|} \hline x & 0 & -5 \\ \hline y & 5 /4 & 0 \\ \hline \end{array}$

समीकरण (i) और (ii) को हल करने पर हम प्राप्त करते हैं

$ \begin{matrix} 4 x+5 =5-x \\ \Rightarrow x =0 \text{ और } y=5 \end{matrix} $

$\therefore$ बिंदु $A=(0,5)$ के निर्देशांक

समीकरण (ii) और (iii) को हल करने पर

$ \begin{aligned} y & =5-x \\ 4 y & =x+5 \\ 5 y & =10 \end{aligned} $

$\therefore y=2$ और $x=3$

$\therefore$ बिंदु $B=(3,2)$ के निर्देशांक

समीकरण (i) और (iii) को हल करने पर

$ y=4 x+5 $

$ \begin{aligned} & 4 y=x+5 \\ & \Rightarrow \quad 4(4 x+5)=x+5 \\ & \Rightarrow \quad 16 x+20=x+5 \Rightarrow 15 x=-15 \\ & \therefore \quad x=-1 \text{ और } y=1 \end{aligned} $

$\therefore$ बिंदु $C=(-1,1)$ के निर्देशांक।

$\therefore$ आवश्यक क्षेत्र का क्षेत्रफल

$=\int _{-1}^{0} y _{AC} d x+\int_0^{3} y _{AB} d x-\int _{-1}^{3} y _{CB} d x$

$=\int _{-1}^{0}(4 x+5) d x+\int_0^{3}(5-x) d x-\int _{-1}^{3} \dfrac{x+5}{4} d x$

$=[4 \dfrac{x^{2}}{2}+5 x] _{-1}^{0}+[5 x-\dfrac{x^{2}}{2}]_0^{3}-\dfrac{1}{4}[\dfrac{x^{2}}{2}+5 x] _{-1}^{3}$

$=[(0+0)-(2-5)]+[(15-\dfrac{9}{2})-(0-0)]-\dfrac{1}{4}[(\dfrac{9}{2}+15)-(\dfrac{1}{2}-5)]$

$=3+\dfrac{21}{2}-\dfrac{1}{4}[\dfrac{39}{2}+\dfrac{9}{2}]=3+\dfrac{21}{2}-\dfrac{1}{4} \times 24 \Rightarrow 3+\dfrac{21}{2}-6$

$=\dfrac{15}{2}$ वर्ग इकाई

अतः, आवश्यक क्षेत्रफल $=\dfrac{15}{2}$ वर्ग इकाई है।

हल

दी गई वक्र का समीकरण $y=2 \cos x$ है

$\therefore$ छायांकित क्षेत्र का क्षेत्रफल

$ \int_0^{2 \pi} 2 \cos x d x=\int_0^{\pi / 2} 2 \cos x d x+\int _{\pi / 2}^{3 \pi / 2}|2 \cos x| d x+\int _{3 \pi / 2}^{2 \pi} 2 \cos x d x $

$ \begin{aligned} & =2[\sin x]_0^{\pi / 2}+|[2 \sin x] _{\pi / 2}^{3 \pi / 2}|+2[\sin x] _{3 \pi / 2}^{2 \pi} \\ & =2[\sin \dfrac{\pi}{2}-\sin 0]+|2(\sin \dfrac{3 \pi}{2}-\sin \dfrac{\pi}{2})| \\ & +2[\sin 2 \pi-\sin \dfrac{3 \pi}{2}] \\ & =2(1)+|2(-1-1)|+2(0+1)=2+4+2=8 \text{ वर्ग इकाई } \end{aligned} $

हल

दिए गए समीकरण हैं

$y=1+|x+1|, x=-3$

और $x=3, y=0$

लेते हैं $y=1+|x+1|$

$\Rightarrow \quad y=1+x+1$

$\Rightarrow \quad y=x+2$

और $y=1-x-1 \Rightarrow y=-x$

हल करने पर हमें $x=-1$ मिलता है

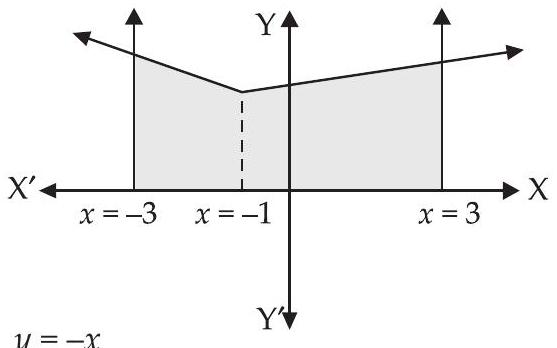
आवश्यक क्षेत्र का क्षेत्रफल

$ \begin{aligned} & =\int _{-3}^{-1}-x d x+\int _{-1}^{3}(x+2) d x \\ & =-[\dfrac{x^{2}}{2}] _{-3}^{-1}+[\dfrac{x^{2}}{2}+2 x] _{-1}^{3}=-[\dfrac{1}{2}-\dfrac{9}{2}]+[(\dfrac{9}{2}+6)-(\dfrac{1}{2}-2)] \\ & =-(-4)+[\dfrac{21}{2}+\dfrac{3}{2}]=4+12=16 \text{ वर्ग इकाई } \end{aligned} $

अतः, आवश्यक क्षेत्र $=16$ वर्ग इकाई है।

हल

दिया गया है $y$-अक्ष, $y=\cos x, y=\sin x, 0 \leq x \leq \dfrac{\pi}{2}$

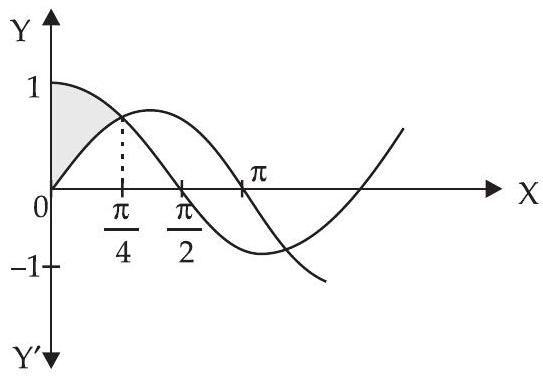
$ \begin{aligned} \text{आवश्यक क्षेत्रफल } & =\int_0^{\pi / 4} \cos x d x-\int_0^{\pi / 4} \sin x d x \\ & =[\sin x]_0^{\pi / 4}-[-\cos x]_0^{\pi / 4} \\ & =[\sin \dfrac{\pi}{4}-\sin 0]+[\cos \dfrac{\pi}{4}-\cos 0] \\ & =[\dfrac{1}{\sqrt{2}}-0+\dfrac{1}{\sqrt{2}}-1]=\dfrac{2}{\sqrt{2}}-1 \\ & =(\sqrt{2}-1) \text{ वर्ग इकाई } \end{aligned} $

अतः, सही विकल्प (c) है।

• विकल्प (a) $\sqrt{2}$ वर्ग इकाई: यह विकल्प गलत है क्योंकि गणना किया गया क्षेत्रफल $\sqrt{2} - 1$ वर्ग इकाई है, न कि $\sqrt{2}$ वर्ग इकाई। अंतिम परिणाम में 1 के घटाव की आवश्यकता है।

• विकल्प (b) $(\sqrt{2}+1)$ वर्ग इकाई: यह विकल्प गलत है क्योंकि गणना किया गया क्षेत्रफल $\sqrt{2} - 1$ वर्ग इकाई है, न कि $\sqrt{2} + 1$ वर्ग इकाई। सही क्षेत्रफल की गणना में 1 के जोड़ का उपयोग नहीं किया जाता है।

• विकल्प (d) $(2 \sqrt{2}-1)$ वर्ग इकाई: यह विकल्प गलत है क्योंकि गणना किया गया क्षेत्रफल $\sqrt{2} - 1$ वर्ग इकाई है, न कि $2 \sqrt{2} - 1$ वर्ग इकाई। $\sqrt{2}$ के सामने 2 के गुणक का उपयोग सही क्षेत्रफल की गणना में नहीं किया जाता है।

हल

दिया गया है: परवलय का समीकरण

$ x^{2}=4 y \qquad…(i)$

और सीधी रेखा का समीकरण

$x=4 y-2 \qquad…(ii)$

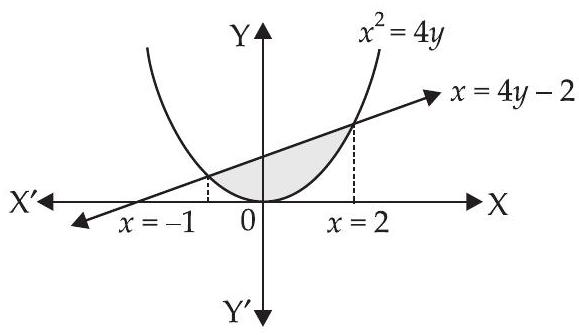
समीकरण (i) और (ii) को हल करने पर हम प्राप्त करते हैं

$$ y=\dfrac{x^{2}}{4} $$

$$ \begin{aligned} & x=4(\dfrac{x^{2}}{4})-2 \\ & \Rightarrow \quad x=x^{2}-2 \\ & \Rightarrow \quad x^{2}-x-2=0 \Rightarrow x^{2}-2 x+x-2=0 \\ & \Rightarrow x(x-2)+1(x-2)=0 \Rightarrow(x-2)(x+1)=0 \therefore x=-1, x=2 \\ & \text{ आवश्यक क्षेत्रफल }=\int _{-1}^{2} \dfrac{x+2}{4} d x-\int _{-1}^{2} \dfrac{x^{2}}{4} d x \\ & =\dfrac{1}{4}[\dfrac{x^{2}}{2}+2 x] _{-1}^{2}-\dfrac{1}{4} \cdot \dfrac{1}{3}[x^{3}] _{-1}^{2} \\ & =\dfrac{1}{4}[(\dfrac{4}{2}+4)-(\dfrac{1}{2}-2)]-\dfrac{1}{12}[8+1] \\ & =\dfrac{1}{4}[6+\dfrac{3}{2}]-\dfrac{1}{12}[9]=\dfrac{1}{4} \times \dfrac{15}{2}-\dfrac{3}{4} \\ & =\dfrac{15}{8}-\dfrac{3}{4}=\dfrac{9}{8} \text{ वर्ग इकाई } \end{aligned} $$

अतः, सही विकल्प $(d)$ है।

• विकल्प (a) $\dfrac{3}{8}$ वर्ग इकाई: यह विकल्प गलत है क्योंकि वक्र और सीधी रेखा द्वारा घिरे क्षेत्र का गणनात्मक क्षेत्रफल $\dfrac{9}{8}$ वर्ग इकाई है, जो $\dfrac{3}{8}$ वर्ग इकाई से बहुत अधिक है। एकीकरण और बीजगणितीय कदम दिखाते हैं कि क्षेत्रफल $\dfrac{3}{8}$ वर्ग इकाई से कम नहीं है।

• विकल्प (b) $\dfrac{5}{8}$ वर्ग इकाई: यह विकल्प गलत है क्योंकि वक्र और सीधी रेखा द्वारा घिरे क्षेत्र का गणनात्मक क्षेत्रफल $\dfrac{9}{8}$ वर्ग इकाई है। विस्तारित एकीकरण प्रक्रिया और बीजगणितीय सरलीकरण पुष्टि करते हैं कि क्षेत्रफल $\dfrac{5}{8}$ वर्ग इकाई से अधिक है।

• विकल्प (c) $\dfrac{7}{8}$ वर्ग इकाई: यह विकल्प गलत है क्योंकि वक्र और सीधी रेखा द्वारा घिरे क्षेत्र का गणनात्मक क्षेत्रफल $\dfrac{9}{8}$ वर्ग इकाई है। एकीकरण और बीजगणितीय कदम स्पष्ट रूप से दिखाते हैं कि क्षेत्रफल $\dfrac{7}{8}$ वर्ग इकाई से थोड़ा अधिक है।

हल

यहाँ, वक्र का समीकरण $y=\sqrt{16-x^{2}}$ है

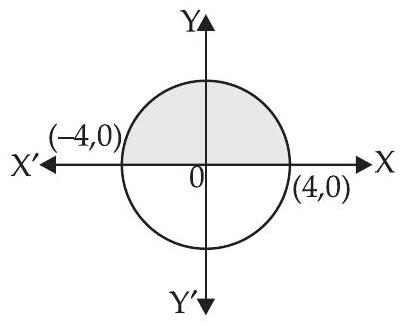
आवश्यक क्षेत्रफल

$$ \begin{aligned} & =2[\int_0^{4} \sqrt{16-x^{2}} d x] \\ & =2[\dfrac{x}{2} \sqrt{16-x^{2}}+\dfrac{16}{2} \sin ^{-1} \dfrac{x}{4}]_0^{4} \\ & =2[(0+8 \sin ^{-1} \dfrac{4}{4})-(0+0)] \\ & =2[8 \sin ^{-1}(1)]=16 \cdot \dfrac{\pi}{2}=8 \pi \text{ वर्ग इकाई } \end{aligned} $$

अतः, सही विकल्प है $(a)$।

• विकल्प (b) $20 \pi$ वर्ग इकाई गलत है क्योंकि अन्तगर्त क्षेत्रफल के अनुपात के अन्तगर्त वक्र $y=\sqrt{16-x^{2}}$ के अंतगर्त क्षेत्रफल $8 \pi$ वर्ग इकाई है, न कि $20 \pi$ वर्ग इकाई।

• विकल्प (c) $16 \pi$ वर्ग इकाई गलत है क्योंकि अन्तगर्त क्षेत्रफल के अनुपात के अन्तगर्त वक्र $y=\sqrt{16-x^{2}}$ के अंतगर्त क्षेत्रफल $8 \pi$ वर्ग इकाई है, न कि $16 \pi$ वर्ग इकाई।

• विकल्प (d) $256 \pi$ वर्ग इकाई गलत है क्योंकि अन्तगर्त क्षेत्रफल के अनुपात के अन्तगर्त वक्र $y=\sqrt{16-x^{2}}$ के अंतगर्त क्षेत्रफल $8 \pi$ वर्ग इकाई है, न कि $256 \pi$ वर्ग इकाई।

हल

दिया गया वृत्त का समीकरण $x^{2}+y^{2}=32 \Rightarrow x^{2}+y^{2}=(4 \sqrt{2})^{2}$ और रेखा $y=x$ और $x$-अक्ष है।

दो समीकरणों को हल करने पर हमें मिलता है

$x^{2}+x^{2} =32$

$\Rightarrow 2 x^{2} =32$

$\Rightarrow x^{2} =16$

$\therefore x = \pm 4$

आवश्यक क्षेत्रफल

$$ \begin{aligned} & =\int_0^{4} x d x+\int_4^{4 \sqrt{2}} \sqrt{(4 \sqrt{2})^{2}-x^{2}} d x \\

& =\dfrac{1}{2}[x^{2}]_0^{4}+[\dfrac{x}{2} \sqrt{(4 \sqrt{2})^{2}-x^{2}}+\dfrac{32}{2} \sin ^{-1} \dfrac{x}{4 \sqrt{2}}]_4^{4 \sqrt{2}} \\ & =\dfrac{1}{2}[16-0]+[0+16 \sin ^{-1}(\dfrac{4 \sqrt{2}}{4 \sqrt{2}})-2 \sqrt{32-16}-16 \sin ^{-1} \dfrac{4}{4 \sqrt{2}}] \\ & =8+[16 \sin ^{-1}(1)-8-16 \sin ^{-1} \dfrac{1}{\sqrt{2}}] \\ & =8+16 \cdot \dfrac{\pi}{2}-8-16 \cdot \dfrac{\pi}{4}=8 \pi-4 \pi=4 \pi \text{ sq. units } \end{aligned} $

अतः, सही विकल्प है $(b)$।

• विकल्प (a) $16 \pi$ sq. units: यह विकल्प गलत है क्योंकि यह क्षेत्रफल को अधिक अनुमानित करता है। वास्तविक क्षेत्रफल की गणना रेखा $y=x$ और वृत्त $x^2 + y^2 = 32$ द्वारा घिरे क्षेत्र के अनुसार की जाती है, जो $4 \pi$ sq. units के छोटे क्षेत्रफल के बराबर होता है।

• विकल्प (c) $32 \pi$ sq. units: यह विकल्प गलत है क्योंकि यह क्षेत्रफल को बहुत अधिक अनुमानित करता है। वृत्त का कुल क्षेत्रफल $32 \pi$ sq. units होता है, लेकिन प्रश्न में बताए गए क्षेत्र केवल वृत्त के एक छोटे हिस्से के बराबर होता है, जो पहले चतुर्थांश में होता है और रेखा $y=x$ और $x$-अक्ष द्वारा घिरा होता है।

• विकल्प (d) 24 sq. units: यह विकल्प गलत है क्योंकि यह वृत्तीय खंड के क्षेत्रफल को सही तरीके से गणना नहीं करता है। क्षेत्रफल की गणना रेखा $y=x$ के तल के त्रिकोणीय क्षेत्र और वृत्त के खंड के बराबर होती है, जो $4 \pi$ sq. units के बराबर होती है, न कि 24 sq. units।

हल

दिया गया है: $y=\cos x, x=0, x=\pi$

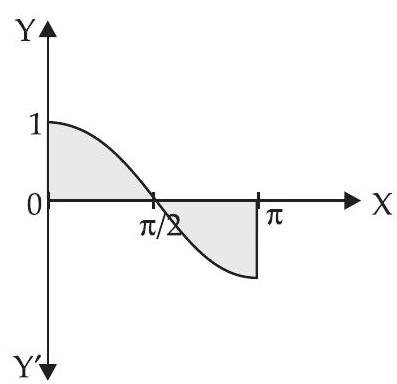
आवश्यक क्षेत्रफल

$ \begin{aligned} & =\int_0^{\pi / 2} \cos x d x+|\int _{\pi / 2}^{\pi} \cos x d x| \\ & =[\sin x]_0^{\pi / 2}+|(\sin x) _{\pi / 2}^{\pi}| \\

& =[\sin \dfrac{\pi}{2}-\sin 0]+|[\sin \pi-\sin \dfrac{\pi}{2}]| \\ & =(1-0)+|0-1|=1+1=2 \text{ वर्ग इकाई } \end{aligned} $

अतः, सही विकल्प है $(a)$।

• विकल्प (b) 4 वर्ग इकाई: यह विकल्प गलत है क्योंकि $x = 0$ से $x = \pi$ तक कोसाइन फलन के समकालीन क्षेत्रफल 2 वर्ग इकाई होता है, न कि 4। गणना दर्शाती है कि इन सीमाओं के बीच $y = \cos x$ वक्र के तल के नीचे क्षेत्रफल 2 वर्ग इकाई होता है।

• विकल्प (c) 3 वर्ग इकाई: यह विकल्प गलत है क्योंकि $x = 0$ से $x = \pi$ तक कोसाइन फलन के समकालीन क्षेत्रफल 2 वर्ग इकाई होता है, न कि 3। गणना पुष्टि करती है कि इन सीमाओं के बीच $y = \cos x$ वक्र के तल के नीचे क्षेत्रफल 2 वर्ग इकाई होता है।

• विकल्प (d) 1 वर्ग इकाई: यह विकल्प गलत है क्योंकि $x = 0$ से $x = \pi$ तक कोसाइन फलन के समकालीन क्षेत्रफल 2 वर्ग इकाई होता है, न कि 1। गणना दर्शाती है कि इन सीमाओं के बीच $y = \cos x$ वक्र के तल के नीचे क्षेत्रफल 2 वर्ग इकाई होता है।

हल

दी गई परबोला का समीकरण $y^{2}=x$ और सीधी रेखा का समीकरण $2 y=x$ है

समीकरण (i) और (ii) को हल करने पर हम प्राप्त करते हैं

$ \begin{aligned} & (\dfrac{x}{2})^{2}=x \Rightarrow \dfrac{x^{2}}{4}=x \Rightarrow x^{2}=4 x \\ & \Rightarrow x(x-4)=0\\ & \therefore x=0,4 \end{aligned} $

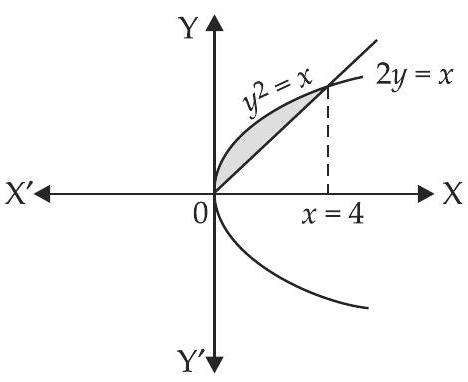
अपेक्षित क्षेत्रफल

$ \begin{aligned} & =\int_0^{4} \sqrt{x} d x-\int_0^{4} \dfrac{x}{2} d x \\ & =\dfrac{2}{3}[x^{3 / 2}]_0^{4}-\dfrac{1}{2} \cdot \dfrac{1}{2}[x^{2}]_0^{4} \end{aligned} $

$=\dfrac{2}{3}[(4)^{3 / 2}-0]-\dfrac{1}{4}[(4)^{2}-0]=\dfrac{2}{3} \times 8-\dfrac{1}{4} \times 16$

$=\dfrac{16}{3}-4=\dfrac{4}{3}$ वर्ग इकाई

अतः, सही उत्तर है $(a)$।

• विकल्प (b) 1 वर्ग इकाई: यह विकल्प गलत है क्योंकि परवलय $ y^2 = x $ और रेखा $ 2y = x $ द्वारा घिरे क्षेत्र का निर्माण करने वाला क्षेत्रफल $\dfrac{4}{3}$ वर्ग इकाई है, न कि 1 वर्ग इकाई। वक्रों के तल के नीचे क्षेत्रफल के अंतर के परिणाम के रूप में 1 वर्ग इकाई नहीं आता है।

• विकल्प (c) $\dfrac{2}{3}$ वर्ग इकाई: यह विकल्प गलत है क्योंकि क्षेत्रफल की गणना फलन $\sqrt{x}$ और $\dfrac{x}{2}$ के बीच 0 से 4 के अंतराल पर समाकलन करके की जाती है। इस समाकलन और अंतर के सही परिणाम $\dfrac{4}{3}$ वर्ग इकाई है, न कि $\dfrac{2}{3}$ वर्ग इकाई।

• विकल्प (d) $\dfrac{1}{3}$ वर्ग इकाई: यह विकल्प गलत है क्योंकि समाकलन प्रक्रिया द्वारा प्राप्त क्षेत्रफल $\dfrac{4}{3}$ वर्ग इकाई है। $\dfrac{1}{3}$ वर्ग इकाई का मान सही गणितीय संचालन के परिणाम से मेल नहीं खाता है।

हल

दिया गया वक्र का समीकरण $y=\sin x$ है, जो $x=0$ और $x=\dfrac{\pi}{2}$ के बीच है

आवश्यक क्षेत्र का क्षेत्रफल

$ \begin{aligned} & =\int_0^{\pi / 2} \sin x d x=-[\cos x]_0^{\pi / 2} \\ & =-[\cos \dfrac{\pi}{2}-\cos 0] \\ & =-[0-1]=1 \text{ वर्ग इकाई } \end{aligned} $

• विकल्प (a) गलत है क्योंकि $\sin x$ के समाकलन के परिणाम $0$ से $\dfrac{\pi}{2}$ तक 2 वर्ग इकाई नहीं होता है। सही समाकलन के परिणाम 1 वर्ग इकाई है।
• विकल्प (b) गलत है क्योंकि $\sin x$ के समाकलन के परिणाम $0$ से $\dfrac{\pi}{2}$ तक 4 वर्ग इकाई नहीं होता है। सही समाकलन के परिणाम 1 वर्ग इकाई है।
• विकल्प (c) गलत है क्योंकि $\sin x$ के समाकलन के परिणाम $0$ से $\dfrac{\pi}{2}$ तक 3 वर्ग इकाई नहीं होता है। सही समाकलन के परिणाम 1 वर्ग इकाई है।

हल

दिया गया वृत्त का समीकरण $\dfrac{x^{2}}{25}+\dfrac{y^{2}}{16}=1$ है

$\Rightarrow \dfrac{y^{2}}{16}=1-\dfrac{x^{2}}{25} \Rightarrow y^{2}=\dfrac{16}{25}(25-x^{2})$

$\therefore \quad y=\dfrac{4}{5} \sqrt{25-x^{2}}$

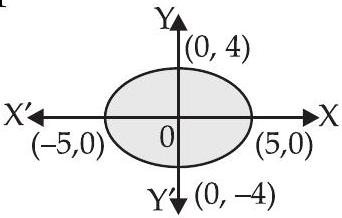
$\therefore$ चूंकि वृत्त अक्षों के संदर्भ में सममित है।

$\therefore$ आवश्यक क्षेत्रफल $=4 \times \int_0^{5} \dfrac{4}{5} \sqrt{25-x^{2}} d x=4 \times \dfrac{4}{5} \int_0^{5} \sqrt{(5)^{2}-x^{2}} d x$

$ \begin{aligned} & =\dfrac{16}{5}[\dfrac{x}{2} \sqrt{(5)^{2}-x^{2}}+\dfrac{25}{2} \sin ^{-1} \dfrac{x}{5}]_0^{5} \\ & =\dfrac{16}{5}[0+\dfrac{25}{2} \cdot \sin ^{-1}(\dfrac{5}{5})-0-0]=\dfrac{16}{5}[\dfrac{25}{2} \cdot \sin ^{-1}(1)] \\ & =\dfrac{16}{5}[\dfrac{25}{2} \cdot \dfrac{\pi}{2}]=20 \pi \text{ वर्ग इकाई } \end{aligned} $

अतः, सही उत्तर (a) है।

• विकल्प (b) $20 \pi^{2}$ वर्ग इकाई: यह विकल्प गलत है क्योंकि एक वृत्त के क्षेत्रफल का सूत्र $\pi \times a \times b$ होता है, जहाँ $a$ और $b$ क्रमशः अक्ष के अर्ध दीर्घ अक्ष और अर्ध लघु अक्ष होते हैं। सही गणना $20 \pi$ वर्ग इकाई देती है, नहीं $20 \pi^{2}$ वर्ग इकाई। $\pi^2$ की उपस्थिति एक गणितीय त्रुटि है।

• विकल्प (c) $16 \pi^{2}$ वर्ग इकाई: यह विकल्प विकल्प (b) के समान कारणों से गलत है। एक वृत्त के क्षेत्रफल की गणना $\pi \times a \times b$ सूत्र का उपयोग करके की जानी चाहिए। सही क्षेत्रफल $20 \pi$ वर्ग इकाई है, और $\pi^2$ के साथ-साथ 16 के बजाय 20 के गलत गुणक के कारण यह विकल्प गलत है।

• विकल्प (d) $25 \pi$ वर्ग इकाई: यह विकल्प गलत है क्योंकि यह वृत्त के क्षेत्रफल की गलत गणना करता है। सही क्षेत्रफल $20 \pi$ वर्ग इकाई है, जो अक्ष के अर्ध दीर्घ अक्ष $a = 5$ और अर्ध लघु अक्ष $b = 4$ से प्राप्त किया जाता है। 25 का गुणक गलत है और वृत्त के क्षेत्रफल के सही सूत्र से मेल नहीं खाता।

हल

दिया गया वृत्त का समीकरण है

$x^{2}+y^{2}=1 \Rightarrow y=\sqrt{1-x^{2}}$

क्योंकि वृत्त अक्षों के सापेक्ष सममित है।

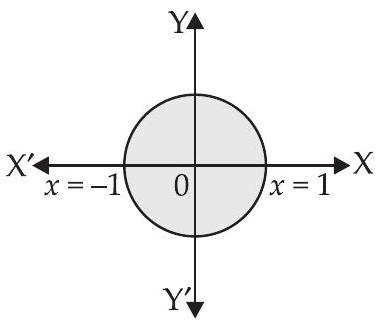
$\therefore$ आवश्यक क्षेत्रफल $=4 \times \int_0^{1} \sqrt{1-x^{2}} d x$

$=4[\dfrac{x}{2} \sqrt{1-x^{2}}+\dfrac{1}{2} \sin ^{-1} x]_0^{1}$

$=4[0+\dfrac{1}{2} \sin ^{-1}(1)-0-0]$

$=4 \times \dfrac{1}{2} \times \dfrac{\pi}{2}=\pi$ वर्ग इकाई

अतः, सही उत्तर $(b)$ है।

• विकल्प (a) $2 \pi$ वर्ग इकाई गलत है क्योंकि त्रिज्या 1 वाले वृत्त का क्षेत्रफल सूत्र $\pi r^2$ द्वारा दिया जाता है। त्रिज्या 1 वाले वृत्त का क्षेत्रफल $\pi \times 1^2 = \pi$ वर्ग इकाई होता है, न कि $2 \pi$ वर्ग इकाई।

• विकल्प (c) $3 \pi$ वर्ग इकाई गलत है क्योंकि, जैसा कि उल्लेख किया गया है, त्रिज्या 1 वाले वृत्त का क्षेत्रफल $\pi$ वर्ग इकाई होता है। $3 \pi$ वर्ग इकाई के लिए कोई गणितीय आधार नहीं है।

• विकल्प (d) $4 \pi$ वर्ग इकाई गलत है क्योंकि त्रिज्या 1 वाले वृत्त का क्षेत्रफल $\pi$ वर्ग इकाई होता है। $4 \pi$ वर्ग इकाई के लिए त्रिज्या 2 वाले वृत्त के लिए होता है, न कि त्रिज्या 1 वाले वृत्त के लिए।

हल

दिया गया रेखाओं का समीकरण है

$y=x+1, x=2 \text{ और } x=3$

आवश्यक क्षेत्रफल

$ \begin{aligned} & =\int_2^{3}(x+1) d x=[\dfrac{x^{2}}{2}+x]_2^{3} \\

& =(\dfrac{9}{2}+3)-(\dfrac{4}{2}+2) \\ & =\dfrac{15}{2}-4=\dfrac{7}{2} \text{ sq.units } \end{aligned} $

अतः, सही विकल्प (a) है।

• विकल्प (b) $\dfrac{9}{2}$ वर्ग इकाई गलत है क्योंकि फलन $y=x+1$ के लिए $x=2$ और $x=3$ के बीच क्षेत्रफल के समाकलन की गणना $\dfrac{7}{2}$ वर्ग इकाई, न कि $\dfrac{9}{2}$ वर्ग इकाई देती है।

• विकल्प (c) $\dfrac{11}{2}$ वर्ग इकाई गलत है क्योंकि फलन $y=x+1$ के लिए $x=2$ और $x=3$ के बीच क्षेत्रफल के समाकलन की गणना $\dfrac{7}{2}$ वर्ग इकाई, न कि $\dfrac{11}{2}$ वर्ग इकाई देती है।

• विकल्प (d) $\dfrac{13}{2}$ वर्ग इकाई गलत है क्योंकि फलन $y=x+1$ के लिए $x=2$ और $x=3$ के बीच क्षेत्रफल के समाकलन की गणना $\dfrac{7}{2}$ वर्ग इकाई, न कि $\dfrac{13}{2}$ वर्ग इकाई देती है।

हल

दिए गए रेखाओं के समीकरण $x=2 y+3, y=1$ और $y=-1$ हैं

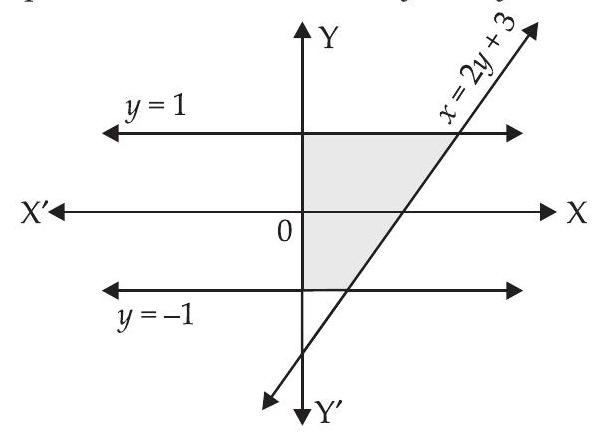
$ \begin{aligned} \text{ आवश्यक क्षेत्रफल } & =\int _{-1}^{1}(2 y+3) d y \\ & =2 \cdot \dfrac{1}{2}[y^{2}] _{-1}^{1}+3[y] _{-1}^{1} \\ & =(1-1)+3(1+1)=6 \text{ वर्ग इकाई } \end{aligned} $

अतः, सही उत्तर (c) है।

• विकल्प (a) 4 वर्ग इकाई: यह विकल्प गलत है क्योंकि दिए गए वक्र और रेखाओं $ y = 1 $ और $ y = -1 $ के बीच क्षेत्रफल के समाकलन की गणना 6 वर्ग इकाई, न कि 4 वर्ग इकाई देती है। समाकलन $\int_{-1}^{1} (2y + 3) , dy$ के मूल्यांकन के परिणाम 6 है, जैसा कि हल में दिखाया गया है।

• विकल्प (b) $\dfrac{3}{2}$ वर्ग इकाई: यह विकल्प गलत है क्योंकि दिए गए वक्र और रेखाओं $ y = 1 $ और $ y = -1 $ के बीच क्षेत्रफल के समाकलन की गणना 6 वर्ग इकाई, न कि $\dfrac{3}{2}$ वर्ग इकाई देती है। समाकलन $\int_{-1}^{1} (2y + 3) , dy$ के मूल्यांकन के परिणाम 6 है, जैसा कि हल में दिखाया गया है।

• विकल्प (d) 8 वर्ग इकाई: यह विकल्प गलत है क्योंकि दी गई वक्र और रेखाओं $ y = 1 $ और $ y = -1 $ के बीच क्षेत्रफल के समाकलन की गणना 6 वर्ग इकाई होती है, न कि 8 वर्ग इकाई। समाकलन $\int_{-1}^{1} (2y + 3) , dy$ का मूल्यांकन 6 होता है, जैसा कि समाधान में दिखाया गया है।