सीधी रेखाएँ
छोटे उत्तर प्रकार प्रश्न
1. बिंदु $(1-2)$ से गुजरने वाली एक सीधी रेखा का समीकरण ज्ञात कीजिए जो अक्षों से बराबर अंतराल काटती हो।
उत्तर दिखाएँ
हल
$X$ और $Y$ अक्षों के अनुदिश अंतराल क्रमशः $a$ और $a$ हैं।
$\therefore\quad$ रेखा का समीकरण $\dfrac{x}{a}+\dfrac{y}{a}=1\qquad\ldots\mathrm{(i)}$
क्योंकि, बिंदु $(1,-2)$ रेखा पर स्थित है,
$\therefore\quad \dfrac{1}{a}-\dfrac{2}{a} =1 $
$\Rightarrow \quad \dfrac{1-2}{a} =1 $
$\Rightarrow \quad a =-1$
$Eq. (i)$ में $a=-1$ रखने पर, हम प्राप्त करते हैं
$\Rightarrow \quad \dfrac{x}{-1}+\dfrac{y}{-1}=1$
$\Rightarrow \quad x+y=-1 $
$\Rightarrow \quad x+y+1=0$
2. बिंदु $(5,2)$ से गुजरने वाली रेखा का समीकरण ज्ञात कीजिए जो बिंदुओं $(2,3)$ और $(3,-1)$ को जोड़ने वाली रेखा के लंबवत हो।
उत्तर दिखाएँ
सोचने की प्रक्रिया
पहले से फॉर्मूला $=\dfrac{y_2-y_1}{x_2-x_1}$ का उपयोग करके ढलान ज्ञात करें।
फिर, लंबवत रेखा की ढलान $-\dfrac{1}{m}$ होती है।
हल
दिए गए बिंदु $A(5,2), B(2,3)$ और $C(3,-1)$ हैं।
बिंदुओं $B$ और $C$ के माध्यम से गुजरने वाली रेखा की ढलान $m_{B C}=\dfrac{-1-3}{3-2}=-4$
इसलिए, अभीष्ट रेखा की ढलान $ ~ \dfrac{1}{4}$ है।
क्योंकि, बिंदु $A(5,2)$ से गुजरने वाली रेखा का समीकरण जो ढलान $\dfrac{1}{4}$ रखती है, है $ \ (y-2)=\dfrac{1}{4}(x-5)$।
$ \begin{matrix} \Rightarrow \quad & 4 y-8=x-5 \\ \\ \Rightarrow \quad & x-4 y+3=0 \end{matrix} $
3. रेखाओं $y=(2-\sqrt{3})(x+5)$ और $y=(2+\sqrt{3})(x-7)$ के बीच कोण ज्ञात कीजिए।
उत्तर दिखाएँ
सोचने की प्रक्रिया
यदि ढलान $m_1$ और $m_2$ वाली रेखाओं के बीच कोण $\theta$ है, तो $\tan \theta=\Big|\dfrac{m_1-m_2}{1+m_1 m_2}\Big|$।
इस फॉर्मूला का उपयोग उपरोक्त समस्या को हल करने के लिए करें।
हल
$ \begin{aligned} \text{दी गई रेखाएँ,}\quad y & =(2-\sqrt{3})(x+5) \\ \\
\text{इस रेखा का ढलान,}\quad m_1 & =(2-\sqrt{3}) \\ \\ \text{और}\quad y & =(2+\sqrt{3})(x-7) \\ \\ \text{इस रेखा का ढलान,}\quad m_2 & =(2+\sqrt{3}) \end{aligned} $
मान लीजिए $\theta$ रेखाओं (i) और (ii) के बीच कोण है, तो
$\qquad \tan \theta =\Big|\dfrac{m_1-m_2}{1+m_1 m_2}\Big| $
$ \Rightarrow \quad \tan \theta =\Big|\dfrac{(2-\sqrt{3})-(2+\sqrt{3})}{1+(2-\sqrt{3})(2+\sqrt{3})}\Big|$
$ \Rightarrow \quad \tan \theta=\Big|\dfrac{-2 \sqrt{3}}{1+4-3}\Big| $
$ \Rightarrow \quad \tan \theta =\sqrt{3} $
$ \Rightarrow \quad \tan \theta =\tan \pi / 3 $
$ \therefore\quad \theta =\pi / 3=60^{\circ} $
अधिक कोण $=\pi-\pi / 3=2 \pi / 3=120^{\circ}$
इसलिए, रेखाओं के बीच कोण $60^{\circ}$ या $120^{\circ}$ है।
4. बिंदु $(3,4)$ से गुजरने वाली रेखाओं का समीकरण ज्ञात कीजिए जो निर्देशांक अक्षों से काटे अंतराल इस प्रकार हो कि उनका योग 14 हो।
उत्तर दिखाएं
हल
मान लीजिए अक्षों के अनुदिश अंतराल $a$ और $b$ हैं।
दिया है, $\quad a+b=14$
$ \Rightarrow \qquad b=14-a$
अब, रेखा का समीकरण $\dfrac{x}{a}+\dfrac{y}{b}=1$ है।
$\Rightarrow \quad \dfrac{x}{a}+\dfrac{y}{14-a}=1$
क्योंकि, बिंदु $(3,4)$ रेखा पर स्थित है।
$ \therefore\quad \dfrac{3}{a}+\dfrac{4}{14-a} =1 $
$\Rightarrow \quad \dfrac{42-3 a+4 a}{a(14-a)} =1 $
$\Rightarrow \quad 42+a=14 a-a^{2} $
$ \Rightarrow \quad a(a-7)-6(a-7) =0$
$ \Rightarrow \quad (a-7)(a-6)=0 $
$\Rightarrow \quad a-7 =0 \text { या } a-6=0 $
$\Rightarrow \quad a =7 \text { या } a=6 $
$\text { जब } a =7, \text { तो } b=7 $
$\text { जब } a =6, \text { तो } b=8$
$\therefore\quad$ जब $a=7$ और $b=7$ हो तो रेखा का समीकरण $ \ \dfrac{x}{7}+\dfrac{y}{7}=1 $ है
$\Rightarrow \quad x+y=7$
इसलिए, जब $a=6$ और $b=8$ हो तो रेखा का समीकरण $ \ \dfrac{x}{6}+\dfrac{y}{8}=1$ है
5. रेखा $x+y=4$ पर बिंदु ज्ञात कीजिए जो रेखा $4 x+3 y=10$ से एक इकाई की दूरी पर स्थित हो।
उत्तर दिखाएं
सोचने की प्रक्रिया
बिंदु $(x_1, y_1)$ की रेखा $A x+B y+C=0$ से लंब दूरी $d^{\prime}$ है,
जहाँ $d=\Big|\dfrac{A x_1+B y_1+C}{\sqrt{A^{2}+B^{2}}}\Big|$।
हल
मान लीजिए आवश्यक बिंदु $(h, k)$ है और बिंदु $(h, k)$ रेखा $x+y=4$ पर स्थित है
अर्थात, $\quad h+k=4\qquad\ldots\mathrm{(i)}$
बिंदु $(h, k)$ की रेखा $4 x+3 y=10$ से दूरी है
धनात्मक चिह्न लेते हुए,
$ \begin{aligned} \Big|\dfrac{4 h+3 k-10}{\sqrt{16+9}} \Big|& =1 \\ \\ 4 h+3 k-10 & = \pm 5 \\ \\ 4 h+3 k & =15\qquad\ldots\mathrm{(ii)} \end{aligned} $
समीकरण (i) से $h=4-k$ को समीकरण (ii) में रखने पर, हमें प्राप्त होता है
$ \begin{aligned} & \Rightarrow \quad 4(4-k)+3 k=15 \\ \\ & \Rightarrow \quad 16-4 k+3 k=15 \\ \\ & \text { समीकरण (i) में } k=1 \text { रखने पर, हमें प्राप्त होता है } \end{aligned} $
इसलिए, बिंदु $(3,1)$ है।
ऋणात्मक चिह्न लेते हुए,
$ \begin{aligned} & 4 h+3 k-10 =-5 \\ \\ \Rightarrow \quad & 4(4-k)+3 k =5 \\ \\ \Rightarrow \quad & 16-4 k+3 k =5 \\ \\ \therefore\quad & -k=5-16 =-11 \\ \\ \therefore\quad & k =11 \end{aligned} $
समीकरण (i) में $k=11$ रखने पर, हमें प्राप्त होता है $ \ h+11=4 $
$\Rightarrow \quad h=-7$
इसलिए, आवश्यक बिंदु $(3,1)$ और $(-7,11)$ हैं।
6. सिद्ध कीजिए कि रेखाओं $\dfrac{x}{a}+\dfrac{y}{b}=1$ और $\dfrac{x}{a}-\dfrac{y}{b}=1$ के बीच कोण का त्रिकोणमितीय अनुपात $\dfrac{2 a b}{a^{2}-b^{2}}$ है।
उत्तर दिखाएं
हल
दी गई रेखाओं के समीकरण हैं
$ \dfrac{x}{a}+\dfrac{y}{b} =1 \ \text { और } \text { ढलान, } m_1 =-\dfrac{b}{a} $
$ \therefore\quad \dfrac{x}{a}-\dfrac{y}{b} =1 \ \text { ढलान, } m_2 =\dfrac{b}{a} $
मान लीजिए $\theta$ दी गई रेखाओं के बीच कोण है, तो
$ \begin{aligned} & \qquad \tan \theta=\left|\dfrac{m_1-m_2}{1+m_1 m_2}\right| \\ \\ & \Rightarrow \quad \tan \theta=\left|\dfrac{-\dfrac{b}{a}-\dfrac{b}{a}}{1+\left(\dfrac{-b}{a}\right)\left(\dfrac{b}{a}\right)}\right| \\ \\ & \Rightarrow \quad \quad \tan \theta=\left|\dfrac{\dfrac{-2 b}{a}}{\dfrac{a^{2}-b^{2}}{a^{2}}}\right| \\ \\ & \Rightarrow \qquad \tan \theta=\dfrac{2 a b}{a^{2}-b^{2}}
\end{aligned} $
इसलिए सिद्ध कर दिया गया है।
7. बिंदु $(1,2)$ से गुजरती रेखाओं का समीकरण ज्ञात कीजिए जो $Y$-अक्ष के साथ $30^{\circ}$ का कोण बनाती हो।
उत्तर दिखाएं
सोचने की प्रक्रिया
बिंदु $(x_1, y_1)$ से गुजरती रेखा जिसका ढलान $m$ हो, का समीकरण $y - y_1 = m(x - x_1)$ होता है।
हल
दिया गया है कि, $Y$-अक्ष के साथ कोण $= 30^{\circ}$
और $X$-अक्ष के साथ कोण $= 60^{\circ}$
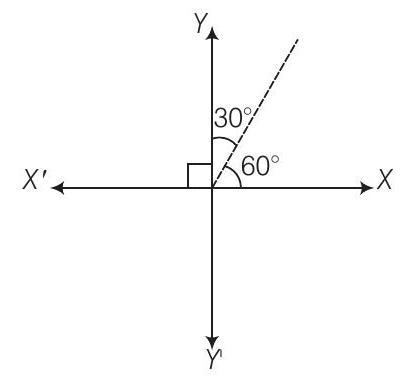
$\therefore\quad$ रेखा का ढलान, $m = \tan 60^{\circ} = \sqrt{3}$
इसलिए, बिंदु $(1,2)$ से गुजरती रेखा जिसका ढलान $\sqrt{3}$ हो, का समीकरण निम्नलिखित है:
$ \begin{matrix} \Rightarrow \quad & y - 2 = \sqrt{3}(x - 1) \\ \\ \Rightarrow \quad & y - 2 = \sqrt{3} x - \sqrt{3} \\ \\ \Rightarrow \quad & y - \sqrt{3} x - 2 + \sqrt{3} = 0 \end{matrix} $
8. रेखाओं $2x + y = 5$ और $x + 3y + 8 = 0$ के प्रतिच्छेद बिंदु से गुजरती रेखा का समीकरण ज्ञात कीजिए जो रेखा $3x + 4y = 7$ के समांतर हो।
उत्तर दिखाएं
सोचने की प्रक्रिया
पहले दी गई रेखाओं के समीकरण को हल करके प्रतिच्छेद बिंदु ज्ञात करें। फिर, यदि एक रेखा का ढलान $m_1$ हो और दूसरी रेखा का ढलान $m_2$ हो तो यदि वे समांतर हों, तो $m_1 = m_2$ होता है। अब, बिंदु $(x_1, y_1)$ से गुजरती रेखा जिसका ढलान $m$ हो, का समीकरण $y - y_1 = m(x - x_1)$ होता है।
हल
दिया गया समीकरण रेखाओं का:
$ \begin{aligned} 2x + y & = 5 \qquad\ldots\mathrm{(i)} \\ \\ x + 3y & = -8 \qquad\ldots\mathrm{(ii)} \end{aligned} $
समीकरण (i) से,
$y = 5 - 2x$
अब, $y$ के मान को समीकरण (ii) में रखने पर, हमें प्राप्त होता है:
$\qquad x + 3(5 - 2x) = -8 $
$ \Rightarrow \quad x + 15 - 6x = -8 $
$ \Rightarrow \quad -5x = -23 $
$\Rightarrow \quad x = \dfrac{23}{5}$
अब, $x = \dfrac{23}{5}$
समीकरण (i) में रखने पर, हमें प्राप्त होता है:
$ y = 5 - \dfrac{46}{5} = \dfrac{25 - 46}{5} = \dfrac{-21}{5} $
चूंकि, अभीष्ट रेखा रेखा $3x + 4y = 7$ के समांतर है। अतः, रेखा का ढलान $m = \dfrac{-3}{4}$ है।
तो, रेखा का समीकरण जो बिंदु $\left(\dfrac{23}{5}\right), \left(\dfrac{-21}{5}\right)$ से गुजरती है और ढाल $\left(\dfrac{-3}{4}\right)$ होती है:
$ \qquad y+\dfrac{21}{5} =\dfrac{-3}{4} \left(x-\dfrac{23}{5}\right) $
$ \Rightarrow \quad 4 y+\dfrac{84}{5} =-3 x+\dfrac{69}{5} $
$ \Rightarrow \quad 3 x+4 y =\dfrac{84-69}{5} $
$\Rightarrow \quad 3 x+4 y+\dfrac{15}{5}=0 $
$ \Rightarrow \quad 3 x+4 y+3 =0 $
9. $a$ और $b$ के किन मानों के लिए रेखा $a x+b y+8=0$ द्वारा निर्देशांक अक्षों पर काटे गए अपवर्तन दूरी एक दूसरे के बराबर होते हैं लेकिन चिह्न में विपरीत होते हैं, जो रेखा $2 x-3 y+6=0$ द्वारा अक्षों पर काटे गए अपवर्तन दूरी के बराबर होते हैं?
उत्तर दिखाएं
हल
दी गई रेखा का समीकरण $a x+b y+8=0 $
$\Rightarrow \quad \dfrac{x}{\dfrac{-8}{a}}+\dfrac{y}{\dfrac{-8}{b}}=1$
इसलिए, अपवर्तन दूरी $\dfrac{-8}{a}$ और $\dfrac{-8}{b}$ हैं।
और दूसरी दी गई रेखा का समीकरण $2 x-3 y+6=0$ है।
$\Rightarrow \quad \quad \dfrac{x}{-3}+\dfrac{y}{2}=1$
इसलिए, अपवर्तन दूरी $-3$ और $2$ हैं।
प्रश्न के अनुसार,
$ \begin{aligned} & \dfrac{-8}{a} =3 \text { और } \dfrac{-8}{b}=-2 \\ \\ \therefore\quad & a =-\dfrac{8}{3}, b=4 \end{aligned} $
10. यदि एक रेखा के निर्देशांक अक्षों के बीच अपवर्तन बिंदु $(-5,4)$ द्वारा $1: 2$ के अनुपात में विभाजित होते हैं, तो रेखा का समीकरण ज्ञात कीजिए।
उत्तर दिखाएं
चिंतन प्रक्रिया
$(x_1, y_1)$ और $(x_2, y_2)$ के बीच बिंदु के निर्देशांक जो $m_1: m_2$ के अनुपात में आंतरिक विभाजन करता है $\left(\dfrac{m_1 x_2+m_2 x_1}{m_1+m_2}, \dfrac{m_1 y_2+m_2 y_1}{m_1+m_2}\right)$।
हल
मान लीजिए रेखा के अपवर्तन $(h, k)$ हैं।
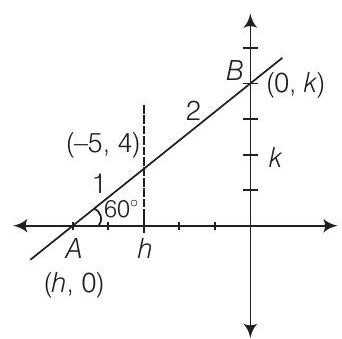
$A$ और $B$ के निर्देशांक क्रमशः $(h, 0)$ और $(0, k)$ हैं। $ -5=\dfrac{1 \times 0+2 \times h}{1+2} $
$ \begin{aligned} & \therefore \quad-5=\dfrac{2 h}{3} \\ \\ & \Rightarrow \quad +h=-\dfrac{15}{2} \\ \\ & \text { and } \quad 4=\dfrac{1 \cdot k+0 \cdot 2}{1+2} \\ \\ & \Rightarrow \quad \quad k=12 \\ \\ & \therefore\quad \quad A=\left(-\dfrac{15}{2}, 0\right) \text { and } \ B=(0,12) \end{aligned} $
अतः, रेखा $AB$ का समीकरण $ \ y-0=\dfrac{12-0}{0+15 / 2} \left(x+\dfrac{15}{2}\right) $ है
$ \begin{aligned} \Rightarrow \quad & y =\dfrac{12 \cdot 2}{15} \left(x+\dfrac{15}{2}\right) \\ \\ \Rightarrow \quad & 5 y =8 x+60 \\ \\ \Rightarrow \quad & 8 x-5 y+60=0 \end{aligned} $
11. मूल बिंदु से लम्ब की लम्बाई चार इकाई है और रेखा X-अक्ष के धनात्मक दिशा के साथ $120^{\circ}$ का कोण बनाती है। ऐसी सीधी रेखा का समीकरण ज्ञात कीजिए।
उत्तर दिखाएँ
सोचने की प्रक्रिया
मूल बिंदु से दूरी P वाली रेखा के समीकरण $x \cos \alpha+y \sin \alpha=p$ होता है, जहाँ $\alpha$ लम्ब द्वारा X-अक्ष के धनात्मक दिशा के साथ बनाया गया कोण है। उपरोक्त समस्या को हल करने के लिए इस सूत्र का उपयोग करें।
हल
दिया गया है, $OC=P=4$ इकाई

$ \begin{aligned} & \angle B A X=120^{\circ} \\ \\ & \text { माना, } \quad \angle C O A=\alpha, \angle O C A=90^{\circ} \\ \\ & \because \quad \angle B A X=\angle C O A+\angle O C A \quad \text { [बाह्य कोण गुणधर्म] } \\ \\ & \Rightarrow \quad \quad 120^{\circ}=\alpha+90^{\circ} \\ \\ & \therefore\quad \quad \alpha=30^{\circ} \\ \\ & \text{ अब, अभीष्ट रेखा का समीकरण है} \\ \\ & x \cos 30^{\circ}+y \sin 30^{\circ}=4 \\ \\ & \Rightarrow \quad x \cdot \dfrac{\sqrt{3}}{2}+y \cdot \dfrac{1}{2}=4 \\ \\ & \Rightarrow \quad \sqrt 3 x+y=8 \end{aligned} $
12. एक समकोण त्रिभुज के एक भुजा का समीकरण ज्ञात कीजिए जिसका कर्ण $3 x+4 y=4$ द्वारा दिया गया है और कर्ण के विपरीत शीर्ष $(2,2)$ है।
उत्तर दिखाएँ
हल
रेखा $AC$ की ढलान $m$ और रेखा $BC$ की ढलान $\dfrac{-3}{4}$ हो और रेखा $AC$ और $BC$ के बीच कोण $\theta$ हो।
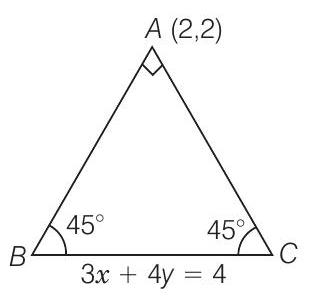
$ \therefore\quad \tan \theta=\left|\dfrac{m+\dfrac{3}{4}}{1-\dfrac{3 m}{4}}\right| $
$\Rightarrow \quad \tan 45^{\circ} = \pm \left[\dfrac{m+\dfrac{3}{4}}{1-\dfrac{3 m}{4}} \right]$
$ \text { धनात्मक चिह्न लेते हुए, } 1 =\dfrac{m+\dfrac{3}{4}}{1-\dfrac{3 m}{4}} $
$ \Rightarrow \quad m+\dfrac{3}{4} =1-\dfrac{3 m}{4}$
$ \Rightarrow \quad m+\dfrac{3 m}{4} =1-\dfrac{3}{4} $
$ \Rightarrow \quad \dfrac{7 m}{4} =\dfrac{1}{4}$
$ \Rightarrow \quad m=\dfrac{1}{7}$
ऋणात्मक चिह्न लेते हुए,
$ \begin{aligned} & \qquad 1=-\left(\dfrac{m+\dfrac{3}{4}}{1-\dfrac{3 m}{4}}\right) \\ \\ & \Rightarrow \quad 1-\dfrac{3 m}{4}=-m-\dfrac{3}{4} \\ \\ & \Rightarrow \quad \quad m-\dfrac{3 m}{4}=-1-\dfrac{3}{4} \\ \\ & \Rightarrow \quad \quad \dfrac{m}{4}=\dfrac{-7}{4} \\ \\ & \Rightarrow \qquad m=-7 \\ \\ & \begin{matrix} \therefore\quad \text { भुजा } A C \text { के लिए समीकरण जिसकी ढलान } \left(\dfrac{1}{7}\right) \text { है } \end{matrix} \\ \\ & \qquad \quad y-2=\dfrac{1}{7}(x-2) \\ \\ & \Rightarrow \quad \quad 7 y-14=x-2 \\ \\ & \text { और भुजा } A B \text { के लिए समीकरण जिसकी ढलान }(-7) \text { है } \\ \\ & \Rightarrow \quad \quad y-2=-7(x-2) \\ \\ & \Rightarrow \quad \quad y-2=-7 x+14 \\ \\ & \Rightarrow \quad \quad 7 x+y-16=0 \end{aligned} $
लंबा उत्तर प्रकार प्रश्न
13. यदि एक समबाहु त्रिभुज के आधार का समीकरण $x+y=2$ है और शीर्ष $(2,-1)$ है, तो त्रिभुज की भुजा की लंबाई ज्ञात कीजिए।
उत्तर दिखाएँ
सोचने की प्रक्रिया
$(2,-1)$ से रेखा पर लंब की लंबाई $( p )$ ज्ञात करें और $p=l \sin 60^{\circ}$ का उपयोग करें, जहाँ $l$ त्रिभुज की भुजा की लंबाई है।
हल
दिया गया है कि, एक समबाहु त्रिभुज $\triangle A B C$ के आधार का समीकरण $x+y=2$ है।
$\ln \triangle A B D$,
$ \begin{aligned} \sin 60^{\circ} & =\dfrac{A D}{A B} \\ \\ A D & =A B \sin 60^{\circ}=A B \dfrac{\sqrt{3}}{2} \\ \\ \Rightarrow \quad A D & =A B \dfrac{\sqrt{3}}{2}\qquad\ldots\mathrm{(i)} \end{aligned} $
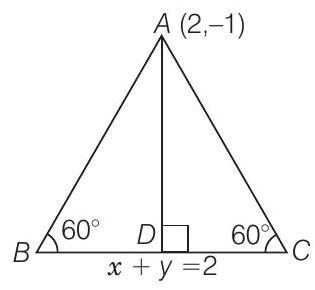
अब, बिंदु $(2,-1)$ से रेखा $x+y=2$ पर लंब की लंबाई निम्नलिखित द्वारा दी गई है
$AD = \Big| \dfrac{2+(-1)-2}{\sqrt{ {1^{2}+1^{2}}}}\Big| = \dfrac{1}{\sqrt 2}$
समीकरण (i) से,
$ \begin{aligned} & \dfrac{1}{\sqrt{2}}=A B \dfrac{\sqrt{3}}{2} \\ \\ & A B=\sqrt{\dfrac{2}{3}} \end{aligned} $
14. एक चर रेखा एक निश्चित बिंदु $P$ से गुजरती है। बिंदुओं $(2,0),(0,2)$ और $(1,1)$ से रेखा पर खींचे गए लंबों के बीजगणितीय योग शून्य है। बिंदु $P$ के निर्देशांक ज्ञात कीजिए।
उत्तर दिखाएं
सोचने की प्रक्रिया
मान लीजिए रेखा की प्रतिशत ढलान $m$ है। तब, निश्चित बिंदु $P(x_1, y_1)$ से गुजरने वाली रेखा का समीकरण $y-y_1=m(x-x_1)$ है। बिंदुओं $(2,0),(0,2),(1,1)$ से रेखा पर खींचे गए लंबों के बीजगणितीय योग शून्य है, इसलिए हमें $y_1-1=m(x_1-1)$ मिलता है। इसलिए, $(x_1, y_1)$ के निर्देशांक $(1,1)$ है।
हल
मान लीजिए चर रेखा $a x+b y=1$ है।
दिया गया है कि बिंदुओं $(2,0),(0,2),(1,1)$ से रेखा पर खींचे गए लंबों के बीजगणितीय योग शून्य है।
$ \begin{aligned} & \therefore \dfrac{2 a+0 b-1}{\sqrt{a^2+b^2}}+\dfrac{a \mathrm{a}+2 \mathrm{~b}-1}{\sqrt{\mathrm{a}^2+\mathrm{b}^2}}+\dfrac{\mathrm{a}+\mathrm{b}-1}{\sqrt{\mathrm{a}^2+\mathrm{b}^2}}=0 \\ \\ & \Rightarrow 3 \mathrm{a}+3 \mathrm{~b}-3=0 \\ \\ & \Rightarrow \mathrm{a}+\mathrm{b}-1=\mathrm{o} \\ \\ & \therefore \mathrm{a}+\mathrm{b}=1 \end{aligned} $
इसलिए, समीकरण $\mathrm{ax}+\mathrm{by}=1$ एक निश्चित बिंदु से गुजरने वाली सीधी रेखाओं के परिवार को प्रस्तुत करता है।
तुलना $\mathrm{ax}+\mathrm{by}=1$ और $\mathrm{a}+\mathrm{b}=1$ करने पर हम प्राप्त करते हैं कि निश्चित बिंदुओं के निर्देशांक $(1,1)$ हैं।
15. बिंदु $(1,2)$ से गुजरने वाली एक रेखा किस दिशा में खींची जानी चाहिए ताकि यह रेखा $x+y=4$ के बिंदु प्रतिच्छेदन की दूरी दिए गए बिंदु से $\dfrac{\sqrt{6}}{3}$ हो?
उत्तर दिखाएं
हल
मान लीजिए रेखा की ढलान $m$ है। रेखा बिंदु $A(1,2)$ से गुजरती है।
$\therefore ~ $ रेखा का समीकरण $\mathrm{y}-2=\mathrm{m}(\mathrm{x}-1)$ है।
$ m \mathrm{x}-\mathrm{y}+2-\mathrm{m}=0 \qquad\ldots\mathrm{(i)} $
इसके अतिरिक्त, दी गई रेखा का समीकरण $\mathrm{x}+\mathrm{y}-4=0 \qquad\ldots\mathrm{(i)} $ है।
मान लीजिए ये रेखाएँ बिंदु $B$ पर मिलती हैं।
समीकरण $\mathrm{(i) \ \& \ (ii)}$ को हल करने पर, हम प्राप्त करते हैं,
$ B \equiv\left(\dfrac{m+2}{m+1}, \dfrac{3 m+2}{m+1}\right) $
अब, दिया गया है $ \ \theta, \ A B=\dfrac{\sqrt{6}}{3}$
$ \begin{aligned} & \Rightarrow A B^2=\dfrac{6}{9} \\ \\ & \Rightarrow\left(\dfrac{\mathrm{ ~ m}+2}{\mathrm{ ~ m}+1}-1\right)^2+\left(\dfrac{3 \mathrm{ ~ m}+2}{\mathrm{ ~ m}+1}-2\right)^2=\dfrac{6}{9} \\ \\ & \Rightarrow\left(\dfrac{1}{\mathrm{ ~ m}+1}\right)^2+\left(\dfrac{\mathrm{m}}{\mathrm{ ~ m}+1}\right)^2=\dfrac{2}{3} \\ \\ & \Rightarrow \dfrac{1+\mathrm{m}^2}{(1+\mathrm{m})^2}=\dfrac{2}{3} \\ \\ & \Rightarrow 3 \mathrm{ ~ m}^2+3=2+2 \mathrm{ ~ m}^2+4 \mathrm{ ~ m} \\ \\ & \Rightarrow \mathrm{ ~ m}^2-4 \mathrm{ ~ m}+1=0 \\ \\ & \therefore \ \mathrm{ ~ m}=\dfrac{4 \pm \sqrt{16-4}}{2}=2 \pm \sqrt{3} \\ \\ & \therefore \ \tan \theta=2+\sqrt{3} \text { or } 2-\sqrt{3} \\ \\ & \qquad\quad \theta=75^{\circ} \text { or } \theta=15^{\circ} \end{aligned} $
16. एक सीधी रेखा ऐसी गति करती है कि अक्षों पर बनाए गए अंतरालों के व्युत्क्रमों का योग नियत होता है। सिद्ध कीजिए कि रेखा एक निश्चित बिंदु से गुजरती है।
उत्तर दिखाएं
चिंतन प्रक्रिया
मान लीजिए रेखा $\dfrac{x}{a}+\dfrac{y}{b}=1, \quad$ जहाँ $\dfrac{1}{a}+\dfrac{1}{b}=$ नियतांक $=\dfrac{1}{k}$ (मान लीजिए)।
इससे यह निर्माण होता है कि $\dfrac{k}{a}+\dfrac{k}{b}=1 $
$\Rightarrow \quad $ रेखा निश्चित बिंदु $(k, k)$ से गुजरती है।
हल
क्योंकि, एक रेखा के अंतिम रूप $\dfrac{x}{a}+\dfrac{y}{b}=1$ होता है।
दिया गया है कि,
$\because \quad \dfrac{1}{a}+\dfrac{1}{b}=\text { स्थिरांक }$
$\Rightarrow \quad \dfrac{1}{a}+\dfrac{1}{b}=\dfrac{1}{k}$
$\Rightarrow \quad \dfrac{k}{a}+\dfrac{k}{b}=1$
इसलिए, $(k, k)$ रेखा $\dfrac{x}{a}+\dfrac{y}{b}=1$ पर स्थित है।
अतः, रेखा निश्चित बिंदु से गुजरती है।
17. बिंदु $(-4,3)$ से गुजरने वाली रेखा का समीकरण ज्ञात कीजिए जो अक्षों के बीच अंतर्गत एक अनुपात $5: 3$ में विभाजित होती है।
उत्तर दिखाएं
सोचने की प्रक्रिया
यदि बिंदु $(h, k)$ बिंदु $A(x_1, y_2)$ और $B(x_2, y_2)$ के बीच अंतर्गत अनुपात $m_1: m_2$ में विभाजित करता है, तो सबसे पहले अंतर्गत विभाजन के सूत्र का उपयोग करके $A$ और $B$ के निर्देशांक ज्ञात करें, अर्थात $h=\dfrac{m_1 x_2+m_2 x_1}{m_1+m_2}, k=\dfrac{m_1 y_2+m_2 y_1}{m_1+m_2}$. फिर, आवश्यक रेखा का समीकरण ज्ञात करें।
हल
क्योंकि, रेखा $X$ और $Y$-अक्ष के क्रमशः बिंदु $A(x, 0)$ और $B(0, y)$ पर काटती है।
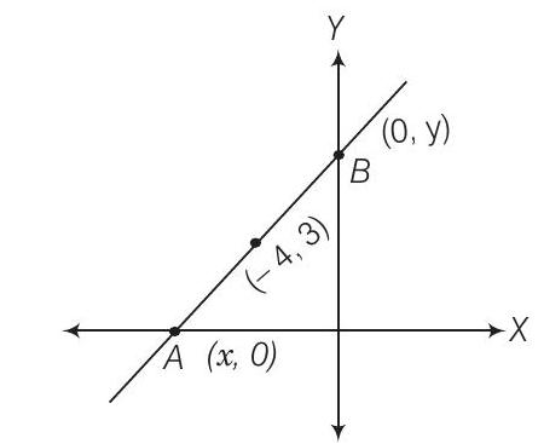
$\begin{aligned}\Rightarrow \quad -4 & =\dfrac{5 \times 0+3 x}{5+3} \\ \\ \Rightarrow \quad -4 & =\dfrac{3 x}{8} \\ \\ \Rightarrow \ \qquad & x=\dfrac{-32}{3} \\ \\ \text{and}\quad 3 & =\dfrac{5 \cdot y+3 \cdot 0}{5+3} \\ \\ \Rightarrow \quad 3 & =\dfrac{5 y}{8} \\ \\ \Rightarrow \qquad & y=\dfrac{24}{5}\end{aligned}$
क्योंकि, $X$ और $Y$-अक्ष पर क्रमशः अंतर $a=\dfrac{-32}{3}$ और $b=\dfrac{24}{5}$ है।
$\therefore\quad$ आवश्यक रेखा का समीकरण है
$ \begin{aligned} & \dfrac{x}{-32 / 3}+\dfrac{y}{24 / 5} & =1 \\ \\ \Rightarrow \quad & \dfrac{-3 x}{32}+\dfrac{5 y}{24} & =1 \\ \\
\Rightarrow \quad & 9 x-20 y+96 & =0 \end{aligned} $
18. बिंदु $x-y+1=0$ और $2 x-3 y+5=0$ के प्रतिच्छेद बिंदु से गुजरने वाली रेखाओं के समीकरण ज्ञात कीजिए जिनकी बिंदु $(3,2)$ से दूरी $\dfrac{7}{5}$ है।
उत्तर दिखाएं
हल
दिए गए रेखाओं के समीकरण
$x-y+1 =0 \qquad\ldots\mathrm{(i)}$
$2 x-3 y+5 =0 \qquad\ldots\mathrm{(ii)}$
$x =y-1$
अब, समीकरण (ii) में $x$ का मान रखें, हमें प्राप्त होता है
$\Rightarrow \quad 2(y-1)-3 y+5 =0 $
$\Rightarrow \quad 2 y-2-3 y+5 =0 $
$\Rightarrow \quad 3-y=0 $
$\Rightarrow \quad y =3 $
$\text { समीकरण (i) में रखने पर, हमें प्राप्त होता है } \quad x =2$
चूंकि, प्रतिच्छेद बिंदु $(2,3)$ है।
अभीष्ट रेखा की ढलान $m$ हो।
$\therefore\quad$ रेखा का समीकरण $y-3=m(x-2)$ है
$\Rightarrow \quad $ $ m x-y+3-2 m=0\qquad\ldots\mathrm{(iii)} $
चूंकि, बिंदु $(3,2)$ से रेखा (iii) की दूरी $\dfrac{7}{5}$ है।
$ \begin{aligned} & \therefore\quad \quad \dfrac{7}{5}=\Big|\dfrac{3 m-2+3-2 m}{\sqrt{1+m^{2}}}\Big| \\ \\ & \Rightarrow \quad \quad \dfrac{49}{25}=\dfrac{(m+1)^{2}}{1+m^{2}} \\ \\ & \Rightarrow \quad \quad 49+49 m^{2}=25(m^{2}+2 m+1) \\ \\ & \Rightarrow \quad \quad 49+49 m^{2}=25 m^{2}+50 m+25 \\ \\ & \Rightarrow \quad \quad 24 m^{2}-50 m+24=0 \\ \\ & \Rightarrow \quad \quad 12 m^{2}-25 m+12=0 \\ \\ & \therefore\quad \quad m=\dfrac{25 \pm \sqrt{625-4 \cdot 12 \cdot 12}}{24}=\dfrac{25 \pm \sqrt{49}}{24} \\ \\ & \qquad \qquad=\dfrac{25 \pm 7}{24}=\dfrac{32}{24} \text { या } \dfrac{18}{24}=\dfrac{4}{3} \text { या } \dfrac{3}{4} \\ \\ & \therefore\quad \text { रेखा का पहला समीकरण } \ y-3=\dfrac{4}{3}(x-2) \\ \\ & \begin{matrix} \Rightarrow \quad & 3 y-9=4 x-8 \end{matrix} \\ \\ & \Rightarrow \quad \quad 4 x-3 y+1=0 \\ \\ & \text { और दूसरा रेखा का समीकरण } \ \left(y-3\right)=\dfrac{3}{4}(x-2) \\ \\ & \Rightarrow \quad 4 y-12=3 x-6 \\ \\ & \Rightarrow \quad 3 x-4 y+6=0 \end{aligned} $
19. यदि तल में एक गतिशील बिंदु की अक्षों से दूरी का योग 1 है, तो बिंदु के बिंदुपथ को ज्ञात कीजिए।
उत्तर दिखाएं
सोचने की प्रक्रिया
दिया गया है कि $|x|+|y|=1$, जो एक वर्ग के चारों ओर भुजाएं देता है।
हल
मान लीजिए गतिशील बिंदु $P$ के निर्देशांक $(x, y)$ हैं। दिया गया है कि तल में इस बिंदु की अक्षों से दूरी का योग 1 है।
$ \begin{matrix} \therefore\quad & |x|+|y|=1 \\ \\ \Rightarrow \quad & \pm x \pm y=1 \\ \\ \Rightarrow \quad & x+y=1 \\ \\ \Rightarrow \quad & -x-y=1 \\ \\ \Rightarrow \quad & -x+y=1 \\ \\ \Rightarrow \quad & x-y=1 \end{matrix} $
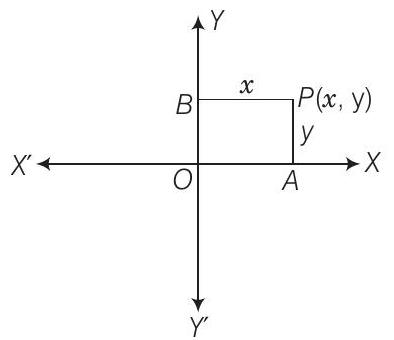
इसलिए, इन समीकरणों से हमें बिंदु के बिंदुपथ के रूप में एक वर्ग मिलता है।
20. $P_1$ और $P_2$ दो रेखाओं $y-\sqrt{3}|x|=2$ पर बिंदु हैं जो उनके प्रतिच्छेद बिंदु से 5 इकाई की दूरी पर हैं। $P_1, P_2$ से दिए गए रेखाओं के बीच कोण के ऐसे ऐसे अक्षर के लंब के पादों के निर्देशांक ज्ञात कीजिए।
उत्तर दिखाएं
सोचने की प्रक्रिया
रेखाएं $y=\sqrt{3} x+2$ और $y=-\sqrt{3} x+2$ हैं जो क्रमशः $x \geq 0$ या $x<0$ के अनुसार हैं। Y-अक्ष दिए गए रेखाओं के बीच कोण के ऐसे अक्षर के लंब के लिए विभाजक है। $P_1, P_2$ इन रेखाओं पर बिंदु हैं जो इन रेखाओं के प्रतिच्छेद बिंदु से 5 इकाई की दूरी पर हैं जो इन बिंदुओं से खींचे गए लंब के एक सामान बिंदु पर पाद हैं। लंब के पाद के y-निर्देशांक $2+5 \cos 30^{\circ}$ द्वारा दिया गया है।
हल
दिए गए रेखाओं के समीकरण हैं
$ \begin{aligned} y-\sqrt{3} x & =2\qquad\ldots\mathrm{(i)} \\ \\ y+\sqrt{3} x & =2\qquad\ldots\mathrm{(ii)} \\ \\ y & =\sqrt{3} x+2 \\ \\ y & =-\sqrt{3} x+2 \\ \\ \sqrt{3} x+2 & =-\sqrt{3} x+2 \qquad[\because\quad x \geq 0] \end{aligned} $
$ \Rightarrow \quad 2 \sqrt{3} x=0 $
$\Rightarrow \qquad x=0 $
$ x=0 $ समीकरण (i) में रखने पर, हम प्राप्त करते हैं
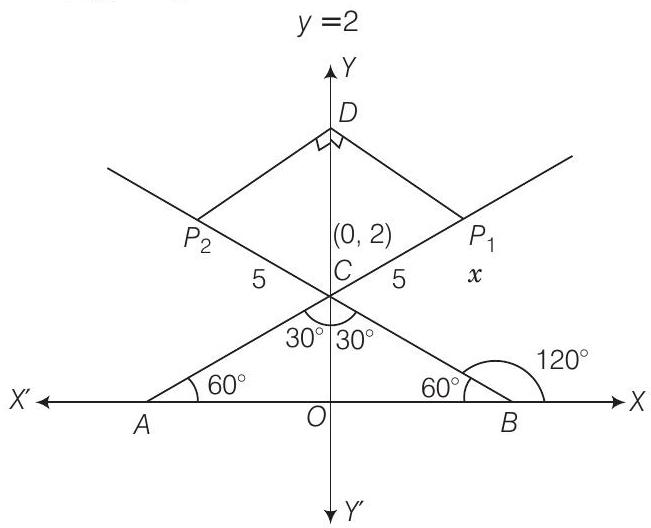
इसलिए, रेखा $\mathrm{(i)}$ और $\mathrm{(ii)}$ के प्रतिच्छेद बिंदु $(0,2)$ है।
यहाँ,
$O C =2 $
$\text{In} \ \triangle \ D E C $
$ \dfrac{C D}{C E} =\cos 30^{\circ}$
$C D =5 \cos 30 $
$\qquad =5 \cdot \dfrac{\sqrt{3}}{2}$
$\therefore\quad C D =5 \cos 30^{\circ} $
$ \qquad\qquad =5 \cdot \dfrac{\sqrt{3}}{2} $
$\Rightarrow \quad O D =O C+C D=2+5 \dfrac{\sqrt{3}}{2}$
इसलिए, लम्ब के पाद के निर्देशांक $\left(0,2+\dfrac{5 \sqrt{3}}{2}\right)$ हैं।
21. यदि $p$ मूल बिंदु से रेखा $\dfrac{x}{a}+\dfrac{y}{b}=1$ पर लम्ब की लंबाई है और $a^{2}, p^{2}$ और $b^{2}$ AP में हैं, तो सिद्ध करें कि $a^{4}+b^{4}=0$।
उत्तर दिखाएं
हल
दी गई रेखा का समीकरण, $\dfrac{x}{a}+\dfrac{y}{b}=1\qquad\ldots\mathrm{(i)}$
मूल बिंदु से रेखा (i) पर लम्ब की लंबाई $p$ द्वारा दी गई है
$\text { अर्थात, } \quad p=\dfrac{1}{\sqrt{\dfrac{1}{a^{2}}+\dfrac{1}{b^{2}}}}=\dfrac{a b}{\sqrt{a^{2}+b^{2}}} $
$\therefore\quad \ p^{2}=\dfrac{a^{2} b^{2}}{a^{2}+b^{2}}$
दिया गया है कि, $a^{2}, p^{2}$ और $b^{2}$ AP में हैं।
$ \begin{aligned} \therefore\quad & 2 p^{2}=a^{2}+b^{2} \\ \\ \Rightarrow \quad & \dfrac{2 a^{2} b^{2}}{a^{2}+b^{2}}=a^{2}+b^{2} \\ \\ \Rightarrow \quad & 2 a^{2} b^{2}=(a^{2}+b^{2})^{2} \\ \\ \Rightarrow \quad & 2 a^{2} b^{2}=a^{4}+b^{4}+2 a^{2} b^{2} \\ \\ \Rightarrow \quad & a^{4}+b^{4}=0 \end{aligned} $
वस्तुनिष्ठ प्रश्न
22. एक रेखा $Y$-अक्ष से $-3$ के अंतराल काटती है और $X$-अक्ष के सापेक्ष झुकाव कोण के त्रिकोणमितीय अनुपात $\dfrac{3}{5}$ है, तो इसका समीकरण है
(a) $5 y-3 x+15=0$
(b) $3 y-5 x+15=0$
(c) $5 y-3 x-15=0$
(d) उपरोक्त में से कोई नहीं
उत्तर दिखाएं
हल
(a) दिया गया है,
$ c=-3 \text { और } m=\dfrac{3}{5} $
$\therefore\quad$ रेखा का समीकरण $y=m x+c$
$ y =\dfrac{3}{5} x-3$
$ \Rightarrow \quad 5 y =3 x-15 $
$ \Rightarrow \quad 5 y-3 x+15 =0 $
23. एक रेखा जो अक्षों पर समान लम्बाई के अंतर्वेध काटती है, की प्रतिशत है
(a) -1
(b) 0
(c) 2
(d) $\sqrt{3}$
उत्तर दिखाएं
हल
(a) रेखा का समीकरण निम्नलिखित है
$ \begin{aligned} \Rightarrow \quad & \dfrac{x}{a}+\dfrac{y}{a}=1 \\ \\ \Rightarrow \quad & x+y=a \end{aligned} $
$ \begin{aligned} \Rightarrow \quad & x+y =a \\ \\ \Rightarrow \quad & y =-x+a \\ \\ \therefore\quad & \text { आवश्यक प्रतिशत } =-1 \end{aligned} $
24. रेखा का समीकरण जो बिंदु $(3,2)$ से गुजरती है और रेखा $y=x$ के लंबवत है, है
(a) $x-y=5$
(b) $x+y=5$
(c) $x+y=1$
(d) $x-y=1$
उत्तर दिखाएं
हल
(b) क्योंकि, रेखा बिंदु $(3,2)$ से गुजरती है और रेखा $y=x$ के लंबवत है।
$\because$ प्रतिशत $(m)=-1 \quad$ [क्योंकि, रेखा रेखा $y=x$ के लंबवत है]
$\therefore\quad \quad$ बिंदु $(3,2)$ से गुजरने वाली रेखा का समीकरण है
$ \begin{aligned} & y-2=-1(x-3) \\ \\ & y-2=-x+3 \end{aligned} $
$ \Rightarrow \quad x+y=5 $
25. रेखा का समीकरण जो बिंदु $(1,2)$ से गुजरती है और रेखा $x+y+1=0$ के लंबवत है, है
(a) $y-x+1=0$
(b) $y-x-1=0$
(c) $y-x+2=0$
(d) $y-x-2=0$
उत्तर दिखाएं
हल
(b) दिया गया बिंदु $(1,2)$ और आवश्यक रेखा की प्रतिशत 1 है ।
$\because\quad x+y+1=0 $
$\Rightarrow \quad y=-x-1$
$ \Rightarrow \quad m_1=-1$
$\therefore\quad$ रेखा की प्रतिशत $=\dfrac{-1}{-1}=1$
$\therefore\quad$ आवश्यक रेखा का समीकरण $ y-2 =1(x-1) $
$ \Rightarrow \quad y-2 =x-1 $
$ \Rightarrow \quad y-x-1 =0 $
26. रेखाओं के बीच कोण के त्रिकोणमिति अनुपात जिनके अक्षों पर अंतर्वेध क्रमशः $a,-b$ और $b,-a$ हैं, है
(a) $\dfrac{a^{2}-b^{2}}{a b}$
(b) $\dfrac{b^{2}-a^{2}}{2}$
(c) $\dfrac{b^{2}-a^{2}}{2 a b}$
(d) इनमें से कोई नहीं
उत्तर दिखाएं
हल
(c) क्योंकि, अक्षों पर अपवार्तियाँ $a,-b$ हैं, तो रेखा का समीकरण $\dfrac{x}{a}-\dfrac{y}{b}=1$ है।
$ \begin{matrix} \Rightarrow \quad & \dfrac{y}{b}=\dfrac{x}{a}-1 \\ \\ \Rightarrow \quad & y=\dfrac{b x}{a}-b \end{matrix} $
इस रेखा की ढलान, अर्थात $m_1=\dfrac{b}{a}$ है।
इसके अलावा, अक्षों पर अपवार्तियाँ $b$ और $-a$ हैं, तो रेखा का समीकरण है
$ \begin{aligned} & \Rightarrow \quad\dfrac{x}{b}-\dfrac{y}{a} =1 \\ \\ & \Rightarrow \quad \dfrac{y}{a} =\dfrac{x}{b}-1 \\ \\ & \Rightarrow \qquad y =\dfrac{a}{b} x-a \end{aligned} $
इस रेखा की ढलान, अर्थात $m_2=\dfrac{a}{b}$ है
$ \therefore\quad \quad \tan \theta=\dfrac{\dfrac{b}{a}-\dfrac{a}{b}}{1+\dfrac{a}{b} \cdot \dfrac{b}{a}}=\dfrac{\dfrac{b^{2}-a^{2}}{a b}}{2}=\dfrac{b^{2}-a^{2}}{2 a b} $
27. यदि रेखा $\dfrac{x}{a}+\dfrac{y}{b}=1$ बिंदुओं $(2,-3)$ और $(4,-5)$ से गुजरती है, तो $(a, b)$ है
(a) $(1,1)$
(b) $(-1,1)$
(c) $(1,-1)$
(d) $(-1,-1)$
उत्तर दिखाएं
हल
(d) दिया गया है, रेखा $\dfrac{x}{a}+\dfrac{y}{b}=1$
क्योंकि, बिंदु $(2,-3)$ और $(4,-5)$ इस रेखा पर स्थित हैं।
$ \begin{matrix} \therefore\quad & \dfrac{2}{a}-\dfrac{3}{b}=1 \\ \\ \text { और } & \dfrac{4}{a}-\dfrac{5}{b}=1 \end{matrix} $
समीकरण (ii) में 2 से गुणा करके और फिर समीकरण (iii) को समीकरण (ii) से घटाकर, हम प्राप्त करते हैं
$\quad -\dfrac{6}{b}+\dfrac{5}{b} =1 $
$ \Rightarrow \quad \dfrac{-1}{b} =1 $
$ \therefore\quad b =-1 $
$ b=-1 $ को समीकरण (ii) में रखने पर, हम प्राप्त करते हैं
$ \begin{aligned} \Rightarrow \quad & \dfrac{2}{a}+3 =1 \\ \\ \therefore\quad & \dfrac{2}{a} =-2 \\ \\ \Rightarrow \quad & a=-1 \\ \\ & (a, b) =(-1,-1) \end{aligned} $
28. रेखाओं $2 x-3 y+5=0$ और $3 x+4 y=0$ के प्रतिच्छेद बिंदु की रेखा $5 x-2 y=0$ से दूरी है
(a) $\dfrac{130}{17 \sqrt{29}}$
(b) $\dfrac{13}{7 \sqrt{29}}$
(c) $\dfrac{130}{7}$
(d) इनमें से कोई नहीं
उत्तर दिखाएं
चिंतन प्रक्रिया
पहले दिए गए पहले दो रेखाओं के प्रतिच्छेद बिंदु को ज्ञात करें, फिर इस बिंदु से तीसरी रेखा की लंब दूरी निकालें। उपयोग किए गए सूत्र के अनुसार, बिंदु $(x_1, y_1)$ से रेखा $a x + b y + c = 0$ की दूरी $d = \dfrac{|a x_1 + b y_1 + c|}{\sqrt{a^{2} + b^{2}}}$ होती है।
हल
(a) दिए गए रेखाओं का समीकरण
और $\quad 2 x - 3 y + 5 = 0 \qquad\ldots\mathrm{(i)}$
$\qquad 3 x + 4 y = 0\qquad\ldots\mathrm{(ii)}$
समीकरण (ii) से, $x = \dfrac{-4 y}{3}$ का मान समीकरण (i) में रखने पर, हम प्राप्त करते हैं
$ 2 \left(\dfrac{-4 y}{3}\right) - 3 y + 5 = 0 $
$ \Rightarrow \quad -8 y - 9 y + 15 = 0 $
$ \Rightarrow \quad y = \dfrac{15}{17} $
समीकरण (ii) से,
$ \begin{aligned} & 3 x + 4 \cdot \dfrac{15}{17} = 0 \\ \\ & \Rightarrow \quad x = \dfrac{-60}{17 \cdot 3} = \dfrac{-20}{17} \end{aligned} $
इसलिए, प्रतिच्छेद बिंदु है $\dfrac{-20}{17}, \dfrac{15}{17}$
$\therefore\quad$ रेखा $5 x - 2 y = 0$ से आवश्यक दूरी है,
$ d = \dfrac{\left|-5 \times \dfrac{20}{17} - 2 \left(\dfrac{15}{17}\right)\right|}{\sqrt{25 + 4}} = \dfrac{\left|\dfrac{-100}{17} - \dfrac{30}{17}\right|}{\sqrt{29}} = \dfrac{130}{17 \sqrt{29}} $
$ \because\quad \text { बिंदु } p(x_1, y_1) \text { से रेखा } a x + b y + c = 0 \text { की दूरी } d = \dfrac{|a x_1 + b y_1 + c|}{\sqrt{a^{2} + b^{2}}} $
29. बिंदु $(3,-2)$ से गुजरने वाली रेखाओं का समीकरण जो रेखा $\sqrt{3} x + y = 1$ के सापेक्ष $60^{\circ}$ के कोण पर झुकी हुई हैं है
(a) $y + 2 = 0, \sqrt{3} x - y - 2 - 3 \sqrt{3} = 0$
(b) $x - 2 = 0, \sqrt{3} x - y + 2 + 3 \sqrt{3} = 0$
(c) $\sqrt{3} x - y - 2 - 3 \sqrt{3} = 0$
(d) इनमें से कोई नहीं
उत्तर दिखाएं
हल
(a) दिया गया बिंदु $A$ है $(3,-2)$।
इसलिए, रेखा का समीकरण $\sqrt{3} x + y = 1$ है।
$ \begin{aligned} \Rightarrow \quad & y = -\sqrt{3} x + 1 \\ \\ \therefore\quad & \text { ढलान, } m_1 = -\sqrt{3} \end{aligned} $
अभीष्ट रेखा की ढलान $m_2$ हो।
$ \begin{aligned}
$$ \begin{aligned} & \therefore\quad \quad \tan \theta=\left|\dfrac{-\sqrt{3}-m_2}{1-\sqrt{3} m_2}\right| \quad \left[\because \tan \theta=\left|\dfrac{m_1-m_2}{1+m_1 m_2}\right|\right] \\ \\ & \Rightarrow \quad \quad \tan 60^{\circ}= \pm \left(\dfrac{-\sqrt{3}-m_2}{1-\sqrt{3} m_2}\right) \\ \\ & \begin{matrix} \Rightarrow \quad & \sqrt{3}=\left(\dfrac{-\sqrt{3}-m_2}{1-\sqrt{3} m_2}\right) \end{matrix} \quad \text { [positive sign के लेने पर] } \\ \\ & \Rightarrow \quad \quad \sqrt{3}-3 m_2=-\sqrt{3}-m_2 \\ \\ & \Rightarrow \quad \quad 2 \sqrt{3}=2 m_2 \\ \\ & \Rightarrow \quad \quad m_2=\sqrt{3} \end{aligned} $$
$$ \therefore\quad \quad $$ बिंदु $(3,-2)$ से गुजरने वाली रेखा का समीकरण $ \ y+2=\sqrt{3}(x-3)$
$$ \Rightarrow \quad \sqrt{3} x-y-2-3 \sqrt{3} =0 $$
$$ \Rightarrow \quad \sqrt{3}-3 m_2 =\sqrt{3}+m_2 $$
$$ \Rightarrow \quad m_2 =0 $$
$$ \therefore\quad $$ रेखा का समीकरण $y+2=0(x-3)$
$$ \Rightarrow \quad \quad y+2=0 $$
इसलिए, आवश्यक रेखाओं के समीकरण $\sqrt{3} x-y-2-3 \sqrt{3}=0$ और $y+2=0$ हैं।
30. बिंदु $(1,0)$ से गुजरने वाली रेखाओं के समीकरण जो मूल बिंदु से $\dfrac{\sqrt{3}}{2}$ की दूरी पर हों, हैं
(a) $\sqrt{3} x+y-\sqrt{3}=0, \sqrt{3} x-y-\sqrt{3}=0$
(b) $\sqrt{3} x+y+\sqrt{3}=0, \sqrt{3} x-y+\sqrt{3}=0$
(c) $x+\sqrt{3} y-\sqrt{3}=0, x-\sqrt{3} y-\sqrt{3}=0$
(d) उपरोक्त में से कोई नहीं
उत्तर दिखाएं
Solution
(a) मान लीजिए रेखा की ढलान $m$ है।
$\because \quad$ बिंदु $(1,0)$ से गुजरने वाली रेखा का समीकरण है
$$ \begin{aligned} &\Rightarrow \quad y-0=m(x-1) \\ \\ &\qquad y-m x+m=0 \end{aligned} $$
क्योंकि, मूल बिंदु से दूरी $\dfrac{\sqrt{3}}{2}$ है।
तब,
$$ \begin{aligned} \Rightarrow \quad & \dfrac{\sqrt{3}}{2} =\dfrac{m}{\sqrt{1+m^{2}}} \\ \\ \Rightarrow \quad & \dfrac{3}{4} =\dfrac{m^{2}}{1+m^{2}} \\ \\ \Rightarrow \quad & 3+3 m^{2} =4 m^{2} \\ \\ \Rightarrow \quad & m^{2} =3 \\ \\ \Rightarrow \quad & m = \pm \sqrt{3} \end{aligned} $$
इसलिए, रेखा का पहला समीकरण है
$ \begin{aligned} & & y=\sqrt{3}(x-1) \\ \\ \Rightarrow \quad & & \sqrt{3} x-y-\sqrt{3}=0 \end{aligned} $
और रेखा के दूसरे समीकरण है
$ \begin{aligned} & & y=-\sqrt{3}(x-1) \\ \\ \Rightarrow \quad & & \sqrt{3} x+y-\sqrt{3}=0 \end{aligned} $
31. रेखाओं $y=m x+c_1$ और $y=m x+c_2$ के बीच दूरी है
(a) $\dfrac{c_1-c_2}{\sqrt{m^{2}+1}}$
(b) $\dfrac{|c_1-c_2|}{\sqrt{1+m^{2}}}$
(c) $\dfrac{c_2-c_1}{\sqrt{1+m^{2}}}$
(d) 0
उत्तर दिखाएं
Solution
(b) दिया गया, रेखाओं के समीकरण हैं
$ \ y =m x+c_1 $ और $ y =m x+c_2$
$\therefore\quad$ उनके बीच दूरी द्वारा दी गई है
$ d=\dfrac{|c_1-c_2|}{\sqrt{1+m^{2}}} $
32. बिंदु $(2,3)$ से रेखा $y=3 x+4$ पर लंब के पाद के निर्देशांक निम्नलिखित में से कौन सा है
(a) $\dfrac{37}{10}, \dfrac{-1}{10}$
(b) $-\dfrac{1}{10}, \dfrac{37}{10}$
(c) $\dfrac{10}{37},-10$
(d) $\dfrac{2}{3},-\dfrac{1}{3}$
उत्तर दिखाएं
Solution
(b) दिया गया, रेखा का समीकरण है
$ y=3 x+4\qquad\ldots\mathrm{(i)} $
$\therefore\quad$ इस रेखा का ढलान, $m_1=3$
इसलिए, रेखा $O P$ का ढलान $-\dfrac{1}{3}$ है।
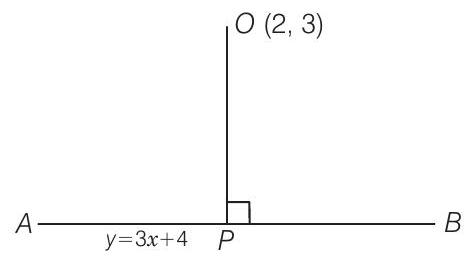
$\therefore\quad$ रेखा $O P$ का समीकरण है
$\Rightarrow \quad y-3 =-\dfrac{1}{3}(x-2) $
$\Rightarrow \quad 3 y-9 =-x+2 $
$\Rightarrow \quad x+3 y-11 =0\qquad\ldots\mathrm{(ii)} $
समीकरण (i) से $y$ के मान को समीकरण (ii) में रखने पर,
हमें प्राप्त होता है, $\quad x+3(3 x+4)-11=0$
$ \begin{matrix} \Rightarrow \quad & x+9 x+12-11=0 \\ \\ \Rightarrow \quad & 10 x+1=0 \\ \\ \Rightarrow \quad & x=-\dfrac{1}{10} \end{matrix} $
$x=\dfrac{-1}{10}$ को समीकरण (i) में रखने पर, हमें प्राप्त होता है
$ y=\dfrac{-3}{10}+4=\dfrac{-3+40}{10}=\dfrac{37}{10} $
इसलिए, लंब का पाद है $\left(-\dfrac{1}{10}, \dfrac{37}{10}\right)$.
33. यदि एक रेखा के निर्देशांक अक्षों के बीच अंतर्ग्रस्थ भाग के मध्य बिंदु के निर्देशांक $(3,2)$ है, तो रेखा का समीकरण होगा
(a) $2 x+3 y=12$
(b) $3 x+2 y=12$
(c) $4 x-3 y=6$
(d) $5 x-2 y=10$
उत्तर दिखाएं
हल
(a) चूंकि, मध्य बिंदु के निर्देशांक $P(3,2)$ हैं।

$ \begin{aligned} & \therefore\quad \quad 3=\dfrac{1 \cdot 0+1 \cdot a}{1+1} \\ \\ & \Rightarrow \quad \quad 3=\dfrac{a}{2} \\ \\ & \Rightarrow \quad a=6 \\ \\ & \text { इसी तरह, } \quad b=4 \\ \\ & \therefore\quad \quad \text { रेखा का समीकरण } \dfrac{x}{6}+\dfrac{y}{4}=1 \\ \\ & \Rightarrow \quad \quad 2 x+3 y=12 \end{aligned} $
34. बिंदु $(1,2)$ से गुजरती तथा रेखा $y=3 x-1$ के समांतर रेखा का समीकरण है
(a) $y+2=x+1$
(b) $y+2=3(x+1)$
(c) $y-2=3(x-1)$
(d) $y-2=x-1$
उत्तर दिखाएं
हल
(c) चूंकि, रेखा $(1,2)$ से गुजरती है तथा रेखा $y=3 x-1$ के समांतर है। अतः, अभीष्ट रेखा की प्रतिशत दर $m=3$ है। अतः, रेखा का समीकरण है $ ~ y-2=3(x-1) $
35. रेखाओं $x=0, y=0, x=1$ तथा $y=1$ द्वारा बने वर्ग के विकर्णों के समीकरण हैं
(a) $y=x, y+x=1$
(b) $y=x, x+y=2$
(c) $2 y=x, y+x=\dfrac{1}{3}$
(d) $y=2 x, y+2 x=1$
उत्तर दिखाएं
हल
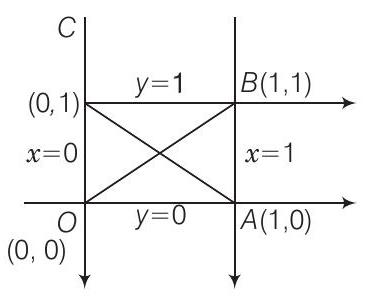
(a) $O B$ का समीकरण है
$ y-0 =\dfrac{1-0}{1-0}(x-0) $
$ \Rightarrow \quad y =x $
$ \text { तथा } A C \text { का समीकरण } $
$ \Rightarrow \quad y-0 =\dfrac{1-0}{0-1}(x-1) $
$ \Rightarrow \quad y+y-1 =0
$
36. सीधी रेखा को निर्धारित करने के लिए कितने ज्यामितीय पैरामीटर जानने आवश्यक हैं?
(a) 1
(b) 2
(c) 4
(d) 3
उत्तर दिखाएं
हल
(b) सीधी रेखा के समीकरण हैं
$ \begin{aligned} & y =m x+c, \text { पैरामीटर }=2 \qquad\ldots\mathrm{(i)}\\ \\ & \dfrac{x}{a}+\dfrac{y}{b} =1, \text { पैरामीटर }=2\qquad \ldots\mathrm{(ii)}\\ \\ & y-y_1 =m(x-x_1), \text { पैरामीटर }=2 \qquad\ldots\mathrm{(iii)}\\ \\ & \text { और } \quad x \cos w +y \sin w=p, \text { पैरामीटर }=2\qquad\ldots\mathrm{(iv)} \end{aligned} $
स्पष्ट रूप से, समीकरणों $\mathrm{(i), \ (ii), \ (iii) \ और \ (iv),} \ $ से सीधी रेखा को निर्धारित करने के लिए दो पैरामीटर जानने आवश्यक हैं।
37. बिंदु $(4,1)$ के निम्नलिखित दो क्रमागत परिवर्तन होते हैं
(i) रेखा $y=x$ के सापेक्ष प्रतिबिंब
(ii) धनात्मक $X$-अक्ष के अनुदिश 2 इकाई की दूरी तक गति
तब, बिंदु के अंतिम निर्देशांक हैं
(a) $(4,3)$
(b) $(3,4)$
(c) $(1,4)$
(d) $\dfrac{7}{2}, \dfrac{7}{2}$
उत्तर दिखाएं
हल
(b) मान लीजिए $A(4,1)$ के प्रतिबिंब $B(h, k)$ है।
अब, $AB$ का मध्य बिंदु $\left(\dfrac{4+h}{2}, \dfrac{1+k}{2}\right)$ जो $y=x$ पर स्थित है।
अर्थात, $\quad \dfrac{4+h}{2}=\dfrac{1+k}{2} $
$\Rightarrow \quad h-k=-3\qquad\ldots\mathrm{(i)}$
इसलिए, रेखा $y=x$ की ढलान 1 है।
$ \text { ढलान } A B =\dfrac{h-4}{k-1} $
$ \Rightarrow \quad 1 \cdot \dfrac{h-4}{k-1} =-1$
$ \Rightarrow \quad h-4 =1-k $
$ \Rightarrow \quad h+k =5 \qquad\ldots\mathrm{(ii)}$
$ \text { और } 2 h =2 \Rightarrow \quad h=1 $
$ h=1 $ को समीकरण (ii) में रखने पर हमें प्राप्त होता है
$ k=4 $
इसलिए, बिंदु $(1,4)$ है।
अतः, परिवर्तन के बाद बिंदु $(1+2,4)$ या $(3,4)$ है।
38. रेखाओं $4 x+3 y+10=0,5 x-12 y+26=0$ और $7 x+24 y-50=0$ के बराबर दूरी पर स्थित बिंदु है
(a) $(1,-1)$
(b) $(1,1)$
(c) $(0,0)$
(d) $(0,1)$
उत्तर दिखाएं
हल
(c) दी गई रेखाओं के समीकरण हैं
$ \Rightarrow \quad 4 x+3 y+10 =0 \qquad\ldots\mathrm{(i)}$
$ \Rightarrow \quad 5 x-12 y+26 =0\qquad\ldots\mathrm{(ii)} $
$ \Rightarrow \quad 7 x+24 y-50 =0\qquad\ldots\mathrm{(iii)} $
मान लीजिए बिंदु $(h, k)$ जो इन रेखाओं से समान दूरी पर है।
रेखा (i) से दूरी $=\dfrac{|4 h+3 k+10|}{\sqrt{16+9}}$
रेखा (ii) से दूरी $=\dfrac{|5 h-12 k+26|}{\sqrt{25+144}}$
रेखा (iii) से दूरी $=\dfrac{|7 h+24 k-50|}{\sqrt{7^{2}+24^{2}}}$
इसलिए, बिंदु $(h, k)$ रेखाओं (i), (ii) और (iii) से समान दूरी पर है।
$ \begin{matrix} \therefore\quad & \dfrac{4 h+3 k+10}{\sqrt{16+9}}=\dfrac{5 h-12 k+26}{\sqrt{25+144}}=\dfrac{7 h+24 k-50}{\sqrt{49+576}} \\ \\ \Rightarrow \quad & \dfrac{|4 h+3 k+10|}{5}=\dfrac{|5 h-12 k+26|}{13}=\dfrac{|7 h+24 k-50|}{25} \end{matrix} $
स्पष्ट रूप से, यदि $h=0, k=0$, तो $\dfrac{10}{5}=\dfrac{26}{13}=\dfrac{50}{25}=2$
अतः, अभीष्ट बिंदु $(0,0)$ है।
39. एक रेखा $(2,2)$ से गुजरती है और रेखा $3 x+y=3$ के लंबवत है। इसका $y$-अक्ष प्रतिच्छेदन बिंदु है
(a) $\dfrac{1}{3}$
(b) $\dfrac{2}{3}$
(c) 1
(d) $\dfrac{4}{3}$
उत्तर दिखाएं
सोचने की प्रक्रिया
पहले आवश्यक रेखा का समीकरण ज्ञात करें फॉर्मूला का उपयोग करके, अर्थात $y-y_1=m(x-x_1)$ फिर $x=0$ रखकर $y$-अक्ष प्रतिच्छेदन बिंदु ज्ञात करें।
हल
(d) दी गई रेखा $y=3-3 x$ है।
तब, आवश्यक रेखा की ढलान $=\dfrac{1}{3}$
$\because$ आवश्यक रेखा का समीकरण है
$ y-2 =\dfrac{1}{3}(x-2) $
$ \Rightarrow \quad 3 y-6 =x-2 $
$ \Rightarrow \quad x-3 y+4 =0 $
$ \text { यदि } y\text{-अक्ष प्रतिच्छेदन बिंदु, } \text { तो } x =0, $
$ \Rightarrow \quad 0-3 y+4 =0$
$ y =\dfrac{4}{3} $
40. रेखा $3 x+4 y+2=0$ द्वारा रेखाओं $3 x+4 y+5=0$ और $3 x+4 y-5=0$ के बीच दूरी को किस अनुपात में विभाजित करती है?
(a) $1: 2$
(b) $3: 7$
(c) $2: 3$
(d) $2: 5$
उत्तर दिखाएं
सोचने की प्रक्रिया
दो समानांतर रेखाओं के बीच दूरी: दो समानांतर रेखाओं $A x+B y+C_1=0$ और $A x+B y+C_2=0$ के बीच दूरी $d$ निम्नलिखित द्वारा दी गई है:
दो समानांतर रेखाओं $A x+B y+C_1=0$ और $A x+B y+C_2=0$ के बीच दूरी $d$ निम्नलिखित द्वारा दी गई है:
d = \dfrac{|C_1 - C_2|}{\sqrt{A^2 + B^2}}
दिए गए रेखाओं $3 x+4 y+5=0$ और $3 x+4 y-5=0$ के बीच दूरी है:
d = \dfrac{|5 - (-5)|}{\sqrt{3^2 + 4^2}} = \dfrac{10}{5} = 2
अब, रेखा $3 x+4 y+2=0$ द्वारा दूरी को विभाजित करने वाले अनुपात की गणना करें। रेखा $3 x+4 y+2=0$ द्वारा दूरी के बीच दो रेखाओं के बीच दूरी के अनुपात के लिए, आप इस तरह गणना कर सकते हैं:
रेखा $3 x+4 y+5=0$ और $3 x+4 y+2=0$ के बीच दूरी है:
d_1 = \dfrac{|5 - 2|}{\sqrt{3^2 + 4^2}} = \dfrac{3}{5}
रेखा $3 x+4 y+2=0$ और $3 x+4 y-5=0$ के बीच दूरी है:
d_2 = \dfrac{|2 - (-5)|}{\sqrt{3^2 + 4^2}} = \dfrac{7}{5}
अतः, अनुपात है:
d_1 : d_2 = 3 : 7
अतः, उत्तर (b) $3: 7$ है।
$ d=\dfrac{\left|C_2-C_1\right|}{\sqrt{A^2+B^2}} $
हल
(b) $3 x+4 y+5=0$ और $3 x+4 y-5=0$ के बीच की दूरी
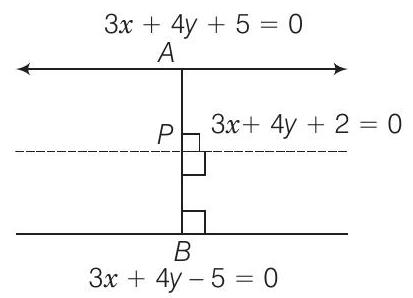
$ d=\dfrac{|5-(-5)|}{\sqrt{3^2+4^2}}=\dfrac{|10|}{\sqrt{9+16}}=\dfrac{10}{5}=2 $
अब, हमें दिए गए समांतर रेखाओं से $3 x+4 y+2=0$ की दूरी ज्ञात करनी होगी और इनका उपयोग करके अनुपात ज्ञात करना होगा।
$3 x+4 y+5=0$ से $3 x+4 y+2=0$ की दूरी
$ d_1=\dfrac{|5-2|}{\sqrt{3^2+4^2}}=\dfrac{3}{5} $
$3 x+4 y-5=0$ से $3 x+4 y+2=0$ की दूरी
$ d_2=\dfrac{|-5-2|}{\sqrt{3^2+4^2}}=\dfrac{7}{5} $
रेखा $3 x+4 y+2=0$ दो रेखाओं के बीच खंड को $d_1: d_2$ के अनुपात में विभाजित करती है।
इसलिए, अनुपात है
$ \dfrac{\dfrac{3}{5}}{\dfrac{7}{5}}=\dfrac{3}{7} $
इसलिए, रेखा दो रेखाओं के बीच दूरी को $3: 7$ के अनुपात में विभाजित करती है।
41. समबाहु त्रिभुज के केंद्रक मूल बिंदु पर है और एक भुजा $x+y-2=0$ है, तो एक शीर्ष है
(a) $(-1,-1)$
(b) $(2,2)$
(c) $(-2,-2)$
(d) $(2,-2)$
उत्तर दिखाएं
चिंतन प्रक्रिया
मान लीजिए $A B C$ एक समबाहु त्रिभुज है जिसका शीर्ष $A(h, k)$ है और $D(\alpha, \beta)$ बिंदु $B C$ पर है।
तब, $\dfrac{2 \alpha+h}{3}=0=\dfrac{2 \beta+k}{3}$.
इसके अलावा, $\alpha+\beta-2=0$ और $\left(\dfrac{k-0}{h-0}\right) \cdot(-1)=-1$।
हल
(c) मान लीजिए $A B C$ एक समबाहु त्रिभुज है जिसका शीर्ष $A(h, k)$ है। मान लीजिए $D$ के निर्देशांक $(a, b)$ हैं।
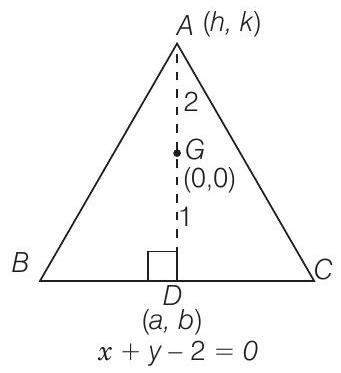
इसके अलावा, केंद्रक $G(0,0)$ है
अब, $A G$ रेखा $B C$ के लंबवत है
रेखा $B C$ या $\boldsymbol{x}+\boldsymbol{y}-\mathbf{2}=\mathbf{0}$ की ढलान $-\mathbf{1}$ है
$\therefore\quad$ $A G$ की ढलान, $\dfrac{k}{h}=1$ या $h=k$
अब, उत्सर्जन के बिंदु से $BC$ की दूरी $=\dfrac{|0+0-2|}{\sqrt{1+1}}=\dfrac{2}{\sqrt{2}}=\sqrt{2}$
$\therefore\quad$ $A$ से $BC$ की दूरी $3 \sqrt{2}=\frac{|h+k-2|}{\sqrt{1+1}}$
$ \therefore\quad |h+k-2|=6 $
$\Rightarrow\quad h+k-8=0$ या $h+k+4=0$
$ \Rightarrow\quad h+h-8=0 \text { या } h+h+4=0 \text { क्योंकि } h=k $
$ \Rightarrow\quad 2 h-8=0 \text { या } 2 h+4=0 $
$ \Rightarrow\quad 2 h=8 \text { या } 2 h=-4 $
$ \Rightarrow\quad h=4 \text { या } h=-2 $
$\therefore\quad$ शीर्ष $(-2,-2)$ है।
भरण पदार्थ
42. यदि $a, b$ और $c$ AP में है, तो सीधी रेखा $a x+b y+c=0$ हमेशा गुजरेगी ……
उत्तर दिखाएं
चिंतन प्रक्रिया
यदि $a, b$ और $c$ AP में है, तो $2 b=a+c$ होता है। इस गुण का उपयोग ऊपरी समस्या को हल करने में करें।
हल
दी गई रेखा $a x+b y+c=0\qquad\ldots\mathrm{(i)}$
क्योंकि, $a, b$ और $c$ AP में है, तो $b=\dfrac{a+c}{2}$
$ \Rightarrow \quad \quad a-2 b+c=0\qquad\ldots\mathrm{(ii)} $
समीकरण (i) और (ii) की तुलना करने पर, हम प्राप्त करते हैं
$ x=1, y=-2 $
इसलिए, $(1,-2)$ रेखा पर स्थित है।
43. अक्षों से समान अंतराल काटती रेखा और बिंदु $(1,-2)$ से गुजरती है, तो रेखा का समीकरण ……
उत्तर दिखाएं
हल
रेखा का समीकरण $\dfrac{x}{a}+\dfrac{y}{a}=1$ है
क्योंकि, यह रेखा $(1,-2)$ से गुजरती है।
$\Rightarrow \quad \dfrac{1}{a}-\dfrac{2}{a} =1 $
$\Rightarrow \quad 1-2 =a$
$\Rightarrow \quad a=-1$
$\therefore\quad$ आवश्यक रेखा का समीकरण $-x-y=1$
$ \Rightarrow \quad \quad x+y+1=0 $
44. बिंदु $(3,2)$ से गुजरती रेखा जो रेखा $x-2 y=3$ के साथ $45^{\circ}$ का कोण बनाती है, तो रेखा के समीकरण ……
उत्तर दिखाएं
हल
दिया गया बिंदु $P(3,2)$ और रेखा $x-2 y=3$ है।
इस रेखा का ढलान $m_1=\dfrac{1}{2}$ है
मान लीजिए अभीष्ट रेखा का ढलान $m$ है।
$ \begin{matrix} \text { तब, } & \tan \theta=\left|\dfrac{m-\dfrac{1}{2}}{1+\dfrac{1}{2} m}\right| \\ \\ \Rightarrow \quad & 1= \pm \left(\dfrac{m-\dfrac{1}{2}}{1+\dfrac{m}{2}}\right)
\end{matrix} $
धनात्मक चिन्ह लेने पर,
$ \Rightarrow \quad 1+\dfrac{m}{2}=m-\dfrac{1}{2} $
$ \begin{aligned} \Rightarrow \quad & m-\dfrac{m}{2} =1+\dfrac{1}{2} \\ \\ \Rightarrow \quad & \dfrac{m}{2} =\dfrac{3}{2} \\ \\ \Rightarrow \quad & m=3 \end{aligned} $
ऋणात्मक चिन्ह लेने पर,
$ \begin{aligned} \Rightarrow \quad & 1=-\left(\dfrac{m-\dfrac{1}{2}}{1+\dfrac{m}{2}}\right) \\ \\ \Rightarrow \quad & 1+\dfrac{m}{2} =-m+\dfrac{1}{2} \\ \\ \Rightarrow \quad & m+\dfrac{m}{2} =\dfrac{1}{2}-1 \\ \\ \Rightarrow \quad & \dfrac{3 m}{2} =\dfrac{-1}{2} \\ \\ \Rightarrow \quad & m=\dfrac{-1}{3} \end{aligned} $
$\therefore\quad \quad$ रेखा का पहला समीकरण है
$\Rightarrow \quad y-2 =3(x-3) $
$\Rightarrow \quad 3 x-y-7 =0$
और रेखा का दूसरा समीकरण है
$ \begin{aligned} \Rightarrow \quad & y-2 =-\dfrac{1}{3}(x-3) \\ \\ \Rightarrow \quad & 3 y-6 =-x+3 \\ \\ \Rightarrow \quad & x+3 y-9 =0 \end{aligned} $
45. बिंदु $(3,4)$ और $(2,-6)$ रेखा $3 x-4 y-8=0$ के …… पर स्थित हैं।
उत्तर दिखाएं
हल
$ \begin{aligned} & \text{दी गई रेखा है}\quad 3 x-4 y-8=0 \\ \\ & \text{बिंदु (3,4) के लिए,} \\ \\ & \Rightarrow \quad 9-4 \cdot 4-8 \\ \\ & \Rightarrow \quad 9-16-8 \\ \\ & \Rightarrow \quad 9-24 \\ \\ & \Rightarrow \quad -15 < 0 \end{aligned} $
बिंदु $(2,-6)$ के लिए,
$ \begin{aligned} & 6+24-8 \\ \\ & 22>0 \end{aligned} $
क्योंकि, मान विपरीत चिन्हों के हैं।
अतः, बिंदु $(3,4)$ और $(2,-6)$ रेखा के विपरीत तरफ स्थित हैं।
46. एक बिंदु इस प्रकार गति करता है कि इसकी बिंदु $(3,-2)$ से दूरी के वर्ग का मान रेखा $5 x-12 y=3$ से दूरी के बराबर होता है। इसके बिंदुपथ का समीकरण निम्नलिखित है।
उत्तर दिखाएं
हल
मान लीजिए बिंदु के निर्देशांक $(h, k)$ हैं,
$\therefore\quad \quad$ बिंदु $(3,-2)$ और $(h, k)$ के बीच दूरी,
$ d_1^{2}=(3-h)^{2}+(-2-k)^{2} $
अब, बिंदु $(h, k)$ की रेखा $5 x-12 y=3$ से दूरी है,
$ \begin{aligned} & \text{Distance from the line } 5x - 12y = 3 \text{ is } \dfrac{|5h - 12k - 3|}{\sqrt{5^2 + (-12)^2}} \\ \\ & \text{According to the problem, } (3 - h)^2 + (-2 - k)^2 = \dfrac{|5h - 12k - 3|}{\sqrt{5^2 + (-12)^2}} \\ \\ & \text{Squaring both sides,} \\ \\ & (3 - h)^2 + (-2 - k)^2 = \dfrac{(5h - 12k - 3)^2}{5^2 + (-12)^2} \\ \\ & \text{Simplify the equation,} \\ \\ & (3 - h)^2 + (k + 2)^2 = \dfrac{(5h - 12k - 3)^2}{169} \\ \\ & \text{Multiply both sides by 169,} \\ \\ & 169[(3 - h)^2 + (k + 2)^2] = (5h - 12k - 3)^2 \end{aligned} $
This is the required equation of the locus.
$ d_2=\Big|\dfrac{5 h-12 k-3}{\sqrt{25+144}}\Big|=\Big|\dfrac{5 h-12 k-3}{13}\Big| $
दिया गया है, $ d_1^{2}=d_2 $
$ \begin{aligned} & \Rightarrow \quad \quad(3-h)^{2}+(2+k)^{2}=\dfrac{5 h-12 k-3}{13} \\ \\ & \Rightarrow \quad \quad 9-6 h+h^{2}+4+4 k+k^{2}=\dfrac{5 h-12 k-3}{13} \\ \\ & \Rightarrow \quad \quad h^{2}+k^{2}-6 h+4 k+13=\dfrac{5 h-12 k-3}{13} \\ \\ & \Rightarrow \quad \quad 13 h^{2}+13 k^{2}-78 h+52 k+169=5 h-12 k-3 \\ \\ & \Rightarrow \quad \quad 13 h^{2}+13 k^{2}-83 h+64 k+172=0 \end{aligned} $
$\therefore\quad$ इस बिंदु के बिंदुपथ है $ \ \ 13 x^{2}+13 y^{2}-83 x+64 y+172=0$
47. रेखा $x \sin \theta+y \cos \theta=p$ के अक्षों के बीच के भाग के मध्य बिंदुओं के बिंदुपथ है ……
उत्तर दिखाएं
हल
दी गई रेखा का समीकरण है
$ x \sin \theta+y \cos \theta=p\qquad\ldots\mathrm{(i)} $
मान लीजिए $AB$ के मध्य बिंदु $p(h, k)$ है।
इसलिए, $AB$ के मध्य बिंदु हैं $\quad\left(\dfrac{a}{2}, \dfrac{b}{2}\right)$
क्योंकि, बिंदु $(a, 0)$ रेखा (i) पर स्थित है, तो $a \sin \theta+0=p$
$\Rightarrow \quad \quad a \sin \theta=p $
$\Rightarrow \qquad a=\dfrac{p}{\sin \theta}$
और बिंदु $(0, b)$ भी रेखा पर स्थित है, तो $0+b\cos \theta=p$
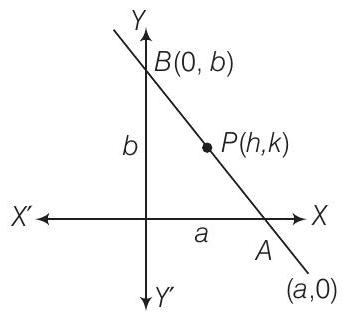
$ \Rightarrow \quad \quad b \cos \theta=p$
$ \Rightarrow \quad b=\dfrac{p}{\cos \theta} $
अब $ \text { AB के मध्य बिंदु }=\left(\dfrac{a}{2}, \dfrac{b}{2}\right) \text { या } \left(\dfrac{p}{2 \sin \theta}, \dfrac{p}{2 \cos \theta}\right) $
$\because\quad$ $ \dfrac{p}{2 \sin \theta}=h $
$\Rightarrow \quad \sin \theta=\dfrac{p}{2 h} $
और $\quad\dfrac{p}{2 \cos \theta}=k $
$\Rightarrow \quad \cos \theta=\dfrac{p}{2 k} $
$\therefore\quad \quad \sin ^{2} \theta+\cos ^{2} \theta=\dfrac{p^{2}}{4 h^{2}}+\dfrac{p^{2}}{4 k^{2}}$
$ \Rightarrow \quad \quad 1=\dfrac{p^{2}}{4}\left( \dfrac{1}{h^{2}}+\dfrac{1}{k^{2}}\right) $
मध्य बिंदु का बिंदुपथ है
$ \Rightarrow\quad 4 =p^{2} \left(\dfrac{1}{x^{2}}+\dfrac{1}{y^{2}}\right) $
$\Rightarrow \quad 4 x^{2} y^{2} =p^{2}\left(x^{2}+y^{2}\right)$
सत्य/असत्य
48. यदि एक त्रिभुज के शीर्ष अपरिमेय समन्वय रखते हैं, तो त्रिभुज समबाहु नहीं हो सकता।
उत्तर दिखाएं
हल
सत्य
हम जानते हैं कि, यदि एक त्रिभुज के शीर्ष अपरिमेय समन्वय रखते हैं, तो त्रिभुज समबाहु नहीं हो सकता। अतः, दिया गया कथन सत्य है।
क्योंकि, समबाहु त्रिभुज में हमें $\tan 60^{\circ}=\sqrt{3}=$ रेखा की प्रतिशत ढलान प्राप्त होती है, इसलिए अपरिमेय समन्वय रखते शीर्षों के साथ त्रिभुज समबाहु नहीं हो सकता।
49. बिंदु $A(-2,1), B(0,5)$ और $C(-1,2)$ संरेख हैं।
उत्तर दिखाएं
हल
असत्य
दिए गए बिंदु $A(-2,1), B(0,5)$ और $C(-1,2)$ हैं।
अब, $ \text { रेखा } AB \text{ की ढलान }=\dfrac{5-1}{0+2}=2 $
रेखा $ BC \text{ की ढलान }=\dfrac{2-5}{-1-0}=3$
रेखा $ AC \text{ की ढलान }=\dfrac{2-1}{-1+2}=1$
क्योंकि, ढलान अलग-अलग हैं।
अतः, $A, B$ और $C$ संरेख नहीं हैं। अतः, कथन असत्य है।
50. बिंदु $(a \cos ^{3} \theta, a \sin ^{3} \theta)$ से गुजरने वाली रेखा जो रेखा $x \sec \theta+y \cosec \theta=a$ के लम्बवत है, उसका समीकरण $x \cos \theta-y \sin \theta=a \sin 2 \theta$ है।
उत्तर दिखाएं
हल
असत्य
दिया गया बिंदु $p(a \cos ^{3} \theta, a \sin ^{3} \theta)$ और रेखा $x \sec \theta+y \cosec \theta=a$
$\because \quad$ रेखा की ढलान $=\dfrac{-\sec \theta}{\cosec \theta}=-\tan \theta$
और
$ \text { अभीष्ट रेखा की ढलान }=\dfrac{1}{\tan \theta}=\cot \theta $
$\therefore\quad \quad$ अभीष्ट रेखा का समीकरण है
$ \begin{aligned} \Rightarrow \quad & y-a \sin ^{3} \theta=\cot \theta(x-a \cos ^{3} \theta) \\ \\ \Rightarrow \quad & y \sin \theta-a \sin ^{4} \theta=x \cos \theta-a\cos^{4} \theta \\ \\
\Rightarrow \quad & x \cos \theta-y \sin \theta=a \cos ^{4} \theta-a\sin^{4} \theta \\ \\ \Rightarrow \quad & x \cos \theta-y \sin \theta=a[(\cos ^{2} \theta+\sin ^{2} \theta)(\cos ^{2} \theta-\sin ^{2} \theta)] \\ \\ \Rightarrow \quad & x \cos \theta-y \sin \theta=a \cos {2} \theta \end{aligned} $
इसलिए, दिए गए कथन गलत है।
51. सीधी रेखा $5 x+4 y=0$ दो सीधी रेखाओं $x+2 y-10=0$ और $2 x+y+5=0$ के प्रतिच्छेद बिंदु से गुजरती है।
उत्तर दिखाएं
हल
सत्य
$\text { दिया गया है, } \quad x+2 y-10=0\qquad\ldots\mathrm{(i)} $
$ \text { और } \quad 2 x+y+5 =0\qquad\ldots\mathrm{(ii)}$
समीकरण $\mathrm{(i)}$ से, $x=10-2 y$ के मान को समीकरण $\mathrm{(ii)}$ में रखने पर, हम प्राप्त करते हैं
$ \begin{aligned} \Rightarrow \quad & 20-4 y+y+5 =0 \\ \\ \Rightarrow \quad & 20-3 y+5 =0 \\ \\ \therefore\quad & x+\dfrac{50}{3}-10 =0 \\ \\ \Rightarrow \quad & x+\dfrac{20}{3}=0 \\ \\ \Rightarrow \quad & x =\dfrac{-20}{3} \end{aligned} $
इसलिए, प्रतिच्छेद बिंदु है $\left(-\dfrac{20}{3}, \dfrac{25}{3}\right)$।
यदि रेखा $5 x+4 y=0$ बिंदु $\left(-\dfrac{20}{3}, \dfrac{25}{3}\right)$ से गुजरती है, तो यह बिंदु इस रेखा पर स्थित होना चाहिए।
$ \because \quad 5\left(\dfrac{-20}{3}\right)+4\left(\dfrac{(25)}{3}\right)=\dfrac{-100}{3}+\dfrac{100}{3}=0 $
इसलिए, यह बिंदु दी गई रेखा पर स्थित है।
इसलिए, कथन सत्य है।
52. एक समबाहु त्रिभुज का शीर्ष $(2,3)$ है और विपरीत भुजा का समीकरण $x+y=2$ है। तब, अन्य दो भुजाएँ $y-3=(2 \pm \sqrt{3})(x-2)$ हैं।
उत्तर दिखाएं
हल
सत्य
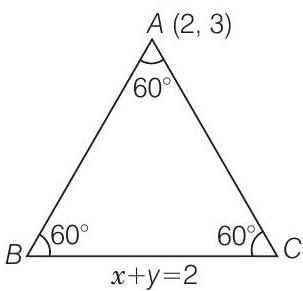
मान लीजिए $A B C$ एक समबाहु त्रिभुज है जिसका शीर्ष $A(2,3)$ है, और $B C$ का समीकरण $x+y=2$ है। अर्थात, ढलान $=-1$ है।
मान लीजिए रेखा $A B$ की ढलान $m$ है।
क्योंकि, रेखा $A B$ और $B C$ के बीच कोण $60^{\circ}$ है।
$ \begin{aligned} & \therefore\quad \quad \tan 60^{\circ}=\Big|\dfrac{m+1}{1-m} \Big|\\ \\ & \Rightarrow \quad \quad \sqrt{3}= \pm \left(\dfrac{m+1}{1-m}\right) \quad \text { [धनात्मक चिह्न लेते हुए] } \\ \\ & \Rightarrow \quad \quad \sqrt{3}-\sqrt{3} m=m+1 \\ \\ & \Rightarrow \quad \quad \sqrt{3}-1=m+\sqrt{3} m \\ \\ & \Rightarrow \quad \quad \sqrt{3}-1=m(1+\sqrt{3}) \\ \\ & \therefore\quad \quad m=\dfrac{(\sqrt{3}-1)(\sqrt{3}-1)}{(\sqrt{3}+1)(\sqrt{3}-1)} =\dfrac{3+1-2 \sqrt{3}}{3-1}=\dfrac{4-2 \sqrt{3}}{2}=2-\sqrt{3} \end{aligned} $
उसी तरह, $A B$ की ढलान $2+\sqrt{3}$ है
$\therefore\quad$ अन्य दो भुजाओं की समीकरण है
[ऋणात्मक चिह्न लेते हुए]
$ y-3=(2 \pm \sqrt{3})(x-2) $
इसलिए, कथन सत्य है।
53. बिंदु $(3,5)$ और रेखाओं $4 x+y-1=0$ और $7 x-3 y-35=0$ के प्रतिच्छेद बिंदु को मिलाने वाली रेखा की समीकरण बिंदुओं $(0,0)$ और $(8,34)$ से समान दूरी पर है।
उत्तर दिखाएं
सोचने की प्रक्रिया
बिंदुओं $(x_1, y_1)$ और $(x_2, y_2)$ से गुजरने वाली रेखा की समीकरण है
$y-y_1=\dfrac{y_2-y_1}{x_2-x_1}(x-x_1)$
हल
सत्य
दी गई रेखाओं की समीकरण $4x+y-1=0$
$ \text { और } \quad 7 x-3 y-35=0 $
समीकरण (i) से, $y=1-4 x$ को समीकरण (ii) में रखने पर, हम प्राप्त करते हैं
$ \Rightarrow \quad \quad 7 x-3+12 x-35=0 $
$ \Rightarrow \quad \quad 19 x-38=0$
$ \Rightarrow \qquad x=2 $
$x=2$ को समीकरण (i) में रखने पर, हम प्राप्त करते हैं
$\Rightarrow \quad 8+y-1=0 $
$\Rightarrow \quad y=-7 $
अब, बिंदुओं $(3,5)$ और $(2,-7)$ से गुजरने वाली रेखा की समीकरण है
$ \begin{aligned} y-5 =\dfrac{-7-5}{2-3}(x-3) \\ \\ \Rightarrow \quad y-5 =12(x-3) \\ \\ \Rightarrow \quad 12 x-y-31 =0 \end{aligned} $
बिंदु $(0,0)$ से रेखा (iii) की दूरी,
$ d_1=\dfrac{|-31|}{\sqrt{144+1}}=\dfrac{31}{\sqrt{145}} $
$\therefore\quad$ बिंदु $(8,34)$ से रेखा (iii) की दूरी,
$ \begin{aligned} d_2 & =\dfrac{|96-34-31|}{\sqrt{145}}=\dfrac{31}{\sqrt{145}} \\ \\
\because \quad d_1 & =d_2 \end{aligned} $
अतः, कथन सत्य है।
54. रेखा $\dfrac{x}{a}+\dfrac{y}{b}=1$ इस प्रकार गति करती है कि $\dfrac{1}{a^{2}}+\dfrac{1}{b^{2}}=\dfrac{1}{c^{2}}$, जहाँ $c$ एक स्थिरांक है। दी गई रेखा पर मूल बिंदु से लम्ब के पाद के बिंदु के अवतरण (locus) $x^{2}+y^{2}=c^{2}$ है।
उत्तर दिखाएं
हल
सत्य
दिया गया कि, रेखा का समीकरण है
$ \dfrac{x}{a}+\dfrac{y}{b}=1\qquad\ldots\mathrm{(i)} $
मूल बिंदु से रेखा (i) पर लम्ब जाने वाली रेखा का समीकरण है
$ \dfrac{x}{b}-\dfrac{y}{a}=0\qquad\ldots\mathrm{(ii)} $
अब, लम्ब का पाद रेखाओं (i) और (ii) के प्रतिच्छेद बिंदु है। इसके अवतरण के लिए हमें चर $a$ और $b$ को बर्बाद करना होगा।
समीकरण (i) और (ii) को वर्ग करके जोड़ने पर हमें प्राप्त होता है
$ \begin{aligned} \Rightarrow \quad & \dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}+\dfrac{2 x y}{a b}+\dfrac{x^{2}}{b^{2}}+\dfrac{y^{2}}{a^{2}}-\dfrac{2 x y}{a b} =1 \\ \\ \Rightarrow \quad & x^{2} \left(\dfrac{1}{a^{2}}+\dfrac{1}{b^{2}}\right)+y^{2} \left(\dfrac{1}{a^{2}}+\dfrac{1}{b^{2}}\right) =1 \\ \\ \Rightarrow \quad & \dfrac{x^{2}}{c^{2}}+\dfrac{y^{2}}{c^{2}} =1 \qquad \left[\because\quad \dfrac{1}{a^{2}}+\dfrac{1}{b^{2}}=\dfrac{1}{c^{2}}\right] \\ \\ \Rightarrow \quad & x^{2}+y^{2} =c^{2} \end{aligned} $
अतः, कथन सत्य है।
55. रेखाएँ $a x+2 y+1=0, \quad b x+3 y+1=0$ और $c x+4 y+1=0$ संगत होंगी, यदि $a, b$ और $c$ एक गुणोत्तर श्रेणी (GP) में हों।
उत्तर दिखाएं
चिंतन प्रक्रिया
पहले दो रेखाओं के प्रतिच्छेद बिंदु को ज्ञात करें। फिर, यदि रेखाएँ संगत हों तो यह बिंदु तीसरी रेखा पर स्थित होना चाहिए।
हल
गलत
दी गई रेखाएँ हैं
$a x+2 y+1=0\qquad\ldots\mathrm{(i)}$
$\mathrm{और}$
$b x+3 y+1=0\qquad\ldots\mathrm{(ii)}$
समीकरण (i) से, $y=\dfrac{-a x-1}{2}$ को समीकरण (ii) में रखने पर हमें प्राप्त होता है
$b x-\dfrac{3}{2}(a x+1)+1=0 $
$\Rightarrow \quad 2 b x-3 a x-3+2=0 $
$\Rightarrow \quad x(2 b-3 a)=1$
$ \Rightarrow \quad x=\dfrac{1}{2 b-3a}$
अब, समीकरण (i) में $x=\dfrac{1}{2 b-3 a}$ का प्रयोग करते हुए, हम प्राप्त करते हैं
$ \Rightarrow \quad \dfrac{a}{2 b-3 a}+2 y+1 =0 $
$ \Rightarrow \quad 2 y =-\Big[\dfrac{a+2 b-3 a}{2 b-3 a}\Big] $
$\Rightarrow \quad 2 y =\dfrac{-(2 b-2 a)}{2 b-3 a} $
$\Rightarrow \quad y =\dfrac{(a-b)}{2 b-3 a}$
इसलिए, प्रतिच्छेद बिंदु है $\left(\dfrac{1}{2 b-3 a}, \dfrac{a-b}{2 b-3 a}\right)$।
क्योंकि, यह बिंदु $c x+4 y+1=0$ पर स्थित है,
$\text{तो}, \quad \dfrac{c}{2 b-3 a}+\dfrac{4(a-b)}{2 b-3 a}+1=0 $
$\Rightarrow \quad c+4 a-4 b+2 b-3 a=0 $
$\Rightarrow \quad -2 b+a+c=0 $
$\Rightarrow \quad 2 b=a+c $
इसलिए, दिया गया कथन गलत है।
56. बिंदुओं $(3,-4)$ और $(-2,6)$ को मिलाने वाली रेखा, बिंदुओं $(-3,6)$ और $(9,-18)$ को मिलाने वाली रेखा के लंबवत है।
उत्तर दिखाएं
Solution
गलत
दिए गए बिंदु $A(3,-4), B(-2,6), P(-3,6)$ और $Q(9,-18)$ हैं।
$\text{अब}$
$ \text { AB का ढलान}=\dfrac{6+4}{-2-3}=-2 $
$\text{और}$
$ \text { PQ का ढलान}=\dfrac{-18-6}{9+3}=-2$
इसलिए, रेखा $AB$ रेखा $PQ$ के समांतर है।
स्तंभों का मिलान
57. निम्नलिखित का मिलान करें।
| स्तंभ I | स्तंभ II |
|---|---|
| (i) रेखा $x+5 y=13$ पर बिंदुओं $P$ और $Q$ के निर्देशांक जो रेखा $12 x-5 y+26=0$ से 2 इकाई की दूरी पर हों | (a) $\quad(3,1),(-7,11)$ |
| (ii) रेखा $x+y=4$ पर बिंदु के निर्देशांक जो रेखा $4 x+3 y-10=0$ से 1 इकाई की दूरी पर हों | (b) $\left(-\dfrac{1}{3}, \dfrac{11}{3}\right), \left(\dfrac{4}{3}, \dfrac{7}{3}\right)$ |
| (iii) बिंदुओं $A(-2,5)$ और $B(3,1)$ को मिलाने वाली रेखा पर बिंदु के निर्देशांक जो $A P=P Q=Q B$ हों | (c) $\left(1, \dfrac{12}{5}\right),\left(-3, \dfrac{16}{5}\right)$ |
उत्तर दिखाएं
Solution
(i) मान लीजिए बिंदु $P(x_1, y_1)$ रेखा $x+5 y=13$ पर है, अर्थात $P(13-5 y_1, y_1)$
$\therefore\quad$ $P$ के बिंदु की रेखा $12 x-5 y+26=0$ से दूरी,
$ \begin{aligned} & \qquad 2=\Big|\dfrac{12(13-5 y_1)-5 y_1+26}{\sqrt{144+25}}\Big| \\ \\ & \Rightarrow \quad 2= \pm \dfrac{156-60 y_1-5 y_1+26}{13} \\ \\ & \Rightarrow \quad -65 y_1=-156 \quad \text { [धनात्मक चिह्न लेते हुए] } \\ \\ & \begin{aligned} \Rightarrow \quad y_1 & =\dfrac{156}{65}=\dfrac{12}{5} \\ \\ \Rightarrow \quad x_1 & =13-5 y_1 \\ \\ & =13-12=1 \end{aligned} \\ \\ & \text { इसलिए, बिंदु } P \begin{aligned} & \left(1, \dfrac{12}{5}\right) . \end{aligned} \\ \\ & \text { इसी तरह, } Q \text { के निर्देशांक } \left(-3, \dfrac{16}{5}\right) \text { हैं } . \end{aligned} $
(ii) रेखा $x+y=4$ पर बिंदु के निर्देशांक $(4-y_1, y_1)$ हों। रेखा $4 x+3 y-10=0$ से दूरी।
$ 1=\Big|\dfrac{4(4-y_1)+3 y_1-10}{\sqrt{16+9}}\Big| $
$ \Rightarrow \quad 1= \pm \dfrac{16-4 y_1+3 y_1-10}{5} $
$ \Rightarrow \quad 5=6-y_1 $
$ \Rightarrow \quad y_1=1 $
$ \text { यदि } y_1=1 \text {, तो } x_1=3 $
इसलिए, बिंदु $(3,1)$ है।
इसी तरह, ऋणात्मक चिह्न लेते हुए बिंदु $(-7,11)$ है।
(iii) दिया गया बिंदु $A(-2,5)$ और $B(3,1)$ है।
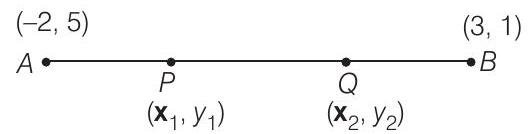
अब, बिंदु $P$ बिंदु $A$ और $B$ को जोड़ने वाली रेखा को $1: 2$ के अनुपात में विभाजित करता है।
$ \begin{aligned} \because \quad & x_1=\dfrac{1 \cdot 3+2(-2)}{1+2}=\dfrac{3-4}{3}=\dfrac{-1}{3} \\ \\ \text { और } & \quad y_1=\dfrac{1 \cdot 1+2 \cdot 5}{1+2}=\dfrac{11}{3} \end{aligned} $
इसलिए, $P$ के निर्देशांक $\left(\dfrac{-1}{3}, \dfrac{11}{3}\right)$ हैं।
इसलिए, बिंदु $Q$ बिंदु $A$ से $B$ को जोड़ने वाली रेखा को $2: 1$ के अनुपात में विभाजित करता है।
$ \begin{matrix} \because & x_2=\dfrac{2 \cdot 3+1(-2)}{2+1}=\dfrac{4}{3} \\ \\ \text { और } & y_2=\dfrac{2 \cdot 1+1 \cdot 5}{2+1}=\dfrac{7}{3} \end{matrix} $
इसलिए, $Q$ के निर्देशांक $\left(\dfrac{4}{3}, \dfrac{7}{3}\right)$ हैं।
अतः, सही मिलान हैं (i) $\rightarrow $ (c), (ii) $\rightarrow $ (a), (iii) $\rightarrow $ (b)।
58. यदि रेखाएँ $(2 x+3 y+4)+\lambda(6 x-y+12)=0$ हैं, तो $\lambda$ का मान है
| स्तंभ I | स्तंभ II |
|---|---|
| (i) $Y$-अक्ष के समांतर है | (a) $\quad \lambda=-\dfrac{3}{4}$ |
| (ii) $7 x+y-4=0$ के लंब है | (b) $\quad \lambda=-\dfrac{1}{3}$ |
| (iii) $(1,2)$ से गुजरती है | (c) $\quad \lambda=-\dfrac{17}{41}$ |
| (iv) $X$-अक्ष के समांतर है | (d) $\quad \lambda=3$ |
उत्तर दिखाएँ
हल
(i) दी गई रेखा का समीकरण है
$ (2 x+3 y+4)+\lambda(6 x-y+12)=0 $
यदि रेखा $Y$-अक्ष के समांतर है, अर्थात यह $X$-अक्ष के लंब है
$ \therefore\quad \quad \text { ढलान }=m=\tan 90^{\circ}=\infty $
$\begin{aligned} & \text { रेखा (i) से, } x(2+6 \lambda)+y(3-\lambda)+4+12 \lambda=0 \\ \\ & \text { और ढलान } =\dfrac{-(2+6 \lambda)}{3-\lambda} \\ \\ & \Rightarrow \quad \quad \dfrac{-2-6 \lambda}{3-\lambda}=\infty \\ \\ & \Rightarrow \quad \quad \dfrac{-2-6 \lambda}{3-\lambda}=\dfrac{1}{0} \\ \\ & \Rightarrow \qquad \lambda=3 \end{aligned}$
(ii) यदि रेखा (i) रेखा $7 x+y-4=0$ या $y=-7 x+4$ के लंब है
$ \begin{aligned} \because \quad & \dfrac{-(2+6 \lambda)}{(3-\lambda)}(-7) =-1 \\ \\ \Rightarrow \quad & 14+42 \lambda =-3+\lambda \\ \\ \Rightarrow \quad & 41 \lambda =-17 \\ \\ \Rightarrow \quad & \lambda =-\dfrac{17}{41} \end{aligned} $
(iii) यदि रेखा (i) बिंदु $(1,2)$ से गुजरती है।
$ \begin{matrix} \text { तो, } & (2+6+4)+\lambda(6-2+12) =0 \\ \\ \Rightarrow \quad & 12+16 \lambda=0 \\ \\ \Rightarrow \quad & \lambda =-\dfrac{3}{4} \end{matrix} $
(iv) यदि रेखा $X$-अक्ष के समांतर है तो ढलान $=0$।
$ \begin{matrix} \text { तो, } & \dfrac{-(2+6 \lambda)}{3-\lambda}=0 \\ \\ \Rightarrow \quad & -(2+6 \lambda)=0 \\ \\ \Rightarrow \quad & \lambda=-\dfrac{1}{3} \end{matrix} $
अतः, सही मिलान हैं (i) $\rightarrow \quad $ (d), (ii) $\rightarrow \quad $ (c), (iii) $\rightarrow \quad $ (a), (iv) $\rightarrow \quad $ (b)।
59. रेखा का समीकरण जो रेखाओं $2 x-3 y=0$ और $4 x-5 y=2$ के प्रतिच्छेद बिंदु से गुजरती है और
| स्तम्भ I | स्तम्भ II |
|---|---|
| (i) बिंदु $(2,1)$ से गुजरती है | (a) $2 x-y=4$ |
| (ii) रेखा $x+2 y+1=0$ के लम्ब है | (b) $x+y-5=0$ |
| (iii) रेखा $3 x-4 y+5=0$ के समानांतर है | (c) $x-y-1=0$ |
| (iv) अक्षों के समान झुकाव वाली है | (d) $3 x-4 y-1=0$ |
उत्तर दिखाएँ
हल
दी गई रेखाओं के समीकरण हैं
$ 2 x-3 y =0\qquad\ldots\mathrm{(i)} $
और $\quad$
$ 4 x-5 y =2\qquad\ldots\mathrm{(ii)} $
समीकरण (i) से, $x=\dfrac{3 y}{2}$ को समीकरण (ii) में रखने पर, हम प्राप्त करते हैं
$\Rightarrow \quad $ $ 4 \cdot \left(\dfrac{3 y}{2}\right)-5 y=2 $
$\Rightarrow \quad $ $ 6 y-5 y=2 $
अब, समीकरण (i) में $y=2$ रखने पर, हम प्राप्त करते हैं $, \ y=2, \ \ x=3$
इसलिए, प्रतिच्छेद बिंदु $(3,2)$ है।
(i) बिंदु $(3,2)$ और $(2,1)$ से गुजरने वाली रेखा का समीकरण है,
$ y-2 =\left(\dfrac{1-2}{2-3}\right)(x-3) $
$ \Rightarrow \quad y-2=x-3 $
$ \Rightarrow \quad x-y-1=0 $
(ii) यदि अभीष्ट रेखा रेखा $x+2 y+1=0$ के लम्ब है
$\because \quad $ अभीष्ट रेखा की प्रतिच्छेद दर $=2$
$\therefore\quad$ रेखा का समीकरण है
$\Rightarrow\quad y-2 =2(x-3) $
$ \Rightarrow \quad 2 x-y-4 =0 $
(iii) यदि अभीष्ट रेखा रेखा $3 x-4 y+5=0$ के समानांतर है,
तो अभीष्ट रेखा की प्रतिच्छेद दर $=\dfrac{3}{4}$
$\therefore\quad$ अभीष्ट रेखा का समीकरण है
$ y-2=\dfrac{3}{4}(x-3) $
$ \Rightarrow \quad 4 y-8=3 x-9 $
$ \Rightarrow \quad 3 x-4 y-1=0 $
(iv) यदि रेखा X-अक्ष के समान झुकाव वाली है, तो
$ m= \pm \tan 45^{\circ}= \pm 1 $
$\therefore\quad$ रेखा का समीकरण है
$y-2$ $=-1(x-3)$
$\Rightarrow \quad $ $y-2$ $=-x+3$
$\Rightarrow \quad $ $x+y-5$ $=0$
इसलिए, सही मिलान (a) $\rightarrow \quad $ (iii), $ \ $ (b) $\rightarrow \quad $ (i), $ \ $ (c) $\rightarrow \quad $ (iv), $ \ $ (d) $\rightarrow \quad $ (ii) है।





