समुच्चय
छोटे उत्तर प्रकार के प्रश्न
1. निम्नलिखित सेट को रोस्टर रूप में लिखिए।
(i) $A=\lbrace x: x \in R, 2 x+11=15\rbrace$
(ii) $B=\lbrace x \mid x^{2}=x, x \in R\rbrace$
(iii) $C=\lbrace x \mid x$ एक अभाज्य संख्या $p$ का धनात्मक गुणनखंड है $\rbrace$
उत्तर दिखाएं
सोचने की प्रक्रिया
दिए गए समीकरण को हल करें और $x$ का मान प्राप्त करें।
हल
(i) हमें दिया गया है,
$A =\lbrace x: x \in R, 2 x+11=15\rbrace$
$\therefore\quad 2 x+11 =15$
$\Rightarrow 2 x =15-11 $
$\Rightarrow 2 x=4$
$\Rightarrow x =2$
$\Rightarrow A =\lbrace 2\rbrace$
$\text{(ii) हमें दिया गया है},$
$ B =\lbrace x \mid x^{2}=x, x \in R\rbrace$
$x^{2} =x$
$\Rightarrow x^{2}-x =0$
$ \Rightarrow x(x-1) =0$
$\Rightarrow x =0,1$
$\therefore\quad B =\lbrace 0,1\rbrace$
(iii) हमें दिया गया है, $C=\lbrace x \mid x$ एक अभाज्य संख्या $p$ का धनात्मक गुणनखंड है $\rbrace$.
क्योंकि, एक अभाज्य संख्या के धनात्मक गुणनखंड 1 और संख्या खुद होते हैं।
$ \therefore\quad C=\lbrace1, p\rbrace $
2. निम्नलिखित सेट को रोस्टर रूप में लिखिए।
(i) $D=\lbrace t \mid t^{3}=t, t \in R\rbrace$
(ii) $E=\lbrace w \vert \ \dfrac{w-2}{w+3}=3, w \in R\rbrace$
(iii) $F=\lbrace x \mid x^{4}-5 x^{2}+6=0, x \in R\rbrace$
उत्तर दिखाएं
सोचने की प्रक्रिया
दिए गए समीकरण को हल करें और संगत चर का मान प्राप्त करें।
हल
(i) हमें दिया गया है,
$\text { हमें दिया गया है, } D =\lbrace t \mid t^{3}=t, t \in R\rbrace $
$\therefore\quad t^{3} =t $
$\Rightarrow t^{3}-t =0 $
$\Rightarrow t(t^{2}-1)=0 $
$\Rightarrow t(t-1)(t+1) =0$
$ \Rightarrow t=0,1,-1 $
$\therefore\quad D =\lbrace-1,0,1\rbrace $
(ii) $ \ \text { हमें दिया गया है, } $
$ \begin{aligned} & E =\left\lbrace w \vert\ \dfrac{w-2}{w+3}=3, w \in R\right\rbrace \\ \\ & \therefore\quad \dfrac{w-2}{w+3}=3 \\ \\ & \Rightarrow \quad w-2=3 w+9 \Rightarrow w-3 w=9+2 \\ \\
& \Rightarrow \quad-2 w=11 \quad \Rightarrow \quad w=\dfrac{-11}{2} \\ \\ & \therefore\quad E=\bigg\lbrace \dfrac{-11}{2} \bigg\rbrace \end{aligned} $
(iii) हमारे पास,
$ F=\lbrace x \mid x^{4}-5 x^{2}+6=0, x \in R\rbrace $
$ \therefore\quad x^{4}-5 x^{2}+6 =0 $
$ \Rightarrow x^{4}-3 x^{2}-2 x^{2}+6 =0 $
$ \Rightarrow x^{2}(x^{2}-3)-2(x^{2}-3) =0 $
$ \Rightarrow (x^{2}-3)(x^{2}-2) =0 $
$ \Rightarrow x = \pm \sqrt{3}, \pm \sqrt{2} $
$ \therefore\quad F =\lbrace -\sqrt{3},-\sqrt{2}, \sqrt{2}, \sqrt{3}\rbrace $
रोस्टर रूप में, तत्वों के व्यवस्था के क्रम के महत्व नहीं होता। इसलिए, हम इस प्रकार लिख सकते हैं $F=\lbrace-\sqrt{3}, \sqrt{2},-\sqrt{2}, \sqrt{3}\rbrace$।
3. यदि $Y=\lbrace x \mid x$ संख्या $2^{p-1}(2^{p}-1)$ का धनात्मक गुणनखंड है, जहाँ $2^{p}-1$ एक अभाज्य संख्या है $\rbrace $. $Y$ को रोस्टर रूप में लिखिए।
उत्तर दिखाएं
चिंतन प्रक्रिया
पहले, $2^{p-1}$ के सभी गुणनखंड लिखिए, जहाँ $p=1,2,3, \ldots, p$ और फिर $Y$ को प्राप्त करें।
हल
$Y=\lbrace x \mid x.$ संख्या $2^{p-1}(2^{p}-1)$ का धनात्मक गुणनखंड है, जहाँ $2^{p}-1$ एक अभाज्य संख्या है $\rbrace$.
इसलिए, $2^{p-1}$ के गुणनखंड $1,2,2^{2}, 2^{3}, \ldots, 2^{p-1}$ हैं।
$ \therefore\quad Y=\lbrace1,2,2^{2}, 2^{3}, \ldots, 2^{p-1}, 2^{p}-1\rbrace $
4. निम्नलिखित कथनों में से कौन से सत्य हैं और कौन से असत्य हैं? अपने उत्तर की व्याख्या करें।
(i) $35 \in\lbrace x \mid x$ के ठीक चार धनात्मक गुणनखंड हैं $\rbrace$।
(ii) $128 \in\lbrace y \mid$ $y$ के सभी धनात्मक गुणनखंडों का योग $2 y$ है $\rbrace$।
(iii) $3 \notin\lbrace x \mid x^{4}-5 x^{3}+2 x^{2}-112 x+6=0\rbrace$
(iv) $496 \notin\lbrace y \mid$ $y$ के सभी धनात्मक गुणनखंडों का योग $2 y$ है $\rbrace$।
उत्तर दिखाएं
हल
(i) क्योंकि, 35 के गुणनखंड $1,5,7$ और 35 हैं। इसलिए, कथन (i) सत्य है।
(ii) क्योंकि, 128 के गुणनखंड 1, 2, 4, 8, 16, 32, 64 और 128 हैं।
$ \begin{aligned}
\therefore\quad \text { गुणनखंडों का योग } & =1+2+4+8+16+32+64+128 \\ & =255 \neq 2 \times 128 \end{aligned} $
इसलिए, कथन $\mathrm{(ii)}$ गलत है।
(iii) हमारे पास,
$ x^{4}-5 x^{3}+2 x^{2}-112 x+6=0 $
$\therefore\quad $ जब $x=3$,
$\Rightarrow \quad 81-135+18-336+6=0$
$\Rightarrow\quad-346=0$
जो सत्य नहीं है।
इसलिए, कथन $\mathrm{(iii)}$ सत्य है।
(iv) $\quad\because \quad 496=2^{4} \times 31$
इसलिए, $496$ के गुणनखंड $1,2,4,8,16,31,62,124,248$ और $496$ हैं।
$\therefore\quad $ गुणनखंडों का योग $=1+2+4+8+16+31+62+124+248+496$
$ \hspace{2.7cm}=992=2(496) $
इसलिए, $496 \in\lbrace y \mid$ $y$ के सभी धनात्मक गुणनखंडों का योग $2 y$ है $\rbrace$।
इसलिए, कथन $\mathrm{(iv)}$ गलत है।
5. दिया गया है $L=\lbrace1,2,3,4\rbrace, M=\lbrace3,4,5,6\rbrace$ और $N=\lbrace1,3,5\rbrace$
प्रमाण करें कि $L-(M \cup N)=(L-M) \cap(L-N)$।
उत्तर दिखाएं
हल
दिया गया है, $\quad L=\lbrace1,2,3,4\rbrace, M=\lbrace3,4,5,6\rbrace$ और $N=\lbrace1,3,5\rbrace$
$\therefore\quad M \cup N=\lbrace1,3,4,5,6\rbrace$
$ L-(M \cup N)=\lbrace2\rbrace $
अब,
$ L-M=\lbrace1,2\rbrace, L-N=\lbrace2,4\rbrace $
$\therefore\quad (L-M) \cap(L-N)=\lbrace2\rbrace$
इसलिए, $\quad L-(M \cup N)=(L-M) \cap(L-N)$।
6. यदि $A$ और $B$ विस्तारित समुच्चय $U$ के उपसमुच्चय हैं, तो सिद्ध करें कि
(i) $A \subset A \cup B$
(ii) $A \subset B \Leftrightarrow A \cup B=B$
(iii) $(A \cap B) \subset A$
उत्तर दिखाएं
हल
(i) मान लीजिए $ x \in A $
$\Rightarrow \quad x \in A$ या $x \in B $
$\Rightarrow \quad x \in A \cup B$
इसलिए, $A \subset A \cup B$
(ii) मान लीजिए $x \in A \cup B$
$\Rightarrow \quad x \in A$ या $x \in B$
$\because \quad A \subset B, \ \ \text{तब}, \ \ x \in B$
$\Rightarrow \quad A \cup B \subset B \qquad\ldots\mathrm{(i)}$
$\text{अब}, \ B \subset A \cup B \qquad\ldots\mathrm{(ii)}$
समीकरण $\mathrm{(i)}$ और $\mathrm{(ii)}$ से, हम प्राप्त करते हैं
$A\cup B = B$
अब, मान लीजिए $y \in A$
$\Rightarrow \quad y \in A \cup B$
क्योंकि, $A \cup B = B,$ हम प्राप्त करते हैं
$\Rightarrow \quad y \in B$
$\Rightarrow \quad A \subset B$
इसलिए, $A \subset B \Leftrightarrow A \cup B = B$
(iii) मान लीजिए $x \in A \cap B$
$\Rightarrow \quad x \in A$ और $x \in B$
$\Rightarrow \quad x \in A$
इसलिए, $A \cap B \subset A$
7. दिया गया है $N=\lbrace1,2,3, \ldots, 100\rbrace$. तब, लिखिए
(i) $N$ का उपसमुच्चय जिसके तत्व सम संख्याएँ हों।
(ii) $N$ का उपसमुच्चय जिसके तत्व पूर्ण वर्ग संख्याएँ हों।
उत्तर दिखाएं
Solution
हमारे पास,
$ N=\lbrace1,2,3,4, \ldots, 100\rbrace $
(i) आवश्यक उपसमुच्चय $=\lbrace2,4,6,8, \ldots, 100\rbrace$
(ii) आवश्यक उपसमुच्चय $=\lbrace1,4,9,16,25,36,49,64,81,100\rbrace$
8. यदि $X=\lbrace1,2,3\rbrace$, और $n$ कोई भी सदस्य है $X$ के, तो निम्नलिखित समुच्चयों को लिखिए जो सभी तत्वों को दर्शाते हैं जो निम्नलिखित व्यंजकों द्वारा प्रस्तुत किए गए हैं
(i) $4 n$
(ii) $n+6$
(iii) $\dfrac{n}{2}$
(iv) $n-1$
उत्तर दिखाएं
Solution
दिया गया है,
$ X=\lbrace1,2,3\rbrace $
(i) $\lbrace4 n \mid n \in X\rbrace=\lbrace4,8,12\rbrace$
(ii) $\lbrace n+6 \mid n \in X\rbrace=\lbrace7,8,9\rbrace$
(iii) $\bigg\lbrace \dfrac{n}{2} \vert n \in X \bigg\rbrace = \bigg\lbrace \dfrac{1}{2}, 1, \dfrac{3}{2} \bigg\rbrace$
(iv) $\lbrace n-1 \mid n \in X\rbrace=\lbrace0,1,2\rbrace$
9. यदि $Y=\lbrace1,2,3, \ldots, 10\rbrace$ और $a$ कोई भी तत्व है $Y$ के, तो निम्नलिखित समुच्चयों को लिखिए, जो सभी तत्वों को दर्शाते हैं जो दिए गए शर्तों को संतुष्ट करते हैं।
(i) $a \in Y$ लेकिन $a^{2} \notin Y$
(ii) $a+1=6, a \in Y$
(iii) $a$ 6 से कम है और $a \in Y$
उत्तर दिखाएं
Solution
दिया गया है,
$ Y=\lbrace 1,2,3, \ldots, 10\rbrace $
(i) $\lbrace a: a \in Y$ और $a^{2} \notin Y\rbrace=\lbrace4,5,6,7,8,9,10\rbrace$
(ii) $\lbrace a: a+1=6, a \in Y\rbrace=\lbrace5\rbrace$
(iii) $\lbrace a:a \ \text{is less than} 6, a \in Y \rbrace = \lbrace 1,2,3,4,5 \rbrace$
10 $A, B$ और $C$ विस्तारित समुच्चय $U$ के उपसमुच्चय हैं। यदि $A=\lbrace2,4,6,8,12,20\rbrace$, $B=\lbrace3,6,9,12,15\rbrace, C=\lbrace5,10,15,20\rbrace$ और $U$ सभी पूर्ण संख्याओं का समुच्चय है, तो $U, A, B$ और $C$ के संबंध को दिखाने वाला वेन आरेख बनाएं।
उत्तर दिखाएं
हल
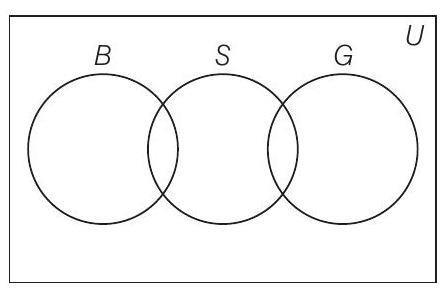
11. मान लीजिए $U$ एक स्कूल में सभी लड़कों और लड़कियों का समुच्चय है, $G$ एक स्कूल में सभी लड़कियों का समुच्चय है, $B$ एक स्कूल में सभी लड़कों का समुच्चय है और $S$ एक स्कूल में स्विमिंग करने वाले सभी छात्रों का समुच्चय है। कुछ लेकिन नहीं सभी छात्र स्विमिंग करते हैं। समुच्चय $U, G, B$ और $S$ के संभावित अंतर्संबंध को दिखाने वाला वेन आरेख बनाएं।
उत्तर दिखाएं
हल
12. सभी समुच्चय $A, B$ और $C$ के लिए सिद्ध करें कि $(A-B) \cap(A-C)=A-(B \cup C)$।
उत्तर दिखाएं
चिंतन प्रक्रिया
इसे सिद्ध करने के लिए हमें दिखाना होगा कि $(A-B) \cap(A-C) \subseteq A-(B \cup C)$ और $A-(B \cup C) \subseteq(A-B) \cap(A-C)$
हल
$\text{मान लीजिए,} \quad x \in(A-B) \cap(A-C)$
$\Rightarrow \quad x \in(A-B)$ और $x \in(A-C)$
$\Rightarrow \quad(x \in A$ और $x \notin B)$ और $(x \in A$ और $x \notin C)$
$\Rightarrow \quad x \in A$ और $(x \notin B$ और $x \notin C)$
$\Rightarrow \quad x \in A$ और $x \notin(B \cup C)$
$\Rightarrow \quad x \in A-(B \cup C)$
$\Rightarrow \quad(A-B) \cap(A-C) \subset A-(B \cup C) \quad \ldots {(i)}$
अब, मान लीजिए $\quad y \in A-(B \cup C)$
$\Rightarrow$ $\quad y \in A$ और $y \notin(B \cup C)$
$\Rightarrow \quad y \in A$ और $(y \notin B$ और $y \notin C)$
$\Rightarrow \quad(y \in A$ और $y \notin B)$ और $(y \in A$ और $y \notin C)$
$\Rightarrow \quad y \in(A-B)$ और $y \in(A-C)$
$\Rightarrow \quad y \in(A-B) \cap(A-C)$
$\Rightarrow \quad A-(B \cup C) \subset(A-B) \cap(A-C) \quad \ldots {(ii)}$
समीकरणों $\mathrm{(i)}$ और $\mathrm{(ii)}$ से,
$A-(B \cup C)=(A-B) \cap(A-C)$
दिशा निर्देश: प्रश्न 13 से 17 तक के प्रत्येक कथन के सत्य या असत्य होने की जांच करें।
अपना उत्तर तर्क सहित दीजिए।
13. सभी समुच्चय $A$ और $B$ के लिए, $(A-B) \cup(A \cap B)=A$
उत्तर दिखाएं
चिंतन प्रक्रिया
उपरोक्त समस्या को हल करने के लिए समुच्चयों पर वितरण नियम का उपयोग करें
अर्थात, $\quad A \cap(B \cup C)=(A \cap B) \cup(A \cap C)$।
हल
$ \begin{aligned} LHS & =(A-B) \cup(A \cap B) \\ & =[(A-B) \cup A] \cap[(A-B) \cup B] \\ & =A \cap(A \cup B)=A=RHS \end{aligned} $
इसलिए, दिया गया कथन सत्य है।
14. सभी समुच्चय $A, B$ और $C$ के लिए, $A-(B-C)=(A-B)-C$
उत्तर दिखाएं
हल
नीचे दिए गए वेन आरेखों को देखें, जहां छायांकित भाग $A-(B-C)$ और $(A-B)-C$ को प्रतिनिधित्व करते हैं।
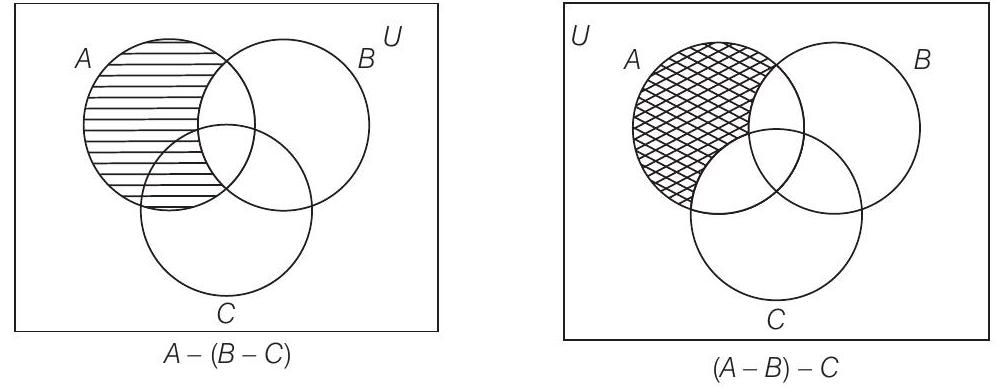
स्पष्ट रूप से, $A-(B-C)\neq (A-B)-C$
इसलिए, दिया गया कथन असत्य है।
15. सभी समुच्चय $A, B$ और $C$ के लिए, यदि $A \subset B$, तो $A \cap C \subset B \cap C$
उत्तर दिखाएं
हल
मान लीजिए $x \in A \cap C$
$\Rightarrow \quad x \in A$ और $x \in C$
$\Rightarrow \quad x \in B$ और $x \in C \quad [\because A \subset B]$
$\Rightarrow \quad x \in(B \cap C)$
$ \Rightarrow\quad(A \cap C) \subset(B \cap C)$
इसलिए, दिया गया कथन सत्य है।
16. सभी समुच्चय $A, B$ और $C$ के लिए, यदि $A \subset B$, तो $A \cup C \subset B \cup C$
उत्तर दिखाएं
हल
$\text{मान लीजिए,} \quad x \in A \cup C$
$\Rightarrow\quad$ $x \in A$ या $x \in C$
$\Rightarrow \quad x \in B$ या $x \in C \quad[\because A \subset B]$
$\Rightarrow \quad x \in B \cup C $
$\Rightarrow \quad A \cup C \subset B \cup C$
इसलिए, दिया गया कथन सत्य है।
17. सभी समुच्चय $A, B$ और $C$ के लिए, यदि $A \subset C$ और $B \subset C$, तो $A \cup B \subset C$।
उत्तर दिखाएं
हल
$\text{मान,}\quad x \in A \cup B$
$\Rightarrow\quad$ $x \in A$ और $x \in B$
$\Rightarrow \quad x \in C$ और $x \in C\quad$ $[\because A \subset C$ और $B \subset C]$
$\Rightarrow$ $x \in C \Rightarrow A \cup B \subset C$
इसलिए, दिया गया कथन सत्य है।
दिशा निर्देश: समुच्चय के गुणों का उपयोग करके अभ्यास प्रश्न $18$ से $22$ में दिए गए कथनों को सिद्ध करें।
18. सभी समुच्चय $A$ और $B$ के लिए, $A \cup(B-A)=A \cup B$
उत्तर दिखाएं
चिंतन प्रक्रिया
उपरोक्त समस्या को हल करने के लिए, वितरण नियम का उपयोग करें, अर्थात, $A \cup(B \cap C)=(A \cup B) \cap(A \cup C)$।
हल
$\text{LHS} = A \cup(B-A)=A \cup(B \cap A^{\prime})\qquad \left[\because A-B=A \cap B^{\prime}\right]$
$\qquad =(A \cup B) \cap(A \cup A^{\prime}) $
$\qquad=(A \cup B) \cap U \qquad{[\because A \cup A^{\prime}=\cup]} $
$\qquad=A \cup B \qquad {[\because A \cap U=A]} $
$\qquad=R H S$
19. सभी समुच्चय $A$ और $B$ के लिए, $A-(A-B)=A \cap B$
उत्तर दिखाएं
हल
$ \begin{aligned} LHS & =A-(A-B)=A-(A \cap B^{\prime}) \\ \\ & =A \cap(A \cap B^{\prime})^{\prime}\\ \\ & =A \cap[A^{\prime} \cup(B^{\prime})^{\prime}] \\ \\ & =A \cap(A^{\prime} \cup B) \\ \\ & =(A \cap A^{\prime}) \cup(A \cap B)\\ \\ & =\phi \cup(A \cap B) \\ \\ & =A \cap B=RHS \end{aligned} $
20. सभी समुच्चय $A$ और $B$ के लिए, $A-(A \cap B)=A-B$
उत्तर दिखाएं
हल
$ \begin{aligned} LHS & =A-(A \cap B)=A \cap(A \cap B)^{\prime} \qquad [\because A-B=A \cap B^{\prime}]\\ \\ & =A \cap(A^{\prime} \cup B^{\prime}) \qquad [\because (A \cap B)^{\prime}=A^{\prime} \cup B^{\prime}] \\ \\ & =(A \cap A^{\prime}) \cup(A \cap B^{\prime})=\phi \cup(A \cap B^{\prime}) \qquad [\because(A^{\prime})^{\prime}=A]\\ \\ `
& =A \cap B^{\prime} \\ \\ & =A-B=RHS \end{aligned} $
21. सभी समुच्चय $A$ और $B$ के लिए, $(A \cup B)-B=A-B$
उत्तर दिखाएं
हल
$ \begin{aligned} LHS & =(A \cup B)-B=(A \cup B) \cap B^{\prime}\quad [\because A-B=A \cap B^{\prime}] \\ \\ & =(A \cap B^{\prime}) \cup(B \cap B^{\prime})=(A \cap B^{\prime}) \cup \phi \quad [\because B \cap B^{\prime}=\phi] \\ \\ & =A \cap B^{\prime} \quad [\because A \cup \phi=A] \\ \\ & =A-B=RHS \end{aligned} $
22. $ \ \ \text{मान लीजिए,} \ T= \left\lbrace x \vert\ \dfrac{x+5}{x-7}-5=\dfrac{4 x-40}{13-x}\right\rbrace.$ $T$ एक खाली समुच्चय है? अपने उत्तर की व्याख्या कीजिए।
उत्तर दिखाएं
चिंतन प्रक्रिया
पहले दिए गए समीकरण को हल करें और $x$ का मान प्राप्त करें।
हल
$\text{क्योंकि}$
$ \begin{aligned} T=\bigg\lbrace x \bigg\vert, \dfrac{x+5}{x-7}-5 =\dfrac{4 x-40}{13-x} \bigg\rbrace \qquad \left[\because \dfrac{x+5}{x-7}-5 =\dfrac{4 x-40}{13-x}\right] \end{aligned} $
$ \begin{aligned} & \Rightarrow \quad \dfrac{x+5-5(x-7)}{x-7}=\dfrac{4 x-40}{13-x} \\ \\ & \Rightarrow \quad \dfrac{x+5-5 x+35}{x-7}=\dfrac{4 x-40}{13-x} \\ \\ & \Rightarrow \quad \dfrac{-4 x+40}{x-7}=\dfrac{4 x-40}{13-x} \\ \\ & \Rightarrow \quad-(4 x-40)(13-x)=(4 x-40)(x-7) \\ \\ & \Rightarrow \quad(4 x-40)(x-7)+(4 x-40)(13-x)=0 \\ \\ & \Rightarrow \quad(4 x-40)(x-7+13-x)=0 \\ \\ & \Rightarrow \quad 4(x-10) 6=0 \\ \\ & \Rightarrow \quad 24(x-10)=0 \\ \\ & \Rightarrow \quad x=10 \\ \\ & \therefore\quad T=\lbrace10\rbrace \end{aligned} $
इसलिए, $T$ एक खाली समुच्चय नहीं है।
लंबे उत्तर प्रकार के प्रश्न
23. यदि $A, B$ और $C$ समुच्चय हों, तो सिद्ध कीजिए कि $A \cap(B \cup C)=(A \cap B) \cup(A \cap C)$।
उत्तर दिखाएं
हल
$\text{मान लीजिए,} \ \ x \in A \cap (B \cup C)$
$\Rightarrow x \in A$ और $x \in(B \cup C)$
$\Rightarrow x \in A$ और $(x \in B$ या $x \in C)$
$\Rightarrow (x \in A$ और $x \in B)$ या $(x \in A$ और $x \in C)$
$\Rightarrow x \in A \cap B$ या $x \in A \cap C$
$\Rightarrow x \in(A \cap B) \cup(A \cap C)$
$\Rightarrow A \cap(B \cup C) \subset(A \cap B) \cup(A \cap C) \quad \qquad\ldots\mathrm{(i)}$
पुनः, $\ \text{let}$
$\Rightarrow y \in(A \cap B) \cup(A \cap C)$
$\Rightarrow y \in(A \cap B)$ या $y \in(A \cap C)$
$\Rightarrow (y \in A$ और $y \in B)$ या $(y \in A$ और $y \in C)$
$\Rightarrow y \in A$ और $(y \in B$ या $y \in C)$
$\Rightarrow y \in A$ और $y \in B \cup C$
$\Rightarrow y \in A \cap(B \cup C)$
$\Rightarrow (A \cap B) \cup(A \cap C) \subset A \cap(B \cup C) \qquad \qquad\ldots\mathrm{(ii)}$
समीकरण (i) और (ii) से
$A \cap(B \cup C)=(A \cap B) \cup(A \cap C)$
24. 100 छात्रों में से; 15 छात्र अंग्रेजी में पास हुए, 12 गणित में पास हुए, 8 विज्ञान में पास हुए, 6 अंग्रेजी और गणित में पास हुए, 7 गणित और विज्ञान में पास हुए, 4 अंग्रेजी और विज्ञान में पास हुए, 4 सभी तीन में पास हुए। बताइए कि कितने छात्र
(i) अंग्रेजी और गणित में पास हुए लेकिन विज्ञान में नहीं।
(ii) गणित और विज्ञान में पास हुए लेकिन अंग्रेजी में नहीं।
(iii) केवल गणित में पास हुए।
(iv) केवल एक से अधिक विषय में पास हुए।
उत्तर दिखाएं
Solution
मान लीजिए कि कुल छात्रों की संख्या $=U$
मान लीजिए कि अंग्रेजी में पास हुए छात्रों की संख्या $=E$
मान लीजिए कि गणित में पास हुए छात्रों की संख्या $=M$
मान लीजिए कि विज्ञान में पास हुए छात्रों की संख्या $=S$
कुल छात्रों की संख्या $n(U)= 100$
अंग्रेजी में पास हुए छात्रों की संख्या $n(E)=15$
गणित में पास हुए छात्रों की संख्या $n(M)=12$
विज्ञान में पास हुए छात्रों की संख्या $n(S)=8$
अंग्रेजी और गणित में पास हुए छात्रों की संख्या $n(E \cap M)=6$
गणित और विज्ञान में पास हुए छात्रों की संख्या $n(M \cap S)=7$
अंग्रेजी और विज्ञान में पास हुए छात्रों की संख्या $n(E \cap S)=4$
सभी तीन में पास हुए छात्रों की संख्या $n(E \cap M \cap S )=4$
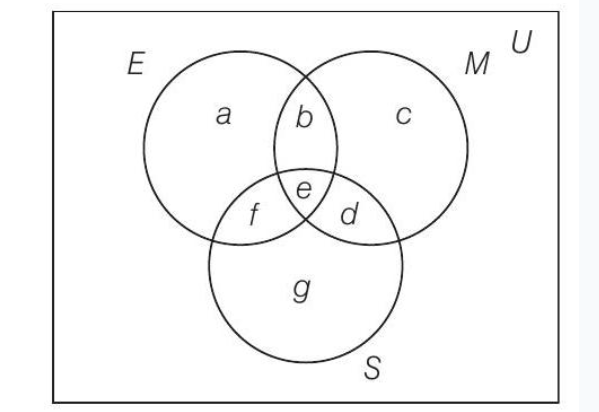
$n(M \cap S \cap E) = e =4$
$n(M \cap S) = e+d =7$
$\Rightarrow \quad 4+d =7$
$\Rightarrow \quad d =3$
अब, $ \ n(M \cap E) = b+e =6$
$\Rightarrow \quad b+4 = 6$
$\Rightarrow \quad b= 2$
साथ ही, $ \ n(S \cap E) = e+f =4$
$\Rightarrow \quad 4+f =4$
$\Rightarrow \quad f= 0$
अब, $ \ n(M) = b+c+e+d =12$
$\Rightarrow \quad 2+c+4+3=12$
$\Rightarrow \quad c=3$
$n(E) = a+b+e+f =15$
$\Rightarrow \quad a+2+4+0 =15$
$\Rightarrow \quad a =9$
$n(S) = f+e+d+g =8$
$\Rightarrow \quad 0+4+3+g =8$
$\Rightarrow \quad g=1$
(i) विषयों में से अंग्रेजी और गणित में पास हुए लेकिन विज्ञान में नहीं हुए छात्रों की संख्या $=b=2$
(ii) विषयों में से गणित और विज्ञान में पास हुए लेकिन अंग्रेजी में नहीं हुए छात्रों की संख्या $=d=3$
(iii) केवल गणित में पास हुए छात्रों की संख्या $=c=3$
(iv) एक से अधिक विषयों में पास हुए छात्रों की संख्या
$ \begin{aligned} & =b+e+d+f \\ \\ & =2+4+3+0=9 \end{aligned} $
वैकल्पिक विधि
मान लीजिए $E$ अंग्रेजी में पास हुए छात्रों के समुच्चय को दर्शाता है। $M$ गणित में पास हुए छात्रों के समुच्चय को दर्शाता है। $S$ विज्ञान में पास हुए छात्रों के समुच्चय को दर्शाता है।
अब,
$ \begin{aligned} \Rightarrow \quad n(U) & =100, n(E)=15, n(m)=12, n(S)=8 \\ \\ n(E \cap M) & =6, n(M \cap S)=7 \\ \\ n(E \cap S) & =4, n(E \cap M \cap S)=4 \end{aligned} $
(i) अंग्रेजी और गणित में पास हुए लेकिन विज्ञान में नहीं हुए छात्रों की संख्या
$ \text { अर्थात, } \quad \begin{aligned} n(E \cap M \cap S^{\prime}) & =n(E \cap M)-n(E \cap M \cap S) \quad[\because A \cap B^{\prime}=A-(A \cap B)] \\ & =6-4=2 \end{aligned} $
(ii) गणित और विज्ञान में पास हुए लेकिन अंग्रेजी में नहीं हुए छात्रों की संख्या।
$ \text { अर्थात, } \quad n(M \cap S \cap E^{\prime})=n(M \cap S)-n(M \cap S \cap E) $
$ \hspace{3.4cm}=7-4=3 $
(iii) केवल गणित में पास हुए छात्रों की संख्या
$ \text { अर्थात, } \quad \begin{aligned} n(M \cap S^{\prime} \cap E^{\prime}) & =n(M)-n(M \cap S)-n(M \cap E)+n(M \cap S \cap E) \\ & =12-7-6+4=3 \end{aligned} $
(iv) एक से अधिक विषयों में पास हुए छात्रों की संख्या (केवल)
$ \text { अर्थात, } \quad \begin{aligned} n(E \cap M)+n(M & \cap S)+n(E \cap S)-3 n(E \cap M \cap S)+n(E \cap M \cap S) \\ & =6+7+4-4 \times 3+4 \\ & =17-12+4=5+4=9 \end{aligned} $
25. 60 छात्रों की कक्षा में, 25 छात्र क्रिकेट खेलते हैं और 20 छात्र टेनिस खेलते हैं और 10 छात्र दोनों खेल खेलते हैं। ज्ञात कीजिए जो छात्र न तो क्रिकेट न ही टेनिस खेलते हैं।
उत्तर दिखाएं
हल
मान लीजिए $C$ वह समुच्चय है जो क्रिकेट खेलने वाले छात्रों को दर्शाता है और $T$ वह समुच्चय है जो टेनिस खेलने वाले छात्रों को दर्शाता है। तब
$ n(U)=60, n(C)=25, n(T)=20 \text {, और } n(C \cap T)=10 $
$ \begin{aligned} \therefore\quad n(C \cup T) & =n(C)+n(T)-n(C \cap T) \\ & =25+20-10=35 \end{aligned} $
$\therefore\quad $ जो छात्र न तो क्रिकेट न ही टेनिस खेलते हैं $=n(U)-n(C \cup T)$
$ \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad =60-35=25 $
26. एक विद्यालय के 200 छात्रों के सर्वेक्षण में पाया गया कि 120 छात्र गणित अध्ययन करते हैं, 90 छात्र भौतिक विज्ञान अध्ययन करते हैं और 70 छात्र रसायन विज्ञान अध्ययन करते हैं, 40 छात्र गणित और भौतिक विज्ञान अध्ययन करते हैं, 30 छात्र भौतिक विज्ञान और रसायन विज्ञान अध्ययन करते हैं, 50 छात्र रसायन विज्ञान और गणित अध्ययन करते हैं और 20 छात्र इन विषयों में से कोई भी अध्ययन नहीं करते हैं। तीनों विषयों के अध्ययन करने वाले छात्रों की संख्या ज्ञात कीजिए।
उत्तर दिखाएं
चिंतन प्रक्रिया
इस समस्या को हल करने के लिए, तीनों विषयों के लिए सूत्र का उपयोग करें
$n(A \cup B \cup C)=n(A)+n(B)+n(C)-n(A \cap B)-n(B \cap C)-n(C \cap A)+n(A \cap B \cap C)$।
हल
मान लीजिए $M$ वह समुच्चय है जो गणित अध्ययन करने वाले छात्रों को दर्शाता है, $P$ वह समुच्चय है जो भौतिक विज्ञान अध्ययन करने वाले छात्रों को दर्शाता है और $C$ वह समुच्चय है जो रसायन विज्ञान अध्ययन करने वाले छात्रों को दर्शाता है।
तब, $n(U)=200,n(M)=120,n(P)=90$
$n(C) =70, n(M \cap P)=40, n(P \cap C)=30, n(C \cap M) =50 $
और $ \quad n(M^{\prime} \cap P^{\prime} \cap C^{\prime})=20 $
$\Rightarrow \quad n(U)-n(M \cup P \cup C) =20 $
$\because \quad n(M \cup P \cup C) =200-20=180$
$\Rightarrow n(M \cup P \cup C) =n(M)+n(P)+n(C)-n(C \cap M)+n(M \cap P \cap C) $
$\Rightarrow 180 =120+90+70-40-30-50+n(M \cap P \cap C) $
$\Rightarrow n(M \cap P \cap C) =180-160=20$
तो, तीनों विषयों के अध्ययन करने वाले छात्रों की संख्या $20$ है।
27. एक शहर में 10,000 परिवार हैं, जहां ज्ञात हुआ कि $40 \%$ परिवार अखबार $A$ खरीदते हैं, $20 \%$ परिवार अखबार $B$ खरीदते हैं, $10 \%$ परिवार अखबार $C$ खरीदते हैं, $5 \%$ परिवार $A$ और $B$ खरीदते हैं, $3 \%$ परिवार $B$ और $C$ खरीदते हैं और $4 \%$ परिवार $A$ और $C$ खरीदते हैं। यदि $2 \%$ परिवार सभी तीन अखबार खरीदते हैं। ज्ञात कीजिए
(i) केवल अखबार $A$ खरीदने वाले परिवारों की संख्या।
(ii) $A, B$ और $C$ में से कोई भी अखबार नहीं खरीदने वाले परिवारों की संख्या।
उत्तर दिखाएं
हल
मान लीजिए $A$ वह समुच्चय है जो अखबार $A$ खरीदने वाले परिवारों को दर्शाता है, $B$ वह समुच्चय है जो अखबार $B$ खरीदने वाले परिवारों को दर्शाता है और $C$ वह समुच्चय है जो अखबार $C$ खरीदने वाले परिवारों को दर्शाता है।
तब,
$n(U) =10000, n(A)=40 \% n(B)=20 \% और n(C)=10 \%$
$n(A \cap B) =5 \%$
$n(B \cap C) =3 \%$
$n(A \cap C) =4 \%$
$n(A \cap B \cap C) =2 \%$
(i) केवल अखबार $A$ खरीदने वाले परिवारों की संख्या
$=n(A)-n(A \cap B)-n(A \cap C)+n(A \cap B \cap C) $
$=(40-5-4+2) \%=33 \%$
$ 10000 \times 33 / 100 =3300 $
(ii) $A, B$ और $C$ में से कोई भी अखबार नहीं खरीदने वाले परिवारों की संख्या
$=n(U)-n(A \cup B \cup C) $
$=n(U)-[n(A)+n(B)+n(C)-n(A \cap B)-n(B \cap C) -n(A \cap C)+n(A \cap B \cap C)]$
$=100-[40+20+10-5-3-4+2]=100-60 \%=40 \%$
$ =10000 \times \dfrac{40}{100}=4000 $
28. 50 छात्रों के एक समूह में, फ्रेंच, अंग्रेजी, संस्कृत के अध्ययन करने वाले छात्रों की संख्या निम्नलिखित है:
फ्रेंच $=17$, अंग्रेजी $=13$, संस्कृत $=15$
फ्रेंच और अंग्रेजी $=09$, अंग्रेजी और संस्कृत =4,
फ्रेंच और संस्कृत $=5$, अंग्रेजी, फ्रेंच और संस्कृत $=3$. ज्ञात कीजिए छात्रों की संख्या जो
(i) केवल फ्रेंच अध्ययन करते हैं।
(ii) केवल अंग्रेजी अध्ययन करते हैं।
(iii) केवल संस्कृत अध्ययन करते हैं।
(iv) अंग्रेजी और संस्कृत लेकिन फ्रेंच नहीं अध्ययन करते हैं।
(v) फ्रेंच और संस्कृत लेकिन अंग्रेजी नहीं अध्ययन करते हैं।
(vi) फ्रेंच और अंग्रेजी लेकिन संस्कृत नहीं अध्ययन करते हैं।
(vii) तीनों भाषाओं में से कम से कम एक भाषा अध्ययन करते हैं।
(viii) तीनों भाषाओं में से कोई भी भाषा अध्ययन नहीं करते हैं।
उत्तर दिखाएं
हल
मान लीजिए छात्रों की संख्या $=U$
मान लीजिए अंग्रेजी के अध्ययन करने वाले छात्रों की संख्या $=E$
मान लीजिए फ्रेंच के अध्ययन करने वाले छात्रों की संख्या $=F$
मान लीजिए संस्कृत के अध्ययन करने वाले छात्रों की संख्या $=S$
कुल छात्रों की संख्या $n(U)=50$
अंग्रेजी के अध्ययन करने वाले छात्रों की संख्या $n(E)=13$
फ्रेंच के अध्ययन करने वाले छात्रों की संख्या $n(F)=17$
संस्कृत के अध्ययन करने वाले छात्रों की संख्या $n(S)=15$
अंग्रेजी और फ्रेंच के अध्ययन करने वाले छात्रों की संख्या $n(E \cap F)=9$
फ्रेंच और संस्कृत के अध्ययन करने वाले छात्रों की संख्या $n(F \cap S)=5$
अंग्रेजी और संस्कृत के अध्ययन करने वाले छात्रों की संख्या $n(E \cap S)=4$
सभी तीन विषयों के अध्ययन करने वाले छात्रों की संख्या $n(E \cap F \cap S)=3$
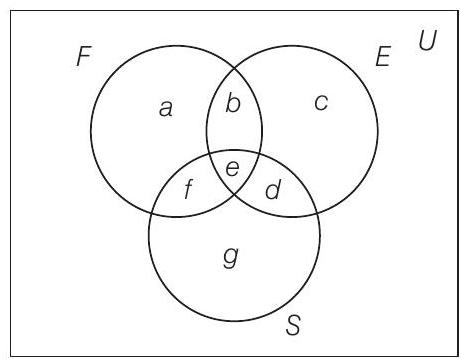
$n(F \cap S \cap E) =e=3$
$n(F \cap S ) = e+f=5$
$\Rightarrow \quad 3+f =5$
$\Rightarrow \quad f=2$
$n(F \cap E) = e+b =9$
$\Rightarrow \quad 3+b=9$
$\Rightarrow \quad b=6$
$n(S \cap E) = e+d =4$
$\Rightarrow \quad 3+d =4$
$\Rightarrow \quad d=1$
$n(F) = a+b+e+f=17$
$\Rightarrow \quad a+6+3+2 =17$
$\Rightarrow \quad a=17-11 = 6$
$n(E)= b+c+e+d =13$
$\Rightarrow \quad 6+c+3+1 =13$
$\Rightarrow \quad c=13-10=3$
$n(S) = f+e+d+g = 15$
$\Rightarrow \quad 2+3+1+g=15$
$\Rightarrow \quad g=15-6=9$
(i) केवल फ्रेंच के अध्ययन करने वाले छात्रों की संख्या, $a=6$
(ii) केवल अंग्रेजी के अध्ययन करने वाले छात्रों की संख्या, $c=3$
(iii) केवल संस्कृत के अध्ययन करने वाले छात्रों की संख्या, $g=9$
(iv) अंग्रेजी और संस्कृत के अध्ययन करने वाले छात्रों की संख्या जो फ्रेंच के अध्ययन न करें, $d=1$
(v) फ्रेंच और संस्कृत के अध्ययन करने वाले छात्रों की संख्या जो अंग्रेजी के अध्ययन न करें, $f=2$
(vi) फ्रेंच और अंग्रेजी के अध्ययन करने वाले छात्रों की संख्या जो संस्कृत के अध्ययन न करें, $b=6$
(vii) तीन भाषाओं में से कम से कम एक भाषा के अध्ययन करने वाले छात्रों की संख्या
$ \begin{aligned} & =a+b+c+d+e+f+g \\ \\ & =6+6+3+1+3+2+9=30 \end{aligned} $
(viii) तीन भाषाओं में से कोई भी अध्ययन न करने वाले छात्रों की संख्या $=$ कुल छात्रों की संख्या - तीन भाषाओं में से कम से कम एक भाषा के अध्ययन करने वाले छात्रों की संख्या
$ =50-30=20 $
वस्तुनिष्ठ प्रश्न
29. मान लीजिए, $A_1, A_2, \ldots, A_{30}$ तीस समुच्चय हैं जिनमें प्रत्येक में 5 तत्व हैं और $B_1, B_2, \ldots, B_{n}$ $n$ समुच्चय हैं जिनमें प्रत्येक में 3 तत्व हैं, इस प्रकार $\displaystyle \bigcup_{i=1}^{30} A_{i}=\bigcup_{j=1}^{n} B_{j}=S$ और $S$ के प्रत्येक तत्व केवल 10 बार $A_{i}$ के में आता है और 9 बार $B_{j}$ के में आता है। तब, $n$ किसके बराबर है
(a) 15
(b) 3
(c) 45
(d) 35
उत्तर दिखाएँ
चिंतन प्रक्रिया
पहले दोनों समुच्चयों के तत्वों की कुल संख्या ज्ञात करें, फिर उन्हें तुलना करें।
हल
विकल्प (c): यदि तत्व दोहराए नहीं जाते, तो $A_1 \cup A_2 \cup A_3, \ldots \cup A_{30}$ के तत्वों की संख्या $30 \times 5$ होती है।
लेकिन प्रत्येक तत्व 10 बार उपयोग किया जाता है, इसलिए
$ \qquad S=\dfrac{30 \times 5}{10}=15 $
यदि $B_1, B_2, \ldots, B_{n}$ में तत्व दोहराए नहीं जाते, तो कुल तत्वों की संख्या $3 n$ होती है लेकिन प्रत्येक तत्व 9 बार दोहराया जाता है, इसलिए
$ \begin{aligned} & S=\dfrac{3 n}{9} \Rightarrow 15=\dfrac{3 n}{9} \\ \\ \therefore\quad & n=45 \end{aligned} $
-
विकल्प (a) 15: यह विकल्प गलत है क्योंकि यदि $ n = 15 $, तो $ B_1, B_2, \ldots, B_{15} $ में कुल तत्वों की संख्या $ 3 \times 15 = 45 $ होती है। चूंकि प्रत्येक तत्व 9 बार दोहराया जाता है, तो अद्वितीय तत्वों की संख्या $ \dfrac{45}{9} = 5 $ होती है, जो दिए गए शर्त के विपरीत है कि $ S $ में 15 अद्वितीय तत्व हैं।
-
विकल्प (b) 3: यह विकल्प गलत है क्योंकि यदि $ n = 3 $, तो $ B_1, B_2, \ldots, B_3 $ में कुल तत्वों की संख्या $ 3 \times 3 = 9 $ होती है। चूंकि प्रत्येक तत्व 9 बार दोहराया जाता है, तो अद्वितीय तत्वों की संख्या $ \dfrac{9}{9} = 1 $ होती है, जो दिए गए शर्त के विपरीत है कि $ S $ में 15 अद्वितीय तत्व हैं।
-
विकल्प (d) 35: यह विकल्प गलत है क्योंकि यदि $ n = 35 $, तो $ B_1, B_2, \ldots, B_{35} $ में कुल तत्वों की संख्या $ 3 \times 35 = 105 $ होती है। चूंकि प्रत्येक तत्व 9 बार दोहराया जाता है, तो अद्वितीय तत्वों की संख्या $ \dfrac{105}{9} \approx 11.67 $ होती है, जो पूर्णांक नहीं है और दिए गए शर्त के विपरीत है कि $ S $ में 15 अद्वितीय तत्व हैं।
30. दो अंतिम समुच्चयों में $m$ और $n$ तत्व हैं। पहले समुच्चय के उपसमुच्चयों की संख्या दूसरे समुच्चय के उपसमुच्चयों की संख्या से 112 अधिक है। $m$ और $n$ के मान क्रमशः हैं
(a) 4,7
(b) 7,4
(c) 4,4
(d) 7,7
उत्तर दिखाएं
विचार प्रक्रिया
हम जानते हैं कि, यदि एक समुच्चय $A$ में $n$ तत्व हो, तो $A$ के उपसमुच्चयों की संख्या $2^{n}$ के बराबर होती है।
हल
विकल्प (a): एक समुच्चय में $m$ तत्व होने पर उपसमुच्चयों की संख्या दूसरे समुच्चय में $n$ तत्व होने पर उपसमुच्चयों की संख्या से 112 अधिक होती है।
$ \because \quad 2^{m}-2^{n} =112 $
$ \Rightarrow\quad 2^{n} \cdot(2^{m-n}-1) =2^{4} \cdot 7 $
$ \Rightarrow\quad 2^{n}=2^{4} \text { और } 2^{m-n}-1 =7 $
$ \Rightarrow\quad n=4 \text { और } 2^{m-n} =8 $
$ \Rightarrow\quad 2^{m-n} =2^{3}$
$\Rightarrow\quad m-n=3 $
$ \Rightarrow\quad m-4 =3 $
$\Rightarrow\quad m=4+3 $
$ \therefore\quad m =7 $
-
विकल्प (b) 7,4: यह विकल्प गलत है क्योंकि यदि $ m = 7 $ और $ n = 4 $, तो पहले समुच्चय के उपसमुच्चयों की संख्या $ 2^7 = 128 $ होती है और दूसरे समुच्चय के उपसमुच्चयों की संख्या $ 2^4 = 16 $ होती है। उपसमुच्चयों की संख्या के बीच अंतर $ 128 - 16 = 112 $ होता है, जो दिए गए शर्त के साथ मेल खाता है। इसलिए, यह विकल्प वास्तव में सही है, न कि गलत।
-
विकल्प (c) 4,4: यह विकल्प गलत है क्योंकि यदि $ m = 4 $ और $ n = 4 $, तो दोनों समुच्चयों के उपसमुच्चयों की संख्या $ 2^4 = 16 $ होती है। उपसमुच्चयों की संख्या के बीच अंतर $ 16 - 16 = 0 $ होता है, जो दिए गए शर्त के साथ मेल नहीं खाता है।
-
विकल्प (d) 7,7: यह विकल्प गलत है क्योंकि यदि $ m = 7 $ और $ n = 7 $, तो दोनों समुच्चयों के उपसमुच्चयों की संख्या $ 2^7 = 128 $ होती है। उपसमुच्चयों की संख्या के बीच अंतर $ 128 - 128 = 0 $ होता है, जो दिए गए शर्त के साथ मेल नहीं खाता है।
31. समुच्चय $(A \cap B^{\prime})^{\prime} \cup(B \cap C)$ बराबर है
(a) $A^{\prime} \cup B \cup C$
(ब) $A^{\prime} \cup B$
(स) $A^{\prime} \cup C^{\prime}$
(द) $A^{\prime} \cap B$
उत्तर दिखाएँ
हल
विकल्प (ब): हम जानते हैं कि, $(A \cap B)^{\prime}=(A^{\prime} \cup B^{\prime})$ और $(A^{\prime})^{\prime}=A$
$ \begin{aligned} \therefore\quad A & =(A \cap B^{\prime})^{\prime} \cup(B \cap C) \\ \\ & =[A^{\prime} \cup(B^\prime)^{\prime}] \cup(B \cap C) \\ \\ & =(A^{\prime} \cup B) \cup(B \cap C)=A^{\prime} \cup B \end{aligned} $
-
विकल्प (अ): $A^{\prime} \cup B \cup C$ गलत है क्योंकि मूल व्यंजक $(A \cap B^{\prime})^{\prime} \cup (B \cap C)$ में $C$ के साथ गैर-संयोजन के लिए शामिल नहीं है। सही सरलीकरण केवल $A^{\prime} \cup B$ ही है।
-
विकल्प (स): $A^{\prime} \cup C^{\prime}$ गलत है क्योंकि मूल व्यंजक में $C$ के पूरक के साथ कोई संबंध नहीं है। सही सरलीकरण $A^{\prime}$ और $B$ के संयोजन के लिए है, न कि $C^{\prime}$ के लिए।
-
विकल्प (द): $A^{\prime} \cap B$ गलत है क्योंकि मूल व्यंजक में $A^{\prime}$ और $B$ के संयोजन के लिए है, न कि उनके कटाच। सही सरलीकरण $A^{\prime} \cup B$ है।
32. मान लीजिए $F_1$ समांतर चतुर्भुजों का समुच्चय है, $F_2$ आयतों का समुच्चय है, $F_3$ वर्गों का समुच्चय है, $F_4$ वर्गों का समुच्चय है और $F_5$ ट्रेज़मियमों का समुच्चय है एक तल में। तब, $F_1$ के बराबर हो सकता है
(अ) $F_2 \cap F_3$
(ब) $F_3 \cap F_4$
(स) $F_2 \cup F_5$
(द) $F_2 \cup F_3 \cup F_4 \cup F_1$
उत्तर दिखाएँ
हल
विकल्प (द): एक तल में प्रत्येक आयत, वर्ग और वर्ग एक समांतर चतुर्भुज होते हैं लेकिन प्रत्येक ट्रेज़मियम एक समांतर चतुर्भुज नहीं होता है।
इसलिए, $F_1$ के बराबर $F_1, F_2, F_3$ और $F_4$ में से कोई एक हो सकता है।
$ \therefore\quad F_1=F_2 \cup F_3 \cup F_4 \cup F_1 $
-
विकल्प (अ): $F_2 \cap F_3$: यह विकल्प गलत है क्योंकि आयतों ($F_2$) और वर्गों ($F_3$) के संयोजन का समुच्चय वर्गों ($F_4$) का समुच्चय होता है, न कि सभी समांतर चतुर्भुजों ($F_1$) का समुच्चय। सभी समांतर चतुर्भुज वर्ग नहीं होते।
-
विकल्प (ब): $F_3 \cap F_4$: यह विकल्प गलत है क्योंकि वर्गों ($F_4$) और समचतुर्भुजों ($F_3$) के कटाच के समूह ($F_4$) है, न कि सभी समांतर चतुर्भुजों ($F_1$) के समूह। सभी समांतर चतुर्भुज वर्ग नहीं होते।
-
विकल्प (स): $F_2 \cup F_5$: यह विकल्प गलत है क्योंकि आयतों ($F_2$) और त्रिभुजों ($F_5$) के संघ सभी समांतर चतुर्भुजों ($F_1$) को नहीं शामिल करता। विशेष रूप से, यह वह वर्ग जो आयत नहीं हैं और वह समांतर चतुर्भुज जो आयत या त्रिभुज नहीं हैं छोड़ देता है।
33. मान लीजिए $S=$ वर्ग के अंदर बिंदुओं का समुच्चय, $T=$ त्रिभुज के अंदर बिंदुओं का समुच्चय और $C=$ वृत्त के अंदर बिंदुओं का समुच्चय है। यदि त्रिभुज और वृत्त एक दूसरे को काटते हैं और एक वर्ग में समाहित हैं। तो,
(a) $S \cap T \cap C=\phi$
(b) $S \cup T \cup C=C$
(c) $S \cup T \cup C=S$
(d) $S \cup T=S \cap C$
उत्तर दिखाएं
हल
विकल्प (स): दिए गए समुच्चयों को नीचे दिखाए गए वेन आरेख में प्रस्तुत किया जा सकता है
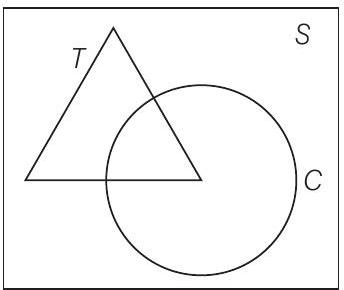
आरेख से स्पष्ट है कि, $S \cup T \cup C=S$।
-
विकल्प (a): $S \cap T \cap C=\phi$: यह विकल्प गलत है क्योंकि त्रिभुज और वृत्त के कटाच आवश्यक रूप से खाली नहीं हो सकता। चूंकि त्रिभुज और वृत्त दोनों वर्ग में समाहित हैं, तो तीनों समुच्चय $S$, $T$, और $C$ के अंदर बिंदु भी हो सकते हैं।
-
विकल्प (b): $S \cup T \cup C=C$: यह विकल्प गलत है क्योंकि वर्ग, त्रिभुज और वृत्त के संघ आवश्यक रूप से वृत्त के बराबर नहीं हो सकता। वर्ग $S$ में वृत्त के बाहर के बिंदु भी हो सकते हैं, और त्रिभुज $T$ में भी वृत्त के बाहर के बिंदु हो सकते हैं। अतः $S \cup T \cup C$ केवल $C$ से बड़ा हो सकता है।
-
विकल्प (d): $S \cup T=S \cap C$: यह विकल्प गलत है क्योंकि वर्ग और त्रिभुज के संघ आवश्यक रूप से वर्ग और वृत्त के कटाच के बराबर नहीं हो सकता। संघ $S \cup T$ में वर्ग और त्रिभुज के अंदर सभी बिंदु शामिल होते हैं, जबकि कटाच $S \cap C$ में केवल वर्ग और वृत्त के अंदर बिंदु शामिल होते हैं। इन दो समुच्चयों के बराबर नहीं हो सकते।
34. मान लीजिए $R$ एक आयत के अंतर्गत बिंदुओं के समुच्चय है जिसकी भुजाएँ $a$ और $b(a, b>1)$ हैं जिसके दो भुजाएँ धनात्मक $X$-अक्ष और $Y$-अक्ष की दिशा में हैं। तब,
(a) $R=\lbrace(x, y): 0 \leq x \leq a, 0 \leq y \leq b\rbrace$
(b) $R=\lbrace(x, y): 0 \leq x<a, 0 \leq y \leq b\rbrace$
(c) $R=\lbrace(x, y): 0 \leq x \leq a, 0<y<b\rbrace$
(d) $R=\lbrace(x, y): 0<x<a, 0<y<b\rbrace$
उत्तर दिखाएँ
हल
विकल्प (d): क्योंकि, $R$ एक आयत के अंतर्गत बिंदुओं के समुच्चय है।
$\therefore\quad R=\lbrace(x, y): 0<x<a$ और $0<y<b\rbrace$
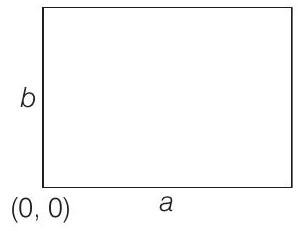
-
विकल्प (a): गलत है क्योंकि यह आयत के सीमा बिंदुओं को शामिल करता है, अर्थात इसमें $ x = 0 $, $ x = a $, $ y = 0 $, और $ y = b $ के बिंदु शामिल हैं। समस्या में आयत के अंतर्गत बिंदुओं का उल्लेख किया गया है, जो सीमा बिंदुओं को छोड़ देता है।
-
विकल्प (b): गलत है क्योंकि यह आयत के सीमा बिंदुओं को शामिल करता है जहाँ $ y = 0 $ और $ y = b $ हैं। समस्या में आयत के अंतर्गत बिंदुओं का उल्लेख किया गया है, जो सीमा बिंदुओं को छोड़ देता है।
-
विकल्प (c): गलत है क्योंकि यह आयत के सीमा बिंदुओं को शामिल करता है जहाँ $ x = 0 $ और $ x = a $ हैं। समस्या में आयत के अंतर्गत बिंदुओं का उल्लेख किया गया है, जो सीमा बिंदुओं को छोड़ देता है।
35. 840 लोगों वाले एक शहर में, 450 लोग हिंदी पढ़ते हैं, 300 लोग अंग्रेजी पढ़ते हैं और 200 लोग दोनों पढ़ते हैं। तब, न तो हिंदी और न ही अंग्रेजी पढ़ने वाले लोगों की संख्या है
(a) 210
(b) 290
(c) 180
(d) 260
उत्तर दिखाएँ
हल
विकल्प (b): मान लीजिए $H$ हिंदी पढ़ने वाले लोगों का समुच्चय है और $E$ अंग्रेजी पढ़ने वाले लोगों का समुच्चय है।
तब, $n(U)=840, n(H)=450, n(E)=300, n(H \cap E)=200$
न तो हिंदी और न ही अंग्रेजी पढ़ने वाले लोगों की संख्या $=n(H^{\prime} \cap F^{\prime})$
$\hspace{4.8cm}=n(H \cup E)^{\prime}$
$\hspace{4.8cm}=n(U)-n(H \cup E)$
$\hspace{4.8cm}=840-[n(H)+n(E)-n(H \cap E)]$
$\hspace{4.8cm}=840-(450+300-200)$
$\hspace{4.8cm}=840-550=290$
-
विकल्प (a) 210: यह विकल्प गलत है क्योंकि उन व्यक्तियों की संख्या जो हिंदी और अंग्रेजी दोनों के बाहर पढ़ते हैं, शामिल करने के सिद्धांत के आधार पर गणना की जाती है। सही गणना दिखाती है कि 290 व्यक्तियों ने दोनों के बाहर पढ़ाई की, न कि 210। इस विकल्प में त्रुटि संभवतः गणना में त्रुटि या सिद्धांत के गलत समझ के कारण हो सकती है।
-
विकल्प (c) 180: यह विकल्प विकल्प (a) के लिए उतना ही गलत है। शामिल करने के सिद्धांत के आधार पर उन व्यक्तियों की संख्या जो हिंदी और अंग्रेजी दोनों के बाहर पढ़ते हैं, 290 है। संख्या 180 सही गणना के अनुरूप नहीं है और इसलिए गलत है।
-
विकल्प (d) 260: यह विकल्प भी गलत है क्योंकि शामिल करने के सिद्धांत के आधार पर उन व्यक्तियों की संख्या जो हिंदी और अंग्रेजी दोनों के बाहर पढ़ते हैं, 290 है। संख्या 260 गलत गणना या सिद्धांत के गलत समझ के कारण हो सकती है।
36. यदि $X=\lbrace8^{n}-7 n-1 \mid n \in N\rbrace$ और $Y=\lbrace49 n-49 \mid n \in N\rbrace$. तो,
(a) $X \subset Y$
(b) $Y \subset X$
(c) $X=Y$
(d) $X \cap Y=\phi$
उत्तर दिखाएं
सोचने की प्रक्रिया
यदि $A$ के प्रत्येक तत्व $B$ के एक तत्व है, तो $A \subseteq B$।
हल
विकल्प (a):
$ \begin{aligned} & X=\lbrace8^{n}-7 n-1 \mid n \in N\rbrace=\lbrace0,49,490, \ldots\rbrace \\ \\ & Y=\lbrace49 n-49 \mid n \in N\rbrace=\lbrace0,49,98,147, \ldots 490, \ldots\rbrace \end{aligned} $
स्पष्ट रूप से, $X$ के प्रत्येक तत्व $Y$ में है लेकिन $Y$ के प्रत्येक तत्व $X$ में नहीं है।
$ \therefore\quad X \subset Y $
-
विकल्प (b): $Y \subset X$: यह विकल्प गलत है क्योंकि $Y$ के प्रत्येक तत्व $X$ में नहीं है। उदाहरण के लिए, 98 $Y$ में है लेकिन $X$ में नहीं है।
-
विकल्प (c): $X=Y$: यह विकल्प गलत है क्योंकि समुच्चय $X$ और $Y$ बराबर नहीं हैं। जबकि $X$ के प्रत्येक तत्व $Y$ में है, $Y$ के प्रत्येक तत्व $X$ में नहीं है। उदाहरण के लिए, 98 $Y$ में है लेकिन $X$ में नहीं है।
-
विकल्प (d): $X \cap Y=\phi$: यह विकल्प गलत है क्योंकि $X$ और $Y$ का उभयनिष्ठ निर्माण खाली नहीं है। उदाहरण के लिए, 0 और 49 दोनों $X$ और $Y$ में सामान्य तत्व हैं।
37. एक सर्वेक्षण दिखाता है कि $63 \%$ लोग एक न्यूज़ चैनल देखते हैं जबकि $76 \%$ लोग दूसरे चैनल देखते हैं। यदि $x \%$ लोग दोनों चैनल देखते हैं, तो
(a) $x=35$
(b) $x=63$
(c) $39 \leq x \leq 63$
(d) $x=39$
उत्तर दिखाएं
हल
विकल्प (c): मान लीजिए $A$ वह समुच्चय है जो उन लोगों के प्रतिशत को दर्शाता है जो एक न्यूज़ चैनल देखते हैं और $B$ वह समुच्चय है जो उन लोगों के प्रतिशत को दर्शाता है जो दूसरे चैनल देखते हैं।
$ n(A)=63 \%, \ n(B) =76 \%, \ $ और मान लीजिए $ \ n(A \cap B)=x $
$ \because\quad n(A \cup B) \leq 100 $
$ \Rightarrow\quad n(A)+n(B)-n(A \cap B) \leq 100 $
$ \Rightarrow\quad 63+76-x \leq 100 $
$\Rightarrow\quad 139-x \leq 100 $
$ \Rightarrow\quad 139-100 \leq x $
$\Rightarrow\quad 39 \leq x $
$\therefore\quad $ $x$ का न्यूनतम मान $39$ है।
इसलिए, $x$ के मान के लिए श्रेणी, $\quad 39 \leq x \leq 63$
-
विकल्प (a): $x=35$: यह गलत है क्योंकि $x$ का न्यूनतम मान $39$ है, जो असमिका $139 - x \leq 100 \Rightarrow x \geq 39$ से निर्मित है।
-
विकल्प (b): $x=63$: यह गलत है क्योंकि भले ही $63$ $x$ का अधिकतम संभावित मान है, लेकिन यह एकमात्र संभावित मान नहीं है। $x$ के सही श्रेणी है $39 \leq x \leq 63$।
-
विकल्प (d): $x=39$: यह गलत है क्योंकि भले ही $39$ $x$ का न्यूनतम संभावित मान है, लेकिन यह एकमात्र संभावित मान नहीं है। $x$ के सही श्रेणी है $39 \leq x \leq 63$।
38. यदि समुच्चय $A$ और $B$ निम्न प्रकार परिभाषित हैं
$A=\lbrace(x, y) \vert\ y=\dfrac{1}{x}, 0 \neq x \in R\rbrace, B=\lbrace(x, y) \mid y=-x, x \in R$ $\rbrace $ तो,
(a) $A \cap B=A$
(b) $A \cap B=B$
(c) $A \cap B=\phi$
(d) $A \cup B=A$
उत्तर दिखाएं
हल
विकल्प (c): दिया गया है, $A=\lbrace(x, y) \vert\ y=\dfrac{1}{x}, 0 \neq x \in R\rbrace \ \text{and} \ B=\lbrace(x, y) \mid y=-x, x \in R$ $\rbrace $
हम जानते हैं कि, किसी भी $x \in R$ के मान के लिए
$
\begin{matrix}
\text { } & -x \neq \dfrac{1}{x} \\ \\
\therefore\quad & A \cap B=\phi
\end{matrix}
$
-
विकल्प (a): $A \cap B \neq A$: समुच्चय $A$ और $B$ के प्रतिच्छेदन के लिए $A$ के बराबर नहीं हो सकता क्योंकि $A$ के सभी तत्व $B$ में नहीं होते हैं। विशेष रूप से, $A$ वह बिंदु होते हैं जहाँ $y = \dfrac{1}{x}$ होता है, जबकि $B$ वह बिंदु होते हैं जहाँ $y = -x$ होता है। इन दोनों स्थितियाँ आम तौर पर एक साथ संतुष्ट नहीं होती, इसलिए $A \cap B$ $A$ के बराबर नहीं हो सकता।
-
विकल्प (b): $A \cap B \neq B$: समुच्चय $A$ और $B$ के प्रतिच्छेदन के लिए $B$ के बराबर नहीं हो सकता क्योंकि $B$ के सभी तत्व $A$ में नहीं होते हैं। $B$ में बिंदु $y = -x$ को संतुष्ट करते हैं, जो किसी भी $x \in R$ के लिए $y = \dfrac{1}{x}$ के बराबर नहीं होता। इसलिए, $A \cap B$ $B$ के बराबर नहीं हो सकता।
-
विकल्प (d): $A \cup B \neq A$: समुच्चय $A$ और $B$ के संयोजन के लिए $A$ के बराबर नहीं हो सकता क्योंकि $B$ में $A$ में नहीं होने वाले बिंदु होते हैं। विशेष रूप से, $B$ में $y = -x$ के बिंदु होते हैं, जो $A$ में $y = \dfrac{1}{x}$ के बिंदु नहीं होते। इसलिए, $A \cup B$ $A$ के बराबर नहीं हो सकता।
39. यदि $A$ और $B$ दो समुच्चय हैं, तो $A \cap(A \cup B)$ के बराबर होता है
(a) $A$
(b) $B$
(c) $\phi$
(d) $A \cap B$
उत्तर दिखाएं
हल
विकल्प (a): $\because$ $ A \cap(A \cup B)=A $
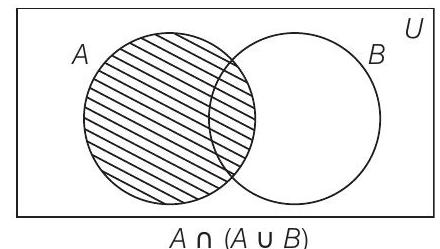
-
विकल्प (b) $B$ गलत है क्योंकि $A$ के साथ $A$ और $B$ के संयोजन के प्रतिच्छेदन में केवल $A$ में तत्व होते हैं, न कि $B$ में।
-
विकल्प (c) $\phi$ गलत है क्योंकि $A$ के साथ $A$ और $B$ के संयोजन के प्रतिच्छेदन कभी खाली समुच्चय नहीं होता, बर्ताव तब होता है जब $A$ खाली समुच्चय हो, जो समस्या में निर्दिष्ट नहीं है।
-
विकल्प (d) $A \cap B$ गलत है क्योंकि $A$ के साथ $A$ और $B$ के संयोजन के प्रतिच्छेदन में $A$ के सभी तत्व शामिल होते हैं, न कि केवल उन तत्वों के जो $A$ और $B$ दोनों में सामान्य होते हैं।
40. यदि $A=\lbrace1,3,5,7,9,11,13,15,17\rbrace, B=\lbrace2,4, \ldots, 18\rbrace$ और $N$ प्राकृत संख्याओं का समुच्चय विस्तार समुच्चय है, तो $A^{\prime} \cup[(A \cup B) \cap B^{\prime}]$ है
(a) $\phi$
(b) $N$
(c) A
(d) B
उत्तर दिखाएं
सोचने की प्रक्रिया
इस समस्या को हल करने के लिए, वितरण नियम का उपयोग करें, अर्थात $A \cap(B \cup C)=(A \cap B) \cup(A \cap C.)$
हल
विकल्प (b):
$A^{\prime} \cup (A \cup B) \cap B^{\prime} = A^{\prime} \cup [(A \cap B^{\prime} )\cup(B \cap B^{\prime})]$
$\qquad \qquad \qquad \qquad =A^{\prime} \cup (A \cap B^{\prime})\cup \phi \qquad \qquad [\because \quad B \cap B^{\prime } = \phi]$
$\qquad \qquad \qquad \qquad = A^{\prime} \cup (A \cap B^{\prime})$
$\qquad \qquad \qquad \qquad =(A^{\prime} \cup A) \cap (A^{\prime} \cup B^{\prime}) $
$\qquad \qquad \qquad \qquad = N \cup (A^{\prime} \cup B^{\prime})$
$\qquad \qquad \qquad \qquad = A^{\prime} \cup B^{\prime} $
$\qquad \qquad \qquad \qquad =(A \cap B)^{\prime } = {\phi}^{\prime} = N$
-
विकल्प (a) $\phi$: यह विकल्प गलत है क्योंकि व्यक्तिगत $(A^{\prime} \cup(A \cup B) \cap B^{\prime})$ विस्तार समुच्चय $N$ के बराबर होता है, न कि खाली समुच्चय $\phi$। खाली समुच्चय का अर्थ होता है कि परिणामी समुच्चय में कोई भी तत्व नहीं होते, जो यहाँ पर सच नहीं है।
-
विकल्प (c) A: यह विकल्प गलत है क्योंकि व्यक्तिगत $(A^{\prime} \cup(A \cup B) \cap B^{\prime})$ समुच्चय $A$ के बराबर नहीं होता। समुच्चय $A$ प्राकृत संख्याओं का एक विशिष्ट उपसमुच्चय है, जबकि व्यक्तिगत विस्तार समुच्चय $N$ के बराबर होता है।
-
विकल्प (d) B: यह विकल्प गलत है क्योंकि व्यक्तिगत $(A^{\prime} \cup(A \cup B) \cap B^{\prime})$ समुच्चय $B$ के बराबर नहीं होता। समुच्चय $B$ एक अन्य विशिष्ट प्राकृत संख्याओं का उपसमुच्चय है, जबकि व्यक्तिगत विस्तार समुच्चय $N$ के बराबर होता है।
41. मान लीजिए $S=\lbrace x \mid x$ 100 से कम एक धनात्मक 3 का गुणज है $\rbrace$ और $P=\lbrace x \mid x$ 20 से कम एक अभाज्य संख्या है $\rbrace$. तब, $n(S)+n(P)$ किसके बराबर है
(a) 34
(b) 31
(c) 33
(d) 41
उत्तर दिखाएं
हल
विकल्प (d):
$\because \quad S=\lbrace x \mid x$ एक धनात्मक 3 का गुणज है जो 100 से कम है $\rbrace$
$\qquad S= \lbrace 3,6,9, \ldots , 99 \rbrace$
$ \therefore\quad n(S)=33 \ $ और $ \ P=\lbrace x \mid x$ एक अभाज्य संख्या है जो 20 से कम है $\rbrace$
$\qquad P= \lbrace 2,3,5,7,11,13,17,19 \rbrace$
$\therefore\quad n(P) =8$
$\qquad n(S)+n(P) =33+8=41$
-
विकल्प (a) 34: यह विकल्प गलत है क्योंकि इसकी धारणा है कि समुच्चय $ S $ और $ P $ में तत्वों की कुल संख्या 34 है। हालांकि, सही कुल संख्या 41 है, क्योंकि $ n(S) = 33 $ और $ n(P) = 8 $, जिससे $ n(S) + n(P) = 41 $ होता है।
-
विकल्प (b) 31: यह विकल्प गलत है क्योंकि इसकी धारणा है कि समुच्चय $ S $ और $ P $ में तत्वों की कुल संख्या 31 है। हालांकि, सही कुल संख्या 41 है, क्योंकि $ n(S) = 33 $ और $ n(P) = 8 $, जिससे $ n(S) + n(P) = 41 $ होता है।
-
विकल्प (c) 33: यह विकल्प गलत है क्योंकि इसकी धारणा है कि समुच्चय $ S $ और $ P $ में तत्वों की कुल संख्या 33 है। हालांकि, सही कुल संख्या 41 है, क्योंकि $ n(S) = 33 $ और $ n(P) = 8 $, जिससे $ n(S) + n(P) = 41 $ होता है।
42. यदि $X$ और $Y$ दो समुच्चय हैं और $X^{\prime}$ का अर्थ $X$ का पूरक है, तो $X \cap(X \cup Y)^{\prime}$ किसके बराबर है?
(a) $X$
(b) $Y$
(c) $\phi$
(d) $X \cap Y$
उत्तर दिखाएं
हल
विकल्प (c):
$ \begin{aligned} X \cap(X \cup Y)^{\prime} & =X \cap(X^{\prime} \cap Y^{\prime}) \qquad [\because(A \cup B)^{\prime}=A^{\prime} \cap B^{\prime}]\\ & =(X \cap X^{\prime}) \cap(X \cap Y^{\prime}) \\ & =\phi \cap(X \cap Y^{\prime})=\phi \qquad [\because \phi \cap A=\phi] \end{aligned} $
-
विकल्प (a) $X$: यह विकल्प गलत है क्योंकि व्यंजक $X \cap(X \cup Y)^{\prime}$ सरलीकृत $\phi$ होता है, न कि $X$। $X \cup Y$ का पूरक $X^{\prime} \cap Y^{\prime}$ है, और $X$ के $X^{\prime} \cap Y^{\prime}$ के साथ कटाव के परिणाम स्वरूप खाली समुच्चय $\phi$ होता है।
-
विकल्प (b) $Y$: यह विकल्प गलत है क्योंकि अभिव्यक्ति $X \cap(X \cup Y)^{\prime}$ $Y$ के बराबर सरल नहीं होती। $X$ के $X \cup Y$ के पूरक के साथ कटाव के परिणाम स्वयं खाली समुच्चय $\phi$ होता है, न कि $Y$।
-
विकल्प (d) $X \cap Y$: यह विकल्प गलत है क्योंकि अभिव्यक्ति $X \cap(X \cup Y)^{\prime}$ $\phi$ के बराबर सरल होती है, न कि $X \cap Y$। $X \cup Y$ का पूरक $X^{\prime} \cap Y^{\prime}$ होता है, और $X$ के $X^{\prime} \cap Y^{\prime}$ के साथ कटाव के परिणाम स्वयं खाली समुच्चय $\phi$ होता है।
रिक्त स्थान भरें
43. समुच्चय $\lbrace x \in R: 1 \leq x<2\rbrace$ को लिखा जा सकता है ……
उत्तर दिखाएं
हल
समुच्चय $\lbrace x \in R: 1 \leq x<2\rbrace$ को लिखा जा सकता है $[1,2)$
44. जब $A=\phi$, तो $P(A)$ में तत्वों की संख्या ……
उत्तर दिखाएं
हल
$ \begin{aligned} A & =\phi \Rightarrow n(A)=0 \\ \\ \therefore\quad & n\lbrace P(A)\rbrace =2^{n(A)}=2^{0}=1 \end{aligned} $
इसलिए, $P(A)$ में तत्वों की संख्या 1 है ।
45. यदि $A$ और $B$ समाप्ति समुच्चय हैं, जैसे कि $A \subset B$, तो $n(A \cup B)=$ ……
उत्तर दिखाएं
हल
यदि $A$ और $B$ दो समाप्ति समुच्चय हैं जैसे कि $A \subset B$, तो $n(A \cup B)=n(B)$।
46. यदि $A$ और $B$ कोई दो समुच्चय हैं, तो $A-B$ के बराबर है ……
उत्तर दिखाएं
हल

यदि $A$ और $B$ कोई दो समुच्चय हैं, तो $A-B=A \cap B^{`}$
47. समुच्चय $A=\lbrace1,2\rbrace$ का शक्ति समुच्चय ……
उत्तर दिखाएं
चिंतन प्रक्रिया
हम जानते हैं कि, शक्ति समुच्चय एक समुच्चय के सभी उपसमुच्चयों के संग्रह होता है। इस समस्या को हल करने के लिए, दिए गए समुच्चय के सभी उपसमुच्चय लिखें।
हल
$\therefore\quad A=\lbrace1,2\rbrace$
तो, $A$ के उपसमुच्चय हैं $\phi , \lbrace1\rbrace,\lbrace2\rbrace$ और $\lbrace1,2\rbrace$।
$\therefore\quad P(A)=\lbrace\phi,\lbrace1\rbrace,\lbrace2\rbrace,\lbrace1,2\rbrace\rbrace$
48. दिए गए समुच्चय $A=\lbrace1,3,5\rbrace, B=\lbrace2,4,6\rbrace$ और $C=\lbrace0,2,4,6,8\rbrace$ हैं। तब, तीनों समुच्चय $A, B$ और $C$ के सार्व समुच्चय को बताइए।
उत्तर दिखाएं
Solution
समुच्चय $A, B$ और $C$ के सार्व समुच्चय $U=\lbrace0,1,2,3,4,5,6,8\rbrace$ द्वारा दिया गया है।
49. यदि $U=\lbrace1,2,3,4,5,6,7,8,9,10\rbrace, A=\lbrace1,2,3,5\rbrace, B=\lbrace2,4,6,7\rbrace$ और $C=\lbrace2,3,4,8\rbrace$ हैं। तब,
(i) $(B \cup C)^{\prime}$ है ……
(ii) $(C-A)^{\prime}$ है ……
उत्तर दिखाएं
Solution
दिया गया है, $U=\lbrace1,2,3,4,5, \ldots, 10\rbrace$,
$A=\lbrace1,2,3,5\rbrace, B=\lbrace2,4,6,7\rbrace$ और $C=\lbrace2,3,4,8\rbrace$
$\therefore\quad B \cup C=\lbrace2,3,4,6,7,8\rbrace$
(i) $(B \cup C)^{\prime}=U-(B \cup C)=\lbrace1,5,9,10\rbrace$
(ii) $C-A=\lbrace4,8\rbrace$
$\therefore\quad (C-A)^{\prime}=U-(C-A)=\lbrace1,2,3,5,6,7,9,10\rbrace$
50. सभी समुच्चय $A$ और $B$ के लिए, $A-(A \cap B)$ के बराबर है ……
उत्तर दिखाएं
Solution
$A-(A \cap B)=A \cap B^{\prime}$
51. सभी समुच्चय $A, B$ और $C$ के लिए निम्नलिखित समुच्चयों का मिलान कीजिए
| Column I | Column II | ||
|---|---|---|---|
| (i) | $((A^{\prime} \cup B^{\prime})-A)^{\prime}$ | (a) | $A-B$ |
| (ii) | $[B^{\prime} \cup(B^{\prime}-A)]^{\prime}$ | (b) | $A$ |
| (iii) | $(A-B)-(B-C)$ | (c) | $B$ |
| (iv) | $(A-B) \cap(C-B)$ | (d) | $(A \times B) \cap(A \times C)$ |
| (v) | $A \times(B \cap C)$ | (e) | $(A \times B) \cup(A \times C)$ |
| (vi) | $A \times(B \cup C)$ | (f) | $(A \cap C)-B$ |
उत्तर दिखाएं
Solution
(i) $[(A^{\prime} \cup B^{\prime})-A]^{\prime}=[(A^{\prime} \cup B^{\prime}) \cap A^{\prime}]^{\prime}$ $ \qquad [\because A-B=A \cap B^{\prime}]$
$\hspace{2.8cm}=[(A \cap B)^{\prime} \cap A^{\prime}]^{\prime}$ $\qquad [\because(A \cap B)^{\prime}=A^{\prime} \cup B^{\prime}]$
$\hspace{2.8cm}=[(A \cap B)^{\prime}]^{\prime} \cup(A^{\prime})^{\prime}=(A \cap B) \cup A$
$\hspace{2.8cm}=A$
(ii) $[B^{\prime} \cup(B^{\prime}-A)]^{\prime}=[B^{\prime} \cup(B^{\prime} \cap A^{\prime})]^{\prime}$ $\qquad [\because A-B=A \cap B^{\prime}]$
$\hspace{2.8cm}=[B^{\prime} \cup(B \cup A)^{\prime}]^{\prime} $ $\qquad [\because A^{\prime} \cap B^{\prime}=(A \cup B)^{\prime}]$
$\hspace{2.8cm}=(B^{\prime})^{\prime} \cap[(B \cup A)^{\prime}]^{\prime}$ $\qquad [\because(A \cup B)^{\prime}=A^{\prime} \cap B^{\prime}]$
$\hspace{2.8cm}=B \cap(B \cup A)$ $\qquad [\because(A^{\prime})^{\prime}=A]$
$\hspace{2.8cm}=B$
(iii) $(A-B)-(B-C)=(A \cap B^{\prime})-(B \cap C^{\prime})$
$\hspace{3.5cm}=(A \cap B^{\prime}) \cap(B \cap C^{\prime})^{\prime}$
$\hspace{3.5cm}=(A \cap B^{\prime}) \cap[B^{\prime} \cup(C^{\prime})^{\prime}]$
$\hspace{3.5cm}=(A \cap B^{\prime}) \cap(B^{\prime} \cup C)$
$\hspace{3.5cm}=[A \cap(B^{\prime} \cup C)] \cap[B^{\prime} \cap(B^{\prime} \cup C)]$
$\hspace{3.5cm}=[A \cap(B^{\prime} \cup C)] \cap B^{\prime}$
$\hspace{3.5cm}=(A \cap B^{\prime}) \cap[(B^{\prime} \cup C) \cap B^{\prime}]$
$\hspace{3.5cm}=(A \cap B^{\prime}) \cap B^{\prime}=A \cap B^{\prime}=A-B$
Alternate Method
आरेख से स्पष्ट है, $(A-B)-(B-C)=A-B$
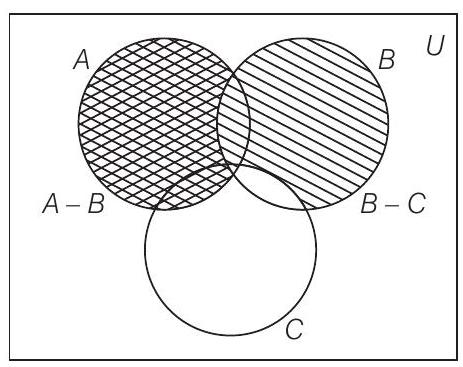
(iv) $(A-B) \cap(C-B)=(A \cap B^{\prime}) \cap(C \cap B^{\prime})$ $\qquad [\because A-B=A \cap B^{\prime}]$
$\hspace{3.5cm}= (A \cap C) \cup (B^{\prime} \cap B^{\prime })$
$\hspace{3.5cm}= (A \cap C) \cap B^{\prime }$
$\hspace{3.5cm}= \quad(A \cap C)-B$ $\qquad [\because A \cap B^{\prime}=A-B]$
(v) $A \times B \cap C=(A \times B) \cap(A \times C)$
(vi) $A \times(B \cup C)=(A \times B) \cup(A \times C)$
इसलिए, सही मिलान हैं
(i) $\rightarrow$ (b),
(ii) $\rightarrow$ (c),
(iii) $\rightarrow(a)$,
(iv) $\rightarrow$ (f),
(v) $\rightarrow(d)$,
(vi) $\rightarrow(e)$
सत्य/असत्य
52. यदि $A$ कोई भी समुच्चय है, तो $A \subset A$
उत्तर दिखाएं
हल
सत्य
क्योंकि, प्रत्येक समुच्चय अपने आप का उपसमुच्चय होता है।
इसलिए, कोई भी समुच्चय $A$ के लिए, $A \subset A$ होता है।
53. दिया गया है कि $M=\lbrace1,2,3,4,5,6,7,8,9\rbrace$ और यदि $B=\lbrace1,2,3,4,5,6,7,8,9\rbrace$, तो $B \not \subset M$
उत्तर दिखाएं
हल
गलत
$ \begin{aligned} & M=\lbrace1,2,3,4,5,6,7,8,9\rbrace \\ \\ & B=\lbrace1,2,3,4,5,6,7,8,9\rbrace \end{aligned} $
क्योंकि, $B$ के प्रत्येक तत्व $M$ में भी हैं
$ \therefore\quad B \subset M $
54. समुच्चय $\lbrace1,2,3,4\rbrace$ और $\lbrace3,4,5,6\rbrace$ बराबर हैं
उत्तर दिखाएं
हल
गलत
क्योंकि, $2 \in\lbrace1,2,3,4\rbrace$
लेकिन $2 \notin\lbrace3,4,5,6\rbrace$
$\therefore\quad $ $ \quad \lbrace1,2,3,4\rbrace \neq\lbrace3,4,5,6\rbrace$
55. $Q \cup Z=Q$, जहाँ $Q$ परिमेय संख्याओं का समुच्चय है और $Z$ पूर्णांकों का समुच्चय है।
उत्तर दिखाएं
हल
सत्य
क्योंकि, प्रत्येक पूर्णांक एक परिमेय संख्या भी होता है, तो $Z \subset Q$
जहाँ, $Z$ पूर्णांकों का समुच्चय है और $Q$ परिमेय संख्याओं का समुच्चय है।
$\therefore\quad $ $Q \cup Z=Q$
56. मान लीजिए समुच्चय $R$ और $T$ निम्न प्रकार परिभाषित हैं
$ \begin{aligned} & R=\lbrace x \in Z \mid x \text { is divisible by } 2\rbrace \\ \\ & T=\lbrace x \in Z \mid x \text { is divisible by } 6\rbrace . \text { Then } T \subset R \end{aligned} $
उत्तर दिखाएं
हल
सत्य
$ \begin{aligned} & R=\lbrace x \in Z \mid x \text { is divisible by } 2\rbrace=\lbrace\ldots-6,-4,-2,0,2,4,6, \ldots\rbrace \\ \\ & T=\lbrace x \in Z \mid x \text { is divisible by } 6\rbrace=\lbrace\ldots,-12,-6,0,6,12, \ldots\rbrace
\end{aligned} $
इसलिए, $T$ के प्रत्येक तत्व $R$ में भी है।
$\therefore\quad T \subset R$
57. दिया गया है $A=\lbrace 0,1,2\rbrace, B=\lbrace x \in R \mid 0 \leq x \leq 2\rbrace$. तो $A=B$.
उत्तर दिखाएं
Solution
गलत
$A=\lbrace0,1,2\rbrace \Rightarrow n(A)=3 \ $ और $ \ B =\lbrace x \in R \mid 0 \leq x \leq 2\rbrace $
इसलिए, $A$ एक समुच्चय है। क्योंकि, 0 से 2 तक के वास्तविक संख्याओं की संख्या अपरिमित है। इसलिए, $B$ अपरिमित है।
$\therefore\quad A \neq B$





