रैखिक असमिकाएँ
छोटे उत्तर प्रकार के प्रश्न
$ x $ के लिए निम्नलिखित प्रश्नों में असमिकाएँ हल कीजिए।
1. $\dfrac{4}{x+1} \leq 3 \leq \dfrac{6}{x+1}(x>0)$
उत्तर दिखाएँ
चिंतन प्रक्रिया
पहले दो असमिकाओं को हल करें, फिर अंतिम दो असमिकाओं को हल करके $ x $ के परिसर को प्राप्त करें।
हल
पहले दो असमिकाओं को लें,
$\dfrac{4}{x+1} \leq 3 $
$\Rightarrow 4 \leq 3(x+1) $
$\Rightarrow 4 \leq 3 x+3 $
$\Rightarrow 4-3 \leq 3 x $
$\Rightarrow 1 \leq 3 x $
$\therefore \ x \geq \dfrac{1}{3} \quad \ldots (i)$
अब, अंतिम दो असमिकाओं को लें,
$ 3 \leq \dfrac{6}{x+1} $
$\Rightarrow \ 3(x+1) \leq 6 $
$\Rightarrow \ 3 x+3 \leq 6 $
$\Rightarrow \ 3 x \leq 6-3 $
$\Rightarrow \ 3 x \leq 3 $
$\therefore \ x \leq 1 \quad \ldots (ii)$
समीकरण (i) और (ii) से,
$ \begin{aligned} & \dfrac{1}{3} \leq x \leq 1 \end{aligned} $
$\Rightarrow \ x \in \left[\dfrac{1}{3}, 1 \right]$
2. $\dfrac{|x-2|-1}{|x-2|-2} \leq 0$
उत्तर दिखाएँ
हल
मान, $|x-2|=y$
$\dfrac{y-1}{y-2} \leq 0, \quad y-2 \neq 0$
केस (1): $ \ y-1 \leq 0, \quad y-2 > 0$
$\Rightarrow \ y \leq 1, \quad y >2$
केस (2): $ \ y-1 \geq 0, \quad y-2 < 0$
$\Rightarrow \ y \geq 1 , \quad y <2$
$\therefore \ 1 \leq y < 2 $
$\Rightarrow \ 1 \leq |x-2| < 2$
केस (1): $ \ |x-2| \geq 1$
$\Rightarrow \ x-2 \geq 1 \Rightarrow x \geq 3$
या $ \ x-2 \leq -1 \Rightarrow x \leq 1$
केस (2): $ \ |x-2| < 2$
$x-2 < 2 \Rightarrow x <4$
या $ \ x-2 > -2 \Rightarrow x >0$
केस (1) और केस (2) से
$\therefore \ x \in (0,1] \cup [3,4)$
3. $\dfrac{1}{|x|-3} \leq \dfrac{1}{2}$
उत्तर दिखाएँ
हल
दिया है, $ \ \dfrac{1}{|x|-3} \leq \dfrac{1}{2} $
$\begin{aligned} & \Rightarrow \quad|x|-3 \geq 2 \quad \left[\because \dfrac{1}{a}<\dfrac{1}{b} \Rightarrow a>b \right] \\ \\ & \Rightarrow \quad |x| \geq 5 \quad \text { [दोनों ओर } 3 \text { जोड़कर] } \\ \\ & \Rightarrow \quad x \leq-5 \text { या } x \geq 5 \quad[\because|x| \geq a \Rightarrow|x| \leq-a \Rightarrow|x| \geq a] \ & \end{aligned}$

$\Rightarrow \ x \in(-\infty,-5] \cup[5, \infty)\quad \ldots (i)$
$\begin{array}{ll} \text { Here, } & |x|-3 \neq 0 \\ \\ \Rightarrow & |x|-3<0 \ \text { or } \ |x|-3>0 \\ \\ \Rightarrow & |x|<3 \ \text { or } \ |x|>3 \\ \\ \Rightarrow & -3<x<3 \ \text { or } \ x<-3 \ \text { or } \ x>3 \quad \ldots (ii) \\ \\ & [\because|x|<a \Rightarrow-a<x<a \ \text { and } \ |x|>a \Rightarrow x<-a \ \text { or } \ x>a] \end{array}$
Eqs. (i) और (ii) के परिणामों को मिलाने पर हम प्राप्त करते हैं
$ x \in(-\infty,-5] \cup(-3,3) \cup[5, \infty) $
4. $|x-1| \leq 5,|x| \geq 2$
उत्तर दिखाएं
Solution
$|x-1| \leq 5$
$\Rightarrow \ -5 \leq x-1 \leq 5$
$\Rightarrow \ -4 \leq x \leq 6$
$\Rightarrow \ x \in [-4,6] \quad \ldots (i)$

और $|x| \geq 2$
$\Rightarrow \ x \leq -2 \ \text{or} \ x \geq 2$
$\Rightarrow \ x \in (- \infty , -2] \cup[2, \infty) \quad \ldots (ii)$

Eqs. (i) और (ii) को मिलाने पर हम प्राप्त करते हैं
$ x \in[-4,-2] \cup[2,6] $
5. $-5 \leq \dfrac{2-3 x}{4} \leq 9$
उत्तर दिखाएं
Solution
हम लेते हैं, $ \ -5 \leq \dfrac{2-3 x}{4} $
$ \Rightarrow \ -20 \leq 2-3 x $
$ \Rightarrow \ 3 x \leq 2+20 $
$ \Rightarrow \ 3 x \leq 22 $
$ \Rightarrow \ x \leq \dfrac{22}{3} \quad \ldots (i)$
इसके अलावा, $ \ \dfrac{2-3 x}{4} \leq 9 $
$ \Rightarrow \ 2-3 x \leq 36 $
$ \Rightarrow \ -3 x \leq 36-2 $
$\Rightarrow \ -3 x \leq 34 $
$\Rightarrow \ 3 x \geq-34 $
$\Rightarrow \ x \geq-\dfrac{34}{3} \quad \ldots (ii)$
Eqs. (i) और (ii) को मिलाने पर हम प्राप्त करते हैं
$-\dfrac{34}{3} \leq x \leq \dfrac{22}{3} $
$\Rightarrow \ x \in \left[\dfrac{-34}{3}, \dfrac{22}{3}\right]$
6. $4 x+3 \geq 2 x+17,3 x-5<-2$
उत्तर दिखाएं
Solution
हमें, $ \ 4 x+3 \geq 2 x+17 $
$\Rightarrow \ 4 x-2 x \geq 17-3 $
$ \Rightarrow \ 2 x \geq 14 $
$\Rightarrow \ x \geq \dfrac{14}{2} $
$\Rightarrow \ x \geq 7 \quad \ldots (i)$
इसके अतिरिक्त, $ \ 3 x-5 <-2 $
$\Rightarrow \ 3 x <-2+5 $
$\Rightarrow \ 3 x<3 $
$\Rightarrow \ x <1 \quad \ldots (ii)$
समीकरण (i) और (ii) को मिलाने पर, हम देखते हैं कि कोई समाधान संभव नहीं है क्योंकि इन दोनों समाधानों के बीच कोई उभयनिष्ठ नहीं है। (अर्थात, $x<1 \ \text{और} \ x \geq 7$ )।
7. एक कंपनी कैसेट बनाती है। इसके लागत और आय फंक्शन क्रमशः $C(x)=26000+30 x$ और $R(x)=43 x$ हैं, जहाँ $x$ एक सप्ताह में उत्पादित और बेचे गए कैसेट की संख्या है। कंपनी को कितने कैसेट बेचने होंगे ताकि कुछ लाभ हो सके?
उत्तर दिखाएं
Solution
लागत फंक्शन, $C(x) = 26000 + 30x$
और आय फंक्शन, $R(x) = 43x$
लाभ के लिए, $R(x) > C(x)$
$\Rightarrow$ $ 26000 + 30x < 43x$
$\Rightarrow$ $ 30x - 43x < -26000$
$\Rightarrow$ $ -13x < -26000$
$\Rightarrow$ $ 13x > 26000$
$\Rightarrow$ $x > \dfrac{26000}{13}$
$\therefore \ x > 2000$
$\therefore \ $ अतः, लाभ प्राप्त करने के लिए 2000 से अधिक कैसेट उत्पादित करने होंगे।
8. एक पूल में पानी की अम्लता तब सामान्य मानी जाती है जब तीन दैनिक मापनों के औसत pH माप 8.2 और 8.5 के बीच हो। यदि पहले दो pH माप 8.48 और 8.35 हैं, तो तीसरे माप के pH मान के क्षेत्र को ज्ञात कीजिए जिससे अम्लता स्तर सामान्य हो जाए।
उत्तर दिखाएं
Solution
दिया गया है, पहला pH मान $=8.48$
और दूसरा pH मान $=8.35$
मान लीजिए तीसरा pH मान $x$ है।
क्योंकि दिया गया है कि औसत pH मान 8.2 और 8.5 के बीच है।
$\therefore \ 8.2<\dfrac{8.48+8.35+x}{3}<8.5 $
$\Rightarrow \ 8.2<\dfrac{16.83+x}{3}<8.5 $
$\Rightarrow \ 3 \times 8.2<16.83+x<8.5 \times 3 $
$\Rightarrow \ 24.6<16.83+x<25.5 $
$\Rightarrow \ 24.6-16.83<x<25.5-16.83 $
$\Rightarrow \ 7.77<x<8.67$
इसलिए, तीसरा pH मान $7.77$ और $8.67$ के बीच होगा ।
9. 9% अम्ल के विलयन को 3% अम्ल के विलयन के जोड़कर तनु करना है। बने हुए मिश्रण में अम्ल की सांद्रता 5% से अधिक लेकिन 7% से कम होनी चाहिए। यदि 9% विलयन की मात्रा 460 लीटर है, तो कितने लीटर 3% विलयन को मिलाना पड़ेगा?
उत्तर दिखाएं
हल
$x$ लीटर 3% विलयन मिलाया गया
460 लीटर 9% विलयन मिलाया गया
कुल विलयन $= (460+x)$ लीटर
मिश्रण की प्रतिशतता $= \dfrac{\left(460 \times \dfrac{9}{100}+ x \times \dfrac{3}{100}\right)}{(460+x)}\times 100$
प्रश्न के अनुसार,
$5 < \text{मिश्रण की प्रतिशतता} <7$
$\Rightarrow \ 5 < \dfrac{(460 \times 9+3x)}{(460+x)} <7$
$\Rightarrow \ 5 \times (460+x) < (460 \times 9 +3x) < 7 \times (460+x)$
$\Rightarrow \ 2300+5x < 4140+3x < 3220+7x$
अब, $ \ 2300+5x < 4140+3x $
$\Rightarrow \ 2x < 4140-2300$
$\Rightarrow \ 2x < 1840$
$\Rightarrow \ x < 920 \quad \ldots (i)$
और $ \ 4140+3x < 3220 +7x$
$\Rightarrow \ 4x > 4140-3220$
$\Rightarrow \ 4x > 920$
$\Rightarrow \ x > 230 \quad \ldots (ii)$
समीकरण (i) और (ii) से,
$920 > x > 230$
इसलिए, 3% अम्ल के विलयन की मात्रा 230 लीटर से अधिक लेकिन 920 लीटर से कम होनी चाहिए।
10. एक विलयन को 40°C और 45°C के बीच बरकरार रखना है। तापमान की डिग्री फ़ेरनहाइट में श्रेणी क्या होगी, यदि परिवर्तन सूत्र $F=\dfrac{9}{5} C+32$ है?
उत्तर दिखाएं
हल
मान लीजिए आवश्यक तापमान $x^{\circ} F$ है।
दिया गया है : $ F= \dfrac{9}{5} C+32 $
$ \begin{array}{l} \Rightarrow \ 5 F=9 C+160 \\ \\ \Rightarrow \ C=\dfrac{(5 F-160)}{9} \end{array} $
$ \because \ $ डिग्री सेल्सियस में तापमान $ 40^{\circ} \mathrm{C} $ से $ 45^{\circ} \mathrm{C} $ के बीच है
$ \begin{array}{l} \therefore \ 40^{\circ}<(5 \mathrm{~F}-160) / 9<45^{\circ} \\ \\ \Rightarrow \ 360^{\circ}<5 \mathrm{~F}-160<405^{\circ} \\ \\ \Rightarrow \ 520^{\circ}<5 \mathrm{~F}<565^{\circ} \\ \\
\Rightarrow \ 104^{\circ}<\mathrm{F}<113^{\circ} \end{array} $
इसलिए, फ़ेरनहाइट में तापमान की श्रेणी $104^{\circ} F$ से $113^{\circ} F$ तक है।
11. एक त्रिभुज की सबसे लंबी भुजा सबसे छोटी भुजा के दुगुनी है और तीसरी भुजा सबसे छोटी भुजा से $2 cm$ लंबी है। यदि त्रिभुज का परिमाप $166 cm$ से अधिक है, तो सबसे छोटी भुजा की न्यूनतम लंबाई ज्ञात कीजिए।
उत्तर दिखाएं
हल
मान लीजिए सबसे छोटी भुजा की लंबाई $x cm$ है।
दिए गए जानकारी के अनुसार,
सबसे लंबी भुजा $=2 \times$ सबसे छोटी भुजा $ =2 x cm $
और तीसरी भुजा $=2+$ सबसे छोटी भुजा $ =(2+x) cm $
त्रिभुज का परिमाप $=x+2 x+(x+2)=4 x+2$
प्रश्न के अनुसार,
परिमाप $>166 cm$
$ \begin{matrix} \Rightarrow & 4 x+2>166 \\ \\ \Rightarrow & 4 x>166-2 \\ \\ \Rightarrow & 4 x>164 \\ \\ \therefore & x>\dfrac{164}{4}=41 cm \end{matrix} $
इसलिए, सबसे छोटी भुजा की न्यूनतम लंबाई $41 cm$ है।
12. विश्व की सबसे गहरी गड्ढा खुदाई करते समय पाया गया कि पृथ्वी की सतह से $x km$ नीचे तापमान $T$ सेल्सियस में द्वारा $T=30+25(x-3), 3 \leq x \leq 15$ द्वारा दिया गया है। कितनी गहराई पर तापमान $155^{\circ} C$ और $205^{\circ} C$ के बीच होगा?
उत्तर दिखाएं
हल
दिया गया है, $ \ T=30+25(x-3), 3 \leq x \leq 15 $
प्रश्न के अनुसार,
$ \begin{aligned} & 155<T<205 \\ \\ & \begin{matrix} \Rightarrow & 155<30+25(x-3)<205 \\ \\ \Rightarrow & 155-30<25(x-3)<205-30 \end{matrix} \\ \\ & \Rightarrow \quad 155-30<25(x-3)<205-30 \quad \text {[ whole में 30 घटाना ]} \\ \\ & \Rightarrow \quad 125<25(x-3)<175 \\ \\ & \Rightarrow \quad \dfrac{125}{25}<x-3<\dfrac{175}{25} \quad \text { [ whole में 25 से विभाजित करना ]} \\ \\ & \Rightarrow \quad 5<x-3<7 \\ \\ & \Rightarrow \quad 5+3<x<7+3 \quad \text {[ whole में 3 जोड़ना ]} \\ \\ & \Rightarrow \quad 8<x<10 \end{aligned} $
इसलिए, $8 km$ से $10 km$ गहराई पर तापमान $155^{\circ}$ से $205^{\circ} C$ के बीच होगा।
लंबा उत्तर प्रकार प्रश्न
13. निम्नलिखित असमिकाओं के निकाय को हल करें $\dfrac{2 x+1}{7 x-1}>5, \dfrac{x+7}{x-8}>2$.
उत्तर दिखाएं
हल
दी गई असमिकाओं के निकाय है
$\dfrac{2 x+1}{7 x-1}>5 $
और $\quad \dfrac{x+7}{x-8}>2 $
अब, $\quad \dfrac{2 x+1}{7 x-1}-5>0 $
$\Rightarrow \quad \dfrac{(2 x+1)-5(7 x-1)}{7 x-1}>0 $
$\Rightarrow \quad \dfrac{2 x+1-35 x+5}{7 x-1}>0 $
$\Rightarrow \quad \dfrac{-33 x+6}{7 x-1}>0 $
$\Rightarrow \quad \dfrac{33 x-6}{7 x-1}<0 $
$\Rightarrow \quad \dfrac{33 \left(x-\dfrac{6}{33}\right)}{7 \left(x-\dfrac{1}{7}\right)} < 0$
$\Rightarrow \quad \dfrac{x-\dfrac{6}{33}}{x- \dfrac{1}{7}} < 0$
$\Rightarrow \quad x \in \left(\dfrac{1}{7}, \dfrac{6}{33} \right)$
$\Rightarrow \quad x \in \left(\dfrac{1}{7}, \dfrac{2}{11} \right) \quad \ldots (i)$
$ \dfrac{x+7}{x-8}>2 $
$\Rightarrow \ \dfrac{x+7}{x-8}-2>0 $
$\Rightarrow \ \dfrac{x+7-2(x-8)}{x-8}>0 $
$\Rightarrow \ \dfrac{x+7-2 x+16}{x-8}>0 $
$\Rightarrow \ \dfrac{-x+23}{x-8}>0 $
$\Rightarrow \ \dfrac{x-23}{x-8}<0 \quad \ldots (ii)$

$x \in(8,23) $
क्योंकि, समीकरण (i) और (ii) के प्रतिच्छेदन शून्य समुच्चय है। अतः, दिए गए असमिकाओं के निकाय का कोई हल नहीं है।
14. दिए गए चित्र में छायांकित क्षेत्र के लिए रैखिक असमिकाएं ज्ञात करें।
उत्तर दिखाएं
हल
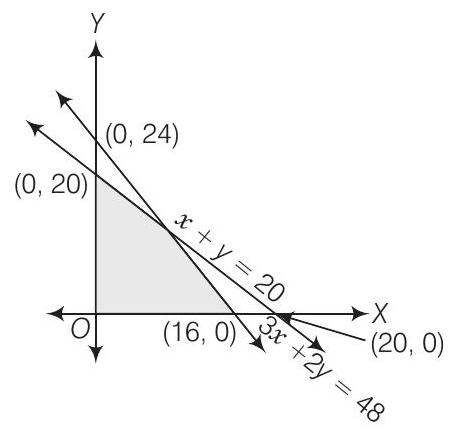
दिए गए चित्र में, छायांकित क्षेत्र प्रथम चतुर्थांश में है। अतः $ x \geq 0, y \geq $ 0।
छायांकित क्षेत्र प्रथम चतुर्थांश में रेखाओं $ x+y \leq 20,3 x+2 y \leq 48 $ के सामान्य क्षेत्र है।
तो, दिए गए छायांकित क्षेत्र को प्रस्तुत करने वाली रैखिक असमिकाएं हैं, $ x+y \leq 20,3 x+2 y \leq 48, x \geq 0, y \geq 0 $
15. दिए गए चित्र में छायांकित क्षेत्र को समाधान समुच्चय के रूप में दर्शाने वाली रैखिक असमिकाएं ज्ञात कीजिए।
उत्तर दिखाएं
हल
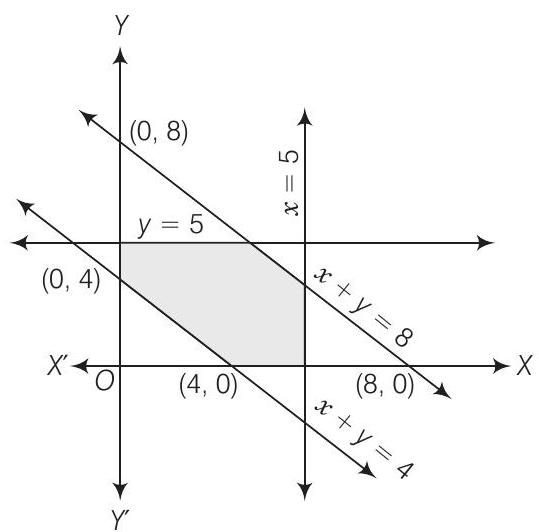
रेखा $x+y=4$ को ध्यान में रखें।
हम देखते हैं कि छायांकित क्षेत्र और मूल बिंदु इस रेखा के विपरीत ओर है और $(0,0)$ असमिका $x+y \leq 4$ को संतुष्ट करता है। अतः, हमें रेखा $x+y=4$ के लिए असमिका $x+y \geq 4$ होनी चाहिए।
रेखा $x+y=8$ को ध्यान में रखें, स्पष्ट रूप से छायांकित क्षेत्र और मूल बिंदु इस रेखा के समान ओर है और $(0,0)$ असमिका $x+y \leq 8$ को संतुष्ट करता है। अतः, हमें रेखा $x+y=8$ के लिए असमिका $x+y \leq 8$ होनी चाहिए।
रेखा $x=5$ को ध्यान में रखें। ग्राफ से स्पष्ट है कि छायांकित क्षेत्र और मूल बिंदु इस रेखा के बाईं ओर है और $(0,0)$ असमिका $x \leq 5$ को संतुष्ट करता है।
अतः, $x \leq 5$ रेखा $x=5$ के लिए असमिका है।
रेखा $y=5$ को ध्यान में रखें, स्पष्ट रूप से छायांकित क्षेत्र और मूल बिंदु इस रेखा के समान ओर (ऊपर) है और $(0,0)$ असमिका $y \leq 5$ को संतुष्ट करता है।
अतः, $y \leq 5$ रेखा $y=5$ के लिए असमिका है।
हम यह भी देखते हैं कि छायांकित क्षेत्र X-अक्ष के ऊपर और Y-अक्ष के दाईं ओर है, अर्थात छायांकित क्षेत्र पहले चतुर्थांश में है। अतः, हमें $x \geq 0, y \geq 0$ होना चाहिए।
इस प्रकार, दिए गए समाधान समुच्चय को बनाने वाली रैखिक असमिकाएं हैं
$ x+y \geq 4 ; x+y \leq 8 ; x \leq 5 ; y \leq 5 ; x \geq 0 \text { और } y \geq 0 $
16. दिखाइए कि निम्नलिखित रैखिक असमिकाओं के निकाय के कोई समाधान नहीं होता $x+2 y \leq 3,3 x+4 y \geq 12, x \geq 0, y \geq 1$।
उत्तर दिखाएं
हल
असमिका $x+2 y \leq 3$ को समीकरण के रूप में लें, हमें प्राप्त होता है
एक समीकरण के रूप में लें, हमें प्राप्त होता है
x + 2y = 3
इस रेखा के लिए, छायांकित क्षेत्र और मूल बिंदु इस रेखा के विपरीत ओर है और $(0,0)$ असमिका $x + 2y \leq 3$ को संतुष्ट करता है। अतः, हमें असमिका $x + 2y \leq 3$ के लिए असमिका $x + 2y \leq 3$ होनी चाहिए।
असमिका $3x + 4y \geq 12$ को समीकरण के रूप में लें, हमें प्राप्त होता है
3x + 4y = 12
इस रेखा के लिए, छायांकित क्षेत्र और मूल बिंदु इस रेखा के विपरीत ओर है और $(0,0)$ असमिका $3x + 4y \geq 12$ को संतुष्ट करता है। अतः, हमें असमिका $3x + 4y \geq 12$ के लिए असमिका $3x + 4y \geq 12$ होनी चाहिए।
असमिका $x \geq 0$ के लिए, छायांकित क्षेत्र और मूल बिंदु इस रेखा के विपरीत ओर है और $(0,0)$ असमिका $x \geq 0$ को संतुष्ट करता है। अतः, हमें असमिका $x \geq 0$ के लिए असमिका $x \geq 0$ होनी चाहिए।
असमिका $y \geq 1$ के लिए, छायांकित क्षेत्र और मूल बिंदु इस रेखा के विपरीत ओर है और $(0,0)$ असमिका $y \geq 1$ को संतुष्ट करता है। अतः, हमें असमिका $y \geq 1$ के लिए असमिका $y \geq 1$ होनी चाहिए।
इस प्रकार, दिए गए निकाय के कोई समाधान नहीं होता है।
$x+2y=3$
$\begin{array}{|c|c|c|c|} \hline x & 0 & 1 & 3 \\ \\ \hline y & 1.5 & 1 & 0 \\ \\ \hline \end{array}$
अब, $(0,0)$ समीकरण $x+2 y \leq 3$ को संतुष्ट करता है।
इसलिए, आधा तल $(0,0)$ को समाधान के रूप में शामिल करता है और रेखा $x+2 y=3$ निर्देशांक अक्ष को $(3,0)$ और $(0,3 / 2)$ पर काटती है।
समीकरण $3 x+4 y \geq 12$ के रूप में समीकरण $3 x+4 y=12$ को लें।
$\begin{array}{|c|c|c|c|} \hline x & 0 & 2 & 4 \\ \\ \hline y & 3 & \dfrac{3}{2} & 0 \\ \\ \hline \end{array}$
इसलिए, रेखा $3 x+4 y=12$ निर्देशांक अक्ष को बिंदु $(4,0)$ और $(0,3)$ पर काटती है।
अब, $(0,0)$ समीकरण $3 x+4 y=12$ को संतुष्ट नहीं करता है।
इसलिए, समाधान के आधा तल $(0,0)$ को शामिल नहीं करता है।
समीकरण $y \geq 1$ के रूप में, हमें $y=1$ मिलता है।
यह एक सीधी रेखा है जो $X$-अक्ष के समानांतर है और बिंदु $(0,1)$ से गुजरती है।
अब, $(0,0)$ समीकरण $y \geq 1$ को संतुष्ट नहीं करता है।
इसलिए, समाधान के आधा तल $(0,0)$ को शामिल नहीं करता है।
स्पष्ट रूप से $x \geq 0$ वह क्षेत्र दर्शाता है जो $Y$-अक्ष के दाईं ओर स्थित है।
दिए गए रैखिक संरेखण के समाधान समुच्चय उपरोक्त क्षेत्र के प्रतिच्छेदन होगा।
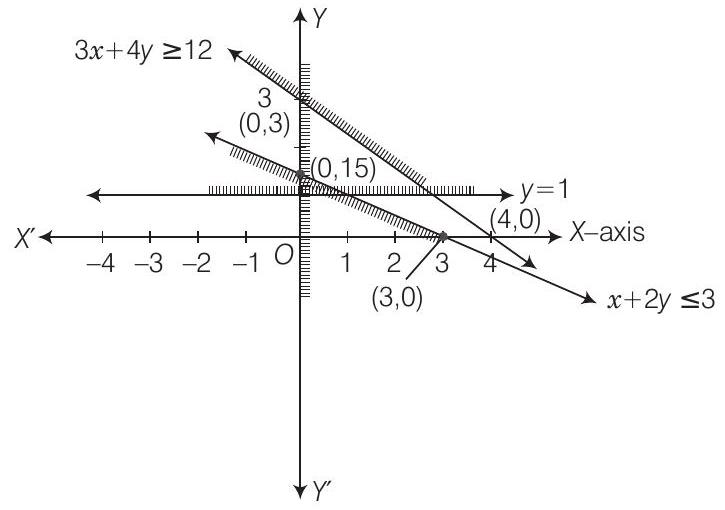
ग्राफ से स्पष्ट है कि छाया वाले भागों में सामान्य क्षेत्र नहीं है।
इसलिए, समाधान समुच्चय शून्य समुच्चय है।
17. निम्नलिखित रैखिक असमिकाओं के निकाय को हल करें
$3 x+2 y \geq 24,3 x+y \leq 15, x \geq 4$.
उत्तर दिखाएं
हल
समीकरण $3 x+2 y \geq 24$ के रूप में, हमें $3 x+2 y=24$ मिलता है।
$\begin{array}{|c|c|c|c|} \hline x & 0 & 8 & 4 \\ \\ \hline y & 12 & 0 & 6 \\ \\ \hline \end{array}$
इसलिए, रेखा $3 x+y=24$ निर्देशांक अक्ष को बिंदु $(8,0)$ और $(0,12)$ पर काटती है।
अब, $(0,0)$ समीकरण $3 x+2 y \geq 24$ को संतुष्ट नहीं करता है।
इसलिए, समाधान समुच्चय के आधा तल $(0,0)$ को नहीं शामिल करता है।
असमिका $3 x+y \leq 15$ को समीकरण के रूप में लें, हमारे पास है
$ 3 x+y=15 $
$\begin{array}{|c|c|c|c|} \hline x & 0 & 5 & 3 \\ \\ \hline y & 15 & 0 & 6 \\ \\ \hline \end{array}$
रेखा $3 x+y=15$ निर्देशांक अक्षों को बिंदु $(5,0)$ और $(0,15)$ पर काटती है।
अब, बिंदु $(0,0)$ असमिका $3 x+y \leq 15$ को संतुष्ट करता है।
इसलिए, समाधान के आधा तल मूल बिंदु को शामिल करता है।
असमिका $x \geq 4$ को समीकरण के रूप में लें, हमारे पास है
$ x=4 $
यह एक सीधी रेखा है जो $Y$-अक्ष के समानांतर है और $(4,0)$ से गुजरती है। अब, बिंदु $(0,0)$ असमिका $x \geq 4$ को संतुष्ट नहीं करता है।
इसलिए, आधा तल $(0,0)$ को नहीं शामिल करता है,
ऊपर की असमिकाओं के ग्राफ नीचे दिया गया है।
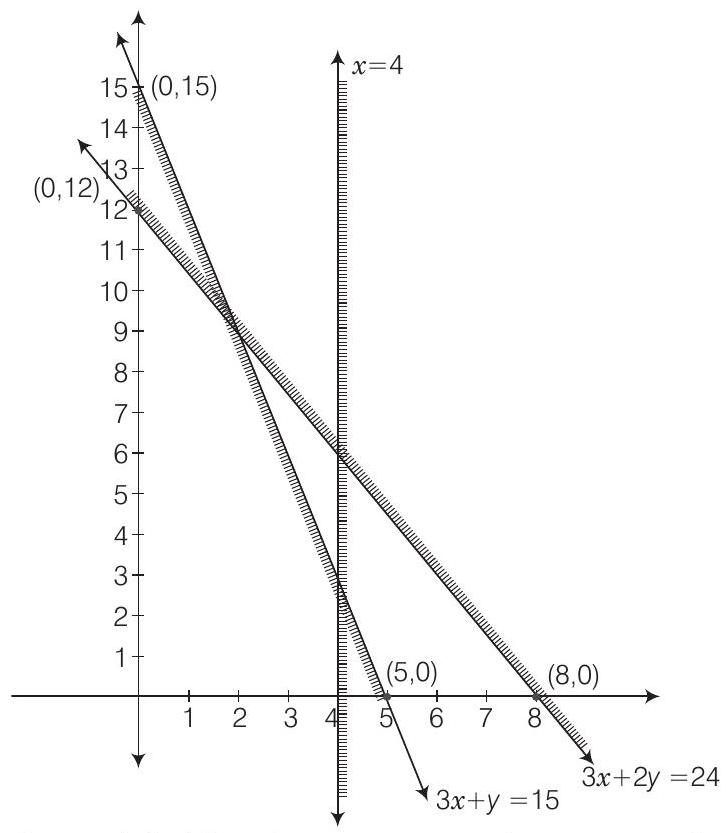
ग्राफ से स्पष्ट है कि इन असमिकाओं के लिए कोई उभयनिष्ठ क्षेत्र नहीं है। इसलिए, दी गई असमिकाओं के तंत्र के कोई समाधान नहीं है।
18. दिखाइए कि निम्नलिखित रैखिक असमिकाओं के तंत्र के समाधान समुच्चय एक असीमित क्षेत्र है $2 x+y \geq 8, x+2 y \geq 10, x \geq 0, y \geq 0$।
उत्तर दिखाएं
हल
असमिका $2 x+y \geq 8$ को समीकरण के रूप में लें, हमारे पास है
$2x + y = 8$
$\begin{array}{|c|c|c|c|} \hline x & 0 & 4 & 3 \\ \\ \hline y & 8 & 0 & 2 \\ \\ \hline \end{array}$
रेखा $2 x+y=8$ निर्देशांक अक्षों को बिंदु $(4,0)$ और $(0,8)$ पर काटती है। अब, बिंदु $(0,0)$ असमिका $2 x+y \geq 8$ को संतुष्ट नहीं करता है। इसलिए, आधा तल मूल बिंदु को नहीं शामिल करता है।
असमिका $x+2 y \geq 10$ को समीकरण के रूप में लें, हमारे पास है
$ x+2 y=10 $
$\begin{array}{|c|c|c|c|} \hline x & 0 & 10 & 8 \\ \\ \hline y & 5 & 0 & 1 \\ \\ \hline \end{array}$
रेखा $2 x+y=8$ निर्देशांक अक्षों को बिंदु $(10,0)$ और $(0,5)$ पर काटती है।
अब, बिंदु $(0,0)$ असमिका $x+2 y \geq 10$ को संतुष्ट नहीं करता है।
इसलिए, आधा तल $(0,0)$ को नहीं शामिल करता है।
असमानुपात $x \geq 0$ और $y \geq 0$ स्पष्ट रूप से पहले चतुर्थांश में क्षेत्र को दर्शाता है। उपरोक्त असमानुपात के ग्राफ नीचे दिया गया है
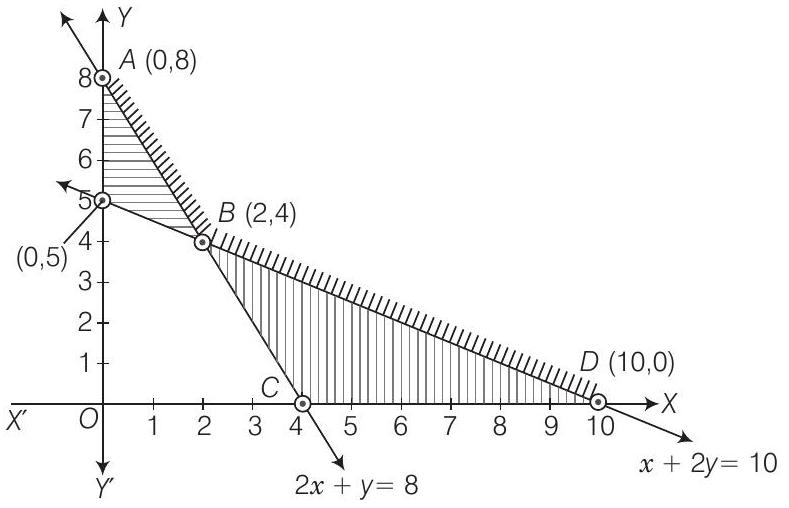
ग्राफ से स्पष्ट है कि सामान्य छायांकित क्षेत्र असीमित है।
वस्तुनिष्ठ प्रश्न
19. यदि $x<5$, तो
(a) $-x<-5$
(b) $-x \leq-5$
(c) $-x>-5$
(d) $-x \geq-5$
उत्तर दिखाएं
हल
विकल्प (c) यदि $x<5$, तो $-x>-5$
[यदि हम नकारात्मक संख्या से गुणा करते हैं, तो असमानता उलट जाती है]
-
विकल्प (a) $-x < -5$: यह गलत है क्योंकि यदि $x<5$, तो दोनों ओर $-1$ से गुणा करने पर असमानता उलट जाती है, जिसके परिणामस्वरूप $-x>-5$ होता है, न कि $-x<-5$।
-
विकल्प (b) $-x \leq-5$: यह गलत है क्योंकि यदि $x<5$, तो दोनों ओर $-1$ से गुणा करने पर असमानता उलट जाती है, जिसके परिणामस्वरूप $-x>-5$ होता है, न कि $-x \leq-5$।
-
विकल्प (d) $-x \geq-5$: यह गलत है क्योंकि यदि $x<5$, तो दोनों ओर $-1$ से गुणा करने पर असमानता उलट जाती है, जिसके परिणामस्वरूप $-x>-5$ होता है, न कि $-x \geq-5$।
20. यह दिया गया है कि $x, y$ और $b$ वास्तविक संख्याएँ हैं और $x<y, b<0$, तो
(a) $\dfrac{x}{b}<\dfrac{y}{b}$
(b) $\dfrac{x}{b} \leq \dfrac{y}{b}$
(c) $\dfrac{x}{b}>\dfrac{y}{b}$
(d) $\dfrac{x}{b} \geq \dfrac{y}{b}$
उत्तर दिखाएं
हल
विकल्प (c) यह दिया गया है कि,
$ x<y, b<0 $
$\Rightarrow \quad \dfrac{x}{b}>\dfrac{y}{b}$ $\quad [\because b<0]$
-
विकल्प (a) $\dfrac{x}{b}<\dfrac{y}{b}$: यह विकल्प गलत है क्योंकि जब $b < 0$, तो एक नकारात्मक संख्या से विभाजन असमानता को उलट देता है। चूंकि $x < y$, $\dfrac{x}{b}$ बराबर $\dfrac{y}{b}$ से अधिक होता है, न कि कम।
-
विकल्प (b) $\dfrac{x}{b} \leq \dfrac{y}{b}$: यह विकल्प विकल्प (a) के लिए उतना ही गलत है। एक नकारात्मक संख्या से विभाजन असमानता को उलट देता है, इसलिए $\dfrac{x}{b}$ बराबर $\dfrac{y}{b}$ से अधिक होता है, न कि कम या बराबर।
-
विकल्प (d) $\dfrac{x}{b} \geq \dfrac{y}{b}$: यह विकल्प गलत है क्योंकि जब एक नकारात्मक संख्या से विभाजन करते हैं तो असमानता के उलट होने के बारे में यह सही रूप से लेखता है, लेकिन बराबरी की संभावना $(\geq)$ को शामिल करता है। क्योंकि $x < y$ और $b < 0$, $\dfrac{x}{b}$ ठीक उतना बड़ा होगा जितना $\dfrac{y}{b}$, न कि बड़ा या बराबर।
21. यदि $-3 x+17<-13$, तो
(a) $x \in(10, \infty)$
(b) $x \in[10, \infty)$
(c) $x \in(-\infty, 10]$
(d) $x \in[-10,10)$
उत्तर दिखाएं
हल
विकल्प (a) दिया गया है, $-3 x+17<-13$
$\Rightarrow$ $3 x-17>13 \quad $ $[$ दोनों ओर $-1$ से गुणा करने पर $]$
$\Rightarrow$ $3 x>13+17 \quad $ $[$ दोनों ओर 17 जोड़ने पर $]$
$\Rightarrow$ $3 x>30$
$\Rightarrow x>10$
-
विकल्प (b) $x \in[10, \infty)$ गलत है क्योंकि असमानता $x > 10$ में मान $10$ को शामिल नहीं होता, जबकि अंतराल नोटेशन $[10, ∞)$ में $10$ शामिल होता है।
-
विकल्प (c) $x \in(-\infty, 10]$ गलत है क्योंकि असमानता $x > 10$ बताती है कि $x$ 10 से बड़ा होना चाहिए, न कि 10 से कम या बराबर होना चाहिए।
-
विकल्प (d) $x \in(-10, 10)$ गलत है क्योंकि असमानता $x > 10$ बताती है कि $x$ 10 से बड़ा होना चाहिए, जबकि अंतराल नोटेशन $(-10, 10)$ में 10 से कम मान शामिल होते हैं और 10 से बड़े मान शामिल नहीं होते हैं।
22. यदि $x$ एक वास्तविक संख्या है और $|x|<3$, तो
(a) $x \geq 3$
(b) $-3<x<3$
(c) $x \leq-3$
(d) $-3 \leq x \leq 3$
उत्तर दिखाएं
हल
विकल्प (b) दिया गया है, $ \ |x|<3 $
$ \Rightarrow \ -3<x<3 \quad[\because|x|<a \Rightarrow-a<x<a] $
-
विकल्प (a) $x \geq 3$ गलत है क्योंकि शर्त $|x|<3$ बताती है कि $x$ के मान $-3$ और $3$ के बीच होना चाहिए, न कि $3$ से बड़ा या बराबर होना चाहिए।
-
विकल्प (c) $x \leq -3$ गलत है क्योंकि शर्त $|x|<3$ बताती है कि $x$ के मान $-3$ और $3$ के बीच होना चाहिए, न कि $-3$ से कम या बराबर होना चाहिए।
-
विकल्प (d) $-3 \leq x \leq 3$ गलत है क्योंकि शर्त $|x|<3$ बताती है कि $x$ के मान $-3$ और $3$ के बीच होना चाहिए, जबकि अंतराल नोटेशन $-3$ और $3$ को शामिल करता है।
23. $x$ और $b$ वास्तविक संख्याएँ हैं। यदि $b>0$ और $|x|>b$, तो
(a) $x \in(-b, \infty)$
(b) $x \in(-\infty, b)$
(c) $x \in(-b, b)$
(d) $x \in(-\infty,-b) \cup(b, \infty)$
उत्तर दिखाएं
Solution
Option (d) दिया गया है, $|x| >b \ \text { और } \ b>0 $
$\Rightarrow \ x <-b \ \text { या } \ x>b$
$\Rightarrow \ x \in(-\infty,-b) \cup(b, \infty)$
-
Option (a) $x \in(-b, \infty)$ गलत है क्योंकि इसमें $x$ के अंतराल $(-b, b)$ में मान शामिल हैं, जो $|x| > b$ को संतुष्ट नहीं करते हैं।
-
Option (b) $x \in(-\infty, b)$ गलत है क्योंकि इसमें $x$ के अंतराल $(-b, b)$ में मान शामिल हैं, जो $|x| > b$ को संतुष्ट नहीं करते हैं।
-
Option (c) $x \in(-b, b)$ गलत है क्योंकि इसमें $x$ के मान जहाँ $|x| \leq b$ शामिल हैं, जो $|x| > b$ को संतुष्ट नहीं करते हैं।
24. यदि $|x-1|>5$, तो
(a) $x \in(-4,6)$
(b) $x \in[-4,6]$
(c) $x \in(-\infty,-4) \cup(6, \infty)$
(d) $x \in(-\infty,-4) \cup[6, \infty)$
उत्तर दिखाएं
Solution
Option (c) दिया गया है, $ \ |x-1| >5 $
$\Rightarrow \ (x-1) <-5 \ \text { या } \ (x-1)>5 \quad[\because|x|>a \Rightarrow x<a \ \text { या } \ x>a] $
$\Rightarrow \ x <-4 \ \text { या } \ x>6 $
$\Rightarrow \ x \in(-\infty,-4) \cup(6, \infty)$
-
Option (a) $x \in(-4,6)$ गलत है क्योंकि इसमें $x$ के मान $-4$ और $6$ के बीच होते हैं, जो $|x-1|>5$ को संतुष्ट नहीं करते हैं। $|x-1|>5$ के लिए $x$ के मान या तो $-4$ से कम होना चाहिए या $6$ से अधिक होना चाहिए।
-
Option (b) $x \in[-4,6]$ गलत है क्योंकि इस अंतराल में $-4$ और $6$ के समावेशी मान शामिल हैं और बीच के मान भी। इसके लिए भी $|x - 1| > 5$ के लिए वही कारण है जो (a) में है।
-
Option (d) $x \in(-\infty,-4) \cup[6, \infty)$ गलत है क्योंकि इसमें $[6, \infty)$ अंतराल शामिल है, जिसका अर्थ है $x \geq 6$। हालाँकि, सही शर्त $|x-1|>5$ के लिए $x > 6$ होना चाहिए, न कि $x \geq 6$।
25. यदि $|x+2| \leq 9$, तो
(a) $x \in(-7,11)$
(b) $x \in[-11,7]$
(c) $x \in(-\infty,-7) \cup(11, \infty)$
(d) $x \in(-\infty,-7) \cup[11, \infty)$
उत्तर दिखाएं
Solution
Option (b) Given, $ \ |x+2| \leq 9,$
$\Rightarrow \ -9 \leq x+2 \leq 9 \quad {[\because \ |x| \leq a \Rightarrow-a \leq x \leq a]}$
$\Rightarrow \ -9-2 \leq x \leq 9-2 \quad \text { [subtracting 2 througout] } $
$\Rightarrow \ -11 \leq x \leq 7 $
$x \in [-11,7]$
-
Option (a) $x \in(-7,11)$: यह विकल्प गलत है क्योंकि अंतराल $(-7, 11)$ अंतिम बिंदुओं $-11$ और $7$ को शामिल नहीं करता है, जो असमिका $|x+2| \leq 9$ के समाधान के हिस्सा हैं। सही अंतराल $[-11, 7]$ होना चाहिए।
-
Option (c) $x \in(-\infty,-7) \cup(11, \infty)$: यह विकल्प गलत है क्योंकि यह $x$ के मानों को अंतराल $[-11, 7]$ के बाहर दर्शाता है। असमिका $|x+2| \leq 9$ अंतराल $[-11, 7]$ के भीतर के मानों को शामिल करती है, न कि बाहर के मानों को।
-
Option (d) $x \in(-\infty,-7) \cup[11, \infty)$: यह विकल्प विकल्प (c) के लिए उतना ही गलत है। यह $x$ के मानों को अंतराल $[-11, 7]$ के बाहर दर्शाता है। असमिका $|x+2| \leq 9$ अंतराल $[-11, 7]$ के भीतर के मानों को शामिल करती है, न कि बाहर के मानों को।
26. निम्नलिखित ग्राफ को प्रस्तुत करने वाली असमिका है:

(a) $|x|<5$
(b) $|x| \leq 5$
(c) $|x|>5$
(d) $|x| \geq 5$
उत्तर दिखाएं
Solution
Option (a) दिया गया ग्राफ $x > -5$ और $x < 5$ को प्रस्तुत करता है।
इन दोनों परिणामों को मिलाने पर हमें प्राप्त होता है
$ |x|<5 \quad [\because -a < x < -a \Rightarrow |x|<a ;a >0] $
-
Option (b) $|x| \leq 5$: यह विकल्प गलत है क्योंकि ग्राफ $x = -5$ और $x = 5$ के बिंदुओं को शामिल नहीं करता है। ग्राफ इन बिंदुओं पर खुले वृत्त के रूप में दिखाई देता है, जो इस बात को दर्शाता है कि ये मान समाधान सेट के हिस्सा नहीं हैं।
-
Option (c) $|x| > 5$: यह विकल्प गलत है क्योंकि ग्राफ $-5$ और $5$ के बीच क्षेत्र को दर्शाता है, न कि इसके बाहर। ग्राफ $x$ के मानों को $5$ से अधिक या $-5$ से कम नहीं शामिल करता है।
-
विकल्प (d) $|x| \geq 5$: यह विकल्प गलत है क्योंकि ग्राफ में $x = -5$ और $x = 5$ के बिंदु शामिल नहीं हैं, और इसके अलावा $-5 < x < 5$ के बाहर कोई मान भी शामिल नहीं है। ग्राफ केवल $-5$ और $5$ के बीच क्षेत्र को दर्शाता है।
एक चर $x$ में रैखिक असमिका के समाधान को अभ्यास 27 से 30 में संख्या रेखा पर दर्शाया गया है।
27.

(a) $x \in(-\infty, 5)$
(b) $x \in(-\infty, 5]$
(c) $x \in [5, \infty)$
(d) $x \in(5, \infty)$
उत्तर दिखाएं
समाधान
विकल्प (d) दिए गए ग्राफ में सभी मान दर्शाए गए हैं जो 5 से बड़े हैं लेकिन 5 को छोड़कर। अतः,
अर्थात $ \ x \in(5, \infty)$।
-
विकल्प (a) $x \in(-\infty, 5)$ गलत है क्योंकि यह 5 से कम सभी मानों को दर्शाता है, जो दिए गए ग्राफ में दर्शाए गए मानों के साथ मेल नहीं खाता है जो 5 से बड़े हैं।
-
विकल्प (b) $x \in(-\infty, 5]$ गलत है क्योंकि यह 5 से कम या बराबर सभी मानों को दर्शाता है, जो दिए गए ग्राफ में दर्शाए गए मानों के साथ मेल नहीं खाता है जो 5 से बड़े हैं और 5 को छोड़कर हैं।
-
विकल्प (c) $x \in [5, \infty)$ गलत है क्योंकि यह अंतराल $x$ को 5 से बड़े या बराबर दर्शाता है जो दिए गए ग्राफ में दर्शाए गए मानों के साथ मेल नहीं खाता है जो 5 से बड़े हैं लेकिन 5 को छोड़कर हैं।
28.

(a) $x \in \left(\dfrac{9}{2}, \infty \right)$
(b) $x \in \left[\dfrac{9}{2}, \infty \right)$
(c) $x \in \left(-\infty, \dfrac{9}{2} \right)$
(d) $x \in \left(-\infty, \dfrac{9}{2} \right]$
उत्तर दिखाएं
समाधान
विकल्प (b) दिए गए ग्राफ में सभी मान दर्शाए गए हैं जो $\dfrac{9}{2}$ से बड़े हैं और $\dfrac{9}{2}$ को शामिल करते हैं।
अर्थात $ \ x \in \left[\dfrac{9}{2}, \infty \right) $
-
विकल्प (a) $x \in \left(\dfrac{9}{2}, \infty \right)$ गलत है क्योंकि यह सही उत्तर के समान नोटेशन का उपयोग करता है लेकिन सही अंतराल नोटेशन को दर्शाता है। सही अंतराल $\left[\dfrac{9}{2}, \infty \right)$ होना चाहिए, जो दर्शाता है कि $\dfrac{9}{2}$ शामिल है।
-
विकल्प (c) $x \in \left(-\infty, \dfrac{9}{2} \right)$ गलत है क्योंकि यह अंतराल $\left(-\infty, \dfrac{9}{2} \right)$ को प्रस्तुत करता है, जो $\dfrac{9}{2}$ से कम सभी मानों को शामिल करता है, न कि अधिक।
-
विकल्प (d) $x \in \left(-\infty, \dfrac{9}{2} \right]$ विकल्प (c) के लिए उतनी ही गलत है; यह अंतराल $\left(-\infty, \dfrac{9}{2} \right)$ को प्रस्तुत करता है, जो $\dfrac{9}{2}$ से कम सभी मानों को शामिल करता है, न कि अधिक।
29.
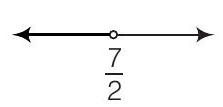
(a) $x \in \left(-\infty, \dfrac{7}{2}\right)$
(b) $x \in \left(-\infty, \dfrac{7}{2} \right]$
(c) $x \in \left[\dfrac{7}{2}, \infty \right)$
(d) $x \in \left(\dfrac{7}{2}, \infty \right)$
उत्तर दिखाएं
हल
विकल्प (a) दिए गए ग्राफ सभी मानों को प्रस्तुत करता है जो $\dfrac{7}{2}$ से कम हैं वास्तविक रेखा पर।
अर्थात, $ \ x \in \left(-\infty, \dfrac{7}{2} \right) $
-
विकल्प (b) $x \in \left(-\infty, \dfrac{7}{2} \right]$ गलत है क्योंकि यह अंतराल $\dfrac{7}{2}$ से कम या बराबर सभी वास्तविक संख्याओं को शामिल करता है। यह $\dfrac{7}{2}$ स्वयं को भी शामिल करता है, जो $\dfrac{7}{2}$ से सख्ती से कम होने की शर्त के विपरीत है।
-
विकल्प (c) $x \in \left[\dfrac{7}{2}, \infty \right)$ गलत है क्योंकि यह अंतराल $\dfrac{7}{2}$ से बड़ी या बराबर सभी वास्तविक संख्याओं को प्रस्तुत करता है। यह हमारे लिए विपरीत है क्योंकि यह वे मान शामिल करता है जो $\dfrac{7}{2}$ से कम नहीं हैं।
-
विकल्प (d) $x \in \left(\dfrac{7}{2}, \infty \right)$ गलत है क्योंकि यह बताता है कि $ x $ अंतराल $ \left(\dfrac{7}{2}, \infty\right) $ में है, जो $\dfrac{7}{2}$ से बड़े सभी मानों को प्रस्तुत करता है, जो दिए गए ग्राफ के विपरीत है जो $\dfrac{7}{2}$ से कम मानों को प्रस्तुत करता है।
30.

(a) $x \in(-\infty,-2)$
(b) $x \in(-\infty,-2]$
(c) $x \in(-2, \infty]$
(d) $x \in[-2, \infty)$
उत्तर दिखाएँ
हल
विकल्प (b) दिए गए ग्राफ सभी मानों को प्रस्तुत करता है जो $-2$ से कम हैं और $-2$ को भी शामिल करता है।
अर्थात, $ \ x \in(-\infty,-2] $
-
विकल्प (a) $x \in(-\infty,-2)$ गलत है क्योंकि यह $-2$ के मान को शामिल नहीं करता, जबकि ग्राफ $-2$ को शामिल करता है।
-
विकल्प (c) $x \in(-2, \infty]$ गलत है क्योंकि यह $-2$ से बड़े मानों को प्रस्तुत करता है, जबकि ग्राफ $-2$ से कम मानों को प्रस्तुत करता है।
-
विकल्प (d) $x \in(-2, \infty)$ गलत है क्योंकि यह $-2$ से बड़े मानों को प्रस्तुत करता है और $-2$ को शामिल नहीं करता, जबकि ग्राफ $-2$ से कम मानों को प्रस्तुत करता है और $-2$ को शामिल करता है।
सत्य/असत्य
31. निम्नलिखित कथनों में से कौन सा सत्य है और कौन सा असत्य है।
(i) यदि $x<y$ और $b<0$, तो $\dfrac{x}{b}<\dfrac{y}{b}$।
(ii) यदि $x y>0$, तो $x>0$ और $y<0$
(iii) यदि $x y>0$, तो $x<0$ और $y<0$
(iv) यदि $x y<0$, तो $x<0$ और $y<0$
(v) यदि $x<-5$ और $x<-2$, तो $x \in(-\infty,-5)$
(vi) यदि $x<-5$ और $x>2$, तो $x \in(-5,2)$
(vii) यदि $x>-2$ और $x<9$, तो $x \in(-2,9)$
(viii) यदि $|x|>5$, तो $x \in(-\infty,-5) \cup[5, \infty)$
(ix) यदि $|x| \leq 4$, तो $x \in[-4, 4]$
(x) $x<3$ के ग्राफ है

(xi) $x \geq 0$ के ग्राफ है

(xii) $y \leq 0$ के ग्राफ है

(xiii) $x \geq 0$ और $y \leq 0$ के समाधान समुच्चय है

(xiv) $x \geq 0$ और $y \leq 1$ के समाधान समुच्चय है

(xv) $x+y \geq 0$ के समाधान समुच्चय का चित्र नीचे दिया गया है:

उत्तर दिखाएं
हल
(i) यदि $x<y$ और $b<0$ $\Rightarrow$ $\dfrac{x}{b}>\dfrac{y}{b}$
अतः कथन (i) गलत है।
(ii) यदि $x y>0$, तो, $x>0, y>0$ या $x<0, y<0$ होता है।
अतः कथन (ii) गलत है।
(iii) यदि $x y>0$, तो $x<0$ और $y<0$ होता है।
अतः कथन (iii) सही है।
(iv) यदि $x y<0 \Rightarrow x<0, y>0$ या $x>0, y<0$ होता है।
अतः कथन (iv) गलत है।
(v) यदि $x<-5$ और $x<-2$
$x<−5$ का अर्थ है कि $x$ कम से कम $−5$ से कम होता है।
$x<−2$ का अर्थ है कि $x$ कम से कम $−2$ से कम होता है।
तब $ x \in(-\infty,-5) $
अतः कथन (v) सही है।
(vi) यदि $x<-5$ और $x>2$, तो $x$ के कोई मान नहीं होता।
अतः कथन (vi) गलत है।
(vii) यदि $x>-2$ और $x<9$, तो $x \in(-2,9)$।
अतः कथन (vii) सही है।
(viii) यदि $|x|>5$, तो या तो $x<-5$ या $x>5$ होता है।
$ \Rightarrow \ x \in(-\infty,-5) \cup(5, \infty) $
अतः कथन (viii) गलत है।
(ix) यदि $|x| \leq 4$, तो
$-4 \leq x \leq 4 $
$\Rightarrow x \in [-4,4] $
अतः कथन (ix) सही है।
(x)

दिया गया ग्राफ $x \leq 3$ को प्रस्तुत करता है।
अतः कथन $(x)$ गलत है।
(xi)

दिया गया ग्राफ $x \geq 0$ को प्रस्तुत करता है।
अतः कथन (xi) सही है।
(xii)

दिया गया ग्राफ $y \geq 0$ को प्रस्तुत करता है।
अतः कथन (xii) गलत है।
(xiii) $ x \geq 0 $ और $ y \leq 0 $ के समाधान समुच्चय पहले चतुर्थांश के समावेशी अक्षों को दर्शाता है। दिया गया ग्राफ इसे सही तरीके से प्रस्तुत नहीं करता।
$x \geq 0$ और $y \leq 0$ के समाधान समुच्चय का चित्र नीचे दिया गया है:
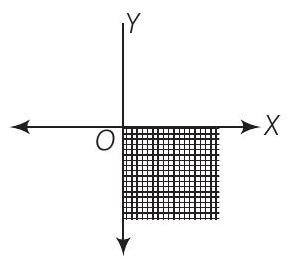
इसलिए, कथन (xiii) गलत है।
(xiv) $ x \geq 0 $ और $ y \leq 1 $ के समाधान समुच्चय वह क्षेत्र है जहाँ $ x $ गैर-ऋणात्मक है और $ y $ 1 से कम या बराबर है।
$ x \geq 0 $ और $ y \leq 1 $ के समाधान समुच्चय है
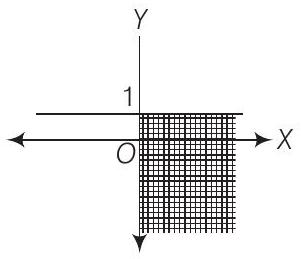
इसलिए, कथन (xiv) गलत है।
(xv)

दिए गए ग्राफ $ x + y \geq 0 $ को प्रस्तुत करता है।
इसलिए, कथन (xv) सही है।
रिक्त स्थान भरें
32. निम्नलिखित के रिक्त स्थान भरें:
(i) यदि $-4 x \geq 12$, तो $x \ldots-3$।
(ii) यदि $\dfrac{-3}{4} x \leq-3$, तो $x \ldots 4$।
(iii) यदि $\dfrac{2}{x+2}>0$, तो $x \ldots-2$।
(iv) यदि $x>-5$, तो $4 x \ldots-20$।
(v) यदि $x>y$ और $z<0$, तो $-x z \ldots-y z$।
(vi) यदि $p>0$ और $q<0$, तो $p-q \ldots p$।
(vii) यदि $|x+2|>5$, तो $x \ldots-7$ या $x \ldots 3$।
(viii) यदि $-2 x+1 \geq 9$, तो $x \ldots-4$।
उत्तर दिखाएं
हल
(i) यदि $-4 x \geq 12 $
$\Rightarrow x \leq-3$
(ii) यदि $\dfrac{-3}{4} x \leq-3$
$ \Rightarrow x \geq(-3) \times \dfrac{4}{-3} $
$\Rightarrow x \geq 4 $
(iii) $\dfrac{2}{x+2}>0$
संपूर्ण भिन्न $\dfrac{2}{x+2}$ धनात्मक होने के लिए, हर $x+2$ भी धनात्मक होना चाहिए।
अर्थात $ \ x+2 >0$
$\Rightarrow \ x > -2$
(iv) यदि $x>-5 \Rightarrow 4 x>-20$
(v) यदि $x>y$ और $z<0$, तो
$ \ -x z>-y z \quad [ \because z \ \text{एक नकारात्मक संख्या है}] $
(vi) यदि $p>0$ और $q<0$, तो
$ p-q>p $
उदाहरण के लिए, $2>0$ और $-3<0$ को लें।
$ 2-(-3)=2+3=5>2 $
(vii) यदि $|x+2|>5$, तो
$ x+2<-5 \text { या } x+2>5 $
$\Rightarrow x<-5-2 \text { या } x>5-2 $
$\Rightarrow x<-7 \text { या } x>3 $
(viii) यदि $-2 x+1 \geq 9$, तो
$ \begin{aligned} &-2 x \geq 9-1 & \\ \\ & \Rightarrow \ -2 x \geq 8 \\ \\ &\Rightarrow \ 2 x \leq-8 & \\ \\ & \Rightarrow \ x \leq-4 `
\end{aligned} $





