त्रि-विमीय ज्यामिति का परिचय
छोटे उत्तर प्रकार के प्रश्न
1. निम्नलिखित बिंदुओं को स्थित करें
(i) $(1,-1,3)$
(ii) $(-1,2,4)$
(iii) $(-2,-4,-7)$
(iv) $(-4,2,-5)$
उत्तर दिखाएं
हल
दिया गया, निर्देशांक हैं
(i) $(1,-1,3)$
(ii) $B(-1,2,4)$
(iii) $C(-2,-4,-7)$
(iv) $D(-4,2,-5)$

X-वृद्धि $=Y$-वृद्धि $=Z$-वृद्धि $=1$
2. निम्नलिखित बिंदुओं के प्रत्येक अक्षांश में नाम बताएं।
(i) $(1,2,3)$
(ii) $(4,-2,3)$
(iii) $(4,-2,-5)$
(iv) $(4,2,-5)$
(v) $(-4,2,5)$
(vi) $(-3,-1,6)$
(vii) $(2,-4,-7)$
(viii) $(-4,2,-5)$.
उत्तर दिखाएं
हल
(i) बिंदु $(1,2,3)$ पहले अक्षांश में स्थित है।
(ii) $(4,-2,3)$ चौथे अक्षांश में है।
(iii) $(4,-2,-5)$ आठवें अक्षांश में है।
(iv) $(4,2,-5)$ पांचवें अक्षांश में है।
(v) $(-4,2,5)$ दूसरे अक्षांश में है।
(vi) $(-3,-1,6)$ तीसरे अक्षांश में है।
(vii) $(2,-4,-7)$ आठवें अक्षांश में है।
(viii) $(-4,2,-5)$ छठे अक्षांश में है।
3. यदि $A, B, C$ एक बिंदु $P$ से $X, Y$ और $Z$-अक्ष पर लंब के पाद हों, तो प्रत्येक में $A, B$ और $C$ के निर्देशांक ज्ञात करें जहां बिंदु $P$ है
(i) $A(3,4,2)$
(ii) $B(-5,3,7)$
(iii) $C(4,-3,-5)$
उत्तर दिखाएं
हल
$A, B$ और $C$ के निर्देशांक निम्नलिखित हैं
(i) $A(3,0,0), B(0,4,0), C(0,0,2)$
(ii) $A(4,0,0), B(0,-3,0), C(0,0,-5)$
(iii) $A(-5,0,0), B(0,3,0), C(0,0,7)$
4. यदि $A, B$, और $C$ एक बिंदु $P$ से $XY, YZ$ और $ZX$-तलों पर लंब के पाद हों, तो प्रत्येक में $A, B$ और $C$ के निर्देशांक ज्ञात करें जहां बिंदु $P$ है
(i) $(3,4,5)$
(ii) $(-5,3,7)$
(iii) $(4,-3,-5)$
उत्तर दिखाएं
Solution
हम जानते हैं कि, $X Y$-समतल पर $z=0$, $YZ$-समतल पर $x=0$ और $ZX$-समतल पर $y=0$ होता है। इसलिए, $A, B$ और $C$ के निर्देशांक निम्नलिखित हैं
(i) $A(3,4,0), B(0,4,5), C(3,0,5)$
(ii) $A(-5,3,0), B(0,3,7), C(-5,0,7)$
(iii) $A(4,-3,0), B(0,-3,-5), C(4,0,-5)$
5. $(2,0,0)$ और $(-3,0,0)$ के बीच की दूरी कितनी है?
उत्तर दिखाएं
Thinking Process
दो बिंदुओं $(x_1, y_1, z_1)$ और $(x_2, y_2, z_2)$ के बीच दूरी
$ d=\sqrt{(x_1-x_2)^{2}+(y_1-y_2)^{2}+(z_1-z_2)^{2}} $
Solution
दिए गए बिंदु, $A(2,0,0)$ और $B(-3,0,0)$
$ A B=\sqrt{(2+3)^{2}+0^{2}+0^{2}}=5 $
6. $(6,6,7)$ के बिंदु के उत्सर्जन से दूरी ज्ञात कीजिए।
उत्तर दिखाएं
Solution
उत्सर्जन से बिंदु $(6,6,7)$ की दूरी
$ \begin{aligned} & =\sqrt{(0-6)^{2}+(0-6)^{2}+(0-7)^{2}} \qquad\big[\because d=\sqrt{(x_1-x_2)^{2}+(y_1-y_2)^{2}+(z_1-z_2)^{2}}\big] \\ \\ & =\sqrt{36+36+49} \\ \\ & =\sqrt{121}=11 \end{aligned} $
7. दिखाइए कि, यदि $x^{2}+y^{2}=1$, तो बिंदु $(x, y, \sqrt{1-x^{2}-y^{2}})$ उत्सर्जन से 1 इकाई की दूरी पर होता है।
उत्तर दिखाएं
Solution
दिया गया है, $x^{2}+y^{2}=1$
$\therefore \quad$ बिंदु $(x, y, \sqrt{1-x^{2}-y^{2}})$ की उत्सर्जन से दूरी निम्नलिखित है
$ \begin{aligned} d & =|\sqrt{x^{2}+y^{2}+(\sqrt{1-x^{2}-y^{2}})^{2}}| \\ \\ & =|\sqrt{x^{2}+y^{2}+1-x^{2}-y^{2}}|=1 \end{aligned} $
इसलिए सिद्ध कर दिया गया है।
8. दिखाइए कि बिंदु $A(1,-1,3), B(2,-4,5)$ और $C(5,-13,11)$ संरेख हैं।
Thinking Process
यदि तीन बिंदु $A, B$ और $C$ संरेख हैं, तो $AB + BC = AC$ होता है।
उत्तर दिखाएं
Solution
दिए गए बिंदु, $A(1,-1,3), B(2,-4,5)$ और $C(5,-13,11)$।
$ \begin{aligned} A B & =\sqrt{(1-2)^{2}+(-1+4)^{2}+(3-5)^{2}} \\ \\ & =\sqrt{1+9+4}=\sqrt{14} \\ \\ B C & =\sqrt{(2-5)^{2}+(-4+13)^{2}+(5-11)^{2}} \\ \\ & =\sqrt{9+81+36}=\sqrt{126} \\ \\
एक समकोण त्रिभुज में दो भुजाओं के वर्गों का योग तीसरी भुजा के वर्ग के बराबर होता है।
उत्तर दिखाएँ
हल
दिया गया है कि, त्रिभुज $ \triangle ABC $ के शीर्ष $ A(0,4,1), B(2,3,-1) $ और $ C(4,5,0) $ हैं। अब,
$$ \begin{aligned} AB & =\sqrt{(0-2)^{2}+(4-3)^{2}+(1+1)^{2}} \\ \\ & =\sqrt{4+1+4}=3 \\ \\ BC & =\sqrt{(2-4)^{2}+(3-5)^{2}+(-1-0)^{2}} \\ \\ & =\sqrt{4+4+1}=3 \\ \\ AC & =\sqrt{(0-4)^{2}+(4-5)^{2}+(1-0)^{2}} \\ \\ & =\sqrt{16+1+1}=\sqrt{18} \end{aligned} $$
$$ \begin{matrix} \because & AC^{2}=AB^{2}+BC^{2} \\ \\ \end{matrix} $$
इसलिए, त्रिभुज $ \triangle ABC $ समकोण त्रिभुज है।
\Rightarrow & 18=9+9 \end{matrix} $
अतः, शीर्ष $\triangle A B C$ एक समकोण त्रिभुज है।
11. एक त्रिभुज के तीसरे शीर्ष को ज्ञात कीजिए जिसका केंद्रक मूल बिंदु है तथा दो शीर्ष $(2,4,6)$ और $(0,-2,5)$ हैं।
उत्तर दिखाएँ
चिंतन प्रक्रिया
$\triangle A B C$ के शीर्ष $A(x_1, y_1, z_1), B(x_2, y_2, z_2)$ और $C(x_3, y_3, z_3)$ हैं, तो केंद्रक $G$ के निर्देशांक $\dfrac{x_1+x_2+x_3}{3}, \dfrac{y_1+y_2+y_3}{3}, \dfrac{z_1+z_2+z_3}{3}$ होते हैं।
हल
मान लीजिए $\triangle A B C$ के तीसरे शीर्ष $A(x, y, z)$ है।
$(2,4,6)$

दिया गया है कि केंद्रक $G$ के निर्देशांक $(0,0,0)$ हैं।
$\because \quad \begin{aligned} 0 & =\dfrac{x+2+0}{3} \Rightarrow x=-2 \\ \\ 0 & =\dfrac{y+4-2}{3} \Rightarrow y=-2 \\ \\ 0 & =\dfrac{z+6-5}{2} \Rightarrow z=-1\end{aligned}$
अतः, त्रिभुज के तीसरे शीर्ष $(-2,-2,-1)$ है।
12. एक त्रिभुज के भुजाओं के मध्य बिंदु $D(1,2,-3), E(3,0,1)$ और $F(-1,1,-4)$ हैं। त्रिभुज का केंद्रक ज्ञात कीजिए।
उत्तर दिखाएँ
हल
दिया गया है कि भुजाओं के मध्य बिंदु $D(1,2,-3), E(3,0,1)$ और $F(-1,1,-4)$ हैं।
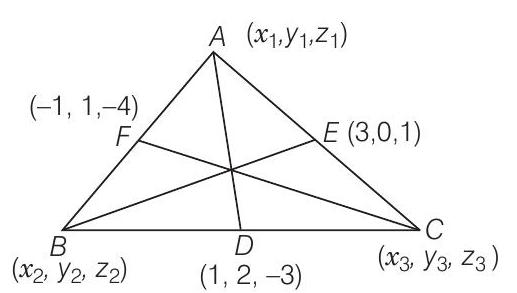
मान लीजिए $\triangle A B C$ के शीर्ष $A(x_1, y_1, z_1), B(x_2, y_2, z_3)$ और $C(x_3, y_3, z_3)$ हैं।
तो, $B C$ के मध्य बिंदु $(1,2,-3)$ हैं।
$ \begin{aligned} 1 & =\dfrac{x_2+x_3}{2} \Rightarrow x_2+x_3=2\qquad\ldots\mathrm{(i)} \\ \\ 2 & =\dfrac{y_2+y_3}{2} \Rightarrow y_2+y_3=4\qquad\ldots\mathrm{(ii)} \\ \\ -3 & =\dfrac{z_2+z_3}{2} \Rightarrow z_2+z_3=-6\qquad\ldots\mathrm{(iii) } \end{aligned} $
इसी तरह भुजाओं $A B$ और $A C$ के लिए,
$ \begin{matrix} \Rightarrow & -1=\dfrac{x_1+x_2}{2} \Rightarrow x_1+x_2=-2\qquad\ldots\mathrm{(iv)} \\ \\
\Rightarrow & 1=\dfrac{y_1+y_2}{2} \Rightarrow y_1+y_2=2\qquad\ldots\mathrm{(v)} \\ \\ \Rightarrow & -4=\dfrac{z_1+z_2}{2} \Rightarrow z_1+z_2=-8\qquad\ldots\mathrm{(vi)} \\ \\ \Rightarrow & 3=\dfrac{x_1+x_3}{2} \Rightarrow x_1+x_3=6\qquad\ldots\mathrm{(vii)} \\ \\ \Rightarrow & 0=\dfrac{y_1+y_3}{2} \Rightarrow y_1+y_3=0\qquad\ldots\mathrm{(viii)} \\ \\ \Rightarrow & 1=\dfrac{z_1+z_3}{2} \Rightarrow z_1+z_3=2 \qquad\ldots\mathrm{(ix) } \end{matrix} $
Eqs. $\mathrm{(i)}$ और $\mathrm{(iv)}$ को जोड़ने पर हम प्राप्त करते हैं
$ x_1+2 x_2+x_3=0\qquad\ldots\mathrm{(x) } $
Eqs. $\mathrm{(ii)}$ और $\mathrm{(v)}$ को जोड़ने पर हम प्राप्त करते हैं
$ y_1+2 y_2+y_3=6\qquad\ldots\mathrm{(xi)} $
Eqs. $\mathrm{(iii)}$ और $\mathrm{(ix)}$ को जोड़ने पर हम प्राप्त करते हैं
$ z_1+2 z_2+z_3=-14\qquad\ldots\mathrm{(xii)} $
Eqs. $\mathrm{(vii)}$ और $\mathrm{(x)}$ से,
$ 2 x_2=-6 \Rightarrow x_2=-3 $
यदि $x_2=-3$, तो $x_3=5$
यदि $x_3=5$, तो $x_1=1, x_2=-3, x_3=5$
Eqs. $\mathrm{(xi)}$ और $\mathrm{(viii)}$ से,
$ 2 y_2=6 \Rightarrow y_2=3 $
यदि $y_2=3$, तो $y_1=-1 $
यदि $y_1=-1$, तो $y_3=1, \quad y_2=3, y_3=1$
Eqs. $\mathrm{(xii)}$ और $\mathrm{(ix)}$ से,
$ \begin{gathered} 2 z_2=-16 \Rightarrow z_2=-8 \\ \\ z_2=-8, \text { तो } z_1=0 \\ \\ z_1=0, \text { तो } z_3=2 \\ \\ z_1=0, z_2=-8, z_3=2 \end{gathered} $
इसलिए, बिंदु $A(1-1,0), B(-3,3,-8)$ और $C(5,1,2)$ हैं।
$\therefore$ त्रिभुज का केंद्रक $G \left(\dfrac{1-3+5}{3}, \dfrac{-1+3+1}{3}, \dfrac{0-8+2}{3}\right)$ अर्थात $G(1,1,-2)$
13. एक त्रिभुज की भुजाओं के मध्य बिंदु $(5,7,11),(0,8,5)$ और $(2,3,-1)$ हैं। इसके शीर्ष बिंदु ज्ञात कीजिए।
उत्तर दिखाएं
हल
मान लीजिए त्रिभुज $\triangle ABC$ के शीर्ष $A(x_1, y_1, z_1), B(x_2, y_2, z_2)$ और $C(x_3, y_3, z_3)$ हैं, तो $BC$ का मध्य बिंदु $(5,7,11)$ है।
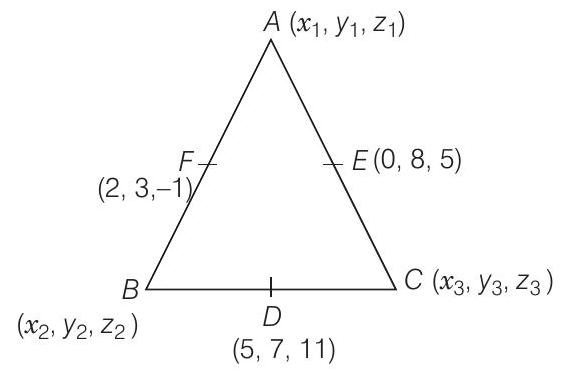
$ \begin{aligned} & 5=\dfrac{x_2+x_3}{2} \Rightarrow x_2+x_3=10 \qquad\ldots\mathrm{(i)} \\ \\ & 7=\dfrac{y_2+y_3}{2} \Rightarrow y_2+y_3=14 \qquad\ldots\mathrm{(ii)} \\ \\ & 11=\dfrac{z_2+z_3}{2} \Rightarrow z_2+z_3=22\qquad\ldots\mathrm{(iii)} \end{aligned} $
इसी तरह भुजाओं $AB$ और $AC$ के लिए,
$ \begin{gathered} 2=\dfrac{x_1+x_2}{2} \Rightarrow x_1+x_2=4 \qquad\ldots\mathrm{(iv)} \\ \\ 3=\dfrac{y_1+y_2}{2} \Rightarrow y_1+y_2=6 \qquad\ldots\mathrm{(v)} \\ \\ -1=\dfrac{z_1+z_2}{2} \Rightarrow z_1+z_2=-2 \qquad\ldots\mathrm{(vi)} \\ \\ 0=\dfrac{x_1+x_3}{2} \Rightarrow x_1+x_3=0 \qquad\ldots\mathrm{(vii)} \\ \\ 8=\dfrac{y_1+y_3}{2} \Rightarrow y_1+y_3=16 \qquad\ldots\mathrm{(viii)} \\ \\ 5=\dfrac{z_1+z_3}{2} \Rightarrow z_1+z_3=10\qquad\ldots\mathrm{(ix)} \end{gathered} $
समीकरणों $\mathrm{(i)}$ और $\mathrm{(iv)}$ से,
$ x_1+2 x_2+x_3=14\qquad\ldots\mathrm{(x)} $
समीकरणों $\mathrm{(ii)}$ और $\mathrm{(v)}$ से,
$y_1+2 y_2+y_3=20\qquad\ldots\mathrm{(xi)}$
समीकरणों $\mathrm{(iii)}$ और $\mathrm{(vi)}$ से,
$z_1+2 z_2+z_3=20\qquad\ldots\mathrm{(xii)}$
समीकरणों $\mathrm{(vii)}$ और $\mathrm{(x)}$ से,
$ \begin{aligned} 2 x_2 & =14 \Rightarrow x_2=7 \\ \\ x_2 & =7, \text { तब, } x_3=10-7=3 \\ \\ x_3 & =3, \text { तब, } x_1=-3 \\ \\ x_1 & =-3, x_2=7, x_3=3 \end{aligned} $
समीकरणों $(viii)$ और $(xi)$ से,
$ \begin{aligned} 2 y_2 & =4 \Rightarrow y_2=2 \\ \\ y_2 & =2, \text { तब, } y_1=4 \\ \\ y_1 & =4, \text { तब, } y_3=12 \\ \\ y_1 & =4, y_2=2, y_3=12 \end{aligned} $
समीकरणों $\mathrm{(ix)}$ और $(xii)$ से,
$ \begin{aligned} 2 z_2 & =10 \Rightarrow z_2=5 \\ \\ z_2 & =5, \text { तब } z_1=-7 \\ \\ z_1 & =-7, \text { तब } z_3=17 \\ \\ z_1 & =-7, z_2=5, z_3=17 \end{aligned} $
इसलिए, शीर्ष हैं $A(-3,4,-7), B(7,2,5)$ और $C(3,12,17)$।
14. यदि एक समांतर चतुर्भुज $ABCD$ के शीर्ष $A(1,2,3), B(-1,-2,-1)$ और $C(2,3,2)$ हैं, तो चौथा शीर्ष $D$ ज्ञात कीजिए।
उत्तर दिखाएं
Thinking Process
एक समांतर चतुर्भुज के विकर्ण एक ही शीर्षों के होते हैं। इस गुण का उपयोग करके समस्या को हल करें।
हल
मान लीजिए समांतर चतुर्भुज $A B C D$ के चौथे शीर्ष $D(x, y, z)$ है।
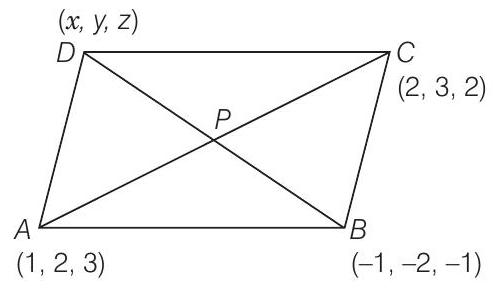
तो, $A C$ के मध्य बिंदु हैं
$ P\left( \dfrac{1+2}{2}, \dfrac{2+3}{2}, \dfrac{3+2}{2}\right) \text { अर्थात } \ P\left( \dfrac{3}{2}, \dfrac{5}{2}, \dfrac{5}{2} \right) $
अब, $B D$ के मध्य बिंदु,
$ \begin{aligned} & \dfrac{3}{2}=\dfrac{-1+x}{2} \Rightarrow x=4 \\ \\ & \dfrac{5}{2}=\dfrac{-2+y}{2} \Rightarrow y=7 \\ \\ & \dfrac{5}{2}=\dfrac{-1+z}{2} \Rightarrow z=6 \end{aligned} $
इसलिए, चौथे शीर्ष के निर्देशांक $(4,7,6)$ हैं।
15. बिंदु $A(2,1,-3)$ और $B(5,-8,3)$ को जोड़ने वाले रेखाखंड के बिंदुओं के निर्देशांक ज्ञात कीजिए जो रेखाखंड को तिसरे बराबर भागों में विभाजित करते हैं।
उत्तर दिखाएं
चिंतन प्रक्रिया
यदि बिंदु $P$ बिंदु $A(x_1, y_1, z_1)$ और $B(x_2, y_2, z_2)$ को $m_1: m_2$ के अनुपात में आंतरिक रूप से विभाजित करता है, तो $P$ के निर्देशांक हैं $\left(\dfrac{m_1 x_2+m_2 x_1}{m_1+m_2}, \dfrac{m_1 y_2+m_2 y_1}{m_1+m_2}, \dfrac{m_1 z_2+m_2 z_1}{m_1+m_2}\right)$
हल
मान लीजिए $P(x_1, y_1, z_1)$ और $Q(x_2, y_2, z_2)$ रेखाखंड $A B$ के तिसरे बराबर भागों में विभाजित करते हैं।
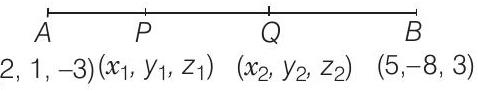
क्योंकि, बिंदु $P$ रेखा $A B$ को $1: 2$ के अनुपात में आंतरिक रूप से विभाजित करता है, तो
$ \begin{aligned} & x_1=\dfrac{2 \times 2+1 \times 5}{1+2}=\dfrac{9}{3}=3 \\ \\ & y_1=\dfrac{2 \times 1+1 \times(-8)}{3}=\dfrac{-6}{3}=-2 \\ \\ & z_1=\dfrac{2 \times(-3)+1 \times 3}{3}=\dfrac{-6+3}{3}=\dfrac{-3}{3}=-1 \end{aligned} $
क्योंकि, बिंदु $Q$ रेखाखंड $A B$ को $2: 1$ के अनुपात में विभाजित करता है, तो
$ \begin{aligned}
& x_2=\dfrac{1 \times 2+2 \times 5}{3}=4, \\ \\ & y_2=\dfrac{1 \times 1+(-8 \times 2)}{3}=-5 \\ \\ & z_2=\dfrac{1 \times(-3)+2 \times 3}{3}=-1 \end{aligned} $
इसलिए, $P$ के निर्देशांक $(3,-2,-1)$ हैं और $Q$ के निर्देशांक $(4,-5,1)$ हैं।
16. यदि मूल बिंदु त्रिभुज $ \triangle A B C $ के केंद्रक है जिसके शीर्ष $A(a, 1,3)$, $B(-2, b,-5)$ और $C(4,7, c)$ हैं, तो $a, b, c$ के मान ज्ञात कीजिए।
उत्तर दिखाएं
हल
दिया गया है कि मूल बिंदु त्रिभुज $ \triangle A B C $ के केंद्रक है, अर्थात $G(0,0,0)$ है।
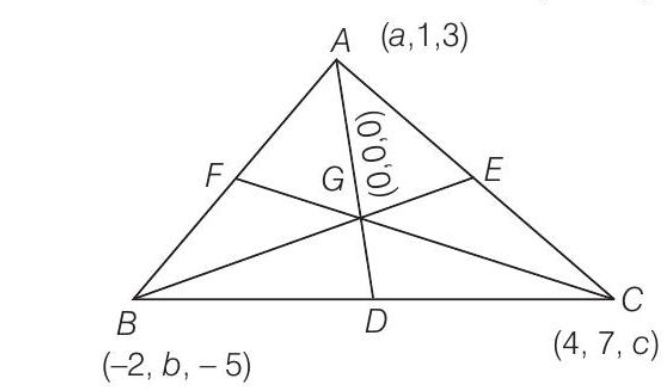
$\begin{aligned} \because \quad 0=\dfrac{a-2+4}{3} \Rightarrow a=-2 \\ \\ 0=\dfrac{1+b+7}{3} \Rightarrow b=-8 \\ \\ \quad 0=\dfrac{3-5+c}{3} \Rightarrow c=+2 \\ \\ \therefore \quad a=-2, b=-8 \text { और } c=2 \end{aligned}$
17. यदि $A(2,2,-3), B(5,6,9), C(2,7,9)$ एक त्रिभुज के शीर्ष हों, तो कोण $A$ के आंतरिक कोण द्विभाजक $BC$ को बिंदु $D$ पर मिलता है, तो $D$ के निर्देशांक ज्ञात कीजिए।
उत्तर दिखाएं
हल
मान लीजिए $D$ के निर्देशांक $(x, y, z)$ हैं।
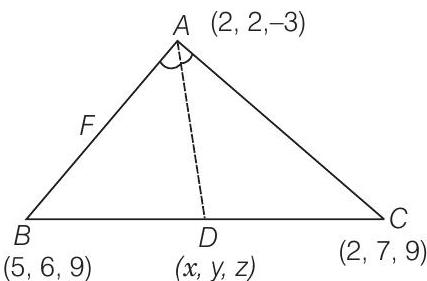
हमारे पास, बिंदु
$ \begin{aligned} & \mathrm{A}\left(\mathrm{x}_1, \mathrm{y}_1, \mathrm{z}_1\right)=(2,2,-3) \\ \\ & \mathrm{B}\left(\mathrm{x}_2, \mathrm{y}_2, \mathrm{z}_2\right)=(5,6,9) \\ \\ & \mathrm{C}\left(\mathrm{x}_3, \mathrm{y}_3, \mathrm{z}_3\right)=(2,7,9) \end{aligned} $
बिंदु $\mathrm{D}(\mathrm{x}, \mathrm{y}, \mathrm{z})$ के निर्देशांक हैं।
इसलिए, प्रश्न के अनुसार,
$ \begin{aligned} & A B=\sqrt{(5-2)^2+(6-2)^2+(9-3)^2} \\ \\ & A B=\sqrt{9+16+149}=\sqrt{13^2}=13 \\ \\
& A C=\sqrt{(2-2)^2+(7-2)^2+(9+3)^2} \\ \\ & A C=\sqrt{0+25+144}=\sqrt{169}=13 \end{aligned} $
इसलिए $A B C$ एक समद्विबाहु त्रिभुज है जहां $A B=A C$ इसलिए, कोण समद्विभाजक $A D$ भुजा $B C$ को दो भागों में बांटता है
$ \mathrm{D} \equiv\left(\dfrac{5+2}{2}, \dfrac{6+7}{2}, \dfrac{9+9}{2}\right) \equiv\left(\dfrac{7}{2}, \dfrac{13}{2}, 9\right) $
इसलिए, यह उत्तर है।
लंबा उत्तर प्रकार प्रश्न
18. दिखाइए कि तीन बिंदु $A(2,3,4), B(1,2,-3)$ और $C(-4,1,-10)$ संरेख हैं और $C$ बिंदु $A B$ को किस अनुपात में विभाजित करता है।
उत्तर दिखाएं
हल
दिए गए बिंदु $A(2,3,4), B(-1,2,-3)$ और $C(-4,1,-10)$ हैं।
$ \begin{aligned} \therefore \ A B & =\sqrt{(2+1)^{2}+(3-2)^{2}+(4+3)^{2}} \\ \\ & =\sqrt{9+1+49}=\sqrt{59} \\ \\ B C & =\sqrt{(-1+4)^{2}+(2-1)^{2}+(-3+10)^{2}} \\ \\ & =\sqrt{9+1+49}=\sqrt{59} \\ \\ A C & =\sqrt{(2+4)^{2}+(3-1)^{2}+(4+10)^{2}} \\ \\ & =\sqrt{36+4+196} \\ \\ & =\sqrt{236}=2 \sqrt{59} \\ \\ A B+B C & =\sqrt{59}+\sqrt{59}=2 \sqrt{59} \end{aligned} $
19. एक त्रिभुज की भुजाओं के मध्य बिंदु $(1,5,-1),(0,4,-2)$ और $(2,3,4)$ हैं। इसके शीर्ष बिंदु ज्ञात कीजिए और त्रिभुज के केंद्रक की भी गणना कीजिए।
उत्तर दिखाएं
हल
मान लीजिए $\triangle A B C$ के शीर्ष $A(x_1, y_1, z_1), B(x_2, y_2, z_2)$ और $C(x_3, y_3, z_3)$ हैं।
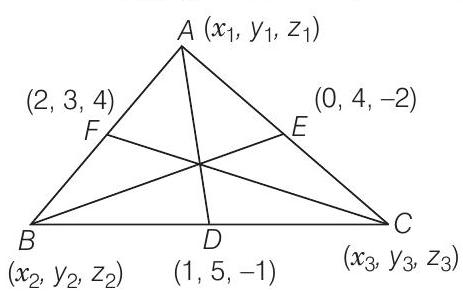
क्योंकि, भुजा $B C$ का मध्य बिंदु $D(1,5,-1)$ है।
तो,
$ \begin{aligned} & \dfrac{x_2+x_3}{2}=1 \Rightarrow x_2+x_3=2 \qquad\ldots\mathrm{(i)}\\ \\ & \dfrac{y_2+y_3}{2}=5 \Rightarrow y_2+y_3=10 \qquad\ldots\mathrm{(ii)}\\ \\ & \dfrac{z_2+z_3}{2}=-1 \Rightarrow z_2+z_3=-2\qquad\ldots\mathrm{(iii)} \end{aligned} $
इसी तरह, $A B$ और $A C$ के मध्य बिंदु $F(2,3,4)$ और $E(0,4,-2)$ हैं,
और
$ \begin{aligned} & \dfrac{x_1+x_2}{2}=2 \Rightarrow x_1+x_2=4 \qquad\ldots\mathrm{(iv)}\\ \\
$$ \begin{aligned} & \dfrac{y_1+y_2}{2}=3 \Rightarrow y_1+y_2=6 \qquad\ldots\mathrm{(v)}\\ \\ & \dfrac{z_1+z_2}{2}=4 \Rightarrow z_1+z_2=8\qquad\ldots\mathrm{(vi)} \end{aligned} $$
अब,
$$ \begin{gathered} \dfrac{x_1+x_3}{2}=0 \Rightarrow x_1+x_3=0 \qquad\ldots\mathrm{(vii)}\\ \\ \dfrac{y_1+y_3}{2}=4 \Rightarrow y_1+y_3=8 \qquad\ldots\mathrm{(viii)}\\ \\ \dfrac{z_1+z_3}{2}=-2 \Rightarrow z_1+z_3=-4\qquad\ldots\mathrm{(ix)} \end{gathered} $$
समीकरणों $\mathrm{(i)}$ और $\mathrm{(iv)}$ से,
$$ x_1+2 x_2+x_3=6\qquad\ldots\mathrm{(x)} $$
समीकरणों $\mathrm{(ii)}$ और $\mathrm{(v)}$ से,
$$ y_1+2 y_2+y_3=16\qquad\ldots\mathrm{(xi)} $$
समीकरणों $\mathrm{(iii)}$ और $\mathrm{(vi)}$ से,
$$ z_1+2 z_2+z_3=6\qquad\ldots\mathrm{(xii)} $$
समीकरणों $\mathrm{(vii)}$ और $\mathrm{(x)}$ से,
$$
\begin{aligned}
2 x_2 & =6
\Rightarrow x_2 =3 \\ \\
x_2 & =3, \ \text { तब, } \ x_3 =-1 \\ \\
x_3 & =-1 \ \text { तब, }
x_1 =1 \\ \\
\Rightarrow x_1 & =1, x_2=3, x_2=-1
\end{aligned}
$$
समीकरणों $\mathrm{(viii)}$ और $\mathrm{(xi)}$ से,
$$ \begin{aligned} 2 y_2 & =8 \Rightarrow y_2=4 \\ \\ y_2 & =4 \ \text { तब, } \ y_1 =2 \\ \\ y_1 & =2 \ \text { तब, } \ y_3 =6 \\ \\ y_1 & =2, y_2=4, y_3=6 \end{aligned} $$
समीकरणों (ix) और (xii) से,
तो,
$$ 2 z_2 =10 \Rightarrow z_2=5 $$
$$ z_1=3,z_2=5,z_3=-7 $$
इसलिए, त्रिभुज के शीर्ष $A(1,2,3), B(3,4,5)$ और $C(-1,6,-7)$ हैं।
इसलिए, त्रिभुज के केंद्रक $G\left(\dfrac{1+3-1}{3}, \dfrac{2+4+6}{3}, \dfrac{3+5-7}{3}\right)$ अर्थात $G(1,4,1 / 3)$ है।
20. सिद्ध कीजिए कि बिंदु $(0,-1,-7),(2,1,-9)$ और $(6,5,-13)$ संरेख हैं। दूसरे दो बिंदुओं के जुड़े रेखाखंड को पहला बिंदु किस अनुपात में विभाजित करता है?
उत्तर दिखाएं
सोचने की प्रक्रिया
पहले सभी बिंदुओं $A, B$ और $C$ के बीच दूरी के मान $AB, AC$ और $BC$ को दूरी सूत्र के उपयोग द्वारा ज्ञात करें अर्थात $\sqrt{(x_1-x_2)^{2}+(y_1-y_2)^{2}+(z_1-z_2)^{2}}$, फिर दिखाएं कि $AB + BC = AC$ बिंदुओं $A, B$ और $C$ के संरेख होने के लिए।
हल
दिए गए बिंदु $A(0,-1,-7), B(2,1,-9)$ और $C(6,5,-13)$ हैं
$ \begin{aligned} & A B=\sqrt{(0-2)^{2}+(-1-1)^{2}+(-7+9)^{2}}=\sqrt{4+4+4}=2 \sqrt{3} \\ \\ & B C=\sqrt{(2-6)^{2}+(1-5)^{2}+(-9+13)^{2}}=\sqrt{16+16+16}=4 \sqrt{3} \\ \\ & A C=\sqrt{(0-6)^{2}+(-1-5)^{2}+(-7+13)^{2}}=\sqrt{36+36+36}=6 \sqrt{3} \end{aligned} $
$ \begin{aligned} & \because \ \ A B+B C=2 \sqrt{3}+4 \sqrt{3}=6 \sqrt{3} \\ \\ & \text { इसलिए, } \ \ A B+B C=A C \\ \\ & \text { इसलिए, बिंदु } A, B \text { और } C \text { संरेख हैं। } \\ \\ & A B: A C=2 \sqrt{3}: 6 \sqrt{3}=1: 3 \end{aligned} $
इसलिए, बिंदु $A$ बिंदु $B$ और $C$ को $1: 3$ के अनुपात में बाहरी विभाजित करता है,
21. एक घन के शीर्षों के निर्देशांक क्या हैं, जिसके किनारे $2$ इकाई है, जिसका एक शीर्ष मूल बिंदु से संगत है और मूल बिंदु से गुजरने वाले तीन किनारे, मूल बिंदु से गुजरने वाले अक्षों की धनात्मक दिशा में संगत हैं?
उत्तर दिखाएं
हल
$2$ इकाई के किनारे वाले घन के शीर्षों के निर्देशांक $(2,0,0),(2,2,0),(0,2,0)$, $(0,2,2),(0,0,2),(2,0,2),(0,0,0)$ और $(2,2,2)$ हैं।
उद्देश्य प्रकार के प्रश्न
22. बिंदु $P(3,4,5)$ की $Y Z$-तल से दूरी क्या है?
(a) $3$ इकाई
(b) $4$ इकाई
(c) $5$ इकाई
(d) $550$
उत्तर दिखाएं
हल
(a) दिया गया, बिंदु $P(3,4,5)$ है।
$P$ की $YZ$-तल से दूरी, $\quad[\because YZ$-तल, $x=0]$
$ d=\sqrt{(0-3)^{2}+(4-4)^{2}+(5-5)^{2}}=3 $
23. बिंदु $P$ $(3,4,5)$ से $Y$-अक्ष पर लंब के पाद की लंबाई क्या है?
(a) $\sqrt{41}$
(b) $\sqrt{34}$
(c) $5$
(d) इनमें से कोई नहीं
उत्तर दिखाएं
हल
(b) हम जानते हैं कि, $Y$-अक्ष पर $x=0$ और $z=0$ होता है।
$\therefore \ \ $ बिंदु $A(0,4,0)$,
$ \begin{aligned} P A & =\sqrt{(0-3)^{2}+(4-4)^{2}+(0-5)^{2}} \\ \\ & =\sqrt{9+0+25}=\sqrt{34} \end{aligned} $
24. बिंदु $(3,4,5)$ की मूल बिंदु $(0,0,0)$ से दूरी क्या है?
(a) $\sqrt{50}$
(b) $3$
(c) $4$
(d) $5$
उत्तर दिखाएं
Solution
(a) दिया गया, बिंदु $P(3,4,5)$ और $O(0,0,0)$,
$ \begin{aligned} P O & =\sqrt{(0-3)^{2}+(0-4)^{2}+(0-5)^{2}} \\ \\ & =\sqrt{9+16+25}=\sqrt{50} \end{aligned} $
25. यदि बिंदु $(a, 0,1)$ और $(0,1,2)$ के बीच की दूरी $\sqrt{27}$ है, तो $a$ का मान है
(a) $5$
(b) $\pm 5$
(c) $-5$
(d) इनमें से कोई नहीं
उत्तर दिखाएं
Solution
(b) दिया गया, बिंदु $A(a, 0,1)$ और $B(0,1,2)$ हैं।
$ \begin{aligned} \therefore \ \ & A B=\sqrt{(a-0)^{2}+(0-1)^{2}+(1-2)^{2}} \\ \\ \Rightarrow \ \ & \sqrt{27}=\sqrt{a^{2}+1+1} \\ \\ \Rightarrow \ \ & 27=a^{2}+2 \\ \\ \Rightarrow \ \ & a^{2}=25 \\ \\ \Rightarrow \ \ & a= \pm 5 \end{aligned} $
26. $X$-अक्ष दो समतलों का प्रतिच्छेदन है
(a) $X Y$ और $X Z$
(b) $Y Z$ और $Z X$
(c) $X Y$ और $Y Z$
(d) इनमें से कोई नहीं
उत्तर दिखाएं
Solution
(a) हम जानते हैं कि, $X Y$ और $X Z$ समतलों पर, प्रतिच्छेदन रेखा $X$-अक्ष होती है।
- विकल्प (b) गलत है क्योंकि समतल $ YZ $ और $ ZX $ का प्रतिच्छेदन $ Z $-अक्ष होता है, न कि $ X $-अक्ष।
- विकल्प (c) गलत है क्योंकि समतल $ XY $ और $ YZ $ का प्रतिच्छेदन $ Y $-अक्ष होता है, न कि $ X $-अक्ष।
- विकल्प (d) गलत है क्योंकि विकल्प (a) सही है, इसलिए “इनमें से कोई नहीं” एक अमान्य चयन है।
27. $Y$-अक्ष का समीकरण माना जाता है
(a) $x=0, y=0$
(b) $y=0, z=0$
(c) $z=0, x=0$
(d) इनमें से कोई नहीं
उत्तर दिखाएं
Solution
(c) $Y$-अक्ष पर, $x=0$ और $z=0$ होता है।
28. बिंदु $(-2,-3,-4)$ किस आठवें चतुर्थांश में स्थित है
(a) पहला आठवें चतुर्थांश
(b) सातवां आठवें चतुर्थांश
(c) दूसरा आठवाँ चतुर्थक
(d) आठवाँ आठवाँ चतुर्थक
उत्तर दिखाएं
हल
(b) बिंदु $(-2,-3,-4)$ सातवाँ आठवाँ चतुर्थक में स्थित है।
29. एक समतल $YZ$-समतल के समानांतर है, इसलिए यह लंब है
(a) $X$-अक्ष
(b) $Y$-अक्ष
**( ज) $Z$-अक्ष
(d) इनमें से कोई नहीं
उत्तर दिखाएं
हल
(a) एक समतल $YZ$-समतल के समानांतर है, इसलिए यह $X$-अक्ष के लंब है।
30. एक बिंदु के लिए $y=0$ और $z=0$ के लिए बिंदु का बिंदुपथ है
(a) $X$-अक्ष का समीकरण
(b) $Y$-अक्ष का समीकरण
(c) $Z$-अक्ष का समीकरण
(d) इनमें से कोई नहीं
उत्तर दिखाएं
हल
(a) हम जानते हैं कि, $X$-अक्ष पर समीकरण $y=0, z=0$ है। इसलिए, बिंदु के बिंदुपथ $X$-अक्ष का समीकरण है।
31. एक बिंदु के लिए $x=0$ के लिए बिंदु का बिंदुपथ है
(a) $XY$-समतल
(b) $YZ$-समतल
(c) $ZX$-समतल
(d) इनमें से कोई नहीं
उत्तर दिखाएं
हल
(b) $YZ$-समतल पर $x=0$, इसलिए बिंदु के बिंदुपथ $YZ$-समतल है।
32. एक समांतर चतुर्भुज जो बिंदुओं $(5,8,10)$ और $(3,6,8)$ से गुजरने वाले तलों द्वारा बनाया गया है, तो समांतर चतुर्भुज के विकर्ण की लंबाई है
(a) $2 \sqrt{3}$
(b) $3 \sqrt{2}$
(c) $\sqrt{2}$
(d) $\sqrt{3}$
उत्तर दिखाएं
हल
(a) समांतर चतुर्भुज के दिए गए बिंदु $A(5,8,10)$ और $B(3,6,8)$ हैं।
$ \begin{aligned} \therefore \quad AB & =\sqrt{(5-3)^{2}+(6-8)^{2}+(10-8)^{2}} \\ \\ & =\sqrt{4+4+4}=2 \sqrt{3} \end{aligned} $
33. $L$ एक बिंदु $P(3,4,5)$ से $XY$-समतल पर खींचे गए लंब का पाद है। बिंदु $L$ के निर्देशांक हैं
(a) $(3,0,0)$
(b) $(0,4,5)$
(c) $(3,0,5)$
(d) इनमें से कोई नहीं
उत्तर दिखाएं
हल
(d) हम जानते हैं कि, $XY$-समतल पर $z=0$ होता है। इसलिए, बिंदु $L$ के निर्देशांक $(3,4,0)$ हैं।
34. $L$ एक बिंदु $(3,4,5)$ से खींचे गए लम्ब का पाद है। $X$-अक्ष पर $L$ के निर्देशांक हैं
(a) $(3,0,0)$
(b) $(0,4,0)$
(c) $(0,0,5)$
(d) इनमें से कोई नहीं
उत्तर दिखाएं
हल
(a) $X$-अक्ष पर, $y=0$ और $z=0$
अतः, आवश्यक निर्देशांक $(3,0,0)$ हैं।
भरण पदार्थ
35. तीन अक्ष $O X, O Y$ और $O Z$ निर्धारित करते हैं ……
उत्तर दिखाएं
हल
तीन अक्ष $O X, O Y$ और $O Z$ तीन निर्देशांक समतल निर्धारित करते हैं।
36. तीन समतल एक आयतन घन के रूप में एक आयताकार समानांतर चतुर्भुज को निर्धारित करते हैं जो …… आयताकार फलकों के रूप में हैं।
उत्तर दिखाएं
हल
तीन बिंदु
37. एक बिंदु के निर्देशांक अक्षों पर विशेष रूप से लम्ब दूरी होते हैं।
उत्तर दिखाएं
हल
दिया गया बिंदु
38. तीन निर्देशांक समतल स्थान को …… भागों में विभाजित करते हैं।
उत्तर दिखाएं
हल
आठ भाग
39. यदि बिंदु $P$ $YZ$-समतल में है, तो $YZ$-समतल पर बिंदु के निर्देशांक निम्न रूप के होते हैं ……
उत्तर दिखाएं
हल
हम जानते हैं कि, $YZ$-समतल पर $x=0$ होता है। अतः, आवश्यक बिंदु के निर्देशांक $(0, y, z)$ होते हैं।
40. $YZ$-समतल का समीकरण ……
उत्तर दिखाएं
हल
$YZ$-समतल का समीकरण $x=0$ है।
41. यदि बिंदु $P$ $Z$-अक्ष पर है, तो $P$ के निर्देशांक निम्न रूप के होते हैं ……
उत्तर दिखाएं
हल
$Z$-अक्ष पर, $x=0$ और $y=0$ होता है। अतः, आवश्यक निर्देशांक $(0,0, z)$ होते हैं।
42. $Z$-अक्ष का समीकरण, है ……
उत्तर दिखाएं
हल
$Z$-अक्ष का समीकरण, $x=0$ और $y=0$।
43. $A$ रेखा $XY$-तल के समानांतर होगी यदि रेखा पर सभी बिंदुओं के समान ……
उत्तर दिखाएं
हल
$z$-निर्देशांक।
44. $A$ रेखा $X$-अक्ष के समानांतर होगी, यदि रेखा पर सभी बिंदुओं के समान ……
उत्तर दिखाएं
हल
$y$ और $z$-निर्देशांक।
45. $x=a$ एक तल को निरूपित करता है जो ……
उत्तर दिखाएं
हल
$ x = a $ एक तल को निरूपित करता है जो $YZ$-तल के समानांतर है।
46. $YZ$-तल के समानांतर तल $X$-अक्ष के लंबवत होता है।
उत्तर दिखाएं
हल
$YZ$-तल के समानांतर तल $X$-अक्ष के लंबवत होता है।
47. एक आयताकार कमरे के आयतन $10, 13$ और $8$ इकाई हैं, तो एक तार के सबसे लंबे टुकड़े की लंबाई जो एक सीधी रेखा में खींची जा सकती है, हैं ……
उत्तर दिखाएं
हल
दिए गए आयाम $a=10, b=13$ और $c=8$ हैं।
$ \begin{aligned} \therefore \quad \text { आवश्यक लंबाई } & =\sqrt{a^{2}+b^{2}+c^{2}} \\ \\ & =\sqrt{100+169+64}=\sqrt{333} \end{aligned} $
48. बिंदुओं $(a, 2,1)$ और $(1,-1,1)$ के बीच की दूरी 5 है, तो $a$ ……
उत्तर दिखाएं
हल
दिए गए बिंदु $(a, 2,1)$ और $(1,-1,1)$ हैं।
$ \begin{aligned} & \therefore \ \sqrt{(a-1)^{2}+(2+1)^{2}+(1-1)^{2}} =5 \\ \\ & \Rightarrow \ (a-1)^{2}+9+0 =25 \\ \\ & \Rightarrow \ a^{2}-2 a+1+9 =25 \\ \\ & \Rightarrow \ a^{2}-2 a-15 =0 \\ \\ & \Rightarrow \ a^{2}-5 a+3 a-15 =0 \\ \\ & \Rightarrow \ a(a-5)+3(a-5) =0 \\ \\ & \Rightarrow \ (a-5)(a+3) =0 \\ \\ & \Rightarrow \ a-5=0 \text { या } a+3 =0 \\ \\ & \therefore \ a =+5 \text { या }-3 \end{aligned} $
49. एक त्रिभुज $ABC$ के भुजाओं $AB, BC$ और $CA$ के मध्य बिंदु $D(1,2,-3)$, $E(3,0,1)$ और $F(-1,1,-4)$ हैं, तो त्रिभुज $ABC$ का केंद्रक ……
उत्तर दिखाएँ
हल
मान लीजिए $\triangle A B C$ के शीर्ष $A(x_1, y_1, z_1), B(x_2, y_2, z_2)$ और $C(x_3, y_3, z_3)$ हैं।
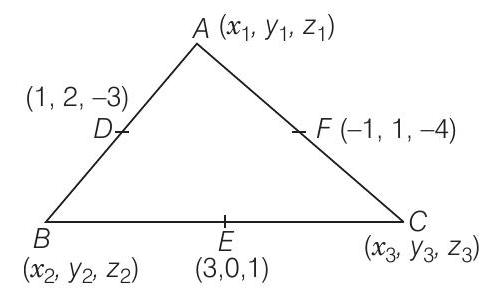
क्योंकि, $D$ भुजा $AB$ का मध्य-बिंदु है, तो
$ \begin{aligned} & \dfrac{x_1+x_2}{2}=1 \Rightarrow x_1+x_2=2 \qquad\ldots\mathrm{(i)} \\ \\ & \dfrac{y_1+y_2}{2}=2 \Rightarrow y_1+y_2=4 \qquad\ldots\mathrm{(ii)} \\ \\ & \dfrac{z_1+z_2}{2}=-3 \Rightarrow z_1+z_2=-6\qquad\ldots\mathrm{(iii)} \end{aligned} $
इसी तरह, $E$ और $F$ क्रमशः भुजा $BC$ और $AC$ के मध्य-बिंदु हैं।
$ \begin{aligned} & \dfrac{x_2+x_3}{2}=3 \Rightarrow x_2+x_3=6 \qquad\ldots\mathrm{(vi)} \\ \\ & \dfrac{y_2+y_3}{2}=0 \Rightarrow y_2+y_3=0 \qquad\ldots\mathrm{(v)} \\ \\ & \dfrac{z_2+z_3}{2}=1 \Rightarrow z_2+z_3=2 \qquad\ldots\mathrm{(vi)} \\ \\ & \dfrac{x_1+x_3}{2}=-1 \Rightarrow x_1+x_3=-2 \qquad\ldots\mathrm{(vii)} \\ \\ & \dfrac{y_1+y_3}{2}=1 \Rightarrow y_1+y_3=2 \qquad\ldots\mathrm{(viii)} \\ \\ & \dfrac{z_1+z_3}{2}=-4 \Rightarrow z_1+z_3=-8\qquad\ldots\mathrm{(ix)} \end{aligned} $
समीकरण $\mathrm{(i)}$ और $\mathrm{(iv)}$ से,
$ x_1+2 x_2+x_3=8\qquad\ldots\mathrm{(x)} $
समीकरण $\mathrm{(ii)}$ और $\mathrm{(v)}$ से,
$ y_1+2 y_2+y_3=4\qquad\ldots\mathrm{(xi)} $
समीकरण $\mathrm{(iii)}$ और $\mathrm{(ix)}$ से,
$ z_1+2 z_2+z_3=-4\qquad\ldots\mathrm{(xii)} $
समीकरण $\mathrm{(vii)}$ और $\mathrm{(x)}$ से,
$ 2 x_2=10 \Rightarrow x_2=5 $
$x_2=5$, तो $x_1=-3$
यदि $ x_1=-3, x_2=5 \Rightarrow x_3=1 $
$\because \ \ $ समीकरण $\mathrm{(viii)}$ और $\mathrm{(xi)}$ से,
$ \begin{aligned} 2 y_2 & =2 \Rightarrow y_2=1 \\ \\ y_2 & =1, \text { तो } y_3=-1 \\ \\ y_3 & =-1, \text { तो } y_1=3 \\ \\ y_1 & =3, y_2=1, y_3=-1 \end{aligned} $
समीकरण $\mathrm{(ix)}$ और $\mathrm{(xii)}$ से,
$ \begin{aligned}
2 z_2 & =4 \Rightarrow z_2=2 \\ \\ z_2 & =2, \text { तब, } z_3=0 \\ \\ z_3 & =0, \text { तब, } z_1=-8 \\ \\ z_1 & =-8, z_2=2, z_3=0 \end{aligned} $
अतः, त्रिभुज $\triangle A B C$ के शीर्ष $A(-3,3,-8), B(5,1,2)$ और $C(1,-1,0)$ हैं।
अतः, त्रिभुज $\triangle A B C$ के केंद्रक $G \left(\dfrac{-3+5+1}{3}, \dfrac{3+1-1}{3}, \dfrac{-8+2+0}{3}\right)=(1,1,-1)$ है।
अर्थात, $ \ G(1,1,-2)$।
50. स्तंभ I में दिए गए प्रत्येक आइटम को स्तंभ II में दिए गए सही उत्तर से मिलाएं।
| स्तंभ I | स्तंभ II | ||
|---|---|---|---|
| (i) | $XY$-समतल में | (a) | प्रथम आठवाँ |
| (ii) | बिंदु $(2,3,4)$ किस आठवाँ में स्थित है | (b) | $YZ$-समतल |
| (iii) | $X$ निर्देशांक शून्य होने वाले बिंदुओं के बिंदुपथ | (c) | $z$-निर्देशांक शून्य हो |
| (iv) | एक रेखा $X$-अक्ष के समांतर होगी यदि और केवल यदि | (d) | $Z$-अक्ष |
| (v) | यदि $X=0, y=0$ एक साथ लिया जाए तो यह | (e) | $XY$-समतल के समांतर समतल |
| (vi) | $z=c$ एक समतल को प्रदर्शित करता है | (f) | रेखा पर सभी बिंदुओं के $y$ और $z$-निर्देशांक समान हो |
| (vii) | समतल $X=a, Y=b$ एक रेखा को प्रदर्शित करते हैं | (f) | संगत बिंदु से |
| (viii) | एक बिंदु के निर्देशांक उस बिंदु से मूल बिंदु तक लंब के पाद तक की दूरियाँ होती हैं | (h) | $Z$-अक्ष के समांतर |
| (ix) | एक गेंद अंतरिक अंतराल में एक | (i) | वृत्त |
| (x) | एक वृत्त द्वारा घिरे क्षेत्र को एक | (j) | गोला |
उत्तर दिखाएं
हल
(i) $XY$-समतल में, $z$-निर्देशांक शून्य होता है।
(ii) बिंदु $(2,3,4)$ प्रथम आठवाँ में स्थित है।
(iii) $x$-निर्देशांक शून्य होने वाले बिंदुओं के बिंदुपथ $YZ$-समतल होता है।
(iv) एक रेखा $X$-अक्ष के समांतर होगी यदि और केवल यदि रेखा पर सभी बिंदुओं के $y$ और $z$-निर्देशांक समान हो।
(v) $x=0, y=0$ $Z$-अक्ष को प्रदर्शित करते हैं।
(vi) $z=c$ $XY$-समतल के समांतर समतल को प्रदर्शित करता है।
(vii) समतल $x=a, y=b$ $Z$-अक्ष के समांतर रेखा को प्रदर्शित करते हैं।
(viii) एक बिंदु के निर्देशांक उस बिंदु से मूल बिंदु तक लंब के पाद तक की दूरियाँ होती हैं।
(ix) एक गेंद एक गोले द्वारा घिरे अंतरिक अंतराल क्षेत्र को कहते हैं।
(x) एक वृत्त द्वारा घिरे तल में क्षेत्र को डिस्क कहते हैं।





