हल

दिया गया है कि वृत्त की त्रिज्या $a$ है अर्थात $(h, k)=(a, a)$

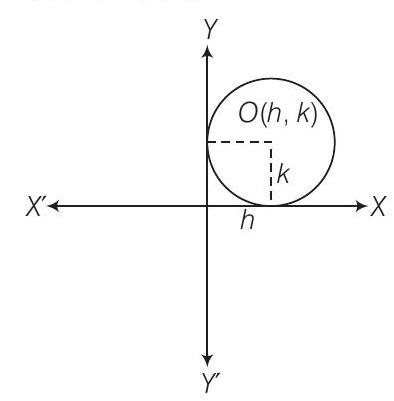
इसलिए, अभीष्ट वृत्त का समीकरण $(x-a)^{2}+(y-a)^{2} =a^{2}$ है

$\Rightarrow x^{2}-2 a x+a^{2}+y^{2}-2 a y+a^{2} =a^{2}$

$\Rightarrow x^{2}+y^{2}-2 a x-2 a y+a^{2} =0 $

हल

दिए गए बिंदु हैं

$ \begin{aligned} x & =\dfrac{2 a t}{1+t^{2}} \text { और } y=\dfrac{a(1-t^{2})}{1+t^{2}} \\ \\ x^{2}+y^{2} & =\dfrac{4 a^{2} t^{2}}{(1+t^{2})^{2}}+\dfrac{a^{2}(1-t^{2})^{2}}{(1+t^{2})^{2}} \end{aligned} $

$ \Rightarrow \quad \dfrac{1}{a^{2}}(x^{2}+y^{2})=\dfrac{4 t^{2}+1+t^{4}-2 t^{2}}{(1+t^{2})^{2}} $

$ \begin{aligned} \Rightarrow \quad & \dfrac{1}{a^{2}}(x^{2}+y^{2})=\dfrac{t^{4}+2 t^{2}+1}{(1+t^{2})^{2}} \\ \\ \Rightarrow \quad & \dfrac{1}{a^{2}}(x^{2}+y^{2})=\dfrac{(1+t^{2})^{2}}{(1+t^{2})^{2}} \\ \\ \Rightarrow \quad & x^{2}+y^{2}=a^{2}, \text { जो अभीष्ट वृत्त है। } \end{aligned} $

चिंतन प्रक्रिया

मूल बिंदु से गुजरने वाले वृत्त का सामान्य समीकरण $x^{2}+y^{2}+2 g x+2 f y=0$ है।

अब, दिए गए बिंदुओं को संतुष्ट करके $g$ और $f$ के मान प्राप्त करें। वृत्त का केंद्र $(-g,-f)$ है।

हल

मान लीजिए वृत्त का समीकरण $

x^{2}+y^{2}+2 g x+2 f y=0 \qquad \ldots(i)$

क्योंकि, यह वृत्त बिंदुओं $A(0,0), B(a, 0)$ और $C(0, b)$ से गुजरता है।

$ \therefore \quad a^{2}+2 a g=0\quad \qquad \ldots(ii)$

$ \text { और } \quad b^{2}+2 b f=0\qquad \ldots(iii)$

समीकरण (ii) से, $a+2 g=0 \Rightarrow g=-a / 2$

समीकरण (iii) से, $b+2 f=0 \Rightarrow f=-b / 2$

इसलिए, वृत्त (i) के केंद्र के निर्देशांक $\dfrac{a}{2}, \dfrac{b}{2}$ हैं।

हल

दिया गया है कि वृत्त का केंद्र $(1,2)$ है।

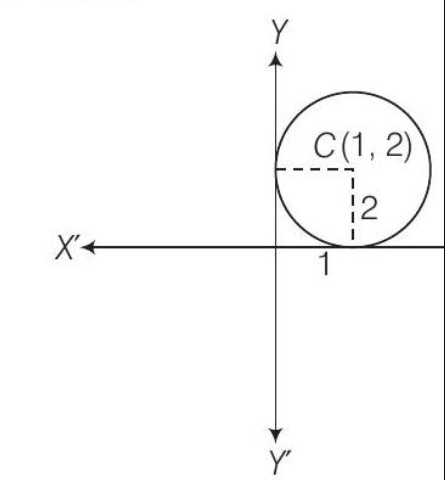
$\because \quad$ त्रिज्या $=2$

इसलिए, वृत्त का समीकरण $(x-1)^2+(y-2)^2 =2^2$

$\begin{aligned} & \Rightarrow \quad x^2-2 x+1+y^2-4 y+4 =4 \\ \\ & \Rightarrow \quad x^2-2 x+y^2-4 y+1 =0 \\ \\ & \Rightarrow \quad x^2+y^2-2 x-4 y+1 =0 \end{aligned}$

चिंतन प्रक्रिया

दो समांतर रेखाओं $a x+b y+c_1=0$ और $a x+b y+c_2=0$ के बीच की दूरी निम्नलिखित द्वारा दी गई है,

अर्थात, $d=\left|\dfrac{c_1-c_2}{\sqrt{a^{2}+b^{2}}}\right|$ इस सूत्र का उपयोग उपरोक्त समस्या को हल करने के लिए करें।

हल

दी गई रेखाएँ, $ \ 3 x-4 y+4=0 \qquad \ldots(i)$

$3 x-4 y-7 / 2=0\quad$ या $\quad 6 x-8 y-7=0 \qquad \ldots(ii)$

स्पष्ट रूप से रेखाएँ (i) और (ii) समांतर हैं।

अब, उनके बीच की दूरी अर्थात,

$ d=\left|\dfrac{4+7 / 2}{\sqrt{9+16}}\right|=\left|\dfrac{\dfrac{8+7}{2}}{5}\right|=\dfrac{3}{2} $

$\therefore \quad$ इन रेखाओं के बीच की दूरी $=$ वृत्त के व्यास

$\therefore \quad$ वृत्त का व्यास $=\dfrac{3}{2}$

और वृत्त की त्रिज्या $=\dfrac{3}{4}$

हल

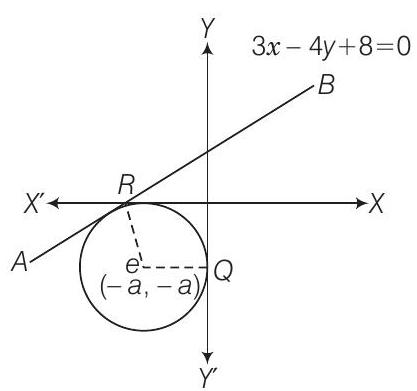
मान लीजिए $a$ वृत्त की त्रिज्या है। तब, वृत्त के केंद्र के निर्देशांक $(-a,-a)$ हैं। अब, $C$ से रेखा $AB$ की लम्ब दूरी = वृत्त की त्रिज्या है

$ d=\bigg|\dfrac{-3 a+4 a+8}{\sqrt{9+16}}\bigg|=\bigg|\dfrac{a+8}{5}\bigg|$

$\because\quad a= \pm \left(\dfrac{a+8}{5}\right)$

$\text { धनात्मक चिन्ह लेते हुए, } a=\dfrac{a+8}{5}$

$\Rightarrow 5 a=a+8$

$\Rightarrow 4 a=8$

$ \Rightarrow a=2$

$\text { ऋणात्मक चिन्ह लेते हुए, } a=\dfrac{-a-8}{5}$

$\Rightarrow 5 a=-a-8$

$\Rightarrow 6 a=-8 $

$\Rightarrow a=\dfrac{-4}{3} $

लेकिन $a \neq\dfrac{-4}{3}$

$\because\quad$ $a=2$

इसलिए, वृत्त का समीकरण है

$ \begin{aligned} & \Rightarrow \quad (x+2)^{2}+(y+2)^{2}=2^{2} \quad[\because a=2] \\ \\ & \Rightarrow \quad x^{2}+4 x+4+y^{2}+4 y+4=4 \\ \\ & \Rightarrow \quad x^{2}+y^{2}+4 x+4 y+4=0 \end{aligned} $

चिंतन प्रक्रिया

पहले दिए गए समीकरण से वृत्त के केंद्र को प्राप्त करें, फिर वृत्त के व्यास के मध्य बिंदु की गणना करें।

हल

दिया गया वृत्त का समीकरण है

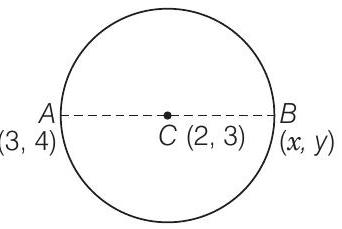
$ x^{2}+y^{2}-4 x-6 y+11=0 . $

$\therefore \quad 2 g=-4$ और $2 f=-6$

इसलिए, वृत्त के केंद्र के निर्देशांक $(-g,-f)$ अर्थात $(2,3)$ हैं।

क्योंकि, $AB$ के मध्य बिंदु $(2,3)$ है।

तब, $2=\dfrac{3+x_1}{2}$

$\Rightarrow$ $4=3+x_1$

$\therefore \quad$ $x_1=1$

और

$\Rightarrow$ $3=\dfrac{4+y_1}{2}$

$\Rightarrow 6=4+y_1 $

$\Rightarrow y_1=2$

इसलिए, व्यास के दूसरे सिरे के निर्देशांक $(1,2)$ होंगे।

हल

दिया गया है कि, वृत्त का केंद्र $(1,-2)$ है और वृत्त रेखाओं के माध्यम से गुजरता है

$ 3 x+y=14\qquad \ldots(i) $

और

$ 2 x+5 y=18\qquad \ldots(ii) $

समीकरण (i) से $y=14-3 x$ को समीकरण (ii) में रखने पर, हम प्राप्त करते हैं

$ \Rightarrow 2 x+70-15 x=18 $

$\Rightarrow -13 x=-52 $

$\Rightarrow x=4$

अब, $x=4$ समीकरण (i) में रखने पर, हम प्राप्त करते हैं

$ \Rightarrow 12+y=14$

$ \Rightarrow y=2 $

क्योंकि, बिंदु $(4,2)$ इन रेखाओं पर स्थित है और वृत्त पर भी स्थित है।

$ \begin{aligned} \therefore \quad \text { वृत्त की त्रिज्या } & =\sqrt{(4-1)^{2}+(2+2)^{2}} \\ \\ & =\sqrt{9+16}=5 \end{aligned} $

अब, वृत्त का समीकरण $(x-1)^{2}+(y+2)^{2} =5^{2} $

$\Rightarrow x^{2}-2 x+1+y^{2}+4 y+4 =25 $

$\Rightarrow x^{2}+y^{2}-2 x+4 y-20 =0 $

हल

दिया गया वृत्त का समीकरण, $x^{2}+y^{2}=16$

$\therefore \quad$ त्रिज्या $=4$ और केंद्र $=(0,0)$

अब, $(0,0)$ से रेखा $y=\sqrt{3} x+k$ पर लंब की लंबाई वृत्त की त्रिज्या के बराबर होती है

$\bigg|\dfrac{0-0+k}{\sqrt{3+1}}\bigg|=4$

क्योंकि बिंदु $(m, n)$ से रेखा $A x+B y+k=0$ की दूरी $d=\bigg|\dfrac{A m+B n+C}{A^{2}+B^{2}}\bigg|$ होती है

$ \begin{aligned} & \Rightarrow \pm \dfrac{k}{2} =4 \\ \\ & \therefore \ \ k = \pm 8 \end{aligned} $

हल

दिया गया वृत्त का समीकरण $x^{2}+y^{2}-6 x+12 y+15=0$

$ \begin{aligned} & \therefore \quad 2 g=-6 \Rightarrow g=-3 \\ \\ & \text { और } \\ \\ & 2 f=12 \Rightarrow f=6 \\ \\ & c=15

\end{aligned} $

[क्योंकि, वृत्त संकेंद्रित हैं]

अपेक्षित वृत्त की त्रिज्या $=r_1$

$\therefore \quad 2 \times$ दिए गए वृत्त का क्षेत्रफल $=$ अपेक्षित वृत्त का क्षेत्रफल

$ \begin{aligned} & \Rightarrow \ 2[\pi(\sqrt{30})^{2}] =\pi (r_1)^{2} \\ \\ & \Rightarrow \ 60 =(r_1)^{2} \\ \\ & \Rightarrow \ r_1 =\sqrt{60} \\ \\ & \therefore \ \ \sqrt{g^{2}+f^{2}-c_1} =\sqrt{60} \\ \\ & \Rightarrow \ 9+36-c_1 =60 \\ \\ & \Rightarrow \ c_1 =-15 \end{aligned} $

इसलिए, अपेक्षित वृत्त का समीकरण $x^{2}+y^{2}-6 x+12 y-15=0$ है।

हल

मान लीजिए अतिपरवलय का समीकरण $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1$ है

$\therefore \quad$ मुख्य अक्ष की लंबाई $=2 a$

कम अक्ष की लंबाई $=2 b$

और लैटसरेक्टम की लंबाई $=\dfrac{2 b^{2}}{a}$

दिया गया है कि, $\dfrac{2 b^{2}}{a} =\dfrac{2 b}{2}$

$ \begin{aligned} \Rightarrow a & =2 b \Rightarrow b=\dfrac{a} {2} \\ \\ \Rightarrow b^{2} & =a^{2}(1-e^{2}) \end{aligned} $

हम जानते हैं कि,

$\Rightarrow\quad$ $\dfrac{a}2^{2}=a^{2}(1-e^{2})$

$\Rightarrow \quad \dfrac{a^{2}}{4}=a^{2}(1-e^{2})$

$\Rightarrow \quad 1-e^{2}=\dfrac{1}{4}$

$\Rightarrow\quad$ $e^{2}=1-\dfrac{1}{4}$

$\Rightarrow\quad e=\sqrt{\dfrac{3}{4}}=\sqrt{\dfrac{3}{2}}$

चिंतन प्रक्रिया

अतिपरवलय के दिए गए समीकरण से $a$ और $b$ के मान ज्ञात कीजिए, फिर $b^{2}=a^{2}(1-e^{2})$ के सूत्र का उपयोग करके $e$ का मान ज्ञात कीजिए।

हल

दिया गया अतिपरवलय का समीकरण,

$ \begin{aligned} 9 x^{2}+25 y^{2} & =225 \\ \\ \dfrac{x^{2}}{25}+\dfrac{y^{2}}{9} & =1 \\ \\ a=5, b & =3 \\ \\ b^{2} & =a^{2}(1-e^{2}) \\ \\ 9 & =25(1-e^{2}) \\ \\ \dfrac{9}{25} & =1-e^{2} \\ \\ e^{2} & =1-9 / 25 \\ \\ & =\sqrt{1-9 / 25} \\ \\ & =\sqrt{\dfrac{25-9}{25}} \\ \\

& =\sqrt{\dfrac{16}{25}}=4 / 5 \end{aligned} $

$ \begin{aligned} & \Rightarrow \ \dfrac{x^{2}}{25}+\dfrac{y^{2}}{9} =1 \\ \\ & \Rightarrow \ a=5, b =3 \\ \\ & \text { हम जानते हैं कि, } \\ \\ & \Rightarrow \ b^{2} =a^{2}(1-e^{2}) \\ \\ & \Rightarrow \ 9 =25(1-e^{2}) \\ \\ & \Rightarrow \ \dfrac{9}{25} =1-e^{2} \\ \\ & \Rightarrow \ e^{2} =1-9 / 25 \\ \\ \therefore & e=\sqrt{1-9 / 25} =\sqrt{\dfrac{25-9}{25}} \end{aligned} $

फोकस $=( \pm a e, 0)=( \pm 5 \times 4 / 5,0)=( \pm 4,0)$

हल

दिया गया है, विस्तार अनुपात $=\dfrac{5}{8}$, अर्थात, $e=\dfrac{5}{8}$

मान लीजिए अतिपरवलय का समीकरण $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1$ है,

क्योंकि इस अतिपरवलय के फोकस $( \pm a e, 0)$ हैं।

$\therefore \quad$ फोकस के बीच की दूरी $=\sqrt{(a e+a e)^{2}}$

$\Rightarrow \quad 2 \sqrt{a^2 e^2}=10 \quad[\because$ फोकस के बीच की दूरी $=10]$

$\Rightarrow \quad \sqrt{a^{2} e^{2}}=5$

$\Rightarrow \quad a^{2} e^{2}=25$

$\Rightarrow \quad a^{2}=\dfrac{25 \times 64}{25}$

$\therefore \ \quad a=8$

हम जानते हैं कि,

$\Rightarrow\quad$ $b^{2}=a^{2}(1-e^{2})$

$\Rightarrow \quad b^{2}=64 \left(1-\dfrac{25}{64}\right)$

$\Rightarrow \quad b^{2}=64 \left(\dfrac{64-25}{64}\right)$

$\Rightarrow \quad b^{2}=39$

$\therefore \quad$ अतिपरवलय के लैटसरेक्टम की लंबाई $=\dfrac{2 b^{2}}{a}=2\times \dfrac{39}{8}=\dfrac{39}{4}$

चिंतन प्रक्रिया

पहले सभी मान $a$ और $b$ के मान को फॉर्मूला $b^{2}=a^{2}(1-e^{2})$ का उपयोग करके ज्ञात कीजिए, फिर अतिपरवलय का समीकरण ज्ञात कीजिए।

हल

दिया गया है, $e=\dfrac{2}{3}$ और लैटसरेक्टम $=5$

$ \begin{aligned} & \text { अर्थात, } \ \dfrac{2 b^{2}}{a}=5 \\ \\ & \Rightarrow b^{2}=\dfrac{5 a}{2} \\ \\

हम जानते हैं कि, $ {b^{2}}{}=a^{2}(1-e^{2}) $\\ \\ & $\Rightarrow \dfrac{5 a}{2}=a^{2} \left(1-\dfrac{4}{9} \right) $\\ \\ & $\Rightarrow \dfrac{5}{2}=\dfrac{5 a}{9} $\\ \\ & $\Rightarrow a=\dfrac{9}{2} $\\ \\ & $\Rightarrow a^{2}=\dfrac{81}{4} $\\ \\ & $\Rightarrow b^{2}=\dfrac{5 \times 9}{2 \times 2}=\dfrac{45}{4}$ \end{aligned} $

इसलिए, अवतल वृत्त का अभीष्ट समीकरण $\dfrac{4 x^{2}}{81}+\dfrac{4 y^{2}}{45}=1$ है।

हल

अवतल वृत्त का समीकरण $\dfrac{x^{2}}{36}+\dfrac{y^{2}}{20}=1$ है।

इस समीकरण को $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1$ के साथ तुलना करने पर, हम प्राप्त करते हैं:

हम जानते हैं कि, $a=6, b=2 \sqrt{5}$

$\Rightarrow\quad$ $b^{2}=a^{2}(1-e^{2})$

$\Rightarrow \quad \dfrac{20}{36}=1-e^{2}$

$\Rightarrow\quad 20=36(1-e^{2})$

$\therefore \quad e=\sqrt{1-\dfrac{20}{36}}=\sqrt{\dfrac{16}{36}}$

$\qquad e=\dfrac{4}{6}=\dfrac{2}{3}$

अब,

$\therefore \quad \dfrac{a}{e}=\dfrac{\dfrac{6}{2}}{3}=\dfrac{6 \times 3}{2}=9\quad$ और $ \quad-\dfrac{a}{e}=-9 $

$\therefore \quad$ नियामकों के बीच दूरी $=|9-(-9)|=18$

हल

दिया गया वृत्त $y^{2}=8 x$ है।

इस वृत्त को $y^{2}=4 a x$ के साथ तुलना करने पर,

हम प्राप्त करते हैं, $\quad 8 x=4 a x \Rightarrow a=2 $

$\therefore \quad \ $ फोकस दूरी $ \ = \ |x+a|=4$

$ \begin{aligned} & \Rightarrow |x+2| =4 \\ \\ & \Rightarrow x+2 = \pm 4 \\ \\ & \Rightarrow x =2,-6 \\ \\ & \text { लेकिन } x \neq-6 \\ \\ & \text { जब } x=2, y^{2} =8 \times 2 \\ \\ & \therefore \ \ y^{2} =16 \Rightarrow y= \pm 4

\end{aligned} $

इसलिए, बिंदु $(2,4)$ और $(2,-4)$ हैं।

हल

दिया गया परवलय का समीकरण $y^{2}=4 a x$ है।

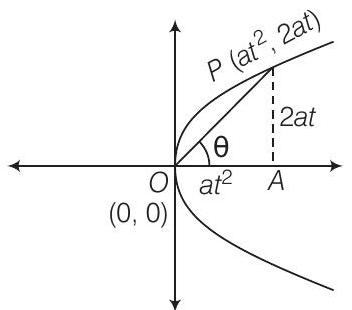
मान लीजिए कि परवलय पर कोई बिंदु $P$ के निर्देशांक $(a t^{2}, 2 a t)$ हैं।

$ \begin{aligned} & \text { त्रिभुज } \triangle P O A \text { में, } \quad \tan \theta=\dfrac{2 \text { at }}{a t^{2}}=\dfrac{2}{t} \\ \\ & \Rightarrow \quad \tan \theta=\dfrac{2}{t} \\ \\ & \Rightarrow \quad t=2 \cot \theta \end{aligned} $

$ \begin{aligned} \therefore \text { लंबाई } O P & =\sqrt{(0-a t^{2})^{2}+(0-2 a t)^{2}} \\ \\ & =\sqrt{a^{2} t^{4}+4 a^{2} t^{2}} \\ \\ & =a t \sqrt{t^{2}+4} \\ \\ & =2 a \cot \theta \sqrt{4 \cot ^{2} \theta+4} \\ \\ & =4 a \cot \theta \sqrt{1+\cot ^{2} \theta} \\ \\ & =4 a \cot \theta \cdot \text{cosec} \theta \\ \\ & =\dfrac{4 a \cos \theta}{\sin \theta} \cdot \dfrac{1}{\sin \theta}=\dfrac{4 a \cos \theta}{\sin ^{2} \theta} \end{aligned} $

हल

दिया गया कि परवलय के शीर्ष के निर्देशांक $(0,4)$ और फोकस के निर्देशांक $(0,2)$ हैं।

परवलय के परिभाषा के अनुसार, $\quad P N=P F$

$ \begin{aligned} & \Rightarrow \ \left|\dfrac{0+y-6}{\sqrt{0+1}}\right| =\sqrt{(x-0)^{2}+(y-2)^{2}} \\ \\ & \Rightarrow \ |y-6| =\sqrt{x^{2}+y^{2}-4 y+4} \\ \\ & \Rightarrow \ x^{2}+y^{2}-4 y+4 =y^{2}+36-12 y \\ \\

Solution

दिया गया अतिपरवलय का समीकरण है

$ \begin{aligned} & \Rightarrow \ 9 y^{2}-4 x^{2} =36 \\ \\ & \Rightarrow \ \dfrac{9 y^{2}}{36}-\dfrac{4 x^{2}}{36} =\dfrac{36}{36} \\ \\ & \Rightarrow \ \dfrac{y^{2}}{4}-\dfrac{x^{2}}{9} =1 \\ \\ & \Rightarrow \ -\dfrac{x^{2}}{9}+\dfrac{y^{2}}{4} =1

\end{aligned} $

क्योंकि, यह समीकरण $-\dfrac{x^{2}}{a^2}+\dfrac{y^{2}}{b^{2}}=1$ के रूप में है, जहाँ $a=3$ और $b=2$ है।

$ \begin{aligned} \therefore \quad e & =\sqrt{1+\dfrac{a^2}{b^{2}}} \\ \\ & =\sqrt{1+\dfrac{9}{4}}=\dfrac{\sqrt{13}}{2} \end{aligned} $

हल

दिया गया है कि विस्तारितता, अर्थात $e=3 / 2$ और $( \pm a e, 0)=( \pm 2,0)$

$ \begin{aligned} & \therefore\quad a e =2 \\ \\ & \Rightarrow\quad a \cdot \dfrac{3}{2} =2 \\ \\ & \Rightarrow \quad a=4 / 3 \\ \\ & \because\quad b^{2} =a^{2}(e^{2}-1) \\ \\ & \Rightarrow\quad b^{2} =\dfrac{16}{9} \left(\dfrac{9}{4}-1\right) \\ \\ & \Rightarrow\quad b^{2} =\dfrac{16}{9} \left(\dfrac{5}{4}\right)=+\dfrac{20}{9} \end{aligned} $

इसलिए, हाइपरबोला का समीकरण है

$\Rightarrow\quad \dfrac{x^2}{\dfrac{16}{9}}-\dfrac{y^2}{\dfrac{20}{9}}=1$

$\Rightarrow \quad\dfrac{x^2}{4}-\dfrac{y^2}{5}=\dfrac{4}{9}$

चिंतन प्रक्रिया

पहले दी गई रेखाओं के प्रतिच्छेद बिंदु को ज्ञात करें, फिर दिए गए क्षेत्रफल से वृत्त की त्रिज्या को ज्ञात करें। अब, केंद्र $(h, k)$ और त्रिज्या $a$ वाले वृत्त के समीकरण के लिए सूत्र $(x-h)^{2}+$ $(y-k)^{2}=a^{2}$ का उपयोग करें।

हल

दी गई रेखाएँ हैं

$ \begin{aligned} & 2 x-3 y-5 =0 \quad\text{और}\quad 3 x-4 y-7 =0 \\ \\ & \dfrac{x}{21-20} =\dfrac{y}{-15+14}=\dfrac{1}{-8+9} \\ \\ & \dfrac{x}{1} =\dfrac{y}{-1}=\dfrac{1}{+1} \\ \\ & x = 1, \ \ y=-1 \end{aligned} $

इन रेखाओं के प्रतिच्छेद बिंदु वृत्त के केंद्र के निर्देशांक होंगे, अर्थात वृत्त के केंद्र के निर्देशांक $(1,-1)$ हैं।

मान लीजिए वृत्त की त्रिज्या $r$ है।

तब, $ \ \pi r^{2}=154 $

$ \begin{aligned} & \Rightarrow\quad \dfrac{22}{7} \times r^{2} =154 \\ \\

& \Rightarrow\quad r^{2} =\dfrac{154 \times 7}{22} \\ \\ & \Rightarrow\quad r^{2} =\dfrac{14 \times 7}{2} \Rightarrow r^{2}=49 \end{aligned} $

तो, वृत्त का समीकरण है

$ \Rightarrow \quad (x-1)^{2}+(y+1)^{2}=49 $

$ \begin{aligned} \Rightarrow \quad & x^{2}-2 x+1+y^{2}+2 y+1=49 \\ \\ \Rightarrow \quad & x^{2}+y^{2}-2 x+2 y=47 \end{aligned} $

हल केंद्र रेखा $y-4 x+3=0$ पर स्थित है

मान लीजिए $\mathrm{x}=\mathrm{h}$

$ \Rightarrow y=4 h-3 $

तो केंद्र के रूप में $(h, 4 h-3)$ है

केंद्र से $(2,3)$ और $(4,5)$ की दूरी बराबर होती है

$ \begin{aligned} & \Rightarrow(h-2)^2+(4 h-3-3)^2=(h-4)^2+(4 h-3-5)^2 \\ \\ & \Rightarrow h=2 \end{aligned} $

तो केंद्र $(2,5)$ है

$ r=\sqrt{(2-2)^2+(5-3)^2}=2 $

तो वृत्त का समीकरण है

$ \begin{aligned} & (x-2)^2+(y-5)^2=2^2 \\ \\ & x^2+y^2-4 x-10 y+25=0 \end{aligned} $

हल

दिया गया वृत्त का केंद्र $(3,-1)$ है

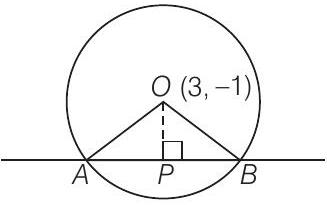
अब,

$ O P=\left|\dfrac{6+5+18}{\sqrt{4+25}}\right|=\dfrac{29}{\sqrt{29}}=\sqrt{29} $

$\ln \triangle O P B$

$ \begin{aligned} & O B^{2}=O P^{2}+P B^{2} \qquad {[\because A B=6 \Rightarrow P B=3]} \\ \\ & O B^{2}=29+9 \\ \\ & O B^{2}=38 \end{aligned} $

तो, वृत्त की त्रिज्या $\sqrt{38}$ है,

$\therefore \quad$ त्रिज्या $r=\sqrt{38}$ और केंद्र $(3,-1)$ वाले वृत्त का समीकरण है

$\Rightarrow \quad(x-3)^{2}+(y+1)^{2}=38$

$\Rightarrow \quad x^{2}-6 x+9+y^{2}+2 y+1=38$

$\Rightarrow \quad x^{2}+y^{2}-6 x+2 y=28$

हल

अभीष्ट वृत्त के केंद्र के निर्देशांक $(h, k)$ हैं, तो दूसरे वृत्त के केंद्र के निर्देशांक $(1,2)$ हैं

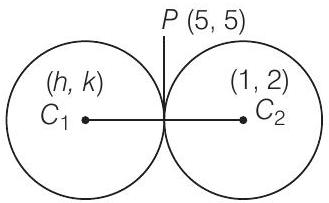
त्रिज्या $=\sqrt{1+4+20}=5$

इसलिए, स्पष्ट है कि $P$ बिंदु $C_1 C_2$ का मध्य बिंदु है।

$\begin{aligned} \therefore \ \ 5=\dfrac{1+h}{2} \Rightarrow h=9 \ \ \text { और } \ \ 5=\dfrac{2+k}{2} \Rightarrow k=8\end{aligned} $

इसलिए, अभीष्ट वृत्त का समीकरण $(x-9)^{2}+(y-8)^{2} =25 $

$\Rightarrow x^{2}-18 x+81+y^{2}-16 y+64 =25 $

$\Rightarrow x^{2}+y^{2}-18 x-16 y+120 =0 $

चिंतन प्रक्रिया

पहले एक वृत्त के समीकरण को अपने केंद्र $(h, k)$ और त्रिज्या $r$ के साथ लिखें $(x-h)^{2}+(y-h)^{2}=r^{2}$, फिर दिए गए शर्तों का उपयोग करके $(h, k)$ का मान प्राप्त करें।

हल

दिया गया वृत्त का समीकरण $ (x-h)^2+(y-k)^2=r^2 $

यहाँ $(h, k ) \rightarrow$ केंद्र

केंद्र से गुजरने वाली रेखा का समीकरण

$\mathrm{k}=\mathrm{h}-1\qquad \ldots(i)$

$ \because \quad ( x, y )$ वृत्त पर बिंदु है

इसलिए, दिया गया $(x, y)=(7,3)$

इसलिए, $(7-h)^2+(3-h+1)^2=3^2$

समीकरण $(i)$ का उपयोग करके हम प्राप्त करते हैं,

$ \begin{aligned} & 28+h^2-11 \mathrm{h}=0 \\ \\ & \mathrm{h}=7 \quad\mathrm{or}\quad 4 \\ \\ & \mathrm{k}=6 \quad \mathrm{or}\quad 3 \end{aligned} $

बिंदु $( 7,6 )$ के संगत वृत्त का समीकरण $ x^2+y^2-14 x-12 y+76=0 $

बिंदु $( 4,3 )$ के संगत वृत्त का समीकरण $ x^2+y^2-8 x-6 y+16=0 $

हल

(i): दिया गया है, directrix $=0$ और focus $=(6,0)$

इसलिए, परवलय का समीकरण $ (x-6)^{2}+y^{2}=x^{2} $

$ \begin{aligned} \Rightarrow \ & x^{2}+36-12 x+y^{2}=x^{2} \\ \\ \Rightarrow \ & y^{2}-12 x+36=0 \end{aligned} $

(ii): दिया गया है, vertex $=(0,4)$ और focus $=(0,2)$

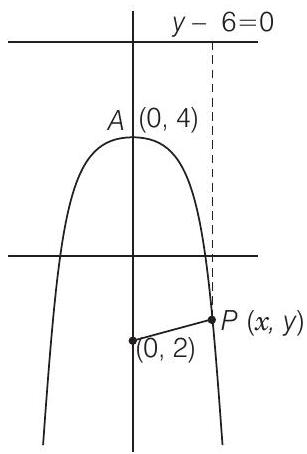
इसलिए, परवलय का समीकरण $\sqrt{(x-0)^{2}+(y-2)^{2}} =|y-6| $

$\Rightarrow x^{2}+y^{2}-4 y+4 =y^{2}-12 y+36 $

$\Rightarrow x^{2}-4 y+12 y-32 =0 $

$\Rightarrow x^{2}+8 y-32 =0 $

$\Rightarrow x^{2} =32-8 y $

(iii): दिया गया है, focus $(-1,-2)$ और directrix $x-2 y+3=0$

इसलिए, परवलय का समीकरण $\sqrt{(x+1)^{2}+(y+2)^{2}}=\bigg|\dfrac{x-2 y+3}{\sqrt{1+4}}\bigg|$

$ \begin{aligned} \Rightarrow \ \ & x^{2}+2 x+1+y^{2}+4 y+4=\dfrac{1}{5}[x^{2}+4 y^{2}+9-4 x y-12 y+6 x] \\ \\ \Rightarrow \ \ & 4 x^{2}+4 x y+y^{2}+4 x+32 y+16=0 \end{aligned} $

हल

मान लीजिए बिंदु के निर्देशांक $(x, y)$ हैं, तो प्रश्न के अनुसार,

$\Rightarrow \sqrt{(x-3)^{2}+y^{2}}+\sqrt{(x-9)^{2}+y^{2}}=12 $

$\Rightarrow \sqrt{(x-3)^{2}+y^{2}}=12-\sqrt{(x-9)^{2}+y^{2}} $

दोनों ओर वर्ग करने पर हमें प्राप्त होता है

$ x^{2}-6 x+9+y^{2} =144+(x^{2}-18 x+81+y^{2})-24 \sqrt{(x-9)^{2}+y^{2}}$

$\Rightarrow 12 x-216 =-24 \sqrt{(x-9)^{2}+y^{2}}$

$\Rightarrow x-18 =-2 \sqrt{(x-9)^{2}+y^{2}}$

$\Rightarrow x^{2}-36 x+324 =4(x^{2}-18 x+81+y^{2})$

$\Rightarrow 3 x^{2}+4 y^{2}-36 x =0 $

सोचने की प्रक्रिया

बिंदु $(x, y)$ को लें और समस्या में दिए गए शर्त को लागू करें, फिर सभी बिंदुओं के समुच्चय को प्राप्त करें।

उत्तर

मान लीजिए बिंदु $P(x, y)$ है।

$\therefore \quad$ बिंदु $(0,4)$ से दूरी $= \sqrt{x^{2}+(y-4)^{2}}$

इसलिए, रेखा $y=9$ से दूरी $\left|\dfrac{y-9}{\sqrt{1}}\right|$

$ \begin{aligned} \therefore \ \ & \sqrt{x^{2}+(y-4)^ {2}}=\dfrac{2}{3}\left|\dfrac{y-9}{1}\right| \\ \\ \Rightarrow \ \ & x^{2}+y^{2}-8 y+10=\dfrac{4}{9}(y^{2}-18 y+81) \\ \\ \Rightarrow \ \ & 9 x^{2}+9 y^{2}-72 y+144=4 y^{2}-72 y+324 \\ \\ \Rightarrow \ \ & 9 x^{2}+5 y^{2}=180 \end{aligned} $

उत्तर

मान लीजिए बिंदु $P(x, y)$ है।

$\therefore \quad$ $P$ की $(4,0)$ से दूरी $\sqrt{(x-4)^{2}+y^{2}}$ और $P$ की $(-4,0)$ से दूरी $\sqrt{(x+4)^{2}+y^{2}}$

अब, $ \ \sqrt{(x+4)^{2}+y^{2}}-\sqrt{(x-4)^{2}+y^{2}}=2 $

$\Rightarrow \ \sqrt{(x+4)^{2}+y^{2}}=2+\sqrt{(x-4)^{2}+y^{2}}$

दोनों ओर वर्ग करने पर हमें प्राप्त होता है

$x^{2}+8 x+16+y^{2} =4+x^{2}-8 x+16+y^{2}+4 \sqrt{(x-4)^{2}+y^{2}} $

$\Rightarrow 16 x-4 =4 \sqrt{(x-4)^{2}+y^{2}} $

$\Rightarrow 4(4 x-1) =4 \sqrt{(x-4)^{2}+y^{2}} $

$\Rightarrow 16 x^{2}-8 x+1 =x^{2}+16-8 x+y^{2} $

$\Rightarrow 15x^{2}-y^{2} =15 \text { जो एक हाइपरबोला है। } $

उत्तर

(i): दिया गया है कि, शीर्ष $=( \pm 5,0)$, फोकस $=( \pm 7,0)$ और $a= \pm 5$

$ \begin{aligned} &\therefore \ \ ( \pm a e, 0)=( \pm 7,0) \\ \\ &\text { अब, } \ \ a e=7 \\ \\ & \Rightarrow 5 e=7 \\ \\ &\Rightarrow \ \ e=7 / 5 \\ \\

&\because \ \ b^{2}=a^{2}(e^{2}-1) \\ \\ &\Rightarrow \ \ b^{2}=25 \left(\dfrac{49}{25}-1\right) \\ \\ &\Rightarrow \ \ b^{2}=25\left( \dfrac{49-25}{25}\right) \\ \\ &\Rightarrow \ \ b^{2}=24 \end{aligned} $

तो, परवलय का समीकरण है

$ \dfrac{x^{2}}{25}-\dfrac{y^{2}}{24}=1 \quad[\because a^{2}=25 \text { और } b^{2}=24] $

(ii): शीर्ष $=(0, \pm 7), e=4 / 3$

$ \begin{aligned} & \therefore \ \ b =7, e=4 / 3 \\ \\ & \ddots \ \ e^{2} =1+\dfrac{a^{2}}{b^{2}} \\ \\ & \Rightarrow \ \ \dfrac{16}{9}-1 =\dfrac{a^{2}}{49} \\ \\ & \Rightarrow \ \ \dfrac{7}{9} =\dfrac{a^{2}}{49} \\ \\ & \Rightarrow a^{2}=\dfrac{343}{9} \end{aligned} $

तो, हाइपरबोला का समीकरण है $-\dfrac{x^{2} \times 9}{343}+\dfrac{y^{2}}{49} =1 $

$\Rightarrow \ -\dfrac{9 x^{2}}{7}+y^{2} =49 $

$\Rightarrow \ 9 x^{2}-7 y^{2}+343 =0 $

(iii): दिया गया है कि, फोकस $=(0, \pm \sqrt{10})$

$ \begin{aligned} & \because b e =\sqrt{10} \\ \\ & \Rightarrow a^{2}+b^{2} =10 \\ \\ & \Rightarrow a^{2} =10-b^{2} \end{aligned} $

$\therefore \quad$ हाइपरबोला का समीकरण है $ -\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1 $

क्योंकि, यह हाइपरबोला बिंदु $(2,3)$ से गुजरती है।

$ \begin{aligned} & \therefore \quad -\dfrac{4}{a^{2}}+\dfrac{9}{b^{2}}=1 \\ \\ & \Rightarrow \quad \dfrac{-4}{10-b^{2}}+\dfrac{9}{b^{2}}=1 \end{aligned} $

$ \begin{aligned} & \Rightarrow \ \ \dfrac{-4 b^{2}+90-9 b^{2}}{b^{2}(10-b^{2})}=1 \\ \\ & \Rightarrow \ \ -13 b^{2}+90=10 b^{2}+b^{4} \\ \\ & \Rightarrow \ \ b^{4}-23 b^{2}+90=0 \\ \\ & \Rightarrow \ \ b^{4}-18 b^{2}-5 b^{2}+90=0 \\ \\ & \Rightarrow \ \ b^{2}(b^{2}-18)-5(b^{2}-18)=0 \\ \\ & \Rightarrow \ \ (b^{2}-18)(b^{2}-5)=0 \\ \\ & \Rightarrow \ \ b^{2}=18 \Rightarrow b= \pm 3 \sqrt{2} \\ \\ & \text { या, } \ \ b^{2}=5 \Rightarrow b=\pm\sqrt{5} \\ \\ & \therefore \ \ b^{2}=18, \ \text { तब, } \ a^{2}=-8 \\ \\ & \text { जब, } \ \ a^{2}=5, \ \text { तब, } \ b^{2}=5 \end{aligned} $

\therefore \quad b^{2}=18 \text { तब } a^{2}=-8 \quad \text { [संभव नहीं] } $

इसलिए, हाइपरबोला का समीकरण है $ \ -\dfrac{x^{2}}{5}+\dfrac{y^{2}}{5} =1 $

$\Rightarrow y^{2}-x^{2} =5 $

चिंतन प्रक्रिया

यदि एक रेखा वृत्त का व्यास है, तो वृत्त के केंद्र रेखा पर स्थित होना चाहिए। इस गुण का उपयोग दिए गए समस्या को हल करने में करें।

हल

असत्य

दिए गए वृत्त का समीकरण है

$ \begin{aligned} & \therefore x^{2}+y^{2}+6 x+2 y =0 \\ \\ & \text { चूंकि दी गई रेखा } x+3 y=0 \qquad \text { केंद्र }=(-3,-1) \\ \\ & \Rightarrow \quad -3-3 \neq 0 \end{aligned} $

इसलिए, यह रेखा वृत्त का व्यास नहीं है।

हल

असत्य

दिया गया वृत्त $x^{2}+y^{2}-14 x-10 y-151=0$ है।

$\therefore \quad$ केंद्र $=(7,5)$ और त्रिज्या $=\sqrt{49+25+151}=\sqrt{225}=15$

इसलिए, बिंदु $(2,-7)$ और वृत्त के केंद्र $(7,5)$ के बीच की दूरी निम्नलिखित द्वारा दी गई है

$\sqrt{(7-2)^2+(5+7)^2}=\sqrt{28+144}=\sqrt{169}=13$

$\therefore \quad$ सबसे कम दूरी, $d=|13-15|=2$

हल

सत्य

दिया गया वृत्त $x^{2}+y^{2}=a^{2}$ है।

$\therefore \quad$ वृत्त की त्रिज्या $=a$ और केंद्र $=(0,0)$

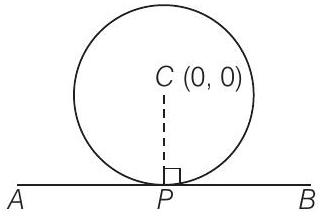
$\therefore \quad$ बिंदु $(l, m)$ और केंद्र के बीच की दूरी $\sqrt{(0-l)^{2}+(0-m)^{2}}=a$

$\Rightarrow \quad l^{2}+m^{2}=a^{2}$

इसलिए, $l, m$ एक वृत्त पर स्थित हैं।

चिंतन प्रक्रिया

यदि $x_1, y_1$ वृत्त $S \equiv x^{2}+y^{2}+2 g x+2 f y+c=0$ के अंदर स्थित हो, तो $x_1^{2}+y_1^{2}+2 g x_1+2 f y_1+c<0$ और यदि $S>0$, तो बिंदु वृत्त के बाहर स्थित होता है।

हल

गलत

दिया गया वृत्त $S \equiv x^{2}+y^{2}-2 x+6 y+1=0$ है।

क्योंकि, बिंदु $(1,2)$ है।

अब,

$ \begin{aligned} & S_1 \equiv 1+4-2+12+1 \\ \\ & \Rightarrow \quad S_1>0 \end{aligned} $

इसलिए, $(1,2)$ वृत्त के बाहर स्थित है।

हल

सत्य

दी गई रेखा का समीकरण

$l x+m y+n=0\qquad \ldots(i)$

और $\text { पराबोला } y^{2}=4 a x\qquad \ldots(ii)$

समीकरण (i) से, $x=-\dfrac{m y+n}{l}$ समीकरण (ii) में रखने पर, हम प्राप्त करते हैं

$\Rightarrow y^{2} =-\dfrac{4 a(m y+n)}{l}$

$\Rightarrow l y^{2} =-4 a m y-4 a n$

$\Rightarrow l y^{2}+4 a m y+4 a n =0$

$\text { स्पर्श रेखा के लिए, } D =0$

$\Rightarrow 16 a^{2} m^{2} =4 l \times 4 a n$

$\Rightarrow 16 a^{2} m^{2} =16$ $ anl $

$\Rightarrow a m^{2} =n l $

हल

गलत

दी गई दीर्घवृत्त का समीकरण $\dfrac{x}{16}+\dfrac{y^{2}}{25}=1$ है।

जो $ \dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1$ के रूप में है, जहाँ $b>a$

$ \begin{aligned} & \therefore \quad \text { फोकस, } \ S=(0, b e),\quad S^{\prime}=(0,-b e) \\ \\ & \therefore \quad e=\sqrt{1-\dfrac{a^{2}}{b^{2}}} =\sqrt{\dfrac{25-16}{25}}=\dfrac{3}{5} \end{aligned} $

$\text { फोकस } S=\left(0, \dfrac{3 \times 5}{5}\right), \quad S^{\prime}=\left(0,-\dfrac{3 \times 5}{5}\right) $

$\text { अर्थात, } S=(0,3), S^{\prime}=(0,-3)$

मान लीजिए बिंदु $P$ के निर्देशांक $(x, y)$ हैं तो $P S+P S^{\prime}=2 b=2 \times 5=10$

हल

सत्य

दी गई रेखा का समीकरण $2 x+3 y =12 $ और $\text { वृत्त } \dfrac{x^{2}}{9}+\dfrac{y^{2}}{4} =2$

क्योंकि, बिंदु $(x_1, y_1)$ पर स्पर्श रेखा का समीकरण $\dfrac{x x_1}{9}+\dfrac{y y_1}{4}=2$ होता है।

$\therefore \quad$ बिंदु $(3,2)$ पर स्पर्श रेखा,

$ \begin{aligned} & \Rightarrow \dfrac{3 x}{9}+\dfrac{2 y}{4}=2 \\ \\ & \Rightarrow \dfrac{x}{3}+\dfrac{y}{2} =2 \\ \\ & \Rightarrow 2 x+3 y =12 \text {, जो दी गई रेखा है। } \end{aligned} $

अतः, कथन सत्य है।

चिंतन प्रक्रिया

पहले सभी दी गई रेखा के समीकरणों से $k$ को बर्बाद करें, फिर हाइपरबोला का समीकरण प्राप्त करें।

हल

सत्य

दी गई रेखा के समीकरण हैं

$ \begin{aligned} & \sqrt{3} x-y-4 \sqrt{3} k =0 \qquad \ldots(i)\\ \\ & \sqrt{3} k x+k y-4 \sqrt{3} =0 \qquad \ldots(ii)\\ \\ &\text{समीकरण (i) से}\\ \\ & \Rightarrow \ 4 \sqrt{3} k =\sqrt{3} x-y \end{aligned} $

$ \begin{aligned} \Rightarrow \ \ & k=\dfrac{\sqrt{3} x-y}{4 \sqrt{3}}\\ \\ & \text{ समीकरण (ii) में रखने पर, हमें प्राप्त होता है } \\ \\ \Rightarrow \ \ & \sqrt{3} x \left(\dfrac{\sqrt{3} x-y}{4 \sqrt{3}}\right)+\left(\dfrac{\sqrt{3} x-y}{4 \sqrt{3}}\right) y-4 \sqrt{3}=0 \\ \\ \Rightarrow \ \ & \dfrac{1}{4}\left(\sqrt{3} x^{2}-x y\right)+\left(\dfrac{1}{4}\right) x y-\dfrac{y^{2}}{\sqrt{3}}-4 \sqrt{3}=0 \\ \\ \Rightarrow \ \ & \left(\dfrac{\sqrt{3}}{4}\right) x^{2}-\left(\dfrac{y^{2}}{4 \sqrt{3}}\right)-4 \sqrt{3}=0 \\ \\ \Rightarrow \ \ & 3 x^{2}-y^2-48=0 \\ \\ \Rightarrow \ \ & 3 x^{2}-y^2=48, \text { जो एक हाइपरबोला है। } \end{aligned} $

हल

केंद्र $(3,-4)$ से रेखा की लम्ब दूरी, $d=\bigg|\dfrac{ 15-48-12}{\sqrt{25+144}}\bigg|=\dfrac{45}{13}$

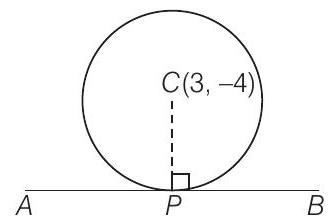
इसलिए, अभीष्ट वृत्त के समीकरण $(x-3)^{2}+(y+4)^{2}=\left(\dfrac{45}{13}\right)^{2}$ है।

हल

दी गई रेखाओं के समीकरण हैं

$y =x+2 \qquad \ldots(i)$

$3 y =4 x \qquad \ldots(ii)$

$2 y =3 x \qquad \ldots(iii)$

समीकरण (i) और (ii) से,

$\Rightarrow$ $ \dfrac{4 x}{3}=x+2 $

$\Rightarrow x=6$

$x=6$ को समीकरण (i) में रखने पर,

हमें प्राप्त होता है, $ \ y =8$

$ \therefore \ \text { बिंदु, } A =(6,8)$

समीकरण (i) और (iii) से,

$ \begin{aligned} & \dfrac{3 x}{2}=x+2 \\ \\ & 3 x=2 x+4 \\ \\ & x=4 \end{aligned} $

समीकरण (ii) और (iii) से

अब,

मान लीजिए वृत्त का समीकरण है

$ \begin{aligned} & x =4, \text { तब, } y=6 \\ \\ & \text { बिंदु, } B =(4,6) \\ \\ & x =0, y=0 \\ \\ & C =(0,0) \end{aligned} $

$ x^{2}+y^{2}+2 g x +2 f y+c=0 $

क्योंकि, बिंदु $A(6,8), B(4,6)$ और $C(0,0)$ इस वृत्त पर स्थित हैं।

$ \ \Rightarrow
36+64+12 g+16 f+c=0 $

$ \begin{aligned} & \Rightarrow 12 g+16 f+c =-100 \qquad \ldots(iv) \\ \\ & \text { और } \ 16+36+8 g+12 f+c =0 \\ \\ & \Rightarrow 8 g+12 f+c =-52 \qquad \ldots(v) \\ \\ & \Rightarrow c =0 \end{aligned} $

समीकरण (iv) और (v) से

$ \begin{aligned} & \Rightarrow \ 12 g+16 f =-100 \\ \\ & \Rightarrow \ 8 g+12 f=-52 \\ \\ & \text {ऊपर के समीकरणों को हल करने पर} \ \ \text{हमें प्राप्त होता है,} \\ \\ & \Rightarrow \ g =-23, f=11 \end{aligned} $

इसलिए, वृत्त का समीकरण है

$ \Rightarrow \quad x^{2}+y^{2}-46 x+22 y+0 =0$

$\Rightarrow \quad x^{2}+y^{2}-46 x+22 y =0$

हल

हम जानते हैं $ \ \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$

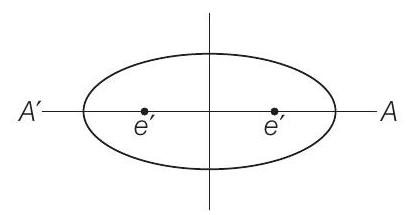
$ \begin{aligned} & \therefore \ \ \mathrm{a}=6 \mathrm{cm, \ a^2}=36 \\ \\ & \mathrm{ ~ b}=4, \ \quad \therefore \ \ \mathrm{ ~ b}^2=16 \\ \\ & \therefore \ \ \mathrm{ ~ b}^2=\mathrm{a}^2\left(1-\mathrm{e}^2\right) \\ \\ & \Rightarrow \mathrm{e}^2=1-\dfrac{\mathrm{b}^2}{\mathrm{a}^2}=1-\dfrac{16}{36}=\dfrac{5}{9} \\ \\ & \therefore \ \ \mathrm{e}=\sqrt{\dfrac{5}{9}}=\dfrac{\sqrt{5}}{3} \\ \\ & \therefore \ \ \mathrm{ae}=\dfrac{6 \times \sqrt{5}}{3} =2{\sqrt{5}} \end{aligned} $

$\therefore$ रस्सी की लंबाई और नुक्कड़ों के बीच की दूरी $6+2 \sqrt{5}, 2 \sqrt{5}$ हैं

चिंतन प्रक्रिया

पहले समस्या में दिए गए शर्तों के मदद से $a$ और $b$ के मान प्राप्त करें, फिर आवश्यक वृत्त का समीकरण प्राप्त करें।

हल

दिया गया है कि, वृत्त के फोकस $(0, \pm b e)$ हैं।

$\because \quad$ be $\equiv 1$

$\therefore \quad$ छोटी अक्ष की लंबाई, $2 a=1$

$ \begin{aligned} & \Rightarrow a=\dfrac{1}{2} \\ \\ & \Rightarrow e^{2} =1-\dfrac{a^{2}}{b^{2}} \\ \\ & \Rightarrow (b e)^{2} =b^{2}-a^{2} \\ \\ & \Rightarrow 1=b^{2}-\dfrac{1}{4} \\ \\ & \Rightarrow 1+\dfrac{1}{4} =b^{2} \\ \\ & \Rightarrow \dfrac{5}{4}=b^{2} \end{aligned} $

इसलिए, वृत्त का समीकरण है $ \dfrac{x^{2}}{\dfrac{1}{4}}+\dfrac{y^{2}}{\dfrac{5}{4}}=1 $

$\Rightarrow \dfrac{4 x^{2}}{1}+\dfrac{4 y^{2}}{5}=1 `

$

हल

दिया गया है, फोकस $F(-1,-2)$ और निर्देशांक रेखा $x-2 y+3=0$

मान लीजिए कोई बिंदु परवलय पर $(x, y)$ है।

$ \begin{aligned} & \therefore \quad P F=\bigg|\dfrac{x-2 y+3}{\sqrt{1+4}}\bigg| \\ \\ & \Rightarrow \quad(x+1)^{2}+(y+2)^{2}=\dfrac{(x-2 y+3)^{2}}{5} \\ \\ & \Rightarrow \quad 5[x^{2}+2 x+1+y^{2}+4 y+4]=x^{2}+4 y^{2}+9-4 x y-12 y+6 x \\ \\ & \Rightarrow \quad 4 x^{2}+y^{2}+4 x+32 y+16=0 \end{aligned} $

हल

मान लीजिए हाइपरबोला का समीकरण $-\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1$ है।

तब शीर्ष $=(0, \pm b)=(0, \pm 6)$

$\therefore \ \ b =6 \text { और } e=5 / 3 $

$\because \ \ e =\sqrt{1+\dfrac{a^{2}}{b^{2}}}$

$ \Rightarrow \dfrac{25}{9}=1+\dfrac{a^{2}}{36} $

$\Rightarrow \dfrac{25-9}{9} =\dfrac{a^{2}}{36} $

$\Rightarrow 16=\dfrac{a^{2}}{4} $

$\Rightarrow a^{2}=48 $

इसलिए, हाइपरबोला का समीकरण है,

$ \begin{aligned} & \dfrac{-x^{2}}{48}+\dfrac{y^{2}}{36} =1 \\ \\ & \Rightarrow \dfrac{y^{2}}{36}-\dfrac{x^{2}}{48}=1 \\ \\ & \because \quad \text { फोकस } =(0, \pm b e)=\left(0, \ \ \pm \dfrac{5}{3} \times 6\right)=(0, \pm 10) \end{aligned} $

हल

(c): दिया गया है, वृत्त केंद्र $(1,2)$ है।

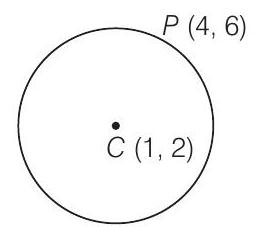
$\because \quad C P=\sqrt{9+16}=5=$ वृत्त की त्रिज्या

$\therefore \quad$ आवश्यक क्षेत्रफल $=\pi r^{2}=25 \pi$

हल

(c): मान लीजिए वृत्त केंद्र $(a, a)$ है, तो वृत्त का समीकरण $(x-a)^{2}+(y-a)^{2}=a^{2}$ है।

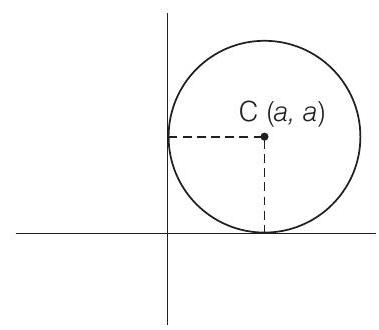
चूंकि, बिंदु $(3,6)$ इस वृत्त पर स्थित है, तो $(3-a)^{2}+(6-a)^{2} =a^{2}$

$ \Rightarrow a^{2}+9-6 a+36-12 a+a^{2} =a^{2}$

$ \Rightarrow a^{2}-18 a+45 =0$

$ \Rightarrow a^{2}-15 a-3 a+45 =0$

$ \Rightarrow a(a-15)-3(a-15) =0$

$ \Rightarrow (a-3)(a-15) =0$

$ \Rightarrow a =3, a=15 $

इसलिए, वृत्त का समीकरण है $(x-3)^{2}+(y-3)^{2} =9$

$\Rightarrow x^{2}-6 x+9+y^{2}-6 y+9 =9$

$\Rightarrow x^{2}+y^{2}-6 x-6 y+9 =0 $

हल

(c): मान लीजिए वृत्त का सामान्य समीकरण $x^{2}+y^{2}+2 g x+2 f y+c=0$ है।

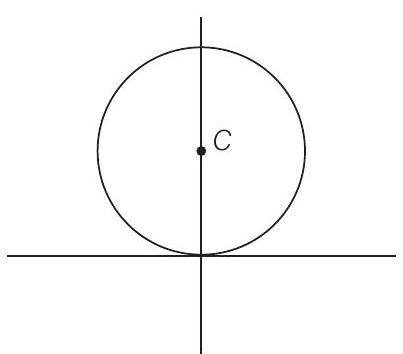
चूंकि बिंदु $(0,0)$ और $(2,3)$ इस पर स्थित है, तो $c=0$ है।

$ \begin{aligned} & \therefore \ 4+9+4 g +6 f=0 \\ \\ & \Rightarrow \ 2 g +3 f=-13 / 2 \\ \\ & \text { केंद्र Y-अक्ष पर है, तो } g =0 \\ \\ & \therefore \ 3 f =-13 / 2 \\ \\ & \Rightarrow \ f =-13 / 6 `

\end{aligned} $

अतः, वृत्त का समीकरण है

$ \Rightarrow \quad 6 x^{2}+6 y^{2}-13 y=0 $

हल

(c): दिया गया है कि, मध्य बिंदु $A D=3 a$

$\because \quad$ वृत्त की त्रिज्या $=\dfrac{2}{3} \times$ मध्य बिंदु की लंबाई $ =\dfrac{2}{3} \times 3 a=2 a $

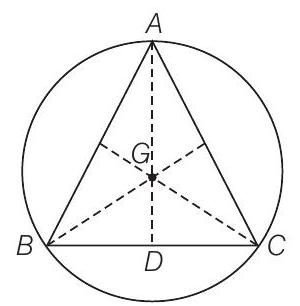
अतः, वृत्त का समीकरण $x^{2}+y^{2}=4 a^{2}$ है।

हल

(a): दिया गया है कि, परवलय का फोकस $F(0,-3)$ तथा नियता का समीकरण $y=3$ है।

मान लीजिए कि परवलय पर कोई बिंदु $P(x, y)$ है।

तब, $ P F=|y-3| $

$ \begin{aligned} & \Rightarrow \ \sqrt{(x-0)^{2}+(y+3)^{2}} =|y-3| \\ \\ & \Rightarrow \ x^{2}+y^{2}+6 y+9 =y^{2}-6 y+9 \\ \\ & \Rightarrow \ x^{2}+12 y =0 \\ \\ & \Rightarrow \ x^{2} =-12 y \end{aligned} $

हल

(b): दिया गया है कि, परवलय है $ y^{2}=4 a x $

$\therefore \quad$ लैटरेक्टम की लंबाई $=4 a$

क्योंकि, परवलय बिंदु $(3,2)$ से गुजरता है।

तब, $4=4 a(3) $

$ \begin{aligned} \Rightarrow \ a=\dfrac{1}{3} \\ \\

\ \ 4 a=\dfrac{4}{3} \\ \\ \therefore \ \ a=\dfrac{1}{3} \end{aligned} $

हल

(a): यहाँ, शीर्ष $=(-3,0)$

$\therefore a=-3$ और नियता, $x+5=0$

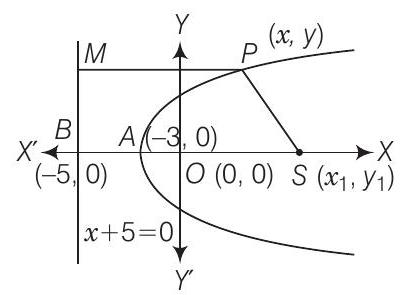
क्योंकि, परवलय के अक्ष नियता के लंबवत रेखा होती है और $A$ बिंदु $AS$ का मध्य बिंदु है।

$ \begin{aligned} & \text { तब, } \ -3 =\dfrac{x_1-5}{2} \\ \\ & \Rightarrow -6 =x_1-5 \Rightarrow x_1=-1, \\ \\ & \therefore \ 0 =\dfrac{0+y_1}{2} \Rightarrow y_1=0 \\ \\ & \therefore \ S =(-1,0) \\ \\ & \Rightarrow P M =P S \quad\left(\to\text{परवलय की स्थिति के द्वारा} \right) \\ \\ & \Rightarrow x+5 =\sqrt{(x+1)^{2}+y^{2}} \\ \\ & \Rightarrow x^{2}+2 x+1+y^{2} =x^{2}+10 x+25 \\ \\ & \Rightarrow y^{2} =+8 x+24 \\ \\ & y^{2} =+8(x+3) \end{aligned} $

हल

(a): दिया गया है कि, अतिपरवलय का फोकस $(1,-1)$ है और नियता रेखा का समीकरण $x-y-3=0$ है और $e=\dfrac{1}{2}$

मान लीजिए $P(x, y)$ और $F(1,-1)$.

$\therefore \quad \dfrac{P F}{\text { Distance of } P \text { from }(x-y-3=0)}=\dfrac{1}{2}$

$ \begin{aligned} & \Rightarrow \ \dfrac{\sqrt{(x-1)^{2}+(y+1)^{2}}}{\dfrac{|x-y-3|}{\sqrt{2}}}=\dfrac{1}{2} \\ \\ & \Rightarrow \ \dfrac{2[x^{2}-2 x+1+y^{2}+2 y+1]}{(x-y-3)^{2}}=\dfrac{1}{4} \\ \\

$$ \begin{aligned} & \Rightarrow \ 8 x^{2}-16 x+16+8 y^{2}+16 y=x^{2}+y^{2}+9-2 x y+6 y-6 x \\ \\ & \Rightarrow \ 7 x^{2}+7 y^{2}+2 x y-10 x+10 y+7=0 \end{aligned} $$

चिंतन प्रक्रिया

पहले दिए गए समीकरण से $a$ और $b$ के मान ज्ञात करें, फिर अक्षय चाप की लम्बाई के सूत्र $\dfrac{2 a^{2}}{b}$ का उपयोग करके लम्बाई ज्ञात करें।

हल

(d): दिया गया वृत्त का समीकरण है $ 3 x^{2}+y^{2}=12 $

$ \begin{aligned} & \Rightarrow \quad \dfrac{x^{2}}{4}+\dfrac{y^{2}}{12}=1 \\ \\ & \therefore \quad a^{2}=4 \Rightarrow a=2 \quad \text { और } \quad b^{2}=12 \Rightarrow b=2 \sqrt{3} \\ \\ & \because \quad b>a \\ \\ & \therefore \quad \text { अक्षय चाप की लम्बाई }=\dfrac{2 a^{2}}{b}=\dfrac{2 \times 4}{2 \sqrt{3}}=\dfrac{4}{\sqrt{3}} \end{aligned} $

हल

(b): दिया गया है,

$ \dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1, a<b $

हम जानते हैं कि, $ e=\sqrt{1-\dfrac{a^{2}}{b^{2}}} $

$ \begin{aligned} & \Rightarrow e^{2}=\dfrac{(b^{2}-a^{2})}{b^{2}} \\ \\ & \Rightarrow b^{2} e^{2}=b^{2}-a^{2} \\ \\ & \Rightarrow a^{2}=b^{2}(1-e^{2}) \end{aligned} $

हल

c:

दिया गया है कि अक्षय चाप की लम्बाई $8$ है और संयुग्मी अक्ष की लम्बाई फोकसों के बीच दूरी के आधा है।

$ \begin{aligned} & \Rightarrow \dfrac{2 b^2}{a}=8 \text { और } 2 b=\dfrac{1}{2}(2 a e) \\ \\ & \therefore \dfrac{2}{a}\left(\dfrac{a e^2}{2}\right)^2=8 \\ \\ & \Rightarrow a e^2=16 \qquad \ldots(i) \end{aligned} $

हमारे पास $ \ \dfrac{2 b^2}{a}=8$ है

$ \begin{aligned} & \Rightarrow \mathrm{b}^2=4 \mathrm{a} \\ \\ & \Rightarrow \mathrm{a}^2\left(\mathrm{e}^2-1\right)=4 \mathrm{a} \\ \\ & \Rightarrow \mathrm{ae}^2-\mathrm{a}=4 \\ \\ & \Rightarrow 16-\mathrm{a}=4 \ \text { (समीकरण (i) से) } \\ \\ & \Rightarrow \mathrm{a}=12 \end{aligned} $

समीकरण (i) में $a = 12 $ को रखें

$ \Rightarrow 12 \mathrm{e}^2=16 $

$ \Rightarrow \mathrm{e}^2=\dfrac{4}{3} $

$ \therefore \ \ \mathrm{e}=\dfrac{2}{\sqrt{3}} $

चिंतन प्रक्रिया

हाइपरबोला के फोकस के बीच की दूरी $2 ae$ होती है और $b^{2}=a^{2}(e^{2}-1)$. इन संबंधों का उपयोग करके $a$ और $b$ के मान को सेट करें।

हल

(a): दिया गया है कि, हाइपरबोला के फोकस के बीच की दूरी

$ \begin{aligned} & \text { अर्थात, } 2 a e =16 \\ \\ & \Rightarrow a e=8 \ \ \text { और } \ \ e =\sqrt{2} \\ \\ & \text { अब, } \ \sqrt{2} a =8 \\ \\ & \Rightarrow a =4 \sqrt{2} \\ \\ & \because \ b^{2} =a^{2}(e^{2}-1) \\ \\ & \Rightarrow b^{2} =32(2-1) \\ \\ & \Rightarrow b^{2} =32 \\ \\ & \therefore \ \dfrac{x^{2}}{32}-\dfrac{y^{2}}{32} =1 \\ \\ & \Rightarrow x^{2}-y^{2} =32 \end{aligned} $

हल

(a): $\dfrac{x^{2}}{4}-\dfrac{y^{2}}{5}=\dfrac{4}{9}$

हाइपरबोला के फोकस $( \pm 2,0)$ दिए गए हैं। इसका अर्थ है कि केंद्र से प्रत्येक फोकस तक की दूरी, जिसे $c$ से नोट किया जाता है, $c=2$ है।

हाइपरबोला के उत्केंद्रता $e$ को निम्नलिखित तरह परिभाषित किया जाता है:

$ e=\dfrac{c}{a} $

दिया गया है कि $e=\dfrac{3}{2}$ और $c=2$, हम निम्नलिखित समीकरण बना सकते हैं:

$ \dfrac{2}{a}=\dfrac{3}{2} $

$ 2 \cdot 2=3 \cdot a \Longrightarrow 4=3 a \Longrightarrow a=\dfrac{4}{3} $

हम जानते हैं कि $c^2=a^2+b^2$

$ a^2=\left(\dfrac{4}{3}\right)^2=\dfrac{16}{9} $

अब, $c=2$ को समीकरण में प्रतिस्थापित करने पर देखें:

$ 2^2=\dfrac{16}{9}+b^2 \Longrightarrow 4=\dfrac{16}{9}+b^2 $

$b^2$ के लिए हल करने के लिए हम पहले 4 को 9 के हर वाली भिन्न में बदलते हैं

$ \Longrightarrow\dfrac{36}{9}=\dfrac{16}{9}+b^2 $

$\Longrightarrow b^2=\dfrac{36}{9}-\dfrac{16}{9}=\dfrac{20}{9} $

केंद्र में बराबर अक्ष के साथ हाइपरबोला के समीकरण के मानक रूप है

$ \dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1 $

$a^2=\dfrac{16}{9}$ और $b^2=\dfrac{20}{9}$ को प्रतिस्थापित करने पर

$ \dfrac{x^2}{\dfrac{16}{9}}-\dfrac{y^2}{\dfrac{20}{9}}=1 $

हर को हटाने के लिए 9 से गुणा करने पर

$ \dfrac{9 x^2}{16}-\dfrac{9 y^2}{20}=9 $

इसे सरल करने पर

$ \dfrac{x^2}{\dfrac{16}{9}}-\dfrac{y^2}{\dfrac{20}{9}}=1 $

इसलिए, हम इसे लिख सकते हैं

$\dfrac{x^{2}}{4}-\dfrac{y^{2}}{5}=\dfrac{4}{9}$