कम्प्लेक्स संख्याएँ एवं द्विघात समीकरण
छोटे उत्तर प्रकार के प्रश्न
1. एक धनात्मक पूर्णांक $n$ के लिए, $(1-i)^{n} (1-\dfrac{1}{i})^{n}$ का मान ज्ञात कीजिए।
उत्तर दिखाएँ
हल
दिया गया व्यंजक $=(1-i)^{n} (1-\dfrac{1}i)^{n}$
$ \begin{aligned} & =(1-i)^{n}(i-1)^{n} \cdot i^{-n}=(1-i)^{n}(1-i)^{n}(-1)^{n} \cdot i^{-n} \\ \\ & =[(1-i)^{2}]^{n}(-1)^{n} \cdot i^{-n}=(1+i^{2}-2 i)^{n}(-1)^{n} i^{-n} \\ \\ & =(1-1-2 i)^{n}(-1)^{n} i^{-n} \quad[\because i^{2}=-1] \\ \\ &=(-2)^{n} \cdot i^{n}(-1)^{n} i^{-n} \\ \\ & =(-1)^{2 n} \cdot 2^{n}=2^{n} \end{aligned} $
2. $\displaystyle \sum_{n=1}^{13}(i^{n}+i^{n+1})$, जहाँ $n \in N$ का मूल्यांकन कीजिए।
उत्तर दिखाएँ
चिंतन प्रक्रिया
इसे हल करने के लिए $i^{2}=-1, i^{4}=(-1)^{2}=1, i^{3}=-i \text {, और } i^{5}=i$ का उपयोग करें।
हल
दिया गया है, $\displaystyle \sum_{n=1}^{13}(i^{n}+i^{n+1}), n \in N$
$=(i+i^{2}+i^{3}+i^{4}+i^{5}+i^{6}+i^{7}+i^{8}+i^{9}+i^{10}+i^{11}+i^{12}+i^{13}) $
$\quad+(i^{2}+i^{3}+i^{4}+i^{5}+i^{6}+i^{7}+i^{8}+i^{9}+i^{10}+i^{11}+i^{12}+i^{13}+i^{14}) $
$=(i+2 i^{2}+2 i^{3}+2 i^{4}+2 i^{5}+2 i^{6}+2 i^{7}+2 i^{8}+2 i^{9}+2 i^{10}+2 i^{11}+2 i^{12}+2 i^{13}+i^{14}) $
$=i-2-2 i+2+2 i+2(i^{4}) i^{2}+2(i)^{4} i^{3}+2(i^{2})^{4}+2(i^{2})^{4} i+2(i^{2})^{5} $
$\quad+2(i^{2})^{5} \cdot i+2(i^{2})^{6}+2(i^{2})^{6} \cdot i+(i^{2})^{7} $
$=i-2-2 i+2+2 i-2-2 i+2+2 i-2-2 i+2+2 i-1$
$=-1+i$
वैकल्पिक विधि
$ \begin{aligned} & \sum_{n=1}^{13}(i^{n}+i^{n+1}), n \in N=\sum_{n=1}^{13} i^{n}(1+i) \\ \\ & =(1+i)[i+i^{2}+i^{3}+i^{4}+i^{5}+i^{6}+i^{7}+i^{8}+i^{9}+i^{10}+i^{11}+i^{12}+i^{13}] \\ \\ & =(1+i)[i^{13}] \quad[\because i^{n}+i^{n+1}+i^{n+2}+i^{n+3}=0, \text { where } n \in N \text { i.e., } \sum_{n=1}^{12} i^{n}=0] \\ \\ & =(1+i) i \quad [\because i^{13}=(i^4)^3 . i = i] \\ \\ & =(i^{2}+i)=i-1 \end{aligned} $
3. यदि $\left(\dfrac{1+i}{1-i}\right)^{3}-\left(\dfrac{1-i}{1+i}\right)^{3}=x+i y$, तो $(x, y)$ का मान ज्ञात कीजिए।
उत्तर दिखाएँ
सोचने की प्रक्रिया
यदि दो समिश्र संख्याएँ $z_1=x_1+i y_{1}$ और $z_2=x_2 +iy_{2}$ समान हों
$ \text { अर्थात, } \quad z_1=z_2 \Rightarrow x_1+i y_1=x_2+i y_2 \text {, तो } x_1=x_2 \text { और } y_1=y_2 \text {. } $
हल
दिया गया है, $\left(\dfrac{1+i}{1-i}\right)^{3}-\left(\dfrac{1-i}{1+i}\right)^{3}=x+i y \quad \ldots (i)$
$ \begin{aligned} \therefore \quad \left(\dfrac{1+i}{1-i}\right)^3 & =\dfrac{1+i^{3}+3 i(1+i)}{1-i^{3}-3 i(1-i)}=\dfrac{1-i+3 i+3 i^{2}}{1+i-3 i+3 i^{2}} \\ \\ & =\dfrac{2 i-2}{-2 i-2}=\dfrac{i-1}{-i-1}=\dfrac{1-i}{1+i} \\ \\ & =\dfrac{(1-i)}{(1+i)} \dfrac{(1-i)}{(1-i)}=\dfrac{1+i^{2}-2 i}{1+1}=\dfrac{1-1-2 i}{2} \end{aligned} $
$\left(\dfrac{1+i}{1-i}\right)^{3}=-i \quad \ldots (ii)$
उसी तरह, $\quad \left(\dfrac{1-i}{1+i}\right)^3=\dfrac{1+i}{1-i}=\dfrac{2i}{2}=i \quad \ldots (iii)$
समीकरण (ii) और (iii) को समीकरण (i) में उपयोग करने पर, हम प्राप्त करते हैं
$ \begin{aligned} -i-i & =x+i y \\ \\ \Rightarrow -2 i & =x+i y \end{aligned} $
समिश्र संख्या के वास्तविक और काल्पनिक भाग की तुलना करने पर, हम प्राप्त करते हैं
$ x=0 \text { और } y=-2 $
इसलिए, $ \quad (x, y)=(0,-2)$
4. यदि $\dfrac{(1+i)^{2}}{2-i}=x+i y$, तो $x+y$ का मान ज्ञात कीजिए।
उत्तर दिखाएँ
हल
दिया गया है, $ \dfrac{(1+i)^{2}}{2-i}=x+i y $
$ \begin{matrix} \Rightarrow & \dfrac{(1+i^{2}+2 i)}{2-i}=x+i y \\ \\ \Rightarrow & \dfrac{2 i}{2-i}=x+i y \\ \\ \Rightarrow & \dfrac{2 i(2+i)}{(2-i)(2+i)}=x+i y \\ \\ \Rightarrow & \dfrac{4 i+2 i^{2}}{4-i^{2}}=x+i y \end{matrix} $
$\Rightarrow \quad \dfrac{4 i-2}{4+1}=x+i y \\ \\Rightarrow \quad \dfrac{-2}{5}+\dfrac{4 i}{5}=x+i y$
समिश्र संख्या के वास्तविक और काल्पनिक भाग की तुलना करने पर, हम प्राप्त करते हैं
$ x=-\dfrac{2}{5} \Rightarrow y=\dfrac{4}{5} $
$ \Rightarrow \quad x+y=\dfrac{-2}{5}+\dfrac{4}{5}=\dfrac{2}{5} $
5. यदि $\left(\dfrac{1-i}{1+i}\right)^{100}=a+i b$, तो $(a, b)$ ज्ञात कीजिए।
उत्तर दिखाएँ
हल
दिया गया है, $\left(\dfrac{1-i}{1+i}\right)^{100}=a+i b$
$ \begin{aligned} & \Rightarrow \quad \left[\dfrac{(1-i)}{(1+i)} \cdot \dfrac{(1-i)}{(1-i)}\right]^{100}=a+i b \\ \\ & \Rightarrow \quad {\left(\dfrac{1+i^{2}-2 i}{1-i^{2}}\right)}^{100}=a+i b \\ \\ & \Rightarrow \quad \left(\dfrac{-2 i}{2}\right)^{100}=a+i b \quad[\because i^{2}=-1] \\ \\ & \Rightarrow \quad(i^{4})^{25}=a+i b \\ \\ & \Rightarrow \quad 1=a+i b \quad[\because i^{4}=1] \end{aligned} $
कम्प्लेक्स संख्या के वास्तविक और काल्पनिक भाग की तुलना करने पर, हम प्राप्त करते हैं
$ \begin{aligned} & \quad a=1 \text { और } b=0 \\ \\ & \therefore \quad(a, b)=(1,0) \end{aligned} $
6. यदि $a=\cos \theta+i \sin \theta$, तो $\dfrac{1+a}{1-a}$ का मान ज्ञात कीजिए।
उत्तर दिखाएँ
चिंतन प्रक्रिया
उपरोक्त समस्या को हल करने के लिए त्रिकोणमितीय सूत्र का उपयोग करें
$\cos \theta=2 \cos ^{2} \theta /2$ $-1=1-2 \sin ^{2} \theta / 2$ और $\sin \theta=2 \sin \theta / 2 \cdot \cos \theta / 2$।
हल
दिया गया है, $a=\cos \theta+i \sin \theta$
$ \begin{aligned} \therefore \quad \dfrac{1+a}{1-a} & =\dfrac{1+\cos \theta+i \sin \theta}{1-\cos \theta-i \sin \theta} \\ \\ & =\dfrac{1+2 \cos ^{2} \theta / 2-1+2 i \sin \theta / 2 \cdot \cos \theta / 2}{1-1+2 \sin ^{2} \theta / 2-2 i \sin \theta / 2 \cdot \cos \theta / 2}=\dfrac{2 \cos \theta / 2(\cos \theta / 2+i \sin \theta / 2)}{2 \sin \theta / 2(\sin \theta / 2-i \cos \theta / 2)} \\ \\ & =-\dfrac{2 \cos \theta / 2(\cos \theta / 2+i \sin \theta / 2)}{2 i \sin \theta / 2(\cos \theta / 2+i \sin \theta / 2)}=-\dfrac{1}{i} \cot \theta / 2 \\ \\ & =\dfrac{i^{2}}{i} \cot \theta / 2 \quad \left[\because \dfrac{-1}{i}=\dfrac{i^{2}}{i}\right] \\ \\ & =i \cot \theta / 2 \end{aligned} $
7. यदि $(1+i) z=(1-i) \bar{z}$, तो सिद्ध कीजिए कि $z=-i \bar{z}$।
उत्तर दिखाएँ
हल
हमें, $(1+i) z=(1-i) \bar{z} $ दिया गया है
$\Rightarrow \dfrac{z}{\bar{z}}=\dfrac{(1-i)}{(1+i)}$
$\Rightarrow \dfrac{z}{\bar{z}}=\dfrac{(1-i)}{(1+i)} \dfrac{(1-i)}{(1-i)} $
$\Rightarrow \dfrac{z}{\bar{z}}=\dfrac{1+i^{2}-2 i}{1-i^{2}} \quad {[\because i^{2}=-1]} $
$\Rightarrow \dfrac{z}{\bar{z}}=\dfrac{1-1-2 i}{2}$
$ \Rightarrow \dfrac{z}{\bar{z}}=-i $
$\therefore \quad z=-i \bar{z}$
इसलिए सिद्ध कर दिया गया है।
8. यदि $z=x+i y$, तो सिद्ध करें कि $z \bar{z}+2(z+\bar{z})+b=0$, जहाँ $b \in R$, एक वृत्त को निरूपित करता है।
उत्तर दिखाएं
हल
दिया गया है, $z=x+iy$
तब, $\bar{z} = x-iy$
अब, $ z \bar{z}+2(z+\bar{z})+b=0$
$\Rightarrow \quad(x+i y)(x-i y)+2(x+i y+x-i y)+b=0$
$\Rightarrow \quad x^{2}+y^{2}+4 x+b=0$, जो एक वृत्त का समीकरण है।
9. यदि $\dfrac{\bar{z}+2}{\bar{z}-1}$ के वास्तविक भाग का मान 4 है, तो सिद्ध करें कि बिंदु $z$ का बिंदुपथ जटिल तल में एक वृत्त है।
उत्तर दिखाएं
हल
मान लीजिए $\quad z =x+i y $ और $\bar{z} = x-iy$
अब, $\quad \dfrac{\bar{z}+2}{\bar{z}-1} =\dfrac{x-i y+2}{x-i y-1} $
$=\dfrac{[(x+2)-i y][(x-1)+i y]}{[(x-1)-i y][(x-1)+i y]} $
$=\dfrac{(x-1)(x+2)-i y(x-1)+i y(x+2)+y^{2}}{(x-1)^{2}+y^{2}} $
$ =\dfrac{(x-1)(x+2)+y^{2}+i[(x+2) y-(x-1) y]}{(x-1)^{2}+y^{2}} \quad[\because-i^{2}=1]$
प्रश्न के अनुसार, हमें वास्तविक भाग $=4$ है
$\therefore \quad \dfrac{(x-1)(x+2)+y^{2}}{(x-1)^{2}+y^{2}}=4$
$\Rightarrow \quad x^{2}-x+2 x-2+y^{2}=4(x^{2}-2 x+1+y^{2})$
$\Rightarrow \quad 3 x^{2}+3 y^{2}-9 x+6=0$, जो एक वृत्त को निरूपित करता है।
इसलिए, $z$ वृत्त पर स्थित है।
10. सिद्ध करें कि जटिल संख्या $z$, जो शर्त arg $\left(\dfrac{z-1}{z+1}\right)=\dfrac{\pi}{4}$ को संतुष्ट करती है, एक वृत्त पर स्थित है।
उत्तर दिखाएं
चिंतन प्रक्रिया
पहले उपयोग करें, $\arg \left(\dfrac{z_1}{z_2}\right)=\arg (z_1)-\arg (z_2)$.
इसके अलावा उपयोग करें $\arg (z)=\theta=\tan ^{-1} (\dfrac{y}{x})$, जहाँ $z=x+i y$
और फिर गुणधर्म $\tan ^{-1} x-\tan ^{-1} y=\tan ^{-1} \left(\dfrac{x-y}{1+x y}\right)$ का उपयोग करें।
हल
मान लीजिए $\quad z =x+i y $
दिया गया है, $\quad \arg \left(\dfrac{z-1}{z+1}\right) =\dfrac{\pi}{4}$
$\Rightarrow \arg (z-1)-\arg (z+1)=\dfrac{\pi}{4} $
$\Rightarrow \arg (x+i y-1)-\arg (x+i y+1)=\dfrac{\pi}{4} $
$\Rightarrow \arg (x-1+i y)-\arg (x+1+i y)=\dfrac{\pi}{4}$
$\Rightarrow \tan ^{-1} \left(\dfrac{y}{x-1}\right)-\tan ^{-1} \left(\dfrac{y}{x+1}\right)=\dfrac{\pi}{4} $
$\Rightarrow \tan ^{-1} \left[\dfrac{\dfrac{y}{x-1}-\dfrac{y}{x+1}}{1+\left(\dfrac{y}{x-1} \right)\left(\dfrac{y}{x+1}\right)}\right]=\dfrac{\pi}{4} $
$\Rightarrow \dfrac{y \left[\dfrac{x+1-x+1}{x^{2}-1}\right]}{\dfrac{x^{2}-1+y^{2}}{x^{2}-1}}=\tan \left(\dfrac{\pi}{4}\right) $
$\Rightarrow \dfrac{2 y}{x^{2}+y^{2}-1}=1 $
$\Rightarrow x^{2}+y^{2}-1=2 y $
$\Rightarrow x^{2}+y^{2}-2 y-1=0,$ जो एक वृत्त को प्रस्तुत करता है।
11. समीकरण $|z|=z+1+2 i$ को हल कीजिए।
उत्तर दिखाएं
हल
दी गई समीकरण $|z|=z+1+2 i \quad \ldots (i)$
मान लीजिए $\quad z=x+i y$
समीकरण (i) से, $\quad|x+i y|=x+i y+1+2 i$
$ \begin{matrix} \Rightarrow & \sqrt{x^{2}+y^{2}}=x+i y+1+2 i & [\because|z|+\sqrt{x^{2}=y^{2}}] \\ \\ \Rightarrow & \sqrt{x^{2}+y^{2}}=(x+1)+i(y+2) & \end{matrix} $
दोनों ओर वर्ग करने पर, हमें प्राप्त होता है
$x^{2}+y^{2}=(x+1)^{2}+i^{2}(y+2)^{2}+2 i(x+1)(y+2) $
$\Rightarrow x^{2}+y^{2}=x^{2}+2 x+1-y^{2}-4 y-4+2 i(x+1)(y+2)$
वास्तविक और काल्पनिक भाग की तुलना करने पर,
$x^{2}+y^{2} =x^{2}+2 x+1-y^{2}-4 y-4 $
अर्थात, $\quad 2y^2 = 2x-4y-3\quad \ldots (ii)$
और $\quad 2(x+1)(y+2) =0$
$(x+1)=0 \text { या }(y+2) =0$
$\Rightarrow x=-1, \text { या } y=-2$
$ x= -1 $ के लिए, $ 2y^2 = -2-4y-3 $
$2y^2+ 4y + 5 =0 \qquad$ [समीकरण (ii) का उपयोग करते हुए]
$\Rightarrow y =\dfrac{-4 \pm \sqrt{16-2 \times 4 \times 5}}{4} $
$y =\dfrac{-4 \pm \sqrt{-24}}{4} \notin R$
$ y=-2 $ के लिए,
$2(-2)^{2} =2 x-4(-2)-3 \qquad$ [समीकरण (ii) का उपयोग करते हुए]
$\Rightarrow 8 =2 x+8-3$
$\Rightarrow 2 x =3 \Rightarrow x=\dfrac{3}{2}$
$\therefore \quad z= x+iy=\dfrac{3}{2}-2i$
लंबे उत्तर प्रकार प्रश्न
12. यदि $|z+1|=z+2(1+i)$, तो $z$ का मान ज्ञात कीजिए।
उत्तर दिखाएं
हल
दिया गया है,
$|z+1| =z+2(1+i) \quad \ldots {(i)}$
मान लीजिए, $z =x+i y$
तब,
$ |x+i y+1|=x+i y+2(1+i) $
$ \begin{aligned} & \Rightarrow \quad|x+1+i y|=(x+2)+i(y+2) \\ \\ & \Rightarrow \quad \sqrt{(x+1)^{2}+y^{2}}=(x+2)+i(y+2) \end{aligned} $
अनुपातिक वास्तविक और काल्पनिक भाग की तुलना करने पर, हम प्राप्त करते हैं
$\sqrt{(x+1)^2+y^2} = (x+2) \quad \ldots (ii)$
और $y+2 = 0$
$\Rightarrow y=-2$
समीकरण (ii) से
$\sqrt{(x+1)^2+(-2)^2} = (x+2)$
दोनों ओर वर्ग करने पर, हम प्राप्त करते हैं
$\Rightarrow \quad (x+1)^2+4 = x^2+4x+4$
$\Rightarrow \quad x^2+2x+1+4 = x^2+4x+4$
$\Rightarrow \quad -2x+1=0$
$\Rightarrow \quad x=\dfrac{1}{2}$
$\therefore \quad z=x+iy = \dfrac{1}{2}-2i$
13. यदि $\arg (z-1)=\arg (z+3 i)$, तो $x-1: y$ ज्ञात कीजिए, जहाँ $z=x+i y$।
उत्तर दिखाएं
हल
दिया गया है, $\arg (z-1)=\arg (z+3 i)$
$\text{और } \quad \text { मान लीजिए } z =x+i y$
$\text{अब } \quad \arg (z-1) =\arg (z+3 i) $
$\Rightarrow \arg (x+i y-1) =\arg (x+i y+3 i) $
$\Rightarrow \arg (x-1+i y) =\arg [x+i(y+3)] $
$ \Rightarrow\tan ^{-1} \left(\dfrac{y}{x-1} \right) =\tan ^{-1} \left(\dfrac{y+3}{x} \right)$
$\Rightarrow \dfrac{y}{x-1} =\dfrac{y+3}{x} $
$\Rightarrow x y=(x-1)(y+3) $
$\Rightarrow x y =x y-y+3 x-3 $
$\Rightarrow 3 x-3=y$
$\Rightarrow \dfrac{3(x-1)}{y}=1 $
$\Rightarrow \dfrac{x-1}{y}=\dfrac{1}{3} $
$\therefore (x-1): y=1: 3$
14. दिखाइए कि $|\dfrac{z-2}{z-3}|=2$ एक वृत्त को प्रस्तुत करता है। इसके केंद्र और त्रिज्या ज्ञात कीजिए।
उत्तर दिखाएं
चिंतन प्रक्रिया
हम जानते हैं कि एक वृत्त के सामान्य समीकरण $x^{2}+y^{2}+2 g x+2 f y+c=0$ होता है, जिसका केंद्र $(-g,-f)$ और त्रिज्या $=\sqrt{g^{2}+f^{2}-c}$ होती है।
हल
मान लीजिए $z=x+i y$
दिया गया समीकरण $\left|\dfrac{z-2}{z-3}\right|=2 $
$\Rightarrow \quad \left|\dfrac{x+i y-2}{x+i y-3}\right|=2$
$\Rightarrow \quad|x-2+i y|=2 | x-3+i y |$
$\Rightarrow \quad \sqrt{(x-2)^{2}+y^{2}}=2 \sqrt{(x-3)^{2}+y^{2}} \quad [\because|x+i y|=\sqrt{x^{2}+y^{2}}]$
दोनों ओर वर्ग करने पर, हम प्राप्त करते हैं
$ \begin{aligned} & & x^{2}-4 x+4+y^{2} & =4(x^{2}-6 x+9+y^{2}) \\ \\ \Rightarrow & & 3 x^{2}+3 y^{2}-20 x+32 & =0 \\ \\
\Rightarrow & & x^{2}+y^{2}-\dfrac{20}{3} x+\dfrac{32}{3} & =0 \end{aligned} $
ऊपर के समीकरण को $x^{2}+y^{2}+2 g x+2 f y+c=0$ के साथ तुलना करने पर, हम प्राप्त करते हैं
$\Rightarrow \quad 2 g=\dfrac{-20}{3} \Rightarrow g=\dfrac{-10}{3} $
और $\quad 2 f=0 \Rightarrow f=0 \text { और } c=\dfrac{32}{3} $
$\therefore \quad \text { केंद्र }=(-g,-f)=\left(\dfrac{10}{3},0 \right)$
इसके अतिरिक्त, $\quad \text { त्रिज्या }(r)=\sqrt{\left(\dfrac{10}{3}\right)^{2}+0-\dfrac{32}3} \qquad[\because r=\sqrt{g^{2}+f^{2}-c}] $
$\qquad \qquad \qquad =\dfrac{1}{3} \sqrt{(100-96)}=\dfrac{2}{3}$
15. यदि $\dfrac{z-1}{z+1}$ एक शुद्ध काल्पनिक संख्या है $(z \neq-1)$, तो $|z|$ का मान ज्ञात कीजिए।
उत्तर दिखाएं
चिंतन प्रक्रिया
यदि $z=x +iy$ एक शुद्ध काल्पनिक संख्या है, तो इसके वास्तविक भाग शून्य होना चाहिए, अर्थात $x=0$,
हल
मान लीजिए $z =x+i y $
$\dfrac{z-1}{z+1} =\dfrac{x+i y-1}{x+i y+1}, z \neq-1 $
$=\dfrac{x-1+i y}{x+1+i y}=\dfrac{(x-1+i y)(x+1-i y)}{(x+1+i y)(x+1-i y)}$
$ =\dfrac{(x^{2}-1)+i y(x+1)-i y(x-1)-i^{2} y^{2}}{(x+1)^{2}-(i y)^{2}} $
$\Rightarrow \quad \dfrac{z-1}{z+1} =\dfrac{(x^{2}-1)+y^{2}+i[y(x+1)-y(x-1)]}{(x+1)^{2}+y^{2}}$
दिया गया है कि, $\dfrac{z-1}{z+1}$ एक शुद्ध काल्पनिक संख्या है।
तब, $\quad \dfrac{(x^{2}-1)+y^{2}}{(x+1)^{2}+y^{2}}=0$
$\Rightarrow x^{2}-1+y^{2}=0 \Rightarrow x^{2}+y^{2}=1 $
$\Rightarrow \sqrt{x^{2}+y^{2}}=\sqrt{1} $
$\Rightarrow|z|=1 \quad {[\because|z|=\sqrt{x^{2}+y^{2}}]}$
16. $z_1$ और $z_2$ दो कम्प्लेक्स संख्याएं हैं जैसे कि $|z_1|=|z_2|$ और $\arg (z_1)+\arg (z_2)=\pi$, तो सिद्ध कीजिए कि $z_1=-\bar{z}_2$।
उत्तर दिखाएं
हल
मान लीजिए $z_1=r_1(\cos \theta_1+i \sin \theta_1)$ और $z_2=r_2(\cos \theta_2+i \sin \theta_2)$ दो कम्प्लेक्स संख्याएं हैं।
दिया गया है कि, $\quad |z_1| =|z_2| $
और $\quad \arg (z_1)+\arg (z_2) =\pi $
यदि $\quad |z_1| =|z_2| $
$\Rightarrow r_1 =r_2 $
और यदि $\quad \arg (z_1)+\arg (z_2) =\pi $
$\Rightarrow \theta_1+\theta_2 =\pi$
$\Rightarrow \theta_1 =\pi-\theta_2$
अब $\quad z_1=r_1(\cos \theta_1+i \sin \theta_1)$
$\Rightarrow z_1=r_2(\cos (\pi-\theta_2)+i \sin (\pi-\theta_2)] \quad [\because r_1=r_2 \text { और } \theta_1=(\pi-\theta_2)] $
$\Rightarrow z_1=r_2(-\cos \theta_2+i \sin \theta_2) $
$\Rightarrow z_1=-r_2(\cos \theta_2-i \sin \theta_2) $
$\Rightarrow z_1=-[r_2(\cos \theta_2-i \sin \theta_2)] \quad {[\because \bar{z}_2=r_2(\cos \theta_2-i \sin \theta_2)]} $
$\Rightarrow z_1=-\bar{z}_2 $
17. यदि $|z_1|=1(z_1 \neq-1)$ और $z_2=\dfrac{z_1-1}{z_1+1}$, तो सिद्ध कीजिए कि $z_2$ का वास्तविक भाग शून्य है।
उत्तर दिखाएं
हल
मान लीजिए $z_1 =x+i y $
$\Rightarrow |z_1| =\sqrt{x^{2}+y^{2}}=1 \qquad [\because |z_1| = 1, \text{दिया गया}] \quad \ldots (i)$
अब, $z_2 =\dfrac{z_1-1}{z_1+1}=\dfrac{x+i y-1}{x+i y+1} $
$=\dfrac{x-1+i y}{x+1+i y}=\dfrac{(x-1+i y)(x+1-i y)}{(x+1+i y)(x+1-i y)} $
$=\dfrac{x^{2}-1+i y(x+1)-i y(x-1)-i^{2} y^{2}}{(x+1)^{2}-i^{2} y^{2}} $
$=\dfrac{x^{2}-1+i x y+i y-i x y+i y+y^{2}}{(x+1)^{2}+y^{2}}$
$=\dfrac{x^{2}+y^{2}-1+2 i y}{(x+1)^{2}+y^{2}}=\dfrac{1-1+2 i y}{(x+1)^{2}+y^{2}} \quad[\because x^{2}+y^{2}=1] $
$=0+\dfrac{2 y i}{(x+1)^{2}+y^{2}}$
इसलिए, $z_2$ का वास्तविक भाग शून्य है।
18. यदि $z_1, z_2$ और $z_3, z_4$ दो संयुग्मी समिश्र संख्याओं के युग्म हैं, तो $\arg (\dfrac{z_1}{z_4})+\arg (\dfrac{z_2}{z_3})$ का मान ज्ञात कीजिए।
उत्तर दिखाएं
चिंतन प्रक्रिया
पहले मान लीजिए $z=r(\cos \theta+i \sin \theta)$, तो $z$ का संयुग्मी, $\bar{z}=r(\cos \theta-i \sin \theta)$ होता है।
गुणधर्म $\arg (\dfrac{z_1}{z_2})=\arg (z_1)-\arg (z_2)$ का उपयोग करें।
हल
मान लीजिए $z_1=r_1(\cos \theta_1+i \sin \theta_1)$,
तो, $\quad z_2=\bar{z}_1=r_1(\cos \theta_1-i \sin \theta_1)=r_1[\cos (-\theta_1)+\sin (-\theta_1)]$
इसके अतिरिक्त, $\quad$ मान लीजिए $\quad z_3=r_2(\cos \theta_2+i \sin \theta_2)$,
तो, $\quad z_4=\bar{z}_3=r_2(\cos \theta_2-i \sin \theta_2)=r_2 [\cos (- \theta _2)+i \sin (- \theta _2)]$
$ \begin{aligned}
\arg \dfrac{z_1}{z_4}+\arg \dfrac{z_2}{z_3} & =\arg (z_1)-\arg (z_4)+\arg (z_2)-\arg (z_3) \\ \\ & =\theta_1-(-\theta_2)+(-\theta_1)-\theta_2 \quad[\because \arg (z)=\theta] \\ \\ & =\theta_1+\theta_2-\theta_1-\theta_2=0 \end{aligned} $
19. यदि $|z_1|=|z_2|=\cdots=|z_{n}|=1$, तो दिखाइए कि
$ |z_1+z_2+z_3+\cdots+z_{n}|=\left|\dfrac{1}{z_1}+\dfrac{1}{z_2}+\dfrac{1}{z_3}+\cdots+\dfrac{1}{z_{n}}\right| . $
उत्तर दिखाएं
हल
दिया गया है,
$ |z_1| =|z_2|=\cdots=|z_{n}|=1 $
$\Rightarrow |z_1|^{2} =|z_2|^{2}=\cdots=|z_{n}|^{2}=1$
$\Rightarrow z_1 \bar z_1 =z_2 \bar z_2=z_3 \bar z_3=\cdots=z_{n} \bar z_n=1 $
$\Rightarrow z_1 =\dfrac{1}{\bar z_1}, z_2=\dfrac{1}{\bar z_2}=\cdots=z_{n}=\dfrac{1}{\overline{z_n}}$
अब, $|z_1+z_2+z_3+z_4+\cdots+z_{n}|$
$=|\overline{z_1+z_2+z_3+ \ldots + z_n}| \quad [\because |z|=|\bar{z}|]$
$=|\bar{z_1}+\bar{z_2}+\bar{z_3}+ \ldots + \bar{z_n}|$
$=\left|\dfrac{1}{z_1}+\dfrac{1}{z_2}+\dfrac{1}{z_3}+ \ldots +\dfrac{1}{z_n}\right|$
इसलिए, सिद्ध कर दिया गया।
20. यदि सम复数 $z_1$ और $z_2$, $\arg (z_1)-\arg (z_2)=0$, तो दिखाइए कि $|z_1-z_2|=|z_1|-|z_2|$.
उत्तर दिखाएं
हल
मान लीजिए $ \ z_1=r_1(\cos \theta_1+i \sin \theta_1)$
और $\ z_2=r_2(\cos \theta_2+i \sin \theta_2)$
$\Rightarrow \arg (z_1)=\theta_1 \text { और } \arg (z_2)=\theta_2$
दिया गया है, $\ \arg (z_1) - \arg(z_2) = 0$
$ \theta_1-\theta_2=0 \Rightarrow \theta_1=\theta_2 $
$ z_2=r_2(\cos \theta_1+i \sin \theta_1) $
$ z_1-z_2=(r_1 \cos \theta_1-r_2 \cos \theta_1)+i(r_1 \sin \theta_1-r_2 \sin \theta_1) $
$ \begin{aligned} |z_1-z_2| & =\sqrt{(r_1 \cos \theta_1-r_2 \cos \theta_1)^{2}+(r_1 \sin \theta_1-r_2 \sin \theta_1)^{2}} \\ \\ & =\sqrt{r_1^{2}+r_2^{2}-2 r_1 r_2 \cos ^{2} \theta_1-2 r_1 r_2 \sin ^{2} \theta_1} \\ \\ & =\sqrt{r_1^{2}+r_2^{2}-2 r_1 r_2(\sin ^{2} \theta_1+\cos ^{2} \theta_1)} \\ \\ & =\sqrt{r_1^{2}+r_2^{2}-2 r_1 r_2}=\sqrt{(r_1-r_2)^{2}} \end{aligned} $
$ \begin{aligned} \Rightarrow |z_1-z_2| & =r_1-r_2 \\ \\ & =|z_1|-|z_2| \end{aligned} $
21. समीकरण के तंत्र को हल करें $Re(z^{2})=0,|z|=2$।
उत्तर दिखाएं
हल
दिया गया है, $\ Re(z^{2})=0,|z|=2$
मान लीजिए $z=x+iy$
$ \begin{matrix} \because & \sqrt{x^{2}+y^{2}}=2 \\ \\ \Rightarrow & x^{2}+y^{2}=4 \quad \ldots (i) \end{matrix} $
और $\ Re(z)=x$
इसके अतिरिक्त, $\ z=x+i y$
$\Rightarrow z^{2}=x^{2}+2 i x y-y^{2}$
$\Rightarrow z^{2}=(x^{2}-y^{2})+2 i x y$
$\Rightarrow Re(z^{2})=x^{2}-y^{2}$
$\Rightarrow x^{2}-y^{2}=0$ $\qquad [\because Re(z^{2})=0]$ $\quad \ldots (ii)$
समीकरण (i) और (ii) से,
$ x^{2}+x^{2} =4 $
$\Rightarrow 2 x^{2} =4 \Rightarrow x^{2}=2 $
$\Rightarrow x = \pm \sqrt{2} $
$\therefore y = \pm \sqrt{2} $
$\because z =x+i y $
$\Rightarrow z =\sqrt{2} \pm i \sqrt{2},-\sqrt{2} \pm i \sqrt{2}$
22. समीकरण $z+\sqrt{2}|(z+1)|+i=0$ को संतुष्ट करने वाली सम复 संख्या ज्ञात करें।
उत्तर दिखाएं
हल
दिया गया समीकरण $\ z+\sqrt{2}|(z+1)|+i=0$
मान लीजिए $\ z=x+iy$
$\Rightarrow \quad x+i y+\sqrt{2}|x+i y+1|+i=0$
$\Rightarrow \quad x+i(1+y)+\sqrt{2} \sqrt{(x+1)^{2}+y^{2}}=0$
$\Rightarrow \quad x+i(1+y)+\sqrt{2} \sqrt{(x^{2}+2 x+1+y^{2})}=0$
$\Rightarrow \quad x+\sqrt{2} \sqrt{(x^2+2x+1+y^2)}+i (1+y)=0 \quad \ldots (i)$
तुलना करते हुए वास्तविक और काल्पनिक भाग, हम प्राप्त करते हैं
$\Rightarrow \quad x+\sqrt{2} \sqrt{x^{2}+2 x+1+y^{2}}=0$
$\Rightarrow \quad x^{2}=2(x^{2}+2 x+1+y^{2})$
$\Rightarrow \quad x^{2}+4 x+2 y^{2}+2=0 \quad \ldots (ii)$
और $ \ 1+y=0 $
$\Rightarrow \quad y=-1$
$ \ y=-1, \quad x^{2}+4 x+2+2=0 \qquad$ [समीकरण (ii) का उपयोग करते हुए]
$\Rightarrow \quad x^{2}+4 x+4=0 \Rightarrow(x+2)^{2}=0$
$\Rightarrow \quad x+2=0 \Rightarrow x=-2$
$\therefore \quad z=x+i y=-2-i$
23. सम复 संख्या $z=\dfrac{1-i}{\cos \dfrac{\pi}{3}+i \sin \dfrac{\pi}{3}}$ को ध्रुवीय रूप में लिखें।
उत्तर दिखाएं
हल
दिया गया है, $z=\dfrac{1-i}{\cos \left(\dfrac{\pi}{3}\right)+i \sin \left(\dfrac{\pi}{3}\right)}=\dfrac{-\sqrt{2} \left[\dfrac{-1}{\sqrt{2}}+i \dfrac{1}{\sqrt{2}}\right]}{\cos \left(\dfrac{\pi}{3}\right)+i \sin \left(\dfrac{\pi}{3}\right)}$
$=\dfrac{-\sqrt{2}\left[\cos \left(\pi-\dfrac{\pi}{4}\right)+i \sin \left(\pi-\dfrac{\pi}{4}\right)\right]}{\cos \left(\dfrac{\pi}{3}\right)+i \sin \left(\dfrac{\pi}{3}\right)}$
$=\dfrac{-\sqrt{2}\left[\cos \left(\dfrac{3 \pi}{4}\right)+i \sin \left(\dfrac{3 \pi}{4}\right)\right]}{\cos \left(\dfrac{\pi}{3}\right)+i \sin \left(\dfrac{\pi}{3}\right)}$
$=-\sqrt{2} \left[\cos \left(\dfrac{3 \pi}{4}-\dfrac{\pi}{3}\right)+i \sin \left(\dfrac{3 \pi}{4}-\dfrac{\pi}{3}\right)\right]$
$=-\sqrt{2} \left[\cos \left(\dfrac{5 \pi}{12}\right)+i \sin \left(\dfrac{5 \pi}{12}\right)\right]$
24. यदि $z$ और $w$ दो ऐसी सम复 संख्याएँ हैं जैसे कि $|z w|=1$ और $\arg (z)-\arg (w)=\dfrac{\pi}{2}$, तो दिखाइए कि $\bar{z} w=-i$।
उत्तर दिखाएँ
हल
मान लीजिए $\ z=r_1(\cos \theta_1+i \sin \theta_1) \ $ और $ \ w=r_2(\cos \theta_2+i \sin \theta_2)$
इसके अतिरिक्त, $\ |z w|=|z||w|=r_1 r_2=1$
$\therefore \ r_1 r_2=1$
इसके अतिरिक्त, $\ \arg (z)=\theta_1 \ $ और $ \ \arg (w)=\theta_2$
लेकिन $\ \arg (z)-\arg (w) =\dfrac{\pi}{2}$
$\Rightarrow \quad \theta_1-\theta_2 =\dfrac{\pi}{2}$
$\Rightarrow \quad \arg (\dfrac{z}{w}) =\dfrac{\pi}{2} $
अब, सिद्ध करना है कि $\ \bar{z} w =-i $
$\text { LHS } =\bar{z} w $
$=r_1(\cos \theta_1-i \sin \theta_1) r_2(\cos \theta_2+i \sin \theta_2) $
$=r_1 r_2[\cos (\theta_2-\theta_1)+i \sin (\theta_2-\theta_1)] $
$=r_1 r_2[\cos (-\pi / 2)+i \sin (-\pi / 2)] $
$=1[0-i] $
$=-i=\text{RHS}$
सिद्ध कर दिया।
रिक्त स्थान भरें
25. निम्नलिखित के रिक्त स्थान भरें।
(i) कोई भी दो सम复 संख्याएँ $z_1, z_2$ और कोई भी वास्तविक संख्याएँ $a, b$, $|a z_1-b z_2|^{2}+|b z_1+a z_2|^{2}=$ ……
(ii) $\sqrt{-25} \times \sqrt{-9}$ का मान ……
(iii) संख्या $\dfrac{(1-i)^{3}}{1-i^{3}}$ के बराबर ……
(iv) श्रेणी $i+i^{2}+i^{3}+$ …… के 1000 पदों तक के योगफल ……
(v) $1+i$ का गुणनात्मक प्रतिलोम ……
(vi) यदि $z_1$ और $z_2$ दो सम复 संख्याएँ हैं जैसे कि $z_1+z_2$ एक वास्तविक संख्या है, तो $z_2=$ ……
(vii) $\arg (z)+\arg \bar{z}$ जहाँ, $(\bar{z} \neq 0)$ है ……
(viii) यदि $|z+4| \leq 3$, तो $|z+1|$ के सबसे बड़े और सबसे छोटे मान ……
(ix) यदि $|\dfrac{z-2}{z+2}|=\dfrac{\pi}{6}$, तो $z$ का बिंदुपथ ……
(x) यदि $|z|=4$ और $\arg (z)=\dfrac{5 \pi}{6}$, तो $z=$ ……
उत्तर दिखाएँ
हल
(i) $|a z_1-b z_2|^{2}+|b z_1+a z_2|^{2}$
$ \begin{aligned} & =|a z_1|^{2}+|b z_2|^{2}-2 Re(a z_1 \cdot b \bar{z}_2)+|b z_1|^{2}+|a z_2|^{2}+2 Re(a z_1 \cdot b \bar{z}_2) \\ \\ & =(a^{2}+b^{2})|z_1|^{2}+(a^{2}+b^{2})|z_2|^{2} \\ \\ & =(a^{2}+b^{2})(|z_1|^{2}+|z_2|^{2}) \end{aligned} $
(ii) $\sqrt{-25} \times \sqrt{-9}=i \sqrt{25} \times i \sqrt{9}=i^{2}(5 \times 3)=-15$
(iii) $\dfrac{(1-i)^{3}}{1-i^{3}}=\dfrac{(1-i)^{3}}{(1-i)(1+i+i^{2})}$
$ =\dfrac{(1-i)^{2}}{i}=\dfrac{1+i^{2}-2 i}{i}=\dfrac{-2 i}{i}=-2 $
(iv) $i+i^{2}+i^{3}+\ldots$ लगातार 1000 पदों तक $=i+i^{2}+i^{3}+i^{4}+\ldots i^{1000}=0$
$\displaystyle [\because i^{n}+i^{n+1}+i^{n+2}+i^{n+3}=0 \text {, जहाँ } n \in N \ i . e ., \sum_{n=1}^{1000} i^{n}=0] $
(v) $1+i$ का गुणनाधिकरण प्रतिलोम $\dfrac{1}{1+i}=\dfrac{1-i}{1-i^{2}}=\dfrac{1}{2}(1-i)$
(vi) मान लीजिए $z_1=x_1+i y_1$ और $z_2=x_2+i y_2$
$z_1+z_2=(x_1+x_2)+i(y_1+y_2)$, जो वास्तविक है।
यदि $\quad z_1+z_2$ वास्तविक है, तो $y_1+y_2=0$
$\Rightarrow \quad y_1=-y_2$
$\because \quad z_2=x_2-i y_1$
$\Rightarrow \quad z_2=\bar{z}_1 \quad$ [जब $x_1=x_2$ ]
(vii) $\arg (z)+\arg (\bar{z}),(\bar{z} \neq 0)$
$\Rightarrow \quad \theta+(-\theta)=0$
(viii) दिया गया है, $|z+4| \leq 3$
सबसे बड़े मान के लिए $|z+1|$ के लिए।
$ \begin{aligned} \Rightarrow \quad|z+1| & =|z+4-3| \\ \\ & \leq|z+4|+|-3| \\ \\ & \leq 3+3 \\ \\ & \leq 6 \end{aligned} $
इसलिए, $|z+1|$ का सबसे बड़ा मान $6$ है।
सबसे छोटे मान के लिए $|z+1|$, हम जानते हैं कि किसी भी समिश्र संख्या के माप का सबसे छोटा मान शून्य होता है। इसलिए, $|z+1|$ का सबसे छोटा मान शून्य है।
(ix) दिया गया है,
$ |\dfrac{z-2}{z+2}|=\dfrac{\pi}{6} $
$\Rightarrow \dfrac{|x+i y-2|}{|x+i y+2|}=\dfrac{\pi}{6} \Rightarrow \dfrac{|x-2+i y|}{|x+2+i y|}=\dfrac{\pi}{6} $
$\Rightarrow 6|x-2+i y|=\pi|x+2+i y| $
$\Rightarrow 6 \sqrt{(x-2)^{2}+y^{2}}=\pi \sqrt{(x+2)^{2}+y^{2}} $
$\Rightarrow 36[x^{2}+4-4 x+y^{2}]=\pi^{2}[x^{2}+4 x+4+y^{2}] $
$\Rightarrow(36-\pi^{2}) x^{2}+(36-\pi^{2}) y^{2}-(144+4 \pi^{2}) x+144+4 \pi^{2}=0, \text { जो कि एक वृत्त है। }$
(x) दिया गया है कि, $|z|=4$ और $\arg (z)=\dfrac{5 \pi}{6}$
$\text { मान लीजिए } z =x+i y=r(\cos \theta+i \sin \theta) $
$\Rightarrow |z| =r=4 \text { और } \arg (z)=\theta =\dfrac{5 \pi}{6}$
$\Rightarrow z =4 \left[\cos \left(\dfrac{5 \pi}{6}\right)+i \sin \left(\dfrac{ 5 \pi}{6}\right)\right]$
$\qquad =4 \left[\dfrac{-\sqrt{3}}{2}+i \dfrac{1}{2}\right]=-2 \sqrt{3}+2 i$
सत्य/असत्य
26. निम्नलिखित के लिए सत्य या असत्य कहिए।
(i) कम्प्लेक्स संख्याओं के समुच्चय पर क्रम विवेक निर्धारित किया गया है।
(ii) एक गैर-शून्य कम्प्लेक्स संख्या को $-i$ से गुणा करने से बिंदु मूल बिंदु के संदर्भ में एक दाई ओर कोण में घूमता है।
(iii) किसी भी कम्प्लेक्स संख्या $z$ के लिए $|z|+|z-1|$ का न्यूनतम मान 1 है।
(iv) $|z-1|=|z-i|$ द्वारा प्रकट किया गया बिंदु बिंदु $(1,0)$ और $(0,1)$ के मिलाने वाली रेखा के लंबवत रेखा है।
(v) यदि $z$ एक कम्प्लेक्स संख्या है जैसे कि $z \neq 0$ और $Re(z)=0$, तो $Im(z^{2})=0$ है।
(vi) असमानुपात $|z-4|<|z-2|$ द्वारा प्रदर्शित क्षेत्र $x>3$ है।
(vii) मान लीजिए $z_1$ और $z_2$ दो कम्प्लेक्स संख्याएं हैं जैसे कि $|z_1+z_2|=|z_1|+|z_2|$, तो $\arg (z_1-z_2)=0$ है।
(viii) 2 एक कम्प्लेक्स संख्या नहीं है।
उत्तर दिखाएं
हल
(i) असत्य
हम दो कम्प्लेक्स संख्याओं की तुलना कर सकते हैं जब वे शुद्ध वास्तविक हों। अन्यथा कम्प्लेक्स संख्याओं की तुलना संभव नहीं है।
(ii) असत्य
$z=x+iy, \quad x > 0,y > 0$
$-iz = -i(x+iy)$
$\quad \quad =-xi +y$
(iii) सत्य
मान लीजिए $ \ z =x+i y $
$|z|+|z-1| =\sqrt{x^{2}+y^{2}}+\sqrt{(x-1)^{2}+y^{2}}$
यदि $x=0, y=0$, तो $|z|+|z-1|$ का मान 1 होता है।
(iv) सत्य
मान लीजिए $\ z =x+i y $
दिया गया है, $|z-1| =|z-i| $
तब, $ \ |x-1+i y| =|x-i(1-y)| $
$(x-1)^{2}+y^{2} =x^{2}+(1-y)^{2} $
$x^{2}-2 x+1+y^{2} =x^{2}+1+y^{2}-2 y $
$-2 x+1 =1-2 y $
$-2 x+2 y =0 $
$x-y =0 \quad \ldots (i)$
बिंदुओं $(1,0)$ और $(0,1)$ से गुजरने वाली रेखा का समीकरण,
$ \begin{aligned} & y-0=\dfrac{1-0}{0-1}(x-1) \\ \\ & \Rightarrow \quad y=-(x-1) \Rightarrow x+y=1 \qquad \ldots (ii) \end{aligned} $
जो $x-y=0$ के लंबवत है।
(v) गलत
मान लीजिए $ \ z=x+i y, z \neq 0$ और $Re(z)=0$
अर्थात, $ \ x=0$
$\therefore \quad z=i y$
$Im(z^{2})=i^{2} y^{2}=-y^{2} \neq 0$
(vi) सही
दिया गया असमिका, $ \ |z-4|<|z-2|$
मान लीजिए $ \ z=x+i y$
$\therefore \quad |x-4+i y| <|x-2+i y| $
$\Rightarrow \sqrt{(x-4)^{2}+y^{2}} <\sqrt{(x-2)^{2}+y^{2}}$
$\Rightarrow (x-4)^{2}+y^{2}<(x-2)^{2}+y^{2}$
$\Rightarrow x^{2}-8 x+16+y^{2}<x^{2}-4 x+4+y^{2}$
$\Rightarrow -8 x+16<-4 x+4$
$\Rightarrow -8 x<-4 x-12$
$\Rightarrow -4 x<-12$
$\Rightarrow 4 x>12$
$\Rightarrow x>3$
(vii) गलत
मान लीजिए $z_1=x_1+i y_1 \ \text { और } \ z_2=x_2+i y_2 $
दिया गया है, $ \ |z_1+z_2|=|z_1|+|z_2|$
$|x_1+i y_1+x_2+i y_2| =|x_1+i y_1|+|x_2+i y_2| $
$\Rightarrow \quad \sqrt{(x_1+x_2)^{2}+(y_1+y_2)^{2}} =\sqrt{(x_1^{2}+y_1^{2})}+\sqrt{(x_2^{2}+y_2^{2})}$
दोनों ओर वर्ग करने पर हमें प्राप्त होता है
$(x_1+x_2)^{2}+(y_1+y_2)^{2}=(x_1^{2}+y_1^{2})+(x_2^{2}+y_2^{2})+2 \sqrt{(x_1^{2}+y_1^{2})(x_2^{2}+y_2^{2})} $
$\Rightarrow x_1^{2}+x_2^{2}+2 x_1 x_2+y_1^{2}+y_2^{2}+2 y_1 y_2=x_1^{2}+y_1^{2}+x_2^{2}+y_2^{2}+2 \sqrt{(x_1^{2}+y_1^{2})(x_2^{2}+y_2^{2})} $
$\Rightarrow 2 x_1 x_2+2 y_1 y_2=2 \sqrt{(x_1^{2}+y_1^{2})(x_2^{2}+y_2^{2})} $
$\Rightarrow x_1 x_2+y_1 y_2=\sqrt{(x_1^{2}+y_1^{2})(x_2^{2}+y_2^{2})}$
दोनों ओर वर्ग करने पर हमें प्राप्त होता है
$x_1^{2} x_2^{2}+y_1^{2} y_2^{2}+2 x_1 x_2 y_1 y_2 =x_1^{2} x_2^{2}+y_1^{2} x_2^{2}+x_1^{2} y_2^{2}+y_1^{2} y_2^{2} $
$\Rightarrow (x_1 y_2-x_2 y_1)^{2} =0 $
$\Rightarrow x_1 y_2 =x_2 y_1 $
$\Rightarrow \dfrac{y_1}{x_1} =\dfrac{y_2}{x_2} $
$\Rightarrow \left(\dfrac{y_1}{x_1}\right)-\left(\dfrac{y_2}{x_2}\right) =0 $
$\Rightarrow \arg (z_1)-\arg (z_2) =0$
(viii) गलत
क्योंकि, प्रत्येक वास्तविक संख्या एक जटिल संख्या भी होती है।
इसलिए, 2 एक समिश्र संख्या है।
27. स्तंभ A और स्तंभ B के कथनों का मिलान करें।
| स्तंभ A | स्तंभ B | ||
|---|---|---|---|
| (a) | $i+\sqrt{3}$ का ध्रुवीय रूप है | (i) | बिंदुओं $(-2,0)$ और $(2,0)$ के जुड़े खंड का लंब समद्विभाजक। |
| (b) | $-1+\sqrt{-3}$ का कोण (amplitude) है | (ii) | केंद्र $(0,-4)$ और त्रिज्या 3 वाले वृत्त के बाहर या उस पर। |
| (c) | यदि $|z+2|=|z-2|$, तो $z$ का बिंदुपथ है | (iii) | $\dfrac{2 \pi}{3}$ |
| (d) | यदि $|z+2 i|=|z-2 i|$, तो $z$ का बिंदुपथ है | (iv) | बिंदुओं $(0,-2)$ और $(0,2)$ के जुड़े खंड का लंब समद्विभाजक। |
| (e) | $\mid z+4i \mid \geq 3 $ द्वारा प्रदर्शित क्षेत्र है | (v) | $2 \left[\cos \left(\dfrac{\pi}{6}\right)+i \sin \left(\dfrac{\pi}{6}\right)\right]$ |
| (f) | $|z+4| \leq 3$ द्वारा प्रदर्शित क्षेत्र है | $(vi)$ | केंद्र $(-4,0)$ और त्रिज्या 3 इकाई वाले वृत्त के अंदर या उस पर। |
| (g) | $\dfrac{1+2 i}{1-i}$ का संयोजक निम्नलिखित में से किस चतुर्थांश में है | (vii) | प्रथम चतुर्थांश |
| (h) | $1-i$ के व्युत्क्रम निम्नलिखित में से किस चतुर्थांश में है | (viii) | तृतीय चतुर्थांश |
उत्तर दिखाएं
हल
(a) दिया गया है, $\ z =i+\sqrt{3}=r(\cos \theta+\sin \theta) $
$\because \quad r \cos \theta =\sqrt{3}, r \sin \theta=1$
$\Rightarrow \quad r^{2} =1+3=4 \Rightarrow r=2 \quad [\because r>0]$
$\tan \theta = \left|\dfrac{r \sin \theta}{r \cos \theta}\right|=\dfrac{1}{\sqrt{3}}$
$\Rightarrow \quad \tan \theta =\dfrac{1}{\sqrt{3}} \Rightarrow \theta=\dfrac{\pi}{6}$
$\therefore \ \arg (z) =\theta=\dfrac{\pi}{6}$
इसलिए, $z$ का ध्रुवीय रूप $2 \left[\cos \left(\dfrac{\pi}{6}\right)+i \sin \left(\dfrac{\pi}{6}\right)\right]$ है।
(b) मान लीजिए $ \ z=x+iy$
तो कोण $= \tan^{-1}\left(\left|\dfrac{y}{x}\right|\right)$
$\qquad = \pi- \tan^{-1}\left(\left|\dfrac{y}{x}\right|\right) \quad ( \text{जब} \ x <0, y >0)$
दिया गया है $z= -1+\sqrt{-3}$
$z=-1+i \sqrt{3}$
$\therefore \quad \text{amp}(z)= \pi- \tan^{-1} \left(\dfrac{\sqrt{3}}{1}\right)$
$\qquad =\pi- \tan^{-1}(\sqrt{3})$
$\text{amp}(z)= \pi - \dfrac{\pi}{3} = \dfrac{2 \pi}{3}$
(c) दिया गया है, $ \ |z+2|=|z-2|$
मान लीजिए $ \ z=x+iy$
$\therefore \quad |x+2+i y| =|x-2+i y| $
$\Rightarrow (x+2)^{2}+y^{2} =(x-2)^{2}+y^{2} $
$\Rightarrow x^{2}+4 x+4 =x^{2}-4 x+4 \quad \Rightarrow \quad 8 x=0$
$\therefore x =0$
यह $y-$ अक्ष के समीकरण को प्रदर्शित करता है और यह बिंदुओं $(-2,0)$ और $(0,2)$ को जोड़ने वाली रेखा के लंबवत है।
(d) दिया गया है, $ \ |z+2 i|=|z-2 i|$
मान लीजिए $ \ z=x+iy$
$\therefore \quad |x+i(y+2)| =|x+i(y-2)| $
$\Rightarrow x^{2}+(y+2)^{2} =x^{2}+(y-2)^{2} $
$\Rightarrow 4 y =0 \Rightarrow y=0$
यह $x-$ अक्ष के समीकरण को प्रदर्शित करता है और यह बिंदुओं $(0,-2)$ और $(0,2)$ को जोड़ने वाले रेखा खण्ड के लंबवत है।
(e) दिया गया है, $\quad |z+4 i| \geq 3 $
मान लीजिए $\ z=x+iy$
$\therefore \quad |x+i y+4 i| \geq 3$
$\Rightarrow \quad |x+i(y+4)| \geq 3 $
$\Rightarrow \quad \sqrt{x^{2}+(y+4)^{2}} \geq 3 $
$\Rightarrow \quad x^{2}+(y+4)^{2} \geq 9 $
$\Rightarrow \quad x^{2}+y^{2}+8 y+16 \geq 9 $
$\Rightarrow \quad x^{2}+y^{2}+8 y+7 \geq 0$
यह केंद्र $(0,-4)$ और त्रिज्या 3 वाले वृत्त के बाहर या उस पर वाले क्षेत्र को प्रदर्शित करता है।
(f) दिया गया है, $ \ |z+4| \leq 3$
मान लीजिए $ \ z= x+iy$
$\therefore \quad |x+i y+4| \leq 3 $
$\Rightarrow |x+4+i y| \leq 3 $
$\Rightarrow \sqrt{(x+4)^{2}+y^{2}} \leq 3 $
$\Rightarrow (x+4)^{2}+y^{2} \leq 9 $
$\Rightarrow x^{2}+8 x+16+y^{2} \leq 9 $
$\Rightarrow x^{2}+8 x+y^{2}+7 \leq 0$
यह केंद्र $(-4,0)$ और त्रिज्या 3 वाले वृत्त के अंदर या उस पर वाले क्षेत्र को प्रदर्शित करता है।
(g) दिया गया है,
$z =\dfrac{1+2 i}{1-i}=\dfrac{(1+2 i)(1+i)}{(1-i)(1+i)} $
$=\dfrac{1+2 i+i+2 i^{2}}{1-i^{2}}$
$=\dfrac{1-2+3 i}{1+1}=\dfrac{-1+3 i}{2}$
$ \therefore \quad \bar{z}=\dfrac{-1}{2}-\dfrac{3 i}{2} $
इसलिए, $\left(\dfrac{-1}{2}, \dfrac{-3}{2}\right)$ तीसरे चतुर्थांश में स्थित है।
(h) दिया गया है, $z=1-i$
$\therefore \quad \dfrac{1}{z}=\dfrac{1}{1-i}=\dfrac{1+i}{(1-i)(1+i)}$
$=\dfrac{1+i}{1-i^{2}}=\dfrac{1}{2}(1+i)$
इसलिए, $\quad \left(\dfrac{1}{2}, \dfrac{1}{2}\right)$ प्रथम चतुर्थांश में स्थित है।
इसलिए, सही मिलान हैं
(a) $\rightarrow$(v),
(b) $\rightarrow$ (iii),
(c) $\rightarrow$ (i),
(d) $\rightarrow$(iv),
(e) $\rightarrow$(ii),
(f) $\rightarrow$ (vi),
(g) $\rightarrow$(viii),
(h) $\rightarrow$(vii)
28. $\dfrac{2-i}{(1-2 i)^{2}}$ का संयुग्मी क्या है ?
उत्तर दिखाएं
Solution
$ \begin{aligned} &\text{दिया गया है, } \ z=\dfrac{2-i}{(1-2 i)^{2}}=\dfrac{2-i}{1+4 i^{2}-4 i} \\ \\ & =\dfrac{2-i}{1-4-4 i}=\dfrac{2-i}{-3-4 i} \\ \\ & =\dfrac{(2-i)}{-(3+4 i)}=-\left[\dfrac{(2-i)(3-4 i)}{(3+4 i)(3-4 i)}\right] \\ \\ & =-\left(\dfrac{6-8 i-3 i+4 i^{2}}{9+16}\right)=-\dfrac{(-11 i+2)}{25} \\ \\ & =\dfrac{-1}{25}(2-11 i) \\ \\ & \Rightarrow z=\dfrac{1}{25}(-2+11 i) \\ \\ & \therefore \quad \bar{z}=\dfrac{1}{25}(-2-11 i)=\dfrac{-2}{25}-\dfrac{11}{25} i \end{aligned} $
29. यदि $|z_1|=|z_2|$, तो क्या आवश्यक है कि $z_1=z_2$ ?
उत्तर दिखाएं
Solution
दिया गया है, $ \ |z_1| =|z_2| $
मान लीजिए $ \ z_1 =x_1+i y_1 \text { और } z_2=x_2+i y_2 $
$\Rightarrow |x_1+i y_1| =|x_2+i y_2|$
$\Rightarrow x_1^{2}+y_1^{2} =x_2^{2}+y_2^{2}$
$\Rightarrow x_1^{2} =x_2^{2}, y_1^{2}=y_2^{2} $
$\Rightarrow x_1 = \pm x_2, y_1= \pm y_2 $
$\Rightarrow z_1 =x_1+i y_1 \text { या } z_1= \pm x_2 \pm i y_2$
$\therefore \quad z_1 \neq z_2$
इसलिए, आवश्यक नहीं है कि $z_1=z_2$.
30. यदि $\dfrac{(a^{2}+1)^{2}}{2 a-i}=x+i y$, तो $x^{2}+y^{2}$ का मान क्या है ?
उत्तर दिखाएं
Solution
दिया गया है, $\ \dfrac{(a^{2}+1)^{2}}{2 a-i}=x+i y $
दोनों ओर मापदंड लेने पर, हमें प्राप्त होता है
$\left| \dfrac{(a^2+1)^2}{2a-i} \right| = |x+iy|$
$\Rightarrow \quad \dfrac{(a^2+1)^2}{\sqrt{4a^2+1}} = \sqrt{x^2+y^2}$
दोनों ओर वर्ग करने पर, हमें प्राप्त होता है
$\dfrac{(a^2+1)^4}{4a^2+1} = x^2+y^2$
31. यदि $|z|=4$ और $\arg (z)=\dfrac{5 \pi}{6}$, तो $z$ का मान ज्ञात कीजिए।
उत्तर दिखाएं
Solution
दिया गया है $ \ |z|=4$ और $\text{arg}(z)= \dfrac{5 \pi}{6}$
मान लीजिए $\quad z= r(\cos\theta+i \sin \theta)$
$ \begin{matrix} \begin{aligned} \therefore \quad |z| & =r=4 \text { और } \theta=\dfrac{5 \pi}{6} \quad[\because \arg (z)=\theta] \\ \\ \text{अब,} & \quad z =4 \left[\cos \dfrac{5 \pi}{6}+i \sin \dfrac{5 \pi}{6}\right] \quad[\because z=r(\cos \theta+i \sin \theta)] \\ \\ & =4 \left[\cos \left(\pi-\dfrac{\pi}{6}\right)+i \sin \left(\pi-\dfrac{\pi}{6}\right)\right] \\ \\ & =4\left[-\cos \dfrac{\pi}{6}+i \sin \dfrac{\pi}{6}\right] \\ \\ & =4\left[-\dfrac{\sqrt{3}}{2}+i \dfrac{1}{2}\right]=-2 \sqrt{3}+2 i \end{aligned} \end{matrix} $
32. $\left|(1+i) \dfrac{(2+i)}{(3+i)}\right|$ ज्ञात कीजिए।
उत्तर दिखाएं
सोचने की प्रक्रिया
पहले, दिए गए व्यंजक को $a+i b$ के रूप में बदलें, फिर $|a+i b|=\sqrt{a^{2}+b^{2}}$ का उपयोग करें।
हल
दिया गया है, $ \ \left|(1+i) \dfrac{(2+i)}{(3+i)}\right|=\left|\dfrac{(2+i+2 i+i^{2})}{(3+i)}\right| \\ \\ = \left|\dfrac{2+3 i-1}{3+i}\right|$
$ \begin{aligned} & =\left|\dfrac{1+3 i}{3+i}\right|=\left|\dfrac{(1+3 i)(3-i)}{(3+i)(3-i)}\right| \\ \\ & =\left|\dfrac{3+9 i-i-3 i^{2}}{9-i^{2}}\right| \\ \\ &= \left|\dfrac{3+8 i+3}{9+1}\right|=\left|\dfrac{6+8 i}{10}\right| \\ \\ & =\sqrt{\dfrac{6^{2}}{100}+\dfrac{8^{2}}{100}} \\ \\ &=\sqrt{\dfrac{36+64}{100}}=\sqrt{\dfrac{100}{100}}=1 \end{aligned} $
33. $(1+i \sqrt{3})^{2}$ का मुख्य त्रिकोणमितीय तर्क ज्ञात कीजिए।
उत्तर दिखाएं
सोचने की प्रक्रिया
मान लीजिए $z=a+i b$, तो $z$ का ध्रुवीय रूप $r(\cos \theta+i \sin \theta)$ होता है, जहाँ $r=|z|=\sqrt{a^{2}+b^{2}}$ और $\tan \theta=\dfrac{b}{a} \cdot$ यहाँ, $\theta$ $z$ का तर्क या आम्पलीता होता है, अर्थात $\arg (z)=\theta$। मुख्य तर्क वह एकमात्र $\theta$ का मान होता है जहाँ $-\pi \leq \theta \leq \pi$।
हल
दिया गया है,
$ \begin{aligned} & z=(1+i \sqrt{3})^{2} \\ \\ & z=1-3+2 i \sqrt{3} \\ \\ & z=-2+i 2 \sqrt{3} \end{aligned} $
$\Rightarrow \tan \alpha=\left|\dfrac{2 \sqrt{3}}{-2}\right|=\left|-\sqrt{3}\right|=\sqrt{3} \qquad \left[\because \tan \alpha = \left|\dfrac{Im(z)}{Re(z)}\right|\right] $
$\Rightarrow \tan \alpha=\tan \dfrac{\pi}{3} \Rightarrow \alpha=\dfrac{\pi}{3} $
$\because \quad Re(z)<0 \text { and } Im(z)>0 $
$\therefore \quad \arg (z)=\pi-\dfrac{\pi}{3} =\dfrac{2 \pi}{3}$
34. $z$ कहाँ स्थित है, यदि $\left|\dfrac{z-5 i}{z+5 i}\right|=1$ ?
उत्तर दिखाएं
सोचने की प्रक्रिया
$ \begin{aligned} & \text { यदि } z_1=x_1+iy_1 \ \text { और } \ z_2=x_2+i y_2 \text {, तो }|z_1|=\sqrt{x_1^{2}+y_1^{2}} \text { और }|z_2|=\sqrt{x_2^{2}+y_2^{2}} . \\ \\ & \text { अतः, मापांक के गुणधर्म का उपयोग करें, अर्थात, } \left|\dfrac{z_1}{z_2}\right|=\dfrac{|z_1|}{|z_2|} \end{aligned} $
हल
मान लीजिए $z=x+iy$
दिया गया है, $\quad \left|\dfrac{z-5 i}{z+5 i}\right|=\dfrac{|x+iy-i5|}{|x+iy+i5|}$
$\Rightarrow \quad \left|\dfrac{z-5 i}{z+5 i}\right|=\dfrac{|x+i(y-5)|}{|x+i(y+5)|}=1 \quad \Big[\because \left|\dfrac{z-5 i}{z+5 i} \right|=1 \Big]$
$\Rightarrow \quad \left|\dfrac{z-5 i}{z+5 i}\right|=\dfrac{\sqrt{x^{2}+(y-5)^{2}}}{\sqrt{x^{2}+(y+5)^{2}}} = 1$
दोनों ओर वर्ग करने पर, हमें प्राप्त होता है
$\dfrac{x^2+(y-5)^2}{x^2+(y+5)^2} =1$
$ \Rightarrow x^{2}+(y-5)^{2}=x^{2}+(y+5)^{2} $
$\Rightarrow -10 y =+10 y $
$\Rightarrow 20 y =0 $
$\therefore \quad y =0$
अतः, $z$ वास्तविक अक्ष पर स्थित है।
उद्देश्य प्रकार के प्रश्न
35. $\sin x+i \cos 2 x$ और $\cos x-i \sin 2 x$ एक दूसरे के संयुग्मी होते हैं यदि
(a) $x=n \pi$
(b) $x=(n+\dfrac{1}{2}) \dfrac{\pi}{2}$
(c) $x=0$
(d) $x$ के कोई मान नहीं
उत्तर दिखाएं
हल
विकल्प (d) मान लीजिए $z=\sin x+i \cos 2 x$
और $\bar{z}=\sin x-i \cos 2 x$
दिया गया है, $\bar{z}=\cos x-i \sin 2 x$
$\therefore \sin x-i \cos 2 x=\cos x-i \sin 2 x$
$\Rightarrow \sin x=\cos x$ और $\cos 2 x=\sin 2 x$
$\Rightarrow \tan x=1$ और $\tan 2 x=1$
$\Rightarrow \tan x=\tan \dfrac{\pi}{4}$ और $\tan 2 x=\tan \dfrac{\pi}{4}$
$\Rightarrow x=n \pi+\dfrac{\pi}{4}$ और $2 x=n \pi+\dfrac{\pi}{4}$
$\Rightarrow 2 x-x=0 \Rightarrow x=0$
-
विकल्प (a) $ x = n\pi $: यदि $ x = n\pi $, तो $ \sin x = 0 $ और $ \cos x = (-1)^n $.
इसके फलस्वरूप $ z = 0 + i \cos 2x $ और $ \bar{z} = 0 - i \cos 2x $ होंगे।
हालांकि, $ \bar{z} $ के $ \cos x - i \sin 2x $ के बराबर होने के लिए $ \cos x $ और $ \sin 2x $ दिए गए शर्तों को संतुष्ट करना चाहिए, जो $ x = n\pi $ के लिए संतुष्ट नहीं होते हैं। -
विकल्प (b) $ x = (n + \dfrac{1}{2}) \dfrac{\pi}{2} $: इस व्यंजक का फॉर्मेट सही नहीं है। $ x=\left(n+\dfrac{1}{2}\right) \dfrac{\pi}{2} $ पर, पूर्णांक $ n $ के लिए $ \sin x $ और $ \cos x $ बराबर नहीं होते हैं, क्योंकि ये बिंदु $ \dfrac{\pi}{4} $ के विषम गुणक होते हैं। इन बिंदुओं पर काल्पकिक भाग $ \cos 2 x $ और $ -\sin 2 x $ भी संयुग्मी शर्त को संतुष्ट नहीं करेंगे।
-
विकल्प (c) $ x = 0 $: यदि $ x = 0 $, तो $ \sin x = 0 $ और $ \cos x = 1 $.
इसके फलस्वरूप $ z = 0 + i \cos 0 = i $ और $ \bar{z} = 0 - i \cos 0 = -i $ होंगे।
हालांकि, $ \bar{z} $ के $ \cos x - i \sin 2x $ के बराबर होने के लिए $ \cos x $ और $ \sin 2x $ दिए गए शर्तों को संतुष्ट करना चाहिए, जो $ x = 0 $ के लिए संतुष्ट नहीं होते हैं।
36. व्यंजक $\dfrac{1-i \sin \alpha}{1+2 i \sin \alpha}$ के लिए वास्तविक मान $\alpha$ के लिए जो व्यंजक शुद्ध वास्तविक हो उसके लिए है
(a) $(n+1) \dfrac{\pi}{2}$
(b) $(2 n+1) \dfrac{\pi}{2}$
(c) $n \pi$
(d) इनमें से कोई नहीं
जहां, $n \in N$
उत्तर दिखाएं
सोचने की प्रक्रिया
पहले, दिए गए व्यंजक को $a +ib$ रूप में बदलें और फिर जांच करें कि कौन सा जटिल संख्या $a +ib$ शुद्ध वास्तविक हो।
हल
विकल्प (c) दिया गया व्यंजक, $z=\dfrac{1-i \sin \alpha}{1+2 i \sin \alpha}$
$ \begin{aligned} & =\dfrac{(1-i \sin \alpha)(1-2 i \sin \alpha)}{(1+2 i \sin \alpha)(1-2 i \sin \alpha)} \\ \\ & =\dfrac{1-i \sin \alpha-2 i \sin \alpha+2 i^{2} \sin ^{2} \alpha}{1-4 i^{2} \sin ^{2} \alpha} \\ \\ & =\dfrac{1-3 i \sin \alpha-2 \sin ^{2} \alpha}{1+4 \sin ^{2} \alpha} \\ \\ & =\dfrac{1-2 \sin ^{2} \alpha}{1+4 \sin ^{2} \alpha}-\dfrac{3 i \sin \alpha}{1+4 \sin ^{2} \alpha}
\end{aligned} $
दिया गया है कि $z$ एक शुद्ध वास्तविक संख्या है।
$\therefore \ \dfrac{-3 \sin \alpha}{1+4 \sin ^{2} \alpha} =0 $
$\Rightarrow \ -3 \sin \alpha =0 \Rightarrow \sin \alpha=0 $
$\quad \alpha =n \pi$
-
विकल्प (a) $(n+1) \dfrac{\pi}{2}$: यह विकल्प इस बात की सुचारु रूप से अनुमति देता है कि $\alpha$ के रूप में $(n+1) \dfrac{\pi}{2}$ हो। इन मानों के लिए $\sin \alpha$ 1 या -1 हो सकता है, जो शर्त $\sin \alpha = 0$ को संतुष्ट नहीं करता है। अतः व्यंजक $\dfrac{1-i \sin \alpha}{1+2 i \sin \alpha}$ शुद्ध वास्तविक नहीं होगा।
-
विकल्प (b) $(2 n+1) \dfrac{\pi}{2}$: यह विकल्प इस बात की सुचारु रूप से अनुमति देता है कि $\alpha$ के रूप में $(2 n+1) \dfrac{\pi}{2}$ हो। इन मानों के लिए $\sin \alpha$ 1 या -1 हो सकता है, जो शर्त $\sin \alpha = 0$ को संतुष्ट नहीं करता है। अतः व्यंजक $\dfrac{1-i \sin \alpha}{1+2 i \sin \alpha}$ शुद्ध वास्तविक नहीं होगा।
-
विकल्प (d) इनमें से कोई नहीं: यह विकल्प गलत है क्योंकि वास्तव में $\alpha$ के एक सही मान है जो व्यंजक को शुद्ध वास्तविक बनाता है, जो कि $\alpha = n \pi$ है जैसा कि समाधान में दिखाया गया है।
37. यदि $z=x +iy$ तीसरे चतुर्थांश में स्थित है, तो $\dfrac{\bar{z}}{z}$ भी तीसरे चतुर्थांश में स्थित होगा, यदि
(a) $x>y>0$
(b) $x<y<0$
(c) $y<x<0$
(d) $y>x>0$
उत्तर दिखाएं
समाधान
विकल्प (b) दिया गया है कि, $z=x+i y$ तीसरे चतुर्थांश में स्थित है।
$ x<0 \ \text { और } \ y<0 \text {. } $
अब, $\quad \dfrac{\bar{z}}{z}=\dfrac{x-i y}{x+i y}=\dfrac{(x-i y)(x-i y)}{(x+i y)(x-i y)}=\dfrac{x^{2}-y^{2}-2 i x y}{x^{2}+y^{2}}$
$ \dfrac{\bar{z}}{z}=\dfrac{x^{2}-y^{2}}{x^{2}+y^{2}}-\dfrac{2 i x y}{x^{2}+y^{2}} $
क्योंकि, $\dfrac{\bar{z}}{z}$ भी तीसरे चतुर्थांश में स्थित है।
$\therefore \quad \dfrac{x^{2}-y^{2}}{x^{2}+y^{2}}<0 \ \text { और } \ \dfrac{-2 x y}{x^{2}+y^{2}}<0 $
$x^{2}-y^{2}<0 \ \text { और } \ -2 x y<0 $
$\Rightarrow x^{2}<y^{2} \ \text { और } \ x y>0 $
$\text { इसलिए, } x<y<0$
-
विकल्प (a) $x>y>0$: यह विकल्प गलत है क्योंकि यदि $x$ और $y$ दोनों धनात्मक होते हैं, तो $z = x + iy$ पहले चतुर्थांश में स्थित होता, न कि तीसरे चतुर्थांश में। $z$ के तीसरे चतुर्थांश में स्थित होने के लिए, $x$ और $y$ दोनों नकारात्मक होना चाहिए।
-
विकल्प (c) $y<x<0$: यह विकल्प गलत है क्योंकि यह वही बताता है कि $x$ और $y$ दोनों नकारात्मक हैं (जिससे $z$ तीसरे चतुर्थांश में आता है), लेकिन इसकी शर्त $x^2 < y^2$ को संतुष्ट नहीं करता। यदि $y < x < 0$, तो $|y| > |x|$ होता है, जिसका अर्थ है $y^2 > x^2$, जो शर्त $x^2 < y^2$ के विपरीत है।
-
विकल्प (d) $y>x>0$: यह विकल्प गलत है क्योंकि यदि $x$ और $y$ दोनों धनात्मक हैं, तो $z = x + iy$ पहले चतुर्थांश में आता है, न कि तीसरे चतुर्थांश में। तीसरे चतुर्थांश में $z$ के लिए $x$ और $y$ दोनों नकारात्मक होना चाहिए।
38. $(z+3)(\bar{z}+3)$ का मान बराबर है
(a) $|z+3|^{2}$
(b) $|z-3|$
(c) $z^{2}+3$
(d) इनमें से कोई नहीं
उत्तर दिखाएं
हल
विकल्प (a) दिया गया है, $(z+3)(\bar{z}+3)$
मान लीजिए $z = x + iy$ और $\bar{z} = x - iy$
$\therefore \quad (z+3)(\bar{z}+3) = (x + iy + 3)(x - iy + 3)$
$= (x+3)^{2} - (iy)^{2}$
$= (x+3)^{2} + y^{2}$
$= |x+3 + iy|^{2} = |z+3|^{2}$
-
विकल्प (b) $|z-3|$: यह विकल्प गलत है क्योंकि व्यंजक $(z+3)(\bar{z}+3)$ में $z$ और 3 के योग का उल्लेख है, न कि अंतर। माप $|z-3|$ कम्प्लेक्स समतल में $z$ और 3 के बीच की दूरी को दर्शाता है, जो दिए गए व्यंजक से संबंधित नहीं है।
-
विकल्प (c) $z^{2}+3$: यह विकल्प गलत है क्योंकि व्यंजक $(z+3)(\bar{z}+3)$ में $z+3$ और उसके संयुग्मी के गुणन का उल्लेख है, जो एक वास्तविक संख्या होती है। व्यंजक $z^2 + 3$ संयुग्मी को ध्यान में नहीं लेता है और इसका रूप $(z+3)(\bar{z}+3)$ के समान नहीं होता।
-
विकल्प (d) इनमें से कोई नहीं: यह विकल्प गलत है क्योंकि सही उत्तर विकल्प (a) में दिया गया है, जो $|z+3|^2$ है। अतः “इनमें से कोई नहीं” लागू नहीं होता।
39. यदि $\left(\dfrac{1+i}{1-i}\right)^{x}=1$, तो
(a) $x=2 n+1$
(b) $x=4 n$
(c) $x=2 n$
(d) $x=4 n+1$
जहाँ, $n \in N$
उत्तर दिखाएं
हल
विकल्प (b) दिया गया है, $ \ \left(\dfrac{1+i}{1-i}\right)^{x}=1$
$\Rightarrow \left[\dfrac{(1+i)(1+i)}{(1-i)(1+i)}\right]^x =1 $
$\Rightarrow \left[{\dfrac{1+2 i+i^{2}}{1-i^{2}}}\right]^{x}=1 $
$\Rightarrow \left[\dfrac{2 i}{1+1}\right]^{x} =1 $
$\Rightarrow \left[\dfrac{2 i}2\right]^{x}=1$
$\Rightarrow i^{x} =1 \Rightarrow i^{x}=(i^{4 n}) $
$\Rightarrow x =4 n \ $ जहाँ, $n \in N$
-
विकल्प (a) $ x = 2n + 1 $: यह विकल्प गलत है क्योंकि $ i^{2n+1} $ सभी प्राकृतिक संख्या $ n $ के लिए 1 नहीं होता। $ i $ के घातें प्रत्येक चार शब्दों के बाद $ i, -1, -i, 1 $ के चक्र में चलती हैं। $ i^{2n+1} $ के लिए परिणाम या तो $ i $ या $ -i $ होता है, नहीं 1।
-
विकल्प (c) $ x = 2n $: यह विकल्प गलत है क्योंकि $ i^{2n} $ सभी प्राकृतिक संख्या $ n $ के लिए 1 नहीं होता। $ i $ के घातें प्रत्येक चार शब्दों के बाद $ i, -1, -i, 1 $ के चक्र में चलती हैं। $ i^{2n} $ के लिए परिणाम या तो $ 1 $ या $ -1 $ होता है, नहीं सांतर्गत 1।
-
विकल्प (d) $ x = 4n + 1 $: यह विकल्प गलत है क्योंकि $ i^{4n+1} $ सभी प्राकृतिक संख्या $ n $ के लिए 1 नहीं होता। $ i $ के घातें प्रत्येक चार शब्दों के बाद $ i, -1, -i, 1 $ के चक्र में चलती हैं। $ i^{4n+1} $ के लिए परिणाम $ i $ होता है, नहीं 1।
40. $A$ वास्तविक मान $x$ समीकरण $\left(\dfrac{3-4 i x}{3+4 i x}\right)=\alpha-i \beta \ (\alpha, \beta \in R)$ को संतुष्ट करता है, यदि $\alpha^{2}+\beta^{2}=$
(a) $1$
(b) $-1$
(c) $2$
(d) $-2$
उत्तर दिखाएं
हल
विकल्प (a) दिया गया समीकरण, $\left(\dfrac{3-4 i x}{3+4 i x}\right)=\alpha-i \beta(\alpha, \beta \in R)$
$\text { अब, } (\alpha-i \beta)=\dfrac{(3-4 i x)(3-4 i x)}{(3+4 i x)(3-4 i x)}=\dfrac{9+16 i^{2} x^{2}-24 i x}{9-16 i^{2} x^{2}} $
$\Rightarrow \alpha-i \beta=\dfrac{9-16 x^{2}-24 i x}{9+16 x^{2}} $
$\Rightarrow \alpha-i \beta=\dfrac{9-16 x^{2}}{9+16 x^{2}}-\dfrac{i 24 x}{9+16 x^{2}} \quad \ldots (i)$
$\therefore \ \alpha+i \beta=\dfrac{9-16 x^{2}}{9+16 x^{2}}+\dfrac{i 24 x}{9+16 x^{2}} \quad \ldots (ii)$
इसलिए, $ \ (\alpha -i \beta)(\alpha +i \beta) = \left(\dfrac{9-16x^2}{9+16x^2}- i \dfrac{24x}{9+16x^2}\right) \left( \dfrac{9-16x^2}{9+16x^2}+i \dfrac{24x}{9+16x^2}\right)$
$\alpha ^2+ \beta ^2 = \left(\dfrac{9-16x^2}{9+16x^2}\right)^2+ \left(\dfrac{24x}{9+16x^2}\right)^2$
$= \dfrac{(9-16x^2)^2+(24x)^2}{(9+16x^2)^2}$
$= \dfrac{81+256x^4+288x^2}{(9+16x^2)^2}$
$\alpha ^2+ \beta ^2 = \dfrac{(9+16x^2)^2}{(9+16x^2)^2} =1$
-
विकल्प (b) $-1$: अभिव्यक्ति $\alpha^2 + \beta^2$ एक समिश्र संख्या के वास्तविक और काल्पनिक भाग के वर्गों का योग दर्शाती है। यह योग हमेशा गैर-ऋणात्मक होता है क्योंकि यह समिश्र संख्या के परिमाण के वर्ग होता है। अतः, $\alpha^2 + \beta^2$ नकारात्मक नहीं हो सकता, इसलिए $-1$ एक संभव मान नहीं है।
-
विकल्प (c) $2$: समाधान में दिखाए गए गणना से पता चलता है कि $\alpha^2 + \beta^2$ सरलीकृत करने पर $1$ हो जाता है। कोई बीजगणितीय अपवाद या $x$ के कोई मान इस परिणाम को $2$ बनाने में सक्षम नहीं हो सकते। अतः, $2$ $\alpha^2 + \beta^2$ के सही मान नहीं है।
-
विकल्प (d) $-2$: विकल्प (b) के समान रूप से, $\alpha^2 + \beta^2$ हमेशा गैर-ऋणात्मक होता है क्योंकि यह एक समिश्र संख्या के परिमाण के वर्ग को दर्शाता है। अतः, यह नकारात्मक नहीं हो सकता, इसलिए $-2$ एक संभव मान नहीं है।
41. किसी दो समिश्र संख्याओं $z_1$ और $z_2$ के लिए निम्नलिखित में से कौन सा सही है?
(a) $|z_1 z_2|=|z_1||z_2|$
(b) $\arg (z_1 z_2)=\arg (z_1) \cdot \arg (z_2)$
(c) $|z_1+z_2|=|z_1|+|z_2|$
(d) $|z_1+z_2| \geq|z_1|-|z_2|$
उत्तर दिखाएं
समाधान
विकल्प (a) मान लीजिए $z_1=r_1(\cos \theta_1+i \sin \theta_1)$
$\Rightarrow \quad|z_1|=r_1 \quad \ldots (i)$
और $z_2=r_2(\cos \theta_2+i \sin \theta_2)$
$\Rightarrow \quad|z_2|=r_2 \quad \ldots (ii)$
अब, $\quad z_1 z_2=r_1 r_2[\cos \theta_1 \cos \theta_2+i \sin \theta_1 \cos \theta_2+i \cos \theta_1 \sin \theta_2+i^{2} \sin \theta_1 \sin \theta_2]$ $=r_1 r_2[\cos (\theta_1+\theta_2)+i \sin (\theta_1+\theta_2)]$
$\Rightarrow \quad|z_1 z_2|=r_1 r_2$
$\therefore \quad|z_1 z_2|=|z_1||z_2| \qquad$ [समीकरण (i) और (ii) का उपयोग करते हुए]
-
विकल्प (b) $\arg (z_1 z_2)=\arg (z_1) \cdot \arg (z_2)$: दो समिश्र संख्याओं के गुणन के कोण दोनों कोणों के योग के बराबर होता है, न कि गुणन के बराबर। अतः, $\arg (z_1 z_2) = \arg (z_1) + \arg (z_2)$, न कि $\arg (z_1) \cdot \arg (z_2)$।
-
विकल्प (c) $|z_1+z_2|=|z_1|+|z_2|$: दो सम复 संख्याओं के योग के परिमाण के लिए आवश्यक रूप से उनके परिमाणों के योग के बराबर नहीं होता। वास्तव में, $|z_1+z_2| \leq |z_1| + |z_2|$ त्रिभुज असमानता के द्वारा होता है।
-
विकल्प (d) $|z_1+z_2| \geq|z_1|-|z_2|$: दो सम复 संख्याओं के योग के परिमाण के संबंध में सही असमानता $|z_1+z_2| \leq |z_1| + |z_2|$ होती है। दिए गए असमानता $|z_1+z_2| \geq |z_1| - |z_2|$ हमेशा सत्य नहीं होती।
42. सम复 संख्या $(2-i)$ द्वारा प्रस्तुत बिंदु को मूल बिंदु के चारों ओर $\dfrac{\pi}{2}$ कोण के घड़ी के विपरीत दिशा में घुमाया जाता है, तो बिंदु की नई स्थिति होगी
(a) $1+2i$
(b) $-1-2i$
(c) $2+i$
(d) $-1+2i$
उत्तर दिखाएं
सोचने की प्रक्रिया
यहाँ, $z<\alpha$ एक सम复 संख्या है, जहाँ परिमाण $r$ और त्रिज्या $(\theta+\alpha)$ है। यदि $P(z)$ घड़ी के विपरीत दिशा में कोण $\boldsymbol{\alpha}$ द्वारा घुमाया जाता है, तो इसकी नई स्थिति $z(\boldsymbol{\theta}-i \boldsymbol{\alpha})$ होगी।
हल
विकल्प (b) दिया गया है, $z=2-i$
इसे मूल बिंदु के चारों ओर $\dfrac{\pi}{2}$ कोण के घड़ी के विपरीत दिशा में घुमाया जाता है
$\therefore \quad$ नई स्थिति $=z e^{-i \pi / 2}=(2-i) e^{-i \pi / 2}$
$ \begin{aligned} & =(2-i) \left[\cos \left(\dfrac{-\pi}{2}\right)+i \sin \left(\dfrac{-\pi}{2}\right)\right]=(2-i)[0-i] \\ \\ & =-2 i-1=-1-2 i \end{aligned} $
-
विकल्प (a) $1+2i$: यह विकल्प गलत है क्योंकि सम复 संख्या $(2-i)$ को $\dfrac{\pi}{2}$ कोण के घड़ी के विपरीत दिशा में घुमाने पर एक सम复 संख्या जो ऋणात्मक वास्तविक भाग और ऋणात्मक काल्पकिक भाग के साथ होनी चाहिए, न कि धनात्मक वास्तविक भाग और धनात्मक काल्पकिक भाग के साथ।
-
विकल्प (c) $2+i$: यह विकल्प गलत है क्योंकि सम复 संख्या $(2-i)$ को $\dfrac{\pi}{2}$ कोण के घड़ी के विपरीत दिशा में घुमाने पर एक सम复 संख्या जो दोनों वास्तविक और काल्पकिक भाग ऋणात्मक होनी चाहिए, न कि धनात्मक वास्तविक भाग और धनात्मक काल्पकिक भाग के साथ।
-
विकल्प (d) $-1+2i$: यह विकल्प गलत है क्योंकि सम复 संख्या $(2-i)$ को $\dfrac{\pi}{2}$ कोण के घड़ी के विपरीत दिशा में घुमाने पर एक सम复 संख्या जो दोनों वास्तविक और काल्पकिक भाग ऋणात्मक होनी चाहिए, न कि ऋणात्मक वास्तविक भाग और धनात्मक काल्पकिक भाग के साथ।
43. यदि $x, y \in R$, तो $x+i y$ एक अ-वास्तविक समिश्र संख्या होगी, यदि
(a) $x=0$
(b) $y=0$
(c) $x \neq 0$
(d) $y \neq 0$
उत्तर दिखाएं
हल
विकल्प (d) दिया गया है कि, $x, y \in R$
तब, $x+i y$ अ-वास्तविक समिश्र संख्या होगी यदि और केवल यदि $y \neq 0$।
-
विकल्प (a) x=0 : यदि $x=0,$ तो समिश्र संख्या $iy$ बन जाती है। संख्या अ-वास्तविक होगी यदि $y \neq 0$। यह विकल्प $x+iy$ के अ-वास्तविक होने की गारंटी नहीं देता बिना $y \neq 0$ के।
-
विकल्प (b) $y=0$ : यदि $y=0,$ तो समिश्र संख्या $x$ बन जाती है। इसका अर्थ है कि यह एक वास्तविक संख्या है। यह विकल्प एक अ-वास्तविक समिश्र संख्या नहीं देता।
-
विकल्प (c) $x \neq 0$: यदि $x \neq 0,$ तो समिश्र संख्या अभी भी वास्तविक हो सकती है यदि $y=0$। यह विकल्प अकेले संख्या के अ-वास्तविक होने की गारंटी नहीं देता।
44. यदि $a+i b=c+i d$, तो
(a) $a^{2}+c^{2}=0$
(b) $b^{2}+c^{2}=0$
(c) $b^{2}+d^{2}=0$
(d) $a^{2}+b^{2}=c^{2}+d^{2}$
उत्तर दिखाएं
चिंतन प्रक्रिया
दो समिश्र संख्याएँ $z_1=x_1+i y_1$ और $z_2=x_2+i y_2$ बराबर होती हैं, तो
$ |z_1|=|z_2| \Rightarrow \sqrt{x_1^{2}+y_1^{2}}=\sqrt{x_2^{2}+y_2^{2}} $
हल
विकल्प (d) दिया गया है कि,
$a+i b=c+i d $
$\Rightarrow |a+i b|=|c+i d| $
$\Rightarrow \sqrt{a^{2}+b^{2}}=\sqrt{c^{2}+d^{2}}$
दोनों ओर वर्ग करने पर हम प्राप्त करते हैं
$ a^{2}+b^{2}=c^{2}+d^{2} $
-
विकल्प (a) $a^{2}+c^{2}=0$ गलत है क्योंकि इसका अर्थ है कि $a$ और $c$ दोनों शून्य होंगे, जो समीकरण $a + i b = c + i d$ के अनुसार आवश्यक नहीं है।
-
विकल्प (b) $b^{2}+c^{2}=0$ गलत है क्योंकि इसका अर्थ है कि $b$ और $c$ दोनों शून्य होंगे, जो समीकरण $a + i b = c + i d$ के अनुसार आवश्यक नहीं है।
-
विकल्प (c) $b^{2}+d^{2}=0$ गलत है क्योंकि इसका अर्थ है कि $b$ और $d$ दोनों शून्य होंगे, जो समीकरण $a + i b = c + i d$ के अनुसार आवश्यक नहीं है।
45. वह समिश्र संख्या $z$ जो शर्त $\left|\dfrac{i+z}{i-z}\right|=1$ को संतुष्ट करती है, निम्नलिखित में से किस पर स्थित होती है?
(a) वृत्त $x^{2}+y^{2}=1$
(b) $X$-अक्ष
(c) $Y$-अक्ष
(d) रेखा $x+y=1$
उत्तर दिखाएं
हल
विकल्प (b) दिया गया है, $ \ \left|\dfrac{i+z}{i-z}\right|=1$
मान लीजिए $z = x+iy$
$ \begin{aligned} & \therefore \quad \left|\dfrac{x+i(y+1)}{-x-i(y-1)}\right|=1 \\ \\ & \Rightarrow \quad \dfrac{x^{2}+(y+1)^{2}}{x^{2}+(y-1)^{2}}=1 \\ \\ & \Rightarrow \quad x^{2}+(y+1)^{2}=x^{2}+(y-1)^{2} \\ \\ & \Rightarrow \quad 4 y=0 \Rightarrow y=0 \end{aligned} $
इसलिए, $z$ $X$-अक्ष (वास्तविक अक्ष) पर स्थित है।
-
विकल्प (a) वृत्त $x^{2}+y^{2}=1$: यह विकल्प गलत है क्योंकि शर्त $\left|\dfrac{i+z}{i-z}\right|=1$ सरलता से $y=0$ बनती है, जिसका अर्थ है कि $z$ वास्तविक अक्ष पर स्थित है। वृत्त $x^{2}+y^{2}=1$ पर बिंदु आमतौर पर शून्य नहीं होते हैं, बल्कि बिंदु $(1,0)$ और $(-1,0)$ के अलावा। हालांकि, दी गई शर्त $x$ को $\pm 1$ तक सीमित नहीं करती है, इसलिए वृत्त पर सभी बिंदु शर्त को संतुष्ट नहीं करते हैं।
-
विकल्प (c) $Y$-अक्ष: यह विकल्प गलत है क्योंकि शर्त $\left|\dfrac{i+z}{i-z}\right|=1$ सरलता से $y=0$ बनती है, जिसका अर्थ है कि $z$ वास्तविक अक्ष पर स्थित है। $Y$-अक्ष पर बिंदु $x=0$ और शून्य नहीं होते हैं, जो शर्त $y=0$ के विरोधाभास है।
-
विकल्प (d) रेखा $x+y=1$: यह विकल्प गलत है क्योंकि शर्त $\left|\dfrac{i+z}{i-z}\right|=1$ सरलता से $y=0$ बनती है, जिसका अर्थ है कि $z$ वास्तविक अक्ष पर स्थित है। रेखा $x+y=1$ पर बिंदु आमतौर पर शून्य नहीं होते हैं, बल्कि बिंदु $(1,0)$ के अलावा। हालांकि, दी गई शर्त $x$ को 1 तक सीमित नहीं करती है, इसलिए रेखा पर सभी बिंदु शर्त को संतुष्ट नहीं करते हैं।
46. यदि $z$ एक सम复 संख्या है, तो
(a) $|z^{2}|>|z|^2$
(b) $|z^{2}|=|z|^{2}$
(c) $|z^{2}|<|z|^{2}$
(d) $|z^{2}| \geq|z|^{2}$
उत्तर दिखाएं
हल
विकल्प (b) यदि $z$ एक समपद संख्या है, तो $z=x+i y$
$ \begin{aligned} & |z|=|x+i y| \text { और }|z|^{2}=|x+i y|^{2} \\ \\ & \Rightarrow \quad|z|^{2}=x^{2}+y^{2} \quad \ldots (i)\\ \\ `
$$ \begin{aligned} & \text{ और } \quad z^{2}=(x+i y)^{2}=x^{2}+i^{2} y^{2}+i 2 x y \\ \\ & z^{2}=x^{2}-y^{2}+i 2 x y \\ \\ & \Rightarrow \quad|z^{2}|=\sqrt{(x^{2}-y^{2})^{2}+(2 x y)^{2}} \\ \\ & \Rightarrow \quad|z^{2}|=\sqrt{x^{4}+y^{4}-2 x^{2} y^{2}+4 x^{2} y^{2}} \\ \\ & \Rightarrow \quad|z^{2}|=\sqrt{x^{4}+y^{4}+2 x^{2} y^{2}}=\sqrt{(x^{2}+y^{2})^{2}} \\ \\ & \Rightarrow \quad|z^{2}|=x^{2}+y^{2} \quad \ldots (ii) \end{aligned} $$
समीकरण (i) और (ii) से,
$$ |z|^{2}=|z^{2}| $$
-
विकल्प (a) $|z^{2}|>|z|$: यह विकल्प गलत है क्योंकि $ z^2 $ के मापदंड के मान $ z $ के मापदंड के वर्ग के बराबर होता है। विशेष रूप से, $ |z^2| = |z|^2 $. क्योंकि $ |z|^2 $ आवश्यक रूप से $ |z| $ से अधिक नहीं हो सकता है (यह बराबर या कम हो सकता है, जो $ |z| $ के मान पर निर्भर करता है), इस कथन के अनुसार यह गलत है।
-
विकल्प (c) $|z^{2}|<|z|^{2}$: यह विकल्प गलत है क्योंकि, जैसा कि निर्मित किया गया है, $ |z^2| = |z|^2 $. इसलिए, $ |z^2| $ ठीक $ |z|^2 $ के बराबर होता है, न कि इससे कम होता है।
-
विकल्प (d) $|z^{2}| \geq|z|^{2}$: यह विकल्प गलत है क्योंकि यह इंगित करता है कि $ |z^2| $ $ |z|^2 $ से अधिक हो सकता है। हालांकि, जैसा कि दिखाया गया है, $ |z^2| = |z|^2 $, इसलिए सही संबंध समानता है, न कि असमानता है।
47. $|z_1+z_2|=|z_1|+|z_2|$ संभव हो सकता है, यदि
(a) $z_2=\bar{z}_1$
(b) $z_2=\dfrac{1}{z_1}$
(c) $\arg (z_1)=\arg (z_2)$
(d) $|z_1|=|z_2|$
उत्तर दिखाएं
हल
विकल्प (c) दिया गया है कि, $ \ |z_1+z_2|=|z_1|+|z_2| \quad \ldots (i)$
मान, $z_1= r_1(\cos \theta _1 + i \sin \theta _1)$
और $z_2 = r_2(\cos \theta _2 + i \sin \theta _2)$
अब, $|z_1|=r_1$ और $|z_2|=r_2 \quad \ldots (ii)$
$\text{arg}|z_1|= \theta _1$ और $\text{arg}|z_2|= \theta _2 \quad \ldots (iii)$
$\therefore$ समीकरण (i) से $\ |r_1(\cos \theta_1+i \sin \theta_1)+r_2(\cos \theta_2+i \sin \theta_2)|=|r_1(\cos \theta_1+i \sin \theta_1)| +|r_2(\cos \theta_2+i \sin \theta_2)|$
$\Rightarrow \ |(r_1 \cos \theta _1 + r_2 \cos \theta _2)+ i (r_1 \sin \theta _1+r_2 \sin \theta _2)| = r_1+r_2 \quad $ [समीकरण (ii) का उपयोग करते हुए]
$\Rightarrow \ \sqrt{r_1^2 \cos ^2 \theta _1+ r_2^2 \cos^2 \theta _2 +2r_1 r_2 \cos \theta _1 \cos \theta _2 + r_1^2 \sin ^2 \theta _1+ r_2^2 \sin ^2 \theta _2 + 2r_1r_2 \sin \theta _1 \sin \theta _2} = r_1+r_2$
$\Rightarrow \ \sqrt{r_1^2+r_2^2+2r_1r_2 [\cos \theta _1 \cos \theta _2 + \sin \theta _1 \sin \theta _2]} = r_1+r_2$
$\Rightarrow \ \sqrt{r_1^2+r_2^2+2r_1r_2 \cos (\theta _1 - \theta _2)} = r_1+r_2$
दोनों ओर वर्ग करने पर, हम प्राप्त करते हैं
$ \begin{aligned} & r_1^{2}+r_2^{2}+2 r_1 r_2 \cos (\theta_1-\theta_2)=r_1^{2}+r_2^{2}+2 r_1 r_2 \\ \\ \Rightarrow & \ 2 r_1 r_2[1-\cos (\theta_1-\theta_2)] =0 \\ \\ \Rightarrow & \ 1-\cos (\theta_1-\theta_2) =0 \\ \\ \Rightarrow & \ \cos (\theta_1-\theta_2) =1 \\ \\ \Rightarrow & \ \cos (\theta_1-\theta_2) =\cos 0^{\circ} \\ \\ \Rightarrow & \ \theta_1-\theta_2 =0^{\circ} \\ \\ \Rightarrow & \ \theta_1 =\theta_2 \\ \\ \therefore & \ \arg (z_1) =\arg (z_2) \quad [\text{समीकरण (iii) का उपयोग करते हुए}] \end{aligned} $
-
विकल्प (a) $z_2=\bar{z}_1$: यह विकल्प गलत है क्योंकि यदि $ z_2 = \bar{z}_1 $, तो $ z_1 + z_2 $ एक वास्तविक संख्या होगी (क्योंकि $ z_1 + \bar{z}_1 $ वास्तविक होता है)। हालांकि, $ |z_1| $ और $ |z_2| $ के मापदंड आमतौर पर $ |z_1 + z_2| $ के मापदंड के बराबर नहीं होंगे, बिना $ z_1 $ केवल काल्पक्ति हो, जो एक सामान्य मामला नहीं है।
-
विकल्प (b) $z_2=\dfrac{1}{z_1}$: यह विकल्प गलत है क्योंकि यदि $ z_2 = \dfrac{1}{z_1} $, तो $ z_1 z_2 = 1 $ होगा। $ |z_1| $ और $ |z_2| $ के मापदंड $ |z_1| \cdot |z_2| = 1 $ को संतुष्ट करेंगे, लेकिन यह बताता नहीं कि $ |z_1 + z_2| = |z_1| + |z_2| $ होगा। समान दिशा में (अर्थात, समान तर्क) होने पर $ |z_1 + z_2| = |z_1| + |z_2| $ के समान रहता है, जो $ z_2 = \dfrac{1}{z_1} $ द्वारा निश्चित नहीं किया जाता है।
-
विकल्प (d) $|z_1|=|z_2|$: यह विकल्प गलत है क्योंकि समान मापदंड $ |z_1| = |z_2| $ के कारण $ |z_1 + z_2| = |z_1| + |z_2| $ आवश्यक रूप से नहीं होता। $ |z_1 + z_2| = |z_1| + |z_2| $ के लिए $ z_1 $ और $ z_2 $ समान दिशा में होना आवश्यक है (अर्थात, समान तर्क), जो केवल समान मापदंड के कारण निश्चित नहीं होता।
48. ऐसे वास्तविक मान $\theta$ का वास्तविक मान ज्ञात कीजिए जिसके लिए व्यंजक $\dfrac{1+i \cos \theta}{1-2 i \cos \theta}$ एक वास्तविक संख्या हो।
(a) $n \pi+\dfrac{\pi}{4}$
(b) $n \pi+(-1)^{n} \dfrac{\pi}{4}$
(c) $2 n \pi \pm \dfrac{\pi}{2}$
(d) इनमें से कोई नहीं
उत्तर दिखाएं
हल
विकल्प (c) दिया गया व्यंजक $=\dfrac{1+i \cos \theta}{1-2 i \cos \theta}=\dfrac{(1+i \cos \theta)(1+2 i \cos \theta)}{(1-2 i \cos \theta)(1+2 i \cos \theta)}$
$ \begin{aligned} & =\dfrac{1+i \cos \theta+2 i \cos \theta+2 i^{2} \cos ^{2} \theta}{1-4 i^{2} \cos ^{2} \theta} \\ \\ & =\dfrac{1+3 i \cos \theta-2 \cos ^{2} \theta}{1+4 \cos ^{2} \theta} \end{aligned} $
वास्तविक मान $\theta$ के लिए $\dfrac{3 \cos \theta}{1+4 \cos ^{2} \theta}=0$
$\Rightarrow 3 \cos \theta =0 $
$\Rightarrow \cos \theta =\cos \dfrac{\pi}{2}$
$\Rightarrow \theta =2 n \pi \pm \dfrac{\pi}{2}$
-
विकल्प (a): $n \pi+\dfrac{\pi}{4}$ गलत है क्योंकि इसका अर्थ है कि $\cos \theta = \cos \left(n \pi + \dfrac{\pi}{4}\right)$. हालांकि, $\cos \left(n \pi + \dfrac{\pi}{4}\right)$ कोई भी पूर्णांक $n$ के लिए शून्य नहीं होता, जो दिए गए व्यंजक के वास्तविक होने की आवश्यकता के विरोधाभास है।
-
विकल्प (b): $n \pi+(-1)^{n} \dfrac{\pi}{4}$ गलत है क्योंकि इसका अर्थ है कि $\cos \theta = \cos \left(n \pi + (-1)^n \dfrac{\pi}{4}\right)$. विकल्प (a) के जैसे, $\cos \left(n \pi + (-1)^n \dfrac{\pi}{4}\right)$ कोई भी पूर्णांक $n$ के लिए शून्य नहीं होता, जो आवश्यकता $\cos \theta = 0$ की उपेक्षा करता है।
-
विकल्प (d): इनमें से कोई नहीं गलत है क्योंकि एक सही विकल्प दिया गया है, जो विकल्प (c) है। दिए गए व्यंजक के वास्तविक होने के लिए $\theta$ का सही मान वास्तविक रूप से $2 n \pi \pm \dfrac{\pi}{2}$ है।
49. जब $x<0$ हो तो $\arg (x)$ का मान है:
(a) 0
(b) $\dfrac{\pi}{2}$
(c) $\pi$
(d) इनमें से कोई नहीं
उत्तर दिखाएं
हल
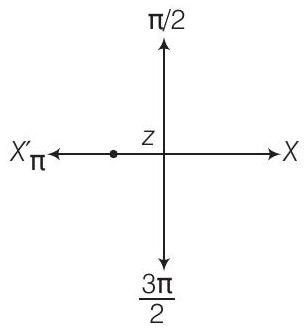
विकल्प (c) मान लीजिए $ \ z =x+i(0) \text { और } x<0 $
$\text{arg}(z) = \tan^{-1} \left(\dfrac{y}{x}\right)$
$\qquad = \tan^{-1} \left(\dfrac{0}{x}\right)$
$\qquad = \tan^{-1} (0)$
यदि $x <0,$ तो $\text{arg}(z)$ का मान $ \pi $ होता है क्योंकि संख्या नकारात्मक वास्तविक अक्ष पर स्थित होती है।
-
विकल्प (a) 0: यह गलत है क्योंकि एक नकारात्मक वास्तविक संख्या का त्रिकोणमितीय तर्क 0 नहीं होता। त्रिकोणमितीय तर्क 0 वास्तविक अक्ष के धनात्मक ओर स्थित धनात्मक वास्तविक संख्याओं को संबोधित करता है।
-
विकल्प (b) $\dfrac{\pi}{2}$: यह गलत है क्योंकि त्रिकोणमितीय तर्क $\dfrac{\pi}{2}$ धनात्मक काल्पकिक अक्ष पर शुद्ध काल्पकिक संख्याओं को संबोधित करता है, नकारात्मक वास्तविक संख्याओं को नहीं।
-
विकल्प (d) इनमें से कोई नहीं: यह गलत है क्योंकि एक सही विकल्प उपलब्ध है, जो (c) $\pi$ है। एक नकारात्मक वास्तविक संख्या का त्रिकोणमितीय तर्क वास्तविक रूप से $\pi$ होता है।
50. यदि $f(z)=\dfrac{7-z}{1-z^{2}}$, जहाँ $z=1+2 i$, तो $|f(z)|$ है
(a) $\dfrac{|z|}{2}$
(b) $|z|$
(c) $2 |z|$
(d) इनमें से कोई नहीं
उत्तर दिखाएं
हल
विकल्प (a)
$ \begin{aligned} \text{मान लीजिए } \quad z & =1+2 i \\ \\ \Rightarrow \quad |z| & =\sqrt{1+4}=\sqrt{5} \\ \\ \text{अब, } \quad f(z) & =\dfrac{7-z}{1-z^{2}}=\dfrac{7-1-2 i}{1-(1+2 i)^{2}} \\ \\ & =\dfrac{6-2 i}{1-1-4 i^{2}-4 i}=\dfrac{6-2 i}{4-4 i} \\ \\ & =\dfrac{(3-i)(2+2 i)}{(2-2 i)(2+2 i)} \\ \\ & =\dfrac{6-2 i+6 i-2 i^{2}}{4-4 i^{2}}=\dfrac{6+4 i+2}{4+4} \\ \\ & =\dfrac{8+4 i}{8}=1+\dfrac{1}{2} i \\ \\ f(z) & =1+\dfrac{1}{2} i \end{aligned} $
$ \begin{aligned} & \therefore \quad|f(z)|=\sqrt{1+\dfrac{1}{4}}=\sqrt{\dfrac{4+1}{4}}=\dfrac{\sqrt{5}}{2}=\dfrac{|z|}{2} \end{aligned} $
-
विकल्प (b) $|z|$: यह विकल्प गलत है क्योंकि $ f(z) $ के परिमाण की गणना $ \dfrac{|z|}{2} $ निकलती है, न कि $ |z| $. गणना दिखाती है कि $ |f(z)| = \dfrac{\sqrt{5}}{2} $, जो $ |z| $ के आधा है।
-
विकल्प (c) $2 |z|$: यह विकल्प गलत है क्योंकि $ f(z) $ के परिमाण $ z $ के परिमाण के दोगुना नहीं होता। $ f(z) $ का सही परिमाण $ \dfrac{|z|}{2} $ होता है, न कि $ 2|z| $.
-
विकल्प (d) इनमें से कोई नहीं: इस विकल्प को सही नहीं माना जा सकता क्योंकि एक विकल्प (a) है जो $ f(z) $ के गणनात्मक मापदंड $ \dfrac{|z|}{2} $ के सही मिलान करता है। इसलिए, “इनमें से कोई नहीं” सही उत्तर नहीं है।





