ऊष्मागतिकी
बहुविकल्पीय प्रश्न (MCQs)
1. ऊष्मागतिकी किसके संबंध में नहीं है
(a) रासायनिक अभिक्रिया में ऊर्जा परिवर्तन
(b) रासायनिक अभिक्रिया कितनी दूर तक चल सकती है
(c) अभिक्रिया के चलने की दर
(d) रासायनिक अभिक्रिया की संभावना
उत्तर दिखाएं
उत्तर: (c) अभिक्रिया के चलने की दर
स्पष्टीकरण:
ऊष्मागतिकी अभिक्रिया के चलने की दर के संबंध में नहीं है। ऊष्मागतिकी ऊर्जा परिवर्तन, संभावना और अभिक्रिया के विस्तार के अध्ययन में होती है, लेकिन अभिक्रिया की दर और यह कैसे होता है इसके बारे में नहीं है।
अब, गलत विकल्पों के बारे में विचार करें:
(a) ऊष्मागतिकी रासायनिक अभिक्रिया में ऊर्जा परिवर्तन के संबंध में है क्योंकि यह अध्ययन करती है कि रासायनिक प्रक्रियाओं के दौरान ऊर्जा कैसे परिवर्तित और स्थानांतरित होती है।
(b) ऊष्मागतिकी रासायनिक अभिक्रिया कितनी दूर तक चल सकती है इसके संबंध में है क्योंकि इसमें संतुलन अवस्थाओं के अध्ययन शामिल होता है और अभिक्रिया कितनी दूर तक चल सकती है इसके बारे में जानकारी होती है।
(d) ऊषजागतिकी रासायनिक अभिक्रिया की संभावना के संबंध में है क्योंकि यह अभिक्रिया के स्वतंत्र रूप से होने की संभावना का निर्धारण करती है, जो एंथैल्पी, एंट्रॉपी और मुक्त ऊर्जा में परिवर्तन पर आधारित होती है।
2. निम्नलिखित में से कौन सा कथन सही है?
(a) एक ढके हुए बरतन में अभिकर्मक वस्तुओं की उपस्थिति एक खुले प्रणाली का उदाहरण है।
(b) एक बंद प्रणाली में प्रणाली और परिवेश के बीच ऊर्जा और पदार्थ का आदान-प्रदान होता है।
(c) एक तांबे के बने बंद बरतन में अभिकर्मकों की उपस्थिति एक बंद प्रणाली का उदाहरण है।
(d) एक थर्मोस फ्लास्क या किसी अन्य बंद आइसोलेटेड बरतन में अभिकर्मकों की उपस्थिति एक बंद प्रणाली का उदाहरण है।
उत्तर दिखाएं
उत्तर: (c) एक तांबे के बने बंद बरतन में अभिकर्मकों की उपस्थिति एक बंद प्रणाली का उदाहरण है।
स्पष्टीकरण:
एक तांबे के बने बंद बरतन में, प्रणाली और परिवेश के बीच कोई पदार्थ आदान-प्रदान नहीं होता, लेकिन ऊर्जा इसकी दीवारों के माध्यम से आदान-प्रदान हो सकती है।
उपस्थिति अभिक्रिया विषयों के एक कवर किए गए बीकर में-बंद प्रणाली और पदार्थ तथा ऊर्जा के आदान-प्रदान खुली प्रणाली। अभिकारक के उपस्थिति बंद बर्तन में-बंद प्रणाली और अभिकारक के उपस्थिति थर्मोस फ्लास्क में-अलग प्रणाली।
अब, गलत विकल्पों को ध्यान में लें:
(a) कवर किए गए बीकर में अभिक्रिया विषयों की उपस्थिति खुली प्रणाली का उदाहरण नहीं है क्योंकि कवर किए गए बीकर परिवेश के साथ पदार्थ के आदान-प्रदान को रोकता है, इसलिए यह एक बंद प्रणाली है।
(b) बंद प्रणाली में प्रणाली और परिवेश के बीच पदार्थ का आदान-प्रदान नहीं होता; केवल ऊर्जा का आदान-प्रदान हो सकता है। इसलिए, कथन गलत है।
(d) थर्मोस फ्लास्क या किसी अन्य बंद आइसोलेटेड बर्तन में अभिकारक की उपस्थिति एक अलग प्रणाली का उदाहरण है, न कि बंद प्रणाली, क्योंकि यह पदार्थ और ऊर्जा दोनों के आदान-प्रदान को रोकता है।
3. गैस की स्थिति को दबाव, आयतन और तापमान के बीच संबंध का उल्लेख करके वर्णित किया जा सकता है।
(a) दबाव, आयतन, तापमान
(b) तापमान, मात्रा, दबाव
(c) मात्रा, आयतन, तापमान
(d) दबाव, आयतन, तापमान, मात्रा
उत्तर दिखाएं
उत्तर: (d) दबाव, आयतन, तापमान, मात्रा
स्पष्टीकरण:
गैस की स्थिति को दबाव, आयतन, तापमान और मात्रा के बीच संबंध का उल्लेख करके वर्णित किया जा सकता है। आदर्श गैस समीकरण है
$ p V = n R T $
इसलिए, $p, V, T$ और $n$ प्रणाली की स्थिति को वर्णित करते हैं।
अब, गलत विकल्पों को ध्यान में लें:
(a) दबाव, आयतन, तापमान: यह विकल्प गलत है क्योंकि इसमें गैस की मात्रा (n) को शामिल नहीं किया गया है, जो गैस की स्थिति का वर्णन करने में एक महत्वपूर्ण चर है। आदर्श गैस समीकरण $ ( pV = nRT ) $ में गैस की मात्रा को शामिल करना आवश्यक है ताकि स्थिति का पूर्ण वर्णन किया जा सके।
(b) तापमान, मात्रा, दबाव: यह विकल्प गलत है क्योंकि इसमें गैस के आयतन (V) को शामिल नहीं किया गया है। आयतन आदर्श गैस समीकरण $ ( pV = nRT ) $ के अनुसार गैस की स्थिति का वर्णन करने के लिए आवश्यक है।
(c) मात्रा, आयतन, तापमान: यह विकल्प गलत है क्योंकि इसमें गैस के दबाव (p) को शामिल नहीं किया गया है। दबाव आदर्श गैस समीकरण $ ( pV = nRT ) $ में एक महत्वपूर्ण चर है और गैस की स्थिति का पूर्ण वर्णन करने के लिए आवश्यक है।
4. गैस का आयतन अपने मूल आयतन के आधा कर दिया जाता है। विशिष्ट ऊष्मा होगी
(a) आधा हो जाएगी
(b) दुगुनी हो जाएगी
(c) स्थिर रहेगी
(d) चार गुना बढ़ जाएगी
उत्तर दिखाएं
Answer: (c) स्थिर रहेगी
Explanation:
गैस का आयतन अपने मूल आयतन के आधा कर दिया जाता है। विशिष्ट ऊष्मा स्थिर रहेगी।
विशिष्ट ऊष्मा एक तीव्र गुणधर्म है जो केवल गैस की प्रकृति पर निर्भर करती है।
5. ब्यूटेन के एक मोल के पूर्ण दहन के दौरान, $2658 \mathrm{~kJ}$ ऊष्मा उत्सर्जित होती है। उपरोक्त परिवर्तन के ऊष्मारसायनिक अभिक्रिया है
(a) $2 C_{4} H_{10}(~g)+13 O_{2}(~g) \rightarrow 8 CO_{2}(~g)+10 H_{2} O(l) ;\ \Delta_{C} H=-2658.0 ~kJ ~mol^{-1}$
(b) $C_{4} H_{10}(~g)+\dfrac{13}{2} O_{2}(~g) \rightarrow 4 CO_{2}(~g)+5 H_{2} O(l) ;\ \Delta_{C} H=-1329.0 ~kJ ~mol^{-1}$
(c) $C_{4} H_{10}(~g)+\dfrac{13}{2} O_{2}(~g) \rightarrow 4 CO_{2}(~g)+5 H_{2} O(l) ;\ \Delta_{C} H=-2658.0 ~kJ ~mol^{-1}$
(d) $C_{4} H_{10}(~g)+\dfrac{13}{2} O_{2}(~g) \rightarrow 4 CO_{2}(~g)+5 H_{2} O(l) ;\ \Delta_{C} H=+2658.0 ~kJ ~mol^{-1}$
उत्तर दिखाएं
Answer: (c) $C_{4} H_{10}(~g)+\dfrac{13}{2} O_{2}(~g) \rightarrow 4 CO_{2}(~g)+5 H_{2} O(l) ;\ \Delta_{C} H=-2658.0 ~kJ ~mol^{-1}$
Explanation:
दिया गया है कि, ब्यूटेन के एक मोल के पूर्ण दहन को ऊष्मारसायनिक अभिक्रिया द्वारा प्रस्तुत किया गया है
$ C_{4} H_{10}(g)+\dfrac{13}{2} O_{2}(g) \rightarrow 4 CO_{2}(g)+5 H_{2} O(l) $
हमें ब्यूटेन के एक मोल के दहन को लेना होगा और $\Delta_{C} H$ नकारात्मक होना चाहिए और इसका मान $2658 ~kJ ~mol^{-1}$ होना चाहिए।
6. $ \Delta_{f} U^{\ominus}$ के निर्माण के लिए $CH_{4}(~g)$ का निश्चित ताप पर मान $-393 ~kJ ~mol^{-1}$ है। $\Delta_{f} H^{\ominus}$ का मान है
(a) शून्य
(b) $<\Delta_{f} U^{\ominus}$
(c) $>\Delta_{f} U^{\ominus}$
(d) $\Delta_{f} U^{\ominus }$ के बराबर
उत्तर दिखाएं
Answer: (b) $<\Delta_{f} U^{\ominus}$
स्पष्टीकरण:
प्रतिक्रिया है $CH_{4}(g)+2 O_{2}(g) \rightarrow CO_{2}(g)+2 H_{2} O(l)$
$ \Delta n_{g} =\left(n_{p}-n_{r}\right)_{g}=1-3=-2 $
$ \Delta_{f} H^{\ominus} =\Delta_{f} U^{\ominus}+\Delta n_{g} R T $
$ \text { जबकि } \quad \Delta n_{g} =-2 $
$\therefore \quad\Delta_{f} H^{\ominus} <\Delta_{f} U^{\ominus} $
7. एक अनुवर्ती प्रक्रम में, प्रणाली और परिवेश के बीच ऊष्मा का कोई स्थानांतरण नहीं होता। निम्नलिखित में से कौन सा विकल्प आदर्श गैस के अनुवर्ती परिस्थितियों में मुक्त विस्तार के लिए सही है?
(a) $q=0, \Delta T \neq 0, w=0$
(b) $q \neq 0, \Delta T=0, w=0$
(c) $q=0, \Delta T=0, w=0$
(d) $q=0, \Delta T<0, w \neq 0$
उत्तर दिखाएं
उत्तर: (c) $q=0, \Delta T=0, w=0$
स्पष्टीकरण:
मुक्त विस्तार, $w=0$
अनुवर्ती प्रक्रम, $q=0$
$\Delta U=q+w=0$, इसका अर्थ है कि आंतरिक ऊर्जा स्थिर रहती है। अतः, $\Delta T=0$. आदर्श गैस में अणुओं के बीच आकर्षण नहीं होता।
इसलिए, जब ऐसी गैस एक वैक्यूम में अनुवर्ती परिस्थितियों में विस्तार करती है, तो अणुओं को अलग करने के लिए कोई बाह्य कार्य नहीं किया जाता है, इसलिए कोई ऊष्मा अवशोषित या उत्सर्जित नहीं होती।
8. आदर्श गैस के दबाव-आयतन कार्य की गणना व्यंजक $w=-\int_{V_{i}}^{V_{f}} p_{e x} d V$ का उपयोग करके की जा सकती है। कार्य की गणना निर्धारित सीमाओं के भीतर वक्र के तल के नीचे क्षेत्रफल का उपयोग करके भी की जा सकती है। जब एक आदर्श गैस को आयतन $V_{i}$ से $V_{f}$ तक संपीड़ित किया जाता है (a) व्युत्क्रमणीय या (b) अव्युत्क्रमणीय। निम्नलिखित में से कौन सा विकल्प सही है।
(a) $w$ (व्युत्क्रमणीय) $=w$ (अव्युत्क्रमणीय)
(b) $w$ (व्युत्क्रमणीय) $<w$ (अव्युत्क्रमणीय)
(c) $w$ (व्युत्क्रमणीय) $>w$ (अव्युत्क्रमणीय)
(d) $w$ (व्युत्क्रमणीय) $=w$ (अव्युत्क्रमणीय) $+p_{\mathrm{ex}} \cdot \Delta V$
उत्तर दिखाएं
उत्तर: (c) $w$ (व्युत्क्रमणीय) $>w$ (अव्युत्क्रमणीय)
स्पष्टीकरण:
सही विकल्प $w$ (व्युत्क्रमणीय) $>w$ (अव्युत्क्रमणीय) है। इसका कारण यह है कि वक्र के तल के नीचे क्षेत्रफल व्युत्क्रमणीय संपीड़न में हमेशा अधिक होता है।

$p V$-plot जब दबाव नियत नहीं हो और संपीड़न के दौरान शुरूआती आयतन, $V_{i}$ से अंतिम आयतन, $V_{f}$ तक अपरिमित कदमों में बदलता रहे (व्युत्क्रमणीय शर्तों के अंतर्गत)। गैस पर किया गया कार्य छायांकित क्षेत्र द्वारा प्रदर्शित किया गया है।

$P V$ -plot जब दबाव नियत रहे (अव्युत्क्रमणीय शर्तों के अंतर्गत) संपीड़न के दौरान शुरूआती आयतन, $V_{i}$ से अंतिम आयतन, $V_{f}$ तक। गैस पर किया गया कार्य छायांकित क्षेत्र द्वारा प्रदर्शित किया गया है।
9. एन्ट्रॉपी परिवर्तन की गणना व्यंजक $\Delta S=\dfrac{q_{\text {rev }}}{T}$ का उपयोग करके की जा सकती है। जब जल एक ग्लास बीकर में जम जाता है, निम्नलिखित में से सही कथन का चयन करें।
(a) $\Delta S$ (सिस्टम) घटता है लेकिन $\Delta S$ (परिवेश) समान रहता है
(b) $\Delta S$ (सिस्टम) बढ़ता है लेकिन $\Delta S$ (परिवेश) घटता है
(c) $\Delta S$ (सिस्टम) घटता है लेकिन $\Delta S$ (परिवेश) बढ़ता है
(d) $\Delta S$ (सिस्टम) घटता है लेकिन $\Delta S$ (परिवेश) भी घटता है
उत्तर दिखाएं
Answer: (c) $\Delta S$ (सिस्टम) घटता है लेकिन $\Delta S$ (परिवेश) बढ़ता है
Explanation:
एन्ट्रॉपी परिवर्तन की गणना व्यंजक
$ \Delta S=\dfrac{q_{\mathrm{rev}}}{T} $
का उपयोग करके की जा सकती है। जब जल एक ग्लास बीकर में जम जाता है, $\Delta S$ (सिस्टम) घटता है क्योंकि ठोस बर्फ में अणु तरल पानी की तुलना में कम अस्थिर होते हैं। हालांकि, जब जल बर्फ में जमता है, तो ऊष्मा उत्सर्जित होती है जो परिवेश द्वारा अवशोषित की जाती है। इसलिए, परिवेश की एन्ट्रॉपी बढ़ती है।
10. ऊष्मारसायनिक समीकरण (1), (2) और (3) के आधार पर, विकल्प (a) से (d) में से कौन सा बीजगणितीय संबंध सही है
-
$C$ (ग्राफाइट) $+O_{2}(g) \rightarrow CO_{2}(g) ;\ \Delta_{r} H=x ~kJ ~mol^{-1}$
-
$C$ (ग्राफाइट) $+\dfrac{1}{2} O_{2}(g) \rightarrow CO(g) ;\ \Delta_{r} H=y ~kJ ~mol^{-1}$
-
$CO(g)+\dfrac{1}{2} O_{2}(g) \rightarrow CO_{2}(g) ;\ \Delta_{r} H=z ~kJ ~mol^{-1}$
(a) $z=x+y$
(b) $x=y-z$
(c) $x=y+z$
(d) $y=2 z-x$
उत्तर दिखाएं
Answer: (c) $x=y+z$
Explanation:
दिए गए अभिक्रिया के बीजगणितीय संबंध समीकरण (1) - समीकरण (2) = समीकरण (3) है
$C$ (graphite) $+O_{2}(g) \rightarrow CO_{2}(g) ;\ \Delta_{r} H=x ~kJ ~mol^{-1}$
$ CO(g) \rightarrow C (graphite) +\dfrac{1}{2} O_{2}(g) ;\ \Delta_{r} H=-y ~kJ ~mol^{-1}$
$CO(g)+\dfrac{1}{2} O_{2}(g) \rightarrow CO_{2}(g) ;\ \Delta_{r} H=z ~kJ ~mol^{-1}=(x-y) ~kJ ~mol^{-1}$
अतः, $x-y=z$ या $x=y+z$
11. नीचे दिए गए अभिक्रियाओं के आधार पर विकल्प (a) से (d) में से कौन सा बीजगणितीय संबंध सही है?
-
$C(g)+4 H(g) \rightarrow CH_{4}(g) ;\ \Delta_{r} H=x ~kJ ~mol^{-1}$
-
$C$ (graphite,s) $+2 H_{2}(g) \rightarrow CH_{4}(g) ;\ \Delta_{r} H=y ~kJ ~mol^{-1}$
(a) $x=y$
(b) $x=2 y$
(c) $x>y$
(d) $x<y$
उत्तर दिखाएं
Answer: (c) $x>y$
Explanation:
अभिक्रिया (1) और (2) में समान बंध बनते हैं लेकिन अभिक्रिया (1) में कोई बंध नहीं टूटते हैं जबकि अभिकारक अणुओं में बंध टूटते हैं अभिक्रिया (2) में। बंध टूटने पर ऊर्जा अवशोषित होती है, अतः अभिक्रिया (1) में विमुक्त ऊर्जा अभिक्रिया (2) की तुलना में अधिक होती है अतः, $x>y$
12. तत्वों के अपने मानक अवस्था में एंथैल्पी को शून्य मान लिया जाता है। एक यौगिक की एंथैल्पी निर्माण
(a) हमेशा नकारात्मक होती है
(b) हमेशा धनात्मक होती है
(c) धनात्मक या नकारात्मक हो सकती है
(d) कभी नकारात्मक नहीं होती
उत्तर दिखाएं
Answer: (c) धनात्मक या नकारात्मक हो सकती है
Explanation:
तत्वों के एक यौगिक में जलाना हमेशा ऊष्माक्षेपी होता है। उदाहरण के लिए, $C+O_{2} \rightarrow CO_{2}$ ऊष्माक्षेपी होता है।
जबकि, $\mathrm{C}+2 \mathrm{~S} \rightarrow \mathrm{CS}_{2}$ ऊष्माशोषी होता है।
अतः, एंथैल्पी निर्माण धनात्मक या नकारात्मक हो सकती है।
13. किसी पदार्थ के वाष्पीकरण की एंथैल्पी बराबर होती है
(a) विलय एंथैल्पी + वाष्पीकरण एंथैल्पी
(b) विलय एंथैल्पी
(c) वाष्पीकरण एंथैल्पी
(d) वाष्पीकरण एंथैल्पी के दुगुनी
उत्तर दिखाएं
उत्तर: (a) विलय एंथैल्पी + वाष्पीकरण एंथैल्पी
स्पष्टीकरण:
किसी पदार्थ के वाष्पीकरण की एंथैल्पी विलय एंथैल्पी + वाष्पीकरण एंथैल्पी के बराबर होती है।
वाष्पीकरण, ठोस से वाष्प में अप्रत्यक्ष परिवर्तन होता है। ठोस $\rightarrow$ वाष्प
दो चरणों में लिखे जाने पर, हमें ठोस $\rightarrow$ द्रव $\rightarrow$ वाष्प मिलता है,
ठोस $\rightarrow$ द्रव के लिए विलय एंथैल्पी की आवश्यकता होती है
द्रव $\rightarrow$ वाष्प के लिए वाष्पीकरण एंथैल्पी की आवश्यकता होती है
14. निम्नलिखित में से कौन सा गलत है?
(a) $\Delta \mathrm{G}$ व्युत्क्रमी अभिक्रिया के लिए शून्य होता है।
(b) $\Delta \mathrm{G}$ आत्मस्पंदन अभिक्रिया के लिए धनात्मक होता है।
(c) $\Delta G$ आत्मस्पंदन अभिक्रिया के लिए नकारात्मक होता है।
(d) $\Delta \mathrm{G}$ अनात्मस्पंदन अभिक्रिया के लिए धनात्मक होता है।
उत्तर दिखाएं
उत्तर: (b) $\Delta \mathrm{G}$ आत्मस्पंदन अभिक्रिया के लिए धनात्मक होता है।
स्पष्टीकरण:
$\Delta G$ निर्धारित करता है कि दबाव और तापमान स्थिर रहते हुए आत्मस्पंदन की शर्त क्या है।
(i) यदि $\Delta G$ नकारात्मक $(<0)$ होता है, तो प्रक्रिया आत्मस्पंदन होती है।
(ii) यदि $\Delta G$ धनात्मक ( $>0$ ) होता है, तो प्रक्रिया अनात्मस्पंदन होती है।
(iii) यदि $\Delta G$ शून्य होता है तो अभिक्रिया संतुलन में होती है।
अब, सही विकल्पों के बारे में विचार करें:
(a) सही है क्योंकि $\Delta \mathrm{G}$ व्युत्क्रमी अभिक्रिया के लिए वास्तव में शून्य होता है, जो इंगित करता है कि प्रणाली संतुलन में है।
(c) सही है क्योंकि $\Delta \mathrm{G}$ के नकारात्मक होने का अर्थ है कि अभिक्रिया आत्मस्पंदन होती है।
(d) सही है क्योंकि $\Delta \mathrm{G}$ के धनात्मक होने का अर्थ है कि अभिक्रिया अनात्मस्पंदन होती है।
बहुविकल्पीय प्रश्न (एक से अधिक विकल्प)
15. ऊष्मागतिकी मुख्य रूप से संबंधित होती है
(a) ऊर्जा के विभिन्न रूपों के बीच संबंध और एक रूप से दूसरे रूप में परिवर्तन।
(b) ऊर्जा परिवर्तन प्रक्रियाओं में जो केवल विकीर्ण तंतुओं वाले छोटे अणुओं वाले प्रणालियों के प्रारंभिक और अंतिम अवस्थाओं पर निर्भर करते हैं।
(c) ऊर्जा परिवर्तन कैसे और किस दर पर किया जाता है।
(d) संतुलन अवस्था में प्रणाली या एक संतुलन अवस्था से दूसरी संतुलन अवस्था तक चल रही प्रणाली।
उत्तर दिखाएं
उत्तर: (a, d)
स्पष्टीकरण:
ऊष्मागतिकी विभिन्न ऊर्जा रूपों के बीच संबंध और एक दूसरे में उनके परिवर्तन के बारे में अध्ययन करती है। यह तापीय या यांत्रिक संतुलन के बारे में भी अध्ययन करती है। हालांकि, इसके बारे में कोई भी जानकारी अभिक्रिया की दर के बारे में नहीं होती है।
अब, गलत विकल्पों के बारे में विचार करें:
(b) गलत है क्योंकि ऊष्मागतिकी छोटे अणुओं वाले प्रक्रियाओं पर ध्यान नहीं देती है; यह आमतौर पर बड़ी संख्या में अणुओं वाले मैक्रोस्कोपिक प्रणालियों के बारे में अध्ययन करती है।
(c) गलत है क्योंकि ऊष्मागतिकी ऊर्जा परिवर्तन की दर के बारे में चिंता नहीं करती है; यह विस्थापन के क्षेत्र में है।
16. एक ऊष्माक्षेपी अभिक्रिया में ऊष्मा उत्पन्न होती है, और प्रणाली आसपास के वातावरण में ऊष्मा खो देती है। ऐसी प्रणाली के लिए
(a) $q_{p}$ नकारात्मक होगा
(b) $\Delta_{r} H$ नकारात्मक होगा
(c) $q_{p}$ धनात्मक होगा
(d) $\Delta_{r} H$ धनात्मक होगा
उत्तर दिखाएं
उत्तर: (a, b)
स्पष्टीकरण:
ऊष्माक्षेपी अभिक्रियाएं वे अभिक्रियाएं होती हैं जिनमें ऊष्मा के उत्पादन के साथ अभिक्रिया होती है।
उदाहरण के लिए,
$ C(s)+O_{2}(g) \rightarrow CO_{2}(g)+393.5 ~kJ $
$ H_{2}(g)+\dfrac{1}{2} O_{2}(g) \rightarrow H_{2} O(l)+285.8 ~kJ $
ऊष्माक्षेपी अभिक्रिया के लिए $q_{p}$ और $\Delta_{r} H$ नकारात्मक होते हैं।
17. स्वतंत्रता का अर्थ है, बाह्य एजेंसी के सहायता के बिना चलने की क्षमता रखना। जो प्रक्रियाएं स्वतंत्र रूप से होती हैं वे हैं
(a) ठंडे शरीर से गरम शरीर में ऊष्मा का प्रवाह
(b) एक पात्र में गैस एक कोने में संकुचित हो जाती है
(c) गैस उपलब्ध आयतन भर लेती है
(d) ऑक्सीजन में कार्बन के जलने से कार्बन डाइऑक्साइड बनती है
उत्तर दिखाएं
उत्तर: (c, d)
स्पष्टीकरण:
विकल्प (a) और (b) अकेले या प्रारंभ करके नहीं हो सकते, (c) अकेले हो सकता है,
(d) प्रारंभ करके हो सकता है। गरम शरीर से ठंडे शरीर में ऊष्मा का प्रवाह, गैस का विस्तार और कार्बन के जलने से कार्बन डाइऑक्साइड बनना, सभी अप्राप्त अभिक्रियाएं हैं।
अब, गलत विकल्पों के बारे में सोचें:
(a) गलत है क्योंकि ऊष्मा प्राकृतिक रूप से गरम शरीर से ठंडे शरीर में प्रवाहित होती है, न कि उलटा। ठंडे शरीर से गरम शरीर में ऊष्मा का प्रवाह करने के लिए बाहरी कार्य या अंतरवेध की आवश्यकता होती है, जिसके कारण यह अप्राप्त होता है।
(b) गलत है क्योंकि गैस प्राकृतिक रूप से उपलब्ध आयतन को भरने के लिए विस्तार करती है। एक बरतन के एक कोने में गैस के संकुचित होने के लिए बाहरी कार्य या अंतरवेध की आवश्यकता होती है, जिसके कारण यह अप्राप्त होता है।
18. आदर्श गैस के लिए, एक समान तापमान पर व्युत्क्रमणीय विस्तार के कार्य की गणना व्यंजक $W=-n R T \ln \dfrac{V_{f}}{V_{i}}$ का उपयोग करके की जा सकती है।
एक नमूना जो $1.0 \mathrm{~mol}$ के आदर्श गैस का नमूना है, अपने मूल आयतन के दस गुना आयतन तक एक समान तापमान पर व्युत्क्रमणीय रूप से विस्तार करता है, दो अलग-अलग प्रयोग में। विस्तार $300 \mathrm{~K}$ और $600 \mathrm{~K}$ पर क्रमशः किया जाता है। सही विकल्प का चयन करें।
(a) $600 \mathrm{~K}$ पर कार्य $300 \mathrm{~K}$ पर कार्य का 20 गुना है
(b) $300 \mathrm{~K}$ पर कार्य $600 \mathrm{~K}$ पर कार्य का दुगुना है
(c) $600 \mathrm{~K}$ पर कार्य $300 \mathrm{~K}$ पर कार्य का दुगुना है
(d) दोनों मामलों में $\Delta U=0$
उत्तर दिखाएं
उत्तर: (c, d)
स्पष्टीकरण:
दिया गया है कि, एक समान तापमान पर व्युत्क्रमणीय विस्तार के कार्य की गणना व्यंजक का उपयोग करके की जा सकती है
$ W =-n R T \ln \dfrac{V_{f}}{V_{i}} $
$ V_{f} =10 V_{i} $
$T_{2} =600 \mathrm{~K} $
$ T_{1} =300 \mathrm{~K} $
ऊपर व्यंजक में इन मानों को रखने पर
$ W_{600 \mathrm{~K}}=1 \times R \times 600 \mathrm{~K} \ln \dfrac{10}{1} $
$ W_{300 \mathrm{~K}}=1 \times R \times 300 \mathrm{~K} \ln \dfrac{10}{1} $
$ \text { अनुपात }=\dfrac{W_{600 \mathrm{~K}}}{W_{300 \mathrm{~K}}}=\dfrac{1 \times R \times 600 \mathrm{~K} \ln \dfrac{10}{1}}{1 \times R \times 300 \mathrm{~K} \ln \dfrac{10}{1}}=\dfrac{600}{300}=2 $
आइसोथर्मल विस्तार के लिए आदर्श गैसों के लिए, $\Delta U=0$. क्योंकि, तापमान नियत रहता है इसका अर्थ है कि आंतरिक ऊर्जा में कोई परिवर्तन नहीं होता है अतः $\Delta U=0$
19. जिंक और ऑक्सीजन के निम्नलिखित प्रतिक्रिया को ध्यान में रखते हुए नीचे दिए गए विकल्पों में से सही विकल्प का चयन करें
$ 2 \mathrm{Zn}(s)+\mathrm{O}_{2}(g) \rightarrow 2 \mathrm{ZnO}(s) ;\ \Delta H=-693.8 \mathrm{~kJ} \mathrm{~mol}^{-1} $
(a) दो मोल के $\mathrm{ZnO}$ की एंथैल्पी दो मोल के $\mathrm{Zn}$ और एक मोल ऑक्सीजन की कुल एंथैल्पी से $693.8 \mathrm{~kJ}$ कम है
(b) दो मोल के $\mathrm{ZnO}$ की एंथैल्पी दो मोल के $\mathrm{Zn}$ और एक मोल ऑक्सीजन की कुल एंथैल्पी से $693.8 \mathrm{~kJ}$ अधिक है
(c) प्रतिक्रिया में $693.8 \mathrm{~kJ} \mathrm{~mol}^{-1}$ ऊर्जा उत्सर्जित होती है
(d) प्रतिक्रिया में $693.8 \mathrm{~kJ} \mathrm{~mol}^{-1}$ ऊर्जा अवशोषित होती है
उत्तर दिखाएं
Answer: (a, c)
Explanation:
प्रतिक्रिया के लिए,
$ 2 \mathrm{Zn}(s)+\mathrm{O}_{2}(g) \rightarrow 2 \mathrm{ZnO}(\mathrm{s}) ;\ \Delta H=-693.8\ \mathrm{~kJ} \mathrm{~mol}^{-1} $
हम जानते हैं कि,
$ \Delta H=H_{p}-H_{R} $
$\Delta H$ के नकारात्मक मान से स्पष्ट है कि $H_{R}>H_{P}$ या $H_{P}<H_{R}$, अर्थात दो मोल के $\mathrm{ZnO}$ की एंथैल्पी दो मोल के जिंक और एक मोल ऑक्सीजन की एंथैल्पी से $693.8\ kJ$ कम है। जबकि $H_{R}>H_{P}$, तो प्रतिक्रिया में $693.8\ \mathrm{~kJ} \mathrm{~mol}^{-1}$ ऊर्जा उत्सर्जित होती है।
छोटे उत्तर प्रकार प्रश्न
20. $18.0 ~g$ पानी $100^{\circ} C$ और 1 बार दबाव पर पूरी तरह से वाष्प बन जाता है और प्रक्रम में एंथैल्पी परिवर्तन $40.79 ~kJ ~mol^{-1}$ है। एक ही शर्तों के तहत दो मोल पानी के वाष्पीकरण के लिए एंथैल्पी परिवर्तन क्या होगा? पानी की मानक वाष्पीकरण एंथैल्पी क्या है?
उत्तर दिखाएं
उत्तर:
दिया गया है, पानी की मात्रा $=18.0\ \mathrm{~g}$, दबाव $=1$ बार
हम जानते हैं कि, $18.0\ g\ H_{2} O=1$ मोल $H_{2} O$
$1$ मोल $\mathrm{H}_{2} \mathrm{O}$ के वाष्पीकरण के लिए एंथैल्पी परिवर्तन $=40.79 \mathrm{~kJ} \mathrm{~mol}^{-1}$
$\therefore$ $2$ मोल $\mathrm{H}_{2} \mathrm{O}$ के वाष्पीकरण के लिए एंथैल्पी परिवर्तन $=2 \times 40.79 \mathrm{~kJ}=81.58 \mathrm{~kJ}$
$100^{\circ} \mathrm{C}$ तापमान और $1$ बार दबाव पर मानक वाष्पीकरण एंथैल्पी, $\Delta_{\text {vap }} H^{\circ}=+40.79 \mathrm{~kJ} \mathrm{~mol}^{-1}$
21. एक मोल एसिटोन के वाष्पीकरण के लिए कम ऊष्मा की आवश्यकता होती है जबकि एक मोल पानी के वाष्पीकरण के लिए अधिक ऊष्मा की आवश्यकता होती है। इन दो द्रवों में से किसकी वाष्पीकरण एंथैल्पी अधिक होती है?
उत्तर दिखाएं
उत्तर:
एक मोल एसिटोन के वाष्पीकरण के लिए कम ऊष्मा की आवश्यकता होती है जबकि एक मोल पानी के वाष्पीकरण के लिए अधिक ऊष्मा की आवश्यकता होती है। अतः, एसिटोन की वाष्पीकरण एंथैल्पी कम होती है और पानी की वाष्पीकरण एंथैल्पी अधिक होती है। इसे $\left(\Delta H_{V}\right)$ पानी $>\left(\Delta H_{V}\right)$ एसिटोन के रूप में प्रस्तुत किया जा सकता है।
22. मानक मोलर एंथैल्पी उत्पादन, $\Delta_{f} H^{\mathrm{\ominus}}$ एंथैल्पी प्रतिक्रिया, $\Delta_{r} H^{\mathrm{\ominus}}$ का एक विशेष मामला है। दिए गए अभिक्रिया के लिए $\Delta_{r} H^{\mathrm{\ominus}}$ $\Delta_{f} H^{\mathrm{\ominus}}$ के समान है? अपने उत्तर के लिए कारण दीजिए।
$ CaO(s)+CO_{2}(g) \rightarrow CaCO_{3}(s) ;\ \Delta_{f} H^{\ominus}=-178.3 ~kJ ~mol^{-1} $
उत्तर दिखाएं
उत्तर:
नहीं, दिए गए अभिक्रिया के लिए $\Delta_{r} H^{\mathrm{\ominus}}$ $\Delta_{f} H^{\mathrm{\ominus}}$ के समान नहीं है। अतिरिक्त अवस्था में एक यौगिक के अपने सबसे स्थायी अवस्था में तत्वों से बनने के लिए मानक एंथैल्पी परिवर्तन को मानक मोलर एंथैल्पी उत्पादन, $\Delta_{f} H^{\mathrm{\ominus}}$ कहा जाता है।
$ Ca(s)+C(s)+\dfrac{3}{2} O_{2}(g) \rightarrow CaCO_{3}(~s) ;\ \Delta_{f} H^\ominus $
इस अभिक्रिया के साथ दी गई अभिक्रिया अलग है।
अतः,
$\Delta_{r} H^{\circ} \neq \Delta_{f} H^{\circ}$
23. $\mathrm{NH}{3}$ के लिए $\Delta{f} H^{\mathrm{\ominus}}$ का मान $-91.8 \mathrm{~kJ} \mathrm{~mol}^{-1}$ है। निम्नलिखित अभिक्रिया के लिए एंथैल्पी परिवर्तन की गणना कीजिए।
$ 2 NH_{3}(g) \rightarrow N_{2}(g)+3 H_{2}(g) $
उत्तर दिखाएं
उत्तर:
दिया गया है, $\dfrac{1}{2} ~N_{2}(g)+\dfrac{3}{2} H_{2}(g) \rightarrow NH_{3}(g) ;\ \Delta_{f} H^{\ominus}=-91.8 ~kJ ~mol^{-1}$
$\left(\Delta_{f} H^{\ominus}\right.$ का अर्थ 1 मोल $\left.\mathrm{NH}_{3}\right)$ के निर्माण की एंथैल्पी है।
$\therefore \quad$ 2 मोल $\mathrm{NH}_{3}$ के निर्माण के लिए एंथैल्पी परिवर्तन
$ N_{2}(g)+3 H_{2}(g) \rightarrow 2 NH_{3}(g) ;\ \Delta_{f} H^{\ominus}=2 \times-91.8=-183.6 ~kJ ~mol^{-1} $
और विपरीत अभिक्रिया के लिए,
$ 2 NH_{3}(g) \rightarrow N_{2}(g)+3 H_{2}(g) ;\ \Delta_{f} H^{\ominus}=+183.6 ~kJ ~mol^{-1} $
अतः, $\mathrm{NH}{3}$ के लिए $\Delta{f} H^{\mathrm{\ominus}}$ का मान $+183.6 \mathrm{~kJ} \mathrm{~mol}^{-1}$ है।
24. एंथैल्पी एक विस्तार गुण है। सामान्यतः, यदि एक मार्ग के माध्यम से अभिक्रिया $A \rightarrow B$ की एंथैल्पी $\Delta_{r} H$ है और $\Delta_{r} H_{1}, \Delta_{r} H_{2}, \Delta_{r} H_{3} \ldots$ उत्पाद $B$ के निर्माण के लिए अंतराल अभिक्रियाओं की एंथैल्पियाँ हैं, तो $\Delta_{r} H$ के साथ अंतराल अभिक्रियाओं के $\Delta_{r} H_{1}, \Delta_{r} H_{2} \ldots$ आदि के बीच क्या संबंध होगा?
उत्तर दिखाएं
उत्तर:
सामान्यतः, यदि एक मार्ग के माध्यम से अभिक्रिया $A \rightarrow B$ की एंथैल्पी $\Delta_{r} H$ है और $\Delta_{r} H_{1}, \Delta_{r} H_{2}, \Delta_{r} H_{3} \ldots$ उत्पाद $B$ के निर्माण के लिए अंतराल अभिक्रियाओं की एंथैल्पियाँ हैं, तो हम निम्नलिखित प्राप्त करते हैं:
$ \Delta_{r} H=\Delta_{r} H_{1}+\Delta_{r} H_{2}+\Delta_{r} H_{3}+\ldots $
नोट: एक सामान्य अभिक्रिया के लिए हेस के नियम को निरंतर ऊष्मा योग के रूप में निम्नलिखित रूप में प्रस्तुत किया जा सकता है:

25. अभिक्रिया $\mathrm{CH}_{4}(g) \rightarrow \mathrm{C}(g)+4 \mathrm{H}(g)$ के अपघटन एन्थैल्पी का मान $1665 \mathrm{~kJ} \mathrm{~mol}^{-1}$ है। $\mathrm{C}-\mathrm{H}$ बंध की बंध ऊर्जा कितनी है?
उत्तर दिखाएं
उत्तर:
$CH_{4}$ में चार $C-H$ बंध होते हैं। 1 मोल $CH_{4}$ के अपघटन की एन्थैल्पी का अर्थ चार मोल $C-H$ बंध के वियोजन होता है।
$ \therefore \quad \mathrm{C}-\mathrm{H} \text { बंध ऊर्जा प्रति } \mathrm{mol} =\dfrac{1665 \mathrm{~kJ}}{4 \mathrm{~mol}} $
$ =416.25 \mathrm{~kJ} \mathrm{~mol}^{-1} $
26. निम्नलिखित डेटा का उपयोग करके NaBr के लिए $\Delta_{\text {lattice }} H^{\mathrm{\ominus}}$ की गणना कीजिए।
सोडियम धातु के उत्पादन एन्थैल्पी $\Delta_{\text {sub }} H^{\mathrm{\ominus}} =108.4 \mathrm{~kJ} \mathrm{~mol}^{-1}$
सोडियम की आयनन एन्थैल्पी $=496 \mathrm{~kJ} \mathrm{~mol}^{-1}$,
ब्रोमीन की इलेक्ट्रॉन ग्रहण एन्थैल्पी $=-325 \mathrm{~kJ} \mathrm{~mol}^{-1}$,
ब्रोमीन के बंध वियोजन एन्थैल्पी $=192 \mathrm{~kJ} \mathrm{~mol}^{-1}$,
$\mathrm{NaBr}(s)$ की विरचन एन्थैल्पी $\Delta_{f} H^{\mathrm{\ominus}}=-360.1 \mathrm{~kJ} \mathrm{~mol}^{-1}$
उत्तर दिखाएं
उत्तर:
इस प्रश्न के आधार पर बर्न-हैबर चक्र तथा हेस के नियम की अवधारणा है। इस समस्या को हल करने के लिए निम्नलिखित कदम लिए गए हैं।
(i) $\mathrm{Na}(\mathrm{s}) \rightarrow \mathrm{Na}(g) ;\ \Delta_{\text {sub }} H^{\mathrm{s}}$
(ii) $\mathrm{Na}(g) \rightarrow \mathrm{Na}^{+}(g)+\mathrm{e}^{-}(g);\ I E$
(iii) $\dfrac{1}{2} Br_{2}(g) \rightarrow Br(g) ;\ \Delta_{\text {diss }} H^{\ominus}$
(iv) $\mathrm{Br}(g)+\mathrm{e}^{-}(g) \rightarrow \mathrm{Br}^{-}(g) ;\ \Delta_{\mathrm{eg}} H^{\mathrm{\ominus}}$
(v) हेस के नियम के अनुसार $\Delta_{f} H^{\mathrm{\ominus}}=\Delta_{\text {sub }} H^{\mathrm{\ominus}}+I \mathrm{E}+\Delta_{\text {diss }} H^{\mathrm{\ominus}}+\Delta_{\text {eg }} H^{\mathrm{\ominus}}+U$
दिया गया है कि, $\Delta_{\text {sub }} H^{\mathrm{\ominus}}$ लिए $\mathrm{Na}$ धातु $=108.4\ \mathrm{k} \mathrm{J} \mathrm{mol}^{-1}$
IE of $\mathrm{Na}=496\ \mathrm{k} \mathrm{J} \mathrm{mol}^{-1}, \Delta_{\text {eg }} H^{\mathrm{\ominus}}$ of $\mathrm{Br}=-325\ \mathrm{k} \mathrm{J}\ \mathrm{mol}^{-1}, \Delta_{\text {diss }} H^{\mathrm{\ominus}}$ of $\mathrm{Br}=192\ \mathrm{k} \mathrm{J}\ \mathrm{mol}^{-1}, \Delta_{f} H^{\mathrm{\ominus}}$ for $\mathrm{NaBr}=-360.1 \mathrm{~kJ} \mathrm{~mol}^{-1}$
Born-Haber cycle for the formation of $\mathrm{NaBr}$ is as

By applying Hess’s law,
$ \Delta_{f} H^{\mathrm{\ominus}} =\Delta_{\text {sub }} H^{\mathrm{\ominus}}+I E+\Delta_{\text {diss }} H^{\mathrm{\ominus}}+\Delta_{\mathrm{eg}} H^{\mathrm{\ominus}}-U $
$ -360.1 =108.4+496+96+(-325)-U $
$ U =+735.5 \mathrm{~kJ} \mathrm{~mol}^{-1} $
27. दिया गया है कि दो गैसों के मिश्रण के लिए $\Delta H=0$। स्पष्ट करें कि इन गैसों के एक बंद बरतन में एक दूसरे में विसरण एक स्पॉन्टेनेस प्रक्रिया है या नहीं?
उत्तर दिखाएं
Answer:
दो गैसों के मिश्रण के लिए $\Delta H$ शून्य के बराबर होता है। इसलिए, यह एक स्पॉन्टेनेस प्रक्रिया है क्योंकि ऊर्जा कारक कोई भूमिका नहीं निभाता है लेकिन असंगठितता बढ़ जाती है, अर्थात असंगठितता कारक प्रक्रिया को समर्थन देता है।
28. ऊष्मा एक तंत्र पर असंगठितता के प्रभाव डालती है और तापमान तंत्र में कणों के औसत असंगठित गति का माप होता है। इन तीन परिमाणों को संबंधित करने वाली गणितीय संबंध को लिखें।
उत्तर दिखाएं
Answer:
ऊष्मा एक तंत्र पर असंगठितता के प्रभाव डालती है और तापमान तंत्र में कणों के औसत असंगठित गति का माप होता है। इन तीन परिमाणों को संबंधित करने वाली गणितीय संबंध है
$ \Delta S=\dfrac{q_{\text {rev }}}{T} $
यहाँ, $\Delta S=$ एंट्रॉपी में परिवर्तन
$q_{\text {rev }}=$ उत्क्रमणीय अभिक्रिया की ऊष्मा
$T=$ तापमान
29. परिवेश के एंथैल्पी में वृद्धि प्रणाली के एंथैल्पी में कमी के बराबर होती है। जब प्रणाली और परिवेश थर्मल संतुलन में होंगे तो उनके तापमान समान होंगे या नहीं?
उत्तर दिखाएं
उत्तर:
हाँ, जब प्रणाली और परिवेश थर्मल संतुलन में होंगे तो उनके तापमान समान होंगे।
नोट: थर्मल संतुलन को तब परिभाषित किया जाता है जब दो भौतिक प्रणालियों को एक ऐसे संबंध में लाया जाता है जो पदार्थ के परिवहन को रोकता हो, ऐसे संबंध को ऊष्मा के रूप में ऊर्जा परिवहन की अनुमति देता है और इसे दीथेरल कहते हैं।
यदि दो भौतिक प्रणालियों के बीच एक दीथेरल संबंध बनाया जाता है और संबंध के बनाने के बाद कोई भी प्रणाली के अवस्था परिवर्तन नहीं होता है, तो दोनों प्रणालियों को थर्मल संतुलन में कहा जाता है। यह ताप विज्ञान के शून्य वेध के नियम का पालन करता है।
30. $298 ~K$ पर, प्रतिक्रिया $N_{2} O_{4}(g) \rightleftharpoons 2 NO_{2}(g)$ के लिए $K_{p}$ 0.98 है। यह प्रतिक्रिया स्पॉन्टेनेस के अनुसार किस प्रकार की है?
उत्तर दिखाएं
उत्ज्ञ:
प्रतिक्रिया के लिए, $N_{2} O_{4}(g) \rightleftharpoons 2 NO_{2}(g), K_{p}=0.98$
हम जानते हैं कि $\quad \Delta_{r} \mathrm{G}^{\mathrm{\ominus}}=-2.303 \mathrm{RT} \log K_{p}$
यहाँ, $K_{p}=0.98$ अर्थात $K_{p}<1$ अतः, $\Delta_{r} G^{\circ}$ धनात्मक होता है, अतः प्रतिक्रिया अस्पॉन्टेनेस होती है।
31. एक मोनोएटोमिक आदर्श गैस के 1.0 मोल के नमूने को चक्रीय प्रक्रम के माध्यम से विस्तार और संपीड़न के माध्यम से ले जाया जाता है जैसा कि चित्र में दिखाया गया है। पूरे चक्र के लिए $\Delta H$ का मान क्या होगा?
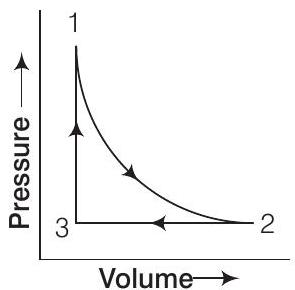
उत्तर दिखाएं
उत्तर:
साइकिल प्रक्रम के लिए शुद्ध एंथैल्पी परिवर्तन, $\Delta H$ शून्य होता है क्योंकि एंथैल्पी परिवर्तन एक अवस्था फलन है, अर्थात $\Delta H($ साइकिल $)=0$
32. $H_{2} O(l)$ के मानक मोलर एन्ट्रॉपी का मान $70\ J\ K^{-1}\ ~mol^{-1}$ है। $H_{2} O(s)$ के मानक मोलर एन्ट्रॉपी का मान $70\ J\ K^{-1}\ ~mol^{-1}$ से अधिक होगा या कम?
उत्तर दिखाएं
Answer:
$H_{2} O(l)$ के मानक मोलर एन्ट्रॉपी का मान $70\ J\ K^{-3}\ ~mol^{-1}$ है। $H_{2} O$ के ठोस रूप को बर्फ कहते हैं। बर्फ में $H_{2} O$ के अणु तरल पानी के अणु की तुलना में कम अस्थिर होते हैं।
इसलिए, $H_{2} O(s)$ के मोलर एन्ट्रॉपी $H_{2} O(l)$ के मोलर एन्ट्रॉपी से कम होता है। $H_{2} O(s)$ के मानक मोलर एन्ट्रॉपी का मान $70 ~J ~K^{-1} ~mol^{-1}$ से कम होता है।
33. निम्नलिखित में से स्थिति फ़ंक्शन और पथ फ़ंक्शन की पहचान करें:
ऊष्मांशल, एन्ट्रॉपी, ऊष्मा, तापमान, कार्य, मुक्त ऊर्जा।
उत्तर दिखाएं
Answer:
स्थिति फ़ंक्शन वे मान होते हैं जो प्रणाली की स्थिति पर निर्भर करते हैं और इसके कैसे प्राप्त किया गया है उस पर निर्भर नहीं करते हैं, उदाहरण के लिए, ऊष्मांशल, एन्ट्रॉपी, तापमान और मुक्त ऊर्जा। पथ फ़ंक्शन वे मान होते हैं जो प्रणाली के पथ पर निर्भर करते हैं। उदाहरण के लिए, ऊष्मा और कार्य।
34. एसीटोन के मोलर वाष्पीकरण ऊष्मा का मान पानी के मोलर वाष्पीकरण ऊष्मा के मान से कम होता है। क्यों?
उत्तर दिखाएं
Answer:
एक तरल के एक मोल के वाष्पीकरण के लिए आवश्यक ऊष्मा की मात्रा नियत तापमान और मानक दबाव (1 बार) पर इसके मोलर वाष्पीकरण ऊष्मा $\Delta_{\text {vap }} H^{\ominus}$ कहलाती है। पानी के मोलर वाष्पीकरण ऊष्मा एसीटोन के मोलर वाष्पीकरण ऊष्मा से अधिक होती है क्योंकि $H_{2} O$ अणु में मजबूत हाइड्रोजन बंधन होते हैं।
35. संतुलन पर $\Delta_{r} G$ और $\Delta_{r} G^{\mathrm{\ominus}}$ में से कौन सी राशि शून्य होगी?
उत्तर दिखाएं
Answer:
एक अभिक्रिया के लिए जिसमें सभी अभिकर्मक और उत्पाद आयतन में हों, गिब्स ऊर्जा $\Delta_{r} G^{s}$ अभिक्रिया के संतुलन स्थिरांक के साथ निम्नलिखित तरह संबंधित होती है
$ \Delta_{r} G=\Delta_{r} G^{\mathrm{\ominus}}+R T \ln K $
$ \text{संतुलन पर} \quad 0 =\Delta_{r} G^{\ominus}+R T \ln K \quad (\therefore \Delta_r G= 0)$
$ \text{या} \quad \Delta_{r} G^{\mathrm{\ominus}} =-R T \ln K $
$ \Delta_{r} G^{\mathrm{\ominus}} =0 \text { जब } K=1 $
सभी अन्य $K$ के मानों के लिए $ \Delta_{r} G^{\ominus} $ शून्य नहीं होगा।
36. एक अन्तर्निहित तंत्र के लिए नियत आयतन पर आंतरिक ऊर्जा में परिवर्तन की भविषेद करें।
उत्तर दिखाएं
उत्तर:
अन्तर्निहित तंत्र में ऊष्मा के परिवहन के लिए कोई ऊष्मा प्रस्तुत नहीं होती, अर्थात $q=0$ और कार्य के रूप में ऊर्जा के परिवहन के लिए भी कोई कार्य नहीं होता, अर्थात $w=0$। ऊष्मागतिकी के प्रथम कानून के अनुसार
$ \Delta U=q+w $
$ \Delta U=0+0=0 $
37. भले ही ऊष्मा एक पथ फलन है, लेकिन एक निश्चित शर्तों के तहत तंत्र द्वारा अवशोषित ऊष्मा पथ से स्वतंत्र होती है। ये कौन सी शर्त हैं? समझाइए।
उत्तर दिखाएं
उत्तर:
ऊष्मा पथ से स्वतंत्र हो जाने के दो शर्त हैं
(i) जब आयतन स्थिर रहता है
(ii) जब दबाव स्थिर रहता है
स्पष्टीकरण
(i) स्थिर आयतन पर: ऊष्मागतिकी के प्रथम कानून के अनुसार, $\Delta U=q+w$ या $q=\Delta U-w$. लेकिन $w=-p \Delta V$ इसलिए, $q=\Delta U+p \Delta V$. लेकिन आयतन स्थिर रहता है तो $\Delta V=0$
$\therefore q_{V}=\Delta U$ लेकिन $\Delta U$ एक अवस्था फलन है।
इसलिए, $q_{v}$ एक अवस्था फलन है।
(ii) स्थिर दबाव पर: जैसा कि हम जानते हैं, $q_{p}=\Delta U+p \Delta V$. लेकिन $\Delta U+p \Delta V=\Delta H$.
$\therefore q_{p}=\Delta H$. जैसे $\Delta H$ एक अवस्था फलन है इसलिए, $q_{p}$ एक अवस्था फलन है।
38. गैस के वैक्यूम में विस्तार को मुक्त विस्तार कहा जाता है। जब $1 \mathrm{~L}$ के आदर्श गैस के विस्तार के लिए $5 \mathrm{~L}$ तक आयतन हो जाता है तो कार्य किया गया और आंतरिक ऊर्जा में परिवर्तन की गणना करें?
उत्तर दिखाएं
उत्तर:
वैक्यूम में गैस के द्वारा किया गया कार्य, $w=-p_{\text {ext }}\left(V_{2}-V_{1}\right)$. जैसे $p_{\text {ext }}=0$ तो $w=-0(5-1)=0$ आदर्श गैस के आंतरिक ऊर्जा केवल तापमान पर निर्भर करती है, इसलिए, आदर्श गैस के आइसोथर्मल विस्तार के लिए आंतरिक ऊर्जा स्थिर रहती है,
i.e.,
$ \Delta U=0 . $
It is to be remember that as $H=U+p V, \Delta H=\Delta(U+p V)=\Delta U+p \Delta V=\Delta U+n R(\Delta T)$. For isothermal process, $\Delta T=0$ and also $\Delta U=0$, as stated above, therefore, $\Delta H=0$.
39. Heat capacity $\left(C_{p}\right)$ is an extensive property but specific heat $(c)$ is intensive property. What will be the relation between $C_{p}$ and $c$ for 1 mole of water?
उत्तर दिखाएं
Answer:
For water, molar heat capacity, $C_{p}=18 \times$ Specific heat, $c$
$ C_{p} =18 \times c\ \text { Specific heat } $
$ c =4.18\ \mathrm{Jg}^{-1} \mathrm{~K}^{-1} \quad \text{(for work)}$
$\text { Heat capacity, } \quad C_{p} =18 \times 4.18\ \mathrm{JK}^{-1} \mathrm{~mol}^{-1} $
$ =75.3\ \mathrm{JK}^{-1}\ \mathrm{~mol}^{-1} $
40. The difference between $C_{p}$ and $C_{v}$ can be derived using the empirical relation $H=U+p V$. Calculate the difference between $C_{p}$ and $C_{v}$ for 10 moles of an ideal gas.
उत्तर दिखाएं
Answer:
Given that, $C_{v}=$ heat capacity at constant volume, $C_{p}=$ heat capacity at constant pressure. Difference between $C_{p}$ and $C_{v}$ is equal to no. of moles times gas constant $(R)$.
$ \therefore \quad C_{p}-C_{v} =n R \quad \text { (where, } n=\text { no. of moles) }$
$ =10 \times 8.314 \mathrm{~J} $
$ =83.14 \mathrm{~J} $
41. If the combustion of $1 \mathrm{~g}$ of graphite produces $20.7\ \mathrm{~kJ}$ of heat, what will be molar enthalpy change? Give the significance of sign also.
उत्तर दिखाएं
Answer:
Given that, enthalpy of combustion of $1 \mathrm{~g}$ graphite $=20.7\ \mathrm{~kJ}$
Molar enthalpy change for the combustion of graphite, $\Delta H=$ enthalpy of combustion of $1 \mathrm{~g}$ graphite $\times$ molar mass
$ \Delta H=-20.7\ \mathrm{kJ\ g}^{-1} \times 12\ \mathrm{~g} \mathrm{~mol}^{-1} $
$ \Delta H=-2.48 \times 10^{2} \mathrm{~kJ} \mathrm{~mol}^{-1} $
नकारात्मक चिह्न $\Delta H$ के मान में इंगित करता है कि अभिक्रिया उष्माक्षेपी है।
42. अभिक्रिया के शुद्ध एन्थैल्पी परिवर्तन अभिकारक अणुओं में सभी बंधों को तोड़ने के लिए आवश्यक ऊर्जा की मात्रा के बराबर होता है घटक अणुओं में सभी बंधों के निर्माण के लिए आवश्यक ऊर्जा की मात्रा के अंतर। निम्नलिखित अभिक्रिया के लिए एन्थैल्पी परिवर्तन क्या होगा?
$H_{2}(g)+Br_{2}(g) \rightarrow 2 HBr(g)$
दिया गया है कि, $H_{2}, Br_{2}$ और $HBr$ के बंध ऊर्जा क्रमशः $435 ~kJ ~mol^{-1}$, $192 ~kJ ~mol^{-1}$ और $368 ~kJ ~mol^{-1}$ है।
उत्तर दिखाएं
Answer:
ऊष्मा परिवर्तन की गणना करने के लिए, जब अभिकारक और उत्पाद गैस अवस्था में हों तो निम्नलिखित सूत्र का उपयोग करें:
$ \Delta_{r} H^{\mathrm{\ominus}}=\Sigma \text { bond energy (reactants) }-\Sigma \text { bond energy (products) } $
दिया गया है कि, $H_{2}$ के बंध ऊर्जा $435 \mathrm{~kJ} \mathrm{~mol}^{-1}$ है
$Br_{2}$ के बंध ऊर्जा $192 \mathrm{~kJ} \mathrm{~mol}^{-1}$ है
$HBr$ के बंध ऊर्जा $368 \mathrm{~kJ} \mathrm{~mol}^{-1}$ है
अभिक्रिया के लिए
$ H_{2}(g)+Br_{2}(g) \rightarrow 2 HBr(g) $
$ \Delta_{r} H^{s}=\Sigma BE(\operatorname{Reactants})-\Sigma BE(\text { Products }) $
$=BE\left(H_{2}\right)+BE\left(Br_{2}\right)-2 BE(HBr) $
$=435+192-(2 \times 368)\ kJ\ mol^{-1} $
$=-109\ ~kJ ~mol^{-1} $
43. $CCl_{4}$ के वाष्पीकरण की एन्थैल्पी $30.5 ~kJ ~mol^{-1}$ है। $284 ~g$ $CCl_{4}$ के वाष्पीकरण के लिए आवश्यक ऊष्मा की गणना करें। ( $CCl_{4}$ का मोलर द्रव्यमान $154 ~g ~mol^{-1}$ है )
उत्तर दिखाएं
Answer:
दिया गया है कि, $1\ \text{mol of}\ CCl_{4}=154 ~g$
$ \Delta_{\text {vap }} H \text { for } 154\ ~g\ CCl_{4}=30.5 ~kJ $
$ \therefore \quad \Delta_{\text {vap }} H \text { for } 284\ ~g\ CCl_{4}=\dfrac{30.5 \times 284}{154}\ ~kJ=56.25\ ~kJ $
44. अभिक्रिया
$ 2 H_{2}(g)+O_{2}(g) \rightarrow 2 H_{2} O(l) \text { के लिए एन्थैल्पी } \Delta_{r} H^{\ominus}=-572\ ~kJ ~mol^{-1}
$
$\mathrm{H}_{2} \mathrm{O}(l)$ के मानक एन्थैल्पी उत्पादन क्या होगा?
उत्तर दिखाएँ
उत्तर:
दिया गया है,
$ 2 H_{2}(g)+O_{2}(g) \rightarrow 2 H_{2} O(l),\ \Delta_{r} H^{\ominus}=-572 ~kJ ~mol^{-1} $
एन्थैल्पी उत्पादन वह एन्थैल्पी परिवर्तन है जब 1 मोल यौगिक अपने तत्वों से बनता है तब
$ H_{2}(g)+\dfrac{1}{2} O_{2}(g) \rightarrow H_{2} O(l),\ \Delta_{r} H^{\ominus}=? $
इसे दिए गए समीकरण को 2 से विभाजित करके प्राप्त किया जा सकता है।
इसलिए,
$ \Delta_{f} H^{\ominus}\left(\mathrm{H}_{2} \mathrm{O}\right)=-\dfrac{572\ \mathrm{kJ\ mol}^{-1}}{2}=-286\ \mathrm{~kJ} \mathrm{~mol}^{-1} $
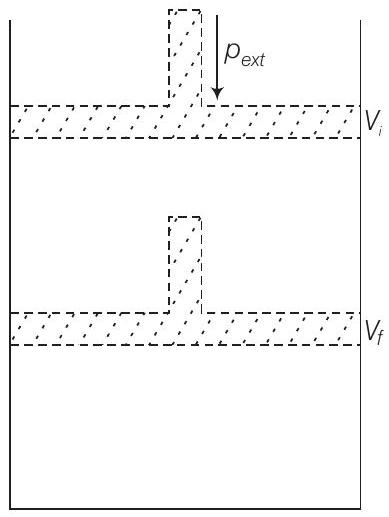
45. चित्र में दिखाए गए अनुसार, एक बर्तन में बंद एक आदर्श गैस को एक स्टेप में एक स्थिर बाह्य दबाव $p_{\text {ext }}$ द्वारा संपीड़ित करने पर बर्तन पर किया गया कार्य क्या होगा? आलेखीय रूप से समझाइए।
उत्तर दिखाएँ
उत्तर:
मान लीजिए गैस के कुल आयतन $V_{i}$ है और बर्तन में गैस का दबाव $p$ है। संपीड़न के बाद बाह्य दबाव $p_{\text {ext }}$ के एक स्टेप में गैस का अंतिम आयतन $V_{f}$ हो जाता है।
तब आयतन परिवर्तन, $\Delta V=\left(V_{f}-V_{i}\right)$
यदि $w$ पिस्टन के गति द्वारा प्रणाली पर किया गया कार्य है, तो
$ w=-p_{\text {ext }}(\Delta V) $
$ w=-p_{\text {ext }}\left(V_{f}-V_{i}\right) $
इसे चित्र में दिखाए गए $p-V$ आलेख से गणना की जा सकती है। कार्य आलेख में छायांकित क्षेत्र $A B V_{f} V_{i}$ के बराबर होता है।

इस व्यंजक में ऋणात्मक चिह्न उत्पादन चिह्न के लिए $w$ के सामान्य चिह्न को प्राप्त करने के लिए आवश्यक है जो धनात्मक होगा। कारण यह है कि संपीड़न के दौरान प्रणाली पर कार्य किया जाता है, इसलिए $\Delta V$ नकारात्मक होगा।
46. आदर्श गैस के संपीड़न के दौरान कार्य की गणना कैसे करेंगे, जब दबाव में परिवर्तन अपरिमित चरणों में किया जाता है?
उत्तर दिखाएं
उत्तर:
जब संपीड़न अपरिमित चरणों में किया जाता है तथा दबाव में परिवर्तन किया जाता है, तो यह एक उत्क्रमणीय प्रक्रम होता है। कार्य की गणना चित्र में दिखाए गए $p-V$ आरेख से की जा सकती है। वक्र के तल के नीचे क्षेत्रफल गैस पर किए गए कार्य का प्रतिनिधित्व करता है।

47. निम्नलिखित प्रक्रमों में संभावन ऊर्जा/ऊष्माशोषण परिवर्तन को ग्राफ़िकल रूप से प्रस्तुत करें।
(a) जमीन से एक पत्थर को छत तक फेंकना।
(b) $\dfrac{1}{2} H_{2}(g)+\dfrac{1}{2} Cl_{2}(g) \rightleftharpoons HCl(g)\quad \Delta_{r} H^{\ominus}=-92.32 ~kJ ~mol^{-1}$
इन प्रक्रमों में संभावन ऊर्जा/ऊष्माशोषण परिवर्तन किस प्रक्रम में स्पॉन्टेनियत के निर्धारण में योगदानकर्ता कारक है?
उत्तर दिखाएं
उत्तर:
निम्नलिखित प्रक्रमों में संभावन ऊर्जा/ऊष्माशोषण परिवर्तन का प्रतिनिधित्व
(a) जमीन से एक पत्थर को छत तक फेंकना।

(b) $\dfrac{1}{2} H_{2}(g)+\dfrac{1}{2} Cl_{2}(g) \rightleftharpoons HCl(g) ;\ \Delta_{r} H^{\ominus}=-92.32 ~kJ ~mol^{-1}$

ऊर्जा (a) में बढ़ती है और (b) प्रक्रम में घटती है। अतः, (b) प्रक्रम में ऊष्माशोषण परिवर्तन स्पॉन्टेनियत के निर्धारण में योगदानकर्ता कारक है।
48. किसी विशिष्ट अभिक्रिया के लिए एंथैल्पी आरेख चित्र में दिया गया है। क्या दिए गए आरेख से अभिक्रिया के स्वतंत्रता के निर्णय किया जा सकता है? समझाइए।
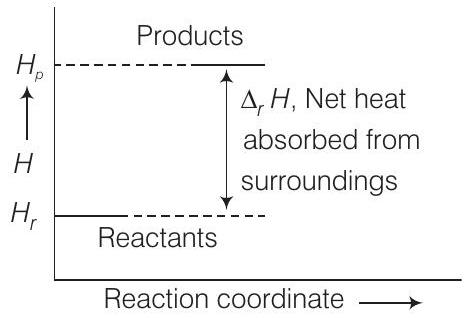
उत्तर दिखाएं
उत्तर:
नहीं, एंथैल्पी अभिक्रिया के स्वतंत्रता के निर्णय के लिए एक योगदानकर्ता कारक है लेकिन यह एकमात्र कारक नहीं है। एक अन्य योगदानकर्ता कारक, एन्ट्रॉपी कारक को भी ध्यान में लेना पड़ता है।
49. एक मोनोएटोमिक आदर्श गैस के 1.0 मोल को चित्र में दिखाए गए अवस्था (1) से अवस्था (2) तक विस्तारित किया जाता है। 298 K पर गैस के अवस्था (1) से अवस्था (2) तक विस्तार के लिए कार्य की गणना कीजिए।
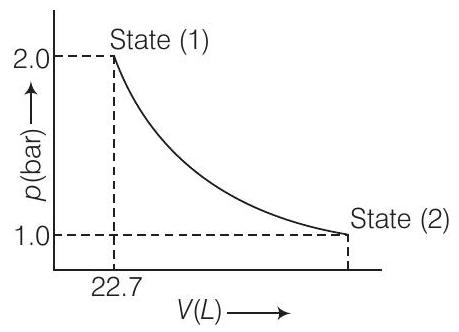
उत्तर दिखाएं
उत्तर:
दिए गए आरेख से स्पष्ट है कि प्रक्रिया अपरिमित चरणों में ले जाए जा रही है, इसलिए यह आदर्श गैस के तापमान 298 K पर दबाव 2.0 वॉट बार से 1.0 वॉट बार तक की आत्मसात विस्तार है।
$$ w=-2.303\ n R T\ \log \dfrac{p_{1}}{p_{2}} $$
$$ w=-2.303 \times 1 \mathrm{~mol} \times 8.314\ \mathrm{JK}^{-1} \mathrm{~mol}^{-1} \times 298\ \mathrm{K\times log} 2 \quad\left(\because \dfrac{p_{1}}{p_{2}}=\dfrac{2}{1}\right) $$
$$ w=-2.303 \times 1 \times 8.314 \times 298 \times 0.3010 \mathrm{~J} $$
$$ w=-1717.63 \mathrm{~J} $$
50. एक आदर्श गैस को 2 बार के नियत दबाव के खिलाफ 10 लीटर से 50 लीटर तक एक ही चरण में विस्तारित किया जाता है। गैस द्वारा किए गए कार्य की गणना कीजिए। यदि इस विस्तार को उत्क्रमणीय रूप से किया जाए, तो कार्य की मात्रा पहले के मुकाबले अधिक होगी या कम?
(दिया गया है, $1 \mathrm{~L}$ बार $=100 \mathrm{~J}$ )
उत्तर दिखाएँ
उत्तर:
पहले मामले में, विस्तार नियत बाह्य दबाव के खिलाफ होता है
$ w =-p_{\text {ext }}\left(V_{2}-V_{1}\right)=-2\ \operatorname{bar} \times(50-10)\ \mathrm{L} $
$ =-80 \mathrm{~L} \text { bar } \quad \quad (1\ L\ bar = 100\ J)$
$ =-80 \times 100 \mathrm{~J} $
$ =-8 \mathrm{~kJ} $
यदि दिया गया विस्तार उत्क्रमणीय रूप से किया जाता, तो गैस के आंतरिक दबाव को प्रत्येक चरण में बाह्य दबाव से अधिक होना चाहिए। इसलिए, कार्य किया गया होगा अधिक होगा।
स्तम्भों का मिलान
51. निम्नलिखित का मिलान करें।
| सूची I | सूची II | ||
|---|---|---|---|
| A. | अनुवर्ती प्रक्रम | 1. | ऊष्मा |
| B. | अलगाव निकाय | 2. | नियत आयतन पर |
| C. | नियत ताप परिवर्तन | 3. | ऊष्मागतिकी का प्रथम कानून |
| D. | पथ फ़ंक्शन | 4. | ऊर्जा और पदार्थ के आदान-प्रदान के बिना |
| E. | अवस्था फ़ंक्शन | 5. | ऊष्मा का स्थानांतरण नहीं होता |
| F. | $\Delta U=q$ | 6. | नियत तापमान |
| G. | ऊर्जा संरक्षण का कानून | 7. | आंतरिक ऊर्जा |
| H. | उत्क्रमणीय प्रक्रम | 8. | $P_{ext}$ = 0 |
| I. | मुक्त विस्तार | 9. | नियत दबाव पर |
| J. | $\Delta H=q$ | 10. | अनंत धीरे धीरे प्रक्रम जो |
| एक श्रृंखला के संतुलन अवस्था से गुजरता है। | |||
| K. | गुणांक गुणधर्म | 11. | एन्ट्रॉपी |
| L. | विस्तार गुणधर्म | 12. | दबाव |
| 13. | विशिष्ट ऊष्माधारिता |
उत्तर दिखाएँ
उत्तर:
A. $\rightarrow(5)$
B. $\rightarrow(4)$
C. $\rightarrow(6)$
D. $\rightarrow(1)$
E. $\rightarrow(7,11,12)$
F. $\rightarrow(2)$
G. $\rightarrow(3)$
H. $\rightarrow(10)$
I. $\rightarrow(8)$
J. $\rightarrow (9) $
K. $\rightarrow(1,12,13)$
L. $\rightarrow(7,11)$
सही मिलान इस प्रकार किया जा सकता है
| A. | अनुवर्ती प्रक्रम | ऊष्मा का स्थानांतरण नहीं होता |
|---|---|---|
| B. | अलगाव निकाय | ऊर्जा और पदार्थ के आदान-प्रदान के बिना |
| C. | नियत ताप परिवर्तन | नियत तापमान |
| डी। | पथ फ़ंक्शन | ऊष्मा | | ई। | स्टेट फ़ंक्शन | आंतरिक ऊर्जा | | | | एंट्रॉपी | | | | दबाव | | एफ। | $\Delta U=q$ | नियत आयतन पर | | जे। | ऊर्जा संरक्षण का नियम | ऊष्मागतिकी का पहला नियम | | एच। | व्युत्क्रमणीय प्रक्रम | एक अनंत धीरे धीरे प्रक्रम जो | | | | एक श्रृंखला के माध्यम से चलता है | | आई। | स्वतंत्र प्रसार | संतुलन अवस्थाओं के माध्यम से | | जे। | $\Delta H=q$ | $P_{ext} =0$ | | के। | तीव्र गुण | नियत दबाव पर | | | | ऊष्मा | | | | दबाव | | एल। | विस्तार गुण | विशिष्ट ऊष्मा |
52. निम्नलिखित प्रक्रमों को एंट्रॉपी परिवर्तन के साथ मिलाएं
| प्रतिक्रिया | एंट्रॉपी परिवर्तन | ||
|---|---|---|---|
| ए। | एक तरल वाष्प बन जाता है | 1. | $\Delta S=0$ |
| ब। | प्रतिक्रिया सभी तापमानों पर अस्पष्ट होती है और $\Delta H$ धनात्मक होता है | 2. | $\Delta S=$ धनात्मक |
| सी। | आदर्श गैस के व्युत्क्रमणीय प्रसार | 3. | $\Delta S=$ नकारात्मक |
उत्तर दिखाएं
उत्तर:
ए। $\rightarrow(2) $
ब। $\rightarrow(3) $
सी। $\rightarrow(1)$
ए। जब एक तरल वाष्प बन जाता है, अर्थात तरल $\rightarrow$ वाष्प, एंट्रॉपी बढ़ जाती है, अर्थात $\Delta S=$ धनात्मक
ब। जब $\Delta H=$ धनात्मक होता है, अर्थात ऊर्जा कारक विरोध करता है। यदि एंट्रॉपी कारक भी प्रक्रम के विरुद्ध होता है, तो प्रक्रम सभी तापमानों पर अस्पष्ट होता है, अर्थात $\Delta S=$ नकारात्मक
सी। आदर्श गैस के व्युत्क्रमणीय प्रसार में, प्रणाली प्रत्येक चरण में संतुलन में रहती है। अतः $\Delta S=0$
53. निम्नलिखित पैरामीटरों को अपस्पष्टता के वर्णन के साथ मिलाएं।
| $\Delta_{r} \boldsymbol{H}^{\mathrm{\ominus}}$ | $\Delta_{r} S^{\mathrm{\ominus}}$ | $\Delta_{r} G^{\mathrm{\ominus}}$ | वर्णन | |
|---|---|---|---|---|
| ए। | + | - | + | 1. उच्च तापमान पर अपस्पष्ट |
| ब। | - | - | + उच्च $T$ पर | $\qquad$ 2. सभी तापमानों पर अपस्पष्ट |
| सी। | - | + | - | 3. सभी तापमानों पर अपस्पष्ट |
उत्तर दिखाएं
उत्तर:
ए। $\rightarrow(3)$
बी। $\rightarrow(1)$
सी। $\rightarrow(2)$
ए। जब $\Delta_{r} G^{\ominus}$ धनात्मक होता है, तो अभिक्रिया सभी तापमानों पर अस्पष्ट होती है
बी। जब $\Delta_{r} G^{\omin’t}$ उच्च तापमान पर धनात्मक होता है, तो अभिक्रिया उच्च तापमान पर अस्पष्ट होती है।
सी। जब $\Delta_{r} H^{\mathrm{\ominus}}=$ नकारात्मक होता है, तो इसका फायदा होता है, $\Delta_{r} S^{\mathrm{\ominus}}=$ धनात्मक होता है, जिसका भी फायदा होता है। $\Delta_{r} G^{\ominus}=$ नकारात्मक होता है, जिसका अभिक्रिया सभी तापमानों पर स्पष्ट होती है।
54। निम्नलिखित का मिलान करें
| A. | वाष्पीकरण की एन्ट्रॉपी | 1. | घटता है |
| B. | अपस्पष्ट प्रक्रिया के लिए $K$ | 2. | हमेशा धनात्मक होता है |
| C. | क्रिस्टलीय ठोस अवस्था | 3. | सबसे कम एन्ट्रॉपी |
| D. | आदर्श गैस के अनुत्क्रमणीय विस्तार में $\Delta U$ | 4. | $\dfrac{\Delta H_{\text {vap }}}{T_{b}}$ |
उत्तर दिखाएं
उत्तर:
A. $\rightarrow(2,4)$
B. $\rightarrow(2)$
C. $\rightarrow(3)$
D. $\rightarrow(1)$
A. वाष्पीकरण की एन्ट्रॉपी हमेशा धनात्मक होती है। यह $\Delta H_{\text {vap }} / T_{b}$ के बराबर होती है
B. $\Delta_{r} G^{\ominus}=-R T \ln K$
यदि $K$ धनात्मक होता है, $\Delta_{r} G^{\ominus}=$ नकारात्मक होता है और अभिक्रिया अपस्पष्ट होती है।
C. क्रिस्टलीय ठोस अवस्था के सबसे कम एन्ट्रॉपी होती है।
D. आदर्श गैस के अनुत्क्रमणीय विस्तार के दौरान, $q=0$। अतः, $\Delta U=q+w$ देता है $\Delta U=w$, अर्थात, कार्य आंतरिक ऊर्जा के खर्च पर होता है जो कम हो जाता है।
अभिकथन और कारण
निम्नलिखित प्रश्नों में एक अभिकथन (A) और एक कारण (R) के बारे में बताया गया है। प्रत्येक प्रश्न में दिए गए विकल्पों में से सही विकल्प चुनें।
55। अभिकथन (A) सभी आवरणीय यौगिकों के ज्वलन एक ऊष्माक्षेपी अभिक्रिया होती है।
कारण (R) सभी तत्वों की ऊष्मांतर ऊर्जा उनके मानक अवस्था में शून्य होती है।
(a) दोनों $A$ और $R$ सत्य हैं और $R$ $A$ का सही स्पष्टीकरण है
(b) दोनों $\mathrm{A}$ और $\mathrm{R}$ सत्य हैं लेकिन $\mathrm{R}$ $\mathrm{A}$ का सही स्पष्टीकरण नहीं है
(c) $A$ सत्य है लेकिन $R$ गलत है
(d) $A$ गलत है लेकिन $R$ सत्य है
उत्तर दिखाएं
उत्तर: (b) दोनों दावा और कारण सत्य हैं लेकिन कारण दावे का सही स्पष्टीकरण नहीं है।
सही स्पष्टीकरण एक दहन अभिक्रिया में, अभिकर्मकों के एंथैल्पी के योग उत्पादों के एंथैल्पी के योग से अधिक होता है।
56. दावा (A) अप्रतिस्पर्धी प्रक्रिया एक अव्यापारी प्रक्रिया होती है और बाह्य एजेंसी द्वारा उलट जा सकती है।
कारण (R) एंथैल्पी में कमी अप्रतिस्पर्धी व्यवहार के एक योगदानकर्ता कारक होती है।
(a) दोनों $A$ और $R$ सत्य हैं और $R$ $A$ का सही स्पष्टीकरण है
(b) दोनों $A$ और $R$ सत्य हैं लेकिन $R$ $A$ का सही स्पष्टीकरण नहीं है
(c) $A$ सत्य है लेकिन $R$ गलत है
(d) $A$ गलत है लेकिन $R$ सत्य है
उत्तर दिखाएं
उत्तर: (b) दोनों दावा और कारण सत्य हैं लेकिन कारण दावे का सही स्पष्टीकरण नहीं है।
अप्रतिस्पर्धी प्रक्रियाओं के साथ ऊर्जा में कमी और असंगठितता में वृद्धि होती है।
57. दावा (A) एक तरल ठोस में ठहरता है और इसके साथ एंट्रॉपी में कमी होती है।
कारण (R) क्रिस्टल में अणु एक क्रमबद्ध ढंग से संगठित होते हैं।
(a) दोनों $A$ और $R$ सत्य हैं और $R$ $A$ का सही स्पष्टीकरण है
(b) दोनों $\mathrm{A}$ और $\mathrm{R}$ सत्य हैं लेकिन $\mathrm{R}$ $\mathrm{A}$ का सही स्पष्टीकरण नहीं है
(c) $A$ सत्य है लेकिन $R$ गलत है
(d) $A$ गलत है लेकिन $R$ सत्य है
उत्तर दिखाएं
उत्तर: (a) दोनों दावा और कारण सत्य हैं और कारण दावे का सही स्पष्टीकरण है।
जब एक तरल ठोस में ठहरता है, तो एंट्रॉपी कम हो जाती है क्योंकि क्रिस्टलीय रूप में अणु तरल की तुलना में अधिक क्रमबद्ध होते हैं।
लंबे उत्तर प्रकार प्रश्न
58. आदर्श गैस के लिए $\Delta H$ और $\Delta U$ के बीच संबंध को निर्माण करें। समीकरण में शामिल हर पद की व्याख्या करें।
उत्तर दिखाएं
उत्तर:
ऊष्मागतागत नियम के अनुसार, $\quad q=\Delta U+p \Delta V$
If the process carried out at constant volume, $\Delta V=0$
Hence,
[Here, $q_v=$ Heat absorbed at constant volume, $\Delta U=$ change in internal energy]
$ q_v=\Delta U $
Similarly,
Here, $q_p=$ heat absorbed at constant pressure
$\Delta H=$ enthalpy change of the system.
Enthalpy change of a system is equal to the heat absorbed or evolved by the system at constant pressure.
As we know that at constant pressure, $\Delta H=\Delta U+p \Delta V$
where, $\Delta V$ is the change in volume.
This equation can be rewritten as $\Delta H=\Delta U+p\left(V_f-V_i\right)=\Delta U+\left(p V_f-p V_i\right)$
where, $V_i=$ initial volume of the system $V_f=$ final volume of the system
But for the ideal gases,
$ p V=n R T $
So that
$ V_1=n_1 R T$
and
$ p V_2=n_2 R T $
where, $n_1=$ number of moles of the gaseous reactants
$n_2=$ number of moles of the gaseous products.
Substituting these values in Eq. (i), we get
$ \Delta H=\Delta U+\left(n_{2} R T-n_{1} R T\right) $
$ \Delta H=\Delta U+\left(n_{2}-n_{1}\right) R T $
$ or \quad \Delta H=\Delta U+\Delta n_{g} R T $
where, $\Delta n_{g}=n_{2}-n_{1}$ is the difference between the number of moles of the gaseous products and gaseous reactants.
Putting the values of $\Delta H$ and $\Delta U$ we get
$ q_{p}=q_{v}+\Delta n_{g} R T $
Note: Conditions under which $q_{p}=q_{v}$ or $\Delta H=\Delta U$
(i) When reaction is carried out in a closed vessel so that volume remains constant i.e., $\Delta V=0$
(ii) When reaction involves only solids or liquids or solutions but no gaseous reactant or product. This is because the volume changes of the solids and liquids during a chemical reaction are negligible.
(iii) When reaction involves gaseous reactants and products but their number of moles are equal (i.e., $n_{p}=n_{r}$ ) e.g.,
$ H_{2}(~g)+Cl_{2}(~g) \longrightarrow 2 HCl(g) $
$ C(s)+O_{2}(~g) \longrightarrow CO_{2}(~g) $
Since, $q_{p}$ is different from $q_{v}$ only in those reactions which involves gaseous reactants and products and $\left(n_{p}\right)$ gaseous $\neq\left(n_{r}\right)$ gaseous.
59. विस्तारित गुणधर्म द्रव्यमान की मात्रा पर निर्भर करते हैं लेकिन घनत्व गुणधर्म नहीं। बताइए कि निम्नलिखित गुणधर्म विस्तारित या घनत्व गुणधर्म हैं।
द्रव्यमान, आंतरिक ऊर्जा, दबाव, ऊष्माधारिता, मोलर ऊष्माधारिता, घनत्व, मोल अनुपात, विशिष्ट ऊष्माधारिता, तापमान और मोलरिता।
उत्तर दिखाएं
उत्तर:
विस्तारित गुणधर्म: वे गुणधर्म जिनका मान प्रणाली में उपस्थित द्रव्यमान की मात्रा या आकार पर निर्भर करता है, विस्तारित गुणधर्म कहलाते हैं।
उदाहरण: द्रव्यमान, आंतरिक ऊर्जा, ऊष्माधारिता।
घनत्व गुणधर्म: वे गुणधर्म जिनका मान प्रणाली में उपस्थित द्रव्यमान की मात्रा या आकार पर निर्भर नहीं करता है, घनत्व गुणधर्म कहलाते हैं। उदाहरण: दबाव, मोलर ऊष्माधारिता, घनत्व, मोल अनुपात, विशिष्ट ऊष्माधारिता, तापमान और मोलरिता।
किसी विलयन के मोल अनुपात या मोलरिता विलयन की छोटी मात्रा या बड़ी मात्रा लेने पर एक समान होती है।
दो विस्तारित गुणधर्म के अनुपात हमेशा घनत्व गुणधर्म होता है।
$ \dfrac{\text { विस्तारित }}{\text { विस्तारित }}=\text { घनत्व } $
इसलिए, मोल अनुपात और मोलरिता घनत्व गुणधर्म हैं।
$ \text { उदाहरण, \quad मोल अनुपात }=\dfrac{\text { घटक के मोल }}{\text { कुल मोलों की संख्या }}=\dfrac{\text { विस्तारित }}{\text { विस्तारित }} $
$ \text { और \quad मोलरिता }=\dfrac{\text { मोल }}{\text { आयतन }}=\dfrac{\text { विस्तारित }}{\text { विस्तारित }} $
60. आयनिक यौगिक की जालक एंथैल्पी वह एंथैल्पी होती है जब एक मोल आयनिक यौगिक अपने गैस अवस्था में अपने आयनों में विखंडित होता है। इसे प्रयोग के माध्यम से सीधे निर्धारित नहीं किया जा सकता। $\mathrm{NaCl}(s)$ की जालक एंथैल्पी को मापने के अप्रत्यक्ष तरीके की सलाह दें और समझाएं।
उत्तर दिखाएं
उत्तर:
आयनिक यौगिक की जालक एंथैल्पी वह एंथैल्पी परिवर्तन होता है जब एक मोल आयनिक यौगिक अपने आयनों में विखंडित होता है अपने गैस अवस्था में। अभिक्रिया के लिए
$ \mathrm{Na}^{+} \mathrm{Cl}^{-}(s) \rightarrow \mathrm{Na}^{+}(g)+\mathrm{Cl}^{-}(g) ;\ \Delta_{\text {lattice }} H^{\mathrm{\ominus}}=+788\ \mathrm{k} \mathrm{J}\ \mathrm{mol}^{-1}
$
क्योंकि, प्रयोग के माध्यम से जालक एन्थैल्पी के निर्धारण की असंभवता है, हम एक अप्रत्यक्ष विधि का उपयोग करते हैं जहां हम एक बर्न-हैबर चक्र के रूप में जाना जाने वाला एन्थैल्पी आरेख बनाते हैं।
अब हम निम्नलिखित चरणों के अनुसार $\mathrm{Na}^{+} \mathrm{Cl}^{-}$(s) की जालक एन्थैल्पी की गणना करेंगे
(i) $\mathrm{Na}(\mathrm{s}) \rightarrow \mathrm{Na}(g);\ $ सोडियम धातु के ठोस से वाष्पीकरण, $\Delta_{\text {sub }} H^{\mathrm{\ominus}}=108.4 \mathrm{~kJ} \mathrm{~mol}^{-1}$
(ii) $\mathrm{Na}(g) \rightarrow \mathrm{Na}^{+}(g)+e^{-}(g);\ $ सोडियम परमाणुओं का आयनन, आयनन एन्थैल्पी $\Delta_{i} H^{\mathrm{\ominus}}=496 \mathrm{~kJ} \mathrm{~mol}^{-1}$
(iii) $\dfrac{1}{2} Cl_{2}(g) \rightarrow Cl(g);\ $ क्लोरीन के वियोजन, अभिक्रिया एन्थैल्पी बंधन वियोजन एन्थैल्पी के आधा होती है $\dfrac{1}{2} \Delta_{\text {bond }} H^{\ominus}=121 ~kJ ~mol^{-1} $
(iv) $\mathrm{Cl}(g)+e^{-}(g) \rightarrow \mathrm{Cl}^{-}(g)$; क्लोरीन परमाणुओं द्वारा इलेक्ट्रॉन के लेने के लिए। इलेक्ट्रॉन लेने की एन्थैल्पी, $\Delta_{\text {eg }} H^{\mathrm{\ominus}}=-348.6 \mathrm{~kJ} \mathrm{~mol}^{-1}$
(v) $\mathrm{Na}^{+}(g)+\mathrm{Cl}^{-}(g) \longrightarrow \mathrm{Na}^{+} \mathrm{Cl}^{-}(s)$
चरणों का क्रम दिए गए चित्र में दिखाया गया है और इसे बर्न-हैबर चक्र के रूप में जाना जाता है। चक्र के महत्व यह है कि, चक्र के चारों ओर एन्थैल्पी परिवर्तन के योग शून्य होता है।
हेस के नियम के अनुसार, हम प्राप्त करते हैं
$ \Delta_{\text {lattice }} H^{\mathrm{\ominus}}=411.2+108.4+121+496-348.6 $
$\Delta_{\text {latitice }} H^{\mathrm{\ominus}}=+788 \mathrm{~kJ}$
61. $ \Delta G$ उपयोगी कार्य करने के लिए उपलब्ध शुद्ध ऊर्जा होती है और इसलिए यह “मुक्त ऊर्जा” के मापदंड होता है। गणितीय रूप से दिखाएं कि $\Delta G$ मुक्त ऊर्जा का मापदंड है। $\Delta G$ की इकाई ज्ञात करें। यदि एक अभिक्रिया में धनात्मक एन्थैल्पी परिवर्तन और धनात्मक एन्ट्रॉपी परिवर्तन हो, तो अभिक्रिया कब स्वतंत्र होगी?
उत्तर दिखाएं
Answer:
गिब्स मुक्त ऊर्जा एक तंत्र की वह तापीय मात्रा होती है, जिसके मूल्य के कम होने के दौरान एक प्रक्रम के दौरान तंत्र से प्राप्त किए जा सकने वाले अधिकतम उपयोगी कार्य के बराबर होती है।
Mathematically, इन परिणामों को निम्नलिखित तरीके से निर्देशित किया जा सकता है
एक प्रणाली द्वारा अवशोषित ऊष्मा $q$, इसकी आंतरिक ऊर्जा में परिवर्तन, $\Delta U$ और प्रणाली द्वारा किए गए कार्य के बीच संबंध ताप विज्ञान के प्रथम कानून के समीकरण द्वारा दिया जाता है, इसलिए,
$ q=\Delta U+w_{\text {expansion }}+w_{\text {non-expansion }} \quad …(i) $
स्थिर दबाव की स्थिति में, विस्तार कार्य $p \Delta V$ द्वारा दिया जाता है।
$ \therefore \quad q =\Delta U+p \Delta V+w_{\text {nonexpansion }} \quad (\because \Delta U+p \Delta V=\Delta H) $
$ =\Delta H+w_{\text {non-expansion }} \quad …(ii)$
एक व्युत्क्रमणीय परिवर्तन जो स्थिर तापमान पर होता है,
$ \Delta S=\dfrac{q_{\text {rev }}}{T} \text { or } q_{\text {rev }}=T \Delta S \quad …(iii) $
समीकरण (iii) में $q$ के मान को समीकरण (ii) में बदलकर, हम प्राप्त करते हैं
$ T \Delta S =\Delta H+w_{\text {non-expansion }} $
$ or \quad \Delta H-T \Delta S =-w_{\text {non expansion }} \quad …(iv) $
एक परिवर्तन जो स्थिर तापमान और दबाव की स्थिति में होता है,
$ \Delta G=\Delta H-T \Delta S $
समीकरण (iv) में इस मान को बदलकर, हम प्राप्त करते हैं
$ \Delta G=-w_{\text {non-expansion }} \quad …(v) $
इस प्रकार, मुक्त ऊर्जा परिवर्तन को विस्तार कार्य के अलावा अन्य कार्य के माप के रूप में लिया जा सकता है। अधिकांश परिवर्तनों में, विस्तार कार्य को अन्य उपयोगी कार्य में नहीं बदला जा सकता, जबकि अन्य विस्तार कार्य उपयोगी कार्य में बदला जा सकता है।
समीकरण $(\mathrm{v})$ को पुनर्व्यवस्थित करके, इसे लिखा जा सकता है
$ -\Delta G=w_{\text {non-expansion }}=w_{\text {useful }} $
जैसे कि $-\Delta G=w_{\text {useful }}$ अतः, $\Delta G$ के इकाई उसी होंगी जैसे कार्य के इकाई, अर्थात जूल
$ \Delta G=\Delta H-T \Delta S . $
यदि $\Delta H=$ धनात्मक और $\Delta S=$ धनात्मक है, तो
$\Delta G$ नकारात्मक होगा अर्थात, प्रक्रम केवल तब स्वतंत्र होगा जब $T \Delta S>\Delta H$ के मान में, जो तब होगा जब तापमान उच्च हो।
62. एक आदर्श गैस के अवस्था को व्युत्क्रमणीय और समतापीय रूप से $ \left(p_{i}, V_{i}\right) $ से $ \left(p_{f}, V_{f}\right) $ तक परिवर्तित करने पर कुल कार्य को ग्राफिक रूप से दिखाइए। एक $p V$ आरेख के साथ ऊपरी मामले में किए गए कार्य की तुलना एक स्थिर दबाव $p_{f}$ के विरुद्ध किए गए कार्य के साथ करें।
उत्तर दिखाएँ
उत्तर:
(i) एक आदर्श गैस के अवस्था के परिवर्तन के दौरान विस्तार के दौरान कुल कार्य किया गया है जब अवस्था व्युत्क्रमी और समतापी रूप से $\left(p_{i}, V_{i}\right)$ से $\left(p_{f}, V_{f}\right)$ तक परिवर्तित होती है। व्युत्क्रमी कार्य को एक संयुक्त क्षेत्र $AB C$ और $BC V_{i} V_{f}$ द्वारा प्रकट किया जाता है।
(ii) स्थिर दबाव के खिलाफ कार्य, $p_{f}$ को क्षेत्र $BC V_{i} V_{f}$ द्वारा प्रकट किया जाता है।
कार्य (i) $>$ कार्य (ii)