परमाणु की संरचना
बहुविकल्पीय प्रश्न (MCQs)
1. निम्नलिखित में से कौन-सा निष्कर्ष रदरफोर्ड के $\alpha$-कण प्रकीर्णन प्रयोग से नहीं प्राप्त किया जा सकता था?
(a) परमाणु में अधिकांश स्थान खाली होता है
(b) परमाणु की त्रिज्या लगभग $10^{-10} \mathrm{~m}$ होती है जबकि नाभिक की त्रिज्या $10^{-15} \mathrm{~m}$ होती है
(c) इलेक्ट्रॉन निश्चित ऊर्जा के वृत्ताकार पथ में घूमते हैं जिन्हें कक्षा कहते हैं
(d) इलेक्ट्रॉन और नाभिक विद्युत आकर्षण बलों द्वारा एक दूसरे से बंधे रहते हैं
उत्तर दिखाएं
उत्तर: (c) इलेक्ट्रॉन निश्चित ऊर्जा के वृत्ताकार पथ में घूमते हैं जिन्हें कक्षा कहते हैं
स्पष्टीकरण:
इलेक्ट्रॉन निश्चित ऊर्जा के वृत्ताकार पथ में घूमते हैं जिन्हें कक्षा कहते हैं इस अवधारणा को बोहर द्वारा प्रस्तुत किया गया था और रदरफोर्ड के प्रकीर्णन प्रयोग से नहीं प्राप्त किया जा सकता था।
नाभिक के आसपास बहुत सारे वृत्ताकार कक्षाएँ संभव हैं, लेकिन इलेक्ट्रॉन केवल उन कक्षाओं में घूमते हैं जिनमें ऊर्जा का निश्चित मान होता है। इसलिए, इन कक्षाओं को ऊर्जा स्तर या स्थायी अवस्था कहते हैं।
अब, गलत विकल्पों के बारे में विचार करें:
(a) परमाणु में अधिकांश स्थान खाली होता है: यह निष्कर्ष सही है और रदरफोर्ड के प्रयोग से प्राप्त किया गया था। प्रयोग दिखाया कि अधिकांश $\alpha$-कण सोने के चादर के माध्यम से गुजरे बिना विक्षेपित नहीं हुए, जिससे पता चला कि परमाणु अधिकांशतः खाली स्थान होते हैं।
(b) परमाणु की त्रिज्या लगभग $10^{-10} \mathrm{~m}$ होती है जबकि नाभिक की त्रिज्या $10^{-15} \mathrm{~m}$ होती है: यह निष्कर्ष भी सही है और रदरफोर्ड के प्रयोग से प्राप्त किया गया था। कुछ $\alpha$-कणों के विक्षेपण से एक बहुत ही छोटे, घनत्व वाले नाभिक की उपस्थिति का अनुमान लगाया गया, जिससे परमाणु और नाभिक की त्रिज्याओं का अनुमान लगाया गया।
(d) इलेक्ट्रॉन और नाभिक विद्युत आकर्षण बलों द्वारा एक दूसरे से बंधे रहते हैं: यह निष्कर्ष भी सही है और रदरफोर्ड के प्रयोग से प्राप्त किया गया था। $\alpha$-कणों के विक्षेपण पैटर्न से यह पता चला कि धनावेशित नाभिक और नकारात्मक आवेशित इलेक्ट्रॉन विद्युत आकर्षण बलों द्वारा एक दूसरे से बंधे रहते हैं।
2. निम्नलिखित में से कौन सा विकल्प परमाणु के आधार अवस्था इलेक्ट्रॉनिक विन्यास का प्रतिनिधित्व नहीं करता है?
(a) $1 s^{2} 2 s^{2} 2 p^{6} 3 s^{2} 3 p^{6} 3 d^{8} 4 s^{2}$
(b) $1 s^{2} 2 s^{2} 2 p^{6} 3 s^{2} 3 p^{6} 3 d^{9} 4 s^{2}$
(c) $1 s^{2} 2 s^{2} 2 p^{6} 3 s^{2} 3 p^{6} 3 d^{10} 4 s^{1}$
(d) $1 s^{2} 2 s^{2} 2 p^{6} 3 s^{2} 3 p^{6} 3 d^{5} 4 s^{1}$
उत्तर दिखाएं
Answer:(b) $1 s^{2} 2 s^{2} 2 p^{6} 3 s^{2} 3 p^{6} 3 d^{9} 4 s^{2}$
Explanation:
सही विन्यास $1 s^{2} 2 s^{2} 2 p^{6} 3 s^{2} 3 p^{6} 3 d^{10} 4 s^{1}$ होना चाहिए जो कॉपर के लिए है जिसकी परमाणु संख्या $29\left({ }_{29} \mathrm{Cu}\right)$ है। $d$-उप-शेल के पूर्ण भरे हुए ऑर्बिटल के अतिरिक्त स्थिरता के कारण, अंतिम इलेक्ट्रॉन $d$-ऑर्बिटल में जाता है बजाय $s$-ऑर्बिटल में।
अब, गलत विकल्पों के बारे में विचार करें:
(a) विन्यास $1s^2 2s^2 2p^6 3s^2 3p^6 3d^8 4s^2$ गलत है क्योंकि यह किसी भी तत्व के आधार अवस्था विन्यास के संगत नहीं है। उदाहरण के लिए, प्रतिरोध (Ni) के परमाणु क्रमांक 28 के लिए आधार अवस्था विन्यास $1s^2 2s^2 2p^6 3s^2 3p^6 3d^8 4s^2$ होता है, लेकिन यह विन्यास किसी भी तत्व के आधार अवस्था में नहीं है।
(c) विन्यास $1s^2 2s^2 2p^6 3s^2 3p^6 3d^{10} 4s^1$ वास्तव में परमाणु क्रमांक 29 के कॉपर (Cu) के आधार अवस्था विन्यास है। इसलिए, यह विकल्प गलत नहीं है।
(d): विन्यास $1s^2 2s^2 2p^6 3s^2 3p^6 3d^5 4s^1$ परमाणु क्रमांक 24 के क्रोमियम (Cr) के आधार अवस्था विन्यास है। इसलिए, यह विकल्प गलत नहीं है।
3. $1 s$ और $2 s$ ऑर्बिटल के संभावना घनत्व आरेख चित्र में दिए गए हैं।

एक क्षेत्र में बिंदुओं की घनत्व उस क्षेत्र में इलेक्ट्रॉन के पाए जाने की संभावना घनत्व का प्रतिनिधित्व करता है।
उपरोक्त आरेख के आधार पर निम्नलिखित में से कौन सा कथन गलत है?
(a) $1 \mathrm{~s}$ और $2 \mathrm{~s}$ कक्षक समाकारी आकार के होते हैं
(b) इलेक्ट्रॉन के नाभिक के पास पाए जाने की संभावना अधिकतम होती है
(c) दिए गए दूरी पर इलेक्ट्रॉन के पाए जाने की संभावना सभी दिशाओं में समान होती है
(d) $2 s$ कक्षक के इलेक्ट्रॉन के संभावना घनत्व नाभिक से दूरी बढ़ने के साथ एकसमान रूप से घटता जाता है
उत्तर दिखाएँ
उत्तर: (d) $2 s$ कक्षक के इलेक्ट्रॉन के संभावना घनत्व नाभिक से दूरी बढ़ने के साथ एकसमान रूप से घटता जाता है
स्पष्टीकरण:
$1 s$ कक्षक के लिए, इलेक्ट्रॉन के पाए जाने की संभावना नाभिक पर अधिकतम होती है और इसे नाभिक से दूर जाने के साथ-साथ तीव्र रूप से घटती जाती है। दूसरी ओर, $2 s$ कक्षक के लिए, इलेक्ट्रॉन के पाए जाने की संभावना नाभिक के पास तीव्र रूप से घटकर शून्य हो जाती है और फिर एक बार बढ़ना शुरू हो जाती है।
अब, गलत विकल्पों के बारे में विचार करें:
(a) यह विकल्प सही है। $1s$ और $2s$ कक्षक वास्तव में समाकारी आकार के होते हैं, इसलिए इसे गलत मानने के कारण नहीं है।
(b) यह विकल्प गलत है। $1s$ कक्षक के लिए, इलेक्ट्रॉन के नाभिक के पास पाए जाने की संभावना वास्तव में अधिकतम होती है। हालांकि, $2s$ कक्षक के लिए, नाभिक के पास एक नोड (संभावना शून्य क्षेत्र) होता है और इलेक्ट्रॉन के पाए जाने की संभाना नाभिक के पास नहीं बल्कि इससे कुछ दूरी पर अधिकतम होती है।
(c) यह विकल्प सही है। $1s$ और $2s$ कक्षक के लिए, दिए गए दूरी पर इलेक्ट्रॉन के पाए जाने की संभावना सभी दिशाओं में समान होती है, क्योंकि वे समाकारी सममिति रखते हैं। इसलिए, इसे गलत मानने के कारण नहीं है।
उत्तर दिखाएँ
उत्तर: (d) कैथोड किरणों के गुण उस गैस के प्रकृति पर निर्भर करते हैं जो कैथोड किरण ट्यूब में मौजूद होती है
स्पष्टीकरण:
कैथोड किरणें नकारात्मक आवेशित मात्रा के कणों, इलेक्ट्रॉनों से बनी होती हैं। यह विलियम क्रूक्स द्वारा खोज निकली थी। कैथोड किरणों के गुण इलेक्ट्रोड के मैटेरियल और कैथोड किरण ट्यूब में मौजूद गैस के प्रकृति पर निर्भर नहीं करते हैं।
अब, सही विकल्पों को ध्यान में रखें:
(a) यह कथन सही है। कैथोड किरणें वास्तव में कैथोड से शुरू होती हैं और कैथोड किरण ट्यूब में एनोड की ओर चलती हैं।
(b) यह कथन सही है। कैथोड किरणें बाहरी विद्युत या चुंबकीय क्षेत्र के बिना सीधी रेखा में चलती हैं।
(c) यह कथन सही है। कैथोड किरणों के गुण कैथोड किरण ट्यूब में इलेक्ट्रोड के मैटेरियल पर निर्भर नहीं करते हैं।
5. इलेक्ट्रॉन के बारे में निम्नलिखित कथनों में से कौन सा गलत है?
(a) यह एक नकारात्मक आवेशित कण है
(b) इलेक्ट्रॉन के द्रव्यमान का न्यूट्रॉन के द्रव्यमान के बराबर होता है
(c) यह सभी परमाणुओं का मूल घटक है
(d) यह कैथोड किरणों का घटक है
उत्तर दिखाएँ
उत्तर: (b) इलेक्ट्रॉन के द्रव्यमान का न्यूट्रॉन के द्रव्यमान के बराबर होता है
स्पष्टीकरण:
इलेक्ट्रॉन का द्रव्यमान न्यूट्रॉन के द्रव्यमान की तुलना में बहुत हल्का होता है।
इलेक्ट्रॉन का द्रव्यमान $=9.1 \times 10^{-31} \mathrm{~kg}$
न्यूट्रॉन का द्रव्यमान $=1.67 \times 10^{-27} \mathrm{~kg}$
अब, सही विकल्पों को ध्यान में रखें:
(a) यह एक नकारात्मक आवेशित कण है: यह कथन सही है। इलेक्ट्रॉन वास्तव में नकारात्मक आवेशित कण होते हैं।
(c) यह सभी परमाणुओं का मूल घटक है: यह कथन सही है। इलेक्ट्रॉन सभी परमाणुओं के मूल घटक होते हैं, जो नाभिक के चारों ओर घूमते हैं।
(d) यह कैथोड किरणों का घटक है: यह कथन सही है। कैथोड किरणें वैक्यूम ट्यूब में देखे जाने वाले इलेक्ट्रॉन के धारा रूप में होती हैं।
6. परमाणु के निम्नलिखित गुणों में से कौन सा थॉमसन परमाणु मॉडल द्वारा सही तौर पर समझाया जा सकता है?
(a) परमाणु की सामान्य उदासीनता
(b) हाइड्रोजन परमाणु के स्पेक्ट्रम
(c) परमाणु में इलेक्ट्रॉन, प्रोटॉन और न्यूट्रॉन की स्थिति
(d) परमाणु की स्थायित्व
उत्तर दिखाएं
उत्तर:(a) परमाणु की सामान्य उदासीनता
स्पष्टीकरण:
जे. जे. थॉमसन, 1898 में, परमाणु के बर्फी लॉरी (अंगूठी बर्फी या अंगूठी बर्फी) मॉडल को प्रस्तावित करते हैं। इस मॉडल की एक महत्वपूर्ण विशेषता यह है कि परमाणु के द्रव्यमान को परमाणु के एकसमान वितरण के रूप में माना जाता है। यह मॉडल परमाणु की सामान्य उदासीनता को समझने में सक्षम था।
अब, गलत विकल्पों के बारे में विचार करें:
(b) हाइड्रोजन परमाणु के स्पेक्ट्रम: थॉमसन के मॉडल ने हाइड्रोजन परमाणु में दृश्य अपवाद रेखाओं को समझने में असमर्थ रहे। यह मॉडल इलेक्ट्रॉन के क्वांटम ऊर्जा स्तरों के बारे में बताने में असमर्थ रहा, जो उत्सर्जन और अवशोषण स्पेक्ट्रम को समझने के लिए आवश्यक हैं।
(c) परमाणु में इलेक्ट्रॉन, प्रोटॉन और न्यूट्रॉन की स्थिति: थॉमसन के मॉडल ने परमाणु में इलेक्ट्रॉन, प्रोटॉन और न्यूट्रॉन की स्थिति के स्पष्ट चित्र को प्रदान नहीं किया। यह केवल इलेक्ट्रॉन के एक धनावेशित ‘बर्फी’ में विस्थापित होने के बारे में सुझाव देता है, जिसमें इन उप-परमाणु कणों की विशिष्ट व्यवस्था या स्थिति के बारे में विस्तार से बताया गया नहीं है।
(d) परमाणु की स्थायित्व: थॉमसन के मॉडल ने परमाणु की स्थायित्व को समझने में असमर्थ रहे। यह इलेक्ट्रॉन के ऋणावेशित होने के कारण धनावेशित ‘बर्फी’ के कारण घूमते हुए अपने आप के विस्थापन के कारण परमाणु के संकुचन के कारण बारे में बताने में असमर्थ रहा।
7. दो परमाणु को आइसोबार कहा जाता है यदि
(a) वे समान परमाणु संख्या लेकिन अलग द्रव्यमान संख्या रखते हैं
(b) वे समान संख्या में इलेक्ट्रॉन लेकिन अलग संख्या में न्यूट्रॉन रखते हैं
(c) वे समान संख्या में न्यूट्रॉन लेकिन अलग संख्या में इलेक्ट्रॉन रखते हैं
(d) प्रोटॉन और न्यूट्रॉन की संख्या के योग समान हो लेकिन प्रोटॉन की संख्या अलग हो
उत्तर दिखाएं
उत्तर:(d) प्रोटॉन और न्यूट्रॉन की संख्या के योग समान हो लेकिन प्रोटॉन की संख्या अलग हो
स्पष्टीकरण:
आइसोबार के द्रव्यमान संख्या (अर्थात प्रोटॉन और न्यूट्रॉन के योग) समान होती है लेकिन परमाणु संख्या (अर्थात प्रोटॉन की संख्या) अलग होती है। उदाहरण के लिए, ${18} Ar^{40}$ और ${19} K^{40}$ आइसोबार हैं।
| ${ }_{18} \mathbf{A r}^{\mathbf{4 0}}$ | ${ }_{19} \mathbf{K}^{\mathbf{4 0}}$ |
|---|---|
| परमाणु संख्या $=18$ | परमाणु संख्या $=19$ |
| द्रव्यमान संख्या $=40$ | द्रव्यमान संख्या $=40$ |
अब, गलत विकल्पों को ध्यान में रखें:
(a) वे एक ही परमाणु संख्या लेकिन अलग द्रव्यमान संख्या रखते हैं: यह समस्थानिक (isotopes) का वर्णन करता है, न कि समद्रव्यमान (isobars)। समस्थानिक एक ही प्रोटॉन की संख्या (परमाणु संख्या) लेकिन अलग न्यूट्रॉन की संख्या रखते हैं, जिसके कारण अलग द्रव्यमान संख्या होती है।
(b) वे एक ही इलेक्ट्रॉन की संख्या लेकिन अलग न्यूट्रॉन की संख्या रखते हैं: यह अलग तत्वों के आयन या उदासीन परमाणुओं का वर्णन करता है, न कि समद्रव्यमान। इलेक्ट्रॉन की संख्या आयनीकरण के कारण बदल सकती है, लेकिन यह समद्रव्यमान की परिभाषा नहीं है।
(c) वे एक ही न्यूट्रॉन की संख्या लेकिन अलग इलेक्ट्रॉन की संख्या रखते हैं: यह समद्रव्यमान या कोई विशिष्ट परमाणु श्रेणी का वर्णन नहीं करता है। न्यूट्रॉन की संख्या एक ही होने के साथ अलग इलेक्ट्रॉन की संख्या समद्रव्यमान की परिभाषा के अनुरूप नहीं है।
8. $3 p$ ऑर्बिटल के त्रिज्यी नोड की संख्या है
(a) 3
(b) 4
(c) 2
(d) 1
उत्तर दिखाएं
उत्तर: (d) 1
स्पष्टीकरण:
त्रिज्यी नोड की संख्या $==n-l-1$
जहाँ $ \mathrm{n}=$ मुख्य क्वांटम संख्या, $ \mathrm{l}=$ अक्षीय क्वांटम संख्या
$3 p$ ऑर्बिटल के लिए $ \mathrm{n}=3$ और $l=1$
$\therefore$ $3 p$ ऑर्बिटल के त्रिज्यी नोड की संख्या $=3-1-1=3-2=1$
अब, गलत विकल्पों को ध्यान में रखें:
(a) गलत है क्योंकि $3p$ ऑर्बिटल के त्रिज्यी नोड की संख्या $n - l - 1$ के द्वारा गणना की जाती है। $n = 3$ और $l = 1$ के लिए गणना $3 - 1 - 1 = 1$ होती है, न कि 3।
(b) गलत है क्योंकि $3p$ ऑर्बिटल के त्रिज्यी नोड की संख्या $n - l - 1$ के द्वारा गणना की जाती है। $n = 3$ और $l = 1$ के लिए गणना $3 - 1 - 1 = 1$ होती है, न कि 4।
(c) गलत है क्योंकि $3p$ ऑर्बिटल के त्रिज्यी नोड की संख्या $n - l - 1$ के द्वारा गणना की जाती है। $n = 3$ और $l = 1$ के लिए गणना $3 - 1 - 1 = 1$ होती है, न कि 2।
9. $4 d$ ऑर्बिटल के कोणीय नोड की संख्या है
(a) 4
(b) 3
(c) 2
(d) 1
उत्तर दिखाएं
Answer:(c) 2
Explanation:
अंगुलीय नोड की संख्या $=l$
जहाँ $ \mathrm{l}=$ अक्षाई क्वांटम संख्या
4 d ऑर्बिटल के लिए, $ \mathrm{l}=2$
$\therefore$ 4 d ऑर्बिटल के लिए अंगुलीय नोड की संख्या $=l=2$
अब, गलत विकल्पों के बारे में सोचें:
(a) गलत है क्योंकि अंगुलीय नोड की संख्या अक्षाई क्वांटम संख्या $( l )$ द्वारा दी जाती है। एक (d) ऑर्बिटल के लिए $( l = 2 )$ होता है, न कि 4।
(b) गलत है क्योंकि एक $ d $-ऑर्बिटल के लिए अंगुलीय नोड की संख्या $( l )$ द्वारा निर्धारित की जाती है, जो 2 होती है, न कि 3।
(d) गलत है क्योंकि एक $d$ -ऑर्बिटल के लिए अंगुलीय नोड की संख्या $( l = 2 )$ द्वारा दी जाती है, न कि 1।
10. निम्नलिखित में से कौन इलेक्ट्रॉन के निश्चित पथ या कक्षाओं के अस्तित्व को निरस्त करता है?
(a) पॉली के अपवाद सिद्धांत
(b) हाइजेनबर्ग के अनिश्चितता सिद्धांत
(c) हंड के अधिकतम गुणप्रसरण नियम
(d) अफबाउ प्रिंसिपल
उत्तर दिखाएं
Answer:(b) हाइजेनबर्ग के अनिश्चितता सिद्धांत
Explanation:
जर्मन भौतिकविद वर्नर हाइजेनबर्ग ने 1927 में अनिश्चितता सिद्धांत को प्रस्तुत किया, जिसके अनुसार इलेक्ट्रॉन के ठीक अवस्थिति और ठीक संवेग के एक साथ निर्धारण करना संभव नहीं है।
गणितीय रूप से,
$ \Delta x \times \Delta p \geq \frac{h}{4 \pi} $
हाइजेनबर्ग अनिश्चितता सिद्धांत के महत्वपूर्ण अर्थ यह है कि इसके कारण इलेक्ट्रॉन और अन्य समान कणों के निश्चित पथ या कक्षाओं के अस्तित्व को निरस्त कर दिया जाता है।
अब, गलत विकल्पों के बारे में सोचें:
(a) पॉली के अपवाद सिद्धांत: यह सिद्धांत बताता है कि परमाणु में कोई दो इलेक्ट्रॉन चार क्वांटम संख्याओं के समान सेट के साथ नहीं हो सकते। यह परमाणु में इलेक्ट्रॉनों के विन्यास और उनके अद्वितीय क्वांटम अवस्थाओं के संबंध में है, लेकिन इलेक्ट्रॉन के निश्चित पथ या कक्षाओं के अस्तित्व के बारे में नहीं बताता है।
(c) हंड के अधिकतम गुणप्रसरण नियम: यह नियम बताता है कि इलेक्ट्रॉन एक समान ऊर्जा वाले ऑर्बिटल (एक ही ऊर्जा वाले ऑर्बिटल) में एकल रूप से भरे जाएंगे जितना संभव हो। यह ऑर्बिटल में इलेक्ट्रॉनों के वितरण के बारे में है जिससे कुल चुंबकीय घूमने को अधिकतम किया जाए, लेकिन इलेक्ट्रॉन के निश्चित पथ या कक्षाओं के अस्तित्व के बारे में नहीं बताता है।
(d) आधुनिकीकरण सिद्धांत: यह सिद्धांत बताता है कि इलेक्ट्रॉन परमाणु कक्षकों में उपलब्ध सबसे कम ऊर्जा स्तरों में भरे जाते हैं जबकि उच्च ऊर्जा स्तरों में भरे जाते हैं। यह इलेक्ट्रॉनों के कक्षकों में जोड़े जाने के क्रम के लिए एक दिशा देता है, लेकिन इलेक्ट्रॉनों के निश्चित पथ या परिक्रमा के अवधारणा को नहीं बताता है।
11. तीसरे कोश से संबंधित कक्षकों की कुल संख्या होगी
(a) 2
(b) 4
(c) 9
(d) 3
उत्तर दिखाएं
Answer:(c) 9
Explanation:
$n^{\text {th }}$ कोश से संबंधित कक्षकों की कुल संख्या $=n^{2}$
$\therefore$ तीसरे कोश से संबंधित कक्षकों की कुल संख्या $=(3)^{2}=9$
अब, गलत विकल्पों के बारे में सोचें:
(a) गलत है क्योंकि तीसरे कोश से संबंधित कक्षकों की कुल संख्या 2 नहीं होती। $n$ वें कोश में कक्षकों की कुल संख्या के लिए सूत्र $n^{2}$ होता है। $n = 3$ के लिए कक्षकों की कुल संख्या $3^{2} = 9$ होती है, न कि 2।
(b) गलत है क्योंकि तीसरे कोश से संबंधित कक्षकों की कुल संख्या 4 नहीं होती। $n^{2}$ सूत्र का उपयोग करते हुए, $n = 3$ के लिए कक्षकों की कुल संख्या $3^{2} = 9$ होती है, न कि 4।
(d) गलत है क्योंकि तीसरे कोश से संबंधित कक्षकों की कुल संख्या 3 नहीं होती। $n^{2}$ सूत्र के अनुसार, $n = 3$ के लिए कक्षकों की कुल संख्या $3^{2} = 9$ होती है, न कि 3।
12. कक्षकीय कोणीय संवेग किस पर निर्भर करता है
(a) $l$
(b) $n$ और $l$
(c) $n$ और $m$
(d) $m$ और $s$
उत्तर दिखाएं
Answer:(a) $l$
Explanation:
कक्षकीय कोणीय संवेग $m v r=\frac{h}{2 \pi} \sqrt{l(l+1)}$। इसलिए, यह केवल ’ $l$ ’ पर निर्भर करता है। $l$ के मान 0 से $(n-1)$ तक हो सकते हैं।
जब $l=0$ होता है, तो उपकोश $s$ होता है और कक्षक गोलाकार आकार का होता है।
अब, गलत विकल्पों के बारे में सोचें:
(b) गलत है क्योंकि मुख्य क्वांटम संख्या $(n)$ कक्षकीय कोणीय संवेग को बर्बाद नहीं करती। कक्षकीय कोणीय संवेग केवल अक्षीय क्वांटम संख्या $(l)$ पर निर्भर करता है।
जब $l=1$ हो, तो उप-शेल $p$ होता है और ऑर्बिटल डम्ब-बेल आकार का होता है।
(c) गलत है क्योंकि चुंबकीय क्वांटम संख्या $(m)$ ऑर्बिटल कोणीय संवेग के मापदंड के मान को प्रभावित नहीं करती। यह केवल ऑर्बिटल कोणीय संवेग के अंतरिक अभिविन्यास को निर्धारित करती है।
जब $l=2$ हो, तो उप-शेल $d$ होता है और ऑर्बिटल दो डम्ब-बेल आकार का होता है।
(d) गलत है क्योंकि चुंबकीय क्वांटम संख्या $(m)$ और चुंबकीय क्वांटम संख्या $(s)$ ऑर्बिटल कोणीय संवेग को प्रभावित नहीं करते। चुंबकीय क्वांटम संख्या $(s)$ इलेक्ट्रॉन के अंतर्निहित चुंबकीय घूर्णन के संबंध में होती है, न कि इसके ऑर्बिटल गति के संबंध में।
जब $l=3$ हो, तो उप-शेल $f$ होता है और ऑर्बिटल आकार में जटिल होता है।
13. क्लोरीन दो आइसोटोपिक रूपों में उपलब्ध है। $ \mathrm{Cl}-37$ और $ \mathrm{Cl}-35$ लेकिन इसका परमाणु द्रव्यमान 35.5 है। यह इंगित करता है कि $ \mathrm{Cl}-37$ और $ \mathrm{Cl}-35$ के अनुपात लगभग है
(a) $1: 2$
(b) $1: 1$
(c) $1: 3$
(d) $3: 1$
उत्तर दिखाएं
Answer:(c) $1: 3$
Explanation:
चलो,
$x=$ $ \mathrm{Cl}-35$ की भिन्नता
$y=$ $ \mathrm{Cl}-37$ की भिन्नता
क्योंकि ये दोनों ही आइसोटोप हैं, हम लिख सकते हैं:
$ x+y=1 $
औसत परमाणु द्रव्यमान को निम्नलिखित तरीके से व्यक्त किया जा सकता है:
$ \text { औसत परमाणु द्रव्यमान }=(x \cdot 35)+(y \cdot 37) $
दिया गया है कि क्लोरीन का औसत परमाणु द्रव्यमान 35.5 है, इसलिए हम लिख सकते हैं:
$ 35.5=(x \cdot 35)+(y \cdot 37) $
$y$ को $1-x$ से बदल दें
पहले समीकरण से हम $y$ को इस तरह व्यक्त कर सकते हैं:
$ y=1-x $
अब औसत परमाणु द्रव्यमान समीकरण में $y$ को बदल दें:
$ 35.5=(x \cdot 35)+((1-x) \cdot 37) $
$ 35.5=35 x+37-37 x $
$ 35.5=37-2 x $
$ 2 x=37-35.5 $
$ 2 x=1.5 $
$ x=0.75 $
$y=1-x$ का उपयोग करते हुए:
$ y=1-0.75=0.25 $
$ \mathrm{Cl}-35$ और $ \mathrm{Cl}-37$ के अनुपात को इस तरह व्यक्त किया जा सकता है:
$ \frac{x}{y}=\frac{0.75}{0.25}=3 $
इसलिए, $ \mathrm{Cl}-37$ और $ \mathrm{Cl}-35$ के अनुपात को इस तरह व्यक्त किया जा सकता है:
$ \frac{y}{x}=\frac{0.25}{0.75}=\frac{1}{3} $
इसलिए,
$ \mathrm{Cl}-37$ के $ \mathrm{Cl}-35$ के सापेक्ष अनुपात लगभग $\mathbf{1 : 3}$ है।
अब, गलत विकल्पों का ध्यान दें:
(a) $1: 2$: यदि $ \mathrm{Cl}-37$ के $ \mathrm{Cl}-35$ के अनुपात $1: 2$ होता, तो औसत परमाणु द्रव्यमान निम्नलिखित तरीके से गणना किया जाता:
$ \text{औसत परमाणु द्रव्यमान } \mathrm{Cl} = \frac{1 \times 37 + 2 \times 35}{3} = \frac{37 + 70}{3} = \frac{107}{3} \approx 35.67 \ \text{amu} $
इस मान को दिए गए परमाणु द्रव्यमान 35.5 amu के बराबर नहीं माना जा सकता।
(b) $1: 1$: यदि $ \mathrm{Cl}-37$ के $ \mathrm{Cl}-35$ के अनुपात $1: 1$ होता, तो औसत परमाणु द्रव्यमान निम्नलिखित तरीके से गणना किया जाता:
$ \text{औसत परमाणु द्रव्यमान } \mathrm{Cl} = \frac{1 \times 37 + 1 \times 35}{2} = \frac{37 + 35}{2} = \frac{72}{2} = 36 \ \text{amu} $
इस मान को दिए गए परमाणु द्रव्यमान 35.5 amu के बराबर नहीं माना जा सकता।
(d) $3: 1$: यदि $ \mathrm{Cl}-37$ के $ \mathrm{Cl}-35$ के अनुपात $3: 1$ होता, तो औसत परमाणु द्रव्यमान निम्नलिखित तरीके से गणना किया जाता:
$ \text{औसत परमाणु द्रव्यमान } \mathrm{Cl} = \frac{3 \times 37 + 1 \times 35}{4} = \frac{111 + 35}{4} = \frac{146}{4} = 36.5 \ \text{amu} $
इस मान को दिए गए परमाणु द्रव्यमान 35.5 amu के बराबर नहीं माना जा सकता।
14. वह आयन युग्म जिनके इलेक्ट्रॉनिक विन्यास समान होते हैं:
(a) $ \mathrm{Cr}^{3+}, \mathrm{Fe}^{3+}$
(b) $ \mathrm{Fe}^{3+}, \mathrm{Mn}^{2+}$
(c) $ \mathrm{Fe}^{3+}, \mathrm{Co}^{3+}$
(d) $ \mathrm{Sc}^{3+}, \mathrm{Cr}^{3+}$
उत्तर दिखाएं
उत्तर: (b) $ \mathrm{Fe}^{3+}, \mathrm{Mn}^{2+}+$
स्पष्टीकरण:
दिए गए परमाणु और उनके संगत आयन के बाहरी कोश के इलेक्ट्रॉनिक विन्यास निम्नलिखित हैं:
$ \mathrm{Fe}, \mathrm{Z}=26: 3 \mathrm{~d}^6 4 \mathrm{~s}^2$ और $ \mathrm{Fe}^{3+}: 3 \mathrm{~d}^5$
$ \mathrm{Mn}, \mathrm{Z}=25: 3 \mathrm{~d}^5 4 \mathrm{~s}^2$ और $ \mathrm{Mn}^{2+}: 3 \mathrm{~d}^5$
इसलिए, $ \mathrm{Mn}^{2+}$ और $ \mathrm{Fe}^{3+}$ के इलेक्ट्रॉनिक विन्यास समान होते हैं।
इसलिए, विकल्प (b) सही विकल्प है।
अब, गलत विकल्पों को ध्यान से देखें:
(a) $\operatorname{Cr}\left(Z=24: 3 \mathrm{~d}^5 4 \mathrm{~s}^1\right.$ और $ \mathrm{Cr}^{3+}: 3 \mathrm{~d}^3$
$ \mathrm{Fe}, \mathrm{Z}=26: 3 \mathrm{~d}^6 4 \mathrm{~s}^2$ और $ \mathrm{Fe}^{3^{+}}: 3 \mathrm{~d}^5$
इसलिए, $ \mathrm{Cr}^{3+}$ और $ \mathrm{Fe}^{3+}$ के विभिन्न इलेक्ट्रॉनिक विन्यास हैं।
(c) $ \mathrm{Fe}, \mathrm{Z}=26: 3 \mathrm{~d}^6 4 \mathrm{~s}^2$ और $ \mathrm{Fe}^{3+}: 3 \mathrm{~d}^5$
$ \mathrm{Co}, \mathrm{Z}=27: 3 \mathrm{~d}^7 4 \mathrm{~s}^2$ और $ \mathrm{Co}^{3^{+}}: 3 \mathrm{~d}^6$
इसलिए, $ \mathrm{Co}^{3+}$ और $ \mathrm{Fe}^{3+}$ के विभिन्न इलेक्ट्रॉनिक विन्यास हैं।
(d) $\operatorname{Cr}\left(Z=24: 3 \mathrm{~d}^5 4 \mathrm{~s}^1\right.$ और $ \mathrm{Cr}^{3+}: 3 \mathrm{~d}^3$
$ \mathrm{Sc}, \mathrm{Z}=21: 3 \mathrm{~d}^1 4 \mathrm{~s}^2$ और $ \mathrm{Sc}^{3+}: 3 \mathrm{~d}^0$
इसलिए, $ \mathrm{Cr}^{3^{+}}$ और $ \mathrm{Sc}^{3+}$ के विभिन्न इलेक्ट्रॉनिक विन्यास हैं।
इसलिए $ \mathrm{Fe}^{3+}$ और $ \mathrm{Mn}^{2+}$ के समान इलेक्ट्रॉनिक विन्यास हैं।
15. ऑक्सीजन परमाणु के इलेक्ट्रॉनों के लिए, निम्नलिखित में से कौन सा कथन सही है?
(a) $2 s$ कक्षक में एक इलेक्ट्रॉन के लिए $Z_{\text {eff }}$ एक $2 p$ कक्षक में एक इलेक्ट्रॉन के लिए $Z_{\text {eff }}$ के समान है
(b) $2 s$ कक्षक में एक इलेक्ट्रॉन की ऊर्जा $2 p$ कक्षक में एक इलेक्ट्रॉन की ऊर्जा के समान है
(c) $1 s$ कक्षक में एक इलेक्ट्रॉन के लिए $Z_{\text {eff }}$ एक $2 s$ कक्षक में एक इलेक्ट्रॉन के लिए $Z_{\text {eff }}$ के समान है
(d) $2 s$ कक्षक में उपस्थित दो इलेक्ट्रॉनों के विपरीत चिह्न वाले $m_{s}$ चुंबकीय क्वांटम संख्या हैं
उत्तर दिखाएं
उत्तर: (d) $2 s$ कक्षक में उपस्थित दो इलेक्ट्रॉनों के विपरीत चिह्न वाले $m_{s}$ चुंबकीय क्वांटम संख्या हैं
स्पष्टीकरण:
$2 s$ कक्षक के दो इलेक्ट्रॉनों के लिए $m_{s}$ का मान $+\frac{1}{2}$ और $-\frac{1}{2}$ है।
अब, गलत विकल्पों को ध्यान से देखें:
(अ) $2s$ और $2p$ कक्षकों में इलेक्ट्रॉन के अलग-अलग स्क्रीनिंग प्रभाव होते हैं। इसलिए, उनका $Z_{\text{eff}}$ अलग-अलग होता है। $2s$ कक्षक का $Z_{\text{eff}}$ $2p$ कक्षक के $Z_{\text{eff}}$ से अधिक होता है। इसलिए, यह कथन गलत है।
(ब) $2s$ कक्षक की ऊर्जा $2p$ कक्षक की ऊर्जा से कम होती है। इसलिए, यह कथन गलत है।
(स) $1s$ कक्षक का $Z_{\text{eff}}$ $2s$ कक्षक के $Z_{\text{eff}}$ से अलग होता है। इसलिए, यह कथन गलत है।
16. एक ही गति के साथ चल रहे निम्नलिखित मैटर तरंगों में से कौन सी तरंग कम सबसे छोटी तरंगदैर्ध्य रखती है?
(अ) इलेक्ट्रॉन
(ब) अल्फा कण $\left(\mathrm{He}^{2+}\right)$
(स) न्यूट्रॉन
(द) प्रोटॉन
उत्तर दिखाएं
उत्तर: (ब) अल्फा कण $\left(\mathrm{He}^{2+}\right)$
स्पष्टीकरण:
डी-ब्रोग्ली समीकरण से,
$ \text { तरंगदैर्ध्य, } \lambda=\frac{h}{m v} $
अलग-अलग कणों (इलेक्ट्रॉन, प्रोटॉन, न्यूट्रॉन और अल्फा कण) के एक ही गति के लिए,
$ \lambda \propto \frac{1}{m} $
जब $h$ स्थिर होता है। अधिक द्रव्यमान वाले मैटर तरंगों की तरंगदैर्ध्य कम होती है और विपरीत। इन मैटर तरंगों में, अल्फा कण $\left(\mathrm{He}^{2+}\right)$ का द्रव्यमान सबसे अधिक होता है, इसलिए इसकी तरंगदैर्ध्य सबसे कम होती है।
अब, गलत विकल्पों के बारे में विचार करें:
इलेक्ट्रॉन: इलेक्ट्रॉन का द्रव्यमान अल्फा कण के तुलना में काफी कम होता है। डी-ब्रोग्ली समीकरण के अनुसार, छोटा द्रव्यमान एक ही गति के लिए लंबी तरंगदैर्ध्य के लिए जिम्मेदार होता है।
न्यूट्रॉन: न्यूट्रॉन का द्रव्यमान इलेक्ट्रॉन के तुलना में अधिक होता है लेकिन अल्फा कण के तुलना में अभी भी कम होता है। इसलिए, एक ही गति के लिए उनकी तरंगदैर्ध्य अल्फा कण की तुलना में लंबी होती है।
प्रोटॉन: प्रोटॉन का द्रव्यमान इलेक्ट्रॉन के तुलना में अधिक होता है लेकिन अल्फा कण के तुलना में कम होता है। इसलिए, एक ही गति के लिए उनकी तरंगदैर्ध्य अल्फा कण की तुलना में लंबी होती है।
बहुविकल्पीय प्रश्न (एक से अधिक विकल्प सही हो सकते हैं)
17. निम्नलिखित में से कौन-से युग्म समस्थानिक नहीं हैं?
(अ) $ _{6}^{12} X, _{6}^{13} Y$
(ब) $ _{17}^{35} X, _{17}^{37} Y$
(c) $ _{6}^{14} X, _{7}^{14} Y$
(d) $ _{4}^{8} X, _{5}^{8} Y$
उत्तर दिखाएं
उत्तर: (c, d)
स्पष्टीकरण:
इसोटोप वे तत्व होते हैं जिनकी परमाणु संख्या $(Z)$ समान होती है लेकिन द्रव्यमान संख्या (A) अलग-अलग होती है।
उस संख्या जो अंडरस्क्रिप्ट में लिखी गई है वह परमाणु संख्या $(Z)$ को दर्शाती है और जो सुपरस्क्रिप्ट में लिखी गई है वह द्रव्यमान संख्या (A) को दर्शाती है।
(c) $ _{6}^{14} X$ और $ _{7}^{14} Y$ के परमाणु संख्या अलग-अलग है लेकिन द्रव्यमान संख्या समान है।
(d) $ _{4}^{8} X$ और $ _{5}^{8} Y$ के परमाणु संख्या अलग-अलग है लेकिन द्रव्यमान संख्या समान है।
इन दोनों जोड़े एक दूसरे के इसोबार हैं।
अब, गलत विकल्पों के बारे में विचार करें:
(a) $ _{6}^{12} X$ और $ _{6}^{13} Y$ के परमाणु संख्या समान है लेकिन द्रव्यमान संख्या अलग-अलग है।
(b) $ _{17}^{35} X$ और $ _{17}^{37} Y$ के परमाणु संख्या समान है लेकिन द्रव्यमान संख्या अलग-अलग है। इन दोनों जोड़े एक दूसरे के इसोटोप हैं।
18. निम्नलिखित इलेक्ट्रॉन युग्मों में से, उन युग्मों की पहचान करें जो एक दूसरे के अपसामान ऑर्बिटल में उपस्थित हैं।
(a) (i) $n=3, l=2, m_{l}=-2, m_{s}=-\frac{1}{2}$
(ii) $n=3, l=2, m_{l}=-1, m_{s}=-\frac{1}{2}$
(b) (i) $n=3, l=1, m_{l}=1, m_{s}=+\frac{1}{2}$
(ii) $n=3, l=2, m_{l}=1, m_{s}=+\frac{1}{2}$
(c) (i) $n=4, l=1, m_{l}=1, m_{s}=+\frac{1}{2}$
(ii) $n=3, l=2, m_{l}=1, m_{s}=+\frac{1}{2}$
(d) (i) $n=3, l=2, m_{l}=+2, m_{s}=-\frac{1}{2}$
(ii) $n=3, l=2, m_{l}=+2, m_{s}=+\frac{1}{2}$
उत्तर दिखाएं
उत्तर: (a, d)
स्पष्टीकरण:
अपसामान ऑर्बिटल का अर्थ है कि एक ही मुख्य शेल के एक ही उपशेल के ऑर्बिटल, अर्थात उनके $n$ और $l$ मान।
(a)
(i) $3 d_{x y} \quad$
(ii) $3 d_{y z}$
(d)
(i) $3 d_{x^{2}-y^{2}} \quad$
(ii) $3 d_{x^{2}-y^{2}}$
इस प्रकार, $3 d_{x y}$ और $3 d_{y z} ; 3 d_{x^{2}-y^{2}}$ और $3 d_{x^{2}-y^{2}}$ अपसामान ऑर्बिटल के युग्म को दर्शाते हैं।
अब, गलत विकल्पों के बारे में विचार करें:
(b) इलेक्ट्रॉन अलग-अलग उपशेल में हैं। एक इलेक्ट्रॉन 3p उपशेल में है ($l=1$) और दूसरा इलेक्ट्रॉन 3d उपशेल में है ($l=2$)। अपसामान ऑर्बिटल एक ही उपशेल में होना चाहिए।
(i) $3 p_{x} $
(ii) $3 d_{x y}$
(c) इलेक्ट्रॉन अलग-अलग मुख्य क्वांटम स्तर में हैं। एक इलेक्ट्रॉन 4s सबशेल में है ($n=4$) और दूसरा 3d सबशेल में है ($n=3$)। समावयवी ऑर्बिटल एक ही मुख्य क्वांटम स्तर में होना चाहिए।
(i) $4 s $
(ii) $3 d_{x y}$
19. निम्नलिखित में से कौन-से क्वांटम संख्या के सेट सही हैं?
| $n$ | $l$ | $m$ | $n$ | $l$ | $m$ |
|---|---|---|---|---|---|
| (a) 1 | 1 | +2 | (b) 2 | 1 | +1 |
| (c) 3 | 2 | -2 | (d) 3 | 4 | -2 |
उत्तर दिखाएं
Answer:(b, c)
Explanation:
यदि $\quad n=2, l=0,1$, $l=1$ के लिए $m=-1,0,+1$ होते हैं।
इसलिए, (b) सही है।
यदि $\quad n=3, l=0,1,2$
$ l=2 $ के लिए $ m=-2,-1,0,+1,+2 $ होते हैं।
$(\because l < n)$.
इसलिए, (c) सही है।
अब, गलत विकल्पों के बारे में विचार करें:
(a) यदि $(n = 1 )$, $( l = 1 )$ क्योंकि $( l )$ के लिए $( n )$ से कम होना चाहिए। इसलिए, $( l )$ केवल 0 हो सकता है जब $( n = 1 )$ हो। इसलिए, (a) गलत है।
(d) यदि $( n = 3 )$, $( l )$ 4 नहीं हो सकता क्योंकि $( l )$ के लिए $( n )$ से कम होना चाहिए। इसलिए, $( l )$ केवल 0, 1 या 2 हो सकता है जब $( n = 3 )$ हो। इसलिए, (d) गलत है।
20. निम्नलिखित युग्मों में से कौन-से आयन समवेबी हैं?
(a) $ \mathrm{Na}^{+}, \mathrm{Mg}^{2+}$
(b) $ \mathrm{Al}^{3+}, \mathrm{O}^{-}$
(c) $ \mathrm{Na}^{+}, \mathrm{O}^{2-}$
(d) $ \mathrm{N}^{3-}, \mathrm{Cl}^{-}$
उत्तर दिखाएं
Answer:(a, c)
Explanation:
$ \mathrm{Na}^{+} =11-1=10 e^{-} $
$ \mathrm{Mg}^{2+} =12-2=10 e^{-} $
इसलिए, वे एक ही संख्या में इलेक्ट्रॉन हैं।
$ \mathrm{Na}^{+}=10 e^{-}$
$ \mathrm{O}^{2-}=8+2=10 e^{-}$
इसलिए, वे एक ही संख्या में इलेक्ट्रॉन हैं।
इसलिए, $ \mathrm{Na}^{+}$ $ \mathrm{Mg}^{2+}$ और $ \mathrm{O}^{2-}$ के समवेबी है।
अब, गलत विकल्पों के बारे में विचार करें:
(b)
$ \mathrm{Al}^{3+}$ में 10 इलेक्ट्रॉन होते हैं ($13-3 = 10$).
$ \mathrm{O}^{-}$ में 9 इलेक्ट्रॉन होते हैं ($8 + 1 = 9$).
इनमें से एक ही संख्या में इलेक्ट्रॉन नहीं होते।
(d)
$ \mathrm{N}^{3-}$ में 10 इलेक्ट्रॉन होते हैं ($7 + 3 = 10$)।
$ \mathrm{Cl}^{-}$ में 18 इलेक्ट्रॉन होते हैं ($17 + 1 = 18$)।
वे एक समान इलेक्ट्रॉन संख्या नहीं रखते।
21. निम्नलिखित में से कौन-से कथन क्वांटम संख्या के संबंध में सही हैं?
(a) कोणीय क्वांटम संख्या ऑर्बिटल के तीन आयामी आकार को निर्धारित करती है
(b) मुख्य क्वांटम संख्या ऑर्बिटल के उन्नति और ऊर्जा को निर्धारित करती है
(c) चुंबकीय क्वांटम संख्या ऑर्बिटल के आकार को निर्धारित करती है
(d) इलेक्ट्रॉन के चुंबकीय क्वांटम संख्या इलेक्ट्रॉन के चुंबकीय घूमने के उत्पादन के संबंध में चुने गए अक्ष के संबंध में निर्धारित करती है
उत्तर दिखाएं
Answer:(a, d)
Explanation:
(a) अक्षीय क्वांटम संख्या ’ $l$ ’ ऑर्बिटल के तीन आयामी आकार को निर्धारित करती है।
(d) एक इलेक्ट्रॉन अपने अक्ष के चारों ओर घूमता है, जैसे धरा अपने अक्ष के चारों ओर घूमती है जबकि सूर्य के चारों ओर घूमती है। अन्य शब्दों में, एक इलेक्ट्रॉन के अलावा आवेश और द्रव्यमान के अतिरिक्त, अंतर्निहित चुंबकीय घूमने के क्वांटम संख्या होती है।
अब, गलत विकल्पों के बारे में विचार करें:
(b) मुख्य क्वांटम संख्या ऑर्बिट के आकार को निर्धारित करती है, न कि ऑर्बिटल के उन्नति और ऊर्जा को।
(c) चुंबकीय क्वांटम संख्या एक उप-शेल में इलेक्ट्रॉन क्लाउड के उन्नति को निर्धारित करती है, न कि ऑर्बिटल के आकार को।
छोटे उत्तर प्रकार प्रश्न
22. एक शेल में $s, p$ और $d$ उप-शेल के बढ़ते क्रम में इलेक्ट्रॉन द्वारा अनुभव किए गए प्रभावी नाभिकीय आवेश ( $Z_{\text {eff }}$ ) के क्रम को व्यवस्थित करें।
उत्तर दिखाएं
Answer:
s-ऑर्बिटल गोलाकार आकार का होता है, जो इलेक्ट्रॉन को नाभिक से अधिक प्रभावी रूप से छुपाता है, जो $p$-ऑर्बिटल की तुलना में अधिक प्रभावी रूप से छुपाता है, जो फिर $d$-ऑर्बिटल की तुलना में अधिक प्रभावी रूप से छुपाता है। इलेक्ट्रॉन शेल के नाभिक के निकट अधिक निकट होने पर, इसके द्वारा अनुभव किए गए प्रभावी नाभिकीय आवेश ( $Z_{\text {eff }}$ ) अधिक होता है।
इसलिए, उनमें उपस्थित इलेक्ट्रॉन द्वारा अनुभव किए गए प्रभावी नाभिकीय आवेश $\left(Z_{\text {eff }}\right)$ का क्रम $d < p < s$ होता है।
23. ऑक्सीजन परमाणु (परमाणु क्रमांक 8) में इलेक्ट्रॉन के वितरण को ऑर्बिटल आरेख के माध्यम से दिखाइए।
उत्तर दिखाएं
उत्तर:

ऑर्बिटल आरेख से यह देखा जा सकता है कि दो असुमेलित इलेक्ट्रॉन हैं।
24. निकेल परमाणु दो इलेक्ट्रॉन खोकर $ \mathrm{Ni}^{2+}$ आयन बना सकता है। निकेल का परमाणु क्रमांक 28 है। निकेल दो इलेक्ट्रॉन कहाँ से खोएगा?
उत्तर दिखाएं
उत्तर:
${ }_{28} \mathrm{Ni}=1 s^{2}, 2 s^{2}, 2 p^{6}, 3 s^{2}, 3 p^{6}, 3 d^{8}, 4 s^{2}$.
निकेल $4 s$ (बाहरी संतृप्त बर्तन) से दो इलेक्ट्रॉन खोकर $ \mathrm{Ni}^{2+}$ आयन बनाएगा।
अतः,
$ { }_{28} \mathrm{Ni}^{2+}=1 s^{2}, 2 s^{2}, 2 p^{6}, 3 s^{2}, 3 p^{6}, 3 d^{8}, 4 s^{0} . $
25. निम्नलिखित में से कौन से ऑर्बिटल अपचायक हैं?
$ 3 d_{x y}, 4 d_{x y}, 3 d_{z^{2}}, 3 d_{y z}, 4 d_{y z}, 4 d_{z^{2}} $
उत्तर दिखाएं
उत्तर:
उसी उप-शेल और उसी शेल के ऑर्बिटल अपचायक ऑर्बिटल कहलाते हैं। $\left(3 d_{x y}, 3 d_{z^{2}}, 3 d_{y z}\right)$ और $\left(4 d_{x y}, 4 d_{y z}, 4 d_{z^{2}}\right)$ दो सेट अपचायक ऑर्बिटल हैं।
26. $3 p$ ऑर्बिटल में कुल कोणीय नोड और त्रिज्यीय नोड की संख्या की गणना कीजिए।
उत्तर दिखाएं
उत्तर:
मुख्य क्वांटम संख्या $n$ के लिए कुल नोड और त्रिज्यीय नोड की संख्या की गणना करने के लिए निम्नलिखित सूत्र का उपयोग किया जाता है
(i) त्रिज्यीय नोड (या गोलीय नोड) $=n-l-1$
(ii) कोणीय नोड (या अगोलीय नोड) $=l$
(iii) कुल नोड $=n-1$
$3 p$-ऑर्बिटल के लिए, मुख्य क्वांटम संख्या, $n=3$ और चुंबकीय क्वांटम संख्या $l=1$
कोणीय नोड की संख्या $=l=1$
त्रिज्यीय नोड की संख्या $=n-l-1=3-1-1=1$
27. ऊर्जा के आधार पर ऑर्बिटल के विन्यास के आधार पर उनके $(n+l)$ मान पर निर्भर करता है। $(n+l)$ का मान कम होने पर ऊर्जा कम होती है। उन ऑर्बिटलों के लिए जिनके $(n+l)$ के मान समान होते हैं, उन ऑर्बिटलों में जिसका $n$ मान कम होता है वह ऊर्जा कम होती है।
I. उपरोक्त जानकारी के आधार पर, निम्नलिखित ऑर्बिटल को ऊर्जा के बढ़ते क्रम में व्यवस्थित करें।
(a) $1 s, 2 s, 3 s, 2 p$
(b) $4 s, 3 s, 3 p, 4 d$
(c) $5 p, 4 d, 5 d, 4 f, 6 s$
(d) $5 f, 6 d, 7 s, 7 p$
II. उपरोक्त जानकारी के आधार पर, नीचे दिए गए प्रश्नों को हल करें।
(a) निम्नलिखित में से कौन सा ऑर्बिटल सबसे कम ऊर्जा का है?
$ 4 d, 4 f, 5 s, 5 p $
(b) निम्नलिखित में से कौन सा ऑर्बिटल सबसे अधिक ऊर्जा का है?
$ 5 p, 5 d, 5 f, 6 s, 6 p $
उत्तर दिखाएं
Answer:
I.
(a) $(n+l)$ मान हैं
$1 s=1+0=1$
$2 s=2+0=2$
$3 s=3+0=3$
$2 p=2+1=3$
इसलिए, उनके ऊर्जा के बढ़ते क्रम में व्यवस्था है
$ 1 s<2 s<2 p<3 s $
(b) $4 s=4+0=4,$
$3 s=3+0=3,$
$3 p=3+1=4,$
$4 d=4+2=6$
इसलिए, उनके ऊर्जा के बढ़ते क्रम में व्यवस्था है
$ 3 s<3 p<4 s<4 d $
(c) $5 p=5+1=6$
$4 d=4+2=6$
$5 d=5+2=7$
$4 f=4+3=7$
$6 s=6+0=6$
इसलिए, उनके ऊर्जा के बढ़ते क्रम में व्यवस्था है
$4 d<5 p<6 s<4 f<5 d$
(d) $5 f=5+3=8$
$6 d=6+2=8$
$7 s=7+0=7$
$7 p=7+1=8$.
इसलिए, उनके ऊर्जा के बढ़ते क्रम में व्यवस्था है
$7 s<5 f<6 d<7 p$
II.
(a) $(n+l)$ मान हैं
$4 d=4+2=6$
$4 f=4+3=7$
$5 s=5+0=5$
$7 p=7+1=8$
इसलिए, $5 s$ सबसे कम ऊर्जा का है।
(b) $5 p=5+1=6$
$5 d=5+2=7$
$5 f=5+3=8$
$6 s=6+0=6$
$6 p=6+1=7$
इसलिए, $5 f$ सबसे अधिक ऊर्जा का है।
28. निम्नलिखित में से कौन विद्युत क्षेत्र से गुजरते हुए पथ से विक्षेपित नहीं होगा?
प्रोटॉन, कैथोड किरणें, इलेक्ट्रॉन, न्यूट्रॉन।
उत्तर दिखाएं
Answer:
न्यूट्रॉन अक्षम होने के कारण विद्युत क्षेत्र से गुजरते हुए पथ से विक्षेपित नहीं होगा।
प्रोटॉन, कैथोड किरणें और इलेक्ट्रॉन आवेशित कण होने के कारण विद्युत क्षेत्र से गुजरते हुए पथ से विक्षेपित होंगे।
29. एक परमाणु के परमाणु द्रव्यमान संख्या 13 है और इसमें 7 न्यूट्रॉन हैं। परमाणु की परमाणु संख्या क्या है?
उत्तर दिखाएं
Answer:
परमाणु द्रव्यमान $(A)=$ न्यूट्रॉन की संख्या $(n)+$ प्रोटॉन की संख्या $(p)$
प्रोटॉन की संख्या परमाणु की परमाणु संख्या के बराबर होती है।
एक परमाणु जिसकी परमाणु द्रव्यमान संख्या 13 है और न्यूट्रॉन की संख्या 7 है ।
$i.e.,$
$\quad A=13, n=7 $
$\text{ जैसे हम जानते हैं},\quad A=n+p $
$\therefore \quad p=A-n%$
$=13-7$
$=6 $
$अतः,$
$ Z=p =6$
परमाणु की परमाणु संख्या 6 है।
30. विभिन्न विकिरणों की तरंगदैर्घ्य नीचे दी गई है।
$\lambda(\mathrm{A})=300 \mathrm{~nm}$
$\lambda(B)$ $=300 \mu \mathrm{m}$
$\lambda(\mathrm{C})=3 \mathrm{~nm}$
$\lambda(D)$ $=30 \mathrm{~Å}$
इन विकिरणों को उनकी ऊर्जा के बढ़ते क्रम में व्यवस्थित करें।
उत्तर दिखाएं
Answer:
$\lambda(A)=300 \mathrm{~nm}=300 \times 10^{-9} \mathrm{~m}, $
$ \lambda(B)=300 \mu \mathrm{m}=300 \times 10^{-6} \mathrm{~m}$
$\lambda(\mathrm{C})=3 \mathrm{~nm}=3 \times 10^{-9} \mathrm{~m}$,
$\lambda(\mathrm{D})=30\textÅ=30 \times 10^{-10} \mathrm{~m}=3 \times 10^{-9} \mathrm{~m}$
$ऊर्जा, E=\frac{h c}{\lambda}$
$ अतः,\quad E \propto \frac{1}{\lambda}$
ऊर्जा के बढ़ते क्रम में $B<A<C=D$ है।
31. $ \mathrm{Cu}$ के बाह्य कोश की इलेक्ट्रॉनिक विन्यास $3 d^{10} 4 s^{1}$ है और नहीं $3 d^{9} 4 s^{2}$. इस विन्यास को कैसे समझाएंगे?
उत्तर दिखाएं
Answer:
इलेक्ट्रॉनिक विन्यास जो ठीक आधा भरा हो या पूर्ण रूप से भरा हो अधिक स्थायी होता है क्योंकि इलेक्ट्रॉनों के सममित वितरण और अधिकतम आदान-प्रदान ऊर्जा होती है। $3 d^{10} 4 s^{1}$ में, d-कक्षक पूर्ण रूप से भरे हुए हैं और s-कक्षक आधा भरा हुआ है।
अतः, यह अधिक स्थायी विन्यास है।
32. हाइड्रोजन स्पेक्ट्रम में बाल्मर श्रेणी $n_{1}=2$ से $n_{2}=3,4, \ldots$ तक के संक्रमण के संगत होती है। यह श्रेणी दृश्य क्षेत्र में होती है। जब इलेक्ट्रॉन $n=4$ कक्षा में जाता है तो बाल्मर श्रेणी के रेखा के तरंग संख्या की गणना करें।
$\left(R_{\mathrm{H}}=109677 \mathrm{~cm}^{-1}\right)$
उत्तर दिखाएं
Answer:
रिडबर्ग सूत्र से,
तरंग संख्या, $\quad \bar{v}=109677\left[\frac{1}{n_{i}^{2}}-\frac{1}{n_{f}^{2}}\right] \mathrm{cm}^{-1}$
$दिया गया, {~n_{i}} =2 \text { और } n_{f}=4 \quad \text{(बैल्मर श्रेणी में परिवर्तन)}$
$\bar{v} =109677\left[\frac{1}{2^{2}}-\frac{1}{4^{2}}\right] \mathrm{cm}^{-1}$
$\Rightarrow \bar{v}=109677\left[\frac{1}{4}-\frac{1}{16}\right] \mathrm{cm}^{-1} $
$\Rightarrow \bar{v}=109677 \times\left[\frac{4-1}{16}\right] \mathrm{cm}^{-1} $
$\Rightarrow \bar{v}=20564.44 \mathrm{~cm}^{-1}$
33. डी-ब्रोग्ली के अनुसार, पदार्थ दोनों तरह का व्यवहार दिखाना चाहिए, अर्थात पारंपरिक और तरंग गुण। हालांकि, एक क्रिकेट बॉल जिसका द्रव्यमान $100 \mathrm{~g}$ है, जब एक बोलर द्वारा $100 \mathrm{~km} / \mathrm{h}$ की गति से फेंका जाता है, तो तरंग के रूप में गति नहीं करता। बॉल की तरंग दैर्घ्य की गणना करें और समझाएं कि क्यों यह तरंग गुण नहीं दिखाता।
उत्तर दिखाएं
Answer:
दिया गया,
$ m=100 \mathrm{~g}=0.1 \mathrm{~kg} $
$v=100 \mathrm{~km} / \mathrm{h}=\dfrac{100 \times 1000}{60 \times 60}=\dfrac{1000}{36} \mathrm{~ms}^{-1}$
डी-ब्रोग्ली समीकरण से, तरंग दैर्घ्य, $\lambda=\dfrac{h}{m v}$
$ \lambda=\dfrac{6.626 \times 10^{-34} \mathrm{~kg} \mathrm{~m}^{2} \mathrm{~s}^{-1}}{0.1 \mathrm{~kg} \times \frac{1000}{36} \mathrm{~ms}^{-1}}=238.5 \times 10^{-36} \mathrm{~m} $
क्योंकि तरंग दैर्घ्य बहुत छोटी है, इसलिए तरंग गुण नहीं पहचाना जा सकता।
34. परमाणु में इलेक्ट्रॉनिक ऊर्जा के क्वांटीकरण के विचार के समर्थन में कौन से प्रयोगात्मक प्रमाण हैं?
उत्तर दिखाएं
Answer:
परमाणु भौतिकी में क्वांटीकरण की अवधारणा का अर्थ है कि परमाणु में इलेक्ट्रॉन केवल विशिष्ट ऊर्जा स्तरों पर ही रह सकते हैं। ये इन स्तरों के बीच में नहीं रह सकते, जो इस बात को संकेत देता है कि ऊर्जा असतत होती है न कि सतत।
इलेक्ट्रॉनिक ऊर्जा के क्वांटीकरण के लिए प्रमुख प्रयोगात्मक प्रमाण में तत्वों के चमकदार रेखीय स्पेक्ट्रम (या उत्सर्जन स्पेक्ट्रम) के अवलोकन को शामिल करता है। जब एक परमाणु को उत्तेजित किया जाता है, तो इसके इलेक्ट्रॉन उच्च ऊर्जा स्तरों में जाते हैं। जब ये इलेक्ट्रॉन अपने मूल (कम) ऊर्जा स्तरों में वापस आ जाते हैं, तो वे विशिष्ट तरंगदैर्घ्यों पर प्रकाश उत्सर्जित करते हैं।
द्वारा उत्सर्जित प्रकाश एक विशिष्ट तरंगदैर्घ्यों पर अलग-अलग रेखाएँ (ज्वलंत रेखाएँ) वाला एक स्पेक्ट्रम उत्पन्न करता है। प्रत्येक रेखा परमाणु के क्वांटाइज़ड ऊर्जा स्तरों के बीच परिवर्तन को दर्शाती है। इन अलग-अलग रेखाओं की उपस्थिति यह दर्शाती है कि ऊर्जा स्तर क्वांटाइज़ड होते हैं।
इसलिए, ज्वलंत रेखा स्पेक्ट्रम एक प्रयोगात्मक प्रमाण है जो परमाणु में इलेक्ट्रॉनिक ऊर्जा के क्वांटाइज़ड होने के विचार को समर्थन देता है, क्योंकि यह दर्शाता है कि इलेक्ट्रॉन केवल विशिष्ट ऊर्जा स्तरों के बीच परिवर्तन कर सकते हैं, जिसके परिणामस्वरूप विशिष्ट तरंगदैर्घ्यों पर प्रकाश की उत्सर्जन होती है।
35. इलेक्ट्रॉन और प्रोटॉन में से कौन एक ही तरंगदैर्घ्य के द्रव्य तरंग उत्पन्न करने के लिए अधिक वेग रखेगा? समझाइए।
उत्तर दिखाएं
उत्तर:
देब्रॉग्ली समीकरण से, तरंगदैर्घ्य, $\lambda=\frac{h}{m v}$
दो अलग-अलग कणों, अर्थात इलेक्ट्रॉन और प्रोटॉन के लिए एक ही तरंगदैर्घ्य के लिए, $m_{1} v_{1}=m_{2} v_{2}$ (h नियतांक है)। कण के द्रव्यमान कम होने पर वेग अधिक होता है। इसलिए, इलेक्ट्रॉन के वेग अधिक होंगे।
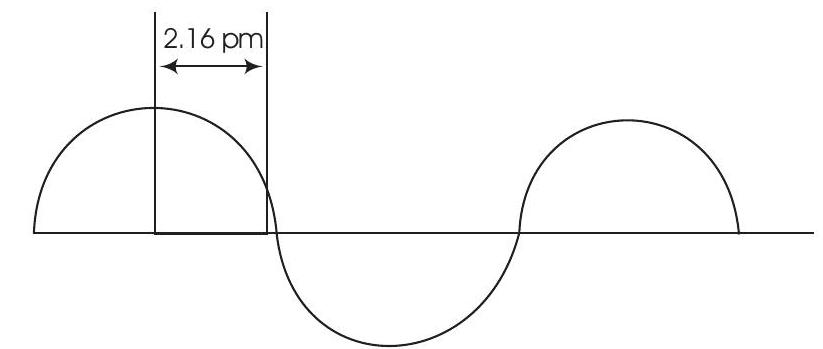
36. एक अनुमानित विद्युत चुंबकीय तरंग के चित्र के रूप में दिखाया गया है। विकिरण की तरंगदैर्घ्य ज्ञात कीजिए।
उत्तर दिखाएं
उत्तर:
तरंगदैर्घ्य: यह एक तरंग के दो आसंजित शिखर या घुटन के बीच की दूरी को परिभाषित करता है, जैसा कि चित्र में दिखाया गया है। इसे $\lambda$ से नोट किया जाता है।
$\lambda=4 \times 2.16 \mathrm{pm}$
$=8.64 \mathrm{pm}$
37. पौधों के हरे पत्तों में उपस्थित क्लोरोफिल, $4.620 \times 10^{14} \mathrm{~Hz}$ के प्रकाश को अवशोषित करता है। नैनोमीटर में विकिरण की तरंगदैर्घ्य की गणना कीजिए।
इस विकिरण को विद्युत चुंबकीय विकिरण के किस भाग में वर्गीकृत किया जाएगा?
उत्तर दिखाएं
उत्तर:
$ Wavelength, \quad\lambda=\frac{C}{V} $
दिया गया है,
$
\text { आवृत्ति } v =4.620 \times 10^{14} \mathrm{~Hz} \text { या } 4.620 \times 10^{14} \mathrm{~s}^{-1} $
$\lambda =\dfrac{c}{v}$
$=\dfrac{3 \times 10^{8} \mathrm{~ms}^{-1}}{4.620 \times 10^{14} \mathrm{~s}^{-1}} $
$=0.6494 \times 10^{-6} \mathrm{~m} $
$=649.4 \mathrm{~nm} \quad \quad\left[\because 1 \mathrm{~nm}=10^{-6} \mathrm{~m}\right]$
इसलिए, यह दृश्य क्षेत्र में स्थित है।
38. “ओर्बिट” और “ओर्बिटल” के बीच अंतर क्या है?
उत्तर दिखाएं
उत्तर:
“ओर्बिट” और “ओर्बिटल” के बीच अंतर नीचे दिया गया है
| ओर्बिट | ओर्बिटल |
|---|---|
| एक ओर्बिट एक स्पष्ट वृत्ताकार पथ होता है नाभिक के चारों ओर जहां इलेक्ट्रॉन घूमते हैं। |
एक ओर्बिटल नाभिक के चारों ओर एक तीन-आयामी अंतराल होता है जहां इलेक्ट्रॉन के पाए जाने की संभावना अधिकतम होती है (लगभग 90%) सभी ओर्बिट वृत्ताकार और डिस्क जैसे होते हैं। |
| ओर्बिट की अवधारणा इलेक्ट्रॉन के तरंग गुण के साथ संगत नहीं होती है ओर्बिटल अलग-अलग आकार के होते हैं। |
ओर्बिटल की अवधारणा इलेक्ट्रॉन के तरंग गुण और अनिश्चितता सिद्धांत के साथ संगत होती है। |
| किसी भी ओर्बिट में अधिकतम इलेक्ट्रॉन की संख्या $2 n^{2}$ द्वारा दी जाती है जहां $n$ ओर्बिट की संख्या होती है। | किसी भी ओर्बिटल में अधिकतम इलेक्ट्रॉन की संख्या दो होती है। |
39. टेबल टेनिस बॉल का द्रव्यमान $10 \mathrm{~g}$ है और गति $90 \mathrm{~m} / \mathrm{s}$ है। यदि गति को मापने की त्रुटि $4 $% है, तो गति और स्थिति में अनिश्चितता क्या होगी?
उत्तर दिखाएं
उत्तर:
दिया गया है, गति $=90 \mathrm{~m} / \mathrm{s}$
द्रव्यमान $=10 \mathrm{~g}=10 \times 10^{-3} \mathrm{~kg}$
गति में अनिश्चितता $(\Delta v)=4 $% के $90 \mathrm{~ms}^{-1}=\frac{4 \times 90}{100}=3.6 \mathrm{~ms}^{-1}$
हाइजेनबर्ग अनिश्चितता सिद्धांत से,
$ \Delta x \cdot \Delta v =\dfrac{h}{4 \pi m} $
$ या \quad \Delta x =\dfrac{h}{4 \pi m \Delta v} $
अस्थिरता स्थिति में,
$ \Delta x =\dfrac{6.626 \times 10^{-34} \mathrm{kgm}^{2} \mathrm{~s}^{-1}}{4 \times 3.14 \times 10 \times 10^{-3} \mathrm{~kg} \times 3.6 \mathrm{~ms}^{-1}} $
$ =1.46 \times 10^{-33} \mathrm{~m} $
40. अस्थिरता सिद्धांत का प्रभाव माइक्रोस्कोपिक कणों के गति के लिए महत्वपूर्ण होता है और मैक्रोस्कोपिक कणों के लिए नगण्य होता है। एक उपयुक्त उदाहरण की सहायता से इस कथन की व्याख्या करें।
उत्तर दिखाएं
Answer:
एक वस्तु के द्रव्यमान के लिए अस्थिरता सिद्धांत के अनुप्रयोग करते हुए, जैसे कि एक मिलीग्राम $\left(10^{-6} \mathrm{~kg}\right)$ के लिए, तो
$ \Delta \cdot \Delta x =\dfrac{h}{4 \pi m} $
$ \Delta v \cdot \Delta x =\dfrac{6.626 \times 10^{-34} \mathrm{kgm}^{2} \mathrm{~s}^{-1}}{4 \times 3.14 \times 10^{-6} \mathrm{~kg}} $
$ =0.52 \times 10^{-28} \mathrm{~m}^{2} \mathrm{~s}^{-1} $
$\Delta v \cdot \Delta x$ के मान बहुत छोटा है और नगण्य है। अतः, मिलीग्राम आकार के या उससे भारी वस्तुओं के लिए संबंधित अस्थिरताएं कोई वास्तविक परिणाम नहीं देती हैं।
41. हाइड्रोजन परमाणु में केवल एक इलेक्ट्रॉन होता है। अतः, इलेक्ट्रॉनों के बीच पारस्परिक प्रतिरोध की अनुपस्थिति होती है। हालांकि, बहुइलेक्ट्रॉन परमाणु में इलेक्ट्रॉनों के बीच पारस्परिक प्रतिरोध महत्वपूर्ण होता है। इसका बहुइलेक्ट्रॉन परमाणु के एक ही मुख्य क्वांटम संख्या वाले ऑर्बिटल में इलेक्ट्रॉन की ऊर्जा पर क्या प्रभाव पड़ता है?
उत्तर दिखाएं
Answer:
हाइड्रोजन परमाणु में इलेक्ट्रॉन की ऊर्जा मुख्य क्वांटम संख्या द्वारा निर्धारित होती है। अतः, ऑर्बिटल की ऊर्जा निम्नलिखित क्रम में बढ़ती है:
$1s<2s=2p<3s=3p=3d<4s=4p<4d=4f$
हालांकि, बहुइलेक्ट्रॉन परमाणु में इलेक्ट्रॉन की ऊर्जा मुख्य क्वांटम संख्या (शेल) के अलावा अक्षीय क्वांटम संख्या (उपशेल) पर भी निर्भर होती है, जो हाइड्रोजन परमाणु के विपरीत बिलकुल अलग होती है। इसका अर्थ यह है कि एक ही मुख्य क्वांटम संख्या के लिए, s, p, d, f सभी अलग-अलग ऊर्जा के होते हैं।
स्तम्भों का मिलान
42. निम्नलिखित तत्वों को उनके संगत भूमि अवस्था इलेक्ट्रॉनिक विन्यास से मिलाएं।
| परमाणु / आयन | इलेक्ट्रॉनिक विन्यास | ||
|---|---|---|---|
| A. | $ \mathrm{Cu}$ | 1. | $1 s^{2} 2 s^{2} 2 p^{6} 3 s^{2} 3 p^{6} 3 d^{10}$ |
| B. | $ \mathrm{Cu}^{2+}$ | 2. | $1 s^{2} 2 s^{2} 2 p^{6} 3 s^{2} 3 p^{6} 3 d^{10} 4 s^{2}$ |
| C. | $ \mathrm{Zn}^{2+}$ | 3. | $1 s^{2} 2 s^{2} 2 p^{6} 3 s^{2} 3 p^{6} 3 d^{10} 4 s^{1}$ |
| D. | $ \mathrm{Cr}^{3+}$ | 4. | $1 s^{2} 2 s^{2} 2 p^{6} 3 s^{2} 3 p^{6} 3 d^{9}$ |
| 5. | $1 s^{2} 2 s^{2} 2 p^{6} 3 s^{2} 3 p^{6} 3 d^{3}$ |
उत्तर दिखाएं
उत्तर:
A. $\rightarrow(3)$
B. $\rightarrow(4)$
C. $\rightarrow(1)$
D. $\rightarrow(5)$
A. $ \mathrm{Cu}(Z=29) \quad: \quad 1 s^{2} 2 s^{2} 2 p^{6} 3 s^{2} 3 p^{6} 3 d^{10} 4 s^{1}$
B. $ \mathrm{Cu}^{2+}(Z=29): 1 s^{2} 2 s^{2} 2 p^{6} 3 s^{2} 3 p^{6} 3 d^{9}$
C. $ \mathrm{Zn}^{2+}(Z=30): 1 s^{2} 2 s^{2} 2 p^{6} 3 s^{2} 3 p^{6} 3 d^{10}$
D. $ \mathrm{Cr}^{3+}(Z=24): 1 s^{2} 2 s^{2} 2 p^{6} 3 s^{2} 3 p^{6} 3 d^{3}$
43. क्वांटम संख्या को उनके द्वारा प्रदान किए गए जानकारी से मिलाएं।
| क्वांटम संख्या | प्रदान की गई जानकारी | ||
|---|---|---|---|
| A. | मुख्य क्वांटम संख्या | 1. | ऑर्बिटल के उपांत विन्यास |
| B. | अक्षीय क्वांटम संख्या | 2. | ऑर्बिटल की ऊर्जा और आकार |
| C. | चुंबकीय क्वांटम संख्या | 3. | इलेक्ट्रॉन का घूर्णन |
| D. | घूर्णन क्वांटम संख्या | 4. | ऑर्बिटल के आकार |
उत्तर दिखाएं
उत्तर:
A. $\rightarrow(2)$
B. $\rightarrow(4)$
C. $\rightarrow(1)$
D. $\rightarrow(3)$
A. मुख्य क्वांटम संख्या सबसे महत्वपूर्ण क्वांटम संख्या है क्योंकि यह ऑर्बिटल के आकार और बहुत बड़े अंश से ऊर्जा को निर्धारित करती है।
B. अक्षीय क्वांटम संख्या इलेक्ट्रॉन के कोणीय संवेग को निर्धारित करती है और ऑर्बिटल के तीन आयामी आकार को परिभाषित करती है।
C. चुंबकीय क्वांटम संख्या ऑर्बिटल के अंतर्गत निर्देशांक अक्ष के संबंध में अंतर्गत विन्यास के बारे में जानकारी प्रदान करती है।
D. चक्रण चुंबकीय संख्या उस स्पेक्ट्रम के प्रमाण से उत्पन्न होती है जिसमें एक इलेक्ट्रॉन अपने नाभिक के चारों ओर एक कक्षा में घूमते हुए अपने अक्ष के चारों ओर भी घूमता है।
44. निम्नलिखित नियमों को उनके कथनों से मिलाएं।
| नियम | कथन | |
|---|---|---|
| A. | Hund का नियम | 1. परमाणु में कोई भी दो इलेक्ट्रॉन चारों तरफ के चार चुंबकीय संख्या के समान सेट के अनुसार नहीं हो सकते। |
| B. | Aufbau सिद्धांत | 2. आधे भरे और पूरी तरह से भरे ऑर्बिटल अतिरिक्त स्थिरता रखते हैं। |
| C. | Pauli विरोधाभास सिद्धांत | 3. एक ही उपकक्षा के ऑर्बिटल में इलेक्ट्रॉन के युग्मन के लिए पहले प्रत्येक ऑर्बिटल में एक इलेक्ट्रॉन होना आवश्यक है, अर्थात इसके एकल रूप से भरे हुए होना आवश्यक है। |
| D. | Heisenberg के अनिश्चितता सिद्धांत | 4. एक उप-परमाणु कण के ठीक स्थिति और ठीक संवेग के एक साथ निर्धारण करना संभव नहीं है। 5. परमाणु के आध्यात्मिक अवस्था में, ऑर्बिटल उनकी बढ़ती ऊर्जा के क्रम में भरे जाते हैं। |
उत्तर दिखाएं
Answer:
A. $\rightarrow(3)$
B. $\rightarrow (5) $
C. $\rightarrow(1)$
D. $\rightarrow(4)$
A. Hund के नियम के अनुसार, एक ही उपकक्षा ( $p, d$ या $f$ ) के ऑर्बिटल में इलेक्ट्रॉन के युग्मन के लिए पहले प्रत्येक ऑर्बिटल में एक इलेक्ट्रॉन होना आवश्यक है, अर्थात इसके एकल रूप से भरे हुए होना आवश्यक है।
B. Aufbau सिद्धांत के अनुसार, परमाणु के आध्यात्मिक अवस्था में, ऑर्बिटल उनकी बढ़ती ऊर्जा के क्रम में भरे जाते हैं।
C. Pauli विरोधाभास सिद्धांत के अनुसार, परमाणु में कोई भी दो इलेक्ट्रॉन चारों तरफ के चार चुंबकीय संख्या के समान सेट के अनुसार नहीं हो सकते।
D. Heisenberg के अनिश्चितता सिद्धांत के अनुसार, एक उप-परमाणु कण के ठीक स्थिति और ठीक संवेग के एक साथ निर्धारण करना संभव नहीं है।
45. निम्नलिखित को मिलाएं।
| स्तम्भ I | स्तम्भ II | ||
|---|---|---|---|
| A. | X-किरणें | 1. | $v=10^{0}-10^{4} \mathrm{~Hz}$ |
| B. | अपवर्तन तरंग (UV) | 2. | $v=10^{10} \mathrm{~Hz}$ |
| सी। | लंब रेडियो तरंगें | 3। | $v=10^{16} \mathrm{~Hz}$ | | डी। | माइक्रोवेव | 4। | $v=10^{18} \mathrm{~Hz}$ |
उत्तर दिखाएं
उत्तर:
A. $\rightarrow(4)$
B. $\rightarrow(3)$
C. $\rightarrow (1)$
D. $\rightarrow(2)$
| नाम | आवृत्ति | उपयोग | |
|---|---|---|---|
| A. | X-rays | $2 \times 10^{16}-3 \times 10^{19} \mathrm{~Hz}$ | चिकित्सा चित्र, सामग्री परीक्षण |
| B. | अल्ट्रावायलेट तरंग $(\mathrm{UV})$ | $7.9 \times 10^{14}-2 \times 10^{16} \mathrm{~Hz}$ | जर्मिसीडल लैंप |
| C. | लंब रेडियो तरंगें | $10^{0}-10^{4} \mathrm{~Hz}$ | संकेत प्रसारण |
| D. | माइक्रोवेव | $1 \times 10^{9}-5 \times 10^{11} \mathrm{~Hz}$ | बनावट, रेडार |
46. निम्नलिखित को मिलाएं।
| स्तंभ I | स्तंभ II | ||
|---|---|---|---|
| A. | फोटॉन | 1. | $N$-शेल के लिए मान 4 होता है |
| B. | इलेक्ट्रॉन | 2. | प्रायिकता घनत्व |
| C. | $\psi^{2}$ | 3. | हमेशा धनात्मक मान |
| D. | मुख्य क्वांटम संख्या $n$ |
4. | संवेग और तरंगदैर्घ्य दोनों दर्शाता है |
उत्तर दिखाएं
उत्तर:
A. $\rightarrow(4)$
B. $\rightarrow(4)$
C. $\rightarrow(2,3)$
D. $\rightarrow(1,3)$
A. फोटॉन के दोनों प्रकार के गुण होते हैं: कण और तरंग। इसके दोनों संवेग और तरंगदैर्घ्य दर्शाता है।
B. इलेक्ट्रॉन में भी कण और तरंग दोनों गुण होते हैं। इसलिए इसमें भी संवेग और तरंगदैर्घ्य दोनों दिखाई देते हैं।
C. $\psi^{2}$ इलेक्ट्रॉन के प्रायिकता घनत्व को दर्शाता है और हमेशा धनात्मक मान रखता है।
D. मुख्य क्वांटम संख्या $n=4$ $N$-शेल के लिए होती है।
$ \hspace{1cm} \hspace{1cm} K\hspace{1cm} L\hspace{1cm} M\hspace{1cm} N $
$ n=\hspace{1cm} 1 \hspace{1.2cm} 2 \hspace{1.4cm} 3 \hspace{1cm} 4 $
यह हमेशा धनात्मक मान रखता है।
47. स्तंभ I में दिए गए विशिष्ट अणुओं को स्तंभ II में दिए गए इलेक्ट्रॉनिक विन्यास के साथ मिलाएं।
| स्तंभ I | स्तंभ II | ||
|---|---|---|---|
| A. | $ \mathrm{Cr}$ | 1. | $[\mathrm{Ar}] 3 d^{8} 4 s^{0}$ |
| बी। | $ \mathrm{Fe}^{2+}$ | 2. | $[\mathrm{Ar}] 3 d^{10} 4 s^{1}$ | | सी। | $ \mathrm{Ni}^{2+}$ | 3. | $[\mathrm{Ar}] 3 d^{6} 4 s^{0}$ | | डी। | $ \mathrm{Cu}$ | 4. | $[\mathrm{Ar}] 3 d^{5} 4 s^{1}$ | | | | 5. | $[\mathrm{Ar}] 3 d^{6} 4 s^{2}$ |
उत्तर दिखाएं
उत्तर:
अ। $\rightarrow(4)$
बी। $\rightarrow(3)$
सी। $\rightarrow(1)$
डी। $\rightarrow(2)$
अ। $\operatorname{Cr}(Z=24)=1 s^{2} 2 s^{2} 2 p^{6} 3 s^{2} 3 p^{6} 3 d^{5} 4 s^{1}=[\operatorname{Ar}] 3 d^{5} 4 s^{1}$
बी। $ \mathrm{Fe}^{2+}(Z=26)=1 s^{2} 2 s^{2} 2 p^{6} 3 s^{2} 3 p^{6} 3 d^{6} 4 s^{0}=[\operatorname{Ar}] 3 d^{6} 4 s^{0}$
सी। $ \mathrm{Ni}^{2+}(Z=28)=1 s^{2} 2 s^{2} 2 p^{6} 3 s^{2} 3 p^{6} 3 d^{8} 4 s^{0}=[\operatorname{Ar}] 3 d^{8} 4 s^{0}$
डी। $ \mathrm{Cu}(Z=29)=1 s^{2} 2 s^{2} 2 p^{6} 3 s^{2} 3 p^{6} 3 d^{10} 4 s^{1}=[\mathrm{Ar}] 3 d^{10} 4 s^{1}$
असर्थकथन और कारण
निम्नलिखित प्रश्नों में असर्थकथन (A) के एक कथन के बाद कारण (R) के एक कथन दिया गया है। प्रत्येक प्रश्न में नीचे दिए गए विकल्पों में से सही विकल्प चुनें।
48. असर्थकथन (A) एक तत्व के सभी समस्थानिक एक ही प्रकार के रासायनिक व्यवहार दिखाते हैं।
कारण (R) एक परमाणु के रासायनिक गुण उस परमाणु में उपस्थित इलेक्ट्रॉनों की संख्या द्वारा नियंत्रित होते हैं।
(ए) दोनों A और R सत्य हैं और R, A का सही स्पष्टीकरण है
(ब) दोनों A और R सत्य हैं लेकिन R, A का सही स्पष्टीकरण नहीं है
(स) A सत्य है लेकिन R गलत है
(द) दोनों A और R गलत हैं
उत्तर दिखाएं
उत्तर: (ए) दोनों A और R सत्य हैं और R, A का सही स्पष्टीकरण है
समस्थानिक एक ही परमाणु संख्या रखते हैं अर्थात एक ही इलेक्ट्रॉनों की संख्या जो उनके रासायनिक व्यवहार के लिए जिम्मेदार है। इसलिए, ये समान रासायनिक गुण दिखाते हैं।
49. असर्थकथन (A) काला शरीर एक आदर्श वस्तु है जो सभी आवृत्तियों के विकिरण को उत्सर्जित और अवशोषित करता है।
कारण (R) एक वस्तु द्वारा उत्सर्जित विकिरण की आवृत्ति तापमान में वृद्धि के साथ एक निम्न आवृत्ति से एक उच्च आवृत्ति तक जाती है।
(a) $A$ और $R$ दोनों सत्य हैं और $R$ $A$ का सही स्पष्टीकरण है
(b) $A$ और $R$ दोनों सत्य हैं लेकिन $R$ $A$ का सही स्पष्टीकरण नहीं है
(c) $A$ सत्य है लेकिन $R$ गलत है
(d) $A$ और $R$ दोनों गलत हैं
उत्तर दिखाएं
उत्तर:(b) $A$ और $R$ दोनों सत्य हैं लेकिन $R$ $A$ का सही स्पष्टीकरण नहीं है
एक काला शरीर वह आदर्श शरीर है जो सभी आवृत्तियों के विकिरण को अवशोषित और उत्सर्जित करता है। इसके उत्सर्जित विकिरण को काला शरीर विकिरण कहा जाता है।
तापमान में वृद्धि के साथ-साथ काला शरीर विकिरण की आवृत्ति बढ़ जाती है।
50. अस्थायी कथन (A) एक इलेक्ट्रॉन की सटीक स्थिति और सटीक संवेग को एक साथ निर्धारित नहीं किया जा सकता।
कारण (R) परमाणु में इलेक्ट्रॉन के पथ को स्पष्ट रूप से परिभाषित किया गया है।
(a) $A$ और $R$ दोनों सत्य हैं और $R$ $A$ का सही स्पष्टी रण है
(b) $A$ और $R$ दोनों सत्य हैं लेकिन $R$ $A$ का सही स्पष्टीकरण नहीं है
(c) $A$ सत्य है लेकिन $R$ गलत है
(d) $A$ और $R$ दोनों गलत हैं
उत्तर दिखाएं
उत्तर:(c) $A$ सत्य है और $R$ गलत है
अस्थायी कथन सत्य है और कारण गलत है।
हाइजेनबर्ग के अनिश्चितता सिद्धांत के अनुसार, एक इलेक्ट्रॉन की सटीक स्थिति और सटीक संवेग को एक साथ निर्धारित नहीं किया जा सकता। इसलिए, परमाणु में इलेक्ट्रॉन के पथ को स्पष्ट रूप से परिभाषित नहीं किया जा सकता।
लंबे उत्तर प्रकार प्रश्न
51. फोटोइलेक्ट्रिक प्रभाव क्या है? फोटोइलेक्ट्रिक प्रभाव प्रयोग के उन परिणामों का वर्णन करें जो क्लासिकल भौतिकी के नियमों के आधार पर समझे जा सकते हैं। इस प्रभाव को विद्युत चुंबकीय विकिरण के क्वांटम सिद्धांत के आधार पर समझाइए।
उत्तर दिखाएं
उत्तर:
फोटोइलेक्ट्रिक प्रभाव जब किसी धातु के सतह पर निश्चित न्यूनतम आवृत्ति $(v_{0})$ के विकिरण के प्रहार होते हैं, तो इलेक्ट्रॉन धातु के सतह से निकल जाते हैं। इस घटना को फोटोइलेक्ट्रिक प्रभाव कहा जाता है। निकले इलेक्ट्रॉन को फोटोइलेक्ट्रॉन कहा जाता है।

इस प्रयोग के परिणाम निम्नलिखित थे:
(i) इलेक्ट्रॉन केवल तभी धातु सतह से निकलते हैं जब प्रकाश की किरण सतह पर प्रहार करती है।
(ii) इलेक्ट्रॉन की संख्या विकिरण की तीव्रता के अनुक्रमानुपाती होती है।
(iii) प्रत्येक धातु के लिए एक न्यूनतम आवृत्ति, $v_0$ होती है जिसके नीचे फोटोइलेक्ट्रॉन प्रभाव देखा नहीं जा सकता।
(iv) इलेक्ट्रॉन की कार्यशक्ति $\alpha$ प्रकाश की आवृत्ति के अनुक्रमानुपाती होती है।
क्वांटम सिद्धांत के आधार पर फोटोइलेक्ट्रॉन प्रभाव की व्याख्या:
जब एक फोटॉन जो उच्च ऊर्जा रखता है धातु के परमाणु के इलेक्ट्रॉन पर प्रहार करता है, तो इस फोटॉन की ऊर्जा इलेक्ट्रॉन में स्थानांतरित हो जाती है और इलेक्ट्रॉन तुरंत निकल जाता है। फोटॉन की ऊर्जा अधिक होगी तो निकले इलेक्ट्रॉन की कार्यशक्ति भी अधिक होगी।
52. श्रेणी आवृत्ति, $v_{0}$ वह न्यूनतम आवृत्ति होती है जिसके लिए एक फोटॉन के धातु के इलेक्ट्रॉन को निकालने के लिए आवश्यक होती है। यह विभिन्न धातुओं के लिए अलग-अलग होती है। जब एक फोटॉन जिसकी आवृत्ति $1.0 \times 10^{15} \mathrm{~s}^{-1}$ है धातु की सतह पर प्रहार करता है, तो एक इलेक्ट्रॉन जिसकी कार्यशक्ति $1.988 \times 10^{-19} \mathrm{~J}$ है उत्सर्जित होता है। इस धातु की श्रेणी आवृत्ति की गणना कीजिए।
दिखाइए कि एक फोटॉन जिसकी तरंगदैर्ध्य $600 \mathrm{~nm}$ है धातु की सतह पर प्रहार करता है तो इलेक्ट्रॉन के उत्सर्जन के लिए नहीं देखा जा सकता।
उत्तर दिखाएं
Answer:
हम जानते हैं कि,
$ h v =h v_{0}+\mathrm{KE} $
$ or \quad h v-\mathrm{KE} =h v_{0}=\left(6.626 \times 10^{-34} \mathrm{Js} \times 1 \times 10^{15} \mathrm{~s}^{-1}\right)-1.988 \times 10^{-19} \mathrm{~J} $
$ h v_{0} =6.626 \times 10^{-19}-1.988 \times 10^{-19} \mathrm{~J} $
$ h v_{0} =4.638 \times 10^{-19} \mathrm{~J} $
$v_{0} =\frac{4.638 \times 10^{-19} \mathrm{~J}}{6.626 \times 10^{-34} \mathrm{Js}}=0.699 \times 10^{15} \mathrm{~s}^{-1}$
$When, \quad \lambda =600 \mathrm{~nm}=600 \times 10^{-19} \mathrm{~m} $
$v =\frac{c}{\lambda}=\frac{3.0 \times 10^{8} \mathrm{~ms}^{-1}}{6.0 \times 10^{-7} \mathrm{~m}}=0.5 \times 10^{15} \mathrm{~s}^{-1}$
अतः, $v<v_{0}$. अतः, कोई इलेक्ट्रॉन उत्सर्जित नहीं होगा।
53. जब विद्युत चालकता के माध्यम से हाइड्रोजन गैस में विद्युत चालकता प्रवाहित की जाती है, तो हाइड्रोजन अणु विघटित होकर उत्तेजित हाइड्रोजन परमाणु उत्पन्न करते हैं। इन उत्तेजित परमाणुओं द्वारा उत्सर्जित विद्युत चुम्बकीय तरंग विशिष्ट आवृत्तियों के रूप में होती है जिसे एक सामान्य सूत्र द्वारा दिया जा सकता है
$ \bar{v}=109677\left[\frac{1}{n_{i}^{2}}-\frac{1}{n_{f}^{2}}\right] $
इस सूत्र के लिए बोहर के परमाणु मॉडल के कौन से बिंदु उपयोग किए जा सकते हैं? इन बिंदुओं के आधार पर उपरोक्त सूत्र के व्युत्पन्न करें और प्रत्येक चरण और प्रत्येक शब्द का विवरण दें।
उत्तर दिखाएं
उत्तर:
दिए गए सूत्र के व्युत्पन्न के लिए बोहर के मॉडल के दो महत्वपूर्ण बिंदु निम्नलिखित हैं:
(i) इलेक्ट्रॉन नाभिक के चारों ओर निश्चित त्रिज्या और ऊर्जा के वृत्ताकार पथ में घूमते हैं। ये पथ निर्माण अवस्था या अनुमत ऊर्जा अवस्था कहलाते हैं।
(ii) जब एक इलेक्ट्रॉन उच्च निर्माण अवस्था से निम्न निर्माण अवस्था या विपरीत रूप से निम्न निर्माण अवस्था से उच्च निर्माण अवस्था में चलता है, तो ऊर्जा उत्सर्जित या अवशोषित होती है।
उत्पन्न करना:
$ n^{\text {th }} $ निर्माण अवस्था में इलेक्ट्रॉन की ऊर्जा को निम्नलिखित सूत्र द्वारा दिया जाता है।
$ E_{n}=-R_{H}\left(\frac{1}{n^{2}}\right) \quad n=1,2,3 \quad …(i) $
जहाँ, $ R_{\mathrm{H}} $ रिडबर्ग नियतांक कहलाता है और इसका मान $ 2.18 \times 10^{-18} \mathrm{~J} $ है। सबसे कम ऊर्जा अवस्था, जिसे भूमि अवस्था कहा जाता है, की ऊर्जा निम्नलिखित है
$E_{n}=-2.18 \times 10^{-18}\left(\frac{1}{1^{2}}\right)$
$=-2.18 \times 10^{-18} \mathrm{~J} \quad …(ii)$
दो निर्माण अवस्थाओं के बीच ऊर्जा अंतर को निम्नलिखित समीकरण द्वारा दिया जाता है,
$ \Delta E=E_{f}-E_{i} \quad …(iii) $
समीकरण (i) और (iii) के संयोजन से
$ \Delta E=\left(-\frac{R_{H}}{n_{f}^{2}}\right)-\left(-\frac{R_{H}}{n_{i}^{2}}\right) $
जहाँ, $ n_{i} $ और $ n_{f} $ आरंभिक अवस्था और अंतिम अवस्था के लिए अवस्था के लिए निर्देशक हैं।
$\Delta E=R_{\mathrm{H}}\left[\frac{1}{n_{i}^{2}}-\frac{1}{n_{f}^{2}}\right]$
$=2.18 \times 10^{-18} \mathrm{~J}\left[\frac{1}{n_{i}^{2}}-\frac{1}{n_{f}^{2}}\right]$
ऊर्जा, $ v $ फोटॉन के अवशोषण और उत्सर्जन के साथ संबंधित आवृत्ति की गणना निम्नलिखित रूप में की जा सकती है
$\quad v =\frac{\Delta E}{h}$
$=\frac{R_{H}}{h}\left[\frac{1}{n_{i}^{2}}-\frac{1}{n_{f}^{2}}\right] $
$\Rightarrow \quad v =\frac{2.18 \times 10^{-18} \mathrm{~J}}{6.626 \times 10^{-34} \mathrm{Js}}\left[\frac{1}{n_{i}^{2}}-\frac{1}{n_{f}^{2}}\right] $
$v =3.29 \times 10^{15}\left[\frac{1}{n_{i}^{2}}-\frac{1}{n_{f}^{2}}\right] \mathrm{Hz} $
$\Rightarrow \bar{v} =\frac{v}{c}=\frac{3.29 \times 10^{15}}{3 \times 10^{8} \mathrm{~ms}^{-1}}\left[\frac{1}{n_{i}^{2}}-\frac{1}{n_{f}^{2}}\right] $
$\bar{v} =1.09677 \times 10^{7}\left[\frac{1}{n_{i}^{2}}-\frac{1}{n_{f}^{2}}\right] \mathrm{m}^{-1} $
$\bar{v}=109677\left[\frac{1}{n_{i}^{2}}-\frac{1}{n_{f}^{2}}\right] \mathrm{cm}^{-1}$
54. एक हाइड्रोजन परमाणु में इलेक्ट्रॉन $n=3$ से $n=2$ तक जाने पर उत्सर्जित विकिरण की ऊर्जा और आवृत्ति की गणना कीजिए।
उत्तर दिखाएं
उत्तर:
हाइड्रोजन परमाणु के ऊर्जा स्तरों के बीच इलेक्ट्रॉन के परिवर्तन के दौरान विकिरण के रूप में ऊर्जा उत्सर्जित या अवशोषित होती है। दो स्तरों के बीच ऊर्जा अंतर को रिडबर्ग सूत्र का उपयोग करके गणना की जा सकती है।
उत्सर्जित विकिरण की तरंगदैर्ध्य ($\lambda$) के लिए रिडबर्ग सूत्र निम्नलिखित है:
$ \frac{1}{\lambda}=R_H\left(\frac{1}{n_i^2}-\frac{1}{n_f^2}\right) $
जहाँ:
$R_H$ रिडबर्ग नियतांक है (लगभग $1.097 \times 10^7 \mathrm{~m}^{-1}$),
$n_i$ प्रारंभिक ऊर्जा स्तर है (इस मामले में 3 है),
$n_f$ अंतिम ऊर्जा स्तर है (इस मामले में 2 है)।
सूत्र में मान बदल देने पर:
$ \frac{1}{\lambda}=R_H\left(\frac{1}{3^2}-\frac{1}{2^2}\right) $
$ \frac{1}{\lambda}=R_H\left(\frac{1}{9}-\frac{1}{4}\right) $
$ \frac{1}{\lambda}=R_H\left(\frac{4-9}{36}\right)=R_H\left(-\frac{5}{36}\right) $
अब $R_H$ के मान को बदल देने पर:
$ \frac{1}{\lambda}=1.097 \times 10^7\left(-\frac{5}{36}\right) $
गणना करने पर:
$ \frac{1}{\lambda}=-1.52 \times 10^6 \mathrm{~m}^{-1} $
$\lambda$ के लिए व्युत्क्रम लेने पर :
$ \lambda=\frac{1}{-1.52 \times 10^6} \approx 6.56 \times 10^{-7} \mathrm{~m} `
$
ऊत्सर्जित विकिरण की ऊर्जा (E) की गणना निम्नलिखित सूत्र का उपयोग करके की जा सकती है:
$ E=\frac{h c}{\lambda} $
जहाँ:
$h$ प्लैंक के नियतांक है ( $6.626 \times 10^{-34} \mathrm{~J} \mathrm{~s}$ ),
$c$ प्रकाश की गति $\left(3.00 \times 10^8 \mathrm{~m} / \mathrm{s}\right)$ है।
मानों को बदलकर:
$ E=\frac{\left(6.626 \times 10^{-34}\right)\left(3.00 \times 10^8\right)}{6.56 \times 10^{-7}} $
गणना करने पर:
$ E \approx 3.03 \times 10^{-19} \mathrm{~J} $
आवृत्ति (v) की गणना निम्नलिखित सूत्र का उपयोग करके की जा सकती है:
$ \nu=\frac{c}{\lambda} $
मानों को बदलकर:
$ \nu=\frac{3.00 \times 10^8}{6.56 \times 10^{-7}} \approx 4.57 \times 10^{14} \mathrm{~s}^{-1} $
इसलिए,
ऊत्सर्जित ऊर्जा: $E \approx 3.03 \times 10^{-19} \mathrm{~J}$
ऊत्सर्जित विकिरण की आवृत्ति: $\nu \approx 4.57 \times 10^{14} \mathrm{~s}^{-1}$
55. परमाणु के बोहर मॉडल में क्यों परिवर्तन करना पड़ा? किस महत्वपूर्ण विकास के कारण इलेक्ट्रॉन के वृत्ताकार कक्षा में गति के अवधारणा को इलेक्ट्रॉन के ऑर्बिटल में पाए जाने की संभावना के अवधारणा से बदल दिया गया? परमाणु के बदले गए मॉडल के नाम क्या है?
उत्तर दिखाएं
उत्तर:
बोहर मॉडल में इलेक्ट्रॉन को एक चार्जित कण के रूप में देखा जाता है जो नाभिक के चारों ओर निश्चित वृत्ताकार कक्षाओं में गति करता है। एक कक्षा को केवल तभी पूरी तरह से परिभाषित किया जा सकता है जब इलेक्ट्रॉन की स्थिति और गति दोनों के एक ही समय में ठीक ज्ञात हो।
इसके विपरीत हेइजेनबर्ग अनिश्चितता सिद्धांत के अनुसार यह संभव नहीं है। इसके अतिरिक्त, बोहर मॉडल में इलेक्ट्रॉन के तरंग गुण को ध्यान में नहीं लिया गया है।
इसलिए, इलेक्ट्रॉन के वृत्ताकार कक्षा में गति के अवधारणा को इलेक्ट्रॉन के ऑर्बिटल में पाए जाने की संभावना के अवधारणा से बदल दिया गया कारण डी-ब्रोग्ली के इलेक्ट्रॉन के द्विगुण अवधारणा और हेइजेनबर्ग के अनिश्चितता सिद्धांत है। बदले गए मॉडल को परमाणु के क्वांटम यांत्रिक मॉडल के रूप में जाना जाता है।





