द्रव्य स्थिति
बहुविकल्पीय प्रश्न (MCQs)
1. शिमला में रहने वाले एक व्यक्ति ने देखा कि दबाव चलाने वाले बरतन के बिना खाना बनाने में अधिक समय लगता है। इस अवलोकन के कारण है कि उच्च ऊंचाई पर
(a) दबाव बढ़ जाता है
(b) तापमान घट जाता है
(c) दबाव घट जाता है
(d) तापमान बढ़ जाता है
उत्तर दिखाएं
उत्तर
(c) पर्वत के शीर्ष [या उच्च ऊंचाई पर] दबाव कम होता है। इससे बर्फ के उबलने के तापमान कम हो जाता है, जिस कारण चीजें बर्फ उबलने में अधिक समय लेती हैं।
हालांकि, दबाव चलाने वाले बरतन में दबाव बढ़ा दिया जाता है और इसलिए, उबलने के बिंदु बढ़ जाता है। इस कारण, दबाव चलाने वाले बरतन में चीजें कम समय में उबल जाती हैं।
-
(a) दबाव बढ़ जाता है: यह गलत है क्योंकि उच्च ऊंचाई पर वायुमंडलीय दबाव वास्तव में कम होता है, न कि बढ़ता है। बढ़े हुए दबाव के कारण उबलने के बिंदु बढ़ जाता है, जो उच्च ऊंचाई पर नहीं होता है।
-
(b) तापमान घट जाता है: यह वास्तव में उच्च ऊंचाई पर तापमान कम हो सकता है, लेकिन यह खाना बनाने में अधिक समय लगने के मुख्य कारण नहीं है। मुख्य कारण वायुमंडलीय दबाव कम होना है, जो पानी के उबलने के बिंदु को कम कर देता है।
-
(d) तापमान बढ़ जाता है: यह गलत है क्योंकि ऊंचाई के साथ तापमान आमतौर पर घटता है। यहां तक कि तापमान बढ़े हों, यह खाना बनाने में अधिक समय लगने के मुख्य कारण नहीं हो सकता है, जो मुख्य रूप से घटे हुए दबाव के कारण पानी के उबलने के बिंदु कम होने के कारण है।
2. निम्नलिखित में से कौन सी जल की गुणधर्म वर्षा के बूंदों के गोलाकार आकार को समझाने में प्रयोग किया जा सकता है?
(a) चिकनाई
(b) सतह तनाव
(c) क्रिटिकल घटनाएं
(d) दबाव
उत्तर दिखाएं
उत्तर
(b) वर्षा के बूंदों के गोलाकार आकार सतह तनाव के कारण होता है। तरल के न्यूनतम ऊर्जा अवस्था तब होती है जब सतह क्षेत्रफल न्यूनतम हो। सतह तनाव तरल के सतह क्षेत्रफल को न्यूनतम करने की कोशिश करता है। वर्षा के बूंद गोलाकार होते हैं क्योंकि दिए गए आयतन के लिए गोला न्यूनतम सतह क्षेत्रफल के रूप में होता है।
-
गुरुत्वाकर्षण: गुरुत्वाकर्षण एक तरल के प्रवाह के विरोध के माप के रूप में है। यह बूंदों के आकार के लिए बर्बाद नहीं होता, बल्कि यह बूंदों के गति या फैलाव की गति को प्रभावित करता है। इसलिए, यह वर्षा की बूंदों के गोल आकार के लिए जिम्मेदार नहीं है।
-
क्रिटिकल घटनाएं: क्रिटिकल घटनाएं भौतिक तंत्र के अवस्था परिवर्तन के व्यवहार को संदर्भित करती हैं, जैसे कि तरल से गैस में परिवर्तन। इस अवधारणा के बूंदों के आकार को समझाने के बजाए अवस्थाओं के सह-संगठन के शर्तों को समझाती है। इसलिए, यह वर्षा की बूंदों के गोल आकार के संबंध में संबंधित नहीं है।
-
दबाव: दबाव क्षेत्रफल पर बल के अनुपात में होता है। यहां दबाव बूंदों के निर्माण और व्यवहार को प्रभावित कर सकता है, लेकिन इनके आकार को निर्धारित नहीं करता है। गोल आकार विशेष रूप से सतह तनाव के कारण होता है जो सतह के क्षेत्रफल को न्यूनतम करता है, न कि दबाव।
3. एक गैस के आयतन $(V)$ तापमान $(T)$ के लिए नियत दबाव पर एक आयतन-तापमान ग्राफ एक बिंदु से गुजरने वाली सीधी रेखा होती है। विभिन्न दबाव के मानों के लिए ग्राफ चित्र में दिखाए गए हैं। इस गैस के लिए निम्नलिखित में से कौन सा दबाव के क्रम सही है?
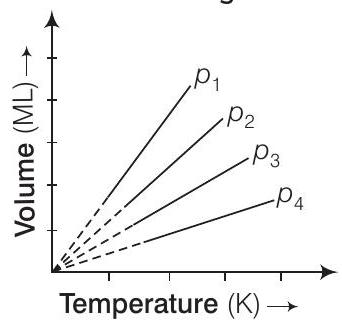
(a) $p_{1}>p_{2}>p_{3}>p_{4}$
(b) $p_{1}=p_{2}=p_{3}=p_{4}$
(c) $p_{1}<p_{2}<p_{3}<p_{4}$
(d) $p_{1}<p_{2}=p_{3}<p_{4}$
उत्तर दिखाएं
सोचने की प्रक्रिया
प्रश्न बॉयल के नियम पर आधारित है। यह कहता है कि नियत तापमान पर, एक निश्चित द्रव्यमान के आयतन उसके दबाव के व्युत्क्रमानुपाती होता है। अर्थात, $V \propto \frac{1}{p}$ या, $p V=$ स्थिरांक
उत्तर
(c) एक निश्चित तापमान पर, $p V=$ स्थिरांक
$$ \begin{aligned} इसलिए, \quad p_{1} V_{1} & =p_{2} V_{2}=p_{3} V_{3}=p_{4} V_{4} \\ जैसे कि \quad V_{1} & >V_{2}>V_{3}>V_{4} \\ इसलिए, \quad p_{1} & <p_{2}<p_{3}<p_{4} \end{aligned} $$
$$
-
विकल्प (a) $p_{1}>p_{2}>p_{3}>p_{4}$: यह विकल्प गलत है क्योंकि इसका अर्थ यह होता है कि आयतन बढ़ने के साथ दबाव घटता है। हालांकि, आदर्श गैस के नियम (PV = नियतांक नियत तापमान पर) के अनुसार, यदि आयतन बढ़ता है, तो दबाव घटना चाहिए। इसलिए, इस विकल्प में दिए गए क्रम के विपरीत क्रम होना चाहिए।
-
विकल्प (b) $p_{1}=p_{2}=p_{3}=p_{4}$: यह विकल्प गलत है क्योंकि इसका अर्थ यह होता है कि सभी आयतनों के लिए दबाव समान है। यदि दबाव समान होता, तो एक निश्चित तापमान पर आयतन भी समान होता, जो दिए गए ग्राफ में अलग-अलग रेखाएँ जो अलग-अलग दबाव को दर्शाती हैं, इसके विपरीत होता है।
-
विकल्प (d) $p_{1}<p_{2}=p_{3}<p_{4}$: यह विकल्प गलत है क्योंकि इसका अर्थ यह होता है कि दबाव के दो भाग समान हैं (अर्थात $p_{2}$ और $p_{3}$)। हालांकि, ग्राफ में प्रत्येक दबाव के लिए अलग-अलग रेखाएँ दिखाई देती हैं, जो इस बात को दर्शाती हैं कि सभी दबाव अलग-अलग हैं। इसलिए, यह विकल्प ग्राफ में दबाव और आयतन के बीच संबंध को सही तरीके से दर्शाता नहीं है।
4. लंडन बल के संग्राम ऊर्जा दो अंतरक्रिया कणों के बीच दूरी के छठे घन के व्युत्क्रमानुपाती होती है, लेकिन उनके मान निर्भर करते हैं
(a) अंतरक्रिया कणों के आवेश
(b) अंतरक्रिया कणों के द्रव्यमान
(c) अंतरक्रिया कणों की पोलरिज़ेबिलिटी
(d) कणों में स्थायी द्विध्रुवों की ताकत
उत्तर दिखाएं
उत्तर
(c) लंडन विस्थापन बल केवल बहुत छोटी दूरी पर कार्य करते हैं। अंतरक्रिया ऊर्जा $\frac{1}{\text { (दो अंतरक्रिया कणों के बीच दूरी) }^{6}}$ के अनुपात में बदलती है।
बड़े या अधिक जटिल अणु, लंडन बल के मान के अधिक होते हैं। यह बात निश्चित रूप से इस तथ्य के कारण है कि बड़े इलेक्ट्रॉन बादल आसानी से विकृत या ध्रुवीकृत हो जाते हैं।
इसलिए, अंतरक्रिया कणों की बड़ी पोलरिज़ेबिलिटी, अंतरक्रिया ऊर्जा के मान के बड़े होने के कारण होती है।
-
(a) अंतरक्रिया कणों के आवेश: लंडन विस्थापन बल वैन डर वाल्स बल के एक प्रकार है जो अणुओं या परमाणुओं में अस्थायी द्विध्रुवों के उत्पन्न होने के कारण उत्पन्न होते हैं। ये बल अंतरक्रिया कणों के आवेश पर निर्भर नहीं करते हैं, क्योंकि ये ताजगी अणुओं और परमाणुओं के बीच भी उत्पन्न होते हैं।
-
(ब) परस्पर कार्य करते कणों का द्रव्यमान: कणों के द्रव्यमान के अप्रत्यक्ष रूप से लंडन विस्थापन बलों के सामान्य बल को प्रभावित कर सकता है (क्योंकि बड़ा द्रव्यमान आमतौर पर बड़े आकार और अधिक इलेक्ट्रॉनों के साथ संबंधित होता है), लेकिन अंतर के ऊर्जा के स्वयं के रूप में द्रव्यमान पर अप्रत्यक्ष रूप से निर्भर नहीं होता। यह इलेक्ट्रॉन क्षमता के विपरीत अधिक सीधे संबंधित होता है।
-
(द) कणों में स्थायी द्विध्रुव के बल की शक्ति: लंडन विस्थापन बल विशेष रूप से अस्थायी द्विध्रुव के कारण होते हैं और नहीं स्थायी द्विध्रुव के कारण होते हैं। स्थायी द्विध्रुव के बल की शक्ति अन्य प्रकार के अंतर-अणुक बलों, जैसे द्विध्रुव-द्विध्रुव अंतरक्रियाओं के लिए उपयोगी होती है, लेकिन लंडन विस्थापन बल के लिए नहीं होती है।
5. द्विध्रुव-द्विध्रुव बल अंतर अणुओं में स्थायी द्विध्रुव के अणुओं के बीच कार्य करते हैं। द्विध्रुव के सिरों में ‘अंशक आवेश’ होता है। अंशक आवेश है
(a) इकाई इलेक्ट्रॉनिक आवेश से अधिक
(b) इकाई इलेक्ट्रॉनिक आवेश के बराबर
(c) इकाई इल ट्रॉनिक आवेश से कम
(d) इकाई इलेक्ट्रॉनिक आवेश के दोगुना
उत्तर दिखाएँ
उत्तर
(c) द्विध्रुव-द्विध्रुव बल अंतर अणुओं में स्थायी द्विध्रुव के अणुओं के बीच कार्य करते हैं और द्विध्रुव के सिरों में ‘अंशक आवेश’ होता है। एक द्विध्रुव के सिरों पर उपस्थित अंशक आवेश हमेशा इकाई इलेक्ट्रॉनिक आवेश से कम होते हैं।
उदाहरण के लिए,
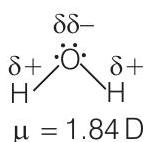
-
(a) इकाई इलेक्ट्रॉनिक आवेश से अधिक: यह विकल्प गलत है क्योंकि एक द्विध्रुव के सिरों पर अंशक आवेश हमेशा इकाई इलेक्ट्रॉनिक आवेश से कम होते हैं। इकाई इलेक्ट्रॉनिक आवेश एक इलेक्ट्रॉन या प्रोटॉन के आवेश को संदर्भित करता है, जो एक मूलभूत नियतांक है। अंशक आवेश अणु में परमाणुओं के बीच इलेक्ट्रॉन के असमान बांटन के कारण उत्पन्न होते हैं और हमेशा इकाई इलेक्ट्रॉनिक आवेश के एक भिन्न होते हैं।
-
(b) इकाई इलेक्ट्रॉनिक आवेश के बराबर: यह विकल्प गलत है क्योंकि अंशक आवेश इकाई इलेक्ट्रॉनिक आवेश के बराबर नहीं होते। इकाई इलेक्ट्रॉनिक आवेश एक निश्चित मान है (लगभग 1.602 x 10^-19 कूलॉम), जबकि अंशक आवेश छोटे होते हैं और अणु में इलेक्ट्रॉन घनत्व के वितरण के कारण उत्पन्न होते हैं। वे इकाई इलेक्ट्रॉनिक आवेश के एक भिन्न को प्रतिनिधित करते हैं।
-
(d) इकाई इलेक्ट्रॉनिक चार्ज के दोगुना: यह विकल्प गलत है क्योंकि आंशिक चार्ज इकाई इलेक्ट्रॉनिक चार्ज से अधिक नहीं हो सकते, और बराबर इकाई इलेक्ट्रॉनिक चार्ज के दोगुना भी नहीं हो सकते। आंशिक चार्ज हमेशा इकाई इलेक्ट्रॉनिक चार्ज से कम होते हैं, क्योंकि इन्हें अणु में परमाणुओं के इलेक्ट्रॉन वितरण के थोड़े से असंतुलन को दर्शाते हैं, न कि इलेक्ट्रॉनों के पूर्ण स्थानांतर को।
6. एक बरतन में डाइहाइड्रोजन और डाइऑक्सीजन के 1:4 मिश्रण के दबाव के एक वायुमंडल है। डाइऑक्सीजन के आंशिक दबाव कितना होगा?
(a) $0.8 \times 10^{5} \mathrm{~atm}$
(b) $0.008 \mathrm{Nm}^{-2}$
(c) $8 \times 10^{4} \mathrm{Nm}^{-2}$
(d) $0.25 \mathrm{~atm}$
उत्तर दिखाएं
Answer
(c) दिया गया है कि, एक बरतन में $H_{2}$ और $O_{2}$ के $1: 4$ मिश्रण के दबाव के एक वायुमंडल है। इससे अंतर्गत $H_{2}$ और $O_{2}$ के मोल अनुपात $1: 4$ है। इसलिए, डाइऑक्सीजन $\left(O_{2}\right)$ के आंशिक दबाव को निम्नलिखित द्वारा दिया जाता है
$\therefore$ डाइऑक्सीजन $O_{2}$ के आंशिक दबाव = $O_{2}$ के मोल अनुपात $\times$ मिश्रण के कुल दबाव
$$ \begin{aligned} & =\frac{4}{1+4} \times 1=\frac{4}{5} \times 1 \mathrm{~atm} \\ & =0.8 \mathrm{~atm}=0.8 \times 10^{5} \mathrm{Nm}^{-2}=8 \times 10^{4} \mathrm{Nm}^{-2} \end{aligned} $$
-
विकल्प (a) $0.8 \times 10^{5} \mathrm{~atm}$: यह विकल्प गलत है क्योंकि इसमें दबाव की इकाई को गलत रूप से प्रस्तुत किया गया है। डाइऑक्सीजन के सही आंशिक दबाव $0.8 \mathrm{~atm}$ है, न कि $0.8 \times 10^{5} \mathrm{~atm}$।
-
विकल्प (b) $0.008 \mathrm{Nm}^{-2}$: यह विकल्प गलत है क्योंकि यह डाइऑक्सीजन के आंशिक दबाव को बहुत कम अनुमानित करता है। सही आंशिक दबाव $8 \times 10^{4} \mathrm{Nm}^{-2}$ है, जो $0.008 \mathrm{Nm}^{-2}$ से बहुत अधिक है।
-
विकल्प (d) $0.25 \mathrm{~atm}$: यह विकल्प गलत है क्योंकि यह डाइऑक्सीजन के आंशिक दबाव की गलत गणना करता है। $H_{2}$ और $O_{2}$ के $1:4$ मोल अनुपात के अनुसार, डाइऑक्सीजन के सही आंशिक दबाव $0.8 \mathrm{~atm}$ है, न कि $0.25 \mathrm{~atm}$।
7. तापमान बढ़ता है, तो अणुओं की औसत गतिज ऊर्जा बढ़ती है। यदि आयतन स्थिर रहे, तो तापमान में वृद्धि के परिणामस्वरूप दबाव पर क्या प्रभाव पड़ेगा?
(a) बढ़ेगा
(b) घटेगा
(c) समान रहेगा
(d) आधा हो जाएगा
उत्तर दिखाएं
सोचने की प्रक्रिया
इस समस्या के आधार पर गैस लुसैक के नियम है जो कहता है कि “आयतन स्थिर रहते हुए, एक निश्चित द्रव्यमान के गैस के दबाव उसके केल्विन में तापमान के सीधे अनुपाती होता है”।
उत्तर
(a) जब तापमान बढ़ता है, तो अणुओं की औसत गतिज ऊर्जा बढ़ती है। गैस लुसैक के नियम के अनुसार, आयतन स्थिर रहते हुए, जब तापमान बढ़ता है, तो दबाव बढ़ता है।
-
(b) घटेगा: यह विकल्प गलत है क्योंकि गैस लुसैक के नियम के अनुसार, आयतन स्थिर रहते हुए, तापमान में वृद्धि दबाव में वृद्धि के लिए नहीं घटने के लिए जिम्मेदार होती है।
-
(c) समान रहेगा: यह विकल्प गलत है क्योंकि गैस लुसैक के नियम के अनुसार, आयतन स्थिर रहते हुए, तापमान में वृद्धि दबाव में वृद्धि के लिए नहीं समान रहने के लिए जिम्मेदार होती है।
-
(d) आधा हो जाएगा: यह विकल्प गलत है क्योंकि गैस लुसैक के नियम के अनुसार, आयतन स्थिर रहते हुए, तापमान में वृद्धि दबाव में वृद्धि के लिए नहीं आधा हो जाने के लिए जिम्मेदार होती है।
8. गैसें अपने अणुओं के बीच अंतराणुक बल के मापदंड पर निर्भर करते हुए विशिष्ट आइसोथर्मल तापमान के लिए ज्ञात होती हैं। नीचे कुछ गैसों के आइसोथर्मल तापमान दिए गए हैं।
| गैसें | $\mathbf{H}_{\mathbf{2}}$ | $\mathbf{H e}$ | $\mathbf{O}_{\mathbf{2}}$ | $\mathbf{N}_{\mathbf{2}}$ |
|---|---|---|---|---|
| केल्विन में आइसोथर्मल तापमान | 33.2 | 5.3 | 154.3 | 126 |
उपरोक्त डेटा के आधार पर इन गैसों के द्रवीकरण के क्रम क्या होगा? द्रवीकरण करने वाली गैस से शुरू करते हुए क्रम लिखें
(a) $H_{2}, He, O_{2}, N_{2}$
(b) $He, O_{2}, H_{2}, N_{2}$
(c) $N_{2}, O_{2}, He, H_{2}$
(d) $O_{2}, N_{2}, H_{2}, He$
उत्तर दिखाएं
उत्तर
(द) उच्चतर क्रिटिकल तापमान, गैस के द्रवीकरण के लिए आसानी से होता है। अतः द्रवीकरण के क्रम के शुरुआत में पहले द्रवीकृत होने वाली गैस के क्रम के रूप में $O_{2}, N_{2}, H_{2}$, $He$ होंगे।
नोट गैस के क्रिटिकल तापमान को उस तापमान के रूप में परिभाषित किया जा सकता है जिसके ऊपर गैस को चाहे कितना भी उच्च दबाव लगाओ वह द्रवीकृत नहीं किया जा सकता।
-
विकल्प (अ) $H_{2}, He, O_{2}, N_{2}$:
- गलत कारण $H_{2}$ और $He$ के क्रिटिकल तापमान सबसे कम हैं (क्रमशः 33.2 K और 5.3 K), जिसका अर्थ है कि वे द्रवीकरण के क्रम में सबसे पहले नहीं होने चाहिए क्योंकि वे सबसे कठिन द्रवीकृत होते हैं।
-
विकल्प (ब) $He, O_{2}, H_{2}, N_{2}$:
- गलत कारण $He$ के क्रिटिकल तापमान सबसे कम है (5.3 K), जिसका अर्थ है कि वह सबसे कठिन द्रवीकृत होता है। अतः वह द्रवीकरण के क्रम में अंत में नहीं होना चाहिए, बल्कि पहले होना चाहिए।
-
विकल्प (स) $N_{2}, O_{2}, He, H_{2}$:
- गलत कारण $N_{2}$ के क्रिटिकल तापमान 126 K है, जो $O_{2}$ (154.3 K) के तुलना में कम है। अतः $N_{2}$ को $O_{2}$ के पहले नहीं होना चाहिए द्रवीकरण के क्रम में।
9. शीर्षक घनत्व गुणांक $(\eta)$ की SI इकाई क्या है?
(अ) पास्कल
(ब) $\mathrm{Nsm}^{-2}$
(स) $\mathrm{km}^{-2} \mathrm{~s}$
(द) $\mathrm{Nm}^{-2}$
उत्तर दिखाएं
उत्तर
(ब) शीर्षक घनत्व गुणांक $(\eta)$ की SI इकाई $\mathrm{Nm}^{-2} \mathrm{~s}$ या $\mathrm{Nsm}^{-2}$ होती है।
$\begin{array}{rlrl} & \text { जैसा कि हम जानते हैं, } & f & =\eta A \frac{d v}{d x} \\ \text { जहाँ, } & f =\text { बल } \\ \eta & =\text { शीर्षक घनत्व गुणांक } \\ \frac{d v}{d x} & =\text { वेग ढलान }\end{array}$
ऊपर दी गई समीकरण में $f=N, d x=m, A=m^{2}$ और $v=m s^{-1}$ की SI इकाइयों को समायोजित करके, हमें प्राप्त होता है,
$$ \eta=\frac{\mathrm{N} \times \mathrm{m}}{\mathrm{m}^{2} \times \mathrm{ms}^{-1}}=\mathrm{Nm}^{-2} \mathrm{~s} $$
अतः $\eta=$ की SI इकाई $n s m^{-2}$ होती है।
-
(अ) पास्कल: पास्कल (Pa) दबाव की SI इकाई है, न कि शीर्षक घनत्व गुणांक। शीर्षक घनत्व गुणांक एक तरल के प्रवाह के विरोध का माप है, जबकि दबाव एक इकाई क्षेत्र पर लगाए गए बल को दर्शाता है।
-
(c) $\mathrm{km}^{-2} \mathrm{~s}$: इकाई गलत है क्योंकि इसमें किलोमीटर (लंबाई की इकाई) के साथ सेकंड के ऐसे संयोजन का उपयोग किया गया है जो श्यानता के भौतिक आयामों के संगत नहीं है। श्यानता में बल, क्षेत्रफल और वेग ढलान के संबंध होते हैं, न केवल लंबाई और समय के।
-
(d) $\mathrm{Nm}^{-2}$: न्यूटन प्रति वर्ग मीटर (Nm$^{-2}$) दबाव (पास्कल) की इकाई है, न कि श्यानता। श्यानता के लिए एक अतिरिक्त समय आयाम (सेकंड) की आवश्यकता होती है ताकि तरल के विकृति की दर को ध्यान में रखा जा सके।
10. विभिन्न शहरों में वायुमंडलीय दबाव के निकले आंकड़े निम्नलिखित हैं
| शहर | शिमला | बैंगलोर | दिल्ली | मुंबई |
|---|---|---|---|---|
| $\boldsymbol{p}$ इं $\mathbf{N} / \mathbf{m}^{\mathbf{2}}$ | $1.01 \times 10^{5}$ | $1.2 \times 10^{5}$ | $1.02 \times 10^{5}$ | $1.21 \times 10^{5}$ |
उपरोक्त डेटा को ध्यान में रखते हुए बताएं कि कौन सी जगह पहले तरल पदार्थ उबलेगा।
(a) शिमला
(b) बैंगलोर
(c) दिल्ली
(d) मुंबई
उत्तर दिखाएं
सोचने की प्रक्रिया
(i) एक तरल उबलता है जब इसके ऊपर वापोर दबाव वायुमंडलीय दबाव के बराबर हो जाता है। निम्न वायुमंडलीय दबाव कम उबलने के बिंदु को दर्शाता है।
(ii) चार शहरों को वायुमंडलीय दबाव के बढ़ते क्रम में व्यवस्थित करें और सबसे कम वाले को चुनें।
उत्तर
(a) शिमला चारों शहरों में सबसे कम वायुमंडलीय दबाव के साथ है। इसलिए, शिमला में तरल पदार्थ पहले उबलेगा क्योंकि निम्न वायुमंडलीय दबाव कम उबलने के बिंदु को दर्शाता है।
-
बैंगलोर: बैंगलोर में शिमला की तुलना में उच्च वायुमंडलीय दबाव है ($1.2 \times 10^{5} , \text{N/m}^2$)। उच्च वायुमंडलीय दबाव तरल के उबलने के बिंदु को बढ़ा देता है, इसलिए बैंगलोर में तरल पदार्थ पहले उबलेगा नहीं।
-
दिल्ली: दिल्ली में शिमला की तुलना में थोड़ा उच्च वायुमंडलीय दबाव है ($1.02 \times 10^{5} , \text{N/m}^2$)। इसका अर्थ है कि तरल के उबलने के बिंदु शिमला के मुकाबले थोड़ा अधिक होगा, इसलिए दिल्ली में तरल पदार्थ पहले उबलेगा नहीं।
-
मुंबई: मुंबई में सभी शहरों में सबसे अधिक वायुमंडलीय दबाव है ($1.21 \times 10^{5} , \text{N/m}^2$)। उच्च वायुमंडलीय दबाव तरल के उबलने के बिंदु को बढ़ा देता है, इसलिए मुंबई में तरल पदार्थ पहले उबलेगा नहीं।
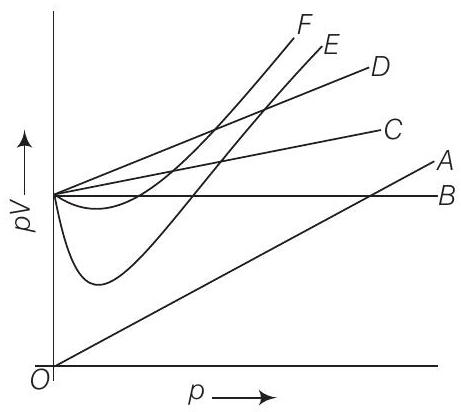
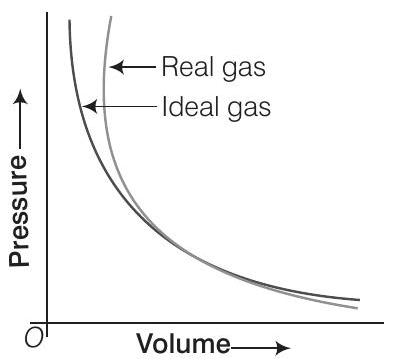
11. चित्र में कौन सी वक्र आदर्श गैस की वक्र को प्रस्तुत करती है?
(a) केवल B
(b) $C$ और $D$
(c) $E$ और $F$
(d) $A$ और $B$
उत्तर दिखाएं
सोचने की प्रक्रिया
(i) प्रश्न में दी गई ग्राफ बॉयल के नियम पर निर्भर करती है।
(ii) स्थिर तापमान पर, सभी दबावों पर $\mathrm{pV}$ vs $\mathrm{p}$ के बीच ग्राफ आदर्श गैस के लिए $x$-अक्ष के समानांतर सीधी रेखा होगी।
(iii) स्थिर तापमान पर वास्तविक गैस के लिए $p \vee v s p$ ग्राफ सीधी रेखा नहीं होती।
उत्तर
(a) आदर्श गैस के लिए $p V=$ सभी दबावों पर स्थिर होता है। अतः, केवल $B$ आदर्श गैस को प्रस्तुत करती है।
-
विकल्प (b) $C$ और $D$: ये वक्र आदर्श गैस को प्रस्तुत नहीं करते क्योंकि वे सभी दबावों पर स्थिर $pV$ उत्पाद नहीं दिखाते हैं। आदर्श गैस के लिए $pV$ उत्पाद स्थिर रहना चाहिए, लेकिन ये वक्र $pV$ के साथ दबाव में परिवर्तन दिखाते हैं, जो गैस के अनादर्श व्यवहार को दर्शाता है।
-
विकल्प (c) $E$ और $F$: विकल्प (b) के समान, ये वक्र आदर्श गैस को प्रस्तुत नहीं करते क्योंकि वे सभी दबावों पर स्थिर $pV$ उत्पाद नहीं दिखाते हैं। $pV$ के साथ दबाव में परिवर्तन गैस के अनादर्श व्यवहार को दर्शाता है।
-
विकल्प (d) $A$ और $B$: जबकि वक्र $B$ आदर्श गैस को प्रस्तुत करती है जिसके लिए $pV$ उत्पाद स्थिर होता है, वक्र $A$ नहीं है। वक्र $A$ के लिए $pV$ उत्पाद दबाव के साथ परिवर्तित हो सकता है, जो अनादर्श गैस व्यवहार को दर्शाता है।
12. गतिज ऊर्जा की वृद्धि अंतरमोलेकुलर आकर्षण बलों को पराभूत कर सकती है। तापमान में वृद्धि द्वारा तरल के श्यानता कैसे प्रभावित होगी?
(a) वृद्धि
(b) कोई प्रभाव नहीं
(c) कमी
(d) कोई नियमित पैटर्न नहीं रहेगा
उत्तर दिखाएं
उत्तर
(c) तापमान में वृद्धि के साथ, तरल के अणुओं की गतिज ऊर्जा बढ़ जाती है जो अंतरमोलेकुलर आकर्षण बलों को पराभूत कर सकती है। अतः, तरल बहने लगता है।
अन्य शब्दों में, तरल के श्यानता कम होती जाती है तापमान में वृद्धि के साथ। यह पाया गया है कि कमी लगभग $2$% प्रति डिग्री तापमान की वृद्धि के साथ होती है।
-
(a) वृद्धि: यह विकल्प गलत है क्योंकि तापमान में वृद्धि अणुओं की गतिज ऊर्जा में वृद्धि करती है, जो अणुओं के बीच आकर्षण बल को कम करती है, जिसके परिणामस्वरूप तरल आसानी से बहता है और इसका श्यानता कम हो जाती है, न कि बढ़ती है।
-
(b) कोई प्रभाव नहीं: यह विकल्प गलत है क्योंकि तापमान अणुओं की गतिज ऊर्जा पर एक महत्वपूर्ण प्रभाव डालता है। जब तापमान बढ़ता है, तो गतिज ऊर्जा बढ़ती है, जो अणुओं के बीच आकर्षण बल को कम करती है और तरल के श्यानता को कम करती है।
-
(d) कोई नियमित पैटर्न नहीं अनुसरण करेगा: यह विकल्प गलत है क्योंकि तापमान और श्यानता के बीच एक अच्छी तरह से स्थापित संबंध है। जब तापमान बढ़ता है, तो तरल के श्यानता कम होती जाती है, जो एक नियमित पैटर्न के अनुसार होती है।
13. तरल के सतही तनाव किस प्रकार तापमान में वृद्धि के साथ बदलता है?
(a) समान रहता है
(b) कम होता है
(c) बढ़ता है
(d) कोई नियमित पैटर्न अनुसरण नहीं करेगा
उत्तर दिखाएं
Answer
(b) तरल के सतही तनाव की विशिष्टता तापमान में वृद्धि के साथ सामान्यतः कम होती है और आलस्य तापमान पर शून्य हो जाती है। तापमान में वृद्धि के साथ सतही तनाव में कमी के कारण यह स्पष्ट है कि तापमान में वृद्धि के साथ अणुओं की गतिज ऊर्जा बढ़ती है और इसलिए अणुओं के बीच आकर्षण कम हो जाता है।
Note तरल के सतही तनाव को तापमान में वृद्धि के साथ एक सेंटीमीटर लंबाई के सतह के लंबवत लगने वाले बल के रूप में परिभाषित किया गया है। सतही तनाव के इकाई डाइन प्रति सेंटीमीटर (या न्यूटन प्रति मीटर अर्थात $\mathrm{Nm}^{-1}$ एस आई प्रणाली में) होते हैं।
-
(a) समान रहता है: यह विकल्प गलत है क्योंकि सतही तनाव तापमान पर प्रभावित होता है। जब तापमान बढ़ता है, तो अणुओं की गतिज ऊर्जा भी बढ़ती है, जो अणुओं के बीच आकर्षण बल को कम करती है और इसलिए सतही तनाव कम हो जाता है। इसलिए, तापमान में वृद्धि के साथ सतही तनाव समान रहता है नहीं।
-
(c) वृद्धि: यह विकल्प गलत है क्योंकि तापमान में वृद्धि के परिणामस्वरूप अणुओं की गतिज ऊर्जा बढ़ जाती है, जो अंतराणुक बलों को कम कर देती है। इस प्रकार, सतही तनाव तापमान में वृद्धि के साथ घटता है बल्कि बढ़ता है।
-
(d) कोई नियमित पैटर्न नहीं अनुसरण करता: यह विकल्प गलत है क्योंकि सतही तनाव तापमान में वृद्धि के साथ घटता है इसका एक ठीक ढंग से स्थापित पैटर्न होता है। तापमान और सतही तनाव के बीच संबंध अनुमान योग्य और सांतर्गत होता है, जो इस विकल्प के अनुसार कि कोई नियमित पैटर्न नहीं अनुसरण करता है, के विपरीत है।
बहुविकल्पीय प्रश्न (एक से अधिक विकल्प सही हो सकते हैं)
14. गैसीय अवस्था के संबंध में निम्नलिखित में से कौन से कथन सही हैं?
(a) अणुओं की पूर्ण क्रमबद्धता
(b) अणुओं की पूर्ण बेक्रमबद्धता
(c) अणुओं की यादृच्छिक गति
(d) अणुओं की निश्चित स्थिति
उत्तर दिखाएं
उत्तर
$(b, c)$
गैसीय अवस्था में, अणु यादृच्छिक गति में होते हैं, अर्थात यह अवस्था जहां अणु बेक्रमबद्ध रूप से व्यवस्थित होते हैं। गैसीय अवस्था के एन्ट्रॉपी तरल और ठोस के बराबर या अधिक होता है।
-
(a) अणुओं की पूर्ण क्रमबद्धता: यह गलत है क्योंकि गैसीय अवस्था में अणु पूर्ण क्रमबद्ध नहीं होते हैं। बजाए इसके, वे पूर्ण बेक्रमबद्ध अवस्था में होते हैं और यादृच्छिक रूप से गति करते हैं।
-
(d) अणुओं की निश्चित स्थिति: यह गलत है क्योंकि गैसीय अवस्था में अणु निश्चित स्थिति में नहीं होते हैं। वे उपलब्ध स्थान के अनुसार मुक्त रूप से और यादृच्छिक रूप से गति करते हैं।
15. निम्नलिखित में से कौन सा चित्र 1 मोल डाइऑक्सीजन गैस के STP पर नहीं प्रतिनिधित्व करता है?
(a) $16 \mathrm{~g}$ गैस
(b) $22.7 \mathrm{~L}$ गैस
(c) $6.022 \times 10^{23}$ डाइऑक्सीजन अणु
(d) $11.2 \mathrm{~L}$ गैस
उत्तर दिखाएं
उत्तर
$(a, b, d)$
यह ज्ञात है कि, 1 मोल गैस = ग्राम अणुक द्रव्यमान = अवोगाड्रो संख्या के अणु $=22.4$ लीटर एसटीपी पर
इसलिए, 1 मोल $O_{2}$ गैस $=32 g$ के $O_2=6.02 \times 10^{23}$ अणु $=22.4 ~L$ के $O_{2}$ एसटीपी पर
-
(a) $16 \mathrm{~g}$ गैस: यह गलत है क्योंकि डाइऑक्सीजन गैस ($O_2$) के 1 मोल का मोलर द्रव्यमान 32 ग्राम होता है, न कि 16 ग्राम। अतः, $O_2$ के 16 ग्राम केवल 0.5 मोल डाइऑक्सीजन गैस को निरूपित करते हैं।
-
(b) $22.7 \mathrm{~L}$ गैस: यह गलत है क्योंकि STP (स्टैंडर्ड टेम्परेचर एंड प्रेशर) पर, किसी आदर्श गैस के 1 मोल के आयतन 22.4 लीटर होता है, न कि 22.7 लीटर। अतः, $O_2$ के 22.7 लीटर डाइऑक्सीजन गैस के लगभग 1 मोल को निरूपित करते हैं।
-
(d) $11.2 \mathrm{~L}$ गैस: यह गलत है क्योंकि STP पर, किसी आदर्श गैस के 1 मोल के आयतन 22.4 लीटर होता है। अतः, $O_2$ के 11.2 लीटर केवल 0.5 मोल डाइऑक्सीजन गैस को निरूपित करते हैं।
16. निम्नलिखित में से कौन सी स्थितियों के संयोजन में, गैस आदर्श व्यवहार से सबसे अधिक विचलित होती है?
(a) कम दबाव
(c) कम तापमान
(b) उच्च दबाव
(d) उच्च तापमान
उत्तर दिखाएं
Answer
( $b, c$ )
एक गैस जो सभी तापमान और दबाव की स्थितियों में आदर्श गैस समीकरण $p V = n R T$ का पालन करती है, एक ‘आदर्श गैस’ कहलाती है।
हालांकि, कोई गैस जो सभी तापमान और दबाव की स्थितियों में आदर्श गैस समीकरण का पालन करती है, वह नहीं होती। अतः, आदर्श गैस की अवधारणा केवल सैद्धांतिक या कल्पनात्मक है। जब दबाव कम हो या तापमान उच्च हो, तब गैस नियमों का अधिक अच्छा पालन करती है।
इसलिए, ऐसी गैसें ‘वास्तविक गैसें’ कहलाती हैं। सभी गैसें वास्तविक गैसें होती हैं। अतः, उच्च दबाव और कम तापमान पर एक वास्तविक गैस आदर्श व्यवहार से सबसे अधिक विचलित होती है।
- कम दबाव पर, गैस अणु दूर दूर होते हैं, और अंतराणुक बल नगण्य होते हैं, इसलिए गैस अधिक आदर्श व्यवहार दर्शाती है।
- उच्च तापमान पर, गैस अणुओं की किणेतज ऊर्जा उच्च होती है, जो अंतराणुक बल को पराभुषित करती है, जिसके परिणामस्वरूप गैस अधिक आदर्श व्यवहार दर्शाती है।
17. निम्नलिखित में से कौन से परिवर्तन एक सील किए गए बर्तन में रखी गई पानी के वाष्प दाब को कम करते हैं?
(a) पानी की मात्रा कम करना
(b) पानी में नमक मिलाना
(c) बर्तन के आयतन को आधा कर देना
(d) पानी के तापमान को कम करना
उत्तर दिखाएं
उत्तर
$(b, d)$
नमक मिलाने पर, पानी के अणुओं के वाष्पीकरण के लिए उपलब्ध सतह क्षेत्र कम हो जाता है क्योंकि नमक के अणु पानी के अणुओं के स्थान पर बैठ जाते हैं। इसलिए, पानी के वाष्प दबाव कम हो जाता है।
इसके अतिरिक्त, तापमान कम होने पर वाष्प दबाव भी कम हो जाता है क्योंकि अणुओं की गतिज ऊर्जा कम हो जाती है।
-
पानी की मात्रा कम करना: एक बंद बरतन में तरल के वाष्प दबाव के लिए तापमान और तरल की प्रकृति पर निर्भर करता है, न कि तरल की मात्रा। इसलिए, पानी की मात्रा कम करना वाष्प दबाव पर कोई प्रभाव नहीं डालता।
-
बरतन के आयतन को आधा कर देना: एक बंद बरतन में तरल के वाष्प दबाव के लिए बरतन के आयतन पर निर्भर नहीं करता। यह तापमान और तरल की प्रकृति द्वारा निर्धारित किया जाता है। इसलिए, बरतन के आयतन को कम करने से वाष्प दबाव में कोई परिवर्तन नहीं होता।
छोटे उत्तर प्रकार के प्रश्न
18. यदि निम्नलिखित गैसों में से प्रत्येक के 1 ग्राम को STP पर लिया जाए, तो निम्नलिखित में से कौन सी गैस (a) सबसे बड़ा आयतन और (b) सबसे छोटा आयतन घेरेगी?
$$ CO, H_{2} O, CH_{4}, NO $$
उत्तर आवोगाड्रो के नियम से हम जानते हैं कि 1 मोल गैस का आयतन $=$ आणविक द्रव्यमान $=22.4 \mathrm{~L}$ STP पर $28 \mathrm{~g} \mathrm{CO}(1 \mathrm{~mol} \mathrm{CO})$ द्वारा घेरा गया आयतन $=22.4 \mathrm{~L}$ STP पर $$
\left(\because \text { Molar mass of } C O=12+16=28 \mathrm{~g} \mathrm{~mol}^{-1}\right)
$$ $\therefore \quad$ $1 \mathrm{~g} \mathrm{CO}$ द्वारा घेरा गया आयतन $=\frac{22.4}{28} \mathrm{~L}$ STP पर उसी तरह, $1 \mathrm{~g} \mathrm{H}_{2} \mathrm{O}$ द्वारा घेरा गया आयतन $=\frac{22.4}{18} \mathrm{~L}$ STP पर $$
\left(\because \text { Molar mass of } \mathrm{H}_{2} \mathrm{O}=(2 \times 1)+16=18 \mathrm{~g} \mathrm{~mol}^{-1}\right)
$$ $1 \mathrm{~g} \mathrm{CH}_{4}$ द्वारा घेरा गया आयतन $=\frac{22.4}{16} \mathrm{~L}$ STP पर $$
\left(\because \text { मोलर द्रव्यमान } \mathrm{CH}_{4}=12+(4 \times 1)=16 \mathrm{~g} \mathrm{~mol}^{-1}\right)
$$ $1 \mathrm{~g} \mathrm{NO}$ द्वारा उपलब्ध आयतन $=\frac{22.4}{30} \mathrm{~L}$ STP पर $$
\left(\because \text { मोलर द्रव्यमान } \mathrm{NO}=14+16=30 \mathrm{~g} \mathrm{~mol}^{-1}\right)
$$ अतः, $1 \mathrm{~g} \mathrm{CH}_{4}$ STP पर अधिकतम आयतन घेरेगा जबकि $1 \mathrm{~g}$ के $\mathrm{NO}$ के लिए न्यूनतम आयतन घेरेगा।उत्तर दिखाएं
उत्तर बर्फ, पानी और भाप के भौतिक गुण बहुत अलग होते हैं क्योंकि वे अलग-अलग अवस्थाओं में पाए जाते हैं। बर्फ ठोस अवस्था में, पानी तरल अवस्था में और भाप वाष्प अवस्था में पाए जाते हैं। तीनों अवस्थाओं (बर्फ, पानी और भाप) में पानी का रासायनिक संघटन समान होता है, अर्थात $\mathrm{H}_{2} \mathrm{O}$ होता है।उत्तर दिखाएं
उत्तर तापमान, दबाव, द्रव्यमान और आयतन विभिन्न अवस्थाओं (ठोस, तरल और गैस) को निर्धारित करने वाले कारक हैं।उत्तर दिखाएं
अधिक मजबूत अंतरमोलेकुलर बल अधिक क्वथनांक के लिए ज़िम्मेदार होते हैं।
लंडन बल की शक्ति अणु में इलेक्ट्रॉन की संख्या के साथ बढ़ती जाती है।
$\mathrm{HF}, \mathrm{HCl}, \mathrm{HBr}$ और $\mathrm{HI}$ के क्वथनांक क्रमशः $293 \mathrm{~K}, 189 \mathrm{~K}, 206 \mathrm{~K}$ और $238 \mathrm{~K}$ हैं।
(a) $\mathrm{HF}, \mathrm{HCl}, \mathrm{HBr}$ और $\mathrm{HI}$ अणुओं में कौन से प्रकार के अंतरमोलेकुलर बल उपस्थित होते हैं?
(b) $\mathrm{HCl}, \mathrm{HBr}$ और $\mathrm{HI}$ के क्वथनांक के प्रवृत्ति के अनुसार, द्विध्रुव-द्विध्रुव संपर्क और लंडन संपर्क में से कौन सा यहां प्रमुख है?
(c) हाइड्रोजन फ्लूओराइड का क्वथनांक सबसे अधिक होता है जबकि हाइड्रोजन क्लोराइड का क्वथनांक सबसे कम होता है? कारण बताइए।
उत्तर प्रश्न में दिए गए जानकारी और डेटा के आधार पर हम निष्कर्ष निकालते हैं कि (a) $\mathrm{HCl}, \mathrm{HBr}$ और $\mathrm{HI}$ में द्विध्रुव-द्विध्रुव और लॉन्डन बल उपस्थित होते हैं क्योंकि अणुओं में स्थायी द्विध्रुव होता है। HF में द्विध्रुव-द्विध्रुव, लॉन्डन बल और हाइड्रोजन बंधन उपस्थित होते हैं। (b) क्लोरीन, ब्रोमीन और आयोडीन के विद्युत ऋणात्मकता का क्रम इस प्रकार होता है: $$
\mathrm{Cl}>\mathrm{Br}>\mathrm{I}
$$ इसलिए, द्विध्रुव आघूर्ण $\mathrm{HCl}$ से $\mathrm{HI}$ की ओर घटता है। इसलिए, द्विध्रुव-द्विध्रुव अंतरक्रिया $\mathrm{HCl}$ से $\mathrm{HI}$ की ओर घटती है। लेकिन $\mathrm{HCl}$ से $\mathrm{HI}$ की ओर जाने पर क्वथनांक बढ़ता है। इसका अर्थ है कि लॉन्डन बल प्रधान होते हैं। इसका कारण यह है कि लॉन्डन बल अणु में इलेक्ट्रॉन की संख्या बढ़ने के साथ बढ़ते हैं और इस मामले में इलेक्ट्रॉन की संख्या $\mathrm{HCl}$ से $\mathrm{HI}$ की ओर बढ़ती है। (c) हाइड्रोजन फ्लूओराइड में सबसे अधिक द्विध्रुव आघूर्ण होता है क्योंकि फ्लूओरीन की सबसे अधिक विद्युत ऋणात्मकता होती है और HF में हाइड्रोजन बंधन उपस्थित होता है। इसलिए, HF का क्वथनांक सबसे अधिक होता है।उत्तर दिखाएं
उत्तर जब गैस का ताप और दबाव 273.15 K (या 0°C) और 1 atm (या 1 बार या $10^{5}$ पास्कल) होता है, तो ऐसी स्थितियों को मानक ताप और दबाव स्थितियाँ (STP) कहते हैं। इन स्थितियों में, प्रत्येक और प्रत्येक गैस द्वारा उपलब्ध आयतन 22.4 लीटर होता है। इसलिए, 273.15 K और 1 atm पर $\mathrm{N}_{2}$ और $\mathrm{Ar}$ के मोलर आयतन 22.4 लीटर होता है।उत्तर दिखाएं
उत्तर कम दबाव और उच्च तापमान पर, एक वास्तविक गैस आदर्श गैस के रूप में व्यवहार करती है। लगभग सभी गैसें वास्तविक गैस होती हैं।उत्तर दिखाएँ
उत्तर एक गैस के लिए जिस तापमान के ऊपर गैस को चाहे कितना ऊँचा दबाव लगाया जाए वह द्रव नहीं हो सकती, इस तापमान को आलोचनात्मक तापमान कहते हैं। चूंकि गैस ‘A’ आसानी से द्रव बन जाती है, इससे यह सुझाव देता है कि गैस ’ $A$ ’ अपने आलोचनात्मक तापमान से नीचे है। दूसरी ओर, गैस ’ $B$ ’ उच्च दबाव लगाए जाने पर भी आसानी से द्रव नहीं बनती। इससे यह सुझाव देता है कि गैस ’ $\mathrm{B}$ ’ अपने आलोचनात्मक तापमान से ऊपर है।उत्त दिखाएँ
उत्तर $R$ की इकाई $p, V$ और $T$ के मापन के इकाई पर निर्भर करती है, क्योंकि $R=\frac{p V}{n T}$. यदि दबाव पास्कल में मापा जाता है, प्रति मोल आयतन $\mathrm{m}^{3}$ में मापा जाता है और तापमान केल्विन में मापा जाता है तो ’ $R$ ’ की इकाई $\mathrm{Pam}^{3} \mathrm{~K}^{-1} \mathrm{~mol}^{-1}$ या $\mathrm{J} \mathrm{mol}^{-1} \mathrm{~K}^{-1}$ होती है। चूंकि जूल कार्य के इकाई होती है, इसलिए ’ $R$ ’ एक मोल प्रति केल्विन पर गैस द्वारा किए गए कार्य को दर्शाता है।उत्तर दिखाएँ
उत्तर इस कथन केवल आदर्श गैसों के लिए सही है। एक आदर्श गैस को द्रवीकृत नहीं किया जा सकता क्योंकि आदर्श गैस के अणुओं के बीच कोई अंतराणुक आकर्षण बल नहीं होता।उत्तर दिखाएँ
पानी, एल्कोहल $\left(C_{2} H_{5} OH\right)$ और हेक्सेन $[CH_3(CH_2)_4 CH_3)]$।
Answer उपरोक्त अणुओं में, केवल हेक्सेन $(CH_3(CH_2)_4 CH3)$ एक अध्रुवीय अणु है जहां केवल लैंडन विस्थापन बल होते हैं। ये बल बहुत कमजोर होते हैं जबकि पानी और एल्कोहल ध्रुवीय अणु हैं जहां द्विध्रुव-द्विध्रुव प्रतिक्रिया तथा $H$-बंधन उपस्थित होते हैं। हालांकि, $\mathrm{H}$-बंधन प्रतिक्रिया पानी में $\mathrm{H}_{2} \mathrm{O}$ की तुलना में काफी अधिक मजबूत होती है, इसलिए, यह अणुओं के बीच अधिक मजबूत आकर्षण बल रखता है और एल्कोहल और हेक्सेन की तुलना में अधिक तनाव रखता है। इसलिए, सतही तनाव के बढ़ते क्रम है: हेक्सेन $<$ एल्कोहल $<$ पानी अणुओं के बीच आकर्षण बल जितना अधिक होता है, तरल के सतही तनाव के मापदंड उतना ही अधिक होता है।उत्तर दिखाएं
Answer जब कोई गैस पानी के ऊपर एकत्रित की जाती है, तो यह नम और जल वाष्प संतृप्त होती है जो अपने आप के दबाव को आरोपित करती है। जल वाष्प के कारण दबाव को जलीय तनाव कहते हैं, इसलिए, गैस के कुल दबाव ( $p$ नम गैस) है इसलिए, $p_{\text {dry gas }}$ निम्नलिखित द्वारा दिया जाता है $$
P_{\text {moist gas }}=p_{\text {dry gas }}+\text { aqueous tension }
$$ $P_{\text {dry gas }}=P_{\text {moist gas }}-$ aqueous tension इसलिए, गैस के कुल दबाव में लगाए जाने वाले संशोधन पद को सूखे गैस के दबाव की गणना के लिए $p$ moist gas - aqueous tension कहते हैं।उत्तर दिखाएं
Answer एक शरीर में परमाणुओं या अणुओं के गति के कारण उत्पन्न ऊर्जा को थर्मल ऊर्जा कहते हैं। यह अणुओं के औसत गतिज ऊर्जा का माप है। तापमान में वृद्धि के साथ यह ऊर्जा बढ़ती जाती है।उत्तर दिखाएं
उत्तर $\mathrm{H}-\mathrm{F}$ एक ध्रुवीय सहसंयोजक अणु है जिसमें द्विध्रुव-द्विध्रुव प्रतिक्रिया उपस्थित होती है। क्योंकि, इसमें एक विद्युत ऋणात्मक परमाणु $\mathrm{F}$, $\mathrm{H}$ परमाणु के साथ बंधे होते हैं, इसलिए इसके अणुओं के बीच $\mathrm{H}$-बंध उपस्थित होते हैं। इन $\mathrm{H}$-बंधों के कारण, $\mathrm{HF}$ अणु तरल अवस्था में रहते हैं। अतः, तरल अवस्था में $\mathrm{HF}$ अणुओं के बीच $\mathrm{H}$-बंध एवं द्विध्रुव-द्विध्रुव प्रतिक्रिया उपस्थित होती है।उत्तर दिखाएं
एक प्रमाण बताइए जो इस अनुमान के लिए वास्तविक गैसों के लिए अनुपयोगी होता है।
उत्तर वास्तविक गैसों को ठंडा करके एवं संपीड़ित करके तरल किया जा सकता है। यह बताता है कि अणुओं के बीच आकर्षण बल उपस्थित होता है। $$
\ldots \stackrel{S t}{H}-F \ldots \underset{H \text {-bonds } \rightarrow}{\stackrel{S t}{H}}-\stackrel{S-}{F} \ldots \stackrel{S T}{H}-F \ldots . H-\stackrel{S t}{H} \ldots
$$उत्तर दिखाएं
(i) आदर्श गैस के लिए $Z$ का मान क्या होता है?
(ii) बॉयल के ताप से ऊपर वास्तविक गैस के लिए $Z$ का मान कैसे प्रभावित होता है?
उत्तर (i) आदर्श गैस के लिए संपीड़न गुणांक, $Z=1$ होता है। (ii) बॉयल के ताप से ऊपर वास्तविक गैसें धनात्मक विचलन दिखाती हैं। अतः, $Z>1$ नोट संपीड़न गुणांक, $Z=\frac{p V}{n R T}$ से निम्नलिखित महत्वपूर्ण बिंदु निकलते हैं। (i) आदर्श गैस के लिए $Z=1$ सभी ताप एवं दबाव पर होता है क्योंकि $p V=n R T$ होता है। (ii) बहुत कम दबाव पर सभी गैसें $Z \simeq 1$ दिखाती हैं एवं आदर्श गैस के रूप में व्यवहार करती हैं। (iii) उच्च दबाव पर सभी गैसें $Z>1$ दिखाती हैं। ये अधिक कठिनता से संपीड़ित होती हैं। (iv) मध्यम दबाव पर अधिकांश गैसें $Z<1$ दिखाती हैं।उत्तर दिखाएं
Answer $CO_{2}$ गैस के दिए गए क्रिटिकल तापमान और दबाव क्रमशः $30.98^{\circ} C$ और $73 ~atm$ हैं। इससे यह सुझाव देता है कि $CO_{2}$ गैस को $30.98^{\circ} C$ से ऊपर और $73 ~atm$ से अधिक दबाव पर द्रवीय नहीं किया जा सकता है, चाहे आप कितना भी उच्च तापमान और दबाव लगाएं। अतः $CO_{2}$ गैस को $32^{\circ} C$ तापमान और $80 ~atm$ दबाव पर द्रवीय नहीं किया जा सकता है।उत्तर दिखाएं
$$ \left(p+\frac{a n^{2}}{V^{2}}\right)(V-n b)=n R T $$
जहाँ, ’ $a$ ’ और ’ $b$ ’ वान डर वॉल्स नियतांक हैं, ’ $n b$ ’ गैस के अणुओं के कुल आयतन के लगभग बराबर होता है। ’ $a$ ’ अणुओं के बीच आकर्षण के माप को दर्शाता है।
(i) निम्नलिखित गैसों को ’ $b$ ’ के बढ़ते क्रम में व्यवस्थित करें। कारण दें।
$$ O_{2}, CO_{2}, H_{2}, He $$
(ii) निम्नलिखित गैसों को ’ $a$ ’ के माप के घटते क्रम में व्यवस्थित करें। कारण दें।
$$ CH_{4}, O_{2}, H_{2} $$
उत्तर दिखाएं
Answer
(i) गैस अणुओं द्वारा उपलब्ध मोलर आयतन $\propto$ अणुओं के आकार और वान डर वॉल्स नियतांक ’ $b$ ’ गैस अणुओं के मोलर आयतन को प्रदर्शित करता है। अतः ’ $b$ ’ के मान निम्न क्रम में बढ़ते हैं
$$ H_{2}<He<O_{2}<CO_{2} $$
(ii) वान डर वॉल्स नियतांक ’ $a$ ’ अणुओं के बीच आकर्षण के माप को दर्शाता है। अणु के इलेक्ट्रॉन क्षमता के आकार के साथ अणुओं के बीच आकर्षण के माप बढ़ता है। अतः दिए गए गैसों के लिए ’ $a$ ’ के माप निम्न क्रम में घटते हैं
$$ CH_{4}>O_{2}>H_{2} $$
अधिक इलेक्ट्रॉन क्षमता वाले अणुओं के लिए अणु के विपरीत बल अधिक होते हैं और लंडन बल या प्रसरण बल अधिक होते हैं।
35. आदर्श गैस द्वारा आरोपित दबाव $\left(p_{\text {ideal }}\right)$ और अवलोकित दबाव ( $p_{\text {real }}$ ) के बीच संबंध निम्न समीकरण द्वारा दिया गया है,
$$ p_{\text {ideal }}=p_{\text {real }}+\frac{a n^{2}}{V^{2}} $$
(i) यदि दबाव को $\mathrm{Nm}^{-2}$ में लिया जाता है, मोल को मोल में और आयतन को $\mathrm{m}^{3}$ में लिया जाता है, तो ’ $a$ ’ की इकाई की गणना करें।
(ii) जब दबाव वातावरण में हो और आयतन $\mathrm{dm}^{3}$ में हो, तो ’ $a$ ’ की इकाई क्या होगी?
उत्तर दिया गया है, $p_{\text {ideal }}=p_{\text {real }}+\frac{a n^{2}}{V^{2}}$ (i) $a=\frac{p V^{2}}{n^{2}}$ यदि $p=\mathrm{Nm}^{-2}$ की इकाई हो, $V=\mathrm{m}^{3}$ की इकाई हो, $n=\mathrm{mol}$ की इकाई हो, तो, $a$ की इकाई $=\frac{\mathrm{Nm}^{-2}\left(\mathrm{~m}^{3}\right)^{2}}{(\mathrm{~mol})^{2}}=\mathrm{Nm}^{4} \mathrm{~mol}^{-2}$ (ii) यदि $p=\operatorname{atm}$ की इकाई हो, $V=\mathrm{dm}^{3}$ की इकाई हो, $n=\mathrm{mol}$ की इकाई हो, तो, $a$ की इकाई $=\frac{p V^{2}}{n^{2}}=\frac{\text { atm. }\left(\mathrm{dm}^{3}\right)^{2}}{(\mathrm{~mol})^{2}}=\mathrm{atm} \mathrm{dm}^{6} \mathrm{~mol}^{-2}$उत्तर दिखाएं
उत्तर सतह तनाव के आधार पर समझी जा सकने वाली दो घटनाएं निम्नलिखित हैं: (i) कैपिलरी में द्रव के उठाव या गिराव (कैपिलरी क्रिया)। (ii) छोटे द्रव की बूंदों की गोली आकृति।उत्तर दिखाएं
चिंतन प्रक्रिया द्रवों के बीच उपस्थित अंतराणुक बल जितने मजबूत होंगे, द्रव उतना ही श्यान होगा। उत्तर जल और ग्लिसरीन - हाइड्रोजन बंधन और दोलन-दोलन प्रतिक्रिया उपस्थित होती हैं क्योंकि दोनों ध्रुवीय अणु हैं। हेक्सेन - अपने अध्रुवीय प्रकृति के कारण वितरण बल/लंडन बल उपस्थित होते हैं। दिए गए द्रवों में अंतरमोलर बलों के क्रम, हेक्सेन $<$ जल $<$ ग्लिसरीन है। क्योंकि, हेक्सेन के अंतरमोलर बल सबसे कम होते हैं और ग्लिसरीन के अंतरमोलर बल सबसे अधिक होते हैं (तीन $\mathrm{OH}$ समूह) अंतरमोलर बल। अतः, हेक्सेन के श्यानता सबसे कम होती है और ग्लिसरीन के श्यानता सबसे अधिक होती है।उत्तर दिखाएं
उत्तर जब एक द्रव के तापमान में वृद्धि होती है, तो अणुओं की गतिज ऊर्जा बढ़ जाती है जो अंतरमोलर बलों को पराभुषित कर सकती है। अतः, द्रव आसानी से बह सकता है, जिसके परिणामस्वरूप द्रव की श्यानता में कमी होती है।उत्तर दिखाएं
(i) एक गैस के दबाव को नियत तापमान पर बढ़ाने पर उसका आयतन कैसे बदलेगा?
(ii) नियत दबाव पर, एक गैस के आयतन कैसे बदलेगा यदि तापमान को $200 \mathrm{~K}$ से $400 \mathrm{~K}$ तक बढ़ा दिया जाए?
उत्तर (i) बॉयल के नियम के अनुसार, तापमान को नियत रखते हुए गैस के दबाव उसके आयतन के व्युत्क्रमानुपाती होता है। अतः, नियत तापमान पर गैस के दबाव को बढ़ाने पर उसका आयतन कम हो जाएगा। उदाहरण के लिए, $200 \mathrm{~K}$ पर जब दबाव $p_{1}$ से $p_{2}$ तक बढ़ जाता है, तो गैस का आयतन कम हो जाता है, $V_{2}<V_{1}$। (ii) आइडियल गैस के लिए चार्ल्स के नियम के अनुसार, दबाव स्थिर रहने पर गैस का आयतन उसके तापमान के सीधे अनुपाती होता है। इसलिए, तापमान में वृद्धि होने पर, दबाव स्थिर रहने पर गैस का आयतन बढ़ेगा। स्थिर $p$ पर जब हम तापमान को $200 \mathrm{~K}$ से $400 \mathrm{~K}$ तक बढ़ाते हैं, तो गैस का आयतन बढ़ जाता है, $V_{4}>V_{3}$।उत्तर दिखाएं

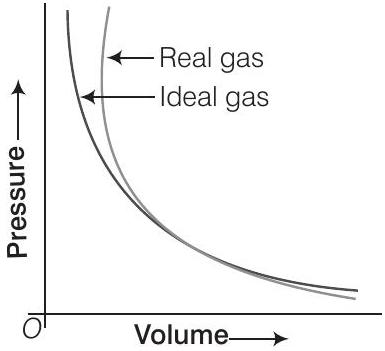
(i) निम्न दबाव पर वास्तविक गैस के आइडियल गैस के सापेक्ष व्यवहार की व्याख्या करें।
(ii) उच्च दबाव पर वास्तविक गैस के आइडियल गैस के सापेक्ष व्यवहार की व्याख्या करें।
(iii) वास्तविक गैस आइडियल गैस के व्यवहार करती है बिंदु पर एक रेखा खींचकर दबाव और आयतन को चिह्नित करें।
उत्तर दिखाएं
Answer
(i) निम्न दबाव पर वास्तविक गैस आइडियल व्यवहार से बहुत छोटा विचलन दिखाती है क्योंकि निम्न दबाव पर दोनों वक्र लगभग एक ही रहते हैं।
(ii) उच्च दबाव पर वास्तविक गैस आइडियल व्यवहार से बहुत बड़े विचलन दिखाती है क्योंकि वक्र एक दूसरे से दूर होते हैं।
(iii) बिंदु ’ $A$ ’ पर दोनों वक्र एक दूसरे को प्रतिच्छेद करते हैं। इस बिंदु पर वास्तविक गैस आइडियल गैस के रूप में व्यवहार करती है। $p_{1}$ और $V_{1}$ इस बिंदु $A$ के संगत दबाव और आयतन हैं।
स्तंभों का मिलान
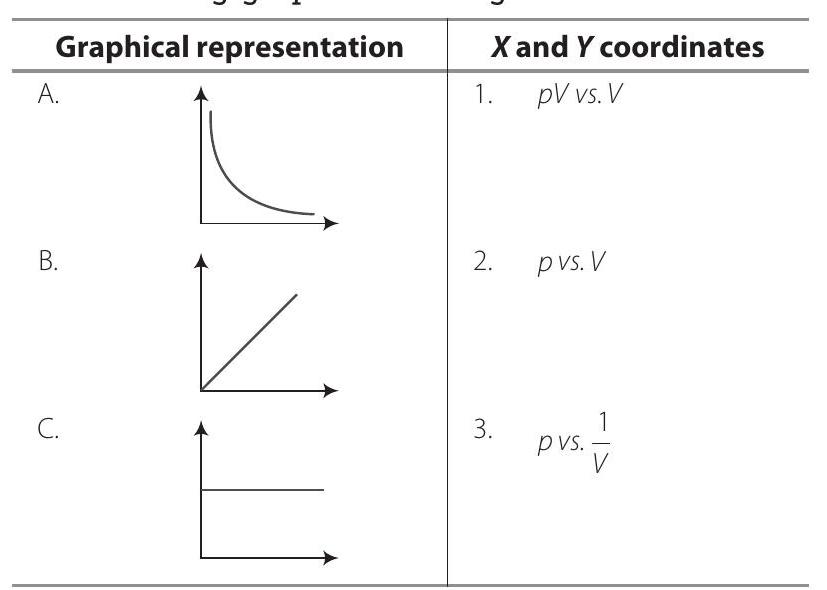
41. निम्नलिखित चर और उनके नाम के बीच ग्राफ का मिलान करें।
| ग्राफ | नाम | |
|---|---|---|
| A. स्थिर मोलर आयतन पर दबाव और तापमान के ग्राफ | 1. | आइसोथर्म |
| B. स्थिर तापमान पर दबाव और आयतन के ग्राफ | 2. | स्थिर तापमान वक्र |
| C. स्थिर दबाव पर आयतन और तापमान के ग्राफ | 3. | आइसोचोर |
उत्तर A. $\rightarrow(3)$ B. $\rightarrow(1)$ C. $\rightarrow(4)$ A. जब मोलर आयतन स्थिर होता है, तो $p-T$ ग्राफ को आइसोचोर कहते हैं। B. जब तापमान स्थिर होता है, तो $p-V$ ग्राफ को आइसोथर्म कहते हैं। C. जब दबाव स्थिर होता है, तो $V-T$ ग्राफ को आइसोबार कहते हैं।उत्तर दिखाएं
| A. | बॉयल का नियम | 1. | $V \propto n$ स्थिर $T$ और $p$ पर |
|---|---|---|---|
| B. | चार्ल्स का नियम | 2. | $p_{\text {Total }}=p_{1}+p_{2}+p_{3}+\ldots$ स्थिर $T, V$ पर |
| C. | डाल्टन का नियम | 3. | $\frac{p V}{T}=$ स्थिर |
| D. | आवोगाड्रो का नियम | 4. | $V \propto T$ स्थिर $n$ और $p$ पर |
| 5. | $p \propto \frac{1}{V}$ स्थिर $n$ और $T$ पर |
उत्तर A. $\rightarrow(5)$ B. $\rightarrow(4)$ C. $\rightarrow(2)$ D. $\rightarrow(1)$ A. बॉयल का नियम, $p \propto \frac{1}{V}$ स्थिर $T$ और $n$ पर। B. चार्ल्स का नियम, $V \propto T$ स्थिर $p$ और $n$ पर। C. डाल्टन का नियम, $p_{\text {Total }}=p_{1}+p_{2}+p_{3}+\ldots$ स्थिर $T$, V पर। D. आवोगाड्रो का नियम, $V \propto n$ स्थिर $T$ और $p$ पर।उत्तर दिखाएं
उत्तर A. $\rightarrow(2)$ B. $\rightarrow(3)$ C. $\rightarrow(1)$ अस्थिरता और कारण निम्नलिखित प्रश्नों में अस्थिरता (A) के कथन के बाद कारण (R) के कथन दिया गया है। प्रत्येक प्रश्न में नीचे दिए गए विकल्पों में से सही विकल्प चुनें।उत्तर दिखाएं

कारण (R) परमाणु बल अणुओं को एक साथ रखने की ओर ले जाते हैं लेकिन अणुओं की थर्मल ऊर्जा उन्हें अलग रखने की ओर ले जाती है।
(a) दोनों $A$ और $R$ सही हैं और $R$ $A$ की सही व्याख्या है
(b) दोनों $A$ और $R$ सही हैं लेकिन $R$ $A$ की सही व्याख्या नहीं है
(c) $A$ सही है लेकिन $R$ गलत है
(d) $A$ गलत है लेकिन $R$ सही है
उत्तर (a) दोनों अस्थिरता और कारण सही हैं और कारण अस्थिरता की सही व्याख्या है। परमाणु बल और थर्मल ऊर्जा अवस्था के निर्धारण करते हैं क्योंकि पहले अणुओं को एक साथ रखते हैं लेकिन बाद वाले उन्हें अलग रखते हैं।उत्तर दिखाएं
कारण (R) उच्च दबाव पर सभी गैसों के $Z>1$ होता है लेकिन मध्यम दबाव पर अधिकांश गैसों के $Z<1$ होता है।
(a) दोनों $A$ और $R$ सही हैं और $R$ $A$ की सही व्याख्या है
(b) दोनों $A$ और $R$ सही हैं लेकिन $R$ $A$ की सही व्याख्या नहीं है
(c) $A$ सही है लेकिन $R$ गलत है
(d) $A$ गलत है लेकिन $R$ सही है
उत्तर (b) दोनों अस्थिरता और कारण सही हैं लेकिन कारण अस्थिरता की सही व्याख्या नहीं है। नियत तापमान पर, वास्तविक गैसों के $p V v s V$ एक सीधी रेखा नहीं होता है क्योंकि वास्तविक गैसों में अणुओं के आकर्षण बल होते हैं।उत्तर दिखाएं
कारण (R) उच्च ऊंचाई पर वायुमंडलीय दबाव उच्च होता है।
(a) दोनों $A$ और $R$ सत्य हैं और $R$ $A$ का सही स्पष्टीकरण है
(b) दोनों $A$ और $R$ सत्य हैं लेकिन $R$ $A$ का सही स्पष्टीकरण नहीं है
(c) $A$ सत्य है लेकिन $R$ गलत है
(d) $A$ गलत है लेकिन $R$ सत्य है
उत्तर (c) अस्थिरता सत्य है लेकिन कारण गलत है। उच्च ऊंचाई पर वायुमंडलीय दबाव कम होता है।उत्तर दिखाएं
कारण (R) आइसोथर्मल ताप के ऊपर, अणुओं की गति तेज होती है और अंतराणुक आकर्षण अणुओं को एक साथ रखने में असमर्थ हो जाते हैं क्योंकि उच्च गति के कारण वे भाप में बदल जाते हैं।
(a) दोनों $A$ और $R$ सत्य हैं और $R$ $A$ का सही स्पष्टीकरण है
(b) दोनों $A$ और $R$ सत्य हैं लेकिन $R$ $A$ का सही स्पष्टीकरण नहीं है
(c) $A$ सत्य है लेकिन $R$ गलत है
(d) $A$ गलत है लेकिन $R$ सत्य है
उत्तर (a) दोनों अस्थिरता और कारण सत्य हैं और कारण अस्थिरता का सही स्पष्टीकरण है। गैसें अपने आइसोथर्मल ताप के ऊपर, भले ही उच्च दबाव लगाए जाए, तरल नहीं हो जातीं क्योंकि आइसोथर्मल ताप के ऊपर, अणुओं की गति तेज होती है और अंतराणुक आकर्षण अणुओं को एक साथ रखने में असमर्थ हो जाते हैं क्योंकि उच्च गति के कारण वे भाप में बदल जाते हैं।उत्तर दिखाएं
कारण (R) तरल और गैसीय अवस्था के घनत्व आइसोथर्मल ताप पर समान होते हैं।
(a) दोनों $A$ और $R$ सत्य हैं और $R$ $A$ का सही स्पष्टीकरण है
(b) दोनों $A$ और $R$ सत्य हैं लेकिन $R$ $A$ का सही स्पष्टीकरण नहीं है
(c) $A$ सत्य है लेकिन $R$ गलत है
(d) $A$ गलत है लेकिन $R$ सत्य है
उत्तर (a) दोनों अस्थिरता और कारण सत्य हैं और कारण अस्थिरता का सही स्पष्टीकरण है। आइसोथर्मल ताप पर, तरल और गैसीय अवस्था के घनत्व समान हो जाते हैं। इस कारण तरल गैसीय अवस्था में अप्रत्यक्ष रूप से बदल जाता है।उत्तर दिखाएं
कारण (R) छोटे तरल बूंदों के गोलाकार आकार होता है।
(a) दोनों $A$ और $R$ सत्य हैं और $R$ $A$ का सही स्पष्टीकरण है
(b) दोनों $A$ और $R$ सत्य हैं लेकिन $R$ $A$ का सही स्पष्टीकरण नहीं है
(c) $A$ सत्य है लेकिन $R$ गलत है
(d) $A$ गलत है लेकिन $R$ सत्य है
उत्तर दिखाएं
उत्तर
(d) अस्थिरता गलत है लेकिन कारण सत्य है।
तरल पदार्थ सतह पर अणुओं की संख्या या सतह तनाव को कम करने की कोशिश करते हैं, इसलिए छोटे तरल बूंदों के गोलाकार आकार होता है।
लंबे उत्तर प्रकार प्रश्न
50. कार्बन डाइऑक्साइड के विभिन्न तापमानों पर आइसोथर्म के चित्र में प्रस्तुत किए गए हैं। इस चित्र के आधार पर निम्नलिखित प्रश्नों के उत्तर दीजिए।
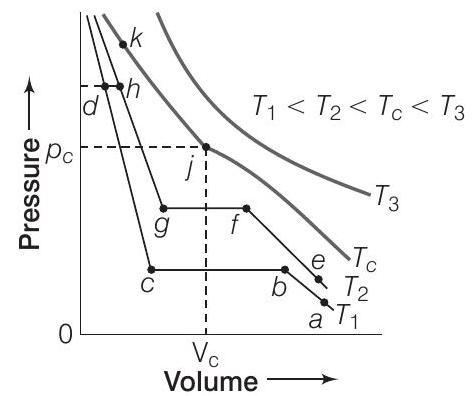
(i) तापमान $T_{1}$ पर बिंदुओं $a$ और $b$ के बीच $CO_{2}$ किस अवस्था में होगा?
(ii) तापमान $T_{1}$ पर $CO_{2}$ किस बिंदु पर द्रव रूप लेना शुरू होगा?
(iii) तापमान $T_{2}$ पर $CO_{2}$ किस बिंदु पर पूरी तरह से द्रव रूप लेगा?
(iv) तापमान $T_{3}$ पर अपसादन होगा या नहीं?
(v) $T_{1}$ तापमान के आइसोथर्म के कौन सा भाग $CO_{2}$ के द्रव और गैसीय रूप के संतुलन को प्रतिनिधित्व करता है?
उत्तर (i) तापमान $T_{1}$ पर बिंदुओं $a$ और $b$ के बीच $CO_{2}$ गैसीय अवस्था में होगा। (ii) बिंदु $b$ पर ग्राफ सीधी रेखा बनती है, जो अवस्था परिवर्तन को दर्शाती है, अर्थात $\mathrm{CO}_{2}$ के द्रवीकरण की शुरुआत होती है और बिंदु $c$ पर यह पूरी तरह से द्रव रूप ले लेता है। (iii) समान रूप से, तापमान $T_{2}$ पर $g$ बिंदु वह बिंदु है जहां $\mathrm{CO}_{2}$ पूरी तरह से द्रव रूप लेगा। (iv) $T_{3}$ तापमान पर अपसादन नहीं होगा क्योंकि $T_{3}>T_{C}$ (क्रिटिकल तापमान) है। (v) $b$ और $c$ के बीच, तरल और गैसीय $\mathrm{CO}_{2}$ संतुलन में होते हैं।उत्तर दिखाएं
(i) तरल $A$ और $B$ के क्वथनांक ग्राफिकल रूप से गणना करें।
(ii) यदि हम एक बंद बरतन में तरल $C$ लेकर इसे निरंतर गरम करते हैं। किस तापमान पर यह क्वथित होगा?
(iii) उच्च ऊंचाई पर, वायुमंडलीय दबाव कम होता है (मान लीजिए $60 \mathrm{~mm} \mathrm{Hg}$)। तरल $D$ किस तापमान पर क्वथित होगा?
(iv) चढ़ाई वाले क्षेत्र में खाना बनाने के लिए दबाव बरतन का उपयोग किया जाता है। वाष्प दबाव के आधार पर इसके कारण क्या है?
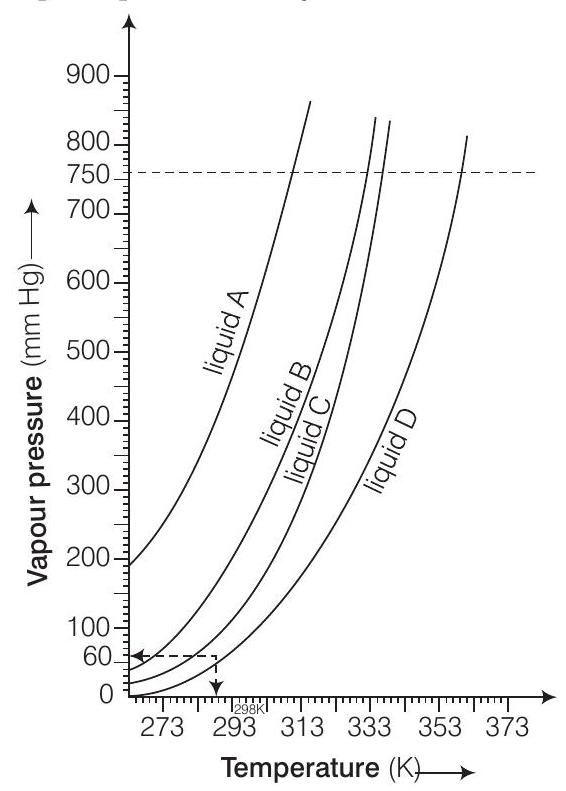
Answer (i) $A$ का क्वथनांक लगभग $315 \mathrm{~K}$ है, $B$ का क्वथनांक लगभग $345 \mathrm{~K}$ है। (ii) बंद बरतन में, तरल $C$ क्वथित नहीं होगा क्योंकि बरतन के अंदर दबाव निरंतर बढ़ता रहता है (iii) $60 \mathrm{~mm}$ संगत तापमान $313 \mathrm{~K}$ है। (iv) एक तरल तब क्वथित होता है जब इसका वाष्प दबाव वायुमंडलीय दबाव के बराबर हो जाता है। हालांकि, उच्च ऊंचाई पर, अर्थात खुले पहाड़ों पर, कम वायुमंडलीय दबाव के कारण पानी कम तापमान पर क्वथित होता है। लेकिन जब दबाव बरतन का उपयोग किया जाता है, तो पानी के वाष्प दबाव को बढ़ा दिया जाता है जिसके कारण पानी छोटे समय में अधिक कम तापमान पर क्वथित हो जाता हैउत्तर दिखाएं
Answer एक बंद बरतन में, यह ध्यान रखना आवश्यक है कि क्रिटिकल बिंदु (अर्थात क्रिटिकल तापमान और क्रिटिकल दबाव) के नीचे, तरल और इसके वाष्प के बीच संपर्क सतह स्पष्ट रूप से दिखाई देती है। जैसे-जैसे हम क्रिटिकल बिंदु की ओर बढ़ते हैं, तरल के घनत्व कम होता जाता है जबकि वाष्प के घनत्व बढ़ता जाता है इसके कारण संपीड़न। निम्न आइसोथर्मिक बिंदु (मेनिसकस स्पष्ट रूप से दिखाई दे रहा है) ऊपर आइसोथर्मिक बिंदु (मेनिसकस चले जाते हैं) आइसोथर्मिक बिंदु पर, तरल और वाष्प के घनत्व बराबर हो जाते हैं और विभाजन सतह चले जाते हैं, अर्थात तरल और गैसीय अवस्था अलग नहीं हो सकते। अन्य शब्दों में, मेनिसकस अब दिखाई नहीं देता। अब एक समान मिश्रण बन चुके तरल को सुपरक्रिटिकल तरल कहते हैं। इसलिए, किसी तरल के उसके आइसोथर्मिक ताप और दबाव से ऊपर वाले तरल को सुपरक्रिटिकल तरल कहते हैं। इन सुपरक्रिटिकल तरलों के बहुत सारे आगनिक पदार्थों को घोल सकते हैं। वे एक मिश्रण के घटकों के तेजी से अलग करने के लिए उपयोग किए जाते हैं। उदाहरण के लिए, $31.1^{\circ} \mathrm{C}$ से ऊपर और 600 बार दबाव से ऊपर $ \mathrm{CO}_{2} $ का घनत्व लगभग $1 \mathrm{~g} / \mathrm{cm}^{3}$ होता है। इसका उपयोग कॉफी बीन से कैफीन को घोलने के लिए किया जाता है क्योंकि यह वातावरण के लिए हानिकारक क्लोरोफ्लूरोकार्बन की बजाए एक बेहतर विकल्प है।उत्तर दिखाएं


उत्तर तीखे गिलास के किनारे गरम करके चिकना कर दिया जाता है। क्योंकि गिलास को गरम करने पर यह पिघल जाता है और तरल के सतह के किनारे न्यूनतम सतह क्षेत्र के वृत्ताकार आकार ले लेता है। इसे गिलास के आग के चमकाने कहते हैं।उत्तर दिखाएं
उत्तर दिखाएं
उत्तर
जब एक तरल पदार्थ एक स्थिर सतह पर बहता है, तो सतह के तुरंत संपर्क में अणुओं के आवरण अपने स्थान पर रहते हैं। ऊपरी आवरण के अणुओं की गति उनकी स्थिति के आधार पर बढ़ती जाती है जब वे स्थिर आवरण से दूर होते जाते हैं।
इस प्रकार के प्रवाह में जहां एक आवरण से दूसरे आवरण तक गति के नियमित अंतर होता है, इसे लैमिनर प्रवाह कहते हैं।
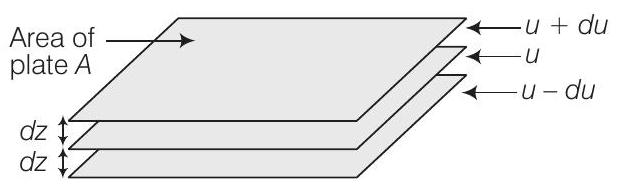
लैमिनर प्रवाह में, अणुओं की गति सभी आवरण में समान नहीं होती क्योंकि प्रत्येक आवरण नीचे के आवरण के लिए कुछ प्रतिरोध या घर्षण प्रदान करता है।
55. कार्बन डाइऑक्साइड गैस के आइसोथर्म्स चित्र में दिखाए गए हैं। एक गैस को तरल में बदलने के लिए एक पथ चिह्नित करें जिसमें कोई भी समय बिंदु पर केवल एक अवस्था (अर्थात या तो गैस या तरल) हो। परिवर्तन के लिए तापमान, आयतन और दबाव को कैसे बदला जाए इसकी व्याख्या करें?
उत्तर दिखाएं
उत्तर
एक गैस को तरल में बदलने या एक तरल को गैस में बदलने के लिए एक प्रक्रिया के माध्यम से ऐसा किया जा सकता है जहां हमेशा एक अवस्था मौजूद रहती है।
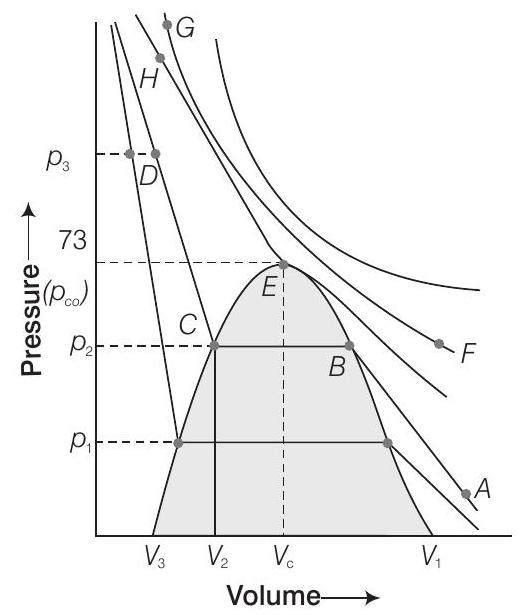
उदाहरण के लिए, ऊपर दिए गए चित्र में, हम $A$ से ऊर्ध्वाधर रूप से बढ़कर तापमान को बढ़ाकर बिंदु तक पहुंच सकते हैं, फिर हम नियत तापमान पर गैस को संपीड़ित करके आइसोथर्म (31.1°C की आइसोथर्म) के अनुसार बिंदु तक पहुंच सकते हैं। दबाव बढ़ जाएगा।
अब, हम तापमान को कम करके बिंदु $D$ की ओर ऊर्ध्वाधर रूप से बढ़ सकते हैं। जैसे ही हम क्रिटिकल आइसोथर्म पर बिंदु $H$ को पार करते हैं, हमें तरल प्राप्त हो जाता है। इस प्रक्रिया के कोई भी चरण में हम दो अवस्था क्षेत्र में नहीं पहुंच सकते।
इस प्रक्रिया को क्रिटिकल तापमान पर किया जाता है, जहां पदार्थ हमेशा एक ही अवस्था में रहता है। इसे गैसीय और तरल अवस्था के बीच अवस्था के सतत रहने के रूप में जाना जाता है।





