10.1 परिचय

1637 में डेसकार्ट ने प्रकाश के कण मॉडल को प्रस्तुत किया और स्नेल के नियम का निर्वचन किया। यह प्रकाश के एक संपर्क सतह पर परावर्तन और अपवर्तन के नियमों की व्याख्या कर सकता था। कण मॉडल का अनुमान था कि यदि प्रकाश की किरण (अपवर्तन के द्वारा) अभिलंब की ओर झुकती है तो दूसरे माध्यम में प्रकाश की गति अधिक होगी। इस प्रकाश के कण मॉडल को आइजैक न्यूटन ने अपनी प्रसिद्ध किताब “ऑप्टिक्स” में आगे ले गए और इस किताब की विशाल लोकप्रियता के कारण इस मॉडल को बहुत अक्सर न्यूटन के नाम से जोड़ दिया गया।

1678 में, डच भौतिकविज्ञानी क्रिस्टियान ह्यूगेंस ने प्रकाश के तरंग सिद्धांत को प्रस्तुत किया - इस तरंग मॉडल के बारे में हम इस पाठ्यक्रम में चर्चा करेंगे। जैसा कि हम देखेंगे, तरंग मॉडल द्वारा प्रतिबिंब और अपवर्तन के घटनाओं की संतुलित व्याख्या की जा सकती है; हालांकि, यह अपवर्तन के दौरान यदि तरंग अभिलंब की ओर झुकती है तो दूसरे माध्यम में प्रकाश की गति कम होगी इसकी भविष्यवाणी करता है। यह तब तक विरोधाभासी होता है जब तक कि प्रकाश के कण मॉडल का उपयोग करके अपेक्षित भविष्यवाणी नहीं की जाती। यह बहुत बाद एक प्रयोग द्वारा पुष्टि की गई जहां दिखाया गया कि पानी में प्रकाश की गति हवा में गति से कम होती है, जो तरंग मॉडल की भविष्यवाणी की पुष्टि करता है; फूको ने 1850 में इस प्रयोग को किया।

तरंग सिद्धांत को मुख्य रूप से न्यूटन के विश्वास के कारण और भी एक कारण भी था कि प्रकाश वैक्यूम में भी यात्रा कर सकता है और एक तरंग के लिए एक माध्यम की आवश्यकता होती है जिससे एक बिंदु से दूसरे बिंदु तक यात्रा कर सके। हालांकि, जब थॉमस यंग ने 1801 में अपने प्रसिद्ध तरंग प्रतिक्रिया प्रयोग को किया तो यह स्पष्ट हो गया कि प्रकाश वास्तव में एक तरंग घटना है। दृश्य प्रकाश की तरंग दैर्घ्य को मापा गया और यह बहुत छोटी पाया गया; उदाहरण के लिए, पीले प्रकाश की तरंग दैर्घ्य लगभग $0.6 \mu \mathrm{m}$ होती है। दृश्य प्रकाश की तरंग दैर्घ्य के कारण (सामान्य दर्पण और लेंस के आकार की तुलना में) प्रकाश को सीधी रेखा में यात्रा करते हुए माना जा सकता है। यह ज्यामितीय प्रकाशिकी के क्षेत्र है, जिसके बारे में हम पिछले अध्याय में चर्चा कर चुके हैं। वास्तव में, जिस प्रकाशिकी के अंतर्गत तरंग दैर्घ्य के अंतर को अनदेखा कर दिया जाता है, उसे ज्यामितीय प्रकाशिकी कहा जाता है और एक किरण को तरंग दैर्घ्य शून्य की सीमा में ऊर्जा प्रसार के मार्ग के रूप में परिभाषित किया जाता है।

1801 में यंग के अनुत्साह एक्सपेरिमेंट के बाद, अगले 40 साल तक, कई एक्सपेरिमेंट लाइट वेव के अनुत्साह और विवर्तन के संबंध में किए गए; इन एक्सपेरिमेंट केवल एक तरंग मॉडल के आधार पर संतुलित ढंग से समझे जा सकते थे। इसलिए, नौंवीं सदी के मध्य तक, तरंग सिद्धांत की तरह बहुत ठोस आधार लग गया लगता था। एकमात्र बड़ी कठिनाई यह थी कि चूंकि यह माना जाता था कि एक तरंग के प्रसार के लिए एक माध्यम की आवश्यकता होती है, तो वैक्यूम में लाइट तरंग कैसे प्रसारित हो सकती है। इसे जब मैक्सवेल ने अपने प्रसिद्ध विद्युत चुंबकत्व सिद्धांत के बारे में बताया तो समझ आई। मैक्सवेल ने विद्युत और चुंबकत्व के नियमों के बारे में एक सेट के समीकरण विकसित किए और इन समीकरणों का उपयोग करके वह जो विद्युत चुंबकीय तरंगों के बारे में जाना जाता है उसे विद्युत चुंबकीय तरंजों के बारे में बताया। विद्युत चुंबकीय तरंगों की गति की गणना मैक्सवेल ने आवर्ती अंतरिक्ष में की और उन्होंने पाया कि सिद्धांतिक मान विद्युत चुंबकीय तरंगों की गति के मापे गए मान के बहुत करीब था। इस बात से वह निष्कर्ष निकाले कि विद्युत चुंबकीय तरंग अवश्य होती है। इसलिए, मैक्सवेल के अनुसार, विद्युत चुंबकीय तरंग बदलते विद्युत और चुंबकीय क्षेत्रों के साथ संबंधित होती है; बदलते विद्युत क्षेत्र एक समय और अंतरिक्ष विशिष्ट चुंबकीय क्षेत्र उत्पन्न करते हैं और बदलते चुंबकीय क्षेत्र एक समय और अंतरिक्ष विशिष्ट विद्युत क्षेत्र उत्पन्न करते हैं। बदलते विद्युत और चुंबकीय क्षेत्र वैक्यूम में भी विद्युत चुंबकीय तरंगों के प्रसार के लिए उत्प्रेरक के रूप में कार्य करते हैं।

इस अध्याय में हम सबसे पहले ह्यूगनस सिद्धांत के मूल संस्करण के बारे में चर्चा करेंगे और परावर्तन और अपवर्तन के नियम निखारेंगे। अनुच्छेद 10.4 और 10.5 में हम अनुप्रस्थ सुपरपोजिशन के सिद्धांत पर आधारित विस्थापन के घटना के बारे में चर्चा करेंगे। अनुच्छेद 10.6 में हम अपवर्तन के घटना के बारे में चर्चा करेंगे जो ह्यूगनस फ्रेस्नेल सिद्धांत पर आधारित है। अंत में अनुच्छेद 10.7 में हम विवरण के घटना के बारे में चर्चा करेंगे जो यह तथ्य पर आधारित है कि प्रकाश तरंगें अनुप्रस्थ विद्युत चुंबकीय तरंगें होती हैं।

• मैक्सवेल ने लगभग 1855 के आसपास विद्युत चुंबकीय तरंगों के अस्तित्व की भविष्यवाणी की थी; इसके काफी बाद (लगभग 1890 में) हेनरिख हर्ट्ज ने प्रयोगशाला में रेडियो तरंगों को उत्पन्न किया। जे.सी. बोस और जी. मार्कोनी ने हर्ट्जियन तरंगों के व्यावहारिक अनुप्रयोग की रचना की।

10.2 हाइगेन्स के सिद्धांत

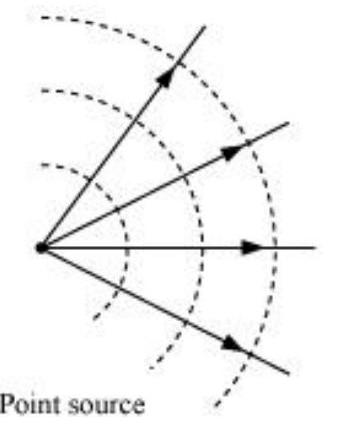
हम सबसे पहले एक तरंग सतह की परिभाषा देंगे: जब हम एक छोटी सी चट्टान को एक शांत झील पर गिराते हैं, तो तरंगें टकराव बिंदु से फैलती हैं। सतह पर किसी भी बिंदु आवर्ती गति करता है। किसी भी क्षण, सतह का एक फोटो गोलाकार वलयों को दिखाएगा जहां अव्यवहारिकता अधिकतम होती है। स्पष्ट रूप से, ऐसे वलय के सभी बिंदु एक साथ आवर्ती गति करते हैं क्योंकि वे स्रोत से समान दूरी पर होते हैं। ऐसे बिंदुओं के संग्रह, जो एक साथ आवर्ती गति करते हैं, एक तरंग सतह कहलाते हैं; इसलिए एक तरंग सतह को एक नियत तरंग अवस्था के सतह के रूप में परिभाषित किया जाता है। तरंग सतह के स्रोत से बाहर चलने की गति को तरंग की गति कहते हैं। तरंग की ऊर्जा तरंग सतह के लंबवत दिशा में चलती है।

चित्र 10.1 (a) एक बिंदु स्रोत से निकलने वाला विस्तारित गोलीय तरंग। तरंग सतहें गोलीय होती हैं।

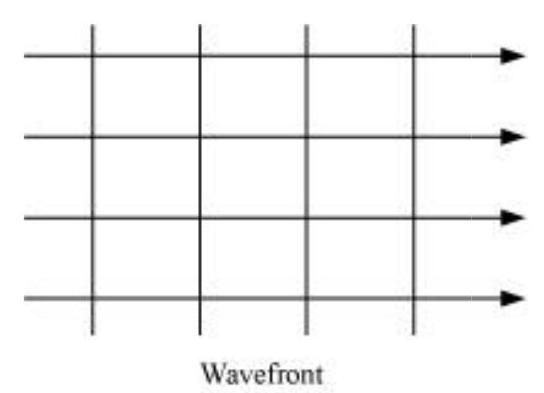
चित्र 10.1 (b) स्रोत से बहुत दूर जाने पर गोलीय तरंग के एक छोटे भाग को तल तरंग के रूप में अपेक्षित किया जा सकता है।

अगर हम एक बिंदु स्रोत के बारे में बात करते हैं जो सभी दिशाओं में समान रूप से तरंगें उत्सर्जित करता है, तो उन बिंदुओं के समूह जो समान आयाम रखते हैं और समान चरण में झूलते हैं, गोलाई वाले गोले होते हैं और इसे ज्ञात तरंग के गोलीय तरंग के रूप में जाना जाता है, जैसा कि चित्र 10.1(a) में दिखाया गया है। एक बड़ी दूरी पर स्रोत से, गोले के एक छोटे भाग को एक समतल के रूप में माना जा सकता है और इसे ज्ञात तरंग के समतल तरंग के रूप में जाना जाता है [चित्र 1 बी]।

अब, अगर हम $t=0$ पर तरंग के आकार को जानते हैं, तो हुएन्स के सिद्धांत हमें बाद में एक समय $\tau$ पर तरंग के आकार को निर्धारित करने की अनुमति देता है। इसलिए, हुएन्स के सिद्धांत आधारिक रूप से एक ज्यामितीय निर्माण है, जो किसी भी समय तरंग के आकार को देता है और बाद में तरंग के आकार को निर्धारित करने की अनुमति देता है। अब हम एक विस्तार वाली तरंग के बारे में विचार करते हैं और $\mathrm{F_1} \mathrm{~F_2}$ को $t=0$ पर एक गोलीय तरंग के एक भाग के रूप में प्रतिनिधित्व करते हैं (चित्र 10.2)। अब, हुएन्स के सिद्धांत के अनुसार, तरंग के प्रत्येक बिंदु एक द्वितीयक विक्षोभ के स्रोत होता है और इन बिंदुओं से उत्सर्जित तरंगों के छोटे तरंग अपनी गति के अनुसार सभी दिशाओं में फैलते हैं। इन तरंगों को आमतौर पर द्वितीयक तरंग के रूप में संदर्भित किया जाता है और यदि हम इन सभी गोलाओं के एक सामान्य स्पर्शरेखा खींचते हैं, तो हमें बाद में एक समय पर तरंग के नए स्थान को प्राप्त करते हैं।

चित्र 10.2 $\mathrm{F_1} \mathrm{~F_2}$, $t=0$ पर $\mathrm{O}$ के केंद्र के साथ गोलीय तरंगदृढ़ता को प्रदर्शित करता है। $F_{1} F_{2}$ से उत्सर्जित द्वितीयक तरंगों के आवरण आगे बढ़ती तरंगदृढ़ता $G_{1} G_{2}$ को उत्पन्न करता है। पीछे बढ़ती तरंग $\mathrm{D_1} \mathrm{~D_2}$ नहीं मौजूद है।

इस प्रकार, यदि हम $t=\tau$ पर तरंग सामूहिक के आकार का निर्धारण करना चाहते हैं, तो हम प्रत्येक बिंदु से त्रिज्या $v \tau$ के गोलाई गोले खींचते हैं, जहाँ $v$ माध्यम में तरंगों की चाल को प्रदर्शित करता है। अब यदि हम इन सभी गोलों के एक सामान्य स्पर्शरेखा खींचते हैं, तो हमें $t=\tau$ पर तरंग सामूहिक के नए स्थान को प्राप्त होता है। चित्र 10.2 में दिखाए गए नए तरंग सामूहिक $\mathrm{G_1} \mathrm{G_2}$ फिर एक गोलाकार तरंग सामूहिक है जिसका केंद्र बिंदु $\mathrm{O}$ है।

चित्र 10.3 एक समतल तरंग के दाहिने ओर चलने के लिए ह्यूगनिस के ज्यामितीय निर्माण। $\mathrm{F_1} \mathrm{~F_2}$ $t=0$ पर समतल तरंग सतह है और $\mathrm{G_1} \mathrm{~G_2}$ बाद के समय $\tau$ पर तरंग सतह है। रेखाएँ $\mathrm{A_1} \mathrm{~A_2}$, $\mathrm{B_1} \mathrm{~B_2} \ldots$ आदि, $\mathrm{F_1} \mathrm{~F_2}$ और $\mathrm{G_1} \mathrm{~G_2}$ दोनों के लंबवत हैं और रेखाएँ को निरूपित करती हैं।

उपरोक्त मॉडल में एक कमी है: हमें एक पीछे की तरंग भी होती है जो चित्र 10.2 में $\mathrm{D_1} \mathrm{~D_2}$ के रूप में दिखाई देती है। ह्यूगनिस ने तरंग के आगे दिशा में द्वितीयक तरंग के आयाम अधिकतम होता है और पीछे दिशा में शून्य होता है के अड़होक अनुमान के आधार पर तरंग के अनुपस्थिति की व्याख्या कर सकते हैं। हालांकि, यह अड़होक अनुमान संतोषजनक नहीं है और तरंग के अनुपस्थिति की वास्तविक व्याख्या अधिक गहरी तरंग सिद्धांत से की जाती है।

एक तरह के तरीके से, हम ह्यूगन और सिद्धांत का उपयोग करके एक समतल तरंग के तरंग सीमा के आकार का निर्धारण कर सकते हैं जो एक माध्यम में चल रही है (चित्र 10.3)।

10.3 समतल तरंग के प्रकीर्णन और परावर्तन के लिए ह्यूगन सिद्धांत का उपयोग

10.3.1 समतल तरंग के प्रकीर्णन

अब हम ह्यूगन सिद्धांत का उपयोग करके प्रकीर्णन के नियमों का निर्वचन करेंगे। माध्यम 1 और माध्यम 2 के बीच सतह को $\mathrm{PP}^{\prime}$ द्वारा प्रदर्शित करेंगे, जैसा कि चित्र 10.4 में दिखाया गया है। माध्यम 1 और माध्यम 2 में प्रकाश की गति को क्रमशः $v_{1}$ और $v_{2}$ द्वारा प्रदर्शित करेंगे। हम एक समतल तरंग सीमा $\mathrm{AB}$ को माध्यम में दिशा $\mathrm{A}^{\prime} \mathrm{A}$ में चलते हुए दिखाए गए चित्र में एक सतह पर कोण $i$ पर आपतित मान लेंगे। मान लें कि $\tau$ वह समय है जिसमें तरंग सीमा दूरी BC के लिए यात्रा करती है। इसलिए,

$B C=v _{1} \tau$

चित्र 10.4 एक समतल तरंग $\mathrm{AB}$, माध्यम 1 और माध्यम 2 के बीच सतह $\mathrm{PP}^{\prime}$ पर कोण $i$ पर आपतित होती है। समतल तरंग के अपवर्तन होता है और $\mathrm{CE}$ अपवर्तित तरंग का अग्रसरी भाग दर्शाता है। चित्र $v_{2}<v_{1}$ के लिए संगत है ताकि अपवर्तित तरंग अभिलम्ब की ओर मुड़ जाए।

क्रिस्टियान ह्यूगेंस (1629 – 1695) डच भौतिकज्ञ, खगोलशास्त्री, गणितज्ञ और प्रकाश के तरंग सिद्धांत के जनक। उनकी किताब, प्रकाश पर ट्रीटीज़, आज भी बहुत रोचक पढ़ने लायक है। इस कार्य में वे अपनी चमत्कारी तर्कसंगत व्याख्या के साथ-साथ चैटलाइट नामक खनिज के द्वारा दिखाए गए द्विप्रतिस्थापन के बारे में भी बताते हैं। वे पहले व्यक्ति थे जिन्होंने वृत्तीय और सरल अवधि गति के विश्लेषण किया और सुधारित घड़ियाँ और दूरबीन बनाए। उन्होंने सैटर्न के अंगारों की सही ज्यामिति की खोज की।

ताकि अपवर्तित तरंगपृष्ठ के आकार का निर्धारण किया जा सके, हम द्वितीय माध्यम में बिंदु $A$ से त्रिज्या $v_{2} \tau$ के एक गोले को खींचते हैं (द्वितीय माध्यम में तरंग की चाल $v_{2}$ होती है)। मान लीजिए $\mathrm{CE}$ बिंदु $\mathrm{C}$ से गोले पर खींची गई स्पर्श रेखा को निरूपित करती है। तब, $\mathrm{AE}=v_{2} \tau$ और $\mathrm{CE}$ अपवर्तित तरंगपृष्ठ को निरूपित करती है। अब हम त्रिभुज $\mathrm{ABC}$ और $\mathrm{AEC}$ को ध्यान में रखते हैं, तो हम आसानी से प्राप्त करते हैं

$\sin i=\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{v_{1} \tau}{\mathrm{AC}}\hspace{12cm}\ldots{(10.1)}$

and

$\sin r=\frac{\mathrm{AE}}{\mathrm{AC}}=\frac{v_{2} \tau}{\mathrm{AC}}\hspace{12cm}\ldots{(10.2)}$

जहाँ $i$ और $r$ क्रमशः आपतन कोण और अपवर्तन कोण हैं। इस प्रकार हम प्राप्त करते हैं

$\dfrac{\sin i}{\sin r}=\frac{v_{1}}{v_{2}}\hspace{13cm}\ldots{(10.3)}$

उपरोक्त समीकरण से हमें महत्वपूर्ण परिणाम मिलता है कि यदि $r<i$ (अर्थात यदि किरण अभिलम्ब की ओर मुड़ती है), तो दूसरे माध्यम में प्रकाश तरंग की चाल $\left(v_{2}\right)$ पहले माध्यम में प्रकाश तरंग की चाल $\left(v_{1}\right)$ से कम होगी। यह अनुमान बूढ़े कण मॉडल के अनुमान के विपरीत है और बाद के प्रयोगों ने दिखाया कि तरंग सिद्धांत का अनुमान सही है। अब, यदि $c$ निर्वात में प्रकाश की चाल को प्रदर्शित करता है, तो,

$n_{1}=\dfrac{c}{v_{1}}\hspace{13cm}\ldots{(10.4)}$

और

$n_{2}=\dfrac{c}{v_{2}}\hspace{13cm}\ldots{(10.5)}$

माध्यम 1 और माध्यम 2 के अपवर्तनांक के रूप में जाने जाते हैं। अपवर्तनांक के संदर्भ में, समीकरण (10.3) को लिखा जा सकता है:

$n_{1} \sin i=n_{2} \sin r \hspace{12cm}\ldots{(10.6)}$

यह अपवर्तन के स्नेल के नियम है। इसके अतिरिक्त, यदि $\lambda_{1}$ और $\lambda_{2}$ क्रमशः माध्यम 1 और माध्यम 2 में प्रकाश के तरंगदैर्ध्य को दर्शाते हैं, और यदि दूरी $\mathrm{BC}$, $\lambda_{1}$ के बराबर हो तो दूरी $\mathrm{AE}$, $\lambda_{2}$ के बराबर होगी (क्योंकि यदि $\mathrm{B}$ से उठे तरंग का शिखर $\tau$ समय में $\mathrm{C}$ पर पहुँच जाता है, तो $\mathrm{A}$ से उठे तरंग का शिखर भी $\tau$ समय में $E$ पर पहुँच जाएगा); इसलिए,

$ \dfrac{\lambda_{1}}{\lambda_{2}}=\frac{\mathrm{BC}}{\mathrm{AE}}=\frac{v_{1}}{v_{2}} $

या

$\dfrac{v_{1}}{\lambda_{1}}=\frac{v_{2}}{\lambda_{2}}\hspace{13cm}\ldots{(10.7)}$

उपरोक्त समीकरण यह दर्शाता है कि जब एक तरंग घनीय माध्यम में अपवर्तित होती है $\left(v_{1}>v_{2}\right)$, तो तरंगदैर्घ्य और प्रसार गति कम हो जाती है, लेकिन आवृत्ति $v(=v / \lambda)$ अपरिवर्तित रहती है।

10.3.2 एक दुर्लक माध्यम पर अपवर्तन

अब हम एक समतल तरंग के एक दुर्लक माध्यम पर अपवर्तन की विवेचना करते हैं, अर्थात, $v_{2}>v_{1}$. एक ठीक तरह से समान प्रकार चलते हुए हम चित्र 10.5 में दिखाए गए अपवर्तित तरंग सामन्तर को निर्मित कर सकते हैं। अब अपवर्तन कोण आपतन कोण से अधिक होगा; हालांकि, हम अभी भी $n_{1} \sin i=n_{2} \sin r$ के साथ रहेंगे। हम एक कोण $i_{c}$ को निम्नलिखित समीकरण द्वारा परिभाषित करते हैं

$\sin i_{c}=d\frac{n_{2}}{n_{1}}\hspace{13cm}\ldots{(10.8)}$

इसलिए, यदि $i=i_{c}$ तो $\sin r=1$ और $r=90^{\circ}$ होगा। स्पष्ट रूप से, $i>i_{c}$ के लिए कोई भी अपवर्तित तरंग नहीं हो सकती। कोण $i_{c}$ को आवर्धक कोण कहा जाता है और सभी आपतन कोणों के लिए जो आवर्धक कोण से अधिक होते हैं, हमें कोई अपवर्तित तरंग नहीं मिलेगी और तरंग को जो कुल आंतरिक प्रतिबिंब कहलाता है, उसके अधीन चलना पड़ेगा। कुल आंतरिक प्रतिबिंब के घटना और उसके अनुप्रयोगों के बारे में अनुच्छेद 9.4 में चर्चा की गई थी।

चित्र 10.5 एक समतल तरंग जो एक बेहतर वाहिनी माध्यम में आपतित होती है जहां $v_{2}>v_{1}$ है। तरंग अभिलम्ब से दूर मुड़ जाती है।

10.3.3 समतल तरंग के समतल सतह द्वारा परावर्तन

हम अब एक समतल तरंग $\mathrm{AB}$ को एक परावर्तक सतह MN पर कोण $i$ पर आपतित होने के बारे में विचार करते हैं। यदि $v$ तरंग की गति को माध्यम में दर्शाता है और यदि $\tau$ तरंग तरंग बिंदु $B$ से $C$ तक आगे बढ़ने के लिए लिए गए समय को दर्शाता है तो दूरी

$$ \mathrm{BC}=v \tau $$

उत्पन्न अपवर्तित तरंग पृष्ठ के निर्माण के लिए हम चित्र 10.6 में दिखाए गए तरीके से बिंदु $\mathrm{A}$ से त्रिज्या $v \tau$ के एक गोले को खींचते हैं। मान लीजिए $\mathrm{CE}$ बिंदु $\mathrm{C}$ से इस गोले पर खींची गई स्पर्श तल को दर्शाता है। स्पष्ट रूप से

$$ \mathrm{AE}=\mathrm{BC}=v \tau $$

 तल तरंग $A B$ के द्वारा प्रतिबिंब तल MN द्वारा प्रतिबिंबित हो रही है। $\mathrm{AB}$ और $\mathrm{CE}$ प्रतिगमन और प्रतिबिंब तरंगों को प्रतिनिधित करते हैं।

अब हम त्रिभुज $\mathrm{EAC}$ और $\mathrm{BAC}$ को ध्यान में रखते हैं, तो हम देखेंगे कि वे समान हैं और इसलिए, आंकड़ा 10.6 में दिखाए गए कोण $i$ और $r$ बराबर होंगे। यह प्रतिबिंब के कानून है।

जब हम प्रतिबिंब और अपवर्तन के कानून को जान लेंगे, तो प्रिज्म, लेंस और दर्पण के व्यवहार को समझ सकते हैं। इन घटनाओं के बारे में विस्तार से चैप्टर 9 में प्रकाश के सीधे प्रसार के आधार पर चर्चा की गई थी। यहां हम केवल तरंगों के व्यवहार का वर्णन करते हैं जब वे प्रतिबिंब या अपवर्तन के माध्यम से गुजरते हैं। आंकड़ा 10.7(a) में हम एक समतल तरंग को एक पतले प्रिज्म के माध्यम से गुजरते हुए देखते हैं। स्पष्ट रूप से, क्योंकि प्रकाश तरंगों की गति काँच में कम होती है, प्रवेश करने वाली तरंग के नीचले हिस्से (जो काँच के सबसे अधिक मोटे भाग के माध्यम से गुजरता है) देर से आएंगे जिसके कारण निर्गत तरंग के आकार में झुकाव हो जाएगा जैसा कि आंकड़ा में दिखाया गया है। आंकड़ा 10.7(b) में हम एक समतल तरंग को एक पतले उत्तल लेंस पर आपतित देखते हैं; प्रवेश करने वाली समतल तरंग के केंद्रीय हिस्सा लेंस के सबसे मोटे भाग के माध्यम से गुजरता है और इसके लिए अधिक देर लगती है। निर्गत तरंग के केंद्र में अवमुखी वक्रता होती है और इसलिए तरंग गोलीय बन जाती है और बिंदु F पर संगत हो जाती है जिसे फोकस कहते हैं। आंकड़ा 10.7(c) में एक समतल तरंग एक अवतल दर्पण पर आपतित होती है और प्रतिबिंब के द्वारा एक गोलीय तरंग बनती है जो फोकस बिंदु $\mathrm{F}$ पर संगत हो जाती है। इसी तरह, हम अवतल लेंस और उत्तल दर्पण के माध्यम से अपवर्तन और प्रतिबिंब को समझ सकते हैं।

ऊपर के विवरण से स्पष्ट होता है कि वस्तु के किसी बिंदु से चित्र के संगत बिंदु तक कुल समय किसी भी किरण के अनुसार एक ही होता है। उदाहरण के लिए, जब एक उत्तल लेंस प्रकाश को एक वास्तविक चित्र बनाने के लिए फोकस करता है, तो एक किरण जो केंद्र से गुजरती है एक छोटा रास्ता तय करती है, लेकिन काँच में धीमी गति के कारण लेंस के किनारे के किरणों के मुकाबले लिया गया समय एक ही होता है।

FIGURE 10.7 तलीय तरंग के द्वारा (a) एक पतले प्रिज्म, (b) एक उत्तल लेंस द्वारा अपवर्तन, (c) एक अवतल दर्पण द्वारा परावर्तन।

उदाहरण 10.1 (a) एक एकल रंग वाली प्रकाश तरंग दो माध्यमों के संपर्क तल पर आपतित होती है, तो उत्पन्न एवं अपवर्तित प्रकाश दोनों आपतित आवृत्ति के समान आवृत्ति रखते हैं। क्यों?

(b) जब प्रकाश एक कम घनत्व वाले माध्यम से एक घनत्व वाले माध्यम में चलता है, तो इसकी चाल कम हो जाती है। चाल में कमी के अर्थ यह है कि प्रकाश तरंग द्वारा वाहक ऊर्जा में कमी होती है?

(c) प्रकाश के तरंग चित्र में, प्रकाश की तीव्रता तरंग के आम्पलीटूड के वर्ग द्वारा निर्धारित होती है। प्रकाश के फोटॉन चित्र में प्रकाश की तीव्रता के निर्धारक क्या है?

हल (अ) प्रतिध्वनि और प्रकाश के अपवर्तन द्रव्य के परमाणु घटकों के साथ प्रतिपादित प्रकाश के अंतर्क्रिया के माध्यम से उत्पन्न होते हैं। परमाणुओं को बाहरी एजेंसी (प्रकाश) के आवर्तन आवृत्ति को ग्रहण करने वाले दोलनकर्ता के रूप में देखा जा सकता है, जो बलपूर्वक दोलन के कारण उत्पन्न होते हैं। एक आवेशित दोलनकर्ता द्वारा उत्सर्जित प्रकाश की आवृत्ति उसकी दोलन आवृत्ति के बराबर होती है। इसलिए, विक्षेपित प्रकाश की आवृत्ति आपतित प्रकाश की आवृत्ति के बराबर होती है।

(ब) नहीं। एक तरंग द्वारा वहन की गई ऊर्जा तरंग के आयाम पर निर्भर करती है, न कि तरंग प्रसारण की गति पर।

(c) एक दिए गए आवृत्ति के लिए, फोटॉन चित्र में प्रकाश की तीव्रता एक इकाई क्षेत्र के प्रति इकाई समय में फोटॉनों की संख्या द्वारा निर्धारित की जाती है।

10.4 तरंगों के समभावी एवं असमभावी योग

चित्र 10.8 (a) जल में दो छोटी छोटी छड़ियाँ जो एक दूसरे के साथ अपने आवर्त गति में घुम रही हैं, दो समभावी स्रोत को दर्शाती हैं। (b) जल के सतह पर एक समय पर जल के अणुओं के विस्थापन के पैटर्न को दर्शाता है जिसमें नोडल $\mathrm{N}$ (कोई विस्थापन) और अंतर्नोडल A (अधिकतम विस्थापन) रेखाएँ दिखाई देती हैं।

इस अनुच्छेद में हम दो तरंगों के अध्यारोपण द्वारा उत्पन्न विस्थापन पैटर्न के बारे में चर्चा करेंगे। आप याद कर सकते हैं कि हम अपने कक्षा XI के पाठ्यपुस्तक के अध्याय 14 में अध्यारोपण सिद्धांत के बारे में चर्चा कर चुके हैं। वास्तव में, विस्थापन के पूरे क्षेत्र के आधार अध्यारोपण सिद्धांत पर है, जिसके अनुसार माध्यम में किसी विशेष बिंदु पर एक संख्या के तरंगों द्वारा उत्पन्न विस्थापन के परिणामी विस्थापन के वेक्टर योग के बराबर होता है।

चित्र 10.9 (a) बिंदु $Q$ पर निर्माणात्मक विवर्धन जिसके लिए पथ अंतर $2 \lambda$ है। (b) बिंदु $\mathrm{R}$ पर विनाशी विवर्धन जिसके लिए पथ अंतर $2.5 \lambda$ है।

दो सुई $\mathrm{S_1}$ और $\mathrm{S_2}$ एक जल के गड्ढे में एक जैसे तरीके से आवर्ती रूप से ऊपर और नीचे गति कर रही हैं [चित्र 10.8(a)]। वे दो जल तरंगें उत्पन्न करती हैं, और एक निश्चित बिंदु पर, प्रत्येक तरंग द्वारा उत्पन्न विस्थापन के बीच अपवर्तन एक समय के साथ बदलता रहता है; जब ऐसा होता है तो दो स्रोतों को सहभाजी कहा जाता है। चित्र 10 बी 10.8(b) एक निश्चित समय के बिंदु पर चरमों (ठोस वृत्त) और गड्ढों (चित्रित वृत्त) की स्थिति दिखाता है। एक बिंदु $P$ के लिए विचार करें जिसके लिए

$ \mathrm{S_1} \mathrm{P}=\mathrm{S_2} \mathrm{P} $

क्योंकि $\mathrm{S_1} \mathrm{P}$ और $\mathrm{S_2} \mathrm{P}$ की दूरियाँ समान हैं, तो $\mathrm{S_1}$ और $\mathrm{S_2}$ से निकलने वाले तरंगें बिंदु $\mathrm{P}$ तक पहुँचने में समान समय लेंगी और $\mathrm{S_1}$ और $\mathrm{S_2}$ से निकलने वाली तरंगें अपने अपने चरण में निकलती हैं तो वे बिंदु $\mathrm{P}$ पर भी अपने अपने चरण में पहुँचेंगी।

इसलिए, यदि स्रोत $S_{1}$ द्वारा बिंदु $P$ पर उत्पन्न विस्थापन को निम्नलिखित द्वारा दिया जाता है

$ y_{1}=a \cos \omega t $

तो स्रोत $S_{2}$ द्वारा बिंदु $P$ पर उत्पन्न विस्थापन भी निम्नलिखित द्वारा दिया जाएगा

$ y_{2}=a \cos \omega t $

इसलिए, $\mathrm{P}$ पर विस्थापन के परिणाम को निम्नलिखित द्वारा दिया जाएगा

$ y=y_{1}+y_{2}=2 a \cos \omega t $

क्योंकि तीव्रता आयाम के वर्ग के समानुपाती होती है, परिणामी तीव्रता निम्नलिखित द्वारा दी जाएगी

$ I=4 I_{0} $

जहाँ $I_{0}$ प्रत्येक व्यक्तिगत स्रोत द्वारा उत्पन्न तीव्रता को प्रतिनिधित्व करता है; $I_{0}$, $a^{2}$ के समानुपाती होता है। वास्तव में, $\mathrm{S_1} \mathrm{~S_2}$ के लम्ब समद्विभाजक पर किसी भी बिंदु पर तीव्रता $4 I_{0}$ होगी। दो स्रोतों के अंतर्वेशन कहलाता है और हम अंतर्वेशन के अंतर्वेशन के बारे में बात कर रहे हैं। हम अब एक बिंदु $Q$ के बारे में विचार करते हैं [चित्र 10.9(a)] जहाँ

$ \mathrm{S_2} \mathrm{Q}-\mathrm{S_1} \mathrm{Q}=2 \lambda $

$\mathrm{S_1}$ से निकलने वाले तरंगें $\mathrm{S_2}$ से निकलने वाली तरंगों के तुलना में ठीक दो चक्र पहले पहुँचेंगी और फिर से एक दूसरे के समान चरण में होंगी [चित्र 10.9(a)]। इसलिए, यदि $\mathrm{S_1}$ द्वारा उत्पन्न विस्थापन को निम्नलिखित द्वारा दिया जाता है

$ y_{1}=a \cos \omega t $

तो $\mathrm{S_2}$ द्वारा उत्पन्न विस्थापन निम्नलिखित द्वारा दिया जाएगा

$ y_{2}=a \cos (\omega t-4 \pi)=a \cos \omega t $

जहाँ हम यह तथ्य का उपयोग करते हैं कि 2λ के पथ अंतर के लिए 4π के चरण अंतर संगत होता है। दोनों विस्थापन फिर से एक दूसरे के समान चरण में होंगे और तीव्रता फिर से $4 I_{0}$ होगी जो निर्माणात्मक अपवाह के उत्पन्न करेगी। उपरोक्त विश्लेषण में हम निर्धारित करते हैं कि $\mathrm{S_1} \mathrm{Q}$ और $\mathrm{S_2} \mathrm{Q}$ की दूरियाँ $d$ (जो $\mathrm{S_1}$ और $\mathrm{S_2}$ के बीच दूरी को प्रदर्शित करता है) की तुलना में बहुत अधिक हैं ताकि यद्यपि $\mathrm{S_1} \mathrm{Q}$ और $\mathrm{S_2} \mathrm{Q}$ बराबर नहीं हैं, परन्तु प्रत्येक तरंग द्वारा उत्पन्न विस्थापन के आयाम बहुत निकट रूप से समान होंगे।

हम अब एक बिंदु R [चित्र 10.9(b)] के बारे में विचार करते हैं जहाँ

$ \mathrm{S_2} \mathrm{R}-\mathrm{S_1} \mathrm{R}=-2.5 \lambda $

चित्र 10.10 बिंदुओं के बर्ताव के बारे में जहाँ $\mathrm{S_1} \mathrm{P}-\mathrm{S_2} \mathrm{P}$ शून्य, $\pm \lambda, \pm 2 \lambda, \pm 3 \lambda$ के बराबर होता है।

$S_{1}$ से निकलने वाले तरंगें $S_{2}$ से निकलने वाली तरंगों के तुलना में ठीक दो और आधे चक्र बाद पहुँचेंगी [चित्र 10.10(b)]। इसलिए यदि $S_{1}$ द्वारा उत्पन्न विस्थापन को निम्नलिखित द्वारा दिया जाता है

$ y_{1}=a \cos \omega t $

तो $\mathrm{S_2}$ द्वारा उत्पन्न विस्थापन निम्नलिखित द्वारा दिया जाएगा

$ y_{2}=a \cos (\omega t+5 \pi)=-a \cos \omega t $

जहाँ हम यह तथ्य का उपयोग कर रहे हैं कि $2.5 \lambda$ के पथान्तर के लिए $5 \pi$ के दोलनान्तर के संगत होता है। अब दो विस्थापन असंगत हो गए हैं और दोनों विस्थापन शून्य तीव्रता देंगे। इसे विनाशकारी तरंग प्रतिक्रिया कहा जाता है।

सारांश: यदि हम दो समानांतर स्रोत $\mathrm{S_1}$ और $\mathrm{S_2}$ के दोलन एक दूसरे के समान अवस्था में हो, तो किसी भी बिंदु $P$ के लिए जब पथान्तर,

$\mathrm{S_1} \mathrm{P} \sim \mathrm{S_2} \mathrm{P}=n \lambda \quad(n=0,1,2,3, \ldots)\hspace{09cm}\ldots{(10.9)}$

हम निर्माणात्मक व्यतिकरण पाएंगे और परिणामी तीव्रता $4 I_{0}$ होगी; $\mathrm{S_1} \mathrm{P}$ और $\mathrm{S_2} \mathrm{P}$ के बीच $\sim$ चिह्न $\mathrm{S_1} \mathrm{P}$ और $\mathrm{S_2} \mathrm{P}$ के अंतर को दर्शाता है। दूसरी ओर, यदि बिंदु $\mathrm{P}$ इस तरह हो कि पथ अंतर,

$\mathrm{S_1} \mathrm{P} \sim \mathrm{S_2} \mathrm{P}=\left(n+\frac{1}{2}\right) \lambda \quad(n=0,1,2,3, \ldots)\hspace{08cm}\ldots{(10.10)}$

हम नष्ट करने वाले विरोधाभास का सामना करेंगे और परिणामी तीव्रता शून्य होगी। अब, किसी भी अन्य अस्पष्ट बिंदु G (चित्र 10.10) के लिए, दो विस्थापनों के बीच चर अंतर $\phi$ होगा। इसलिए, यदि $\mathrm{S_1}$ द्वारा उत्पन्न विस्थापन $\mathrm{S_1}$ द्वारा उत्पन्न विस्थापन निम्नलिखित है

$ y_{1}=a \cos \omega t $

तो, $\mathrm{S_2}$ द्वारा उत्पन्न विस्थापन निम्नलिखित होगा

$ y_{2}=a \cos (\omega t+\phi) $

और परिणामी विस्थापन निम्नलिखित होगा

$ \begin{aligned} y & =y _{1}+y _{2} \\ & =a[\cos \omega t+\cos (\omega t+\phi)] \\

& =2 a \cos (\phi / 2) \cos (\omega t+\phi / 2)\left[\because \cos \mathrm{A}+\cos \mathrm{B}=2 \cos \left(\frac{\mathrm{A}+\mathrm{B}}{2}\right) \cos \left(\frac{\mathrm{A}-\mathrm{B}}{2}\right)\right] \end{aligned} $

परिणामी विस्थापन का आयाम $2 a \cos (\phi / 2)$ होता है और अतः उस बिंदु पर तीव्रता होगी

$I=4 I_{0} \cos ^{2}(\phi / 2)\hspace{12cm}\ldots{(10.11)}$

यदि $\phi=0, \pm 2 \pi, \pm 4 \pi, \ldots$ जो कि समीकरण (10.9) द्वारा दिए गए स्थिति के संगत है, तो निर्माणात्मक व्यतिकरण होगा जिसके परिणामस्वरूप अधिकतम तीव्रता होगी। दूसरी ओर, यदि $\phi= \pm \pi, \pm 3 \pi, \pm 5 \pi \ldots$ [जो कि समीकरण (10.10) द्वारा दिए गए स्थिति के संगत है] तो विनाशी व्यतिकरण होगा जिसके परिणामस्वरूप तीव्रता शून्य होगी।

अब यदि दो स्रोत सहसंगत हैं (अर्थात, यदि दो सुई नियमित रूप से ऊपर और नीचे जा रही हैं) तो किसी भी बिंदु पर फेज अंतर $\phi$ समय के साथ बदलेगा और हमें एक स्थिर अपवर्तन पैटर्न प्राप्त होगा; अर्थात, अधिकतम और न्यूनतम के स्थान समय के साथ बदलेंगे। हालांकि, यदि दो सुई एक नियत फेज अंतर बनाए रखे बिना रहती हैं, तो अपवर्तन पैटर्न भी समय के साथ बदल जाएगा और, यदि फेज अंतर समय के साथ बहुत तेजी से बदलता है, तो अधिकतम और न्यूनतम के स्थान भी समय के साथ तेजी से बदल जाएंगे और हम एक “समय के औसत” तीव्रता वितरण देखेंगे। जब ऐसा होता है, तो हम एक औसत तीव्रता देखेंगे जो द्वारा दिया जाएगा

$I=2 I_{0} \hspace{14cm}\ldots{(10.12)}$

जब दो दोलन करते स्रोतों के बीच फेज अंतर तेजी से समय के साथ बदलता है, तो हम कहते हैं कि दो स्रोत असंगत हैं और जब ऐसा होता है तो तीव्रताएँ बस जोड़ देती हैं। यह वास्तव में दो अलग-अलग प्रकाश स्रोतों द्वारा एक दीवार पर प्रकाश के बर्बादी के समय होता है।

10.5 प्रकाश तरंगों के बर्बादी और यॉंग के प्रयोग

अब हम प्रकाश तरंगों के बर्बादी के बारे में चर्चा करेंगे। यदि हम दो सोडियम लैंप का उपयोग करते हैं जो दो छेदों (चित्र 10.11) को प्रकाशित करते हैं, तो हम कोई भी बर्बादी बैंड नहीं देखेंगे। इसके कारण यह है कि एक सामान्य स्रोत (जैसे सोडियम लैंप) से उत्सर्जित प्रकाश तरंगें $10^{-10}$ सेकंड के क्रम में अचानक फेज परिवर्तन होते हैं। इसलिए दो छेदों से निकलने वाली प्रकाश तरंगें एक दूसरे के संबंध में असंगत होंगी और जब ऐसा होता है, तो पिछले अनुच्छेद में चर्चा की गई तरह, स्क्रीन पर तीव्रताएँ जोड़ देंगी।

चित्र 10.11 यदि दो सोडियम लैंप दो पिनहोल $\mathrm{S_1}$ और $\mathrm{S_2}$ को प्रकाशित करती हैं, तो तीव्रताएँ एक साथ जुड़ जाएंगी और स्क्रीन पर तरंग विवर्तन के कोई बैंड नहीं दिखाई देंगे।

अंग्रेज भौतिक विज्ञानी थॉमस यंग ने एक चतुर तकनीक का उपयोग किया जिससे तरंगों के चरण बरकरार रह सकें। वह $\mathrm{S_1}$ और $\mathrm{S_2}$ से उत्पन्न तरंगों के चरण को “लॉक” कर सकते हैं। वह एक अपारदर्शी पट्टी पर दो पिनहोल $\mathrm{S_1}$ और $S_{2}$ (एक दूसरे के बहुत करीब) बनाए [चित्र 10.12(a)]। इन्हें एक अन्य पिनहोल द्वारा प्रकाशित किया जाता है जो फिर एक चमकीले स्रोत द्वारा प्रकाशित होता है। प्रकाश तरंगें $S$ से फैलती हैं और दोनों $S_{1}$ और $S_{2}$ पर पड़ती हैं। तब $S_{1}$ और $S_{2}$ दो समानांतर स्रोत के रूप में व्यवहार करते हैं क्योंकि $S_{1}$ और $S_{2}$ से निकलने वाली प्रकाश तरंगें एक ही मूल स्रोत से आती हैं और $S$ में कोई अचानक चरण परिवर्तन हो जाए तो इसका ठीक तरह से समान चरण परिवर्तन $S_{1}$ और $S_{2}$ से निकलने वाली प्रकाश तरंगों में दिखाई देगा। इस प्रकार, दो स्रोत $\mathrm{S_1}$ और $\mathrm{S_2}$ चरण में बरकरार रहेंगे; अर्थात, वे हमारे पानी के तरंग के उदाहरण में दो झूलते हुए सुई के जैसे समानांतर होंगे [चित्र 10.8(a)]।

स्पष्ट रूप से, आपके द्वारा प्रस्तुत किए गए मार्कडाउन दस्तावेज़ को हिंदी में अनुवाद करने के लिए आपके निर्देशों के अनुसार, मैं आपके लिए अनुवादित मार्कडाउन दस्तावेज़ प्रदान करता हूं।

स्पष्ट रूप से, $\mathrm{S_1}$ और $\mathrm{S_2}$ से निकलने वाले गोलीय तरंगें चित्र 10.12 (b) में दिखाए गए अनुसार छड़ी $\mathrm{GG}^{\prime}$ पर व्यतिकरण बैंड उत्पन्न करेंगी। अधिकतम और न्यूनतम तीव्रता के स्थान की गणना अनुच्छेद 10.4 में दिए गए विश्लेषण का उपयोग करके की जा सकती है।

चित्र 10.12 यंग की व्यवस्था व्यतिकरण पैटर्न उत्पन्न करने के लिए।

हम एक चमकदार क्षेत्र प्राप्त करेंगे जब $\frac{x d}{D}=n \lambda$। अर्थात,

$$ \begin{equation*} x=x_{n}=\frac{n \lambda D}{d} ; \mathrm{n}=0, \pm 1, \pm 2, \ldots \tag{10.13} \end{equation*} $$

दूसरी ओर, हम एक गहरा क्षेत्र प्राप्त करेंगे जब

$$\frac{x d}{D}=\left(n+\frac{1}{2}\right) \lambda$$

अर्थात,

$$ \begin{equation*} x=x_{\mathrm{n}}=\left(n+\frac{1}{2}\right) \frac{\lambda D}{d} ; n=0, \pm 1, \pm 2 \tag{10.14}

\end{equation*} $$

अत: छाया और प्रकाश बैंड एक परदे पर दिखाई देते हैं, जैसा कि आकृति 10.13 में दिखाया गया है। ऐसे बैंड को फ्रिंज कहते हैं। समीकरण (10.13) और (10 बराबर 14) दर्शाते हैं कि छाया और प्रकाश फ्रिंज समान दूरी पर स्थित होते हैं।

थॉमस यंग (1773 – 1829) एक ब्रिटिश भौतिक विज्ञानी, चिकित्सक और मिस्र विशेषज्ञ। यंग ने आंख के संरचना और दृष्टि के यंत्र के से लेकर रोजेट स्टोन के अनुवाद तक विभिन्न वैज्ञानिक समस्याओं पर काम किया। उन्होंने प्रकाश के तरंग सिद्धांत को फिर से जीवित किया और अध्ययन किया कि विवर्तन घटनाएं प्रकाश के तरंग गुणों के प्रमाण प्रदान करती हैं।

$$ d=0.025 \mathrm{~mm}(\beta \approx 1 \mathrm{~mm}) $$

चित्र 10.13 कंप्यूटर द्वारा उत्पन्न फ्रिंज पैटर्न, जो दो बिंदु स्रोत $S_{1}$ और $S_{2}$ द्वारा स्क्रीन GG’ $^{\prime}$ पर उत्पन्न होता है (चित्र 10.12); जो $d=0.025$ $\mathrm{mm}, D=5 \mathrm{~cm}$ और $\lambda=5 \times 10^{-5} \mathrm{~cm}$ के संगत हैं। (OPTICS द्वारा A. Ghatak, Tata McGraw Hill Publishing Co. Ltd., New Delhi, 2000 से अपनाया गया।)

10.6 विवर्तन

यदि हम एक अपारगम्य वस्तु द्वारा छाया के बर्फ के क्षेत्र के पास छाया को स्पष्ट रूप से देखते हैं, तो वहां विवर्तन के कारण एकांतर गहरे और चमकदार क्षेत्र होते हैं, जैसे कि विवर्तन में। यह घटना विवर्तन के कारण होती है। विवर्तन सभी प्रकार के तरंगों द्वारा दिखाई गई एक सामान्य विशेषता है, चाहे वह ध्वनि तरंगें, प्रकाश तरंगें, जल तरंगें या पदार्थ तरंगें हों। चूंकि प्रकाश की तरंगदैर्ध्य अधिकांश अवरोधों की तुलना में कम होती है, इसलिए हम दैनिक जीवन में प्रकाश के विवर्तन प्रभावों के सामना नहीं करते।

अवलोकन। हालांकि, हमारी आंख या ऑप्टिकल उपकरणों जैसे टेलीस्कोप या माइक्रोस्कोप की सीमित विराम शक्ति विस्थापन के परिघटना के कारण सीमित होती है। वास्तव में, जब आप एक CD को देखते हैं तो आप देखते हैं जो रंग विस्थापन प्रभाव के कारण होते हैं। अब हम विस्थापन के परिघटना के बारे में चर्चा करेंगे।

10.6.1 एकल छेद

यॉंग के प्रयोग के चर्चा में, हम निर्धारित कर चुके हैं कि एक चौड़ा छेद एक नए स्रोत के रूप में कार्य करता है जिससे प्रकाश फैलता है। यॉंग से पहले, प्रारंभिक प्रयोगकर्ता - जिनमें न्यूटन भी शामिल थे - ने ध्यान दिया था कि प्रकाश चौड़े छेद और छेद से फैलता है। यह आपको घुमक्कड़ी और छाया के क्षेत्र में प्रवेश करता हुआ लगता है। इन प्रभावों को विस्थापन के रूप में जाना जाता है और इन्हें तरंग विचारों का उपयोग करके केवल सही ढंग से समझा जा सकता है। बाद में, आपको कोने के पार बात करते हुए ध्वनि तरंगों की आवाज सुनना बहुत आश्चर्य नहीं होता!

जब यांग के प्रयोग में दो छेदों के स्थान पर एक चौड़ा नहीं छेद (एकल छेद) का उपयोग किया जाता है (जो एक एकल रंग वाले स्रोत द्वारा प्रकाशित होता है), तो एक चौड़ा पैटर्न दिखाई देता है जिसमें केंद्रीय चमकीला क्षेत्र होता है। केंद्र के दोनों ओर, विकल्पतः अंधेरे और चमकीले क्षेत्र होते हैं, जिसकी तीव्रता केंद्र से दूर बढ़ती जाती है (चित्र 10.15)। इसे समझने के लिए चित्र 10.14 पर जाएं, जो एक समान बीम के प्रकाश को एकल छेद LN के ऊपर एक सीधी रेखा में गिरते हुए दिखाता है, जिसकी चौड़ाई $a$ है। विवर्तन वाला प्रकाश एक स्क्रीन पर पहुंचता है। छेद के मध्य बिंदु $\mathrm{M}$ होता है।

एक सीधी रेखा M से लंब गुजरती है

मूल विचार यह है कि छिद्र को बहुत छोटे भागों में विभाजित कर दें और उनके योगदान को $\mathrm{P}$ पर सही तरंग के अंतर के साथ जोड़ दें। हम छिद्र पर विभिन्न भागों को द्वितीयक स्रोत के रूप में बर्बाद कर रहे हैं। चूंकि आगत तरंग छिद्र के तल के समानांतर है, इन स्रोतों के बीच अनुपात एक है।

यह देखा गया है कि तीव्रता केंद्रीय अधिकतम होती है $\theta=0$ पर और अन्य द्वितीयक अधिकतम $\theta \approx$ $(n+1 / 2) \lambda / a$ पर होते हैं, जो $n$ के बढ़ते होने के साथ-साथ कमजोर होते जाते हैं। न्यूनतम (शून्य तीव्रता) $\theta \approx$ $n \lambda / a, n= \pm 1, \pm 2, \pm 3, \ldots$ पर होते हैं। चित्र 10.15 में फोटोग्राफ और इसके संगत तीव्रता पैटर्न दिखाए गए हैं।

दो संकेतों के बीच अंतर के बारे में लंबे समय तक चर्चा चल रही है जो वैज्ञानिकों द्वारा इन घटनाओं के खोज के बाद शुरू हुई थी। इस संदर्भ में रिचर्ड फेनमैन* के अपने प्रसिद्ध भौतिक विज्ञान के विवरण में कहे गए बातों के बारे में ध्यान देने वाली बात रोचक है:

चित्र 10.15 एकल छिद्र पर विवर्तन के कारण तीव्रता वितरण और बैंड के फोटो।

कोई भी अभी तक अवरोधन और विवर्तन के बीच अंतर को संतोषजनक तौर पर परिभाषित नहीं कर सका है। यह केवल उपयोग के सवाल है, और उनमें कोई विशिष्ट, महत्वपूर्ण भौतिक अंतर नहीं है। हम बेहतर तरीका अपनाकर कह सकते हैं कि जब केवल कुछ स्रोत होते हैं, जैसे कि दो अवरोधन करने वाले स्रोत, तो आमतौर पर इसके परिणाम को अवरोधन कहा जाता है, लेकिन जब इनकी संख्या बहुत अधिक होती है, तो लगता है कि शब्द “विवर्तन” अधिक बार उपयोग किया जाता है।

• रिचार्ड फेनमैन को 1965 के भौतिक विज्ञान के नोबेल पुरस्कार के लिए अपने क्वांटम विद्युत चुंबकत्व विज्ञान में मूल कार्य के लिए एक प्राप्तकर्ता थे।

द्वि-शीतल अनुभाग प्रयोग में, हम ध्यान देना चाहिए कि स्क्रीन पर पैटर्न वास्तव में प्रत्येक शीतल या छेद से एकल-शीतल विवर्तन के अधिकांश अधिकांश रूप में होता है, और द्वि-शीतल अन्तर्वेशन पैटर्न होता है।

10.6.2 एकल-शीतल विवर्तन पैटर्न को देखना

एकल-शीतल विवर्तन पैटर्न को अपने आप देखना आश्चर्यजनक रूप से आसान है। आवश्यक उपकरण अधिकांश घरों में पाए जा सकते हैं - दो रेजर ब्लेड और एक स्पष्ट ग्लास विद्युत बल्ब, जिसमें सीधा फिलामेंट हो। एक व्यक्ति को दो ब्लेड को इस तरह से धारण करना होता है कि किनारे समानांतर हों और बीच में एक चौड़ा छेद हो। यह आसानी से अंगूठे और अंगूठे के साथ किया जा सकता है (चित्र 10.16)।

चित्र 10.16 दो छोटी चाकू को एकल छेद के रूप में बनाए रखें। इसके माध्यम से एक बल्ब के फिलामेंट को देखने पर स्पष्ट विवर्तन बैंड दिखाई देते हैं।

छेद को फिलामेंट के समानांतर रखें और आंख के ठीक सामने रखें। अगर आप अक्सर चश्मा पहनते हैं तो उसका उपयोग करें। छेद के चौड़ाई और किनारों के समानांतरता के थोड़ा सा समायोजन करके, आप अपने आंखों से इस पैटर्न को देख सकते हैं जिसमें चमकदार और अंधेरे बैंड होते हैं। चूंकि सभी बैंडों (केंद्रीय बैंड के अलावा) की स्थिति तरंगदैर्घ्य पर निर्भर करती है, इनमें कुछ रंग दिखाई देंगे। लाल या नीला फ़िल्टर का उपयोग करके बैंड अधिक स्पष्ट दिखाई देंगे। दोनों फ़िल्टर उपलब्ध होने पर, लाल के तुलना में नीले के चौड़े बैंड को देखा जा सकता है।

इस प्रयोग में, फिलामेंट चित्र 10.15 में पहले स्लिट $S$ की भूमिका निभाता है। आंख के लेंस ने पैटर्न को स्क्रीन पर (आंख के रेटिना) फोकस कर देता है।

कुछ प्रयत्न के साथ, एक डबल स्लिट एल्यूमिनियम फोइल में एक ब्लेड के साथ काटा जा सकता है। बल्ब फिलामेंट को पहले जैसा देखा जा सकता है ताकि यूंग के प्रयोग को दोहराया जा सके। दिन में, आंख के लिए एक अन्य उपयुक्त चमकदार स्रोत होता है जो छोटे कोण पर आंख के साथ अवतल चमकदार सतह (जैसे, साइकिल बेल) में सूरज के परावर्तन के कारण होता है। सूरज के प्रत्यक्ष रोशनी को न देखें - यह आंख को नुकसान पहुंचा सकता है और फ्रिंज भी नहीं दिखाई देंगे क्योंकि सूरज आंख के लिए $(1 / 2)^{\circ}$ के कोण पर अवतल होता है।

प्रकाश की ऊर्जा विवर्तन और व्यापकता में पुनर्वितरित होती है। यदि एक क्षेत्र में यह कम हो जाती है, तो एक गहरा बैंड बनता है, जबकि दूसरे क्षेत्र में यह बढ़ जाती है, जिसके परिणामस्वरूप एक चमकदार बैंड बनता है। ऊर्जा के कोई भी लाभ या नुकसान नहीं होता, जो ऊर्जा संरक्षण के सिद्धांत के साथ संगत है।[^0]

10.7 ध्रुवीकरण

एक लंबी स्ट्रिंग को ध्यान में रखें जो क्षैतिज रूप से रखी गई है, जिसका दूसरा सिरा मान लीजिए निश्चित है। यदि हम स्ट्रिंग के सिरे को आवर्ती रूप से ऊपर और नीचे ले जाएं, तो हम एक तरंग के उत्पन्न करेंगे जो $+x$ दिशा में चलती है (चित्र 10.17)। ऐसी तरंग को निम्नलिखित समीकरण द्वारा वर्णित किया जा सकता है

चित्र 10.17 (a) वक्र एक साइनस तरंग के +x दिशा में चलने के दौरान एक स्ट्रिंग के विस्थापन को दर्शाते हैं, क्रमशः $t=0$ और $t=\Delta t$ के लिए। (b) वक्र $x=0$ पर विस्थापन के समय परिवर्तन को दर्शाता है जब एक साइनस तरंग +x दिशा में चल रही है। $x=\Delta x$ पर विस्थापन के समय परिवर्तन के लिए वक्र दाहिने ओर थोड़ा विस्थापित होगा।

$y(x, t)=a \sin (k x-\omega t)\hspace{11cm}\ldots{(10.15)}$

जहाँ $a$ और $\omega(=2 \pi v)$ क्रमशः तरंग के आयाम और कोणीय आवृत्ति को प्रदर्शित करते हैं; आगे,

$\lambda=\dfrac{2 \pi}{k}\hspace{13cm}\ldots{(10.16)}$

तरंग के संगत तरंगदैर्घ्य को प्रदर्शित करता है। हम अपने कक्षा XI के पाठ्यक्रम के अध्याय 14 में ऐसी तरंगों के प्रसार के बारे में चर्चा कर चुके हैं। क्योंकि विस्थापन (जो $y$ दिशा में होता है) तरंग के प्रसार की दिशा के लंबवत होता है, इसलिए इसे एक अनुप्रस्थ तरंग कहा जाता है। इसके अतिरिक्त, क्योंकि विस्थापन $y$ दिशा में होता है, इसे अक्सर $y$-पोलराइज़्ड तरंग के रूप में संदर्भित किया जाता है। क्योंकि डोरी के प्रत्येक बिंदु सीधी रेखा में गति करता है, तरंग को एक रैखिक रूप से पोलराइज़्ड तरंग के रूप में भी संदर्भित किया जाता है।

ढलान. इसके अतिरिक्त, तार की चैनल हमेशा $x-y$ समतल में सीमित रहती है और इसलिए इसे एक तलीय विस्थापित तरंग के रूप में भी संदर्भित किया जाता है।

इसी तरह, हम तार के विस्थापन के लिए $x$ - $z$ समतल में तार के विस्थापन को विचार कर सकते हैं जो एक $z$-विस्थापित तरंग उत्पन्न करता है जिसका विस्थापन निम्नलिखित द्वारा दिया जाता है

$z(x, t)=a \sin (k x-\omega t) \hspace{11cm}\ldots{(10.17)}$

यह ध्यान देने योग्य है कि रेखीय विस्थापित तरंगें [समीकरण (10.15) और (10.17) द्वारा वर्णित] सभी अनुप्रस्थ तरंगें होती हैं; अर्थात, तार के प्रत्येक बिंदु का विस्थापन हमेशा तरंग के प्रसार की दिशा के लंबवत होता है। अंत में, यदि तार के विस्थापन के समतल को बहुत छोटे समय अंतराल में अनियमित रूप से बदल दिया जाए, तो हमें अप्रसारित तरंग के रूप में जाना जाता है। इसलिए, अप्रसारित तरंग के लिए विस्थापन समय के साथ अनियमित रूप से बदलता रहता है, हालांकि यह हमेशा प्रसार की दिशा के लंबवत रहता है।

प्रकाश तरंगें प्रकृति में अनुप्रस्थ होती हैं; अर्थात, एक चलती हुई प्रकाश तरंग के साथ संबद्ध विद्युत क्षेत्र हमेशा तरंग के प्रसार की दिशा के लंब दिशा में होता है। इसका आसान रूप से दर्शाना एक सरल पोलरॉइड का उपयोग करके संभव है। आपने ऐसे पतले प्लास्टिक जैसे शीट देखे होंगे, जिन्हें पोलरॉइड कहा जाता है। एक पोलरॉइड में लंबी श्रृंखला अणु एक निश्चित दिशा में व्यवस्थित होते हैं। विद्युत वेक्टर (चलती हुई प्रकाश तरंग के साथ संबद्ध) अलग किए गए अणुओं की दिशा के अनुदिश अवशोषित हो जाते हैं। इसलिए, यदि एक अपolarised प्रकाश तरंग ऐसे पोलरॉइड पर आपतित होती है तो तरंग रेखीय रूप से पोलराइज़ कर देती है जिसमें विद्युत वेक्टर व्यवस्थित अणुओं के लंब दिशा में दोलन करता है; इस दिशा को पोलरॉइड के पास अक्ष कहा जाता है।

इसलिए, यदि एक सामान्य स्रोत (जैसे सोडियम लैंप) के प्रकाश के माध्यम से एक पोलरॉइड शीट $P_{1}$ गुजरे, तो देखा जाता है कि इसकी तीव्रता आधा हो जाती है। $P_{1}$ को घुमाने पर प्रसारित बeam पर कोई प्रभाव नहीं पड़ता और प्रसारित तीव्रता स्थिर रहती है। अब, एक समान टुकड़ा पोलरॉइड $P_{2}$ को $P_{1}$ के सामने रख दें। अपेक्षित रूप से, लैंप के प्रकाश की तीव्रता $P_{2}$ के माध्यम से गुजरते हुए घट जाती है। लेकिन अब $P_{1}$ को घुमाने पर $P_{2}$ से आने वाले प्रकाश पर एक बड़ा प्रभाव पड़ता है। एक स्थिति में, $P_{2}$ द्वारा प्रसारित तीव्रता जो $P_{1}$ के माध्यम से गुजरती है, लगभग शून्य हो जाती है। जब इस स्थिति से $90^{\circ}$ घुमा दिया जाता है, तो $P_{1}$ लगभग पूरी तीव्रता को $P_{2}$ से निकले प्रकाश को प्रसारित करता है (चित्र 10.18)।

चित्र 10.18 में वर्णित प्रयोग को आसानी से समझा जा सकता है यदि मान लिया जाए कि पोलरॉइड $P_{2}$ के माध्यम से गुजरने वाला प्रकाश $P_{2}$ के पास अक्ष के अनुदिश ध्रुवित हो जाता है। यदि $P_{2}$ के पास अक्ष $P_{1}$ के पास अक्ष से कोण $\theta$ बनाता है, तो जब ध्रुवित किरण बeam $P_{2}$ के माध्यम से गुजरती है, तो $E \cos \theta$ (जो $P_{2}$ के पास अक्ष के अनुदिश होता है) $P_{2}$ के माध्यम से गुजर सकता है। इस प्रकार, जब हम पोलरॉइड $P_{1}$ (या $P_{2}$) को घुमाते हैं, तो तीव्रता निम्नलिखित रूप में बदलती है:

$I=I_{0} \cos ^{2} \theta \hspace{13cm}\ldots{(10.18)}$

जहाँ $I_{0}$ वह तीव्रता है जो $P_{1}$ के माध्यम से गुजरने के बाद पोलराइज्ड प्रकाश की होती है। इसे मैलस के नियम के रूप में जाना जाता है। उपरोक्त चर्चा दर्शाती है कि एक अकेले पोलरॉइड से निकलने वाली तीव्रता आपतित तीव्रता के आधा होती है। दूसरे पोलरॉइड को रखकर, आपतित तीव्रता के 50% से शून्य तक तीव्रता को नियंत्रित किया जा सकता है, दो पोलरॉइड के पास-अक्षों के बीच कोण को समायोजित करके।

चित्र 10.18 (a) प्रकाश के दो पोलरॉइड $P_{2}$ और $P_{1}$ के माध्यम से गुजरना। जब दोनों के बीच कोण $0^{\circ}$ से $90^{\circ}$ तक बदलता है, तो पारगमन भिन्नता 1 से 0 तक घटती है। ध्यान दें कि एक अकेले पोलरॉइड $P_{1}$ के माध्यम से देखे गए प्रकाश की तीव्रता कोण पर निर्भर नहीं करती। (b) जब प्रकाश दो पोलरॉइड के माध्यम से गुजरता है तो विद्युत वेक्टर के व्यवहार। पारगमन विद्युत वेक्टर के अक्ष के समानांतर घटक होता है। दोनों डबल तीर विद्युत वेक्टर के दोलन को दर्शाते हैं।

पोलरॉइड का उपयोग सूंघनी चश्मों, खिड़कियों आदि में तीव्रता को नियंत्रित करने के लिए किया जा सकता है। पोलरॉइड फोटोग्राफी कैमरों और 3D फिल्म कैमरों में भी उपयोग किए जाते हैं।

उदाहरण 10.2 जब एक पोलरॉइड शीट दो परस्पर लंब वाले पोलरॉइडों के बीच घुमाई जाती है, तो अपवर्तित प्रकाश की तीव्रता के बारे में चर्चा करें?

हल मान लीजिए $I_{0}$ पहले पोलराइजर $P_{1}$ के माध्यम से गुजरने के बाद विपरीत प्रकाश की तीव्रता है। फिर दूसरे पोलराइजर $P_{2}$ के माध्यम से गुजरने के बाद प्रकाश की तीव्रता होगी

$I=I_{0} \cos ^{2} \theta$

जहाँ $\theta$ $P_{1}$ और $P_{2}$ के पास अक्षों के बीच कोण है। क्योंकि $P_{1}$ और $P_{3}$ परस्पर लंब हैं, इसलिए $P_{2}$ और $P_{3}$ के पास अक्षों के बीच कोण $(\pi / 2-\theta)$ होगा। इसलिए $P_{3}$ से निकलने वाले प्रकाश की तीवरता होगी

$ \begin{aligned} I & =I_{0} \cos ^{2} \theta \cos ^{2} \frac{\pi}{2}-\theta \\ & =I_{0} \cos ^{2} \theta \sin ^{2} \theta=\left(I_{0} / 4\right) \sin ^{2} 2 \theta \end{aligned} $

इसलिए, जब $\theta=\pi / 4$ होगा तो प्रसारित तीव्रता अधिकतम होगी।

सारांश

1. हाइगेंस के सिद्धांत के अनुसार, एक तरंग सतह के प्रत्येक बिंदु एक द्वितीयक तरंग के उत्सर्जक होता है, जो बाद के समय में तरंग सतह को बनाने में सहायता करते हैं।

2. हाइगेंस के निर्माण के अनुसार, नई तरंग सतह द्वितीयक तरंगों के आगे के आवरण होती है। जब प्रकाश की गति दिशा से स्वतंत्र होती है, तो द्वितीयक तरंगें गोलाकार होती हैं। तब किरणें तरंग सतहों और समय के यात्रा के लंबवत होती हैं और किरण के अनुसार किसी भी बिंदु पर समय की माप एक समान होती है। इस सिद्धांत से परावर्तन और अपवर्तन के ज्ञात नियम प्राप्त होते हैं।

3. तरंगों के अधिग्रहण के सिद्धांत केवल तभी लागू होता है जब दो या अधिक प्रकाश के स्रोत एक ही बिंदु पर प्रकाश फैलाते हैं। जब हम इन स्रोतों के कारण दिए गए बिंदु पर प्रकाश की तीव्रता को विचार करते हैं, तो व्यक्तिगत तीव्रताओं के योग के अतिरिक्त एक असंयोजन पद भी होता है। लेकिन यह पद केवल तभी महत्वपूर्ण होता है जब इसका औसत शून्य नहीं होता, जो केवल तभी होता है जब स्रोतों की आवृत्ति समान हो और उनका स्थिर अपवार्ती अंतर हो।

4. अल्प दूरी के यंग के द्विस्लिट द्वारा समान रूप से विभाजित अपवार्ती बैंड उत्पन्न होते हैं।

5. एक एकल छेद जिसकी चौड़ाई $a$ होती है, विवर्तन पैटर्न बनाता है जिसमें केंद्रीय अधिकतम होता है। तीव्रता को शून्य हो जाता है जब कोण $\pm \frac{\lambda}{a}, \pm \frac{2 \lambda}{a}$, आदि पर होते हैं, और बीच में क्रमशः कमजोर द्वितीयक अधिकतम होते हैं।

6. प्राकृतिक प्रकाश, जैसे सूर्य से, अप्रकाशित होता है। इसका अर्थ है कि विद्युत वेक्टर एक मापन के दौरान अनुप्रस्थ तल में सभी संभावित दिशाओं में तेजी से और यादृच्छिक रूप से चलता है। एक पोलरॉइड केवल एक घटक (विशेष अक्ष के समानांतर) को पार करता है। इस प्रकार के प्रकाश को रैखिक रूप से प्रकाशित या समतल प्रकाशित कहा जाता है। जब इस प्रकार के प्रकाश को एक द्वितीय पोलरॉइड के माध्यम से देखा जाता है जिसका अक्ष $2 \pi$ के माध्यम से घूमता है, तो तीव्रता के दो उच्चतम और दो निम्नतम देखे जाते हैं।

सोचने वाले बिंदु

1. एक बिंदु स्रोत से निकलने वाले तरंगें सभी दिशाओं में फैलती हैं, जबकि प्रकाश को चौड़े किरणों के रूप में चलते हुए देखा गया। इस बात को समझने के लिए कि एक तरंग सिद्धांत कैसे सभी प्रकाश के व्यवहार के पहलूओं को समझ सकता है, हुइगेन्स, यंग और फ्रेस्नेल के द्वारा दिए गए दृष्टिकोण और प्रयोग की आवश्यकता थी।

2. तरंगों के नए महत्वपूर्ण विशेषता विभिन्न स्रोतों से आ रहे आयामों के अंतर्वेशन (interference) है, जो निर्माणात्मक और नष्टकारी दोनों हो सकते हैं, जैसा कि यंग के प्रयोग में दिखाया गया है।

3. विवर्तन (diffraction) घटनाएं किरण प्रकाशिकी की सीमा निर्धारित करती हैं। सूक्ष्मदर्शी और दूरदर्शी के बहुत निकट वस्तुओं को अलग करने की क्षमता की सीमा प्रकाश की तरंगदैर्ध्य द्वारा निर्धारित की जाती है।

4. अधिकांश अपसारण एवं विवर्तन प्रभाव वायु में ध्वनि जैसे अनुप्रस्थ तरंगों के लिए भी मौजूद होते हैं। लेकिन ध्रुवीकरण घटनाएं विशेष रूप से प्रकाश तरंगों जैसे अनुप्रस्थ तरंगों के लिए होती हैं।

अभ्यास

10.1 एक एकल रंग वाले प्रकाश की तरंगदैर्ध्य $589 \mathrm{~nm}$ है जो हवा से जल के सतह पर आपतित होता है। इसकी

(a) प्रतिध्वनि, और (b) अपवर्तित प्रकाश की तरंगदैर्ध्य, आवृत्ति और चाल क्या हैं? जल का अपवर्तनांक 1.33 है।

10.2 निम्नलिखित परिस्थितियों में तरंग सामग्री के आकार क्या होता है:

(a) एक बिंदु स्रोत से विस्तारित प्रकाश।

(b) एक उत्तल लेंस से बाहर निकलने वाला प्रकाश जब एक बिंदु स्रोत को उसके फोकस पर रखा जाता है।

(c) एक दूर के तारे से आने वाले प्रकाश के तरंग सामग्री का भाग पृथ्वी द्वारा पकड़ा गया है।

उत्तर दिखाएं

उत्तर

एक बिंदु स्रोत से विस्तारित प्रकाश के मामले में तरंग सामग्री के आकार गोलाकार होता है। बिंदु स्रोत से निकलने वाली तरंग सामग्री को दिए गए चित्र में दिखाया गया है।

किरण के तरंग सामन्तर जाल के रूप में होता है जब एक बिंदु स्रोत को उत्तल लेंस के फोकस पर रखा जाता है। इसका चित्र दिया गया है।

एक दूर के तारे से आने वाली किरण के तरंग सामन्तर जाल के रूप में होता है जब यह पृथ्वी द्वारा पकड़ लिया जाता है।

10.3 (a) काँच का अपवर्तनांक 1.5 है। काँच में प्रकाश की गति क्या है? (एक रिक्त स्थान में प्रकाश की गति $3.0 \times 10^{8} \mathrm{~m} \mathrm{~s}^{-1}$ है)

(b) काँच में प्रकाश की गति रंग के अनुसार स्वतंत्र है या नहीं? यदि नहीं, तो लाल और बैंगनी दोनों रंगों में से कौन एक ग्लास प्रिज्म में धीमी गति से चलता है?

10.4 यंग के द्विस्लिट प्रयोग में, स्लिट के बीच की दूरी $0.28 \mathrm{~mm}$ है और पर्दा $1.4 \mathrm{~m}$ की दूरी पर रखा गया है। केंद्रीय चमकीले बैंदी और चौथे चमकीले बैंदी के बीच की दूरी मापी गई है जो $1.2 \mathrm{~cm}$ है। प्रयोग में प्रयुक्त प्रकाश की तरंगदैर्ध्य निर्धारित कीजिए।

10.5 एक एकल तरंगदैर्ध्य $\lambda$ के एकल तरंगदैर्ध्य वाले प्रकाश का यंग के द्विस्लिट प्रयोग में, स्क्रीन पर एक बिंदु पर जहाँ पथातर $\lambda$ है, प्रकाश की तीव्रता $K$ इकाई है। एक बिंदु पर जहाँ पथांतर $\lambda / 3$ है, प्रकाश की तीव्रता कितनी होगी?

10.6 एक प्रकाश किरण बंडल जिसमें दो तरंगदैर्घ्य, $650 \mathrm{~nm}$ और $520 \mathrm{~nm}$ हैं, का उपयोग यूंग के द्विस्लिट प्रयोग में व्यतिकरण बैंड प्राप्त करने के लिए किया जाता है।

(a) तरंगदैर्घ्य $650 \mathrm{~nm}$ के लिए स्क्रीन पर केंद्रीय अधिकतम से तीसरे चमकीले बैंड की दूरी ज्ञात कीजिए।

(b) दोनों तरंगदैर्घ्यों के कारण चमकीले बैंड कहाँ मिलेंगे जो केंद्रीय अधिकतम से सबसे कम दूरी पर होंगे?