अध्याय 1 विद्युत आवेश एवं क्षेत्र
1.1 परिचय
हम सभी के अनुभव में एक चमक या एक चक्रकार आवाज देखना या सुनना होता है जब हम अपने संश्लेषित कपड़ों या स्वेटर को उतारते हैं, विशेषकर शुष्क मौसम में। यह लेडीज कपड़ों में जैसे पॉलीएस्टर साड़ी के साथ लगभग अपरिहार्य होता है। क्या आपने इस घटना के लिए कोई व्याख्या खोजने की कोशिश की है? विद्युत विस्थापन के एक और सामान्य उदाहरण बिजली के बिजली चमक जो हम तूफान के दौरान आकाश में देखते हैं। हम अपने कार के दरवाजे को खोलते हुए या बस के लौह बार को धरते हुए बैठकर अपने सीट से फिसलकर भी एक विद्युत चक्र का अनुभव करते हैं। इन अनुभवों के कारण हमारे शरीर के माध्यम से विद्युत आवेश के विस्थापन होता है, जो विद्युत चालक सतहों के घर्षण के कारण जमा हो जाता है। आपने भी सुना होगा कि इसके कारण इस्तेमाल की जाने वाली विद्युत की चूषण होती है। यह ठीक वह विषय है जिसके बारे में हम इस अध्याय और अगले अध्याय में चर्चा करेंगे। चूषण का अर्थ है कुछ भी जो समय के साथ नहीं चलता या बदलता है। विद्युत चूषण के अध्ययन में विद्युत आवेशों से उत्पन्न बल, क्षेत्र और संभावनाओं का अध्ययन किया जाता है।
1.2 विद्युत आवेश
इतिहास में यह खोज के श्रेय ग्रीक देश के मिलेटस के थेल्स को जाता है, जिन्होंने लगभग 600 ई.पू. में यह खोज की कि रेशम या सूती कपड़े से रगड़े गए एम्बर लघु वस्तुओं को आकर्षित करता है। विद्युत शब्द का नाम ग्रीक शब्द elektron से लिया गया है, जिसका अर्थ एम्बर होता है। कई ऐसे सामग्री के जोड़े जाने जाते थे जिन्हें रगड़ने पर लघु वस्तुओं जैसे चावल के तार, चावल के गोलियाँ और कागज के टुकड़े आकर्षित करते थे। आप घर पर निम्नलिखित गतिविधि करके इस प्रभाव का अनुभव कर सकते हैं। सफेद कागज के लंबे चौड़े टुकड़े काट लें और उन्हें हल्के से आईरन कर दें। उन्हें टीवी स्क्रीन या कंप्यूटर मॉनिटर के पास ले जाएं। आप देखेंगे कि टुकड़े स्क्रीन के तेजी से आकर्षित हो जाते हैं। वास्तव में वे स्क्रीन पर कुछ समय तक चिपके रहते हैं।

यह देखा गया कि यदि दो काँच के छड़ियों को बाल या सिल्क के कपड़े से रगड़कर एक दूसरे के पास लाया जाता है, तो वे एक दूसरे को बाहर करती हैं [चित्र 1.1(a)]। बाल या सिल्क के दो टुकड़ों, जिनसे छड़ियों को रगड़ा गया था, एक दूसरे को भी बाहर करते हैं। हालांकि, काँच की छड़ और बाल एक दूसरे को आकर्षित करते हैं। इसी तरह, दो प्लास्टिक की छड़ियों को बिल्ली के बाल से रगड़कर एक दूसरे के पास लाया जाता है, तो वे एक दूसरे को बाहर करती हैं [चित्र 1.1(b)] लेकिन बाल को आकर्षित करती हैं। दूसरी ओर, प्लास्टिक की छड़ काँच की छड़ को आकर्षित करती है [चित्र 1.1(c)] और सिल्क या बाल से जिनसे काँच की छड़ रगड़ी गई थी, उनसे बाहर करती है। काँच की छड़ बाल को बाहर करती है। यदि बिल्ली के बाल से रगड़ी गई प्लास्टिक की छड़ को दो छोटे पिथ गेंदों (अब हम पॉलीस्टीरीन गेंदों का उपयोग कर सकते हैं) के सिल्क या नाइलॉन धागे से लटकाए गए गेंदों को स्पर्श कराया जाता है, तो गेंदें एक दूसरे को बाहर करती हैं [चित्र 1.1(d)] और छड़ से भी बाहर करती हैं। यदि पिथ गेंदों को सिल्क से रगड़ी गई काँच की छड़ से स्पर्श कराया जाता है [चित्र 1.1(e)] तो एक समान प्रभाव पाया जाता है। एक दमकील अवलोकन यह है कि एक पिथ गेंद को काँच की छड़ से स्पर्श कराकर दूसरी पिथ गेंद को प्लास्टिक की छड़ से स्पर्श कराने पर एक दूसरे को आकर्षित करती है [चित्र 1.1(f)]।
इन आसान तथ्यों के लिए कई वर्षों के प्रयास और ध्यान से किए गए प्रयोगों और उनके विश्लेषण के आधार पर निष्कर्ष निकाले गए। विभिन्न वैज्ञानिकों द्वारा कई ध्यान से अध्ययनों के बाद निष्कर्ष निकाला गया कि विद्युत आवेश के नाम से जाने वाले एक पदार्थ के केवल दो प्रकार हो सकते हैं। हम कहते हैं कि जैसे कि काँच या प्लास्टिक के छड़, सिल्क, बालू और पिथ गेंद आदि वस्तुएं विद्युत आवेशित हो जाती हैं। इन वस्तुओं को रगड़ने पर विद्युत आवेश प्राप्त हो जाता है। पिथ गेंदों पर किए गए प्रयोगों से यह सुझाव दिया गया कि विद्युत आवेश के दो प्रकार होते हैं और हम देखते हैं कि (i) समान आवेश परस्पर विपरीत होते हैं और (ii) विपरीत आवेश परस्पर आकर्षित होते हैं। प्रयोगों ने यह भी दिखाया कि छड़ से पिथ गेंदों पर संपर्क के द्वारा आवेश परिवहन होता है। कहा जाता है कि पिथ गें आवेशित या आवेशित हो जाती हैं। दो प्रकार के आवेश को अलग करने वाली गुण को आवेश की ध्रुवता कहते हैं।
जब एक काँच की छड़ को रेशम के साथ रगड़ा जाता है, तो छड़ एक प्रकार का आवेश अर्जित कर लेती है और रेशम दूसरा प्रकार का आवेश अर्जित कर लेती है। यह किसी भी वस्तु के जोड़े के लिए सत्य होता है जिन्हें आवेशित करने के लिए रगड़ा जाता है। अब यदि आवेशित काँच की छड़ को उस रेशम के संपर्क में लाया जाता है जिसके साथ यह रगड़ा गया था, तो वे एक दूसरे को आकर्षित नहीं करते हैं। वे अन्य आवेशित होने पर आकर्षित या विकर्षित करने वाले हल्के वस्तुओं को भी आकर्षित या विकर्षित नहीं करते हैं।
इसलिए, जब आवेशित वस्तुएँ एक दूसरे के संपर्क में लाई जाती हैं तो उनके द्वारा अर्जित आवेश खो देते हैं। इन अवलोकनों से आप क्या निष्कर्ष निकाल सकते हैं? यह केवल बताता है कि वस्तुओं द्वारा अर्जित विपरीत आवेश एक दूसरे के प्रभाव को निरस्त कर देते हैं या उनके प्रभाव को शून्य कर देते हैं। इसलिए, अमेरिकी वैज्ञानिक बेंजामिन फ्रांकलिन द्वारा आवेशों को धनात्मक और नकारात्मक कहे गए। हम जानते हैं कि जब हम एक धनात्मक संख्या को उसके बराबर मापदंड के एक नकारात्मक संख्या के योग में जोड़ते हैं, तो योग शून्य हो जाता है। यह आवेशों को धनात्मक और नकारात्मक कहे जाने के नामकरण के दर्शन के बारे में बताता हो सकता है। परंपरा के अनुसार, काँच की छड़ या कैट के बाल के आवेश को धनात्मक कहा जाता है और प्लास्टिक की छड़ या रेशम के आवेश को नकारात्मक कहा जाता है। यदि कोई वस्तु विद्युत आवेश के साथ अवस्थित होती है, तो उसे आवेशित या आवेशित कहा जाता है। जब वह आवेश के बिना होती है, तो उसे विद्युत रूप से उदासीन कहा जाता है।
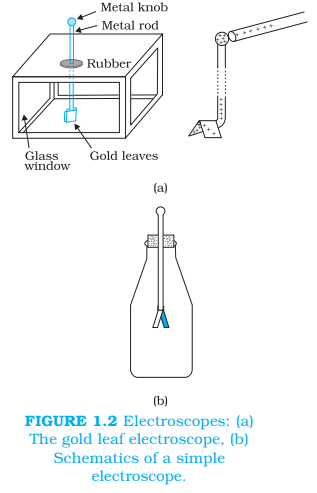
एक सरल उपकरण आवेश के उपस्थिति का पता लगाने के लिए गोल्ड-लीफ इलेक्ट्रोस्कोप [चित्र 1.2(a)] है। इसमें एक ऊर्ध्वाधर धातु की छड़ एक बॉक्स में रखी होती है, जिसके नीचे छोर पर दो पतली गोल्ड शीट लगी होती हैं। जब कोई आवेशित वस्तु छड़ के शीर्ष पर धातु के छोटे छिन्नक से संपर्क करती है, तो आवेश शीट पर प्रवाहित हो जाता है और वे अलग हो जाते हैं। अलग होने की मात्रा आवेश की मात्रा का सूचक होती है।
यह हमारे जीवन के लगभग हर एक क्षेत्र को समावेश करता है। इसलिए ऐसे बल के बारे में अधिक जानना आवश्यक है।
एक उदासीन शरीर को विद्युत आवेशित करने के लिए हमें एक प्रकार के आवेश को जोड़ना या हटाना पड़ता है। जब हम कहते हैं कि एक शरीर आवेशित है, तो हम हमेशा इस आवेश के अतिरिक्त या अभाव के बारे में संदर्भित करते हैं। ठोस में, कुछ इलेक्ट्रॉन, परमाणु में कम तीव्रता से बंधे होने के कारण, एक शरीर से दूसरे शरीर तक परिवहन किए जाने वाले आवेश होते हैं। एक शरीर इलेक्ट्रॉनों के कुछ अंश के नुकसान से धनात्मक आवेशित हो सकता है। इसी तरह, एक शरीर ऋणात्मक आवेशित हो सकता है।
इलेक्ट्रॉन प्राप्त करके। जब हम एक कांच के छड़ को रेशम के साथ रगड़ते हैं, तो छड़ से कुछ इलेक्ट्रॉन रेशम के कपड़े में चले जाते हैं। इसलिए छड़ धनावेशित हो जाती है और रेशम ऋणावेशित हो जाती है। रगड़ने की प्रक्रिया में कोई नया चार्ज नहीं बनता। इसके अलावा, चले जाने वाले इलेक्ट्रॉनों की संख्या, सामग्री में कुल इलेक्ट्रॉनों की संख्या के बहुत कम भाग होती है।
1.3 चालक और अचालक
कुछ पदार्थ बिजली के प्रवाह को आसानी से अनुमति देते हैं, जबकि कुछ नहीं। वे पदार्थ जो बिजली के प्रवाह को आसानी से अनुमति देते हैं, चालक कहलाते हैं। इनमें विद्युत चार्ज (इलेक्ट्रॉन) आसानी से आंतरिक पदार्थ में गति कर सकते हैं। धातुएं, मानव और पशु शरीर और जमीन चालक होते हैं। अधिकांश अधातुएं जैसे कांच, सिरामिक, प्लास्टिक, नाइलॉन, लकड़ी बिजली के प्रवाह के लिए उच्च प्रतिरोध प्रदान करते हैं। वे अचालक कहलाते हैं। अधिकांश पदार् ऊपर दिए गए दो वर्गों में से एक में आते हैं।*
जब कोई आवेश एक चालक पर स्थानांतरित किया जाता है, तो यह चालक के सम्पूर्ण सतह पर आसानी से वितरित हो जाता है। विपरीत रूप से, यदि कोई आवेश एक अचालक पर रखा जाता है, तो यह उसी स्थान पर रह जाता है। आप अगले अध्याय में जानेंगे कि ऐसा क्यों होता है।
इस गुण के कारण हम जानते हैं कि नाइलॉन या प्लास्टिक के ब्रश को सूखे बालों के साथ बांधने या रगड़ने पर आवेशित हो जाते हैं, लेकिन एक धातु के वस्तु जैसे चम्मच ऐसा नहीं करते। धातु के आवेश दोनों चालक होने के कारण हमारे शरीर के माध्यम से जमीन तक बह जाते हैं। हालांकि, यदि एक धातु के छड़ को उसके धातु के हिस्से को छूए बिना लकड़ी या प्लास्टिक के हाथ के साथ रगड़ा जाए, तो इसके चारों ओर आवेश के लक्षण दिखाई देते हैं।
1.4 विद्युत आवेश के मूल गुण
हम देख चुके हैं कि आवेश दो प्रकार के होते हैं, अर्थात धनात्मक और नकारात्मक, और उनके प्रभाव एक दूसरे को बरकरार रखते हैं। यहां, हम विद्युत आवेश के कुछ अन्य गुणों का वर्णन करेंगे।
अगर आवेशित वस्तुओं के आकार उनके बीच की दूरी की तुलना में बहुत छोटे हों, तो हम उन्हें बिंदु आवेश मानते हैं। वस्तु के सभी आवेश को एक बिंदु पर केंद्रित माना जाता है।
1.4.1 आवेशों की जोड़ के गुण
हम अब तक आवेश की एक मात्रात्मक परिभाषा नहीं दे चुके हैं; हम अगले अनुच्छेद में इसके बारे में चर्चा करेंगे। हम इसके बारे में अस्थायी रूप से मान लेंगे और आगे बढ़ेंगे। यदि
एक निकाय में दो बिंदु आवेश $\mathrm{q_1}$ और $\mathrm{q_2}$ होते हैं, निकाय का कुल आवेश बस $\mathrm{q_1}$ और $\mathrm{q_2}$ को बीजगणितीय रूप से जोड़कर प्राप्त किया जाता है, अर्थात, आवेश वास्तविक संख्याओं की तरह जोड़े जाते हैं या वे द्रव्यमान की तरह अदिश राशियाँ होते हैं। यदि एक निकाय में n आवेश $\mathrm{q_1}$, $\mathrm{q_2}$, $\mathrm{q_3}$, …, qn होते हैं, तो निकाय का कुल आवेश $\mathrm{q_1}$ + $\mathrm{q_2}$ + $\mathrm{q_3}$ + … + qn होता है। आवेश के मात्रा होती है लेकिन दिशा नहीं, द्रव्यमान के समान। हालांकि,
एक बॉडी के द्रव्यमान हमेशा धनात्मक होता है, जबकि आवेश या तो धनात्मक या नकारात्मक हो सकता है। एक सिस्टम में आवेशों को जोड़ते समय सही चिह्नों का उपयोग करना आवश्यक होता है। उदाहरण के लिए, एक सिस्टम में पांच आवेश +1, +2, –3, +4 और –5 हैं, जो कि कुछ असंगत इकाई में हैं, तो इस सिस्टम का कुल आवेश (+1) + (+2) + (–3) + (+4) + (–5) = –1 होता है, इसी इकाई में।
1.4.2 आवेश संरक्षित होता है
हमने पहले ही इस बात की ओर इशारा कर चुके हैं कि जब वस्तुएं घर्षण के द्वारा आवेशित होती हैं, तो एक वस्तु से दूसरी वस्तु में इलेक्ट्रॉनों का स्थानांतरण होता है; कोई नए
आवेश या बनाया जा सकता है या नष्ट कर दिया जा सकता है। विद्युत आवेश के कणों के चित्र से हमें आवेश के संरक्षण के विचार को समझने में मदद मिलती है। जब हम दो वस्तुओं को घर्षित करते हैं, तो एक वस्तु द्वारा आवेश के लाभ दूसरी वस्तु द्वारा आवेज के नुकसान के रूप में होता है। एक आइसोलेटेड सिस्टम में बहुत सारे आवेशित वस्तुओं के एक सिस्टम में, वस्तुओं के बीच अंतरक्रियाओं के कारण आवेशों का वितरण हो सकता है, लेकिन यह पाया गया है कि आइसोलेटेड सिस्टम के कुल आवेश हमेशा संरक्षित रहता है। आवेश के संरक्षण को प्रयोगों द्वारा स्थापित किया गया है।
कोई आइसोलेटेड वस्तु द्वारा ले जाए गए नेट आवेश को बनाना या नष्ट करना संभव नहीं है।
सिस्टम हालांकि चार्ज वाहक कण एक प्रक्रिया में बनाए जा सकते हैं या नष्ट कर दिए जा सकते हैं। कभी-कभी प्रकृति चार्जित कण बनाती है: एक न्यूट्रॉन एक प्रोटॉन और एक इलेक्ट्रॉन में बदल जाता है। इस प्रकार बनाए गए प्रोटॉन और इलेक्ट्रॉन के बराबर और विपरीत चार्ज होते हैं और बनाने से पहले और बनाने के बाद कुल चार्ज शून्य होता है।
1.4.3 चार्ज के क्वांटीकरण
प्रयोग के आधार पर स्थापित किया गया है कि सभी मुक्त चार्ज एक मूल इकाई चार्ज के पूर्ण गुणज होते हैं, जिसे e द्वारा नोट किया जाता है। इसलिए किसी वस्तु पर चार्ज q हमेशा इस प्रकार दिया जाता है:
$$ q=n e $$
जहाँ n कोई भी पूर्णांक हो सकता है, धनात्मक या ऋणात्मक। इस बुनियादी आवेश के इकाई को एक इलेक्ट्रॉन या प्रोटॉन के आवेश के रूप में लिया जाता है। परंपरा के अनुसार, इलेक्ट्रॉन पर आवेश ऋणात्मक माना जाता है; इसलिए इलेक्ट्रॉन पर आवेश –e के रूप में लिखा जाता है और प्रोटॉन पर आवेश +e के रूप में लिखा जाता है।
विद्युत आवेश हमेशा e के एक पूर्णांक गुणक होता है, इस तथ्य को आवेश के क्वांटीकरण के रूप में जाना जाता है। भौतिकी में एक बड़ी संख्या में स्थितियाँ होती हैं जहाँ कुछ भौतिक राशियाँ क्वांटीकृत होती हैं। आवेश के क्वांटीकरण
पहले फैराडे द्वारा खोजे गए विद्युत अपघटन के प्रयोगात्मक कानूनों द्वारा सुझाया गया था। 1912 में मिल्लिकन द्वारा इसका प्रयोगात्मक प्रमाण दिया गया था।
अंतरराष्ट्रीय मात्रक पद्धति (SI) में, आवेश के एक मात्रक को कूलॉम कहा जाता है और इसे प्रतीक C द्वारा निरूपित किया जाता है। कूलॉम की परिभाषा विद्युत धारा के मात्रक पर आधारित होती है, जिसके बारे में आप एक आगामी अध्याय में सीखेंगे। इस परिभाषा के अनुसार, एक कूलॉम वह आवेश होता है जो 1 सेकंड में 1 A (एम्पियर) की धारा वाले तार में प्रवाहित होता है (अध्याय 1 के देखें)
कक्षा XI के भौतिक विज्ञान पाठ्यक्रम के भाग I में दिया गया है। इस प्रणाली में, आवेश के मूल इकाई के मान है
$$ e=1.602192 \times 10^{-19} \mathrm{C} $$
इस प्रकार, -1C आवेश के लिए लगभग 6 × 10¹⁸ इलेक्ट्रॉन होते हैं। विद्युत चुंबकत्व में, ऐसे बड़े मान के आवेश बहुत घटिया आम नहीं होते हैं और इसलिए हम छोटी इकाइयों का उपयोग करते हैं, जैसे 1 मीक्रोकूलॉम (mC) = 10⁻⁶ C या 1 मिलीकूलॉम (mC) = 10⁻³ C।
यदि वैज्ञानिक और इलेक्ट्रॉन ब्रह्मांड में एकमात्र मूल आवेश हों, तो सभी देखे जा सकने वाले आवेश e के पूर्णांक गुणक होने चाहिए। इसलिए, यदि एक वस्तु में n₁ इलेक्ट्रॉन और n₂ प्रोटॉन हों, तो वस्तु पर कुल आवेश n₂ × e + n₁ × (–e) = (n₂ – n₁) e होता है। क्योंकि n₁ और n₂ पूर्णांक हैं, उनके अंतर भी एक पूर्णांक होता है। इसलिए, किसी भी वस्तु पर आवेश हमेशा e के पूर्णांक गुणक होता है और इसे e के चरणों में बढ़ाया या घटाया जा सकता है।
संचय के चरण आकार e बहुत छोटा है क्योंकि मैक्रोस्कोपिक स्तर पर हम कई मिलीकूलॉम (mC) के चार्ज के साथ काम करते हैं। इस स्तर पर एक वस्तु के चार्ज के बढ़ या घट सकने के इकाई e के रूप में नहीं दिखाई देता। इस दृष्टि से, चार्ज के बर्न गुण के रूप में खो जाता है और यह लगता है कि यह सतत है।
इस स्थिति को बिंदु और रेखा के ज्यामितीय अवधारणाओं के साथ तुलना की जा सकती है। दूर से देखे जाने पर एक बिंदु वाली रेखा हमें सतत दिखाई देती है लेकिन वास्तव में यह सतत नहीं है। आमतौर पर बहुत कम दूरी पर एक दूसरे के बराबर बिंदुओं के संग्रह के लिए एक सतत रेखा की छवि बनती है, इसी तरह बहुत छोटे चार्जों के संग्रह के रूप में एक सतत चार्ज वितरण के रूप में दिखाई देता है।
मैक्रोस्कोपिक स्तर पर, एक व्यक्ति ऐसे चार्ज के साथ काम करता है जो चार्ज e के मान की तुलना में बहुत बड़े होते हैं। क्योंकि e = 1.6 × 10–19 C, एक चार्ज के मान, जैसे कि 1 मिलीकूलॉम (mC), में इलेक्ट्रॉनिक चार्ज के लगभग 1013 गुना होता है। इस स्तर पर, चार्ज केवल e के इकाइयों में बढ़ या घट सकता है इस तथ्य के कारण यह बहुत अलग नहीं होता है जैसे कि चार्ज के निरंतर मान ले सकता है। इसलिए, मैक्रोस्कोपिक स्तर पर, चार्ज के क्वांटीकरण के कोई व्यावहारिक परिणाम नहीं होते हैं और इसे नगण्य माना जा सकता है। हालांकि, माइक्रोस्कोपिक स्तर पर, जहां शामिल चार्ज के मान कई दहाई या सैकड़ों e के क्रम में होते हैं, अर्थात उन्हें गिना जा सकता है, वे अलग-अलग गुच्छों में दिखाई देते हैं और चार्ज के क्वांटीकरण को नगण्य नहीं माना जा सकता है। यह अंतर अंतर्गत अंक के मान के आधार पर होता है
संलग्न जो काफी महत्वपूर्ण है।
उदाहरण 1.1 यदि प्रति सेकंड $10^9$ इलेक्ट्रॉन एक वस्तु से दूसरी वस्तु की ओर चले जाते हैं, तो दूसरी वस्तु पर कुल $1 \mathrm{C}$ आवेश प्राप्त करने के लिए कितना समय लगेगा?
हल एक सेकंड में $10^9$ इलेक्ट्रॉन वस्तु से बाहर चले जाते हैं। अतः एक सेकंड में दी गई आवेश की मात्रा $1.6 \times 10^{-19} \times 10^9 \mathrm{C}=1.6 \times 10^{-10} \mathrm{C}$ होती है।
$1 \mathrm{C}$ आवेश एकत्र करने के लिए आवश्यक समय $1 \mathrm{C} \div\left(1.6 \times 10^{-10} \mathrm{C} / \mathrm{s}\right)$ $=6.25 \times 10^9 \mathrm{~s}=6.25 \times 10^9 \div(365 \times 24 \times$ 3600) वर्ष $=198$ वर्ष होगा। अतः $10^9$ इलेक्ट्रॉन प्रति सेकंड एक वस्तु से बाहर चले जाने पर, एक कूलॉम आवेश एकत्र करने के लिए हमें लगभग 200 वर्ष की आवश्यकता होगी। अतः एक कूलॉम आवेश कई व्यावहारिक उद्देश्यों के लिए बहुत बड़ा इकाई है।
हालांकि, यह भी महत्वपूर्ण है कि ज्ञात करें कि किसी सामग्री के एक घन सेंटीमीटर के टुकड़े में लगभग कितने इलेक्ट्रॉन होते हैं। $1 \mathrm{~cm}$ भुजा वाले एक घनाकार कॉपर के टुकड़े में लगभग $2.5 \times 10^{24}$ इलेक्ट्रॉन होते हैं।
उदाहरण 1.2 एक कप पानी में कितना धनात्मक और नकारात्मक आवेश होता है?
हल मान लीजिए कि एक कप पानी का द्रव्यमान $250 \mathrm{~g}$ है। पानी के अणुभार $18 \mathrm{~g}$ है। इसलिए, एक मोल $(=6.02 \times 10^{23}$ अणु) पानी $18 \mathrm{~g}$ होता है। इसलिए, एक कप पानी में अणुओं की संख्या $(250 / 18) \times 6.02 \times 10^{23}$ होती है।
प्रत्येक पानी के अणु में दो हाइड्रोजन परमाणु और एक ऑक्सीजन परमाणु होते हैं, अर्थात 10 इलेक्ट्रॉन और 10 प्रोटॉन। इसलिए कुल धनात्मक और कुल नकारात्मक आवेश के मान बराबर होते हैं। यह बराबर होता है $(250 / 18) \times 6.02 \times 10^{23} \times 10 \times 1.6 \times 10^{-19} \mathrm{C}=1.34 \times 10^7 \mathrm{C}$
1.5 कूलॉम के नियम
कूलॉम के नियम दो बिंदु आवेशों के बीच बल के बारे में एक मात्रात्मक कथन है। जब आवेशित वस्तुओं के रैखिक आकार उनके बीच की दूरी की तुलना में बहुत छोटे होते हैं, तो आकार को नगण्य मान लिया जाता है और आवेशित वस्तुओं को बिंदु आवेश के रूप में लिया जाता है। कूलॉम ने दो बिंदु आवेशों के बीच बल को मापा और पाया कि यह आवेशों के बीच की दूरी के वर्ग के व्युत्क्रमानुपाती होता है और दोनों आवेशों के मान के गुणनफल के सीधे अनुपाती होता है और दोनों आवेशों को जोड़ने वाली रेखा के अनुदिश कार्य करता है। इसलिए, यदि दो बिंदु आवेश $\mathrm{q_1}$, $\mathrm{q_2}$ एक रिक्त स्थान में दूरी r पर अलग होते हैं, तो उनके बीच बल (F) के मान को निम्नलिखित द्वारा दिया जाता है
$$ \begin{equation*} F=k \frac{\mid q _{1} q _{2} \mid}{r^{2}} \tag{1.1} \end{equation*} $$
कूलॉम ने अपने प्रयोगों से इस कानून को कैसे प्राप्त किया? कूलॉम ने बल के मापन के लिए एक बल घुमावदार तंतु का उपयोग किया। जब दो आवेशित धातु गोलियों के बीच की दूरी प्रत्येक गोली के त्रिज्या से काफी बड़ी होती है, तो आवेशित गोलियों को बिंदु आवेश के रूप में देखा जा सकता है। हालांकि, आवेशों के मान शुरू में अज्ञात थे। तो फिर कूलॉम ने ऐसे संबंध की खोज कैसे की? कूलॉम ने निम्नलिखित सरल तरीका चिंतन किया: मान लीजिए एक धातु गोली पर आवेश q है। यदि गोली को एक समान अनावेशित गोली के संपर्क में लाया जाता है, तो आवेश दोनों गोलियों के बीच वितरित हो जाता है। सममिति के कारण, प्रत्येक गोली पर आवेश q/2 होता है। इस प्रक्रिया को दोहराकर, हम q/2, q/4 आदि आवेश प्राप्त कर सकते हैं। कूलॉम ने एक स्थिर आवेश युग्म के लिए दूरी को बदलते हुए विभिन्न दूरियों के लिए बल को मापा। फिर वह आवेशों के युग्म को बदलते हुए, प्रत्येक युग्म के लिए दूरी को स्थिर रखते हुए बल को मापते रहे। विभिन्न दूरियों पर विभिन्न आवेश युग्मों के बल की तुलना करके कूलॉम ने समीकरण (1.1) के संबंध को प्राप्त किया।
कूलॉम के नियम, एक सरल गणितीय कथन, पहले ऊपर बताए गए तरीके से प्रयोगों के माध्यम से पहचाना गया था। जबकि मूल प्रयोग एक मैक्रोस्कोपिक स्तर पर इसे स्थापित करते हैं, इसे एक उप-परमाणु स्तर $(r ~ 10^{–10} m)$ तक भी स्थापित किया गया है।
कूलॉम ने अपने नियम की खोज चार्ज के स्पष्ट मान के बिना की थी। वास्तव में, यह उलटा है: कूलॉम के नियम को अब चार्ज के एक इकाई की परिभाषा प्रदान करने के लिए उपयोग किया जा सकता है। समीकरण (1.1) में, k अब तक अस्पष्ट है। हम किसी भी धनात्मक मान का चयन कर सकते हैं। k के चयन के आधार पर चार्ज की इकाई के आकार का निर्धारण होता है। SI इकाइयों में, k का मान लगभग $9 × 10^9 \frac{Nm^2}{C^2}$ होता है। इस चयन से प्राप्त चार्ज की इकाई को कूलॉम कहते हैं, जिसे हम पहले अनुच्छेद 1.4 में परिभाषित कर चुके हैं। समीकरण (1.1) में इस मान के k को रखने पर, हम देख सकते हैं कि $q _{1}=q _{2}=1 \mathrm{C}$, $r=1 \mathrm{~m}$ के लिए,
$$ F=9 \times 10^{9} \mathrm{~N} $$

चार्ल्स ऑगस्टिन डी कूलॉम्ब (1736 – 1806) एक फ्रांसीसी भौतिकविद थे, जिन्होंने वेस्ट इंडीज में सैन्य अभियंता के रूप में अपना करियर शुरू किया। 1776 में वे पेरिस वापस लौट आए और एक छोटे बागान में अपने वैज्ञानिक अनुसंधान के लिए बर्खास्त हो गए। उन्होंने एक घूर्णन तुलना बनाई जिसके माध्यम से बल की मात्रा को मापा जा सकता है और इसे छोटे आवेशित गोलियों के बीच विद्युत आकर्षण या प्रतिकर्षण बल की निर्धारण के लिए उपयोग किया। इस प्रकार वे 1785 में व्युत्क्रम वर्ग नियम के संबंध में पहुंच गए, जिसे अब कूलॉम के नियम के रूप में जाना जाता है। यह नियम प्रिस्टले द्वारा भी आगे बढ़ा गया गया था और इसके पहले गैवेंडिश द्वारा भी अनुमान लगाया गया था, हालांकि गैवेंडिश ने अपने परिणामों को कभी प्रकाशित नहीं किया। कूलॉम ने अलग-अलग और समान चुंबकीय ध्रुवों के बीच बल के व्युत्क्रम वर्ग नियम की खोज भी की।
उस प्रकार, 1 C वह आवेश है जो एक खाली स्थान में एक दूसरे आवेश के समान मात्रा में 1 मीटर की दूरी पर रखे जाने पर $9 × 10^9$ N के प्रतिकर्षण बल का अनुभव करता है। स्पष्ट रूप से, 1 कूलॉम एक बहुत बड़ा इकाई है जिसका उपयोग करना सुविधाजनक नहीं है। व्यावहारिक रूप से, विद्युत चालकता में, आप छोटी इकाइयों जैसे 1 मिलीकूलॉम या 1 माइक्रोकूलॉम का उपयोग करते हैं।

चित्र 1.3 (a) भौतिक रूप और (b) आवेशों के बीच बल।
समीकरण (1.1) में स्थिरांक $k$ को आगामी सुविधा के लिए आमतौर पर $k=1 / 4 \pi \varepsilon _{0}$ के रूप में लिखा जाता है, ताकि कूलॉम के नियम को लिखा जा सके:
$$ \begin{equation*} F=\frac{1}{4 \pi \varepsilon _{0}} \quad \frac{\left|q _{1} q _{2}\right|}{r^{2}} \tag{1.2} \end{equation*} $$
$ε_0$ को मुक्त अंतरिक या रिक्त अंतरिक की प्रवृत्ति कहा जाता है। $ε_0$ का मान SI इकाइयों में है
$$ \varepsilon _{0}=8.854 \times 10^{-12} \mathrm{C}^{2} \mathrm{~N}^{-1} \mathrm{~m}^{-2} $$
$$
क्योंकि बल एक सदिश होता है, इसलिए कूलॉम के नियम को सदिश रूप में लिखना बेहतर होता है। मान लीजिए आवेश $q_1$ और $q_2$ के स्थिति सदिश क्रमशः $r_1$ और $r_2$ हैं [चित्र 1.6(a) देखें]। हम $q_1$ पर $q_2$ के कारण बल को $F_{12}$ और $q_2$ पर $q_1$ के कारण बल को $F_{21}$ से दर्शाते हैं। $q_1$ और $q_2$ को सुविधा के लिए 1 और 2 क्रमशः संख्या दी गई है और 1 से 2 तक जाने वाले सदिश को $r_{21}$ से दर्शाया जाता है:
$$ \mathbf{r} _{21}=\mathbf{r} _{2}-\mathbf{r} _{1} $$
उतनी ही तरह, 2 से 1 तक जाने वाले सदिश को $r_{12}$ से दर्शाया जाता है:
$r_{12} = r_1 - r_2 = - r_{21}$
वेक्टर $r_{21}$ और $r_{12}$ के परिमाण को क्रमशः $r_{21}$ और $r_{13}$ द्वारा नोट किया जाता है $(r_{12} = r_{21})$। एक वेक्टर की दिशा उस वेक्टर के अनुदिश एक इकाई वेक्टर द्वारा निर्धारित की जाती है। 1 से 2 (या 2 से 1) की दिशा को निर्दिष्ट करने के लिए, हम इकाई वेक्टर परिभाषित करते हैं:
$$\hat{r_{21}}=\frac{r_{21}}{r_{21}},\quad \hat{r_{12}}=\frac{r_{12}}{r_{12}}, \quad \hat{r_{21}}-\hat{r_{12}}$$
दो बिंदु आवेश $\mathrm{q_1}$ और $\mathrm{q_2}$ जो क्रमशः r1 और r2 पर स्थित हैं, के बीच कूलॉम बल कानून को निम्नलिखित तरह से व्यक्त किया जाता है:
$$ \begin{equation*} \mathbf{F} _{21}=\frac{1}{4 \pi \varepsilon _{o}} \frac{q _{1} q _{2}}{r _{21}^{2}} \hat{\mathbf{r}} _{21} \tag{1.3} \end{equation*} $$
समीकरण (1.3) पर कुछ टिप्पणियाँ महत्वपूर्ण हैं:
-
समीकरण (1.3) कोई भी $\mathrm{q_1}$ और $\mathrm{q_2}$ के चिन्ह के लिए लागू होता है, चाहे वे धनात्मक या नकारात्मक हों। यदि $\mathrm{q_1}$ और $\mathrm{q_2}$ एक ही चिन्ह के हों (दोनों धनात्मक या दोनों नकारात्मक), तो $\mathbf{F}{21}$, $r^{21}$ के अनुदिश होता है, जो समान चार्जों के बीच प्रतिकर्षण को दर्शाता है। यदि $\mathrm{q_1}$ और $\mathrm{q_2}$ विपरीत चिन्ह के हों, तो $\mathbf{F}{21}$, $-r_{21}$ ($= r_{12}$) के अनुदिश होता है, जो विपरीत चार्जों के बीच आकर्षण को दर्शाता है। इसलिए, हमें समान और विपरीत चार्जों के मामलों के लिए अलग-अलग समीकरण लिखने की आवश्यकता नहीं होती। समीकरण (1.3) दोनों मामलों को सही तरीके से संभाल लेता है [चित्र 1.6(b)]।
-
आवेश $\mathrm{q_2}$ के कारण $\mathrm{q_1}$ पर बल $\mathrm{F_12}$, समीकरण (1.3) से प्राप्त किया जा सकता है, बस 1 और 2 को आपस में बदल देने से, अर्थात,
$\mathbf{F} _{12}=\frac{1}{4 \pi \varepsilon _{0}} \frac{q _{1} q _{2}}{r _{12}^{2}} \hat{\mathbf{r}} _{12}=-\mathbf{F} _{21}$
इस प्रकार, कूलॉम के नियम न्यूटन के तीसरे नियम के साथ सहमत है।
कूलॉम के नियम [समीकरण (1.3)] एक आवेश $\mathrm{q_1}$ और $\mathrm{q_2}$ के बीच बल को निर्वात में देता है। यदि आवेश वस्तु में रखे जाते हैं या बीच के अंतराल में वस्तु होती है, तो वस्तु के आवेशित घटकों की उपस्थिति के कारण स्थिति जटिल हो जाती है। हम अगले अध्याय में वस्तु में विद्युत स्थैतिकता के बारे में चर्चा करेंगे।
उदाहरण 1.3 दो बिंदु आवेशों के बीच विद्युत बल के कूलॉम के नियम और दो स्थैतिक बिंदु द्रव्यमानों के बीच गुरुत्वाकर्षण बल के न्यूटन के नियम, दोनों आवेशों और द्रव्यमानों के बीच दूरी के वर्ग के व्युत्क्रमानुपाती निर्भरता रखते हैं। (a) इन बलों की तीव्रता की तुलना करें द्वारा उनके परिमाण के अनुपात की गणना करके (i) एक इलेक्ट्रॉन और एक प्रोटॉन के लिए और (ii) दो प्रोटॉन के लिए। (b) जब वे 1 Å (= 10⁻¹⁰ मीटर) की दूरी पर हों तो इलेक्ट्रॉन और प्रोटॉन के आपसी आकर्षण के विद्युत बल के कारण त्वरण का अनुमान लगाएं? (m_p = 1.67 × 10⁻²⁷ किग्रा, m_e = 9.11 × 10⁻³¹ किग्रा)
हल (a) (i) एक इलेक्ट्रॉन और एक प्रोटॉन के बीच विद्युत बल $ r $ दूरी पर:
$$ F_{e}=-\frac{1}{4 \pi \varepsilon_{0}} \frac{e^{2}}{r^{2}} $$
जहाँ नकारात्मक चिह्न इस बल के आकर्षण प्रकृति को दर्शाता है। संगत गुरुत्वाकर्षण बल (हमेशा आकर्षण वाला) है:
$$ F_{G}=-G \frac{m_{p} m_{e}}{r^{2}} $$
जहाँ $ m_{p} $ और $ m_{e} $ क्रमशः प्रोटॉन और इलेक्ट्रॉन के द्रव्यमान हैं।
$$ \left|\frac{F_{e}}{F_{G}}\right|=\frac{e^{2}}{4 \pi \varepsilon_{0} G m_{p} m_{e}}=2.4 \times 10^{39} $$
$$
(ii) इसी तरह, दो प्रोटॉन के बीच दूरी $r$ पर विद्युत बल और गुरुत्वाकर्षण बल के परिमाणों के अनुपात को निम्नलिखित द्वारा दर्शाया जा सकता है:
$\left|\frac{F_{e}}{F_{G}}\right|=\frac{e^{2}}{4 \pi \varepsilon_{0} G m_{p} m_{p}}=1.3 \times 10^{36}$
हालांकि, यहां ध्यान देने योग्य है कि दोनों बलों के चिह्न अलग हैं। दो प्रोटॉन के बीच गुरुत्वाकर्षण बल आकर्षण प्रकृति का होता है और कूलॉम बल विकर्षण प्रकृति का होता है। एक नाभिक के अंदर दो प्रोटॉन के बीच बलों के वास्तविक मान (दो प्रोटॉन के बीच दूरी $\sim 10^{-15} \mathrm{~m}$ होती है) $F_{\mathrm{e}} \sim 230 \mathrm{~N}$ है, जबकि $F_{\mathrm{G}} \sim 1.9 \times 10^{-34} \mathrm{~N}$ है।
दो बलों के (अपरिमाणहीन) अनुपात के अनुसार, विद्युत बल गुरुत्वाकर्षण बलों की तुलना में बहुत अधिक मजबूत होते हैं।
(b) एक प्रोटॉन द्वारा एक इलेक्ट्रॉन पर लगाए गए विद्युत बल $\mathbf{F}$, एक इलेक्ट्रॉन द्वारा एक प्रोटॉन पर लगाए गए बल के बराबर होता है; हालांकि, इलेक्ट्रॉन और प्रोटॉन के द्रव्यमान अलग होते हैं। इसलिए, बल के मापदंड के आकार के लिए
$$ \begin{aligned} |\mathbf{F}| & =\frac{1}{4 \pi \varepsilon_{0}} \frac{e^{2}}{r^{2}}=8.987 \times 10^{9} \mathrm{Nm}^{2} / \mathrm{C}^{2} \times\left(1.6 \times 10^{-19} \mathrm{C}\right)^{2} /\left(10^{-10} \mathrm{~m}\right)^{2} \\
$$ \begin{aligned} & =2.3 \times 10^{-8} \mathrm{~N} \end{aligned} $$
न्यूटन के गति के द्वितीय नियम के अनुसार, $F=m a$, इलेक्ट्रॉन द्वारा अनुभव किया गया त्वरण निम्नलिखित होगा: $a=2.3 \times 10^{-8} \mathrm{~N} / 9.11 \times 10^{-31} \mathrm{~kg}=2.5 \times 10^{22} \mathrm{~m} / \mathrm{s}^{2}$
इसकी तुलना गुरुत्वीय त्वरण के मान के साथ करने पर, हम निष्कर्ष निकाल सकते हैं कि गुरुत्वीय क्षेत्र का प्रभाव इलेक्ट्रॉन के गति पर नगण्य होता है और एक प्रोटॉन के कूलॉम बल के कारण इलेक्ट्रॉन बहुत बड़े त्वरण अनुभव करता है।
में त्वरण के मान के लिए मान है
$2.3 \times 10^{-8} \mathrm{~N} / 1.67 \times 10^{-27} \mathrm{~kg}=1.4 \times 10^{19} \mathrm{~m} / \mathrm{s}^{2}$
उदाहरण 1.4 एक चार्जित धातु के गोला A नाइलॉन धागे से लटकाया गया है। एक अन्य चार्जित धातु के गोला B, एक आइसोलेटिंग हैंडल के द्वारा पकड़े गए हैं, जो A के पास ले जाया जाता है ताकि उनके केंद्रों के बीच की दूरी 10 सेमी हो, जैसा कि चित्र 1.7(a) में दिखाया गया है। फलस्वरूप A के प्रतिकर्षण का नोट किया जाता है (उदाहरण के लिए, एक प्रकाश किरण के बीम को चमकाकर उसके छाया के विक्षेपण को एक स्क्रीन पर मापकर)। गोले A और B क्रमशः अनुदिप्त गोले C और D द्वारा स्पर्श किए जाते हैं, जैसा कि चित्र 1.7(b) में दिखाया गया है। C और D फिर से हटा दिए जाते हैं और B को A के पास ले जाया जाता है ताकि उनके केंद्रों के बीच की दूरी 5.0 सेमी हो, जैसा कि चित्र 1.7(c) में दिखाया गया है। कूलॉम के नियम के आधार पर A के प्रतिकर्षण का अनुमान लगाएं। गोले A और C और गोले B और D के आकार समान हैं। उनके केंद्रों के बीच के अंतर की तुलना में A और B के आकार को नगण्य मान लें।

हल मान लीजिए कि गोले A पर मूल आवेश $q$ है और गोले B पर $q^{\prime}$ है। उनके केंद्रों के बीच दूरी $r$ होने पर, प्रत्येक पर विद्युत बल के परिमाण को निम्नलिखित द्वारा दिया जाता है
$$ F=\frac{1}{4 \pi \varepsilon_{0}} \frac{q q^{\prime}}{r^{2}} $$
गोले A और B के आकार को $r$ की तुलना में नगण्य मान लें। जब एक समान लेकिन अनुत्तर आवेशित गोला $\mathrm{C}$ गोला $\mathrm{A}$ से स्पर्श करता है, तो आवेश A और C पर वितरित हो जाता है और, सममिति के कारण, प्रत्येक गोले पर आवेश $q/2$ हो जाता है। इसी तरह, D गोला B से स्पर्श करते हुए, प्रत्येक गोले पर वितरित आवेश $q^{\prime} / 2$ हो जाता है। अब, यदि A और B के बीच दूरी आधी कर दी जाए, तो प्रत्येक पर विद्युत बल के परिमाण को निम्नलिखित द्वारा दिया जाता है
$$ F^{\prime}=\frac{1}{4 \pi \varepsilon_{0}} \frac{(q / 2)\left(q^{\prime} / 2\right)}{(r / 2)^{2}}=\frac{1}{4 \pi \varepsilon_{0}} \frac{\left(q q^{\prime}\right)}{r^{2}}=F $$
इसलिए $\mathrm{A}$ के ऊपर $\mathrm{B}$ के कारण विद्युत बल अपरिवर्तित रहता है।
1.6 विभिन्न आवेशों के बीच बल
दो आवेशों के बीच पारस्परिक विद्युत बल को कूलॉम के नियम द्वारा दिया जाता है। एक आवेश पर विभिन्न आवेशों के कारण बल कैसे गणना करें? एक निर्वात में n स्थिर आवेशों के एक प्रणाली की विचार करें $\mathrm{q_1}$, $\mathrm{q_2}$, $\mathrm{q_3}$, …, qn। $\mathrm{q_1}$ पर $\mathrm{q_2}$, $\mathrm{q_3}$, …, qn के कारण बल क्या होगा? कूलॉम के नियम केवल इस प्रश्न का उत्तर देने के लिए पर्याप्त नहीं है। याद रखें कि यांत्रिक बलों को विस्तार विधि के अनुसार जोड़ा जाता है। विद्युत बलों के लिए भी यही वैसी बात है?

चित्र 1.5 एक चार्ज के तंत्र के (a) तीन चार्ज (b) अनेक चार्ज।
प्रयोग के आधार पर यह सत्यापित किया गया है कि किसी चार्ज पर अनेक अन्य चार्जों के कारण बल उन अन्य चार्जों के कारण उस चार्ज पर लगने वाले सभी बलों के सदिश योग होता है, एक-एक करके। अन्य चार्जों की उपस्थिति के कारण व्यक्तिगत बल प्रभावित नहीं होते। इसे सुपरपोजिशन के सिद्धांत के रूप में जाना जाता है।
To better understand the concept, consider a system of three charges $\mathrm{q_1}$, $\mathrm{q_2}$ and $\mathrm{q_3}$, as shown in Fig. 1.8(a). The force on one charge, say $\mathrm{q_1}$, due to two other charges $\mathrm{q_2}$, $\mathrm{q_3}$ can therefore be obtained by performing a vector addition of the forces due to each one of these charges. Thus, if the force on $\mathrm{q_1}$ due to $\mathrm{q_2}$ is denoted by $\mathrm{F_{12}}$, $\mathrm{F_{12}}$ is given by Eq. (1.3) even though other charges are present. Thus,
$$ \mathbf{F} _{12}=\frac{1}{4 \pi \varepsilon _{0}} \frac{q _{1} q _{2}}{r _{12}^{2}} \hat{\mathbf{r}} _{12} $$
उतनी ही तरह, $\mathrm{q_1}$ के कारण $\mathrm{q_3}$ द्वारा बल, जिसे $\mathrm{F_{13}}$ से नोट किया जाता है, निम्नलिखित द्वारा दिया जाता है
$$ \mathbf{F} _{13}=\frac{1}{4 \pi \varepsilon _{0}} \frac{q _{1} q _{3}}{r _{13}^{2}} \hat{\mathbf{r}} _{13} $$
जो फिर से $\mathrm{q_3}$ के कारण $\mathrm{q_1}$ पर कूलॉम बल है, भले ही अन्य आवेश $\mathrm{q_2}$ मौजूद हो।
इसलिए, दो आवेश $\mathrm{q_2}$ और $\mathrm{q_3}$ के कारण $\mathrm{q_1}$ पर कुल बल $\mathrm{F_1}$ निम्नलिखित द्वारा दिया जाता है
$$ \begin{equation*} \mathbf{F} _{1}=\mathbf{F} _{12}+\mathbf{F} _{13}=\frac{1}{4 \pi \varepsilon _{0}} \frac{q _{1} q _{2}}{r _{12}^{2}} \hat{\mathbf{r}} _{12}+\frac{1}{4 \pi \varepsilon _{0}} \frac{q _{1} q _{3}}{r _{13}^{2}} \hat{\mathbf{r}} _{13} \tag{1.4} \end{equation*} $$
ऊपर की बल की गणना तीन से अधिक आवेशों के एक तंत्र तक सामान्यीकृत की जा सकती है, जैसा कि चित्र 1.8(b) में दिखाया गया है।
सुपरपोजिशन के सिद्धांत के अनुसार, आवेशों के एक तंत्र $\mathrm{q_1}$, $\mathrm{q_2}$, …, qn में, $\mathrm{q_1}$ पर $\mathrm{q_2}$ के कारण बल $\mathrm{q_2}$ के उपस्थिति के कारण बदले बिना कूलॉम के नियम द्वारा दिया गया होता है। अतः आवेश $\mathrm{q_1}$ पर अन्य सभी आवेशों के कारण कुल बल F 1 बलों $\mathrm{F_12}$, F13, …, F1n के सदिश योग द्वारा दिया जाता है, अर्थात,
$$ \begin{align*} & \mathbf{F} _{1}=\mathbf{F} _{12}+\mathbf{F} _{13}+\ldots+\mathbf{F} _{1 n}=\frac{1}{4 \pi \varepsilon _{0}}\left[\frac{q _{1} q _{2}}{r _{12}^{2}} \hat{\mathbf{r}} _{12}+\frac{q _{1} q _{3}}{r _{13}^{2}} \hat{\mathbf{r}} _{13}+\ldots+\frac{q _{1} q _{n}}{r _{1 n}^{2}} \hat{\mathbf{r}} _{1 n}\right] \\ & =\frac{q _{1}}{4 \pi \varepsilon _{0}} \sum _{i=2}^{n} \frac{q _{i}}{r _{1 i}^{2}} \hat{\mathbf{r}} _{1 i} \tag{1.5} \end{align*} $$
सामान्य तरीके से सदिश योग के लिए समान्तर चतुर्भुज नियम का उपयोग करके प्राप्त किया जाता है। विद्युत चुंबकत्व के सभी तत्व बूढ़े काल के कूलॉम के नियम और सुपरपोजिशन के सिद्धांत के परिणाम हैं।
उदाहरण 1.5 तीन आवेश $\mathrm{q_1}$, $\mathrm{q_2}$, $\mathrm{q_3}$, प्रत्येक के मान q है, जो एक समबाहु त्रिभुज के शीर्षों पर स्थित हैं जिसकी भुजा की लंबाई l है। त्रिभुज के केंद्र पर रखे आवेश Q पर बल क्या होगा, जहाँ Q का चिन्ह q के समान है, जैसा कि चित्र 1.9 में दिखाया गया है?

चित्र 1.6
हल दिए गए समबाहु त्रिभुज $\mathrm{ABC}$ की भुजाओं की लंबाई $l$ है, यदि हम भुजा $BC$ पर लंब $AD$ खींचे,
$\mathrm{AD}=\mathrm{AC} \cos 30^{\circ}=(\sqrt{3} / 2) l$ और गुरुत्व केंद्र $\mathrm{O}$ के बिंदु $\mathrm{A}$ से दूरी $\mathrm{AO} = (2 / 3) \mathrm{AD} = (1 / \sqrt{3})$ l है। सममिति के कारण $\mathrm{AO}=\mathrm{BO}=\mathrm{CO}$ है।
इसलिए,
$Q$ पर $A$ पर स्थित $q$ आवेश के कारण बल $\mathbf{F_1} = \frac{3}{4 \pi \varepsilon_{0}} \frac{Q q}{l^{2}}$ बिंदु $\mathrm{AO}$ के अनुदिश है
$Q$ पर $B$ पर स्थित $q$ आवेश के कारण बल $\mathbf{F_2} = \frac{3}{4 \pi \varepsilon_{0}} \frac{Q q}{l^{2}}$ बिंदु $\mathrm{BO}$ के अनुदिश है
$Q$ पर $C$ पर स्थित $q$ आवेश के कारण बल $\mathbf{F_3} = \frac{3}{4 \pi \varepsilon_{0}} \frac{Q q}{l^{2}}$ बिंदु $\mathrm{CO}$ के अनुदिश है
संकेंद्रित बल $\mathbf{F_2}$ और $\mathbf{F_3}$ का परिणाम $\frac{3}{4 \pi \varepsilon_{0}} \frac{Q q}{l^{2}}$ $OA$ के अनुदिश होता है, समानांतर चतुर्भुज के नियम द्वारा।
इसलिए, $Q$ पर कुल बल $\frac{3}{4 \pi \varepsilon_{0}} \frac{Q q}{l^{2}}(\hat{\mathbf{r}}-\hat{\mathbf{r}})$ $=0$ होता है, जहाँ $\hat{\mathbf{r}}$ $OA$ के अनुदिश एक इकाई सदिश है।
सममिति के आधार पर भी स्पष्ट है कि तीन बलों का योग शून्य होता है। मान लीजिए कि परिणामी बल शून्य नहीं है लेकिन किसी दिशा में है। यदि प्रणाली को O के चारों ओर 60° घुमाया जाए, तो इसका क्या होगा इसका विचार करें।
उदाहरण 1.6 एक समबाहु त्रिभुज के शीर्षों पर q, q और –q आवेश रखे गए हैं, जैसा कि चित्र 1.7 में दिखाया गया है। प्रत्येक आवेश पर बल कितना होगा?

चित्र 1.7
हल आवेश $q$ बिंदु A पर आवेश $q$ बिंदु B और $-q$ बिंदु C के कारण बल $\mathbf{F} _{12}$ बिंदु BA के अनुदिश और $\mathbf{F} _{13}$ बिंदु AC के अनुदिश क्रमशः कार्य करता है, जैसा कि चित्र 1.7 में दिखाया गया है। समानांतर चतुर्भुज के नियम द्वारा, आवेश $q$ बिंदु A पर कुल बल $F_1$ द्वारा दिया जाता है $\mathbf{F} _1=F \tilde{\mathbf{r}} _1$ जहाँ $\tilde{\mathbf{r}} _1$ बिंदु BC के अनुदिश एक इकाई सदिश है।
The force of attraction or repulsion for each pair of charges has the same magnitude $F=\frac{q^2}{4 \pi \varepsilon _0 l^2}$
The total force $\mathbf{F} _2$ on charge $q$ at $\mathrm{B}$ is thus $\mathbf{F} _2=F \hat{\mathbf{r}} _2$, where $\hat{\mathbf{r}} _2$ is a unit vector along AC.
Similarly the total force on charge $-q$ at $\mathrm{C}$ is $\mathbf{F}_3=\sqrt{3} F \hat{\mathbf{n}}$, where $\hat{\mathbf{n}}$ is the unit vector along the direction bisecting the $\angle \mathrm{BCA}$. It is interesting to see that the sum of the forces on the three charges is zero, i.e.,
$ \mathbf{F}_1+\mathbf{F}_2+\mathbf{F}_3=0 $
इस परिणाम के बारे में बिलकुल अनुमान लगाना आश्चर्यजनक नहीं है। यह तथ्य के अनुसार है कि कूलॉम के नियम न्यूटन के तीसरे नियम के साथ संगत है। इसका साक्षात्कार आपको एक अभ्यास के रूप में छोड़ दिया गया है।
1.7 विद्युत क्षेत्र
मान लीजिए कि हम एक बिंदु आवेश Q को एक रेखीय रिक्त स्थान में मूल बिंदु O पर रखते हैं। अगर हम एक अन्य बिंदु आवेश q को बिंदु P पर रखते हैं, जहां OP = r है, तो आवेश Q के बल के कारण q पर बल लगता है। हम यह प्रश्न रख सकते हैं: यदि आवेश q हटा दिया जाए, तो आसपास के क्षेत्र में क्या बच जाता है? क्या कुछ भी नहीं बचता है? यदि बिंदु P पर कुछ भी नहीं होता है, तो बल कैसे कार्य करता है जब हम आवेश q को बिंदु P पर रखते हैं। इस प्रकार के प्रश्नों के उत्तर देने के लिए, प्रारंभिक वैज्ञानिकों ने क्षेत्र के अवधारणा को परिचय दिया। इसके अनुसार, हम कहते हैं कि आवेश Q आसपास के सभी स्थानों में एक विद्युत क्षेत्र उत्पन्न करता है। जब एक अन्य आवेश q को किसी बिंदु P पर लाया जाता है, तो वहां के क्षेत्र उस पर बल लगाता है और बल उत्पन्न करता है। आवेश Q द्वारा बिंदु r पर उत्पन्न विद्युत क्षेत्र को निम्नलिखित द्वारा दिया जाता है:
$$ \begin{equation*} \mathbf{E}(\mathbf{r})=\frac{1}{4 \pi \varepsilon_{0}} \frac{Q}{r^{2}} \hat{\mathbf{r}}=\frac{1}{4 \pi \varepsilon_{0}} \frac{Q}{r^{2}} \hat{\mathbf{r}} \tag{1.6} \end{equation*} $$
जहाँ $\hat{\mathbf{r}}=\mathbf{r} / \mathrm{r}$, एक इकाई सदिश है जो मूल बिंदु से बिंदु r तक की दिशा को दर्शाता है। इस प्रकार, समीकरण (1.6) स्थिति सदिश r के प्रत्येक मान के लिए विद्युत क्षेत्र के मान को निर्दिष्ट करता है। शब्द “field” (क्षेत्र) यह दर्शाता है कि कुछ वितरित मात्रा (जो एक अदिश या सदिश हो सकती है) स्थिति के साथ कैसे बदलती है। आवेश के प्रभाव को विद्युत क्षेत्र के अस्तित्व में शामिल कर लिया गया है। हम एक आवेश Q द्वारा आवेश q पर बल F को प्राप्त करते हैं, जैसे कि

चित्र 1.8 विद्युत क्षेत्र (a) आवेश Q के कारण, (b) आवेश –Q के कारण।
$$ \begin{equation*} \mathbf{F}=\frac{1}{4 \pi \varepsilon_{0}} \frac{Q q}{r^{2}} \hat{\mathbf{r}} \tag{1.7} \end{equation*} $$
ध्यान दें कि आवेश $q$ आवेश $Q$ पर बराबर और विपरीत बल भी लगाता है। आवेश $Q$ और $q$ के बीच विद्युत बल को आवेश $q$ और $Q$ के विद्युत क्षेत्र के बीच अंतरक्रिया के रूप में देखा जा सकता है। यदि हम आवेश $q$ की स्थिति को सदिश $\mathbf{r}$ द्वारा निरूपित करते हैं, तो आवेश $q$ पर लगने वाला बल $\mathbf{F}$ आवेश $q$ के आवेश के बराबर होता है जो आवेश $q$ के स्थान पर विद्युत क्षेत्र $\mathbf{E}$ के गुणनफल के बराबर होता है। इसलिए,
$$ \begin{equation*} \mathbf{F}(\mathbf{r})=q \mathbf{E}(\mathbf{r}) \tag{1.8} \end{equation*} $$
समीकरण (1.8) विद्युत क्षेत्र के SI इकाई को न्यूटन/कूलॉम (N/C) के रूप में परिभाषित करता है।
(i) समीकरण (1.8) से हम यह निष्कर्ष निकाल सकते हैं कि यदि q एकता हो, तो आवेश Q के कारण विद्युत क्षेत्र संख्यातः Q आवेश द्वारा लगाए गए बल के बराबर होता है। अतः एक आवेश Q के कारण अंतरिक बिंदु पर विद्युत क्षेत्र को उस बिंदु पर रखे गए एक इकाई धनावेश के द्वारा अनुभव किए गए बल के बराबर माना जा सकता है। आवेश Q, जो विद्युत क्षेत्र उत्पन्न करता है, को स्रोत आवेश कहा जाता है और आवेश q, जो स्रोत आवेश के प्रभाव का परीक्षण करता है, को परीक्षण आवेश कहा जाता है। ध्यान दें कि स्रोत आवेश Q अपनी मूल स्थिति पर रहना आवश्यक है। हालांकि, यदि कोई आवेश q Q के आसपास किसी बिंदु पर लाया जाता है, तो Q खुद q के कारण विद्युत बल का अनुभव करेगा और गति करने की ओर झुकेगा। इस कठिनाई से बचने के एक तरीके को आवेश q को बहुत छोटा बनाना है। तब बल F भी बहुत छोटा हो जाता है, लेकिन F/q का अनुपात अंतर्निहित होता है और विद्युत क्षेत्र को परिभाषित करता है:
$\mathbf{E}=\lim _{q \rightarrow 0}\left(\frac{\mathbf{F}}{q}\right)$ (1.9)
एक व्यावहारिक तरीका इस समस्या (Q को q की उपस्थिति में अनिवार्य रूप से अपरिवर्तित रखे रहने की) के आसपास जाने के लिए Q को अपने स्थान पर अनिर्धारित बलों द्वारा बरकरार रखना है! यह अजीब लग सकता है लेकिन वास्तव में यह व्यावहारिक रूप से होता है। जब हम एक परीक्षण आवेश q के कारण एक आवेशित तल के कारण विद्युत बल के बारे में विचार करते हैं (अनुच्छेद 1.15), तो तल पर आवेश अपने स्थान पर अनिर्धारित आवेशों के कारण बलों द्वारा बरकरार रखे रहते हैं।
(ii) ध्यान दें कि आवेश Q के कारण विद्युत क्षेत्र E, हालांकि कुछ परीक्षण आवेश q के आधार पर परिभाषित किया गया है, लेकिन q पर निर्भर नहीं करता। इसका कारण यह है कि F, q के समानुपाती होता है, इसलिए F/q का अनुपात q पर निर्भर नहीं करता। आवेश Q के कारण आवेश q पर बल F, आवेश q के स्थिति पर निर्भर करता है जो आवेश Q के चारों ओर अंतरिका में कहीं भी हो सकता है। इसलिए, आवेश Q के कारण विद्युत क्षेत्र E, अंतरिका के स्थानीय निर्देशांक r पर भी निर्भर करता है। आवेश q के अलग-अलग स्थितियों के कारण विद्युत क्षेत्र E के अलग-अलग मान प्राप्त होते हैं। विद्युत क्षेत्र तीन-विमीय अंतरिका में प्रत्येक बिंदु पर उपस्थित होता है।
(iii) एक धनात्मक आवेश के लिए, विद्युत क्षेत्र आवेश से बाहर केंद्रित रेडियल रूप से बाहर की ओर दिशा में होता है। दूसरी ओर, यदि स्रोत आवेश नकारात्मक है, तो विद्युत क्षेत्र वेक्टर, प्रत्येक बिंदु पर, आवेश से बाहर केंद्रित रेडियल रूप से अंदर की ओर दिशा में होता है।
(iv) चार्ज q पर चार्ज Q द्वारा बल F के मापदंड के माप केवल चार्ज q और चार्ज Q के बीच की दूरी r पर निर्भर करता है, इसलिए विद्युत क्षेत्र E के माप केवल दूरी r पर निर्भर करता है। इसलिए, चार्ज Q से समान दूरी पर, इसके विद्युत क्षेत्र E के माप समान होता है। एक बिंदु आवेश के कारण विद्युत क्षेत्र E के माप केंद्र पर बिंदु आवेश के एक गोलाकार गोले पर समान होता है; अन्य शब्दों में, इसकी सममिति गोलीय होती है।
1.7.1 आवेशों के एक प्रणाली के कारण विद्युत क्षेत्र
एक आवेशों के प्रणाली $q_{1}, q_{2}, \ldots, q_{n}$ को एक काल्पनिक मूल बिंदु $\mathrm{O}$ के संबंध में स्थिति सदिश $\mathbf{r_1}$, $\mathbf{r_2}, \ldots, \mathbf{r_n}$ से व्यक्त किया जाता है। एक अकेले आवेश के कारण एक बिंदु पर विद्युत क्षेत्र की तरह, एक बिंदु पर विद्युत क्षेत्र को परिभाषित किया जाता है जो एक इकाई परीक्षण आवेश के द्वारा उस बिंदु पर अनुभव किए गए बल के बराबर होता है, जबकि आवेशों $q_{1}, q_{2}, \ldots, q_{n}$ के मूल स्थितियों को बिगाड़े बिना। हम आवेशों के कारण विद्युत क्षेत्र को निर्धारित करने के लिए कूलॉम के नियम और अधिस्थिति सिद्धांत का उपयोग कर सकते हैं। एक बिंदु $\mathrm{P}$ पर विद्युत क्षेत्र को उस बिंदु के स्थिति सदिश $\mathbf{r}$ द्वारा निर्दिष्ट किया जाता है।

चित्र 1.9 आवेशों के एक प्रणाली के कारण एक बिंदु पर विद्युत क्षेत्र, विभिन्न आवेशों के कारण उस बिंदु पर विद्युत क्षेत्र के सदिश योग होता है।
$ q_{1} $ के कारण $ \mathbf{r} $ पर विद्युत क्षेत्र $ \mathbf{E_1} $ निम्नलिखित द्वारा दिया जाता है
$$ \mathbf{E_1}=\frac{1}{4 \pi \varepsilon _{0}} \frac{q _{1}}{r _{1 \mathrm{P}}^{2}} \hat{\mathbf{r}} _{1 \mathrm{P}} $$
$$
जहाँ $\hat{\mathbf{r _1}} \mathrm{P}$, $q _{1}$ से $\mathrm{P}$ की दिशा में एक इकाई सदिश है, और $r _{1} \mathrm{P}$, $q _{1}$ और $\mathrm{P}$ के बीच की दूरी है। इसी तरह, $q _{2}$ के कारण $\mathbf{r}$ पर विद्युत क्षेत्र $\mathbf{E}v _{2}$ है
$$ \mathbf{E_2}=\frac{1}{4 \pi \varepsilon_{0}} \frac{q_{2}}{r_{2 \mathrm{P}}^{2}} \hat{\mathbf{r}}_{2 \mathrm{P}} $$
जहाँ $\hat{\mathbf{r _2} \mathrm{P}}$ $q _{2}$ से $\mathrm{P}$ की दिशा में एक इकाई सदिश है और $r _{2 \mathrm{P}}$ $q _{2}$ और $\mathrm{P}$ के बीच की दूरी है। चार्ज $q _{3}, q _{4}, \ldots, q _{n}$ के कारण क्षेत्र $\mathbf{E _3}, \mathbf{E _4}, \ldots, \mathbf{E _n}$ के लिए भी ऐसी समान अभिव्यक्तियाँ लागू होती हैं।
सुपरपोज़िशन सिद्धांत के अनुसार, आवेशों के एक निकाय के कारण $\mathbf{r}$ पर विद्युत क्षेत्र $\mathbf{E}$ (चित्र 1.9 में दिखाया गया है) है:
$$ \begin{align*} \mathbf{E}(\mathbf{r}) & =\mathbf{E} _{1}(\mathbf{r})+\mathbf{E} _{2}(\mathbf{r})+\ldots+\mathbf{E} _{\mathrm{n}}(\mathbf{r}) \\ & =\frac{1}{4 \pi \varepsilon _{0}} \frac{q _{1}}{r _{1 \mathrm{P}}^{2}} \hat{\mathbf{r}} _{1 \mathrm{P}}+\frac{1}{4 \pi \varepsilon _{0}} \frac{q _{2}}{r _{2 \mathrm{P}}^{2}} \hat{\mathbf{r}} _{2 \mathrm{P}}+\ldots+\frac{1}{4 \pi \varepsilon _{0}} \frac{q _{n}}{r _{n \mathrm{P}}^{2}} \hat{\mathbf{r}} _{n \mathrm{P}} \\ $$
$$ \mathbf{E}(\mathbf{r}) & =\frac{1}{4 \pi \varepsilon _{0}} \sum _{i=1}^{n} \frac{q _{i}}{r _{i \mathrm{P}}^{2}} \hat{\mathbf{r}} _{\mathrm{iP}} \tag{1.10} \end{align*} $$
$$ \mathbf{E} $$ एक सदिश राशि है जो अंतरिक अंतर के बीच बदलती रहती है और आवेश के स्रोत के स्थानों से निर्धारित की जाती है।
1.7.2 विद्युत क्षेत्र के भौतिक महत्व
आप यह चिंतित हो सकते हैं कि यहाँ विद्युत क्षेत्र की अवधारणा क्यों प्रस्तुत की गई है। बर्बाद, किसी आवेश प्रणाली के लिए माप्य राशि एक आवेश पर बल होता है जिसे कूलॉम के नियम और अधिवृत्ति सिद्धांत [समीकरण (1.5)] का प्रयोग करके सीधे निर्धारित किया जा सकता है। तो फिर इस बीच राशि के रूप में विद्युत क्षेत्र की अवधारणा क्यों प्रस्तुत की गई है?
इलेक्ट्रोस्टैटिक्स के लिए, विद्युत क्षेत्र की अवधारणा सुविधाजनक होती है, लेकिन वास्तव में आवश्यक नहीं होती। विद्युत क्षेत्र एक सुंदर तरीका है जिसके माध्यम से आवेशों के एक प्रणाली के विद्युत वातावरण की विशेषता को वर्णित किया जा सकता है। आवेशों के एक प्रणाली के आसपास अंतरिक बिंदु पर विद्युत क्षेत्र आपको बताता है कि यदि आप उस बिंदु पर एक इकाई धनात्मक परीक्षण आवेश को रखते हैं (तो प्रणाली को बिगाड़े बिना), तो उस बिंदु पर आवेश के द्वारा अनुभव किए जाने वाले बल के बारे में क्या होता है। विद्युत क्षेत्र आवेशों के प्रणाली की विशेषता होता है और इसके निर्धारण के लिए आप जो बिंदु पर परीक्षण आवेश रखते हैं उसके आधार पर निर्भर नहीं होता। भौतिकी में “क्षेत्र” शब्द आमतौर पर एक राशि को बताता है जो अंतरिक के प्रत्येक बिंदु पर परिभाषित होती है और बिंदु से बिंदु तक भिन्न हो सकती है। विद्युत क्षेत्र एक सदिश क्षेत्र होता है, क्योंकि बल एक सदिश राशि होती है।
किसी भी विद्युत क्षेत्र के वास्तविक भौतिक अर्थ केवल तभी स्पष्ट होता है जब हम विद्युत स्थैतिक विज्ञान से बाहर निकलकर समय-संवेदी विद्युत-चुंबकीय घटनाओं के साथ लड़ाई लड़ते हैं। मान लीजिए हम दूर के दो आवेश $\mathrm{q_1}$, $\mathrm{q_2}$ के बीच बल के बारे में सोच रहे हैं जो त्वरित गति में हैं। अब किसी भी संकेत या सूचना के एक बिंदु से दूसरे बिंदु तक सबसे तेज गति c होती है, जो प्रकाश की गति है। इसलिए, $\mathrm{q_1}$ की कोई गति $\mathrm{q_2}$ पर प्रभाव तुरंत नहीं उत्पन्न कर सकती। कारण ( $\mathrm{q_1}$ की गति) और परिणाम ( $\mathrm{q_2}$ पर बल) के बीच कुछ समय लगेगा। यहीं पर विद्युत क्षेत्र (कठिन रूप से विद्युत-चुंबकीय क्षेत्र) की अवधारणा प्राकृतिक और बहुत उपयोगी होती है। क्षेत्र के चित्र यह है: $\mathrm{q_1}$ के त्वरित गति के कारण विद्युत-चुंबकीय तरंगें उत्पन्न होती हैं, जो तेजी से c के गति से चलती हैं, $\mathrm{q_2}$ पर पहुंचती हैं और $\mathrm{q_2}$ पर बल उत्पन्न करती हैं। क्षेत्र की अवधारणा समय देरी के लिए सुंदर रूप से खाता है। इसलिए, हालांकि विद्युत और चुंबकीय क्षेत्र केवल आवेशों पर बल के प्रभावों द्वारा खोजे जा सकते हैं, वे भौतिक पिण्ड के रूप में देखे जाते हैं, न कि केवल गणितीय रचनाओं के रूप में। वे अपने आप में स्वतंत्र भौतिक गति के अधीन होते हैं, अर्थात वे अपने नियमों के अनुसार विकसित होते हैं। वे ऊर्जा के वाहक भी हो सकते हैं। इसलिए, एक समय-संवेदी विद्युत-चुंबकीय क्षेत्र के स्रोत को एक छोटे समय अंतराल के लिए चालू कर दिया जाता है और फिर बंद कर दिया जाता है, तो वह ऊर्जा वाहक विद्युत-चुंबकीय क्षेत्र के रूप में छोड़ देता है। क्षेत्र की अवधारणा पहले फैराडे द्वारा प्रस्तुत की गई थी और अब भौतिकी के केंद्रीय अवधारणाओं में से एक है।
उदाहरण 1.8 एक इलेक्ट्रॉन एक समान विद्युत क्षेत्र में $1.5 \mathrm{~cm}$ की दूरी तय करता है जिसका परिमाण $2.0 \times 10^{4} \mathrm{~N} \mathrm{C}^{-1}$ है [चित्र 1.10(a)]। क्षेत्र की दिशा विपरीत रखते हुए उसके परिमाण को अपरिवर्तित रखा जाता है और एक प्रोटॉन उसी दूरी तक गिरता है [चित्र 1.10(b)]। प्रत्येक स्थिति में गिरने के समय की गणना कीजिए। ‘गुरुत्वाकर्षण के अंतर्गत मुक्त गिरावट’ के साथ इस स्थिति की तुलना कीजिए।

चित्र 1.10
हल क्षेत्र ऊपर की ओर है, इसलिए नकारात्मक आवेश वाले इलेक्ट्रॉन पर नीचे की ओर बल कार्य करता है जिसका मान $e E$ है, जहाँ $E$ विद्युत क्षेत्र के मान को दर्शाता है। इलेक्ट्रॉन के त्वरण को निम्नलिखित द्वारा दर्शाया जा सकता है:
$$ a _{e}=e E / m _{e} $$
जहाँ $m_{e}$ इलेक्ट्रॉन के द्रव्यमान को दर्शाता है।
शुरू से विराम में, इलेक्ट्रॉन द्वारा दूरी $h$ के माध्यम से गिरने के लिए आवश्यक समय निम्नलिखित द्वारा दिया जाता है:
$$ \begin{aligned} t _{e} & =\sqrt{\frac{2 h}{a _{e}}}=\sqrt{\frac{2 h m _{e}}{e E}} \\ e & =1.6 \times 10^{-19} \mathrm{C}, m _{\mathrm{e}}=9.11 \times 10^{-31} \mathrm{~kg}, \\
$$ E & =2.0 \times 10^{4} \mathrm{~N} \mathrm{C}^{-1}, h=1.5 \times 10^{-2} \mathrm{~m}, \\ t _{\mathrm{e}} & =2.9 \times 10^{-9} \mathrm{~s} \end{aligned} $$
चित्र 1.13 (b) में, क्षेत्र नीचे की ओर है, और धनावेशित प्रोटॉन के लिए बल का परिमाण $e E$ है। प्रोटॉन के त्वरण को निम्नलिखित द्वारा दिया जाता है:
$$ a_{p}=e E / m_{p} $$
जहाँ $m_{p}$ प्रोटॉन के द्रव्यमान है; $m_{p}=1.67 \times 10^{-27} \mathrm{~kg}$. प्रोटॉन के गिरने के समय $t_{p}=\sqrt{\frac{2 h}{a_{p}}}=\sqrt{\frac{2 h m_{p}}{e E}}=1.3 \times 10^{-7} \mathrm{~s}$
इसलिए, भारी कण (प्रोटॉन) एक ही दूरी के माध्यम से गिरने में अधिक समय लेता है। यह ‘गुरुत्वाकर्षण के अंतर्गत मुक्त गिरावट’ की स्थिति के मूलभूत विरोध में है, जहाँ गिरावट के समय के लिए वस्तु के द्रव्यमान के अधिकार के बारे में निरपेक्ष होता है। ध्यान दें कि इस उदाहरण में हम गिरावट के समय की गणना के लिए गुरुत्वाकर्षण के कारण त्वरण को नगण्य मान रहे हैं। इसकी योग्यता की जांच करने के लिए, दिए गए विद्युत क्षेत्र में प्रोटॉन के त्वरण की गणना करें:
$$a_{p}=\frac{e E}{m_{p}}$$
$$ \begin{aligned} & =\frac{\left(1.6 \times 10^{-19} \mathrm{C}\right) \times\left(2.0 \times 10^{4} \mathrm{~N} \mathrm{C}^{-1}\right)}{1.67 \times 10^{-27} \mathrm{~kg}} \\
$$ a =1.9 \times 10^{12} \mathrm{~m} \mathrm{~s}^{-2} $$
$$ \end{aligned} $$
जो कि $g\left(9.8 \mathrm{~m} \mathrm{~s}^{-2}\right)$, गुरुत्वाकर्षण के कारण त्वरण के मान की तुलना में बहुत बड़ा है। इलेक्ट्रॉन का त्वरण इतना अधिक है कि इस उदाहरण में गुरुत्वाकर्षण के कारण त्वरण का प्रभाव नगण्य माना जा सकता है।
उदाहरण 1.9 दो बिंदु आवेश $q_{1}$ और $q_{2}$, जिनके परिमाण क्रमशः $+10^{-8} \mathrm{C}$ और $-10^{-8} \mathrm{C}$ हैं, को एक-दूसरे से $0.1 \mathrm{~m}$ की दूरी पर रखा गया है। चित्र 1.14 में दिखाए गए बिंदुओं A, B और C पर विद्युत क्षेत्र की गणना कीजिए।

चित्र 1.10
हल धनात्मक आवेश $q_{1}$ के कारण बिंदु $\mathrm{A}$ पर विद्युत क्षेत्र सदिश $\mathbf{E_1} \mathrm{~A}$ दाहिने ओर बिंदु तक इंगित करता है और इसका परिमाण निम्नलिखित है
$$ E_{1 \mathrm{~A}}=\frac{\left(9 \times 10^{9} \mathrm{Nm}^{2} \mathrm{C}^{-2}\right) \times\left(10^{-8} \mathrm{C}\right)}{(0.05 \mathrm{~m})^{2}}=3.6 \times 10^{4} \mathrm{~N} \mathrm{C}^{-1} $$
$$
A बिंदु पर नकारात्मक आवेश $q_{2}$ के कारण विद्युत क्षेत्र सदिश $\mathbf{E_2} \mathrm{~A}$ दाहिना दिशा में बिंदु तक बिंदु बराबर मापदंड है। अतः बिंदु A पर कुल विद्युत क्षेत्र $E_{\mathrm{A}}$ के मापदंड है
$E_{\mathrm{A}}=E_1 \mathrm{~A}+E_{2 \mathrm{~A}}=7.2 \times 10^{4} \mathrm{~N} \mathrm{C}^{-1}$ $\mathbf{E}_{\mathrm{A}}$ दाहिना दिशा में दिशित है।
बिंदु B पर धनात्मक आवेश $q _{1}$ के कारण विद्युत क्षेत्र सदिश $\mathbf{E} _{1 \mathrm{~B}}$ बाएं दिशा में बिंदु तक बिंदु बराबर मापदंड है और इसके मापदंड है
$$ E _{1 \mathrm{~B}}=\frac{\left(9 \times 10^{9} \mathrm{Nm}^{2} \mathrm{C}^{-2}\right) \times\left(10^{-8} \mathrm{C}\right)}{(0.05 \mathrm{~m})^{2}}=3.6 \times 10^{4} \mathrm{~N} \mathrm{C}^{-1} $$
बिंदु B पर नकारात्मक आवेश $q _{2}$ के कारण विद्युत क्षेत्र सदिश $\mathbf{E} _{2 \mathrm{~B}}$ के दाईं ओर इंगित करता है और इसका परिमाण निम्नलिखित है
$$ E_{2 \mathrm{~B}}=\frac{\left(9 \times 10^{9} \mathrm{Nm}^{2} \mathrm{C}^{-2}\right) \times\left(10^{-8} \mathrm{C}\right)}{(0.15 \mathrm{~m})^{2}}=4 \times 10^{3} \mathrm{~N} \mathrm{C}^{-1} $$
$$
$\mathrm{B}$ पर कुल विद्युत क्षेत्र के परिमाण को
$$ E_{\mathrm{B}}=E_{1 \mathrm{~B}}-E_{2 \mathrm{~B}}=3.2 \times 10^{4} \mathrm{~N} \mathrm{C}^{-1} $$
$\mathbf{E}_{\mathrm{B}}$ बाईं ओर दिशा में है।
बिंदु $\mathrm{C}$ पर प्रत्येक विद्युत क्षेत्र सदिश के परिमाण, $q_{1}$ और $q_{2}$ आवेश के कारण है
$$ E_{1 \mathrm{C}}=E_{2 \mathrm{C}}=\frac{\left(9 \times 10^{9} \mathrm{Nm}^{2} \mathrm{C}^{-2}\right) \times\left(10^{-8} \mathrm{C}\right)}{(0.10 \mathrm{~m})^{2}}=9 \times 10^{3} \mathrm{~N} \mathrm{C}^{-1}
$$
इन दो वेक्टरों के दिशा चित्र 1.11 में दिखाई गई है। इन दो वेक्टरों का परिणाम है
$$ E_{C}=E_{1 c} \cos \frac{\pi}{3}+E_{2 c} \cos \frac{\pi}{3}=9 \times 10^{3} \mathrm{~N} \mathrm{C}^{-1} $$
$\mathbf{E}_{\mathrm{C}}$ दाईं ओर बिंदु बताता है।

चित्र 1.12 बिंदु आवेश के क्षेत्र।
हम चित्र को कागज के तल पर बनाते हैं, अर्थात द्विविमीय में, लेकिन हम त्रिविमीय में रहते हैं। इसलिए यदि किसी को क्षेत्र रेखाओं की घनत्व का अनुमान लगाना हो, तो उसे रेखाओं के लंब अनुप्रस्थ काट के क्षेत्रफल पर रेखाओं की संख्या को ध्यान में रखना पड़ता है। चूंकि विद्युत क्षेत्र बिंदु आवेश से दूरी के वर्ग के अनुपात में कम होता है और आवेश के घेरे के क्षेत्रफल दूरी के वर्ग के अनुपात में बढ़ता है, इसलिए आवेश के घेरे के क्षेत्रफल के माध्यम से गुजरने वाली रेखाओं की संख्या आवेश से क्षेत्र की दूरी के बावजूद स्थिर रहती है।

चित्र 1.13 विद्युत क्षेत्र के तीव्रता के दूरी पर निर्भरता और इसका क्षेत्र रेखाओं की संख्या से संबंध।
हम शुरू करते हैं कि क्षेत्र रेखाएँ विद्युत क्षेत्र की दिशा के बारे में जानकारी ले आती हैं जो अंतरिक्ष में विभिन्न बिंदुओं पर होती हैं। एक निश्चित सेट की क्षेत्र रेखाओं के बाद, विभिन्न बिंदुओं पर क्षेत्र रेखाओं की सापेक्ष घनत्व (अर्थात, कुछ निकटता) उन बिंदुओं पर विद्युत क्षेत्र की सापेक्ष तीव्रता को दर्शाता है। क्षेत्र रेखाएँ जहाँ क्षेत्र तीव्र होता है घनी होती हैं और जहाँ क्षेत्र कम होता है वहाँ वे दूर फैली होती हैं। चित्र 1.16 एक सेट क्षेत्र रेखाओं को दर्शाता है। हम दो बराबर और छोटे क्षेत्र के तत्वों को बिंदु R और S पर रख सकते हैं जहाँ वे क्षेत्र रेखाओं के लंबवत होते हैं। हमारी छवि में क्षेत्र रेखाओं की संख्या जो क्षेत्र तत्वों को काटती है उन बिंदुओं पर क्षेत्र के मान के समानुपाती होती है। छवि दर्शाती है कि R पर क्षेत्र R पर क्षेत्र अधिक तीव्र है। क्षेत्र रेखाओं के क्षेत्र के आधार पर निर्भरता, या बल्कि एक क्षेत्र तत्व द्वारा घन खंड के द्वारा बनाए गए ठोस कोण के आधार पर निर्भरता को समझने के लिए हम एक क्षेत्र को ठोस कोण से संबंधित करने की कोशिश करेंगे, जो तीन आयामों में कोण के सामान्यीकरण है।
याद करें कि दो-आयाम में एक (समतल) कोण किस प्रकार परिभाषित किया जाता है। मान लीजिए कि एक छोटा अपरिवर्ती रेखा तत्व $\Delta l$ बिंदु $O$ से दूरी $r$ पर रखा गया है। तब इस $\Delta l$ द्वारा $\mathrm{O}$ पर बनाया गया कोण लगभग $\Delta \theta = \Delta l / r$ के बराबर होता है। इसी तरह, तीन आयाम में एक ठोस कोण* द्वारा एक छोटे लंब तल क्षेत्रफल $\Delta S$ द्वारा बनाया गया ठोस कोण दूरी $r$ पर लिखा जा सकता है $\Delta \Omega = \Delta S / r^{2}$. हम जानते हैं कि एक दिए गए ठोस कोण में विराम वृत्त रेखाओं की संख्या समान होती है। चित्र 1.13 में, आवेश से दूरी $r_{1}$ और $r_{2}$ पर दो बिंदुओं $\mathrm{P_1}$ और $\mathrm{P_2}$ के लिए, ठोस कोण $\Delta \Omega$ बनाने वाले क्षेत्रफल के तत्व क्रमशः $\mathrm{P_1}$ पर $r_{1^2} \Delta \Omega$ और $\mathrm{P_2}$ पर $r_{2^2} \Delta \Omega$ होते हैं। इन क्षेत्रफल तत्वों को काटने वाली रेखाओं की संख्या (मान लीजिए $n$) समान होती है। इसलिए, इकाई क्षेत्रफल तत्व को काटने वाली रेखाओं की संख्या क्रमशः $\mathrm{P_1}$ पर $n / \left(r_{1^2} \Delta \Omega\right)$ और $\mathrm{P_2}$ पर $n / \left(r_{2^2} \Delta \Omega\right)$ होती है। चूंकि और $\Delta \Omega$ सामान हैं, इसलिए स्पष्ट रूप से क्षेत्र की तीव्रता $1 / r^{2}$ के अनुपात में होती है।
चुंबकीय क्षेत्र के लिए फैराडे द्वारा बनाई गई चुंबकीय रेखाओं की छवि के बारे में बात करते हैं। फैराडे ने इन्हें बल रेखाएं कहा। यह शब्द कुछ तरीके से गलत अर्थ देता है, विशेष रूप से चुंबकीय क्षेत्र के मामले में। इसके बजाय अधिक उपयुक्त शब्द “क्षेत्र रेखाएं” (इलेक्ट्रिक या मैग्नेटिक) हैं, जिन्हें हम इस किताब में अपनाया है।
- ठोस कोण एक शंकु के माप को दर्शाता है। एक दिए गए शंकु को त्रिज्या $R$ के गोले के साथ कटाव करें। शंकु के ठोस कोण $\Delta \Omega$ को परिभाषित किया गया है जो $ \Delta S / R^2 $ के बराबर होता है, जहां $\Delta S$ शंकु द्वारा गोले पर काटे गए क्षेत्र का क्षेत्रफल है।
विद्युत क्षेत्र रेखाएँ इस प्रकार एक चित्र द्वारा आवेशों के एक व्यवस्था के आसपास विद्युत क्षेत्र को नक्शा बनाने का एक तरीका है। एक विद्युत क्षेत्र रेखा आमतौर पर एक ऐसी वक्र होती है जिसे इस प्रकार खींचा जाता है कि इसके प्रत्येक बिंदु पर इसकी स्पर्श रेखा उस बिंदु पर शुद्ध क्षेत्र की दिशा में होती है। एक वक्र पर एक तीर निश्चित रूप से आवश्यक होता है ताकि विद्युत क्षेत्र की दिशा को दो संभावित दिशाओं में से एक को निर्दिष्ट किया जा सके जो वक्र की स्पर्श रेखा द्वारा दर्शाई गई होती है। एक क्षेत्र रेखा एक अंतरिक वक्र होती है, अर्थात तीन आयामों में एक वक्र होती है।
चित्र 1.17 कुछ सरल आवेश व्यवस्थाओं के आसपास क्षेत्र रेखाओं को दिखाता है। जैसा कि पहले उल्लेख किया गया है, क्षेत्र रेखाएँ तीन आयामी अंतरिक स्थान में होती हैं, हालांकि चित्र उन्हें केवल एक तल में दिखाता है। एक धनावेश के क्षेत्र रेखाएँ त्रिज्यागत रूप से बाहर की ओर होती हैं, जबकि एक नकारात्मक आवेश के क्षेत्र रेखाएँ त्रिज्यागत रूप से अंदर की ओर होती हैं। दो धनावेशों (q, q) की व्यवस्था के आसपास क्षेत्र रेखाएँ उनके परस्पर विरोधाभास का एक जोरदार चित्र देती हैं, जबकि दो समान आवेशों (q, –q) की व्यवस ती जो एक द्विध्रुव (dipole) के रूप में होती है, आवेशों के परस्पर आकर्षण को स्पष्ट रूप से दिखाती है। क्षेत्र रेखाएँ कुछ महत्वपूर्ण सामान्य गुणों का पालन करती हैं:
(i) चुंबकीय रेखाएँ धनात्मक आवेश से शुरू होती हैं और ऋणात्मक आवेश पर समाप्त होती हैं। यदि केवल एक आवेश हो, तो वे अपरिमित दूरी पर शुरू या समाप्त हो सकती हैं।
(ii) आवेश रहित क्षेत्र में, विद्युत क्षेत्र रेखाएँ कोई भी ब्रेक बिना लगातार वक्र हो सकती हैं।
(iii) दो विद्युत क्षेत्र रेखाएँ कभी एक दूसरे को काट नहीं सकती हैं। (यदि वे काटती हैं, तो कटान बिंदु पर क्षेत्र के एक अद्वितीय दिशा होना आवश्यक है, जो असंभव है।)
(iv) विद्युत स्थैतिक क्षेत्र रेखाएँ कोई बंद लूप नहीं बनाती हैं। यह विद्युत क्षेत्र के संरक्षित प्रकृति से आता है (अध्याय 2)।

चित्र 1.14 कुछ सरल आवेश विन्यास के कारण क्षेत्र रेखाएँ।
1.9 विद्युत फ्लक्स
एक तरल के प्रवाह को विचार करें जिसकी चाल $\mathbf{v}$ है, एक छोटे से समतल क्षेत्र $\mathrm{d} S$ के माध्यम से एक दिशा में जो कि उस सतह के लम्बवत है। तरल के प्रवाह की दर एक इकाई समय में क्षेत्रफल के माध्यम से पारित आयतन $v \mathrm{~d} S$ द्वारा दी जाती है और यह तल के माध्यम से प्रवाहित हो रहे तरल के फ्लक्स को प्रदर्शित करती है। यदि सतह के लम्ब किसी भी दिशा में तरल के प्रवाह के समानांतर नहीं है, अर्थात तरल के प्रवाह की दिशा $\mathbf{v}$ के समानांतर नहीं है, बल्कि इसके साथ कोण $\theta$ बनाता है, तो $\mathbf{v}$ के लम्बवत तल में प्रक्षेपित क्षेत्रफल $\delta \mathrm{d} S \cos \theta$ होता है। अतः, $\mathrm{d} S$ सतह से बाहर जाने वाला फ्लक्स $\mathbf{v} \cdot \hat{\mathbf{n}} \mathrm{d} S$ होता है। विद्युत क्षेत्र के मामले में, हम एक समान राशि परिभाषित करते हैं जिसे हम विद्युत फ्लक्स कहते हैं। हालांकि, हम ध्यान रखें कि वास्तविक रूप से देखे जा सकने वाली राशि के प्रवाह के विपरीत, तरल के प्रवाह के मामले में ऐसा नहीं होता।
ऊपर वर्णित विद्युत क्षेत्र रेखाओं के चित्र में हम देखा कि एक बिंदु पर विद्युत क्षेत्र के लंब दिशा में रखे एक इकाई क्षेत्रफल के माध्यम से गुजरने वाली रेखाओं की संख्या उस बिंदु पर विद्युत क्षेत्र की ताकत का मापदंड है। इसका अर्थ है कि यदि हम एक छोटे तल के क्षेत्रफल के एक अवयव ∆S को विद्युत क्षेत्र E के लंब दिशा में एक बिंदु पर रखे, तो इसके माध्यम से गुजरने वाली रेखाओं की संख्या E ∆S के समानुपाती होती है। अब मान लीजिए कि हम क्षेत्रफल के अवयव को कोण θ के कारण झुका देते हैं। स्पष्ट रूप से, क्षेत्रफल के अवयव के माध्यम से गुजरने वाली रेखाओं की संख्या कम हो जाएगी। क्षेत्रफल के अवयव के विद्युत क्षेत्र के लंब दिशा में प्रक्षेप निर्देशांक ∆S cosθ होता है। अतः, क्षेत्रफल के अवयव ∆S के माध्यम से गुजरने वाली रेज़ की संख्या E ∆S cosθ के समानुपाती होती है। जब θ = 90° होता है, तो रेखाएँ ∆S के समानांतर होती हैं और इनके माध्यम से गुजरने वाली रेखाएँ नहीं होती हैं (चित्र 1.15)।

चित्र 1.15 विद्युत क्षेत्र $\mathbf{E}$ और $\hat{\mathrm{n}}$ के बीच कोण $\theta$ पर फ्लक्स के निर्भरता।
क्षेत्र के तत्व के उपरितल के आकार के बराबर नहीं, बल्कि उसकी दिशा भी कई संदर्भों में महत्वपूर्ण होती है। उदाहरण के लिए, एक नदी में, एक वलय के माध्यम से पानी के प्रवाह की मात्रा वलय के तरीके पर निर्भर करती है। यदि आप वलय को प्रवाह के लंबवत धारण करते हैं, तो उसके माध्यम से अधिकतम पानी प्रवाहित होगा, जबकि आप अन्य दिशा में धारण करते हैं तो न्यूनतम पानी प्रवाहित होगा। यह दिखाता है कि एक क्षेत्र के तत्व को एक सदिश के रूप में लेना चाहिए। इसके आकार और दिशा दोनों होते हैं। एक समतल क्षेत्र की दिशा कैसे निर्धारित करें? स्पष्ट रूप से, समतल के लंबवत दिशा समतल की दिशा को निर्धारित करती है। इसलिए, एक समतल क्षेत्र सदिश की दिशा उसके लंबवत दिशा में होती है।
कैसे एक वेक्टर को वक्र पृष्ठ के क्षेत्रफल के साथ संबंधित किया जाए? हम अपने मन में इस पृष्ठ को बहुत छोटे क्षेत्र तत्वों में विभाजित करते हैं। प्रत्येक छोटे क्षेत्र तत्व को तल के रूप में ले लिया जा सकता है और इसके साथ एक वेक्टर को जोड़ा जा सकता है, जैसा कि पहले समझाया गया है।
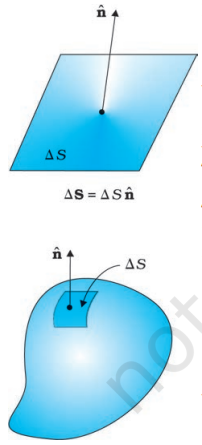
चित्र 1.16 नॉर्मल $\hat{\mathrm{n}}$ और $\Delta \mathrm{S}$ को परिभाषित करने की संवाद।
यहाँ एक अस्पष्टता ध्यान में रखें। क्षेत्र के एक तत्व की दिशा उसके अभिलम्ब के अनुदिश होती है। लेकिन एक अभिलम्ब दो दिशाओं में बिंदु सकता है। इस दिशा के चयन के लिए हमें किस दिशा को क्षेत्र तत्व के संगत सदिश की दिशा माना जाए? इस समस्या को किसी भी दिए गए संदर्भ के अनुरूप एक संमति द्वारा हल किया जाता है। बंद सतह के मामले में यह संमति बहुत सरल होती है। बंद सतह के प्रत्येक क्षेत्र तत्व के संगत सदिश को बाहरी अभिलम्ब की दिशा में लिया जाता है। यह आकृति 1.19 में उपयोग की गई संमति है। इसलिए, बंद सतह पर एक बिंदु पर क्षेत्र तत्व सदिश ∆S, बिंदु पर बाहरी अभिलम्ब की दिशा में इकाई सदिश nˆ के साथ ∆S nˆ के बराबर होता है, जहाँ ∆S क्षेत्र तत्व के परिमाण है और nˆ बिंदु पर बाहरी अभिलम्ब की दिशा में इकाई सदिश है।
अब हम विद्युत फ्लक्स के परिभाषा पर आ गए हैं। एक क्षेत्र के तत्व ∆S के माध्यम से विद्युत फ्लक्स ∆φ निम्नलिखित द्वारा परिभाषित किया जाता है
$$ \begin{equation*} \Delta \phi=\mathbf{E} \cdot \Delta \mathbf{S}=E \Delta S \cos \theta \tag{1.11} \end{equation*} $$
जैसा कि पहले देखा गया है, यह क्षेत्र रेखाओं की संख्या के समानुपाती होता है जो क्षेत्र के तत्व को काटती हैं। यहाँ कोण $\theta$ विद्युत क्षेत्र $\mathbf{E}$ और क्षेत्र के तत्व $\Delta \mathbf{S}$ के बीच का कोण है। एक बंद सतह के लिए, जैसा कि पहले बताया गया है, $\theta$ विद्युत क्षेत्र $\mathbf{E}$ और क्षेत्र के तत्व के बाहरी अभिलम्ब के बीच का कोण होता है। ध्यान दें कि हम अभिव्यक्ति $E \Delta S \cos \theta$ को दो तरीकों से देख सकते हैं: $E(\Delta S \cos \theta)$ अर्थात $E$ के गुणनफल के रूप में[^3] क्षेत्र के लंब अभिलम्ब के प्रक्षेप के अर्थात या $E_{\perp} \Delta S$, अर्थात क्षेत्र के तत्व के अभिलम्ब के अनुदिश $\mathbf{E}$ के घटक के अर्थात क्षेत्र के तत्व के आकार के परिमाण के गुणनफल। विद्युत फ्लक्स की इकाई $\mathrm{N} \mathrm{C}^{-1} \mathrm{~m}^{2}$ होती है।
- कहना अनुचित होगा कि क्षेत्र रेखाओं की संख्या $E \Delta S$ के बराबर होती है। क्षेत्र रेखाओं की संख्या बिलकुल एक विषय है जो विचार करते हुए हम कितनी क्षेत्र रेखाओं को खींचना चाहते हैं। भौतिक रूप से महत्वपूर्ण बात विभिन्न बिंदुओं पर एक दिए गए क्षेत्र के माध्यम से क्रॉसिंग करने वाली क्षेत्र रेखाओं की संख्या के संबंध में है।
समीकरण (1.11) द्वारा दिए गए विद्युत फ्लक्स के मूल परिभाषा का उपयोग सिद्धांत रूप से किसी भी दिए गए सतह के माध्यम से कुल फ्लक्स की गणना करने के लिए किया जा सकता है। हमें केवल यह करना होगा कि सतह को छोटे क्षेत्र तत्वों में विभाजित कर दें, प्रत्येक तत्व पर फ्लक्स की गणना करें और उन्हें जोड़ दें। इस प्रकार, एक सतह $S$ के माध्यम से कुल फ्लक्स $\phi$ होता है:
$$ \begin{equation*} \phi \simeq \Sigma \mathbf{E} \cdot \Delta \mathbf{S} \tag{1.12} \end{equation*} $$
अंकन चिह्न के उपयोग का कारण यह है कि विद्युत क्षेत्र $\mathbf{E}$ को छोटे क्षेत्र के तत्व पर स्थिर मान लिया जाता है। यह गणितीय रूप से सटीक केवल तब होता है जब आप $\Delta S \rightarrow 0$ की सीमा लेते हैं और समीकरण (1.12) में योग को एक समाकलन के रूप में लिखा जाता है।
1.10 विद्युत द्विध्रुव
एक विद्युत द्विध्रुव एक समान और विपरीत बिंदु आवेश q और –q के जोड़े को कहते हैं, जो 2a की दूरी पर अलग होते हैं। दो आवेशों को जोड़ने वाली रेखा अंतरिक अंतर के एक दिशा को परिभाषित करती है। संमवाद के अनुसार, –q से q की दिशा को द्विध्रुव की दिशा कहा जाता है। –q और q के स्थान के मध्य बिंदु को द्विध्रुव के केंद्र कहते हैं।
विद्युत द्विध्रुव के आवेश कुल स्पष्ट रूप से शून्य होता है। यह नहीं मतलब कि विद्युत द्विध्रुव के क्षेत्र शून्य होता है। चूंकि आवेश q और –q कुछ दूरी पर अलग होते हैं, इनके कारण विद्युत क्षेत्र, जब जोड़े जाते हैं, ठीक रूप से विपरीत नहीं होते। हालांकि, दो आवेशों के बीच की दूरी के बहुत बड़े दूरी पर (r » 2a), q और –q के कारण क्षेत्र लगभग विपरीत हो जाते हैं। इसलिए विद्युत द्विध्रुव के कारण क्षेत्र, बड़ी दूरी पर, एक विद्युत आवेश q के कारण क्षेत्र के तुलना में तेजी से घटता है (1/r² के अनुपात में)। इन गुणात्मक विचारों को निम्नलिखित व्यापक गणना द्वारा सत्यापित किया जाता है:
1.10.1 विद्युत द्विध्रुव के क्षेत्र
कोई बिंदु वायु में हो या नहीं, विद्युत द्विध्रुव के आवेश युग्म ( $-q$ और $q$ ) के विद्युत क्षेत्र को कूलॉम के नियम और सुपरपोजिशन सिद्धांत के द्वारा निर्धारित किया जा सकता है। निम्नलिखित दो मामलों में परिणाम सरल होते हैं: (i) जब बिंदु द्विध्रुव अक्ष पर हो, और (ii) जब बिंदु द्विध्रुव के भूमि तल में हो, अर्थात द्विध्रुव अक्ष के केंद्र से गुजरने वाले तल में हो जो अक्ष के लंबवत हो। कोई सामान्य बिंदु $\mathrm{P}$ पर विद्युत क्षेत्र $\mathbf{E} _{-q}$ के कारण $-q$ आवेश के विद्युत क्षेत्र और $\mathbf{E} _{+q}$ के कारण $q$ आवेश के विद्युत क्षेत्र के वेक्टर योग द्वारा प्राप्त किया जाता है।
(i) अक्ष पर बिंदुओं के लिए
मान लीजिए बिंदु $\mathrm{P}$, चार्ज $q$ के ओर द्विध्रुव के केंद्र से दूरी $r$ पर है, जैसा कि चित्र 1.17(a) में दिखाया गया है। तब
$$ \begin{equation*} \mathbf{E_-q}=-\frac{q}{4} \pi \varepsilon_{0}(r+a)^{2} \mathbf{p} \tag{1.13 a} \end{equation*} $$
जहाँ $\hat{\mathbf{p}}$ द्विध्रुव अक्ष के अनुदिश एक इकाई सदिश है (से $-q$ से $q$ तक)। इसके अलावा
$$ \begin{equation*} \mathbf{E_+q}=\frac{q}{4} \pi \varepsilon_{0}(r-a)^{2} \mathbf{p} \tag{1.13 b} \end{equation*} $$
$$

चित्र 1.17 द्विध्रुव के विद्युत क्षेत्र (a) द्विध्रुव के अक्ष पर बिंदु पर, (b) द्विध्रुव के भूमि समतल पर बिंदु पर। p, द्विध्रुव क्षेत्र के परिमाण p = q × 2a के सदिश है और इसकी दिशा -q से q तक होती है।
बिंदु P पर कुल क्षेत्र है
$$ \begin{align*} \mathbf{E} & =\mathbf{E} _{+q}+\mathbf{E} _{-q}=\frac{q}{4 \pi \varepsilon _{o}}\left[\frac{1}{(r-a)^{2}}-\frac{1}{(r+a)^{2}}\right] \mathbf{p} \\
$$ & =\frac{q}{4 \pi \varepsilon _{o}} \frac{4 a r}{\left(r^{2}-a^{2}\right)^{2}} \hat{\mathbf{p}} \tag{1.14} \end{align*} $$
जब $r > > a$
$$ \begin{equation*} \mathbf{E}=\frac{4 q a}{4 \pi \varepsilon _{o} r^{3}} \hat{\mathbf{p}} \quad(r»a) \tag{1.15} \end{equation*} $$
(ii) बराबरीय तल पर बिंदुओं के लिए
$+q$ और $-q$ आवेशों के कारण विद्युत क्षेत्र के परिमाण निम्नलिखित द्वारा दिए जाते हैं
$$ \begin{align*} & E_{+q}=\frac{q}{4} \pi \varepsilon_{0} \frac{1}{r^{2}+a^{2}} \tag{16(a)}\\
$$ & E_{-q}=\frac{q}{4} \pi \varepsilon_{0} \frac{1}{r^{2}+a^{2}} \tag{16(b)} \end{align*} $$
और बराबर हैं।
$\mathbf{E_{+q}}$ और $\mathbf{E_{-q}}$ की दिशाएँ चित्र 1.17(b) में दिखाई गई हैं। स्पष्ट रूप से, दोलन अक्ष के लम्ब घटक एक दूसरे को बर्बाद कर देते हैं। दोलन अक्ष के अनुदिश घटक जुड़ जाते हैं। कुल विद्युत क्षेत्र $\hat{\mathbf{p}}$ के विपरीत होता है। हम लिख सकते हैं:
$$ \begin{align*} \mathbf{E} & =-\left(E_{+q}+E_{-q}\right) \cos \theta \hat{\mathbf{p}} \\ & =-\frac{2 q a}{4 \pi \varepsilon_{o}\left(r^{2}+a^{2}\right)^{3 / 2}} \mathbf{p} \tag{1.17} $$
\end{align*} $$
बड़ी दूरी पर $(r > > a)$, यह समीकरण घट जाता है
$$ \begin{equation*} \mathbf{E}=-\frac{2 q a}{4 \pi \varepsilon_{o} r^{3}} \hat{\mathbf{p}} \quad(r > > a) \tag{1.18} \end{equation*} $$
समीकरण (1.15) और (1.18) से स्पष्ट है कि दोलन चुंबकीय क्षेत्र बड़ी दूरी पर $q$ और $a$ के अलग-अलग निर्भर नहीं होता; यह $q a$ के उत्पाद पर निर्भर करता है। यह प्रस्तावित करता है कि दोलन क्षेत्र के परिभाषा के बारे में। एक विद्युत दोलन के दोलन आघूर्ण सदिश $\mathbf{p}$ को निम्नलिखित द्वारा परिभाषित किया जाता है
$$ \begin{equation*}
\mathbf{p}=q \times 2 a \hat{\mathbf{p}} \tag{1.19} \end{equation*} $$
अर्थात, यह एक वेक्टर है जिसका परिमाण आवेश $q$ के बराबर होता है जो दो आवेशों $q,-q$ के बीच के अंतर $2 a$ के गुणनफल के बराबर होता है और दिशा $-q$ से $q$ की रेखा के अनुदिश होती है। $\mathbf{p}$ के संदर्भ में, द्विध्रुव के विद्युत क्षेत्र के बड़ी दूरी पर सरल रूप में लिखा जा सकता है:
द्विध्रुव अक्ष पर एक बिंदु पर
$$ \begin{equation*} \mathbf{E}=\frac{2 \mathbf{p}}{4 \pi \varepsilon _{o} r^{3}} \quad(r > > a) \tag{1.20} \end{equation*} $$
एक विमान में भूमध्य रेखा पर एक बिंदु पर
$$ \begin{equation*} \mathbf{E}=-\frac{\mathbf{p}}{4 \pi \varepsilon _{o} r^{3}} \quad(r > > a) \tag{1.21} \end{equation*} $$
ध्यान दें कि द्विध्रुवी क्षेत्र बड़ी दूरी पर $1 / r^{2}$ नहीं बल्कि $1 / r^{3}$ के अनुपात में घटता है। इसके अतिरिक्त, द्विध्रुवी क्षेत्र के मापदंड और दिशा न केवल दूरी $r$ पर निर्भर करते हैं बल्कि अक्ष के स्थिति सदिश $\mathbf{r}$ और द्विध्रुवी आघूर्ण $\mathbf{p}$ के बीच कोण पर भी निर्भर करते हैं।
हम विचार कर सकते हैं कि जब द्विध्रुवी के आकार $2 a$ शून्य की ओर बढ़ता है, आवेश $q$ अपरिमित तक बढ़ता है ताकि उत्पाद $p=q \times 2 a$ सीमित रहे। ऐसे द्विध्रुवी को बिंदु द्विध्रुवी कहा जाता है। एक बिंदु द्विध्रुवी के लिए, समीकरण (1.20) और (1.21) सटीक होते हैं, जो किसी भी $r$ के लिए सत्य होते हैं।
1.10.2 डाइपोल के भौतिक अर्थ
अधिकांश अणुओं में, धनात्मक आवेश के केंद्र और नकारात्मक आवेश के केंद्र एक ही स्थान पर होते हैं। इसलिए, उनके डाइपोल आघूर्ण शून्य होता है। $\mathrm{CO_2}$ और $\mathrm{CH_4}$ इस प्रकार के अणुओं के उदाहरण हैं। हालांकि, जब विद्युत क्षेत्र लगाया जाता है तो ये डाइपोल आघूर्ण विकसित करते हैं। लेकिन कुछ अणुओं में, नकारात्मक आवेश के केंद्र और धनात्मक आवेश के केंद्र एक ही स्थान पर नहीं होते। इसलिए, वे विद्युत क्षेत्र की अनुपस्थिति में भी एक स्थायी विद्युत डाइपोल आघूर्ण रखते हैं। ऐसे अणुओं को ध्रुवी अणु कहा जाता है। पानी के अणु, $\mathrm{H_2} \mathrm{O}$, इस प्रकार के अणुओं का एक उदाहरण है। विभिन्न पदार्थ विद्युत क्षेत्र की उपस्थिति या अनुपस्थिति में रोचक गुणों और महत्वपूर्ण अनुप्रयोगों के कारण उत्पन्न होते हैं।
- धनात्मक बिंदु आवेशों के संग्रह के केंद्र को द्रव्यमान केंद्र के लगभग उसी तरह परिभाषित किया जाता है:
$\mathbf{r}_{\mathrm{cm}}=\frac{\sum_i q_i \mathbf{r}_i}{\sum_i q_i}$.
उदाहरण 1.9 दो आवेश ±10 मीलीकूलों को 5.0 मिमी की दूरी पर रखा गया है। निर्धारित करें (a) द्विध्रुव के अक्ष के अक्ष पर एक बिंदु P जो इसके केंद्र O से 15 सेमी की दूरी पर है और धनात्मक आवेश के ओर है, जैसा कि चित्र 1.18(a) में दिखाया गया है, और (b) एक बिंदु Q जो O से 15 सेमी की दूरी पर है और द्विध्रुव के अक्ष के लंबवत एक रेखा पर है जो O से गुजरती है, जैसा कि चित्र 1.18(b) में दिखाया गया है।

चित्र 1.18
हल (a) $+10 \mu \mathrm{C}$ आवेश के कारण P पर विद्युत क्षेत्र
$$ \begin{aligned} & =\frac{10^{-5} \mathrm{C}}{4 \pi\left(8.854 \times 10^{-12} \mathrm{C}^2 \mathrm{~N}^{-1} \mathrm{~m}^{-2}\right)} \times \frac{1}{(15-0.25)^2 \times 10^{-1} \mathrm{~m}^2} \\ & =4.13 \times 10^6 \mathrm{~N} \mathrm{C}^{-1} \text { along } \mathrm{BP} $$
\end{aligned} $$
$P$ पर $-10 \mu \mathrm{C}$ आवेश के कारण क्षेत्र
$$ \begin{aligned} & =\frac{10^{-5} \mathrm{C}}{4 \pi\left(8.854 \times 10^{-12} \mathrm{C}^2 \mathrm{~N}^{-1} \mathrm{~m}^{-2}\right)} \times \frac{1}{(15+0.25)^2 \times 10^{-4} \mathrm{~m}^2} \\ & =3.86 \times 10^6 \mathrm{~N} \mathrm{C}^{-1} \text { PA के अक्ष के अनुदिश } \end{aligned} $$
$A$ और $B$ पर आवेश के कारण $P$ पर परिणामी विद्युत क्षेत्र $=2.7 \times 10^5 \mathrm{~N} \mathrm{C}^{-1}$ $\mathrm{BP}$ के अक्ष के अनुदिश है। इस उदाहरण में, OP/OB का अनुपात बहुत बड़ा है $(=60)$. इसलिए, हम द्विध्रुव के अक्ष पर दूर बिंदु पर विद्युत क्षेत्र के सूत्र का प्रयोग करके ऊपर के नतीजे के लगभग समान परिणाम प्राप्त कर सकते हैं। एक द्विध्रुव जो आवेश $\pm q$ द्वारा बना हो जो $2 a$ की दूरी पर अलग हो, तो द्विध्रुव के अक्ष पर केंद्र से $r$ दूरी पर विद्युत क्षेत्र के परिमाण के लिए:
$$ E=\frac{2 p}{4 \pi \varepsilon_0 r^3} \quad(r / a > > 1) $$
जहाँ $p=2 a q$ द्विध्रुव आघूर्ण के परिमाण को दर्शाता है। द्विध्रुव अक्ष पर विद्युत क्षेत्र की दिशा हमेशा द्विध्रुव आघूर्ण सदिश की दिशा में होती है (अर्थात, $-q$ से q तक)। यहाँ, $p=10^{-5} \mathrm{C} \times 5 \times 10^{-3} \mathrm{~m}=5 \times 10^{-8} \mathrm{C} \mathrm{m}$ इसलिए, $$ E=\frac{2 \times 5 \times 10^{-8} \mathrm{Cm}}{4 \pi\left(8.854 \times 10^{-12} \mathrm{C}^2 \mathrm{~N}^{-1} \mathrm{~m}^2\right)} \times \frac{1}{(15)^3 \times 10^6 \mathrm{~m}^3}=2.6 \times 10^5 \mathrm{~N} \mathrm{C}^{-1} $$
$$
$\mathrm{AB}$ दिशा में, जो पहले प्राप्त किए गए नतीजे के करीब है। (b) $\mathrm{B}$ पर $+10 \mu \mathrm{C}$ आवेश के कारण $Q$ पर चुंबकीय क्षेत्र
$$ \begin{aligned} & =\frac{10^{-5} \mathrm{C}}{4 \pi\left(8.854 \times 10^{-12} \mathrm{C}^2 \mathrm{~N}^{-1} \mathrm{~m}^{-2}\right)} \times \frac{1}{\left[15^2+(0.25)^2\right] \times 10^{-4} \mathrm{~m}^2} \end{aligned} $$
$$ \begin{aligned} & =3.99 \times 10^6 \mathrm{~N} \mathrm{C}^{-1} \mathrm{BQ} \text { लंबवत} \end{aligned} $$
$$
$\mathrm{A}$ पर $-10 \mu \mathrm{C}$ आवेश के कारण $\mathrm{Q}$ पर क्षेत्र
$$ \begin{aligned} & =\frac{10^{-5} \mathrm{C}}{4 \pi\left(8.854 \times 10^{-12} \mathrm{C}^2 \mathrm{~N}^{-1} \mathrm{~m}^{-2}\right)} \times \frac{1}{\left[15^2+(0.25)^2\right] \times 10^{-4} \mathrm{~m}^2} \ \end{aligned} $$
$$ \begin{aligned} & =3.99 \times 10^6 \mathrm{~N} \mathrm{C}^{-1} \text { along } \mathrm{gA} . \end{aligned} $$
स्पष्ट रूप से, इन दो बलों के बराबर मापदंड भाग दिशा $O Q$ के अनुदिश विपरीत होते हैं लेकिन $B A$ के समानांतर दिशा में जुड़ते हैं। अतः, $A$ और $B$ पर आवेश के कारण $Q$ पर परिणामी विद्युत क्षेत्र है:
$$ \begin{aligned} & =2 \times \frac{0.25}{\sqrt{15^2+(0.25)^2}} \times 3.99 \times 10^6 \mathrm{~N} \mathrm{C}^{-1} \text { लंबवत } \mathrm{BA} \\ & =1.33 \times 10^5 \mathrm{~N} \mathrm{C}^{-1} \text { लंबवत } \mathrm{BA} . \end{aligned} $$
(a) के तुलना में, हम अपेक्षा कर सकते हैं कि दोलन के अक्ष के लंबवत बिंदु पर दोलन के क्षेत्र के फॉर्मूला का प्रयोग करके लगभग समान परिणाम प्राप्त कर सकेंगे:
$$ \begin{aligned} & E=\frac{p}{4 \pi \varepsilon_0 r^3} \quad(r / a \gg 1) \\ = & \frac{5 \times 10^{-8} \mathrm{Cm}}{4 \pi\left(8.854 \times 10^{-12} \mathrm{C}^2 \mathrm{~N}^{-1} \mathrm{~m}^{-2}\right)} \times \frac{1}{(15)^3 \times 10^{-6} \mathrm{~m}^3} \\
= & 1.33 \times 10^5 \mathrm{~N} \mathrm{C}^{-1} . \end{aligned} $$
इस मामले में विद्युत क्षेत्र की दिशा द्विध्रुवी आघूर्ण सदिश की दिशा के विपरीत होती है। फिर भी, परिणाम पहले से प्राप्त किए गए परिणाम के साथ सहमत है।
1.11 समान बाह्य क्षेत्र में द्विध्रुव
एक स्थायी द्विध्रुव जिसका द्विध्रुवी आघूर्ण $\mathbf{p}$ है, एक समान बाह्य क्षेत्र E में रखा गया है, जैसा कि चित्र 1.19 में दिखाया गया है। (स्थायी द्विध्रुव के अर्थ में, $\mathbf{p}$ का अस्तित्व $\mathbf{E}$ के बिना भी होता है; यह $\mathbf{E}$ द्वारा uced नहीं होता है।)

चित्र 1.19 विद्युत क्षेत्र में द्विध्रुव
$ q $ पर $ q \mathbf{E} $ बल लगता है और $ -q $ पर $ -q \mathbf{E} $ बल लगता है। चूंकि $ \mathbf{E} $ समान विद्युत क्षेत्र है, इसलिए द्विध्रुव पर शुद्ध बल शून्य होता है। हालांकि, आवेश अलग-अलग हैं, इसलिए बल अलग-अलग बिंदुओं पर कार्य करते हैं, जिसके परिणामस्वरूप द्विध्रुव पर एक बल-युग्म (torque) उत्पन्न होता है। जब शुद्ध बल शून्य होता है, तो बल-युग्म का मान उत्पन्न बल के मान के गुणनफल के बराबर होता है जो दो विपरीत दिशा वाले बलों के बीच लंब दूरी (couple के अrm) के बराबर होता है।
Magnitude of torque $=q E \times 2 a \sin \theta$
$$ =2 q a E \sin \theta $$
इसकी दिशा कागज के तल के लम्बवत है, कागज से बाहर निकलती है। p × E के मान की भी दिशा कागज के तल के लम्बवत है, कागज से बाहर निकलती है। इसलिए,
$$ \begin{equation*} \tau=\mathbf{p} \times \mathbf{E} \tag{1.22} \end{equation*} $$

 E, p के समानांतर, (b) E, p के विपरीत समानांतर।)
इस टॉर्क के कारण द्विध्रुव को क्षेत्र $\mathbf{E}$ के साथ समानांतर करने की ओर बल लगता है। जब $\mathbf{p}$, $\mathbf{E}$ के समानांतर होता है, तो टॉर्क शून्य हो जाता है।
यदि क्षेत्र असमान हो तो क्या होता है? ऐसे मामले में, समग्र बल निश्चित रूप से शून्य नहीं होगा। इसके अतिरिक्त, सामान्यतः पहले जैसे टॉर्क द्विध्रुव पर लगता रहेगा। सामान्य मामला जटिल है, इसलिए हम उन सरल स्थितियों का अध्ययन करेंगे जब $\mathbf{p}$, $\mathbf{E}$ के समानांतर या विपरीत समानांतर हो। दोनों मामलों में समग्र टॉर्क शून्य होता है, लेकिन यदि $\mathbf{E}$ असमान हो तो द्विध्रुव पर समग्र बल लगता है।
चित्र 1.20 स्वयं स्पष्ट है। यह आसानी से देखा जा सकता है कि जब $\mathbf{p}$, $\mathbf{E}$ के समानांतर होता है, तो द्विध्रुव बल के एक नेट बल के दिशा में बढ़ते क्षेत्र की ओर बल अनुभव करता है। जब $\mathbf{p}$, $\mathbf{E}$ के विपरीत दिशा में होता है, तो द्विध्रुव पर नेट बल क्षेत्र के घटते दिशा में होता है। सामान्य रूप से, बल $\mathbf{p}$ के $\mathbf{E}$ के संबंध में व्यवस्था पर निर्भर करता है।
इससे हम घर्षण विद्युत के एक सामान्य अवलोकन तक पहुंचते हैं। एक कम्ब शुष्क बालों के माध्यम से गुजरते हुए कागज के टुकड़ों को आकर्षित करता है। हम जानते हैं कि कम्ब घर्षण के माध्यम से आवेश अर्जित करता है। लेकिन कागज आवेशित नहीं होता। तो आकर्षण बल के लिए क्या व्याख्या होती है? पिछले विवरण के संकेत को लेते हुए, आवेशित कम्ब ‘पॉलराइज़ करता है’ कागज के टुकड़े को, अर्थात बल के दिशा में एक नेट द्विध्रुव आघूर्ण को प्रेरित करता है। इसके अतिरिक्त, कम्ब के कारण विद्युत क्षेत्र एकसमान नहीं होता। इस क्षेत्र की असमानता के कारण द्विध्रुव पर एक नेट बल अनुभव करता है। इस स्थिति में, आसानी से देखा जा सकता है कि कागज कम्ब की ओर गति करता है!
1.12 निरंतर आवेश वितरण
हम अब तक विलक्षण आवेशों $q_{1}, q_{2}, \ldots, q_{n}$ के साथ आवेश विन्यासों के साथ काम किया है। एक कारण जिसके कारण हम विलक्षण आवेशों के साथ सीमित रहे हैं, यह है कि गणितीय विवेचन सरल होता है और इसमें कलन की आवश्यकता नहीं होती। हालांकि, कई उद्देश्यों के लिए विलक्षण आवेशों के साथ काम करना असंभव होता है और हमें निरंतर आवेश वितरण के साथ काम करना पड़ता है। उदाहरण के लिए, एक आवेशित चालक के सतह पर, विलक्षण आवेशों के स्थानों के आधार पर आवेश वितरण को निर्धारित करना असंभव होता है। यह अधिक सुविधाजनक होता है कि चालक के सतह पर एक क्षेत्र के तत्व $\Delta S$ (चित्र 1.21) को विचार करें (जो मैक्रोस्कोपिक अंश के लिए बहुत छोटा होता है लेकिन बहुत सारे इलेक्ट्रॉनों को शामिल करने वाला बड़ा होता है) और उस तत्व पर आवेश $\Delta Q$ को निर्धारित करें। फिर हम उस क्षेत्र तत्व पर सतह आवेश घनत्व $\sigma$ को परिभाषित करते हैं:

चित्र 1.21 रेखीय, सतह और आयतन आवेश घनत्व की परिभाषा। प्रत्येक मामले में, चयनित तत्व (Dl, DS, DV) मैक्रोस्कोपिक अंश के लिए छोटा होता है लेकिन माइक्रोस्कोपिक घटकों के बहुत बड़ी संख्या को शामिल करता है।
$$ \begin{equation*} \sigma=\frac{\Delta Q}{\Delta S} \tag{1.23} \end{equation*} $$
$$ \begin{equation*} \rho=\frac{\Delta Q}{\Delta V} \tag{1.25} \end{equation*} $$
जहाँ $\Delta Q$ वह आवेश है जो मैक्रोस्कोपिक रूप से छोटे आयतन तत्व $\Delta V$ में शामिल है जिसमें बहुत सारे माइक्रोस्कोपिक आवेश घटक होते हैं। $\rho$ के इकाई $\mathrm{C} / \mathrm{m}^{3}$ होते हैं।
सतत आवेश वितरण की अवधारणा भौतिकी में सतत द्रव्यमान वितरण की अवधारणा के समान है। जब हम किसी तरल के घनत्व का उल्लेख करते हैं, तो हम उसके मैक्रोस्कोपिक घनत्व का उल्लेख कर रहे होते हैं। हम इसे एक सतत द्रव मान लेते हैं और इसके अलग-अलग अणुओं के संगठन को नगण्य मान लेते हैं।
- माइक्रोस्कोपिक स्तर पर, आवेश वितरण असतत होता है, क्योंकि वे एक दूसरे से अलग आवेश होते हैं जो एक दूसरे के बीच आवेश रहित अंतराल द्वारा अलग होते हैं
एक सतत आवेश वितरण के कारण क्षेत्र को एक विस्थापित आवेश प्रणाली के लिए समीकरण (1.10) के जैसे तरीके से प्राप्त किया जा सकता है। मान लीजिए कि एक स्थान में सतत आवेश वितरण के लिए आवेश घनत्व $\rho$ है। कोई आवेश वितरण के किसी बिंदु के स्थिति सदिश को $\mathbf{r}$ लें और कोई सुविधाजनक मूल बिंदु $\mathrm{O}$ चुन लें। आवेश घनत्व $\rho$ बिंदु से बिंदु तक बदल सकता है, अर्थात यह $\mathbf{r}$ के फलन है। आवेश वित, आवेश वितरण को छोटे आयतन तत्वों $\Delta V$ में विभाजित कर दें। आयतन तत्व $\Delta V$ में आवेश $\rho \Delta V$ होता है।
अब, किसी भी सामान्य बिंदु $\mathrm{P}$ (वितरण के अंदर या बाहर) को विचार करें जिसका स्थिति सदिश $\mathbf{R}$ है (चित्र 1.21)। आवेश $\rho \Delta V$ के कारण विद्युत क्षेत्र द्वारा कूलॉम के नियम द्वारा दिया जाता है:
$$ \begin{equation*} \Delta \mathbf{E}=\frac{1}{4 \pi \varepsilon_{0}} \frac{\rho \Delta V}{r^{\prime 2}} \hat{\mathbf{r^\prime} }\tag{1.26} \end{equation*} $$
जहाँ $r^{\prime}$ आवेश तत्व और $P$ के बीच की दूरी है, और $\hat{\mathbf{r}}^{\prime}$ आवेश तत्व से $P$ की दिशा में एक एकक सदिश है। सुपरपोजिशन सिद्धांत के अनुसार, आवेश वितरण के कारण कुल विद्युत क्षेत्र को विभिन्न आयतन तत्वों के कारण विद्युत क्षेत्रों के योग द्वारा प्राप्त किया जाता है:
$$ \begin{equation*} \mathbf{E} \cong \frac{1}{4 \pi \varepsilon _{0}} \sum _{\text {all } \Delta V} \frac{\rho \Delta V}{r^{\prime 2}} \hat{\mathbf{r}}^{\prime} \tag{1.27} \end{equation*} $$
ध्यान दें कि $\rho, r^{\prime}, \quad \hat{\mathbf{r}}^{\prime}$ सभी बिंदु से बिंदु तक बदल सकते हैं। एक सख्त गणितीय विधि में, हमें $\Delta V \rightarrow 0$ करना चाहिए और तब योग एक समाकलन बन जाता है; लेकिन यहां सरलता के लिए इस विवरण को छोड़ देंगे। शॉर्ट करें, कूलॉम के नियम और अधिस्थलन सिद्धांत का उपयोग करके, किसी भी आवेश वितरण के लिए विद्युत क्षेत्र निर्धारित किया जा सकता है, चाहे वह असतत हो या सतत हो या आंशिक रूप से असतत और आंशिक रूप से सतत हो।
1.13 गॉस के नियम
इलेक्ट्रिक फ्लक्स की अवधारणा के एक सरल अनुप्रयोग के रूप में, हम एक त्रिज्या $r$ के गोले पर विचार करें जो इसके केंद्र पर एक बिंदु आवेश $q$ को घेरता है। चित्र 1.22 में दिखाए गए तरीके से गोले को छोटे क्षेत्र तत्वों में विभाजित करें।
एक क्षेत्र तत्व $\Delta \mathbf{S}$ के माध्यम से फ्लक्स है
$$ \begin{equation*} \Delta \phi=\mathbf{E} \Delta \mathbf{S}=\frac{q}{4 \pi \varepsilon _{0} r^{2}} \hat{\mathbf{r}} \Delta \mathbf{S} \tag{1.28} \end{equation*} $$
जहाँ हम एक अकेले आवेश $q$ के कारण विद्युत क्षेत्र के लिए कूलॉम के नियम का उपयोग करते हैं। एकक वेक्टर $\hat{\mathbf{r}}$ केंद्र से क्षेत्र तत्व तक त्रिज्या वेक्टर के अनुदिश होता है। अब, क्योंकि गोले के प्रत्येक बिंदु पर अभिलम्ब उस बिंदु के त्रिज्या वेक्टर के अनुदिश होता है, इसलिए क्षेत्र तत्व $\Delta \mathbf{S}$ और $\hat{\mathbf{r}}$ एक ही दिशा में होते हैं। इसलिए,
$$ \begin{equation*} \Delta \phi=\frac{q}{4 \pi \varepsilon _{0} r^{2}} \Delta S \tag{1.29} \end{equation*} $$
क्योंकि एक इकाई सदिश के मापदंड का मान 1 होता है।

चित्र 1.22 एक बिंदु आवेश q के वितरण के एक गोले के माध्यम से फ्लक्स।

FIGURE 1.23 एक सिलेंडर के सतह के माध्यम से समान विद्युत क्षेत्र के फ्लक्स की गणना।
गोले के माध्यम से कुल फ्लक्स की गणना विभिन्न क्षेत्र तत्वों के माध्यम से फ्लक्स को जोड़कर की जाती है:
$$ \varphi=\sum_{\text {all } \Delta S} \frac{q}{4 \pi \varepsilon_{0} r^{2}} \Delta S $$
क्योंकि गोले के प्रत्येक क्षेत्र तत्व आवेश से समान दूरी $r$ पर होते हैं,
$$ \varphi=\frac{q}{4 \pi \varepsilon_{o} r^{2}} \sum_{\text {all } \Delta S} \Delta S=\frac{q}{4 \pi \varepsilon_{0} r^{2}} S $$
$$
अब $S$, गोले के कुल क्षेत्रफल, $4 \pi r^{2}$ के बराबर होता है। इसलिए,
$$ \begin{equation*} \phi=\frac{q}{4 \pi \varepsilon _{o} r^{2}} \times 4 \pi r^{2}=\frac{q}{\varepsilon _{o}} \tag{1.30} \end{equation*} $$
समीकरण (1.30) विद्युत चुंबकत्व के एक सामान्य परिणाम का एक सरल उदाहरण है, जिसे गॉस के नियम के रूप में जाना जाता है।
हम बिना साबित किए गॉस के नियम को इस प्रकार देते हैं:
एक बंद सतह $S$ के माध्यम से विद्युत फ्लक्स
$$ \begin{equation*} =q / \varepsilon _{0} \tag{1.31} \end{equation*} $$
$q=$ $\mathrm{S}$ द्वारा घिरे कुल आवेश।
कानून यह अर्थ देता है कि एक बंद सतह के माध्यम से कुल विद्युत फ्लक्स शून्य होता है यदि सतह के भीतर कोई आवेश न हो। हम इसे चित्र 1.23 में एक सरल स्थिति में अपेक्षाकृत देख सकते हैं।
यहाँ विद्युत क्षेत्र समान है और हम एक बंद बेलनाकार सतह के बारे में विचार कर रहे हैं, जिसकी धुरी समान क्षेत्र $\mathbf{E}$ के समानांतर है। सतह के माध्यम से कुल फ्लक्स $\phi$ होता है $\phi=\phi_{1}+\phi_{2}+\phi_{3}$, जहाँ $\phi_{1}$ और $\phi_{2}$ बेलन के सतह 1 और 2 (वृताकार काट के साथ) के माध्यम से फ्लक्स को दर्शाते हैं और $\phi_{3}$ बंद सतह के वक्र बेलनाकार हिस्से के माध्यम से फ्लक्स को दर्शाता है। अब सतह 3 के प्रत्येक बिंदु पर अभिलम्ब लम्बवत $\mathbf{E}$ के होता है, इसलिए फ्लक्स के परिभाषा के अनुसार, $\phi_{3}=0$ होता है। इसके अतिरिक्त, 2 के बाहरी अभिलम्ब $\mathbf{E}$ के समानांतर होता है जबकि 1 के बाहरी अभिलम्ब $\mathbf{E}$ के विपरीत होता है। इसलिए,
$$ \begin{aligned} & \phi_{1}=-E S_{1}, \quad \phi_{2}=+E S_{2} \\ & S_{1}=S_{2}=S \end{aligned} $$
जहाँ $S$ वृताकार परिच्छेद का क्षेत्रफल है। इस प्रकार, कुल फ्लक्स शून्य होता है, जैसा कि गॉस के नियम द्वारा अपेक्षित है। इसलिए, जब आप किसी बंद सतह के माध्य विद्युत फ्लक्स को शून्य पाते हैं, तो निष्कर्ष लेते हैं कि बंद सतह में समाहित कुल आवेश शून्य है।
गॉस के नियम के समीकरण (1.31) के बहुत बड़े महत्व के कारण यह यह यह व्यापक रूप से सत्य होता है और ऊपर चर्चा किए गए सरल मामलों के लिए ही नहीं। इस नियम के बारे में कुछ महत्वपूर्ण बिंदु ध्यान में रखें:
(i) गॉस के नियम के दाएं ओर वाला पद q, सतह के आंतरिक सभी आवेशों के योग को शामिल करता है। आवेश बिलकुल भी आंतरिक सतह के कहीं भी हो सकते हैं।
(ii) जब सतह के आंतरिक और बाहरी दोनों आवेश होते हैं, तो विद्युत क्षेत्र [जो समीकरण (1.31) के बाएं ओर धारित विद्युत धारा के रूप में दिखाई देता है] आंतरिक और बाहरी दोनों आवेशों के कारण होता है। लेकिन गॉस के नियम के दाएं ओर वाला पद q केवल आंतरिक आवेश के कुल योग को प्रस्तुत करता है।
(iv) गॉस के नियम के अनुप्रयोग के लिए हम चुने गए सतह को गॉसीय सतह कहते हैं। आप किसी भी गॉसीय सतह का चयन कर सकते हैं और गॉस के नियम के अनुप्रयोग कर सकते हैं। हालांकि, ध्यान रखें कि गॉसीय सतह को किसी भी विच्छिन्न आवेश के माध्यम से न गुजरे। इसका कारण यह है कि विच्छिन्न आवेशों के एक प्रणाली के कारण विद्युत क्षेत्र के किसी आवेश के स्थान पर अच्छी तरह से परिभाषित नहीं होता है। (जैसे ही आप आवेश के पास जाते हैं, क्षेत्र असीमित रूप से बढ़ता जाता है।) हालांकि, गॉसीय सतह एक सतत आवेश वितरण के माध्यम से गुजर सकती है।
(v) गॉस के नियम का उपयोग विद्युत क्षेत्र की गणना करते समय बहुत सारे समय एक आसान तरीका होता है जब व्यवस्था कुछ सममिति के अनुसार होती है। इसे सुगम बनाने के लिए एक उपयुक्त गॉसीय सतह का चयन किया जाता है।
(vi) अंत में, गॉस के नियम को कूलॉम के नियम में दूरी के व्युत्क्रम वर्ग निर्भरता पर आधारित होता है। गॉस के नियम के कोई भी उल्लंघन व्युत्क्रम वर्ग नियम से विचलन को दर्शाएगा।
उदाहरण 1.10 चित्र 1.24 में विद्युत क्षेत्र के घटक $E_x=\alpha x^{1 / 2}, E_y=E_z=0$ हैं, जहाँ $\alpha=80,000 \mathrm{~N} / \mathrm{C} \mathrm{m}^{1 / 2}$ है। (a) घन के माध्यम से फ्लक्स की गणना करें और (b) घन के भीतर आवेश की गणना करें। मान लें कि $a=0.1 \mathrm{~m}$।

चित्र 1.24
हल (अ) चूंकि विद्युत क्षेत्र केवल $x$ घटक रखता है, तो $x$ दिशा के लम्ब तलों के लिए, $\mathbf{E}$ और $\Delta \mathbf{S}$ के बीच कोण $\pm \pi / 2$ होता है। अतः, घन के प्रत्येक तल के लिए फ्लक्स $\phi=\mathbf{E} . \Delta \mathbf{S}$ अलग-अलग शून्य होता है, बचे हुए दो छायांकित तलों के अतिरिक्त। अब बाएँ तल पर विद्युत क्षेत्र के मान का आयाम
$$ E_L=\alpha x^{1 / 2}=\alpha a^{1 / 2} $$
$(x=a$ बाईं तल पर)। दाईं तल पर विद्युत क्षेत्र के परिमाण के लिए
$$E_R=\alpha x^{1 / 2}=\alpha(2 a)^{1 / 2}$$
($x=2 a$ दाईं तल पर)। संगत फ्लक्स हैं
$$ \begin{aligned} \phi_L & =\mathbf{E}_L \cdot \Delta \mathbf{S}=\Delta \mathbf{S} \mathbf{E}_L \cdot \hat{\mathbf{n}}_L=E_L \Delta S \cos \theta=-E_L \Delta S, \text { क्योंकि } \theta=18 $$
$$ & =E_R a^2 \end{aligned} $$ क्यूब के माध्यम से शुद्ध प्रवाह।
$$ \begin{aligned} & =\phi_R+\phi_L=E_R a^2-E_L a^2=a^2\left(E_R-E_L\right)=\alpha a^2\left[(2 a)^{1 / 2}-a^{1 / 2}\right] \\ & =\alpha a^{5 / 2}(\sqrt{2}-1) \\ & =800(0.1)^{5 / 2}(\sqrt{2}-1) \\ & =1.05 \mathrm{~N} \mathrm{~m}^2 \mathrm{C}^{-1} \end{aligned} $$
(b) हम गॉस के नियम का उपयोग करके क्यूब के भीतर कुल आवेश $q$ निर्धारित कर सकते हैं। हमें $\phi=q / \varepsilon_0$ या $q=\phi \varepsilon_0$ मिलता है। इसलिए,
$$ q=1.05 \times 8.854 \times 10^{-12} \mathrm{C}=9.27 \times 10^{-12} \mathrm{C} \text {. }
$$
उदाहरण 1.11 एक विद्युत क्षेत्र समान है, और धनात्मक $x$ दिशा में धनात्मक $x$ के लिए, और ऋणात्मक $x$ के लिए एक ही मात्रा के साथ ऋणात्मक $x$ दिशा में समान है। यह दिया गया है कि $x>0$ के लिए $\mathbf{E}=200 \hat{\mathbf{i}}$ N/C और $x<0$ के लिए $\mathbf{E}=-200 \overline{\mathbf{i}}$ N/C है। एक दाहिना वृत्तीय बेलन, जिसकी लंबाई $20 \mathrm{~cm}$ और त्रिज्या $5 \mathrm{~cm}$ है, मूल बिंदु पर केंद्रित है और अक्ष $x$-अक्ष के अनुदिश है ताकि एक फलक $x=+10 \mathrm{~cm}$ पर है और दूसरा फलक $x=-10 \mathrm{~cm}$ पर है (चित्र 1.25)। (a) प्रत्येक समतल फलक से नेट बाहरी प्रवाह क्या है? (b) बेलन के तल से प्रवाह क्या है? (c) बेलन से नेट बाहरी प्रवाह क्या है? (d) बेलन के अंदर नेट आवेश क्या है?
हल (अ) हम चित्र से देख सकते हैं कि बाएँ फलक पर $\mathbf{E}$ और $\Delta \mathbf{S}$ समानांतर हैं। इसलिए, बाहरी प्रवाह है
$$ \begin{aligned} & \phi_L=\mathbf{E} \cdot \Delta \mathbf{S}=-200 \hat{\mathbf{i}} \cdot \Delta \mathbf{S} \ \end{aligned} $$
$$ \begin{aligned} & =+200 \Delta \mathbf{S}, \text { क्योंकि } \hat{\mathbf{i}} \cdot \Delta \mathbf{S}=-\Delta \mathrm{S} \ \end{aligned} $$
$$ \begin{aligned} & =+200 \times \pi(0.05)^2=+1.57 \mathrm{~N} \mathrm{~m}^2 \mathrm{C}^{-1}
\end{aligned} $$
दाहिने फलक पर, $\mathbf{E}$ और $\Delta \mathbf{S}$ समानांतर हैं और अतः $$ \phi_R=\mathbf{E} \cdot \Delta \mathbf{S}=+1.57 \mathrm{~N} \mathrm{~m}^2 \mathrm{C}^{-1} . $$
(b) सिलेंडर के किसी बिंदु पर $\mathbf{E}$, $\Delta \mathbf{S}$ के लंबवत होता है और अतः $\mathbf{E} \cdot \Delta \mathbf{S}=0$। अतः सिलेंडर के तल से बाहर जाने वाला फ्लक्स शून्य होता है।
(c) सिलेंडर के माध्यम से कुल बाहरी फ्लक्स $$ \phi=1.57+1.57+0=3.14 \mathrm{~N} \mathrm{~m}^2 \mathrm{C}^{-1}
$$

चित्र 1.25
(d) बेलन के भीतर कुल आवेश की गणना गॉस के नियम का उपयोग करके की जा सकती है, जो निम्नलिखित देता है
$$ \begin{aligned} q & =\varepsilon_0 \phi \\ & =3.14 \times 8.854 \times 10^{-12} \mathrm{C} \\ & =2.78 \times 10^{-11} \mathrm{C} \end{aligned} $$
1.14 गॉस के नियम के अनुप्रयोग
एक सामान्य आवेश वितरण के कारण विद्युत क्षेत्र, जैसा कि ऊपर देखा गया है, समीकरण (1.27) द्वारा दिया जाता है। व्यावहारिक दृष्टिकोण से, अपवाद के अतिरिक्त, इस समीकरण में शामिल योग (या समाकलन) को अंतरिक अंकन के प्रत्येक बिंदु पर विद्युत क्षेत्र की गणना करने के लिए लागू नहीं किया जा सकता है। हालांकि, कुछ सममिति आवेश विन्यास के लिए, गॉस के नियम का उपयोग करके विद्युत क्षेत्र की आसान गणना संभव हो सकती है। यह कुछ उदाहरणों के माध्यम से सबसे अच्छा समझा जा सकता है।
1.14.1 एक अपरिमित लंबे सीधे एकसमान आवेशित तार के कारण क्षेत्र
एक अपरिमित लंबे सीधे तार की बात करें जिसकी एकसमान रैखिक आवेश घनत्व λ है। यह तार निश्चित रूप से सममिति के अक्ष है। मान लीजिए हम O से P तक वृत्तीय सदिश ले लें और इसे तार के चारों ओर घुमाएं। इस प्रकार प्राप्त बिंदु P, P′, P′′ आवेशित तार के संबंध में पूर्ण रूप से समान हैं। इसका अर्थ है कि इन बिंदुओं पर विद्युत क्षेत्र के परिमाण समान होना चाहिए। प्रत्येक बिंदु पर विद्युत क्षेत्र की दिशा वृत्तीय होनी चाहिए (λ > 0 के लिए बाहरी, λ < 0 के लिए अंदरी)। यह चित्र 1.29 से स्पष्ट है।
एक तार के दो रेखीय तत्व P1 और P2 के जोड़ को देखिए, जैसा कि चित्र में दिखाया गया है। दो तत्वों द्वारा उत्पन्न विद्युत क्षेत्र के योग एक परिणामी विद्युत क्षेत्र देता है जो वृत्तीय (अक्षीय वेक्टर के लंबवत घटक विपरीत दिशा में रह जाते हैं) होता है। यह किसी भी ऐसे जोड़ के लिए सत्य है और इसलिए किसी बिंदु P पर कुल विद्युत क्षेत्र अक्षीय होता है। अंत में, क्योंकि तार अनंत है, विद्युत क्षेत्र तार के लंबाई के अनुदिश P की स्थिति पर निर्भर नहीं करता है। संक्षेप में, विद्युत क्षेत्र तार के लंबवत काट वाले तल में हर जगह अक्षीय होता है, और इसका मान केवल अक्षीय दूरी r पर निर्भर करता है।
चुंबकीय क्षेत्र की गणना करने के लिए, चित्र 1.29 (b) में दिखाए गए एक बेलनाकार गाउसीय सतह को कल्पना करें। चूंकि क्षेत्र सभी बिंदुओं पर वृत्तीय है, इसलिए बेलनाकार गाउसीय सतह के दो सिरों से फ्लक्स शून्य होता है। बेलनाकार भाग के सतह पर, E प्रत्येक बिंदु पर सतह के लंबवत होता है और इसके मान के तीव्रता के लिए निरंतर होता है, क्योंकि यह केवल r पर निर्भर करता है। वक्र भाग के सतह क्षेत्रफल 2πrl होता है, जहां l बेलन की लंबाई है।

चित्र 1.26 (a) एक अपरिमित लंबे सीधे तार के कारण विद्युत क्षेत्र वृत्तीय होता है, (b) एक समान रेखीय आवेश घनत्व वाले लंबे सीधे तार के गॉसीय पृष्ठ। पृष्ठ से बाहर निकलने वाला विद्युत फ्लक्स
$=$ पृष्ठ के वक्र बेलनाकार भाग से बाहर निकलने वाला विद्युत फ्लक्स
$=E \times 2 \pi r l$
पृष्ठ में आवेश के मान के बराबर होता है $\lambda l$। गॉस के नियम द्वारा यह दिया जाता है $E \times 2 \pi r l=\lambda l / \varepsilon_{0}$
अर्थात,
$$E=\frac{\lambda}{2 \pi \varepsilon_{0} r}$$
सदिश रूप में, किसी बिंदु पर $\mathbf{E}$ द्वारा दिया जाता है
$$\mathbf{E}=\frac{\lambda}{2 \pi \varepsilon_{0} r} \hat{\mathbf{n}}$$
जहाँ $\hat{\mathbf{n}}$ वर्तिका के लंबवत समतल में बिंदु के माध्यम से गुजरने वाले बिंदु पर वृत्तीय एकक वेक्टर है। $\mathbf{E}$ यदि $\lambda$ धनात्मक है तो बाहर की ओर तथा यदि $\lambda$ नकारात्मक है तो अंदर की ओर दिशा लेता है।
ध्यान दें कि जब हम एक वेक्टर $\mathbf{A}$ को एक अदिश के गुणनफल के रूप में लिखते हैं, अर्थात $\mathbf{A}=A \hat{\mathbf{a}}$ के रूप में, तो अदिश $A$ एक बीजगणितीय संख्या होती है। यह धनात्मक या ऋणात्मक हो सकती है। यदि $A>0$ है तो $\mathbf{A}$ की दिशा एकक वेक्टर $\hat{\mathbf{a}}$ के समान होती है तथा यदि $A<0$ है तो इसकी दिशा $\hat{\mathbf{a}}$ के विपरीत होती है। जब हम धनात्मक मानों के लिए संरक्षण करना चाहते हैं, तो हम $|\mathbf{A}|$ का चिह्न उपयोग करते हैं और इसे $\mathbf{A}$ के मापदंड कहते हैं। इस प्रकार, $|\mathbf{A}| \geq 0$।
ध्यान दें कि उपरोक्त में केवल सतह द्वारा घिरे चार्ज $(\lambda l)$ को ही शामिल किया गया है, लेकिन विद्युत क्षेत्र $\mathbf{E}$ पूरे तार पर विद्युत चार्ज के कारण होता है। इसके अतिरिक्त, तार के अपरिमित लंबाई के अनुमान के आधार पर अनुमान बहुत महत्वपूर्ण है। इस अनुमान के बिना, हम $\mathbf{E}$ को बेलनाकार गाउसीय सतह के वक्र भाग के लंब रूप में नहीं ले सकते। हालांकि, समीकरण (1.32) एक लंबे तार के केंद्रीय भागों के आसपास विद्युत क्षेत्र के लिए लगभग सही होता है, जहां सिर के प्रभाव को नगण्य मान लिया जाता है।
1.14.2 एक समान आवेशित अपरिमित तल के कारण क्षेत्र
मान लीजिए कि एक अपरिमित तल के समान तलीय आवेश घनत्व σ है (चित्र 1.30)। हम दिए गए तल के लंब अक्ष के रूप में x-अक्ष को लेंगे। सममिति के कारण, विद्युत क्षेत्र y और z निर्देशांक पर निर्भर नहीं करेगा और प्रत्येक बिंदु पर इसकी दिशा x-दिशा के समान्तर होगी।


हम गॉसीय सतह के रूप में एक आयताकार समानांतर चतुर्भुज ले सकते हैं, जिसका काट-क्षेत्रफल A है, जैसा कि चित्र में दिखाया गया है। (एक बेलनाकार सतह भी ठीक होगी।) चित्र से देखा जा सकता है कि केवल दो सतह 1 और 2 फ्लक्स के योगदानकर्ता होंगी; विद्युत क्षेत्र रेखाएँ अन्य सतहों के समानांतर होती हैं और इनके कारण कुल फ्लक्स में योगदान नहीं होता।
सतह 1 के लंब एकक वेक्टर -x दिशा में है जबकि सतह 2 के लंब एकक वेक्टर +x दिशा में है। अतः दोनों सतहों के माध्यम से फ्लक्स E.∆S बराबर होता है और एक साथ जोड़ लिया जाता है। अतः गॉसीय सतह के माध्यम से कुल फ्लक्स 2 EA होता है। बंद सतह द्वारा घिरे आवेश का मान σA है। अतः गॉस के नियम के अनुसार
$2 E A=\sigma A / \varepsilon_{0}$ या, $E=\sigma / 2 \varepsilon_{0}$
सदिश रूप में,
$$ \begin{equation*} \mathbf{E}=\frac{\sigma}{2 \varepsilon_{0}} \hat{\mathbf{n}} \end{equation*} $$
जहाँ $\hat{\mathbf{n}}$ एक इकाई सदिश है जो तल के लम्बवत है और इससे बाहर जाता है।
$\mathbf{E}$ यदि $\sigma$ धनात्मक है तो तल से बाहर तथा यदि $\sigma$ नकारात्मक है तो तल की ओर दिशा लेता है। ध्यान दें कि गॉस के नियम के उपयोग ने एक अतिरिक्त तथ्य को भी खोल दिया है: $E$ भी $x$ के स्वतंत्र है। एक अंतिम विशाल समतलीय पट्टी के लिए, समीकरण (1.33) समतलीय पट्टी के मध्य भाग में, सिरों से दूर लगभग सत्य होता है।
1.14.3 एक समान आवेशित पतली गोलीय खोल के कारण क्षेत्र
मान लीजिए $\sigma$ एक पतली गोलीय खोल के समतल आवेश घनत्व है, जिसकी त्रिज्या $R$ है (चित्र 1.28)। यह स्थिति स्पष्ट रूप से गोलीय सममिति के अंतर्गत है। कोई बिंदु $\mathrm{P}$, बाहर या अंदर, जहां विद्युत क्षेत्र केवल $r$ (खोल के केंद्र से बिंदु तक की त्रिज्या) पर निर्भर कर सकता है और यह त्रिज्य वेक्टर के अनुदिश होना चाहिए (अर्थात, त्रिज्य वेक्टर के अनुदिश)।
(i) खोल के बाहर बिंदु पर क्षेत्र: मान लीजिए बिंदु $\mathrm{P}$ खोल के बाहर है और इसका त्रिज्य वेक्टर $\mathbf{r}$ है। $\mathrm{P}$ पर $\mathbf{E}$ की गणना करने के लिए, हम गॉसीय सतह के रूप में एक गोला लेते हैं, जिसकी त्रिज्या $r$ है और जो केंद्र $\mathrm{O}$ के केंद्र पर है और $\mathrm{P}$ के माध्यम से गुजरता है। इस गोले के सभी बिंदु दिए गए आवेश विन्यास के संबंध में समान हैं। (यह हमारे गोलीय सममिति के अर्थ है।) इसलिए, गॉसीय सतह के प्रत्येक बिंदु पर विद्युत क्षेत्र के मान $E$ के समान होता है और यह प्रत्येक बिंदु पर त्रिज्य वेक्टर के अनुदिश होता है। इसलिए, $\mathbf{E}$ और $\Delta \mathbf{S}$ के प्रत्येक बिंदु पर समान्तर होते हैं और प्रत्येक तत्व के माध्यम से फ्लक्स $E \Delta S$ होता है। सभी $\Delta S$ के लिए योग करने पर, गॉसीय सतह के माध्यम से फ्लक्स $E \times 4 \pi r^{2}$ होता है। आवेश घेरा गया है $\sigma \times 4 \pi R^{2}$।
गॉस के नियम द्वारा
$$ E \times 4 \pi r^2=\frac{\sigma}{\varepsilon_0} 4 \pi R^2 $$
या,
$$ E=\frac{\sigma R^2}{\varepsilon_0 r^2}=\frac{q}{4 \pi \varepsilon_0 r^2} $$
जहाँ $q=4 \pi R^2 \sigma$ गोलीय खोल पर कुल आवेश है। सदिश रूप में,
$$ \mathbf{E}=\frac{q}{4 \pi \varepsilon_0 r^2} \hat{\mathbf{r}} $$

चित्र: 1.28 एक बिंदु के लिए गाउसीय सतहें (a) r > R, (b) r < R के लिए।
विद्युत क्षेत्र $q>0$ के लिए बाहर की ओर दिशात्मक होता है और $q<0$ के लिए अंदर की ओर दिशात्मक होता है। हालांकि, यह ठीक तौर पर एक आवेश $q$ के केंद्र $\mathrm{O}$ पर रखे आवेश द्वारा उत्पन्न क्षेत्र होता है। इसलिए, शेल के बाहर के बिंदुओं के लिए, एक समान आवेशित शेल के कारण क्षेत्र जैसे ही लगता है मान लें कि शेल का पूरा आवेश उसके केंद्र पर संकेंद्रित है।
(ii) शेल के अंदर क्षेत्र: चित्र 1.28 (b) में, बिंदु $\mathrm{P}$ शेल के अंदर है। गाउसीय सतह फिर भी $\mathrm{P}$ के माध्यम से गुजरती हुई $\mathrm{O}$ केंद्रित एक गोला है।
फ्लक्स गॉसियन सतह के माध्यम से, पहले के तरह गणना की जाती है, $E \times 4 \pi r^{2}$. हालांकि, इस मामले में, गॉसियन सतह कोई भी आवेश नहीं घेरती है। तब गॉस के नियम के अनुसार
$E \times 4 \pi r^{2}=0$
अर्थात, $E=0 \quad(r<R)$
अर्थात, एक समान आवेशित पतली शेल के कारण शेल के अंदर के सभी बिंदुओं पर क्षेत्र शून्य होता है। यह महत्वपूर्ण परिणाम गॉस के नियम का एक व्युत्पन्न परिणाम है, जो कूलॉम के नियम से आता है। इस परिणाम की प्रयोगात्मक जांच कूलॉम के नियम में $1 / r^{2}$ आश्रितता की पुष्टि करती है।
उदाहरण 1.13 एक प्रारंभिक परमाणु के मॉडल के लिए, इसे एक धनावेशित बिंदु नाभिक के रूप में विचार किया गया जिसका आवेश Ze होता है, जो एक त्रिज्या R तक एकसमान नकारात्मक आवेश के घेरे में होता है। पूरा परमाणु उदासीन होता है। इस मॉडल के लिए, नाभिक से r दूरी पर विद्युत क्षेत्र क्या होगा?

चित्र 1.29
हल इस परमाणु के मॉडल के लिए आवेश वितरण चित्र 1.29 में दिखाया गया है। त्रिज्या $R$ के समान गोलीय आवेश वितरण में कुल नकारात्मक आवेश $-Z e$ होना चाहिए, क्योंकि परमाणु (आवेश $Z e+$ नकारात्मक आवेश के नाभिक) उदासीन होता है। इससे तुरंत हमें नकारात्मक आवेश घनत्व $\rho$ मिल जाता है, क्योंकि हमें निम्नलिखित होना चाहिए:
$$ \frac{4 \pi R^{3}}{3} \rho=0-Z e $$
या $\rho=-\frac{3 Z e}{4 \pi R^{3}}$
एक बिंदु $\mathrm{P}$ पर विद्युत क्षेत्र $\mathbf{E}(\mathbf{r})$ की गणना करने के लिए, जो नाभिक से दूरी $r$ पर होता है, हम गॉस के नियम का उपयोग करते हैं। आवेश वितरण के गोलीय सममिति के कारण, विद्युत क्षेत्र $\mathbf{E}(\mathbf{r})$ के मान केवल त्रिज्यीय दूरी पर निर्भर करता है, बिंदु $\mathbf{r}$ की दिशा के बावजूद। इसकी दिशा नाभिक से बिंदु $\mathrm{P}$ तक त्रिज्या सदिश $\mathbf{r}$ की दिशा में (या विपरीत दिशा में) होती है। स्पष्ट गॉसीय सतह एक गोलीय सतह है जो नाभिक केंद्रित होती है। हम दो स्थितियों की विचार करते हैं, अर्थात $r<R$ और $r>R$।
(i) $r<R$ : गोलीय सतह द्वारा घिरे विद्युत फ्लक्स $\phi$ है
$$ \phi=E(r) \times 4 \pi r^{2} $$
जहाँ E (r) वह बिंदु पर विद्युत क्षेत्र के परिमाण को दर्शाता है। इसका कारण यह है कि गोलीय गॉसीय सतह के किसी बिंदु पर विद्युत क्षेत्र की दिशा उस बिंदु पर सतह के अभिलम्ब की दिशा के समान होती है और सतह के सभी बिंदुओं पर इसका परिमाण समान होता है।
- इसे वर्ग 11 के भौतिक विज्ञान के अध्याय 7.5 में चर्चा किए गए समान द्रव्यमान के ढक्कन के साथ तुलना करें।
गॉसीय सतह द्वारा घिरे आवेश q धनात्मक नाभिकीय आवेश और त्रिज्या r के गोले के भीतर नकारात्मक आवेश है,
i.e., $q=Z e+\frac{4 \pi r^{3}}{3} \rho$
पहले प्राप्त की गई आवेश घनत्व $\rho$ के लिए प्रतिस्थापित करने पर, हमारे पास है
$q=Z e-Z e \frac{r^{3}}{R^{3}}$
गॉस के नियम द्वारा, हमें देते हैं,
$E(r)=\frac{Z e}{4 \pi \varepsilon_{0}} \quad \frac{1}{r^{2}}-\frac{r}{R^{3}} \quad ; \quad r<R$
इलेक्ट्रिक क्षेत्र त्रिज्या के बाहर दिशा में होता है।
(ii) $r>R$ : इस स्थिति में, गॉसीय गोलीय सतह द्वारा घेरे गए कुल आवेश शून्य है क्योंकि परमाणु उदासीन है। इसलिए, गॉस के नियम से,
$E(r) \times 4 \pi r^{2}=0$ या $E(r)=0 ; \quad r>R$
$ r=R $ पर, दोनों मामलों में एक ही परिणाम प्राप्त होता है: $ E=0 $।
सारांश
1. विद्युत और चुंबकीय बल परमाणु, अणु और ठोस पदार्थ के गुणों को निर्धारित करते हैं।
2. घर्षण विद्युत के सरल प्रयोगों से यह अनुमान लगाया जा सकता है कि प्रकृति में दो प्रकार के आवेश होते हैं; और एक ही प्रकार के आवेश परस्पर विपरीत तथा असमान आवेश आकर्षित करते हैं। संवाद के अनुसार, रेशम से घर्षित काँच के छड़ के आवेश धनात्मक होता है; और बालू से घर्षित प्लास्टिक के छड़ के आवेश ऋणात्मक होता है।
3. चालक पदार्थ विद्युत आवेश के गति के लिए अनुमति देते हैं, जबकि अचालक पदार्थ नहीं। धातुओं में गतिशील आवेश इलेक्ट्रॉन होते हैं; विद्युत अपघट्यों में धनात्मक और ऋणात्मक आयन दोनों गतिशील होते हैं।
4. विद्युत आवेश के तीन मूल गुण होते हैं: क्वांटीकरण, अद्वितीयता और संरक्षण।
विद्युत आवेश के क्वांटीकरण का अर्थ यह है कि किसी वस्तु के कुल आवेश $(q)$ हमेशा आवेश के मूल क्वांटम $(e)$ के पूर्णांक गुणक होता है, अर्थात $q = n e$, जहाँ $n = 0, \pm 1, \pm 2, \pm 3, \ldots$ प्रोटॉन और इलेक्ट्रॉन के आवेश क्रमशः $+e$ और $-e$ होते हैं। विशाल आवेशों के लिए, जहाँ $n$ एक बहुत बड़ी संख्या होती है, आवेश के क्वांटीकरण को नगण्य मान लिया जाता है।
विद्युत आवेश की अद्वितीयता का अर्थ यह है कि किसी तंत्र के कुल आवेश तंत्र में सभी व्यक्तिगत आवेशों के बीजगणितीय योग (अर्थात सही चिह्न के साथ योग) होता है।
विद्युत आवेशों के संरक्षण का अर्थ यह है कि एक अलगाव वाले निकाय के कुल आवेश समय के साथ अपरिवर्तित रहता है। इसका अर्थ यह है कि जब वस्तुएं घर्षण के माध्यम से आवेशित होती हैं, तो एक वस्तु से दूसरी वस्तु में विद्युत आवेश के परिवर्तन होता है, लेकिन आवेश के निर्माण या विनाश नहीं होता।
5. कूलॉम का नियम: दो बिंदु आवेश $q_{1}$ और $q_{2}$ के बीच आपसी विद्युत स्थैतिक बल उत्परिवर्तन $q_{1} q_{2}$ के गुणनफल और उनके बीच दूरी $r_{21}$ के वर्ग के व्युत्क्रमानुपाती होता है। गणितीय रूप से,
$ \mathbf{F_{21}}= \text{force on }q_{2} \text{ due to } q_{1}=\frac{k\left(q_{1} q_{2}\right)}{r_{21}^2} \hat{\mathbf{r_{21}}}$
जहाँ $\hat{\mathbf{r _{21}}}$ एक इकाई सदिश है, जो $q _{1}$ से $q _{2}$ की दिशा में होता है और $k=\frac{1}{4 \pi \varepsilon _{0}}$ समानुपाती स्थिरांक है।
SI इकाइयों में, आवेश की इकाई कूलॉम होती है। समानुपाती स्थिरांक $\varepsilon_{0}$ का प्रयोगकर्ता मूल्य है
$$ \varepsilon _{0}=8.854 \times 10^{-12} \mathrm{C}^{2} \mathrm{~N} ^{-1} \mathrm{~m} ^{-2} $$
$ k $ का अनुमानित मान है
$$ k=9 \times 10^{9} \mathrm{~N} \mathrm{~m}^{2} \mathrm{C}^{-2} $$
6. प्रोटॉन और इलेक्ट्रॉन के बीच विद्युत बल और गुरुत्वाकर्षण बल का अनुपात है
$$ \frac{k e^{2}}{G \quad m_{e} m_{p}} \cong 2.4 \times 10^{39} $$
7. सुपरपोजिशन सिद्धांत: यह सिद्धांत यह गुण है पर आधारित है कि दो आवेशों के बीच आकर्षण या प्रतिकर्षण बल तीसरे (या अधिक) आवेश की उपस्थिति से प्रभावित नहीं होते। आवेशों के एक संग्रह $q_{1}, q_{2}, q_{3}, \ldots$ के लिए, किसी आवेश, जैसे $q_{1}$ पर बल वह सदिश योग है जो $q_{1}$ पर $q_{2}$ के कारण बल, $q_{1}$ पर $q_{3}$ के कारण बल आदि द्वारा लगता है। प्रत्येक युग्म के लिए, बल पहले उल्लेखित दो आवेशों के लिए कूलॉम के नियम द्वारा दिया गया है।
8. एक आवेश विन्यास के कारण एक बिंदु पर विद्युत क्षेत्र $\mathbf{E}$, उस बिंदु पर रखे छोटे धनावेशी परीक्षण आवेश $q$ पर बल को आवेश के परिमाण से विभाजित करके प्राप्त किया जाता है। एक बिंदु आवेश $q$ के कारण विद्युत क्षेत्र का परिमाण $|q| / 4 \pi \varepsilon_{0} r^{2}$ होता है; यह $q$ के बराबर त्रिज्या दिशा में बाहर की ओर होता है, यदि $q$ धनावेशित हो, और यदि $q$ नकारात्मक हो तो त्रिज्या दिशा में अंदर की ओर होता है। कूलॉम बल के जैसे ही, विद्युत क्षेत्र भी सुपरपोजिशन सिद्धांत को संतुष्ट करता है।
9. एक विद्युत क्षेत्र रेखा एक ऐसी वक्र होती है जिसका प्रत्येक बिंदु पर स्पर्श रेखा उस बिंदु पर विद्युत क्षेत्र की दिशा दर्शाती है। विद्युत क्षेत्र रेखाओं की सापेक्ष घनत्वता विभिन्न बिंदुओं पर विद्युत क्षेत्र की सापेक्ष शक्ति को दर्शाती है; वे तीव्र विद्युत क्षेत्र के क्षेत्र में एक दूसरे के पास घनिष्ठ होती हैं और कम विद्युत क्षेत्र के क्षेत्र में दूर दूर फैली होती हैं। विद्युत क्षेत्र के स्थिर क्षेत्र में विद्युत क्षेत्र रेखाएँ समान दूरी पर समांतर सीधी रेखाएँ होती हैं।
10. क्षेत्र रेखाओं के कुछ महत्वपूर्ण गुण हैं: (i) क्षेत्र रेखाएँ कोई भी ब्रेक बिना जारी रहते हुए लगातार वक्र होती हैं। (ii) दो क्षेत्र रेखाएँ एक दूसरे को काट नहीं सकतीं। (iii) विद्युत क्षेत्र रेखाएँ धनात्मक आवेश से नकारात्मक आवेश तक शुरू होती हैं और समाप्त होती हैं - वे बंद लूप बनाने में सक्षम नहीं हैं।
11. एक विद्युत द्विध्रुव एक समान और विपरीत आवेश $q$ और $-q$ के एक जोड़े को कहते हैं जो कुछ दूरी $2a$ पर अलग होते हैं। इसके द्विध्रुव आघूर्ण सदिश $\mathbf{p}$ के परिमाण $2 q a$ होता है और यह द्विध्रुव अक्ष के दिशा में होता है, जो $-q$ से $q$ तक होता है।
12. विद्युत द्विध्रुव के चुंबकीय क्षेत्र के बराबर तल में (अर्थात अक्ष के लंबवत तल जो इसके केंद्र से गुजरता है) केंद्र से दूरी $r$ पर:
$$\mathbf{E}=\frac{-\mathbf{p}}{4 \pi \varepsilon_{o}} \frac{1}{\left(a^{2}+r^{2}\right)^{3 / 2}}$$ $$\cong \frac{-\mathbf{p}}{4 \pi \varepsilon_{o} r^{3}}, \quad$ जब $r > > a$$
केंद्र से दूरी $r$ पर अक्ष पर द्विध्रुव के विद्युत क्षेत्र:
$$ \begin{aligned} & \mathbf{E}=\frac{2 \mathbf{p} r}{4 \pi \varepsilon_{0}\left(r^{2}-a^{2}\right)^{2}} \\
$$ & \cong \frac{2 \mathbf{p}}{4 \pi \varepsilon_{0} r^{3}} \quad \text { for } \quad r > > a \end{aligned} $$
द्विध्रुव विद्युत क्षेत्र के $1 / r^{3}$ आश्रितता का ध्यान रखना चाहिए, जो बिंदु आवेश के कारण विद्युत क्षेत्र के $1 / r^{2}$ आश्रितता के विपरीत है।
13. एक समान विद्युत क्षेत्र $\mathbf{E}$ में, एक द्विध्रुव एक बल距 $\tau$ अनुभव करता है जो द्वारा दिया जाता है
$$ \tau=\mathbf{p} \times \mathbf{E} $$
लेकिन कोई शुद्ध बल अनुभव नहीं करता है।
14. विद्युत क्षेत्र $\mathbf{E}$ के माध्यम से छोटे क्षेत्र के तत्व $\Delta \mathbf{S}$ के माध्यम से फ्लक्स $\Delta \phi$ द्वारा दिया जाता है
$ \Delta \phi=\mathbf{E} \cdot \Delta \mathbf{S} $ वेक्टर क्षेत्र के अवयव $\Delta \mathbf{S}$ है $ \Delta \mathbf{S}=\Delta S \hat{\mathbf{n}} $
जहाँ $\Delta S$ क्षेत्र के अवयव के मापदंड है और $\hat{\mathbf{n}}$ क्षेत्र के अवयव के लम्ब दिशा में है, जिसे अत्यधिक छोटे $\Delta S$ के लिए समतल माना जा सकता है। एक बंद सतह के क्षेत्र अवयव के लिए, $\hat{\mathbf{n}}$ को बाहरी लम्ब दिशा के रूप में लिया जाता है, इसके लिए परिपाटी है।
15. गॉस के नियम: किसी भी बंद सतह $S$ के माध्यम से विद्युत क्षेत्र के फ्लक्स $1 / \varepsilon_{0}$ के गुणक में $S$ द्वारा घेरे गए कुल आवेश के बराबर होता है। यह नियम विद्युत क्षेत्र $\mathbf{E}$ के निर्धारण में विशेष रूप से उपयोगी होता है, जब स्रोत वितरण की सरल सममिति होती है:
(i) एक समान रेखीय आवेश घनत्व $\lambda$ के बेहद लंबे सीधे तार के लिए
$$\mathbf{E}=\frac{\lambda}{2 \pi \varepsilon_{0} r} \hat{\mathbf{n}}$$
जहाँ $r$ बिंदु के तार से लंबवत दूरी है और $\hat{\mathbf{n}}$ बिंदु के माध्यम से गुजरते हुए तार के लंबवत समतल में एक इकाई वेक्टर है।
(ii) एक अपरिमित बेहद पतले समतल आवेश घनत्व $\sigma$ के तल के लिए
$$\mathbf{E}=\frac{\sigma}{2 \varepsilon_{0}} \hat{\mathbf{n}}$$
जहाँ $\hat{\mathbf{n}}$ तल के लंबवत एक इकाई वेक्टर है, जो दोनों ओर बाहर की ओर बिंदु तक बढ़ता है।
(iii) एक समान सतह आवेश घनत्व $\sigma$ वाले पतले गोलीय खोल के लिए
$$ \begin{array}{ll} \mathbf{E}=\frac{q}{4 \pi \varepsilon_{0} r^{2}} \hat{\mathbf{r}} & (r \geq R) \\ \mathbf{E}=0 & (r<R) \end{array} $$
जहाँ $r$ बिंदु के केंद्र से दूरी है और $R$ खोल की त्रिज्या है। $q$ खोल का कुल आवेश है: $q=4 \pi R^{2} \sigma$। खोल के बाहर विद्युत क्षेत्र ऐसा लगता है जैसे कुल आवेश केंद्र पर संकेंद्रित हो। एक समान आयतन आवेश घनत्व वाले ठोस गोले के लिए भी यही परिणाम सत्य है। खोल के आंतरिक सभी बिंदुओं पर विद्युत क्षेत्र शून्य होता है।
| भौतिक राशि | प्रतीक | आयाम | इकाई | टिप्पणियाँ |
|---|---|---|---|---|
| सदिश क्षेत्र का तत्व | $\Delta \mathbf{S}$ | $\left[\mathrm{L}^2\right]$ | $\mathrm{m}^2$ | $\Delta \mathbf{S}=\Delta S \mathbf{n}$ |
| विद्युत क्षेत्र | $\mathbf{E}$ | VIL 121 | $\mathrm{~V} \mathrm{~m}^{-1}$ | |
| विद्युत फ्लक्स | $\phi$ | $\left[\mathrm{ML}^3 \mathrm{~T}^{-3} \mathrm{~A}^{-1}\right]$ | $\mathrm{V} \mathrm{m}$ | $\Delta \phi=\mathbf{E} . \Delta \mathbf{S}$ |
| द्विध्रुव आघूर्ण | $\mathbf{p}$ | [LTA] | $\mathrm{C} \mathrm{m}$ | सदिश ऋणात्मक आवेश से धनात्मक आवेश की ओर दिशा में |
| आवेश घनत्व: | | | | | | रेखीय | $\lambda$ | $\left[\mathrm{L}^{-1} \mathrm{TA}\right]$ | $\mathrm{C} \mathrm{m}^{-1}$ | आवेश/लंबाई | | सतह | $\sigma$ | $\left[\mathrm{L}^{-2} \mathrm{TA}\right]$ | $\mathrm{C} \mathrm{m}^{-2}$ | आवेश/क्षेत्रफल | | आयतन | $\rho$ | $\left[\mathrm{L}^{-3} \mathrm{TA}\right]$ | $\mathrm{C} \mathrm{m}^{-3}$ | आवेश/आयतन |
सोचने वाले बिंदु
1. आप विचार कर सकते हैं कि क्यों प्रोटॉन, सभी धनावेशित होते हैं, एक साथ नाभिक में घनिष्ठ रूप से रहते हैं। क्यों वे नहीं उड़ जाते? आप जानेंगे कि एक तीसरा मूल बल, जिसे मजबूत बल कहा जाता है, जो उन्हें एक साथ रखता है। लेकिन इस बल की कार्यक्षमता की दूरी बहुत छोटी होती है $\sim 10^{-14}$ $\mathrm{m}$. यह ठीक तरह से नाभिक के आकार के बराबर है। इसके अलावा, क्वांटम यांत्रिकी के नियमों के कारण इलेक्ट्रॉन भी प्रोटॉन के ऊपर बैठे नहीं रह सकते, अर्थात नाभिक में नहीं। इससे प्रकृति में अपने रूप में अपनी संरचना के साथ परमाणु बनते हैं।
4. $k$ का बहुत बड़ा मान, अर्थात् विद्युत प्रभावों के दृष्टिकोण से आवेश के इकाई (1C) के बड़े आकार के कारण होता है। यह वही कारण है जिसके बारे में बिंदु 3 में जा चुके हैं (जैसा कि उल्लेख किया गया है) कि आवेश की इकाई चुंबकीय बलों (धारा वाहक तारों पर बल) के आधार पर परिभाषित की गई है, जो आमतौर पर विद्युत बलों की तुलना में कमजोर होते हैं। इसलिए जबकि 1 ऐम्पियर चुंबकीय प्रभावों के लिए एक उचित आकार की इकाई है, $1 \mathrm{C}=1 \mathrm{~A} \mathrm{~s}$, विद्युत प्रभावों के लिए इतनी बड़ी इकाई है।
5. आवेश के योगात्मक गुण कोई ‘स्पष्ट’ गुण नहीं है। इसके साथ यह तथ्य संबंधित है कि विद्युत आवेश के साथ कोई दिशा संबंधित नहीं होती; आवेश एक अदिश है।
6. आवेश न केवल घूर्णन के तहत एक अदिश (या अपरिवर्ती) होता है; बल्कि एक दूसरे के संबंध में गतिमान अंकगणितीय ढांचों के लिए भी अपरिवर्ती होता है। यह प्रत्येक अदिश के लिए हमेशा सत्य नहीं होता। उदाहरण के लिए, कार्यशक्ति घूर्णन के तहत एक अदिश होती है, लेकिन एक दूसरे के संबंध में गतिमान अंकगणितीय ढांचों के लिए अपरिवर्ती नहीं होती।
7. एक अनुच्छेदित प्रणाली के कुल आवेश के संरक्षण की गुणधर्म अंक 6 में आवेश के अदिश प्रकृति के स्वतंत्र गुण है। संरक्षण एक दिए गए अंकगणितीय ढांचे में समय के संबंध में अपरिवर्तीता को संदर्भित करता है। एक मात्रा अदिश हो सकती है लेकिन संरक्षित नहीं हो सकती (जैसे कि एक अप्रत्यावर्ती टकराव में कार्यशक्ति)। दूसरी ओर, आप एक संरक्षित सदिश मात्रा के साथ भी हो सकते हैं (जैसे कि एक अनुच्छेदित प्रणाली के कोणीय संवेग)।
8. विद्युत आवेश के क्वांटीकरण का एक मूलभूत (समझा नहीं जा सकता) प्रकृति का नियम है; दिलचस्प बात यह है कि द्रव्यमान के क्वांटीकरण के लिए कोई ऐसा समान नियम नहीं है।
9. सुपरपोजिशन सिद्धांत को ‘स्पष्ट’ नहीं माना जाना चाहिए, या सदिशों के जोड़ के नियम के बराबर नहीं माना जाना चाहिए। यह दो बातें कहता है: एक आवेश पर दूसरे आवेश के कारण बल अन्य आवेशों की उपस्थिति से प्रभावित नहीं होता, और दो से अधिक आवेशों के उपस्थिति में केवल तीन-केंद्रीय, चार-केंद्रीय, आदि बल नहीं होते।
10. एक विस्थापित आवेश विन्यास के कारण विद्युत क्षेत्र विस्थापित आवेशों के स्थान पर निर्धारित नहीं होता। एक सतत आयतन आवेश वितरण के लिए, विद्युत क्षेत्र वितरण के किसी भी बिंदु पर निर्धारित होता है। एक सतह आवेश वितरण के लिए, विद्युत क्षेत्र सतह के पार असतत होता है।
11. एक आवेश विन्यास के कारण विद्युत क्षेत्र जिसका कुल आवेश शून्य होता है, शून्य नहीं होता; लेकिन विन्यास के आकार की तुलना में बहुत बड़ी दूरियों पर इसका क्षेत्र $1 / r^{2}$ से तेजी से घटता है, जो एक अकेले आवेश के कारण विद्युत क्षेत्र के लिए आम बात होती है। विद्युत द्विध्रुव इस तथ्य का सरलतम उदाहरण है।
अभ्यास
1.1 दो छोटे आवेशित गोलियों के बीच बल क्या होगा जिनके आवेश $2 \times 10^{-7} \mathrm{C}$ और $3 \times 10^{-7} \mathrm{C}$ हैं और वे हवा में 30 सेमी की दूरी पर स्थित हैं?
उत्तर दिखाएं
उत्तर
प्रतिकर्षण बल का परिमाण = $6 \times 10^{-3} \mathrm{~N}$
पहले गोली का आवेश, $q_{1}=2 \times 10^{-7} \mathrm{C}$
दूसरे गोली का आवेश, $q_{2}=3 \times 10^{-7} \mathrm{C}$
गोलियों के बीच दूरी, $r=30 \mathrm{~cm}=0.3 \mathrm{~m}$
गोलियों के बीच विद्युत बल को निम्न संबंध द्वारा दिया जाता है,
$$ F=\frac{q_{1} q_{2}}{4 \pi \in_{0} r^{2}} $$
जहाँ, $\epsilon_{0}=$ रिक्त स्थान की प्रवैगता
$$ \begin{aligned} & \frac{1}{4 \pi \epsilon_{0}}=9 \times 10^{9} \mathrm{~N} \mathrm{~m}^{2} \mathrm{C}^{-2} \\ & F=\frac{9 \times 10^{9} \times 2 \times 10^{-7} \times 3 \times 10^{-7}}{(0.3)^{2}}=6 \times 10^{-3} \mathrm{~N} \end{aligned} $$
अतः, दो छोटे आवेशित गोलियों के बीच बल $6 \times 10^{-3} \mathrm{~N}$ है। आवेश समान प्रकृति के हैं। अतः, उनके बीच बल प्रतिकर्षण होगा।
1.2 एक छोटे गोली के आवेश $0.4 \mu \mathrm{C}$ है जो दूसरे छोटे गोली के आवेश $-0.8 \mu \mathrm{C}$ के कारण हवा में $0.2 \mathrm{~N}$ के विद्युत बल का अनुभव करती है। (a) दो गोलियों के बीच दूरी क्या है? (b) पहले गोली के कारण दूसरे गोली पर बल क्या है?
उत्तर दिखाएं
उत्तर
पहले गोली पर विद्युत बल, $F=0.2 \mathrm{~N}$
इस गोली का आवेश, $q_{1}=0.4 \mu \mathrm{C}=0.4 \times 10^{-6} \mathrm{C}$
दूसरे गोली का आवेश, $q_{2}=-0.8 \mu \mathrm{C}=-0.8 \times 10^{-6} \mathrm{C}$
गोलियों के बीच विद्युत बल को निम्न संबंध द्वारा दिया जाता है,
$$ F=\frac{q_{1} q_{2}}{4 \pi \in_{0} r^{2}} $$
जहाँ, $\epsilon_{0}=$ रिक्त स्थान की प्रवैगता
$$ \begin{aligned} & \text { और, } \frac{1}{4 \pi \epsilon_{0}}=9 \times 10^{9} \mathrm{~N} \mathrm{~m}^{2} \mathrm{C}^{-2} \\
$$ \begin{aligned} r^{2} & =\frac{q_{1} q_{2}}{4 \pi \in_{0} F} \\ & =\frac{0.4 \times 10^{-6} \times 8 \times 10^{-6} \times 9 \times 10^{9}}{0.2} \\ & =144 \times 10^{-4} \\ r & =\sqrt{144 \times 10^{-4}}=0.12 \mathrm{~m} \end{aligned} $$
दो गोलियों के बीच की दूरी $0.12 \mathrm{~m}$ है।
दोनों गोलियाँ एक दूसरे को एक ही बल से आकर्षित करती हैं। इसलिए, पहली गोली के कारण दूसरी गोली पर बल $0.2 \mathrm{~N}$ है।
1.3 जांच करें कि अनुपात $k e^{2} / G m_{e} m_{p}$ विमाहीन है। भौतिक नियतांकों के तालिका को देखकर इस अनुपात का मान निर्धारित करें। इस अनुपात का क्या अर्थ है?
उत्तर दिखाएं
उत्तर
दिए गए अनुपात है $\frac{k e^{2}}{\mathrm{G} m_{\mathrm{e}} m_{\mathrm{p}}}$।
जहाँ,
$\mathrm{G}=$ गुरुत्वाकर्षण नियतांक
इसकी इकाई $\mathrm{N} \mathrm{m}^{2} \mathrm{~kg}^{-2}$ है।
$m_{\mathrm{e}}$ और $m_{\mathrm{p}}=$ इलेक्ट्रॉन और प्रोटॉन के द्रव्यमान।
इनकी इकाई $\mathrm{kg}$ है।
$e=$ विद्युत आवेश। इसकी इकाई C है।
$k=\mathrm{A}$ नियतांक
$=\frac{1}{4 \pi \epsilon_{0}}$
$\epsilon_{0}=$ रिक्त स्थान की प्रवेश्यता
इसकी इकाई $\mathrm{N} \mathrm{m}^{2} \mathrm{C}^{-2}$ है।
इसलिए, दिए गए अनुपात की इकाई $\frac{k e^{2}}{\mathrm{G} m_{\mathrm{e}} m_{\mathrm{p}}}=\frac{\left[\mathrm{Nm}^{2} \mathrm{C}^{-2}\right]\left[\mathrm{C}^{-2}\right]}{\left[\mathrm{Nm}^{2} \mathrm{~kg}^{-2}\right][\mathrm{kg}][\mathrm{kg}]}$ $=\mathrm{M}^{0} \mathrm{~L}^{0} \mathrm{~T}^{0}$
इसलिए, दिए गए अनुपात विमाहीन है।
$e=1.6 \times 10^{-19} \mathrm{C}$
$\mathrm{G}=6.67 \times 10^{-11} \mathrm{~N} \mathrm{~m}^{2} \mathrm{~kg}^{-2}$
$m_{\mathrm{e}}=9.1 \times 10^{-31} \mathrm{~kg}$
$m_{\mathrm{p}}=1.66 \times 10^{-27} \mathrm{~kg}$
इसलिए, दिए गए अनुपात का संख्यात्मक मान है
$\frac{k e^{2}}{\mathrm{G} m_{e} m_{p}}=\frac{9 \times 10^{9} \times\left(1.6 \times 10^{-19}\right)^{2}}{6.67 \times 10^{-11} \times 9.1 \times 10^{-3} \times 1.67 \times 10^{-22}} \approx 2.3 \times 10^{39}$
This is the ratio of electric force to the gravitational force between a proton and an electron, keeping distance between them constant.
1.4 (a) Explain the meaning of the statement ’electric charge of a body is quantised'.
(b) Why can one ignore quantisation of electric charge when dealing with macroscopic i.e., large scale charges?
उत्तर दिखाएं
Answer
“electric charge of a body is quantised” के कथन का अर्थ यह है कि विद्युत आवेश एक सतत श्रेणी में नहीं बल्कि एक डिस्क्रीट इकाइयों में मौजूद होता है। विशेषकर, किसी वस्तु का आवेश कोई पूर्णांक गुणक होता है, जो तत्वावेश $ e $ के बराबर होता है, जो लगभग $ 1.6 \times 10^{-19} $ कूलॉम होता है। इसका अर्थ यह है कि किसी वस्तु के कुल आवेश $ Q $ को इस प्रकार व्यक्त किया जा सकता है: $ Q = n \cdot e $
जहाँ $ n $ एक पूर्णांक होता है (जो धनात्मक, ऋणात्मक या शून्य हो सकता है)। इस आवेश के डिस्क्रीट होने का कारण यह है कि आवेश को तत्वावेश वाले कणों, जैसे इलेक्ट्रॉन और प्रोटॉन द्वारा वहन किया जाता है, जो अपने आवेश के निश्चित होते हैं। इस कारण, कोई मैक्रोस्कोपिक वस्तु केवल इन तत्वावेश के पूर्णांक गुणकों के आवेश के मान रख सकती है।
मैक्रोस्कोपिक या बड़े पैमाने के आवेशों के मामले में, आवेशों के मान विद्युत आवेश के मान के तुलना में बहुत बड़े होते हैं। इसलिए, विद्युत आवेश के डिस्क्रीट होने के बारे में ध्यान नहीं दिया जाता है। इसलिए, यह माना जाता है कि विद्युत आवेश सतत होता है।
1.5 जब एक कांच के छड़ को सूत के कपड़े के साथ रगड़ा जाता है, तो दोनों पर आवेश उत्पन्न होते हैं। अनेक अन्य वस्तु युग्मों के साथ एक समान घटना देखी जाती है। बताइए कि यह देखना कैसे आवेश के संरक्षण के नियम के साथ संवेदनशील है।
उत्तर दिखाएं
Answer
रगड़ना दो वस्तुओं पर बराबर मात्रा में विपरीत प्रकृति के आवेश उत्पन्न करता है क्योंकि आवेश जोड़ी के रूप में उत्पन्न होते हैं। इस आवेश के चार्ज करने की घटना को फ्रेक्शन द्वारा चार्ज करना कहा जाता है। दो रगड़े गए वस्तुओं के तंत्र का कुल आवेश शून्य होता है। इसका कारण यह है कि बराबर मात्रा में विपरीत आवेश एक दूसरे को नष्ट कर देते हैं। जब कांच के छड़ को सूत के कपड़े के साथ रगड़ा जाता है, तो दोनों वस्तुओं पर विपरीत प्रकृति के आवेश उत्पन्न होते हैं। यह घटना आवेश के संरक्षण के नियम के साथ संवेदनशील है। अनेक अन्य वस्तु युग्मों के साथ एक समान घटना देखी जाती है।
1.6 चार बिंदु आवेश $q_{\mathrm{A}}=2 \mu \mathrm{C}, q_{\mathrm{B}}=-5 \mu \mathrm{C}, q_{\mathrm{C}}=2 \mu \mathrm{C}$, और $q_{\mathrm{D}}=-5 \mu \mathrm{C}$ एक वर्ग $ABCD$ के कोनों पर स्थित हैं, जिसकी भुजा $10 \mathrm{~cm}$ है। एक $1 \mu \mathrm{C}$ के आवेश को वर्ग के केंद्र पर रखने पर आवेश पर बल कितना होगा?
उत्तर दिखाएं
उत्तर
दी गई आकृति में एक वर्ग दिखाया गया है, जिसकी भुजा $10 \mathrm{~cm}$ है और इसके कोनों पर चार आवेश रखे गए हैं। $\mathrm{O}$ वर्ग का केंद्र है।

जहाँ,
(भुजाएँ) $\mathrm{AB}=\mathrm{BC}=\mathrm{CD}=\mathrm{AD}=10 \mathrm{~cm}$
(कर्ण) $\mathrm{AC}=\mathrm{BD}=10 \sqrt{2} \mathrm{~cm}$
$\mathrm{AO}=\mathrm{OC}=\mathrm{DO}=\mathrm{OB}=5 \sqrt{2} \mathrm{~cm}$
बिंदु $\mathrm{O}$ पर $1 \mu \mathrm{C}$ का आवेश रखा गया है।
कोने $\mathrm{A}$ पर रखे आवेश और केंद्र $\mathrm{O}$ पर रखे आवेश के बीच प्रतिकर्षण बल के मान के बराबर है लेकिन दिशा विपरीत है, जो कोने $\mathrm{C}$ पर रखे आवेश और केंद्र $\mathrm{O}$ पर रखे आवेश के बीच प्रतिकर्षण बल के विपरीत है। इसलिए, वे एक दूसरे को विपरीत दिशा में बराबर मान के बल देंगे और एक दूसरे को विपरीत दिशा में बराबर मान के बल देंगे। इसलिए, वे एक दूसरे को विपरीत दिशा में बराबर मान के बल देंगे और एक दूसरे को विपरीत दिशा में बराबर मान के बल देंगे। इसलिए, वर्ग के कोनों पर रखे चार आवेशों द्वारा केंद्र $\mathrm{O}$ पर रखे $1 \mu \mathrm{C}$ आवेश पर लगने वाला नेट बल शून्य होगा।
1.7 (a) एक विद्युत चुंबकीय क्षेत्र रेखा एक अंतर्विरोधी वक्र होती है। अर्थात, एक क्षेत्र रेखा अचानक ब्रेक नहीं लगा सकती। क्यों नहीं?
(b) समझाइए कि क्षेत्र रेखाएँ कहीं भी एक दूसरे को काट नहीं सकतीं?
उत्तर दिखाएं
उत्तर
एक विद्युत चुंबकीय क्षेत्र रेखा एक अंतर्विराम वक्र होती है क्योंकि जब एक आवेश को विद्युत क्षेत्र में ट्रेस किया जाता है तो उसे एक निरंतर बल अनुभव होता है। चुंबकीय क्षेत्र रेखा अचानक ब्रेक नहीं लग सकती क्योंकि आवेश निरंतर गति करता है और एक बिंदु से दूसरे बिंदु तक कूद नहीं सकता।
यदि दो चुंबकीय क्षेत्र रेखाएं एक बिंदु पर प्रतिच्छेद करती हैं, तो विद्युत क्षेत्र की तीव्रता उस बिंदु पर दो दिशाओं को दर्शाएगी। यह संभव नहीं है। इसलिए, दो चुंबकीय क्षेत्र रेखाएं कभी एक दूसरे को प्रतिच्छेद नहीं करती हैं।
1.8 दो बिंदु आवेश $q_{\mathrm{A}}=3 \mu \mathrm{C}$ और $q_{\mathrm{B}}=-3 \mu \mathrm{C}$ वैक्यूम में 20 सेमी की दूरी पर स्थित हैं।
(a) दो आवेशों को जोड़ने वाली रेखा $\mathrm{AB}$ के मध्य बिंदु $\mathrm{O}$ पर विद्युत क्षेत्र का मान क्या होगा?
(b) यदि इस बिंदु पर एक नकारात्मक परीक्षण आवेश $1.5 \times 10^{-9} \mathrm{C}$ का मान रखा जाता है, तो परीक्षण आवेश द्वारा अनुभव किया गया बल क्या होगा?
उत्तर दिखाएं
उत्तर
स्थिति दी गई आकृति में प्रस्तुत की गई है। $\mathrm{O}$, रेखा $\mathrm{AB}$ का मध्य बिंदु है।

दो आवेशों के बीच दूरी, $\mathrm{AB}=20 \mathrm{~cm}$
$\therefore \mathrm{AO}=\mathrm{OB}=10 \mathrm{~cm}$
बिंदु $\mathrm{O}$ पर शुद्ध विद्युत क्षेत्र $E$ है।
बिंदु $\mathrm{O}$ पर $+3 \mu \mathrm{C}$ आवेश द्वारा उत्पन्न विद्युत क्षेत्र,
$E_{1}=\frac{3 \times 10^{-6}}{4 \pi \epsilon_{0}(\mathrm{AO})^{2}}=\frac{3 \times 10^{-6}}{4 \pi \epsilon_{0}\left(10 \times 10^{-2}\right)^{2}} \mathrm{~N} / \mathrm{C} \quad$ बिंदु $\mathrm{OB}$ के अनुदिश
जहाँ,
$\epsilon_{0}=$ मुक्त अंतरिका की प्रवृत्ति
$\frac{1}{4 \pi \epsilon_{0}}=9 \times 10^{9} \mathrm{Nm}^{2} \mathrm{C}^{-2}$
बिंदु $\mathrm{O}$ पर $-3 \mu \mathrm{C}$ आवेश द्वारा उत्पन्न विद्युत क्षेत्र का मान,
$E_{2}=\left|\frac{-3 \times 10^{-6}}{4 \pi \epsilon_{0}(\mathrm{OB})^{2}}\right|=\frac{3 \times 10^{-6}}{4 \pi \epsilon_{0}\left(10 \times 10^{-2}\right)^{2}} \mathrm{~N} / \mathrm{C} \quad$ बिंदु $\mathrm{OB}$ के अनुदिश
$\therefore E=E_{1}+E_{2}$
$=2 \times\left[\left(9 \times 10^{9}\right) \times \frac{3 \times 10^{-6}}{\left(10 \times 10^{-2}\right)^{2}}\right] \quad\left[\right.$ क्योंकि $E_{1}$ और $E_{2}$ के मान समान हैं, इसलिए मान को 2 से गुणा किया गया है]
$=5.4 \times 10^{6} \mathrm{~N} / \mathrm{C}$ बिंदु $\mathrm{OB}$ के अनुदिश
इसलिए, बिंदु $\mathrm{O}$ पर विद्युत क्षेत्र $5.4 \times 10^{6} \mathrm{~N} \mathrm{C}^{-1}$ बिंदु $\mathrm{OB}$ के अनुदिश है।
मध्य बिंदु $\mathrm{O}$ पर $1.5 \times 10^{-9} \mathrm{C}$ का परीक्षण आवेश रखा गया है।
$q=1.5 \times 10^{-9} \mathrm{C}$
परीक्षण आवेश द्वारा अनुभव किया गया बल $=F$
$\therefore F=q E$
$=1.5 \times 10^{-9} \times 5.4 \times 10^{6}$
$=8.1 \times 10^{-3} \mathrm{~N}$
बल रेखा OA के अनुदिश है। इसका कारण यह है कि नकारात्मक परीक्षण आवेश बिंदु $B$ पर रखे आवेश से दूर धकेला जाता है लेकिन बिंदु $A$ की ओर आकर्षित होता है।
इसलिए, परीक्षण आवेश द्वारा अनुभव किया गया बल $8.1 \times 10^{-3} \mathrm{~N}$ बिंदु $\mathrm{OA}$ के अनुदिश है।
1.9 एक निकाय में दो आवेश $q_{\mathrm{A}}=2.5 \times 10^{-7} \mathrm{C}$ और $q_{\mathrm{B}}=-2.5 \times 10^{-7} \mathrm{C}$ बिंदु A: $(0,0,-15 \mathrm{~cm})$ और $B:(0,0,+15 \mathrm{~cm})$ पर स्थित हैं। निकाय का कुल आवेश और विद्युत द्विध्रुव आघूर्ण क्या है?
उत्तर दिखाएं
उत्तर
दोनों आवेश दिए गए चित्र में दिखाए गए निर्देशांक फ्रेम में स्थित हो सकते हैं।

A पर आवेश की मात्रा, $q_{\mathrm{A}}=2.5 \times 10^{-7} \mathrm{C}$
बी पर आवेश की मात्रा, $q_{\mathrm{B}}=-2.5 \times 10^{-7} \mathrm{C}$
सिस्टम का कुल आवेश,
$q=q_{\mathrm{A}}+q_{\mathrm{B}}$
$=2.5 \times 10^{7} \mathrm{C}-2.5 \times 10^{-7} \mathrm{C}$
$=0$
बिंदु A और B पर आवेश के बीच दूरी,
$d=15+15=30 \mathrm{~cm}=0.3 \mathrm{~m}$
सिस्टम के विद्युत द्विध्रुवी आघूर्ण को निम्नलिखित सूत्र द्वारा दिया जाता है, $p=q_{\mathrm{A}} \times d=q_{\mathrm{B}} \times d$
$=2.5 \times 10^{-7} \times 0.3$
$=7.5 \times 10^{-8} \mathrm{C} \mathrm{m}$ धनात्मक $z$-अक्ष के अनुदिश
इसलिए, सिस्टम के विद्युत द्विध्रुवी आघूर्ण $7.5 \times 10^{-8} \mathrm{C} \mathrm{m}$ धनात्मक $z$-अक्ष के अनुदिश है।
1.10 एक विद्युत द्विध्रुवी जिसका द्विध्रुवी आघूर्ण $4 \times 10^{-9} \mathrm{C} \mathrm{m}$ है, एक समान विद्युत क्षेत्र की दिशा के साथ $30^{\circ}$ कोण पर समायोजित है जिसका परिमाण $5 \times 10^{4} \mathrm{NC}^{-1}$ है। द्विध्रुवी पर कार्य कर रहे बलाघूर्ण के परिमाण की गणना कीजिए।
उत्तर दिखाएं
उत्तर
विद्युत द्विध्रुवी आघूर्ण, $p=4 \times 10^{-9} \mathrm{C} \mathrm{m}$
$p$ द्वारा एक समान विद्युत क्षेत्र के साथ बनाया गया कोण, $\theta=30^{\circ}$
विद्युत क्षेत्र, $E=5 \times 10^{4} \mathrm{~N} \mathrm{C}^{-1}$
द्विध्रुवी पर कार्य कर रहे बलाघूर्ण को निम्नलिखित संबंध द्वारा दिया जाता है,
$\tau=p E \sin \theta$
$=4 \times 10^{-9} \times 5 \times 10^{4} \times \sin 30$
$=20 \times 10^{-5} \times \frac{1}{2}$
$=10^{-4} \mathrm{~N} \mathrm{~m}$
इसलिए, द्विध्रुवी पर कार्य कर रहे बलाघूर्ण का परिमाण $10^{-4} \mathrm{~N} \mathrm{~m}$ है।
1.11 पॉलीथीन के एक टुकड़े को रेशम के साथ रगड़ा जाता है जिसके परिणामस्वरूप इसका नकारात्मक आवेश $3 \times 10^{-7} \mathrm{C}$ हो जाता है।
(a) आवेश के परिमाण के आधार पर इलेक्ट्रॉनों की संख्या का अनुमान लगाइए (किस से किस में स्थानांतरित होते हैं?)
(b) रेशम से पॉलीथीन में द्रव्यमान के स्थानांतरण की क्या संभावना है?
उत्तर दिखाएं
उत्तर
जब पॉलीथीन को रेशम के साथ रगड़ा जाता है तो कई इलेक्ट्रॉन रेशम से पॉलीथीन में स्थानांतरित हो जाते हैं। इसलिए, रेशम धनात्मक आवेशित हो जाता है और पॉलीथीन नकारात्मक आवेशित हो जाता है।
पॉलीथीन टुकड़े पर आवेश की मात्रा, $q=-3 \times 10^{-7} \mathrm{C}$
आवेश इलेक्ट्रॉन पर, $e=-1.6 \times 10^{-19} \mathrm{C}$
वॉल के तूफान से पॉलीथीन में आवेशित इलेक्ट्रॉन की संख्या $=n$
$n$ की गणना निम्नलिखित संबंध का उपयोग करके की जा सकती है,
$q=n e$
$n=\frac{q}{e}$
$=\frac{-3 \times 10^{-7}}{-1.6 \times 10^{-19}}$
$=1.87 \times 10^{12}$
इसलिए, वॉल से पॉलीथीन में आवेशित इलेक्ट्रॉन की संख्या $1.87 \times 10^{12}$ है।
हाँ।
मास के परिवहन की घटना हो रही है। इसका कारण यह है कि एक इलेक्ट्रॉन के मास होता है,
$m_{e}=9.1 \times 10^{-3} \mathrm{~kg}$
पॉलीथीन में वॉल से कुल मास परिवहन,
$m=m_{e} \times n$
$=9.1 \times 10^{-31} \times 1.85 \times 10^{12}$
$=1.6835 \times 10^{-18} \mathrm{~kg}$
इसलिए, वॉल से पॉलीथीन में एक नगण्य मात्रा में मास परिवहन होता है।
1.12 (a) दो आइसोलेटेड चार्ज तांबे के गोले A और B के केंद्रों के बीच दूरी $50 \mathrm{~cm}$ है। यदि प्रत्येक गोले पर आवेश $6.5 \times 10^{-7} \mathrm{C}$ है, तो उनके बीच विद्युत बल के परस्पर प्रतिकर्षण क्या होगा? A और B की त्रिज्याएँ अलग करने वाली दूरी की तुलना में नगण्य हैं।
(b) यदि प्रत्येक गोले का आवेश ऊपरी मात्रा के दुगुना हो जाए और उनके बीच की दूरी आधी हो जाए, तो प्रतिकर्षण बल क्या होगा?
उत्तर दिखाएं
उत्तर
गोले A पर आवेश $(q_{\mathrm{A}})=$ गोले B पर आवेश $(q_{\mathrm{B}})=6.5 \times 10^{-7} \mathrm{C}$
गोलों के बीच दूरी, $r=50 \mathrm{~cm}=0.5 \mathrm{~m}$
दो गोलों के बीच प्रतिकर्षण बल,
$$ F=\frac{q_{\mathrm{A}} q_{\mathrm{B}}}{4 \pi \in_{0} r^{2}} $$
जहाँ,
$\epsilon_{0}=$ रिक्त स्थान की प्रवैगता
$$ \begin{aligned} & \frac{1}{4 \pi \epsilon_{0}}=9 \times 10^{9} \mathrm{~N} \mathrm{~m}^{2} \mathrm{C}^{-2} \\ & \quad F=\frac{9 \times 10^{9} \times\left(6.5 \times 10^{-7}\right)^{2}}{(0.5)^{2}} \\ & \therefore \quad \\ & =1.52 \times 10^{-2} \mathrm{~N} \end{aligned} $$
इसलिए, दो गोलों के बीच बल $1.52 \times 10^{-2} \mathrm{~N}$ है।
आवेश को दुगुना करने के बाद, गोले A पर आवेश $(q_{\mathrm{A}})=$ गोले B पर आवेश $(q_{\mathrm{B}})=2 \times 6.5 \times$ $10^{-7} \mathrm{C}=1.3 \times 10^{-6} \mathrm{C}$
दो गोलियों के बीच की दूरी आधी कर दी गई है।
$$ \therefore \quad r=\frac{0.5}{2}=0.25 \mathrm{~m} $$
दो गोलियों के बीच प्रतिकर्षण बल,
$$ \begin{aligned} & F=\frac{q_{\mathrm{A}} q_{\mathrm{B}}}{4 \pi \epsilon_{0} r^{2}} \\ & =\frac{9 \times 10^{9} \times 1.3 \times 10^{-6} \times 1.3 \times 10^{-6}}{(0.25)^{2}} \\ & =16 \times 1.52 \times 10^{-2} \\ & =0.243 \mathrm{~N} \end{aligned} $$
इसलिए, दो गोलियों के बीच बल $0.243 \mathrm{~N}$ है।
1.13 चित्र 1.30 में एक समान विद्युत क्षेत्र में तीन आवेशित कणों के पथ दिखाए गए हैं। तीनों आवेशों के चिह्न बताइए। कौन सा कण आवेश और द्रव्यमान के अनुपात के लिए सबसे अधिक है?

चित्र 1.30
उत्तर दिखाएं
उत्तर
विपरीत आवेश एक दूसरे को आकर्षित करते हैं और समान आवेश एक दूसरे को विकर्षित करते हैं। यह देखा जा सकता है कि कण 1 और 2 दोनों धनावेशित प्लेट की ओर गति करते हैं और ऋणावेशित प्लेट से विकर्षित होते हैं। इसलिए, ये दोनों कण ऋणावेशित हैं। यह भी देखा जा सकता है कि कण 3 ऋणावेशित प्लेट की ओर गति करता है और धनावेशित प्लेट से विकर्षित होता है। इसलिए, कण 3 धनावेशित है।
आवेश और द्रव्यमान के अनुपात (e/m) दिए गए वेग के लिए विस्थापन या विक्षेपण के मात्रा के सीधे अनुपात में होता है। क्योंकि कण 3 के विक्षेपण सबसे अधिक है, इसलिए इसका आवेश और द्रव्यमान का अनुपात सबसे अधिक है।
1.14 एक समान विद्युत क्षेत्र $\mathbf{E}=3 \times 10^{3} \hat{\mathbf{i}} \quad \mathrm{N} / \mathrm{C}$ का विचार करें।
(a) इस क्षेत्र के माध्यम से एक वर्ग के बराबर क्षेत्रफल $10 \mathrm{~cm}$ भुजा वाले वर्ग के लिए फ्लक्स क्या है जिसकी सतह या तल $y z$ तल के समानांतर है?
(b) यदि वर्ग के तल के लंब के तल के साथ $60^{\circ}$ का कोण बनता है, तो इस वर्ग के माध्यम से फ्लक्स क्या है?
उत्तर दिखाएं
उत्तर
विद्युत क्षेत्र तीव्रता, $\vec{E}=3 \times 10^{3} \hat{\imath} \quad \mathrm{N} / \mathrm{C}$
विद्युत क्षेत्र तीव्रता के परिमाण, $|\vec{E}|_{=3 \times 10^{3} \mathrm{~N} / \mathrm{C}}$
वर्ग की भुजा, $s=10 \mathrm{~cm}=0.1 \mathrm{~m}$
वर्ग का क्षेत्रफल, $A=\mathrm{s}^{2}=0.01 \mathrm{~m}^{2}$
वर्ग के तल के तल के समानांतर है $y-z$ तल के। अतः तल के तल के एकक सदिश और विद्युत क्षेत्र के बीच कोण, $\theta=0^{\circ}$
तल के माध्यम से फ्लक्स $(\Phi)$ के संबंध में निम्नलिखित संबंध द्वारा दिया गया है,
$\Phi=|\vec{E}| A \cos \theta$
$=3 \times 10^{3} \times 0.01 \times \cos 0^{\circ}$
$=30 \mathrm{~N} \mathrm{~m}^{2} / \mathrm{C}$
तल $x$-अक्ष के साथ $60^{\circ}$ का कोण बनाता है। अतः $\theta=60^{\circ}$
फ्लक्स, $\Phi=|\vec{E}| A \cos \theta$
$=3 \times 10^{3} \times 0.01 \times \cos 60^{\circ}$ $=30 \times \frac{1}{2}=15 \mathrm{~N} \mathrm{~m}^{2} / \mathrm{C}$
1.15 एक घन जिसकी भुजा $20 \mathrm{~cm}$ है और जो निर्देशांक तलों के समानांतर अभिविन्यस्त है, के माध्यम से एक समान विद्युत क्षेत्र के नेट फ्लक्स क्या होगा?
उत्तर दिखाएं
उत्तर
एक घन के सभी फलक निर्देशांक अक्षों के समानांतर होते हैं। अतः घन में प्रवेश करने वाली विद्युत क्षेत्र रेखाओं की संख्या घन से बाहर निकलने वाली विद्युत क्षेत्र रेखाओं की संख्या के बराबर होती है। इसलिए घन के माध्यम से नेट फ्लक्स शून्य होता है।
1.16 काला बॉक्स के सतह पर विद्युत क्षेत्र के सावधान मापन के अनुसार, बॉक्स के सतह के माध्यम से नेट बाहरी फ्लक्स $8.0 \times 10^{3} \ \mathrm{Nm}^{2} / \mathrm{C}$ है।
(a) बॉक्स के भीतर नेट आवेश क्या है?
(b) यदि बॉक्स के सतह के माध्यम से नेट बाहरी फ्लक्स शून्य हो जाए, तो आप क्या निष्कर्ष निकाल सकते हैं कि बॉक्स के भीतर कोई आवेश नहीं है? क्यों या क्यों नहीं?
उत्तर दिखाएं
उत्तर
(a) बॉक्स के सतह के माध्यम से नेट बाहरी फ्लक्स, $\Phi=8.0 \times 10^{3} \mathrm{~N} \mathrm{~m}^{2} / \mathrm{C}$
एक वस्तु के लिए जिसमें नेट आवेश $q$ हो, फ्लक्स के संबंध में निम्नलिखित संबंध द्वारा दिया गया है,
$\phi=\frac{q}{\epsilon_{0}}$
$\epsilon_{0}=$ रिक्त स्थान की प्रवैगता
$=8.854 \times 10^{-12} \mathrm{~N}^{-1} \mathrm{C}^{2} \mathrm{~m}^{-2}$ $q=\epsilon_{0} \Phi$
$=8.854 \times 10^{-12} \times 8.0 \times 10^{3}$
$=7.08 \times 10^{-8}$
$=0.07 \mu \mathrm{C}$
अतः, बॉक्स के भीतर कुल आवेश $0.07 \mu \mathrm{C}$ है।
(b) नहीं
किसी वस्तु के माध्यम से निकलने वाला विद्युत फ्लक्स उस वस्तु के भीतर उपस्थित कुल आवेश पर निर्भर करता है। यदि कुल फ्लक्स शून्य है, तो इसका निष्कर्ष लिया जा सकता है कि वस्तु के भीतर कुल आवेश शून्य है। वस्तु में धनात्मक और ऋणात्मक आवेश के समान मात्रा हो सकती है।
1.17 एक बिंदु आवेश $+10 \mu \mathrm{C}$ एक वर्ग के केंद्र के ठीक ऊपर $5 \mathrm{~cm}$ की दूरी पर है, जिसकी भुजा $10 \mathrm{~cm}$ है, जैसा कि चित्र 1.31 में दिखाया गया है। वर्ग के माध्यम से विद्युत फ्लक्स का परिमाण क्या है? (संकेत: वर्ग को एक घन के एक फलक के रूप में सोचें जिसका किनारा $10 \mathrm{~cm}$ है।)

उत्तर दिखाएं
उत्तर
वर्ग को एक घन के एक फलक के रूप में माना जा सकता है, जिसका किनारा $10 \mathrm{~cm}$ है और जिसके केंद्र पर आवेश $q$ रखा गया है। घन के लिए गॉस के प्रमेय के अनुसार, कुल विद्युत फ्लक्स सभी छह फलकों के माध्यम से होता है।
$$ \phi_{\text {Total }}=\frac{q}{\epsilon_{0}} $$
अतः, घन के एक फलक के माध्यम से विद्युत फ्लक्स, अर्थात वर्ग के माध्यम से विद्युत फ्लक्स, $\phi=\frac{\phi_{\text {Total }}}{6}$ $=\frac{1}{6} \frac{q}{\epsilon_{0}}$
जहाँ,
$\epsilon_{0}=$ रिक्त स्थान की प्रवैगता
$=8.854 \times 10^{-12} \mathrm{~N}^{-1} \mathrm{C}^{2} \mathrm{~m}^{-2}$
$q=10 \mu \mathrm{C}=10 \times 10^{-6} \mathrm{C}$
$\therefore \phi=\frac{1}{6} \times \frac{10 \times 10^{-6}}{8.854 \times 10^{-12}}$
$=1.88 \times 10^{5} \mathrm{~N} \mathrm{~m}^{2} \mathrm{C}^{-1}$
अतः, वर्ग के माध्यम से विद्युत फ्लक्स $1.88 \times 10^{5} \mathrm{~N} \mathrm{~m}^{2} \mathrm{C}^{-1}$ है।
1.18 9.0 सेमी किनारे वाले घन गॉस तल के केंद्र पर 2.0 μC के बिंदु आवेश के कारण तल के माध्यम से कुल विद्युत फ्लक्स कितना होगा?
उत्तर दिखाएं
उत्तर
घन तल के माध्यम से कुल विद्युत फ्लक्स ( $\left.\Phi_{\mathrm{Net}}\right)$ निम्नलिखित सूत्र द्वारा दिया गया है,
$$ \phi_{\mathrm{Net}}=\frac{q}{\epsilon_{0}} $$
जहाँ,
$\epsilon_{0}=$ रिक्त स्थान की प्रवैगता
$=8.854 \times 10^{-12} \mathrm{~N}^{-1} \mathrm{C}^{2} \mathrm{~m}^{-2}$
$q=$ घन के भीतर स्थित कुल आवेश $=2.0 \mu \mathrm{C}=2 \times 10^{-6} \mathrm{C}$ $\therefore \phi_{\text {Net }}=\frac{2 \times 10^{-6}}{8.854 \times 10^{-12}}$
$=2.26 \times 10^{5} \mathrm{~N} \mathrm{~m}^{2} \mathrm{C}^{-1}$
तल के माध्यम से कुल विद्युत फ्लक्स $2.26 \times 10^{5} \mathrm{~N} \mathrm{~m}^{2} \mathrm{C}^{-1}$ है।
1.19 एक बिंदु आवेश द्वारा 10.0 सेमी त्रिज्या वाले गोलीय गॉस तल के माध्यम से $-1.0 \times 10^{3} \mathrm{Nm}^{2} / \mathrm{C}$ का विद्युत फ्लक्स पार जाता है। (a) यदि गॉस तल की त्रिज्या दोगुनी कर दी जाए, तो तल के माध्यम से कितना फ्लक्स पार जाएगा? (b) बिंदु आवेश का मान क्या है?
उत्तर दिखाएं
उत्तर
विद्युत फ्लक्स, $\Phi=-1.0 \times 10^{3} \mathrm{~N} \mathrm{~m}^{2} / \mathrm{C}$
गॉस तल की त्रिज्या, $r=10.0 \mathrm{~cm}$
एक तल के माध्यम से विद्युत फ्लक्स तल के आकार पर निर्भर नहीं करता, बल्कि तल के भीतर स्थित कुल आवेश पर निर्भर करता है। यदि गॉस तल की त्रिज्या दोगुनी कर दी जाए, तो तल के माध्यम से पार जाने वाला फ्लक्स समान रहेगा, अर्थात $-10^{3} \mathrm{~N} \mathrm{~m}^{2} / \mathrm{C}$ होगा।
विद्युत फ्लक्स को निम्नलिखित संबंध द्वारा दिया गया है,
$\phi=\frac{q}{\epsilon_{0}}$
जहाँ,
$q=$ गोलीय तल के भीतर स्थित कुल आवेश
$\epsilon_{0}=$ रिक्त स्थान की प्रवैगता $=8.854 \times 10^{-12} \mathrm{~N}^{-1} \mathrm{C}^{2} \mathrm{~m}^{-2}$
$\therefore q=\phi \in_{0}$
$=-1.0 \times 10^{3} \times 8.854 \times 10^{-12}$
$=-8.854 \times 10^{-9} \mathrm{C}$
$=-8.854 \mathrm{nC}$
इसलिए, बिंदु आवेश का मान $-8.854 \mathrm{nC}$ है।
1.20 एक चालक गोले की त्रिज्या $10 \mathrm{~cm}$ है और इसका अज्ञात आवेश है। यदि गोले के केंद्र से $20 \mathrm{~cm}$ की दूरी पर विद्युत क्षेत्र $1.5 \times 10^{3} \mathrm{~N} / \mathrm{C}$ है और इसकी दिशा त्रिज्या के अंदर की ओर है, तो गोले पर शुद्ध आवेश कितना है?
उत्तर दिखाएं
Answer
एक गोले के केंद्र से दूरी $(d)$ पर विद्युत क्षेत्र तीव्रता $(E)$ जो गोले पर शुद्ध आवेश $q$ के कारण होती है, निम्नलिखित संबंध द्वारा दी जाती है,
$$ E=\frac{q}{4 \pi \in_{0} d^{2}} $$
जहाँ,
$q=$ शुद्ध आवेश $=1.5 \times 10^{3} \mathrm{~N} / \mathrm{C}$
$d=$ केंद्र से दूरी $=20 \mathrm{~cm}=0.2 \mathrm{~m}$
$\epsilon_{0}=$ रिक्त स्थान की प्रवैगता
और, $\frac{1}{4 \pi \epsilon_{0}}=9 \times 10^{9} \mathrm{~N} \mathrm{~m}^{2} \mathrm{C}^{-2}$
$\therefore q=E\left(4 \pi \epsilon_{0}\right) d^{2}$
$=\frac{1.5 \times 10^{3} \times(0.2)^{2}}{9 \times 10^{9}}$
$=6.67 \times 10^{9} \mathrm{C}$
$=6.67 \mathrm{nC}$
इसलिए, गोले पर शुद्ध आवेश $6.67 \mathrm{nC}$ है।
1.21 एक समान रूप से आवेशित चालक गोले का व्यास $2.4 \mathrm{~m}$ है और इसकी सतह पर आवेश घनत्व $80.0 \mu \mathrm{C} / \mathrm{m}^{2}$ है।
(a) गोले पर आवेश कितना है?
(b) गोले की सतह से निकलने वाली कुल विद्युत फ्लक्स कितना है?
उत्तर दिखाएं
Answer
गोले का व्यास, $d=2.4 \mathrm{~m}$
गोले की त्रिज्या, $r=1.2 \mathrm{~m}$
सतह पर आवेश घनत्व, $\sigma=80.0 \mu \mathrm{C} / \mathrm{m}^{2}=80 \times 10^{-6} \mathrm{C} / \mathrm{m}^{2}$
गोले की सतह पर कुल आवेश,
$Q=$ आवेश घनत्व $\times$ सतह का क्षेत्रफल
$=\sigma \times 4 \pi r^{2}$
$=80 \times 10^{-6} \times 4 \times 3.14 \times(1.2)^{2}$
$=1.447 \times 10^{-3} \mathrm{C}$
इसलिए, गोले पर आवेश $1.447 \times 10^{-3} \mathrm{C}$ है।
एक गोले की सतह से निकलने वाली कुल विद्युत फ्लक्स ( $\phi_{\text {Total }}$ ) जो शुद्ध आवेश $Q$ के कारण होती है, निम्नलिखित संबंध द्वारा दी जाती है,
$$ \phi_{\text {TOtal }}=\frac{Q}{\epsilon_{0}} $$
जहाँ,
$\epsilon_{0}=$ रिक्त स्थान की प्रवृत्ति
$=8.854 \times 10^{-12} \mathrm{~N}^{-1} \mathrm{C}^{2} \mathrm{~m}^{-2}$
$$ \begin{aligned} & Q=1.447 \times 10^{-3} \mathrm{C} \\ & \phi_{\text {Total }}=\frac{1.44 \times 10^{-3}}{8.854 \times 10^{-12}} \\ & =1.63 \times 10^{8} \mathrm{~N} \mathrm{C}^{-1} \mathrm{~m}^{2} \end{aligned} $$
इसलिए, गोले के सतह से छूट रहे कुल विद्युत फ्लक्स $1.63 \times 10^{8} \mathrm{~N} \mathrm{C}^{-1} \mathrm{~m}^{2}$ है।
1.22 अनंत रेखीय आवेश द्वारा 2 सेमी की दूरी पर $9 \times 10^{4} \mathrm{~N} / \mathrm{C}$ के विद्युत क्षेत्र उत्पन्न किया जाता है। रेखीय आवेश घनत्व की गणना कीजिए।
उत्तर दिखाएं
उत्तर
अनंत रेखीय आवेश द्वारा दूरी $d$ पर उत्पन्न विद्युत क्षेत्र रेखीय आवेश घनत्व $\lambda$ के साथ निम्नलिखित संबंध द्वारा दिया जाता है,
$$ \begin{aligned} & E=\frac{\lambda}{2 \pi \epsilon_{0} d} \\ & \lambda=2 \pi \epsilon_{0} d E \end{aligned} $$
जहाँ,
$d=2 \mathrm{~cm}=0.02 \mathrm{~m}$
$E=9 \times 10^{4} \mathrm{~N} / \mathrm{C}$
$\epsilon_{0}=$ रिक्त स्थान की प्रवृत्ति
$$ \begin{aligned} & \frac{1}{4 \pi \epsilon_{0}}=9 \times 10^{9} \mathrm{~N} \mathrm{~m}^{2} \mathrm{C}^{-2} \\ & \lambda=\frac{0.02 \times 9 \times 10^{4}}{2 \times 9 \times 10^{9}} \\ & =10 \mu \mathrm{C} / \mathrm{m} \end{aligned} $$
इसलिए, रेखीय आवेश घनत्व $10 \mu \mathrm{C} / \mathrm{m}$ है।
1.23 दो बड़े, चौड़े धातु के पट्टी एक दूसरे के समानांतर और निकट रहते हैं। उनके आंतरिक तलों पर विपरीत चिह्न और $17.0 \times 10^{-22} \mathrm{C} / \mathrm{m}^{2}$ के मान के सतह आवेश घनत्व होते हैं। पहले पट्टी के बाहरी क्षेत्र में $\mathbf{E}$, (a) पहले पट्टी के बाहरी क्षेत्र में, (b) दूसरे पट्टी के बाहरी क्षेत्र में, और (c) पट्टियों के बीच में क्या है?
उत्तर दिखाएं
उत्तर
मान लीजिए $A$ और $B$ दो बड़े, चौड़े धातु के पट्टी हैं जो एक दूसरे के समानांतर और निकट रहते हैं जैसा कि चित्र में दिखाया गया है। चार्ज के सतह घनत्व $A$ पर $\sigma=+17.0 \times 10^{-22} \mathrm{C} / \mathrm{m}^2$ है। और चार्ज के सतह घनत्व $B$ पर $-\sigma=-17.0 \times 10^{-22} \mathrm{C} / \mathrm{m}^2$ है। किसी बिंदु $K$ पर पहले पट्टी $A$ के बाहरी क्षेत्र में हमें $\left|\overrightarrow{E_A}\right|=\left|\overrightarrow{E_B}\right|=\frac{\sigma}{2 \epsilon_0}$ लेकिन उनके दिशा एक दूसरे के विपरीत होती है।
इसलिए, $\left(E_k\right)=\overrightarrow{E_A}+\overrightarrow{E_B}=\overrightarrow{0}$
(b) मान लीजिए $\mathrm{A}$ और $\mathrm{B}$ दो बड़े, चोटी धातु के प्लेट हैं जो एक दूसरे के पास और समानांतर रखे गए हैं जैसा कि चित्र में दिखाया गया है। चार्ज के सतह घनत्व पर A पर, $ \sigma=+17.0 \times 10^{-22} \mathrm{C} / \mathrm{m}^2$ है। और चार्ज के सतह घनत्व पर B,
$ -\sigma=-17.0 \times 10^{-22} C / m^2 $
फिर दूसरे प्लेट के बाहरी क्षेत्र में बिंदु $M$ पर, कुल विद्युत क्षेत्र शून्य है (c) मान लीजिए $\mathrm{A}$ और $\mathrm{B}$ दो बड़े, चोटी धातु के प्लेट हैं जो एक दूसरे के पास और समानांतर रखे गए हैं जैसा कि चित्र में दिखाया गया है। चार्ज के सतह घनत्व पर A, $ \sigma=+17.0 \times 10^{-22} \mathrm{C} / \mathrm{m}^2$ है। और चार्ज के सतह घनत्व पर
$ B,-\sigma=-17.0 \times 10^{-22} C / m^2 $
प्लेटों $\mathrm{A}$ और $\mathrm{B}$ के बीच बिंदु $\mathrm{N}$ पर, $\overrightarrow{E_B}$ के परिमाण समान हैं और दोनों एक ही दिशा में दिखाई देते हैं और इसलिए एक दूसरे के जोड़ में होते हैं, इसलिए कुल विद्युत क्षेत्र निम्नलिखित द्वारा दिया जाता है,
$$ \begin{aligned} & \vec{E}=\overrightarrow{E_A}+\overrightarrow{E_B}=\frac{\sigma}{2 \epsilon_0}+\frac{\sigma}{2 \epsilon_0}=\frac{\sigma}{\epsilon_0} \\ & =\frac{1.70 \times 10^{-22}}{8.85 \times 10^{-12}}=1.9 \times 10^{-10} N C^{-1} \end{aligned} $$





